UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
|
|
|
- Ilene Chandler
- 6 years ago
- Views:
Transcription
1 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ZNÁME NEROVNOSTI V MATEMATIKE BAKALÁRSKA PRÁCA 014 Zuzana FRONCOVÁ
2 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ZNÁME NEROVNOSTI V MATEMATIKE BAKALÁRSKA PRÁCA tudijný program: tudijný odbor: koliace pracovisko: Vedúci práce: Ekonomická a nan ná matematika 1114 Aplikovaná matematika Katedra aplikovanej matematiky a ²tatistiky RNDr. Mária Trnovská, PhD Bratislava 014 Zuzana FRONCOVÁ
3 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky ZADANIE ZÁVEREČNEJ PRÁCE Meno a priezvisko študenta: Študijný program: Študijný odbor: Typ záverečnej práce: Jazyk záverečnej práce: Zuzana Froncová ekonomická a finančná matematika Jednoodborové štúdium, bakalársky I. st., denná forma) aplikovaná matematika bakalárska slovenský Názov: Cieľ: Známe nerovnosti v matematike / Well-known inequalities in mathematics Spracovanie prehľadu najznámejších nerovností v matematike s ich zovšeobecneniami, alternatívnymi dôkazmi, súvislosťami. Vedúci: Katedra: Vedúci katedry: Dátum zadania: RNDr. Mária Trnovská, PhD. FMFI.KAMŠ - Katedra aplikovanej matematiky a štatistiky prof. RNDr. Daniel Ševčovič, CSc. Dátum schválenia: doc. RNDr. Margaréta Halická, CSc. garant študijného programu študent vedúci práce
4 Po akovanie Touto cestou sa chcem po akovat svojej vedúcej bakalárskej práce RNDr. Márii Trnovskej, PhD za ochotu, pomoc, odborné rady a podnetné pripomienky, ktoré mi pomohli pri písaní tejto práce. akujem aj svojej rodine a priate om za ich trpezlivos a podporu.
5 Abstrakt v ²tátnom jazyku FRONCOVÁ, Zuzana: Známe nerovnosti v matematike [Bakalárska práca], Univerzita Komenského v Bratislave, Fakulta matematiky, fyziky a informatiky, Katedra aplikovanej matematiky a ²tatistiky; ²kolite : RNDr. Mária Trnovská, PhD., Bratislava, 014, 60 s. V na²ej práci sa zaoberáme dvomi z najznámej²ích a najpouºívanej²ích nerovností. Sú to Cauchy-Schwarzova nerovnos a nerovnos aritmetického a geometrického priemeru. Na²im cie om je zozbieranie a spracovanie mnoºstva informácií z rôznych zdrojov a vytvorenie jedného celku, ktorý itate ovi predstaví dané nerovnosti aj s ich zov²eobecneniami, alternatívnymi dôkazmi a súvislos ami medzi nimi a im podobnými nerovnos ami. Okrem zozbierania a spracovania je cie om tejto práce aj podrobné a o najzrozumite nej²ie podanie informácií itate ovi, ktorý s touto problematikou nemusí ma skúsenosti. Význam práce spo íva v tom, ºe itate ovi so záujmom o túto tému poskytuje viac informácií ako iné, v²eobecnej²ie zamerané publikácie. K ú ové slová: Cauchy-Schwarzova nerovnos, AG nerovnos, alternatívne dôkazy, aplikácie
6 Abstract FRONCOVÁ, Zuzana: Well-known inequalities in mathematics [Bachelor Thesis], Comenius University in Bratislava, Faculty of Mathematics, Physics and Informatics, Department of Applied Mathematics and Statistics; Supervisor: RNDr. Mária Trnovská, PhD., Bratislava, 014, 60 p. Our thesis is dedicated to two of the best-known and most widely used inequalities, which are the Cauchy-Schwarz inequality and the Inequality of arithmetic mean and geometric mean. Our objective is collecting and processing information from dierent sources and creating one unit, that makes the reader acquainted with these inequalities with their generalizations, alternative proofs and connections to other similar inequalities. Besides collecting and processing information, the aim of this work is to present the information in the most detailed and comprehensible form to a reader, who might not have any previous knowledge of this subject. The purpose of this thesis lies in oering an interested reader more on the subject than other, more generally aimed publications. Keywords: Cauchy-Schwarz inequality, Arithmetic Mean-Geometric Mean inequality, alternative proofs, applications
7 OBSAH OBSAH Obsah Zoznam obrázkov 9 Úvod 10 1 Cauchy-Schwarzova nerovnos História V²eobecný tvar Alternatívne dôkazy a odvodenia Odvodenie pomocou Lagrangeovej identity Dôkaz matematickou indukciou Dôkaz pomocou postupnosti sú tov Dôkaz pomocou Jensenovej nerovnosti Dôkaz pomocou AG nerovnosti Dôkaz pomocou permuta nej nerovnosti Odvodenie z úlohy na viazaný extrém Aplikácie Trojuholníková nerovnos Kosínus uhla dvoch vektorov Korela ný koecient Úloha o kladne denitných maticiach Súvis s Hölderovou nerovnos ou AG nerovnos 36.1 V²eobecný tvar Jednoduché dôkazy pre premenné Geometrický dôkaz Geometrický dôkaz Geometrický dôkaz Geometrický dôkaz Dôkaz pomocou doty nice hyperboly Cauchyho dôkaz spätnou indukciou
8 OBSAH OBSAH.4 Dôkaz pomocou pre²kálovania prvkov Dôkazy vyuºívajúce konvexnos alebo konkávnos Dôkaz pomocou konkávnosti geometrického priemeru Dôkaz pomocou Jensenovej nerovnosti Dôkaz pomocou doty nice konvexnej funkcie Aplikácie Maximaliza ná úloha Eulerove íslo Analógia s izoperimetrickou nerovnos ou Záver 56 Zoznam pouºitej literatúry 58 8
9 ZOZNAM OBRÁZKOV ZOZNAM OBRÁZKOV Zoznam obrázkov 1 Z ava: Augustin Louis Cauchy [8], Viktor Jakovlevi Bunyakovskij [7] a Hermann Amandus Schwarz [8] Komplexné íslo z a k nemu komplexne zdruºené z [30] Mnoºina prípustných rie²ení f 1 u) = u T u 1 = 0, kde u R a vrstevnice ú elovej funkcie f 0 u) = v T u, pre v = 1, 1) a hodnoty f 0 u) = 0, f 0 u) = 1, f 0u) = 1 a f 0 u) = Projekcia vektora v na vektor u Korela ný koecient pre rôzne sady dát Geometrický dôkaz.1, [31] Geometrický dôkaz., [31] Geometrický dôkaz.4, [5] Geometrický dôkaz Dôkaz pomocou doty nice hyperboly, [31] Aritmetický a geometrický priemer Doty nica k y = e x v bode x = 0, [5] Zvä ²enie plochy ohrani enej krivkou bez zmeny obvodu [1] Rovnaká plocha ohrani ená kruºnicou a inou krivkou [9] Obd ºnik a ²tvorec s plochou x 1 x Obd ºnik a ²tvorec s obvodom x 1 + x
10 ÚVOD ÚVOD Úvod Rovnosti neexistujú, dokonca aj v udskom ºivote sa vºdy stretávame s nerovnos ami. Dragoslav S. Mitrinovi Ako tvrdí jeden z uznávaných matematikov, ktorý venoval ve kú as svojej práce práve nerovnostiam, Dragoslav S. Mitrinovi, s nerovnos ami sa stretávame kaºdodenne bez toho, aby sme si to uvedomili a pritom zohrávajú v na²om ºivote celkom významnú úlohu. V obchode môºeme minú najviac celú výplatu, ak cesta do ²koly trvá 5 minút, musíme z domu vyrazi aspo 5 minút pred za iatkom vyu ovania... Nerovnosti sú uº oddávna povaºované taktieº za dôleºitú oblas matematiky a ich platnos sa asto vyuºíva aj v iných matematických odvetviach. Predstavujú neustále sa meniace a ve mi atraktívne pole pre výskum. Pod a publikácie [1] boli základy teórie nerovností vybudované v 18. a 19. storo í matematikmi K. F. Gauss ), A. L. Cauchy ) a P. L. ƒeby²ev ). V nasledujúcich rokoch nerovnosti oslovili aj al²ích významných matematikov ako H. Poincaré ), A. M. Lyapunov ), O. Hölder ) alebo J. Hadamard ). 0. storo ie, ako sa môºeme do íta v rôznych zdrojoch ako napríklad [17], [18] a [], bolo obdobím ve kého pokroku a to hlavne v aka siedmim konferenciám o nerovnostiach, ktoré sa konali v Nemeckom Oberwolfachu v rokoch 1976 aº Vyvinula sa celkom nová vetva modernej matematiky nerovnosti. Prvou knihou venovanou výlu ne nerovnostiam bola práca Inequalities od autorov G. H. Hardy ), J. E. Littlewood ) a G. Pólya ), prvýkrát publikovaná v roku Táto kniha podnietila vydanie mnohých al²ích kníh, napríklad Inequalities 1961) od E. F. Beckenbacha ) a R. Bellmana ), Analytic Inequalities 1970) od D. S. Mitrinovi a ) alebo Classical and New Inequalities in Analysis 1993) od D. S. Mitrinovi a, J. E Pe ari a a A. M. Finka [18], z ktorej budeme aj alej v tejto práci erpa. Objavili sa aj knihy zamerané na ²peciálne typy 10
11 ÚVOD ÚVOD nerovností, ako napríklad diferenciálne nerovnosti alebo nerovnosti priemerov. Medzi takéto patria napríklad publikácie od P.S. Bullena a P. M. Vasi a Means and Their Inequalities a od D. S. Mitrinovi a, J. E. Pe ari a ) a A. M. Finka ) Inequalities Involving Functions and Their Integrals and Derivatives 1991). V sú asnosti existujú zoskupenia matematikov z celého sveta zamerané na matematické nerovnosti a ich aplikácie. Pokra ujú konferencie pod a príkladu tých zo 70-tych aº 90-tych rokov minulého storo ia venované nerovnostiam a moºnostiam ich vylep²enia. Objavujú sa stále nové nerovnosti a nové dôkazy tých star²ích. Cie om tejto práce bolo vytvori ucelený preh ad nieko kých najznámej²ích a najvyuºívanej²ích nerovností. Konkrétne sme vybrali dve nerovnosti, a to Cauchy-Schwarzovu nerovnos a nerovnos aritmetického a geometrického priemeru, skrátene nazývanú AG nerovnos. O týchto nerovnostiach uº existuje ve a rôznych kníh, lánkov a ²kolských prác. Kaºdý zdroj uvádza iné dôkazy, odvodenia, dôsledky a aplikácie. Na²im cie om teda bolo zozbiera viaceré alternatívne dôkazy, aplikácie a poukáza na súvislosti s inými nerovnos ami. Prácu sme rozdelili na dve hlavné kapitoly. Prvá kapitola bude celá venovaná Cauchy- Schwarzovej nerovnosti. Na za iatok oboznámime itate a s jej autormi, historickým pozadím a postupnými zov²eobecneniami. Následne dokáºeme v²eobecný tvar Cauchy- Schwarzovej nerovnosti a uvedieme nieko ko ²peciálnych prípadov. alej bude nasledova as s viacerými alternatívnymi dôkazmi. Nakoniec pridáme nieko ko aplikácií Cauchy-Schwarzovej nerovnosti a jej súvis so v²eobecnej²ou Hölderovou nerovnos ou. V druhej kapitole itate a oboznámime s AG nerovnos ou. V úvode tejto kapitoly uvedieme tri základné tvary tejto nerovnosti. Potom nasledujú dôkazy, usporiadané od najjednoduch²ích po zloºitej²ie. alej budú nasledova aplikácie AG nerovnosti a úplne na záver uvedieme analógiu AG nerovnosti s izoperimetrickou nerovnos ou. 11
12 1 CAUCHY-SCHWARZOVA NEROVNOS 1 Cauchy-Schwarzova nerovnos Nerovnos, s ktorou sa zoznámime v tejto kapitole je vo vysoko²kolskej matematike povaºovaná za dôleºitý pojem. Významnú rolu, ako sa pí²e aj v lánku [3], zohráva v teórii Hilbertových priestorov, matematickej analýze, numerickej analýze, pravdepodobnosti a ²tatistike alebo kvalitatívnej teórii diferenciálnych rovníc. Naj astej²ie sa jej platnos vyuºíva pri odhadoch matematických výrazov, dôkazoch tvrdení a je jedným zo základných nástrojov pri práci s nerovnos ami. V literatúre býva ozna ovaná ako Cauchyho nerovnos, Schwarzova nerovnos, Cauchy-Schwarzova nerovnos alebo Cauchy-Schwarzova-Bunyakovského nerovnos, pod a troch slávnych matematikov, ktorým v a íme za jej objavenie a viaceré roz²írenia. Obr. 1: Z ava: Augustin Louis Cauchy [8], Viktor Jakovlevi Bunyakovskij [7] a Hermann Amandus Schwarz [8] 1.1 História Prvýkrát bola Cauchy-Schwarzova nerovnos, ako uvádza práca [15], z ktorej sme v tejto podkapitole erpali, publikovaná v roku 181 v diele Augustina Louisa Cauchyho Cours d' Analyse Algébrique [7], kde ju pouºil v zopár ilustratívnych príkladoch. O 8 rokov neskôr ju pouºil znovu pri overovaní Newtonovej metódy na h adanie kore ov algebraických rovníc. Cauchy odvodil túto nerovnos v nasledovnom znení: Nech u 1,..., u n, v 1,..., v n sú reálne ísla, potom platí n ) u i v i n u i n v i. 1) 1
13 1.1 História 1 CAUCHY-SCHWARZOVA NEROVNOS Rovnos nastáva vtedy a len vtedy, ak u i = 0 pre v²etky i = 1,..., n alebo existuje t R také, ºe v i = tu i pre v²etky i = 1,..., n. Tento tvar je aj dnes naj astej²ie pouºívaným tvarom Cauchy-Schwarzovej nerovnosti. Neskôr ju Viktor Jakovlevi Bunyakovskij v roku 1859 vo svojom diele Mémoires [6] roz²íril aj na sú ty nekone ných radov a integrály pomocou aproximácie sumami. Pre nekone né rady teda nadobudla znenie: Nech u 1, u,..., v 1, v,... sú reálne ísla, potom platí ) u i v i vi. ) Rovnos nastáva vtedy a len vtedy, ak u i = 0 pre v²etky i = 1,,... alebo existuje t R také, ºe v i = tu i pre v²etky i = 1,,.... Uvedieme aj integrálnu formu pre funkcie: Nech f, g sú reálne integrovate né funkcie na intervale [a, b], potom b b fx)gx)dx) a a u i ) b ) f x)dx g x)dx, 3) a pri om rovnos platí práve vtedy, ke f a g sú lineárne závislé funkcie, teda gx) = λfx), kde λ R. Jedným z mien, ktoré sa s touto nerovnos ou spájajú je aj meno matematika Hermanna Amandusa Schwarza. Schwarz vo svojom lánku [3] sformuloval Cauchyho nerovnos pre vektorové priestory, skalárny sú in a jeho normu. Nech V je vektorový priestor nad po om F so skalárnym sú inom.,. : V V F a normou., odvodenou od tohto skalárneho sú inu ako u = u, u. Potom pre ubovo né vektory u, v V platí u, v u v. 4) Rovnos nastáva práve vtedy, ke u a v sú lineárne závislé vektory, teda ak existujú také reálne ísla k 1, k, ºe aspo jedno z nich je rôzne od nuly a zárove platí k 1.u + k.v = 0. 13
14 1. V²eobecný tvar 1 CAUCHY-SCHWARZOVA NEROVNOS 1. V²eobecný tvar Predtým, ako vyslovíme a dokáºeme tvrdenie o v²eobecnom tvare Cauchy-Schwarzovej nerovnosti pre ubovo ný vektorový priestor so skalárnym sú inom a od neho odvodenou normou, si pripomenieme pojmy vektorový priestor, skalárny sú in a norma. Hovoríme, ºe V je vektorový priestor nad po om F, ak neprázdna mnoºina V spolu s binárnou operáciou +, V, +) je komutatívna grupa a kaºdej dvojici c F, v V je priradený prvok c.v V, pri om pre ubovo né c, d F a u, v V platí: i) c.u + v) = c.u + c.v, ii) c + d).v = c.v + d.v, iii) c.d).v = c.d.v), iv) 1.v = v. Skalárny sú in na vektorovom priestore V nad po om reálnych ísel R je zobrazenie g : V V R. Zobrazenie g je kladne denitná symetrická bilineárna forma, to znamená, ºe pre ubovo né u, v, w V a c R platí: i) gu, v) = gv, u) ii) gu + v, w) = gu, w) + gv, w) iii) gcu, v) = cgu, v) iv) ak u 0, tak gu, u) > 0. Vektorový priestor V spolu so skalárnym sú inom g alebo inak povedané, usporiadanú dvojicu V, g), nazývame unitárnym vektorovým priestorom. alej budeme pre skalárny sú in pouºíva namiesto gu, v) ozna enie u, v. Norma vektora, teda jeho ve kos je pre ubovo ný prvok unitárneho vektorového priestoru V denovaná ako funkcia. : V R, ktorá pre ubovo né u, v V a pre ubovo né α R sp a vlastnosti: i) u 0, u = 0 práve vtedy, ak u = 0, ii) αu = α u, iii) u + v u + v. My budeme uvaºova len normy odvodené od niektorého skalárneho sú inu nasledovným spôsobom u = u, u. 14
15 1. V²eobecný tvar 1 CAUCHY-SCHWARZOVA NEROVNOS Teraz prejdeme ku v²eobecnému tvaru Cauchy-Schwarzovej nerovnosti pre unitárny vektorový priestor s normou. Tvrdenie 1.1. Nech V je unitárny vektorový priestor nad R. Potom pre ubovo né vektory u, v V platí u, v u v. Rovnos nastáva vtedy a len vtedy, ak u a v sú lineárne závislé vektory, t.j. existuje k R, ºe u = kv. Dôkaz: Vlastnos iv) skalárneho sú inu nám zabezpe í, ºe u 0 a u = 0 práve vtedy, ke u = 0. Tento poznatok pouºijeme pre vektor u + cv, kde c je ubovo né reálne íslo. V aka vlastnostiam skalárneho sú inu môºeme urobi tieto úpravy u + cv = u + cv, u + cv = u, u + c u, v + c v, v = = u + c u, v + c v 0. Ke ºe uvedená nerovnos mala plati pre ubovo né c, môºeme ju chápa ako kvadratickú nerovnicu s neznámou c. Diskriminant tejto nerovnice musí by nekladný D = 4 u, v 4 u v 0. Z tejto nerovnosti dostaneme u, v u v a po odmocnení máme u, v u v, o je práve nerovnos 4). Tým sme dokázali platnos Cauchy-Schwarzovej nerovnosti pre ubovo ný vektorový priestor a skalárny sú in s normou. Pre rôzne vektorové priestory a skalárne sú iny nadobúda Cauchy-Schwarzova nerovnos rôzne tvary. Ke napríklad zoberieme za V reálny n-rozmerný vektorový priestor R n a ²tandardný skalárny sú in denovaný ako 15
16 1. V²eobecný tvar 1 CAUCHY-SCHWARZOVA NEROVNOS u, v = u T v = n u i v i s Euklidovskou normou n u = u i, tak dostaneme Cauchyho tvar 1). Bunyakovského tvar pre nekone né sumy ) dostaneme, ak vezmeme ako V nekone norozmerný reálny vektorový priestor a skalárny sú in denovaný nasledovne u, v = u T v = u i v i s normou u = u i. Ak chceme dosta druhý Bunyakovského tvar pre funkcie 3), zoberieme za V priestor C a, b v²etkých spojitých reálnych funkcií denovaných na uzavretom intervale a, b, kde a < b sú reálne ísla. Pre f, g V denujeme skalárny sú in nasledovne s normou f, g = f = b a b fx)gx)dx a f x)dx. Overíme, ºe takto denovaný skalárny sú in sp a potrebné vlastnosti. Násobenie reálnych ísel je komutatívne a integrál má vlastnos homogenity a aditivity. Z toho vyplýva, ºe f, g je symetrická bilineárna forma na V, teda sp a prvé tri vlastnosti skalárneho sú inu. alej pre f 0, je f x) 0 pre kaºdé x a, b. Zo spojitosti f, a teda aj f, vyplýva existencia uzavretého podintervalu c, d a, b takého, ºe f x) > 0 pre v²etky x c, d. Na tomto podintervale f zárove nadobúda svoje minimum, teda f, f = b a f x)dx d c f x)dx d c) min c x d f x) > 0. 16
17 1. V²eobecný tvar 1 CAUCHY-SCHWARZOVA NEROVNOS To znamená, ºe tento skalárny sú in sp a aj podmienku kladnej denitnosti, teda je korektne denovaný. al²ím príkladom skalárneho sú inu sú kladne denitné bilineárne formy denované nasledovne s normou tvaru u, v = u T Av u = u T Au, kde A je kladne denitná n n matica a u, v R n sú n-rozmerné reálne vektory. Cauchy-Schwarzova nerovnos má pre n-rozmerný reálny vektorový priestor R n a takto denovaný skalárny sú in nasledovný tvar u T Av ut Au v T Av, s rovnos ou pre lineárne závislé vektory u a v. Ak uvaºujeme priestor reálnych m n matíc R m n a na om denovaný skalárny sú in matíc U, V R m n ako U, V = tru T V ), kde tra) je stopa matice A R n n, t.j. tra) = n a ii. Norma odvodená od tohto skalárneho sú inu vyzerá nasledovne U = U, U = tru T U). Cauchy-Schwarzova nerovnos v tomto prípade nadobúda tvar tru T V ) tru T U) trv T V ). Rovnos nastáva vtedy a len vtedy, ke je jedna z matíc nulová alebo je skalárnym násobkom druhej U = cv, 17
18 1. V²eobecný tvar 1 CAUCHY-SCHWARZOVA NEROVNOS kde c je reálne íslo. Napokon, Cauchy-Schwarzova nerovnos sa dá zov²eobecni pre vektorový priestor nad komplexnými íslami a Hermitovský skalárny sú in. Hermitovský skalárny sú in je zobrazenie h : V V C na n-rozmernom komplexnom vektorovom priestore V denované ako hu, v) = u, v = n u i v i, kde u, v C n. Hermitovský skalárny sú in sp a pre ubovo né u, v, w C n a c C nasledujúce vlastnosti: i) u + v, w = u, w + v, w ii) u, v + w = u, v + u, w iii) cu, v = c u, v iv) u, cv = c u, v v) u, v = v, u vi) u, u 0, s rovnos ou iba pre u = 0. Norma pre hermitovský skalárny sú in má tvar n n u = u i u i = u. Cauchy-Schwarzova nerovnos pri takejto denícii vektorového priestoru a skalárneho sú inu vyzerá pre u, v V nasledovne n n n u j v j u j u j v j v j. 5) j=1 j=1 V²eobecný tvar Cauchy-Schwarzovej nerovnosti sme v²ak mali dokázaný len pre skalárne sú iny na vektorových priestoroch nad R. Uvedieme preto aj analógiu tohoto dôkazu pre komplexný priestor. Dôkaz: Vyuºijúc vlastnosti hermitovského sú inu robíme úpravy u + cv, u + cv = u, u + u, cv + cv, u + cv, cv = u, u + c u, v + c v, u + cc v, v = u + c u, v + c u, v + c v = u + Rec u, v ) + c v. j=1 18
19 1. V²eobecný tvar 1 CAUCHY-SCHWARZOVA NEROVNOS Kladná denitnos hermitovského skalárneho sú inu nám pre ubovo né u, v C n a c C zabezpe í nezápornos výrazu u + cv, u + cv, teda dostaneme nerovnos u + Rec u, v ) + c v 0. 6) Vieme, ºe reálna as komplexného ísla je vºdy men²ia ako jeho absolútna hodnota, teda Rec u, v ) c u, v = c u, v. Ke takto nahradíme prostredný len v nerovnosti 6) máme novú nerovnos c v + c u, v + u 0, ktorú uº vieme ahko vyrie²i rovnakým spôsobom ako v reálnom prípade. Z nekladného diskriminantu dostaneme nerovnos 5). Na druhej strane si môºeme v²imnú, ºe ke jednotlivé zloºky u = u 1, u,..., u n ) prepí²eme ako u k = x k +y k i, dá sa o C n uvaºova ako o R n. Teda komplexný vektorový priestor sa dá zreálni na n rozmerný vektorový priestor nad R. Obr. : Komplexné íslo z a k nemu komplexne zdruºené z [30] V tom prípade je reálna as hermitovského skalárneho sú inu Reh) ²tandardný skalárny sú in a jeho imaginárna as Imh) je nedegenerovaná nulová len pre nulový prvok) bilineárna forma s meniacimi sa znamienkami. 19
20 1.3 Alternatívne dôkazy a odvodenia 1 CAUCHY-SCHWARZOVA NEROVNOS 1.3 Alternatívne dôkazy a odvodenia Spôsobov dokazovania tejto nerovnosti je skuto ne ve mi ve a a vznikajú stále nové, i uº podobné tým star²ím alebo s celkom odli²nou technikou. V tejto práci ur ite nie je priestor, aby sme sa venovali kaºdému z nich, tak uvedieme aspo tie jednoduch²ie alebo zaujímavej²ie.v²etky dôkazy sa týkajú tvaru 1) Odvodenie pomocou Lagrangeovej identity Tento dôkaz vyuºíva platnos Lagrangeovej identity 1 n n u i v j u j v i ) = j=1 alebo inak zapísané ako n u i n n ) v i u i v i. 7) u v = u v u, v Uvedieme odvodenie in²pirované lánkom [3]. Po umocnení a usporiadaní výrazu n n j=1 n u i v i j=1 n u i v j u j v i ) = n n j=1 dostaneme Lagrangeovu identitu 7). n u i v j u j v i ) u n i j=1 v j + n v n i j=1 u j n ) n ) n ) v j u j = u i v i u i v i Vidíme, ºe výraz na avej strane 7) je nezáporný pre v²etky reálne ísla, teda n u n n i v i u i v i) = 1 n n u i v j u j v i ) 0. Z toho vyplýva o je presne tvar 1). n u n i j=1 n v i ) u i v i, 0
21 1.3 Alternatívne dôkazy a odvodenia 1 CAUCHY-SCHWARZOVA NEROVNOS 1.3. Dôkaz matematickou indukciou Úplne odli²ným spôsobom dokazovania je matematická indukcia, no aj takýmto spôsobom sa dá Cauchy-Schwarzova nerovnos dokáza. In²pirovali sme sa dôkazom na stránke [0] a v lánku [3]. Prípad n = 1 je triviálny. Pre n = máme u 1 v 1 + u v ) = u 1 v 1 + u 1 v 1 u v + u v. V aka nezápornosti výrazu u 1 v u v 1 ) 0 alebo ekvivalentne u 1 u v 1 v u 1v + u v 1 dostaneme u 1 v 1 + u 1 v 1 u v + u v u 1 v 1 + u 1 v + u v 1 + u v = u 1 + u )v 1 + v ), teda platí nerovnos u 1 v 1 + u v ) u 1 + u )v 1 + v ). Predpokladajme, ºe takáto nerovnos platí pre nejaké prirodzené íslo k, teda k ) k u i v i u i ) k Dokáºeme platnos tohto tvrdenia pre k + 1, teda k+1 ) k+1 ) k+1 u i v i u i v i v i ) ). 8) Za neme od induk ného predpokladu 8), ktorý odmocníme a pripo ítame k + 1-vé leny k k u i v i + u k+1 v k+1 u i ) 1 k Teraz vyuºijeme uº dokázanú Cauchyho nerovnos pre n = v tvare v i ) 1 a 1 b 1 + a b a 1 + a ) 1 b 1 + b ) 1. + u k+1 v k+1. 9) 1
22 1.3 Alternatívne dôkazy a odvodenia 1 CAUCHY-SCHWARZOVA NEROVNOS Za a 1, a, b 1, b dosadíme nasledovné výrazy: a 1 = k u i, a = u k+1, b 1 = k vi, b = v k+1 a z pravej strany nerovnosti 9) dostaneme o je to isté ako k k u i v i + u k+1 v k+1 k+1 u i v i ) u i + u k+1 k+1 u i ) 1 k ) 1 k+1 v i v i + v k+1 To znamená, ºe Cauchy-Schwarzova nerovnos platí pre n = k+1, teda platí pre v²etky prirodzené ísla. Po umocnení dostaneme nerovnos 1). ) 1. ) 1, Dôkaz pomocou postupnosti sú tov V nasledujúcom dôkaze pod a príkladu autora lánku [3] vytvoríme monotónnu postupnos {S n }. Denujeme ju nasledovne S n = u 1 v u n v n ) u u n)v vn). Potom rozdiel po sebe idúcich lenov vyzerá takto S n+1 S n = u 1 v u n+1 v n+1 ) u u n+1)v vn+1) u 1 v u n v n ) + u u n)v vn) = u 1v u n+1vn+1 + u 1 v 1 u v u n v n u n+1 v n+1 u 1v1... u n+1vn+1 u 1v1... u nvn u 1 v 1 u v... u n v n u n+1 v n+1 + u 1v u nvn a dá sa zjednodu²i na S n+1 S n = [u 1 v n+1 v 1 u n+1 ) + u v n+1 v u n+1 ) u n v n+1 v n u n+1 ) ]. Z toho vidno, ºe
23 1.3 Alternatívne dôkazy a odvodenia 1 CAUCHY-SCHWARZOVA NEROVNOS S n+1 S n a ke ºe to platí pre v²etky n N, tak S n S n 1... S 1 = 0, o implikuje na²u nerovnos 1) Dôkaz pomocou Jensenovej nerovnosti al²ím zaujímavým prístupom je dôkaz pomocou Jensenovej nerovnosti pre konvexné funkcie, ktorá znie nasledovne: Funkcia f je konvexná na intervale J, ak pre ubovo né x 1,..., x n J a pre ubovo né n θ 1,..., θ n, θ i 0, θ i = 1 platí n ) n f θ i x i θ i fx i ). 10) Funkcia je konkávna, ak v uvedenom výraze platí opa ná nerovnos. A teraz k dôkazu Cauchyho nerovnosti, uvedenému v lánku [3]. Uvaºujeme reálne ísla u 1,..., u n, v 1,..., v n. Vieme, ºe funkcia fx) = x je konvexná na intervale, ). Pouºitím Jensenovej nerovnosti dostaneme θ 1 x 1 + θ x θ n x n ) θ 1 x 1 + θ x θ n x n, kde θ i 0, θ 1 + θ θ n = 1, x i R. Dôkaz rozdelíme na dve asti: I. v i 0 pre i = 1,..., n v i Poloºíme θ i = a x v vn i = u i pre i = 1,..., n dosadíme do Jensenovej nerovnosti v i pre fx) = x a dostaneme Po úprave dostaneme ) u1 v u n v n u u n. v vn v vn u 1 v u n v n ) u u n)v v n). 3
24 1.3 Alternatívne dôkazy a odvodenia 1 CAUCHY-SCHWARZOVA NEROVNOS II. Ak existujú v i1 = v i =... = v ik = 0 dostaneme n ) ) u i v i = u i v i i i 1,...,i k,1 i n Tým je nerovnos 1) dokázaná. n u i u i i i 1,...,i k,1 i n ) n v i ). ) v i i i 1,...,i k,1 i n ) Dôkaz pomocou AG nerovnosti al²ia nerovnos, pomocou ktorej sa dá dokáza platnos Cauchy-Schwarzovej nerovnosti je AG nerovnos, teda nerovnos aritmetického a geometrického priemeru, o ktorej budeme písa v kapitole. Najprv uvedieme jej znenie: Pre nezáporné reálne ísla x 1, x platí s rovnos ou len pre x 1 = x. x1 x x 1 + x, Dôkaz Cauchy-Schwarzovej nerovnosti prevedieme nasledovne ako v lánku [3]. Poloºíme A = u 1 + u u n a B = v 1 + v v n, pre u i, v i R. Napí²eme AG nerovnosti pre jednotlivé dvojice u i A, vi B u i v i AB 1 u i A + v i B Ke tieto nerovnosti s ítame pre v²etky i = 1,..., n dostaneme n u i v i AB 1 ) n u i A + v i = 1, B teda n u i v i AB = u 1 + u un v 1 + v vn. Po umocnení dostane poºadovaný tvar nerovnosti 1). ) Dôkaz pomocou permuta nej nerovnosti Permuta ná nerovnos, ktorej platnos vyuºíva nasledujúci dôkaz, znie nasledovne: 4
25 1.3 Alternatívne dôkazy a odvodenia 1 CAUCHY-SCHWARZOVA NEROVNOS Lema 1.. Nech x 1... x N, y 1... y N sú reálne ísla a x σ1),..., x σn) je nejaká permutácia x 1,..., x N. Potom platí x 1 y x N y N x σ1) y x σn) y N x N y x 1 y N. Uvádzame postup dôkazu z lánku [3]. Pre N-tice x i, y i a x σi) z lemy 1. zavedieme ozna enie A = x 1,..., x N ), B = y 1,..., y N ), Ã = x σ1),..., x σn) ). Bez ujmy na v²eobecnosti môºeme predpoklada, ºe prvky u i v i, i = 1,,..., n sú usporiadané tak, ºe u 1 v 1... u 1 v n u v 1... u v n... u n v 1... u n v n. Za N-tice z lemy 1. zoberieme A = B = u 1 v 1,..., u 1 v n, u v 1,..., u v n,..., u n v 1,..., u n v n ), Ã = u 1 v 1,..., u n v 1, u 1 v,..., u n v,..., u 1 v n,..., u n v n ). Ke na ne aplikujeme permuta nú nerovnos, dostaneme u 1 v 1 )u 1 v 1 ) u 1 v n )u 1 v n ) + u v 1 )u v 1 ) u v n )u v n ) u n v 1 )u n v 1 ) u n v n )u n v n ) u 1 v 1 )u 1 v 1 ) u 1 v n )u n v 1 ) + u v 1 )u 1 v ) u v n )u n v ) u n v 1 )u 1 v n ) u n v n )u n v n ). Ke roznásobíme jednotlivé zátvorky dostaneme u 1v u 1vn + u v u vn u nv u nvn u 1v u 1 u n v 1 v n + u 1 u v 1 v u u n v v n u 1 u n v 1 v n u nvn, o sa dá napísa ako u 1 + u u n)v1 + v vn) u 1 v 1 + u v u n v n ) a to je opä tvar 1), ktorý sme chceli dosiahnu Odvodenie z úlohy na viazaný extrém In²piráciu pre nasledovné odvodenie sme na²li v publikácii [11], str. 6. Majme optimaliza nú úlohu s lineárnou ú elovou funkciou f 0 u) = v T u, kde u, v R n a v je 5
26 1.3 Alternatívne dôkazy a odvodenia 1 CAUCHY-SCHWARZOVA NEROVNOS pevný vektor. Mnoºina prípustných rie²ení denovaná rovnos ou f 1 u) = u T u 1 = 0 je kruºnica, teda kompaktná mnoºina. Úlohu budeme rie²i pomocou Lagrangeovej funkcie Lu, λ) = f 0 u) λf 1 u), λ R. Obr. 3: Mnoºina prípustných rie²ení f 1 u) = u T u 1 = 0, kde u R a vrstevnice ú elovej funkcie f 0 u) = v T u, pre v = 1, 1) a hodnoty f 0 u) = 0, f 0 u) = 1, f 0u) = 1 a f 0 u) = Lagrangeova funkcia pre túto úlohu má tvar Lu, λ) = v T u λu T u 1), λ R. Stacionárny bod Lagrangeovej funkcie sp a rovnice Z prvého vz ahu si vyjadríme u a dosadíme do ohrani enia f 1 u) L = v λu = 0, u L λ = ut u 1 = 0. u = v λ u T u = vt v λ λ = vt v 4λ = 1. 6
27 1.3 Alternatívne dôkazy a odvodenia 1 CAUCHY-SCHWARZOVA NEROVNOS Vyjadríme λ v T v λ = ± 4 = ± v a dosadíme do vz ahu pre u. Tým dostaneme dva stacionárne body Lagrangeovej funkcie L u 1 = v, v u = v. v V aka spojitosti Lagrangeovej funkcie L a kompaktnosti mnoºiny prípustných rie²ení, z Weierstrassovej vety vieme, ºe na tejto mnoºine Lagrangeova funkcia nadobúda svoje minimum aj maximum. To znamená, ºe získané stacionárne body budú bodmi minima a maxima û 1, û 1 = v, v û = v. v Dosadením do ú elovej funkcie f 0 u) dostaneme optimálne hodnoty f 0 û 1 ) = v T û 1 = vt v v = v, f 0 û ) = v T û = vt v v = v. Ke ºe f 0 û 1, ) sú maximom a minimom f 0 u), tak platí v v T u v. Z ohrani enia vyplýva, ºe u = 1 pre v²etky u, tak môºeme predo²lý vz ah prepísa na a odtia po jednoduchej úprave dostaneme v vt u u v v T u v u a to je práve nerovnos 1). 7
28 1.4 Aplikácie 1 CAUCHY-SCHWARZOVA NEROVNOS 1.4 Aplikácie Ako sme uº v úvode spomenuli, Cauchy-Schwarzova nerovnos má bohaté vyuºitie v rôznych matematických disciplínach Trojuholníková nerovnos Ve mi známou a asto pouºívanou napríklad v matematickej analýze je trojuholníková nerovnos, ktorá znie nasledovne: Pre ubovo né vektory u, v z unitárneho vektorového priestoru V platí u + v u + v. 11) Ukáºeme jej platnos pomocou Cauchy-Schwarzovej nerovnosti. Budeme upravova výraz u + v u + v = u + v, u + v = u, u + u, v + v, v = u + u, v + v Teraz vyuºijeme Cauchy-Schwarzovu nerovnos 4) a nahradíme len u, v u + u, v + v u + u v + v = u + v ). Dostávame nerovnos u + v u + v ), odkia uº ahko vyplýva nerovnos 11), o sme chceli dosta Kosínus uhla dvoch vektorov Jednou z dôleºitých aplikácií je dobrá denícia kosínusu uhla dvoch vektorov. Majme dva vektory u a v so spolo ným po iatkom, ktoré zvierajú uhol θ. Spolu s vektorom u v tvoria trojuholník. Vieme, ºe kosínus uhla je v pravouhlom trojuholníku podiel pri ahlej odvesny ku prepone. Potrebujeme teda nejako vytvori pravouhlý trojuholník. Urobíme projekciu vektora v na u, ím dostaneme nový vektor v, ktorý je k násobkom vektora u v = ku. 8
29 1.4 Aplikácie 1 CAUCHY-SCHWARZOVA NEROVNOS Rozdiel vektorov v v je kolmý na vektor u, ím sme dostali pravouhlý trojuholník, zobrazený na obrázku 4). Obr. 4: Projekcia vektora v na vektor u Ke ºe vektor v v je kolmý na vektor u, tak platí Dosadíme v = ku odkia vyplýva v v, u = 0. ku v, u = ku T u u T v = 0, v = ku = ut v u T u u = uut u T u v. Teraz vyjadríme kosínus uhla θ ako podiel odvesny v a prepony v cos θ = v v. Dosadíme v = uut u T u v cos θ = uu T u T u v v a postupne upravujeme cos θ v = uu T v u = u u, v u = u, v u. Dostaneme vzorec na výpo et kosínusu uhla ubovo ných dvoch vektorov u a v cos θ = u, v u v. 9
30 1.4 Aplikácie 1 CAUCHY-SCHWARZOVA NEROVNOS V prípade, ºe je niektorý z vektorov nulový, poloºíme θ = 0. Teraz príde na rad vyuzitie Cauchy-Schwarzovej nerovnosti 4) tak, ako uvádza aj autor predná²ky [1]. V aka nej platí 1 u, v u v 1. Ke ºe cos θ nadobúda len tieto hodnoty, takýto uhol vºdy existuje. Tým sme ukázali, ºe takáto denícia kosínusu dvoch uhlov je korektná Korela ný koecient al²ím príkladom vyuºitia tejto nerovnosti je z oblasti pravdepodobnosti a ²tatistiky. Pomocou ²peciálneho tvaru Cauchy-Schwarzovej nerovnosti pre náhodné premenné ukáºeme, ºe korela ný koecient je vºdy íslo z intervalu 1, 1. Najprv je potrebné pripomenú si niektoré pojmy. Mnoºinu v²etkých moºných výsledkov experimentu nazývame mnoºinou elementárnych udalostí a ozna ujeme Ω. V prípade, ºe je Ω kone ná, udalos ou rozumieme ubovo nú podmnoºinu Ω a systém v²etkých udalostí ozna ujeme S. Náhodná premenná X je priradenie íselných hodnôt elementárnym výsledkom experimentu. Pre íselný výsledok x, ktorý náhodná premenná X nadobúda, ozna ujeme symbolom P [X = x] pravdepodobnos tej mnoºiny elementárnych výsledkov, ktorým X prira uje hodnotu x. Strednou hodnotou náhodnej premennej nazývame váºený priemer moºných íselných výsledkov experimentu, kde váhy sú pravdepodobnosti nadobudnutia týchto výsledkov. Teda, ak íselnými výsledkami experimentu môºu by hodnoty x 1,..., x m, potom stredná hodnota je EX) = m x i P [X = x i ]. Disperzia náhodnej premennej X je íslo DX) = EX EX)). 30
31 1.4 Aplikácie 1 CAUCHY-SCHWARZOVA NEROVNOS Ke máme náhodné premenné X a Y so strednými hodnotami a disperziami, potom stredná hodnota covx, Y ) = EX EX))Y EY ))) existuje a nazýva sa kovariancia X a Y. Ak majú náhodné premenné X a Y stredné hodnoty EX), EY ) a nenulové disperzie DX), DY ), tak koecient korelácie medzi X a Y je íslo X EX) ρ X,Y = cov, Y ). EY ) DX) DY ) Obr. 5: Korela ný koecient pre rôzne sady dát Lema 1.3. [13], str.50, Veta 7.7) Nech X má strednú hodnotu EX) a disperziu DX). Ozna me X = X EX) DX). Potom EX ) = 0 a DX ) = 1. Ozna me teda 31
32 1.4 Aplikácie 1 CAUCHY-SCHWARZOVA NEROVNOS X = X EX) DX), Y = Y EY ) DY ). Tvar Cauchy-Schwarzovej nerovnosti pre stredné hodnoty pod a [13], str.50 vyzerá nasledovne: Nech náhodné veli iny X, Y majú stredné hodnoty EX), EY ), EX ), EY ). Potom platí E XY ) EX )EY ), 1) pri om rovnos platí vtedy a len vtedy, ke existujú a, b R, z ktorých aspo jedno je nenulové a pravdepodobnos P {ω : axω) + bxω) = 0}) = 1. Teraz odvodíme spomínané ohrani enie pre korela ný koecient. Chceme teda dokáza, ºe ρ X,Y 1. Postupne rozpisujeme ρ X,Y = covx, Y ) = EX Y ) EX )EY ). V aka leme 1.3 vieme, ºe EX ) = EY ) = 0, DX ) = DY ) = 1, teda EX Y ) EX )EY ) = EX Y ). Teraz pouºijeme Cauchy-Schwarzovu nerovnos 1) ρ X,Y = EX Y ) EX ) EY ) = DX ) DY ) = 1, teda ρ X,Y 1, o sme chceli dosiahnu Úloha o kladne denitných maticiach Úloha zo zdroja [4] znie nasledovne: Úloha: Nájdite nutnú a posta ujúcu podmienku pre α a β tak, aby 3
33 1.4 Aplikácie 1 CAUCHY-SCHWARZOVA NEROVNOS T + αt + βi bola kladne denitná matica pre ubovo nú symetrickú maticu T. Rie²enie: Pre prípad 1 1 matice T = t, t R nutnú a posta ujúcu podmienku dostaneme z nerovnosti t + αt + β > 0. Tá platí práve vtedy, ke je jej diskriminant záporný, teda α < 4β. 13) Pod a vzoru jednorozmerného prípadu chceme ukáza, ºe pre ubovo né n prirodzené platí, ºe matica T + αt + βi je kladne denitná pre ubovo nú symetrickú n n maticu T práve vtedy, ke α < 4β. Pre symetrickú n n maticu môºeme nájs jej spektrálny rozklad T = QΛQ T, kde Λ je diagonálna matica s vlastnými íslami matice T a Q je ortogonálna matica jej vlastných vektorov. Pre jej druhú mocninu platí T = QΛ Q T. Matica T + αt + βi bude kladne denitná práve vtedy, ke bude kladne denitná matica Q Λ + αλ + βi) Q T 0. Ke ºe ortogonálna matica zachováva d ºku vektora, sta í aby Λ + αλ + βi 0, odkia uº vyplýva podmienka 13). Na²im cie om v²ak bolo vyuºi Cauchy-Schwarzovu nerovnos, tak pouºijeme iný postup. 33
34 1.4 Aplikácie 1 CAUCHY-SCHWARZOVA NEROVNOS Zaujíma nás kladná denitnos matice T +αt +βi, o znamená, kedy pre ubovo né v 0 platí v T T + αt + βi)v > 0. Budeme teda skúma hodnotu výrazu v T T + αt + βi)v. Po roznásobení dostaneme v T T + αt + βi)v = T v, T v + α T v, v + β v, v = T v + α T v, v + β v, teda matica T + αt + βi je kladne denitná ke platí 0 < T v + α T v, v + β v. 14) Teraz pouºijeme Cauchy-Schwarzovu nerovnos. Ke ºe platí alebo inak zapísané α T v, v α T v v α T v v α T v, v α T v v, prostredný len pravej strany 14) α T v, v môºeme nahradi nasledovne o je to isté ako T v α T v v + β v T v + α T v, v + β v T v + α T v v + β v, T v α T v v + β v v T T + αt + βi)v T v + α T v v + β v. Po úprave ohrani ení na ²tvorec máme ) α v T v + β α 4 T v + ) v v T T + αt + βi)v 15) α v ) ) + β α v. 4 Z prvej nerovnosti 15) vyplýva posta ujúca podmienka pre α a β. To znamená, platnos podmienky 13) sta í na to, aby v T T + αt + βi)v > 0. Z druhej nerovnosti 15) zas vyplýva nutná podmienka. Teda, ak platí v T T + αt + βi)v > 0, potom nutne α a β sp a o je presne podmienka 13). β α 4 > 0, 34
35 1.5 Súvis s Hölderovou nerovnos ou 1 CAUCHY-SCHWARZOVA NEROVNOS 1.5 Súvis s Hölderovou nerovnos ou Cauchy-Schwarzova nerovnos je ²peciálnym tvarom Hölderovej nerovnosti. Aj ke Cauchyho nerovnos bola publikovaná uº v roku 181, kým Hölderove zov²eobecnenie sa pod a [6] neobjavilo do roku Hölderova nerovnos má nasledovné znenie: Nech p, q > 0 sú ísla sp ajúce rovnos Potom platí 1 p + 1 q = 1. s rovnos ou pre n n ) 1 u i v i u i p p n v i q ) 1 q, v i = c u i p 1. Ak poloºíme p = q =, dostaneme Cauchy-Schwarzovu nerovnos 1). Hölderova nerovnos sa tieº niekedy uvádza v tvare s integrálmi: Nech p, q > 0 sú ísla sp ajúce rovnos Potom platí nerovnos 1 p + 1 q = 1. Rovnos platí ak b a fx)gx) dx b a ) 1 ) fx) p p b 1 dx gx) q q dx. a gx) = c fx) p 1. Opä pre p = q = dosiahneme tvar Cauchy-Schwarzovej nerovnosti 3). 35
36 AG NEROVNOS AG nerovnos Nerovnos aritmetického a geometrického priemeru alebo AG nerovnos, ako sa astej²ie nazýva, je jednou z najznámej²ích a najpouºívanej²ích nerovností. Jej prvé formy boli pod a publikácie [19] známe pravdepodobne uº v antike. Neskôr, e²te pred zavedením innitezimálneho po tu, sa vyuºívala na rie²enie optimaliza ných úloh, ktoré by inak vyºadovali výpo et derivácie. Jej v²eobecný tvar s váºenými priemermi pre n premenných sa prvýkrát objavil v tla i aº v 19. storo í v poznámkach z Cauchyho ²kolenia, ktoré viedol na École Royale Polytechnique. V sú asnosti sa pouºíva hlavne pri dôkazoch iných nerovností a pri rie²ení minimaliza ných a maximaliza ných úloh..1 V²eobecný tvar Najprv pripomenieme pojmy aritmetický, geometrický, váºený aritmetický a váºený geometrický priemer v²eobecne pre n prvkov: Majme n-ticu kladných ísel x = x 1,..., x n ). Potom veli iny A n x) = x 1 + x x n ; n G n x) = n x 1 x...x n nazývame aritmetickým a geometrickým priemerom prvkov x 1,..., x n v tomto poradí. Majme dve n-tice ísel x = x 1,..., x n ), kde x i > 0 pre i = 1,..., n a w = w 1,..., w n ) tak, ºe w i 0 pre i = 1,..., n a n w i = 1. Potom veli iny A n x; w) = w 1 x 1 + w x w n x n ; G n x; w) = x w 1 1 x w...x wn n nazývame váºeným aritmetickým a váºeným geometrickým priemerom prvkov x 1,..., x n, s nezápornými váhami w 1,..., w n v tomto poradí. AG nerovnos sa zvykne uvádza vo viacerých tvaroch. Najjednoduch²ím z nich je tvar pre premenné: 36
37 . Jednoduché dôkazy pre premenné AG NEROVNOS Nech x 1 a x sú kladné reálne ísla, potom platí x 1 + x x 1 x 16) s rovnos ou pre x 1 = x. Rovnako astý je aj tvar pre n premenných: Nech x 1,..., x n sú kladné reálne ísla, potom platí medzi nimi nasledujúca nerovnos A n x) = x 1 + x x n n n x 1 x...x n = G n x), 17) pri om rovnos je splnená vtedy a len vtedy, ak sú v²etky x i pre i = 1,..., n rovnaké. Najv²eobecnej²í tvar AG nerovnosti je tvar s váºenými priemermi: Majme dve n-tice kladných ísel x = x 1,..., x n ) a w = w 1,..., w n ) tak, ºe w 0, n w i = 1. Potom platí nerovnos A n x; w) = w 1 x 1 + w x w n x n x w 1 1 x w...x wn n = G n x; w). 18) Rovnos je splnená práve vtedy, ak sú v²etky x i rovnaké.. Jednoduché dôkazy pre premenné Za neme od najjednoduch²ích dôkazov pre dva rozmery. Nasledujúce dva dôkazy sme prebrali z lánku [31]...1 Geometrický dôkaz.1 Plocha ve kého ²tvorca na obrázku 6) je x 1 + x ). Plocha v²etkých ºltých trojuholníkov dohromady je x 1 x a ke ºe modré trojuholníky sú zrkadlovými obrazmi ºltých, ich plocha je takisto x 1 x. Celková plocha trojuholníkov je teda 4x 1 x. alej vidíme, ºe plocha bieleho ²tvorca v strede je x 1 x ). D ºky x 1 a x sú zvolené 37
38 . Jednoduché dôkazy pre premenné AG NEROVNOS Obr. 6: Geometrický dôkaz.1, [31] tak, ºe x 1 > x. Ak by sme tieto d ºky postupne menili tak, ºe x 1 sa bude blíºi k x, tak plocha bieleho ²tvorca sa bude zmen²ova. Nulová bude práve vtedy, ke x 1 = x. Zrejme platí nerovnos x 1 + x ) 4x 1 x, s rovnos ou nastávajúcou pre x 1 = x. Po nieko kých ekvivalentných úpravách sa dopracujeme k tvaru nerovnosti 16)... Geometrický dôkaz. V al²om dôkaze AG nerovnos vyplýva priamo z rovnosti dvoch rôznych zápisov tej istej plochy. Plocha ve kého ²tvorca na obrázku 7) sa dá zapísa bu ako x 1 +x ), alebo ako sú et plôch obd ºnikov 4x 1 x a plochy malého ºltého ²tvorca x 1 x ). Platí teda rovnos x 1 + x ) = x 1 x ) + 4x 1 x. 38
39 . Jednoduché dôkazy pre premenné AG NEROVNOS Obr. 7: Geometrický dôkaz., [31] Je zrejmé, ºe len x 1 x ) je nezáporný, teda ur te bude plati nerovnos x 1 + x ) 4x 1 x, odkia uº ahko dostaneme tvar nerovnosti 16)...3 Geometrický dôkaz.3 Nasledujúci dôkaz sme prebrali z publikácie [5]. Nech ABCD je ²tvorec so stranou x 1 a ABF E je obd ºnik so stranami x 1 a x. Obr. 8: Geometrický dôkaz.4, [5] 39
40 . Jednoduché dôkazy pre premenné AG NEROVNOS Plochu obd ºnika ABF E ozna íme P ABF E. Je zrejmé, ºe platí nasledovný vz ah to znamená o uº je dokazovaná nerovnos 16). P ABF E = P AGE + P ABF G P AGE + P ABC, x 1 x x + x 1,..4 Geometrický dôkaz.4 al²í dôkaz, ktorý je in²pirovaný dôkazom z lánku [16] vyuºíva vlastnosti Tálesovej kruºnice a Euklidovu vetu o vý²ke. Môºeme si ich v skratke pripomenú. Tálesova veta hovorí, ºe ak A, B, C sú body na kruºnici, kde AC je priemer kruºnice, potom uhol ABC je pravý uhol. Euklidova veta o vý²ke hovorí, ºe obsah ²tvorca zostrojeného nad vý²kou pravouhlého trojuholníka sa rovná obsahu obd ºnika zostrojeného z oboch úsekov na prepone. Bez ujmy na v²eobecnosti môºeme predpoklada, ºe pre reálne ísla x 1, x platí x 1 > x. Skon²truujeme kruºnicu s priemerom x 1 + x. Polomer preto bude x 1+x, teda aritmetický priemer x 1 a x. alej urobíme kolmicu na priemer v spolo nom bode P úse iek x 1 a x a jej priese ník s kruºnicou nazveme C. Obr. 9: Geometrický dôkaz.3 40
41 . Jednoduché dôkazy pre premenné AG NEROVNOS Pod a Tálesovej vety bude uhol ACB na obrázku 9) pravým uhlom, o nám umoºní pouºi Euklidovu vetu na výpo et vý²ky trojuholníka ABC, ktorá bude ma d ºku x 1 x. Z obrázka 9) alej vidíme, ºe d ºka x 1 x ervenej úse ky vý²ky) bude ur ite men²ia ako d ºka modrej úse ky polomer kruºnice) x 1+x, ktorá je zárove preponou trojuholníka SP C. Okrem prípadu a = b, ke je vý²ka trojuholníka ABC totoºná s jeho polomerom. Opä sme tým dokázali nerovnos 16)...5 Dôkaz pomocou doty nice hyperboly Nasledujúci dôkaz je opä prebraný z lánku [31]. Zvolíme ubovo ný bod x, y) v prvom kvadrante roviny R. Na obrázku 10) vidno, ºe ak priamka x + y = m má nejaký spolo ný bod s niektorou z hyperbol xy = c, tak bu sú to dva body, v ktorých ju pretína, alebo práve jeden dotykový bod. Obr. 10: Dôkaz pomocou doty nice hyperboly, [31] Ak je priamka x + y = m doty nicou ku jednej z hyperbol, tak sa dotýkajú v bode m, m). Pre dotykový bod m, m) potom platí 41
42 .3 Cauchyho dôkaz spätnou indukciou AG NEROVNOS c = xy = m a teda ) x + y xy =. Kaºdý iný bod tejto priamky je priese níkom s niektorou z hyperbol xy = c pre nejaké iné, men²ie c, c < m. Teda ak za x, y) zvolíme ubovo né x 1, x ), x 1, x 0, tak alebo platí nerovnos ) x1 + x x 1 x <, alebo rovnos ak x 1 = x ) x1 + x x 1 x =. Tým sme dokázali AG nerovnos v tvare 16). Teraz uvedieme dôkazy AG nerovnosti pre v²eobecný po et n premenných..3 Cauchyho dôkaz spätnou indukciou Cauchyho dôkaz sa uvádza v literatúre naj astej²ie zo v²etkých dôkazov AG nerovnosti. My sme si ako predlohu vybrali publikácie [4] a [5]. Pre n = nerovnos vyplýva z nezápornosti výrazu 0 x 1 x ) = x 1 x 1 x + x. Dokáza platnos pre n = 3 sa nám teraz e²te nepodarí, tak skúsime prejs na n = 4. Môºeme si v²imnú, ºe ak AG nerovnos aplikujeme dvakrát, tak máme 4 x1 x x 3 x 4 = x1 x + x 3 x 4 x1 x x3 x 4 x 1 + x + x 3 + x 4 = x 1 + x + x 3 + x 4, 4 o dokazuje na²u nerovnos pre n = 4. Skúsme sa teraz vráti k prípadu n = 3. Uº vieme, ºe AG nerovnos platí pre ubovo né ²tyri kladné ísla. 4
43 .3 Cauchyho dôkaz spätnou indukciou AG NEROVNOS Skúsme teda ku x 1, x, x 3 prida kladné íslo, ktoré nezmení ich aritmetický priemer a vyuºi tento poznatok x 1 + x + x 3 3 = x 1 + x + x 3 + x 1 + x + x Dostali sme nerovnos )) 1 x1 + x + x 4 3 x 1 + x + x 3 x 1 x x 3, 3 3 ktorú môºeme postupne upravi x 1 x x 3 x1 + x + x 3 3 ) x1 + x + x 3 3 )) 1 x1 + x + x 4 3 x 1 x x 3. 3 ) 4 na nerovnos x1 + x + x 3 x 1 x x 3 3 ) 3 ktorú sme potrebovali. 3 x1 x x 3 x 1 + x + x 3, 3 Vyzerá, ºe by sa podobný postup dal pouºi aj v al²ích prípadoch pre vä ²ie n. Ke AG aplikujeme k-krát, dokáºeme platnos pre n = k. pre ubovo né k 1. x 1 x...x k) 1 k x 1 + x x k k, Medzery medzi druhými mocninami vyplníme nasledovne. Vezmeme nejaké m < k a skúsime nájs spôsob ako pouºi m ísel x 1, x,..., x m na vytvorenie dlh²ej postupnosti α 1, α,..., α k, na ktorú by sme aplikovali AG nerovnos. Zvo me teda postupnos {α i } nasledovne α i = x i pre 1 i m, α i = x 1 + x x m m A pre m < i k, inak povedané, len doplníme na miesta chýbajúcich k m lenov pôvodnej postupnosti aritmetické priemery A. Po aplikovaní AG dostaneme x 1 x...x m A k m ) 1 k x 1 + x x m + k m)a k = k A k = A. 43
44 .4 Dôkaz pomocou pre²kálovania prvkov AG NEROVNOS Mocniny A presunieme na pravú stranu nerovnosti x 1 x...x m ) 1 k A m k a ke umocníme obe strany na k, dostaneme presne poºadovaný tvar dokazovanej m nerovnosti 17)..4 Dôkaz pomocou pre²kálovania prvkov Dôkaz, ktorý teraz nasleduje je uvedený v publikácii [14]. Najskôr dokáºeme platnos nasledovného tvrdenia. Tvrdenie.1. Ak je sú in n kladných reálnych ísel x 1, x,..., x n rovný 1, potom ich sú et nie je men²í ako n, teda ak x 1 x...x n = 1, potom platí nerovnos x 1 + x x n n. Na dôkaz pouºijeme matematickú indukciu. Najprv skontrolujeme platnos pre n =, to znamená, ºe volíme len také x 1, x, ºe x 1 x = 1 a overíme, i vºdy platí x 1 + x. Pre x 1 = x = 1 je platnos zrejmá. Ak x 1 x, bez ujmy na v²eobecnosti môºeme predpoklada, ºe x 1 < x, potom musí by x 1 < 1 a x > 1, ke ºe ich sú in má by rovný 1. Z rovnosti 1 x 1 )x 1) = x 1 + x x 1 x 1 vyplýva x 1 + x = x 1 x x 1 )x 1) = + 1 x 1 )x 1) a ke ºe x 1 < 1 < x, tak sú in 1 x 1 )x 1) je kladný, teda x 1 + x >, ím je tvrdenie.1 pre n = dokázané. Teraz predpokladajme, ºe tvrdenie.1 platí pre n = k a dokáºeme, ºe potom platí aj pre n = k
45 .4 Dôkaz pomocou pre²kálovania prvkov AG NEROVNOS Ako prvé si treba v²imnú, ºe ak x 1 x...x k+1 = 1, tak môºu nasta dva prípady: I. Ke sú v²etky initele rovné 1 x 1 = x =... = x k = x k+1 = 1. Vtedy sa ich sú et rovná k + 1. II. V prípade, ºe nie sú v²etky initele rovnaké, musia niektoré z nich by vä ²ie ako 1 a niektoré men²ie ako 1. Napríklad, predpokladajme, ºe x 1 < 1 a x k+1 > 1. Poloºme y = x 1 x k+1. Potom máme yx...x k = 1. Ide o sú in k ísel rovný 1, teda pod a induk ného predpokladu o ich sú te platí y + x x k k. alej je zrejmé, ºe platí x 1 + x x k + x k+1 = y + x x k ) + x k+1 y + x 1 k + x k+1 y + x 1 = k + 1) + x k+1 y + x 1 1. V nasledujúcom kroku vyuºijeme, ºe y = x 1 x k+1 x 1 +x +...+x k +x k+1 k +1)+x k+1 x 1 x k+1 +x 1 1 = k +1)+x k+1 1)1 x 1 ). Ke ºe x 1 < 1 a x k+1 > 1, sú in x k+1 1)1 x 1 ) je kladný a preto x 1 + x x k + x k+1 k + 1) + x k+1 1)1 x 1 ) > k + 1, ím je tvrdenie.1 dokázané. Teraz prejdeme k samotnému dôkazu AG nerovnosti. Ozna íme G n x) = g. 45
46 .5 Dôkazy vyuºívajúce konvexnos alebo konkávnos AG NEROVNOS Z rovnosti vyplýva alebo po umocnení g = n x 1 x...x n 1 = n x1 g 1 = x 1 g x g...x n g, x g...x n g. V aka tvrdeniu.1 vieme, ºe sú et lenov x 1 g, x g,..., x n g x 1 g + x g x n g n. je aspo n, teda platí Prenásobením oboch strán g dostaneme poºadovaný tvar 17). n Rovnos je splnená práve vtedy, ke x 1 g = x g =... = x n g = 1, teda x 1 = x =... = x n = g, kde g ozna uje geometrický priemer x i, i = 1,..., n..5 Dôkazy vyuºívajúce konvexnos alebo konkávnos.5.1 Dôkaz pomocou konkávnosti geometrického priemeru Prvú as nasledovného dôkazu sme prebrali z publikácie [3]. Ako prvý krok dokáºeme, ºe geometrický priemer G n x) je konkávna funkcia na kladnom ortante R ++ ) n. Na to aby funkcia denovaná na n-rozmernom priestore bola konkávna, musí by jej Hessova matica, teda matica druhých derivácií G n x) záporne denitná. To znamená, ºe pre ubovo ný vektor y R n platí: y T G n x)y 0. Jednotlivé prvky matice druhých derivácií G n x) vyzerajú nasledovne n ) 1 n x i G n x) = n 1) = G nx) x k n x k n x k G n x) = G nx), pre k l. x k x l n x k x l 46
47 .5 Dôkazy vyuºívajúce konvexnos alebo konkávnos AG NEROVNOS G n x) = G nx) n n 1) 1 x 1 x 1 x 1 n 1) x x 1 x x n x 1 x n x 1 x 1 x n 1 x x n. n 1) x n Dá sa napísa nasledovným spôsobom kde D je diagonálna matica s prvkami q i = 1 x i, i = 1,..., n. G n x) = G nx) n nd qq T ), 1 x 1, 1,..., 1 na diagonále a q je vektor s prvkami x x n Teraz chceme ukáza zápornú denitnos G n x), to znamená ºe y T G n x)y = G nx) n n y n ) ) i y i 0, n x i x i pre kaºdé y. Predo²lá nerovnos vyplýva z Cauchy-Schwarzovej nerovnosti 1), o ktorej y1 sme písali v kapitole 1, ke ju aplikujeme na vektory u = 1 a v =, y,..., y ) n. x 1 x x n Tým sme dokázali, ºe geometrický priemer G n x) je konkávna funkcia. Vieme, ºe ke skon²truujeme dotykovú rovinu ku konkávnej funkcii, tak v kaºdom bode okrem dotykového bude ma táto funkcia men²iu hodnotu, ako dotyková rovina. Skon²truujme dotykovú rovinu ²peciálne v bode x = x 1, x,..., x n) takom, ºe x 1 = x =... = x n = a G n x) G n x ) + G n x )x x ). Po dosadení hodnôt G n x ) a G n x ) dostaneme G n x) a + x 1 a) + x a) x n a) = a + x x n ) na n n a + x 1 + x x n a = A n x). n = Na obrázku 11) máme geometrický priemer a aritmetický priemer, ktorý je zárove jeho dotykovou rovinou v bode x = x 1, x,..., x n). 47
48 .5 Dôkazy vyuºívajúce konvexnos alebo konkávnos AG NEROVNOS Obr. 11: Aritmetický a geometrický priemer Tým sme dokázali, ºe geometrický priemer G n x) je vºdy men²í ako aritmetický priemer A n x), okrem prípadu, ke x 1 = x =... = x n. To je presne nerovnos 17). alej nasleduje nieko ko dôkazov pre najv²eobecnej²í tvar AG nerovnosti pre n prvkov s váhami. Nasledovné dva dôkazy, ktoré teraz uvedieme sa dajú nájs na internetovej stránke []..5. Dôkaz pomocou Jensenovej nerovnosti V²imnime si, ºe funkcia fx) = ln x je rýdzo konkávna. Vyberieme n kladných ísel x 1,..., x n a budeme skúma vz ahy medzi funk nými hodnotami v týchto bodoch. Pod a Jensenovej nerovnosti 10), ktorú sme si pripomenuli v podkapitole 1.3, platí n ) ln w i x i n n ) w i ln x i = ln x w i i, kde w 0, n w i = 1, pri om rovnos nastáva len v prípade, ºe v²etky x i sú rovnaké. Ke ºe ln x je ostro rastúca funkcia, tak platí: n w i x i n x w i i, s rovnos ou len v prípade, ºe v²etky x i sú rovnaké, o je presne nerovnos 18). 48
49 .5 Dôkazy vyuºívajúce konvexnos alebo konkávnos AG NEROVNOS.5.3 Dôkaz pomocou doty nice konvexnej funkcie al²í dôkaz pouºíva konvexnos. Vieme, ºe funkcia fx) = e x je rýdzo konvexná, to znamená, ºe doty nica v ubovo nom bode leºí celá pod krivkou y = e x. Nájdeme teda doty nicu napríklad v bode x 0 = 0 pomocou známeho vzorca y = fx 0 ) + f x 0 )x x 0 ). Dostaneme y = 1 + x. Teda pre v²etky x reálne platí 1 + x e x 19) s rovnos ou v bode x = 0. Obrázok 1) nám môºe pomôc predstavi si danú situáciu. Obr. 1: Doty nica k y = e x v bode x = 0, [5] Pre lep²iu preh adnos zavedieme nasledovná ozna enia: Teraz poloºme Sx) = n w i x i, P x) = n r i = x w i i. x i Sx) 1 0, 49
50 .6 Aplikácie AG NEROVNOS kde x i 0 pre i = 1,..., n a n w i = 1, w i 0. Vz ah 19) potom hovorí, ºe a tieº r i + 1 e r i, pre i = 1,,..., n r i + 1) w i e w ir i, lebo w i 0. Vynásobením n takýchto nerovností dostaneme n n r i + 1) w i e w ir i. 0) Nerovnos sa zachová v aka nezápornosti r i. Po dosadení za r i do avej strany 0) máme n r i + 1) w i = P x) n = P x) w j Sx) j=1 Sx) Po dosadení za r i do pravej strany 0) zas máme n e w ir i = n e x i w i Sx) w Sx) i = e Sx) n Ke opä spojíme obe strany 0), tak dostamene alebo o je presne nerovnos 18). n P x) Sx) 1 x w i i n w i x i, pre n w j = 1. j=1 w i = e 0 = 1..6 Aplikácie.6.1 Maximaliza ná úloha Ako sme v úvode kapitoly spomenuli, jedným z vyuºití AG nerovnosti je pri rie²ení maximaliza ných úloh. Uvedieme príklad rie²enia takejto úlohy bez pouºitia diferenciálneho po tu, len pomocou AG. Prebrali sme ho z predná²ky [9]. Úloha: Nájdite maximálnu hodnotu x 5 sp ajúceho podmienky x 1 + x + x 3 + x 4 + x 5 = 0 1) x 1 + x + x 3 + x 4 + x 5 = 80. ) 50
51 .6 Aplikácie AG NEROVNOS Rie²enie: Z AG nerovnosti pre n = máme x 1 + x x 1 x, x 1 + x 3 x 1 x 3,..., x 3 + x 4 x 3 x 4, s rovnos ami pre x 1 = x = x 3 = x 4. Vyjadríme x 5 z prvej rovnice 1) x 5 = x 1 + x + x 3 + x 4 ), dosadíme ho do druhej rovnice ), nahradíme leny x 1 x, x 1 x 3,..., x 3 x 4 a dostaneme x 5 = x 1 +x +x 3 +x 4 ) = x 1 +x +x 3 +x 4 +x 1 x +x 1 x x 3 x 4 x 1 +x +x 3 + x 4 +x 1 +x ) + x 1 +x 3) + x 1 +x 4)+... +x 3 +x 4) = 4x 1 +x +x 3 +x 4) = 480 x 5). Teda dostávame nerovnos x x 5), z ktorej uº len ekvivalentnými úpravami dostaneme rie²enie úlohy: 5x x 5 8, s rovnos ou pre x 1 = x = x 3 = x 4 =..6. Eulerove íslo Eulerove íslo e zohráva v matematike dôleºitú rolu. Je denované ako limita postupnosti x n = n )n e = lim x n = lim n. 3) n n n) Dokázaním zopár tvrdení s vyuºitím AG nerovnosti ukáºeme, ºe táto limita existuje, a teda Eulerove íslo je korektne denované. Predlohou nám bola publikácia [14]. Tvrdenie.. Pre ubovo né kladné ísla a, b, a b platí nerovnos n+1 ab n < a + nb n
52 .6 Aplikácie AG NEROVNOS Dôkaz: Pod a AG nerovnosti platí n+1 ab n < a + b b n + 1 = a + nb n + 1. Tvrdenie.3. S rastúcim n rastú aj hodnoty postupností x n = ) n n a to znamená z n = 1 1 n) n, x n < x n+1 = ) n+1, n + 1 z n < z n+1 = 1 1 ) n+1. n + 1 Dôkaz: Do nerovnosti z tvrdenia. dosadíme a = 1, b = a dostaneme n n n) 1 n < 1 + n ) n = n + n + 1 n + 1 = n + 1. Ke umocníme obe strany na n + 1), dostaneme 1 + n) 1 n < ) n+1, n + 1 o bolo treba dokáza. Druhá nerovnos sa ukáºe analogicky. Tvrdenie.4. Postupnos y n = n) n+1 klesá s rastúcim n, teda y n > y n+1 = ) n+. n + 1 Dôkaz: Máme y n = 1 + n) 1 n+1 ) n+1 n + 1 = = n Ke ºe z n rastie s n, potom y n s n klesá. 1 ) n+1 = n n ) n+1 = 1. z n+1 n + 1 5
53 .7 Analógia s izoperimetrickou nerovnos ou AG NEROVNOS V tvrdeniach.3 a.4 sme dokázali, ºe x 1 = = < x = 1 + 1) 1 =, 5 < x 3 <... < x n <..., ) y 1 = 1 + 1) 1 = 4 > y = = 3, 375 > y 3 >... > y n >... ) Zárove = x 1 < x n = 1 + n) 1 n < 1 + n) 1 n+1 = y n < y 1 = 4. Postupnos x n je teda monotónne rastúca a ohrani ená < x n < 4. Vieme, ºe kaºdá monotónna ohrani ená postupnos má kone nú limitu. Preto existuje aj limita x n, ktorá je ozna ovaná e, teda Takisto aj limita y n je rovná e e = lim n Nie je aºké overi, ºe e < 3 teda e = lim x n = lim n. n n n) n) n+1 = lim n x n < y n < y 5 = ) n ) = e.1 = e. n n ) 6 =, , e = lim n x n <, < 3. Presná hodnota Eulerovho ísla je e =, Analógia s izoperimetrickou nerovnos ou AG nerovnos je istou obdobou známej izoperimetrickej nerovnosti. Izoperimetrická nerovnos znie nasledovne: Majme v rovine uzavretú, nepresekajúcu sa krivku Γ. Ozna íme L = LΓ) d ºku krivky Γ a A = AΓ) plochu ohrani enú touto krivkou. Potom platí nerovnos L 4πA 1. 53
54 .7 Analógia s izoperimetrickou nerovnos ou AG NEROVNOS Rovnos platí vtedy a len vtedy, ke Γ je kruºnica. Inak povedané izoperimetrická nerovnos hovorí: 1. Spomedzi v²etkých rovinných útvarov s rovnakým obvodom, kruh má najvä ²iu plochu. Obr. 13: Zvä ²enie plochy ohrani enej krivkou bez zmeny obvodu [1]. Spomedzi v²etkých rovinných útvarov s rovnakou plochou, kruh má najmen²í obvod. Obr. 14: Rovnaká plocha ohrani ená kruºnicou a inou krivkou [9] AG nerovnos v tvare 16) pod a autora publikácie [5] tvrdí to isté o ²tvorci. Uvaºujme mnoºinu v²etkých obd ºnikov s plochou A a d ºkami strán x 1 a x. 54
55 .7 Analógia s izoperimetrickou nerovnos ou AG NEROVNOS Obr. 15: Obd ºnik a ²tvorec s plochou x 1 x Pretoºe A = x 1 x, nerovnos 16) nám hovorí, ºe ²tvorec s d ºkou strany s = x 1 x musí ma najmen²í obvod spomedzi v²etkých obd ºnikov s plochou x 1 x 4s = 4 x 1 x x 1 + x. Teraz zoberme mnoºinu obd ºnikov s rovnakým obvodom p a stranami x 1 a x. Potom p = x 1 + x. Obr. 16: Obd ºnik a ²tvorec s obvodom x 1 + x tvorec so stranou s = p 4 potom dosahuje maximálnu plochu spomedzi obd ºnikov s obvodom x 1 + x s = p 16 = x 1 + x ) 4 x 1 x. 55
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MOCNINOVÉ RADY A ICH VYUšITIE BAKALÁRSKA PRÁCA 04 Sára MINÁROVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MOCNINOVÉ RADY A ICH VYUšITIE BAKALÁRSKA PRÁCA 04 Sára MINÁROVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Vlastnosti spektrahedrálnych mnoºín a ich aplikácie v nelineárnej optimalizácii DIPLOMOVÁ PRÁCA 2016 Bc. Andrej Iring UNIVERZITA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Vlastnosti spektrahedrálnych mnoºín a ich aplikácie v nelineárnej optimalizácii DIPLOMOVÁ PRÁCA 2016 Bc. Andrej Iring UNIVERZITA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY. Kritéria nezápornosti Fourierových radov BAKALÁRSKA PRÁCA
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kritéria nezápornosti Fourierových radov BAKALÁRSKA PRÁCA Bratislava 2014 Andrej Iring UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kritéria nezápornosti Fourierových radov BAKALÁRSKA PRÁCA Bratislava 2014 Andrej Iring UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
Metódy vol nej optimalizácie
 Matematické programovanie Metódy vol nej optimalizácie p. 1/35 Informácie o predmete Informácie o predmete p. 2/35 Informácie o predmete METÓDY VOL NEJ OPTIMALIZÁCIE Prednášajúca: M. Trnovská (M 267) Cvičiaci:
Matematické programovanie Metódy vol nej optimalizácie p. 1/35 Informácie o predmete Informácie o predmete p. 2/35 Informácie o predmete METÓDY VOL NEJ OPTIMALIZÁCIE Prednášajúca: M. Trnovská (M 267) Cvičiaci:
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VZ AHY SPEKTIER MATICE A JEJ PODMATÍC Bakalárska práca 2013 Viktor GREGOR UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VZ AHY SPEKTIER MATICE A JEJ PODMATÍC Bakalárska práca 2013 Viktor GREGOR UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
Matematika 17. a 18. storočia
 Matematika 17. a 18. storočia René Descartes Narodený : 31 Marec 1596 v La Haye (teraz Descartes),Touraine, France Zomrel : 11 Feb 1650 v Stockholm, Sweden Riešenie kvadratických rovníc podľa Descarta
Matematika 17. a 18. storočia René Descartes Narodený : 31 Marec 1596 v La Haye (teraz Descartes),Touraine, France Zomrel : 11 Feb 1650 v Stockholm, Sweden Riešenie kvadratických rovníc podľa Descarta
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MATEMATIKA NA POH ADNICIACH BAKALÁRSKA PRÁCA 2014 Katarína IVANOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MATEMATIKA NA POH ADNICIACH BAKALÁRSKA PRÁCA 2014 Katarína IVANOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY
The Golden Ratio and Signal Quantization
 The Golden Ratio and Signal Quantization Tom Hejda, tohecz@gmail.com based on the work of Ingrid Daubechies et al. Doppler Institute & Department of Mathematics, FNSPE, Czech Technical University in Prague
The Golden Ratio and Signal Quantization Tom Hejda, tohecz@gmail.com based on the work of Ingrid Daubechies et al. Doppler Institute & Department of Mathematics, FNSPE, Czech Technical University in Prague
Kapitola S5. Skrutkovica na rotačnej ploche
 Kapitola S5 Skrutkovica na rotačnej ploche Nech je rotačná plocha určená osou rotácie o a meridiánom m. Skrutkový pohyb je pohyb zložený z rovnomerného rotačného pohybu okolo osi o a z rovnomerného translačného
Kapitola S5 Skrutkovica na rotačnej ploche Nech je rotačná plocha určená osou rotácie o a meridiánom m. Skrutkový pohyb je pohyb zložený z rovnomerného rotačného pohybu okolo osi o a z rovnomerného translačného
PSEUDOINVERZNÁ MATICA
 PSEUDOINVERZNÁ MATICA Jozef Fecenko, Michal Páleš Abstrakt Cieľom príspevku je podať základnú informácie o pseudoinverznej matici k danej matici. Ukázať, že bázický rozklad matice na súčin matíc je skeletným
PSEUDOINVERZNÁ MATICA Jozef Fecenko, Michal Páleš Abstrakt Cieľom príspevku je podať základnú informácie o pseudoinverznej matici k danej matici. Ukázať, že bázický rozklad matice na súčin matíc je skeletným
Teória grafov. RNDr. Milan Stacho, PhD.
 Teória grafov RNDr. Milan Stacho, PhD. Literatúra Plesník: Grafové algoritmy, Veda Bratislava 1983 Sedláček: Úvod do teórie grafů, Academia Praha 1981 Bosák: Grafy a ich aplikácie, Alfa Bratislava 1980
Teória grafov RNDr. Milan Stacho, PhD. Literatúra Plesník: Grafové algoritmy, Veda Bratislava 1983 Sedláček: Úvod do teórie grafů, Academia Praha 1981 Bosák: Grafy a ich aplikácie, Alfa Bratislava 1980
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY 80e687db-77df-4b93-992e-b291c6457462 Vyuºitie SATsolverov pri rie²ení aºkých úloh 2011 Matú² Kukan UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY 80e687db-77df-4b93-992e-b291c6457462 Vyuºitie SATsolverov pri rie²ení aºkých úloh 2011 Matú² Kukan UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY REKURENTNÉ POSTUPNOSTI
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Evidenčné číslo: 74b93af3-8dd5-43d9-b3f2-05523e0ba177 REKURENTNÉ POSTUPNOSTI 2011 András Varga UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Evidenčné číslo: 74b93af3-8dd5-43d9-b3f2-05523e0ba177 REKURENTNÉ POSTUPNOSTI 2011 András Varga UNIVERZITA KOMENSKÉHO V BRATISLAVE
METRICKÉ ÚLOHY V PRIESTORE
 1. ÚVOD METRICKÉ ÚLOHY V PRIESTORE Monika ĎURIKOVIČOVÁ 1 Katedra Matematiky, Strojnícka fakulta STU, Abstrakt: Popisujeme možnosti použitia programového systému Mathematica pri riešení špeciálnych metrických
1. ÚVOD METRICKÉ ÚLOHY V PRIESTORE Monika ĎURIKOVIČOVÁ 1 Katedra Matematiky, Strojnícka fakulta STU, Abstrakt: Popisujeme možnosti použitia programového systému Mathematica pri riešení špeciálnych metrických
FILTRÁCIA GEODETICKÝCH DÁT NA POVRCHU ZEME POMOCOU NELINEÁRNYCH DIFÚZNYCH ROVNÍC
 Úvod FILTRÁCIA GEODETICKÝCH DÁT NA POVRCHU ZEME POMOCOU NELINEÁRNYCH DIFÚZNYCH ROVNÍC Martin Tunega, Róbert ƒunderlík, Karol Mikula V lánku vytvoríme metódu kone ných objemov na numerické rie²enie parabolických
Úvod FILTRÁCIA GEODETICKÝCH DÁT NA POVRCHU ZEME POMOCOU NELINEÁRNYCH DIFÚZNYCH ROVNÍC Martin Tunega, Róbert ƒunderlík, Karol Mikula V lánku vytvoríme metódu kone ných objemov na numerické rie²enie parabolických
Matematická analýza II.
 V. Diferenciálny počet (prezentácia k prednáške MANb/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prednáška 8 6. marca 2018 It has apparently not yet been observed, that...
V. Diferenciálny počet (prezentácia k prednáške MANb/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prednáška 8 6. marca 2018 It has apparently not yet been observed, that...
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS A PRIORI ESTIMATES OF SOLUTIONS OF SUPERLINEAR ELLIPTIC AND PARABOLIC PROBLEMS Dissertation thesis 015 Július Pa uta COMENIUS
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS A PRIORI ESTIMATES OF SOLUTIONS OF SUPERLINEAR ELLIPTIC AND PARABOLIC PROBLEMS Dissertation thesis 015 Július Pa uta COMENIUS
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY HADAMARDOVE MATICE A ICH APLIKÁCIE V OPTIMÁLNOM DIZAJNE BAKALÁRSKA PRÁCA 2012 Samuel ROSA UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY HADAMARDOVE MATICE A ICH APLIKÁCIE V OPTIMÁLNOM DIZAJNE BAKALÁRSKA PRÁCA 2012 Samuel ROSA UNIVERZITA KOMENSKÉHO V BRATISLAVE
Maticové algoritmy I maticová algebra operácie nad maticami súčin matíc
 Maticové algoritmy I maticová algebra operácie nad maticami súčin matíc priesvitka Maurits Cornelis Escher (898-97) Ascending and Descending, 960, Lithograph priesvitka Matice V mnohých prípadoch dáta
Maticové algoritmy I maticová algebra operácie nad maticami súčin matíc priesvitka Maurits Cornelis Escher (898-97) Ascending and Descending, 960, Lithograph priesvitka Matice V mnohých prípadoch dáta
Aplikácie subriemannovskej geometrie
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Aplikácie subriemannovskej geometrie Luká² Tomek 2011 Aplikácie subriemannovskej geometrie DIPLOMOVÁ PRÁCA (Eviden né íslo:
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Aplikácie subriemannovskej geometrie Luká² Tomek 2011 Aplikácie subriemannovskej geometrie DIPLOMOVÁ PRÁCA (Eviden né íslo:
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY DIPLOMOVÁ PRÁCA ZDENKA ZUBÁƒOVÁ
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY DIPLOMOVÁ PRÁCA 2011 ZDENKA ZUBÁƒOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Spracovanie
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY DIPLOMOVÁ PRÁCA 2011 ZDENKA ZUBÁƒOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Spracovanie
Dokonalé a spriatelené čísla
 Dokonalé a spriatelené čísla 1. kapitola. Niektoré poznatky z teorie čísel In: Tibor Šalát (author): Dokonalé a spriatelené čísla. (Slovak). Praha: Mladá fronta, 1969. pp. 5 17. Persistent URL: http://dml.cz/dmlcz/403668
Dokonalé a spriatelené čísla 1. kapitola. Niektoré poznatky z teorie čísel In: Tibor Šalát (author): Dokonalé a spriatelené čísla. (Slovak). Praha: Mladá fronta, 1969. pp. 5 17. Persistent URL: http://dml.cz/dmlcz/403668
Comenius University, Bratislava Faculty of Mathematics, Physics and Informatics. Multi-head Automata. Bachelor Thesis.
 Comenius University, Bratislava Faculty of Mathematics, Physics and Informatics Multi-head Automata Bachelor Thesis 2013 Boris Vida Comenius University, Bratislava Faculty of Mathematics, Physics and Informatics
Comenius University, Bratislava Faculty of Mathematics, Physics and Informatics Multi-head Automata Bachelor Thesis 2013 Boris Vida Comenius University, Bratislava Faculty of Mathematics, Physics and Informatics
ADM a logika. 4. prednáška. Výroková logika II, logický a sémantický dôsledok, teória a model, korektnosť a úplnosť
 ADM a logika 4. prednáška Výroková logika II, logický a sémantický dôsledok, teória a model, korektnosť a úplnosť 1 Odvodzovanie formúl výrokovej logiky, logický dôsledok, syntaktický prístup Logický dôsledok
ADM a logika 4. prednáška Výroková logika II, logický a sémantický dôsledok, teória a model, korektnosť a úplnosť 1 Odvodzovanie formúl výrokovej logiky, logický dôsledok, syntaktický prístup Logický dôsledok
Aplikácie teórie množín Martin Sleziak 24. februára 2015
 Aplikácie teórie množín Martin Sleziak 24. februára 2015 Obsah 1 Úvod 5 1.1 Sylaby a literatúra................................. 5 1.1.1 Literatúra.................................. 5 1.1.2 Sylaby predmetu..............................
Aplikácie teórie množín Martin Sleziak 24. februára 2015 Obsah 1 Úvod 5 1.1 Sylaby a literatúra................................. 5 1.1.1 Literatúra.................................. 5 1.1.2 Sylaby predmetu..............................
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS ULTIMATE EFFICIENCY OF DESIGNS FOR MULTIVARIATE ORNSTEIN-UHLENBECK PROCESSES MASTER S THESIS 2014 Bc. Michal Hojčka COMENIUS
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS ULTIMATE EFFICIENCY OF DESIGNS FOR MULTIVARIATE ORNSTEIN-UHLENBECK PROCESSES MASTER S THESIS 2014 Bc. Michal Hojčka COMENIUS
Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava THEILOVA REGRESIA
 Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava THEILOVA REGRESIA Róbert Tóth Bratislava 2013 Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava THEILOVA
Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava THEILOVA REGRESIA Róbert Tóth Bratislava 2013 Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava THEILOVA
Univerzita Karlova v Praze Matematicko-fyzikální fakulta. Michal Kesely. Katedra matematické analýzy. Studijní program: Obecná matematika
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Michal Kesely Slavné neřešitelné problémy Katedra matematické analýzy Vedoucí bakalářské práce: RNDr. Dalibor Pražák, Ph.D. Studijní
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Michal Kesely Slavné neřešitelné problémy Katedra matematické analýzy Vedoucí bakalářské práce: RNDr. Dalibor Pražák, Ph.D. Studijní
Odhady veľkosti pokrytí náhodne indukovaných podgrafov n-rozmernej hyperkocky
 KATEDRA INFORMATIKY FAKULTA MATEMATIKY FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO Odhady veľkosti pokrytí náhodne indukovaných podgrafov nrozmernej hyperkocky Diplomová práca Bc. Ján Kliman študijný odbor:
KATEDRA INFORMATIKY FAKULTA MATEMATIKY FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO Odhady veľkosti pokrytí náhodne indukovaných podgrafov nrozmernej hyperkocky Diplomová práca Bc. Ján Kliman študijný odbor:
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
THIS PAGE DECLASSIFIED IAW E
 THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
2 u Du, k Hu Dv Hu, y H. u Cu j u qu u. Nv. v uy. Cu Hu F A H. qu Cu.. Cu j 1980, u V, v Nu My O k. v u u. A G C. My u v k, 2.5 H v v u / u v u v k y
 H HE 1016 M EEING OF HE ODIE CLU 1,016 Cu 7:30.. D 11, 2007 y W L Uvy. C : Pu A y: Ov 25 x u. Hk, u k MA k D u y Hu, u G, u C C, MN C, Nk Dv Hu, MN, u K A u vu v. W y A Pku G, G u. N EW UINE: D, Cu, 22
H HE 1016 M EEING OF HE ODIE CLU 1,016 Cu 7:30.. D 11, 2007 y W L Uvy. C : Pu A y: Ov 25 x u. Hk, u k MA k D u y Hu, u G, u C C, MN C, Nk Dv Hu, MN, u K A u vu v. W y A Pku G, G u. N EW UINE: D, Cu, 22
Stavba Lobačevského planimetrie
 Stavba Lobačevského planimetrie Riešenie úloh In: Ján Gatial (author); Milan Hejný (author): Stavba Lobačevského planimetrie. (Slovak). Praha: Mladá fronta, 1969. pp. 78 109. Persistent URL: http://dml.cz/dmlcz/403691
Stavba Lobačevského planimetrie Riešenie úloh In: Ján Gatial (author); Milan Hejný (author): Stavba Lobačevského planimetrie. (Slovak). Praha: Mladá fronta, 1969. pp. 78 109. Persistent URL: http://dml.cz/dmlcz/403691
LINEAR ALGEBRA W W L CHEN
 LINEAR ALGEBRA W W L CHEN c W W L Chen, 1997, 2008. This chapter is available free to all individuals, on the understanding that it is not to be used for financial gain, and may be downloaded and/or photocopied,
LINEAR ALGEBRA W W L CHEN c W W L Chen, 1997, 2008. This chapter is available free to all individuals, on the understanding that it is not to be used for financial gain, and may be downloaded and/or photocopied,
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS BIFURCATION AND ASYMPTOTIC PROPERTIES OF PERIODIC SOLUTIONS IN DISCONTINUOUS SYSTEMS Dissertation thesis 212 RNDr. Michal
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS BIFURCATION AND ASYMPTOTIC PROPERTIES OF PERIODIC SOLUTIONS IN DISCONTINUOUS SYSTEMS Dissertation thesis 212 RNDr. Michal
Obsah. 2 Určenie objemu valčeka Teoretický úvod Postup merania a spracovanie výsledkov... 10
 Obsah 1 Chyby merania 1 1.1 áhodné a systematické chyby.................... 1 1.2 Aritmetický priemer a stredná kvadratická chyba......... 1 1.3 Rozdelenie nameraných dát..................... 3 1.4 Limitné
Obsah 1 Chyby merania 1 1.1 áhodné a systematické chyby.................... 1 1.2 Aritmetický priemer a stredná kvadratická chyba......... 1 1.3 Rozdelenie nameraných dát..................... 3 1.4 Limitné
Algoritmy metód vnútorného bodu v lineárnom programovaní
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Algoritmy metód vnútorného bodu v lineárnom programovaní RIGORÓZNA PRÁCA 14 Mgr. Marek KABÁT UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Algoritmy metód vnútorného bodu v lineárnom programovaní RIGORÓZNA PRÁCA 14 Mgr. Marek KABÁT UNIVERZITA KOMENSKÉHO V BRATISLAVE
Analýza investi ného rozhodovania pri uplatnení reálnej opcie
 FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO V BRATISLAVE Katedra aplikovanej matematiky a ²tatistiky Analýza investi ného rozhodovania pri uplatnení reálnej opcie DIPLOMOVÁ PRÁCA BRATISLAVA
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO V BRATISLAVE Katedra aplikovanej matematiky a ²tatistiky Analýza investi ného rozhodovania pri uplatnení reálnej opcie DIPLOMOVÁ PRÁCA BRATISLAVA
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics. Learning in finance. Master s thesis Bc.
 Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Learning in finance Master s thesis 2013 Bc. Vladimír Novák Comenius University in Bratislava Faculty of Mathematics, Physics
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Learning in finance Master s thesis 2013 Bc. Vladimír Novák Comenius University in Bratislava Faculty of Mathematics, Physics
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
 OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
1 Matice a ich vlastnosti
 Pojem sústavy a jej riešenie 1 Matice a ich vlastnosti 11 Sústavy lineárnych rovníc a matice Príklad 11 V množine reálnych čísel riešte sústavu rovníc x - 2y + 4z + t = -6 2x + 3y - z + 2t = 13 2x + 5y
Pojem sústavy a jej riešenie 1 Matice a ich vlastnosti 11 Sústavy lineárnych rovníc a matice Príklad 11 V množine reálnych čísel riešte sústavu rovníc x - 2y + 4z + t = -6 2x + 3y - z + 2t = 13 2x + 5y
MASTER THESIS. Vlastnosti k-intervalových booleovských funkcí Properties of k-interval Boolean functions
 Charles University in Prague Faculty of Mathematics and Physics MASTER THESIS Pavol Gál Vlastnosti k-intervalových booleovských funkcí Properties of k-interval Boolean functions Department of Theoretical
Charles University in Prague Faculty of Mathematics and Physics MASTER THESIS Pavol Gál Vlastnosti k-intervalových booleovských funkcí Properties of k-interval Boolean functions Department of Theoretical
Spectral Techniques for Economic Time Series
 COMENIUS UNIVERSITY, BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS Spectral Techniques for Economic Time Series DISSERTATION THESIS 1688f35e-4a28-4223-a35f-0e25eb955301 2012 Ivana Bátorová
COMENIUS UNIVERSITY, BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS Spectral Techniques for Economic Time Series DISSERTATION THESIS 1688f35e-4a28-4223-a35f-0e25eb955301 2012 Ivana Bátorová
Samuel Flimmel. Univerzita Karlova v Praze Matematicko-fyzikální fakulta. Katedra pravděpodobnosti a matematické statistiky
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Samuel Flimmel Log-optimální investování Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: doc. RNDr.
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Samuel Flimmel Log-optimální investování Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: doc. RNDr.
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A. Ήχος Πα. to os se e e na aș te e e slă ă ă vi i i i i
 CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
Kapitola P2. Rozvinuteľné priamkové plochy
 Kapitola P2 Rozvinuteľné priamkové plochy 1 Priamková plocha je rozvinuteľná, ak na nej ležia iba torzálne priamky. Rozvinuteľné priamkové plochy rozdeľujeme na: rovinu, valcové plochy, kužeľové plochy,
Kapitola P2 Rozvinuteľné priamkové plochy 1 Priamková plocha je rozvinuteľná, ak na nej ležia iba torzálne priamky. Rozvinuteľné priamkové plochy rozdeľujeme na: rovinu, valcové plochy, kužeľové plochy,
Lecture 20: 6.1 Inner Products
 Lecture 0: 6.1 Inner Products Wei-Ta Chu 011/1/5 Definition An inner product on a real vector space V is a function that associates a real number u, v with each pair of vectors u and v in V in such a way
Lecture 0: 6.1 Inner Products Wei-Ta Chu 011/1/5 Definition An inner product on a real vector space V is a function that associates a real number u, v with each pair of vectors u and v in V in such a way
h : sh +i F J a n W i m +i F D eh, 1 ; 5 i A cl m i n i sh» si N «q a : 1? ek ser P t r \. e a & im a n alaa p ( M Scanned by CamScanner
 m m i s t r * j i ega>x I Bi 5 n ì r s w «s m I L nk r n A F o n n l 5 o 5 i n l D eh 1 ; 5 i A cl m i n i sh» si N «q a : 1? { D v i H R o s c q \ l o o m ( t 9 8 6) im a n alaa p ( M n h k Em l A ma
m m i s t r * j i ega>x I Bi 5 n ì r s w «s m I L nk r n A F o n n l 5 o 5 i n l D eh 1 ; 5 i A cl m i n i sh» si N «q a : 1? { D v i H R o s c q \ l o o m ( t 9 8 6) im a n alaa p ( M n h k Em l A ma
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE
 FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE PÍSOMNÁ PRÁCA K DIZERTAČNEJ SKÚŠKE 2005 Zuzana Holeščáková FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE PÍSOMNÁ PRÁCA K DIZERTAČNEJ SKÚŠKE 2005 Zuzana Holeščáková FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
Fuzzy Reasoning and Optimization Based on a Generalized Bayesian Network
 Fuy R O B G By Nw H-Y K D M Du M Hu Cu Uvy 48 Hu Cu R Hu 300 Tw. @w.u.u.w A By w v wy u w w uy. Hwv u uy u By w y u v w uu By w w w u vu vv y. T uy v By w w uy v v uy. B By w uy. T uy v uy. T w w w- uy.
Fuy R O B G By Nw H-Y K D M Du M Hu Cu Uvy 48 Hu Cu R Hu 300 Tw. @w.u.u.w A By w v wy u w w uy. Hwv u uy u By w y u v w uu By w w w u vu vv y. T uy v By w w uy v v uy. B By w uy. T uy v uy. T w w w- uy.
Short time oscillations of exchange rates
 Univerzita Komenského v Bratislave, Fakulta matematiky, fyziky a informatiky Short time oscillations of exchange rates Diploma Thesis Bratislava 2007 Tomáš Bokes Short time oscillations of exchange rates
Univerzita Komenského v Bratislave, Fakulta matematiky, fyziky a informatiky Short time oscillations of exchange rates Diploma Thesis Bratislava 2007 Tomáš Bokes Short time oscillations of exchange rates
Technické rezervy v neºivotnom poistení
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Technické rezervy v neºivotnom poistení DIPLOMOVÁ PRÁCA 2012 Bc JAROSLAVA GATIALOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Technické rezervy v neºivotnom poistení DIPLOMOVÁ PRÁCA 2012 Bc JAROSLAVA GATIALOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
Errors-in-variables models
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Ida Fürjesová Errors-in-variables models Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: RNDr. Michal
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Ida Fürjesová Errors-in-variables models Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: RNDr. Michal
VÝUČBA DIFFERENCIÁLNEHO POČTU FUNKCIE VIAC PREMENNÝCH POMOCOU PG. SYST. MATHEMATICA
 VÝUČBA DIFFERENCIÁLNEHO POČTU FUNKCIE VIAC PREMENNÝCH POMOCOU PG. SYST. MATHEMATICA Monika Kováčová Katedra Matematiky SjF STU Bratislava kovacova_v@dekan.sjf.stuba.sk Abstrakt. V článku popisujeme možnosti
VÝUČBA DIFFERENCIÁLNEHO POČTU FUNKCIE VIAC PREMENNÝCH POMOCOU PG. SYST. MATHEMATICA Monika Kováčová Katedra Matematiky SjF STU Bratislava kovacova_v@dekan.sjf.stuba.sk Abstrakt. V článku popisujeme možnosti
RNDr. Petr Tomiczek CSc.
 HABILITAČNÍ PRÁCE RNDr. Petr Tomiczek CSc. Plzeň 26 Nonlinear differential equation of second order RNDr. Petr Tomiczek CSc. Department of Mathematics, University of West Bohemia 5 Contents 1 Introduction
HABILITAČNÍ PRÁCE RNDr. Petr Tomiczek CSc. Plzeň 26 Nonlinear differential equation of second order RNDr. Petr Tomiczek CSc. Department of Mathematics, University of West Bohemia 5 Contents 1 Introduction
1 Úvod Úvod Sylaby a literatúra Označenia a pomocné tvrdenia... 4
 Obsah 1 Úvod 3 1.1 Úvod......................................... 3 1. Sylaby a literatúra................................. 3 1.3 Označenia a omocné tvrdenia.......................... 4 Prvočísla 6.1 Deliteľnosť......................................
Obsah 1 Úvod 3 1.1 Úvod......................................... 3 1. Sylaby a literatúra................................. 3 1.3 Označenia a omocné tvrdenia.......................... 4 Prvočísla 6.1 Deliteľnosť......................................
Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCA. Bc. Roman Cinkais. Aplikace samoopravných kódů v steganografii
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCA Bc. Roman Cinkais Aplikace samoopravných kódů v steganografii Katedra algebry Vedúcí diplomovej práce: prof. RNDr. Aleš Drápal,
Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCA Bc. Roman Cinkais Aplikace samoopravných kódů v steganografii Katedra algebry Vedúcí diplomovej práce: prof. RNDr. Aleš Drápal,
DEA modely a meranie eko-efektívnosti
 Fakulta matematiky, fyziky a informatiky Univerzita Komenského v Bratislave DEA modely a meranie eko-efektívnosti 2008 Veronika Lennerová DEA modely a meranie eko-efektívnosti DIPLOMOVÁ PRÁCA Diplomant:
Fakulta matematiky, fyziky a informatiky Univerzita Komenského v Bratislave DEA modely a meranie eko-efektívnosti 2008 Veronika Lennerová DEA modely a meranie eko-efektívnosti DIPLOMOVÁ PRÁCA Diplomant:
Solution Methods for Beam and Frames on Elastic Foundation Using the Finite Element Method
 Solution Methods for Beam and Frames on Elastic Foundation Using the Finite Element Method Spôsoby riešenie nosníkov a rámov na pružnom podklade pomocou metódy konečných prvkov Roland JANČO 1 Abstract:
Solution Methods for Beam and Frames on Elastic Foundation Using the Finite Element Method Spôsoby riešenie nosníkov a rámov na pružnom podklade pomocou metódy konečných prvkov Roland JANČO 1 Abstract:
ANOTÁCIA ZHLUKOV GÉNOV
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY ANOTÁCIA ZHLUKOV GÉNOV 2011 Milan Mikula UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY ANOTÁCIA ZHLUKOV
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY ANOTÁCIA ZHLUKOV GÉNOV 2011 Milan Mikula UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY ANOTÁCIA ZHLUKOV
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA VZ AHOV MEDZI ƒasovými RADMI METÓDAMI SIE OVEJ ANALÝZY A ZHLUKOVANIA DIPLOMOVÁ PRÁCA 2018 Radka LITVAJOVÁ UNIVERZITA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA VZ AHOV MEDZI ƒasovými RADMI METÓDAMI SIE OVEJ ANALÝZY A ZHLUKOVANIA DIPLOMOVÁ PRÁCA 2018 Radka LITVAJOVÁ UNIVERZITA
Ayuntamiento de Madrid
 9 v vx-xvv \ ü - v q v ó - ) q ó v Ó ü " v" > - v x -- ü ) Ü v " ñ v é - - v j? j 7 Á v ü - - v - ü
9 v vx-xvv \ ü - v q v ó - ) q ó v Ó ü " v" > - v x -- ü ) Ü v " ñ v é - - v j? j 7 Á v ü - - v - ü
Le classeur à tampons
 Le classeur à tampons P a s à pa s Le matériel 1 gr a n d cla s s e u r 3 pa pi e r s co o r d o n n é s. P o u r le m o d è l e pr é s e n t é P a p i e r ble u D ai s y D s, pa pi e r bor d e a u x,
Le classeur à tampons P a s à pa s Le matériel 1 gr a n d cla s s e u r 3 pa pi e r s co o r d o n n é s. P o u r le m o d è l e pr é s e n t é P a p i e r ble u D ai s y D s, pa pi e r bor d e a u x,
Jádrové odhady gradientu regresní funkce
 Monika Kroupová Ivana Horová Jan Koláček Ústav matematiky a statistiky, Masarykova univerzita, Brno ROBUST 2018 Osnova Regresní model a odhad gradientu Metody pro odhad vyhlazovací matice Simulace Závěr
Monika Kroupová Ivana Horová Jan Koláček Ústav matematiky a statistiky, Masarykova univerzita, Brno ROBUST 2018 Osnova Regresní model a odhad gradientu Metody pro odhad vyhlazovací matice Simulace Závěr
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS Prediction of future events for companies by analysing articles of financial newspapers MASTER THESIS 2018 Ján Siviček
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS Prediction of future events for companies by analysing articles of financial newspapers MASTER THESIS 2018 Ján Siviček
A l g o r i t m i c k y n e r i e š i t e ľ n é p r o b l é m y
 A l g o r i t m i c k y n e r i e š i t e ľ n é p r o b l é m y Lev Bukovský Ústav matematických vied, Prírodovedecká fakulta UPJŠ Košice, 20. apríla 2004 Obsah 1 Úvod 2 2 Čiastočne rekurzívne funkcie
A l g o r i t m i c k y n e r i e š i t e ľ n é p r o b l é m y Lev Bukovský Ústav matematických vied, Prírodovedecká fakulta UPJŠ Košice, 20. apríla 2004 Obsah 1 Úvod 2 2 Čiastočne rekurzívne funkcie
História nekonečne malej veličiny PROJEKTOVÁ PRÁCA. Martin Čulen. Alex Fleško. Konzultant: Vladimír Repáš
 História nekonečne malej veličiny PROJEKTOVÁ PRÁCA Martin Čulen Alex Fleško Konzultant: Vladimír Repáš Škola pre mimoriadne nadané deti a Gymnázium, Skalická 1, Bratislava BRATISLAVA 2013 1. Obsah 1. Obsah
História nekonečne malej veličiny PROJEKTOVÁ PRÁCA Martin Čulen Alex Fleško Konzultant: Vladimír Repáš Škola pre mimoriadne nadané deti a Gymnázium, Skalická 1, Bratislava BRATISLAVA 2013 1. Obsah 1. Obsah
Súťaž PALMA junior a programovanie v jazyku Python
 Súťaž PALMA junior a programovanie v jazyku Python Ján Guniš Ľubomír Šnajder Prírodovedecká fakulta Univerzity P. J. Šafárika v Košiciach DidInfo + DidactIG 2017, Banská Bystrica Obsah Súťaž PALMA junior
Súťaž PALMA junior a programovanie v jazyku Python Ján Guniš Ľubomír Šnajder Prírodovedecká fakulta Univerzity P. J. Šafárika v Košiciach DidInfo + DidactIG 2017, Banská Bystrica Obsah Súťaž PALMA junior
Úlohy o veľkých číslach
 Úlohy o veľkých číslach Ivan Korec (author): Úlohy o veľkých číslach. (Slovak). Praha: Mladá fronta, 1988. Persistent URL: http://dml.cz/dmlcz/404175 Terms of use: Ivan Korec, 1988 Institute of Mathematics
Úlohy o veľkých číslach Ivan Korec (author): Úlohy o veľkých číslach. (Slovak). Praha: Mladá fronta, 1988. Persistent URL: http://dml.cz/dmlcz/404175 Terms of use: Ivan Korec, 1988 Institute of Mathematics
CLASSIFICATION AND PRINCIPLE OF SUPERPOSITION FOR SECOND ORDER LINEAR PDE
 CLASSIFICATION AND PRINCIPLE OF SUPERPOSITION FOR SECOND ORDER LINEAR PDE 1. Linear Partial Differential Equations A partial differential equation (PDE) is an equation, for an unknown function u, that
CLASSIFICATION AND PRINCIPLE OF SUPERPOSITION FOR SECOND ORDER LINEAR PDE 1. Linear Partial Differential Equations A partial differential equation (PDE) is an equation, for an unknown function u, that
Structural aspects of FeSi
 Comenius university in Bratislava Faculty of mathematics, physics and informatics Structural aspects of FeSi bachelor s thesis 2015 Andrej Vlček Comenius university in Bratislava Faculty of mathematics,
Comenius university in Bratislava Faculty of mathematics, physics and informatics Structural aspects of FeSi bachelor s thesis 2015 Andrej Vlček Comenius university in Bratislava Faculty of mathematics,
Univerzita Karlova v Praze. Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE. Matúš Kepič
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Matúš Kepič Webová aplikace pro výuku goniometrických funkcí, rovnic a nerovnic Katedra didaktiky matematiky Vedoucí diplomové práce:
Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Matúš Kepič Webová aplikace pro výuku goniometrických funkcí, rovnic a nerovnic Katedra didaktiky matematiky Vedoucí diplomové práce:
Tvorba efekt vnych algoritmov
 Tvorba efekt vnych algoritmov RNDr. Pavol uri, CSc. Katedra informatiky MFF UK e-mail: duris@fmph.uniba.sk December 1997 Abstrakt Tento text vznikol ako materi l ku predn ke "Tvorba efekt vnych algoritmov"
Tvorba efekt vnych algoritmov RNDr. Pavol uri, CSc. Katedra informatiky MFF UK e-mail: duris@fmph.uniba.sk December 1997 Abstrakt Tento text vznikol ako materi l ku predn ke "Tvorba efekt vnych algoritmov"
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UIVERZITA KOMESKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A IFORMATIKY VÝPOČET FOURIEROVÝCH RADOV POMOCOU DISKRÉTEJ FOURIEROVEJ TRASFORMÁCIE BAKALÁRSKA PRÁCA 2013 Andrej ZUBAL UIVERZITA KOMESKÉHO V BRATISLAVE
UIVERZITA KOMESKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A IFORMATIKY VÝPOČET FOURIEROVÝCH RADOV POMOCOU DISKRÉTEJ FOURIEROVEJ TRASFORMÁCIE BAKALÁRSKA PRÁCA 2013 Andrej ZUBAL UIVERZITA KOMESKÉHO V BRATISLAVE
Index Policies for Dynamic and Stochastic Problems
 Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Index Policies for Dynamic and Stochastic Problems 2011 Vladimír Novák Comenius University in Bratislava Faculty of Mathematics,
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Index Policies for Dynamic and Stochastic Problems 2011 Vladimír Novák Comenius University in Bratislava Faculty of Mathematics,
Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava. Multiparty Communication Complexity (Master thesis)
 Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Multiparty Communication Complexity (Master thesis) František Ďuriš Study programme: 921 Informatics Supervisor:
Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Multiparty Communication Complexity (Master thesis) František Ďuriš Study programme: 921 Informatics Supervisor:
FAKULTA HUMANITNÝCH VIED, ŽILINSKÁ UNIVERZITA V ŽILINE INFORMAČNÝ LIST PREDMETU. Názov: Matematická analýza 1 (povinný) Zabezpečuje:
 Názov: Matematická analýza 1 (povinný) prof. RNDr. Miroslava Růžičková, CSc. Semester: 1. rok štúdia: 1. Týždenný: 4 2 0 Za semester: 52 26 0 Prerekvizity: Stredoškolská matematika v rozsahu osnov gymnázií.
Názov: Matematická analýza 1 (povinný) prof. RNDr. Miroslava Růžičková, CSc. Semester: 1. rok štúdia: 1. Týždenný: 4 2 0 Za semester: 52 26 0 Prerekvizity: Stredoškolská matematika v rozsahu osnov gymnázií.
Kybernetika. Peter Hudzovič Súčasná kontrola stability a kvality impulznej regulácie. Terms of use:
 Kybernetika Peter Hudzovič Súčasná kontrola stability a kvality impulznej regulácie Kybernetika, Vol. 3 (1967), No. 2, (175)--194 Persistent URL: http://dml.cz/dmlcz/125051 Terms of use: Institute of Information
Kybernetika Peter Hudzovič Súčasná kontrola stability a kvality impulznej regulácie Kybernetika, Vol. 3 (1967), No. 2, (175)--194 Persistent URL: http://dml.cz/dmlcz/125051 Terms of use: Institute of Information
Eva Baranová, Kamil Maleček OD STREDOVÉHO PRIEMETU KRUŽNICE KU STREDOVÝM CYKLIDÁM. 1 Priemet kružnice v stredovom premietaní
 25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Eva Baranová, Kamil Maleček OD STREDOVÉHO PRIEMETU KRUŽNICE KU STREDOVÝM CYKLIDÁM Abstrakt V prvej časti príspevku odvodzujeme podmienku, kedy je v danom
25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Eva Baranová, Kamil Maleček OD STREDOVÉHO PRIEMETU KRUŽNICE KU STREDOVÝM CYKLIDÁM Abstrakt V prvej časti príspevku odvodzujeme podmienku, kedy je v danom
EXTREME SEVERAL-DAY PRECIPITATION TOTALS AT HURBANOVO DURING THE TWENTIETH CENTURY
 Rožnovský, J., Litschmann, T. (ed.): XIV. Česko-slovenská bioklimatologická konference, Lednice na Moravě 2.-4. září 2, ISBN -85813-99-8, s. 9-19 EXTREME SEVERAL-DAY PRECIPITATION TOTALS AT HURBANOVO DURING
Rožnovský, J., Litschmann, T. (ed.): XIV. Česko-slovenská bioklimatologická konference, Lednice na Moravě 2.-4. září 2, ISBN -85813-99-8, s. 9-19 EXTREME SEVERAL-DAY PRECIPITATION TOTALS AT HURBANOVO DURING
Jádrové odhady regresní funkce pro korelovaná data
 Jádrové odhady regresní funkce pro korelovaná data Ústav matematiky a statistiky MÚ Brno Finanční matematika v praxi III., Podlesí 3.9.-4.9. 2013 Obsah Motivace Motivace Motivace Co se snažíme získat?
Jádrové odhady regresní funkce pro korelovaná data Ústav matematiky a statistiky MÚ Brno Finanční matematika v praxi III., Podlesí 3.9.-4.9. 2013 Obsah Motivace Motivace Motivace Co se snažíme získat?
Teória kvantifikácie a binárne predikáty
 Teória kvantifikácie a binárne predikáty Miloš Kosterec Univerzita Komenského v Bratislave Abstract: The paper deals with a problem in formal theory of quantification. Firstly, by way of examples, I introduce
Teória kvantifikácie a binárne predikáty Miloš Kosterec Univerzita Komenského v Bratislave Abstract: The paper deals with a problem in formal theory of quantification. Firstly, by way of examples, I introduce
MEDZINÁRODNÝ VEDECKÝ ČASOPIS MLADÁ VEDA / YOUNG SCIENCE
 MEDZINÁRODNÝ VEDECKÝ ČASOPIS MLADÁ VEDA / YOUNG SCIENCE November 2014 (číslo 3) Ročník druhý ISSN 1339-3189 Kontakt: info@mladaveda.sk, tel.: +421 908 546 716, www.mladaveda.sk Fotografia na obálke: Kuala
MEDZINÁRODNÝ VEDECKÝ ČASOPIS MLADÁ VEDA / YOUNG SCIENCE November 2014 (číslo 3) Ročník druhý ISSN 1339-3189 Kontakt: info@mladaveda.sk, tel.: +421 908 546 716, www.mladaveda.sk Fotografia na obálke: Kuala
Ur enie faktora kvality seizmických P-v n na základe analýzy seizmogramov
 Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Katedra astronómie, fyziky Zeme a meteorológie Oddelenie fyziky Zeme Ur enie faktora kvality seizmických P-v n na základe analýzy
Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Katedra astronómie, fyziky Zeme a meteorológie Oddelenie fyziky Zeme Ur enie faktora kvality seizmických P-v n na základe analýzy
Radka Sabolová Znaménkový test
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Radka Sabolová Znaménkový test Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: Mgr. Martin Schindler
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Radka Sabolová Znaménkový test Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: Mgr. Martin Schindler
R a. Aeolian Church. A O g C. Air, Storm, Wind. P a h. Affinity: Clan Law. r q V a b a. R 5 Z t 6. c g M b. Atroxic Church. d / X.
 A M W A A A A R A O C A () A 6 A A G A A A A A A-C Au A A P 0 V A T < Au J Az01 Az02 A Au A A A A R 5 Z 6 M B G B B B P T Bu B B B B S B / X B A Cu A, S, W A: S Hu Ru A: C L A, S, F, S A, u F C, R C F
A M W A A A A R A O C A () A 6 A A G A A A A A A-C Au A A P 0 V A T < Au J Az01 Az02 A Au A A A A R 5 Z 6 M B G B B B P T Bu B B B B S B / X B A Cu A, S, W A: S Hu Ru A: C L A, S, F, S A, u F C, R C F
Econometric modelling and forecasting of intraday electricity prices
 E y y Xv:1812.09081v1 [q-.st] 21 D 2018 M Nw Uvy Duu-E F Z Uvy Duu-E D 24, 2018 A I w w y ID 3 -P G Iy Cuu Ey M u. A uv u uy qu-uy u y. W u qu u-- vy - uy. T w u. F u v w G Iy Cuu Ey M y ID 3 -P vu. T
E y y Xv:1812.09081v1 [q-.st] 21 D 2018 M Nw Uvy Duu-E F Z Uvy Duu-E D 24, 2018 A I w w y ID 3 -P G Iy Cuu Ey M u. A uv u uy qu-uy u y. W u qu u-- vy - uy. T w u. F u v w G Iy Cuu Ey M y ID 3 -P vu. T
Lecture 23: 6.1 Inner Products
 Lecture 23: 6.1 Inner Products Wei-Ta Chu 2008/12/17 Definition An inner product on a real vector space V is a function that associates a real number u, vwith each pair of vectors u and v in V in such
Lecture 23: 6.1 Inner Products Wei-Ta Chu 2008/12/17 Definition An inner product on a real vector space V is a function that associates a real number u, vwith each pair of vectors u and v in V in such
2-UMA-115 Teória množín. Martin Sleziak
 2-UMA-115 Teória množín Martin Sleziak 23. septembra 2010 Obsah 1 Úvod 4 1.1 Predhovor...................................... 4 1.2 Sylaby a literatúra................................. 5 1.2.1 Literatúra..................................
2-UMA-115 Teória množín Martin Sleziak 23. septembra 2010 Obsah 1 Úvod 4 1.1 Predhovor...................................... 4 1.2 Sylaby a literatúra................................. 5 1.2.1 Literatúra..................................
Charles University in Prague Faculty of Mathematics and Physics MASTER THESIS. Martin Babka. Properties of Universal Hashing
 Charles University in Prague Faculty of Mathematics and Physics MASTER THESIS Martin Babka Properties of Universal Hashing Department of Theoretical Computer Science and Mathematical Logic Supervisor:
Charles University in Prague Faculty of Mathematics and Physics MASTER THESIS Martin Babka Properties of Universal Hashing Department of Theoretical Computer Science and Mathematical Logic Supervisor:
Computational Complexity and Practical Implementation of RNA Motif Search
 Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Department of Computer Science Computational Complexity and Practical Implementation of RNA Motif Search (Master s Thesis)
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Department of Computer Science Computational Complexity and Practical Implementation of RNA Motif Search (Master s Thesis)
Recall: Dot product on R 2 : u v = (u 1, u 2 ) (v 1, v 2 ) = u 1 v 1 + u 2 v 2, u u = u u 2 2 = u 2. Geometric Meaning:
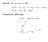 Recall: Dot product on R 2 : u v = (u 1, u 2 ) (v 1, v 2 ) = u 1 v 1 + u 2 v 2, u u = u 2 1 + u 2 2 = u 2. Geometric Meaning: u v = u v cos θ. u θ v 1 Reason: The opposite side is given by u v. u v 2 =
Recall: Dot product on R 2 : u v = (u 1, u 2 ) (v 1, v 2 ) = u 1 v 1 + u 2 v 2, u u = u 2 1 + u 2 2 = u 2. Geometric Meaning: u v = u v cos θ. u θ v 1 Reason: The opposite side is given by u v. u v 2 =
VYHLÁSENIE O PARAMETROCH. č SK
 VYHLÁSENIE O PARAMETROCH č. 0048 SK 1. Jedi eč ý ide tifikač ý k d typu výro ku: rá ová h oždi ka fischer SXR/SXRL 2. )a ýšľa é použitie/použitia: Produkt Plastové kotvy pre použitie v betóne a murive
VYHLÁSENIE O PARAMETROCH č. 0048 SK 1. Jedi eč ý ide tifikač ý k d typu výro ku: rá ová h oždi ka fischer SXR/SXRL 2. )a ýšľa é použitie/použitia: Produkt Plastové kotvy pre použitie v betóne a murive
Analýza multispektrálnych dát z konfokálnej mikroskopie. DIPLOMOVÁ PRÁCA
 Analýza multispektrálnych dát z konfokálnej mikroskopie. DIPLOMOVÁ PRÁCA Kamil Paulíny UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ INFORMATIKY Študijný
Analýza multispektrálnych dát z konfokálnej mikroskopie. DIPLOMOVÁ PRÁCA Kamil Paulíny UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ INFORMATIKY Študijný
Matematická analýza II.
 V. Diferenciálny počet (prezentácia k prednáške MANb/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prezentácie k prednáškam čast II 21. februára 2018 The extent of this calculus
V. Diferenciálny počet (prezentácia k prednáške MANb/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prezentácie k prednáškam čast II 21. februára 2018 The extent of this calculus
Ash Wednesday. First Introit thing. * Dómi- nos. di- di- nos, tú- ré- spi- Ps. ne. Dó- mi- Sál- vum. intra-vé-runt. Gló- ri-
 sh Wdsdy 7 gn mult- tú- st Frst Intrt thng X-áud m. ns ní- m-sr-cór- Ps. -qu Ptr - m- Sál- vum m * usqu 1 d fc á-rum sp- m-sr-t- ó- num Gló- r- Fí- l- Sp-rí- : quó-n- m ntr-vé-runt á- n-mm c * m- quó-n-
sh Wdsdy 7 gn mult- tú- st Frst Intrt thng X-áud m. ns ní- m-sr-cór- Ps. -qu Ptr - m- Sál- vum m * usqu 1 d fc á-rum sp- m-sr-t- ó- num Gló- r- Fí- l- Sp-rí- : quó-n- m ntr-vé-runt á- n-mm c * m- quó-n-
Prednáška 3. Optimalizačné metódy pre funkcie n-premenných. Študujme reálnu funkciu n-premenných. f: R R
 Prednáška 3 Optimalizačné metódy pre funkcie n-premenných Študujme reálnu funkciu n-premenných n f: R R Našou úlohou bude nájsť také x opt R n, pre ktoré má funkcia f minimum x opt = arg min ( f x) Túto
Prednáška 3 Optimalizačné metódy pre funkcie n-premenných Študujme reálnu funkciu n-premenných n f: R R Našou úlohou bude nájsť také x opt R n, pre ktoré má funkcia f minimum x opt = arg min ( f x) Túto
ANALÝZA VLASTNÝCH FREKVENCIÍ DYCHOVÉHO HUDOBNÉHO NÁSTROJA FUJARY
 SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE STAVEBNÁ FAKULTA ANALÝZA VLASTNÝCH FREKVENCIÍ DYCHOVÉHO HUDOBNÉHO NÁSTROJA FUJARY Diplomová práca tudijný program: tudijný odbor: koliace pracovisko: Vedúci
SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE STAVEBNÁ FAKULTA ANALÝZA VLASTNÝCH FREKVENCIÍ DYCHOVÉHO HUDOBNÉHO NÁSTROJA FUJARY Diplomová práca tudijný program: tudijný odbor: koliace pracovisko: Vedúci
