Matematická analýza II.
|
|
|
- Cameron Fisher
- 5 years ago
- Views:
Transcription
1 V. Diferenciálny počet (prezentácia k prednáške MANb/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prednáška 8 6. marca 2018
2 It has apparently not yet been observed, that... continuity at any single point... is not the continuity... which can be called uniform continuity, because it extends uniformly to all points and in all directions. Heine: Ueber trigonometrische Reihen (1870), p. 361 Definícia rovnomerná spojitost funkcie na množine Funkciu f nazývame rovnomerne spojitá na množine M D f, akk ( ε > 0) ( δ > 0) ( x, y M, x y < δ) f (x) f (y) < ε. Budeme písat f C u (M). Príklady: Vyšetrite rovnomernú spojitost funkcie f na množine M, ak f (x) = sin x, kde M = R; f (x) = 1 x na M = 1, + ); f (x) = 1 x na M = (0, + );
3 It has apparently not yet been observed, that... continuity at any single point... is not the continuity... which can be called uniform continuity, because it extends uniformly to all points and in all directions. Heine: Ueber trigonometrische Reihen (1870), p. 361 Definícia rovnomerná spojitost funkcie na množine Funkciu f nazývame rovnomerne spojitá na množine M D f, akk ( ε > 0) ( δ > 0) ( x, y M, x y < δ) f (x) f (y) < ε. Budeme písat f C u (M). Príklady: Vyšetrite rovnomernú spojitost funkcie f na množine M, ak f (x) = sin x, kde M = R; f (x) = 1 x na M = 1, + ); f (x) = 1 x na M = (0, + );
4 It has apparently not yet been observed, that... continuity at any single point... is not the continuity... which can be called uniform continuity, because it extends uniformly to all points and in all directions. Heine: Ueber trigonometrische Reihen (1870), p. 361 Definícia rovnomerná spojitost funkcie na množine Funkciu f nazývame rovnomerne spojitá na množine M D f, akk ( ε > 0) ( δ > 0) ( x, y M, x y < δ) f (x) f (y) < ε. Budeme písat f C u (M). Príklady: Vyšetrite rovnomernú spojitost funkcie f na množine M, ak f (x) = sin x, kde M = R; f (x) = 1 x na M = 1, + ); f (x) = 1 x na M = (0, + );
5 It has apparently not yet been observed, that... continuity at any single point... is not the continuity... which can be called uniform continuity, because it extends uniformly to all points and in all directions. Heine: Ueber trigonometrische Reihen (1870), p. 361 Definícia rovnomerná spojitost funkcie na množine Funkciu f nazývame rovnomerne spojitá na množine M D f, akk ( ε > 0) ( δ > 0) ( x, y M, x y < δ) f (x) f (y) < ε. Budeme písat f C u (M). Príklady: Vyšetrite rovnomernú spojitost funkcie f na množine M, ak f (x) = sin x, kde M = R; f (x) = 1 x na M = 1, + ); f (x) = 1 x na M = (0, + );
6 It has apparently not yet been observed, that... continuity at any single point... is not the continuity... which can be called uniform continuity, because it extends uniformly to all points and in all directions. Heine: Ueber trigonometrische Reihen (1870), p. 361 Definícia rovnomerná spojitost funkcie na množine Funkciu f nazývame rovnomerne spojitá na množine M D f, akk ( ε > 0) ( δ > 0) ( x, y M, x y < δ) f (x) f (y) < ε. Budeme písat f C u (M). Pozorovanie: f C u(m) ( x n, y n M) lim x n n y n = 0 pohrajte sa interaktívne: Veta V.10 C u (M) C (M) lim f (x n n) f (y n) = 0
7 It has apparently not yet been observed, that... continuity at any single point... is not the continuity... which can be called uniform continuity, because it extends uniformly to all points and in all directions. Heine: Ueber trigonometrische Reihen (1870), p. 361 Definícia rovnomerná spojitost funkcie na množine Funkciu f nazývame rovnomerne spojitá na množine M D f, akk ( ε > 0) ( δ > 0) ( x, y M, x y < δ) f (x) f (y) < ε. Budeme písat f C u (M). Pozorovanie: f C u(m) ( x n, y n M) lim x n n y n = 0 pohrajte sa interaktívne: Veta V.10 C u (M) C (M) lim f (x n n) f (y n) = 0
8 It has apparently not yet been observed, that... continuity at any single point... is not the continuity... which can be called uniform continuity, because it extends uniformly to all points and in all directions. Heine: Ueber trigonometrische Reihen (1870), p. 361 Definícia rovnomerná spojitost funkcie na množine Funkciu f nazývame rovnomerne spojitá na množine M D f, akk ( ε > 0) ( δ > 0) ( x, y M, x y < δ) f (x) f (y) < ε. Budeme písat f C u (M). Pozorovanie: f C u(m) ( x n, y n M) lim x n n y n = 0 pohrajte sa interaktívne: Veta V.10 C u (M) C (M) lim f (x n n) f (y n) = 0
9 The general ideas of the proof of several theorems in 3 according to the principles of Mr. Weierstrass are known to me by oral communications from himself, from Mr. Schwarz and Mr. Cantor, so that... Heine: Die Elemente der Funktionenlehre (1872), p. 182 Veta (Heineho-Cantorova, 1872) C u a, b = C a, b EDUARD HEINE ( ) GEORG CANTOR ( )
10 The general ideas of the proof of several theorems in 3 according to the principles of Mr. Weierstrass are known to me by oral communications from himself, from Mr. Schwarz and Mr. Cantor, so that... Heine: Die Elemente der Funktionenlehre (1872), p. 182 Veta (Heineho-Cantorova, 1872) C u a, b = C a, b Poznámky: Heineho-Cantorova veta neplatí na otvorenom intervale, napr. f (x) = cos 1 x na M = (0, 1 je spojitá, ale nie rovnomerne! Čo vieme povedat o natiahnutí spojitosti do krajných bodov intervalu? Tvrdenie: bod nespojitosti rovnomerne spojitej funkcie na otvorenom intervale je odstránitel ný Nech f C (a, b), kde a, b R. Potom f sa dá spojite rozšírit na a, b (t.j. existujú vlastné jednostranné limity v krajných bodoch) práve vtedy, ked f C u(a, b). Náčrt dôkazu: zrejmé, lebo ak sa dá spojite rozšírit na a, b, tak podl a Heineho-Cantorovej vety je f C u a, b, teda aj f C u(a, b) Ked že f C u(a, b), tak ( ε > 0)( δ > 0)( x, y (a, b)) ( x y < δ f (x) f (y) < ε), a teda to platí aj pre intervaly (a, a + δ) a (b δ, b), čiže podl a Dirichletovej vety existujú vlastné jednostranné limity v krajných bodoch. Predchádzajúci výsledok neplatí na neohraničenom intervale, napr. f (x) = sin x je rovnomerne spojitá na R, ale neexistujú jej limity v ±!
11 The general ideas of the proof of several theorems in 3 according to the principles of Mr. Weierstrass are known to me by oral communications from himself, from Mr. Schwarz and Mr. Cantor, so that... Heine: Die Elemente der Funktionenlehre (1872), p. 182 Veta (Heineho-Cantorova, 1872) C u a, b = C a, b Poznámky: Heineho-Cantorova veta neplatí na otvorenom intervale, napr. f (x) = cos 1 x na M = (0, 1 je spojitá, ale nie rovnomerne! Čo vieme povedat o natiahnutí spojitosti do krajných bodov intervalu? Tvrdenie: bod nespojitosti rovnomerne spojitej funkcie na otvorenom intervale je odstránitel ný Nech f C (a, b), kde a, b R. Potom f sa dá spojite rozšírit na a, b (t.j. existujú vlastné jednostranné limity v krajných bodoch) práve vtedy, ked f C u(a, b). Náčrt dôkazu: zrejmé, lebo ak sa dá spojite rozšírit na a, b, tak podl a Heineho-Cantorovej vety je f C u a, b, teda aj f C u(a, b) Ked že f C u(a, b), tak ( ε > 0)( δ > 0)( x, y (a, b)) ( x y < δ f (x) f (y) < ε), a teda to platí aj pre intervaly (a, a + δ) a (b δ, b), čiže podl a Dirichletovej vety existujú vlastné jednostranné limity v krajných bodoch. Predchádzajúci výsledok neplatí na neohraničenom intervale, napr. f (x) = sin x je rovnomerne spojitá na R, ale neexistujú jej limity v ±!
12 The general ideas of the proof of several theorems in 3 according to the principles of Mr. Weierstrass are known to me by oral communications from himself, from Mr. Schwarz and Mr. Cantor, so that... Heine: Die Elemente der Funktionenlehre (1872), p. 182 Veta (Heineho-Cantorova, 1872) C u a, b = C a, b Poznámky: Heineho-Cantorova veta neplatí na otvorenom intervale, napr. f (x) = cos 1 x na M = (0, 1 je spojitá, ale nie rovnomerne! Čo vieme povedat o natiahnutí spojitosti do krajných bodov intervalu? Tvrdenie: bod nespojitosti rovnomerne spojitej funkcie na otvorenom intervale je odstránitel ný Nech f C (a, b), kde a, b R. Potom f sa dá spojite rozšírit na a, b (t.j. existujú vlastné jednostranné limity v krajných bodoch) práve vtedy, ked f C u(a, b). Náčrt dôkazu: zrejmé, lebo ak sa dá spojite rozšírit na a, b, tak podl a Heineho-Cantorovej vety je f C u a, b, teda aj f C u(a, b) Ked že f C u(a, b), tak ( ε > 0)( δ > 0)( x, y (a, b)) ( x y < δ f (x) f (y) < ε), a teda to platí aj pre intervaly (a, a + δ) a (b δ, b), čiže podl a Dirichletovej vety existujú vlastné jednostranné limity v krajných bodoch. Predchádzajúci výsledok neplatí na neohraničenom intervale, napr. f (x) = sin x je rovnomerne spojitá na R, ale neexistujú jej limity v ±!
13 The general ideas of the proof of several theorems in 3 according to the principles of Mr. Weierstrass are known to me by oral communications from himself, from Mr. Schwarz and Mr. Cantor, so that... Heine: Die Elemente der Funktionenlehre (1872), p. 182 Veta (Heineho-Cantorova, 1872) C u a, b = C a, b Poznámky: Heineho-Cantorova veta neplatí na otvorenom intervale, napr. f (x) = cos 1 x na M = (0, 1 je spojitá, ale nie rovnomerne! Čo vieme povedat o natiahnutí spojitosti do krajných bodov intervalu? Tvrdenie: bod nespojitosti rovnomerne spojitej funkcie na otvorenom intervale je odstránitel ný Nech f C (a, b), kde a, b R. Potom f sa dá spojite rozšírit na a, b (t.j. existujú vlastné jednostranné limity v krajných bodoch) práve vtedy, ked f C u(a, b). Náčrt dôkazu: zrejmé, lebo ak sa dá spojite rozšírit na a, b, tak podl a Heineho-Cantorovej vety je f C u a, b, teda aj f C u(a, b) Ked že f C u(a, b), tak ( ε > 0)( δ > 0)( x, y (a, b)) ( x y < δ f (x) f (y) < ε), a teda to platí aj pre intervaly (a, a + δ) a (b δ, b), čiže podl a Dirichletovej vety existujú vlastné jednostranné limity v krajných bodoch. Predchádzajúci výsledok neplatí na neohraničenom intervale, napr. f (x) = sin x je rovnomerne spojitá na R, ale neexistujú jej limity v ±!
14 The general ideas of the proof of several theorems in 3 according to the principles of Mr. Weierstrass are known to me by oral communications from himself, from Mr. Schwarz and Mr. Cantor, so that... Heine: Die Elemente der Funktionenlehre (1872), p. 182 Veta (Heineho-Cantorova, 1872) C u a, b = C a, b Poznámky: Heineho-Cantorova veta neplatí na otvorenom intervale, napr. f (x) = cos 1 x na M = (0, 1 je spojitá, ale nie rovnomerne! Čo vieme povedat o natiahnutí spojitosti do krajných bodov intervalu? Tvrdenie: bod nespojitosti rovnomerne spojitej funkcie na otvorenom intervale je odstránitel ný Nech f C (a, b), kde a, b R. Potom f sa dá spojite rozšírit na a, b (t.j. existujú vlastné jednostranné limity v krajných bodoch) práve vtedy, ked f C u(a, b). Náčrt dôkazu: zrejmé, lebo ak sa dá spojite rozšírit na a, b, tak podl a Heineho-Cantorovej vety je f C u a, b, teda aj f C u(a, b) Ked že f C u(a, b), tak ( ε > 0)( δ > 0)( x, y (a, b)) ( x y < δ f (x) f (y) < ε), a teda to platí aj pre intervaly (a, a + δ) a (b δ, b), čiže podl a Dirichletovej vety existujú vlastné jednostranné limity v krajných bodoch. Predchádzajúci výsledok neplatí na neohraničenom intervale, napr. f (x) = sin x je rovnomerne spojitá na R, ale neexistujú jej limity v ±!
15 Spojitost a d alšie vlastnosti funkcií Zopakovanie Veta II.4 Ak f je rýdzomonotónna na M D f, tak f je injektívna na M. y x Čo je potrebné pridat k injektívnosti, aby sme dostali rýdzomonotónnost??? Veta V.11 Ak f je injektívna na M D f a f C (M), tak f je rýdzomonotónna na M.
16 Spojitost a d alšie vlastnosti funkcií Zopakovanie Veta II.4 Ak f je rýdzomonotónna na M D f, tak f je injektívna na M. y x Čo je potrebné pridat k injektívnosti, aby sme dostali rýdzomonotónnost??? Veta V.11 Ak f je injektívna na M D f a f C (M), tak f je rýdzomonotónna na M.
17 Spojitost a d alšie vlastnosti funkcií Zopakovanie Veta II.4 Ak f je rýdzomonotónna na M D f, tak f je injektívna na M. y x Čo je potrebné pridat k injektívnosti, aby sme dostali rýdzomonotónnost??? Veta V.11 Ak f je injektívna na M D f a f C (M), tak f je rýdzomonotónna na M.
18 Dôsledok = Veta II.4 + Veta V.11 Nech f C (M). Potom f je injektívna na M práve vtedy, ked f je rýdzomonotónna na M. Zopakovanie Dôsledok Darbouxovej vety Nech f C (M), kde M je interval. Potom N = {y = f (x); x M} je jednoprvková množina alebo interval. JEAN GASTON DARBOUX ( ) Za akých okolností sa dá tento výsledok obrátit?
19 Dôsledok = Veta II.4 + Veta V.11 Nech f C (M). Potom f je injektívna na M práve vtedy, ked f je rýdzomonotónna na M. Zopakovanie Dôsledok Darbouxovej vety Nech f C (M), kde M je interval. Potom N = {y = f (x); x M} je jednoprvková množina alebo interval. JEAN GASTON DARBOUX ( ) Za akých okolností sa dá tento výsledok obrátit?
20 Dôsledok = Veta II.4 + Veta V.11 Nech f C (M). Potom f je injektívna na M práve vtedy, ked f je rýdzomonotónna na M. Veta V.12 Nech f je monotónna na intervale M D f a N = {y = f (x); x M} je jednoprvková množina alebo interval. Potom f C (M). Veta (o spojitosti inverznej funkcie) Nech f C (M) je injektívna na intervale M D f a N = {y = f (x); x M}. Potom f C (N) je rýdzomonotónna. Veta V.9 Všetky základné elementárne funkcie sú spojité v každom bode svojho definičného oboru. všeobecná mocninná funkcia, logaritmická funkcia, cyklometrické a hyperbolometrické funkcie
21 Dôsledok = Veta II.4 + Veta V.11 Nech f C (M). Potom f je injektívna na M práve vtedy, ked f je rýdzomonotónna na M. Veta V.12 Nech f je monotónna na intervale M D f a N = {y = f (x); x M} je jednoprvková množina alebo interval. Potom f C (M). Veta (o spojitosti inverznej funkcie) Nech f C (M) je injektívna na intervale M D f a N = {y = f (x); x M}. Potom f C (N) je rýdzomonotónna. Veta V.9 Všetky základné elementárne funkcie sú spojité v každom bode svojho definičného oboru. všeobecná mocninná funkcia, logaritmická funkcia, cyklometrické a hyperbolometrické funkcie
22 Dôsledok = Veta II.4 + Veta V.11 Nech f C (M). Potom f je injektívna na M práve vtedy, ked f je rýdzomonotónna na M. Veta V.12 Nech f je monotónna na intervale M D f a N = {y = f (x); x M} je jednoprvková množina alebo interval. Potom f C (M). Veta (o spojitosti inverznej funkcie) Nech f C (M) je injektívna na intervale M D f a N = {y = f (x); x M}. Potom f C (N) je rýdzomonotónna. Veta V.9 Všetky základné elementárne funkcie sú spojité v každom bode svojho definičného oboru. všeobecná mocninná funkcia, logaritmická funkcia, cyklometrické a hyperbolometrické funkcie
23 The extent of this calculus is immense: it applies to curves both mechanical and geometrical; radical signs cause it no difficulty, and even are often convenient; it extends to as many variables as one wishes; the comparison of infinitely small quantities of all sorts is easy. And it gives rise to an infinity of surprising discoveries concerning curved or straight tangents, questions De maximis & minimis, inflexion points and cusps of curves, envelopes, caustics from reflexion or refraction, &c. as we shall see in this work. Marquis de L Hospital: Analyse des infiniment petits (1696)
24 Infinitezimálny počet motivácia And I dare say that this is not only the most useful and most general problem in geometry that I know, but even that I ever desired to know. Descartes: La Geometrie, Appendix to the Discours de la methode (1637) What contempt for the non-english! We have found these methods, without any help from the English. Joh. Bernoulli: Opera, vol. IV (1735), p. 70 Isaac Newton was not a pleasant man. His relations with other academics were notorious, with most of his later life spent embroiled in heated disputes... A serious dispute arose with the German philosopher Gottfried Leibniz. Both Leibniz and Newton had independently developed a branch of mathematics called calculus, which underlies most of modern physics... Hawking: A Brief History of Time (1988) Problém: Nech y = f (x) je daná krivka. V každom bode x chceme poznat sklon krivky, dotyčnicu ku krivke a normálu ku krivke. Motivácie: výpočet uhla, pod ktorým sa dve krivky pretínajú (Descartes); konštrukcia d alekohl adov (Galilei) a hodín (Huygens 1673); nájdenie maxima a minima funkcie (Fermat 1638); rýchlost a zrýchlenie pohybu (Galilei 1638, Newton 1686); astronómia, overenie gravitačného zákona (Kepler, Newton).
25 Infinitezimálny počet okolnosti vzniku a historické súvislosti NEWTON (1671, publikované až v roku 1736): Uvažuje premenné v, x, y, z ako as gradually and indefinitely increasing,... And the velocities by which every Fluent is increased by its general motion, (which I may call Fluxions) I shall represent by the same Letters pointed thus v, ẋ, ẏ, ż. Hodnoty dostal spôsobom rejecting the Terms... as being equal to nothing.
26 Infinitezimálny počet okolnosti vzniku a historické súvislosti LEIBNIZ (1684): Nech y = x 2. Ak x narastie o x, tak y narastie na y + y = (x + x) 2 = x 2 + 2x x + ( x) 2 y = 2x x + ( x) 2. Podl a Leibniza x a y predstavujú nekonečne malé veličiny, ktoré označil dx a dy. Zanedbaním výrazu (dx) 2, ktorý je nekonečne menší ako 2xdx dostal dy = 2xdx alebo dy dx = 2x.
27 Infinitezimálny počet okolnosti vzniku a historické súvislosti JACOB A JOHANN BERNOULLI: tretie znovuobjavenie diferenciálneho kalkulu na základe Leibnizovho článku z roku Johann dáva v roku 1691/92 súkromné hodiny nového kalkulu markízovi de L Hospitalovi, pričom nekonečne malé veličiny chápal ako veličiny, ktoré sa môžu pripočítat ku konečným veličinám bez zmeny ich hodnôt kritika tejto novej matematiky od B. NIEVENTIJTA z roku 1694
28 Infinitezimálny počet okolnosti vzniku a historické súvislosti GUILLAUME DE L HOSPITAL (1696): vydal knihu Analyse des infiniment petits, ktorá sa stala prvou učebnicou diferenciálneho počtu a znamenala prelom v používaní nového kalkulu dokonca aj vo Francúzsku, kde veda bola ovplyvnená dlhé desat ročia karteziánmi (abbé Catelan, Papin, Rolle, atd.)
29 Derivácia rodiaca sa: derivácia umožňuje popis fyzikálnych dejov a geometrické správanie sa funkcií ISAAC NEWTON ( ) GOTTFRIED WILHELM LEIBNIZ ( )
30 Derivácia uháňajúca: derivácia udáva rýchlost zmien fyzikálnych veličín derivácia umožňuje merat rýchlost dejov najrôznejšieho druhu
31 Derivácia tvarujúca: derivácia funkcie v bode je smernica jej dotyčnice v danom bode, t.j. udáva ako rýchlo funkcia rastie alebo klesá druhá derivácia udává mieru konvexnosti či konkávnosti derivácia je vhodný nástroj pre popis kriviek najrôznejšieho druhu
32 Derivácia zjednodušujúca: derivácia slúži na aproximáciu funkcie, ak ju nahradíme jej dotyčnicou namiesto všeobecne komplikovaných závislostí medzi veličinami pracujeme s lineárnymi funkciami a rovnicami
33 Derivácia všeobklopujúca: ked že väčšina fyzikálnych dejov prebieha tak, že zmena jednej veličiny vyvoláva zmenu či prítomnost inej veličiny, je derivácia ideálnym prostriedkom pre formulovanie fyzikálnych zákonov popisuje všetko, čo nás obklopuje
34 ... tangentem invenire, esse rectam ducere, quæ duo curvæ puncta distantiam infinite parvam habentia, jungat,... Leibniz: Nova methodus pro maximis et minimis... (1684) Definícia derivácia funkcie v bode Nech x 0 D f je hromadný bod D f. Deriváciou funkcie f v bode x 0 nazývame f (x) f (x 0 ) vlastnú limitu lim a označujeme ju f (x 0 ). x x0 x x 0
35 ... tangentem invenire, esse rectam ducere, quæ duo curvæ puncta distantiam infinite parvam habentia, jungat,... Leibniz: Nova methodus pro maximis et minimis... (1684) Definícia derivácia funkcie v bode Nech x 0 D f je hromadný bod D f. Deriváciou funkcie f v bode x 0 nazývame f (x) f (x 0 ) vlastnú limitu lim a označujeme ju f (x 0 ). x x0 x x 0
36 f f (x) f (x 0 ) f (x 0 + h) f (x 0 ) (x 0 ) = lim = lim x x0 x x 0 h 0 h Príklady: Nájdite deriváciu funkcie f v l ubovol nom bode x 0 R, ak f (x) = c, kde c R; f (x) = x n pre n N; f (x) = a x pre a > 0, a 1;
37 f f (x) f (x 0 ) f (x 0 + h) f (x 0 ) (x 0 ) = lim = lim x x0 x x 0 h 0 h Príklady: Nájdite deriváciu funkcie f v l ubovol nom bode x 0 R, ak f (x) = c, kde c R; f (x) = x n pre n N; f (x) = a x pre a > 0, a 1;
38 f f (x) f (x 0 ) f (x 0 + h) f (x 0 ) (x 0 ) = lim = lim x x0 x x 0 h 0 h Príklady: Nájdite deriváciu funkcie f v l ubovol nom bode x 0 R, ak f (x) = c, kde c R; f (x) = x n pre n N; f (x) = a x pre a > 0, a 1;
Matematická analýza II.
 V. Diferenciálny počet (prezentácia k prednáške MANb/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prezentácie k prednáškam čast II 21. februára 2018 The extent of this calculus
V. Diferenciálny počet (prezentácia k prednáške MANb/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prezentácie k prednáškam čast II 21. februára 2018 The extent of this calculus
Historical notes on calculus
 Historical notes on calculus Dr. Vladimir Dotsenko Dr. Vladimir Dotsenko Historical notes on calculus 1 / 9 Descartes: Describing geometric figures by algebraic formulas 1637: René Descartes publishes
Historical notes on calculus Dr. Vladimir Dotsenko Dr. Vladimir Dotsenko Historical notes on calculus 1 / 9 Descartes: Describing geometric figures by algebraic formulas 1637: René Descartes publishes
Beyond Newton and Leibniz: The Making of Modern Calculus. Anthony V. Piccolino, Ed. D. Palm Beach State College Palm Beach Gardens, Florida
 Beyond Newton and Leibniz: The Making of Modern Calculus Anthony V. Piccolino, Ed. D. Palm Beach State College Palm Beach Gardens, Florida Calculus Before Newton & Leibniz Four Major Scientific Problems
Beyond Newton and Leibniz: The Making of Modern Calculus Anthony V. Piccolino, Ed. D. Palm Beach State College Palm Beach Gardens, Florida Calculus Before Newton & Leibniz Four Major Scientific Problems
O1 History of Mathematics Lecture VI Successes of and difficulties with the calculus: the 18th-century beginnings of rigour
 O1 History of Mathematics Lecture VI Successes of and difficulties with the calculus: the 18th-century beginnings of rigour Monday 22nd October 2018 (Week 3) Summary Publication and acceptance of the calculus
O1 History of Mathematics Lecture VI Successes of and difficulties with the calculus: the 18th-century beginnings of rigour Monday 22nd October 2018 (Week 3) Summary Publication and acceptance of the calculus
Teória grafov. RNDr. Milan Stacho, PhD.
 Teória grafov RNDr. Milan Stacho, PhD. Literatúra Plesník: Grafové algoritmy, Veda Bratislava 1983 Sedláček: Úvod do teórie grafů, Academia Praha 1981 Bosák: Grafy a ich aplikácie, Alfa Bratislava 1980
Teória grafov RNDr. Milan Stacho, PhD. Literatúra Plesník: Grafové algoritmy, Veda Bratislava 1983 Sedláček: Úvod do teórie grafů, Academia Praha 1981 Bosák: Grafy a ich aplikácie, Alfa Bratislava 1980
Leibniz and the Discovery of Calculus. The introduction of calculus to the world in the seventeenth century is often associated
 Leibniz and the Discovery of Calculus The introduction of calculus to the world in the seventeenth century is often associated with Isaac Newton, however on the main continent of Europe calculus would
Leibniz and the Discovery of Calculus The introduction of calculus to the world in the seventeenth century is often associated with Isaac Newton, however on the main continent of Europe calculus would
In today s world, people with basic calculus knowledge take the subject for granted. As
 Ziya Chen Math 4388 Shanyu Ji Calculus In today s world, people with basic calculus knowledge take the subject for granted. As long as they plug in numbers into the right formula and do the calculation
Ziya Chen Math 4388 Shanyu Ji Calculus In today s world, people with basic calculus knowledge take the subject for granted. As long as they plug in numbers into the right formula and do the calculation
Historical Reflections On Teaching Calculus/Analysis David Bressoud Macalester College St. Paul, MN
 Historical Reflections On Teaching Calculus/Analysis David Bressoud Macalester College St. Paul, MN University of Utrecht The Netherlands April 23, 2010 PowerPoint available at www.macalester.edu/~bressoud/talks
Historical Reflections On Teaching Calculus/Analysis David Bressoud Macalester College St. Paul, MN University of Utrecht The Netherlands April 23, 2010 PowerPoint available at www.macalester.edu/~bressoud/talks
Calculus Trivia: Historic Calculus Texts
 Calculus Trivia: Historic Calculus Texts Archimedes of Syracuse (c. 287 BC - c. 212 BC) - On the Measurement of a Circle : Archimedes shows that the value of pi (π) is greater than 223/71 and less than
Calculus Trivia: Historic Calculus Texts Archimedes of Syracuse (c. 287 BC - c. 212 BC) - On the Measurement of a Circle : Archimedes shows that the value of pi (π) is greater than 223/71 and less than
Slopes, Derivatives, and Tangents. Matt Riley, Kyle Mitchell, Jacob Shaw, Patrick Lane
 Slopes, Derivatives, and Tangents Matt Riley, Kyle Mitchell, Jacob Shaw, Patrick Lane S Introduction Definition of a tangent line: The tangent line at a point on a curve is a straight line that just touches
Slopes, Derivatives, and Tangents Matt Riley, Kyle Mitchell, Jacob Shaw, Patrick Lane S Introduction Definition of a tangent line: The tangent line at a point on a curve is a straight line that just touches
Math 4388 Amber Pham 1. The Birth of Calculus. for counting. There are two major interrelated topics in calculus known as differential and
 Math 4388 Amber Pham 1 The Birth of Calculus The literal meaning of calculus originated from Latin, which means a small stone used for counting. There are two major interrelated topics in calculus known
Math 4388 Amber Pham 1 The Birth of Calculus The literal meaning of calculus originated from Latin, which means a small stone used for counting. There are two major interrelated topics in calculus known
Reflections on the Fundamental Theorem Of Integral Calculus
 Reflections on the Fundamental Theorem Of Integral Calculus David Bressoud St. Paul, MN MAA Wisconsin Sec,on Ripon College, Ripon, WI April 25, 2015 Mathematical Association of America PowerPoint available
Reflections on the Fundamental Theorem Of Integral Calculus David Bressoud St. Paul, MN MAA Wisconsin Sec,on Ripon College, Ripon, WI April 25, 2015 Mathematical Association of America PowerPoint available
A history of Topology
 A history of Topology Version for printing Geometry and topology index History Topics Index Topological ideas are present in almost all areas of today's mathematics. The subject of topology itself consists
A history of Topology Version for printing Geometry and topology index History Topics Index Topological ideas are present in almost all areas of today's mathematics. The subject of topology itself consists
Mathematical Misnomers: Hey, who really discovered that theorem!
 Mathematical Misnomers: Hey, who really discovered that theorem! Mike Raugh mikeraugh.org LACC Math Contest 24th March 2007 Who was buried in Grant s tomb? Ulysss S. Grant, of course! These are true too:
Mathematical Misnomers: Hey, who really discovered that theorem! Mike Raugh mikeraugh.org LACC Math Contest 24th March 2007 Who was buried in Grant s tomb? Ulysss S. Grant, of course! These are true too:
Zentrum für Technomathematik Fachbereich 3 Mathematik und Informatik. R, dx and ε. Derivatives and Infinitesimal Numbers
 R, dx and ε Derivatives and Infinitesimal Numbers 1 We use derivatives all day Looking for extrema: f (x) = 0 Expressing conntection between quantities: y = f(y, x) Calculating norms or constaints: f =
R, dx and ε Derivatives and Infinitesimal Numbers 1 We use derivatives all day Looking for extrema: f (x) = 0 Expressing conntection between quantities: y = f(y, x) Calculating norms or constaints: f =
Kapitola S5. Skrutkovica na rotačnej ploche
 Kapitola S5 Skrutkovica na rotačnej ploche Nech je rotačná plocha určená osou rotácie o a meridiánom m. Skrutkový pohyb je pohyb zložený z rovnomerného rotačného pohybu okolo osi o a z rovnomerného translačného
Kapitola S5 Skrutkovica na rotačnej ploche Nech je rotačná plocha určená osou rotácie o a meridiánom m. Skrutkový pohyb je pohyb zložený z rovnomerného rotačného pohybu okolo osi o a z rovnomerného translačného
The Leibniz Catenary Construction: Geometry vs Analysis in the 17 th Century
 The Leibniz Catenary Construction: Geometry vs Analysis in the 17 th Century Mike Raugh www.mikeraugh.org JMM: Joint Mathematics Meetings, Atlanta January 4, 2017 Copyright 2017 Mike Raugh Catenary: Derived
The Leibniz Catenary Construction: Geometry vs Analysis in the 17 th Century Mike Raugh www.mikeraugh.org JMM: Joint Mathematics Meetings, Atlanta January 4, 2017 Copyright 2017 Mike Raugh Catenary: Derived
Chapter 1 INTRODUCTION TO CALCULUS
 Chapter 1 INTRODUCTION TO CALCULUS In the English language, the rules of grammar are used to speak and write effectively. Asking for a cookie at the age of ten was much easier than when you were first
Chapter 1 INTRODUCTION TO CALCULUS In the English language, the rules of grammar are used to speak and write effectively. Asking for a cookie at the age of ten was much easier than when you were first
MATH1014 Calculus II. A historical review on Calculus
 MATH1014 Calculus II A historical review on Calculus Edmund Y. M. Chiang Department of Mathematics Hong Kong University of Science & Technology September 4, 2015 Instantaneous Velocities Newton s paradox
MATH1014 Calculus II A historical review on Calculus Edmund Y. M. Chiang Department of Mathematics Hong Kong University of Science & Technology September 4, 2015 Instantaneous Velocities Newton s paradox
These slides will be available at
 David Bressoud Macalester College St. Paul, MN Moravian College February 20, 2009 These slides will be available at www.macalester.edu/~bressoud/talks The task of the educator is to make the child s spirit
David Bressoud Macalester College St. Paul, MN Moravian College February 20, 2009 These slides will be available at www.macalester.edu/~bressoud/talks The task of the educator is to make the child s spirit
Concepts in Engineering Mathematics: Lecture 39
 Concepts in Engineering Mathematics: Lecture 39 Part IV: Vector Calculus Lecture 39 Version: 0.94 Dec7.15 Jont B. Allen; UIUC Urbana IL, USA December 9, 2015 Jont B. Allen; UIUC Urbana IL, USA Concepts
Concepts in Engineering Mathematics: Lecture 39 Part IV: Vector Calculus Lecture 39 Version: 0.94 Dec7.15 Jont B. Allen; UIUC Urbana IL, USA December 9, 2015 Jont B. Allen; UIUC Urbana IL, USA Concepts
The integral test and estimates of sums
 The integral test Suppose f is a continuous, positive, decreasing function on [, ) and let a n = f (n). Then the series n= a n is convergent if and only if the improper integral f (x)dx is convergent.
The integral test Suppose f is a continuous, positive, decreasing function on [, ) and let a n = f (n). Then the series n= a n is convergent if and only if the improper integral f (x)dx is convergent.
O1 History of Mathematics Lecture IV The beginnings of calculus, part 2: quadrature. Monday 17th October 2016 (Week 2)
 O1 History of Mathematics Lecture IV The beginnings of calculus, part 2: quadrature Monday 17th October 2016 (Week 2) Summary Quadrature (finding areas) The method of indivisibles Infinitesimals Newton
O1 History of Mathematics Lecture IV The beginnings of calculus, part 2: quadrature Monday 17th October 2016 (Week 2) Summary Quadrature (finding areas) The method of indivisibles Infinitesimals Newton
1230, notes 16. Karl Theodor Wilhelm Weierstrass, November 18, / 18
 1230, notes 16 Karl Theodor Wilhelm Weierstrass, 1815-1897 November 18, 2014 1 / 18 1230, notes 16 Karl Theodor Wilhelm Weierstrass, 1815-1897 Left university without a degree (ignored what he was supposed
1230, notes 16 Karl Theodor Wilhelm Weierstrass, 1815-1897 November 18, 2014 1 / 18 1230, notes 16 Karl Theodor Wilhelm Weierstrass, 1815-1897 Left university without a degree (ignored what he was supposed
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UIVERZITA KOMESKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A IFORMATIKY VÝPOČET FOURIEROVÝCH RADOV POMOCOU DISKRÉTEJ FOURIEROVEJ TRASFORMÁCIE BAKALÁRSKA PRÁCA 2013 Andrej ZUBAL UIVERZITA KOMESKÉHO V BRATISLAVE
UIVERZITA KOMESKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A IFORMATIKY VÝPOČET FOURIEROVÝCH RADOV POMOCOU DISKRÉTEJ FOURIEROVEJ TRASFORMÁCIE BAKALÁRSKA PRÁCA 2013 Andrej ZUBAL UIVERZITA KOMESKÉHO V BRATISLAVE
ADM a logika. 4. prednáška. Výroková logika II, logický a sémantický dôsledok, teória a model, korektnosť a úplnosť
 ADM a logika 4. prednáška Výroková logika II, logický a sémantický dôsledok, teória a model, korektnosť a úplnosť 1 Odvodzovanie formúl výrokovej logiky, logický dôsledok, syntaktický prístup Logický dôsledok
ADM a logika 4. prednáška Výroková logika II, logický a sémantický dôsledok, teória a model, korektnosť a úplnosť 1 Odvodzovanie formúl výrokovej logiky, logický dôsledok, syntaktický prístup Logický dôsledok
Module 3 : Differentiation and Mean Value Theorems. Lecture 7 : Differentiation. Objectives. In this section you will learn the following :
 Module 3 : Differentiation and Mean Value Theorems Lecture 7 : Differentiation Objectives In this section you will learn the following : The concept of derivative Various interpretations of the derivatives
Module 3 : Differentiation and Mean Value Theorems Lecture 7 : Differentiation Objectives In this section you will learn the following : The concept of derivative Various interpretations of the derivatives
Celebrating Torricelli
 On the Occasion of His 400th Birthday Chuck, Ph.D. Department of Mathematics Rockdale Magnet School for Science and Technology October 16, 2008 / Georgia Mathematics Conference Outline 1 Torricelli s Life
On the Occasion of His 400th Birthday Chuck, Ph.D. Department of Mathematics Rockdale Magnet School for Science and Technology October 16, 2008 / Georgia Mathematics Conference Outline 1 Torricelli s Life
The Brachistochrone Curve
 The Brachistochrone Curve Paige R MacDonald May 16, 2014 Paige R MacDonald The Brachistochrone Curve May 16, 2014 1 / 1 The Problem In 1696, Johann Bernoulli posed the following problem to the scientific
The Brachistochrone Curve Paige R MacDonald May 16, 2014 Paige R MacDonald The Brachistochrone Curve May 16, 2014 1 / 1 The Problem In 1696, Johann Bernoulli posed the following problem to the scientific
Introduction to Calculus
 Introduction to Calculus Contents 1 Introduction to Calculus 3 11 Introduction 3 111 Origin of Calculus 3 112 The Two Branches of Calculus 4 12 Secant and Tangent Lines 5 13 Limits 10 14 The Derivative
Introduction to Calculus Contents 1 Introduction to Calculus 3 11 Introduction 3 111 Origin of Calculus 3 112 The Two Branches of Calculus 4 12 Secant and Tangent Lines 5 13 Limits 10 14 The Derivative
Stories from the Development of Real Analysis
 Stories from the Development of Real Analysis David Bressoud Macalester College St. Paul, MN PowerPoint available at www.macalester.edu/~bressoud/talks Texas Sec)on University of Texas Tyler Tyler, TX
Stories from the Development of Real Analysis David Bressoud Macalester College St. Paul, MN PowerPoint available at www.macalester.edu/~bressoud/talks Texas Sec)on University of Texas Tyler Tyler, TX
2.8 Linear Approximations and Differentials
 Arkansas Tech University MATH 294: Calculus I Dr. Marcel B. Finan 2.8 Linear Approximations and Differentials In this section we approximate graphs by tangent lines which we refer to as tangent line approximations.
Arkansas Tech University MATH 294: Calculus I Dr. Marcel B. Finan 2.8 Linear Approximations and Differentials In this section we approximate graphs by tangent lines which we refer to as tangent line approximations.
= π + sin π = π + 0 = π, so the object is moving at a speed of π feet per second after π seconds. (c) How far does it go in π seconds?
 Mathematics 115 Professor Alan H. Stein April 18, 005 SOLUTIONS 1. Define what is meant by an antiderivative or indefinite integral of a function f(x). Solution: An antiderivative or indefinite integral
Mathematics 115 Professor Alan H. Stein April 18, 005 SOLUTIONS 1. Define what is meant by an antiderivative or indefinite integral of a function f(x). Solution: An antiderivative or indefinite integral
THE RISE OF MODERN SCIENCE CHAPTER 20, SECTION 2
 THE RISE OF MODERN SCIENCE CHAPTER 20, SECTION 2 ORIGINS OF THE SCIENTIFIC REVOLUTION 335 BCE-1687 CE A New View of the Universe Scientists of the 1500s asked same questions as Greeks: What is the universe
THE RISE OF MODERN SCIENCE CHAPTER 20, SECTION 2 ORIGINS OF THE SCIENTIFIC REVOLUTION 335 BCE-1687 CE A New View of the Universe Scientists of the 1500s asked same questions as Greeks: What is the universe
Johann Bernoulli ( )he established the principle of the so-called virtual work for static systems.
 HISTORICAL SURVEY Wilhelm von Leibniz (1646-1716): Leibniz s approach to mechanics was based on the use of mathematical operations with the scalar quantities of energy, as opposed to the vector quantities
HISTORICAL SURVEY Wilhelm von Leibniz (1646-1716): Leibniz s approach to mechanics was based on the use of mathematical operations with the scalar quantities of energy, as opposed to the vector quantities
2.5 Exponential Functions and Trigonometric Functions
 5 CHAPTER. COMPLEX-VALUED FUNCTIONS.5 Exponential Functions and Trigonometric Functions Exponential Function and Its Properties By the theory of power series, we can define e z := which is called the exponential
5 CHAPTER. COMPLEX-VALUED FUNCTIONS.5 Exponential Functions and Trigonometric Functions Exponential Function and Its Properties By the theory of power series, we can define e z := which is called the exponential
4.3. Riemann Sums. Riemann Sums. Riemann Sums and Definite Integrals. Objectives
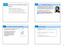 4.3 Riemann Sums and Definite Integrals Objectives Understand the definition of a Riemann sum. Evaluate a definite integral using limits & Riemann Sums. Evaluate a definite integral using geometric formulas
4.3 Riemann Sums and Definite Integrals Objectives Understand the definition of a Riemann sum. Evaluate a definite integral using limits & Riemann Sums. Evaluate a definite integral using geometric formulas
How Euler Did It. by Ed Sandifer. Foundations of Calculus. September 2006
 How Euler Did It Foundations of Calculus September 2006 by Ed Sandifer As we begin a new academic year, many of us are introducing another generation of students to the magic of calculus. As always, those
How Euler Did It Foundations of Calculus September 2006 by Ed Sandifer As we begin a new academic year, many of us are introducing another generation of students to the magic of calculus. As always, those
The Fundamental Theorem of Calculus
 The Fundamental Theorem of Calculus Objectives Evaluate a definite integral using the Fundamental Theorem of Calculus. Understand and use the Mean Value Theorem for Integrals. Find the average value of
The Fundamental Theorem of Calculus Objectives Evaluate a definite integral using the Fundamental Theorem of Calculus. Understand and use the Mean Value Theorem for Integrals. Find the average value of
Calculus. Central role in much of modern science Physics, especially kinematics and electrodynamics Economics, engineering, medicine, chemistry, etc.
 Calculus Calculus - the study of change, as related to functions Formally co-developed around the 1660 s by Newton and Leibniz Two main branches - differential and integral Central role in much of modern
Calculus Calculus - the study of change, as related to functions Formally co-developed around the 1660 s by Newton and Leibniz Two main branches - differential and integral Central role in much of modern
An Introduction to a Rigorous Definition of Derivative
 Ursinus College Digital Commons @ Ursinus College Analysis Transforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) 017 An Introduction to a Rigorous Definition of
Ursinus College Digital Commons @ Ursinus College Analysis Transforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) 017 An Introduction to a Rigorous Definition of
MthEd/Math 300 Williams Fall 2011 Midterm Exam 3
 Name: MthEd/Math 300 Williams Fall 2011 Midterm Exam 3 Closed Book / Closed Note. Answer all problems. You may use a calculator for numerical computations. Section 1: For each event listed in the first
Name: MthEd/Math 300 Williams Fall 2011 Midterm Exam 3 Closed Book / Closed Note. Answer all problems. You may use a calculator for numerical computations. Section 1: For each event listed in the first
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MOCNINOVÉ RADY A ICH VYUšITIE BAKALÁRSKA PRÁCA 04 Sára MINÁROVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MOCNINOVÉ RADY A ICH VYUšITIE BAKALÁRSKA PRÁCA 04 Sára MINÁROVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY
A l g o r i t m i c k y n e r i e š i t e ľ n é p r o b l é m y
 A l g o r i t m i c k y n e r i e š i t e ľ n é p r o b l é m y Lev Bukovský Ústav matematických vied, Prírodovedecká fakulta UPJŠ Košice, 20. apríla 2004 Obsah 1 Úvod 2 2 Čiastočne rekurzívne funkcie
A l g o r i t m i c k y n e r i e š i t e ľ n é p r o b l é m y Lev Bukovský Ústav matematických vied, Prírodovedecká fakulta UPJŠ Košice, 20. apríla 2004 Obsah 1 Úvod 2 2 Čiastočne rekurzívne funkcie
Introduction to ODE's (0A) Young Won Lim 3/9/15
 Introduction to ODE's (0A) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2
Introduction to ODE's (0A) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY HADAMARDOVE MATICE A ICH APLIKÁCIE V OPTIMÁLNOM DIZAJNE BAKALÁRSKA PRÁCA 2012 Samuel ROSA UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY HADAMARDOVE MATICE A ICH APLIKÁCIE V OPTIMÁLNOM DIZAJNE BAKALÁRSKA PRÁCA 2012 Samuel ROSA UNIVERZITA KOMENSKÉHO V BRATISLAVE
Math 121 Calculus 1 Fall 2009 Outcomes List for Final Exam
 Math 121 Calculus 1 Fall 2009 Outcomes List for Final Exam This outcomes list summarizes what skills and knowledge you should have reviewed and/or acquired during this entire quarter in Math 121, and what
Math 121 Calculus 1 Fall 2009 Outcomes List for Final Exam This outcomes list summarizes what skills and knowledge you should have reviewed and/or acquired during this entire quarter in Math 121, and what
Lecture 6, September 1, 2017
 Engineering Mathematics Fall 07 Lecture 6, September, 07 Escape Velocity Suppose we have a planet (or any large near to spherical heavenly body) of radius R and acceleration of gravity at the surface of
Engineering Mathematics Fall 07 Lecture 6, September, 07 Escape Velocity Suppose we have a planet (or any large near to spherical heavenly body) of radius R and acceleration of gravity at the surface of
f(x)dx = lim f n (x)dx.
 Chapter 3 Lebesgue Integration 3.1 Introduction The concept of integration as a technique that both acts as an inverse to the operation of differentiation and also computes areas under curves goes back
Chapter 3 Lebesgue Integration 3.1 Introduction The concept of integration as a technique that both acts as an inverse to the operation of differentiation and also computes areas under curves goes back
Integral. For example, consider the curve y = f(x) between x = 0 and x = 1, with f(x) = x. We ask:
 Integral Integration is an important concept in mathematics, specifically in the field of calculus and, more broadly, mathematical analysis. Given a function ƒ of a real variable x and an interval [a,
Integral Integration is an important concept in mathematics, specifically in the field of calculus and, more broadly, mathematical analysis. Given a function ƒ of a real variable x and an interval [a,
2.1 How Do We Measure Speed? Student Notes HH6ed. Time (sec) Position (m)
 2.1 How Do We Measure Speed? Student Notes HH6ed Part I: Using a table of values for a position function The table below represents the position of an object as a function of time. Use the table to answer
2.1 How Do We Measure Speed? Student Notes HH6ed Part I: Using a table of values for a position function The table below represents the position of an object as a function of time. Use the table to answer
History of the Derivative
 Parabola Volume 46, Issue 1(2010) History of the Derivative Milan Pahor 1 Measure what is measurable, and make measurable what is not so. Galileo Galilei The 17th century was a revolutionary period in
Parabola Volume 46, Issue 1(2010) History of the Derivative Milan Pahor 1 Measure what is measurable, and make measurable what is not so. Galileo Galilei The 17th century was a revolutionary period in
Chapter 10. Definition of the Derivative Velocity and Tangents
 Chapter 10 Definition of the Derivative 10.1 Velocity and Tangents 10.1 Notation. If E 1 (x, y) and E 2 (x, y) denote equations or inequalities in x and y, we will use the notation {E 1 (x, y)} = {(x,
Chapter 10 Definition of the Derivative 10.1 Velocity and Tangents 10.1 Notation. If E 1 (x, y) and E 2 (x, y) denote equations or inequalities in x and y, we will use the notation {E 1 (x, y)} = {(x,
Integration. Copyright Cengage Learning. All rights reserved.
 4 Integration Copyright Cengage Learning. All rights reserved. 1 4.3 Riemann Sums and Definite Integrals Copyright Cengage Learning. All rights reserved. 2 Objectives Understand the definition of a Riemann
4 Integration Copyright Cengage Learning. All rights reserved. 1 4.3 Riemann Sums and Definite Integrals Copyright Cengage Learning. All rights reserved. 2 Objectives Understand the definition of a Riemann
ODE Background: Differential (1A) Young Won Lim 12/29/15
 ODE Background: Differential (1A Copyright (c 2011-2015 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version
ODE Background: Differential (1A Copyright (c 2011-2015 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version
A Preview Of Calculus & 2.1 Rates of Change
 Math 180 www.timetodare.com A Preview Of Calculus &.1 Rates of Change Calculus is one of the greatest achievements of the human intellect. Inspired by problems in astronomy, Newton and Leibniz developed
Math 180 www.timetodare.com A Preview Of Calculus &.1 Rates of Change Calculus is one of the greatest achievements of the human intellect. Inspired by problems in astronomy, Newton and Leibniz developed
MATH1013 Calculus I. Limits (part I) 1
 MATH1013 Calculus I Limits (part I) 1 Edmund Y. M. Chiang Department of Mathematics Hong Kong University of Science & Technology March 5, 2014 2013 1 Based on Briggs, Cochran and Gillett: Calculus for
MATH1013 Calculus I Limits (part I) 1 Edmund Y. M. Chiang Department of Mathematics Hong Kong University of Science & Technology March 5, 2014 2013 1 Based on Briggs, Cochran and Gillett: Calculus for
Kapitola P2. Rozvinuteľné priamkové plochy
 Kapitola P2 Rozvinuteľné priamkové plochy 1 Priamková plocha je rozvinuteľná, ak na nej ležia iba torzálne priamky. Rozvinuteľné priamkové plochy rozdeľujeme na: rovinu, valcové plochy, kužeľové plochy,
Kapitola P2 Rozvinuteľné priamkové plochy 1 Priamková plocha je rozvinuteľná, ak na nej ležia iba torzálne priamky. Rozvinuteľné priamkové plochy rozdeľujeme na: rovinu, valcové plochy, kužeľové plochy,
YET ANOTHER ELEMENTARY SOLUTION OF THE BRACHISTOCHRONE PROBLEM
 YET ANOTHER ELEMENTARY SOLUTION OF THE BRACHISTOCHRONE PROBLEM GARY BROOKFIELD In 1696 Johann Bernoulli issued a famous challenge to his fellow mathematicians: Given two points A and B in a vertical plane,
YET ANOTHER ELEMENTARY SOLUTION OF THE BRACHISTOCHRONE PROBLEM GARY BROOKFIELD In 1696 Johann Bernoulli issued a famous challenge to his fellow mathematicians: Given two points A and B in a vertical plane,
1. Introduction. 2. Outlines
 1. Introduction Graphs are beneficial because they summarize and display information in a manner that is easy for most people to comprehend. Graphs are used in many academic disciplines, including math,
1. Introduction Graphs are beneficial because they summarize and display information in a manner that is easy for most people to comprehend. Graphs are used in many academic disciplines, including math,
Samuel Flimmel. Univerzita Karlova v Praze Matematicko-fyzikální fakulta. Katedra pravděpodobnosti a matematické statistiky
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Samuel Flimmel Log-optimální investování Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: doc. RNDr.
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Samuel Flimmel Log-optimální investování Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: doc. RNDr.
Exam 3 MATH Calculus I
 Trinity College December 03, 2015 MATH 131-01 Calculus I By signing below, you attest that you have neither given nor received help of any kind on this exam. Signature: Printed Name: Instructions: Show
Trinity College December 03, 2015 MATH 131-01 Calculus I By signing below, you attest that you have neither given nor received help of any kind on this exam. Signature: Printed Name: Instructions: Show
Inventors and Scientists: Sir Isaac Newton
 Inventors and Scientists: Sir Isaac Newton By Cynthia Stokes Brown, Big History Project on 07.30.16 Word Count 909 Portrait of Sir Isaac Newton circa 1715-1720 Bonhams Synopsis: Sir Isaac Newton developed
Inventors and Scientists: Sir Isaac Newton By Cynthia Stokes Brown, Big History Project on 07.30.16 Word Count 909 Portrait of Sir Isaac Newton circa 1715-1720 Bonhams Synopsis: Sir Isaac Newton developed
GRAFICKÉ ZOBRAZENIE MATEMATICKÝCH FUNKCIÍ DRAWING OF MATHEMATICS FUNCTIONS GRAPHS
 GRAFICKÉ ZOBRAZENIE MATEMATICKÝCH FUNKCIÍ DRAWING OF MATHEMATICS FUNCTIONS GRAPHS Dana ORSZÁGHOVÁ (SR) ABSTRACT Graphs of functions are the topic that is the part of mathematics study. The graphics software
GRAFICKÉ ZOBRAZENIE MATEMATICKÝCH FUNKCIÍ DRAWING OF MATHEMATICS FUNCTIONS GRAPHS Dana ORSZÁGHOVÁ (SR) ABSTRACT Graphs of functions are the topic that is the part of mathematics study. The graphics software
AP Calculus BC Syllabus Course Overview
 AP Calculus BC Syllabus Course Overview Textbook Anton, Bivens, and Davis. Calculus: Early Transcendentals, Combined version with Wiley PLUS. 9 th edition. Hoboken, NJ: John Wiley & Sons, Inc. 2009. Course
AP Calculus BC Syllabus Course Overview Textbook Anton, Bivens, and Davis. Calculus: Early Transcendentals, Combined version with Wiley PLUS. 9 th edition. Hoboken, NJ: John Wiley & Sons, Inc. 2009. Course
Computation of Information Value for Credit Scoring Models
 Jedovnice 20 Computation of Information Value for Credit Scoring Models Martin Řezáč, Jan Koláček Dept. of Mathematics and Statistics, Faculty of Science, Masaryk University Information value The special
Jedovnice 20 Computation of Information Value for Credit Scoring Models Martin Řezáč, Jan Koláček Dept. of Mathematics and Statistics, Faculty of Science, Masaryk University Information value The special
LOOKING AT GRAPHS THROUGH INFINITESIMAL MICROSCOPES WINDOWS AND TELESCOPES
 LOOKING AT GRAPHS THROUGH INFINITESIMAL MICROSCOPES WINDOWS AND TELESCOPES An Introduction to Calculus using Infinitesimals David Tall Mathematics Education Research Centre University of Warwick CV4 7AL
LOOKING AT GRAPHS THROUGH INFINITESIMAL MICROSCOPES WINDOWS AND TELESCOPES An Introduction to Calculus using Infinitesimals David Tall Mathematics Education Research Centre University of Warwick CV4 7AL
VÝUČBA DIFFERENCIÁLNEHO POČTU FUNKCIE VIAC PREMENNÝCH POMOCOU PG. SYST. MATHEMATICA
 VÝUČBA DIFFERENCIÁLNEHO POČTU FUNKCIE VIAC PREMENNÝCH POMOCOU PG. SYST. MATHEMATICA Monika Kováčová Katedra Matematiky SjF STU Bratislava kovacova_v@dekan.sjf.stuba.sk Abstrakt. V článku popisujeme možnosti
VÝUČBA DIFFERENCIÁLNEHO POČTU FUNKCIE VIAC PREMENNÝCH POMOCOU PG. SYST. MATHEMATICA Monika Kováčová Katedra Matematiky SjF STU Bratislava kovacova_v@dekan.sjf.stuba.sk Abstrakt. V článku popisujeme možnosti
Ing. Tomasz Kanik. doc. RNDr. Štefan Peško, CSc.
 Ing. Tomasz Kanik Školiteľ: doc. RNDr. Štefan Peško, CSc. Pracovisko: Študijný program: KMMOA, FRI, ŽU 9.2.9 Aplikovaná informatika 1 identifikácia problémovej skupiny pacientov, zlepšenie kvality rozhodovacích
Ing. Tomasz Kanik Školiteľ: doc. RNDr. Štefan Peško, CSc. Pracovisko: Študijný program: KMMOA, FRI, ŽU 9.2.9 Aplikovaná informatika 1 identifikácia problémovej skupiny pacientov, zlepšenie kvality rozhodovacích
Segmentace textury. Jan Kybic
 Segmentace textury Případová studie Jan Kybic Zadání Mikroskopický obrázek segmentujte do tříd: Příčná vlákna Podélná vlákna Matrice Trhliny Zvolená metoda Deskriptorový popis Učení s učitelem ML klasifikátor
Segmentace textury Případová studie Jan Kybic Zadání Mikroskopický obrázek segmentujte do tříd: Příčná vlákna Podélná vlákna Matrice Trhliny Zvolená metoda Deskriptorový popis Učení s učitelem ML klasifikátor
INTRO TO LIMITS & CALCULUS MR. VELAZQUEZ AP CALCULUS
 INTRO TO LIMITS & CALCULUS MR. VELAZQUEZ AP CALCULUS WHAT IS CALCULUS? Simply put, Calculus is the mathematics of change. Since all things change often and in many ways, we can expect to understand a wide
INTRO TO LIMITS & CALCULUS MR. VELAZQUEZ AP CALCULUS WHAT IS CALCULUS? Simply put, Calculus is the mathematics of change. Since all things change often and in many ways, we can expect to understand a wide
1). To introduce and define the subject of mechanics. 2). To introduce Newton's Laws, and to understand the significance of these laws.
 2 INTRODUCTION Learning Objectives 1). To introduce and define the subject of mechanics. 2). To introduce Newton's Laws, and to understand the significance of these laws. 3). The review modeling, dimensional
2 INTRODUCTION Learning Objectives 1). To introduce and define the subject of mechanics. 2). To introduce Newton's Laws, and to understand the significance of these laws. 3). The review modeling, dimensional
Rules for Differentiation Finding the Derivative of a Product of Two Functions. What does this equation of f '(
 Rules for Differentiation Finding the Derivative of a Product of Two Functions Rewrite the function f( = ( )( + 1) as a cubic function. Then, find f '(. What does this equation of f '( represent, again?
Rules for Differentiation Finding the Derivative of a Product of Two Functions Rewrite the function f( = ( )( + 1) as a cubic function. Then, find f '(. What does this equation of f '( represent, again?
Matematika 17. a 18. storočia
 Matematika 17. a 18. storočia René Descartes Narodený : 31 Marec 1596 v La Haye (teraz Descartes),Touraine, France Zomrel : 11 Feb 1650 v Stockholm, Sweden Riešenie kvadratických rovníc podľa Descarta
Matematika 17. a 18. storočia René Descartes Narodený : 31 Marec 1596 v La Haye (teraz Descartes),Touraine, France Zomrel : 11 Feb 1650 v Stockholm, Sweden Riešenie kvadratických rovníc podľa Descarta
Types of Curves. From `A Short Account of the History of Mathematics' (4th edition, 1908) by W. W. Rouse Ball.
 Calculus CURVES Types of Curves In the second book Descartes divides curves into two classes, namely, geometrical and mechanical curves. He defines geometrical curves as those which can be generated by
Calculus CURVES Types of Curves In the second book Descartes divides curves into two classes, namely, geometrical and mechanical curves. He defines geometrical curves as those which can be generated by
The Limit of Humanly Knowable Mathematical Truth
 The Limit of Humanly Knowable Mathematical Truth Gödel s Incompleteness Theorems, and Artificial Intelligence Santa Rosa Junior College December 12, 2015 Another title for this talk could be... An Argument
The Limit of Humanly Knowable Mathematical Truth Gödel s Incompleteness Theorems, and Artificial Intelligence Santa Rosa Junior College December 12, 2015 Another title for this talk could be... An Argument
Periodic Solutions Averaging Methods in Nonlinear Ordinary Differential Equations
 Volume: 4 Issue: 7 23 3 Periodic Solutions Averaging Methods in Nonlinear Ordinary Differential Equations Dr. V. Ramadoss, M.Sc., M.Phil., Ph.D.,* & D.Sinduja** *Professor, Department of Mathematics, PRIST
Volume: 4 Issue: 7 23 3 Periodic Solutions Averaging Methods in Nonlinear Ordinary Differential Equations Dr. V. Ramadoss, M.Sc., M.Phil., Ph.D.,* & D.Sinduja** *Professor, Department of Mathematics, PRIST
1 Úvod Úvod Sylaby a literatúra Označenia a pomocné tvrdenia... 4
 Obsah 1 Úvod 3 1.1 Úvod......................................... 3 1. Sylaby a literatúra................................. 3 1.3 Označenia a omocné tvrdenia.......................... 4 Prvočísla 6.1 Deliteľnosť......................................
Obsah 1 Úvod 3 1.1 Úvod......................................... 3 1. Sylaby a literatúra................................. 3 1.3 Označenia a omocné tvrdenia.......................... 4 Prvočísla 6.1 Deliteľnosť......................................
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY. Kritéria nezápornosti Fourierových radov BAKALÁRSKA PRÁCA
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kritéria nezápornosti Fourierových radov BAKALÁRSKA PRÁCA Bratislava 2014 Andrej Iring UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kritéria nezápornosti Fourierových radov BAKALÁRSKA PRÁCA Bratislava 2014 Andrej Iring UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
9.2 Taylor Polynomials
 9.2 Taylor Polynomials Taylor Polynomials and Approimations Polynomial functions can be used to approimate other elementary functions such as sin, Eample 1: f at 0 Find the equation of the tangent line
9.2 Taylor Polynomials Taylor Polynomials and Approimations Polynomial functions can be used to approimate other elementary functions such as sin, Eample 1: f at 0 Find the equation of the tangent line
Principles of Spherical Trigonometry Drawn from the Method of the Maxima and Minima
 TRANSLATOR S NOTE In preparing this translation my assumption has been that the interested audience likely consists of both mathematicians and historians of mathematics. To satisfy the latter I have attempted
TRANSLATOR S NOTE In preparing this translation my assumption has been that the interested audience likely consists of both mathematicians and historians of mathematics. To satisfy the latter I have attempted
Invariant Lagrangian Systems on Lie Groups
 Invariant Lagrangian Systems on Lie Groups Dennis Barrett Geometry and Geometric Control (GGC) Research Group Department of Mathematics (Pure and Applied) Rhodes University, Grahamstown 6140 Eastern Cape
Invariant Lagrangian Systems on Lie Groups Dennis Barrett Geometry and Geometric Control (GGC) Research Group Department of Mathematics (Pure and Applied) Rhodes University, Grahamstown 6140 Eastern Cape
From Newton s Fluxions to Virtual Microscopes
 From Newton s Fluxions to Virtual Microscopes Jacques Bair and Valerie Henry J.Bair@ulg.ac.be V.Henry@ulg.ac.be Key words : Fluxions ; tangent lines ; hyperreal numbers ; dual numbers ; virtual microscopes
From Newton s Fluxions to Virtual Microscopes Jacques Bair and Valerie Henry J.Bair@ulg.ac.be V.Henry@ulg.ac.be Key words : Fluxions ; tangent lines ; hyperreal numbers ; dual numbers ; virtual microscopes
Calculus with the TI-89. Sample Activity: Exploration 6. Brendan Kelly
 Calculus with the TI-89 Saple Activity: Exploration 6 Brendan Kelly EXPLORATION 6 The Derivative as a Liit THE BETTMANN ARCHIVE Isaac Newton, Karl Gauss, and Archiedes are rated by historians of atheatics
Calculus with the TI-89 Saple Activity: Exploration 6 Brendan Kelly EXPLORATION 6 The Derivative as a Liit THE BETTMANN ARCHIVE Isaac Newton, Karl Gauss, and Archiedes are rated by historians of atheatics
Časopis pro pěstování matematiky a fysiky
 Časopis pro pěstování matematiky a fysiky Felix Adalbert Behrend On sequences of integers containing no arithmetic progression Časopis pro pěstování matematiky a fysiky, Vol. 67 (1938), No. 4, 235--239
Časopis pro pěstování matematiky a fysiky Felix Adalbert Behrend On sequences of integers containing no arithmetic progression Časopis pro pěstování matematiky a fysiky, Vol. 67 (1938), No. 4, 235--239
Appendix III 1. Chr. Huygens Pages T. XIV [1665]
![Appendix III 1. Chr. Huygens Pages T. XIV [1665] Appendix III 1. Chr. Huygens Pages T. XIV [1665]](/thumbs/93/113210581.jpg) Appendix III 1 Chr. Huygens Pages 102-107 T. XIV [1665] J[an] has 2 white tokens and 1 black, but 1 white and 2 black. And each in his turn chooses blindly one of his tokens. The one who obtains a black
Appendix III 1 Chr. Huygens Pages 102-107 T. XIV [1665] J[an] has 2 white tokens and 1 black, but 1 white and 2 black. And each in his turn chooses blindly one of his tokens. The one who obtains a black
8 Differential Calculus 1 Introduction
 8 Differential Calculus Introduction The ideas that are the basis for calculus have been with us for a ver long time. Between 5 BC and 5 BC, Greek mathematicians were working on problems that would find
8 Differential Calculus Introduction The ideas that are the basis for calculus have been with us for a ver long time. Between 5 BC and 5 BC, Greek mathematicians were working on problems that would find
Math Lecture 1: Differential Equations - What Are They, Where Do They Come From, and What Do They Want?
 Math 2280 - Lecture 1: Differential Equations - What Are They, Where Do They Come From, and What Do They Want? Dylan Zwick Fall 2013 Newton s fundamental discovery, the one which he considered necessary
Math 2280 - Lecture 1: Differential Equations - What Are They, Where Do They Come From, and What Do They Want? Dylan Zwick Fall 2013 Newton s fundamental discovery, the one which he considered necessary
Two dimensional oscillator and central forces
 Two dimensional oscillator and central forces September 4, 04 Hooke s law in two dimensions Consider a radial Hooke s law force in -dimensions, F = kr where the force is along the radial unit vector and
Two dimensional oscillator and central forces September 4, 04 Hooke s law in two dimensions Consider a radial Hooke s law force in -dimensions, F = kr where the force is along the radial unit vector and
THE CALCULUS OF VARIATIONS*
 1925.] THE CALCULUS OF VARIATIONS 163 THE CALCULUS OF VARIATIONS* BY LEONIDA TONELLI 1. The Purpose of this Note. It is proposed to explain briefly here the method followed in my Fondamenti di Calcolo
1925.] THE CALCULUS OF VARIATIONS 163 THE CALCULUS OF VARIATIONS* BY LEONIDA TONELLI 1. The Purpose of this Note. It is proposed to explain briefly here the method followed in my Fondamenti di Calcolo
Development of Thought continued. The dispute between rationalism and empiricism concerns the extent to which we
 Development of Thought continued The dispute between rationalism and empiricism concerns the extent to which we are dependent upon sense experience in our effort to gain knowledge. Rationalists claim that
Development of Thought continued The dispute between rationalism and empiricism concerns the extent to which we are dependent upon sense experience in our effort to gain knowledge. Rationalists claim that
VII. Table of Contents
 TABLE OF CONTENTS LEIBNIZ AND THE INVENTION OF MATHEMATICAL TRANSCENDENCE. THE ADVENTURES OF AN IMPOSSIBLE INVENTORY... XIII The discovery of the transcendence... XIII Transcendence and Symbolism... XIII
TABLE OF CONTENTS LEIBNIZ AND THE INVENTION OF MATHEMATICAL TRANSCENDENCE. THE ADVENTURES OF AN IMPOSSIBLE INVENTORY... XIII The discovery of the transcendence... XIII Transcendence and Symbolism... XIII
1.1 Introduction to Limits
 Chapter 1 LIMITS 1.1 Introduction to Limits Why Limit? Suppose that an object steadily moves forward, with s(t) denotes the position at time t. The average speed over the interval [1,2] is The average
Chapter 1 LIMITS 1.1 Introduction to Limits Why Limit? Suppose that an object steadily moves forward, with s(t) denotes the position at time t. The average speed over the interval [1,2] is The average
PSEUDOINVERZNÁ MATICA
 PSEUDOINVERZNÁ MATICA Jozef Fecenko, Michal Páleš Abstrakt Cieľom príspevku je podať základnú informácie o pseudoinverznej matici k danej matici. Ukázať, že bázický rozklad matice na súčin matíc je skeletným
PSEUDOINVERZNÁ MATICA Jozef Fecenko, Michal Páleš Abstrakt Cieľom príspevku je podať základnú informácie o pseudoinverznej matici k danej matici. Ukázať, že bázický rozklad matice na súčin matíc je skeletným
UNIVERSITY OF REGINA Department of Mathematics and Statistics. Calculus I Mathematics 110. Final Exam, Winter 2013 (April 25 th )
 UNIVERSITY OF REGINA Department of Mathematics and Statistics Calculus I Mathematics 110 Final Exam, Winter 2013 (April 25 th ) Time: 3 hours Pages: 11 Full Name: Student Number: Instructor: (check one)
UNIVERSITY OF REGINA Department of Mathematics and Statistics Calculus I Mathematics 110 Final Exam, Winter 2013 (April 25 th ) Time: 3 hours Pages: 11 Full Name: Student Number: Instructor: (check one)
Infinity. Newton, Leibniz & the Calculus
 Infinity Newton, Leibniz & the Calculus Aristotle: Past time can t be infinite because there can t be an endless chain of causes (movements) preceding the present. Descartes: Space as extension; the res
Infinity Newton, Leibniz & the Calculus Aristotle: Past time can t be infinite because there can t be an endless chain of causes (movements) preceding the present. Descartes: Space as extension; the res
mass vs. weight. 392 dependent variable, 2 derivative(s) of a power series. 459 Descartes, René, 201 Devil s curve, 126 Difference Law of limits, 36 D
 # #, # definition of a limit, 31,64 A absolute maximum and minimum, 199 absolute maximum and minimum values, 199 absolute value function, 5 absolutely convergent series, 446 acceleration, 282 Airy function,
# #, # definition of a limit, 31,64 A absolute maximum and minimum, 199 absolute maximum and minimum values, 199 absolute value function, 5 absolutely convergent series, 446 acceleration, 282 Airy function,
Section 3.2 The Derivative as a Function Graphing the Derivative
 Math 80 www.timetodare.com Derivatives Section 3. The Derivative as a Function Graphing the Derivative ( ) In the previous section we defined the slope of the tangent to a curve with equation y= f ( )
Math 80 www.timetodare.com Derivatives Section 3. The Derivative as a Function Graphing the Derivative ( ) In the previous section we defined the slope of the tangent to a curve with equation y= f ( )
Visualizing Differentials in Integration to Picture the Fundamental Theorem of Calculus
 Visualizing Differentials in Integration to Picture the Fundamental Theorem of Calculus David Tall Introduction Mathematics Education Research Centre University of Warwick COVENTRY CV4 7AL What is a differential?
Visualizing Differentials in Integration to Picture the Fundamental Theorem of Calculus David Tall Introduction Mathematics Education Research Centre University of Warwick COVENTRY CV4 7AL What is a differential?
Isaac Newton. Translated into English by
 THE MATHEMATICAL PRINCIPLES OF NATURAL PHILOSOPHY (BOOK 2, LEMMA 2) By Isaac Newton Translated into English by Andrew Motte Edited by David R. Wilkins 2002 NOTE ON THE TEXT Lemma II in Book II of Isaac
THE MATHEMATICAL PRINCIPLES OF NATURAL PHILOSOPHY (BOOK 2, LEMMA 2) By Isaac Newton Translated into English by Andrew Motte Edited by David R. Wilkins 2002 NOTE ON THE TEXT Lemma II in Book II of Isaac
