Inequalities for Some Classes of Hardy Type Operators and Compactness in Weighted Lebesgue Spaces
|
|
|
- Curtis Dennis
- 5 years ago
- Views:
Transcription
1 DOCTORAL T H E SIS Ineuliies for Some Clsses of Hrdy Tye Oerors nd Comcness in Weighed Lebesgue Sces Abo Abylyev Mhemics
2
3 Ineuliies for some clsses of Hrdy ye oerors nd comcness in weighed Lebesgue sces by Abo Muhmediyrovn Abylyev Dermen of Engineering Sciences nd Mhemics Luleå Universiy of Technology Luleå, Sweden & Dermen of Fundmenl Mhemics Fculy of Mechnics nd Mhemics Eursin Nionl Universiy Asn 8, Kzhsn December 26
4 Keywords: Ineuliies, oerors, weighs, weighed Lebesgue sces, Hrdy-ye ineuliy, weighed differenil Hrdy ineuliy, Hrdy oeror, Rimnn-Liouville oeror, Weyl oeror, inegrl oeror wih vrible limis of inegrion, logrihmic singulriies, Oinrov ernels, boundedness, comcness. Prined by Luleå Universiy of Technology, Grhic Producion 26 ISSN ISBN (rin) ISBN (df) Luleå 26
5 To my rens nd fmily
6
7 Absrc This PhD hesis is devoed o invesige weighed differenil Hrdy ineuliies nd Hrdy-ye ineuliies wih ernel when he ernel hs n inegrble singulriy, nd lso he ddiiviy of he esime of Hrdy ye oeror wih ernel. The hesis consiss of seven ers (Pers, 2, 3, 4, 5, 6, 7) nd n inroducion where review on he subjec of he hesis is given. In Per weighed differenil Hrdy ye ineuliies re invesiged on he se of comcly suored smooh funcions, where necessry nd sufficien condiions on he weigh funcions re esblished for which his ineuliy nd wo-sided esimes for he bes consn hold. In Pers 2, 3, 4 more generl clss of α - order frcionl inegrion oerors re considered including he well-nown clssicl Weyl, Riemnn-Liouville, Erdelyi-Kober nd Hdmrd oerors. Here <α<. In Pers 2 nd 3 he boundedness nd comcness of wo clsses of such oerors re invesiged nmely of Weyl nd Riemnn-Liouville ye, resecively, in weighed Lebesgue sces for < < nd < < <. As licions some new resuls for he frcionl inegrion oerors of Weyl, Riemnn-Liouville, Erdelyi-Kober nd Hdmrd re given nd discussed. In Per 4 he Riemnn-Liouville ye oeror wih vrible uer limi is considered. The min resuls re roved by using loclizion mehod euied wih he uer limi funcion nd he ernel of he oeror. In Pers 5 nd 6 he Hrdy oeror wih ernel is considered, where he ernel hs logrihmic singulriy. The crieri of he boundedness nd comcness of he oeror in weighed Lebesgue sces re given for < < nd < < <, resecively. In Per 7 we invesiged he weighed ddiive esimes uk ± f C ( ρ f + vh ± f ), f ( ) for inegrl oerors K + nd K defined by K + f () := K(, s) f (s)ds, K f () := K(, s) f (s)ds. I is ssumed h he ernel K = K(, s) of he oeror K ± belongs o he generl Oinrov clss. We derived he crieri for he vlidiy of he ineuliy ( ) when <. v
8
9 Prefce This PhD hesis is minly devoed o inroduce nd sudy weighed differenil Hrdy ineuliies nd new Hrdy ye inegrl ineuliies involving Riemnn-Liouville ye oeror nd is conjuge Weyl ye oeror. Furher we invesige boundedness nd comcness of Hrdy ye oerors wih vrible uer limi nd inegrl oerors wih logrihmic singulriy in weighed Lebesgue sces. Moreover, we hve found ddiive esimes of clss of inegrl oerors, which is much wider hn reviously sudied. We lso resen some licions, which cover much wider clsses of inegrl oerors hn sudied before. The hesis consiss of n inroducion nd he following seven ers: [] A.M. Abylyev, A.O. Birysnov nd R. Oinrov, A weighed differenil Hrdy ineuliy on AC(I), Siberin Mh. J. 55 (24), No.3, [2] A.M. Abylyev, Boundedness, comcness for clss of frcionl inegrion oerors of Weyl ye, Eursin Mh. J. 7 (26), No., [3] A.M. Abylyev, R. Oinrov, nd L.-E. Persson, Boundedness nd comcness of clss of Hrdy ye oerors, Reserch reor 26 (submied). [4] A.M. Abylyev, Boundedness nd comcness of he Hrdy ye oeror wih vrible uer limi in weighed Lebesgue sces, Reserch reor 26-4, ISSN: 4-43, Dermen of Engineering Sciences nd Mhemics, Luleå Universiy of Technology, Sweden. Submied o n Inernionl Journl. [5] A.M. Abylyev nd L.-E. Persson, Hrdy ye ineuliies wih logrihmic singulriies, Reserch reor 26-5, ISSN: 4-43, Dermen of Engineering Sciences nd Mhemics, Luleå Universiy of Technology, Sweden. [6] A.M. Abylyev, Comcness of clss of inegrl oerors wih logrihmic singulriies, Reserch reor 26-6, ISSN: 4-43, Dermen of Engineering Sciences nd Mhemics, Luleå Universiy of Technology, Sweden. [7] A.M. Abylyev, A.O. Birysnov, L.-E. Persson nd P. Wll, Addiive weighed L esimes of some clsses of inegrl oerors involving generlized Oinrov ernels, J. Mh. Ineul. (JMI), o er 26. vii
10
11 Acnowledgemens Firs of ll, I would lie o eress my dee griude o my suervisors Professor Lrs-Eri Persson (Dermen of Engineering Sciences nd Mhemics, Luleå Universiy of Technology, Sweden) nd Professor Rysul Oinrov (L.N. Gumilyov Eursin Nionl Universiy, Kzhsn) for heir consn suor, hel, ience, undersnding nd encourgemen during my sudies. I lso hn hem for heir wise suggesions nd helful discussions. They devoed mny hours of heir gold ime for dvising me. I hn God h I me such clever, ind, comeen nd wise rofessors in my life. I will forever be hnful o hem. I lso sincere hns my hird suervisor Professor Peer Wll (Dermen of Engineering Sciences nd Mhemics, Luleå Universiy of Technology, Sweden) for suoring nd heling me in vrious wys nd for giving me such mzing ossibiliy o visi nd wor he Dermen of Mhemics of Luleå Universiy of Technology. Everybody of hem re remendous menors. I is gre honour for me o be one of heir sudens. Secondly, my secil hns goes o Professor Lech Mligrnd for his ind dvices nd vluble remrs. I lso would lie o hn Luleå Universiy of Technology for heir gre suor nd for cceing me s PhD suden in heir inernionl PhD rogrm. I m lso greful o L.N. Gumilyov Eursin Nionl Universiy for cceing me s PhD suden in heir inernionl PhD rogrm, which mde my PhD sudies ossible. Furhermore, I would lie o hn everybody he Dermen of Engineering Sciences nd Mhemics Luleå Universiy of Technology, esecilly Professor Nsh Smo nd Elen Miroshniov, for heling me in differen wys nd for lwys being so wrm, suorive nd friendly. I m lso very greful o collegues nd friends he Dermen of Fundmenl Mhemics in L.N. Gumilyov Eursin Nionl Universiy for heling nd suoring me. Moreover, I wn o eress my sincere reciion o my echer of English Professor Krlygsh Zhzibev for siriul suor nd fih in me. Finlly, I give my hery hns o my der rens nd fmily. Esecilly I ronounce my invluble griude o my husbnd PhD docor of mhemics Mdi Murbeov nd my dughers for love nd regulr encourgemen during ll of my sudy. i
12
13 Inroducion Inegrl oerors re wide clss of liner oerors h hve licions in vrious fields of science, such s hysics, economics, echnicl sciences nd mny ohers. Therefore he sudy of inegrl oerors e n imorn lce in modern mhemics. In he ls decdes he issues of finding necessry nd sufficien condiions for he weighed ineuliy K f,u C f,v (.) nd wo-sided esimes for he bes consn C in (.) re inensively sudied for vrious inegrl oerors K, where f,v := f () v()d <. In he cse when one of he rmeers nd is eul o or, here is generl resul ([28] Cher XI,.5, Theorem 4, see lso [8], Theorem.) esblishing he ec vlue of he bes consns in (.). However, when <, < in he generl cse his roblem remins oen. Therefore soluion of his roblem for vrious clsses of inegrl oerors is urgen. In 925 G.H.Hrdy [24] obined he ineuliy (.) when = for he Hrdy oeror defined by K f () Hf() := f ()d wih he weighed funcions u() =, v wih he ec vlue C = for he bes consn C in (.), i.e. he ineuliy ( ( ) f ()d) d f ()d, f, (.2) holds which is clled he clssicl Hrdy ineuliy. In 928 G.H.Hrdy [25] roved he firs weigh modificion of ineuliy (.2), nmely he ineuliy ( ( ) f ()d) α d α f () α d, f, (.3)
14 wih he bes consn C = (, α ) when > α> (see [26], Theorem 33). I is nowdys nown h he ineuliies (.2) nd (.3) re in sense euivlen nd lso euivlen o some oher ower weighed vrins of Hrdy s ineuliy, see [56]. Since he middle of he ls cenury he suding of generl weighed form of ineuliy (.) wih he Hrdy oeror H i.e. he ineuliy ( u() ( f ()d d) C f () ) v()d (.4) for = ws iniied (see for insnce [8] by P.R. Beesc, [27] by J. Kdlec nd A. Kufner, [57] by V.R. Pornov, [63] by V.N. Sedov nd [76] by F.A. Sysoev). However, for he cse = he necessry nd sufficien condiion for he vlidiy of ineuliy (.4) ws firs obined, indeendenly, in he wors of G.Tleni [77] nd G.Tomselli [78]. In 972 B.Mucenhou in [42] gve simle ecellen roof of his resul, even in he more generl cse, when u ()d nd v ()d were relced by generl Borel mesures dμ() nd dν(), resecively. A crierion for he ineuliy (.4) o hold when < < ws given indeendenly by J.Brdley [], V.Koilshvili [29] nd B.Mz y [39]. And he cse < < < ws firs described by B.Mz y nd A.Rozin in he le sevenies, see [38] nd [39]. These resuls hve been eended by G. Sinnmon [64] o he vlues of he rmeers < < <, >, nd he cse < < = hs been described by G.Sinnmon nd V.D.Senov [65]. G.Tomselli [78] gve n lernive crierion for he weighed Hrdy ineuliy (.4) o hold when =, which V. Senov nd L.-E. Persson generlized his resul o he cses < < nd < < < in [54]. There re sudies on he descriion of he ineuliies in oher erms [5] nd [32], differen from he bove uhors nd lso for negive vlues of he rmeers, see e.g. [6]. Le us sum u some of he resuls bove in he following Theorem: Theorem A. (i) If <, hen he ineuliy (.4) holds for ll mesurble funcions f () on (, b) if nd only if ( A := su <<b ) ( u()d v ()d 2 ) <
15 or A PS := su > w() v (y)dy d v (y)dy <. (ii) If < < <, hen he ineuliy (.4) holds if nd only if A 2 := ( ) r ( ) r r u()d v ()d v ()d < or B PS := r w() v (y)dy d r v (y)dy v ()d r <, where r =. (iii) If < < < <, hen he ineuliy (.4) holds if nd only if A 3 := ( ) r ( ) r r u()d v ()d u()d <. (iv) If < < =, hen he ineuliy (.4) holds if nd only if A 4 := where v() = ess su <<. v() [ ) v() u()d u()d <, I is nowdys nown h he condiions in (i)-(ii) in fc cn be relced by infinie mny euivlen condiions, even by four differen scles of condiions, see [5] (he cse (i)), [55] (he cse (ii)) nd for even more informion of his ye he review ricle [34]. In connecion wih he invesigion of oerors in Lorenz sces since 99 he Hrdy-ye oerors were cively sudied on he clss of monoone funcions, see for emle [8], [9], [2], [2], [22] nd he references herein. Moreover, oerors including he suremum, hs begn o be invesiged recenly, see for emle [3], [6], [7], [53] nd he references herein. 3
16 The ineuliy (.4) nd is dul ineuliy re euivlen o he differenil ineuliy y,u C y,v (.5) resecively for y() = nd for y( ) =. We remr h P.Gur [23] described he ineuliy (.5) under he condiion y() =, y( ) =. (.6) Hisoricl bcground, review of he reserch, he min resuls nd heir licions re given in he boos [], [2], [26], [3], [33], [4] nd [5]. The ineuliy (.5) wih condiion (.6) ws considered in [5], [3], bu only in [5] n ended version of he wor of P. Gur [23] ws considered nd wo-sided esimes for he bes consn C of (.5) ws sed. The im of his PhD hesis is o comlemen nd eend severl resuls in he re described bove which is ody clled Hrdy ye ineuliies nd reled boundedness nd comcness resuls. Below we give shor descriion nd moivion for hese new conribuions resened in his PhD hesis. In Per, using new mehod, we obined necessry nd sufficien condiions for he vlidiy of he ineuliy (.5) wih condiion (.6) for he cses < < nd < < <, >. We lso derived wo-sided esimes for he bes consn C of (.5), which re beer hn hose in [5]. In 979 O.D.Ayshev nd M.Oelbev [7] considered he ineuliy (.5) for higher order derivive, nmely he ineuliy y,u C y n,v, n > (.7) y (i) () =, i =,,...n. (.8) Bu crierion for he ineuliy (.7) o hold ws obined only under cerin resricions on he weigh funcions. We menion h Cher 4 of he boo [3] is devoed only o such higher order Hrdy ye ineuliies. We remr h he ossible boundry vlues (of ye (.8)) re very crucil o me such invesigions ossible (see [3]). The ineuliy (.7) wih he condiion (.8) is euivlen o he ineuliy (.), when he inegrl oeror K is eul o he Riemnn-Liouville 4
17 oeror I α defined by for α = n, i.e. I α f () := ( y) (α ) f (y)dy, >, (.9) Γ(α) I α f,u C f,v. (.) A sisfcory crierion for he ineuliy (.) o hold for he Riemnn- Liouville oeror when α>ws obined in he ers [67], [7] nd [69] of V.D.Senov. An oher generlizion of (.4) is norm ineuliy of he form (, y) f (y)dy u()d C f (y)v(y)dy for he Hrdy-Volerr inegrl oeror K given by Kf() :=, f, (.) (, y) f (y)dy,, (.2) wih ernel (, y), which is ssumed o be non-negive nd mesurble on he ringle {(, y) : y }. A number of uhors hve sudied in heir wors severl differen clsses of such oerors. In [37] i ws obined chrcerizion of (.) in he cse < < wih he secil ernel (, y) = ϕ(/y), where ϕ :(, ) (, ) is non-incresing nd sisfying h ϕ(b) D(ϕ() + ϕ(b)) for ll <, b <. Moreover, crierion of he L,v L,w boundedness ws given in [7] nd [72] by V.D. Senov for he Volerr convoluion oeror (.2) wih (, y) = ( y) for boh he cses < < nd < < <. An oher clss of sudied oerors of he ye (.2) hs ernels sisfying some ddiionl monooniciy nd coninuiy condiions (see e.g. [9] by S. Bloom nd R. Kermn). In he nineies i ered some imorn wors (see e.g. [45], [46] by R. Oinrov nd [73], [74] by V.D. Senov) devoed o he clss of he oerors (.2) wih so clled Oinrov ernels. A ernel (, y) sisfies he Oinrov condiion if here is consn D indeenden on, y, z such h D (, y) (, z) + (z, y) D(, y), y z. (.3) 5
18 Le he ernel (, y) of he oeror (.2) sisfy he Oinrov condiion (.3). If nd A (α) := su > A (α) := su > B (α) := B (α) := hen i is nown h K (, )u()d u()d K (, )u()d u()d v (y)dy K (, y)v (y)dy v (y)dy ( ) K (, y)v (y)dy ( ),, v ()d u()d K L,v L,u A (α) + A (α), < <, (.4) nd K L,v L,u B (α) + B (α), < < <. (.5) Ler on wo-sided esimes of he yes (.4) nd (.5) were derived for more generl oerors nd sces, see e.g. [37], [35], [75], [3], [4], [2], [3], [47], [48] nd [49]. The clss of Oinrov ernels includes ll bove menioned clsses of ernels ece Riemnn-Liouville ernels for <α<. The Riemnn-Liouville oeror is wely singulr inegrl oeror when <α<nd behves very differenly hn when α>. For ower weigh funcion v() nd u(y) he following clssicl resul [26], Theorem 42, is well nown: If >, <α</, /( α) or α /, < <, hen ( +α) (I α f ) ()d 6 C f. (.6),,
19 The ineuliy (.6) hs been generlized in he following wy in er [6] of K.F.Andersen nd E.T.Swyer: Le <α< nd < < =. Then ( α) ui α (uf) C f if nd only if K <, where K := su h <h<α +h u ()d h h u ()d Moreover, in [59] D.V.Prohorov nd V.D.Senov roved he followings resul: Le <α< nd < < =. Then ( α) ui α f C,v f, (.7) if nd only if v <. When α, = = 2 nd v he ineuliy (.7) hs been 2 chrcerized by S. Newmn nd M. Solomy wihin he secrl heory of seudo-differenil oerors on he hlf-is, see [44] nd lso references herein. A crierion for he ineuliy (.) o hold for < < ws derived by M.Loreni [36]. However, due o imliciness of he condiions he crieri in [36] me hem difficul o verify. Therefore, we se gol o derive elici L,v L,u crieri for he boundedness of he Riemnn- Liouville oeror in subseuen wors. In he cse < <, < <, α> nd v( ) elici crieri for L,v L,u boundedness of he Riemnn-Liouville nd Weyl oerors re obined indeendenly in wors of A.Meshi [4] nd D.V.Prohorov [58], see lso [66]. A generlizion of hese resuls o he cse when he funcion u( ) is no incresing ws climed in he er [3] of S.M.Frsni. In he er [59] of D.V.Prohorov nd V.D.Senov crieri for L,v L,u boundedness nd comcness of he Riemnn-Liouville oeror re given for < < in he following cses: ) < <α nd he funcion v is no decresing; b) < <α nd he funcion u is no incresing. 7.
20 A generlizion of hese crieri for L L boundedness of he Riemnn-Liouville oeror in he cse of convoluion ye oeror K, defined by K f () := v() K( s)u(s) f (s)ds, >, re given in he ers of N.A.Ruin [52] nd R.Oinrov [5]. For he cse when he ernel of he oeror K, defined by (.2) is (, y) = ( y) nd he funcion ( ) hs n inegrble singulriy in zero lie he Riemnn- Liouville oeror he resuls in [52] were generlized by D.V.Prohorov nd V.D.Senov [59] in he cse of ineuliy (.). Moreover, R.Oinrov [5] roved generl resul of he ye climed by S.M.Frsni [3]. In ddiion o he Riemnn-Liouville nd Weyl oerors he Erdey- Kober nd Hdmrd oerors re imorn boh in mhemics nd for severl licions. One of he generlizions nd unificions of hese oerors is he frcionl inegrion oeror I α g defined by: I α gϕ() := Γ(α) ϕ()g ()d, [g() g()] α >, α >, (.8) where g( ) is locl bsolue coninuous nd incresing funcion on I (, ). In [62] he oeror I α g is clled frcionl inegrl of he funcion ϕ wih resec o he funcion g of order α. In riculr, in (.8) when g() =, g() = σ, σ> nd g() = ln, we obin he frcionl inegrl Riemnn- Liouville, Erdelyi-Kober ye nd Hdmrd oeror, resecively. In Pers 2 nd 3 of his PhD hesis we consider he more generl oerors K α,β nd T α,β defined s follows: nd K α,β f () := T α,β f () := u(s)w β (s) f (s)w(s)ds, I, α (W(s) W()) u(s)w β () f (s)v(s)ds, I, α (W(s) W()) 8
21 where <α<, β R, I = (, b), < b nd W( ) is loclly bsoluely coninuous nd monooniclly incresing funcion on I, dw() = d w() nd u( ) - non-negive mesurble funcion in I. In Per 2 when <α<, >, β (β< α, ifw(b) = ) nd α u is non-decresing funcion we obined necessry nd sufficien condiions for he boundedness nd comcness of he oeror K α,β from L,w ino L,v, for he cses < < nd < < <, when b < α nd for he cse < < < when b =. Conseuenly, from hese semens we obin necessry nd sufficien condiions for he boundedness nd comcness of he weighed Weyl oeror Iα, defined by Iα f () := w() u(s)s β f (s)ds, >, <α<, α (s ) from L o L. Noe h from hese resuls i seems h Theorems 3, 4, 7 nd 8 of er [3] re no rue in generl. Similrly, in Per 3 when <α<, >, β nd u is nonincresing funcion we derived necessry nd sufficien condiions for he α boundedness nd comcness of he oeror T α,β from L,w ino L,v, for he cses < < nd < < <, when b < nd for he cse α < < < when b =. Conseuenly, we obined in riculr necessry nd sufficien condiions for he boundedness nd comcness of he weighed Riemnn- Liouville, Erdelyi-Kober nd Hdmrd oerors from L ino L, which generlize he well nown resuls for hese oerors when >. α In Per 4 we considered he roblem of boundedness nd comcness of he oeror K α,ϕ, defined in he following wy K α,ϕ f () := ϕ() f (s)w(s)ds (W() W(s)) α, <α<, from L,w ino L,v, where ϕ() is sricly incresing loclly bsoluely coninuous funcion, which sisfies he following condiions lim ϕ() =, lim + ϕ() = b, nd ϕ(). b 9
22 Obviously, he resuls resened in his er clerly generlizes he resuls in [] nd [4]. In Pers 5 nd 6 we considered he oeror K γ wih logrihmic singulriy defined by K γ f () := v() u(s)s γ ln f (s)ds, >. s When γ =, v( ) u( ) his oeror is clled frcionl inegrion oeror of infiniesiml order nd i hs wide licions in mhemicl biology, see [43]. In Per 5 we ssumed h he funcion u is non-incresing nd derived necessry nd sufficien condiions for he boundedness of he oeror K γ from L ino L, when < < nd < < <, >. Moreover, he comcness of he oeror K γ from L ino L ws roved in Per 6 when < <. We remr h he resuls in ers 5 nd 6 clerly generlizes he min resuls in [5] nd [2], resecively. In Per 7 we considered he weighed ddiive esimes uk ± f C ( ρ f + vh ± f ), f (.9) for he inegrl oerors K + nd K defined by K + f () := K(, s) f (s)ds, K f () := K(, s) f (s)ds, where he secil cses H + nd H re he usul Hrdy oerors defined by H + f () := f (s)ds, H f () := f (s)ds. We ssumed h ernel of he oerors K + nd K belong o he generlised Oinrov clss [48] nd hus found ec crieri for he vlidiy of he ineuliy (.9) when < in much more generl cses hn reviously nown.
23 References [] A.M. Abylyev nd G.Zh. Ismgulov. Crieri such s he limi oeror of frcionl inegrion wih vrible uer limi in weighed Lebesgue sces. Eursin Mh. J. (28), No., 2-2 (in Russin). [2] A.M. Abylyev nd A.O. Birysnov. Comcness crierion for frcionl inegrion oeror of infiniesiml order. Uf Mh. J. 5 (23), No., 3. [3] A.M. Abylyev nd A.O. Birysnov. Hrdy ye ineuliies conining suremum. Mh. J. 4 (24), No.4 (54), 5-7 (in Russin). [4] A.M. Abylyev. Crierion of he boundedness of frcionl inegrion ye oeror wih vrible uer limi in weighed Lebesgue sces. Inernionl Conference on Anlysis nd Alied Mhemics (ICAAM 26) AIP Conf. Proc. 759, Published by AIP Publishing 26. [5] A.M. Abylyev. Weighed esimes for he inegrl oeror wih logrihmic singulriy. Inernionl Conference on Anlysis nd Alied Mhemics (ICAAM 26) AIP Conf. Proc. 759, Published by AIP Publishing 26. [6] K.F. Andersen nd E.T. Swyer. Weighed norm ineuliies for he Riemnn - Liouville nd Weyl frcionl inegrl oerors. Trns. Amer. Mh. Soc. 38 (988), No.2, [7] O.D. Ayshev nd M.O. Oelbyev. On he secrum of clss of differenil oerors nd some embedding heorems. Izv. Ad. Nu SSSR Ser. M. 43 (979), No.4, (in Russin). [8] P.R. Beesc. Hrdy s ineuliy nd is eensions. Pcific J. Mh., (96), [9] S. Bloom nd R. Kermn. Weighed norm ineuliies for oerors of Hrdy ye. Proc. Amer. Mh. Soc. 3 (99), No., [] J.S. Brdley. Hrdy ineuliies wih mied norms. Cnd. Mh. Bull. 2 (978), No., [] D.E. Edmunds nd W.D. Evns. Hrdy oerors, funcion sces nd embeddings. Sringer-Verlg, Berlin, 24. [2] D.E. Edmunds, V. Koilshvili nd A. Meshi. Bounded nd comc inegrl oerors. Kluwer Acdemic Publishers, Dordrech, 22.
24 [3] S.M. Frsni. On he boundedness nd comcness of he frcionl Riemnn-Liouville oerors. Sibirs. M. Zh. 54 (23), No.2, (in Russin); rnslion in Sib. Mh. J. 54 (23), No.2, [4] I. Genebshvili, A. Gogishvili, V. Koilshvili nd M. Krbec. Weigh heory for inegrl rnsforms on sces of homogeneous ye, Longmn, Hrlow, 998. [5] A. Gogishvili, A. Kufner, L.-E. Persson nd A. Wedesig. An euivlence heorem for inegrl condiions reled o Hrdy s ineuliy. Rel Anl. Echnge 29 (23/4), [6] A. Gogishvili, B. Oic nd L. Pic. Weighed ineuliies for Hrdy-ye oerors involving surem. Collec. Mh. 57 (26), No.3, [7] A. Gogishvili nd L. Pic. A reducion heorem for suremum oerors. J. Comu. Al. Mh. 28 : (27), [8] A. Gogishvili nd V.D. Senov. Reducion heorems for weighed inegrl ineuliies on he cone of monoone funcions. Russin Mh. Surveys 68 (23), [9] M. L. Goldmn. Order-shr esimes for Hrdy-ye oerors on cones of usimonoone funcions. Eursin Mh. J. 2:3 (2), [2] M. L. Goldmn. Order-shr esimes for Hrdy-ye oerors on he cones of funcions wih roeries of monooniciy. Eursin Mh. J. 3:2 (22), [2] M. L. Goldmn. Some euivlen crieri for he boundedness of Hrdyye oerors on he cone of usimonoone funcions. Eursin Mh. J. 4:4 (23), [22] M. L. Goldmn. Esimes for resricions monoone oerors on he cone decresing funcions in Orlicz sce. Mh. Zm. : (26), [23] P. Gur. Generlized Hrdy s ineuliy. Csois Pěs. M. 9 (984), [24] G.H. Hrdy. Noes on some oins in he inegrl clculus, LX. An ineuliy beween inegrls, Messenger of Mh. 54 (925), [25] G.H. Hrdy. Remrs on hree recen noes in he journl. J. London Mh. Soc. 3 (928),
25 [26] G.H. Hrdy, J.E. Lilewood, G. Póly. Ineuliies. Cmbridge Univ. Press, 324 (952). [27] J. Kdlec nd A.Kufner. Chrcerizion of funcions wih zero rces by inegrls wih weigh funcions II. Csois Pěs. M. 92 (967), [28] L.V. Knrovich nd G.R. Ailov. Funcionl nlysis. Nu, Moscow, 977 (in Russin). [29] V.M. Koilshvili. On Hrdy s ineuliies in weighed sces. Soobsch. Acd. Nu Gruzin. SSR, 96 (979), No., [3] V. Koilshvili, L-E. Persson nd A. Meshi. Weighed norm ineuliies for inegrl rnsforms wih roduc ernels. Nov Science Publishers, Inc. NY, 29. [3] A. Kufner nd L.-E. Persson. Weighed ineuliies of Hrdy ye. World Scienific, New Jersey-London-Singore-Hong Kong, 23. [32] A. Kufner, L.-E. Persson nd A. Wedesig. A sudy of some consns chrcerizing he weighed Hrdy ineuliy. Bnch Cener Publ. 64, Orlicz Cenenry Volume, Polish Acd. Sci., Wrsw (24), [33] A. Kufner, L. Mligrnd nd L-E. Persson. The Hrdy Ineuliy. Abou is Hisory nd Some Reled Resuls. Vydvelsý Servis, Plzeˆn, 27. [34] A.Kufner, L.E.Persson nd N.Smo. Some new scles of weigh chrcerizions of Hrdy-ye ineuliies, Oeror Theory, Pseudo- Differenil Euions, nd Mhemicl Physics, , Oeror Theory: Adv. Al. 228, Birhöuser/Sringer, Bse/ A.G.,Bsel, 23. [35] E. Lomin nd V.D. Senov. On he Hrdy-ye inegrl oerors in Bnch funcion sces. Publ. M. 42 (998), [36] M. Lorene. A chrcerizion of wo weigh norm ineuliies for one-sided oerors of frcionl ye. Cn. J. Mh. 49 (997), No. 5, -33. [37] P.J. Mrin-Reyes nd E. Swyer. Weighed ineuliies for Riemnn- Liouville frcionl inegrls of order one nd greer. Proc. Amer. Mh. Soc. 6 (989), [38] V.G. Mz y. Einbeungssäze für Sobolewsche Räume. Teil [Imbedding Theorems for Sobolev Sces. Pr ], Teubner -Tee zur Mhemics, Leizig,
26 [39] V.G. Mz y. Sobolev sces. Sringer-Verlg, Berlin, Heidelberg, 985. [4] A. Meshi. Soluion of some weigh roblems for he Riemnn-Liouville nd Weyl oerors. Georgin Mh. J. 5 (998), No.6, [4] D.S. Mirinovic, J.E. Pečrić nd A.M. Fin. Ineuliies involving funcions nd heir inegrls nd derivives. Kluver Acd. Publishers, Dordrech, 99. [42] B. Mucenhou. Hrdy s ineuliies wih weighs. Sudi Mh. 34 (972), No., [43] A.M.Nhushev. Euions of mhemicl biology. M.: Vysshy shol, 995 (in Russin). [44] J. Newmn nd M. Solomy. Two-sided esimes on singulr vlues for clss of inegrl oerors on he semi-is. J. Func. Anl. 5 (997), [45] R. Oinrov. Weighed ineuliies for clss of inegrl oerors. Sovie Mh. Dol. 44 (992), (in Russin). [46] R. Oinrov. Two-sided esimes of cerin clss of inegrl oerors. Proc. Selov Ins. Mh. 24 (993), (in Russin). [47] R. Oinrov. A weighed esime for n inermedie oeror on he cone of nonnegive funcions. Siberin Mh. J. 43 (2), No., [48] R. Oinrov. Boundedness nd comcness of Volerr-ye inegrl oerors, Siberin Mh. J. 48 (27), No. 5, [49] R. Oinrov. Boundedness nd comcness in weighed Lebesgue sces of inegrl oerors wih vrible inegrion limis, Siberin Mh. J. 52 (2), No. 6, [5] R. Oinrov. Boundedness nd comcness of clss of convoluion inegrl oerors of frcionl inegrion ye. Proc. Selov Ins. Mh. 293 (26), No., (in Russin). [5] B. Oic nd A. Kufner. Hrdy-ye Ineuliies. Longmn, Hrlow, 99. [52] N.A. Ruin. On he boundedness of clss of frcionl ye inegrl oerors. Sborni Mhemics. 2 (29), No.2,
27 [53] E. Pernecá nd L. Pic. Comcness of Hrdy oerors involving surem. Boll. Unione M. Il. Ser. 9, 6: (23), [54] L.E. Persson nd V.D.Senov. Weighed inegrl ineuliies wih he geomeric men oeror. J. Ineul. Al. 7 (22), No.5, [55] L.E. Persson, V.D. Senov nd P. Wll. Some scles of euivlen weighed chrcerizion of Hrdy s ineuliy, he cse <. Mh. Ineul. Al. (27), No.2, [56] L.E. Persson nd N. Smo. Wh should hve hened if Hrdy hd discovered his? J. Ineul. Al. 22, 22:29. [57] V.R. Pornov. Two imbedding heorems for sces L,b (Ω R +) nd heir licions. Dol. Ad. Nu SSSR, 55 (964), [58] D.V. Prohorov. On he boundedness nd comcness of clss of inegrl oerors. J. London Mh. Soc. 6 (2), [59] D.V. Prohorov nd V.D.Senov. Weighed esimes for Riemnn- Liouville oerors nd some of heir licions. Proc. Selov Ins. Mh. 243 (23), No.4, [6] D.V. Prohorov. Weighed esimes for he Riemnn-Liouville oerors wih vrible limis. Siberin Mh. J. 44 (23), No.6, [6] D.V. Prohorov. Weighed Hrdy s ineuliies for negive indices. Publiccions M. 48 (24), [62] S.G. Smo, A.A. Kilbs nd O.I. Mrichev. Frcionl order inegrls nd derivives, nd some licions. Mins: Science nd Technology, 987. [63] V.N. Sedov. Weighed sces. The imbedding heorem. Diff. Urvneniy, 8 (972), (in Russin). [64] G. Sinnmon. A weighed grdien ineuliy. Proc. Roy. Soc. Edinburgh Sec. A (989), No. 3-4, [65] G. Sinnmon nd V.D. Senov. The weighed Hrdy ineuliy: new roofs nd he cse =. J. London Mh. Soc. 54 (996), No., 89-. [66] M. Solomy. Esimes for he roimion numbers of he weighed Riemnn-Liouville oeror in he sces L. Oer. Theory: Adv. nd Al. 3 (2),
28 [67] V.D. Senov. Two-weighed esimes for he Riemnn-Liouville inegrls. Czesoslovens Ademie Ved Memicy Usv. 39 (988), 28. [68] V.D.Senov. Weighed ineuliies of Hrdy ye for higher order derivives. Proc. Selov Ins. Mh. 3 (99), [69] V.D. Senov. On weighed ineuliy of Hrdy ye for frcionl Riemnn-Liouville inegrls. Sib. Mh. J. 3 (99), No. 3, (in Russin). [7] V.D. Senov. Two-weighed esimes of Riemnn-Liouville inegrls. Izv. Ad. Nu SSSR Ser. M. 54 (99), No. 3, ; rnslion in Mh. USSR-Izv. 36 (99), No. 3, [7] V.D. Senov. Weighed ineuliies for clss of Volerr convoluion oerors. J. London Mh. Soc. 45 (992), No.2, [72] V.D. Senov. On weighed esimes for clss of inegrl oerors. Siberin Mh. J. 34 (993), [73] V.D. Senov. Weighed norm ineuliies of Hrdy ye for clss of inegrl oerors. J. London Mh. Soc. 5 (994), No.2, 5 2. [74] V.D. Senov. Weighed norm ineuliies for inegrl oerors nd reled oics. Proceedings of he sring school on Nonliner Anlysis, Funcionl sces nd Alicions, Prgue: Promeheus Publishing House 5 (994), [75] V.D. Senov nd E.P. Ushov. On inegrl oerors wih vrible limis of inegrion. Proc. Selov Ins. Mh. 232 (2), [76] F.A. Sysoev. Generlizions of cerin Hrdy ineuliy. Izv. Vysš. Učeb. Zved. Memi 49 (965), No.6, 4 43 (in Russin). [77] G.Tleni. Osservzione sor un clsse di disuguglinze. Rend. Sem. M. Fiz. Milno 39 (969), [78] G.Tomsselli. A clss of ineuliies. Boll. Unione M. Il. 2 (969),
29 Per A weighed differenil Hrdy ineuliy on AC(I) Siberin Mhemicl Journl 55 (24), No.3, Remr: The e is he sme bu he form hs been modified o fi he syle in his PhD hesis.
30
31 Siberin Mhemicl Journl, Vol. 55, No. 3, , 24 Originl Russin Te Coyrigh c 24 Abylyev A.M., Birysnov A.O., nd Oinrov R. A WEIGHTED DIFFERENTIAL HARDY INEQUALITY ON AC(I) A. M. Abylyev, A. O. Birysnov, nd R. Oinrov Absrc: A weighed differenil Hrdy ineuliy is emined on he se of loclly bsoluely coninuous funcions vnishing he endoins of n inervl. Some generlizions of he vilble resuls nd shrer esimes for he bes consn re obined. DOI:.34/S X Keywords: weighed differenil Hrdy ineuliy, Lebesgue sce, loclly bsoluely coninuous funcions. Inroducion Assume h I = (, b), < b,<, <, + =, ρ, υ nd ρ = re nonnegive loclly summble funcions on I nd υ. ρ Le < < nd le L,ρ L,ρ (I) be he sce of mesurble funcions f on I such h he norm f,ρ ρ () f () d is finie. The symbol W,ρ W(ρ, I), >, snds for he collecion of f loclly bsolluely coninuous on I nd hving he norm f W = f,ρ + f ( ) (2),ρ finie, where I is fied oin. Assume h lim + f () f (), lim b f () f (b), nd AC (ρ, I) = { f W,ρ : f () = f (b) = }, AC,l (ρ, I) = { f W,ρ : f () = }, AC,r (ρ, I) = { f W,ρ : f (b) = }. The closures of AC (ρ, I), AC,l (ρ, I) nd AC,r (ρ, I) under (2) re denoed resecively by W (ρ, I), W (ρ, I) nd,l W,r(ρ, I).
32 2 We consider he weighed Hrdy ineuliy in differenil form on AC (ρ, I) [] : υ() f () d C ρ() f () d. (2) Ineuliy (2) nd is generlizions were he subjec of invesigions of mny seciliss in he ls 5 yers, nd so hese re sudied well on AC,l (ρ, I) nd AC,r (ρ, I). The hisory of he roblem nd he resuls cn be found in [, 2, 3]. In he recen yers numerous euivlen crierions, ensuring his ineuliy, re obined (for insnce, see [4, 5]). Bu (2) is AC (ρ, I). Some resuls cn be found in [, 2] no sudied deuely on nd only in he ricle [] wo-sided esimes for he bes consn C > of (2) re given. Vrious licions of (2) in he uliive heory of differenil eu- AC (ρ, I) wih shrer es- ions (see [6, 7, 8, 9]) necessie sudying i on imes for he bes consn. In he resen ricle by mehod differen from h in [] we esblish more genrl resul generlizing hose in he bove ers nd give shrer wo-sided esimes for he bes consn C > in (2). 2. Necessry Noions nd Semens We sudy (2) on AC (ρ, I) in deendence on he behvior of ρ he endoins of I. The weighed funcion ρ my vnish he endoins of I nd hus we hve Theorem A. Le < <. Then ( ) (i) if ρ L (I) hen, for every f W ρ, I, here eis lim + f () f (), lim b f () f (b), nd W (ρ, I) = { f W(ρ, I) : f () = f (b) = } AC (ρ, I); ( ) (ii) if ρ L (, c) nd ρ L (c, b), c I, hen, for every f W ρ, I, here eis f () nd W (ρ, I) = W ( ) {,l ρ, I = f W (ρ, I) : f () = } ( ) AC,l ρ, I ; ( ) (iii) if ρ L (, c) nd ρ L (c, b), c I, hen, for every f W ρ, I, here eis f (b) nd
33 3 W (ρ, I) = W,r ( ) { ρ, I = f W (ρ, I) : f (b) = } ( ) AC,r ρ, I ; (iv) if ρ L (, c) nd ρ L (c, b), c I, hen W (ρ, I) = W ( ),l ρ, I = W ( ),r ρ, I = f W ( ) ρ, I. Generlly seing, he semens of Theorem A re nown nd hey cn be deduced from he resuls in [,, 2]. We resen he roof of (ii). The remining semens re roven by nlogy. Assume ( ) h ρ L (, c) nd ρ L (c, b), c I. Then for f ρ, I we hve W c f () c d ρ b ρ() f () d <. Therefore, f () is ( defined. ) { } ( ) Le f W,l ρ, I. Then here eiss seuence fn AC,l ρ, I such h W f fn sn. Since,ρ f () f n () for < < < b, he Hölder ineuliy yields f () f n () m, Hence, f () =. Le <α < b. In his cse or f (α) α f (α) α f (s) f n(s) ds + f ( ) f n ( ) ρ ρ ρ α α W f f n.,ρ ρ() f d ρ() f d
34 4 Le oin α = α (,α) (,α) sisfy he relion α α ρ = ρ. α Inroduce funcion, < α, ( )( α ) f α () = f (α) ρ ρ, α α, α α f (), α < b. Obviously, f α AC,l ( ρ, I ). We hve f f α W = α ρ f f α α ρ f + f (α) α α ρ ) ( α + 2 ρ f, nd so W ( ) ( ) f fα sα. Hence f W,l ρ, I nd W,l ρ, I = { ( ) } f W ρ, I : f () =. ( ) ( ) ( ) ( ) Demonsre h W ρ, I = W,l ρ, I. Since W ρ, I W,l ρ, I, ( ) ( ) ( ) i suffices o esblish h W ρ, I W,l ρ, I. Le f W,l ρ, I nd <α <β<b. Since β = β ( β, b ) ( β, b ) such h β ρ ds =, for every β I here eiss oin f (β) β β ρ ρ() f () d. β
35 5 Consruc f α,β In his cse AC ( ρ, I ) such h f α (), < β, β β f α,β () = f (β) ρ ρ, β β, β, β < b. f f α,β W,ρ α ) ( α + 2 ρ f f α ρ f ) ( α β β β ρ f ρ f ρ f f α,β f (β) β ρ f + β β. β ρ ρ f Hence, W f fα,β sα nd β b. There fore, f ( ) W ρ, I.,ρ Theorem A is roven. Le α<β b. Pu ( ) A α, β, = ( ) A 2 α, β, = α α ρ β A ( ) α, β, = ρ ρ α β υ() α υ()d α ρ, υ()d, d,
36 6 β A ( ) 2 α, β, = A i ρ β υ() β ρ ( ) ( ) A i α, β = su A i α, β,, α<<β ( ) α, β = su A i α<<β ( γ = min ( ), d ( α, β, ), i =, 2, ( ) ),γ 2 =.,α< <β; The bes consns C in (2) on AC ( ( )) ( ( )) ( ( )) ( ) ρ, α, β (, AC,l ) ρ, α, β ( nd ) AC,r ρ, α, β re denoed by C = J α, β, C = Jl α, β, nd C = Jr α, β, resecively. In view of [3, 3], we cn sy h Theorem B. Le < <. Then m { ( ) ( )} ( ) { ( ) ( )} A α, β, A2 α, β Jl α, β min γ A α, β,γ2 A 2 α, β, (22) m { A ( ) α, β, A ( ) } ( ) { 2 α, β J r α, β min γ A ( ) α, β,γ2 A ( ) } 2 α, β. (23) Assume h B ( α, β ) = B ( α, β ) = β α β α β α υ υ α β ρ ρ ( ) ( ) ρ()d ρ()d Since ρ is loclly summble on I, weby[3, 4] hve (see [4], Remr) Theorem C. Le < < <, >. Then μ B ( α, β ) J l ( α, β ) μ + B ( α, β ), μ B ( α, β ) J r ( α, β ) μ + B ( α, β ), where μ = ( ( ) μ + = ), μ + = ( ) ( for < < < nd μ = ) ( ) for < < < <.,.,
37 7 3. The Min Resuls 3.. The cse of < <. Le ρ (s)ds <. (24) Definiion. A oin c i I, i =, 2, is clled midoin for ( A i, A i) if A i (, c i ) = A i (c i, b) T ci (, b) <, i =, 2. Theorem. Assume h < < nd (24) holds. Then (2) is fulfilled on AC ( ) ρ, I if nd only if here eis midoin ci I for ( A i, Ai) les for one of he numbers i =, 2 nd he bes consn J (, b) in (2) in his cse sisfies he esime 2 m { Tc (, b), T c2 (, b) } J (, b) min { γ T c (, b),γ 2 T c2 (, b) }. (25) Corollry [9]. In he cse of =, we hve m { T c (, b), T c2 (, b) } { ( J (, b) min ) } T c (, b), T c2 (, b). To rove Theorem, we use Lemm. Le < < nd ssume h (24) holds. Then midoin for ( A i, A i), i=,2, eiss if nd only if, for given c I, here eis lim su A i (, c, ) <, lim su A i (c, b, ) <, i =, 2. (26) b Proof of Lemm. Sufficiency: (26) yields lim c A i (, c) <, lim A i (c, b) <, i =, 2. c b Demonsre h lim A i (, c) > lim A i (c, b), i =, 2. (27) c b c b Indeed, if lim A i (, c) lim A i (c, b) < (28) c b c b
38 8 hen (24) imlies h υ()d <, c I. c Hence, lim A i (c, b) =, i =, 2. (29) c b For i =, (29) is obvious nd, for i = 2, i follows from he ineuliy h c ρ c υ() ρ d c ρ b c υ()d Since A i (, c) is nonnegive nondecresing coninuous funcion in c I, from (28) nd (29) i follows h A i (, b), i =, 2. Thus, υ () on I nd he ler conrdics he condiions on υ. Hence, (27) holds. In he sme wy, we jusify he ineuliy lim A c i (c, b) > lim A i (, c), i =, 2. (3) c b In view of (27) nd (3), he coninuiy nd monooniciy of A i (, c) nd A (c, b) in c I imly he eisence of oins c i i I such h A i (, c i ) = A (c i i, b), i =, 2. Necessiy: Le midoin c i I for ( A i, Ai), i =, 2, eis. The definiion of c i yields A i (, c i ) = A i (c i, b) <, i =, 2. If c c hen (24) imlies h su <<c lim su A (, c, ) = lim ρ = A (, c ) + lim c su ρ << υ()d ρ + lim c su ρ << c c υ()d c c. υ()d υ()d = A (, c ) <,
39 9 lim b su A su c <<b (c, b, ) = lim ρ su ρ b <<b c υ()d In he cse of c < c we similrly hve lim b su A A (c, b) + lim c υ()d = A (c, b) <. lim su A (, c, ) A (, c ) <, (c, b, ) = lim su ρ b <<b ρ In he cse of A 2 nd A 2 we hve c c υ()d c υ()d = A (c, b) <. lim su A 2 (, c, ) = lim su ρ << υ() ρ d su <<c 2 ρ for every c I nd similrly υ() ρ d = A 2 (, c 2 ) < lim su A 2 (c, b, ) A 2 (c 2, b) <. b Lemm is roven. Proof of Theorem. Necessiy: Le (2) hold on AC ( ) ρ, I wih he bes consn C = J (, b). Assume h < c < c < c + < b. Pu
40 c ρ ρ, < < c, f () =, c c +, ρ, c + < b. c + ρ The funcion f is loclly bsoluely coninuous on I nd (3) ρ(s) c f (s) ds = ρ(s) c+ f (s) ds + ρ(s) f (s) ds + = c ρ c c c ρρ ( ) + = ρ + ( ) Hence, f W ρ, I nd lim f () f () =, + by consrucion. In his cse f J (, b) The direc clculion yields υ() f () d = c c + c + ρ ρ c + c + lim f () f (b) = b b ρρ ( ) ρ(s) f (s) ds <. (32) AC ( ρ, I ). Insering f in (2), we hve υ() f () c+ d + υ() f () d ρ() f () d υ() f () d + b υ() f () d (33) = c ρ c c υ() ρ d c +
41 c+ + υ()d + c c + ρ By (32) - (34), we obin he ineuliies J (, b) c c ρ υ() c ρ + J (, b) ( ρ c + c + υ() ρ ρ c + ) ρ d υ() c + + c ρ b + c c + υ()d + c c c ρ + υ()d ρ c + d. (34) ρ c + ρ d, (35). (36) Mulilying he numeror nd denominor of he righ-hnd sides in c (35) nd (36) by ρ, we derive J (, b) c ρ + c c υ() ( b ρ J (, b) c ρ c + ρ ) d + c ρ b + c ρ c + b ρ υ() c + ρ c + ρ d (37) ρ c c υ()d + ρ c + υ()d c c c + b ρ. (38) c + ρ Since he lef-hnd sides of (37) nd (38) re indeende of c (, c), ssing o he limi s c on he righ-hnd sides, we infer,
42 2 lim su J (, b) + lim c c ( + lim c ρ b + lim c ) ρ c υ() b ρ ρ c + c b ρ υ() c + ( ρ c + ρ c + ρ ) d ρ d = lim su ρ υ() ρ d = lim su A (, c, ), (39) 2 J (, b) lim su = lim su ( ρ ) + lim ρ c c c c υ()d + lim c b ρ c ρ c + ρ υ()d υ()d = lim su A (, c, ). (4) Mulilying he numeror nd denominor of he righ-hnd sides in (35) nd (36) by nd ssing o he limi s c + b, we obin c + ρ lim c J + (, b) b ρ c + lim c + b c ρ c + c ρ υ() ( c ρ + ρ ) d
43 = lim b su + lim su b ρ lim c J + (, b) b = lim b su lim c + b b ρ c + ρ c + υ() ρ b υ() ρ d c ρ + ρ 3 d = lim b su ( A 2 (c, b, )), (4) c υ()d + lim su b ρ c lim c ρ + c + b ρ c + ρ c c υ()d υ()d = lim b su ( A (c, b, )). (42) Relions (39) - (42) ensure (26). By Lemm, here eis midoins c i I for ( A i, A i), i=,2. Definiion yields he euliy Ai (, c i ) = A i (c i, b) T ci (, b) <, i =, 2. Since A i (, c i, ) nd A i (c i, b, ) re coninuous in on (, c i ] nd [c i, b), resecively, nd A i (, c i ) lim su A i (, c i, ), A i (c i, b) lim b su A i (c i, b, ), he wo ossibiliies re oen: If A i (, c i ) = lim su A i (, c i, ) or A (c i i, b) = lim b su A (c i i, b, ) hen (39) - (42) imly he esime J (, b) T ci (, b), i =, 2, i.e., he lef r of (25) holds. Oherwise, here eis oins c, i ( c+, < i ) c c i i, c i c + < b, such h c c i, c + c, A i (, c i ) = A i, ci, c i, nd A (c ( ) i i, b) = A ci, b, c + i i. To jusify he lef esime in (25), we esime T c (, b) nd T c2 (, b) serely. Firs, we emine T c2 (, b). Le c = c 2 in (35). Esime (37) yields
44 4 J (, b) c 2 c ρ 2 c + 2 υ() ( ) ρ d c ρ 2 + ρ c + 2 ρ + c + 2 ρ c + 2 b c + 2 υ() c ρ 2 d ρ c ρ 2 + ρ ( ) ( ) (we e he eressions for A 2, c2, c 2 nd A 2 c2, b, c + 2 ino ccoun) = ( ( )) b A2, c2, c 2 c + 2 c + 2 ρ + ( A 2 ( )) c c2, b, c c ρ 2 + ρ ρ ( ) (by he definiion of c 2, we hve A 2 (, c 2 ) = A 2, c2, c 2 nd A (, 2 c 2) = ( ) A 2 c2, b, c + 2 ) = (A 2 (, c 2, )) b c + 2 c + 2 ρ + ( A (c 2 2, b) ) c 2 ρ c ρ 2 + ρ
45 5 (since c 2 is midoin for ( A 2, A 2) ) = ( T c2 (, b) ) c + 2 c + 2 ρ + c 2 ρ c ρ 2 + ρ 2 ( T c2 (, b) ). (43) Esime T c (, b). Similrly, uing c = c, c = c, nd c+ = c + 2 view of (38) we obin in (36), in J (, b) = c ρ c + 2 c c υ()d c + ρ c ρ 2 + ρ ( ( )) b A, c, c = c + 2 c + (A (, c, )) b c + 2 ρ + + ( A c + ρ c + 2 c υ()d ρ c + c c ρ 2 + ρ c ( )) c, b, c + c ρ 2 + ρ c + ρ ρ + ( A (c, b) ) c ρ c ρ 2 + ρ ρ = ( T c (, b) ) c + c ρ + c ρ 2 + ρ c ( T c (, b) ). (44)
46 6 The lef esime in (25) resuls from (43) nd (44). The necessiy is roven. Sufficiency: Assume he eisence of midoin c i I for (A i, A ), i =, 2. i In his cse we hve A i (, c i ) = A (c i i, b) = T ci (, b) <, i =, 2. Since f () = f (b) = for f AC ( ) ( ) ρ, I, he resricion of AC ρ, I o (, ci ) ( nd (c i, b) belongs o AC,l ρ, (, ci ) ) ( nd AC,r ρ, (ci, b) ), resecively. Theorem 8 imlies h ( γ i A i (, c i ) ) υ() f () d = c i ( γ i T ci (, b) ) ci ρ(s) f (s) ds c i υ() f () d + = ( γ i T ci (, c i ) ) b c i + ( γ i A i (c i, b) ) ρ(s) f (s) ds + b c i υ() f () d ρ(s) f (s) ds c i ρ(s) f (s) ds, ρ(s) f (s) ds i.e., (2) holds nd he bes consn C = J (, b) in (2) mees he esime J (, b) min { γ T c (, b), γ 2 T c2 (, b) }, which defines he righ-hnd side of (25). Theorem is roven. Remr. Theorem imroves he esime for J (, b) in []. For emle, in Theorem 8.8 of [], under he ssumion A (, ) = A (b, b) = (he ler is euivlen o he condiions lim A (, c, ) = nd lim b A (c, b, ) = ), i is esblished h 2 A J (, b) ( + ) ( ) + A, where A = inf <c<b m { A (, c), A (c, b)}. Under our condiions, i is esily seen h A = T (, b). Le c ρ (s)ds <, ρ (s)ds =, c I, (45) c
47 7 or c ρ (s)ds =, ρ (s)ds <, c I. (46) c Theorem 2. Le < <. If (45) or (46) holds hen he bes consn J (, b) in (2) mees he esime m {A (, b), A 2 (, b)} J (, b) min { γ A (, b),γ 2 A 2 (, b) } (47) m { A (, b), A 2 (, b)} J (, b) min { γ A (, b),γ 2A (, b)} (48) PROOF OF THEOREM 2. ( ) W ρ, I, Since AC ( ρ, I ) is dense everywhere in J (, b) = su f AC (ρ,i) υ() f () d ρ() f () d = su f W (ρ,i) υ() f () d. (49) ρ() f () d ( ) { Le (45) hold. In view of iem (ii) of Theorem A, W ρ, I = ( ) } ( ) f W ρ, I : f () = = AC,l ρ, I. Hence, J (I) = J l (I) nd (47) follows from Theorem B. By nlogy we jusify (48) in he cse (46). Theorem 2 is roven. Finlly, le c ρ (s)ds =, c ρ (s)ds =, c I. (5) Theorem 3. Assume h < < nd (5) is vlid. Then (2) fils on he se W ( ) ρ, I, i.e., J (, b) =. PROOF OF THEOREM 3. By condiion, (5) holds. By Theorem A (iem (iv)) W ( ) ( ) ( ) ρ, I = W ρ, I. Since f () W ρ, I, (49) yields J (, b) =. Theorem 3 is roven The cse of < < <.
48 8 Definiion 2. A oin c I is clled midoin for (B, B ) if B (, c) = B (c, b) T (, b) <. Obviously, for midoin for (B, B ) o eis, i is necessry nd sufficien h B (,β ) <, β I, nd B (α, b) <, α I. Theorem 4. Assume h < < <, >, nd (24) holds. Then (2) is fulfilled on AC ( ) ρ, I if nd only if here eiss midoin c I for (B, B ) ; in his cse he bes consn J (, b) in (2) sisfies he esime ( ) T (, b) J (, b) 2 μ + T (, b). (5) PROOF. Necessiy: Assume h < < <, >, nd (2) holds on ( ) AC ρ, I wih C = J (, b). Le <α<β<b. In view of he condiions on he weighed funcions υ nd ρ, he uniies B (α, c), c (α, b), B ( c,β ), nd c (,β ) re finie. Hence, here eiss midoin c = c ( α, β ) ( α, β ) for B ( α, β ) nd B ( α, β ), i.e., c α c υ α ρ Inroduce he funcion where f () = b α ( ) ρ ()d = α β c c υ β ρ ( ), < α, ( c ) ( ) ( ) υ ρ ρ ()d, α c, ( ) β ( ) β b 2 υ ρ ρ ()d, c β, c, β b, b = b 2 = c α β c c c υ υ ρ α β ρ ( ) ( ) ρ ()d, ρ ()d. ρ ()d. (52)
49 9 Obviously, f AC ( ) ρ, I. For funcion f we hve ρ() f () d = b (B(α, c)) + ( B b (c,β) ) 2 Since c = α f () b f c υ() f () d = ( f () ) c υ α for α c nd similrly for c β, we infer β c Hence, (54) yields c α α = ( T(α, β) ) b c α β υ(s)dsd + ρ + b 2 υ() ( β f () ) d + f () b f () ( f () ) c ( f ()) ( f () ) υ() f () d c c c, (53) υ() ( f () ) d ( f ()) ( f () ) ρ ()d = b c υ υ(s)dsd υ(s)dsd β ρ c c υ(s)dsd. (54) υ ( ) (B(α, c)), b ρ ( ) ( B (c,β) ). b 2 ( ) b (B(α, c)) + b (B (c,β)) 2 α
50 2 = [ ( ) ] Since >, we hve + b b 2 υ() f () d ( ) ( ) T(α, β) b ( b Relions (2), (53) nd (55) imly h + b. 2 + b 2 ). Hence, ( ) ( ) T(α, β) b + b 2. (55) ( ) T(α, β) J (, b). (56) The bsolue coninuiy of he inegrl ensures he coninuiy of T ( α, β ) in α nd β for α<β b. In view of he indeendence of he righ-hnd side (56) of α nd β, <α<β<b, we hve ( ) T(, b) J (, b), (57) i.e., here eiss midoin c I for (B, B ) nd (57) is rue. Sufficiency: Le midoin c I for (B, B ) eis, i.e., B (, c) = B (c, b) = T(, b) <. Arguing s in he sufficiency r of Theorem nd involing Theorem C, we derive h ( μ + B(, c) ) υ() f () d = c ( μ + T(, b) ) 2 c α ρ(s) f (s) ds c α υ() f () d + β + ( μ + B (c, b) ) ρ(s) f (s) ds + c β c υ() f () d c ρ(s) f (s) ds ρ(s) f (s) ds i.e., (2) is fulfilled nd J (, b) μ + 2 T(, b); he ls esime nd (57) ensure (5). Theorem 4 is roven.,
51 2 Remr 2. The comrision of (5) nd he esime ( ) 2 B J (, b) 2 ( ) B, where B = min <c<b m {B(, c), B(b, c)}, obined in he cse of < < in Theorem 8.7 of [], shows h he esime in (5) is beer hn h of []. Theorem 5. Le < < <, >. If (26) or (27) holds hen he bes consn J (, b) in (2) sisfies he esime μ B(, b) J (, b) μ + B(, b) or μ B (, b) J (, b) μ + B (, b), resecively. Theorem 6. Assume h < < <, >, nd (5) holds. Then (2) fils on AC ( ) ρ, I ; i.e., J (, b) =. Theorems 5 nd 6 re roven by nlogy wih Theorem 2 nd 3. References [] Oic B. nd Kufner A. Hrdy-Tye Ineuliies, Longmn, Hrlow (99). [2] Kufner A. nd Persson L.-E. Weighed Ineuliies of Hrdy Tye, Word Sci., New Jersey, London, Singore nd Hong Kong (23). [3] Kufner A., Mligrnd L., nd Persson L-E. The Hrdy Ineuliy: Abou Is Hisory nd Some Reled Resuls, Pilseń (27). [4] Gogishvili A., Kufner A., Persson L.-E., nd Wedesig A. An euivlence heorem for inegrl condiions reled o Hrdy s ineuliy, Rel Anl. Echnge, 29, (23/24), No.2, [5] Kufner A., Persson L.-E. nd Wedesig A. A sudy of some consns chrcerizing he weighed Hrdy ineuliy, in: Bnch Cener Publ. Vol.64. Orlicz Cenenry Volume, Polish Acd. Sci., Wrsw, 24, [6] Drbe P. nd Kufner A. Hrdy ineuliy nd roeries of he usiliner Surm-Liouville roblem, Rend. Lincei M. Al. 8 (27), [7] Oinrov R. nd Rhimov S.Y. Weighed Hrdy ineuliies nd heir licion o oscillion heory of hlf-liner differenil euions, Eursin Mh. J. (2), No.2, -24. [8] Oinrov R. nd Rhimov S.Y. Oscillion nd nonoscillion of wo erms liner nd hlf-liner euions of higher order, Elecron. J. Qul. Theory Differ. Eu. 49 (2), -5.
52 22 [9] Kudbyev S.Y. nd Oinrov R. The crieri of disconjuge of hlfliner second order differenil euions, Mh. J. Kzhsn, (2), No.2, [] Lizorin P.I. On he closure of he se of comcly suored funcions in he weighed sce W, l, Dol. Ad. Nu SSSR, 239 (978), No.4, [] Kudryvsev L.D. On he densiy of comcly suored funcions in weighed sces, Sovie Mh. Dol. 9 (978), No., [2] Oinrov R. On weighed norm ineuliies wih hree weighs, J. London Mh. Soc. 48 (993) No.2, 3-6. [3] Persson L.-E. nd Senov V.D. Weighed inegrl ineuliies wih he geomeric men oeror, J. Ineul. Al. 7 (22), No.5, [4] Sinnmon G. nd Senov V.D. The weighed Hrdy ineuliy: new roofs nd he cse =, J.Mh. Soc. 54 (996), No.2, 89-. A.M. Abylyev; A.O. Birysnov; R.Oinrov L.N. Gumilyov Eursin Nionl Universiy, Asn, Kzhsn E-mil ddress: bylyev b@mil.ru; osr 62@mil.ru; o rysul@mil.ru
53 Per 2 Boundedness, comcness for clss of frcionl inegrion oerors of Weyl ye. Eursin Mhemicl Journl 7 (26), No., Remr: The e is he sme bu he form hs been modified o fi he syle in his PhD hesis.
54
55 EURASIAN MATHEMATICAL JOURNAL ISSN Volume 7, Number (26), 9 27 BOUNDEDNESS, COMPACTNESS FOR A CLASS OF FRACTIONAL INTEGRATION OPERATORS OF WEYL TYPE A.M. Abylyev Communiced by E.D. Nursulnov Key words: frcionl inegrion oeror, Weyl oeror, Riemnn- Liouville oeror, Hdmrd oeror, Erdelyi-Kober oeror, boundedness, comcness. AMS Mhemics Subjec Clssificion: 26A33, 26D, 47G. Absrc. We esblish crieri for he boundedness nd comcness for clss of oerors of frcionl inegrion involving he Weyl oeror. Inroducion Le I = (, b), < b,<, <, + =. Le u, v be lmos everywhere osiive nd loclly inegrble funcions on I. ByL,u L (u, I) we denoe he se of ll mesurble funcions f on I such h f,u = f () u()d <. In he cse u we wrie L L (I). Le W be osiive sricly incresing nd loclly bsoluely coninuous funcion on I. Suose dw() w() for d lmos everywhere I. Le >α>. We consider he oeror u(s)w β (s) f (s)w(s)ds K α,β f () =, I. () α (W(s) W()) In he cse β =, u he dul oeror o oeror () hs he form K α,β f () = f (s)w(s)ds, I. (2) α (W() W(s))
56 2 A.M. Abylyev Oeror (2) is clled [5] he oeror of frcionl inegrion of he funcion f of he funcion W. Weighed esimes for oeror (2) were reviously considered in [2], []. When W() =, u, β = oeror () is he Weyl oeror I α f () = which is dul o he Riemnn-Liouville oeror I α g(s) = s f (s)ds, (s ) α I, (3) g()d, (s ) α s I. (4) Oerors (3) nd (4) cing from he weighed sce L,u o he weighed sce L,v re invesiged in ers [3], [3], [7], [5], [2], [2] nd ohers, where necessry nd sufficien condiions for heir boundedness, comcness re obined for vrious relions beween he rmeers α,, nd under vrious ssumions regrding he weigh funcions u nd v. Two-sided esimes of heir norms re lso obined. We invesige oeror () cing from he sce L,w o L,v. From he obined resuls new sserions follow, in simle erms, for oerors (3) nd (4), generlizing he resuls of [7], [5], [2]. The osiiviy nd monooniciy of W imlies he eisence of he nonnegive limi lim + W() W(). Fuher, we ssume W() = nd oherwise, we consider he oeror K α,β in he form, where funcion W() is relced by he funcion W () = W() W(), I. Furher, he norm of he liner oeror T from normed sce o noher one is denoed briefly by T. Which sces re men will be cler from he cone. Throughou he er he roducs of he form re suosed be eul o zero. Relions A B, A B men A cb wih consn c deending only on,, α which cn be differen in differen lces. If A B nd A B hen we wrie A B. By Z we denoe he se of ll ineger numbers, χ E denoes he chrcerisic funcion of he se E. 2 Auiliry sserions To rove he min resuls we need some well-nown sserions. Along wih oeror () we consider he Hrdy oeror
57 Boundedness, comcness of clss frcionl inegrion oeror of Weyl ye 3 H α,β f () = u(s)w β+α (s) f (s)w(s)ds. () I is esy o see h for f K α,β f () H α,β f (), I. (2) Issues of boundedness nd comcness of oeror () in weighed Lebesgue sces were sudied uie comleely. A summry of he resuls cn be found in [5]. The following Theorem A nd Theorem B re corollries of Theorem 5 nd Theorem 6 in [5]. Theorem A. Le < <. The oeror H α,β is bounded from L,w o L,v if nd only if z A α,β = su v()d z I b u (s)w (α+β ) (s)w(s)ds <. Moreover, H α,β A α,β. z Theorem B. Le < < <, >. The oeror H α,β is bounded from L,w o L,v if nd only if B α,β = z u (s)w (α+β ) w(s)ds ( ) ( z v()d ) v(z)dz <. Moreover, H α,β B α,β. Remr 2.. In he cse < < <,> he vlue B α,β is euivlen o he vlue B α,β (, b) = z u (s)w (α+β ) (s)w(s)ds ( z v()d ) ( ) u (z)w (α+β ) (z)w(z)dz.
REAL ANALYSIS I HOMEWORK 3. Chapter 1
 REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
Convergence of Singular Integral Operators in Weighted Lebesgue Spaces
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS
 - TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
- TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
How to Prove the Riemann Hypothesis Author: Fayez Fok Al Adeh.
 How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
On The Hermite- Hadamard-Fejér Type Integral Inequality for Convex Function
 Turkish Journl o Anlysis nd Numer Theory, 4, Vol., No. 3, 85-89 Aville online h://us.scieu.com/jn//3/6 Science nd Educion Pulishing DOI:.69/jn--3-6 On The Hermie- Hdmrd-Fejér Tye Inegrl Ineuliy or Convex
Turkish Journl o Anlysis nd Numer Theory, 4, Vol., No. 3, 85-89 Aville online h://us.scieu.com/jn//3/6 Science nd Educion Pulishing DOI:.69/jn--3-6 On The Hermie- Hdmrd-Fejér Tye Inegrl Ineuliy or Convex
How to prove the Riemann Hypothesis
 Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Hermite-Hadamard-Fejér type inequalities for convex functions via fractional integrals
 Sud. Univ. Beş-Bolyi Mh. 6(5, No. 3, 355 366 Hermie-Hdmrd-Fejér ype inequliies for convex funcions vi frcionl inegrls İmd İşcn Asrc. In his pper, firsly we hve eslished Hermie Hdmrd-Fejér inequliy for
Sud. Univ. Beş-Bolyi Mh. 6(5, No. 3, 355 366 Hermie-Hdmrd-Fejér ype inequliies for convex funcions vi frcionl inegrls İmd İşcn Asrc. In his pper, firsly we hve eslished Hermie Hdmrd-Fejér inequliy for
Weighted Hardy-Type Inequalities on Time Scales with Applications
 Medierr J Mh DOI 0007/s00009-04-054-y c Sringer Bsel 204 Weighed Hrdy-Tye Ineuliies on Time Scles wih Alicions S H Sker, R R Mhmoud nd A Peerson Absrc In his er, we will rove some new dynmic Hrdy-ye ineuliies
Medierr J Mh DOI 0007/s00009-04-054-y c Sringer Bsel 204 Weighed Hrdy-Tye Ineuliies on Time Scles wih Alicions S H Sker, R R Mhmoud nd A Peerson Absrc In his er, we will rove some new dynmic Hrdy-ye ineuliies
ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX
 Journl of Applied Mhemics, Sisics nd Informics JAMSI), 9 ), No. ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX MEHMET ZEKI SARIKAYA, ERHAN. SET
Journl of Applied Mhemics, Sisics nd Informics JAMSI), 9 ), No. ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX MEHMET ZEKI SARIKAYA, ERHAN. SET
Refinements to Hadamard s Inequality for Log-Convex Functions
 Alied Mhemics 899-93 doi:436/m7 Pulished Online Jul (h://wwwscirporg/journl/m) Refinemens o Hdmrd s Ineuli for Log-Convex Funcions Asrc Wdllh T Sulimn Dermen of Comuer Engineering College of Engineering
Alied Mhemics 899-93 doi:436/m7 Pulished Online Jul (h://wwwscirporg/journl/m) Refinemens o Hdmrd s Ineuli for Log-Convex Funcions Asrc Wdllh T Sulimn Dermen of Comuer Engineering College of Engineering
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR IAN KNOWLES
 A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
Positive and negative solutions of a boundary value problem for a
 Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Mathematics 805 Final Examination Answers
 . 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
. 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
1. Introduction. 1 b b
 Journl of Mhemicl Inequliies Volume, Number 3 (007), 45 436 SOME IMPROVEMENTS OF GRÜSS TYPE INEQUALITY N. ELEZOVIĆ, LJ. MARANGUNIĆ AND J. PEČARIĆ (communiced b A. Čižmešij) Absrc. In his pper some inequliies
Journl of Mhemicl Inequliies Volume, Number 3 (007), 45 436 SOME IMPROVEMENTS OF GRÜSS TYPE INEQUALITY N. ELEZOVIĆ, LJ. MARANGUNIĆ AND J. PEČARIĆ (communiced b A. Čižmešij) Absrc. In his pper some inequliies
INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).
![INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q). INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).](/thumbs/78/77677920.jpg) INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE BOUNDARY-VALUE PROBLEM
 Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
ON THE OSTROWSKI-GRÜSS TYPE INEQUALITY FOR TWICE DIFFERENTIABLE FUNCTIONS
 Hceepe Journl of Mhemics nd Sisics Volume 45) 0), 65 655 ON THE OSTROWSKI-GRÜSS TYPE INEQUALITY FOR TWICE DIFFERENTIABLE FUNCTIONS M Emin Özdemir, Ahme Ock Akdemir nd Erhn Se Received 6:06:0 : Acceped
Hceepe Journl of Mhemics nd Sisics Volume 45) 0), 65 655 ON THE OSTROWSKI-GRÜSS TYPE INEQUALITY FOR TWICE DIFFERENTIABLE FUNCTIONS M Emin Özdemir, Ahme Ock Akdemir nd Erhn Se Received 6:06:0 : Acceped
ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX.
 ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX. MEHMET ZEKI SARIKAYA?, ERHAN. SET, AND M. EMIN OZDEMIR Asrc. In his noe, we oin new some ineuliies
ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX. MEHMET ZEKI SARIKAYA?, ERHAN. SET, AND M. EMIN OZDEMIR Asrc. In his noe, we oin new some ineuliies
FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m)
![FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m) FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m)](/thumbs/75/72845579.jpg) Univ. Beogrd. Pul. Elekroehn. Fk. Ser. M. 8 (997), 79{83 FUTHE GENEALIZATIONS OF INEQUALITIES FO AN INTEGAL QI Feng Using he Tylor's formul we prove wo inegrl inequliies, h generlize K. S. K. Iyengr's
Univ. Beogrd. Pul. Elekroehn. Fk. Ser. M. 8 (997), 79{83 FUTHE GENEALIZATIONS OF INEQUALITIES FO AN INTEGAL QI Feng Using he Tylor's formul we prove wo inegrl inequliies, h generlize K. S. K. Iyengr's
CALDERON S REPRODUCING FORMULA FOR DUNKL CONVOLUTION
 Avilble online hp://scik.org Eng. Mh. Le. 15, 15:4 ISSN: 49-9337 CALDERON S REPRODUCING FORMULA FOR DUNKL CONVOLUTION PANDEY, C. P. 1, RAKESH MOHAN AND BHAIRAW NATH TRIPATHI 3 1 Deprmen o Mhemics, Ajy
Avilble online hp://scik.org Eng. Mh. Le. 15, 15:4 ISSN: 49-9337 CALDERON S REPRODUCING FORMULA FOR DUNKL CONVOLUTION PANDEY, C. P. 1, RAKESH MOHAN AND BHAIRAW NATH TRIPATHI 3 1 Deprmen o Mhemics, Ajy
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
 Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
New Inequalities in Fractional Integrals
 ISSN 1749-3889 (prin), 1749-3897 (online) Inernionl Journl of Nonliner Science Vol.9(21) No.4,pp.493-497 New Inequliies in Frcionl Inegrls Zoubir Dhmni Zoubir DAHMANI Lborory of Pure nd Applied Mhemics,
ISSN 1749-3889 (prin), 1749-3897 (online) Inernionl Journl of Nonliner Science Vol.9(21) No.4,pp.493-497 New Inequliies in Frcionl Inegrls Zoubir Dhmni Zoubir DAHMANI Lborory of Pure nd Applied Mhemics,
Green s Functions and Comparison Theorems for Differential Equations on Measure Chains
 Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
MTH 146 Class 11 Notes
 8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
Integral Transform. Definitions. Function Space. Linear Mapping. Integral Transform
 Inegrl Trnsform Definiions Funcion Spce funcion spce A funcion spce is liner spce of funcions defined on he sme domins & rnges. Liner Mpping liner mpping Le VF, WF e liner spces over he field F. A mpping
Inegrl Trnsform Definiions Funcion Spce funcion spce A funcion spce is liner spce of funcions defined on he sme domins & rnges. Liner Mpping liner mpping Le VF, WF e liner spces over he field F. A mpping
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Hermite-Hadamard and Simpson Type Inequalities for Differentiable Quasi-Geometrically Convex Functions
 Trkish Jornl o Anlysis nd Nmer Theory, 4, Vol, No, 4-46 Aville online h://ssciecom/jn/// Science nd Edcion Plishing DOI:69/jn--- Hermie-Hdmrd nd Simson Tye Ineliies or Dierenile Qsi-Geomericlly Convex
Trkish Jornl o Anlysis nd Nmer Theory, 4, Vol, No, 4-46 Aville online h://ssciecom/jn/// Science nd Edcion Plishing DOI:69/jn--- Hermie-Hdmrd nd Simson Tye Ineliies or Dierenile Qsi-Geomericlly Convex
Solutions of half-linear differential equations in the classes Gamma and Pi
 Soluions of hlf-liner differenil equions in he clsses Gmm nd Pi Pvel Řehák Insiue of Mhemics, Acdemy of Sciences CR CZ-6662 Brno, Czech Reublic; Fculy of Educion, Msryk Universiy CZ-60300 Brno, Czech Reublic
Soluions of hlf-liner differenil equions in he clsses Gmm nd Pi Pvel Řehák Insiue of Mhemics, Acdemy of Sciences CR CZ-6662 Brno, Czech Reublic; Fculy of Educion, Msryk Universiy CZ-60300 Brno, Czech Reublic
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
Solutions to Problems from Chapter 2
 Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Application on Inner Product Space with. Fixed Point Theorem in Probabilistic
 Journl of Applied Mhemics & Bioinformics, vol.2, no.2, 2012, 1-10 ISSN: 1792-6602 prin, 1792-6939 online Scienpress Ld, 2012 Applicion on Inner Produc Spce wih Fixed Poin Theorem in Probbilisic Rjesh Shrivsv
Journl of Applied Mhemics & Bioinformics, vol.2, no.2, 2012, 1-10 ISSN: 1792-6602 prin, 1792-6939 online Scienpress Ld, 2012 Applicion on Inner Produc Spce wih Fixed Poin Theorem in Probbilisic Rjesh Shrivsv
3. Renewal Limit Theorems
 Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
..,..,.,
 57.95. «..» 7, 9,,. 3 DOI:.459/mmph7..,..,., E-mil: yshr_ze@mil.ru -,,. -, -.. -. - - ( ). -., -. ( - ). - - -., - -., - -, -., -. -., - - -, -., -. : ; ; - ;., -,., - -, []., -, [].,, - [3, 4]. -. 3 (
57.95. «..» 7, 9,,. 3 DOI:.459/mmph7..,..,., E-mil: yshr_ze@mil.ru -,,. -, -.. -. - - ( ). -., -. ( - ). - - -., - -., - -, -., -. -., - - -, -., -. : ; ; - ;., -,., - -, []., -, [].,, - [3, 4]. -. 3 (
Journal of Mathematical Analysis and Applications. Two normality criteria and the converse of the Bloch principle
 J. Mh. Anl. Appl. 353 009) 43 48 Conens liss vilble ScienceDirec Journl of Mhemicl Anlysis nd Applicions www.elsevier.com/loce/jm Two normliy crieri nd he converse of he Bloch principle K.S. Chrk, J. Rieppo
J. Mh. Anl. Appl. 353 009) 43 48 Conens liss vilble ScienceDirec Journl of Mhemicl Anlysis nd Applicions www.elsevier.com/loce/jm Two normliy crieri nd he converse of he Bloch principle K.S. Chrk, J. Rieppo
On Hadamard and Fejér-Hadamard inequalities for Caputo k-fractional derivatives
 In J Nonliner Anl Appl 9 8 No, 69-8 ISSN: 8-68 elecronic hp://dxdoiorg/75/ijn8745 On Hdmrd nd Fejér-Hdmrd inequliies for Cpuo -frcionl derivives Ghulm Frid, Anum Jved Deprmen of Mhemics, COMSATS Universiy
In J Nonliner Anl Appl 9 8 No, 69-8 ISSN: 8-68 elecronic hp://dxdoiorg/75/ijn8745 On Hdmrd nd Fejér-Hdmrd inequliies for Cpuo -frcionl derivives Ghulm Frid, Anum Jved Deprmen of Mhemics, COMSATS Universiy
Anatoly A. Kilbas. tn 1. t 1 a. dt 2. a t. log x
 J. Koren Mh. So. 38 200) No. 6. 9 204 HADAMARD-TYPE FRACTIONAL CALCULUS Anoly A. Kilbs Absr. The er is devoed o he sudy of frionl inegrion nd differeniion on finie inervl [ b] of he rel xis in he frme
J. Koren Mh. So. 38 200) No. 6. 9 204 HADAMARD-TYPE FRACTIONAL CALCULUS Anoly A. Kilbs Absr. The er is devoed o he sudy of frionl inegrion nd differeniion on finie inervl [ b] of he rel xis in he frme
Procedia Computer Science
 Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
Exponential Decay for Nonlinear Damped Equation of Suspended String
 9 Inernionl Symoium on Comuing, Communicion, nd Conrol (ISCCC 9) Proc of CSIT vol () () IACSIT Pre, Singore Eonenil Decy for Nonliner Dmed Equion of Suended Sring Jiong Kemuwn Dermen of Mhemic, Fculy of
9 Inernionl Symoium on Comuing, Communicion, nd Conrol (ISCCC 9) Proc of CSIT vol () () IACSIT Pre, Singore Eonenil Decy for Nonliner Dmed Equion of Suended Sring Jiong Kemuwn Dermen of Mhemic, Fculy of
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
A Simple Method to Solve Quartic Equations. Key words: Polynomials, Quartics, Equations of the Fourth Degree INTRODUCTION
 Ausrlin Journl of Bsic nd Applied Sciences, 6(6): -6, 0 ISSN 99-878 A Simple Mehod o Solve Quric Equions Amir Fhi, Poo Mobdersn, Rhim Fhi Deprmen of Elecricl Engineering, Urmi brnch, Islmic Ad Universi,
Ausrlin Journl of Bsic nd Applied Sciences, 6(6): -6, 0 ISSN 99-878 A Simple Mehod o Solve Quric Equions Amir Fhi, Poo Mobdersn, Rhim Fhi Deprmen of Elecricl Engineering, Urmi brnch, Islmic Ad Universi,
6. Gas dynamics. Ideal gases Speed of infinitesimal disturbances in still gas
 6. Gs dynmics Dr. Gergely Krisóf De. of Fluid echnics, BE Februry, 009. Seed of infiniesiml disurbnces in sill gs dv d, dv d, Coninuiy: ( dv)( ) dv omenum r r heorem: ( ( dv) ) d 3443 4 q m dv d dv llievi
6. Gs dynmics Dr. Gergely Krisóf De. of Fluid echnics, BE Februry, 009. Seed of infiniesiml disurbnces in sill gs dv d, dv d, Coninuiy: ( dv)( ) dv omenum r r heorem: ( ( dv) ) d 3443 4 q m dv d dv llievi
Some Inequalities variations on a common theme Lecture I, UL 2007
 Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Analytic solution of linear fractional differential equation with Jumarie derivative in term of Mittag-Leffler function
 Anlyic soluion of liner frcionl differenil equion wih Jumrie derivive in erm of Mig-Leffler funcion Um Ghosh (), Srijn Sengup (2), Susmi Srkr (2b), Shnnu Ds (3) (): Deprmen of Mhemics, Nbdwip Vidysgr College,
Anlyic soluion of liner frcionl differenil equion wih Jumrie derivive in erm of Mig-Leffler funcion Um Ghosh (), Srijn Sengup (2), Susmi Srkr (2b), Shnnu Ds (3) (): Deprmen of Mhemics, Nbdwip Vidysgr College,
Some Hardy Type Inequalities with Weighted Functions via Opial Type Inequalities
 Advnces in Dynmicl Systems nd Alictions ISSN 0973-5321, Volume 10, Number 1,. 1 9 (2015 htt://cmus.mst.edu/ds Some Hrdy Tye Inequlities with Weighted Functions vi Oil Tye Inequlities Rvi P. Agrwl Tes A&M
Advnces in Dynmicl Systems nd Alictions ISSN 0973-5321, Volume 10, Number 1,. 1 9 (2015 htt://cmus.mst.edu/ds Some Hrdy Tye Inequlities with Weighted Functions vi Oil Tye Inequlities Rvi P. Agrwl Tes A&M
EÜFBED - Fen Bilimleri Enstitüsü Dergisi Cilt-Sayı: 3-2 Yıl:
 63 EÜFBED - Fen Bilimleri Ensiüsü Dergisi Cil-Syı: 3- Yıl: 63-7 SOME INEQUALITIES OF HERMITE-HADAMARD TYPE FOR FUNCTIONS WHOSE DERIVATIVES ABSOLUTE VALUES ARE QUASI-CONVEX TÜREVİNİN MUTLAK DEĞERİ QUASI-KONVEKS
63 EÜFBED - Fen Bilimleri Ensiüsü Dergisi Cil-Syı: 3- Yıl: 63-7 SOME INEQUALITIES OF HERMITE-HADAMARD TYPE FOR FUNCTIONS WHOSE DERIVATIVES ABSOLUTE VALUES ARE QUASI-CONVEX TÜREVİNİN MUTLAK DEĞERİ QUASI-KONVEKS
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
Power Transformations and Unit Mean and Constant Variance Assumptions of the Multiplicative Error Model: The Generalized Gamma Distribution
 Briish Journl of Mhemics & Comuer Science (): 88-06, 0 SCIENCEDOMAIN inernionl www.sciencedomin.org Power Trnsformions nd Uni Men nd Consn Vrince Assumions of he Mulilicive Error Model: The Generlized
Briish Journl of Mhemics & Comuer Science (): 88-06, 0 SCIENCEDOMAIN inernionl www.sciencedomin.org Power Trnsformions nd Uni Men nd Consn Vrince Assumions of he Mulilicive Error Model: The Generlized
Chapter Direct Method of Interpolation
 Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
C 0 Approximation on the Spatially Homogeneous Boltzmann Equation for Maxwellian Molecules*
 Alied Mhemics,,, 54-59 doi:.46/m..666 Published Online December (h://www.scip.org/journl/m) C Aroximion on he Silly Homogeneous Bolzmnn Equion or Mxwellin Molecules Absrc Minling Zheng School o Science,
Alied Mhemics,,, 54-59 doi:.46/m..666 Published Online December (h://www.scip.org/journl/m) C Aroximion on he Silly Homogeneous Bolzmnn Equion or Mxwellin Molecules Absrc Minling Zheng School o Science,
MATH 124 AND 125 FINAL EXAM REVIEW PACKET (Revised spring 2008)
 MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
LAPLACE TRANSFORM OVERCOMING PRINCIPLE DRAWBACKS IN APPLICATION OF THE VARIATIONAL ITERATION METHOD TO FRACTIONAL HEAT EQUATIONS
 Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
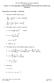 .615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
Journal of Mathematical Inequalities
 Journl of Mhemicl Inequliies Wih Comlimens of he Auhor Zgreb, Croi Volume 10, Number 2, June 2016 Mrin J. Bohner nd Smir H. Sker Snek-ou rincile on ime scles JMI-10-30 393 403 JOURNAL OF MATHEMATICAL INEQUALITIES
Journl of Mhemicl Inequliies Wih Comlimens of he Auhor Zgreb, Croi Volume 10, Number 2, June 2016 Mrin J. Bohner nd Smir H. Sker Snek-ou rincile on ime scles JMI-10-30 393 403 JOURNAL OF MATHEMATICAL INEQUALITIES
Hadamard-Type Inequalities for s Convex Functions I
 Punjb University Journl of Mthemtics ISSN 6-56) Vol. ). 5-6 Hdmrd-Tye Ineulities for s Convex Functions I S. Hussin Dertment of Mthemtics Institute Of Sce Technology, Ner Rwt Toll Plz Islmbd Highwy, Islmbd
Punjb University Journl of Mthemtics ISSN 6-56) Vol. ). 5-6 Hdmrd-Tye Ineulities for s Convex Functions I S. Hussin Dertment of Mthemtics Institute Of Sce Technology, Ner Rwt Toll Plz Islmbd Highwy, Islmbd
Communications inmathematicalanalysis
 Communicions inmhemicanysis Voume 11, Number 2,. 23 35 (211) ISSN 1938-9787 www.mh-res-ub.org/cm GRONWALL-LIKE INEQUALITIES ON TIME SCALES WITH APPLICATIONS ELVAN AKIN-BOHNER Dermen of Mhemics nd Sisics
Communicions inmhemicanysis Voume 11, Number 2,. 23 35 (211) ISSN 1938-9787 www.mh-res-ub.org/cm GRONWALL-LIKE INEQUALITIES ON TIME SCALES WITH APPLICATIONS ELVAN AKIN-BOHNER Dermen of Mhemics nd Sisics
LAPLACE TRANSFORMS. 1. Basic transforms
 LAPLACE TRANSFORMS. Bic rnform In hi coure, Lplce Trnform will be inroduced nd heir properie exmined; ble of common rnform will be buil up; nd rnform will be ued o olve ome dierenil equion by rnforming
LAPLACE TRANSFORMS. Bic rnform In hi coure, Lplce Trnform will be inroduced nd heir properie exmined; ble of common rnform will be buil up; nd rnform will be ued o olve ome dierenil equion by rnforming
Research Article New General Integral Inequalities for Lipschitzian Functions via Hadamard Fractional Integrals
 Hindwi Pulishing orporion Inernionl Journl of Anlysis, Aricle ID 35394, 8 pges hp://d.doi.org/0.55/04/35394 Reserch Aricle New Generl Inegrl Inequliies for Lipschizin Funcions vi Hdmrd Frcionl Inegrls
Hindwi Pulishing orporion Inernionl Journl of Anlysis, Aricle ID 35394, 8 pges hp://d.doi.org/0.55/04/35394 Reserch Aricle New Generl Inegrl Inequliies for Lipschizin Funcions vi Hdmrd Frcionl Inegrls
Average & instantaneous velocity and acceleration Motion with constant acceleration
 Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
f(x) dx with An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples dx x x 2
 Impope Inegls To his poin we hve only consideed inegls f() wih he is of inegion nd b finie nd he inegnd f() bounded (nd in fc coninuous ecep possibly fo finiely mny jump disconinuiies) An inegl hving eihe
Impope Inegls To his poin we hve only consideed inegls f() wih he is of inegion nd b finie nd he inegnd f() bounded (nd in fc coninuous ecep possibly fo finiely mny jump disconinuiies) An inegl hving eihe
Asymptotic relationship between trajectories of nominal and uncertain nonlinear systems on time scales
 Asympoic relionship beween rjecories of nominl nd uncerin nonliner sysems on ime scles Fim Zohr Tousser 1,2, Michel Defoor 1, Boudekhil Chfi 2 nd Mohmed Djemï 1 Absrc This pper sudies he relionship beween
Asympoic relionship beween rjecories of nominl nd uncerin nonliner sysems on ime scles Fim Zohr Tousser 1,2, Michel Defoor 1, Boudekhil Chfi 2 nd Mohmed Djemï 1 Absrc This pper sudies he relionship beween
HUI-HSIUNG KUO, ANUWAT SAE-TANG, AND BENEDYKT SZOZDA
 Communicions on Sochsic Anlysis Vol 6, No 4 2012 603-614 Serils Publicions wwwserilspublicionscom THE ITÔ FORMULA FOR A NEW STOCHASTIC INTEGRAL HUI-HSIUNG KUO, ANUWAT SAE-TANG, AND BENEDYKT SZOZDA Absrc
Communicions on Sochsic Anlysis Vol 6, No 4 2012 603-614 Serils Publicions wwwserilspublicionscom THE ITÔ FORMULA FOR A NEW STOCHASTIC INTEGRAL HUI-HSIUNG KUO, ANUWAT SAE-TANG, AND BENEDYKT SZOZDA Absrc
NEW FRACTIONAL DERIVATIVES WITH NON-LOCAL AND NON-SINGULAR KERNEL Theory and Application to Heat Transfer Model
 Angn, A., e l.: New Frcionl Derivives wih Non-Locl nd THERMAL SCIENCE, Yer 216, Vol. 2, No. 2, pp. 763-769 763 NEW FRACTIONAL DERIVATIVES WITH NON-LOCAL AND NON-SINGULAR KERNEL Theory nd Applicion o He
Angn, A., e l.: New Frcionl Derivives wih Non-Locl nd THERMAL SCIENCE, Yer 216, Vol. 2, No. 2, pp. 763-769 763 NEW FRACTIONAL DERIVATIVES WITH NON-LOCAL AND NON-SINGULAR KERNEL Theory nd Applicion o He
Research Article Generalized Fractional Integral Inequalities for Continuous Random Variables
 Journl of Proiliy nd Sisics Volume 2015, Aricle ID 958980, 7 pges hp://dx.doi.org/10.1155/2015/958980 Reserch Aricle Generlized Frcionl Inegrl Inequliies for Coninuous Rndom Vriles Adullh Akkur, Zeynep
Journl of Proiliy nd Sisics Volume 2015, Aricle ID 958980, 7 pges hp://dx.doi.org/10.1155/2015/958980 Reserch Aricle Generlized Frcionl Inegrl Inequliies for Coninuous Rndom Vriles Adullh Akkur, Zeynep
ECE Microwave Engineering. Fall Prof. David R. Jackson Dept. of ECE. Notes 10. Waveguides Part 7: Transverse Equivalent Network (TEN)
 EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
On the Pseudo-Spectral Method of Solving Linear Ordinary Differential Equations
 Journl of Mhemics nd Sisics 5 ():136-14, 9 ISS 1549-3644 9 Science Publicions On he Pseudo-Specrl Mehod of Solving Liner Ordinry Differenil Equions B.S. Ogundre Deprmen of Pure nd Applied Mhemics, Universiy
Journl of Mhemics nd Sisics 5 ():136-14, 9 ISS 1549-3644 9 Science Publicions On he Pseudo-Specrl Mehod of Solving Liner Ordinry Differenil Equions B.S. Ogundre Deprmen of Pure nd Applied Mhemics, Universiy
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
An Introduction to Malliavin calculus and its applications
 An Inroducion o Malliavin calculus and is applicaions Lecure 5: Smoohness of he densiy and Hörmander s heorem David Nualar Deparmen of Mahemaics Kansas Universiy Universiy of Wyoming Summer School 214
An Inroducion o Malliavin calculus and is applicaions Lecure 5: Smoohness of he densiy and Hörmander s heorem David Nualar Deparmen of Mahemaics Kansas Universiy Universiy of Wyoming Summer School 214
Solutions for Nonlinear Partial Differential Equations By Tan-Cot Method
 IOSR Journl of Mhemics (IOSR-JM) e-issn: 78-578. Volume 5, Issue 3 (Jn. - Feb. 13), PP 6-11 Soluions for Nonliner Pril Differenil Equions By Tn-Co Mehod Mhmood Jwd Abdul Rsool Abu Al-Sheer Al -Rfidin Universiy
IOSR Journl of Mhemics (IOSR-JM) e-issn: 78-578. Volume 5, Issue 3 (Jn. - Feb. 13), PP 6-11 Soluions for Nonliner Pril Differenil Equions By Tn-Co Mehod Mhmood Jwd Abdul Rsool Abu Al-Sheer Al -Rfidin Universiy
An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples.
 Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Fractional Calculus. Connor Wiegand. 6 th June 2017
 Frcionl Clculus Connor Wiegnd 6 h June 217 Absrc This pper ims o give he reder comforble inroducion o Frcionl Clculus. Frcionl Derivives nd Inegrls re defined in muliple wys nd hen conneced o ech oher
Frcionl Clculus Connor Wiegnd 6 h June 217 Absrc This pper ims o give he reder comforble inroducion o Frcionl Clculus. Frcionl Derivives nd Inegrls re defined in muliple wys nd hen conneced o ech oher
Boundary layer problem for system of first order of ordinary differential equations with linear non-local boundary conditions
 IJS 3 37A3 Secil issue-mheics: 389-396 Irnin Journl of Science & echnology h://ijssshirzucir Boundry lyer role for syse of firs order of ordinry differenil euions wih liner non-locl oundry condiions M
IJS 3 37A3 Secil issue-mheics: 389-396 Irnin Journl of Science & echnology h://ijssshirzucir Boundry lyer role for syse of firs order of ordinry differenil euions wih liner non-locl oundry condiions M
MAT 266 Calculus for Engineers II Notes on Chapter 6 Professor: John Quigg Semester: spring 2017
 MAT 66 Clculus for Engineers II Noes on Chper 6 Professor: John Quigg Semeser: spring 7 Secion 6.: Inegrion by prs The Produc Rule is d d f()g() = f()g () + f ()g() Tking indefinie inegrls gives [f()g
MAT 66 Clculus for Engineers II Noes on Chper 6 Professor: John Quigg Semeser: spring 7 Secion 6.: Inegrion by prs The Produc Rule is d d f()g() = f()g () + f ()g() Tking indefinie inegrls gives [f()g
FM Applications of Integration 1.Centroid of Area
 FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
2k 1. . And when n is odd number, ) The conclusion is when n is even number, an. ( 1) ( 2 1) ( k 0,1,2 L )
 Scholrs Journl of Engineering d Technology SJET) Sch. J. Eng. Tech., ; A):8-6 Scholrs Acdemic d Scienific Publisher An Inernionl Publisher for Acdemic d Scienific Resources) www.sspublisher.com ISSN -X
Scholrs Journl of Engineering d Technology SJET) Sch. J. Eng. Tech., ; A):8-6 Scholrs Acdemic d Scienific Publisher An Inernionl Publisher for Acdemic d Scienific Resources) www.sspublisher.com ISSN -X
Numerical Approximations to Fractional Problems of the Calculus of Variations and Optimal Control
 Numericl Approximions o Frcionl Problems of he Clculus of Vriions nd Opiml Conrol Shkoor Pooseh, Ricrdo Almeid, Delfim F. M. Torres To cie his version: Shkoor Pooseh, Ricrdo Almeid, Delfim F. M. Torres.
Numericl Approximions o Frcionl Problems of he Clculus of Vriions nd Opiml Conrol Shkoor Pooseh, Ricrdo Almeid, Delfim F. M. Torres To cie his version: Shkoor Pooseh, Ricrdo Almeid, Delfim F. M. Torres.
Temperature Rise of the Earth
 Avilble online www.sciencedirec.com ScienceDirec Procedi - Socil nd Behviorl Scien ce s 88 ( 2013 ) 220 224 Socil nd Behviorl Sciences Symposium, 4 h Inernionl Science, Socil Science, Engineering nd Energy
Avilble online www.sciencedirec.com ScienceDirec Procedi - Socil nd Behviorl Scien ce s 88 ( 2013 ) 220 224 Socil nd Behviorl Sciences Symposium, 4 h Inernionl Science, Socil Science, Engineering nd Energy
A Structural Approach to the Enforcement of Language and Disjunctive Constraints
 A Srucurl Aroch o he Enforcemen of Lnguge nd Disjuncive Consrins Mrin V. Iordche School of Engineering nd Eng. Tech. LeTourneu Universiy Longview, TX 7607-700 Pnos J. Ansklis Dermen of Elecricl Engineering
A Srucurl Aroch o he Enforcemen of Lnguge nd Disjuncive Consrins Mrin V. Iordche School of Engineering nd Eng. Tech. LeTourneu Universiy Longview, TX 7607-700 Pnos J. Ansklis Dermen of Elecricl Engineering
A FINITE-DIFFERENCE SCHEME FOR SOLUTION OF A FRACTIONAL HEAT DIFFUSION-WAVE EQUATION WITHOUT INITIAL CONDITIONS
 Beilev, V. D., e l.: A Finie-Difference Scheme for Soluion of... THERMAL SCIENCE: Yer 5, Vol. 9, No.,. 53-536 53 A FINITE-DIFFERENCE SCHEME FOR SOLUTION OF A FRACTIONAL HEAT DIFFUSION-WAVE EQUATION WITHOUT
Beilev, V. D., e l.: A Finie-Difference Scheme for Soluion of... THERMAL SCIENCE: Yer 5, Vol. 9, No.,. 53-536 53 A FINITE-DIFFERENCE SCHEME FOR SOLUTION OF A FRACTIONAL HEAT DIFFUSION-WAVE EQUATION WITHOUT
Example on p. 157
 Example 2.5.3. Le where BV [, 1] = Example 2.5.3. on p. 157 { g : [, 1] C g() =, g() = g( + ) [, 1), var (g) = sup g( j+1 ) g( j ) he supremum is aken over all he pariions of [, 1] (1) : = < 1 < < n =
Example 2.5.3. Le where BV [, 1] = Example 2.5.3. on p. 157 { g : [, 1] C g() =, g() = g( + ) [, 1), var (g) = sup g( j+1 ) g( j ) he supremum is aken over all he pariions of [, 1] (1) : = < 1 < < n =
Tax Audit and Vertical Externalities
 T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
( ) ( ) ( ) ( ) ( ) ( y )
 8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
SOME HARDY TYPE INEQUALITIES WITH WEIGHTED FUNCTIONS VIA OPIAL TYPE INEQUALITIES
 SOME HARDY TYPE INEQUALITIES WITH WEIGHTED FUNCTIONS VIA OPIAL TYPE INEQUALITIES R. P. AGARWAL, D. O REGAN 2 AND S. H. SAKER 3 Abstrct. In this pper, we will prove severl new ineulities of Hrdy type with
SOME HARDY TYPE INEQUALITIES WITH WEIGHTED FUNCTIONS VIA OPIAL TYPE INEQUALITIES R. P. AGARWAL, D. O REGAN 2 AND S. H. SAKER 3 Abstrct. In this pper, we will prove severl new ineulities of Hrdy type with
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
On asymptotic behavior of composite integers n = pq Yasufumi Hashimoto
 Journal of Mah-for-Indusry Vol1009A-6 45 49 On asymoic behavior of comosie inegers n = q Yasufumi Hashimoo Received on March 1 009 Absrac In his aer we sudy he asymoic behavior of he number of comosie
Journal of Mah-for-Indusry Vol1009A-6 45 49 On asymoic behavior of comosie inegers n = q Yasufumi Hashimoo Received on March 1 009 Absrac In his aer we sudy he asymoic behavior of he number of comosie
A Time Truncated Improved Group Sampling Plans for Rayleigh and Log - Logistic Distributions
 ISSNOnline : 39-8753 ISSN Prin : 347-67 An ISO 397: 7 Cerified Orgnizion Vol. 5, Issue 5, My 6 A Time Trunced Improved Group Smpling Plns for Ryleigh nd og - ogisic Disribuions P.Kvipriy, A.R. Sudmni Rmswmy
ISSNOnline : 39-8753 ISSN Prin : 347-67 An ISO 397: 7 Cerified Orgnizion Vol. 5, Issue 5, My 6 A Time Trunced Improved Group Smpling Plns for Ryleigh nd og - ogisic Disribuions P.Kvipriy, A.R. Sudmni Rmswmy
The Asymptotic Behavior of Nonoscillatory Solutions of Some Nonlinear Dynamic Equations on Time Scales
 Advances in Dynamical Sysems and Applicaions. ISSN 0973-5321 Volume 1 Number 1 (2006, pp. 103 112 c Research India Publicaions hp://www.ripublicaion.com/adsa.hm The Asympoic Behavior of Nonoscillaory Soluions
Advances in Dynamical Sysems and Applicaions. ISSN 0973-5321 Volume 1 Number 1 (2006, pp. 103 112 c Research India Publicaions hp://www.ripublicaion.com/adsa.hm The Asympoic Behavior of Nonoscillaory Soluions
arxiv: v1 [math.gm] 7 Nov 2017
![arxiv: v1 [math.gm] 7 Nov 2017 arxiv: v1 [math.gm] 7 Nov 2017](/thumbs/72/67237961.jpg) A TOUR ON THE MASTER FUNCTION THEOPHILUS AGAMA arxiv:7.0665v [mah.gm] 7 Nov 07 Absrac. In his aer we sudy a funcion defined on naural numbers having eacly wo rime facors. Using his funcion, we esablish
A TOUR ON THE MASTER FUNCTION THEOPHILUS AGAMA arxiv:7.0665v [mah.gm] 7 Nov 07 Absrac. In his aer we sudy a funcion defined on naural numbers having eacly wo rime facors. Using his funcion, we esablish
Yan Sun * 1 Introduction
 Sun Boundry Vlue Problems 22, 22:86 hp://www.boundryvlueproblems.com/conen/22//86 R E S E A R C H Open Access Posiive soluions of Surm-Liouville boundry vlue problems for singulr nonliner second-order
Sun Boundry Vlue Problems 22, 22:86 hp://www.boundryvlueproblems.com/conen/22//86 R E S E A R C H Open Access Posiive soluions of Surm-Liouville boundry vlue problems for singulr nonliner second-order
An Integral Two Space-Variables Condition for Parabolic Equations
 Jornl of Mhemics nd Sisics 8 (): 85-9, ISSN 549-3644 Science Pblicions An Inegrl Two Spce-Vribles Condiion for Prbolic Eqions Mrhone, A.L. nd F. Lkhl Deprmen of Mhemics, Lborory Eqions Differenielles,
Jornl of Mhemics nd Sisics 8 (): 85-9, ISSN 549-3644 Science Pblicions An Inegrl Two Spce-Vribles Condiion for Prbolic Eqions Mrhone, A.L. nd F. Lkhl Deprmen of Mhemics, Lborory Eqions Differenielles,
ASYMPTOTIC BEHAVIOR OF INTERMEDIATE SOLUTIONS OF FOURTH-ORDER NONLINEAR DIFFERENTIAL EQUATIONS WITH REGULARLY VARYING COEFFICIENTS
 Elecronic Journl of Differenil Equions, Vol. 06 06), No. 9, pp. 3. ISSN: 07-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu ASYMPTOTIC BEHAVIOR OF INTERMEDIATE SOLUTIONS OF FOURTH-ORDER NONLINEAR
Elecronic Journl of Differenil Equions, Vol. 06 06), No. 9, pp. 3. ISSN: 07-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu ASYMPTOTIC BEHAVIOR OF INTERMEDIATE SOLUTIONS OF FOURTH-ORDER NONLINEAR
Chapter 2. First Order Scalar Equations
 Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Extension of Hardy Inequality on Weighted Sequence Spaces
 Jourl of Scieces Islic Reublic of Ir 20(2): 59-66 (2009) Uiversiy of ehr ISS 06-04 h://sciecesucir Eesio of Hrdy Iequliy o Weighed Sequece Sces R Lshriour d D Foroui 2 Dere of Mheics Fculy of Mheics Uiversiy
Jourl of Scieces Islic Reublic of Ir 20(2): 59-66 (2009) Uiversiy of ehr ISS 06-04 h://sciecesucir Eesio of Hrdy Iequliy o Weighed Sequece Sces R Lshriour d D Foroui 2 Dere of Mheics Fculy of Mheics Uiversiy
On New Inequalities of Hermite-Hadamard-Fejér Type for Harmonically s-convex Functions via Fractional Integrals
 Krelm en ve Müh. Derg. 6(:879 6 Krelm en ve Mühendili Dergii Jornl home ge: h://fd.en.ed.r eerch Aricle n New Ineliie of HermieHdmrdejér ye for Hrmoniclly Convex ncion vi rcionl Inegrl Keirli İnegrller
Krelm en ve Müh. Derg. 6(:879 6 Krelm en ve Mühendili Dergii Jornl home ge: h://fd.en.ed.r eerch Aricle n New Ineliie of HermieHdmrdejér ye for Hrmoniclly Convex ncion vi rcionl Inegrl Keirli İnegrller
Magnetostatics Bar Magnet. Magnetostatics Oersted s Experiment
 Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
f(t) dt, x > 0, is the best value and it is the norm of the
 MATEMATIQKI VESNIK 66, 1 (214), 19 32 March 214 originalni nauqni rad research aer GENERALIZED HAUSDORFF OPERATORS ON WEIGHTED HERZ SPACES Kuang Jichang Absrac. In his aer, we inroduce new generalized
MATEMATIQKI VESNIK 66, 1 (214), 19 32 March 214 originalni nauqni rad research aer GENERALIZED HAUSDORFF OPERATORS ON WEIGHTED HERZ SPACES Kuang Jichang Absrac. In his aer, we inroduce new generalized
