Journal of Mathematical Inequalities
|
|
|
- Elfreda Welch
- 5 years ago
- Views:
Transcription
1 Journl of Mhemicl Inequliies Wih Comlimens of he Auhor Zgreb, Croi Volume 10, Number 2, June 2016 Mrin J. Bohner nd Smir H. Sker Snek-ou rincile on ime scles JMI
2 JOURNAL OF MATHEMATICAL INEQUALITIES AIMS AND SCOPE Journl of Mhemicl Inequliies (JMI, J. Mh. Inequl.) resens crefully seleced originl reserch ricles from ll res of ure nd lied mhemics, rovided hey re concerned wih mhemicl inequliies. JMI will lso eriodiclly ublish invied survey ricles wih ineresing resuls reing he heory of inequliies, s well s relevn book reviews. JMI is ublished qurerly, in Mrch, June, Seember, nd December. SUBMISSION OF MANUSCRIPTS Auhors re requesed o submi heir ricles elecroniclly s T E X@/L A T E X@files, wih enclosed Adobe Acrob PDF form hrough he rovided web inerfce on journl web ge. The uhor who submied he ricle for ublicion will be denoed s corresonding uhor. He/She mnges ll communicion nd corresondence wih he JMI regrding he ricle, mkes ny revisions, nd reviews nd releses he uhor roofs. Auhors my indice member of he Edioril Bord whom hey consider rorie for he ricle. However, ssignmen o h riculr edior is no ssured. COPYRIGHT The ccence of he ricle uomiclly imlies he coyrigh rnsfer o he JMI. Mnuscris re cceed for review wih he undersnding h he sme work hs no been ublished (exce in he form of n bsrc), h i is no under considerion for ublicion elsewhere, h i will no be submied o noher journl while under review for he JMI, nd h is submission for ublicion hs been roved by ll of he uhors. OPEN ACCESS Journl of Mhemicl Inequliies is ublished s oen ccess journl. All ineresed reders re llowed o view, downlod, rin, nd redisribue ny ricle wihou ying for subscriion. Offrins of ech ricle my be ordered from JMI rior o ublicion. PREPARATION OF MANUSCRIPTS Mnuscris should be wrien in English, using rered journl LTeX syle. The firs ge should conin he ricle ile, uhors nmes (comlee firs nmes nd fmily nmes), comlee ffiliions (nme of insiuion, ddress, ciy, se, nd zi code), e-mil ddresses, roosed running hed (no more hn 40 chrcers), shor bsrc (no more hn 150 words), lis of key words nd hrses, nd he AMS 2010 Mhemics Subjec Clssificion rimry (nd secondry) codes. Avoid bbreviions, mhemicl symbols nd formuls, digrms, nd reference o he ex of he ricle. Figures should be rered in digil form suible for direc reroducion, resoluion of 300 di or higher, nd in EPS, TIFF or JPEG form. Bibliogrhic references should be lised lhbeiclly he end of he ricle, ech numbered by n Arbic number beween squre brckes. The following informion should be rovided for references o journls: nmes of uhors, full ile of he ricle, bbrevied nme of he journl, volume, yer of ublicion, nd rnge of ge numbers. For sndrd bbreviions of journl nmes, he uhors should consul he les Abbreviions of Nmes nd Serils reviewed in Mhemicl Reviews. SOURCE FILE, PROOFS Uon ccence of he ricle, he uhors will be sked o send he reled LTeX source file o he Edioril Office, in ccordnce o he journl syle. In order o ccelere he ublicion rocess, he AMS LTeX ckge is srongly referred. PDF roofs will be sen by e-mil o he corresonding uhor. FORTHCOMING PAPERS Pers cceed nd rered for ublicion will er in he forhcoming secion of Journl Web ge. They re idenicl in form s finl rined ers, exce volume, issue nd ge numbers. JMI is ublished by Publishing House ELEMENT, Zgreb, Croi. All corresondence nd subscriion orders should be ddressed o he Edioril Office: e-mil: jmi@ele-mh.com Journl of Mhemicl Inequliies Edioril Office Menceicev 2, Zgreb, Croi Fx: The conen of his ublicion is indexed in Mhemicl Reviews (MhSciNe), Zenrlbl für Mhemik, Referivny жurnl Memik, Curren Conens, Science Ciion Index Exnded, nd Scous.
3 Journl of Mhemicl Inequliies Volume 10, Number 2 (2016), doi: /jmi SNEAK OUT PRINCIPLE ON TIME SCALES MARTIN J. BOHNER AND SAMIR H. SAKER (Communiced by A. Peerson) Absrc. In his er, we show h he so-clled snek-ou rincile for discree inequliies is vlid lso on generl ime scle. In riculr, we rove some new dynmic inequliies on ime scles which s secil cses conin discree inequliies obined by Benne nd Grosse- Erdmnn. The min resuls lso re used o formule he corresonding coninuous inegrl inequliies, nd hese re essenilly new. The echniques emloyed in his er re elemenry nd rely minly on he ime scles inegrion by rs rule, he ime scles chin rule, he ime scles Hölder inequliy, nd he ime scles Minkowski inequliy. 1. Inroducion In [4], Benne nd Grosse-Erdmnn sudied he roblem of deducing he convergence of one series from h of noher during he course of heir invesigions on Hrdy ye inequliies. In riculr, hey hve considered generl yes of series which cnno be reed by ny of he usul convergence ess (rio es, comrison es, Rbe s es, ec.). Afer hey hd severl successes, hey noiced somehing quie remrkble in subjec s old s his: The emergence of new echniques. They clled hese he five series heorem, he snek-ou rincile nd he heds/ils oion (see [3]). All hree re vlid in considerble generliy nd ll hve significn licions beyond Hrdy s inequliy. Now he following quesion rises: Is i ossible o exend hese echniques o ime scles? In oher words, is i ossible o exend hese echniques o conin corresonding inegrl inequliies nd summion inequliies s secil cses? Our im in his er is o give n ffirmive nswer for he second one which is he snek-ou rincile. The obined resuls will suor he dvice of Hrdy, Lilewood nd Póly [12, ge 11] by giving unificion of he coninuous nd he discree inequliies nd showing h wh goes for sums goes for inegrls nd vise vers. The snek-ou rincile h hs been considered by Benne nd Grosse-Erdmnn [3] ws concerned wih he equivlence of he wo series ( n Ak k) n=1 α x (1.1) k=n Mhemics subjec clssificion (2010): 26A15, 26D10, 26D15, 39A13, 34A40, 34N05. Keywords nd hrses: Coson s inequliy, Hrdy s inequliy, ime scles. c D l,zgreb Per JMI
4 394 M. J. BOHNER AND S. H. SAKER nd n=1 n A α n ( ) x k. k=n In oher words, when is i ossible o snek he erm Ak α ou of he inner sum in (1.1). Benne nd Grosse-Erdmnn, using his rincile, roved severl inequliies of he form n=1 n ( k=n A α k x k) K(α, ) n=1 n A α n ( k=nx k ) nd heir inverses for differen vlues of nd α. Our im in his er is concerned wih he equivlence of he wo ime scles inegrls ( () A (σ(s))x(s)δs) α Δ (1.2) nd ( ()A α (σ(s)) x(s)δs) Δ, where he domin of he unknown funcion is so-clled ime scle T (which is n rbirry nonemy closed subse of he rel numbers R). In oher words, we wn o deermine recisely when i is ossible o snek A α (σ(s)) ouside of he inner inegrl in (1.2). More recisely, we re concerned wih new dynmic inequliies of he form ( ( () A (σ(s))x(s)δs) α Δ K ()A α (σ(s)) x(s)δs) Δ (1.3) nd heir converses on ime scles for differen vlues of nd α, which s secil cses wih T = N conin he discree inequliies obined by Benne nd Grosse- Erdmnn [3, Secion 6] nd cn be lied lso wih T = R o formule he corresonding inegrl inequliies. The resuls lso cn be lied o oher ime scles such s T = hz for h > 0ndT = q N 0 wih q > 1. We include he deils of he roofs since hey rovide sregy which cn be used in oher siuions. For reled dynmic inequliies on ime scles, we refer he reder o [1, 2, 5, 8, 13 17]. This er is orgnizeds follows: In Secion 2, we rovide some uxiliry resuls such s he ime scles inegrion by rs rule, he ime scles chin rule, he ime scles Hölder inequliy, nd he ime scles Minkowski inequliy. Secion 3 feures wo new dynmic inequliies of Coson ye h re needed in he roofs of our min resuls. In Secion 4, we resenourmin resuls, which re hreedynmicinequliies of he ye (1.3) for differen vlues of 1ndα. Firs he cse α 1 is reed (see Theorem 4.1 below), hen he cse 0 α 1 (see Theorem 4.4 below), nd finlly he cse 1/ < α 0 (see Theorem 4.6 below). The corresonding cses when 0 < < 1 re sill oen roblems nd will be considered in he fuure.
5 SNEAK-OUT PRINCIPLE Auxiliry resuls For comleeness, we recll he following conces reled o he noion of ime scles. For more deils of ime scle nlysis, we refer he reder o he wo books by Bohner nd Peerson [6, 7]. A ime scle T is n rbirry nonemy closed subse of he rel numbers R. The cses when T = R nd T = Z reresen he clssicl heories of differenil nd difference clculus. In his er, we ssume h sut = nd define he forwrd jum oeror by σ() := inf{s T : s > }. For ny funcion f : T R, we wrie f σ for f σ.for T, wedefine f Δ () o be he number (if i exiss) wih he roery h given ny ε > 0, here is neighborhood U of wih f (σ()) f (s) f Δ ()(σ() s) ε σ() s for ll s U. In his cse, we sy f Δ () is he (del) derivive of f.if f is (del) differenible ny T,hen f Δ : T R is clled he del derivive of f. Nex, if F : T R is n niderivive of f, i.e., F Δ = f, hen he Cuchy del inegrl of f is defined by f (s)δs := F() F(), where T is fixed. I is known [6, Theorem 1.74] h so-clled rd-coninuous funcions lwys ossess niderivives. EXAMPLE 2.1. Noe h if T = R,hen σ()=, f Δ = f, nd for,b R wih < b. IfT = Z, hen b b f ()Δ = f ()d σ()= + 1, f Δ = Δ f, nd b for,b Z wih < b. IfT = hz wih h > 0, hen b 1 f ()Δ = = f () σ()= + h nd b f ()Δ = h b h h k=0 f ( + kh) for,b hz. IfT = q N 0 wih q > 1, hen σ()=q nd b log q (b) 1 f ()Δ =(q 1) k=log q () q k f (q k ) for,b q N 0.
6 396 M. J. BOHNER AND S. H. SAKER Now we collec hose known ime scles resuls h will be used frequenly hroughou his er. The roduc nd quoien rules [6, Theorem 1.20] for he derivive of he roduc fg nd he quoien f /g (wih g() 0forll T) of wo differenible funcions f,g : T R se ( fg) Δ = f Δ g + f σ g Δ = fg Δ + f Δ g σ nd ( ) f Δ = f Δ g fg Δ g gg σ. (2.1) The chin rule [6, Theorem 1.90] for he γ -h ower (γ R) of differenible funcion f : T R sys (see [6, Theorem 1.90]) 1 ( f γ ) Δ = γ f Δ (hf σ +(1 h) f ) γ 1 dh. (2.2) 0 The inegrion by rs formul [6, Theorem 1.77] for wo differenible funcions f,g : T R is given (,b T) by b f ()g Δ ()Δ = f ()g() b b f Δ ()g σ ()Δ. (2.3) Hölder s inequliy [6, Theorem 6.13] ses h wo rd-coninuous funcions f,g : T R sisfy b { b { 1 b q f ()g() Δ f () Δ g() Δ} q, (2.4) where > 1, q = /( 1),nd,b T. Minkowski s inequliy [6, Theorem 6.16] ssers h hree rd-coninuous funcions f,g,h : T R sisfy { b { b { 1 b h() f ()+g() Δ h() f () Δ + h() g() Δ}, (2.5) where > 1nd,b T. Inequliies (2.6)nd(2.7) below re simle consequences of he chin rule (2.2), bu for convenience of furher reference, we now se hese four imorn inequliies (which re subsiues for he ower rule from differenil clculus) in he following lemm, sulemened by wo new inequliies which re, however, merely simle consequences of he roduc rule (2.1). LEMMA 2.2. Suose f : T R is differenible nd osiive. Le γ R. If f Δ is eiher lwys osiive or lwys negive, hen γ f Δ ( f γ 1) σ ( f γ ) Δ γ f Δ f γ 1 if 0 γ 1 (2.6) nd γ f Δ f γ 1 ( f γ ) Δ γ f Δ ( f γ 1) σ if γ 1. (2.7)
7 SNEAK-OUT PRINCIPLE 397 If f Δ is lwys osiive, hen nd ( f γ ) Δ f Δ ( f γ 1) σ ( f γ ) Δ f Δ ( f γ 1) σ if 0 γ 1 (2.8) if γ 1. (2.9) Proof. Inequliies (2.6)nd(2.7) follow direcly from (2.2). Nex, if f is incresing nd if 0 γ 1, hen f γ 1 is decresing nd hus ( f γ 1) Δ < 0soh ( f γ ) Δ = ( ff γ 1) Δ (2.1) = f Δ ( f γ 1) σ + f ( f γ 1 ) Δ. This shows (2.8), nd (2.9) follows similrly. 3. Dynmic inequliies of Coson ye In his secion, we rove wo new dynmic inequliies of Coson ye (see [9, 10] for he originl Coson inequliies). These will be used in he roofs of our min resuls in he nex secion. Throughou, we re using he following ssumions: sut =, T, : T (0, ) is rd-coninuous, A() := (3.1) (s)δs, T. THEOREM 3.1. Assume (3.1). Suose ϕ : T R is such h (s) Φ() := A(σ(s)) ϕ(s)δs, T is well defined. Le k 1. Then ()Φ k ()Δ k k ()ϕ k ()Δ. (3.2) Proof. We use inegrion by rs (2.3), he lef r of he inequliy (2.7) wih f = Φ nd γ = k, ndhölder s inequliy (2.4) wih = k nd q = k/(k 1) (unless k = 1 in which cse (2.4) is no needed) o obin ()Φ k ()Δ = (2.3) A Δ ()Φ k ()Δ = A()Φ k () = (2.7) A(σ()) ( A(σ()) Φ k) Δ ()Δ ( Φ k) Δ ()Δ A(σ())kΦ Δ ()Φ k 1 ()Δ
8 398 M. J. BOHNER AND S. H. SAKER = k ()ϕ()φ k 1 ()Δ = k 0 [ { (2.4) k 1 k ()ϕ() ][ k 1 k ] ()Φ k 1 () Δ [ ] { 1 k k [ k ()ϕ() Δ { { = k ()ϕ k k ()Δ k 1 k 1 ()Φ k k ()Δ. ] k } k 1 ()Φ k 1 () k 1 k Δ Dividing he enire inequliy by he righ-hnd fcor of he ls exression nd hen rising he resuling inequliy o he k-h owerconfirms he vlidiy of (3.2). REMARK 3.2. I is worh o menion here h our echnique of he roof of Theorem 3.1 is differen from he echnique due o Coson o rove he discree form of (3.2). In riculr, he followed he echnique due o Ellio [11] h hs been used o rove he Hrdy inequliy. THEOREM 3.3. Assume (3.1). Suose ϕ : T R is such h Φ() := (s)ϕ(s)δs, T is well defined. Le k 1 nd 0 c < 1. Then ( ) () k k A c (σ()) Φk ()Δ ()A k c (σ())ϕ k ()Δ. (3.3) 1 c Proof. Firs we define n uxiliry funcion à : T R by (s) Ã() := A c Δs, T. (σ(s)) Noe h he lef r of he inequliy (2.6) wih f = A nd γ = 1 c imlies σ() Ã(σ()) = ( (s) σ() A 1 c ) Δ (s) A c (σ(s)) Δs 1 c Δs = A1 c (σ()). (3.4) 1 c Now we use inegrion by rs (2.3), he lef r of he inequliy (2.7) wih f = Φ nd γ = k, (3.4), nd Hölder s inequliy (2.4) wih = k nd q = k/(k 1) (unless
9 SNEAK-OUT PRINCIPLE 399 k = 1 in which cse (2.4) is no needed) o obin () A c (σ()) Φk ()Δ = Ã Δ ()Φ k ()Δ (2.3) = Ã()Φ k () ( Ã(σ()) Φ k) Δ ()Δ ( = Ã(σ()) Φ k) Δ ()Δ (3.4) (2.7) = k 1 c = k 1 c (2.4) A 1 c (σ()) kφ Δ ()Φ k 1 ()Δ 1 c ()A 1 c (σ())ϕ()φ k 1 ()Δ [ ] [ 1 k ()A 1 c k (σ())ϕ() k { 1 c [ 1 k ()A 1 c k (σ())ϕ() ] k Δ k [ k 1 k () A c(k 1) k (σ()) Φ k 1 () k 1 k () A c(k 1) k (σ()) ] k k 1 Δ k 1 k ] Φ k 1 () Δ = k { { ()A k c (σ())ϕ k k } () 1 1 k ()Δ 1 c A c (σ()) Φk ()Δ. Dividing he enire inequliy by he righ-hnd fcor of he ls exression nd hen rising he resuling inequliy o he k-h owerconfirms he vlidiy of (3.3). 4. Dynmic snek-ou inequliies In his secion, we rove he min resuls of his er. We lso ly hese resuls o he secil ime scles T = R nd T = Z. The resuls for T = Z re known (see [3]) while he resuls for T = R re new. Throughou his secion, we le 1. For he cses α 1, 0 α 1, nd 1/ < α 0, we resen hree disinc inequliies. In ddiion o (3.1), for given vlueof α, we requirehe ssumions x : T (0, ) is rd-coninuous, y() := x(s)δs nd Ψ() := A α (σ(s))x(s)δs, T (4.1) re well defined. THEOREM 4.1. Le 1 nd α 1. Assume (3.1) nd (4.1). Then ()Ψ ()Δ (1 + α ) ()A α (σ())y ()Δ. (4.2)
10 400 M. J. BOHNER AND S. H. SAKER Proof. We use inegrion by rs (2.3) nd he righ r of he inequliy (2.7) wih f = A nd γ = α o obin Ψ() = A α (σ(s))y Δ (s)δs { (2.3) = A α (s)y(s) = A α ()y()+ (2.7) A α ()y()+ A α (σ())y()+α (A α ) Δ (s)y(s)δs (A α ) Δ (s)y(s)δs } αa Δ (s)a α 1 (σ(s))y(s)δs (s)a α 1 (σ(s))y(s)δs, where we hve uilized A A σ in he ls inequliy. Now we use Minkowski s inequliy (2.5) ndtheorem3.1 wih k = nd ϕ =(A α ) σ y o find he esime { ()Ψ ()Δ (2.5) = (3.2) { { { { [ () A α (σ())y()+α (s)a (σ(s))y(s)δs] α 1 Δ ()[A α (σ())y()] { Δ + () ()A α (σ())y { [ ()Δ +α () { ()A α (σ())y ()Δ + α { = (1 + α ) ()A α (σ())y ()Δ. [ α (s)a (σ(s))y(s)δs] α 1 Δ ] (s) A(σ(s)) Aα (σ(s))y(s)δs Δ ()A α (σ())y ()Δ Rising his inequliy o he -h ower confirms he vlidiy of (4.2). EXAMPLE 4.2. Le T = Z nd = 1. As secil cse of Theorem 4.1,wehve from (4.2) he inequliy ( ( (n) A α (k + 1)x(k)) (1 + α ) (n)a α (n + 1) x(n)), (4.3) n=1 k=n n=1 k=n where n 1 A(n)= (k), n N. k=1 Noe h (4.3) is he discree inequliy [3, Theorem 8] due o Benne nd Grosse- Erdmnn.
11 SNEAK-OUT PRINCIPLE 401 EXAMPLE 4.3. Le T = R. As secil cse of Theorem 4.1, we hve from (4.2) he inequliy ( ) ( () A α (s)x(s)ds d (1 + α ) ()A α () x(s)ds) d, (4.4) where A()= (s)ds, R. Noe h (4.4) is new inequliy. THEOREM 4.4. Le 1 nd 0 α 1. Assume (3.1) nd (4.1). Then ()Ψ ()Δ (1 + ) ()A α (σ())y ()Δ. (4.5) Proof. In his cse, we cnno use he righ r of he inequliy (2.7) wih f = A nd γ = α s we did in he roof of Theorem 4.1. However, we cn use inequliy (2.8) wih f = A nd γ = α nd follow he exc sme ses s in he roof of Theorem 4.1 o obin (4.5). REMARK 4.5. For T = Z, Theorem 4.4 reduces o he corresonding discree inequliy by Benne nd Grosse-Erdmnn [3, Theorem 9]. For T = R, (4.5) is new. THEOREM 4.6. Le 1 nd 1/ < α 0. Assume (3.1) nd (4.1). Then ( ) 1 + α ()Ψ ()Δ ()A α (σ())y ()Δ. (4.6) 1 + α + Proof. We use inegrion by rs (2.3) nd he inequliy (2.8) wih f = A nd γ = α o obin y() = A α (σ(s))ψ Δ (s)δs { (2.3) = A α (s)ψ(s) ( A α ) } Δ (s)ψ(s)δs = A α ( ()Ψ()+ A α ) Δ (s)ψ(s)δs (2.8) A α ()Ψ()+ A α (σ())ψ()+ A Δ (s)a α 1 (σ(s))ψ(s)δs (s)a α 1 (σ(s))ψ(s)δs, where we hve uilized A A σ in he ls inequliy. Now we use Minkowski s inequliy (2.5) ndtheorem3.3 wih k =, c = α, ndϕ = ( A α 1) σ Ψ o find
12 402 M. J. BOHNER AND S. H. SAKER he esime { ()A α (σ())y ()Δ (2.5) { [ ()A α (σ()) A α (σ())ψ()+ (s)a (σ(s))ψ(s)δs] α 1 Δ { ()A α (σ()) [ A α (σ())ψ() ] Δ { + [ ()A α (σ()) (s)a (σ(s))ψ(s)δs] α 1 Δ { [ + { = ()Ψ () ()Δ A α (σ()) { (3.3) {( ) ()Ψ ()Δ + ()Ψ ()Δ 1 + α ( ){ 1 + α + = ()Ψ ()Δ. 1 + α Rising his inequliy o he -h ower confirms he vlidiy of (4.6). (s)a (σ(s))ψ(s)δs] α 1 Δ EXAMPLE 4.7. Le T = Z nd = 1. As secil cse of Theorem 4.6,wehve from (4.6) he inequliy ( ( 1 + α ( (n) A α (k + 1)x(k)) (n)a n=1 k=n 1 + α + ) α (n + 1) x(n)), n=1 k=n (4.7) where n 1 A(n)= (k), n N. k=1 Noe h (4.7) is he discree inequliy [3, Theorem 10] due o Benne nd Grosse- Erdmnn. EXAMPLE 4.8. Le T = R. As secil cse of Theorem 4.6, we hve from (4.6) he inequliy ( ( ) 1 + α ( () A (s)x(s)ds) α d ()A α () x(s)ds) d, 1 + α + (4.8) where A()= (s)ds, R. Noe h (4.8) is new inequliy.
13 SNEAK-OUT PRINCIPLE 403 REFERENCES [1] R. P. AGARWAL, M. BOHNER, AND S. H. SAKER, Dynmic Lilewood-ye inequliies, Proc. Amer. Mh. Soc., 143 (2): , [2] M. R. S. AMMI AND D. F. M. TORRES, Hölder s nd Hrdy s wo dimensionl dimond-lh inequliies on ime scles, An. Univ. Criov Ser. M. Inform., 37 (1): 1 11, [3] G. BENNETT AND K.-G. GROSSE-ERDMANN, On series of osiive erms, Houson J. Mh., 31 (2): , [4] G. BENNETT AND K.-G. GROSSE-ERDMANN, Weighed Hrdy inequliies for decresing sequences nd funcions, Mh. Ann., 334 (3): , [5] M. BOHNER, R. A. FERREIRA, AND D. F. M. TORRES, Inegrl inequliies nd heir licions o he clculus of vriions on ime scles, Mh. Inequl. Al., 13 (3): , [6] M. BOHNER AND A. PETERSON, Dynmic Equions on Time Scles: An Inroducion wih Alicions, Birkhäuser, Boson, [7] M. BOHNER AND A. PETERSON, Advnces in Dynmic Equions on Time Scles, Birkhäuser, Boson, [8] M. BOHNER AND A. ZAFER, Lyunov ye inequliies for lnr liner Hmilonin sysems on ime scles, Al. Anl. Discree Mh., 7 (1): , [9] E. T. COPSON, Noe on series of osiive erms, J. London Mh. Soc., S1 2 (1): 9 12, [10] E. T. COPSON, Noe on series of osiive erms, J. London Mh. Soc., S1 3 (1): 49 51, [11] E. B. ELLIOTT, A simle exnsion of some recenly roved fcs s o convergency, J. London Mh. Soc., S1 1 (1): 93 96, [12] G. H. HARDY, J. E. LITTLEWOOD, AND G. PÓLYA, Inequliies, Cmbridge Universiy Press, Cmbridge, [13] U. M. ÖZKAN AND H. YILDIRIM, Hrdy-Kno-ye inequliies on ime scles, Dynm. Sysems Al., 17 (3 4): , [14] S. H. SAKER, Hrdy Leindler ye inequliies on ime scles, Al. Mh. Inf. Sci., 8 (6): , [15] S. H. SAKER AND J. GRAEF, A new clss of dynmic inequliies of Hrdy s ye on ime scles, Dynm. Sysems Al., 23 (1): 83 99, [16] S. H. SAKER, D. O REGAN, AND R. AGARWAL, Generlized Hrdy, Coson, Leindler nd Benne inequliies on ime scles, Mh. Nchr., 287 (5 6): , [17] A. TUNA AND S. KÜTÜKÇÜ, Some inegrl inequliies on ime scles, Al. Mh. Mech. (English Ed.), 29 (1): 23 29, (Received Ocober 21, 2014) Mrin J. Bohner Missouri Universiy of Science nd Technology Dermen of Mhemics nd Sisics Roll, Missouri , USA e-mil: bohner@ms.edu Smir H. Sker Mnsour Universiy, Dermen of Mhemics Fculy of Science Mnsour, Egy e-mil: shsker@mns.edu.eg
14 Journl of Mhemicl Inequliies
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Green s Functions and Comparison Theorems for Differential Equations on Measure Chains
 Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
1. Introduction. 1 b b
 Journl of Mhemicl Inequliies Volume, Number 3 (007), 45 436 SOME IMPROVEMENTS OF GRÜSS TYPE INEQUALITY N. ELEZOVIĆ, LJ. MARANGUNIĆ AND J. PEČARIĆ (communiced b A. Čižmešij) Absrc. In his pper some inequliies
Journl of Mhemicl Inequliies Volume, Number 3 (007), 45 436 SOME IMPROVEMENTS OF GRÜSS TYPE INEQUALITY N. ELEZOVIĆ, LJ. MARANGUNIĆ AND J. PEČARIĆ (communiced b A. Čižmešij) Absrc. In his pper some inequliies
Weighted Hardy-Type Inequalities on Time Scales with Applications
 Medierr J Mh DOI 0007/s00009-04-054-y c Sringer Bsel 204 Weighed Hrdy-Tye Ineuliies on Time Scles wih Alicions S H Sker, R R Mhmoud nd A Peerson Absrc In his er, we will rove some new dynmic Hrdy-ye ineuliies
Medierr J Mh DOI 0007/s00009-04-054-y c Sringer Bsel 204 Weighed Hrdy-Tye Ineuliies on Time Scles wih Alicions S H Sker, R R Mhmoud nd A Peerson Absrc In his er, we will rove some new dynmic Hrdy-ye ineuliies
How to Prove the Riemann Hypothesis Author: Fayez Fok Al Adeh.
 How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
How to prove the Riemann Hypothesis
 Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Hermite-Hadamard-Fejér type inequalities for convex functions via fractional integrals
 Sud. Univ. Beş-Bolyi Mh. 6(5, No. 3, 355 366 Hermie-Hdmrd-Fejér ype inequliies for convex funcions vi frcionl inegrls İmd İşcn Asrc. In his pper, firsly we hve eslished Hermie Hdmrd-Fejér inequliy for
Sud. Univ. Beş-Bolyi Mh. 6(5, No. 3, 355 366 Hermie-Hdmrd-Fejér ype inequliies for convex funcions vi frcionl inegrls İmd İşcn Asrc. In his pper, firsly we hve eslished Hermie Hdmrd-Fejér inequliy for
On The Hermite- Hadamard-Fejér Type Integral Inequality for Convex Function
 Turkish Journl o Anlysis nd Numer Theory, 4, Vol., No. 3, 85-89 Aville online h://us.scieu.com/jn//3/6 Science nd Educion Pulishing DOI:.69/jn--3-6 On The Hermie- Hdmrd-Fejér Tye Inegrl Ineuliy or Convex
Turkish Journl o Anlysis nd Numer Theory, 4, Vol., No. 3, 85-89 Aville online h://us.scieu.com/jn//3/6 Science nd Educion Pulishing DOI:.69/jn--3-6 On The Hermie- Hdmrd-Fejér Tye Inegrl Ineuliy or Convex
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
Convergence of Singular Integral Operators in Weighted Lebesgue Spaces
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
Refinements to Hadamard s Inequality for Log-Convex Functions
 Alied Mhemics 899-93 doi:436/m7 Pulished Online Jul (h://wwwscirporg/journl/m) Refinemens o Hdmrd s Ineuli for Log-Convex Funcions Asrc Wdllh T Sulimn Dermen of Comuer Engineering College of Engineering
Alied Mhemics 899-93 doi:436/m7 Pulished Online Jul (h://wwwscirporg/journl/m) Refinemens o Hdmrd s Ineuli for Log-Convex Funcions Asrc Wdllh T Sulimn Dermen of Comuer Engineering College of Engineering
ON THE OSTROWSKI-GRÜSS TYPE INEQUALITY FOR TWICE DIFFERENTIABLE FUNCTIONS
 Hceepe Journl of Mhemics nd Sisics Volume 45) 0), 65 655 ON THE OSTROWSKI-GRÜSS TYPE INEQUALITY FOR TWICE DIFFERENTIABLE FUNCTIONS M Emin Özdemir, Ahme Ock Akdemir nd Erhn Se Received 6:06:0 : Acceped
Hceepe Journl of Mhemics nd Sisics Volume 45) 0), 65 655 ON THE OSTROWSKI-GRÜSS TYPE INEQUALITY FOR TWICE DIFFERENTIABLE FUNCTIONS M Emin Özdemir, Ahme Ock Akdemir nd Erhn Se Received 6:06:0 : Acceped
FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m)
![FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m) FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m)](/thumbs/75/72845579.jpg) Univ. Beogrd. Pul. Elekroehn. Fk. Ser. M. 8 (997), 79{83 FUTHE GENEALIZATIONS OF INEQUALITIES FO AN INTEGAL QI Feng Using he Tylor's formul we prove wo inegrl inequliies, h generlize K. S. K. Iyengr's
Univ. Beogrd. Pul. Elekroehn. Fk. Ser. M. 8 (997), 79{83 FUTHE GENEALIZATIONS OF INEQUALITIES FO AN INTEGAL QI Feng Using he Tylor's formul we prove wo inegrl inequliies, h generlize K. S. K. Iyengr's
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
Mathematics 805 Final Examination Answers
 . 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
. 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE BOUNDARY-VALUE PROBLEM
 Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS
 - TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
- TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
 Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Communications inmathematicalanalysis
 Communicions inmhemicanysis Voume 11, Number 2,. 23 35 (211) ISSN 1938-9787 www.mh-res-ub.org/cm GRONWALL-LIKE INEQUALITIES ON TIME SCALES WITH APPLICATIONS ELVAN AKIN-BOHNER Dermen of Mhemics nd Sisics
Communicions inmhemicanysis Voume 11, Number 2,. 23 35 (211) ISSN 1938-9787 www.mh-res-ub.org/cm GRONWALL-LIKE INEQUALITIES ON TIME SCALES WITH APPLICATIONS ELVAN AKIN-BOHNER Dermen of Mhemics nd Sisics
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR IAN KNOWLES
 A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).
![INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q). INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).](/thumbs/78/77677920.jpg) INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
( ) ( ) ( ) ( ) ( ) ( y )
 8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Solutions to Problems from Chapter 2
 Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Solutions of half-linear differential equations in the classes Gamma and Pi
 Soluions of hlf-liner differenil equions in he clsses Gmm nd Pi Pvel Řehák Insiue of Mhemics, Acdemy of Sciences CR CZ-6662 Brno, Czech Reublic; Fculy of Educion, Msryk Universiy CZ-60300 Brno, Czech Reublic
Soluions of hlf-liner differenil equions in he clsses Gmm nd Pi Pvel Řehák Insiue of Mhemics, Acdemy of Sciences CR CZ-6662 Brno, Czech Reublic; Fculy of Educion, Msryk Universiy CZ-60300 Brno, Czech Reublic
Chapter Direct Method of Interpolation
 Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples.
 Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
3. Renewal Limit Theorems
 Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
MTH 146 Class 11 Notes
 8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
REAL ANALYSIS I HOMEWORK 3. Chapter 1
 REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
Hermite-Hadamard and Simpson Type Inequalities for Differentiable Quasi-Geometrically Convex Functions
 Trkish Jornl o Anlysis nd Nmer Theory, 4, Vol, No, 4-46 Aville online h://ssciecom/jn/// Science nd Edcion Plishing DOI:69/jn--- Hermie-Hdmrd nd Simson Tye Ineliies or Dierenile Qsi-Geomericlly Convex
Trkish Jornl o Anlysis nd Nmer Theory, 4, Vol, No, 4-46 Aville online h://ssciecom/jn/// Science nd Edcion Plishing DOI:69/jn--- Hermie-Hdmrd nd Simson Tye Ineliies or Dierenile Qsi-Geomericlly Convex
Application on Inner Product Space with. Fixed Point Theorem in Probabilistic
 Journl of Applied Mhemics & Bioinformics, vol.2, no.2, 2012, 1-10 ISSN: 1792-6602 prin, 1792-6939 online Scienpress Ld, 2012 Applicion on Inner Produc Spce wih Fixed Poin Theorem in Probbilisic Rjesh Shrivsv
Journl of Applied Mhemics & Bioinformics, vol.2, no.2, 2012, 1-10 ISSN: 1792-6602 prin, 1792-6939 online Scienpress Ld, 2012 Applicion on Inner Produc Spce wih Fixed Poin Theorem in Probbilisic Rjesh Shrivsv
ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX
 Journl of Applied Mhemics, Sisics nd Informics JAMSI), 9 ), No. ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX MEHMET ZEKI SARIKAYA, ERHAN. SET
Journl of Applied Mhemics, Sisics nd Informics JAMSI), 9 ), No. ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX MEHMET ZEKI SARIKAYA, ERHAN. SET
Asymptotic relationship between trajectories of nominal and uncertain nonlinear systems on time scales
 Asympoic relionship beween rjecories of nominl nd uncerin nonliner sysems on ime scles Fim Zohr Tousser 1,2, Michel Defoor 1, Boudekhil Chfi 2 nd Mohmed Djemï 1 Absrc This pper sudies he relionship beween
Asympoic relionship beween rjecories of nominl nd uncerin nonliner sysems on ime scles Fim Zohr Tousser 1,2, Michel Defoor 1, Boudekhil Chfi 2 nd Mohmed Djemï 1 Absrc This pper sudies he relionship beween
CALDERON S REPRODUCING FORMULA FOR DUNKL CONVOLUTION
 Avilble online hp://scik.org Eng. Mh. Le. 15, 15:4 ISSN: 49-9337 CALDERON S REPRODUCING FORMULA FOR DUNKL CONVOLUTION PANDEY, C. P. 1, RAKESH MOHAN AND BHAIRAW NATH TRIPATHI 3 1 Deprmen o Mhemics, Ajy
Avilble online hp://scik.org Eng. Mh. Le. 15, 15:4 ISSN: 49-9337 CALDERON S REPRODUCING FORMULA FOR DUNKL CONVOLUTION PANDEY, C. P. 1, RAKESH MOHAN AND BHAIRAW NATH TRIPATHI 3 1 Deprmen o Mhemics, Ajy
Journal of Mathematical Analysis and Applications. Two normality criteria and the converse of the Bloch principle
 J. Mh. Anl. Appl. 353 009) 43 48 Conens liss vilble ScienceDirec Journl of Mhemicl Anlysis nd Applicions www.elsevier.com/loce/jm Two normliy crieri nd he converse of he Bloch principle K.S. Chrk, J. Rieppo
J. Mh. Anl. Appl. 353 009) 43 48 Conens liss vilble ScienceDirec Journl of Mhemicl Anlysis nd Applicions www.elsevier.com/loce/jm Two normliy crieri nd he converse of he Bloch principle K.S. Chrk, J. Rieppo
On Hadamard and Fejér-Hadamard inequalities for Caputo k-fractional derivatives
 In J Nonliner Anl Appl 9 8 No, 69-8 ISSN: 8-68 elecronic hp://dxdoiorg/75/ijn8745 On Hdmrd nd Fejér-Hdmrd inequliies for Cpuo -frcionl derivives Ghulm Frid, Anum Jved Deprmen of Mhemics, COMSATS Universiy
In J Nonliner Anl Appl 9 8 No, 69-8 ISSN: 8-68 elecronic hp://dxdoiorg/75/ijn8745 On Hdmrd nd Fejér-Hdmrd inequliies for Cpuo -frcionl derivives Ghulm Frid, Anum Jved Deprmen of Mhemics, COMSATS Universiy
A General Dynamic Inequality of Opial Type
 Appl Mth Inf Sci No 3-5 (26) Applied Mthemtics & Informtion Sciences An Interntionl Journl http://dxdoiorg/2785/mis/bos7-mis A Generl Dynmic Inequlity of Opil Type Rvi Agrwl Mrtin Bohner 2 Donl O Regn
Appl Mth Inf Sci No 3-5 (26) Applied Mthemtics & Informtion Sciences An Interntionl Journl http://dxdoiorg/2785/mis/bos7-mis A Generl Dynmic Inequlity of Opil Type Rvi Agrwl Mrtin Bohner 2 Donl O Regn
Question Details Int Vocab 1 [ ] Question Details Int Vocab 2 [ ]
![Question Details Int Vocab 1 [ ] Question Details Int Vocab 2 [ ] Question Details Int Vocab 1 [ ] Question Details Int Vocab 2 [ ]](/thumbs/92/109283538.jpg) /3/5 Assignmen Previewer 3 Bsic: Definie Inegrls (67795) Due: Wed Apr 5 5 9: AM MDT Quesion 3 5 6 7 8 9 3 5 6 7 8 9 3 5 6 Insrucions Red ody's Noes nd Lerning Gols. Quesion Deils In Vocb [37897] The chnge
/3/5 Assignmen Previewer 3 Bsic: Definie Inegrls (67795) Due: Wed Apr 5 5 9: AM MDT Quesion 3 5 6 7 8 9 3 5 6 7 8 9 3 5 6 Insrucions Red ody's Noes nd Lerning Gols. Quesion Deils In Vocb [37897] The chnge
The Asymptotic Behavior of Nonoscillatory Solutions of Some Nonlinear Dynamic Equations on Time Scales
 Advances in Dynamical Sysems and Applicaions. ISSN 0973-5321 Volume 1 Number 1 (2006, pp. 103 112 c Research India Publicaions hp://www.ripublicaion.com/adsa.hm The Asympoic Behavior of Nonoscillaory Soluions
Advances in Dynamical Sysems and Applicaions. ISSN 0973-5321 Volume 1 Number 1 (2006, pp. 103 112 c Research India Publicaions hp://www.ripublicaion.com/adsa.hm The Asympoic Behavior of Nonoscillaory Soluions
Procedia Computer Science
 Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
Average & instantaneous velocity and acceleration Motion with constant acceleration
 Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
C 0 Approximation on the Spatially Homogeneous Boltzmann Equation for Maxwellian Molecules*
 Alied Mhemics,,, 54-59 doi:.46/m..666 Published Online December (h://www.scip.org/journl/m) C Aroximion on he Silly Homogeneous Bolzmnn Equion or Mxwellin Molecules Absrc Minling Zheng School o Science,
Alied Mhemics,,, 54-59 doi:.46/m..666 Published Online December (h://www.scip.org/journl/m) C Aroximion on he Silly Homogeneous Bolzmnn Equion or Mxwellin Molecules Absrc Minling Zheng School o Science,
14. The fundamental theorem of the calculus
 4. The funmenl heorem of he clculus V 20 00 80 60 40 20 0 0 0.2 0.4 0.6 0.8 v 400 200 0 0 0.2 0.5 0.8 200 400 Figure : () Venriculr volume for subjecs wih cpciies C = 24 ml, C = 20 ml, C = 2 ml n (b) he
4. The funmenl heorem of he clculus V 20 00 80 60 40 20 0 0 0.2 0.4 0.6 0.8 v 400 200 0 0 0.2 0.5 0.8 200 400 Figure : () Venriculr volume for subjecs wih cpciies C = 24 ml, C = 20 ml, C = 2 ml n (b) he
MATH 124 AND 125 FINAL EXAM REVIEW PACKET (Revised spring 2008)
 MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
A Simple Method to Solve Quartic Equations. Key words: Polynomials, Quartics, Equations of the Fourth Degree INTRODUCTION
 Ausrlin Journl of Bsic nd Applied Sciences, 6(6): -6, 0 ISSN 99-878 A Simple Mehod o Solve Quric Equions Amir Fhi, Poo Mobdersn, Rhim Fhi Deprmen of Elecricl Engineering, Urmi brnch, Islmic Ad Universi,
Ausrlin Journl of Bsic nd Applied Sciences, 6(6): -6, 0 ISSN 99-878 A Simple Mehod o Solve Quric Equions Amir Fhi, Poo Mobdersn, Rhim Fhi Deprmen of Elecricl Engineering, Urmi brnch, Islmic Ad Universi,
Some Inequalities variations on a common theme Lecture I, UL 2007
 Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
PHYSICS 1210 Exam 1 University of Wyoming 14 February points
 PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
Power Transformations and Unit Mean and Constant Variance Assumptions of the Multiplicative Error Model: The Generalized Gamma Distribution
 Briish Journl of Mhemics & Comuer Science (): 88-06, 0 SCIENCEDOMAIN inernionl www.sciencedomin.org Power Trnsformions nd Uni Men nd Consn Vrince Assumions of he Mulilicive Error Model: The Generlized
Briish Journl of Mhemics & Comuer Science (): 88-06, 0 SCIENCEDOMAIN inernionl www.sciencedomin.org Power Trnsformions nd Uni Men nd Consn Vrince Assumions of he Mulilicive Error Model: The Generlized
Oscillation of an Euler Cauchy Dynamic Equation S. Huff, G. Olumolode, N. Pennington, and A. Peterson
 PROCEEDINGS OF THE FOURTH INTERNATIONAL CONFERENCE ON DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS May 4 7, 00, Wilmingon, NC, USA pp 0 Oscillaion of an Euler Cauchy Dynamic Equaion S Huff, G Olumolode,
PROCEEDINGS OF THE FOURTH INTERNATIONAL CONFERENCE ON DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS May 4 7, 00, Wilmingon, NC, USA pp 0 Oscillaion of an Euler Cauchy Dynamic Equaion S Huff, G Olumolode,
Probability, Estimators, and Stationarity
 Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
Temperature Rise of the Earth
 Avilble online www.sciencedirec.com ScienceDirec Procedi - Socil nd Behviorl Scien ce s 88 ( 2013 ) 220 224 Socil nd Behviorl Sciences Symposium, 4 h Inernionl Science, Socil Science, Engineering nd Energy
Avilble online www.sciencedirec.com ScienceDirec Procedi - Socil nd Behviorl Scien ce s 88 ( 2013 ) 220 224 Socil nd Behviorl Sciences Symposium, 4 h Inernionl Science, Socil Science, Engineering nd Energy
HUI-HSIUNG KUO, ANUWAT SAE-TANG, AND BENEDYKT SZOZDA
 Communicions on Sochsic Anlysis Vol 6, No 4 2012 603-614 Serils Publicions wwwserilspublicionscom THE ITÔ FORMULA FOR A NEW STOCHASTIC INTEGRAL HUI-HSIUNG KUO, ANUWAT SAE-TANG, AND BENEDYKT SZOZDA Absrc
Communicions on Sochsic Anlysis Vol 6, No 4 2012 603-614 Serils Publicions wwwserilspublicionscom THE ITÔ FORMULA FOR A NEW STOCHASTIC INTEGRAL HUI-HSIUNG KUO, ANUWAT SAE-TANG, AND BENEDYKT SZOZDA Absrc
Research Article New General Integral Inequalities for Lipschitzian Functions via Hadamard Fractional Integrals
 Hindwi Pulishing orporion Inernionl Journl of Anlysis, Aricle ID 35394, 8 pges hp://d.doi.org/0.55/04/35394 Reserch Aricle New Generl Inegrl Inequliies for Lipschizin Funcions vi Hdmrd Frcionl Inegrls
Hindwi Pulishing orporion Inernionl Journl of Anlysis, Aricle ID 35394, 8 pges hp://d.doi.org/0.55/04/35394 Reserch Aricle New Generl Inegrl Inequliies for Lipschizin Funcions vi Hdmrd Frcionl Inegrls
P441 Analytical Mechanics - I. Coupled Oscillators. c Alex R. Dzierba
 Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
A Structural Approach to the Enforcement of Language and Disjunctive Constraints
 A Srucurl Aroch o he Enforcemen of Lnguge nd Disjuncive Consrins Mrin V. Iordche School of Engineering nd Eng. Tech. LeTourneu Universiy Longview, TX 7607-700 Pnos J. Ansklis Dermen of Elecricl Engineering
A Srucurl Aroch o he Enforcemen of Lnguge nd Disjuncive Consrins Mrin V. Iordche School of Engineering nd Eng. Tech. LeTourneu Universiy Longview, TX 7607-700 Pnos J. Ansklis Dermen of Elecricl Engineering
Honours Introductory Maths Course 2011 Integration, Differential and Difference Equations
 Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
New Inequalities in Fractional Integrals
 ISSN 1749-3889 (prin), 1749-3897 (online) Inernionl Journl of Nonliner Science Vol.9(21) No.4,pp.493-497 New Inequliies in Frcionl Inegrls Zoubir Dhmni Zoubir DAHMANI Lborory of Pure nd Applied Mhemics,
ISSN 1749-3889 (prin), 1749-3897 (online) Inernionl Journl of Nonliner Science Vol.9(21) No.4,pp.493-497 New Inequliies in Frcionl Inegrls Zoubir Dhmni Zoubir DAHMANI Lborory of Pure nd Applied Mhemics,
Ann. Funct. Anal. 2 (2011), no. 2, A nnals of F unctional A nalysis ISSN: (electronic) URL:
 Ann. Func. Anal. 2 2011, no. 2, 34 41 A nnals of F uncional A nalysis ISSN: 2008-8752 elecronic URL: www.emis.de/journals/afa/ CLASSIFICAION OF POSIIVE SOLUIONS OF NONLINEAR SYSEMS OF VOLERRA INEGRAL EQUAIONS
Ann. Func. Anal. 2 2011, no. 2, 34 41 A nnals of F uncional A nalysis ISSN: 2008-8752 elecronic URL: www.emis.de/journals/afa/ CLASSIFICAION OF POSIIVE SOLUIONS OF NONLINEAR SYSEMS OF VOLERRA INEGRAL EQUAIONS
Magnetostatics Bar Magnet. Magnetostatics Oersted s Experiment
 Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
1. Find a basis for the row space of each of the following matrices. Your basis should consist of rows of the original matrix.
 Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
Positive and negative solutions of a boundary value problem for a
 Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
Some Improvements of Hölder s Inequality on Time Scales
 DOI: 0.55/uom-207-0037 An. Şt. Univ. Ovidius Constnţ Vol. 253,207, 83 96 Some Improvements of Hölder s Inequlity on Time Scles Cristin Dinu, Mihi Stncu nd Dniel Dănciulescu Astrct The theory nd pplictions
DOI: 0.55/uom-207-0037 An. Şt. Univ. Ovidius Constnţ Vol. 253,207, 83 96 Some Improvements of Hölder s Inequlity on Time Scles Cristin Dinu, Mihi Stncu nd Dniel Dănciulescu Astrct The theory nd pplictions
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Solutions for Nonlinear Partial Differential Equations By Tan-Cot Method
 IOSR Journl of Mhemics (IOSR-JM) e-issn: 78-578. Volume 5, Issue 3 (Jn. - Feb. 13), PP 6-11 Soluions for Nonliner Pril Differenil Equions By Tn-Co Mehod Mhmood Jwd Abdul Rsool Abu Al-Sheer Al -Rfidin Universiy
IOSR Journl of Mhemics (IOSR-JM) e-issn: 78-578. Volume 5, Issue 3 (Jn. - Feb. 13), PP 6-11 Soluions for Nonliner Pril Differenil Equions By Tn-Co Mehod Mhmood Jwd Abdul Rsool Abu Al-Sheer Al -Rfidin Universiy
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
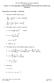 .615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
Chapter 2. First Order Scalar Equations
 Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
EÜFBED - Fen Bilimleri Enstitüsü Dergisi Cilt-Sayı: 3-2 Yıl:
 63 EÜFBED - Fen Bilimleri Ensiüsü Dergisi Cil-Syı: 3- Yıl: 63-7 SOME INEQUALITIES OF HERMITE-HADAMARD TYPE FOR FUNCTIONS WHOSE DERIVATIVES ABSOLUTE VALUES ARE QUASI-CONVEX TÜREVİNİN MUTLAK DEĞERİ QUASI-KONVEKS
63 EÜFBED - Fen Bilimleri Ensiüsü Dergisi Cil-Syı: 3- Yıl: 63-7 SOME INEQUALITIES OF HERMITE-HADAMARD TYPE FOR FUNCTIONS WHOSE DERIVATIVES ABSOLUTE VALUES ARE QUASI-CONVEX TÜREVİNİN MUTLAK DEĞERİ QUASI-KONVEKS
6. Gas dynamics. Ideal gases Speed of infinitesimal disturbances in still gas
 6. Gs dynmics Dr. Gergely Krisóf De. of Fluid echnics, BE Februry, 009. Seed of infiniesiml disurbnces in sill gs dv d, dv d, Coninuiy: ( dv)( ) dv omenum r r heorem: ( ( dv) ) d 3443 4 q m dv d dv llievi
6. Gs dynmics Dr. Gergely Krisóf De. of Fluid echnics, BE Februry, 009. Seed of infiniesiml disurbnces in sill gs dv d, dv d, Coninuiy: ( dv)( ) dv omenum r r heorem: ( ( dv) ) d 3443 4 q m dv d dv llievi
..,..,.,
 57.95. «..» 7, 9,,. 3 DOI:.459/mmph7..,..,., E-mil: yshr_ze@mil.ru -,,. -, -.. -. - - ( ). -., -. ( - ). - - -., - -., - -, -., -. -., - - -, -., -. : ; ; - ;., -,., - -, []., -, [].,, - [3, 4]. -. 3 (
57.95. «..» 7, 9,,. 3 DOI:.459/mmph7..,..,., E-mil: yshr_ze@mil.ru -,,. -, -.. -. - - ( ). -., -. ( - ). - - -., - -., - -, -., -. -., - - -, -., -. : ; ; - ;., -,., - -, []., -, [].,, - [3, 4]. -. 3 (
Existence of positive solution for a third-order three-point BVP with sign-changing Green s function
 Elecronic Journal of Qualiaive Theory of Differenial Equaions 13, No. 3, 1-11; hp://www.mah.u-szeged.hu/ejqde/ Exisence of posiive soluion for a hird-order hree-poin BVP wih sign-changing Green s funcion
Elecronic Journal of Qualiaive Theory of Differenial Equaions 13, No. 3, 1-11; hp://www.mah.u-szeged.hu/ejqde/ Exisence of posiive soluion for a hird-order hree-poin BVP wih sign-changing Green s funcion
Fractional Calculus. Connor Wiegand. 6 th June 2017
 Frcionl Clculus Connor Wiegnd 6 h June 217 Absrc This pper ims o give he reder comforble inroducion o Frcionl Clculus. Frcionl Derivives nd Inegrls re defined in muliple wys nd hen conneced o ech oher
Frcionl Clculus Connor Wiegnd 6 h June 217 Absrc This pper ims o give he reder comforble inroducion o Frcionl Clculus. Frcionl Derivives nd Inegrls re defined in muliple wys nd hen conneced o ech oher
ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX.
 ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX. MEHMET ZEKI SARIKAYA?, ERHAN. SET, AND M. EMIN OZDEMIR Asrc. In his noe, we oin new some ineuliies
ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX. MEHMET ZEKI SARIKAYA?, ERHAN. SET, AND M. EMIN OZDEMIR Asrc. In his noe, we oin new some ineuliies
ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER 2
 ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER Seion Eerise -: Coninuiy of he uiliy funion Le λ ( ) be he monooni uiliy funion defined in he proof of eisene of uiliy funion If his funion is oninuous y hen
ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER Seion Eerise -: Coninuiy of he uiliy funion Le λ ( ) be he monooni uiliy funion defined in he proof of eisene of uiliy funion If his funion is oninuous y hen
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 9: The High Beta Tokamak
 .65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
.65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
Transforms II - Wavelets Preliminary version please report errors, typos, and suggestions for improvements
 EECS 3 Digil Signl Processing Universiy of Cliforni, Berkeley: Fll 007 Gspr November 4, 007 Trnsforms II - Wveles Preliminry version plese repor errors, ypos, nd suggesions for improvemens We follow n
EECS 3 Digil Signl Processing Universiy of Cliforni, Berkeley: Fll 007 Gspr November 4, 007 Trnsforms II - Wveles Preliminry version plese repor errors, ypos, nd suggesions for improvemens We follow n
Matrix Versions of Some Refinements of the Arithmetic-Geometric Mean Inequality
 Marix Versions of Some Refinemens of he Arihmeic-Geomeric Mean Inequaliy Bao Qi Feng and Andrew Tonge Absrac. We esablish marix versions of refinemens due o Alzer ], Carwrigh and Field 4], and Mercer 5]
Marix Versions of Some Refinemens of he Arihmeic-Geomeric Mean Inequaliy Bao Qi Feng and Andrew Tonge Absrac. We esablish marix versions of refinemens due o Alzer ], Carwrigh and Field 4], and Mercer 5]
LAPLACE TRANSFORM OVERCOMING PRINCIPLE DRAWBACKS IN APPLICATION OF THE VARIATIONAL ITERATION METHOD TO FRACTIONAL HEAT EQUATIONS
 Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
MAT 266 Calculus for Engineers II Notes on Chapter 6 Professor: John Quigg Semester: spring 2017
 MAT 66 Clculus for Engineers II Noes on Chper 6 Professor: John Quigg Semeser: spring 7 Secion 6.: Inegrion by prs The Produc Rule is d d f()g() = f()g () + f ()g() Tking indefinie inegrls gives [f()g
MAT 66 Clculus for Engineers II Noes on Chper 6 Professor: John Quigg Semeser: spring 7 Secion 6.: Inegrion by prs The Produc Rule is d d f()g() = f()g () + f ()g() Tking indefinie inegrls gives [f()g
A note to the convergence rates in precise asymptotics
 He Journal of Inequaliies and Alicaions 203, 203:378 h://www.journalofinequaliiesandalicaions.com/conen/203//378 R E S E A R C H Oen Access A noe o he convergence raes in recise asymoics Jianjun He * *
He Journal of Inequaliies and Alicaions 203, 203:378 h://www.journalofinequaliiesandalicaions.com/conen/203//378 R E S E A R C H Oen Access A noe o he convergence raes in recise asymoics Jianjun He * *
CHARACTERIZATION OF REARRANGEMENT INVARIANT SPACES WITH FIXED POINTS FOR THE HARDY LITTLEWOOD MAXIMAL OPERATOR
 Annales Academiæ Scieniarum Fennicæ Mahemaica Volumen 31, 2006, 39 46 CHARACTERIZATION OF REARRANGEMENT INVARIANT SPACES WITH FIXED POINTS FOR THE HARDY LITTLEWOOD MAXIMAL OPERATOR Joaquim Marín and Javier
Annales Academiæ Scieniarum Fennicæ Mahemaica Volumen 31, 2006, 39 46 CHARACTERIZATION OF REARRANGEMENT INVARIANT SPACES WITH FIXED POINTS FOR THE HARDY LITTLEWOOD MAXIMAL OPERATOR Joaquim Marín and Javier
Some Hardy Type Inequalities with Weighted Functions via Opial Type Inequalities
 Advnces in Dynmicl Systems nd Alictions ISSN 0973-5321, Volume 10, Number 1,. 1 9 (2015 htt://cmus.mst.edu/ds Some Hrdy Tye Inequlities with Weighted Functions vi Oil Tye Inequlities Rvi P. Agrwl Tes A&M
Advnces in Dynmicl Systems nd Alictions ISSN 0973-5321, Volume 10, Number 1,. 1 9 (2015 htt://cmus.mst.edu/ds Some Hrdy Tye Inequlities with Weighted Functions vi Oil Tye Inequlities Rvi P. Agrwl Tes A&M
Chickens vs. Eggs: Replicating Thurman and Fisher (1988) by Arianto A. Patunru Department of Economics, University of Indonesia 2004
 Chicens vs. Eggs: Relicaing Thurman and Fisher (988) by Ariano A. Paunru Dearmen of Economics, Universiy of Indonesia 2004. Inroducion This exercise lays ou he rocedure for esing Granger Causaliy as discussed
Chicens vs. Eggs: Relicaing Thurman and Fisher (988) by Ariano A. Paunru Dearmen of Economics, Universiy of Indonesia 2004. Inroducion This exercise lays ou he rocedure for esing Granger Causaliy as discussed
Properties of Logarithms. Solving Exponential and Logarithmic Equations. Properties of Logarithms. Properties of Logarithms. ( x)
 Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
MISCELLANEOUS DYNAMIC EQUATIONS. Elvan Akın Bohner and Martin Bohner. 1. Introduction
 MISCELLANEOUS DYNAMIC EQUATIONS Elvan Akın Bohner and Marin Bohner We consider several dynamic equaions and resen mehods on how o solve hese equaions. Among hem are linear equaions of higher order, Euler
MISCELLANEOUS DYNAMIC EQUATIONS Elvan Akın Bohner and Marin Bohner We consider several dynamic equaions and resen mehods on how o solve hese equaions. Among hem are linear equaions of higher order, Euler
FRACTIONAL DYNAMIC INEQUALITIES HARMONIZED ON TIME SCALES
 FRACTIONAL DYNAMIC INEQUALITIES HARMONIZED ON TIME SCALES M JIBRIL SHAHAB SAHIR Accepted Mnuscript Version This is the unedited version of the rticle s it ppered upon cceptnce by the journl. A finl edited
FRACTIONAL DYNAMIC INEQUALITIES HARMONIZED ON TIME SCALES M JIBRIL SHAHAB SAHIR Accepted Mnuscript Version This is the unedited version of the rticle s it ppered upon cceptnce by the journl. A finl edited
Tax Audit and Vertical Externalities
 T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
Think of the Relationship Between Time and Space Again
 Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
1 jordan.mcd Eigenvalue-eigenvector approach to solving first order ODEs. -- Jordan normal (canonical) form. Instructor: Nam Sun Wang
 jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
= ( ) ) or a system of differential equations with continuous parametrization (T = R
 XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
RESPONSE UNDER A GENERAL PERIODIC FORCE. When the external force F(t) is periodic with periodτ = 2π
 RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
A new model for limit order book dynamics
 Anewmodelforlimiorderbookdynmics JeffreyR.Russell UniversiyofChicgo,GrdueSchoolofBusiness TejinKim UniversiyofChicgo,DeprmenofSisics Absrc:Thispperproposesnewmodelforlimiorderbookdynmics.Thelimiorderbookconsiss
Anewmodelforlimiorderbookdynmics JeffreyR.Russell UniversiyofChicgo,GrdueSchoolofBusiness TejinKim UniversiyofChicgo,DeprmenofSisics Absrc:Thispperproposesnewmodelforlimiorderbookdynmics.Thelimiorderbookconsiss
