(UKÁŽKY V JAZYKU TURBO PASCAL) Zoltán Zalabai, SR - Milan Pokorný, SR
|
|
|
- Nickolas Burke
- 6 years ago
- Views:
Transcription
1 Mtemtik jej plikácie inžinierskom zdelání 006 APLIKÁCIA n-rozmerných INEGRÁLOV (UKÁŽKY V JAZYKU URBO PASCAL) Zoltán Zli, SR - Miln Pokorný, SR Astrkt Poítom podporoné yuonie mtemtiky má nezstupitené miesto j o yuoní mtemtickej nlýzy. V lánku opisujeme des úloh n nájdenie žisk, pri ktorých je potrené zisti priližnú hodnotu icrozmerných integrálo. Nkoko pri riešení prktických prolémo je ýpoet presnej hodnoty icrozmerného integrálu emi nároný, je ýhodné použi poíte n nájdenie jeho priližnej hodnoty. Kúoé sloá: icrozmerný integrál, priližné riešenie, žisko teles, súrdnice žisk, poítom podporoné yuonie. Úod Poítom podporoná ýu predmete mtemtik má soje nezstupitené miesto súste yuocích metód. Dnes už existuje celý rd n profesijnej úroni zostených progrmo. kéto progrmy yužíme j my. V tomto lánku šk chceme uprimi pozornos n ýznm tz. krátkych progrmo, ktoré môžeme npís primo niektorom progrmocom jzyku. káto prác emi úzko súisí s primou ýuou mtemtiky. Metodiku prípry tkýchto progrmo ez äších prolémo zládnu j žici stredných škôl študenti ysokých škôl. Potom už môžu pís progrmy smosttne pod lstných predstá. V lánku udeme poít integrály. V plikáciách šk ýpoet jedného integrálu nestí. Npr. pri ýpote súrdníc žisk teles potreujeme ypoít štyri trojné integrály! Ide tu ždy o priližný ýpoet! Uedieme príkldy tké, pri ktorých je známy presný ýsledok. Zároe uedieme j tké úlohy, ktoré klsickými mtemtickými postupmi nie je možné yrieši. Úloh je niekedy prehdnejši, k k nej dokážeme nkresli hodný nárt, i orázok. Poít umožuje tkéto orázky nkresli. ým s zýši úroe názornosti pri smotnej ýue. Ukážky Úloh 1. Vypoítjme súrdnice žisk roinného útru, ktorý je ohrniený sinusoidou osou x pre x 0,π. ([1], str. 57, pr. 60; ýsledok x = π /, y = π / 8 = 0, 3969 ) Pre n = 1000 dostneme tkéto priližné hodnoty: x 1,5708, y = 0, = Vypoítli sme tri urité integrály: S x = y dx, S y = xydx, m = ydx. S y S x Pre súrdnice žisk pltí: x =, y =. m m Uedieme prconú erziu progrmu (Progrm. 1) príslušný orázok (Orázok. 1). 160
2 Mtemtik jej plikácie inžinierskom zdelání 006 uses Crt, Grph, GenGrph, SclGrph; r x,s,,,h,h1,d,t,xt,yt:rel; n,k,i,k1,k,k3,w:integer; u: rry [1..3] of rel; Function f(x:rel):rel; egin f:=k1*sin(x)+k*x*sin(x)+k3*0.5*sin(x)*sin(x); end; egin for w:=1 to 3 do egin write('zdjte k1,k,k3:'); redln(k1,k,k3); n:=1000; :=0; := ; CLRSCR; s:=0; for k:=0 to n-1 do egin h:=(-)/n; d:=h/; s:=s+f(+k*h+d); end; u[w]:=s*h; writeln('u[',w,']=',s*h); writeln('integrl sucet=',s*h::5); Redln; end; xt:=u[]/u[1]; yt:=u[3]/u[1]; writeln ('xt=',u[]/u[1]); writeln('yt=',u[3]/u[1]); redln; initgrphics; scle (-5,4,5,-4); sclexis; for i:=0 to n do egin t:=+i*h; ScleputPixel (t,sin(t),15); end; redln; h1:=0.05; scleline (xt-h1,yt-h1,xt+h1,yt-h1); scleline (xt+h1,yt-h1,xt+h1,yt+h1); scleline (xt+h1,yt+h1,xt-h1,yt+h1); scleline (xt-h1,yt+h1,xt-h1,yt-h1); redln; end. Progrm. 1 Orázok. 1 Orázok. Úloh. Vypoítjme súrdnice žisk roinného útru, ktorý je ohrniený grfom funkcie y = x sin x osou x, pre x 0, π. Progrm. 1 hodne upríme. Pre n = 1000 dostneme tkýto ýsledok: x 1,868, y = 0, 697. Pozri orázok.. = Úloh 3. Urme súrdnice žisk olúk kriky y = 1x, y 0, x 1,. ([1], str. 48, pr. 55, ide o emi žký príkld, pretože x y mjú komplikoný tr) y dx. Vypoítme: S x = y + y dx, S y = x 1+ y dx, m = S y S x Súrdnice žisk sú: x = ; y =. m m Pre n = 1000 dostneme tkýto ýsledok: x 1,4807, y = 4, 195. Pozri orázok. 3. = 161
3 Mtemtik jej plikácie inžinierskom zdelání 006 Orázok. 3 Orázok.4 Orázok.5 Úloh 4. Vypoítjme súrdnice žisk roinného útru, ktorý je ohrniený krikmi y = x, x + y = ( > 0). 8 ([], str. 361, pr. 405, ýsledok: x =, y = ) 5 Pre = 1, n = 300 dostneme tkýto ýsledok: x 0,5001, y = 1, 601. Pozri orázok. 4. = Úloh 5. 1 Z olsti D predošlej úlohy ( = 1) yerieme kruh: ( x 0,1) + ( y 1). Vznikne noá π * * ols: D. Vypoítjme súrdnice žisk olsti D. Dostneme tkýto ýsledok: x 0,671, y = 1, 777. Pozri orázok. 5. = Poznámk: Vypoítli sme tri dojné integrály Pre súrdnice žisk pltí: x M y M x =, y. M M = dxdy M x = ydxdy M y = M =,, xdxdy. Úloh 6. Roinný útr je ohrniený krikou: 9x + 36y + 4xy + 34x 48y 139 = 0. Vypoítjme jeho osh súrdnice žisk. x y ([3], str. 19, elips, stred: S [ 1;1 ]; + = 1). 4 9 P = π = π 3 = 18,849 ; pre n = 300 dostneme: P = 18,84; x = 1, y = 1. (Súrdnice žisk sú súrdnicmi stredu elipsy). Pozri orázok. 6. Uedieme s prconej erzie progrmu pre ýpoet trojných integrálo. uses Crt, Grph, GenGrph, SclGrph; r k1,k,k3,k4,w:integer; i,j,k,n:longint;,,c,d,e,f,s,h1,h,h3:rel; x,y,z:rry[1..500] of rel; u:rry[1..4] of rel; function Fx (x,y,z:rel):rel; egin Fx :=k1+k*x+k3*y+k4*z; end; D D D 16
4 Mtemtik jej plikácie inžinierskom zdelání 006 egin for w:=1 to 4 do egin clrscr; Write ('Zdj n,k1,k,k3,k4 = '); RedLn (n,k1,k,k3,k4); :=-; :=; c:=-; d:=; e:=0; f:=; writeln('prcujem'); s:=0; for i:=1 to n do egin x[i]:= +i*(-)/n; y[i]:= c+i*(d-c)/n; z[i]:= e+i*(f-e)/n; end; for i:=1 to n do for j:=1 to n do for k:=1 to n do If ((x[i]*x[i]+y[j]*y[j]+z[k]*z[k]-4<=0) nd (x[i]*x[i]+y[j]*y[j]-z[k]*z[k]<=0)) then s := s+fx(x[i],y[j],z[k])*(-)*(d-c)*(f-e)/(n*n*n); u[w]:=s; WriteLn ('s = ',s); writeln ('u[',w,']=',s); redln; end; writeln ('xt=',u[]/u[1]); writeln ('yt=',u[3]/u[1]); writeln ('zt=',u[4]/u[1]); redln; end. Progrm. Orázok. 6 Orázok. 7 Úloh 7. Vypoítjme súrdnice žisk teles, ktoré je ohrniené zhor guoou plochou, zdol kužeoou plochou ( z 0) : x + y + z = 4; x + y = z. Pre n = 30 dostneme tkýto ýsledok x y = 0, z = 1, 80. Pozri orázok. 7. = Bolo potrené ypoít 4 trojné integrály : 1 1 m = dxdydz, x = xdxdydz, y = m m ydxdydz, z = 1 m zdxdydz Úloh 8. Vypoítjme súrdnice žisk teles, ktoré je ohrniené zhor grfom funkcie 3 h ( x, y) = +, zdol grfom funkcie x y + 1 x 1 / + y + ( ) ( ) 1 x y g ( x, y) = + 0, 5. Výsledok: x = 0,08, y = 0, z = 1, 19 (pre n = 30). Šikmý priemet teles idíme n orázku
5 Mtemtik jej plikácie inžinierskom zdelání 006 Úloh 9. Orázok. 8 Orázok. 9 eleso je ohrniené zhor proloidom h ( x, y) = + 3 ( x, y) 4x 4y g = +. Vypoítjme súrdnice žisk. Výsledok: x = 0, y = 0, z =, 05. Šikmý priemet teles je n orázku. 9. Úloh 10. eleso je ohrniené zhor roinou x y h( x, y) = 3, zdol kužeoou plochou 5 5 ( x, y) 4x 4y g = +. Vypoítjme súrdnice žisk. Výsledok: x = 0,116, y = 0,116, z =,98. Šikmý priemet teles je n orázku. 10. x 3 y 3, zdol kužeoou plochou Orázok. 10 Litertúr 1. Hláek, A: Sírk ešených píkld z yšší mtemtiky I, II. SPN, Prh Demidoi, B. P.: Sornik zd i upržnenij po mtemtieskomu nlizu. Izdtesto Nuk, Mosk Bydžoský, B.: Úod do nlytické geometrie. Jednot eskosloenských mtemtik fysik, Prometheus, Prh Zli, Z.: Ukážky yužiti produkto KM n ýpoet dojného trojného integrálu. Zorník edeckých prác z medzinárodnej konferencie SF U Košicich, SROFEK, Košice Zli, Z. Pokorný, M.: n-rozmerný integrál jeho priližný ýpoet. Act Mthemtic 8, UKF, Nitr 005, s ISBN
6 Mtemtik jej plikácie inžinierskom zdelání 006 Adres utoro prof. RNDr. Zoltán Zli, CSc., rnská unierzit, Pedgogická fkult, Ktedr mtemtiky informtiky, Priemyselná 4, P.O.BOX 9, rn E-mil: PedDr. Miln Pokorný, rnská unierzit, Pedgogická fkult, Ktedr mtemtiky informtiky, Priemyselná 4, P.O.BOX 9, rn E-mil: APPLICAION OF MULIDIMENSIONAL INEGRALS Astrct Computer supported lerning plys n importnt role in mthemticl nlysis teching. he pper dels with ten prolems in which it is necessry to find n pproximte lue of multidimensionl integrls to find centre of mss co-ordintes. As it is usully ery difficult to clculte exct lues of multidimensionl integrls, it cn e useful to use computers to find pproximte lues. Keywords: multidimensionl integrl, pproximte lue, centre of mss, centre of mss co-ordintes, computer supported lerning. Oponol: doc. RNDr. Dn Országhoá, CSc. 165
r 0 ( ) cos( ) r( )sin( ). 1. Last time, we calculated that for the cardioid r( ) =1+sin( ),
Wrm up Recll from lst time, given polr curve r = r( ),, dx dy dx = dy d = (r( )sin( )) d (r( ) cos( )) = r0 ( )sin( )+r( ) cos( ) r 0 ( ) cos( ) r( )sin( ).. Lst time, we clculted tht for crdioid r( )
Section 17.2 Line Integrals
Section 7. Line Integrls Integrting Vector Fields nd Functions long urve In this section we consider the problem of integrting functions, both sclr nd vector (vector fields) long curve in the plne. We
JUST THE MATHS UNIT NUMBER INTEGRATION APPLICATIONS 6 (First moments of an arc) A.J.Hobson
JUST THE MATHS UNIT NUMBER 13.6 INTEGRATION APPLICATIONS 6 (First moments of n rc) by A.J.Hobson 13.6.1 Introduction 13.6. First moment of n rc bout the y-xis 13.6.3 First moment of n rc bout the x-xis
An Alternative Approach to Estimating the Bounds of the Denominators of Egyptian Fractions
Leonrdo Journl of Sciences ISSN 58-0 Issue, Jnury-June 0 p. -0 An Alterntive Approch to Estimting the Bounds of the Denomintors of Egyptin Frctions School of Humn Life Sciences, University of Tsmni, Locked
Definite Integrals. The area under a curve can be approximated by adding up the areas of rectangles = 1 1 +
Definite Integrls --5 The re under curve cn e pproximted y dding up the res of rectngles. Exmple. Approximte the re under y = from x = to x = using equl suintervls nd + x evluting the function t the left-hnd
SAINT IGNATIUS COLLEGE
SAINT IGNATIUS COLLEGE Directions to Students Tril Higher School Certificte 0 MATHEMATICS Reding Time : 5 minutes Totl Mrks 00 Working Time : hours Write using blue or blck pen. (sketches in pencil). This
x = a To determine the volume of the solid, we use a definite integral to sum the volumes of the slices as we let!x " 0 :
Clculus II MAT 146 Integrtion Applictions: Volumes of 3D Solids Our gol is to determine volumes of vrious shpes. Some of the shpes re the result of rotting curve out n xis nd other shpes re simply given
CREATIVE USE OF MATHEMATICAL STRATEGIES IN PROOFS IN UNDERGRADUATE CALCULUS
CREATIVE USE OF MATHEMATICAL STRATEGIES IN PROOFS IN UNDERGRADUATE CALCULUS VARGA Mrek (SK), NAŠTICKÁ Zuzn (SK) Abstrct Mthemticl theories could be developed neither without mthemticl proofs, nor without
The Fundamental Theorem of Calculus
The Fundmentl Theorem of Clculus MATH 151 Clculus for Mngement J. Robert Buchnn Deprtment of Mthemtics Fll 2018 Objectives Define nd evlute definite integrls using the concept of re. Evlute definite integrls
FINAL REVIEW. 1. Vector Fields, Work, and Flux Suggested Problems:
FINAL EVIEW 1. Vector Fields, Work, nd Flux uggested Problems: { 14.1 7, 13, 16 14.2 17, 25, 27, 29, 36, 45 We dene vector eld F (x, y) to be vector vlued function tht mps ech point in the plne to two
Undergraduate Research
Undergrdute Reserch A Trigonometric Simpson s Rule By Ctherine Cusimno Kirby nd Sony Stnley Biogrphicl Sketch Ctherine Cusimno Kirby is the dughter of Donn nd Sm Cusimno. Originlly from Vestvi Hills, Albm,
7. Numerical evaluation of definite integrals
7. Numericl evlution of definite integrls Tento učení text yl podpořen z Operčního progrmu Prh - Adptilit Hn Hldíková Numericl pproximtion of definite integrl is clled numericl qudrture, the formuls re
A sequence is a list of numbers in a specific order. A series is a sum of the terms of a sequence.
Core Module Revision Sheet The C exm is hour 30 minutes long nd is in two sections. Section A (36 mrks) 8 0 short questions worth no more thn 5 mrks ech. Section B (36 mrks) 3 questions worth mrks ech.
Objectives. Materials
Techer Notes Activity 17 Fundmentl Theorem of Clculus Objectives Explore the connections between n ccumultion function, one defined by definite integrl, nd the integrnd Discover tht the derivtive of the
How Kayak Stability Works
How Kyk Stility Works When I tip in my kyk it wnts to right me up to point eyond tht I tip over. How cn I find the ngle of mximum tip? Dgger Nomd 8.1: 68 gllons x 8.35 ls./gl (wter weight) 568 pounds of
Main topics for the First Midterm
Min topics for the First Midterm The Midterm will cover Section 1.8, Chpters 2-3, Sections 4.1-4.8, nd Sections 5.1-5.3 (essentilly ll of the mteril covered in clss). Be sure to know the results of the
a < a+ x < a+2 x < < a+n x = b, n A i n f(x i ) x. i=1 i=1
Mth 33 Volume Stewrt 5.2 Geometry of integrls. In this section, we will lern how to compute volumes using integrls defined by slice nlysis. First, we recll from Clculus I how to compute res. Given the
On New Inequalities of Hermite-Hadamard-Fejer Type for Harmonically Quasi-Convex Functions Via Fractional Integrals
X th Interntionl Sttistics Dys Conference ISDC 6), Giresun, Turkey On New Ineulities of Hermite-Hdmrd-Fejer Type for Hrmoniclly Qusi-Convex Functions Vi Frctionl Integrls Mehmet Kunt * nd İmdt İşcn Deprtment
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER /2019
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS MATH00030 SEMESTER 208/209 DR. ANTHONY BROWN 7.. Introduction to Integrtion. 7. Integrl Clculus As ws the cse with the chpter on differentil
We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.
![We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.](/thumbs/93/114277851.jpg "We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.")
Mth 255 - Vector lculus II Notes 4.2 Pth nd Line Integrls We begin with discussion of pth integrls (the book clls them sclr line integrls). We will do this for function of two vribles, but these ides cn
n f(x i ) x. i=1 In section 4.2, we defined the definite integral of f from x = a to x = b as n f(x i ) x; f(x) dx = lim i=1
The Fundmentl Theorem of Clculus As we continue to study the re problem, let s think bck to wht we know bout computing res of regions enclosed by curves. If we wnt to find the re of the region below the
Lecture 14 Numerical integration: advanced topics
Lecture 14 Numericl integrtion: dvnced topics Weinn E 1,2 nd Tiejun Li 2 1 Deprtment of Mthemtics, Princeton University, weinn@princeton.edu 2 School of Mthemticl Sciences, Peking University, tieli@pku.edu.cn
4.4 Areas, Integrals and Antiderivatives
. res, integrls nd ntiderivtives 333. Ares, Integrls nd Antiderivtives This section explores properties of functions defined s res nd exmines some connections mong res, integrls nd ntiderivtives. In order
Review of Calculus, cont d
Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Edexcel GCE Core Mathematics (C2) Required Knowledge Information Sheet. Daniel Hammocks
Edexcel GCE Core Mthemtics (C) Required Knowledge Informtion Sheet C Formule Given in Mthemticl Formule nd Sttisticl Tles Booklet Cosine Rule o = + c c cosine (A) Binomil Series o ( + ) n = n + n 1 n 1
QUADRATURE is an old-fashioned word that refers to
World Acdemy of Science Engineering nd Technology Interntionl Journl of Mthemticl nd Computtionl Sciences Vol:5 No:7 011 A New Qudrture Rule Derived from Spline Interpoltion with Error Anlysis Hdi Tghvfrd
10. AREAS BETWEEN CURVES
. AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
A Modified ADM for Solving Systems of Linear Fredholm Integral Equations of the Second Kind
Applied Mthemticl Sciences, Vol. 6, 2012, no. 26, 1267-1273 A Modified ADM for Solving Systems of Liner Fredholm Integrl Equtions of the Second Kind A. R. Vhidi nd T. Dmercheli Deprtment of Mthemtics,
Definite integral. Mathematics FRDIS MENDELU
Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová Brno 1 Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function defined on [, b]. Wht is the re of the
Riemann Sums and Riemann Integrals
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
The Riemann Integral
Deprtment of Mthemtics King Sud University 2017-2018 Tble of contents 1 Anti-derivtive Function nd Indefinite Integrls 2 3 4 5 Indefinite Integrls & Anti-derivtive Function Definition Let f : I R be function
(6.5) Length and area in polar coordinates
86 Chpter 6 SLICING TECHNIQUES FURTHER APPLICATIONS Totl mss 6 x ρ(x)dx + x 6 x dx + 9 kg dx + 6 x dx oment bout origin 6 xρ(x)dx x x dx + x + x + ln x ( ) + ln 6 kg m x dx + 6 6 x x dx Centre of mss +
Definite integral. Mathematics FRDIS MENDELU. Simona Fišnarová (Mendel University) Definite integral MENDELU 1 / 30
Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová (Mendel University) Definite integrl MENDELU / Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function
Tangent Line and Tangent Plane Approximations of Definite Integral
Rose-Hulmn Undergrdute Mthemtics Journl Volume 16 Issue 2 Article 8 Tngent Line nd Tngent Plne Approximtions of Definite Integrl Meghn Peer Sginw Vlley Stte University Follow this nd dditionl works t:
METHODS OF APPROXIMATING THE RIEMANN INTEGRALS AND APPLICATIONS
Journl of Young Scientist Volume III 5 ISSN 44-8; ISSN CD-ROM 44-9; ISSN Online 44-5; ISSN-L 44 8 METHODS OF APPROXIMATING THE RIEMANN INTEGRALS AND APPLICATIONS An ALEXANDRU Scientific Coordintor: Assist
We know that if f is a continuous nonnegative function on the interval [a, b], then b
![We know that if f is a continuous nonnegative function on the interval [a, b], then b](/thumbs/72/66633133.jpg "We know that if f is a continuous nonnegative function on the interval [a, b], then b")
1 Ares Between Curves c 22 Donld Kreider nd Dwight Lhr We know tht if f is continuous nonnegtive function on the intervl [, b], then f(x) dx is the re under the grph of f nd bove the intervl. We re going
Math 32B Discussion Session Week 8 Notes February 28 and March 2, f(b) f(a) = f (t)dt (1)
Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
Section 6.1 Definite Integral
Section 6.1 Definite Integrl Suppose we wnt to find the re of region tht is not so nicely shped. For exmple, consider the function shown elow. The re elow the curve nd ove the x xis cnnot e determined
New Expansion and Infinite Series
Interntionl Mthemticl Forum, Vol. 9, 204, no. 22, 06-073 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/0.2988/imf.204.4502 New Expnsion nd Infinite Series Diyun Zhng College of Computer Nnjing University
Review of Riemann Integral
1 Review of Riemnn Integrl In this chpter we review the definition of Riemnn integrl of bounded function f : [, b] R, nd point out its limittions so s to be convinced of the necessity of more generl integrl.
Review of Gaussian Quadrature method
Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Green function and Eigenfunctions
Green function nd Eigenfunctions Let L e regulr Sturm-Liouville opertor on n intervl (, ) together with regulr oundry conditions. We denote y, φ ( n, x ) the eigenvlues nd corresponding normlized eigenfunctions
Riemann Sums and Riemann Integrals
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
HIGHER SCHOOL CERTIFICATE EXAMINATION MATHEMATICS 4 UNIT (ADDITIONAL) Time allowed Three hours (Plus 5 minutes reading time)
HIGHER SCHOOL CERTIFICATE EXAMINATION 999 MATHEMATICS UNIT (ADDITIONAL) Time llowed Three hours (Plus 5 minutes reding time) DIRECTIONS TO CANDIDATES Attempt ALL questions ALL questions re of equl vlue
x = b a n x 2 e x dx. cdx = c(b a), where c is any constant. a b
CHAPTER 5. INTEGRALS 61 where nd x = b n x i = 1 (x i 1 + x i ) = midpoint of [x i 1, x i ]. Problem 168 (Exercise 1, pge 377). Use the Midpoint Rule with the n = 4 to pproximte 5 1 x e x dx. Some quick
On the Decomposition Method for System of Linear Fredholm Integral Equations of the Second Kind
Applied Mthemticl Sciences, Vol. 2, 28, no. 2, 57-62 On the Decomposition Method for System of Liner Fredholm Integrl Equtions of the Second Kind A. R. Vhidi 1 nd M. Mokhtri Deprtment of Mthemtics, Shhr-e-Rey
An iterative method for solving nonlinear functional equations
J. Mth. Anl. Appl. 316 (26) 753 763 www.elsevier.com/locte/jm An itertive method for solving nonliner functionl equtions Vrsh Dftrdr-Gejji, Hossein Jfri Deprtment of Mthemtics, University of Pune, Gneshkhind,
Improper Integrals, and Differential Equations
Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
STEP FUNCTIONS, DELTA FUNCTIONS, AND THE VARIATION OF PARAMETERS FORMULA. 0 if t < 0, 1 if t > 0.
STEP FUNCTIONS, DELTA FUNCTIONS, AND THE VARIATION OF PARAMETERS FORMULA STEPHEN SCHECTER. The unit step function nd piecewise continuous functions The Heviside unit step function u(t) is given by if t
Lab 11 Approximate Integration
Nme Student ID # Instructor L Period Dte Due L 11 Approximte Integrtion Ojectives 1. To ecome fmilir with the right endpoint rule, the trpezoidl rule, nd Simpson's rule. 2. To compre nd contrst the properties
ROB EBY Blinn College Mathematics Department
ROB EBY Blinn College Mthemtics Deprtment Mthemtics Deprtment 5.1, 5.2 Are, Definite Integrls MATH 2413 Rob Eby-Fll 26 Weknowthtwhengiventhedistncefunction, wecnfindthevelocitytnypointbyfindingthederivtiveorinstntneous
Section 7.1 Area of a Region Between Two Curves
Section 7.1 Are of Region Between Two Curves White Bord Chllenge The circle elow is inscried into squre: Clcultor 0 cm Wht is the shded re? 400 100 85.841cm White Bord Chllenge Find the re of the region
Unit #9 : Definite Integral Properties; Fundamental Theorem of Calculus
Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Mathematics Extension 2
S Y D N E Y B O Y S H I G H S C H O O L M O O R E P A R K, S U R R Y H I L L S 005 HIGHER SCHOOL CERTIFICATE TRIAL PAPER Mthemtics Extension Generl Instructions Totl Mrks 0 Reding Time 5 Minutes Attempt
6.5 Numerical Approximations of Definite Integrals
Arknss Tech University MATH 94: Clculus II Dr. Mrcel B. Finn 6.5 Numericl Approximtions of Definite Integrls Sometimes the integrl of function cnnot be expressed with elementry functions, i.e., polynomil,
Chapter 8. Numerical Solution of Ordinary Differential Equations. Module No. 2. Predictor-Corrector Methods
Numerical Analysis by Dr. Anita Pal Assistant Professor Department of Matematics National Institute of Tecnology Durgapur Durgapur-7109 email: anita.buie@gmail.com 1 . Capter 8 Numerical Solution of Ordinary
Overview of Calculus I
Overview of Clculus I Prof. Jim Swift Northern Arizon University There re three key concepts in clculus: The limit, the derivtive, nd the integrl. You need to understnd the definitions of these three things,
B.Sc. in Mathematics (Ordinary)
R48/0 DUBLIN INSTITUTE OF TECHNOLOGY KEVIN STREET, DUBLIN 8 B.Sc. in Mthemtics (Ordinry) SUPPLEMENTAL EXAMINATIONS 01 Numericl Methods Dr. D. Mckey Dr. C. Hills Dr. E.A. Cox Full mrks for complete nswers
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
1 The fundamental theorems of calculus.
The fundmentl theorems of clculus. The fundmentl theorems of clculus. Evluting definite integrls. The indefinite integrl- new nme for nti-derivtive. Differentiting integrls. Theorem Suppose f is continuous
Space Curves. Recall the parametric equations of a curve in xy-plane and compare them with parametric equations of a curve in space.
Clculus 3 Li Vs Spce Curves Recll the prmetric equtions of curve in xy-plne nd compre them with prmetric equtions of curve in spce. Prmetric curve in plne x = x(t) y = y(t) Prmetric curve in spce x = x(t)
Review: Velocity: v( t) r '( t) speed = v( t) Initial speed v, initial height h, launching angle : 1 Projectile motion: r( ) j v r
13.3 Arc Length Review: curve in spce: r t f t i g t j h t k Tngent vector: r '( t ) f ' t i g ' t j h' t k Tngent line t t t : s r( t ) sr '( t ) Velocity: v( t) r '( t) speed = v( t) Accelertion ( t)
MAS 4156 Lecture Notes Differential Forms
MAS 4156 Lecture Notes Differentil Forms Definitions Differentil forms re objects tht re defined on mnifolds. For this clss, the only mnifold we will put forms on is R 3. The full definition is: Definition:
DEFINITION The inner product of two functions f 1 and f 2 on an interval [a, b] is the number. ( f 1, f 2 ) b DEFINITION 11.1.
![DEFINITION The inner product of two functions f 1 and f 2 on an interval [a, b] is the number. ( f 1, f 2 ) b DEFINITION 11.1.](/thumbs/81/83893993.jpg "DEFINITION The inner product of two functions f 1 and f 2 on an interval [a, b] is the number. ( f 1, f 2 ) b DEFINITION 11.1.")
398 CHAPTER 11 ORTHOGONAL FUNCTIONS AND FOURIER SERIES 11.1 ORTHOGONAL FUNCTIONS REVIEW MATERIAL The notions of generlized vectors nd vector spces cn e found in ny liner lger text. INTRODUCTION The concepts
TOPPER SAMPLE PAPER - 5 CLASS XI MATHEMATICS. Questions. Time Allowed : 3 Hrs Maximum Marks: 100
TOPPER SAMPLE PAPER - 5 CLASS XI MATHEMATICS Questions Time Allowed : 3 Hrs Mximum Mrks: 100 1. All questions re compulsory.. The question pper consist of 9 questions divided into three sections A, B nd
dt. However, we might also be curious about dy
Section 0. The Clculus of Prmetric Curves Even though curve defined prmetricly my not be function, we cn still consider concepts such s rtes of chnge. However, the concepts will need specil tretment. For
MA 124 January 18, Derivatives are. Integrals are.
MA 124 Jnury 18, 2018 Prof PB s one-minute introduction to clculus Derivtives re. Integrls re. In Clculus 1, we lern limits, derivtives, some pplictions of derivtives, indefinite integrls, definite integrls,
Math 107H Topics for the first exam. csc 2 x dx = cot x + C csc x cotx dx = csc x + C tan x dx = ln secx + C cot x dx = ln sinx + C e x dx = e x + C
Integrtion Mth 07H Topics for the first exm Bsic list: x n dx = xn+ + C (provided n ) n + sin(kx) dx = cos(kx) + C k sec x dx = tnx + C sec x tnx dx = sec x + C /x dx = ln x + C cos(kx) dx = sin(kx) +
Bulletin of the. Iranian Mathematical Society
ISSN: 07-060X Print ISSN: 735-855 Online Bulletin of the Irnin Mthemticl Society Vol 3 07, No, pp 09 5 Title: Some extended Simpson-type ineulities nd pplictions Authors: K-C Hsu, S-R Hwng nd K-L Tseng
WHEN IS A FUNCTION NOT FLAT? 1. Introduction. {e 1 0, x = 0. f(x) =
WHEN IS A FUNCTION NOT FLAT? YIFEI PAN AND MEI WANG Abstrct. In this pper we prove unique continution property for vector vlued functions of one vrible stisfying certin differentil inequlity. Key words:
AN INEQUALITY OF OSTROWSKI TYPE AND ITS APPLICATIONS FOR SIMPSON S RULE AND SPECIAL MEANS. I. Fedotov and S. S. Dragomir
RGMIA Reserch Report Collection, Vol., No., 999 http://sci.vu.edu.u/ rgmi AN INEQUALITY OF OSTROWSKI TYPE AND ITS APPLICATIONS FOR SIMPSON S RULE AND SPECIAL MEANS I. Fedotov nd S. S. Drgomir Astrct. An
Test , 8.2, 8.4 (density only), 8.5 (work only), 9.1, 9.2 and 9.3 related test 1 material and material from prior classes
Test 2 8., 8.2, 8.4 (density only), 8.5 (work only), 9., 9.2 nd 9.3 relted test mteril nd mteril from prior clsses Locl to Globl Perspectives Anlyze smll pieces to understnd the big picture. Exmples: numericl
SPECIALIST MATHEMATICS
Victorin Certificte of Euction 009 SUPERVISOR TO ATTACH PROCESSING LABEL HERE STUDENT NUMBER Letter Figures Wors SPECIALIST MATHEMATICS Written exmintion Friy 30 October 009 Reing time: 3.00 pm to 3.5
The Solution of Volterra Integral Equation of the Second Kind by Using the Elzaki Transform
Applied Mthemticl Sciences, Vol. 8, 214, no. 11, 525-53 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/1.12988/ms.214.312715 The Solution of Volterr Integrl Eqution of the Second Kind by Using the Elzki
Math& 152 Section Integration by Parts
Mth& 5 Section 7. - Integrtion by Prts Integrtion by prts is rule tht trnsforms the integrl of the product of two functions into other (idelly simpler) integrls. Recll from Clculus I tht given two differentible
Suppose we want to find the area under the parabola and above the x axis, between the lines x = 2 and x = -2.
Mth 43 Section 6. Section 6.: Definite Integrl Suppose we wnt to find the re of region tht is not so nicely shped. For exmple, consider the function shown elow. The re elow the curve nd ove the x xis cnnot
POSITIVE SOLUTIONS FOR SINGULAR THREE-POINT BOUNDARY-VALUE PROBLEMS
Electronic Journl of Differentil Equtions, Vol. 27(27), No. 156, pp. 1 8. ISSN: 172-6691. URL: http://ejde.mth.txstte.edu or http://ejde.mth.unt.edu ftp ejde.mth.txstte.edu (login: ftp) POSITIVE SOLUTIONS
Numerical Integration
Numericl Integrtion Wouter J. Den Hn London School of Economics c 2011 by Wouter J. Den Hn June 3, 2011 Qudrture techniques I = f (x)dx n n w i f (x i ) = w i f i i=1 i=1 Nodes: x i Weights: w i Qudrture
I. INTEGRAL THEOREMS. A. Introduction
1 U Deprtment of Physics 301A Mechnics - I. INTEGRAL THEOREM A. Introduction The integrl theorems of mthemticl physics ll hve their origin in the ordinry fundmentl theorem of clculus, i.e. xb x df dx dx
Sample Questions PREPARING FOR THE AP (AB) CALCULUS EXAMINATION. tangent line, a+h. a+h
Smple Questions PREPARING FOR THE AP (AB) CALCULUS EXAMINATION B B A B tngent line,, f '() = lim h f( + h) f() h +h f(x) dx = lim [f(x ) x + f(x ) x + f(x ) x +...+ f(x ) x n] n B B A B tngent line,, f
A. Limits - L Hopital s Rule ( ) How to find it: Try and find limits by traditional methods (plugging in). If you get 0 0 or!!, apply C.! 1 6 C.
A. Limits - L Hopitl s Rule Wht you re finding: L Hopitl s Rule is used to find limits of the form f ( x) lim where lim f x x! c g x ( ) = or lim f ( x) = limg( x) = ". ( ) x! c limg( x) = 0 x! c x! c
Integration Techniques
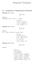Integrtion Techniques. Integrtion of Trigonometric Functions Exmple. Evlute cos x. Recll tht cos x = cos x. Hence, cos x Exmple. Evlute = ( + cos x) = (x + sin x) + C = x + 4 sin x + C. cos 3 x. Let u
Coimisiún na Scrúduithe Stáit State Examinations Commission
M 30 Coimisiún n Scrúduithe Stáit Stte Exmintions Commission LEAVING CERTIFICATE EXAMINATION, 005 MATHEMATICS HIGHER LEVEL PAPER ( 300 mrks ) MONDAY, 3 JUNE MORNING, 9:30 to :00 Attempt FIVE questions
Line Integrals. Partitioning the Curve. Estimating the Mass
Line Integrls Suppose we hve curve in the xy plne nd ssocite density δ(p ) = δ(x, y) t ech point on the curve. urves, of course, do not hve density or mss, but it my sometimes be convenient or useful to
D. Correct! This is the correct answer. It is found by dy/dx = (dy/dt)/(dx/dt).
Calculus II - Problem Solving Drill 4: Calculus for Parametric Equations Question No. of 0 Instructions: () Read the problem and answer choices carefully () Work the problems on paper as. Find dy/dx where
Main topics for the Second Midterm
Min topics for the Second Midterm The Midterm will cover Sections 5.4-5.9, Sections 6.1-6.3, nd Sections 7.1-7.7 (essentilly ll of the mteril covered in clss from the First Midterm). Be sure to know the
Section 3.6. Definite Integrals
The Clulus of Funtions of Severl Vribles Setion.6 efinite Integrls We will first define the definite integrl for funtion f : R R nd lter indite how the definition my be extended to funtions of three or
The Dirac distribution
A DIRAC DISTRIBUTION A The Dirc distribution A Definition of the Dirc distribution The Dirc distribution δx cn be introduced by three equivlent wys Dirc [] defined it by reltions δx dx, δx if x The distribution
(uv) = u v + uv, (1) u vdx + b [uv] b a = u vdx + u v dx. (8) u vds =
![(uv) = u v + uv, (1) u vdx + b [uv] b a = u vdx + u v dx. (8) u vds =](/thumbs/88/115374676.jpg "(uv) = u v + uv, (1) u vdx + b [uv] b a = u vdx + u v dx. (8) u vds =")
Integrtion by prts Integrting the both sides of yields (uv) u v + uv, (1) or b (uv) dx b u vdx + b uv dx, (2) or b [uv] b u vdx + Eqution (4) is the 1-D formul for integrtion by prts. Eqution (4) cn be
Distance And Velocity
Unit #8 - The Integrl Some problems nd solutions selected or dpted from Hughes-Hllett Clculus. Distnce And Velocity. The grph below shows the velocity, v, of n object (in meters/sec). Estimte the totl
Reversing the Chain Rule. As we have seen from the Second Fundamental Theorem ( 4.3), the easiest way to evaluate an integral b
Mth 32 Substitution Method Stewrt 4.5 Reversing the Chin Rule. As we hve seen from the Second Fundmentl Theorem ( 4.3), the esiest wy to evlute n integrl b f(x) dx is to find n ntiderivtive, the indefinite
f(x) dx, If one of these two conditions is not met, we call the integral improper. Our usual definition for the value for the definite integral
Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
DUNKL WAVELETS AND APPLICATIONS TO INVERSION OF THE DUNKL INTERTWINING OPERATOR AND ITS DUAL
IJMMS 24:6, 285 293 PII. S16117124212285 http://ijmms.hindwi.com Hindwi Publishing Corp. UNKL WAVELETS AN APPLICATIONS TO INVESION OF THE UNKL INTETWINING OPEATO AN ITS UAL ABELLATIF JOUINI eceived 28
SPECIALIST MATHEMATICS
Victorin CertiÞcte of Euction 007 SUPERVISOR TO ATTACH PROCESSING LABEL HERE STUDENT NUMBER Letter Figures Wors SPECIALIST MATHEMATICS Written exmintion Mony 5 November 007 Reing time: 3.00 pm to 3.5 pm
Scientific notation is a way of expressing really big numbers or really small numbers.
Scientific Nottion (Stndrd form) Scientific nottion is wy of expressing relly big numbers or relly smll numbers. It is most often used in scientific clcultions where the nlysis must be very precise. Scientific
Positive Integral Operators with Analytic Kernels
Int. Journl of Mth. Anlysis, Vol. 5, 2, no. 34, 683-688 Positive Integrl Opertors with Anlytic Kernels Cn Murt Dikmen onguldk Krelms University Art nd Science Fculty Deprtment of Mthemtics 67, onguldk,
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H. Thomas Shores Department of Mathematics University of Nebraska Spring 2007
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
Sections 5.2: The Definite Integral
Sections 5.2: The Definite Integrl In this section we shll formlize the ides from the lst section to functions in generl. We strt with forml definition.. The Definite Integrl Definition.. Suppose f(x)
5.1 How do we Measure Distance Traveled given Velocity? Student Notes
. How do we Mesure Distnce Trveled given Velocity? Student Notes EX ) The tle contins velocities of moving cr in ft/sec for time t in seconds: time (sec) 3 velocity (ft/sec) 3 A) Lel the x-xis & y-xis
Math Calculus with Analytic Geometry II
orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem