PHYSICS 149: Lecture 21
|
|
|
- Aron Shelton
- 6 years ago
- Views:
Transcription
1 PHYSICS 149: Lecture 21 Chapter 8: Torque and Angular Momentum 8.2 Torque 8.4 Equilibrium Revisited 8.8 Angular Momentum Lecture 21 Purdue University, Physics 149 1
2 Midterm Exam 2 Wednesday, April 6, 6:30 PM 7:30 PM Place: PHY 333 Chapters 5-8 The exam is closed book. The exam is a multiple-choice test. There will be ~15 multiple-choice problems. Each problem is worth 10 points. Note that total possible score for the course is 1,000 points (see the course syllabus) The difficulty level is about the same as the level of textbook problems. You may make a single crib sheet you may write on both sides of an sheet Lecture 20 Purdue University, Physics 149 2
3 Rotational Kinetic Energy Consider a mass M on the end of a string being spun around in a circle with radius r and angular frequency ω Mass has speed v = ω r Mass has kinetic energy K = ½ M v 2 = ½ M ω 2 r 2 Consider a disk with radius R and mass M, spinning with angular frequency ω Each piece of disk has speed v i = ωr i Each piece has kinetic energy K i = ½ m i v 2 = ½ m i ω 2 r 2 i Combine all the pieces ΣK i = Σ ½ m i ω 2 r 2 = ½ (Σ m i r i2 ) ω 2 = ½ I ω 2 Rotational Inertia r i I = Σ m i r 2 i (units kg m 2 ) M Lecture 21 Purdue University, Physics 149 3
4 Rotational Inertia Table For objects with finite number of masses, use I = Σ m r 2. For continuous objects, use table below. Lecture 20 Purdue University, Physics 149 4
5 Torque Rotational effect of force. Tells how effective force is at twisting or rotating an object. τ = ± r F perpendicular = r F sin θ τ = ±r perpendicular F r perpendicular = lever arm Units N m Sign, CCW rotation is positive F Lecture 20 Purdue University, Physics 149 5
6 Torque Torque measures the effectiveness of a force for twisting or turning an object. Magnitude: lever arm Sign: If a torque causes a CCW rotation, assign + sign. If a torque causes a CW rotation, assign - sign. Direction: If a torque causes a CCW rotation, the torque s direction is out of the plane and normal to the plane. If a torque causes a CW rotation, the torque s direction is into the plane and normal to the plane. Torque is a vector quantity. Units: N m But, torque is not a form of energy. Torque is denoted by τ beyond the scope of this class Lecture 20 Purdue University, Physics 149 6
7 Torque Rotational effect of force. Tells how effective force is at twisting or rotating an object. τ = ± r F perpendicular = r F sin θ Units N m Sign, CCW rotation is positive Work done by torque Recall W = F d cos θ For a wheel W = F tangential d = F tangential 2 π r θ / (2 π) (θ in radians) = F tangential r θ = τ θ P = W/t = τ θ/t = τ ω Lecture 21 Purdue University, Physics 149 7
8 The picture below shows three different ways of using a wrench to loosen a stuck nut. Assume the applied force F is the same in each case. In which of the cases is the torque on the nut the biggest? A) Case 1 B) Case 2 C) Case 3 ILQ: Torque In which of the cases is the torque on the nut the smallest? A) Case 1 B) Case 2 C) Case 3 Lecture 20 Purdue University, Physics 149 8
9 ILQ 1 Two forces produce the same torque. Does it follow that they have the same magnitude? A) Yes B) No Lecture 21 Purdue University, Physics 149 9
10 ILQ 2 Which of the forces in the figure produces a negative (clockwise) torque about the rotation axis indicated? A) 1 and 2 B) 1, 2, and 4 C) 3 only D) 4 only Lecture 21 Purdue University, Physics
11 ILQ The figure shows an overhead view of a meter stick that can pivot about the dot shown at the position marked 20 (for 20 cm). All five horizontal forces on the stick have the same magnitude. Rank those forces according to the magnitude of the torque they produce, greatest first. a) 2 and 3 tie, 1, then 1 and 5 tie b) 1 and 3 tie, 4, then 2 and 5 tie c) All tie d) 1, 4, then 2 and 3 tie, 5 Lecture 21 Purdue University, Physics
12 ILQ A heavy box is resting on the floor. You would like to push the box to tip it over on its side, using the minimum force possible. Which of the force vectors in the diagram shows the correct location and direction of the force? Assume enough friction so that the box does not slide; instead it rotates about point P. a) a b) b c) c r Lecture 21 Purdue University, Physics
13 Example The pull cord of a lawnmower engine is wound around a drum of radius of 6.00 cm. While the cord is pulled with a force of 75 N to start the engine, what magnitude torque does the cord apply to the drum? 75 N F = 75.0 N r = 6.00 cm = m θ = 90 6 cm τ = F r sinθ = 4.5 N m Lecture 21 Purdue University, Physics
14 Torque Example A person raises one leg to an angle of 30 degrees. An ankle weight (89 N) is attached a distance of 0.84 m from her hip. What is the torque due to this weight? 1) Draw Diagram 2) τ = F r sin θ = F r sin(90 30) 30 = 65 N m If she raises her leg higher, the torque due to the weight will A) Increase B) Same C) Decrease F=89 N Lecture 21 Purdue University, Physics
15 Equilibrium Conditions for Equilibrium Σ F = 0 Translational EQ (Center of Mass) Στ= 0 Rotational EQ Can choose any axis of rotation. Choose Wisely! A meter stick is suspended at the center. If a 1 kg weight is placed at x=0. Where do you need to place a 2 kg weight to balance it? A) x = 25 B) x=50 C) x=75 D) x=100 E) Impossible y 50 cm d 9.8 N pivot 19.6 N x Σ τ = (0.5) (19.6)d = 0 d = 25 Lecture 21 Purdue University, Physics
16 Static Equilibrium and Center of Mass Gravitational Force Weight = mg Acts as force at center of mass Torque about pivot due to gravity τ = mgd Object not in static equilibrium pivot d W=mg Center of mass Lecture 21 Purdue University, Physics
17 Static Equilibrium Not in equilibrium Equilibrium pivot pivot d W=mg Center of mass Center of mass Torque about pivot 0 Torque about pivot = 0 A method to find center of mass of an irregular object Lecture 21 Purdue University, Physics
18 Equilibrium Acts A rod is lying on a table and has two equal but opposite forces acting on it. What is the net force on the rod? A) Up B) Down C) Zero y-direction: Σ F y = ma y +F F = 0 Will the rod move? A) Yes B) No y F Yes, it rotates! Lecture 21 Purdue University, Physics F x
19 Example 8.6 The beam s weight is 425 N. For equilibrium, what should be the magnitudes of the forces? The entire gravitational force acts at the center of mass (recall in Ch 7). Choose a rotation axis. For Στ = 0 (rotational equilibrium), calculate and add all the torques. * torque due to gravity: τ g = (lever arm) (force) = +(2.44m / 2) (425N) = N m (We assign + sign, because this torque causes a CCW rotation.) * torque due to F 1 : τ F1 = (lever arm) (force) = (2.44m 1.00m) (F 1 ) = (1.44m) (F 1 ) (We assign sign, because this torque causes a CW rotation.) Στ = τ g + τ F1 + τ F2 = N m (1.44m) (F 1 ) + 0 = 0 F 1 = 360 N For ΣF = 0 (translational equilibrium), calculate and add all the forces. ΣF y = F 1 + F 2 mg = 360 N + F N = 0 F 2 = 65 N Lecture 21 Purdue University, Physics
20 Example 8.6: Different Axis The beam s weight is 425 N. For equilibrium, what should be the magnitudes of the forces? The entire gravitational force acts at the center of mass (recall in Ch 7). Choose a rotation axis. For Στ = 0 (rotational equilibrium), calculate and add all the torques. * torque due to gravity: τ g = (lever arm) (force) = (2.44m / m) (425N) = 93.5 N m (We assign sign, because this torque causes a CW rotation.) * torque due to F 2 : τ F2 = (lever arm) (force) = +(2.44m 1.00m) (F 2 ) = +(1.44m) (F 2 ) (We assign + sign, because this torque causes a CCW rotation.) Στ = τ g + τ F1 + τ F2 = 93.5 N m (1.44m) (F 2 )= 0 F 2 = 65 N For ΣF = 0 (translational equilibrium), calculate and add all the forces. Lecture 21 ΣF y = F 1 + F 2 mg = Purdue F University, N 425 Physics N = F 1 = 360 N 20
21 ILQ A 1 kg ball is hung at the end of a rod 1 m long. If the system balances at a point on the rod one third of the distance from the end holding the mass, what is the mass of the rod? a) 0.25 kg b) 0.50 kg c) 1.0 kg d) 2.0 kg Lecture 21 Purdue University, Physics
22 ILQ Find the mass of the tomatoes which make this mobile a "balanced meal." Assume the rods are massless with the lengths indicated. a) 0.5 kg b) 1.0 kg c) 1.5 kg d) 2.0 kg Lecture 21 Purdue University, Physics
23 Equilibrium Example A 50 kg diver stands at the end of a 4.6 m diving board. Neglecting the weight of the board, what are the forces acted by the supports? Draw a FBD. Choose a rotation axis. Στ = 0 (rotational equilibrium) Στ = +(1.2m) (F 1 ) (4.6m) (50kg 9.8m/s 2 ) = 0 F 1 = 1880 N F 1 ΣF = 0 (translational equilibrium) ΣF y = F 1 F 2 mg = 1880 N F 2 (50kg 9.8m/s 2 )= 0 F 2 = 1390 N F 2 mg Lecture 21 Purdue University, Physics
24 ILQ A child's pull-toy has two wheels attached to an axle, which has a string wrapped around it. A cut-away view is shown. Assume that friction exists between the wheels and floor. When the string is pulled to the right, the wheels will roll to the a) right, winding up the string. b) left, unwinding the string. Lecture 21 Purdue University, Physics
25 Example: Dumbbell Consider a rotational motion around a point P. For normal force and F 3, θ = 0. So τ=0 no rotation For gravity, θ = 180. So τ=0 no rotation F 1 and F 2 cause CCW rotations. F 4 causes a CW rotation. Lecture 21 Purdue University, Physics
26 The Hammer You want to balance a hammer on the tip of your finger, which way is easier A) Head up B) Head down C) Same τ = I α m g R sin(θ) = mr 2 α Torque increases with R g sin(θ) / R = α Inertia increases as R 2 Lecture 21 Purdue University, Physics R mg Angular acceleration decreases with R!, so large R is easier to balance.
27 Energy Conservation Friction causes an object to roll, but if it rolls w/o slipping friction does NO work! W = F d cos θ θ is zero for point in contact No dissipated work, energy is conserved Need to include both translation and rotation kinetic energy. K = ½ m v 2 + ½ I ω 2 Lecture 21 Purdue University, Physics
28 Translational + Rotational KE Consider a cylinder with radius R and mass M, rolling w/o slipping down a ramp. Determine the ratio of the translational to rotational KE. Translational: K T = ½ M v 2 Rotational: K R = ½ I ω 2 use and K R = ½ (½ M R 2 ) (V/R) 2 = ¼ M v 2 H = ½ K T Energy conservation: K i + U i = K f + U f Lecture 21 Purdue University, Physics
29 Rolling Act Two uniform cylinders are machined out of solid aluminum. One has twice the radius of the other. If both are placed at the top of the same ramp and released, which is moving faster at the bottom? A) bigger one B) smaller one C) same K i + U i = K f + U f Lecture 21 Purdue University, Physics
30 Define Angular Momentum Momentum Angular Momentum p = mv L = Iω conserved if ΣF ext = 0 conserved if Στ ext = 0 Vector Vector units: kg-m/s units: kg-m 2 /s For a particle: Lecture 21 Purdue University, Physics
31 Linear and Angular Linear Angular Displacement x θ Velocity v ω Acceleration a α Inertia m I Kinetic Energy ½ m v 2 ½ I ω 2 Newton s 2 nd Law F = ma τ = Iα Momentum p = mv L = Iω Lecture 21 Purdue University, Physics
32 Act: Two Disks A disk of mass M and radius R rotates around the z axis with angular velocity ω i. A second identical disk, initially not rotating, is dropped on top of the first. There is friction between the disks, and eventually they rotate together with angular velocity ω f. A) ω f = ω i B) ω f = ½ ω i C) ω f = ¼ ω i z z ω i ω f Lecture 21 Purdue University, Physics
33 Act: Two Disks First realize that there are no external torques acting on the two-disk system. Angular momentum will be conserved! z 2 1 z ω 0 ω f Lecture 21 Purdue University, Physics
34 Demo You are sitting on a freely rotating bar-stool with your arms stretched out and a heavy glass mug in each hand. Your friend gives you a twist and you start rotating around a vertical axis though the center of the stool. You can assume that the bearing the stool turns on is frictionless, and that there is no net external torque present once you have started spinning. You now pull your arms and hands (and mugs) close to your body. Lecture 21 Purdue University, Physics
Physics 101: Lecture 14 Torque and Equilibrium
 Exam II Physics 101: Lecture 14 Torque and Equilibrium Today s lecture will cover Textbook Chapter 8.2-8.4 Physics 101: Lecture 14, Pg 1 Hour Exam 1 Results Average = 75 Number of students 20 0 20 40 60
Exam II Physics 101: Lecture 14 Torque and Equilibrium Today s lecture will cover Textbook Chapter 8.2-8.4 Physics 101: Lecture 14, Pg 1 Hour Exam 1 Results Average = 75 Number of students 20 0 20 40 60
PHYSICS 220. Lecture 15. Textbook Sections Lecture 15 Purdue University, Physics 220 1
 PHYSICS 220 Lecture 15 Angular Momentum Textbook Sections 9.3 9.6 Lecture 15 Purdue University, Physics 220 1 Last Lecture Overview Torque = Force that causes rotation τ = F r sin θ Work done by torque
PHYSICS 220 Lecture 15 Angular Momentum Textbook Sections 9.3 9.6 Lecture 15 Purdue University, Physics 220 1 Last Lecture Overview Torque = Force that causes rotation τ = F r sin θ Work done by torque
Physics 101: Lecture 15 Torque, F=ma for rotation, and Equilibrium
 Physics 101: Lecture 15 Torque, F=ma for rotation, and Equilibrium Strike (Day 10) Prelectures, checkpoints, lectures continue with no change. Take-home quizzes this week. See Elaine Schulte s email. HW
Physics 101: Lecture 15 Torque, F=ma for rotation, and Equilibrium Strike (Day 10) Prelectures, checkpoints, lectures continue with no change. Take-home quizzes this week. See Elaine Schulte s email. HW
Review session for Exam 2 Monday 3/25 6:00 PM in Loomis 151 (here) Print out/bring Exam 2, Fall 2005
 Physics 101: Lecture 16 Rolling Objects and Angular Momentum No checkpoints today. Review session for Exam 2 Monday 3/25 6:00 PM in Loomis 151 (here) Print out/bring Exam 2, Fall 2005 Linear and Angular
Physics 101: Lecture 16 Rolling Objects and Angular Momentum No checkpoints today. Review session for Exam 2 Monday 3/25 6:00 PM in Loomis 151 (here) Print out/bring Exam 2, Fall 2005 Linear and Angular
Chapter 8 - Rotational Dynamics and Equilibrium REVIEW
 Pagpalain ka! (Good luck, in Filipino) Date Chapter 8 - Rotational Dynamics and Equilibrium REVIEW TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1) When a rigid body
Pagpalain ka! (Good luck, in Filipino) Date Chapter 8 - Rotational Dynamics and Equilibrium REVIEW TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1) When a rigid body
Physics 207: Lecture 24. Announcements. No labs next week, May 2 5 Exam 3 review session: Wed, May 4 from 8:00 9:30 pm; here.
 Physics 07: Lecture 4 Announcements No labs next week, May 5 Exam 3 review session: Wed, May 4 from 8:00 9:30 pm; here Today s Agenda ecap: otational dynamics and torque Work and energy with example Many
Physics 07: Lecture 4 Announcements No labs next week, May 5 Exam 3 review session: Wed, May 4 from 8:00 9:30 pm; here Today s Agenda ecap: otational dynamics and torque Work and energy with example Many
Chapter 9-10 Test Review
 Chapter 9-10 Test Review Chapter Summary 9.2. The Second Condition for Equilibrium Explain torque and the factors on which it depends. Describe the role of torque in rotational mechanics. 10.1. Angular
Chapter 9-10 Test Review Chapter Summary 9.2. The Second Condition for Equilibrium Explain torque and the factors on which it depends. Describe the role of torque in rotational mechanics. 10.1. Angular
Physics 111. Tuesday, November 2, Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy
 ics Tuesday, ember 2, 2002 Ch 11: Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy Announcements Wednesday, 8-9 pm in NSC 118/119 Sunday, 6:30-8 pm in CCLIR 468 Announcements This
ics Tuesday, ember 2, 2002 Ch 11: Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy Announcements Wednesday, 8-9 pm in NSC 118/119 Sunday, 6:30-8 pm in CCLIR 468 Announcements This
Chapter 6, Problem 18. Agenda. Rotational Inertia. Rotational Inertia. Calculating Moment of Inertia. Example: Hoop vs.
 Agenda Today: Homework quiz, moment of inertia and torque Thursday: Statics problems revisited, rolling motion Reading: Start Chapter 8 in the reading Have to cancel office hours today: will have extra
Agenda Today: Homework quiz, moment of inertia and torque Thursday: Statics problems revisited, rolling motion Reading: Start Chapter 8 in the reading Have to cancel office hours today: will have extra
ΣF = ma Στ = Iα ½mv 2 ½Iω 2. mv Iω
 Thur Oct 22 Assign 9 Friday Today: Torques Angular Momentum x θ v ω a α F τ m I Roll without slipping: x = r Δθ v LINEAR = r ω a LINEAR = r α ΣF = ma Στ = Iα ½mv 2 ½Iω 2 I POINT = MR 2 I HOOP = MR 2 I
Thur Oct 22 Assign 9 Friday Today: Torques Angular Momentum x θ v ω a α F τ m I Roll without slipping: x = r Δθ v LINEAR = r ω a LINEAR = r α ΣF = ma Στ = Iα ½mv 2 ½Iω 2 I POINT = MR 2 I HOOP = MR 2 I
Rolling, Torque, Angular Momentum
 Chapter 11 Rolling, Torque, Angular Momentum Copyright 11.2 Rolling as Translational and Rotation Combined Motion of Translation : i.e.motion along a straight line Motion of Rotation : rotation about a
Chapter 11 Rolling, Torque, Angular Momentum Copyright 11.2 Rolling as Translational and Rotation Combined Motion of Translation : i.e.motion along a straight line Motion of Rotation : rotation about a
Physics 111. Lecture 23 (Walker: 10.6, 11.1) Conservation of Energy in Rotation Torque March 30, Kinetic Energy of Rolling Object
 Physics 111 Lecture 3 (Walker: 10.6, 11.1) Conservation of Energy in Rotation Torque March 30, 009 Lecture 3 1/4 Kinetic Energy of Rolling Object Total kinetic energy of a rolling object is the sum of
Physics 111 Lecture 3 (Walker: 10.6, 11.1) Conservation of Energy in Rotation Torque March 30, 009 Lecture 3 1/4 Kinetic Energy of Rolling Object Total kinetic energy of a rolling object is the sum of
= o + t = ot + ½ t 2 = o + 2
 Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
We define angular displacement, θ, and angular velocity, ω. What's a radian?
 We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
Torque rotational force which causes a change in rotational motion. This force is defined by linear force multiplied by a radius.
 Warm up A remote-controlled car's wheel accelerates at 22.4 rad/s 2. If the wheel begins with an angular speed of 10.8 rad/s, what is the wheel's angular speed after exactly three full turns? AP Physics
Warm up A remote-controlled car's wheel accelerates at 22.4 rad/s 2. If the wheel begins with an angular speed of 10.8 rad/s, what is the wheel's angular speed after exactly three full turns? AP Physics
Chapter 10. Rotation
 Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
Chapter 8 Rotational Motion and Equilibrium. 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction
 Chapter 8 Rotational Motion and Equilibrium Name 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction 1. The distance between a turning axis and the
Chapter 8 Rotational Motion and Equilibrium Name 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction 1. The distance between a turning axis and the
Rolling, Torque & Angular Momentum
 PHYS 101 Previous Exam Problems CHAPTER 11 Rolling, Torque & Angular Momentum Rolling motion Torque Angular momentum Conservation of angular momentum 1. A uniform hoop (ring) is rolling smoothly from the
PHYS 101 Previous Exam Problems CHAPTER 11 Rolling, Torque & Angular Momentum Rolling motion Torque Angular momentum Conservation of angular momentum 1. A uniform hoop (ring) is rolling smoothly from the
Rotation. PHYS 101 Previous Exam Problems CHAPTER
 PHYS 101 Previous Exam Problems CHAPTER 10 Rotation Rotational kinematics Rotational inertia (moment of inertia) Kinetic energy Torque Newton s 2 nd law Work, power & energy conservation 1. Assume that
PHYS 101 Previous Exam Problems CHAPTER 10 Rotation Rotational kinematics Rotational inertia (moment of inertia) Kinetic energy Torque Newton s 2 nd law Work, power & energy conservation 1. Assume that
General Physics (PHY 2130)
 General Physics (PHY 130) Lecture 0 Rotational dynamics equilibrium nd Newton s Law for rotational motion rolling Exam II review http://www.physics.wayne.edu/~apetrov/phy130/ Lightning Review Last lecture:
General Physics (PHY 130) Lecture 0 Rotational dynamics equilibrium nd Newton s Law for rotational motion rolling Exam II review http://www.physics.wayne.edu/~apetrov/phy130/ Lightning Review Last lecture:
Exam 3 Practice Solutions
 Exam 3 Practice Solutions Multiple Choice 1. A thin hoop, a solid disk, and a solid sphere, each with the same mass and radius, are at rest at the top of an inclined plane. If all three are released at
Exam 3 Practice Solutions Multiple Choice 1. A thin hoop, a solid disk, and a solid sphere, each with the same mass and radius, are at rest at the top of an inclined plane. If all three are released at
31 ROTATIONAL KINEMATICS
 31 ROTATIONAL KINEMATICS 1. Compare and contrast circular motion and rotation? Address the following Which involves an object and which involves a system? Does an object/system in circular motion have
31 ROTATIONAL KINEMATICS 1. Compare and contrast circular motion and rotation? Address the following Which involves an object and which involves a system? Does an object/system in circular motion have
TutorBreeze.com 7. ROTATIONAL MOTION. 3. If the angular velocity of a spinning body points out of the page, then describe how is the body spinning?
 1. rpm is about rad/s. 7. ROTATIONAL MOTION 2. A wheel rotates with constant angular acceleration of π rad/s 2. During the time interval from t 1 to t 2, its angular displacement is π rad. At time t 2
1. rpm is about rad/s. 7. ROTATIONAL MOTION 2. A wheel rotates with constant angular acceleration of π rad/s 2. During the time interval from t 1 to t 2, its angular displacement is π rad. At time t 2
= 2 5 MR2. I sphere = MR 2. I hoop = 1 2 MR2. I disk
 A sphere (green), a disk (blue), and a hoop (red0, each with mass M and radius R, all start from rest at the top of an inclined plane and roll to the bottom. Which object reaches the bottom first? (Use
A sphere (green), a disk (blue), and a hoop (red0, each with mass M and radius R, all start from rest at the top of an inclined plane and roll to the bottom. Which object reaches the bottom first? (Use
 AP Physics 1- Torque, Rotational Inertia, and Angular Momentum Practice Problems FACT: The center of mass of a system of objects obeys Newton s second law- F = Ma cm. Usually the location of the center
AP Physics 1- Torque, Rotational Inertia, and Angular Momentum Practice Problems FACT: The center of mass of a system of objects obeys Newton s second law- F = Ma cm. Usually the location of the center
Static Equilibrium; Torque
 Static Equilibrium; Torque The Conditions for Equilibrium An object with forces acting on it, but that is not moving, is said to be in equilibrium. The first condition for equilibrium is that the net force
Static Equilibrium; Torque The Conditions for Equilibrium An object with forces acting on it, but that is not moving, is said to be in equilibrium. The first condition for equilibrium is that the net force
Lecture 14. Rotational dynamics Torque. Give me a lever long enough and a fulcrum on which to place it, and I shall move the world.
 Lecture 14 Rotational dynamics Torque Give me a lever long enough and a fulcrum on which to place it, and I shall move the world. Archimedes, 87 1 BC EXAM Tuesday March 6, 018 8:15 PM 9:45 PM Today s Topics:
Lecture 14 Rotational dynamics Torque Give me a lever long enough and a fulcrum on which to place it, and I shall move the world. Archimedes, 87 1 BC EXAM Tuesday March 6, 018 8:15 PM 9:45 PM Today s Topics:
Name Date Period PROBLEM SET: ROTATIONAL DYNAMICS
 Accelerated Physics Rotational Dynamics Problem Set Page 1 of 5 Name Date Period PROBLEM SET: ROTATIONAL DYNAMICS Directions: Show all work on a separate piece of paper. Box your final answer. Don t forget
Accelerated Physics Rotational Dynamics Problem Set Page 1 of 5 Name Date Period PROBLEM SET: ROTATIONAL DYNAMICS Directions: Show all work on a separate piece of paper. Box your final answer. Don t forget
Torque. Introduction. Torque. PHY torque - J. Hedberg
 Torque PHY 207 - torque - J. Hedberg - 2017 1. Introduction 2. Torque 1. Lever arm changes 3. Net Torques 4. Moment of Rotational Inertia 1. Moment of Inertia for Arbitrary Shapes 2. Parallel Axis Theorem
Torque PHY 207 - torque - J. Hedberg - 2017 1. Introduction 2. Torque 1. Lever arm changes 3. Net Torques 4. Moment of Rotational Inertia 1. Moment of Inertia for Arbitrary Shapes 2. Parallel Axis Theorem
Cutnell/Johnson Physics
 Cutnell/Johnson Physics Classroom Response System Questions Chapter 9 Rotational Dynamics Interactive Lecture Questions 9.1.1. You are using a wrench in an attempt to loosen a nut by applying a force as
Cutnell/Johnson Physics Classroom Response System Questions Chapter 9 Rotational Dynamics Interactive Lecture Questions 9.1.1. You are using a wrench in an attempt to loosen a nut by applying a force as
Chapter 8 Rotational Motion and Equilibrium
 Chapter 8 Rotational Motion and Equilibrium 8.1 Rigid Bodies, Translations, and Rotations A rigid body is an object or a system of particles in which the distances between particles are fixed (remain constant).
Chapter 8 Rotational Motion and Equilibrium 8.1 Rigid Bodies, Translations, and Rotations A rigid body is an object or a system of particles in which the distances between particles are fixed (remain constant).
Physics 111. Lecture 22 (Walker: ) Torque Rotational Dynamics Static Equilibrium Oct. 28, 2009
 Physics 111 Lecture 22 (Walker: 11.1-3) Torque Rotational Dynamics Static Equilibrium Oct. 28, 2009 Lecture 22 1/26 Torque (τ) We define a quantity called torque which is a measure of twisting effort.
Physics 111 Lecture 22 (Walker: 11.1-3) Torque Rotational Dynamics Static Equilibrium Oct. 28, 2009 Lecture 22 1/26 Torque (τ) We define a quantity called torque which is a measure of twisting effort.
Circular Motion, Pt 2: Angular Dynamics. Mr. Velazquez AP/Honors Physics
 Circular Motion, Pt 2: Angular Dynamics Mr. Velazquez AP/Honors Physics Formulas: Angular Kinematics (θ must be in radians): s = rθ Arc Length 360 = 2π rads = 1 rev ω = θ t = v t r Angular Velocity α av
Circular Motion, Pt 2: Angular Dynamics Mr. Velazquez AP/Honors Physics Formulas: Angular Kinematics (θ must be in radians): s = rθ Arc Length 360 = 2π rads = 1 rev ω = θ t = v t r Angular Velocity α av
AP Physics 1 Rotational Motion Practice Test
 AP Physics 1 Rotational Motion Practice Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) A spinning ice skater on extremely smooth ice is able
AP Physics 1 Rotational Motion Practice Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) A spinning ice skater on extremely smooth ice is able
Exercise Torque Magnitude Ranking Task. Part A
 Exercise 10.2 Calculate the net torque about point O for the two forces applied as in the figure. The rod and both forces are in the plane of the page. Take positive torques to be counterclockwise. τ 28.0
Exercise 10.2 Calculate the net torque about point O for the two forces applied as in the figure. The rod and both forces are in the plane of the page. Take positive torques to be counterclockwise. τ 28.0
It will be most difficult for the ant to adhere to the wheel as it revolves past which of the four points? A) I B) II C) III D) IV
 AP Physics 1 Lesson 16 Homework Newton s First and Second Law of Rotational Motion Outcomes Define rotational inertia, torque, and center of gravity. State and explain Newton s first Law of Motion as it
AP Physics 1 Lesson 16 Homework Newton s First and Second Law of Rotational Motion Outcomes Define rotational inertia, torque, and center of gravity. State and explain Newton s first Law of Motion as it
Test 7 wersja angielska
 Test 7 wersja angielska 7.1A One revolution is the same as: A) 1 rad B) 57 rad C) π/2 rad D) π rad E) 2π rad 7.2A. If a wheel turns with constant angular speed then: A) each point on its rim moves with
Test 7 wersja angielska 7.1A One revolution is the same as: A) 1 rad B) 57 rad C) π/2 rad D) π rad E) 2π rad 7.2A. If a wheel turns with constant angular speed then: A) each point on its rim moves with
Chapter 9 Rotational Dynamics
 Chapter 9 ROTATIONAL DYNAMICS PREVIEW A force acting at a perpendicular distance from a rotation point, such as pushing a doorknob and causing the door to rotate on its hinges, produces a torque. If the
Chapter 9 ROTATIONAL DYNAMICS PREVIEW A force acting at a perpendicular distance from a rotation point, such as pushing a doorknob and causing the door to rotate on its hinges, produces a torque. If the
CHAPTER 8 TEST REVIEW MARKSCHEME
 AP PHYSICS Name: Period: Date: 50 Multiple Choice 45 Single Response 5 Multi-Response Free Response 3 Short Free Response 2 Long Free Response MULTIPLE CHOICE DEVIL PHYSICS BADDEST CLASS ON CAMPUS AP EXAM
AP PHYSICS Name: Period: Date: 50 Multiple Choice 45 Single Response 5 Multi-Response Free Response 3 Short Free Response 2 Long Free Response MULTIPLE CHOICE DEVIL PHYSICS BADDEST CLASS ON CAMPUS AP EXAM
Moment of Inertia Race
 Review Two points, A and B, are on a disk that rotates with a uniform speed about an axis. Point A is closer to the axis than point B. Which of the following is NOT true? 1. Point B has the greater tangential
Review Two points, A and B, are on a disk that rotates with a uniform speed about an axis. Point A is closer to the axis than point B. Which of the following is NOT true? 1. Point B has the greater tangential
Chapter 8 continued. Rotational Dynamics
 Chapter 8 continued Rotational Dynamics 8.6 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Chapter 8 continued Rotational Dynamics 8.6 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Webreview Torque and Rotation Practice Test
 Please do not write on test. ID A Webreview - 8.2 Torque and Rotation Practice Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A 0.30-m-radius automobile
Please do not write on test. ID A Webreview - 8.2 Torque and Rotation Practice Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A 0.30-m-radius automobile
Chapter 8 Lecture Notes
 Chapter 8 Lecture Notes Physics 2414 - Strauss Formulas: v = l / t = r θ / t = rω a T = v / t = r ω / t =rα a C = v 2 /r = ω 2 r ω = ω 0 + αt θ = ω 0 t +(1/2)αt 2 θ = (1/2)(ω 0 +ω)t ω 2 = ω 0 2 +2αθ τ
Chapter 8 Lecture Notes Physics 2414 - Strauss Formulas: v = l / t = r θ / t = rω a T = v / t = r ω / t =rα a C = v 2 /r = ω 2 r ω = ω 0 + αt θ = ω 0 t +(1/2)αt 2 θ = (1/2)(ω 0 +ω)t ω 2 = ω 0 2 +2αθ τ
Big Idea 4: Interactions between systems can result in changes in those systems. Essential Knowledge 4.D.1: Torque, angular velocity, angular
 Unit 7: Rotational Motion (angular kinematics, dynamics, momentum & energy) Name: Big Idea 3: The interactions of an object with other objects can be described by forces. Essential Knowledge 3.F.1: Only
Unit 7: Rotational Motion (angular kinematics, dynamics, momentum & energy) Name: Big Idea 3: The interactions of an object with other objects can be described by forces. Essential Knowledge 3.F.1: Only
Rolling, Torque, and Angular Momentum
 AP Physics C Rolling, Torque, and Angular Momentum Introduction: Rolling: In the last unit we studied the rotation of a rigid body about a fixed axis. We will now extend our study to include cases where
AP Physics C Rolling, Torque, and Angular Momentum Introduction: Rolling: In the last unit we studied the rotation of a rigid body about a fixed axis. We will now extend our study to include cases where
Textbook Reference: Wilson, Buffa, Lou: Chapter 8 Glencoe Physics: Chapter 8
 AP Physics Rotational Motion Introduction: Which moves with greater speed on a merry-go-round - a horse near the center or one near the outside? Your answer probably depends on whether you are considering
AP Physics Rotational Motion Introduction: Which moves with greater speed on a merry-go-round - a horse near the center or one near the outside? Your answer probably depends on whether you are considering
Welcome back to Physics 211
 Welcome back to Physics 211 Today s agenda: Moment of Inertia Angular momentum 13-2 1 Current assignments Prelecture due Tuesday after Thanksgiving HW#13 due next Wednesday, 11/24 Turn in written assignment
Welcome back to Physics 211 Today s agenda: Moment of Inertia Angular momentum 13-2 1 Current assignments Prelecture due Tuesday after Thanksgiving HW#13 due next Wednesday, 11/24 Turn in written assignment
Rotation. Kinematics Rigid Bodies Kinetic Energy. Torque Rolling. featuring moments of Inertia
 Rotation Kinematics Rigid Bodies Kinetic Energy featuring moments of Inertia Torque Rolling Angular Motion We think about rotation in the same basic way we do about linear motion How far does it go? How
Rotation Kinematics Rigid Bodies Kinetic Energy featuring moments of Inertia Torque Rolling Angular Motion We think about rotation in the same basic way we do about linear motion How far does it go? How
III. Angular Momentum Conservation (Chap. 10) Rotation. We repeat Chap. 2-8 with rotatiing objects. Eqs. of motion. Energy.
 Chap. 10: Rotational Motion I. Rotational Kinematics II. Rotational Dynamics - Newton s Law for Rotation III. Angular Momentum Conservation (Chap. 10) 1 Toward Exam 3 Eqs. of motion o To study angular
Chap. 10: Rotational Motion I. Rotational Kinematics II. Rotational Dynamics - Newton s Law for Rotation III. Angular Momentum Conservation (Chap. 10) 1 Toward Exam 3 Eqs. of motion o To study angular
τ net l = r p L = Iω = d L dt = I α ΔL Angular momentum (one) Angular momentum (system, fixed axis) Newton s second law (system)
 l = r p L = Iω = d L dt = I α ΔL = 0 Angular momentum (one) Angular momentum (system, fixed axis) Newton s second law (system) Conserva
l = r p L = Iω = d L dt = I α ΔL = 0 Angular momentum (one) Angular momentum (system, fixed axis) Newton s second law (system) Conserva
Big Ideas 3 & 5: Circular Motion and Rotation 1 AP Physics 1
 Big Ideas 3 & 5: Circular Motion and Rotation 1 AP Physics 1 1. A 50-kg boy and a 40-kg girl sit on opposite ends of a 3-meter see-saw. How far from the girl should the fulcrum be placed in order for the
Big Ideas 3 & 5: Circular Motion and Rotation 1 AP Physics 1 1. A 50-kg boy and a 40-kg girl sit on opposite ends of a 3-meter see-saw. How far from the girl should the fulcrum be placed in order for the
Angular Momentum L = I ω
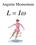 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
3. A bicycle tire of radius 0.33 m and a mass 1.5 kg is rotating at 98.7 rad/s. What torque is necessary to stop the tire in 2.0 s?
 Practice 8A Torque 1. Find the torque produced by a 3.0 N force applied at an angle of 60.0 to a door 0.25 m from the hinge. What is the maximum torque this force could exert? 2. If the torque required
Practice 8A Torque 1. Find the torque produced by a 3.0 N force applied at an angle of 60.0 to a door 0.25 m from the hinge. What is the maximum torque this force could exert? 2. If the torque required
Physics 2210 Fall smartphysics Rotational Statics 11/18/2015
 Physics 2210 Fall 2015 smartphysics 17-18 Rotational Statics 11/18/2015 τ TT = L T 1 sin 150 = 1 T 2 1L Poll 11-18-01 τ TT = L 2 T 2 sin 150 = 1 4 T 2L 150 150 τ gg = L 2 MM sin +90 = 1 2 MMM +90 MM τ
Physics 2210 Fall 2015 smartphysics 17-18 Rotational Statics 11/18/2015 τ TT = L T 1 sin 150 = 1 T 2 1L Poll 11-18-01 τ TT = L 2 T 2 sin 150 = 1 4 T 2L 150 150 τ gg = L 2 MM sin +90 = 1 2 MMM +90 MM τ
Name (please print): UW ID# score last first
 Name (please print): UW ID# score last first Question I. (20 pts) Projectile motion A ball of mass 0.3 kg is thrown at an angle of 30 o above the horizontal. Ignore air resistance. It hits the ground 100
Name (please print): UW ID# score last first Question I. (20 pts) Projectile motion A ball of mass 0.3 kg is thrown at an angle of 30 o above the horizontal. Ignore air resistance. It hits the ground 100
Rotation review packet. Name:
 Rotation review packet. Name:. A pulley of mass m 1 =M and radius R is mounted on frictionless bearings about a fixed axis through O. A block of equal mass m =M, suspended by a cord wrapped around the
Rotation review packet. Name:. A pulley of mass m 1 =M and radius R is mounted on frictionless bearings about a fixed axis through O. A block of equal mass m =M, suspended by a cord wrapped around the
Chapter 8. Rotational Motion
 Chapter 8 Rotational Motion Rotational Work and Energy W = Fs = s = rθ Frθ Consider the work done in rotating a wheel with a tangential force, F, by an angle θ. τ = Fr W =τθ Rotational Work and Energy
Chapter 8 Rotational Motion Rotational Work and Energy W = Fs = s = rθ Frθ Consider the work done in rotating a wheel with a tangential force, F, by an angle θ. τ = Fr W =τθ Rotational Work and Energy
Chapter 8. Rotational Equilibrium and Rotational Dynamics
 Chapter 8 Rotational Equilibrium and Rotational Dynamics Wrench Demo Torque Torque, τ, is the tendency of a force to rotate an object about some axis τ = Fd F is the force d is the lever arm (or moment
Chapter 8 Rotational Equilibrium and Rotational Dynamics Wrench Demo Torque Torque, τ, is the tendency of a force to rotate an object about some axis τ = Fd F is the force d is the lever arm (or moment
Angular Momentum L = I ω
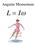 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Solution Only gravity is doing work. Since gravity is a conservative force mechanical energy is conserved:
 8) roller coaster starts with a speed of 8.0 m/s at a point 45 m above the bottom of a dip (see figure). Neglecting friction, what will be the speed of the roller coaster at the top of the next slope,
8) roller coaster starts with a speed of 8.0 m/s at a point 45 m above the bottom of a dip (see figure). Neglecting friction, what will be the speed of the roller coaster at the top of the next slope,
PSI AP Physics I Rotational Motion
 PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
End-of-Chapter Exercises
 End-of-Chapter Exercises Exercises 1 12 are conceptual questions that are designed to see if you have understood the main concepts of the chapter. 1. Figure 11.21 shows four different cases involving a
End-of-Chapter Exercises Exercises 1 12 are conceptual questions that are designed to see if you have understood the main concepts of the chapter. 1. Figure 11.21 shows four different cases involving a
Rotational Motion. Chapter 8: Rotational Motion. Angular Position. Rotational Motion. Ranking: Rolling Cups 9/21/12
 Rotational Motion Chapter 8: Rotational Motion In physics we distinguish two types of motion for objects: Translational Motion (change of location): Whole object moves through space. Rotational Motion
Rotational Motion Chapter 8: Rotational Motion In physics we distinguish two types of motion for objects: Translational Motion (change of location): Whole object moves through space. Rotational Motion
Review questions. Before the collision, 70 kg ball is stationary. Afterward, the 30 kg ball is stationary and 70 kg ball is moving to the right.
 Review questions Before the collision, 70 kg ball is stationary. Afterward, the 30 kg ball is stationary and 70 kg ball is moving to the right. 30 kg 70 kg v (a) Is this collision elastic? (b) Find the
Review questions Before the collision, 70 kg ball is stationary. Afterward, the 30 kg ball is stationary and 70 kg ball is moving to the right. 30 kg 70 kg v (a) Is this collision elastic? (b) Find the
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Rotational N.2 nd Law
 Lecture 0 Chapter 1 Physics I Rotational N. nd Law Torque Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi IN THIS CHAPTER, you will continue discussing rotational dynamics Today
Lecture 0 Chapter 1 Physics I Rotational N. nd Law Torque Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi IN THIS CHAPTER, you will continue discussing rotational dynamics Today
Name Student ID Score Last First. I = 2mR 2 /5 around the sphere s center of mass?
 NOTE: ignore air resistance in all Questions. In all Questions choose the answer that is the closest!! Question I. (15 pts) Rotation 1. (5 pts) A bowling ball that has an 11 cm radius and a 7.2 kg mass
NOTE: ignore air resistance in all Questions. In all Questions choose the answer that is the closest!! Question I. (15 pts) Rotation 1. (5 pts) A bowling ball that has an 11 cm radius and a 7.2 kg mass
Chapter 8, Rotational Equilibrium and Rotational Dynamics. 3. If a net torque is applied to an object, that object will experience:
 CHAPTER 8 3. If a net torque is applied to an object, that object will experience: a. a constant angular speed b. an angular acceleration c. a constant moment of inertia d. an increasing moment of inertia
CHAPTER 8 3. If a net torque is applied to an object, that object will experience: a. a constant angular speed b. an angular acceleration c. a constant moment of inertia d. an increasing moment of inertia
Chapter 11 Motion in a Circle
 Lecture Outline Chapter 11 Motion in a Circle Remaining Schedule (tentative) 29 Mar torque 12.1-5 31 Mar torque 12.6-8 5Apr periodic motion 15.1-7 7 Apr fluids 18.1-5 12 Apr fluids 18.6-8 14 Apr EXAM 3
Lecture Outline Chapter 11 Motion in a Circle Remaining Schedule (tentative) 29 Mar torque 12.1-5 31 Mar torque 12.6-8 5Apr periodic motion 15.1-7 7 Apr fluids 18.1-5 12 Apr fluids 18.6-8 14 Apr EXAM 3
AP Physics Multiple Choice Practice Torque
 AP Physics Multiple Choice Practice Torque 1. A uniform meterstick of mass 0.20 kg is pivoted at the 40 cm mark. Where should one hang a mass of 0.50 kg to balance the stick? (A) 16 cm (B) 36 cm (C) 44
AP Physics Multiple Choice Practice Torque 1. A uniform meterstick of mass 0.20 kg is pivoted at the 40 cm mark. Where should one hang a mass of 0.50 kg to balance the stick? (A) 16 cm (B) 36 cm (C) 44
PSI AP Physics I Rotational Motion
 PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
Name: Date: Period: AP Physics C Rotational Motion HO19
 1.) A wheel turns with constant acceleration 0.450 rad/s 2. (9-9) Rotational Motion H19 How much time does it take to reach an angular velocity of 8.00 rad/s, starting from rest? Through how many revolutions
1.) A wheel turns with constant acceleration 0.450 rad/s 2. (9-9) Rotational Motion H19 How much time does it take to reach an angular velocity of 8.00 rad/s, starting from rest? Through how many revolutions
Chapter 9- Static Equilibrium
 Chapter 9- Static Equilibrium Changes in Office-hours The following changes will take place until the end of the semester Office-hours: - Monday, 12:00-13:00h - Wednesday, 14:00-15:00h - Friday, 13:00-14:00h
Chapter 9- Static Equilibrium Changes in Office-hours The following changes will take place until the end of the semester Office-hours: - Monday, 12:00-13:00h - Wednesday, 14:00-15:00h - Friday, 13:00-14:00h
Exam II. Spring 2004 Serway & Jewett, Chapters Fill in the bubble for the correct answer on the answer sheet. next to the number.
 Agin/Meyer PART I: QUALITATIVE Exam II Spring 2004 Serway & Jewett, Chapters 6-10 Assigned Seat Number Fill in the bubble for the correct answer on the answer sheet. next to the number. NO PARTIAL CREDIT:
Agin/Meyer PART I: QUALITATIVE Exam II Spring 2004 Serway & Jewett, Chapters 6-10 Assigned Seat Number Fill in the bubble for the correct answer on the answer sheet. next to the number. NO PARTIAL CREDIT:
Physics 131: Lecture 21. Today s Agenda
 Physics 131: Lecture 21 Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 201: Lecture 10, Pg 1 Newton s second law in rotation land Sum of the torques will equal the moment of inertia
Physics 131: Lecture 21 Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 201: Lecture 10, Pg 1 Newton s second law in rotation land Sum of the torques will equal the moment of inertia
1. An object is dropped from rest. Which of the five following graphs correctly represents its motion? The positive direction is taken to be downward.
 Unless otherwise instructed, use g = 9.8 m/s 2 Rotational Inertia about an axis through com: Hoop about axis(radius=r, mass=m) : MR 2 Hoop about diameter (radius=r, mass=m): 1/2MR 2 Disk/solid cyllinder
Unless otherwise instructed, use g = 9.8 m/s 2 Rotational Inertia about an axis through com: Hoop about axis(radius=r, mass=m) : MR 2 Hoop about diameter (radius=r, mass=m): 1/2MR 2 Disk/solid cyllinder
Classical Mechanics Lecture 15
 Classical Mechanics Lecture 5 Today s Concepts: a) Parallel Axis Theorem b) Torque & Angular Acceleration Mechanics Lecture 5, Slide Unit 4 Main Points Mechanics Lecture 4, Slide Unit 4 Main Points Mechanics
Classical Mechanics Lecture 5 Today s Concepts: a) Parallel Axis Theorem b) Torque & Angular Acceleration Mechanics Lecture 5, Slide Unit 4 Main Points Mechanics Lecture 4, Slide Unit 4 Main Points Mechanics
Physics 201. Professor P. Q. Hung. 311B, Physics Building. Physics 201 p. 1/1
 Physics 201 p. 1/1 Physics 201 Professor P. Q. Hung 311B, Physics Building Physics 201 p. 2/1 Rotational Kinematics and Energy Rotational Kinetic Energy, Moment of Inertia All elements inside the rigid
Physics 201 p. 1/1 Physics 201 Professor P. Q. Hung 311B, Physics Building Physics 201 p. 2/1 Rotational Kinematics and Energy Rotational Kinetic Energy, Moment of Inertia All elements inside the rigid
Slide 1 / 37. Rotational Motion
 Slide 1 / 37 Rotational Motion Slide 2 / 37 Angular Quantities An angle θ can be given by: where r is the radius and l is the arc length. This gives θ in radians. There are 360 in a circle or 2π radians.
Slide 1 / 37 Rotational Motion Slide 2 / 37 Angular Quantities An angle θ can be given by: where r is the radius and l is the arc length. This gives θ in radians. There are 360 in a circle or 2π radians.
Rotation. Rotational Variables
 Rotation Rigid Bodies Rotation variables Constant angular acceleration Rotational KE Rotational Inertia Rotational Variables Rotation of a rigid body About a fixed rotation axis. Rigid Body an object that
Rotation Rigid Bodies Rotation variables Constant angular acceleration Rotational KE Rotational Inertia Rotational Variables Rotation of a rigid body About a fixed rotation axis. Rigid Body an object that
. d. v A v B. e. none of these.
 General Physics I Exam 3 - Chs. 7,8,9 - Momentum, Rotation, Equilibrium Oct. 28, 2009 Name Rec. Instr. Rec. Time For full credit, make your work clear to the grader. Show the formulas you use, the essential
General Physics I Exam 3 - Chs. 7,8,9 - Momentum, Rotation, Equilibrium Oct. 28, 2009 Name Rec. Instr. Rec. Time For full credit, make your work clear to the grader. Show the formulas you use, the essential
FALL TERM EXAM, PHYS 1211, INTRODUCTORY PHYSICS I Saturday, 14 December 2013, 1PM to 4 PM, AT 1003
 FALL TERM EXAM, PHYS 1211, INTRODUCTORY PHYSICS I Saturday, 14 December 2013, 1PM to 4 PM, AT 1003 NAME: STUDENT ID: INSTRUCTION 1. This exam booklet has 14 pages. Make sure none are missing 2. There is
FALL TERM EXAM, PHYS 1211, INTRODUCTORY PHYSICS I Saturday, 14 December 2013, 1PM to 4 PM, AT 1003 NAME: STUDENT ID: INSTRUCTION 1. This exam booklet has 14 pages. Make sure none are missing 2. There is
Work and kinetic Energy
 Work and kinetic Energy Problem 66. M=4.5kg r = 0.05m I = 0.003kgm 2 Q: What is the velocity of mass m after it dropped a distance h? (No friction) h m=0.6kg mg Work and kinetic Energy Problem 66. M=4.5kg
Work and kinetic Energy Problem 66. M=4.5kg r = 0.05m I = 0.003kgm 2 Q: What is the velocity of mass m after it dropped a distance h? (No friction) h m=0.6kg mg Work and kinetic Energy Problem 66. M=4.5kg
PHY131H1S - Class 20. Pre-class reading quiz on Chapter 12
 PHY131H1S - Class 20 Today: Gravitational Torque Rotational Kinetic Energy Rolling without Slipping Equilibrium with Rotation Rotation Vectors Angular Momentum Pre-class reading quiz on Chapter 12 1 Last
PHY131H1S - Class 20 Today: Gravitational Torque Rotational Kinetic Energy Rolling without Slipping Equilibrium with Rotation Rotation Vectors Angular Momentum Pre-class reading quiz on Chapter 12 1 Last
Rotational N.2 nd Law
 Lecture 19 Chapter 12 Rotational N.2 nd Law Torque Newton 2 nd Law again!? That s it. He crossed the line! Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi IN THIS CHAPTER, you will
Lecture 19 Chapter 12 Rotational N.2 nd Law Torque Newton 2 nd Law again!? That s it. He crossed the line! Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi IN THIS CHAPTER, you will
Chapter 9: Rotational Dynamics Tuesday, September 17, 2013
 Chapter 9: Rotational Dynamics Tuesday, September 17, 2013 10:00 PM The fundamental idea of Newtonian dynamics is that "things happen for a reason;" to be more specific, there is no need to explain rest
Chapter 9: Rotational Dynamics Tuesday, September 17, 2013 10:00 PM The fundamental idea of Newtonian dynamics is that "things happen for a reason;" to be more specific, there is no need to explain rest
Midterm 3 Thursday April 13th
 Welcome back to Physics 215 Today s agenda: Angular momentum Rolling without slipping Midterm Review Physics 215 Spring 2017 Lecture 12-2 1 Midterm 3 Thursday April 13th Material covered: Ch 9 Ch 12 Lectures
Welcome back to Physics 215 Today s agenda: Angular momentum Rolling without slipping Midterm Review Physics 215 Spring 2017 Lecture 12-2 1 Midterm 3 Thursday April 13th Material covered: Ch 9 Ch 12 Lectures
Physics 131: Lecture 21. Today s Agenda
 Physics 131: Lecture 1 Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 01: Lecture 10, Pg 1 Newton s second law in rotation land Sum of the torques will equal the moment of inertia
Physics 131: Lecture 1 Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 01: Lecture 10, Pg 1 Newton s second law in rotation land Sum of the torques will equal the moment of inertia
AP Physics QUIZ Chapters 10
 Name: 1. Torque is the rotational analogue of (A) Kinetic Energy (B) Linear Momentum (C) Acceleration (D) Force (E) Mass A 5-kilogram sphere is connected to a 10-kilogram sphere by a rigid rod of negligible
Name: 1. Torque is the rotational analogue of (A) Kinetic Energy (B) Linear Momentum (C) Acceleration (D) Force (E) Mass A 5-kilogram sphere is connected to a 10-kilogram sphere by a rigid rod of negligible
Torque. Objectives. Assessment. Assessment. Equations. Physics terms 6/2/14
 Objectives Calculate torque given the lever arm (perpendicular distance) and the force. Calculate torque in newton meters and in pound feet. Interpret positive and negative signs in the context of torque.
Objectives Calculate torque given the lever arm (perpendicular distance) and the force. Calculate torque in newton meters and in pound feet. Interpret positive and negative signs in the context of torque.
CHAPTER 8: ROTATIONAL OF RIGID BODY PHYSICS. 1. Define Torque
 7 1. Define Torque 2. State the conditions for equilibrium of rigid body (Hint: 2 conditions) 3. Define angular displacement 4. Define average angular velocity 5. Define instantaneous angular velocity
7 1. Define Torque 2. State the conditions for equilibrium of rigid body (Hint: 2 conditions) 3. Define angular displacement 4. Define average angular velocity 5. Define instantaneous angular velocity
Chap. 10: Rotational Motion
 Chap. 10: Rotational Motion I. Rotational Kinematics II. Rotational Dynamics - Newton s Law for Rotation III. Angular Momentum Conservation (Chap. 10) 1 Newton s Laws for Rotation n e t I 3 rd part [N
Chap. 10: Rotational Motion I. Rotational Kinematics II. Rotational Dynamics - Newton s Law for Rotation III. Angular Momentum Conservation (Chap. 10) 1 Newton s Laws for Rotation n e t I 3 rd part [N
Phys 106 Practice Problems Common Quiz 1 Spring 2003
 Phys 106 Practice Problems Common Quiz 1 Spring 2003 1. For a wheel spinning with constant angular acceleration on an axis through its center, the ratio of the speed of a point on the rim to the speed
Phys 106 Practice Problems Common Quiz 1 Spring 2003 1. For a wheel spinning with constant angular acceleration on an axis through its center, the ratio of the speed of a point on the rim to the speed
A uniform rod of length L and Mass M is attached at one end to a frictionless pivot. If the rod is released from rest from the horizontal position,
 A dentist s drill starts from rest. After 3.20 s of constant angular acceleration, it turns at a rate of 2.51 10 4 rev/min. (a) Find the drill s angular acceleration. (b) Determine the angle (in radians)
A dentist s drill starts from rest. After 3.20 s of constant angular acceleration, it turns at a rate of 2.51 10 4 rev/min. (a) Find the drill s angular acceleration. (b) Determine the angle (in radians)
Fall 2007 RED Barcode Here Physics 105, sections 1 and 2 Please write your CID Colton
 Fall 007 RED Barcode Here Physics 105, sections 1 and Exam 3 Please write your CID Colton -3669 3 hour time limit. One 3 5 handwritten note card permitted (both sides). Calculators permitted. No books.
Fall 007 RED Barcode Here Physics 105, sections 1 and Exam 3 Please write your CID Colton -3669 3 hour time limit. One 3 5 handwritten note card permitted (both sides). Calculators permitted. No books.
Rotational Dynamics. Slide 2 / 34. Slide 1 / 34. Slide 4 / 34. Slide 3 / 34. Slide 6 / 34. Slide 5 / 34. Moment of Inertia. Parallel Axis Theorem
 Slide 1 / 34 Rotational ynamics l Slide 2 / 34 Moment of Inertia To determine the moment of inertia we divide the object into tiny masses of m i a distance r i from the center. is the sum of all the tiny
Slide 1 / 34 Rotational ynamics l Slide 2 / 34 Moment of Inertia To determine the moment of inertia we divide the object into tiny masses of m i a distance r i from the center. is the sum of all the tiny
PHYS 185 Final Exam December 4, 2012
 PHYS 185 Final Exam December 4, 2012 Name: Answer the questions in the spaces provided on the question sheets. If you run out of room for an answer, continue on the back of the page. Please make an effort
PHYS 185 Final Exam December 4, 2012 Name: Answer the questions in the spaces provided on the question sheets. If you run out of room for an answer, continue on the back of the page. Please make an effort
Angular Momentum System of Particles Concept Questions
 Question 1: Angular Momentum Angular Momentum System of Particles Concept Questions A non-symmetric body rotates with an angular speed ω about the z axis. Relative to the origin 1. L 0 is constant. 2.
Question 1: Angular Momentum Angular Momentum System of Particles Concept Questions A non-symmetric body rotates with an angular speed ω about the z axis. Relative to the origin 1. L 0 is constant. 2.
Review for 3 rd Midterm
 Review for 3 rd Midterm Midterm is on 4/19 at 7:30pm in the same rooms as before You are allowed one double sided sheet of paper with any handwritten notes you like. The moment-of-inertia about the center-of-mass
Review for 3 rd Midterm Midterm is on 4/19 at 7:30pm in the same rooms as before You are allowed one double sided sheet of paper with any handwritten notes you like. The moment-of-inertia about the center-of-mass
