Chapter 8 continued. Rotational Dynamics
|
|
|
- Lambert Barton
- 5 years ago
- Views:
Transcription
1 Chapter 8 continued Rotational Dynamics
2 8.6 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω : angular velocity of rotation (same for entire object) α : angular acceleration (same for entire object) v T = ωr : tangential velocity a T = αr : tangential acceleration According to Newton s second law, a net force causes an object to have a linear acceleration. What causes an object to have an angular acceleration? TORQUE
3 8.6 The Action of Forces and Torques on Rigid Objects The amount of torque depends on where and in what direction the force is applied, as well as the location of the axis of rotation. Maximum rotational effect of the force F. Smaller rotational effect of the force F. Rotational effect of the force F is minimal; it compresses more than rotates the bar
4 8.6 The Action of Forces and Torques on Rigid Objects DEFINITION OF TORQUE Magnitude of Torque = r ( Component of Force to r ) τ = rf = rf sinθ Direction: The torque is positive when the force tends to produce a counterclockwise rotation about the axis. SI Unit of Torque: newton x meter (N m) r F θ θ θ is the angle between F and r F = F sinθ r L
5 8.6 The Action of Forces and Torques on Rigid Objects Example: The Achilles Tendon The tendon exerts a force of magnitude 720 N. Determine the torque (magnitude and direction) of this force about the ankle joint. Assume the angle is 35. τ = r( F sinθ ) = (.036 m)(720 N)(sin35 ) = 15.0 N m θ is the angle between F and r Direction is clockwise ( ) around ankle joint θ = 35 F sinθ r F Torque vector τ = 15.0 N m L = m
6 8.7 Rigid Objects in Equilibrium If a rigid body is in equilibrium, neither its linear motion nor its rotational motion changes. All equilibrium problems use these equations no net force and no net torque.
7 8.7 Rigid Objects in Equilibrium EQUILIBRIUM OF A RIGID BODY A rigid body is in equilibrium if it has zero translational acceleration and zero angular acceleration. In equilibrium, the sum of the externally applied forces is zero, and the sum of the externally applied torques is zero. Note: constant linear speed or constant rotational speed are allowed for an object in equilibrium.
8 8.7 Rigid Objects in Equilibrium Reasoning Strategy 1. Select the object to which the equations for equilibrium are to be applied. 2. Draw a free-body diagram that shows all of the external forces acting on the object. 3. Choose a convenient set of x, y axes and resolve all forces into components that lie along these axes. 4. Apply the equations that specify the balance of forces at equilibrium. (Set the net force in the x and y directions equal to zero.) 5. Select a convenient axis of rotation. Set the sum of the torques about this axis equal to zero. 6. Solve the equations for the desired unknown quantities.
9 8.7 Rigid Objects in Equilibrium Example A Diving Board A woman whose weight is 530 N is poised at the right end of a diving board with length 3.90 m. The board has negligible weight and is supported by a fulcrum 1.40 m away from the left end. Find the forces that the bolt and the fulcrum exert on the board. F 1 acts on rotation axis - produces no torque. Counter-clockwise torque is positive τ = 0 = 2 F 2 W W F 2 = ( W 2 )W = ( )530N = 1480 N F y = 0 = F 1 + F 2 W F 1 = F 2 W = ( )N = 950 N
10 8.7 Rigid Objects in Equilibrium Choice of pivot is arbitary (most convenient) Pivot at fulcum: F 2 produces no torque. Counter-clockwise torque is positive τ = 0 = F 1 2 W ( W 2 ) F 1 = W ( W 2 1) = (530N)(1.8) = 950N F y = 0 = F 1 + F 2 W F 2 = F 1 +W = ( )N = 1480 N Yields the same answers as with pivot at Bolt.
11 8.7 Rigid Objects in Equilibrium All forces acting on the arm Counter-clockwise torque is positive Only those contributing torque Example 5 Bodybuilding The arm is horizontal and weighs 31.0 N. The deltoid muscle can supply 1840 N of force. What is the weight of the heaviest dumbell he can hold?
12 8.7 Rigid Objects in Equilibrium positive torque negative torques τ = M ( sin13 ) M W a a W d d = 0 W d = + M ( sin13 ) M W a a d = 1840N(.225)(0.15m) 31N(0.28m) 0.62m = 86.1N
13 8.7 Center of Gravity DEFINITION OF CENTER OF GRAVITY The center of gravity of a rigid body is the point at which its weight can be considered to act when the torque due to the weight is being calculated.
14 8.7 Center of Gravity When an object has a symmetrical shape and its weight is distributed uniformly, the center of gravity lies at its geometrical center.
15 8.7 Center of Gravity General Form of x cg Balance point is under x cg Center of Gravity, x cg, for 2 masses x cg = W 1 x 1 +W 2 x 2 W 1 +W 2
16 8.7 Center of Gravity Example: The Center of Gravity of an Arm The horizontal arm is composed of three parts: the upper arm (17 N), the lower arm (11 N), and the hand (4.2 N). Find the center of gravity of the arm relative to the shoulder joint. x cg = W 1 x 1 +W 2 x 2 +W 3 x 3 W 1 +W 2 +W 3 = ( ) +11( 0.38) + 4.2( 0.61) ( ) N N m = 0.28 m
17 8.7 Center of Gravity Finding the center of gravity of an irregular shape.
18 Clicker Question 8.4 Torque and Equilibrium (no clickers today) A 4-kg ball and a 1-kg ball are positioned a distance L apart on a bar of negligible mass. How far from the 4-kg mass should the fulcum be placed to balance the bar? a) 1 2 L b) 1 3 L c) 1 4 L d) 1 5 L e) 1 6 L m 1 = 1kg L m 2 = 4kg
19 Clicker Question 8.4 Torque and Equilibrium A 4-kg ball and a 1-kg ball are positioned a distance L apart on a bar of negligible mass. How far from the 4-kg mass should the fulcum be placed to balance the bar? a) 1 2 L b) 1 3 L c) 1 4 L d) 1 5 L m 1 = 1kg positive torque e) 1 L For equilibrium the sum of the torques must be zero 6 Need to separate length into 4 parts on 1-kg mass side 4 L 1 W 1 W 2 m 2 = 4kg negative torque and 1 part on the 4-kg mass side. Total is 5 parts. Fulcum must be 1/5 of the total length from the 4-kg mass.
20 Clicker Question 8.4 Torque and Equilibrium A 4-kg ball and a 1-kg ball are positioned a distance L apart on a bar of negligible mass. How far from the 4-kg mass should the fulcum be placed to balance the bar? a) 1 2 L b) 1 3 L c) 1 4 L d) 1 5 L L m = 1kg 1 L x x m = 4kg 2 positive torque W 1 W 2 For equilibrium the sum of the torques must be zero negative torque e) 1 6 L Let x be the distance of fulcum from 4-kg mass. τ = 0 = m 1 g(l x) + ( m 2 gx) ( m 1 + m 2 )x = m 1 L x = m 1 ( ) L = 1 m 1 + m 2 (1+ 4) L = 1 5 L
21 8.8 Newton s Second Law for Rotational Motion About a Fixed Axis τ = F T r = ma T r = mαr 2 = ( mr 2 )α = Iα I = mr 2 Moment of Inertia Moment of Inertia, I =mr 2, for a point-mass, m, at the end of a massless arm of length, r. τ = Iα Newton s 2 nd Law for rotations
22 8.8 Newton s Second Law for Rotational Motion About a Fixed Axis Break object into N individual masses τ Net = Net external torque i (mr 2 ) α i Moment of inertia τ 1 = ( 2 m 1 r 1 )α τ 2 = ( 2 m 2 r 2 )α τ N = ( 2 m N r N )α
23 8.8 Newton s Second Law for Rotational Motion About a Fixed Axis ROTATIONAL ANALOG OF NEWTON S SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS τ Net = I α I = (mr 2 ) i i Requirement: Angular acceleration must be expressed in radians/s 2.
24 From Ch.8.4 Rotational Kinetic Energy Moments of Inertia of Rigid Objects Mass M Solid sphere through center I = 2 5 MR2 Solid sphere through surface tangent I = MR 2 I = 1 2 MR2 Thin walled hollow cylinder Solid cylinder or disk Thin rod length through center I = 7 5 MR2 Thin walled sphere through center I = 2 3 MR2 Thin plate width, through center I = 1 12 M2 I = 1 12 M2 Thin rod length through end Thin plate width through edge I = 1 3 M2 I = 1 3 M2
25 8.8 Newton s Second Law for Rotational Motion About a Fixed Axis Example: Hoisting a Crate The combined moment of inertia of the dual pulley is 50.0 kg m 2. The crate weighs 4420 N. A tension of 2150 N is maintained in the cable attached to the motor. Find the angular acceleration of the dual Pulley (radius-1 = 0.600m, radius-2 = m). up is positive Tension 1 Motor Dual Pulley Tension 2 Forces on Pulley P 1 = 0.600m T 1 Post 2 = 0.200m Forces on Crate T2 Axis W P a y T2 Crate W magnitude mg
26 8.8 Newton s Second Law for Rotational Motion About a Fixed Axis 2nd law for linear motion of crate F y = T 2 mg = ma y 2nd law for rotation of the pulley T 2 mg = m 2 α T 1 1 T 2 2 = Iα T 2 = m 2 α + mg & T 2 = T 1 1 Iα 2 m 2 2 α + Iα = T 1 1 mg 2 α = T 1 1 mg 2 m I = 6.3 rad/s 2 a y = 2 α Motor I = 46kg m 2 mg = 4420 N T 1 = 2150 N Dual Pulley Crate 1 = 0.600m T 1 Axis W P T2 P 2 = 0.200m = T2,down T2 = T 2,up (+) a y T 2 = m 2 α + mg = ( 451(.6)(6.3) )N = 6125 N mg
27 8.9 Angular Momentum DEFINITION OF ANGULAR MOMENTUM The angular momentum L of a body rotating about a fixed axis is the product of the body s moment of inertia and its angular velocity with respect to that axis: Requirement: The angular speed must be expressed in rad/s. SI Unit of Angular Momentum: kg m 2 /s
28 8.9 Angular Momentum PRINCIPLE OF CONSERVATION OF ANGULAR MOMENTUM The angular momentum of a system remains constant (is conserved) if the net external torque acting on the system is zero. Angular momentum, L L i = I i ω i ; L f = I f ω f No external torque Angular momentum conserved L f = L i Moment of Inertia decreases I = mr 2, r f < r i I f < I i I i I f > 1 I f ω f = I i ω i ω f = I i I f ω i ; I i I f > 1 ω f > ω i (angular speed increases)
29 8.9 Angular Momentum From Angular Momentum Conservation ω f = ( I i I f )ω i I i I f > 1 Angular velocity increases Is Energy conserved? KE f = 1 2 I f ω 2 f ( ) 2 ω 2 i ( )( 1 I ω 2 ) KE 2 i i i = 1 I ω 2 ; 2 i i ( ) KE i Kinetic Energy increases = 1 2 I f I i I f = I i I f = I i I f Energy is not conserved because pulling in the arms does (NC) work on their mass and increases the kinetic energy of rotation
30 8.9 Angular Momentum Example: A Satellite in an Elliptical Orbit An artificial satellite is placed in an elliptical orbit about the earth. Its point of closest approach is 8.37x10 6 m from the center of the earth, and its point of greatest distance is 25.1x10 6 m from the center of the earth.the speed of the satellite at the perigee is 8450 m/s. Find the speed at the apogee. Gravitational force along L (no torque) Angular momentum conserved I A ω A = I P ω P ( ) = mr 2 P ( v P r P ) I A = mr A 2 ; I P = mr P 2 ω A = v A r A ; ω P = v P r P mr 2 A v A r A r A v A = r P v P v A = ( r P r A )v P = ( ) / ( ) ( 8450 m/s) = 2820 m/s
31 8.9 The Vector Nature of Angular Variables Right-Hand Rule: Grasp the axis of rotation with your right hand, so that your fingers circle the axis in the same sense as the rotation. Your extended thumb points along the axis in the direction of the angular velocity. Vector Quantities in Rotational Motion Angular Acceleration Angular Momentum Torque α = Δ ω Δt L = Iω τ = I α = Δ L Δt Changes Angular Momentum If torque is perpendicular to the angular momentum, only the direction of the angular momentum changes (precession) no changes to the magnitude.
32 Rotational/Linear Dynamics Summary linear rotational x θ v a m F p ω α I = mr 2 (point m) τ = Fr sinθ L = Iω linear F = ma p = mv W = rf cosθ rotational τ = Iα L = Iω W rot = τθ KE = 1 KE rot = 1 Iω 2 2 mv2 2 W ΔKE W rot ΔKE rot FΔt Δp τδt ΔL Potential Energies U G = mgy or U G = GM E m/r E U S = 1 2 kx2 Conserved quantity: If W NC = 0, E = K +U Conservation laws If F ext = 0, P system = p If τ ext = 0, L = I ω
Rotational Dynamics continued
 Chapter 9 Rotational Dynamics continued 9.1 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Chapter 9 Rotational Dynamics continued 9.1 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Chapter 8 continued. Rotational Dynamics
 Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = s = rφ = Frφ Fr = τ (torque) = τφ r φ s F to s θ = 0 DEFINITION
Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = s = rφ = Frφ Fr = τ (torque) = τφ r φ s F to s θ = 0 DEFINITION
Chapter 8 continued. Rotational Dynamics
 Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = rφ = Frφ Fr = τ (torque) = τφ r φ s F to x θ = 0 DEFINITION OF
Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = rφ = Frφ Fr = τ (torque) = τφ r φ s F to x θ = 0 DEFINITION OF
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
Rotational Dynamics continued
 Chapter 9 Rotational Dynamics continued 9.4 Newton s Second Law for Rotational Motion About a Fixed Axis ROTATIONAL ANALOG OF NEWTON S SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS I = ( mr 2
Chapter 9 Rotational Dynamics continued 9.4 Newton s Second Law for Rotational Motion About a Fixed Axis ROTATIONAL ANALOG OF NEWTON S SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS I = ( mr 2
Chapter 8. Rotational Motion
 Chapter 8 Rotational Motion The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of
Chapter 8 Rotational Motion The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 8. Rotational Kinematics
 Chapter 8 Rotational Kinematics 8.3 The Equations of Rotational Kinematics 8.4 Angular Variables and Tangential Variables The relationship between the (tangential) arc length, s, at some radius, r, and
Chapter 8 Rotational Kinematics 8.3 The Equations of Rotational Kinematics 8.4 Angular Variables and Tangential Variables The relationship between the (tangential) arc length, s, at some radius, r, and
Chapter 8. Rotational Motion
 Chapter 8 Rotational Motion Rotational Work and Energy W = Fs = s = rθ Frθ Consider the work done in rotating a wheel with a tangential force, F, by an angle θ. τ = Fr W =τθ Rotational Work and Energy
Chapter 8 Rotational Motion Rotational Work and Energy W = Fs = s = rθ Frθ Consider the work done in rotating a wheel with a tangential force, F, by an angle θ. τ = Fr W =τθ Rotational Work and Energy
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
= o + t = ot + ½ t 2 = o + 2
 Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
Lecture 14. Rotational dynamics Torque. Give me a lever long enough and a fulcrum on which to place it, and I shall move the world.
 Lecture 14 Rotational dynamics Torque Give me a lever long enough and a fulcrum on which to place it, and I shall move the world. Archimedes, 87 1 BC EXAM Tuesday March 6, 018 8:15 PM 9:45 PM Today s Topics:
Lecture 14 Rotational dynamics Torque Give me a lever long enough and a fulcrum on which to place it, and I shall move the world. Archimedes, 87 1 BC EXAM Tuesday March 6, 018 8:15 PM 9:45 PM Today s Topics:
31 ROTATIONAL KINEMATICS
 31 ROTATIONAL KINEMATICS 1. Compare and contrast circular motion and rotation? Address the following Which involves an object and which involves a system? Does an object/system in circular motion have
31 ROTATIONAL KINEMATICS 1. Compare and contrast circular motion and rotation? Address the following Which involves an object and which involves a system? Does an object/system in circular motion have
Solution Only gravity is doing work. Since gravity is a conservative force mechanical energy is conserved:
 8) roller coaster starts with a speed of 8.0 m/s at a point 45 m above the bottom of a dip (see figure). Neglecting friction, what will be the speed of the roller coaster at the top of the next slope,
8) roller coaster starts with a speed of 8.0 m/s at a point 45 m above the bottom of a dip (see figure). Neglecting friction, what will be the speed of the roller coaster at the top of the next slope,
AP Physics QUIZ Chapters 10
 Name: 1. Torque is the rotational analogue of (A) Kinetic Energy (B) Linear Momentum (C) Acceleration (D) Force (E) Mass A 5-kilogram sphere is connected to a 10-kilogram sphere by a rigid rod of negligible
Name: 1. Torque is the rotational analogue of (A) Kinetic Energy (B) Linear Momentum (C) Acceleration (D) Force (E) Mass A 5-kilogram sphere is connected to a 10-kilogram sphere by a rigid rod of negligible
Torque rotational force which causes a change in rotational motion. This force is defined by linear force multiplied by a radius.
 Warm up A remote-controlled car's wheel accelerates at 22.4 rad/s 2. If the wheel begins with an angular speed of 10.8 rad/s, what is the wheel's angular speed after exactly three full turns? AP Physics
Warm up A remote-controlled car's wheel accelerates at 22.4 rad/s 2. If the wheel begins with an angular speed of 10.8 rad/s, what is the wheel's angular speed after exactly three full turns? AP Physics
Chapter 10. Rotation
 Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
AP Physics 1 Rotational Motion Practice Test
 AP Physics 1 Rotational Motion Practice Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) A spinning ice skater on extremely smooth ice is able
AP Physics 1 Rotational Motion Practice Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) A spinning ice skater on extremely smooth ice is able
Handout 7: Torque, angular momentum, rotational kinetic energy and rolling motion. Torque and angular momentum
 Handout 7: Torque, angular momentum, rotational kinetic energy and rolling motion Torque and angular momentum In Figure, in order to turn a rod about a fixed hinge at one end, a force F is applied at a
Handout 7: Torque, angular momentum, rotational kinetic energy and rolling motion Torque and angular momentum In Figure, in order to turn a rod about a fixed hinge at one end, a force F is applied at a
Rotational Kinetic Energy
 Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
PHYSICS 149: Lecture 21
 PHYSICS 149: Lecture 21 Chapter 8: Torque and Angular Momentum 8.2 Torque 8.4 Equilibrium Revisited 8.8 Angular Momentum Lecture 21 Purdue University, Physics 149 1 Midterm Exam 2 Wednesday, April 6, 6:30
PHYSICS 149: Lecture 21 Chapter 8: Torque and Angular Momentum 8.2 Torque 8.4 Equilibrium Revisited 8.8 Angular Momentum Lecture 21 Purdue University, Physics 149 1 Midterm Exam 2 Wednesday, April 6, 6:30
Chapter 8. Rotational Equilibrium and Rotational Dynamics
 Chapter 8 Rotational Equilibrium and Rotational Dynamics Wrench Demo Torque Torque, τ, is the tendency of a force to rotate an object about some axis τ = Fd F is the force d is the lever arm (or moment
Chapter 8 Rotational Equilibrium and Rotational Dynamics Wrench Demo Torque Torque, τ, is the tendency of a force to rotate an object about some axis τ = Fd F is the force d is the lever arm (or moment
We define angular displacement, θ, and angular velocity, ω. What's a radian?
 We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
AP Pd 3 Rotational Dynamics.notebook. May 08, 2014
 1 Rotational Dynamics Why do objects spin? Objects can travel in different ways: Translation all points on the body travel in parallel paths Rotation all points on the body move around a fixed point An
1 Rotational Dynamics Why do objects spin? Objects can travel in different ways: Translation all points on the body travel in parallel paths Rotation all points on the body move around a fixed point An
Chapter 8 - Rotational Dynamics and Equilibrium REVIEW
 Pagpalain ka! (Good luck, in Filipino) Date Chapter 8 - Rotational Dynamics and Equilibrium REVIEW TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1) When a rigid body
Pagpalain ka! (Good luck, in Filipino) Date Chapter 8 - Rotational Dynamics and Equilibrium REVIEW TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1) When a rigid body
Chapter 8. Rotational Equilibrium and Rotational Dynamics
 Chapter 8 Rotational Equilibrium and Rotational Dynamics 1 Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related 2 Torque The door is free to rotate
Chapter 8 Rotational Equilibrium and Rotational Dynamics 1 Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related 2 Torque The door is free to rotate
Topic 1: Newtonian Mechanics Energy & Momentum
 Work (W) the amount of energy transferred by a force acting through a distance. Scalar but can be positive or negative ΔE = W = F! d = Fdcosθ Units N m or Joules (J) Work, Energy & Power Power (P) the
Work (W) the amount of energy transferred by a force acting through a distance. Scalar but can be positive or negative ΔE = W = F! d = Fdcosθ Units N m or Joules (J) Work, Energy & Power Power (P) the
Translational vs Rotational. m x. Connection Δ = = = = = = Δ = = = = = = Δ =Δ = = = = = 2 / 1/2. Work
 Translational vs Rotational / / 1/ Δ m x v dx dt a dv dt F ma p mv KE mv Work Fd / / 1/ θ ω θ α ω τ α ω ω τθ Δ I d dt d dt I L I KE I Work / θ ω α τ Δ Δ c t s r v r a v r a r Fr L pr Connection Translational
Translational vs Rotational / / 1/ Δ m x v dx dt a dv dt F ma p mv KE mv Work Fd / / 1/ θ ω θ α ω τ α ω ω τθ Δ I d dt d dt I L I KE I Work / θ ω α τ Δ Δ c t s r v r a v r a r Fr L pr Connection Translational
Physics A - PHY 2048C
 Physics A - PHY 2048C and 11/15/2017 My Office Hours: Thursday 2:00-3:00 PM 212 Keen Building Warm-up Questions 1 Did you read Chapter 12 in the textbook on? 2 Must an object be rotating to have a moment
Physics A - PHY 2048C and 11/15/2017 My Office Hours: Thursday 2:00-3:00 PM 212 Keen Building Warm-up Questions 1 Did you read Chapter 12 in the textbook on? 2 Must an object be rotating to have a moment
Physics 101 Lecture 12 Equilibrium and Angular Momentum
 Physics 101 Lecture 1 Equilibrium and Angular Momentum Ali ÖVGÜN EMU Physics Department www.aovgun.com Static Equilibrium q Equilibrium and static equilibrium q Static equilibrium conditions n Net external
Physics 101 Lecture 1 Equilibrium and Angular Momentum Ali ÖVGÜN EMU Physics Department www.aovgun.com Static Equilibrium q Equilibrium and static equilibrium q Static equilibrium conditions n Net external
 AP Physics 1- Torque, Rotational Inertia, and Angular Momentum Practice Problems FACT: The center of mass of a system of objects obeys Newton s second law- F = Ma cm. Usually the location of the center
AP Physics 1- Torque, Rotational Inertia, and Angular Momentum Practice Problems FACT: The center of mass of a system of objects obeys Newton s second law- F = Ma cm. Usually the location of the center
Physics 111. Tuesday, November 2, Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy
 ics Tuesday, ember 2, 2002 Ch 11: Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy Announcements Wednesday, 8-9 pm in NSC 118/119 Sunday, 6:30-8 pm in CCLIR 468 Announcements This
ics Tuesday, ember 2, 2002 Ch 11: Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy Announcements Wednesday, 8-9 pm in NSC 118/119 Sunday, 6:30-8 pm in CCLIR 468 Announcements This
Review questions. Before the collision, 70 kg ball is stationary. Afterward, the 30 kg ball is stationary and 70 kg ball is moving to the right.
 Review questions Before the collision, 70 kg ball is stationary. Afterward, the 30 kg ball is stationary and 70 kg ball is moving to the right. 30 kg 70 kg v (a) Is this collision elastic? (b) Find the
Review questions Before the collision, 70 kg ball is stationary. Afterward, the 30 kg ball is stationary and 70 kg ball is moving to the right. 30 kg 70 kg v (a) Is this collision elastic? (b) Find the
Ch 8. Rotational Dynamics
 Ch 8. Rotational Dynamics Rotational W, P, K, & L (a) Translation (b) Combined translation and rotation ROTATIONAL ANALOG OF NEWTON S SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS = τ Iα Requirement:
Ch 8. Rotational Dynamics Rotational W, P, K, & L (a) Translation (b) Combined translation and rotation ROTATIONAL ANALOG OF NEWTON S SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS = τ Iα Requirement:
PHYSICS 220. Lecture 15. Textbook Sections Lecture 15 Purdue University, Physics 220 1
 PHYSICS 220 Lecture 15 Angular Momentum Textbook Sections 9.3 9.6 Lecture 15 Purdue University, Physics 220 1 Last Lecture Overview Torque = Force that causes rotation τ = F r sin θ Work done by torque
PHYSICS 220 Lecture 15 Angular Momentum Textbook Sections 9.3 9.6 Lecture 15 Purdue University, Physics 220 1 Last Lecture Overview Torque = Force that causes rotation τ = F r sin θ Work done by torque
Kinematics (special case) Dynamics gravity, tension, elastic, normal, friction. Energy: kinetic, potential gravity, spring + work (friction)
 Kinematics (special case) a = constant 1D motion 2D projectile Uniform circular Dynamics gravity, tension, elastic, normal, friction Motion with a = constant Newton s Laws F = m a F 12 = F 21 Time & Position
Kinematics (special case) a = constant 1D motion 2D projectile Uniform circular Dynamics gravity, tension, elastic, normal, friction Motion with a = constant Newton s Laws F = m a F 12 = F 21 Time & Position
Chapter 9-10 Test Review
 Chapter 9-10 Test Review Chapter Summary 9.2. The Second Condition for Equilibrium Explain torque and the factors on which it depends. Describe the role of torque in rotational mechanics. 10.1. Angular
Chapter 9-10 Test Review Chapter Summary 9.2. The Second Condition for Equilibrium Explain torque and the factors on which it depends. Describe the role of torque in rotational mechanics. 10.1. Angular
Torque. Physics 6A. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB
 Physics 6A Torque is what causes angular acceleration (just like a force causes linear acceleration) Torque is what causes angular acceleration (just like a force causes linear acceleration) For a torque
Physics 6A Torque is what causes angular acceleration (just like a force causes linear acceleration) Torque is what causes angular acceleration (just like a force causes linear acceleration) For a torque
Static Equilibrium, Gravitation, Periodic Motion
 This test covers static equilibrium, universal gravitation, and simple harmonic motion, with some problems requiring a knowledge of basic calculus. Part I. Multiple Choice 1. 60 A B 10 kg A mass of 10
This test covers static equilibrium, universal gravitation, and simple harmonic motion, with some problems requiring a knowledge of basic calculus. Part I. Multiple Choice 1. 60 A B 10 kg A mass of 10
Chapter 8. Centripetal Force and The Law of Gravity
 Chapter 8 Centripetal Force and The Law of Gravity Centripetal Acceleration An object traveling in a circle, even though it moves with a constant speed, will have an acceleration The centripetal acceleration
Chapter 8 Centripetal Force and The Law of Gravity Centripetal Acceleration An object traveling in a circle, even though it moves with a constant speed, will have an acceleration The centripetal acceleration
Name Student ID Score Last First. I = 2mR 2 /5 around the sphere s center of mass?
 NOTE: ignore air resistance in all Questions. In all Questions choose the answer that is the closest!! Question I. (15 pts) Rotation 1. (5 pts) A bowling ball that has an 11 cm radius and a 7.2 kg mass
NOTE: ignore air resistance in all Questions. In all Questions choose the answer that is the closest!! Question I. (15 pts) Rotation 1. (5 pts) A bowling ball that has an 11 cm radius and a 7.2 kg mass
Chapter 8. Rotational Equilibrium and Rotational Dynamics. 1. Torque. 2. Torque and Equilibrium. 3. Center of Mass and Center of Gravity
 Chapter 8 Rotational Equilibrium and Rotational Dynamics 1. Torque 2. Torque and Equilibrium 3. Center of Mass and Center of Gravity 4. Torque and angular acceleration 5. Rotational Kinetic energy 6. Angular
Chapter 8 Rotational Equilibrium and Rotational Dynamics 1. Torque 2. Torque and Equilibrium 3. Center of Mass and Center of Gravity 4. Torque and angular acceleration 5. Rotational Kinetic energy 6. Angular
Center of Gravity Pearson Education, Inc.
 Center of Gravity = The center of gravity position is at a place where the torque from one end of the object is balanced by the torque of the other end and therefore there is NO rotation. Fulcrum Point
Center of Gravity = The center of gravity position is at a place where the torque from one end of the object is balanced by the torque of the other end and therefore there is NO rotation. Fulcrum Point
Rotational Motion and Torque
 Rotational Motion and Torque Introduction to Angular Quantities Sections 8- to 8-2 Introduction Rotational motion deals with spinning objects, or objects rotating around some point. Rotational motion is
Rotational Motion and Torque Introduction to Angular Quantities Sections 8- to 8-2 Introduction Rotational motion deals with spinning objects, or objects rotating around some point. Rotational motion is
III. Work and Energy
 Rotation I. Kinematics - Angular analogs II. III. IV. Dynamics - Torque and Rotational Inertia Work and Energy Angular Momentum - Bodies and particles V. Elliptical Orbits The student will be able to:
Rotation I. Kinematics - Angular analogs II. III. IV. Dynamics - Torque and Rotational Inertia Work and Energy Angular Momentum - Bodies and particles V. Elliptical Orbits The student will be able to:
Rotation. Rotational Variables
 Rotation Rigid Bodies Rotation variables Constant angular acceleration Rotational KE Rotational Inertia Rotational Variables Rotation of a rigid body About a fixed rotation axis. Rigid Body an object that
Rotation Rigid Bodies Rotation variables Constant angular acceleration Rotational KE Rotational Inertia Rotational Variables Rotation of a rigid body About a fixed rotation axis. Rigid Body an object that
Chapter 8. Rotational Equilibrium and Rotational Dynamics
 Chapter 8 Rotational Equilibrium and Rotational Dynamics Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related Torque The door is free to rotate about
Chapter 8 Rotational Equilibrium and Rotational Dynamics Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related Torque The door is free to rotate about
FALL TERM EXAM, PHYS 1211, INTRODUCTORY PHYSICS I Thursday, 11 December 2014, 6 PM to 9 PM, Field House Gym
 FALL TERM EXAM, PHYS 1211, INTRODUCTORY PHYSICS I Thursday, 11 December 2014, 6 PM to 9 PM, Field House Gym NAME: STUDENT ID: INSTRUCTION 1. This exam booklet has 13 pages. Make sure none are missing 2.
FALL TERM EXAM, PHYS 1211, INTRODUCTORY PHYSICS I Thursday, 11 December 2014, 6 PM to 9 PM, Field House Gym NAME: STUDENT ID: INSTRUCTION 1. This exam booklet has 13 pages. Make sure none are missing 2.
Chapter 8 Lecture Notes
 Chapter 8 Lecture Notes Physics 2414 - Strauss Formulas: v = l / t = r θ / t = rω a T = v / t = r ω / t =rα a C = v 2 /r = ω 2 r ω = ω 0 + αt θ = ω 0 t +(1/2)αt 2 θ = (1/2)(ω 0 +ω)t ω 2 = ω 0 2 +2αθ τ
Chapter 8 Lecture Notes Physics 2414 - Strauss Formulas: v = l / t = r θ / t = rω a T = v / t = r ω / t =rα a C = v 2 /r = ω 2 r ω = ω 0 + αt θ = ω 0 t +(1/2)αt 2 θ = (1/2)(ω 0 +ω)t ω 2 = ω 0 2 +2αθ τ
Chapter 12 Static Equilibrium
 Chapter Static Equilibrium. Analysis Model: Rigid Body in Equilibrium. More on the Center of Gravity. Examples of Rigid Objects in Static Equilibrium CHAPTER : STATIC EQUILIBRIUM AND ELASTICITY.) The Conditions
Chapter Static Equilibrium. Analysis Model: Rigid Body in Equilibrium. More on the Center of Gravity. Examples of Rigid Objects in Static Equilibrium CHAPTER : STATIC EQUILIBRIUM AND ELASTICITY.) The Conditions
Torque. Introduction. Torque. PHY torque - J. Hedberg
 Torque PHY 207 - torque - J. Hedberg - 2017 1. Introduction 2. Torque 1. Lever arm changes 3. Net Torques 4. Moment of Rotational Inertia 1. Moment of Inertia for Arbitrary Shapes 2. Parallel Axis Theorem
Torque PHY 207 - torque - J. Hedberg - 2017 1. Introduction 2. Torque 1. Lever arm changes 3. Net Torques 4. Moment of Rotational Inertia 1. Moment of Inertia for Arbitrary Shapes 2. Parallel Axis Theorem
General Physics (PHY 2130)
 General Physics (PHY 130) Lecture 0 Rotational dynamics equilibrium nd Newton s Law for rotational motion rolling Exam II review http://www.physics.wayne.edu/~apetrov/phy130/ Lightning Review Last lecture:
General Physics (PHY 130) Lecture 0 Rotational dynamics equilibrium nd Newton s Law for rotational motion rolling Exam II review http://www.physics.wayne.edu/~apetrov/phy130/ Lightning Review Last lecture:
Chapter 8- Rotational Kinematics Angular Variables Kinematic Equations
 Chapter 8- Rotational Kinematics Angular Variables Kinematic Equations Chapter 9- Rotational Dynamics Torque Center of Gravity Newton s 2 nd Law- Angular Rotational Work & Energy Angular Momentum Angular
Chapter 8- Rotational Kinematics Angular Variables Kinematic Equations Chapter 9- Rotational Dynamics Torque Center of Gravity Newton s 2 nd Law- Angular Rotational Work & Energy Angular Momentum Angular
ΣF = ma Στ = Iα ½mv 2 ½Iω 2. mv Iω
 Thur Oct 22 Assign 9 Friday Today: Torques Angular Momentum x θ v ω a α F τ m I Roll without slipping: x = r Δθ v LINEAR = r ω a LINEAR = r α ΣF = ma Στ = Iα ½mv 2 ½Iω 2 I POINT = MR 2 I HOOP = MR 2 I
Thur Oct 22 Assign 9 Friday Today: Torques Angular Momentum x θ v ω a α F τ m I Roll without slipping: x = r Δθ v LINEAR = r ω a LINEAR = r α ΣF = ma Στ = Iα ½mv 2 ½Iω 2 I POINT = MR 2 I HOOP = MR 2 I
Chapter 8, Rotational Equilibrium and Rotational Dynamics. 3. If a net torque is applied to an object, that object will experience:
 CHAPTER 8 3. If a net torque is applied to an object, that object will experience: a. a constant angular speed b. an angular acceleration c. a constant moment of inertia d. an increasing moment of inertia
CHAPTER 8 3. If a net torque is applied to an object, that object will experience: a. a constant angular speed b. an angular acceleration c. a constant moment of inertia d. an increasing moment of inertia
Recap I. Angular position: Angular displacement: s. Angular velocity: Angular Acceleration:
 Recap I Angular position: Angular displacement: s Angular velocity: Angular Acceleration: Every point on a rotating rigid object has the same angular, but not the same linear motion! Recap II Circular
Recap I Angular position: Angular displacement: s Angular velocity: Angular Acceleration: Every point on a rotating rigid object has the same angular, but not the same linear motion! Recap II Circular
Circular Motion, Pt 2: Angular Dynamics. Mr. Velazquez AP/Honors Physics
 Circular Motion, Pt 2: Angular Dynamics Mr. Velazquez AP/Honors Physics Formulas: Angular Kinematics (θ must be in radians): s = rθ Arc Length 360 = 2π rads = 1 rev ω = θ t = v t r Angular Velocity α av
Circular Motion, Pt 2: Angular Dynamics Mr. Velazquez AP/Honors Physics Formulas: Angular Kinematics (θ must be in radians): s = rθ Arc Length 360 = 2π rads = 1 rev ω = θ t = v t r Angular Velocity α av
. d. v A v B. e. none of these.
 General Physics I Exam 3 - Chs. 7,8,9 - Momentum, Rotation, Equilibrium Oct. 28, 2009 Name Rec. Instr. Rec. Time For full credit, make your work clear to the grader. Show the formulas you use, the essential
General Physics I Exam 3 - Chs. 7,8,9 - Momentum, Rotation, Equilibrium Oct. 28, 2009 Name Rec. Instr. Rec. Time For full credit, make your work clear to the grader. Show the formulas you use, the essential
Definition. is a measure of how much a force acting on an object causes that object to rotate, symbol is, (Greek letter tau)
 Torque Definition is a measure of how much a force acting on an object causes that object to rotate, symbol is, (Greek letter tau) = r F = rfsin, r = distance from pivot to force, F is the applied force
Torque Definition is a measure of how much a force acting on an object causes that object to rotate, symbol is, (Greek letter tau) = r F = rfsin, r = distance from pivot to force, F is the applied force
Physics 201, Lecture 18
 q q Physics 01, Lecture 18 Rotational Dynamics Torque Exercises and Applications Rolling Motion Today s Topics Review Angular Velocity And Angular Acceleration q Angular Velocity (ω) describes how fast
q q Physics 01, Lecture 18 Rotational Dynamics Torque Exercises and Applications Rolling Motion Today s Topics Review Angular Velocity And Angular Acceleration q Angular Velocity (ω) describes how fast
Physics 1A Lecture 10B
 Physics 1A Lecture 10B "Sometimes the world puts a spin on life. When our equilibrium returns to us, we understand more because we've seen the whole picture. --Davis Barton Cross Products Another way to
Physics 1A Lecture 10B "Sometimes the world puts a spin on life. When our equilibrium returns to us, we understand more because we've seen the whole picture. --Davis Barton Cross Products Another way to
Dynamics of Rotational Motion
 Chapter 10 Dynamics of Rotational Motion To understand the concept of torque. To relate angular acceleration and torque. To work and power in rotational motion. To understand angular momentum. To understand
Chapter 10 Dynamics of Rotational Motion To understand the concept of torque. To relate angular acceleration and torque. To work and power in rotational motion. To understand angular momentum. To understand
General Definition of Torque, final. Lever Arm. General Definition of Torque 7/29/2010. Units of Chapter 10
 Units of Chapter 10 Determining Moments of Inertia Rotational Kinetic Energy Rotational Plus Translational Motion; Rolling Why Does a Rolling Sphere Slow Down? General Definition of Torque, final Taking
Units of Chapter 10 Determining Moments of Inertia Rotational Kinetic Energy Rotational Plus Translational Motion; Rolling Why Does a Rolling Sphere Slow Down? General Definition of Torque, final Taking
ω = 0 a = 0 = α P = constant L = constant dt = 0 = d Equilibrium when: τ i = 0 τ net τ i Static Equilibrium when: F z = 0 F net = F i = ma = d P
 Equilibrium when: F net = F i τ net = τ i a = 0 = α dp = 0 = d L = ma = d P = 0 = I α = d L = 0 P = constant L = constant F x = 0 τ i = 0 F y = 0 F z = 0 Static Equilibrium when: P = 0 L = 0 v com = 0
Equilibrium when: F net = F i τ net = τ i a = 0 = α dp = 0 = d L = ma = d P = 0 = I α = d L = 0 P = constant L = constant F x = 0 τ i = 0 F y = 0 F z = 0 Static Equilibrium when: P = 0 L = 0 v com = 0
Rotational Kinematics and Dynamics. UCVTS AIT Physics
 Rotational Kinematics and Dynamics UCVTS AIT Physics Angular Position Axis of rotation is the center of the disc Choose a fixed reference line Point P is at a fixed distance r from the origin Angular Position,
Rotational Kinematics and Dynamics UCVTS AIT Physics Angular Position Axis of rotation is the center of the disc Choose a fixed reference line Point P is at a fixed distance r from the origin Angular Position,
Angular velocity and angular acceleration CHAPTER 9 ROTATION. Angular velocity and angular acceleration. ! equations of rotational motion
 Angular velocity and angular acceleration CHAPTER 9 ROTATION! r i ds i dθ θ i Angular velocity and angular acceleration! equations of rotational motion Torque and Moment of Inertia! Newton s nd Law for
Angular velocity and angular acceleration CHAPTER 9 ROTATION! r i ds i dθ θ i Angular velocity and angular acceleration! equations of rotational motion Torque and Moment of Inertia! Newton s nd Law for
ω avg [between t 1 and t 2 ] = ω(t 1) + ω(t 2 ) 2
![ω avg [between t 1 and t 2 ] = ω(t 1) + ω(t 2 ) 2 ω avg [between t 1 and t 2 ] = ω(t 1) + ω(t 2 ) 2](/thumbs/94/120561024.jpg) PHY 302 K. Solutions for problem set #9. Textbook problem 7.10: For linear motion at constant acceleration a, average velocity during some time interval from t 1 to t 2 is the average of the velocities
PHY 302 K. Solutions for problem set #9. Textbook problem 7.10: For linear motion at constant acceleration a, average velocity during some time interval from t 1 to t 2 is the average of the velocities
Physics 101 Lecture 11 Torque
 Physics 101 Lecture 11 Torque Dr. Ali ÖVGÜN EMU Physics Department www.aovgun.com Force vs. Torque q Forces cause accelerations q What cause angular accelerations? q A door is free to rotate about an axis
Physics 101 Lecture 11 Torque Dr. Ali ÖVGÜN EMU Physics Department www.aovgun.com Force vs. Torque q Forces cause accelerations q What cause angular accelerations? q A door is free to rotate about an axis
Chapter 10: Rotation
 Chapter 10: Rotation Review of translational motion (motion along a straight line) Position x Displacement x Velocity v = dx/dt Acceleration a = dv/dt Mass m Newton s second law F = ma Work W = Fdcosφ
Chapter 10: Rotation Review of translational motion (motion along a straight line) Position x Displacement x Velocity v = dx/dt Acceleration a = dv/dt Mass m Newton s second law F = ma Work W = Fdcosφ
Rotation review packet. Name:
 Rotation review packet. Name:. A pulley of mass m 1 =M and radius R is mounted on frictionless bearings about a fixed axis through O. A block of equal mass m =M, suspended by a cord wrapped around the
Rotation review packet. Name:. A pulley of mass m 1 =M and radius R is mounted on frictionless bearings about a fixed axis through O. A block of equal mass m =M, suspended by a cord wrapped around the
Welcome back to Physics 211
 Welcome back to Physics 211 Today s agenda: Torque Rotational Dynamics Current assignments Prelecture Thursday, Nov 20th at 10:30am HW#13 due this Friday at 5 pm. Clicker.1 What is the center of mass of
Welcome back to Physics 211 Today s agenda: Torque Rotational Dynamics Current assignments Prelecture Thursday, Nov 20th at 10:30am HW#13 due this Friday at 5 pm. Clicker.1 What is the center of mass of
= 2 5 MR2. I sphere = MR 2. I hoop = 1 2 MR2. I disk
 A sphere (green), a disk (blue), and a hoop (red0, each with mass M and radius R, all start from rest at the top of an inclined plane and roll to the bottom. Which object reaches the bottom first? (Use
A sphere (green), a disk (blue), and a hoop (red0, each with mass M and radius R, all start from rest at the top of an inclined plane and roll to the bottom. Which object reaches the bottom first? (Use
PSI AP Physics I Rotational Motion
 PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
Application of Forces. Chapter Eight. Torque. Force vs. Torque. Torque, cont. Direction of Torque 4/7/2015
 Raymond A. Serway Chris Vuille Chapter Eight Rotational Equilibrium and Rotational Dynamics Application of Forces The point of application of a force is important This was ignored in treating objects as
Raymond A. Serway Chris Vuille Chapter Eight Rotational Equilibrium and Rotational Dynamics Application of Forces The point of application of a force is important This was ignored in treating objects as
Rotation. I. Kinematics - Angular analogs
 Rotation I. Kinematics - Angular analogs II. III. IV. Dynamics - Torque and Rotational Inertia Work and Energy Angular Momentum - Bodies and particles V. Elliptical Orbits The student will be able to:
Rotation I. Kinematics - Angular analogs II. III. IV. Dynamics - Torque and Rotational Inertia Work and Energy Angular Momentum - Bodies and particles V. Elliptical Orbits The student will be able to:
Review for 3 rd Midterm
 Review for 3 rd Midterm Midterm is on 4/19 at 7:30pm in the same rooms as before You are allowed one double sided sheet of paper with any handwritten notes you like. The moment-of-inertia about the center-of-mass
Review for 3 rd Midterm Midterm is on 4/19 at 7:30pm in the same rooms as before You are allowed one double sided sheet of paper with any handwritten notes you like. The moment-of-inertia about the center-of-mass
t = g = 10 m/s 2 = 2 s T = 2π g
 Annotated Answers to the 1984 AP Physics C Mechanics Multiple Choice 1. D. Torque is the rotational analogue of force; F net = ma corresponds to τ net = Iα. 2. C. The horizontal speed does not affect the
Annotated Answers to the 1984 AP Physics C Mechanics Multiple Choice 1. D. Torque is the rotational analogue of force; F net = ma corresponds to τ net = Iα. 2. C. The horizontal speed does not affect the
FALL TERM EXAM, PHYS 1211, INTRODUCTORY PHYSICS I Saturday, 14 December 2013, 1PM to 4 PM, AT 1003
 FALL TERM EXAM, PHYS 1211, INTRODUCTORY PHYSICS I Saturday, 14 December 2013, 1PM to 4 PM, AT 1003 NAME: STUDENT ID: INSTRUCTION 1. This exam booklet has 14 pages. Make sure none are missing 2. There is
FALL TERM EXAM, PHYS 1211, INTRODUCTORY PHYSICS I Saturday, 14 December 2013, 1PM to 4 PM, AT 1003 NAME: STUDENT ID: INSTRUCTION 1. This exam booklet has 14 pages. Make sure none are missing 2. There is
Welcome back to Physics 211
 Welcome back to Physics 211 Today s agenda: Moment of Inertia Angular momentum 13-2 1 Current assignments Prelecture due Tuesday after Thanksgiving HW#13 due next Wednesday, 11/24 Turn in written assignment
Welcome back to Physics 211 Today s agenda: Moment of Inertia Angular momentum 13-2 1 Current assignments Prelecture due Tuesday after Thanksgiving HW#13 due next Wednesday, 11/24 Turn in written assignment
Rotation. PHYS 101 Previous Exam Problems CHAPTER
 PHYS 101 Previous Exam Problems CHAPTER 10 Rotation Rotational kinematics Rotational inertia (moment of inertia) Kinetic energy Torque Newton s 2 nd law Work, power & energy conservation 1. Assume that
PHYS 101 Previous Exam Problems CHAPTER 10 Rotation Rotational kinematics Rotational inertia (moment of inertia) Kinetic energy Torque Newton s 2 nd law Work, power & energy conservation 1. Assume that
Q1. For a completely inelastic two-body collision the kinetic energy of the objects after the collision is the same as:
 Coordinator: Dr.. Naqvi Monday, January 05, 015 Page: 1 Q1. For a completely inelastic two-body collision the kinetic energy of the objects after the collision is the same as: ) (1/) MV, where M is the
Coordinator: Dr.. Naqvi Monday, January 05, 015 Page: 1 Q1. For a completely inelastic two-body collision the kinetic energy of the objects after the collision is the same as: ) (1/) MV, where M is the
Name (please print): UW ID# score last first
 Name (please print): UW ID# score last first Question I. (20 pts) Projectile motion A ball of mass 0.3 kg is thrown at an angle of 30 o above the horizontal. Ignore air resistance. It hits the ground 100
Name (please print): UW ID# score last first Question I. (20 pts) Projectile motion A ball of mass 0.3 kg is thrown at an angle of 30 o above the horizontal. Ignore air resistance. It hits the ground 100
PSI AP Physics I Rotational Motion
 PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
6. Find the net torque on the wheel in Figure about the axle through O if a = 10.0 cm and b = 25.0 cm.
 1. During a certain period of time, the angular position of a swinging door is described by θ = 5.00 + 10.0t + 2.00t 2, where θ is in radians and t is in seconds. Determine the angular position, angular
1. During a certain period of time, the angular position of a swinging door is described by θ = 5.00 + 10.0t + 2.00t 2, where θ is in radians and t is in seconds. Determine the angular position, angular
Static Equilibrium; Torque
 Static Equilibrium; Torque The Conditions for Equilibrium An object with forces acting on it, but that is not moving, is said to be in equilibrium. The first condition for equilibrium is that the net force
Static Equilibrium; Torque The Conditions for Equilibrium An object with forces acting on it, but that is not moving, is said to be in equilibrium. The first condition for equilibrium is that the net force
Chapter 8 Rotational Motion and Equilibrium. 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction
 Chapter 8 Rotational Motion and Equilibrium Name 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction 1. The distance between a turning axis and the
Chapter 8 Rotational Motion and Equilibrium Name 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction 1. The distance between a turning axis and the
Angular Momentum L = I ω
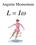 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Slide 1 / 37. Rotational Motion
 Slide 1 / 37 Rotational Motion Slide 2 / 37 Angular Quantities An angle θ can be given by: where r is the radius and l is the arc length. This gives θ in radians. There are 360 in a circle or 2π radians.
Slide 1 / 37 Rotational Motion Slide 2 / 37 Angular Quantities An angle θ can be given by: where r is the radius and l is the arc length. This gives θ in radians. There are 360 in a circle or 2π radians.
Equilibrium. For an object to remain in equilibrium, two conditions must be met. The object must have no net force: and no net torque:
 Equilibrium For an object to remain in equilibrium, two conditions must be met. The object must have no net force: F v = 0 and no net torque: v τ = 0 Worksheet A uniform rod with a length L and a mass
Equilibrium For an object to remain in equilibrium, two conditions must be met. The object must have no net force: F v = 0 and no net torque: v τ = 0 Worksheet A uniform rod with a length L and a mass
Chapter 8 Rotational Equilibrium and Rotational Dynamics Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and
 Chapter 8 Rotational Equilibrium and Rotational Dynamics Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related Torque The door is free to rotate about
Chapter 8 Rotational Equilibrium and Rotational Dynamics Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related Torque The door is free to rotate about
Physics 201. Professor P. Q. Hung. 311B, Physics Building. Physics 201 p. 1/1
 Physics 201 p. 1/1 Physics 201 Professor P. Q. Hung 311B, Physics Building Physics 201 p. 2/1 Rotational Kinematics and Energy Rotational Kinetic Energy, Moment of Inertia All elements inside the rigid
Physics 201 p. 1/1 Physics 201 Professor P. Q. Hung 311B, Physics Building Physics 201 p. 2/1 Rotational Kinematics and Energy Rotational Kinetic Energy, Moment of Inertia All elements inside the rigid
Chapter 8 Lecture. Pearson Physics. Rotational Motion and Equilibrium. Prepared by Chris Chiaverina Pearson Education, Inc.
 Chapter 8 Lecture Pearson Physics Rotational Motion and Equilibrium Prepared by Chris Chiaverina Chapter Contents Describing Angular Motion Rolling Motion and the Moment of Inertia Torque Static Equilibrium
Chapter 8 Lecture Pearson Physics Rotational Motion and Equilibrium Prepared by Chris Chiaverina Chapter Contents Describing Angular Motion Rolling Motion and the Moment of Inertia Torque Static Equilibrium
Torque and Static Equilibrium
 Torque and Static Equilibrium Rigid Bodies Rigid body: An extended object in which the distance between any two points in the object is constant in time. Examples: sphere, disk Effect of external forces
Torque and Static Equilibrium Rigid Bodies Rigid body: An extended object in which the distance between any two points in the object is constant in time. Examples: sphere, disk Effect of external forces
PHYSICS 218 Exam 3 Fall, 2013
 PHYSICS 218 Exam 3 Fall, 2013 Wednesday, November 20, 2013 Please read the information on the cover page BUT DO NOT OPEN the exam until instructed to do so! Name: Signature: Student ID: E-mail: Section
PHYSICS 218 Exam 3 Fall, 2013 Wednesday, November 20, 2013 Please read the information on the cover page BUT DO NOT OPEN the exam until instructed to do so! Name: Signature: Student ID: E-mail: Section
Physics 101: Lecture 15 Torque, F=ma for rotation, and Equilibrium
 Physics 101: Lecture 15 Torque, F=ma for rotation, and Equilibrium Strike (Day 10) Prelectures, checkpoints, lectures continue with no change. Take-home quizzes this week. See Elaine Schulte s email. HW
Physics 101: Lecture 15 Torque, F=ma for rotation, and Equilibrium Strike (Day 10) Prelectures, checkpoints, lectures continue with no change. Take-home quizzes this week. See Elaine Schulte s email. HW
Write your name legibly on the top right hand corner of this paper
 NAME Phys 631 Summer 2007 Quiz 2 Tuesday July 24, 2007 Instructor R. A. Lindgren 9:00 am 12:00 am Write your name legibly on the top right hand corner of this paper No Books or Notes allowed Calculator
NAME Phys 631 Summer 2007 Quiz 2 Tuesday July 24, 2007 Instructor R. A. Lindgren 9:00 am 12:00 am Write your name legibly on the top right hand corner of this paper No Books or Notes allowed Calculator
III. Angular Momentum Conservation (Chap. 10) Rotation. We repeat Chap. 2-8 with rotatiing objects. Eqs. of motion. Energy.
 Chap. 10: Rotational Motion I. Rotational Kinematics II. Rotational Dynamics - Newton s Law for Rotation III. Angular Momentum Conservation (Chap. 10) 1 Toward Exam 3 Eqs. of motion o To study angular
Chap. 10: Rotational Motion I. Rotational Kinematics II. Rotational Dynamics - Newton s Law for Rotation III. Angular Momentum Conservation (Chap. 10) 1 Toward Exam 3 Eqs. of motion o To study angular
Rotational Dynamics, Moment of Inertia and Angular Momentum
 Rotational Dynamics, Moment of Inertia and Angular Momentum Now that we have examined rotational kinematics and torque we will look at applying the concepts of angular motion to Newton s first and second
Rotational Dynamics, Moment of Inertia and Angular Momentum Now that we have examined rotational kinematics and torque we will look at applying the concepts of angular motion to Newton s first and second
PHYSICS 221, FALL 2011 EXAM #2 SOLUTIONS WEDNESDAY, NOVEMBER 2, 2011
 PHYSICS 1, FALL 011 EXAM SOLUTIONS WEDNESDAY, NOVEMBER, 011 Note: The unit vectors in the +x, +y, and +z directions of a right-handed Cartesian coordinate system are î, ĵ, and ˆk, respectively. In this
PHYSICS 1, FALL 011 EXAM SOLUTIONS WEDNESDAY, NOVEMBER, 011 Note: The unit vectors in the +x, +y, and +z directions of a right-handed Cartesian coordinate system are î, ĵ, and ˆk, respectively. In this
