PHYSICS 220. Lecture 15. Textbook Sections Lecture 15 Purdue University, Physics 220 1
|
|
|
- Stanley Damon Flynn
- 5 years ago
- Views:
Transcription
1 PHYSICS 220 Lecture 15 Angular Momentum Textbook Sections Lecture 15 Purdue University, Physics 220 1
2 Last Lecture Overview Torque = Force that causes rotation τ = F r sin θ Work done by torque W = τ θ Equilibrium Σ F = 0 Σ τ = 0 (Can choose any axis) Στ = Iα Rolling Object Two objects of the same mass rolling at the same translational speed do not necessarily have the same kinetic energy Today Angular Momentum L = Iω ΔL = 0 if Σ τ = 0 Lecture 15 Purdue University, Physics 220 2
3 Linear and Angular Linear Angular Displacement x θ Velocity v ω Acceleration a α Inertia m I Kinetic Energy ½ m v 2 ½ I ω 2 Newton s 2 nd Law F = ma τ = Iα Momentum p = mv L = Iω Lecture 15 Purdue University, Physics 220 3
4 Quiz 1) A uniform bar of mass m is supported by a pivot at its top, about which the bar can swing like a pendulum. If a force F is applied perpendicularly to the lower end of the bar as in the diagram, how big must F be in order to hold the bar in equilibrium at an angle from the vertical? A) 2mg B) mg sinθ C) 2mg sinθ D) (mg/2) sinθ E) (mg/2) cosθ Lecture 15 Purdue University, Physics 220 4
5 Quiz 2) You decide to roll two objects down a ramp to see which one gets to the bottom first. Object A is a solid cylinder and object B is a hollow cylinder. A and B have the same mass and radius. Suppose you released them from rest at the top of the ramp at same time, which has the most kinetic energy when it gets to the bottom of the ramp? A) Solid cylinder B) Hollow cylinder I solid = 1/2MR 2 C) Same I hollow = MR 2 Lecture 15 Purdue University, Physics 220 5
6 Define Angular Momentum Momentum Angular Momentum p = mv L = Iωω conserved if ΣF ext = 0 conserved if Στ ext = 0 Vector Vector units: kg-m/s units: kg-m 2 /s For a particle: L= Iω = mr = mvr = pr r Lecture 15 Purdue University, Physics v
7 Right Hand Rule In general, for an object rotating about a fixed (z) axis we can write L z =I Iω The direction of L z is + CCW, - CW Wrap fingers on right hand, around angle of rotation, thumb points in direction of L L z =Iω Lecture 15 Purdue University, Physics ω
8 Spinning Disks A disk of mass M and radius R rotates around the z axis with angular velocity ω i. A second identical disk, initially not rotating, is dropped on top of the first. There is friction between the disks, and eventually they rotate together with angular velocity ω f. A) ω f = ω i B) ω f = ½ ω i C) ω f = ¼ ω i z z ω i ω f Lecture 15 Purdue University, Physics 220 8
9 Two Spinning Disks First realize that there are no external torques acting on the two-disk system. Angular momentum will be conserved! L i = I + 0= = = 1ω1+ MR ω L i f I1ω1+ I2ω2 MR ω f z 2 ω MR ω = MR i 1 ω = ω 2 i f ω z ω f Lecture 15 Purdue University, Physics 220 9
10 Demo: Spin Up/Down You are sitting on a freely rotating bar-stool with your arms stretched out and a heavy glass mug in each hand. Your friend gives you a twist and you start rotating around a vertical axis though the center of the stool. You can assume that the bearing the stool turns on is frictionless, and that there is no net external torque present once you have started spinning. You now pull your arms and hands (and mugs) close to your body. Lecture 15 Purdue University, Physics
11 Demo There are no external forces acting on the student+stool system. A) True B) False C) What!? FBD has gravity and normal force. Key is no external torques! Lecture 15 Purdue University, Physics
12 Demo: Spin Up/Down What happens to the angular momentum as you pull in your arms? A) it increases B) it decreases C) it stays the same torques no external forces gives constant angular momentum L 1 L 2 Lecture 15 Purdue University, Physics
13 Demo: Spin Up/Down What happens to your angular velocity as you pull in your arms? A) it increases B) it decreases ω ω 1 C) it stays the same 2 I 1 I 2 L L Angular velocity increases because inertia decreases Pulling in your arms decreases your moment of inertia. Therefore, you will have an increased angular velocity Lecture 15 Purdue University, Physics
14 Demo: Spin Up/Down What happens to your kinetic energy as you pull in your arms? A) it increases B) it decreases C) it stays the same ω 1 ω 2 KE = 1 I 2 ω = 2 1 I 2 2 ω 2I = 1 2I L 2 (using L = Iω ) I 1 I 2 L L The mass is closer so you have less inertia and you speed up. If you speed up then, your kinetic energy must increase as well. Lecture 15 Purdue University, Physics
15 Sliding Puck A puck slides in a circular path on a horizontal frictionless table. It is held at a constant radius by a string threaded d through a frictionless hole at the center of the table. If you pull on the string such that the radius decreases by a factor of 2, by what factor does the angular velocity of the puck increase? A) 2 B) 4 C) 8 ω Lecture 15 Purdue University, Physics
16 Solution Since the string is pulled through a hole at the center of rotation, ti there is no torque: Angular momentum is conserved. L 1 = I 1 ω 1 = mr 2 ω 1 = R 2 L 2 = I 2 ω 2 = m ω 2 2 mr 2 ω = 2 1 1/4 mr ω 2 ω 1 =1/4 ω 2 ω 2 = 4ω 1 m R ω 1 m R/2 ω 2 Lecture 15 Purdue University, Physics
17 Turning the Bike Wheel A student sits on a barstool holding a bike wheel. The wheel is initially spinning CCW in the horizontal plane (as viewed from above) L= 25 kg m 2 /s. She now turns the bike wheel over. What happens? A) She starts to spin CCW B) She starts to spin CW C) Nothing Start with angular momentum L pointing up from wheel. When wheel is flipped, no more angular momentum from it pointing up, so need to spin person/stool to conserve L! Lecture 15 Purdue University, Physics
18 Turning the Bike Wheel She is holding the bike wheel and spinning counter clockwise. What happens if she turns it the other ½ rotation (so it is basically upside down from how it started). A) Spins Faster B) Stays same C) Stops Lecture 15 Purdue University, Physics
19 Turning the Bike Wheel Since there is no net external torque acting on the studentstool system, angular momentum is conserved. Remenber, L has a direction as well as a magnitude! Initially: L INI = L WI W,I = + 25 kg m 2 /s Finally: L FIN = L W,F + L S = -25 kg m 2 /s +L s L s = 50 kg m 2 /s L S L W,I L W,F L W,I = L W,F + L S Lecture 15 Purdue University, Physics
20 Gyroscopic Motion Suppose you have a spinning gyroscope in the configuration shown below: If the left support is removed, what will happen? support g ω pivot Lecture 15 Purdue University, Physics
21 Gyroscopic Motion Suppose you have a spinning gyroscope in the configuration shown below: If the left support is removed, what will happen? The gyroscope does not fall down! ω pivot g Lecture 15 Purdue University, Physics
22 Gyroscopic Motion... instead it precesses around its pivot axis! ω pivot Lecture 15 Purdue University, Physics
23 Gyroscope Because of the way the wheel is mounted in the frame, the torque on the wheel is zero Even when the frame is moved or rotated The wheel s angular momentum is conserved The orientation of the gyroscope provides a direction finder Lecture 15 Purdue University, Physics
24 Earth as a Gyroscope The Earth acts as a gyroscope as it spins on its axis This is a spin angular momentum, separate from its orbital angular momentum The spin angular momentum points in the direction of the north pole There e is no external torque on the Earth so its spin angular momentum is conserved The Earth s spin axis is tilted about 23.5 from the perpendicular to the orbital axis Since its spin angular momentum is conserved, the rotational axis remains tilted at a fixed angle with respect to the orbital plane This produces seasons on the Earth Lecture 15 Purdue University, Physics
25 Spinning Wheel A spinning wheel is more stable than a stationary one The increased stability is due to its angular momentum The angular momentum is directed along the axis of the wheel and so, ideally, there is no external torque on the wheel and it would remain in the same direction and never fall over However, in reality there is some small external torque and so the wheel will eventually tip over This torque could be from friction or deviations in the shape of the wheel, etc. Lecture 15 Purdue University, Physics
26 Precession The external torque on a rotating object can be substantial This leads to an effect called precession At rest, the device s stability is very low Its angular momentum adds to its stability, although the gravitational forceactingonitislarge on it is Assume the gravitational force acts on the center of mass of the system The center of mass of the system is close to the center of the wheel The applied torque leads to a change in the angular momentum of the system τ Δ t =Δ L Lecture 15 Purdue University, Physics
27 Example: Bullet Hitting Stick A uniform stick of mass M and length D is pivoted at the center. A bullet of mass m is shot through the stick at a point halfway between the pivot and the end. The initial speed of the bullet is v 1, and the final speed is v 2. What is the angular speed ω F of the stick after the collision? (Ignore friction and gravity) M m D D/4 ω F v 1 v 2 initial final Lecture 15 Purdue University, Physics
28 Example: Bullet Hitting Stick Conserve angular momentum around the pivot (z) axis! The total angular momentum before the collision is due only to the bullet (since the stick is not rotating gy yet). M m D D/4 v 1 initial Lecture 15 Purdue University, Physics
29 Example: Bullet Hitting Stick Conserve angular momentum around the pivot (z) axis! The total angular momentum after the collision has contributions from both the bullet and the stick where I is the moment of inertia of the stick about the pivot. D/4 ω F v 2 final Lecture 15 Purdue University, Physics
30 Example: Bullet Hitting Stick Set L i = L f : mv 1 (D/4) = mv 2 (D/4) + Iω F m M D D/4 ω F v 1 v 2 initial final Lecture 15 Purdue University, Physics
31 Example: Bullet Hitting Stick Set L i = L f using m M D D/4 ω F v 1 v 2 initial final Lecture 15 Purdue University, Physics
32 Στ = I α Summary of Concepts Energy is Conserved Need to include translational and rotational L = I ω Right Hand Rule gives direction If Στ = 0, L is conserved Lecture 15 Purdue University, Physics
Review session for Exam 2 Monday 3/25 6:00 PM in Loomis 151 (here) Print out/bring Exam 2, Fall 2005
 Physics 101: Lecture 16 Rolling Objects and Angular Momentum No checkpoints today. Review session for Exam 2 Monday 3/25 6:00 PM in Loomis 151 (here) Print out/bring Exam 2, Fall 2005 Linear and Angular
Physics 101: Lecture 16 Rolling Objects and Angular Momentum No checkpoints today. Review session for Exam 2 Monday 3/25 6:00 PM in Loomis 151 (here) Print out/bring Exam 2, Fall 2005 Linear and Angular
PHYSICS 149: Lecture 21
 PHYSICS 149: Lecture 21 Chapter 8: Torque and Angular Momentum 8.2 Torque 8.4 Equilibrium Revisited 8.8 Angular Momentum Lecture 21 Purdue University, Physics 149 1 Midterm Exam 2 Wednesday, April 6, 6:30
PHYSICS 149: Lecture 21 Chapter 8: Torque and Angular Momentum 8.2 Torque 8.4 Equilibrium Revisited 8.8 Angular Momentum Lecture 21 Purdue University, Physics 149 1 Midterm Exam 2 Wednesday, April 6, 6:30
Angular Momentum L = I ω
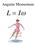 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Physics 131: Lecture 22. Today s Agenda
 Physics 131: Lecture Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 01: Lecture 10, Pg 1 An Unfair Race A frictionless block and a rolling (without slipping) disk are released at
Physics 131: Lecture Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 01: Lecture 10, Pg 1 An Unfair Race A frictionless block and a rolling (without slipping) disk are released at
Physics 131: Lecture 22. Today s Agenda
 Physics 131: Lecture 22 Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 201: Lecture 10, Pg 1 An Unfair Race A frictionless block and a rolling (without slipping) disk are released
Physics 131: Lecture 22 Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 201: Lecture 10, Pg 1 An Unfair Race A frictionless block and a rolling (without slipping) disk are released
Angular Momentum L = I ω
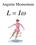 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Exam 3 Practice Solutions
 Exam 3 Practice Solutions Multiple Choice 1. A thin hoop, a solid disk, and a solid sphere, each with the same mass and radius, are at rest at the top of an inclined plane. If all three are released at
Exam 3 Practice Solutions Multiple Choice 1. A thin hoop, a solid disk, and a solid sphere, each with the same mass and radius, are at rest at the top of an inclined plane. If all three are released at
ΣF = ma Στ = Iα ½mv 2 ½Iω 2. mv Iω
 Thur Oct 22 Assign 9 Friday Today: Torques Angular Momentum x θ v ω a α F τ m I Roll without slipping: x = r Δθ v LINEAR = r ω a LINEAR = r α ΣF = ma Στ = Iα ½mv 2 ½Iω 2 I POINT = MR 2 I HOOP = MR 2 I
Thur Oct 22 Assign 9 Friday Today: Torques Angular Momentum x θ v ω a α F τ m I Roll without slipping: x = r Δθ v LINEAR = r ω a LINEAR = r α ΣF = ma Στ = Iα ½mv 2 ½Iω 2 I POINT = MR 2 I HOOP = MR 2 I
= o + t = ot + ½ t 2 = o + 2
 Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
Rolling, Torque, Angular Momentum
 Chapter 11 Rolling, Torque, Angular Momentum Copyright 11.2 Rolling as Translational and Rotation Combined Motion of Translation : i.e.motion along a straight line Motion of Rotation : rotation about a
Chapter 11 Rolling, Torque, Angular Momentum Copyright 11.2 Rolling as Translational and Rotation Combined Motion of Translation : i.e.motion along a straight line Motion of Rotation : rotation about a
Gyroscopes and statics
 Gyroscopes and statics Announcements: Welcome back from Spring Break! CAPA due Friday at 10pm We will finish Chapter 11 in H+R on angular momentum and start Chapter 12 on stability. Friday we will begin
Gyroscopes and statics Announcements: Welcome back from Spring Break! CAPA due Friday at 10pm We will finish Chapter 11 in H+R on angular momentum and start Chapter 12 on stability. Friday we will begin
Rolling without slipping Angular Momentum Conservation of Angular Momentum. Physics 201: Lecture 19, Pg 1
 Physics 131: Lecture Today s Agenda Rolling without slipping Angular Momentum Conservation o Angular Momentum Physics 01: Lecture 19, Pg 1 Rolling Without Slipping Rolling is a combination o rotation and
Physics 131: Lecture Today s Agenda Rolling without slipping Angular Momentum Conservation o Angular Momentum Physics 01: Lecture 19, Pg 1 Rolling Without Slipping Rolling is a combination o rotation and
Last 6 lectures are easier
 Your Comments I love you. Seriously. I do. And you never post it. I felt really bad whilst completing the checkpoint for this. This stuff is way above my head and I struggled with the concept of precession.
Your Comments I love you. Seriously. I do. And you never post it. I felt really bad whilst completing the checkpoint for this. This stuff is way above my head and I struggled with the concept of precession.
Chapter 10. Rotation
 Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
Physics 101: Lecture 15 Torque, F=ma for rotation, and Equilibrium
 Physics 101: Lecture 15 Torque, F=ma for rotation, and Equilibrium Strike (Day 10) Prelectures, checkpoints, lectures continue with no change. Take-home quizzes this week. See Elaine Schulte s email. HW
Physics 101: Lecture 15 Torque, F=ma for rotation, and Equilibrium Strike (Day 10) Prelectures, checkpoints, lectures continue with no change. Take-home quizzes this week. See Elaine Schulte s email. HW
Chapter 8. Rotational Motion
 Chapter 8 Rotational Motion Rotational Work and Energy W = Fs = s = rθ Frθ Consider the work done in rotating a wheel with a tangential force, F, by an angle θ. τ = Fr W =τθ Rotational Work and Energy
Chapter 8 Rotational Motion Rotational Work and Energy W = Fs = s = rθ Frθ Consider the work done in rotating a wheel with a tangential force, F, by an angle θ. τ = Fr W =τθ Rotational Work and Energy
Torque. Introduction. Torque. PHY torque - J. Hedberg
 Torque PHY 207 - torque - J. Hedberg - 2017 1. Introduction 2. Torque 1. Lever arm changes 3. Net Torques 4. Moment of Rotational Inertia 1. Moment of Inertia for Arbitrary Shapes 2. Parallel Axis Theorem
Torque PHY 207 - torque - J. Hedberg - 2017 1. Introduction 2. Torque 1. Lever arm changes 3. Net Torques 4. Moment of Rotational Inertia 1. Moment of Inertia for Arbitrary Shapes 2. Parallel Axis Theorem
General Physics (PHY 2130)
 General Physics (PHY 130) Lecture 0 Rotational dynamics equilibrium nd Newton s Law for rotational motion rolling Exam II review http://www.physics.wayne.edu/~apetrov/phy130/ Lightning Review Last lecture:
General Physics (PHY 130) Lecture 0 Rotational dynamics equilibrium nd Newton s Law for rotational motion rolling Exam II review http://www.physics.wayne.edu/~apetrov/phy130/ Lightning Review Last lecture:
Chapter 9-10 Test Review
 Chapter 9-10 Test Review Chapter Summary 9.2. The Second Condition for Equilibrium Explain torque and the factors on which it depends. Describe the role of torque in rotational mechanics. 10.1. Angular
Chapter 9-10 Test Review Chapter Summary 9.2. The Second Condition for Equilibrium Explain torque and the factors on which it depends. Describe the role of torque in rotational mechanics. 10.1. Angular
Rotational Kinetic Energy
 Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
Chapter 12. Recall that when a spring is stretched a distance x, it will pull back with a force given by: F = -kx
 Chapter 1 Lecture Notes Chapter 1 Oscillatory Motion Recall that when a spring is stretched a distance x, it will pull back with a force given by: F = -kx When the mass is released, the spring will pull
Chapter 1 Lecture Notes Chapter 1 Oscillatory Motion Recall that when a spring is stretched a distance x, it will pull back with a force given by: F = -kx When the mass is released, the spring will pull
Review for 3 rd Midterm
 Review for 3 rd Midterm Midterm is on 4/19 at 7:30pm in the same rooms as before You are allowed one double sided sheet of paper with any handwritten notes you like. The moment-of-inertia about the center-of-mass
Review for 3 rd Midterm Midterm is on 4/19 at 7:30pm in the same rooms as before You are allowed one double sided sheet of paper with any handwritten notes you like. The moment-of-inertia about the center-of-mass
Concept Question: Normal Force
 Concept Question: Normal Force Consider a person standing in an elevator that is accelerating upward. The upward normal force N exerted by the elevator floor on the person is 1. larger than 2. identical
Concept Question: Normal Force Consider a person standing in an elevator that is accelerating upward. The upward normal force N exerted by the elevator floor on the person is 1. larger than 2. identical
Rolling, Torque & Angular Momentum
 PHYS 101 Previous Exam Problems CHAPTER 11 Rolling, Torque & Angular Momentum Rolling motion Torque Angular momentum Conservation of angular momentum 1. A uniform hoop (ring) is rolling smoothly from the
PHYS 101 Previous Exam Problems CHAPTER 11 Rolling, Torque & Angular Momentum Rolling motion Torque Angular momentum Conservation of angular momentum 1. A uniform hoop (ring) is rolling smoothly from the
Chapter 8. Rotational Equilibrium and Rotational Dynamics
 Chapter 8 Rotational Equilibrium and Rotational Dynamics 1 Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related 2 Torque The door is free to rotate
Chapter 8 Rotational Equilibrium and Rotational Dynamics 1 Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related 2 Torque The door is free to rotate
Energy and Angular Momentum
 Notes 13 Rotation Page 1 Energy and Angular Momentum The kinetic energy associate with a rotating object is simply the sum of the regular kinetic energies. Our goal is to state the rotational kinetic energy
Notes 13 Rotation Page 1 Energy and Angular Momentum The kinetic energy associate with a rotating object is simply the sum of the regular kinetic energies. Our goal is to state the rotational kinetic energy
Webreview Torque and Rotation Practice Test
 Please do not write on test. ID A Webreview - 8.2 Torque and Rotation Practice Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A 0.30-m-radius automobile
Please do not write on test. ID A Webreview - 8.2 Torque and Rotation Practice Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A 0.30-m-radius automobile
Angular Momentum System of Particles Concept Questions
 Question 1: Angular Momentum Angular Momentum System of Particles Concept Questions A non-symmetric body rotates with an angular speed ω about the z axis. Relative to the origin 1. L 0 is constant. 2.
Question 1: Angular Momentum Angular Momentum System of Particles Concept Questions A non-symmetric body rotates with an angular speed ω about the z axis. Relative to the origin 1. L 0 is constant. 2.
Chapter 8 continued. Rotational Dynamics
 Chapter 8 continued Rotational Dynamics 8.6 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Chapter 8 continued Rotational Dynamics 8.6 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Physics 111. Tuesday, November 2, Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy
 ics Tuesday, ember 2, 2002 Ch 11: Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy Announcements Wednesday, 8-9 pm in NSC 118/119 Sunday, 6:30-8 pm in CCLIR 468 Announcements This
ics Tuesday, ember 2, 2002 Ch 11: Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy Announcements Wednesday, 8-9 pm in NSC 118/119 Sunday, 6:30-8 pm in CCLIR 468 Announcements This
CHAPTER 8: ROTATIONAL OF RIGID BODY PHYSICS. 1. Define Torque
 7 1. Define Torque 2. State the conditions for equilibrium of rigid body (Hint: 2 conditions) 3. Define angular displacement 4. Define average angular velocity 5. Define instantaneous angular velocity
7 1. Define Torque 2. State the conditions for equilibrium of rigid body (Hint: 2 conditions) 3. Define angular displacement 4. Define average angular velocity 5. Define instantaneous angular velocity
PH1104/PH114S MECHANICS
 PH04/PH4S MECHANICS SEMESTER I EXAMINATION 06-07 SOLUTION MULTIPLE-CHOICE QUESTIONS. (B) For freely falling bodies, the equation v = gh holds. v is proportional to h, therefore v v = h h = h h =.. (B).5i
PH04/PH4S MECHANICS SEMESTER I EXAMINATION 06-07 SOLUTION MULTIPLE-CHOICE QUESTIONS. (B) For freely falling bodies, the equation v = gh holds. v is proportional to h, therefore v v = h h = h h =.. (B).5i
PHY131H1S - Class 20. Pre-class reading quiz on Chapter 12
 PHY131H1S - Class 20 Today: Gravitational Torque Rotational Kinetic Energy Rolling without Slipping Equilibrium with Rotation Rotation Vectors Angular Momentum Pre-class reading quiz on Chapter 12 1 Last
PHY131H1S - Class 20 Today: Gravitational Torque Rotational Kinetic Energy Rolling without Slipping Equilibrium with Rotation Rotation Vectors Angular Momentum Pre-class reading quiz on Chapter 12 1 Last
Big Ideas 3 & 5: Circular Motion and Rotation 1 AP Physics 1
 Big Ideas 3 & 5: Circular Motion and Rotation 1 AP Physics 1 1. A 50-kg boy and a 40-kg girl sit on opposite ends of a 3-meter see-saw. How far from the girl should the fulcrum be placed in order for the
Big Ideas 3 & 5: Circular Motion and Rotation 1 AP Physics 1 1. A 50-kg boy and a 40-kg girl sit on opposite ends of a 3-meter see-saw. How far from the girl should the fulcrum be placed in order for the
PHYSICS 221, FALL 2011 EXAM #2 SOLUTIONS WEDNESDAY, NOVEMBER 2, 2011
 PHYSICS 1, FALL 011 EXAM SOLUTIONS WEDNESDAY, NOVEMBER, 011 Note: The unit vectors in the +x, +y, and +z directions of a right-handed Cartesian coordinate system are î, ĵ, and ˆk, respectively. In this
PHYSICS 1, FALL 011 EXAM SOLUTIONS WEDNESDAY, NOVEMBER, 011 Note: The unit vectors in the +x, +y, and +z directions of a right-handed Cartesian coordinate system are î, ĵ, and ˆk, respectively. In this
Chapter 8 - Rotational Dynamics and Equilibrium REVIEW
 Pagpalain ka! (Good luck, in Filipino) Date Chapter 8 - Rotational Dynamics and Equilibrium REVIEW TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1) When a rigid body
Pagpalain ka! (Good luck, in Filipino) Date Chapter 8 - Rotational Dynamics and Equilibrium REVIEW TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1) When a rigid body
End-of-Chapter Exercises
 End-of-Chapter Exercises Exercises 1 12 are conceptual questions that are designed to see if you have understood the main concepts of the chapter. 1. Figure 11.21 shows four different cases involving a
End-of-Chapter Exercises Exercises 1 12 are conceptual questions that are designed to see if you have understood the main concepts of the chapter. 1. Figure 11.21 shows four different cases involving a
Chapter 10: Dynamics of Rotational Motion
 Chapter 10: Dynamics of Rotational Motion What causes an angular acceleration? The effectiveness of a force at causing a rotation is called torque. QuickCheck 12.5 The four forces shown have the same strength.
Chapter 10: Dynamics of Rotational Motion What causes an angular acceleration? The effectiveness of a force at causing a rotation is called torque. QuickCheck 12.5 The four forces shown have the same strength.
Static Equilibrium; Torque
 Static Equilibrium; Torque The Conditions for Equilibrium An object with forces acting on it, but that is not moving, is said to be in equilibrium. The first condition for equilibrium is that the net force
Static Equilibrium; Torque The Conditions for Equilibrium An object with forces acting on it, but that is not moving, is said to be in equilibrium. The first condition for equilibrium is that the net force
Angular Momentum Conservation of Angular Momentum
 Lecture 22 Chapter 12 Physics I Angular Momentum Conservation of Angular Momentum Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi IN THIS CHAPTER, you will continue discussing rotational
Lecture 22 Chapter 12 Physics I Angular Momentum Conservation of Angular Momentum Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi IN THIS CHAPTER, you will continue discussing rotational
I 2 comω 2 + Rolling translational+rotational. a com. L sinθ = h. 1 tot. smooth rolling a com =αr & v com =ωr
 Rolling translational+rotational smooth rolling a com =αr & v com =ωr Equations of motion from: - Force/torque -> a and α - Energy -> v and ω 1 I 2 comω 2 + 1 Mv 2 = KE 2 com tot a com KE tot = KE trans
Rolling translational+rotational smooth rolling a com =αr & v com =ωr Equations of motion from: - Force/torque -> a and α - Energy -> v and ω 1 I 2 comω 2 + 1 Mv 2 = KE 2 com tot a com KE tot = KE trans
In the absence of an external force, the momentum of an object remains unchanged conservation of momentum. In this. rotating objects tend to
 Rotating objects tend to keep rotating while non- rotating objects tend to remain non-rotating. In the absence of an external force, the momentum of an object remains unchanged conservation of momentum.
Rotating objects tend to keep rotating while non- rotating objects tend to remain non-rotating. In the absence of an external force, the momentum of an object remains unchanged conservation of momentum.
= 2 5 MR2. I sphere = MR 2. I hoop = 1 2 MR2. I disk
 A sphere (green), a disk (blue), and a hoop (red0, each with mass M and radius R, all start from rest at the top of an inclined plane and roll to the bottom. Which object reaches the bottom first? (Use
A sphere (green), a disk (blue), and a hoop (red0, each with mass M and radius R, all start from rest at the top of an inclined plane and roll to the bottom. Which object reaches the bottom first? (Use
Review questions. Before the collision, 70 kg ball is stationary. Afterward, the 30 kg ball is stationary and 70 kg ball is moving to the right.
 Review questions Before the collision, 70 kg ball is stationary. Afterward, the 30 kg ball is stationary and 70 kg ball is moving to the right. 30 kg 70 kg v (a) Is this collision elastic? (b) Find the
Review questions Before the collision, 70 kg ball is stationary. Afterward, the 30 kg ball is stationary and 70 kg ball is moving to the right. 30 kg 70 kg v (a) Is this collision elastic? (b) Find the
We define angular displacement, θ, and angular velocity, ω. What's a radian?
 We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
Chapter 8. Rotational Equilibrium and Rotational Dynamics
 Chapter 8 Rotational Equilibrium and Rotational Dynamics Wrench Demo Torque Torque, τ, is the tendency of a force to rotate an object about some axis τ = Fd F is the force d is the lever arm (or moment
Chapter 8 Rotational Equilibrium and Rotational Dynamics Wrench Demo Torque Torque, τ, is the tendency of a force to rotate an object about some axis τ = Fd F is the force d is the lever arm (or moment
Physics 131: Lecture 21. Today s Agenda
 Physics 131: Lecture 21 Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 201: Lecture 10, Pg 1 Newton s second law in rotation land Sum of the torques will equal the moment of inertia
Physics 131: Lecture 21 Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 201: Lecture 10, Pg 1 Newton s second law in rotation land Sum of the torques will equal the moment of inertia
Rotational Dynamics. Slide 2 / 34. Slide 1 / 34. Slide 4 / 34. Slide 3 / 34. Slide 6 / 34. Slide 5 / 34. Moment of Inertia. Parallel Axis Theorem
 Slide 1 / 34 Rotational ynamics l Slide 2 / 34 Moment of Inertia To determine the moment of inertia we divide the object into tiny masses of m i a distance r i from the center. is the sum of all the tiny
Slide 1 / 34 Rotational ynamics l Slide 2 / 34 Moment of Inertia To determine the moment of inertia we divide the object into tiny masses of m i a distance r i from the center. is the sum of all the tiny
31 ROTATIONAL KINEMATICS
 31 ROTATIONAL KINEMATICS 1. Compare and contrast circular motion and rotation? Address the following Which involves an object and which involves a system? Does an object/system in circular motion have
31 ROTATIONAL KINEMATICS 1. Compare and contrast circular motion and rotation? Address the following Which involves an object and which involves a system? Does an object/system in circular motion have
8.012 Physics I: Classical Mechanics Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
Physics 8 Wednesday, October 30, 2013
 Physics 8 Wednesday, October 30, 2013 HW9 (due Friday) is 7 conceptual + 8 calculation problems. Of the 8 calculation problems, 4 or 5 are from Chapter 11, and 3 or 4 are from Chapter 12. 7pm HW sessions:
Physics 8 Wednesday, October 30, 2013 HW9 (due Friday) is 7 conceptual + 8 calculation problems. Of the 8 calculation problems, 4 or 5 are from Chapter 11, and 3 or 4 are from Chapter 12. 7pm HW sessions:
Physics 6A Winter 2006 FINAL
 Physics 6A Winter 2006 FINAL The test has 16 multiple choice questions and 3 problems. Scoring: Question 1-16 Problem 1 Problem 2 Problem 3 55 points total 20 points 15 points 10 points Enter the solution
Physics 6A Winter 2006 FINAL The test has 16 multiple choice questions and 3 problems. Scoring: Question 1-16 Problem 1 Problem 2 Problem 3 55 points total 20 points 15 points 10 points Enter the solution
Chapter 11. Angular Momentum
 Chapter 11 Angular Momentum Angular Momentum The Vector Nature of Rotation Torque and Angular Momentum Conservation of Angular Momentum MFMcGraw-PHY 2425 Chap_11Ha_Angular_Momentum-Revised 10/13/2012 2
Chapter 11 Angular Momentum Angular Momentum The Vector Nature of Rotation Torque and Angular Momentum Conservation of Angular Momentum MFMcGraw-PHY 2425 Chap_11Ha_Angular_Momentum-Revised 10/13/2012 2
Physics 131: Lecture 21. Today s Agenda
 Physics 131: Lecture 1 Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 01: Lecture 10, Pg 1 Newton s second law in rotation land Sum of the torques will equal the moment of inertia
Physics 131: Lecture 1 Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 01: Lecture 10, Pg 1 Newton s second law in rotation land Sum of the torques will equal the moment of inertia
Chapter 6, Problem 18. Agenda. Rotational Inertia. Rotational Inertia. Calculating Moment of Inertia. Example: Hoop vs.
 Agenda Today: Homework quiz, moment of inertia and torque Thursday: Statics problems revisited, rolling motion Reading: Start Chapter 8 in the reading Have to cancel office hours today: will have extra
Agenda Today: Homework quiz, moment of inertia and torque Thursday: Statics problems revisited, rolling motion Reading: Start Chapter 8 in the reading Have to cancel office hours today: will have extra
Announcements Oct 27, 2009
 Announcements Oct 7, 009 1. HW 14 due tonight. Reminder: some of your HW answers will need to be written in scientific notation. Do this with e notation, not with x signs. a. 6.57E33 correct format b.
Announcements Oct 7, 009 1. HW 14 due tonight. Reminder: some of your HW answers will need to be written in scientific notation. Do this with e notation, not with x signs. a. 6.57E33 correct format b.
Slide 1 / 37. Rotational Motion
 Slide 1 / 37 Rotational Motion Slide 2 / 37 Angular Quantities An angle θ can be given by: where r is the radius and l is the arc length. This gives θ in radians. There are 360 in a circle or 2π radians.
Slide 1 / 37 Rotational Motion Slide 2 / 37 Angular Quantities An angle θ can be given by: where r is the radius and l is the arc length. This gives θ in radians. There are 360 in a circle or 2π radians.
Physics 111. Lecture 23 (Walker: 10.6, 11.1) Conservation of Energy in Rotation Torque March 30, Kinetic Energy of Rolling Object
 Physics 111 Lecture 3 (Walker: 10.6, 11.1) Conservation of Energy in Rotation Torque March 30, 009 Lecture 3 1/4 Kinetic Energy of Rolling Object Total kinetic energy of a rolling object is the sum of
Physics 111 Lecture 3 (Walker: 10.6, 11.1) Conservation of Energy in Rotation Torque March 30, 009 Lecture 3 1/4 Kinetic Energy of Rolling Object Total kinetic energy of a rolling object is the sum of
PHY2020 Test 2 November 5, Name:
 1 PHY2020 Test 2 November 5, 2014 Name: sin(30) = 1/2 cos(30) = 3/2 tan(30) = 3/3 sin(60) = 3/2 cos(60) = 1/2 tan(60) = 3 sin(45) = cos(45) = 2/2 tan(45) = 1 sin(37) = cos(53) = 0.6 cos(37) = sin(53) =
1 PHY2020 Test 2 November 5, 2014 Name: sin(30) = 1/2 cos(30) = 3/2 tan(30) = 3/3 sin(60) = 3/2 cos(60) = 1/2 tan(60) = 3 sin(45) = cos(45) = 2/2 tan(45) = 1 sin(37) = cos(53) = 0.6 cos(37) = sin(53) =
Rotation Quiz II, review part A
 Rotation Quiz II, review part A 1. A solid disk with a radius R rotates at a constant rate ω. Which of the following points has the greater angular velocity? A. A B. B C. C D. D E. All points have the
Rotation Quiz II, review part A 1. A solid disk with a radius R rotates at a constant rate ω. Which of the following points has the greater angular velocity? A. A B. B C. C D. D E. All points have the
Physics 207: Lecture 24. Announcements. No labs next week, May 2 5 Exam 3 review session: Wed, May 4 from 8:00 9:30 pm; here.
 Physics 07: Lecture 4 Announcements No labs next week, May 5 Exam 3 review session: Wed, May 4 from 8:00 9:30 pm; here Today s Agenda ecap: otational dynamics and torque Work and energy with example Many
Physics 07: Lecture 4 Announcements No labs next week, May 5 Exam 3 review session: Wed, May 4 from 8:00 9:30 pm; here Today s Agenda ecap: otational dynamics and torque Work and energy with example Many
Physics 121, March 27, Angular Momentum, Torque, and Precession. Department of Physics and Astronomy, University of Rochester
 Physics 121, March 27, 2008. Angular Momentum, Torque, and Precession. Physics 121. March 27, 2008. Course Information Quiz Topics to be discussed today: Review of Angular Momentum Conservation of Angular
Physics 121, March 27, 2008. Angular Momentum, Torque, and Precession. Physics 121. March 27, 2008. Course Information Quiz Topics to be discussed today: Review of Angular Momentum Conservation of Angular
Chapter 12: Rotation of Rigid Bodies. Center of Mass Moment of Inertia Torque Angular Momentum Rolling Statics
 Chapter 12: Rotation of Rigid Bodies Center of Mass Moment of Inertia Torque Angular Momentum Rolling Statics Translational vs Rotational 2 / / 1/ 2 m x v dx dt a dv dt F ma p mv KE mv Work Fd P Fv 2 /
Chapter 12: Rotation of Rigid Bodies Center of Mass Moment of Inertia Torque Angular Momentum Rolling Statics Translational vs Rotational 2 / / 1/ 2 m x v dx dt a dv dt F ma p mv KE mv Work Fd P Fv 2 /
Physics A - PHY 2048C
 Physics A - PHY 2048C and 11/15/2017 My Office Hours: Thursday 2:00-3:00 PM 212 Keen Building Warm-up Questions 1 Did you read Chapter 12 in the textbook on? 2 Must an object be rotating to have a moment
Physics A - PHY 2048C and 11/15/2017 My Office Hours: Thursday 2:00-3:00 PM 212 Keen Building Warm-up Questions 1 Did you read Chapter 12 in the textbook on? 2 Must an object be rotating to have a moment
1 MR SAMPLE EXAM 3 FALL 2013
 SAMPLE EXAM 3 FALL 013 1. A merry-go-round rotates from rest with an angular acceleration of 1.56 rad/s. How long does it take to rotate through the first rev? A) s B) 4 s C) 6 s D) 8 s E) 10 s. A wheel,
SAMPLE EXAM 3 FALL 013 1. A merry-go-round rotates from rest with an angular acceleration of 1.56 rad/s. How long does it take to rotate through the first rev? A) s B) 4 s C) 6 s D) 8 s E) 10 s. A wheel,
8.012 Physics I: Classical Mechanics Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
Rolling, Torque, and Angular Momentum
 AP Physics C Rolling, Torque, and Angular Momentum Introduction: Rolling: In the last unit we studied the rotation of a rigid body about a fixed axis. We will now extend our study to include cases where
AP Physics C Rolling, Torque, and Angular Momentum Introduction: Rolling: In the last unit we studied the rotation of a rigid body about a fixed axis. We will now extend our study to include cases where
Lecture 11 - Advanced Rotational Dynamics
 Lecture 11 - Advanced Rotational Dynamics A Puzzle... A moldable blob of matter of mass M and uniform density is to be situated between the planes z = 0 and z = 1 so that the moment of inertia around the
Lecture 11 - Advanced Rotational Dynamics A Puzzle... A moldable blob of matter of mass M and uniform density is to be situated between the planes z = 0 and z = 1 so that the moment of inertia around the
Topic 1: Newtonian Mechanics Energy & Momentum
 Work (W) the amount of energy transferred by a force acting through a distance. Scalar but can be positive or negative ΔE = W = F! d = Fdcosθ Units N m or Joules (J) Work, Energy & Power Power (P) the
Work (W) the amount of energy transferred by a force acting through a distance. Scalar but can be positive or negative ΔE = W = F! d = Fdcosθ Units N m or Joules (J) Work, Energy & Power Power (P) the
Physics 121, March 25, Rotational Motion and Angular Momentum. Department of Physics and Astronomy, University of Rochester
 Physics 121, March 25, 2008. Rotational Motion and Angular Momentum. Physics 121. March 25, 2008. Course Information Topics to be discussed today: Review of Rotational Motion Rolling Motion Angular Momentum
Physics 121, March 25, 2008. Rotational Motion and Angular Momentum. Physics 121. March 25, 2008. Course Information Topics to be discussed today: Review of Rotational Motion Rolling Motion Angular Momentum
6. Find the net torque on the wheel in Figure about the axle through O if a = 10.0 cm and b = 25.0 cm.
 1. During a certain period of time, the angular position of a swinging door is described by θ = 5.00 + 10.0t + 2.00t 2, where θ is in radians and t is in seconds. Determine the angular position, angular
1. During a certain period of time, the angular position of a swinging door is described by θ = 5.00 + 10.0t + 2.00t 2, where θ is in radians and t is in seconds. Determine the angular position, angular
Translational vs Rotational. m x. Connection Δ = = = = = = Δ = = = = = = Δ =Δ = = = = = 2 / 1/2. Work
 Translational vs Rotational / / 1/ Δ m x v dx dt a dv dt F ma p mv KE mv Work Fd / / 1/ θ ω θ α ω τ α ω ω τθ Δ I d dt d dt I L I KE I Work / θ ω α τ Δ Δ c t s r v r a v r a r Fr L pr Connection Translational
Translational vs Rotational / / 1/ Δ m x v dx dt a dv dt F ma p mv KE mv Work Fd / / 1/ θ ω θ α ω τ α ω ω τθ Δ I d dt d dt I L I KE I Work / θ ω α τ Δ Δ c t s r v r a v r a r Fr L pr Connection Translational
AP Physics C: Rotation II. (Torque and Rotational Dynamics, Rolling Motion) Problems
 AP Physics C: Rotation II (Torque and Rotational Dynamics, Rolling Motion) Problems 1980M3. A billiard ball has mass M, radius R, and moment of inertia about the center of mass I c = 2 MR²/5 The ball is
AP Physics C: Rotation II (Torque and Rotational Dynamics, Rolling Motion) Problems 1980M3. A billiard ball has mass M, radius R, and moment of inertia about the center of mass I c = 2 MR²/5 The ball is
Unit 8 Notetaking Guide Torque and Rotational Motion
 Unit 8 Notetaking Guide Torque and Rotational Motion Rotational Motion Until now, we have been concerned mainly with translational motion. We discussed the kinematics and dynamics of translational motion
Unit 8 Notetaking Guide Torque and Rotational Motion Rotational Motion Until now, we have been concerned mainly with translational motion. We discussed the kinematics and dynamics of translational motion
Rotation review packet. Name:
 Rotation review packet. Name:. A pulley of mass m 1 =M and radius R is mounted on frictionless bearings about a fixed axis through O. A block of equal mass m =M, suspended by a cord wrapped around the
Rotation review packet. Name:. A pulley of mass m 1 =M and radius R is mounted on frictionless bearings about a fixed axis through O. A block of equal mass m =M, suspended by a cord wrapped around the
Chapter 8 Lecture Notes
 Chapter 8 Lecture Notes Physics 2414 - Strauss Formulas: v = l / t = r θ / t = rω a T = v / t = r ω / t =rα a C = v 2 /r = ω 2 r ω = ω 0 + αt θ = ω 0 t +(1/2)αt 2 θ = (1/2)(ω 0 +ω)t ω 2 = ω 0 2 +2αθ τ
Chapter 8 Lecture Notes Physics 2414 - Strauss Formulas: v = l / t = r θ / t = rω a T = v / t = r ω / t =rα a C = v 2 /r = ω 2 r ω = ω 0 + αt θ = ω 0 t +(1/2)αt 2 θ = (1/2)(ω 0 +ω)t ω 2 = ω 0 2 +2αθ τ
Physics 2210 Fall smartphysics Conservation of Angular Momentum 11/20/2015
 Physics 2210 Fall 2015 smartphysics 19-20 Conservation of Angular Momentum 11/20/2015 Poll 11-18-03 In the two cases shown above identical ladders are leaning against frictionless walls and are not sliding.
Physics 2210 Fall 2015 smartphysics 19-20 Conservation of Angular Momentum 11/20/2015 Poll 11-18-03 In the two cases shown above identical ladders are leaning against frictionless walls and are not sliding.
Torque rotational force which causes a change in rotational motion. This force is defined by linear force multiplied by a radius.
 Warm up A remote-controlled car's wheel accelerates at 22.4 rad/s 2. If the wheel begins with an angular speed of 10.8 rad/s, what is the wheel's angular speed after exactly three full turns? AP Physics
Warm up A remote-controlled car's wheel accelerates at 22.4 rad/s 2. If the wheel begins with an angular speed of 10.8 rad/s, what is the wheel's angular speed after exactly three full turns? AP Physics
Big Idea 4: Interactions between systems can result in changes in those systems. Essential Knowledge 4.D.1: Torque, angular velocity, angular
 Unit 7: Rotational Motion (angular kinematics, dynamics, momentum & energy) Name: Big Idea 3: The interactions of an object with other objects can be described by forces. Essential Knowledge 3.F.1: Only
Unit 7: Rotational Motion (angular kinematics, dynamics, momentum & energy) Name: Big Idea 3: The interactions of an object with other objects can be described by forces. Essential Knowledge 3.F.1: Only
Class XI Chapter 7- System of Particles and Rotational Motion Physics
 Page 178 Question 7.1: Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie
Page 178 Question 7.1: Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie
Recap: Solid Rotational Motion (Chapter 8) displacement velocity acceleration Newton s 2nd law τ = I.α N.s τ = F. l moment of inertia mass size
 Recap: Solid Rotational Motion (Chapter 8) We have developed equations to describe rotational displacement θ, rotational velocity ω and rotational acceleration α. We have used these new terms to modify
Recap: Solid Rotational Motion (Chapter 8) We have developed equations to describe rotational displacement θ, rotational velocity ω and rotational acceleration α. We have used these new terms to modify
Chap. 10: Rotational Motion
 Chap. 10: Rotational Motion I. Rotational Kinematics II. Rotational Dynamics - Newton s Law for Rotation III. Angular Momentum Conservation (Chap. 10) 1 Newton s Laws for Rotation n e t I 3 rd part [N
Chap. 10: Rotational Motion I. Rotational Kinematics II. Rotational Dynamics - Newton s Law for Rotation III. Angular Momentum Conservation (Chap. 10) 1 Newton s Laws for Rotation n e t I 3 rd part [N
FINAL EXAM CLOSED BOOK
 Physics 7A- Section 2, Fall 2008. Instructor Lanzara FINAL EXAM CLOSED BOOK GOOD LUCK! Print Name Discussion Section# or Time Signature Discussion Section GSI Student ID# Problem Points Score 1 20 2 20
Physics 7A- Section 2, Fall 2008. Instructor Lanzara FINAL EXAM CLOSED BOOK GOOD LUCK! Print Name Discussion Section# or Time Signature Discussion Section GSI Student ID# Problem Points Score 1 20 2 20
Lecture PowerPoints. Chapter 11. Physics for Scientists and Engineers, with Modern Physics, 4 th edition Giancoli
 Lecture PowerPoints Chapter 11 Physics for Scientists and Engineers, with Modern Physics, 4 th edition Giancoli 2009 Pearson Education, Inc. This work is protected by United States copyright laws and is
Lecture PowerPoints Chapter 11 Physics for Scientists and Engineers, with Modern Physics, 4 th edition Giancoli 2009 Pearson Education, Inc. This work is protected by United States copyright laws and is
It will be most difficult for the ant to adhere to the wheel as it revolves past which of the four points? A) I B) II C) III D) IV
 AP Physics 1 Lesson 16 Homework Newton s First and Second Law of Rotational Motion Outcomes Define rotational inertia, torque, and center of gravity. State and explain Newton s first Law of Motion as it
AP Physics 1 Lesson 16 Homework Newton s First and Second Law of Rotational Motion Outcomes Define rotational inertia, torque, and center of gravity. State and explain Newton s first Law of Motion as it
Name: Date: Period: AP Physics C Rotational Motion HO19
 1.) A wheel turns with constant acceleration 0.450 rad/s 2. (9-9) Rotational Motion H19 How much time does it take to reach an angular velocity of 8.00 rad/s, starting from rest? Through how many revolutions
1.) A wheel turns with constant acceleration 0.450 rad/s 2. (9-9) Rotational Motion H19 How much time does it take to reach an angular velocity of 8.00 rad/s, starting from rest? Through how many revolutions
Chapter 8. Rotational Equilibrium and Rotational Dynamics. 1. Torque. 2. Torque and Equilibrium. 3. Center of Mass and Center of Gravity
 Chapter 8 Rotational Equilibrium and Rotational Dynamics 1. Torque 2. Torque and Equilibrium 3. Center of Mass and Center of Gravity 4. Torque and angular acceleration 5. Rotational Kinetic energy 6. Angular
Chapter 8 Rotational Equilibrium and Rotational Dynamics 1. Torque 2. Torque and Equilibrium 3. Center of Mass and Center of Gravity 4. Torque and angular acceleration 5. Rotational Kinetic energy 6. Angular
 AP Physics 1- Torque, Rotational Inertia, and Angular Momentum Practice Problems FACT: The center of mass of a system of objects obeys Newton s second law- F = Ma cm. Usually the location of the center
AP Physics 1- Torque, Rotational Inertia, and Angular Momentum Practice Problems FACT: The center of mass of a system of objects obeys Newton s second law- F = Ma cm. Usually the location of the center
Last Name: First Name Network-ID Discussion Section: Discussion TA Name:
 Last Name: First Name Network-ID Discussion Section: Discussion TA Name: Instructions Turn off your cell phone and put it out of sight. Keep your calculator on your own desk. Calculators cannot be shared.
Last Name: First Name Network-ID Discussion Section: Discussion TA Name: Instructions Turn off your cell phone and put it out of sight. Keep your calculator on your own desk. Calculators cannot be shared.
Chapter 8: Momentum, Impulse, & Collisions. Newton s second law in terms of momentum:
 linear momentum: Chapter 8: Momentum, Impulse, & Collisions Newton s second law in terms of momentum: impulse: Under what SPECIFIC condition is linear momentum conserved? (The answer does not involve collisions.)
linear momentum: Chapter 8: Momentum, Impulse, & Collisions Newton s second law in terms of momentum: impulse: Under what SPECIFIC condition is linear momentum conserved? (The answer does not involve collisions.)
A solid disk and a ring roll down an incline. The ring is slower than the disk if
 A solid disk and a ring roll down an incline. The ring is slower than the disk if A. mring= mdisk, where m is the mass. B. rring = rdisk, where r is the radius. C. mring = mdisk and rring = rdisk. D.The
A solid disk and a ring roll down an incline. The ring is slower than the disk if A. mring= mdisk, where m is the mass. B. rring = rdisk, where r is the radius. C. mring = mdisk and rring = rdisk. D.The
Lecture 13 REVIEW. Physics 106 Spring What should we know? What should we know? Newton s Laws
 Lecture 13 REVIEW Physics 106 Spring 2006 http://web.njit.edu/~sirenko/ What should we know? Vectors addition, subtraction, scalar and vector multiplication Trigonometric functions sinθ, cos θ, tan θ,
Lecture 13 REVIEW Physics 106 Spring 2006 http://web.njit.edu/~sirenko/ What should we know? Vectors addition, subtraction, scalar and vector multiplication Trigonometric functions sinθ, cos θ, tan θ,
Rotational Dynamics continued
 Chapter 9 Rotational Dynamics continued 9.4 Newton s Second Law for Rotational Motion About a Fixed Axis ROTATIONAL ANALOG OF NEWTON S SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS I = ( mr 2
Chapter 9 Rotational Dynamics continued 9.4 Newton s Second Law for Rotational Motion About a Fixed Axis ROTATIONAL ANALOG OF NEWTON S SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS I = ( mr 2
W13D1-1 Reading Quiz and Concept Questions
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics Physics 8.01 Fall Term 2009 W13D1-1 Reading Quiz and Concept Questions A person spins a tennis ball on a string in a horizontal circle (so that
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics Physics 8.01 Fall Term 2009 W13D1-1 Reading Quiz and Concept Questions A person spins a tennis ball on a string in a horizontal circle (so that
Physics 201, Practice Midterm Exam 3, Fall 2006
 Physics 201, Practice Midterm Exam 3, Fall 2006 1. A figure skater is spinning with arms stretched out. A moment later she rapidly brings her arms close to her body, but maintains her dynamic equilibrium.
Physics 201, Practice Midterm Exam 3, Fall 2006 1. A figure skater is spinning with arms stretched out. A moment later she rapidly brings her arms close to her body, but maintains her dynamic equilibrium.
Show all work in answering the following questions. Partial credit may be given for problems involving calculations.
 Physics 3210, Spring 2018 Final Exam Name: Signature: UID: Please read the following before continuing: Show all work in answering the following questions. Partial credit may be given for problems involving
Physics 3210, Spring 2018 Final Exam Name: Signature: UID: Please read the following before continuing: Show all work in answering the following questions. Partial credit may be given for problems involving
Rotation. I. Kinematics - Angular analogs
 Rotation I. Kinematics - Angular analogs II. III. IV. Dynamics - Torque and Rotational Inertia Work and Energy Angular Momentum - Bodies and particles V. Elliptical Orbits The student will be able to:
Rotation I. Kinematics - Angular analogs II. III. IV. Dynamics - Torque and Rotational Inertia Work and Energy Angular Momentum - Bodies and particles V. Elliptical Orbits The student will be able to:
Circular Motion, Pt 2: Angular Dynamics. Mr. Velazquez AP/Honors Physics
 Circular Motion, Pt 2: Angular Dynamics Mr. Velazquez AP/Honors Physics Formulas: Angular Kinematics (θ must be in radians): s = rθ Arc Length 360 = 2π rads = 1 rev ω = θ t = v t r Angular Velocity α av
Circular Motion, Pt 2: Angular Dynamics Mr. Velazquez AP/Honors Physics Formulas: Angular Kinematics (θ must be in radians): s = rθ Arc Length 360 = 2π rads = 1 rev ω = θ t = v t r Angular Velocity α av
Solution Only gravity is doing work. Since gravity is a conservative force mechanical energy is conserved:
 8) roller coaster starts with a speed of 8.0 m/s at a point 45 m above the bottom of a dip (see figure). Neglecting friction, what will be the speed of the roller coaster at the top of the next slope,
8) roller coaster starts with a speed of 8.0 m/s at a point 45 m above the bottom of a dip (see figure). Neglecting friction, what will be the speed of the roller coaster at the top of the next slope,
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
