Chapter 9. Rotational Dynamics
|
|
|
- Jody Blankenship
- 5 years ago
- Views:
Transcription
1 Chapter 9 Rotational Dynamics
2 In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation.
3 1) Torque Produces angular acceleration F1 F2 If F1 = - F2,! F 1 +! F 2 = m! a CM 0 = m! a CM Object rotates about CM (or fixed axis) ==> CM remains at rest
4 The amount of torque depends on where and in what direction the force is applied, as well as the location of the axis of rotation.
5 φ r DEFINITION OF TORQUE Magnitude of Torque = (Magnitude of the force) x (Lever arm) τ = Frsinφ Direction: The torque is positive when the force tends to produce a counterclockwise rotation about the axis. SI Unit of Torque: newton x meter (N m)
6 Example In San Francisco a very simple technique is used to turn around a cable car when it reaches the end of its route. The car rolls onto a turntable, which can rotate about a vertical axis through its center. Then, two people push perpendicularly on the car, one at each end, as shown in the drawing. The turntable is rotated one-half of a revolution to turn the car around. If the length of the car is 9.20 m and each person pushes with a 185-N force, what is the magnitude of the net torque applied to the car?
7 Example You are installing a new spark plug in your car, and the manual specifies that it be tightened to a torque that has a magnitude of 45 N m. Using the data in the drawing, determine the magnitude, F, of the force that you must exert on the wrench.
8 2) Rigid objects in equilibrium A rigid body is in equilibrium if it has zero translational acceleration and zero angular acceleration. In equilibrium, the sum of the externally applied forces is zero, and the sum of the externally applied torques is zero. ax = a y = 0 α = 0
9 Reasoning Strategy 1. Select the object to which the equations for equilibrium are to be applied. 2. Draw a free-body diagram that shows all of the external forces acting on the object. 3. Choose a convenient set of x, y axes and resolve all forces into components that lie along these axes. 4. Apply the equations that specify the balance of forces at equilibrium. (Set the net force in the x and y directions equal to zero.) 5. Select a convenient axis of rotation. Set the sum of the torques about this axis equal to zero. 6. Solve the equations for the desired unknown quantities.
10 Example A person exerts a horizontal force of 190 N in the test apparatus shown in the drawing. Find the horizontal force M (magnitude and direction) that his flexor muscle exerts on his forearm.
11 Example A woman whose weight is 530 N is poised at the right end of a diving board with length 3.90 m. The board has negligible weight and is supported by a fulcrum 1.40 m away from the left end. Find the forces that the bolt and the fulcrum exert on the board.
12 3) Torque due to gravity; centre-of-gravity a) Torque due to discrete point masses m1 m2 axis W1 W2 r2 r1 τ 1 = W 1 r 1 τ 2 = W 2 r 2 τ = τ 1 + τ 2
13 (b) Continuous mass Wi ri τ = ΔW i r i
14 (c) Centre-of-gravity (definition) The center of gravity of a rigid body is the point at which its weight can be considered to act when the torque due to the weight is being calculated. Wr cg = ΔW i r i r cg = ΔW i r i W
15 (d) Locating the c.g. For 2 discrete masses (extends to any number) τ = Wr cg = W 1 r 1 + W 2 r 2 r cg = W 1 r 1 + W 2 r 2 W 1 + W 2 Uniform gravity W i = m i g r cg = m 1r 1 + m 2 r 2 m 1 + m 2 = r cm For symmetrical objects, cg is at the geometrical centre
16 Example Find the torque of a symmetrical meter stick with a mass of 1 kg about a fulcrum 15 cm from one end.
17 Balancing r cg = W 1 r 1 + W 2 r 2 W 1 + W 2
18 Finding the centre of gravity Image reprinted with permission of John Wiley and Sons, Inc.
19 Example The drawing shows a person (weight 584 N) doing push-ups. Find the normal force exerted by the floor on each hand and each foot, assuming the person holds this position.
20 Example A uniform board is leaning against a smooth vertical wall. The board is at an angle θ above the horizontal ground. The coefficient of static friction between the ground and the lower end of the board is Find the smallest value for the angle θ, such that the lower end of the board does not slide along the ground.
21 4) Moment of Inertia; 2nd law for rotation Translation F = ma m resists acceleration Rotation τ = Iα - I resists angular acceleration
22 Moment of inertia of a point object I = mr 2 FT m r F T = ma T rf T = ma T r τ = mr 2 α τ = Iα Moment of inertia of a rigid object I = 2 m i r i
23
24 5) Angular momentum linear momentum: p = mv angular momentum: τ = Iα = I Δω Δt τ = ΔL Δt L = Iω For a point particle on a circular path, L = mvr Units: kg m 2 /s
25 Conservation of angular momentum τ = ΔL Δt If external torque is zero, L is constant. L = Iω I = 2 m i r i If I decreases, angular speed increases.
26 Example Satellite in elliptical orbit L = Iω L A = L P I A ω A = I P ω P mv A r A = mv P r P v A = r P r A v P Image reprinted with permission of John Wiley and Sons, Inc.
27 Example A uniform board is leaning against a smooth vertical wall. The board is at an angle θ above the horizontal ground. The coefficient of static friction between the ground and the lower end of the board is Find the smallest value for the angle θ, such that the lower end of the board does not slide along the ground.
28 Example C&J In outer space two identical space modules are joined together by a massless cable. These modules are rotating about their center of mass, which is at the center of the cable because the modules are identical (see the drawing). In each module, the cable is connected to a motor, so that the modules can pull each other together. The initial tangential speed of each module is v 0 = 17 m/s. Then they pull together until the distance between them is reduced by a factor of two. Determine the final tangential speed v f for each module. Answer: 34 m/s
29 Example A small kg object moves on a frictionless horizontal table in a circular path of radius 1.00 m The angular speed is 6.28 rad/s. The object is attached to a string of negligible mass that passes through a small hole in the centre of the circle. Someone under the table begins to pull the string downward to make the circle smaller. If the string will tolerate a tension of no more than 105 N, what is the radius of the smallest possible circle on which the object can move?
30 Example A thin rod has a length of 0.25 m and rotates in a circle on a frictionless table-top. The axis is perpendicular to the length of the rod at one of its ends. The rod has angular velocity of 0.32 rad/s and a moment of inertia of kg m 2. A bug standing on the axis decides to crawl out to the other end of the rod. When the bug ( mass = kg) gets where it s going, what is the angular velocity of the rod? Answer: 0.26 rad/s
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 8 continued. Rotational Dynamics
 Chapter 8 continued Rotational Dynamics 8.6 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Chapter 8 continued Rotational Dynamics 8.6 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Rotational Dynamics continued
 Chapter 9 Rotational Dynamics continued 9.1 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Chapter 9 Rotational Dynamics continued 9.1 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Chapter 8 continued. Rotational Dynamics
 Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = s = rφ = Frφ Fr = τ (torque) = τφ r φ s F to s θ = 0 DEFINITION
Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = s = rφ = Frφ Fr = τ (torque) = τφ r φ s F to s θ = 0 DEFINITION
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
Torque rotational force which causes a change in rotational motion. This force is defined by linear force multiplied by a radius.
 Warm up A remote-controlled car's wheel accelerates at 22.4 rad/s 2. If the wheel begins with an angular speed of 10.8 rad/s, what is the wheel's angular speed after exactly three full turns? AP Physics
Warm up A remote-controlled car's wheel accelerates at 22.4 rad/s 2. If the wheel begins with an angular speed of 10.8 rad/s, what is the wheel's angular speed after exactly three full turns? AP Physics
Chapter 8 continued. Rotational Dynamics
 Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = rφ = Frφ Fr = τ (torque) = τφ r φ s F to x θ = 0 DEFINITION OF
Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = rφ = Frφ Fr = τ (torque) = τφ r φ s F to x θ = 0 DEFINITION OF
Lecture 14. Rotational dynamics Torque. Give me a lever long enough and a fulcrum on which to place it, and I shall move the world.
 Lecture 14 Rotational dynamics Torque Give me a lever long enough and a fulcrum on which to place it, and I shall move the world. Archimedes, 87 1 BC EXAM Tuesday March 6, 018 8:15 PM 9:45 PM Today s Topics:
Lecture 14 Rotational dynamics Torque Give me a lever long enough and a fulcrum on which to place it, and I shall move the world. Archimedes, 87 1 BC EXAM Tuesday March 6, 018 8:15 PM 9:45 PM Today s Topics:
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
Table of Contents. Pg. # Momentum & Impulse (Bozemanscience Videos) 1 1/11/16
 Table of Contents g. # 1 1/11/16 Momentum & Impulse (Bozemanscience Videos) 2 1/13/16 Conservation of Momentum 3 1/19/16 Elastic and Inelastic Collisions 4 1/19/16 Lab 1 Momentum 5 1/26/16 Rotational Dynamics
Table of Contents g. # 1 1/11/16 Momentum & Impulse (Bozemanscience Videos) 2 1/13/16 Conservation of Momentum 3 1/19/16 Elastic and Inelastic Collisions 4 1/19/16 Lab 1 Momentum 5 1/26/16 Rotational Dynamics
= o + t = ot + ½ t 2 = o + 2
 Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
Chapter 8. Rotational Kinematics
 Chapter 8 Rotational Kinematics 8.3 The Equations of Rotational Kinematics 8.4 Angular Variables and Tangential Variables The relationship between the (tangential) arc length, s, at some radius, r, and
Chapter 8 Rotational Kinematics 8.3 The Equations of Rotational Kinematics 8.4 Angular Variables and Tangential Variables The relationship between the (tangential) arc length, s, at some radius, r, and
Mechanics II. Which of the following relations among the forces W, k, N, and F must be true?
 Mechanics II 1. By applying a force F on a block, a person pulls a block along a rough surface at constant velocity v (see Figure below; directions, but not necessarily magnitudes, are indicated). Which
Mechanics II 1. By applying a force F on a block, a person pulls a block along a rough surface at constant velocity v (see Figure below; directions, but not necessarily magnitudes, are indicated). Which
Name Date Period PROBLEM SET: ROTATIONAL DYNAMICS
 Accelerated Physics Rotational Dynamics Problem Set Page 1 of 5 Name Date Period PROBLEM SET: ROTATIONAL DYNAMICS Directions: Show all work on a separate piece of paper. Box your final answer. Don t forget
Accelerated Physics Rotational Dynamics Problem Set Page 1 of 5 Name Date Period PROBLEM SET: ROTATIONAL DYNAMICS Directions: Show all work on a separate piece of paper. Box your final answer. Don t forget
Circular Motion, Pt 2: Angular Dynamics. Mr. Velazquez AP/Honors Physics
 Circular Motion, Pt 2: Angular Dynamics Mr. Velazquez AP/Honors Physics Formulas: Angular Kinematics (θ must be in radians): s = rθ Arc Length 360 = 2π rads = 1 rev ω = θ t = v t r Angular Velocity α av
Circular Motion, Pt 2: Angular Dynamics Mr. Velazquez AP/Honors Physics Formulas: Angular Kinematics (θ must be in radians): s = rθ Arc Length 360 = 2π rads = 1 rev ω = θ t = v t r Angular Velocity α av
Chapter 8. Rotational Motion
 Chapter 8 Rotational Motion The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of
Chapter 8 Rotational Motion The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of
Part 1 of 1. (useful for homework)
 Chapter 9 Part 1 of 1 Example Problems & Solutions Example Problems & Solutions (useful for homework) 1 1. You are installing a spark plug in your car, and the manual specifies that it be tightened to
Chapter 9 Part 1 of 1 Example Problems & Solutions Example Problems & Solutions (useful for homework) 1 1. You are installing a spark plug in your car, and the manual specifies that it be tightened to
31 ROTATIONAL KINEMATICS
 31 ROTATIONAL KINEMATICS 1. Compare and contrast circular motion and rotation? Address the following Which involves an object and which involves a system? Does an object/system in circular motion have
31 ROTATIONAL KINEMATICS 1. Compare and contrast circular motion and rotation? Address the following Which involves an object and which involves a system? Does an object/system in circular motion have
Q1. For a completely inelastic two-body collision the kinetic energy of the objects after the collision is the same as:
 Coordinator: Dr.. Naqvi Monday, January 05, 015 Page: 1 Q1. For a completely inelastic two-body collision the kinetic energy of the objects after the collision is the same as: ) (1/) MV, where M is the
Coordinator: Dr.. Naqvi Monday, January 05, 015 Page: 1 Q1. For a completely inelastic two-body collision the kinetic energy of the objects after the collision is the same as: ) (1/) MV, where M is the
Chapter 9-10 Test Review
 Chapter 9-10 Test Review Chapter Summary 9.2. The Second Condition for Equilibrium Explain torque and the factors on which it depends. Describe the role of torque in rotational mechanics. 10.1. Angular
Chapter 9-10 Test Review Chapter Summary 9.2. The Second Condition for Equilibrium Explain torque and the factors on which it depends. Describe the role of torque in rotational mechanics. 10.1. Angular
Chapter 8. Rotational Equilibrium and Rotational Dynamics. 1. Torque. 2. Torque and Equilibrium. 3. Center of Mass and Center of Gravity
 Chapter 8 Rotational Equilibrium and Rotational Dynamics 1. Torque 2. Torque and Equilibrium 3. Center of Mass and Center of Gravity 4. Torque and angular acceleration 5. Rotational Kinetic energy 6. Angular
Chapter 8 Rotational Equilibrium and Rotational Dynamics 1. Torque 2. Torque and Equilibrium 3. Center of Mass and Center of Gravity 4. Torque and angular acceleration 5. Rotational Kinetic energy 6. Angular
CHAPTER 8 TEST REVIEW MARKSCHEME
 AP PHYSICS Name: Period: Date: 50 Multiple Choice 45 Single Response 5 Multi-Response Free Response 3 Short Free Response 2 Long Free Response MULTIPLE CHOICE DEVIL PHYSICS BADDEST CLASS ON CAMPUS AP EXAM
AP PHYSICS Name: Period: Date: 50 Multiple Choice 45 Single Response 5 Multi-Response Free Response 3 Short Free Response 2 Long Free Response MULTIPLE CHOICE DEVIL PHYSICS BADDEST CLASS ON CAMPUS AP EXAM
Test 7 wersja angielska
 Test 7 wersja angielska 7.1A One revolution is the same as: A) 1 rad B) 57 rad C) π/2 rad D) π rad E) 2π rad 7.2A. If a wheel turns with constant angular speed then: A) each point on its rim moves with
Test 7 wersja angielska 7.1A One revolution is the same as: A) 1 rad B) 57 rad C) π/2 rad D) π rad E) 2π rad 7.2A. If a wheel turns with constant angular speed then: A) each point on its rim moves with
Physics 111. Tuesday, November 2, Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy
 ics Tuesday, ember 2, 2002 Ch 11: Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy Announcements Wednesday, 8-9 pm in NSC 118/119 Sunday, 6:30-8 pm in CCLIR 468 Announcements This
ics Tuesday, ember 2, 2002 Ch 11: Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy Announcements Wednesday, 8-9 pm in NSC 118/119 Sunday, 6:30-8 pm in CCLIR 468 Announcements This
Chapter 9 Rotational Dynamics
 Chapter 9 ROTATIONAL DYNAMICS PREVIEW A force acting at a perpendicular distance from a rotation point, such as pushing a doorknob and causing the door to rotate on its hinges, produces a torque. If the
Chapter 9 ROTATIONAL DYNAMICS PREVIEW A force acting at a perpendicular distance from a rotation point, such as pushing a doorknob and causing the door to rotate on its hinges, produces a torque. If the
Slide 1 / 37. Rotational Motion
 Slide 1 / 37 Rotational Motion Slide 2 / 37 Angular Quantities An angle θ can be given by: where r is the radius and l is the arc length. This gives θ in radians. There are 360 in a circle or 2π radians.
Slide 1 / 37 Rotational Motion Slide 2 / 37 Angular Quantities An angle θ can be given by: where r is the radius and l is the arc length. This gives θ in radians. There are 360 in a circle or 2π radians.
Rotational Dynamics continued
 Chapter 9 Rotational Dynamics continued 9.4 Newton s Second Law for Rotational Motion About a Fixed Axis ROTATIONAL ANALOG OF NEWTON S SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS I = ( mr 2
Chapter 9 Rotational Dynamics continued 9.4 Newton s Second Law for Rotational Motion About a Fixed Axis ROTATIONAL ANALOG OF NEWTON S SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS I = ( mr 2
Chapter 8. Centripetal Force and The Law of Gravity
 Chapter 8 Centripetal Force and The Law of Gravity Centripetal Acceleration An object traveling in a circle, even though it moves with a constant speed, will have an acceleration The centripetal acceleration
Chapter 8 Centripetal Force and The Law of Gravity Centripetal Acceleration An object traveling in a circle, even though it moves with a constant speed, will have an acceleration The centripetal acceleration
We define angular displacement, θ, and angular velocity, ω. What's a radian?
 We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
Class XI Chapter 7- System of Particles and Rotational Motion Physics
 Page 178 Question 7.1: Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie
Page 178 Question 7.1: Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie
Chapter 8, Rotational Equilibrium and Rotational Dynamics. 3. If a net torque is applied to an object, that object will experience:
 CHAPTER 8 3. If a net torque is applied to an object, that object will experience: a. a constant angular speed b. an angular acceleration c. a constant moment of inertia d. an increasing moment of inertia
CHAPTER 8 3. If a net torque is applied to an object, that object will experience: a. a constant angular speed b. an angular acceleration c. a constant moment of inertia d. an increasing moment of inertia
Angular Momentum L = I ω
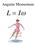 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Rotational Dynamics. Slide 2 / 34. Slide 1 / 34. Slide 4 / 34. Slide 3 / 34. Slide 6 / 34. Slide 5 / 34. Moment of Inertia. Parallel Axis Theorem
 Slide 1 / 34 Rotational ynamics l Slide 2 / 34 Moment of Inertia To determine the moment of inertia we divide the object into tiny masses of m i a distance r i from the center. is the sum of all the tiny
Slide 1 / 34 Rotational ynamics l Slide 2 / 34 Moment of Inertia To determine the moment of inertia we divide the object into tiny masses of m i a distance r i from the center. is the sum of all the tiny
Torque. Physics 6A. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB
 Physics 6A Torque is what causes angular acceleration (just like a force causes linear acceleration) Torque is what causes angular acceleration (just like a force causes linear acceleration) For a torque
Physics 6A Torque is what causes angular acceleration (just like a force causes linear acceleration) Torque is what causes angular acceleration (just like a force causes linear acceleration) For a torque
Topic 1: Newtonian Mechanics Energy & Momentum
 Work (W) the amount of energy transferred by a force acting through a distance. Scalar but can be positive or negative ΔE = W = F! d = Fdcosθ Units N m or Joules (J) Work, Energy & Power Power (P) the
Work (W) the amount of energy transferred by a force acting through a distance. Scalar but can be positive or negative ΔE = W = F! d = Fdcosθ Units N m or Joules (J) Work, Energy & Power Power (P) the
Chapter 8. Rotational Motion
 Chapter 8 Rotational Motion Rotational Work and Energy W = Fs = s = rθ Frθ Consider the work done in rotating a wheel with a tangential force, F, by an angle θ. τ = Fr W =τθ Rotational Work and Energy
Chapter 8 Rotational Motion Rotational Work and Energy W = Fs = s = rθ Frθ Consider the work done in rotating a wheel with a tangential force, F, by an angle θ. τ = Fr W =τθ Rotational Work and Energy
-- Angular momentum. -- Equilibrium. Final Exam. During class (1-3:55 pm) on 6/27, Mon Room: 412 FMH (classroom)
 inal Exam During class (1-3:55 pm) on 6/27, Mon Room: 412 MH (classroom) Bring scientific calculators No smart phone calculators l are allowed. Exam covers everything learned in this course. tomorrow s
inal Exam During class (1-3:55 pm) on 6/27, Mon Room: 412 MH (classroom) Bring scientific calculators No smart phone calculators l are allowed. Exam covers everything learned in this course. tomorrow s
Physics 2210 Fall smartphysics Conservation of Angular Momentum 11/20/2015
 Physics 2210 Fall 2015 smartphysics 19-20 Conservation of Angular Momentum 11/20/2015 Poll 11-18-03 In the two cases shown above identical ladders are leaning against frictionless walls and are not sliding.
Physics 2210 Fall 2015 smartphysics 19-20 Conservation of Angular Momentum 11/20/2015 Poll 11-18-03 In the two cases shown above identical ladders are leaning against frictionless walls and are not sliding.
Physics 2210 Fall smartphysics Rotational Statics 11/18/2015
 Physics 2210 Fall 2015 smartphysics 17-18 Rotational Statics 11/18/2015 τ TT = L T 1 sin 150 = 1 T 2 1L Poll 11-18-01 τ TT = L 2 T 2 sin 150 = 1 4 T 2L 150 150 τ gg = L 2 MM sin +90 = 1 2 MMM +90 MM τ
Physics 2210 Fall 2015 smartphysics 17-18 Rotational Statics 11/18/2015 τ TT = L T 1 sin 150 = 1 T 2 1L Poll 11-18-01 τ TT = L 2 T 2 sin 150 = 1 4 T 2L 150 150 τ gg = L 2 MM sin +90 = 1 2 MMM +90 MM τ
Chapter 4. Forces and Newton s Laws of Motion. continued
 Chapter 4 Forces and Newton s Laws of Motion continued Quiz 3 4.7 The Gravitational Force Newton s Law of Universal Gravitation Every particle in the universe exerts an attractive force on every other
Chapter 4 Forces and Newton s Laws of Motion continued Quiz 3 4.7 The Gravitational Force Newton s Law of Universal Gravitation Every particle in the universe exerts an attractive force on every other
Practice. Newton s 3 Laws of Motion. Recall. Forces a push or pull acting on an object; a vector quantity measured in Newtons (kg m/s²)
 Practice A car starts from rest and travels upwards along a straight road inclined at an angle of 5 from the horizontal. The length of the road is 450 m and the mass of the car is 800 kg. The speed of
Practice A car starts from rest and travels upwards along a straight road inclined at an angle of 5 from the horizontal. The length of the road is 450 m and the mass of the car is 800 kg. The speed of
Chapter 10 Practice Test
 Chapter 10 Practice Test 1. At t = 0, a wheel rotating about a fixed axis at a constant angular acceleration of 0.40 rad/s 2 has an angular velocity of 1.5 rad/s and an angular position of 2.3 rad. What
Chapter 10 Practice Test 1. At t = 0, a wheel rotating about a fixed axis at a constant angular acceleration of 0.40 rad/s 2 has an angular velocity of 1.5 rad/s and an angular position of 2.3 rad. What
 AP Physics 1- Torque, Rotational Inertia, and Angular Momentum Practice Problems FACT: The center of mass of a system of objects obeys Newton s second law- F = Ma cm. Usually the location of the center
AP Physics 1- Torque, Rotational Inertia, and Angular Momentum Practice Problems FACT: The center of mass of a system of objects obeys Newton s second law- F = Ma cm. Usually the location of the center
Chapter 9 TORQUE & Rotational Kinematics
 Chapter 9 TORQUE & Rotational Kinematics This motionless person is in static equilibrium. The forces acting on him add up to zero. Both forces are vertical in this case. This car is in dynamic equilibrium
Chapter 9 TORQUE & Rotational Kinematics This motionless person is in static equilibrium. The forces acting on him add up to zero. Both forces are vertical in this case. This car is in dynamic equilibrium
Physics 201 Midterm Exam 3
 Physics 201 Midterm Exam 3 Information and Instructions Student ID Number: Section Number: TA Name: Please fill in all the information above. Please write and bubble your Name and Student Id number on
Physics 201 Midterm Exam 3 Information and Instructions Student ID Number: Section Number: TA Name: Please fill in all the information above. Please write and bubble your Name and Student Id number on
ΣF = ma Στ = Iα ½mv 2 ½Iω 2. mv Iω
 Thur Oct 22 Assign 9 Friday Today: Torques Angular Momentum x θ v ω a α F τ m I Roll without slipping: x = r Δθ v LINEAR = r ω a LINEAR = r α ΣF = ma Στ = Iα ½mv 2 ½Iω 2 I POINT = MR 2 I HOOP = MR 2 I
Thur Oct 22 Assign 9 Friday Today: Torques Angular Momentum x θ v ω a α F τ m I Roll without slipping: x = r Δθ v LINEAR = r ω a LINEAR = r α ΣF = ma Στ = Iα ½mv 2 ½Iω 2 I POINT = MR 2 I HOOP = MR 2 I
1 MR SAMPLE EXAM 3 FALL 2013
 SAMPLE EXAM 3 FALL 013 1. A merry-go-round rotates from rest with an angular acceleration of 1.56 rad/s. How long does it take to rotate through the first rev? A) s B) 4 s C) 6 s D) 8 s E) 10 s. A wheel,
SAMPLE EXAM 3 FALL 013 1. A merry-go-round rotates from rest with an angular acceleration of 1.56 rad/s. How long does it take to rotate through the first rev? A) s B) 4 s C) 6 s D) 8 s E) 10 s. A wheel,
Torque and Static Equilibrium
 Torque and Static Equilibrium Rigid Bodies Rigid body: An extended object in which the distance between any two points in the object is constant in time. Examples: sphere, disk Effect of external forces
Torque and Static Equilibrium Rigid Bodies Rigid body: An extended object in which the distance between any two points in the object is constant in time. Examples: sphere, disk Effect of external forces
Chapter 6, Problem 18. Agenda. Rotational Inertia. Rotational Inertia. Calculating Moment of Inertia. Example: Hoop vs.
 Agenda Today: Homework quiz, moment of inertia and torque Thursday: Statics problems revisited, rolling motion Reading: Start Chapter 8 in the reading Have to cancel office hours today: will have extra
Agenda Today: Homework quiz, moment of inertia and torque Thursday: Statics problems revisited, rolling motion Reading: Start Chapter 8 in the reading Have to cancel office hours today: will have extra
Chapter 8. Rotational Equilibrium and Rotational Dynamics
 Chapter 8 Rotational Equilibrium and Rotational Dynamics Wrench Demo Torque Torque, τ, is the tendency of a force to rotate an object about some axis τ = Fd F is the force d is the lever arm (or moment
Chapter 8 Rotational Equilibrium and Rotational Dynamics Wrench Demo Torque Torque, τ, is the tendency of a force to rotate an object about some axis τ = Fd F is the force d is the lever arm (or moment
Chapter 9: Rotational Dynamics Tuesday, September 17, 2013
 Chapter 9: Rotational Dynamics Tuesday, September 17, 2013 10:00 PM The fundamental idea of Newtonian dynamics is that "things happen for a reason;" to be more specific, there is no need to explain rest
Chapter 9: Rotational Dynamics Tuesday, September 17, 2013 10:00 PM The fundamental idea of Newtonian dynamics is that "things happen for a reason;" to be more specific, there is no need to explain rest
Review for 3 rd Midterm
 Review for 3 rd Midterm Midterm is on 4/19 at 7:30pm in the same rooms as before You are allowed one double sided sheet of paper with any handwritten notes you like. The moment-of-inertia about the center-of-mass
Review for 3 rd Midterm Midterm is on 4/19 at 7:30pm in the same rooms as before You are allowed one double sided sheet of paper with any handwritten notes you like. The moment-of-inertia about the center-of-mass
It will be most difficult for the ant to adhere to the wheel as it revolves past which of the four points? A) I B) II C) III D) IV
 AP Physics 1 Lesson 16 Homework Newton s First and Second Law of Rotational Motion Outcomes Define rotational inertia, torque, and center of gravity. State and explain Newton s first Law of Motion as it
AP Physics 1 Lesson 16 Homework Newton s First and Second Law of Rotational Motion Outcomes Define rotational inertia, torque, and center of gravity. State and explain Newton s first Law of Motion as it
AP Physics QUIZ Chapters 10
 Name: 1. Torque is the rotational analogue of (A) Kinetic Energy (B) Linear Momentum (C) Acceleration (D) Force (E) Mass A 5-kilogram sphere is connected to a 10-kilogram sphere by a rigid rod of negligible
Name: 1. Torque is the rotational analogue of (A) Kinetic Energy (B) Linear Momentum (C) Acceleration (D) Force (E) Mass A 5-kilogram sphere is connected to a 10-kilogram sphere by a rigid rod of negligible
Use the following to answer question 1:
 Use the following to answer question 1: On an amusement park ride, passengers are seated in a horizontal circle of radius 7.5 m. The seats begin from rest and are uniformly accelerated for 21 seconds to
Use the following to answer question 1: On an amusement park ride, passengers are seated in a horizontal circle of radius 7.5 m. The seats begin from rest and are uniformly accelerated for 21 seconds to
Webreview Torque and Rotation Practice Test
 Please do not write on test. ID A Webreview - 8.2 Torque and Rotation Practice Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A 0.30-m-radius automobile
Please do not write on test. ID A Webreview - 8.2 Torque and Rotation Practice Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A 0.30-m-radius automobile
PHYSICS 149: Lecture 21
 PHYSICS 149: Lecture 21 Chapter 8: Torque and Angular Momentum 8.2 Torque 8.4 Equilibrium Revisited 8.8 Angular Momentum Lecture 21 Purdue University, Physics 149 1 Midterm Exam 2 Wednesday, April 6, 6:30
PHYSICS 149: Lecture 21 Chapter 8: Torque and Angular Momentum 8.2 Torque 8.4 Equilibrium Revisited 8.8 Angular Momentum Lecture 21 Purdue University, Physics 149 1 Midterm Exam 2 Wednesday, April 6, 6:30
Rolling, Torque & Angular Momentum
 PHYS 101 Previous Exam Problems CHAPTER 11 Rolling, Torque & Angular Momentum Rolling motion Torque Angular momentum Conservation of angular momentum 1. A uniform hoop (ring) is rolling smoothly from the
PHYS 101 Previous Exam Problems CHAPTER 11 Rolling, Torque & Angular Momentum Rolling motion Torque Angular momentum Conservation of angular momentum 1. A uniform hoop (ring) is rolling smoothly from the
General Physics (PHY 2130)
 General Physics (PHY 130) Lecture 0 Rotational dynamics equilibrium nd Newton s Law for rotational motion rolling Exam II review http://www.physics.wayne.edu/~apetrov/phy130/ Lightning Review Last lecture:
General Physics (PHY 130) Lecture 0 Rotational dynamics equilibrium nd Newton s Law for rotational motion rolling Exam II review http://www.physics.wayne.edu/~apetrov/phy130/ Lightning Review Last lecture:
Page 2. Q1.A satellite X is in a circular orbit of radius r about the centre of a spherical planet of mass
 Q1. satellite X is in a circular orbit of radius r about the centre of a spherical planet of mass M. Which line, to, in the table gives correct expressions for the centripetal acceleration a and the speed
Q1. satellite X is in a circular orbit of radius r about the centre of a spherical planet of mass M. Which line, to, in the table gives correct expressions for the centripetal acceleration a and the speed
Chapter 12 Static Equilibrium
 Chapter Static Equilibrium. Analysis Model: Rigid Body in Equilibrium. More on the Center of Gravity. Examples of Rigid Objects in Static Equilibrium CHAPTER : STATIC EQUILIBRIUM AND ELASTICITY.) The Conditions
Chapter Static Equilibrium. Analysis Model: Rigid Body in Equilibrium. More on the Center of Gravity. Examples of Rigid Objects in Static Equilibrium CHAPTER : STATIC EQUILIBRIUM AND ELASTICITY.) The Conditions
Chapter 8 Rotational Motion and Equilibrium. 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction
 Chapter 8 Rotational Motion and Equilibrium Name 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction 1. The distance between a turning axis and the
Chapter 8 Rotational Motion and Equilibrium Name 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction 1. The distance between a turning axis and the
Angular Momentum L = I ω
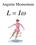 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
PSI AP Physics I Rotational Motion
 PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
Physics 201. Professor P. Q. Hung. 311B, Physics Building. Physics 201 p. 1/1
 Physics 201 p. 1/1 Physics 201 Professor P. Q. Hung 311B, Physics Building Physics 201 p. 2/1 Rotational Kinematics and Energy Rotational Kinetic Energy, Moment of Inertia All elements inside the rigid
Physics 201 p. 1/1 Physics 201 Professor P. Q. Hung 311B, Physics Building Physics 201 p. 2/1 Rotational Kinematics and Energy Rotational Kinetic Energy, Moment of Inertia All elements inside the rigid
Uniform Circular Motion
 Uniform Circular Motion Motion in a circle at constant angular speed. ω: angular velocity (rad/s) Rotation Angle The rotation angle is the ratio of arc length to radius of curvature. For a given angle,
Uniform Circular Motion Motion in a circle at constant angular speed. ω: angular velocity (rad/s) Rotation Angle The rotation angle is the ratio of arc length to radius of curvature. For a given angle,
Handout 7: Torque, angular momentum, rotational kinetic energy and rolling motion. Torque and angular momentum
 Handout 7: Torque, angular momentum, rotational kinetic energy and rolling motion Torque and angular momentum In Figure, in order to turn a rod about a fixed hinge at one end, a force F is applied at a
Handout 7: Torque, angular momentum, rotational kinetic energy and rolling motion Torque and angular momentum In Figure, in order to turn a rod about a fixed hinge at one end, a force F is applied at a
Chapter 8. Rotational Equilibrium and Rotational Dynamics
 Chapter 8 Rotational Equilibrium and Rotational Dynamics 1 Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related 2 Torque The door is free to rotate
Chapter 8 Rotational Equilibrium and Rotational Dynamics 1 Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related 2 Torque The door is free to rotate
Chapter 10: Dynamics of Rotational Motion
 Chapter 10: Dynamics of Rotational Motion What causes an angular acceleration? The effectiveness of a force at causing a rotation is called torque. QuickCheck 12.5 The four forces shown have the same strength.
Chapter 10: Dynamics of Rotational Motion What causes an angular acceleration? The effectiveness of a force at causing a rotation is called torque. QuickCheck 12.5 The four forces shown have the same strength.
Torque. Introduction. Torque. PHY torque - J. Hedberg
 Torque PHY 207 - torque - J. Hedberg - 2017 1. Introduction 2. Torque 1. Lever arm changes 3. Net Torques 4. Moment of Rotational Inertia 1. Moment of Inertia for Arbitrary Shapes 2. Parallel Axis Theorem
Torque PHY 207 - torque - J. Hedberg - 2017 1. Introduction 2. Torque 1. Lever arm changes 3. Net Torques 4. Moment of Rotational Inertia 1. Moment of Inertia for Arbitrary Shapes 2. Parallel Axis Theorem
Practice Test 3. Name: Date: ID: A. Multiple Choice Identify the choice that best completes the statement or answers the question.
 Name: Date: _ Practice Test 3 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A wheel rotates about a fixed axis with an initial angular velocity of 20
Name: Date: _ Practice Test 3 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A wheel rotates about a fixed axis with an initial angular velocity of 20
AP Physics C: Rotation II. (Torque and Rotational Dynamics, Rolling Motion) Problems
 AP Physics C: Rotation II (Torque and Rotational Dynamics, Rolling Motion) Problems 1980M3. A billiard ball has mass M, radius R, and moment of inertia about the center of mass I c = 2 MR²/5 The ball is
AP Physics C: Rotation II (Torque and Rotational Dynamics, Rolling Motion) Problems 1980M3. A billiard ball has mass M, radius R, and moment of inertia about the center of mass I c = 2 MR²/5 The ball is
Practice Test 3. Multiple Choice Identify the choice that best completes the statement or answers the question.
 Practice Test 3 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A wheel rotates about a fixed axis with an initial angular velocity of 20 rad/s. During
Practice Test 3 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A wheel rotates about a fixed axis with an initial angular velocity of 20 rad/s. During
Chapter 8 Lecture Notes
 Chapter 8 Lecture Notes Physics 2414 - Strauss Formulas: v = l / t = r θ / t = rω a T = v / t = r ω / t =rα a C = v 2 /r = ω 2 r ω = ω 0 + αt θ = ω 0 t +(1/2)αt 2 θ = (1/2)(ω 0 +ω)t ω 2 = ω 0 2 +2αθ τ
Chapter 8 Lecture Notes Physics 2414 - Strauss Formulas: v = l / t = r θ / t = rω a T = v / t = r ω / t =rα a C = v 2 /r = ω 2 r ω = ω 0 + αt θ = ω 0 t +(1/2)αt 2 θ = (1/2)(ω 0 +ω)t ω 2 = ω 0 2 +2αθ τ
Exercise Torque Magnitude Ranking Task. Part A
 Exercise 10.2 Calculate the net torque about point O for the two forces applied as in the figure. The rod and both forces are in the plane of the page. Take positive torques to be counterclockwise. τ 28.0
Exercise 10.2 Calculate the net torque about point O for the two forces applied as in the figure. The rod and both forces are in the plane of the page. Take positive torques to be counterclockwise. τ 28.0
ROTATIONAL DYNAMICS AND STATIC EQUILIBRIUM
 ROTATIONAL DYNAMICS AND STATIC EQUILIBRIUM Chapter 11 Units of Chapter 11 Torque Torque and Angular Acceleration Zero Torque and Static Equilibrium Center of Mass and Balance Dynamic Applications of Torque
ROTATIONAL DYNAMICS AND STATIC EQUILIBRIUM Chapter 11 Units of Chapter 11 Torque Torque and Angular Acceleration Zero Torque and Static Equilibrium Center of Mass and Balance Dynamic Applications of Torque
Name: Date: Period: AP Physics C Rotational Motion HO19
 1.) A wheel turns with constant acceleration 0.450 rad/s 2. (9-9) Rotational Motion H19 How much time does it take to reach an angular velocity of 8.00 rad/s, starting from rest? Through how many revolutions
1.) A wheel turns with constant acceleration 0.450 rad/s 2. (9-9) Rotational Motion H19 How much time does it take to reach an angular velocity of 8.00 rad/s, starting from rest? Through how many revolutions
Physics 2210 Homework 18 Spring 2015
 Physics 2210 Homework 18 Spring 2015 Charles Jui April 12, 2015 IE Sphere Incline Wording A solid sphere of uniform density starts from rest and rolls without slipping down an inclined plane with angle
Physics 2210 Homework 18 Spring 2015 Charles Jui April 12, 2015 IE Sphere Incline Wording A solid sphere of uniform density starts from rest and rolls without slipping down an inclined plane with angle
Definition. is a measure of how much a force acting on an object causes that object to rotate, symbol is, (Greek letter tau)
 Torque Definition is a measure of how much a force acting on an object causes that object to rotate, symbol is, (Greek letter tau) = r F = rfsin, r = distance from pivot to force, F is the applied force
Torque Definition is a measure of how much a force acting on an object causes that object to rotate, symbol is, (Greek letter tau) = r F = rfsin, r = distance from pivot to force, F is the applied force
is the study of and. We study objects. is the study of and. We study objects.
 Static Equilibrium Translational Forces Torque Unit 4 Statics Dynamics vs Statics is the study of and. We study objects. is the study of and. We study objects. Recall Newton s First Law All objects remain
Static Equilibrium Translational Forces Torque Unit 4 Statics Dynamics vs Statics is the study of and. We study objects. is the study of and. We study objects. Recall Newton s First Law All objects remain
Physics Fall Mechanics, Thermodynamics, Waves, Fluids. Lecture 20: Rotational Motion. Slide 20-1
 Physics 1501 Fall 2008 Mechanics, Thermodynamics, Waves, Fluids Lecture 20: Rotational Motion Slide 20-1 Recap: center of mass, linear momentum A composite system behaves as though its mass is concentrated
Physics 1501 Fall 2008 Mechanics, Thermodynamics, Waves, Fluids Lecture 20: Rotational Motion Slide 20-1 Recap: center of mass, linear momentum A composite system behaves as though its mass is concentrated
III. Work and Energy
 Rotation I. Kinematics - Angular analogs II. III. IV. Dynamics - Torque and Rotational Inertia Work and Energy Angular Momentum - Bodies and particles V. Elliptical Orbits The student will be able to:
Rotation I. Kinematics - Angular analogs II. III. IV. Dynamics - Torque and Rotational Inertia Work and Energy Angular Momentum - Bodies and particles V. Elliptical Orbits The student will be able to:
Physics. Chapter 8 Rotational Motion
 Physics Chapter 8 Rotational Motion Circular Motion Tangential Speed The linear speed of something moving along a circular path. Symbol is the usual v and units are m/s Rotational Speed Number of revolutions
Physics Chapter 8 Rotational Motion Circular Motion Tangential Speed The linear speed of something moving along a circular path. Symbol is the usual v and units are m/s Rotational Speed Number of revolutions
PSI AP Physics I Rotational Motion
 PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
Translational vs Rotational. m x. Connection Δ = = = = = = Δ = = = = = = Δ =Δ = = = = = 2 / 1/2. Work
 Translational vs Rotational / / 1/ Δ m x v dx dt a dv dt F ma p mv KE mv Work Fd / / 1/ θ ω θ α ω τ α ω ω τθ Δ I d dt d dt I L I KE I Work / θ ω α τ Δ Δ c t s r v r a v r a r Fr L pr Connection Translational
Translational vs Rotational / / 1/ Δ m x v dx dt a dv dt F ma p mv KE mv Work Fd / / 1/ θ ω θ α ω τ α ω ω τθ Δ I d dt d dt I L I KE I Work / θ ω α τ Δ Δ c t s r v r a v r a r Fr L pr Connection Translational
Chapter 10. Rotation
 Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
PHYSICS - CLUTCH 1E CH 12: TORQUE & ROTATIONAL DYNAMICS.
 !! www.clutchprep.com INTRO TO TORQUE TORQUE is a twist that a Force gives an object around an axis of rotation. - For example, when you push on a door, it rotates around its hinges. - When a Force acts
!! www.clutchprep.com INTRO TO TORQUE TORQUE is a twist that a Force gives an object around an axis of rotation. - For example, when you push on a door, it rotates around its hinges. - When a Force acts
PHYSICS - CLUTCH CH 12: TORQUE & ROTATIONAL DYNAMICS.
 !! www.clutchprep.com TORQUE & ACCELERATION (ROTATIONAL DYNAMICS) When a Force causes rotation, it produces a Torque. Think of TORQUE as the equivalent of FORCE! FORCE (F) TORQUE (τ) - Causes linear acceleration
!! www.clutchprep.com TORQUE & ACCELERATION (ROTATIONAL DYNAMICS) When a Force causes rotation, it produces a Torque. Think of TORQUE as the equivalent of FORCE! FORCE (F) TORQUE (τ) - Causes linear acceleration
Center of Gravity Pearson Education, Inc.
 Center of Gravity = The center of gravity position is at a place where the torque from one end of the object is balanced by the torque of the other end and therefore there is NO rotation. Fulcrum Point
Center of Gravity = The center of gravity position is at a place where the torque from one end of the object is balanced by the torque of the other end and therefore there is NO rotation. Fulcrum Point
Solution Only gravity is doing work. Since gravity is a conservative force mechanical energy is conserved:
 8) roller coaster starts with a speed of 8.0 m/s at a point 45 m above the bottom of a dip (see figure). Neglecting friction, what will be the speed of the roller coaster at the top of the next slope,
8) roller coaster starts with a speed of 8.0 m/s at a point 45 m above the bottom of a dip (see figure). Neglecting friction, what will be the speed of the roller coaster at the top of the next slope,
Physics 201, Practice Midterm Exam 3, Fall 2006
 Physics 201, Practice Midterm Exam 3, Fall 2006 1. A figure skater is spinning with arms stretched out. A moment later she rapidly brings her arms close to her body, but maintains her dynamic equilibrium.
Physics 201, Practice Midterm Exam 3, Fall 2006 1. A figure skater is spinning with arms stretched out. A moment later she rapidly brings her arms close to her body, but maintains her dynamic equilibrium.
Question 7.1: Answer. Geometric centre; No
 Question 7.1: Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring,, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside
Question 7.1: Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring,, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside
6. Find the net torque on the wheel in Figure about the axle through O if a = 10.0 cm and b = 25.0 cm.
 1. During a certain period of time, the angular position of a swinging door is described by θ = 5.00 + 10.0t + 2.00t 2, where θ is in radians and t is in seconds. Determine the angular position, angular
1. During a certain period of time, the angular position of a swinging door is described by θ = 5.00 + 10.0t + 2.00t 2, where θ is in radians and t is in seconds. Determine the angular position, angular
Chapter 8 Lecture. Pearson Physics. Rotational Motion and Equilibrium. Prepared by Chris Chiaverina Pearson Education, Inc.
 Chapter 8 Lecture Pearson Physics Rotational Motion and Equilibrium Prepared by Chris Chiaverina Chapter Contents Describing Angular Motion Rolling Motion and the Moment of Inertia Torque Static Equilibrium
Chapter 8 Lecture Pearson Physics Rotational Motion and Equilibrium Prepared by Chris Chiaverina Chapter Contents Describing Angular Motion Rolling Motion and the Moment of Inertia Torque Static Equilibrium
Review PHYS114 Chapters 4-7
 Review PHYS114 Chapters 4-7 MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) A 27 kg object is accelerated at a rate of 1.7 m/s 2. What force does
Review PHYS114 Chapters 4-7 MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) A 27 kg object is accelerated at a rate of 1.7 m/s 2. What force does
1. Which of the following is the unit for angular displacement? A. Meters B. Seconds C. Radians D. Radian per second E. Inches
 AP Physics B Practice Questions: Rotational Motion Multiple-Choice Questions 1. Which of the following is the unit for angular displacement? A. Meters B. Seconds C. Radians D. Radian per second E. Inches
AP Physics B Practice Questions: Rotational Motion Multiple-Choice Questions 1. Which of the following is the unit for angular displacement? A. Meters B. Seconds C. Radians D. Radian per second E. Inches
Rotation. PHYS 101 Previous Exam Problems CHAPTER
 PHYS 101 Previous Exam Problems CHAPTER 10 Rotation Rotational kinematics Rotational inertia (moment of inertia) Kinetic energy Torque Newton s 2 nd law Work, power & energy conservation 1. Assume that
PHYS 101 Previous Exam Problems CHAPTER 10 Rotation Rotational kinematics Rotational inertia (moment of inertia) Kinetic energy Torque Newton s 2 nd law Work, power & energy conservation 1. Assume that
Angular velocity and angular acceleration CHAPTER 9 ROTATION. Angular velocity and angular acceleration. ! equations of rotational motion
 Angular velocity and angular acceleration CHAPTER 9 ROTATION! r i ds i dθ θ i Angular velocity and angular acceleration! equations of rotational motion Torque and Moment of Inertia! Newton s nd Law for
Angular velocity and angular acceleration CHAPTER 9 ROTATION! r i ds i dθ θ i Angular velocity and angular acceleration! equations of rotational motion Torque and Moment of Inertia! Newton s nd Law for
Physics 2211 ABC Quiz #3 Solutions Spring 2017
 Physics 2211 ABC Quiz #3 Solutions Spring 2017 I. (16 points) A block of mass m b is suspended vertically on a ideal cord that then passes through a frictionless hole and is attached to a sphere of mass
Physics 2211 ABC Quiz #3 Solutions Spring 2017 I. (16 points) A block of mass m b is suspended vertically on a ideal cord that then passes through a frictionless hole and is attached to a sphere of mass
PHYSICS 221, FALL 2011 EXAM #2 SOLUTIONS WEDNESDAY, NOVEMBER 2, 2011
 PHYSICS 1, FALL 011 EXAM SOLUTIONS WEDNESDAY, NOVEMBER, 011 Note: The unit vectors in the +x, +y, and +z directions of a right-handed Cartesian coordinate system are î, ĵ, and ˆk, respectively. In this
PHYSICS 1, FALL 011 EXAM SOLUTIONS WEDNESDAY, NOVEMBER, 011 Note: The unit vectors in the +x, +y, and +z directions of a right-handed Cartesian coordinate system are î, ĵ, and ˆk, respectively. In this
