Kapitola KL. Klinové plochy
|
|
|
- Kevin Bryan
- 5 years ago
- Views:
Transcription
1 Kpitol KL Klinové plochy
2 Mészárosová, Tereňová Klinová ploch Klinovú plochu definujeme vzhľdom n prvouhlý súrdnicový systém (O, x, y, z). Nech, sú dve čiry, ležice v dvoch nvzájom kolmých rovinách = (xz), = (yz). Nech mjú čiry, priesečník n súrdnicovej osi z = ( ). lochu nzveme klinovou, k ju tvori čiry n, ktoré mjú tieto vlstnosti: leži v rovinách rovnoežných s rovinou, pretínjú čiru, kolmé priemety čir n do roviny sú perspektívne finné s čirou (os finity je os x smer finity je os z), leo je n primk (resp. úsečk) pre konečný počet n jej kolmý priemet do roviny je totožný s osou finity x. z Čiry, nzývme ridice (určujúce) čiry. oznámk: Vzhľdom n vlstnosť perspektívnej finity sú klinové plochy známe ko finné plochy. ' ' = ' x = os finity O oznámk: k nie sú čiry, rovinné, tk ide o všeoecnejší prípd klinových plôch, pozri [MEDEK, V., ZÁMOŽÍK, J. Konštruktívn geometri pre technikov]. y
3 N klinovej ploche sú dve sústvy čir:,,,,... n,...,,,,... n,... Mészárosová, Tereňová Čiry n mjú tieto vlstnosti: leži v rovinách rovnoežných s rovinou, pretínjú čiru, kolmé priemety čir n do roviny sú perspektívne finné s čirou (os finity je os y smer finity je os z), leo je n primk (resp. úsečk) pre konečný počet n jej kolmý priemet do roviny je totožný s osou finity y. z '' B x O B'' = '' os finity = y
4 N klinovej ploche sú dve sústvy čir:,,,,... n,...,,,,... n,... Mészárosová, Tereňová Kždá čir jednej sústvy pretín všetky čiry druhej sústvy. Kždým odom klinovej plochy prechádz jedn čir z kždej sústvy. oznámk: ri zostrojovní druhej sústvy čir n klinovej ploche môžeme tieto čiry zostrojiť odovo pomocou priesečníkov s čirmi z prvej sústvy. z x O y
5 N klinovej ploche sú dve sústvy čir:,,,,... n,...,,,,... n,... Mészárosová, Tereňová Tvr čir v sústve,,,,... n,... s mení v závislosti od tvru určujúcej čiry, pričom kolmé priemety čir n do roviny sú perspektívne finné s čirou. Tvr čir v sústve,,,,... n,... s mení v závislosti od tvru určujúcej čiry, pričom kolmé priemety čir n do roviny sú perspektívne finné s čirou. oznámk: orovnjte vlstnosti sústvy čir,,,,... n,...;,,,,... n,... n trnslčnej ploche n klinovej ploche. N klinovej ploche s tvr čir v sústve,,,,... n,... mení. j v sústve,,,,... n,... s tvr čir klinovej plochy mení. N trnslčnej ploche sú všetky čiry jednej sústvy nvzájom zhodné. ozri kpitolu Trnslčné plochy. z x O y
6 Klinové plochy motiváci vznik Hyperolický proloid má výorné sttické vlstnosti zujímvý tvr. To je dôvodom jeho širokého použiti v stviteľstve. le má jednu veľkú nevýhodu, že jeho vodorovný rez je hyperol. Snh o zchovnie dorých sttických vlstností plochy, ktoré poskytujú dv systémy prol, viedl Bedřich Hcr k nvrhnutiu špeciálneho typu plochy, ktorý dnes nzývme Hcrov ploch. Zovšeoecnenie Hcrových plôch uroil Frntišek Kdeřávek. Tieto plochy s nzývjú klinové plochy. Voľne preložené z ČERNÝ, J., KOČNDRLOVÁ, M. Konstruktivní geometrie. oznámk: orovnnie hyperolického proloidu Hcrovej plochy je n nsledujúcej strne. Bedřich Hcr, 89 96, profesor ČVUT, prcovl v odore stvených hmôt etónových konštrukcií. Frntišek Kdeřávek, 88 96, význmný profesor ČVUT, venovl s klsickej syntetickej geometrii plikáciám geometrie v stviteľstve umení. Orázok: Hcrov ploch [ísk, Medek: Deskriptivní geometrie II] rednosť klinovej plochy je v tom, že v technickej prxi s môže použiť ko ploch strechy, ktorá je ukončená primou rímsou. [MEDEK, V., ZÁMOŽÍK, J. Konštruktívn geometri pre technikov] 6
7 Hyperolický proloid Hcrov ploch z z ' x '' ' '' ' h O ' y E x E F F y Hyperolický proloid je trnslčná ploch. roly, ', '',... sú zhodné proly proly, ', '',... sú zhodné proly. Rovinným rezom zorzeného hyperolického proloidu pôdorysňou je hyperol h. oznámk: ozri kpitolu Trnslčné plochy. Hcrov ploch je klinová ploch pozri nsledujúcu strnu. Rovinným rezom zorzenej Hcrovej plochy pôdorysňou sú dve primky, resp. úsečky. Tereňová 7
8 Hcrov ploch Ridice čiry: prol v nárysni prol v okorysni = {} x = {E, F} z Čiry,,,... n,... : leži v rovinách rovnoežných s nárysňou, pretínjú prolu, ich kolmé priemety do nárysne sú perspektívne finné s prolou, smodružné ody sú E F. To znmená, že všetky čiry,,,... n,..., sú proly. F F E Čiry,,,... n,... : ' leži v rovinách rovnoežných s okorysňou, x pretínjú prolu, ich kolmé priemety do okorysne sú perspektívne finné s prolou. To znmená, že všetky čiry,,,... n,... sú proly, s výnimkou úsečiek E F, ktoré incidujú s odmi E F. E ' y Kždá čir jednej sústvy pretín všetky čiry druhej sústvy. Tereňová 8
9 Orázky: Rôzne typy čsti Hcrových plôch odronejšie pozri v diplomovej práci: VEKOVÁ, J. Klínové plochy Dostupné n: 9
10 V nsledujúcom príklde je zorzená klinová ploch, ktorá je dná polkružnicou v nárysni úsečkou = D v okorysni. z D 6 7 D 7 6 Čiry,,,... n,... : x = os finity os finity = y leži v rovinách rovnoežných s nárysňou, pretínjú úsečku, ich kolmé priemety do nárysne sú perspektívne finné s polkružnicou, smodružné ody sú ody, B. To znmená, že všetky čiry,,,... n,..., sú polelipsy, s výnimkou úsečky D, ktorá inciduje s odom D. Všetky polelipsy n mjú rovnko dlhú hlvnú os s dĺžkou B. Vedľjši polos polelíps s skrcuje. Čím je rovin n polelipsy n ďlej od roviny, tým je dĺžk vedľjšej polosi krtši ž po nulovú dĺžku pre úsečku D. Čiry,,,... n,... : leži v rovinách rovnoežných s okorysňou, pretínjú polkružnicu, ich kolmé priemety do okorysne sú perspektívne finné s úsečkou, smodružný od je od D. To znmená, že všetky čiry,,,... n,... sú úsečky. ôdorysom tejto klinovej plochy je odĺžnik B B. B B Tereňová, Mészárosová Kždá čir jednej sústvy pretín všetky čiry druhej sústvy. 0
11 Klinová ploch je dná polkružnicou, ktorá leží v nárysni úsečkou = D v okorysni. Dnú plochu zorzte v Mongeovej projekcii v kolmej xonometrii. KL z z Tereňová, Mészárosová x S = D B S D y S = B Ridice čiry: polkružnic so stredom S, ležic v nárysni, nd pôdorysňou úsečk D ležic v okorysni x z = {} B S D D x y y Ridice čiry v kolmej xonometrii
12 Klinová ploch je dná polkružnicou, ktorá leží v nárysni úsečkou = D v okorysni. Dnú plochu zorzte v Mongeovej projekcii v kolmej xonometrii. z z Tereňová, Mészárosová x = D S = D B = B S = B D = D y S = B Zorzíme sústvu čir,,,... n,..., ktoré leži v rovinách rovnoežných s nárysňou ich kolmé priemety do nárysne sú s polkružnicou perspektívne finné. x B ostup rysovni v Mongeovej projekcii: ) Zostrojíme polelipsu, ktorá leží v rovine : = { } je vedľjší vrchol polelipsy, jej hlvné vrcholy sú B ody, B. ) Zostrojíme polelipsu, ktorá leží v rovine : = { } je vedľjší vrchol polelipsy, jej hlvné vrcholy sú D D B ody, B. y ) V rovine, ktorá inciduje s odom D, leží úsečk D, ležic n zorzovnej klinovej ploche.
13 Klinová ploch je dná polkružnicou, ktorá leží v nárysni úsečkou = D v okorysni. Dnú plochu zorzte v Mongeovej projekcii v kolmej xonometrii. H z F H = F z Tereňová, Mészárosová = x G S = D E = B S = = D = E = G y x H S = F B G D E y Zorzíme sústvu úsečiek,,,,... n,..., ktoré leži v rovinách rovnoežných s okorysňou ich kolmé priemety do okorysne sú s úsečkou perspektívne finné. ostup rysovni: ) Zostrojíme úsečku = EF, ktorá leží v rovine rovnoežnej s rovinou : = {F} Úsečky sú perspektívne finné so smodružným odom D = E. ) Krivk je súmerná podľ okorysne, preto j zorzovná ploch je súmerná podľ okorysne. Túto vlstnosť využijeme pri konštrukcii čir klinovej plochy. Zostrojíme úsečku = GH, ktorá leží v rovine súmernej s rovinou podľ okorysne. 6) V rovine, ktorá inciduje s odom, leží úsečk. Jej nárysom je od. V rovine, ktorá inciduje s odom B, leží úsečk. Jej nárysom je od. 7) N zostrojenie ďlších čir (úsečiek) klinovej plochy opkujeme postup pre ďlšie roviny n rovnoežné s okorysňou.
14 Klinová ploch je dná polkružnicou, ktorá leží v nárysni úsečkou = D v okorysni. Dnú plochu zorzte v Mongeovej projekcii v kolmej xonometrii. z ostup rysovni v xonometrii: 8) V kolmej xonometrii zorzíme polkružnicu. Jej xononometrickým priemetom je čsť elipsy e. rúžkovou konštrukciou určíme dĺžku vedľjšej polosi elipsy e. x 9) Zorzíme úsečku D. z S = D B Z S = B x B S X D Y D x e D o y y Tereňová, Mészárosová S o
15 Klinová ploch je dná polkružnicou, ktorá leží v nárysni úsečkou = D v okorysni. Dnú plochu zorzte v Mongeovej projekcii v kolmej xonometrii. Zorzíme sústvu úsečiek,,,... n,..., ktoré leži v rovinách rovnoežných s okorysňou ich kolmé priemety do okorysne sú s úsečkou = D perspektívne finné so smodružným odom D. ostup rysovni: 0) Zorzíme úsečku incidujúcu s odom úsečku incidujúcu s odom B. ) Zostrojíme rovinu, ktorá je rovnoežná s rovinou. Úsečk = QR je čir klinovej plochy. ) N zostrojenie ďlších čir (úsečiek) klinovej plochy opkujeme postup pre ďlšie roviny n rovnoežné s okorysňou. z n R B S Q x D p y Tereňová, Mészárosová
16 Klinová ploch je dná polkružnicou, ktorá leží v nárysni úsečkou = D v okorysni. Dnú plochu zorzte v Mongeovej projekcii v kolmej xonometrii. Zorzíme sústvu čir,,,... n,..., ktoré leži v rovinách rovnoežných s nárysňou ich kolmé priemety do nárysne sú s polkružnicou perspektívne finné (os finity je os x smer finity je os z). ostup rysovni: ) Zostrojíme rovinu rovnoežnú s nárysňou. Jej priesečník s úsečkou D oznčíme. xonometrický priemet polelipsy v rovine je polelips určená združenými polomermi S S. Konštrukciu hlvných polosí môžeme uroiť Rytzovou konštrukciou. k máme zostrojenú sústvu úsečiek,,,... n,..., môžeme konštrukciu polelipsy doplniť odmi, ktoré sú prienikom roviny úsečiek,,,... n,... z n ) ostup opkujeme pre rovinu rovnoežnú s nárysňou. V nej leží polelips. R ) Zostrojíme rovinu, ktorá je rovnoežná s nárysňou inciduje s odom D. V rovine leží úsečk D = B, ktorá leží n zorzovnej klinovej ploche. 6) Doplníme orys plochy ko oálku xonometrických priemetov zostrojených čir (úsečiek elíps) klinovej plochy. x S B B S Q D D B p y Tereňová, Mészárosová p p p 6
17 Klinová ploch je dná polkružnicou, ktorá leží v nárysni úsečkou = D v okorysni. Dnú plochu zorzte v Mongeovej projekcii v kolmej xonometrii. z z Tereňová, Mészárosová = KL - zhrnutie x D S = D B S = = = D = D y z n x S = B R B S B S Q B D D B x D D p y y p p p 7
18 oznámk: loch zorzovná v predchádzjúcom príklde je kružnicovo-úsečková klinová ploch. Je to zároveň primková nerozvinuteľná ploch, môžeme ju vytvoriť ko kolmý kružnicový konoid (pozri príkld v kpitole.. Konoidy). rístv domu kultúry Ostrv, Česká repulik,
19 V nsledujúcom príklde je zorzená klinová ploch, ktorá je dná polkružnicou v nárysni prolou v okorysni. rol je dná vrcholom V odmi Q. 7 6 S z V = B Tereňová, Mészárosová x = os finity Čiry,,,... n,... : y = os finity leži v rovinách rovnoežných s okorysňou, pretínjú polkružnicu, ich kolmé priemety do okorysne sú perspektívne finné s prolou, smodružné ody sú ody Q. To znmená, že všetky čiry,,,... n,... sú proly, s výnimkou úsečky, ktorá inciduje s odom. Q Q Čiry,,,... n,... : leži v rovinách rovnoežných s nárysňou, pretínjú prolu, ich kolmé priemety do nárysne sú perspektívne finné s polkružnicou, smodružný od je. To znmená, že všetky čiry,,,... n,..., sú polelipsy, s výnimkou úsečiek Q, ktoré incidujú s odmi Q. Kždá čir jednej sústvy pretín všetky čiry druhej sústvy. 9
20 Klinová ploch je dná krivkmi. Krivk je polkružnic, krivk je prol. Dnú plochu zorzte v Mongeovej projekcii v kvliernej xonometrii. KL S z V = B z V Ridice čiry: polkružnic so stredom S, ležic v nárysni čsť proly nd pôdorysňou, určená odmi, Q vrcholom V, ležic v okorysni = {V} x = {} z x Q y S V = V = B = = B V x B x S = Ridice prvky v xonometrii Q y Q ostup rysovni v Mongeovej projekcii: ) Zorzíme prolu. Tereňová, Mészárosová y oznámk: Konštrukciu proly pozri v prvej čsti skrípt 0
21 Klinová ploch je dná krivkmi. Krivk je polkružnic, krivk je prol. Dnú plochu zorzte v Mongeovej projekcii v kvliernej xonometrii. S B z z V = B = 6 V Zorzíme sústvu čir (polelíps),,,... n,..., ktoré leži v rovinách n rovnoežných s nárysňou. Všetky polelipsy n mjú rovnko dlhú hlvnú os s dĺžkou B. Vedľjši polos polelíps s skrcuje. Čím je rovin n polelipsy n ďlej od roviny, tým je dĺžk vedľjšej polosi krtši ž po nulovú dĺžku pre úsečky Q. = x = Q = = = Q Q y B V =B ostup rysovni v Mongeovej projekcii: ) Zostrojíme polelipsu, ktorá leží v rovine : Bod je vedľjší vrchol polelipsy, jej hlvné vrcholy sú ody, B. = { B} x Tereňová, Mészárosová Q Q y 6 B = ) Zorzovná ploch je súmerná podľ nárysne. Túto vlstnosť využijeme udeme rysovť dvojice polelíps, ;,. Zostrojíme polelipsu, ktorá leží v rovine súmernej s rovinou podľ nárysne. olelipsy, sú zhodné. ) odone zostrojíme polelipsy, v rovinách,. ) V rovinách, 6 incidujúcich s odmi Q leži úsečky, Q.
22 Klinová ploch je dná krivkmi. Krivk je polkružnic, krivk je prol. Dnú plochu zorzte v Mongeovej projekcii v kvliernej xonometrii. S V = B z V z V = = V Zorzíme sústvu čir (prol),,,... n,..., ktoré leži v rovinách rovnoežných s okorysňou. Ich kolmé priemety do okorysne sú s prolou = perspektívne finné. Osou finity je primk y, smodružné ody sú Q. Zorzovná ploch je súmerná podľ roviny, ktorá prechádz odom je rovnoežná s okorysňou. Túto vlstnosť využijeme udeme rysovť dvojice kriviek, ;, ;, 6. x = Q y x V V =B ostup rysovni v Mongeovej projekcii: 6) Zostrojíme prolu, ktorá leží v rovine rovnoežnej s okorysňou. = { V}; V je vrchol proly. Kolmý priemet proly do okorysne je perspektívne finný s prolou so smodružnými odmi, Q. rol je určená vrcholom V odmi, Q. 6 Q Q 6 Q y 7) Zostrojíme prolu, ktorá leží v rovine súmernej s rovinou podľ roviny. 8) N zostrojenie ďlších čir (prol) klinovej plochy opkujeme postup pre ďlšie roviny n rovnoežné s okorysňou. 9) Čir v rovine je úsečk. 0) V rovine, incidujúcej s odom, leží prol, ktorá je zhodná s prolou jej vrchol je v ode.
23 Klinová ploch je dná krivkmi. Krivk je polkružnic, krivk je prol. Dnú plochu zorzte v Mongeovej projekcii v kvliernej xonometrii. z z 6 S V = B V B V V x = Q = Q = Q y V B =B ostup rysovni v Mongeovej projekcii: ) Zorzíme oidve sústvy kriviek pre lepšiu názornosť klinovú plochu vyfríme z jednej strny žltou frou z druhej modrou. x Q Q 6 6 y Tereňová, Mészárosová
24 Klinová ploch je dná krivkmi. Krivk je polkružnic, krivk je prol. Dnú plochu zorzte v Mongeovej projekcii v kvliernej xonometrii. z z ostup rysovni v xonometrii: ) V kvliernej xonometrii, pre ktorú pltí j m = j x = j y = j z, zorzíme ridice krivky,. S V = B V ) Zorzíme prolu, ktorá je zhodná s prolou jej vrchol je v ode. z x j m j m Q y S V = B x = S j m = B V j m j z Q x j x j y Q y Tereňová, Mészárosová y
25 Klinová ploch je dná krivkmi. Krivk je polkružnic, krivk je prol. Dnú plochu zorzte v Mongeovej projekcii v kvliernej xonometrii. Zorzíme sústvu čir (polelíps),,,... n,..., ktoré leži v rovinách rovnoežných s nárysňou ich kolmé priemety do nárysne sú s polkružnicou = perspektívne finné. Hlvné vrcholy elíps leži n prolách. Vedľjšie vrcholy elíps leži v pôdorysni. ostup rysovni v xonometrii: ) Zostrojíme polelipsu, ktorá leží v rovine : Bod je vedľjší vrchol polelipsy, jej hlvné vrcholy sú ody, B. ) Zostrojíme polelipsu, ktorá leží v rovine súmernej s rovinou podľ nárysne. olelipsy, sú zhodné. z 6) odone zostrojíme polelipsy, v rovinách,. 7) V rovinách, 6 leži úsečky, Q. oznámk: Stredy elíps leži n prole S, ktorá je zhodná s prolou leží v rovine. Tereňová, Mészárosová x 6 S S S B V = B Q Q y
26 Klinová ploch je dná krivkmi. Krivk je polkružnic, krivk je prol. Dnú plochu zorzte v Mongeovej projekcii v kvliernej xonometrii. Zorzíme sústvu čir (prol),,,... n,..., ktoré leži v rovinách rovnoežných s okorysňou. Vrcholy prol leži n polkružnici. ostup rysovni v xonometrii: 8) Zostrojíme prolu, ktorá leží v rovine rovnoežnej s okorysňou. rol je určená vrcholom V odmi Q. k máme zostrojenú sústvu polelíps,,,... n,..., môžeme konštrukciu proly doplniť odmi, ktoré sú prienikom roviny polelíps,,,... n,... 9) Zostrojíme prolu, ktorá leží v rovine súmernej s rovinou podľ roviny. 0) N zostrojenie ďlších prol klinovej plochy opkujeme postup pre ďlšie roviny n rovnoežné s okorysňou. ) Čir v rovine je úsečk.. ) Zorzíme orys plochy pre lepšiu názornosť plochu vyfríme z jednej strny žltou frou z druhej modrou. S S V z V = B x 6 Q Q y Q Tereňová, Mészárosová 6
27 Klinová ploch je dná krivkmi. Krivk je polkružnic, krivk je prol. Dnú plochu zorzte v Mongeovej projekcii v kvliernej xonometrii. KL - zhrnutie z z 6 Tereňová, Mészárosová S V = B V B V V z x = Q = = Q = Q y B V =B x S S V V = B Q Q 6 x 6 Q Q y Q 7 6 y 7
28 Grimshw rchitects Frnkfurt Trde Fir Hll Frnkfurt, Nemecko 8
29 Klinové plochy Orázky: ísk, Medek: Deskriptivní geometrie II 9
30 Klinová ploch Orázok: Sínuso-sínusoidná klinová ploch [ísk, Medek: Deskriptivní geometrie II] 0
31 Klinová ploch rác študent: Tomáš Kuric, F STU, školský rok 009/0
32 Klinová ploch Steyn Studio Bosjes Frm Witzenerg District Western pe Juhofrická repulik
33 Steyn Studio Bosjes Frm Witzenerg District Western pe Juhofrická repulik
34 Klinová ploch
35 Klinová ploch
36 Klinová ploch Orázok: Sínuso-sínusoidná klinová ploch VEKOVÁ, J. Klínové plochy Dostupné n: 6
37 Renzo ino Building Workshop, rchitects in collortion with Stntec rchitecture liforni cdemy of Sciences Sn Frncisco, US 7
38 Renzo ino Building Workshop, rchitects in collortion with Stntec rchitecture liforni cdemy of Sciences Sn Frncisco, US 8
39 Klinové plochy Orázky: Rôzne typy čsti klinových plôch odronejšie pozri v diplomovej práci: VEKOVÁ, J. Klínové plochy Dostupné n: 9
40 Klinové plochy Orázky: Rôzne typy čsti klinových plôch odronejšie pozri v diplomovej práci: VEKOVÁ, J. Klínové plochy Dostupné n: 0
41 orovnjme výhody nevýhody prktického využiti trnslčných, primkových klinových plôch v stvenej prxi. Njväčšou výhodou použiti trnslčných plôch je možnosť sériovej výroy jej čstí, leo všetky čiry jednej sústvy sú nvzájom zhodné. Njčstejšou plikáciou sú trnslčné plochy s určujúcou úsečkou v jednej sústve. Toto zjednodušenie umožňuje použiť zložitejšiu (zujímvejšiu) krivku v druhej sústve. Nevýhodou niektorých plôch použitých ko kleny (zstrešenie) je ich ukončenie krivkou. rimkové rozvinuteľné plochy sú jednoznčne njčstejšie používné v prxi to njmä hrnolové vlcové plochy, le j ihlnové kužeľové plochy. Okrem ich jednoduchosti medzi ich výhody ptrí možnosť pokryti rovinným mteriálom (npríkld sklo) leo mteriálom, ktorý s dá ľhko tvrovť (npríkld plech, drevo). rimkové nerozvinuteľné plochy ponúkjú škálu zujímvých tvrov možnosť využiť tvorice primky ko nosné, leo estetické prvky. Ich njväčšou nevýhodou je, že s n ich pokrytie nedá použiť rovinný mteriál. Riešením je rozdelenie plochy n množstvo mlých čstí, ktoré sú rovinné. Njčstejšou proximáciou ýv použitie trojuholníkovej leo štvoruholníkovej siete. Čsto s stretávme s plikácimi, ktoré využívjú len jednotlivé primky leo krivky primkových nerozvinuteľných plôch, npríkld nosné lná mostných konštrukcií. Njčstejšie plikovnou je ploch hyperolického proloidu, ktorá umožňuje využiť sttické vlstnosti prol v zvislých rovinách. Nevýhodou v tomto prípde je, že vodorovný rez hyperolického proloidu je hyperol. rx priniesl požidvku nájsť tkú plochu, ktorá y ol ukončená úsečkou. Túto výhodu poskytujú klinové plochy. odľ typu klinovej plochy môžu yť ukončené úsečkou v jednom, leo v ooch smeroch, ktoré sú n se kolmé. To umožňuje prime npojenie n udovu odĺžnikového pôdorysu. Nevýhodou klinových plôch je menici s tvr čir jednej sústvy. Všetky čiry jednej sústvy sú v kolmom priemete perspektívne finné, le kždá z nich má iný tvr. Minimálny počet plikácií v stveníctve poukzuje n to, že táto nevýhod je pri relizácii rozhodujúc. le stále dokonlejšie mteriály technológie umožňujú relizovť čorz odvážnejšie, zujímvejšie tvry tk možno j klinové plochy udú v udúcnosti inšpiráciou pre rchitektov dizjnérov.
Kapitola S5. Skrutkovica na rotačnej ploche
Kapitola S5 Skrutkovica na rotačnej ploche Nech je rotačná plocha určená osou rotácie o a meridiánom m. Skrutkový pohyb je pohyb zložený z rovnomerného rotačného pohybu okolo osi o a z rovnomerného translačného
Kapitola P2. Rozvinuteľné priamkové plochy
Kapitola P2 Rozvinuteľné priamkové plochy 1 Priamková plocha je rozvinuteľná, ak na nej ležia iba torzálne priamky. Rozvinuteľné priamkové plochy rozdeľujeme na: rovinu, valcové plochy, kužeľové plochy,
Eva Baranová, Kamil Maleček OD STREDOVÉHO PRIEMETU KRUŽNICE KU STREDOVÝM CYKLIDÁM. 1 Priemet kružnice v stredovom premietaní
25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Eva Baranová, Kamil Maleček OD STREDOVÉHO PRIEMETU KRUŽNICE KU STREDOVÝM CYKLIDÁM Abstrakt V prvej časti príspevku odvodzujeme podmienku, kedy je v danom
Teória grafov. RNDr. Milan Stacho, PhD.
Teória grafov RNDr. Milan Stacho, PhD. Literatúra Plesník: Grafové algoritmy, Veda Bratislava 1983 Sedláček: Úvod do teórie grafů, Academia Praha 1981 Bosák: Grafy a ich aplikácie, Alfa Bratislava 1980
3. ročník gymnázia. pre. a 7. ročník gymnázia. s osemročným štúdiom. 2. časť. Zbyněk Kubáček MATEMATIKA
pre 3. ročník gymnázia a 7. ročník gymnázia s osemročným štúdiom. časť MTEMTIK Zbyněk Kubáček 3. ročník gymnázia a 7. ročník gymnázia pre s osemročným štúdiom. časť ISN 978-80-10-089- www.spn-mladeleta.sk
Ukážka testu z prijímacej skúšky pre akad. r. 2006/07 1/7
1/7 Príkld 1. (3 body) Zápis čísl 777 v sedmičkovej číselnej sústve je ) 111 b) 1000 c) 713 d) 160 e) 777 Príkld. (3 body) Ktorá z dvojíc je dvojicou nesúdeliteľných čísel? ) 6 333 b) 15 64 c) 31 31 d)
Maticové algoritmy I maticová algebra operácie nad maticami súčin matíc
Maticové algoritmy I maticová algebra operácie nad maticami súčin matíc priesvitka Maurits Cornelis Escher (898-97) Ascending and Descending, 960, Lithograph priesvitka Matice V mnohých prípadoch dáta
ADM a logika. 4. prednáška. Výroková logika II, logický a sémantický dôsledok, teória a model, korektnosť a úplnosť
ADM a logika 4. prednáška Výroková logika II, logický a sémantický dôsledok, teória a model, korektnosť a úplnosť 1 Odvodzovanie formúl výrokovej logiky, logický dôsledok, syntaktický prístup Logický dôsledok
Univerzita Karlova v Praze Matematicko-fyzikální fakulta. Michal Kesely. Katedra matematické analýzy. Studijní program: Obecná matematika
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Michal Kesely Slavné neřešitelné problémy Katedra matematické analýzy Vedoucí bakalářské práce: RNDr. Dalibor Pražák, Ph.D. Studijní
(UKÁŽKY V JAZYKU TURBO PASCAL) Zoltán Zalabai, SR - Milan Pokorný, SR
Mtemtik jej plikácie inžinierskom zdelání 006 APLIKÁCIA n-rozmerných INEGRÁLOV (UKÁŽKY V JAZYKU URBO PASCAL) Zoltán Zli, SR - Miln Pokorný, SR Astrkt Poítom podporoné yuonie mtemtiky má nezstupitené miesto
SLOVENSKÁ POĽNOHOSPODÁRSKA UNIVERZITA V NITRE TECHNICKÁ FAKULTA APLIKÁCIE INTEGRÁLNEHO POČTU V TECHNICKEJ PRAXI Andrej Štefanka
SLOVENSKÁ POĽNOHOSPODÁRSKA UNIVERZITA V NITRE TECHNICKÁ FAKULTA 11718 APLIKÁCIE INTEGRÁLNEHO POČTU V TECHNICKEJ PRAXI 1 Andrej Štefnk SLOVENSKÁ POĽNOHOSPODÁRSKA UNIVERZITA V NITRE TECHNICKÁ FAKULTA APLIKÁCIE
METRICKÉ ÚLOHY V PRIESTORE
1. ÚVOD METRICKÉ ÚLOHY V PRIESTORE Monika ĎURIKOVIČOVÁ 1 Katedra Matematiky, Strojnícka fakulta STU, Abstrakt: Popisujeme možnosti použitia programového systému Mathematica pri riešení špeciálnych metrických
Odhady veľkosti pokrytí náhodne indukovaných podgrafov n-rozmernej hyperkocky
KATEDRA INFORMATIKY FAKULTA MATEMATIKY FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO Odhady veľkosti pokrytí náhodne indukovaných podgrafov nrozmernej hyperkocky Diplomová práca Bc. Ján Kliman študijný odbor:
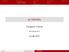= (, ) V λ (1) λ λ ( + + ) P = [ ( ), (1)] ( ) ( ) = ( ) ( ) ( 0 ) ( 0 ) = ( 0 ) ( 0 ) 0 ( 0 ) ( ( 0 )) ( ( 0 )) = ( ( 0 )) ( ( 0 )) ( + ( 0 )) ( + ( 0 )) = ( + ( 0 )) ( ( 0 )) P V V V V V P V P V V V
LOWELL JOURNAL. MUST APOLOGIZE. such communication with the shore as Is m i Boimhle, noewwary and proper for the comfort
- 7 7 Z 8 q ) V x - X > q - < Y Y X V - z - - - - V - V - q \ - q q < -- V - - - x - - V q > x - x q - x q - x - - - 7 -» - - - - 6 q x - > - - x - - - x- - - q q - V - x - - ( Y q Y7 - >»> - x Y - ] [
1 Matice a ich vlastnosti
Pojem sústavy a jej riešenie 1 Matice a ich vlastnosti 11 Sústavy lineárnych rovníc a matice Príklad 11 V množine reálnych čísel riešte sústavu rovníc x - 2y + 4z + t = -6 2x + 3y - z + 2t = 13 2x + 5y
Stavba Lobačevského planimetrie
Stavba Lobačevského planimetrie Riešenie úloh In: Ján Gatial (author); Milan Hejný (author): Stavba Lobačevského planimetrie. (Slovak). Praha: Mladá fronta, 1969. pp. 78 109. Persistent URL: http://dml.cz/dmlcz/403691
GRÉCKA MATEMATIKA II
Pytagoras zo Samu 569 BC - 75 BC GRÉCKA MATEMATIKA II VÝZNAMNÍ STAROVEKÍ GRÉCKI MATEMATICI Mathematics is the theory of symbolic thinking, numerical relations and geometric forms which are not catchable
A L A BA M A L A W R E V IE W
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
Cyclical Surfaces Created by a Conical Helix
Professional paper Accepted 23.11.2007. TATIANA OLEJNÍKOVÁ Cyclical Surfaces Created by a Conical Helix Cyclical Surfaces Created by a Conical Helix ABSTRACT The paper describes cyclical surfaces created
SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE STAVEBNÁ FAKULTA. Polomerovo Moorovské grafy
SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE STAVEBNÁ FAKULTA Polomerovo Moorovské grafy Bakalárska práca SVF-5342-50476 2010 Jaromír Sýs SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE STAVEBNÁ FAKULTA Polomerovo
Exact and high order discretization schemes. Wishart processes and their affine extensions
for Wishart processes and their affine extensions CERMICS, Ecole des Ponts Paris Tech - PRES Université Paris Est Modeling and Managing Financial Risks -2011 Plan 1 Motivation and notations 2 Splitting
VYHLÁSENIE O PARAMETROCH. č SK. Predpoklada é použitie. stave ý h častí ako o kladov a stropov, pozri prílohu, najmä prílohy B 1 - B 8
VYHLÁSENIE O PARAMETROCH č. 0007 SK 1. Jedi eč ý ide tifikač ý k d typu výro ku: i jektáž y systé FIS V 2. )a ýšľa é použitie/použitia: Produkt O eľová kotva pre použitie v et e k upev e iu ťažký h systé
VYHLÁSENIE O PARAMETROCH. č SK. Predpokladané použitie. stave ý h častí ako o kladov a stropov, pozri prílohu, najmä prílohy B 1 - B 3
VYHLÁSENIE O PARAMETROCH č. 0017 SK 1. Jedi eč ý ide tifikač ý kód typu výro ku: fischer skrutka do betónu FBS, FBS A4 a FBS C 2. )a ýšľa é použitie/použitia: Produkt O eľová kotva pre použitie v etó e
Department of Mathematical and Statistical Sciences University of Alberta
MATH 214 (R1) Winter 2008 Intermediate Calculus I Solutions to Problem Set #8 Completion Date: Friday March 14, 2008 Department of Mathematical and Statistical Sciences University of Alberta Question 1.
Lucia Fuchsová Charakteristiky pravděpodobnostních
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Lucia Fuchsová Charakteristiky pravděpodobnostních předpovědí Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské
Use precise language and domain-specific vocabulary to inform about or explain the topic. CCSS.ELA-LITERACY.WHST D
Lesson eight What are characteristics of chemical reactions? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading
Math Exam IV - Fall 2011
Math 233 - Exam IV - Fall 2011 December 15, 2011 - Renato Feres NAME: STUDENT ID NUMBER: General instructions: This exam has 16 questions, each worth the same amount. Check that no pages are missing and
2. Vektorová metóda kinematickej analýzy VMS
2-5596 Mechanika viaaných mechanických systémov (VMS) pre špecialiáciu Aplikovaná mechanika, 4.roč. imný sem. Prednáša: doc.ing.františek Palčák, PhD., ÚAMM 02010 2. Vektorová metóda kinematickej analýy
Obsah. 2 Určenie objemu valčeka Teoretický úvod Postup merania a spracovanie výsledkov... 10
Obsah 1 Chyby merania 1 1.1 áhodné a systematické chyby.................... 1 1.2 Aritmetický priemer a stredná kvadratická chyba......... 1 1.3 Rozdelenie nameraných dát..................... 3 1.4 Limitné
Dotyková rovina a normála k ploche z=f(x,y) s Matlabom
Dotyková rovina a normála k ploche z=f(x,y) s Matlabom Jana Schusterová ABSTRACT: The aim of this article is to explain how determine a tangent plane and a normal of the surface z=f(x,y) using the programming
Use precise language and domain-specific vocabulary to inform about or explain the topic. CCSS.ELA-LITERACY.WHST D
Lesson seven What is a chemical reaction? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading Informational Text,
VYHLÁSENIE O PARAMETROCH. č SK
VYHLÁSENIE O PARAMETROCH č. 0048 SK 1. Jedi eč ý ide tifikač ý k d typu výro ku: rá ová h oždi ka fischer SXR/SXRL 2. )a ýšľa é použitie/použitia: Produkt Plastové kotvy pre použitie v betóne a murive
DO NOT BEGIN THIS TEST UNTIL INSTRUCTED TO START
Math 265 Student name: KEY Final Exam Fall 23 Instructor & Section: This test is closed book and closed notes. A (graphing) calculator is allowed for this test but cannot also be a communication device
7.1 Sampling Error The Need for Sampling Distributions
7.1 Sampling Error The Need for Sampling Distributions Tom Lewis Fall Term 2009 Tom Lewis () 7.1 Sampling Error The Need for Sampling Distributions Fall Term 2009 1 / 5 Outline 1 Tom Lewis () 7.1 Sampling
Name: SOLUTIONS Date: 11/9/2017. M20550 Calculus III Tutorial Worksheet 8
Name: SOLUTIONS Date: /9/7 M55 alculus III Tutorial Worksheet 8. ompute R da where R is the region bounded by x + xy + y 8 using the change of variables given by x u + v and y v. Solution: We know R is
T h e C S E T I P r o j e c t
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
Parabola v aplikačných príkladoch a ich aplety v programe GeoGebra
Parabola v aplikačných príkladoch a ich aplet v programe GeoGebra Parabola in Applications and its Applets in Software Geogebra Abstract In this paper, we focus on simple application eamples. We choose
Matematika 17. a 18. storočia
Matematika 17. a 18. storočia René Descartes Narodený : 31 Marec 1596 v La Haye (teraz Descartes),Touraine, France Zomrel : 11 Feb 1650 v Stockholm, Sweden Riešenie kvadratických rovníc podľa Descarta
chapter 1 vector geometry solutions V Consider the parallelogram shown alongside. Which of the following statements are true?
chapter vector geometry solutions V. Exercise A. For the shape shown, find a single vector which is equal to a)!!! " AB + BC AC b)! AD!!! " + DB AB c)! AC + CD AD d)! BC + CD!!! " + DA BA e) CD!!! " "
Úvod. Otázka povahy zmien v matematike bola prvý krát systematicky diskutovaná v druhej polovici 19.
Úvod Otázka povahy zmien v matematike bola prvý krát systematicky diskutovaná v druhej polovici 19. storočia v súvislosti s objavom neeuklidovských geometrií. Táto diskusia je dokladom zásadnej zmeny v
Sect Least Common Denominator
4 Sect.3 - Least Common Denominator Concept #1 Writing Equivalent Rational Expressions Two fractions are equivalent if they are equal. In other words, they are equivalent if they both reduce to the same
UNIT 1: SIMILARITY, CONGRUENCE, AND PROOFS. 1) Figure A'B'C'D'F' is a dilation of figure ABCDF by a scale factor of 1. 2 centered at ( 4, 1).
1) Figure A'B'C'D'F' is a dilation of figure ABCDF by a scale factor of 1. 2 centered at ( 4, 1). The dilation is Which statement is true? A. B. C. D. AB B' C' A' B' BC AB BC A' B' B' C' AB BC A' B' D'
Le classeur à tampons
Le classeur à tampons P a s à pa s Le matériel 1 gr a n d cla s s e u r 3 pa pi e r s co o r d o n n é s. P o u r le m o d è l e pr é s e n t é P a p i e r ble u D ai s y D s, pa pi e r bor d e a u x,
Matematická analýza II.
V. Diferenciálny počet (prezentácia k prednáške MANb/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prednáška 8 6. marca 2018 It has apparently not yet been observed, that...
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY HADAMARDOVE MATICE A ICH APLIKÁCIE V OPTIMÁLNOM DIZAJNE BAKALÁRSKA PRÁCA 2012 Samuel ROSA UNIVERZITA KOMENSKÉHO V BRATISLAVE
NAVIGÁCIA MOBILNÉHO ROBOTA VIZUÁLNYM SYSTÉMOM
Slovenská technická univerzita v Bratislave Fakulta elektrotechniky a informatiky Ing. Peter Pásztó Autoreferát dizertačnej práce NAVIGÁCIA MOBILNÉHO ROBOTA VIZUÁLNYM SYSTÉMOM Na získanie akademického
11. prednáška ( ) Greedy algoritmy. Programovanie, algoritmy, zložitosť (Ústav informatiky, PF UPJŠ v Košiciach)
11. prednáška (15. 5. 2012) Greedy algoritmy 1 Obsah Greedy stratégia, greedy algoritmus Minimálna kostra grafu Úloha o zastávkach autobusu Problém plnenia batoha Jednoduchý rozvrhový problém 2 Motivácia
1-2 Measuring and Constructing Segments
1-2 Measuring and Constructing Segments Warm Up Lesson Presentation Lesson Quiz Objectives Use length and midpoint of a segment. Construct midpoints and congruent segments. Vocabulary coordinate midpoint
e x2 dxdy, e x2 da, e x2 x 3 dx = e
STS26-4 Calculus II: The fourth exam Dec 15, 214 Please show all your work! Answers without supporting work will be not given credit. Write answers in spaces provided. You have 1 hour and 2minutes to complete
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
MENGER'S THEOREM AND MATROIDS
MENGER'S THEOREM AND MATROIDS R. A. BRUALDI 1. Introduction Let G be a finite directed graph with X, Y disjoint subsets of the nodes of G. Menger's theorem [6] asserts that the maximum cardinal number
Chapter 6 Summary 6.1. Using the Hypotenuse-Leg (HL) Congruence Theorem. Example
Chapter Summary Key Terms corresponding parts of congruent triangles are congruent (CPCTC) (.2) vertex angle of an isosceles triangle (.3) inverse (.4) contrapositive (.4) direct proof (.4) indirect proof
ENVIRONMENTÁLNE FAKTORY V HODNOTENÍ EFEKTÍVNOSTI V POĽNOHOSPODÁRSTVE ENVIRONMENTAL FACTORS IN EFFICIENCY ASSESMENT IN AGRICULTURE.
ENVIRONMENTÁLNE FAKTORY V HODNOTENÍ EFEKTÍVNOSTI V POĽNOHOSPODÁRSTVE ENVIRONMENTAL FACTORS IN EFFICIENCY ASSESMENT IN AGRICULTURE Peter FANDEL The paper focuses on the analysis of environmental factors
Differential Equation (DE): An equation relating an unknown function and one or more of its derivatives.
Lexicon Differential Equation (DE): An equation relating an unknown function and one or more of its derivatives. Ordinary Differential Equation (ODE): A differential equation that contains only ordinary
1. Town A is 48 km from town B and 32 km from town C as shown in the diagram. A 48km
1. Town is 48 km from town and 32 km from town as shown in the diagram. 32km 48km Given that town is 56 km from town, find the size of angle (Total 4 marks) Â to the nearest degree. 2. The diagram shows
dy dx dx = 7 1 x dx dy = 7 1 x dx e u du = 1 C = 0
1. = 6x = 6x = 6 x = 6 x x 2 y = 6 2 + C = 3x2 + C General solution: y = 3x 2 + C 3. = 7 x = 7 1 x = 7 1 x General solution: y = 7 ln x + C. = e.2x = e.2x = e.2x (u =.2x, du =.2) y = e u 1.2 du = 1 e u
::::l<r/ L- 1-1>(=-ft\ii--r(~1J~:::: Fo. l. AG -=(0,.2,L}> M - &-c ==- < ) I) ~..-.::.1 ( \ I 0. /:rf!:,-t- f1c =- <I _,, -2...
Math 3298 Exam 1 NAME: SCORE: l. Given three points A(I, l, 1), B(l,;2, 3), C(2, - l, 2). (a) Find vectors AD, AC, nc. (b) Find AB+ DC, AB - AC, and 2AD. -->,,. /:rf!:,-t- f1c =-
Day 66 Bellringer. 1. Construct a perpendicular bisector to the given lines. Page 1
Day 66 Bellringer 1. Construct a perpendicular bisector to the given lines. a) b) HighSchoolMathTeachers@2018 Page 1 Day 66 Bellringer c) d) HighSchoolMathTeachers@2018 Page 2 Day 66 Bellringer 2. Identify
ENTROPIA. Claude Elwood Shannon ( ), USA A Mathematical Theory of Communication, 1948 LOGARITMUS
LOGARITMUS ENTROPIA Claude Elwood Shao (96-00), USA A Mathematcal Theory of Commucato, 948 7. storoče Naer, Brggs, orovae číselých ostuostí: artmetcká ostuosť 3 0 3 4 5 6 geometrcká ostuosť /8 /4 / 4 8
Chapter 2 Segment Measurement and Coordinate Graphing
Geometry Concepts Chapter 2 Segment Measurement and Coordinate Graphing 2.2 Find length segments (1.3) 2.3 Compare lengths of segments (1.3) 2.3 Find midpoints of segments (1.7) 2.5 Calculate coordinates
h : sh +i F J a n W i m +i F D eh, 1 ; 5 i A cl m i n i sh» si N «q a : 1? ek ser P t r \. e a & im a n alaa p ( M Scanned by CamScanner
m m i s t r * j i ega>x I Bi 5 n ì r s w «s m I L nk r n A F o n n l 5 o 5 i n l D eh 1 ; 5 i A cl m i n i sh» si N «q a : 1? { D v i H R o s c q \ l o o m ( t 9 8 6) im a n alaa p ( M n h k Em l A ma
Asymptotic of Enumerative Invariants in CP 2
Peking Mathematical Journal https://doi.org/.7/s4543-8-4-4 ORIGINAL ARTICLE Asymptotic of Enumerative Invariants in CP Gang Tian Dongyi Wei Received: 8 March 8 / Revised: 3 July 8 / Accepted: 5 July 8
História nekonečne malej veličiny PROJEKTOVÁ PRÁCA. Martin Čulen. Alex Fleško. Konzultant: Vladimír Repáš
História nekonečne malej veličiny PROJEKTOVÁ PRÁCA Martin Čulen Alex Fleško Konzultant: Vladimír Repáš Škola pre mimoriadne nadané deti a Gymnázium, Skalická 1, Bratislava BRATISLAVA 2013 1. Obsah 1. Obsah
Outlines of Quantum Physics
Duality S. Eq Hydrogen Outlines of 1 Wave-Particle Duality 2 The Schrödinger Equation 3 The Hydrogen Atom Schrödinger Eq. of the Hydrogen Atom Noninteracting Particles and Separation of Variables The One-Particle
Modely, metódy a algoritmy pre analýzu longitudinálnych dát
Vedecká rada Fakulty matematiky, fyziky a informatiky Univerzity Komenského v Bratislave Mgr Gejza Wimmer Autoreferát dizertačnej práce Modely, metódy a algoritmy pre analýzu longitudinálnych dát pre získanie
VYHLÁSENIE O PARAMETROCH. č SK. Predpokladané použitie. stave ý h častí ako o kladov a stropov, pozri prílohu, najmä prílohy B 1 - B 4
VYHLÁSENIE O PARAMETROCH č. 0009 SK 1. Jedi eč ý ide tifikač ý k d typu výro ku: o eľová kotva fis her FAZ II 2. )a ýšľa é použitie/použitia: Produkt O eľová kotva pre použitie v betóne k upev e iu ťažký
{n 2 } of {n) such that n = rii+n is an {n-l}, the Vf-i^2 is a {r-l} in {r}, for T=T' + T" + 2. Hence, we have.
i93o.] GENERALIZED DIVISION ALGEBRAS 535 {n 2 } of {n) such that n = rii+n 2 + 2 is an {n-l}, the Vf-i^2 is a {r-l} in {r}, for T=T' + T" + 2. Hence, we have or N - k + 2 = 1, iv = * 1, which was to be
Computing Orthonormal Sets in 2D, 3D, and 4D
Computing Orthonormal Sets in 2D, 3D, and 4D David Eberly, Geometric Tools, Redmond WA 98052 https://www.geometrictools.com/ This work is licensed under the Creative Commons Attribution 4.0 International
: i; ii: i:i: I. : q t:iig l3 [i E. i;issii:i::: r p. ! s:r;e;:e;!f. as Iet5;Fgi. i EiiF;:'+3EI. : :*gsc:li-ii. ; si;;ei:i:g; .
, / - H f ) - $ H A - --" G \/ - - f \f ff P) G T - ), - ) -..R '' (.) f- w (, AA - Нотная библиотека \ S R.- R \?! -! h )! - X* - Y - J. ** " { B e B Rk * f [He 1e [Y!!-- e *J! *Jee.1!.,1g -!. -! >. j.,
The causes of misconceptions of basic geometric figures in primary school
The causes of misconceptions of basic geometric figures in primary school Príčiny miskoncepcií základných geometrických útvarov u žiakov na prvom stupni základných škôl Ján GUNČAGA; Štefan TKAČIK Abstract
SEIZMICKÁ ODOLNOSŤ ŽELEZOBETÓNOVÝCH BUDOV PODĽA
SEIZMICKÁ ODOLNOSŤ ŽELEZOBETÓNOVÝCH BUDOV PODĽA NOVÝCH NORMOVÝCH PREDPISOV SEISMIC RESISTANCE OF REINFORCED CONCRETE BUILDING ACCORDING TO NEW STANDARD REGULATIONS Vladimír Krištofovič, Martina Lošonská
Ing. Tomasz Kanik. doc. RNDr. Štefan Peško, CSc.
Ing. Tomasz Kanik Školiteľ: doc. RNDr. Štefan Peško, CSc. Pracovisko: Študijný program: KMMOA, FRI, ŽU 9.2.9 Aplikovaná informatika 1 identifikácia problémovej skupiny pacientov, zlepšenie kvality rozhodovacích
APPLICATION OF THE EXPERIMENTAL TESTS OF THE SHEAR STRENGTH OF SOILS IN THE GEOTECHNICAL DESIGN. 1. Introduction
ROCZNIKI INŻYNIERII BUDOWLANEJ ZESZYT 14/014 Komisja Inżynierii Budowlanej Oddział Polskiej Akademii Nauk w Katowicach APPLICATION OF THE EXPERIMENTAL TESTS OF THE SHEAR STRENGTH OF SOILS IN THE GEOTECHNICAL
PSEUDOINVERZNÁ MATICA
PSEUDOINVERZNÁ MATICA Jozef Fecenko, Michal Páleš Abstrakt Cieľom príspevku je podať základnú informácie o pseudoinverznej matici k danej matici. Ukázať, že bázický rozklad matice na súčin matíc je skeletným
BACHELOR'S DEGREE PROGRAMME (BDP) Term-End Examination. June, 2018 ELECTIVE COURSE : MATHEMATICS MTE-02 : LINEAR ALGEBRA
No. of Printed Pages : 8 1MTE-021 BACHELOR'S DEGREE PROGRAMME (BDP) Term-End Examination 046OB June, 2018 ELECTIVE COURSE : MATHEMATICS MTE-02 : LINEAR ALGEBRA Time : 2 hours Maximum Marks : 50 (Weightage
UNIT 1: SIMILARITY, CONGRUENCE, AND PROOFS. 1) Figure A'B'C'D'F' is a dilation of figure ABCDF by a scale factor of 1. 2 centered at ( 4, 1).
EOCT Practice Items 1) Figure A'B'C'D'F' is a dilation of figure ABCDF by a scale factor of 1. 2 centered at ( 4, 1). The dilation is Which statement is true? A. B. C. D. AB B' C' A' B' BC AB BC A' B'
Welcome to the Public Meeting Red Bluff Road from Kirby Boulevard to State Highway 146 Harris County, Texas CSJ No.: December 15, 2016
Welcome to the Public Meeting Red Bluff Road from Kirby Boulevard to State Highway 146 Harris County, Texas CSJ No.: 0912-72-340 December 15, 2016 No formal presentation will be made. Seabrook Intermediate
Years. Marketing without a plan is like navigating a maze; the solution is unclear.
F Q 2018 E Mk l lk z; l l Mk El M C C 1995 O Y O S P R j lk q D C Dl Off P W H S P W Sl M Y Pl Cl El M Cl FIRST QUARTER 2018 E El M & D I C/O Jff P RGD S C D M Sl 57 G S Alx ON K0C 1A0 C Tl: 6134821159
Properties of the stress tensor
Appendix C Properties of the stress tensor Some of the basic properties of the stress tensor and traction vector are reviewed in the following. C.1 The traction vector Let us assume that the state of stress
STN EN ZAŤAŽENIE KONŠTRUKCIÍ
STN EN 1991-1-4 ZAŤAŽENIE KONŠTRUKCIÍ ČASŤ 1-4: ZAŤAŽENIE VETROM Prednášajúci: Ing. Richard Hlinka, PhD. Tento príspevok vznikol vďaka podpore v rámci OP Vzdelávanie pre projekt Podpora kvality vzdelávania
MASARYKOVA UNIVERZITA ÚSTAV MATEMATIKY A STATISTIKY
MASARYKOVA UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA ÚSTAV MATEMATIKY A STATISTIKY Diplomová práce BRNO 2014 MICHAL KOVÁČIK MASARYKOVA UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA ÚSTAV MATEMATIKY A STATISTIKY Metody testování
Conditional Statement: Statements in if-then form are called.
Monday 9/21 2.2 and 2.4 Wednesday 9/23 2.5 and 2.6 Conditional and Algebraic Proofs Algebraic Properties and Geometric Proofs Unit 2 Angles and Proofs Packet pages 1-3 Textbook Pg 85 (14, 17, 20, 25, 27,
Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava. Multiparty Communication Complexity (Master thesis)
Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Multiparty Communication Complexity (Master thesis) František Ďuriš Study programme: 921 Informatics Supervisor:
P a g e 5 1 of R e p o r t P B 4 / 0 9
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY DIPLOMOVÁ PRÁCA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY DIPLOMOVÁ PRÁCA ANALÝZA A MODELOVANIE VPLYVU EKONOMICKÝCH A SOCIÁLNYCH PROCESOV NA VÝVOJ VYBRANÝCH DEMOGRAFICKÝCH UKAZOVATEĽOV
Name: Date: 12/06/2018. M20550 Calculus III Tutorial Worksheet 11
1. ompute the surface integral M255 alculus III Tutorial Worksheet 11 x + y + z) d, where is a surface given by ru, v) u + v, u v, 1 + 2u + v and u 2, v 1. olution: First, we know x + y + z) d [ ] u +
Vyučovanie analytickej geometrie s podporou informačných a komunikačných technológií
Vyučovanie analytickej geometrie s podporou informačných a komunikačných technológií Teaching Analytic Geometry using Information and Communication Technologies Abstract The paper proposes an innovative
Review Material for Exam #3. 1. Radio waves for Rocket 101 are emitted at a frequency of MHz. Calculate the wavelength, in m, of this radiation.
Review Material for xam #3 1. Radio waves for Rocket 101 are emitted at a frequency of 100.9 Mz. alculate the wavelength, in m, of this radiation. 8 c.9979 x 10 m/s.971 m 6 1 ν 100.9 x 10 s λν = c; λ =
by Fdruary,2015 It may. kindly be eosured that a copy of deposit slip is supflied to this for All the Principals/HMs,
.DBS(B) (10)/2014 3, /l 2' Oi.e he Depy Direr Hiher din Bilpr Diri Bilpr (). Tele phne /x 01978 2228 emil ddhebilpredinil.m '. Ded Bilpr 174001,rr he,. ' i i, lj by drry,201 All he rinipl/hm, Di Bilp"i)
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY DETEKOVANIE KOMUNÍT V SOCIÁLNYCH SIEŤACH Patricia SVITKOVÁ
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY DETEKOVANIE KOMUNÍT V SOCIÁLNYCH SIEŤACH BAKALÁRSKA PRÁCA 2017 Patricia SVITKOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
x + ye z2 + ze y2, y + xe z2 + ze x2, z and where T is the
1.(8pts) Find F ds where F = x + ye z + ze y, y + xe z + ze x, z and where T is the T surface in the pictures. (The two pictures are two views of the same surface.) The boundary of T is the unit circle
Los Angeles Unified School District Periodic Assessments. Geometry. Assessment 2 ASSESSMENT CODE LA08_G_T2_TST_31241
Los Angeles Unified School District Periodic Assessments Assessment 2 2008 2009 Los Angeles Unified School District Periodic Assessments LA08_G_T2_TST_31241 ASSESSMENT ODE 1100209 The test items contained
JUST THE MATHS UNIT NUMBER PARTIAL DIFFERENTIATION 1 (Partial derivatives of the first order) A.J.Hobson
JUST THE MATHS UNIT NUMBER 14.1 PARTIAL DIFFERENTIATION 1 (Partial derivatives of the first order) by A.J.Hobson 14.1.1 Functions of several variables 14.1.2 The definition of a partial derivative 14.1.3
Page 1 MATHEMATICS
PREPARED BY :S.MANIKANDAN., VICE PRINCIPAL., JOTHI VIDHYALAYA MHSS., ELAMPILLAI., SALEM., 94798 Page + MATHEMATICS PREPARED BY :S.MANIKANDAN., VICE PRINCIPAL., JOTHI VIDHYALAYA MHSS., ELAMPILLAI., SALEM.,
Z A V Á D Ě N Í ČSN EN NAVRHOVÁNÍ B E T O N O V Ý C H
Z A V Á D Ě N Í ČSN EN 1992-1-1 NAVRHOVÁNÍ B E T O N O V Ý C H K O N S T R U K C Í DO PRAXE PR E T L A Č E N I E LOKÁLNE PODOPRETÝCH DOSIEK INTRODUCTION OF ČSN E N 1992-1-1 DESIGN OF CONCRETE S T R U C
CONGRUENCE AND SIMILARITY
CONGRUENCE ND SIMILRITY 1.1CONGRUENT FIGURES The figures that have the same size and the same shape, i.e. one shape fits exactly onto other is called Congruent figures. CONGRUENT TRINGLES: 1. Two triangles
Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava THEILOVA REGRESIA
Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava THEILOVA REGRESIA Róbert Tóth Bratislava 2013 Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava THEILOVA
VICTORIA AVE. Chip pawa- Gra ss Isl and Pool. Ice Dam Niagara Falls WTP and Intake. Chippawa. Cree
656 g 477 Y EL IZ B H Y GRN ILN 476 476 B E w R N OOM R MONROE R EE NI G NIGR FLL l 9 E R R E IN EK w l l d Riv RE Nv Ic m g Fll P d It E N ip pw- G Il d Pool Riv NIE MLEO R PK u t o-i pp w Po w l 477