PARAMETRIC EQUATIONS, POLAR COORDINATES, AND VECTOR FUNCTIONS
|
|
|
- Isabel Fitzgerald
- 5 years ago
- Views:
Transcription
1 PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS. Parameric Equaions Preliminar Quesions. escribe he shae of he curve cos ; sin. For all, C. cos / C. sin / 9.cos C sin / 9 9; herefore he curve is on he circle C 9. Also,eachoinonhecircle C 9 can be reresened in he form. cos ;sin / for some value of. Weconcludehahecurve cos, sin is he circle of radius cenered a he origin.. How does C cos ; 5 C sin differ from he curve in he revious quesion? In his case we have. / C. 5/. cos / C. sin / 9.cos C sin / 9 9 Therefore, he given equaions aramerize he circle of radius cenered a he oin.; 5/.. Wha is he maimum heigh of a aricle whose ah has arameric equaions 9,? The aricle s heigh is.tofindhemaimumheighwesehederivaiveequalozeroandsolve: The maimum heigh is.0/ 0. d d d d. / 0 or 0. Can he arameric curve.; sin / be reresened as a grah f./?whaabou.sin ;/? In he arameric curve.; sin / we have and sin, herefore, sin. Thais,hecurvecanbe reresened as a grah of a funcion. In he arameric curve.sin ;/ we have sin,, herefore sin. This equaion does no define as a funcion of,hereforehearamericcurve.sin ;/ canno be reresened as a grah of a funcion f./. 5. Mach he derivaives wih a verbal descriion: (a) d (b) d d d (i) Sloe of he angen line o he curve (ii) Verical rae of change wih resec o ime (iii) Horizonal rae of change wih resec o ime (a) The derivaive d d ishehorizonalraeofchangewihresecoime. (b) The derivaive d d ishevericalraeofchangewihresecoime. (c) The derivaive d d ishesloeofheangenlineohecurve. Hence, (a) $ (iii), (b) $ (ii), (c) $ (i) (c) d d
2 8 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS Eercises. Find he coordinaes a imes 0,,ofaariclefollowingheah C, 9. Subsiuing 0,, and ino C, 9 gives he coordinaes of he aricle a hese imes resecivel. Tha is,. 0/ C 0 ; ).; 9/. / C 9; 9 ).9; /. / C 65; 9 9 ).65; 9/:. Find he coordinaes a 0; ; of a aricle moving along he ah c./.cos ; sin /. Seing 0,, and in c./.cos ; sin / we obain he following coordinaes of he aricle: 0W.cos 0; sin 0/.; 0/ W.cos ; sin /.0; / W.cos ; sin /.; 0/. Show ha he ah raced b he bulle in Eamle is a arabola b eliminaing he arameer. The ah raced b he bulle is given b he following arameric equaions: 80; 00 :9 We eliminae he arameer. Since 80, wehave 80. Subsiuing ino he equaion for we obain: 00 : :9 5 : The equaion 5 :9 600 isheequaionofaarabola.. Use he able of values o skech he arameric curve../;.//,indicainghedirecionofmoion We markhegivenoinsonhe-lane and connec he oins corresonding o successive values of in he direcion of increasing. Wegehefollowingrajecor(hereareohercorrecanswers): = 6 = = = = = 0 5. Grah he arameric curves. Include arrows indicaing he direcion of moion. (a).; /, << (b).sin ;sin /, 0 (c).e ;e /, << (d). ; /, (a) For he rajecor c./.; /, << we have. Alsohewocoordinaesendo and as!and! resecivel. The grah is shown ne: =
3 SECTION. Parameric Equaions 9 (b) For he curve c./.sin ;sin /, 0, wehave.sin is increasing for 0, decreasing for and increasing again for. Henceheariclemovesfromc.0/.0; 0/ o c. /.; /, henmovesbacko c. /. ; / and hen reurns o c./.0; 0/.Weobainhefollowingrajecor: π = (,) π = (,) = 0 0< = π (, ) = π (, ) < These hree ars of he rajecor are shown ogeher in he ne figure: π = (,) = 0 = π = π (, ) (c) For he rajecor c./.e ;e /, <<, wehave. Howeversince rajecor is he ar of he line, 0<. lim! e 0 and lim! e,he (d) For he rajecor c./. ; /,, wehaveagain. Sincehefuncion is increasing he aricle moves in one direcion saring a.. / ;. / /. ; / and ending a. ; /.; /. Therajecorisshownne: = (,) = (, ) 6. Give wo differen aramerizaions of he line hrough.; / wih sloe. The equaion of he line hrough.; / wih sloe is. / or 7. Onearamerizaionis obained b choosing he coordinae as he arameer. Tha is,. Hence 7 and we ge, 7, <<.Anoheraramerizaionisgivenb, 7, <<. In Eercises 7, eress in he form f./b eliminaing he arameer. 7. C, We eliminae he arameer. Since C, wehave. Subsiuingino we obain. / )
4 50 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS 8., From,wehave.Subsiuingin we obain 9., an. C e /. / ) ; 0: Relacing b in he equaion for we obain an. C e /. 0., C From we ge. Subsiuing ino C we obain C. / C C ; 0: Since we mus have afuncionof,weshouldrobablchooseeiherheosiiveornegaiveroo.. e, 6e. C, We eliminae he arameer. Since e,wehave ln or ln.subsiuingin 6e we ge 6e 6e. ln / 6e ln 6e ln 6 ) 6 ; >0: From C,wege or. We now subsiue in o obain ). / ; :. ln, Since ln we have e.subsiuingin we obain e.. cos, an We use he rigonomeric ideni sin cos o wrie We noweress in erms of : an sin cos cos : cos an ) ; 0: Since we mus have afuncionof,weshouldrobablchooseeiherheosiiveornegaiveroo. In Eercises 5 8, grah he curve and draw an arrow secifing he direcion corresonding o moion. 5., Le c./../;.//. ; /.Thenc. /../;.// so he curve is smmeric wih resec o he -ais. Also, he funcion is increasing.hencehereisonlonedirecionofmoiononhecurve.thecorresondingfuncion is he arabola./ 8.Weobainhefollowingrajecor: = 0 6. C, C
5 SECTION. Parameric Equaions 5 We find he funcion b eliminaing he arameer. Since C we have, hence C. / or C. Also, since C and C are increasing funcions, he direcion of moion is he direcion of increasing. We obain he following curve: 6 = 0 = (6, 5) (, ) , sin We find he funcion b eliminaing. Since,wehave. Subsiuing sin. We obain he following curve: ino sin we ge ( π,0) (π,0) 8., From we have =.Hence, =.Sincehefuncions and are increasing, here is onl one direcion of moion, which is he direcion of increasing. Noicehaforc./. ; / we have c. /. ; /../;.//.Hencehecurveissmmericwihresecohe ais. We obain he following curve: 9. Mach he aramerizaions (a) (d) below wih heir los in Figure, and draw an arrow indicaing he direcion of moion π (I) (II) FIGURE (III) (IV) (a) c./.sin ; / (b) c./. 9; 8 / (c) c./. ; 9/ (d) c./. C ; 5 / (a) In he curve c./.sin ; /he -coordinae is varing beween and so his curve corresonds o lo IV. As increases, he -coordinae is decreasing so he direcion of moion is downward.
6 5 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS π π (IV) c./.sin ; / (b) The curve c./. 9; 8 / inersecs he -ais where 8 0; or ; 0, and. These are he oins. ; 0/ and. 9; 0/.The-inerces are obained where 9; or : The -inerces are.0; / and.0; /.As increases from o 0, decreases, and as increases from 0 o, increases. We obain he following rajecor: (c) The curve c./. ; 9/ inersecs he -ais where 0, or. The-inerce is.0; 8/. The -inerces are obained where 9 0 or. Theseareheoins. ; 0/ and.; 0/.Seing we ge 9. / 9 8: As increases he coordinae decreases and we obain he following rajecor: 0 5 (III) (d) The curve c./. C ; 5 / is a sraigh line, since eliminaing in C and subsiuing in 5 gives 5 C which is he equaion of a line. As increases, he coordinae C increases and he -coordinae 5 decreases. We obain he following rajecor: 5 5 (I)
7 SECTION. Parameric Equaions 5 0. Aariclefollowsherajecor./ C ;./ 0 wih in seconds and disance in cenimeers. (a) Wha is he aricle s maimum heigh? (b) When does he aricle hi he ground and how far from he origin does i land? (a) To find he maimum heigh./,wesehederivaiveof./ equal o zero and solve: d d d d.0 / 0 0 ) 0: The maimum heigh is.0/ cm. (b) The objec his he ground when is heigh is zero. Tha is, when./ 0. Solvingfor we ge 0.0 / 0 ) 0; 0: 0 is he iniial ime, so he soluion is 0.Ahaime,heobjec s coordinae is.0/ 0 C 0 00.Thus, when i his he ground, he objec is 00 cm awa from he origin.. Find an inerval of -values such ha c./.cos ;sin / races he lower half of he uni circle. For, wehavec./. ; 0/. As increases from o, he-coordinae of c./ increases from o, and he -coordinae decreases from 0 o (a =) andhenreurnso0.thus,for in Œ;, heequaionraceshe lower ar of he circle.. Find an inerval of -values such ha c./. C ; 5/ aramerizes he segmen from.0; 7/ o.7; 7/. Noe ha C 0 a =, and C 7 a. Also, 5 akes on he values of 7 and 7 a = and.thus,heinervalisœ =;. In Eercises 8, find arameric equaions for he given curve.. 9 This is a line hrough P.0; 9/ wih sloe m. Usinghearamericreresenaionofaline,asgivenin Eamle, we obain c./.; 9 / C 9 Leing ields he arameric reresenaion c./.; 8 /. We define he arameer. Then, 5 C 5 C, giving us he aramerizaion c./ 5 C The curve C 9 is a circle of radius 7 cenered a he origin. We use he arameric reresenaion of a circle o obain he reresenaion c./.7 cos ;7sin /. 7.. C 9/ C. / 9 This is a circle of radius 7 cenered a. 9; /. Usinghearamericreresenaionofacirclewegec./. 9 C 7 cos ; C 7 sin /. 8. C 5 This is an ellise cenered a he origin wih a 5 and b. Usinghearamericreresenaionofanellisewe ge c./.5 cos ;sin / for. 9. Line of sloe 8 hrough. ; 9/ Using he arameric reresenaion of a line given in Equaion, we ge he aramerizaion c./. C ;9C 8/. 0. Line hrough.; 5/ erendicular o The line erendicular o has sloe m. We use he arameric reresenaion of a line given in Equaion oobainhearamerizaionc./. C ;5 /. ;.
8 5 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS. Line hrough.; / and. 5; / We use he wo-oin aramerizaion of a line wih P.a; b/.; / and Q.c; d/. 5; /. Thenc./. 8; C / for <<.. Line hrough ; 6 and 7 6 ; 5 We use he wo-oin aramerizaion of a line wih P.a; b/ ; 6 and Q.c; d/ 7 6 ; 5. Then for <<.. Segmen joining.; / and.; / c./ ; 6 C We use he wo-oin aramerizaion of a line wih P.a; b/.; / and Q.c; d/.; /. Thenc./. C ; C /;sincewewanonlhesegmenjoininghewooins,wewan0.. Segmen joining. ; 0/ and.0; / We use he wo-oin aramerizaion of a line wih P.a; b/. ; 0/ and Q.c; d/.0; /. Thenc./. C ; /; sincewewanonlhesegmenjoininghewooins,wewan0. 5. Circle of radius wih cener.; 9/ Subsiuing.a; b/.; 9/ and R in he arameric equaion of he circle we ge c./. C cos ;9C sin /. 6. Ellise of Eercise 8, wih is cener ranslaed o.7; / Since he cener is ranslaed b.7; /, soiseveroin.thusheoriginalaramerizaionbecomesc./.7 C 5 cos ; C sin / for. 7.,ranslaedsohaheminimumoccursa. ; 8/ We ma aramerize b.; / for <<. Theminimumof occurs a.0; 0/, sohedesired curve is ranslaed b. ; 8/ from.thusaaramerizaionofhedesiredcurveisc./. C ; 8 C /. 8. cos ranslaed so ha a maimum occurs a.; 5/ Amaimumvalueof cos occurs a 0. Hence,hecurve cos. /, or C cos. / has a maimum a he oin.; 5/. Wele, hen C and C cos. Weobainhereresenaionc./. C ; C cos /. In Eercises 9, find a aramerizaion c./ of he curve saisfing he given condiion. 9., c.0/.; / Le./ C a and./. C a/. Wewan.0/, huswemususea. Ourlineis c./../;.//. C ;. C / /. C ; C /. 0., c./.; / Le./ C a; since./ we have C a so ha a. Then. / 7, so ha he line is c./. ; 7/ for <<.., c.0/.; 9/ Le./ C a and./. C a/.wewan.0/, huswemususea. Ourcurveis c./../;.//. C ;. C / /. C ; C 6 C 9/.. C, c.0/.; / This is a circle of radius cenered a he origin, so we are looking for a aramerizaion of ha circle ha sars a a differen oin. Thus insead of he sandard aramerizaion. cos ;sin /, 0 mus corresond o some oher angle!. We choose he aramerizaion. cos. C!/;sin. C!// and mus deermine he value of!. Now, Since.0/ ; so cos.0 C!/ cos! and! cos or 5.0/ ; we have sin.0 C!/ sin! and! sin or Comaring hese resuls we see ha we mus have! sohahearamerizaionis c./ cos C ; sin C
9 SECTION. Parameric Equaions 55. escribe c./.sec ;an / for 0 < inheform f./.secifhedomainof. The funcion sec has eriod and an has eriod. Thegrahsofhesefuncionsinheinerval, areshownbelow: sec an sec ) sec an ) an sin cos cos cos sec Hence he grah of he curve is he herbola. Thefuncion sec is an even funcion while an is odd. Also has eriod and has eriod.ifollowshaheinervals <, < < and < <race he curve eacl once. The corresonding curve is shown ne: = = = (, 0) (, 0) = 0 = + = + c./.sec ;an /. Find a aramerizaion of he righ branch ( >0)ofheherbola a b using he funcions cosh and sinh.how can ou aramerize he branch < 0? We show firs ha cosh, sinh aramerizes he herbola when a b : hen.cosh /.sinh / : using he ideni cosh sinh. Generalizehisaramerizaionogeaaramerizaionforhegeneralherbola. a /. b / : a cosh ; b sinh : We mus of course check ha his aramerizaion indeed aramerizes he curve, i.e. ha a cosh and b sin saisf he equaion. a /. b / : a cosh b sinh.cosh /.sinh / : a b a b The lef branch of he herbola is he reflecion of he righ branch around he line 0, soiclearlhashearamerizaion a cosh ; b sinh : 5. The grahs of./ and./ as funcions of are shown in Figure (A). Which of (I) (III) is he lo of c./../;.//? Elain. () () (A) (I) FIGURE (II) (III)
10 56 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS As seen in Figure (A), he -coordinae is an increasing funcion of,while./ is firs increasing and hen decreasing. In Figure I, and are boh increasing or boh decreasing (deending on he direcion on he curve). In Figure II, does no mainain one endenc, raher, i is decreasing and increasing for cerain values of. Theloc./../;.// is lo III. 6. Which grah, (I) or (II), is he grah of./ and which is he grah of./ for he arameric curve in Figure (A)? (A) (I) FIGURE (II) As indicaed b Figure (A), he -coordinae is decreasing and hen increasing, so lo I is he grah of. Figure (A) also shows ha he -coordinae is increasing, decreasing and hen increasing, so lo II is he grah for. 7. Skech c./. ; / following he ses in Eamle 7. We noe ha./ is odd and./ is even, hence c. /.. /;. //../;.//.I follows ha c. / is he reflecion of c./ across -ais. Tha is, c. / and c./ are smmeric wih resec o he -ais; hus, i suffices o grah he curve for 0. For 0, wehavec.0/.0; 0/ and he -coordinae./ ends o as!.to analze he -coordinae, we grah./ for 0: 8 6 We see ha./ < 0 and decreasing for 0<<=,./ < 0 and increasing for = <<and./ > 0 and increasing for >.Also./ ends o as!.therefore,saringaheorigin,hecurvefirsdirecsohelefofhe-ais, hen a = i urnsoherigh,alwaskeeinganuwarddirecion.thearofheahfor 0 is obained b reflecing across he -ais. We also use he oins c.0/.0; 0/, c./. ; /, c./.0; / o obain he following grah for c./: = (0, ) = = = (, ) = 0 = = 0 = Grah of c./ for 0. Grahof c./ for all. 8. Skech c./. ; 9 / for 0. The grahs of./ and./ 9 for 0 are shown in he following figures: /./ 9
11 SECTION. Parameric Equaions 57 The curve sars a c. /.; 7/. For <<0,./ is decreasing and./ is increasing, so he grah urns o he lef and uwards o c.0/.0; 9/. Thenfor0<<,./ is decreasing and so is./,hencehegrahurnsohelefanddownwards owards c./. ; 5/. For <<0,./ is increasing and./ is decreasing, hence he grah urns o he righ and downwards, ending a c.0/.60; 9/. Theinerceareheoinswhere. / 0 or 9 0, hais 0; ;. Thesearehe oins c.0/.0; 9/, c./.0; 7/, c./. ; 0/, c. /.; 0/.Theseroeriesleadohefollowingah: = 0 (0, 9) =, (, 5) (, 0) =, (, 0) = = (0, 7) = (, 7) In Eercises 9 5, use Eq. (7) o find d=d a he given oin. 9.. ; /, B Eq. (7) we have Subsiuing we ge 50.. C 9; 7 9/, We find d d : 5..s s; s /, s Using Eq. (7) we ge Subsiuing s we obain d d 0./ 0./. 0 /. / 0 d d ˇ ˇ. / 6 : d.7 9/0 d. C 9/ 0 7 ) d ˇ 7 d ˇ : d d 0.s/ 0.s/.s 0 /.s s/ 0 s d d s ˇ s ˇs s s s. /. / : 5..sin ; cos /, 6 Using Eq. (7) we ge d d 0./ sin 0./ cos Subsiuing 6 wege d d sin cos ˇ sin ˇ=6 cos
12 58 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS In Eercises 5 56, find an equaion f./for he arameric curve and comue d=d in wo was: using Eq. (7) and b differeniaing f./. 5. c./. C ; 9/ Since C,wehave. Subsiuing in 9 we have 9 9 C iffereniaing 9 C 5. c./ ; d gives d 9 d. We now find using Eq. (7): d d d 0./. 9/0 0./. C / 0 9 Since we have. Subsiuingin ields./ : We differeniae : Now, we find d using Eq. (7). Thus, d d d 0./ 0./ d d 0 0 : Since,henhis is he same as. 55. s, s 6 C s We find as a funcion of : We now differeniae C.Thisgives s 6 C s s C s C : d d : Alernaivel, we can use Eq. (7) o obain he following derivaive: d d 0.s/ s 6 0.s/ C s 0 s 0 6s5 s s s s 6 : Hence, since s, 56. cos, cos C sin d d : To find as a funcion of,wefirsuseherigonomericidenisin cos o wrie cos C cos : We subsiue cos o obain C.iffereniainghisfuncionields Alernaivel, we can comue d using Eq. (7). Tha is, d Hence, since cos, d d 0./ 0./ cos C sin 0.cos / 0 d : d d : d sin C sin cos sin cos :
13 SECTION. Parameric Equaions Find he oins on he curve c./. ; 6/ where he angen line has sloe. We solve d d 6 6 or 6 8 6, or 6 0, sohesloeis a 0; 6 and he oins are.0; 0/ and.96; 80/ 58. Find he equaion of he angen line o he ccloid generaed b a circle of radius a. The ccloid generaed b a circle of radius can be aramerized b c./. sin ; cos / Then we comue d ˇ sin ˇ d ˇ= cos ˇ= sohahesloeofheangenlineis and he equaion of he angen line is cos sin or C 8 In Eercises 59 6, le c./. 9; 8/ (see Figure ) FIGURE Plo of c./. 9; 8/. 59. raw an arrow indicaing he direcion of moion, and deermine he inerval of -values corresonding o he orion of he curve in each of he four quadrans. We lo he funcions./ 9 and./ 8: We noe carefull where each of hese grahs are osiive or negaive, increasing or decreasing. In aricular,./ is decreasing for <0,increasingfor>0,osiiveforjj >,andnegaiveforjj <.Likewise,./ is decreasing for <,increasingfor >,osiivefor>8or <0,andnegaivefor0<<8.Wenowdrawarrowsonheahfollowinghedecreasing/increasing behavior of he coordinaes as indicaed above. We obain: 60 = 0 ( 9,0) 0 0 = (0, 5) 0 = (0,) 0 0 = (7, 6) = 8 (55,0) 0 60
14 60 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS This lo also shows ha: The grah is in he firs quadran for < or >8. The grah is in he second quadran for <<0. The grah is in he hird quadran for 0<<. The grah is in he fourh quadran for << Find he equaion of he angen line a. Using he formula for he sloe m of he angen line we have: m d ˇ 8 0 d ˇ 9 ˇ 0 ˇ 8 j j 0: Since he sloe is zero, he angen line is horizonal. The -coordinae corresonding o is 8 6.Hencehe equaion of he angen line is Find he oins where he angen has sloe. The sloe of he angen a is d d The oin where he angen has sloe corresonds o he value of ha saisfies d d ) ) 8: We subsiue 8 in./ 9 and./ 8 o obain he following oin:.8/ / Find he oins where he angen is horizonal or verical. In Eercise 6 we found ha he sloe of he angen a is d d ).55; 0/ The angen is horizonal where is sloe is zero. We se he sloe equal o zero and solve for. Thisgives The corresonding oin is 0 ) :../;.//. 9; 8 /.7; 6/: The angen is verical where i has infinie sloe; ha is, a 0. Thecorresondingoinis..0/;.0//.0 9; 0 8 0/. 9; 0/: 6. Le A and B be he oins where he ra of angle inersecs he wo concenric circles of radii r < R cenered a he origin (Figure 5). Le P be he oin of inersecion of he horizonal line hrough A and he verical line hrough B. Eresshe coordinaes of P as a funcion of and describe he curve raced b P for 0. B A r P R FIGURE 5
15 SECTION. Parameric Equaions 6 We use he arameric reresenaion of a circle o deermine he coordinaes of he oins A and B. Thais, A.r cos ;r sin /; B.R cos ;R sin / The coordinaes of P are herefore P.R cos ;r sin / In order o idenif he curve raced b P,wenoicehahe and coordinaes of P saisf R cos and r C cos C sin : R r sin. Hence The equaion R C r is heequaionofellise.hence,hecoordinaesofp,.r cos ;r sin / describe an ellise for A0-fladderslidesdownawallasisboomB is ulled awa from he wall (Figure 6). Using he angle as arameer, find he arameric equaions for he ah followed b (a) he o of he ladder A, (b)heboomofheladderb, and(c)heoinp locaed ffrom he o of he ladder. Show ha P describes an ellise. A P = (, ) 6 FIGURE 6 B (a) We define he -coordinae ssem as shown in he figure: A 0 0 B As he ladder slides down he wall, he -coordinae of A is alwas zero and he -coordinae is 0 sin. Thearameric equaions for he ah followed b A are hus 0; 0 sin ; is beween and 0. The ah described b A is he segmen Œ0; 0 on he -ais. 0 0
16 6 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS (b) As he ladder slides down he wall, he -coordinae of B is alwas zero and he -coordinae is 0 cos. Thearameric equaions for he ah followed b B are herefore 0 cos ; 0; is beween and 0. The ah is he segmen Œ0; 0 on he -ais. 0 0 (c) The and coordinaes of P are cos, 6 sin. The ah followed b P has he following aramerizaion: c./. cos ;6sin /; is beween and 0. P(, ) 6 0 As shown in Eamle, he corresonding ah is a ar of an ellise. Since is varing beween he ellise in he firs quadran. and 0, weobainhearof 6 0 In Eercises 65 68, refer o he Bézier curve defined b Eqs. (8) and (9). 65. Show ha he Bézier curve wih conrol oins has aramerizaion P 0.; /; P.; /; P.6; 5/; P.7; / c./. C 6 C ;C 5 9 / Verif ha he sloe a 0 is equal o he sloe of he segmen P 0 P. For he given Bézier curve we have a 0, a, a 6, a 7, andb 0, b, b 5, b. Subsiuing hese values in Eq. (8) (9) and simlifing gives./. / C 9. / C 8. /C 7 C C 9. C / C 8 8 C 7 C C 9 8 C 9 C 8 8 C 7 C C 6 C
17 SECTION. Parameric Equaions 6./. / C 6. / C 5. /C. C / C 6. C / C 5 5 C C C 6 7 C 6 C 5 5 C C 5 9 Then c./. C 6 C ;C 5 9 /; 0 : We find he sloe a 0. Usingheformulaforsloeofheangenlinewege d d. C 5 9 / C 6 C / 0 6 C 6 9 ) d ˇ d ˇ0 6 : The sloe of he segmen P 0 P ishesloeofhelinedeerminedbheoinsp 0.; / and P.; /. Thais, 8. We see ha he sloe of he angen line a 0 is equal o he sloe of he segmen P 0P, as eeced. 66. Find an equaion of he angen line o he Bézier curve in Eercise 65 a. so ha a, and We have Thus he angen line is d d./0 0 7./ 0 6 C 6 9 d ˇ d ˇ= C 6 9 ˇ ˇ= ; or 7 C Find and lo he Bézier curve c./ assing hrough he conrol oins P 0.; /; P.0; /; P.5; /; P.; / gives Seing a 0, a 0, a 5, a, andb 0, b, b, b ino Eq. (8) (9) and simlifing./. / C 0 C 5. /C. C / C 5 5 C 9 C 6./. / C 6. / C. / C. C / C 6. C / C C 6 C 6 C 6 C 6 C C C 6 We obain he following equaion The grah of he Bézier curve is shown in he following figure: c./. 9 C 6 ;C 6 /; 0 :
18 6 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS 68. Show ha a cubic Bézier curve is angen o he segmen P P a P. The equaions of he cubic Bézier curve are./ a 0. / C a. / C a. / C a./ b 0. / C b. / C b. / C b We use he formula for he sloe of he angen line o find he sloe of he angen line a P.Weobain d d 0./ 0./ b 0. / C b.. /. //C b.. / / C b a 0. / C a.. /. //C a.. / / C a () The sloe of he angen line a P is obained b seing in (). Tha is, m 0 C 0 b C b 0 C 0 a C a b b a a () We comue he sloe of he segmen P P for P.a ;b / and P.a ;b /.Wege m b b a a Since he wo sloes are equal, we conclude ha he angen line o he curve a he oin P is he segmen P P. 69. Abullefiredfromagunfollowsherajecor a; b 6.a; b > 0/ Show ha he bulle leaves he gun a an angle an b a and lands a a disance ab=6 from he origin. The heigh of he bulle equals he value of he -coordinae. When he bulle leaves he gun,./.b 6/ 0. Thesoluionsohisequaionare 0 and 6 b, wih 0 corresonding o he momen he bulle leaves he gun. We find he sloe m of he angen line a 0: d d 0./ b 0./ a ) m b a ˇ b ˇ0 a I followshaan b a or an b a. The bulle lands a 6 b. We find he disance of he bulle from he origin a his ime, b subsiuing 6 b in./ a. Thisgives b ab Plo c./. ; C 8/ for.findheoinswhereheangenlineishorizonalorverical. The grah of c./. ; C 8/, is shown in he following figure: = 0 (0, 8) =.5 (.,.8) = ( 5, ) =.5 (.,.8) =, (5, ) =.5 0 (.9, ) =.5 (.9, ) We find he sloe of he angen line a : d d 0./ 0./. 0 C 8/. / 0 () The angen line is horizonal where d 0. Tha is, d 0 ). 6/ 0 ) 0; 6; 6:
19 SECTION. Parameric Equaions 65 We findhecorresondingoinsbsubsiuinghesevaluesof in c./.weobain: c.0/.0; 8/; c. 6/. :9; /; c. 6/.:9; /: The angen line is verical where he sloe in () is infinie, ha is, where 0 or :5. Wefindheoins b seing in c./.wege c. :; :8/; c.:; :8/: 7. Plo he asroid cos, sin and find he equaion of he angen line a. The grah of he asroid cos, sin is shown in he following figure: π = (0, ) = π (, 0) = 0 (, 0) π = (0, ) The sloe of he angen line a is m d ˇ.sin / 0 ˇ d ˇ=.cos / 0 sin cos ˇ ˇ= cos sin ˇ an ˇ. sin / ˇ= cos ˇ= ˇ= We findheoinofangenc:! ; cos ; sin 8 ; 8 The equaion of he angen line a is, hus, 8 ) C 8 7. Find he equaion of he angen line a oheccloidgeneraedbheunicirclewiharamericequaion(5). We find he equaion of he angen line a oheccloid sin, cos.wefirsfindhederiva- ive d d : The sloe of he angen line a isherefore: We findheoinofangenc: The equaion of he angen line is, hus,! d d 0./. cos /0 0./. sin / 0 sin cos m d ˇ sin d ˇ= cos ; sin ; cos ;!! )! C 7. Find he oins wih horizonal angen line on he ccloid wih arameric equaion (5).
20 66 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS The arameric equaions of he ccloid are sin ; cos We find he sloe of he angen line a : The angen line is horizonal where i has sloe zero. Tha is, d. cos /0 d. sin / 0 sin cos d d sin cos 0 ) sin 0 cos ).k /; k 0; ; ; : : : We find he coordinaes of he oins wih horizonal angen line, b subsiuing.k / in./ and./.thisgives The required oins are.k / sin.k /.k / cos..k //. /..k /; /; k 0; ; ; : :: 7. Proer of he Ccloid Prove ha he angen line a a oin P on he ccloid alwas asses hrough he o oin on he rolling circle as indicaed in Figure 7. Assume he generaing circle of he ccloid has radius. Tangen line Ccloid FIGURE 7 The definiion of he ccloid is such ha a ime, heoofhecirclehascoordinaesq.; / (since a ime he circle has roaed eacl once, and is circumference is ). Le L be he line hrough P and Q. ToshowhaL is angen o he ccloid a P i suffices o show ha he sloe of L equals he sloe of he angen a P.Recallhaheccloidis aramerized b c./. sin ; cos /.ThenhesloeofL is and he sloe of he angen line is and he wo are equal. 0./. cos /0 0./. sin / 0 sin cos. cos /. sin / C cos sin sin. C cos / cos sin. C cos / sin C cos sin 75. A curae ccloid (Figure 8) is he curve raced b a oin a a disance h from he cener of a circle of radius R rolling along he -ais where h<r.showhahiscurvehasaramericequaions R h sin, R h cos. h R π π FIGURE 8 Curae ccloid. Le P be a oin a a disance h from he cener C of he circle. Assume ha a 0, helineofcp is assing hrough he origin. When he circle rolls a disance R along he -ais, he lengh of he arc c SQ (see figure) is also R and he angle SCQ has radian measure.wecomuehecoordinaes and of P. C S h P A C R 0 R Q
21 SECTION. Parameric Equaions 67 We obain he following aramerizaion: R PA R h sin. / R h sin R C AC R C h cos. / R h cos R h sin ; R h cos : 76. Use a comuer algebra ssem o elore wha haens when h >Rin he arameric equaions of Eercise 75. escribe he resul. Look firs a he arameric equaions hsin, hcos.thesedescribeacircleofradiush.seeforinsance he grahs below obained for h and h c() = ( h*sin(), h*cos()) h =, 5 Adding R o he coordinae o obain he arameric equaions h sin, R h cos, ieldsacirclewihiscener moved u b R unis: c() = ( h*sin(), R h*cos()) R =, 5 h = 5 Now, we add R o he coordinae o obain he given arameric equaion; he curve becomes a sring. The figure below shows he grahs obained for R and various values of h. We see he inner loo formed for h > R Show ha he line of sloe hrough. ; 0/ inersecs he uni circle in he oin wih coordinaes C ; C Conclude ha hese equaions aramerize he uni circle wih he oin. ; 0/ ecluded (Figure 9). Show furher ha =. C /. 0
22 68 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS (, ) Sloe (, 0) FIGURE 9 Uni circle. The equaion of he line of sloe hrough. ; 0/ is. C /. Theequaionofheunicircleis C. Hence, he line inersecs he uni circle a he oins.; / ha saisf he equaions: Subsiuing from equaion () ino equaion () and solving for we obain This gives. C / () C () C. C / C C C. C / C C. / 0 ;. C /. /. C /. C / C So and. The soluion corresonds o he oin. ; 0/. Weareineresedinhesecondoinof C inersecion ha is varing as varies. Hence he aroriae soluion is C We findhe-coordinae b subsiuing in equaion (). This gives!. C / C C C C C C We concludehahelineandheunicircleinersec,besidesa. ; 0/, aheoinwihhefollowingcoordinaes: C ; () C Since hese oins deermine all he oins on he uni circle ece for. ; 0/ and no oher oins, he equaions in () aramerize he uni circle wih he oin. ; 0/ ecluded. We show ha. Using () we have C C C C C C C C C C C : 78. The folium of escares is he curve wih equaion C a, wherea 0 is a consan (Figure 0). (a) Show ha he line inersecs he folium a he origin and a one oher oin P for all ; 0.Eresshecoordinaes of P in erms of o obain a aramerizaion of he folium. Indicae he direcion of he aramerizaion on he grah. (b) escribe he inerval of -values aramerizing he ars of he curve in quadrans I, II, and IV. Noe ha is a oin of disconinui of he aramerizaion. (c) Calculae d=d as a funcion of and find he oins wih horizonal or verical angen. II I III IV FIGURE 0 Folium C a.
23 SECTION. Parameric Equaions 69 (a) We find he oins where he line ( ; 0) andhefoliuminersec,bsolvinghefollowingequaions: Subsiuing from () in () and solving for we ge () C a () C a. C / a 0.. C / a/ 0 ) 0; Subsiuing in () we find he corresonding -coordinaes. Tha is, 0 0; a C a C a C Weconcludehaheline, 0; inersecs he folium in a unique oin P besides he origin. The coordinaes of P are: a C ; a ; 0; C The coordinaes of P deermine a aramerizaion for he folium. We add he origin so 0 mus be included in he inerval of. We ge! a c./ C ; a C ; To indicae he direcion on he curve (for a>0), we firs consider he following limis: lim./ lim!./! lim./ lim./ 0 lim./ lim./ 0!!!! lim./ lim! C./! C lim./ 0 lim./ 0!0!0 These limis deermine he direcions of he wo ars of he folium in he second and fourh quadran. The loo in he firs quadran, corresonds o he values 0 <, andiisdirecedfromc./. a ; a / o c./. a ; a / where and are wo chosen values in he inerval 0 <.Thefollowinggrahshowshedirecedfolium: < < 0 < < 0 < = + = 0 = = = (b) The limis comued in ar (a) indicae ha he ars of he curve in he second and fourh quadrans corresond o he values <<0and << resecivel. The loo in he firs quadran corresonds o he remaining inerval 0 <. (c) We find he derivaive d, using he Formula for he Sloe of he Tangen Line. We ge d a 0 d d 0./ 0./ C 0 a C Horizonal angen occurs when d 0. Tha is, d 6a.C / a.c / a.c / a.c / 6a a a 6a. /. / 0 ). / 0; 0 ) 0; :
24 70 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS The corresonding oins are: c.0/..0/;.0//.0; 0/ c ; a C ; a! C Verical angen line occurs when d d isinfinie.thais, The corresonding oin is 0 ) c ; 0 a C ; A C a ; a a; a : 79. Use he resuls of Eercise 78 o show ha he asmoe of he folium is he line C a. Hin: Show ha lim. C /! a. We mus show ha as!or! he grah of he folium is geing arbiraril close o he line C a, and he derivaive d isaroachinghesloe of he line. d In Eercise 78 we showed ha!when!. / and! when!. C /.Wefirsshowhahegrahis aroaching he line C a as!or!,bshowingha lim C lim C a.!! C For./ a a,./ C C, a >0,calculaedinEercise78,weobainusingL Hôial srule: We now show ha d d obain lim. C / lim! lim. C / lim! C!! C a C a C lim! a C a C lim! C a C 6a a C 6a a 6a a 6a a a d 6a a isaroaching as! and as! C. Weuse d a 6a comued in Eercise 78 o d lim! d lim 6a a! a 6a 9a 9a d lim! C d lim 6a a! C a 6a 9a 9a We conclude ha he line C a is an asmoe of he folium as!and as!. 80. Find a aramerizaion of nc C nc a n n,wherea and n are consans. Following he mehod in Eercise 78, we firs find he coordinaes of he oin P where he curve and he line inersec. We solve he following equaions: nc C nc a n n Subsiuing in he second equaion and solving for ields nc C nc nc a n n n. C nc / nc a n n 0 n.. C nc / a n / 0 ) 0; a n C nc We assume ha (so C nc 0) andobainonesoluionbesidesheorigin.thecorresonding coordinaes are Hence, he oins aramerizaion: a n anc C nc C nc a n anc,,, areeaclheoinsonhecurve.weobainhefollowing C nc C nc a n anc ; ; : C nc C nc
25 SECTION. Parameric Equaions 7 8. Second erivaive for a Paramerized Curve Given a aramerized curve c./../;.//,showha Use his o rove he formula d d d 0./ 00./ 0./ 00./ d 0./ d d 0./ 00./ 0./ 00./ 0./ Bheformulaforhesloeofheangenlinewehave d d 0./ 0./ iffereniaing wih resec o,usinghequoienrule,gives d d d 0./ d d d 0 0./ 00./ 0./ 00././ 0./ B he Chain Rule we have d d d d d d d d d d Subsiuing ino he above equaion and using d d d=d 0 gives./ d d d d 0./ 00./ 0./ 00./ 0./ 0./ 0./ 00./ 0./ 00./ 0./ 8. The second derivaive of is d =d. VerifhaEq.()aliedoc./.; / ields d =d.infac, an aramerizaion ma be used. Check ha c./. ; 6 / and c./.an ;an / also ield d =d. so ha indeed For he aramerizaion c./.; /,wehave For c./. ; 6 /,wehave so ha again Finall, for c./.an ;an /, and 0./ ; 00./ 0; 0./ ; 00./ 0./ 00./ 0./ 00./ 0 0./ 0./ ; 00./ 6; 0./ 6 5 ; 00./ 0 0./ 00./ 0./ 00./ 0./ / / sec ; 00./ an sec ; 0./ an sec ; 00./ 6 sec sec 0./ 00./ 0./ 00./ 0./ sec.6sec sec / an sec.an sec / sec 6 6 sec6 sec sec an sec 6 sec6 sec 6 6 sec6 sec.. C sec /// sec 6
26 7 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS In Eercises 8 86, use Eq. () o find d =d. 8. C, 7, Using Eq. () we ge We find he firs and second derivaives of./ and./: 8. s C s, s, s 0./ C ) 0./ C 6 00./ 6 C ) 00./ 6 C 0./ ) 0./ 8 00./ ) 00./ d ˇ d 0./ 00./ 0./ 00./ ˇ ˇ 0./ ˇ Since 0.s/ s C s, we have 0./ 0.Hence,Eq.()cannobeusedocomue d a s. d C 9,, We comue he firs and second derivaives of./ and./: 0./ 8 ) 0. / 8 00./ 0 ) 00. / 0 0./ ) 0. / 00./ 0 ) 00. / 0 Using Eq. () we ge d ˇ d 0. / 00. / 0. / 00. / ˇ 0. / 8 0. / cos, sin, Using Eq. () we ge We find he firs and second derivaives of./ and./: d ˇ d ˇ 0./ sin ) 0 00./ cos ) 00 0./ cos ) 0 00./ sin ) Use Eq. () o find he -inervals on which c./. ; / is concave u. The curve is concave u where d d > 0.Thus, We comue he firs and second derivaives: 0./ 00./ 0./ 00./ 0./ >0 () 0./ ; 00./ 0./ ; 00./ 6
27 SECTION. Parameric Equaions 7 Subsiuing in () and solving for gives.6 8/ 8 6 C 8 8 Since 6 C 8>0for all,hequoienisosiiveif8 >0.Weconcludehahecurveisconcaveufor> Use Eq. () o find he -inervals on which c./. ; / is concave u. The curve is concave u where d d > 0.Thais, We comue he firs and second derivaives: Subsiuing in () and solving for gives 0./ 00./ 0./ 00./ 0./ >0 () 0./ ; 00./ 0./ ; 00./.8 8/ 8 6 C 8 8 C This is clearl osiive for >0.For<0,wewanC > 0,whichmeans >, so < (b aking he recirocal of boh sides), so <. Thus, we see ha our curve is concave u for < and for > Area Under a Paramerized Curve Le c./../;.//, where./ > 0 and 0./ > 0 (Figure ). Show ha he area A under c./ for 0 is Z A./ 0./ d 0 Hin: Because i is increasing, he funcion./ has an inverse g./ and c./ is he grah of.g.//. Al he change-of-variables formula o A R. /. 0 /.g.//d. c() ( 0 ) FIGURE ( ) Le 0. 0 / and. /.Wearegivenha 0./ > 0,hence./ is an increasing funcion of,soihas.g.//d.recallha is a funcion of and g./, soheheigh an inverse funcion g./. TheareaA is given b R 0 a an oin is given b.g.//.wefindhenewlimisofinegraion.since 0. 0 / and. /,helimisfor are 0 and,resecivel.alsosince 0./ d d, we have d 0./d.Performinghissubsiuiongives Since g./,wehavea Z 0 Z A.g.//d 0./ 0./ d. Z 0.g.// 0./ d: 90. Calculae he area under over Œ0; using Eq. () wih he aramerizaions. ; 6 / and. ; /. The area A under on Œ0; is given b he inegral Z A./ 0./ d 0 where. 0 / 0 and. /.Wefirsusehearamerizaion. ; 6 /.Wehave./,./ 6.Hence, 0. 0 / 0 ) 0 0
28 7 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS. / ) Also 0./.SubsiuinghesevaluesinEq.()weobain Z Z A 6 d 8 d ˇˇˇˇ 0 9 Using he aramerizaion./,./,wehave 0./.Wefind 0 and : 0. 0 / 0 ) 0 0. / ) or : Equaion () is valid if 0./ > 0, haisif>0.hencewechooseheosiivevalue,. WenowuseEq.()oobain Z Z A d 5 d ˇˇˇˇ 0 6 Boh answers agree, as eeced. 9. Wha does Eq. () sa if c./.; f.//? In he aramerizaion./,./ f./we have 0./, 0. 0 /,. /.HenceEq.()becomes A Z 0 Z../ 0 /./ d f./d. 0 / We see ha in his aramerizaion Eq. () is he familiar formula for he area under he grah of a osiive funcion. 9. Skech he grah of c./.ln ; / for and comue he area under he grah using Eq. (). We use he following grahs of./ ln and./ for :./ ln./ We see ha for <<,./ is osiive and increasing and./ is osiive and decreasing. Also c./.ln ; /.0; / and c./.ln ; /.ln ; 0/. Addiionalinformaionisobainedfromhederivaive d. /0 d.ln / 0 = ; ielding d ˇ d ˇ and d ˇ : d ˇ We obain he following grah: (0, ) = = (ln, 0)
29 SECTION. Parameric Equaions 75 WenowuseEq.()ocomueheareaA under he grah. We have./ ln, 0./,./, 0,.Hence, Z Z A./ 0./ d. / Z 0 d d ln ˇ. ln /. ln / ln 0:86 9. Galileo ried unsuccessfull o find he area under a ccloid. Around 60, Gilles de Roberval roved ha he area under one arch of he ccloid c./.r R sin ;R R cos / generaed b a circle of radius R is equal o hree imes he area of he circle (Figure ). Verif Roberval s resul using Eq. (). R πr πr FIGURE The area of one arch of he ccloid equals hree imes he area of he generaing circle. This reduces o Z 0 Z.R R cos /.R R sin / 0 d R. cos / d R : 0 Furher Insighs and Challenges 9. Prove he following generalizaion of Eercise 9: For all >0,heareaofheccloidalsecorOP C is equal o hree imes he area of he circular segmen cu b he chord PC in Figure. P R P R O C = (R, 0) O C = (R, 0) (A) Ccloidal secor OPC FIGURE (B) Circular segmen cu b he chord PC ro a erendicular from oin P o he -ais and label he oin of inersecion T,anddenoeb he cener of he circle. Then he area of he ccloidal secor is equal o he area of OP T lus he area of PTC.Thelaerisarianglewih heigh./ R R cos and base R.R R sin / R sin, soisareais R sin. cos /.TheareaofOP T,using Eq. (), is Z Z Z.u/ 0.u/ du.r R cos u/.ru R sin u/ 0 du R. cos u/ du R sin C sin cos so ha he oal area of he ccloidal secor is R sin C sin cos C R sin. cos / R R sin R. sin / The area of he circular segmen is he area of he circular secor P C subended b he angle less he area of he riangle P C. The riangle P C has heigh R cos and base R sin sohaisareaisr cos sin R sin,andheareaofhecircular secor is R R. Thus he area of he circular segmen is which is one hird he area of he ccloidal secor. R. sin /
30 76 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS 95. erive he formula for he sloe of he angen line o a arameric curve c./../;.// using a mehod differen from ha resened in he e. Assume ha 0. 0 / and 0. 0 / eis and ha 0. 0 / 0. Showha. 0 C h/. 0 / lim h!0. 0 C h/. 0 / 0. 0 / 0. 0 / Then elain wh his limi is equal o he sloe d=d. rawadiagramshowinghaheraioinhelimiishesloeofasecan line. Since 0. 0 / and 0. 0 / eis, we have he following limis:. 0 C h/. 0 / lim 0. 0 C h/. 0 /. 0 /; lim 0. 0 / () h!0 h h!0 h We use Basic Limi Laws, he limis in () and he given daa 0. 0 / 0,owrie.. 0 C h/. 0 / 0 Ch/. 0 / lim h!0. 0 C h/. 0 / lim h h!0. 0 Ch/. 0 / h lim h!0. 0Ch/. 0 / h. lim 0 Ch/. 0 / h!0 h 0. 0 / 0. 0 /. 0 C h/. 0 / Noice ha he quoien. 0 C h/. 0 / is he sloe of he secan line deermined b he oins P.. 0/;. 0 // and Q.. 0 C h/;. 0 C h//. Hence,helimiofhequoienash! 0 is he sloe of he angen line a P,haishederivaive d d. ( 0, h) Q ( 0 ) P ( 0 ) ( 0 + h) 96. Verif ha he racri curve (` >0) c./ ` anh ; ` sech ` ` has he following roer: For all, hesegmenfromc./ o.; 0/ is angen o he curve and has lengh ` (Figure ). c() FIGURE The racri c./ ` anh `; ` sech. ` Le P c./ and Q.; 0/. P((), ()) Q = (, 0) The sloe of he segmen PQ is./ 0 m./ ` sech ` ` anh sinh ` `
31 SECTION. Parameric Equaions 77 We comuehesloeofheangenlineap : m d 0 d 0./ ` sech ` 0./ 0 ` ` sech ` anh ` ` anh ` ` ` sech ` sech anh ` ` sech sech anh ` ` anh sech ` anh sinh ` ` ` ` Since m m,weconcludehahesegmenfromc./ o.; 0/ is angen o he curve. We now show ha jpqj `: s q jpqj../ / C../ 0/ ` anh s ` ` sech C ` sech ` ` s anh ` C sech ` ` sech ` sinh ` C sech ` ` s sinh C ` sech ` cosh ` 97. In Eercise 58 of Secion 9., we described he racri b he differenial equaion d d ` ` ` ` Show ha he curve c./ idenified as he racri in Eercise 96 saisfies his differenial equaion. Noe ha he derivaive on he lef is aken wih resec o,no. Noe ha d=d sech.=`/ anh.=`/ and d=d sech.=`/ anh.=`/.thus, Muliling o and boom b `=` gives d d d=d d=d sech.=`/ anh.=`/ d d ` =` =` InEercises98and99,referoFigure In he aramerizaion c./.a cos ;b sin / of an ellise, is no an angular arameer unless a b (in which case he ellise is a circle). However, can be inerreed in erms of area: Show ha if c./.; /, hen.=ab/a, wherea is he area of he shaded region in Figure 5. Hin: Use Eq. (). (, ) FIGURE 5 The arameer on he ellise C. a b We comue he area A of he shaded region as he sum of he area S of he riangle and he area S of he region under he curve. The area of he riangle is S.a cos /.bsin / ab sin () (, ) S S
32 78 C H A P TE R PARAMETRIC EQUATIONS, POLAR COORINATES, AN VECTOR FUNCTIONS The area S under he curve can be comued using Eq. (). The lower limi of he inegraion is 0 0 (corresonds o.a; 0/) and he uer limi is (corresonds o../;.//). Also./ b sin and 0./ asin. Since 0./ < 0 on he inerval 0<< (which reresens he ellise on he firs quadran), we use he osiive value a sin o obain a osiive value for he area. This gives Z S 0 Z b sin u a sin udu ab 0 cos u du ab Z ab 0 sin ab 0 ab sin udu u ab sin ˇˇˇˇ sin u 0 () Combining () and () we obain A S C S ab sin Hence, A ab. 99. Show ha he aramerizaion of he ellise b he angle is C ab ab sin ab ab cos a sin C b cos ab sin a sin C b cos We consider he ellise a C b : For he angle we have an, hence, Subsiuing in he equaion of he ellise and solving for we obain a C an b b C a an a b.a an C b / a b a b a an C b an () a b cos a sin C b cos We now ake he square roo. Since he sign of he -coordinae is he same as he sign of cos,weakeheosiiveroo,obaining Hence b (), he -coordinae is ab cos a sin C b cos () ab cos an an a sin C b cos Equaliies () and () give he following aramerizaion for he ellise: c./ ab cos ; a sin C b cos ab sin a sin C b cos ab sin a sin C b cos! ()
Check in: 1 If m = 2(x + 1) and n = find y when. b y = 2m n 2
 7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
10.1 EXERCISES. y 2 t 2. y 1 t y t 3. y e
 66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
15. Vector Valued Functions
 1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
Chapters 6 & 7: Trigonometric Functions of Angles and Real Numbers. Divide both Sides by 180
 Algebra Chapers & : Trigonomeric Funcions of Angles and Real Numbers Chapers & : Trigonomeric Funcions of Angles and Real Numbers - Angle Measures Radians: - a uni (rad o measure he size of an angle. rad
Algebra Chapers & : Trigonomeric Funcions of Angles and Real Numbers Chapers & : Trigonomeric Funcions of Angles and Real Numbers - Angle Measures Radians: - a uni (rad o measure he size of an angle. rad
11 PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS
 PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS. Parametric Equations Preliminar Questions. Describe the shape of the curve = cos t, = sin t. For all t, + = cos t + sin t = 9cos t + sin t =
PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS. Parametric Equations Preliminar Questions. Describe the shape of the curve = cos t, = sin t. For all t, + = cos t + sin t = 9cos t + sin t =
AP Calculus BC Chapter 10 Part 1 AP Exam Problems
 AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
10.6 Parametric Equations
 0_006.qd /8/05 9:05 AM Page 77 Secion 0.6 77 Parameric Equaions 0.6 Parameric Equaions Wha ou should learn Evaluae ses of parameric equaions for given values of he parameer. Skech curves ha are represened
0_006.qd /8/05 9:05 AM Page 77 Secion 0.6 77 Parameric Equaions 0.6 Parameric Equaions Wha ou should learn Evaluae ses of parameric equaions for given values of he parameer. Skech curves ha are represened
!!"#"$%&#'()!"#&'(*%)+,&',-)./0)1-*23)
 "#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
"#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
WEEK-3 Recitation PHYS 131. of the projectile s velocity remains constant throughout the motion, since the acceleration a x
 WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
Math 2142 Exam 1 Review Problems. x 2 + f (0) 3! for the 3rd Taylor polynomial at x = 0. To calculate the various quantities:
 Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Ground Rules. PC1221 Fundamentals of Physics I. Kinematics. Position. Lectures 3 and 4 Motion in One Dimension. A/Prof Tay Seng Chuan
 Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
3, so θ = arccos
 Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
KEY. Math 334 Midterm I Fall 2008 sections 001 and 003 Instructor: Scott Glasgow
 1 KEY Mah 4 Miderm I Fall 8 secions 1 and Insrucor: Sco Glasgow Please do NOT wrie on his eam. No credi will be given for such work. Raher wrie in a blue book, or on our own paper, preferabl engineering
1 KEY Mah 4 Miderm I Fall 8 secions 1 and Insrucor: Sco Glasgow Please do NOT wrie on his eam. No credi will be given for such work. Raher wrie in a blue book, or on our own paper, preferabl engineering
ln 2 1 ln y x c y C x
 Lecure 14 Appendi B: Some sample problems from Boas Here are some soluions o he sample problems assigned for Chaper 8 8: 6 Soluion: We wan o find he soluion o he following firs order equaion using separaion
Lecure 14 Appendi B: Some sample problems from Boas Here are some soluions o he sample problems assigned for Chaper 8 8: 6 Soluion: We wan o find he soluion o he following firs order equaion using separaion
Answers to 1 Homework
 Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
PROBLEMS FOR MATH 162 If a problem is starred, all subproblems are due. If only subproblems are starred, only those are due. SLOPES OF TANGENT LINES
 PROBLEMS FOR MATH 6 If a problem is sarred, all subproblems are due. If onl subproblems are sarred, onl hose are due. 00. Shor answer quesions. SLOPES OF TANGENT LINES (a) A ball is hrown ino he air. Is
PROBLEMS FOR MATH 6 If a problem is sarred, all subproblems are due. If onl subproblems are sarred, onl hose are due. 00. Shor answer quesions. SLOPES OF TANGENT LINES (a) A ball is hrown ino he air. Is
KINEMATICS IN ONE DIMENSION
 KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
SOLUTIONS TO ECE 3084
 SOLUTIONS TO ECE 384 PROBLEM 2.. For each sysem below, specify wheher or no i is: (i) memoryless; (ii) causal; (iii) inverible; (iv) linear; (v) ime invarian; Explain your reasoning. If he propery is no
SOLUTIONS TO ECE 384 PROBLEM 2.. For each sysem below, specify wheher or no i is: (i) memoryless; (ii) causal; (iii) inverible; (iv) linear; (v) ime invarian; Explain your reasoning. If he propery is no
Additional Exercises for Chapter What is the slope-intercept form of the equation of the line given by 3x + 5y + 2 = 0?
 ddiional Eercises for Caper 5 bou Lines, Slopes, and Tangen Lines 39. Find an equaion for e line roug e wo poins (, 7) and (5, ). 4. Wa is e slope-inercep form of e equaion of e line given by 3 + 5y +
ddiional Eercises for Caper 5 bou Lines, Slopes, and Tangen Lines 39. Find an equaion for e line roug e wo poins (, 7) and (5, ). 4. Wa is e slope-inercep form of e equaion of e line given by 3 + 5y +
and v y . The changes occur, respectively, because of the acceleration components a x and a y
 Week 3 Reciaion: Chaper3 : Problems: 1, 16, 9, 37, 41, 71. 1. A spacecraf is raveling wih a veloci of v0 = 5480 m/s along he + direcion. Two engines are urned on for a ime of 84 s. One engine gives he
Week 3 Reciaion: Chaper3 : Problems: 1, 16, 9, 37, 41, 71. 1. A spacecraf is raveling wih a veloci of v0 = 5480 m/s along he + direcion. Two engines are urned on for a ime of 84 s. One engine gives he
15. Bicycle Wheel. Graph of height y (cm) above the axle against time t (s) over a 6-second interval. 15 bike wheel
 15. Biccle Wheel The graph We moun a biccle wheel so ha i is free o roae in a verical plane. In fac, wha works easil is o pu an exension on one of he axles, and ge a suden o sand on one side and hold he
15. Biccle Wheel The graph We moun a biccle wheel so ha i is free o roae in a verical plane. In fac, wha works easil is o pu an exension on one of he axles, and ge a suden o sand on one side and hold he
F x 3-4x 2 >25-6x + 6 = 0, whose only real root is x a. relative minimum of at x 1.404; c. 3p2 - p3
 or Use Onl in Pilo Program F Seleced Answers A-7. 7. Abs min (, ) Local and abs ma (, ) Inflecion oin (, ) Inflecion oin (, ) Abs min (, ) Local and abs ma ((),.) Inflecion oin ((), 9.9) -inerce (, ) -inerce
or Use Onl in Pilo Program F Seleced Answers A-7. 7. Abs min (, ) Local and abs ma (, ) Inflecion oin (, ) Inflecion oin (, ) Abs min (, ) Local and abs ma ((),.) Inflecion oin ((), 9.9) -inerce (, ) -inerce
Review Exercises for Chapter 3
 60_00R.qd //0 :9 M age CHATER Applicaions of Differeniaion Review Eercises for Chaper. Give he definiion of a criical number, and graph a funcion f showing he differen pes of criical numbers.. Consider
60_00R.qd //0 :9 M age CHATER Applicaions of Differeniaion Review Eercises for Chaper. Give he definiion of a criical number, and graph a funcion f showing he differen pes of criical numbers.. Consider
1. VELOCITY AND ACCELERATION
 1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
3.6 Derivatives as Rates of Change
 3.6 Derivaives as Raes of Change Problem 1 John is walking along a sraigh pah. His posiion a he ime >0 is given by s = f(). He sars a =0from his house (f(0) = 0) and he graph of f is given below. (a) Describe
3.6 Derivaives as Raes of Change Problem 1 John is walking along a sraigh pah. His posiion a he ime >0 is given by s = f(). He sars a =0from his house (f(0) = 0) and he graph of f is given below. (a) Describe
Solutions from Chapter 9.1 and 9.2
 Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
Solution: b All the terms must have the dimension of acceleration. We see that, indeed, each term has the units of acceleration
 PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
Some Basic Information about M-S-D Systems
 Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
MEI STRUCTURED MATHEMATICS 4758
 OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
Math 2214 Sol Test 2B Spring 2015
 Mah 14 Sol Tes B Sring 015 roblem 1: An objec weighing ounds sreches a verical sring 8 fee beond i naural lengh before coming o res a equilibrium The objec is ushed u 6 fee from i s equilibrium osiion
Mah 14 Sol Tes B Sring 015 roblem 1: An objec weighing ounds sreches a verical sring 8 fee beond i naural lengh before coming o res a equilibrium The objec is ushed u 6 fee from i s equilibrium osiion
4.5 Constant Acceleration
 4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
ACCUMULATION. Section 7.5 Calculus AP/Dual, Revised /26/2018 7:27 PM 7.5A: Accumulation 1
 ACCUMULATION Secion 7.5 Calculus AP/Dual, Revised 2019 vie.dang@humbleisd.ne 12/26/2018 7:27 PM 7.5A: Accumulaion 1 APPLICATION PROBLEMS A. Undersand he quesion. I is ofen no necessary o as much compuaion
ACCUMULATION Secion 7.5 Calculus AP/Dual, Revised 2019 vie.dang@humbleisd.ne 12/26/2018 7:27 PM 7.5A: Accumulaion 1 APPLICATION PROBLEMS A. Undersand he quesion. I is ofen no necessary o as much compuaion
The equation to any straight line can be expressed in the form:
 Sring Graphs Par 1 Answers 1 TI-Nspire Invesigaion Suden min Aims Deermine a series of equaions of sraigh lines o form a paern similar o ha formed by he cables on he Jerusalem Chords Bridge. Deermine he
Sring Graphs Par 1 Answers 1 TI-Nspire Invesigaion Suden min Aims Deermine a series of equaions of sraigh lines o form a paern similar o ha formed by he cables on he Jerusalem Chords Bridge. Deermine he
2.1: What is physics? Ch02: Motion along a straight line. 2.2: Motion. 2.3: Position, Displacement, Distance
 Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Chapter 2. First Order Scalar Equations
 Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
23.5. Half-Range Series. Introduction. Prerequisites. Learning Outcomes
 Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
Phys 221 Fall Chapter 2. Motion in One Dimension. 2014, 2005 A. Dzyubenko Brooks/Cole
 Phys 221 Fall 2014 Chaper 2 Moion in One Dimension 2014, 2005 A. Dzyubenko 2004 Brooks/Cole 1 Kinemaics Kinemaics, a par of classical mechanics: Describes moion in erms of space and ime Ignores he agen
Phys 221 Fall 2014 Chaper 2 Moion in One Dimension 2014, 2005 A. Dzyubenko 2004 Brooks/Cole 1 Kinemaics Kinemaics, a par of classical mechanics: Describes moion in erms of space and ime Ignores he agen
SMT 2014 Calculus Test Solutions February 15, 2014 = 3 5 = 15.
 SMT Calculus Tes Soluions February 5,. Le f() = and le g() =. Compue f ()g (). Answer: 5 Soluion: We noe ha f () = and g () = 6. Then f ()g () =. Plugging in = we ge f ()g () = 6 = 3 5 = 5.. There is a
SMT Calculus Tes Soluions February 5,. Le f() = and le g() =. Compue f ()g (). Answer: 5 Soluion: We noe ha f () = and g () = 6. Then f ()g () =. Plugging in = we ge f ()g () = 6 = 3 5 = 5.. There is a
k 1 k 2 x (1) x 2 = k 1 x 1 = k 2 k 1 +k 2 x (2) x k series x (3) k 2 x 2 = k 1 k 2 = k 1+k 2 = 1 k k 2 k series
 Final Review A Puzzle... Consider wo massless springs wih spring consans k 1 and k and he same equilibrium lengh. 1. If hese springs ac on a mass m in parallel, hey would be equivalen o a single spring
Final Review A Puzzle... Consider wo massless springs wih spring consans k 1 and k and he same equilibrium lengh. 1. If hese springs ac on a mass m in parallel, hey would be equivalen o a single spring
Motion along a Straight Line
 chaper 2 Moion along a Sraigh Line verage speed and average velociy (Secion 2.2) 1. Velociy versus speed Cone in he ebook: fer Eample 2. Insananeous velociy and insananeous acceleraion (Secions 2.3, 2.4)
chaper 2 Moion along a Sraigh Line verage speed and average velociy (Secion 2.2) 1. Velociy versus speed Cone in he ebook: fer Eample 2. Insananeous velociy and insananeous acceleraion (Secions 2.3, 2.4)
IB Physics Kinematics Worksheet
 IB Physics Kinemaics Workshee Wrie full soluions and noes for muliple choice answers. Do no use a calculaor for muliple choice answers. 1. Which of he following is a correc definiion of average acceleraion?
IB Physics Kinemaics Workshee Wrie full soluions and noes for muliple choice answers. Do no use a calculaor for muliple choice answers. 1. Which of he following is a correc definiion of average acceleraion?
4.6 One Dimensional Kinematics and Integration
 4.6 One Dimensional Kinemaics and Inegraion When he acceleraion a( of an objec is a non-consan funcion of ime, we would like o deermine he ime dependence of he posiion funcion x( and he x -componen of
4.6 One Dimensional Kinemaics and Inegraion When he acceleraion a( of an objec is a non-consan funcion of ime, we would like o deermine he ime dependence of he posiion funcion x( and he x -componen of
1. Kinematics I: Position and Velocity
 1. Kinemaics I: Posiion and Velociy Inroducion The purpose of his eperimen is o undersand and describe moion. We describe he moion of an objec by specifying is posiion, velociy, and acceleraion. In his
1. Kinemaics I: Posiion and Velociy Inroducion The purpose of his eperimen is o undersand and describe moion. We describe he moion of an objec by specifying is posiion, velociy, and acceleraion. In his
MA 366 Review - Test # 1
 MA 366 Review - Tes # 1 Fall 5 () Resuls from Calculus: differeniaion formulas, implici differeniaion, Chain Rule; inegraion formulas, inegraion b pars, parial fracions, oher inegraion echniques. (1) Order
MA 366 Review - Tes # 1 Fall 5 () Resuls from Calculus: differeniaion formulas, implici differeniaion, Chain Rule; inegraion formulas, inegraion b pars, parial fracions, oher inegraion echniques. (1) Order
Section 3.5 Nonhomogeneous Equations; Method of Undetermined Coefficients
 Secion 3.5 Nonhomogeneous Equaions; Mehod of Undeermined Coefficiens Key Terms/Ideas: Linear Differenial operaor Nonlinear operaor Second order homogeneous DE Second order nonhomogeneous DE Soluion o homogeneous
Secion 3.5 Nonhomogeneous Equaions; Mehod of Undeermined Coefficiens Key Terms/Ideas: Linear Differenial operaor Nonlinear operaor Second order homogeneous DE Second order nonhomogeneous DE Soluion o homogeneous
Week 1 Lecture 2 Problems 2, 5. What if something oscillates with no obvious spring? What is ω? (problem set problem)
 Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
Chapter 7: Solving Trig Equations
 Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
Solutions to Assignment 1
 MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
a. Show that these lines intersect by finding the point of intersection. b. Find an equation for the plane containing these lines.
 Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
CHAPTER 12 DIRECT CURRENT CIRCUITS
 CHAPTER 12 DIRECT CURRENT CIUITS DIRECT CURRENT CIUITS 257 12.1 RESISTORS IN SERIES AND IN PARALLEL When wo resisors are conneced ogeher as shown in Figure 12.1 we said ha hey are conneced in series. As
CHAPTER 12 DIRECT CURRENT CIUITS DIRECT CURRENT CIUITS 257 12.1 RESISTORS IN SERIES AND IN PARALLEL When wo resisors are conneced ogeher as shown in Figure 12.1 we said ha hey are conneced in series. As
AP Calculus BC - Parametric equations and vectors Chapter 9- AP Exam Problems solutions
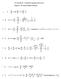 AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
23.2. Representing Periodic Functions by Fourier Series. Introduction. Prerequisites. Learning Outcomes
 Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
Differential Equations
 Mah 21 (Fall 29) Differenial Equaions Soluion #3 1. Find he paricular soluion of he following differenial equaion by variaion of parameer (a) y + y = csc (b) 2 y + y y = ln, > Soluion: (a) The corresponding
Mah 21 (Fall 29) Differenial Equaions Soluion #3 1. Find he paricular soluion of he following differenial equaion by variaion of parameer (a) y + y = csc (b) 2 y + y y = ln, > Soluion: (a) The corresponding
INSTANTANEOUS VELOCITY
 INSTANTANEOUS VELOCITY I claim ha ha if acceleraion is consan, hen he elociy is a linear funcion of ime and he posiion a quadraic funcion of ime. We wan o inesigae hose claims, and a he same ime, work
INSTANTANEOUS VELOCITY I claim ha ha if acceleraion is consan, hen he elociy is a linear funcion of ime and he posiion a quadraic funcion of ime. We wan o inesigae hose claims, and a he same ime, work
Be able to sketch a function defined parametrically. (by hand and by calculator)
 Pre Calculus Uni : Parameric and Polar Equaions (7) Te References: Pre Calculus wih Limis; Larson, Hoseler, Edwards. B he end of he uni, ou should be able o complee he problems below. The eacher ma provide
Pre Calculus Uni : Parameric and Polar Equaions (7) Te References: Pre Calculus wih Limis; Larson, Hoseler, Edwards. B he end of he uni, ou should be able o complee he problems below. The eacher ma provide
Chapter 3 Kinematics in Two Dimensions
 Chaper 3 KINEMATICS IN TWO DIMENSIONS PREVIEW Two-dimensional moion includes objecs which are moing in wo direcions a he same ime, such as a projecile, which has boh horizonal and erical moion. These wo
Chaper 3 KINEMATICS IN TWO DIMENSIONS PREVIEW Two-dimensional moion includes objecs which are moing in wo direcions a he same ime, such as a projecile, which has boh horizonal and erical moion. These wo
( ) 2. Review Exercise 2. cos θ 2 3 = = 2 tan. cos. 2 x = = x a. Since π π, = 2. sin = = 2+ = = cotx. 2 sin θ 2+
 Review Eercise sin 5 cos sin an cos 5 5 an 5 9 co 0 a sinθ 6 + 4 6 + sin θ 4 6+ + 6 + 4 cos θ sin θ + 4 4 sin θ + an θ cos θ ( ) + + + + Since π π, < θ < anθ should be negaive. anθ ( + ) Pearson Educaion
Review Eercise sin 5 cos sin an cos 5 5 an 5 9 co 0 a sinθ 6 + 4 6 + sin θ 4 6+ + 6 + 4 cos θ sin θ + 4 4 sin θ + an θ cos θ ( ) + + + + Since π π, < θ < anθ should be negaive. anθ ( + ) Pearson Educaion
Review - Quiz # 1. 1 g(y) dy = f(x) dx. y x. = u, so that y = xu and dy. dx (Sometimes you may want to use the substitution x y
 Review - Quiz # 1 (1) Solving Special Tpes of Firs Order Equaions I. Separable Equaions (SE). d = f() g() Mehod of Soluion : 1 g() d = f() (The soluions ma be given implicil b he above formula. Remember,
Review - Quiz # 1 (1) Solving Special Tpes of Firs Order Equaions I. Separable Equaions (SE). d = f() g() Mehod of Soluion : 1 g() d = f() (The soluions ma be given implicil b he above formula. Remember,
1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.
![1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx. 1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.](/thumbs/71/65799522.jpg) . Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
. Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
Math Spring 2015 PRACTICE FINAL EXAM (modified from Math 2280 final exam, April 29, 2011)
 ame ID number Mah 8- Sring 5 PRACTICE FIAL EXAM (modified from Mah 8 final exam, Aril 9, ) This exam is closed-book and closed-noe You may use a scienific calculaor, bu no one which is caable of grahing
ame ID number Mah 8- Sring 5 PRACTICE FIAL EXAM (modified from Mah 8 final exam, Aril 9, ) This exam is closed-book and closed-noe You may use a scienific calculaor, bu no one which is caable of grahing
Brock University Physics 1P21/1P91 Fall 2013 Dr. D Agostino. Solutions for Tutorial 3: Chapter 2, Motion in One Dimension
 Brock Uniersiy Physics 1P21/1P91 Fall 2013 Dr. D Agosino Soluions for Tuorial 3: Chaper 2, Moion in One Dimension The goals of his uorial are: undersand posiion-ime graphs, elociy-ime graphs, and heir
Brock Uniersiy Physics 1P21/1P91 Fall 2013 Dr. D Agosino Soluions for Tuorial 3: Chaper 2, Moion in One Dimension The goals of his uorial are: undersand posiion-ime graphs, elociy-ime graphs, and heir
(π 3)k. f(t) = 1 π 3 sin(t)
 Mah 6 Fall 6 Dr. Lil Yen Tes Show all our work Name: Score: /6 No Calculaor permied in his par. Read he quesions carefull. Show all our work and clearl indicae our final answer. Use proper noaion. Problem
Mah 6 Fall 6 Dr. Lil Yen Tes Show all our work Name: Score: /6 No Calculaor permied in his par. Read he quesions carefull. Show all our work and clearl indicae our final answer. Use proper noaion. Problem
AP CALCULUS BC 2016 SCORING GUIDELINES
 6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
d = ½(v o + v f) t distance = ½ (initial velocity + final velocity) time
 BULLSEYE Lab Name: ANSWER KEY Dae: Pre-AP Physics Lab Projecile Moion Weigh = 1 DIRECTIONS: Follow he insrucions below, build he ramp, ake your measuremens, and use your measuremens o make he calculaions
BULLSEYE Lab Name: ANSWER KEY Dae: Pre-AP Physics Lab Projecile Moion Weigh = 1 DIRECTIONS: Follow he insrucions below, build he ramp, ake your measuremens, and use your measuremens o make he calculaions
Displacement ( x) x x x
 Kinemaics Kinemaics is he branch of mechanics ha describes he moion of objecs wihou necessarily discussing wha causes he moion. 1-Dimensional Kinemaics (or 1- Dimensional moion) refers o moion in a sraigh
Kinemaics Kinemaics is he branch of mechanics ha describes he moion of objecs wihou necessarily discussing wha causes he moion. 1-Dimensional Kinemaics (or 1- Dimensional moion) refers o moion in a sraigh
Kinematics Vocabulary. Kinematics and One Dimensional Motion. Position. Coordinate System in One Dimension. Kinema means movement 8.
 Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Parametrics and Vectors (BC Only)
 Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
a 10.0 (m/s 2 ) 5.0 Name: Date: 1. The graph below describes the motion of a fly that starts out going right V(m/s)
 Name: Dae: Kinemaics Review (Honors. Physics) Complee he following on a separae shee of paper o be urned in on he day of he es. ALL WORK MUST BE SHOWN TO RECEIVE CREDIT. 1. The graph below describes he
Name: Dae: Kinemaics Review (Honors. Physics) Complee he following on a separae shee of paper o be urned in on he day of he es. ALL WORK MUST BE SHOWN TO RECEIVE CREDIT. 1. The graph below describes he
One-Dimensional Kinematics
 One-Dimensional Kinemaics One dimensional kinemaics refers o moion along a sraigh line. Een hough we lie in a 3-dimension world, moion can ofen be absraced o a single dimension. We can also describe moion
One-Dimensional Kinemaics One dimensional kinemaics refers o moion along a sraigh line. Een hough we lie in a 3-dimension world, moion can ofen be absraced o a single dimension. We can also describe moion
MOMENTUM CONSERVATION LAW
 1 AAST/AEDT AP PHYSICS B: Impulse and Momenum Le us run an experimen: The ball is moving wih a velociy of V o and a force of F is applied on i for he ime inerval of. As he resul he ball s velociy changes
1 AAST/AEDT AP PHYSICS B: Impulse and Momenum Le us run an experimen: The ball is moving wih a velociy of V o and a force of F is applied on i for he ime inerval of. As he resul he ball s velociy changes
2.7. Some common engineering functions. Introduction. Prerequisites. Learning Outcomes
 Some common engineering funcions 2.7 Inroducion This secion provides a caalogue of some common funcions ofen used in Science and Engineering. These include polynomials, raional funcions, he modulus funcion
Some common engineering funcions 2.7 Inroducion This secion provides a caalogue of some common funcions ofen used in Science and Engineering. These include polynomials, raional funcions, he modulus funcion
UCLA: Math 3B Problem set 3 (solutions) Fall, 2018
 UCLA: Mah 3B Problem se 3 (soluions) Fall, 28 This problem se concenraes on pracice wih aniderivaives. You will ge los of pracice finding simple aniderivaives as well as finding aniderivaives graphically
UCLA: Mah 3B Problem se 3 (soluions) Fall, 28 This problem se concenraes on pracice wih aniderivaives. You will ge los of pracice finding simple aniderivaives as well as finding aniderivaives graphically
Lecture 2-1 Kinematics in One Dimension Displacement, Velocity and Acceleration Everything in the world is moving. Nothing stays still.
 Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
AP CALCULUS AB 2003 SCORING GUIDELINES (Form B)
 SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
In this chapter the model of free motion under gravity is extended to objects projected at an angle. When you have completed it, you should
 Cambridge Universiy Press 978--36-60033-7 Cambridge Inernaional AS and A Level Mahemaics: Mechanics Coursebook Excerp More Informaion Chaper The moion of projeciles In his chaper he model of free moion
Cambridge Universiy Press 978--36-60033-7 Cambridge Inernaional AS and A Level Mahemaics: Mechanics Coursebook Excerp More Informaion Chaper The moion of projeciles In his chaper he model of free moion
Solutions for homework 12
 y Soluions for homework Secion Nonlinear sysems: The linearizaion of a nonlinear sysem Consider he sysem y y y y y (i) Skech he nullclines Use a disincive marking for each nullcline so hey can be disinguished
y Soluions for homework Secion Nonlinear sysems: The linearizaion of a nonlinear sysem Consider he sysem y y y y y (i) Skech he nullclines Use a disincive marking for each nullcline so hey can be disinguished
Math 116 Practice for Exam 2
 Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
Physics 235 Chapter 2. Chapter 2 Newtonian Mechanics Single Particle
 Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Position, Velocity, and Acceleration
 rev 06/2017 Posiion, Velociy, and Acceleraion Equipmen Qy Equipmen Par Number 1 Dynamic Track ME-9493 1 Car ME-9454 1 Fan Accessory ME-9491 1 Moion Sensor II CI-6742A 1 Track Barrier Purpose The purpose
rev 06/2017 Posiion, Velociy, and Acceleraion Equipmen Qy Equipmen Par Number 1 Dynamic Track ME-9493 1 Car ME-9454 1 Fan Accessory ME-9491 1 Moion Sensor II CI-6742A 1 Track Barrier Purpose The purpose
ME 391 Mechanical Engineering Analysis
 Fall 04 ME 39 Mechanical Engineering Analsis Eam # Soluions Direcions: Open noes (including course web posings). No books, compuers, or phones. An calculaor is fair game. Problem Deermine he posiion of
Fall 04 ME 39 Mechanical Engineering Analsis Eam # Soluions Direcions: Open noes (including course web posings). No books, compuers, or phones. An calculaor is fair game. Problem Deermine he posiion of
Math 2214 Solution Test 1B Fall 2017
 Mah 14 Soluion Tes 1B Fall 017 Problem 1: A ank has a capaci for 500 gallons and conains 0 gallons of waer wih lbs of sal iniiall. A soluion conaining of 8 lbsgal of sal is pumped ino he ank a 10 galsmin.
Mah 14 Soluion Tes 1B Fall 017 Problem 1: A ank has a capaci for 500 gallons and conains 0 gallons of waer wih lbs of sal iniiall. A soluion conaining of 8 lbsgal of sal is pumped ino he ank a 10 galsmin.
University Physics with Modern Physics 14th Edition Young TEST BANK
 Universi Phsics wih Modern Phsics 14h Ediion Young SOLUTIONS MANUAL Full clear download (no formaing errors) a: hps://esbankreal.com/download/universi-phsics-modern-phsics- 14h-ediion-oung-soluions-manual-/
Universi Phsics wih Modern Phsics 14h Ediion Young SOLUTIONS MANUAL Full clear download (no formaing errors) a: hps://esbankreal.com/download/universi-phsics-modern-phsics- 14h-ediion-oung-soluions-manual-/
1.6. Slopes of Tangents and Instantaneous Rate of Change
 1.6 Slopes of Tangens and Insananeous Rae of Change When you hi or kick a ball, he heigh, h, in meres, of he ball can be modelled by he equaion h() 4.9 2 v c. In his equaion, is he ime, in seconds; c represens
1.6 Slopes of Tangens and Insananeous Rae of Change When you hi or kick a ball, he heigh, h, in meres, of he ball can be modelled by he equaion h() 4.9 2 v c. In his equaion, is he ime, in seconds; c represens
Decimal moved after first digit = 4.6 x Decimal moves five places left SCIENTIFIC > POSITIONAL. a) g) 5.31 x b) 0.
 PHYSICS 20 UNIT 1 SCIENCE MATH WORKSHEET NAME: A. Sandard Noaion Very large and very small numbers are easily wrien using scienific (or sandard) noaion, raher han decimal (or posiional) noaion. Sandard
PHYSICS 20 UNIT 1 SCIENCE MATH WORKSHEET NAME: A. Sandard Noaion Very large and very small numbers are easily wrien using scienific (or sandard) noaion, raher han decimal (or posiional) noaion. Sandard
BOX-JENKINS MODEL NOTATION. The Box-Jenkins ARMA(p,q) model is denoted by the equation. pwhile the moving average (MA) part of the model is θ1at
 BOX-JENKINS MODEL NOAION he Box-Jenkins ARMA(,q) model is denoed b he equaion + + L+ + a θ a L θ a 0 q q. () he auoregressive (AR) ar of he model is + L+ while he moving average (MA) ar of he model is
BOX-JENKINS MODEL NOAION he Box-Jenkins ARMA(,q) model is denoed b he equaion + + L+ + a θ a L θ a 0 q q. () he auoregressive (AR) ar of he model is + L+ while he moving average (MA) ar of he model is
Roller-Coaster Coordinate System
 Winer 200 MECH 220: Mechanics 2 Roller-Coaser Coordinae Sysem Imagine you are riding on a roller-coaer in which he rack goes up and down, wiss and urns. Your velociy and acceleraion will change (quie abruply),
Winer 200 MECH 220: Mechanics 2 Roller-Coaser Coordinae Sysem Imagine you are riding on a roller-coaer in which he rack goes up and down, wiss and urns. Your velociy and acceleraion will change (quie abruply),
3.1.3 INTRODUCTION TO DYNAMIC OPTIMIZATION: DISCRETE TIME PROBLEMS. A. The Hamiltonian and First-Order Conditions in a Finite Time Horizon
 3..3 INRODUCION O DYNAMIC OPIMIZAION: DISCREE IME PROBLEMS A. he Hamilonian and Firs-Order Condiions in a Finie ime Horizon Define a new funcion, he Hamilonian funcion, H. H he change in he oal value of
3..3 INRODUCION O DYNAMIC OPIMIZAION: DISCREE IME PROBLEMS A. he Hamilonian and Firs-Order Condiions in a Finie ime Horizon Define a new funcion, he Hamilonian funcion, H. H he change in he oal value of
u(x) = e x 2 y + 2 ) Integrate and solve for x (1 + x)y + y = cos x Answer: Divide both sides by 1 + x and solve for y. y = x y + cos x
 . 1 Mah 211 Homework #3 February 2, 2001 2.4.3. y + (2/x)y = (cos x)/x 2 Answer: Compare y + (2/x) y = (cos x)/x 2 wih y = a(x)x + f(x)and noe ha a(x) = 2/x. Consequenly, an inegraing facor is found wih
. 1 Mah 211 Homework #3 February 2, 2001 2.4.3. y + (2/x)y = (cos x)/x 2 Answer: Compare y + (2/x) y = (cos x)/x 2 wih y = a(x)x + f(x)and noe ha a(x) = 2/x. Consequenly, an inegraing facor is found wih
3 at MAC 1140 TEST 3 NOTES. 5.1 and 5.2. Exponential Functions. Form I: P is the y-intercept. (0, P) When a > 1: a = growth factor = 1 + growth rate
 1 5.1 and 5. Eponenial Funcions Form I: Y Pa, a 1, a > 0 P is he y-inercep. (0, P) When a > 1: a = growh facor = 1 + growh rae The equaion can be wrien as The larger a is, he seeper he graph is. Y P( 1
1 5.1 and 5. Eponenial Funcions Form I: Y Pa, a 1, a > 0 P is he y-inercep. (0, P) When a > 1: a = growh facor = 1 + growh rae The equaion can be wrien as The larger a is, he seeper he graph is. Y P( 1
Constant Acceleration
 Objecive Consan Acceleraion To deermine he acceleraion of objecs moving along a sraigh line wih consan acceleraion. Inroducion The posiion y of a paricle moving along a sraigh line wih a consan acceleraion
Objecive Consan Acceleraion To deermine he acceleraion of objecs moving along a sraigh line wih consan acceleraion. Inroducion The posiion y of a paricle moving along a sraigh line wih a consan acceleraion
Morning Time: 1 hour 30 minutes Additional materials (enclosed):
 ADVANCED GCE 78/0 MATHEMATICS (MEI) Differenial Equaions THURSDAY JANUARY 008 Morning Time: hour 30 minues Addiional maerials (enclosed): None Addiional maerials (required): Answer Bookle (8 pages) Graph
ADVANCED GCE 78/0 MATHEMATICS (MEI) Differenial Equaions THURSDAY JANUARY 008 Morning Time: hour 30 minues Addiional maerials (enclosed): None Addiional maerials (required): Answer Bookle (8 pages) Graph
Dynamics. Option topic: Dynamics
 Dynamics 11 syllabusref Opion opic: Dynamics eferenceence In his cha chaper 11A Differeniaion and displacemen, velociy and acceleraion 11B Inerpreing graphs 11C Algebraic links beween displacemen, velociy
Dynamics 11 syllabusref Opion opic: Dynamics eferenceence In his cha chaper 11A Differeniaion and displacemen, velociy and acceleraion 11B Inerpreing graphs 11C Algebraic links beween displacemen, velociy
4.3 Trigonometry Extended: The Circular Functions
 8 CHAPTER Trigonomeric Funcions. Trigonomer Eended: The Circular Funcions Wha ou ll learn abou Trigonomeric Funcions of An Angle Trigonomeric Funcions of Real Numbers Periodic Funcions The 6-Poin Uni Circle...
8 CHAPTER Trigonomeric Funcions. Trigonomer Eended: The Circular Funcions Wha ou ll learn abou Trigonomeric Funcions of An Angle Trigonomeric Funcions of Real Numbers Periodic Funcions The 6-Poin Uni Circle...
Reading from Young & Freedman: For this topic, read sections 25.4 & 25.5, the introduction to chapter 26 and sections 26.1 to 26.2 & 26.4.
 PHY1 Elecriciy Topic 7 (Lecures 1 & 11) Elecric Circuis n his opic, we will cover: 1) Elecromoive Force (EMF) ) Series and parallel resisor combinaions 3) Kirchhoff s rules for circuis 4) Time dependence
PHY1 Elecriciy Topic 7 (Lecures 1 & 11) Elecric Circuis n his opic, we will cover: 1) Elecromoive Force (EMF) ) Series and parallel resisor combinaions 3) Kirchhoff s rules for circuis 4) Time dependence
Ch.1. Group Work Units. Continuum Mechanics Course (MMC) - ETSECCPB - UPC
 Ch.. Group Work Unis Coninuum Mechanics Course (MMC) - ETSECCPB - UPC Uni 2 Jusify wheher he following saemens are rue or false: a) Two sreamlines, corresponding o a same insan of ime, can never inersec
Ch.. Group Work Unis Coninuum Mechanics Course (MMC) - ETSECCPB - UPC Uni 2 Jusify wheher he following saemens are rue or false: a) Two sreamlines, corresponding o a same insan of ime, can never inersec
Two Coupled Oscillators / Normal Modes
 Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Challenge Problems. DIS 203 and 210. March 6, (e 2) k. k(k + 2). k=1. f(x) = k(k + 2) = 1 x k
 Challenge Problems DIS 03 and 0 March 6, 05 Choose one of he following problems, and work on i in your group. Your goal is o convince me ha your answer is correc. Even if your answer isn compleely correc,
Challenge Problems DIS 03 and 0 March 6, 05 Choose one of he following problems, and work on i in your group. Your goal is o convince me ha your answer is correc. Even if your answer isn compleely correc,
THE 2-BODY PROBLEM. FIGURE 1. A pair of ellipses sharing a common focus. (c,b) c+a ROBERT J. VANDERBEI
 THE 2-BODY PROBLEM ROBERT J. VANDERBEI ABSTRACT. In his shor noe, we show ha a pair of ellipses wih a common focus is a soluion o he 2-body problem. INTRODUCTION. Solving he 2-body problem from scrach
THE 2-BODY PROBLEM ROBERT J. VANDERBEI ABSTRACT. In his shor noe, we show ha a pair of ellipses wih a common focus is a soluion o he 2-body problem. INTRODUCTION. Solving he 2-body problem from scrach
Physics 221 Fall 2008 Homework #2 Solutions Ch. 2 Due Tues, Sept 9, 2008
 Physics 221 Fall 28 Homework #2 Soluions Ch. 2 Due Tues, Sep 9, 28 2.1 A paricle moving along he x-axis moves direcly from posiion x =. m a ime =. s o posiion x = 1. m by ime = 1. s, and hen moves direcly
Physics 221 Fall 28 Homework #2 Soluions Ch. 2 Due Tues, Sep 9, 28 2.1 A paricle moving along he x-axis moves direcly from posiion x =. m a ime =. s o posiion x = 1. m by ime = 1. s, and hen moves direcly
