11 PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS
|
|
|
- Walter Nathaniel Johnston
- 5 years ago
- Views:
Transcription
1 PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS. Parametric Equations Preliminar Questions. Describe the shape of the curve = cos t, = sin t. For all t, + = cos t + sin t = 9cos t + sin t = 9 = 9, therefore the curve is on the circle + = 9. Also, each point on the circle + = 9 can be represented in the form cos t, sin t for some value of t. We conclude that the curve = cos t, = sin t is the circle of radius centered at the origin.. How does = + cos t, = 5 + sin t differ from the curve in the previous question? In this case we have + 5 = cos t + sin t = 9cos t + sin t = 9 = 9 Therefore, the given equations parametrize the circle of radius centered at the point, 5.. What is the maimum height of a particle whose path has parametric equations = t 9, = t? solve: The particle s height is = t. To find the maimum height we set the derivative equal to zero and d dt = d dt t = t = or t = The maimum height is = =.. Can the parametric curve t, sin t be represented as a graph = f? What about sin t,t? In the parametric curve t, sin t we have = t and = sin t, therefore, = sin. That is, the curve can be represented as a graph of a function. In the parametric curve sin t,t we have = sin t, = t, therefore = sin. This equation does not define as a function of, therefore the parametric curve sin t,t cannot be represented as a graph of a function = f. 5. Match the derivatives with a verbal description: a d b d dt dt i Slope of the tangent line to the curve ii Vertical rate of change with respect to time iii Horizontal rate of change with respect to time c d d a The derivative d is the horizontal rate of change with respect to time. dt b The derivative d is the vertical rate of change with respect to time. dt c The derivative d is the slope of the tangent line to the curve. d Hence, a iii, b ii, c i 8 April,
2 SECTION. Parametric Equations 8 Eercises. Find the coordinates at times t =,, of a particle following the path = + t, = 9 t. Substituting t =, t =, and t = into = + t, = 9 t gives the coordinates of the particle at these times respectivel. That is, t = = + =, = 9 = 9, 9 t = = + = 9, = 9 = 9, t = = + = 65, = 9 = 9 65, 9.. Find the coordinates at t =,, of a particle moving along the path ct = cos t,sin t. Setting t =, t =, and t = in ct = cos t,sin twe obtain the following coordinates of the particle: t = : cos, sin =, t = : cos, sin =, t = : cos, sin =,. Show that the path traced b the bullet in Eample is a parabola b eliminating the parameter. The path traced b the bullet is given b the following parametric equations: = t, = t 6t We eliminate the parameter. Since = t, we have t =. Substituting into the equation for we obtain: = t 6t = 6 = 5 The equation = + is the equation of a parabola. 5. Use the table of values to sketch the parametric curve t, t, indicating the direction of motion. t We mark the given points on the -plane and connect the points corresponding to successive values of t in the direction of increasing t. We get the following trajector there are other correct answers: t = 6 t = t = 5 5 t = t = t = t = 5. Graph the parametric curves. Include arrows indicating the direction of motion. a t, t, <t< b sin t,sin t, t c e t,e t, <t< d t,t, t a For the trajector ct = t, t, <t< we have =. Also the two coordinates tend to and as t and t respectivel. The graph is shown net: April,
3 8 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS b For the curve ct = sin t,sin t, t, we have =. sin t is increasing for t, decreasing for t and increasing again for t. Hence the particle moves from c =, to c =,, then moves back to c =, and then returns to c =,. We obtain the following trajector: t =, t =, t = t =, t =, <t t t< These three parts of the trajector are shown together in the net figure: t =, t = t = t =, c For the trajector ct = e t,e t, <t<, we have =. However since lim t et = and lim t et =, the trajector is the part of the line =, <. d For the trajector ct = t,t, t, we have again =. Since the function t is increasing the particle moves in one direction starting at, =, and ending at, =,. The trajector is shown net: t =, t =, 6. Give two different parametrizations of the line through, with slope. The equation of the line through, with slope is = or = 7. One parametrization is obtained b choosing the coordinate as the parameter. That is, = t. Hence = t 7 and we get = t, = t 7, <t<. Another parametrization is given b = t, = t 7, <t<. April,
4 SECTION. Parametric Equations 85 In Eercises 7, epress in the form = fb eliminating the parameter. 7. = t +, = t We eliminate the parameter. Since = t +, we have t =. Substituting into = t we obtain 8. = t, = t = t = = From = t, we have t =. Substituting in = t we obtain = t = = =, =. 9. = t, = tan t + e t Replacing t b in the equation for we obtain = tan + e.. = t, = t + From = t we get t =±. Substituting into = t + we obtain = t + = ± + =± +,. Since we must have a function of, we should probabl choose either the positive or negative root.. = e t, = 6e t we get We eliminate the parameter. Since = e t, we have t = ln or t = ln. Substituting in = 6et = 6e t = 6e ln = 6e ln = 6e ln = 6 = 6, >.. = + t, = t From = + t,wegett = ort =. We now substitute t = in = t to obtain = t = =, =.. = ln t, = t Since = ln t we have t = e. Substituting in = t we obtain = e.. = cos t, = tan t We use the trigonometric identit sin t =± cos t to write We now epress in terms of : = tan t = sin t cos cos t =± t cos t. = tan t =± =±, =. Since we must have a function of, we should probabl choose either the positive or negative root. In Eercises 5 8, graph the curve and draw an arrow specifing the direction corresponding to motion. 5. = t, = t Let ct = t, t = t,t. Then c t = t, t so the curve is smmetric with respect to the -ais. Also, the function t is increasing. Hence there is onl one direction of motion on the curve. The corresponding function is the parabola = = 8. We obtain the following trajector: t = April,
5 86 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS 6. = + t, = + t We find the function b eliminating the parameter. Since = + t we have t =, hence = + or = +. Also, since + t and + t are increasing functions, the direction of motion is the direction of increasing t. We obtain the following curve: 6 t = t = 6, 5, = t, = sin t We find the function b eliminating t. Since = t, we have t =. Substituting t = get = sin. We obtain the following curve: into = sin t we,, 8. = t, = t From = t we have t = ± /. Hence, = ± /. Since the functions t and t are increasing, there is onl one direction of motion, which is the direction of increasing t. Notice that for ct = t,t we have c t = t, t = t, t. Hence the curve is smmetric with respect to the ais. We obtain the following curve: 9. Match the parametrizations a d below with their plots in Figure, and draw an arrow indicating the direction of motion I II FIGURE III IV a ct = sin t, t b ct = t 9, 8t t c ct = t,t 9 d ct = t +, 5 t a In the curve ct = sin t, t the -coordinate is varing between and so this curve corresponds to plot IV. As t increases, the -coordinate = t is decreasing so the direction of motion is downward. April,
6 SECTION. Parametric Equations 87 IV ct = sin t, t b The curve ct = t 9, t 8 intersects the -ais where = t 8 =, or t =. The -intercept is 5,. The -intercepts are obtained where = t 9 =, or t =±. The -intercepts are, 5 and, 9.As t increases from to, and decrease, and as t increases from to, increases and decreases. We obtain the following trajector: 9 t =, 9, 8 5 II c The curve ct = t,t 9 intersects the -ais where = t =, or t =. The -intercept is, 8. The -intercepts are obtained where t 9 = ort =±. These are the points, and,. Setting t = we get = t 9 = 9 = 8. As t increases the coordinate decreases and we obtain the following trajector: 5 III d The curve ct = t +, 5 t is a straight line, since eliminating t in = t + and substituting in = 5 t gives = 5 = + which is the equation of a line. As t increases, the coordinate = t + increases and the -coordinate = 5 t decreases. We obtain the following trajector: 5 5 I April,
7 88 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS. A particle follows the trajector t = t + t, t = t t with t in seconds and distance in centimeters. a What is the particle s maimum height? b When does the particle hit the ground and how far from the origin does it land? a To find the maimum height t, we set the derivative of t equal to zero and solve: d = d dt dt t t = t = t =. The maimum height is = = cm. b The object hits the ground when its height is zero. That is, when t =. Solving for t we get t t = t t = t =,t =. t = is the initial time, so the is t =.At that time, the object s coordinate is = + =. Thus, when it hits the ground, the object is cm awa from the origin.. Find an interval of t-values such that ct = cos t,sin t traces the lower half of the unit circle. For t =, we have c =,.Ast increases from to, the -coordinate of ct increases from to, and the -coordinate decreases from to at t = / and then returns to. Thus, for t in [, ], the equation traces the lower part of the circle.. Find an interval of t-values such that ct = t +, t 5 parametrizes the segment from, 7 to 7, 7. Note that t + = att = /, and t + = 7att =. Also, t 5 takes on the values of 7and7at t = / and t =. Thus, the interval is [ /, ]. In Eercises 8, find parametric equations for the given curve.. = 9 This is a line through P =, 9 with slope m =. Using the parametric representation of a line, as given in Eample, we obtain ct = t, 9 t.. = 8 Letting t = ields the parametric representation ct = t, 8t t. 5. = 5 We define the parameter t =. Then, = 5 + = 5 + t, giving us the parametrization ct = 5 + t,t = 9 The curve + = 9 is a circle of radius 7 centered at the origin. We use the parametric representation of a circle to obtain the representation ct = 7 cos t,7 sin t = 9 This is a circle of radius 7 centered at 9,. Using the parametric representation of a circle we get ct = cos t, + 7 sin t = 5 This is an ellipse centered at the origin with a = 5 and b =. Using the parametric representation of an ellipse we get ct = 5 cos t, sin t for t. 9. Line of slope 8 through, 9 Using the parametric representation of a line given in Eample, we get the parametrization ct = + t,9 + 8t.. Line through, 5 perpendicular to = The line perpendicular to = has slope m =. We use the parametric representation of a line given in Eample to obtain the parametrization ct = + t,5 t. April,
8 SECTION. Parametric Equations 89. Line through, and 5, We use the two-point parametrization of a line with P = a, b =, and Q = c, d = 5,. Then ct = 8t, + t for <t<.. Line through, 6 and 7 6, 5 We use the two-point parametrization of a line with P = a, b =, 6 and Q = c, d = 7 6, 5. Then ct = t, 6 + t for <t<.. Segment joining, and, We use the two-point parametrization of a line with P = a, b =, and Q = c, d =,. Then ct = + t, + t; since we want onl the segment joining the two points, we want t.. Segment joining, and, We use the two-point parametrization of a line with P = a, b =, and Q = c, d =,. Then ct = + t,t; since we want onl the segment joining the two points, we want t. 5. Circle of radius with center, 9 Substituting a, b =, 9 and R = in the parametric equation of the circle we get ct = + cos t,9 + sin t. 6. Ellipse of Eercise 8, with its center translated to 7, Since the center is translated b 7,, so is ever point. Thus the original parametrization becomes ct = cos t, + sin t for t. 7. =, translated so that the minimum occurs at, 8 We ma parametrize = b t, t for <t<. The minimum of = occurs at,, so the desired curve is translated b, 8 from =. Thus a parametrization of the desired curve is ct = + t, 8 + t. 8. = cos translated so that a maimum occurs at, 5 A maimum value of = cos occurs at =. Hence, the curve = cos, or = + cos has a maimum at the point, 5. We let t =, then = t + and = + cos t. We obtain the representation ct = t +, + cos t. In Eercises 9, find a parametrization ct of the curve satisfing the given condition. 9. =, c =, Let t = t + a and t = = t + a. We want =, thus we must use a =. Our line is ct = t, t = t +, t + = t +, t +.. =, c =, Let t = t + a; since = we have = + a so that a =. Then = = t = t 7, so that the line is ct = t, t 7 for <t<.. =, c =, 9 Let t = t + a and t = = t + a. We want =, thus we must use a =. Our curve is ct = t, t = t +,t + = t +,t + 6t =, c =, This is a circle of radius centered at the origin, so we are looking for a parametrization of that circle that starts at a different point. Thus instead of the standard parametrization cos θ,sin θ, θ = must correspond to some other angle ω. We choose the parametrization cosθ + ω, sinθ + ω and must determine the value of ω. Now, Since =, so = cos + ω = cos ω and ω = cos = or 5 =, we have = sin + ω = sin ω and ω = sin = or Comparing these results we see that we must have ω = so that the parametrization is ct = cos θ +, sin θ + April,
9 9 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS. Describe ct = sec t,tan t for t< in the form = f. Specif the domain of. The function = sec t has period and = tan t has period. The graphs of these functions in the interval t, are shown below: p p p p p p p p = sec t = tan t = sec t = sec t = tan t = tan t = sin t cos t = cos t cos = sec t = t Hence the graph of the curve is the hperbola =. The function = sec t is an even function while = tan t is odd. Also has period and has period. It follows that the intervals t<, <t< and <t< trace the curve eactl once. The corresponding curve is shown net: p t = t = p t = p t = t = p +,, p t = + ct = sec t,tan t. Find a parametrization of the right branch > of the hperbola = a b using the functions cosh t and sinh t. How can ou parametrize the branch <? We show first that = cosh t, = sinh t parametrizes the hperbola when a = b = : then = cosh t sinh t =. using the identit cosh sinh =. Generalize this parametrization to get a parametrization for the general hperbola a b = : = a cosh t, = b sinh t. We must of course check that this parametrization indeed parametrizes the curve, i.e. that = a cosh t and = b sin t satisf the equation a b = : a cosh t b sinh t = = cosh t sinh t =. a b a b The left branch of the hperbola is the reflection of the right branch around the line =, so it clearl has the parametrization = a cosh t, = b sinh t. 5. The graphs of t and t as functions of t are shown in Figure 5A. Which of I III is the plot of ct = t, t? Eplain. t t t A I FIGURE 5 II III April,
10 SECTION. Parametric Equations 9 As seen in Figure 5A, the -coordinate is an increasing function of t, while t is first increasing and then decreasing. In Figure I, and are both increasing or both decreasing depending on the direction on the curve. In Figure II, does not maintain one tendenc, rather, it is decreasing and increasing for certain values of t. The plot ct = t, t is plot III. 6. Which graph, I or II, is the graph of t and which is the graph of t for the parametric curve in Figure 6A? t t A I FIGURE 6 II As indicated b Figure 6A, the -coordinate is decreasing and then increasing, so plot I is the graph of. Figure 6A also shows that the -coordinate is increasing, decreasing and then increasing, so plot II is the graph for. 7. Sketch ct = t t,t following the steps in Eample 7. We note that t = t t is odd and t = t is even, hence c t = t, t = t, t. It follows that c tis the reflection of ct across -ais. That is, c tand ct are smmetric with respect to the -ais; thus, it suffices to graph the curve for t. For t =, we have c =, and the -coordinate t = t tends to as t. To analze the -coordinate, we graph t = t t for t : 8 6 = t t We see that t < and decreasing for <t</, t < and increasing for / <t< and t > and increasing for t>. Also t tends to as t. Therefore, starting at the origin, the curve first directs to the left of the -ais, then at t = / it turns to the right, alwas keeping an upward direction. The part of the path for t is obtained b reflecting across the -ais. We also use the points c =,, c =,, c =, to obtain the following graph for ct: t =, t = t = t =, t = t = t = t = Graph of ct for t. Graph of ct for all t. 8. Sketch ct = t t,9 t for t. The graphs of t = t t and t = 9 t for t are shown in the following figures: April,
11 9 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS t = t t t = 9 t The curve starts at c =, 7. For <t<, t is decreasing and t is increasing, so the graph turns to the left and upwards to c =, 9. Then for <t<, t is decreasing and so is t, hence the graph turns to the left and downwards towards c =, 5. For <t<, t is increasing and t is decreasing, hence the graph turns to the right and downwards, ending at c = 6, 9. The intercept are the points where t t = tt = or9 t =, that is t =,, ±. These are the points c =, 9, c =, 7, c =,, c =,. These properties lead to the following path: t =, 9 t =,, 5, t =,, t = t =, 7 t =, 7 In Eercises 9 5, use Eq. 7 to find d/d at the given point. 9. t,t, t = B Eq. 7 we have d d = t t = t t = t t = t Substituting t = weget d d = t = t= = t + 9, 7t 9, t = We find d d : d 7t 9 = d t + 9 = 7 d d = 7 t=. 5. s s, s, s = Using Eq. 7 we get d d = s s = s s s = s s = s s Substituting s = we obtain d d = s s = s= =. April,
12 SECTION. Parametric Equations 9 5. sin θ,cos θ, θ = 6 Using Eq. 7 we get d d = θ sin θ = θ cos θ Substituting θ = 6 we get d d = sin θ cos θ = sin θ=/6 cos = = In Eercises 5 56, find an equation = ffor the parametric curve and compute d/d in two was: using Eq. 7 and b differentiating f. 5. ct = t +, 9t Since = t +, we have t =. Substituting in = 9t we have = 9 = 9 + Differentiating = ct = t, t t d gives d = 9 d. We now find using Eq. 7: d d d = t 9t = t t + = 9 Since = t we have t =. Substituting in = t t ields = =. We differentiate = : Now, we find d d using Eq. 7. Thus, d d = t t = Since t =, then this t is the same as. 55. = s, = s 6 + s d d = t t t = t = t. We find as a function of : = s 6 + s = s + s = +. We now differentiate = +. This gives d d =. Alternativel, we can use Eq. 7 to obtain the following derivative: d d = s s 6 + s s = s = 6s5 s s = s s 6. Hence, since = s, d d =. April,
13 9 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS 56. = cos θ, = cos θ + sin θ To find as a function of, we first use the trigonometric identit sin θ = cos θ to write = cos θ + cos θ. We substitute = cos θ to obtain = +. Differentiating this function ields d d =. Alternativel, we can compute d d using Eq. 7. That is, Hence, since = cos θ, d d = θ θ = cos θ + sin θ cos θ = d d =. sin θ + sin θ cos θ sin θ = cos θ. 57. Find the points on the curve ct = t t,t 6t where the tangent line has slope. We solve d d = t 6 6t = or t 6 = 8t 6, or t 6t =, so the slope is at t =, 6 and the points are, and 96, Find the equation of the tangent line to the ccloid generated b a circle of radius at t =. The ccloid generated b a circle of radius can be parametrized b ct = t sin t, cos t Then we compute d d = sin t t=/ cos t = t=/ = so that the slope of the tangent line is and the equation of the tangent line is cos = sin or = + 8 In Eercises 59 6, let ct = t 9,t 8t see Figure 7. 6 FIGURE 7 Plot of ct = t 9,t 8t. 59. Draw an arrow indicating the direction of motion, and determine the interval of t-values corresponding to the portion of the curve in each of the four quadrants. We plot the functions t = t 9 and t = t 8t: 6 t t = t 9 = t 8t April,
14 SECTION. Parametric Equations 95 We note carefull where each of these graphs are positive or negative, increasing or decreasing. In particular, t is decreasing for t<, increasing for t>, positive for t >, and negative for t <. Likewise, t is decreasing for t<, increasing for t>, positive for t>8ort<, and negative for <t<8. We now draw arrows on the path following the decreasing/increasing behavior of the coordinates as indicated above. We obtain: 6 t = 9, t =, 5 t =, t = 7, 6 t = 8 55, 6 This plot also shows that: The graph is in the first quadrant for t< ort>8. The graph is in the second quadrant for <t<. The graph is in the third quadrant for <t<. The graph is in the fourth quadrant for <t<8. 6. Find the equation of the tangent line at t =. Using the formula for the slope m of the tangent line we have: m = d t 8t d = t= t 9 = t 8 t= = t= t t t= =. Since the slope is zero, the tangent line is horizontal. The -coordinate corresponding to t = is = 8 = 6. Hence the equation of the tangent line is = Find the points where the tangent has slope. The slope of the tangent at t is d t 8t d = t 9 = t 8 t = t The point where the tangent has slope corresponds to the value of t that satisfies d d = t = t = t = 8. We substitute t = 8int = t 9 and t = t 8t to obtain the following point: 8 = 8 9 = 55 8 = = 55, 6. Find the points where the tangent is horizontal or vertical. In Eercise 6 we found that the slope of the tangent at t is d d = t = t t The tangent is horizontal where its slope is zero. We set the slope equal to zero and solve for t. This gives t = t =. t The corresponding point is, = 9, 8 = 7, 6. The tangent is vertical where it has infinite slope; that is, at t =. The corresponding point is, = 9, 8 = 9,. April,
15 96 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS 6. Let A and B be the points where the ra of angle θ intersects the two concentric circles of radii r<rcentered at the origin Figure 8. Let P be the point of intersection of the horizontal line through A and the vertical line through B. Epress the coordinates of P as a function of θ and describe the curve traced b P for θ. B A r P R FIGURE 8 We use the parametric representation of a circle to determine the coordinates of the points A and B. That is, A = r cos θ,r sin θ, B = R cos θ,rsin θ The coordinates of P are therefore P = R cos θ,r sin θ In order to identif the curve traced b P, we notice that the and coordinates of P satisf R = cos θ and r Hence + = cos θ + sin θ =. R r = sin θ. The equation + = R r is the equation of ellipse. Hence, the coordinates of P, R cos θ,r sin θ describe an ellipse for θ. 6. A -ft ladder slides down a wall as its bottom B is pulled awa from the wall Figure 9. Using the angle θ as parameter, find the parametric equations for the path followed b a the top of the ladder A, b the bottom of the ladder B, and c the point P located ft from the top of the ladder. Show that P describes an ellipse. A P =, 6 q B FIGURE 9 a We define the -coordinate sstem as shown in the figure: A q B April,
16 SECTION. Parametric Equations 97 As the ladder slides down the wall, the -coordinate of A is alwas zero and the -coordinate is = sin θ. The parametric equations for the path followed b A are thus =, = sin θ, θ is between and. The path described b A is the segment [, ] on the -ais. b As the ladder slides down the wall, the -coordinate of B is alwas zero and the -coordinate is = cos θ. The parametric equations for the path followed b B are therefore = cos θ, =, θ is between and. The path is the segment [, ] on the -ais. c The and coordinates of P are = cos θ, = 6 sin θ. The path followed b P has the following parametrization: cθ = cos θ,6 sin θ, θ is between and. q P, 6 q As shown in Eample, the corresponding path is a part of an ellipse. Since θ is varing between part of the ellipse in the first quadrant. and, we obtain the 6 April,
17 98 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS In Eercises 65 68, refer to the Bézier curve defined b Eqs. 8 and Show that the Bézier curve with control points has parametrization P =,, P =,, P = 6, 5, P = 7, ct = + 6t + t t, + t 5t 9t Verif that the slope at t = is equal to the slope of the segment P P. For the given Bézier curve we have a =, a =, a = 6, a = 7, and b =, b =, b = 5, b =. Substituting these values in Eq. 8 9 and simplifing gives t = t + 9t t + 8t t + 7t Then = t + t t + 9t t + t + 8t 8t + 7t = t + t t + 9t 8t + 9t + 8t 8t + 7t = t + t + 6t + t = t + 6t t + 5t t + t = t + t t + 6t t + t + 5t 5t + t = t + t t + 6t 7t + 6t + 5t 5t + t = + t 5t 9t ct = + 6t + t t, + t 5t 9t, t. We find the slope at t =. Using the formula for slope of the tangent line we get d d = + t 5t 9t t 7t + 6t + t t = 6 + 6t 9t d d = t= 6 =. The slope of the segment P P is the slope of the line determined b the points P =, and P =,. That is, = 8 =. We see that the slope of the tangent line at t = is equal to the slope of the segment P P, as epected. 66. Find an equation of the tangent line to the Bézier curve in Eercise 65 at t =. We have d d = t t 7t t = 6 6 t 9t so that at t =, d d = t=/ t 7t 6 + 6t 9t = t=/ 7 and = 9 9, = Thus the tangent line is = 9 or = Find and plot the Bézier curve ct passing through the control points P =,, P =,, P = 5,, P =, Setting a =, a =, a = 5, a =, and b =, b =, b =, b = into Eq. 8 9 and simplifing gives t = t + + 5t t + t = t + t t + 5t 5t + t = 9t + t 6t April,
18 SECTION. Parametric Equations 99 t = t + 6t t + t t + t = t + t t + 6t t + t + t t + t = 6t + 6t t + 6t t + 6t + t t + t = + 6t t We obtain the following equation ct = 9t + t 6t, + 6t t, t. The graph of the Bézier curve is shown in the following figure: 68. Show that a cubic Bézier curve is tangent to the segment P P at P. The equations of the cubic Bézier curve are t = a t + a t t + a t t + a t t = b t + b t t + b t t + b t We use the formula for the slope of the tangent line to find the slope of the tangent line at P. We obtain d d = t t = b t + b t t t + b t t t + b t a t + a t t t + a t t t + a t The slope of the tangent line at P is obtained b setting t = in. That is, m = + b + b + a + a = b b a a We compute the slope of the segment P P for P = a,b and P = a,b. We get m = b b a a Since the two slopes are equal, we conclude that the tangent line to the curve at the point P is the segment P P. 69. A bullet fired from a gun follows the trajector = at, = bt 6t a, b > Show that the bullet leaves the gun at an angle θ = tan b a and lands at a distance ab/6 from the origin. The height of the bullet equals the value of the -coordinate. When the bullet leaves the gun, t = tb 6t =. The s to this equation are t = and t = 6 b, with t = corresponding to the moment the bullet leaves the gun. We find the slope m of the tangent line at t = : d d = t t = b t m = b t a a = b t= a It follows that tan θ = a b or θ = tan b a. The bullet lands at t = 6 b. We find the distance of the bullet from the origin at this time, b substituting t = 6 b in t = at. This gives b = ab 6 6 April,
19 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS 7. Plot ct = t t,t t + 8 for t. Find the points where the tangent line is horizontal or vertical. The graph of ct = t t,t t + 8, t is shown in the following figure: 6 5 t =, 8 t =.5.,.8 t = 5, t =.5.,.8 t =, 5, t =.5.9, 5 5 t =.5.9, 5 5 We find the slope of the tangent line at t: d d = t = t t + 8 t t = t t t The tangent line is horizontal where d d =. That is, t t t = tt 6 = t =, t= 6,t= 6. We find the corresponding points b substituting these values of t in ct. We obtain: c =, 8, c 6.9,, c 6.9,. The tangent line is vertical where the slope in is infinite, that is, where t = ort =± ±.5. We find the points b setting t =± in ct. We get c.,.8, c., Plot the astroid = cos θ, = sin θ and find the equation of the tangent line at θ =. The graph of the astroid = cos θ, = sin θ is shown in the following figure: =, =, =, =, The slope of the tangent line at θ = is m = d d = sin θ θ=/ cos θ = sin θ cos θ θ=/ cos θ sin θ = sin θ θ=/ cos θ = tan θ = θ=/ / We find the point of tangenc:, = cos, sin = 8, 8 The equation of the tangent line at θ = is, thus, = = Find the equation of the tangent line at t = to the ccloid generated b the unit circle with parametric equation 5. We find the equation of the tangent line at t = to the ccloid = t sin t, = cos t. We first find the derivative d d : April,
20 SECTION. Parametric Equations d d = t cos t = t t sin t = sin t cos t The slope of the tangent line at t = is therefore: m = d d = sin t=/ cos = = We find the point of tangenc: The equation of the tangent line is, thus, =, = sin, cos = =, + 7. Find the points with horizontal tangent line on the ccloid with parametric equation 5. The parametric equations of the ccloid are = t sin t, = cos t We find the slope of the tangent line at t: d cos t = d t sin t = sin t cos t The tangent line is horizontal where it has slope zero. That is, d d = sin t cos t = sin t = cos t = t = k, k =, ±, ±,... We find the coordinates of the points with horizontal tangent line, b substituting t = k in t and t. This gives The required points are = k sink = k = cosk = = k,, k =, ±, ±, Propert of the Ccloid Prove that the tangent line at a point P on the ccloid alwas passes through the top point on the rolling circle as indicated in Figure. Assume the generating circle of the ccloid has radius. Tangent line Ccloid FIGURE The definition of the ccloid is such that at time t, the top of the circle has coordinates Q = t, since at time t = the circle has rotated eactl once, and its circumference is. Let L be the line through P and Q. To show that L is tangent to the ccloid at P it suffices to show that the slope of L equals the slope of the tangent at P. Recall that the ccloid is parametrized b ct = t sin t, cos t. Then the slope of L is cos t t t sin t = + cos t sin t and the slope of the tangent line is t cos t = t t sin t = sin t sin t + cos t sin t + cos t = cos t cos = t sin = + cos t t sin t and the two are equal. April,
21 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS 75. A curtate ccloid Figure is the curve traced b a point at a distance h from the center of a circle of radius R rolling along the -ais where h<r. Show that this curve has parametric equations = Rt h sin t, = R h cos t. h R FIGURE Curtate ccloid. Let P be a point at a distance h from the center C of the circle. Assume that at t =, the line of CP is passing through the origin. When the circle rolls a distance Rt along the -ais, the length of the arc ŜQ see figure is also Rt and the angle SCQ has radian measure t. We compute the coordinates and of P. C S P h t A C R Rt Q = Rt PA = Rt h sin t = Rt h sin t = R + AC = R + h cos t = R h cos t We obtain the following parametrization: = Rt h sin t, = R h cos t. 76. Use a computer algebra sstem to eplore what happens when h>rin the parametric equations of Eercise 75. Describe the result. Look first at the parametric equations = hsin t, = hcos t. These describe a circle of radius h. See for instance the graphs below obtained for h = and h = ct = h*sint, h*cost h =, 5 Adding R to the coordinate to obtain the parametric equations = h sin t, = R h cos t, ields a circle with its center moved up b R units: ct = h*sint, R h*cost R =, 5 h = 5 April,
22 SECTION. Parametric Equations Now, we add Rt to the coordinate to obtain the given parametric equation; the curve becomes a spring. The figure below shows the graphs obtained for R = and various values of h. We see the inner loop formed for h>r Show that the line of slope t through, intersects the unit circle in the point with coordinates = t t +, = t t + Conclude that these equations parametrize the unit circle with the point, ecluded Figure. Show further that t = / +., Slope t, FIGURE Unit circle. The equation of the line of slope t through, is = t +. The equation of the unit circle is + =. Hence, the line intersects the unit circle at the points, that satisf the equations: Substituting from equation into equation and solving for we obtain This gives = t + + = + t + = + t + t + t = + t + t + t =, = t ± t t + t + t = t ± ± t + t = + t So = and = t t. The = corresponds to the point,. We are interested in the second + point of intersection that is varing as t varies. Hence the appropriate is = t t + We find the -coordinate b substituting in equation. This gives t = t + = t t + + = t t + t + t + = t t + We conclude that the line and the unit circle intersect, besides at,, at the point with the following coordinates: = t t +, = t t + April,
23 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS Since these points determine all the points on the unit circle ecept for, and no other points, the equations in parametrize the unit circle with the point, ecluded. We show that t =. Using we have + + = t t + t t + + = t t + t +t + t + = t t + t + = t = t. 78. The folium of Descartes is the curve with equation + = a, where a = is a constant Figure. a Show that the line = t intersects the folium at the origin and at one other point P for all t =,. Epress the coordinates of P in terms of t to obtain a parametrization of the folium. Indicate the direction of the parametrization on the graph. b Describe the interval of t-values parametrizing the parts of the curve in quadrants I, II, and IV. Note that t = isa point of discontinuit of the parametrization. c Calculate d/d as a function of t and find the points with horizontal or vertical tangent. II I III IV FIGURE Folium + = a. a We find the points where the line = t t =, and the folium intersect, b solving the following equations: Substituting from in and solving for we get = t + = a + t = at + t at = + t at = =, = Substituting in we find the corresponding -coordinates. That is, at + t at = t =, = t + t = at + t We conclude that the line = t, t =, intersects the folium in a unique point P besides the origin. The coordinates of P are: = at at,=, t =, + t + t The coordinates of P determine a parametrization for the folium. We add the origin so t = must be included in the interval of t. We get at ct = + t, at + t, t = To indicate the direction on the curve for a>, we first consider the following limits: lim t = lim t lim t = lim t t t = lim t = lim t + lim t = t t = t t lim t = lim t t = t = t + lim t = t April,
24 SECTION. Parametric Equations 5 These limits determine the directions of the two parts of the folium in the second and fourth quadrant. The loop in the first quadrant, corresponds to the values t<, and it is directed from c = a, a to c = a, a where t = and t = are two chosen values in the interval t<. The following graph shows the directed folium: < t < < t < t < t = + t = t = t = b The limits computed in part a indicate that the parts of the curve in the second and fourth quadrants correspond to the values <t< and <t< respectivel. The loop in the first quadrant corresponds to the remaining interval t<. c We find the derivative d d, using the Formula for the Slope of the Tangent Line. We get at d d = t t = +t at = +t t = 6at+t at t +t 6at at = a+t at t a 6at = t t t +t Horizontal tangent occurs when d d =. That is, t t t = t t =, t = t =,t =. The corresponding points are: c =, =, c =, = Vertical tangent line occurs when d d is infinite. That is, t = t = The corresponding point is c =, = a +, a = a,a + a a +, + = a, a. 79. Use the results of Eercise 78 to show that the asmptote of the folium is the line + = a. Hint: Show that lim + = a. t We must show that as or the graph of the folium is getting arbitraril close to the line + = a, and the derivative d d is approaching the slope of the line. In Eercise 78 we showed that when t and when t +. We first show that the graph is approaching the line + = a as or, b showing that lim + = lim + = a. t t + For t = at at, t =, a>, calculated in Eercise 78, we obtain using L Hôpital s Rule: + t + t We now show that d d 78 to obtain lim + = lim t lim + = lim t + t t + at + at + t = lim t at + at + t = lim t + a + 6at t a + 6at t is approaching ast and as t +. We use d d d lim t d = lim 6at at t a 6at = = = 9a 9a = a 6a a 6a = a = a 6at at = computed in Eercise a 6at April,
25 6 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS d lim t + d = lim 6at at t + a 6at = 9a 9a = We conclude that the line + = a is an asmptote of the folium as and as. 8. Find a parametrization of n+ + n+ = a n n, where a and n are constants. Following the method in Eercise 78, we first find the coordinates of the point P where the curve and the line = t intersect. We solve the following equations: = t n+ + n+ = a n n Substituting = t in the second equation and solving for ields n+ + t n+ n+ = a n t n n + t n+ n+ at n n = n + t n+ at n = =, = at n + t n+ We assume that t = so + t n+ = and obtain one besides the origin. The corresponding coordinates are at n atn+ = t = t = + tn+ + t n+ at n atn+ Hence, the points =, =, t =, are eactl the points on the curve. We obtain the following + tn+ + tn+ parametrization: at n atn+ =,=, t =. + tn+ + tn+ 8. Second Derivative for a Parametrized Curve Given a parametrized curve ct = t, t, show that Use this to prove the formula d dt d = t t t t d t d d = t t t t t B the formula for the slope of the tangent line we have d d = t t Differentiating with respect to t, using the Quotient Rule, gives B the Chain Rule we have d dt d = d d dt d d = d d t = t t t t t t d = d d dt d dt d d Substituting into the above equation and using dt d = d/dt = gives t d d = t t t t t t = t t t t t April,
26 SECTION. Parametric Equations 7 8. The second derivative of = is d /d =. Verif that Eq. applied to ct = t, t ields d /d =. In fact, an parametrization ma be used. Check that ct = t,t 6 and ct = tan t,tan t also ield d /d =. For the parametrization ct = t, t, we have so that indeed For ct = t,t 6, we have so that again Finall, for ct = tan t,tan t, and t =, t =, t = t, t = t t t t t = t = t = t, t = 6t, t = 6t 5, t = t t t t t t = t t 6t 5 6t t = 5t6 7t 6 = t = sec t, t = tan t sec t, t = tan t sec t, t = 6 sec t sec t t t t t t = sec t6 sec t sec t tan t sec t tan t sec t sec 6 t = 6 sec6 t sec t sec t tan t sec 6 t = sec6 t sec 6 = t = 6 sec6 t sec t + sec t sec 6 t In Eercises 8 86, use Eq. to find d /d. 8. = t + t, = 7t, t = We find the first and second derivatives of t and t: t = t + t = + = 6 t = 6t + = 6 + = t = t = = 8 t = = Using Eq. we get d d = t t t t t= t = t= = 5 8. = s + s, = s, s = s =. Since s = s + = s, we have =. Hence, Eq. cannot be used to compute d d at 85. = 8t + 9, = t, t = We compute the first and second derivatives of t and t: t = 8 = 8 t = = t = = t = = April,
27 8 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS Using Eq. we get d d = t= = 8 8 = 86. = cos θ, = sin θ, θ = We find the first and second derivatives of θ and θ: θ = sin θ = θ = cos θ = θ = cos θ = θ = sin θ = Using Eq. we get d d = θ= = 87. Use Eq. to find the t-intervals on which ct = t,t t is concave up. = The curve is concave up where d >. Thus, d t t t t t > We compute the first and second derivatives: t = t, t = t = t, t = 6t Substituting in and solving for t gives t 6t 8 8t = 6t + 8 8t Since 6t + 8 > for all t, the quotient is positive if 8t >. We conclude that the curve is concave up for t>. 88. Use Eq. to find the t-intervals on which ct = t,t t is concave up. The curve is concave up where d >. That is, d t t t t t > We compute the first and second derivatives: Substituting in and solving for t gives t = t, t = t = t, t = t t 8t 8 8t = 6t + 8 8t = + t This is clearl positive for t>. For t<, we want + t >, which means t >, so t < b taking the reciprocal of both sides, so t<. Thus, we see that our curve is concave up for t< and for t>. April,
28 SECTION. Parametric Equations Area Under a Parametrized Curve Let ct = t, t, where t > and t > Figure. Show that the area A under ct for t t t is t A = t t dt t Hint: Because it is increasing, the function t has an inverse t = g and ct is the graph of = g. Appl the change-of-variables formula to A = t t gd. ct t FIGURE t Let = t and = t. We are given that t >, hence = t is an increasing function of t, so it has an inverse function t = g. The area A is given b gd. Recall that is a function of t and t = g, so the height at an point is given b = g. We find the new limits of integration. Since = t and = t, the limits for t are t and t, respectivel. Also since t = d dt, we have d = tdt. Performing this substitution gives t A = gd = g t dt. Since g = t, we have A = t t t t dt. 9. Calculate the area under = over [, ] using Eq. with the parametrizations t,t 6 and t,t. The area A under = on [, ] is given b the integral A = t t t t t dt where t = and t =. We first use the parametrization t,t 6. We have t = t, t = t 6. Hence, = t = t t = = t = t t = Also t = t. Substituting these values in Eq. we obtain A = t 6 t dt = t 8 dt = 9 t9 = 9 = Using the parametrization t = t, t = t, we have t = t. We find t and t : = t = t t = = t = t t = or t =. Equation is valid if t >, that is if t>. Hence we choose the positive value, t =. We now use Eq. to obtain A = t t dt= t 5 dt = 6 t6 = 6 = Both answers agree, as epected. 9. What does Eq. sa if ct = t, f t? In the parametrization t = t, t = ft we have t =, t = t, t = t. Hence Eq. becomes t t A = t t dt = ftdt t t We see that in this parametrization Eq. is the familiar formula for the area under the graph of a positive function. April,
29 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS 9. Sketch the graph of ct = ln t, t for t and compute the area under the graph using Eq.. We use the following graphs of t = ln t and t = t for t : t t t = ln t t = t We see that for <t<, t is positive and increasing and t is positive and decreasing. Also c = ln, =, and c = ln, = ln,. Additional information is obtained from the derivative d t = d ln t = /t = t, ielding d d t= and d d. t= We obtain the following graph:, t = ln, t = t We now use Eq. to compute the area A under the graph. We have t = ln t, t = t, t = t, t =, t =. Hence, t A = t t dt = t t t dt = t dt = lnt t = ln ln = ln Galileo tried unsuccessfull to find the area under a ccloid. Around 6, Gilles de Roberval proved that the area under one arch of the ccloid ct = Rt R sin t,r R cos t generated b a circle of radius R is equal to three times the area of the circle Figure 5. Verif Roberval s result using Eq.. R R R FIGURE 5 The area of one arch of the ccloid equals three times the area of the generating circle. This reduces to R R cos trt R sin t dt = R cos t dt = R. April,
30 SECTION. Parametric Equations Further Insights and Challenges 9. Prove the following generalization of Eercise 9: For all t>, the area of the ccloidal sector OPC is equal to three times the area of the circular segment cut b the chord PC in Figure 6. P t R P t R O C = Rt, O C = Rt, A Ccloidal sector OPC FIGURE 6 B Circular segment cut b the chord PC Drop a perpendicular from point P to the -ais and label the point of intersection T, and denote b D the center of the circle. Then the area of the ccloidal sector is equal to the area of OPT plus the area of PTC. The latter is a triangle with height t = R R cos t and base Rt Rt R sin t = R sin t, so its area is R sin t cos t. The area of OPT, using Eq., is t t t u u du = R R cos uru R sin u du = R cos u du = R t sin t + sin t cos t so that the total area of the ccloidal sector is R t sin t + sin t cos t + R sin t cos t = R t R sin t = R t sin t The area of the circular segment is the area of the circular sector DPC subtended b the angle t less the area of the triangle DPC. The triangle DPC has height R cos t and base R sin t so that its area is R cos t sin t = R sin t, and the area of the circular sector is R which is one third the area of the ccloidal sector. t = R t. Thus the area of the circular segment is R t sin t 95. Derive the formula for the slope of the tangent line to a parametric curve ct = t, t using a method different from that presented in the tet. Assume that t and t eist and that t =. Show that t lim + h t h t + h t = t t Then eplain wh this limit is equal to the slope d/d. Draw a diagram showing that the ratio in the limit is the slope of a secant line. Since t and t eist, we have the following limits: t lim + h t = t t, lim + h t = t h h h h We use Basic Limit Laws, the limits in and the given data t =, to write t t lim + h t +h t h t + h t = lim h h t +h t h = lim h t +h t h t lim +h t h h = t t Notice that the quotient t + h t t + h t is the slope of the secant line determined b the points P = t, t and Q = t + h, t + h. Hence, the limit of the quotient as h is the slope of the tangent line at P, that is the derivative d d. April,
31 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS t, h Q t P t t + h 96. Verif that the tractri curve l > ct = t l tanh t l,lsech t l has the following propert: For all t, the segment from ct to t, is tangent to the curve and has length l Figure 7. ct FIGURE 7 The tractri ct = t t l tanh t l,lsech t. l Let P = ct and Q = t,. Pt, t Q = t, The slope of the segment PQis m = t t t = l sech t l l tanh t l = sinh t l We compute the slope of the tangent line at P : m = d d = t l sech tl t = t l tanh tl = l l sech tl tanh tl l l sech t l = sech t l tanh tl sech t = sech tl tanh tl l tanh t l = sech tl tanh t = l sinh t l Since m = m, we conclude that the segment from ct to t, is tangent to the curve. We now show that PQ =l: PQ = t t + t = = = l sech l tanh t l t l l tanh t t + l sech l l + sech t = l sech t sinh t + sech t l l l l sinh t + = l sech l t cosh l t = l = l l April,
32 SECTION. Parametric Equations 97. In Eercise 5 of Section. ET Eercise 5 of Section 9., we described the tractri b the differential equation d d = l Show that the curve ct identified as the tractri in Eercise 96 satisfies this differential equation. Note that the derivative on the left is taken with respect to, not t. Note that d/dt = sech t/l = tanh t/l and d/dt = secht/l tanht/l. Thus, Multipling top and bottom b l/l gives d d = d/dt d/dt = secht/l /l = tanht/l /l d d = l In Eercises 98 and 99, refer to Figure In the parametrization ct = a cos t,bsin t of an ellipse, t is not an angular parameter unless a = b in which case the ellipse is a circle. However, t can be interpreted in terms of area: Show that if ct =,, then t = /aba, where A is the area of the shaded region in Figure 8. Hint: Use Eq.., q FIGURE 8 The parameter θ on the ellipse + =. a b We compute the area A of the shaded region as the sum of the area S of the triangle and the area S of the region under the curve. The area of the triangle is S = = a cos tb sin t = ab sin t, S S The area S under the curve can be computed using Eq.. The lower limit of the integration is t = corresponds to a, and the upper limit is t corresponds to t, t. Also t = b sin t and t = asin t. Since t < on the interval <t< which represents the ellipse on the first quadrant, we use the positive value a sin t to obtain a positive value for the area. This gives Combining and we obtain t S = t b sin u a sin udu= ab cos u du = ab ] t = ab [ t sin t = ab = abt sin udu [ ] u sin u t ab sin t Hence, t = A ab. A = S + S = ab sin t + abt ab sin t = abt April,
33 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS 99. Show that the parametrization of the ellipse b the angle θ is ab cos θ = a sin θ + b cos θ ab sin θ = a sin θ + b cos θ We consider the ellipse a + b =. For the angle θ we have tan θ =, hence, Substituting in the equation of the ellipse and solving for we obtain a + tan θ b = b + a tan θ = a b a tan θ + b = a b = a b a tan θ + b = = tan θ a b cos θ a sin θ + b cos θ We now take the square root. Since the sign of the -coordinate is the same as the sign of cos θ, we take the positive root, obtaining ab cos θ = a sin θ + b cos θ Hence b, the -coordinate is ab cos θ tan θ = tan θ = a sin = θ + b cos θ ab sin θ a sin θ + b cos θ Equalities and give the following parametrization for the ellipse: ab cos θ ab sin θ c θ = a sin, θ + b cos θ a sin θ + b cos θ. Arc Length and Speed Preliminar Questions. What is the definition of arc length? A curve can be approimated b a polgonal path obtained b connecting points p = ct, p = ct,...,p N = ct N on the path with segments. One gets an approimation b summing the lengths of the segments. The definition of arc length is the limit of that approimation when increasing the number of points so that the lengths of the segments approach zero. In doing so, we obtain the following theorem for the arc length: b S = t + t dt, a which is the length of the curve ct = t, t for a t b.. What is the interpretation of t + t for a particle following the trajector t, t? The epression t + t denotes the speed at time t of a particle following the trajector t, t. April,
34 SECTION. Arc Length and Speed 5. A particle travels along a path from, to,. What is the displacement? Can the distance traveled be determined from the information given? The net displacement is the distance between the initial point, and the endpoint,. That is + = 5 = 5. The distance traveled can be determined onl if the trajector ct = t, t of the particle is known.. A particle traverses the parabola = with constant speed cm/s. What is the distance traveled during the first minute? Hint: No computation is necessar. Since the speed is constant, the distance traveled is the following product: L = st = 6 = 8 cm. Eercises In Eercises, use Eq. to find the length of the path over the given interval.. t +, 9 t, t Since = t + and = 9 t we have = and =. Hence, the length of the path is S = + dt = 5 dt =.. + t, + t, t We have = + t and = + t, hence = and =. Using the formula for arc length we obtain S = + dt = dt = = 6 5. t, t, t Since = t and = t, we have = t and = 6t. B the formula for the arc length we get S = t + t dt = 6t + 6t dt = 5 tdt= 5 t = 6. t,t /, t We have = t and = t /, hence = and = 6t /. Using the formula for the arc length we obtain S = t + t dt = + 6t / dt = 9 + 6t dt= + t dt Setting u = + t we get S = 5 udu= 5 u/ = 5/ t, t, t We have = t and = t. Hence = 6t and = t. B the formula for the arc length we get S = t + t dt = 6t + t dt = 6 + t tdt. Using the substitution u = + t, du = 8t dtwe obtain S = 6 65 udu= u/ = 5 65/ 5 / 56. April,
35 6 CHAPTER PARAMETRIC EQUATIONS, POLAR COORDINATES, AND CONIC SECTIONS 6. t +,t, t We have = t +, = t, hence, = t and = t. B the formula for the arc length we get S = t + t dt = 9t + t dt = t 9t + dt We compute the integral using the substitution u = + 9t. This gives S = udu= 8 8 u/ = 7 / / = 7 / sin t,cos t, t We have = sin t, = cos t, hence = cos t and = sin t. B the formula for the arc length we obtain: S = t + t dt = 9 cos t + 9 sin tdt= 9 dt = 8. sin θ θ cos θ,cos θ + θ sin θ, θ We have = sin θ θ cos θ and = cos θ + θ sin θ. Hence, = cos θ cos θ θ sin θ = θ sin θ and = sin θ + sin θ + θ cos θ = θ cos θ. Using the formula for the arc length we obtain: S = θ + θ dθ = θ sin θ + θ cos θ dθ = θ sin θ + cos θdθ = θdθ= θ = In Eercises 9 and, use the identit cos t = sin t 9. cos t cos t, sin t sin t, t We have = cos t cos t, = sin t sin t. Thus, = sin t + sin t and = cos t cos t. We get t + t = sin t + sin t + cos t cos t = sin t 8 sin t sin t + sin t + cos t 8 cos t cos t + cos t = sin t + cos t + sin t + cos t 8sin t sin t + cos t cos t = + 8 cost t = 8 8 cos t = 8 cos t We now use the formula for the arc length to obtain / / S = t + t / = 8 cos tdt = 6 sin t / dt = sin t dt = 8cos t / = 8 cos cos = 8.. 5θ sin θ,5 cos θ, θ Since = 5θ sin θand = 5 cos θ, we have = 5 cos θand = 5 sin θ. Using the formula for the arc length we obtain: S = θ + θ dθ = 5 cos θ + 5 sin θdθ = 5 cos θ + cos θ + sin θdθ= 5 cos θdθ = 5 sin θ dθ = sin θ dθ = sin udu = cos u = =. April,
6 = 1 2. The right endpoints of the subintervals are then 2 5, 3, 7 2, 4, 2 9, 5, while the left endpoints are 2, 5 2, 3, 7 2, 4, 9 2.
 5 THE ITEGRAL 5. Approimating and Computing Area Preliminar Questions. What are the right and left endpoints if [, 5] is divided into si subintervals? If the interval [, 5] is divided into si subintervals,
5 THE ITEGRAL 5. Approimating and Computing Area Preliminar Questions. What are the right and left endpoints if [, 5] is divided into si subintervals? If the interval [, 5] is divided into si subintervals,
APPM 1360 Final Exam Spring 2016
 APPM 36 Final Eam Spring 6. 8 points) State whether each of the following quantities converge or diverge. Eplain your reasoning. a) The sequence a, a, a 3,... where a n ln8n) lnn + ) n!) b) ln d c) arctan
APPM 36 Final Eam Spring 6. 8 points) State whether each of the following quantities converge or diverge. Eplain your reasoning. a) The sequence a, a, a 3,... where a n ln8n) lnn + ) n!) b) ln d c) arctan
CHAPTER 11 Vector-Valued Functions
 CHAPTER Vector-Valued Functions Section. Vector-Valued Functions...................... 9 Section. Differentiation and Integration of Vector-Valued Functions.... Section. Velocit and Acceleration.....................
CHAPTER Vector-Valued Functions Section. Vector-Valued Functions...................... 9 Section. Differentiation and Integration of Vector-Valued Functions.... Section. Velocit and Acceleration.....................
Math 323 Exam 2 - Practice Problem Solutions. 2. Given the vectors a = 1,2,0, b = 1,0,2, and c = 0,1,1, compute the following:
 Math 323 Eam 2 - Practice Problem Solutions 1. Given the vectors a = 2,, 1, b = 3, 2,4, and c = 1, 4,, compute the following: (a) A unit vector in the direction of c. u = c c = 1, 4, 1 4 =,, 1+16+ 17 17
Math 323 Eam 2 - Practice Problem Solutions 1. Given the vectors a = 2,, 1, b = 3, 2,4, and c = 1, 4,, compute the following: (a) A unit vector in the direction of c. u = c c = 1, 4, 1 4 =,, 1+16+ 17 17
Review Exercises for Chapter 3. Review Exercises for Chapter r v 0 2. v ft sec. x 1 2 x dx f x x 99.4.
 Review Eercises for Chapter 6. r v 0 sin. Let f, 00, d 0.6. v 0 00 ftsec changes from 0 to dr 00 cos d 6 0 d 0 r dr 80 00 6 96 feet 80 cos 0 96 feet 8080 f f fd d f 99. 00 0.6 9.97 00 Using a calculator:
Review Eercises for Chapter 6. r v 0 sin. Let f, 00, d 0.6. v 0 00 ftsec changes from 0 to dr 00 cos d 6 0 d 0 r dr 80 00 6 96 feet 80 cos 0 96 feet 8080 f f fd d f 99. 00 0.6 9.97 00 Using a calculator:
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
13.1. For further details concerning the physics involved and animations of the trajectories of the particles, see the following websites:
 8 CHAPTER VECTOR FUNCTIONS N Some computer algebra sstems provide us with a clearer picture of a space curve b enclosing it in a tube. Such a plot enables us to see whether one part of a curve passes in
8 CHAPTER VECTOR FUNCTIONS N Some computer algebra sstems provide us with a clearer picture of a space curve b enclosing it in a tube. Such a plot enables us to see whether one part of a curve passes in
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
Chapter 1 Prerequisites for Calculus
 Section. Chapter Prerequisites for Calculus Section. Lines (pp. ) Quick Review.. + ( ) + () +. ( +). m. m ( ) ( ). (a) ( )? 6 (b) () ( )? 6. (a) 7? ( ) + 7 + Yes (b) ( ) + 9 No Yes No Section. Eercises.
Section. Chapter Prerequisites for Calculus Section. Lines (pp. ) Quick Review.. + ( ) + () +. ( +). m. m ( ) ( ). (a) ( )? 6 (b) () ( )? 6. (a) 7? ( ) + 7 + Yes (b) ( ) + 9 No Yes No Section. Eercises.
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 78 Section. Rolle s Theorem and the Mean Value Theorem. 8 Section. Increasing and Decreasing Functions and the First
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 78 Section. Rolle s Theorem and the Mean Value Theorem. 8 Section. Increasing and Decreasing Functions and the First
17.3. Parametric Curves. Introduction. Prerequisites. Learning Outcomes
 Parametric Curves 7.3 Introduction In this Section we eamine et another wa of defining curves - the parametric description. We shall see that this is, in some was, far more useful than either the Cartesian
Parametric Curves 7.3 Introduction In this Section we eamine et another wa of defining curves - the parametric description. We shall see that this is, in some was, far more useful than either the Cartesian
Infinite Limits. Let f be the function given by. f x 3 x 2.
 0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
APPENDIXES. B Coordinate Geometry and Lines C. D Trigonometry E F. G The Logarithm Defined as an Integral H Complex Numbers I
 APPENDIXES A Numbers, Inequalities, and Absolute Values B Coordinate Geometr and Lines C Graphs of Second-Degree Equations D Trigonometr E F Sigma Notation Proofs of Theorems G The Logarithm Defined as
APPENDIXES A Numbers, Inequalities, and Absolute Values B Coordinate Geometr and Lines C Graphs of Second-Degree Equations D Trigonometr E F Sigma Notation Proofs of Theorems G The Logarithm Defined as
CHAPTER 5 Logarithmic, Exponential, and Other Transcendental Functions
 CHAPTER 5 Logarithmic, Eponential, and Other Transcendental Functions Section 5. The Natural Logarithmic Function: Differentiation.... 9 Section 5. The Natural Logarithmic Function: Integration...... 98
CHAPTER 5 Logarithmic, Eponential, and Other Transcendental Functions Section 5. The Natural Logarithmic Function: Differentiation.... 9 Section 5. The Natural Logarithmic Function: Integration...... 98
Review of Essential Skills and Knowledge
 Review of Essential Skills and Knowledge R Eponent Laws...50 R Epanding and Simplifing Polnomial Epressions...5 R 3 Factoring Polnomial Epressions...5 R Working with Rational Epressions...55 R 5 Slope
Review of Essential Skills and Knowledge R Eponent Laws...50 R Epanding and Simplifing Polnomial Epressions...5 R 3 Factoring Polnomial Epressions...5 R Working with Rational Epressions...55 R 5 Slope
C H A P T E R 9 Topics in Analytic Geometry
 C H A P T E R Topics in Analtic Geometr Section. Circles and Parabolas.................... 77 Section. Ellipses........................... 7 Section. Hperbolas......................... 7 Section. Rotation
C H A P T E R Topics in Analtic Geometr Section. Circles and Parabolas.................... 77 Section. Ellipses........................... 7 Section. Hperbolas......................... 7 Section. Rotation
APPENDIX D Rotation and the General Second-Degree Equation
 APPENDIX D Rotation and the General Second-Degree Equation Rotation of Aes Invariants Under Rotation After rotation of the - and -aes counterclockwise through an angle, the rotated aes are denoted as the
APPENDIX D Rotation and the General Second-Degree Equation Rotation of Aes Invariants Under Rotation After rotation of the - and -aes counterclockwise through an angle, the rotated aes are denoted as the
11.4 Polar Coordinates
 11. Polar Coordinates 917 11. Polar Coordinates In Section 1.1, we introduced the Cartesian coordinates of a point in the plane as a means of assigning ordered pairs of numbers to points in the plane.
11. Polar Coordinates 917 11. Polar Coordinates In Section 1.1, we introduced the Cartesian coordinates of a point in the plane as a means of assigning ordered pairs of numbers to points in the plane.
Coordinate geometry. + bx + c. Vertical asymptote. Sketch graphs of hyperbolas (including asymptotic behaviour) from the general
 A Sketch graphs of = a m b n c where m = or and n = or B Reciprocal graphs C Graphs of circles and ellipses D Graphs of hperbolas E Partial fractions F Sketch graphs using partial fractions Coordinate
A Sketch graphs of = a m b n c where m = or and n = or B Reciprocal graphs C Graphs of circles and ellipses D Graphs of hperbolas E Partial fractions F Sketch graphs using partial fractions Coordinate
17.3. Parametric Curves. Introduction. Prerequisites. Learning Outcomes
 Parametric Curves 17.3 Introduction In this section we eamine et another wa of defining curves - the parametric description. We shall see that this is, in some was, far more useful than either the Cartesian
Parametric Curves 17.3 Introduction In this section we eamine et another wa of defining curves - the parametric description. We shall see that this is, in some was, far more useful than either the Cartesian
Department of Mathematical and Statistical Sciences University of Alberta
 MATH 4 (R) Winter 8 Intermediate Calculus I Solutions to Problem Set #5 Completion Date: Frida Februar 5, 8 Department of Mathematical and Statistical Sciences Universit of Alberta Question. [Sec.., #
MATH 4 (R) Winter 8 Intermediate Calculus I Solutions to Problem Set #5 Completion Date: Frida Februar 5, 8 Department of Mathematical and Statistical Sciences Universit of Alberta Question. [Sec.., #
McKinney High School AP Calculus Summer Packet
 McKinne High School AP Calculus Summer Packet (for students entering AP Calculus AB or AP Calculus BC) Name:. This packet is to be handed in to our Calculus teacher the first week of school.. ALL work
McKinne High School AP Calculus Summer Packet (for students entering AP Calculus AB or AP Calculus BC) Name:. This packet is to be handed in to our Calculus teacher the first week of school.. ALL work
Solutions to the Exercises of Chapter 4
 Solutions to the Eercises of Chapter 4 4A. Basic Analtic Geometr. The distance between (, ) and (4, 5) is ( 4) +( 5) = 9+6 = 5 and that from (, 6) to (, ) is ( ( )) +( 6 ( )) = ( + )=.. i. AB = (6 ) +(
Solutions to the Eercises of Chapter 4 4A. Basic Analtic Geometr. The distance between (, ) and (4, 5) is ( 4) +( 5) = 9+6 = 5 and that from (, 6) to (, ) is ( ( )) +( 6 ( )) = ( + )=.. i. AB = (6 ) +(
KEY IDEAS. Chapter 1 Function Transformations. 1.1 Horizontal and Vertical Translations Pre-Calculus 12 Student Workbook MHR 1
 Chapter Function Transformations. Horizontal and Vertical Translations A translation can move the graph of a function up or down (vertical translation) and right or left (horizontal translation). A translation
Chapter Function Transformations. Horizontal and Vertical Translations A translation can move the graph of a function up or down (vertical translation) and right or left (horizontal translation). A translation
PARAMETRIC EQUATIONS AND POLAR COORDINATES
 PARAMETRIC EQUATINS AND PLAR CRDINATES Parametric equations and polar coordinates enable us to describe a great variet of new curves some practical, some beautiful, some fanciful, some strange. So far
PARAMETRIC EQUATINS AND PLAR CRDINATES Parametric equations and polar coordinates enable us to describe a great variet of new curves some practical, some beautiful, some fanciful, some strange. So far
REVIEW OF CONIC SECTIONS
 REVIEW OF CONIC SECTIONS In this section we give geometric definitions of parabolas, ellipses, and hperbolas and derive their standard equations. The are called conic sections, or conics, because the result
REVIEW OF CONIC SECTIONS In this section we give geometric definitions of parabolas, ellipses, and hperbolas and derive their standard equations. The are called conic sections, or conics, because the result
Systems of Linear Equations: Solving by Graphing
 8.1 Sstems of Linear Equations: Solving b Graphing 8.1 OBJECTIVE 1. Find the solution(s) for a set of linear equations b graphing NOTE There is no other ordered pair that satisfies both equations. From
8.1 Sstems of Linear Equations: Solving b Graphing 8.1 OBJECTIVE 1. Find the solution(s) for a set of linear equations b graphing NOTE There is no other ordered pair that satisfies both equations. From
Not for reproduction
 REVIEW OF CONIC SECTIONS In this section we give geometric definitions of parabolas, ellipses, and hperbolas and derive their standard equations. The are called conic sections, or conics, because the result
REVIEW OF CONIC SECTIONS In this section we give geometric definitions of parabolas, ellipses, and hperbolas and derive their standard equations. The are called conic sections, or conics, because the result
3.7 InveRSe FUnCTIOnS
 CHAPTER functions learning ObjeCTIveS In this section, ou will: Verif inverse functions. Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
CHAPTER functions learning ObjeCTIveS In this section, ou will: Verif inverse functions. Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
Calculus III. George Voutsadakis 1. LSSU Math 251. Lake Superior State University. 1 Mathematics and Computer Science
 Calculus III George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 251 George Voutsadakis (LSSU) Calculus III January 2016 1 / 76 Outline 1 Parametric Equations,
Calculus III George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 251 George Voutsadakis (LSSU) Calculus III January 2016 1 / 76 Outline 1 Parametric Equations,
Lesson 9.1 Using the Distance Formula
 Lesson. Using the Distance Formula. Find the eact distance between each pair of points. a. (0, 0) and (, ) b. (0, 0) and (7, ) c. (, 8) and (, ) d. (, ) and (, 7) e. (, 7) and (8, ) f. (8, ) and (, 0)
Lesson. Using the Distance Formula. Find the eact distance between each pair of points. a. (0, 0) and (, ) b. (0, 0) and (7, ) c. (, 8) and (, ) d. (, ) and (, 7) e. (, 7) and (8, ) f. (8, ) and (, 0)
9.1. Click here for answers. Click here for solutions. PARAMETRIC CURVES
 SECTION 9. PARAMETRIC CURVES 9. PARAMETRIC CURVES A Click here for answers. S Click here for solutions. 5 (a) Sketch the curve b using the parametric equations to plot points. Indicate with an arrow the
SECTION 9. PARAMETRIC CURVES 9. PARAMETRIC CURVES A Click here for answers. S Click here for solutions. 5 (a) Sketch the curve b using the parametric equations to plot points. Indicate with an arrow the
DIFFERENTIATION. 3.1 Approximate Value and Error (page 151)
 CHAPTER APPLICATIONS OF DIFFERENTIATION.1 Approimate Value and Error (page 151) f '( lim 0 f ( f ( f ( f ( f '( or f ( f ( f '( f ( f ( f '( (.) f ( f '( (.) where f ( f ( f ( Eample.1 (page 15): Find
CHAPTER APPLICATIONS OF DIFFERENTIATION.1 Approimate Value and Error (page 151) f '( lim 0 f ( f ( f ( f ( f '( or f ( f ( f '( f ( f ( f '( (.) f ( f '( (.) where f ( f ( f ( Eample.1 (page 15): Find
UNCORRECTED SAMPLE PAGES. 3Quadratics. Chapter 3. Objectives
 Chapter 3 3Quadratics Objectives To recognise and sketch the graphs of quadratic polnomials. To find the ke features of the graph of a quadratic polnomial: ais intercepts, turning point and ais of smmetr.
Chapter 3 3Quadratics Objectives To recognise and sketch the graphs of quadratic polnomials. To find the ke features of the graph of a quadratic polnomial: ais intercepts, turning point and ais of smmetr.
Chapter 8 More About the Trigonometric Functions
 Relationships Among Trigonometric Functions Section 8. 8 Chapter 8 More About the Trigonometric Functions Section 8. Relationships Among Trigonometric Functions. The amplitude of the graph of cos is while
Relationships Among Trigonometric Functions Section 8. 8 Chapter 8 More About the Trigonometric Functions Section 8. Relationships Among Trigonometric Functions. The amplitude of the graph of cos is while
I. Degrees and Radians minutes equal 1 degree seconds equal 1 minute. 3. Also, 3600 seconds equal 1 degree. 3.
 0//0 I. Degrees and Radians A. A degree is a unit of angular measure equal to /80 th of a straight angle. B. A degree is broken up into minutes and seconds (in the DMS degree minute second sstem) as follows:.
0//0 I. Degrees and Radians A. A degree is a unit of angular measure equal to /80 th of a straight angle. B. A degree is broken up into minutes and seconds (in the DMS degree minute second sstem) as follows:.
Mathematics 309 Conic sections and their applicationsn. Chapter 2. Quadric figures. ai,j x i x j + b i x i + c =0. 1. Coordinate changes
 Mathematics 309 Conic sections and their applicationsn Chapter 2. Quadric figures In this chapter want to outline quickl how to decide what figure associated in 2D and 3D to quadratic equations look like.
Mathematics 309 Conic sections and their applicationsn Chapter 2. Quadric figures In this chapter want to outline quickl how to decide what figure associated in 2D and 3D to quadratic equations look like.
Trigonometric Functions
 Trigonometric Functions This section reviews radian measure and the basic trigonometric functions. C ' θ r s ' ngles ngles are measured in degrees or radians. The number of radians in the central angle
Trigonometric Functions This section reviews radian measure and the basic trigonometric functions. C ' θ r s ' ngles ngles are measured in degrees or radians. The number of radians in the central angle
13.1. For further details concerning the physics involved and animations of the trajectories of the particles, see the following websites:
 8 CHAPTER 3 VECTOR FUNCTIONS N Some computer algebra sstems provie us with a clearer picture of a space curve b enclosing it in a tube. Such a plot enables us to see whether one part of a curve passes
8 CHAPTER 3 VECTOR FUNCTIONS N Some computer algebra sstems provie us with a clearer picture of a space curve b enclosing it in a tube. Such a plot enables us to see whether one part of a curve passes
Differentiation and applications
 FS O PA G E PR O U N C O R R EC TE D Differentiation and applications. Kick off with CAS. Limits, continuit and differentiabilit. Derivatives of power functions.4 C oordinate geometr applications of differentiation.5
FS O PA G E PR O U N C O R R EC TE D Differentiation and applications. Kick off with CAS. Limits, continuit and differentiabilit. Derivatives of power functions.4 C oordinate geometr applications of differentiation.5
+ 4 Ex: y = v = (1, 4) x = 1 Focus: (h, k + ) = (1, 6) L.R. = 8 units We can have parabolas that open sideways too (inverses) x = a (y k) 2 + h
 Unit 7 Notes Parabolas: E: reflectors, microphones, (football game), (Davinci) satellites. Light placed where ras will reflect parallel. This point is the focus. Parabola set of all points in a plane that
Unit 7 Notes Parabolas: E: reflectors, microphones, (football game), (Davinci) satellites. Light placed where ras will reflect parallel. This point is the focus. Parabola set of all points in a plane that
HIGHER SCHOOL CERTIFICATE EXAMINATION MATHEMATICS 4 UNIT (ADDITIONAL) Time allowed Three hours (Plus 5 minutes reading time)
 N E W S O U T H W A L E S HIGHER SCHOOL CERTIFICATE EXAMINATION 996 MATHEMATICS 4 UNIT (ADDITIONAL) Time allowed Three hours (Plus 5 minutes reading time) DIRECTIONS TO CANDIDATES Attempt ALL questions.
N E W S O U T H W A L E S HIGHER SCHOOL CERTIFICATE EXAMINATION 996 MATHEMATICS 4 UNIT (ADDITIONAL) Time allowed Three hours (Plus 5 minutes reading time) DIRECTIONS TO CANDIDATES Attempt ALL questions.
8 Differential Calculus 1 Introduction
 8 Differential Calculus Introduction The ideas that are the basis for calculus have been with us for a ver long time. Between 5 BC and 5 BC, Greek mathematicians were working on problems that would find
8 Differential Calculus Introduction The ideas that are the basis for calculus have been with us for a ver long time. Between 5 BC and 5 BC, Greek mathematicians were working on problems that would find
Created by T. Madas. Candidates may use any calculator allowed by the regulations of this examination.
 IYGB GCE Mathematics SYN Advanced Level Snoptic Paper C Difficult Rating: 3.895 Time: 3 hours Candidates ma use an calculator allowed b the regulations of this eamination. Information for Candidates This
IYGB GCE Mathematics SYN Advanced Level Snoptic Paper C Difficult Rating: 3.895 Time: 3 hours Candidates ma use an calculator allowed b the regulations of this eamination. Information for Candidates This
Math 2250 Final Exam Practice Problem Solutions. f(x) = ln x x. 1 x. lim. lim. x x = lim. = lim 2
 Math 5 Final Eam Practice Problem Solutions. What are the domain and range of the function f() = ln? Answer: is only defined for, and ln is only defined for >. Hence, the domain of the function is >. Notice
Math 5 Final Eam Practice Problem Solutions. What are the domain and range of the function f() = ln? Answer: is only defined for, and ln is only defined for >. Hence, the domain of the function is >. Notice
Vector-Valued Functions
 Vector-Valued Functions 1 Parametric curves 8 ' 1 6 1 4 8 1 6 4 1 ' 4 6 8 Figure 1: Which curve is a graph of a function? 1 4 6 8 1 8 1 6 4 1 ' 4 6 8 Figure : A graph of a function: = f() 8 ' 1 6 4 1 1
Vector-Valued Functions 1 Parametric curves 8 ' 1 6 1 4 8 1 6 4 1 ' 4 6 8 Figure 1: Which curve is a graph of a function? 1 4 6 8 1 8 1 6 4 1 ' 4 6 8 Figure : A graph of a function: = f() 8 ' 1 6 4 1 1
EXERCISES Chapter 7: Transcendental Functions. Hyperbolic Function Values and Identities
 54 Chapter 7: ranscendental Functions EXERCISES 7.8 perbolic Function Values and Identities Each of Eercises 4 gives a value of sinh or cosh. Use the definitions and the identit cosh - sinh = to find the
54 Chapter 7: ranscendental Functions EXERCISES 7.8 perbolic Function Values and Identities Each of Eercises 4 gives a value of sinh or cosh. Use the definitions and the identit cosh - sinh = to find the
Section 1.2: A Catalog of Functions
 Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
39. (a) Use trigonometric substitution to verify that. 40. The parabola y 2x divides the disk into two
 35. Prove the formula A r for the area of a sector of a circle with radius r and central angle. [Hint: Assume 0 and place the center of the circle at the origin so it has the equation. Then is the sum
35. Prove the formula A r for the area of a sector of a circle with radius r and central angle. [Hint: Assume 0 and place the center of the circle at the origin so it has the equation. Then is the sum
STUDY KNOWHOW PROGRAM STUDY AND LEARNING CENTRE. Functions & Graphs
 STUDY KNOWHOW PROGRAM STUDY AND LEARNING CENTRE Functions & Graphs Contents Functions and Relations... 1 Interval Notation... 3 Graphs: Linear Functions... 5 Lines and Gradients... 7 Graphs: Quadratic
STUDY KNOWHOW PROGRAM STUDY AND LEARNING CENTRE Functions & Graphs Contents Functions and Relations... 1 Interval Notation... 3 Graphs: Linear Functions... 5 Lines and Gradients... 7 Graphs: Quadratic
LESSON #42 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART 2 COMMON CORE ALGEBRA II
 LESSON #4 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART COMMON CORE ALGEBRA II You will recall from unit 1 that in order to find the inverse of a function, ou must switch and and solve for. Also,
LESSON #4 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART COMMON CORE ALGEBRA II You will recall from unit 1 that in order to find the inverse of a function, ou must switch and and solve for. Also,
Math 2414 Activity 1 (Due by end of class Jan. 26) Precalculus Problems: 3,0 and are tangent to the parabola axis. Find the other line.
 Math Activity (Due by end of class Jan. 6) Precalculus Problems: 3, and are tangent to the parabola ais. Find the other line.. One of the two lines that pass through y is the - {Hint: For a line through
Math Activity (Due by end of class Jan. 6) Precalculus Problems: 3, and are tangent to the parabola ais. Find the other line.. One of the two lines that pass through y is the - {Hint: For a line through
1.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS
 .6 Continuit of Trigonometric, Eponential, and Inverse Functions.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS In this section we will discuss the continuit properties of trigonometric
.6 Continuit of Trigonometric, Eponential, and Inverse Functions.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS In this section we will discuss the continuit properties of trigonometric
Math 2414 Activity 1 (Due by end of class July 23) Precalculus Problems: 3,0 and are tangent to the parabola axis. Find the other line.
 Math 44 Activity (Due by end of class July 3) Precalculus Problems: 3, and are tangent to the parabola ais. Find the other line.. One of the two lines that pass through y is the - {Hint: For a line through
Math 44 Activity (Due by end of class July 3) Precalculus Problems: 3, and are tangent to the parabola ais. Find the other line.. One of the two lines that pass through y is the - {Hint: For a line through
1993 AP Calculus AB: Section I
 99 AP Calculus AB: Section I 90 Minutes Scientific Calculator Notes: () The eact numerical value of the correct answer does not always appear among the choices given. When this happens, select from among
99 AP Calculus AB: Section I 90 Minutes Scientific Calculator Notes: () The eact numerical value of the correct answer does not always appear among the choices given. When this happens, select from among
4.317 d 4 y. 4 dx d 2 y dy. 20. dt d 2 x. 21. y 3y 3y y y 6y 12y 8y y (4) y y y (4) 2y y 0. d 4 y 26.
 38 CHAPTER 4 HIGHER-ORDER DIFFERENTIAL EQUATIONS sstems are also able, b means of their dsolve commands, to provide eplicit solutions of homogeneous linear constant-coefficient differential equations.
38 CHAPTER 4 HIGHER-ORDER DIFFERENTIAL EQUATIONS sstems are also able, b means of their dsolve commands, to provide eplicit solutions of homogeneous linear constant-coefficient differential equations.
Analytic Geometry in Three Dimensions
 Analtic Geometr in Three Dimensions. The Three-Dimensional Coordinate Sstem. Vectors in Space. The Cross Product of Two Vectors. Lines and Planes in Space The three-dimensional coordinate sstem is used
Analtic Geometr in Three Dimensions. The Three-Dimensional Coordinate Sstem. Vectors in Space. The Cross Product of Two Vectors. Lines and Planes in Space The three-dimensional coordinate sstem is used
The details of the derivation of the equations of conics are com-
 Part 6 Conic sections Introduction Consider the double cone shown in the diagram, joined at the verte. These cones are right circular cones in the sense that slicing the double cones with planes at right-angles
Part 6 Conic sections Introduction Consider the double cone shown in the diagram, joined at the verte. These cones are right circular cones in the sense that slicing the double cones with planes at right-angles
4 The Cartesian Coordinate System- Pictures of Equations
 The Cartesian Coordinate Sstem- Pictures of Equations Concepts: The Cartesian Coordinate Sstem Graphs of Equations in Two Variables -intercepts and -intercepts Distance in Two Dimensions and the Pthagorean
The Cartesian Coordinate Sstem- Pictures of Equations Concepts: The Cartesian Coordinate Sstem Graphs of Equations in Two Variables -intercepts and -intercepts Distance in Two Dimensions and the Pthagorean
CHAPTER 6 Applications of Integration
 PART II CHAPTER Applications of Integration Section. Area of a Region Between Two Curves.......... Section. Volume: The Disk Method................. 7 Section. Volume: The Shell Method................
PART II CHAPTER Applications of Integration Section. Area of a Region Between Two Curves.......... Section. Volume: The Disk Method................. 7 Section. Volume: The Shell Method................
AP Calculus (BC) Summer Assignment (169 points)
 AP Calculus (BC) Summer Assignment (69 points) This packet is a review of some Precalculus topics and some Calculus topics. It is to be done NEATLY and on a SEPARATE sheet of paper. Use your discretion
AP Calculus (BC) Summer Assignment (69 points) This packet is a review of some Precalculus topics and some Calculus topics. It is to be done NEATLY and on a SEPARATE sheet of paper. Use your discretion
REVIEW, pages
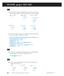 REVIEW, pages 5 5.. Determine the value of each trigonometric ratio. Use eact values where possible; otherwise write the value to the nearest thousandth. a) tan (5 ) b) cos c) sec ( ) cos º cos ( ) cos
REVIEW, pages 5 5.. Determine the value of each trigonometric ratio. Use eact values where possible; otherwise write the value to the nearest thousandth. a) tan (5 ) b) cos c) sec ( ) cos º cos ( ) cos
2018 Midterm Review Trigonometry: Midterm Review A Missive from the Math Department Trigonometry Work Problems Study For Understanding Read Actively
 Summer . Fill in the blank to correctl complete the sentence..4 written in degrees and minutes is..4 written in degrees and minutes is.. Find the complement and the supplement of the given angle. The complement
Summer . Fill in the blank to correctl complete the sentence..4 written in degrees and minutes is..4 written in degrees and minutes is.. Find the complement and the supplement of the given angle. The complement
D sin x. (By Product Rule of Diff n.) ( ) D 2x ( ) 2. 10x4, or 24x 2 4x 7 ( ) ln x. ln x. , or. ( by Gen.
 SOLUTIONS TO THE FINAL - PART MATH 50 SPRING 07 KUNIYUKI PART : 35 POINTS, PART : 5 POINTS, TOTAL: 50 POINTS No notes, books, or calculators allowed. 35 points: 45 problems, 3 pts. each. You do not have
SOLUTIONS TO THE FINAL - PART MATH 50 SPRING 07 KUNIYUKI PART : 35 POINTS, PART : 5 POINTS, TOTAL: 50 POINTS No notes, books, or calculators allowed. 35 points: 45 problems, 3 pts. each. You do not have
9.1 VECTORS. A Geometric View of Vectors LEARNING OBJECTIVES. = a, b
 vectors and POLAR COORDINATES LEARNING OBJECTIVES In this section, ou will: View vectors geometricall. Find magnitude and direction. Perform vector addition and scalar multiplication. Find the component
vectors and POLAR COORDINATES LEARNING OBJECTIVES In this section, ou will: View vectors geometricall. Find magnitude and direction. Perform vector addition and scalar multiplication. Find the component
The region enclosed by the curve of f and the x-axis is rotated 360 about the x-axis. Find the volume of the solid formed.
 Section A ln. Let g() =, for > 0. ln Use the quotient rule to show that g ( ). 3 (b) The graph of g has a maimum point at A. Find the -coordinate of A. (Total 7 marks) 6. Let h() =. Find h (0). cos 3.
Section A ln. Let g() =, for > 0. ln Use the quotient rule to show that g ( ). 3 (b) The graph of g has a maimum point at A. Find the -coordinate of A. (Total 7 marks) 6. Let h() =. Find h (0). cos 3.
Arc-length of a curve on the plane (Sect. 11.2) Review: Parametric curves on the plane
 Arc-length of a curve on the plane (Sect. 11.2) Review: Parametric curves on the plane. The slope of tangent lines to curves. The arc-length of a curve. The arc-length function and differential. Review:
Arc-length of a curve on the plane (Sect. 11.2) Review: Parametric curves on the plane. The slope of tangent lines to curves. The arc-length of a curve. The arc-length function and differential. Review:
Math 121. Practice Questions Chapters 2 and 3 Fall Find the other endpoint of the line segment that has the given endpoint and midpoint.
 Math 11. Practice Questions Chapters and 3 Fall 01 1. Find the other endpoint of the line segment that has the given endpoint and midpoint. Endpoint ( 7, ), Midpoint (, ). Solution: Let (, ) denote the
Math 11. Practice Questions Chapters and 3 Fall 01 1. Find the other endpoint of the line segment that has the given endpoint and midpoint. Endpoint ( 7, ), Midpoint (, ). Solution: Let (, ) denote the
SOLUTIONS TO THE FINAL - PART 1 MATH 150 FALL 2016 KUNIYUKI PART 1: 135 POINTS, PART 2: 115 POINTS, TOTAL: 250 POINTS
 SOLUTIONS TO THE FINAL - PART MATH 5 FALL 6 KUNIYUKI PART : 5 POINTS, PART : 5 POINTS, TOTAL: 5 POINTS No notes, books, or calculators allowed. 5 points: 45 problems, pts. each. You do not have to algebraically
SOLUTIONS TO THE FINAL - PART MATH 5 FALL 6 KUNIYUKI PART : 5 POINTS, PART : 5 POINTS, TOTAL: 5 POINTS No notes, books, or calculators allowed. 5 points: 45 problems, pts. each. You do not have to algebraically
Answer Key 1973 BC 1969 BC 24. A 14. A 24. C 25. A 26. C 27. C 28. D 29. C 30. D 31. C 13. C 12. D 12. E 3. A 32. B 27. E 34. C 14. D 25. B 26.
 Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
Lines, Conics, Tangents, Limits and the Derivative
 Lines, Conics, Tangents, Limits and te Derivative Te Straigt Line An two points on te (,) plane wen joined form a line segment. If te line segment is etended beond te two points ten it is called a straigt
Lines, Conics, Tangents, Limits and te Derivative Te Straigt Line An two points on te (,) plane wen joined form a line segment. If te line segment is etended beond te two points ten it is called a straigt
REVISION SHEET FP2 (MEI) CALCULUS. x x 0.5. x x 1.5. π π. Standard Calculus of Inverse Trig and Hyperbolic Trig Functions = + = + arcsin x = +
 the Further Mathematics network www.fmnetwork.org.uk V 07 REVISION SHEET FP (MEI) CALCULUS The main ideas are: Calculus using inverse trig functions & hperbolic trig functions and their inverses. Maclaurin
the Further Mathematics network www.fmnetwork.org.uk V 07 REVISION SHEET FP (MEI) CALCULUS The main ideas are: Calculus using inverse trig functions & hperbolic trig functions and their inverses. Maclaurin
PreCalculus Final Exam Review Revised Spring 2014
 PreCalculus Final Eam Review Revised Spring 0. f() is a function that generates the ordered pairs (0,0), (,) and (,-). a. If f () is an odd function, what are the coordinates of two other points found
PreCalculus Final Eam Review Revised Spring 0. f() is a function that generates the ordered pairs (0,0), (,) and (,-). a. If f () is an odd function, what are the coordinates of two other points found
Chapter One. Chapter One
 Chapter One Chapter One CHAPTER ONE Hughes Hallett et al c 005, John Wile & Sons ConcepTests and Answers and Comments for Section.. Which of the following functions has its domain identical with its range?
Chapter One Chapter One CHAPTER ONE Hughes Hallett et al c 005, John Wile & Sons ConcepTests and Answers and Comments for Section.. Which of the following functions has its domain identical with its range?
Conic Section: Circles
 Conic Section: Circles Circle, Center, Radius A circle is defined as the set of all points that are the same distance awa from a specific point called the center of the circle. Note that the circle consists
Conic Section: Circles Circle, Center, Radius A circle is defined as the set of all points that are the same distance awa from a specific point called the center of the circle. Note that the circle consists
Amherst College, DEPARTMENT OF MATHEMATICS Math 11, Final Examination, May 14, Answer Key. x 1 x 1 = 8. x 7 = lim. 5(x + 4) x x(x + 4) = lim
 Amherst College, DEPARTMENT OF MATHEMATICS Math, Final Eamination, May 4, Answer Key. [ Points] Evaluate each of the following limits. Please justify your answers. Be clear if the limit equals a value,
Amherst College, DEPARTMENT OF MATHEMATICS Math, Final Eamination, May 4, Answer Key. [ Points] Evaluate each of the following limits. Please justify your answers. Be clear if the limit equals a value,
10.2 The Unit Circle: Cosine and Sine
 0. The Unit Circle: Cosine and Sine 77 0. The Unit Circle: Cosine and Sine In Section 0.., we introduced circular motion and derived a formula which describes the linear velocit of an object moving on
0. The Unit Circle: Cosine and Sine 77 0. The Unit Circle: Cosine and Sine In Section 0.., we introduced circular motion and derived a formula which describes the linear velocit of an object moving on
4.3 Mean-Value Theorem and Monotonicity
 .3 Mean-Value Theorem and Monotonicit 1. Mean Value Theorem Theorem: Suppose that f is continuous on the interval a, b and differentiable on the interval a, b. Then there eists a number c in a, b such
.3 Mean-Value Theorem and Monotonicit 1. Mean Value Theorem Theorem: Suppose that f is continuous on the interval a, b and differentiable on the interval a, b. Then there eists a number c in a, b such
Green s Theorem Jeremy Orloff
 Green s Theorem Jerem Orloff Line integrals and Green s theorem. Vector Fields Vector notation. In 8.4 we will mostl use the notation (v) = (a, b) for vectors. The other common notation (v) = ai + bj runs
Green s Theorem Jerem Orloff Line integrals and Green s theorem. Vector Fields Vector notation. In 8.4 we will mostl use the notation (v) = (a, b) for vectors. The other common notation (v) = ai + bj runs
Methods of Integration
 U96-b)! Use the substitution u = - to evaluate U95-b)! 4 Methods of Integration d. Evaluate 9 d using the substitution u = + 9. UNIT MATHEMATICS (HSC) METHODS OF INTEGRATION CSSA «8» U94-b)! Use the substitution
U96-b)! Use the substitution u = - to evaluate U95-b)! 4 Methods of Integration d. Evaluate 9 d using the substitution u = + 9. UNIT MATHEMATICS (HSC) METHODS OF INTEGRATION CSSA «8» U94-b)! Use the substitution
Conic Sections CHAPTER OUTLINE. The Circle Ellipses and Hyperbolas Second-Degree Inequalities and Nonlinear Systems FIGURE 1
 088_0_p676-7 /7/0 :5 PM Page 676 (FPG International / Telegraph Colour Librar) Conic Sections CHAPTER OUTLINE. The Circle. Ellipses and Hperbolas.3 Second-Degree Inequalities and Nonlinear Sstems O ne
088_0_p676-7 /7/0 :5 PM Page 676 (FPG International / Telegraph Colour Librar) Conic Sections CHAPTER OUTLINE. The Circle. Ellipses and Hperbolas.3 Second-Degree Inequalities and Nonlinear Sstems O ne
Math 123 Summary of Important Algebra & Trigonometry Concepts Chapter 1 & Appendix D, Stewart, Calculus Early Transcendentals
 Math Summar of Important Algebra & Trigonometr Concepts Chapter & Appendi D, Stewart, Calculus Earl Transcendentals Function a rule that assigns to each element in a set D eactl one element, called f (
Math Summar of Important Algebra & Trigonometr Concepts Chapter & Appendi D, Stewart, Calculus Earl Transcendentals Function a rule that assigns to each element in a set D eactl one element, called f (
Name Please print your name as it appears on the class roster.
 Berkele Cit College Practice Problems Math 1 Precalculus - Final Eam Preparation Name Please print our name as it appears on the class roster. SHORT ANSWER. Write the word or phrase that best completes
Berkele Cit College Practice Problems Math 1 Precalculus - Final Eam Preparation Name Please print our name as it appears on the class roster. SHORT ANSWER. Write the word or phrase that best completes
Edexcel GCE A Level Maths. Further Maths 3 Coordinate Systems
 Edecel GCE A Level Maths Further Maths 3 Coordinate Sstems Edited b: K V Kumaran kumarmaths.weebl.com 1 kumarmaths.weebl.com kumarmaths.weebl.com 3 kumarmaths.weebl.com 4 kumarmaths.weebl.com 5 1. An ellipse
Edecel GCE A Level Maths Further Maths 3 Coordinate Sstems Edited b: K V Kumaran kumarmaths.weebl.com 1 kumarmaths.weebl.com kumarmaths.weebl.com 3 kumarmaths.weebl.com 4 kumarmaths.weebl.com 5 1. An ellipse
Unit 3 Notes Mathematical Methods
 Unit 3 Notes Mathematical Methods Foundational Knowledge Created b Triumph Tutoring Copright info Copright Triumph Tutoring 07 Triumph Tutoring Pt Ltd ABN 60 607 0 507 First published in 07 All rights
Unit 3 Notes Mathematical Methods Foundational Knowledge Created b Triumph Tutoring Copright info Copright Triumph Tutoring 07 Triumph Tutoring Pt Ltd ABN 60 607 0 507 First published in 07 All rights
Answers to Some Sample Problems
 Answers to Some Sample Problems. Use rules of differentiation to evaluate the derivatives of the following functions of : cos( 3 ) ln(5 7 sin(3)) 3 5 +9 8 3 e 3 h 3 e i sin( 3 )3 +[ ln ] cos( 3 ) [ln(5)
Answers to Some Sample Problems. Use rules of differentiation to evaluate the derivatives of the following functions of : cos( 3 ) ln(5 7 sin(3)) 3 5 +9 8 3 e 3 h 3 e i sin( 3 )3 +[ ln ] cos( 3 ) [ln(5)
Identifying second degree equations
 Chapter 7 Identifing second degree equations 71 The eigenvalue method In this section we appl eigenvalue methods to determine the geometrical nature of the second degree equation a 2 + 2h + b 2 + 2g +
Chapter 7 Identifing second degree equations 71 The eigenvalue method In this section we appl eigenvalue methods to determine the geometrical nature of the second degree equation a 2 + 2h + b 2 + 2g +
Mathematics Extension 2
 0 HIGHER SCHL CERTIFICATE EXAMINATIN Mathematics Etension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Black pen is preferred Board-approved calculators
0 HIGHER SCHL CERTIFICATE EXAMINATIN Mathematics Etension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Black pen is preferred Board-approved calculators
4.3. Differentiation Rules for Sinusoidal Functions. How do the differentiation rules apply to sinusoidal functions?
 .3 Differentiation Rules for Sinusoidal Functions Sinusoidal patterns occur frequentl in nature. Sinusoidal functions and compound sinusoidal functions are used to describe the patterns found in the stu
.3 Differentiation Rules for Sinusoidal Functions Sinusoidal patterns occur frequentl in nature. Sinusoidal functions and compound sinusoidal functions are used to describe the patterns found in the stu
TMTA Calculus and Advanced Topics Test 2010
 . Evaluate lim Does not eist - - 0 TMTA Calculus and Advanced Topics Test 00. Find the period of A 6D B B y Acos 4B 6D, where A 0, B 0, D 0. Solve the given equation for : ln = ln 4 4 ln { } {-} {0} {}
. Evaluate lim Does not eist - - 0 TMTA Calculus and Advanced Topics Test 00. Find the period of A 6D B B y Acos 4B 6D, where A 0, B 0, D 0. Solve the given equation for : ln = ln 4 4 ln { } {-} {0} {}
Section 1.5 Formal definitions of limits
 Section.5 Formal definitions of limits (3/908) Overview: The definitions of the various tpes of limits in previous sections involve phrases such as arbitraril close, sufficientl close, arbitraril large,
Section.5 Formal definitions of limits (3/908) Overview: The definitions of the various tpes of limits in previous sections involve phrases such as arbitraril close, sufficientl close, arbitraril large,
Mathematics. Mathematics 2. hsn.uk.net. Higher HSN22000
 Higher Mathematics UNIT Mathematics HSN000 This document was produced speciall for the HSN.uk.net website, and we require that an copies or derivative works attribute the work to Higher Still Notes. For
Higher Mathematics UNIT Mathematics HSN000 This document was produced speciall for the HSN.uk.net website, and we require that an copies or derivative works attribute the work to Higher Still Notes. For
CHAPTER P Preparation for Calculus
 CHAPTER P Preparation for Calculus Section P. Graphs and Models...................... Section P. Linear Models and Rates of Change............ Section P. Functions and Their Graphs................. Section
CHAPTER P Preparation for Calculus Section P. Graphs and Models...................... Section P. Linear Models and Rates of Change............ Section P. Functions and Their Graphs................. Section
Section 4.1 Increasing and Decreasing Functions
 Section.1 Increasing and Decreasing Functions The graph of the quadratic function f 1 is a parabola. If we imagine a particle moving along this parabola from left to right, we can see that, while the -coordinates
Section.1 Increasing and Decreasing Functions The graph of the quadratic function f 1 is a parabola. If we imagine a particle moving along this parabola from left to right, we can see that, while the -coordinates
Open the TI-Nspire file: Astroid. Navigate to page 1.2 of the file. Drag point A on the rim of the bicycle wheel and observe point P on the rim.
 Astroid Student Activity 7 9 TI-Nspire Investigation Student min Introduction How is the motion of a ladder sliding down a wall related to the motion of the valve on a bicycle wheel or to a popular amusement
Astroid Student Activity 7 9 TI-Nspire Investigation Student min Introduction How is the motion of a ladder sliding down a wall related to the motion of the valve on a bicycle wheel or to a popular amusement
5.6 RATIOnAl FUnCTIOnS. Using Arrow notation. learning ObjeCTIveS
 CHAPTER PolNomiAl ANd rational functions learning ObjeCTIveS In this section, ou will: Use arrow notation. Solve applied problems involving rational functions. Find the domains of rational functions. Identif
CHAPTER PolNomiAl ANd rational functions learning ObjeCTIveS In this section, ou will: Use arrow notation. Solve applied problems involving rational functions. Find the domains of rational functions. Identif
MATH 115: Final Exam Review. Can you find the distance between two points and the midpoint of a line segment? (1.1)
 MATH : Final Eam Review Can ou find the distance between two points and the midpoint of a line segment? (.) () Consider the points A (,) and ( 6, ) B. (a) Find the distance between A and B. (b) Find the
MATH : Final Eam Review Can ou find the distance between two points and the midpoint of a line segment? (.) () Consider the points A (,) and ( 6, ) B. (a) Find the distance between A and B. (b) Find the
Polynomial and Rational Functions
 Name Date Chapter Polnomial and Rational Functions Section.1 Quadratic Functions Objective: In this lesson ou learned how to sketch and analze graphs of quadratic functions. Important Vocabular Define
Name Date Chapter Polnomial and Rational Functions Section.1 Quadratic Functions Objective: In this lesson ou learned how to sketch and analze graphs of quadratic functions. Important Vocabular Define
Ready To Go On? Skills Intervention 10-1 Introduction to Conic Sections
 Find this vocabular word in Lesson 10-1 and the Multilingual Glossar. Graphing Parabolas and Hperbolas on a Calculator A is a single curve, whereas a has two congruent branches. Identif and describe each
Find this vocabular word in Lesson 10-1 and the Multilingual Glossar. Graphing Parabolas and Hperbolas on a Calculator A is a single curve, whereas a has two congruent branches. Identif and describe each
