A Linear-Space Top-down Algorithm for Tree Inclusion Problem
|
|
|
- Gordon Wilkinson
- 5 years ago
- Views:
Transcription
1 A Linr-Spc Top-own Algorithm for Tr Inclusion Prolm Yngjun Chn 1, Yiin Chn 2 Dpt. Appli Computr Scinc, Univrsity of Winnipg, Cn 1 y.chn@uwinnipg.c, 2 chnyiin@gmil.com Astrct W consir th following tr-mtching prolm: Givn ll, orr trs P n T, cn P otin from T y lting nos? Dlting no v ntils rmoving ll gs incint to v n, if v hs prnt u, rplcing th gs from u to v y gs from u to th chilrn of v. Th st known lgorithm for this prolm ns O( T lvs(p) ) tim n O( lvs(p) min{d T, lvs(t) } + T + P ) spc, whr lvs(t) (rsp. lvs(p)) stns for th st of th lvs of T (rsp. P), n D T (rsp. D P ) for th hight of T (rsp. P). In this ppr, w prsnt n fficint lgorithm tht rquirs O( T lvs(p) ) tim n O( T + P ) spc. I. INTRODUCTION Lt T tr n v no iffrnt of root in T with prnt no u. Dnot y lt(t, v) th tr otin from T y rmoving th no v. Th chilrn of v com th chilrn of u s illustrt in Fig. 1. T: lt(t, v) c () f () illustrtion. Th orr tr inclusion prolm ws initilly introuc y Knuth [10], whr only sufficint conition for this prolm is givn. Th tr inclusion hs n suggst s n importnt primitiv for xprssing quris on structur ocumnt tss [4, 5, 6, 12]. A structur ocumnt ts is consir s collction of prs trs tht rprsnt th structur of th stor txts n th tr inclusion is us s mns of rtriving informtion from thm. Anothr ppliction of th orr tr mtching is th vio contnt-s rtrivl. Accoring to Rui t l. [14], vio cn succssfully compos into hirrchicl tr structur, in which ch no rprsnts scn, group, shot, frm, ftur, n so on. Espcilly, such tr is n orr on sinc th tmporl orr is vry importnt for vio. In ition, th orr tr mtching cn lso ppli in th scn nlysis, th computtionl iology (such s th RNA structur mtching [11]), s wll s in th t mining (such s th tr mining [15]). np t n v s vp np v f Th stunt rs t j n intnsivly Fig. 1 Th ffct of rmoving no from tr vp th intrsting ook () Givn two orr ll trs P n T, cll th pttrn n th trgt, rspctivly. An intrsting prolm is: Cn w otin pttrn P y lting som nos from trgt T? Tht is, is thr squnc v 1,..., v k of nos such tht for T 0 = T n T i+1 = lt(t i, v i+1 ) for i = 0,..., k - 1, w hv T k = P? If this is th cs, w sy, P is inclu in T [9]. Such prolm is cll th tr inclusion prolm. Orr ll trs ppr in vrious rsrch fils, incluing progrmming lngug implmnttion, nturl lngug procssing, n molculr iology. As n xmpl [9], consir qurying grmmticl structurs s shown in Fig. 2(), which is th prs tr of nturl lngug sntnc. On might wnt to loct, sy, thos sntncs tht inclu vr phrs contining th vr rs n ftr it noun ook follow y ny vr. This is xctly th sntncs whos prs tr cn otin y lting som nos from th tr shown in Fig. 2(). S Fig. 2() for v rs n ook v () Fig. 2 Illustrtion for orr tr inclusion This prolm hs n th ttntion of much rsrch. Kilpläinn n Mnnil [9] prsnt th first polynomil tim lgorithm using O( T P ) tim n spc. Most of th ltr improvmnts r rfinmnts of this lgorithm. In [13], Richtr gv n lgorithm using O( α(p) T + m(p, T) D T ) tim, whr α(p) is th lpht of th lls of P, m(p, T) is th siz of st cll mtchs, fin s ll th pirs (v, w) P T such tht ll(v) = ll(w), n D T (rsp. D P ) is th pth of T (rsp. P). Hnc, if th numr of mtchs is smll, th tim complxity of this lgorithm is ttr thn O(T P ). Th spc complxity of th lgorithm is O( α(p) T + m(p, T)). In [3], mor sophistict lgorithm ws prsnt using O( T lvs(p) ) tim n O( lvs(p) min{d T, lvs(t) } + T + P ) spc. In [1], n fficint vrg cs lgorithm ws iscuss. Its vrg tim complxity is O( T /12/$ IEEE 2127
2 + C(P, T) P ), whr C(P, T) rprsnts th numr of T s nos tht hv n xmin uring th inclusion srch. Howvr, its worst tim complxity is still O( T P ). In [2], nothr ottom-up lgorithm is propos. Th tim complxity of th lgorithm is oun y min O( T lvs(p) ) O( lvs(t) lvs(p) loglog lvs(p) + lvs(p)) O( T P /(log T ) + T log T ) But it is clim tht th lgorithm ns only O( T + P ) spc. A crful nlysis rvls tht th spc complxity of th lgorithm is th sm s tht of [3]. In th lgorithm, t structur EMB(v) for ch v in P is us to rcor p occurrncs of P[v] in T. It is of siz O( lvs(t) ) in th worst cs. EMB(v) is gnrt rcursivly n works in wy similr to th concpt of shll iscuss in [3]. So th nlysis of shll pplis to EMB(v) s. In our rlir work [7], top-own lgorithm ws propos with O( T + P ) spc rquirmnt. Howvr, its tim complxity is not polynomil, s shown in [11]. In this ppr, w rvisit this issu n prsnt nw topown lgorithm to rmov ny runncy of [10]. Th tim complxity of th nw on is oun y O( T lvs(p) ). Although th tim complxity of our lgorithm is comprl to Chn s lgorithm [3], it is mor fficint thn Chn s sinc in Chn s lgorithm ch no in T will chck ginst, sis som intrnl nos, ll th lf nos in P. But in our lgorithm, no in T my chck so mny tims only whn som conitions r stisfi. Mor importntly, our lgorithm ns only linr spc O( T + P ). Th tr inclusion prolm on unorr trs is NPcomplt [9] n not iscuss in this ppr. II. BASIC DEFINIION W concntrt on ll trs tht r orr, i.., th orr twn silings is significnt. Tchniclly, it is convnint to consir slight gnrliztion of trs, nmly forsts. A forst is finit orr squnc of isjoint finit trs. A tr T consists of spcilly signt no root(t) cll th root of th tr, n forst <T 1,..., T k >, whr k 0. Th trs T 1,..., T k r th sutrs of th root of T or th immit sutrs of tr T, n k is th outgr of th root of T. A tr with th root t n th sutrs T 1,..., T k is not y <t; T 1,..., T k >. Th roots of th trs T 1,..., T k r th chilrn of t n silings of ch othr. Also, w cll T 1,..., T k th siling trs of ch othr. In ition, T 1,..., T i-1 r cll th lft siling trs of T i, n T i-1 th immit lft siling tr of T i. Th root is n ncstor of ll th nos in its sutrs, n th nos in th sutrs r scnnts of th root. Th st of scnnts of no v is not y sc(v). A lf is no with n mpty st of scnnts. Somtims w trt tr T s th forst <T>. W my lso not th st of nos in forst F y V(F). For xmpl, if w spk of functions from forst G to forst F, w mn functions mpping th nos of G onto th nos of F. Th siz of forst F, not y F, is th numr of th nos in F. Th rstriction of forst F to no v with its scnnts sc(v) is cll sutr of F root t v, not y F[v]. Lt F = <T 1,..., T k > forst. Th prorr of forst F is th orr of th nos visit uring prorr trvrsl. A prorr trvrsl of forst <T 1,..., T k > is s follows. Trvrs th trs T 1,..., T k in scning orr of th inics in prorr. To trvrs tr in prorr, first visit th root n thn trvrs th forst of its sutrs in prorr. Th postorr is fin similrly, xcpt tht in postorr trvrsl th root is visit ftr trvrsing th forst of its sutrs in postorr. W not th prorr n postorr numrs of no v y pr(v) n post(v), rspctivly. Using prorr n postorr numrs, th ncstorship cn sily chck. If thr is pth from no u to no v, w sy, u is n ncstor of v n v is scnnt of u. In this ppr, y ncstor ( scnnt ), w mn propr ncstor (scnnt), i.., u v. Lmm 1 Lt v n u nos in forst F. Thn, v is n ncstor of u if n only if pr(v) < pr(u) n post(u) < post(v). Proof. S Exrcis in [10] (pg 347). Similrly, w chck th lft-to-right orring s follows. Lmm 2 Lt v n u nos in forst F. v is si to to th lft of u if thy r not rlt y th ncstor-scnnt rltionship n u follows v whn w trvrs F in prorr. Thn, v is to th lft of u if n only if pr(v) < pr(u) n post(v) < post(u). Proof. Th proof is trivil. In th following, w us th postorr numrs to fin n orring of th nos of forst F givn y v p v iff post(v) < post(v ). Also, v p v iff v p v or v = v. Furthrmor, w xtn this orring with two spcil nos 7 p v p 6. Th lft rltivs, lr(v), of no v V(F) is th st of nos tht r to th lft of v n similrly th right rltivs, rr(v), r th st of nos tht r to th right of v. Th following finition is u to [9]. Dfinition 1 Lt F n G ll orr forsts. W fin n orr ming (ϕ, G, F) s n injctiv function ϕ: V(G) V(F) such tht for ll nos v, u V(G), i) ll(v) = ll(ϕ(v)); (ll prsrvtion conition) ii) v is n ncstor of u iff ϕ(v) is n ncstor of ϕ(u), i.., pr(v) < pr(u) n post(u) < post(v) iff pr(ϕ(v)) < pr(ϕ(u)) n post(ϕ(u)) < post(ϕ(v)); (ncstor conition) iii) v is to th lft of u iff ϕ(v) is to th lft of ϕ(u), i.., pr(v) < pr(u) n post(v) < post(u) iff pr(ϕ(v)) < pr(ϕ(u)) n post(ϕ(v)) < post(ϕ(u)). (Siling conition) If thr xists such n injctiv function from V(G) to V(F), w sy, F inclus G, F contins G, F covrs G, or sy, G cn m in F. Fig. 3 shows n xmpl of n orr inclusion. Lt P n T two ll orr trs. An ming ϕ of P in T is si to root-prsrving if ϕ(root(p)) = root(t). If thr is root-prsrving ming of P in T, w sy tht th root of T is n occurrnc of P. Fig. 3() lso shows n xmpl of root prsrving ming. Accoring to [9], rstricting to root-prsrving 2128
3 ming os not los gnrlity. In fct, wht cn foun y th top-own lgorithm to iscuss is rootprsrving tr ming. Throughout th rst of th ppr, w rfr to th ll orr trs simply s trs. III. ALGORITHM DESCRIPTION Lt T = <t; T 1,..., T k > (k 0) tr n G = <P 1,..., P q > (q 0) forst. W hnl G s tr P = <p v ; P 1,..., P q >, whr p v rprsnt virtul no, mtching ny no in T. Not tht vn though G contins only on singl tr it is consir to forst. So virtul root is. Thrfor, ch no in G, xcpt th virtul no, hs prnt. Consir no v in G = <P 1,..., P q > with chilrn v 1,..., v j. W us pir <i, v> (i j) to rprsnt n orr forst contining th first i sutrs of v: <G[v 1 ],..., G[v i ]>. If v is p v, or no on th lft-most pth in P 1, <i, v> is cll lft cornr of G. Espcilly, <i, p v > is lft cornr, rprsnting th first i trs in G: P 1,..., P i. In ition, δ(v) rprsnts link from no v to th lft-most lf no in G[v], s illustrt in Fig. 4. Lt v lf no in G. δ(v ) is fin to link to v itslf. So in Fig. 5, w hv δ(v 1 ) = δ(v 2 ) = δ(v 3 ) = v 3. W lso not y δ -1 (v ) st of nos x such tht for ch v x δ(v) = v. Thrfor, in Fig. 5, δ -1 (v 3 ) = {v 1, v 2, v 3 }, δ -1 (v 4 ) = {v 4 }, n δ -1 (v 5 ) = {v 5 }. Th out-gr of v in tr is not y (v) whil th hight of v is not y h(v), fin to th numr of gs on th longst ownwr pth from v to lf. Th hight of lf no is st to 0. As with [7], w rrng two functions: top-own(t, G) n ottom-up(t, G) to chck tr inclusion, whr T is tr, n T n G r two forsts. Howvr, iffrnt from [7], ch of th two functions rturns lft cornr <i, v> of G with th following proprtis: Lt v th lft-most lf in G[v]. If i > 0, it shows tht th first i sutrs of v in G cn m in T (or in T ), n for ny i > i, <i, v> cnnot m in T (or in T ), n for ny v s ncstor u δ -1 (v ) thr xists no j > 0 such tht <j, u> is l to m in T (or in T ). If i = 0, v is th lft-most lf in G, inicting tht no lft cornr of G cn m in T (or in T ). Fig. 3: () Th tr on th lft cn inclu in th tr on th right y lting th nos lll :,, n ; () th ming corrsponing to (). () () In this sns, w sy, <i, v> is th highst n wist lft cornr which cn m in T (or in T ). P: δ(v 2) δ(v 1) v 3 v 1 v 2 v 5 v 4 Fig. 4 A pttrn tr W notic tht if v = p v n i > 0, it shows tht P 1,..., P i cn inclu. In [7], oth top-own(t, G) n ottom-up(t, G) rturn n intgr i to inict tht T ms th first i trs in G. Although our lgorithm follows th rrngmnt of [7], th min i is quit iffrnt. It is not ncssry to rfr to [7] to unrstn th following iscussion. If th trgt is tr n th pttrn is forst, w cll th function top-own. If oth th trgt n th pttrn r forsts, w cll th function ottom-up. But uring th computtion, thy will cll from ch othr. In top-own(t, G), w n to hnl two css. Cs 1: G = <P 1 >; or G = <P 1,..., P q > (q > 1), ut T P 1 + P 2. In this cs, to fin th highst n wist lft cornr <i, v> tht cn m in T = <t; T 1,..., T k >, th following chckings will conuct: i) If t is lf no, w will chck whthr ll(t) = ll(δ(p 1 )), whr p 1 is th root of P 1. If it is th cs, rturn <1, prnt of δ(p 1 )>. Othrwis, rturn <0, δ(p 1 )>. ii) If T < P 1 or h(t) < h(p 1 ), w will mk rcursiv cll top-own(t, <P 11,..., P 1j >), whr <P 11,..., P 1j > is forst of th sutrs of p 1. Th rturn vlu of top-own(t, <P 11,..., P 1j >) is us s th rturn vlu of top-own(t, G). iii) If T P 1 n h(t) h(p 1 ), w furthr istinguish twn two sucss: ll(t) = ll(p 1 ). In this cs, w will cll ottomup(<t 1,..., T k >, <P 11,..., P 1j >). ll(t) ll(p 1 ). In this cs, w will cll ottomup(<t 1,..., T k >, <P 1 >). In oth css, ssum tht th rturn vlu of ottom-up( ) is <i, v>. W n to prform furthr chcking: - If ll(t) = ll(v) n i = (v), th rturn vlu of top-own(t, G) is st to <1, v s prnt>. - Othrwis, th rturn vlu of top-own(t, G) is th sm s <i, v>. Cs 2: G = <P 1,..., P q > (q > 1), n T > P 1 + P 2. In this cs, w will cll ottom-up(<t 1,..., T k >, G). Assum tht th rturn vlu of ottom-up(<t 1,..., T k >, G) is <i, v>. Th following chckings will continully conuct. iv) If v p 1 s prnt, chck whthr ll(t) = ll(v) n i = (v). If so, th rturn vlu of top-own(t, G) will st to <1, v s prnt>. Othrwis, th rturn vlu of topown(t, G) is th sm s <i, v>. v) If v = p 1 s prnt, th rturn vlu of top-own(t, G) is th sm s <i, v>. 2129
4 Th following is forml scription of th lgorithm. In th procss, ch no t in T is ssocit with t structur, rfrr to s κ(t). Initilly, ch κ(t) is st to φ. Ech tim cll of th form top-own(t[t], G ) rturns lft cornr <i, v>, κ(t) will chng to <i, v>, whr G is forst m up of st of sutrs root rspctivly t st of conscutiv chil nos (strting from spcific chil to th lst chil) of crtin no in G. This vlu is minly us in ottom-up( ) to voi runncy. Howvr, for simplicity, in th following lgorithm κ(t) is not xplicitly rprsnt. function top-own(t, G) input: T = <t; T 1,..., T k >, G = <P 1,..., P q >. output: <i, v> spcifi ov. gin 1. if (q = 1 or T P 1 + P 2 ) 2. thn { lt P 1 = <p 1 ; P 11,..., P 1j >; (*Cs 1*) 3. if t is lf thn { { lt δ(p 1 ) = v; (*Cs 1 - (i)*) 4. if ll(t) = ll(v) thn rturn <1, v s prnt> ls rturn <0, v>; } 5. if ( T < P 1 or h(t) < h(p 1 )) thn rturn top-own(t, <P 11,..., P 1j >); (*Cs 1 - (ii)*) 6. if ll(t) = ll(p 1 ) (*Cs 1 - (iii)*) 7. thn { if p 1 is lf thn {v := p 1 s prnt; i := 1;} 8. ls {<i, v> := ottom-up(<t 1,..., T k >, <P 11,..., P 1j >); 9. if ll(t) = ll(v) n i = (v) thn {v := v s prnt; i := 1; } 10. } 11. ls <i, v> := ottom-up(<t 1,..., T k >, <P 1 >); (*If ll(t) ll(p 1 ), cll ottom-up( ).*) 12. rturn <i, v>; 13. } 14. ls {<i, v> := ottom-up(<t 1,..., T k >, G); (*Cs 2*) 15. if v p 1 s prnt thn (*Cs 2 - (iv)*) 16. if (ll(t) = ll(v)) n i = (v) thn rturn <1, v s prnt>; 17. rturn <i, v>; (*Cs 2 - (v)*) 18. } n In th ov lgorithm, w first chck whthr q = 1 or T P 1 + P 2 (s lin 1). If it is th cs w hv Cs 1 n thn lins 2-13 r xcut. In this procss, ll th thr sucss (i), (ii), n (iii) r chck. If q > 1 n T > P 1 + P 2, w hv Cs 2 n lins will crri out, in which w first cll ottom-up(<t 1,..., T k >, G). Dpning on its rturn vlu, (vi) or (v) is conuct. ottom-up(t, G) is sign to hnl th cs tht oth T n G r forsts m up of st of sutrs root t nos tht r conscutiv silings in T n P, rspctivly. Lt T = <T 1,..., T k > n G = <P 1,..., P q >. Dnot y t l th root of T l (l = 1,..., k). Dnot y p j th root of P j (j = 1,..., q). In ottom-up(t, G), w will mk sris of clls topown(t l, < P,..., P q >), whr l = 1,..., k, j 1 = 1, n j 1 j 2... j l j h q (for som h k), controll s follows. 1. Two inx vrils l, j r us to scn T 1,..., T k n P 1,..., P q, rspctivly. (Initilly, l is st to 1, n j is st to 0.) Thy lso inict tht <P 1,..., P j > hs n succssfully m in <T 1,..., T l >. 2. Lt <i l, v l > th rturn vlu of top-own(t l, <P j+1,..., P q >). If v l = p 1 s prnt, st j to j + i l. Othrwis, j is not chng. St l to l + 1. Go to (2). 3. Th loop trmints whn ll T l s or ll P j s r xmin. If j > 0 whn th loop trmints, ottom-up(t, G) rturns <j, p 1 s prnt>, inicting tht T contins P 1,..., P j. Othrwis, j = 0, inicting tht vn P 1 lon cnnot m in ny T l (l {1,..., k}). Howvr, in this cs, w n to continu to srch for highst n wist lft cornr <i, v> in G, which cn m in T. This is on s scri low. i) Lt <i 1, v 1 >,..., <i k, v k > th rturn vlus of topown(t 1, <P 1,..., P q >),..., top-own(t k, <P 1,..., P q >), rspctivly. Sinc j = 0, ch v l δ -1 (v ) (l = 1,..., k), whr v is th lft-most lf in P 1. ii) If ch i l = 0, rturn <0, lft-most lf of P 1 >. Othrwis, thr must som v l s such tht i l > 0. W cll such no non-zro point. Fin th first non-zro point v f with chilrn w 1,..., w s such tht v f is not scnnt of ny othr non-zro point. Thn, w will chck <T f+1,..., T k > ginst <P[ w + 1 ],..., P[w s ]>. Lt x (0 x s - i ) f numr such tht <P[ w + 1 ],..., P[ w + x ]> cn m in <T f+1,..., T k >. Th rturn vlu of ottom-up(t, G) shoul st to < + x, v f >. In th ottom-up procss, κ(t) cn us to voi runnt computtion. Concrtly, ch tim for w mk cll of th form top-own(t l, <P j,..., P q >), w will clcult function κ-chcking(t l, p j ) fin low to trmin whthr this cll cn skipp ovr, whr t l n p j r th roots of T l n P j, rspctivly. function κ-chcking(t, p) input: t - no in T; p - no in G. output: φ or <i, v> spcifi ov. gin 1. if κ(t l ) φ thn { 2. lt κ(t l ) = <i, v>; 3. if i = 0 thn rturn φ; 4. if i > 0, δ(v) = δ(p), n p is qul to v s first chil or n ncstor of v s first chil 5. thn rturn <i, v>; 6. if i > 0, δ(v) = δ(p), n p is scnnt of v s first chil 7. thn rturn <(p s prnt), p s prnt>. 8. ls rturn φ. n Only whn κ-chcking(t l, p j ) rturns φ, top-own(t l, <P j,..., P q >) will crri out. Othrwis, w us th vlu of κ- chcking(t l, p j ) s th rturn vlu of top-own(t l, <P j,..., P q >). In trms of th ov iscussion, w rrng nw suprocur to chck T l ginst forst <P j,..., P q >, oing th sm work s th top-own procss ut with κ-chcking(t l, p j ) ing us to voi unncssry chckings. function top-own-κ(t, <P 1,..., P q >) input: T - tr; <P 1,..., P q > - forst. output: <v, i> spcifi ov. gin 1. if κ-chcking(t, p 1 ) = φ 2130
5 thn <i, v> := top-own(t, <P 1,..., P q >) 2. ls <i, v> = κ-chcking(t, p 1 ); 3. rturn <i, v>; n In th following lgorithm, w us top-own-κ( ), inst of top-own( ), to chck tr ginst forst. function ottom-up(t, G) input: T = <T 1,..., T k >, G = <P 1,..., P q > output: <i, v> spcifi ov. gin 1. l := 1; j := 0; 2. whil (j < q n l k) o (*min chcking*) 3. { <i l, v l > := top-own-κ(t l, <P j+1,..., P q >) 4. if (v l = p 1 s prnt n i l > 0) thn j := j + i l ; 5. l := l + 1; } 6. if j > 0 thn rturn <j, p 1 s prnt>; 7. if for ll <i l, v l > s i l = 0 thn rturn <0, lft-most lf in G> 8. ls { lt v f th first non-zro point such tht it is not scnnt of ny othr non-zro point; 9. lt w 1,..., w s th chilrn of v f ; 10. l := f + 1; j := ; 11. whil (j < s n l k) o (*supplmnt chcking*) 12. { <i l, v l > := top-own-κ(t l, <G[w j+1 ],..., G[w s ]>); 13. if (v l = v f n i l > 0) thn j := j + i l ; 14. l := l + 1; } 15. rturn <j, v f >; 16. } n In ottom-up(t, G), w hv two whil-loops: on from lin 2 to 5 n nothr from lin 11 to 14. In th first whilloop, w chck <T 1,..., T k > ginst <P 1,..., P q >, rfrr to s th min ottom-up chcking (or simply th min chcking). In this chcking, ch T l is chck on y on, y rptly clling top-own-κ(t l, <P j+1,..., P q >) (lin 3), y which κ- chcking(t l, p j+1 ) is us to rmov runncy (s lins 1-2 in top-own-κ( )). In th scon whil-loop, w o supplmnt chcking. This is crri out only whn th following two conitions r stisfi (s lins 6 n 7): (1) j = 0, n (2) Thr xists t lst non-zro point <i l, v l > (rturn vlu of top-own-κ(t l, <P 1,..., P q >) such tht i l > 0. W rfr to ths two conitions s th supplmnt chcking conition. Lt v f th first non-zro point such tht v f is not scnnt of ny othr non-zro point. Lt w 1,..., w s th chilrn of v f. In th supplmnt chcking, w will chck <T f+1,..., T k > ginst <G[ w + 1 ],..., G[w s ]> (s lins ) computtion to voi ny uslss ffort, high prformnc is chiv. Th tim complxity of th nw lgorithm is oun y O( T lvs(p) ) whil th spc rquirmnt is oun y O( T + P ), whr T n P r trgt n pttrn tr, rspctivly. REFERENCES [1] L. Alonso n R. Schott. On th tr inclusion prolm. In Procings of Mthmticl Fountions of Computr Scinc, pgs , [2] P. Bill n I.L. Gørtz, An Orr Tr Inclusion Algorithm Bs on Dynmic Tr Lling, in Proc.32th Intl. Colloquium on Automt, Lngugs n Progrmming, Lctur Nots in Computr Scinc, vol. 3580, 2005, pp [3] W. Chn. Mor fficint lgorithm for orr tr inclusion. Journl of Algorithms, 26: , [4] Y. Chn n Y.B. Chn, Sutr Rconstruction, Qury No Intrvls n Tr Pttrn Qury Evlution, Journl of Informtion Scinc n Enginring 28, (2012). [5] Y. Chn n L. Zou, n Unorr tr mtching n orr tr mtching: th vlution of tr pttrn quris, Int. J. Informtion Tchnology, Communictions n Convrgnc, Vol. 1, No. 3, 2011, pp [6] Y. Chn, A Nw Algorithm for Twig Pttrn Mtching, in: Proc. of Int. Conf. on Entrpris Informtion Systms (ICEIS 2007), IEEE, Funchl-mir, Portugl, Jun 2007, pp [7] Y. Chn n Y.B. Chn, A Nw Tr Inclusion Algorithm, Informtion Procssing Lttrs 98(2006) , Elsvir Scinc B.V. [8] H.L Chng n B.F Wng, On Chn n Chn's nw tr inclusion lgorithm, Informtion Procssing Lttrs, 2007, Vol. 103, 14-18, Elsvir Scinc B.V. [9] P. Kilpläinn n H. Mnnil. Orr n unorr tr inclusion. SIAM J. Comput, 24: , [10] D.E. Knuth, Th Art of Computr Progrmming, Vol. 1 (1st ition), Aison-Wsly, Ring, MA, [11] R.B. Lyngs, M. Zukr & C.N.S. Prsn, Intrnl loops in RNA sconry structur priction, in Procings of th 3r nnul intrntionl confrnc on computtionl molculr iology (RECOMB), (1999). [12] H. Mnnil n K.-J. Räih, On Qury Lngugs for th p-string t mol, in Informtion Molling n Knowlg Bss (H. Kngsslo, S. Ohsug, n H. Jkol, Es.), pp , IOS Prss, Amstrm, [13] Thorstn Richtr. A nw lgorithm for th orr tr inclusion prolm. In Procings of th 8th Annul Symposium on Comintoril Pttrn Mtching (CPM), in Lctur Nots of Computr Scinc (LNCS), volum 1264, pgs Springr, [14] Y. Rui, T.S. Hung, n S. Mhrotr, Constructing tl-of-contnt for vios, ACM Multimi Systms Journl, Spcil Issu Multimi Systms on Vio Lirris, 7(5): , Spt [15] M. Zki, Efficintly mining frqunt trs in forst. In Proc. of KDD, IV. CONCLUSION In this ppr, nw lgorithm is propos to improv th lgorithm iscuss in [7]. Th min i hin it is to lt ny suprocur cll rturn pir to inict sutr (suforst) ming whil in [7], only singl intgr is rturn to inict whthr whol forst (or th first svrl sutrs of th forst) is m y th corrsponing trgt sutr. Togthr with simpl t structur ssocit with ch no in th trgt tr to trnsfr th rsult otin in prvious stp to th nxt stp 2131
CSI35 Chapter 11 Review
 1. Which of th grphs r trs? c f c g f c x y f z p q r 1 1. Which of th grphs r trs? c f c g f c x y f z p q r . Answr th qustions out th following tr 1) Which vrtx is th root of c th tr? ) wht is th hight
1. Which of th grphs r trs? c f c g f c x y f z p q r 1 1. Which of th grphs r trs? c f c g f c x y f z p q r . Answr th qustions out th following tr 1) Which vrtx is th root of c th tr? ) wht is th hight
Similarity Search. The Binary Branch Distance. Nikolaus Augsten.
 Similrity Srh Th Binry Brnh Distn Nikolus Augstn nikolus.ugstn@sg..t Dpt. of Computr Sins Univrsity of Slzurg http://rsrh.uni-slzurg.t Vrsion Jnury 11, 2017 Wintrsmstr 2016/2017 Augstn (Univ. Slzurg) Similrity
Similrity Srh Th Binry Brnh Distn Nikolus Augstn nikolus.ugstn@sg..t Dpt. of Computr Sins Univrsity of Slzurg http://rsrh.uni-slzurg.t Vrsion Jnury 11, 2017 Wintrsmstr 2016/2017 Augstn (Univ. Slzurg) Similrity
Winter 2016 COMP-250: Introduction to Computer Science. Lecture 23, April 5, 2016
 Wintr 2016 COMP-250: Introduction to Computr Scinc Lctur 23, April 5, 2016 Commnt out input siz 2) Writ ny lgorithm tht runs in tim Θ(n 2 log 2 n) in wors cs. Explin why this is its running tim. I don
Wintr 2016 COMP-250: Introduction to Computr Scinc Lctur 23, April 5, 2016 Commnt out input siz 2) Writ ny lgorithm tht runs in tim Θ(n 2 log 2 n) in wors cs. Explin why this is its running tim. I don
Module graph.py. 1 Introduction. 2 Graph basics. 3 Module graph.py. 3.1 Objects. CS 231 Naomi Nishimura
 Moul grph.py CS 231 Nomi Nishimur 1 Introution Just lik th Python list n th Python itionry provi wys of storing, ssing, n moifying t, grph n viw s wy of storing, ssing, n moifying t. Bus Python os not
Moul grph.py CS 231 Nomi Nishimur 1 Introution Just lik th Python list n th Python itionry provi wys of storing, ssing, n moifying t, grph n viw s wy of storing, ssing, n moifying t. Bus Python os not
V={A,B,C,D,E} E={ (A,D),(A,E),(B,D), (B,E),(C,D),(C,E)}
 s s of s Computr Sin & Enginring 423/823 Dsign n Anlysis of Ltur 03 (Chptr 22) Stphn Sott (Apt from Vinohnrn N. Vriym) s of s s r strt t typs tht r pplil to numrous prolms Cn ptur ntitis, rltionships twn
s s of s Computr Sin & Enginring 423/823 Dsign n Anlysis of Ltur 03 (Chptr 22) Stphn Sott (Apt from Vinohnrn N. Vriym) s of s s r strt t typs tht r pplil to numrous prolms Cn ptur ntitis, rltionships twn
V={A,B,C,D,E} E={ (A,D),(A,E),(B,D), (B,E),(C,D),(C,E)}
 Introution Computr Sin & Enginring 423/823 Dsign n Anlysis of Algorithms Ltur 03 Elmntry Grph Algorithms (Chptr 22) Stphn Sott (Apt from Vinohnrn N. Vriym) I Grphs r strt t typs tht r pplil to numrous
Introution Computr Sin & Enginring 423/823 Dsign n Anlysis of Algorithms Ltur 03 Elmntry Grph Algorithms (Chptr 22) Stphn Sott (Apt from Vinohnrn N. Vriym) I Grphs r strt t typs tht r pplil to numrous
CSE 373: More on graphs; DFS and BFS. Michael Lee Wednesday, Feb 14, 2018
 CSE 373: Mor on grphs; DFS n BFS Mihl L Wnsy, F 14, 2018 1 Wrmup Wrmup: Disuss with your nighor: Rmin your nighor: wht is simpl grph? Suppos w hv simpl, irt grph with x nos. Wht is th mximum numr of gs
CSE 373: Mor on grphs; DFS n BFS Mihl L Wnsy, F 14, 2018 1 Wrmup Wrmup: Disuss with your nighor: Rmin your nighor: wht is simpl grph? Suppos w hv simpl, irt grph with x nos. Wht is th mximum numr of gs
a b c cat CAT A B C Aa Bb Cc cat cat Lesson 1 (Part 1) Verbal lesson: Capital Letters Make The Same Sound Lesson 1 (Part 1) continued...
 Progrssiv Printing T.M. CPITLS g 4½+ Th sy, fun (n FR!) wy to tch cpitl lttrs. ook : C o - For Kinrgrtn or First Gr (not for pr-school). - Tchs tht cpitl lttrs mk th sm souns s th littl lttrs. - Tchs th
Progrssiv Printing T.M. CPITLS g 4½+ Th sy, fun (n FR!) wy to tch cpitl lttrs. ook : C o - For Kinrgrtn or First Gr (not for pr-school). - Tchs tht cpitl lttrs mk th sm souns s th littl lttrs. - Tchs th
Walk Like a Mathematician Learning Task:
 Gori Dprtmnt of Euction Wlk Lik Mthmticin Lrnin Tsk: Mtrics llow us to prform mny usful mthmticl tsks which orinrily rquir lr numbr of computtions. Som typs of problms which cn b on fficintly with mtrics
Gori Dprtmnt of Euction Wlk Lik Mthmticin Lrnin Tsk: Mtrics llow us to prform mny usful mthmticl tsks which orinrily rquir lr numbr of computtions. Som typs of problms which cn b on fficintly with mtrics
Section 3: Antiderivatives of Formulas
 Chptr Th Intgrl Appli Clculus 96 Sction : Antirivtivs of Formuls Now w cn put th is of rs n ntirivtivs togthr to gt wy of vluting finit intgrls tht is ct n oftn sy. To vlut finit intgrl f(t) t, w cn fin
Chptr Th Intgrl Appli Clculus 96 Sction : Antirivtivs of Formuls Now w cn put th is of rs n ntirivtivs togthr to gt wy of vluting finit intgrls tht is ct n oftn sy. To vlut finit intgrl f(t) t, w cn fin
CSC Design and Analysis of Algorithms. Example: Change-Making Problem
 CSC 801- Dsign n Anlysis of Algorithms Ltur 11 Gry Thniqu Exmpl: Chng-Mking Prolm Givn unlimit mounts of oins of nomintions 1 > > m, giv hng for mount n with th lst numr of oins Exmpl: 1 = 25, 2 =10, =
CSC 801- Dsign n Anlysis of Algorithms Ltur 11 Gry Thniqu Exmpl: Chng-Mking Prolm Givn unlimit mounts of oins of nomintions 1 > > m, giv hng for mount n with th lst numr of oins Exmpl: 1 = 25, 2 =10, =
b. How many ternary words of length 23 with eight 0 s, nine 1 s and six 2 s?
 MATH 3012 Finl Exm, My 4, 2006, WTT Stunt Nm n ID Numr 1. All our prts o this prolm r onrn with trnry strings o lngth n, i.., wors o lngth n with lttrs rom th lpht {0, 1, 2}.. How mny trnry wors o lngth
MATH 3012 Finl Exm, My 4, 2006, WTT Stunt Nm n ID Numr 1. All our prts o this prolm r onrn with trnry strings o lngth n, i.., wors o lngth n with lttrs rom th lpht {0, 1, 2}.. How mny trnry wors o lngth
Math 61 : Discrete Structures Final Exam Instructor: Ciprian Manolescu. You have 180 minutes.
 Nm: UCA ID Numr: Stion lttr: th 61 : Disrt Struturs Finl Exm Instrutor: Ciprin nolsu You hv 180 minuts. No ooks, nots or lultors r llow. Do not us your own srth ppr. 1. (2 points h) Tru/Fls: Cirl th right
Nm: UCA ID Numr: Stion lttr: th 61 : Disrt Struturs Finl Exm Instrutor: Ciprin nolsu You hv 180 minuts. No ooks, nots or lultors r llow. Do not us your own srth ppr. 1. (2 points h) Tru/Fls: Cirl th right
FSA. CmSc 365 Theory of Computation. Finite State Automata and Regular Expressions (Chapter 2, Section 2.3) ALPHABET operations: U, concatenation, *
 CmSc 365 Thory of Computtion Finit Stt Automt nd Rgulr Exprssions (Chptr 2, Sction 2.3) ALPHABET oprtions: U, conctntion, * otin otin Strings Form Rgulr xprssions dscri Closd undr U, conctntion nd * (if
CmSc 365 Thory of Computtion Finit Stt Automt nd Rgulr Exprssions (Chptr 2, Sction 2.3) ALPHABET oprtions: U, conctntion, * otin otin Strings Form Rgulr xprssions dscri Closd undr U, conctntion nd * (if
CS61B Lecture #33. Administrivia: Autograder will run this evening. Today s Readings: Graph Structures: DSIJ, Chapter 12
 Aministrivi: CS61B Ltur #33 Autogrr will run this vning. Toy s Rings: Grph Struturs: DSIJ, Chptr 12 Lst moifi: W Nov 8 00:39:28 2017 CS61B: Ltur #33 1 Why Grphs? For xprssing non-hirrhilly rlt itms Exmpls:
Aministrivi: CS61B Ltur #33 Autogrr will run this vning. Toy s Rings: Grph Struturs: DSIJ, Chptr 12 Lst moifi: W Nov 8 00:39:28 2017 CS61B: Ltur #33 1 Why Grphs? For xprssing non-hirrhilly rlt itms Exmpls:
CSE303 - Introduction to the Theory of Computing Sample Solutions for Exercises on Finite Automata
 CSE303 - Introduction to th Thory of Computing Smpl Solutions for Exrciss on Finit Automt Exrcis 2.1.1 A dtrministic finit utomton M ccpts th mpty string (i.., L(M)) if nd only if its initil stt is finl
CSE303 - Introduction to th Thory of Computing Smpl Solutions for Exrciss on Finit Automt Exrcis 2.1.1 A dtrministic finit utomton M ccpts th mpty string (i.., L(M)) if nd only if its initil stt is finl
CSE 373: AVL trees. Warmup: Warmup. Interlude: Exploring the balance invariant. AVL Trees: Invariants. AVL tree invariants review
 rmup CSE 7: AVL trs rmup: ht is n invrint? Mihl L Friy, Jn 9, 0 ht r th AVL tr invrints, xtly? Disuss with your nighor. AVL Trs: Invrints Intrlu: Exploring th ln invrint Cor i: xtr invrint to BSTs tht
rmup CSE 7: AVL trs rmup: ht is n invrint? Mihl L Friy, Jn 9, 0 ht r th AVL tr invrints, xtly? Disuss with your nighor. AVL Trs: Invrints Intrlu: Exploring th ln invrint Cor i: xtr invrint to BSTs tht
Outline. 1 Introduction. 2 Min-Cost Spanning Trees. 4 Example
 Outlin Computr Sin 33 Computtion o Minimum-Cost Spnnin Trs Prim's Alorithm Introution Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #33 3 Alorithm Gnrl Constrution Mik Joson (Univrsity o Clry)
Outlin Computr Sin 33 Computtion o Minimum-Cost Spnnin Trs Prim's Alorithm Introution Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #33 3 Alorithm Gnrl Constrution Mik Joson (Univrsity o Clry)
CSE 373. Graphs 1: Concepts, Depth/Breadth-First Search reading: Weiss Ch. 9. slides created by Marty Stepp
 CSE 373 Grphs 1: Conpts, Dpth/Brth-First Srh ring: Wiss Ch. 9 slis rt y Mrty Stpp http://www.s.wshington.u/373/ Univrsity o Wshington, ll rights rsrv. 1 Wht is grph? 56 Tokyo Sttl Soul 128 16 30 181 140
CSE 373 Grphs 1: Conpts, Dpth/Brth-First Srh ring: Wiss Ch. 9 slis rt y Mrty Stpp http://www.s.wshington.u/373/ Univrsity o Wshington, ll rights rsrv. 1 Wht is grph? 56 Tokyo Sttl Soul 128 16 30 181 140
Why the Junction Tree Algorithm? The Junction Tree Algorithm. Clique Potential Representation. Overview. Chris Williams 1.
 Why th Juntion Tr lgorithm? Th Juntion Tr lgorithm hris Willims 1 Shool of Informtis, Univrsity of Einurgh Otor 2009 Th JT is gnrl-purpos lgorithm for omputing (onitionl) mrginls on grphs. It os this y
Why th Juntion Tr lgorithm? Th Juntion Tr lgorithm hris Willims 1 Shool of Informtis, Univrsity of Einurgh Otor 2009 Th JT is gnrl-purpos lgorithm for omputing (onitionl) mrginls on grphs. It os this y
Linear Algebra Existence of the determinant. Expansion according to a row.
 Lir Algbr 2270 1 Existc of th dtrmit. Expsio ccordig to row. W dfi th dtrmit for 1 1 mtrics s dt([]) = (1) It is sy chck tht it stisfis D1)-D3). For y othr w dfi th dtrmit s follows. Assumig th dtrmit
Lir Algbr 2270 1 Existc of th dtrmit. Expsio ccordig to row. W dfi th dtrmit for 1 1 mtrics s dt([]) = (1) It is sy chck tht it stisfis D1)-D3). For y othr w dfi th dtrmit s follows. Assumig th dtrmit
An undirected graph G = (V, E) V a set of vertices E a set of unordered edges (v,w) where v, w in V
 Unirt Grphs An unirt grph G = (V, E) V st o vrtis E st o unorr gs (v,w) whr v, w in V USE: to mol symmtri rltionships twn ntitis vrtis v n w r jnt i thr is n g (v,w) [or (w,v)] th g (v,w) is inint upon
Unirt Grphs An unirt grph G = (V, E) V st o vrtis E st o unorr gs (v,w) whr v, w in V USE: to mol symmtri rltionships twn ntitis vrtis v n w r jnt i thr is n g (v,w) [or (w,v)] th g (v,w) is inint upon
Graphs. CSC 1300 Discrete Structures Villanova University. Villanova CSC Dr Papalaskari
 Grphs CSC 1300 Disrt Struturs Villnov Univrsity Grphs Grphs r isrt struturs onsis?ng of vr?s n gs tht onnt ths vr?s. Grphs n us to mol: omputr systms/ntworks mthm?l rl?ons logi iruit lyout jos/prosss f
Grphs CSC 1300 Disrt Struturs Villnov Univrsity Grphs Grphs r isrt struturs onsis?ng of vr?s n gs tht onnt ths vr?s. Grphs n us to mol: omputr systms/ntworks mthm?l rl?ons logi iruit lyout jos/prosss f
# 1 ' 10 ' 100. Decimal point = 4 hundred. = 6 tens (or sixty) = 5 ones (or five) = 2 tenths. = 7 hundredths.
 How os it work? Pl vlu o imls rprsnt prts o whol numr or ojt # 0 000 Tns o thousns # 000 # 00 Thousns Hunrs Tns Ons # 0 Diml point st iml pl: ' 0 # 0 on tnth n iml pl: ' 0 # 00 on hunrth r iml pl: ' 0
How os it work? Pl vlu o imls rprsnt prts o whol numr or ojt # 0 000 Tns o thousns # 000 # 00 Thousns Hunrs Tns Ons # 0 Diml point st iml pl: ' 0 # 0 on tnth n iml pl: ' 0 # 00 on hunrth r iml pl: ' 0
Cycles and Simple Cycles. Paths and Simple Paths. Trees. Problem: There is No Completely Standard Terminology!
 Outlin Computr Sin 331, Spnnin, n Surphs Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #30 1 Introution 2 3 Dinition 4 Spnnin 5 6 Mik Joson (Univrsity o Clry) Computr Sin 331 Ltur #30 1 / 20 Mik
Outlin Computr Sin 331, Spnnin, n Surphs Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #30 1 Introution 2 3 Dinition 4 Spnnin 5 6 Mik Joson (Univrsity o Clry) Computr Sin 331 Ltur #30 1 / 20 Mik
Kernels. ffl A kernel K is a function of two objects, for example, two sentence/tree pairs (x1; y1) and (x2; y2)
 Krnls krnl K is a function of two ojcts, for xampl, two sntnc/tr pairs (x1; y1) an (x2; y2) K((x1; y1); (x2; y2)) Intuition: K((x1; y1); (x2; y2)) is a masur of th similarity (x1; y1) twn (x2; y2) an ormally:
Krnls krnl K is a function of two ojcts, for xampl, two sntnc/tr pairs (x1; y1) an (x2; y2) K((x1; y1); (x2; y2)) Intuition: K((x1; y1); (x2; y2)) is a masur of th similarity (x1; y1) twn (x2; y2) an ormally:
Garnir Polynomial and their Properties
 Univrsity of Cliforni, Dvis Dprtmnt of Mthmtis Grnir Polynomil n thir Proprtis Author: Yu Wng Suprvisor: Prof. Gorsky Eugny My 8, 07 Grnir Polynomil n thir Proprtis Yu Wng mil: uywng@uvis.u. In this ppr,
Univrsity of Cliforni, Dvis Dprtmnt of Mthmtis Grnir Polynomil n thir Proprtis Author: Yu Wng Suprvisor: Prof. Gorsky Eugny My 8, 07 Grnir Polynomil n thir Proprtis Yu Wng mil: uywng@uvis.u. In this ppr,
Algorithmic and NP-Completeness Aspects of a Total Lict Domination Number of a Graph
 Intrntionl J.Mth. Comin. Vol.1(2014), 80-86 Algorithmi n NP-Compltnss Aspts of Totl Lit Domintion Numr of Grph Girish.V.R. (PES Institut of Thnology(South Cmpus), Bnglor, Krntk Stt, Ini) P.Ush (Dprtmnt
Intrntionl J.Mth. Comin. Vol.1(2014), 80-86 Algorithmi n NP-Compltnss Aspts of Totl Lit Domintion Numr of Grph Girish.V.R. (PES Institut of Thnology(South Cmpus), Bnglor, Krntk Stt, Ini) P.Ush (Dprtmnt
CS 461, Lecture 17. Today s Outline. Example Run
 Prim s Algorithm CS 461, Ltur 17 Jr Si Univrsity o Nw Mxio In Prim s lgorithm, th st A mintin y th lgorithm orms singl tr. Th tr strts rom n ritrry root vrtx n grows until it spns ll th vrtis in V At h
Prim s Algorithm CS 461, Ltur 17 Jr Si Univrsity o Nw Mxio In Prim s lgorithm, th st A mintin y th lgorithm orms singl tr. Th tr strts rom n ritrry root vrtx n grows until it spns ll th vrtis in V At h
, each of which is a tree, and whose roots r 1. , respectively, are children of r. Data Structures & File Management
 nrl tr T is init st o on or mor nos suh tht thr is on sint no r, ll th root o T, n th rminin nos r prtition into n isjoint susts T, T,, T n, h o whih is tr, n whos roots r, r,, r n, rsptivly, r hilrn o
nrl tr T is init st o on or mor nos suh tht thr is on sint no r, ll th root o T, n th rminin nos r prtition into n isjoint susts T, T,, T n, h o whih is tr, n whos roots r, r,, r n, rsptivly, r hilrn o
Present state Next state Q + M N
 Qustion 1. An M-N lip-lop works s ollows: I MN=00, th nxt stt o th lip lop is 0. I MN=01, th nxt stt o th lip-lop is th sm s th prsnt stt I MN=10, th nxt stt o th lip-lop is th omplmnt o th prsnt stt I
Qustion 1. An M-N lip-lop works s ollows: I MN=00, th nxt stt o th lip lop is 0. I MN=01, th nxt stt o th lip-lop is th sm s th prsnt stt I MN=10, th nxt stt o th lip-lop is th omplmnt o th prsnt stt I
The second condition says that a node α of the tree has exactly n children if the arity of its label is n.
 CS 6110 S14 Hanout 2 Proof of Conflunc 27 January 2014 In this supplmntary lctur w prov that th λ-calculus is conflunt. This is rsult is u to lonzo Church (1903 1995) an J. arkly Rossr (1907 1989) an is
CS 6110 S14 Hanout 2 Proof of Conflunc 27 January 2014 In this supplmntary lctur w prov that th λ-calculus is conflunt. This is rsult is u to lonzo Church (1903 1995) an J. arkly Rossr (1907 1989) an is
Minimum Spanning Trees
 Minimum Spnning Trs Minimum Spnning Trs Problm A town hs st of houss nd st of rods A rod conncts nd only houss A rod conncting houss u nd v hs rpir cost w(u, v) Gol: Rpir nough (nd no mor) rods such tht:
Minimum Spnning Trs Minimum Spnning Trs Problm A town hs st of houss nd st of rods A rod conncts nd only houss A rod conncting houss u nd v hs rpir cost w(u, v) Gol: Rpir nough (nd no mor) rods such tht:
Exam 1 Solution. CS 542 Advanced Data Structures and Algorithms 2/14/2013
 CS Avn Dt Struturs n Algorithms Exm Solution Jon Turnr //. ( points) Suppos you r givn grph G=(V,E) with g wights w() n minimum spnning tr T o G. Now, suppos nw g {u,v} is to G. Dsri (in wors) mtho or
CS Avn Dt Struturs n Algorithms Exm Solution Jon Turnr //. ( points) Suppos you r givn grph G=(V,E) with g wights w() n minimum spnning tr T o G. Now, suppos nw g {u,v} is to G. Dsri (in wors) mtho or
A Simple Code Generator. Code generation Algorithm. Register and Address Descriptors. Example 3/31/2008. Code Generation
 A Simpl Co Gnrtor Co Gnrtion Chptr 8 II Gnrt o for singl si lok How to us rgistrs? In most mhin rhitturs, som or ll of th oprnsmust in rgistrs Rgistrs mk goo tmporris Hol vlus tht r omput in on si lok
A Simpl Co Gnrtor Co Gnrtion Chptr 8 II Gnrt o for singl si lok How to us rgistrs? In most mhin rhitturs, som or ll of th oprnsmust in rgistrs Rgistrs mk goo tmporris Hol vlus tht r omput in on si lok
Chapter 16. 1) is a particular point on the graph of the function. 1. y, where x y 1
 Prctic qustions W now tht th prmtr p is dirctl rltd to th mplitud; thrfor, w cn find tht p. cos d [ sin ] sin sin Not: Evn though ou might not now how to find th prmtr in prt, it is lws dvisl to procd
Prctic qustions W now tht th prmtr p is dirctl rltd to th mplitud; thrfor, w cn find tht p. cos d [ sin ] sin sin Not: Evn though ou might not now how to find th prmtr in prt, it is lws dvisl to procd
1 Introduction to Modulo 7 Arithmetic
 1 Introution to Moulo 7 Arithmti Bor w try our hn t solvin som hr Moulr KnKns, lt s tk los look t on moulr rithmti, mo 7 rithmti. You ll s in this sminr tht rithmti moulo prim is quit irnt rom th ons w
1 Introution to Moulo 7 Arithmti Bor w try our hn t solvin som hr Moulr KnKns, lt s tk los look t on moulr rithmti, mo 7 rithmti. You ll s in this sminr tht rithmti moulo prim is quit irnt rom th ons w
Paths. Connectivity. Euler and Hamilton Paths. Planar graphs.
 Pths.. Eulr n Hmilton Pths.. Pth D. A pth rom s to t is squn o gs {x 0, x 1 }, {x 1, x 2 },... {x n 1, x n }, whr x 0 = s, n x n = t. D. Th lngth o pth is th numr o gs in it. {, } {, } {, } {, } {, } {,
Pths.. Eulr n Hmilton Pths.. Pth D. A pth rom s to t is squn o gs {x 0, x 1 }, {x 1, x 2 },... {x n 1, x n }, whr x 0 = s, n x n = t. D. Th lngth o pth is th numr o gs in it. {, } {, } {, } {, } {, } {,
(2) If we multiplied a row of B by λ, then the value is also multiplied by λ(here lambda could be 0). namely
 . DETERMINANT.. Dtrminnt. Introution:I you think row vtor o mtrix s oorint o vtors in sp, thn th gomtri mning o th rnk o th mtrix is th imnsion o th prlllppi spnn y thm. But w r not only r out th imnsion,
. DETERMINANT.. Dtrminnt. Introution:I you think row vtor o mtrix s oorint o vtors in sp, thn th gomtri mning o th rnk o th mtrix is th imnsion o th prlllppi spnn y thm. But w r not only r out th imnsion,
Graph Isomorphism. Graphs - II. Cayley s Formula. Planar Graphs. Outline. Is K 5 planar? The number of labeled trees on n nodes is n n-2
 Grt Thortil Is In Computr Sin Vitor Amhik CS 15-251 Ltur 9 Grphs - II Crngi Mllon Univrsity Grph Isomorphism finition. Two simpl grphs G n H r isomorphi G H if thr is vrtx ijtion V H ->V G tht prsrvs jny
Grt Thortil Is In Computr Sin Vitor Amhik CS 15-251 Ltur 9 Grphs - II Crngi Mllon Univrsity Grph Isomorphism finition. Two simpl grphs G n H r isomorphi G H if thr is vrtx ijtion V H ->V G tht prsrvs jny
12/3/12. Outline. Part 10. Graphs. Circuits. Euler paths/circuits. Euler s bridge problem (Bridges of Konigsberg Problem)
 12/3/12 Outlin Prt 10. Grphs CS 200 Algorithms n Dt Struturs Introution Trminology Implmnting Grphs Grph Trvrsls Topologil Sorting Shortst Pths Spnning Trs Minimum Spnning Trs Ciruits 1 Ciruits Cyl 2 Eulr
12/3/12 Outlin Prt 10. Grphs CS 200 Algorithms n Dt Struturs Introution Trminology Implmnting Grphs Grph Trvrsls Topologil Sorting Shortst Pths Spnning Trs Minimum Spnning Trs Ciruits 1 Ciruits Cyl 2 Eulr
5/9/13. Part 10. Graphs. Outline. Circuits. Introduction Terminology Implementing Graphs
 Prt 10. Grphs CS 200 Algorithms n Dt Struturs 1 Introution Trminology Implmnting Grphs Outlin Grph Trvrsls Topologil Sorting Shortst Pths Spnning Trs Minimum Spnning Trs Ciruits 2 Ciruits Cyl A spil yl
Prt 10. Grphs CS 200 Algorithms n Dt Struturs 1 Introution Trminology Implmnting Grphs Outlin Grph Trvrsls Topologil Sorting Shortst Pths Spnning Trs Minimum Spnning Trs Ciruits 2 Ciruits Cyl A spil yl
Outline. Computer Science 331. Computation of Min-Cost Spanning Trees. Costs of Spanning Trees in Weighted Graphs
 Outlin Computr Sin 33 Computtion o Minimum-Cost Spnnin Trs Prim s Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #34 Introution Min-Cost Spnnin Trs 3 Gnrl Constrution 4 5 Trmintion n Eiiny 6 Aitionl
Outlin Computr Sin 33 Computtion o Minimum-Cost Spnnin Trs Prim s Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #34 Introution Min-Cost Spnnin Trs 3 Gnrl Constrution 4 5 Trmintion n Eiiny 6 Aitionl
SOLVED EXAMPLES. be the foci of an ellipse with eccentricity e. For any point P on the ellipse, prove that. tan
 LOCUS 58 SOLVED EXAMPLES Empl Lt F n F th foci of n llips with ccntricit. For n point P on th llips, prov tht tn PF F tn PF F Assum th llips to, n lt P th point (, sin ). P(, sin ) F F F = (-, 0) F = (,
LOCUS 58 SOLVED EXAMPLES Empl Lt F n F th foci of n llips with ccntricit. For n point P on th llips, prov tht tn PF F tn PF F Assum th llips to, n lt P th point (, sin ). P(, sin ) F F F = (-, 0) F = (,
Chem 104A, Fall 2016, Midterm 1 Key
 hm 104A, ll 2016, Mitrm 1 Ky 1) onstruct microstt tl for p 4 configurtion. Pls numrt th ms n ml for ch lctron in ch microstt in th tl. (Us th formt ml m s. Tht is spin -½ lctron in n s oritl woul writtn
hm 104A, ll 2016, Mitrm 1 Ky 1) onstruct microstt tl for p 4 configurtion. Pls numrt th ms n ml for ch lctron in ch microstt in th tl. (Us th formt ml m s. Tht is spin -½ lctron in n s oritl woul writtn
Outline. Binary Tree
 Outlin Similrity Srh Th Binry Brnh Distn Nikolus Austn nikolus.ustn@s..t Dpt. o Computr Sins Univrsity o Slzur http://rsrh.uni-slzur.t 1 Binry Brnh Distn Binry Rprsnttion o Tr Binry Brnhs Lowr Boun or
Outlin Similrity Srh Th Binry Brnh Distn Nikolus Austn nikolus.ustn@s..t Dpt. o Computr Sins Univrsity o Slzur http://rsrh.uni-slzur.t 1 Binry Brnh Distn Binry Rprsnttion o Tr Binry Brnhs Lowr Boun or
Graphs. Graphs. Graphs: Basic Terminology. Directed Graphs. Dr Papalaskari 1
 CSC 00 Disrt Struturs : Introuon to Grph Thory Grphs Grphs CSC 00 Disrt Struturs Villnov Univrsity Grphs r isrt struturs onsisng o vrs n gs tht onnt ths vrs. Grphs n us to mol: omputr systms/ntworks mthml
CSC 00 Disrt Struturs : Introuon to Grph Thory Grphs Grphs CSC 00 Disrt Struturs Villnov Univrsity Grphs r isrt struturs onsisng o vrs n gs tht onnt ths vrs. Grphs n us to mol: omputr systms/ntworks mthml
ECE COMBINATIONAL BUILDING BLOCKS - INVEST 13 DECODERS AND ENCODERS
 C 24 - COMBINATIONAL BUILDING BLOCKS - INVST 3 DCODS AND NCODS FALL 23 AP FLZ To o "wll" on this invstition you must not only t th riht nswrs ut must lso o nt, omplt n onis writups tht mk ovious wht h
C 24 - COMBINATIONAL BUILDING BLOCKS - INVST 3 DCODS AND NCODS FALL 23 AP FLZ To o "wll" on this invstition you must not only t th riht nswrs ut must lso o nt, omplt n onis writups tht mk ovious wht h
CS200: Graphs. Graphs. Directed Graphs. Graphs/Networks Around Us. What can this represent? Sometimes we want to represent directionality:
 CS2: Grphs Prihr Ch. 4 Rosn Ch. Grphs A olltion of nos n gs Wht n this rprsnt? n A omputr ntwork n Astrtion of mp n Soil ntwork CS2 - Hsh Tls 2 Dirt Grphs Grphs/Ntworks Aroun Us A olltion of nos n irt
CS2: Grphs Prihr Ch. 4 Rosn Ch. Grphs A olltion of nos n gs Wht n this rprsnt? n A omputr ntwork n Astrtion of mp n Soil ntwork CS2 - Hsh Tls 2 Dirt Grphs Grphs/Ntworks Aroun Us A olltion of nos n irt
Lecture 11 Waves in Periodic Potentials Today: Questions you should be able to address after today s lecture:
 Lctur 11 Wvs in Priodic Potntils Tody: 1. Invrs lttic dfinition in 1D.. rphicl rprsnttion of priodic nd -priodic functions using th -xis nd invrs lttic vctors. 3. Sris solutions to th priodic potntil Hmiltonin
Lctur 11 Wvs in Priodic Potntils Tody: 1. Invrs lttic dfinition in 1D.. rphicl rprsnttion of priodic nd -priodic functions using th -xis nd invrs lttic vctors. 3. Sris solutions to th priodic potntil Hmiltonin
0.1. Exercise 1: the distances between four points in a graph
 Mth 707 Spring 2017 (Drij Grinrg): mitrm 3 pg 1 Mth 707 Spring 2017 (Drij Grinrg): mitrm 3 u: W, 3 My 2017, in lss or y mil (grinr@umn.u) or lss S th wsit or rlvnt mtril. Rsults provn in th nots, or in
Mth 707 Spring 2017 (Drij Grinrg): mitrm 3 pg 1 Mth 707 Spring 2017 (Drij Grinrg): mitrm 3 u: W, 3 My 2017, in lss or y mil (grinr@umn.u) or lss S th wsit or rlvnt mtril. Rsults provn in th nots, or in
10. EXTENDING TRACTABILITY
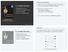 Coping with NP-compltnss 0. EXTENDING TRACTABILITY ining small vrtx covrs solving NP-har problms on trs circular arc covrings vrtx covr in bipartit graphs Q. Suppos I n to solv an NP-complt problm. What
Coping with NP-compltnss 0. EXTENDING TRACTABILITY ining small vrtx covrs solving NP-har problms on trs circular arc covrings vrtx covr in bipartit graphs Q. Suppos I n to solv an NP-complt problm. What
Planar Upward Drawings
 C.S. 252 Pro. Rorto Tmssi Computtionl Gomtry Sm. II, 1992 1993 Dt: My 3, 1993 Sri: Shmsi Moussvi Plnr Upwr Drwings 1 Thorm: G is yli i n only i it hs upwr rwing. Proo: 1. An upwr rwing is yli. Follow th
C.S. 252 Pro. Rorto Tmssi Computtionl Gomtry Sm. II, 1992 1993 Dt: My 3, 1993 Sri: Shmsi Moussvi Plnr Upwr Drwings 1 Thorm: G is yli i n only i it hs upwr rwing. Proo: 1. An upwr rwing is yli. Follow th
Examples and applications on SSSP and MST
 Exampls an applications on SSSP an MST Dan (Doris) H & Junhao Gan ITEE Univrsity of Qunslan COMP3506/7505, Uni of Qunslan Exampls an applications on SSSP an MST Dijkstra s Algorithm Th algorithm solvs
Exampls an applications on SSSP an MST Dan (Doris) H & Junhao Gan ITEE Univrsity of Qunslan COMP3506/7505, Uni of Qunslan Exampls an applications on SSSP an MST Dijkstra s Algorithm Th algorithm solvs
TOPIC 5: INTEGRATION
 TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
COMP108 Algorithmic Foundations
 Grdy mthods Prudn Wong http://www.s.liv..uk/~pwong/thing/omp108/01617 Coin Chng Prolm Suppos w hv 3 typs of oins 10p 0p 50p Minimum numr of oins to mk 0.8, 1.0, 1.? Grdy mthod Lrning outoms Undrstnd wht
Grdy mthods Prudn Wong http://www.s.liv..uk/~pwong/thing/omp108/01617 Coin Chng Prolm Suppos w hv 3 typs of oins 10p 0p 50p Minimum numr of oins to mk 0.8, 1.0, 1.? Grdy mthod Lrning outoms Undrstnd wht
ME 522 PRINCIPLES OF ROBOTICS. FIRST MIDTERM EXAMINATION April 19, M. Kemal Özgören
 ME 522 PINCIPLES OF OBOTICS FIST MIDTEM EXAMINATION April 9, 202 Nm Lst Nm M. Kml Özgörn 2 4 60 40 40 0 80 250 USEFUL FOMULAS cos( ) cos cos sin sin sin( ) sin cos cos sin sin y/ r, cos x/ r, r 0 tn 2(
ME 522 PINCIPLES OF OBOTICS FIST MIDTEM EXAMINATION April 9, 202 Nm Lst Nm M. Kml Özgörn 2 4 60 40 40 0 80 250 USEFUL FOMULAS cos( ) cos cos sin sin sin( ) sin cos cos sin sin y/ r, cos x/ r, r 0 tn 2(
Last time: introduced our first computational model the DFA.
 Lctur 7 Homwork #7: 2.2.1, 2.2.2, 2.2.3 (hnd in c nd d), Misc: Givn: M, NFA Prov: (q,xy) * (p,y) iff (q,x) * (p,) (follow proof don in clss tody) Lst tim: introducd our first computtionl modl th DFA. Tody
Lctur 7 Homwork #7: 2.2.1, 2.2.2, 2.2.3 (hnd in c nd d), Misc: Givn: M, NFA Prov: (q,xy) * (p,y) iff (q,x) * (p,) (follow proof don in clss tody) Lst tim: introducd our first computtionl modl th DFA. Tody
More Foundations. Undirected Graphs. Degree. A Theorem. Graphs, Products, & Relations
 Mr Funtins Grphs, Pruts, & Rltins Unirt Grphs An unirt grph is pir f 1. A st f ns 2. A st f gs (whr n g is st f tw ns*) Friy, Sptmr 2, 2011 Ring: Sipsr 0.2 ginning f 0.4; Stughtn 1.1.5 ({,,,,}, {{,}, {,},
Mr Funtins Grphs, Pruts, & Rltins Unirt Grphs An unirt grph is pir f 1. A st f ns 2. A st f gs (whr n g is st f tw ns*) Friy, Sptmr 2, 2011 Ring: Sipsr 0.2 ginning f 0.4; Stughtn 1.1.5 ({,,,,}, {{,}, {,},
Constructive Geometric Constraint Solving
 Construtiv Gomtri Constrint Solving Antoni Soto i Rir Dprtmnt Llngutgs i Sistms Inormàtis Univrsitt Politèni Ctluny Brlon, Sptmr 2002 CGCS p.1/37 Prliminris CGCS p.2/37 Gomtri onstrint prolm C 2 D L BC
Construtiv Gomtri Constrint Solving Antoni Soto i Rir Dprtmnt Llngutgs i Sistms Inormàtis Univrsitt Politèni Ctluny Brlon, Sptmr 2002 CGCS p.1/37 Prliminris CGCS p.2/37 Gomtri onstrint prolm C 2 D L BC
12. Traffic engineering
 lt2.ppt S-38. Introution to Tltrffi Thory Spring 200 2 Topology Pths A tlommunition ntwork onsists of nos n links Lt N not th st of nos in with n Lt J not th st of nos in with j N = {,,,,} J = {,2,3,,2}
lt2.ppt S-38. Introution to Tltrffi Thory Spring 200 2 Topology Pths A tlommunition ntwork onsists of nos n links Lt N not th st of nos in with n Lt J not th st of nos in with j N = {,,,,} J = {,2,3,,2}
Integration Continued. Integration by Parts Solving Definite Integrals: Area Under a Curve Improper Integrals
 Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
DFA (Deterministic Finite Automata) q a
 Big pictur All lngugs Dcidl Turing mchins NP P Contxt-fr Contxt-fr grmmrs, push-down utomt Rgulr Automt, non-dtrministic utomt, rgulr xprssions DFA (Dtrministic Finit Automt) 0 q 0 0 0 0 q DFA (Dtrministic
Big pictur All lngugs Dcidl Turing mchins NP P Contxt-fr Contxt-fr grmmrs, push-down utomt Rgulr Automt, non-dtrministic utomt, rgulr xprssions DFA (Dtrministic Finit Automt) 0 q 0 0 0 0 q DFA (Dtrministic
Analysis of Algorithms - Elementary graphs algorithms -
 Analysis of Algorithms - Elmntary graphs algorithms - Anras Ermahl MRTC (Mälaralns Ral-Tim Rsarch Cntr) anras.rmahl@mh.s Autumn 004 Graphs Graphs ar important mathmatical ntitis in computr scinc an nginring
Analysis of Algorithms - Elmntary graphs algorithms - Anras Ermahl MRTC (Mälaralns Ral-Tim Rsarch Cntr) anras.rmahl@mh.s Autumn 004 Graphs Graphs ar important mathmatical ntitis in computr scinc an nginring
Seven-Segment Display Driver
 7-Smnt Disply Drivr, Ron s in 7-Smnt Disply Drivr, Ron s in Prolm 62. 00 0 0 00 0000 000 00 000 0 000 00 0 00 00 0 0 0 000 00 0 00 BCD Diits in inry Dsin Drivr Loi 4 inputs, 7 outputs 7 mps, h with 6 on
7-Smnt Disply Drivr, Ron s in 7-Smnt Disply Drivr, Ron s in Prolm 62. 00 0 0 00 0000 000 00 000 0 000 00 0 00 00 0 0 0 000 00 0 00 BCD Diits in inry Dsin Drivr Loi 4 inputs, 7 outputs 7 mps, h with 6 on
Flat Splicing Array Grammar Systems Generating Picture Arrays
 Intrntionl Journl of Computr Informtion Systms n Inustril Mngmnt Applictions. ISSN 2150-7988 Volum 8 (2016) pp. 336 344 c MIR Ls, www.mirls.nt/ijcisim/inx.html Flt Splicing Arry Grmmr Systms Gnrting Pictur
Intrntionl Journl of Computr Informtion Systms n Inustril Mngmnt Applictions. ISSN 2150-7988 Volum 8 (2016) pp. 336 344 c MIR Ls, www.mirls.nt/ijcisim/inx.html Flt Splicing Arry Grmmr Systms Gnrting Pictur
QUESTIONS BEGIN HERE!
 Points miss: Stunt's Nm: Totl sor: /100 points Est Tnnss Stt Univrsity Dprtmnt of Computr n Informtion Sins CSCI 710 (Trnoff) Disrt Struturs TEST for Fll Smstr, 00 R this for strtin! This tst is los ook
Points miss: Stunt's Nm: Totl sor: /100 points Est Tnnss Stt Univrsity Dprtmnt of Computr n Informtion Sins CSCI 710 (Trnoff) Disrt Struturs TEST for Fll Smstr, 00 R this for strtin! This tst is los ook
The University of Sydney MATH2969/2069. Graph Theory Tutorial 5 (Week 12) Solutions 2008
 Th Univrsity o Syny MATH2969/2069 Grph Thory Tutoril 5 (Wk 12) Solutions 2008 1. (i) Lt G th isonnt plnr grph shown. Drw its ul G, n th ul o th ul (G ). (ii) Show tht i G is isonnt plnr grph, thn G is
Th Univrsity o Syny MATH2969/2069 Grph Thory Tutoril 5 (Wk 12) Solutions 2008 1. (i) Lt G th isonnt plnr grph shown. Drw its ul G, n th ul o th ul (G ). (ii) Show tht i G is isonnt plnr grph, thn G is
Analysis of Algorithms - Elementary graphs algorithms -
 Analysis of Algorithms - Elmntary graphs algorithms - Anras Ermahl MRTC (Mälaralns Ral-Tim Rsach Cntr) anras.rmahl@mh.s Autumn 00 Graphs Graphs ar important mathmatical ntitis in computr scinc an nginring
Analysis of Algorithms - Elmntary graphs algorithms - Anras Ermahl MRTC (Mälaralns Ral-Tim Rsach Cntr) anras.rmahl@mh.s Autumn 00 Graphs Graphs ar important mathmatical ntitis in computr scinc an nginring
Multi-Section Coupled Line Couplers
 /0/009 MultiSction Coupld Lin Couplrs /8 Multi-Sction Coupld Lin Couplrs W cn dd multipl coupld lins in sris to incrs couplr ndwidth. Figur 7.5 (p. 6) An N-sction coupld lin l W typiclly dsign th couplr
/0/009 MultiSction Coupld Lin Couplrs /8 Multi-Sction Coupld Lin Couplrs W cn dd multipl coupld lins in sris to incrs couplr ndwidth. Figur 7.5 (p. 6) An N-sction coupld lin l W typiclly dsign th couplr
Notes on Finite Automata Department of Computer Science Professor Goldberg Textbooks: Introduction to the Theory of Computation by Michael Sipser
 Nots on Finit Automt Dprtmnt of Computr Scinc Profssor Goldrg Txtooks: Introduction to th Thory of Computtion y Michl Sipsr Elmnts of th Thory of Computtion y H. Lwis nd C. Ppdimitriou Ths nots contin
Nots on Finit Automt Dprtmnt of Computr Scinc Profssor Goldrg Txtooks: Introduction to th Thory of Computtion y Michl Sipsr Elmnts of th Thory of Computtion y H. Lwis nd C. Ppdimitriou Ths nots contin
CS September 2018
 Loil los Distriut Systms 06. Loil los Assin squn numrs to msss All ooprtin prosss n r on orr o vnts vs. physil los: rport tim o y Assum no ntrl tim sour Eh systm mintins its own lol lo No totl orrin o
Loil los Distriut Systms 06. Loil los Assin squn numrs to msss All ooprtin prosss n r on orr o vnts vs. physil los: rport tim o y Assum no ntrl tim sour Eh systm mintins its own lol lo No totl orrin o
arxiv: v1 [cs.ds] 20 Feb 2008
![arxiv: v1 [cs.ds] 20 Feb 2008 arxiv: v1 [cs.ds] 20 Feb 2008](/thumbs/91/107110294.jpg) Symposium on Thortil Aspts of Computr Sin 2008 (Borux), pp. 361-372 www.sts-onf.org rxiv:0802.2867v1 [s.ds] 20 F 2008 FIXED PARAMETER POLYNOMIAL TIME ALGORITHMS FOR MAXIMUM AGREEMENT AND COMPATIBLE SUPERTREES
Symposium on Thortil Aspts of Computr Sin 2008 (Borux), pp. 361-372 www.sts-onf.org rxiv:0802.2867v1 [s.ds] 20 F 2008 FIXED PARAMETER POLYNOMIAL TIME ALGORITHMS FOR MAXIMUM AGREEMENT AND COMPATIBLE SUPERTREES
Weighted graphs -- reminder. Data Structures LECTURE 15. Shortest paths algorithms. Example: weighted graph. Two basic properties of shortest paths
 Dt Strutur LECTURE Shortt pth lgorithm Proprti of hortt pth Bllmn-For lgorithm Dijktr lgorithm Chptr in th txtook (pp ). Wight grph -- rminr A wight grph i grph in whih g hv wight (ot) w(v i, v j ) >.
Dt Strutur LECTURE Shortt pth lgorithm Proprti of hortt pth Bllmn-For lgorithm Dijktr lgorithm Chptr in th txtook (pp ). Wight grph -- rminr A wight grph i grph in whih g hv wight (ot) w(v i, v j ) >.
Outline. Circuits. Euler paths/circuits 4/25/12. Part 10. Graphs. Euler s bridge problem (Bridges of Konigsberg Problem)
 4/25/12 Outlin Prt 10. Grphs CS 200 Algorithms n Dt Struturs Introution Trminology Implmnting Grphs Grph Trvrsls Topologil Sorting Shortst Pths Spnning Trs Minimum Spnning Trs Ciruits 1 2 Eulr s rig prolm
4/25/12 Outlin Prt 10. Grphs CS 200 Algorithms n Dt Struturs Introution Trminology Implmnting Grphs Grph Trvrsls Topologil Sorting Shortst Pths Spnning Trs Minimum Spnning Trs Ciruits 1 2 Eulr s rig prolm
First order differential equation Linear equation; Method of integrating factors
 First orr iffrntial quation Linar quation; Mtho of intgrating factors Exampl 1: Rwrit th lft han si as th rivativ of th prouct of y an som function by prouct rul irctly. Solving th first orr iffrntial
First orr iffrntial quation Linar quation; Mtho of intgrating factors Exampl 1: Rwrit th lft han si as th rivativ of th prouct of y an som function by prouct rul irctly. Solving th first orr iffrntial
Numbering Boundary Nodes
 Numring Bounry Nos Lh MBri Empori Stt Univrsity August 10, 2001 1 Introution Th purpos of this ppr is to xplor how numring ltril rsistor ntworks ffts thir rspons mtrix, Λ. Morovr, wht n lrn from Λ out
Numring Bounry Nos Lh MBri Empori Stt Univrsity August 10, 2001 1 Introution Th purpos of this ppr is to xplor how numring ltril rsistor ntworks ffts thir rspons mtrix, Λ. Morovr, wht n lrn from Λ out
Section 10.4 Connectivity (up to paths and isomorphism, not including)
 Toy w will isuss two stions: Stion 10.3 Rprsnting Grphs n Grph Isomorphism Stion 10.4 Conntivity (up to pths n isomorphism, not inluing) 1 10.3 Rprsnting Grphs n Grph Isomorphism Whn w r working on n lgorithm
Toy w will isuss two stions: Stion 10.3 Rprsnting Grphs n Grph Isomorphism Stion 10.4 Conntivity (up to pths n isomorphism, not inluing) 1 10.3 Rprsnting Grphs n Grph Isomorphism Whn w r working on n lgorithm
Instructions for Section 1
 Instructions for Sction 1 Choos th rspons tht is corrct for th qustion. A corrct nswr scors 1, n incorrct nswr scors 0. Mrks will not b dductd for incorrct nswrs. You should ttmpt vry qustion. No mrks
Instructions for Sction 1 Choos th rspons tht is corrct for th qustion. A corrct nswr scors 1, n incorrct nswr scors 0. Mrks will not b dductd for incorrct nswrs. You should ttmpt vry qustion. No mrks
S i m p l i f y i n g A l g e b r a SIMPLIFYING ALGEBRA.
 S i m p l i y i n g A l g r SIMPLIFYING ALGEBRA www.mthltis.o.nz Simpliying SIMPLIFYING Algr ALGEBRA Algr is mthmtis with mor thn just numrs. Numrs hv ix vlu, ut lgr introus vrils whos vlus n hng. Ths
S i m p l i y i n g A l g r SIMPLIFYING ALGEBRA www.mthltis.o.nz Simpliying SIMPLIFYING Algr ALGEBRA Algr is mthmtis with mor thn just numrs. Numrs hv ix vlu, ut lgr introus vrils whos vlus n hng. Ths
INTEGRALS. Chapter 7. d dx. 7.1 Overview Let d dx F (x) = f (x). Then, we write f ( x)
 Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
On the Role of Fitness, Precision, Generalization and Simplicity in Process Discovery
 On th Rol of Fitnss, Prcision, Gnrliztion n Simplicity in Procss Discovry Joos Buijs Bouwijn vn Dongn Wil vn r Alst http://www.win.tu.nl/coslog/ Avncs in Procss ining ny procss iscovry n conformnc chcking
On th Rol of Fitnss, Prcision, Gnrliztion n Simplicity in Procss Discovry Joos Buijs Bouwijn vn Dongn Wil vn r Alst http://www.win.tu.nl/coslog/ Avncs in Procss ining ny procss iscovry n conformnc chcking
Floating Point Number System -(1.3)
 Floting Point Numbr Sstm -(.3). Floting Point Numbr Sstm: Comutrs rrsnt rl numbrs in loting oint numbr sstm: F,k,m,M 0. 3... k ;0, 0 i, i,...,k, m M. Nottions: th bs 0, k th numbr o igts in th bs xnsion
Floting Point Numbr Sstm -(.3). Floting Point Numbr Sstm: Comutrs rrsnt rl numbrs in loting oint numbr sstm: F,k,m,M 0. 3... k ;0, 0 i, i,...,k, m M. Nottions: th bs 0, k th numbr o igts in th bs xnsion
Case Study VI Answers PHA 5127 Fall 2006
 Qustion. A ptint is givn 250 mg immit-rls thophyllin tblt (Tblt A). A wk ltr, th sm ptint is givn 250 mg sustin-rls thophyllin tblt (Tblt B). Th tblts follow on-comprtmntl mol n hv first-orr bsorption
Qustion. A ptint is givn 250 mg immit-rls thophyllin tblt (Tblt A). A wk ltr, th sm ptint is givn 250 mg sustin-rls thophyllin tblt (Tblt B). Th tblts follow on-comprtmntl mol n hv first-orr bsorption
Using the Printable Sticker Function. Using the Edit Screen. Computer. Tablet. ScanNCutCanvas
 SnNCutCnvs Using th Printl Stikr Funtion On-o--kin stikrs n sily rt y using your inkjt printr n th Dirt Cut untion o th SnNCut mhin. For inormtion on si oprtions o th SnNCutCnvs, rr to th Hlp. To viw th
SnNCutCnvs Using th Printl Stikr Funtion On-o--kin stikrs n sily rt y using your inkjt printr n th Dirt Cut untion o th SnNCut mhin. For inormtion on si oprtions o th SnNCutCnvs, rr to th Hlp. To viw th
XML and Databases. Outline. Recall: Top-Down Evaluation of Simple Paths. Recall: Top-Down Evaluation of Simple Paths. Sebastian Maneth NICTA and UNSW
 Smll Pth Quiz ML n Dtss Cn you giv n xprssion tht rturns th lst / irst ourrn o h istint pri lmnt? Ltur 8 Strming Evlution: how muh mmory o you n? Sstin Mnth NICTA n UNSW
Smll Pth Quiz ML n Dtss Cn you giv n xprssion tht rturns th lst / irst ourrn o h istint pri lmnt? Ltur 8 Strming Evlution: how muh mmory o you n? Sstin Mnth NICTA n UNSW
On Testing Satisfiability of Tree Pattern Queries
 On Tsting Stisfiility of Tr Pttrn Quris Lks V.S. Lkshmnn, Gnsh Rmsh, Hui (wny) Wng, Zhng (Jssic) Zho Dprtmnt of Computr Scinc Univrsity of ritish Columi {lks,rmsh,hwng,zzho}@cs.uc.c strct XPth n XQury
On Tsting Stisfiility of Tr Pttrn Quris Lks V.S. Lkshmnn, Gnsh Rmsh, Hui (wny) Wng, Zhng (Jssic) Zho Dprtmnt of Computr Scinc Univrsity of ritish Columi {lks,rmsh,hwng,zzho}@cs.uc.c strct XPth n XQury
QUESTIONS BEGIN HERE!
 Points miss: Stunt's Nm: Totl sor: /100 points Est Tnnss Stt Univrsity Dprtmnt o Computr n Inormtion Sins CSCI 2710 (Trno) Disrt Struturs TEST or Sprin Smstr, 2005 R this or strtin! This tst is los ook
Points miss: Stunt's Nm: Totl sor: /100 points Est Tnnss Stt Univrsity Dprtmnt o Computr n Inormtion Sins CSCI 2710 (Trno) Disrt Struturs TEST or Sprin Smstr, 2005 R this or strtin! This tst is los ook
CS 241 Analysis of Algorithms
 CS 241 Anlysis o Algorithms Prossor Eri Aron Ltur T Th 9:00m Ltur Mting Lotion: OLB 205 Businss HW6 u lry HW7 out tr Thnksgiving Ring: Ch. 22.1-22.3 1 Grphs (S S. B.4) Grphs ommonly rprsnt onntions mong
CS 241 Anlysis o Algorithms Prossor Eri Aron Ltur T Th 9:00m Ltur Mting Lotion: OLB 205 Businss HW6 u lry HW7 out tr Thnksgiving Ring: Ch. 22.1-22.3 1 Grphs (S S. B.4) Grphs ommonly rprsnt onntions mong
Lecture contents. Bloch theorem k-vector Brillouin zone Almost free-electron model Bands Effective mass Holes. NNSE 508 EM Lecture #9
 Lctur contnts Bloch thorm -vctor Brillouin zon Almost fr-lctron modl Bnds ffctiv mss Hols Trnsltionl symmtry: Bloch thorm On-lctron Schrödingr qution ch stt cn ccommo up to lctrons: If Vr is priodic function:
Lctur contnts Bloch thorm -vctor Brillouin zon Almost fr-lctron modl Bnds ffctiv mss Hols Trnsltionl symmtry: Bloch thorm On-lctron Schrödingr qution ch stt cn ccommo up to lctrons: If Vr is priodic function:
Chapter Finding Small Vertex Covers. Extending the Limits of Tractability. Coping With NP-Completeness. Vertex Cover
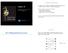 Coping With NP-Compltnss Chaptr 0 Extning th Limits o Tractability Q. Suppos I n to solv an NP-complt problm. What shoul I o? A. Thory says you'r unlikly to in poly-tim algorithm. Must sacriic on o thr
Coping With NP-Compltnss Chaptr 0 Extning th Limits o Tractability Q. Suppos I n to solv an NP-complt problm. What shoul I o? A. Thory says you'r unlikly to in poly-tim algorithm. Must sacriic on o thr
Floating Point Number System -(1.3)
 Floting Point Numbr Sstm -(.3). Floting Point Numbr Sstm: Comutrs rrsnt rl numbrs in loting oint numbr sstm: F,k,m,M 0. 3... k ;0, 0 i, i,...,k, m M. Nottions: th bs 0, k th numbr o igits in th bs xnsion
Floting Point Numbr Sstm -(.3). Floting Point Numbr Sstm: Comutrs rrsnt rl numbrs in loting oint numbr sstm: F,k,m,M 0. 3... k ;0, 0 i, i,...,k, m M. Nottions: th bs 0, k th numbr o igits in th bs xnsion
Parallel Computation for Managing Transitive Relations. Yijie Han and Yugyung Lee. University of Missouri at Kansas City.
 Prlll Computtion or Mnging Trnsitiv Rltions Yiji Hn n Yugyung L Computr Scinc Tlcommunictions Progrm Univrsity o Missouri t Knss City Knss City, Missouri 64110-2499 hn,yugig@cstp.umkc.u My 24, 2000 Abstrct
Prlll Computtion or Mnging Trnsitiv Rltions Yiji Hn n Yugyung L Computr Scinc Tlcommunictions Progrm Univrsity o Missouri t Knss City Knss City, Missouri 64110-2499 hn,yugig@cstp.umkc.u My 24, 2000 Abstrct
COMPLEXITY OF COUNTING PLANAR TILINGS BY TWO BARS
 OMPLXITY O OUNTING PLNR TILINGS Y TWO RS KYL MYR strt. W show tht th prolm o trmining th numr o wys o tiling plnr igur with horizontl n vrtil r is #P-omplt. W uil o o th rsults o uquir, Nivt, Rmil, n Roson
OMPLXITY O OUNTING PLNR TILINGS Y TWO RS KYL MYR strt. W show tht th prolm o trmining th numr o wys o tiling plnr igur with horizontl n vrtil r is #P-omplt. W uil o o th rsults o uquir, Nivt, Rmil, n Roson
Compression. Compression. Compression. This part of the course... Ifi, UiO Norsk Regnesentral Vårsemester 2005 Wolfgang Leister
 Kurs INF5080 Ifi, UiO Norsk Rgnsntrl Vårsmstr 2005 Wolfgng Listr This prt of th ours...... is hl t Ifi, UiO... (Wolfgng Listr) n t ontins mtril from Univrsity Collg Krlsruh (Ptr Ol, Clmns Knorzr) Informtion
Kurs INF5080 Ifi, UiO Norsk Rgnsntrl Vårsmstr 2005 Wolfgng Listr This prt of th ours...... is hl t Ifi, UiO... (Wolfgng Listr) n t ontins mtril from Univrsity Collg Krlsruh (Ptr Ol, Clmns Knorzr) Informtion
( ) Geometric Operations and Morphing. Geometric Transformation. Forward v.s. Inverse Mapping. I (x,y ) Image Processing - Lesson 4 IDC-CG 1
 Img Procssing - Lsson 4 Gomtric Oprtions nd Morphing Gomtric Trnsformtion Oprtions dpnd on Pil s Coordints. Contt fr. Indpndnt of pil vlus. f f (, ) (, ) ( f (, ), f ( ) ) I(, ) I', (,) (, ) I(,) I (,
Img Procssing - Lsson 4 Gomtric Oprtions nd Morphing Gomtric Trnsformtion Oprtions dpnd on Pil s Coordints. Contt fr. Indpndnt of pil vlus. f f (, ) (, ) ( f (, ), f ( ) ) I(, ) I', (,) (, ) I(,) I (,
DUET WITH DIAMONDS COLOR SHIFTING BRACELET By Leslie Rogalski
 Dut with Dimons Brlt DUET WITH DIAMONDS COLOR SHIFTING BRACELET By Lsli Roglski Photo y Anrw Wirth Supruo DUETS TM from BSmith rt olor shifting fft tht mks your work tk on lif of its own s you mov! This
Dut with Dimons Brlt DUET WITH DIAMONDS COLOR SHIFTING BRACELET By Lsli Roglski Photo y Anrw Wirth Supruo DUETS TM from BSmith rt olor shifting fft tht mks your work tk on lif of its own s you mov! This
Minimum Spanning Trees
 Yufi Tao ITEE Univrsity of Qunslan In tis lctur, w will stuy anotr classic prolm: finin a minimum spannin tr of an unirct wit rap. Intrstinly, vn tou t prolm appars ratr iffrnt from SSSP (sinl sourc sortst
Yufi Tao ITEE Univrsity of Qunslan In tis lctur, w will stuy anotr classic prolm: finin a minimum spannin tr of an unirct wit rap. Intrstinly, vn tou t prolm appars ratr iffrnt from SSSP (sinl sourc sortst
13. Binary tree, height 4, eight terminal vertices 14. Full binary tree, seven vertices v 7 v13. v 19
 0. Spnning Trs n Shortst Pths 0. Consir th tr shown blow with root v 0.. Wht is th lvl of v 8? b. Wht is th lvl of v 0? c. Wht is th hight of this root tr?. Wht r th chilrn of v 0?. Wht is th prnt of v
0. Spnning Trs n Shortst Pths 0. Consir th tr shown blow with root v 0.. Wht is th lvl of v 8? b. Wht is th lvl of v 0? c. Wht is th hight of this root tr?. Wht r th chilrn of v 0?. Wht is th prnt of v
The Plan. Honey, I Shrunk the Data. Why Compress. Data Compression Concepts. Braille Example. Braille. x y xˆ
 h ln ony, hrunk th t ihr nr omputr in n nginring nivrsity of shington t omprssion onpts ossy t omprssion osslss t omprssion rfix os uffmn os th y 24 2 t omprssion onpts originl omprss o x y xˆ nor or omprss
h ln ony, hrunk th t ihr nr omputr in n nginring nivrsity of shington t omprssion onpts ossy t omprssion osslss t omprssion rfix os uffmn os th y 24 2 t omprssion onpts originl omprss o x y xˆ nor or omprss
