In applications, we encounter many constrained optimization problems. Examples Basis pursuit: exact sparse recovery problem
|
|
|
- Kristian Logan
- 5 years ago
- Views:
Transcription
1 1 Conve Analsis Main references: Vandenberghe UCLA): EECS236C - Optimiation methods for large scale sstems, vandenbe/ee236c.html Parikh and Bod, Proimal algorithms, slides and note. bod/papers/pro_algs.html Bod, ADMM bod/admm.html Simon Foucart and Holger Rauhut, Appendi B. 1.1 Motivations: Conve optimiation problems In applications, we encounter man constrained optimiation problems. Eamples Basis pursuit: eact sparse recover problem or robust recover problem Image processing: The constrained can be a conve set C. That is we can define an indicator function min 1 subject to A = b. min 1 subject to A b 2 2 ɛ. min 1 subject to A b 2 2 ɛ. min f 0 ) subject to A C ι C ) = { 0 if C + otherwise. We can rewrite the constrained minimiation problem as a unconstrained minimiation problem: This can be reformulated as In abstract form, we encounter we can epress it as For more applications, see Bod s book. min f 0 ) + ι C A). min, f 0) + ι C ) subject to A =. min f) + ga) min f) + g) subject to A =. A standard conve optimiation problem can be formulated as min f 0) X subject to A = and f i ) b i, i = 1,..., M Here, f i s are conve. The space X is a Hilbert space. Here, we just take X = R N. 1
2 1.2 Conve functions Goal: We want to etend theor of smooth conve analsis to non-differentiable conve functions. Let X be a separable Hilbert space, f : X, + ] be a function. Proper: f is called proper if f) < for at least one. The domain of f is defined to be: domf = { f) < }. Lower Semi-continuit: f is called lower semi-continuous if lim inf n f n ) f ). The set epif := {, η) f) η} is called the epigraph of f. Prop: f is l.s.c. if and onl if epif is closed. Sometimes, we call such f closed. proofwiki.org/wiki/characteriation_of_lower_semicontinuit) The indicator function ι C of a set C is closed if and onl if C is closed. Conve function f is called conve if dom f is conve and Jensen s inequalit holds: f1 θ) + θ) 1 θ)f) + θf) for all 0 θ 1 and an, X. Proposition: f is conve if and onl if epif is conve. First-order condition: for f C 1, epif being conve is equivalent to f) f) + f), for all, X. Second-order condition: for f C 2, Jensen s inequalit is equivalent to 2 f) 0. If f α is a famil of conve function, then sup α f α is again a conve function. Strictl conve: f is called strictl conve if the strict Jensen inequalit holds: for and t 0, 1), f1 t) + t) < 1 t)f) + tf). First-order condition: for f C 1, the strict Jensen inequalit is equivalent to f) > f) + f), for all, X. Second-order condition: for f C 2, 2 f) 0) = strict Jensen s inequalit is equivalent to. Proposition 1.1. A conve function f : R N R is continuous. Proposition 1.2. Let f : R N, ] be conve. Then 1. a local minimier of f is also a global minimier; 2. the set of minimiers is conve; 3. if f is strictl conve, then the minimier is unique. 2
3 1.3 Gradients of conve functions Proposition 1.3 Monotonicit of f)). Suppose f C 1. Then f is conve if and onl if domf is conve and f) is a monotone operator: f) f), 0. Proof. 1. ) From conveit f) f) + f),, f) f) + f),. Add these two, we get monotonicit of f). 2. ) Let gt) = f+t )). Then g t) = f+t )), g 0) b monotonicit. Hence f) = g1) = g0) g t) dt g0) g 0) dt = f) + f), Proposition 1.4. Suppose f is conve and in C 1. The following statements are equivalent. a) Lipschit continuit of f): there eists an L > 0 such that f) f) L for all, domf. b) g) := L 2 2 f) is conve. c) Quadratic upper bound f) f) + f), + L 2 2. d) Co-coercivit f) f), 1 L f) f) 2. Proof. 1. a) b): f) f), f) f) L 2 g) g), = L ) f) f)), 0 Therefore, g) is monotonic and thus g is conve. 2. b) c): g is conve g) g) + g), L 2 2 f) L 2 2 f) + L f), f) f) + f), + L
4 3. b) d): Define f ) = f) f),, f ) = f) f),. From b), both L/2) 2 f ) and L/2) 2 f ) are conve, and = minimies f. Thus from the proposition below f) f) f), = f ) f ) 1 2L f ) 2 = 1 2L f) f) 2. Similarl, = minimies f ), we get f) f) f), 1 2L f) f) 2. Adding these two together, we get the co-coercivit. 4. d) a): b Cauch inequalit. Proposition 1.5. Suppose f is conve and in C 1 with f) being Lipschit continuous with parameter L. Suppose is a global minimum of f. Then Proof. 1 2L f) 2 f) f ) L Right-hand inequalit follows from quadratic upper bound. 2. Left-hand inequalit follows b minimiing quadratic upper bound f) + f), + L2 ) 2 f ) = inf f) inf = f) 1 2L f) Strong conveit f is called strongl conve if domf is conve and the strong Jensen inequalit holds: there eists a constant m > 0 such that for an, domf and t [0, 1], ft + 1 t)) tf) + 1 t)f) m 2 t1 t) 2. This definition is equivalent to the conveit of g) := f) m 2 2. This comes from the calculation 1 t) 2 + t 2 1 t) + t 2 = t1 t) 2. Whenf C 2, then strong conveit of f is equivalent to 2 f) mi for an domf. Proposition 1.6. Suppose f C 1. The following statements are equivalent: a) f is strongl conve, i.e. g) = f) m 2 2 is conve, b) for an, domf, f) f), m 2. c) quadratic lower bound): f) f) + f), + m
5 Proposition 1.7. If f is strongl conve, then f has a unique global minimier which satisfies Proof. m 2 2 f) f ) 1 2m f) 2 1. For lelf-hand inequalit, we appl quadratic lower bound for all domf. f) f ) + f ), + m 2 2 = m For right-hand inequalit, quadratic lower bound gives f ) = inf f) inf f) + f), + m 2 2) f) 1 2m f) 2 We take infimum in then get the left-hand inequalit. Proposition 1.8. Suppose f is both strongl conve with parameter m and f) is Lipschit continuous with parameter L. Then f satisfies stronger co-coercivit condition f) f), ml m + L m + L f) f) 2. Proof. 1. Consider g) = f) m 2 2. From strong conveit of f, we get g) is conve. 2. From Lipschit of f, we get g is also Lipschit continuous with parameter L m. 3. We appl co-coercivit to g): g) g), 1 g) g) 2 L m f) f) m ), 1 f) f) m ) 2 L m 1 + 2m ) f) f), 1 ) m 2 L m L m f) f) 2 + L m + m Subdifferential Let f be conve. The subdifferential of f at a point is a set defined b f) = {u X X) f) + u, f)} f) is also called subgradients of f at. Proposition 1. a) If f is conve and differentiable at, then f) = { f)}. b) If f is conve, then f) is a closed conve set. Let f) =. Then f0) = [ 1, 1]. Let C be a closed conve set on R N. Then C is locall rectifiable. Moreover, ι C ) = {λn λ 0, n is the unit outer normal of C at }. 5
6 Proposition 1.9. Let f : R n, ] be conve and closed. Then is a minimum of f if and onl if 0 f ). Proposition The subdifferential of a conve function f is a set-valued monotone operator. That is, if u f), v f), then u v, 0. Proof. From f) f) + u,, Combining these two inequalit, we get monotonicit. Proposition The following statements are equivalent. 1) f is strongl conve i.e. f m 2 2 is conve); 2) quadratic lower bound) f) f) + v,, f) f) + u, + m 2 for 2 an, where u f); 3) Strong monotonicit of f): 1.6 Proimal operator u v, m 2, for an, with an u f), v f). Definition 1.1. Given a conve function f, the proimal mapping of f is defined as pro f ) := argmin u fu) + 1 ) 2 u 2. Since fu) + 1/2 u 2 is strongl conve in u, we get unique minimum. Thus, pro f ) is welldefined. Eamples Let C be a conve set. Define indicator function ι C ) as { 0 if C ι C ) = otherwise. Then pro ιc ) is the projection of onto C. f) = 1 : pro f is the soft-thresholding: P C C and C), P C ), P C ) 0. i 1 if i 1 pro f ) i = 0 if i 1 i + 1 if i 1 6
7 Properties Let f be conve. Then = pro f ) = argmin u fu) u 2 ) if and onl if or Sometimes, we epress this as 0 f) + + f). pro f ) = = I + f) 1 ). Co-coercivit: pro f ), pro f ), pro f ) pro f ) 2. Let + = pro f ) := argmin f) We have + f + ). Similarl, + := pro f ) satisfies + f + ). From monotonicit of f, we get u v, for an u f + ), v f + ). Taking u = + and v = +, we obtain co-coercivit. The co-coercivit of pro f implies that pro f is Lipschit continuous. pro f ) pro f ) 2, pro f ) pro f ) implies pro f ) pro f ). 1.7 Conjugate of a conve function For a function f : R N, ], we define its conjugate f b f ) = sup, f)). Eamples { b if = a 1. f) = a, b, f ) = sup, a, + b) = otherwise. 2. f) = { a if < 0 b if > 0., a < 0 < b. { f 0 if a < < b ) = otherwise. 7
8 3. f) = 1 2, A + b, + c, where A is smmteric and non-singular, then In general, if A 0, then f ) = 1 2 b, A 1 b) c. f ) = 1 2 b, A b) c, A := A A) 1 A and dom f = range A + b. 4. f) = 1 p p, p 1, then f u) = 1 p u p, where 1/p + 1/p = f) = e, f ) = sup e ) = ln if > 0 0 if = 0 if < 0 6. C = { A, 1}, where A is s smmetric positive definite matri. ι C = A 1 u, u. Properties f is conve and l.s.c. Note that f is the supremum of linear functions. We have seen that supremum of a famil of closed functions is closed; and supremum of a famil of conve functions is also conve. Fenchel s inequalit: This follows directl from the definition of f : f) + f ),. f ) = sup, f)), f). This can be viewed as an etension of the Cauch inequalit ,. Proposition ) f ) is closed and conve. 2) f ) f). 3) f ) = f) if and onl if f is closed and conve. Proof. 1. From Fenchel s inequalit Taking sup in gives f ) f)., f ) f). 2. f ) = f) if and onl if epif = epif. We have seen f f. This leads to eps f eps f. Suppose f is closed and conve and suppose, f )) epif. That is f ) < f) and there is a strict separating hperplane: {, s) : a ) + bs f ) = 0} such that with b 0. a b ), s f ) ) c < 0 8 for all, s) epif
9 3. If b < 0, we ma normalie it such that a, b) =, 1). Then we have Taking supremum over, s) epif, Thus, we get sup,s) epif This contradicts to Fenchel s inequalit., s, + f ) c < 0., s) sup, f)) = f ). f ), + f ) c < If b = 0, choose ŷ dom f and add ɛŷ, 1) to a, b), we can get ) ) a + ɛŷ, ɛ s f c ) 1 < 0 Now, we appl the argument for b < 0 and get contradiction. 5. If f = f, then f is closed and conve because f is closed and conve no matter what f is. Proposition If f is closed and conve, then Proof. 1. f) f ), = f) + f ). f) f) f) +,, f), f) for all, f) = sup, f)), f) = f ) 2. For the equivalence of f ), = f) + f ), we use f ) = f) and appl the previous argument. 1.8 Method of Lagrange multiplier for constrained optimiation problems A standard conve optimiation problem can be formulated as inf 0) subject to f i ) 0, i = 1,..., m and h i ) = 0 i = 1,..., p. We assume the domain D := i domf i i domh i is a closed conve set in R n. A point D satisfing the constraints is called a feasible point. We assume D and denote p the optimal value. 9
10 The method of Lagrange multiplier is to introduce augmented variables λ, µ and a Lagrangian so that the problem is transformed to a unconstrained optimiation problem. Let us define the Lagrangian to be m p L, λ, µ) = f 0 ) + λ i f i ) + µ i h i ). Here, λ and µ are the augmented variables, called the Lagrange multipliers or the dual variables. Primal problem From this Lagrangian, we notice that m ) sup λ i f i ) = ι Cf ), C f = λ 0 i { f i ) 0} and Hence p ) sup µ i h i ) = ι Ch ), C h = { h i ) = 0}. µ i sup L, λ, µ) = f 0 ) + ι Cf ) + ι Ch ) λ 0,µ Thus, the original optimiation problem can be written as p = inf f0 ) + ι Cf ) + ι Ch ) ) = inf sup L, λ, µ). D D λ 0,µ This problem is called the primal problem. Dual problem From this Lagrangian, we define the dual function gλ, µ) := inf L, λ, µ). D This is an infimum of a famil of concave closed functions in λ and µ, thus gλ, µ) is a concave closed function. The dual problem is d = sup gλ, µ). λ 0,µ This dual problem is the same as sup gλ, µ) subject to λ 0. λ,µ We refer λ, µ) dom g with λ 0 as dual feasible variables. The primal problem and dual problem are connected b the following dualit propert. Weak Dualit Propert Proposition 2. For an λ 0 and an µ, we have that gλ, µ) p. In other words, d p 10
11 Proof. Suppose is feasible point i.e. D, or equivalentl, f i ) 0 and h i ) = 0). Then for an λ i 0 and an µ i, we have m p λ i f i ) + µ i h i ) 0. This leads to Hence Hence for all feasible pair λ, µ) L, λ, µ) = f 0 ) + m λ i f i ) + p µ i h i ) f 0 ). gλ, µ) := inf D L, λ, µ) f 0), for all D. gλ, µ) p This is called weak dualit propert. Thus, the weak dualit can also be read as sup inf λ 0,µ D L, λ, µ) inf sup L, λ, µ). D λ 0,µ Definition 1.2. a) A point is called a primal optimal if it minimies sup λ 0,µ L, λ, µ). b) A dual pair λ, µ ) with λ 0 is said to be a dual optimal if it maimies inf D L, λ, µ). Strong dualit Definition 1.3. When d = p, we sa the strong dualit holds. A sufficient condition for strong dualit is the Slater condition: there eists a feasible in relative interior of domd: f i ) < 0, i = 1,..., m and h i ) = 0, i = 1,..., p. Such a point is called a strictl feasible point. Theorem 1.1. Suppose f 0,..., f m are conve, h) = A b, and assume the Slater condition holds: there eists D with A b = 0 and f i ) < 0 for all i = 1,..., m. Then the strong dualit holds. sup inf λ 0,µ D Proof. See pp , Bod s Conve Optimiation. L, λ, µ) = inf sup L, λ, µ). D λ 0,µ Complementar slackness Suppose there eist, λ 0 and µ such that is the optimal primal point and λ, µ ) is the optimal dual point and the strong dualit gap p d = 0. In this case, f 0 ) = gλ, µ ) := inf f 0 ) + f 0 ). f 0 ) + m λ i f i ) + m λ i f i ) + ) p µ i h i ) p µ i h i ) 11
12 The last line follows from m λ i f i ) + for an feasible pair, λ, µ). This leads to m λ i f i ) + p µ i h i ) 0. p µ i h i ) = 0. Since h i ) = 0 for i = 1,..., p, λ i 0 and f i ) 0, we then get λ i f i ) = 0 for all i = 1,..., m. This is called complementar slackness. It holds for an optimal solutions, λ, µ ). KKT condition Proposition When f 0, f i and h i are differentiable, then the optimal points to the primal problem and λ, µ ) to the dual problem satisf the Karush-Kuhn-Tucker KKT) condition: f 0 ) + m λ i f i ) + f i ) 0, i = 1,..., m λ i 0, i = 1,..., m, λ i f i ) = 0, h i ) = 0, p µ i g i ) = 0. i = 1,..., m i = 1,..., p Remark. If f 0, f i, i = 0,..., m are closed and conve, but ma not be differentiable, then the last KKT condition is replaced b 0 f 0 ) + m λ i f i ) + We call the triple, λ, µ ) satisfies the optimalit condition. p µ i g i ). Theorem 1.2. If f 0, f i are closed and conve and h are affine. Then the KKT condition is also a sufficient condition for optimal solutions. That is, if ˆ, ˆλ, ˆµ) satisfies KKT condition, then ˆ is primal optimal and ˆλ, ˆµ) is dual optimal, and there is ero dualit gap. Proof. 1. From f i ˆ) 0 and hˆ) = 0, we get that ˆ is feasible. 2. From ˆλ i 0 and f i being conve and h i are linear, we get L, ˆλ, ˆµ) = f 0 ) + i ˆλ i f i ) + i ˆµ i h i ) is also conve in. 12
13 3. The last KKT condition states that ˆ minimies L, ˆλ, ˆµ). Thus gˆλ, ˆµ) = Lˆ, ˆλ, ˆµ) m = f 0 ˆ) + ˆλ i f i ˆ) + = f 0 ˆ) p ˆµ i h i ˆ) This shows that ˆ and ˆλ, ˆµ) have ero dualit gap and therefore are primal optimal and dual optimal, respectivel. 2 Optimiation algorithms 2.1 Gradient Methods Assumptions f C 1 R N ) and conve f) is Lipschit continuous with parameter L Optimal value f = inf f) is finite and attained at. Gradient method Forward method k = k 1 t k f k 1 ) Fied step sie: if t k is constant Backtracking line search: Choose 0 < β < 1, initialie t k = 1; take t k := βt k until f t k f)) < f) 1 2 t k f) 2 Optimal line search: Backward method t k = argmin t f t f)). k = k 1 t k f k ). Analsis for the fied step sie case Proposition Suppose f C 1, conve and f is Lipschit with constant L. If the step sie t satisfies t 1/L, then the fied-step sie gradient descent method satisfies f k ) f ) 1 2kt
14 Remarks Proof. The sequence { k } is bounded. Thus, it has convergent subsequence to some which is an optimal solution. If in addition f is strongl conve, then the sequence { k } converges to the unique optimal solution linearl. 1. Let + := t f). 2. From quadratic upper bound: choose = + and t < 1/L, we get f + ) f) + f) f) + f), + L 2 2 t + Lt2 2 ) f) 2 f) t 2 f) From we get f ) f) + f), f + ) f) t 2 f) 2 f + f), t 2 f) 2 = f t f) 2) 2t = f ). 2t 4. Define i 1 =, i = +, sum this inequalities from i = 1,..., k, we get k f i ) f ) 1 2t k i 1 2 i 2) = 1 2t 0 2 k 2) 1 2t Since f i ) f is a decreasing sequence, we then get f k ) f 1 k k f i ) f ) 1 2kt 0 2. Proposition Suppose f C 1 and conve. The fied-step sie backward gradient method satisfies f k ) f ) 1 2kt 0 2. Here, no assumption on Lipschit continuit of f) is needed. 14
15 Proof. 1. Define + = t f + ). 2. For an, we have f) f + ) + f + ), + = f + ) + f + ), + t f + ) Take =, we get f + ) f) t f + ) 2 Thus, f + ) < f) unless f + ) = Take =, we obtain f + ) f ) + f + ), t f + ) 2 f ) + f + ), t 2 f+ ) 2 = f ) 1 2t t f + ) t 2 = f ) ). 2t Proposition Suppose f is strongl conve with parameter m and f) is Lipschit continuous with parameter L. Suppose the minimum of f is attended at. Then the gradient method converges linearl, namel k 2 c k 0 2 where Proof. 1. For 0 < t 2/m + L): f k ) f ) ck L 2 0 2, c = 1 t 2mL 2 < 1 if the step sie t m + L m + L. + 2 = t f) 2 = 2 2t f), + t 2 f) 2 1 t 2mL ) 2 + t t 2 ) f) 2 m + L m + L 1 t 2mL ) 2 = c 2. m + L t is chosen so that c < 1. Thus, the sequence k converges linearl with rate c. 2. From quadratic upper bound f k ) f ) L 2 k 2 ck L we get f k ) f ) also converges to 0 with linear rate. 15
16 2.2 Subgradient method Assumptions f is closed and conve Optimal value f = inf f) is finite and attained at. Subgradient method k = k 1 t k v k 1, v k 1 f k 1 ). t k is chosen so that f k ) < f k 1 ). This is a forward sub)gradient method. It ma not converge. If it converges, the optimal rate is f k ) f ) O1/ k), which is ver slow. 2.3 Proimal point method Assumptions f is closed and conve Optimal value f = inf f) is finite and attained at. Proimal point method: Let + := pro tf ) := tg t ). From we get k = pro tf k 1 ) = k 1 tg t k 1 ) pro tf ) := argmin tf) ) G t ) f + ). Thus, we ma view proimal point method is a backward subgradient method. Proposition Suppose f is closed and conve and suppose an ptimal solution of min f is attainable. Then the proimal point method k = pro tf k 1 ) with t > 0 satisfies f k ) f ) 1 2kt 0. 16
17 Convergence proof: 1. Given, let + := pro tf ). Let G t ) := + )/t. Then G t ) f + ). We then have, for an, f) f + ) + G t ), + = G t ), + t G t ) Take =, we get Thus, f + ) < f) unless f + ) = Take =, we obtain f + ) f) t f + ) 2 f + ) f ) + G t ), t G t ) 2 f ) + G t ), t 2 G t) 2 = f ) + 1 2t tg t ) 2 1 2t 2 = f ) + 1 2t + 2 2). 4. Taking = i 1, + = i, sum over i = 1,..., k, we get k f k ) f )) 1 2t Since f k ) is non-increasing, we get ) 0 k. kf k ) f )) k f k ) f )) 1 2t Accelerated Proimal point method The proimal point method is a first order method. With a small modification, it can be accelerated to a second order method. This is the work of Nesterov in 1980s. 2.5 Fied point method The proimal point method can be viewed as a fied point of the proimal map: F ) := pro f ). Let G) = + = I F )). Both F and G are firml non-epansive, i.e. F ) F ), F ) F ) 2 G) G), G) G) 2 17
18 Proof. 1). + = pro f ) = F ), + = pro f ) = F ). G) = + f + ). From monotonicit of f, we have This gives That is 2). From G = I F, we have G) G), , F ) F ), F ) F ) 2. G) G), = G) G), F + G)) F + G)) = G) G) 2 + G) G), F ) F ) = G) G) 2 + F ) + F ), F ) F ) = G) G) 2 +, F ) F ) F ) F ) 2 G) G) 2 Theorem 2.3. Assume F is firml non-epansive. Let Suppose a fied point of F eists and Then k converges to a fied point of F. Proof. k = 1 t k ) k 1 + t k F k 1 ), 0 arbitrar. t k [t min, t ma ], 0 < t min t ma < Let us define G = I F ). We have seen that G is also firml non-epansive. k = k 1 t k G k 1 ). 2. Suppose is a fied point of F, or equivalentl, G ) = 0. From firml nonepansive propert of F and G, we get with = k 1, + = k, t = t k ) = where M = t min 2 t ma ). 3. Let us sum this inequalit over k: This implies M = 2 +, = 2 tg), + t 2 G) 2 = 2 tg) G )), + t 2 G) 2 2t G) G ) 2 + t 2 G) 2 = t2 t) G) 2 M G) 2 0. G l ) l=0 G k ) 0 as k, and k is non-increasing; hence k is bounded; and k C as k. 18
19 4. Since the sequence { k } is bounded, an convergent subsequence, sa ȳ k, converges to ȳ satisfing Gȳ) = lim k Gȳk ) = 0, b the continuit of G. Thus, an cluster point ȳ of { k } satisfies Gȳ) = 0. Hence, b the previous argument with replaced b ȳ, the sequence k ȳ is also non-increasing and has a limit. 5. We claim that there is onl one limiting point of { k }. Suppose ȳ 1 and ȳ 2 are two cluster points of { k }. Then both sequences { k ȳ 1 } and { k ȳ 2 } are non-increasing and have limits. Since ȳ i are limiting points, there eist subsequences {ki 1} and {k2 i } such that k1 i ȳ 1 and k2 i ȳ 2 as i. We can choose subsequences again so that we have k 2 i 1 < k 1 i < k 2 i < k 1 i+1 for all i With this and the non-increasing of k ȳ 1 and k ȳ 2 we get k1 i+1 ȳ1 k2 i ȳ1 k1 i ȳ1 0 as i. On the other hand, k2 i ȳ 2. Therefore, we get ȳ 1 = ȳ 2. This shows that there is onl one limiting point, sa, and k. 2.6 Proimal gradient method This method is to minimie h) := f) + g). Assumptions: g C 1 conve, g) Lipschit continuous with parameter L f is closed and conve Proimal gradient method: This is also known as the Forward-backward method k = pro tf k 1 t g k 1 )) We can epress pro tf as I + t f) 1. Therefore the proimal gradient method can be epressed as k = I + t f) 1 I t g) k 1 Thus, the proimal gradient method is also called the forward-backward method. Theorem 2.4. The forward-backward method converges provided Lt 1. Proof. 1. Given a point, define Then = t g), + = pro tf ). t = g), + t f + ). Combining these two, we define a gradient G t ) := + t. Then G t ) g) f + ). 19
20 2. From the quadratic upper bound of g, we have g + ) g) + g), + + L = g) + g), + + Lt2 2 G t) 2 g) + g), + + t 2 G t) 2, The last inequalit holds provided Lt 1. Combining this with g) g) + g), we get g + ) g) + g), + + t 2 G t) From first-order condition at + of f f) f + ) + p, + for all p f + ). Choosing p = G t ) g), we get f + ) f) + G t ) g), Adding the above two inequalities, we get h + ) h) + G t ), + + t 2 G t) 2 Taking =, we get h + ) h) t 2 G t) 2. Taking =, we get h + ) h ) G t ), + + t 2 G t) 2 = tg t ) 2 + 2) 2t = ) 2t 2.7 Augmented Lagrangian Method Problem min F P ) := f) + ga) Equivalent to the primal problem with constraint min f) + g) subject to A = Assumptions f and g are closed and conve. 20
21 Eamples: { 0 if = b g) = ι {b} ) = otherwise The corresponding g ) =, b. g) = ι C ) g) = b 2. The Lagrangian is The primal function is The primal problem is The dual problem is sup inf, L,, ) := f) + g) +, A. inf [ L,, ) = sup [ = sup = sup F P ) = inf F P ) = inf inf Thus, the dual function F D ) is defined as and the dual problem is sup L,, ). inf sup L,, ). ] f) +, A ) + inf g), ) sup A, f)) sup, g)) f A ) g )) = sup F D )) F D ) := inf, L,, ) = f A ) + g )). sup P D ). We shall solve this dual problem b proimal point method: k = pro tfd k 1 ) = argma u [ f A T u) g u) 1 2t u k 1 2 ] ] We have sup f A T u) g u) 12t ) u 2 u = sup inf L,, u) 1 ) u 2 u, 2t = sup inf f) + g) + u, A 12t ) u u, 2 = inf f) + g) + u, A 12t ) u 2 sup, u = inf, f) + g) +, A + t2 A 2 ). 21
22 Here, the maimum u = + ta ). Thus, we define the augmented Lagrangian to be The augmented Lagrangian method is L t,, ) := f) + g) +, A + t A 2 2 k, k ) = argmin, L t,, k 1 ) k = k 1 + ta k k ) Thus, the Augmented Lagrangian method is equivalent to the proimal point method applied to the dual problem: sup f A ) g )). 2.8 Alternating direction method of multipliersadmm) Problem min f 1 1 ) + f 2 2 ) subject to A A 2 2 b = 0. Assumptions f i are closed and conve. ADMM Define ADMM: L t 1, 2, ) := f 1 1 ) + f 2 2 ) +, A A 2 2 b + t 2 A A 2 2 b 2. k 1 = argmin 1 L t 1, k 1 2, k 1 ) = argmin 1 f 1 1 ) + t 2 A A 2 k 1 2 b + 1 t k 1 2 ) k 2 = argmin 2 L t k 1, 2, k 1 ) = argmin 2 f 2 2 ) + t 2 A 1 k 1 + A 2 2 b + 1 t k 1 2 ) k = k 1 + ta 1 k 1 + A 2 k 2 b) ADMM is the Douglas-Rachford method applied to the dual problem: ma b, f 1 A T 1 ) ) + f2 A T 2 ) ) := h 1 ) h 2 ). Douglas-Rachford method min h 1 ) + h 2 ) k = pro h1 k 1 ) k = k 1 + pro h2 2 k k 1 ) k. If we call I + h 1 ) 1 = A and I + h 2 ) 1 = B. These two operators are firml nonepansive. The Douglas-Rachford method is to find the fied point of k = T k 1. T = I + A + B2A I). 22
23 2.9 Primal dual formulation Consider Let inf f) + ga)) F P ) := f) + ga) Define = A consider inf, f) + g) subject to = A. Now, introduce method of Lagrange multiplier: consider L P,, ) = f) + g) +, A Then The problem is The dual problem is We find that F P ) = inf inf B assuming optimalit condition, we have If we take inf first inf L P,, ) = inf Then the problem is inf sup L P,, ) sup L P,, ) sup inf L P,, ), inf L P,, ) = f A ) g ). := F D ), sup inf L P,, ) = sup F D )., f) + g) +, A ) = f) +, A g ) := L P D, ). inf sup L P D, ). On the other hand, we can start from F D ) := f A ) g ). Consider then we have If instead, we echange the order of inf and sup, sup,w L D, w, ) = f w) g ), A w sup inf L D, w, ) = F D ). w L D, w, ) = sup f w) g ), A w ) = f) + ga) = F P ).,w We can also take sup w first, then we get sup w L D, w, ) = sup f w) g ), A w ) = f) g ) + A, = L P D, ). w 23
24 Let us summarie F P ) = f) + ga) F D ) = f A) g ) L P,, ) := f) + g) +, A L D, w, ) := f w) g ), A w L P D, ) := inf F P ) = sup L P D, ) F D ) = inf L P D, ) B assuming optimalit condition, we have L P,, ) = sup L D, w, ) = f) g ) +, A w inf sup L P D, ) = sup inf L P, ). 24
A set C R n is convex if and only if δ C is convex if and only if. f : R n R is strictly convex if and only if f is convex and the inequality (1.
 ONVEX OPTIMIZATION SUMMARY ANDREW TULLOH 1. Eistence Definition. For R n, define δ as 0 δ () = / (1.1) Note minimizes f over if and onl if minimizes f + δ over R n. Definition. (ii) (i) dom f = R n f()
ONVEX OPTIMIZATION SUMMARY ANDREW TULLOH 1. Eistence Definition. For R n, define δ as 0 δ () = / (1.1) Note minimizes f over if and onl if minimizes f + δ over R n. Definition. (ii) (i) dom f = R n f()
1. Gradient method. gradient method, first-order methods. quadratic bounds on convex functions. analysis of gradient method
 L. Vandenberghe EE236C (Spring 2016) 1. Gradient method gradient method, first-order methods quadratic bounds on convex functions analysis of gradient method 1-1 Approximate course outline First-order
L. Vandenberghe EE236C (Spring 2016) 1. Gradient method gradient method, first-order methods quadratic bounds on convex functions analysis of gradient method 1-1 Approximate course outline First-order
Convex Optimization & Lagrange Duality
 Convex Optimization & Lagrange Duality Chee Wei Tan CS 8292 : Advanced Topics in Convex Optimization and its Applications Fall 2010 Outline Convex optimization Optimality condition Lagrange duality KKT
Convex Optimization & Lagrange Duality Chee Wei Tan CS 8292 : Advanced Topics in Convex Optimization and its Applications Fall 2010 Outline Convex optimization Optimality condition Lagrange duality KKT
Math 273a: Optimization Subgradients of convex functions
 Math 273a: Optimization Subgradients of convex functions Made by: Damek Davis Edited by Wotao Yin Department of Mathematics, UCLA Fall 2015 online discussions on piazza.com 1 / 42 Subgradients Assumptions
Math 273a: Optimization Subgradients of convex functions Made by: Damek Davis Edited by Wotao Yin Department of Mathematics, UCLA Fall 2015 online discussions on piazza.com 1 / 42 Subgradients Assumptions
Introduction to Alternating Direction Method of Multipliers
 Introduction to Alternating Direction Method of Multipliers Yale Chang Machine Learning Group Meeting September 29, 2016 Yale Chang (Machine Learning Group Meeting) Introduction to Alternating Direction
Introduction to Alternating Direction Method of Multipliers Yale Chang Machine Learning Group Meeting September 29, 2016 Yale Chang (Machine Learning Group Meeting) Introduction to Alternating Direction
Subgradient. Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes. definition. subgradient calculus
 1/41 Subgradient Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes definition subgradient calculus duality and optimality conditions directional derivative Basic inequality
1/41 Subgradient Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes definition subgradient calculus duality and optimality conditions directional derivative Basic inequality
Constrained Optimization and Lagrangian Duality
 CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization
 Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization Compiled by David Rosenberg Abstract Boyd and Vandenberghe s Convex Optimization book is very well-written and a pleasure to read. The
Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization Compiled by David Rosenberg Abstract Boyd and Vandenberghe s Convex Optimization book is very well-written and a pleasure to read. The
Lecture: Duality of LP, SOCP and SDP
 1/33 Lecture: Duality of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2017.html wenzw@pku.edu.cn Acknowledgement:
1/33 Lecture: Duality of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2017.html wenzw@pku.edu.cn Acknowledgement:
Lecture 23: November 19
 10-725/36-725: Conve Optimization Fall 2018 Lecturer: Ryan Tibshirani Lecture 23: November 19 Scribes: Charvi Rastogi, George Stoica, Shuo Li Charvi Rastogi: 23.1-23.4.2, George Stoica: 23.4.3-23.8, Shuo
10-725/36-725: Conve Optimization Fall 2018 Lecturer: Ryan Tibshirani Lecture 23: November 19 Scribes: Charvi Rastogi, George Stoica, Shuo Li Charvi Rastogi: 23.1-23.4.2, George Stoica: 23.4.3-23.8, Shuo
5. Duality. Lagrangian
 5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
Duality. Lagrange dual problem weak and strong duality optimality conditions perturbation and sensitivity analysis generalized inequalities
 Duality Lagrange dual problem weak and strong duality optimality conditions perturbation and sensitivity analysis generalized inequalities Lagrangian Consider the optimization problem in standard form
Duality Lagrange dual problem weak and strong duality optimality conditions perturbation and sensitivity analysis generalized inequalities Lagrangian Consider the optimization problem in standard form
CSCI : Optimization and Control of Networks. Review on Convex Optimization
 CSCI7000-016: Optimization and Control of Networks Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one
CSCI7000-016: Optimization and Control of Networks Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one
STATIC LECTURE 4: CONSTRAINED OPTIMIZATION II - KUHN TUCKER THEORY
 STATIC LECTURE 4: CONSTRAINED OPTIMIZATION II - KUHN TUCKER THEORY UNIVERSITY OF MARYLAND: ECON 600 1. Some Eamples 1 A general problem that arises countless times in economics takes the form: (Verbally):
STATIC LECTURE 4: CONSTRAINED OPTIMIZATION II - KUHN TUCKER THEORY UNIVERSITY OF MARYLAND: ECON 600 1. Some Eamples 1 A general problem that arises countless times in economics takes the form: (Verbally):
Lagrange duality. The Lagrangian. We consider an optimization program of the form
 Lagrange duality Another way to arrive at the KKT conditions, and one which gives us some insight on solving constrained optimization problems, is through the Lagrange dual. The dual is a maximization
Lagrange duality Another way to arrive at the KKT conditions, and one which gives us some insight on solving constrained optimization problems, is through the Lagrange dual. The dual is a maximization
A Brief Review on Convex Optimization
 A Brief Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one convex, two nonconvex sets): A Brief Review
A Brief Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one convex, two nonconvex sets): A Brief Review
A. Derivation of regularized ERM duality
 A. Derivation of regularized ERM dualit For completeness, in this section we derive the dual 5 to the problem of computing proximal operator for the ERM objective 3. We can rewrite the primal problem as
A. Derivation of regularized ERM dualit For completeness, in this section we derive the dual 5 to the problem of computing proximal operator for the ERM objective 3. We can rewrite the primal problem as
Course Notes for EE227C (Spring 2018): Convex Optimization and Approximation
 Course otes for EE7C (Spring 018): Conve Optimization and Approimation Instructor: Moritz Hardt Email: hardt+ee7c@berkeley.edu Graduate Instructor: Ma Simchowitz Email: msimchow+ee7c@berkeley.edu October
Course otes for EE7C (Spring 018): Conve Optimization and Approimation Instructor: Moritz Hardt Email: hardt+ee7c@berkeley.edu Graduate Instructor: Ma Simchowitz Email: msimchow+ee7c@berkeley.edu October
Convex Optimization M2
 Convex Optimization M2 Lecture 3 A. d Aspremont. Convex Optimization M2. 1/49 Duality A. d Aspremont. Convex Optimization M2. 2/49 DMs DM par email: dm.daspremont@gmail.com A. d Aspremont. Convex Optimization
Convex Optimization M2 Lecture 3 A. d Aspremont. Convex Optimization M2. 1/49 Duality A. d Aspremont. Convex Optimization M2. 2/49 DMs DM par email: dm.daspremont@gmail.com A. d Aspremont. Convex Optimization
On the Method of Lagrange Multipliers
 On the Method of Lagrange Multipliers Reza Nasiri Mahalati November 6, 2016 Most of what is in this note is taken from the Convex Optimization book by Stephen Boyd and Lieven Vandenberghe. This should
On the Method of Lagrange Multipliers Reza Nasiri Mahalati November 6, 2016 Most of what is in this note is taken from the Convex Optimization book by Stephen Boyd and Lieven Vandenberghe. This should
Math 273a: Optimization Lagrange Duality
 Math 273a: Optimization Lagrange Duality Instructor: Wotao Yin Department of Mathematics, UCLA Winter 2015 online discussions on piazza.com Gradient descent / forward Euler assume function f is proper
Math 273a: Optimization Lagrange Duality Instructor: Wotao Yin Department of Mathematics, UCLA Winter 2015 online discussions on piazza.com Gradient descent / forward Euler assume function f is proper
Linear programming: Theory
 Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analsis and Economic Theor Winter 2018 Topic 28: Linear programming: Theor 28.1 The saddlepoint theorem for linear programming The
Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analsis and Economic Theor Winter 2018 Topic 28: Linear programming: Theor 28.1 The saddlepoint theorem for linear programming The
Lecture: Duality.
 Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
CS-E4830 Kernel Methods in Machine Learning
 CS-E4830 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 27. September, 2017 Juho Rousu 27. September, 2017 1 / 45 Convex optimization Convex optimisation This
CS-E4830 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 27. September, 2017 Juho Rousu 27. September, 2017 1 / 45 Convex optimization Convex optimisation This
Shiqian Ma, MAT-258A: Numerical Optimization 1. Chapter 4. Subgradient
 Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 4 Subgradient Shiqian Ma, MAT-258A: Numerical Optimization 2 4.1. Subgradients definition subgradient calculus duality and optimality conditions Shiqian
Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 4 Subgradient Shiqian Ma, MAT-258A: Numerical Optimization 2 4.1. Subgradients definition subgradient calculus duality and optimality conditions Shiqian
Convex Optimization Boyd & Vandenberghe. 5. Duality
 5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
Convex Optimization. Dani Yogatama. School of Computer Science, Carnegie Mellon University, Pittsburgh, PA, USA. February 12, 2014
 Convex Optimization Dani Yogatama School of Computer Science, Carnegie Mellon University, Pittsburgh, PA, USA February 12, 2014 Dani Yogatama (Carnegie Mellon University) Convex Optimization February 12,
Convex Optimization Dani Yogatama School of Computer Science, Carnegie Mellon University, Pittsburgh, PA, USA February 12, 2014 Dani Yogatama (Carnegie Mellon University) Convex Optimization February 12,
Lecture 14: Newton s Method
 10-725/36-725: Conve Optimization Fall 2016 Lecturer: Javier Pena Lecture 14: Newton s ethod Scribes: Varun Joshi, Xuan Li Note: LaTeX template courtesy of UC Berkeley EECS dept. Disclaimer: These notes
10-725/36-725: Conve Optimization Fall 2016 Lecturer: Javier Pena Lecture 14: Newton s ethod Scribes: Varun Joshi, Xuan Li Note: LaTeX template courtesy of UC Berkeley EECS dept. Disclaimer: These notes
Convex Optimization. Newton s method. ENSAE: Optimisation 1/44
 Convex Optimization Newton s method ENSAE: Optimisation 1/44 Unconstrained minimization minimize f(x) f convex, twice continuously differentiable (hence dom f open) we assume optimal value p = inf x f(x)
Convex Optimization Newton s method ENSAE: Optimisation 1/44 Unconstrained minimization minimize f(x) f convex, twice continuously differentiable (hence dom f open) we assume optimal value p = inf x f(x)
Duality Uses and Correspondences. Ryan Tibshirani Convex Optimization
 Duality Uses and Correspondences Ryan Tibshirani Conve Optimization 10-725 Recall that for the problem Last time: KKT conditions subject to f() h i () 0, i = 1,... m l j () = 0, j = 1,... r the KKT conditions
Duality Uses and Correspondences Ryan Tibshirani Conve Optimization 10-725 Recall that for the problem Last time: KKT conditions subject to f() h i () 0, i = 1,... m l j () = 0, j = 1,... r the KKT conditions
Dual Methods. Lecturer: Ryan Tibshirani Convex Optimization /36-725
 Dual Methods Lecturer: Ryan Tibshirani Conve Optimization 10-725/36-725 1 Last time: proimal Newton method Consider the problem min g() + h() where g, h are conve, g is twice differentiable, and h is simple.
Dual Methods Lecturer: Ryan Tibshirani Conve Optimization 10-725/36-725 1 Last time: proimal Newton method Consider the problem min g() + h() where g, h are conve, g is twice differentiable, and h is simple.
Primal-dual Subgradient Method for Convex Problems with Functional Constraints
 Primal-dual Subgradient Method for Convex Problems with Functional Constraints Yurii Nesterov, CORE/INMA (UCL) Workshop on embedded optimization EMBOPT2014 September 9, 2014 (Lucca) Yu. Nesterov Primal-dual
Primal-dual Subgradient Method for Convex Problems with Functional Constraints Yurii Nesterov, CORE/INMA (UCL) Workshop on embedded optimization EMBOPT2014 September 9, 2014 (Lucca) Yu. Nesterov Primal-dual
Convex Optimization and Modeling
 Convex Optimization and Modeling Duality Theory and Optimality Conditions 5th lecture, 12.05.2010 Jun.-Prof. Matthias Hein Program of today/next lecture Lagrangian and duality: the Lagrangian the dual
Convex Optimization and Modeling Duality Theory and Optimality Conditions 5th lecture, 12.05.2010 Jun.-Prof. Matthias Hein Program of today/next lecture Lagrangian and duality: the Lagrangian the dual
Math 273a: Optimization Convex Conjugacy
 Math 273a: Optimization Convex Conjugacy Instructor: Wotao Yin Department of Mathematics, UCLA Fall 2015 online discussions on piazza.com Convex conjugate (the Legendre transform) Let f be a closed proper
Math 273a: Optimization Convex Conjugacy Instructor: Wotao Yin Department of Mathematics, UCLA Fall 2015 online discussions on piazza.com Convex conjugate (the Legendre transform) Let f be a closed proper
Optimization for Machine Learning
 Optimization for Machine Learning (Problems; Algorithms - A) SUVRIT SRA Massachusetts Institute of Technology PKU Summer School on Data Science (July 2017) Course materials http://suvrit.de/teaching.html
Optimization for Machine Learning (Problems; Algorithms - A) SUVRIT SRA Massachusetts Institute of Technology PKU Summer School on Data Science (July 2017) Course materials http://suvrit.de/teaching.html
Optimization and Optimal Control in Banach Spaces
 Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
Motivation. Lecture 2 Topics from Optimization and Duality. network utility maximization (NUM) problem:
 CDS270 Maryam Fazel Lecture 2 Topics from Optimization and Duality Motivation network utility maximization (NUM) problem: consider a network with S sources (users), each sending one flow at rate x s, through
CDS270 Maryam Fazel Lecture 2 Topics from Optimization and Duality Motivation network utility maximization (NUM) problem: consider a network with S sources (users), each sending one flow at rate x s, through
ICS-E4030 Kernel Methods in Machine Learning
 ICS-E4030 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 28. September, 2016 Juho Rousu 28. September, 2016 1 / 38 Convex optimization Convex optimisation This
ICS-E4030 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 28. September, 2016 Juho Rousu 28. September, 2016 1 / 38 Convex optimization Convex optimisation This
Introduction to Machine Learning Lecture 7. Mehryar Mohri Courant Institute and Google Research
 Introduction to Machine Learning Lecture 7 Mehryar Mohri Courant Institute and Google Research mohri@cims.nyu.edu Convex Optimization Differentiation Definition: let f : X R N R be a differentiable function,
Introduction to Machine Learning Lecture 7 Mehryar Mohri Courant Institute and Google Research mohri@cims.nyu.edu Convex Optimization Differentiation Definition: let f : X R N R be a differentiable function,
Convex Functions. Pontus Giselsson
 Convex Functions Pontus Giselsson 1 Today s lecture lower semicontinuity, closure, convex hull convexity preserving operations precomposition with affine mapping infimal convolution image function supremum
Convex Functions Pontus Giselsson 1 Today s lecture lower semicontinuity, closure, convex hull convexity preserving operations precomposition with affine mapping infimal convolution image function supremum
Lecture 18: Optimization Programming
 Fall, 2016 Outline Unconstrained Optimization 1 Unconstrained Optimization 2 Equality-constrained Optimization Inequality-constrained Optimization Mixture-constrained Optimization 3 Quadratic Programming
Fall, 2016 Outline Unconstrained Optimization 1 Unconstrained Optimization 2 Equality-constrained Optimization Inequality-constrained Optimization Mixture-constrained Optimization 3 Quadratic Programming
Nash Equilibrium and the Legendre Transform in Optimal Stopping Games with One Dimensional Diffusions
 Nash Equilibrium and the Legendre Transform in Optimal Stopping Games with One Dimensional Diffusions J. L. Seton This version: 9 Januar 2014 First version: 2 December 2011 Research Report No. 9, 2011,
Nash Equilibrium and the Legendre Transform in Optimal Stopping Games with One Dimensional Diffusions J. L. Seton This version: 9 Januar 2014 First version: 2 December 2011 Research Report No. 9, 2011,
Lecture 23: Conditional Gradient Method
 10-725/36-725: Conve Optimization Spring 2015 Lecture 23: Conditional Gradient Method Lecturer: Ryan Tibshirani Scribes: Shichao Yang,Diyi Yang,Zhanpeng Fang Note: LaTeX template courtesy of UC Berkeley
10-725/36-725: Conve Optimization Spring 2015 Lecture 23: Conditional Gradient Method Lecturer: Ryan Tibshirani Scribes: Shichao Yang,Diyi Yang,Zhanpeng Fang Note: LaTeX template courtesy of UC Berkeley
Improved Fast Dual Gradient Methods for Embedded Model Predictive Control
 Preprints of the 9th World Congress The International Federation of Automatic Control Improved Fast Dual Gradient Methods for Embedded Model Predictive Control Pontus Giselsson Electrical Engineering,
Preprints of the 9th World Congress The International Federation of Automatic Control Improved Fast Dual Gradient Methods for Embedded Model Predictive Control Pontus Giselsson Electrical Engineering,
ON A CLASS OF NONSMOOTH COMPOSITE FUNCTIONS
 MATHEMATICS OF OPERATIONS RESEARCH Vol. 28, No. 4, November 2003, pp. 677 692 Printed in U.S.A. ON A CLASS OF NONSMOOTH COMPOSITE FUNCTIONS ALEXANDER SHAPIRO We discuss in this paper a class of nonsmooth
MATHEMATICS OF OPERATIONS RESEARCH Vol. 28, No. 4, November 2003, pp. 677 692 Printed in U.S.A. ON A CLASS OF NONSMOOTH COMPOSITE FUNCTIONS ALEXANDER SHAPIRO We discuss in this paper a class of nonsmooth
m x n matrix with m rows and n columns is called an array of m.n real numbers
 LINEAR ALGEBRA Matrices Linear Algebra Definitions m n matri with m rows and n columns is called an arra of mn real numbers The entr a a an A = a a an = ( a ij ) am am amn a ij denotes the element in the
LINEAR ALGEBRA Matrices Linear Algebra Definitions m n matri with m rows and n columns is called an arra of mn real numbers The entr a a an A = a a an = ( a ij ) am am amn a ij denotes the element in the
The Lagrangian L : R d R m R r R is an (easier to optimize) lower bound on the original problem:
 HT05: SC4 Statistical Data Mining and Machine Learning Dino Sejdinovic Department of Statistics Oxford Convex Optimization and slides based on Arthur Gretton s Advanced Topics in Machine Learning course
HT05: SC4 Statistical Data Mining and Machine Learning Dino Sejdinovic Department of Statistics Oxford Convex Optimization and slides based on Arthur Gretton s Advanced Topics in Machine Learning course
Lagrange Duality. Daniel P. Palomar. Hong Kong University of Science and Technology (HKUST)
 Lagrange Duality Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Lagrangian Dual function Dual
Lagrange Duality Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Lagrangian Dual function Dual
Dual Ascent. Ryan Tibshirani Convex Optimization
 Dual Ascent Ryan Tibshirani Conve Optimization 10-725 Last time: coordinate descent Consider the problem min f() where f() = g() + n i=1 h i( i ), with g conve and differentiable and each h i conve. Coordinate
Dual Ascent Ryan Tibshirani Conve Optimization 10-725 Last time: coordinate descent Consider the problem min f() where f() = g() + n i=1 h i( i ), with g conve and differentiable and each h i conve. Coordinate
Convex Optimization Overview (cnt d)
 Conve Optimization Overview (cnt d) Chuong B. Do November 29, 2009 During last week s section, we began our study of conve optimization, the study of mathematical optimization problems of the form, minimize
Conve Optimization Overview (cnt d) Chuong B. Do November 29, 2009 During last week s section, we began our study of conve optimization, the study of mathematical optimization problems of the form, minimize
Lecture 6: Conic Optimization September 8
 IE 598: Big Data Optimization Fall 2016 Lecture 6: Conic Optimization September 8 Lecturer: Niao He Scriber: Juan Xu Overview In this lecture, we finish up our previous discussion on optimality conditions
IE 598: Big Data Optimization Fall 2016 Lecture 6: Conic Optimization September 8 Lecturer: Niao He Scriber: Juan Xu Overview In this lecture, we finish up our previous discussion on optimality conditions
Some Properties of the Augmented Lagrangian in Cone Constrained Optimization
 MATHEMATICS OF OPERATIONS RESEARCH Vol. 29, No. 3, August 2004, pp. 479 491 issn 0364-765X eissn 1526-5471 04 2903 0479 informs doi 10.1287/moor.1040.0103 2004 INFORMS Some Properties of the Augmented
MATHEMATICS OF OPERATIONS RESEARCH Vol. 29, No. 3, August 2004, pp. 479 491 issn 0364-765X eissn 1526-5471 04 2903 0479 informs doi 10.1287/moor.1040.0103 2004 INFORMS Some Properties of the Augmented
LECTURE 25: REVIEW/EPILOGUE LECTURE OUTLINE
 LECTURE 25: REVIEW/EPILOGUE LECTURE OUTLINE CONVEX ANALYSIS AND DUALITY Basic concepts of convex analysis Basic concepts of convex optimization Geometric duality framework - MC/MC Constrained optimization
LECTURE 25: REVIEW/EPILOGUE LECTURE OUTLINE CONVEX ANALYSIS AND DUALITY Basic concepts of convex analysis Basic concepts of convex optimization Geometric duality framework - MC/MC Constrained optimization
Convex Optimization. Convex Analysis - Functions
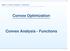 Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
ABOUT THE WEAK EFFICIENCIES IN VECTOR OPTIMIZATION
 ABOUT THE WEAK EFFICIENCIES IN VECTOR OPTIMIZATION CRISTINA STAMATE Institute of Mathematics 8, Carol I street, Iasi 6600, Romania cstamate@mail.com Abstract: We present the principal properties of the
ABOUT THE WEAK EFFICIENCIES IN VECTOR OPTIMIZATION CRISTINA STAMATE Institute of Mathematics 8, Carol I street, Iasi 6600, Romania cstamate@mail.com Abstract: We present the principal properties of the
Lecture 16: October 22
 0-725/36-725: Conve Optimization Fall 208 Lecturer: Ryan Tibshirani Lecture 6: October 22 Scribes: Nic Dalmasso, Alan Mishler, Benja LeRoy Note: LaTeX template courtesy of UC Berkeley EECS dept. Disclaimer:
0-725/36-725: Conve Optimization Fall 208 Lecturer: Ryan Tibshirani Lecture 6: October 22 Scribes: Nic Dalmasso, Alan Mishler, Benja LeRoy Note: LaTeX template courtesy of UC Berkeley EECS dept. Disclaimer:
Optimality Conditions for Constrained Optimization
 72 CHAPTER 7 Optimality Conditions for Constrained Optimization 1. First Order Conditions In this section we consider first order optimality conditions for the constrained problem P : minimize f 0 (x)
72 CHAPTER 7 Optimality Conditions for Constrained Optimization 1. First Order Conditions In this section we consider first order optimality conditions for the constrained problem P : minimize f 0 (x)
1.1 The Equations of Motion
 1.1 The Equations of Motion In Book I, balance of forces and moments acting on an component was enforced in order to ensure that the component was in equilibrium. Here, allowance is made for stresses which
1.1 The Equations of Motion In Book I, balance of forces and moments acting on an component was enforced in order to ensure that the component was in equilibrium. Here, allowance is made for stresses which
Subgradients. subgradients and quasigradients. subgradient calculus. optimality conditions via subgradients. directional derivatives
 Subgradients subgradients and quasigradients subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE392o, Stanford University Basic inequality recall basic
Subgradients subgradients and quasigradients subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE392o, Stanford University Basic inequality recall basic
Lecture Notes on Support Vector Machine
 Lecture Notes on Support Vector Machine Feng Li fli@sdu.edu.cn Shandong University, China 1 Hyperplane and Margin In a n-dimensional space, a hyper plane is defined by ω T x + b = 0 (1) where ω R n is
Lecture Notes on Support Vector Machine Feng Li fli@sdu.edu.cn Shandong University, China 1 Hyperplane and Margin In a n-dimensional space, a hyper plane is defined by ω T x + b = 0 (1) where ω R n is
Master 2 MathBigData. 3 novembre CMAP - Ecole Polytechnique
 Master 2 MathBigData S. Gaïffas 1 3 novembre 2014 1 CMAP - Ecole Polytechnique 1 Supervised learning recap Introduction Loss functions, linearity 2 Penalization Introduction Ridge Sparsity Lasso 3 Some
Master 2 MathBigData S. Gaïffas 1 3 novembre 2014 1 CMAP - Ecole Polytechnique 1 Supervised learning recap Introduction Loss functions, linearity 2 Penalization Introduction Ridge Sparsity Lasso 3 Some
UC Berkeley Department of Electrical Engineering and Computer Science. EECS 227A Nonlinear and Convex Optimization. Solutions 6 Fall 2009
 UC Berkele Department of Electrical Engineering and Computer Science EECS 227A Nonlinear and Convex Optimization Solutions 6 Fall 2009 Solution 6.1 (a) p = 1 (b) The Lagrangian is L(x,, λ) = e x + λx 2
UC Berkele Department of Electrical Engineering and Computer Science EECS 227A Nonlinear and Convex Optimization Solutions 6 Fall 2009 Solution 6.1 (a) p = 1 (b) The Lagrangian is L(x,, λ) = e x + λx 2
BASICS OF CONVEX ANALYSIS
 BASICS OF CONVEX ANALYSIS MARKUS GRASMAIR 1. Main Definitions We start with providing the central definitions of convex functions and convex sets. Definition 1. A function f : R n R + } is called convex,
BASICS OF CONVEX ANALYSIS MARKUS GRASMAIR 1. Main Definitions We start with providing the central definitions of convex functions and convex sets. Definition 1. A function f : R n R + } is called convex,
EE/AA 578, Univ of Washington, Fall Duality
 7. Duality EE/AA 578, Univ of Washington, Fall 2016 Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
7. Duality EE/AA 578, Univ of Washington, Fall 2016 Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
Self Equivalence of the Alternating Direction Method of Multipliers
 Self Equivalence of the Alternating Direction Method of Multipliers Ming Yan and Wotao Yin Abstract The alternating direction method of multipliers (ADM or ADMM) breaks a comple optimization problem into
Self Equivalence of the Alternating Direction Method of Multipliers Ming Yan and Wotao Yin Abstract The alternating direction method of multipliers (ADM or ADMM) breaks a comple optimization problem into
Maximal Monotone Inclusions and Fitzpatrick Functions
 JOTA manuscript No. (will be inserted by the editor) Maximal Monotone Inclusions and Fitzpatrick Functions J. M. Borwein J. Dutta Communicated by Michel Thera. Abstract In this paper, we study maximal
JOTA manuscript No. (will be inserted by the editor) Maximal Monotone Inclusions and Fitzpatrick Functions J. M. Borwein J. Dutta Communicated by Michel Thera. Abstract In this paper, we study maximal
Introduction to Machine Learning Spring 2018 Note Duality. 1.1 Primal and Dual Problem
 CS 189 Introduction to Machine Learning Spring 2018 Note 22 1 Duality As we have seen in our discussion of kernels, ridge regression can be viewed in two ways: (1) an optimization problem over the weights
CS 189 Introduction to Machine Learning Spring 2018 Note 22 1 Duality As we have seen in our discussion of kernels, ridge regression can be viewed in two ways: (1) an optimization problem over the weights
Chapter 11 Optimization with Equality Constraints
 Ch. - Optimization with Equalit Constraints Chapter Optimization with Equalit Constraints Albert William Tucker 95-995 arold William Kuhn 95 oseph-ouis Giuseppe odovico comte de arane 76-. General roblem
Ch. - Optimization with Equalit Constraints Chapter Optimization with Equalit Constraints Albert William Tucker 95-995 arold William Kuhn 95 oseph-ouis Giuseppe odovico comte de arane 76-. General roblem
Convex Optimization Theory. Chapter 5 Exercises and Solutions: Extended Version
 Convex Optimization Theory Chapter 5 Exercises and Solutions: Extended Version Dimitri P. Bertsekas Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Convex Optimization Theory Chapter 5 Exercises and Solutions: Extended Version Dimitri P. Bertsekas Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Convex Analysis Notes. Lecturer: Adrian Lewis, Cornell ORIE Scribe: Kevin Kircher, Cornell MAE
 Convex Analysis Notes Lecturer: Adrian Lewis, Cornell ORIE Scribe: Kevin Kircher, Cornell MAE These are notes from ORIE 6328, Convex Analysis, as taught by Prof. Adrian Lewis at Cornell University in the
Convex Analysis Notes Lecturer: Adrian Lewis, Cornell ORIE Scribe: Kevin Kircher, Cornell MAE These are notes from ORIE 6328, Convex Analysis, as taught by Prof. Adrian Lewis at Cornell University in the
Coordinate Update Algorithm Short Course Subgradients and Subgradient Methods
 Coordinate Update Algorithm Short Course Subgradients and Subgradient Methods Instructor: Wotao Yin (UCLA Math) Summer 2016 1 / 30 Notation f : H R { } is a closed proper convex function domf := {x R n
Coordinate Update Algorithm Short Course Subgradients and Subgradient Methods Instructor: Wotao Yin (UCLA Math) Summer 2016 1 / 30 Notation f : H R { } is a closed proper convex function domf := {x R n
Lecture 3: Lagrangian duality and algorithms for the Lagrangian dual problem
 Lecture 3: Lagrangian duality and algorithms for the Lagrangian dual problem Michael Patriksson 0-0 The Relaxation Theorem 1 Problem: find f := infimum f(x), x subject to x S, (1a) (1b) where f : R n R
Lecture 3: Lagrangian duality and algorithms for the Lagrangian dual problem Michael Patriksson 0-0 The Relaxation Theorem 1 Problem: find f := infimum f(x), x subject to x S, (1a) (1b) where f : R n R
Karush-Kuhn-Tucker Conditions. Lecturer: Ryan Tibshirani Convex Optimization /36-725
 Karush-Kuhn-Tucker Conditions Lecturer: Ryan Tibshirani Convex Optimization 10-725/36-725 1 Given a minimization problem Last time: duality min x subject to f(x) h i (x) 0, i = 1,... m l j (x) = 0, j =
Karush-Kuhn-Tucker Conditions Lecturer: Ryan Tibshirani Convex Optimization 10-725/36-725 1 Given a minimization problem Last time: duality min x subject to f(x) h i (x) 0, i = 1,... m l j (x) = 0, j =
Lecture 3. Optimization Problems and Iterative Algorithms
 Lecture 3 Optimization Problems and Iterative Algorithms January 13, 2016 This material was jointly developed with Angelia Nedić at UIUC for IE 598ns Outline Special Functions: Linear, Quadratic, Convex
Lecture 3 Optimization Problems and Iterative Algorithms January 13, 2016 This material was jointly developed with Angelia Nedić at UIUC for IE 598ns Outline Special Functions: Linear, Quadratic, Convex
6. Proximal gradient method
 L. Vandenberghe EE236C (Spring 2016) 6. Proximal gradient method motivation proximal mapping proximal gradient method with fixed step size proximal gradient method with line search 6-1 Proximal mapping
L. Vandenberghe EE236C (Spring 2016) 6. Proximal gradient method motivation proximal mapping proximal gradient method with fixed step size proximal gradient method with line search 6-1 Proximal mapping
Newton s Method. Javier Peña Convex Optimization /36-725
 Newton s Method Javier Peña Convex Optimization 10-725/36-725 1 Last time: dual correspondences Given a function f : R n R, we define its conjugate f : R n R, f ( (y) = max y T x f(x) ) x Properties and
Newton s Method Javier Peña Convex Optimization 10-725/36-725 1 Last time: dual correspondences Given a function f : R n R, we define its conjugate f : R n R, f ( (y) = max y T x f(x) ) x Properties and
Numerical Optimization
 Constrained Optimization Computer Science and Automation Indian Institute of Science Bangalore 560 012, India. NPTEL Course on Constrained Optimization Constrained Optimization Problem: min h j (x) 0,
Constrained Optimization Computer Science and Automation Indian Institute of Science Bangalore 560 012, India. NPTEL Course on Constrained Optimization Constrained Optimization Problem: min h j (x) 0,
Primal/Dual Decomposition Methods
 Primal/Dual Decomposition Methods Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2018-19, HKUST, Hong Kong Outline of Lecture Subgradients
Primal/Dual Decomposition Methods Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2018-19, HKUST, Hong Kong Outline of Lecture Subgradients
Iterative Convex Optimization Algorithms; Part One: Using the Baillon Haddad Theorem
 Iterative Convex Optimization Algorithms; Part One: Using the Baillon Haddad Theorem Charles Byrne (Charles Byrne@uml.edu) http://faculty.uml.edu/cbyrne/cbyrne.html Department of Mathematical Sciences
Iterative Convex Optimization Algorithms; Part One: Using the Baillon Haddad Theorem Charles Byrne (Charles Byrne@uml.edu) http://faculty.uml.edu/cbyrne/cbyrne.html Department of Mathematical Sciences
I.3. LMI DUALITY. Didier HENRION EECI Graduate School on Control Supélec - Spring 2010
 I.3. LMI DUALITY Didier HENRION henrion@laas.fr EECI Graduate School on Control Supélec - Spring 2010 Primal and dual For primal problem p = inf x g 0 (x) s.t. g i (x) 0 define Lagrangian L(x, z) = g 0
I.3. LMI DUALITY Didier HENRION henrion@laas.fr EECI Graduate School on Control Supélec - Spring 2010 Primal and dual For primal problem p = inf x g 0 (x) s.t. g i (x) 0 define Lagrangian L(x, z) = g 0
Dual Proximal Gradient Method
 Dual Proximal Gradient Method http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes Outline 2/19 1 proximal gradient method
Dual Proximal Gradient Method http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes Outline 2/19 1 proximal gradient method
Descent methods. min x. f(x)
 Gradient Descent Descent methods min x f(x) 5 / 34 Descent methods min x f(x) x k x k+1... x f(x ) = 0 5 / 34 Gradient methods Unconstrained optimization min f(x) x R n. 6 / 34 Gradient methods Unconstrained
Gradient Descent Descent methods min x f(x) 5 / 34 Descent methods min x f(x) x k x k+1... x f(x ) = 0 5 / 34 Gradient methods Unconstrained optimization min f(x) x R n. 6 / 34 Gradient methods Unconstrained
Bregman Divergence and Mirror Descent
 Bregman Divergence and Mirror Descent Bregman Divergence Motivation Generalize squared Euclidean distance to a class of distances that all share similar properties Lots of applications in machine learning,
Bregman Divergence and Mirror Descent Bregman Divergence Motivation Generalize squared Euclidean distance to a class of distances that all share similar properties Lots of applications in machine learning,
Lecture 15 Newton Method and Self-Concordance. October 23, 2008
 Newton Method and Self-Concordance October 23, 2008 Outline Lecture 15 Self-concordance Notion Self-concordant Functions Operations Preserving Self-concordance Properties of Self-concordant Functions Implications
Newton Method and Self-Concordance October 23, 2008 Outline Lecture 15 Self-concordance Notion Self-concordant Functions Operations Preserving Self-concordance Properties of Self-concordant Functions Implications
too, of course, but is perhaps overkill here.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR OPTIMERING 018-01-11 kl 08-13 1. a) CQ points are shown as A and B below. Graphically: they are the only points that share the same tangent line for both active
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR OPTIMERING 018-01-11 kl 08-13 1. a) CQ points are shown as A and B below. Graphically: they are the only points that share the same tangent line for both active
1. f(β) 0 (that is, β is a feasible point for the constraints)
 xvi 2. The lasso for linear models 2.10 Bibliographic notes Appendix Convex optimization with constraints In this Appendix we present an overview of convex optimization concepts that are particularly useful
xvi 2. The lasso for linear models 2.10 Bibliographic notes Appendix Convex optimization with constraints In this Appendix we present an overview of convex optimization concepts that are particularly useful
4TE3/6TE3. Algorithms for. Continuous Optimization
 4TE3/6TE3 Algorithms for Continuous Optimization (Duality in Nonlinear Optimization ) Tamás TERLAKY Computing and Software McMaster University Hamilton, January 2004 terlaky@mcmaster.ca Tel: 27780 Optimality
4TE3/6TE3 Algorithms for Continuous Optimization (Duality in Nonlinear Optimization ) Tamás TERLAKY Computing and Software McMaster University Hamilton, January 2004 terlaky@mcmaster.ca Tel: 27780 Optimality
Newton-Type Algorithms for Nonlinear Constrained Optimization
 Newton-Type Algorithms for Nonlinear Constrained Optimization Angelika Altmann-Dieses Faculty of Management Science and Engineering Karlsruhe University of Applied Sciences Moritz Diehl Department of Microsystems
Newton-Type Algorithms for Nonlinear Constrained Optimization Angelika Altmann-Dieses Faculty of Management Science and Engineering Karlsruhe University of Applied Sciences Moritz Diehl Department of Microsystems
Uses of duality. Geoff Gordon & Ryan Tibshirani Optimization /
 Uses of duality Geoff Gordon & Ryan Tibshirani Optimization 10-725 / 36-725 1 Remember conjugate functions Given f : R n R, the function is called its conjugate f (y) = max x R n yt x f(x) Conjugates appear
Uses of duality Geoff Gordon & Ryan Tibshirani Optimization 10-725 / 36-725 1 Remember conjugate functions Given f : R n R, the function is called its conjugate f (y) = max x R n yt x f(x) Conjugates appear
Lecture 8: February 9
 0-725/36-725: Convex Optimiation Spring 205 Lecturer: Ryan Tibshirani Lecture 8: February 9 Scribes: Kartikeya Bhardwaj, Sangwon Hyun, Irina Caan 8 Proximal Gradient Descent In the previous lecture, we
0-725/36-725: Convex Optimiation Spring 205 Lecturer: Ryan Tibshirani Lecture 8: February 9 Scribes: Kartikeya Bhardwaj, Sangwon Hyun, Irina Caan 8 Proximal Gradient Descent In the previous lecture, we
Convex Optimization Lecture 6: KKT Conditions, and applications
 Convex Optimization Lecture 6: KKT Conditions, and applications Dr. Michel Baes, IFOR / ETH Zürich Quick recall of last week s lecture Various aspects of convexity: The set of minimizers is convex. Convex
Convex Optimization Lecture 6: KKT Conditions, and applications Dr. Michel Baes, IFOR / ETH Zürich Quick recall of last week s lecture Various aspects of convexity: The set of minimizers is convex. Convex
UNIVERSIDAD CARLOS III DE MADRID MATHEMATICS II EXERCISES (SOLUTIONS )
 UNIVERSIDAD CARLOS III DE MADRID MATHEMATICS II EXERCISES (SOLUTIONS ) CHAPTER : Limits and continuit of functions in R n. -. Sketch the following subsets of R. Sketch their boundar and the interior. Stud
UNIVERSIDAD CARLOS III DE MADRID MATHEMATICS II EXERCISES (SOLUTIONS ) CHAPTER : Limits and continuit of functions in R n. -. Sketch the following subsets of R. Sketch their boundar and the interior. Stud
Proximal methods. S. Villa. October 7, 2014
 Proximal methods S. Villa October 7, 2014 1 Review of the basics Often machine learning problems require the solution of minimization problems. For instance, the ERM algorithm requires to solve a problem
Proximal methods S. Villa October 7, 2014 1 Review of the basics Often machine learning problems require the solution of minimization problems. For instance, the ERM algorithm requires to solve a problem
Math 273a: Optimization Subgradients of convex functions
 Math 273a: Optimization Subgradients of convex functions Made by: Damek Davis Edited by Wotao Yin Department of Mathematics, UCLA Fall 2015 online discussions on piazza.com 1 / 20 Subgradients Assumptions
Math 273a: Optimization Subgradients of convex functions Made by: Damek Davis Edited by Wotao Yin Department of Mathematics, UCLA Fall 2015 online discussions on piazza.com 1 / 20 Subgradients Assumptions
Support Vector Machines: Maximum Margin Classifiers
 Support Vector Machines: Maximum Margin Classifiers Machine Learning and Pattern Recognition: September 16, 2008 Piotr Mirowski Based on slides by Sumit Chopra and Fu-Jie Huang 1 Outline What is behind
Support Vector Machines: Maximum Margin Classifiers Machine Learning and Pattern Recognition: September 16, 2008 Piotr Mirowski Based on slides by Sumit Chopra and Fu-Jie Huang 1 Outline What is behind
QUADRATIC AND CONVEX MINIMAX CLASSIFICATION PROBLEMS
 Journal of the Operations Research Societ of Japan 008, Vol. 51, No., 191-01 QUADRATIC AND CONVEX MINIMAX CLASSIFICATION PROBLEMS Tomonari Kitahara Shinji Mizuno Kazuhide Nakata Toko Institute of Technolog
Journal of the Operations Research Societ of Japan 008, Vol. 51, No., 191-01 QUADRATIC AND CONVEX MINIMAX CLASSIFICATION PROBLEMS Tomonari Kitahara Shinji Mizuno Kazuhide Nakata Toko Institute of Technolog
CONSTRAINT QUALIFICATIONS, LAGRANGIAN DUALITY & SADDLE POINT OPTIMALITY CONDITIONS
 CONSTRAINT QUALIFICATIONS, LAGRANGIAN DUALITY & SADDLE POINT OPTIMALITY CONDITIONS A Dissertation Submitted For The Award of the Degree of Master of Philosophy in Mathematics Neelam Patel School of Mathematics
CONSTRAINT QUALIFICATIONS, LAGRANGIAN DUALITY & SADDLE POINT OPTIMALITY CONDITIONS A Dissertation Submitted For The Award of the Degree of Master of Philosophy in Mathematics Neelam Patel School of Mathematics
Review of Optimization Basics
 Review of Optimization Basics. Introduction Electricity markets throughout the US are said to have a two-settlement structure. The reason for this is that the structure includes two different markets:
Review of Optimization Basics. Introduction Electricity markets throughout the US are said to have a two-settlement structure. The reason for this is that the structure includes two different markets:
Newton s Method. Ryan Tibshirani Convex Optimization /36-725
 Newton s Method Ryan Tibshirani Convex Optimization 10-725/36-725 1 Last time: dual correspondences Given a function f : R n R, we define its conjugate f : R n R, Properties and examples: f (y) = max x
Newton s Method Ryan Tibshirani Convex Optimization 10-725/36-725 1 Last time: dual correspondences Given a function f : R n R, we define its conjugate f : R n R, Properties and examples: f (y) = max x
Extended Monotropic Programming and Duality 1
 March 2006 (Revised February 2010) Report LIDS - 2692 Extended Monotropic Programming and Duality 1 by Dimitri P. Bertsekas 2 Abstract We consider the problem minimize f i (x i ) subject to x S, where
March 2006 (Revised February 2010) Report LIDS - 2692 Extended Monotropic Programming and Duality 1 by Dimitri P. Bertsekas 2 Abstract We consider the problem minimize f i (x i ) subject to x S, where
