A set C R n is convex if and only if δ C is convex if and only if. f : R n R is strictly convex if and only if f is convex and the inequality (1.
|
|
|
- Kellie Freeman
- 5 years ago
- Views:
Transcription
1 ONVEX OPTIMIZATION SUMMARY ANDREW TULLOH 1. Eistence Definition. For R n, define δ as 0 δ () = / (1.1) Note minimizes f over if and onl if minimizes f + δ over R n. Definition. (ii) (i) dom f = R n f() < }, arg min f = f R n f() = f} f < (1.2) (iii) f is proper if and onl if dom f and f() > for all R n. Definition. For f : R n R, denote epi f = (, α) R n R f() α} (1.3) Theorem. A set is an epigraph if and onl if for ever there is an α R such that ( R) = [α, ] - so all vertical one-dimensional sections must be closed upper half-lines. If f is proper then epi f is not empt and does not include a complete vertical line. Definition. For f : R n R, define lim f() = lim δ 0 2 δ f() = lim k 2 1 k f() (1.4) f is lower semicontinuous at if and onl if f( ) lim f(). f is lower semicontinuous if f is lower semicontinuous at ever R n. Theorem. lim f() = minα R ( k ) : f( k ) α} (1.5) In particular, f is lower semi-continuous at if and onl if f( ) lim k f( k ) for all convergence sequences k. Theorem. Let f : R n R. Then the following are equivalent: (i) f is lsc on R n (ii) epi f is closed in R n R (iii) The sub level sets lev α f = R n f() α} are closed in R n for all α R. Proof. epi f can onl be not closed along vertical lines. Definition. f : R n R is level bounded if and onl if lev α f is bounded for all α R. Theorem. f : R n R is level-bounded if and onl if f( k ) for all sequences ( k ) satisfing k 2. Proof. K(α) such that k / lev α f for k K(α) b boundedness. In reverse, find α with lev α f unbounded and choose k in this set with f( k ) α. Theorem. Assume f : R n R is lsc, level-bounded, and proper. Then f() (, + ) and arg min f is nonempt and compact. Proof. onsider α R,a> f = arg min f, then this is countable intersection of nonempt, compact sets, so intersection is nonempt. Finiteness of is shown as for an arg min f, must have f() = contradicting properness. Theorem. (i) f, g lsc, proper implies f + g is lsc. (ii) f lsc, λ 0 implies λf is lsc (iii) f : R n R is lsc and g : R m R n is continuous implies f g is lsc. 2. onveit Definition. f : R n R is conve if and onl if f((1 τ) + τ) (1 τ)f() + τf() (2.1) for all, R n, τ (0, 1). A set R n is conve if and onl if δ is conve if and onl if (1 τ) + τ for all,, τ (0, 1). f : R n R is strictl conve if and onl if f is conve and the inequalit is strict for all and τ (0, 1). Definition. Let 0,..., m R n and λ 0,..., λ m 0, m i=0 λ i = 1. The linear combination m i=0 λ i i is a conve combination of the points 0,..., m. Theorem. (i) f : R n R is conve if and onl if m m f( λ i i ) λ i f( i ) (2.2) i=0 i=0 for all m 0, i R n, λ i 0, m i=0 λ i = 1. (ii) R n is conve if and onl if contains all conve combinations of its elements. Theorem. f : R n R is conve implies dom f is conve. Theorem. (i) f : R n R is conve if and onl if epi f is conve in R n R. (ii) f : R n R is strictl conve if and onl if (, α) R n R f() < α} is conve in R n R. (iii) f : R n R is conve implies lev α f is conve for all α R. Theorem. Assume f : R n R is conve. Then (i) arg min f is conve. (ii) is a local minimizer of f implies is a global minimize of f. (iii) f is strictl conve and proper implies f has at most one global minimizer. Theorem. Let I be an arbitrar inde set. Then (i) f i, i I conve implies sup i I f i () is conve. (ii) f i, i I strictl conve, I finite implies sup i I f i () is strictl conve. (iii) i, i I is conve implies i I i is conve. (iv) f k, k N is conve implies lim sup k f k () is conve. Theorem. Assume R n is open and conve, and f : R is differentiable. Then the following are equivalent: (i) f is [strictl] conve (ii), f() f() 0 for all, [and > 0 if ] (iii) f()+, f() f() for all, [and < f() if ] (iv) If f is additionall twice differentiable, then 2 f() is positive semidefinite for all. Proof. Reduce to one-dimensional sections g(t) = f( + t( )). Take g( + h), use conveit to show g () g() g(). Use g() = sup dom g g() + ( )g () to show the supremum over conve functions is conve. Theorem. (i) Assume f 1,..., f m : R n R are conve, λ 1,..., λ m 0. Then f = m i=1 λ if i is conve. If at least one of the f i with λ i > 0 is strictl conve, then f is strictl conve. (ii) Assume f i : R n i R are conve. Then m f : R n 1... R nm Rf( 1,..., m) = f i ( i ) (2.3) i=1 is conve. If all f i are strictl conve, then f is strictl conve. (iii) If f : R m R is conve, A R m n, b R m. Then g() = f(a + b) is conve. Theorem. (i) 1,..., m conve implies 1 m is conve. (ii) R n conve, A R m n, b R m, L() = A + b implies L() is conve. (iii) R m conve, A R m n, b R m, L() = A + b implies L 1 () is conve. (iv) 1, 2 is conve implies is conve. (v) conve, λ R implies λ is conve. 1
2 ONVEX OPTIMIZATION SUMMARY 2 Definition. For a set S R n and R n, define the projection of onto S as Π() = arg min 2. (2.4) S S Theorem. Assume R n is conve, closed, and. Then Π is single-valued - that is, the projection of onto is unique for ever R n. Proof. f is lsc, level-bounded, and proper, so arg min f. f is strictl conve so has at most one minimizer. Definition. For an arbitrar set S R n, con S = conve, S (2.5) is the conve hull of S. It is the smallest conve set that contains S. Theorem. con S = p i=0 λ i i i S, λ i 0, p i=0 λ i = 1, p 0} = D Proof. D con S as a conve set contains all conve combinations of points in S, thus D con S. con S D as taking linear combination of, D, we have a conve combination of elements in D, which is in D, so con S D. Theorem. We have (i) cl = R n open neighborhoods N of, N } (ii) int = R n open neighborhood N of such that N } (iii) bnd = cl \. Theorem. cl = S closed, S S. 3. ones and Generalized Inequalities Definition. K R n is a cone if and onl if 0 K and λ K for all K, λ 0. A cone K is pointed if and onl if m 0=1 i = 0, i K implies i = 0 for all i. Theorem. Let K R n be arbitrar. Then the following are equivalent: (i) K is a conve cone. (ii) K is a cone and K + K K. (iii) K and m i=0 α i i K for all i K and α i 0 (not necessaril summing to 1). Proof. = m i=0 α i i K, a i 0 m a i i=0 j α K, which is a j conve combination. Theorem. Assume K is a conve cone. Then K is pointed if and onl if K K = 0}. Proof m K, 1 0, m = 1, m K, so 1 K K. Theorem. For a closed conve cone K R n we define the generalized inequalit Then K K (3.1) (i) K (ii) K, K z K z (iii) K K (iv) K, λ 0 λ K λ (v) K, K + K + (vi) k, k with k K K for all k N, then K. (vii) K, K = (antismmetr) holds if and onl if K is pointed. Definition (Kn LP ). For an pointed, closed, conve cone K R m, a matri A R m n, and vectors c R n, b R m, define the conic problem c T s.t.a K b. Definition (K SOP n ). K SOP n = R n } n n 1. (3.2) 4. Subgradients Definition. For an f : R n R and R n, f() = v R n f() + v, f() R n } (4.1) is the set of subgradients of f at. Theorem. Assume f, g : R n R are conve. Then (i) If f is differentiable at, then f() = f()} (ii) If f is differentiable at and g() R, then (f +g)() = g()+ f(). Theorem. Assume f : R n R is proper. Then arg min f 0 f(). Proof. 0 f() f() f() arg min f (4.2) where properness was required since arg min + = b definition. Definition. For a conve set R n and, the normal cone N () at is N ( = v R n v, 0 }) (4.3) N () = for /. Note that N () is a cone if. Theorem. Assume R n is conve with. Then δ () = N (). Proof. For, this follows easil, and for /, choosing shows that δ () =. Theorem. Assume R n is closed and conve with and R n. Then Π () N (). Proof. Follows from being the unique minimizer of f( ) = δ ( ). Theorem. Assume f : R n R is proper and conve. Then / dom f f() = v R n (v, 1) N epi f (, f())} dom f If dom f then N dom f () = v R n (v, 0) N epi f (, f())}. (4.4) Proof. / dom f: choose f() <, then f() =. dom f: v T ( ) + ( 1)( f()) 0 (, α) epi f (v, 1) N epi f (, f()). Definition. For an set R n, define the affine hull and relative interior b aff = A affine, A A (4.5) rint = R n open neighborhood N of with N aff }. (4.6) Theorem. (i) Assume f : R n R is conve. Then g() = f( + ) g() = f( + ) (4.7) g() = f(λ) g() = λ f(λ), λ 0 (4.8) g() = λf() g() = λ f(), λ > 0 (4.9) (4.10) (ii) Assume f : R n R is proper and conve, and A R n m is such that A R m } rint dom f (4.11) If dom(f A) = R m A dom f}, then (f A)() = A T f(a). (iii) Assume f 0,..., f m : R n R are proper and conve, and rint dom f 0 rint dom f m. If dom f, then ( m i=0 f i)() = m i=0 f i(). 5. onjugate Functions Definition. For f : R n R, con f() = sup g f, g conve is the conve hull of f. con f is the greatest conve function majorized b f. Definition. For f : R n R, the lower closure cl f is defined as (cl f)() = lim f(). Alternativel, (cl f)() = sup g f, g lsc g(). Theorem. For f : R n R, we have epi(cl f) = cl(epi f). Moreover, if f is conve then cl f is conve. Proof. (, α) cl(epi f) k, α k α, f( k α k ) lim f() α (, α) epi(cl f).
3 ONVEX OPTIMIZATION SUMMARY 3 Theorem. Assume R n is closed and conve. Then = H b,β (5.1) (b,β), H b,β where B b,β = R n, b β 0} Proof. Separating hperplane theorem - then is the intersection. If / consider the separating hperplane of and }. Theorem. Assume f : R n R is proper, lsc, and conve. Then f() = sup g affine, f f g(). Proof. f lsc implies epi f is closed, f is conve implies epi f is conve, so epi f is the intersection of all half spaces containing it. Show g affine there eists (b, c), β with c <, epi g = H (b,c),β. Then as epi(sup g f g()) = g f epi g where g is affine and g f epi f epi g, we need onl show I 1 = (b,c),β S H (b,c),β = (b,c),β S,c<0 H (b,c),β = I 2. Definition. Let f : R n R, then f : R n R (5.2) f (v) = sup R n v, f() (5.3) is the conjugate to f. The mapping f f is the Legendre-Fenchel transform. Theorem. Assume f : R n R. Then f = (con f) = (cl f) = (cl con f) and f = (f ) f. If con f is proper, then f and f are proper, lsc, and conve, and f = cl con f. If f : R n R is proper, lsc, and conve, then f = f. Proof. (v, β) epi f (v, ) β f() so (v, β) epi f define all affine functions majorized b f. Thus for ever affine function h, h f h cl f h con f h cl con f. Which gives our result. For the inequalit, epand f () = sup v v, + (f() v, ) f() at =. As con f is proper, then cl con f is proper, lsc, and conve, so cl con f = sup g cl con f g() where g is affine,which equals f b definition. Finall, if f is conve, then con f = f, so con fis proper, and con f = f is lsc, so f = cl con f = cl f = f. Theorem. Assume f : R n R. Then (i) con f is not proper implies f + or f. (ii) In particular, f proper implies con f is proper. Proof. If con f =, then f (v) =. f (v) = (con f) (v) +. If con f( ) =, then Theorem. Assume f : R n R is proper, lsc, and conve. Then f = ( f) 1, specificall, Moreover, v f() f() + f (v) = v, f (v). (5.4) f() = arg ma v v, f (v ) f () = arg ma v, f() (5.5) Proof. f() + f (v) = v, iff arg ma v, f( ) v f(). Theorem. For a proper, lsc, conve f : R n R, we have (f( ) a, ) = f ( + a) (5.6) (f( + b)) = f ( ), b, (5.7) (f( ) + c) = f ( ) c (5.8) (λf( )) = λf star ( ), λ > 0 λ (5.9) (λf( λ )) = λf ( ), λ > 0 (5.10) Theorem. Let f i : R n i R, i = 0,..., m be proper and f( 0,..., m) = m i=0 f i( i ). Then f (v 1,..., v m) = m i=0 f i (v i). Proof. For support functions, f () = σ (), so nonempt closed conve implies f is proper lsc conve with f (0) = 0 and f (λv) = λf (v), so f = σ is positivel homogeneous. If g is positivel homogeneous lower semicontinuous, g () 0, }, so g is an indicator function, which must be conve and nonempt b properness lsc conveit of g. One to one follows from δ = δ. For cones, show g is positivel homogeneous lsc conve proper indicator function g = δ K for Ka conve closed cone. Taking an such indicator function δ K, then δk is an indicator function, with δk (v) < v K. Definition. For an set S R n define the support function supp S (v) = sup S v, = (δ S )(v) Definition. A function f : R n R is said to be positivel homogeneous if and onl if 0 dom f and f(λ) = λf() for all R n and λ > 0. Theorem. The set of positivel homogeneous proper lsc conve functions and the set of closed conve nonempt sets are in one-to-one correspondence through the Legendre-Fenchel transform: δ supp (5.11) supp(v) (5.12) supp(v) = v, v N (). (5.13) In particular, the set of closed conve cones is in one-to-one correspondence with itself - for an cone K define the polar cone or dual cone as K = v R d v, 0 K}. Then TODO: fill net condition/implication in. δ K δ K (5.14) N K (v) v N K () (5.15) 6. Dualit in Optimization Definition. Assume f : R n R m R is proper, lsc, and conve. Define the primal problem as the dual problem as and the -projections φ(), φ() = f(, 0), (6.1) Rn sup R n ψ(), ψ() = f (0, ) (6.2) q(v) = f (v, ) = sup p(u) = f(, u) (6.3) ( f (v, )) (6.4) f is sometimes called a perturbation function for ψ, and p the associated marginal function. Theorem. Assume f : R n R m R is proper, lsc, and conve. Then (i) φ and ψ are lsc and conve. (ii) p, q are conve. (iii) p(0) and p (0) are the optimal values of the primal and dual problems - p(0) = φ(), p (0) = sup ψ(). (6.5) (iv) The primal and dual problems are feasible if and onl if their associated marginal function contains 0: φ() < 0 dom p (6.6) sup ψ() > 0 dom q (6.7) Proof. f proper lsc conve implies f is proper lsc conve implies π, ψ lsc conve. p, q are conve from the strict epigraph set, with E = (u, a) R m R p(u) = R n f(, u) < α} = A(E ), where A is the linear projection mapping A(, u, α) = (u, α), and E is the strict epigraph of f and thus conve, so A(E ) is conve. p () = ψ(), so p (0) = sup ψ(). 0 dom p p(0) < f(, 0) < ψ <. Theorem. Assume f : R n R m R is proper, lsc, and conve. Then weak dualit alwas holds, φ() sup ψ(), (6.8) and under certain conditions the imum and supremum are equal and finite - strong dualit p(0) R, p lsc in 0 The difference φ sup ψ is the dualit gap. φ() = sup ψ() R. (6.9)
4 ONVEX OPTIMIZATION SUMMARY 4 Proof. φ() = p(0) p (0) = sup ψ() so must show p(0) R and p lsc in 0 if and onl if p(0) = p (0) R. ( ) follows as p (0) cl p(0) p(0), so lim 0 p() = cl p(0) = p(0) R, so p is lsc in 0. ( ) follows from the claim that if it holds then cl p is proper lsc conve. onveit, lsc is clear, and an improper conve lsc function is alwas constant or, contradiction p(0) R. So (p ) (0) = ((cl p) ) (0) = cl p(0) = p(0). Theorem. Assume f : R n R m R is proper, lsc, and conve. Then we have the primal-dual optimalit conditions, (0, ) f(, 0) (6.10) arg min φ(), arg ma ψ(), ψ() = sup ψ()} (6.11) (, 0) f (0, ). (6.12) The set of primal-dual optimal points (, ) satisfing this equation is either empt or equal to (arg min φ) (arg ma ψ). Proof. Follows from invertibilit of subgradient in terms of conjugate functions, showing f(, 0) = f (0, ) φ( ) = ψ( ) R, and equalit with inite value is eplicitl ecluded b definition of arg min. Theorem. Assume f : R n R m R is proper, lsc, and conve. Then (i) 0 int dom p or 0 int dom q implies φ() = sup ψ(). (S ) (ii) 0 int dom p and 0 int dom q implies φ() = sup ψ() R. (S) (iii) 0 dom p and φ() R if and onl if arg ma ψ() is nonempt and bounded. (P ) (iv) 0 dom q and sup ψ() R if and onl if arg min φ() is nonempt and bounded. (D) In particular, if an of S, P, D hold, then strong dualit holds - φ = sup ψ R. If S, or (P and D) hold, then there eists, satisfing the primal-dual optimalit conditions. Also, P implies p(0) = arg ma ψ(), and D implies q(0) = arg min φ(). Proof. (i): If p(0) =, then p (0) p(0) = Use cl p = p on dom p, so sup ψ = ψ =. Otherwise, p(0) R so as cl p = p on dom p, we have p is lsc in 0 and so p (0) = p(0) R. This follows smmetricall on f (, ) = f (, ). If both 0 dom p, 0 dom q, then + > p(0) p (0) = sup ψ = q(0) >, which is finite. Nonemptness and boundedness follows from 0 dom p if and onl if ψ is proper lsc conve and level bounded. Subdifferential: if (iii) then p(0) R, so cl p(0) = p(0) R, cl p is then proper and lsc conve, so (cl p)(0) = arg ma ψ, but p(0) = (cl p)(0). Theorem. Assume k : R n R and h : R m R are both proper, lsc, conve, and A R m n, b R m, c R n. For f(, u) = c, + k() + h(a b + u), the primal and dual problems are of the form with φ(), φ() = c, + k() + h(a b) (6.13) sup ψ(), ψ() = b, h () k ( A T c) (6.14) and optimalit conditions dom p = (dom h A dom k) + b (6.15) dom q = (dom k ( A T ) dom h ) + c (6.16) A T c k( ), h(a b)} (6.17) arg min φ(), arg ma ψ(), φ() = sup ψ()} (6.18) A b h ( ), k ( A T c)} (6.19) Theorem. Assume f : R n R m R is proper, lsc, conve. Define the associated Lagrangian as l(, ) = f(, ) (), so l(, ) = u(f(, u), u ). Then l(, ) is conve for ever, l(, ) is lsc and conve for ever, and f(, ) = ( l(, )), and (v, ) f(, u) v l(, ) and u ( l)(, ). Proof. onsider g(,, u) = f(, u), u, which is proper lsc conve. Then l(, ) = u g(,, u) is conve.then f () = f(, ), then l(, ) = f ( ) so f is either + or proper lsc conve, and l(, ) is either or proper lsc conve, but alwas lsc conve. B subgradient definition, (v, ) f(, u) u f(, u ), u f(, u), u + v,, which evaluated at = implies u f(, u ), u = f(, u), u. ontinuing, we obtain (v, ) f(, u) uf(, u), l(, ), and the first condition is equivalent to u f (), or u ( l(, )) = ( l)(, ) as required. Definition. For an function l : R n R m R we sa that (, ) is a saddle point of l if l(, ) l(, ) l(, ) for all,. The set of all saddle points is denoted b sp l. Evquivalentl, (, ) sp l if l(, ) = l(, ) = sup l(, ). Theorem. Assume f is proper, lsc, and conve with associated Lagrangian l. Then φ() = sup l(, ), and ψ() = l(, ), and the primal problem is φ() = sup l(, ), and the dual problem is sup ψ() = sup l(, ). Moreover, the optimalit condition arg min φ(), arg ma ψ(), φ() = sup ψ()} (6.20) (, ) sp l (6.21) 0 l(, ), 0 ( l)(, )} (6.22) Theorem. Assume X R n, Y R m are nonempt, closed, conve, and L : X Y R is a continuous function with L(, ) is conve for ever and L(, ) conve for ever. Then l(, ) = L(, ) + δ X () δ Y () with the convention + = + on the right, is the Lagrangian to f(, u) = sup l(, ) + u, = ( l(, )) (u). f is proper, lsc, and conve, so the previous result applies with primal and dual problems φ() = δ X () + sup Y L(, ), ψ() = δ Y () + X L(, ). Moreover, if X and Y are bounded, then sp l is nonempt and bounded. Proof. For a fied, l(, ) = f (0, ) = ψ(), and for a fied, sup l(, ) = f(, 0) = f (0) = f(, 0) = φ() as f is either proper lsc conve or +. The optimalit condition is equivalent to (0, ) f(, 0) 0 l(, ), 0 ( l)(, ), which is the saddle point condition. 7. Numerical Optimalit Definition. For φ : R n R, a point is an ɛ-optimal solution if φ() φ ɛ. Definition. Assume ( k, k ) is a primal-dual feasible pair - so k dom φ and k dom ψ. Then φ( k ) ψ( k ), and 0 φ( k ) φ φ( k ) ψ k = γ( k, k ) := γ. γ is the numerical primal-dual gap. If γ < ɛ then k is an ɛ-optimal solution with optimalit certificate k. The normalized gap is γ = γ( k, k ) = φ(k ) ψ( k ). ψ( k ) Definition. Assume φ() = φ 0 () = n p i=1 δ g i () 0, ψ() = ψ 0 () nd i=1 δ h i () 0 where dom φ 0 = dom ψ 0 = R n and g i : R n R, h i : R m R are suitable continuous real-valued conve functions, so the primal and dual constraints are of the form g i () 0, h i () 0. Then the primal and dual easibilities are defined as η p = ma0, g 1 ( k ),..., g np ( k )} and η d = ma0, h 1 ( k ),..., h nd ( k )}. 8. First-Order Methods Definition. For f : R n R, we define (i) The forward step, F τk f ( k ) = (I τ k f) k (ii) The backward step, B τk f ( k ) = (I + τ k f) 1 k. Theorem. If f : R n R is proper lsc conve with τ > 0, then the backward step is B τf () = arg min τf()} and is therefore unique. Proof. B τf () 0 + τ f() arg min τf( )} Theorem. Assume f is proper lsc conve and arg min f. The forward step is k+1 F τk f ( k ). The sequence is not unique, can get stuck if k is easible. The backward step is k+1 = B τk f ( k ) - which is a unique sequence, and cannot get stuck. Sub-steps are as hard as the original problem (but strictl conve).
5 ONVEX OPTIMIZATION SUMMARY 5 (i) Forward stepping: k+1 F τk f ( k ): (ii) Backward stepping: k+1 = B τk f ( k ). If f = g + h, f = g + h with f, g, h proper lsc conve, arg min f, we can do: (i) Backward-Backward stepping: k+1 = B τk hb τk g( k ). (ii) Forward-Backward stepping: k+1 B τk hf τk g( k ). If f() = g() + δ (), g differentiable, closed and conve, then k+1 arg min 1 2 (k τ k g( k )) δ ()} = Π ( k τ k g( k )), which is a gradient projection. 9. Interior-Point Methods Definition. For a cone K we define the canonical barriers F = F K and associated parameters θ F. (i) K = Kn LP θ F = n. (ii) K = Kn SOP = R n n = R n 1,..., n 0}, F () = n i=1 log i, n 1 }, F () = log( 2 n n 1 ), θ F = 2. (iii) K = Kn SDP = X R n n X smmetric positive semidefinite}, F () = log det X, θ F = n. (iv) K = K 1 K 2, then F K ( 1, 2 ) = F K 1( 1 ) + F K 2( 2 ), with θ F = θ F 1 + θ F 2. Theorem. If F is a canonical barrier for K, then F is smooth on dom F = K and strictl conve, F (t) = F () θf log t for all dom F, and for dom F, we have (i) F () dom F (ii) F (), = θ F, (iii) F ( F ()) =, (iv) F (t) = 1 t F () Proof. Differentiate with respect to t and let t = 1. Theorem. onsider the problem c, s.t. A b K 0. The dual problem is sup b, s.t. A T = c, K 0. Replacing b and assuming K is self-dual K = K we obtain the dual as sup b, such that A T = c, K 0. The primal central path is the mapping t (t) = arg min t b, + F () + δ A T =c } (9.1) The dual central path is the mapping t (t) = arg min t b, + F () + δ A T =c } The primal-dual central path is the mapping t z(t) = ((t), (t)) for some t > 0, if and onl if A b dom F (9.2) A T = c (9.3) t + F (A b) = 0 (9.4) Proof. = 1 f(a b) dom F as A b dom F and dom F is a cone. We also have that if is on the primal path, then A T = c, so is feasible. For dual optimalit, we need 0 tb + F () + N A T =c. As tb + F () = ta range A, is the unique dual solution. Multipling the dual optimalit result b A T gives the optimalit condition for the primal central point. Theorem. For feasible, (so A b K, A T = c, K), the dualit gap is φ() ψ() =, A b. Moreover, for points ((t), (t)) on the central path, the dualit gap is φ((t)) ψ((t)) = θ F t. Proof. φ() ψ() = c, b, (9.5) =, A b (9.6) = 1t F (A(t) b), A(t) b (9.7) = θ F t. (9.8) Theorem. We define v = (vt 2 F (A b) 1 v) 1 2, z = (, ), so z(t) is the primal-dual central path, and dist(z, z(t)) = t + F (A b). Then for A b dom F, dom F, A T = c, we have dist(z, z(t)) 1 implies φ() ψ() 2(φ((t)) ψ((t))) = 2 θ F t. Proof. If we linearize F (A k+1 b) = F (A k b+a ) F (A k b)+ 2 F (A k b)a, and solve the constraints A T () = c, t+ F (A b) = 0. Theorem. Assume 0 < ρ κ < 1 10, tk > 0 fied, and z k = ( k, k ) strictl feasible, so A k b dom F, k dom f, such that dist(z k, z(t k )) < κ. If we appl a full Newton step with τ k = 1 and t k+1 = (1 + ρ )t k to θf generate z k+1, then k+1, k+1 are strictl primal and dual feasible, and dist(z k+1, z(t k+1 )) > κ as well. 10. Support Vector Machines Definition. The primal formulation of an SVM is 1 w,b 2 w 2 2 (10.1) such that 1 i ( w, i + b) for all 1 i n. The dual formulation is 1 n z R n 2 i i z i et z (10.2) i=1 such that z i 0, n i=1 i z i = Total Variation and Applications Definition. For u L 1 (Ω, R m ), the total variation of u is defined as T V (u) = sup u, div v d (11.1) Ω v 1 c (Ω,Rm n ), v 1 Theorem. Assume A Ω is a set so that its boundar is 1 and satisfies H n 1 (Ω A) <. Define 1 A 1 A () = (11.2) 0 / A then T V (1 A ) = H n 1 (Ω A). Proof. The lower bound follows from T V (1 A ) = sup v, n ds (11.3) v c 1(Ω,Rn ), v 1 A b Gauss s theorem. Theorem (oarea formula). If u BV (Ω), then T V (1 u()>t ) < for L 1 -a.e. t R, and T V (u) = R T V (1u>t)dt. Definition. For Ω R d and k 1, define the space BV k (Ω) as BV k = u W k 1,1 k 1 u BV (Ω, R dk 1 )} and the higher-order total variation as T V k (u) = sup u div k vd = T V ( k 1 u) v c k(ω,smk (R d )), v 1 Ω (11.4) 12. Relaation Definition. onsider the han-vese model f V (, c 1, c 2 ) = (g c 2 1 d + = (g c 2 ) 2 d + λh d 1 ()). (12.1) Ω\ Theorem. Let c 1, c 2 be fied, and consider u:ω [0,1],u BV (Ω) f(u), f(u) = u, s L 1 + λt V (u). Then if u is a minimizer of f, and u() 0, 1}a.e., then is a minimizer of f V (,c1,c 2 ). Proof. Follows b definitions - must have u = 1. Definition. Let = BV (Ω, [0, 1]) = u BV (Ω) u() [0, 1]a.e.}. Then for u, α [0, 1]. Define u α = 1 u>α}. Then f : R satisfies the generalized coarea condition if and onl if 1 f(u) = f(u α)dα (12.2) 0 for all u. Theorem. Let f u = T V (u), the condition is the cooarea formula. As the condition is additive, we need onl show Ω s()u() = 1 0 Ω s()1 u()>α}dα, where we use Fubini due to s L (Ω). Theorem. Assume f : R satisfies the generalized coarea condition, and u satisfies u arg min u f(u). Then for almost ever α [0, 1], the thresholded function satisfies u α arg min u BV (Ω,0,1}) f(u).
6 ONVEX OPTIMIZATION SUMMARY 6 Proof. Follows b considering the set S ɛ = α [0, 1] f(u ) f(u α ) ɛ} for some ɛ > 0, and showing that this implies f(u 1 0 f(u α))dα ɛl 1 (S ɛ) which contradicts the generalized coarea formula. References
In applications, we encounter many constrained optimization problems. Examples Basis pursuit: exact sparse recovery problem
 1 Conve Analsis Main references: Vandenberghe UCLA): EECS236C - Optimiation methods for large scale sstems, http://www.seas.ucla.edu/ vandenbe/ee236c.html Parikh and Bod, Proimal algorithms, slides and
1 Conve Analsis Main references: Vandenberghe UCLA): EECS236C - Optimiation methods for large scale sstems, http://www.seas.ucla.edu/ vandenbe/ee236c.html Parikh and Bod, Proimal algorithms, slides and
Contents. 1 Introduction 5. 2 Convexity 9. 3 Cones and Generalized Inequalities Conjugate Functions Duality in Optimization 27
 A N D R E W T U L L O C H C O N V E X O P T I M I Z AT I O N T R I N I T Y C O L L E G E T H E U N I V E R S I T Y O F C A M B R I D G E Contents 1 Introduction 5 1.1 Setup 5 1.2 Convexity 6 2 Convexity
A N D R E W T U L L O C H C O N V E X O P T I M I Z AT I O N T R I N I T Y C O L L E G E T H E U N I V E R S I T Y O F C A M B R I D G E Contents 1 Introduction 5 1.1 Setup 5 1.2 Convexity 6 2 Convexity
Convex Optimization. Convex Analysis - Functions
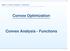 Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Convex Functions. Pontus Giselsson
 Convex Functions Pontus Giselsson 1 Today s lecture lower semicontinuity, closure, convex hull convexity preserving operations precomposition with affine mapping infimal convolution image function supremum
Convex Functions Pontus Giselsson 1 Today s lecture lower semicontinuity, closure, convex hull convexity preserving operations precomposition with affine mapping infimal convolution image function supremum
LECTURE 25: REVIEW/EPILOGUE LECTURE OUTLINE
 LECTURE 25: REVIEW/EPILOGUE LECTURE OUTLINE CONVEX ANALYSIS AND DUALITY Basic concepts of convex analysis Basic concepts of convex optimization Geometric duality framework - MC/MC Constrained optimization
LECTURE 25: REVIEW/EPILOGUE LECTURE OUTLINE CONVEX ANALYSIS AND DUALITY Basic concepts of convex analysis Basic concepts of convex optimization Geometric duality framework - MC/MC Constrained optimization
LECTURE 12 LECTURE OUTLINE. Subgradients Fenchel inequality Sensitivity in constrained optimization Subdifferential calculus Optimality conditions
 LECTURE 12 LECTURE OUTLINE Subgradients Fenchel inequality Sensitivity in constrained optimization Subdifferential calculus Optimality conditions Reading: Section 5.4 All figures are courtesy of Athena
LECTURE 12 LECTURE OUTLINE Subgradients Fenchel inequality Sensitivity in constrained optimization Subdifferential calculus Optimality conditions Reading: Section 5.4 All figures are courtesy of Athena
Optimality Conditions for Nonsmooth Convex Optimization
 Optimality Conditions for Nonsmooth Convex Optimization Sangkyun Lee Oct 22, 2014 Let us consider a convex function f : R n R, where R is the extended real field, R := R {, + }, which is proper (f never
Optimality Conditions for Nonsmooth Convex Optimization Sangkyun Lee Oct 22, 2014 Let us consider a convex function f : R n R, where R is the extended real field, R := R {, + }, which is proper (f never
Local strong convexity and local Lipschitz continuity of the gradient of convex functions
 Local strong convexity and local Lipschitz continuity of the gradient of convex functions R. Goebel and R.T. Rockafellar May 23, 2007 Abstract. Given a pair of convex conjugate functions f and f, we investigate
Local strong convexity and local Lipschitz continuity of the gradient of convex functions R. Goebel and R.T. Rockafellar May 23, 2007 Abstract. Given a pair of convex conjugate functions f and f, we investigate
Optimization and Optimal Control in Banach Spaces
 Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
Some Properties of the Augmented Lagrangian in Cone Constrained Optimization
 MATHEMATICS OF OPERATIONS RESEARCH Vol. 29, No. 3, August 2004, pp. 479 491 issn 0364-765X eissn 1526-5471 04 2903 0479 informs doi 10.1287/moor.1040.0103 2004 INFORMS Some Properties of the Augmented
MATHEMATICS OF OPERATIONS RESEARCH Vol. 29, No. 3, August 2004, pp. 479 491 issn 0364-765X eissn 1526-5471 04 2903 0479 informs doi 10.1287/moor.1040.0103 2004 INFORMS Some Properties of the Augmented
3.1 Convexity notions for functions and basic properties
 3.1 Convexity notions for functions and basic properties We start the chapter with the basic definition of a convex function. Definition 3.1.1 (Convex function) A function f : E R is said to be convex
3.1 Convexity notions for functions and basic properties We start the chapter with the basic definition of a convex function. Definition 3.1.1 (Convex function) A function f : E R is said to be convex
Semi-infinite programming, duality, discretization and optimality conditions
 Semi-infinite programming, duality, discretization and optimality conditions Alexander Shapiro School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332-0205,
Semi-infinite programming, duality, discretization and optimality conditions Alexander Shapiro School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332-0205,
Introduction to Alternating Direction Method of Multipliers
 Introduction to Alternating Direction Method of Multipliers Yale Chang Machine Learning Group Meeting September 29, 2016 Yale Chang (Machine Learning Group Meeting) Introduction to Alternating Direction
Introduction to Alternating Direction Method of Multipliers Yale Chang Machine Learning Group Meeting September 29, 2016 Yale Chang (Machine Learning Group Meeting) Introduction to Alternating Direction
BASICS OF CONVEX ANALYSIS
 BASICS OF CONVEX ANALYSIS MARKUS GRASMAIR 1. Main Definitions We start with providing the central definitions of convex functions and convex sets. Definition 1. A function f : R n R + } is called convex,
BASICS OF CONVEX ANALYSIS MARKUS GRASMAIR 1. Main Definitions We start with providing the central definitions of convex functions and convex sets. Definition 1. A function f : R n R + } is called convex,
Convex Optimization M2
 Convex Optimization M2 Lecture 3 A. d Aspremont. Convex Optimization M2. 1/49 Duality A. d Aspremont. Convex Optimization M2. 2/49 DMs DM par email: dm.daspremont@gmail.com A. d Aspremont. Convex Optimization
Convex Optimization M2 Lecture 3 A. d Aspremont. Convex Optimization M2. 1/49 Duality A. d Aspremont. Convex Optimization M2. 2/49 DMs DM par email: dm.daspremont@gmail.com A. d Aspremont. Convex Optimization
5. Duality. Lagrangian
 5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
ABOUT THE WEAK EFFICIENCIES IN VECTOR OPTIMIZATION
 ABOUT THE WEAK EFFICIENCIES IN VECTOR OPTIMIZATION CRISTINA STAMATE Institute of Mathematics 8, Carol I street, Iasi 6600, Romania cstamate@mail.com Abstract: We present the principal properties of the
ABOUT THE WEAK EFFICIENCIES IN VECTOR OPTIMIZATION CRISTINA STAMATE Institute of Mathematics 8, Carol I street, Iasi 6600, Romania cstamate@mail.com Abstract: We present the principal properties of the
On duality theory of conic linear problems
 On duality theory of conic linear problems Alexander Shapiro School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia 3332-25, USA e-mail: ashapiro@isye.gatech.edu
On duality theory of conic linear problems Alexander Shapiro School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia 3332-25, USA e-mail: ashapiro@isye.gatech.edu
ON A CLASS OF NONSMOOTH COMPOSITE FUNCTIONS
 MATHEMATICS OF OPERATIONS RESEARCH Vol. 28, No. 4, November 2003, pp. 677 692 Printed in U.S.A. ON A CLASS OF NONSMOOTH COMPOSITE FUNCTIONS ALEXANDER SHAPIRO We discuss in this paper a class of nonsmooth
MATHEMATICS OF OPERATIONS RESEARCH Vol. 28, No. 4, November 2003, pp. 677 692 Printed in U.S.A. ON A CLASS OF NONSMOOTH COMPOSITE FUNCTIONS ALEXANDER SHAPIRO We discuss in this paper a class of nonsmooth
Subgradients. subgradients and quasigradients. subgradient calculus. optimality conditions via subgradients. directional derivatives
 Subgradients subgradients and quasigradients subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE392o, Stanford University Basic inequality recall basic
Subgradients subgradients and quasigradients subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE392o, Stanford University Basic inequality recall basic
Nonsymmetric potential-reduction methods for general cones
 CORE DISCUSSION PAPER 2006/34 Nonsymmetric potential-reduction methods for general cones Yu. Nesterov March 28, 2006 Abstract In this paper we propose two new nonsymmetric primal-dual potential-reduction
CORE DISCUSSION PAPER 2006/34 Nonsymmetric potential-reduction methods for general cones Yu. Nesterov March 28, 2006 Abstract In this paper we propose two new nonsymmetric primal-dual potential-reduction
Nash Equilibrium and the Legendre Transform in Optimal Stopping Games with One Dimensional Diffusions
 Nash Equilibrium and the Legendre Transform in Optimal Stopping Games with One Dimensional Diffusions J. L. Seton This version: 9 Januar 2014 First version: 2 December 2011 Research Report No. 9, 2011,
Nash Equilibrium and the Legendre Transform in Optimal Stopping Games with One Dimensional Diffusions J. L. Seton This version: 9 Januar 2014 First version: 2 December 2011 Research Report No. 9, 2011,
Chapter 2 Convex Analysis
 Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
Subgradient. Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes. definition. subgradient calculus
 1/41 Subgradient Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes definition subgradient calculus duality and optimality conditions directional derivative Basic inequality
1/41 Subgradient Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes definition subgradient calculus duality and optimality conditions directional derivative Basic inequality
Convex Optimization Theory. Chapter 5 Exercises and Solutions: Extended Version
 Convex Optimization Theory Chapter 5 Exercises and Solutions: Extended Version Dimitri P. Bertsekas Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Convex Optimization Theory Chapter 5 Exercises and Solutions: Extended Version Dimitri P. Bertsekas Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
UNIVERSIDAD CARLOS III DE MADRID MATHEMATICS II EXERCISES (SOLUTIONS )
 UNIVERSIDAD CARLOS III DE MADRID MATHEMATICS II EXERCISES (SOLUTIONS ) CHAPTER : Limits and continuit of functions in R n. -. Sketch the following subsets of R. Sketch their boundar and the interior. Stud
UNIVERSIDAD CARLOS III DE MADRID MATHEMATICS II EXERCISES (SOLUTIONS ) CHAPTER : Limits and continuit of functions in R n. -. Sketch the following subsets of R. Sketch their boundar and the interior. Stud
Lecture 5. The Dual Cone and Dual Problem
 IE 8534 1 Lecture 5. The Dual Cone and Dual Problem IE 8534 2 For a convex cone K, its dual cone is defined as K = {y x, y 0, x K}. The inner-product can be replaced by x T y if the coordinates of the
IE 8534 1 Lecture 5. The Dual Cone and Dual Problem IE 8534 2 For a convex cone K, its dual cone is defined as K = {y x, y 0, x K}. The inner-product can be replaced by x T y if the coordinates of the
New formulas for the Fenchel subdifferential of the conjugate function
 New formulas for the Fenchel subdifferential of the conjugate function Rafael Correa, Abderrahim Hantoute Centro de Modelamiento Matematico, Universidad de Chile (CNRS UMI 2807), Avda Blanco Encalada 2120,
New formulas for the Fenchel subdifferential of the conjugate function Rafael Correa, Abderrahim Hantoute Centro de Modelamiento Matematico, Universidad de Chile (CNRS UMI 2807), Avda Blanco Encalada 2120,
Proximal methods. S. Villa. October 7, 2014
 Proximal methods S. Villa October 7, 2014 1 Review of the basics Often machine learning problems require the solution of minimization problems. For instance, the ERM algorithm requires to solve a problem
Proximal methods S. Villa October 7, 2014 1 Review of the basics Often machine learning problems require the solution of minimization problems. For instance, the ERM algorithm requires to solve a problem
On the p-laplacian and p-fluids
 LMU Munich, Germany Lars Diening On the p-laplacian and p-fluids Lars Diening On the p-laplacian and p-fluids 1/50 p-laplacian Part I p-laplace and basic properties Lars Diening On the p-laplacian and
LMU Munich, Germany Lars Diening On the p-laplacian and p-fluids Lars Diening On the p-laplacian and p-fluids 1/50 p-laplacian Part I p-laplace and basic properties Lars Diening On the p-laplacian and
Convex Optimization Boyd & Vandenberghe. 5. Duality
 5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
DUALITY, OPTIMALITY CONDITIONS AND PERTURBATION ANALYSIS
 1 DUALITY, OPTIMALITY CONDITIONS AND PERTURBATION ANALYSIS Alexander Shapiro 1 School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332-0205, USA, E-mail: ashapiro@isye.gatech.edu
1 DUALITY, OPTIMALITY CONDITIONS AND PERTURBATION ANALYSIS Alexander Shapiro 1 School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332-0205, USA, E-mail: ashapiro@isye.gatech.edu
The local equicontinuity of a maximal monotone operator
 arxiv:1410.3328v2 [math.fa] 3 Nov 2014 The local equicontinuity of a maximal monotone operator M.D. Voisei Abstract The local equicontinuity of an operator T : X X with proper Fitzpatrick function ϕ T
arxiv:1410.3328v2 [math.fa] 3 Nov 2014 The local equicontinuity of a maximal monotone operator M.D. Voisei Abstract The local equicontinuity of an operator T : X X with proper Fitzpatrick function ϕ T
Maximal Monotone Inclusions and Fitzpatrick Functions
 JOTA manuscript No. (will be inserted by the editor) Maximal Monotone Inclusions and Fitzpatrick Functions J. M. Borwein J. Dutta Communicated by Michel Thera. Abstract In this paper, we study maximal
JOTA manuscript No. (will be inserted by the editor) Maximal Monotone Inclusions and Fitzpatrick Functions J. M. Borwein J. Dutta Communicated by Michel Thera. Abstract In this paper, we study maximal
Lecture: Duality.
 Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
Constrained optimization
 Constrained optimization DS-GA 1013 / MATH-GA 2824 Optimization-based Data Analysis http://www.cims.nyu.edu/~cfgranda/pages/obda_fall17/index.html Carlos Fernandez-Granda Compressed sensing Convex constrained
Constrained optimization DS-GA 1013 / MATH-GA 2824 Optimization-based Data Analysis http://www.cims.nyu.edu/~cfgranda/pages/obda_fall17/index.html Carlos Fernandez-Granda Compressed sensing Convex constrained
CONVEX OPTIMIZATION VIA LINEARIZATION. Miguel A. Goberna. Universidad de Alicante. Iberian Conference on Optimization Coimbra, November, 2006
 CONVEX OPTIMIZATION VIA LINEARIZATION Miguel A. Goberna Universidad de Alicante Iberian Conference on Optimization Coimbra, 16-18 November, 2006 Notation X denotes a l.c. Hausdorff t.v.s and X its topological
CONVEX OPTIMIZATION VIA LINEARIZATION Miguel A. Goberna Universidad de Alicante Iberian Conference on Optimization Coimbra, 16-18 November, 2006 Notation X denotes a l.c. Hausdorff t.v.s and X its topological
Shiqian Ma, MAT-258A: Numerical Optimization 1. Chapter 4. Subgradient
 Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 4 Subgradient Shiqian Ma, MAT-258A: Numerical Optimization 2 4.1. Subgradients definition subgradient calculus duality and optimality conditions Shiqian
Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 4 Subgradient Shiqian Ma, MAT-258A: Numerical Optimization 2 4.1. Subgradients definition subgradient calculus duality and optimality conditions Shiqian
Chapter 2: Preliminaries and elements of convex analysis
 Chapter 2: Preliminaries and elements of convex analysis Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-14-15.shtml Academic year 2014-15
Chapter 2: Preliminaries and elements of convex analysis Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-14-15.shtml Academic year 2014-15
Convex Stochastic optimization
 Convex Stochastic optimization Ari-Pekka Perkkiö January 30, 2019 Contents 1 Practicalities and background 3 2 Introduction 3 3 Convex sets 3 3.1 Separation theorems......................... 5 4 Convex
Convex Stochastic optimization Ari-Pekka Perkkiö January 30, 2019 Contents 1 Practicalities and background 3 2 Introduction 3 3 Convex sets 3 3.1 Separation theorems......................... 5 4 Convex
Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem
 56 Chapter 7 Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem Recall that C(X) is not a normed linear space when X is not compact. On the other hand we could use semi
56 Chapter 7 Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem Recall that C(X) is not a normed linear space when X is not compact. On the other hand we could use semi
Semicontinuous functions and convexity
 Semicontinuous functions and convexity Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto April 3, 2014 1 Lattices If (A, ) is a partially ordered set and S is a subset
Semicontinuous functions and convexity Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto April 3, 2014 1 Lattices If (A, ) is a partially ordered set and S is a subset
Master 2 MathBigData. 3 novembre CMAP - Ecole Polytechnique
 Master 2 MathBigData S. Gaïffas 1 3 novembre 2014 1 CMAP - Ecole Polytechnique 1 Supervised learning recap Introduction Loss functions, linearity 2 Penalization Introduction Ridge Sparsity Lasso 3 Some
Master 2 MathBigData S. Gaïffas 1 3 novembre 2014 1 CMAP - Ecole Polytechnique 1 Supervised learning recap Introduction Loss functions, linearity 2 Penalization Introduction Ridge Sparsity Lasso 3 Some
Duality. Lagrange dual problem weak and strong duality optimality conditions perturbation and sensitivity analysis generalized inequalities
 Duality Lagrange dual problem weak and strong duality optimality conditions perturbation and sensitivity analysis generalized inequalities Lagrangian Consider the optimization problem in standard form
Duality Lagrange dual problem weak and strong duality optimality conditions perturbation and sensitivity analysis generalized inequalities Lagrangian Consider the optimization problem in standard form
Constraint qualifications for convex inequality systems with applications in constrained optimization
 Constraint qualifications for convex inequality systems with applications in constrained optimization Chong Li, K. F. Ng and T. K. Pong Abstract. For an inequality system defined by an infinite family
Constraint qualifications for convex inequality systems with applications in constrained optimization Chong Li, K. F. Ng and T. K. Pong Abstract. For an inequality system defined by an infinite family
Optimality, identifiability, and sensitivity
 Noname manuscript No. (will be inserted by the editor) Optimality, identifiability, and sensitivity D. Drusvyatskiy A. S. Lewis Received: date / Accepted: date Abstract Around a solution of an optimization
Noname manuscript No. (will be inserted by the editor) Optimality, identifiability, and sensitivity D. Drusvyatskiy A. S. Lewis Received: date / Accepted: date Abstract Around a solution of an optimization
NATIONAL UNIVERSITY OF SINGAPORE Department of Mathematics MA4247 Complex Analysis II Lecture Notes Part I
 NATIONAL UNIVERSITY OF SINGAPORE Department of Mathematics MA4247 Comple Analsis II Lecture Notes Part I Chapter 1 Preliminar results/review of Comple Analsis I These are more detailed notes for the results
NATIONAL UNIVERSITY OF SINGAPORE Department of Mathematics MA4247 Comple Analsis II Lecture Notes Part I Chapter 1 Preliminar results/review of Comple Analsis I These are more detailed notes for the results
Optimality Conditions for Constrained Optimization
 72 CHAPTER 7 Optimality Conditions for Constrained Optimization 1. First Order Conditions In this section we consider first order optimality conditions for the constrained problem P : minimize f 0 (x)
72 CHAPTER 7 Optimality Conditions for Constrained Optimization 1. First Order Conditions In this section we consider first order optimality conditions for the constrained problem P : minimize f 0 (x)
Lagrange duality. The Lagrangian. We consider an optimization program of the form
 Lagrange duality Another way to arrive at the KKT conditions, and one which gives us some insight on solving constrained optimization problems, is through the Lagrange dual. The dual is a maximization
Lagrange duality Another way to arrive at the KKT conditions, and one which gives us some insight on solving constrained optimization problems, is through the Lagrange dual. The dual is a maximization
ANALYTIC CENTER CUTTING PLANE METHODS FOR VARIATIONAL INEQUALITIES OVER CONVEX BODIES
 ANALYI ENER UING PLANE MEHODS OR VARIAIONAL INEQUALIIES OVER ONVE BODIES Renin Zen School of Mathematical Sciences honqin Normal Universit honqin hina ABSRA An analtic center cuttin plane method is an
ANALYI ENER UING PLANE MEHODS OR VARIAIONAL INEQUALIIES OVER ONVE BODIES Renin Zen School of Mathematical Sciences honqin Normal Universit honqin hina ABSRA An analtic center cuttin plane method is an
DUALIZATION OF SUBGRADIENT CONDITIONS FOR OPTIMALITY
 DUALIZATION OF SUBGRADIENT CONDITIONS FOR OPTIMALITY R. T. Rockafellar* Abstract. A basic relationship is derived between generalized subgradients of a given function, possibly nonsmooth and nonconvex,
DUALIZATION OF SUBGRADIENT CONDITIONS FOR OPTIMALITY R. T. Rockafellar* Abstract. A basic relationship is derived between generalized subgradients of a given function, possibly nonsmooth and nonconvex,
Math 273a: Optimization Subgradients of convex functions
 Math 273a: Optimization Subgradients of convex functions Made by: Damek Davis Edited by Wotao Yin Department of Mathematics, UCLA Fall 2015 online discussions on piazza.com 1 / 42 Subgradients Assumptions
Math 273a: Optimization Subgradients of convex functions Made by: Damek Davis Edited by Wotao Yin Department of Mathematics, UCLA Fall 2015 online discussions on piazza.com 1 / 42 Subgradients Assumptions
Convex Analysis and Optimization Chapter 2 Solutions
 Convex Analysis and Optimization Chapter 2 Solutions Dimitri P. Bertsekas with Angelia Nedić and Asuman E. Ozdaglar Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Convex Analysis and Optimization Chapter 2 Solutions Dimitri P. Bertsekas with Angelia Nedić and Asuman E. Ozdaglar Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
A. Derivation of regularized ERM duality
 A. Derivation of regularized ERM dualit For completeness, in this section we derive the dual 5 to the problem of computing proximal operator for the ERM objective 3. We can rewrite the primal problem as
A. Derivation of regularized ERM dualit For completeness, in this section we derive the dual 5 to the problem of computing proximal operator for the ERM objective 3. We can rewrite the primal problem as
STABLE AND TOTAL FENCHEL DUALITY FOR CONVEX OPTIMIZATION PROBLEMS IN LOCALLY CONVEX SPACES
 STABLE AND TOTAL FENCHEL DUALITY FOR CONVEX OPTIMIZATION PROBLEMS IN LOCALLY CONVEX SPACES CHONG LI, DONGHUI FANG, GENARO LÓPEZ, AND MARCO A. LÓPEZ Abstract. We consider the optimization problem (P A )
STABLE AND TOTAL FENCHEL DUALITY FOR CONVEX OPTIMIZATION PROBLEMS IN LOCALLY CONVEX SPACES CHONG LI, DONGHUI FANG, GENARO LÓPEZ, AND MARCO A. LÓPEZ Abstract. We consider the optimization problem (P A )
Subgradients. subgradients. strong and weak subgradient calculus. optimality conditions via subgradients. directional derivatives
 Subgradients subgradients strong and weak subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE364b, Stanford University Basic inequality recall basic inequality
Subgradients subgradients strong and weak subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE364b, Stanford University Basic inequality recall basic inequality
Duality revisited. Javier Peña Convex Optimization /36-725
 Duality revisited Javier Peña Conve Optimization 10-725/36-725 1 Last time: barrier method Main idea: approimate the problem f() + I C () with the barrier problem f() + 1 t φ() tf() + φ() where t > 0 and
Duality revisited Javier Peña Conve Optimization 10-725/36-725 1 Last time: barrier method Main idea: approimate the problem f() + I C () with the barrier problem f() + 1 t φ() tf() + φ() where t > 0 and
The proximal mapping
 The proximal mapping http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes Outline 2/37 1 closed function 2 Conjugate function
The proximal mapping http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes Outline 2/37 1 closed function 2 Conjugate function
12. Interior-point methods
 12. Interior-point methods Convex Optimization Boyd & Vandenberghe inequality constrained minimization logarithmic barrier function and central path barrier method feasibility and phase I methods complexity
12. Interior-point methods Convex Optimization Boyd & Vandenberghe inequality constrained minimization logarithmic barrier function and central path barrier method feasibility and phase I methods complexity
Translative Sets and Functions and their Applications to Risk Measure Theory and Nonlinear Separation
 Translative Sets and Functions and their Applications to Risk Measure Theory and Nonlinear Separation Andreas H. Hamel Abstract Recently defined concepts such as nonlinear separation functionals due to
Translative Sets and Functions and their Applications to Risk Measure Theory and Nonlinear Separation Andreas H. Hamel Abstract Recently defined concepts such as nonlinear separation functionals due to
Duality, Geometry, and Support Vector Regression
 ualit, Geometr, and Support Vector Regression Jinbo Bi and Kristin P. Bennett epartment of Mathematical Sciences Rensselaer Poltechnic Institute Tro, NY 80 bij@rpi.edu, bennek@rpi.edu Abstract We develop
ualit, Geometr, and Support Vector Regression Jinbo Bi and Kristin P. Bennett epartment of Mathematical Sciences Rensselaer Poltechnic Institute Tro, NY 80 bij@rpi.edu, bennek@rpi.edu Abstract We develop
Convex Analysis Notes. Lecturer: Adrian Lewis, Cornell ORIE Scribe: Kevin Kircher, Cornell MAE
 Convex Analysis Notes Lecturer: Adrian Lewis, Cornell ORIE Scribe: Kevin Kircher, Cornell MAE These are notes from ORIE 6328, Convex Analysis, as taught by Prof. Adrian Lewis at Cornell University in the
Convex Analysis Notes Lecturer: Adrian Lewis, Cornell ORIE Scribe: Kevin Kircher, Cornell MAE These are notes from ORIE 6328, Convex Analysis, as taught by Prof. Adrian Lewis at Cornell University in the
Directional derivatives and gradient vectors (Sect. 14.5). Directional derivative of functions of two variables.
 Directional derivatives and gradient vectors (Sect. 14.5). Directional derivative of functions of two variables. Partial derivatives and directional derivatives. Directional derivative of functions of
Directional derivatives and gradient vectors (Sect. 14.5). Directional derivative of functions of two variables. Partial derivatives and directional derivatives. Directional derivative of functions of
Lecture 23: November 19
 10-725/36-725: Conve Optimization Fall 2018 Lecturer: Ryan Tibshirani Lecture 23: November 19 Scribes: Charvi Rastogi, George Stoica, Shuo Li Charvi Rastogi: 23.1-23.4.2, George Stoica: 23.4.3-23.8, Shuo
10-725/36-725: Conve Optimization Fall 2018 Lecturer: Ryan Tibshirani Lecture 23: November 19 Scribes: Charvi Rastogi, George Stoica, Shuo Li Charvi Rastogi: 23.1-23.4.2, George Stoica: 23.4.3-23.8, Shuo
On smoothness properties of optimal value functions at the boundary of their domain under complete convexity
 On smoothness properties of optimal value functions at the boundary of their domain under complete convexity Oliver Stein # Nathan Sudermann-Merx June 14, 2013 Abstract This article studies continuity
On smoothness properties of optimal value functions at the boundary of their domain under complete convexity Oliver Stein # Nathan Sudermann-Merx June 14, 2013 Abstract This article studies continuity
Contents: 1. Minimization. 2. The theorem of Lions-Stampacchia for variational inequalities. 3. Γ -Convergence. 4. Duality mapping.
 Minimization Contents: 1. Minimization. 2. The theorem of Lions-Stampacchia for variational inequalities. 3. Γ -Convergence. 4. Duality mapping. 1 Minimization A Topological Result. Let S be a topological
Minimization Contents: 1. Minimization. 2. The theorem of Lions-Stampacchia for variational inequalities. 3. Γ -Convergence. 4. Duality mapping. 1 Minimization A Topological Result. Let S be a topological
Lecture 5. Theorems of Alternatives and Self-Dual Embedding
 IE 8534 1 Lecture 5. Theorems of Alternatives and Self-Dual Embedding IE 8534 2 A system of linear equations may not have a solution. It is well known that either Ax = c has a solution, or A T y = 0, c
IE 8534 1 Lecture 5. Theorems of Alternatives and Self-Dual Embedding IE 8534 2 A system of linear equations may not have a solution. It is well known that either Ax = c has a solution, or A T y = 0, c
A SET OF LECTURE NOTES ON CONVEX OPTIMIZATION WITH SOME APPLICATIONS TO PROBABILITY THEORY INCOMPLETE DRAFT. MAY 06
 A SET OF LECTURE NOTES ON CONVEX OPTIMIZATION WITH SOME APPLICATIONS TO PROBABILITY THEORY INCOMPLETE DRAFT. MAY 06 CHRISTIAN LÉONARD Contents Preliminaries 1 1. Convexity without topology 1 2. Convexity
A SET OF LECTURE NOTES ON CONVEX OPTIMIZATION WITH SOME APPLICATIONS TO PROBABILITY THEORY INCOMPLETE DRAFT. MAY 06 CHRISTIAN LÉONARD Contents Preliminaries 1 1. Convexity without topology 1 2. Convexity
IE 521 Convex Optimization
 Lecture 5: Convex II 6th February 2019 Convex Local Lipschitz Outline Local Lipschitz 1 / 23 Convex Local Lipschitz Convex Function: f : R n R is convex if dom(f ) is convex and for any λ [0, 1], x, y
Lecture 5: Convex II 6th February 2019 Convex Local Lipschitz Outline Local Lipschitz 1 / 23 Convex Local Lipschitz Convex Function: f : R n R is convex if dom(f ) is convex and for any λ [0, 1], x, y
Dedicated to Michel Théra in honor of his 70th birthday
 VARIATIONAL GEOMETRIC APPROACH TO GENERALIZED DIFFERENTIAL AND CONJUGATE CALCULI IN CONVEX ANALYSIS B. S. MORDUKHOVICH 1, N. M. NAM 2, R. B. RECTOR 3 and T. TRAN 4. Dedicated to Michel Théra in honor of
VARIATIONAL GEOMETRIC APPROACH TO GENERALIZED DIFFERENTIAL AND CONJUGATE CALCULI IN CONVEX ANALYSIS B. S. MORDUKHOVICH 1, N. M. NAM 2, R. B. RECTOR 3 and T. TRAN 4. Dedicated to Michel Théra in honor of
Conjugate duality in stochastic optimization
 Ari-Pekka Perkkiö, Institute of Mathematics, Aalto University Ph.D. instructor/joint work with Teemu Pennanen, Institute of Mathematics, Aalto University March 15th 2010 1 / 13 We study convex problems.
Ari-Pekka Perkkiö, Institute of Mathematics, Aalto University Ph.D. instructor/joint work with Teemu Pennanen, Institute of Mathematics, Aalto University March 15th 2010 1 / 13 We study convex problems.
A Dual Condition for the Convex Subdifferential Sum Formula with Applications
 Journal of Convex Analysis Volume 12 (2005), No. 2, 279 290 A Dual Condition for the Convex Subdifferential Sum Formula with Applications R. S. Burachik Engenharia de Sistemas e Computacao, COPPE-UFRJ
Journal of Convex Analysis Volume 12 (2005), No. 2, 279 290 A Dual Condition for the Convex Subdifferential Sum Formula with Applications R. S. Burachik Engenharia de Sistemas e Computacao, COPPE-UFRJ
Conic Linear Optimization and its Dual. yyye
 Conic Linear Optimization and Appl. MS&E314 Lecture Note #04 1 Conic Linear Optimization and its Dual Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A.
Conic Linear Optimization and Appl. MS&E314 Lecture Note #04 1 Conic Linear Optimization and its Dual Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A.
Lecture 14: Optimality Conditions for Conic Problems
 EE 227A: Conve Optimization and Applications March 6, 2012 Lecture 14: Optimality Conditions for Conic Problems Lecturer: Laurent El Ghaoui Reading assignment: 5.5 of BV. 14.1 Optimality for Conic Problems
EE 227A: Conve Optimization and Applications March 6, 2012 Lecture 14: Optimality Conditions for Conic Problems Lecturer: Laurent El Ghaoui Reading assignment: 5.5 of BV. 14.1 Optimality for Conic Problems
EE/AA 578, Univ of Washington, Fall Duality
 7. Duality EE/AA 578, Univ of Washington, Fall 2016 Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
7. Duality EE/AA 578, Univ of Washington, Fall 2016 Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
Primal-dual IPM with Asymmetric Barrier
 Primal-dual IPM with Asymmetric Barrier Yurii Nesterov, CORE/INMA (UCL) September 29, 2008 (IFOR, ETHZ) Yu. Nesterov Primal-dual IPM with Asymmetric Barrier 1/28 Outline 1 Symmetric and asymmetric barriers
Primal-dual IPM with Asymmetric Barrier Yurii Nesterov, CORE/INMA (UCL) September 29, 2008 (IFOR, ETHZ) Yu. Nesterov Primal-dual IPM with Asymmetric Barrier 1/28 Outline 1 Symmetric and asymmetric barriers
Hyperbolic Systems of Conservation Laws. in One Space Dimension. II - Solutions to the Cauchy problem. Alberto Bressan
 Hyperbolic Systems of Conservation Laws in One Space Dimension II - Solutions to the Cauchy problem Alberto Bressan Department of Mathematics, Penn State University http://www.math.psu.edu/bressan/ 1 Global
Hyperbolic Systems of Conservation Laws in One Space Dimension II - Solutions to the Cauchy problem Alberto Bressan Department of Mathematics, Penn State University http://www.math.psu.edu/bressan/ 1 Global
9. Interpretations, Lifting, SOS and Moments
 9-1 Interpretations, Lifting, SOS and Moments P. Parrilo and S. Lall, CDC 2003 2003.12.07.04 9. Interpretations, Lifting, SOS and Moments Polynomial nonnegativity Sum of squares (SOS) decomposition Eample
9-1 Interpretations, Lifting, SOS and Moments P. Parrilo and S. Lall, CDC 2003 2003.12.07.04 9. Interpretations, Lifting, SOS and Moments Polynomial nonnegativity Sum of squares (SOS) decomposition Eample
Convex Optimization & Lagrange Duality
 Convex Optimization & Lagrange Duality Chee Wei Tan CS 8292 : Advanced Topics in Convex Optimization and its Applications Fall 2010 Outline Convex optimization Optimality condition Lagrange duality KKT
Convex Optimization & Lagrange Duality Chee Wei Tan CS 8292 : Advanced Topics in Convex Optimization and its Applications Fall 2010 Outline Convex optimization Optimality condition Lagrange duality KKT
SYMBOLIC CONVEX ANALYSIS
 SYMBOLIC CONVEX ANALYSIS by Chris Hamilton B.Sc., Okanagan University College, 2001 a thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in the Department of
SYMBOLIC CONVEX ANALYSIS by Chris Hamilton B.Sc., Okanagan University College, 2001 a thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in the Department of
Lecture: Duality of LP, SOCP and SDP
 1/33 Lecture: Duality of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2017.html wenzw@pku.edu.cn Acknowledgement:
1/33 Lecture: Duality of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2017.html wenzw@pku.edu.cn Acknowledgement:
Douglas-Rachford splitting for nonconvex feasibility problems
 Douglas-Rachford splitting for nonconvex feasibility problems Guoyin Li Ting Kei Pong Jan 3, 015 Abstract We adapt the Douglas-Rachford DR) splitting method to solve nonconvex feasibility problems by studying
Douglas-Rachford splitting for nonconvex feasibility problems Guoyin Li Ting Kei Pong Jan 3, 015 Abstract We adapt the Douglas-Rachford DR) splitting method to solve nonconvex feasibility problems by studying
Duality Uses and Correspondences. Ryan Tibshirani Convex Optimization
 Duality Uses and Correspondences Ryan Tibshirani Conve Optimization 10-725 Recall that for the problem Last time: KKT conditions subject to f() h i () 0, i = 1,... m l j () = 0, j = 1,... r the KKT conditions
Duality Uses and Correspondences Ryan Tibshirani Conve Optimization 10-725 Recall that for the problem Last time: KKT conditions subject to f() h i () 0, i = 1,... m l j () = 0, j = 1,... r the KKT conditions
Convex Optimization Conjugate, Subdifferential, Proximation
 1 Lecture Notes, HCI, 3.11.211 Chapter 6 Convex Optimization Conjugate, Subdifferential, Proximation Bastian Goldlücke Computer Vision Group Technical University of Munich 2 Bastian Goldlücke Overview
1 Lecture Notes, HCI, 3.11.211 Chapter 6 Convex Optimization Conjugate, Subdifferential, Proximation Bastian Goldlücke Computer Vision Group Technical University of Munich 2 Bastian Goldlücke Overview
too, of course, but is perhaps overkill here.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR OPTIMERING 018-01-11 kl 08-13 1. a) CQ points are shown as A and B below. Graphically: they are the only points that share the same tangent line for both active
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR OPTIMERING 018-01-11 kl 08-13 1. a) CQ points are shown as A and B below. Graphically: they are the only points that share the same tangent line for both active
CPS 616 ITERATIVE IMPROVEMENTS 10-1
 CPS 66 ITERATIVE IMPROVEMENTS 0 - APPROACH Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change
CPS 66 ITERATIVE IMPROVEMENTS 0 - APPROACH Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change
LECTURE 9 LECTURE OUTLINE. Min Common/Max Crossing for Min-Max
 Min-Max Problems Saddle Points LECTURE 9 LECTURE OUTLINE Min Common/Max Crossing for Min-Max Given φ : X Z R, where X R n, Z R m consider minimize sup φ(x, z) subject to x X and maximize subject to z Z.
Min-Max Problems Saddle Points LECTURE 9 LECTURE OUTLINE Min Common/Max Crossing for Min-Max Given φ : X Z R, where X R n, Z R m consider minimize sup φ(x, z) subject to x X and maximize subject to z Z.
NONSMOOTH ANALYSIS AND PARAMETRIC OPTIMIZATION. R. T. Rockafellar*
 NONSMOOTH ANALYSIS AND PARAMETRIC OPTIMIZATION R. T. Rockafellar* Abstract. In an optimization problem that depends on parameters, an important issue is the effect that perturbations of the parameters
NONSMOOTH ANALYSIS AND PARAMETRIC OPTIMIZATION R. T. Rockafellar* Abstract. In an optimization problem that depends on parameters, an important issue is the effect that perturbations of the parameters
15. Conic optimization
 L. Vandenberghe EE236C (Spring 216) 15. Conic optimization conic linear program examples modeling duality 15-1 Generalized (conic) inequalities Conic inequality: a constraint x K where K is a convex cone
L. Vandenberghe EE236C (Spring 216) 15. Conic optimization conic linear program examples modeling duality 15-1 Generalized (conic) inequalities Conic inequality: a constraint x K where K is a convex cone
Exam: Continuous Optimisation 2015
 Exam: Continuous Optimisation 215 1. Let f : C R, C R n convex, be a convex function. Show that then the following holds: A local imizer of f on C is a global imizer on C. And a strict local imizer of
Exam: Continuous Optimisation 215 1. Let f : C R, C R n convex, be a convex function. Show that then the following holds: A local imizer of f on C is a global imizer on C. And a strict local imizer of
MAT389 Fall 2016, Problem Set 2
 MAT389 Fall 2016, Problem Set 2 Circles in the Riemann sphere Recall that the Riemann sphere is defined as the set Let P be the plane defined b Σ = { (a, b, c) R 3 a 2 + b 2 + c 2 = 1 } P = { (a, b, c)
MAT389 Fall 2016, Problem Set 2 Circles in the Riemann sphere Recall that the Riemann sphere is defined as the set Let P be the plane defined b Σ = { (a, b, c) R 3 a 2 + b 2 + c 2 = 1 } P = { (a, b, c)
Continuous Sets and Non-Attaining Functionals in Reflexive Banach Spaces
 Laboratoire d Arithmétique, Calcul formel et d Optimisation UMR CNRS 6090 Continuous Sets and Non-Attaining Functionals in Reflexive Banach Spaces Emil Ernst Michel Théra Rapport de recherche n 2004-04
Laboratoire d Arithmétique, Calcul formel et d Optimisation UMR CNRS 6090 Continuous Sets and Non-Attaining Functionals in Reflexive Banach Spaces Emil Ernst Michel Théra Rapport de recherche n 2004-04
Victoria Martín-Márquez
 A NEW APPROACH FOR THE CONVEX FEASIBILITY PROBLEM VIA MONOTROPIC PROGRAMMING Victoria Martín-Márquez Dep. of Mathematical Analysis University of Seville Spain XIII Encuentro Red de Análisis Funcional y
A NEW APPROACH FOR THE CONVEX FEASIBILITY PROBLEM VIA MONOTROPIC PROGRAMMING Victoria Martín-Márquez Dep. of Mathematical Analysis University of Seville Spain XIII Encuentro Red de Análisis Funcional y
CONVERGENCE AND STABILITY OF A REGULARIZATION METHOD FOR MAXIMAL MONOTONE INCLUSIONS AND ITS APPLICATIONS TO CONVEX OPTIMIZATION
 Variational Analysis and Appls. F. Giannessi and A. Maugeri, Eds. Kluwer Acad. Publ., Dordrecht, 2004 CONVERGENCE AND STABILITY OF A REGULARIZATION METHOD FOR MAXIMAL MONOTONE INCLUSIONS AND ITS APPLICATIONS
Variational Analysis and Appls. F. Giannessi and A. Maugeri, Eds. Kluwer Acad. Publ., Dordrecht, 2004 CONVERGENCE AND STABILITY OF A REGULARIZATION METHOD FOR MAXIMAL MONOTONE INCLUSIONS AND ITS APPLICATIONS
SWFR ENG 4TE3 (6TE3) COMP SCI 4TE3 (6TE3) Continuous Optimization Algorithm. Convex Optimization. Computing and Software McMaster University
 SWFR ENG 4TE3 (6TE3) COMP SCI 4TE3 (6TE3) Continuous Optimization Algorithm Convex Optimization Computing and Software McMaster University General NLO problem (NLO : Non Linear Optimization) (N LO) min
SWFR ENG 4TE3 (6TE3) COMP SCI 4TE3 (6TE3) Continuous Optimization Algorithm Convex Optimization Computing and Software McMaster University General NLO problem (NLO : Non Linear Optimization) (N LO) min
Lecture 1: Background on Convex Analysis
 Lecture 1: Background on Convex Analysis John Duchi PCMI 2016 Outline I Convex sets 1.1 Definitions and examples 2.2 Basic properties 3.3 Projections onto convex sets 4.4 Separating and supporting hyperplanes
Lecture 1: Background on Convex Analysis John Duchi PCMI 2016 Outline I Convex sets 1.1 Definitions and examples 2.2 Basic properties 3.3 Projections onto convex sets 4.4 Separating and supporting hyperplanes
BREGMAN DISTANCES, TOTALLY
 BREGMAN DISTANCES, TOTALLY CONVEX FUNCTIONS AND A METHOD FOR SOLVING OPERATOR EQUATIONS IN BANACH SPACES DAN BUTNARIU AND ELENA RESMERITA January 18, 2005 Abstract The aim of this paper is twofold. First,
BREGMAN DISTANCES, TOTALLY CONVEX FUNCTIONS AND A METHOD FOR SOLVING OPERATOR EQUATIONS IN BANACH SPACES DAN BUTNARIU AND ELENA RESMERITA January 18, 2005 Abstract The aim of this paper is twofold. First,
Lectures for the Course on Foundations of Mathematical Finance
 Definitions and properties of Lectures for the Course on Foundations of Mathematical Finance First Part: Convex Marco Frittelli Milano University The Fields Institute, Toronto, April 2010 Definitions and
Definitions and properties of Lectures for the Course on Foundations of Mathematical Finance First Part: Convex Marco Frittelli Milano University The Fields Institute, Toronto, April 2010 Definitions and
Lecture 3: Lagrangian duality and algorithms for the Lagrangian dual problem
 Lecture 3: Lagrangian duality and algorithms for the Lagrangian dual problem Michael Patriksson 0-0 The Relaxation Theorem 1 Problem: find f := infimum f(x), x subject to x S, (1a) (1b) where f : R n R
Lecture 3: Lagrangian duality and algorithms for the Lagrangian dual problem Michael Patriksson 0-0 The Relaxation Theorem 1 Problem: find f := infimum f(x), x subject to x S, (1a) (1b) where f : R n R
Lecture 7: Weak Duality
 EE 227A: Conve Optimization and Applications February 7, 2012 Lecture 7: Weak Duality Lecturer: Laurent El Ghaoui 7.1 Lagrange Dual problem 7.1.1 Primal problem In this section, we consider a possibly
EE 227A: Conve Optimization and Applications February 7, 2012 Lecture 7: Weak Duality Lecturer: Laurent El Ghaoui 7.1 Lagrange Dual problem 7.1.1 Primal problem In this section, we consider a possibly
