Convex Functions. Pontus Giselsson
|
|
|
- Miranda Boyd
- 6 years ago
- Views:
Transcription
1 Convex Functions Pontus Giselsson 1
2 Today s lecture lower semicontinuity, closure, convex hull convexity preserving operations precomposition with affine mapping infimal convolution image function supremum of convex functions (example: conjugate functions) support functions sublinearity directional derivative 2
3 Domain assume that f : X R is finite-valued then X R n is the domain of f 3
4 Extending the domain we want to avoid to explicitly state domain in f : X R extend domain of functions with X = R n by constructing: { f(x) if x X ˆf(x) = else (extension works well in convex analysis) obviously ˆf : R n R {+ } define R := R {+ } can compare function values on all of R n using R arithmetics ( = and c < for all c R) 4
5 Standing assumptions throughout this course we assume that all functions f: may be extended valued, i.e., have range R have extended domain, R n are proper, i.e., f + are minorized by an affine function, i.e., there exist s R n and r R such that f(x) s, x + r for all x or r inf x example, affine minorizer: {f(x) s, x } or 0 inf{f(x) s, x r} x f(x) s, x + r 5
6 Effective domain the effective domain of f : R n R is the set dom f = {x R n f(x) < } 6
7 Convex functions function f : R n R is convex if for all x, y R n and θ [0, 1]: f(θx + (1 θ)y) θf(x) + (1 θ)f(y) (in extended valued arithmetics) every convex combination of two points on the graph of f is above the graph a nonconvex function a convex function 7
8 Comparison to other definition a function f : X R (without extended domain) is convex if f(θx + (1 θ)y) θf(x) + (1 θ)f(y) holds for all x, y X and θ [0, 1], and if X is convex equivalent to definition for functions with extended domain for f : R n R, convexity of dom f is implicit in convexity definition 8
9 Why convexity? local minima are also global minima! can search for local minima to minimize the function much easier to devise algorithms 9
10 Jensen s inequality assume that f : R n R is convex then for all collections {x 1,..., x k } of points ( k ) f θ i x i i=1 k θ i f(x i ) i=1 where θ i 0 and k i=1 θ i = 1 for k = 2 this reduces to the convexity definition 10
11 Strict and strong convexity a function is strictly convex if convex with strict inequality f(θx + (1 θ)y) < θf(x) + (1 θ)f(y) for all x y and θ (0, 1) a function is σ-strongly convex if there exists σ > 0 such that f(θx + (1 θ)y) θf(x) + (1 θ)f(y) σ 2 θ(1 θ) x y 2 for every x, y R n and θ [0, 1] strongly convex functions are strictly convex a function is σ-strongly convex iff f σ 2 2 is convex prove by inserting f σ 2 2 in convexity definition a strongly convex function has at least curvature σ
12 Uniqueness of minimizers if a function is strictly (strongly) convex the minimizers are unique proof: assume that x 1 x 2 and that both satisfy x 2 = x 1 = argmin f(x) x i.e., f(x 1 ) = f(x 2 ) = inf x f(x), then contradiction! f( 1 2 x x 2) < 1 2 (f(x 1) + f(x 2 )) = inf f(x) x (minimizer might not exist for strictly convex, but always for strongly convex) 12
13 Smoothness a convex function is β-smooth if there exists β > 0 such that f(θx + (1 θ)y) θf(x) + (1 θ)f(y) β 2 θ(1 θ) x y 2 for every x, y R n and θ [0, 1] (and convexity definition holds) inequality flipped compared to strong convexity a convex function f is β-smooth iff β 2 2 f is convex a smooth function is continuously differentiable (sometimes higher order differentiability required in smoothness definitions) 13
14 Graphs and epigraphs the graph of f is the set of all couples (x, f(x)) R n R the epigraph of a (proper) function f is the nonempty set epi f = {(x, r) f(x) r} (note dimension of epi f is n + 1 when dimension of dom f is n) epif 14
15 Epigraphs and convexity let f : R n R then f is convex if and only epi f is a convex set in R n R epif epif nonconvex convex 15
16 Level-sets a (sub)level-set S r (f) to the function f is defined as S r (f) = {x R n f(x) r} r S r(f) (slice epigraph and project back to R n )) level-sets of convex functions are convex even if all level-sets convex, function might be nonconvex if all level-sets convex, function is quasi-convex 16
17 Level-sets and constraint qualification assume that f : R n R is convex (and finite-valued) Slater s constraint qualification assumes existence of x such that f( x) < 0 (0 is often used to define constraints, any level can be used) this clearly implies that the level-set S 0 (f) is nonempty in fact, it implies the following statements: cl {x f(x) < 0} = {x f(x) 0} {x f(x) < 0} = int {x f(x) 0} consequently: bd {x f(x) 0} = {x f(x) = 0} 17
18 Affine functions affine functions f(x) = s, x b for any x 0 R n affine functions can be written as f(x) = f(x 0 ) + s, x x 0 (since b = s, x 0 f(x 0 )) epigraph of affine function is closed half-space with non-horizontal normal vector (s, 1) R n R epif = {(x, r) : r s, x b} = {(x, r) : b (s, 1), (x, r) } s, x b = f(x 0 ) + s, x x 0 (s, 1) 18
19 Affine minorizers any proper, convex f is minorized by some affine function more precisely: for any x 0 ri dom f, there is s such that f(x) f(x 0 ) + s, x x 0 which coincides with f at x 0 i.e., there is an affine function whose epigraph covers epi f convex epigraph supported by non-vertical hyperplanes normal vector s is called subgradient, much more on this later 19
20 Lower semicontinuity a function f : R n R is lower semicontinuous if lim inf f(y) f(x) y x consider the following function f which is not defined on x = 0: construct a lower semicontinuous function { f(x) if x 0 g(x) = c else what can c be? at or below lower circle (upper semicontinuous if inequality flipped) 20
21 Lower semicontinuity The following are equivalent for f : R n R: f is lower semicontinuous (l.s.c.) epi f is a closed set all level-sets S r (f) are closed (may be empty) will call lower semicontinuous functions closed l.s.c. not l.s.c. 21
22 Closure (lower-semicontinuous hull) the closure cl f of the function f is defined as epi(clf) := cl(epif) a function is closed iff cl f = f, i.e., if epi(f) := cl(epif) the closure is really the lower-semicontinuous hull: cl f = sup{h(x) h lower-semicontinuous, h f} what is the closure of g 1? g 1 cl g 1 22
23 Outer construction the closure of a convex function f is the supremum of all minorizing affine functions, i.e., cl f = g where g(x) = sup { s, x b : s, y b f(y) for all y R n } s,b let Σ 1 be all non-vertical hyperplanes that support epi f (solid) epi g is intersection of halfspaces defined by hyperplanes in Σ 1 let Σ 0 be all vertical hyperplanes that support epi f (dashed) cl(epif) is intersection of all halfspaces defined by Σ 1 and Σ 0 (consequence of strict separating hyperplane theorem) prove result by showing that halfspaces defined by Σ 0 redundant (i.e., dashed line not needed, then epi(clf) = cl(epif)) 23
24 Continuity for convex functions for convex f, cl f(x) = f(x) for x ri dom f for finite-valued convex functions, ri dom f = R n l.s.c. we can say more: convex f are locally Lipschitz continuous for each compact convex subset S ri dom f there exists L(S): f(x) f(y) L(S) x y for all x and y in S consequence: convex functions f are continuous on ri dom f 24
25 Why closed functions? a closed function defined on a nonempty closed and bounded set is bounded below and attains its infimum generalization of Weierstrass extreme value theorem inf attained inf not attained left figure: closed, right figure: not closed (supremum not attained, needs upper semicontinuity) 25
26 Convex hull the convex hull is the largest convex minorizing function, i.e.: the closed convex hull: conv f(x) = sup{h(x) : h convex, h f} conv f(x) = sup{h(x) : h closed convex, h f} the closed convex hull can equivalently be written as: conv f(x) = sup{ s, x b : s, x b f(y) for all y R n } s,b (supremum of affine functions minorizing f) 26
27 Convex hull Example the figure shows the closed convex hull conv f(x) = sup{ s, x b : s, x b f(y) for all y R n } s,b of a nonconvex function f(x) f(1) conv f(1) 27
28 First-order conditions for convexity a differentiable function f : R n R is convex iff holds for all x, y R n f(y) f(x) + f(x), y x f(y) (x, f(x)) f(x) + f(x), y x function has affine minorizer defined by f 28
29 Second-order conditions for convexity a twice differentiable function is convex if and only if 2 f(x) 0 for all x R n (i.e., the Hessian is positive semi-definite) the function has non-negative curvature 29
30 Examples of convex functions indicator function ι S (x) = { 0 if x S else [closed] and convex iff S [closed] and convex norms: x norm-squared: x 2 (shortest) distance to convex set: dist S (y) = inf x S { x y } linear functions: f(x) = q, x quadratic forms: f(x) = 1 2 Qx, x with Q positive semi-definite linear operator matrix fractional function: f(x, Y ) = x T Y 1 x 30
31 How to conclude convexity different ways to conclude convexity use convexity definition show that epigraph is convex set use first or second order condition for convexity show that function built by convexity preserving operations (next) 31
32 Operations that preserve convexity assume that f j are convex for j = {1,..., m} assume that there exists x such that f j (x) < for all j then positive combination m f = t j f j j=1 with t j > 0 is convex proof : add convexity definitions t j f j (θx + (1 θ)y) t j (θf j (x) + (1 θ)f j (y)) 32
33 Precomposition with affine mapping let f be convex and L be affine, then (f L)(x) := f(l(x)) is convex if ImL domf then f L proper 33
34 Infimal convolution the infimal convolution of two functions f, g is defined as (f g)(x) := inf y Rn{f(y) + g(x y)} convex if f and g are convex with a common affine minorizer closed and convex if f, g closed and convex and, e.g.: f(x) as x (coercive) and g bounded from below f(x)/ x as x (super-coercive) in this case, infimal convolution is set addition of epi-graphs (in other case, strict epigraphs are equal) 34
35 Moreau envelope let γ > 0 and f be closed and convex infimal convolution with g = 1 2γ 2 is called Moreau envelope (f )(x) := min y R n{f(y) + 1 2γ x y 2 } argmin of this is called proximal operator (more on this later) the Moreau envelope is a smooth under-estimator of f minimizers coincide (can minimize smooth envelope instead of f) example f(x) = x : γ = 2 γ = 1, 2, 4 35
36 Image of function under linear mapping the image function Lf : R m R { } is defined as (Lf)(x) := inf{f(y) : Ly = x} y where L : R m R n is linear and f : R m R { } convex if f convex and bounded below for all x on inverse image 36
37 Examples of image functions marginal function: let F : R n R m R { } be convex then (if f is bounded below) the marginal function is convex f : R n R {± } : x inf F (x, y) y Rm why? marginal function f = (LF ) where L(x, y) = x (LF )(z) = inf{f (x, y) L(x, y) = z} x,y = inf{f (x, y) x = z} x,y = inf{f (z, y)} = f(z) y 37
38 Infimal convolution also the infimal convolution is an image function infimal convolution of f 1 and f 2 : (f 1 f 2 )(z) = inf x {f 1(x) + f 2 (z x)} introduce g(x, y) = f 1 (x) + f 2 (y) and L(x, y) = x + y, then (Lg)(z) = inf{g(x, y) : L(x, y) = z} x,y = inf x,y {f 1(x) + f 2 (y) : x + y = z} = inf x {f 1(x) + f 2 (z x)} = (f 1 f 2 )(z) (therefore image function is not closed in general case) 38
39 Supremum of convex functions point-wise supremum of convex functions from family {f j } j J : f := sup{f j : j J} example: f 1 = 1 2 x2 3x, f 2 = x + 2, f 3 = 1 4 x2 + 2x f 3 (x) f 2 (x) f 1 (x) convex since intersection of convex epigraphs! 39
40 Example Conjugate functions the conjugate function f is defined as f (s) := sup x R n { s, x f(x)} for each x j R n, let r j = f(x j ), then f (s) := sup x j { s, x j r j } s, x j r j convex (affine) in s (independent of convexity of f) supremum of family of affine functions convex epigraph of conjugate is intersection of (closed) affine functions 40
41 Draw the conjugate recall: f (s) := sup x R n { s, x f(x)} draw conjugate of f (f(x) = outside points) s + 0 s + 0 ( 1, 0) (0, 0.2) (1, 0) 0s 0.2 what if f(0) = 0.2 instead? what if f(0) = 0.2 and points are connected with straight lines? each feasible x defines a slope, f(x) defines vertical translation 41
42 Support functions the support function to a set C is defined as it can be written as σ C (s) := sup s, x x C σ C (s) := sup{ s, x ι C (x)} =: ι C(x) x i.e., it is the conjugate of the indicator function (more on general conjugate functions later) 42
43 Support function properties graphical interpretation (σ C (s) = sup x C s, x = s, x in figure) s s C x σ C (s) s, x = r 2 s, x = r 1 s, x = σ C (s) put inequalities between r 2, r 1, and σ C (s) 0 σ C (s) r 1 r 2 suppose that σ C (s) = r, what is σ C (2s)? 2r suppose that σ C (s) = r, what is σ C ( s)? don t know! support function is positively homogeneous of degree 1, i.e. σ C (tx) = tσ C (x) if t > 0 43
44 Closure and convexity assume that C is nonempty then σ C (s) = σ cl C (s) = σ conv C (s) example: the same if (closed) convex hull considered instead s s, x = σ C (s) = σ conv C (s) 0 therefore only necessary to consider closed and convex sets 44
45 Further properties the support function is convex (since a conjugate function) functions that are convex and positively homogeneous of degree 1 are called sublinear 45
46 1D example consider the set C = [0.2, 1]: C draw the support function (σ C (s) = sup x C s, x ) σ C x 0.2x s the epigraph of this support function is a convex cone actually: f is sublinear if and only if epi f is a convex cone 46
47 Directional derivative assume that f : R n R is finite-valued and convex the directional derivative of f at x in the direction d is d f (x, d) := lim t 0 f(x + td) f(x) t the directional derivative is convex in d for fixed x 47
48 Positive homogeneity the directional derivative is positively homogeneous of degree 1 proof: let f (x, d 1 ) = lim t 0 f(x + td 1 ) f(x) t set d 2 = αd 1 for some α > 0, then f f(x + td 2 ) f(x) (x, d 2 ) = lim t 0 t f(x + tαd 1 ) f(x) = lim t 0 t f(x + sd 1 ) f(x) = lim s 0 s/α = αf (x, d 1 ) 48
49 Sublinearity f (x, d) is convex, positively homogeneous, hence sublinear (in d) it is also finite it is the support function for the subdifferential (next lecture) 49
50 Example 1D example f(x) = 1 2 x2 + x 2 : compute f (2, 1) and f (2, 1): f 0.5(2 + t) 2 + t t + t 2 2 (2, 1) = lim = lim = 3 t 0 t t 0 t f 0.5(2 t) 2 + t 2 2 t + t 2 2 (2, 1) = lim = lim = 1 t 0 t t 0 t 50
51 Example cont d use that f (2, d) positively homogeneous to get explicit expression { f 3d if d 0 (2, d) = 1d if d 0 (since f (2, 1) = 1, then f (2, 2) = 2, etc) with origin shifted to point of interest (2, f(2)), we get tangent cone to epigraph of f is epigraph of directional derivative 51
52 Example Levelsets assume that f is convex with the following levelsets (increasing values for larger sets) x draw the set of directions d (from x) for with f (x, d) 0 x set of d for which f (x, d) 0 is tangent cone to levelset (under some additional assumptions) 52
Optimality Conditions for Nonsmooth Convex Optimization
 Optimality Conditions for Nonsmooth Convex Optimization Sangkyun Lee Oct 22, 2014 Let us consider a convex function f : R n R, where R is the extended real field, R := R {, + }, which is proper (f never
Optimality Conditions for Nonsmooth Convex Optimization Sangkyun Lee Oct 22, 2014 Let us consider a convex function f : R n R, where R is the extended real field, R := R {, + }, which is proper (f never
Optimization and Optimal Control in Banach Spaces
 Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
A Brief Review on Convex Optimization
 A Brief Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one convex, two nonconvex sets): A Brief Review
A Brief Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one convex, two nonconvex sets): A Brief Review
Subgradients. subgradients and quasigradients. subgradient calculus. optimality conditions via subgradients. directional derivatives
 Subgradients subgradients and quasigradients subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE392o, Stanford University Basic inequality recall basic
Subgradients subgradients and quasigradients subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE392o, Stanford University Basic inequality recall basic
Lecture 1: Background on Convex Analysis
 Lecture 1: Background on Convex Analysis John Duchi PCMI 2016 Outline I Convex sets 1.1 Definitions and examples 2.2 Basic properties 3.3 Projections onto convex sets 4.4 Separating and supporting hyperplanes
Lecture 1: Background on Convex Analysis John Duchi PCMI 2016 Outline I Convex sets 1.1 Definitions and examples 2.2 Basic properties 3.3 Projections onto convex sets 4.4 Separating and supporting hyperplanes
CSCI : Optimization and Control of Networks. Review on Convex Optimization
 CSCI7000-016: Optimization and Control of Networks Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one
CSCI7000-016: Optimization and Control of Networks Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one
Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization
 Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization Compiled by David Rosenberg Abstract Boyd and Vandenberghe s Convex Optimization book is very well-written and a pleasure to read. The
Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization Compiled by David Rosenberg Abstract Boyd and Vandenberghe s Convex Optimization book is very well-written and a pleasure to read. The
EC9A0: Pre-sessional Advanced Mathematics Course. Lecture Notes: Unconstrained Optimisation By Pablo F. Beker 1
 EC9A0: Pre-sessional Advanced Mathematics Course Lecture Notes: Unconstrained Optimisation By Pablo F. Beker 1 1 Infimum and Supremum Definition 1. Fix a set Y R. A number α R is an upper bound of Y if
EC9A0: Pre-sessional Advanced Mathematics Course Lecture Notes: Unconstrained Optimisation By Pablo F. Beker 1 1 Infimum and Supremum Definition 1. Fix a set Y R. A number α R is an upper bound of Y if
1. Gradient method. gradient method, first-order methods. quadratic bounds on convex functions. analysis of gradient method
 L. Vandenberghe EE236C (Spring 2016) 1. Gradient method gradient method, first-order methods quadratic bounds on convex functions analysis of gradient method 1-1 Approximate course outline First-order
L. Vandenberghe EE236C (Spring 2016) 1. Gradient method gradient method, first-order methods quadratic bounds on convex functions analysis of gradient method 1-1 Approximate course outline First-order
LECTURE 25: REVIEW/EPILOGUE LECTURE OUTLINE
 LECTURE 25: REVIEW/EPILOGUE LECTURE OUTLINE CONVEX ANALYSIS AND DUALITY Basic concepts of convex analysis Basic concepts of convex optimization Geometric duality framework - MC/MC Constrained optimization
LECTURE 25: REVIEW/EPILOGUE LECTURE OUTLINE CONVEX ANALYSIS AND DUALITY Basic concepts of convex analysis Basic concepts of convex optimization Geometric duality framework - MC/MC Constrained optimization
3.1 Convexity notions for functions and basic properties
 3.1 Convexity notions for functions and basic properties We start the chapter with the basic definition of a convex function. Definition 3.1.1 (Convex function) A function f : E R is said to be convex
3.1 Convexity notions for functions and basic properties We start the chapter with the basic definition of a convex function. Definition 3.1.1 (Convex function) A function f : E R is said to be convex
3. Convex functions. basic properties and examples. operations that preserve convexity. the conjugate function. quasiconvex functions
 3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
LECTURE 12 LECTURE OUTLINE. Subgradients Fenchel inequality Sensitivity in constrained optimization Subdifferential calculus Optimality conditions
 LECTURE 12 LECTURE OUTLINE Subgradients Fenchel inequality Sensitivity in constrained optimization Subdifferential calculus Optimality conditions Reading: Section 5.4 All figures are courtesy of Athena
LECTURE 12 LECTURE OUTLINE Subgradients Fenchel inequality Sensitivity in constrained optimization Subdifferential calculus Optimality conditions Reading: Section 5.4 All figures are courtesy of Athena
Chapter 2 Convex Analysis
 Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
Lecture 2: Convex functions
 Lecture 2: Convex functions f : R n R is convex if dom f is convex and for all x, y dom f, θ [0, 1] f is concave if f is convex f(θx + (1 θ)y) θf(x) + (1 θ)f(y) x x convex concave neither x examples (on
Lecture 2: Convex functions f : R n R is convex if dom f is convex and for all x, y dom f, θ [0, 1] f is concave if f is convex f(θx + (1 θ)y) θf(x) + (1 θ)f(y) x x convex concave neither x examples (on
Subgradients. subgradients. strong and weak subgradient calculus. optimality conditions via subgradients. directional derivatives
 Subgradients subgradients strong and weak subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE364b, Stanford University Basic inequality recall basic inequality
Subgradients subgradients strong and weak subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE364b, Stanford University Basic inequality recall basic inequality
In Progress: Summary of Notation and Basic Results Convex Analysis C&O 663, Fall 2009
 In Progress: Summary of Notation and Basic Results Convex Analysis C&O 663, Fall 2009 Intructor: Henry Wolkowicz November 26, 2009 University of Waterloo Department of Combinatorics & Optimization Abstract
In Progress: Summary of Notation and Basic Results Convex Analysis C&O 663, Fall 2009 Intructor: Henry Wolkowicz November 26, 2009 University of Waterloo Department of Combinatorics & Optimization Abstract
A function(al) f is convex if dom f is a convex set, and. f(θx + (1 θ)y) < θf(x) + (1 θ)f(y) f(x) = x 3
 Convex functions The domain dom f of a functional f : R N R is the subset of R N where f is well-defined. A function(al) f is convex if dom f is a convex set, and f(θx + (1 θ)y) θf(x) + (1 θ)f(y) for all
Convex functions The domain dom f of a functional f : R N R is the subset of R N where f is well-defined. A function(al) f is convex if dom f is a convex set, and f(θx + (1 θ)y) θf(x) + (1 θ)f(y) for all
Math 273a: Optimization Subgradients of convex functions
 Math 273a: Optimization Subgradients of convex functions Made by: Damek Davis Edited by Wotao Yin Department of Mathematics, UCLA Fall 2015 online discussions on piazza.com 1 / 42 Subgradients Assumptions
Math 273a: Optimization Subgradients of convex functions Made by: Damek Davis Edited by Wotao Yin Department of Mathematics, UCLA Fall 2015 online discussions on piazza.com 1 / 42 Subgradients Assumptions
A SET OF LECTURE NOTES ON CONVEX OPTIMIZATION WITH SOME APPLICATIONS TO PROBABILITY THEORY INCOMPLETE DRAFT. MAY 06
 A SET OF LECTURE NOTES ON CONVEX OPTIMIZATION WITH SOME APPLICATIONS TO PROBABILITY THEORY INCOMPLETE DRAFT. MAY 06 CHRISTIAN LÉONARD Contents Preliminaries 1 1. Convexity without topology 1 2. Convexity
A SET OF LECTURE NOTES ON CONVEX OPTIMIZATION WITH SOME APPLICATIONS TO PROBABILITY THEORY INCOMPLETE DRAFT. MAY 06 CHRISTIAN LÉONARD Contents Preliminaries 1 1. Convexity without topology 1 2. Convexity
Convex Analysis and Optimization Chapter 2 Solutions
 Convex Analysis and Optimization Chapter 2 Solutions Dimitri P. Bertsekas with Angelia Nedić and Asuman E. Ozdaglar Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Convex Analysis and Optimization Chapter 2 Solutions Dimitri P. Bertsekas with Angelia Nedić and Asuman E. Ozdaglar Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
3. Convex functions. basic properties and examples. operations that preserve convexity. the conjugate function. quasiconvex functions
 3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
The proximal mapping
 The proximal mapping http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes Outline 2/37 1 closed function 2 Conjugate function
The proximal mapping http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes Outline 2/37 1 closed function 2 Conjugate function
Lecture 3: Lagrangian duality and algorithms for the Lagrangian dual problem
 Lecture 3: Lagrangian duality and algorithms for the Lagrangian dual problem Michael Patriksson 0-0 The Relaxation Theorem 1 Problem: find f := infimum f(x), x subject to x S, (1a) (1b) where f : R n R
Lecture 3: Lagrangian duality and algorithms for the Lagrangian dual problem Michael Patriksson 0-0 The Relaxation Theorem 1 Problem: find f := infimum f(x), x subject to x S, (1a) (1b) where f : R n R
Shiqian Ma, MAT-258A: Numerical Optimization 1. Chapter 4. Subgradient
 Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 4 Subgradient Shiqian Ma, MAT-258A: Numerical Optimization 2 4.1. Subgradients definition subgradient calculus duality and optimality conditions Shiqian
Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 4 Subgradient Shiqian Ma, MAT-258A: Numerical Optimization 2 4.1. Subgradients definition subgradient calculus duality and optimality conditions Shiqian
BASICS OF CONVEX ANALYSIS
 BASICS OF CONVEX ANALYSIS MARKUS GRASMAIR 1. Main Definitions We start with providing the central definitions of convex functions and convex sets. Definition 1. A function f : R n R + } is called convex,
BASICS OF CONVEX ANALYSIS MARKUS GRASMAIR 1. Main Definitions We start with providing the central definitions of convex functions and convex sets. Definition 1. A function f : R n R + } is called convex,
Chapter 2: Preliminaries and elements of convex analysis
 Chapter 2: Preliminaries and elements of convex analysis Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-14-15.shtml Academic year 2014-15
Chapter 2: Preliminaries and elements of convex analysis Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-14-15.shtml Academic year 2014-15
Convex Functions. Wing-Kin (Ken) Ma The Chinese University of Hong Kong (CUHK)
 Convex Functions Wing-Kin (Ken) Ma The Chinese University of Hong Kong (CUHK) Course on Convex Optimization for Wireless Comm. and Signal Proc. Jointly taught by Daniel P. Palomar and Wing-Kin (Ken) Ma
Convex Functions Wing-Kin (Ken) Ma The Chinese University of Hong Kong (CUHK) Course on Convex Optimization for Wireless Comm. and Signal Proc. Jointly taught by Daniel P. Palomar and Wing-Kin (Ken) Ma
Constrained Optimization and Lagrangian Duality
 CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
ZERO DUALITY GAP FOR CONVEX PROGRAMS: A GENERAL RESULT
 ZERO DUALITY GAP FOR CONVEX PROGRAMS: A GENERAL RESULT EMIL ERNST AND MICHEL VOLLE Abstract. This article addresses a general criterion providing a zero duality gap for convex programs in the setting of
ZERO DUALITY GAP FOR CONVEX PROGRAMS: A GENERAL RESULT EMIL ERNST AND MICHEL VOLLE Abstract. This article addresses a general criterion providing a zero duality gap for convex programs in the setting of
8. Conjugate functions
 L. Vandenberghe EE236C (Spring 2013-14) 8. Conjugate functions closed functions conjugate function 8-1 Closed set a set C is closed if it contains its boundary: x k C, x k x = x C operations that preserve
L. Vandenberghe EE236C (Spring 2013-14) 8. Conjugate functions closed functions conjugate function 8-1 Closed set a set C is closed if it contains its boundary: x k C, x k x = x C operations that preserve
Concave and Convex Functions 1
 John Nachbar Washington University March 6, 2017 Concave and Convex Functions 1 1 Basic Definitions Definition 1 Let C R N be convex and let f : C R 1 (a) f is concave iff for any a, b C and any θ [0,
John Nachbar Washington University March 6, 2017 Concave and Convex Functions 1 1 Basic Definitions Definition 1 Let C R N be convex and let f : C R 1 (a) f is concave iff for any a, b C and any θ [0,
Iterative Convex Optimization Algorithms; Part One: Using the Baillon Haddad Theorem
 Iterative Convex Optimization Algorithms; Part One: Using the Baillon Haddad Theorem Charles Byrne (Charles Byrne@uml.edu) http://faculty.uml.edu/cbyrne/cbyrne.html Department of Mathematical Sciences
Iterative Convex Optimization Algorithms; Part One: Using the Baillon Haddad Theorem Charles Byrne (Charles Byrne@uml.edu) http://faculty.uml.edu/cbyrne/cbyrne.html Department of Mathematical Sciences
Convex Analysis and Optimization Chapter 4 Solutions
 Convex Analysis and Optimization Chapter 4 Solutions Dimitri P. Bertsekas with Angelia Nedić and Asuman E. Ozdaglar Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Convex Analysis and Optimization Chapter 4 Solutions Dimitri P. Bertsekas with Angelia Nedić and Asuman E. Ozdaglar Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Dedicated to Michel Théra in honor of his 70th birthday
 VARIATIONAL GEOMETRIC APPROACH TO GENERALIZED DIFFERENTIAL AND CONJUGATE CALCULI IN CONVEX ANALYSIS B. S. MORDUKHOVICH 1, N. M. NAM 2, R. B. RECTOR 3 and T. TRAN 4. Dedicated to Michel Théra in honor of
VARIATIONAL GEOMETRIC APPROACH TO GENERALIZED DIFFERENTIAL AND CONJUGATE CALCULI IN CONVEX ANALYSIS B. S. MORDUKHOVICH 1, N. M. NAM 2, R. B. RECTOR 3 and T. TRAN 4. Dedicated to Michel Théra in honor of
Convex Functions. Daniel P. Palomar. Hong Kong University of Science and Technology (HKUST)
 Convex Functions Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Definition convex function Examples
Convex Functions Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Definition convex function Examples
Subdifferential representation of convex functions: refinements and applications
 Subdifferential representation of convex functions: refinements and applications Joël Benoist & Aris Daniilidis Abstract Every lower semicontinuous convex function can be represented through its subdifferential
Subdifferential representation of convex functions: refinements and applications Joël Benoist & Aris Daniilidis Abstract Every lower semicontinuous convex function can be represented through its subdifferential
ON A CLASS OF NONSMOOTH COMPOSITE FUNCTIONS
 MATHEMATICS OF OPERATIONS RESEARCH Vol. 28, No. 4, November 2003, pp. 677 692 Printed in U.S.A. ON A CLASS OF NONSMOOTH COMPOSITE FUNCTIONS ALEXANDER SHAPIRO We discuss in this paper a class of nonsmooth
MATHEMATICS OF OPERATIONS RESEARCH Vol. 28, No. 4, November 2003, pp. 677 692 Printed in U.S.A. ON A CLASS OF NONSMOOTH COMPOSITE FUNCTIONS ALEXANDER SHAPIRO We discuss in this paper a class of nonsmooth
Convex Optimization & Lagrange Duality
 Convex Optimization & Lagrange Duality Chee Wei Tan CS 8292 : Advanced Topics in Convex Optimization and its Applications Fall 2010 Outline Convex optimization Optimality condition Lagrange duality KKT
Convex Optimization & Lagrange Duality Chee Wei Tan CS 8292 : Advanced Topics in Convex Optimization and its Applications Fall 2010 Outline Convex optimization Optimality condition Lagrange duality KKT
Convex Analysis Notes. Lecturer: Adrian Lewis, Cornell ORIE Scribe: Kevin Kircher, Cornell MAE
 Convex Analysis Notes Lecturer: Adrian Lewis, Cornell ORIE Scribe: Kevin Kircher, Cornell MAE These are notes from ORIE 6328, Convex Analysis, as taught by Prof. Adrian Lewis at Cornell University in the
Convex Analysis Notes Lecturer: Adrian Lewis, Cornell ORIE Scribe: Kevin Kircher, Cornell MAE These are notes from ORIE 6328, Convex Analysis, as taught by Prof. Adrian Lewis at Cornell University in the
Descent methods. min x. f(x)
 Gradient Descent Descent methods min x f(x) 5 / 34 Descent methods min x f(x) x k x k+1... x f(x ) = 0 5 / 34 Gradient methods Unconstrained optimization min f(x) x R n. 6 / 34 Gradient methods Unconstrained
Gradient Descent Descent methods min x f(x) 5 / 34 Descent methods min x f(x) x k x k+1... x f(x ) = 0 5 / 34 Gradient methods Unconstrained optimization min f(x) x R n. 6 / 34 Gradient methods Unconstrained
4. Convex optimization problems (part 1: general)
 EE/AA 578, Univ of Washington, Fall 2016 4. Convex optimization problems (part 1: general) optimization problem in standard form convex optimization problems quasiconvex optimization 4 1 Optimization problem
EE/AA 578, Univ of Washington, Fall 2016 4. Convex optimization problems (part 1: general) optimization problem in standard form convex optimization problems quasiconvex optimization 4 1 Optimization problem
Subgradient. Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes. definition. subgradient calculus
 1/41 Subgradient Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes definition subgradient calculus duality and optimality conditions directional derivative Basic inequality
1/41 Subgradient Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes definition subgradient calculus duality and optimality conditions directional derivative Basic inequality
Chapter 1. Optimality Conditions: Unconstrained Optimization. 1.1 Differentiable Problems
 Chapter 1 Optimality Conditions: Unconstrained Optimization 1.1 Differentiable Problems Consider the problem of minimizing the function f : R n R where f is twice continuously differentiable on R n : P
Chapter 1 Optimality Conditions: Unconstrained Optimization 1.1 Differentiable Problems Consider the problem of minimizing the function f : R n R where f is twice continuously differentiable on R n : P
Some Properties of the Augmented Lagrangian in Cone Constrained Optimization
 MATHEMATICS OF OPERATIONS RESEARCH Vol. 29, No. 3, August 2004, pp. 479 491 issn 0364-765X eissn 1526-5471 04 2903 0479 informs doi 10.1287/moor.1040.0103 2004 INFORMS Some Properties of the Augmented
MATHEMATICS OF OPERATIONS RESEARCH Vol. 29, No. 3, August 2004, pp. 479 491 issn 0364-765X eissn 1526-5471 04 2903 0479 informs doi 10.1287/moor.1040.0103 2004 INFORMS Some Properties of the Augmented
LECTURE SLIDES ON BASED ON CLASS LECTURES AT THE CAMBRIDGE, MASS FALL 2007 BY DIMITRI P. BERTSEKAS.
 LECTURE SLIDES ON CONVEX ANALYSIS AND OPTIMIZATION BASED ON 6.253 CLASS LECTURES AT THE MASSACHUSETTS INSTITUTE OF TECHNOLOGY CAMBRIDGE, MASS FALL 2007 BY DIMITRI P. BERTSEKAS http://web.mit.edu/dimitrib/www/home.html
LECTURE SLIDES ON CONVEX ANALYSIS AND OPTIMIZATION BASED ON 6.253 CLASS LECTURES AT THE MASSACHUSETTS INSTITUTE OF TECHNOLOGY CAMBRIDGE, MASS FALL 2007 BY DIMITRI P. BERTSEKAS http://web.mit.edu/dimitrib/www/home.html
Lecture: Duality of LP, SOCP and SDP
 1/33 Lecture: Duality of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2017.html wenzw@pku.edu.cn Acknowledgement:
1/33 Lecture: Duality of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2017.html wenzw@pku.edu.cn Acknowledgement:
Concave and Convex Functions 1
 John Nachbar Washington University March 27, 2018 Concave and Convex Functions 1 1 Basic Definitions. Definition 1. Let C R N be non-empty and convex and let f : C R. 1. (a) f is concave iff for any a,
John Nachbar Washington University March 27, 2018 Concave and Convex Functions 1 1 Basic Definitions. Definition 1. Let C R N be non-empty and convex and let f : C R. 1. (a) f is concave iff for any a,
Convex Functions and Optimization
 Chapter 5 Convex Functions and Optimization 5.1 Convex Functions Our next topic is that of convex functions. Again, we will concentrate on the context of a map f : R n R although the situation can be generalized
Chapter 5 Convex Functions and Optimization 5.1 Convex Functions Our next topic is that of convex functions. Again, we will concentrate on the context of a map f : R n R although the situation can be generalized
Semi-infinite programming, duality, discretization and optimality conditions
 Semi-infinite programming, duality, discretization and optimality conditions Alexander Shapiro School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332-0205,
Semi-infinite programming, duality, discretization and optimality conditions Alexander Shapiro School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332-0205,
Local strong convexity and local Lipschitz continuity of the gradient of convex functions
 Local strong convexity and local Lipschitz continuity of the gradient of convex functions R. Goebel and R.T. Rockafellar May 23, 2007 Abstract. Given a pair of convex conjugate functions f and f, we investigate
Local strong convexity and local Lipschitz continuity of the gradient of convex functions R. Goebel and R.T. Rockafellar May 23, 2007 Abstract. Given a pair of convex conjugate functions f and f, we investigate
Strongly convex functions, Moreau envelopes and the generic nature of convex functions with strong minimizers
 University of Wollongong Research Online Faculty of Engineering and Information Sciences - Papers: Part B Faculty of Engineering and Information Sciences 206 Strongly convex functions, Moreau envelopes
University of Wollongong Research Online Faculty of Engineering and Information Sciences - Papers: Part B Faculty of Engineering and Information Sciences 206 Strongly convex functions, Moreau envelopes
IE 521 Convex Optimization
 Lecture 5: Convex II 6th February 2019 Convex Local Lipschitz Outline Local Lipschitz 1 / 23 Convex Local Lipschitz Convex Function: f : R n R is convex if dom(f ) is convex and for any λ [0, 1], x, y
Lecture 5: Convex II 6th February 2019 Convex Local Lipschitz Outline Local Lipschitz 1 / 23 Convex Local Lipschitz Convex Function: f : R n R is convex if dom(f ) is convex and for any λ [0, 1], x, y
Convex Optimization Theory. Chapter 5 Exercises and Solutions: Extended Version
 Convex Optimization Theory Chapter 5 Exercises and Solutions: Extended Version Dimitri P. Bertsekas Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Convex Optimization Theory Chapter 5 Exercises and Solutions: Extended Version Dimitri P. Bertsekas Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Convex Optimization Conjugate, Subdifferential, Proximation
 1 Lecture Notes, HCI, 3.11.211 Chapter 6 Convex Optimization Conjugate, Subdifferential, Proximation Bastian Goldlücke Computer Vision Group Technical University of Munich 2 Bastian Goldlücke Overview
1 Lecture Notes, HCI, 3.11.211 Chapter 6 Convex Optimization Conjugate, Subdifferential, Proximation Bastian Goldlücke Computer Vision Group Technical University of Munich 2 Bastian Goldlücke Overview
Brøndsted-Rockafellar property of subdifferentials of prox-bounded functions. Marc Lassonde Université des Antilles et de la Guyane
 Conference ADGO 2013 October 16, 2013 Brøndsted-Rockafellar property of subdifferentials of prox-bounded functions Marc Lassonde Université des Antilles et de la Guyane Playa Blanca, Tongoy, Chile SUBDIFFERENTIAL
Conference ADGO 2013 October 16, 2013 Brøndsted-Rockafellar property of subdifferentials of prox-bounded functions Marc Lassonde Université des Antilles et de la Guyane Playa Blanca, Tongoy, Chile SUBDIFFERENTIAL
5. Duality. Lagrangian
 5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
Proximal methods. S. Villa. October 7, 2014
 Proximal methods S. Villa October 7, 2014 1 Review of the basics Often machine learning problems require the solution of minimization problems. For instance, the ERM algorithm requires to solve a problem
Proximal methods S. Villa October 7, 2014 1 Review of the basics Often machine learning problems require the solution of minimization problems. For instance, the ERM algorithm requires to solve a problem
Optimisation convexe: performance, complexité et applications.
 Optimisation convexe: performance, complexité et applications. Introduction, convexité, dualité. A. d Aspremont. M2 OJME: Optimisation convexe. 1/128 Today Convex optimization: introduction Course organization
Optimisation convexe: performance, complexité et applications. Introduction, convexité, dualité. A. d Aspremont. M2 OJME: Optimisation convexe. 1/128 Today Convex optimization: introduction Course organization
Math 273a: Optimization Subgradients of convex functions
 Math 273a: Optimization Subgradients of convex functions Made by: Damek Davis Edited by Wotao Yin Department of Mathematics, UCLA Fall 2015 online discussions on piazza.com 1 / 20 Subgradients Assumptions
Math 273a: Optimization Subgradients of convex functions Made by: Damek Davis Edited by Wotao Yin Department of Mathematics, UCLA Fall 2015 online discussions on piazza.com 1 / 20 Subgradients Assumptions
LECTURE SLIDES ON CONVEX OPTIMIZATION AND DUALITY THEORY TATA INSTITUTE FOR FUNDAMENTAL RESEARCH MUMBAI, INDIA JANUARY 2009 PART I
 LECTURE SLIDES ON CONVEX OPTIMIZATION AND DUALITY THEORY TATA INSTITUTE FOR FUNDAMENTAL RESEARCH MUMBAI, INDIA JANUARY 2009 PART I BY DIMITRI P. BERTSEKAS M.I.T. http://web.mit.edu/dimitrib/www/home.html
LECTURE SLIDES ON CONVEX OPTIMIZATION AND DUALITY THEORY TATA INSTITUTE FOR FUNDAMENTAL RESEARCH MUMBAI, INDIA JANUARY 2009 PART I BY DIMITRI P. BERTSEKAS M.I.T. http://web.mit.edu/dimitrib/www/home.html
EE 546, Univ of Washington, Spring Proximal mapping. introduction. review of conjugate functions. proximal mapping. Proximal mapping 6 1
 EE 546, Univ of Washington, Spring 2012 6. Proximal mapping introduction review of conjugate functions proximal mapping Proximal mapping 6 1 Proximal mapping the proximal mapping (prox-operator) of a convex
EE 546, Univ of Washington, Spring 2012 6. Proximal mapping introduction review of conjugate functions proximal mapping Proximal mapping 6 1 Proximal mapping the proximal mapping (prox-operator) of a convex
Rockefellar s Closed Functions
 Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory Fall 2018 Winter 2019 Topic 21: Rockefellar s Closed Functions 21.1 Closed convex functions Convex analysts
Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory Fall 2018 Winter 2019 Topic 21: Rockefellar s Closed Functions 21.1 Closed convex functions Convex analysts
g 2 (x) (1/3)M 1 = (1/3)(2/3)M.
 COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
In English, this means that if we travel on a straight line between any two points in C, then we never leave C.
 Convex sets In this section, we will be introduced to some of the mathematical fundamentals of convex sets. In order to motivate some of the definitions, we will look at the closest point problem from
Convex sets In this section, we will be introduced to some of the mathematical fundamentals of convex sets. In order to motivate some of the definitions, we will look at the closest point problem from
Coordinate Update Algorithm Short Course Subgradients and Subgradient Methods
 Coordinate Update Algorithm Short Course Subgradients and Subgradient Methods Instructor: Wotao Yin (UCLA Math) Summer 2016 1 / 30 Notation f : H R { } is a closed proper convex function domf := {x R n
Coordinate Update Algorithm Short Course Subgradients and Subgradient Methods Instructor: Wotao Yin (UCLA Math) Summer 2016 1 / 30 Notation f : H R { } is a closed proper convex function domf := {x R n
Convex Optimization M2
 Convex Optimization M2 Lecture 3 A. d Aspremont. Convex Optimization M2. 1/49 Duality A. d Aspremont. Convex Optimization M2. 2/49 DMs DM par email: dm.daspremont@gmail.com A. d Aspremont. Convex Optimization
Convex Optimization M2 Lecture 3 A. d Aspremont. Convex Optimization M2. 1/49 Duality A. d Aspremont. Convex Optimization M2. 2/49 DMs DM par email: dm.daspremont@gmail.com A. d Aspremont. Convex Optimization
Lower semicontinuous and Convex Functions
 Lower semicontinuous and Convex Functions James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University October 6, 2017 Outline Lower Semicontinuous Functions
Lower semicontinuous and Convex Functions James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University October 6, 2017 Outline Lower Semicontinuous Functions
Convex Optimization and Modeling
 Convex Optimization and Modeling Duality Theory and Optimality Conditions 5th lecture, 12.05.2010 Jun.-Prof. Matthias Hein Program of today/next lecture Lagrangian and duality: the Lagrangian the dual
Convex Optimization and Modeling Duality Theory and Optimality Conditions 5th lecture, 12.05.2010 Jun.-Prof. Matthias Hein Program of today/next lecture Lagrangian and duality: the Lagrangian the dual
CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS. W. Erwin Diewert January 31, 2008.
 1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
Division of the Humanities and Social Sciences. Supergradients. KC Border Fall 2001 v ::15.45
 Division of the Humanities and Social Sciences Supergradients KC Border Fall 2001 1 The supergradient of a concave function There is a useful way to characterize the concavity of differentiable functions.
Division of the Humanities and Social Sciences Supergradients KC Border Fall 2001 1 The supergradient of a concave function There is a useful way to characterize the concavity of differentiable functions.
Convex Optimization Boyd & Vandenberghe. 5. Duality
 5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
1 Convexity, concavity and quasi-concavity. (SB )
 UNIVERSITY OF MARYLAND ECON 600 Summer 2010 Lecture Two: Unconstrained Optimization 1 Convexity, concavity and quasi-concavity. (SB 21.1-21.3.) For any two points, x, y R n, we can trace out the line of
UNIVERSITY OF MARYLAND ECON 600 Summer 2010 Lecture Two: Unconstrained Optimization 1 Convexity, concavity and quasi-concavity. (SB 21.1-21.3.) For any two points, x, y R n, we can trace out the line of
Mathematics 530. Practice Problems. n + 1 }
 Department of Mathematical Sciences University of Delaware Prof. T. Angell October 19, 2015 Mathematics 530 Practice Problems 1. Recall that an indifference relation on a partially ordered set is defined
Department of Mathematical Sciences University of Delaware Prof. T. Angell October 19, 2015 Mathematics 530 Practice Problems 1. Recall that an indifference relation on a partially ordered set is defined
Convex analysis and profit/cost/support functions
 Division of the Humanities and Social Sciences Convex analysis and profit/cost/support functions KC Border October 2004 Revised January 2009 Let A be a subset of R m Convex analysts may give one of two
Division of the Humanities and Social Sciences Convex analysis and profit/cost/support functions KC Border October 2004 Revised January 2009 Let A be a subset of R m Convex analysts may give one of two
DYNAMIC DUALIZATION IN A GENERAL SETTING
 Journal of the Operations Research Society of Japan Vol. 60, No. 2, April 2017, pp. 44 49 c The Operations Research Society of Japan DYNAMIC DUALIZATION IN A GENERAL SETTING Hidefumi Kawasaki Kyushu University
Journal of the Operations Research Society of Japan Vol. 60, No. 2, April 2017, pp. 44 49 c The Operations Research Society of Japan DYNAMIC DUALIZATION IN A GENERAL SETTING Hidefumi Kawasaki Kyushu University
Self-equilibrated Functions in Dual Vector Spaces: a Boundedness Criterion
 Self-equilibrated Functions in Dual Vector Spaces: a Boundedness Criterion Michel Théra LACO, UMR-CNRS 6090, Université de Limoges michel.thera@unilim.fr reporting joint work with E. Ernst and M. Volle
Self-equilibrated Functions in Dual Vector Spaces: a Boundedness Criterion Michel Théra LACO, UMR-CNRS 6090, Université de Limoges michel.thera@unilim.fr reporting joint work with E. Ernst and M. Volle
Convex Analysis Background
 Convex Analysis Background John C. Duchi Stanford University Park City Mathematics Institute 206 Abstract In this set of notes, we will outline several standard facts from convex analysis, the study of
Convex Analysis Background John C. Duchi Stanford University Park City Mathematics Institute 206 Abstract In this set of notes, we will outline several standard facts from convex analysis, the study of
CONSTRAINT QUALIFICATIONS, LAGRANGIAN DUALITY & SADDLE POINT OPTIMALITY CONDITIONS
 CONSTRAINT QUALIFICATIONS, LAGRANGIAN DUALITY & SADDLE POINT OPTIMALITY CONDITIONS A Dissertation Submitted For The Award of the Degree of Master of Philosophy in Mathematics Neelam Patel School of Mathematics
CONSTRAINT QUALIFICATIONS, LAGRANGIAN DUALITY & SADDLE POINT OPTIMALITY CONDITIONS A Dissertation Submitted For The Award of the Degree of Master of Philosophy in Mathematics Neelam Patel School of Mathematics
Robust Duality in Parametric Convex Optimization
 Robust Duality in Parametric Convex Optimization R.I. Boţ V. Jeyakumar G.Y. Li Revised Version: June 20, 2012 Abstract Modelling of convex optimization in the face of data uncertainty often gives rise
Robust Duality in Parametric Convex Optimization R.I. Boţ V. Jeyakumar G.Y. Li Revised Version: June 20, 2012 Abstract Modelling of convex optimization in the face of data uncertainty often gives rise
CONTINUOUS CONVEX SETS AND ZERO DUALITY GAP FOR CONVEX PROGRAMS
 CONTINUOUS CONVEX SETS AND ZERO DUALITY GAP FOR CONVEX PROGRAMS EMIL ERNST AND MICHEL VOLLE ABSTRACT. This article uses classical notions of convex analysis over euclidean spaces, like Gale & Klee s boundary
CONTINUOUS CONVEX SETS AND ZERO DUALITY GAP FOR CONVEX PROGRAMS EMIL ERNST AND MICHEL VOLLE ABSTRACT. This article uses classical notions of convex analysis over euclidean spaces, like Gale & Klee s boundary
Lectures on Geometry
 January 4, 2001 Lectures on Geometry Christer O. Kiselman Contents: 1. Introduction 2. Closure operators and Galois correspondences 3. Convex sets and functions 4. Infimal convolution 5. Convex duality:
January 4, 2001 Lectures on Geometry Christer O. Kiselman Contents: 1. Introduction 2. Closure operators and Galois correspondences 3. Convex sets and functions 4. Infimal convolution 5. Convex duality:
Convex Optimization Theory
 Convex Optimization Theory A SUMMARY BY DIMITRI P. BERTSEKAS We provide a summary of theoretical concepts and results relating to convex analysis, convex optimization, and duality theory. In particular,
Convex Optimization Theory A SUMMARY BY DIMITRI P. BERTSEKAS We provide a summary of theoretical concepts and results relating to convex analysis, convex optimization, and duality theory. In particular,
Lecture: Duality.
 Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
Almost Convex Functions: Conjugacy and Duality
 Almost Convex Functions: Conjugacy and Duality Radu Ioan Boţ 1, Sorin-Mihai Grad 2, and Gert Wanka 3 1 Faculty of Mathematics, Chemnitz University of Technology, D-09107 Chemnitz, Germany radu.bot@mathematik.tu-chemnitz.de
Almost Convex Functions: Conjugacy and Duality Radu Ioan Boţ 1, Sorin-Mihai Grad 2, and Gert Wanka 3 1 Faculty of Mathematics, Chemnitz University of Technology, D-09107 Chemnitz, Germany radu.bot@mathematik.tu-chemnitz.de
Epiconvergence and ε-subgradients of Convex Functions
 Journal of Convex Analysis Volume 1 (1994), No.1, 87 100 Epiconvergence and ε-subgradients of Convex Functions Andrei Verona Department of Mathematics, California State University Los Angeles, CA 90032,
Journal of Convex Analysis Volume 1 (1994), No.1, 87 100 Epiconvergence and ε-subgradients of Convex Functions Andrei Verona Department of Mathematics, California State University Los Angeles, CA 90032,
Maximal Monotone Inclusions and Fitzpatrick Functions
 JOTA manuscript No. (will be inserted by the editor) Maximal Monotone Inclusions and Fitzpatrick Functions J. M. Borwein J. Dutta Communicated by Michel Thera. Abstract In this paper, we study maximal
JOTA manuscript No. (will be inserted by the editor) Maximal Monotone Inclusions and Fitzpatrick Functions J. M. Borwein J. Dutta Communicated by Michel Thera. Abstract In this paper, we study maximal
On Semicontinuity of Convex-valued Multifunctions and Cesari s Property (Q)
 On Semicontinuity of Convex-valued Multifunctions and Cesari s Property (Q) Andreas Löhne May 2, 2005 (last update: November 22, 2005) Abstract We investigate two types of semicontinuity for set-valued
On Semicontinuity of Convex-valued Multifunctions and Cesari s Property (Q) Andreas Löhne May 2, 2005 (last update: November 22, 2005) Abstract We investigate two types of semicontinuity for set-valued
4. Convex optimization problems
 Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
GEOMETRIC APPROACH TO CONVEX SUBDIFFERENTIAL CALCULUS October 10, Dedicated to Franco Giannessi and Diethard Pallaschke with great respect
 GEOMETRIC APPROACH TO CONVEX SUBDIFFERENTIAL CALCULUS October 10, 2018 BORIS S. MORDUKHOVICH 1 and NGUYEN MAU NAM 2 Dedicated to Franco Giannessi and Diethard Pallaschke with great respect Abstract. In
GEOMETRIC APPROACH TO CONVEX SUBDIFFERENTIAL CALCULUS October 10, 2018 BORIS S. MORDUKHOVICH 1 and NGUYEN MAU NAM 2 Dedicated to Franco Giannessi and Diethard Pallaschke with great respect Abstract. In
New formulas for the Fenchel subdifferential of the conjugate function
 New formulas for the Fenchel subdifferential of the conjugate function Rafael Correa, Abderrahim Hantoute Centro de Modelamiento Matematico, Universidad de Chile (CNRS UMI 2807), Avda Blanco Encalada 2120,
New formulas for the Fenchel subdifferential of the conjugate function Rafael Correa, Abderrahim Hantoute Centro de Modelamiento Matematico, Universidad de Chile (CNRS UMI 2807), Avda Blanco Encalada 2120,
LECTURE SLIDES ON CONVEX ANALYSIS AND OPTIMIZATION BASED ON LECTURES GIVEN AT THE MASSACHUSETTS INSTITUTE OF TECHNOLOGY CAMBRIDGE, MASS
 LECTURE SLIDES ON CONVEX ANALYSIS AND OPTIMIZATION BASED ON LECTURES GIVEN AT THE MASSACHUSETTS INSTITUTE OF TECHNOLOGY CAMBRIDGE, MASS BY DIMITRI P. BERTSEKAS http://web.mit.edu/dimitrib/www/home.html
LECTURE SLIDES ON CONVEX ANALYSIS AND OPTIMIZATION BASED ON LECTURES GIVEN AT THE MASSACHUSETTS INSTITUTE OF TECHNOLOGY CAMBRIDGE, MASS BY DIMITRI P. BERTSEKAS http://web.mit.edu/dimitrib/www/home.html
DEFINABLE VERSIONS OF THEOREMS BY KIRSZBRAUN AND HELLY
 DEFINABLE VERSIONS OF THEOREMS BY KIRSZBRAUN AND HELLY MATTHIAS ASCHENBRENNER AND ANDREAS FISCHER Abstract. Kirszbraun s Theorem states that every Lipschitz map S R n, where S R m, has an extension to
DEFINABLE VERSIONS OF THEOREMS BY KIRSZBRAUN AND HELLY MATTHIAS ASCHENBRENNER AND ANDREAS FISCHER Abstract. Kirszbraun s Theorem states that every Lipschitz map S R n, where S R m, has an extension to
Convex Optimization in Communications and Signal Processing
 Convex Optimization in Communications and Signal Processing Prof. Dr.-Ing. Wolfgang Gerstacker 1 University of Erlangen-Nürnberg Institute for Digital Communications National Technical University of Ukraine,
Convex Optimization in Communications and Signal Processing Prof. Dr.-Ing. Wolfgang Gerstacker 1 University of Erlangen-Nürnberg Institute for Digital Communications National Technical University of Ukraine,
Convex Optimization. Convex Analysis - Functions
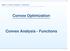 Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
DUALITY, OPTIMALITY CONDITIONS AND PERTURBATION ANALYSIS
 1 DUALITY, OPTIMALITY CONDITIONS AND PERTURBATION ANALYSIS Alexander Shapiro 1 School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332-0205, USA, E-mail: ashapiro@isye.gatech.edu
1 DUALITY, OPTIMALITY CONDITIONS AND PERTURBATION ANALYSIS Alexander Shapiro 1 School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332-0205, USA, E-mail: ashapiro@isye.gatech.edu
Structural and Multidisciplinary Optimization. P. Duysinx and P. Tossings
 Structural and Multidisciplinary Optimization P. Duysinx and P. Tossings 2018-2019 CONTACTS Pierre Duysinx Institut de Mécanique et du Génie Civil (B52/3) Phone number: 04/366.91.94 Email: P.Duysinx@uliege.be
Structural and Multidisciplinary Optimization P. Duysinx and P. Tossings 2018-2019 CONTACTS Pierre Duysinx Institut de Mécanique et du Génie Civil (B52/3) Phone number: 04/366.91.94 Email: P.Duysinx@uliege.be
Franco Giannessi, Giandomenico Mastroeni. Institute of Mathematics University of Verona, Verona, Italy
 ON THE THEORY OF VECTOR OPTIMIZATION AND VARIATIONAL INEQUALITIES. IMAGE SPACE ANALYSIS AND SEPARATION 1 Franco Giannessi, Giandomenico Mastroeni Department of Mathematics University of Pisa, Pisa, Italy
ON THE THEORY OF VECTOR OPTIMIZATION AND VARIATIONAL INEQUALITIES. IMAGE SPACE ANALYSIS AND SEPARATION 1 Franco Giannessi, Giandomenico Mastroeni Department of Mathematics University of Pisa, Pisa, Italy
Convex Optimization Theory. Chapter 3 Exercises and Solutions: Extended Version
 Convex Optimization Theory Chapter 3 Exercises and Solutions: Extended Version Dimitri P. Bertsekas Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Convex Optimization Theory Chapter 3 Exercises and Solutions: Extended Version Dimitri P. Bertsekas Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Convex Optimization and Modeling
 Convex Optimization and Modeling Convex Optimization Fourth lecture, 05.05.2010 Jun.-Prof. Matthias Hein Reminder from last time Convex functions: first-order condition: f(y) f(x) + f x,y x, second-order
Convex Optimization and Modeling Convex Optimization Fourth lecture, 05.05.2010 Jun.-Prof. Matthias Hein Reminder from last time Convex functions: first-order condition: f(y) f(x) + f x,y x, second-order
