Chapter 8. Rotational Equilibrium and Rotational Dynamics
|
|
|
- Kerry Day
- 6 years ago
- Views:
Transcription
1 Chapter 8 Rotational Equilibrium and Rotational Dynamics 1
2 Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related 2
3 Torque The door is free to rotate about an axis through O There are three factors that determine the effectiveness of the force in opening the door: The magnitude of the force The position of the application of the force The angle at which the force is applied 3
4 Torque, cont Torque, τ, is the tendency of a force to rotate an object about some axis τ = r F τ is the torque F is the force symbol is the Greek tau r is the length of the position vector SI unit is N. m 4
5 QQ1 Using a screwdriver, you try to remove a screw from a piece of furniture, but can t get it to turn. To increase the chances of success, you should use a screwdriver that (a) is longer, (b) is shorter, (c) has a narrower handle (d) has a wider handle. 5
6 Direction of Torque Torque is a vector quantity The direction is perpendicular to the plane determined by the position vector and the force If the turning tendency of the force is counterclockwise, the torque will be positive If the turning tendency is clockwise, the torque will be negative 6
7 Right Hand Rule Point the fingers in the direction of the position vector (beginning from the axis of rotation) Curl the fingers toward the force vector The thumb points in the direction of the torque Out of the page for the figure 7
8 Multiple Torques When two or more torques are acting on an object, the torques are added As vectors. Take sign into account If the net torque is zero, the object s rate of rotation doesn t change 8
9 General Definition of Torque The applied force is not always perpendicular to the position vector When the force is parallel to the position vector, no rotation occurs When the force is at some angle, the perpendicular component causes the rotation 9
10 General Definition of Torque, final Taking the angle into account leads to a more general definition of torque: τ = r F sin θ F is the force r is the position vector θ is the angle between the force and the position vector 10
11 Lever Arm The lever arm, d, is the perpendicular distance from the axis of rotation to a line drawn along the direction of the force d = r sin θ Formula for torque may be rearranged to show that the torque is proportional to the force F times lever arm τ = r F sin θ = F (r sin θ) = F d 11
12 Net Torque The net torque is the sum of all the torques produced by all the forces Remember to account for the direction of the tendency for rotation which gives the sign: Counterclockwise torques are positive Clockwise torques are negative 12
13 Torque and Equilibrium First Condition of Equilibrium r Σ F = 0 or r r Σ F = 0 and Σ F = 0 The net external force must be zero x This is a statement of translational equilibrium (we know it from previous chapters) This is a necessary, but not sufficient, condition to ensure that an object is in complete mechanical equilibrium: the object may rotate! y 13
14 Torque and Equilibrium, cont To ensure mechanical equilibrium, you need to ensure rotational equilibrium as well as translational The Second Condition of Equilibrium (for rotation) states The net external torque must be zero r Σ τ = 0 14
15 Equilibrium Example (8.3) The woman, mass m, sits on the left end of the see-saw The man, mass M, sits where the seesaw will be balanced Apply the Second Condition of Equilibrium and solve for the unknown distance, x Free body diagram 15
16 Axis of Rotation If the object is in equilibrium, it does not matter where you put the axis of rotation for calculating the net torque The location of the axis of rotation is completely arbitrary Often the nature of the problem will suggest a convenient location for the axis When solving a problem, you must specify an axis of rotation Once you have chosen an axis, you must maintain that choice consistently throughout the problem 16
17 Example (8.7 page 235) Beam The free body diagram includes the directions of the forces The weights act through the centers of gravity of their objects Fig 8.12, p.228 Slide 17 17
18 Fig. P8-20, 18p.256
19 Fig. 8-2, 19p.228
20 Fig. P8-58, 20p.260
21 Center of Gravity The force of gravity acting on an object must be considered In finding the torque produced by the force of gravity, all of the weight of the object can be considered to be concentrated at a single point, called the center of gravity 21
22 Calculating the Center of Gravity The object is divided up into a large number of very small particles with small weight Each particle will have a set of coordinates indicating its location (x,y) 22
23 Calculating the Center of Gravity, cont. We assume the object is free to rotate about its center The torque produced by each particle about the axis of rotation is equal to its weight times its lever arm For example, for a particle 1 with mass m 1 τ 1 = m 1 g x 1 23
24 Calculating the Center of Gravity, cont. We wish to locate the point of application of the single force whose magnitude is equal to the total weight of the object, and whose effect on the rotation is the same as all the individual particles. This point is called the center of gravity of the object 24
25 Coordinates of the Center of Gravity The coordinates of the center of gravity can be found from the sum of the torques acting on the individual particles being set equal to the torque produced by the weight of the object Σmx i i Σmy i i xcg = and ycg = Σm Σm i i 25
26 Center of Gravity (C.G.)of a Uniform Object The center of gravity of a homogenous, symmetric body must lie on the axis of symmetry. Often, the center of gravity of such an object is the geometric center of the object. Example: for the ring, the c.g. is in the center of the ring 26
27 Experimentally Determining the Center of Gravity The wrench is hung freely from two different pivots The intersection of the lines indicates the center of gravity A rigid object can be balanced by a single force equal in magnitude to its weight as long as the force is acting upward through the object s center of gravity 27
28 28p.230
29 Fig. Q8-12,29p.253
30 Notes About Equilibrium A zero net torque does not mean the absence of rotational motion An object that rotates at uniform angular velocity can be under the influence of a zero net torque This is analogous to the translational situation where a zero net force does not mean the object is not in motion 30
31 Solving Equilibrium Problems Draw a diagram of the system Include coordinates and choose a rotation axis Isolate the object being analyzed and draw a free body diagram showing all the external forces acting on the object For systems containing more than one object, draw a separate free body diagram for each object 31
32 Problem Solving, cont. Apply the Second Condition of Equilibrium This will yield a single equation, often with one unknown which can be solved immediately Apply the First Condition of Equilibrium This will give you two more equations Solve the resulting simultaneous equations for all of the unknowns 32
33 Example of a Free Body Diagram (Ladder) The free body diagram shows the normal force and the force of static friction acting on the ladder at the ground The last diagram shows the lever arms for the forces 33
34 Torque and Angular Acceleration When a rigid object is subject to a net torque ( 0), it undergoes an angular acceleration The angular acceleration is directly proportional to the net torque 34
35 Moment of Inertia The analog for force for rotation is torque The mass analog for the rotation is called the moment of inertia, I, of the object I Σmr SI units are kg m
36 Newton s Second Law for a Rotating Object Σ τ = I α The angular acceleration is directly proportional to the net torque The relationship is similar to F = ma Newton s Second Law for translation 36
37 QQ2 A constant net torque is applied to an object. Which one of the following will not be constant? (a) angular acceleration (b) angular velocity (c) moment of inertia (d) center of gravity 37
38 More About Moment of Inertia There is a major difference between moment of inertia and mass: the moment of inertia depends on the quantity of matter and its distribution in the rigid object. The moment of inertia also depends upon the location of the axis of rotation Also the units are different 38
39 Moment of Inertia of a Uniform Ring Image the hoop is divided into a number of small segments, m 1 These segments are equidistant from the axis I =Σ mr = MR 2 2 i i 39
40 Other Moments of Inertia 40
41 QQ3 The two rigid objects shown in Figure have the same mass, radius, and angular speed. If the same braking torque is applied to each, which takes longer to stop? (a) A (b) B (c) more information is needed 41
42 Fig. 8-16, 42p.238
43 Example, Newton s Second Law for Rotation Draw free body diagrams of each object Only the cylinder is rotating, so apply Στ = I α The bucket is falling, but not rotating, so apply ΣF = m a Remember that a = α r and solve the resulting equations 43
44 Rotational Kinetic Energy An object rotating about some axis with an angular speed, ω, has rotational kinetic energy ½Iω 2 Similar= to the formula for a known formula for kinetic energy (for translational motion) Ek = ½mv 2 Energy concepts can be useful for simplifying the analysis of rotational motion 44
45 QQ4 Two spheres, one hollow and one solid, are rotating with the same angular speed around an axis through their centers. Both spheres have the same mass and radius. Which sphere, if either, has the higher rotational kinetic energy? (a) The hollow sphere. (b) The solid sphere. (c) They both have the same kinetic energy. 45
46 Total Energy of a System Conservation of Mechanical Energy ( KE + KE + PE ) = ( KE + KE + PE ) t r g i t r g f Remember, this is for conservative forces, no dissipative (non-conservative) forces such as friction can be present Potential energies of any other conservative forces could be added (e.g. spring) 46
47 QQ 5 (Modified) Which arrives at the bottom first: (a) a ball (hollow inside) rolling without sliding down a certain incline A, (b) a solid cylinder rolling without sliding down incline A, or (c) a box sliding down a frictionless incline B having the same dimensions as A? Assume that all objects have the same mass and each object is released from rest at the top of its incline. 47
48 Work-Energy in a Rotating System In the case where there are dissipative forces such as friction, use the generalized Work-Energy Theorem instead of Conservation of Energy W nc = ΔKE t + ΔKE R + ΔPE 48
49 General Problem Solving Hints The same basic techniques that were used in linear motion can be applied to rotational motion. τ α Analogies: F becomes, m becomes I and a becomes, v becomes ω and x becomes θ 49
50 Problem Solving Hints for Energy Methods Choose two points of interest One where all the necessary information is given The other where information is desired Identify the conservative and non-conservative forces 50
51 Problem Solving Hints for Energy Methods, cont Write the general equation for the Work-Energy theorem if there are non-conservative forces Alternatively use Conservation of Energy if there are no non-conservative forces Use v =rω if necessary to combine translational and rotational terms Solve for the unknown 51
52 Fig. 8-25, 52p.245
53 Fig. P8-36, 53p.258
54 Angular Momentum Similarly to the relationship between force and momentum in a linear system, we can show the relationship between torque and angular momentum Angular momentum is defined as L = I ω (similar to M=mv) r ΔL Δ p mv ( f v) r i and Σ τ = (similar to = = Fnet ) Δ t Δt Δt 54
55 Angular Momentum, cont Conservation of Angular Momentum states: The angular momentum of a system is conserved (remains constant) when the net external torque acting on the systems is zero. That is, when Σ τ = = ω = ω 0, Li Lf or Ii i If f 55
56 Conservation of Angular Momentum, Example With hands and feet drawn closer to the body, the skater s angular speed increases L is conserved, I decreases, ω increases 56
57 QQ (Example 8.15) A student walks toward the center of the rotating platform. The angular speed of the platform will: (a) increase (b) decrease (c) stay the same 57
58 Fig. 8-30, 58p.249
59 QQ7 Al Gore quiz If global warming continues, it s likely that some ice from the polar ice caps of the Earth will melt and the water will be distributed closer to the Equator. If this occurs, would the length of the day (one revolution) (a) increase, (b) decrease, or (c) remain the same? 59
60 Conservation Rules, Summary In an isolated system (with no external forces acting on the system, and no internal dissipation of energy), the following quantities are conserved: Mechanical energy Linear momentum Angular momentum 60
Chapter 8. Rotational Equilibrium and Rotational Dynamics
 Chapter 8 Rotational Equilibrium and Rotational Dynamics Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related Torque The door is free to rotate about
Chapter 8 Rotational Equilibrium and Rotational Dynamics Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related Torque The door is free to rotate about
Application of Forces. Chapter Eight. Torque. Force vs. Torque. Torque, cont. Direction of Torque 4/7/2015
 Raymond A. Serway Chris Vuille Chapter Eight Rotational Equilibrium and Rotational Dynamics Application of Forces The point of application of a force is important This was ignored in treating objects as
Raymond A. Serway Chris Vuille Chapter Eight Rotational Equilibrium and Rotational Dynamics Application of Forces The point of application of a force is important This was ignored in treating objects as
Chapter 8 Rotational Equilibrium and Rotational Dynamics Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and
 Chapter 8 Rotational Equilibrium and Rotational Dynamics Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related Torque The door is free to rotate about
Chapter 8 Rotational Equilibrium and Rotational Dynamics Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related Torque The door is free to rotate about
General Physics (PHY 2130)
 General Physics (PHY 130) Lecture 0 Rotational dynamics equilibrium nd Newton s Law for rotational motion rolling Exam II review http://www.physics.wayne.edu/~apetrov/phy130/ Lightning Review Last lecture:
General Physics (PHY 130) Lecture 0 Rotational dynamics equilibrium nd Newton s Law for rotational motion rolling Exam II review http://www.physics.wayne.edu/~apetrov/phy130/ Lightning Review Last lecture:
Chapter 8. Rotational Equilibrium and Rotational Dynamics. 1. Torque. 2. Torque and Equilibrium. 3. Center of Mass and Center of Gravity
 Chapter 8 Rotational Equilibrium and Rotational Dynamics 1. Torque 2. Torque and Equilibrium 3. Center of Mass and Center of Gravity 4. Torque and angular acceleration 5. Rotational Kinetic energy 6. Angular
Chapter 8 Rotational Equilibrium and Rotational Dynamics 1. Torque 2. Torque and Equilibrium 3. Center of Mass and Center of Gravity 4. Torque and angular acceleration 5. Rotational Kinetic energy 6. Angular
Physics A - PHY 2048C
 Physics A - PHY 2048C and 11/15/2017 My Office Hours: Thursday 2:00-3:00 PM 212 Keen Building Warm-up Questions 1 Did you read Chapter 12 in the textbook on? 2 Must an object be rotating to have a moment
Physics A - PHY 2048C and 11/15/2017 My Office Hours: Thursday 2:00-3:00 PM 212 Keen Building Warm-up Questions 1 Did you read Chapter 12 in the textbook on? 2 Must an object be rotating to have a moment
Rotational Motion and Torque
 Rotational Motion and Torque Introduction to Angular Quantities Sections 8- to 8-2 Introduction Rotational motion deals with spinning objects, or objects rotating around some point. Rotational motion is
Rotational Motion and Torque Introduction to Angular Quantities Sections 8- to 8-2 Introduction Rotational motion deals with spinning objects, or objects rotating around some point. Rotational motion is
Chapter 8. Rotational Equilibrium and Rotational Dynamics
 Chapter 8 Rotational Equilibrium and Rotational Dynamics Wrench Demo Torque Torque, τ, is the tendency of a force to rotate an object about some axis τ = Fd F is the force d is the lever arm (or moment
Chapter 8 Rotational Equilibrium and Rotational Dynamics Wrench Demo Torque Torque, τ, is the tendency of a force to rotate an object about some axis τ = Fd F is the force d is the lever arm (or moment
= o + t = ot + ½ t 2 = o + 2
 Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
We define angular displacement, θ, and angular velocity, ω. What's a radian?
 We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
Rotational Motion About a Fixed Axis
 Rotational Motion About a Fixed Axis Vocabulary rigid body axis of rotation radian average angular velocity instantaneous angular average angular Instantaneous angular frequency velocity acceleration acceleration
Rotational Motion About a Fixed Axis Vocabulary rigid body axis of rotation radian average angular velocity instantaneous angular average angular Instantaneous angular frequency velocity acceleration acceleration
General Definition of Torque, final. Lever Arm. General Definition of Torque 7/29/2010. Units of Chapter 10
 Units of Chapter 10 Determining Moments of Inertia Rotational Kinetic Energy Rotational Plus Translational Motion; Rolling Why Does a Rolling Sphere Slow Down? General Definition of Torque, final Taking
Units of Chapter 10 Determining Moments of Inertia Rotational Kinetic Energy Rotational Plus Translational Motion; Rolling Why Does a Rolling Sphere Slow Down? General Definition of Torque, final Taking
AP Physics 1 Rotational Motion Practice Test
 AP Physics 1 Rotational Motion Practice Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) A spinning ice skater on extremely smooth ice is able
AP Physics 1 Rotational Motion Practice Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) A spinning ice skater on extremely smooth ice is able
PSI AP Physics I Rotational Motion
 PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
Chapter 8 Lecture Notes
 Chapter 8 Lecture Notes Physics 2414 - Strauss Formulas: v = l / t = r θ / t = rω a T = v / t = r ω / t =rα a C = v 2 /r = ω 2 r ω = ω 0 + αt θ = ω 0 t +(1/2)αt 2 θ = (1/2)(ω 0 +ω)t ω 2 = ω 0 2 +2αθ τ
Chapter 8 Lecture Notes Physics 2414 - Strauss Formulas: v = l / t = r θ / t = rω a T = v / t = r ω / t =rα a C = v 2 /r = ω 2 r ω = ω 0 + αt θ = ω 0 t +(1/2)αt 2 θ = (1/2)(ω 0 +ω)t ω 2 = ω 0 2 +2αθ τ
PSI AP Physics I Rotational Motion
 PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
Chapter 12: Rotation of Rigid Bodies. Center of Mass Moment of Inertia Torque Angular Momentum Rolling Statics
 Chapter 1: Rotation of Rigid Bodies Center of Mass Moment of Inertia Torque Angular Momentum Rolling Statics Translational vs Rotational / / 1/ m x v dx dt a dv dt F ma p mv KE mv Work Fd P Fv / / 1/ I
Chapter 1: Rotation of Rigid Bodies Center of Mass Moment of Inertia Torque Angular Momentum Rolling Statics Translational vs Rotational / / 1/ m x v dx dt a dv dt F ma p mv KE mv Work Fd P Fv / / 1/ I
Rotation Quiz II, review part A
 Rotation Quiz II, review part A 1. A solid disk with a radius R rotates at a constant rate ω. Which of the following points has the greater angular velocity? A. A B. B C. C D. D E. All points have the
Rotation Quiz II, review part A 1. A solid disk with a radius R rotates at a constant rate ω. Which of the following points has the greater angular velocity? A. A B. B C. C D. D E. All points have the
Chapter 8. Rotational Motion
 Chapter 8 Rotational Motion Rotational Work and Energy W = Fs = s = rθ Frθ Consider the work done in rotating a wheel with a tangential force, F, by an angle θ. τ = Fr W =τθ Rotational Work and Energy
Chapter 8 Rotational Motion Rotational Work and Energy W = Fs = s = rθ Frθ Consider the work done in rotating a wheel with a tangential force, F, by an angle θ. τ = Fr W =τθ Rotational Work and Energy
Chapter 8 continued. Rotational Dynamics
 Chapter 8 continued Rotational Dynamics 8.6 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Chapter 8 continued Rotational Dynamics 8.6 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
PHYSICS 220. Lecture 15. Textbook Sections Lecture 15 Purdue University, Physics 220 1
 PHYSICS 220 Lecture 15 Angular Momentum Textbook Sections 9.3 9.6 Lecture 15 Purdue University, Physics 220 1 Last Lecture Overview Torque = Force that causes rotation τ = F r sin θ Work done by torque
PHYSICS 220 Lecture 15 Angular Momentum Textbook Sections 9.3 9.6 Lecture 15 Purdue University, Physics 220 1 Last Lecture Overview Torque = Force that causes rotation τ = F r sin θ Work done by torque
Torque rotational force which causes a change in rotational motion. This force is defined by linear force multiplied by a radius.
 Warm up A remote-controlled car's wheel accelerates at 22.4 rad/s 2. If the wheel begins with an angular speed of 10.8 rad/s, what is the wheel's angular speed after exactly three full turns? AP Physics
Warm up A remote-controlled car's wheel accelerates at 22.4 rad/s 2. If the wheel begins with an angular speed of 10.8 rad/s, what is the wheel's angular speed after exactly three full turns? AP Physics
Recap I. Angular position: Angular displacement: s. Angular velocity: Angular Acceleration:
 Recap I Angular position: Angular displacement: s Angular velocity: Angular Acceleration: Every point on a rotating rigid object has the same angular, but not the same linear motion! Recap II Circular
Recap I Angular position: Angular displacement: s Angular velocity: Angular Acceleration: Every point on a rotating rigid object has the same angular, but not the same linear motion! Recap II Circular
Chapter 6, Problem 18. Agenda. Rotational Inertia. Rotational Inertia. Calculating Moment of Inertia. Example: Hoop vs.
 Agenda Today: Homework quiz, moment of inertia and torque Thursday: Statics problems revisited, rolling motion Reading: Start Chapter 8 in the reading Have to cancel office hours today: will have extra
Agenda Today: Homework quiz, moment of inertia and torque Thursday: Statics problems revisited, rolling motion Reading: Start Chapter 8 in the reading Have to cancel office hours today: will have extra
Mechanics II. Which of the following relations among the forces W, k, N, and F must be true?
 Mechanics II 1. By applying a force F on a block, a person pulls a block along a rough surface at constant velocity v (see Figure below; directions, but not necessarily magnitudes, are indicated). Which
Mechanics II 1. By applying a force F on a block, a person pulls a block along a rough surface at constant velocity v (see Figure below; directions, but not necessarily magnitudes, are indicated). Which
Chapter 8 - Rotational Dynamics and Equilibrium REVIEW
 Pagpalain ka! (Good luck, in Filipino) Date Chapter 8 - Rotational Dynamics and Equilibrium REVIEW TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1) When a rigid body
Pagpalain ka! (Good luck, in Filipino) Date Chapter 8 - Rotational Dynamics and Equilibrium REVIEW TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1) When a rigid body
Chapter 10. Rotation
 Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
Rotational Kinematics and Dynamics. UCVTS AIT Physics
 Rotational Kinematics and Dynamics UCVTS AIT Physics Angular Position Axis of rotation is the center of the disc Choose a fixed reference line Point P is at a fixed distance r from the origin Angular Position,
Rotational Kinematics and Dynamics UCVTS AIT Physics Angular Position Axis of rotation is the center of the disc Choose a fixed reference line Point P is at a fixed distance r from the origin Angular Position,
Physics 1A Lecture 10B
 Physics 1A Lecture 10B "Sometimes the world puts a spin on life. When our equilibrium returns to us, we understand more because we've seen the whole picture. --Davis Barton Cross Products Another way to
Physics 1A Lecture 10B "Sometimes the world puts a spin on life. When our equilibrium returns to us, we understand more because we've seen the whole picture. --Davis Barton Cross Products Another way to
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 8 continued. Rotational Dynamics
 Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = rφ = Frφ Fr = τ (torque) = τφ r φ s F to x θ = 0 DEFINITION OF
Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = rφ = Frφ Fr = τ (torque) = τφ r φ s F to x θ = 0 DEFINITION OF
Chapter 8- Rotational Kinematics Angular Variables Kinematic Equations
 Chapter 8- Rotational Kinematics Angular Variables Kinematic Equations Chapter 9- Rotational Dynamics Torque Center of Gravity Newton s 2 nd Law- Angular Rotational Work & Energy Angular Momentum Angular
Chapter 8- Rotational Kinematics Angular Variables Kinematic Equations Chapter 9- Rotational Dynamics Torque Center of Gravity Newton s 2 nd Law- Angular Rotational Work & Energy Angular Momentum Angular
PHY131H1S - Class 20. Pre-class reading quiz on Chapter 12
 PHY131H1S - Class 20 Today: Gravitational Torque Rotational Kinetic Energy Rolling without Slipping Equilibrium with Rotation Rotation Vectors Angular Momentum Pre-class reading quiz on Chapter 12 1 Last
PHY131H1S - Class 20 Today: Gravitational Torque Rotational Kinetic Energy Rolling without Slipping Equilibrium with Rotation Rotation Vectors Angular Momentum Pre-class reading quiz on Chapter 12 1 Last
Chapter 8 continued. Rotational Dynamics
 Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = s = rφ = Frφ Fr = τ (torque) = τφ r φ s F to s θ = 0 DEFINITION
Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = s = rφ = Frφ Fr = τ (torque) = τφ r φ s F to s θ = 0 DEFINITION
Physics 111. Lecture 23 (Walker: 10.6, 11.1) Conservation of Energy in Rotation Torque March 30, Kinetic Energy of Rolling Object
 Physics 111 Lecture 3 (Walker: 10.6, 11.1) Conservation of Energy in Rotation Torque March 30, 009 Lecture 3 1/4 Kinetic Energy of Rolling Object Total kinetic energy of a rolling object is the sum of
Physics 111 Lecture 3 (Walker: 10.6, 11.1) Conservation of Energy in Rotation Torque March 30, 009 Lecture 3 1/4 Kinetic Energy of Rolling Object Total kinetic energy of a rolling object is the sum of
Chapter 9-10 Test Review
 Chapter 9-10 Test Review Chapter Summary 9.2. The Second Condition for Equilibrium Explain torque and the factors on which it depends. Describe the role of torque in rotational mechanics. 10.1. Angular
Chapter 9-10 Test Review Chapter Summary 9.2. The Second Condition for Equilibrium Explain torque and the factors on which it depends. Describe the role of torque in rotational mechanics. 10.1. Angular
Physics 201. Professor P. Q. Hung. 311B, Physics Building. Physics 201 p. 1/1
 Physics 201 p. 1/1 Physics 201 Professor P. Q. Hung 311B, Physics Building Physics 201 p. 2/1 Rotational Kinematics and Energy Rotational Kinetic Energy, Moment of Inertia All elements inside the rigid
Physics 201 p. 1/1 Physics 201 Professor P. Q. Hung 311B, Physics Building Physics 201 p. 2/1 Rotational Kinematics and Energy Rotational Kinetic Energy, Moment of Inertia All elements inside the rigid
Chapter 8 Rotational Motion and Equilibrium. 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction
 Chapter 8 Rotational Motion and Equilibrium Name 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction 1. The distance between a turning axis and the
Chapter 8 Rotational Motion and Equilibrium Name 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction 1. The distance between a turning axis and the
Handout 7: Torque, angular momentum, rotational kinetic energy and rolling motion. Torque and angular momentum
 Handout 7: Torque, angular momentum, rotational kinetic energy and rolling motion Torque and angular momentum In Figure, in order to turn a rod about a fixed hinge at one end, a force F is applied at a
Handout 7: Torque, angular momentum, rotational kinetic energy and rolling motion Torque and angular momentum In Figure, in order to turn a rod about a fixed hinge at one end, a force F is applied at a
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
 AP Physics 1- Torque, Rotational Inertia, and Angular Momentum Practice Problems FACT: The center of mass of a system of objects obeys Newton s second law- F = Ma cm. Usually the location of the center
AP Physics 1- Torque, Rotational Inertia, and Angular Momentum Practice Problems FACT: The center of mass of a system of objects obeys Newton s second law- F = Ma cm. Usually the location of the center
Lecture 14. Rotational dynamics Torque. Give me a lever long enough and a fulcrum on which to place it, and I shall move the world.
 Lecture 14 Rotational dynamics Torque Give me a lever long enough and a fulcrum on which to place it, and I shall move the world. Archimedes, 87 1 BC EXAM Tuesday March 6, 018 8:15 PM 9:45 PM Today s Topics:
Lecture 14 Rotational dynamics Torque Give me a lever long enough and a fulcrum on which to place it, and I shall move the world. Archimedes, 87 1 BC EXAM Tuesday March 6, 018 8:15 PM 9:45 PM Today s Topics:
Class XI Chapter 7- System of Particles and Rotational Motion Physics
 Page 178 Question 7.1: Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie
Page 178 Question 7.1: Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie
Physics 111. Tuesday, November 2, Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy
 ics Tuesday, ember 2, 2002 Ch 11: Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy Announcements Wednesday, 8-9 pm in NSC 118/119 Sunday, 6:30-8 pm in CCLIR 468 Announcements This
ics Tuesday, ember 2, 2002 Ch 11: Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy Announcements Wednesday, 8-9 pm in NSC 118/119 Sunday, 6:30-8 pm in CCLIR 468 Announcements This
Rotational Dynamics. Slide 2 / 34. Slide 1 / 34. Slide 4 / 34. Slide 3 / 34. Slide 6 / 34. Slide 5 / 34. Moment of Inertia. Parallel Axis Theorem
 Slide 1 / 34 Rotational ynamics l Slide 2 / 34 Moment of Inertia To determine the moment of inertia we divide the object into tiny masses of m i a distance r i from the center. is the sum of all the tiny
Slide 1 / 34 Rotational ynamics l Slide 2 / 34 Moment of Inertia To determine the moment of inertia we divide the object into tiny masses of m i a distance r i from the center. is the sum of all the tiny
Unit 8 Notetaking Guide Torque and Rotational Motion
 Unit 8 Notetaking Guide Torque and Rotational Motion Rotational Motion Until now, we have been concerned mainly with translational motion. We discussed the kinematics and dynamics of translational motion
Unit 8 Notetaking Guide Torque and Rotational Motion Rotational Motion Until now, we have been concerned mainly with translational motion. We discussed the kinematics and dynamics of translational motion
31 ROTATIONAL KINEMATICS
 31 ROTATIONAL KINEMATICS 1. Compare and contrast circular motion and rotation? Address the following Which involves an object and which involves a system? Does an object/system in circular motion have
31 ROTATIONAL KINEMATICS 1. Compare and contrast circular motion and rotation? Address the following Which involves an object and which involves a system? Does an object/system in circular motion have
III. Work and Energy
 Rotation I. Kinematics - Angular analogs II. III. IV. Dynamics - Torque and Rotational Inertia Work and Energy Angular Momentum - Bodies and particles V. Elliptical Orbits The student will be able to:
Rotation I. Kinematics - Angular analogs II. III. IV. Dynamics - Torque and Rotational Inertia Work and Energy Angular Momentum - Bodies and particles V. Elliptical Orbits The student will be able to:
Physics. Chapter 8 Rotational Motion
 Physics Chapter 8 Rotational Motion Circular Motion Tangential Speed The linear speed of something moving along a circular path. Symbol is the usual v and units are m/s Rotational Speed Number of revolutions
Physics Chapter 8 Rotational Motion Circular Motion Tangential Speed The linear speed of something moving along a circular path. Symbol is the usual v and units are m/s Rotational Speed Number of revolutions
Torque. Introduction. Torque. PHY torque - J. Hedberg
 Torque PHY 207 - torque - J. Hedberg - 2017 1. Introduction 2. Torque 1. Lever arm changes 3. Net Torques 4. Moment of Rotational Inertia 1. Moment of Inertia for Arbitrary Shapes 2. Parallel Axis Theorem
Torque PHY 207 - torque - J. Hedberg - 2017 1. Introduction 2. Torque 1. Lever arm changes 3. Net Torques 4. Moment of Rotational Inertia 1. Moment of Inertia for Arbitrary Shapes 2. Parallel Axis Theorem
Chapter 8 Rotational Motion
 Chapter 8 Rotational Motion Chapter 8 Rotational Motion In this chapter you will: Learn how to describe and measure rotational motion. Learn how torque changes rotational velocity. Explore factors that
Chapter 8 Rotational Motion Chapter 8 Rotational Motion In this chapter you will: Learn how to describe and measure rotational motion. Learn how torque changes rotational velocity. Explore factors that
Chapter 12 Static Equilibrium
 Chapter Static Equilibrium. Analysis Model: Rigid Body in Equilibrium. More on the Center of Gravity. Examples of Rigid Objects in Static Equilibrium CHAPTER : STATIC EQUILIBRIUM AND ELASTICITY.) The Conditions
Chapter Static Equilibrium. Analysis Model: Rigid Body in Equilibrium. More on the Center of Gravity. Examples of Rigid Objects in Static Equilibrium CHAPTER : STATIC EQUILIBRIUM AND ELASTICITY.) The Conditions
Chapter 8 Lecture. Pearson Physics. Rotational Motion and Equilibrium. Prepared by Chris Chiaverina Pearson Education, Inc.
 Chapter 8 Lecture Pearson Physics Rotational Motion and Equilibrium Prepared by Chris Chiaverina Chapter Contents Describing Angular Motion Rolling Motion and the Moment of Inertia Torque Static Equilibrium
Chapter 8 Lecture Pearson Physics Rotational Motion and Equilibrium Prepared by Chris Chiaverina Chapter Contents Describing Angular Motion Rolling Motion and the Moment of Inertia Torque Static Equilibrium
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
Rotational Motion Test
 Rotational Motion Test Multiple Choice: Write the letter that best answers the question. Each question is worth 2pts. 1. Angular momentum is: A.) The sum of moment of inertia and angular velocity B.) The
Rotational Motion Test Multiple Choice: Write the letter that best answers the question. Each question is worth 2pts. 1. Angular momentum is: A.) The sum of moment of inertia and angular velocity B.) The
Circular Motion, Pt 2: Angular Dynamics. Mr. Velazquez AP/Honors Physics
 Circular Motion, Pt 2: Angular Dynamics Mr. Velazquez AP/Honors Physics Formulas: Angular Kinematics (θ must be in radians): s = rθ Arc Length 360 = 2π rads = 1 rev ω = θ t = v t r Angular Velocity α av
Circular Motion, Pt 2: Angular Dynamics Mr. Velazquez AP/Honors Physics Formulas: Angular Kinematics (θ must be in radians): s = rθ Arc Length 360 = 2π rads = 1 rev ω = θ t = v t r Angular Velocity α av
Test 7 wersja angielska
 Test 7 wersja angielska 7.1A One revolution is the same as: A) 1 rad B) 57 rad C) π/2 rad D) π rad E) 2π rad 7.2A. If a wheel turns with constant angular speed then: A) each point on its rim moves with
Test 7 wersja angielska 7.1A One revolution is the same as: A) 1 rad B) 57 rad C) π/2 rad D) π rad E) 2π rad 7.2A. If a wheel turns with constant angular speed then: A) each point on its rim moves with
Big Ideas 3 & 5: Circular Motion and Rotation 1 AP Physics 1
 Big Ideas 3 & 5: Circular Motion and Rotation 1 AP Physics 1 1. A 50-kg boy and a 40-kg girl sit on opposite ends of a 3-meter see-saw. How far from the girl should the fulcrum be placed in order for the
Big Ideas 3 & 5: Circular Motion and Rotation 1 AP Physics 1 1. A 50-kg boy and a 40-kg girl sit on opposite ends of a 3-meter see-saw. How far from the girl should the fulcrum be placed in order for the
PHYSICS 149: Lecture 21
 PHYSICS 149: Lecture 21 Chapter 8: Torque and Angular Momentum 8.2 Torque 8.4 Equilibrium Revisited 8.8 Angular Momentum Lecture 21 Purdue University, Physics 149 1 Midterm Exam 2 Wednesday, April 6, 6:30
PHYSICS 149: Lecture 21 Chapter 8: Torque and Angular Momentum 8.2 Torque 8.4 Equilibrium Revisited 8.8 Angular Momentum Lecture 21 Purdue University, Physics 149 1 Midterm Exam 2 Wednesday, April 6, 6:30
ΣF = ma Στ = Iα ½mv 2 ½Iω 2. mv Iω
 Thur Oct 22 Assign 9 Friday Today: Torques Angular Momentum x θ v ω a α F τ m I Roll without slipping: x = r Δθ v LINEAR = r ω a LINEAR = r α ΣF = ma Στ = Iα ½mv 2 ½Iω 2 I POINT = MR 2 I HOOP = MR 2 I
Thur Oct 22 Assign 9 Friday Today: Torques Angular Momentum x θ v ω a α F τ m I Roll without slipping: x = r Δθ v LINEAR = r ω a LINEAR = r α ΣF = ma Στ = Iα ½mv 2 ½Iω 2 I POINT = MR 2 I HOOP = MR 2 I
Rotation. I. Kinematics - Angular analogs
 Rotation I. Kinematics - Angular analogs II. III. IV. Dynamics - Torque and Rotational Inertia Work and Energy Angular Momentum - Bodies and particles V. Elliptical Orbits The student will be able to:
Rotation I. Kinematics - Angular analogs II. III. IV. Dynamics - Torque and Rotational Inertia Work and Energy Angular Momentum - Bodies and particles V. Elliptical Orbits The student will be able to:
Slide 1 / 37. Rotational Motion
 Slide 1 / 37 Rotational Motion Slide 2 / 37 Angular Quantities An angle θ can be given by: where r is the radius and l is the arc length. This gives θ in radians. There are 360 in a circle or 2π radians.
Slide 1 / 37 Rotational Motion Slide 2 / 37 Angular Quantities An angle θ can be given by: where r is the radius and l is the arc length. This gives θ in radians. There are 360 in a circle or 2π radians.
Physics 8 Wednesday, October 30, 2013
 Physics 8 Wednesday, October 30, 2013 HW9 (due Friday) is 7 conceptual + 8 calculation problems. Of the 8 calculation problems, 4 or 5 are from Chapter 11, and 3 or 4 are from Chapter 12. 7pm HW sessions:
Physics 8 Wednesday, October 30, 2013 HW9 (due Friday) is 7 conceptual + 8 calculation problems. Of the 8 calculation problems, 4 or 5 are from Chapter 11, and 3 or 4 are from Chapter 12. 7pm HW sessions:
Chapter 7. Rotational Motion
 Chapter 7 Rotational Motion In This Chapter: Angular Measure Angular Velocity Angular Acceleration Moment of Inertia Torque Rotational Energy and Work Angular Momentum Angular Measure In everyday life,
Chapter 7 Rotational Motion In This Chapter: Angular Measure Angular Velocity Angular Acceleration Moment of Inertia Torque Rotational Energy and Work Angular Momentum Angular Measure In everyday life,
Physics 8 Wednesday, October 25, 2017
 Physics 8 Wednesday, October 25, 2017 HW07 due Friday. It is mainly rotation, plus a couple of basic torque questions. And there are only 8 problems this week. For today, you read (in Perusall) Onouye/Kane
Physics 8 Wednesday, October 25, 2017 HW07 due Friday. It is mainly rotation, plus a couple of basic torque questions. And there are only 8 problems this week. For today, you read (in Perusall) Onouye/Kane
Moment of Inertia Race
 Review Two points, A and B, are on a disk that rotates with a uniform speed about an axis. Point A is closer to the axis than point B. Which of the following is NOT true? 1. Point B has the greater tangential
Review Two points, A and B, are on a disk that rotates with a uniform speed about an axis. Point A is closer to the axis than point B. Which of the following is NOT true? 1. Point B has the greater tangential
Physics 101 Lecture 11 Torque
 Physics 101 Lecture 11 Torque Dr. Ali ÖVGÜN EMU Physics Department www.aovgun.com Force vs. Torque q Forces cause accelerations q What cause angular accelerations? q A door is free to rotate about an axis
Physics 101 Lecture 11 Torque Dr. Ali ÖVGÜN EMU Physics Department www.aovgun.com Force vs. Torque q Forces cause accelerations q What cause angular accelerations? q A door is free to rotate about an axis
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination
PHYSICS. Chapter 12 Lecture FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E RANDALL D. KNIGHT Pearson Education, Inc.
 PHYSICS FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E Chapter 12 Lecture RANDALL D. KNIGHT Chapter 12 Rotation of a Rigid Body IN THIS CHAPTER, you will learn to understand and apply the physics
PHYSICS FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E Chapter 12 Lecture RANDALL D. KNIGHT Chapter 12 Rotation of a Rigid Body IN THIS CHAPTER, you will learn to understand and apply the physics
CHAPTER 9 ROTATIONAL DYNAMICS
 CHAPTER 9 ROTATIONAL DYNAMICS PROBLEMS. REASONING The drawing shows the forces acting on the person. It also shows the lever arms for a rotational axis perpendicular to the plane of the paper at the place
CHAPTER 9 ROTATIONAL DYNAMICS PROBLEMS. REASONING The drawing shows the forces acting on the person. It also shows the lever arms for a rotational axis perpendicular to the plane of the paper at the place
Chapter 10. Rotation of a Rigid Object about a Fixed Axis
 Chapter 10 Rotation of a Rigid Object about a Fixed Axis Angular Position Axis of rotation is the center of the disc Choose a fixed reference line. Point P is at a fixed distance r from the origin. A small
Chapter 10 Rotation of a Rigid Object about a Fixed Axis Angular Position Axis of rotation is the center of the disc Choose a fixed reference line. Point P is at a fixed distance r from the origin. A small
Big Idea 4: Interactions between systems can result in changes in those systems. Essential Knowledge 4.D.1: Torque, angular velocity, angular
 Unit 7: Rotational Motion (angular kinematics, dynamics, momentum & energy) Name: Big Idea 3: The interactions of an object with other objects can be described by forces. Essential Knowledge 3.F.1: Only
Unit 7: Rotational Motion (angular kinematics, dynamics, momentum & energy) Name: Big Idea 3: The interactions of an object with other objects can be described by forces. Essential Knowledge 3.F.1: Only
Chapter 8. Centripetal Force and The Law of Gravity
 Chapter 8 Centripetal Force and The Law of Gravity Centripetal Acceleration An object traveling in a circle, even though it moves with a constant speed, will have an acceleration The centripetal acceleration
Chapter 8 Centripetal Force and The Law of Gravity Centripetal Acceleration An object traveling in a circle, even though it moves with a constant speed, will have an acceleration The centripetal acceleration
Rotational Kinetic Energy
 Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
Moment of Inertia & Newton s Laws for Translation & Rotation
 Moment of Inertia & Newton s Laws for Translation & Rotation In this training set, you will apply Newton s 2 nd Law for rotational motion: Στ = Σr i F i = Iα I is the moment of inertia of an object: I
Moment of Inertia & Newton s Laws for Translation & Rotation In this training set, you will apply Newton s 2 nd Law for rotational motion: Στ = Σr i F i = Iα I is the moment of inertia of an object: I
Rotational Dynamics continued
 Chapter 9 Rotational Dynamics continued 9.4 Newton s Second Law for Rotational Motion About a Fixed Axis ROTATIONAL ANALOG OF NEWTON S SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS I = ( mr 2
Chapter 9 Rotational Dynamics continued 9.4 Newton s Second Law for Rotational Motion About a Fixed Axis ROTATIONAL ANALOG OF NEWTON S SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS I = ( mr 2
Welcome back to Physics 211
 Welcome back to Physics 211 Today s agenda: Moment of Inertia Angular momentum 13-2 1 Current assignments Prelecture due Tuesday after Thanksgiving HW#13 due next Wednesday, 11/24 Turn in written assignment
Welcome back to Physics 211 Today s agenda: Moment of Inertia Angular momentum 13-2 1 Current assignments Prelecture due Tuesday after Thanksgiving HW#13 due next Wednesday, 11/24 Turn in written assignment
α = p = m v L = I ω Review: Torque Physics 201, Lecture 21 Review: Rotational Dynamics a = Στ = I α
 Physics 1, Lecture 1 Today s Topics q Static Equilibrium of Rigid Objects(Ch. 1.1-3) Review: Rotational and Translational Motion Conditions for Translational and Rotational Equilibrium Demos and Exercises
Physics 1, Lecture 1 Today s Topics q Static Equilibrium of Rigid Objects(Ch. 1.1-3) Review: Rotational and Translational Motion Conditions for Translational and Rotational Equilibrium Demos and Exercises
Translational vs Rotational. m x. Connection Δ = = = = = = Δ = = = = = = Δ =Δ = = = = = 2 / 1/2. Work
 Translational vs Rotational / / 1/ Δ m x v dx dt a dv dt F ma p mv KE mv Work Fd / / 1/ θ ω θ α ω τ α ω ω τθ Δ I d dt d dt I L I KE I Work / θ ω α τ Δ Δ c t s r v r a v r a r Fr L pr Connection Translational
Translational vs Rotational / / 1/ Δ m x v dx dt a dv dt F ma p mv KE mv Work Fd / / 1/ θ ω θ α ω τ α ω ω τθ Δ I d dt d dt I L I KE I Work / θ ω α τ Δ Δ c t s r v r a v r a r Fr L pr Connection Translational
Rotational Motion. Every quantity that we have studied with translational motion has a rotational counterpart
 Rotational Motion & Angular Momentum Rotational Motion Every quantity that we have studied with translational motion has a rotational counterpart TRANSLATIONAL ROTATIONAL Displacement x Angular Displacement
Rotational Motion & Angular Momentum Rotational Motion Every quantity that we have studied with translational motion has a rotational counterpart TRANSLATIONAL ROTATIONAL Displacement x Angular Displacement
Chapter 10: Dynamics of Rotational Motion
 Chapter 10: Dynamics of Rotational Motion What causes an angular acceleration? The effectiveness of a force at causing a rotation is called torque. QuickCheck 12.5 The four forces shown have the same strength.
Chapter 10: Dynamics of Rotational Motion What causes an angular acceleration? The effectiveness of a force at causing a rotation is called torque. QuickCheck 12.5 The four forces shown have the same strength.
P12 Torque Notes.notebook. March 26, Torques
 Torques The size of a torque depends on two things: 1. The size of the force being applied (a larger force will have a greater effect) 2. The distance away from the pivot point (the further away from this
Torques The size of a torque depends on two things: 1. The size of the force being applied (a larger force will have a greater effect) 2. The distance away from the pivot point (the further away from this
Angular Momentum L = I ω
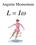 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
A. Incorrect! It looks like you forgot to include π in your calculation of angular velocity.
 High School Physics - Problem Drill 10: Rotational Motion and Equilbrium 1. If a bike wheel of radius 50 cm rotates at 300 rpm what is its angular velocity and what is the linear speed of a point on the
High School Physics - Problem Drill 10: Rotational Motion and Equilbrium 1. If a bike wheel of radius 50 cm rotates at 300 rpm what is its angular velocity and what is the linear speed of a point on the
Textbook Reference: Wilson, Buffa, Lou: Chapter 8 Glencoe Physics: Chapter 8
 AP Physics Rotational Motion Introduction: Which moves with greater speed on a merry-go-round - a horse near the center or one near the outside? Your answer probably depends on whether you are considering
AP Physics Rotational Motion Introduction: Which moves with greater speed on a merry-go-round - a horse near the center or one near the outside? Your answer probably depends on whether you are considering
Dynamics of Rotational Motion
 Chapter 10 Dynamics of Rotational Motion To understand the concept of torque. To relate angular acceleration and torque. To work and power in rotational motion. To understand angular momentum. To understand
Chapter 10 Dynamics of Rotational Motion To understand the concept of torque. To relate angular acceleration and torque. To work and power in rotational motion. To understand angular momentum. To understand
Definition. is a measure of how much a force acting on an object causes that object to rotate, symbol is, (Greek letter tau)
 Torque Definition is a measure of how much a force acting on an object causes that object to rotate, symbol is, (Greek letter tau) = r F = rfsin, r = distance from pivot to force, F is the applied force
Torque Definition is a measure of how much a force acting on an object causes that object to rotate, symbol is, (Greek letter tau) = r F = rfsin, r = distance from pivot to force, F is the applied force
Exam 3 Practice Solutions
 Exam 3 Practice Solutions Multiple Choice 1. A thin hoop, a solid disk, and a solid sphere, each with the same mass and radius, are at rest at the top of an inclined plane. If all three are released at
Exam 3 Practice Solutions Multiple Choice 1. A thin hoop, a solid disk, and a solid sphere, each with the same mass and radius, are at rest at the top of an inclined plane. If all three are released at
Chapter 12: Rotation of Rigid Bodies. Center of Mass Moment of Inertia Torque Angular Momentum Rolling Statics
 Chapter 12: Rotation of Rigid Bodies Center of Mass Moment of Inertia Torque Angular Momentum Rolling Statics Translational vs Rotational 2 / / 1/ 2 m x v dx dt a dv dt F ma p mv KE mv Work Fd P Fv 2 /
Chapter 12: Rotation of Rigid Bodies Center of Mass Moment of Inertia Torque Angular Momentum Rolling Statics Translational vs Rotational 2 / / 1/ 2 m x v dx dt a dv dt F ma p mv KE mv Work Fd P Fv 2 /
AP Pd 3 Rotational Dynamics.notebook. May 08, 2014
 1 Rotational Dynamics Why do objects spin? Objects can travel in different ways: Translation all points on the body travel in parallel paths Rotation all points on the body move around a fixed point An
1 Rotational Dynamics Why do objects spin? Objects can travel in different ways: Translation all points on the body travel in parallel paths Rotation all points on the body move around a fixed point An
Rolling, Torque, and Angular Momentum
 AP Physics C Rolling, Torque, and Angular Momentum Introduction: Rolling: In the last unit we studied the rotation of a rigid body about a fixed axis. We will now extend our study to include cases where
AP Physics C Rolling, Torque, and Angular Momentum Introduction: Rolling: In the last unit we studied the rotation of a rigid body about a fixed axis. We will now extend our study to include cases where
Torque. Physics 6A. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB
 Physics 6A Torque is what causes angular acceleration (just like a force causes linear acceleration) Torque is what causes angular acceleration (just like a force causes linear acceleration) For a torque
Physics 6A Torque is what causes angular acceleration (just like a force causes linear acceleration) Torque is what causes angular acceleration (just like a force causes linear acceleration) For a torque
Angular Momentum L = I ω
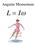 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Rotational Dynamics, Moment of Inertia and Angular Momentum
 Rotational Dynamics, Moment of Inertia and Angular Momentum Now that we have examined rotational kinematics and torque we will look at applying the concepts of angular motion to Newton s first and second
Rotational Dynamics, Moment of Inertia and Angular Momentum Now that we have examined rotational kinematics and torque we will look at applying the concepts of angular motion to Newton s first and second
Physics 201, Lecture 21
 Physics 201, Lecture 21 Today s Topics q Static Equilibrium of Rigid Objects(Ch. 12.1-3) Review: Rotational and Translational Motion Conditions for Translational and Rotational Equilibrium Demos and Exercises
Physics 201, Lecture 21 Today s Topics q Static Equilibrium of Rigid Objects(Ch. 12.1-3) Review: Rotational and Translational Motion Conditions for Translational and Rotational Equilibrium Demos and Exercises
Chapter 9- Static Equilibrium
 Chapter 9- Static Equilibrium Changes in Office-hours The following changes will take place until the end of the semester Office-hours: - Monday, 12:00-13:00h - Wednesday, 14:00-15:00h - Friday, 13:00-14:00h
Chapter 9- Static Equilibrium Changes in Office-hours The following changes will take place until the end of the semester Office-hours: - Monday, 12:00-13:00h - Wednesday, 14:00-15:00h - Friday, 13:00-14:00h
Rolling, Torque & Angular Momentum
 PHYS 101 Previous Exam Problems CHAPTER 11 Rolling, Torque & Angular Momentum Rolling motion Torque Angular momentum Conservation of angular momentum 1. A uniform hoop (ring) is rolling smoothly from the
PHYS 101 Previous Exam Problems CHAPTER 11 Rolling, Torque & Angular Momentum Rolling motion Torque Angular momentum Conservation of angular momentum 1. A uniform hoop (ring) is rolling smoothly from the
Question 7.1: Answer. Geometric centre; No
 Question 7.1: Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring,, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside
Question 7.1: Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring,, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside
Rotational Motion What is the difference between translational and rotational motion? Translational motion.
 Rotational Motion 1 1. What is the difference between translational and rotational motion? Translational motion Rotational motion 2. What is a rigid object? 3. What is rotational motion? 4. Identify and
Rotational Motion 1 1. What is the difference between translational and rotational motion? Translational motion Rotational motion 2. What is a rigid object? 3. What is rotational motion? 4. Identify and
Chap. 10: Rotational Motion
 Chap. 10: Rotational Motion I. Rotational Kinematics II. Rotational Dynamics - Newton s Law for Rotation III. Angular Momentum Conservation (Chap. 10) 1 Newton s Laws for Rotation n e t I 3 rd part [N
Chap. 10: Rotational Motion I. Rotational Kinematics II. Rotational Dynamics - Newton s Law for Rotation III. Angular Momentum Conservation (Chap. 10) 1 Newton s Laws for Rotation n e t I 3 rd part [N
