1. THE CALCULUS OF VARIATIONS
|
|
|
- Timothy Franklin
- 5 years ago
- Views:
Transcription
1 1. HE CALCULUS OF VARIAIONS During he cold wr (s I her he sory), couple of nmeless superpowers invesed gre del of reserch monies ino solving opimizion prolems involving rjecories nmely, ino finding he opiml wy o lunch missiles ino your opponens living rooms nd schools. Ech of hese superpowers independenly developed sregy for solving hese prolems. his redundncy llows us o ckle simple dynmic opimizion prolems wih he dynmic progrmming pproch dvnced y Bellmn nd ohers or lernively wih he mximum principle of Ponrygin nd his crew. One of my fvorie quoes is on Mr. Ponrygin s recion o lerning ou he Bellmn sregy in less delice erms, he uhor of his line likened Ponrygin s recion o person hndling ded r. Being le o ell his sory is one of my fvorie prs of eing le o lk ou he pproches o dynmic prolems, s well s eing le o ell my friends nd fmily h I prcice rocke science in my spre ime. While he mximum principle nd dynmic progrmming hve heir own srengh nd limiions in solving hese prolems, I hve menioned lredy heir common wekness: s hey re wrien, hey work well only in simple vriionl prolems. he clculus of vriions ws pioneered y such noles s he Bernoulli Brohers, heir suden Euler, nd some of heir drinking uddies. Originlly someone ws posed wih he sk of designing curved werslide for seveneenhcenury werprk: he prolem ws o pick he shpe h go people from poin A o poin B s quickly s possile, ccelered only y grviy. his is known s he rchisochrone prolem. he soluion is no srigh line i is slide shped like cycloid, priculr funcion h is iniilly firly seep, geing shllower. he generl vriionl prolem is h we would like o pick ph for prmerized vrile o mximize he inegrl of some given funcion of h vrile. he simple cse (s I deem i) presens his inegrl: J( x)= f( x(),«( x ), ) d
2 he chllenge is o find n exremum ( mximum or minimum) of Jx ( ) wih respec o some funcion x (); Jx ( ) is ofen clled he cos funcion of he conrol x (). he noion x «( ) denoes he firs pril derivive of x () wih respec o ime. here is n ddiionl requiremen for he funcion x (): we re given he endpoins x ( ) nd x ( ). In he rchisochrone prolem, hese were wo poins in spce nd we were sked o find he ph eween hem h hd he les ime cos (ime is money when you re werprk). his form works for ny dynmic prolem in which one mus consider oh he effecs of some vrile s well s chnging i for insnce, hink of firm h ries o mximize profis, which re funcion of cpil nd lor, over numer of ime periods. I is lso fced wih cos of djusing is workforce or cpil rining nd lyoff coss for lor, insllion nd removl coss for mchinery. In he sence of such djusmen coss, he profi funcion over yer migh look like: ( )= [ ( ) ] Π k, l p y k ( ), l( ) w l() r k () d where y is producion funcion from kpil nd lor, nd p is he price of oupu. he second nd hird erms in he inegrnd re he coss of hiring hese inpus. Of course, we re old he moun of ech h we sred he yer wih, nd our consulns hve dvised us wh our rges should e he end. Now consider djusmen coss, which my look like: [ ] ( )= ( ) ( ) Π k, l p y k ( ), l ( ) w l () r k () c «l(), k «() d his is very rel prolem fcing firms ouside simple sic models of producion. he hing wihin rckes fis ino he form specified for he simple cse, nd we mus use he clculus of vriions (in one form or noher) o solve i. he soluion o he simple cse sisfies he Euler-Lgrnge equion; ll vriionl prolems re solved wih some generlizion of his. Here is n lmos heorem for he simple cse: provided we don hve differeniiliy prolems, in order for x () = rg mx J( x)= rg mx f( x ( ), x «( ), d ), sujec o iniil nd erminl condiions on x, i is necessry h he funcion lso sisfy he equion:
3 f d f = x d x«h s he punchline, he sis ool of he clculus of vriions! How is his derived, he ineresed reder my sk? (he unineresed reder my choose o skip his lmos proof.) he generl ide is h we ke he differenil of he cos funcion nd se i equl o zero: f δj x δ δ δ δ x x f x xd f x x d f ( )= + x x d = + = ««««he ide conveyed y δx is h we hve vried he funcion x lile i hroughou, hough we were required o hold down he endpoins. For no ppren reson, some very clever person ried inegring he ls erm in his equion y prs. He found h: = = f x x d f x x d f δ xd ««δ δ «d x«= his goes ck ino he differenil of J: = = f δj x δ δ δ x x d d f f ( )= x d d x x x + = ««he ls erm requires us o evlue he differenil δx is endpoins. Bu when we were vrying he funcion x, we were required o keep he iniil nd erminl vlues unchnged nd his mens h he ls erm equls zero! hen he pproprie condiion for opimliy is f d f δj( x)= δx d x d x = «One wy o solve his, clerly, is o se he erm in rckes equl o zero for ll [, ]. he firs fundmenl lemm of he clculus of vriions ells us h his is he only wy o chieve h condiion for ll dmissile choices of δx h is, for ll he possile wys o vry he funcion x, keeping i differenile enough nd keeping is endpoins unchnged. QED! (More or less.) Knowing how he simple resul is derived llows us o derive our own opimliy condiions when he prolem doesn fi ino he form of he simple cse. However, le s look couple of exmples firs.
4 Exmple: he mximum principle. Le s reurn o he generl opiml conrol prolem. Recll h in he generl cse, we were sked o solve (his funcion f is differen from he funcion f in he vriionl prolem): ( ) mx u f x( ), u( ), d sujec o: x«() g x(), u(), My inclinion is o re his like plin old consrined opimizion prolem excep wih consrin for ech ime period. he Lgrnge muliplier for ime is represened y λ( ). My inuiion is o define his Lgrngin funcion: = ( ) ( )= ( ) + [ ( ) ] L x (), u (), f x (), u (), d λ() g x (), u (), x «( ) d [ ] = ( )+ [ ( ) ] f x(), u(), λ() g x(), u(), x«( ) d he second line ppers o e in form similr o he simple cse. Since x () nd u () nd heir ime derivives re he only vriles showing up in he inegrnd, I wrie ou he Euler-Lgrnge equions for opimliy: ( f u)+ λ( ) ( g u)= ( f x)+ λ() ( g x)+ ( dλ d)= Wih sligh rerrngemen of he second condiion, hese ecome: f u+ λ( ) g u = f x+ λ() g x= λ«() I is lef s n exercise o he reder o flip ck secion or wo nd verify h hese re excly he sme opimliy condiions required y he Ponrygin mximum principle. Exmple: djusmen coss. Le s go ck o he cse of our firm h hd o mximize profis, sujec o coss of djusing heir cpil nd lor socks: [ ] ( )= ( ) ( ) Π k, l p y k ( ), l ( ) w l () r k () c «l(), k «() d he necessry condiions o opimize his prolem re: p yk d c k ( (), l() ) («l (), «() ) r + = k () d k «() p yk w d c k ( (), l() ) («l (), «() ) + = () d «l l () he firm will generlly no se he mrginl revenue produc of fcor equl o he fcor price in he presence of djusmen coss. his will e he cse only if he djusmen cos is he sme ll imes; wih decresing reurns o scle i will e he cse only if he firm is mking no chnges in cpil nd lor.
5 Exmple: squndering n inherince. A =, our friend gins ccess o his rus fund, sses vlued A. He wns o live off of his for he res of his life wihou working. Le c () denoe his consumpion ime. he cn -ke-iwih-you heorem sys h no erminl sses or des re permied: A ( )=. His lifeime uiliy is represened s: ( )= ( ) β Uc e uc () d he chnge in his sses wih ime cn e descried y: A «() = ρa () c () where ρ is he insnneous ineres re. Susiuing his ck ino his uiliy funcion, we ge h lifeime uiliy depends on he chosen ph A () nd A. «() ( ) β Uc ( )= e uρ A () A «() d his is vriion on he Solow growh model. he rue Euler-Lgrnge equion here ers some similriy o wh mcroeconomiss imprecisely descrie s Euler equions : β d β ρe u c d e ( ())+ [ u ( c () )]= ρ β u c() u c ()«( c) ( ) ( ) ( ) = hose re nice resuls, hough generlly his pproch hs no dvnge over he Bellmn nd Ponrygin sregies. Wh, however, hppens when good prolems go d when he simple Euler-Lgrnge formul fils us, or does no go fr enough? Here re some vriions on h equion. Vriion 1. A simple rewriing of he equion h my or my no provide more insigh ino he simple cse: f d f = x d x«+ + f = xx x f xx x f f ««««««x«x his is essenilly wh I did in order o derive he implicion of he Euler equion of he inherince squndering exmple: proceeding o olly differenie he derivive wih respec o A. «()
6 Vriion. he cos funcion my conin higher-order derivives of x, wih he inerpreion h here is some cos o djusing he sock nd ddiionl coss o chnging he re of djusmen: ( d n )= ( d d d n ) d d n n dx dx d x dx dx d x J x,,, K,, f x,,, K,, d hen we require iniil nd erminl condiions for x s well s for he firs n-1 ime derivives. he generlizion of he Euler-Lgrnge equion is: n f d f ( ) + d f ( ) + ( n d f K 1) x d d d ( ) = dx dx n n d x d n d d Exmple: inherince squndering wih he persisence of memory. Le s revisi his prolem, dding wis: our idle rich friend grows ccusomed o his sndrd of living, nd so here is some psychic cos of chnging his consumpion eween periods. I model his hi-forming uiliy funcion s: ( )= ( ) β Uc e uc (),«( c) d he udge consrin in his prolem gives us he chnge in consumpion: c () = ρ A () A «() c «() = ρ A «() A ««() We would hve o mke some sor of ssumpions or inferences ou he iniil nd erminl vlues of c «( ), u hen lifeime uiliy cn e wrien s funcion of he ime ph of sses, s well s is firs wo derivives: β Uc ( )= e uρa () A «(), ρa «() A ««() d ( ) he opimliy condiion is: β u d u u d u e e e e c + β d c β β ρ ρ = c «d c «Expnding his is relly messy, which is one of mny good reson no o work wih hi-forming preferences. Vriion 3. he cos funcion my e inegred over region in Ω R k, nd x is funcion of k prmeers h I cll,, K, : 1 k ( d n )= ( d d 1 k d1 d dk 1 k) 1 k n dx dx d x dx dx dx J x,,, K,, K f x(,, K, );,, K, ;,, K, d d Kd Ω wih n iniil nd erminl condiion for x. he necessry condiion for his prolem is:
7 f d f x d dx d ( ) d d f dx ( d ) 1 1 d f K dk dx ( d k ) = Exmple: inherince squndering wih your spouse. As is oo ofen he cse, our chelor friend hs kicked ll his es his nd gone nd goen himself mrried. Wih discouning included in he funcion u (, i ), his lifeime is once gin given y: U1( c)= u1( c1(), ) d And his spouse hs similr uiliy. Becuse of some rgining rrngemen, hey wn o mximize he produc of heir lifeime uiliies. his is known s he Nsh socil welfre funcion: 1 ( )= ( ) ( ) Nc (), cs ( ) u c (), u cs ( ), sdsd
8 HINK SMALL WHEN HINKING VARIAIONALLY n he clssicl vriionl prolems is o find funcion x: R o solve prolem of he form: mx f( x( ), x«( ), ) d s.. x( ) =, x() 1 = Admissile soluions o he prolem, s fr s we re concerned, re in suse of C. Unless non-exisen or corner, he soluion x * will sisfy he Euler- Lgrnge equion: f () d f () = ƒ [, 1] * * x () d x«() he derivion of his formul comes s follows. Firs, we define loss funcion for priculr conrol x; h is, JC R defined y: ( ) = ( ) J x : f x( ),«( x ), d : hen we consider some funcions which re wee iny perurions δx of he funcion x. he chnge in he loss is: f () f () δj( x; δx) : = ( δx ()) d+ ( δx «( )) d x () x «( ) Nurlly, his loss will e zero for sionry x *. In order o ge rid of h nsy erm δ«x, we re going o hve o rememer o use some inegrion-y-prs rick: = f () d f () f () δj( x; δx) : = δx () d δx () d δx () ( ) x () ( ) + d x «( ) x «( ) Bu if we re only considering perurions which leve he endpoins unchnged he only sensile ones we ll hve h ( δx() ) = nd ( δx() ) = =, so =1 h he ls erm disppers. A his poin we ll invoke he firs fundmenl lemm of vriionl clculus, which siclly sys: ( g ())( δy ()) d= δy () smll { g () ƒ } And so we hve he desired resul, f () d f () = * * x () d x«() Unless we wn o prove he lemm, h s more or less QED. = 1 Bu his isn he wy h Euler did i. Bck in his dy, infiniesimls were ll he rge. Ldies in Pris frequenly wore hem on heir hs. A h ime, we would
9 hve hough ou picking some relly, relly ig ineger N (infiniely lrge!) nd hen se = 1 N. he ide of n inegrl ws inerchngele wih h of sum: = N + f x x d f x x x ( (),«( ),) =,, = If we wn o exremize his prolem, we would seek sequence of { x } o solve he prolem. We don even need o ssume nyhing ou he disnce eween x nd x + nmely, i doesn even hve o e coninuous, or coninuously differenile. Believe i or no, his is n dvnge when working wih so-clled swooh prolems nd oher cses in which he soluion requires somehing like chering. So how does one find he sequence of { x } o mximize he funcion? Essenilly, jus find he sionry x on heir own, which should sisfy: = N + f x x x =,, x = f + f f = x x«x«f f 1 f x x«x«= f f : = x x«h s jus so slick, i s hrd o elieve h i cully plces fewer resricions on se of dmissile conrols. I lso kes ou 9 seconds o derive on he ck of n envelope, when you cn recll he formul. We hve sor of glossed over wheher ll x eing sionry is necessry o mximize he prolem, u i urns ou o e lmos necessry. Prolem: Using he usul mehod, find he necessry condiion for conrol x () o mximize he prolem: [ o, 1] ( ) f x(), x( s),«( x ),«( x s) ds d hen ry finding he necessry condiions using Euler s infiniesiml mehod. Prolem: Using he oh mehods, find he soluion o he prolem: min ( 1+ x ) 1+ («1) x d wih x = x1 =. In ech cse, verify h his is in fc soluion.
10 n he clssicl vriionl prolems is o find funcion x: R o solve prolem of he form: mx f( x( ), x«( ), ) d s.. x( ) =, x() 1 = Admissile soluions o he prolem, s fr s we re concerned, re in suse of C. Unless non-exisen or corner, he soluion x * will sisfy he Euler- Lgrnge equion: f () d f () = ƒ [, 1] * * x () d x«() he derivion of his formul comes s follows. Firs, we define loss funcion for priculr conrol x; h is, JC R defined y: ( ) = ( ) J x : f x( ),«( x ), d : hen we consider some funcions which re wee iny perurions δx of he funcion x. he chnge in he loss is: f () f () δj( x; δx) : = ( δx ()) d+ ( δx «( )) d x () x «( ) Nurlly, his loss will e zero for sionry x *. In order o ge rid of h nsy erm δ«x, we re going o hve o rememer o use some inegrion-y-prs rick: = f () d f () f () δj( x; δx) : = δx () d δx () d δx () ( ) x () ( ) + d x «( ) x «( ) Bu if we re only considering perurions which leve he endpoins unchnged he only sensile ones we ll hve h ( δx() ) = nd ( δx() ) = =, so =1 h he ls erm disppers. A his poin we ll invoke he firs fundmenl lemm of vriionl clculus, which siclly sys: ( g ())( δy ()) d= δy () smll { g () ƒ } And so we hve he desired resul, f () d f () = * * x () d x«() Unless we wn o prove he lemm, h s more or less QED. = 1 Bu his isn he wy h Euler did i. Bck in his dy, infiniesimls were ll he rge. Ldies in Pris frequenly wore hem on heir hs. A h ime, we would
11 hve hough ou picking some relly, relly ig ineger N (infiniely lrge!) nd hen se = 1 N. he ide of n inegrl ws inerchngele wih h of sum: = N + f x x d f x x x ( (),«( ),) =,, = If we wn o exremize his prolem, we would seek sequence of { x } o solve he prolem. We don even need o ssume nyhing ou he disnce eween x nd x + nmely, i doesn even hve o e coninuous, or coninuously differenile. Believe i or no, his is n dvnge when working wih so-clled swooh prolems nd oher cses in which he soluion requires somehing like chering. So how does one find he sequence of { x } o mximize he funcion? Essenilly, jus find he sionry x on heir own, which should sisfy: = N + f x x x =,, x = f + f f = x x«x«f f 1 f x x«x«= f f : = x x«h s jus so slick, i s hrd o elieve h i cully plces fewer resricions on se of dmissile conrols. I lso kes ou 9 seconds o derive on he ck of n envelope, when you cn recll he formul. We hve sor of glossed over wheher ll x eing sionry is necessry o mximize he prolem, u i urns ou o e lmos necessry. Prolem: Using he usul mehod, find he necessry condiion for conrol x () o mximize he prolem: [ o, 1] ( ) f x(), x( s),«( x ),«( x s) ds d hen ry finding he necessry condiions using Euler s infiniesiml mehod. Prolem: Using he oh mehods, find he soluion o he prolem: min ( 1+ x ) 1+ («1) x d wih x = x1 =. In ech cse, verify h his is in fc soluion.
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
( ) ( ) ( ) ( ) ( ) ( y )
 8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
MTH 146 Class 11 Notes
 8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
 Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Mathematics 805 Final Examination Answers
 . 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
. 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
Properties of Logarithms. Solving Exponential and Logarithmic Equations. Properties of Logarithms. Properties of Logarithms. ( x)
 Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Chapter 2: Evaluative Feedback
 Chper 2: Evluive Feedbck Evluing cions vs. insrucing by giving correc cions Pure evluive feedbck depends olly on he cion ken. Pure insrucive feedbck depends no ll on he cion ken. Supervised lerning is
Chper 2: Evluive Feedbck Evluing cions vs. insrucing by giving correc cions Pure evluive feedbck depends olly on he cion ken. Pure insrucive feedbck depends no ll on he cion ken. Supervised lerning is
Honours Introductory Maths Course 2011 Integration, Differential and Difference Equations
 Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
Some Inequalities variations on a common theme Lecture I, UL 2007
 Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples.
 Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).
![INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q). INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).](/thumbs/78/77677920.jpg) INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
the approaches to dynamic problems, as well as being able to tell my friends and family that I practice rocket science in my spare time.
 6. Calculus of variaions and opimal conrol heory So you ve heard my sory aou he Cold War superpowers solving opimizaion prolems involving rajecories namely, ino finding he opimal way o launch missiles
6. Calculus of variaions and opimal conrol heory So you ve heard my sory aou he Cold War superpowers solving opimizaion prolems involving rajecories namely, ino finding he opimal way o launch missiles
Chapter 2. First Order Scalar Equations
 Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Magnetostatics Bar Magnet. Magnetostatics Oersted s Experiment
 Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE BOUNDARY-VALUE PROBLEM
 Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
3D Transformations. Computer Graphics COMP 770 (236) Spring Instructor: Brandon Lloyd 1/26/07 1
 D Trnsformions Compuer Grphics COMP 770 (6) Spring 007 Insrucor: Brndon Lloyd /6/07 Geomery Geomeric eniies, such s poins in spce, exis wihou numers. Coordines re nming scheme. The sme poin cn e descried
D Trnsformions Compuer Grphics COMP 770 (6) Spring 007 Insrucor: Brndon Lloyd /6/07 Geomery Geomeric eniies, such s poins in spce, exis wihou numers. Coordines re nming scheme. The sme poin cn e descried
Math 2142 Exam 1 Review Problems. x 2 + f (0) 3! for the 3rd Taylor polynomial at x = 0. To calculate the various quantities:
 Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Average & instantaneous velocity and acceleration Motion with constant acceleration
 Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
REAL ANALYSIS I HOMEWORK 3. Chapter 1
 REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
PHYSICS 1210 Exam 1 University of Wyoming 14 February points
 PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
Chapter Direct Method of Interpolation
 Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 9: The High Beta Tokamak
 .65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
.65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
= ( ) ) or a system of differential equations with continuous parametrization (T = R
 XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
1 jordan.mcd Eigenvalue-eigenvector approach to solving first order ODEs. -- Jordan normal (canonical) form. Instructor: Nam Sun Wang
 jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
3. Renewal Limit Theorems
 Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
How to Prove the Riemann Hypothesis Author: Fayez Fok Al Adeh.
 How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
Some basic notation and terminology. Deterministic Finite Automata. COMP218: Decision, Computation and Language Note 1
 COMP28: Decision, Compuion nd Lnguge Noe These noes re inended minly s supplemen o he lecures nd exooks; hey will e useful for reminders ou noion nd erminology. Some sic noion nd erminology An lphe is
COMP28: Decision, Compuion nd Lnguge Noe These noes re inended minly s supplemen o he lecures nd exooks; hey will e useful for reminders ou noion nd erminology. Some sic noion nd erminology An lphe is
MAT 266 Calculus for Engineers II Notes on Chapter 6 Professor: John Quigg Semester: spring 2017
 MAT 66 Clculus for Engineers II Noes on Chper 6 Professor: John Quigg Semeser: spring 7 Secion 6.: Inegrion by prs The Produc Rule is d d f()g() = f()g () + f ()g() Tking indefinie inegrls gives [f()g
MAT 66 Clculus for Engineers II Noes on Chper 6 Professor: John Quigg Semeser: spring 7 Secion 6.: Inegrion by prs The Produc Rule is d d f()g() = f()g () + f ()g() Tking indefinie inegrls gives [f()g
Essential Microeconomics : OPTIMAL CONTROL 1. Consider the following class of optimization problems
 Essenial Microeconomics -- 6.5: OPIMAL CONROL Consider he following class of opimizaion problems Max{ U( k, x) + U+ ( k+ ) k+ k F( k, x)}. { x, k+ } = In he language of conrol heory, he vecor k is he vecor
Essenial Microeconomics -- 6.5: OPIMAL CONROL Consider he following class of opimizaion problems Max{ U( k, x) + U+ ( k+ ) k+ k F( k, x)}. { x, k+ } = In he language of conrol heory, he vecor k is he vecor
( ) a system of differential equations with continuous parametrization ( T = R + These look like, respectively:
 XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
() t. () t r () t or v. ( t) () () ( ) = ( ) or ( ) () () () t or dv () () Section 10.4 Motion in Space: Velocity and Acceleration
 Secion 1.4 Moion in Spce: Velociy nd Acceleion We e going o dive lile deepe ino somehing we ve ledy inoduced, nmely () nd (). Discuss wih you neighbo he elionships beween posiion, velociy nd cceleion you
Secion 1.4 Moion in Spce: Velociy nd Acceleion We e going o dive lile deepe ino somehing we ve ledy inoduced, nmely () nd (). Discuss wih you neighbo he elionships beween posiion, velociy nd cceleion you
TEACHING STUDENTS TO PROVE BY USING ONLINE HOMEWORK Buma Abramovitz 1, Miryam Berezina 1, Abraham Berman 2
 TEACHING STUDENTS TO PROVE BY USING ONLINE HOMEWORK Bum Armoviz 1, Mirym Berezin 1, Arhm Bermn 1 Deprmen of Mhemics, ORT Brude College, Krmiel, Isrel Deprmen of Mhemics, Technion IIT, Hf, Isrel Asrc We
TEACHING STUDENTS TO PROVE BY USING ONLINE HOMEWORK Bum Armoviz 1, Mirym Berezin 1, Arhm Bermn 1 Deprmen of Mhemics, ORT Brude College, Krmiel, Isrel Deprmen of Mhemics, Technion IIT, Hf, Isrel Asrc We
Hermite-Hadamard-Fejér type inequalities for convex functions via fractional integrals
 Sud. Univ. Beş-Bolyi Mh. 6(5, No. 3, 355 366 Hermie-Hdmrd-Fejér ype inequliies for convex funcions vi frcionl inegrls İmd İşcn Asrc. In his pper, firsly we hve eslished Hermie Hdmrd-Fejér inequliy for
Sud. Univ. Beş-Bolyi Mh. 6(5, No. 3, 355 366 Hermie-Hdmrd-Fejér ype inequliies for convex funcions vi frcionl inegrls İmd İşcn Asrc. In his pper, firsly we hve eslished Hermie Hdmrd-Fejér inequliy for
Solutions to Problems from Chapter 2
 Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
3 Motion with constant acceleration: Linear and projectile motion
 3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
1. Consider a PSA initially at rest in the beginning of the left-hand end of a long ISS corridor. Assume xo = 0 on the left end of the ISS corridor.
 In Eercise 1, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 1. Consider PSA iniilly res in he beginning of he lef-hnd
In Eercise 1, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 1. Consider PSA iniilly res in he beginning of he lef-hnd
Question Details Int Vocab 1 [ ] Question Details Int Vocab 2 [ ]
![Question Details Int Vocab 1 [ ] Question Details Int Vocab 2 [ ] Question Details Int Vocab 1 [ ] Question Details Int Vocab 2 [ ]](/thumbs/92/109283538.jpg) /3/5 Assignmen Previewer 3 Bsic: Definie Inegrls (67795) Due: Wed Apr 5 5 9: AM MDT Quesion 3 5 6 7 8 9 3 5 6 7 8 9 3 5 6 Insrucions Red ody's Noes nd Lerning Gols. Quesion Deils In Vocb [37897] The chnge
/3/5 Assignmen Previewer 3 Bsic: Definie Inegrls (67795) Due: Wed Apr 5 5 9: AM MDT Quesion 3 5 6 7 8 9 3 5 6 7 8 9 3 5 6 Insrucions Red ody's Noes nd Lerning Gols. Quesion Deils In Vocb [37897] The chnge
Green s Functions and Comparison Theorems for Differential Equations on Measure Chains
 Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
A 1.3 m 2.5 m 2.8 m. x = m m = 8400 m. y = 4900 m 3200 m = 1700 m
 PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
Tax Audit and Vertical Externalities
 T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
f(x) dx with An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples dx x x 2
 Impope Inegls To his poin we hve only consideed inegls f() wih he is of inegion nd b finie nd he inegnd f() bounded (nd in fc coninuous ecep possibly fo finiely mny jump disconinuiies) An inegl hving eihe
Impope Inegls To his poin we hve only consideed inegls f() wih he is of inegion nd b finie nd he inegnd f() bounded (nd in fc coninuous ecep possibly fo finiely mny jump disconinuiies) An inegl hving eihe
Economics 8105 Macroeconomic Theory Recitation 6
 Economics 8105 Macroeconomic Theory Reciaion 6 Conor Ryan Ocober 11h, 2016 Ouline: Opimal Taxaion wih Governmen Invesmen 1 Governmen Expendiure in Producion In hese noes we will examine a model in which
Economics 8105 Macroeconomic Theory Reciaion 6 Conor Ryan Ocober 11h, 2016 Ouline: Opimal Taxaion wih Governmen Invesmen 1 Governmen Expendiure in Producion In hese noes we will examine a model in which
A new model for solving fuzzy linear fractional programming problem with ranking function
 J. ppl. Res. Ind. Eng. Vol. 4 No. 07 89 96 Journl of pplied Reserch on Indusril Engineering www.journl-prie.com new model for solving fuzzy liner frcionl progrmming prolem wih rning funcion Spn Kumr Ds
J. ppl. Res. Ind. Eng. Vol. 4 No. 07 89 96 Journl of pplied Reserch on Indusril Engineering www.journl-prie.com new model for solving fuzzy liner frcionl progrmming prolem wih rning funcion Spn Kumr Ds
LAPLACE TRANSFORMS. 1. Basic transforms
 LAPLACE TRANSFORMS. Bic rnform In hi coure, Lplce Trnform will be inroduced nd heir properie exmined; ble of common rnform will be buil up; nd rnform will be ued o olve ome dierenil equion by rnforming
LAPLACE TRANSFORMS. Bic rnform In hi coure, Lplce Trnform will be inroduced nd heir properie exmined; ble of common rnform will be buil up; nd rnform will be ued o olve ome dierenil equion by rnforming
Chapter 2. Motion along a straight line. 9/9/2015 Physics 218
 Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
MATH 124 AND 125 FINAL EXAM REVIEW PACKET (Revised spring 2008)
 MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS
 - TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
- TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
How to prove the Riemann Hypothesis
 Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Problem Set 5. Graduate Macro II, Spring 2017 The University of Notre Dame Professor Sims
 Problem Se 5 Graduae Macro II, Spring 2017 The Universiy of Nore Dame Professor Sims Insrucions: You may consul wih oher members of he class, bu please make sure o urn in your own work. Where applicable,
Problem Se 5 Graduae Macro II, Spring 2017 The Universiy of Nore Dame Professor Sims Insrucions: You may consul wih oher members of he class, bu please make sure o urn in your own work. Where applicable,
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR IAN KNOWLES
 A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
p-adic Egyptian Fractions
 p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
This document was generated at 1:04 PM, 09/10/13 Copyright 2013 Richard T. Woodward. 4. End points and transversality conditions AGEC
 his documen was generaed a 1:4 PM, 9/1/13 Copyrigh 213 Richard. Woodward 4. End poins and ransversaliy condiions AGEC 637-213 F z d Recall from Lecure 3 ha a ypical opimal conrol problem is o maimize (,,
his documen was generaed a 1:4 PM, 9/1/13 Copyrigh 213 Richard. Woodward 4. End poins and ransversaliy condiions AGEC 637-213 F z d Recall from Lecure 3 ha a ypical opimal conrol problem is o maimize (,,
Numerical Approximations to Fractional Problems of the Calculus of Variations and Optimal Control
 Numericl Approximions o Frcionl Problems of he Clculus of Vriions nd Opiml Conrol Shkoor Pooseh, Ricrdo Almeid, Delfim F. M. Torres To cie his version: Shkoor Pooseh, Ricrdo Almeid, Delfim F. M. Torres.
Numericl Approximions o Frcionl Problems of he Clculus of Vriions nd Opiml Conrol Shkoor Pooseh, Ricrdo Almeid, Delfim F. M. Torres To cie his version: Shkoor Pooseh, Ricrdo Almeid, Delfim F. M. Torres.
More on Magnetically C Coupled Coils and Ideal Transformers
 Appenix ore on gneiclly C Couple Coils Iel Trnsformers C. Equivlen Circuis for gneiclly Couple Coils A imes, i is convenien o moel mgneiclly couple coils wih n equivlen circui h oes no involve mgneic coupling.
Appenix ore on gneiclly C Couple Coils Iel Trnsformers C. Equivlen Circuis for gneiclly Couple Coils A imes, i is convenien o moel mgneiclly couple coils wih n equivlen circui h oes no involve mgneic coupling.
white strictly far ) fnf regular [ with f fcs)8( hs ) as function Preliminary question jointly speaking does not exist! Brownian : APA Lecture 1.
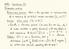 Am : APA Lecure 13 Brownin moion Preliminry quesion : Wh is he equivlen in coninuous ime of sequence of? iid Ncqe rndom vribles ( n nzn noise ( 4 e Re whie ( ie se every fm ( xh o + nd covrince E ( xrxs
Am : APA Lecure 13 Brownin moion Preliminry quesion : Wh is he equivlen in coninuous ime of sequence of? iid Ncqe rndom vribles ( n nzn noise ( 4 e Re whie ( ie se every fm ( xh o + nd covrince E ( xrxs
3.1.3 INTRODUCTION TO DYNAMIC OPTIMIZATION: DISCRETE TIME PROBLEMS. A. The Hamiltonian and First-Order Conditions in a Finite Time Horizon
 3..3 INRODUCION O DYNAMIC OPIMIZAION: DISCREE IME PROBLEMS A. he Hamilonian and Firs-Order Condiions in a Finie ime Horizon Define a new funcion, he Hamilonian funcion, H. H he change in he oal value of
3..3 INRODUCION O DYNAMIC OPIMIZAION: DISCREE IME PROBLEMS A. he Hamilonian and Firs-Order Condiions in a Finie ime Horizon Define a new funcion, he Hamilonian funcion, H. H he change in he oal value of
A new model for limit order book dynamics
 Anewmodelforlimiorderbookdynmics JeffreyR.Russell UniversiyofChicgo,GrdueSchoolofBusiness TejinKim UniversiyofChicgo,DeprmenofSisics Absrc:Thispperproposesnewmodelforlimiorderbookdynmics.Thelimiorderbookconsiss
Anewmodelforlimiorderbookdynmics JeffreyR.Russell UniversiyofChicgo,GrdueSchoolofBusiness TejinKim UniversiyofChicgo,DeprmenofSisics Absrc:Thispperproposesnewmodelforlimiorderbookdynmics.Thelimiorderbookconsiss
Inventory Management Models with Variable Holding Cost and Salvage value
 OSR Journl of Business nd Mngemen OSR-JBM e-ssn: -X p-ssn: 9-. Volume ssue Jul. - Aug. PP - www.iosrjournls.org nvenory Mngemen Models wi Vrile Holding os nd Slvge vlue R.Mon R.Venkeswrlu Memics Dep ollege
OSR Journl of Business nd Mngemen OSR-JBM e-ssn: -X p-ssn: 9-. Volume ssue Jul. - Aug. PP - www.iosrjournls.org nvenory Mngemen Models wi Vrile Holding os nd Slvge vlue R.Mon R.Venkeswrlu Memics Dep ollege
The average rate of change between two points on a function is d t
 SM Dae: Secion: Objecive: The average rae of change beween wo poins on a funcion is d. For example, if he funcion ( ) represens he disance in miles ha a car has raveled afer hours, hen finding he slope
SM Dae: Secion: Objecive: The average rae of change beween wo poins on a funcion is d. For example, if he funcion ( ) represens he disance in miles ha a car has raveled afer hours, hen finding he slope
IX.1.1 The Laplace Transform Definition 700. IX.1.2 Properties 701. IX.1.3 Examples 702. IX.1.4 Solution of IVP for ODEs 704
 Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 6, 8 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 6, 8 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Physics 2A HW #3 Solutions
 Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
dt = C exp (3 ln t 4 ). t 4 W = C exp ( ln(4 t) 3) = C(4 t) 3.
 Mah Rahman Exam Review Soluions () Consider he IVP: ( 4)y 3y + 4y = ; y(3) = 0, y (3) =. (a) Please deermine he longes inerval for which he IVP is guaraneed o have a unique soluion. Soluion: The disconinuiies
Mah Rahman Exam Review Soluions () Consider he IVP: ( 4)y 3y + 4y = ; y(3) = 0, y (3) =. (a) Please deermine he longes inerval for which he IVP is guaraneed o have a unique soluion. Soluion: The disconinuiies
Seminar 4: Hotelling 2
 Seminar 4: Hoelling 2 November 3, 211 1 Exercise Par 1 Iso-elasic demand A non renewable resource of a known sock S can be exraced a zero cos. Demand for he resource is of he form: D(p ) = p ε ε > A a
Seminar 4: Hoelling 2 November 3, 211 1 Exercise Par 1 Iso-elasic demand A non renewable resource of a known sock S can be exraced a zero cos. Demand for he resource is of he form: D(p ) = p ε ε > A a
The Brock-Mirman Stochastic Growth Model
 c December 3, 208, Chrisopher D. Carroll BrockMirman The Brock-Mirman Sochasic Growh Model Brock and Mirman (972) provided he firs opimizing growh model wih unpredicable (sochasic) shocks. The social planner
c December 3, 208, Chrisopher D. Carroll BrockMirman The Brock-Mirman Sochasic Growh Model Brock and Mirman (972) provided he firs opimizing growh model wih unpredicable (sochasic) shocks. The social planner
Bridging the gap: GCSE AS Level
 Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
FM Applications of Integration 1.Centroid of Area
 FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
Two Coupled Oscillators / Normal Modes
 Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER 2
 ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER Seion Eerise -: Coninuiy of he uiliy funion Le λ ( ) be he monooni uiliy funion defined in he proof of eisene of uiliy funion If his funion is oninuous y hen
ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER Seion Eerise -: Coninuiy of he uiliy funion Le λ ( ) be he monooni uiliy funion defined in he proof of eisene of uiliy funion If his funion is oninuous y hen
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
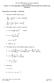 .615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
Review of Gaussian Quadrature method
 Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
LAPLACE TRANSFORM OVERCOMING PRINCIPLE DRAWBACKS IN APPLICATION OF THE VARIATIONAL ITERATION METHOD TO FRACTIONAL HEAT EQUATIONS
 Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
10. State Space Methods
 . Sae Space Mehods. Inroducion Sae space modelling was briefly inroduced in chaper. Here more coverage is provided of sae space mehods before some of heir uses in conrol sysem design are covered in he
. Sae Space Mehods. Inroducion Sae space modelling was briefly inroduced in chaper. Here more coverage is provided of sae space mehods before some of heir uses in conrol sysem design are covered in he
1. Find a basis for the row space of each of the following matrices. Your basis should consist of rows of the original matrix.
 Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
Intermediate Macro In-Class Problems
 Inermediae Macro In-Class Problems Exploring Romer Model June 14, 016 Today we will explore he mechanisms of he simply Romer model by exploring how economies described by his model would reac o exogenous
Inermediae Macro In-Class Problems Exploring Romer Model June 14, 016 Today we will explore he mechanisms of he simply Romer model by exploring how economies described by his model would reac o exogenous
IX.1.1 The Laplace Transform Definition 700. IX.1.2 Properties 701. IX.1.3 Examples 702. IX.1.4 Solution of IVP for ODEs 704
 Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 4, 7 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 4, 7 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Lecture 2e Orthogonal Complement (pages )
 Lecture 2e Orthogonl Complement (pges -) We hve now seen tht n orthonorml sis is nice wy to descrie suspce, ut knowing tht we wnt n orthonorml sis doesn t mke one fll into our lp. In theory, the process
Lecture 2e Orthogonl Complement (pges -) We hve now seen tht n orthonorml sis is nice wy to descrie suspce, ut knowing tht we wnt n orthonorml sis doesn t mke one fll into our lp. In theory, the process
Online Appendix to Solution Methods for Models with Rare Disasters
 Online Appendix o Soluion Mehods for Models wih Rare Disasers Jesús Fernández-Villaverde and Oren Levinal In his Online Appendix, we presen he Euler condiions of he model, we develop he pricing Calvo block,
Online Appendix o Soluion Mehods for Models wih Rare Disasers Jesús Fernández-Villaverde and Oren Levinal In his Online Appendix, we presen he Euler condiions of he model, we develop he pricing Calvo block,
1B40 Practical Skills
 B40 Prcticl Skills Comining uncertinties from severl quntities error propgtion We usully encounter situtions where the result of n experiment is given in terms of two (or more) quntities. We then need
B40 Prcticl Skills Comining uncertinties from severl quntities error propgtion We usully encounter situtions where the result of n experiment is given in terms of two (or more) quntities. We then need
P441 Analytical Mechanics - I. Coupled Oscillators. c Alex R. Dzierba
 Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Problem 1 / 25 Problem 2 / 20 Problem 3 / 10 Problem 4 / 15 Problem 5 / 30 TOTAL / 100
 eparmen of Applied Economics Johns Hopkins Universiy Economics 602 Macroeconomic Theory and Policy Miderm Exam Suggesed Soluions Professor Sanjay hugh Fall 2008 NAME: The Exam has a oal of five (5) problems
eparmen of Applied Economics Johns Hopkins Universiy Economics 602 Macroeconomic Theory and Policy Miderm Exam Suggesed Soluions Professor Sanjay hugh Fall 2008 NAME: The Exam has a oal of five (5) problems
graph of unit step function t
 .5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
.5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
Appendix 14.1 The optimal control problem and its solution using
 1 Appendix 14.1 he opimal conrol problem and is soluion using he maximum principle NOE: Many occurrences of f, x, u, and in his file (in equaions or as whole words in ex) are purposefully in bold in order
1 Appendix 14.1 he opimal conrol problem and is soluion using he maximum principle NOE: Many occurrences of f, x, u, and in his file (in equaions or as whole words in ex) are purposefully in bold in order
Lecture 3: Equivalence Relations
 Mthcmp Crsh Course Instructor: Pdric Brtlett Lecture 3: Equivlence Reltions Week 1 Mthcmp 2014 In our lst three tlks of this clss, we shift the focus of our tlks from proof techniques to proof concepts
Mthcmp Crsh Course Instructor: Pdric Brtlett Lecture 3: Equivlence Reltions Week 1 Mthcmp 2014 In our lst three tlks of this clss, we shift the focus of our tlks from proof techniques to proof concepts
FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m)
![FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m) FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m)](/thumbs/75/72845579.jpg) Univ. Beogrd. Pul. Elekroehn. Fk. Ser. M. 8 (997), 79{83 FUTHE GENEALIZATIONS OF INEQUALITIES FO AN INTEGAL QI Feng Using he Tylor's formul we prove wo inegrl inequliies, h generlize K. S. K. Iyengr's
Univ. Beogrd. Pul. Elekroehn. Fk. Ser. M. 8 (997), 79{83 FUTHE GENEALIZATIONS OF INEQUALITIES FO AN INTEGAL QI Feng Using he Tylor's formul we prove wo inegrl inequliies, h generlize K. S. K. Iyengr's
Positive and negative solutions of a boundary value problem for a
 Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
14. The fundamental theorem of the calculus
 4. The funmenl heorem of he clculus V 20 00 80 60 40 20 0 0 0.2 0.4 0.6 0.8 v 400 200 0 0 0.2 0.5 0.8 200 400 Figure : () Venriculr volume for subjecs wih cpciies C = 24 ml, C = 20 ml, C = 2 ml n (b) he
4. The funmenl heorem of he clculus V 20 00 80 60 40 20 0 0 0.2 0.4 0.6 0.8 v 400 200 0 0 0.2 0.5 0.8 200 400 Figure : () Venriculr volume for subjecs wih cpciies C = 24 ml, C = 20 ml, C = 2 ml n (b) he
Improper Integrals. The First Fundamental Theorem of Calculus, as we ve discussed in class, goes as follows:
 Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
Solutions Problem Set 3 Macro II (14.452)
 Soluions Problem Se 3 Macro II (14.452) Francisco A. Gallego 04/27/2005 1 Q heory of invesmen in coninuous ime and no uncerainy Consider he in nie horizon model of a rm facing adjusmen coss o invesmen.
Soluions Problem Se 3 Macro II (14.452) Francisco A. Gallego 04/27/2005 1 Q heory of invesmen in coninuous ime and no uncerainy Consider he in nie horizon model of a rm facing adjusmen coss o invesmen.
