1. The vibrating string problem revisited.
|
|
|
- Shon Atkinson
- 5 years ago
- Views:
Transcription
1 Weeks 7 8: S eprtion of Vribes In the pst few weeks we hve expored the possibiity of soving first nd second order PDEs by trnsforming them into simper forms ( method of chrcteristics. Unfortuntey, this process often does not hep much. If we strt with n rbitrry second order PDE, nd reduce it to cnonic form, most ikey we sti do not know how to find the gener soutions. In the foowing few weeks, we wi introduce method tht re much more powerfu t finding soutions thn the method of chrcteristics. The min ide is seprtion of vribes.. The vibrting string probem revisited. We consider the system u t t c u x x =, < x <, t > ( u( x, = f( x, x, ( u t ( x, = g( x, x, ( 3 u(, t =, t, ( 4 u(, t =, t. ( 5 In the pst week we hve tried to sove this system using the gener soution formus of the wve equtions. We hve seen tht it is not possibe to write cen formu for the soution nd therefore very hrd to extrct much informtion from it. Now we try nother pproch. Insted of trying to get the gener soution, we sk, wht is the simpest nontrivi soution of the wve eqution ( without considering the initi nd boundry conditions? One possibiity is the speci form u( x, t = X( x T( t. ( 6 We pug this into the eqution to see when we wi be so ucky to hve such soutions. We obtin which eds to X T = c X T ( 7 X X = c T T. ( 8 This seems to be compicted eqution unti we reized tht X /X is function of x ony nd T /T is function of t ony. The equity cn hod ony if both X /X nd T /T re constnts. From this we see tht u( x, t = X( x T( t is soution to the wve eqution if there is constnt λ such tht From ODE theory we know tht the soutions re X λ X =, ( 9 T λ c T =. ( X( x = A e λ / x + B e λ / x, T( t = A e λ / c t + B e λ / c t. ( To fix the rbitrry constnts, we now consider the boundry conditions u(, t = u(, t = ( but sti negect the initi conditions, which gives X( = X( =. ( Discussing the cses λ >, =, < ( see pp of the textbook we see tht this cn be stisfied by nonzero X ony if. A =, nd λ = ( 3 Therefore. To see this, differentite the eqution by, we hve x of x ony. X( x = X n ( x for some n N, ( 4 x ( X = which gives X X X = constnt becuse it is function
2 where X n ( x = B n sin x for some rbitrry constnt B n. It foows tht c c T( t = T n ( t = C n cos t + D n sin t for rbitrry constnts C n nd D n. We hve shown tht soutions of the form X( t T( t re ( c c α cos t + β sin t sin x where α, β re constnts. Now it s time to tke into ccount the initi conditions. If we tke t =, we hve f( x = u( x, = α sin x g( x = u t ( x, = β n c sin ( 5 ( 6 ( 7, ( 8 x. ( 9 which re cery not true for most f nd g! Does this men the method fis? Not so fst. Rec tht for iner equtions, finite or even infinite sums of soutions re sti soutions ( certin conditions ppy. Therefore, if we cn find finitey mny constnts α n, β n : n =,, m or infinitey mny constnts α n, β n such tht or m f( x = f( x = α n sin x, g( x = m α n sin x, g( x = β n n c β n n c sin x, ( sin x, ( then the soution u cn be written s either u( x, t = m ( c c α n cos t + β n sin t sin x ( or u( x, t = ( c c α n cos t + β n sin t sin x. ( 3 It turns out tht finite sum representtion is in gener not possibe, we hve to rey on the infinite sums. To indeed crry this out, we need to nswer the foowing questions:. Cn we represent rbitrry f, g?. If we cn, how to compute the coefficients α n, β n? 3. Does the infinite sum represent function? Tht is, does the sum converge? 4. If the infinite sum converges to function, does this function sove the eqution nd stisfy the initi nd boundry conditions? The nswers to these questions form the bsics of the theory of Fourier series. We wi study Fourier series in the foowing one to two ectures before returning to the method of seprtion of vribes. Remrk. Wht is the retion between our new formu u( x, t = ( c c α n cos t + β n sin t sin x ( 4 nd our previous one using gener soutions? Using bsic trignometric formus: cos( x ± y = cos x cos y sin x sin y, sin( x ± y = sin x cos y ± cos x sin y ( 5
3 we esiy obtin u( x, t = or equiventy with { α n } sin ( x + c t sin ( x c t + β n cos ( x c t cos ( x + c t φ( x = u( x, t = φ( x + c t + ψ( x c t ( 6 α n sin x β n cos x, ( 7 ψ( x = β n cos x α n sin x. ( 8 We see tht ψ( x = φ( x nd φ( x = ψ( x s we know. Remrk. As we wi soon see, oftentimes we cnnot obtin cosed form formu for u nd hve to ive with the infinite sum. Recing our motivtion to do better thn the method of chrcteristics one my wonder wht the difference is. The difference is the foowing. When we cnnot sove the probem by method of chrcteristics, we re toty stuck; On the other hnd, the coefficients in the infinite sum te us much informtion of the soution.. Fourier Series. Rec the issues we woud ike to sette.. Cn we represent rbitrry f, g?. If we cn, how to compute the coefficients α n, β n? 3. Does the infinite sum represent function? Tht is, does the sum converge? 4. If the infinite sum converges to function, does this function sove the eqution nd stisfy the initi nd boundry conditions?.. Representtion of functions by Fourier series. We first try to sette the first two questions. We study whether ny function f cn be represented in the form f( x = α n sin x. ( 9 First we notice tht, for ny f representbe in the bove fshion, formy ( tht is negecting ny convergence issues reted to infinite sums f( k = f( x + = α n sin k = α n f( x = α n sin ( x + = In other words, ny function tht is possibe to be represented must stisfy i. f( k =, ii. f( x dx =, α n sin( k n =, ( 3 sin x dx =, ( 3 α n sin x + n. ( 3
4 iii. f( x + = f( x tht is f is periodic function with period ; Or equiventy, we cn ony represent functions defined over interv of ength. As we woud ike to represent s mny functions s possibe, we woud try to fix the bove restrictions. i. f( k = : The reson for this restriction is tht sin k =, it is esiy fixed by introducing cos x into the series. ii. f( x dx = : Even with cos s introduced, we sti hve f( x dx =. Therefore we need to introduce one more term constnt reting to f( x dx into the series. iii. f( x + = f( x : There is currenty no wy to fix this. We wi mention bit bout this in few ectures. Now the representtion becomes ( we hve chnged the nottions bit to be consistent with the textbook f( x = + ( x x n cos + b k sin. ( 33 for f with period. In the foowing we wi show how to find the coefficients.. We strt with. As we hve seen, the introduction of is to ow us to represent function with nonzero men. Therefore we integrte the representtion over (, : f( x dx = dx + ( ( k x ( k x k cos dx + b k sin dx =. ( 34 k = Therefore = f( x dx. ( 35 To obtin n nd b n, we notice x ( m x { n = m cos cos dx = ( 36 n m x ( m x cos sin dx = ( 37 x ( m x { n = m sin sin dx = ( 38 n m Therefore n = x f( x cos dx; b k = Remrk 3. The interv (, cn be repced by ny interv of ength. From the bove formus, we cery see tht x f( x sin dx. ( 39 f( x is odd n = n =,,, ( 4 f( x is even b n = n =,, ( 4 Tht is, when f is odd, ony sin s re invoved in the Fourier series nd when f is even ony cos s re invoved. In these cses, we ony need hf of f to determine the coefficients: f even: n = x f( x cos dx, b n =, n =,,, ( 4 f odd: b n = x f( x sin dx, n =, n =,, ( 43
5 Exmpe 4. ( 6. 4 Find the Fourier series of the foowing function { x < x < f( x = h is constnt. ( 44 h < x < Soution. As f is defined over (,, =. We compute = f( x dx = x dx + h dx = + h = h ; ( 45 n = f( x cos( n x dx = x cos( n x dx + h cos( n x dx = x dsin( n x + h n n sin( n x = n x sin( n x sin( n x dx + h n n sin( n x = n ( cos( n x = ( n n. ( 46 b k = f( x sin( n x dx = x sin( n x dx + h sin( n x dx = x dcos( n x + h sin( n x dx n = x cos( n x cos( n x dx + h cos( n x n = ( ( n n n sin( n x + h ( ( n = ( n + h ( ( n n = h ( h + ( n. ( 47 n Therefore the representtion is f( x = h 4 + ( n ( n cos( n x + n h ( h + ( sin( n x. ( 48 n Exmpe 5. ( c Obtin the Fourier cosine series representtion for the foowing functions: f( x = x, < x <. ( 49 Soution. Obtin the Fourier cosine series effectivey mens extending f eveny nd obtin its Fourier series. Or equiventy, use the formus n = x f( x cos dx, b n =, n =,,, ( 5 Thus =. We compute = x dx = 3. ( 5
6 nd n = x cos( n x dx = x dsin( n x n = x sin( n x n 4 = n x dcos( n x 4 = n x cos( n x The Fourier cosine series representtion is then x sin( n x dx cos( n x dx = 4 ( n n. ( ( n n cos( n x. ( 53 Remrk 6. Mthemticy speking, wht we hve done is the foowing. We hve shown tht, if function f( x cn be represented by f( x = + ( x x n cos + b n sin. ( 54 Then the coefficients must be given by n = x f( x cos dx, n =,,, ( 55 b n = x f( x sin dx, n =,, ( 56 To estbish sound mthemtic theory, we hve to study whether the sequence + ( x x n cos + b n sin, ( 57 with coefficients given by the bove formus, converges to the function f... C onvergence nd other issues. We mention quicky theories reting the 3rd nd 4th questions. In fct, due to imited time, we wi ony mention quicky the questions tht wi be nswered by the theory of Fourier series. First we review wht we hve so fr. We re concerned with soving the initi-boundry probem u t t c u x x =, < x <, t > ( 58 u( x, = f( x, x, ( 59 u t ( x, = g( x, x, ( 6 u(, t =, t, ( 6 u(, t =, t. ( 6 We re be to construct the foowing infinite sum: ( c c α n cos t + β n sin t sin x ( 63
7 nd hope tht this is our soution. Mthemticy the foowing re required:. The sum gives function. Tht is we cn define u( x, t = ( c c α n cos t + β n sin. The eqution is stisfies by this function. Tht is i. t t u( x, t nd x x u( x, t re we-defined for < x <, t >, ii. u t t c u x x = for < x <, t >. t sin x. ( 64 We note tht if we cn differentite the sum termwise, then the eqution wi be stisfied. 3. Correct initi vues re tken. f( x = g( x = in pproprite senses, nd furthermore im u( x, t = u( x,, im t α n sin x β n n c sin x ( 65 ( 66 t u t( x, t = u t ( x,. ( 67 Tht is, the t imit is the sme s the resut of setting t = in ech term of the infinite sum. 4. Correct boundry vues re tken. im u( x, t = u(, t, im x u( x, t = u(, t ( 68 x where u(, t, u(, t re the vues of the infinite sum when we repce x by nd in the infinite sum. From the bove we see tht the foowing questions need to be nswered for Fourier series:. Given function, is the corresponding Fourier series converging to this function?. Given n infinite sum of sin s nd cos s, when is it convergent to resonbe function? 3. If the series converges to function, when is this function differentibe? Does the derivtive coincide with the sum of termwise derivtive of ech term? Tht is if f( x = + ( n cos x + b n sin x ( 69 when do we hve the existence of f, f, etc. nd furthermore when do we hve ( d p dx p f( x = 4. Cn we tke termwise imits. Tht is ( x x im n cos + b n sin =? = x x ( d p ( d p n dx pcos x + b n dx psin x. ( 7 ( x x n cos + b n sin. ( 7 Of course in fct the bove questions need to be nswered for doube Fourier series. The nswers to the bove questions re highy invoved. We just give the shortest ( reds: crudest nswers here. Answer to. If f is piecewise continuous, then its Fourier series converges to f t of its continuous points, nd converges to f ( x + + f ( x t discontinuous points. In prticur, if f is uniformy continuous, the convergence is uniform.
8 Answer to nd 4. Yes s ong s n + b n <. Answer to 3. Yes s ong s p ( n + b n <. Remrk 7. Finy we mention few resons why Fourier series is widey ppied in modern mthemtics nd science. Fourier series cn be obtined for wide css of functions. b The prti sum f N = + N ( x x n cos + b n sin is the best pproximnt of f in the foowing sense f N = rgmin g VN ( f g dx ( 73 where V N is the spce of functions of the form α + N ( x x α n cos + β n sin. ( 74 ( 7 Furthermore we hve the Prsev s retion + ( n + b n = f( x dx. ( 75 c Most importnty, the sin s nd cos s re eigenfunctions of derivtive opertors. In prticur, differentition of one Fourier series resuts in nother Fourier series. This is why Fourier series is ubiquitous in modern theory of PDEs.. 3. C ompex Fourier series. Recing we hve cos x = ei x + e i x + ( n cos x + b n sin x where, sin x = eix e ix, ( 76 ( = c + k = c n e inx / + c n e inx / = c n e i nx/. ( 77 c =, c n = n i b n, c n = n + i b n. ( 78 This series is ced the compex Fourier series. Note tht, insted of computing c k from k nd b k, we cn obtin the coefficients directy: c = f( x dx, ( 79 c n = f( x e inx / dx, n = ±, ±, ( 8 Remrk 8. We emphsize gin tht the interv (, cn be repced by ny interv of ength. In this cse the Prsev s retion tkes more estheticy stisfctory form: c n = f( x dx. ( 8
9 Exmpe 9. ( 6. 4, 5 b Expnd the foowing function to compex Fourier series f( x = cosh x, < x <. ( 8 Soution. We hve =. Rec tht cosh x = e x + e x. We compute c = e x + e x dx = ( e e ; ( 83 c k = e x + e x e ik x dx = e ( ik x dx + e ( + ik x dx 4 = 4 i k e( ik x + i k e ( + ik x = ( e ( k e ( k ( e ( k e ( k 4 i k + i k = 4 ( i k + + i k ( e e ( k = ( k ( e + k e. ( 84 Noticing + =, the compex Fourier series cn be written in the foowing compct form: f( x = k = ( k ( e + k e e ik x. ( Doube Fourier series. We just mention tht the theory of Fourier series cn be extended to functions with more thn one vribes. For exmpe, in D, insted of cos x nd sin x, we hve four combintions cos x cos y, cos x sin y, sin x cos y, sin x sin y. ( 86 See 6. of the textbook for detis. Remrk. In higher dimensions, the compex representtion becomes more convenient to use, s insted of d combintions of sin s nd cos s ( d is the dimension, we cn simpy write the gener form of the bsis function s where k = k k d, x = x x d. e i k x ( Non-periodic functions nd Fourier trnsform. We hve presented stisfctory theory for periodic functions. Now how bout non-periodic functions? Here we give hint of wht hppens in this gener cse. We tke the interv to be (,. Rec the compex Fourier series formus for f with period : with c n = Furthermore we hve the Prsev s retion f( x = c n = c n e i n x, ( 88 f( x e inx / dx. ( 89 f( x dx. ( 9
10 Now setting we hve λ = n, c λ = c n, ( 9 dλ = dn =, ( 9 nd the bove formus cn be formy re-written s ( tking λ f( x = c n e i n = c n e i λ x dn = c λ e iλ x dn = c λ e iλ x dλ, ( 93 c λ = c n = f( x e iλ x dx f( x e iλ x dx, ( 94 c ( λ dλ = c n dn = cn = f( x dx f( x dx. ( 95 The formus c λ = f( x e iλ x dx, f( x = c λ e iλ x dλ ( 96 re ced the Fourier trnsform. It turns out tht these formus, incuding the Prsev s retion c λ dλ = f( x dx ( 97 cn be rigorousy derived for resonby rge css of functions. For trignometric version of the Fourier trnsform theory, see 6. 3 of the textbook. 3. Appictions of the Fourier series theory. The theory of Fourier series cn be ppied to mny PDE probems. 3.. The wve eqution. We return to the probem u t t c u x x =, < x <, t > ( 98 We hve seen tht the soution cn be represented by u( x, t = ( ( n cos n c c t + b n sin with the coefficients determined from u( x, = f( x, x, ( 99 u t ( x, = g( x, x, ( u(, t =, t, ( u(, t =, t. ( f( x = u( x, = n sin b n c x t sin x ( 3 ( 4 sin x. ( 5 g( x = u t ( x, = Now we try to compute n, b n. First we shoud note probem here. The formu determining the coefficients for the Fourier series reds n = f( x sin x dx, ( 6. In fct, the Fourier trnsform theory is the foundtion of compete gener theory of iner prti differenti equtions, the deveoper L. Hörmnder ws wrded the Fieds Med due to this contribution.
11 but our f( x is ony defined on (,. Therefore we need to extend f( x to (, in n pproprite wy. This extension must not produce ny cos terms. Therefore we shoud extend f oddy, { f( x < x < f ( x = ( 7 f( x < x < which eds to n = f ( x sin x dx = f( x sin x dx. ( 8 Simiry we hve b n = g( x sin x dx. ( 9 n c Exmpe. ( 7. 9 Sove u t t = c u x x, < x <, t > ( u( x, = x ( x, x, ( u t ( x, =, x, ( Soution. We hve =. Compute n = x ( x sin x dx = x ( x dcos x n = x ( x cos x n = ( x dsin x = ( x sin x 4 = sin x dx 4 = 3 cos x It is cer tht b n = s u t ( x, =. Therefore the soution is u(, t =, t, ( 3 u(, t =, t. ( 4 cos x ( x dx sin x ( dx = 4 ( ( n 3. ( 5 u( x, t = 4 ( ( n 3.. The het eqution. We consider the initi-boundry probem of the her eqution 3 cos c t sin x. ( 6 u t k u x x =, < x <, t > ( 7 u(, t =, t ( 8 u(, t =, t ( 9 u( x, = f( x, x. (
12 We consider soution of the form Substituting into the eqution we obtin u( x, t = X( x T( t. ( X T = k X T Simir to wht we hve done for the wve eqution, we concude for some constnt λ. Now considering the boundry condition, we hve nd consequenty ( up to constnt fctor X = X n sin nd ( up to constnt fctor T T = k X X. ( T = k λ T, X = λ X ( 3 X = λ X, X( = X( = ( 4 x ( 5 T = k n T T( t = e k t. ( 6 Thus we expect the gener soution to tke the form u( x, t = n e ( k t n sin x. ( 7 where the coefficients n = f( x sin x dx The Lpce eqution. Consider the probem We sove it using seprtion of vribes. Consider Substituting into the eqution we obtin which eds to u x x + u y y =, < x <, < x < b, ( 8 u( x, = f( x, x ( 9 u( x, b =, x, ( 3 u x (, y =, y b, ( 3 u x (, y =, y b. ( 3 u( x, y = X( x Y( y. ( 33 X Y + X Y = X X = Y Y ( 34 X λ X =, Y + λ Y = ( 35 for some constnt λ. Tking into ccount the boundry conditions for X, we hve, X λ X =, X ( = X ( = λ = X = An cos x ( 36 nd therefore, when n, Y Y =, Y(, Y( b = Y = B n e n y e n b e n y n = B n sinh( ( y b. ( 37
13 When n =, Thus the soution shoud be represented by Y =, Y( =, Y( b = Y = B ( y/b. ( 38 u( x, y = ( b y b To determine the coefficients, we use + f( x = u( x, = + n cos x sinh ( y b. ( 39 ( n sinh n b cos x which gives ( note tht we re expnding into cosine series here = x f( x dx, n = ( n b f( x cos. ( 4 sinh Nonhomogeneous probems. Now we show the power of the method of seprtion of vribes ( more precisey, the power of Fourier series by studying probem tht is beyond the power of the method of chrcteristics we hve erned. ( 4 u t t c u x x = h( x, t, < x <, t > ( 4 u( x, = f( x, x ( 43 u t ( x, = g( x, x ( 44 u(, t =, t ( 45 u(, t =, t. ( 46 As h( x, t is not seprted, it is not possibe to find ny soution of form u( x, t = X( x T( t for the eqution u t t c u x x = h( x, t. ( 47 However, it is sti possibe to sove this probem using our knowedge of Fourier series. We ssume the soution tkes the form 3 u( x, t = u n ( t sin x. ( 48 Reders fmiir with ODE theory my recognize this s PDE version of the vrition of constnts method. Aso note tht We need to represent h( x, t by sin x too. h( x, t = h n ( t sin x, h n ( t = h( x, t sin x dx. ( 49 Now the eqution becomes Now it is cer tht with initi conditions u n ( t + c un ( t sin x = h n ( t sin x. ( 5 u n ( t + c un ( t = h n ( t ( 5 c u n ( = n, u n ( = b n ( 5 ( n 3. Note tht, s we hve u(, t = u(, t =, Fourier sine series is reevnt. Therefore we ony keep the sin x terms.
14 where n nd b n re from the sine series of f nd g: f( x = n sin x n = g( x = c b n sin x To sove this eqution, we notice tht b n = n c f( x sin x dx, ( 53 g( x sin x dx. ( 54 u n ( t = v n ( t + w n ( t ( 55 where v n nd w n sove c c v n ( t + vn ( t =, v n ( = n, v n ( = b n, ( 56 c w n ( t + vn ( t = h n ( t, w n ( =, w n ( =. ( 57 The former eqution yieds c c v n ( t = n cos t + b n sin t ; ( 58 To sove the second eqution, we need the foowing Duhme s principe: The soution to the eqution is given by where w( t; s soves v ( t + λ v( t = h( t, v( =, v ( = ( 59 v( t = Using the bove principe we hve c w n ( t = Therefore the soution is { n u( x, t = } s ds sin x. t w( t; s ds ( 6 w ( t + λ w( t =, w( s =, w ( s = h( s. ( 6 c cos t Exmpe. ( 7. 9 Sove the probem t c h n ( s sin ( t s ds. ( 6 c + b n sin Soution. Rec tht we shoud use the formu u( x, t = { c c n cos x + b n sin } s ds sin x. t + c t h n ( s c sin ( t ( 63 u t t c u x x = A x, < x <, t > ( 64 u( x, =, x ( 65 u t ( x, =, x ( 66 u(, t =, t > ( 67 u(, t =, t > ( 68 x + c t h n ( s c sin ( t ( 69
15 with n = f( x sin x dx, b n = n c g( x sin x dx, h n ( t = Now tht f = g =, h( x, t = A x, =, we hve n = b n = nd h n ( t = A x sin x dx = A x dcos x n = A x cos x cos x dx n Therefore We cn check h( x, t sin x dx. ( 7 = A ( n+. ( 7 n u( x, t = { } t A ( n+ sin c ( t s ds sin x n c n = { ( } A ( n+ cos c ( t s t sin x n c n = n+ A ( n 3 3 c cos c t sin x. ( 7 u t t c u x x = { } A ( n+ cos c t sin x n c A ( n+ n c cos c t sin x = n+ A ( sin x = A x. ( 73 n
Math 124B January 24, 2012
 Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
MAGIC058 & MATH64062: Partial Differential Equations 1
 MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
Suggested Solution to Assignment 5
 MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
Mutipy by r sin RT P to get sin R r r R + T sin (sin T )+ P P = (7) ffi So we hve P P ffi = m (8) choose m re so tht P is sinusoi. If we put this in b
 Topic 4: Lpce Eqution in Spheric Co-orintes n Mutipoe Expnsion Reing Assignment: Jckson Chpter 3.-3.5. Lpce Eqution in Spheric Coorintes Review of spheric por coorintes: x = r sin cos ffi y = r sin sin
Topic 4: Lpce Eqution in Spheric Co-orintes n Mutipoe Expnsion Reing Assignment: Jckson Chpter 3.-3.5. Lpce Eqution in Spheric Coorintes Review of spheric por coorintes: x = r sin cos ffi y = r sin sin
Statistical Physics. Solutions Sheet 5.
 Sttistic Physics. Soutions Sheet 5. Exercise. HS 04 Prof. Mnfred Sigrist Ide fermionic quntum gs in hrmonic trp In this exercise we study the fermionic spiness ide gs confined in three-dimension hrmonic
Sttistic Physics. Soutions Sheet 5. Exercise. HS 04 Prof. Mnfred Sigrist Ide fermionic quntum gs in hrmonic trp In this exercise we study the fermionic spiness ide gs confined in three-dimension hrmonic
Lecture 6 Notes, Electromagnetic Theory I Dr. Christopher S. Baird University of Massachusetts Lowell
 Lecture 6 Notes, Eectrognetic Theory I Dr. Christopher S. Bird University of Msschusetts Lowe. Associted Legendre Poynois - We now return to soving the Lpce eqution in spheric coordintes when there is
Lecture 6 Notes, Eectrognetic Theory I Dr. Christopher S. Bird University of Msschusetts Lowe. Associted Legendre Poynois - We now return to soving the Lpce eqution in spheric coordintes when there is
Fluid Flow through a Tube
 . Theory through Tube In this experiment we wi determine how we physic retionship (so ced w ), nmey Poiseue s eqution, ppies. In the suppementry reding mteri this eqution ws derived s p Q 8 where Q is
. Theory through Tube In this experiment we wi determine how we physic retionship (so ced w ), nmey Poiseue s eqution, ppies. In the suppementry reding mteri this eqution ws derived s p Q 8 where Q is
Physics 116C Solution of inhomogeneous ordinary differential equations using Green s functions
 Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Fourier Series in Complex notation. cos(x) = eix + e ix 2. A n cos + B n sin l. i 2 B n. e inx=l + A n + ib n 2 8. ( 0 m 6= n. C n = 1 2l.
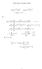 Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
1 1D heat and wave equations on a finite interval
 1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
Summary: Method of Separation of Variables
 Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Consequently, the temperature must be the same at each point in the cross section at x. Let:
 HW 2 Comments: L1-3. Derive the het eqution for n inhomogeneous rod where the therml coefficients used in the derivtion of the het eqution for homogeneous rod now become functions of position x in the
HW 2 Comments: L1-3. Derive the het eqution for n inhomogeneous rod where the therml coefficients used in the derivtion of the het eqution for homogeneous rod now become functions of position x in the
PhysicsAndMathsTutor.com
 M Dynmics - Dmped nd forced hrmonic motion. A P α B A ight estic spring hs ntur ength nd moduus of esticity mg. One end of the spring is ttched to point A on pne tht is incined to the horizont t n nge
M Dynmics - Dmped nd forced hrmonic motion. A P α B A ight estic spring hs ntur ength nd moduus of esticity mg. One end of the spring is ttched to point A on pne tht is incined to the horizont t n nge
Conservation Law. Chapter Goal. 5.2 Theory
 Chpter 5 Conservtion Lw 5.1 Gol Our long term gol is to understnd how mny mthemticl models re derived. We study how certin quntity chnges with time in given region (sptil domin). We first derive the very
Chpter 5 Conservtion Lw 5.1 Gol Our long term gol is to understnd how mny mthemticl models re derived. We study how certin quntity chnges with time in given region (sptil domin). We first derive the very
arxiv: v1 [math.co] 5 Jun 2015
![arxiv: v1 [math.co] 5 Jun 2015 arxiv: v1 [math.co] 5 Jun 2015](/thumbs/78/77492077.jpg) First non-trivi upper bound on the circur chromtic number of the pne. Konstnty Junosz-Szniwski, Fcuty of Mthemtics nd Informtion Science, Wrsw University of Technoogy, Pond Abstrct rxiv:1506.01886v1 [mth.co]
First non-trivi upper bound on the circur chromtic number of the pne. Konstnty Junosz-Szniwski, Fcuty of Mthemtics nd Informtion Science, Wrsw University of Technoogy, Pond Abstrct rxiv:1506.01886v1 [mth.co]
In this appendix, we evaluate the derivative of Eq. 9 in the main text, i.e., we need to calculate
 Supporting Tet Evoution of the Averge Synptic Updte Rue In this ppendi e evute the derivtive of Eq. 9 in the min tet i.e. e need to ccute Py ( ) Py ( Y ) og γ og. [] P( y Y ) P% ( y Y ) Before e strt et
Supporting Tet Evoution of the Averge Synptic Updte Rue In this ppendi e evute the derivtive of Eq. 9 in the min tet i.e. e need to ccute Py ( ) Py ( Y ) og γ og. [] P( y Y ) P% ( y Y ) Before e strt et
1.2. Linear Variable Coefficient Equations. y + b "! = a y + b " Remark: The case b = 0 and a non-constant can be solved with the same idea as above.
 1 12 Liner Vrible Coefficient Equtions Section Objective(s): Review: Constnt Coefficient Equtions Solving Vrible Coefficient Equtions The Integrting Fctor Method The Bernoulli Eqution 121 Review: Constnt
1 12 Liner Vrible Coefficient Equtions Section Objective(s): Review: Constnt Coefficient Equtions Solving Vrible Coefficient Equtions The Integrting Fctor Method The Bernoulli Eqution 121 Review: Constnt
1 E3102: a study guide and review, Version 1.0
 1 E3102: study guide nd review, Version 1.0 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in very
1 E3102: study guide nd review, Version 1.0 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in very
Review SOLUTIONS: Exam 2
 Review SOUTIONS: Exm. True or Flse? (And give short nswer ( If f(x is piecewise smooth on [, ], we cn find series representtion using either sine or cosine series. SOUTION: TRUE. If we use sine series,
Review SOUTIONS: Exm. True or Flse? (And give short nswer ( If f(x is piecewise smooth on [, ], we cn find series representtion using either sine or cosine series. SOUTION: TRUE. If we use sine series,
Improper Integrals. Type I Improper Integrals How do we evaluate an integral such as
 Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Chapter 0. What is the Lebesgue integral about?
 Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Fourier Series. with the period 2π, given that sin nx and cos nx are period functions with the period 2π. Then we.
 . Definition We c the trigonometric series the series of the form + cos x+ b sin x+ cos x+ b sin x+ or more briefy + ( ncos nx+ bnsin nx) () n The constnts, n nd b, n ( n,, ) re coefficients of the series
. Definition We c the trigonometric series the series of the form + cos x+ b sin x+ cos x+ b sin x+ or more briefy + ( ncos nx+ bnsin nx) () n The constnts, n nd b, n ( n,, ) re coefficients of the series
f(x) dx, If one of these two conditions is not met, we call the integral improper. Our usual definition for the value for the definite integral
 Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
7.2 The Definite Integral
 7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
Development of the Sinc Method for Nonlinear Integro-Differential Eequations
 Austrin Journ of Bsic nd Appied Sciences, 4(): 558-555, ISS 99-878 Deveopment of the Sinc Method for oniner Integro-Differenti Eequtions K. Jei, M. Zrebni, 3 M. Mirzee Chi,3 Ismic Azd University Brnch
Austrin Journ of Bsic nd Appied Sciences, 4(): 558-555, ISS 99-878 Deveopment of the Sinc Method for oniner Integro-Differenti Eequtions K. Jei, M. Zrebni, 3 M. Mirzee Chi,3 Ismic Azd University Brnch
potentials A z, F z TE z Modes We use the e j z z =0 we can simply say that the x dependence of E y (1)
 3e. Introduction Lecture 3e Rectngulr wveguide So fr in rectngulr coordintes we hve delt with plne wves propgting in simple nd inhomogeneous medi. The power density of plne wve extends over ll spce. Therefore
3e. Introduction Lecture 3e Rectngulr wveguide So fr in rectngulr coordintes we hve delt with plne wves propgting in simple nd inhomogeneous medi. The power density of plne wve extends over ll spce. Therefore
1 2-D Second Order Equations: Separation of Variables
 Chpter 12 PDEs in Rectngles 1 2-D Second Order Equtions: Seprtion of Vribles 1. A second order liner prtil differentil eqution in two vribles x nd y is A 2 u x + B 2 u 2 x y + C 2 u y + D u 2 x + E u +
Chpter 12 PDEs in Rectngles 1 2-D Second Order Equtions: Seprtion of Vribles 1. A second order liner prtil differentil eqution in two vribles x nd y is A 2 u x + B 2 u 2 x y + C 2 u y + D u 2 x + E u +
c n φ n (x), 0 < x < L, (1) n=1
 SECTION : Fourier Series. MATH4. In section 4, we will study method clled Seprtion of Vribles for finding exct solutions to certin clss of prtil differentil equtions (PDEs. To do this, it will be necessry
SECTION : Fourier Series. MATH4. In section 4, we will study method clled Seprtion of Vribles for finding exct solutions to certin clss of prtil differentil equtions (PDEs. To do this, it will be necessry
Math Fall 2006 Sample problems for the final exam: Solutions
 Mth 42-5 Fll 26 Smple problems for the finl exm: Solutions Any problem my be ltered or replced by different one! Some possibly useful informtion Prsevl s equlity for the complex form of the Fourier series
Mth 42-5 Fll 26 Smple problems for the finl exm: Solutions Any problem my be ltered or replced by different one! Some possibly useful informtion Prsevl s equlity for the complex form of the Fourier series
Energy Bands Energy Bands and Band Gap. Phys463.nb Phenomenon
 Phys463.nb 49 7 Energy Bnds Ref: textbook, Chpter 7 Q: Why re there insultors nd conductors? Q: Wht will hppen when n electron moves in crystl? In the previous chpter, we discussed free electron gses,
Phys463.nb 49 7 Energy Bnds Ref: textbook, Chpter 7 Q: Why re there insultors nd conductors? Q: Wht will hppen when n electron moves in crystl? In the previous chpter, we discussed free electron gses,
Improper Integrals, and Differential Equations
 Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
V. More General Eigenfunction Series. A. The Sturm-Liouville Family of Problems
 V. More Gener Eigenfunction Series c 214, Phiip D. Loewen A. The Sturm-Liouvie Fmiy of Probems Given n re interv, b], functions p(x), q(x), r(x), nd constnts c, c 1, d, d 1, consider (ODE) (p(x)y (x))
V. More Gener Eigenfunction Series c 214, Phiip D. Loewen A. The Sturm-Liouvie Fmiy of Probems Given n re interv, b], functions p(x), q(x), r(x), nd constnts c, c 1, d, d 1, consider (ODE) (p(x)y (x))
The Dirichlet Problem in a Two Dimensional Rectangle. Section 13.5
 The Dirichlet Prolem in Two Dimensionl Rectngle Section 13.5 1 Dirichlet Prolem in Rectngle In these notes we will pply the method of seprtion of vriles to otin solutions to elliptic prolems in rectngle
The Dirichlet Prolem in Two Dimensionl Rectngle Section 13.5 1 Dirichlet Prolem in Rectngle In these notes we will pply the method of seprtion of vriles to otin solutions to elliptic prolems in rectngle
Exam 2, Mathematics 4701, Section ETY6 6:05 pm 7:40 pm, March 31, 2016, IH-1105 Instructor: Attila Máté 1
 Exm, Mthemtics 471, Section ETY6 6:5 pm 7:4 pm, Mrch 1, 16, IH-115 Instructor: Attil Máté 1 17 copies 1. ) Stte the usul sufficient condition for the fixed-point itertion to converge when solving the eqution
Exm, Mthemtics 471, Section ETY6 6:5 pm 7:4 pm, Mrch 1, 16, IH-115 Instructor: Attil Máté 1 17 copies 1. ) Stte the usul sufficient condition for the fixed-point itertion to converge when solving the eqution
ENGI 9420 Lecture Notes 7 - Fourier Series Page 7.01
 ENGI 940 ecture Notes 7 - Fourier Series Pge 7.0 7. Fourier Series nd Fourier Trnsforms Fourier series hve multiple purposes, including the provision of series solutions to some liner prtil differentil
ENGI 940 ecture Notes 7 - Fourier Series Pge 7.0 7. Fourier Series nd Fourier Trnsforms Fourier series hve multiple purposes, including the provision of series solutions to some liner prtil differentil
Introduction to statically indeterminate structures
 Sttics of Buiding Structures I., EASUS Introduction to stticy indeterminte structures Deprtment of Structur echnics Fcuty of Civi Engineering, VŠB-Technic University of Ostrv Outine of Lecture Stticy indeterminte
Sttics of Buiding Structures I., EASUS Introduction to stticy indeterminte structures Deprtment of Structur echnics Fcuty of Civi Engineering, VŠB-Technic University of Ostrv Outine of Lecture Stticy indeterminte
Section 6.1 INTRO to LAPLACE TRANSFORMS
 Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Theoretical foundations of Gaussian quadrature
 Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
UNIFORM CONVERGENCE. Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3
 UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
Math 31S. Rumbos Fall Solutions to Assignment #16
 Mth 31S. Rumbos Fll 2016 1 Solutions to Assignment #16 1. Logistic Growth 1. Suppose tht the growth of certin niml popultion is governed by the differentil eqution 1000 dn N dt = 100 N, (1) where N(t)
Mth 31S. Rumbos Fll 2016 1 Solutions to Assignment #16 1. Logistic Growth 1. Suppose tht the growth of certin niml popultion is governed by the differentil eqution 1000 dn N dt = 100 N, (1) where N(t)
Chapter 14. Matrix Representations of Linear Transformations
 Chpter 4 Mtrix Representtions of Liner Trnsformtions When considering the Het Stte Evolution, we found tht we could describe this process using multipliction by mtrix. This ws nice becuse computers cn
Chpter 4 Mtrix Representtions of Liner Trnsformtions When considering the Het Stte Evolution, we found tht we could describe this process using multipliction by mtrix. This ws nice becuse computers cn
Advanced Calculus: MATH 410 Notes on Integrals and Integrability Professor David Levermore 17 October 2004
 Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
1 E3102: A study guide and review, Version 1.2
 1 E3102: A study guide nd review, Version 1.2 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in
1 E3102: A study guide nd review, Version 1.2 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in
Analytical Methods Exam: Preparatory Exercises
 Anlyticl Methods Exm: Preprtory Exercises Question. Wht does it men tht (X, F, µ) is mesure spce? Show tht µ is monotone, tht is: if E F re mesurble sets then µ(e) µ(f). Question. Discuss if ech of the
Anlyticl Methods Exm: Preprtory Exercises Question. Wht does it men tht (X, F, µ) is mesure spce? Show tht µ is monotone, tht is: if E F re mesurble sets then µ(e) µ(f). Question. Discuss if ech of the
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Reversing the Chain Rule. As we have seen from the Second Fundamental Theorem ( 4.3), the easiest way to evaluate an integral b
 Mth 32 Substitution Method Stewrt 4.5 Reversing the Chin Rule. As we hve seen from the Second Fundmentl Theorem ( 4.3), the esiest wy to evlute n integrl b f(x) dx is to find n ntiderivtive, the indefinite
Mth 32 Substitution Method Stewrt 4.5 Reversing the Chin Rule. As we hve seen from the Second Fundmentl Theorem ( 4.3), the esiest wy to evlute n integrl b f(x) dx is to find n ntiderivtive, the indefinite
Review of Riemann Integral
 1 Review of Riemnn Integrl In this chpter we review the definition of Riemnn integrl of bounded function f : [, b] R, nd point out its limittions so s to be convinced of the necessity of more generl integrl.
1 Review of Riemnn Integrl In this chpter we review the definition of Riemnn integrl of bounded function f : [, b] R, nd point out its limittions so s to be convinced of the necessity of more generl integrl.
(4.1) D r v(t) ω(t, v(t))
 1.4. Differentil inequlities. Let D r denote the right hnd derivtive of function. If ω(t, u) is sclr function of the sclrs t, u in some open connected set Ω, we sy tht function v(t), t < b, is solution
1.4. Differentil inequlities. Let D r denote the right hnd derivtive of function. If ω(t, u) is sclr function of the sclrs t, u in some open connected set Ω, we sy tht function v(t), t < b, is solution
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
GEOMETRIC PROBABILITY MODELS TO ANALYZE STRATEGIES FOR FINDING A BURIED CABLE
 Journ of the Opertions Reserch Society of Jpn Vo. 6, No. 3, Juy 17, pp. 4 417 c The Opertions Reserch Society of Jpn GEOMETRIC PROBABILITY MODELS TO ANALYZE STRATEGIES FOR FINDING A BURIED CABLE Ken-ichi
Journ of the Opertions Reserch Society of Jpn Vo. 6, No. 3, Juy 17, pp. 4 417 c The Opertions Reserch Society of Jpn GEOMETRIC PROBABILITY MODELS TO ANALYZE STRATEGIES FOR FINDING A BURIED CABLE Ken-ichi
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chapter 5. , r = r 1 r 2 (1) µ = m 1 m 2. r, r 2 = R µ m 2. R(m 1 + m 2 ) + m 2 r = r 1. m 2. r = r 1. R + µ m 1
 Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
Section 6.1 INTRO to LAPLACE TRANSFORMS
 Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
The Wave Equation I. MA 436 Kurt Bryan
 1 Introduction The Wve Eqution I MA 436 Kurt Bryn Consider string stretching long the x xis, of indeterminte (or even infinite!) length. We wnt to derive n eqution which models the motion of the string
1 Introduction The Wve Eqution I MA 436 Kurt Bryn Consider string stretching long the x xis, of indeterminte (or even infinite!) length. We wnt to derive n eqution which models the motion of the string
Linearity, linear operators, and self adjoint eigenvalue problems
 Linerity, liner opertors, nd self djoint eigenvlue problems 1 Elements of liner lgebr The study of liner prtil differentil equtions utilizes, unsurprisingly, mny concepts from liner lgebr nd liner ordinry
Linerity, liner opertors, nd self djoint eigenvlue problems 1 Elements of liner lgebr The study of liner prtil differentil equtions utilizes, unsurprisingly, mny concepts from liner lgebr nd liner ordinry
Best Approximation. Chapter The General Case
 Chpter 4 Best Approximtion 4.1 The Generl Cse In the previous chpter, we hve seen how n interpolting polynomil cn be used s n pproximtion to given function. We now wnt to find the best pproximtion to given
Chpter 4 Best Approximtion 4.1 The Generl Cse In the previous chpter, we hve seen how n interpolting polynomil cn be used s n pproximtion to given function. We now wnt to find the best pproximtion to given
Linear Systems COS 323
 Liner Systems COS 33 Soving Liner Systems of Equtions Define iner system Singurities in iner systems Gussin Eimintion: A gener purpose method Nïve Guss Guss with pivoting Asymptotic nysis Tringur systems
Liner Systems COS 33 Soving Liner Systems of Equtions Define iner system Singurities in iner systems Gussin Eimintion: A gener purpose method Nïve Guss Guss with pivoting Asymptotic nysis Tringur systems
We know that if f is a continuous nonnegative function on the interval [a, b], then b
![We know that if f is a continuous nonnegative function on the interval [a, b], then b We know that if f is a continuous nonnegative function on the interval [a, b], then b](/thumbs/72/66633133.jpg) 1 Ares Between Curves c 22 Donld Kreider nd Dwight Lhr We know tht if f is continuous nonnegtive function on the intervl [, b], then f(x) dx is the re under the grph of f nd bove the intervl. We re going
1 Ares Between Curves c 22 Donld Kreider nd Dwight Lhr We know tht if f is continuous nonnegtive function on the intervl [, b], then f(x) dx is the re under the grph of f nd bove the intervl. We re going
PHYSICS 116C Homework 4 Solutions
 PHYSICS 116C Homework 4 Solutions 1. ( Simple hrmonic oscilltor. Clerly the eqution is of the Sturm-Liouville (SL form with λ = n 2, A(x = 1, B(x =, w(x = 1. Legendre s eqution. Clerly the eqution is of
PHYSICS 116C Homework 4 Solutions 1. ( Simple hrmonic oscilltor. Clerly the eqution is of the Sturm-Liouville (SL form with λ = n 2, A(x = 1, B(x =, w(x = 1. Legendre s eqution. Clerly the eqution is of
Lecture 1. Functional series. Pointwise and uniform convergence.
 1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
1 Probability Density Functions
 Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Review of Gaussian Quadrature method
 Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
VI. The Heat Equation. A. The Diffusion Equation Conservation in Action
 VI. The Het Eqution c 214, Phiip D. Loewen A. The Diffusion Eqution Conservtion in Action The simpest PDE describing diffusion (of het, perfume, poutnt) ong the x-xis is u t = α 2 u xx. ( ) Theme: Concvity
VI. The Het Eqution c 214, Phiip D. Loewen A. The Diffusion Eqution Conservtion in Action The simpest PDE describing diffusion (of het, perfume, poutnt) ong the x-xis is u t = α 2 u xx. ( ) Theme: Concvity
u t = k 2 u x 2 (1) a n sin nπx sin 2 L e k(nπ/l) t f(x) = sin nπx f(x) sin nπx dx (6) 2 L f(x 0 ) sin nπx 0 2 L sin nπx 0 nπx
 Chpter 9: Green s functions for time-independent problems Introductory emples One-dimensionl het eqution Consider the one-dimensionl het eqution with boundry conditions nd initil condition We lredy know
Chpter 9: Green s functions for time-independent problems Introductory emples One-dimensionl het eqution Consider the one-dimensionl het eqution with boundry conditions nd initil condition We lredy know
Chapter 28. Fourier Series An Eigenvalue Problem.
 Chpter 28 Fourier Series Every time I close my eyes The noise inside me mplifies I cn t escpe I relive every moment of the dy Every misstep I hve mde Finds wy it cn invde My every thought And this is why
Chpter 28 Fourier Series Every time I close my eyes The noise inside me mplifies I cn t escpe I relive every moment of the dy Every misstep I hve mde Finds wy it cn invde My every thought And this is why
Review of Calculus, cont d
 Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS.
 THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS RADON ROSBOROUGH https://intuitiveexplntionscom/picrd-lindelof-theorem/ This document is proof of the existence-uniqueness theorem
THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS RADON ROSBOROUGH https://intuitiveexplntionscom/picrd-lindelof-theorem/ This document is proof of the existence-uniqueness theorem
Physics 215 Quantum Mechanics 1 Assignment 2
 Physics 15 Quntum Mechnics 1 Assignment Logn A. Morrison Jnury, 16 Problem 1 Clculte p nd p on the Gussin wve pcket α whose wve function is x α = 1 ikx x 1/4 d 1 Solution Recll tht where ψx = x ψ. Additionlly,
Physics 15 Quntum Mechnics 1 Assignment Logn A. Morrison Jnury, 16 Problem 1 Clculte p nd p on the Gussin wve pcket α whose wve function is x α = 1 ikx x 1/4 d 1 Solution Recll tht where ψx = x ψ. Additionlly,
Candidates must show on each answer book the type of calculator used.
 UNIVERSITY OF EAST ANGLIA School of Mthemtics My/June UG Exmintion 2007 2008 ELECTRICITY AND MAGNETISM Time llowed: 3 hours Attempt FIVE questions. Cndidtes must show on ech nswer book the type of clcultor
UNIVERSITY OF EAST ANGLIA School of Mthemtics My/June UG Exmintion 2007 2008 ELECTRICITY AND MAGNETISM Time llowed: 3 hours Attempt FIVE questions. Cndidtes must show on ech nswer book the type of clcultor
and that at t = 0 the object is at position 5. Find the position of the object at t = 2.
 7.2 The Fundmentl Theorem of Clculus 49 re mny, mny problems tht pper much different on the surfce but tht turn out to be the sme s these problems, in the sense tht when we try to pproimte solutions we
7.2 The Fundmentl Theorem of Clculus 49 re mny, mny problems tht pper much different on the surfce but tht turn out to be the sme s these problems, in the sense tht when we try to pproimte solutions we
The solutions of the single electron Hamiltonian were shown to be Bloch wave of the form: ( ) ( ) ikr
 Lecture #1 Progrm 1. Bloch solutions. Reciprocl spce 3. Alternte derivtion of Bloch s theorem 4. Trnsforming the serch for egenfunctions nd eigenvlues from solving PDE to finding the e-vectors nd e-vlues
Lecture #1 Progrm 1. Bloch solutions. Reciprocl spce 3. Alternte derivtion of Bloch s theorem 4. Trnsforming the serch for egenfunctions nd eigenvlues from solving PDE to finding the e-vectors nd e-vlues
Advanced Calculus: MATH 410 Uniform Convergence of Functions Professor David Levermore 11 December 2015
 Advnced Clculus: MATH 410 Uniform Convergence of Functions Professor Dvid Levermore 11 December 2015 12. Sequences of Functions We now explore two notions of wht it mens for sequence of functions {f n
Advnced Clculus: MATH 410 Uniform Convergence of Functions Professor Dvid Levermore 11 December 2015 12. Sequences of Functions We now explore two notions of wht it mens for sequence of functions {f n
Homework Assignment #5 Solutions
 Physics 506 Winter 008 Textbook probems: Ch. 9: 9., 9., 9.4 Ch. 10: 10.1 Homework Assignment #5 Soutions 9. A spheric hoe of rdius in conducting medium cn serve s n eectromgnetic resonnt cvity. Assuming
Physics 506 Winter 008 Textbook probems: Ch. 9: 9., 9., 9.4 Ch. 10: 10.1 Homework Assignment #5 Soutions 9. A spheric hoe of rdius in conducting medium cn serve s n eectromgnetic resonnt cvity. Assuming
1.1. Linear Constant Coefficient Equations. Remark: A differential equation is an equation
 1 1.1. Liner Constnt Coefficient Equtions Section Objective(s): Overview of Differentil Equtions. Liner Differentil Equtions. Solving Liner Differentil Equtions. The Initil Vlue Problem. 1.1.1. Overview
1 1.1. Liner Constnt Coefficient Equtions Section Objective(s): Overview of Differentil Equtions. Liner Differentil Equtions. Solving Liner Differentil Equtions. The Initil Vlue Problem. 1.1.1. Overview
Combined RKDG and LDG Method for the Simulation of the Bipolar Charge Transport in Solid Dielectrics
 PIERS ONLINE, VOL. 5, NO. 1, 009 51 Combined RKDG nd LDG Method for the Simution of the Bipor Chrge Trnsport in Soid Dieectrics Jihun Tin, Jun Zou, nd Jinsheng Yun Deprtment of Eectric Engineering, Tsinghu
PIERS ONLINE, VOL. 5, NO. 1, 009 51 Combined RKDG nd LDG Method for the Simution of the Bipor Chrge Trnsport in Soid Dieectrics Jihun Tin, Jun Zou, nd Jinsheng Yun Deprtment of Eectric Engineering, Tsinghu
MA 124 January 18, Derivatives are. Integrals are.
 MA 124 Jnury 18, 2018 Prof PB s one-minute introduction to clculus Derivtives re. Integrls re. In Clculus 1, we lern limits, derivtives, some pplictions of derivtives, indefinite integrls, definite integrls,
MA 124 Jnury 18, 2018 Prof PB s one-minute introduction to clculus Derivtives re. Integrls re. In Clculus 1, we lern limits, derivtives, some pplictions of derivtives, indefinite integrls, definite integrls,
HOMEWORK SOLUTIONS MATH 1910 Sections 7.9, 8.1 Fall 2016
 HOMEWORK SOLUTIONS MATH 9 Sections 7.9, 8. Fll 6 Problem 7.9.33 Show tht for ny constnts M,, nd, the function yt) = )) t ) M + tnh stisfies the logistic eqution: y SOLUTION. Let Then nd Finlly, y = y M
HOMEWORK SOLUTIONS MATH 9 Sections 7.9, 8. Fll 6 Problem 7.9.33 Show tht for ny constnts M,, nd, the function yt) = )) t ) M + tnh stisfies the logistic eqution: y SOLUTION. Let Then nd Finlly, y = y M
20 MATHEMATICS POLYNOMIALS
 0 MATHEMATICS POLYNOMIALS.1 Introduction In Clss IX, you hve studied polynomils in one vrible nd their degrees. Recll tht if p(x) is polynomil in x, the highest power of x in p(x) is clled the degree of
0 MATHEMATICS POLYNOMIALS.1 Introduction In Clss IX, you hve studied polynomils in one vrible nd their degrees. Recll tht if p(x) is polynomil in x, the highest power of x in p(x) is clled the degree of
ODE: Existence and Uniqueness of a Solution
 Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Indefinite Integral. Chapter Integration - reverse of differentiation
 Chpter Indefinite Integrl Most of the mthemticl opertions hve inverse opertions. The inverse opertion of differentition is clled integrtion. For exmple, describing process t the given moment knowing the
Chpter Indefinite Integrl Most of the mthemticl opertions hve inverse opertions. The inverse opertion of differentition is clled integrtion. For exmple, describing process t the given moment knowing the
A BRIEF INTRODUCTION TO UNIFORM CONVERGENCE. In the study of Fourier series, several questions arise naturally, such as: c n e int
 A BRIEF INTRODUCTION TO UNIFORM CONVERGENCE HANS RINGSTRÖM. Questions nd exmples In the study of Fourier series, severl questions rise nturlly, such s: () (2) re there conditions on c n, n Z, which ensure
A BRIEF INTRODUCTION TO UNIFORM CONVERGENCE HANS RINGSTRÖM. Questions nd exmples In the study of Fourier series, severl questions rise nturlly, such s: () (2) re there conditions on c n, n Z, which ensure
1 The Lagrange interpolation formula
 Notes on Qudrture 1 The Lgrnge interpoltion formul We briefly recll the Lgrnge interpoltion formul. The strting point is collection of N + 1 rel points (x 0, y 0 ), (x 1, y 1 ),..., (x N, y N ), with x
Notes on Qudrture 1 The Lgrnge interpoltion formul We briefly recll the Lgrnge interpoltion formul. The strting point is collection of N + 1 rel points (x 0, y 0 ), (x 1, y 1 ),..., (x N, y N ), with x
21.6 Green Functions for First Order Equations
 21.6 Green Functions for First Order Equtions Consider the first order inhomogeneous eqution subject to homogeneous initil condition, B[y] y() = 0. The Green function G( ξ) is defined s the solution to
21.6 Green Functions for First Order Equtions Consider the first order inhomogeneous eqution subject to homogeneous initil condition, B[y] y() = 0. The Green function G( ξ) is defined s the solution to
Math Lecture 23
 Mth 8 - Lecture 3 Dyln Zwick Fll 3 In our lst lecture we delt with solutions to the system: x = Ax where A is n n n mtrix with n distinct eigenvlues. As promised, tody we will del with the question of
Mth 8 - Lecture 3 Dyln Zwick Fll 3 In our lst lecture we delt with solutions to the system: x = Ax where A is n n n mtrix with n distinct eigenvlues. As promised, tody we will del with the question of
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H. Thomas Shores Department of Mathematics University of Nebraska Spring 2007
 A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
g i fφdx dx = x i i=1 is a Hilbert space. We shall, henceforth, abuse notation and write g i f(x) = f
 1. Appliction of functionl nlysis to PEs 1.1. Introduction. In this section we give little introduction to prtil differentil equtions. In prticulr we consider the problem u(x) = f(x) x, u(x) = x (1) where
1. Appliction of functionl nlysis to PEs 1.1. Introduction. In this section we give little introduction to prtil differentil equtions. In prticulr we consider the problem u(x) = f(x) x, u(x) = x (1) where
Math Calculus with Analytic Geometry II
 orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER /2019
 ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS MATH00030 SEMESTER 208/209 DR. ANTHONY BROWN 7.. Introduction to Integrtion. 7. Integrl Clculus As ws the cse with the chpter on differentil
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS MATH00030 SEMESTER 208/209 DR. ANTHONY BROWN 7.. Introduction to Integrtion. 7. Integrl Clculus As ws the cse with the chpter on differentil
Abstract inner product spaces
 WEEK 4 Abstrct inner product spces Definition An inner product spce is vector spce V over the rel field R equipped with rule for multiplying vectors, such tht the product of two vectors is sclr, nd the
WEEK 4 Abstrct inner product spces Definition An inner product spce is vector spce V over the rel field R equipped with rule for multiplying vectors, such tht the product of two vectors is sclr, nd the
Variational Techniques for Sturm-Liouville Eigenvalue Problems
 Vritionl Techniques for Sturm-Liouville Eigenvlue Problems Vlerie Cormni Deprtment of Mthemtics nd Sttistics University of Nebrsk, Lincoln Lincoln, NE 68588 Emil: vcormni@mth.unl.edu Rolf Ryhm Deprtment
Vritionl Techniques for Sturm-Liouville Eigenvlue Problems Vlerie Cormni Deprtment of Mthemtics nd Sttistics University of Nebrsk, Lincoln Lincoln, NE 68588 Emil: vcormni@mth.unl.edu Rolf Ryhm Deprtment
Massachusetts Institute of Technology Quantum Mechanics I (8.04) Spring 2005 Solutions to Problem Set 6
 Msschusetts Institute of Technology Quntum Mechnics I (8.) Spring 5 Solutions to Problem Set 6 By Kit Mtn. Prctice with delt functions ( points) The Dirc delt function my be defined s such tht () (b) 3
Msschusetts Institute of Technology Quntum Mechnics I (8.) Spring 5 Solutions to Problem Set 6 By Kit Mtn. Prctice with delt functions ( points) The Dirc delt function my be defined s such tht () (b) 3
Unit #9 : Definite Integral Properties; Fundamental Theorem of Calculus
 Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
New Expansion and Infinite Series
 Interntionl Mthemticl Forum, Vol. 9, 204, no. 22, 06-073 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/0.2988/imf.204.4502 New Expnsion nd Infinite Series Diyun Zhng College of Computer Nnjing University
Interntionl Mthemticl Forum, Vol. 9, 204, no. 22, 06-073 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/0.2988/imf.204.4502 New Expnsion nd Infinite Series Diyun Zhng College of Computer Nnjing University
Goals: Determine how to calculate the area described by a function. Define the definite integral. Explore the relationship between the definite
 Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
UNIFORM CONVERGENCE MA 403: REAL ANALYSIS, INSTRUCTOR: B. V. LIMAYE
 UNIFORM CONVERGENCE MA 403: REAL ANALYSIS, INSTRUCTOR: B. V. LIMAYE 1. Pointwise Convergence of Sequence Let E be set nd Y be metric spce. Consider functions f n : E Y for n = 1, 2,.... We sy tht the sequence
UNIFORM CONVERGENCE MA 403: REAL ANALYSIS, INSTRUCTOR: B. V. LIMAYE 1. Pointwise Convergence of Sequence Let E be set nd Y be metric spce. Consider functions f n : E Y for n = 1, 2,.... We sy tht the sequence
Conservation Law. Chapter Goal. 6.2 Theory
 Chpter 6 Conservtion Lw 6.1 Gol Our long term gol is to unerstn how mthemticl moels re erive. Here, we will stuy how certin quntity chnges with time in given region (sptil omin). We then first erive the
Chpter 6 Conservtion Lw 6.1 Gol Our long term gol is to unerstn how mthemticl moels re erive. Here, we will stuy how certin quntity chnges with time in given region (sptil omin). We then first erive the
Name Solutions to Test 3 November 8, 2017
 Nme Solutions to Test 3 November 8, 07 This test consists of three prts. Plese note tht in prts II nd III, you cn skip one question of those offered. Some possibly useful formuls cn be found below. Brrier
Nme Solutions to Test 3 November 8, 07 This test consists of three prts. Plese note tht in prts II nd III, you cn skip one question of those offered. Some possibly useful formuls cn be found below. Brrier
( ) 2. ( ) is the Fourier transform of! ( x). ( ) ( ) ( ) = Ae i kx"#t ( ) = 1 2" ( )"( x,t) PC 3101 Quantum Mechanics Section 1
 1. 1D Schrödinger Eqution G chpters 3-4. 1.1 the Free Prticle V 0 "( x,t) i = 2 t 2m x,t = Ae i kxt "( x,t) x 2 where = k 2 2m. Normliztion must hppen: 2 x,t = 1 Here, however: " A 2 dx " " As this integrl
1. 1D Schrödinger Eqution G chpters 3-4. 1.1 the Free Prticle V 0 "( x,t) i = 2 t 2m x,t = Ae i kxt "( x,t) x 2 where = k 2 2m. Normliztion must hppen: 2 x,t = 1 Here, however: " A 2 dx " " As this integrl
We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.
![We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b. We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.](/thumbs/93/114277851.jpg) Mth 255 - Vector lculus II Notes 4.2 Pth nd Line Integrls We begin with discussion of pth integrls (the book clls them sclr line integrls). We will do this for function of two vribles, but these ides cn
Mth 255 - Vector lculus II Notes 4.2 Pth nd Line Integrls We begin with discussion of pth integrls (the book clls them sclr line integrls). We will do this for function of two vribles, but these ides cn
7.3 Problem 7.3. ~B(~x) = ~ k ~ E(~x)=! but we also have a reected wave. ~E(~x) = ~ E 2 e i~ k 2 ~x i!t. ~B R (~x) = ~ k R ~ E R (~x)=!
 7. Problem 7. We hve two semi-innite slbs of dielectric mteril with nd equl indices of refrction n >, with n ir g (n ) of thickness d between them. Let the surfces be in the x; y lne, with the g being
7. Problem 7. We hve two semi-innite slbs of dielectric mteril with nd equl indices of refrction n >, with n ir g (n ) of thickness d between them. Let the surfces be in the x; y lne, with the g being
