V. More General Eigenfunction Series. A. The Sturm-Liouville Family of Problems
|
|
|
- Jordan Richard
- 5 years ago
- Views:
Transcription
1 V. More Gener Eigenfunction Series c 214, Phiip D. Loewen A. The Sturm-Liouvie Fmiy of Probems Given n re interv, b], functions p(x), q(x), r(x), nd constnts c, c 1, d, d 1, consider (ODE) (p(x)y (x)) q(x)y(x) + λr(x)y(x) =, < x < b, BC() c y() + c 1 y () =, BC(b) d y(b) + d 1 y (b) =. (EVP) Assume wys tht p(x) > nd r(x) > for x, b], nd tht (c, c 1 ) (, ), (d, d 1 ) (, ). This is the prototype for Sturm-Liouvie eigenvue probem. Terminoogy. () A constnt λ is n eigenvue in (EVP) if using this prticur vue in (ODE) ows for some nonzero soution function y in (ODE)+(BC). (Any such function is ced n eigenfunction corresponding to λ.) (b) A nonzero function y defined on, b] is n eigenfunction in (EVP) if this prticur function stisfies both (BC) nd (ODE) for some choice of constnt λ. (Tht constnt is then ced the eigenvue corresponding to y.) Prcticities. () Testing some given number λ for the sttus of eigenvue in (EVP) is not esy. Typicy it requires soving the differenti eqution (ODE) nd ppying the boundry conditions (BC) to see if nontrivi function is comptibe. We hve seen exmpes, nd there wi be more. (b) Testing some given function y for the sttus of eigenfunction in (EVP) is very esy. Checking the boundry vues nd verifying (BC) is extremey simpe, nd substition into (ODE) reduces tht identity to n eqution in which the constnt λ is the ony unknown. Aterntivey, one coud rerrnge (ODE) ike this: λ = q(x)y(x) (p(x)y (x)), < x < b. ( ) r(x)y(x) When y(x) is given, everything on the right side is known. If tht rtio simpifies to produce constnt, then y is n eigenfunction nd the rtio is the eigenvue; if not, then y is not n eigenfunction. As consequence of () (b) here, it is often enough to remember ony the eigenfunctions in (EVP). The eigenvues re wys esiy ccessibe from quick ccution nogous to ( ). Exmpe. When the interv hs = nd the coefficient functions re the constnts p(x) = 1, q(x) =, r(x) = 1, the ODE becomes to get y + λy =. Mking the further choices (c, c 1 ) = (1, ) nd (d, d 1 ) = (1, ) turns the BC s into y() = = y(b). Thus the eigenvue probem tht produces the Fourier Sine Series fits into the Fie 214notes, version of 17 Juy 24, pge 1. Typeset t 22:2 Juy 17, 214.
2 2 PHILIP D. LOEWEN frmework bove. Ech function y n (x) = sin(nπx/b) is n eigenfunction, nd the corresponding eigenvue comes from λ n = y n(x) y(x) = sin(nπx/b) (nπ/b)2 sin(nπx/b) = n2 π 2 b 2. The eigenvue probems ssocited with the FCS, HPSS, nd HPCS hve Sturm- Liouvie form s we they just invove different choices of (c, c 1 ) nd (d, d 1 ). Derivtive Pcking. In (EVP), the derivtives re concentrted in the first term, (py ). Using the product rue eds to this equivent eqution: p(x)y (x) + p (x)y (x) q(x)y(x) + λr(x)y(x) =, < x < b. () The speci retionship between the coefficients of y nd y here is critic in deriving the foowing ist of fcts. (See beow for detis.) Notice how these correspond to known properties of the eigenfunction fmiies we hve redy worked with. Theorem (Sturm-Liouvie). Under the stted conditions governing (EVP), () A the eigenvues re re numbers. (b) The eigenvues form n infinite sequence λ 1 < λ 2 < λ 3 < such tht im λ n = +. n (c) For ech eigenvue λ n, soutions of (ODE)/(BC) with λ = λ n cn be expressed s constnt mutipes of singe representtive eigenfunction y n. Tht is, the eigenspce E(λ n ) is one-dimension.] (d) Eigenfunctions with distinct eigenvues re orthogon with weight r. Tht is, if y m, y n re eigenfunctions for eigenvues λ m, λ n, (y m, y n ) r def = y m (x)y n (x)r(x) dx = whenever λ m λ n. Note the presence of r(x) in this orthogonity retion. (e) Eigenfunction series give rbitrriy good men-squre pproximtions for ny Riemnn-integrbe f:, b] R. Sturm-Liouvie/Sef-Adjoint Form. When derivtives re condensed into the term (py ) s shown in (ODE), the differenti eqution is sid to be in Sturm- Liouvie Form or Sef-Adjoint Form. This rrngement is ide for integrtion by prts. Here s why. Suppose u(x) nd v(x) re ny differentibe functions defined on, b]. Integrtion by prts gives ( b u(x) p(x)v (x)) dx = u(x)(p(x)v (x)) (p(x)v (x))u (x) dx. (1) Swpping the etters u nd v eds to different-ooking, but equivent, sttement: ( b v(x) p(x)u (x)) dx = v(x)(p(x)u (x)) (p(x)u (x))v (x) dx. (2) x= x= Fie 214notes, version of 17 Juy 24, pge 2. Typeset t 22:2 Juy 17, 214.
3 V. More Gener Eigenfunction Series 3 The integrs on the fr right in (1) nd (2) re equ, so these two equtions cn be combined to produce n identity tht shows the discrepncy introduced by moving the pckged-derivtive opertion from one fctor to the other: u(x) ( (p(x)v (x)) dx = ( p(x)u (x)) v(x) dx ( ) ] b p(x) u(x)v (x) u (x)v(x). (3) x= If the functions u nd v hppen to stisfy both BC() nd BC(b), the brcketed terms in (3) equ exercise!] nd the identity becomes u(x)(p(x)v (x)) dx = (p(x)u (x)) v(x) dx (ssuming (BC)). In prticur, if we choose eigenfunctions y m nd y n (with eigenvues λ m nd λ n ) for the functions u nd v in the ccution bove, we cn use (ODE) to repce the pckged derivtive terms: y m (x) ( p(x)y n (x) ) dx = ( ) y m (x) q(x)y n (x) λ n r(x)y n (x) dx = ( p(x)y m (x) ) y n (x) dx ( ) q(x)y m (x) λ m r(x)y m (x) y n (x) dx λ n y m (x)y n (x)r(x) dx = λ m y m (x)y n (x)r(x) dx. This is equivent to (λ m λ n ) y m (x)y n (x)r(x) dx =. (4) If we hve λ m λ n, this forces the integr to equ, nd tht proves sttement (d) in the Sturm-Liouvie theorem. Exercise Soution. To hnde the evuted terms shown in ine (3), rewrite the sttement tht both functions u nd v stisfy BC() s the pir of equtions In mtrix form, this is equivent to u() u () v() v () c u() + c 1 u () = c v() + c 1 v () =. ] c c 1 ] = ]. Since (c, c 1 ) (, ), this eqution cn ony hod if the mtrix on the eft is noninvertibe. Tht is, we must hve ( ]) u() u () = det v() v = u()v () u ()v(). () This shows tht the evuted term in (3) vnishes t the eft endpoint, x =. The sme ine of rgument ppies t the right endpoint, x = b. //// Fie 214notes, version of 17 Juy 24, pge 3. Typeset t 22:2 Juy 17, 214.
4 4 PHILIP D. LOEWEN Ccution (1) cn be interesting even when u nd v re equ. Suppose y n is some eigenfunction for (EVP). Using u = y n = v, nd expoiting the identity in (ODE), we hve y n (x) ( ) b y n (x) p(x)y n(x) dx = p(x)y n (x)y n(x) x= ( ) q(x)y n (x) λ n r(x)y n (x) dx = p(x)y n (x)y n(x) b x= Rerrnging this produces n eqution invoving the eigenvue λ n : λ n = p(x)y n(x) 2 dx p(x)y n(x) 2 dx ) ] (p(x)y n (x)2 + q(x)y n (x) 2 dx p(b)y n (b)y n (b) p()y n()y n (). (5) r(x)y n (x) 2 dx To see how usefu this cn be, consider the simpe constnt functions p(x) = 1, q(x) =, r(x) = 1 nd boundry conditions y() =, y(b) = tht we ssocite with Fourier Sine Series. Without knowing nything bout the eigenfunction y n, we cn see tht its corresponding eigenvue is λ n = y n(x) 2 dx. (6) y n (x) 2 dx The integrs on the top nd bottom of this frction must both be non-negtive, so λ n is gurnteed. In fct, λ n = woud require y n (x) = for x, nd tht (together with the BC s) woud force y n be the constnt function which is incomptibe with the hypothesis tht y n is nontrivi in the first pce. So we cn t hve λ n = fter. Therefore λ n > must hod for ech n. Of course this is no surprise for the FSS exmpe, but the possibiity of predicting eigenvue signs in probems were the form of the eigenfunctions is not known in dvnce cn be re sset. Prctice. In the Trench textbook, try exercise 13.2 #8. Arrnging Sturm-Liouvie Form. Differenti equtions encountered in the wid my not hve their derivtives pcked into the first term s shown in (ODE). To reorgnize given eqution into this form, use the expnded version () s trget: p(x)y + p (x)y q(x)y + λr(x)y =. Tht is, given ny second-order iner ODE, try to mtch it with the form bove by introducing new unknown p(x) nd then mtching the coefficients of y nd y. Exmpe. Find orthogonity weight for y + 4y + (4 + 9λ)y =. Fie 214notes, version of 17 Juy 24, pge 4. Typeset t 22:2 Juy 17, 214.
5 V. More Gener Eigenfunction Series 5 Soution. Mutipy the given eqution by p(x). Tht mkes the y coefficient excty wht we wnt: p(x)y + 4p(x)y + (4 + 9λ)p(x)y =. To mtch the coefficient on y, we wnt p (x) = 4p(x). This is simpe differenti eqution for p(x). The gener soution is p(x) = Ae 4x, A R. Any constnt A wi work; we tke A = 1 becuse it s simpe. (Admittedy, A = woud be simper, but tht choice woud reduce our origin differenti eqution to = profound oss of informtion bout y!) Then the given eqution is equivent to = e 4x y + 4e 4x y + (4 + 9λ)e 4x y = ( e 4x y ) + 4e 4x y + λ ( 9e 4x) y =. It foows tht eigenfunctions on the interv < x < b, with distinct eigenvues, re orthogon with weight r(x) = 9e 4x : y m (x)y n (x)9e 4x dx = whenever m n. (You cn drop the fctor 9 here nd the sttement remins true.) //// Exmpe. Find the orthogonity weight for Lguerre s eqution, xy + (1 x)y + λy =. Soution. Know the terminoogy: In the nottion of (EVP) bove, orthogonity weight mens function r(x). Mutipy through Lguerr s eqution by p(x)/x to mtch the y term with the form in (): ( ) 1 x p(x)y + p(x)y + λ x ( p(x) To mtch the y -term, we need p (x) = 1 x p(x), i.e., x x ) y =. dp p = 1 x dx n(p) = nx x + C p(x) = Axe x. x Choose A = 1 for simpicity, to get = xe x y + (1 x)e x y + λe x y = ( xe x y ) + λe x y. Hence the orthogonity weight is r(x) = e x. This function is not cery visibe in the given eqution, but it s very importnt. In ny version of (EVP) bsed on this ODE with some interv, b], eigenfunctions y m nd y n wi hve the orthogonity property y m (x)y n (x)e x dx = whenever m n. (Think bout this: the sttement just mde ony works if is not point in the interv, b]. Why?) //// Fie 214notes, version of 17 Juy 24, pge 5. Typeset t 22:2 Juy 17, 214.
6 6 PHILIP D. LOEWEN Prctice. In the Trench textbook, try exercises 13.2 #1 7. Exmpe (Euer Series from Lpce Eqn). For the foowing eigenvue probem bsed on n Euer-type eqution, x 2 y (x) + xy (x) + λy(x) =, 1 < x < b, y(1) = = y(b), ( nπ ) the eigenfunctions turn out to be (prctice!) y n (x) = sin nb nx, with corresponding eigenvues ( ) 2 nπ λ n =, n = 1, 2, 3,.... nb From FSS theory pus chnge of vribes, or from gener SL theory, we hve the orthogonity retion = 1 y m (x)y n (x) dx x, m n. Orthogonity nd Coefficient Extrction. Suppose we know fu ist of representtive eigenfunctions y 1, y 2,... in probem (EVP). Then, et f(x) be given on, b]. Wht coefficients c n wi mke correct eigenfunction series identity beow? f(x) = c n y n (x), < x < b. ( ) Orthogonity provides the nswer. Pick ny prticur subscript k, mutipy ( ) by y k (x)r(x) nd integrte: f(x)y k (x)r(x) dx = c n y n (x)y k (x)r(x) dx = c k y k (x) 2 r(x) dx. Thnks to orthogonity, terms in the sum except the one where n = k equ zero. This expins the second step bove, nd eds to c k = f(x)y k(x)r(x) dx y k(x) 2 r(x) dx. Normiztion. When choosing the eigenfunction y k for λ k, if you set the constnts right you cn rrnge y k (x) 2 r(x) dx = 1. This mkes the formu for c k bove itte cener. Eigenfunctions chosen to stisfy ( ) re ced normized. In our course, normizing eigenfunctions is wste of time: it mkes no difference to the series soutions we ccute. Don t bother! ( ) Fie 214notes, version of 17 Juy 24, pge 6. Typeset t 22:2 Juy 17, 214.
7 V. More Gener Eigenfunction Series 7 Consider this eigenvue probem: B. Extended Exmpe 1 (ODE) x 2 y + xy + λy =, 1 < x < e, (BC) y(1) = = y(e). () Express the eqution in stndrd form nd find the orthogonity retion. Get r(x) = 1/x, deduce tht if y m nd y n re eigenfunctions with different eigenvues, then = e 1 y m (x)y n (x) dx x. (b) Find eigenvues nd eigenfunctions. Grinding cse-by-cse nysis eds to λ n = n 2 π 2, y n (x) = sin(nπ nx), n = 1, 2,.... (c) Tsk 1: Chnge of Bsis/Coefficient Extrction] Given f(x), find formus for the coefficients in f(x) = c n y n (x) = c n sin(nπ nx), 1 < x < e. Evute the c n s expicity for f(x) = Genery, c n = (f, y n) r = (y n, y n ) r = 2 e 1 { nx, 1 < x < e,, otherwise. e 1 f(x) sin(nπ nx) x 1 dx e 1 sin2 (nπ nx) x 1 dx f(x) sin(nπ nx) x 1 dx. For the specific f in question, spitting gives e c n = 2 (nx) sin(nπ nx) dx /2 1 x = 2 u sin(nπu) du = 2 ( ) nπ (nπ) sin 1 ( ) nπ 2 2 nπ cos. 2 n c n 2/π 2 1/2π 2/9π 2 1/4π 2/25π 2 1/6π 2/49π 2 (d) Tsk 2: Eqution-Soving] Use suitbe eigenfunction series to sove x 2 y + xy + 7y = f(x), 1 < x < e; y(1) = = y(e), Fie 214notes, version of 17 Juy 24, pge 7. Typeset t 22:2 Juy 17, 214.
8 8 PHILIP D. LOEWEN with f s given in prt (c) bove. Notice tht y n (x) = sin(nπ nx) gives y n (x) = nπ x cos(nπ nx), y n (x) = nπ x 2 cos(nπ nx) n2 π 2 x 2 sin(nπ nx), so x 2 y n + xy n = n2 π 2 sin(nπ nx) = n 2 π 2 y n. This recpitutes the eigenvue/eigenfunction retionship nd is usefu when guessing y = n y n for the desired soution. Substitution gives x 2 y + xy + 7y = = n x 2 y n + xy n + 7y ] n n n 2 π ] y n. Therefore n 7 n 2 π 2] must mtch the coefficient c n computed bove. Answer ( ) c n n = 7 n 2 π 2 = 1 2 nπ 7 n 2 π 2 (nπ) 2 sin 2 1 nπ cos ( nπ 2 )]. (e) Tsk 3: Dynmics] Sove for u = u(x, t) in this het conduction probem: (PDE) u t = x 2 u xx + xu x, 1 < x < e, t >, with f s bove. (BC) u(1, t) = = u(e, t), t >, (IC) u(x, ) = f(x), 1 < x < e, Answer: Seprtion of vribes eds to the eigenvue probem stted bove, hence to the postute u(x, t) = T n (t) sin(nπ nx). To compete the soution, it suffices to find the functions T n (t). First initiize T n () = c n (see prt (c) bove), then propgte T n = n2 π 2 T n, so with c n s before. u(x, t) = c n e n2 π 2t sin(nπ nx), Fie 214notes, version of 17 Juy 24, pge 8. Typeset t 22:2 Juy 17, 214.
9 V. More Gener Eigenfunction Series 9 Consider this eigenvue probem: C. Extended Exmpe 2 (ODE) y + λy =, < x < 1, (BC) y () = = y(1) y (1). () Express the eqution in sef-djoint form nd find the orthogonity retion. The eqution redy is in sef-djoint (Sturm-Liouvie) form, with p(x) = 1, q(x) =, nd r(x) = 1. In prticur, ny two eigenfunctions y m nd y n hving different eigenvues λ m nd λ n wi obey y m (x)y n (x) dx =. (b) Find eigenvues nd eigenfunctions. Guessing y = e sx for constnt s C eds to soution whenever s 2 + λ =. Three types of s-vues emerge, depending on the sign of λ. Cse λ < : Define α = λ > to get s 2 = α 2, so s = ±α: y = Ae αx + Be αx, A, B R. The eft BC gives = y () = (A B)α. Since α >, B = A nd The right BC requires y = A e αx + e αx], y = αa e αx e αx]. ( ) = y(1) y (1) = A e α + e α α(e α e α ) ]. For nontriviity (see ( )) we must hve A, so this requires e α + e α = α(e α e α 1 ), i.e., α = eα e α e α + e. ( ) α Express this st condition s L(α) = R(α) for the functions L nd R defined by 3 L(α) = 1/α, R(α) = eα e α e α + e α α Grphic soution for α Fie 214notes, version of 17 Juy 24, pge 9. Typeset t 22:2 Juy 17, 214.
10 1 PHILIP D. LOEWEN Potting the curves z = L(α) nd z = R(α) for α > nd ooking for n intersection point gives one soution: c this α , with corresponding eigenvue λ = α A representtive eigenfunction is obtined by tking A = 1 nd α = α in ( ): y (x) = e α x + e α x, α given by ( ). Cse λ = : When λ = the gener soution of the given ODE is y(x) = A + Bx. The eft BC gives = y () = B, so y = A. The right BC gives = y(1) y (1) = A, so y =. Ony the trivi soution obeys both BC s, so λ = is not n eigenvue. Cse λ > : Write ω = λ >, so tht the chrcteristic eqution is s 2 = ω 2, with soutions s = ±iω. Here y = A cos(ωx) + B sin(ωx), A, B R, nd the eft BC requires = y () = Bω. Since ω >, this gives B = nd Now the right BC requires y = A cos(ωx), y = ωa sin(ωx), A R. ( ) = y(1) y (1) = A cos ω + ω sin ω]. For nontriviity (see ( )) we must hve A, so this requires cos ω = ω sin ω i.e., 1 ω = sin ω cos ω. ( ) Express this st condition s L(ω) = R(ω) for the functions L nd R defined by L(ω) = 1/ω, R(ω) = tnω ω 1 ω 2 ω 3 ω Grphic soution for ω 1, ω 2,... Fie 214notes, version of 17 Juy 24, pge 1. Typeset t 22:2 Juy 17, 214.
11 V. More Gener Eigenfunction Series 11 Potting the curves z = L(ω) nd z = R(ω) for ω > nd ooking for intersection points gives n infinite fmiy of soutions: c these ω 1, ω 2,..., with corresponding eigenvues λ n = ωn 2. Representtive eigenfunctions re obtined by tking A = 1 nd ω = ω n in ( ): y n (x) = cos(ω n x), ω n given by ( ), n = 1, 2,.... Since L(ω) s ω, the points where L(ω) = R(ω) get coser nd coser to zeros of R(o) = tnω s ω increses. These zeros re known: they re the integer mutipes of π. Thinking crefuy bout the subscripting scheme introduced bove (see the sketch) eds to the pproximtion ω n nπ, so λ n n 2 π 2, n 1. (c) Tsk 1: Chnge of Bsis/Coefficient Extrction] Outine the construction for gener eigenfunction expnsion f(x) = c n y n (x) nd then evute the coefficients for f(x) = n { 1, x < 1/2,, 1/2 x 1. The gener summtion formu must invove the eigenfunctions for the whoe probem. Our numbering scheme strts with n = : λ = α 2 < whie for n 1, λ n = ωn 2 >. So in our cse the eigenfunction expnsion ooks ike f(x) = c n y n (x) = c y (x) + c 1 y 1 (x) + c 2 y 2 (x) + n= = c e α x + e α x ] + c 1 cos(ω 1 x) + c 2 cos(ω 2 x) +. For ny fixed k, mutipying cross the given identity by y k (x)r(x) = y k (x) nd integrting the resut ets us hrness the power of the orthogonity retion in prt (): f(x)y k (x)r(x) dx = = c k = c n y n (x)y k (x)r(x) dx = c k y k (x) 2 r(x) dx n= f(x)y k (x)r(x) dx, k =, 1, 2,... y k (x) 2 r(x) dx The boxed formu works in ny Sturm-Liouvie probem; here, we hve r(x) = 1. To mtch the subscripts in the origin expnsion bove, copy the coefficient formu with k = n: c n = f(x)y n (x) dx, n =, 1, 2,.... y n (x) 2 dx Fie 214notes, version of 17 Juy 24, pge 11. Typeset t 22:2 Juy 17, 214.
12 12 PHILIP D. LOEWEN Since ech y n is known function, the denomintors here cn be evuted with no reference to whtever function f(x) we hppen to be considering: n 1 = y (x) 2 dx = y n (x) 2 dx = e 2α x e 2α x ] dx = e2α e 2α, 2α 2α cos 2 (ω n x) dx = sin(2ω n) 4ω n. (In contrst to the fmous Big Four eigenvue expnsions, the vue of the denomintor integr now depends on the counter, n.) For the specific f in question, the numertors cn be evuted by spitting: f(x)y (x) dx = f(x)y n (x) dx = /2 /2 e α x + e α x ] dx = eα /2 1 α e α/2 1 α, cos(ω n x) dx = sin(ω n/2) ω n, n = 1, 2,.... Combining numertors nd denomintors gives the foowing resuts. They re not pretty, but they re competey expicit rec tht α = , ω 1 = , ω 2 = , etc., re known constnts. c = α 1 e α /2 e ] α / = 2 e α /2 e ] α /2 2 α 1 e 2α e 2α ] 4α + e 2α e 2α, ωn 1 c n = sin(ω n/2) (1/2) + (1/4)ωn 1 sin(2ω n ) = 4 sin(ω n/2), n = 1, 2,.... 2ω n + sin(2ω n ) (d) Tsk 2: Eqution-Soving] Use suitbe eigenfunction series to sove with f s bove. y 17y = f(x), < x < 1; y () = = y(1) y (1), Here it s critic tht the BC s nd differenti opertor for y hve the sme form s the BC s nd differenti opertor in the origin eigenvue probem. This mkes it sfe to postute series soution of the form y(x) = K n y n (x), ( ) n= using the eigenfunctions found bove, becuse ny choice of constnts K n wi respect the BC s. Finding the constnts K n tht so respects the given ODE wi sove the probem. Notice tht y n(x) = λ n y n (x) for ech n, so using ( ) in the given eqution gives f(x) = y 17y = = n= λ n 17]K n y n (x), n= K n y n (x) 17K ny n (x)] Fie 214notes, version of 17 Juy 24, pge 12. Typeset t 22:2 Juy 17, 214.
13 V. More Gener Eigenfunction Series 13 This is n eigenfunction expnsion for f. We know such expnsions must be unique, nd we redy hve one in hnd from prt (c) bove. This forces K (λ + 17) = c, i.e., K = c λ + 17 = c 17 α 2, K n (λ + 17) = c n, i.e., K n = c n λ n + 17 = c 17 + ωn 2, n = 1, 2, 3,..., with c, c 1,... s found in prt (c) bove. (e) Tsk 3: Dynmics Wve Type] Sove this wve-motion probem, using f(x) s given bove: (PDE) u tt = c 2 u xx, < x < 1, t >, (BC) u x (, t) =, u(1, t) u x (1, t) =, t >, (IC) u(x, ) = f(x), < x < 1, (IC) u t (x, ) =, < x < 1. Eigen-nysis: Since PDE/BC re both homogeneous, we try seprtion of vribes. Putting u(x, t) = X(x)T(t) into PDE/BC produces n eigenvue probem for X(x) of excty the form shown bove. Postute: So we postute series soution of the form u(x, t) = T n (t)y n (x), n= using the eigenfunctions redy identified. Here the functions T (t), T 1 (t),... re not yet known: finding them wi compete the soution. Initiize: The initi conditions require f(x) = u(x, ), so T n () = c n s ccuted in prt (c). Aso, = u t (x, ) gives T n () = for ech n. Propgte: Pugging the postuted series into the PDE produces differenti eqution for ech coefficient function. T n (t) + c 2 λ n T n (t) =, n =, 1, 2,.... For n =, this wi be unstbe becuse λ = α 2 < : using the initi informtion found bove gives T (t) c 2 α 2 T (t) = = T (t) = c e α ct + e α ct ] /2. For n 1, this wi be hrmonic oscitor eqution becuse λ n = ωn 2 initi dt ed to T n (t) + c 2 ω 2 n T n(t) = = T n (t) = c n cos(ω n ct). >. Our Report: The fu soution wi be u(x, t) = c 2 e α ct + e α ct ] e α x + e α x ] + c n cos(ω n ct) cos(ω n x), with the constnts c, c 1,... pproprite for f coming from prt (c) bove. Nonhomogeneous het exmpe not shown.] Fie 214notes, version of 17 Juy 24, pge 13. Typeset t 22:2 Juy 17, 214.
14 14 PHILIP D. LOEWEN D. Extended Exmpe 3 Boyce/DiPrim (7/e) theme exmpe: 11.1 #8; 11.2 #4, 11; 11.3 #4. Discuss: (ODE) y + λy =, < x < 1, (BC()) y () =, (BC(1)) y(1) + y (1) =. Soution. A eigenvues re positive. To see this, first rue out λ = by soving y (x) = nd ppying the BC s to get the unique soution y(x) =. Then imgine tht some eigenvue-eigenfunction pir λ, y stisfies the conditions bove. Mutipy through (ODE) by y, rerrnge, nd integrte by prts to get 1 1 ] 1 λ y(x) 2 dx = y(x)y (x) dx = y(x)y (x) (y (x)) 2 dx. Pug in y () = nd y (1) = y(1) to rrive t λ y(x) 2 dx = y(1) 2 + x= (y (x)) 2 dx. Cery this requires λ, nd we know λ redy. So et ω = λ, etc., nd find tht y n (x) = cos(ω n x) is n eigenfunction for λ n if nd ony if ω n is the nth positive soution of 1 ω = tnω. Sketching the functions of ω in this eqution heps us predict tht ω 1 π/4, ω 2 (π, 3π/2), nd ω n (n 1)π for n 1. 5 z=1/ω nd z=tn(ω), ω> 4 3 z ω Eigenfunction Expnsion. Probem: Find constnts c n such tht x = c n cos(ω n x), < x < 1, for the constnts ω n identified bove. Fie 214notes, version of 17 Juy 214, pge 14. Typeset t 22:2 Juy 17, 214.
15 V. More Gener Eigenfunction Series 15 Soution. The orthogonity of the eigenfunctions y n = cos(ω n x) is critic here. The usu derivtion, bsed on eds to = y m (x)y n (x) dx = c m = cos(ω m x) cos(ω n x) dx whenever m n, Stndrd integrtion by prts wi give top = bot = Thus we hve m=1 f(x)y m (x) dx. y m (x) 2 dx x cos(ω m x) dx = ω k sin ω k + cos ω k 1, cos 2 (ω m x) dx = c m = ω 2 k 1 + cos(2ω m x) 2 ( ) 2 cos ω + ω sin ω 1 ω ω + sin ω cos ω dx = ω m + sin(ω m ) cos(ω m ) 2ω m. ω=ωm The textbook nswer (B/DiP, 11.3 #11) sys ( ) cosωm 1 x = m 1 + sin 2 cos(ω m x), where m = ω m 1 + sin 2. ω m This suggests n expnsion simir to ours, but with coefficients ] 2 2 (2 cos ω 1) m 1 + sin 2 = ω m ω ( sin 2 ω ) ω=ω m. These re the sme vues we ccuted, even though they ook quite different. To expin this, remember tht 1/ω m = tnω m, so ω m sin ω m = cos ω m nd hence ω m + sin ω m cos ω m = ω m (1 + sin 2 ω m ). PDE BVP. It s no troube to invent prti differenti eqution probem for which the ingredients bove turn out to be key. (PDE) u t = α 2 u xx, < x < 1, t >, (BC) u x (, t) =, u(1, t) + u x (1, t) =, t >, (IC) u(x, ) = x, < x < 1. Seprtion of vribes wi show tht u(x, t) = X(x)T(t) stisfies (PDE)+(BC) if nd ony if X(x) hppens to be one of the eigenfunctions found bove. So we postute soution of the form u(x, t) = T n (t) cos(ω n x), ω 2 m Fie 214notes, version of 17 Juy 214, pge 15. Typeset t 22:2 Juy 17, 214.
16 16 PHILIP D. LOEWEN initiize T n () = c n s detied bove, nd then propgte by pugging the series form into the (PDE). The resut: u(x, t) = c n e ω2 n α2t cos(ω n x), c n = ( ) 2 cos ω + ω sin ω 1 ω ω + sinω cos ω. ω=ωn Fie 214notes, version of 17 Juy 214, pge 16. Typeset t 22:2 Juy 17, 214.
17 V. More Gener Eigenfunction Series 17 E. Fu Fourier Series (FFS) Periodic Functions. A function f: R R is periodic if there is some number k comptibe with n identity of the form f(x + k) = f(x), x R. This k is ced the period of f, nd the phrse f is k-periodic succincty describes the sitution. Lemm. Let c, c 1, c 2 be re constnts; et k >. For ny soution y of the differenti eqution c 2 y + c 1 y + c y =, x R, the foowing sttements re equivent: (i) The function y is k-periodic. (ii) For ech nd every open interv (, b) with b = k, one hs y() = y(b) nd y () = y (b). ( ) (iii) There exists some open interv (, b) such tht ( ) hods. Proof. (i ii) Assume (i). This mens tht y(x+k) = y(x) for re x. Differentite both sides: y (x+k) = y (x) for re x. To prove (ii), pick ny open interv (, b) with b = k. Then pug x = into the identities bove, noting tht + k = b: This proves (ii). y(b) = y(), y (b) = y (). (ii iii) Obvious. Assume (ii). One of the intervs comptibe with the setup in (ii) is (, k), so we know y() = y(k) nd y () = y (k). So the interv (, k) shows tht sttement (iii) hods.] (iii i) Assume (iii). Tht is, ssume tht some prticur vues of nd b = + k mke ine ( ) vid. Define u(x) = y(x + k). This identity impies u (x) = y (x + k) nd u (x) = y (x + k). Since the given differenti eqution bout y is true t every point, we hve c 2 u (x) + c 1 u (x) + c u(x) = c 2 y (x + k) + c 1 y (x + k) + c y(x + k) =. Aso, from ( ), u() = y( + k) = y(b) = y(), u () = y ( + k) = y (b) = y (). This shows tht the function u stisfies the sme ODE nd IC s s the function y. Thnks to the uniqueness theorem for ODE s, the functions u nd y must be identic. Tht is, y(x + k) = u(x) = y(x), x R. This proves (i). //// Fie 214notes, version of 17 Juy 214, pge 17. Typeset t 22:2 Juy 17, 214.
18 18 PHILIP D. LOEWEN An Eigenvue Probem. Given constnt k >, we seek nontrivi k-periodic soutions of y + λy =, x R. Which constnts λ work here, nd wht re the corresponding soutions? Thnks to the Lemm, the property of being k-periodic is equivent to the property of stisfying pir of repeting BC s ike y(k) = y() nd y (k) = y (). Any x-vues seprted by k cn be used to set this up, nd symmetric pproch turns out to be convenient ter. So define = k/2 nd set up the probem (ODE) y + λy =, x R, (BC) y() = y( ), y () = y ( ). This probem does not hve Sturm-Liouvie form, becuse its boundry conditions rete behviour t two different endpoints, wheres the Sturm-Liouvie theory requires seprte BC s t ech end: { c y( ) + c 1 y ( ) =, d y() + d 1 y () =. Since (BC) bove is not comptibe with the Sturm-Liouvie setup, we shoud not be stonished tht some of the min concusions of Sturm-Liouvie theory re not vibe in this cse. Some S-L Properties Persist. For the FFS eigenprobem (ODE)+(BC) bove, 1. A the eigenvues re re numbers. 2. There re no negtive eigenvues (review ine (6) in Section A, bove). 3. Eigenfunctions for distinct eigenvues re orthogon on < x <. Home Prctice: Adpt erier proofs to justify these sttements.] Some S-L Properties re Lost. In prticur, the eigenspces re not onedimension. Let s find the eigenfunctions in deti. Cse λ =. When λ =, soutions of (ODE)/(BC) re mutipes of y (x) = 1. Abstrct sttement: Eigenspce E() is one-dimension, with bsis {y }. Cse λ >. Define ω = λ >. Then the gener soution of (ODE) is y(x) = A cos(ωx) + B sin(ωx); note y (x) = Bω cos(ωx) Aω sin(ωx). The BC s require = y() y( ) = 2B sin(ω), = y () y ( ) = 2Aω sin(ω). Fie 214notes, version of 17 Juy 214, pge 18. Typeset t 22:2 Juy 17, 214.
19 V. More Gener Eigenfunction Series 19 If sin(ω), we get A = B = nd y(x) = is the trivi soution. However, if sin(ω) =, i.e., ω = nπ/ for n N, then both BC equtions bove reduce to = no mtter wht constnts A nd B we choose. Therefore the positive eigenvues re precisey λ n = ω 2 n = n2 π 2, n = 1, 2,..., 2 nd for ech integer n 1, ech nd every nonzero function of the form ( ) ( ) nπx nπx y(x) = A cos + B sin, A, B R is n eigenfunction for λ = λ n. In other words, the set of eigenfunctions for λ n consists of (nonzero) iner combintions of the two functions ( ) ( ) y n (x) def nπx = cos, ψ n (x) def nπx = sin. Notice tht (y n, ψ n ) = cos sin dx = (odd symmetry). In bstrct terminoogy, we hve for ech integer n 1 tht the eigenspce E(λ n ) is two-dimension, with orthogon bsis {y n, ψ n }. Eigenfunction Series. Given some function f(x) defined for < x <, we might hope to for n identity of the form ( ) ( )] nπx nπx f(x) = 1 2 y (x) + n cos + b n sin. ( ) For such n identity to hod, orthogonity requires f(x) sin dx b n = ( ) = 1 f(x) sin dx, n = 1, 2,..., nπx sin 2 dx n = 1 f(x) cos dx, n =, 1, 2,.... Convergence. Is ( ) vid identity between functions? Mosty. Given f(x), we cn ccute the coefficients n nd b n from the integrs bove, nd use the resuts to define f(x) = The resuting function f wi obey n cos ( ) ( nπx nπx + b n sin )]. Fie 214notes, version of 17 Juy 214, pge 19. Typeset t 22:2 Juy 17, 214.
20 2 PHILIP D. LOEWEN (i) f(x) = f(x) t ech point x (, ) where f is continuous; (ii) f is 2-periodic; (iii) f is jump-verging t every point. If the origin function f hs properties (ii) (iii), then f wi recover f excty. More genery, properties (i) (iii) chrcterize the best pproximte reconstruction of f tht we cn resonby expect from series with the given form. Even Functions. If the given f: (, ) R hppens to be even, the FFS coefficients described bove cn be expressed s foows: n = 1 f(x) cos dx = 2 f(x) cos dx (even symmetry), b n = 1 f(x) sin dx = (odd symmetry). Since b n = for ech n, the FFS of f invoves ony cosine terms. Further, by symmetry, the FFS coefficient formu for n mtches excty the FCS formu bsed in the interv < x <. In short, the FFS nd the FCS mount to the sme thing for even functions. Odd Functions. If f: (, ) R hppens to be odd, the FFS coefficients described bove cn be expressed s foows: n = 1 f(x) cos dx = (odd symmetry), b n = 1 f(x) sin dx = 2 f(x) sin dx (even symmetry). Since n = for ech n, the FFS of f invoves ony sine terms. Further, by symmetry, the FFS coefficients b n re identic with the FSS coefficients ccuted using the interv < x <. In short, the FFS nd the FSS mount to the sme thing for odd functions. Simir sttements ppy to the HPSS nd HPCS. Thus four pointwise convergence theorems described bove cn be derived s ppictions of the singe resut for the FFS cse. Any resut for FFS hs immedite ppictions for other types. Convergence Anysis. Most textbook presenttion of the Fourier theory strt with the FFS nd then derive the Big Four s consequences. Here we py this deveopment in the reverse order. Suppose > is given nd f: (, ) R. For such n f, define two new functions: f even (x) = 1 f(x) + f( x)], 2 f odd(x) = f(x) f even (x) = 1 f(x) f( x)]. 2 These new functions re nmed fter their symmetry properties: f even ( x) = f even (x), f odd ( x) = f odd (x), so f even is n even function, so f odd is n odd function. Fie 214notes, version of 17 Juy 214, pge 2. Typeset t 22:2 Juy 17, 214.
21 V. More Gener Eigenfunction Series 21 Aso, it s esy to check the identity f(x) = f even (x) + f odd (x), < x <. Intuitivey the definitions bove spit ny given f into the sum of n even function nd n odd function. And we know ot bout Fourier expnsions of functions with symmetry properties. () Since f odd is odd on (, ), its Fourier Sine Series correcty reproduces it (t continuity points) not just in (, ) but indeed in of (, ). Aso, b n = 2 = 1 = 1 = 1 f odd (x) sin dx f odd (x) sin dx f(x) f even (x)]sin f(x) sin dx. dx (b) Since f even is even on (, ), its Fourier Cosine Series correcty reproduces it (t continuity points) not just in (, ) but indeed in of (, ). Aso, n = 2 = 1 = 1 = 1 f even (x) cos dx f even (x) cos dx f(x) f odd (x)]cos f(x) cos dx dx Using the coefficients ccuted bove, we hve the FCS nd FSS reconstructions f even (x) = 2 + n cos, f odd (x) = b n sin. Fie 214notes, version of 17 Juy 214, pge 21. Typeset t 22:2 Juy 17, 214.
22 22 PHILIP D. LOEWEN It foows tht for every continuity point x of f in the interv (, ), f(x) = f even (x) + f odd (x) = f even (x) + f odd (x) = f(x) = 2 + ( ( ) ( )) nπx nπx def n cos + b n sin = f(x), where n = 1 f(x) cos dx, n =, 1, 2,..., b n = 1 f(x) sin dx, n = 1, 2,.... More genery, f is piecewise continuous, 2π-periodic nd jump-verging. Usefu Misceny. 1. DC Offset. For integers n 1, cos dx = (by ccution, or becuse (y, y n ) = ) sin dx = (by odd symmetry, or becuse (y, ψ n ) = ) It foows tht f(x) dx = 2 + ( n cos ( ) ( nπx nπx + b n sin )) ] dx = 2 2. Tht is, 2 = 1 f(x) dx. 2 This shows tht the constnt term in the FS (or the FCS) reves the verge vue of the input function f over one period. 2. Coefficient Decy. For ny resonbe (i.e., piecewise smooth) function f, there is constnt M (independent of n) such tht both n M n nd b n M n for n 1. In prticur, n nd b n s n. Fie 214notes, version of 17 Juy 214, pge 22. Typeset t 22:2 Juy 17, 214.
23 V. More Gener Eigenfunction Series 23 Proof ( n ony; b n simir): Integrte by prts to get n = f(x) cos dx ( ) ( )] nπx = f(x) sin nπ = n = + ( ) nπx sin f (x) dx nπ 1 f (x) dx nπ = n 1 nπ 1 f (x) dx. ( ) ( ) nπx sin nπ f (x) dx This gives the sttement bove, with M = 1 π f (x) dx. Fie 214notes, version of 17 Juy 214, pge 23. Typeset t 22:2 Juy 17, 214.
Math 124B January 24, 2012
 Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
MAGIC058 & MATH64062: Partial Differential Equations 1
 MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
1. The vibrating string problem revisited.
 Weeks 7 8: S eprtion of Vribes In the pst few weeks we hve expored the possibiity of soving first nd second order PDEs by trnsforming them into simper forms ( method of chrcteristics. Unfortuntey, this
Weeks 7 8: S eprtion of Vribes In the pst few weeks we hve expored the possibiity of soving first nd second order PDEs by trnsforming them into simper forms ( method of chrcteristics. Unfortuntey, this
Suggested Solution to Assignment 5
 MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
VI. The Heat Equation. A. The Diffusion Equation Conservation in Action
 VI. The Het Eqution c 214, Phiip D. Loewen A. The Diffusion Eqution Conservtion in Action The simpest PDE describing diffusion (of het, perfume, poutnt) ong the x-xis is u t = α 2 u xx. ( ) Theme: Concvity
VI. The Het Eqution c 214, Phiip D. Loewen A. The Diffusion Eqution Conservtion in Action The simpest PDE describing diffusion (of het, perfume, poutnt) ong the x-xis is u t = α 2 u xx. ( ) Theme: Concvity
Mutipy by r sin RT P to get sin R r r R + T sin (sin T )+ P P = (7) ffi So we hve P P ffi = m (8) choose m re so tht P is sinusoi. If we put this in b
 Topic 4: Lpce Eqution in Spheric Co-orintes n Mutipoe Expnsion Reing Assignment: Jckson Chpter 3.-3.5. Lpce Eqution in Spheric Coorintes Review of spheric por coorintes: x = r sin cos ffi y = r sin sin
Topic 4: Lpce Eqution in Spheric Co-orintes n Mutipoe Expnsion Reing Assignment: Jckson Chpter 3.-3.5. Lpce Eqution in Spheric Coorintes Review of spheric por coorintes: x = r sin cos ffi y = r sin sin
Summary: Method of Separation of Variables
 Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Statistical Physics. Solutions Sheet 5.
 Sttistic Physics. Soutions Sheet 5. Exercise. HS 04 Prof. Mnfred Sigrist Ide fermionic quntum gs in hrmonic trp In this exercise we study the fermionic spiness ide gs confined in three-dimension hrmonic
Sttistic Physics. Soutions Sheet 5. Exercise. HS 04 Prof. Mnfred Sigrist Ide fermionic quntum gs in hrmonic trp In this exercise we study the fermionic spiness ide gs confined in three-dimension hrmonic
Physics 116C Solution of inhomogeneous ordinary differential equations using Green s functions
 Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Fourier Series in Complex notation. cos(x) = eix + e ix 2. A n cos + B n sin l. i 2 B n. e inx=l + A n + ib n 2 8. ( 0 m 6= n. C n = 1 2l.
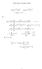 Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
PHYSICS 116C Homework 4 Solutions
 PHYSICS 116C Homework 4 Solutions 1. ( Simple hrmonic oscilltor. Clerly the eqution is of the Sturm-Liouville (SL form with λ = n 2, A(x = 1, B(x =, w(x = 1. Legendre s eqution. Clerly the eqution is of
PHYSICS 116C Homework 4 Solutions 1. ( Simple hrmonic oscilltor. Clerly the eqution is of the Sturm-Liouville (SL form with λ = n 2, A(x = 1, B(x =, w(x = 1. Legendre s eqution. Clerly the eqution is of
Lecture 6 Notes, Electromagnetic Theory I Dr. Christopher S. Baird University of Massachusetts Lowell
 Lecture 6 Notes, Eectrognetic Theory I Dr. Christopher S. Bird University of Msschusetts Lowe. Associted Legendre Poynois - We now return to soving the Lpce eqution in spheric coordintes when there is
Lecture 6 Notes, Eectrognetic Theory I Dr. Christopher S. Bird University of Msschusetts Lowe. Associted Legendre Poynois - We now return to soving the Lpce eqution in spheric coordintes when there is
Consequently, the temperature must be the same at each point in the cross section at x. Let:
 HW 2 Comments: L1-3. Derive the het eqution for n inhomogeneous rod where the therml coefficients used in the derivtion of the het eqution for homogeneous rod now become functions of position x in the
HW 2 Comments: L1-3. Derive the het eqution for n inhomogeneous rod where the therml coefficients used in the derivtion of the het eqution for homogeneous rod now become functions of position x in the
Improper Integrals, and Differential Equations
 Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Review SOLUTIONS: Exam 2
 Review SOUTIONS: Exm. True or Flse? (And give short nswer ( If f(x is piecewise smooth on [, ], we cn find series representtion using either sine or cosine series. SOUTION: TRUE. If we use sine series,
Review SOUTIONS: Exm. True or Flse? (And give short nswer ( If f(x is piecewise smooth on [, ], we cn find series representtion using either sine or cosine series. SOUTION: TRUE. If we use sine series,
Chapter 5. , r = r 1 r 2 (1) µ = m 1 m 2. r, r 2 = R µ m 2. R(m 1 + m 2 ) + m 2 r = r 1. m 2. r = r 1. R + µ m 1
 Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
AMS 212A Applied Mathematical Methods I Lecture 06 Copyright by Hongyun Wang, UCSC. ( ), v (that is, 1 ( ) L i
 AMS A Applied Mthemticl Methods I Lecture 6 Copyright y Hongyun Wng, UCSC Recp of Lecture 5 Clssifiction of oundry conditions Dirichlet eumnn Mixed Adjoint opertor, self-djoint opertor Sturm-Liouville
AMS A Applied Mthemticl Methods I Lecture 6 Copyright y Hongyun Wng, UCSC Recp of Lecture 5 Clssifiction of oundry conditions Dirichlet eumnn Mixed Adjoint opertor, self-djoint opertor Sturm-Liouville
In this appendix, we evaluate the derivative of Eq. 9 in the main text, i.e., we need to calculate
 Supporting Tet Evoution of the Averge Synptic Updte Rue In this ppendi e evute the derivtive of Eq. 9 in the min tet i.e. e need to ccute Py ( ) Py ( Y ) og γ og. [] P( y Y ) P% ( y Y ) Before e strt et
Supporting Tet Evoution of the Averge Synptic Updte Rue In this ppendi e evute the derivtive of Eq. 9 in the min tet i.e. e need to ccute Py ( ) Py ( Y ) og γ og. [] P( y Y ) P% ( y Y ) Before e strt et
1 E3102: a study guide and review, Version 1.0
 1 E3102: study guide nd review, Version 1.0 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in very
1 E3102: study guide nd review, Version 1.0 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in very
1 1D heat and wave equations on a finite interval
 1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
C. Fourier Sine Series Overview
 12 PHILIP D. LOEWEN C. Fourier Sine Series Overview Let some constant > be given. The symboic form of the FSS Eigenvaue probem combines an ordinary differentia equation (ODE) on the interva (, ) with a
12 PHILIP D. LOEWEN C. Fourier Sine Series Overview Let some constant > be given. The symboic form of the FSS Eigenvaue probem combines an ordinary differentia equation (ODE) on the interva (, ) with a
Fluid Flow through a Tube
 . Theory through Tube In this experiment we wi determine how we physic retionship (so ced w ), nmey Poiseue s eqution, ppies. In the suppementry reding mteri this eqution ws derived s p Q 8 where Q is
. Theory through Tube In this experiment we wi determine how we physic retionship (so ced w ), nmey Poiseue s eqution, ppies. In the suppementry reding mteri this eqution ws derived s p Q 8 where Q is
STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS
 STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS Throughout, we let [, b] be bounded intervl in R. C 2 ([, b]) denotes the spce of functions with derivtives of second order continuous up to the endpoints. Cc 2
STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS Throughout, we let [, b] be bounded intervl in R. C 2 ([, b]) denotes the spce of functions with derivtives of second order continuous up to the endpoints. Cc 2
1 Techniques of Integration
 November 8, 8 MAT86 Week Justin Ko Techniques of Integrtion. Integrtion By Substitution (Chnge of Vribles) We cn think of integrtion by substitution s the counterprt of the chin rule for differentition.
November 8, 8 MAT86 Week Justin Ko Techniques of Integrtion. Integrtion By Substitution (Chnge of Vribles) We cn think of integrtion by substitution s the counterprt of the chin rule for differentition.
Chapter 28. Fourier Series An Eigenvalue Problem.
 Chpter 28 Fourier Series Every time I close my eyes The noise inside me mplifies I cn t escpe I relive every moment of the dy Every misstep I hve mde Finds wy it cn invde My every thought And this is why
Chpter 28 Fourier Series Every time I close my eyes The noise inside me mplifies I cn t escpe I relive every moment of the dy Every misstep I hve mde Finds wy it cn invde My every thought And this is why
Lecture 1. Functional series. Pointwise and uniform convergence.
 1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Chapter 0. What is the Lebesgue integral about?
 Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
SUMMER KNOWHOW STUDY AND LEARNING CENTRE
 SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
MA 124 January 18, Derivatives are. Integrals are.
 MA 124 Jnury 18, 2018 Prof PB s one-minute introduction to clculus Derivtives re. Integrls re. In Clculus 1, we lern limits, derivtives, some pplictions of derivtives, indefinite integrls, definite integrls,
MA 124 Jnury 18, 2018 Prof PB s one-minute introduction to clculus Derivtives re. Integrls re. In Clculus 1, we lern limits, derivtives, some pplictions of derivtives, indefinite integrls, definite integrls,
The Wave Equation I. MA 436 Kurt Bryan
 1 Introduction The Wve Eqution I MA 436 Kurt Bryn Consider string stretching long the x xis, of indeterminte (or even infinite!) length. We wnt to derive n eqution which models the motion of the string
1 Introduction The Wve Eqution I MA 436 Kurt Bryn Consider string stretching long the x xis, of indeterminte (or even infinite!) length. We wnt to derive n eqution which models the motion of the string
Math 231E, Lecture 33. Parametric Calculus
 Mth 31E, Lecture 33. Prmetric Clculus 1 Derivtives 1.1 First derivtive Now, let us sy tht we wnt the slope t point on prmetric curve. Recll the chin rule: which exists s long s /. = / / Exmple 1.1. Reconsider
Mth 31E, Lecture 33. Prmetric Clculus 1 Derivtives 1.1 First derivtive Now, let us sy tht we wnt the slope t point on prmetric curve. Recll the chin rule: which exists s long s /. = / / Exmple 1.1. Reconsider
Best Approximation. Chapter The General Case
 Chpter 4 Best Approximtion 4.1 The Generl Cse In the previous chpter, we hve seen how n interpolting polynomil cn be used s n pproximtion to given function. We now wnt to find the best pproximtion to given
Chpter 4 Best Approximtion 4.1 The Generl Cse In the previous chpter, we hve seen how n interpolting polynomil cn be used s n pproximtion to given function. We now wnt to find the best pproximtion to given
Section 7.1 Integration by Substitution
 Section 7. Integrtion by Substitution Evlute ech of the following integrls. Keep in mind tht using substitution my not work on some problems. For one of the definite integrls, it is not possible to find
Section 7. Integrtion by Substitution Evlute ech of the following integrls. Keep in mind tht using substitution my not work on some problems. For one of the definite integrls, it is not possible to find
Math 124B January 31, 2012
 Math 124B January 31, 212 Viktor Grigoryan 7 Inhomogeneous boundary vaue probems Having studied the theory of Fourier series, with which we successfuy soved boundary vaue probems for the homogeneous heat
Math 124B January 31, 212 Viktor Grigoryan 7 Inhomogeneous boundary vaue probems Having studied the theory of Fourier series, with which we successfuy soved boundary vaue probems for the homogeneous heat
STURM-LIOUVILLE PROBLEMS: GENERALIZED FOURIER SERIES
 STURM-LIOUVILLE PROBLEMS: GENERALIZED FOURIER SERIES 1. Regulr Sturm-Liouville Problem The method of seprtion of vribles to solve boundry vlue problems leds to ordinry differentil equtions on intervls
STURM-LIOUVILLE PROBLEMS: GENERALIZED FOURIER SERIES 1. Regulr Sturm-Liouville Problem The method of seprtion of vribles to solve boundry vlue problems leds to ordinry differentil equtions on intervls
f(x) dx, If one of these two conditions is not met, we call the integral improper. Our usual definition for the value for the definite integral
 Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Name Solutions to Test 3 November 8, 2017
 Nme Solutions to Test 3 November 8, 07 This test consists of three prts. Plese note tht in prts II nd III, you cn skip one question of those offered. Some possibly useful formuls cn be found below. Brrier
Nme Solutions to Test 3 November 8, 07 This test consists of three prts. Plese note tht in prts II nd III, you cn skip one question of those offered. Some possibly useful formuls cn be found below. Brrier
PDE Notes. Paul Carnig. January ODE s vs PDE s 1
 PDE Notes Pul Crnig Jnury 2014 Contents 1 ODE s vs PDE s 1 2 Section 1.2 Het diffusion Eqution 1 2.1 Fourier s w of Het Conduction............................. 2 2.2 Energy Conservtion.....................................
PDE Notes Pul Crnig Jnury 2014 Contents 1 ODE s vs PDE s 1 2 Section 1.2 Het diffusion Eqution 1 2.1 Fourier s w of Het Conduction............................. 2 2.2 Energy Conservtion.....................................
ODE: Existence and Uniqueness of a Solution
 Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Math& 152 Section Integration by Parts
 Mth& 5 Section 7. - Integrtion by Prts Integrtion by prts is rule tht trnsforms the integrl of the product of two functions into other (idelly simpler) integrls. Recll from Clculus I tht given two differentible
Mth& 5 Section 7. - Integrtion by Prts Integrtion by prts is rule tht trnsforms the integrl of the product of two functions into other (idelly simpler) integrls. Recll from Clculus I tht given two differentible
3 Mathematics of the Poisson Equation
 3 Mthemtics of the Poisson Eqution 3. Green functions nd the Poisson eqution () The Dirichlet Green function stisfies the Poisson eqution with delt-function chrge 2 G D (r, r o ) = δ 3 (r r o ) (3.) nd
3 Mthemtics of the Poisson Eqution 3. Green functions nd the Poisson eqution () The Dirichlet Green function stisfies the Poisson eqution with delt-function chrge 2 G D (r, r o ) = δ 3 (r r o ) (3.) nd
Differential Equations 2 Homework 5 Solutions to the Assigned Exercises
 Differentil Equtions Homework Solutions to the Assigned Exercises, # 3 Consider the dmped string prolem u tt + 3u t = u xx, < x , u, t = u, t =, t >, ux, = fx, u t x, = gx. In the exm you were supposed
Differentil Equtions Homework Solutions to the Assigned Exercises, # 3 Consider the dmped string prolem u tt + 3u t = u xx, < x , u, t = u, t =, t >, ux, = fx, u t x, = gx. In the exm you were supposed
Math 113 Exam 1-Review
 Mth 113 Exm 1-Review September 26, 2016 Exm 1 covers 6.1-7.3 in the textbook. It is dvisble to lso review the mteril from 5.3 nd 5.5 s this will be helpful in solving some of the problems. 6.1 Are Between
Mth 113 Exm 1-Review September 26, 2016 Exm 1 covers 6.1-7.3 in the textbook. It is dvisble to lso review the mteril from 5.3 nd 5.5 s this will be helpful in solving some of the problems. 6.1 Are Between
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Convergence of Fourier Series and Fejer s Theorem. Lee Ricketson
 Convergence of Fourier Series nd Fejer s Theorem Lee Ricketson My, 006 Abstrct This pper will ddress the Fourier Series of functions with rbitrry period. We will derive forms of the Dirichlet nd Fejer
Convergence of Fourier Series nd Fejer s Theorem Lee Ricketson My, 006 Abstrct This pper will ddress the Fourier Series of functions with rbitrry period. We will derive forms of the Dirichlet nd Fejer
14 Separation of Variables Method
 14 Separation of Variabes Method Consider, for exampe, the Dirichet probem u t = Du xx < x u(x, ) = f(x) < x < u(, t) = = u(, t) t > Let u(x, t) = T (t)φ(x); now substitute into the equation: dt
14 Separation of Variabes Method Consider, for exampe, the Dirichet probem u t = Du xx < x u(x, ) = f(x) < x < u(, t) = = u(, t) t > Let u(x, t) = T (t)φ(x); now substitute into the equation: dt
Improper Integrals. Type I Improper Integrals How do we evaluate an integral such as
 Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Math 100 Review Sheet
 Mth 100 Review Sheet Joseph H. Silvermn December 2010 This outline of Mth 100 is summry of the mteril covered in the course. It is designed to be study id, but it is only n outline nd should be used s
Mth 100 Review Sheet Joseph H. Silvermn December 2010 This outline of Mth 100 is summry of the mteril covered in the course. It is designed to be study id, but it is only n outline nd should be used s
MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1
 MATH34032: Green s Functions, Integrl Equtions nd the Clculus of Vritions 1 Section 1 Function spces nd opertors Here we gives some brief detils nd definitions, prticulrly relting to opertors. For further
MATH34032: Green s Functions, Integrl Equtions nd the Clculus of Vritions 1 Section 1 Function spces nd opertors Here we gives some brief detils nd definitions, prticulrly relting to opertors. For further
LECTURE 3. Orthogonal Functions. n X. It should be noted, however, that the vectors f i need not be orthogonal nor need they have unit length for
 ECTURE 3 Orthogonl Functions 1. Orthogonl Bses The pproprite setting for our iscussion of orthogonl functions is tht of liner lgebr. So let me recll some relevnt fcts bout nite imensionl vector spces.
ECTURE 3 Orthogonl Functions 1. Orthogonl Bses The pproprite setting for our iscussion of orthogonl functions is tht of liner lgebr. So let me recll some relevnt fcts bout nite imensionl vector spces.
Homework Assignment #5 Solutions
 Physics 506 Winter 008 Textbook probems: Ch. 9: 9., 9., 9.4 Ch. 10: 10.1 Homework Assignment #5 Soutions 9. A spheric hoe of rdius in conducting medium cn serve s n eectromgnetic resonnt cvity. Assuming
Physics 506 Winter 008 Textbook probems: Ch. 9: 9., 9., 9.4 Ch. 10: 10.1 Homework Assignment #5 Soutions 9. A spheric hoe of rdius in conducting medium cn serve s n eectromgnetic resonnt cvity. Assuming
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
1 The Lagrange interpolation formula
 Notes on Qudrture 1 The Lgrnge interpoltion formul We briefly recll the Lgrnge interpoltion formul. The strting point is collection of N + 1 rel points (x 0, y 0 ), (x 1, y 1 ),..., (x N, y N ), with x
Notes on Qudrture 1 The Lgrnge interpoltion formul We briefly recll the Lgrnge interpoltion formul. The strting point is collection of N + 1 rel points (x 0, y 0 ), (x 1, y 1 ),..., (x N, y N ), with x
Separation of Variables. A. Three Famous PDE s
 Separation of Variables c 14, Philip D. Loewen A. Three Famous PDE s 1. Wave Equation. Displacement u depends on position and time: u = u(x, t. Concavity drives acceleration: u tt = c u xx.. Heat Equation.
Separation of Variables c 14, Philip D. Loewen A. Three Famous PDE s 1. Wave Equation. Displacement u depends on position and time: u = u(x, t. Concavity drives acceleration: u tt = c u xx.. Heat Equation.
Coordinate Geometry. Coordinate Geometry. Curriculum Ready ACMNA: 178, 214, 294.
 Coordinte Geometr Coordinte Geometr Curricuum Red ACMNA: 78, 4, 94 www.mthetics.com Coordinte COORDINATE Geometr GEOMETRY Shpes ou ve seen in geometr re put onto es nd nsed using gebr. Epect bit of both
Coordinte Geometr Coordinte Geometr Curricuum Red ACMNA: 78, 4, 94 www.mthetics.com Coordinte COORDINATE Geometr GEOMETRY Shpes ou ve seen in geometr re put onto es nd nsed using gebr. Epect bit of both
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
7.2 The Definite Integral
 7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS.
 THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS RADON ROSBOROUGH https://intuitiveexplntionscom/picrd-lindelof-theorem/ This document is proof of the existence-uniqueness theorem
THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS RADON ROSBOROUGH https://intuitiveexplntionscom/picrd-lindelof-theorem/ This document is proof of the existence-uniqueness theorem
Variational Techniques for Sturm-Liouville Eigenvalue Problems
 Vritionl Techniques for Sturm-Liouville Eigenvlue Problems Vlerie Cormni Deprtment of Mthemtics nd Sttistics University of Nebrsk, Lincoln Lincoln, NE 68588 Emil: vcormni@mth.unl.edu Rolf Ryhm Deprtment
Vritionl Techniques for Sturm-Liouville Eigenvlue Problems Vlerie Cormni Deprtment of Mthemtics nd Sttistics University of Nebrsk, Lincoln Lincoln, NE 68588 Emil: vcormni@mth.unl.edu Rolf Ryhm Deprtment
STURM-LIOUVILLE PROBLEMS
 STURM-LIOUVILLE PROBLEMS Mrch 8, 24 We hve seen tht in the process of solving certin liner evolution equtions such s the het or wve equtions we re led in very nturl wy to n eigenvlue problem for second
STURM-LIOUVILLE PROBLEMS Mrch 8, 24 We hve seen tht in the process of solving certin liner evolution equtions such s the het or wve equtions we re led in very nturl wy to n eigenvlue problem for second
UNIFORM CONVERGENCE. Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3
 UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
Math 113 Exam 2 Practice
 Mth Em Prctice Februry, 8 Em will cover sections 6.5, 7.-7.5 nd 7.8. This sheet hs three sections. The first section will remind you bout techniques nd formuls tht you should know. The second gives number
Mth Em Prctice Februry, 8 Em will cover sections 6.5, 7.-7.5 nd 7.8. This sheet hs three sections. The first section will remind you bout techniques nd formuls tht you should know. The second gives number
A-Level Mathematics Transition Task (compulsory for all maths students and all further maths student)
 A-Level Mthemtics Trnsition Tsk (compulsory for ll mths students nd ll further mths student) Due: st Lesson of the yer. Length: - hours work (depending on prior knowledge) This trnsition tsk provides revision
A-Level Mthemtics Trnsition Tsk (compulsory for ll mths students nd ll further mths student) Due: st Lesson of the yer. Length: - hours work (depending on prior knowledge) This trnsition tsk provides revision
The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a).
![The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a). The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a).](/thumbs/78/77467690.jpg) The Fundmentl Theorems of Clculus Mth 4, Section 0, Spring 009 We now know enough bout definite integrls to give precise formultions of the Fundmentl Theorems of Clculus. We will lso look t some bsic emples
The Fundmentl Theorems of Clculus Mth 4, Section 0, Spring 009 We now know enough bout definite integrls to give precise formultions of the Fundmentl Theorems of Clculus. We will lso look t some bsic emples
The Dirichlet Problem in a Two Dimensional Rectangle. Section 13.5
 The Dirichlet Prolem in Two Dimensionl Rectngle Section 13.5 1 Dirichlet Prolem in Rectngle In these notes we will pply the method of seprtion of vriles to otin solutions to elliptic prolems in rectngle
The Dirichlet Prolem in Two Dimensionl Rectngle Section 13.5 1 Dirichlet Prolem in Rectngle In these notes we will pply the method of seprtion of vriles to otin solutions to elliptic prolems in rectngle
A BRIEF INTRODUCTION TO UNIFORM CONVERGENCE. In the study of Fourier series, several questions arise naturally, such as: c n e int
 A BRIEF INTRODUCTION TO UNIFORM CONVERGENCE HANS RINGSTRÖM. Questions nd exmples In the study of Fourier series, severl questions rise nturlly, such s: () (2) re there conditions on c n, n Z, which ensure
A BRIEF INTRODUCTION TO UNIFORM CONVERGENCE HANS RINGSTRÖM. Questions nd exmples In the study of Fourier series, severl questions rise nturlly, such s: () (2) re there conditions on c n, n Z, which ensure
Anti-derivatives/Indefinite Integrals of Basic Functions
 Anti-derivtives/Indefinite Integrls of Bsic Functions Power Rule: In prticulr, this mens tht x n+ x n n + + C, dx = ln x + C, if n if n = x 0 dx = dx = dx = x + C nd x (lthough you won t use the second
Anti-derivtives/Indefinite Integrls of Bsic Functions Power Rule: In prticulr, this mens tht x n+ x n n + + C, dx = ln x + C, if n if n = x 0 dx = dx = dx = x + C nd x (lthough you won t use the second
Heat flux and total heat
 Het flux nd totl het John McCun Mrch 14, 2017 1 Introduction Yesterdy (if I remember correctly) Ms. Prsd sked me question bout the condition of insulted boundry for the 1D het eqution, nd (bsed on glnce
Het flux nd totl het John McCun Mrch 14, 2017 1 Introduction Yesterdy (if I remember correctly) Ms. Prsd sked me question bout the condition of insulted boundry for the 1D het eqution, nd (bsed on glnce
ENGI 9420 Lecture Notes 7 - Fourier Series Page 7.01
 ENGI 940 ecture Notes 7 - Fourier Series Pge 7.0 7. Fourier Series nd Fourier Trnsforms Fourier series hve multiple purposes, including the provision of series solutions to some liner prtil differentil
ENGI 940 ecture Notes 7 - Fourier Series Pge 7.0 7. Fourier Series nd Fourier Trnsforms Fourier series hve multiple purposes, including the provision of series solutions to some liner prtil differentil
221B Lecture Notes WKB Method
 Clssicl Limit B Lecture Notes WKB Method Hmilton Jcobi Eqution We strt from the Schrödinger eqution for single prticle in potentil i h t ψ x, t = [ ] h m + V x ψ x, t. We cn rewrite this eqution by using
Clssicl Limit B Lecture Notes WKB Method Hmilton Jcobi Eqution We strt from the Schrödinger eqution for single prticle in potentil i h t ψ x, t = [ ] h m + V x ψ x, t. We cn rewrite this eqution by using
Energy Bands Energy Bands and Band Gap. Phys463.nb Phenomenon
 Phys463.nb 49 7 Energy Bnds Ref: textbook, Chpter 7 Q: Why re there insultors nd conductors? Q: Wht will hppen when n electron moves in crystl? In the previous chpter, we discussed free electron gses,
Phys463.nb 49 7 Energy Bnds Ref: textbook, Chpter 7 Q: Why re there insultors nd conductors? Q: Wht will hppen when n electron moves in crystl? In the previous chpter, we discussed free electron gses,
Linear Systems COS 323
 Liner Systems COS 33 Soving Liner Systems of Equtions Define iner system Singurities in iner systems Gussin Eimintion: A gener purpose method Nïve Guss Guss with pivoting Asymptotic nysis Tringur systems
Liner Systems COS 33 Soving Liner Systems of Equtions Define iner system Singurities in iner systems Gussin Eimintion: A gener purpose method Nïve Guss Guss with pivoting Asymptotic nysis Tringur systems
Math Fall 2006 Sample problems for the final exam: Solutions
 Mth 42-5 Fll 26 Smple problems for the finl exm: Solutions Any problem my be ltered or replced by different one! Some possibly useful informtion Prsevl s equlity for the complex form of the Fourier series
Mth 42-5 Fll 26 Smple problems for the finl exm: Solutions Any problem my be ltered or replced by different one! Some possibly useful informtion Prsevl s equlity for the complex form of the Fourier series
c n φ n (x), 0 < x < L, (1) n=1
 SECTION : Fourier Series. MATH4. In section 4, we will study method clled Seprtion of Vribles for finding exct solutions to certin clss of prtil differentil equtions (PDEs. To do this, it will be necessry
SECTION : Fourier Series. MATH4. In section 4, we will study method clled Seprtion of Vribles for finding exct solutions to certin clss of prtil differentil equtions (PDEs. To do this, it will be necessry
Chapter 3 Polynomials
 Dr M DRAIEF As described in the introduction of Chpter 1, pplictions of solving liner equtions rise in number of different settings In prticulr, we will in this chpter focus on the problem of modelling
Dr M DRAIEF As described in the introduction of Chpter 1, pplictions of solving liner equtions rise in number of different settings In prticulr, we will in this chpter focus on the problem of modelling
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 5 NOVEMBER 2014
 SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 5 NOVEMBER 014 Mrk Scheme: Ech prt of Question 1 is worth four mrks which re wrded solely for the correct nswer.
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 5 NOVEMBER 014 Mrk Scheme: Ech prt of Question 1 is worth four mrks which re wrded solely for the correct nswer.
Notes on the Eigenfunction Method for solving differential equations
 Notes on the Eigenfunction Metho for solving ifferentil equtions Reminer: Wereconsieringtheinfinite-imensionlHilbertspceL 2 ([, b] of ll squre-integrble functions over the intervl [, b] (ie, b f(x 2
Notes on the Eigenfunction Metho for solving ifferentil equtions Reminer: Wereconsieringtheinfinite-imensionlHilbertspceL 2 ([, b] of ll squre-integrble functions over the intervl [, b] (ie, b f(x 2
MATH 144: Business Calculus Final Review
 MATH 144: Business Clculus Finl Review 1 Skills 1. Clculte severl limits. 2. Find verticl nd horizontl symptotes for given rtionl function. 3. Clculte derivtive by definition. 4. Clculte severl derivtives
MATH 144: Business Clculus Finl Review 1 Skills 1. Clculte severl limits. 2. Find verticl nd horizontl symptotes for given rtionl function. 3. Clculte derivtive by definition. 4. Clculte severl derivtives
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H. Thomas Shores Department of Mathematics University of Nebraska Spring 2007
 A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
Theoretical foundations of Gaussian quadrature
 Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
. Double-angle formulas. Your answer should involve trig functions of θ, and not of 2θ. sin 2 (θ) =
 Review of some needed Trig. Identities for Integrtion. Your nswers should be n ngle in RADIANS. rccos( 1 ) = π rccos( - 1 ) = 2π 2 3 2 3 rcsin( 1 ) = π rcsin( - 1 ) = -π 2 6 2 6 Cn you do similr problems?
Review of some needed Trig. Identities for Integrtion. Your nswers should be n ngle in RADIANS. rccos( 1 ) = π rccos( - 1 ) = 2π 2 3 2 3 rcsin( 1 ) = π rcsin( - 1 ) = -π 2 6 2 6 Cn you do similr problems?
Green function and Eigenfunctions
 Green function nd Eigenfunctions Let L e regulr Sturm-Liouville opertor on n intervl (, ) together with regulr oundry conditions. We denote y, φ ( n, x ) the eigenvlues nd corresponding normlized eigenfunctions
Green function nd Eigenfunctions Let L e regulr Sturm-Liouville opertor on n intervl (, ) together with regulr oundry conditions. We denote y, φ ( n, x ) the eigenvlues nd corresponding normlized eigenfunctions
arxiv: v1 [math.co] 5 Jun 2015
![arxiv: v1 [math.co] 5 Jun 2015 arxiv: v1 [math.co] 5 Jun 2015](/thumbs/78/77492077.jpg) First non-trivi upper bound on the circur chromtic number of the pne. Konstnty Junosz-Szniwski, Fcuty of Mthemtics nd Informtion Science, Wrsw University of Technoogy, Pond Abstrct rxiv:1506.01886v1 [mth.co]
First non-trivi upper bound on the circur chromtic number of the pne. Konstnty Junosz-Szniwski, Fcuty of Mthemtics nd Informtion Science, Wrsw University of Technoogy, Pond Abstrct rxiv:1506.01886v1 [mth.co]
Linearity, linear operators, and self adjoint eigenvalue problems
 Linerity, liner opertors, nd self djoint eigenvlue problems 1 Elements of liner lgebr The study of liner prtil differentil equtions utilizes, unsurprisingly, mny concepts from liner lgebr nd liner ordinry
Linerity, liner opertors, nd self djoint eigenvlue problems 1 Elements of liner lgebr The study of liner prtil differentil equtions utilizes, unsurprisingly, mny concepts from liner lgebr nd liner ordinry
Exam 2, Mathematics 4701, Section ETY6 6:05 pm 7:40 pm, March 31, 2016, IH-1105 Instructor: Attila Máté 1
 Exm, Mthemtics 471, Section ETY6 6:5 pm 7:4 pm, Mrch 1, 16, IH-115 Instructor: Attil Máté 1 17 copies 1. ) Stte the usul sufficient condition for the fixed-point itertion to converge when solving the eqution
Exm, Mthemtics 471, Section ETY6 6:5 pm 7:4 pm, Mrch 1, 16, IH-115 Instructor: Attil Máté 1 17 copies 1. ) Stte the usul sufficient condition for the fixed-point itertion to converge when solving the eqution
AP Calculus Multiple Choice: BC Edition Solutions
 AP Clculus Multiple Choice: BC Edition Solutions J. Slon Mrch 8, 04 ) 0 dx ( x) is A) B) C) D) E) Divergent This function inside the integrl hs verticl symptotes t x =, nd the integrl bounds contin this
AP Clculus Multiple Choice: BC Edition Solutions J. Slon Mrch 8, 04 ) 0 dx ( x) is A) B) C) D) E) Divergent This function inside the integrl hs verticl symptotes t x =, nd the integrl bounds contin this
1 E3102: A study guide and review, Version 1.2
 1 E3102: A study guide nd review, Version 1.2 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in
1 E3102: A study guide nd review, Version 1.2 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in
Advanced Calculus: MATH 410 Notes on Integrals and Integrability Professor David Levermore 17 October 2004
 Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
1 Probability Density Functions
 Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Wave Equation on a Two Dimensional Rectangle
 Wve Eqution on Two Dimensionl Rectngle In these notes we re concerned with ppliction of the method of seprtion of vriles pplied to the wve eqution in two dimensionl rectngle. Thus we consider u tt = c
Wve Eqution on Two Dimensionl Rectngle In these notes we re concerned with ppliction of the method of seprtion of vriles pplied to the wve eqution in two dimensionl rectngle. Thus we consider u tt = c
Abstract inner product spaces
 WEEK 4 Abstrct inner product spces Definition An inner product spce is vector spce V over the rel field R equipped with rule for multiplying vectors, such tht the product of two vectors is sclr, nd the
WEEK 4 Abstrct inner product spces Definition An inner product spce is vector spce V over the rel field R equipped with rule for multiplying vectors, such tht the product of two vectors is sclr, nd the
CMDA 4604: Intermediate Topics in Mathematical Modeling Lecture 19: Interpolation and Quadrature
 CMDA 4604: Intermedite Topics in Mthemticl Modeling Lecture 19: Interpoltion nd Qudrture In this lecture we mke brief diversion into the res of interpoltion nd qudrture. Given function f C[, b], we sy
CMDA 4604: Intermedite Topics in Mthemticl Modeling Lecture 19: Interpoltion nd Qudrture In this lecture we mke brief diversion into the res of interpoltion nd qudrture. Given function f C[, b], we sy
Linear Systems with Constant Coefficients
 Liner Systems with Constnt Coefficients 4-3-05 Here is system of n differentil equtions in n unknowns: x x + + n x n, x x + + n x n, x n n x + + nn x n This is constnt coefficient liner homogeneous system
Liner Systems with Constnt Coefficients 4-3-05 Here is system of n differentil equtions in n unknowns: x x + + n x n, x x + + n x n, x n n x + + nn x n This is constnt coefficient liner homogeneous system
We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.
![We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b. We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.](/thumbs/93/114277851.jpg) Mth 255 - Vector lculus II Notes 4.2 Pth nd Line Integrls We begin with discussion of pth integrls (the book clls them sclr line integrls). We will do this for function of two vribles, but these ides cn
Mth 255 - Vector lculus II Notes 4.2 Pth nd Line Integrls We begin with discussion of pth integrls (the book clls them sclr line integrls). We will do this for function of two vribles, but these ides cn
Section 6.1 INTRO to LAPLACE TRANSFORMS
 Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
1. Gauss-Jacobi quadrature and Legendre polynomials. p(t)w(t)dt, p {p(x 0 ),...p(x n )} p(t)w(t)dt = w k p(x k ),
 1. Guss-Jcobi qudrture nd Legendre polynomils Simpson s rule for evluting n integrl f(t)dt gives the correct nswer with error of bout O(n 4 ) (with constnt tht depends on f, in prticulr, it depends on
1. Guss-Jcobi qudrture nd Legendre polynomils Simpson s rule for evluting n integrl f(t)dt gives the correct nswer with error of bout O(n 4 ) (with constnt tht depends on f, in prticulr, it depends on
PhysicsAndMathsTutor.com
 M Dynmics - Dmped nd forced hrmonic motion. A P α B A ight estic spring hs ntur ength nd moduus of esticity mg. One end of the spring is ttched to point A on pne tht is incined to the horizont t n nge
M Dynmics - Dmped nd forced hrmonic motion. A P α B A ight estic spring hs ntur ength nd moduus of esticity mg. One end of the spring is ttched to point A on pne tht is incined to the horizont t n nge
Fourier Series. with the period 2π, given that sin nx and cos nx are period functions with the period 2π. Then we.
 . Definition We c the trigonometric series the series of the form + cos x+ b sin x+ cos x+ b sin x+ or more briefy + ( ncos nx+ bnsin nx) () n The constnts, n nd b, n ( n,, ) re coefficients of the series
. Definition We c the trigonometric series the series of the form + cos x+ b sin x+ cos x+ b sin x+ or more briefy + ( ncos nx+ bnsin nx) () n The constnts, n nd b, n ( n,, ) re coefficients of the series
