Lecture 6 Notes, Electromagnetic Theory I Dr. Christopher S. Baird University of Massachusetts Lowell
|
|
|
- Madeleine Tate
- 6 years ago
- Views:
Transcription
1 Lecture 6 Notes, Eectrognetic Theory I Dr. Christopher S. Bird University of Msschusetts Lowe. Associted Legendre Poynois - We now return to soving the Lpce eqution in spheric coordintes when there is no ziuth syetry by soving the fu Legendre eqution for = nd : d dx [ x2 d P x dx ] [ 2] 2 x P x = where x=cos - Once this eqution is soved, the gener soution for the Lpce eqution in spheric coordintes wi hve the for: r,, = A r B r A B P = cos A r B r A e i B e i P cos, - Encourged by the Rodrigues' for of the soution to the = Legendre eqution, we try soution of the for P ( x)=( x 2 ) / 2 d g( x) nd substitute in: = x x 2 /2[ d /2 [ d 2 dx dx g x ] 2 d dx g x x2 x 2 /2 d x 2 dx ] g x 2 2 x x2 / 2 d g x dx [ ] x 2 /2 d dx g x 2 x 2 / 2 d dx g x dx g x x2 / 2 - Coect siir ters: = x [ 2 d d 2 dx dx ] g x d d 2 [ ]x g x [ ] 2 dx dx g x - We wnt to ove s uch s possibe inside the derivtives. We cn do this by using the product rue. - The product rue used ties sttes: d dx u v = k=! k! k! [ d k dx ][ u d k k dx ] v k - Let us try to ppy this to rerrnge the first ter in the differenti eqution.
2 - If u= x 2 then d u= 2 x dx, d 2 = 2 dx nd higher derivtives in the expnsion re zero so 2 tht: d dx x2 v = x 2 [ - Moving ters round: x 2 [ d dx v ] 2 x [ d dx v ] [ d 2 d dx v ] = d dx x2 v 2 x[ d - Now if we set v= d 2 x 2 [ d dx d 2 dx 2 g x ] = d dx 2 v ] dx v ] [ d 2 2 g (x) dx this product rue expnsion becoes: dx x2 d 2 dx 2 g x 2 x [ d dx 2 v ] dx g x ] [ d dx g x ] - We cn use this product rue to rerrnge the first ter of the Legendre eqution so it becoes: = d dx [ x2 d 2 dx ] g x 2 d d 2 x g x dx dx g x 2 [ d dx g x ] - Now we wnt to use the product rue expnsion on the second ter of the Legendre eqution. With u=x, du =, higher derivtives re zero nd v= d g( x) dx dx, the gener product rue becoes: d dx [ x d dx ] [ g x =x d dx ] [ g x d dx ] g x - After rerrnging: x[ d dx g x ] = d - Substitute in: dx [ x d dx g x ] [ d dx g x ] = d dx [ x2 d 2 dx [ g x 2 x d 2 dx ] ] g x g x = d dx [ d dx( ( x2 ) d dx g( x) ) + (+) g(x) ] - It is worth noting tht if this is true for =, then it wi utoticy be true for. So
3 we cn set = : = d dx x2 d dx g x g x - Now this is just the = Legendre eqution, which we hve redy soved. We found the soutions to be the ordinry Legendre poynois, P (x), so tht g x =P x. - We now hve the soution to the fu Legendre eqution: P x = x 2 /2 d dx P x - There is n rbitrry phse fctor tht we hve ssued to be one for sipicity, but is conventiony set to, so tht the ssocited Legendre functions becoe: P ( x)=( ) ( x 2 ) /2 d dx P (x) - Or written expicity using Rodrigues' eqution: P ( x)= ( ) 2! ( x2 ) /2 d + dx + ( x2 ) - It is worth noting upon exintion of the eqution = d dx [ d dx x2 d dx ] g x g x tht the highest power of x inside the brckets is, so tht cnnot be greter thn, otherwise the eqution woud be triviy stisfied nd thus there woud be no unique soution. In sury, both nd re integers nd the possibe re -, -(-),...,,..., (-),. - Sever usefu thetic retions invoving the ssocited Legendre functions cn be found (the derivtions re eft to the interested student). P x =!! P x P x = 2 x P x P x x 2 P x = x P x P x x 2 d dx P x = x P x P x - For fixed, the Legendre functions for n orthogon set:
4 P ' x P x dx= 2! 2! ' 2. Spheric Hronics - With the fu Legendre eqution now soved, the gener soution of the Lpce eqution in spheric coordintes hs been found: r,, = A r B r A B P = cos = = = A r B r A e i B e i P cos where P re the ssocited Legendre functions. - Typicy, ost probes require vid soution on the fu rnge of. The singe-vued requireent in this cse forces B =, nd the = ter cn now be incuded in the su with the rest of the ters: r,, = = = A r B r A e i B e i P cos - An ternte wy of presenting this is to et su fro - to nd thus cobine the A nd B ters with the other constnts: r,, = A, r B, r e i P cos = = - The norizing ters re incuded in the undeterined constnts A nd B. When boundry condition is ppied, these constnts becoe specified nd the norizing ters resut ntury. However, to ke the th cener, we cn expicity pu the norizing ters out of the constnts in dvnce. r,, = = = A, r B, r 2! 4! ei P cos - It is now evident tht P (cos θ) ties its noriztion ter fors copete set of orthonor functions in the vribe θ, indexed by for fixed, nd e i φ ties its noriztion ter fors copete set of orthonor functions in the vribe φ, indexed by. The product of both thus cretes orthonor functions tht spns nges of the unit circe. These re known s spheric hronics Y : Y (θ,ϕ)= 2+ 4 π ( )! (+)! ei ϕ P (cosθ) so tht
5 Φ(r,θ, ϕ)= = = ( A, r +B, r )Y (θ,ϕ) - The orthonority of the spheric hronics expicity ens tht: 2 * Y ' ' x, Y x, dx d = ' ' where x=cos or 2π π * Y ' ' (θ,ϕ)y (θ,ϕ)sin θ d θd ϕ=δ ' δ ' - The vidity of this eqution cn be checked triviy by expressing the spheric hronics in ters of its definition nd ppying the orthonority of the ssocited Legendre functions nd the copex exponentis. - Using the definitions of the spheric hronics, the ptient student cn work out the expicit nytic for for ny given nd. The owest-order spheric hronics re especiy sipe nd re typicy tbuted in textbooks. - Becuse the spheric hronics for n orthonor set of equtions, n rbitrry function f, cn be expnded in ters of spheric hronics: f (θ,ϕ)= = = 2π π A Y (θ,ϕ) where A = f (θ, ϕ)y * (θ,ϕ)sin θ d θ d ϕ - There re sever usefu speci cses for spheric hronics tht we shoud keep in ind. - If =, the spheric hronic does not depend on the ziuth nge nd the ssocited Legendre function reduces down to Legendre poynoi: Y, (θ,ϕ)= 2+ 4 π P (cosθ) - If =, the spheric hronic's dependence on por nge becoes especiy sipe, just the sine function to the th power, so there is ony one xiu in this direction: Y, (θ, ϕ)= ( ) (2 +)(2)! e i ϕ sin θ 2! 4π - The spheric hronics with negtive powers of re triviy reted to those with positive powers: Y, (θ,ϕ)=( ) * Y, (θ,ϕ) - Regions of interest incude the positive nd negtive z xis, where the spheric hronics sipify:
6 if Y (,ϕ)={ =} if 2+ 4π if nd Y (π, ϕ)={ 2 + 4π ( ) if =} 3. Boundry Vue Probes in Spheric Coordintes - Consider the probe where there is region of spce without ny chrges, bounded by sphere with rdius r centered t the origin on which there is potenti r=r,, =V,. We wnt to know the potenti inside the sphere. We use the gener soution to the Lpce eqution in spheric coordintes: Φ(r, θ, ϕ)= = = ( A r +B r )Y (θ, ϕ) - The region of interest incudes the origin, thus B = to keep the soution fro bowing up there: Φ(r,θ,ϕ)= = = A r Y (θ, ϕ) - Now ppy the boundry condition: V (θ,ϕ)= = = A r Y (θ,ϕ) - This is n expnsion in spheric hronics, nd the constnts re thus: 2 π π A r = V (θ,ϕ)y * (θ,ϕ)sin θd θd ϕ - The soution is then: Φ(r,θ,ϕ)= = = 2π π A r Y (θ, ϕ) where A =r V (θ,ϕ)y * (θ,ϕ)sin θ d θ d ϕ - Or written in ore intuitive wy by redefining the constnt: Φ(r,θ, ϕ)= = = A ( r r ) 2π π Y (θ,ϕ) where A = V (θ,ϕ)y * (θ, ϕ)sin θd θd ϕ
7 4. The Addition Theore for Spheric Hronics - Consider two coordinte vectors (r, θ, φ) nd (r', θ', φ') which hve the nge γ between the. - The ordinry Legendre poynoi s function of the nge between the, P cos cn be expnded in spheric hronics of the coordinte vectors: P cos = 4 Y * 2 ', ' Y, = - This is known s the ddition theore. - Previousy, we derived the potenti t r in spheric coordintes tht resuts fro unit chrge t soe point r on the z-xis s: r,, = r r = r = r P cos if r r nd r r r = = r P cos if r r - The equtions sti hod when the point r is off the z-xis if the Legendre poynois becoe functions of the nge γ between the observtion point r nd the source point r. r r = r = r P cos if r r nd r r r = = r P cos if r r - This eqution is not terriby usefu becuse the nge γ depends on the spheric coordintes. - We cn use the ddition theore to expnd the ordinry Legendre poynoi so tht the expression is function of spheric coordintes rther thn function of the nge between coordinte vectors: r r =4π = r r =4 π = = = 2+ r r Y * + (θ',ϕ ')Y (θ,ϕ) if r<r nd r r Y * (θ', ϕ ')Y (θ, ϕ) if r>r - This wi be usefu if we wnt to know the potenti produced by utipe point chrges in expicit coordintes. 5. The Lpce Eqution in Cyindric Coordintes - Erier, we soved the Lpce eqution in cyindric coordintes for the speci cse of when the boundry conditions re unifor in the z-diension, nd the probe reduced to por coordintes. - We now revisit the probe for when the boundry conditions re not unifor in the z- diension. - The Lpce eqution in cyindric coordintes is: 2 = z 2 =
8 - Use the ethod of seprtion of vribes by trying soution of the for: r,, z =R Q Z z nd substituting it in: Q Z z R R Z z 2 Q R Q 2 Z z = 2 2 z 2 - Divide by R Q Z z : R R Q 2 Q 2 Z z = 2 2 Z z z 2 - The st ter depends ony on z nd the other ters do not so to be vid for z, they ust be reted by constnt: R R Q - Mutipy the eft eqution by 2 : R 2 Q k 2 = where k 2 = 2 Z z 2 2 Z z z 2 R 2 Q k 2 2 = where k 2 = 2 Z z Q 2 Z z z 2 - The second ter depends now ony on φ nd the rest of the ters do not, so we set it to constnt. A the prti derivtives becoe regur derivtives s the functions re of one vribe ony now: R d d d R d 2 k 2 2 = where 2 = d 2 Q, k 2 = d 2 Z z Q d 2 Z z d z 2 - We put ech eqution in ore intuitive for: d d d R d k 2 2 d 2 R = where 2 Q d 2 = 2 Q, d 2 Z z =k 2 Z z d z 2 - In order to get the ost gener soution, we ust cover four cses: - Cse : If = nd k= then the soutions re: R = A, B, n, Q =C, D, nd Z z = F, G, z - The copete prticur soution is the product of these prts.
9 - Cse 2: If nd k= then the soutions re: R = A, B,, Q =C, e i D, e i nd Z z = F, G, z - The copete prticur soution is the product of these prts. - Cse 3: If = nd k, soutions to the st two equtions re: Q =C,k D, k, Z z = F, k e k z G,k e k z The differenti eqution invoving R hs the se soution s the next cse nd wi be hnded with it. - Cse 4: If nd k, the soutions to the st two equtions re: Q =C, k e i D,k e i Z z = F, k e k z G, k e k z - The differenti eqution invoving R ust be soved by trying series soution. Once found, the gener soution for this cse wi hve the for:,, z = k R, k C, k e i D, k e i F, k e k z G, k e k z - First sipify the eqution by king the substitution: x=k d d R x x d x x d x 2 x 2 R x = - Try soution of the for R x = j x j nd substitute it in: j = j= j x j 2 j 2 2 j x j = j= - Reove the first two ters of the su on the eft nd cobine the reining sus: x x 2 2 x j j 2 j j = j= - Every power of x is independent, thus the coefficient of every power ust vnish: 2 2 =, 2 2 =, j 2 = j j - Fro these it is found tht =±, odd = nd j 2 = j 2 j 2±2 j
10 - Becuse odd powers re zero, we cn iterte over integers nd rewrite the indices: 2 j = 4 j j± 2 j for j=,2,3,... - In sury, one soution to the R eqution is the Besse J function: R, k = J k where J x = 2 j x 2 j, 2 j = 4 j j 2 j nd by convention, = 2 in ters of the G function. j= - One ight think tht the other soution to the R eqution is J -ν, but it turns out tht this is not inery dependent fro J ν when ν is n integer nd we ust find nother soution. - Trditiony, the Neunn function, or Besse function of the second kind is tken s the other inery independent soution. It is defined by: N x = J x cos J x sin x - Usefu properties, incuding the recurrence retions, cn be esiy derived or found in textbooks. - The gener soution for R, in ters of the Besse functions, becoes: R, k = A, k J k B,k N k - The gener soution to the Lpce eqution in cyindric coordintes for cse 4 becoes:,, z = k A, k J k B, k N k C, k e i D, k e i F, k e k z G, k e k z - The ost gener soution to the Lpce eqution in cyindric coordintes is the su of the soutions of the possibe cses: Φ(ρ,ϕ, z)=( A, +B, nρ)(c, + D, ϕ)( F, +G, z) + (A ν, ρ ν + B ν, ρ ν )(C ν, e i ν ϕ +D ν, e i νϕ )(F ν, +G ν, z) ν (A, k J (k ρ)+b, k N (k ρ))(c,k +D, k ϕ)(f,k e k z +G,k e k z ) + k + ν ( A ν, k J ν (k ρ)+b ν,k N ν (k ρ))(c ν,k e i νϕ + D ν, k e i νϕ )(F ν,k e k z +G ν, k e k z ) k - To be usefu, we ust find orthogon sets of functions invoving the Besse functions so tht we cn use the orthogonity condition to invert equtions invoving the boundry conditions. The functions:
11 J x n cn be shown to be orthogon on the interv (, ) for fixed ν nd n =, 2, 3,... where x νn re the roots tht stisfy J x n =. - The orthogonity condition for these functions cn be shown to be: J x n' J x 2 n d = 2 [ J x n ]2 n' n - This cn be used to expnd n rbitrry function in Besse series: f = j= A n J x n where A = 2 n 2 2 J x n f J x n 6. Boundry Vue Probes in Cyindric Coordintes - Consider cyinder with rdius nd height L with its botto centered t the origin. The potenti is everywhere zero on the surfce of the cyinder, except the top where it is potenti V,. This eds to the boundry conditions: =,, z =,,, z= =, nd,, z= L =V, - The gener soution to the Lpce eqution in cyindric coordintes is:,, z = A, B, n C, D, F, G, z A, B, C, e i D, e i F, G, z A, k J k B,k N k C,k D, k F,k e k z G, k e k z k A, k J k B,k N k C,k e i D,k e i F, k e k z G, k e k z k - The region where we need vid soution incudes the origin, so sever of the coefficients ust be zero to keep the soution fro bowing up. This eds to:,, z = C, D, F, G, z C, e i D, e i F, G, z J k C, k D,k F,k e k z G, k e k z k J k C,k e i D,k e i F, k e k z G,k e k z k - The region where we need vid soution spns the fu circe of nges for φ, so we require the function to be singe-vued:,, z =, 2, z
12 - This equity ust hod for vues of of the independent vribes, thus ech ter ust tch. This requireent eds to: D, =, D,k =, nd = where =,,2,3,...,, z = F, G, z C, e i D, e i F, G, z J k F,k e k z G, k e k z k k J k C,k e i D,k e i F, k e k z G,k e k z - Appy the boundry condition:,, z= = =F, C, e i D, e i F, k k J k F,k G, k J k C,k e i D, k e i F, k G, k - This eds to the requireents tht F, =, F, =, G,k = F, k, nd G, k = F,k,, z =G, z C, e i D, e i z k k J k F, k sinh k z J k C,k e i D,k e i sinh k z - A the = ters now hve for for which they cn be cobined with the ters:,, z = C, e i D, e i z J k C, k e i D, k e i sinh k z k - The first ter on the right is just speci cse of the st ter when k = (cose to zero, J hs n syptotic for tht is proportion to ρ ). They cn be cobined:,, z = J k C, k e i D, k e i sinh k z k - Appy the boundry condition: =,, z = : = J k C, k e i D,k e i sinh k z k - This cn ony hod true for vues of the independent vribe nd z if the coefficients re zero:
13 =J k for nd k - There is ony discrete set of soutions to this equtions - its roots. The roots cnnot be found nyticy. When done nuericy, the roots re designted s x for n=, 2, 3... so tht k= x - The soution now becoes:,, z = = n= J x C,n ei D,n e sinh i x z - The fin boundry condition is,, z= L =V, now ppied: V, = = n= J x C, n ei D, n e sinh i x L - This is Fourier series in nd Fourier-Besse series in ρ. We find the coefficients in the usu wy. Mutipy both sides by n exponenti nd integrte: 2 V, e i ' d = = n= J x 2 C, n e i ' D,n e i ' d sinh x L - Use the orthogonity condition e i ' x dx=2,' nd rebe: 2 V, e i d =2 J n= x C sinh,n x L - Mutipy both side by J x ' J x ' 2 nd integrte: V, e i d d =2 - Use the orthogonity condition: J x ' 2 n= J x n' J x ' J x d C sinh, n x L J x n 2 d = 2 [ J x n ]2 n' n V, e i d d =2 2 n= 2 [ J x ]2 n' n C, n sinh x L J x 2 V, e i d d = 2 [ J x n ] 2 C,n sinh x L
14 - Sove for the coefficient: C,n csch x L 2 = 2 [ J x ] 2 d d V, J x e i - In the exct se process the other set of coefficients is found to be: D, n csch x L 2 = d d V, J 2 [ J x n ] 2 x ei * - It is pprent now tht D, n =C,n - In sury, the fin soution is: Φ(ρ,ϕ, z)= where = J ( x ρ n= csch C,n = ( L x ) ) (C, n ei ϕ +C, n 2π π 2 [ J + ( x )] 2 d ϕ * e i ϕ )sinh ( x z ) d ρ ρv (ρ, ϕ) J ( x ρ ) e iϕ
1. The vibrating string problem revisited.
 Weeks 7 8: S eprtion of Vribes In the pst few weeks we hve expored the possibiity of soving first nd second order PDEs by trnsforming them into simper forms ( method of chrcteristics. Unfortuntey, this
Weeks 7 8: S eprtion of Vribes In the pst few weeks we hve expored the possibiity of soving first nd second order PDEs by trnsforming them into simper forms ( method of chrcteristics. Unfortuntey, this
MAGIC058 & MATH64062: Partial Differential Equations 1
 MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
Math 124B January 24, 2012
 Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
Mutipy by r sin RT P to get sin R r r R + T sin (sin T )+ P P = (7) ffi So we hve P P ffi = m (8) choose m re so tht P is sinusoi. If we put this in b
 Topic 4: Lpce Eqution in Spheric Co-orintes n Mutipoe Expnsion Reing Assignment: Jckson Chpter 3.-3.5. Lpce Eqution in Spheric Coorintes Review of spheric por coorintes: x = r sin cos ffi y = r sin sin
Topic 4: Lpce Eqution in Spheric Co-orintes n Mutipoe Expnsion Reing Assignment: Jckson Chpter 3.-3.5. Lpce Eqution in Spheric Coorintes Review of spheric por coorintes: x = r sin cos ffi y = r sin sin
PHYS 601 HW3 Solution
 3.1 Norl force using Lgrnge ultiplier Using the center of the hoop s origin, we will describe the position of the prticle with conventionl polr coordintes. The Lgrngin is therefore L = 1 2 ṙ2 + 1 2 r2
3.1 Norl force using Lgrnge ultiplier Using the center of the hoop s origin, we will describe the position of the prticle with conventionl polr coordintes. The Lgrngin is therefore L = 1 2 ṙ2 + 1 2 r2
Jackson 2.7 Homework Problem Solution Dr. Christopher S. Baird University of Massachusetts Lowell
 Jckson.7 Homework Problem Solution Dr. Christopher S. Bird University of Msschusetts Lowell PROBLEM: Consider potentil problem in the hlf-spce defined by, with Dirichlet boundry conditions on the plne
Jckson.7 Homework Problem Solution Dr. Christopher S. Bird University of Msschusetts Lowell PROBLEM: Consider potentil problem in the hlf-spce defined by, with Dirichlet boundry conditions on the plne
Suggested Solution to Assignment 5
 MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
r = cos θ + 1. dt ) dt. (1)
 MTHE 7 Proble Set 5 Solutions (A Crdioid). Let C be the closed curve in R whose polr coordintes (r, θ) stisfy () Sketch the curve C. r = cos θ +. (b) Find pretriztion t (r(t), θ(t)), t [, b], of C in polr
MTHE 7 Proble Set 5 Solutions (A Crdioid). Let C be the closed curve in R whose polr coordintes (r, θ) stisfy () Sketch the curve C. r = cos θ +. (b) Find pretriztion t (r(t), θ(t)), t [, b], of C in polr
Summary: Method of Separation of Variables
 Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Jackson 2.26 Homework Problem Solution Dr. Christopher S. Baird University of Massachusetts Lowell
 Jckson 2.26 Homework Problem Solution Dr. Christopher S. Bird University of Msschusetts Lowell PROBLEM: The two-dimensionl region, ρ, φ β, is bounded by conducting surfces t φ =, ρ =, nd φ = β held t zero
Jckson 2.26 Homework Problem Solution Dr. Christopher S. Bird University of Msschusetts Lowell PROBLEM: The two-dimensionl region, ρ, φ β, is bounded by conducting surfces t φ =, ρ =, nd φ = β held t zero
Orthogonal functions
 Orthogonl functions Given rel vrible over the intervl (, b nd set of rel or complex functions U n (ξ, n =, 2,..., which re squre integrble nd orthonorml b U n(ξu m (ξdξ = δ n,m ( if the set of of functions
Orthogonl functions Given rel vrible over the intervl (, b nd set of rel or complex functions U n (ξ, n =, 2,..., which re squre integrble nd orthonorml b U n(ξu m (ξdξ = δ n,m ( if the set of of functions
Section 10.2 Angles and Triangles
 117 Ojective #1: Section 10.2 nges n Tringes Unerstning efinitions of ifferent types of nges. In the intersection of two ines, the nges tht re cttycorner fro ech other re vertic nges. Vertic nges wi hve
117 Ojective #1: Section 10.2 nges n Tringes Unerstning efinitions of ifferent types of nges. In the intersection of two ines, the nges tht re cttycorner fro ech other re vertic nges. Vertic nges wi hve
potentials A z, F z TE z Modes We use the e j z z =0 we can simply say that the x dependence of E y (1)
 3e. Introduction Lecture 3e Rectngulr wveguide So fr in rectngulr coordintes we hve delt with plne wves propgting in simple nd inhomogeneous medi. The power density of plne wve extends over ll spce. Therefore
3e. Introduction Lecture 3e Rectngulr wveguide So fr in rectngulr coordintes we hve delt with plne wves propgting in simple nd inhomogeneous medi. The power density of plne wve extends over ll spce. Therefore
Statistical Physics. Solutions Sheet 5.
 Sttistic Physics. Soutions Sheet 5. Exercise. HS 04 Prof. Mnfred Sigrist Ide fermionic quntum gs in hrmonic trp In this exercise we study the fermionic spiness ide gs confined in three-dimension hrmonic
Sttistic Physics. Soutions Sheet 5. Exercise. HS 04 Prof. Mnfred Sigrist Ide fermionic quntum gs in hrmonic trp In this exercise we study the fermionic spiness ide gs confined in three-dimension hrmonic
Fourier Series. with the period 2π, given that sin nx and cos nx are period functions with the period 2π. Then we.
 . Definition We c the trigonometric series the series of the form + cos x+ b sin x+ cos x+ b sin x+ or more briefy + ( ncos nx+ bnsin nx) () n The constnts, n nd b, n ( n,, ) re coefficients of the series
. Definition We c the trigonometric series the series of the form + cos x+ b sin x+ cos x+ b sin x+ or more briefy + ( ncos nx+ bnsin nx) () n The constnts, n nd b, n ( n,, ) re coefficients of the series
UNIQUENESS THEOREMS FOR ORDINARY DIFFERENTIAL EQUATIONS WITH HÖLDER CONTINUITY
 UNIQUENESS THEOREMS FOR ORDINARY DIFFERENTIAL EQUATIONS WITH HÖLDER CONTINUITY YIFEI PAN, MEI WANG, AND YU YAN ABSTRACT We estblish soe uniqueness results ner 0 for ordinry differentil equtions of the
UNIQUENESS THEOREMS FOR ORDINARY DIFFERENTIAL EQUATIONS WITH HÖLDER CONTINUITY YIFEI PAN, MEI WANG, AND YU YAN ABSTRACT We estblish soe uniqueness results ner 0 for ordinry differentil equtions of the
Problems for HW X. C. Gwinn. November 30, 2009
 Problems for HW X C. Gwinn November 30, 2009 These problems will not be grded. 1 HWX Problem 1 Suppose thn n object is composed of liner dielectric mteril, with constnt reltive permittivity ɛ r. The object
Problems for HW X C. Gwinn November 30, 2009 These problems will not be grded. 1 HWX Problem 1 Suppose thn n object is composed of liner dielectric mteril, with constnt reltive permittivity ɛ r. The object
Partial Differential Equations
 Prtil Differentil Equtions Notes by Robert Piché, Tmpere University of Technology reen s Functions. reen s Function for One-Dimensionl Eqution The reen s function provides complete solution to boundry
Prtil Differentil Equtions Notes by Robert Piché, Tmpere University of Technology reen s Functions. reen s Function for One-Dimensionl Eqution The reen s function provides complete solution to boundry
Problem Set 3 Solutions
 Msschusetts Institute of Technology Deprtment of Physics Physics 8.07 Fll 2005 Problem Set 3 Solutions Problem 1: Cylindricl Cpcitor Griffiths Problems 2.39: Let the totl chrge per unit length on the inner
Msschusetts Institute of Technology Deprtment of Physics Physics 8.07 Fll 2005 Problem Set 3 Solutions Problem 1: Cylindricl Cpcitor Griffiths Problems 2.39: Let the totl chrge per unit length on the inner
Theoretische Physik 2: Elektrodynamik (Prof. A.-S. Smith) Home assignment 4
 WiSe 1 8.1.1 Prof. Dr. A.-S. Smith Dipl.-Phys. Ellen Fischermeier Dipl.-Phys. Mtthis Sb m Lehrstuhl für Theoretische Physik I Deprtment für Physik Friedrich-Alexnder-Universität Erlngen-Nürnberg Theoretische
WiSe 1 8.1.1 Prof. Dr. A.-S. Smith Dipl.-Phys. Ellen Fischermeier Dipl.-Phys. Mtthis Sb m Lehrstuhl für Theoretische Physik I Deprtment für Physik Friedrich-Alexnder-Universität Erlngen-Nürnberg Theoretische
Lecture 13 - Linking E, ϕ, and ρ
 Lecture 13 - Linking E, ϕ, nd ρ A Puzzle... Inner-Surfce Chrge Density A positive point chrge q is locted off-center inside neutrl conducting sphericl shell. We know from Guss s lw tht the totl chrge on
Lecture 13 - Linking E, ϕ, nd ρ A Puzzle... Inner-Surfce Chrge Density A positive point chrge q is locted off-center inside neutrl conducting sphericl shell. We know from Guss s lw tht the totl chrge on
PHY 5246: Theoretical Dynamics, Fall Assignment # 5, Solutions. θ = l mr 2 = l
 PHY 546: Theoreticl Dynics, Fll 15 Assignent # 5, Solutions 1 Grded Probles Proble 1 (1.) Using the eqution of the orbit or force lw d ( 1 dθ r)+ 1 r = r F(r), (1) l with r(θ) = ke αθ one finds fro which
PHY 546: Theoreticl Dynics, Fll 15 Assignent # 5, Solutions 1 Grded Probles Proble 1 (1.) Using the eqution of the orbit or force lw d ( 1 dθ r)+ 1 r = r F(r), (1) l with r(θ) = ke αθ one finds fro which
Consequently, the temperature must be the same at each point in the cross section at x. Let:
 HW 2 Comments: L1-3. Derive the het eqution for n inhomogeneous rod where the therml coefficients used in the derivtion of the het eqution for homogeneous rod now become functions of position x in the
HW 2 Comments: L1-3. Derive the het eqution for n inhomogeneous rod where the therml coefficients used in the derivtion of the het eqution for homogeneous rod now become functions of position x in the
New Integral Inequalities through Generalized Convex Functions
 Punjb University Journ of Mthetics ISSN 116-2526) Vo. 462)214) pp. 47-51 New Integr Inequities through Generized Convex Functions Muhd Muddssr, Deprtent of Mthetics, University of Engineering nd Technoogy,
Punjb University Journ of Mthetics ISSN 116-2526) Vo. 462)214) pp. 47-51 New Integr Inequities through Generized Convex Functions Muhd Muddssr, Deprtent of Mthetics, University of Engineering nd Technoogy,
Fluid Flow through a Tube
 . Theory through Tube In this experiment we wi determine how we physic retionship (so ced w ), nmey Poiseue s eqution, ppies. In the suppementry reding mteri this eqution ws derived s p Q 8 where Q is
. Theory through Tube In this experiment we wi determine how we physic retionship (so ced w ), nmey Poiseue s eqution, ppies. In the suppementry reding mteri this eqution ws derived s p Q 8 where Q is
MA 131 Lecture Notes Calculus Sections 1.5 and 1.6 (and other material)
 MA Lecture Notes Clculus Sections.5 nd.6 (nd other teril) Algebr o Functions Su, Dierence, Product, nd Quotient o Functions Let nd g be two unctions with overlpping doins. Then or ll x coon to both doins,
MA Lecture Notes Clculus Sections.5 nd.6 (nd other teril) Algebr o Functions Su, Dierence, Product, nd Quotient o Functions Let nd g be two unctions with overlpping doins. Then or ll x coon to both doins,
Homework Assignment #5 Solutions
 Physics 506 Winter 008 Textbook probems: Ch. 9: 9., 9., 9.4 Ch. 10: 10.1 Homework Assignment #5 Soutions 9. A spheric hoe of rdius in conducting medium cn serve s n eectromgnetic resonnt cvity. Assuming
Physics 506 Winter 008 Textbook probems: Ch. 9: 9., 9., 9.4 Ch. 10: 10.1 Homework Assignment #5 Soutions 9. A spheric hoe of rdius in conducting medium cn serve s n eectromgnetic resonnt cvity. Assuming
PHYSICS 116C Homework 4 Solutions
 PHYSICS 116C Homework 4 Solutions 1. ( Simple hrmonic oscilltor. Clerly the eqution is of the Sturm-Liouville (SL form with λ = n 2, A(x = 1, B(x =, w(x = 1. Legendre s eqution. Clerly the eqution is of
PHYSICS 116C Homework 4 Solutions 1. ( Simple hrmonic oscilltor. Clerly the eqution is of the Sturm-Liouville (SL form with λ = n 2, A(x = 1, B(x =, w(x = 1. Legendre s eqution. Clerly the eqution is of
The Dirichlet Problem in a Two Dimensional Rectangle. Section 13.5
 The Dirichlet Prolem in Two Dimensionl Rectngle Section 13.5 1 Dirichlet Prolem in Rectngle In these notes we will pply the method of seprtion of vriles to otin solutions to elliptic prolems in rectngle
The Dirichlet Prolem in Two Dimensionl Rectngle Section 13.5 1 Dirichlet Prolem in Rectngle In these notes we will pply the method of seprtion of vriles to otin solutions to elliptic prolems in rectngle
Physics 116C Solution of inhomogeneous ordinary differential equations using Green s functions
 Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
ρ θ φ δ δ θ δ φ δ φ π δ φ π δ φ π
 Physics 6 Fin Ex Dec. 6, ( pts Fou point chges with chge ± q e nged s in Figue. (5 pts. Wht is the chge density function ρ (, θφ,? (,, q ( ( cos ( / + ( ( / / ρ θ φ δ δ θ δ φ δ φ π δ φ π δ φ π b (5 pts.
Physics 6 Fin Ex Dec. 6, ( pts Fou point chges with chge ± q e nged s in Figue. (5 pts. Wht is the chge density function ρ (, θφ,? (,, q ( ( cos ( / + ( ( / / ρ θ φ δ δ θ δ φ δ φ π δ φ π δ φ π b (5 pts.
Homework Assignment 3 Solution Set
 Homework Assignment 3 Solution Set PHYCS 44 6 Ferury, 4 Prolem 1 (Griffiths.5(c The potentil due to ny continuous chrge distriution is the sum of the contriutions from ech infinitesiml chrge in the distriution.
Homework Assignment 3 Solution Set PHYCS 44 6 Ferury, 4 Prolem 1 (Griffiths.5(c The potentil due to ny continuous chrge distriution is the sum of the contriutions from ech infinitesiml chrge in the distriution.
In this appendix, we evaluate the derivative of Eq. 9 in the main text, i.e., we need to calculate
 Supporting Tet Evoution of the Averge Synptic Updte Rue In this ppendi e evute the derivtive of Eq. 9 in the min tet i.e. e need to ccute Py ( ) Py ( Y ) og γ og. [] P( y Y ) P% ( y Y ) Before e strt et
Supporting Tet Evoution of the Averge Synptic Updte Rue In this ppendi e evute the derivtive of Eq. 9 in the min tet i.e. e need to ccute Py ( ) Py ( Y ) og γ og. [] P( y Y ) P% ( y Y ) Before e strt et
Math 5440 Problem Set 3 Solutions
 Mth 544 Mth 544 Problem Set 3 Solutions Aron Fogelson Fll, 213 1: (Logn, 1.5 # 2) Repet the derivtion for the eqution of motion of vibrting string when, in ddition, the verticl motion is retrded by dmping
Mth 544 Mth 544 Problem Set 3 Solutions Aron Fogelson Fll, 213 1: (Logn, 1.5 # 2) Repet the derivtion for the eqution of motion of vibrting string when, in ddition, the verticl motion is retrded by dmping
Polynomials and Division Theory
 Higher Checklist (Unit ) Higher Checklist (Unit ) Polynomils nd Division Theory Skill Achieved? Know tht polynomil (expression) is of the form: n x + n x n + n x n + + n x + x + 0 where the i R re the
Higher Checklist (Unit ) Higher Checklist (Unit ) Polynomils nd Division Theory Skill Achieved? Know tht polynomil (expression) is of the form: n x + n x n + n x n + + n x + x + 0 where the i R re the
Math 113 Exam 1-Review
 Mth 113 Exm 1-Review September 26, 2016 Exm 1 covers 6.1-7.3 in the textbook. It is dvisble to lso review the mteril from 5.3 nd 5.5 s this will be helpful in solving some of the problems. 6.1 Are Between
Mth 113 Exm 1-Review September 26, 2016 Exm 1 covers 6.1-7.3 in the textbook. It is dvisble to lso review the mteril from 5.3 nd 5.5 s this will be helpful in solving some of the problems. 6.1 Are Between
Vector Spherical Harmonics
 Vector Spherica Haronics Lecture Introduction Previousy we have seen that the Lapacian operator is different when operating on a vector or a scaar function. We avoided this probe by etting the Lapacian
Vector Spherica Haronics Lecture Introduction Previousy we have seen that the Lapacian operator is different when operating on a vector or a scaar function. We avoided this probe by etting the Lapacian
Lecture 4 Notes, Electromagnetic Theory I Dr. Christopher S. Baird University of Massachusetts Lowell
 Lecture 4 Notes, Electromgnetic Theory I Dr. Christopher S. Bird University of Msschusetts Lowell 1. Orthogonl Functions nd Expnsions - In the intervl (, ) of the vrile x, set of rel or complex functions
Lecture 4 Notes, Electromgnetic Theory I Dr. Christopher S. Bird University of Msschusetts Lowell 1. Orthogonl Functions nd Expnsions - In the intervl (, ) of the vrile x, set of rel or complex functions
Math 5440 Problem Set 3 Solutions
 Mth 544 Mth 544 Problem Set 3 Solutions Aron Fogelson Fll, 25 1: Logn, 1.5 # 2) Repet the derivtion for the eqution of motion of vibrting string when, in ddition, the verticl motion is retrded by dmping
Mth 544 Mth 544 Problem Set 3 Solutions Aron Fogelson Fll, 25 1: Logn, 1.5 # 2) Repet the derivtion for the eqution of motion of vibrting string when, in ddition, the verticl motion is retrded by dmping
Chapter (a) 2. At equilibrium, V = 0. x = (c) V( x) ke bkxe = 0. At equilibrium. b bx bx 2 bx. V = bke bkxe + b kxe = + = < 0.
 Chpter. () V( x) = x + x V = x x At equiibriu, V = x = V = + x V = + = > x= Stbe (b) V( x) = xe bx bx bx V = e bxe At equiibriu bx bx e bxe = x = b bx bx bx V = be bxe + b xe V be be = + = < x= b Unstbe
Chpter. () V( x) = x + x V = x x At equiibriu, V = x = V = + x V = + = > x= Stbe (b) V( x) = xe bx bx bx V = e bxe At equiibriu bx bx e bxe = x = b bx bx bx V = be bxe + b xe V be be = + = < x= b Unstbe
APPENDIX B. Some special functions in low-frequency seismology. 2l +1 x j l (B.2) j l = j l 1 l +1 x j l (B.3) j l = l x j l j l+1
 APPENDIX B Soe specia functions in ow-frequency seisoogy 1. Spherica Besse functions The functions j and y are usefu in constructing ode soutions in hoogeneous spheres (fig B1). They satisfy d 2 j dr 2
APPENDIX B Soe specia functions in ow-frequency seisoogy 1. Spherica Besse functions The functions j and y are usefu in constructing ode soutions in hoogeneous spheres (fig B1). They satisfy d 2 j dr 2
Chapter 28. Fourier Series An Eigenvalue Problem.
 Chpter 28 Fourier Series Every time I close my eyes The noise inside me mplifies I cn t escpe I relive every moment of the dy Every misstep I hve mde Finds wy it cn invde My every thought And this is why
Chpter 28 Fourier Series Every time I close my eyes The noise inside me mplifies I cn t escpe I relive every moment of the dy Every misstep I hve mde Finds wy it cn invde My every thought And this is why
Improper Integrals, and Differential Equations
 Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Review of Gaussian Quadrature method
 Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Physics 712 Electricity and Magnetism Solutions to Final Exam, Spring 2016
 Physics 7 Electricity nd Mgnetism Solutions to Finl Em, Spring 6 Plese note tht some possibly helpful formuls pper on the second pge The number of points on ech problem nd prt is mrked in squre brckets
Physics 7 Electricity nd Mgnetism Solutions to Finl Em, Spring 6 Plese note tht some possibly helpful formuls pper on the second pge The number of points on ech problem nd prt is mrked in squre brckets
ENGI 9420 Lecture Notes 7 - Fourier Series Page 7.01
 ENGI 940 ecture Notes 7 - Fourier Series Pge 7.0 7. Fourier Series nd Fourier Trnsforms Fourier series hve multiple purposes, including the provision of series solutions to some liner prtil differentil
ENGI 940 ecture Notes 7 - Fourier Series Pge 7.0 7. Fourier Series nd Fourier Trnsforms Fourier series hve multiple purposes, including the provision of series solutions to some liner prtil differentil
Space Curves. Recall the parametric equations of a curve in xy-plane and compare them with parametric equations of a curve in space.
 Clculus 3 Li Vs Spce Curves Recll the prmetric equtions of curve in xy-plne nd compre them with prmetric equtions of curve in spce. Prmetric curve in plne x = x(t) y = y(t) Prmetric curve in spce x = x(t)
Clculus 3 Li Vs Spce Curves Recll the prmetric equtions of curve in xy-plne nd compre them with prmetric equtions of curve in spce. Prmetric curve in plne x = x(t) y = y(t) Prmetric curve in spce x = x(t)
Math 473: Practice Problems for the Material after Test 2, Fall 2011
 Mth 473: Prctice Problems for the Mteril fter Test, Fll SOLUTION. Consider the following modified het eqution u t = u xx + u x. () Use the relevnt 3 point pproximtion formuls for u xx nd u x to derive
Mth 473: Prctice Problems for the Mteril fter Test, Fll SOLUTION. Consider the following modified het eqution u t = u xx + u x. () Use the relevnt 3 point pproximtion formuls for u xx nd u x to derive
Edexcel GCE Core Mathematics (C2) Required Knowledge Information Sheet. Daniel Hammocks
 Edexcel GCE Core Mthemtics (C) Required Knowledge Informtion Sheet C Formule Given in Mthemticl Formule nd Sttisticl Tles Booklet Cosine Rule o = + c c cosine (A) Binomil Series o ( + ) n = n + n 1 n 1
Edexcel GCE Core Mthemtics (C) Required Knowledge Informtion Sheet C Formule Given in Mthemticl Formule nd Sttisticl Tles Booklet Cosine Rule o = + c c cosine (A) Binomil Series o ( + ) n = n + n 1 n 1
4 The dynamical FRW universe
 4 The dynmicl FRW universe 4.1 The Einstein equtions Einstein s equtions G µν = T µν (7) relte the expnsion rte (t) to energy distribution in the universe. On the left hnd side is the Einstein tensor which
4 The dynmicl FRW universe 4.1 The Einstein equtions Einstein s equtions G µν = T µν (7) relte the expnsion rte (t) to energy distribution in the universe. On the left hnd side is the Einstein tensor which
set is not closed under matrix [ multiplication, ] and does not form a group.
![set is not closed under matrix [ multiplication, ] and does not form a group. set is not closed under matrix [ multiplication, ] and does not form a group.](/thumbs/78/78412113.jpg) Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Physics 3323, Fall 2016 Problem Set 7 due Oct 14, 2016
 Physics 333, Fll 16 Problem Set 7 due Oct 14, 16 Reding: Griffiths 4.1 through 4.4.1 1. Electric dipole An electric dipole with p = p ẑ is locted t the origin nd is sitting in n otherwise uniform electric
Physics 333, Fll 16 Problem Set 7 due Oct 14, 16 Reding: Griffiths 4.1 through 4.4.1 1. Electric dipole An electric dipole with p = p ẑ is locted t the origin nd is sitting in n otherwise uniform electric
Phys 6321 Final Exam - Solutions May 3, 2013
 Phys 6321 Finl Exm - Solutions My 3, 2013 You my NOT use ny book or notes other thn tht supplied with this test. You will hve 3 hours to finish. DO YOUR OWN WORK. Express your nswers clerly nd concisely
Phys 6321 Finl Exm - Solutions My 3, 2013 You my NOT use ny book or notes other thn tht supplied with this test. You will hve 3 hours to finish. DO YOUR OWN WORK. Express your nswers clerly nd concisely
3 Mathematics of the Poisson Equation
 3 Mthemtics of the Poisson Eqution 3. Green functions nd the Poisson eqution () The Dirichlet Green function stisfies the Poisson eqution with delt-function chrge 2 G D (r, r o ) = δ 3 (r r o ) (3.) nd
3 Mthemtics of the Poisson Eqution 3. Green functions nd the Poisson eqution () The Dirichlet Green function stisfies the Poisson eqution with delt-function chrge 2 G D (r, r o ) = δ 3 (r r o ) (3.) nd
Reversing the Chain Rule. As we have seen from the Second Fundamental Theorem ( 4.3), the easiest way to evaluate an integral b
 Mth 32 Substitution Method Stewrt 4.5 Reversing the Chin Rule. As we hve seen from the Second Fundmentl Theorem ( 4.3), the esiest wy to evlute n integrl b f(x) dx is to find n ntiderivtive, the indefinite
Mth 32 Substitution Method Stewrt 4.5 Reversing the Chin Rule. As we hve seen from the Second Fundmentl Theorem ( 4.3), the esiest wy to evlute n integrl b f(x) dx is to find n ntiderivtive, the indefinite
Identites and properties for associated Legendre functions
 Identites and properties for associated Legendre functions DBW This note is a persona note with a persona history; it arose out off y incapacity to find references on the internet that prove reations that
Identites and properties for associated Legendre functions DBW This note is a persona note with a persona history; it arose out off y incapacity to find references on the internet that prove reations that
STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS
 STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS Throughout, we let [, b] be bounded intervl in R. C 2 ([, b]) denotes the spce of functions with derivtives of second order continuous up to the endpoints. Cc 2
STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS Throughout, we let [, b] be bounded intervl in R. C 2 ([, b]) denotes the spce of functions with derivtives of second order continuous up to the endpoints. Cc 2
Chapter 2. Solving a Nonlinear Equation
 Chpter Soving Noniner Eqtion 1 Bisection Method Ater reding this chpter, yo shod be be to: 1 oow the gorith o the bisection ethod o soving noniner eqtion, se the bisection ethod to sove epes o inding roots
Chpter Soving Noniner Eqtion 1 Bisection Method Ater reding this chpter, yo shod be be to: 1 oow the gorith o the bisection ethod o soving noniner eqtion, se the bisection ethod to sove epes o inding roots
1 1D heat and wave equations on a finite interval
 1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
Prof. Anchordoqui. Problems set # 4 Physics 169 March 3, 2015
 Prof. Anchordoui Problems set # 4 Physics 169 Mrch 3, 15 1. (i) Eight eul chrges re locted t corners of cube of side s, s shown in Fig. 1. Find electric potentil t one corner, tking zero potentil to be
Prof. Anchordoui Problems set # 4 Physics 169 Mrch 3, 15 1. (i) Eight eul chrges re locted t corners of cube of side s, s shown in Fig. 1. Find electric potentil t one corner, tking zero potentil to be
Advanced Calculus: MATH 410 Notes on Integrals and Integrability Professor David Levermore 17 October 2004
 Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
Bernoulli Numbers Jeff Morton
 Bernoulli Numbers Jeff Morton. We re interested in the opertor e t k d k t k, which is to sy k tk. Applying this to some function f E to get e t f d k k tk d k f f + d k k tk dk f, we note tht since f
Bernoulli Numbers Jeff Morton. We re interested in the opertor e t k d k t k, which is to sy k tk. Applying this to some function f E to get e t f d k k tk d k f f + d k k tk dk f, we note tht since f
Practice final exam solutions
 University of Pennsylvni Deprtment of Mthemtics Mth 26 Honors Clculus II Spring Semester 29 Prof. Grssi, T.A. Asher Auel Prctice finl exm solutions 1. Let F : 2 2 be defined by F (x, y (x + y, x y. If
University of Pennsylvni Deprtment of Mthemtics Mth 26 Honors Clculus II Spring Semester 29 Prof. Grssi, T.A. Asher Auel Prctice finl exm solutions 1. Let F : 2 2 be defined by F (x, y (x + y, x y. If
PHYS 705: Classical Mechanics. Small Oscillations: Example A Linear Triatomic Molecule
 PHYS 75: Clssicl echnics Sll Oscilltions: Exple A Liner Tritoic olecule A Liner Tritoic olecule x b b x x3 x Experientlly, one ight be interested in the rdition resulted fro the intrinsic oscilltion odes
PHYS 75: Clssicl echnics Sll Oscilltions: Exple A Liner Tritoic olecule A Liner Tritoic olecule x b b x x3 x Experientlly, one ight be interested in the rdition resulted fro the intrinsic oscilltion odes
Homework Assignment 5 Solution Set
 Homework Assignment 5 Solution Set PHYCS 44 3 Februry, 4 Problem Griffiths 3.8 The first imge chrge gurntees potentil of zero on the surfce. The secon imge chrge won t chnge the contribution to the potentil
Homework Assignment 5 Solution Set PHYCS 44 3 Februry, 4 Problem Griffiths 3.8 The first imge chrge gurntees potentil of zero on the surfce. The secon imge chrge won t chnge the contribution to the potentil
1 E3102: a study guide and review, Version 1.0
 1 E3102: study guide nd review, Version 1.0 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in very
1 E3102: study guide nd review, Version 1.0 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in very
Quantum Physics II (8.05) Fall 2013 Assignment 2
 Quntum Physics II (8.05) Fll 2013 Assignment 2 Msschusetts Institute of Technology Physics Deprtment Due Fridy September 20, 2013 September 13, 2013 3:00 pm Suggested Reding Continued from lst week: 1.
Quntum Physics II (8.05) Fll 2013 Assignment 2 Msschusetts Institute of Technology Physics Deprtment Due Fridy September 20, 2013 September 13, 2013 3:00 pm Suggested Reding Continued from lst week: 1.
The final exam will take place on Friday May 11th from 8am 11am in Evans room 60.
 Mth 104: finl informtion The finl exm will tke plce on Fridy My 11th from 8m 11m in Evns room 60. The exm will cover ll prts of the course with equl weighting. It will cover Chpters 1 5, 7 15, 17 21, 23
Mth 104: finl informtion The finl exm will tke plce on Fridy My 11th from 8m 11m in Evns room 60. The exm will cover ll prts of the course with equl weighting. It will cover Chpters 1 5, 7 15, 17 21, 23
Fourier Series in Complex notation. cos(x) = eix + e ix 2. A n cos + B n sin l. i 2 B n. e inx=l + A n + ib n 2 8. ( 0 m 6= n. C n = 1 2l.
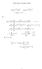 Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
The solutions of the single electron Hamiltonian were shown to be Bloch wave of the form: ( ) ( ) ikr
 Lecture #1 Progrm 1. Bloch solutions. Reciprocl spce 3. Alternte derivtion of Bloch s theorem 4. Trnsforming the serch for egenfunctions nd eigenvlues from solving PDE to finding the e-vectors nd e-vlues
Lecture #1 Progrm 1. Bloch solutions. Reciprocl spce 3. Alternte derivtion of Bloch s theorem 4. Trnsforming the serch for egenfunctions nd eigenvlues from solving PDE to finding the e-vectors nd e-vlues
Improper Integrals. Type I Improper Integrals How do we evaluate an integral such as
 Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
PhysicsAndMathsTutor.com
 M Dynmics - Dmped nd forced hrmonic motion. A P α B A ight estic spring hs ntur ength nd moduus of esticity mg. One end of the spring is ttched to point A on pne tht is incined to the horizont t n nge
M Dynmics - Dmped nd forced hrmonic motion. A P α B A ight estic spring hs ntur ength nd moduus of esticity mg. One end of the spring is ttched to point A on pne tht is incined to the horizont t n nge
Second degree generalized gauss-seidel iteration method for solving linear system of equations. ABSTRACT
 Ethiop. J. Sci. & Technol. 7( 5-, 0 5 Second degree generlized guss-seidel itertion ethod for solving liner syste of equtions Tesfye Keede Bhir Dr University, College of Science, Deprtent of Mthetics tk_ke@yhoo.co
Ethiop. J. Sci. & Technol. 7( 5-, 0 5 Second degree generlized guss-seidel itertion ethod for solving liner syste of equtions Tesfye Keede Bhir Dr University, College of Science, Deprtent of Mthetics tk_ke@yhoo.co
V. More General Eigenfunction Series. A. The Sturm-Liouville Family of Problems
 V. More Gener Eigenfunction Series c 214, Phiip D. Loewen A. The Sturm-Liouvie Fmiy of Probems Given n re interv, b], functions p(x), q(x), r(x), nd constnts c, c 1, d, d 1, consider (ODE) (p(x)y (x))
V. More Gener Eigenfunction Series c 214, Phiip D. Loewen A. The Sturm-Liouvie Fmiy of Probems Given n re interv, b], functions p(x), q(x), r(x), nd constnts c, c 1, d, d 1, consider (ODE) (p(x)y (x))
Chebyshev Functions and their use for two-dimensional electrostatic problems in elliptic coordinates
 Chebyshev Functions nd their use for two-diensionl electrosttic probles in elliptic coordintes RAUL PEREZ-ENRIQUEZ, IVAN MARIN-ENRIQUEZ, J. L. MARIN AND R. RIERA Deprtento de Fisic Universidd de Sonor
Chebyshev Functions nd their use for two-diensionl electrosttic probles in elliptic coordintes RAUL PEREZ-ENRIQUEZ, IVAN MARIN-ENRIQUEZ, J. L. MARIN AND R. RIERA Deprtento de Fisic Universidd de Sonor
, the action per unit length. We use g = 1 and will use the function. gψd 2 x = A 36. Ψ 2 d 2 x = A2 45
 Gbriel Brello - Clssicl Electrodynmics.. For this problem, we compute A L z, the ction per unit length. We use g = nd will use the function Ψx, y = Ax x y y s the form of our pproximte solution. First
Gbriel Brello - Clssicl Electrodynmics.. For this problem, we compute A L z, the ction per unit length. We use g = nd will use the function Ψx, y = Ax x y y s the form of our pproximte solution. First
Math 231E, Lecture 33. Parametric Calculus
 Mth 31E, Lecture 33. Prmetric Clculus 1 Derivtives 1.1 First derivtive Now, let us sy tht we wnt the slope t point on prmetric curve. Recll the chin rule: which exists s long s /. = / / Exmple 1.1. Reconsider
Mth 31E, Lecture 33. Prmetric Clculus 1 Derivtives 1.1 First derivtive Now, let us sy tht we wnt the slope t point on prmetric curve. Recll the chin rule: which exists s long s /. = / / Exmple 1.1. Reconsider
NEW INTEGRAL INEQUALITIES OF THE TYPE OF SIMPSON S AND HERMITE-HADAMARD S FOR TWICE DIFFERENTIABLE QUASI-GEOMETRICALLY CONVEX MAPPINGS
 TJMM 8 6, No., 37-45 NEW INTEGRAL INEQUALITIES OF THE TYPE OF SIMPSON S AND HERMITE-HADAMARD S FOR TWICE DIFFERENTIABLE QUASI-GEOMETRICALLY CONVEX MAPPINGS MUHAMMAD MUDDASSAR AND ZAFFER ELAHI Astrct. In
TJMM 8 6, No., 37-45 NEW INTEGRAL INEQUALITIES OF THE TYPE OF SIMPSON S AND HERMITE-HADAMARD S FOR TWICE DIFFERENTIABLE QUASI-GEOMETRICALLY CONVEX MAPPINGS MUHAMMAD MUDDASSAR AND ZAFFER ELAHI Astrct. In
UNIQUENESS THEOREMS FOR ORDINARY DIFFERENTIAL EQUATIONS WITH HÖLDER CONTINUITY
 UNIQUENESS THEOREMS FOR ORDINARY DIFFERENTIAL EQUATIONS WITH HÖLDER CONTINUITY YIFEI PAN, MEI WANG, AND YU YAN ABSTRACT We study ordinry differentil equtions of the type u n t = fut with initil conditions
UNIQUENESS THEOREMS FOR ORDINARY DIFFERENTIAL EQUATIONS WITH HÖLDER CONTINUITY YIFEI PAN, MEI WANG, AND YU YAN ABSTRACT We study ordinry differentil equtions of the type u n t = fut with initil conditions
Construction of Gauss Quadrature Rules
 Jim Lmbers MAT 772 Fll Semester 2010-11 Lecture 15 Notes These notes correspond to Sections 10.2 nd 10.3 in the text. Construction of Guss Qudrture Rules Previously, we lerned tht Newton-Cotes qudrture
Jim Lmbers MAT 772 Fll Semester 2010-11 Lecture 15 Notes These notes correspond to Sections 10.2 nd 10.3 in the text. Construction of Guss Qudrture Rules Previously, we lerned tht Newton-Cotes qudrture
Math 1051 Diagnostic Pretest Key and Homework
 Mth 1051 Dignostic Pretest Ke nd Hoework HW1 The dignostic test is designed to give us n ide of our level of skill in doing high school lgebr s ou begin Mth 1051. You should be ble to do these probles
Mth 1051 Dignostic Pretest Ke nd Hoework HW1 The dignostic test is designed to give us n ide of our level of skill in doing high school lgebr s ou begin Mth 1051. You should be ble to do these probles
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H. Thomas Shores Department of Mathematics University of Nebraska Spring 2007
 A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Name Solutions to Test 3 November 8, 2017
 Nme Solutions to Test 3 November 8, 07 This test consists of three prts. Plese note tht in prts II nd III, you cn skip one question of those offered. Some possibly useful formuls cn be found below. Brrier
Nme Solutions to Test 3 November 8, 07 This test consists of three prts. Plese note tht in prts II nd III, you cn skip one question of those offered. Some possibly useful formuls cn be found below. Brrier
g i fφdx dx = x i i=1 is a Hilbert space. We shall, henceforth, abuse notation and write g i f(x) = f
 1. Appliction of functionl nlysis to PEs 1.1. Introduction. In this section we give little introduction to prtil differentil equtions. In prticulr we consider the problem u(x) = f(x) x, u(x) = x (1) where
1. Appliction of functionl nlysis to PEs 1.1. Introduction. In this section we give little introduction to prtil differentil equtions. In prticulr we consider the problem u(x) = f(x) x, u(x) = x (1) where
( ) 2. ( ) is the Fourier transform of! ( x). ( ) ( ) ( ) = Ae i kx"#t ( ) = 1 2" ( )"( x,t) PC 3101 Quantum Mechanics Section 1
 1. 1D Schrödinger Eqution G chpters 3-4. 1.1 the Free Prticle V 0 "( x,t) i = 2 t 2m x,t = Ae i kxt "( x,t) x 2 where = k 2 2m. Normliztion must hppen: 2 x,t = 1 Here, however: " A 2 dx " " As this integrl
1. 1D Schrödinger Eqution G chpters 3-4. 1.1 the Free Prticle V 0 "( x,t) i = 2 t 2m x,t = Ae i kxt "( x,t) x 2 where = k 2 2m. Normliztion must hppen: 2 x,t = 1 Here, however: " A 2 dx " " As this integrl
The Spring. Consider a spring, which we apply a force F A to either stretch it or compress it
 The Spring Consider spring, which we pply force F A to either stretch it or copress it F A - unstretched -F A 0 F A k k is the spring constnt, units of N/, different for different terils, nuber of coils
The Spring Consider spring, which we pply force F A to either stretch it or copress it F A - unstretched -F A 0 F A k k is the spring constnt, units of N/, different for different terils, nuber of coils
Differential Equations 2 Homework 5 Solutions to the Assigned Exercises
 Differentil Equtions Homework Solutions to the Assigned Exercises, # 3 Consider the dmped string prolem u tt + 3u t = u xx, < x , u, t = u, t =, t >, ux, = fx, u t x, = gx. In the exm you were supposed
Differentil Equtions Homework Solutions to the Assigned Exercises, # 3 Consider the dmped string prolem u tt + 3u t = u xx, < x , u, t = u, t =, t >, ux, = fx, u t x, = gx. In the exm you were supposed
. Double-angle formulas. Your answer should involve trig functions of θ, and not of 2θ. cos(2θ) = sin(2θ) =.
 Review of some needed Trig Identities for Integrtion Your nswers should be n ngle in RADIANS rccos( 1 2 ) = rccos( - 1 2 ) = rcsin( 1 2 ) = rcsin( - 1 2 ) = Cn you do similr problems? Review of Bsic Concepts
Review of some needed Trig Identities for Integrtion Your nswers should be n ngle in RADIANS rccos( 1 2 ) = rccos( - 1 2 ) = rcsin( 1 2 ) = rcsin( - 1 2 ) = Cn you do similr problems? Review of Bsic Concepts
Candidates must show on each answer book the type of calculator used.
 UNIVERSITY OF EAST ANGLIA School of Mthemtics My/June UG Exmintion 2007 2008 ELECTRICITY AND MAGNETISM Time llowed: 3 hours Attempt FIVE questions. Cndidtes must show on ech nswer book the type of clcultor
UNIVERSITY OF EAST ANGLIA School of Mthemtics My/June UG Exmintion 2007 2008 ELECTRICITY AND MAGNETISM Time llowed: 3 hours Attempt FIVE questions. Cndidtes must show on ech nswer book the type of clcultor
c n φ n (x), 0 < x < L, (1) n=1
 SECTION : Fourier Series. MATH4. In section 4, we will study method clled Seprtion of Vribles for finding exct solutions to certin clss of prtil differentil equtions (PDEs. To do this, it will be necessry
SECTION : Fourier Series. MATH4. In section 4, we will study method clled Seprtion of Vribles for finding exct solutions to certin clss of prtil differentil equtions (PDEs. To do this, it will be necessry
Waveguides Free Space. Modal Excitation. Daniel S. Weile. Department of Electrical and Computer Engineering University of Delaware
 Modl Excittion Dniel S. Weile Deprtment of Electricl nd Computer Engineering University of Delwre ELEG 648 Modl Excittion in Crtesin Coordintes Outline 1 Aperture Excittion Current Excittion Outline 1
Modl Excittion Dniel S. Weile Deprtment of Electricl nd Computer Engineering University of Delwre ELEG 648 Modl Excittion in Crtesin Coordintes Outline 1 Aperture Excittion Current Excittion Outline 1
SOLUTIONS TO CONCEPTS CHAPTER 6
 SOLUIONS O CONCEPS CHAPE 6 1. Let ss of the block ro the freebody digr, 0...(1) velocity Agin 0 (fro (1)) g 4 g 4/g 4/10 0.4 he co-efficient of kinetic friction between the block nd the plne is 0.4. Due
SOLUIONS O CONCEPS CHAPE 6 1. Let ss of the block ro the freebody digr, 0...(1) velocity Agin 0 (fro (1)) g 4 g 4/g 4/10 0.4 he co-efficient of kinetic friction between the block nd the plne is 0.4. Due
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 5 NOVEMBER 2014
 SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 5 NOVEMBER 014 Mrk Scheme: Ech prt of Question 1 is worth four mrks which re wrded solely for the correct nswer.
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 5 NOVEMBER 014 Mrk Scheme: Ech prt of Question 1 is worth four mrks which re wrded solely for the correct nswer.
Physics 9 Fall 2011 Homework 2 - Solutions Friday September 2, 2011
 Physics 9 Fll 0 Homework - s Fridy September, 0 Mke sure your nme is on your homework, nd plese box your finl nswer. Becuse we will be giving prtil credit, be sure to ttempt ll the problems, even if you
Physics 9 Fll 0 Homework - s Fridy September, 0 Mke sure your nme is on your homework, nd plese box your finl nswer. Becuse we will be giving prtil credit, be sure to ttempt ll the problems, even if you
If a is any non zero real or imaginary number and m is the positive integer, then a...
 Idices d Surds.. Defiitio of Idices. If is o ero re or igir uer d is the positive iteger the...... ties. Here is ced the se d the ide power or epoet... Lws of Idices. 0 0 0. where d re rtio uers where
Idices d Surds.. Defiitio of Idices. If is o ero re or igir uer d is the positive iteger the...... ties. Here is ced the se d the ide power or epoet... Lws of Idices. 0 0 0. where d re rtio uers where
x = b a n x 2 e x dx. cdx = c(b a), where c is any constant. a b
 CHAPTER 5. INTEGRALS 61 where nd x = b n x i = 1 (x i 1 + x i ) = midpoint of [x i 1, x i ]. Problem 168 (Exercise 1, pge 377). Use the Midpoint Rule with the n = 4 to pproximte 5 1 x e x dx. Some quick
CHAPTER 5. INTEGRALS 61 where nd x = b n x i = 1 (x i 1 + x i ) = midpoint of [x i 1, x i ]. Problem 168 (Exercise 1, pge 377). Use the Midpoint Rule with the n = 4 to pproximte 5 1 x e x dx. Some quick
The usual algebraic operations +,, (or ), on real numbers can then be extended to operations on complex numbers in a natural way: ( 2) i = 1
 Mth50 Introduction to Differentil Equtions Brief Review of Complex Numbers Complex Numbers No rel number stisfies the eqution x =, since the squre of ny rel number hs to be non-negtive. By introducing
Mth50 Introduction to Differentil Equtions Brief Review of Complex Numbers Complex Numbers No rel number stisfies the eqution x =, since the squre of ny rel number hs to be non-negtive. By introducing
Chapter 5. , r = r 1 r 2 (1) µ = m 1 m 2. r, r 2 = R µ m 2. R(m 1 + m 2 ) + m 2 r = r 1. m 2. r = r 1. R + µ m 1
 Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
