Introduction to statically indeterminate structures
|
|
|
- Robert Hutchinson
- 5 years ago
- Views:
Transcription
1 Sttics of Buiding Structures I., EASUS Introduction to stticy indeterminte structures Deprtment of Structur echnics Fcuty of Civi Engineering, VŠB-Technic University of Ostrv
2 Outine of Lecture Stticy indeterminte structures, degree of indetermincy Force method Simpe stticy indeterminte bem Simpe stticy indeterminte bem xi oding Unitery fixed bem trnsvers oding Bitery fixed bem trnsvers oding Simpy supported bem s n eement of stticy indeterminte structure Simpe stticy indeterminte bem torsion oding Ccution of deformtion of the simpe stticy indeterminte bem Outine of Lecture / 58
3 Possibiity of free motion of physic objects Degree of freedom n v : biity to mke one right-nged component of dispcement or rottion. free mss point in the pne: n v =, coordintes [x, y], different positions free mss point in the spce: n v =3, coordintes [x, y, z], 3 different positions m[x m,z m ] x +x free soid br in the pne: n v =3, coordintes [x, y, ], 3 different positions soid body in the spce: n v =6, coordintes [x, y, z, ], 6 different positions +z z Sttics of structures bsic knowedge 3 / 58
4 Extern constrints to movement Dispcement constrint prevents movement of constrined point in the given direction ( (b (c (d (e (f (g ( (b (c (d (e Sttics of structures bsic knowedge 4 / 58
5 Extern constrints to rottion ottion constrint prevents rottion of constrined br in the given direction ( (b (c Simpe rottion constrints Fu fix (cmp in spce or pne, prti fix in pne ( (b (c Compex dispcement nd rottion constrints Sttics of structures bsic knowedge 5 / 58
6 utipicity of constrints Extern constrints eimintes degrees of freedom of the object. n mutipe constrint eimintes n degrees of freedom (n=,, 3 of object Exmpes of simpe constrints nd their rections of soid br in the pne Nme Pin, swing rod utipicity of constrint Symbo of constrint (support, rections z oer z Hinge z x Siding cmp Fixed (cmped 3 z y z x y Sttics of structures bsic knowedge 6 / 58
7 Ensuring immobiity of the br To sufficienty support some object it is needed v constrints to eiminte n v degrees of freedom. v = n v v < n v v > n v Supporting of the object is kinemticy determinte nd stticy determinte, immobiity of buiding is ensured, structure cn be used s buiding construction. Supporting of the object is kinemticy indeterminte nd stticy overdeterminte, immobiity of buiding is not ensured, structure is indmissibe s the buiding construction. (insufficient number of constrined degrees of freedom Supporting of the object is kinemticy overdeterminte nd stticy indeterminte, immobiity of buiding is ensured, structure cn be used s buiding construction.. Constrints must be propery rrnged to ensure immobiity of structures it must not be Exception cse of kinemticy determinte or overdeterminte structure. Sttics of structures bsic knowedge 7 / 58
8 Kinemticy nd stticy determinte structure v = n v v = 3, n v = 3 Supporting of the structure is kinemticy nd stticy determinte P P x b z bz x y P P z Sttics of structures bsic knowedge 8 / 58
9 Stticy nd kinemticy determinte brs ( (e (i n v = 6 n v = n v = 3 Axi oding (b n v = 3 (f n v = (j n v = 3 Torsion oding (c n v = 3 (g n v = 3 (k n v = 3 (d n v = (h n v = 3 ( n v = 6 Trnsvers oding Sttics of structures bsic knowedge 9 / 58
10 Stticy indeterminte structure v > n v Supporting of the structure is kinemticy overdeterminte nd stticy indeterminte x P P b bx v = 4 n v = 3 z bz x y P P b by bx v = 6 n v = 3 z bz Sttics of structures bsic knowedge / 58
11 Kinemticy indeterminte structure v < n v Supporting of the structure is kinemticy indeterminte nd stticy overdeterminte P P b z bz Equiibrium of the object is ensured ony for specific oding In buiding prctice unusbe structure Sttics of structures bsic knowedge / 58
12 Exception cses of supporting Constrints must be propery rrnged to ensure immobiity of structures it must not be exception cse of supporting tht is unusbe in construction prctice. x P P b bx z P P b c z bz cz Sttics of structures bsic knowedge / 58
13 Exception cses of supporting (c bem is not secured ginst rottion (d 3 constrints ginst movement intersect t one point (e 3 constrints ginst movement ying in one direct ine ( (d (b (c (e Exception cses of supporting Sttics of structures bsic knowedge 3 / 58
14 Equiibrium conditions of oded br Supported br hs to be motioness nd in equiibrium. Number of equiibrium conditions depends on the type of soved tsk. It is equ to degree of freedom of unsupported br n v. Number of rections is equ to number of constrined degrees of freedom v. v = n v Number of unknown rections is equ to number of equiibrium conditions, the br is stticy determinte v < n v Number of unknown rections is smer thn number of equiibrium conditions, the br is kinemticy indeterminte nd cnnot be used s buiding construction. v > n v Number of unknown rections is bigger thn number of equiibrium conditions, the br is stticy indeterminte, it cn be buiding construction. There must be suppemented deformtion conditions to sttic equiibrium conditions. If the determinnt of system of equtions is equ to zero, then it is exception cse of supporting of structure. Sttics of structures bsic knowedge 4 / 58
15 Equiibrium conditions of oded br system For every seprte br cn be written 3 equiibrium conditions Number of intern nd extern constrints: v = v e + v i Number of rections is equ to number of constrined degrees of freedom of structure. Sttics of structures bsic knowedge 5 / 58
16 Kinemtic nd sttic determincy of truss Prctic pproch computtion mode is mde from mss-points (t joints nd intern inks (brs, tht constrin mutu dispcement of both connected joints. Condition of kinemtic determincy:.s p v e br (intern ink joint (mss-point extern constrint (support Truss s system of mss-points nd extern nd intern inks Sttics of structures bsic knowedge 6 / 58
17 Kinemtic nd sttic determincy F F N 4 N 8 e f g F 3 N N 5 N 9 N 3 N 7 N x N N 6 N c d b z. s p. 4 bz s=7 number of joints ( equiibrium conditions in ech of them p= number of brs ( unknown xi force in ech of them = = number of constrints with nd unknown rections Sttics of structures bsic knowedge 7 / 58
18 Kinemtic nd sttic determincy F F c N 5 d s=4 N N 3 N 4 p=5 x N b = = z bz. s 8 p. 8 Stticy nd kinemticy determinte truss.s p. Kinemticy indeterminte truss Sttics of structures bsic knowedge 8 / 58
19 Kinemtic nd sttic determincy F F This is not joint (brs re overpping here c N N 5 N 3 N 6 d N 4 s=4 p=6 = x N b bx = z bz. s 8 p. x stticy indeterminte truss Sttics of structures bsic knowedge 9 / 58
20 Ccution of the degree of sttic indetermincy Pne frme structures nd bems. Open br systems: n s = v 3 p k = p k v number of extern constrints (rections i number of extern constrints with, or 3 rections p k number of intern hinges reccuted to simpe hinges. Cosed br systems: n s = 3.u + v 3 p k u number of cosed res / 58
21 Force method Force method: is used for soution of stticy indeterminte structures, n s, is bsic method for soution of stticy indetermince br structures is direct method Force method utiizes equiibrium conditions deformtion conditions princip of superposition nd princip of proportionity Force method / 58
22 Force method outine of soution of structures by the Force method:. Determintion of degree of sttic indetermincy n s. Creting of Bsic stticy determinte structure by removing of n s constrints (extern or intern 3. emoved constrints re repced by stticy indeterminte forces or moments (stticy indeterminte rections or interctions 4. Formuting of the system of n s deformtion conditions in the form of iner equtions 5. Soving of the system of iner equtions. The soution re vues of stticy indeterminte rections or interctions. 6. Ccution of remining rections nd intern forces Force method / 58
23 Simpe stticy indeterminte bem Assumptions: direct bem of constnt or vribe cross-section b xis of the bem is identic with x-xis c bem is supported in points, d every of extern constrints is pre to one of coordinte xis, e every of extern rottion constrints works in the pne tht is perpendicur to some of the coordinte xis f bem prut cn be sptiy oded Simpe stticy indeterminte bem 3 / 58
24 Simpe stticy indeterminte bem The degree of sttic indetermincy n s = v n v is number of redundnt constrints, i.e. number of constrints tht hs to be removed to mke the bem stticy determinte Spti probem of simpe direct bem Simpe stticy indeterminte bem 4 / 58
25 Simpe stticy indeterminte bem Every probem of simpe stticy indeterminte bem in spce (3D cn be divided into 4 simpifier probems:. Axi probem n v =. Trnsvers probem in xz pne n v = 3. Trnsvers probem in xy pne n v = 4. Torsion probem n v = Simpe stticy indeterminte bem 5 / 58
26 Simpe stticy indeterminte bem xi oding n s v bx n v bx Siové ztížení N E N A dx Siové ztížení E A dx N E N A dx N E N A dx E N A dx Siové ztížení Otepení t N dx t t t Force method in xi probem Simpe stticy indeterminte bem xi oding 6 / 58
27 Simpe stticy indeterminte bem xi oding Dispcement of supports Dispcement in x-xis direction u, Deformtion condition: d ub In this cse ( pre to x-xis: ū nd hve oposite direction ( ( u ( u ū b nd hve sme direction d u b x u b u x u u b x bx u Force method in xi probem 7 / 58
28 Exmpe 3. Force oding EA 9,68 5 kn Deformtion condition bx bx x 4,8kN( ( (4,8,9kN( N E N E x N dx A 4,, 5 9,68 N dx A x E 9,68 A 5,7 3 4,8 9,68 5,9kN( 3 ( 3 N 5 9,68,9 dx 5,7 5,9kN( Simpe stticy indeterminte bem xi oding Probem definition nd soution of the exmpe 3. 8 / 58
29 Exmpe 3. Therm oding The bem is oded by chnge of temperture ong ength of bem. t =5 o C. The temperture is constnt EA 9,68 x kn, 5,4 x 74,58 kn( 4, Deformtion condition: bx x x N t 3 EA 9,68 5 t dx α 5 t t 9,68 3 bx t -5,, 5 Δt ,4 74,58 kn( ( 74,58 74,58 kn( 74,58 kn( C 4 Simpe stticy indeterminte bem xi oding Probem definition nd soution of the exmpe 3. 9 / 58
30 d Exmpe 3., supports shifting Ū = 5 mm =,5 m (to the right Ū b = 8 mm =,8 m (to the right Dispcement Ū nd rection re in opposite direction Dispcement Ū b nd unit force = re in sme direction Deformtion condition: 3 bx x x x u EA b bx ( 9,68,8 bx u b 968, kn( u 968, kn( 5 ( x,8 bx u 3 (,5 968, kn( d u 9,68 u 5,5 968, kn( Probem definition nd soution of the exmpe 3. 3 / 58
31 Trnsversy oded stticy indeterminte bems Degree of sttic indetermin cy : Deformtio n condition - force oding nd therm oding Deformtio n condition - oding by shifting of supports : n s v n v 3 : d One-end fixed stticy indeterminte bem Simpe stticy indeterminte bem trnsvers oding 3 / 58
32 Bitery fixed bem trnsvers oding ns v n v 4 Deformtion conditions for force oding nd therm oding: b b Deformtion conditions for oding by ifting of supports: d d Force method - bitery fixed bem with trnsvers oding 3 / 58
33 Exmpe 3.8 The bem of stee cross-section I is oded by: forces ccording to pict. ( iner chnge of temperture t =5 o K pict. (e supports shifting pict. (h Deformtion conditions for force nd therm oding: Deformtion conditions for oding by supports shifting: d d Probem definition nd soution of the exmpe / 58
34 Exmpe 3.8 soution, force oding Force oding Bsic stticy determinte structure: simpy supported bem Stticy indeterminte vues: = b =- b oding stte: ections z, bz : Bending moment o : z bz for ( x ( x,6 (6 (,6 x 3, z z 4 x x 4,8 3, 4 q q 3, 4 x x,6 for F 3,,6 / 4,8 6 ( x,6 x x,8 / 4,8 F,6 q 8kN ( x 7,6kN x F Cn be so written: where F q F ( x z x x F F q q q q q x ( x for x F for x x F x 34 / 4
35 Exmpe 3.8 soution, force oding st oding x stte nd oding x stte Ccutio n of deformtio n coefficien ts : b, b b b b b E E I I E E dx dx I I 4,8,6 3EI 3EI EI,6 for constnt cross - section 3EI EI 4,8,8 dx 6EI 6EI EI,8 dx 6EI EI,, bsic deformtio n nges of simpy supported bem b b 35 / 4
36 Exmpe 3.8 soution, force oding Ccution of deformtion coefficients, EI EI dx EI dx EI ( ( Integrtio n cn be reized : nytic y, with use of Vereshchgin' s rue, 3 with use of Tbe. In this cse it is : q q 6,3 EI 58,444 EI F F q q dx dx 36 / 4
37 Exmpe 3.8 soution, force oding Soution of iner equtions is: b b ections : 6,667 knm 3,3444 knm b b 6,66 3, ,563 kn 4,8 4,8 b 6,66 3,344 7,6 7,37 kn 4,8 4,8 Probem definition nd soution of the exmpe / 4
38 Exmpe 3.8 therm oding Liner chnge of The Soution For Digrm of ection z probem is EI of t suppied z z symmetric, two iner equtions t bending h z temperture cross the cross - section EI bz dx ( 6,6, 5,8 EI EI 4494 knm therefore moment - see pict. (g., becuse z 5 cn be reduced into 5, 6 4,8,4 konst. nd V ( 5 x dx 4,8 EI 6 4,8 one t : 4,446 knm, or so 5 5 o C Probem definition nd soution of the exmpe / 4
39 Exmpe 3.8 oding by supports shifting Deformtio n conditions : For seected bsic stticy determint e system is : d ( ( ( ( After substituti on :,6,8 d ,8,6 d Soution of equtions is : b b b b Soution - see pictures (i nd (j w w b b 6,5 w ( 4,8 4,8,4 6,5 b w b w b ( 4 w -,kn, 4,65 - (, (8,49 4,8 4,8 d d,4 ( wb,3,6 6,5 4,8 4,8 4 wb,3,6 6,5 4,8 4,8 d b 4 8,49kNm 6,44 kn nd b hve sme direction 4 4 Probem definition nd soution of the exmpe / 4
40 Tbe 3. Fixed-end moment rections of the bem with constnt crosssection Unitery fixed bem trnsvers oding 4 / 58
41 Simpy supported bem s n eement of stticy indeterminte structure Decomposition of simpy supported bem into seprte oding sttes Simpy supported bem s n eement of stticy indeterminte structure 4 / 58
42 Simpy supported bem s n eement of stticy indeterminte structure digrms of intern forces. oding stte (q:. oding stte (P: oment s oding stte: Digrms of bending moments in oding stte nd in moment s oding stte Simpy supported bem s n eement of stticy indeterminte structure 4 / 58
43 Vribe cross-section of the bem Unitery fixed bem trnsvers oding 43 / 58
44 Vribe cross-section - exmpe 3.5 Soution 5 From tbe b, mx by Tbe,4 q Ccutio n of,, b, 3.3 :,3,6 x n q, b q b, ,85, b 5 q b, 4 5 simiry b, Ccutio n of : mx, b 6,5 x,545 m n q 4 3 3,9,,9 recions :,5 x n 4,5 5 q,63,855, 66,85kNm b,,63kn 66, by iner interpot ion cn be obtined 4 48,37kN,545 6,7kNm,9 Unitery fixed bem trnsvers oding 44 / 58
45 Coefficients for moment rection (uniformy distributed oding Tbe 3.3 Unitery fixed bem trnsvers oding 45 / 58
46 Coefficients for moment rection (nod force oding Tbe 3.4 Unitery fixed bem trnsvers oding 46 / 58
47 Coefficients for moment rection (uniformy distributed oding Tbe 3.6 Unitery fixed bem trnsvers oding 47 / 58
48 Coefficients for moment rection (nod force oding Tbe 3.7 Unitery fixed bem trnsvers oding 48 / 58
49 Simpe stticy indeterminte bem torsion oding Degree of indetermin cy : n s ν n v Deformtio n condition for force oding : δ δ b for oding by supports shifting : δ δ d Force method nd torsion oding Simpe stticy indeterminte bem torsion oding 49 / 58
50 Torsion probem exmpe 3. Probem definition: einforced-concrete bem (G=9,4. 6 kp of constnt rectngur crosssection, width b=,4m, height h=,36m. It is oded by: torsion oding ccording pict. ( b supports shifting, rd, b, rd. Torsion stiffness is ( see tb. : I t b 3 h,96,4 3,36 9,75 4 m 4 G I t 93kNm h/b,,,,3,4,5,46,54,66,77,869,958 h/b,6,7,8,9 3,37,9,74,33,87,633 Simpe stticy indeterminte bem torsion oding Probem definition nd soution of the exmpe 3. 5 / 58
51 oment Torsion probem exmpe 3., force oding Deformtio n condition : T T T G T G T I I T t T t ( hs oposite direction compred to oding 4 dx G I G I dx G 3 G 4 G I t t I t I t 4 T 7,75kNm 4 7,75 6,5kNm,5 3 esuting digrm of torsion moments T - see pict. (d t dx,5 (4 9 G I T b t moments 3 G I t Probem definition nd soution of the exmpe 3. Simpe stticy indeterminte bem torsion oding 5 / 58
52 Torsion probem exmpe 3., supports shifting Supports shifting:, rd, b, rd. Deformtion condition: d T 4 ( T, rd T GI T b b t d 4 4, d T ( (,, rd, (, T b 4 4,438 rd/knm 4 6,76 knm,3 4, ,76 knm Probem definition nd soution of the exmpe 3. Simpe stticy indeterminte bem torsion oding 5 / 58
53 Ccution of deformtion of simpe stticy indeterminte bem Force oding stte eduction theorem: When ccution deformtion of stticy indeterminte structure of degree of indetermincy n s thn the unite force oding stte cn be mde on: origin stticy indeterminte bem stticy indeterminte bem with ower degree of indetermincy n sj < n s, (removed ess thn n s inks, stticy determinte bem (removed n s inks. eduction theorem cn be used to ccute the deformtion of ny stticy indeterminte structure exposed to force oding. Ccution of deformtion of the simpe stticy indeterminte bem 53 / 58
54 Ccution of deformtion force oding stte Exmpes of virtu od cse options to ccute the dispcement of stticy indeterminte bem. Ccution of deformtion of the simpe stticy indeterminte bem 54 / 58
55 Ccution of deformtion force oding stte, exmpe 3. Ccute dispceme nt of the bem in point s.. Bending moments were ccuted using tbe 3., Virtu unit force stte choosed s on picture (c. w s 3 5 P dx dx E I E I 96 E I The formu bove cn be soved : nytic y b using Vereshchgin' s rue c using Tbe. Exmpe 3. nd its soution Ccution of deformtion of the simpe stticy indeterminte bem 55 / 58
56 Ccution of deformtion force oding stte, exmpe 3. Ccution using Vereshchgin s rue w s E I dx E I dx w w w w s s s s E I E E E I I I ( A ( ( ( P 8 9 P T 4 P A 7P P T 5P 96 3 EI 3 Probem definition nd soution of the exmpe 3. Ccution of deformtion of the simpe stticy indeterminte bem 56 / 58
57 Ccution of deformtion therm oding esuting deformtion is given by superposition of: estic deformtion w pr b therm deformtion w t on bsic stticy determinte structure w w pr w t Ccution of deformtion of the simpe stticy indeterminte bem 57 / 58
58 Ccution of deformtion therm oding, exmpe 3.3 The bem is oded by chnge of temperture. Ccute dispcement in point c. Soution : EI 4494 knm w c w pr w t w pr EI,3 (,8 4.56,3,35, / 4494 w pr,395 3 m w t t h t dx,, 5 8 5,3 3,36 3 m w c, ,36 3,93 3 m Exmpe 3.3 nd its soution Ccution of deformtion of the simpe stticy indeterminte bem 58 / 58
Statically indeterminate examples - axial loaded members, rod in torsion, members in bending
 Elsticity nd Plsticity Stticlly indeterminte exmples - xil loded memers, rod in torsion, memers in ending Deprtment of Structurl Mechnics Fculty of Civil Engineering, VSB - Technicl University Ostrv 1
Elsticity nd Plsticity Stticlly indeterminte exmples - xil loded memers, rod in torsion, memers in ending Deprtment of Structurl Mechnics Fculty of Civil Engineering, VSB - Technicl University Ostrv 1
ELASTICITY AND PLASTICITY I
 ELASTICITY AD PLASTICITY I Litertur in Czech Ing. Lenk Lusová LPH 407/1 te. 59 73 136 enk.usov@vs.cz http://fst10.vs.cz/usov Literture: Higgeer Sttics nd mechnics of mteri, USA 199 Beer, Johnston, DeWof,
ELASTICITY AD PLASTICITY I Litertur in Czech Ing. Lenk Lusová LPH 407/1 te. 59 73 136 enk.usov@vs.cz http://fst10.vs.cz/usov Literture: Higgeer Sttics nd mechnics of mteri, USA 199 Beer, Johnston, DeWof,
Identification of Axial Forces on Statically Indeterminate Pin-Jointed Trusses by a Nondestructive Mechanical Test
 Send Orders of Reprints t reprints@benthmscience.net 50 The Open Civi Engineering Journ, 0, 7, 50-57 Open Access Identifiction of Axi Forces on Stticy Indeterminte Pin-Jointed Trusses by Nondestructive
Send Orders of Reprints t reprints@benthmscience.net 50 The Open Civi Engineering Journ, 0, 7, 50-57 Open Access Identifiction of Axi Forces on Stticy Indeterminte Pin-Jointed Trusses by Nondestructive
Math 124B January 24, 2012
 Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
BEAM DIAGRAMS AND FORMULAS. Nomenclature
 BEA DIAGAS AND FOULAS Nomencture E = moduus of esticity of stee t 9,000 ksi I = moment of inerti of em (in. 4 ) L = tot ength of em etween rection points (ft) m = mimum moment (kip-in.) = mimum moment
BEA DIAGAS AND FOULAS Nomencture E = moduus of esticity of stee t 9,000 ksi I = moment of inerti of em (in. 4 ) L = tot ength of em etween rection points (ft) m = mimum moment (kip-in.) = mimum moment
MAGIC058 & MATH64062: Partial Differential Equations 1
 MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
1. The vibrating string problem revisited.
 Weeks 7 8: S eprtion of Vribes In the pst few weeks we hve expored the possibiity of soving first nd second order PDEs by trnsforming them into simper forms ( method of chrcteristics. Unfortuntey, this
Weeks 7 8: S eprtion of Vribes In the pst few weeks we hve expored the possibiity of soving first nd second order PDEs by trnsforming them into simper forms ( method of chrcteristics. Unfortuntey, this
Module 2. Analysis of Statically Indeterminate Structures by the Matrix Force Method. Version 2 CE IIT, Kharagpur
 Module Anlysis of Stticlly Indeterminte Structures by the Mtrix Force Method Version CE IIT, Khrgpur esson 8 The Force Method of Anlysis: Bems Version CE IIT, Khrgpur Instructionl Objectives After reding
Module Anlysis of Stticlly Indeterminte Structures by the Mtrix Force Method Version CE IIT, Khrgpur esson 8 The Force Method of Anlysis: Bems Version CE IIT, Khrgpur Instructionl Objectives After reding
Module 1. Energy Methods in Structural Analysis
 Module 1 Energy Methods in Structurl Anlysis Lesson 4 Theorem of Lest Work Instructionl Objectives After reding this lesson, the reder will be ble to: 1. Stte nd prove theorem of Lest Work.. Anlyse stticlly
Module 1 Energy Methods in Structurl Anlysis Lesson 4 Theorem of Lest Work Instructionl Objectives After reding this lesson, the reder will be ble to: 1. Stte nd prove theorem of Lest Work.. Anlyse stticlly
Development of the Sinc Method for Nonlinear Integro-Differential Eequations
 Austrin Journ of Bsic nd Appied Sciences, 4(): 558-555, ISS 99-878 Deveopment of the Sinc Method for oniner Integro-Differenti Eequtions K. Jei, M. Zrebni, 3 M. Mirzee Chi,3 Ismic Azd University Brnch
Austrin Journ of Bsic nd Appied Sciences, 4(): 558-555, ISS 99-878 Deveopment of the Sinc Method for oniner Integro-Differenti Eequtions K. Jei, M. Zrebni, 3 M. Mirzee Chi,3 Ismic Azd University Brnch
PhysicsAndMathsTutor.com
 M Dynmics - Dmped nd forced hrmonic motion. A P α B A ight estic spring hs ntur ength nd moduus of esticity mg. One end of the spring is ttched to point A on pne tht is incined to the horizont t n nge
M Dynmics - Dmped nd forced hrmonic motion. A P α B A ight estic spring hs ntur ength nd moduus of esticity mg. One end of the spring is ttched to point A on pne tht is incined to the horizont t n nge
Coordinate Geometry. Coordinate Geometry. Curriculum Ready ACMNA: 178, 214, 294.
 Coordinte Geometr Coordinte Geometr Curricuum Red ACMNA: 78, 4, 94 www.mthetics.com Coordinte COORDINATE Geometr GEOMETRY Shpes ou ve seen in geometr re put onto es nd nsed using gebr. Epect bit of both
Coordinte Geometr Coordinte Geometr Curricuum Red ACMNA: 78, 4, 94 www.mthetics.com Coordinte COORDINATE Geometr GEOMETRY Shpes ou ve seen in geometr re put onto es nd nsed using gebr. Epect bit of both
V. DEMENKO MECHANICS OF MATERIALS LECTURE 6 Plane Bending Deformation. Diagrams of Internal Forces (Continued)
 V. DEMENKO MECHNCS OF MTERLS 015 1 LECTURE 6 Plne ending Deformtion. Digrms of nternl Forces (Continued) 1 Construction of ending Moment nd Shering Force Digrms for Two Supported ems n this mode of loding,
V. DEMENKO MECHNCS OF MTERLS 015 1 LECTURE 6 Plne ending Deformtion. Digrms of nternl Forces (Continued) 1 Construction of ending Moment nd Shering Force Digrms for Two Supported ems n this mode of loding,
Stability condition of finite difference solution for viscoelastic wave equations
 Erthq Sci (009): 79 85 79 Doi: 0007/s589-009-079- Stbiity condition of finite difference soution for viscoestic wve equtions Chengyu Sun, Yunfei Xio Xingyo Yin nd Hongcho Peng Chin University of Petroeum,
Erthq Sci (009): 79 85 79 Doi: 0007/s589-009-079- Stbiity condition of finite difference soution for viscoestic wve equtions Chengyu Sun, Yunfei Xio Xingyo Yin nd Hongcho Peng Chin University of Petroeum,
Mutipy by r sin RT P to get sin R r r R + T sin (sin T )+ P P = (7) ffi So we hve P P ffi = m (8) choose m re so tht P is sinusoi. If we put this in b
 Topic 4: Lpce Eqution in Spheric Co-orintes n Mutipoe Expnsion Reing Assignment: Jckson Chpter 3.-3.5. Lpce Eqution in Spheric Coorintes Review of spheric por coorintes: x = r sin cos ffi y = r sin sin
Topic 4: Lpce Eqution in Spheric Co-orintes n Mutipoe Expnsion Reing Assignment: Jckson Chpter 3.-3.5. Lpce Eqution in Spheric Coorintes Review of spheric por coorintes: x = r sin cos ffi y = r sin sin
Combined RKDG and LDG Method for the Simulation of the Bipolar Charge Transport in Solid Dielectrics
 PIERS ONLINE, VOL. 5, NO. 1, 009 51 Combined RKDG nd LDG Method for the Simution of the Bipor Chrge Trnsport in Soid Dieectrics Jihun Tin, Jun Zou, nd Jinsheng Yun Deprtment of Eectric Engineering, Tsinghu
PIERS ONLINE, VOL. 5, NO. 1, 009 51 Combined RKDG nd LDG Method for the Simution of the Bipor Chrge Trnsport in Soid Dieectrics Jihun Tin, Jun Zou, nd Jinsheng Yun Deprtment of Eectric Engineering, Tsinghu
1 Bending of a beam with a rectangular section
 1 Bending of bem with rectngulr section x3 Episseur b M x 2 x x 1 2h M Figure 1 : Geometry of the bem nd pplied lod The bem in figure 1 hs rectngur section (thickness 2h, width b. The pplied lod is pure
1 Bending of bem with rectngulr section x3 Episseur b M x 2 x x 1 2h M Figure 1 : Geometry of the bem nd pplied lod The bem in figure 1 hs rectngur section (thickness 2h, width b. The pplied lod is pure
arxiv: v1 [math.co] 5 Jun 2015
![arxiv: v1 [math.co] 5 Jun 2015 arxiv: v1 [math.co] 5 Jun 2015](/thumbs/78/77492077.jpg) First non-trivi upper bound on the circur chromtic number of the pne. Konstnty Junosz-Szniwski, Fcuty of Mthemtics nd Informtion Science, Wrsw University of Technoogy, Pond Abstrct rxiv:1506.01886v1 [mth.co]
First non-trivi upper bound on the circur chromtic number of the pne. Konstnty Junosz-Szniwski, Fcuty of Mthemtics nd Informtion Science, Wrsw University of Technoogy, Pond Abstrct rxiv:1506.01886v1 [mth.co]
Statistical Physics. Solutions Sheet 5.
 Sttistic Physics. Soutions Sheet 5. Exercise. HS 04 Prof. Mnfred Sigrist Ide fermionic quntum gs in hrmonic trp In this exercise we study the fermionic spiness ide gs confined in three-dimension hrmonic
Sttistic Physics. Soutions Sheet 5. Exercise. HS 04 Prof. Mnfred Sigrist Ide fermionic quntum gs in hrmonic trp In this exercise we study the fermionic spiness ide gs confined in three-dimension hrmonic
Where does Oxygen Extinction Occur in a Soil Profile?
 2st Interntion Congress on Modeing nd Simution, God Cost, Austri, 29 Nov to 4 ec 25 www.mssnz.org.u/modsim25 Where does Oxygen Extinction Occur in Soi Profie? Freemn J Cook nd John H Knightb Freemn Cook
2st Interntion Congress on Modeing nd Simution, God Cost, Austri, 29 Nov to 4 ec 25 www.mssnz.org.u/modsim25 Where does Oxygen Extinction Occur in Soi Profie? Freemn J Cook nd John H Knightb Freemn Cook
L v. removal. elastic. the body is. Hooke s force. [ M L 1 T 2 ] (1) (2) (3) Normal Stress Tensile Stress. stress. parallel. Shearing.
![L v. removal. elastic. the body is. Hooke s force. [ M L 1 T 2 ] (1) (2) (3) Normal Stress Tensile Stress. stress. parallel. Shearing. L v. removal. elastic. the body is. Hooke s force. [ M L 1 T 2 ] (1) (2) (3) Normal Stress Tensile Stress. stress. parallel. Shearing.](/thumbs/74/70692816.jpg) Esticity Definition Esticity: A wire is cmped t one end nd oded t its free end. It is found tht the ength of the wire chnges. The force is known s deforming force, the chnges known s deformtion. If fter
Esticity Definition Esticity: A wire is cmped t one end nd oded t its free end. It is found tht the ength of the wire chnges. The force is known s deforming force, the chnges known s deformtion. If fter
Fluid Flow through a Tube
 . Theory through Tube In this experiment we wi determine how we physic retionship (so ced w ), nmey Poiseue s eqution, ppies. In the suppementry reding mteri this eqution ws derived s p Q 8 where Q is
. Theory through Tube In this experiment we wi determine how we physic retionship (so ced w ), nmey Poiseue s eqution, ppies. In the suppementry reding mteri this eqution ws derived s p Q 8 where Q is
Prof. Anchordoqui. Problems set # 4 Physics 169 March 3, 2015
 Prof. Anchordoui Problems set # 4 Physics 169 Mrch 3, 15 1. (i) Eight eul chrges re locted t corners of cube of side s, s shown in Fig. 1. Find electric potentil t one corner, tking zero potentil to be
Prof. Anchordoui Problems set # 4 Physics 169 Mrch 3, 15 1. (i) Eight eul chrges re locted t corners of cube of side s, s shown in Fig. 1. Find electric potentil t one corner, tking zero potentil to be
Suggested Solution to Assignment 5
 MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
Physics 2D Lecture Slides Lecture 30: March 9th 2005
 Physics D Lecture Sides Lecture 3: Mrch 9th 5 Vivek Shrm UCSD Physics Mgnetic Quntum Number m L = r p (Right Hnd Rue) Cssicy, direction & Mgnitude of L wys we defined QM: Cn/Does L hve definite direction?
Physics D Lecture Sides Lecture 3: Mrch 9th 5 Vivek Shrm UCSD Physics Mgnetic Quntum Number m L = r p (Right Hnd Rue) Cssicy, direction & Mgnitude of L wys we defined QM: Cn/Does L hve definite direction?
We will see what is meant by standard form very shortly
 THEOREM: For fesible liner progrm in its stndrd form, the optimum vlue of the objective over its nonempty fesible region is () either unbounded or (b) is chievble t lest t one extreme point of the fesible
THEOREM: For fesible liner progrm in its stndrd form, the optimum vlue of the objective over its nonempty fesible region is () either unbounded or (b) is chievble t lest t one extreme point of the fesible
In this appendix, we evaluate the derivative of Eq. 9 in the main text, i.e., we need to calculate
 Supporting Tet Evoution of the Averge Synptic Updte Rue In this ppendi e evute the derivtive of Eq. 9 in the min tet i.e. e need to ccute Py ( ) Py ( Y ) og γ og. [] P( y Y ) P% ( y Y ) Before e strt et
Supporting Tet Evoution of the Averge Synptic Updte Rue In this ppendi e evute the derivtive of Eq. 9 in the min tet i.e. e need to ccute Py ( ) Py ( Y ) og γ og. [] P( y Y ) P% ( y Y ) Before e strt et
Bending Analysis of Castellated Beams. By Sahar Elaiwi Boksun Kim Long-Yuan Li
 Athens Journ of Technoogy nd Engineering X Y Bending Anysis of Csteted Bems By Shr Eiwi Boksun Kim Long-Yun Li Existing studies hve shown tht the od-crrying cpcity of csteted bems cn be infuenced by the
Athens Journ of Technoogy nd Engineering X Y Bending Anysis of Csteted Bems By Shr Eiwi Boksun Kim Long-Yun Li Existing studies hve shown tht the od-crrying cpcity of csteted bems cn be infuenced by the
GEOMETRIC PROBABILITY MODELS TO ANALYZE STRATEGIES FOR FINDING A BURIED CABLE
 Journ of the Opertions Reserch Society of Jpn Vo. 6, No. 3, Juy 17, pp. 4 417 c The Opertions Reserch Society of Jpn GEOMETRIC PROBABILITY MODELS TO ANALYZE STRATEGIES FOR FINDING A BURIED CABLE Ken-ichi
Journ of the Opertions Reserch Society of Jpn Vo. 6, No. 3, Juy 17, pp. 4 417 c The Opertions Reserch Society of Jpn GEOMETRIC PROBABILITY MODELS TO ANALYZE STRATEGIES FOR FINDING A BURIED CABLE Ken-ichi
CE 160 Lab 2 Notes: Shear and Moment Diagrams for Beams
 E 160 Lb 2 Notes: Sher nd oment Digrms for ems Sher nd moment digrms re plots of how the internl bending moment nd sher vry long the length of the bem. Sign onvention for nd onsider the rbitrrily loded
E 160 Lb 2 Notes: Sher nd oment Digrms for ems Sher nd moment digrms re plots of how the internl bending moment nd sher vry long the length of the bem. Sign onvention for nd onsider the rbitrrily loded
Shear and torsion interaction of hollow core slabs
 Competitive nd Sustinble Growth Contrct Nº G6RD-CT--6 Sher nd torsion interction of hollow core slbs HOLCOTORS Technicl Report, Rev. Anlyses of hollow core floors December The content of the present publiction
Competitive nd Sustinble Growth Contrct Nº G6RD-CT--6 Sher nd torsion interction of hollow core slbs HOLCOTORS Technicl Report, Rev. Anlyses of hollow core floors December The content of the present publiction
Figure XX.1.1 Plane truss structure
 Truss Eements Formution. TRUSS ELEMENT.1 INTRODUTION ne truss struture is ste struture on the sis of tringe, s shown in Fig..1.1. The end of memer is pin juntion whih does not trnsmit moment. As for the
Truss Eements Formution. TRUSS ELEMENT.1 INTRODUTION ne truss struture is ste struture on the sis of tringe, s shown in Fig..1.1. The end of memer is pin juntion whih does not trnsmit moment. As for the
A Slipping and Buried Strike-Slip Fault in a Multi-Layered Elastic Model
 Geosciences 7, 7(): 68-76 DOI:.59/j.geo.77. A Sipping nd Buried Strike-Sip Fut in Muti-Lyered Estic Mode Asish Krmkr,*, Snjy Sen Udirmpur Pisree Sikshytn (H.S.), Udirmpur, P.O. Knyngr, Pin, Indi Deprtment
Geosciences 7, 7(): 68-76 DOI:.59/j.geo.77. A Sipping nd Buried Strike-Sip Fut in Muti-Lyered Estic Mode Asish Krmkr,*, Snjy Sen Udirmpur Pisree Sikshytn (H.S.), Udirmpur, P.O. Knyngr, Pin, Indi Deprtment
Complete Description of the Thelen2003Muscle Model
 Compete Description o the he23usce ode Chnd John One o the stndrd musce modes used in OpenSim is the he23usce ctutor Unortuntey, to my knowedge, no other pper or document, incuding the he, 23 pper describing
Compete Description o the he23usce ode Chnd John One o the stndrd musce modes used in OpenSim is the he23usce ctutor Unortuntey, to my knowedge, no other pper or document, incuding the he, 23 pper describing
Linear Systems COS 323
 Liner Systems COS 33 Soving Liner Systems of Equtions Define iner system Singurities in iner systems Gussin Eimintion: A gener purpose method Nïve Guss Guss with pivoting Asymptotic nysis Tringur systems
Liner Systems COS 33 Soving Liner Systems of Equtions Define iner system Singurities in iner systems Gussin Eimintion: A gener purpose method Nïve Guss Guss with pivoting Asymptotic nysis Tringur systems
P R A S I C ' 02. Simpozionul na.ional cu participare interna.ional/ PRoiectarea ASIstat/ de Calculator
 UNIVERSITTE TRNSILVNI DIN R0OV tedr Design de Produs i Robotic Simpozionu n.ion cu prticipre intern.ion/ PRoiectre SIstt/ de cutor P R S I ' 0 Vo. I Mecnisme i Triboogie 7-8 Noiembrie rov Români ISN 97-65-064-9
UNIVERSITTE TRNSILVNI DIN R0OV tedr Design de Produs i Robotic Simpozionu n.ion cu prticipre intern.ion/ PRoiectre SIstt/ de cutor P R S I ' 0 Vo. I Mecnisme i Triboogie 7-8 Noiembrie rov Români ISN 97-65-064-9
Chapter 5. , r = r 1 r 2 (1) µ = m 1 m 2. r, r 2 = R µ m 2. R(m 1 + m 2 ) + m 2 r = r 1. m 2. r = r 1. R + µ m 1
 Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
KINEMATICS OF RIGID BODIES
 KINEMTICS OF RIGID ODIES Introduction In rigid body kinemtics, e use the reltionships governing the displcement, velocity nd ccelertion, but must lso ccount for the rottionl motion of the body. Description
KINEMTICS OF RIGID ODIES Introduction In rigid body kinemtics, e use the reltionships governing the displcement, velocity nd ccelertion, but must lso ccount for the rottionl motion of the body. Description
Forces from Strings Under Tension A string under tension medites force: the mgnitude of the force from section of string is the tension T nd the direc
 Physics 170 Summry of Results from Lecture Kinemticl Vribles The position vector ~r(t) cn be resolved into its Crtesin components: ~r(t) =x(t)^i + y(t)^j + z(t)^k. Rtes of Chnge Velocity ~v(t) = d~r(t)=
Physics 170 Summry of Results from Lecture Kinemticl Vribles The position vector ~r(t) cn be resolved into its Crtesin components: ~r(t) =x(t)^i + y(t)^j + z(t)^k. Rtes of Chnge Velocity ~v(t) = d~r(t)=
Dynamics: Newton s Laws of Motion
 Lecture 7 Chpter 4 Physics I 09.25.2013 Dynmics: Newton s Lws of Motion Solving Problems using Newton s lws Course website: http://fculty.uml.edu/andriy_dnylov/teching/physicsi Lecture Cpture: http://echo360.uml.edu/dnylov2013/physics1fll.html
Lecture 7 Chpter 4 Physics I 09.25.2013 Dynmics: Newton s Lws of Motion Solving Problems using Newton s lws Course website: http://fculty.uml.edu/andriy_dnylov/teching/physicsi Lecture Cpture: http://echo360.uml.edu/dnylov2013/physics1fll.html
arxiv: v1 [cond-mat.supr-con] 27 Dec 2018
![arxiv: v1 [cond-mat.supr-con] 27 Dec 2018 arxiv: v1 [cond-mat.supr-con] 27 Dec 2018](/thumbs/93/111554339.jpg) Ccution of currents round tringur indenttion by the hodogrph method J. I. Avi 1, B. Venderheyden 2, A. V. Sihnek 3, S. Meinte 1 1 ICTEAM, Université cthoique de Louvin, B-1348, Louvin-L-Neuve, Begium 2
Ccution of currents round tringur indenttion by the hodogrph method J. I. Avi 1, B. Venderheyden 2, A. V. Sihnek 3, S. Meinte 1 1 ICTEAM, Université cthoique de Louvin, B-1348, Louvin-L-Neuve, Begium 2
Section 10.2 Angles and Triangles
 117 Ojective #1: Section 10.2 nges n Tringes Unerstning efinitions of ifferent types of nges. In the intersection of two ines, the nges tht re cttycorner fro ech other re vertic nges. Vertic nges wi hve
117 Ojective #1: Section 10.2 nges n Tringes Unerstning efinitions of ifferent types of nges. In the intersection of two ines, the nges tht re cttycorner fro ech other re vertic nges. Vertic nges wi hve
Plates on elastic foundation
 Pltes on elstic foundtion Circulr elstic plte, xil-symmetric lod, Winkler soil (fter Timoshenko & Woinowsky-Krieger (1959) - Chpter 8) Prepred by Enzo Mrtinelli Drft version ( April 016) Introduction Winkler
Pltes on elstic foundtion Circulr elstic plte, xil-symmetric lod, Winkler soil (fter Timoshenko & Woinowsky-Krieger (1959) - Chpter 8) Prepred by Enzo Mrtinelli Drft version ( April 016) Introduction Winkler
Chapter 5 Bending Moments and Shear Force Diagrams for Beams
 Chpter 5 ending Moments nd Sher Force Digrms for ems n ddition to illy loded brs/rods (e.g. truss) nd torsionl shfts, the structurl members my eperience some lods perpendiculr to the is of the bem nd will
Chpter 5 ending Moments nd Sher Force Digrms for ems n ddition to illy loded brs/rods (e.g. truss) nd torsionl shfts, the structurl members my eperience some lods perpendiculr to the is of the bem nd will
COLLEGE OF ENGINEERING AND TECHNOLOGY
 COLLEGE OF ENGNEERNG ND TECHNOLOGY DEPRTMENT : Construction nd uilding Engineering COURSE : Structurl nlysis 2 COURSE NO : C 343 LECTURER : Dr. Mohmed SFN T. SSSTNT : Eng. Mostf Yossef, Eng. l-hussein
COLLEGE OF ENGNEERNG ND TECHNOLOGY DEPRTMENT : Construction nd uilding Engineering COURSE : Structurl nlysis 2 COURSE NO : C 343 LECTURER : Dr. Mohmed SFN T. SSSTNT : Eng. Mostf Yossef, Eng. l-hussein
(6.5) Length and area in polar coordinates
 86 Chpter 6 SLICING TECHNIQUES FURTHER APPLICATIONS Totl mss 6 x ρ(x)dx + x 6 x dx + 9 kg dx + 6 x dx oment bout origin 6 xρ(x)dx x x dx + x + x + ln x ( ) + ln 6 kg m x dx + 6 6 x x dx Centre of mss +
86 Chpter 6 SLICING TECHNIQUES FURTHER APPLICATIONS Totl mss 6 x ρ(x)dx + x 6 x dx + 9 kg dx + 6 x dx oment bout origin 6 xρ(x)dx x x dx + x + x + ln x ( ) + ln 6 kg m x dx + 6 6 x x dx Centre of mss +
CBE 291b - Computation And Optimization For Engineers
 The University of Western Ontrio Fculty of Engineering Science Deprtment of Chemicl nd Biochemicl Engineering CBE 9b - Computtion And Optimiztion For Engineers Mtlb Project Introduction Prof. A. Jutn Jn
The University of Western Ontrio Fculty of Engineering Science Deprtment of Chemicl nd Biochemicl Engineering CBE 9b - Computtion And Optimiztion For Engineers Mtlb Project Introduction Prof. A. Jutn Jn
Solution Manual. for. Fracture Mechanics. C.T. Sun and Z.-H. Jin
 Solution Mnul for Frcture Mechnics by C.T. Sun nd Z.-H. Jin Chpter rob.: ) 4 No lod is crried by rt nd rt 4. There is no strin energy stored in them. Constnt Force Boundry Condition The totl strin energy
Solution Mnul for Frcture Mechnics by C.T. Sun nd Z.-H. Jin Chpter rob.: ) 4 No lod is crried by rt nd rt 4. There is no strin energy stored in them. Constnt Force Boundry Condition The totl strin energy
VI. The Heat Equation. A. The Diffusion Equation Conservation in Action
 VI. The Het Eqution c 214, Phiip D. Loewen A. The Diffusion Eqution Conservtion in Action The simpest PDE describing diffusion (of het, perfume, poutnt) ong the x-xis is u t = α 2 u xx. ( ) Theme: Concvity
VI. The Het Eqution c 214, Phiip D. Loewen A. The Diffusion Eqution Conservtion in Action The simpest PDE describing diffusion (of het, perfume, poutnt) ong the x-xis is u t = α 2 u xx. ( ) Theme: Concvity
Lecture 6 Notes, Electromagnetic Theory I Dr. Christopher S. Baird University of Massachusetts Lowell
 Lecture 6 Notes, Eectrognetic Theory I Dr. Christopher S. Bird University of Msschusetts Lowe. Associted Legendre Poynois - We now return to soving the Lpce eqution in spheric coordintes when there is
Lecture 6 Notes, Eectrognetic Theory I Dr. Christopher S. Bird University of Msschusetts Lowe. Associted Legendre Poynois - We now return to soving the Lpce eqution in spheric coordintes when there is
RFID Technologies HF Part I
 RFID Technoogies HF Prt I Diprtimento di Ingegneri de Informzione e Scienze Mtemtiche Ampere s w h(r,t) ĉ d = j(r,t) ˆnds t C brt (, ) = µ hrt (, ) S S d(r,t) ˆnds j(r,t) d(r,t) ds ˆn Ø Biot-Svrt (sttic
RFID Technoogies HF Prt I Diprtimento di Ingegneri de Informzione e Scienze Mtemtiche Ampere s w h(r,t) ĉ d = j(r,t) ˆnds t C brt (, ) = µ hrt (, ) S S d(r,t) ˆnds j(r,t) d(r,t) ds ˆn Ø Biot-Svrt (sttic
99/105 Comparison of OrcaFlex with standard theoretical results
 99/105 Comprison of OrcFlex ith stndrd theoreticl results 1. Introduction A number of stndrd theoreticl results from literture cn be modelled in OrcFlex. Such cses re, by virtue of being theoreticlly solvble,
99/105 Comprison of OrcFlex ith stndrd theoreticl results 1. Introduction A number of stndrd theoreticl results from literture cn be modelled in OrcFlex. Such cses re, by virtue of being theoreticlly solvble,
BME 207 Introduction to Biomechanics Spring 2018
 April 6, 28 UNIVERSITY O RHODE ISAND Deprtment of Electricl, Computer nd Biomedicl Engineering BME 27 Introduction to Biomechnics Spring 28 Homework 8 Prolem 14.6 in the textook. In ddition to prts -e,
April 6, 28 UNIVERSITY O RHODE ISAND Deprtment of Electricl, Computer nd Biomedicl Engineering BME 27 Introduction to Biomechnics Spring 28 Homework 8 Prolem 14.6 in the textook. In ddition to prts -e,
In-Class Problems 2 and 3: Projectile Motion Solutions. In-Class Problem 2: Throwing a Stone Down a Hill
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Deprtment of Physics Physics 8T Fll Term 4 In-Clss Problems nd 3: Projectile Motion Solutions We would like ech group to pply the problem solving strtegy with the
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Deprtment of Physics Physics 8T Fll Term 4 In-Clss Problems nd 3: Projectile Motion Solutions We would like ech group to pply the problem solving strtegy with the
SIMULATION OF WOOD DRYING STRESSES USING CVFEM
 Ltin Americn Appied Reserch 4:2- (2) SIMULATION OF WOOD DRYING STRESSES USING CVFEM C. H. SALINAS, C. A. CHAVEZ, Y. GATICA nd R.A. ANANIAS Deprtmento de Ingenierí Mecánic, Universidd de Bío-Bío, Av. Coo
Ltin Americn Appied Reserch 4:2- (2) SIMULATION OF WOOD DRYING STRESSES USING CVFEM C. H. SALINAS, C. A. CHAVEZ, Y. GATICA nd R.A. ANANIAS Deprtmento de Ingenierí Mecánic, Universidd de Bío-Bío, Av. Coo
Space Curves. Recall the parametric equations of a curve in xy-plane and compare them with parametric equations of a curve in space.
 Clculus 3 Li Vs Spce Curves Recll the prmetric equtions of curve in xy-plne nd compre them with prmetric equtions of curve in spce. Prmetric curve in plne x = x(t) y = y(t) Prmetric curve in spce x = x(t)
Clculus 3 Li Vs Spce Curves Recll the prmetric equtions of curve in xy-plne nd compre them with prmetric equtions of curve in spce. Prmetric curve in plne x = x(t) y = y(t) Prmetric curve in spce x = x(t)
State space systems analysis (continued) Stability. A. Definitions A system is said to be Asymptotically Stable (AS) when it satisfies
 Stte spce systems nlysis (continued) Stbility A. Definitions A system is sid to be Asymptoticlly Stble (AS) when it stisfies ut () = 0, t > 0 lim xt () 0. t A system is AS if nd only if the impulse response
Stte spce systems nlysis (continued) Stbility A. Definitions A system is sid to be Asymptoticlly Stble (AS) when it stisfies ut () = 0, t > 0 lim xt () 0. t A system is AS if nd only if the impulse response
Chapter (a) 2. At equilibrium, V = 0. x = (c) V( x) ke bkxe = 0. At equilibrium. b bx bx 2 bx. V = bke bkxe + b kxe = + = < 0.
 Chpter. () V( x) = x + x V = x x At equiibriu, V = x = V = + x V = + = > x= Stbe (b) V( x) = xe bx bx bx V = e bxe At equiibriu bx bx e bxe = x = b bx bx bx V = be bxe + b xe V be be = + = < x= b Unstbe
Chpter. () V( x) = x + x V = x x At equiibriu, V = x = V = + x V = + = > x= Stbe (b) V( x) = xe bx bx bx V = e bxe At equiibriu bx bx e bxe = x = b bx bx bx V = be bxe + b xe V be be = + = < x= b Unstbe
Exam CT3109 STRUCTURAL MECHANICS april 2011, 09:00 12:00 hours
 Subfculty of Civil Engineering rk ech ge with your: Structurl echnics STUDENT NUBER : NAE : Em CT309 STRUCTURAL ECHANICS 4 ril 0, 09:00 :00 hours This em consists of 4 roblems. Use for ech roblem serte
Subfculty of Civil Engineering rk ech ge with your: Structurl echnics STUDENT NUBER : NAE : Em CT309 STRUCTURAL ECHANICS 4 ril 0, 09:00 :00 hours This em consists of 4 roblems. Use for ech roblem serte
Review of Calculus, cont d
 Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Part I: Basic Concepts of Thermodynamics
 Prt I: Bsic Concepts o Thermodynmics Lecture 4: Kinetic Theory o Gses Kinetic Theory or rel gses 4-1 Kinetic Theory or rel gses Recll tht or rel gses: (i The volume occupied by the molecules under ordinry
Prt I: Bsic Concepts o Thermodynmics Lecture 4: Kinetic Theory o Gses Kinetic Theory or rel gses 4-1 Kinetic Theory or rel gses Recll tht or rel gses: (i The volume occupied by the molecules under ordinry
INTRODUCTION. The three general approaches to the solution of kinetics problems are:
 INTRODUCTION According to Newton s lw, prticle will ccelerte when it is subjected to unblnced forces. Kinetics is the study of the reltions between unblnced forces nd the resulting chnges in motion. The
INTRODUCTION According to Newton s lw, prticle will ccelerte when it is subjected to unblnced forces. Kinetics is the study of the reltions between unblnced forces nd the resulting chnges in motion. The
Explain shortly the meaning of the following eight words in relation to shells structures.
 Delft University of Technology Fculty of Civil Engineering nd Geosciences Structurl Mechnics Section Write your nme nd study number t the top right-hnd of your work. Exm CIE4143 Shell Anlysis Tuesdy 15
Delft University of Technology Fculty of Civil Engineering nd Geosciences Structurl Mechnics Section Write your nme nd study number t the top right-hnd of your work. Exm CIE4143 Shell Anlysis Tuesdy 15
Problems for HW X. C. Gwinn. November 30, 2009
 Problems for HW X C. Gwinn November 30, 2009 These problems will not be grded. 1 HWX Problem 1 Suppose thn n object is composed of liner dielectric mteril, with constnt reltive permittivity ɛ r. The object
Problems for HW X C. Gwinn November 30, 2009 These problems will not be grded. 1 HWX Problem 1 Suppose thn n object is composed of liner dielectric mteril, with constnt reltive permittivity ɛ r. The object
Dynamic Analysis of the Turnout Diverging Track for HSR with Variable Curvature Sections
 Word Journ of Engineering nd Technoogy, 07, 5, 4-57 http://www.scirp.org/journ/wjet ISSN Onine: -449 ISSN Print: -4 Dynmic Anysis of the Turnout Diverging Trck for HSR with Vribe Curvture Sections Wdysw
Word Journ of Engineering nd Technoogy, 07, 5, 4-57 http://www.scirp.org/journ/wjet ISSN Onine: -449 ISSN Print: -4 Dynmic Anysis of the Turnout Diverging Trck for HSR with Vribe Curvture Sections Wdysw
Comparison of the Design of Flexural Reinforced Concrete Elements According to Albanian Normative
 ISBN 978-93-84422-22-6 Proceedings of 2015 Interntionl Conference on Innovtions in Civil nd Structurl Engineering (ICICSE'15) Istnbul (Turkey), June 3-4, 2015 pp. 155-163 Comprison of the Design of Flexurl
ISBN 978-93-84422-22-6 Proceedings of 2015 Interntionl Conference on Innovtions in Civil nd Structurl Engineering (ICICSE'15) Istnbul (Turkey), June 3-4, 2015 pp. 155-163 Comprison of the Design of Flexurl
Calculus 2: Integration. Differentiation. Integration
 Clculus 2: Integrtion The reverse process to differentition is known s integrtion. Differentition f() f () Integrtion As it is the opposite of finding the derivtive, the function obtined b integrtion is
Clculus 2: Integrtion The reverse process to differentition is known s integrtion. Differentition f() f () Integrtion As it is the opposite of finding the derivtive, the function obtined b integrtion is
Lecture 8. Newton s Laws. Applications of the Newton s Laws Problem-Solving Tactics. Physics 105; Fall Inertial Frames: T = mg
 Lecture 8 Applictions of the ewton s Lws Problem-Solving ctics http://web.njit.edu/~sireno/ ewton s Lws I. If no net force ocects on body, then the body s velocity cnnot chnge. II. he net force on body
Lecture 8 Applictions of the ewton s Lws Problem-Solving ctics http://web.njit.edu/~sireno/ ewton s Lws I. If no net force ocects on body, then the body s velocity cnnot chnge. II. he net force on body
13: Diffusion in 2 Energy Groups
 3: Diffusion in Energy Groups B. Rouben McMster University Course EP 4D3/6D3 Nucler Rector Anlysis (Rector Physics) 5 Sept.-Dec. 5 September Contents We study the diffusion eqution in two energy groups
3: Diffusion in Energy Groups B. Rouben McMster University Course EP 4D3/6D3 Nucler Rector Anlysis (Rector Physics) 5 Sept.-Dec. 5 September Contents We study the diffusion eqution in two energy groups
Work and energy method. Exercise 1 : Beam with a couple. Exercise 1 : Non-linear loaddisplacement. Exercise 2 : Horizontally loaded frame
 Work and energy method EI EI T x-axis Exercise 1 : Beam with a coupe Determine the rotation at the right support of the construction dispayed on the right, caused by the coupe T using Castigiano s nd theorem.
Work and energy method EI EI T x-axis Exercise 1 : Beam with a coupe Determine the rotation at the right support of the construction dispayed on the right, caused by the coupe T using Castigiano s nd theorem.
Spherical Coordinates
 Sphericl Coordintes This is the coordinte system tht is most nturl to use - for obvious resons (e.g. NWP etc.). λ longitude (λ increses towrd est) ltitude ( increses towrd north) z rdil coordinte, locl
Sphericl Coordintes This is the coordinte system tht is most nturl to use - for obvious resons (e.g. NWP etc.). λ longitude (λ increses towrd est) ltitude ( increses towrd north) z rdil coordinte, locl
Higher Checklist (Unit 3) Higher Checklist (Unit 3) Vectors
 Vectors Skill Achieved? Know tht sclr is quntity tht hs only size (no direction) Identify rel-life exmples of sclrs such s, temperture, mss, distnce, time, speed, energy nd electric chrge Know tht vector
Vectors Skill Achieved? Know tht sclr is quntity tht hs only size (no direction) Identify rel-life exmples of sclrs such s, temperture, mss, distnce, time, speed, energy nd electric chrge Know tht vector
13.4 Work done by Constant Forces
 13.4 Work done by Constnt Forces We will begin our discussion of the concept of work by nlyzing the motion of n object in one dimension cted on by constnt forces. Let s consider the following exmple: push
13.4 Work done by Constnt Forces We will begin our discussion of the concept of work by nlyzing the motion of n object in one dimension cted on by constnt forces. Let s consider the following exmple: push
The Wave Equation I. MA 436 Kurt Bryan
 1 Introduction The Wve Eqution I MA 436 Kurt Bryn Consider string stretching long the x xis, of indeterminte (or even infinite!) length. We wnt to derive n eqution which models the motion of the string
1 Introduction The Wve Eqution I MA 436 Kurt Bryn Consider string stretching long the x xis, of indeterminte (or even infinite!) length. We wnt to derive n eqution which models the motion of the string
Dynamic analysis of an underwater suspension system in ocean currents with method of averaging
 Indin Journ of Geo Mrine Sciences Vo. (),November 7, pp. -7 Dynmic nysis of n underwter suspension system in ocen currents with method of verging Xing Li,, Jifeng ui,, Min Zho,,* & Tong Ge, Stte Key Lbortory
Indin Journ of Geo Mrine Sciences Vo. (),November 7, pp. -7 Dynmic nysis of n underwter suspension system in ocen currents with method of verging Xing Li,, Jifeng ui,, Min Zho,,* & Tong Ge, Stte Key Lbortory
Case (a): Ans Ans. Case (b): ; s 1 = 65(4) Ans. s 1 = pr t. = 1.04 ksi. Ans. s 2 = pr 2t ; s 2 = 65(4) = 520 psi
 8 3. The thin-wlled cylinder cn be supported in one of two wys s shown. Determine the stte of stress in the wll of the cylinder for both cses if the piston P cuses the internl pressure to be 65 psi. The
8 3. The thin-wlled cylinder cn be supported in one of two wys s shown. Determine the stte of stress in the wll of the cylinder for both cses if the piston P cuses the internl pressure to be 65 psi. The
Homework Assignment #5 Solutions
 Physics 506 Winter 008 Textbook probems: Ch. 9: 9., 9., 9.4 Ch. 10: 10.1 Homework Assignment #5 Soutions 9. A spheric hoe of rdius in conducting medium cn serve s n eectromgnetic resonnt cvity. Assuming
Physics 506 Winter 008 Textbook probems: Ch. 9: 9., 9., 9.4 Ch. 10: 10.1 Homework Assignment #5 Soutions 9. A spheric hoe of rdius in conducting medium cn serve s n eectromgnetic resonnt cvity. Assuming
20 MATHEMATICS POLYNOMIALS
 0 MATHEMATICS POLYNOMIALS.1 Introduction In Clss IX, you hve studied polynomils in one vrible nd their degrees. Recll tht if p(x) is polynomil in x, the highest power of x in p(x) is clled the degree of
0 MATHEMATICS POLYNOMIALS.1 Introduction In Clss IX, you hve studied polynomils in one vrible nd their degrees. Recll tht if p(x) is polynomil in x, the highest power of x in p(x) is clled the degree of
Jack Simons, Henry Eyring Scientist and Professor Chemistry Department University of Utah
 1. Born-Oppenheimer pprox.- energy surfces 2. Men-field (Hrtree-Fock) theory- orbitls 3. Pros nd cons of HF- RHF, UHF 4. Beyond HF- why? 5. First, one usully does HF-how? 6. Bsis sets nd nottions 7. MPn,
1. Born-Oppenheimer pprox.- energy surfces 2. Men-field (Hrtree-Fock) theory- orbitls 3. Pros nd cons of HF- RHF, UHF 4. Beyond HF- why? 5. First, one usully does HF-how? 6. Bsis sets nd nottions 7. MPn,
The Predom module. Predom calculates and plots isothermal 1-, 2- and 3-metal predominance area diagrams. Predom accesses only compound databases.
 Section 1 Section 2 The module clcultes nd plots isotherml 1-, 2- nd 3-metl predominnce re digrms. ccesses only compound dtbses. Tble of Contents Tble of Contents Opening the module Section 3 Stoichiometric
Section 1 Section 2 The module clcultes nd plots isotherml 1-, 2- nd 3-metl predominnce re digrms. ccesses only compound dtbses. Tble of Contents Tble of Contents Opening the module Section 3 Stoichiometric
DETERMINATION OF MECHANICAL PROPERTIES OF NANOSTRUCTURES WITH COMPLEX CRYSTAL LATTICE USING MOMENT INTERACTION AT MICROSCALE
 Determintion RevAdvMterSci of mechnicl 0(009) -7 properties of nnostructures with complex crystl lttice using DETERMINATION OF MECHANICAL PROPERTIES OF NANOSTRUCTURES WITH COMPLEX CRYSTAL LATTICE USING
Determintion RevAdvMterSci of mechnicl 0(009) -7 properties of nnostructures with complex crystl lttice using DETERMINATION OF MECHANICAL PROPERTIES OF NANOSTRUCTURES WITH COMPLEX CRYSTAL LATTICE USING
How do you know you have SLE?
 Simultneous Liner Equtions Simultneous Liner Equtions nd Liner Algebr Simultneous liner equtions (SLE s) occur frequently in Sttics, Dynmics, Circuits nd other engineering clsses Need to be ble to, nd
Simultneous Liner Equtions Simultneous Liner Equtions nd Liner Algebr Simultneous liner equtions (SLE s) occur frequently in Sttics, Dynmics, Circuits nd other engineering clsses Need to be ble to, nd
PDE Notes. Paul Carnig. January ODE s vs PDE s 1
 PDE Notes Pul Crnig Jnury 2014 Contents 1 ODE s vs PDE s 1 2 Section 1.2 Het diffusion Eqution 1 2.1 Fourier s w of Het Conduction............................. 2 2.2 Energy Conservtion.....................................
PDE Notes Pul Crnig Jnury 2014 Contents 1 ODE s vs PDE s 1 2 Section 1.2 Het diffusion Eqution 1 2.1 Fourier s w of Het Conduction............................. 2 2.2 Energy Conservtion.....................................
Summary: Method of Separation of Variables
 Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Energy Bands Energy Bands and Band Gap. Phys463.nb Phenomenon
 Phys463.nb 49 7 Energy Bnds Ref: textbook, Chpter 7 Q: Why re there insultors nd conductors? Q: Wht will hppen when n electron moves in crystl? In the previous chpter, we discussed free electron gses,
Phys463.nb 49 7 Energy Bnds Ref: textbook, Chpter 7 Q: Why re there insultors nd conductors? Q: Wht will hppen when n electron moves in crystl? In the previous chpter, we discussed free electron gses,
Improper Integrals. Type I Improper Integrals How do we evaluate an integral such as
 Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Fourier Series in Complex notation. cos(x) = eix + e ix 2. A n cos + B n sin l. i 2 B n. e inx=l + A n + ib n 2 8. ( 0 m 6= n. C n = 1 2l.
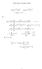 Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram. Drum Brakes. Among the various types of devices to be studied, based on their practical use,
 chine Design II Prof. K.Gointh & Prof...yurm Drum Brkes Among the vrious tyes of devices to be studied, bsed on their rcticl use, the discussion will be limited to Drum brkes of the following tyes which
chine Design II Prof. K.Gointh & Prof...yurm Drum Brkes Among the vrious tyes of devices to be studied, bsed on their rcticl use, the discussion will be limited to Drum brkes of the following tyes which
A-Level Mathematics Transition Task (compulsory for all maths students and all further maths student)
 A-Level Mthemtics Trnsition Tsk (compulsory for ll mths students nd ll further mths student) Due: st Lesson of the yer. Length: - hours work (depending on prior knowledge) This trnsition tsk provides revision
A-Level Mthemtics Trnsition Tsk (compulsory for ll mths students nd ll further mths student) Due: st Lesson of the yer. Length: - hours work (depending on prior knowledge) This trnsition tsk provides revision
Math 8 Winter 2015 Applications of Integration
 Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
Kirchhoff and Mindlin Plates
 Kirchhoff nd Mindlin Pltes A plte significntly longer in two directions compred with the third, nd it crries lod perpendiculr to tht plne. The theory for pltes cn be regrded s n extension of bem theory,
Kirchhoff nd Mindlin Pltes A plte significntly longer in two directions compred with the third, nd it crries lod perpendiculr to tht plne. The theory for pltes cn be regrded s n extension of bem theory,
Calculus - Activity 1 Rate of change of a function at a point.
 Nme: Clss: p 77 Mths Helper Plus Resource Set. Copright 00 Bruce A. Vughn, Techers Choice Softwre Clculus - Activit Rte of chnge of function t point. ) Strt Mths Helper Plus, then lod the file: Clculus
Nme: Clss: p 77 Mths Helper Plus Resource Set. Copright 00 Bruce A. Vughn, Techers Choice Softwre Clculus - Activit Rte of chnge of function t point. ) Strt Mths Helper Plus, then lod the file: Clculus
a a a a a a a a a a a a a a a a a a a a a a a a In this section, we introduce a general formula for computing determinants.
 Section 9 The Lplce Expnsion In the lst section, we defined the determinnt of (3 3) mtrix A 12 to be 22 12 21 22 2231 22 12 21. In this section, we introduce generl formul for computing determinnts. Rewriting
Section 9 The Lplce Expnsion In the lst section, we defined the determinnt of (3 3) mtrix A 12 to be 22 12 21 22 2231 22 12 21. In this section, we introduce generl formul for computing determinnts. Rewriting
Heat flux and total heat
 Het flux nd totl het John McCun Mrch 14, 2017 1 Introduction Yesterdy (if I remember correctly) Ms. Prsd sked me question bout the condition of insulted boundry for the 1D het eqution, nd (bsed on glnce
Het flux nd totl het John McCun Mrch 14, 2017 1 Introduction Yesterdy (if I remember correctly) Ms. Prsd sked me question bout the condition of insulted boundry for the 1D het eqution, nd (bsed on glnce
Math 520 Final Exam Topic Outline Sections 1 3 (Xiao/Dumas/Liaw) Spring 2008
 Mth 520 Finl Exm Topic Outline Sections 1 3 (Xio/Dums/Liw) Spring 2008 The finl exm will be held on Tuesdy, My 13, 2-5pm in 117 McMilln Wht will be covered The finl exm will cover the mteril from ll of
Mth 520 Finl Exm Topic Outline Sections 1 3 (Xio/Dums/Liw) Spring 2008 The finl exm will be held on Tuesdy, My 13, 2-5pm in 117 McMilln Wht will be covered The finl exm will cover the mteril from ll of
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Energy Balance of Solar Collector
 Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Wecome! Energy Bnce of Sor Coector Mohmd Khrseh E-mi:m.Khrseh@gmi.com Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Liuid Ft Pte Coectors. Het
Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Wecome! Energy Bnce of Sor Coector Mohmd Khrseh E-mi:m.Khrseh@gmi.com Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Liuid Ft Pte Coectors. Het
Can the Phase I problem be unfeasible or unbounded? -No
 Cn the Phse I problem be unfesible or unbounded? -No Phse I: min 1X AX + IX = b with b 0 X 1, X 0 By mnipulting constrints nd dding/subtrcting slck/surplus vribles, we cn get b 0 A fesible solution with
Cn the Phse I problem be unfesible or unbounded? -No Phse I: min 1X AX + IX = b with b 0 X 1, X 0 By mnipulting constrints nd dding/subtrcting slck/surplus vribles, we cn get b 0 A fesible solution with
HW Solutions # MIT - Prof. Kowalski. Friction, circular dynamics, and Work-Kinetic Energy.
 HW Solutions # 5-8.01 MIT - Prof. Kowlski Friction, circulr dynmics, nd Work-Kinetic Energy. 1) 5.80 If the block were to remin t rest reltive to the truck, the friction force would need to cuse n ccelertion
HW Solutions # 5-8.01 MIT - Prof. Kowlski Friction, circulr dynmics, nd Work-Kinetic Energy. 1) 5.80 If the block were to remin t rest reltive to the truck, the friction force would need to cuse n ccelertion
#6A&B Magnetic Field Mapping
 #6A& Mgnetic Field Mpping Gol y performing this lb experiment, you will: 1. use mgnetic field mesurement technique bsed on Frdy s Lw (see the previous experiment),. study the mgnetic fields generted by
#6A& Mgnetic Field Mpping Gol y performing this lb experiment, you will: 1. use mgnetic field mesurement technique bsed on Frdy s Lw (see the previous experiment),. study the mgnetic fields generted by
