3D from Photographs: Camera Calibration. Dr Francesco Banterle
|
|
|
- Primrose Adams
- 6 years ago
- Views:
Transcription
1 3D from Photographs: Camera Calibration Dr Francesco Banterle
2 3D from Photographs Automatic Matching of Images Camera Calibration Photographs Surface Reconstruction Dense Matching 3D model
3 3D from Photographs Automatic Matching of Images Camera Calibration Photographs Surface Reconstruction Dense Matching 3D model
4 Camera Pre-Calibration
5 Camera Model: Pinhole Camera Y c X c Image C Z c Plane Hole Y w X w f image-space Z w world-space
6 Camera Model: Pinhole Camera The perspective projection is defined as m = P M m 0 = m/m z P = K[I 0]G = K[R t] K = fk u 0 u 0 0 fk v v t = 2 3 t R = t 2 t 3 2 r > 1 4r > 2 r > Intrinsic Matrix Extrinsic Matrix
7 Pre-Calibration In some cases, when we know the camera, it is useful to avoid intrinsics matrix estimation: It is more precise. We reduce computations.
8 Pre-Calibration: Why? In some cases, when we know the camera, it is useful to avoid intrinsics matrix estimation: It is more precise. We reduce computations.
9 DLT: Direct Linear Transform
10 DLT: Direct Linear Transform Input: a photograph of a non-coplanar calibration with m 2D points with known 3D coordinates. Output: K of the camera.
11 DLT: Direct Linear Transform Y Z X
12 DLT: Direct Linear Transform P = 2 p > 1 4p > < u = p> 1 M p > 3 M p > 3 : v = p> 2 M p > 3 M
13 DLT: Direct Linear Transform ( p > M 1 i u i p > M 3 i =0 p > 2 M i v i p > 3 M i =0 m i =[u i,v i, 1] > $ M i =[x, y, z, 1] > 2D-3D matches
14 DLT: Direct Linear Transform This leads to a matrix: apple M > i 0 u i M > i 0 M > i v i M > i 2 4 p 1 p 2 p = 0 For each point, we need to stack this equations obtaining a matrix A.
15 DLT: Direct Linear Transform We obtain a 2m 12 linear system to solve. The minimum number of points to solve it is 6, but more points are required to have robust and stable solutions.
16 What s the problem with this method?
17 DLT: Direct Linear Transform DLT minimizes an algebraic error! It does not have geometric meaning!! Hang on, is it all wrong? Nope, we can use it as input for a non-linear method.
18 DLT: Non-linear Refinement The non-linear refinement minimizes (at least squares) the distance between 2D points of the image (mi) and projected 3D points (Mi): arg min P mx p > 1 M i i=1 p > 3 M i u i 2 + p > 2 M i p > 3 M i v i 2 Different methods for solving it; e.g., Nelder-Mead s method (MATLAB s fminsearch).
19 Now we have a nice matrix P
20 DLT: Direct Linear Transform Let s recap: K has to be upper-triangular. R is orthogonal. P = K[R t] =[K R K t] =[P 0 p 4 ]
21 DLT: Direct Linear Transform QR decomposition: A = O T where O is orthogonal and T is upper-triangular. In our case, we have: P 0 = K R! (P 0 ) 1 = R 1 K 1
22 DLT: Direct Linear Transform QR decomposition to P : [P 0 ] QR = O T In our case, we have: R = O 1 K = T 1 Note that there is a scale factor!
23 DLT: Direct Linear Transform The scale factor is due to the fact we do not know if are taking a shot to a large object from afar or to a small object in front of the camera! Case 1 Case 2
24 DLT: Direct Linear Transform It makes sense to fix the scale in K because R has to be an orthogonal matrix! This affects also t!
25 How do we compute t?
26 How do we compute t? t = K 1 p 4
27 The Sanity Check If we can have an estimation of K from camera parameters that are available in the camera specifications. K = 2 3 a 0 u 0 4a b v
28 The Sanity Check What do we need? Focal length of the camera in mm ( f ). Resolution of the picture in pixels ( w, h ). CCD/CMOS sensor size in mm ( ws, hs ).
29 The Sanity Check a = ( f w ) / ws. b = ( f h ) / hs. u0 = w / 2. v0 = h / 2.
30 The Sanity Check a = ( f w ) / ws. b = ( f h ) / hs. u0 = w / 2. v0 = h / 2. Assuming it in the center!
31 and what s about the radial distortion?
32 Estimating Radial Distortion Let s start with simple radial distortion (i.e., only a coefficient): ( u 0 =(u u 0 ) (1 + k 1 rd 2)+u 0 r 2 d = ( Can we solve it? v 0 =(v v 0 ) (1 + k 1 r 2 d )+v (u u0 ) + u 2 (v v0 ) u = f k u u = f k v v
33 Estimating Radial Distortion We have only one unknown, which is linear; i.e., k1: ( u 0 u (u u 0 ) rd 2 v 0 v (v v 0 ) rd 2 = k 1 = k 1 In theory, a single point is enough, but it is better to use more points to get a more robust solution.
34 Homography
35 2D Transformations We can have different type of transformation (defined by a matrix) of 2D points: Translation (2 degree of freedom [DoF]): It preserves orientation. Rigid/Euclidian (3 DoF); translation, and rotation: It preserves lengths. Similarity (4DoF); translation, rotation, and scaling: It preserves angles.
36 2D Transformations Affine (6 degree of freedom [DoF]): It reserves parallelism. Projective (8 DoF): It preserves straight lines.
37 2D Transformations: Homography Homography is defined as m = H M m = This is typically expressed as 2 4 x 0 y = 2 3 m 1 /m 3 4m 2 /m m H M where H is a 3 3 non-singular matrix with 8 DoF.
38 2D Transformations: Homography H M m
39 Homography Estimation m H M m = 2 4 x 0 y M = 2 3 x 4y5 1
40 Homography Estimation m H M m = 2 4 x 0 y M = 2 3 x 4y5 1
41 Homography Estimation m H M m = 2 4 x 0 y M = 2 3 x 4y5 1 x 0 = h 11x 1 + h 12 y 1 + h 13 h 31 x 1 + h 32 y 1 + h 33 y 0 = h 21x 1 + h 22 y 1 + h 23 h 31 x 1 + h 32 y 1 + h 33
42 Homography Estimation (h 31 x 1 + h 32 y 1 + h 33 ) x 0 (h 11 x 1 + h 12 y 1 + h 33 )=0 (h 31 x 1 + h 32 y 1 + h 33 ) y 0 (h 21 x 1 + h 22 y 1 + h 23 )=0
43 Homography Estimation (h 31 x 1 + h 32 y 1 + h 33 ) x 0 (h 11 x 1 + h 12 y 1 + h 33 )=0 (h 31 x 1 + h 32 y 1 + h 33 ) y 0 (h 21 x 1 + h 22 y 1 + h 23 )=0 Stacking multiple equations; one for each match (at least 5!)
44 Homography Estimation (h 31 x 1 + h 32 y 1 + h 33 ) x 0 (h 11 x 1 + h 12 y 1 + h 33 )=0 (h 31 x 1 + h 32 y 1 + h 33 ) y 0 (h 21 x 1 + h 22 y 1 + h 23 )=0 Stacking multiple equations; one for each match (at least 5!) A vec(h) =0 A is 2n 9
45 Homography Estimation Again, we have minimized an algebraic error!! Technically speaking, we should run a non-linear optimization.
46 Zhang s Algorithm
47 Zhang s Algorithm Input: a set of n photographs of a checkboard or other patterns. From these, we have to extract m points in each photograph! Output: K of the camera, and [R t] for each photographs.
48 Zhang s Algorithm A set of input images
49 Zhang s Algorithm 2 3 K = 4 fk u 0 u 0 0 fk v v
50 Zhang s Algorithm 2 3 K = 4 c u 0 0 v
51 Zhang s Algorithm 2 3 K = 4 c u 0 0 v
52 Zhang s Algorithm Assumption: We have a set of photographs of a plane so Z is equal 0. So we have 3D points defined as M = 2 3 x 6y
53 Zhang s Algorithm m =P M = =K [R t] 2 3 x 6y =
54 Zhang s Algorithm m 2 3 x =K [r 1 r 2 r 3 t] 6y = x =K [r 1 r 2 t] 4y5 1
55 Zhang s Algorithm m 2 3 x =K [r 1 r 2 r 3 t] 6y = x =K [r 1 r 2 t] 4y5 1
56 Zhang s Algorithm m 2 3 x =K [r 1 r 2 r 3 t] 6y = x =K [r 1 r 2 t] 4y5 1 H = K [r 1 r 2 t]
57 Zhang s Algorithm m 2 3 x =K [r 1 r 2 r 3 t] 6y = x =K [r 1 r 2 t] 4y5 1 It is a homography! H = K [r 1 r 2 t]
58 Zhang s Algorithm m 2 3 x =K [r 1 r 2 r 3 t] 6y = x =K [r 1 r 2 t] 4y5 1 It is a homography! H = K [r 1 r 2 t] H = h 1 h 2 h 3
59 Zhang s Algorithm Now that we know that we need homographies! What to do? For each photograph we compute the homography H between photographed checkerboard corners and its model.
60 Zhang s Algorithm H Model Photograph
61 Zhang s Algorithm Given that r1 and r2 are orthonormal, we have that: h > 1 K > K 1 h 2 =0 h > 1 K > K 1 h 1 = h > 2 K > K 1 h 2
62 Zhang s Algorithm B = K > K 1 = 1 α 2 c α 2 β c α 2 β cv 0 u 0 β α 2 β c 2 α 2 β β 2 c(cv 0 u 0 β) α 2 β 2 v 0 β 2 cv 0 u 0 β α 2 β c(cv 0 u 0 β) α 2 β 2 v 0 β 2 (cv 0 u 0 β) 2 α 2 β 2 + v2 0 β 2 +1 B is symmetric > defined only by six values: b =[B 1,1,B 1,2,B 2,2,B 1,3,B 2,3,B 3,3 ] >
63 Zhang s Algorithm B = K > K 1 = 1 α 2 c α 2 β c α 2 β cv 0 u 0 β α 2 β c 2 α 2 β β 2 c(cv 0 u 0 β) α 2 β 2 v 0 β 2 cv 0 u 0 β α 2 β c(cv 0 u 0 β) α 2 β 2 v 0 β 2 (cv 0 u 0 β) 2 α 2 β 2 + v2 0 β 2 +1 B is symmetric > defined only by six values: b =[B 1,1,B 1,2,B 2,2,B 1,3,B 2,3,B 3,3 ] >
64 Zhang s Algorithm h > i B h j = v > i,j b
65 Zhang s Algorithm h > i B h j = v > i,j b H = h 1 h 2 h 3 h i = h i1 h i2 h i3 > v ij = h i1 h j1 h i1 h j2 + h i2 h j1 h i2 h j2 h i3 h j1 + h i1 h j3 h i3 h j2 + h i2 h j3 h i3 h j
66 Zhang s Algorithm Given that r1 and r2 are orthonormal, we have that: h > 1 K > K 1 h 2 =0 h > 1 K > K 1 h 1 = h > 2 K > K 1 h 2 [ ] v T 12 (v 11 v 22 ) T b = 0
67 Zhang s Algorithm If n images of the model plane are observed, by stacking n of such equations: [ ] v T 12 (v 11 v 22 ) T b = 0 We obtain: V b = 0 V is 2n 6 matrix, so we need n > 2
68 Zhang s Algorithm At this point, we can compute elements of K as v 0 =(B 12 B 13 B 11 B 23 )/(B 11 B 22 B 2 12) λ = B 33 [B v 0 (B 12 B 13 B 11 B 23 )]/B 11 α = λ/b 11 β = λb 11 /(B 11 B 22 B12 2 ) c = B 12 α 2 β/λ u 0 = cv 0 /α B 13 α 2 /λ. 3 3
69 Zhang s Algorithm: Camera Pose Furthermore, we can extract the pose as r 1 = K 1 h 1 r 2 = K 1 h 2 r 3 = r 1 r 2 t = K 1 h 3
70 Zhang s Algorithm: Non-Linear Refinement So far, we have obtained a solution through minimizing an algebraic distance that is not physically meaningful. From that solution, we can use a non-linear method for minimizing the following error: nx mx km i,j m(k, R i, t i, M j )k 2 i=1 j=1
71 Zhang s Algorithm: Non-Linear Refinement So far, we have obtained a solution through minimizing an algebraic distance that is not physically meaningful. From that solution, we can use a non-linear method for minimizing the following error: nx mx i=1 j=1 km i,j m(k, R i, t i, M j )k 2 This is a function projecting Mj points given intrinsics and the pose!
72 Zhang s Algorithm: Optical Distortion What s about the parameters for modeling the radial distortion? As before, first algebraic solution, and then a nonlinear solution.
73 Zhang s Algorithm: Optical Distortion apple (u u0 )r 2 d (u u 0 )r 4 d (v v 0 )r 2 d (v v 0 )r 4 d apple k1 k 2 = apple u 0 v 0 u v D k = d k =(D > D) 1 D > d
74 Zhang s Algorithm: Non-Linear Refinement We extend the previous non-linear model to include optical distortion: nx mx km i,j m(k, R i, t i, k, M j )k 2 i=1 j=1
75 Zhang s Algorithm: Non-Linear Refinement We extend the previous non-linear model to include optical distortion: nx mx i=1 j=1 km i,j m(k, R i, t i, k, M j )k 2 This is a function projecting Mj points given intrinsics and the pose!
76 that s all folks!
Camera calibration by Zhang
 Camera calibration by Zhang Siniša Kolarić September 2006 Abstract In this presentation, I present a way to calibrate a camera using the method by Zhang. NOTE. This
Camera calibration by Zhang Siniša Kolarić September 2006 Abstract In this presentation, I present a way to calibrate a camera using the method by Zhang. NOTE. This
Introduction to pinhole cameras
 Introduction to pinhole cameras Lesson given by Sébastien Piérard in the course Introduction aux techniques audio et vidéo (ULg, Pr JJ Embrechts) INTELSIG, Montefiore Institute, University of Liège, Belgium
Introduction to pinhole cameras Lesson given by Sébastien Piérard in the course Introduction aux techniques audio et vidéo (ULg, Pr JJ Embrechts) INTELSIG, Montefiore Institute, University of Liège, Belgium
Augmented Reality VU Camera Registration. Prof. Vincent Lepetit
 Augmented Reality VU Camera Registration Prof. Vincent Lepetit Different Approaches to Vision-based 3D Tracking [From D. Wagner] [From Drummond PAMI02] [From Davison ICCV01] Consider natural features Consider
Augmented Reality VU Camera Registration Prof. Vincent Lepetit Different Approaches to Vision-based 3D Tracking [From D. Wagner] [From Drummond PAMI02] [From Davison ICCV01] Consider natural features Consider
Theory of Bouguet s MatLab Camera Calibration Toolbox
 Theory of Bouguet s MatLab Camera Calibration Toolbox Yuji Oyamada 1 HVRL, University 2 Chair for Computer Aided Medical Procedure (CAMP) Technische Universität München June 26, 2012 MatLab Camera Calibration
Theory of Bouguet s MatLab Camera Calibration Toolbox Yuji Oyamada 1 HVRL, University 2 Chair for Computer Aided Medical Procedure (CAMP) Technische Universität München June 26, 2012 MatLab Camera Calibration
Camera calibration. Outline. Pinhole camera. Camera projection models. Nonlinear least square methods A camera calibration tool
 Outline Camera calibration Camera projection models Camera calibration i Nonlinear least square methods A camera calibration tool Applications Digital Visual Effects Yung-Yu Chuang with slides b Richard
Outline Camera calibration Camera projection models Camera calibration i Nonlinear least square methods A camera calibration tool Applications Digital Visual Effects Yung-Yu Chuang with slides b Richard
Structure from Motion. CS4670/CS Kevin Matzen - April 15, 2016
 Structure from Motion CS4670/CS5670 - Kevin Matzen - April 15, 2016 Video credit: Agarwal, et. al. Building Rome in a Day, ICCV 2009 Roadmap What we ve seen so far Single view modeling (1 camera) Stereo
Structure from Motion CS4670/CS5670 - Kevin Matzen - April 15, 2016 Video credit: Agarwal, et. al. Building Rome in a Day, ICCV 2009 Roadmap What we ve seen so far Single view modeling (1 camera) Stereo
Camera calibration Triangulation
 Triangulation Perspective projection in homogenous coordinates ~x img I 0 apple R t 0 T 1 ~x w ~x img R t ~x w Matrix transformations in 2D ~x img K R t ~x w K = 2 3 1 0 t u 40 1 t v 5 0 0 1 Translation
Triangulation Perspective projection in homogenous coordinates ~x img I 0 apple R t 0 T 1 ~x w ~x img R t ~x w Matrix transformations in 2D ~x img K R t ~x w K = 2 3 1 0 t u 40 1 t v 5 0 0 1 Translation
Pose estimation from point and line correspondences
 Pose estimation from point and line correspondences Giorgio Panin October 17, 008 1 Problem formulation Estimate (in a LSE sense) the pose of an object from N correspondences between known object points
Pose estimation from point and line correspondences Giorgio Panin October 17, 008 1 Problem formulation Estimate (in a LSE sense) the pose of an object from N correspondences between known object points
Camera Calibration The purpose of camera calibration is to determine the intrinsic camera parameters (c 0,r 0 ), f, s x, s y, skew parameter (s =
 Camera Calibration The purpose of camera calibration is to determine the intrinsic camera parameters (c 0,r 0 ), f, s x, s y, skew parameter (s = cotα), and the lens distortion (radial distortion coefficient
Camera Calibration The purpose of camera calibration is to determine the intrinsic camera parameters (c 0,r 0 ), f, s x, s y, skew parameter (s = cotα), and the lens distortion (radial distortion coefficient
EE Camera & Image Formation
 Electric Electronic Engineering Bogazici University February 21, 2018 Introduction Introduction Camera models Goal: To understand the image acquisition process. Function of the camera Similar to that of
Electric Electronic Engineering Bogazici University February 21, 2018 Introduction Introduction Camera models Goal: To understand the image acquisition process. Function of the camera Similar to that of
Visual Object Recognition
 Visual Object Recognition Lecture 2: Image Formation Per-Erik Forssén, docent Computer Vision Laboratory Department of Electrical Engineering Linköping University Lecture 2: Image Formation Pin-hole, and
Visual Object Recognition Lecture 2: Image Formation Per-Erik Forssén, docent Computer Vision Laboratory Department of Electrical Engineering Linköping University Lecture 2: Image Formation Pin-hole, and
Homographies and Estimating Extrinsics
 Homographies and Estimating Extrinsics Instructor - Simon Lucey 16-423 - Designing Computer Vision Apps Adapted from: Computer vision: models, learning and inference. Simon J.D. Prince Review: Motivation
Homographies and Estimating Extrinsics Instructor - Simon Lucey 16-423 - Designing Computer Vision Apps Adapted from: Computer vision: models, learning and inference. Simon J.D. Prince Review: Motivation
Camera Projection Model
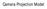 amera Projection Model 3D Point Projection (Pixel Space) O ( u, v ) ccd ccd f Projection plane (, Y, Z ) ( u, v ) img Z img (0,0) w img ( u, v ) img img uimg f Z p Y v img f Z p x y Zu f p Z img img x
amera Projection Model 3D Point Projection (Pixel Space) O ( u, v ) ccd ccd f Projection plane (, Y, Z ) ( u, v ) img Z img (0,0) w img ( u, v ) img img uimg f Z p Y v img f Z p x y Zu f p Z img img x
Linear Algebra & Geometry why is linear algebra useful in computer vision?
 Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Linear Algebra & Geometry why is linear algebra useful in computer vision?
 Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Lecture 4.3 Estimating homographies from feature correspondences. Thomas Opsahl
 Lecture 4.3 Estimating homographies from feature correspondences Thomas Opsahl Homographies induced by central projection 1 H 2 1 H 2 u uu 2 3 1 Homography Hu = u H = h 1 h 2 h 3 h 4 h 5 h 6 h 7 h 8 h
Lecture 4.3 Estimating homographies from feature correspondences Thomas Opsahl Homographies induced by central projection 1 H 2 1 H 2 u uu 2 3 1 Homography Hu = u H = h 1 h 2 h 3 h 4 h 5 h 6 h 7 h 8 h
Pose Tracking II! Gordon Wetzstein! Stanford University! EE 267 Virtual Reality! Lecture 12! stanford.edu/class/ee267/!
 Pose Tracking II! Gordon Wetzstein! Stanford University! EE 267 Virtual Reality! Lecture 12! stanford.edu/class/ee267/!! WARNING! this class will be dense! will learn how to use nonlinear optimization
Pose Tracking II! Gordon Wetzstein! Stanford University! EE 267 Virtual Reality! Lecture 12! stanford.edu/class/ee267/!! WARNING! this class will be dense! will learn how to use nonlinear optimization
ANALYTICAL IMAGE FEATURES
 Chapter 6 ANALYTICAL IMAGE FEATURES Chapter laid the geometric foundations of image formation. This chapter uses analytical geometry to quantify more precisely the relationship between a camera, the objects
Chapter 6 ANALYTICAL IMAGE FEATURES Chapter laid the geometric foundations of image formation. This chapter uses analytical geometry to quantify more precisely the relationship between a camera, the objects
Multi-Frame Factorization Techniques
 Multi-Frame Factorization Techniques Suppose { x j,n } J,N j=1,n=1 is a set of corresponding image coordinates, where the index n = 1,...,N refers to the n th scene point and j = 1,..., J refers to the
Multi-Frame Factorization Techniques Suppose { x j,n } J,N j=1,n=1 is a set of corresponding image coordinates, where the index n = 1,...,N refers to the n th scene point and j = 1,..., J refers to the
CSE 252B: Computer Vision II
 CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Tasha Vanesian LECTURE 3 Calibrated 3D Reconstruction 3.1. Geometric View of Epipolar Constraint We are trying to solve the following problem:
CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Tasha Vanesian LECTURE 3 Calibrated 3D Reconstruction 3.1. Geometric View of Epipolar Constraint We are trying to solve the following problem:
6.801/866. Affine Structure from Motion. T. Darrell
 6.801/866 Affine Structure from Motion T. Darrell [Read F&P Ch. 12.0, 12.2, 12.3, 12.4] Affine geometry is, roughly speaking, what is left after all ability to measure lengths, areas, angles, etc. has
6.801/866 Affine Structure from Motion T. Darrell [Read F&P Ch. 12.0, 12.2, 12.3, 12.4] Affine geometry is, roughly speaking, what is left after all ability to measure lengths, areas, angles, etc. has
3D Computer Vision - WT 2004
 3D Computer Vision - WT 2004 Singular Value Decomposition Darko Zikic CAMP - Chair for Computer Aided Medical Procedures November 4, 2004 1 2 3 4 5 Properties For any given matrix A R m n there exists
3D Computer Vision - WT 2004 Singular Value Decomposition Darko Zikic CAMP - Chair for Computer Aided Medical Procedures November 4, 2004 1 2 3 4 5 Properties For any given matrix A R m n there exists
Camera Models and Affine Multiple Views Geometry
 Camera Models and Affine Multiple Views Geometry Subhashis Banerjee Dept. Computer Science and Engineering IIT Delhi email: suban@cse.iitd.ac.in May 29, 2001 1 1 Camera Models A Camera transforms a 3D
Camera Models and Affine Multiple Views Geometry Subhashis Banerjee Dept. Computer Science and Engineering IIT Delhi email: suban@cse.iitd.ac.in May 29, 2001 1 1 Camera Models A Camera transforms a 3D
Multiple View Geometry in Computer Vision
 Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Scene Planes & Homographies Lecture 19 March 24, 2005 2 In our last lecture, we examined various
Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Scene Planes & Homographies Lecture 19 March 24, 2005 2 In our last lecture, we examined various
Uncertainty Models in Quasiconvex Optimization for Geometric Reconstruction
 Uncertainty Models in Quasiconvex Optimization for Geometric Reconstruction Qifa Ke and Takeo Kanade Department of Computer Science, Carnegie Mellon University Email: ke@cmu.edu, tk@cs.cmu.edu Abstract
Uncertainty Models in Quasiconvex Optimization for Geometric Reconstruction Qifa Ke and Takeo Kanade Department of Computer Science, Carnegie Mellon University Email: ke@cmu.edu, tk@cs.cmu.edu Abstract
Trinocular Geometry Revisited
 Trinocular Geometry Revisited Jean Pounce and Martin Hebert 报告人 : 王浩人 2014-06-24 Contents 1. Introduction 2. Converging Triplets of Lines 3. Converging Triplets of Visual Rays 4. Discussion 1. Introduction
Trinocular Geometry Revisited Jean Pounce and Martin Hebert 报告人 : 王浩人 2014-06-24 Contents 1. Introduction 2. Converging Triplets of Lines 3. Converging Triplets of Visual Rays 4. Discussion 1. Introduction
Linear Algebra (Review) Volker Tresp 2017
 Linear Algebra (Review) Volker Tresp 2017 1 Vectors k is a scalar (a number) c is a column vector. Thus in two dimensions, c = ( c1 c 2 ) (Advanced: More precisely, a vector is defined in a vector space.
Linear Algebra (Review) Volker Tresp 2017 1 Vectors k is a scalar (a number) c is a column vector. Thus in two dimensions, c = ( c1 c 2 ) (Advanced: More precisely, a vector is defined in a vector space.
Practical rotation angle measurement method by monocular vision
 Practical rotation angle measurement method by monocular vision Hongxin Dong,, * Qiang Fu, Xu Zhao, Quan Quan,,2 and Ruifeng Zhang School of Automation Science and Electrical Engineering, Beihang University,
Practical rotation angle measurement method by monocular vision Hongxin Dong,, * Qiang Fu, Xu Zhao, Quan Quan,,2 and Ruifeng Zhang School of Automation Science and Electrical Engineering, Beihang University,
Mysteries of Parameterizing Camera Motion - Part 2
 Mysteries of Parameterizing Camera Motion - Part 2 Instructor - Simon Lucey 16-623 - Advanced Computer Vision Apps Today Gauss-Newton and SO(3) Alternative Representations of SO(3) Exponential Maps SL(3)
Mysteries of Parameterizing Camera Motion - Part 2 Instructor - Simon Lucey 16-623 - Advanced Computer Vision Apps Today Gauss-Newton and SO(3) Alternative Representations of SO(3) Exponential Maps SL(3)
CS4495/6495 Introduction to Computer Vision. 3D-L3 Fundamental matrix
 CS4495/6495 Introduction to Computer Vision 3D-L3 Fundamental matrix Weak calibration Main idea: Estimate epipolar geometry from a (redundant) set of point correspondences between two uncalibrated cameras
CS4495/6495 Introduction to Computer Vision 3D-L3 Fundamental matrix Weak calibration Main idea: Estimate epipolar geometry from a (redundant) set of point correspondences between two uncalibrated cameras
Numerical Linear Algebra
 Numerical Linear Algebra By: David McQuilling; Jesus Caban Deng Li Jan.,31,006 CS51 Solving Linear Equations u + v = 8 4u + 9v = 1 A x b 4 9 u v = 8 1 Gaussian Elimination Start with the matrix representation
Numerical Linear Algebra By: David McQuilling; Jesus Caban Deng Li Jan.,31,006 CS51 Solving Linear Equations u + v = 8 4u + 9v = 1 A x b 4 9 u v = 8 1 Gaussian Elimination Start with the matrix representation
Tracking for VR and AR
 Tracking for VR and AR Hakan Bilen November 17, 2017 Computer Graphics University of Edinburgh Slide credits: Gordon Wetzstein and Steven M. La Valle 1 Overview VR and AR Inertial Sensors Gyroscopes Accelerometers
Tracking for VR and AR Hakan Bilen November 17, 2017 Computer Graphics University of Edinburgh Slide credits: Gordon Wetzstein and Steven M. La Valle 1 Overview VR and AR Inertial Sensors Gyroscopes Accelerometers
Lecture 5. Epipolar Geometry. Professor Silvio Savarese Computational Vision and Geometry Lab. 21-Jan-15. Lecture 5 - Silvio Savarese
 Lecture 5 Epipolar Geometry Professor Silvio Savarese Computational Vision and Geometry Lab Silvio Savarese Lecture 5-21-Jan-15 Lecture 5 Epipolar Geometry Why is stereo useful? Epipolar constraints Essential
Lecture 5 Epipolar Geometry Professor Silvio Savarese Computational Vision and Geometry Lab Silvio Savarese Lecture 5-21-Jan-15 Lecture 5 Epipolar Geometry Why is stereo useful? Epipolar constraints Essential
Algorithms for Computing a Planar Homography from Conics in Correspondence
 Algorithms for Computing a Planar Homography from Conics in Correspondence Juho Kannala, Mikko Salo and Janne Heikkilä Machine Vision Group University of Oulu, Finland {jkannala, msa, jth@ee.oulu.fi} Abstract
Algorithms for Computing a Planar Homography from Conics in Correspondence Juho Kannala, Mikko Salo and Janne Heikkilä Machine Vision Group University of Oulu, Finland {jkannala, msa, jth@ee.oulu.fi} Abstract
A Practical Method for Decomposition of the Essential Matrix
 Applied Mathematical Sciences, Vol. 8, 2014, no. 176, 8755-8770 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.410877 A Practical Method for Decomposition of the Essential Matrix Georgi
Applied Mathematical Sciences, Vol. 8, 2014, no. 176, 8755-8770 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.410877 A Practical Method for Decomposition of the Essential Matrix Georgi
A Study of Kruppa s Equation for Camera Self-calibration
 Proceedings of the International Conference of Machine Vision and Machine Learning Prague, Czech Republic, August 14-15, 2014 Paper No. 57 A Study of Kruppa s Equation for Camera Self-calibration Luh Prapitasari,
Proceedings of the International Conference of Machine Vision and Machine Learning Prague, Czech Republic, August 14-15, 2014 Paper No. 57 A Study of Kruppa s Equation for Camera Self-calibration Luh Prapitasari,
A Multi-Affine Model for Tensor Decomposition
 Yiqing Yang UW Madison breakds@cs.wisc.edu A Multi-Affine Model for Tensor Decomposition Hongrui Jiang UW Madison hongrui@engr.wisc.edu Li Zhang UW Madison lizhang@cs.wisc.edu Chris J. Murphy UC Davis
Yiqing Yang UW Madison breakds@cs.wisc.edu A Multi-Affine Model for Tensor Decomposition Hongrui Jiang UW Madison hongrui@engr.wisc.edu Li Zhang UW Madison lizhang@cs.wisc.edu Chris J. Murphy UC Davis
Position & motion in 2D and 3D
 Position & motion in 2D and 3D! METR4202: Guest lecture 22 October 2014 Peter Corke Peter Corke Robotics, Vision and Control FUNDAMENTAL ALGORITHMS IN MATLAB 123 Sections 11.1, 15.2 Queensland University
Position & motion in 2D and 3D! METR4202: Guest lecture 22 October 2014 Peter Corke Peter Corke Robotics, Vision and Control FUNDAMENTAL ALGORITHMS IN MATLAB 123 Sections 11.1, 15.2 Queensland University
Morphing. Xiao-Ming Fu
 Morphing Xiao-Ming Fu Outlines Definition Angle, length, area, volume, and curvature Example-Driven Deformations Based on Discrete Shells Affine transformation As-Rigid-As-Possible Shape Interpolation
Morphing Xiao-Ming Fu Outlines Definition Angle, length, area, volume, and curvature Example-Driven Deformations Based on Discrete Shells Affine transformation As-Rigid-As-Possible Shape Interpolation
Photometric Stereo: Three recent contributions. Dipartimento di Matematica, La Sapienza
 Photometric Stereo: Three recent contributions Dipartimento di Matematica, La Sapienza Jean-Denis DUROU IRIT, Toulouse Jean-Denis DUROU (IRIT, Toulouse) 17 December 2013 1 / 32 Outline 1 Shape-from-X techniques
Photometric Stereo: Three recent contributions Dipartimento di Matematica, La Sapienza Jean-Denis DUROU IRIT, Toulouse Jean-Denis DUROU (IRIT, Toulouse) 17 December 2013 1 / 32 Outline 1 Shape-from-X techniques
Basic Math for
 Basic Math for 16-720 August 23, 2002 1 Linear Algebra 1.1 Vectors and Matrices First, a reminder of a few basic notations, definitions, and terminology: Unless indicated otherwise, vectors are always
Basic Math for 16-720 August 23, 2002 1 Linear Algebra 1.1 Vectors and Matrices First, a reminder of a few basic notations, definitions, and terminology: Unless indicated otherwise, vectors are always
Nonlinear Dimensionality Reduction
 Nonlinear Dimensionality Reduction Piyush Rai CS5350/6350: Machine Learning October 25, 2011 Recap: Linear Dimensionality Reduction Linear Dimensionality Reduction: Based on a linear projection of the
Nonlinear Dimensionality Reduction Piyush Rai CS5350/6350: Machine Learning October 25, 2011 Recap: Linear Dimensionality Reduction Linear Dimensionality Reduction: Based on a linear projection of the
CS 231A Computer Vision (Fall 2011) Problem Set 2
 CS 231A Computer Vision (Fall 2011) Problem Set 2 Solution Set Due: Oct. 28 th, 2011 (5pm) 1 Some Projective Geometry Problems (15 points) Suppose there are two parallel lines that extend to infinity in
CS 231A Computer Vision (Fall 2011) Problem Set 2 Solution Set Due: Oct. 28 th, 2011 (5pm) 1 Some Projective Geometry Problems (15 points) Suppose there are two parallel lines that extend to infinity in
Lecture 8: Coordinate Frames. CITS3003 Graphics & Animation
 Lecture 8: Coordinate Frames CITS3003 Graphics & Animation E. Angel and D. Shreiner: Interactive Computer Graphics 6E Addison-Wesley 2012 Objectives Learn how to define and change coordinate frames Introduce
Lecture 8: Coordinate Frames CITS3003 Graphics & Animation E. Angel and D. Shreiner: Interactive Computer Graphics 6E Addison-Wesley 2012 Objectives Learn how to define and change coordinate frames Introduce
M3: Multiple View Geometry
 M3: Multiple View Geometry L18: Projective Structure from Motion: Iterative Algorithm based on Factorization Based on Sections 13.4 C. V. Jawahar jawahar-at-iiit.net Mar 2005: 1 Review: Reconstruction
M3: Multiple View Geometry L18: Projective Structure from Motion: Iterative Algorithm based on Factorization Based on Sections 13.4 C. V. Jawahar jawahar-at-iiit.net Mar 2005: 1 Review: Reconstruction
Lecture 4 Orthonormal vectors and QR factorization
 Orthonormal vectors and QR factorization 4 1 Lecture 4 Orthonormal vectors and QR factorization EE263 Autumn 2004 orthonormal vectors Gram-Schmidt procedure, QR factorization orthogonal decomposition induced
Orthonormal vectors and QR factorization 4 1 Lecture 4 Orthonormal vectors and QR factorization EE263 Autumn 2004 orthonormal vectors Gram-Schmidt procedure, QR factorization orthogonal decomposition induced
Image Transform. Panorama Image (Keller+Lind Hall)
 Image Transform Panorama Image (Keller+Lind Hall) Image Warping (Coordinate Transform) u I v 1 I 2 I ( v) = I ( u) 2 1 Image Warping (Coordinate Transform) u I v 1 I 2 I ( v) = I ( u) 2 1 : Piel transport
Image Transform Panorama Image (Keller+Lind Hall) Image Warping (Coordinate Transform) u I v 1 I 2 I ( v) = I ( u) 2 1 Image Warping (Coordinate Transform) u I v 1 I 2 I ( v) = I ( u) 2 1 : Piel transport
(Linear equations) Applied Linear Algebra in Geoscience Using MATLAB
 Applied Linear Algebra in Geoscience Using MATLAB (Linear equations) Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots
Applied Linear Algebra in Geoscience Using MATLAB (Linear equations) Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots
Visual SLAM Tutorial: Bundle Adjustment
 Visual SLAM Tutorial: Bundle Adjustment Frank Dellaert June 27, 2014 1 Minimizing Re-projection Error in Two Views In a two-view setting, we are interested in finding the most likely camera poses T1 w
Visual SLAM Tutorial: Bundle Adjustment Frank Dellaert June 27, 2014 1 Minimizing Re-projection Error in Two Views In a two-view setting, we are interested in finding the most likely camera poses T1 w
Single Exposure Enhancement and Reconstruction. Some slides are from: J. Kosecka, Y. Chuang, A. Efros, C. B. Owen, W. Freeman
 Single Exposure Enhancement and Reconstruction Some slides are from: J. Kosecka, Y. Chuang, A. Efros, C. B. Owen, W. Freeman 1 Reconstruction as an Inverse Problem Original image f Distortion & Sampling
Single Exposure Enhancement and Reconstruction Some slides are from: J. Kosecka, Y. Chuang, A. Efros, C. B. Owen, W. Freeman 1 Reconstruction as an Inverse Problem Original image f Distortion & Sampling
OPPA European Social Fund Prague & EU: We invest in your future.
 OPPA European Social Fund Prague & EU: We invest in your future. 1D Projective Coordinates The 1-D projective coordinate of a point P : [P ] = [P P 0 P I P ] = [p p 0 p I p] = p pi p 0 p I p 0 p p p p
OPPA European Social Fund Prague & EU: We invest in your future. 1D Projective Coordinates The 1-D projective coordinate of a point P : [P ] = [P P 0 P I P ] = [p p 0 p I p] = p pi p 0 p I p 0 p p p p
Recovering Unknown Focal Lengths in Self-Calibration: G.N. Newsam D.Q. Huynh M.J. Brooks H.-P. Pan.
 Recovering Unknown Focal Lengths in Self-Calibration: An Essentially Linear Algorithm and Degenerate Congurations G.N. Newsam D.Q. Huynh M.J. Brooks H.-P. Pan fgnewsam,du,mjb,hepingg@cssip.edu.au Centre
Recovering Unknown Focal Lengths in Self-Calibration: An Essentially Linear Algorithm and Degenerate Congurations G.N. Newsam D.Q. Huynh M.J. Brooks H.-P. Pan fgnewsam,du,mjb,hepingg@cssip.edu.au Centre
Main matrix factorizations
 Main matrix factorizations A P L U P permutation matrix, L lower triangular, U upper triangular Key use: Solve square linear system Ax b. A Q R Q unitary, R upper triangular Key use: Solve square or overdetrmined
Main matrix factorizations A P L U P permutation matrix, L lower triangular, U upper triangular Key use: Solve square linear system Ax b. A Q R Q unitary, R upper triangular Key use: Solve square or overdetrmined
Nonlinear Dimensionality Reduction
 Outline Hong Chang Institute of Computing Technology, Chinese Academy of Sciences Machine Learning Methods (Fall 2012) Outline Outline I 1 Kernel PCA 2 Isomap 3 Locally Linear Embedding 4 Laplacian Eigenmap
Outline Hong Chang Institute of Computing Technology, Chinese Academy of Sciences Machine Learning Methods (Fall 2012) Outline Outline I 1 Kernel PCA 2 Isomap 3 Locally Linear Embedding 4 Laplacian Eigenmap
A Theory of Multi-Layer Flat Refractive Geometry Supplementary Materials
 A Theory of Multi-Layer Flat Refractive Geometry Supplementary Materials Amit Agrawal, Srikumar Ramalingam, Yuichi Taguchi Mitsubishi Electric Research Labs MERL) [agrawal,ramalingam,taguchi] at merl.com
A Theory of Multi-Layer Flat Refractive Geometry Supplementary Materials Amit Agrawal, Srikumar Ramalingam, Yuichi Taguchi Mitsubishi Electric Research Labs MERL) [agrawal,ramalingam,taguchi] at merl.com
16. Analysis and Computation of the Intrinsic Camera Parameters
 16. Analysis and Computation of the Intrinsic Camera Parameters Eduardo Bayro-Corrochano and Bodo Rosenhahn Institute of Computer Science and Applied Mathematics, Christian-Albrechts-University of Kiel
16. Analysis and Computation of the Intrinsic Camera Parameters Eduardo Bayro-Corrochano and Bodo Rosenhahn Institute of Computer Science and Applied Mathematics, Christian-Albrechts-University of Kiel
Maths for Signals and Systems Linear Algebra in Engineering
 Maths for Signals and Systems Linear Algebra in Engineering Lecture 18, Friday 18 th November 2016 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE LONDON Mathematics
Maths for Signals and Systems Linear Algebra in Engineering Lecture 18, Friday 18 th November 2016 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE LONDON Mathematics
Camera Calibration. (Trucco, Chapter 6) -Toproduce an estimate of the extrinsic and intrinsic camera parameters.
 Camera Calibration (Trucco, Chapter 6) What is the goal of camera calibration? -Toproduce an estimate of the extrinsic and intrinsic camera parameters. Procedure -Given the correspondences beteen a set
Camera Calibration (Trucco, Chapter 6) What is the goal of camera calibration? -Toproduce an estimate of the extrinsic and intrinsic camera parameters. Procedure -Given the correspondences beteen a set
Lecture 16: Projection and Cameras. October 17, 2017
 Lecture 6: Projection and Cameras October 7 207 3D Viewing as Virtual Camera To take a picture with a camera or to render an image with computer graphics we need to:. Position the camera/viewpoint in 3D
Lecture 6: Projection and Cameras October 7 207 3D Viewing as Virtual Camera To take a picture with a camera or to render an image with computer graphics we need to:. Position the camera/viewpoint in 3D
Spectral Algorithms I. Slides based on Spectral Mesh Processing Siggraph 2010 course
 Spectral Algorithms I Slides based on Spectral Mesh Processing Siggraph 2010 course Why Spectral? A different way to look at functions on a domain Why Spectral? Better representations lead to simpler solutions
Spectral Algorithms I Slides based on Spectral Mesh Processing Siggraph 2010 course Why Spectral? A different way to look at functions on a domain Why Spectral? Better representations lead to simpler solutions
EPIPOLAR GEOMETRY WITH MANY DETAILS
 EPIPOLAR GEOMERY WIH MANY DEAILS hank ou for the slides. he come mostl from the following source. Marc Pollefes U. of North Carolina hree questions: (i) Correspondence geometr: Given an image point in
EPIPOLAR GEOMERY WIH MANY DEAILS hank ou for the slides. he come mostl from the following source. Marc Pollefes U. of North Carolina hree questions: (i) Correspondence geometr: Given an image point in
Optimisation on Manifolds
 Optimisation on Manifolds K. Hüper MPI Tübingen & Univ. Würzburg K. Hüper (MPI Tübingen & Univ. Würzburg) Applications in Computer Vision Grenoble 18/9/08 1 / 29 Contents 2 Examples Essential matrix estimation
Optimisation on Manifolds K. Hüper MPI Tübingen & Univ. Würzburg K. Hüper (MPI Tübingen & Univ. Würzburg) Applications in Computer Vision Grenoble 18/9/08 1 / 29 Contents 2 Examples Essential matrix estimation
Affine Structure From Motion
 EECS43-Advanced Computer Vision Notes Series 9 Affine Structure From Motion Ying Wu Electrical Engineering & Computer Science Northwestern University Evanston, IL 68 yingwu@ece.northwestern.edu Contents
EECS43-Advanced Computer Vision Notes Series 9 Affine Structure From Motion Ying Wu Electrical Engineering & Computer Science Northwestern University Evanston, IL 68 yingwu@ece.northwestern.edu Contents
Numerical Methods for Inverse Kinematics
 Numerical Methods for Inverse Kinematics Niels Joubert, UC Berkeley, CS184 2008-11-25 Inverse Kinematics is used to pose models by specifying endpoints of segments rather than individual joint angles.
Numerical Methods for Inverse Kinematics Niels Joubert, UC Berkeley, CS184 2008-11-25 Inverse Kinematics is used to pose models by specifying endpoints of segments rather than individual joint angles.
Multiview Geometry and Bundle Adjustment. CSE P576 David M. Rosen
 Multiview Geometry and Bundle Adjustment CSE P576 David M. Rosen 1 Recap Previously: Image formation Feature extraction + matching Two-view (epipolar geometry) Today: Add some geometry, statistics, optimization
Multiview Geometry and Bundle Adjustment CSE P576 David M. Rosen 1 Recap Previously: Image formation Feature extraction + matching Two-view (epipolar geometry) Today: Add some geometry, statistics, optimization
Multiple View Geometry in Computer Vision
 Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Trifocal Tensor Lecture 21 March 31, 2005 2 Lord Shiva is depicted as having three eyes. The
Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Trifocal Tensor Lecture 21 March 31, 2005 2 Lord Shiva is depicted as having three eyes. The
Final Exam, Linear Algebra, Fall, 2003, W. Stephen Wilson
 Final Exam, Linear Algebra, Fall, 2003, W. Stephen Wilson Name: TA Name and section: NO CALCULATORS, SHOW ALL WORK, NO OTHER PAPERS ON DESK. There is very little actual work to be done on this exam if
Final Exam, Linear Algebra, Fall, 2003, W. Stephen Wilson Name: TA Name and section: NO CALCULATORS, SHOW ALL WORK, NO OTHER PAPERS ON DESK. There is very little actual work to be done on this exam if
MATH Linear Algebra
 MATH 304 - Linear Algebra In the previous note we learned an important algorithm to produce orthogonal sequences of vectors called the Gramm-Schmidt orthogonalization process. Gramm-Schmidt orthogonalization
MATH 304 - Linear Algebra In the previous note we learned an important algorithm to produce orthogonal sequences of vectors called the Gramm-Schmidt orthogonalization process. Gramm-Schmidt orthogonalization
Outline. Linear Algebra for Computer Vision
 Outline Linear Algebra for Computer Vision Introduction CMSC 88 D Notation and Basics Motivation Linear systems of equations Gauss Elimination, LU decomposition Linear Spaces and Operators Addition, scalar
Outline Linear Algebra for Computer Vision Introduction CMSC 88 D Notation and Basics Motivation Linear systems of equations Gauss Elimination, LU decomposition Linear Spaces and Operators Addition, scalar
PAijpam.eu EPIPOLAR GEOMETRY WITH A FUNDAMENTAL MATRIX IN CANONICAL FORM Georgi Hristov Georgiev 1, Vencislav Dakov Radulov 2
 International Journal of Pure and Applied Mathematics Volume 105 No. 4 2015, 669-683 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu doi: http://dx.doi.org/10.12732/ijpam.v105i4.8
International Journal of Pure and Applied Mathematics Volume 105 No. 4 2015, 669-683 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu doi: http://dx.doi.org/10.12732/ijpam.v105i4.8
AM 205: lecture 8. Last time: Cholesky factorization, QR factorization Today: how to compute the QR factorization, the Singular Value Decomposition
 AM 205: lecture 8 Last time: Cholesky factorization, QR factorization Today: how to compute the QR factorization, the Singular Value Decomposition QR Factorization A matrix A R m n, m n, can be factorized
AM 205: lecture 8 Last time: Cholesky factorization, QR factorization Today: how to compute the QR factorization, the Singular Value Decomposition QR Factorization A matrix A R m n, m n, can be factorized
Science Insights: An International Journal
 Available online at http://www.urpjournals.com Science Insights: An International Journal Universal Research Publications. All rights reserved ISSN 2277 3835 Original Article Object Recognition using Zernike
Available online at http://www.urpjournals.com Science Insights: An International Journal Universal Research Publications. All rights reserved ISSN 2277 3835 Original Article Object Recognition using Zernike
Mobile Robotics 1. A Compact Course on Linear Algebra. Giorgio Grisetti
 Mobile Robotics 1 A Compact Course on Linear Algebra Giorgio Grisetti SA-1 Vectors Arrays of numbers They represent a point in a n dimensional space 2 Vectors: Scalar Product Scalar-Vector Product Changes
Mobile Robotics 1 A Compact Course on Linear Algebra Giorgio Grisetti SA-1 Vectors Arrays of numbers They represent a point in a n dimensional space 2 Vectors: Scalar Product Scalar-Vector Product Changes
COMS 4721: Machine Learning for Data Science Lecture 19, 4/6/2017
 COMS 4721: Machine Learning for Data Science Lecture 19, 4/6/2017 Prof. John Paisley Department of Electrical Engineering & Data Science Institute Columbia University PRINCIPAL COMPONENT ANALYSIS DIMENSIONALITY
COMS 4721: Machine Learning for Data Science Lecture 19, 4/6/2017 Prof. John Paisley Department of Electrical Engineering & Data Science Institute Columbia University PRINCIPAL COMPONENT ANALYSIS DIMENSIONALITY
Parameterizing the Trifocal Tensor
 Parameterizing the Trifocal Tensor May 11, 2017 Based on: Klas Nordberg. A Minimal Parameterization of the Trifocal Tensor. In Computer society conference on computer vision and pattern recognition (CVPR).
Parameterizing the Trifocal Tensor May 11, 2017 Based on: Klas Nordberg. A Minimal Parameterization of the Trifocal Tensor. In Computer society conference on computer vision and pattern recognition (CVPR).
Conceptual Questions for Review
 Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
Position and orientation of rigid bodies
 Robotics 1 Position and orientation of rigid bodies Prof. Alessandro De Luca Robotics 1 1 Position and orientation right-handed orthogonal Reference Frames RF A A p AB B RF B rigid body position: A p AB
Robotics 1 Position and orientation of rigid bodies Prof. Alessandro De Luca Robotics 1 1 Position and orientation right-handed orthogonal Reference Frames RF A A p AB B RF B rigid body position: A p AB
CE 59700: Digital Photogrammetric Systems
 CE 59700: Digital Photogrammetric Systems Fall 2016 1 Instructor: Contact Information Office: HAMP 4108 Tel: (765) 496-0173 E-mail: ahabib@purdue.edu Lectures (HAMP 2102): Monday, Wednesday & Friday (12:30
CE 59700: Digital Photogrammetric Systems Fall 2016 1 Instructor: Contact Information Office: HAMP 4108 Tel: (765) 496-0173 E-mail: ahabib@purdue.edu Lectures (HAMP 2102): Monday, Wednesday & Friday (12:30
APPENDIX A. Background Mathematics. A.1 Linear Algebra. Vector algebra. Let x denote the n-dimensional column vector with components x 1 x 2.
 APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
5 Linear Algebra and Inverse Problem
 5 Linear Algebra and Inverse Problem 5.1 Introduction Direct problem ( Forward problem) is to find field quantities satisfying Governing equations, Boundary conditions, Initial conditions. The direct problem
5 Linear Algebra and Inverse Problem 5.1 Introduction Direct problem ( Forward problem) is to find field quantities satisfying Governing equations, Boundary conditions, Initial conditions. The direct problem
Applied Linear Algebra in Geoscience Using MATLAB
 Applied Linear Algebra in Geoscience Using MATLAB Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots Programming in
Applied Linear Algebra in Geoscience Using MATLAB Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots Programming in
Orthogonal Laplacianfaces for Face Recognition
 3608 IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 15, NO. 11, NOVEMBER 2006 [29] G. Deng and J. C. Pinoli, Differentiation-based edge detection using the logarithmic image processing model, J. Math. Imag.
3608 IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 15, NO. 11, NOVEMBER 2006 [29] G. Deng and J. C. Pinoli, Differentiation-based edge detection using the logarithmic image processing model, J. Math. Imag.
GEOMETRY FOR 3D COMPUTER VISION
 GEOMETRY FOR 3D COMPUTER VISION 1/29 Válav Hlaváč Czeh Tehnial University, Faulty of Eletrial Engineering Department of Cybernetis, Center for Mahine Pereption 121 35 Praha 2, Karlovo nám. 13, Czeh Republi
GEOMETRY FOR 3D COMPUTER VISION 1/29 Válav Hlaváč Czeh Tehnial University, Faulty of Eletrial Engineering Department of Cybernetis, Center for Mahine Pereption 121 35 Praha 2, Karlovo nám. 13, Czeh Republi
Introduction to Machine Learning. PCA and Spectral Clustering. Introduction to Machine Learning, Slides: Eran Halperin
 1 Introduction to Machine Learning PCA and Spectral Clustering Introduction to Machine Learning, 2013-14 Slides: Eran Halperin Singular Value Decomposition (SVD) The singular value decomposition (SVD)
1 Introduction to Machine Learning PCA and Spectral Clustering Introduction to Machine Learning, 2013-14 Slides: Eran Halperin Singular Value Decomposition (SVD) The singular value decomposition (SVD)
1 Cricket chirps: an example
 Notes for 2016-09-26 1 Cricket chirps: an example Did you know that you can estimate the temperature by listening to the rate of chirps? The data set in Table 1 1. represents measurements of the number
Notes for 2016-09-26 1 Cricket chirps: an example Did you know that you can estimate the temperature by listening to the rate of chirps? The data set in Table 1 1. represents measurements of the number
Multiple Degree of Freedom Systems. The Millennium bridge required many degrees of freedom to model and design with.
 Multiple Degree of Freedom Systems The Millennium bridge required many degrees of freedom to model and design with. The first step in analyzing multiple degrees of freedom (DOF) is to look at DOF DOF:
Multiple Degree of Freedom Systems The Millennium bridge required many degrees of freedom to model and design with. The first step in analyzing multiple degrees of freedom (DOF) is to look at DOF DOF:
ECE295, Data Assimila0on and Inverse Problems, Spring 2015
 ECE295, Data Assimila0on and Inverse Problems, Spring 2015 1 April, Intro; Linear discrete Inverse problems (Aster Ch 1 and 2) Slides 8 April, SVD (Aster ch 2 and 3) Slides 15 April, RegularizaFon (ch
ECE295, Data Assimila0on and Inverse Problems, Spring 2015 1 April, Intro; Linear discrete Inverse problems (Aster Ch 1 and 2) Slides 8 April, SVD (Aster ch 2 and 3) Slides 15 April, RegularizaFon (ch
B553 Lecture 5: Matrix Algebra Review
 B553 Lecture 5: Matrix Algebra Review Kris Hauser January 19, 2012 We have seen in prior lectures how vectors represent points in R n and gradients of functions. Matrices represent linear transformations
B553 Lecture 5: Matrix Algebra Review Kris Hauser January 19, 2012 We have seen in prior lectures how vectors represent points in R n and gradients of functions. Matrices represent linear transformations
Induced Planar Homologies in Epipolar Geometry
 Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 12, Number 4 (2016), pp. 3759 3773 Research India Publications http://www.ripublication.com/gjpam.htm Induced Planar Homologies in
Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 12, Number 4 (2016), pp. 3759 3773 Research India Publications http://www.ripublication.com/gjpam.htm Induced Planar Homologies in
Dimension Reduction and Low-dimensional Embedding
 Dimension Reduction and Low-dimensional Embedding Ying Wu Electrical Engineering and Computer Science Northwestern University Evanston, IL 60208 http://www.eecs.northwestern.edu/~yingwu 1/26 Dimension
Dimension Reduction and Low-dimensional Embedding Ying Wu Electrical Engineering and Computer Science Northwestern University Evanston, IL 60208 http://www.eecs.northwestern.edu/~yingwu 1/26 Dimension
The structure tensor in projective spaces
 The structure tensor in projective spaces Klas Nordberg Computer Vision Laboratory Department of Electrical Engineering Linköping University Sweden Abstract The structure tensor has been used mainly for
The structure tensor in projective spaces Klas Nordberg Computer Vision Laboratory Department of Electrical Engineering Linköping University Sweden Abstract The structure tensor has been used mainly for
Elementary linear algebra
 Chapter 1 Elementary linear algebra 1.1 Vector spaces Vector spaces owe their importance to the fact that so many models arising in the solutions of specific problems turn out to be vector spaces. The
Chapter 1 Elementary linear algebra 1.1 Vector spaces Vector spaces owe their importance to the fact that so many models arising in the solutions of specific problems turn out to be vector spaces. The
LINEAR ALGEBRA KNOWLEDGE SURVEY
 LINEAR ALGEBRA KNOWLEDGE SURVEY Instructions: This is a Knowledge Survey. For this assignment, I am only interested in your level of confidence about your ability to do the tasks on the following pages.
LINEAR ALGEBRA KNOWLEDGE SURVEY Instructions: This is a Knowledge Survey. For this assignment, I am only interested in your level of confidence about your ability to do the tasks on the following pages.
CSE4030 Introduction to Computer Graphics
 CSE4030 Introduction to Computer Graphics Dongguk University Jeong-Mo Hong Week 5 Living in a 3 dimensional world II Geometric coordinate in 3D How to move your cubes in 3D Objectives Introduce concepts
CSE4030 Introduction to Computer Graphics Dongguk University Jeong-Mo Hong Week 5 Living in a 3 dimensional world II Geometric coordinate in 3D How to move your cubes in 3D Objectives Introduce concepts
Structure Report for J. Reibenspies
 X-ray Diffraction Laboratory Center for Chemical Characterization and Analysis Department of Chemistry Texas A & M University Structure Report for J. Reibenspies Project Name: Sucrose Date: January 29,
X-ray Diffraction Laboratory Center for Chemical Characterization and Analysis Department of Chemistry Texas A & M University Structure Report for J. Reibenspies Project Name: Sucrose Date: January 29,
Robust Camera Location Estimation by Convex Programming
 Robust Camera Location Estimation by Convex Programming Onur Özyeşil and Amit Singer INTECH Investment Management LLC 1 PACM and Department of Mathematics, Princeton University SIAM IS 2016 05/24/2016,
Robust Camera Location Estimation by Convex Programming Onur Özyeşil and Amit Singer INTECH Investment Management LLC 1 PACM and Department of Mathematics, Princeton University SIAM IS 2016 05/24/2016,
Distortion mapping correction in aspheric null testing
 Distortion mapping correction in aspheric null testing M. Novak, C. Zhao, J. H. Burge College of Optical Sciences, 1630 East University Boulevard, Tucson, AZ, 85721 ABSTRACT We describe methods to correct
Distortion mapping correction in aspheric null testing M. Novak, C. Zhao, J. H. Burge College of Optical Sciences, 1630 East University Boulevard, Tucson, AZ, 85721 ABSTRACT We describe methods to correct
33AH, WINTER 2018: STUDY GUIDE FOR FINAL EXAM
 33AH, WINTER 2018: STUDY GUIDE FOR FINAL EXAM (UPDATED MARCH 17, 2018) The final exam will be cumulative, with a bit more weight on more recent material. This outline covers the what we ve done since the
33AH, WINTER 2018: STUDY GUIDE FOR FINAL EXAM (UPDATED MARCH 17, 2018) The final exam will be cumulative, with a bit more weight on more recent material. This outline covers the what we ve done since the
Exercise Set 7.2. Skills
 Orthogonally diagonalizable matrix Spectral decomposition (or eigenvalue decomposition) Schur decomposition Subdiagonal Upper Hessenburg form Upper Hessenburg decomposition Skills Be able to recognize
Orthogonally diagonalizable matrix Spectral decomposition (or eigenvalue decomposition) Schur decomposition Subdiagonal Upper Hessenburg form Upper Hessenburg decomposition Skills Be able to recognize
A geometric interpretation of the homogeneous coordinates is given in the following Figure.
 Introduction Homogeneous coordinates are an augmented representation of points and lines in R n spaces, embedding them in R n+1, hence using n + 1 parameters. This representation is useful in dealing with
Introduction Homogeneous coordinates are an augmented representation of points and lines in R n spaces, embedding them in R n+1, hence using n + 1 parameters. This representation is useful in dealing with
