Camera calibration Triangulation
|
|
|
- Juliet Stevenson
- 5 years ago
- Views:
Transcription
1 Triangulation
2 Perspective projection in homogenous coordinates ~x img I 0 apple R t 0 T 1 ~x w ~x img R t ~x w
3 Matrix transformations in 2D ~x img K R t ~x w K = t u 40 1 t v Translation K = K = 2 3 s x t u 4 0 s y t v Added skew if image x and y axes are not perpendicular 2 3 s x 0 t u 4 0 s y t v Scaling of Image x and y (conversion from meters to pixels )
4 Final perspective projection Camera extrinsics: where your camera is relative to the world. Changes if you move the camera ~x img K R t ~x w Camera intrinsics: how your camera handles pixel. Changes if you change your camera ~x img P~x w
5 Final perspective projection ~x img K R t ~x w Camera parameters ~x img P~x w
6 Goal: find the parameters of the camera ~x img K R t ~x w Why? Tells you where the camera is relative to the world/particular objects Equivalently, tells you where objects are relative to the camera Can allow you to render new objects into the scene
7 Y Y Z O O X X Z
8 ~x img P~x w Suppose we know that (X,Y,Z) in the world projects to (x,y) in the image. How many equations does this provide? 2 3 x 4y5 P X 6Y 7 4Z 5 1 Need to convert equivalence into equality.
9 ~x img P~x w Suppose we know that (X,Y,Z) in the world projects to (x,y) in the image. How many equations does this provide? Note: λ is unknown x y5 = P 2 3 X 6Y 7 4Z 5 1
10 ~x img P~x w Suppose we know that (X,Y,Z) in the world projects to (x,y) in the image. How many equations does this provide? x y5 = P 11 P 12 P 13 P 14 4P 21 P 22 P 23 P 5 24 P 31 P 32 P 33 P 34 X 6Y 4Z
11 ~x img P~x w Suppose we know that (X,Y,Z) in the world projects to (x,y) in the image. How many equations does this provide? x = P 11 X + P 12 Y + P 13 Z + P 14 y = P 21 X + P 22 Y + P 23 Z + P 24 = P 31 X + P 32 Y + P 33 Z + P 34
12 Suppose we know that (X,Y,Z) in the world projects to (x,y) in the image. How many equations does this provide? 2 equations! ~x img P~x w (P 31 X + P 32 Y + P 33 Z + P 34 )x = P 11 X + P 12 Y + P 13 Z + P 14 (P 31 X + P 32 Y + P 33 Z + P 34 )y = P 21 X + P 22 Y + P 23 Z + P 24 Are the equations linear in the parameters? How many equations do we need?
13 (P 31 X + P 32 Y + P 33 Z + P 34 )x = P 11 X + P 12 Y + P 13 Z + P 14 (P 31 X + P 32 Y + P 33 Z + P 34 )y = P 21 X + P 22 Y + P 23 Z + P 24 XxP 31 + YxP 32 + ZxP 33 + xp 34 XP 11 Y P 12 ZP 13 P 14 =0 In matrix vector form: Ap = 0 6 points give 12 equations, 12 variables to solve for But can only solve upto scale
14 In matrix vector form: Ap = 0 We want non-trivial solutions If p is a solution, αp is a solution too Let s just search for a solution with unit norm Ap =0 s.t kpk =1 How do you solve this?
15 In matrix vector form: Ap = 0 We want non-trivial solutions If p is a solution, αp is a solution too Let s just search for a solution with unit norm Ap =0 s.t kpk =1
16 What happens if there are more than 6 points? What if there is noise in the point locations? min kapk 2 p Ap =0 s.t kpk =1
17 What happens if there are more than 6 points? What if there is noise in the point locations? min p T A T Ap p Ap =0 s.t kpk =1 Look at eigenvector of A T A with the smallest eigenvalue!
18 >=6 points with known 3D coordinates + known image coordinates XxP 31 + YxP 32 + ZxP 33 + xp 34 XP 11 Y P 12 ZP 13 P 14 =0 In matrix vector form: want Ap = 0 Resilience to noise: min p p T A T Ap s.t kpk =1 Look at eigenvector of A T A with the smallest eigenvalue!
19 We need 6 world points for which we know image locations Would any 6 points work? What if all 6 points are the same? Need at least 6 non-coplanar points!
20 Y Y Z O O X X Z
21 ~x img P~x w ~x img K R t ~x w How do we get K, R and t from P? Need to make some assumptions about K What if K is identity?
22 ~x img P~x w ~x img K R t ~x w How do we get K, R and t from P? Need to make some assumptions about K What if K is upper triangular? 2 3 s x t u K = 4 0 s y t v Added skew if image x and y axes are not perpendicular
23 How do we get K, R and t from P? Need to make some assumptions about K What if K is upper triangular? 2 3 s x t u K = 4 0 s y t v 5 P = K [ R t] First 3 x 3 matrix of P is KR RQ decomposition: decomposes an n x n matrix into product of upper triangular and rotation matrix
24 How do we get K, R and t from P? Need to make some assumptions about K What if K is upper triangular? P = K [ R t] First 3 x 3 matrix of P is KR RQ decomposition: decomposes an n x n matrix into product of upper triangular and rotation matrix t = K -1 P[:,2] ß last column of P
25 Camera calibration and pose estimation
26 Triangulation Suppose we have two cameras Calibrated: parameters known And a pair of corresponding pixels Find 3D location of point!
27 Triangulation Suppose we have two cameras Calibrated: parameters known And a pair of corresponding pixels Find 3D location of point! P (1) P (2) (x 1,y 1 ) (x 2,y 2 )
28 Triangulation 2 3 x 1 4y x 2 4y ~x (1) img P (1) ~x w ~x (2) img P (2) ~x w 2 3 X 6Y 7 4Z 5 1
29 Triangulation ~x (1) img P (1) ~x w x 1 = P (1) 11 X + P (1) 12 Y + P (1) 13 Z + P (1) 14 y 1 = P (1) 21 X + P (1) 22 Y + P (1) 23 Z + P (1) 24 = P (1) 31 X + P (1) 32 Y + P (1) 33 Z + P (1) 34 (P (1) 31 X + P (1) 32 Y + P (1) 33 Z + P (1) 34 )x 1 = P (1) 11 X + P (1) 12 Y + P (1) 13 Z + P (1) 14 X(P (1) 31 x 1 P (1) (1) 11 ) + Y (P 32 x 1 P (1) (1) 12 ) + Z(P 33 x 1 P (1) 13 ) + (P (1) 34 x 1 P (1) 14 ) =0
30 X(P (1) X(P (1) Triangulation 1 image gives 2 equations Need 2 images! ~x (1) img P (1) ~x w 31 x 1 P (1) (1) 11 ) + Y (P 32 x 1 P (1) (1) 12 ) + Z(P 33 x 1 P (1) (1) 13 ) + (P 34 x 1 P (1) 14 ) =0 31 y 1 P (1) (1) 21 ) + Y (P 32 y 1 P (1) (1) 22 ) + Z(P 33 y 1 P (1) (1) 23 ) + (P 34 y 1 P (1) 24 ) =0 Solve linear equations to get 3D point location
31 Linear vs non-linear optimization x 1 = P (1) 11 X + P (1) 12 Y + P (1) 13 Z + P (1) 14 y 1 = P (1) 21 X + P (1) 22 Y + P (1) 23 Z + P (1) 24 = P (1) 31 X + P (1) 32 Y + P (1) 33 Z + P (1) 34 x 1 = P (1) 11 X + P (1) 12 Y + P (1) 13 Z + P (1) 14 P (1) 31 X + P (1) 32 Y + P (1) 33 Z + P (1) 34 y 1 = P (1) 21 X + P (1) 22 Y + P (1) 23 Z + P (1) 24 P (1) 31 X + P (1) 32 Y + P (1) 33 Z + P (1) 34
32 Linear vs non-linear optimization x 1 = P (1) 11 X + P (1) 12 Y + P (1) 13 Z + P (1) 14 P (1) 31 X + P (1) 32 Y + P (1) 33 Z + P (1) 34 y 1 = P (1) 21 X + P (1) 22 Y + P (1) 23 Z + P (1) 24 P (1) 31 X + P (1) 32 Y + P (1) 33 Z + P (1) 34 P (1) 11 (x X + P (1) 12 Y + P (1) 13 Z + P (1) 14 1 P (1) 31 X + P (1) 32 Y + P (1) 33 Z + P (1) 34 P (1) 21 +(y X + P (1) 22 Y + P (1) 23 Z + P (1) 24 1 P (1) 31 X + P (1) 32 Y + P (1) 33 Z + P (1) 34 Reprojection error ) 2 ) 2
33 Linear vs non-linear optimization P (1) 11 (x X + P (1) 12 Y + P (1) 13 Z + P (1) 14 1 P (1) 31 X + P (1) 32 Y + P (1) 33 Z + P (1) 34 P (1) 21 +(y X + P (1) 22 Y + P (1) 23 Z + P (1) 24 1 P (1) 31 X + P (1) 32 Y + P (1) 33 Z + P (1) 34 Reprojection error Reprojection error is the squared error between the true image coordinates of a point and the projected coordinates of hypothesized 3D point Actual error we care about Minimize total sum of reprojection error across all images Non-linear optimization ) 2 ) 2
34
Augmented Reality VU Camera Registration. Prof. Vincent Lepetit
 Augmented Reality VU Camera Registration Prof. Vincent Lepetit Different Approaches to Vision-based 3D Tracking [From D. Wagner] [From Drummond PAMI02] [From Davison ICCV01] Consider natural features Consider
Augmented Reality VU Camera Registration Prof. Vincent Lepetit Different Approaches to Vision-based 3D Tracking [From D. Wagner] [From Drummond PAMI02] [From Davison ICCV01] Consider natural features Consider
Camera Calibration The purpose of camera calibration is to determine the intrinsic camera parameters (c 0,r 0 ), f, s x, s y, skew parameter (s =
 Camera Calibration The purpose of camera calibration is to determine the intrinsic camera parameters (c 0,r 0 ), f, s x, s y, skew parameter (s = cotα), and the lens distortion (radial distortion coefficient
Camera Calibration The purpose of camera calibration is to determine the intrinsic camera parameters (c 0,r 0 ), f, s x, s y, skew parameter (s = cotα), and the lens distortion (radial distortion coefficient
3D from Photographs: Camera Calibration. Dr Francesco Banterle
 3D from Photographs: Camera Calibration Dr Francesco Banterle francesco.banterle@isti.cnr.it 3D from Photographs Automatic Matching of Images Camera Calibration Photographs Surface Reconstruction Dense
3D from Photographs: Camera Calibration Dr Francesco Banterle francesco.banterle@isti.cnr.it 3D from Photographs Automatic Matching of Images Camera Calibration Photographs Surface Reconstruction Dense
EE Camera & Image Formation
 Electric Electronic Engineering Bogazici University February 21, 2018 Introduction Introduction Camera models Goal: To understand the image acquisition process. Function of the camera Similar to that of
Electric Electronic Engineering Bogazici University February 21, 2018 Introduction Introduction Camera models Goal: To understand the image acquisition process. Function of the camera Similar to that of
M3: Multiple View Geometry
 M3: Multiple View Geometry L18: Projective Structure from Motion: Iterative Algorithm based on Factorization Based on Sections 13.4 C. V. Jawahar jawahar-at-iiit.net Mar 2005: 1 Review: Reconstruction
M3: Multiple View Geometry L18: Projective Structure from Motion: Iterative Algorithm based on Factorization Based on Sections 13.4 C. V. Jawahar jawahar-at-iiit.net Mar 2005: 1 Review: Reconstruction
CS 231A Computer Vision (Fall 2011) Problem Set 2
 CS 231A Computer Vision (Fall 2011) Problem Set 2 Solution Set Due: Oct. 28 th, 2011 (5pm) 1 Some Projective Geometry Problems (15 points) Suppose there are two parallel lines that extend to infinity in
CS 231A Computer Vision (Fall 2011) Problem Set 2 Solution Set Due: Oct. 28 th, 2011 (5pm) 1 Some Projective Geometry Problems (15 points) Suppose there are two parallel lines that extend to infinity in
Outline. Linear Algebra for Computer Vision
 Outline Linear Algebra for Computer Vision Introduction CMSC 88 D Notation and Basics Motivation Linear systems of equations Gauss Elimination, LU decomposition Linear Spaces and Operators Addition, scalar
Outline Linear Algebra for Computer Vision Introduction CMSC 88 D Notation and Basics Motivation Linear systems of equations Gauss Elimination, LU decomposition Linear Spaces and Operators Addition, scalar
Lecture 5. Epipolar Geometry. Professor Silvio Savarese Computational Vision and Geometry Lab. 21-Jan-15. Lecture 5 - Silvio Savarese
 Lecture 5 Epipolar Geometry Professor Silvio Savarese Computational Vision and Geometry Lab Silvio Savarese Lecture 5-21-Jan-15 Lecture 5 Epipolar Geometry Why is stereo useful? Epipolar constraints Essential
Lecture 5 Epipolar Geometry Professor Silvio Savarese Computational Vision and Geometry Lab Silvio Savarese Lecture 5-21-Jan-15 Lecture 5 Epipolar Geometry Why is stereo useful? Epipolar constraints Essential
Compatible Systems and Charpit s Method
 MODULE 2: FIRST-ORDER PARTIAL DIFFERENTIAL EQUATIONS 28 Lecture 5 Compatible Systems Charpit s Method In this lecture, we shall study compatible systems of first-order PDEs the Charpit s method for solving
MODULE 2: FIRST-ORDER PARTIAL DIFFERENTIAL EQUATIONS 28 Lecture 5 Compatible Systems Charpit s Method In this lecture, we shall study compatible systems of first-order PDEs the Charpit s method for solving
Linear Algebra Review. Fei-Fei Li
 Linear Algebra Review Fei-Fei Li 1 / 51 Vectors Vectors and matrices are just collections of ordered numbers that represent something: movements in space, scaling factors, pixel brightnesses, etc. A vector
Linear Algebra Review Fei-Fei Li 1 / 51 Vectors Vectors and matrices are just collections of ordered numbers that represent something: movements in space, scaling factors, pixel brightnesses, etc. A vector
Camera Models and Affine Multiple Views Geometry
 Camera Models and Affine Multiple Views Geometry Subhashis Banerjee Dept. Computer Science and Engineering IIT Delhi email: suban@cse.iitd.ac.in May 29, 2001 1 1 Camera Models A Camera transforms a 3D
Camera Models and Affine Multiple Views Geometry Subhashis Banerjee Dept. Computer Science and Engineering IIT Delhi email: suban@cse.iitd.ac.in May 29, 2001 1 1 Camera Models A Camera transforms a 3D
Structure from Motion. CS4670/CS Kevin Matzen - April 15, 2016
 Structure from Motion CS4670/CS5670 - Kevin Matzen - April 15, 2016 Video credit: Agarwal, et. al. Building Rome in a Day, ICCV 2009 Roadmap What we ve seen so far Single view modeling (1 camera) Stereo
Structure from Motion CS4670/CS5670 - Kevin Matzen - April 15, 2016 Video credit: Agarwal, et. al. Building Rome in a Day, ICCV 2009 Roadmap What we ve seen so far Single view modeling (1 camera) Stereo
Final Exam Due on Sunday 05/06
 Final Exam Due on Sunday 05/06 The exam should be completed individually without collaboration. However, you are permitted to consult with the textbooks, notes, slides and even internet resources. If you
Final Exam Due on Sunday 05/06 The exam should be completed individually without collaboration. However, you are permitted to consult with the textbooks, notes, slides and even internet resources. If you
A Practical Method for Decomposition of the Essential Matrix
 Applied Mathematical Sciences, Vol. 8, 2014, no. 176, 8755-8770 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.410877 A Practical Method for Decomposition of the Essential Matrix Georgi
Applied Mathematical Sciences, Vol. 8, 2014, no. 176, 8755-8770 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.410877 A Practical Method for Decomposition of the Essential Matrix Georgi
Camera calibration by Zhang
 Camera calibration by Zhang Siniša Kolarić September 2006 Abstract In this presentation, I present a way to calibrate a camera using the method by Zhang. NOTE. This
Camera calibration by Zhang Siniša Kolarić September 2006 Abstract In this presentation, I present a way to calibrate a camera using the method by Zhang. NOTE. This
Multiple View Geometry in Computer Vision
 Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Scene Planes & Homographies Lecture 19 March 24, 2005 2 In our last lecture, we examined various
Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Scene Planes & Homographies Lecture 19 March 24, 2005 2 In our last lecture, we examined various
Multiview Geometry and Bundle Adjustment. CSE P576 David M. Rosen
 Multiview Geometry and Bundle Adjustment CSE P576 David M. Rosen 1 Recap Previously: Image formation Feature extraction + matching Two-view (epipolar geometry) Today: Add some geometry, statistics, optimization
Multiview Geometry and Bundle Adjustment CSE P576 David M. Rosen 1 Recap Previously: Image formation Feature extraction + matching Two-view (epipolar geometry) Today: Add some geometry, statistics, optimization
Multi-Frame Factorization Techniques
 Multi-Frame Factorization Techniques Suppose { x j,n } J,N j=1,n=1 is a set of corresponding image coordinates, where the index n = 1,...,N refers to the n th scene point and j = 1,..., J refers to the
Multi-Frame Factorization Techniques Suppose { x j,n } J,N j=1,n=1 is a set of corresponding image coordinates, where the index n = 1,...,N refers to the n th scene point and j = 1,..., J refers to the
Theory of Bouguet s MatLab Camera Calibration Toolbox
 Theory of Bouguet s MatLab Camera Calibration Toolbox Yuji Oyamada 1 HVRL, University 2 Chair for Computer Aided Medical Procedure (CAMP) Technische Universität München June 26, 2012 MatLab Camera Calibration
Theory of Bouguet s MatLab Camera Calibration Toolbox Yuji Oyamada 1 HVRL, University 2 Chair for Computer Aided Medical Procedure (CAMP) Technische Universität München June 26, 2012 MatLab Camera Calibration
1. What is the determinant of the following matrix? a 1 a 2 4a 3 2a 2 b 1 b 2 4b 3 2b c 1. = 4, then det
 What is the determinant of the following matrix? 3 4 3 4 3 4 4 3 A 0 B 8 C 55 D 0 E 60 If det a a a 3 b b b 3 c c c 3 = 4, then det a a 4a 3 a b b 4b 3 b c c c 3 c = A 8 B 6 C 4 D E 3 Let A be an n n matrix
What is the determinant of the following matrix? 3 4 3 4 3 4 4 3 A 0 B 8 C 55 D 0 E 60 If det a a a 3 b b b 3 c c c 3 = 4, then det a a 4a 3 a b b 4b 3 b c c c 3 c = A 8 B 6 C 4 D E 3 Let A be an n n matrix
Linear Least-Squares Data Fitting
 CHAPTER 6 Linear Least-Squares Data Fitting 61 Introduction Recall that in chapter 3 we were discussing linear systems of equations, written in shorthand in the form Ax = b In chapter 3, we just considered
CHAPTER 6 Linear Least-Squares Data Fitting 61 Introduction Recall that in chapter 3 we were discussing linear systems of equations, written in shorthand in the form Ax = b In chapter 3, we just considered
Robert Collins CSE486, Penn State. Lecture 25: Structure from Motion
 Lecture 25: Structure from Motion Structure from Motion Given a set of flow fields or displacement vectors from a moving camera over time, determine: the sequence of camera poses the 3D structure of the
Lecture 25: Structure from Motion Structure from Motion Given a set of flow fields or displacement vectors from a moving camera over time, determine: the sequence of camera poses the 3D structure of the
MAT Linear Algebra Collection of sample exams
 MAT 342 - Linear Algebra Collection of sample exams A-x. (0 pts Give the precise definition of the row echelon form. 2. ( 0 pts After performing row reductions on the augmented matrix for a certain system
MAT 342 - Linear Algebra Collection of sample exams A-x. (0 pts Give the precise definition of the row echelon form. 2. ( 0 pts After performing row reductions on the augmented matrix for a certain system
The Jordan Normal Form and its Applications
 The and its Applications Jeremy IMPACT Brigham Young University A square matrix A is a linear operator on {R, C} n. A is diagonalizable if and only if it has n linearly independent eigenvectors. What happens
The and its Applications Jeremy IMPACT Brigham Young University A square matrix A is a linear operator on {R, C} n. A is diagonalizable if and only if it has n linearly independent eigenvectors. What happens
Math Review: parameter estimation. Emma
 Math Review: parameter estimation Emma McNally@flickr Fitting lines to dots: We will cover how Slides provided by HyunSoo Park 1809, Carl Friedrich Gauss What about fitting line on a curved surface? Least
Math Review: parameter estimation Emma McNally@flickr Fitting lines to dots: We will cover how Slides provided by HyunSoo Park 1809, Carl Friedrich Gauss What about fitting line on a curved surface? Least
Introduction to pinhole cameras
 Introduction to pinhole cameras Lesson given by Sébastien Piérard in the course Introduction aux techniques audio et vidéo (ULg, Pr JJ Embrechts) INTELSIG, Montefiore Institute, University of Liège, Belgium
Introduction to pinhole cameras Lesson given by Sébastien Piérard in the course Introduction aux techniques audio et vidéo (ULg, Pr JJ Embrechts) INTELSIG, Montefiore Institute, University of Liège, Belgium
Chapter Practice Test Name: Period: Date:
 Name: Period: Date: 1. Draw the graph of the following system: 3 x+ 5 y+ 13 = 0 29 x 11 y 7 = 0 3 13 y = x 3x+ 5y+ 13= 0 5 5 29x 11y 7 = 0 29 7 y = x 11 11 Practice Test Page 1 2. Determine the ordered
Name: Period: Date: 1. Draw the graph of the following system: 3 x+ 5 y+ 13 = 0 29 x 11 y 7 = 0 3 13 y = x 3x+ 5y+ 13= 0 5 5 29x 11y 7 = 0 29 7 y = x 11 11 Practice Test Page 1 2. Determine the ordered
Linear Algebra & Geometry why is linear algebra useful in computer vision?
 Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
and let s calculate the image of some vectors under the transformation T.
 Chapter 5 Eigenvalues and Eigenvectors 5. Eigenvalues and Eigenvectors Let T : R n R n be a linear transformation. Then T can be represented by a matrix (the standard matrix), and we can write T ( v) =
Chapter 5 Eigenvalues and Eigenvectors 5. Eigenvalues and Eigenvectors Let T : R n R n be a linear transformation. Then T can be represented by a matrix (the standard matrix), and we can write T ( v) =
Linear Algebra Review. Fei-Fei Li
 Linear Algebra Review Fei-Fei Li 1 / 37 Vectors Vectors and matrices are just collections of ordered numbers that represent something: movements in space, scaling factors, pixel brightnesses, etc. A vector
Linear Algebra Review Fei-Fei Li 1 / 37 Vectors Vectors and matrices are just collections of ordered numbers that represent something: movements in space, scaling factors, pixel brightnesses, etc. A vector
Vision 3D articielle Session 2: Essential and fundamental matrices, their computation, RANSAC algorithm
 Vision 3D articielle Session 2: Essential and fundamental matrices, their computation, RANSAC algorithm Pascal Monasse monasse@imagine.enpc.fr IMAGINE, École des Ponts ParisTech Contents Some useful rules
Vision 3D articielle Session 2: Essential and fundamental matrices, their computation, RANSAC algorithm Pascal Monasse monasse@imagine.enpc.fr IMAGINE, École des Ponts ParisTech Contents Some useful rules
Econ Slides from Lecture 7
 Econ 205 Sobel Econ 205 - Slides from Lecture 7 Joel Sobel August 31, 2010 Linear Algebra: Main Theory A linear combination of a collection of vectors {x 1,..., x k } is a vector of the form k λ ix i for
Econ 205 Sobel Econ 205 - Slides from Lecture 7 Joel Sobel August 31, 2010 Linear Algebra: Main Theory A linear combination of a collection of vectors {x 1,..., x k } is a vector of the form k λ ix i for
A Study of Kruppa s Equation for Camera Self-calibration
 Proceedings of the International Conference of Machine Vision and Machine Learning Prague, Czech Republic, August 14-15, 2014 Paper No. 57 A Study of Kruppa s Equation for Camera Self-calibration Luh Prapitasari,
Proceedings of the International Conference of Machine Vision and Machine Learning Prague, Czech Republic, August 14-15, 2014 Paper No. 57 A Study of Kruppa s Equation for Camera Self-calibration Luh Prapitasari,
1 Invariant subspaces
 MATH 2040 Linear Algebra II Lecture Notes by Martin Li Lecture 8 Eigenvalues, eigenvectors and invariant subspaces 1 In previous lectures we have studied linear maps T : V W from a vector space V to another
MATH 2040 Linear Algebra II Lecture Notes by Martin Li Lecture 8 Eigenvalues, eigenvectors and invariant subspaces 1 In previous lectures we have studied linear maps T : V W from a vector space V to another
Math 3191 Applied Linear Algebra
 Math 9 Applied Linear Algebra Lecture 9: Diagonalization Stephen Billups University of Colorado at Denver Math 9Applied Linear Algebra p./9 Section. Diagonalization The goal here is to develop a useful
Math 9 Applied Linear Algebra Lecture 9: Diagonalization Stephen Billups University of Colorado at Denver Math 9Applied Linear Algebra p./9 Section. Diagonalization The goal here is to develop a useful
22.4. Numerical Determination of Eigenvalues and Eigenvectors. Introduction. Prerequisites. Learning Outcomes
 Numerical Determination of Eigenvalues and Eigenvectors 22.4 Introduction In Section 22. it was shown how to obtain eigenvalues and eigenvectors for low order matrices, 2 2 and. This involved firstly solving
Numerical Determination of Eigenvalues and Eigenvectors 22.4 Introduction In Section 22. it was shown how to obtain eigenvalues and eigenvectors for low order matrices, 2 2 and. This involved firstly solving
COMP 558 lecture 18 Nov. 15, 2010
 Least squares We have seen several least squares problems thus far, and we will see more in the upcoming lectures. For this reason it is good to have a more general picture of these problems and how to
Least squares We have seen several least squares problems thus far, and we will see more in the upcoming lectures. For this reason it is good to have a more general picture of these problems and how to
MATH 369 Linear Algebra
 Assignment # Problem # A father and his two sons are together 00 years old. The father is twice as old as his older son and 30 years older than his younger son. How old is each person? Problem # 2 Determine
Assignment # Problem # A father and his two sons are together 00 years old. The father is twice as old as his older son and 30 years older than his younger son. How old is each person? Problem # 2 Determine
2. Griffith s 4.19 a. The commutator of the z-component of the angular momentum with the coordinates are: [L z. + xyp x. x xxp y.
 Physics Homework #8 Spring 6 Due Friday 5/7/6. Download the Mathematica notebook from the notes page of the website (http://minerva.union.edu/labrakes/physics_notes_s5.htm) or the homework page of the
Physics Homework #8 Spring 6 Due Friday 5/7/6. Download the Mathematica notebook from the notes page of the website (http://minerva.union.edu/labrakes/physics_notes_s5.htm) or the homework page of the
1. Suppose that a, b, c and d are four different integers. Explain why. (a b)(a c)(a d)(b c)(b d)(c d) a 2 + ab b = 2018.
 New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
Homographies and Estimating Extrinsics
 Homographies and Estimating Extrinsics Instructor - Simon Lucey 16-423 - Designing Computer Vision Apps Adapted from: Computer vision: models, learning and inference. Simon J.D. Prince Review: Motivation
Homographies and Estimating Extrinsics Instructor - Simon Lucey 16-423 - Designing Computer Vision Apps Adapted from: Computer vision: models, learning and inference. Simon J.D. Prince Review: Motivation
Two-View Segmentation of Dynamic Scenes from the Multibody Fundamental Matrix
 Two-View Segmentation of Dynamic Scenes from the Multibody Fundamental Matrix René Vidal Stefano Soatto Shankar Sastry Department of EECS, UC Berkeley Department of Computer Sciences, UCLA 30 Cory Hall,
Two-View Segmentation of Dynamic Scenes from the Multibody Fundamental Matrix René Vidal Stefano Soatto Shankar Sastry Department of EECS, UC Berkeley Department of Computer Sciences, UCLA 30 Cory Hall,
Coding the Matrix Index - Version 0
 0 vector, [definition]; (2.4.1): 68 2D geometry, transformations in, [lab]; (4.15.0): 196-200 A T (matrix A transpose); (4.5.4): 157 absolute value, complex number; (1.4.1): 43 abstract/abstracting, over
0 vector, [definition]; (2.4.1): 68 2D geometry, transformations in, [lab]; (4.15.0): 196-200 A T (matrix A transpose); (4.5.4): 157 absolute value, complex number; (1.4.1): 43 abstract/abstracting, over
Mathematical Properties of Stiffness Matrices
 Mathematical Properties of Stiffness Matrices CEE 4L. Matrix Structural Analysis Department of Civil and Environmental Engineering Duke University Henri P. Gavin Fall, 0 These notes describe some of the
Mathematical Properties of Stiffness Matrices CEE 4L. Matrix Structural Analysis Department of Civil and Environmental Engineering Duke University Henri P. Gavin Fall, 0 These notes describe some of the
CS 246 Review of Linear Algebra 01/17/19
 1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
Spectral Algorithms I. Slides based on Spectral Mesh Processing Siggraph 2010 course
 Spectral Algorithms I Slides based on Spectral Mesh Processing Siggraph 2010 course Why Spectral? A different way to look at functions on a domain Why Spectral? Better representations lead to simpler solutions
Spectral Algorithms I Slides based on Spectral Mesh Processing Siggraph 2010 course Why Spectral? A different way to look at functions on a domain Why Spectral? Better representations lead to simpler solutions
Linear Algebra Practice Problems
 Linear Algebra Practice Problems Page of 7 Linear Algebra Practice Problems These problems cover Chapters 4, 5, 6, and 7 of Elementary Linear Algebra, 6th ed, by Ron Larson and David Falvo (ISBN-3 = 978--68-78376-2,
Linear Algebra Practice Problems Page of 7 Linear Algebra Practice Problems These problems cover Chapters 4, 5, 6, and 7 of Elementary Linear Algebra, 6th ed, by Ron Larson and David Falvo (ISBN-3 = 978--68-78376-2,
Mathematics for 3D Graphics
 math 1 Topics Mathematics for 3D Graphics math 1 Points, Vectors, Vertices, Coordinates Dot Products, Cross Products Lines, Planes, Intercepts References Many texts cover the linear algebra used for 3D
math 1 Topics Mathematics for 3D Graphics math 1 Points, Vectors, Vertices, Coordinates Dot Products, Cross Products Lines, Planes, Intercepts References Many texts cover the linear algebra used for 3D
Recall : Eigenvalues and Eigenvectors
 Recall : Eigenvalues and Eigenvectors Let A be an n n matrix. If a nonzero vector x in R n satisfies Ax λx for a scalar λ, then : The scalar λ is called an eigenvalue of A. The vector x is called an eigenvector
Recall : Eigenvalues and Eigenvectors Let A be an n n matrix. If a nonzero vector x in R n satisfies Ax λx for a scalar λ, then : The scalar λ is called an eigenvalue of A. The vector x is called an eigenvector
Linear Algebra & Geometry why is linear algebra useful in computer vision?
 Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
21 Symmetric and skew-symmetric matrices
 21 Symmetric and skew-symmetric matrices 21.1 Decomposition of a square matrix into symmetric and skewsymmetric matrices Let C n n be a square matrix. We can write C = (1/2)(C + C t ) + (1/2)(C C t ) =
21 Symmetric and skew-symmetric matrices 21.1 Decomposition of a square matrix into symmetric and skewsymmetric matrices Let C n n be a square matrix. We can write C = (1/2)(C + C t ) + (1/2)(C C t ) =
MATH 167: APPLIED LINEAR ALGEBRA Least-Squares
 MATH 167: APPLIED LINEAR ALGEBRA Least-Squares October 30, 2014 Least Squares We do a series of experiments, collecting data. We wish to see patterns!! We expect the output b to be a linear function of
MATH 167: APPLIED LINEAR ALGEBRA Least-Squares October 30, 2014 Least Squares We do a series of experiments, collecting data. We wish to see patterns!! We expect the output b to be a linear function of
arxiv: v2 [cs.cv] 22 Mar 2019
![arxiv: v2 [cs.cv] 22 Mar 2019 arxiv: v2 [cs.cv] 22 Mar 2019](/thumbs/95/123571131.jpg) Closed-Form Optimal Triangulation Based on Angular Errors Seong Hun Lee Javier Civera IA, University of Zaragoza, Spain {seonghunlee, jcivera}@unizar.es arxiv:190.09115v [cs.cv] Mar 019 Abstract In this
Closed-Form Optimal Triangulation Based on Angular Errors Seong Hun Lee Javier Civera IA, University of Zaragoza, Spain {seonghunlee, jcivera}@unizar.es arxiv:190.09115v [cs.cv] Mar 019 Abstract In this
Linear Algebra: Matrix Eigenvalue Problems
 CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
Principal Components Analysis (PCA)
 Principal Components Analysis (PCA) Principal Components Analysis (PCA) a technique for finding patterns in data of high dimension Outline:. Eigenvectors and eigenvalues. PCA: a) Getting the data b) Centering
Principal Components Analysis (PCA) Principal Components Analysis (PCA) a technique for finding patterns in data of high dimension Outline:. Eigenvectors and eigenvalues. PCA: a) Getting the data b) Centering
Progress, tbe Universal LaW of f'laiare; Tbodgbt. tbe 3olVer)t of fier Problems. C H IC A G O. J U N E
 4 '; ) 6 89 80 pp p p p p ( p ) - p - p - p p p j p p p p - p- q ( p - p p' p ( p ) ) p p p p- p ; R : pp x ; p p ; p p - : p pp p -------- «( 7 p p! ^(/ -) p x- p- p p p p 2p p xp p : / xp - p q p x p
4 '; ) 6 89 80 pp p p p p ( p ) - p - p - p p p j p p p p - p- q ( p - p p' p ( p ) ) p p p p- p ; R : pp x ; p p ; p p - : p pp p -------- «( 7 p p! ^(/ -) p x- p- p p p p 2p p xp p : / xp - p q p x p
Ch 10.1: Two Point Boundary Value Problems
 Ch 10.1: Two Point Boundary Value Problems In many important physical problems there are two or more independent variables, so the corresponding mathematical models involve partial differential equations.
Ch 10.1: Two Point Boundary Value Problems In many important physical problems there are two or more independent variables, so the corresponding mathematical models involve partial differential equations.
In this section again we shall assume that the matrix A is m m, real and symmetric.
 84 3. The QR algorithm without shifts See Chapter 28 of the textbook In this section again we shall assume that the matrix A is m m, real and symmetric. 3.1. Simultaneous Iterations algorithm Suppose we
84 3. The QR algorithm without shifts See Chapter 28 of the textbook In this section again we shall assume that the matrix A is m m, real and symmetric. 3.1. Simultaneous Iterations algorithm Suppose we
Homework 1 Elena Davidson (B) (C) (D) (E) (F) (G) (H) (I)
 CS 106 Spring 2004 Homework 1 Elena Davidson 8 April 2004 Problem 1.1 Let B be a 4 4 matrix to which we apply the following operations: 1. double column 1, 2. halve row 3, 3. add row 3 to row 1, 4. interchange
CS 106 Spring 2004 Homework 1 Elena Davidson 8 April 2004 Problem 1.1 Let B be a 4 4 matrix to which we apply the following operations: 1. double column 1, 2. halve row 3, 3. add row 3 to row 1, 4. interchange
Pose estimation from point and line correspondences
 Pose estimation from point and line correspondences Giorgio Panin October 17, 008 1 Problem formulation Estimate (in a LSE sense) the pose of an object from N correspondences between known object points
Pose estimation from point and line correspondences Giorgio Panin October 17, 008 1 Problem formulation Estimate (in a LSE sense) the pose of an object from N correspondences between known object points
Nonlinear Diffusion. 1 Introduction: Motivation for non-standard diffusion
 Nonlinear Diffusion These notes summarize the way I present this material, for my benefit. But everything in here is said in more detail, and better, in Weickert s paper. 1 Introduction: Motivation for
Nonlinear Diffusion These notes summarize the way I present this material, for my benefit. But everything in here is said in more detail, and better, in Weickert s paper. 1 Introduction: Motivation for
Mobile Robotics 1. A Compact Course on Linear Algebra. Giorgio Grisetti
 Mobile Robotics 1 A Compact Course on Linear Algebra Giorgio Grisetti SA-1 Vectors Arrays of numbers They represent a point in a n dimensional space 2 Vectors: Scalar Product Scalar-Vector Product Changes
Mobile Robotics 1 A Compact Course on Linear Algebra Giorgio Grisetti SA-1 Vectors Arrays of numbers They represent a point in a n dimensional space 2 Vectors: Scalar Product Scalar-Vector Product Changes
EXAMPLES OF PROOFS BY INDUCTION
 EXAMPLES OF PROOFS BY INDUCTION KEITH CONRAD 1. Introduction In this handout we illustrate proofs by induction from several areas of mathematics: linear algebra, polynomial algebra, and calculus. Becoming
EXAMPLES OF PROOFS BY INDUCTION KEITH CONRAD 1. Introduction In this handout we illustrate proofs by induction from several areas of mathematics: linear algebra, polynomial algebra, and calculus. Becoming
Numerical Methods I: Eigenvalues and eigenvectors
 1/25 Numerical Methods I: Eigenvalues and eigenvectors Georg Stadler Courant Institute, NYU stadler@cims.nyu.edu November 2, 2017 Overview 2/25 Conditioning Eigenvalues and eigenvectors How hard are they
1/25 Numerical Methods I: Eigenvalues and eigenvectors Georg Stadler Courant Institute, NYU stadler@cims.nyu.edu November 2, 2017 Overview 2/25 Conditioning Eigenvalues and eigenvectors How hard are they
Extra Problems for Math 2050 Linear Algebra I
 Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
Intro Vectors 2D implicit curves 2D parametric curves. Graphics 2011/2012, 4th quarter. Lecture 2: vectors, curves, and surfaces
 Lecture 2, curves, and surfaces Organizational remarks Tutorials: Tutorial 1 will be online later today TA sessions for questions start next week Practicals: Exams: Make sure to find a team partner very
Lecture 2, curves, and surfaces Organizational remarks Tutorials: Tutorial 1 will be online later today TA sessions for questions start next week Practicals: Exams: Make sure to find a team partner very
Bundle Adjustment for 3-D Reconstruction: Implementation and Evaluation
 Memoirs of the Faculty of Engineering Okayama University Vol 45 pp 1 9 January 2011 Bundle Adjustment for 3-D Reconstruction: Implementation and Evaluation Kenichi KANATANI Department of Computer Science
Memoirs of the Faculty of Engineering Okayama University Vol 45 pp 1 9 January 2011 Bundle Adjustment for 3-D Reconstruction: Implementation and Evaluation Kenichi KANATANI Department of Computer Science
LINEAR ALGEBRA 1, 2012-I PARTIAL EXAM 3 SOLUTIONS TO PRACTICE PROBLEMS
 LINEAR ALGEBRA, -I PARTIAL EXAM SOLUTIONS TO PRACTICE PROBLEMS Problem (a) For each of the two matrices below, (i) determine whether it is diagonalizable, (ii) determine whether it is orthogonally diagonalizable,
LINEAR ALGEBRA, -I PARTIAL EXAM SOLUTIONS TO PRACTICE PROBLEMS Problem (a) For each of the two matrices below, (i) determine whether it is diagonalizable, (ii) determine whether it is orthogonally diagonalizable,
[POLS 8500] Review of Linear Algebra, Probability and Information Theory
![[POLS 8500] Review of Linear Algebra, Probability and Information Theory [POLS 8500] Review of Linear Algebra, Probability and Information Theory](/thumbs/72/67586683.jpg) [POLS 8500] Review of Linear Algebra, Probability and Information Theory Professor Jason Anastasopoulos ljanastas@uga.edu January 12, 2017 For today... Basic linear algebra. Basic probability. Programming
[POLS 8500] Review of Linear Algebra, Probability and Information Theory Professor Jason Anastasopoulos ljanastas@uga.edu January 12, 2017 For today... Basic linear algebra. Basic probability. Programming
CS4495/6495 Introduction to Computer Vision. 3D-L3 Fundamental matrix
 CS4495/6495 Introduction to Computer Vision 3D-L3 Fundamental matrix Weak calibration Main idea: Estimate epipolar geometry from a (redundant) set of point correspondences between two uncalibrated cameras
CS4495/6495 Introduction to Computer Vision 3D-L3 Fundamental matrix Weak calibration Main idea: Estimate epipolar geometry from a (redundant) set of point correspondences between two uncalibrated cameras
c c c c c c c c c c a 3x3 matrix C= has a determinant determined by
 Linear Algebra Determinants and Eigenvalues Introduction: Many important geometric and algebraic properties of square matrices are associated with a single real number revealed by what s known as the determinant.
Linear Algebra Determinants and Eigenvalues Introduction: Many important geometric and algebraic properties of square matrices are associated with a single real number revealed by what s known as the determinant.
Repeated Eigenvalues and Symmetric Matrices
 Repeated Eigenvalues and Symmetric Matrices. Introduction In this Section we further develop the theory of eigenvalues and eigenvectors in two distinct directions. Firstly we look at matrices where one
Repeated Eigenvalues and Symmetric Matrices. Introduction In this Section we further develop the theory of eigenvalues and eigenvectors in two distinct directions. Firstly we look at matrices where one
CS 4495 Computer Vision Principle Component Analysis
 CS 4495 Computer Vision Principle Component Analysis (and it s use in Computer Vision) Aaron Bobick School of Interactive Computing Administrivia PS6 is out. Due *** Sunday, Nov 24th at 11:55pm *** PS7
CS 4495 Computer Vision Principle Component Analysis (and it s use in Computer Vision) Aaron Bobick School of Interactive Computing Administrivia PS6 is out. Due *** Sunday, Nov 24th at 11:55pm *** PS7
A Factorization Method for 3D Multi-body Motion Estimation and Segmentation
 1 A Factorization Method for 3D Multi-body Motion Estimation and Segmentation René Vidal Department of EECS University of California Berkeley CA 94710 rvidal@eecs.berkeley.edu Stefano Soatto Dept. of Computer
1 A Factorization Method for 3D Multi-body Motion Estimation and Segmentation René Vidal Department of EECS University of California Berkeley CA 94710 rvidal@eecs.berkeley.edu Stefano Soatto Dept. of Computer
Chapter 5 Eigenvalues and Eigenvectors
 Chapter 5 Eigenvalues and Eigenvectors Outline 5.1 Eigenvalues and Eigenvectors 5.2 Diagonalization 5.3 Complex Vector Spaces 2 5.1 Eigenvalues and Eigenvectors Eigenvalue and Eigenvector If A is a n n
Chapter 5 Eigenvalues and Eigenvectors Outline 5.1 Eigenvalues and Eigenvectors 5.2 Diagonalization 5.3 Complex Vector Spaces 2 5.1 Eigenvalues and Eigenvectors Eigenvalue and Eigenvector If A is a n n
Linear Algebra Math 221
 Linear Algebra Math 221 Open Book Exam 1 Open Notes 3 Sept, 24 Calculators Permitted Show all work (except #4) 1 2 3 4 2 1. (25 pts) Given A 1 2 1, b 2 and c 4. 1 a) (7 pts) Bring matrix A to echelon form.
Linear Algebra Math 221 Open Book Exam 1 Open Notes 3 Sept, 24 Calculators Permitted Show all work (except #4) 1 2 3 4 2 1. (25 pts) Given A 1 2 1, b 2 and c 4. 1 a) (7 pts) Bring matrix A to echelon form.
Linear Algebra in Actuarial Science: Slides to the lecture
 Linear Algebra in Actuarial Science: Slides to the lecture Fall Semester 2010/2011 Linear Algebra is a Tool-Box Linear Equation Systems Discretization of differential equations: solving linear equations
Linear Algebra in Actuarial Science: Slides to the lecture Fall Semester 2010/2011 Linear Algebra is a Tool-Box Linear Equation Systems Discretization of differential equations: solving linear equations
Linear Combination. v = a 1 v 1 + a 2 v a k v k
 Linear Combination Definition 1 Given a set of vectors {v 1, v 2,..., v k } in a vector space V, any vector of the form v = a 1 v 1 + a 2 v 2 +... + a k v k for some scalars a 1, a 2,..., a k, is called
Linear Combination Definition 1 Given a set of vectors {v 1, v 2,..., v k } in a vector space V, any vector of the form v = a 1 v 1 + a 2 v 2 +... + a k v k for some scalars a 1, a 2,..., a k, is called
Routines for Relative Pose of Two Calibrated Cameras from 5 Points
 Routines for Relative Pose of Two Calibrated Cameras from 5 Points Bill Triggs INRIA Rhône-Alpes, 655 avenue de l Europe, 38330 Montbonnot, France. http://www.inrialpes.fr/movi/people/ Triggs Bill.Triggs@inrialpes.fr
Routines for Relative Pose of Two Calibrated Cameras from 5 Points Bill Triggs INRIA Rhône-Alpes, 655 avenue de l Europe, 38330 Montbonnot, France. http://www.inrialpes.fr/movi/people/ Triggs Bill.Triggs@inrialpes.fr
1 Linear Regression and Correlation
 Math 10B with Professor Stankova Worksheet, Discussion #27; Tuesday, 5/1/2018 GSI name: Roy Zhao 1 Linear Regression and Correlation 1.1 Concepts 1. Often when given data points, we want to find the line
Math 10B with Professor Stankova Worksheet, Discussion #27; Tuesday, 5/1/2018 GSI name: Roy Zhao 1 Linear Regression and Correlation 1.1 Concepts 1. Often when given data points, we want to find the line
Final Exam, Linear Algebra, Fall, 2003, W. Stephen Wilson
 Final Exam, Linear Algebra, Fall, 2003, W. Stephen Wilson Name: TA Name and section: NO CALCULATORS, SHOW ALL WORK, NO OTHER PAPERS ON DESK. There is very little actual work to be done on this exam if
Final Exam, Linear Algebra, Fall, 2003, W. Stephen Wilson Name: TA Name and section: NO CALCULATORS, SHOW ALL WORK, NO OTHER PAPERS ON DESK. There is very little actual work to be done on this exam if
MATH 20F: LINEAR ALGEBRA LECTURE B00 (T. KEMP)
 MATH 20F: LINEAR ALGEBRA LECTURE B00 (T KEMP) Definition 01 If T (x) = Ax is a linear transformation from R n to R m then Nul (T ) = {x R n : T (x) = 0} = Nul (A) Ran (T ) = {Ax R m : x R n } = {b R m
MATH 20F: LINEAR ALGEBRA LECTURE B00 (T KEMP) Definition 01 If T (x) = Ax is a linear transformation from R n to R m then Nul (T ) = {x R n : T (x) = 0} = Nul (A) Ran (T ) = {Ax R m : x R n } = {b R m
Problems. Looks for literal term matches. Problems:
 Problems Looks for literal term matches erms in queries (esp short ones) don t always capture user s information need well Problems: Synonymy: other words with the same meaning Car and automobile 电脑 vs.
Problems Looks for literal term matches erms in queries (esp short ones) don t always capture user s information need well Problems: Synonymy: other words with the same meaning Car and automobile 电脑 vs.
Math Fall Final Exam
 Math 104 - Fall 2008 - Final Exam Name: Student ID: Signature: Instructions: Print your name and student ID number, write your signature to indicate that you accept the honor code. During the test, you
Math 104 - Fall 2008 - Final Exam Name: Student ID: Signature: Instructions: Print your name and student ID number, write your signature to indicate that you accept the honor code. During the test, you
Solve the equation for c: 8 = 9c (c + 24). Solve the equation for x: 7x (6 2x) = 12.
 1 Solve the equation f x: 7x (6 2x) = 12. 1a Solve the equation f c: 8 = 9c (c + 24). Inverse Operations 7x (6 2x) = 12 Given 7x 1(6 2x) = 12 Show distributing with 1 Change subtraction to add (-) 9x =
1 Solve the equation f x: 7x (6 2x) = 12. 1a Solve the equation f c: 8 = 9c (c + 24). Inverse Operations 7x (6 2x) = 12 Given 7x 1(6 2x) = 12 Show distributing with 1 Change subtraction to add (-) 9x =
Basic Math for
 Basic Math for 16-720 August 23, 2002 1 Linear Algebra 1.1 Vectors and Matrices First, a reminder of a few basic notations, definitions, and terminology: Unless indicated otherwise, vectors are always
Basic Math for 16-720 August 23, 2002 1 Linear Algebra 1.1 Vectors and Matrices First, a reminder of a few basic notations, definitions, and terminology: Unless indicated otherwise, vectors are always
Math 2433 Notes Week The Dot Product. The angle between two vectors is found with this formula: cosθ = a b
 Math 2433 Notes Week 2 11.3 The Dot Product The angle between two vectors is found with this formula: cosθ = a b a b 3) Given, a = 4i + 4j, b = i - 2j + 3k, c = 2i + 2k Find the angle between a and c Projection
Math 2433 Notes Week 2 11.3 The Dot Product The angle between two vectors is found with this formula: cosθ = a b a b 3) Given, a = 4i + 4j, b = i - 2j + 3k, c = 2i + 2k Find the angle between a and c Projection
TI89 Titanium Exercises - Part 10.
 TI89 Titanium Exercises - Part. Entering matrices directly in the HOME screen s entry line ) Enter your nxm matrix using this format: [[ a, a 2,,a m ][a 2, a 22, a 2m ] [a n, a n2,, a nm ]] This is a matrix
TI89 Titanium Exercises - Part. Entering matrices directly in the HOME screen s entry line ) Enter your nxm matrix using this format: [[ a, a 2,,a m ][a 2, a 22, a 2m ] [a n, a n2,, a nm ]] This is a matrix
Chapter 4 & 5: Vector Spaces & Linear Transformations
 Chapter 4 & 5: Vector Spaces & Linear Transformations Philip Gressman University of Pennsylvania Philip Gressman Math 240 002 2014C: Chapters 4 & 5 1 / 40 Objective The purpose of Chapter 4 is to think
Chapter 4 & 5: Vector Spaces & Linear Transformations Philip Gressman University of Pennsylvania Philip Gressman Math 240 002 2014C: Chapters 4 & 5 1 / 40 Objective The purpose of Chapter 4 is to think
Camera Projection Model
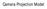 amera Projection Model 3D Point Projection (Pixel Space) O ( u, v ) ccd ccd f Projection plane (, Y, Z ) ( u, v ) img Z img (0,0) w img ( u, v ) img img uimg f Z p Y v img f Z p x y Zu f p Z img img x
amera Projection Model 3D Point Projection (Pixel Space) O ( u, v ) ccd ccd f Projection plane (, Y, Z ) ( u, v ) img Z img (0,0) w img ( u, v ) img img uimg f Z p Y v img f Z p x y Zu f p Z img img x
We will discuss matrix diagonalization algorithms in Numerical Recipes in the context of the eigenvalue problem in quantum mechanics, m A n = λ m
 Eigensystems We will discuss matrix diagonalization algorithms in umerical Recipes in the context of the eigenvalue problem in quantum mechanics, A n = λ n n, (1) where A is a real, symmetric Hamiltonian
Eigensystems We will discuss matrix diagonalization algorithms in umerical Recipes in the context of the eigenvalue problem in quantum mechanics, A n = λ n n, (1) where A is a real, symmetric Hamiltonian
Camera Calibration. (Trucco, Chapter 6) -Toproduce an estimate of the extrinsic and intrinsic camera parameters.
 Camera Calibration (Trucco, Chapter 6) What is the goal of camera calibration? -Toproduce an estimate of the extrinsic and intrinsic camera parameters. Procedure -Given the correspondences beteen a set
Camera Calibration (Trucco, Chapter 6) What is the goal of camera calibration? -Toproduce an estimate of the extrinsic and intrinsic camera parameters. Procedure -Given the correspondences beteen a set
Elementary Linear Algebra
 Matrices J MUSCAT Elementary Linear Algebra Matrices Definition Dr J Muscat 2002 A matrix is a rectangular array of numbers, arranged in rows and columns a a 2 a 3 a n a 2 a 22 a 23 a 2n A = a m a mn We
Matrices J MUSCAT Elementary Linear Algebra Matrices Definition Dr J Muscat 2002 A matrix is a rectangular array of numbers, arranged in rows and columns a a 2 a 3 a n a 2 a 22 a 23 a 2n A = a m a mn We
Theorem A.1. If A is any nonzero m x n matrix, then A is equivalent to a partitioned matrix of the form. k k n-k. m-k k m-k n-k
 I. REVIEW OF LINEAR ALGEBRA A. Equivalence Definition A1. If A and B are two m x n matrices, then A is equivalent to B if we can obtain B from A by a finite sequence of elementary row or elementary column
I. REVIEW OF LINEAR ALGEBRA A. Equivalence Definition A1. If A and B are two m x n matrices, then A is equivalent to B if we can obtain B from A by a finite sequence of elementary row or elementary column
Math 304 Answers to Selected Problems
 Math Answers to Selected Problems Section 6.. Find the general solution to each of the following systems. a y y + y y y + y e y y y y y + y f y y + y y y + 6y y y + y Answer: a This is a system of the
Math Answers to Selected Problems Section 6.. Find the general solution to each of the following systems. a y y + y y y + y e y y y y y + y f y y + y y y + 6y y y + y Answer: a This is a system of the
ANALYTICAL IMAGE FEATURES
 Chapter 6 ANALYTICAL IMAGE FEATURES Chapter laid the geometric foundations of image formation. This chapter uses analytical geometry to quantify more precisely the relationship between a camera, the objects
Chapter 6 ANALYTICAL IMAGE FEATURES Chapter laid the geometric foundations of image formation. This chapter uses analytical geometry to quantify more precisely the relationship between a camera, the objects
(a) II and III (b) I (c) I and III (d) I and II and III (e) None are true.
 1 Which of the following statements is always true? I The null space of an m n matrix is a subspace of R m II If the set B = {v 1,, v n } spans a vector space V and dimv = n, then B is a basis for V III
1 Which of the following statements is always true? I The null space of an m n matrix is a subspace of R m II If the set B = {v 1,, v n } spans a vector space V and dimv = n, then B is a basis for V III
Intro Vectors 2D implicit curves 2D parametric curves. Graphics 2012/2013, 4th quarter. Lecture 2: vectors, curves, and surfaces
 Lecture 2, curves, and surfaces Organizational remarks Tutorials: TA sessions for tutorial 1 start today Tutorial 2 will go online after lecture 3 Practicals: Make sure to find a team partner very soon
Lecture 2, curves, and surfaces Organizational remarks Tutorials: TA sessions for tutorial 1 start today Tutorial 2 will go online after lecture 3 Practicals: Make sure to find a team partner very soon
11.1 Three-Dimensional Coordinate System
 11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
LINEAR ALGEBRA KNOWLEDGE SURVEY
 LINEAR ALGEBRA KNOWLEDGE SURVEY Instructions: This is a Knowledge Survey. For this assignment, I am only interested in your level of confidence about your ability to do the tasks on the following pages.
LINEAR ALGEBRA KNOWLEDGE SURVEY Instructions: This is a Knowledge Survey. For this assignment, I am only interested in your level of confidence about your ability to do the tasks on the following pages.
