Image Transform. Panorama Image (Keller+Lind Hall)
|
|
|
- Bennett Fletcher
- 6 years ago
- Views:
Transcription
1 Image Transform Panorama Image (Keller+Lind Hall)
2 Image Warping (Coordinate Transform) u I v 1 I 2 I ( v) = I ( u) 2 1
3 Image Warping (Coordinate Transform) u I v 1 I 2 I ( v) = I ( u) 2 1 : Piel transport
4 Image Warping (Coordinate Transform) u I v 1 I 2 I ( v) = I ( u) 2 1 : Piel transport
5 Cf) Image Filtering (Piel Transform) I 1 I 2 I = g( I ) 2 1 : Piel transform
6 Uniform Scaling u v I 1 I 2 I ( v) = I ( u) 2 1
7 Uniform Scaling u v I 1 I 2 I ( v) = I ( u) 2 1 v s u v y s? y u y 1 1 1
8 Uniform Scaling u v I 1 I 2 I ( v) = I ( u) 2 1 v s u v y sy u y s = s y
9 Aspect Ratio Change u I 1 I 2 v I ( v) = I ( u) 2 1 v s u v y sy u y s s y
10 Translation t y t u v I 1 I 2 I ( v) = I ( u) 2 1 v 1 t u v y 1? t y u y 1 1 1
11 Translation t y t u v I 1 I 2 I ( v) = I ( u) 2 1 v 1 t u v y 1 t y u y 1 1 1
12 Rotation θ u I 1 v I 2 I ( v) = I ( u) 2 1 v cosθ sinθ u y sin cos v θ? θ uy 1 1 1
13 Rotation θ u I 1 v I 2 I ( v) = I ( u) 2 1 v cosθ sinθ u y sin cos v θ θ uy 1 1 1
14 Euclidean Transform SE(3) I 1 I 2 v cosθ sinθ t u v y sinθ? cosθ t y u y Rotation around the center of image
15 Euclidean Transform SE(3) I 1 I 2 v cosθ sinθ t u v y sinθ cosθ t y u y Rotation around the center of image
16 Euclidean Transform SE(3) I 1 I 2 Invariant properties Length Angle Area v cosθ sinθ t u v y sinθ cosθ t y u y Rotation around the center of image Degree of freedom 3 (2 translation+1 rotation)
17 Euclidean Transform SE(3) I 1 I 2 Invariant properties Length Angle Area v cosθ sinθ t u v y sinθ cosθ t y u y Rotation around the center of image v R t u Degree of freedom 3 (2 translation+1 rotation)
18 Euclidean Transform SE(3) Rotate about the image center v R t u v Ru+ t t? I 2 u v
19 Euclidean Transform SE(3) Rotate about the image center v R t u v Ru+ t t? u v
20 Euclidean Transform SE(3) Rotate about the image center v R t u v Ru+ t p p I 2 u v
21 Euclidean Transform SE(3) Rotate about the image center v R t u v Ru+ t p p u = u-p v Ru v = v -p I 2 u v
22 Euclidean Transform SE(3) Rotate about the image center v R t u v Ru+ t p u v p u = u-p v = v -p v Ru v - p R u- p v Ru-Rp+p I 2
23 Euclidean Transform SE(3) Rotate about the image center v R t u v Ru+ t p u v p u = u-p v = v -p v Ru v - p R u- p v Ru-Rp+p I 2 t -Rp+p
24 Similarity Transform I 1 I 2 v cosθ sinθ t u u y R t v? sinθ cosθ t y u y y 1 u
25 Similarity Transform I 1 I 2 v cosθ sinθ t u u y R t v sinθ cosθ t y u y y 1 u
26 Similarity Transform I 1 I 2 Invariant properties Length ratio Angle v cosθ sinθ t u u y R t v sinθ cosθ t y u y y 1 u Degree of freedom 4 (2 translation+1 rotation+1 scale)
27 Affine Transform I 1 I 2 v u R t vy y 1 u Euclidean transform
28 Affine Transform I 1 I 2 v u R t vy y 1 u Euclidean transform v a11 a12 a13 u u A t v y a21 a22 a23 u y y 1 u
29 Affine Transform I 1 I 2 Invariant properties Parallelism Ratio of area Ratio of length Degree of freedom 6 v u R t vy y 1 u Euclidean transform v a11 a12 a13 u u A t v y a21 a22 a23 u y y 1 u
30 Perspective Transform (Homography) I 1 I 2 v h11 h12 h13 u u v y h21 h22 h23 u y Hu y h h
31 Perspective Transform (Homography) I 1 I 2 v h11 h12 h13 u u v y h21 h22 h23 u y Hu y h h : General form of plane to plane linear mapping
32 Perspective Transform (Homography) u Camera plane u K R t X Camera plane Ground plane X Ground plane u
33 Perspective Transform (Homography) u Camera plane Ground plane X= X Y 0 1 u K R t X Camera plane Ground plane u
34 Perspective Transform (Homography) u Camera plane Ground plane X= X Y 0 1 u K R t X Camera plane Ground plane X Y u Kr r r t 0 1 u
35 Perspective Transform (Homography) u Camera plane X= Ground plane u X Y 0 1 u K R t X Camera plane Ground plane X Y u Kr r r t 0 1 X u K r 1 r2 t Y 1
36 Perspective Transform (Homography) u Camera plane X= Ground plane u X Y 0 1 u K R t X Camera plane Ground plane X Y u Kr r r t 0 1 X u K r 1 r2 t Y 1 u X uy H Y 1 1
37 Perspective Transform (Homography) I 1 I 2 Invariant properties Cross ratio Concurrency Colinearity v h11 h12 h13 u u v y h21 h22 h23 u y Hu y h h Degree of freedom 8 (9 variables 1 scale)
38 Hierarchy of Transformations Euclidean (3 dof) Similarity (4 dof) Affine (6 dof) Projective (8 dof) Length Length ratio Parallelism Cross ratio Angle Angle Ratio of area Concurrency Area Ratio of length Colinearity cosθ sinθ sinθ cosθ t t y 1 cosθ sinθ sinθ cosθ t t y 1 a11 a12 a13 a21 a22 a h h h h h h h h32 1
39 Fun with Homography u 3 v 4 v 3 u 4 u 1 u 2 H v 1 v 2 The image can be rectified as if it is seen from top view.
40 Fun with Homography RectificationViaHomography.m u = [u1'; u2'; u3'; u4']; v = [v1'; v2'; v3'; v4']; % Need at least non-colinear four points H = ComputeHomography(v, u); u 3 im_warped = ImageWarping(im, H); u 4 u 1 u 2
41 Fun with Homography RectificationViaHomography.m u = [u1'; u2'; u3'; u4']; v = [v1'; v2'; v3'; v4']; % Need at least non-colinear four points H = ComputeHomography(v, u); u 3 im_warped = ImageWarping(im, H); u 4 Cf) ImageWarpingEuclidean.m u 1 u 2 u_ = H(1,1)*v_ + H(1,2)*v_y + H(1,3); u_y = H(2,1)*v_ + H(2,2)*v_y + H(2,3); ImageWarping.m u_ = H(1,1)*v_ + H(1,2)*v_y + H(1,3); u_y = H(2,1)*v_ + H(2,2)*v_y + H(2,3); u_z = H(3,1)*v_ + H(3,2)*v_y + H(3,3); u_ = u_./u_z; u_y = u_y./u_z; v u vy Huy 1 1 im_warped(:,:,1) = reshape(interp2(im(:,:,1), u_(:), u_y(:)), [h, w]); im_warped(:,:,2) = reshape(interp2(im(:,:,2), u_(:), u_y(:)), [h, w]); im_warped(:,:,3) = reshape(interp2(im(:,:,3), u_(:), u_y(:)), [h, w]); im_warped = uint8(im_warped);
42 Fun with Homography u 3 v 4 v 3 u 4 u 1 u 2 H v 1 v 2
43 Fun with Homography u 3 u 4 u 1 u 2
44 Fun with Homography
45 Fun with Homography
46 Image Warping
47 Image Inpainting
48 Virtual Advertisement
49 Image Transform via Plane Keller entrance left Keller entrance right
50 Image Transform via 3D Plane u K R t X X Y X= 0 1 u Plane
51 Image Transform via 3D Plane X Y X= 0 1 u K R t X X u = K r 1 r2 t Y 1 X v = Kr 1 r2 t Y 1 u Plane
52 Image Transform via 3D Plane v X Y X= 0 1 u K R t X X u = K r 1 r2 t Y 1 X v = Kr 1 r2 t Y 1 u Plane
53 Image Transform via 3D Plane v Plane u X Y X= 0 1 u K R t X X u = K r 1 r2 t Y 1 X v = Kr 1 r2 t Y 1 How are two image coordinates (u,v) related?
54 Image Transform via 3D Plane v Plane u X Y X= 0 1 u K R t X X u = K r 1 r2 t Y 1 X v = Kr 1 r2 t Y 1 How are two image coordinates (u,v) related? X = = r r t K u Y r1 r2 t K v 1 v = Kr r tr r t K u v = Hu
55 Image Transform via 3D Plane Keller entrance left Keller entrance right
56 Image Transform via 3D Plane Keller entrance left Right image to left
57 Image Transform via 3D Plane
58 Image Transform via 3D Plane Left image to right Right image to left
59 Image Transform via 3D Plane
60 360 Panorama
61 Image Transform by Pure 3D Rotation Camera X
62 Image Transform by Pure 3D Rotation Camera X 1 u = KX
63 Image Transform by Pure 3D Rotation Camera X 1 u = KX v KRX 2 =
64 Image Transform by Pure 3D Rotation Camera X 1 u = KX v KRX 2 = X = K u = R K v -1 T
65 Image Transform by Pure 3D Rotation Camera X 1 u = KX v KRX 2 = X = K u = R K v v = -1 T KRK u
66 Image Transform by Pure 3D Rotation Camera X 1 u = KX v KRX 2 = X = K u = R K v v = -1 T KRK u H = KRK -1
67 Image Transform by Pure 3D Rotation Camera X 1 u = KX v KRX 2 = X = K u = R K v v = -1 T KRK u H = KRK R = -1-1 K HK
68 u = Hv Lind Hall Left Lind Hall Right
69 Euclidean Transform (Translation)
70 Homography
71 Homography Why misalignment?
72 Image Panorama (Cylindrical Projection)
73 Image Panorama (Cylindrical Projection)
74 Image Panorama (Cylindrical Projection) h
75 Image Panorama (Cylindrical Projection) R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 R11 X = -1 T K R u u R = -1 K HK
76 Image Panorama (Cylindrical Projection) h -1 T X = K R u H u u= f cos H h - 2 sin f R = -1 K HK
77 Image Panorama (Cylindrical Projection) h H f u -1 T X = K R u u= f cos H h - 2 sin f R = -1 K HK
78 Image Panorama (Cylindrical Projection) h H f u h -1 T X = K R u u= f cos H h - 2 sin f R = -1 K HK
79 Image Panorama (Cylindrical Projection) h H f u h -1 T X = K R u u= f cos H h - 2 sin f -1 T = K R u R = -1 K HK
80 Image Panorama (Cylindrical Projection) h
Camera Projection Model
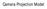amera Projection Model 3D Point Projection (Pixel Space) O ( u, v ) ccd ccd f Projection plane (, Y, Z ) ( u, v ) img Z img (0,0) w img ( u, v ) img img uimg f Z p Y v img f Z p x y Zu f p Z img img x
Homographies and Estimating Extrinsics
Homographies and Estimating Extrinsics Instructor - Simon Lucey 16-423 - Designing Computer Vision Apps Adapted from: Computer vision: models, learning and inference. Simon J.D. Prince Review: Motivation
1. Projective geometry
1. Projective geometry Homogeneous representation of points and lines in D space D projective space Points at infinity and the line at infinity Conics and dual conics Projective transformation Hierarchy
A geometric interpretation of the homogeneous coordinates is given in the following Figure.
Introduction Homogeneous coordinates are an augmented representation of points and lines in R n spaces, embedding them in R n+1, hence using n + 1 parameters. This representation is useful in dealing with
Lines and points. Lines and points
omogeneous coordinates in the plane Homogeneous coordinates in the plane A line in the plane a + by + c is represented as (a, b, c). A line is a subset of points in the plane. All vectors (ka, kb, kc)
Homogeneous Coordinates
Homogeneous Coordinates Basilio Bona DAUIN-Politecnico di Torino October 2013 Basilio Bona (DAUIN-Politecnico di Torino) Homogeneous Coordinates October 2013 1 / 32 Introduction Homogeneous coordinates
Camera: optical system
Camera: optical system Y dαα α ρ ρ curvature radius Z thin lens small angles: α Y ρ α Y ρ lens refraction inde: n Y incident light beam deviated beam θ '' α θ ' α sin( θ '' α ) sin( θ ' α ) n θ α θ α deviation
Augmented Reality VU Camera Registration. Prof. Vincent Lepetit
Augmented Reality VU Camera Registration Prof. Vincent Lepetit Different Approaches to Vision-based 3D Tracking [From D. Wagner] [From Drummond PAMI02] [From Davison ICCV01] Consider natural features Consider
3D from Photographs: Camera Calibration. Dr Francesco Banterle
3D from Photographs: Camera Calibration Dr Francesco Banterle francesco.banterle@isti.cnr.it 3D from Photographs Automatic Matching of Images Camera Calibration Photographs Surface Reconstruction Dense
M2A2 Problem Sheet 3 - Hamiltonian Mechanics
MA Problem Sheet 3 - Hamiltonian Mechanics. The particle in a cone. A particle slides under gravity, inside a smooth circular cone with a vertical axis, z = k x + y. Write down its Lagrangian in a) Cartesian,
Gradient, Divergence and Curl in Curvilinear Coordinates
Gradient, Divergence and Curl in Curvilinear Coordinates Although cartesian orthogonal coordinates are very intuitive and easy to use, it is often found more convenient to work with other coordinate systems.
Pose estimation from point and line correspondences
Pose estimation from point and line correspondences Giorgio Panin October 17, 008 1 Problem formulation Estimate (in a LSE sense) the pose of an object from N correspondences between known object points
Curvilinear coordinates
C Curvilinear coordinates The distance between two points Euclidean space takes the simplest form (2-4) in Cartesian coordinates. The geometry of concrete physical problems may make non-cartesian coordinates
Operations depend on pixel s Coordinates. Context free. Independent of pixel values. I(x,y) I (x,y )
Geometric Transformation Operations depend on piel s Coordinates. Contet free. Independent of piel values. f f (, ) = ' (, ) = ' I(, ) = I' ( f (, ), f ( ) ), (,) (, ) I(,) I (, ) Eample: Translation =
Single view metrology
EECS 44 Computer vision Single view metrology Review calibration Lines and planes at infinity Absolute conic Estimating geometry from a single image Etensions Reading: [HZ] Chapters,3,8 Calibration Problem
The spatial frequency domain
The spatial frequenc /3/5 wk9-a- Recall: plane wave propagation λ z= θ path dela increases linearl with E ep i2π sinθ + λ z i2π cosθ λ z plane of observation /3/5 wk9-a-2 Spatial frequenc angle of propagation?
Homogeneous Transformations
Purpose: Homogeneous Transformations The purpose of this chapter is to introduce you to the Homogeneous Transformation. This simple 4 x 4 transformation is used in the geometry engines of CAD systems and
2D Geometric Transformations. (Chapter 5 in FVD)
2D Geometric Transformations (Chapter 5 in FVD) 2D geometric transformation Translation Scaling Rotation Shear Matri notation Compositions Homogeneous coordinates 2 2D Geometric Transformations Question:
THE DIFFERENTIAL GEOMETRY OF PARAMETRIC PRIMITIVES
THE DIFFERENTIAL GEOMETRY OF PARAMETRIC PRIMITIVES Ken Turkowski Media Technologies: Graphics Software Advanced Technology Group Apple Computer, Inc. (Draft Friday, May 18, 1990) Abstract: We derive the
Chapter 5 Trigonometric Functions of Angles
Chapter 5 Trigonometric Functions of Angles Section 3 Points on Circles Using Sine and Cosine Signs Signs I Signs (+, +) I Signs II (+, +) I Signs II (, +) (+, +) I Signs II (, +) (+, +) I III Signs II
Conformal Clifford Algebras and Image Viewpoints Orbit
Conformal Clifford Algebras and Image Viewpoints Orbit Ghina EL MIR Ph.D in Mathematics Conference on Differential Geometry April 27, 2015 - Notre Dame University, Louaize Context Some viewpoints of a
Math 1501 Calc I Summer 2015 QUP SOUP w/ GTcourses
Math 1501 Calc I Summer 2015 QUP SOUP w/ GTcourses Instructor: Sal Barone School of Mathematics Georgia Tech May 22, 2015 (updated May 22, 2015) Covered sections: 3.3 & 3.5 Exam 1 (Ch.1 - Ch.3) Thursday,
MIT 2.71/2.710 Optics 10/31/05 wk9-a-1. The spatial frequency domain
10/31/05 wk9-a-1 The spatial frequency domain Recall: plane wave propagation x path delay increases linearly with x λ z=0 θ E 0 x exp i2π sinθ + λ z i2π cosθ λ z plane of observation 10/31/05 wk9-a-2 Spatial
CS 378: Computer Game Technology
CS 378: Computer Game Technolog 3D Engines and Scene Graphs Spring 202 Universit of Teas at Austin CS 378 Game Technolog Don Fussell Representation! We can represent a point, p =,), in the plane! as a
Reading. 4. Affine transformations. Required: Watt, Section 1.1. Further reading:
Reading Required: Watt, Section.. Further reading: 4. Affine transformations Fole, et al, Chapter 5.-5.5. David F. Rogers and J. Alan Adams, Mathematical Elements for Computer Graphics, 2 nd Ed., McGraw-Hill,
Visual Object Recognition
Visual Object Recognition Lecture 2: Image Formation Per-Erik Forssén, docent Computer Vision Laboratory Department of Electrical Engineering Linköping University Lecture 2: Image Formation Pin-hole, and
Rural Women Get Invitations For Conference. Playground Opens With Enthusiasm
H M H M v v Y v v v v H 4-H 6 MH U 4 97 Y-H Y H v M U M M M 5 M 5? v -? v 7 q - v < v 9 q U H # v - M - v < M 75 8 v - v 8 M 4-H v U v v M v v - v - v M v v v 4-H 4-H 9 M v 5 v 5 6 - $6 M v - M - v \ v
Fuzzy Reasoning and Optimization Based on a Generalized Bayesian Network
Fuy R O B G By Nw H-Y K D M Du M Hu Cu Uvy 48 Hu Cu R Hu 300 Tw. @w.u.u.w A By w v wy u w w uy. Hwv u uy u By w y u v w uu By w w w u vu vv y. T uy v By w w uy v v uy. B By w uy. T uy v uy. T w w w- uy.
"INDEPENDENT IN AI.L THINOS. NEUTRAI. IN NOTHINO' LOWELL, MICHIGAN, JAM AHV, 19, WHOLE NO. 290.
> HS U H V V 8 W HG J HV 9 899 WH 29 H G S J G W W W WS 4 5 6 898 K H q $ U S S U G 8 G H - J W U S G Y K - «H - W S HW W»U W 8 W H WS H G U Y Y J H q x U 2 VV GV W H W H G 8 H S G K W W W H J? 5? G S-
Ridig Body Motion Homogeneous Transformations
Ridig Body Motion Homogeneous Transformations Claudio Melchiorri Dipartimento di Elettronica, Informatica e Sistemistica (DEIS) Università di Bologna email: claudio.melchiorri@unibo.it C. Melchiorri (DEIS)
Advances in Computer Vision. Prof. Bill Freeman. Image and shape descriptors. Readings: Mikolajczyk and Schmid; Belongie et al.
6.869 Advances in Computer Vision Prof. Bill Freeman March 3, 2005 Image and shape descriptors Affine invariant features Comparison of feature descriptors Shape context Readings: Mikolajczyk and Schmid;
The Double Chooz Project
The Double Chooz Project Progress and Expected Sensitivity David McKee, KSU 13 17 July 2009 TeVPA @ SLAC Outline I. Neutrino mixing and θ 13 II. Existing θ 13 measurements III. This is hard with a single
Why Transforms? Want to animate objects and camera Translations Rotations Shears And more.. Want to be able to use projection transforms
Why Transforms? Want to animate objects and camera Translations Rotations Shears And more.. Want to be able to use projection transforms ITCS 3050:Game Engine Programming 1 Geometric Transformations Implementing
General Vector Space (2A) Young Won Lim 11/4/12
General (2A Copyright (c 2012 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version
EXAM. Practice for Second Exam. Math , Fall Nov 4, 2003 ANSWERS
EXAM Practice for Second Eam Math 135-006, Fall 003 Nov 4, 003 ANSWERS i Problem 1. In each part, find the integral. A. d (4 ) 3/ Make the substitution sin(θ). d cos(θ) dθ. We also have Then, we have d/dθ
COMP 175 COMPUTER GRAPHICS. Lecture 04: Transform 1. COMP 175: Computer Graphics February 9, Erik Anderson 04 Transform 1
Lecture 04: Transform COMP 75: Computer Graphics February 9, 206 /59 Admin Sign up via email/piazza for your in-person grading Anderson@cs.tufts.edu 2/59 Geometric Transform Apply transforms to a hierarchy
with any accuracy. The parameter a of cubic substances is directly proportional to the spacing d of any particular set of lattice planes:
The change in solute concentration or temperature produce only a small change in lattice parameter precise parameter measurements is needed to measure these quantities with any accuracy. The parameter
we must pay attention to the role of the coordinate system w.r.t. which we perform a tform
linear SO... we will want to represent the geometr of points in space we will often want to perform (rigid) transformations to these objects to position them translate rotate or move them in an animation
Math 20C Homework 2 Partial Solutions
Math 2C Homework 2 Partial Solutions Problem 1 (12.4.14). Calculate (j k) (j + k). Solution. The basic properties of the cross product are found in Theorem 2 of Section 12.4. From these properties, we
Camera calibration by Zhang
Camera calibration by Zhang Siniša Kolarić September 2006 Abstract In this presentation, I present a way to calibrate a camera using the method by Zhang. NOTE. This
Derivatives in 2D. Outline. James K. Peterson. November 9, Derivatives in 2D! Chain Rule
Derivatives in 2D James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 9, 2016 Outline Derivatives in 2D! Chain Rule Let s go back to
Linear Algebra & Geometry why is linear algebra useful in computer vision?
Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Matrix Transformation (2A) Young Won Lim 11/9/12
Matrix (A Copyright (c 01 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1. or any later version published
In the presence of viscous damping, a more generalized form of the Lagrange s equation of motion can be written as
2 MODELING Once the control target is identified, which includes the state variable to be controlled (ex. speed, position, temperature, flow rate, etc), and once the system drives are identified (ex. force,
MATH 130 FINAL REVIEW
MATH 130 FINAL REVIEW Problems 1 5 refer to triangle ABC, with C=90º. Solve for the missing information. 1. A = 40, c = 36m. B = 53 30', b = 75mm 3. a = 91 ft, b = 85 ft 4. B = 1, c = 4. ft 5. A = 66 54',
Pose Tracking II! Gordon Wetzstein! Stanford University! EE 267 Virtual Reality! Lecture 12! stanford.edu/class/ee267/!
Pose Tracking II! Gordon Wetzstein! Stanford University! EE 267 Virtual Reality! Lecture 12! stanford.edu/class/ee267/!! WARNING! this class will be dense! will learn how to use nonlinear optimization
MATHEMATICS FOR ENGINEERING DIFFERENTIATION TUTORIAL 2 ADVANCED DIFFERENTIATION
MATHEMATICS FOR ENGINEERING DIFFERENTIATION TUTORIAL ADVANCED DIFFERENTIATION CONTENTS Function of a Function Differentiation of a Sum Differentiation of a Proct Differentiation of a Quotient Turning Points
Robotics - Homogeneous coordinates and transformations. Simone Ceriani
Robotics - Homogeneous coordinates and transformations Simone Ceriani ceriani@elet.polimi.it Dipartimento di Elettronica e Informazione Politecnico di Milano 5 March 0 /49 Outline Introduction D space
Lecture 4.3 Estimating homographies from feature correspondences. Thomas Opsahl
Lecture 4.3 Estimating homographies from feature correspondences Thomas Opsahl Homographies induced by central projection 1 H 2 1 H 2 u uu 2 3 1 Homography Hu = u H = h 1 h 2 h 3 h 4 h 5 h 6 h 7 h 8 h
we must pay attention to the role of the coordinate system w.r.t. which we perform a tform
linear SO... we will want to represent the geometr of points in space we will often want to perform (rigid) transformations to these objects to position them translate rotate or move them in an animation
Notes on multivariable calculus
Notes on multivariable calculus Jonathan Wise February 2, 2010 1 Review of trigonometry Trigonometry is essentially the study of the relationship between polar coordinates and Cartesian coordinates in
Multi-Frame Factorization Techniques
Multi-Frame Factorization Techniques Suppose { x j,n } J,N j=1,n=1 is a set of corresponding image coordinates, where the index n = 1,...,N refers to the n th scene point and j = 1,..., J refers to the
Elementary maths for GMT
Elementary maths for GMT Linear Algebra Part 1: Vectors, Representations Algebra and Linear Algebra Algebra: numbers and operations on numbers 2 + 3 = 5 3 7 = 21 Linear Algebra: tuples, triples... of numbers
Section 8.2 Vector Angles
Section 8.2 Vector Angles INTRODUCTION Recall that a vector has these two properties: 1. It has a certain length, called magnitude 2. It has a direction, indicated by an arrow at one end. In this section
Fact: Every matrix transformation is a linear transformation, and vice versa.
Linear Transformations Definition: A transformation (or mapping) T is linear if: (i) T (u + v) = T (u) + T (v) for all u, v in the domain of T ; (ii) T (cu) = ct (u) for all scalars c and all u in the
Tracking for VR and AR
Tracking for VR and AR Hakan Bilen November 17, 2017 Computer Graphics University of Edinburgh Slide credits: Gordon Wetzstein and Steven M. La Valle 1 Overview VR and AR Inertial Sensors Gyroscopes Accelerometers
The Cartan Dieudonné Theorem
Chapter 7 The Cartan Dieudonné Theorem 7.1 Orthogonal Reflections Orthogonal symmetries are a very important example of isometries. First let us review the definition of a (linear) projection. Given a
THE COMPOUND ANGLE IDENTITIES
TRIGONOMETRY THE COMPOUND ANGLE IDENTITIES Question 1 Prove the validity of each of the following trigonometric identities. a) sin x + cos x 4 4 b) cos x + + 3 sin x + 2cos x 3 3 c) cos 2x + + cos 2x cos
Engineering Notebook
Engineering Notebook miscellaneous problems and solutions compiled by C Bond Vol1 no9 Actuator with zero bend angle Rotary Actuator Equations Given two points at which the track radius and gap skew angle
Keypoint extraction: Corners Harris Corners Pkwy, Charlotte, NC
Kepoint etraction: Corners 9300 Harris Corners Pkw Charlotte NC Wh etract kepoints? Motivation: panorama stitching We have two images how do we combine them? Wh etract kepoints? Motivation: panorama stitching
C3 Exam Workshop 2. Workbook. 1. (a) Express 7 cos x 24 sin x in the form R cos (x + α) where R > 0 and 0 < α < 2
C3 Exam Workshop 2 Workbook 1. (a) Express 7 cos x 24 sin x in the form R cos (x + α) where R > 0 and 0 < α < 2 π. Give the value of α to 3 decimal places. (b) Hence write down the minimum value of 7 cos
Lec 12 Review of Part I: (Hand-crafted) Features and Classifiers in Image Classification
Image Analysis & Retrieval Spring 2017: Image Analysis Lec 12 Review of Part I: (Hand-crafted) Features and Classifiers in Image Classification Zhu Li Dept of CSEE, UMKC Office: FH560E, Email: lizhu@umkc.edu,
Net Wt. 15 lbs. (6.8 kg) Covers 5,000 Sq. Ft. CAUTION CAUTION L AW N Storage and Disposal KEEP OUT OF REACH OF CHILDREN. Spreader Directions
L W OI: h. U y. f uy h u, h Wy h h. If, u h u. uy Hz Hu D UIO u y. v h y h. U v y h u y y. Wh huhy h f h f, k, h u, u. F H y y y h f 1-2 u. IF I Y: v, f, f h f u, h u y. f v. D : F k h f h yu v. h k h.
Vector Calculus. Dr. D. Sukumar
Vector Calculus Dr. D. Sukumar Space co-ordinates Change of variable Cartesian co-ordinates < x < Cartesian co-ordinates < x < < y < Cartesian co-ordinates < x < < y < < z < Cylindrical Cylindrical Cylindrical
FP101 FIRE PROTECTION PLAN FIRE PROTECTION SYMBOL LEGEND FIRE PROTECTION CODES & STANDARDS FIRE PROTECTION ABBREVIATIONS
Y F P Y Y PK PP PU VV P H UH U Z H HK VV F F H Y UP HZ U P F F P & 70 U F U & H UU... (05) U.F.. (05) F FP 3 (03) F H PK Y FP 5 (0) F H P,, F P Y F P V () X F V FH F F P FP F P PK P PU P QU H F QU F U/
Visual features: From Fourier to Gabor
Visual features: From Fourier to Gabor Deep Learning Summer School 2015, Montreal Hubel and Wiesel, 1959 from: Natural Image Statistics (Hyvarinen, Hurri, Hoyer; 2009) Alexnet ICA from: Natural Image Statistics
Linear Algebra & Geometry why is linear algebra useful in computer vision?
Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
The Two -Body Central Force Problem
The Two -Body Central Force Problem Physics W3003 March 6, 2015 1 The setup 1.1 Formulation of problem The two-body central potential problem is defined by the (conserved) total energy E = 1 2 m 1Ṙ2 1
Thin flow over a sphere
1 University of Waterloo, Faculty of Mathematics, Waterloo, Canada 2 Ryerson University, Department of Mathematics, Toronto, Canada IMA8 2016, June 12-16, Bad Honnef, Germany Problem description Related
The choice of origin, axes, and length is completely arbitrary.
Polar Coordinates There are many ways to mark points in the plane or in 3-dim space for purposes of navigation. In the familiar rectangular coordinate system, a point is chosen as the origin and a perpendicular
Practice Exam. 2x 1 + 4x 2 + 2x 3 = 4 x 1 + 2x 2 + 3x 3 = 1 2x 1 + 3x 2 + 4x 3 = 5
Practice Exam. Solve the linear system using an augmented matrix. State whether the solution is unique, there are no solutions or whether there are infinitely many solutions. If the solution is unique,
Multiple Choice. Compute the Jacobian, (u, v), of the coordinate transformation x = u2 v 4, y = uv. (a) 2u 2 + 4v 4 (b) xu yv (c) 3u 2 + 7v 6
.(5pts) y = uv. ompute the Jacobian, Multiple hoice (x, y) (u, v), of the coordinate transformation x = u v 4, (a) u + 4v 4 (b) xu yv (c) u + 7v 6 (d) u (e) u v uv 4 Solution. u v 4v u = u + 4v 4..(5pts)
Quantum Nonlocality Pt. 4: More on the CHSH Inequality
Quantum Nonlocality Pt. 4: More on the CHSH Inequality PHYS 500 - Southern Illinois University May 4, 2017 PHYS 500 - Southern Illinois University Quantum Nonlocality Pt. 4: More on the CHSH Inequality
Totally quasi-umbilic timelike surfaces in R 1,2
Totally quasi-umbilic timelike surfaces in R 1,2 Jeanne N. Clelland, University of Colorado AMS Central Section Meeting Macalester College April 11, 2010 Definition: Three-dimensional Minkowski space R
Image preprocessing in spatial domain
Image preprocessing in spatial domain Sampling theorem, aliasing, interpolation, geometrical transformations Revision: 1.4, dated: May 25, 2006 Tomáš Svoboda Czech Technical University, Faculty of Electrical
Kinematics of a UR5. Rasmus Skovgaard Andersen Aalborg University
Kinematics of a UR5 May 3, 28 Rasmus Skovgaard Andersen Aalborg University Contents Introduction.................................... Notation.................................. 2 Forward Kinematics for
( ) ( ) ( ) ( ) TNM046: Datorgrafik. Transformations. Linear Algebra. Linear Algebra. Sasan Gooran VT Transposition. Scalar (dot) product:
TNM046: Datorgrafik Transformations Sasan Gooran VT 04 Linear Algebra ( ) ( ) =,, 3 =,, 3 Transposition t = 3 t = 3 Scalar (dot) product: Length (Norm): = t = + + 3 3 = = + + 3 Normaliation: ˆ = Linear
Image preprocessing in spatial domain
Image preprocessing in spatial domain Sampling theorem, aliasing, interpolation, geometrical transformations Revision: 1.3, dated: December 7, 2005 Tomáš Svoboda Czech Technical University, Faculty of
Linear Wire Antennas. EE-4382/ Antenna Engineering
EE-4382/5306 - Antenna Engineering Outline Introduction Infinitesimal Dipole Small Dipole Finite Length Dipole Half-Wave Dipole Ground Effect Constantine A. Balanis, Antenna Theory: Analysis and Design
Adaptive fuzzy observer and robust controller for a 2-DOF robot arm
Adaptive fuzzy observer and robust controller for a 2-DOF robot arm S. Bindiganavile Nagesh Zs. Lendek A. A. Khalate R. Babuška Delft University of Technology, Technical University of Cluj-Napoca FUZZ-IEEE-2012
Interpolation of Transformation
Spatial Rotation Interpolation of Transformation I 3,0 U 12 K v V -1 1 11 11-1 Kv B 2 U 11 B 1 Interpolation of Transformation I 3,0 R,t U 12 K v V -1 1 11 11-1 Kv B 2 U 11 B 1 Interpolation of Transformation
Fun With Carbon Monoxide. p. 1/2
Fun With Carbon Monoxide p. 1/2 p. 1/2 Fun With Carbon Monoxide E = 0.25 ± 0.05 ev Electron beam results p. 1/2 Fun With Carbon Monoxide E = 0.25 ± 0.05 ev Electron beam results C V (J/K-mole) 35 30 25
Institute of Structural Engineering Page 1. Method of Finite Elements I. Chapter 2. The Direct Stiffness Method. Method of Finite Elements I
Institute of Structural Engineering Page 1 Chapter 2 The Direct Stiffness Method Institute of Structural Engineering Page 2 Direct Stiffness Method (DSM) Computational method for structural analysis Matrix
Lecture 8: Coordinate Frames. CITS3003 Graphics & Animation
Lecture 8: Coordinate Frames CITS3003 Graphics & Animation E. Angel and D. Shreiner: Interactive Computer Graphics 6E Addison-Wesley 2012 Objectives Learn how to define and change coordinate frames Introduce
Conditions for Segmentation of Motion with Affine Fundamental Matrix
Conditions for Segmentation of Motion with Affine Fundamental Matrix Shafriza Nisha Basah 1, Reza Hoseinnezhad 2, and Alireza Bab-Hadiashar 1 Faculty of Engineering and Industrial Sciences, Swinburne University
Diatomic Molecules. 7th May Hydrogen Molecule: Born-Oppenheimer Approximation
Diatomic Molecules 7th May 2009 1 Hydrogen Molecule: Born-Oppenheimer Approximation In this discussion, we consider the formulation of the Schrodinger equation for diatomic molecules; this can be extended
Mathematics Trigonometry: Unit Circle
a place of mind F A C U L T Y O F E D U C A T I O N Department of Curriculum and Pedagog Mathematics Trigonometr: Unit Circle Science and Mathematics Education Research Group Supported b UBC Teaching and
Kinetic Theory of Gases (1)
Advanced Thermodynamics (M2794.007900) Chapter 11 Kinetic Theory of Gases (1) Min Soo Kim Seoul National University 11.1 Basic Assumption Basic assumptions of the kinetic theory 1) Large number of molecules
HVAC LEGEND F.D. M.D. S.R. L.S.R. D.G. MECHANICAL COMPONENT IMPORTANCE FACTOR (Ip) DESIGNATION X Y
QU F H Y HV U/XHU/U U U / VV U V -0 / -0. P 0. F H 0 F H H, H QUP, PP UPP (U F U & F ) XP H H PU H H U. H QU, H F F U U. F H UU F PF F Y.. QUP HU F PF P P F.. U PP QU F H H P.. F P QU, H P UPP H H Y PF.
7. The Multivariate Normal Distribution
of 5 7/6/2009 5:56 AM Virtual Laboratories > 5. Special Distributions > 2 3 4 5 6 7 8 9 0 2 3 4 5 7. The Multivariate Normal Distribution The Bivariate Normal Distribution Definition Suppose that U and
Discrete Euclidean Curvature Flows
Discrete Euclidean Curvature Flows 1 1 Department of Computer Science SUNY at Stony Brook Tsinghua University 2010 Isothermal Coordinates Relation between conformal structure and Riemannian metric Isothermal
= n. 1 n. Next apply Snell s law at the cylindrical boundary between the core and cladding for the marginal ray. = n 2. sin π 2.
EXERCISE.-9 First, re-derive equation.-5 considering the possibility that the index at the entrance to the fiber bay be different than one. Snell s law at the entrance to the fiber is where all symbols
Omm Al-Qura University Dr. Abdulsalam Ai LECTURE OUTLINE CHAPTER 3. Vectors in Physics
LECTURE OUTLINE CHAPTER 3 Vectors in Physics 3-1 Scalars Versus Vectors Scalar a numerical value (number with units). May be positive or negative. Examples: temperature, speed, height, and mass. Vector
SAVE 9,893 SALE PRICE $12,961 * SAVE 6,354 $22,596 * SAVE 9,833 SALE PRICE $42,864 *
L WY UL - UL L ** L WY UL - UL L ** 3,839 5,649 6,94 L WY * L WY * 017 k,,, 16,800 Hk, f, k.,! 8,45 1,961 * L WY * 017 z L,596 * L WY * 017 k L 4,864 * f,, 49,010 007 L, L...W 4,998... 3,957 007,,...W
Section A brief on transformations
Section 127 A brief on transformations consider the transformation another name for it: change of variable x = rcosθ The determinant y = rsinθ r y r is called the Jacobian determinant of x,y with respect
Study guide for Exam 1. by William H. Meeks III October 26, 2012
Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
A Quantum Mechanical Model for the Vibration and Rotation of Molecules. Rigid Rotor
A Quantum Mechanical Model for the Vibration and Rotation of Molecules Harmonic Oscillator Rigid Rotor Degrees of Freedom Translation: quantum mechanical model is particle in box or free particle. A molecule
CS 354R: Computer Game Technology
CS 354R: Computer Game Technolog Transformations Fall 207 Universit of Teas at Austin CS 354R Game Technolog S. Abraham Transformations What are the? Wh should we care? Universit of Teas at Austin CS 354R
Principal Stresses, Yielding Criteria, wall structures
Principal Stresses, Yielding Criteria, St i thi Stresses in thin wall structures Introduction The most general state of stress at a point may be represented by 6 components, x, y, z τ xy, τ yz, τ zx normal
Complex Numbers Class Work. Complex Numbers Homework. Pre-Calc Polar & Complex #s ~1~ NJCTL.org. Simplify using i b 4 3.
Complex Numbers Class Work Simplify using i. 1. 16 2. 36b 4 3. 8a 2 4. 32x 6 y 7 5. 16 25 6. 8 10 7. 3i 4i 5i 8. 2i 4i 6i 8i 9. i 9 10. i 22 11. i 75 Complex Numbers Homework Simplify using i. 12. 81 13.