Camera: optical system
|
|
|
- Archibald Riley
- 5 years ago
- Views:
Transcription
1 Camera: optical system Y dαα α ρ ρ curvature radius Z thin lens small angles: α Y ρ α Y ρ
2 lens refraction inde: n Y incident light beam deviated beam θ '' α θ ' α sin( θ '' α ) sin( θ ' α ) n θ α θ α deviation angle? Δθ θ θ Δθ ( n ) Y ( + ) ρ ρ sin( θ α) sin( θ ' α ) ' n Z
3 a) Y Δθ b) f Δθ Y hin lens rules f ( n )( ρ + ) ρ parallel rays converge onto a focal plane beams through lens center: undeviated independent of y Y Δθ f
4 Hp: Z >> a r f the image of a point P belongs to the line (P,O) P image plane O p p image of P image plane line(o,p) interpretation line of p: line(o,p) locus of the scene points projecting onto image point p
5 Projective D geometry Notes based on di R.Hartley e A.Zisserman Multiple view geometry
6 Projective D Geometry Points, lines & conics ransformations & invariants D projective geometry and the Cross-ratio
7 Homogeneous coordinates Homogeneous representation of lines a + by + c ( a,b,c) ( ka ) + ( kb) y + kc, k ( a,b,c ) ~ k( a,b,c) equivalence class of vectors, any vector is representative Set of all equivalence classes in R 3 (,,) forms P Homogeneous representation of points, y on l a,b,c if and only if a + by + c ( ) ( ) (,y, )( a,b,c) (,y, ) l (, y,) ~ k(, y,), k he point lies on the line l if and only if ll ( ) Homogeneous coordinates,, Inhomogeneous coordinates (, y) 3 but only DOF
8 Points from lines and vice-versa Intersections of lines he intersection of two lines l and l' is l l' Line joining two points he line through two points and ' is Eample l Line joining two points: parametric equation A point on the line through two points and is y + θ ' y
9 Ideal points and the line at infinity Intersections of parallel lines l ( a, b, c) and l' ( a, b, c' ) l l' ( b, a,) Eample ( b, a) ( a,b) tangent vector normal direction Ideal points (,, ) Line at infinity l (,,) P R l Note that in P there is no distinction between ideal points and others
10 Duality l l l l l' l ' Duality principle: o any theorem of -dimensional projective geometry there corresponds a dual theorem, which may be derived by interchanging the role of points and lines in the original theorem
11 Conics Curve described by nd -degree equation in the plane a + by + cy + d + ey + f or homogenized a α, 3 y α + b + c + d3 + e3 + f3 or in matri form a b / d / C with C b / c e / d / e / f 3 5DOF: { a : b : c : d : e : f }
12 Five points define a conic For each point the conic passes through f ey d cy y b a i i i i i i or ( ),,,,, c f y y y i i i i i i ( ) f e d c b a,,,,, c c y y y y y y y y y y y y y y y stacking constraints yields
13 Pole-polar relationship he polar line lc of the point with respect to the conic C intersects the conic in two points. he two lines tangent to C at these points intersect at
14 Polarity: cross ratio Cross ratio of 4 colinear points y + θ (with i,..,4) ratio of ratios θ θ -θ -θ 3 4 θ θ i -θ -θ 3 4 i Harmonic 4-tuple of colinear points: such that CR-
15 angent lines to conics he line l tangent to C at point on C is given by lc l C
16 Dual conics A line tangent to the conic C satisfies l C * l C * In general (C full rank): in fact Dual conics line conics conic envelopes C Line l is the polar line of y : y C l, but since y Cy - - * - - l C C C l C C C -
17 Degenerate conics A conic is degenerate if matri C is not of full rank e.g. two lines (rank ) C lm + ml e.g. repeated line (rank ) m l C ll l Degenerate line conics: points (rank ), double point (rank) Note that for degenerate conics ( * C ) * C
18 Projective transformations Definition: A projectivity is an invertible mapping h from P to itself such that three points,, 3 lie on the same line if and only if h( ),h( ),h( 3 ) do. heorem: A mapping h:p P is a projectivity if and only if there eist a non-singular 33 matri H such that for any point in P represented by a vector it is true that h()h Definition: Projective transformation ' h ' h ' 3 h 3 h h h 3 h h h or ' H 8DOF projectivitycollineationprojective transformationhomography
19 Mapping between planes central projection may be epressed by H (application of theorem)
20 Removing projective distortion select four points in a plane with known coordinates ' ' ' 3 h h 3 + h + h 3 y + h y + h 3 33 y' ' ' 3 h h 3 + h + h 3 y + h y + h 3 33 ( h3 + h3 y + h33 ) h + h y h3 ( h3 + h3 y + h33 ) h + h y h3 ' + y ' + (linear in h ij ) ( constraints/point, 8DOF 4 points needed) Remark: no calibration at all necessary, better ways to compute (see later)
21 More eamples
22 ransformation of lines and conics For a point transformation ' H ransformation for lines l' H - ransformation for conics l C ' H - CH - ransformation for dual conics * C' * HC H
23 A hierarchy of transformations Projective linear group Affine group (last row (,,)) Euclidean group (upper left orthogonal) Oriented Euclidean group (upper left det ) Alternative, characterize transformation in terms of elements or quantities that are preserved or invariant e.g. Euclidean transformations leave distances unchanged
24 Class I: Isometries (isosame, metricmeasure) ' y' ε cosθ ε sinθ sinθ cosθ t t y y ε ± orientation preserving: orientation reversing: ε ε ' H E R t 3DOF ( rotation, translation) R R special cases: pure rotation, pure translation I Invariants: length, angle, area
25 Class II: Similarities (isometry + scale) cos sin sin cos ' ' y t s s t s s y y θ θ θ θ ' t R H s S I R R also know as equi-form (shape preserving) metric structure structure up to similarity (in literature) 4DOF ( scale, rotation, translation) Invariants: ratios of length, angle, ratios of areas, parallel lines
26 Class III: Affine transformations ' ' y t a a t a a y y ' t A H A non-isotropic scaling! (DOF: scale ratio and orientation) 6DOF ( scale, rotation, translation) Invariants: parallel lines, ratios of parallel segment lengths, ratios of areas ( ) ( ) ( ) φ φ θ DR R R A λ λ D ) )( ( VDV UV UDV A where
27 Action of affinities and projectivities on line at infinity + v v v v A A t v A A t Line at infinity becomes finite, allows to observe vanishing points, horizon, Line at infinity stays at infinity, but points move along line
28 Class VI: Projective transformations ' H P A v t v v ( v v ), 8DOF ( scale, rotation, translation, line at infinity) Action: non-homogeneous over the plane Invariants: cross-ratio of four points on a line (ratio of ratios)
29 Projective geometry of D ( ), ' H 3DOF (-) he cross ratio Cross (,,, ) 3 4,, 3 3,, 4 4, i j i det i j j Invariant under projective transformations
30 Overview transformations Projective 8dof Affine 6dof Similarity 4dof Euclidean 3dof h h h3 a a sr sr r r h h h a a r r 3 sr sr h3 h 3 h 33 t t y t t y t t y Concurrency, collinearity, order of contact (intersection, tangency, inflection, etc.), cross ratio Parallellism, ratio of areas, ratio of lengths on parallel lines (e.g midpoints), linear combinations of vectors (centroids). he line at infinity l Ratios of lengths, angles. he circular points I,J lengths, areas.
31 Number of invariants? he number of functional invariants is equal to, or greater than, the number of degrees of freedom of the configuration less the number of degrees of freedom of the transformation e.g. configuration of 4 points in general position has 8 dof (/pt) and so 4 similarity, affinity and zero projective invariants
32 Recovering metric and affine properties from images Parallelism Parallel length ratios Angles Length ratios
33 he line at infinity l l l A t A H A he line at infinity l is a fied line under a projective transformation H if and only if H is an affinity Note: not fied pointwise
34 Affine properties from images projection (affine) rectification A P l l l H H 3 ' [ ], l' 3 3 l l l l in fact, any point on l is mapped to a point at the
35 Affine rectification v v l l l 3 l l 4 v l3 l4 v l l l v v
36 he circular points I i J i I cos sin sin cos I I i se i t s s t s s i y S θ θ θ θ θ H he circular points I, J are fied points under the projective transformation H iff H is a similarity
37 he circular points circular points l + + d3 + e3 + f3 + 3 I (, i,) Intersection points between any circle and l J, i, Algebraically, encodes orthogonal directions I (,, ) + i(,, ) ( )
38 Circular points invariance {I,J} l any circumference Similarity: circ circ Similarity: circ l circ l Similarity: {I,J} {I,J} circular points: invariant under similarity
39 * C Conic dual to the circular points * C IJ + JI : line conic set of lines through any of the circular points C * C * H C * S H S C he dual conic * is fied conic under the projective transformation H iff H is a similarity * C Note: has 4DOF l is the null vector
40 Angles ( )( ) cos m m l l m l m l θ ( ) 3,, l l l l ( ) 3,, m m m m Euclidean: Projective: ( )( ) m m l l m l cos * * * C C C θ m l * C (orthogonal)
41 Metric properties from images ( ) ( ) ( ) ( ) ( ) ( ) v v v v ' * * * * K K KK H H C H H H H H C H H H H H H C H H H C A P A P A P S S A P S A P S A P U U C ' * Rectifying transformation from SVD H U
42 Normally: SVD (Singular Value Decomposition) U V C c b a ' * But is symmetric ' * C ' ' * * C VDU UDV C and SVD is unique V U with U and V orthogonal U U C ' * Why? Observation : HU orthogonal (33): not a P isometry
43 Once the image has been affinely rectified A H A C H C * * ' ' * t t KK K K C Metric from affine
44 Metric from affine ( ) 3 3 m m m l l l KK ( )( ),,,, + + k k k k k m l m l m l m l
45 Metric from projective ( ) ( ) ( ) ( ) c,,,,, m l m l m l m l m l m l m l m l m l ( ) v v v v 3 3 m m m l l l K K KK
46 Fied points and lines H e λ e (eigenvectors H fied points) (λ λ pointwise fied line) H l λ l (eigenvectors H - fied lines)
47 Projective 3D geometry
48 Singular Value Decomposition n n n m m m n m V Σ U A I U U n σ σ σ Λ I V V m n X V X V Σ X V UΣ n n U n V V U V U A σ σ σ Λ Σ Λ Μ Μ Μ Λ Μ Ο Μ Μ Λ Λ σ n σ σ
49 Singular Value Decomposition Homogeneous least-squares min AX subject to X solution X Vn Span and null-space S L [ U U ]; N [ U ] L 3U4 V V ; R V3V 4 Closest rank r approimation A ~ UΣ ~ V [ ] [ ] S R N Pseudo inverse + A VΣ U A UΣ V ~ Σ diag Σ σ ( σ, σ, Λ, σ,,, ) r Λ + ( Σ + diag σ, σ, Λ, σ,,, ) σ r Λ
50 Projective 3D Geometry Points, lines, planes and quadrics ransformations П, ω and Ω
51 3D points 3D point ( X, Y, Z ) in R 3 X ( X, X, X X ) 3, 4 in P 3 X X X X 3,,, Z X 4 X 4 X 4 ( X, Y,,) ( X 4 ) projective transformation X' H X (44-5 dof)
52 3D plane Planes π X + πy + π3z + π4 π X + πx + π3x 3 + π4x 4 ransformation X' H X - π' H π π X Euclidean n.x ~ representation + d ( π ), π, π3 d n ( ) π 4 X ~ X, Y, Z X 4 d / n Dual: points planes, lines lines
53 Solve X X X Planes from points 3 π from 3 π [ X X X X ] det 3 X π, X π and X π X (solve π as right nullspace of X ) X3 Or implicitly from coplanarity condition X det X X X 3 4 ( X) ( X ) ( X ) 3 ( X) ( X ) ( X ) 3 ( X) ( X ) ( X 3) 3 3 ( X ) ( X ) ( X ) X D 34 X D 34 + X 3 D 4 X π ( D ) 4D3 34, D34, D4, D
54 Points from planes X π π π 3 X M [ ] 3 X X X M π M M I p ( ) d c b a,,, π a d a c a b p,, X π X π, X π X 3 and from Solve (solve as right nullspace of ) X 3 π π π Representing a plane by its span
55 Lines W A B λa+ μb (4dof) W * P Q λp+ μq two points A and B two planes P and Q * * W W WW Eample: X-ais W W *
56 Points, lines and planes W M M π X X W W * M M X π * W π
57 Quadrics and dual quadrics X QX. 9 d.o.f. (Q : 44 symmetric matri). in general 9 points define quadric 3. det Q degenerate quadric 4. pole polar 5. (plane quadric)conic 6. transformation π * Q π π QX Q' H Q ο ο ο ο ο ο C M QM π : X M - QH - * - Q Q * * HQ H. relation to quadric (non-degenerate). transformation Q'
58 Quadric classification Rank Sign. Diagonal Equation Realization 4 4 (,,,) X + Y + Z + No real points (,,,-) X + Y + Z Sphere (,,-,-) X + Y Z + Hyperboloid (S) 3 3 (,,,) X + Y + Z Single point (,,-,) X + Y Z Cone (,,,) X + Y Single line (,-,,) X Y wo planes (,,,) X Single plane
59 Quadric classification Projectively equivalent to sphere: sphere Ruled quadrics: ellipsoid hyperboloid of two sheets paraboloid hyperboloids of one sheet Degenerate ruled quadrics: cone two planes
60 Hierarchy of transformations Projective 5dof A v t v Intersection and tangency Affine dof A t Parallellism of planes, Volume ratios, centroids, he plane at infinity π Similarity 7dof s R t he absolute conic Ω Euclidean 6dof R t Volume
61 Screw decomposition Any particular translation and rotation is equivalent to a rotation about a screw ais and a translation along the screw ais. screw ais // rotation ais t + t t //
62 he plane at infinity A π H A π π A t he plane at infinity π is a fied plane under a projective transformation H iff H is an affinity π (,,,). canical position. contains directions D ( X ), X, X 3, 3. two planes are parallel line of intersection in π 4. line // line (or plane) point of intersection in π
63 he absolute conic he absolute conic Ω is a (point) conic on π. In a metric frame: X or conic for directions: (with no real points) + X X 4 + X he absolute conic Ω is a fied conic under the projective transformation H iff H is a similarity 3 ( X, X, X ) I( X, X X ) 3, 3. Ω is only fied as a set. Circle intersect Ω in two points 3. Spheres intersect π in Ω
64 Absolute conic invariance Ω π any sphere Similarity: sphere sphere Similarity: sphere π sphere π Similarity: Ω Ω Ω : invariant under similarity
65 he absolute conic Euclidean: Projective: cosθ cosθ ( d ) d ( )( d ) d d d ( d ) Ω d ( d d )( Ω d Ω d ) d Ω d (orthogonalityconjugacy) normal plane
66 he absolute dual quadric * I Ω he absolute conic Ω * is a fied conic under the projective transformation H iff H is a similarity. 8 dof. plane at infinity π is the nullvector of Ω 3. Angles: * cosθ ( * )( * π Ω π π Ω π ) π Ω π
67 Y P X p c y f O Z y f f X Z Y Z perspective projection -nonlinear -not shape-preserving -not length-ratio preserving
68 Homogeneous coordinates In D: add a third coordinate, w Point [,y] epanded to [u,v,w] Any two sets of points [u,v,w ] and [u,v,w ] represent the same point if one is multiple of the other [u,v,w] [,y] with u/w, and yv/w [u,v,] is the point at the infinite along direction (u,v)
69 ransformations translation by vector [d,d y ] scaling (by different factors in and y) rotation by angle θ
70 Homogeneous coordinates In 3D: add a fourth coordinate, t Point [X,Y,Z] epanded to [,y,z,t] Any two sets of points [,y,z,t ] and [,y,z,t ] represent the same point if one is multiple of the other [,y,z,t] [X,Y,Z] with X/t, Yy/t, and Zz/t [,y,z,] is the point at the infinite along direction (,y,z)
71 ransformations translation scaling rotation Obs: rotation matri is an orthogonal matri i.e.: R - R
72 Pinhole camera model Z fy Z fx Z Y X ) /, / ( ),, ( α Z Y X f f Z fy fx Z Y X α
73 Scene->Image mapping: perspective transformation u v w f with f X Y Z y u w v w With ad hoc reference frames, for both image and scene
74 Let us recall them O image reference - centered on principal point - - and y-aes parallel to the sensor rows and columns - Euclidean reference c y f Y X scene reference - centered on lens center - Z-ais orthogonal to image plane - X- and Y-aes opposite to image - and y-aes Z
75 principal point c Actual references are generic y f O principal ais Y X image reference - centered on upper left corner - nonsquare piels (aspect ratio) noneuclidean reference Z scene reference - not attached to the camera
76 Principal point offset o o v Z fy u Z fx Z Y X ) /, / ( ),, ( + + α principal point o v o u ), ( + + Z Y X v f u f Z Zv fy Zu fx Z Y X o o o o α
77 CCD camera o y o v f u f K o o v f u f a K
78 Scene-image relationship wrt actual reference frames image u A u v w ( s a) a u v o o u v w normally, s X scene Y Z R t X
79 X t R X P u f f v a u o o t K R K t R I P o o v af u f K upper triangular: intrinsic camera parameters scene-camera tranformation etrinsic camera parameters orthogonal (3D rotation) matri P: - degrees of freedom ( if s)
80 z y o I M X o I M u ) ( o M o I M u i.e., defining [, y, z] o I M o M M m M t K R K P with R K M and m M o
81 Interpretation of o: u is image of if ( o) λm u i.e., if o + λm u he locus of the points whose image is u is a straight line through o having direction d M u o M m is independent of u o is the camera viewpoint (perspective projection center) line(o, d) Interpretation line of image point u
82 M K and R Intrinsic and etrinsic parameters from P M K R M R K R K RQ-decomposition of a matri: as the product between an orthogonal matri and an upper triangular matri M and m t o M m ( KR) Kt R K Kt R t t Ro
83 Camera center null-space camera projection matri P O X λa + ( λ)o PX λpa + ( λ)po For all A all points on AO project on image of A, therefore O is camera center Image of camera center is (,,), i.e. undefined o M m Finite cameras: O d Infinite cameras: o,md
84 Action of projective camera on point Forward projection PX [ M m] D Md PD Back-projection P O + X P P + P ( PP ) ( λ) P + λo X + - d M M X( λ) μ D - (pseudo-inverse) - M + O - m M - + PP I ( μ - m)
85 Camera matri decomposition Finding the camera center P O (use SVD to find null-space) X det( [ p,p3,m] ) Y det( [ p,p3,m] ) Z det( [ p,p,m] ) ([ p,p,m]) det Finding the camera orientation and internal parameters M KR (use RQ decomposition ~QR) (if only QR, invert) ( Q R ) - R - - Q
86 Radial distortion
87 Data normalization 3 X ~ i UX i u~ i u i (i) translate origin to gravity center (ii) (an)isotropic scaling
88 Eterior orientation Calibrated camera, position and orientation unkown Pose estimation 6 dof 3 points minimal (4 solutions in general)
89 Properties of perspective transformations ) vanishing points V image of the point at the along direction d u V M m d M d d M u V the interpretation line of V is parallel to d
90 d P O V he images of parallel lines are concurrent lines
91 Properties of perspective transformations ctd. ) cross ratio invariance Given four colinear points ( p, p, p p ) let (,, ) 3, 4 3, be their abscissae 4 CR ( p, p, p p ) 3,
92 Cross ratio invariance under perspective transformation a point on the line yz X [, y, z, t] [,,, t ] its image its coordinate u det u, u CR( u, u, u3, u4 ) det u, u det u [ u, v, w] 3 3 det u det u P X p u [ u, w] P4 p t 3, u, u detp detp det det,, 3 4 CR(,, 3, 4 ) det,, det det,, 3 belongs to a line detp detp 4 4 det det 3,, 4 4
93 Object localization : three colinear points geometric model of an object a perspective image of the object position and orientation of the object? calibrated camera: known P M known interpretation lines m C A B B A O C B A π C
94 a) orientation C A B C V O A B π Cross ratio invariance: a c solve CR( A', B', C', V ) CR( A, B, C, ) for V (image of ) b c V: vanishing point of the direction of (A,B,C) interpretation line of V parallel to (A,B,C) direction M uv
95 b) position (e.g., distance(o,a)) M u C γ C A B C V O α M u A A B M u V π interpretation lines OA AC sinγ sinα angles α and γ
96 Object localization : four coplanar points D C O E B A (i) orientation of (A,E,C) (ii) orientation of (B,E,D) (iii) distance (O,A)
97 Off-side Find vanishing point of the field-bottom line direction b b a a images of symmetric segments
98 a c b d a and b: c(a+b)/: d : abscissae of the endpoints of a segment abscissa of segment midpoint, point at the infinite along the segment direction CR a c a d b d a c b c ( a, b, c, d ) b c Harmonic 4-tuple (a,b,c,d) (a,b ) and (a, b ) are image of symmetric segments same image of the midpoint c, same vanishing point d
99 solve a' c' ( a', b', c', d' ) b' c' { CR for CR a' ', b'', c', d' a'' c' a' d' b' d' ( ) b'' c' a'' d' b'' d' c, d system of two linear equations in (c d ) and (c +d ) two degree equation, whose solutions are c and d among the two solutions, the one for d is the value eternal to the range [a,b ]
100 What can be told from a single image?
101 Action of projective camera on planes [ ] [ ] p p p p p p p PX Y X Y X he most general transformation that can occur between a scene plane and an image plane under perspective imaging is a plane projective transformation
102 Action of projective camera on lines forward projection ( μ) P(A + μb) PA + μpb a μb X + back-projection l PX l PX with Π P l Π X Interpretation plane of line l
103 [ ] [ ] [ ] P Y X Y X p p p p p p p p p p PX Image of a conic C C - P P therefore - C C' P P
104 Action of projective camera on conics back-projection of a conic C to cone Q co C Q co
105 back-projection of a conic C to cone Qco C PX C X P CPX with X Q co X Interpretation cone of a conic C Q co P CP eample: Q co K C [ K ] K CK
106 Images of smooth surfaces he contour generator Γ is the set of points X on S at which rays are tangent to the surface. he corresponding apparent contour γ is the set of points which are the image of X, i.e. γ is the image of Γ he contour generator Γ depends only on position of projection center, γ depends also on rest of P
107 Action of projective camera on quadrics apparent contour of a quadric Q dual quadric Q * Q is a plane quadric: the set of planes tangent to Q Π Q * Π Let us consider only those planes that are backprojection of image lines Π P l Π Q * Π l * PQ P l with C * * PQ P its dual is C C *
108 he plane containing the apparent contour Γ of a quadric Q from a camera center O follows from pole-polar relationship ΠQO he cone with verte V and tangent to the quadric Q is Q CO (V QV)Q - (QV)(QV) Q CO V back-projection to cone
109 What does calibration give? K[I ] d d K d d cos θ ( )( ) ( )( ) d d d d (K K ) (K K ) (K - K - ) An image line l defines a plane through the camera center with normal nk l measured in the camera s Euclidean frame. In fact the backprojection of l is P l nk l
110 he image of the absolute conic Ω d PX KR[I O] KRd mapping between π to an image is given by the planar homogaphy Hd, with HKR absolute conic (IAC), represented by I 3 within π (w) its image (IAC) ( ) - - KK K K ω ( C α H CH ) (i) IAC depends only on intrinsics (ii) angle between two rays cos θ (iii) DIACω * KK (iv) ω K (Cholesky factorization) (v) image of circular points belong to ω (image of absolute conic) ( ω )( ω ) ω
111 A simple calibration device (i) compute H i for each square (corners (,),(,),(,),(,)) (ii) compute the imaged circular points H i [,±i,] (iii) fit a conic ω to 6 imaged circular points (iv) compute K from ωk - K - through Cholesky factorization ( Zhang s calibration method)
112
113 Orthogonality relation cos θ ( )( ) v ωv v ωv v ωv v ωv * l ω l
114 Calibration from vanishing points and lines
115 Calibration from vanishing points and lines
116
117 wo-view geometry Epipolar geometry F-matri comp. 3D reconstruction Structure comp.
118 hree questions: (i) Correspondence geometry: Given an image point in the first view, how does this constrain the position of the corresponding point in the second image? (ii) Camera geometry (motion): Given a set of corresponding image points { i i }, i,,n, what are the cameras P and P for the two views? (iii) Scene geometry (structure): Given corresponding image points i i and cameras P, P, what is the position of (their pre-image) X in space?
119 he epipolar geometry C,C,, and X are coplanar
120 he epipolar geometry What if only C,C, are known?
121 he epipolar geometry All points on π project on l and l
122 he epipolar geometry Family of planes π and lines l and l Intersection in e and e
123 he epipolar geometry epipoles e,e intersection of baseline with image plane projection of projection center in other image vanishing point of camera motion direction an epipolar plane plane containing baseline (-D family) an epipolar line intersection of epipolar plane with image (always come in corresponding pairs)
124 Eample: converging cameras
125 Eample: motion parallel with image plane
126 Eample: forward motion e e
127 he fundamental matri F algebraic representation of epipolar geometry α l' we will see that mapping is (singular) correlation (i.e. projective mapping from points to lines) represented by the fundamental matri F
128 he fundamental matri F geometric derivation ' H π [ e' ] Hπ F l' e' ' mapping from -D to -D family (rank )
129 he fundamental matri F algebraic derivation ( λ) P λc X + + ( + P P I) l P'C P' P + P + X( λ) F [ ] + e' P' P (note: doesn t work for CC F)
130 he fundamental matri F correspondence condition he fundamental matri satisfies the condition that for any pair of corresponding points in the two images ' F ( ' l' )
131 he fundamental matri F F is the unique 33 rank matri that satisfies F for all (i) ranspose: if F is fundamental matri for (P,P ), then F is fundamental matri for (P,P) (ii) Epipolar lines: l F & lf (iii) Epipoles: on all epipolar lines, thus e F, e F, similarly Fe (iv) F has 7 d.o.f., i.e. 33-(homogeneous)-(rank) (v) F is a correlation, projective mapping from a point to a line l F (not a proper correlation, i.e. not invertible)
132 he epipolar line geometry l,l epipolar lines, k line not through e l F[k] l and symmetrically lf [k ] l l l k k e e' l Fk (pick ke, since e e ) F[ e] l l F [ e' ] l' l'
133 Fundamental matri for pure translation
134 Fundamental matri for pure translation
135 Fundamental matri for pure translation [ e' ] H [ ] F e' ( H K RK) eample: e' (,,) F - ' F y y' PX ' P' X K[I ]X K - K[I t] Z ( X,Y,Z) - K /Z ' + Kt/Z motion starts at and moves towards e, faster depending on Z pure translation: F only d.o.f., [e] auto-epipolar
136 General motion [ e' ] H [ e' ] ˆ ' ' ' K'RK - + K' t/z
137 Geometric representation of F F ( F F )/ ( F F F )/ S + A ( F + ) F S F A F ( F ) A F F s : Steiner conic, 5 d.o.f. F a [ a ] : pole of line ee w.r.t. F s, d.o.f. S
138 Geometric representation of F
139 Pure planar motion Steiner conic F s is degenerate (two lines)
140 Projective transformation and invariance Derivation based purely on projective concepts ˆ H, ˆ' H' ' Fˆ PX ( )( - PH H X) Pˆ Xˆ ( )( - P' H H X) Pˆ' Xˆ H' - FH - F invariant to transformations of projective 3-space ' P' X ( P, P' ) α F F α ( P,P' ) canonical form P' [I ] [M m] unique not unique P [ m] M F
141 Projective ambiguity of cameras given F previous slide: at least projective ambiguity this slide: not more! ~ ~ Show that if F is same for (P,P ) and (P,P ), there eists a projective transformation H so that ~ ~ PHP and P HP lemma: H P' H ~ P [I ] P' [A a] P [I ] P ~ ' F [ a] A [ ~ a] A ~ ~ A ~ a ka k A + av ( ) rank [A ~ ~ a] af a[] a A ~ af ~ a ka a A ~ a A ~ a ka ~ - A ka ~ - A av [ ] [ ] [ ] ( ) ( ) k I k v k [A a] k I k v k [ k ( A - av ) ka] P ~ ' (-57, ok)
142 Canonical cameras given F F matri corresponds to P,P iff P FP is skew-symmetric ( X P' FPX, X) F matri, S skew-symmetric matri P [I ] P' [SF e'] [SF e'] (fund.matrif) F[I ] F S F e' F F S F Possible choice: P [I ] P' [[e'] F e'] Canonical representation: P [I ] P' [[e'] F + e' v λe']
143 he essential matri ~fundamental matri for calibrated cameras (remove K) E ˆ ' [ t] R R[R t] Eˆ - - ( ˆ K ; ˆ' K ' ) E K' FK 5 d.o.f. (3 for R; for t up to scale) E is essential matri if and only if two singularvalues are equal (and third) E Udiag(,,)V
144 Four possible reconstructions from E (only one solution where points is in front of both cameras)
145 wo-view geometry Epipolar geometry F-matri comp. 3D reconstruction Structure comp.
146 hree questions: (i) Correspondence geometry: Given an image point in the first view, how does this constrain the position of the corresponding point in the second image? (ii) Camera geometry (motion): Given a set of corresponding image points { i i }, i,,n, what are the cameras P and P for the two views? (iii) Scene geometry (structure): Given corresponding image points i i and cameras P, P, what is the position of (their pre-image) X in space?
147 he epipolar geometry C,C,, and X are coplanar
148 he epipolar geometry What if only C,C, are known?
149 he epipolar geometry All points on π project on l and l
150 he epipolar geometry Family of planes π and lines l and l Intersection in e and e
151 he epipolar geometry epipoles e,e intersection of baseline with image plane projection of projection center in other image vanishing point of camera motion direction an epipolar plane plane containing baseline (-D family) an epipolar line intersection of epipolar plane with image (always come in corresponding pairs)
152 Eample: converging cameras
153 Eample: motion parallel with image plane
154 Eample: forward motion e e
155 he fundamental matri F algebraic representation of epipolar geometry α l' we will see that mapping is (singular) correlation (i.e. projective mapping from points to lines) represented by the fundamental matri F
156 he fundamental matri F geometric derivation ' H π [ e' ] Hπ F l' e' ' mapping from -D to -D family (rank )
157 l' he fundamental matri F algebraic derivation M + ( ) λc X λ - M [ ] [ ] [ ] M' m' C M' m' M' m' C M' M ' l' ' l' ' F P + X( λ) F [ ] e' M' M (note: doesn t work for CC F)
158 he fundamental matri F correspondence condition he fundamental matri satisfies the condition that for any pair of corresponding points in the two images ' F ( ' l' )
159 he fundamental matri F F is the unique 33 rank matri that satisfies F for all (i) ranspose: if F is fundamental matri for (P,P ), then F is fundamental matri for (P,P) (ii) Epipolar lines: l F & lf (iii) Epipoles: on all epipolar lines, thus e F, e F, similarly Fe (iv) F has 7 d.o.f., i.e. 33-(homogeneous)-(rank) (v) F is a correlation, projective mapping from a point to a line l F (not a proper correlation, i.e. not invertible)
160 he epipolar line geometry l,l epipolar lines, k line not through e l F[k] l and symmetrically lf [k ] l l l k k e e' l Fk (pick ke, since e e ) F[ e] l l F [ e' ] l' l'
161 Fundamental matri for pure translation
162 Fundamental matri for pure translation
163 Fundamental matri for pure translation [ e' ] H [ ] F e' ( H K RK) eample: e' (,,) F - ' F y y' PX ' P' X K[I ]X - K[I t] K Z ( X,Y,Z) - K /Z ' + Kt/Z motion starts at and moves towards e, faster depending on Z pure translation: F only d.o.f., [e] auto-epipolar
164 General motion [ e' ] H [ e' ] ˆ ' ' ' K'RK - + K' t/z
165 Geometric representation of F F ( F F )/ ( F F F )/ S + A ( F + ) F S F A F ( F ) A F F s : Steiner conic, 5 d.o.f. F a [ a ] : pole of line ee w.r.t. F s, d.o.f. S
166 Geometric representation of F
167 Pure planar motion Steiner conic F s is degenerate (two lines)
168 Projective transformation and invariance Derivation based purely on projective concepts ˆ H, ˆ' H' ' Fˆ PX ( )( - PH H X) Pˆ Xˆ ( )( - P' H H X) Pˆ' Xˆ H' - FH - F invariant to transformations of projective 3-space ' P' X ( P, P' ) α F F α ( P,P' ) canonical form P' [I ] [M m] unique not unique P [ m] M F
169 Projective ambiguity of cameras given F previous slide: at least projective ambiguity this slide: not more! ~ ~ Show that if F is same for (P,P ) and (P,P ), there eists a projective transformation H so that ~ ~ PHP and P HP lemma: H P' H ~ P [I ] P' [A a] P ~ [I ] P' F [ a] A [ ~ a] A ~ ~ A ~ a ka k A + av ( ) rank [A ~ ~ a] af a[] a A ~ af ~ a ka a A ~ a A ~ a ka ~ - A ka ~ - A av [ ] [ ] [ ] ( ) ( ) k I k v k [A a] k I k v k [ k ( A - av ) ka] P ~ ' (-57, ok)
170 Canonical cameras given F F matri corresponds to P,P iff P FP is skew-symmetric ( X P' FPX, X) F matri, S skew-symmetric matri P [I ] P' [SF e'] [SF e'] (fund.matrif) F[I ] F S F e' F F S F Possible choice: P [I ] P' [[e'] F e'] Canonical representation: P [I ] P' [[e'] F + e' v λe']
171 he essential matri ~fundamental matri for calibrated cameras (remove K) E ˆ ' [ t] R R[R t] Eˆ - - ( ˆ K ; ˆ' K ' ) E K' FK 5 d.o.f. (3 for R; for t up to scale) E is essential matri if and only if two singularvalues are equal (and third) SVD E Udiag(,,)V
172 Motion from E Given W Four solutions R' UW V and t' U 3 R' ' UWV t' ' U 3
173 Four possible reconstructions from E (only one solution where points is in front of both cameras)
EPIPOLAR GEOMETRY WITH MANY DETAILS
 EPIPOLAR GEOMERY WIH MANY DEAILS hank ou for the slides. he come mostl from the following source. Marc Pollefes U. of North Carolina hree questions: (i) Correspondence geometr: Given an image point in
EPIPOLAR GEOMERY WIH MANY DEAILS hank ou for the slides. he come mostl from the following source. Marc Pollefes U. of North Carolina hree questions: (i) Correspondence geometr: Given an image point in
Lines and points. Lines and points
 omogeneous coordinates in the plane Homogeneous coordinates in the plane A line in the plane a + by + c is represented as (a, b, c). A line is a subset of points in the plane. All vectors (ka, kb, kc)
omogeneous coordinates in the plane Homogeneous coordinates in the plane A line in the plane a + by + c is represented as (a, b, c). A line is a subset of points in the plane. All vectors (ka, kb, kc)
Camera Projection Model
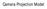 amera Projection Model 3D Point Projection (Pixel Space) O ( u, v ) ccd ccd f Projection plane (, Y, Z ) ( u, v ) img Z img (0,0) w img ( u, v ) img img uimg f Z p Y v img f Z p x y Zu f p Z img img x
amera Projection Model 3D Point Projection (Pixel Space) O ( u, v ) ccd ccd f Projection plane (, Y, Z ) ( u, v ) img Z img (0,0) w img ( u, v ) img img uimg f Z p Y v img f Z p x y Zu f p Z img img x
1. Projective geometry
 1. Projective geometry Homogeneous representation of points and lines in D space D projective space Points at infinity and the line at infinity Conics and dual conics Projective transformation Hierarchy
1. Projective geometry Homogeneous representation of points and lines in D space D projective space Points at infinity and the line at infinity Conics and dual conics Projective transformation Hierarchy
A geometric interpretation of the homogeneous coordinates is given in the following Figure.
 Introduction Homogeneous coordinates are an augmented representation of points and lines in R n spaces, embedding them in R n+1, hence using n + 1 parameters. This representation is useful in dealing with
Introduction Homogeneous coordinates are an augmented representation of points and lines in R n spaces, embedding them in R n+1, hence using n + 1 parameters. This representation is useful in dealing with
Camera Models and Affine Multiple Views Geometry
 Camera Models and Affine Multiple Views Geometry Subhashis Banerjee Dept. Computer Science and Engineering IIT Delhi email: suban@cse.iitd.ac.in May 29, 2001 1 1 Camera Models A Camera transforms a 3D
Camera Models and Affine Multiple Views Geometry Subhashis Banerjee Dept. Computer Science and Engineering IIT Delhi email: suban@cse.iitd.ac.in May 29, 2001 1 1 Camera Models A Camera transforms a 3D
Single view metrology
 EECS 44 Computer vision Single view metrology Review calibration Lines and planes at infinity Absolute conic Estimating geometry from a single image Etensions Reading: [HZ] Chapters,3,8 Calibration Problem
EECS 44 Computer vision Single view metrology Review calibration Lines and planes at infinity Absolute conic Estimating geometry from a single image Etensions Reading: [HZ] Chapters,3,8 Calibration Problem
Lecture 5. Epipolar Geometry. Professor Silvio Savarese Computational Vision and Geometry Lab. 21-Jan-15. Lecture 5 - Silvio Savarese
 Lecture 5 Epipolar Geometry Professor Silvio Savarese Computational Vision and Geometry Lab Silvio Savarese Lecture 5-21-Jan-15 Lecture 5 Epipolar Geometry Why is stereo useful? Epipolar constraints Essential
Lecture 5 Epipolar Geometry Professor Silvio Savarese Computational Vision and Geometry Lab Silvio Savarese Lecture 5-21-Jan-15 Lecture 5 Epipolar Geometry Why is stereo useful? Epipolar constraints Essential
3D from Photographs: Camera Calibration. Dr Francesco Banterle
 3D from Photographs: Camera Calibration Dr Francesco Banterle francesco.banterle@isti.cnr.it 3D from Photographs Automatic Matching of Images Camera Calibration Photographs Surface Reconstruction Dense
3D from Photographs: Camera Calibration Dr Francesco Banterle francesco.banterle@isti.cnr.it 3D from Photographs Automatic Matching of Images Camera Calibration Photographs Surface Reconstruction Dense
A Study of Kruppa s Equation for Camera Self-calibration
 Proceedings of the International Conference of Machine Vision and Machine Learning Prague, Czech Republic, August 14-15, 2014 Paper No. 57 A Study of Kruppa s Equation for Camera Self-calibration Luh Prapitasari,
Proceedings of the International Conference of Machine Vision and Machine Learning Prague, Czech Republic, August 14-15, 2014 Paper No. 57 A Study of Kruppa s Equation for Camera Self-calibration Luh Prapitasari,
Multiple View Geometry in Computer Vision
 Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Scene Planes & Homographies Lecture 19 March 24, 2005 2 In our last lecture, we examined various
Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Scene Planes & Homographies Lecture 19 March 24, 2005 2 In our last lecture, we examined various
Homogeneous Coordinates
 Homogeneous Coordinates Basilio Bona DAUIN-Politecnico di Torino October 2013 Basilio Bona (DAUIN-Politecnico di Torino) Homogeneous Coordinates October 2013 1 / 32 Introduction Homogeneous coordinates
Homogeneous Coordinates Basilio Bona DAUIN-Politecnico di Torino October 2013 Basilio Bona (DAUIN-Politecnico di Torino) Homogeneous Coordinates October 2013 1 / 32 Introduction Homogeneous coordinates
EE Camera & Image Formation
 Electric Electronic Engineering Bogazici University February 21, 2018 Introduction Introduction Camera models Goal: To understand the image acquisition process. Function of the camera Similar to that of
Electric Electronic Engineering Bogazici University February 21, 2018 Introduction Introduction Camera models Goal: To understand the image acquisition process. Function of the camera Similar to that of
Robotics - Homogeneous coordinates and transformations. Simone Ceriani
 Robotics - Homogeneous coordinates and transformations Simone Ceriani ceriani@elet.polimi.it Dipartimento di Elettronica e Informazione Politecnico di Milano 5 March 0 /49 Outline Introduction D space
Robotics - Homogeneous coordinates and transformations Simone Ceriani ceriani@elet.polimi.it Dipartimento di Elettronica e Informazione Politecnico di Milano 5 March 0 /49 Outline Introduction D space
Camera Calibration The purpose of camera calibration is to determine the intrinsic camera parameters (c 0,r 0 ), f, s x, s y, skew parameter (s =
 Camera Calibration The purpose of camera calibration is to determine the intrinsic camera parameters (c 0,r 0 ), f, s x, s y, skew parameter (s = cotα), and the lens distortion (radial distortion coefficient
Camera Calibration The purpose of camera calibration is to determine the intrinsic camera parameters (c 0,r 0 ), f, s x, s y, skew parameter (s = cotα), and the lens distortion (radial distortion coefficient
THE ENVELOPE OF LINES MEETING A FIXED LINE AND TANGENT TO TWO SPHERES
 6 September 2004 THE ENVELOPE OF LINES MEETING A FIXED LINE AND TANGENT TO TWO SPHERES Abstract. We study the set of lines that meet a fixed line and are tangent to two spheres and classify the configurations
6 September 2004 THE ENVELOPE OF LINES MEETING A FIXED LINE AND TANGENT TO TWO SPHERES Abstract. We study the set of lines that meet a fixed line and are tangent to two spheres and classify the configurations
Math 302 Outcome Statements Winter 2013
 Math 302 Outcome Statements Winter 2013 1 Rectangular Space Coordinates; Vectors in the Three-Dimensional Space (a) Cartesian coordinates of a point (b) sphere (c) symmetry about a point, a line, and a
Math 302 Outcome Statements Winter 2013 1 Rectangular Space Coordinates; Vectors in the Three-Dimensional Space (a) Cartesian coordinates of a point (b) sphere (c) symmetry about a point, a line, and a
Linear Algebra & Geometry why is linear algebra useful in computer vision?
 Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Pose estimation from point and line correspondences
 Pose estimation from point and line correspondences Giorgio Panin October 17, 008 1 Problem formulation Estimate (in a LSE sense) the pose of an object from N correspondences between known object points
Pose estimation from point and line correspondences Giorgio Panin October 17, 008 1 Problem formulation Estimate (in a LSE sense) the pose of an object from N correspondences between known object points
Trinocular Geometry Revisited
 Trinocular Geometry Revisited Jean Pounce and Martin Hebert 报告人 : 王浩人 2014-06-24 Contents 1. Introduction 2. Converging Triplets of Lines 3. Converging Triplets of Visual Rays 4. Discussion 1. Introduction
Trinocular Geometry Revisited Jean Pounce and Martin Hebert 报告人 : 王浩人 2014-06-24 Contents 1. Introduction 2. Converging Triplets of Lines 3. Converging Triplets of Visual Rays 4. Discussion 1. Introduction
Conics and their duals
 9 Conics and their duals You always admire what you really don t understand. Blaise Pascal So far we dealt almost exclusively with situations in which only points and lines were involved. Geometry would
9 Conics and their duals You always admire what you really don t understand. Blaise Pascal So far we dealt almost exclusively with situations in which only points and lines were involved. Geometry would
Geometric Modeling Summer Semester 2010 Mathematical Tools (1)
 Geometric Modeling Summer Semester 2010 Mathematical Tools (1) Recap: Linear Algebra Today... Topics: Mathematical Background Linear algebra Analysis & differential geometry Numerical techniques Geometric
Geometric Modeling Summer Semester 2010 Mathematical Tools (1) Recap: Linear Algebra Today... Topics: Mathematical Background Linear algebra Analysis & differential geometry Numerical techniques Geometric
Camera calibration. Outline. Pinhole camera. Camera projection models. Nonlinear least square methods A camera calibration tool
 Outline Camera calibration Camera projection models Camera calibration i Nonlinear least square methods A camera calibration tool Applications Digital Visual Effects Yung-Yu Chuang with slides b Richard
Outline Camera calibration Camera projection models Camera calibration i Nonlinear least square methods A camera calibration tool Applications Digital Visual Effects Yung-Yu Chuang with slides b Richard
Mathematics 309 Conic sections and their applicationsn. Chapter 2. Quadric figures. ai,j x i x j + b i x i + c =0. 1. Coordinate changes
 Mathematics 309 Conic sections and their applicationsn Chapter 2. Quadric figures In this chapter want to outline quickl how to decide what figure associated in 2D and 3D to quadratic equations look like.
Mathematics 309 Conic sections and their applicationsn Chapter 2. Quadric figures In this chapter want to outline quickl how to decide what figure associated in 2D and 3D to quadratic equations look like.
A Practical Method for Decomposition of the Essential Matrix
 Applied Mathematical Sciences, Vol. 8, 2014, no. 176, 8755-8770 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.410877 A Practical Method for Decomposition of the Essential Matrix Georgi
Applied Mathematical Sciences, Vol. 8, 2014, no. 176, 8755-8770 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.410877 A Practical Method for Decomposition of the Essential Matrix Georgi
Linear Algebra & Geometry why is linear algebra useful in computer vision?
 Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
8. Diagonalization.
 8. Diagonalization 8.1. Matrix Representations of Linear Transformations Matrix of A Linear Operator with Respect to A Basis We know that every linear transformation T: R n R m has an associated standard
8. Diagonalization 8.1. Matrix Representations of Linear Transformations Matrix of A Linear Operator with Respect to A Basis We know that every linear transformation T: R n R m has an associated standard
Singular Value Decomposition
 Singular Value Decomposition Motivatation The diagonalization theorem play a part in many interesting applications. Unfortunately not all matrices can be factored as A = PDP However a factorization A =
Singular Value Decomposition Motivatation The diagonalization theorem play a part in many interesting applications. Unfortunately not all matrices can be factored as A = PDP However a factorization A =
Optimisation on Manifolds
 Optimisation on Manifolds K. Hüper MPI Tübingen & Univ. Würzburg K. Hüper (MPI Tübingen & Univ. Würzburg) Applications in Computer Vision Grenoble 18/9/08 1 / 29 Contents 2 Examples Essential matrix estimation
Optimisation on Manifolds K. Hüper MPI Tübingen & Univ. Würzburg K. Hüper (MPI Tübingen & Univ. Würzburg) Applications in Computer Vision Grenoble 18/9/08 1 / 29 Contents 2 Examples Essential matrix estimation
Extra Problems for Math 2050 Linear Algebra I
 Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
CSE 252B: Computer Vision II
 CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Tasha Vanesian LECTURE 3 Calibrated 3D Reconstruction 3.1. Geometric View of Epipolar Constraint We are trying to solve the following problem:
CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Tasha Vanesian LECTURE 3 Calibrated 3D Reconstruction 3.1. Geometric View of Epipolar Constraint We are trying to solve the following problem:
Mobile Robotics 1. A Compact Course on Linear Algebra. Giorgio Grisetti
 Mobile Robotics 1 A Compact Course on Linear Algebra Giorgio Grisetti SA-1 Vectors Arrays of numbers They represent a point in a n dimensional space 2 Vectors: Scalar Product Scalar-Vector Product Changes
Mobile Robotics 1 A Compact Course on Linear Algebra Giorgio Grisetti SA-1 Vectors Arrays of numbers They represent a point in a n dimensional space 2 Vectors: Scalar Product Scalar-Vector Product Changes
Exercises for Unit I I (Vector algebra and Euclidean geometry)
 Exercises for Unit I I (Vector algebra and Euclidean geometry) I I.1 : Approaches to Euclidean geometry Ryan : pp. 5 15 1. What is the minimum number of planes containing three concurrent noncoplanar lines
Exercises for Unit I I (Vector algebra and Euclidean geometry) I I.1 : Approaches to Euclidean geometry Ryan : pp. 5 15 1. What is the minimum number of planes containing three concurrent noncoplanar lines
MATH PROBLEM SET 6
 MATH 431-2018 PROBLEM SET 6 DECEMBER 2, 2018 DUE TUESDAY 11 DECEMBER 2018 1. Rotations and quaternions Consider the line l through p 0 := (1, 0, 0) and parallel to the vector v := 1 1, 1 that is, defined
MATH 431-2018 PROBLEM SET 6 DECEMBER 2, 2018 DUE TUESDAY 11 DECEMBER 2018 1. Rotations and quaternions Consider the line l through p 0 := (1, 0, 0) and parallel to the vector v := 1 1, 1 that is, defined
16. Analysis and Computation of the Intrinsic Camera Parameters
 16. Analysis and Computation of the Intrinsic Camera Parameters Eduardo Bayro-Corrochano and Bodo Rosenhahn Institute of Computer Science and Applied Mathematics, Christian-Albrechts-University of Kiel
16. Analysis and Computation of the Intrinsic Camera Parameters Eduardo Bayro-Corrochano and Bodo Rosenhahn Institute of Computer Science and Applied Mathematics, Christian-Albrechts-University of Kiel
Outline. Linear Algebra for Computer Vision
 Outline Linear Algebra for Computer Vision Introduction CMSC 88 D Notation and Basics Motivation Linear systems of equations Gauss Elimination, LU decomposition Linear Spaces and Operators Addition, scalar
Outline Linear Algebra for Computer Vision Introduction CMSC 88 D Notation and Basics Motivation Linear systems of equations Gauss Elimination, LU decomposition Linear Spaces and Operators Addition, scalar
APPLICATIONS The eigenvalues are λ = 5, 5. An orthonormal basis of eigenvectors consists of
 CHAPTER III APPLICATIONS The eigenvalues are λ =, An orthonormal basis of eigenvectors consists of, The eigenvalues are λ =, A basis of eigenvectors consists of, 4 which are not perpendicular However,
CHAPTER III APPLICATIONS The eigenvalues are λ =, An orthonormal basis of eigenvectors consists of, The eigenvalues are λ =, A basis of eigenvectors consists of, 4 which are not perpendicular However,
Multiple View Geometry in Computer Vision
 Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Basic Information Instructor: Professor Ron Sahoo Office: NS 218 Tel: (502) 852-2731 Fax: (502)
Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Basic Information Instructor: Professor Ron Sahoo Office: NS 218 Tel: (502) 852-2731 Fax: (502)
Hyperbolic Conformal Geometry with Clifford Algebra 1)
 MM Research Preprints, 72 83 No. 18, Dec. 1999. Beijing Hyperbolic Conformal Geometry with Clifford Algebra 1) Hongbo Li Abstract. In this paper we study hyperbolic conformal geometry following a Clifford
MM Research Preprints, 72 83 No. 18, Dec. 1999. Beijing Hyperbolic Conformal Geometry with Clifford Algebra 1) Hongbo Li Abstract. In this paper we study hyperbolic conformal geometry following a Clifford
Augmented Reality VU Camera Registration. Prof. Vincent Lepetit
 Augmented Reality VU Camera Registration Prof. Vincent Lepetit Different Approaches to Vision-based 3D Tracking [From D. Wagner] [From Drummond PAMI02] [From Davison ICCV01] Consider natural features Consider
Augmented Reality VU Camera Registration Prof. Vincent Lepetit Different Approaches to Vision-based 3D Tracking [From D. Wagner] [From Drummond PAMI02] [From Davison ICCV01] Consider natural features Consider
MAT1035 Analytic Geometry
 MAT1035 Analytic Geometry Lecture Notes R.A. Sabri Kaan Gürbüzer Dokuz Eylül University 2016 2 Contents 1 Review of Trigonometry 5 2 Polar Coordinates 7 3 Vectors in R n 9 3.1 Located Vectors..............................................
MAT1035 Analytic Geometry Lecture Notes R.A. Sabri Kaan Gürbüzer Dokuz Eylül University 2016 2 Contents 1 Review of Trigonometry 5 2 Polar Coordinates 7 3 Vectors in R n 9 3.1 Located Vectors..............................................
TWO THEOREMS ON THE FOCUS-SHARING ELLIPSES: A THREE-DIMENSIONAL VIEW
 TWO THEOREMS ON THE FOCUS-SHARING ELLIPSES: A THREE-DIMENSIONAL VIEW ILYA I. BOGDANOV Abstract. Consider three ellipses each two of which share a common focus. The radical axes of the pairs of these ellipses
TWO THEOREMS ON THE FOCUS-SHARING ELLIPSES: A THREE-DIMENSIONAL VIEW ILYA I. BOGDANOV Abstract. Consider three ellipses each two of which share a common focus. The radical axes of the pairs of these ellipses
6.801/866. Affine Structure from Motion. T. Darrell
 6.801/866 Affine Structure from Motion T. Darrell [Read F&P Ch. 12.0, 12.2, 12.3, 12.4] Affine geometry is, roughly speaking, what is left after all ability to measure lengths, areas, angles, etc. has
6.801/866 Affine Structure from Motion T. Darrell [Read F&P Ch. 12.0, 12.2, 12.3, 12.4] Affine geometry is, roughly speaking, what is left after all ability to measure lengths, areas, angles, etc. has
Name of the Student:
 Engineering Mathematics 016 SUBJECT NAME : Engineering Mathematics - I SUBJECT CODE : MA111 MATERIAL NAME : Universit Questions REGULATION : R008 WEBSITE : wwwhariganeshcom UPDATED ON : Januar 016 TEXTBOOK
Engineering Mathematics 016 SUBJECT NAME : Engineering Mathematics - I SUBJECT CODE : MA111 MATERIAL NAME : Universit Questions REGULATION : R008 WEBSITE : wwwhariganeshcom UPDATED ON : Januar 016 TEXTBOOK
Decomposition of Screw-motion Envelopes of Quadrics
 Decomposition of Screw-motion Envelopes of Quadrics Šárka Voráčová * Department of Applied Mathematics Faculty of Transportation, CTU in Prague Study and realization of the construction of the envelope
Decomposition of Screw-motion Envelopes of Quadrics Šárka Voráčová * Department of Applied Mathematics Faculty of Transportation, CTU in Prague Study and realization of the construction of the envelope
Identifying second degree equations
 Chapter 7 Identifing second degree equations 71 The eigenvalue method In this section we appl eigenvalue methods to determine the geometrical nature of the second degree equation a 2 + 2h + b 2 + 2g +
Chapter 7 Identifing second degree equations 71 The eigenvalue method In this section we appl eigenvalue methods to determine the geometrical nature of the second degree equation a 2 + 2h + b 2 + 2g +
QUESTION BANK ON STRAIGHT LINE AND CIRCLE
 QUESTION BANK ON STRAIGHT LINE AND CIRCLE Select the correct alternative : (Only one is correct) Q. If the lines x + y + = 0 ; 4x + y + 4 = 0 and x + αy + β = 0, where α + β =, are concurrent then α =,
QUESTION BANK ON STRAIGHT LINE AND CIRCLE Select the correct alternative : (Only one is correct) Q. If the lines x + y + = 0 ; 4x + y + 4 = 0 and x + αy + β = 0, where α + β =, are concurrent then α =,
Final Exam Due on Sunday 05/06
 Final Exam Due on Sunday 05/06 The exam should be completed individually without collaboration. However, you are permitted to consult with the textbooks, notes, slides and even internet resources. If you
Final Exam Due on Sunday 05/06 The exam should be completed individually without collaboration. However, you are permitted to consult with the textbooks, notes, slides and even internet resources. If you
PAijpam.eu EPIPOLAR GEOMETRY WITH A FUNDAMENTAL MATRIX IN CANONICAL FORM Georgi Hristov Georgiev 1, Vencislav Dakov Radulov 2
 International Journal of Pure and Applied Mathematics Volume 105 No. 4 2015, 669-683 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu doi: http://dx.doi.org/10.12732/ijpam.v105i4.8
International Journal of Pure and Applied Mathematics Volume 105 No. 4 2015, 669-683 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu doi: http://dx.doi.org/10.12732/ijpam.v105i4.8
CLASS XII MATHEMATICS. Weightage (Marks) (i) Relations and Functions 10. Type of Questions Weightage of Number of Total Marks each question questions
 CLASS XII MATHEMATICS Units Weightage (Marks) (i) Relations and Functions 0 (ii) Algebra (Matrices and Determinants) (iii) Calculus 44 (iv) Vector and Three dimensional Geometry 7 (v) Linear Programming
CLASS XII MATHEMATICS Units Weightage (Marks) (i) Relations and Functions 0 (ii) Algebra (Matrices and Determinants) (iii) Calculus 44 (iv) Vector and Three dimensional Geometry 7 (v) Linear Programming
Statistical Geometry Processing Winter Semester 2011/2012
 Statistical Geometry Processing Winter Semester 2011/2012 Linear Algebra, Function Spaces & Inverse Problems Vector and Function Spaces 3 Vectors vectors are arrows in space classically: 2 or 3 dim. Euclidian
Statistical Geometry Processing Winter Semester 2011/2012 Linear Algebra, Function Spaces & Inverse Problems Vector and Function Spaces 3 Vectors vectors are arrows in space classically: 2 or 3 dim. Euclidian
Algorithms for Computing a Planar Homography from Conics in Correspondence
 Algorithms for Computing a Planar Homography from Conics in Correspondence Juho Kannala, Mikko Salo and Janne Heikkilä Machine Vision Group University of Oulu, Finland {jkannala, msa, jth@ee.oulu.fi} Abstract
Algorithms for Computing a Planar Homography from Conics in Correspondence Juho Kannala, Mikko Salo and Janne Heikkilä Machine Vision Group University of Oulu, Finland {jkannala, msa, jth@ee.oulu.fi} Abstract
Lecture 2: Linear Algebra Review
 EE 227A: Convex Optimization and Applications January 19 Lecture 2: Linear Algebra Review Lecturer: Mert Pilanci Reading assignment: Appendix C of BV. Sections 2-6 of the web textbook 1 2.1 Vectors 2.1.1
EE 227A: Convex Optimization and Applications January 19 Lecture 2: Linear Algebra Review Lecturer: Mert Pilanci Reading assignment: Appendix C of BV. Sections 2-6 of the web textbook 1 2.1 Vectors 2.1.1
MECH 576 Geometry in Mechanics September 16, 2009 Using Line Geometry
 MECH 576 Geometry in Mechanics September 16, 2009 Using Line Geometry 1 Deriving Equations in Line Coordinates Four exercises in deriving fundamental geometric equations with line coordinates will be conducted.
MECH 576 Geometry in Mechanics September 16, 2009 Using Line Geometry 1 Deriving Equations in Line Coordinates Four exercises in deriving fundamental geometric equations with line coordinates will be conducted.
Kinematics. Chapter Multi-Body Systems
 Chapter 2 Kinematics This chapter first introduces multi-body systems in conceptual terms. It then describes the concept of a Euclidean frame in the material world, following the concept of a Euclidean
Chapter 2 Kinematics This chapter first introduces multi-body systems in conceptual terms. It then describes the concept of a Euclidean frame in the material world, following the concept of a Euclidean
CSE 252B: Computer Vision II
 CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Hamed Masnadi Shirazi, Solmaz Alipour LECTURE 5 Relationships between the Homography and the Essential Matrix 5.1. Introduction In practice,
CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Hamed Masnadi Shirazi, Solmaz Alipour LECTURE 5 Relationships between the Homography and the Essential Matrix 5.1. Introduction In practice,
ON THE INVERSE KINEMATICS OF A FRAGMENT OF PROTEIN BACKBONE
 ON THE INVERSE KINEMATIS OF A FRAGMENT OF PROTEIN BAKBONE Guanfeng Liu, R.J. Milgram, A. Dhanik, and J.. Latombe Department of omputer Science, Stanford University Department of Mathematics, Stanford University
ON THE INVERSE KINEMATIS OF A FRAGMENT OF PROTEIN BAKBONE Guanfeng Liu, R.J. Milgram, A. Dhanik, and J.. Latombe Department of omputer Science, Stanford University Department of Mathematics, Stanford University
POINT. Preface. The concept of Point is very important for the study of coordinate
 POINT Preface The concept of Point is ver important for the stud of coordinate geometr. This chapter deals with various forms of representing a Point and several associated properties. The concept of coordinates
POINT Preface The concept of Point is ver important for the stud of coordinate geometr. This chapter deals with various forms of representing a Point and several associated properties. The concept of coordinates
Basic Math for
 Basic Math for 16-720 August 23, 2002 1 Linear Algebra 1.1 Vectors and Matrices First, a reminder of a few basic notations, definitions, and terminology: Unless indicated otherwise, vectors are always
Basic Math for 16-720 August 23, 2002 1 Linear Algebra 1.1 Vectors and Matrices First, a reminder of a few basic notations, definitions, and terminology: Unless indicated otherwise, vectors are always
CHAPTER 3. Gauss map. In this chapter we will study the Gauss map of surfaces in R 3.
 CHAPTER 3 Gauss map In this chapter we will study the Gauss map of surfaces in R 3. 3.1. Surfaces in R 3 Let S R 3 be a submanifold of dimension 2. Let {U i, ϕ i } be a DS on S. For any p U i we have a
CHAPTER 3 Gauss map In this chapter we will study the Gauss map of surfaces in R 3. 3.1. Surfaces in R 3 Let S R 3 be a submanifold of dimension 2. Let {U i, ϕ i } be a DS on S. For any p U i we have a
Distance Formula in 3-D Given any two points P 1 (x 1, y 1, z 1 ) and P 2 (x 2, y 2, z 2 ) the distance between them is ( ) ( ) ( )
 Vectors and the Geometry of Space Vector Space The 3-D coordinate system (rectangular coordinates ) is the intersection of three perpendicular (orthogonal) lines called coordinate axis: x, y, and z. Their
Vectors and the Geometry of Space Vector Space The 3-D coordinate system (rectangular coordinates ) is the intersection of three perpendicular (orthogonal) lines called coordinate axis: x, y, and z. Their
(D) (A) Q.3 To which of the following circles, the line y x + 3 = 0 is normal at the point ? 2 (A) 2
 CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
Two-View Segmentation of Dynamic Scenes from the Multibody Fundamental Matrix
 Two-View Segmentation of Dynamic Scenes from the Multibody Fundamental Matrix René Vidal Stefano Soatto Shankar Sastry Department of EECS, UC Berkeley Department of Computer Sciences, UCLA 30 Cory Hall,
Two-View Segmentation of Dynamic Scenes from the Multibody Fundamental Matrix René Vidal Stefano Soatto Shankar Sastry Department of EECS, UC Berkeley Department of Computer Sciences, UCLA 30 Cory Hall,
1 Vectors and the Scalar Product
 1 Vectors and the Scalar Product 1.1 Vector Algebra vector in R n : an n-tuple of real numbers v = a 1, a 2,..., a n. For example, if n = 2 and a 1 = 1 and a 2 = 1, then w = 1, 1 is vector in R 2. Vectors
1 Vectors and the Scalar Product 1.1 Vector Algebra vector in R n : an n-tuple of real numbers v = a 1, a 2,..., a n. For example, if n = 2 and a 1 = 1 and a 2 = 1, then w = 1, 1 is vector in R 2. Vectors
Algebra Workshops 10 and 11
 Algebra Workshops 1 and 11 Suggestion: For Workshop 1 please do questions 2,3 and 14. For the other questions, it s best to wait till the material is covered in lectures. Bilinear and Quadratic Forms on
Algebra Workshops 1 and 11 Suggestion: For Workshop 1 please do questions 2,3 and 14. For the other questions, it s best to wait till the material is covered in lectures. Bilinear and Quadratic Forms on
The structure tensor in projective spaces
 The structure tensor in projective spaces Klas Nordberg Computer Vision Laboratory Department of Electrical Engineering Linköping University Sweden Abstract The structure tensor has been used mainly for
The structure tensor in projective spaces Klas Nordberg Computer Vision Laboratory Department of Electrical Engineering Linköping University Sweden Abstract The structure tensor has been used mainly for
Image Transform. Panorama Image (Keller+Lind Hall)
 Image Transform Panorama Image (Keller+Lind Hall) Image Warping (Coordinate Transform) u I v 1 I 2 I ( v) = I ( u) 2 1 Image Warping (Coordinate Transform) u I v 1 I 2 I ( v) = I ( u) 2 1 : Piel transport
Image Transform Panorama Image (Keller+Lind Hall) Image Warping (Coordinate Transform) u I v 1 I 2 I ( v) = I ( u) 2 1 Image Warping (Coordinate Transform) u I v 1 I 2 I ( v) = I ( u) 2 1 : Piel transport
Vectors Coordinate frames 2D implicit curves 2D parametric curves. Graphics 2008/2009, period 1. Lecture 2: vectors, curves, and surfaces
 Graphics 2008/2009, period 1 Lecture 2 Vectors, curves, and surfaces Computer graphics example: Pixar (source: http://www.pixar.com) Computer graphics example: Pixar (source: http://www.pixar.com) Computer
Graphics 2008/2009, period 1 Lecture 2 Vectors, curves, and surfaces Computer graphics example: Pixar (source: http://www.pixar.com) Computer graphics example: Pixar (source: http://www.pixar.com) Computer
Multi-Frame Factorization Techniques
 Multi-Frame Factorization Techniques Suppose { x j,n } J,N j=1,n=1 is a set of corresponding image coordinates, where the index n = 1,...,N refers to the n th scene point and j = 1,..., J refers to the
Multi-Frame Factorization Techniques Suppose { x j,n } J,N j=1,n=1 is a set of corresponding image coordinates, where the index n = 1,...,N refers to the n th scene point and j = 1,..., J refers to the
Linear algebra for computational statistics
 University of Seoul May 3, 2018 Vector and Matrix Notation Denote 2-dimensional data array (n p matrix) by X. Denote the element in the ith row and the jth column of X by x ij or (X) ij. Denote by X j
University of Seoul May 3, 2018 Vector and Matrix Notation Denote 2-dimensional data array (n p matrix) by X. Denote the element in the ith row and the jth column of X by x ij or (X) ij. Denote by X j
arxiv: v6 [math.mg] 9 May 2014
![arxiv: v6 [math.mg] 9 May 2014 arxiv: v6 [math.mg] 9 May 2014](/thumbs/83/88763528.jpg) arxiv:1311.0131v6 [math.mg] 9 May 2014 A Clifford algebraic Approach to Line Geometry Daniel Klawitter Abstract. In this paper we combine methods from projective geometry, Klein s model, and Clifford algebra.
arxiv:1311.0131v6 [math.mg] 9 May 2014 A Clifford algebraic Approach to Line Geometry Daniel Klawitter Abstract. In this paper we combine methods from projective geometry, Klein s model, and Clifford algebra.
DIRECTORATE OF EDUCATION GOVT. OF NCT OF DELHI
 456789045678904567890456789045678904567890456789045678904567890456789045678904567890 456789045678904567890456789045678904567890456789045678904567890456789045678904567890 QUESTION BANK 456789045678904567890456789045678904567890456789045678904567890456789045678904567890
456789045678904567890456789045678904567890456789045678904567890456789045678904567890 456789045678904567890456789045678904567890456789045678904567890456789045678904567890 QUESTION BANK 456789045678904567890456789045678904567890456789045678904567890456789045678904567890
Methods in Computer Vision: Introduction to Matrix Lie Groups
 Methods in Computer Vision: Introduction to Matrix Lie Groups Oren Freifeld Computer Science, Ben-Gurion University June 14, 2017 June 14, 2017 1 / 46 Definition and Basic Properties Definition (Matrix
Methods in Computer Vision: Introduction to Matrix Lie Groups Oren Freifeld Computer Science, Ben-Gurion University June 14, 2017 June 14, 2017 1 / 46 Definition and Basic Properties Definition (Matrix
11/29/2010. Propagation in Anisotropic Media 3. Introduction. Introduction. Gabriel Popescu
 Propagation in Anisotropic Media Gabriel Popescu University of Illinois at Urbana Champaign Beckman Institute Quantitative Light Imaging Laboratory http://light.ece.uiuc.edu Principles of Optical Imaging
Propagation in Anisotropic Media Gabriel Popescu University of Illinois at Urbana Champaign Beckman Institute Quantitative Light Imaging Laboratory http://light.ece.uiuc.edu Principles of Optical Imaging
Part IB GEOMETRY (Lent 2016): Example Sheet 1
 Part IB GEOMETRY (Lent 2016): Example Sheet 1 (a.g.kovalev@dpmms.cam.ac.uk) 1. Suppose that H is a hyperplane in Euclidean n-space R n defined by u x = c for some unit vector u and constant c. The reflection
Part IB GEOMETRY (Lent 2016): Example Sheet 1 (a.g.kovalev@dpmms.cam.ac.uk) 1. Suppose that H is a hyperplane in Euclidean n-space R n defined by u x = c for some unit vector u and constant c. The reflection
SIAM Conference on Applied Algebraic Geometry Daejeon, South Korea, Irina Kogan North Carolina State University. Supported in part by the
 SIAM Conference on Applied Algebraic Geometry Daejeon, South Korea, 2015 Irina Kogan North Carolina State University Supported in part by the 1 Based on: 1. J. M. Burdis, I. A. Kogan and H. Hong Object-image
SIAM Conference on Applied Algebraic Geometry Daejeon, South Korea, 2015 Irina Kogan North Carolina State University Supported in part by the 1 Based on: 1. J. M. Burdis, I. A. Kogan and H. Hong Object-image
Chapter 3. Riemannian Manifolds - I. The subject of this thesis is to extend the combinatorial curve reconstruction approach to curves
 Chapter 3 Riemannian Manifolds - I The subject of this thesis is to extend the combinatorial curve reconstruction approach to curves embedded in Riemannian manifolds. A Riemannian manifold is an abstraction
Chapter 3 Riemannian Manifolds - I The subject of this thesis is to extend the combinatorial curve reconstruction approach to curves embedded in Riemannian manifolds. A Riemannian manifold is an abstraction
Reading. 4. Affine transformations. Required: Watt, Section 1.1. Further reading:
 Reading Required: Watt, Section.. Further reading: 4. Affine transformations Fole, et al, Chapter 5.-5.5. David F. Rogers and J. Alan Adams, Mathematical Elements for Computer Graphics, 2 nd Ed., McGraw-Hill,
Reading Required: Watt, Section.. Further reading: 4. Affine transformations Fole, et al, Chapter 5.-5.5. David F. Rogers and J. Alan Adams, Mathematical Elements for Computer Graphics, 2 nd Ed., McGraw-Hill,
MATH 1020 WORKSHEET 12.1 & 12.2 Vectors in the Plane
 MATH 100 WORKSHEET 1.1 & 1. Vectors in the Plane Find the vector v where u =, 1 and w = 1, given the equation v = u w. Solution. v = u w =, 1 1, =, 1 +, 4 =, 1 4 = 0, 5 Find the magnitude of v = 4, 3 Solution.
MATH 100 WORKSHEET 1.1 & 1. Vectors in the Plane Find the vector v where u =, 1 and w = 1, given the equation v = u w. Solution. v = u w =, 1 1, =, 1 +, 4 =, 1 4 = 0, 5 Find the magnitude of v = 4, 3 Solution.
1 Differentiable manifolds and smooth maps. (Solutions)
 1 Differentiable manifolds and smooth maps Solutions Last updated: February 16 2012 Problem 1 a The projection maps a point P x y S 1 to the point P u 0 R 2 the intersection of the line NP with the x-axis
1 Differentiable manifolds and smooth maps Solutions Last updated: February 16 2012 Problem 1 a The projection maps a point P x y S 1 to the point P u 0 R 2 the intersection of the line NP with the x-axis
Induced Planar Homologies in Epipolar Geometry
 Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 12, Number 4 (2016), pp. 3759 3773 Research India Publications http://www.ripublication.com/gjpam.htm Induced Planar Homologies in
Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 12, Number 4 (2016), pp. 3759 3773 Research India Publications http://www.ripublication.com/gjpam.htm Induced Planar Homologies in
3. Interpret the graph of x = 1 in the contexts of (a) a number line (b) 2-space (c) 3-space
 MA2: Prepared by Dr. Archara Pacheenburawana Exercise Chapter 3 Exercise 3.. A cube of side 4 has its geometric center at the origin and its faces parallel to the coordinate planes. Sketch the cube and
MA2: Prepared by Dr. Archara Pacheenburawana Exercise Chapter 3 Exercise 3.. A cube of side 4 has its geometric center at the origin and its faces parallel to the coordinate planes. Sketch the cube and
Linear Algebra Primer
 Linear Algebra Primer David Doria daviddoria@gmail.com Wednesday 3 rd December, 2008 Contents Why is it called Linear Algebra? 4 2 What is a Matrix? 4 2. Input and Output.....................................
Linear Algebra Primer David Doria daviddoria@gmail.com Wednesday 3 rd December, 2008 Contents Why is it called Linear Algebra? 4 2 What is a Matrix? 4 2. Input and Output.....................................
Dynamic P n to P n Alignment
 Dynamic P n to P n Alignment Amnon Shashua and Lior Wolf School of Engineering and Computer Science, the Hebrew University of Jerusalem, Jerusalem, 91904, Israel {shashua,lwolf}@cs.huji.ac.il We introduce
Dynamic P n to P n Alignment Amnon Shashua and Lior Wolf School of Engineering and Computer Science, the Hebrew University of Jerusalem, Jerusalem, 91904, Israel {shashua,lwolf}@cs.huji.ac.il We introduce
Matrix Algebra for Engineers Jeffrey R. Chasnov
 Matrix Algebra for Engineers Jeffrey R. Chasnov The Hong Kong University of Science and Technology The Hong Kong University of Science and Technology Department of Mathematics Clear Water Bay, Kowloon
Matrix Algebra for Engineers Jeffrey R. Chasnov The Hong Kong University of Science and Technology The Hong Kong University of Science and Technology Department of Mathematics Clear Water Bay, Kowloon
Study guide for Exam 1. by William H. Meeks III October 26, 2012
 Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
Projection pencils of quadrics and Ivory s theorem
 Projection pencils of quadrics and Ivory s theorem Á.G. Horváth Abstract. Using selfadjoint regular endomorphisms, the authors of [7] defined, for an indefinite inner product, a variant of the notion of
Projection pencils of quadrics and Ivory s theorem Á.G. Horváth Abstract. Using selfadjoint regular endomorphisms, the authors of [7] defined, for an indefinite inner product, a variant of the notion of
ROBOTICS 01PEEQW. Basilio Bona DAUIN Politecnico di Torino
 ROBOTICS 01PEEQW Basilio Bona DAUIN Politecnico di Torino Kinematic Functions Kinematic functions Kinematics deals with the study of four functions(called kinematic functions or KFs) that mathematically
ROBOTICS 01PEEQW Basilio Bona DAUIN Politecnico di Torino Kinematic Functions Kinematic functions Kinematics deals with the study of four functions(called kinematic functions or KFs) that mathematically
Chapter 12. The cross ratio Klein s Erlanger program The projective line. Math 4520, Fall 2017
 Chapter 12 The cross ratio Math 4520, Fall 2017 We have studied the collineations of a projective plane, the automorphisms of the underlying field, the linear functions of Affine geometry, etc. We have
Chapter 12 The cross ratio Math 4520, Fall 2017 We have studied the collineations of a projective plane, the automorphisms of the underlying field, the linear functions of Affine geometry, etc. We have
+ 2gx + 2fy + c = 0 if S
 CIRCLE DEFINITIONS A circle is the locus of a point which moves in such a way that its distance from a fixed point, called the centre, is always a constant. The distance r from the centre is called the
CIRCLE DEFINITIONS A circle is the locus of a point which moves in such a way that its distance from a fixed point, called the centre, is always a constant. The distance r from the centre is called the
Introduction to pinhole cameras
 Introduction to pinhole cameras Lesson given by Sébastien Piérard in the course Introduction aux techniques audio et vidéo (ULg, Pr JJ Embrechts) INTELSIG, Montefiore Institute, University of Liège, Belgium
Introduction to pinhole cameras Lesson given by Sébastien Piérard in the course Introduction aux techniques audio et vidéo (ULg, Pr JJ Embrechts) INTELSIG, Montefiore Institute, University of Liège, Belgium
Numerical Methods for Inverse Kinematics
 Numerical Methods for Inverse Kinematics Niels Joubert, UC Berkeley, CS184 2008-11-25 Inverse Kinematics is used to pose models by specifying endpoints of segments rather than individual joint angles.
Numerical Methods for Inverse Kinematics Niels Joubert, UC Berkeley, CS184 2008-11-25 Inverse Kinematics is used to pose models by specifying endpoints of segments rather than individual joint angles.
Analytic Geometry MAT 1035
 Analytic Geometry MAT 035 5.09.04 WEEKLY PROGRAM - The first week of the semester, we will introduce the course and given a brief outline. We continue with vectors in R n and some operations including
Analytic Geometry MAT 035 5.09.04 WEEKLY PROGRAM - The first week of the semester, we will introduce the course and given a brief outline. We continue with vectors in R n and some operations including
Chapter 8. Rigid transformations
 Chapter 8. Rigid transformations We are about to start drawing figures in 3D. There are no built-in routines for this purpose in PostScript, and we shall have to start more or less from scratch in extending
Chapter 8. Rigid transformations We are about to start drawing figures in 3D. There are no built-in routines for this purpose in PostScript, and we shall have to start more or less from scratch in extending
Mathematical Fundamentals
 Mathematical Fundamentals Ming-Hwa Wang, Ph.D. COEN 148/290 Computer Graphics COEN 166/366 Artificial Intelligence COEN 396 Interactive Multimedia and Game Programming Department of Computer Engineering
Mathematical Fundamentals Ming-Hwa Wang, Ph.D. COEN 148/290 Computer Graphics COEN 166/366 Artificial Intelligence COEN 396 Interactive Multimedia and Game Programming Department of Computer Engineering
APPENDIX A. Background Mathematics. A.1 Linear Algebra. Vector algebra. Let x denote the n-dimensional column vector with components x 1 x 2.
 APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
Q.2 A, B and C are points in the xy plane such that A(1, 2) ; B (5, 6) and AC = 3BC. Then. (C) 1 1 or
 STRAIGHT LINE [STRAIGHT OBJECTIVE TYPE] Q. A variable rectangle PQRS has its sides parallel to fied directions. Q and S lie respectivel on the lines = a, = a and P lies on the ais. Then the locus of R
STRAIGHT LINE [STRAIGHT OBJECTIVE TYPE] Q. A variable rectangle PQRS has its sides parallel to fied directions. Q and S lie respectivel on the lines = a, = a and P lies on the ais. Then the locus of R
Definition: A vector is a directed line segment which represents a displacement from one point P to another point Q.
 THE UNIVERSITY OF NEW SOUTH WALES SCHOOL OF MATHEMATICS AND STATISTICS MATH Algebra Section : - Introduction to Vectors. You may have already met the notion of a vector in physics. There you will have
THE UNIVERSITY OF NEW SOUTH WALES SCHOOL OF MATHEMATICS AND STATISTICS MATH Algebra Section : - Introduction to Vectors. You may have already met the notion of a vector in physics. There you will have
AOL Spring Wavefront Sensing. Figure 1: Principle of operation of the Shack-Hartmann wavefront sensor
 AOL Spring Wavefront Sensing The Shack Hartmann Wavefront Sensor system provides accurate, high-speed measurements of the wavefront shape and intensity distribution of beams by analyzing the location and
AOL Spring Wavefront Sensing The Shack Hartmann Wavefront Sensor system provides accurate, high-speed measurements of the wavefront shape and intensity distribution of beams by analyzing the location and
Mathematics 1. Part II: Linear Algebra. Exercises and problems
 Bachelor Degree in Informatics Engineering Barcelona School of Informatics Mathematics Part II: Linear Algebra Eercises and problems February 5 Departament de Matemàtica Aplicada Universitat Politècnica
Bachelor Degree in Informatics Engineering Barcelona School of Informatics Mathematics Part II: Linear Algebra Eercises and problems February 5 Departament de Matemàtica Aplicada Universitat Politècnica
