Deep Learning. A journey from feature extraction and engineering to end-to-end pipelines. Part 2: Neural Networks. Andrei Bursuc
|
|
|
- Camron Mason
- 5 years ago
- Views:
Transcription
1 Deep Learning A journey from feature extraction and engineering to end-to-end pipelines Part 2: Neural Networks Andrei Bursuc With slides from A. Karpathy, F. Fleuret, J. Johnson, S. Yeung, G. Louppe, Y. Avrithis... 1 / 149
2 Empirical risk minimization Consider a function f:x Y produced by some learning algorithm. The predictions of this function can be evaluated through a loss l:y Y R such that l(y, f(x)) 0 measures how close is the prediction f(x) from y. For example, for classi!cation: for regression: l(y, f(x))=1 y f(x) l(y, f(x))=(y f(x)) 2 2 / 149
3 Let us denote as F the hypothesis space, i.e. the set of all functions f than can be produced by the chosen learning algorithm. We are looking for a function f generalization error) F with a small expected risk (or R(f)=E (x,y) P(X,Y) [l(y, f(x))]. This means that for a given data generating distribution and for a given hypothesis space, the optimal model is f =argmin f F R(f). 3 / 149
4 Unfortunately, since P(X, Y) is unknown, the expected risk cannot be evaluated and the optimal model cannot be determined. However, given training data d={(x i, y i ) i=1,, N}, we can compute an estimate, the empirical risk (or training error) ˆR(f,d)= 1 N l(y i, f(x i )). (x i,y i ) d This estimate can be used for!nding a good enough approximation of f, giving rise to the empirical risk minimization principle: f d =argmin f F ˆR(f, d) 4 / 149
5 Most machine learning algorithms, including neural networks, implement empirical risk minimization. Under regularity assumptions, empirical risk minimizers converge: lim f d = f N This is why tuning the parameters of the model to make it work on the training data is a reasonable thing to do. 5 / 149
6 Neural Networks / 149
7 The neuron Inspired by neuroscience and human brain, but resemblances do not go too far In fact there several types of neurons with di"erent functions and the metaphor does not hold everywhere Slide credit: A. Karpathy 7 / 149
8 The neuron Inspired by neuroscience and human brain, but resemblances do not go too far Slide credit: A. Karpathy 8 / 149
9 Neural Networks Inspired by neuroscience and human brain, but resemblances do not go too far Slide credit: A. Karpathy 9 / 149
10 Discovery of oriented cells in the visual cortex Find out more from video Hubel& Wiesel, / 149
11 Discovery of oriented cells in the visual cortex Hubel& Wiesel, / 149
12 Mark I Perceptron!rst implementation of the perceptron algorithm the machine was connected to a camera that used 20x20 cadmium sul!de photocells to produce a 400-pixel image it recognized letter of the alphabet Rosenblatt, / 149
13 Threshold Logic Unit The Threshold Logic Unit (McCulloch and Pitts, 1943) was the!rst mathematical model for a neuron. Assuming Boolean inputs and outputs, it is de!ned as: f(x)=1 { i w i x i +b 0} This unit can implement: or(a, b)=1 {a+b 0.5 0} and(a, b)=1 {a+b 1.5 0} not(a)=1 { a+0.5 0} Therefore, any Boolean function can be built which such units. 13 / 149
14 Perceptron The perceptron (Rosenblatt, 1957) is very similar, except that the inputs are real: { f(x)= 1 if i w i x i + b 0 0 otherwise This model was originally motivated by biology, with w i being synaptic weights and x i and f!ring rates. This is a cartoonesque biological model. 14 / 149
15 Let us de!ne the activation function: σ(x)= { 1 if x 0 0 otherwise Therefore, the perceptron classi!cation rule can be rewritten as f(x)=σ(w T x+b). 15 / 149
16 Note that the sigmoid function σ(x)= 1 1+exp( x) looks like a soft heavyside: Therefore, the overall model f(x;w, b)=σ(w T x+b) is very similar to the perceptron. 16 / 149
17 In terms of tensor operations, the computational graph of f can be represented as: where white nodes correspond to inputs and outputs; red nodes correspond to model parameters; blue nodes correspond to intermediate operations, which themselves produce intermediate output values (not represented). This unit is the core component all neural networks! 17 / 149
18 Gradient descent LetL(θ) denote a loss function de!ned over model parameters θ (e.g., w and b). To minimize L(θ), gradient descent uses local linear information to iteratively move towards a (local) minimum. For θ 0 R d, a!rst-order approximation around θ 0 can be de!ned as ˆL(θ 0 + ϵ)=l(θ 0 )+ϵ T θ L(θ 0 )+ 1 2η ϵ / 149
19 A minimizer of the approximationˆl(θ 0 + ϵ) is given for ϵˆl(θ 0 + ϵ)=0 = θ L(θ 0 )+ 1 η ϵ, which results in the best improvement for the step ϵ= η θ L(θ 0 ). Therefore, model parameters can be updated iteratively using the update rule: Notes: θ t+1 = θ t η θ L(θ t ) θ 0 are the initial parameters of the model; η is the learning rate; both are critical for the convergence of the update rule. 19 / 149
20 Example 1: Convergence to a global minima Slide credit: F. Fleuret 0 / 149
21 Example 1: Convergence to a global minima Slide credit: F. Fleuret 0 / 149
22 Example 1: Convergence to a global minima Slide credit: F. Fleuret 0 / 149
23 Example 1: Convergence to a global minima Slide credit: F. Fleuret 0 / 149
24 Example 1: Convergence to a global minima Slide credit: F. Fleuret 0 / 149
25 Example 1: Convergence to a global minima Slide credit: F. Fleuret 0 / 149
26 Example 1: Convergence to a global minima Slide credit: F. Fleuret 0 / 149
27 Example 1: Convergence to a global minima Slide credit: F. Fleuret 0 / 149
28 Example 1: Convergence to a global minima Slide credit: F. Fleuret 0 / 149
29 Example 1: Convergence to a global minima Slide credit: F. Fleuret 0 / 149
30 Example 1: Convergence to a global minima Slide credit: F. Fleuret 0 / 149
31 Example 2: Convergence to a local minima Slide credit: F. Fleuret 1 / 149
32 Example 2: Convergence to a local minima Slide credit: F. Fleuret 1 / 149
33 Example 2: Convergence to a local minima Slide credit: F. Fleuret 1 / 149
34 Example 2: Convergence to a local minima Slide credit: F. Fleuret 1 / 149
35 Example 2: Convergence to a local minima Slide credit: F. Fleuret 1 / 149
36 Example 2: Convergence to a local minima Slide credit: F. Fleuret 1 / 149
37 Example 2: Convergence to a local minima Slide credit: F. Fleuret 1 / 149
38 Example 2: Convergence to a local minima Slide credit: F. Fleuret 1 / 149
39 Example 2: Convergence to a local minima Slide credit: F. Fleuret 1 / 149
40 Example 2: Convergence to a local minima Slide credit: F. Fleuret 1 / 149
41 Example 2: Convergence to a local minima Slide credit: F. Fleuret 1 / 149
42 Example 2: Convergence to a local minima Slide credit: F. Fleuret 1 / 149
43 Example 3: Divergence due to a too large learning rate Slide credit: F. Fleuret 22 / 149
44 Example 3: Divergence due to a too large learning rate Slide credit: F. Fleuret 22 / 149
45 Example 3: Divergence due to a too large learning rate Slide credit: F. Fleuret 22 / 149
46 Example 3: Divergence due to a too large learning rate Slide credit: F. Fleuret 22 / 149
47 Example 3: Divergence due to a too large learning rate Slide credit: F. Fleuret 22 / 149
48 Example 3: Divergence due to a too large learning rate Slide credit: F. Fleuret 22 / 149
49 Example 3: Divergence due to a too large learning rate Slide credit: F. Fleuret 22 / 149
50 Example 3: Divergence due to a too large learning rate Slide credit: F. Fleuret 22 / 149
51 Example 3: Divergence due to a too large learning rate Slide credit: F. Fleuret 22 / 149
52 Example 3: Divergence due to a too large learning rate Slide credit: F. Fleuret 22 / 149
53 Example 3: Divergence due to a too large learning rate Slide credit: F. Fleuret 22 / 149
54 Example 3: Divergence due to a too large learning rate Slide credit: F. Fleuret 22 / 149
55 Example 3: Divergence due to a too large learning rate Slide credit: F. Fleuret 22 / 149
56 Slide credit: F. Fleuret3 2 / 149
57 Slide credit: F. Fleuret 24 / 149
58 Slide credit: F. Fleuret 25 / 149
59 Slide credit: F. Fleuret 26 / 149
60 Stochastic gradient descent In the empirical risk minimization setup,l(θ) and its gradient decompose as L(θ)= 1 N x i,y i dl(y i, f(x i ; θ)) L(θ)= 1 N x i,y i d l(y i, f(x i ; θ)). Therefore, in batch gradient descent the complexity of an update grows linearly with the size N of the dataset. More importantly, since the empirical risk is already an approximation of the expected risk, it should not be necessary to carry out the minimization with great accuracy. 27 / 149
61 While it makes sense in principle to compute the gradient exactly, in practice: It takes a lot of time to compute 8 / 149
62 While it makes sense in principle to compute the gradient exactly, in practice: It takes a lot of time to compute It is an empirical estimation of an hidden quantity, and any partial sum would similarly be an unbiased empirical estimate, although more noisy. 29 / 149
63 While it makes sense in principle to compute the gradient exactly, in practice: It takes a lot of time to compute It is an empirical estimation of an hidden quantity, and any partial sum would similarly be an unbiased empirical estimate, although more noisy. It is computed incrementally L(θ)= 1 N x i,y i d l(y i, f(x i ; θ)). 30 / 149
64 Instead, stochastic gradient descent uses as update rule: θ t+1 = θ t η l(y i(t+1), f(x i(t+1) ; θ t )) Iteration complexity is independent of N. The stochastic process {θ t t=1,...} depends on the examples i(t) picked randomly at each iteration. 31 / 149
65 Instead, stochastic gradient descent uses as update rule: θ t+1 = θ t η l(y i(t+1), f(x i(t+1) ; θ t )) Iteration complexity is independent of N. The stochastic process {θ t t=1,...} depends on the examples i(t) picked randomly at each iteration. Batch gradient descent Stochastic gradient descent 32 / 149
66 Why is stochastic gradient descent still a good idea? Informally, averaging the update θ t+1 = θ t η l(y i(t+1), f(x i(t+1) ; θ t )) over all choices i(t+1) restores batch gradient descent. Formally, if the gradient estimate is unbiased, e.g., if E i(t+1) [ l(y i(t+1), f(x i(t+1) ; θ t ))]= 1 N x i,y i d l(y i, f(x i ; θ t )) = L(θ t ) then the formal convergence of SGD can be proved, under appropriate assumptions. 33 / 149
67 The mini-batch stochastic gradient descent is the standard procedure for deep learning. It consists of visiting the samples in "mini-batches", each of a few tens of samples, and updating the parameters each time. θ t+1 = θ t η B b=1 l(y i(t+1), f(x i(t+1) ; θ t )) The order n(t, b) to visit the samples can either be sequential, or uniform sampling, usually without replacement. 34 / 149
68 The mini-batch stochastic gradient descent is the standard procedure for deep learning. It consists of visiting the samples in "mini-batches", each of a few tens of samples, and updating the parameters each time. θ t+1 = θ t η B b=1 l(y i(t+1), f(x i(t+1) ; θ t )) 35 / 149
69 The mini-batch stochastic gradient descent is the standard procedure for deep learning. It consists of visiting the samples in "mini-batches", each of a few tens of samples, and updating the parameters each time. θ t+1 = θ t η B b=1 l(y i(t+1), f(x i(t+1) ; θ t )) The order n(t, b) to visit the samples can either be sequential, or uniform sampling, usually without replacement. 36 / 149
70 The mini-batch stochastic gradient descent is the standard procedure for deep learning. It consists of visiting the samples in "mini-batches", each of a few tens of samples, and updating the parameters each time. θ t+1 = θ t η B b=1 l(y i(t+1), f(x i(t+1) ; θ t )) The order n(t, b) to visit the samples can either be sequential, or uniform sampling, usually without replacement. The stochastic behavior of this procedure helps evade local minima. 37 / 149
71 38 / 149
72 Limitations of gradient descent The gradient descent method makes a strong assumption about the magnitude of the "local curvature" to!x the step size, and about its isotropy so that the same step size makes sense in all directions. 39 / 149
73 Limitations of gradient descent The gradient descent method makes a strong assumption about the magnitude of the "local curvature" to!x the step size, and about its isotropy so that the same step size makes sense in all directions. 40 / 149
74 Limitations of gradient descent The gradient descent method makes a strong assumption about the magnitude of the "local curvature" to!x the step size, and about its isotropy so that the same step size makes sense in all directions. 41 / 149
75 Limitations of gradient descent The gradient descent method makes a strong assumption about the magnitude of the "local curvature" to!x the step size, and about its isotropy so that the same step size makes sense in all directions. 42 / 149
76 Limitations of gradient descent The gradient descent method makes a strong assumption about the magnitude of the "local curvature" to!x the step size, and about its isotropy so that the same step size makes sense in all directions. 43 / 149
77 Limitations of gradient descent The gradient descent method makes a strong assumption about the magnitude of the "local curvature" to!x the step size, and about its isotropy so that the same step size makes sense in all directions. 44 / 149
78 Limitations of gradient descent The gradient descent method makes a strong assumption about the magnitude of the "local curvature" to!x the step size, and about its isotropy so that the same step size makes sense in all directions. 45 / 149
79 Some optimization methods leverage higher-order moments, in particular second order to use a more accurate local model of the functional to optimize. However the resulting computational overhead reduces the number of iterations for a!xed budget, and it is rarely at the advantage of these methods. Deep-learning generally relies on a smarter use of the gradient, using statistics over its past values to make a "smarter step" with the current one. 46 / 149
80 Momentum and moment estimation The "vanilla" mini-batch stochastic gradient descent (SGD) consists of where θ t+1 = θ t ηg t g t = B b=1 l n(t,b) (θ t ) is the gradient summed over a mini-batch 47 / 149
81 Momentum and moment estimation The!rst improvement is the use of a "momentum" to add inertia in the choice of the step direction u t = γu t 1 + ηg t θ t+1 = θ t u t 48 / 149
82 Momentum and moment estimation The!rst improvement is the use of a "momentum" to add inertia in the choice of the step direction u t = γu t 1 + ηg t θ t+1 = θ t u t With γ=0, this is the same as vanilla SGD 49 / 149
83 Momentum and moment estimation The!rst improvement is the use of a "momentum" to add inertia in the choice of the step direction u t = γu t 1 + ηg t θ t+1 = θ t u t With γ=0, this is the same as vanilla SGD With γ>0, this update: can go through local barriers accelerate if the gradient does not change much dampnes oscillations in narrow valleys γ is typically set to 0.9 Rumelhart et al., / 149
84 51 / 149
85 52 / 149
86 Why Momentum Really Works 53 / 149
87 Why Momentum Really Works 54 / 149
88 Why Momentum Really Works 55 / 149
89 Why Momentum Really Works 56 / 149
90 Momentum and moment estimation Another class of methods exploits the statistics over the previous steps to compensate for the anisotropy of the mapping. The Adam algorithm uses moving averages of each coordinate and its square to rescale each coordinate separately. 57 / 149
91 Momentum and moment estimation Another class of methods exploits the statistics over the previous steps to compensate for the anisotropy of the mapping. The Adam algorithm uses moving averages of each coordinate and its square to rescale each coordinate separately. The update rule is, on each coordinate separately Kingma and Ba, / 149
92 Adam m t = β 1 m t 1 +(1 β 1 )g t ^ m t = m t 1 β 1 v t = β 2 v t 1 +(1 β 2 )g 2 t ^ v t = v t 1 β 2 θ t+1 = θ t η ^ m t ^ v t + ϵ This can be seen as a combination of momentum, with ^ m t, and a percoordinate re-scaling with Kingma and Ba, 2014 ^ v t 59 / 149
93 60 / 149
94 61 / 149
95 Optimizers SGD (with Nesterov momentum) Simple to implement Very sensitive to initial value of η Need learning rate scheduling Adam: adaptive learning rate scale for each param Globalηset to often works well enough Good default choice of optimizer (often) But well-tuned SGD with LR scheduling can generalize better than Adam... Active area of research 62 / 149
96 Optimizers Many other derived optimizers readily available in most frameworks: Nesterov's accelerated gradient, Adagrad, Adadelta, RMSprop, AdaMax, Nadam / 149
97 Optimizers 4 / 149
98 Optimizers 5 / 149
99 Layers So far we considered the logistic unit h=σ w T x+b, where h R, x R p, w R p and b R. These units can be composed in parallel to form a layer with q outputs: h=σ(w T x+b) ( ) where h R q, x R p, W R p q, b R q and where σ( ) is upgraded to the element-wise sigmoid function. 66 / 149
100 Multi-layer perceptron Similarly, layers can be composed in series, such that: h 0 =x h 1 = σ(w T 1 h 0 +b 1 )... h L = σ(w T L h L 1 +b L ) f(x; θ)=h L where θ denotes the model parameters {W k,b k,... k=1,...,l}. This model is the multi-layer perceptron, also known as the fully connected feedforward network. Optionally, the last activation σ can be skipped to produce unbounded output values ŷ R. 67 / 149
101 68 / 149
102 To minimize L(θ) with stochastic gradient descent, we need the gradient θ l(θ t ). Therefore, we require the evaluation of the (total) derivatives dl dw k, dl db k of the loss l with respect to all model parametersw k,b k, for k=1,...,l. These derivatives can be evaluated automatically from the computational graph of l using automatic di"erentiation. 69 / 149
103 Automatic di"erentiation Consider a 1-dimensional output composition f g, such that y=f(u) u=g(x)=(g 1 (x),...,g m (x)). The chain rule of total derivatives states that dy dx = m k=1 y u k du k dx recursive case Since a neural network is a composition of di"erentiable functions, the total derivatives of the loss can be evaluated by applying the chain rule recursively over its computational graph. The implementation of this procedure is called (reverse) automatic di"erentiation (AD). AD is not numerical di"erentiation, nor symbolic di"erentiation.70 / 149
104 As a guiding example, let us consider a simpli!ed 2-layer MLP and the following loss function: ( ( )) f(x;w 1,W 2 )=σ W T 2 σ WT 1 x ( ) l(y, ŷ;w 1,W 2 )=cross_entropy(y, ŷ)+λ W W 2 2 for x R p, y R, W 1 R p q and W 2 R q. 71 / 149
105 As a guiding example, let us consider a simpli!ed 2-layer MLP and the following loss function: ( ( )) f(x;w 1,W 2 )=σ W T 2 σ WT 1 x ( ) l(y, ŷ;w 1,W 2 )=cross_entropy(y, ŷ)+λ W W 2 2 for x R p, y R, W 1 R p q and W 2 R q. 72 / 149
106 The total derivative dl dw 1 can be computed backward, by walking through all paths from l tow 1 in the computational graph and accumulating the terms: dl dw 1 = l u 8 du 8 dw 1 + l u 4 du 4 dw 1 du 8 dw 1 = / 149
107 This algorithm is known as reverse-mode automatic di"erentiation, also called backpropagation. An equivalent procedure can be de!ned to evaluate the derivatives in forward mode, from inputs to outputs. Automatic di"erentiation generalizes to N inputs and M outputs. if N M, reverse-mode automatic di"erentiation is computationally more e%cient. otherwise, if M N, forward automatic di"erentiation is better. Since di"erentiation is a linear operator, AD can be implemented e%ciently in terms of matrix operations. 74 / 149
108 Backpropagation Inside a single unit/neuron/function 75 / 149
109 Backpropagation Inside a single unit/neuron/function 76 / 149
110 Backpropagation Inside a single unit/neuron/function 77 / 149
111 Backpropagation Inside a single unit/neuron/function 78 / 149
112 Backpropagation Inside a single unit/neuron/function 79 / 149
113 Backpropagation Inside a single unit/neuron/function 80 / 149
114 Vanishing gradients Training deep MLPs with many layers has for long (pre-2011) been very di%cult due to the vanishing gradient problem. Small gradients slow down, and eventually block, stochastic gradient descent. This results in a limited capacity of learning. Backpropagated gradients normalized histograms (Glorot and Bengio, 2010). Gradients for layers far from the output vanish to zero. 81 / 149
115 Consider a simpli!ed 3-layer MLP, with x, w 1, w 2, w 3 R, such that ( ( ( ))) f(x; w 1, w 2, w 3 )=σ w 3 σ w 2 σ w 1 x. Under the hood, this would be evaluated as and its derivative dŷ dw 1 as u 1 = w 1 x u 2 = σ(u 1 ) u 3 = w 2 u 2 u 4 = σ(u 3 ) u 5 = w 3 u 4 ŷ=σ(u 5 ) 82 / 149
116 The derivative of the sigmoid activation function σ is: dσ dx (x)=σ(x)(1 σ(x)) Notice that 0 dσ dx (x) 1 4 for all x. 83 / 149
117 Assume that weights w 1, w 2, w 3 are initialized randomly from a Gaussian with zero-mean and small variance, such that with high probability 1 w i 1. Then, dŷ dw 1 = σ(u 5 ) u 5 w 3 σ(u 3 ) u 3 w 2 σ(u 1 ) x u This implies that the gradient dŷ the number of layers in the network increases. Hence the vanishing gradient problem. dw 1 exponentially shrinks to zero as In general, bounded activation functions (sigmoid, tanh, etc) are prone to the vanishing gradient problem. Note the importance of a proper initialization scheme. 84 / 149
118 Recti!ed linear units Instead of the sigmoid activation function, modern neural networks are for most based on recti!ed linear units (ReLU) (Glorot et al, 2011): ReLU(x)= max(0, x) 85 / 149
119 Note that the derivative of the ReLU function is { d dx ReLU(x)= 0 if x 0 1 otherwise For x=0, the derivative is unde!ned. In practice, it is set to zero. 86 / 149
120 Therefore, dŷ dw 1 = σ(u 5 ) u 5 w 3 σ(u 3 ) u 3 w 2 σ(u 1 ) u 1 x =1 =1 =1 This solves the vanishing gradient problem, even for deep networks! (provided proper initialization) Note that: The ReLU unit dies when its input is negative, which might block gradient descent. This is actually a useful property to induce sparsity. This issue can also be solved using leaky ReLUs, de!ned as LeakyReLU(x) = max(αx, x) for a small α R + (e.g., α=0.1). 87 / 149
121 Universal approximation Theorem. (Cybenko 1989; Hornik et al, 1991) Let σ( ) be a bounded, non-constant continuous function. Let I p denote the p-dimensional hypercube, and C(I p ) denote the space of continuous functions on I p. Given any f C(I p ) and ϵ>0, there exists q>0 and v i, w i, b i, i=1,...,q such that satis!es sup x Ip f(x) F(x) < ϵ. F(x)= v i σ(w T i x+b i ) i q It guarantees that even a single hidden-layer network can represent any classi!cation problem in which the boundary is locally linear (smooth); It does not inform about good/bad architectures, nor how they relate to the optimization procedure. 88 / 149
122 Theorem (Barron, 1992) The mean integrated square error between the estimated network ˆF and the target function f is bounded by O ( ) C 2 f q + qp N logn where N is the number of training points, q is the number of neurons, p is the input dimension, and C f measures the global smoothness of f. Combines approximation and estimation errors. Provided enough data, it guarantees that adding more neurons will result in a better approximation. 89 / 149
123 Consider the 1-layer MLP f(x)= w i ReLU(x+b i ). This model can approximate any smooth 1D function, provided enough hidden units. 90 / 149
124 Consider the 1-layer MLP f(x)= w i ReLU(x+b i ). This model can approximate any smooth 1D function, provided enough hidden units. 90 / 149
125 Consider the 1-layer MLP f(x)= w i ReLU(x+b i ). This model can approximate any smooth 1D function, provided enough hidden units. 90 / 149
126 Consider the 1-layer MLP f(x)= w i ReLU(x+b i ). This model can approximate any smooth 1D function, provided enough hidden units. 90 / 149
127 Consider the 1-layer MLP f(x)= w i ReLU(x+b i ). This model can approximate any smooth 1D function, provided enough hidden units. 90 / 149
128 Consider the 1-layer MLP f(x)= w i ReLU(x+b i ). This model can approximate any smooth 1D function, provided enough hidden units. 90 / 149
129 Consider the 1-layer MLP f(x)= w i ReLU(x+b i ). This model can approximate any smooth 1D function, provided enough hidden units. 90 / 149
130 Consider the 1-layer MLP f(x)= w i ReLU(x+b i ). This model can approximate any smooth 1D function, provided enough hidden units. 90 / 149
131 Consider the 1-layer MLP f(x)= w i ReLU(x+b i ). This model can approximate any smooth 1D function, provided enough hidden units. 90 / 149
132 Consider the 1-layer MLP f(x)= w i ReLU(x+b i ). This model can approximate any smooth 1D function, provided enough hidden units. 90 / 149
133 Consider the 1-layer MLP f(x)= w i ReLU(x+b i ). This model can approximate any smooth 1D function, provided enough hidden units. 90 / 149
134 Consider the 1-layer MLP f(x)= w i ReLU(x+b i ). This model can approximate any smooth 1D function, provided enough hidden units. 90 / 149
135 Consider the 1-layer MLP f(x)= w i ReLU(x+b i ). This model can approximate any smooth 1D function, provided enough hidden units. 90 / 149
136 Neural Network for classi!cation The neuron Inspired by neuroscience and human brain, but resemblances do not go too far In fact there several types of neurons with di"erent functions and the metaphor does not hold everywhere Slide credit: A. Karpathy 91 / 149
137 Neural Network for classi!cation The neuron Inspired by neuroscience and human brain, but resemblances do not go too far Slide credit: A. Karpathy 92 / 149
138 Neural Network for classi!cation Inspired by neuroscience and human brain, but resemblances do not go too far Slide credit: A. Karpathy 93 / 149
139 Arti!cial Neuron Slide credit: C. Ollion & O. Grisel 4 / 149
140 Arti!cial Neuron x, f(x) input and output z(x) pre-activation w, b weights and bias g activation function z(x)=w T x+b f(x)=g(w T x+b) Slide credit: C. Ollion & O. Grisel 95 / 149
141 More neurons -> more capacity 96 / 149
142 Layer of Neurons Slide credit: C. Ollion & O. Grisel 97 / 149
143 Layer of Neurons f(x)=g(z(x))=g(wx+b) W,b now matrix and vector Slide credit: C. Ollion & O. Grisel 98 / 149
144 One Hidden Layer Network z h (x)=w h x+b h h(x)=g(z h (x))=g(w h x+b h ) z o (x)=w o h(x)+b o f(x)=softmax(z o )=softmax(w o h(x)+b o ) Slide credit: C. Ollion & O. Grisel 9 / 149
145 One Hidden Layer Network z h (x)=w h x+b h h(x)=g(z h (x))=g(w h x+b h ) z o (x)=w o h(x)+b o f(x)=softmax(z o )=softmax(w o h(x)+b o ) Slide credit: C. Ollion & O. Grisel 00 / 149
146 One Hidden Layer Network z h (x)=w h x+b h h(x)=g(z h (x))=g(w h x+b h ) z o (x)=w o h(x)+b o f(x)=softmax(z o )=softmax(w o h(x)+b o ) Slide credit: C. Ollion & O. Grisel 101 / 149
147 One Hidden Layer Network z h (x)=w h x+b h h(x)=g(z h (x))=g(w h x+b h ) z o (x)=w o h(x)+b o f(x)=softmax(z o )=softmax(w o h(x)+b o ) Slide credit: C. Ollion & O. Grisel 02 / 149
148 One Hidden Layer Network Alternate representation Slide credit: C. Ollion & O. Grisel 103 / 149
149 One Hidden Layer Network PyTorch implementation model = torch.nn.sequential( torch.nn.linear(d_in, H), # weight matrix dim [D_in x H] torch.nn.tanh(), torch.nn.linear(h, D_out), # weight matrix dim [H x D_out] torch.nn.softmax(), ) 104 / 149
150 Element-wise activation functions blue: activation function green: derivative Slide credit: C. Ollion & O. Grisel 105 / 149
151 Element-wise activation functions Many other activation functions available: 106 / 149
152 Softmax function softmax(x) = 1 n i=1 ex i [ e x ] 1 e x 2 e x n softmax(x) i x j = { softmax(x) i (1 softmax(x) i ) i=j softmax(x) i softmax(x) j i j 107 / 149
153 Softmax function softmax(x) = 1 n i=1 ex i [ e x ] 1 e x 2 e x n softmax(x) i x j = { softmax(x) i (1 softmax(x) i ) i=j softmax(x) i softmax(x) j i j vector of values in (0, 1) that add up to 1 p(y=c X=x)=softmax(z((x)) c the pre-activation vector z(x) is often called "the logits" Slide credit: C. Ollion & O. Grisel 108 / 149
154 Training the network Find parameters θ=(w h ;b h ;W o ;b o ) that minimize the negative log likelihood (or cross entropy) 09 / 149
155 Training the network Find parameters θ=(w h ;b h ;W o ;b o ) that minimize the negative log likelihood (or cross entropy) The loss function for a given sample s S: l(f(x s ; θ), y s )=nll(θ;x s, y s )= logf(x s ; θ) y s 110 / 149
156 Training the network Find parameters θ=(w h ;b h ;W o ;b o ) that minimize the negative log likelihood (or cross entropy) The loss function for a given sample s S: l(f(x s ; θ), y s )=nll(θ;x s, y s )= logf(x s ; θ) y s example 111 / 149
157 Training the network Find parameters θ=(w h ;b h ;W o ;b o ) that minimize the negative log likelihood (or cross entropy) The loss function for a given sample s S: l(f(x s ; θ), y s )=nll(θ;x s, y s )= logf(x s ; θ) y s The cost function is the negative likelihood of the model computed on the full training set (for i.i.d. samples): L S (θ)= 1 S logf(x s ; θ) y s+λω(θ) s S 112 / 149
158 Training the network Find parameters θ=(w h ;b h ;W o ;b o ) that minimize the negative log likelihood (or cross entropy) The loss function for a given sample s S: l(f(x s ; θ), y s )=nll(θ;x s, y s )= logf(x s ; θ) y s The cost function is the negative likelihood of the model computed on the full training set (for i.i.d. samples): L S (θ)= 1 S logf(x s ; θ) y s+λω(θ) s S λω(θ)=λ( W h 2 + W o 2 ) is an optional regularization term. 113 / 149
159 Stochastic Gradient Descent Initialize θ randomly 114 / 149
160 Stochastic Gradient Descent Initialize θ randomly ForEepochs perform: Randomly select a small batch of samples (B S) 115 / 149
161 Stochastic Gradient Descent Initialize θ randomly ForEepochs perform: Randomly select a small batch of samples (B S) Compute gradients: Δ= θ L B (θ) 116 / 149
162 Stochastic Gradient Descent Initialize θ randomly ForEepochs perform: Randomly select a small batch of samples (B S) Compute gradients: Δ= θ L B (θ) Update parameters: θ θ ηδ η>0 is called the learning rate 117 / 149
163 Stochastic Gradient Descent Initialize θ randomly ForEepochs perform: Randomly select a small batch of samples (B S) Compute gradients: Δ= θ L B (θ) Update parameters: θ θ ηδ η>0 is called the learning rate Stop when reaching criterion nll stops decreasing when computed on validation set 118 / 149
164 Loss functions 119 / 149
165 Discrete output (classi!cation) Binary classi!cation: y [0,1] Y X =x Bernoulli(b = f(x;θ)) output function:logistic(x) = 1+e x loss function: binary cross-entropy Multiclass classi!cation: y [0, K 1] 1 Y X =x Multinoulli(p =f(x;θ)) output function: softmax loss function: categorical cross-entropy 120 / 149
166 Continuous output (regression) Continuous output:y R n Y X =x N(μ =f(x;θ),σ 2 I) output function: Identity loss function: square loss Heteroschedastic if f(x;θ) predicts both μ and σ 2 Mixture Density Network (multimodal output) Y X =x GMM x f(x;θ) predicts all the parameters: the means, covariance matrices and mixture weights 121 / 149
167 Going deeper 122 / 149
168 Dropout First "deep" regularization technique Remove units at random during the forward pass on each sample Put them all back during test Dropout: A Simple Way to Prevent Neural Networks from Over!tting, Srivastava et al., JMLR / 149
169 Dropout Interpretation Reduces the network dependency to individual neurons and distributes representation More redundant representation of data Ensemble interpretation Equivalent to training a large ensemble of shared-parameters, binary-masked models Each model is only trained on a single data point A network with dropout can be interpreted as an ensemble of 2 N models with heavy weight sharing (Goodfellow et al., 2013) 124 / 149
170 Dropout One has to decide on which units/layers to use dropout, and with what probability p units are dropped. During training, for each sample, as many Bernoulli variables as units are sampled independently to select units to remove. To keep the means of the inputs to layers unchanged, the initial version of dropout was multiplying activations by p during test. The standard variant is the "inverted dropout": multiply activations by 1 during training and keep the network 1 p untouched during test. 125 / 149
171 Dropout Over!tting noise Slide credit: C. Ollion & O. Grisel 126 / 149
172 Dropout A bit of Dropout Slide credit: C. Ollion & O. Grisel 127 / 149
173 Dropout Too much: under!tting Slide credit: C. Ollion & O. Grisel 128 / 149
174 Dropout Features learned on MNIST with one hidded layer autoencoders having 256 recti!ed linear units Dropout: A Simple Way to Prevent Neural Networks from Over!tting, Srivastava et al., JMLR / 149
175 Dropout >>> x = Variable(torch.Tensor(3, 9).fill_ (1.0), requires_grad = True) >>> x.data [torch.floattensor of size 3x9] >>> dropout = nn.dropout(p = 0.75) >>> y = dropout(x) >>> y.data [torch.floattensor of size 3x9] >>> l = y.norm(2, 1).sum() >>> l.backward() >>> x.grad.data [torch.floattensor of size 3x9] 130 / 149
176 Dropout For a given network model = nn.sequential(nn.linear(10, 100), nn.relu(), nn.linear(100, 50), nn.relu(), nn.linear(50, 2)); 131 / 149
177 Dropout For a given network model = nn.sequential(nn.linear(10, 100), nn.relu(), nn.linear(100, 50), nn.relu(), nn.linear(50, 2)); we can simply add dropout layers model = nn.sequential(nn.linear(10, 100), nn.relu(), nn.dropout(), nn.linear(100, 50), nn.relu(), nn.dropout(), nn.linear(50, 2)); 132 / 149
178 Dropout A model using dropout has to be set in "train" or "test" mode 133 / 149
179 Dropout A model using dropout has to be set in "train" or "test" mode The method nn.module.train(mode) recursively sets the *ag training to all sub-modules. >>> dropout = nn.dropout() >>> model = nn.sequential(nn.linear(3, 10), dropout, nn.linear(10, 3)) >>> dropout.training True >>> model.train(false) Sequential ( (0): Linear (3 -> 10) (1): Dropout (p = 0.5) (2): Linear (10 -> 3) ) >>> dropout.training False 134 / 149
180 Spatial Dropout As pointed out by Tompson et al. (2015), units in a 2d activation map are generally locally correlated, and dropout has virtually no e"ect. They proposed SpatialDropout, which drops channels instead of individual units. Slide credit: F. Fleuret 135 / 149
181 Spatial Dropout >>> dropout2d = nn.dropout2d() >>> x = Variable(Tensor(2, 3, 2, 2).fill_(1.0)) >>> dropout2d(x) Variable containing: (0,0,.,.) = (0,1,.,.) = (0,2,.,.) = (1,0,.,.) = (1,1,.,.) = (1,2,.,.) = [torch.floattensor of size 2x3x2x2] 136 / 149
182 Batch normalization We saw that maintaining proper statistics of the activations and derivatives was a critical issue to allow the training of deep architectures. It is the main motivation behind weight initialization rules (we'll cover them later). 137 / 149
183 Batch normalization We saw that maintaining proper statistics of the activations and derivatives was a critical issue to allow the training of deep architectures. It is the main motivation behind weight initialization rules (we'll cover them later). A di"erent approach consists of explicitly forcing the activation statistics during the forward pass by re-normalizing them. Batch normalization proposed by Io"e and Szegedy (2015) was the!rst method introducing this idea. 138 / 149
184 Batch normalization Normalize activations in each mini-batch before activation function: speeds up and stabilizes training (less dependent on init) Batch normalization forces the activation!rst and second order moments, so that the following layers do not need to adapt to their drift. 139 / 149
185 Batch normalization Normalize activations in each mini-batch before activation function: speeds up and stabilizes training (less dependent on init) Batch normalization: Accelerating deep network training by reducing internal covariate shift, Io"e and Szegedy, ICML / 149
186 Batch normalization During training batch normalization shifts and rescales according to the mean and variance estimated on the batch. As for dropout, the model behaves di"erently during train and test. 141 / 149
187 Batch normalization At inference time, use average and standard deviation computed on the whole dataset instead of batch Widely used in ConvNets, but requires the mini-batch to be large enough to compute statistics in the minibatch. 142 / 149
188 Batch normalization As dropout, batch normalization is implemented as a separate module torch.batchnorm1d that processes the input components separately. >>> x = torch.tensor(10000, 3).normal_() >>> x = x * torch.tensor([2, 5, 10]) + torch.tensor([-10, 25, 3]) >>> x = Variable(x) >>> x.data.mean(0) [torch.floattensor of size 3] >>> x.data.std(0) [torch.floattensor of size 3] 143 / 149
189 Batch normalization Since the module has internal variables to keep statistics, it must be provided with the sample dimension at creation. >>> bn = nn.batchnorm1d(3) >>> bn.bias.data = torch.tensor([2, 4, 8]) >>> bn.weight.data = torch.tensor([1, 2, 3]) >>> y = bn(x) >>> y.data.mean(0) [torch.floattensor of size 3] >>> y.data.std(0) [torch.floattensor of size 3] 144 / 149
190 Batch normalization BatchNorm2d example >>> x = Variable(torch.randn(20, 100, 35, 45)) >>> bn2d = nn.batchnorm2d(100) >>> y = bn2d(x) >>> x.size() torch.size([20, 100, 35, 45]) >>> bn2d.weight.data.size() torch.size([100]) >>> bn2d.bias.data.size() torch.size([100]) 145 / 149
191 Batch normalization Results on ImageNet LSVRC 2012: Batch normalization: Accelerating deep network training by reducing internal covariate shift, Io"e and Szegedy, ICML / 149
192 Batch normalization Results on ImageNet LSVRC 2012: learning rate can be greater dropout and local normalization are not necessary L 2 regularization in*uence should be reduced Batch normalization: Accelerating deep network training by reducing internal covariate shift, Io"e and Szegedy, ICML / 149
193 Batch normalization Deep MLP on a 2d "disc" toy example, with naive Gaussian weight initialization, cross-entropy, standard SGD, η=0.1. def create_model(with_batchnorm, nc = 32, depth = 16): modules = [] modules.append(nn.linear(2, nc)) if with_batchnorm: modules.append(nn.batchnorm1d(nc)) modules.append(nn.relu()) for d in range(depth): modules.append(nn.linear(nc, nc)) if with_batchnorm: modules.append(nn.batchnorm1d(nc)) modules.append(nn.relu()) modules.append(nn.linear(nc, 2)) return nn.sequential(*modules) Slide credit: F. Fleuret 148 / 149
194 Batch normalization Slide credit: F. Fleuret 149 / 149
Advanced Machine Learning
 Advanced Machine Learning Lecture 4: Deep Learning Essentials Pierre Geurts, Gilles Louppe, Louis Wehenkel 1 / 52 Outline Goal: explain and motivate the basic constructs of neural networks. From linear
Advanced Machine Learning Lecture 4: Deep Learning Essentials Pierre Geurts, Gilles Louppe, Louis Wehenkel 1 / 52 Outline Goal: explain and motivate the basic constructs of neural networks. From linear
Deep Feedforward Networks
 Deep Feedforward Networks Liu Yang March 30, 2017 Liu Yang Short title March 30, 2017 1 / 24 Overview 1 Background A general introduction Example 2 Gradient based learning Cost functions Output Units 3
Deep Feedforward Networks Liu Yang March 30, 2017 Liu Yang Short title March 30, 2017 1 / 24 Overview 1 Background A general introduction Example 2 Gradient based learning Cost functions Output Units 3
Comments. Assignment 3 code released. Thought questions 3 due this week. Mini-project: hopefully you have started. implement classification algorithms
 Neural networks Comments Assignment 3 code released implement classification algorithms use kernels for census dataset Thought questions 3 due this week Mini-project: hopefully you have started 2 Example:
Neural networks Comments Assignment 3 code released implement classification algorithms use kernels for census dataset Thought questions 3 due this week Mini-project: hopefully you have started 2 Example:
Need for Deep Networks Perceptron. Can only model linear functions. Kernel Machines. Non-linearity provided by kernels
 Need for Deep Networks Perceptron Can only model linear functions Kernel Machines Non-linearity provided by kernels Need to design appropriate kernels (possibly selecting from a set, i.e. kernel learning)
Need for Deep Networks Perceptron Can only model linear functions Kernel Machines Non-linearity provided by kernels Need to design appropriate kernels (possibly selecting from a set, i.e. kernel learning)
Deep Neural Networks (3) Computational Graphs, Learning Algorithms, Initialisation
 Deep Neural Networks (3) Computational Graphs, Learning Algorithms, Initialisation Steve Renals Machine Learning Practical MLP Lecture 5 16 October 2018 MLP Lecture 5 / 16 October 2018 Deep Neural Networks
Deep Neural Networks (3) Computational Graphs, Learning Algorithms, Initialisation Steve Renals Machine Learning Practical MLP Lecture 5 16 October 2018 MLP Lecture 5 / 16 October 2018 Deep Neural Networks
Deep Feedforward Networks. Seung-Hoon Na Chonbuk National University
 Deep Feedforward Networks Seung-Hoon Na Chonbuk National University Neural Network: Types Feedforward neural networks (FNN) = Deep feedforward networks = multilayer perceptrons (MLP) No feedback connections
Deep Feedforward Networks Seung-Hoon Na Chonbuk National University Neural Network: Types Feedforward neural networks (FNN) = Deep feedforward networks = multilayer perceptrons (MLP) No feedback connections
Statistical Machine Learning (BE4M33SSU) Lecture 5: Artificial Neural Networks
 Statistical Machine Learning (BE4M33SSU) Lecture 5: Artificial Neural Networks Jan Drchal Czech Technical University in Prague Faculty of Electrical Engineering Department of Computer Science Topics covered
Statistical Machine Learning (BE4M33SSU) Lecture 5: Artificial Neural Networks Jan Drchal Czech Technical University in Prague Faculty of Electrical Engineering Department of Computer Science Topics covered
Topics in AI (CPSC 532L): Multimodal Learning with Vision, Language and Sound. Lecture 3: Introduction to Deep Learning (continued)
 Topics in AI (CPSC 532L): Multimodal Learning with Vision, Language and Sound Lecture 3: Introduction to Deep Learning (continued) Course Logistics - Update on course registrations - 6 seats left now -
Topics in AI (CPSC 532L): Multimodal Learning with Vision, Language and Sound Lecture 3: Introduction to Deep Learning (continued) Course Logistics - Update on course registrations - 6 seats left now -
Understanding Neural Networks : Part I
 TensorFlow Workshop 2018 Understanding Neural Networks Part I : Artificial Neurons and Network Optimization Nick Winovich Department of Mathematics Purdue University July 2018 Outline 1 Neural Networks
TensorFlow Workshop 2018 Understanding Neural Networks Part I : Artificial Neurons and Network Optimization Nick Winovich Department of Mathematics Purdue University July 2018 Outline 1 Neural Networks
Deep Feedforward Networks
 Deep Feedforward Networks Liu Yang March 30, 2017 Liu Yang Short title March 30, 2017 1 / 24 Overview 1 Background A general introduction Example 2 Gradient based learning Cost functions Output Units 3
Deep Feedforward Networks Liu Yang March 30, 2017 Liu Yang Short title March 30, 2017 1 / 24 Overview 1 Background A general introduction Example 2 Gradient based learning Cost functions Output Units 3
Need for Deep Networks Perceptron. Can only model linear functions. Kernel Machines. Non-linearity provided by kernels
 Need for Deep Networks Perceptron Can only model linear functions Kernel Machines Non-linearity provided by kernels Need to design appropriate kernels (possibly selecting from a set, i.e. kernel learning)
Need for Deep Networks Perceptron Can only model linear functions Kernel Machines Non-linearity provided by kernels Need to design appropriate kernels (possibly selecting from a set, i.e. kernel learning)
A summary of Deep Learning without Poor Local Minima
 A summary of Deep Learning without Poor Local Minima by Kenji Kawaguchi MIT oral presentation at NIPS 2016 Learning Supervised (or Predictive) learning Learn a mapping from inputs x to outputs y, given
A summary of Deep Learning without Poor Local Minima by Kenji Kawaguchi MIT oral presentation at NIPS 2016 Learning Supervised (or Predictive) learning Learn a mapping from inputs x to outputs y, given
Apprentissage, réseaux de neurones et modèles graphiques (RCP209) Neural Networks and Deep Learning
 Apprentissage, réseaux de neurones et modèles graphiques (RCP209) Neural Networks and Deep Learning Nicolas Thome Prenom.Nom@cnam.fr http://cedric.cnam.fr/vertigo/cours/ml2/ Département Informatique Conservatoire
Apprentissage, réseaux de neurones et modèles graphiques (RCP209) Neural Networks and Deep Learning Nicolas Thome Prenom.Nom@cnam.fr http://cedric.cnam.fr/vertigo/cours/ml2/ Département Informatique Conservatoire
Machine Learning for Large-Scale Data Analysis and Decision Making A. Neural Networks Week #6
 Machine Learning for Large-Scale Data Analysis and Decision Making 80-629-17A Neural Networks Week #6 Today Neural Networks A. Modeling B. Fitting C. Deep neural networks Today s material is (adapted)
Machine Learning for Large-Scale Data Analysis and Decision Making 80-629-17A Neural Networks Week #6 Today Neural Networks A. Modeling B. Fitting C. Deep neural networks Today s material is (adapted)
Deep Learning & Artificial Intelligence WS 2018/2019
 Deep Learning & Artificial Intelligence WS 2018/2019 Linear Regression Model Model Error Function: Squared Error Has no special meaning except it makes gradients look nicer Prediction Ground truth / target
Deep Learning & Artificial Intelligence WS 2018/2019 Linear Regression Model Model Error Function: Squared Error Has no special meaning except it makes gradients look nicer Prediction Ground truth / target
CS 6501: Deep Learning for Computer Graphics. Basics of Neural Networks. Connelly Barnes
 CS 6501: Deep Learning for Computer Graphics Basics of Neural Networks Connelly Barnes Overview Simple neural networks Perceptron Feedforward neural networks Multilayer perceptron and properties Autoencoders
CS 6501: Deep Learning for Computer Graphics Basics of Neural Networks Connelly Barnes Overview Simple neural networks Perceptron Feedforward neural networks Multilayer perceptron and properties Autoencoders
Deep Learning II: Momentum & Adaptive Step Size
 Deep Learning II: Momentum & Adaptive Step Size CS 760: Machine Learning Spring 2018 Mark Craven and David Page www.biostat.wisc.edu/~craven/cs760 1 Goals for the Lecture You should understand the following
Deep Learning II: Momentum & Adaptive Step Size CS 760: Machine Learning Spring 2018 Mark Craven and David Page www.biostat.wisc.edu/~craven/cs760 1 Goals for the Lecture You should understand the following
ECE G: Special Topics in Signal Processing: Sparsity, Structure, and Inference
 ECE 18-898G: Special Topics in Signal Processing: Sparsity, Structure, and Inference Neural Networks: A brief touch Yuejie Chi Department of Electrical and Computer Engineering Spring 2018 1/41 Outline
ECE 18-898G: Special Topics in Signal Processing: Sparsity, Structure, and Inference Neural Networks: A brief touch Yuejie Chi Department of Electrical and Computer Engineering Spring 2018 1/41 Outline
Lecture 4 Backpropagation
 Lecture 4 Backpropagation CMSC 35246: Deep Learning Shubhendu Trivedi & Risi Kondor University of Chicago April 5, 2017 Things we will look at today More Backpropagation Still more backpropagation Quiz
Lecture 4 Backpropagation CMSC 35246: Deep Learning Shubhendu Trivedi & Risi Kondor University of Chicago April 5, 2017 Things we will look at today More Backpropagation Still more backpropagation Quiz
Neural Networks and Deep Learning
 Neural Networks and Deep Learning Professor Ameet Talwalkar November 12, 2015 Professor Ameet Talwalkar Neural Networks and Deep Learning November 12, 2015 1 / 16 Outline 1 Review of last lecture AdaBoost
Neural Networks and Deep Learning Professor Ameet Talwalkar November 12, 2015 Professor Ameet Talwalkar Neural Networks and Deep Learning November 12, 2015 1 / 16 Outline 1 Review of last lecture AdaBoost
Lecture 5: Logistic Regression. Neural Networks
 Lecture 5: Logistic Regression. Neural Networks Logistic regression Comparison with generative models Feed-forward neural networks Backpropagation Tricks for training neural networks COMP-652, Lecture
Lecture 5: Logistic Regression. Neural Networks Logistic regression Comparison with generative models Feed-forward neural networks Backpropagation Tricks for training neural networks COMP-652, Lecture
Day 3 Lecture 3. Optimizing deep networks
 Day 3 Lecture 3 Optimizing deep networks Convex optimization A function is convex if for all α [0,1]: f(x) Tangent line Examples Quadratics 2-norms Properties Local minimum is global minimum x Gradient
Day 3 Lecture 3 Optimizing deep networks Convex optimization A function is convex if for all α [0,1]: f(x) Tangent line Examples Quadratics 2-norms Properties Local minimum is global minimum x Gradient
4. Multilayer Perceptrons
 4. Multilayer Perceptrons This is a supervised error-correction learning algorithm. 1 4.1 Introduction A multilayer feedforward network consists of an input layer, one or more hidden layers, and an output
4. Multilayer Perceptrons This is a supervised error-correction learning algorithm. 1 4.1 Introduction A multilayer feedforward network consists of an input layer, one or more hidden layers, and an output
DEEP LEARNING AND NEURAL NETWORKS: BACKGROUND AND HISTORY
 DEEP LEARNING AND NEURAL NETWORKS: BACKGROUND AND HISTORY 1 On-line Resources http://neuralnetworksanddeeplearning.com/index.html Online book by Michael Nielsen http://matlabtricks.com/post-5/3x3-convolution-kernelswith-online-demo
DEEP LEARNING AND NEURAL NETWORKS: BACKGROUND AND HISTORY 1 On-line Resources http://neuralnetworksanddeeplearning.com/index.html Online book by Michael Nielsen http://matlabtricks.com/post-5/3x3-convolution-kernelswith-online-demo
Neural Networks. CSE 6363 Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington
 Neural Networks CSE 6363 Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington 1 Perceptrons x 0 = 1 x 1 x 2 z = h w T x Output: z x D A perceptron
Neural Networks CSE 6363 Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington 1 Perceptrons x 0 = 1 x 1 x 2 z = h w T x Output: z x D A perceptron
Machine Learning
 Machine Learning 10-315 Maria Florina Balcan Machine Learning Department Carnegie Mellon University 03/29/2019 Today: Artificial neural networks Backpropagation Reading: Mitchell: Chapter 4 Bishop: Chapter
Machine Learning 10-315 Maria Florina Balcan Machine Learning Department Carnegie Mellon University 03/29/2019 Today: Artificial neural networks Backpropagation Reading: Mitchell: Chapter 4 Bishop: Chapter
text classification 3: neural networks
 text classification 3: neural networks CS 585, Fall 2018 Introduction to Natural Language Processing http://people.cs.umass.edu/~miyyer/cs585/ Mohit Iyyer College of Information and Computer Sciences University
text classification 3: neural networks CS 585, Fall 2018 Introduction to Natural Language Processing http://people.cs.umass.edu/~miyyer/cs585/ Mohit Iyyer College of Information and Computer Sciences University
Lecture 17: Neural Networks and Deep Learning
 UVA CS 6316 / CS 4501-004 Machine Learning Fall 2016 Lecture 17: Neural Networks and Deep Learning Jack Lanchantin Dr. Yanjun Qi 1 Neurons 1-Layer Neural Network Multi-layer Neural Network Loss Functions
UVA CS 6316 / CS 4501-004 Machine Learning Fall 2016 Lecture 17: Neural Networks and Deep Learning Jack Lanchantin Dr. Yanjun Qi 1 Neurons 1-Layer Neural Network Multi-layer Neural Network Loss Functions
Machine Learning. Neural Networks. (slides from Domingos, Pardo, others)
 Machine Learning Neural Networks (slides from Domingos, Pardo, others) For this week, Reading Chapter 4: Neural Networks (Mitchell, 1997) See Canvas For subsequent weeks: Scaling Learning Algorithms toward
Machine Learning Neural Networks (slides from Domingos, Pardo, others) For this week, Reading Chapter 4: Neural Networks (Mitchell, 1997) See Canvas For subsequent weeks: Scaling Learning Algorithms toward
Lecture 2: Learning with neural networks
 Lecture 2: Learning with neural networks Deep Learning @ UvA LEARNING WITH NEURAL NETWORKS - PAGE 1 Lecture Overview o Machine Learning Paradigm for Neural Networks o The Backpropagation algorithm for
Lecture 2: Learning with neural networks Deep Learning @ UvA LEARNING WITH NEURAL NETWORKS - PAGE 1 Lecture Overview o Machine Learning Paradigm for Neural Networks o The Backpropagation algorithm for
Introduction to Neural Networks
 CUONG TUAN NGUYEN SEIJI HOTTA MASAKI NAKAGAWA Tokyo University of Agriculture and Technology Copyright by Nguyen, Hotta and Nakagawa 1 Pattern classification Which category of an input? Example: Character
CUONG TUAN NGUYEN SEIJI HOTTA MASAKI NAKAGAWA Tokyo University of Agriculture and Technology Copyright by Nguyen, Hotta and Nakagawa 1 Pattern classification Which category of an input? Example: Character
Backpropagation Introduction to Machine Learning. Matt Gormley Lecture 12 Feb 23, 2018
 10-601 Introduction to Machine Learning Machine Learning Department School of Computer Science Carnegie Mellon University Backpropagation Matt Gormley Lecture 12 Feb 23, 2018 1 Neural Networks Outline
10-601 Introduction to Machine Learning Machine Learning Department School of Computer Science Carnegie Mellon University Backpropagation Matt Gormley Lecture 12 Feb 23, 2018 1 Neural Networks Outline
Machine Learning Basics III
 Machine Learning Basics III Benjamin Roth CIS LMU München Benjamin Roth (CIS LMU München) Machine Learning Basics III 1 / 62 Outline 1 Classification Logistic Regression 2 Gradient Based Optimization Gradient
Machine Learning Basics III Benjamin Roth CIS LMU München Benjamin Roth (CIS LMU München) Machine Learning Basics III 1 / 62 Outline 1 Classification Logistic Regression 2 Gradient Based Optimization Gradient
Neural Networks with Applications to Vision and Language. Feedforward Networks. Marco Kuhlmann
 Neural Networks with Applications to Vision and Language Feedforward Networks Marco Kuhlmann Feedforward networks Linear separability x 2 x 2 0 1 0 1 0 0 x 1 1 0 x 1 linearly separable not linearly separable
Neural Networks with Applications to Vision and Language Feedforward Networks Marco Kuhlmann Feedforward networks Linear separability x 2 x 2 0 1 0 1 0 0 x 1 1 0 x 1 linearly separable not linearly separable
Machine Learning CS 4900/5900. Lecture 03. Razvan C. Bunescu School of Electrical Engineering and Computer Science
 Machine Learning CS 4900/5900 Razvan C. Bunescu School of Electrical Engineering and Computer Science bunescu@ohio.edu Machine Learning is Optimization Parametric ML involves minimizing an objective function
Machine Learning CS 4900/5900 Razvan C. Bunescu School of Electrical Engineering and Computer Science bunescu@ohio.edu Machine Learning is Optimization Parametric ML involves minimizing an objective function
EVERYTHING YOU NEED TO KNOW TO BUILD YOUR FIRST CONVOLUTIONAL NEURAL NETWORK (CNN)
 EVERYTHING YOU NEED TO KNOW TO BUILD YOUR FIRST CONVOLUTIONAL NEURAL NETWORK (CNN) TARGETED PIECES OF KNOWLEDGE Linear regression Activation function Multi-Layers Perceptron (MLP) Stochastic Gradient Descent
EVERYTHING YOU NEED TO KNOW TO BUILD YOUR FIRST CONVOLUTIONAL NEURAL NETWORK (CNN) TARGETED PIECES OF KNOWLEDGE Linear regression Activation function Multi-Layers Perceptron (MLP) Stochastic Gradient Descent
Introduction to (Convolutional) Neural Networks
 Introduction to (Convolutional) Neural Networks Philipp Grohs Summer School DL and Vis, Sept 2018 Syllabus 1 Motivation and Definition 2 Universal Approximation 3 Backpropagation 4 Stochastic Gradient
Introduction to (Convolutional) Neural Networks Philipp Grohs Summer School DL and Vis, Sept 2018 Syllabus 1 Motivation and Definition 2 Universal Approximation 3 Backpropagation 4 Stochastic Gradient
Neural Networks. Lecture 2. Rob Fergus
 Neural Networks Lecture 2 Rob Fergus Overview Individual neuron Non-linearities (RELU, tanh, sigmoid) Single layer model Multiple layer models Theoretical discussion: representational power Examples shown
Neural Networks Lecture 2 Rob Fergus Overview Individual neuron Non-linearities (RELU, tanh, sigmoid) Single layer model Multiple layer models Theoretical discussion: representational power Examples shown
Reading Group on Deep Learning Session 1
 Reading Group on Deep Learning Session 1 Stephane Lathuiliere & Pablo Mesejo 2 June 2016 1/31 Contents Introduction to Artificial Neural Networks to understand, and to be able to efficiently use, the popular
Reading Group on Deep Learning Session 1 Stephane Lathuiliere & Pablo Mesejo 2 June 2016 1/31 Contents Introduction to Artificial Neural Networks to understand, and to be able to efficiently use, the popular
Overview of gradient descent optimization algorithms. HYUNG IL KOO Based on
 Overview of gradient descent optimization algorithms HYUNG IL KOO Based on http://sebastianruder.com/optimizing-gradient-descent/ Problem Statement Machine Learning Optimization Problem Training samples:
Overview of gradient descent optimization algorithms HYUNG IL KOO Based on http://sebastianruder.com/optimizing-gradient-descent/ Problem Statement Machine Learning Optimization Problem Training samples:
Linear discriminant functions
 Andrea Passerini passerini@disi.unitn.it Machine Learning Discriminative learning Discriminative vs generative Generative learning assumes knowledge of the distribution governing the data Discriminative
Andrea Passerini passerini@disi.unitn.it Machine Learning Discriminative learning Discriminative vs generative Generative learning assumes knowledge of the distribution governing the data Discriminative
Statistical Machine Learning from Data
 January 17, 2006 Samy Bengio Statistical Machine Learning from Data 1 Statistical Machine Learning from Data Multi-Layer Perceptrons Samy Bengio IDIAP Research Institute, Martigny, Switzerland, and Ecole
January 17, 2006 Samy Bengio Statistical Machine Learning from Data 1 Statistical Machine Learning from Data Multi-Layer Perceptrons Samy Bengio IDIAP Research Institute, Martigny, Switzerland, and Ecole
Artificial Neural Networks
 Artificial Neural Networks 鮑興國 Ph.D. National Taiwan University of Science and Technology Outline Perceptrons Gradient descent Multi-layer networks Backpropagation Hidden layer representations Examples
Artificial Neural Networks 鮑興國 Ph.D. National Taiwan University of Science and Technology Outline Perceptrons Gradient descent Multi-layer networks Backpropagation Hidden layer representations Examples
Deep Learning Lab Course 2017 (Deep Learning Practical)
 Deep Learning Lab Course 207 (Deep Learning Practical) Labs: (Computer Vision) Thomas Brox, (Robotics) Wolfram Burgard, (Machine Learning) Frank Hutter, (Neurorobotics) Joschka Boedecker University of
Deep Learning Lab Course 207 (Deep Learning Practical) Labs: (Computer Vision) Thomas Brox, (Robotics) Wolfram Burgard, (Machine Learning) Frank Hutter, (Neurorobotics) Joschka Boedecker University of
Lecture 6 Optimization for Deep Neural Networks
 Lecture 6 Optimization for Deep Neural Networks CMSC 35246: Deep Learning Shubhendu Trivedi & Risi Kondor University of Chicago April 12, 2017 Things we will look at today Stochastic Gradient Descent Things
Lecture 6 Optimization for Deep Neural Networks CMSC 35246: Deep Learning Shubhendu Trivedi & Risi Kondor University of Chicago April 12, 2017 Things we will look at today Stochastic Gradient Descent Things
Optimization for Training I. First-Order Methods Training algorithm
 Optimization for Training I First-Order Methods Training algorithm 2 OPTIMIZATION METHODS Topics: Types of optimization methods. Practical optimization methods breakdown into two categories: 1. First-order
Optimization for Training I First-Order Methods Training algorithm 2 OPTIMIZATION METHODS Topics: Types of optimization methods. Practical optimization methods breakdown into two categories: 1. First-order
Artificial Neural Networks
 Artificial Neural Networks Threshold units Gradient descent Multilayer networks Backpropagation Hidden layer representations Example: Face Recognition Advanced topics 1 Connectionist Models Consider humans:
Artificial Neural Networks Threshold units Gradient descent Multilayer networks Backpropagation Hidden layer representations Example: Face Recognition Advanced topics 1 Connectionist Models Consider humans:
Machine Learning. Neural Networks. (slides from Domingos, Pardo, others)
 Machine Learning Neural Networks (slides from Domingos, Pardo, others) For this week, Reading Chapter 4: Neural Networks (Mitchell, 1997) See Canvas For subsequent weeks: Scaling Learning Algorithms toward
Machine Learning Neural Networks (slides from Domingos, Pardo, others) For this week, Reading Chapter 4: Neural Networks (Mitchell, 1997) See Canvas For subsequent weeks: Scaling Learning Algorithms toward
(Feed-Forward) Neural Networks Dr. Hajira Jabeen, Prof. Jens Lehmann
 (Feed-Forward) Neural Networks 2016-12-06 Dr. Hajira Jabeen, Prof. Jens Lehmann Outline In the previous lectures we have learned about tensors and factorization methods. RESCAL is a bilinear model for
(Feed-Forward) Neural Networks 2016-12-06 Dr. Hajira Jabeen, Prof. Jens Lehmann Outline In the previous lectures we have learned about tensors and factorization methods. RESCAL is a bilinear model for
CSCI567 Machine Learning (Fall 2018)
 CSCI567 Machine Learning (Fall 2018) Prof. Haipeng Luo U of Southern California Sep 12, 2018 September 12, 2018 1 / 49 Administration GitHub repos are setup (ask TA Chi Zhang for any issues) HW 1 is due
CSCI567 Machine Learning (Fall 2018) Prof. Haipeng Luo U of Southern California Sep 12, 2018 September 12, 2018 1 / 49 Administration GitHub repos are setup (ask TA Chi Zhang for any issues) HW 1 is due
Introduction to Convolutional Neural Networks (CNNs)
 Introduction to Convolutional Neural Networks (CNNs) nojunk@snu.ac.kr http://mipal.snu.ac.kr Department of Transdisciplinary Studies Seoul National University, Korea Jan. 2016 Many slides are from Fei-Fei
Introduction to Convolutional Neural Networks (CNNs) nojunk@snu.ac.kr http://mipal.snu.ac.kr Department of Transdisciplinary Studies Seoul National University, Korea Jan. 2016 Many slides are from Fei-Fei
Deep Learning book, by Ian Goodfellow, Yoshua Bengio and Aaron Courville
 Deep Learning book, by Ian Goodfellow, Yoshua Bengio and Aaron Courville Chapter 6 :Deep Feedforward Networks Benoit Massé Dionyssos Kounades-Bastian Benoit Massé, Dionyssos Kounades-Bastian Deep Feedforward
Deep Learning book, by Ian Goodfellow, Yoshua Bengio and Aaron Courville Chapter 6 :Deep Feedforward Networks Benoit Massé Dionyssos Kounades-Bastian Benoit Massé, Dionyssos Kounades-Bastian Deep Feedforward
Lecture 3 Feedforward Networks and Backpropagation
 Lecture 3 Feedforward Networks and Backpropagation CMSC 35246: Deep Learning Shubhendu Trivedi & Risi Kondor University of Chicago April 3, 2017 Things we will look at today Recap of Logistic Regression
Lecture 3 Feedforward Networks and Backpropagation CMSC 35246: Deep Learning Shubhendu Trivedi & Risi Kondor University of Chicago April 3, 2017 Things we will look at today Recap of Logistic Regression
Introduction to Machine Learning
 Introduction to Machine Learning Neural Networks Varun Chandola x x 5 Input Outline Contents February 2, 207 Extending Perceptrons 2 Multi Layered Perceptrons 2 2. Generalizing to Multiple Labels.................
Introduction to Machine Learning Neural Networks Varun Chandola x x 5 Input Outline Contents February 2, 207 Extending Perceptrons 2 Multi Layered Perceptrons 2 2. Generalizing to Multiple Labels.................
Tips for Deep Learning
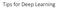 Tips for Deep Learning Recipe of Deep Learning Step : define a set of function Step : goodness of function Step 3: pick the best function NO Overfitting! NO YES Good Results on Testing Data? YES Good Results
Tips for Deep Learning Recipe of Deep Learning Step : define a set of function Step : goodness of function Step 3: pick the best function NO Overfitting! NO YES Good Results on Testing Data? YES Good Results
ECE521 Lectures 9 Fully Connected Neural Networks
 ECE521 Lectures 9 Fully Connected Neural Networks Outline Multi-class classification Learning multi-layer neural networks 2 Measuring distance in probability space We learnt that the squared L2 distance
ECE521 Lectures 9 Fully Connected Neural Networks Outline Multi-class classification Learning multi-layer neural networks 2 Measuring distance in probability space We learnt that the squared L2 distance
COMP 551 Applied Machine Learning Lecture 14: Neural Networks
 COMP 551 Applied Machine Learning Lecture 14: Neural Networks Instructor: Ryan Lowe (ryan.lowe@mail.mcgill.ca) Slides mostly by: Class web page: www.cs.mcgill.ca/~hvanho2/comp551 Unless otherwise noted,
COMP 551 Applied Machine Learning Lecture 14: Neural Networks Instructor: Ryan Lowe (ryan.lowe@mail.mcgill.ca) Slides mostly by: Class web page: www.cs.mcgill.ca/~hvanho2/comp551 Unless otherwise noted,
DeepLearning on FPGAs
 DeepLearning on FPGAs Introduction to Deep Learning Sebastian Buschäger Technische Universität Dortmund - Fakultät Informatik - Lehrstuhl 8 October 21, 2017 1 Recap Computer Science Approach Technical
DeepLearning on FPGAs Introduction to Deep Learning Sebastian Buschäger Technische Universität Dortmund - Fakultät Informatik - Lehrstuhl 8 October 21, 2017 1 Recap Computer Science Approach Technical
1 What a Neural Network Computes
 Neural Networks 1 What a Neural Network Computes To begin with, we will discuss fully connected feed-forward neural networks, also known as multilayer perceptrons. A feedforward neural network consists
Neural Networks 1 What a Neural Network Computes To begin with, we will discuss fully connected feed-forward neural networks, also known as multilayer perceptrons. A feedforward neural network consists
Lecture 3 Feedforward Networks and Backpropagation
 Lecture 3 Feedforward Networks and Backpropagation CMSC 35246: Deep Learning Shubhendu Trivedi & Risi Kondor University of Chicago April 3, 2017 Things we will look at today Recap of Logistic Regression
Lecture 3 Feedforward Networks and Backpropagation CMSC 35246: Deep Learning Shubhendu Trivedi & Risi Kondor University of Chicago April 3, 2017 Things we will look at today Recap of Logistic Regression
Neural Networks Learning the network: Backprop , Fall 2018 Lecture 4
 Neural Networks Learning the network: Backprop 11-785, Fall 2018 Lecture 4 1 Recap: The MLP can represent any function The MLP can be constructed to represent anything But how do we construct it? 2 Recap:
Neural Networks Learning the network: Backprop 11-785, Fall 2018 Lecture 4 1 Recap: The MLP can represent any function The MLP can be constructed to represent anything But how do we construct it? 2 Recap:
Neural Networks. Lecture 6. Rob Fergus
 Neural Networks Lecture 6 Rob Fergus Overview Individual neuron Non-linearities (RELU, tanh, sigmoid) Single layer model Multiple layer models Theoretical discussion: representational power Examples shown
Neural Networks Lecture 6 Rob Fergus Overview Individual neuron Non-linearities (RELU, tanh, sigmoid) Single layer model Multiple layer models Theoretical discussion: representational power Examples shown
Neural Network Training
 Neural Network Training Sargur Srihari Topics in Network Training 0. Neural network parameters Probabilistic problem formulation Specifying the activation and error functions for Regression Binary classification
Neural Network Training Sargur Srihari Topics in Network Training 0. Neural network parameters Probabilistic problem formulation Specifying the activation and error functions for Regression Binary classification
Neural Networks: Optimization Part 2. Intro to Deep Learning, Fall 2017
 Neural Networks: Optimization Part 2 Intro to Deep Learning, Fall 2017 Quiz 3 Quiz 3 Which of the following are necessary conditions for a value x to be a local minimum of a twice differentiable function
Neural Networks: Optimization Part 2 Intro to Deep Learning, Fall 2017 Quiz 3 Quiz 3 Which of the following are necessary conditions for a value x to be a local minimum of a twice differentiable function
Convolutional Neural Network Architecture
 Convolutional Neural Network Architecture Zhisheng Zhong Feburary 2nd, 2018 Zhisheng Zhong Convolutional Neural Network Architecture Feburary 2nd, 2018 1 / 55 Outline 1 Introduction of Convolution Motivation
Convolutional Neural Network Architecture Zhisheng Zhong Feburary 2nd, 2018 Zhisheng Zhong Convolutional Neural Network Architecture Feburary 2nd, 2018 1 / 55 Outline 1 Introduction of Convolution Motivation
Classification CE-717: Machine Learning Sharif University of Technology. M. Soleymani Fall 2012
 Classification CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2012 Topics Discriminant functions Logistic regression Perceptron Generative models Generative vs. discriminative
Classification CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2012 Topics Discriminant functions Logistic regression Perceptron Generative models Generative vs. discriminative
CSC 411 Lecture 10: Neural Networks
 CSC 411 Lecture 10: Neural Networks Roger Grosse, Amir-massoud Farahmand, and Juan Carrasquilla University of Toronto UofT CSC 411: 10-Neural Networks 1 / 35 Inspiration: The Brain Our brain has 10 11
CSC 411 Lecture 10: Neural Networks Roger Grosse, Amir-massoud Farahmand, and Juan Carrasquilla University of Toronto UofT CSC 411: 10-Neural Networks 1 / 35 Inspiration: The Brain Our brain has 10 11
Learning Deep Architectures for AI. Part II - Vijay Chakilam
 Learning Deep Architectures for AI - Yoshua Bengio Part II - Vijay Chakilam Limitations of Perceptron x1 W, b 0,1 1,1 y x2 weight plane output =1 output =0 There is no value for W and b such that the model
Learning Deep Architectures for AI - Yoshua Bengio Part II - Vijay Chakilam Limitations of Perceptron x1 W, b 0,1 1,1 y x2 weight plane output =1 output =0 There is no value for W and b such that the model
Machine Learning
 Machine Learning 10-601 Maria Florina Balcan Machine Learning Department Carnegie Mellon University 02/10/2016 Today: Artificial neural networks Backpropagation Reading: Mitchell: Chapter 4 Bishop: Chapter
Machine Learning 10-601 Maria Florina Balcan Machine Learning Department Carnegie Mellon University 02/10/2016 Today: Artificial neural networks Backpropagation Reading: Mitchell: Chapter 4 Bishop: Chapter
Lecture 2: Modular Learning
 Lecture 2: Modular Learning Deep Learning @ UvA MODULAR LEARNING - PAGE 1 Announcement o C. Maddison is coming to the Deep Vision Seminars on the 21 st of Sep Author of concrete distribution, co-author
Lecture 2: Modular Learning Deep Learning @ UvA MODULAR LEARNING - PAGE 1 Announcement o C. Maddison is coming to the Deep Vision Seminars on the 21 st of Sep Author of concrete distribution, co-author
Neural Networks (Part 1) Goals for the lecture
 Neural Networks (Part ) Mark Craven and David Page Computer Sciences 760 Spring 208 www.biostat.wisc.edu/~craven/cs760/ Some of the slides in these lectures have been adapted/borrowed from materials developed
Neural Networks (Part ) Mark Craven and David Page Computer Sciences 760 Spring 208 www.biostat.wisc.edu/~craven/cs760/ Some of the slides in these lectures have been adapted/borrowed from materials developed
Artificial Neural Networks. MGS Lecture 2
 Artificial Neural Networks MGS 2018 - Lecture 2 OVERVIEW Biological Neural Networks Cell Topology: Input, Output, and Hidden Layers Functional description Cost functions Training ANNs Back-Propagation
Artificial Neural Networks MGS 2018 - Lecture 2 OVERVIEW Biological Neural Networks Cell Topology: Input, Output, and Hidden Layers Functional description Cost functions Training ANNs Back-Propagation
Logistic Regression Review Fall 2012 Recitation. September 25, 2012 TA: Selen Uguroglu
 Logistic Regression Review 10-601 Fall 2012 Recitation September 25, 2012 TA: Selen Uguroglu!1 Outline Decision Theory Logistic regression Goal Loss function Inference Gradient Descent!2 Training Data
Logistic Regression Review 10-601 Fall 2012 Recitation September 25, 2012 TA: Selen Uguroglu!1 Outline Decision Theory Logistic regression Goal Loss function Inference Gradient Descent!2 Training Data
Deep Neural Networks (1) Hidden layers; Back-propagation
 Deep Neural Networs (1) Hidden layers; Bac-propagation Steve Renals Machine Learning Practical MLP Lecture 3 4 October 2017 / 9 October 2017 MLP Lecture 3 Deep Neural Networs (1) 1 Recap: Softmax single
Deep Neural Networs (1) Hidden layers; Bac-propagation Steve Renals Machine Learning Practical MLP Lecture 3 4 October 2017 / 9 October 2017 MLP Lecture 3 Deep Neural Networs (1) 1 Recap: Softmax single
Deep Feedforward Networks
 Deep Feedforward Networks Yongjin Park 1 Goal of Feedforward Networks Deep Feedforward Networks are also called as Feedforward neural networks or Multilayer Perceptrons Their Goal: approximate some function
Deep Feedforward Networks Yongjin Park 1 Goal of Feedforward Networks Deep Feedforward Networks are also called as Feedforward neural networks or Multilayer Perceptrons Their Goal: approximate some function
Machine Learning. Neural Networks. (slides from Domingos, Pardo, others)
 Machine Learning Neural Networks (slides from Domingos, Pardo, others) Human Brain Neurons Input-Output Transformation Input Spikes Output Spike Spike (= a brief pulse) (Excitatory Post-Synaptic Potential)
Machine Learning Neural Networks (slides from Domingos, Pardo, others) Human Brain Neurons Input-Output Transformation Input Spikes Output Spike Spike (= a brief pulse) (Excitatory Post-Synaptic Potential)
Bits of Machine Learning Part 1: Supervised Learning
 Bits of Machine Learning Part 1: Supervised Learning Alexandre Proutiere and Vahan Petrosyan KTH (The Royal Institute of Technology) Outline of the Course 1. Supervised Learning Regression and Classification
Bits of Machine Learning Part 1: Supervised Learning Alexandre Proutiere and Vahan Petrosyan KTH (The Royal Institute of Technology) Outline of the Course 1. Supervised Learning Regression and Classification
<Special Topics in VLSI> Learning for Deep Neural Networks (Back-propagation)
 Learning for Deep Neural Networks (Back-propagation) Outline Summary of Previous Standford Lecture Universal Approximation Theorem Inference vs Training Gradient Descent Back-Propagation
Learning for Deep Neural Networks (Back-propagation) Outline Summary of Previous Standford Lecture Universal Approximation Theorem Inference vs Training Gradient Descent Back-Propagation
Introduction to Neural Networks
 Introduction to Neural Networks Philipp Koehn 3 October 207 Linear Models We used before weighted linear combination of feature values h j and weights λ j score(λ, d i ) = j λ j h j (d i ) Such models
Introduction to Neural Networks Philipp Koehn 3 October 207 Linear Models We used before weighted linear combination of feature values h j and weights λ j score(λ, d i ) = j λ j h j (d i ) Such models
CSC321 Lecture 7: Optimization
 CSC321 Lecture 7: Optimization Roger Grosse Roger Grosse CSC321 Lecture 7: Optimization 1 / 25 Overview We ve talked a lot about how to compute gradients. What do we actually do with them? Today s lecture:
CSC321 Lecture 7: Optimization Roger Grosse Roger Grosse CSC321 Lecture 7: Optimization 1 / 25 Overview We ve talked a lot about how to compute gradients. What do we actually do with them? Today s lecture:
Neural networks COMS 4771
 Neural networks COMS 4771 1. Logistic regression Logistic regression Suppose X = R d and Y = {0, 1}. A logistic regression model is a statistical model where the conditional probability function has a
Neural networks COMS 4771 1. Logistic regression Logistic regression Suppose X = R d and Y = {0, 1}. A logistic regression model is a statistical model where the conditional probability function has a
Stochastic gradient descent; Classification
 Stochastic gradient descent; Classification Steve Renals Machine Learning Practical MLP Lecture 2 28 September 2016 MLP Lecture 2 Stochastic gradient descent; Classification 1 Single Layer Networks MLP
Stochastic gradient descent; Classification Steve Renals Machine Learning Practical MLP Lecture 2 28 September 2016 MLP Lecture 2 Stochastic gradient descent; Classification 1 Single Layer Networks MLP
CSC321 Lecture 8: Optimization
 CSC321 Lecture 8: Optimization Roger Grosse Roger Grosse CSC321 Lecture 8: Optimization 1 / 26 Overview We ve talked a lot about how to compute gradients. What do we actually do with them? Today s lecture:
CSC321 Lecture 8: Optimization Roger Grosse Roger Grosse CSC321 Lecture 8: Optimization 1 / 26 Overview We ve talked a lot about how to compute gradients. What do we actually do with them? Today s lecture:
Introduction to Machine Learning (67577)
 Introduction to Machine Learning (67577) Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem Deep Learning Shai Shalev-Shwartz (Hebrew U) IML Deep Learning Neural Networks
Introduction to Machine Learning (67577) Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem Deep Learning Shai Shalev-Shwartz (Hebrew U) IML Deep Learning Neural Networks
SPSS, University of Texas at Arlington. Topics in Machine Learning-EE 5359 Neural Networks
 Topics in Machine Learning-EE 5359 Neural Networks 1 The Perceptron Output: A perceptron is a function that maps D-dimensional vectors to real numbers. For notational convenience, we add a zero-th dimension
Topics in Machine Learning-EE 5359 Neural Networks 1 The Perceptron Output: A perceptron is a function that maps D-dimensional vectors to real numbers. For notational convenience, we add a zero-th dimension
Data Mining Part 5. Prediction
 Data Mining Part 5. Prediction 5.5. Spring 2010 Instructor: Dr. Masoud Yaghini Outline How the Brain Works Artificial Neural Networks Simple Computing Elements Feed-Forward Networks Perceptrons (Single-layer,
Data Mining Part 5. Prediction 5.5. Spring 2010 Instructor: Dr. Masoud Yaghini Outline How the Brain Works Artificial Neural Networks Simple Computing Elements Feed-Forward Networks Perceptrons (Single-layer,
From perceptrons to word embeddings. Simon Šuster University of Groningen
 From perceptrons to word embeddings Simon Šuster University of Groningen Outline A basic computational unit Weighting some input to produce an output: classification Perceptron Classify tweets Written
From perceptrons to word embeddings Simon Šuster University of Groningen Outline A basic computational unit Weighting some input to produce an output: classification Perceptron Classify tweets Written
ECE521 Lecture 7/8. Logistic Regression
 ECE521 Lecture 7/8 Logistic Regression Outline Logistic regression (Continue) A single neuron Learning neural networks Multi-class classification 2 Logistic regression The output of a logistic regression
ECE521 Lecture 7/8 Logistic Regression Outline Logistic regression (Continue) A single neuron Learning neural networks Multi-class classification 2 Logistic regression The output of a logistic regression
Deep Feedforward Networks. Sargur N. Srihari
 Deep Feedforward Networks Sargur N. srihari@cedar.buffalo.edu 1 Topics Overview 1. Example: Learning XOR 2. Gradient-Based Learning 3. Hidden Units 4. Architecture Design 5. Backpropagation and Other Differentiation
Deep Feedforward Networks Sargur N. srihari@cedar.buffalo.edu 1 Topics Overview 1. Example: Learning XOR 2. Gradient-Based Learning 3. Hidden Units 4. Architecture Design 5. Backpropagation and Other Differentiation
Neural networks. Chapter 20. Chapter 20 1
 Neural networks Chapter 20 Chapter 20 1 Outline Brains Neural networks Perceptrons Multilayer networks Applications of neural networks Chapter 20 2 Brains 10 11 neurons of > 20 types, 10 14 synapses, 1ms
Neural networks Chapter 20 Chapter 20 1 Outline Brains Neural networks Perceptrons Multilayer networks Applications of neural networks Chapter 20 2 Brains 10 11 neurons of > 20 types, 10 14 synapses, 1ms
Multilayer Neural Networks. (sometimes called Multilayer Perceptrons or MLPs)
 Multilayer Neural Networks (sometimes called Multilayer Perceptrons or MLPs) Linear separability Hyperplane In 2D: w x + w 2 x 2 + w 0 = 0 Feature x 2 = w w 2 x w 0 w 2 Feature 2 A perceptron can separate
Multilayer Neural Networks (sometimes called Multilayer Perceptrons or MLPs) Linear separability Hyperplane In 2D: w x + w 2 x 2 + w 0 = 0 Feature x 2 = w w 2 x w 0 w 2 Feature 2 A perceptron can separate
Neural Networks, Computation Graphs. CMSC 470 Marine Carpuat
 Neural Networks, Computation Graphs CMSC 470 Marine Carpuat Binary Classification with a Multi-layer Perceptron φ A = 1 φ site = 1 φ located = 1 φ Maizuru = 1 φ, = 2 φ in = 1 φ Kyoto = 1 φ priest = 0 φ
Neural Networks, Computation Graphs CMSC 470 Marine Carpuat Binary Classification with a Multi-layer Perceptron φ A = 1 φ site = 1 φ located = 1 φ Maizuru = 1 φ, = 2 φ in = 1 φ Kyoto = 1 φ priest = 0 φ
Machine Learning Lecture 14
 Machine Learning Lecture 14 Tricks of the Trade 07.12.2017 Bastian Leibe RWTH Aachen http://www.vision.rwth-aachen.de leibe@vision.rwth-aachen.de Course Outline Fundamentals Bayes Decision Theory Probability
Machine Learning Lecture 14 Tricks of the Trade 07.12.2017 Bastian Leibe RWTH Aachen http://www.vision.rwth-aachen.de leibe@vision.rwth-aachen.de Course Outline Fundamentals Bayes Decision Theory Probability
CSC 578 Neural Networks and Deep Learning
 CSC 578 Neural Networks and Deep Learning Fall 2018/19 3. Improving Neural Networks (Some figures adapted from NNDL book) 1 Various Approaches to Improve Neural Networks 1. Cost functions Quadratic Cross
CSC 578 Neural Networks and Deep Learning Fall 2018/19 3. Improving Neural Networks (Some figures adapted from NNDL book) 1 Various Approaches to Improve Neural Networks 1. Cost functions Quadratic Cross
Machine learning comes from Bayesian decision theory in statistics. There we want to minimize the expected value of the loss function.
 Bayesian learning: Machine learning comes from Bayesian decision theory in statistics. There we want to minimize the expected value of the loss function. Let y be the true label and y be the predicted
Bayesian learning: Machine learning comes from Bayesian decision theory in statistics. There we want to minimize the expected value of the loss function. Let y be the true label and y be the predicted
Multilayer Neural Networks. (sometimes called Multilayer Perceptrons or MLPs)
 Multilayer Neural Networks (sometimes called Multilayer Perceptrons or MLPs) Linear separability Hyperplane In 2D: w 1 x 1 + w 2 x 2 + w 0 = 0 Feature 1 x 2 = w 1 w 2 x 1 w 0 w 2 Feature 2 A perceptron
Multilayer Neural Networks (sometimes called Multilayer Perceptrons or MLPs) Linear separability Hyperplane In 2D: w 1 x 1 + w 2 x 2 + w 0 = 0 Feature 1 x 2 = w 1 w 2 x 1 w 0 w 2 Feature 2 A perceptron
Based on the original slides of Hung-yi Lee
 Based on the original slides of Hung-yi Lee Google Trends Deep learning obtains many exciting results. Can contribute to new Smart Services in the Context of the Internet of Things (IoT). IoT Services
Based on the original slides of Hung-yi Lee Google Trends Deep learning obtains many exciting results. Can contribute to new Smart Services in the Context of the Internet of Things (IoT). IoT Services
Eve: A Gradient Based Optimization Method with Locally and Globally Adaptive Learning Rates
 Eve: A Gradient Based Optimization Method with Locally and Globally Adaptive Learning Rates Hiroaki Hayashi 1,* Jayanth Koushik 1,* Graham Neubig 1 arxiv:1611.01505v3 [cs.lg] 11 Jun 2018 Abstract Adaptive
Eve: A Gradient Based Optimization Method with Locally and Globally Adaptive Learning Rates Hiroaki Hayashi 1,* Jayanth Koushik 1,* Graham Neubig 1 arxiv:1611.01505v3 [cs.lg] 11 Jun 2018 Abstract Adaptive
Deep Feedforward Networks. Lecture slides for Chapter 6 of Deep Learning Ian Goodfellow Last updated
 Deep Feedforward Networks Lecture slides for Chapter 6 of Deep Learning www.deeplearningbook.org Ian Goodfellow Last updated 2016-10-04 Roadmap Example: Learning XOR Gradient-Based Learning Hidden Units
Deep Feedforward Networks Lecture slides for Chapter 6 of Deep Learning www.deeplearningbook.org Ian Goodfellow Last updated 2016-10-04 Roadmap Example: Learning XOR Gradient-Based Learning Hidden Units
CSCI 1951-G Optimization Methods in Finance Part 12: Variants of Gradient Descent
 CSCI 1951-G Optimization Methods in Finance Part 12: Variants of Gradient Descent April 27, 2018 1 / 32 Outline 1) Moment and Nesterov s accelerated gradient descent 2) AdaGrad and RMSProp 4) Adam 5) Stochastic
CSCI 1951-G Optimization Methods in Finance Part 12: Variants of Gradient Descent April 27, 2018 1 / 32 Outline 1) Moment and Nesterov s accelerated gradient descent 2) AdaGrad and RMSProp 4) Adam 5) Stochastic
