Putnam 1997 (Problems and Solutions)
|
|
|
- Merry Gaines
- 5 years ago
- Views:
Transcription
1 Putna 997 (Probles and Solutions) A. A rectangle, HOMF, has sides HO =and OM =5. A triangle ABC has H as the intersection of the altitudes, O the center of the circuscribed circle, M the idpoint of BC, andf the foot of the altitude fro A. What is the length of BC? Solution. In the figure below, let G be such that MG =,letx = BF = GC, and let y = AH. Since O is the circucenter, we have y =5 2 +(+x) 2. The slope of the line AB is (5 + y) /x and the slope of HC is 5/ (22 + x). Since these lines eet at right angles, the product of the slopes is. Thus, 5+y 5 x 22+x =or y =22x + x 2. Hence y =5 2 +(+x) 2 = x + x 2 = y, or y 2 5y 50 = 0 or (y 0) (y +5) =0. Thus, y =0,x=3and BC = = 28.
2 A2. Players, 2, 3,..., n are seated around a table and each has a single penny. Player passes a penny to Player 2, who then passes two pennies to Player 3. Player 3 then passes one penny to player 4, who passes two pennies to Player 5, and so on, players alternately passing one penny or two to the next player who still has pennies. A player who runs out of pennies drops out of the gae and leaves the table. Find an infinite set of nubers n for which soe player ends up with all n pennies. Solution. Suppose that at soe point there are an odd nuber greater than of reaining players, say p,p 2,..., p 2k+ (k ), none in danger of dropping out on their next pass. Then there is an odd nuber of passes starting with p s pass to p 2 and ending with p 2k+ s pass to p. Thus, if p passes 2 coins he will receive 2 coins, and if he passes he will receive. The sae is true for any other player and the gae will not terinate. Thus, we ust avoid this situation, or we are stuck with a nonterinating gae. Suppose that to begin with there are n =2 (where for notational convenience, 3) players, say p,..., p 2. Note that p drops out and p 2 passes his two and drops out, p 3 passes and ends up with 2, p 4 drops out, but p 5 ends up with 2. Continuing, p 3,p 5,..., p 2 each have 2 coins and p 2 drops out when he passes 2 to p 3 who now has 4. There are now players and we are stuck if is odd. Thus, we need =2 for soe. Relabel the players q,..., q 2.Nowq has 4 coins, the rest have 2, andq starts this stage by passing to q 2.Sincethere areanevennuber(2 ) of players, q will eventually receive 2 (for a total of 5) andpass again to q 2 to begin the second round of the stage, but then q 2 drops out, as do q 4,q 6,..., q 2. When q 2 passes 2 to q and drops out, q will have 7 and the rest q 3,q 5,..., q 2 each have 4. At the beginning of this new stage, there are now players left which ust be even, or else =(i.e., we have a winner) or we are stuck. Continuing, we see that the gae terinates if and only if is a power of 2, since half of the players (those repeatedly passing 2) eventually drop out at each stage which necessarily ust have an even nuber of players if not a winner. Observe that all the players passing 2 in a stage, have the sae nuber of coins, and so they all drop out in the sae final round of the stage. Thus, a gae with n =2 players terinates if and only if =2 =2 k for soe k 0, or n =2 =2 2 k + =2 h +2, h =2, 3, 4,... will yield terinating gaes. Of course, n =2and n =4gaes also terinate. Incidentally, for n =2 h +2, the original player p 3 is the winner since each stage ends with p 3 receiving 2. 2
3 A3. Evaluate Z µx µ x3 2 + x5 2 4 x x x x dx 0 Solution. The first series is xe 2 x2. For the second series, we use the fact that for n =0,, 2,..., Z π 0 cos 2n θ dθ = = 3 5 (n ) (2n ) 2n π = n (2n) 2 π (2n)! (2n) 2 π. Then second series is (using R π 0 cos2n+ θ dθ =0), R π R π 0 cos2n θ dθ π x 2n π 0 = cosk θ dθ x k = (2n)! k! π n=0 Thus, the desired integral is Z Z π = π n=0 Z π 0 0 e x cos θ dθ. Z π Z Z π 0 (x cos θ) k dθ k! xe 2 x2 e x cos θ dθ dx = e 2 r2 e r cos θ rdrdθ 0 π 0 π 0 0 = Z Z e 2 (x2 +y 2 ) e x dxdy = Z Z π 0 π e 2 e 2 2x+) (x2 dx e 2 y2 dy 0 = Z Z π e 2 e 2 (x )2 dx e 2 y2 dy = π e ³ 2 2π 2π = e. 2 n=0 3
4 A4. Let G be a group with identity e and φ : G G be a function such that φ (g ) φ (g 2 ) φ (g 3 )=φ (h ) φ (h 2 ) φ (h 3 ) whenever g g 2 g 3 = e = h h 2 h 3. Prove that there exists an eleent a in G such that ψ (x) =aφ (x) is a hooorphis (that is, ψ (xy) =ψ (x) ψ (y) for all x and y in G). Solution. Since x xe = e 3, we have φ x φ (x) φ (e) =φ (e) 3 or φ x φ (x) =φ (e) 2 or φ x = φ (x) φ (e) 2. Since yy e = e 3,wehave φ (y) φ y φ (e) =φ (e) 3 or φ (y) φ y = φ (e) 2 or φ y = φ (e) 2 φ (y). Since x (xy) y = eee,we have φ x φ (xy) φ y = φ (e) 3, and so φ (xy) = φ x φ (e) 3 φ y = φ (x) φ (e) 2 φ (e) 3 φ (e) 2 φ (y) = φ (x) φ (e) φ (y). 4
5 A5. Let N n denote the nuber of ordered n-tuples of positive integers (a,a 2,...,a n ) such that /a +/a /a n =. Deterine whether N 0 is even or odd. Solution. Consider the involution of the set of solutions (a,a 2,a 3,a 4,a 5,a 6,a 7,a 8,a 9,a 0 ) 7 (a 2,a,a 4,a 3,a 6,a 5,a 8,a 7,a 0,a 9 ) The nuber of points that are not fixed is even. Thus, we need only to consider the solutions of the for (a,a,a 3,a 3,a 5,a 5,a 7,a 7,a 9,a 9 ). On this set of reaining solutions, consider the involution (a,a,a 3,a 3,a 5,a 5,a 7,a 7,a 9,a 9 ) 7 (a 3,a 3,a,a,a 7,a 7,a 5,a 5,a 9,a 9 ) The points that are fixed are of the for (a,a,a,a,a 5,a 5,a 5,a 5,a 9,a 9 ). By one ore involution we need only consider the nuber of solutions of the for (a,a,a,a,a,a,a,a,a 9,a 9 ). For these 8 a + 2 a 9 =,andsoa 9 = 2a a 8. The set of possible pairs (a,a 9 ) is {(9, 8), (0, 0), (2, 6), (6, 4), (24, 3)}. Thus,N 0 is odd. 5
6 A6. For a positive integer n and any real nuber c, define x k recursively by x 0 =0, x =, and for k 0, x k+2 = cx k+ (n k)x k. k + Fix n andthentakec to be the largest value for which x n+ =0. Find x k in ters of n and k, k n. Solution. The recurrence relation is as one ight find while solving a differential equation using power series. We have (k +)x k+2 = cx k+ (n k)x k x k+2 (k +)t k = c x k+ t k n x k t k + kx k t k x k+2 (k +)t k = c x k+ t k (n ) x k t k + t 2 k= (k ) x k t k 2 Let f(t) = P x k+t k =+ P x k+2t k+ = P k= x kt k. Then the above says Hence f 0 (t) = cf(t) (n ) tf(t)+t 2 f 0 (t) f 0 (t) c (n )t = f(t) t 2 = B +t + A t = 2 (n +c) +t 2 (n c). t f(t) =( t) 2 (n c) ( + t) 2 (n +c). Now f(t) will be a polynoial of degree n if 2 (n +c) and 2 (n c) are nonnegative integers, say j and n j (i.e., j =0,..., n ). Since f(t) = P x k+t k,wewouldthenhavex n+ =0. Since j = 2 (n +c), c =2j n +. Thus, soe possible values for c for which x n+ (n, c) =0are the n values n +, n +3,..., 2(n ) n +=n. However, it is clear that x k (n, c) is a polynoial of degree at ost k in c. Indeed, x 2 (n, c) =c, and fro x k+2 = cxk+ (n k)xk k+ the result follows fro induction. Thus, the values the above values are the only values of c for which x n+ (n, c) =0. The largest of these values is c = n. Then f(t) =( t) 2 (n c) ( + t) 2 (n +c) =(+t) n, 6
7 and f(t) = P x k+t k x k+ = n k or 0 k =0 x k = k = n k k =2,..., n 0 k>n. 7
8 B. Let {x} denote the distance between the real nuber x and the nearest integer. For each positive integer n, evaluate F n = 6n = in({ 6n }, { 3n }). (Here in(a, b) denotes the iniu of a and b.) Solution. Wehave { 6n } = ½ 6n 3n 6n 3n 6n { 3n 3n/2 3n } = 3n 3n/2 3n 3n 3n 3n 3 2 = 9n 2 2 9n 3n 2 6n Now in({ 6n }, { 6n 3n/2 3n })= in 6n, 3n 3n/2 3n in 6n, 3n 3n 3n 3 2 = 9n 2 in 6n, 2 9n 3n 2 6n Using 6n 3n 2n, 6n 3n 4n 6n 2 3n 6n,. we have in({ 6n }, { 3n })= 6n 3n/2 6n 3n/2 2n 3n 2n 3n 3n 3n 4n 6n 4n 9 2 n 9 6n 2 n 6n 6n 2n = 3n 2n 3n 3n 3n 4n 6n 4n 6n 8
9 Hence, F n = = 6n = 2n = 6n in({ 6n }, { 3n }) 3n 6n + = =2n à 2n 2 = ³ 3n 3n =2n n =3n 4n =3n ³ 6n 3n + 6n =4n =4n! ³ 6n +(3n 2n +) (4n 3n +)+(6n 4n +) = 6n 2 (2n)(2n ) (5n ) n +(7n ) n 2 (0n ) 2n +2n = n. 9
10 B2. Let f be a twice-differentiable real-valued function satisfying f(x)+f 00 (x) = xg(x)f 0 (x), where g(x) 0 for all real x. Provethat f(x) is bounded. Solution. Multiplying by f 0 (x), we get 2 d f(x) 2 + f 0 (x) 2 = f(x)f 0 (x)+f 0 (x)f 00 (x) = xg(x)f 0 (x) 2. dx Thus, f(x) 2 + f 0 (x) 2 is nondecreasing for x 0 and nonincreasing for x 0. Hence f(x) 2 f(x) 2 + f 0 (x) 2 f(0) 2 + f 0 (0) 2. 0
11 B3. For each positive integer n, write the su P n = / in the for p n/q n, where p n and q n are relatively prie positive integers. Deterine all n such that 5 does not divide q n. Solution. WeaywritethesuS n := P n = / in the for S n = = n / K 5 k bn/5 k c 5- bn/5c 5-2 / + bn/5 c 5 2 K / = 5- / k F bn/5 k c, where 5 K is the largest power of 5 not greater than n and M F M :=. Consider a su of reciprocals of integers n,..., n k not divisible by 5, say = n 2...n k + n n 3...n k n n 2...n k = N n n 2 n k n n 2...n k D with D = n n 2...n k. Let n i betheassociateofn i ; i.e., n i n i od(5). Note that D (n + n n k ) = n n 2...n k (n + n n k ) n 2...n k + n n 3...n k n n 2...n k = N (od 5) Thus, D (n + n n k ) N (od 5) Since 5 - D we have 5 N n + n n k 0(od5) Note that =, 2=3, 3=2, 4=4 Working od 5, wehave 5- =, +2 =, +2+3 =, = = = = = 0, etc..
12 Writing F M = NM D M, we have N M,,, 0, 0(od5)if M, 2, 3, 4, 5(od5), respectively. Note that if M 5, thenf M = F M and N M = N M 0(od5). Recall Consider the last ter S n = K 5 k F bn/5 k c ( ) 5 K F bn/5 K c in ( ). We have n/5 K =, 2, 3 or 4. If n/5 K =, 2,or 3, then the nuerator of F bn/5k c is not divisible by 5. In this case, S n ust have a factor of at least 5 K in its denoinator. Thus, K =0in this case and n =, 2,or 3. Henceforth, suppose that n/5 K =4. In this case, we have F 4 =+/2+ /3 +/4 = 25 2 and 5 F K bn/5k c = 2 5. If K =0,thenS K 2 4 = F 4 = 25 2 and n =4has the desired property. If K, the preceding ter in ( ) is 5 F K bn/5 K c,and n/5 K =4 n/5 K =4, 2 5, 22 5, 23 5, 24 5 n/5 K =20, 2,..., 24. If n/5 K =2, 22, 23, then 5 F K bn/5 K c has nuerator not divisible by 5 and the denoinator has a factor of 5 K. As all other denoinators in the su have lower powers of 5 (in particular the last ter is 2 5 ), in this K 2 case S n will have denoinator divisible by 5 unless K. Thus, in the case n/5 K =2, 22, 23, we have n = bnc = n/5 K =2, 22, 23. Now suppose that n/5 K =20, 24. We have F 20 = and F 24 = As the nuerators of F 20 and F 24 are divisible by 25, theter 5 F K bn/5 K c has denoinator with a power of 5 of at least K 3. The su of the two ters in ( ) before and after this ter is 5 K 2 F bn/5 K 2 c + 5 K F bn/5 K c = 5 K 2 µ F bn/5 K 2 c + 2 Since 2 3 and the nuerator of F bn/5 K 2 c can be only be congruent to ± or 0, the denoinator of this su has a factor of at least 5 K 2, and all of the other ters have denoinators with lower powers of 5. Thus, we ust have K = or 2. For K =,n=20, 24 and for K =2,we have bn/5c =20, 24 n = 00 04, Thus, in view of all of the above, the only values for n with the desired property are 4, 20 24, 00 04, and
13 B4. Let a,n denote the coefficient of x n in the expansion of ( + x + x 2 ). Prove that for all k 0, b 2k 3 c 0 ( ) i a k i,i. i=0 Solution. Notethatsincethedegreeof( + x + x 2 ) is 2, wehavea,n =0 for n>2. Hence a k i,i =0for i>2(k i) or 3i >2k. Hence the upper liit on the su only serves to eliinate ters which would be 0 or undefined. Let us define a,n =0for n<0 or <0. Thusinthesuaboveandallsus below, we ay take the index to run over all integers. a +,n x n = (+x + x 2 ) + =(+x + x 2 )( + x + x 2 ) n = (+x + x 2 ) k a,k x k = k a,k (x k + x k+ + x k+2 ) = n a,n x n + n a,n x n + n a,n 2 x n = n (a,n + a,n + a,n 2 ) x n. Thus, a +,n = a,n + a,n + a,n 2. Let s k := P b 2k 3 c i=0 ( )i a k i,i = P i ( )i a k i,i.then s k+ : = ( ) i a k+ i,i = ( ) i (a k i,i + a k i,i + a k i,i 2 ) i i = ( ) i a k i,i ( ) i a (k ) (i ),i +( ) i 2 a (k 2) (i 2),i 2 i We have = s k s k + s k 2 s 2 = i ( ) i a 2 i,i =0,s = i ( ) i a i,i =0,s 0 = i ( ) i a 0 i,i = a 0,0 = Thus, s = s 0 s + s 2 = s 2 = s s 0 + s =0 s 3 = s 2 s + s 0 =0 s 4 = s 3 s 2 + s = s 5 = s 4 s 3 + s 2 = 3
14 Assue that s 4k =,s 4k+ =,s 4k+2 =0,s 4k+3 =0. Then s 4(k+) = s 4k+4 = s 4k+3 s 4k+2 + s 4k+ =0 0+=, s 4(k+)+ = s 4k+5 = s 4k+4 s 4k+3 + s 4k+2 = 0+0=, s 4(k+)+2 = s 4k+6 = s 4k+5 s 4k+4 + s 4k+3 = +0=0, and s 4(k+)+3 = s 4k+7 = s 4k+6 s 4k+5 + s 4k+4 =0 +=0. Thus, s k is 0 or for all k 0, and in particular 0 s k. 4
15 B5. Prove that for n 2, o n o n (odn) Solution. Let t := 2 and let t n := 2 t n. We are to show t n =2 t n t n (od n). We firstchecktheresultinthecasen =2 k. Note that t n 2 2 k 2 tn 2 tn 2 od 2 k t n t n od 2 k Thus, for the case n =2 k, it suffices to check that t 2 k 2 2 k. This is true if k =. If it is true for k, then t 2 k+ 2 >t 2k =2 t 2 k k 2 k+, and so t 2k 2 2 k by induction. We handle the case n =2 k d where d is odd, by using induction on d. The case d =has been done. First note that since (d, 2) =, 2 ϕ(d) (odd). Thus, we have the key observation that t 2 t (od ϕ (d)) 2 t t 2 (odd) 2 t 2 2 t (od d) t t (od d). Now t n t n od 2 k d t n t n od 2 k and t n t n (od d) Since n 2 k, we have already shown t n t n od 2 k. Thus, we need only show that t n t n (od d) and by the key observation it suffices to show that t n 2 t n (od ϕ (d)). We have d n 0 := ϕ (d) =2 k0 d 0, where d 0 is odd. Since d 0 <d,by induction we have t n 0 t n 0 (od n 0 ) or t n 0 t n 0 (od ϕ (d)). However, we need t n 2 t n (od ϕ (d)). Since n d n 0,we have n 2 n 0. Hence, if we could show the stronger result that not only t n t n (od n) but also t n t n t n+ t n+2 (od n), 5
16 (ad infinitu), then we would have t n0 t n 0 t n t n t n+ (od ϕ (d)) The stronger result t n t n t n+ t n+2 (od n) is true in the base case n =2 k. Then assuing it holds for d 0 <dinductively, we have t n 0 t n 0 t n t n t n+ (od ϕ (d)) in which case by the key observation, We already know that Thus, t n 0 t n t n t n+ (od d). t n t n+ od 2 k. t n t n+ t n+2 od 2 k d, and we have proven this stronger result by induction. 6
17 B6. The dissection of the triangle shown below (into four congruent right triangles siilar to the original) has diaeter 5/2. Find the least diaeter of a dissection of this triangle into four parts. (The diaeter of a dissection is the least upper bound of the distances between pairs of points belonging to the sae part.) Solution. Lower bounds on the least diaeter of a dissection of the triangle into 4 parts can be obtained by selecting 5 points and taking the sallest distance between pairs. Indeed, any dissection into four parts ust have one region containing 2 of the 5 points and that region has diaeter at least the distance between the two points. Thus, optiistically, we seek 5 points so that the iniu distance between pairs is as large as possible. Then we attept to find a dissection where no region has diaeter larger than this iniu distance. Let A =(0, 4),B =(0, 0),C =(3, 0). The point on the segent AC which is distance t fro (3, 0) is 5 t (0, 4) + 5 t (3, 0) = t, 4 5 t. The square of the distance fro this point to the point (0, 4 t) on AB (at distance t fro A) is µ3 35 t, 45 t 2 (0, 4 t) =25 8t t2 Setting this equal to t 2 yields 25 8t t2 = t 2 t = 25 3, 5 Thus, A is distance 25 3 fro D:= 0, 27 (0, ) which is at distance 25 3 fro E:= , = 24 3, 3 20 (.8462,.5385). It is easy to verify that 25 3 is the iniu distance between pairs of the five points A,B,C,D,E. 25 Thus, 3 is a lower bound on the diaeter of any dissection of ABC into 4 regions. We try to show that this lower bound is realized. Let F = 3 2, 0 and G = 3 2,h where h>0 is chosen so that BG = CG = µ 2 µ h 2 = 26 3 We find h = Thus,G= 3 2, (.5,.2034). Let H = 0, and let I = , = 5 3, 3 32 (.538, 2.465) be the point on AC at distance 25 3 fro A. Then BG = 25 3, CG =
18 Now, the triangle ADI and the two quadrilaterals BFGH and FGEC clearly have diaeter For the pentagon HGEID, we need to check that HE 3, but the height of E is less than that of the idpoint of DH since µ 3 < Thus, all 4 regions have diaeter equal to the lower bound
A1. Find all ordered pairs (a, b) of positive integers for which 1 a + 1 b = 3
 A. Find all ordered pairs a, b) of positive integers for which a + b = 3 08. Answer. The six ordered pairs are 009, 08), 08, 009), 009 337, 674) = 35043, 674), 009 346, 673) = 3584, 673), 674, 009 337)
A. Find all ordered pairs a, b) of positive integers for which a + b = 3 08. Answer. The six ordered pairs are 009, 08), 08, 009), 009 337, 674) = 35043, 674), 009 346, 673) = 3584, 673), 674, 009 337)
a a a a a a a m a b a b
 Algebra / Trig Final Exa Study Guide (Fall Seester) Moncada/Dunphy Inforation About the Final Exa The final exa is cuulative, covering Appendix A (A.1-A.5) and Chapter 1. All probles will be ultiple choice
Algebra / Trig Final Exa Study Guide (Fall Seester) Moncada/Dunphy Inforation About the Final Exa The final exa is cuulative, covering Appendix A (A.1-A.5) and Chapter 1. All probles will be ultiple choice
12 th Annual Johns Hopkins Math Tournament Saturday, February 19, 2011 Power Round-Poles and Polars
 1 th Annual Johns Hopkins Math Tournaent Saturday, February 19, 011 Power Round-Poles and Polars 1. Definition and Basic Properties 1. Note that the unit circles are not necessary in the solutions. They
1 th Annual Johns Hopkins Math Tournaent Saturday, February 19, 011 Power Round-Poles and Polars 1. Definition and Basic Properties 1. Note that the unit circles are not necessary in the solutions. They
Egyptian Mathematics Problem Set
 (Send corrections to cbruni@uwaterloo.ca) Egyptian Matheatics Proble Set (i) Use the Egyptian area of a circle A = (8d/9) 2 to copute the areas of the following circles with given diaeter. d = 2. d = 3
(Send corrections to cbruni@uwaterloo.ca) Egyptian Matheatics Proble Set (i) Use the Egyptian area of a circle A = (8d/9) 2 to copute the areas of the following circles with given diaeter. d = 2. d = 3
List Scheduling and LPT Oliver Braun (09/05/2017)
 List Scheduling and LPT Oliver Braun (09/05/207) We investigate the classical scheduling proble P ax where a set of n independent jobs has to be processed on 2 parallel and identical processors (achines)
List Scheduling and LPT Oliver Braun (09/05/207) We investigate the classical scheduling proble P ax where a set of n independent jobs has to be processed on 2 parallel and identical processors (achines)
International Mathematical Olympiad. Preliminary Selection Contest 2009 Hong Kong. Outline of Solutions
 International Matheatical Olypiad Preliinary Selection ontest 009 Hong Kong Outline of Solutions nswers:. 03809. 0 3. 0. 333. 00099 00. 37 7. 3 8. 3 9. 3 0. 8 3. 009 00. 3 3. 3. 89. 8077. 000 7. 30 8.
International Matheatical Olypiad Preliinary Selection ontest 009 Hong Kong Outline of Solutions nswers:. 03809. 0 3. 0. 333. 00099 00. 37 7. 3 8. 3 9. 3 0. 8 3. 009 00. 3 3. 3. 89. 8077. 000 7. 30 8.
Analysis of Polynomial & Rational Functions ( summary )
 Analysis of Polynoial & Rational Functions ( suary ) The standard for of a polynoial function is ( ) where each of the nubers are called the coefficients. The polynoial of is said to have degree n, where
Analysis of Polynoial & Rational Functions ( suary ) The standard for of a polynoial function is ( ) where each of the nubers are called the coefficients. The polynoial of is said to have degree n, where
MA304 Differential Geometry
 MA304 Differential Geoetry Hoework 4 solutions Spring 018 6% of the final ark 1. The paraeterised curve αt = t cosh t for t R is called the catenary. Find the curvature of αt. Solution. Fro hoework question
MA304 Differential Geoetry Hoework 4 solutions Spring 018 6% of the final ark 1. The paraeterised curve αt = t cosh t for t R is called the catenary. Find the curvature of αt. Solution. Fro hoework question
arxiv: v1 [math.nt] 14 Sep 2014
![arxiv: v1 [math.nt] 14 Sep 2014 arxiv: v1 [math.nt] 14 Sep 2014](/thumbs/89/98762755.jpg) ROTATION REMAINDERS P. JAMESON GRABER, WASHINGTON AND LEE UNIVERSITY 08 arxiv:1409.411v1 [ath.nt] 14 Sep 014 Abstract. We study properties of an array of nubers, called the triangle, in which each row
ROTATION REMAINDERS P. JAMESON GRABER, WASHINGTON AND LEE UNIVERSITY 08 arxiv:1409.411v1 [ath.nt] 14 Sep 014 Abstract. We study properties of an array of nubers, called the triangle, in which each row
= 10 such triples. If it is 5, there is = 1 such triple. Therefore, there are a total of = 46 such triples.
 . Two externally tangent unit circles are constructed inside square ABCD, one tangent to AB and AD, the other to BC and CD. Compute the length of AB. Answer: + Solution: Observe that the diagonal of the
. Two externally tangent unit circles are constructed inside square ABCD, one tangent to AB and AD, the other to BC and CD. Compute the length of AB. Answer: + Solution: Observe that the diagonal of the
Lecture 21 Principle of Inclusion and Exclusion
 Lecture 21 Principle of Inclusion and Exclusion Holden Lee and Yoni Miller 5/6/11 1 Introduction and first exaples We start off with an exaple Exaple 11: At Sunnydale High School there are 28 students
Lecture 21 Principle of Inclusion and Exclusion Holden Lee and Yoni Miller 5/6/11 1 Introduction and first exaples We start off with an exaple Exaple 11: At Sunnydale High School there are 28 students
Sun Life Financial Canadian Open Mathematics Challenge Section A 4 marks each. Official Solutions
 Sun Life Financial Canadian Open Mathematics Challenge 2015 Official Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2015/practice.html
Sun Life Financial Canadian Open Mathematics Challenge 2015 Official Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2015/practice.html
4 = (0.02) 3 13, = 0.25 because = 25. Simi-
 Theore. Let b and be integers greater than. If = (. a a 2 a i ) b,then for any t N, in base (b + t), the fraction has the digital representation = (. a a 2 a i ) b+t, where a i = a i + tk i with k i =
Theore. Let b and be integers greater than. If = (. a a 2 a i ) b,then for any t N, in base (b + t), the fraction has the digital representation = (. a a 2 a i ) b+t, where a i = a i + tk i with k i =
Polygonal Designs: Existence and Construction
 Polygonal Designs: Existence and Construction John Hegean Departent of Matheatics, Stanford University, Stanford, CA 9405 Jeff Langford Departent of Matheatics, Drake University, Des Moines, IA 5011 G
Polygonal Designs: Existence and Construction John Hegean Departent of Matheatics, Stanford University, Stanford, CA 9405 Jeff Langford Departent of Matheatics, Drake University, Des Moines, IA 5011 G
Bernoulli Numbers. Junior Number Theory Seminar University of Texas at Austin September 6th, 2005 Matilde N. Lalín. m 1 ( ) m + 1 k. B m.
 Bernoulli Nubers Junior Nuber Theory Seinar University of Texas at Austin Septeber 6th, 5 Matilde N. Lalín I will ostly follow []. Definition and soe identities Definition 1 Bernoulli nubers are defined
Bernoulli Nubers Junior Nuber Theory Seinar University of Texas at Austin Septeber 6th, 5 Matilde N. Lalín I will ostly follow []. Definition and soe identities Definition 1 Bernoulli nubers are defined
MULTIPLAYER ROCK-PAPER-SCISSORS
 MULTIPLAYER ROCK-PAPER-SCISSORS CHARLOTTE ATEN Contents 1. Introduction 1 2. RPS Magas 3 3. Ites as a Function of Players and Vice Versa 5 4. Algebraic Properties of RPS Magas 6 References 6 1. Introduction
MULTIPLAYER ROCK-PAPER-SCISSORS CHARLOTTE ATEN Contents 1. Introduction 1 2. RPS Magas 3 3. Ites as a Function of Players and Vice Versa 5 4. Algebraic Properties of RPS Magas 6 References 6 1. Introduction
. The univariate situation. It is well-known for a long tie that denoinators of Pade approxiants can be considered as orthogonal polynoials with respe
 PROPERTIES OF MULTIVARIATE HOMOGENEOUS ORTHOGONAL POLYNOMIALS Brahi Benouahane y Annie Cuyt? Keywords Abstract It is well-known that the denoinators of Pade approxiants can be considered as orthogonal
PROPERTIES OF MULTIVARIATE HOMOGENEOUS ORTHOGONAL POLYNOMIALS Brahi Benouahane y Annie Cuyt? Keywords Abstract It is well-known that the denoinators of Pade approxiants can be considered as orthogonal
Understanding Machine Learning Solution Manual
 Understanding Machine Learning Solution Manual Written by Alon Gonen Edited by Dana Rubinstein Noveber 17, 2014 2 Gentle Start 1. Given S = ((x i, y i )), define the ultivariate polynoial p S (x) = i []:y
Understanding Machine Learning Solution Manual Written by Alon Gonen Edited by Dana Rubinstein Noveber 17, 2014 2 Gentle Start 1. Given S = ((x i, y i )), define the ultivariate polynoial p S (x) = i []:y
THE SUPER CATALAN NUMBERS S(m, m + s) FOR s 3 AND SOME INTEGER FACTORIAL RATIOS. 1. Introduction. = (2n)!
 THE SUPER CATALAN NUMBERS S(, + s FOR s 3 AND SOME INTEGER FACTORIAL RATIOS XIN CHEN AND JANE WANG Abstract. We give a cobinatorial interpretation for the super Catalan nuber S(, + s for s 3 using lattice
THE SUPER CATALAN NUMBERS S(, + s FOR s 3 AND SOME INTEGER FACTORIAL RATIOS XIN CHEN AND JANE WANG Abstract. We give a cobinatorial interpretation for the super Catalan nuber S(, + s for s 3 using lattice
13.2 Fully Polynomial Randomized Approximation Scheme for Permanent of Random 0-1 Matrices
 CS71 Randoness & Coputation Spring 018 Instructor: Alistair Sinclair Lecture 13: February 7 Disclaier: These notes have not been subjected to the usual scrutiny accorded to foral publications. They ay
CS71 Randoness & Coputation Spring 018 Instructor: Alistair Sinclair Lecture 13: February 7 Disclaier: These notes have not been subjected to the usual scrutiny accorded to foral publications. They ay
Curious Bounds for Floor Function Sums
 1 47 6 11 Journal of Integer Sequences, Vol. 1 (018), Article 18.1.8 Curious Bounds for Floor Function Sus Thotsaporn Thanatipanonda and Elaine Wong 1 Science Division Mahidol University International
1 47 6 11 Journal of Integer Sequences, Vol. 1 (018), Article 18.1.8 Curious Bounds for Floor Function Sus Thotsaporn Thanatipanonda and Elaine Wong 1 Science Division Mahidol University International
The Weierstrass Approximation Theorem
 36 The Weierstrass Approxiation Theore Recall that the fundaental idea underlying the construction of the real nubers is approxiation by the sipler rational nubers. Firstly, nubers are often deterined
36 The Weierstrass Approxiation Theore Recall that the fundaental idea underlying the construction of the real nubers is approxiation by the sipler rational nubers. Firstly, nubers are often deterined
Monochromatic images
 CHAPTER 8 Monochroatic iages 1 The Central Sets Theore Lea 11 Let S,+) be a seigroup, e be an idepotent of βs and A e There is a set B A in e such that, for each v B, there is a set C A in e with v+c A
CHAPTER 8 Monochroatic iages 1 The Central Sets Theore Lea 11 Let S,+) be a seigroup, e be an idepotent of βs and A e There is a set B A in e such that, for each v B, there is a set C A in e with v+c A
Functions: Review of Algebra and Trigonometry
 Sec. and. Functions: Review o Algebra and Trigonoetry A. Functions and Relations DEFN Relation: A set o ordered pairs. (,y) (doain, range) DEFN Function: A correspondence ro one set (the doain) to anther
Sec. and. Functions: Review o Algebra and Trigonoetry A. Functions and Relations DEFN Relation: A set o ordered pairs. (,y) (doain, range) DEFN Function: A correspondence ro one set (the doain) to anther
Model Fitting. CURM Background Material, Fall 2014 Dr. Doreen De Leon
 Model Fitting CURM Background Material, Fall 014 Dr. Doreen De Leon 1 Introduction Given a set of data points, we often want to fit a selected odel or type to the data (e.g., we suspect an exponential
Model Fitting CURM Background Material, Fall 014 Dr. Doreen De Leon 1 Introduction Given a set of data points, we often want to fit a selected odel or type to the data (e.g., we suspect an exponential
Poornima University, For any query, contact us at: , 18
 AIEEE//Math S. No Questions Solutions Q. Lets cos (α + β) = and let sin (α + β) = 5, where α, β π, then tan α = 5 (a) 56 (b) 9 (c) 7 (d) 5 6 Sol: (a) cos (α + β) = 5 tan (α + β) = tan α = than (α + β +
AIEEE//Math S. No Questions Solutions Q. Lets cos (α + β) = and let sin (α + β) = 5, where α, β π, then tan α = 5 (a) 56 (b) 9 (c) 7 (d) 5 6 Sol: (a) cos (α + β) = 5 tan (α + β) = tan α = than (α + β +
Putnam problems and solutions A1
 Putnam problems and solutions A1 (Many solutions are taken directly from http://www.unl.edu/amc/a-activities/a7-problems/ putnamindex.shtml where the authors are properly attributed. Others are from The
Putnam problems and solutions A1 (Many solutions are taken directly from http://www.unl.edu/amc/a-activities/a7-problems/ putnamindex.shtml where the authors are properly attributed. Others are from The
1 Proof of learning bounds
 COS 511: Theoretical Machine Learning Lecturer: Rob Schapire Lecture #4 Scribe: Akshay Mittal February 13, 2013 1 Proof of learning bounds For intuition of the following theore, suppose there exists a
COS 511: Theoretical Machine Learning Lecturer: Rob Schapire Lecture #4 Scribe: Akshay Mittal February 13, 2013 1 Proof of learning bounds For intuition of the following theore, suppose there exists a
In this chapter, we consider several graph-theoretic and probabilistic models
 THREE ONE GRAPH-THEORETIC AND STATISTICAL MODELS 3.1 INTRODUCTION In this chapter, we consider several graph-theoretic and probabilistic odels for a social network, which we do under different assuptions
THREE ONE GRAPH-THEORETIC AND STATISTICAL MODELS 3.1 INTRODUCTION In this chapter, we consider several graph-theoretic and probabilistic odels for a social network, which we do under different assuptions
EXPLICIT CONGRUENCES FOR EULER POLYNOMIALS
 EXPLICIT CONGRUENCES FOR EULER POLYNOMIALS Zhi-Wei Sun Departent of Matheatics, Nanjing University Nanjing 10093, People s Republic of China zwsun@nju.edu.cn Abstract In this paper we establish soe explicit
EXPLICIT CONGRUENCES FOR EULER POLYNOMIALS Zhi-Wei Sun Departent of Matheatics, Nanjing University Nanjing 10093, People s Republic of China zwsun@nju.edu.cn Abstract In this paper we establish soe explicit
Solutions of some selected problems of Homework 4
 Solutions of soe selected probles of Hoework 4 Sangchul Lee May 7, 2018 Proble 1 Let there be light A professor has two light bulbs in his garage. When both are burned out, they are replaced, and the next
Solutions of soe selected probles of Hoework 4 Sangchul Lee May 7, 2018 Proble 1 Let there be light A professor has two light bulbs in his garage. When both are burned out, they are replaced, and the next
Characterization of the Line Complexity of Cellular Automata Generated by Polynomial Transition Rules. Bertrand Stone
 Characterization of the Line Coplexity of Cellular Autoata Generated by Polynoial Transition Rules Bertrand Stone Abstract Cellular autoata are discrete dynaical systes which consist of changing patterns
Characterization of the Line Coplexity of Cellular Autoata Generated by Polynoial Transition Rules Bertrand Stone Abstract Cellular autoata are discrete dynaical systes which consist of changing patterns
arxiv: v1 [math.co] 19 Apr 2017
![arxiv: v1 [math.co] 19 Apr 2017 arxiv: v1 [math.co] 19 Apr 2017](/thumbs/72/66647389.jpg) PROOF OF CHAPOTON S CONJECTURE ON NEWTON POLYTOPES OF q-ehrhart POLYNOMIALS arxiv:1704.0561v1 [ath.co] 19 Apr 017 JANG SOO KIM AND U-KEUN SONG Abstract. Recently, Chapoton found a q-analog of Ehrhart polynoials,
PROOF OF CHAPOTON S CONJECTURE ON NEWTON POLYTOPES OF q-ehrhart POLYNOMIALS arxiv:1704.0561v1 [ath.co] 19 Apr 017 JANG SOO KIM AND U-KEUN SONG Abstract. Recently, Chapoton found a q-analog of Ehrhart polynoials,
Related Rates section 3.9
 Related Rate ection 3.9 Iportant Note: In olving the related rate proble, the rate of change of a quantity i given and the rate of change of another quantity i aked for. You need to find a relationhip
Related Rate ection 3.9 Iportant Note: In olving the related rate proble, the rate of change of a quantity i given and the rate of change of another quantity i aked for. You need to find a relationhip
On the Navier Stokes equations
 On the Navier Stokes equations Daniel Thoas Hayes April 26, 2018 The proble on the existence and soothness of the Navier Stokes equations is resolved. 1. Proble description The Navier Stokes equations
On the Navier Stokes equations Daniel Thoas Hayes April 26, 2018 The proble on the existence and soothness of the Navier Stokes equations is resolved. 1. Proble description The Navier Stokes equations
UNIVERSITY OF MICHIGAN UNDERGRADUATE MATH COMPETITION 28 APRIL 7, 2011
 UNIVERSITY OF MICHIGAN UNDERGRADUATE MATH COMPETITION 28 APRIL 7, 20 Instructions. Write on the front of your blue book your student ID number. Do not write your name anywhere on your blue book. Each question
UNIVERSITY OF MICHIGAN UNDERGRADUATE MATH COMPETITION 28 APRIL 7, 20 Instructions. Write on the front of your blue book your student ID number. Do not write your name anywhere on your blue book. Each question
International Mathematics TOURNAMENT OF THE TOWNS
 International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2008. 1. A standard 8 8 chessboard is modified by varying the distances between parallel grid lines, so that the cells are rectangles
International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2008. 1. A standard 8 8 chessboard is modified by varying the distances between parallel grid lines, so that the cells are rectangles
The Euler-Maclaurin Formula and Sums of Powers
 DRAFT VOL 79, NO 1, FEBRUARY 26 1 The Euler-Maclaurin Forula and Sus of Powers Michael Z Spivey University of Puget Sound Tacoa, WA 98416 spivey@upsedu Matheaticians have long been intrigued by the su
DRAFT VOL 79, NO 1, FEBRUARY 26 1 The Euler-Maclaurin Forula and Sus of Powers Michael Z Spivey University of Puget Sound Tacoa, WA 98416 spivey@upsedu Matheaticians have long been intrigued by the su
3.8 Three Types of Convergence
 3.8 Three Types of Convergence 3.8 Three Types of Convergence 93 Suppose that we are given a sequence functions {f k } k N on a set X and another function f on X. What does it ean for f k to converge to
3.8 Three Types of Convergence 3.8 Three Types of Convergence 93 Suppose that we are given a sequence functions {f k } k N on a set X and another function f on X. What does it ean for f k to converge to
11 th Philippine Mathematical Olympiad Questions, Answers, and Hints
 view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
13 Harmonic oscillator revisited: Dirac s approach and introduction to Second Quantization
 3 Haronic oscillator revisited: Dirac s approach and introduction to Second Quantization. Dirac cae up with a ore elegant way to solve the haronic oscillator proble. We will now study this approach. The
3 Haronic oscillator revisited: Dirac s approach and introduction to Second Quantization. Dirac cae up with a ore elegant way to solve the haronic oscillator proble. We will now study this approach. The
UNC Charlotte 2004 Algebra with solutions
 with solutions March 8, 2004 1. Let z denote the real number solution to of the digits of z? (A) 13 (B) 14 (C) 15 (D) 16 (E) 17 3 + x 1 = 5. What is the sum Solution: E. Square both sides twice to get
with solutions March 8, 2004 1. Let z denote the real number solution to of the digits of z? (A) 13 (B) 14 (C) 15 (D) 16 (E) 17 3 + x 1 = 5. What is the sum Solution: E. Square both sides twice to get
Series Solutions of Differential Equations
 Chapter 6 Series Solutions of Differential Equations In this chapter we consider methods for solving differential equations using power series. Sequences and infinite series are also involved in this treatment.
Chapter 6 Series Solutions of Differential Equations In this chapter we consider methods for solving differential equations using power series. Sequences and infinite series are also involved in this treatment.
A Note on Scheduling Tall/Small Multiprocessor Tasks with Unit Processing Time to Minimize Maximum Tardiness
 A Note on Scheduling Tall/Sall Multiprocessor Tasks with Unit Processing Tie to Miniize Maxiu Tardiness Philippe Baptiste and Baruch Schieber IBM T.J. Watson Research Center P.O. Box 218, Yorktown Heights,
A Note on Scheduling Tall/Sall Multiprocessor Tasks with Unit Processing Tie to Miniize Maxiu Tardiness Philippe Baptiste and Baruch Schieber IBM T.J. Watson Research Center P.O. Box 218, Yorktown Heights,
arxiv: v2 [math.nt] 5 Sep 2012
![arxiv: v2 [math.nt] 5 Sep 2012 arxiv: v2 [math.nt] 5 Sep 2012](/thumbs/92/108477280.jpg) ON STRONGER CONJECTURES THAT IMPLY THE ERDŐS-MOSER CONJECTURE BERND C. KELLNER arxiv:1003.1646v2 [ath.nt] 5 Sep 2012 Abstract. The Erdős-Moser conjecture states that the Diophantine equation S k () = k,
ON STRONGER CONJECTURES THAT IMPLY THE ERDŐS-MOSER CONJECTURE BERND C. KELLNER arxiv:1003.1646v2 [ath.nt] 5 Sep 2012 Abstract. The Erdős-Moser conjecture states that the Diophantine equation S k () = k,
The Hydrogen Atom. Nucleus charge +Ze mass m 1 coordinates x 1, y 1, z 1. Electron charge e mass m 2 coordinates x 2, y 2, z 2
 The Hydrogen Ato The only ato that can be solved exactly. The results becoe the basis for understanding all other atos and olecules. Orbital Angular Moentu Spherical Haronics Nucleus charge +Ze ass coordinates
The Hydrogen Ato The only ato that can be solved exactly. The results becoe the basis for understanding all other atos and olecules. Orbital Angular Moentu Spherical Haronics Nucleus charge +Ze ass coordinates
Integration. Tuesday, December 3, 13
 4 Integration 4.3 Riemann Sums and Definite Integrals Objectives n Understand the definition of a Riemann sum. n Evaluate a definite integral using properties of definite integrals. 3 Riemann Sums 4 Riemann
4 Integration 4.3 Riemann Sums and Definite Integrals Objectives n Understand the definition of a Riemann sum. n Evaluate a definite integral using properties of definite integrals. 3 Riemann Sums 4 Riemann
E0 370 Statistical Learning Theory Lecture 5 (Aug 25, 2011)
 E0 370 Statistical Learning Theory Lecture 5 Aug 5, 0 Covering Nubers, Pseudo-Diension, and Fat-Shattering Diension Lecturer: Shivani Agarwal Scribe: Shivani Agarwal Introduction So far we have seen how
E0 370 Statistical Learning Theory Lecture 5 Aug 5, 0 Covering Nubers, Pseudo-Diension, and Fat-Shattering Diension Lecturer: Shivani Agarwal Scribe: Shivani Agarwal Introduction So far we have seen how
Putnam f(x) g(x) + h(x) = 3x +2 if 1 x 0 2x +2 if x > 0
 Putnam 999 A. Find polynomials f(x),g(x), andh(x), iftheyexist, suchthatforallx, if x< f(x) g(x) + h(x) 3x + if x 0 x + if x > 0 Solution. Let h(x) ax + b. Note that there are corners in the graph of this
Putnam 999 A. Find polynomials f(x),g(x), andh(x), iftheyexist, suchthatforallx, if x< f(x) g(x) + h(x) 3x + if x 0 x + if x > 0 Solution. Let h(x) ax + b. Note that there are corners in the graph of this
Math Reviews classifications (2000): Primary 54F05; Secondary 54D20, 54D65
 The Monotone Lindelöf Property and Separability in Ordered Spaces by H. Bennett, Texas Tech University, Lubbock, TX 79409 D. Lutzer, College of Willia and Mary, Williasburg, VA 23187-8795 M. Matveev, Irvine,
The Monotone Lindelöf Property and Separability in Ordered Spaces by H. Bennett, Texas Tech University, Lubbock, TX 79409 D. Lutzer, College of Willia and Mary, Williasburg, VA 23187-8795 M. Matveev, Irvine,
SOUTH AFRICAN TERTIARY MATHEMATICS OLYMPIAD
 SOUTH AFRICAN TERTIARY MATHEMATICS OLYMPIAD. Determine the following value: 7 August 6 Solutions π + π. Solution: Since π
SOUTH AFRICAN TERTIARY MATHEMATICS OLYMPIAD. Determine the following value: 7 August 6 Solutions π + π. Solution: Since π
Putnam n +1 (1 P (O n 1)) 2n +1. 2n +1 (2 (n 1) + 1) 2n +1 = (2 (n 1) + 1) P (O n 1)+1. (2(n 2)+1)P (On 2 )+1 2(n 1)+1. O n (n 1) + n 1 2n +1
 Putnam 00 A. Consider a set S and a binary operation, i.e., for each a, b S, a b S. Assume (a b) a b for all a, b S. Provethata (b a) b for all a, b S. Solution. Wehaveb ((b a) b) (b a) a (b a). A. You
Putnam 00 A. Consider a set S and a binary operation, i.e., for each a, b S, a b S. Assume (a b) a b for all a, b S. Provethata (b a) b for all a, b S. Solution. Wehaveb ((b a) b) (b a) a (b a). A. You
MADHAVA MATHEMATICS COMPETITION, December 2015 Solutions and Scheme of Marking
 MADHAVA MATHEMATICS COMPETITION, December 05 Solutions and Scheme of Marking NB: Part I carries 0 marks, Part II carries 30 marks and Part III carries 50 marks Part I NB Each question in Part I carries
MADHAVA MATHEMATICS COMPETITION, December 05 Solutions and Scheme of Marking NB: Part I carries 0 marks, Part II carries 30 marks and Part III carries 50 marks Part I NB Each question in Part I carries
2016 EF Exam Texas A&M High School Students Contest Solutions October 22, 2016
 6 EF Exam Texas A&M High School Students Contest Solutions October, 6. Assume that p and q are real numbers such that the polynomial x + is divisible by x + px + q. Find q. p Answer Solution (without knowledge
6 EF Exam Texas A&M High School Students Contest Solutions October, 6. Assume that p and q are real numbers such that the polynomial x + is divisible by x + px + q. Find q. p Answer Solution (without knowledge
Homework 4 Solutions
 Hoework 4 s Fall 017 65 Points Proble 6.. (10 points) A plane wave is reflected fro the ocean floor at noral incidence with a level 0 db below that of the incident wave Possible values of the specific
Hoework 4 s Fall 017 65 Points Proble 6.. (10 points) A plane wave is reflected fro the ocean floor at noral incidence with a level 0 db below that of the incident wave Possible values of the specific
(x + 3)(x 1) lim(x + 3) = 4. lim. (x 2)( x ) = (x 2)(x + 2) x + 2 x = 4. dt (t2 + 1) = 1 2 (t2 + 1) 1 t. f(x) = lim 3x = 6,
 Math 140 MT1 Sample C Solutions Tyrone Crisp 1 (B): First try direct substitution: you get 0. So try to cancel common factors. We have 0 x 2 + 2x 3 = x 1 and so the it as x 1 is equal to (x + 3)(x 1),
Math 140 MT1 Sample C Solutions Tyrone Crisp 1 (B): First try direct substitution: you get 0. So try to cancel common factors. We have 0 x 2 + 2x 3 = x 1 and so the it as x 1 is equal to (x + 3)(x 1),
F = 0. x o F = -k x o v = 0 F = 0. F = k x o v = 0 F = 0. x = 0 F = 0. F = -k x 1. PHYSICS 151 Notes for Online Lecture 2.4.
 PHYSICS 151 Notes for Online Lecture.4 Springs, Strings, Pulleys, and Connected Objects Hook s Law F = 0 F = -k x 1 x = 0 x = x 1 Let s start with a horizontal spring, resting on a frictionless table.
PHYSICS 151 Notes for Online Lecture.4 Springs, Strings, Pulleys, and Connected Objects Hook s Law F = 0 F = -k x 1 x = 0 x = x 1 Let s start with a horizontal spring, resting on a frictionless table.
Web Solutions for How to Read and Do Proofs
 Web Solutions for How to Read and Do Proofs An Introduction to Mathematical Thought Processes Sixth Edition Daniel Solow Department of Operations Weatherhead School of Management Case Western Reserve University
Web Solutions for How to Read and Do Proofs An Introduction to Mathematical Thought Processes Sixth Edition Daniel Solow Department of Operations Weatherhead School of Management Case Western Reserve University
Solutions 1. Introduction to Coding Theory - Spring 2010 Solutions 1. Exercise 1.1. See Examples 1.2 and 1.11 in the course notes.
 Solutions 1 Exercise 1.1. See Exaples 1.2 and 1.11 in the course notes. Exercise 1.2. Observe that the Haing distance of two vectors is the iniu nuber of bit flips required to transfor one into the other.
Solutions 1 Exercise 1.1. See Exaples 1.2 and 1.11 in the course notes. Exercise 1.2. Observe that the Haing distance of two vectors is the iniu nuber of bit flips required to transfor one into the other.
ORIGAMI CONSTRUCTIONS OF RINGS OF INTEGERS OF IMAGINARY QUADRATIC FIELDS
 #A34 INTEGERS 17 (017) ORIGAMI CONSTRUCTIONS OF RINGS OF INTEGERS OF IMAGINARY QUADRATIC FIELDS Jürgen Kritschgau Departent of Matheatics, Iowa State University, Aes, Iowa jkritsch@iastateedu Adriana Salerno
#A34 INTEGERS 17 (017) ORIGAMI CONSTRUCTIONS OF RINGS OF INTEGERS OF IMAGINARY QUADRATIC FIELDS Jürgen Kritschgau Departent of Matheatics, Iowa State University, Aes, Iowa jkritsch@iastateedu Adriana Salerno
PERMANENT WEAK AMENABILITY OF GROUP ALGEBRAS OF FREE GROUPS
 PERMANENT WEAK AMENABILITY OF GROUP ALGEBRAS OF FREE GROUPS B. E. JOHNSON ABSTRACT We show that all derivations fro the group algebra (G) of a free group into its nth dual, where n is a positive even integer,
PERMANENT WEAK AMENABILITY OF GROUP ALGEBRAS OF FREE GROUPS B. E. JOHNSON ABSTRACT We show that all derivations fro the group algebra (G) of a free group into its nth dual, where n is a positive even integer,
arxiv:math/ v1 [math.nt] 15 Jul 2003
![arxiv:math/ v1 [math.nt] 15 Jul 2003 arxiv:math/ v1 [math.nt] 15 Jul 2003](/thumbs/94/118551693.jpg) arxiv:ath/0307203v [ath.nt] 5 Jul 2003 A quantitative version of the Roth-Ridout theore Toohiro Yaada, 606-8502, Faculty of Science, Kyoto University, Kitashirakawaoiwakecho, Sakyoku, Kyoto-City, Kyoto,
arxiv:ath/0307203v [ath.nt] 5 Jul 2003 A quantitative version of the Roth-Ridout theore Toohiro Yaada, 606-8502, Faculty of Science, Kyoto University, Kitashirakawaoiwakecho, Sakyoku, Kyoto-City, Kyoto,
Individual Round CHMMC November 20, 2016
 Individual Round CHMMC 20 November 20, 20 Problem. We say that d k d k d d 0 represents the number n in base 2 if each d i is either 0 or, and n d k ( 2) k + d k ( 2) k + + d ( 2) + d 0. For example, 0
Individual Round CHMMC 20 November 20, 20 Problem. We say that d k d k d d 0 represents the number n in base 2 if each d i is either 0 or, and n d k ( 2) k + d k ( 2) k + + d ( 2) + d 0. For example, 0
Legendre s Equation. PHYS Southern Illinois University. October 18, 2016
 Legendre s Equation PHYS 500 - Southern Illinois University October 18, 2016 PHYS 500 - Southern Illinois University Legendre s Equation October 18, 2016 1 / 11 Legendre s Equation Recall We are trying
Legendre s Equation PHYS 500 - Southern Illinois University October 18, 2016 PHYS 500 - Southern Illinois University Legendre s Equation October 18, 2016 1 / 11 Legendre s Equation Recall We are trying
SOLVING LITERAL EQUATIONS. Bundle 1: Safety & Process Skills
 SOLVING LITERAL EQUATIONS Bundle 1: Safety & Process Skills Solving Literal Equations An equation is a atheatical sentence with an equal sign. The solution of an equation is a value for a variable that
SOLVING LITERAL EQUATIONS Bundle 1: Safety & Process Skills Solving Literal Equations An equation is a atheatical sentence with an equal sign. The solution of an equation is a value for a variable that
Probability Distributions
 Probability Distributions In Chapter, we ephasized the central role played by probability theory in the solution of pattern recognition probles. We turn now to an exploration of soe particular exaples
Probability Distributions In Chapter, we ephasized the central role played by probability theory in the solution of pattern recognition probles. We turn now to an exploration of soe particular exaples
THE UNIVERSITY OF TORONTO UNDERGRADUATE MATHEMATICS COMPETITION. Sunday, March 14, 2004 Time: hours No aids or calculators permitted.
 THE UNIVERSITY OF TORONTO UNDERGRADUATE MATHEMATICS COMPETITION Sunday, March 1, Time: 3 1 hours No aids or calculators permitted. 1. Prove that, for any complex numbers z and w, ( z + w z z + w w z +
THE UNIVERSITY OF TORONTO UNDERGRADUATE MATHEMATICS COMPETITION Sunday, March 1, Time: 3 1 hours No aids or calculators permitted. 1. Prove that, for any complex numbers z and w, ( z + w z z + w w z +
1 2n. i=1. 2m+1 i = m, while. 2m + 1 = 1. is the best possible for any odd n.
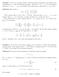 Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
1. The sides of a triangle are in the ratio 3 : 5 : 9. Which of the following words best describes the triangle?
 UNIVERSITY OF NORTH CAROLINA CHARLOTTE 999 HIGH SCHOOL MATHEMATICS CONTEST March 8, 999 The sides of a triangle are in the ratio : 5 : 9 Which of the following words best describes the triangle? (A) obtuse
UNIVERSITY OF NORTH CAROLINA CHARLOTTE 999 HIGH SCHOOL MATHEMATICS CONTEST March 8, 999 The sides of a triangle are in the ratio : 5 : 9 Which of the following words best describes the triangle? (A) obtuse
Answers to assigned problems from Chapter 1
 Answers to assigned probles fro Chapter 1 1.7. a. A colun of ercury 1 in cross-sectional area and 0.001 in height has a volue of 0.001 and a ass of 0.001 1 595.1 kg. Then 1 Hg 0.001 1 595.1 kg 9.806 65
Answers to assigned probles fro Chapter 1 1.7. a. A colun of ercury 1 in cross-sectional area and 0.001 in height has a volue of 0.001 and a ass of 0.001 1 595.1 kg. Then 1 Hg 0.001 1 595.1 kg 9.806 65
2005 Euclid Contest. Solutions
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 2005 Euclid Contest Tuesday, April 19, 2005 Solutions c
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 2005 Euclid Contest Tuesday, April 19, 2005 Solutions c
PUTNAM TRAINING EASY PUTNAM PROBLEMS
 PUTNAM TRAINING EASY PUTNAM PROBLEMS (Last updated: September 24, 2018) Remark. This is a list of exercises on Easy Putnam Problems Miguel A. Lerma Exercises 1. 2017-A1. Let S be the smallest set of positive
PUTNAM TRAINING EASY PUTNAM PROBLEMS (Last updated: September 24, 2018) Remark. This is a list of exercises on Easy Putnam Problems Miguel A. Lerma Exercises 1. 2017-A1. Let S be the smallest set of positive
Notes on Continued Fractions for Math 4400
 . Continued fractions. Notes on Continued Fractions for Math 4400 The continued fraction expansion converts a positive real number α into a sequence of natural numbers. Conversely, a sequence of natural
. Continued fractions. Notes on Continued Fractions for Math 4400 The continued fraction expansion converts a positive real number α into a sequence of natural numbers. Conversely, a sequence of natural
1. Matrices and Determinants
 Important Questions 1. Matrices and Determinants Ex.1.1 (2) x 3x y Find the values of x, y, z if 2x + z 3y w = 0 7 3 2a Ex 1.1 (3) 2x 3x y If 2x + z 3y w = 3 2 find x, y, z, w 4 7 Ex 1.1 (13) 3 7 3 2 Find
Important Questions 1. Matrices and Determinants Ex.1.1 (2) x 3x y Find the values of x, y, z if 2x + z 3y w = 0 7 3 2a Ex 1.1 (3) 2x 3x y If 2x + z 3y w = 3 2 find x, y, z, w 4 7 Ex 1.1 (13) 3 7 3 2 Find
EASY PUTNAM PROBLEMS
 EASY PUTNAM PROBLEMS (Last updated: December 11, 2017) Remark. The problems in the Putnam Competition are usually very hard, but practically every session contains at least one problem very easy to solve
EASY PUTNAM PROBLEMS (Last updated: December 11, 2017) Remark. The problems in the Putnam Competition are usually very hard, but practically every session contains at least one problem very easy to solve
THE AVERAGE NORM OF POLYNOMIALS OF FIXED HEIGHT
 THE AVERAGE NORM OF POLYNOMIALS OF FIXED HEIGHT PETER BORWEIN AND KWOK-KWONG STEPHEN CHOI Abstract. Let n be any integer and ( n ) X F n : a i z i : a i, ± i be the set of all polynoials of height and
THE AVERAGE NORM OF POLYNOMIALS OF FIXED HEIGHT PETER BORWEIN AND KWOK-KWONG STEPHEN CHOI Abstract. Let n be any integer and ( n ) X F n : a i z i : a i, ± i be the set of all polynoials of height and
TEST CODE: MMA (Objective type) 2015 SYLLABUS
 TEST CODE: MMA (Objective type) 2015 SYLLABUS Analytical Reasoning Algebra Arithmetic, geometric and harmonic progression. Continued fractions. Elementary combinatorics: Permutations and combinations,
TEST CODE: MMA (Objective type) 2015 SYLLABUS Analytical Reasoning Algebra Arithmetic, geometric and harmonic progression. Continued fractions. Elementary combinatorics: Permutations and combinations,
The Methods of Solution for Constrained Nonlinear Programming
 Research Inventy: International Journal Of Engineering And Science Vol.4, Issue 3(March 2014), PP 01-06 Issn (e): 2278-4721, Issn (p):2319-6483, www.researchinventy.co The Methods of Solution for Constrained
Research Inventy: International Journal Of Engineering And Science Vol.4, Issue 3(March 2014), PP 01-06 Issn (e): 2278-4721, Issn (p):2319-6483, www.researchinventy.co The Methods of Solution for Constrained
A Self-Organizing Model for Logical Regression Jerry Farlow 1 University of Maine. (1900 words)
 1 A Self-Organizing Model for Logical Regression Jerry Farlow 1 University of Maine (1900 words) Contact: Jerry Farlow Dept of Matheatics Univeristy of Maine Orono, ME 04469 Tel (07) 866-3540 Eail: farlow@ath.uaine.edu
1 A Self-Organizing Model for Logical Regression Jerry Farlow 1 University of Maine (1900 words) Contact: Jerry Farlow Dept of Matheatics Univeristy of Maine Orono, ME 04469 Tel (07) 866-3540 Eail: farlow@ath.uaine.edu
Section 3.5: Implicit Differentiation
 Section 3.5: Implicit Differentiation In the previous sections, we considered the problem of finding the slopes of the tangent line to a given function y = f(x). The idea of a tangent line however is not
Section 3.5: Implicit Differentiation In the previous sections, we considered the problem of finding the slopes of the tangent line to a given function y = f(x). The idea of a tangent line however is not
A nonstandard cubic equation
 MATH-Jan-05-0 A nonstandard cubic euation J S Markoitch PO Box West Brattleboro, VT 050 Dated: January, 05 A nonstandard cubic euation is shown to hae an unusually econoical solution, this solution incorporates
MATH-Jan-05-0 A nonstandard cubic euation J S Markoitch PO Box West Brattleboro, VT 050 Dated: January, 05 A nonstandard cubic euation is shown to hae an unusually econoical solution, this solution incorporates
Chapter 16 Solutions
 Chapter 16 Solutions 16.1 Replace x by x vt = x 4.5t to get y = 6 [(x 4.5t) + 3] 16. y (c) y (c) y (c) 6 4 4 4 t = s t = 1 s t = 1.5 s 0 6 10 14 x 0 6 10 14 x 0 6 10 14 x y (c) y (c) 4 t =.5 s 4 t = 3
Chapter 16 Solutions 16.1 Replace x by x vt = x 4.5t to get y = 6 [(x 4.5t) + 3] 16. y (c) y (c) y (c) 6 4 4 4 t = s t = 1 s t = 1.5 s 0 6 10 14 x 0 6 10 14 x 0 6 10 14 x y (c) y (c) 4 t =.5 s 4 t = 3
A := A i : {A i } S. is an algebra. The same object is obtained when the union in required to be disjoint.
 59 6. ABSTRACT MEASURE THEORY Having developed the Lebesgue integral with respect to the general easures, we now have a general concept with few specific exaples to actually test it on. Indeed, so far
59 6. ABSTRACT MEASURE THEORY Having developed the Lebesgue integral with respect to the general easures, we now have a general concept with few specific exaples to actually test it on. Indeed, so far
An EGZ generalization for 5 colors
 An EGZ generalization for 5 colors David Grynkiewicz and Andrew Schultz July 6, 00 Abstract Let g zs(, k) (g zs(, k + 1)) be the inial integer such that any coloring of the integers fro U U k 1,..., g
An EGZ generalization for 5 colors David Grynkiewicz and Andrew Schultz July 6, 00 Abstract Let g zs(, k) (g zs(, k + 1)) be the inial integer such that any coloring of the integers fro U U k 1,..., g
HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS
 HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
Organization Team Team ID#
 1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
Kernel Methods and Support Vector Machines
 Intelligent Systes: Reasoning and Recognition Jaes L. Crowley ENSIAG 2 / osig 1 Second Seester 2012/2013 Lesson 20 2 ay 2013 Kernel ethods and Support Vector achines Contents Kernel Functions...2 Quadratic
Intelligent Systes: Reasoning and Recognition Jaes L. Crowley ENSIAG 2 / osig 1 Second Seester 2012/2013 Lesson 20 2 ay 2013 Kernel ethods and Support Vector achines Contents Kernel Functions...2 Quadratic
LATTICE POINT SOLUTION OF THE GENERALIZED PROBLEM OF TERQUEi. AND AN EXTENSION OF FIBONACCI NUMBERS.
 i LATTICE POINT SOLUTION OF THE GENERALIZED PROBLEM OF TERQUEi. AND AN EXTENSION OF FIBONACCI NUMBERS. C. A. CHURCH, Jr. and H. W. GOULD, W. Virginia University, Morgantown, W. V a. In this paper we give
i LATTICE POINT SOLUTION OF THE GENERALIZED PROBLEM OF TERQUEi. AND AN EXTENSION OF FIBONACCI NUMBERS. C. A. CHURCH, Jr. and H. W. GOULD, W. Virginia University, Morgantown, W. V a. In this paper we give
ALGEBRA REVIEW. MULTINOMIAL An algebraic expression consisting of more than one term.
 Page 1 of 6 ALGEBRAIC EXPRESSION A cobination of ordinary nubers, letter sybols, variables, grouping sybols and operation sybols. Nubers reain fixed in value and are referred to as constants. Letter sybols
Page 1 of 6 ALGEBRAIC EXPRESSION A cobination of ordinary nubers, letter sybols, variables, grouping sybols and operation sybols. Nubers reain fixed in value and are referred to as constants. Letter sybols
R. L. Ollerton University of Western Sydney, Penrith Campus DC1797, Australia
 FURTHER PROPERTIES OF GENERALIZED BINOMIAL COEFFICIENT k-extensions R. L. Ollerton University of Western Sydney, Penrith Capus DC1797, Australia A. G. Shannon KvB Institute of Technology, North Sydney
FURTHER PROPERTIES OF GENERALIZED BINOMIAL COEFFICIENT k-extensions R. L. Ollerton University of Western Sydney, Penrith Capus DC1797, Australia A. G. Shannon KvB Institute of Technology, North Sydney
SMT Power Round Solutions : Poles and Polars
 SMT Power Round Solutions : Poles and Polars February 18, 011 1 Definition and Basic Properties 1 Note that the unit circles are not necessary in the solutions. They just make the graphs look nicer. (1).0
SMT Power Round Solutions : Poles and Polars February 18, 011 1 Definition and Basic Properties 1 Note that the unit circles are not necessary in the solutions. They just make the graphs look nicer. (1).0
Paper 1 Further Pure Mathematics For Examination from 2016 SPECIMEN MARK SCHEME 3 hours MAXIMUM MARK: 120
 Cabridge International Exainations Cabridge Pre-U Certificate www.xtreepapers.co FURTHER MATHEMATICS (PRINCIPAL) 9795/ Paper Further Pure Matheatics For Exaination fro SPECIMEN MARK SCHEME hours MAXIMUM
Cabridge International Exainations Cabridge Pre-U Certificate www.xtreepapers.co FURTHER MATHEMATICS (PRINCIPAL) 9795/ Paper Further Pure Matheatics For Exaination fro SPECIMEN MARK SCHEME hours MAXIMUM
Lecture 21. Interior Point Methods Setup and Algorithm
 Lecture 21 Interior Point Methods In 1984, Kararkar introduced a new weakly polynoial tie algorith for solving LPs [Kar84a], [Kar84b]. His algorith was theoretically faster than the ellipsoid ethod and
Lecture 21 Interior Point Methods In 1984, Kararkar introduced a new weakly polynoial tie algorith for solving LPs [Kar84a], [Kar84b]. His algorith was theoretically faster than the ellipsoid ethod and
SMT 2011 General Test and Solutions February 19, F (x) + F = 1 + x. 2 = 3. Now take x = 2 2 F ( 1) = F ( 1) = 3 2 F (2)
 SMT 0 General Test and Solutions February 9, 0 Let F () be a real-valued function defined for all real 0, such that ( ) F () + F = + Find F () Answer: Setting =, we find that F () + F ( ) = Now take =,
SMT 0 General Test and Solutions February 9, 0 Let F () be a real-valued function defined for all real 0, such that ( ) F () + F = + Find F () Answer: Setting =, we find that F () + F ( ) = Now take =,
Bernoulli numbers and generalized factorial sums
 Bernoulli nubers and generalized factorial sus Paul Thoas Young Departent of Matheatics, College of Charleston Charleston, SC 29424 paul@ath.cofc.edu June 25, 2010 Abstract We prove a pair of identities
Bernoulli nubers and generalized factorial sus Paul Thoas Young Departent of Matheatics, College of Charleston Charleston, SC 29424 paul@ath.cofc.edu June 25, 2010 Abstract We prove a pair of identities
2. A die is rolled 3 times, the probability of getting a number larger than the previous number each time is
 . If P(A) = x, P = 2x, P(A B) = 2, P ( A B) = 2 3, then the value of x is (A) 5 8 5 36 6 36 36 2. A die is rolled 3 times, the probability of getting a number larger than the previous number each time
. If P(A) = x, P = 2x, P(A B) = 2, P ( A B) = 2 3, then the value of x is (A) 5 8 5 36 6 36 36 2. A die is rolled 3 times, the probability of getting a number larger than the previous number each time
(b) g(x) = 4 + 6(x 3) (x 3) 2 (= x x 2 ) M1A1 Note: Accept any alternative form that is correct. Award M1A0 for a substitution of (x + 3).
 Paper. Answers. (a) METHOD f (x) q x f () q 6 q 6 f() p + 8 9 5 p METHOD f(x) (x ) + 5 x + 6x q 6, p (b) g(x) + 6(x ) (x ) ( + x x ) Note: Accept any alternative form that is correct. Award A for a substitution
Paper. Answers. (a) METHOD f (x) q x f () q 6 q 6 f() p + 8 9 5 p METHOD f(x) (x ) + 5 x + 6x q 6, p (b) g(x) + 6(x ) (x ) ( + x x ) Note: Accept any alternative form that is correct. Award A for a substitution
Block designs and statistics
 Bloc designs and statistics Notes for Math 447 May 3, 2011 The ain paraeters of a bloc design are nuber of varieties v, bloc size, nuber of blocs b. A design is built on a set of v eleents. Each eleent
Bloc designs and statistics Notes for Math 447 May 3, 2011 The ain paraeters of a bloc design are nuber of varieties v, bloc size, nuber of blocs b. A design is built on a set of v eleents. Each eleent
Chapter II TRIANGULAR NUMBERS
 Chapter II TRIANGULAR NUMBERS Part of this work contained in this chapter has resulted in the following publications: Gopalan, M.A. and Jayakuar, P. "Note on triangular nubers in arithetic progression",
Chapter II TRIANGULAR NUMBERS Part of this work contained in this chapter has resulted in the following publications: Gopalan, M.A. and Jayakuar, P. "Note on triangular nubers in arithetic progression",
lecture 36: Linear Multistep Mehods: Zero Stability
 95 lecture 36: Linear Multistep Mehods: Zero Stability 5.6 Linear ultistep ethods: zero stability Does consistency iply convergence for linear ultistep ethods? This is always the case for one-step ethods,
95 lecture 36: Linear Multistep Mehods: Zero Stability 5.6 Linear ultistep ethods: zero stability Does consistency iply convergence for linear ultistep ethods? This is always the case for one-step ethods,
