:i PROPULSION I - I \ distribution unlimited. DAVID W. TAYLOR NAVAL SHIP RESEARCH AND DEVELOPMENT CENTER. z (0l. < Bethesda. Md.
|
|
|
- Phebe Tate
- 5 years ago
- Views:
Transcription
1 DAVID W. TAYLOR NAVAL SHIP RESEARCH AND DEVELOPMENT CENTER < Bethesda. Md a. O o w THE PERFORMANCE GAINS OF USING WIDE, FLUSH BOUNDARY LAYER INLETS ON WATER-JET PROPELLED CRAFT K GO ( by John G. Purnell I - Approved for public release; I \ distribution unlimited. z (0l u. :i PROPULSION AND AUXILIARY SYSTEMS DEPARTMENT Annapolis 1; zresearch AND DEVELOPMENT REPORT I m Ii z<march 1976 Report PAS-7545
2 -L The Naval Ship Research and Development Center is a U. S. Navy center for laboratory effort directed at achievinj'mproved sea and air vehscles. It was formed in March 1967 by merging the David Taylor Model Basin at Carderock, Maryland with the Marine Engineering Laboratory at Annapolis, Maryland. Naval Ship Research and Development Center Bethesda, Md MAJOR NSRDC ORGANIZATIONAL COMPONENTS -I NSRDC CM NDER TECHNICAL DIRECTO%, -7 REPORT ORIGINATOR - - ) OFFICER.IN.CHARGE OFFICER- I N-04ARGE CARDEROCK ANNAPOLIS DEVELOPMENT. DEPARTMENT 1 SHIP PERFORMANCE AVIATION AND ERFRMANT SURFACE EFFECTS 15 DEPARTMENT 16 STRUCTURES DEPARTMENT COMPUTATION 17 AND MATHEMATICS DEPARTMENT 7 SHI ACPROPULSION AND * DEPARTMENT AUXILIARY SYSTEMS 19 DEPARTMENT 27 MATERIALS CENTRAL A1 r DEPARTMENT INSTRUMENTATION w S DEPARTMENT. ':... ch i~t t1l
3 UNCLASSIFIED SECURITY CLASSIFICATION OF THIS PAGE (When Data Entered) REPORT DOCUMENTATION PAGE BEFORE COMPLETING FORM PAS L 2. GOVT ACCESSION No. 3. RECIPIE.T S TALbG NME ID, Research ; 1veopment Y AtLUSf foundary LRER.INLETS ON, ATER-JET PROPEELED CRAFT*, 6. PERFORMING ORG. REPORT NUMBER j 7 AUTHOR( ) 8' T- 7 7Eq Ic John G. Purnell 9 PERFORMING ORGANIZATION NAME AND ADDRESS g._,aeau TP-l R JE- T TASK' David W. Taylor Naval Ship R&D Center TASF4LI3We S4622 Annapolis, i Maryland WU I-152 1=' -n & t4 81 ItI. CONTROLLING OFFICE NAME AND ADDRESS.R David W. Taylor Naval Ship R&D Cente Bethesda, Maryland Mar-X ES 14 MONI ORING AGENCY NAME. ODRESS(If different from Controlling Office) 15 SECURITY CLASS. (of this report) Unclassified 15a. DECL ASSI FICATION/ DOWNGRADING I 16 DISTRIBUTION STATEMENT (of %hi Report) Approved for public release; distribution unlimited. 17. DISTRIBUTION STATEMENT (of the abstract entered In Block 20, t different from Report) 18 SUPPLEMENTARY NOTES j T 19 KEY WORDS (Continue on reverse aide If necessary and identiiy by block number) Performance gains Boundary layer inlets Water-jet propelled craft Boundary layer conditions Pump size a 0. ABSTRACT (Continue on reverse side if necsseary and identify by block number) Water-jet performance ' The application of a wide, flush inlet on a water-jet-propelled craft was investigated to determine performance gains from using primarily low momentum boundary layer flow for producing the propulsion jet. A method of predicting the boundary layer conditions, the pump size, and the overall water-jet system performance is given. Improvement in overall system efficiency or /ly (over) DD JAN EDITION OF I NOV 65IS OBSOLETE UNCLASSIFIED SIN 0102N014A66011 SECURITY CLASSIFICATION OF THIS PAGE (When Data hntsred)
4 UNCLASSIFIED.,.IJITY CLASSIF., ATION OF '.S PAG(H0han Data Entered) 20. ABSTRACT (Cont) Spropulsive coefficient of 10% to 12% over conventional flush inlets is predicted for a planing craft application. (Author) I UNCLASSIFIED SECURITY CLASSIFICATION OF THIS PAGEf'hen Data Entered)
5 I ADMINISTRATIVE INFORMATION This work was performed jointly under the DTNSRDC programs entitled, "Propulsion Technology Development," Program Element 62543N, Task Area SF , Work Unit ; and "Water- Jet Technology," Program Element 63508N, Task Area S4622, Work j Unit LIST OF ABBREVIATIONS IDWDI - double width, double inlet fps - feet per second gpm - gallons per minute lb/hp - pounds per horsepower psf - pounds per square foot I rpm - revolutions per minute P I I I I I PAS-75-45
6 I' TABLE OF CONTENTS [ Page ADMINISTRATIVE INFORMATION i LIST OF ABBREVIATIONS i NOMENCLATURE iv INTRODUCTION 1 WIDE BOUNDARY LAYER INLETS 1 BOUNDARY LAYER CHARACTERISTICS 3 Boundary Layer Thickness 3 Boundary Layer Profiles 4 PERFORMANCE OF BOUNDARY LAYER INLETS 7 WIDE BOUNDARY LAYER INLET DESIGN 11 CRAFT DRAG AND PART POWER OPERATION 14 PUMP DESIGN 16 SENSITIVITY STUDIES 22 EVALUATION OF POTENTIAL WIDE INLET PUMP SYSTEM ARRANGEMENTS 29 T CONCLUSIONS 35 RECOMMENDATIONS 35 TECHNICAL REFERENCES 35 -r INITIAL DISTRIBUTION T PAS iii PRECEDI G PAGE BLANK-NOT FIDi2ED
7 NOMENCLATURE Ai - Inlet area ft 2 - Projected hull area ft 2 c c - Cavitation coefficient CDi - Inlet drag coefficient C w - Weight coefficient -' Di - Inlet drag lb D s - Shaft diameter ft DTI - Pump inlet diameter ft DT 2 - Pump exit diameter ft FV - Froude number g - Acceleration of gravity ft/sec 2 h e - Inlet submergence head ft hv - Vapor pressure ft H i - Inlet height ft H - Off design pump head ft - pump head ft Hpd - design pump head ft Ke - Energy velocity ratio (Ue/Vcj. Kk - Inlet loss coefficient Km - Momentum velocity ratio (Um/V ) K 1 - Pump efficiency parameter sec 2 /ft 5 K 2 - Pump efficiency parameter sec 3 /ftl 5 / 2 L w - Inlet width ft Lx - Wetted hull length upstream of inlet ft n - Exponent N - Pump speed rpm PAS iv ":i
8 Np - Number of pumps I N pi - Number of pump inlets N s - Specific speed rpm-gpm /2/ft3/4 I NPSH - Net positive suction head ft Patm - Atmospheric pressure head ft Pbk - Boundary layer net thrust pressure psf Pi - Input power ft-lb/sec Q - Flow rate cfs Qd - Design flow rate cfs Qod -Off design pump flow rate cfs * Qimp - Flow per impeller inlet gpm R - Jet velocity ratio (Vj/V.) R c - Craft resistance at design displacement lb Rco - Craft resistance at reduced displacement lb -. Re - Reynolds number S - Integral number of pump stages sfc - Specific fuel consumption lb/hp-hr Tc - Craft or gross thrust lb Tnet - Net thrust lb U - Local velocity at distance y from hull fps U a - Average velocity of ingested flow fps U e - Energy velocity of ingested flow fps U m - Momentum velocity of ingested flow fps Utl - Pump inlet tip speed fps U 2 - Pump exit tip speed fps Vax - Pump axial inlet velocity fps V i - Average inlet velocity fps PAS v
9 Vj - Jet velocity fps V, - Free stream or craft velocity fps Wap - Axial pump weight lb Wc - Craft design weight lb Wco - Craft weight at reduced displacement lb Wcp - Centrifugal pump weight lb y - Distance from hull ft L/B - Craft length to beam ratio U/Vo - Local velocity ratio y/6 - Height ratio a - Inlet velocity ratio (Vi/V ) 6 - Boundary layer thickness ft V - Craft displacement at rest ft 3 *n o - Overall efficiency or propulsive coefficient lp - Pump efficiency npo d - Off design pump efficiency r t X - Transmission efficiency - Shaft blockage coefficient (Ds/Dtl) V - Viscosity of seawater ft 2 /sec p - Density of seawater slugs/ft 3 a t T u - Thoma cavitation number - Energy ratio based on Vax - Energy ratio based on Otl 0 - Flow coefficient PAS vi
10 JINTRODUCTION ci Water-jet propulsion systems have found increased application on many types of naval ships, such as surface effect ships, hydrofoils, and planing craft. The attractiveness of the water-jet system lies mostly in its high reliability and basic simplicity compared to alternative systems. The main disadvantage has been that the performance coefficient or overall efficiency of waterjet systems may be on the order of 10% lower than that of propellertype systems. Improvements are desired which will permit the overall efficiency of typical water-jet systems to approach more closely T those of propeller systems. In the area of planing hull craft it appears possible to approach propeller system efficiencies by making use of the low momentum fluid in the craft boundary layer near the stern to reduce the inflow momentum drag of the water-jet system. am This requires that a wide or large width/height ratio inlet be used, spanning as much of the beam as possible in order to minimize the inlet height such that flow would be drawn primarily or entirely from the boundary layer. Planing-type craft have sufficient beam for the flow rates required to make wide boundary layer inlets feasible. This report considers the application of wide boundary layer inlets to water-jet-propelled craft where maximum craft velocities are on the order of 50 knots. Special attention is given to planing craft since they have sufficient beam and high speed; however, results are applicable to displacement vessels. WIDE BOUNDARY LAYER INLETS The application of water-jet propulsion to displacement craft offers important advantages in addition to reliability and simplic- -- ity when compared to a propeller system: e Shallow draft capability. * Elimination of propulsion system damage from striking -* underwater objects. * Reduction of appendage drag. With the use of a wide boundary layer inlet, where water-jet flow is drawn primarily or entirely from the boundary layer, several other advantages are possible: * System efficiency can, in some cases, approach or exceed that of a propeller system. 9 Amount of inflow diffusion required for the flow (as well as diffuser size) is reduced.. Inlet drag can be reduced. PAS
11 Some potential problem areas do exist with wide boundary layer inlets. The distorted boundary layer flow profile coming into the inlet makes efficient diffusion without separation difficult. Because the inlet is very wide and the inlet height is thus very small, the length of diffuser required for a given diffusion ratio will be very short, thus minimizing additional losses, since the pump may be placed physically very close to the inlet. Machinery arrangement can be a problem. If the wide inlet flow is diffused to one (or two) pumps, the diffusion would be three-dimensional, and the transition of diffuser and duct shape between inlet and pump would cause high internal losses. However, it appears that a satisfactory pumping arrangement is obtained with multiple small diameter impellers (i.e., DWDI* centrifugal) mounted in parallel across the beam of the craft on a common shaft as shown in figure 1. With this arrangement the diffusion remains essentially two-dimensional. FOR WARD Figure 1 Wide Boundary Layer Inlet Using Multiple, Parallel, Double Width, Double Inlet Centrifugal Pumps FORWARD, I - *Definitions of abbreviations are on page i. PAS
12 A major problem with this arrangement is the power transmission to the athwartship mounted pump shaft. Another problem area of the wide inlet appears to be the ingestion of debris into the system. Many present inlet systems use inlet grates to block objects from entering the system. How some arrangement such as Tthis would affect a wide boundary layer inlet is presently unknown. Air ingestion, especially in turning maneuvers, is also a potential problem that could significantly limit inlet width. Model tests to determine the magnitude of these problem areas and practical solutions will be needed to fully pursue the application of this concept to high performance planing craft. The analysis approach used in this report was first to determine empirical methods for calculating boundary layer -- thickness and profile at the inlet. With this information the velocities at the inlet can then be determined for any given set of conditions and performance predicted. BOUNDARY LAYER THICKNESS BOUNDARY LAYER CHARACTERISTICS The successful design of a wide boundary layer inlet depends on having some knowledge of the boundary layer on the craft prior - to the inlet. Based on test craft data -5, it is evident that the boundary layer thickness at any point along the craft base can be approximated by Prandtl's equation for boundary layer thickness: ( V COQ-1/5-1/5 - = * = Re (1) L x where Re = Reynolds number = V Lx/v. (la) The boundary layer thickness, 6, varies inversely as the 1/5-power of the free stream velocity. Thus, boundary layer thickness decreases with increasing craft speed. The above equation for boundary layer thickness is applicable basically only to the zero pitch case. It has been shown that craft pitch has considerable effect on the boundary layer., 'Superscripts refer to similarly numbered entries in the Technical References at the end of the text. PAS
13 a 3-degree bow-up pitch resulted in a 40% reduction in boundary layc7 tnickness during model tests. In the zero pitch case, drag is primarily frictional, while in the bow-up pitch, drag has both frictional and pressure components. However, with increasing trim or pitch angle, the bottom pressure is greater than the free stream pressure because the average bottom velocity is less than the forward speed by Bernoulli's equation. Additional study or experimentation will be necessary to determine the boundary layer characteristics of different types of craft, especially planing craft, which are designed with some amount of bow-up pitch. However, equation (1) will be assumed to be applicable, except in extreme cases, since it has shown agreement with experimental craft data. 1-5 BOUNDARY LAYER PROFILES Details of the boundary layer profile are required for determining the average, momentum, and energy velocities of the flow into the inlet. The characteristic boundary layer shapes are assumed to have an exponential boundary layer profile described by: yi/ny - 1 For-, (2) U _ 00 where n =logl 0 Re (3) Figure 2 shows the effect of the value of the exponent n on the shape of the boundary layer profile. Increasing n increases the local velocity ratio, U/V 0, for any given height ratio, y/6. The distance, y, is the depth below the hull from which flow is ingested, as shown in figure 3, and defines the dividing streamline between flow into the inlet and around it. The average velocity in the ingested flow is calculated from: (Y/6)61(4 V" V _ Ua _/ U d() (4) PAS
14 i I I I I I I I, I IA T"0.8-07!0.6 - u (./n : U v Figure 2 - Boundary Layer Profiles as a Function of the Power n STREAMLINE BEWEEN.. -UM---;- -- AROUND IT,. VA.DIVIDING. _ FLOW INTO THE INLET AND i.. :-UE WHERE:!.- =,U:AVERAGE VELOCITY OF INGESTED FLOW oue Um :MOMENTUM VELOCITY OF INGESTED FLOW :ENERGY VELOCITY OF INGESTED FLOW U :LOCAL VELOCITY AT DIVIDING STREAMLINE V :FREE STREAM VELOCITY Figure 3 - Wide Inlet and Boundary Layer PAS
15 The momentum velocity of the ingested flow is obtained from: Um = ML ( d ( - (5) Ur Ua Y()2() (5) The energy velocity of the ingested flow is calculated from: I The local velocity ratio, U/Vw, at the dividing streamline is obtained trom equation (2) for y/6 -< 1; however, for y/6 > 1, equation. (4), (5), and (6) must be integrated over the additional interval of 1 to y/6, where the local velocity ratio is equal to one ac ail Ipoints. The L:y.nential boundary layer profile of equation (2) anq, the basic definition of equations (4), (5, nd (6) ;nay b-- used to derive the following equations; For y/s i, Ua a- = n U n + 1 (7a) U m n + 1 U n + 2 (7b) Ue {n +!V/2 _ = (\ / (7c) U= \n+ 3) For y/{ ' l, Ua l 1= (8a) V (-) (n + 1) PAS
16 U (Y) -1+ n 5 (n + 2) (8b) ( (n + () - 11) _ e _ 6 (n + 3T (8c) V( ) (n + 1) The value y/16 > 1 indicates that flow is also taken from beyond the boundary layer. The exponential boundary layer of equation (2) and the basic definitions of the velocities shown in figure 3 may be used to relate the local height ratio at the dividing streamline to the inlet conditions by: V.) ( n 1)]n/(GI + 1) (nhi) For 1 (9a) and " For > 1. (9b) ( [(n+lit (i) (')] ( PERFORMANCE OF BOUNDARY LAYER INLETS In calculating the performance of a water-jet system, it is a normal first assumption to neglect the effects of the boundary layer. However, the boundary layer reduces the momentum and energy velocities at the inlet and is a most important factor to consider for this concept. Burke, et al, showed the momentum velocity for the XR-lB inlet was about times the free stream velocity. PAS
17 The craft or gross thrust, Tc, is calculated from: Tc = p Q (Vj - U m ) = p Q Vm(R - Km). (10) The drag of the inlet, Di, is obtained from: D A i V 2 CDi D i CD Ai V = p V', Q (11) The net thrust Tnet required by the craft is obtained by subtracting the inlet drag from the craft thrust requirement; thus: Tnet = Tc - D i CD. = p V Q - K m (12) The required input power Pi' is given by: PJ e + e P = 2 +Kz 2 p t p Q - (R2 + K (K9-1) 'p (3 The overall efficiency or propulsive coefficient, no, of the water-jet system is obtained by use of equations (12) and (13), giving: Tnet VD no - Pi CDi _2 (R -Km ±) 2 n t (14) ' 2 R+ Ke 9-1 i PAS
18 WO The effects of boundary layer flow ingestion on the overall efficiency are shown in figures 4 through 6. Reducing the momentum velocity ratio for any jet velocity ratio increases the overall efficiency of the water-jet system. Increasing the drag coefficient and/or system loss coeffic-ent reduces the overall - efficiency as would be expected. The effects of the value of n from equation (3) on the overall efficiency were negligible since the energy velocity ratios calculated for the different a's were very close for a constant momentum velocity ratio. With reducing momentum velocity ratio, the point of peak overall efficiency is shifted to lower jet velocity ratios. Increasing jet velocity ratio minimizes the gains due to boundary layer ingestion since jet velocity now becomes the dominant term in the performance prediction equation (i.e., equations (10), (12), (13), and (14). Thus, a wide inlet system should have a low design jet velocity ratio, approximately 1.6 to 2.0, and is most applicable to a craft that spends a large percentage of its time at or near its design jet velocity ratio, which implies high craft speed. At low speed where the jet velocity ratio is high, * the wide inlet system has performance that is comparable to that of the conventional flush inlet. 'a K.: K, K L =0.15 ~ , I I I DESIGN JET VELOCITY RATIO Figure 4 - Effects of Boundary Layer Flow Ingestion on the Overall Efficiency for CDi/ 2 a = 0.05 a. PAS
19 Km 09 =Pj0.5 K,=l.0 X KL = K : I DESIGN JET VELOCITY RATIO Figure 5 - Effects of Boundary Layer Flow Ingestion on the Overall Efficiency for CDi/ 2 a = Km:O.B KmO/" F~ ; DESIGN JET VELOCITY RATIO Figure 6 - Effects of Boundary Layer Flow Ingestion on the Overall Efficiency for CD./ 2 PAS =0.15
20 IT By equating the net thrust equation at constant flow and velocity for two different Km values, the following is obtained: (CDi - CDi') R'= R - (Km - Ki') - 2 ' (15) with the primed quanlities denoting conditions at the second Km - value-. Thus, if the system is designed for a lower K m value (i.e., wider inlet), it is possible to reduce the jet velocity ratio for the same flow rate and thus have approximately the same size m'stem. The inlet drag coefficient will decrease slightly with decreasing Km, but its effect in equation (15) will be at least an order of magnitude less than the effects of the Km term and may be ignored. Thus, the reduction in jet velocity ratio with decreasing Km can improve efficiency both by minimizing energy lost in the jet and by reduced inlet momentum losses. 4-0 WIDE BOUNDARY LAYER INLET DESIGN The size of the wide boundary layer inlet will depend on several factors, the most important being the available hull width near -ne transom of the craft that is suitable for inl use. Not all of this width can be used since such problems as avoiding broaching in turns can reduce available width. The flow into the inlet can be determined from the net thrust equation (12) by: " Q =(16) Tnet j The flow rate into the inlet can also be determined from any of the following: Q = Ua y Lw Q = H i V i Lw (17a) (17b) Q = Hi a V Lw (17c) If flow is assumed to be taken from the boundary layer region or from the boundary layer region and beyond, then by substitution from equations (2), (4), (7a), (7b), and (8a) in (17a) the following expressions for flow are obtained, respectively: PAS
21 L Qn L+ I [ 1 2 K-nn L n +i m] n (For -) (18a) ~1n + and Q4w+ V W(For >i) (18b) 1 y/6 in equation (18b) may be expressed in terms of Km and n using equation (8b). Equating (16) with (18a) and (18b), the inlet width can be calculated from: Lw (For Y - 1). (19a) P V" 2 6 n + 2 n+1 Di6 n +1 i Km R -K m 2-a and 6 [ n+1 R Km Tnet (For Y > 1). (19b) F :1 = Thus, for a given available inlet width, a range of jet velocity and inlet momentum velocity ratios exist that will satisfy the equations. If the jet velocity ratio is fixed, there will be a minimum inlet momentum velocity ratio below which there is not sufficient inlet width available. Equations (19a) and kl9b) may be rewritten to express what will be called a boundary layer net thrust pressure, Pb,, where: k 1 n K]n l[rc. Tnet pv 2 n + Km C- CDai (For Pb Lw 6 n Km)2a] T ne Sb = Tnet = V 2 [y- F - Km DA (For Y>). (20b) i -ot Lb 6 ns- 6 PAS
22 The net boundary layer thrust pressure is plotted in figures 7 and 8 as a function of jet velocity ratio for different inlet T momentum velocity ratios at 50 and 25 knots, respectively. The n value is representative of the range of Reynolds numbers to be expected. With the basic craft design information, the PbZ value can be calculated and will be constant for a given craft velocity. If the value of Pbt at 50 knots (which is about the maximum velocity for a naval planing hull craft) is checked in figure 7, the range of Km values possible is shown. Decreasing jet velocity ratio increases the minimum attainable Km value and the size and weight of the system since flow rates increase significantly. The overall system efficiency will vary over the allowable Km - range for a given PbZ, and the point of optimum efficiency may be determined from equation (14) or thru figures 4, 5, and 6. Increases in the value of CDi/2a in equations (20a) and (20b) have only a slight effect in reducing PbZ since its value is small in comparison to the other terms. ' 101 CD, /2c:0.05 vo- 50 KNOTS " '"K,= K z085 -' K :0 80 o,'f K :.7 5 Figure 7 - Boundary Layer Net Thrust Pressure as a Function of R and K m -co KW0.0.. /I.-- KmwO 65 I0 3 " '... K O JET VELOCITY RATIO PAS
23 10 1 I I I CD,/2cr-005 VQo25 KNOTSKmO9.09 n:9... Kn =0.85 / /..-- " 1: , -n:9 K Fiur 8 BondryLae, /.f KwO 70 SFigure 8 Boundary Layer CRAFNet Thrust Pressure wa a " 11 d K:06t as a Function of R and Km // K.F JE VELOCITY RATIO CRAFT DRAG AND PART POWER OPERATION As speed increases on a planing hull craft, a point will be reached where enough lifting force is generated by the hull form to start lifting some of the hull clear of the water, thus reducing wetted surface area and slowing the rate of drag increase. This effect causes a hump in the drag curve at the intermediate speeds. Figure 9 shows a plot of craft resistance or drag as a function of Froude number based on the following equation- 6 Rc (7r Fv e= Fv sin 2 \, (21) PAS
24 1where Fv = Froude number ( (22) g V1/3 wc (23) P9 This equation is representative of planing craft in the 20- to 100-ton these conditions displacement range with 50-knot speed capability. For a length/beam ratio of 5.5 appears optimum and was assumed in estimating resistance above.6 A load coefficient (Ap/V 2 / 3 ) of 7.0 was chosen as representative of 20- to 100-ton -" craft in the development of equation (21).6 The resistance values calculated by equation (21) are for a bare hull and have been increased by 25% to account for increased resistance due to 4-* such factors as appendages, roughness, and sea state. I- -- _o L/B: Ap/'/3=70 < Uj 0.12 SEA OGHES T cz z BARE HULL, RESISTANCE U,v U S FROUDE NUMBER, V. /,/gv73 Figure 9 Craft Resistance versus Froude Number PAS
25 by:' Craft resistance at reduced displacement has been estimated CO o1 PUMP DESIGN Axial and double inlet centrifugal pumps are both candidate systems for use with a wide boundary layer inlet. The double width, double inlet centrifugal pumps offer a good combination with the wide inlet since the pumps can be strung in parallel across the transom and mounted on a common shaft as in figure 1. Axial pumps with their high efficiency and light weight could provide an optimum system, and weight tradeoffs between different axial and centrifugal arrangements will be investigated later. In the pump design, care must be taken to avoid cavitation at cruise conditions or pump life will be severely shortened. During periods of craft acceleration, some cavitation can be tolerated as long as it does not degrade pump performance, since the acceleration times are relatively short and no significant damage should result. The cavitation performance of a pump can be characterized by its flow coefficient, 0, and the non-dimensionalized energy ratio, T, where: and V ax (25) Ut 1 NPSH T a22 (26) V ax 2 /2g or NPSH T u 2 (26a) Ut2 /2g where NPSH - K,) + P atm + het -y (27) PAS
26 and = 2 T u T. (28) There exist relationships between energy ratio and flow coefficient that can be used for determining cavitation performance. For cavitation free pump performance: ' a1 + Cc (1 + 1/02) (29) T u 2 + Cc (1 + 02), (30) where Cc = 0.3 for noncavitating flow in general = 0.25 for noncavitating flow with welldesigned pumps. Since some cavitation can be tolerated under transient conditions, such as during acceleration and hump conditions, a smaller and lighter pump design is possible with limited cavitation. Based on data for axial and centrifugal 8 pumps, expressions for energy ratio as a function of flow coefficient at 115% of breakdown NPSH yield over the given ranges of flow coefficient data: For axial pumps, 'U > [ ). (31) u For centrifugal pumps, T 'u [0.08 ' ]. (32) For cruise conditions the pump must be cavitation free as defined by equations (29) and (30). However, for transient conditions, the pump can be allowed to operate down to the limits of equation (31) or (32). by: Pump inlet tip speed, inlet diameters, and rpm are determined.+, 2g NPSH 1/2 ' U u PAS
27 / ) 4Q Dtl = (1 - X 2 ) Vax N pi) 1/2 N = 6. (35) 71 Dtl For axial pumps, an inducer stage plus additional stages can be used. The number of pump stages reqaired is determined by: 4g Hp S 2-0.6, (36) Ut 1 where S = least integral number of stages satisfying equation (36). Axial pump weight, including water weight can be determined from the empirical relation: 9 Wap = [ (S - 5)] Dtl/ 2 (37) For centrifugal pumps the outlet diameter is determined from: 10 D I ] gil 1/2 St Ut 1 2) Dt l, (38) and DWDI centrifugal wet pump weight is determined from: 9 2 Wcp = C N s Dt Np (1.55), (39) p Cw NDt2 [0 where Cw = PAS
28 By combining equations (33), (34), and (35) and dividing by pump head, the following expression for specific speed is obtained: NO1/2-m 12gTCt 3/4 0)1/2 NS im = (i - 2 ) ) (40) T where NPSH = Thoma cavitation number =N Hp Assuming X = 0.3:?- 1/2 3/4 N s = /2 3/ (41) Tu Equation (41) is plotted in figures 10 through 12 for the noncavitating and limited cavitating design cases defined by using the equalities in equations (30), (31), and (32), respectively. Thus, these figures represent upper limits on specific speed for a given Thoma number. Pump designs are usually characterized by their specific speed, where: 9 * 500 : N s s 4,000 for centrifugal pumps. * 4,000 : N s :!i0,000 for mixed flow pumps. * 10,000 s N s s 15,000 for axial pumps. Thus, for higher specific speed designs, figures 10 through 12 show that high Thoma cavitation numbers are required, meaning large NPSH and/or low pump head rise. However, with the increased application of inducers, the characteristic specific speeds of pumps can be reduced. Axial pump inducer stages can now be designed for specific speed as low as about PAS
29 30,000 I I Ii I I I I I 0:0.07 0:0.15 1; 25, H'_ 20,000-0:0.23- =:0.19 S10,000 FOR ,00 0- K / 0J I.J I ll I THMA CAVITATION NUMBER, NPSH / PUMP HEAD ~i Figure 10 Axial Pump Specific Speed Versus Thoma Cavitation Number for Limited Cavitating Designs PAS I rv!
30 20,000 I I I I ~t I0: / /.0=0.24 Tl 0: #040 T IOooo -,. LUJ 9.V) 5, L THOMA CAVITATION NUMBER, NPSH/PUMP HEAD Figure 11 Centrifugal Pump Specific Speed Versus Thoma Cavitation Number for Limited Cavitating Designs 13,000 12, *0 32 *' 11, ,000 *9000 8,000 /JU 7,0000 * 6,000 Uj 5,000 4,000 P01 3,000 -FRX0. 2, e3 S1,000 0~ " IHOMA CAVITATION NUMBER, NPSH/PUMP HEAD - Figure 12 Specific Speed Versus Thoma Cavitation Number for Noncavitating Designs PAS
31 The pump performance at speeds other than the maximum ship design speed condition can be approximated by: K Q2 KQ3 K1 od K 2 od (42) npod Hod Hod3/2 where K 1 = 3np H (43a) and 2np Hd3/2 K 2 p 3 d ' (43b) Qd where npod is the pump efficiency at off design speed conditions. The maximum pump efficiency, flp, for axial and centrifugal pumps is in the 85% to 90% range for well-designed pumps. SENSITIVITY STUDIES The effects of various parameters on a wide boundary layer inlet performance were considered for a representative 70-ton, 50-knot planing craft. The craft net thrust requirements versus speed were obtained from equation (21) with a 25% margin for appendages, sea state, and roughness and are plotted in figure 13, where an additional thrust margin equal to 2% of the craft weight is included to allow for acceleration. The base line craft design conditions at 50 knots were taken as: R = 1.8 = jet velocity ratio = Vj/V. a = 0.7 = inlet velocity ratio =Vi/V Lx = 90 feet Lw = 12 feet np = 85% KZ = 0.3 CDi/2a = 0.05 At the 30-knot design condition, 6 7 inches and (y/6).4 at the inlet for the above conditions. PAS
32 1 30,000 - THRUST ACCELERATION MARGIN =2 %OF 25,000 CRAFT WEIGHT ca 'z' 20,000 I.-,00 CRUISE THRUST v)1500 z U- CRAFT WEIGHT= 140,000 LB 5, CRAFT VELOCITY, KNOTS Figure 13 Net Thrust versus craft velocity PAS
33 Figures 14 and 15 show the effects of craft velocty on inlet aind jet velocity ratio, momentum velocity ratio, overall propulsivc coet LCient, pump efficiency, and horsepower for the cruise and accelerating conlditions %1HERE -CRUISE CONDITION --- ACCELERATING CONDITION I- *--~~JET VELOCITY RATIO i 0- L C - ~ r T F 0 CRAFT VELOCITY, KNOTS Figure 14 wide~ Boundary Layer inlet Ferformfance P~s
34 1.o.86 I I I 1 I I I I i d z ~~~~~~a0.83-iiiii!ii U / z 1 O.8 / <.7/ I r tvo were: H/ -CRUISE CONDITION -- ACCELERATION CONDITION 0.1h 0-" CRAFtVOOCCOY, KNOTS Figure 15 Wide Boundary Layer Inlet Performance The effects of craft velocity on the various parameters are as follows: Jet velocity ratio - increases with decreasing speed, thus making kinetic energy losses proportionally higher. * Inlet velocity ratio - increases with decreasing speed. The CDi/2a term was considered to be constant with speed in the calculations but might actually decrease with decreasing speed due to the increasing a at lower speed and no great expected changes in CDi. This would improve low speed efficiency slightly above values shown. PAS
35 e Momentum velocity ratio - increases slightly with decreasing speed, thus reducing n o slightly. * Overall propulsive coefficient - decreases with decreasing speed due mainly to the increasing jet velocity ratio. * Pump efficiency - is relatively unaffected by craft speed, showing the pump operates close to its optimum over the speed range. * Horsepower requirements - are reduced with decreasing speed due to the lower thrust requirements. Horsepower requirements vary somewhat linearly with speed. At about half speed, power requirements are thus about half of design speed requirements. Thus, on a ship of two or more engines, one or more could be shut off and the remaining unit or units could be operated at higher power where sfc is generally improved. Figure 16 shows the effects of wetted length, inlet width, inlet loss coefficient, and drag coefficient on the overall propulsive coefficient. The effects on overall propulsive coefficient are as follows: o Wetted length - A reduction in wetted length upstream of the inlet causes only slight reductions in no, even for large decreases in wetted length. This is important since planing hulls can have reduced wetted surface with increased speed. o Inlet width - Increasing inlet width will also increase no slightly since a smaller percentage of the boundary layer thickness will be used, an effect that results in a lower inlet momentum velocity. o Inlet loss coefficient - Increasing inlet loss coefficient will cause noticeable decreases in no. Keeping inlet losses very small will be difficult due to the following: There are losses on the ramp directly upstream on the flush inlet which reduce the inlet dynamic head by roughly 10% 3 4' compared to what would be predicted for the ingested portion of the boundary layer. The skewed inlet profile will cause problems in avoiding separation in the inlet diffuser. 4 Separation causes diffuser efficiency to suffer, and undesirable flow patterns are established. 9 Inlet drag coefficient - Increasing drag coefficient will significantly reduce no, especially since the area of interest is a low jet velocity ratio region. However, very low inlet drag PAS
36 coefficients are possible with flush inlets." The wide boundary layer inlet will operate in the lower velocity environment of the boundary layer, resulting in potentially even lower inlet drag coefficients JET VELOCITY RATIO I I ii I_ PERCENT CHANGE IN WETTED LENGTH 1.8 LU _ U- I I I U.j o oj PERCENT CHANGE IN INLET WIDTH J 1_0.60 T I I I I, INLET LOSS COEFFICIENT, KL l D I CDi/2e( Figure 16 Effects of Various Parameters on Wide Boundary Layer Inlet Performance T PAS
37 Figure 17 shows the effects of jet velocity ratio on a wide boundary layer inlet system design at the maximum cruise design speed. The use of low jet velocity ratios (2) at design speed will most likely be necessary to ensure an no high enough to compete with other alternative systems L- 0WIDE BOUNDARY LAYER INLET >U u, CONVENTIONAL INLET (Km0.95) Z1.45 [- XA U._ nic 1.35 i- 6. CENTRIFUGAL II 5500 _1- CENTRIFUGAL DWDI AXIAL _,-, i r f XUJ I,I I DESIGN JET VELOCITY RATIO ACCELERATION CRUISE Figure 17 - Effects of Jet Velocity on a Wide Boundary Layer Inlet Design at Cruise Conditions PAS
38 The effects of jet velocity ratio were: * Overall propulsive coefficient - increases with decreasing jet velocity ratio for the variables investigated. Figure 17 also shows a comparison with what would be expected for a conventional low aspect ratio inlet where boundary layer effects are small and Km is assumed equal to The wide inlet shows a 5- to 6.5-point efficiency advantage over a conventional system. Figures 4 through 6 also show jet velocity ratio effects on no for a wider range of variables. 9 Diffusion ratios - are low and show a tendency to decrease slightly with reduced jet velocity ratio. The low diffusion ratios result from high flow coefficients appearing desirable. Since diffusion ratios can be low, diffuser size and losses may potentially be kept low. 'I o Pump weight - increases rapidly with decreasing jet velocity ratio due to the increased pump mass flows. The pump designs are based on noncavitating flow at the craft design speed. Increasing the number of pumps will reduce pump weight. Axial pumps tend to show a weight advantage over centrifugal pumps; but when the complete system is considered, this advantage may vanish. o Maximum horsepower -increases with increasing jet velocity ratio due to higher jet kinetic energy losses. EVALUATION OF POTENTIAL WIDE INLET PUMP SYSTEM ARRANGEMENTS Three different pump arrangements were investigated for a 70-ton planing craft: o Multiple parallel DWDI centrifugal pumps. * Multiple parallel axial pumps with turning volutes. o Conventionally mounted axial pumps. The three arrangements are shown in figures 18 through 20, respectively. In all three cases, the pumps are driven by two gas turbines. However, the first two arrangements can declutch a turbine to provide improved fuel consumption at lower speed and power conditions. The weight of a combining gear on the conventionally mounted axial pumps was too high in this case to be considered for use. PAS
39 The multiple parallel DWDI centrifugal pump arrangement, figure 18, is attractive since the pumps can be strung on a single shaft. The multiple pump inlets are then in a line which will closely match the inlet width. This will enable the inlet diffusion to be essentially two-dimensional and should keep losses to a minimum. The multiple small diameter pumps should help keep pump weight and elevation losses to a minimum.,,.,coupling [1v, tvj Iv REDUCTION GEAR INLET, DIFFUSER AND TRANSITION Z-I-RIGHTANGL E. DRIVE. CLUTCH TRAIN GTPF GTPF (I Figure 18 Multiple Parallel Double Width, Double Inlet Centrifugal Pump Arrangement PAS
40 I The multiple parallel axial pumps' arrangement of figure 19 enables all the pumps to be mounted on a common shaft. The flow must be turned (turning losses were considered) to get into the pump, and a turning volute is required downstream of the pump to direct the flow toward the transom with minimum losses. This arrangement strings the pumps out to match the inlet width more effectively. The small pump diameters should keep pump weight low. Pump weight has been increased by onethird to account for the turning volute. COUPLING I /AI,',,REDUCTION INL N FFSR TASIINTRAIN - -r ' DRIVE - k CLUTCH GEAR GTPF GTPF Figure 19 Multiple Parallel Axial Pumps With a Turning Volute PAS
41 The conventionally mounted axial pumps' arrangement of figure 20 enabled the realization of a simple compact system. The flow from the wide inlet, however, must be ducted to the narrower pump inlet which will require three-dimensional diffusion and/or transition with their associated losses in a minimum length inlet system to minimize weight. INLET, DIFFUSER AND TR NSITION PLANETARY RDCTION GEARS GTPF GTPF Figure 20 Conventionally Mounted Axial Pumps The craft drag characteristic was assumed to be the same as shown in figure 13. The basic craft design conditions were as follows: Wc = 70 tons V = 50 knots (maximum) R = 1.8 (at 50-knot cruise) a = 0.7 (at 50-knot cruise) PAS
42 L x = 90 feet LW = 12 feet np = 0.85 K--factor = 500 gears Duct weight = 15 psf of surface On all the designs it was assumed that after the inlet there would be a length of constant area duct with area equal to the inlet cross section and running a minimum of five inlet heights. This would allow the skewed boundary layer inlet profile to become more uniform before any diffusion took place. Since the amount of diffusion required in the designs considered turned out to be small, this duct length did not involve any weight penalty. Additional duct would have been required to get to the pump inlet due to the short diffusers. -. The two multiple parallel pump arrangements have similar gear arrangements. Power from the gas turbine is fed to a 1:1 right angle bevel gearbox whose output then drives a reduction gear train. This arrangement appears very desirable since it allows flexibility in where to mount the gas turbines. Also the reduction gear train enables offset so that the input shaft clears the pump and ducting. Most important, the reduction gear train is half the width of any other alternative systems, thus allowing maximum utilization of transom width for stringing out the multiple pumps to match the inlet width. The following tabulation is a comparison of the three arrangements. The weights of the transmission system, including shafting, bearings, etc, were based on Muench.A The tabulation shows that the centrifugal and conventionally mounted axial pumps yield comparable system weights. The multiple parallel axial arrangement was much heavier due to the additional weight of the turning volutes and heavier reduction gears. System losses were assumed to be slightly higher for the axial pump arrangements so they had increased horsepower requirements which appears likely due to their required inlet and/or outlet ducting configurations. The centrifugal pump arrangement appears to offer the most advantages since, in addition to having a weight comparable to the conventional axial arrangement, all the centrifugal pumps can be run from a single gas turbine to improve low power sfc. A combining reduction gear was estimated to add about 3200 more pounds to the conventional axial pump setup. Further study, particularly in the area of system losses, would be needed to assure the selection of the appropriate pump and arrangement. PAS
43 COMPARISON OF PUMP ARRANGEMENTS Multiple Parallel Multiple Parallel Conventionally DWDI Axial Pumps With Mounted Centrifugal Pumps Turning Volutes Axial Pumps No. of pumps Impeller exit tip velocity, fps Pump flow coefficient Inlet axial velocity, fps Inlet loss coefficient Inlet height, in Inlet momentum velocity ratio n o (cruise) ipmax 10,972 11,205 11,205 11Pcruise 9,508 9,731 9,731 Diffusion ratio Pump diameter, ft o.d. x i.d. Shaft blockage coefficient Pump maximum rpm 3,490 2,212 1,310 Pump unit length, ft ea. Reduction gear ratio Wet pump weights 4,555 5,083 4,704 Inlet weight, lb Diffuser and transition weights, lb Pump inlet elbow weights, lb * Bevel gear weights, lb 1,240 1,240 - Reduction gear weights, lb 1,690 3,174 2,636 Weights of shafts, bearings, clutches, etc, lb Weight of gas turbines, lb 6,402 6,402 6,402 Propulsion system weight, lb 15,363 17,817 15,396 Propulsion system weight fraction Propulsion system specific weight, lb/hp , * Included in pump weight. PAS
44 j CONCLUSIONS The use of wide boundary layer inlets should enable realization of improved propulsive coefficients for water-jet systems. This type of inlet is most applicable to displacement-type craft, which have sufficiently wide beam to accommodate it. Propulsion coefficients approaching 0.6 are predicted, with improvements being about 10% to 12% above those of con- Tventional inlets. The biggest improvements in propulsive coefficient for a wide inlet system occur for low design jet velocity ratios on the order of 1.6 to 2.0. As jet velocity ratio increases, the effect of reduced inlet momentum coefficient is minimized and wide inlet performance approaches that of a conventional flush inlet. Thus, wide inlet systems are most applicable to a craft that spends a large percent of its time at or near its design jet velocity ratio. The performance of a wide boundary layer inlet system is most affected by increasing inlet drag, inlet system losses, and jet velocity ratio. Changes in wetted length and inlet width have a lesser effect on overall system efficiency. The 4- multiple parallel centrifugal pumps and the conventionally J mounted axial pumps both appear to have potential application on a wide boundary layer inlet system. In this study the centrifugal setup had low speed powering advantages which could only be obtained in the axial arrangement through increased gear weight. RECOMMENDATIONS * Model testing of a wide inlet system is needed to determine inlet system losses, drag coefficients, and potential air ingestion problems. e Measurements of boundary layer thickness and profile on planing and displacement craft, especially at high speeds, are needed to assure that the reduced velocity which is characteristic of the boundary layer is present in spite of the induced ventilation and broaching that occur during nonideal sea states. TECHNICAL REFERENCES 1 Burke, F. P., et al, "R & D Testcraft: XR-lB Semi Flush Inlets, Final Test Report," Rohr Industries, Inc., Rept RHR (Oct 1972) 2 - Burke, F. P., et al, "R & D Testcraft: XR-lB Semi Flush Inlets, Correlation Report," Rohr Industries, Inc., RHR (Dec 1972) 3 - Johnson, V. E., et al, "Design and Performance of Diffusers, Fixed-Area Inlets and Variable-Area Inlets in Integrated Inlet-Diffuser Subsystems," Hydronautics, Inc., Rept (Aug 1972) PAS
45 4 - Stephens, L. K., et al, "Waterjet Inlet/Duct Development Phase I, Validation Tests," Hydronautics, Inc., Rept (Jan 1973) 5 - Poquette, G. M., and R. J. Etter, "Waterjet Inlet/Duct Development Phase II, XR-lB Correlation Tests," Hydronautics, Inc., Rept (Mar 1973) 6 - Barr, R. A., "State-of-the-Art Technology and Performance Prediction Methods for Waterjet Propulsion Systems for High Speed Naval Ships," Hydronautics, Inc., Rept (June 1974) '7 - Brophy, M. C., "A Theoretical Study of Cavitating Inducers with an Application to Waterjet Propulsion," NSRDC Rept 4431 (Feb 1975) 8 - Gongwer, C. A., "A Theory of Cavitation Flow in Centrifugal Pump Impellers," Trans. of the ASME (Jan 1941) 9 - Carmichael, A. D, and R. C. Percival, "Design Optimization of Waterjet Propulsion Systems for Hydrofoils, Part 3," MIT Ocean Engineering Rept (1972) 10 - Wislicenus, G. F., Fluid Mechanics of Turbomachinery, Vol. 1, New York, Dover Publicaticns, Inc. (1965) 11 - Muench, R. K., "Arctic Surface Effect Vehicle Program: Parametric Data on a Mechanical Transmission Suitable for Large Surface Effect Vehicles," NSRDC Rept (Dec 1973) The Center cannot assume responsibility for the universal availability of all references mentioned in a technical document. Both the age of the document and sensitivity caused by imminent implementation of a system may impose originator's limits on availability. PAS
46 IINITIAL DISTRIBUTION Copies Copies 9 NAVSEA 1 The Boeing Co. 1 SEA 03C) Seattle, Wash. 2 SEA 032) (R. Dixon) 2 SEA 0331G)* 2 SEA 035) 1 Dr. G. F. Wislicenus 2 SEA 09G32) 4641 E. Coronado Dr. Tucson, Ariz NAVSEC 1 (SEC 6144, CENTER DISTRIBUTION Blount) 1 (SEC 6661, Lombardi) Copies 1 Code 1170) 12 DDC 2 15) ) ) 2 Aerojet Liquid ) Rocket Co ) P.O. Box B) Sacramento, Calif (R. G. Siogren) T~W 2 Applied Research Lab. P.O. Box 30 State College, Pa Gearhart) R E. Henderson) 2 Hydronautics, Inc Pindell School Rd. Laurel, Md (R. Barr) (R. Etter) 1 Massachusetts Institute -- of Technology Dept. of Ocean Engr. Cambridge, Mass (Dr. A. D. Carmichael) 2 Rocketdyne 6633 Canoga Ave. Canoga Park, Calif (G. Wong) (L. Barham) *Addressee. PAS-75-45, March
Performance Assessment of the Waterjet Propulsion System through a Combined Analytical and Numerical Approach
 International Journal of Physics, 013, Vol. 1, No., -7 Available online at http://pubs.sciepub.com/ijp/1//1 Science and Education Publishing DOI:10.1691/ijp-1--1 Performance Assessment of the Waterjet
International Journal of Physics, 013, Vol. 1, No., -7 Available online at http://pubs.sciepub.com/ijp/1//1 Science and Education Publishing DOI:10.1691/ijp-1--1 Performance Assessment of the Waterjet
ITTC Recommended Procedures and Guidelines
 Page of Table of Contents Waterjet Propulsion Test and Extrapolation... PURPOSE OF PROCEDURE.... PARAMETERS.... Nomenclature... 3. DESCRIPTION OF PROCEDURE... 3 3. Model and installation... 3 3.. Resistance
Page of Table of Contents Waterjet Propulsion Test and Extrapolation... PURPOSE OF PROCEDURE.... PARAMETERS.... Nomenclature... 3. DESCRIPTION OF PROCEDURE... 3 3. Model and installation... 3 3.. Resistance
Applied Fluid Mechanics
 Applied Fluid Mechanics 1. The Nature of Fluid and the Study of Fluid Mechanics 2. Viscosity of Fluid 3. Pressure Measurement 4. Forces Due to Static Fluid 5. Buoyancy and Stability 6. Flow of Fluid and
Applied Fluid Mechanics 1. The Nature of Fluid and the Study of Fluid Mechanics 2. Viscosity of Fluid 3. Pressure Measurement 4. Forces Due to Static Fluid 5. Buoyancy and Stability 6. Flow of Fluid and
CHAPTER EIGHT P U M P I N G O F L I Q U I D S
 CHAPTER EIGHT P U M P I N G O F L I Q U I D S Pupmps are devices for supplying energy or head to a flowing liquid in order to overcome head losses due to friction and also if necessary, to raise liquid
CHAPTER EIGHT P U M P I N G O F L I Q U I D S Pupmps are devices for supplying energy or head to a flowing liquid in order to overcome head losses due to friction and also if necessary, to raise liquid
TOTAL HEAD, N.P.S.H. AND OTHER CALCULATION EXAMPLES Jacques Chaurette p. eng., June 2003
 TOTAL HEAD, N.P.S.H. AND OTHER CALCULATION EXAMPLES Jacques Chaurette p. eng., www.lightmypump.com June 2003 Figure 1 Calculation example flow schematic. Situation Water at 150 F is to be pumped from a
TOTAL HEAD, N.P.S.H. AND OTHER CALCULATION EXAMPLES Jacques Chaurette p. eng., www.lightmypump.com June 2003 Figure 1 Calculation example flow schematic. Situation Water at 150 F is to be pumped from a
Department of Energy Fundamentals Handbook. THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW, Module 3 Fluid Flow
 Department of Energy Fundamentals Handbook THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW, Module 3 REFERENCES REFERENCES Streeter, Victor L., Fluid Mechanics, 5th Edition, McGraw-Hill, New York, ISBN 07-062191-9.
Department of Energy Fundamentals Handbook THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW, Module 3 REFERENCES REFERENCES Streeter, Victor L., Fluid Mechanics, 5th Edition, McGraw-Hill, New York, ISBN 07-062191-9.
Chapter Four Hydraulic Machines
 Contents 1- Introduction. - Pumps. Chapter Four Hydraulic Machines (لفرع الميكانيك العام فقط ( Turbines. -3 4- Cavitation in hydraulic machines. 5- Examples. 6- Problems; sheet No. 4 (Pumps) 7- Problems;
Contents 1- Introduction. - Pumps. Chapter Four Hydraulic Machines (لفرع الميكانيك العام فقط ( Turbines. -3 4- Cavitation in hydraulic machines. 5- Examples. 6- Problems; sheet No. 4 (Pumps) 7- Problems;
Pressure and Flow Characteristics
 Pressure and Flow Characteristics Continuing Education from the American Society of Plumbing Engineers August 2015 ASPE.ORG/ReadLearnEarn CEU 226 READ, LEARN, EARN Note: In determining your answers to
Pressure and Flow Characteristics Continuing Education from the American Society of Plumbing Engineers August 2015 ASPE.ORG/ReadLearnEarn CEU 226 READ, LEARN, EARN Note: In determining your answers to
Chapter Four Hydraulic Machines
 Contents 1- Introduction. 2- Pumps. Chapter Four Hydraulic Machines (لفرع الميكانيك العام فقط ( Turbines. -3 4- Cavitation in hydraulic machines. 5- Examples. 6- Problems; sheet No. 4 (Pumps) 7- Problems;
Contents 1- Introduction. 2- Pumps. Chapter Four Hydraulic Machines (لفرع الميكانيك العام فقط ( Turbines. -3 4- Cavitation in hydraulic machines. 5- Examples. 6- Problems; sheet No. 4 (Pumps) 7- Problems;
Therefore, the control volume in this case can be treated as a solid body, with a net force or thrust of. bm # V
 When the mass m of the control volume remains nearly constant, the first term of the Eq. 6 8 simply becomes mass times acceleration since 39 CHAPTER 6 d(mv ) CV m dv CV CV (ma ) CV Therefore, the control
When the mass m of the control volume remains nearly constant, the first term of the Eq. 6 8 simply becomes mass times acceleration since 39 CHAPTER 6 d(mv ) CV m dv CV CV (ma ) CV Therefore, the control
7.2 Ship Drive Train and Power
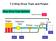 7.2 Ship Drive Train and Power Ship Drive Train System EHP Engine Reduction Gear Bearing Seals Strut Screw THP BHP SHP DHP Ship Drive Train and Power EHP Engine Reduction Gear Bearing Seals Strut Screw
7.2 Ship Drive Train and Power Ship Drive Train System EHP Engine Reduction Gear Bearing Seals Strut Screw THP BHP SHP DHP Ship Drive Train and Power EHP Engine Reduction Gear Bearing Seals Strut Screw
9. Pumps (compressors & turbines) Partly based on Chapter 10 of the De Nevers textbook.
 Lecture Notes CHE 31 Fluid Mechanics (Fall 010) 9. Pumps (compressors & turbines) Partly based on Chapter 10 of the De Nevers textbook. Basics (pressure head, efficiency, working point, stability) Pumps
Lecture Notes CHE 31 Fluid Mechanics (Fall 010) 9. Pumps (compressors & turbines) Partly based on Chapter 10 of the De Nevers textbook. Basics (pressure head, efficiency, working point, stability) Pumps
COURSE NUMBER: ME 321 Fluid Mechanics I 3 credit hour. Basic Equations in fluid Dynamics
 COURSE NUMBER: ME 321 Fluid Mechanics I 3 credit hour Basic Equations in fluid Dynamics Course teacher Dr. M. Mahbubur Razzaque Professor Department of Mechanical Engineering BUET 1 Description of Fluid
COURSE NUMBER: ME 321 Fluid Mechanics I 3 credit hour Basic Equations in fluid Dynamics Course teacher Dr. M. Mahbubur Razzaque Professor Department of Mechanical Engineering BUET 1 Description of Fluid
Teaching sessions week 40
 Teaching sessions week 40 Monday 28 September Lecture: Introduction to propulsion. Momentum theory of propeller action. Friday 2 October Lecture: Screw propeller Introduction of Marine Hydrodynamics 1
Teaching sessions week 40 Monday 28 September Lecture: Introduction to propulsion. Momentum theory of propeller action. Friday 2 October Lecture: Screw propeller Introduction of Marine Hydrodynamics 1
AEROSPACE ENGINEERING DEPARTMENT. Second Year - Second Term ( ) Fluid Mechanics & Gas Dynamics
 AEROSPACE ENGINEERING DEPARTMENT Second Year - Second Term (2008-2009) Fluid Mechanics & Gas Dynamics Similitude,Dimensional Analysis &Modeling (1) [7.2R*] Some common variables in fluid mechanics include:
AEROSPACE ENGINEERING DEPARTMENT Second Year - Second Term (2008-2009) Fluid Mechanics & Gas Dynamics Similitude,Dimensional Analysis &Modeling (1) [7.2R*] Some common variables in fluid mechanics include:
UNIT 4 FLYWHEEL 4.1 INTRODUCTION 4.2 DYNAMICALLY EQUIVALENT SYSTEM. Structure. Objectives. 4.1 Introduction
 UNIT 4 FLYWHEEL Structure 4.1 Introduction Objectives 4. Dynamically Equivalent System 4.3 Turning Moment Diagram 4.3.1 Turning Moment Diagram of a Single Cylinder 4-storke IC Engine 4.3. Turning Moment
UNIT 4 FLYWHEEL Structure 4.1 Introduction Objectives 4. Dynamically Equivalent System 4.3 Turning Moment Diagram 4.3.1 Turning Moment Diagram of a Single Cylinder 4-storke IC Engine 4.3. Turning Moment
Numerical Investigation of the Impact of SES-Waterjet Interactions and Flow Non-uniformity on Pump Performance
 11 th International Conference on Fast Sea Transportation FAST 2011, Honolulu, Hawaii, USA, September 2011 Numerical Investigation of the Impact of SES-Waterjet Interactions and Flow Non-uniformity on
11 th International Conference on Fast Sea Transportation FAST 2011, Honolulu, Hawaii, USA, September 2011 Numerical Investigation of the Impact of SES-Waterjet Interactions and Flow Non-uniformity on
6.1 Propellor e ciency
 Chapter 6 The Turboprop cycle 6. Propellor e ciency The turboprop cycle can be regarded as a very high bypass limit of a turbofan. Recall that the propulsive e ciency of a thruster with P e = P 0 and f
Chapter 6 The Turboprop cycle 6. Propellor e ciency The turboprop cycle can be regarded as a very high bypass limit of a turbofan. Recall that the propulsive e ciency of a thruster with P e = P 0 and f
Offshore Hydromechanics Module 1
 Offshore Hydromechanics Module 1 Dr. ir. Pepijn de Jong 6. Real Flows part 2 Introduction Topics of Module 1 Problems of interest Chapter 1 Hydrostatics Chapter 2 Floating stability Chapter 2 Constant
Offshore Hydromechanics Module 1 Dr. ir. Pepijn de Jong 6. Real Flows part 2 Introduction Topics of Module 1 Problems of interest Chapter 1 Hydrostatics Chapter 2 Floating stability Chapter 2 Constant
Dimensions of propulsion shafts and their permissible torsional vibration stresses
 (Feb 2005) (orr.1 Mar 2012) (orr.2 Nov 2012) Dimensions of propulsion shafts and their permissible torsional vibration stresses.1 Scope This UR applies to propulsion shafts such as intermediate and propeller
(Feb 2005) (orr.1 Mar 2012) (orr.2 Nov 2012) Dimensions of propulsion shafts and their permissible torsional vibration stresses.1 Scope This UR applies to propulsion shafts such as intermediate and propeller
Northern Lesson 2 Gear Pump Terminology. Gear Pump 101. Lesson 2: Gear Pump Terminology. When your reputation depends on it!
 Gear Pump 101 Lesson 2: Gear Pump Terminology When your reputation depends on it! Symbol Term Metric Unit Abbreviation US Customary Unit Abbreviation Conversion factor a A Area square millimeter mm2 square
Gear Pump 101 Lesson 2: Gear Pump Terminology When your reputation depends on it! Symbol Term Metric Unit Abbreviation US Customary Unit Abbreviation Conversion factor a A Area square millimeter mm2 square
DESIGN OPTIMIZATION STUDY ON A CONTAINERSHIP PROPULSION SYSTEM
 DESIGN OPTIMIZATION STUDY ON A CONTAINERSHIP PROPULSION SYSTEM Brian Cuneo Thomas McKenney Morgan Parker ME 555 Final Report April 19, 2010 ABSTRACT This study develops an optimization algorithm to explore
DESIGN OPTIMIZATION STUDY ON A CONTAINERSHIP PROPULSION SYSTEM Brian Cuneo Thomas McKenney Morgan Parker ME 555 Final Report April 19, 2010 ABSTRACT This study develops an optimization algorithm to explore
IJREAS Volume 2, Issue 2 (February 2012) ISSN:
 DESIGN AND CFD ANALYSIS OF SINGLE STAGE, END SUCTION, RADIAL FLOW CENTRIFUGAL PUMP FOR MINE DEWATERING APPLICATION Swapnil Urankar * Dr. H S Shivashankar ** Sourabh Gupta *** ABSTRACT Heavy centrifugal
DESIGN AND CFD ANALYSIS OF SINGLE STAGE, END SUCTION, RADIAL FLOW CENTRIFUGAL PUMP FOR MINE DEWATERING APPLICATION Swapnil Urankar * Dr. H S Shivashankar ** Sourabh Gupta *** ABSTRACT Heavy centrifugal
Machinery Requirements for Polar Class Ships
 (August 2006) (Rev.1 Jan 2007) (Corr.1 Oct 2007) Machinery Requirements for Polar Class Ships.1 Application * The contents of this Chapter apply to main propulsion, steering gear, emergency and essential
(August 2006) (Rev.1 Jan 2007) (Corr.1 Oct 2007) Machinery Requirements for Polar Class Ships.1 Application * The contents of this Chapter apply to main propulsion, steering gear, emergency and essential
INTERNATIONAL JOURNAL OF DESIGN AND MANUFACTURING
 INTERNATIONAL JOURNAL OF DESIGN AND MANUFACTURING Proceedings of the International Conference on Emerging Trends in Engineering and Management TECHNOLOGY (ICETEM14) (IJDMT) 30-31,December, 2014, Ernakulam,
INTERNATIONAL JOURNAL OF DESIGN AND MANUFACTURING Proceedings of the International Conference on Emerging Trends in Engineering and Management TECHNOLOGY (ICETEM14) (IJDMT) 30-31,December, 2014, Ernakulam,
CIVE HYDRAULIC ENGINEERING PART II Pierre Julien Colorado State University
 1 CIVE 401 - HYDRAULIC ENGINEERING PART II Pierre Julien Colorado State University Problems with and are considered moderate and those with are the longest and most difficult. In 2018 solve the problems
1 CIVE 401 - HYDRAULIC ENGINEERING PART II Pierre Julien Colorado State University Problems with and are considered moderate and those with are the longest and most difficult. In 2018 solve the problems
WATERJET PROPULSION SYSEM FOR HIGH SPEED CRAFTS
 ARAB ACADEMY FOR SCIENCE, TECHNOLOGY AND MARITIME TRANSPORT COLLEGE OF ENGINEERING AND TECHNOLOGY WATERJET PROPULSION SYSEM FOR HIGH SPEED CRAFTS Thesis Submitted to The Marine Engineering Department In
ARAB ACADEMY FOR SCIENCE, TECHNOLOGY AND MARITIME TRANSPORT COLLEGE OF ENGINEERING AND TECHNOLOGY WATERJET PROPULSION SYSEM FOR HIGH SPEED CRAFTS Thesis Submitted to The Marine Engineering Department In
CHAPTER 12 Turbomachinery
 CAER urbomachinery Chapter / urbomachinery 800 / 0 8 8 rad /s, u r 8 8 0 0 m /s, u r 8 8 0 0 8 m /s, rbv, but V u since, n n 0 0 0 0 0 0 m / s V V 0 0 m /s, rb 0 0 0 Vn u 0 8 6 77 m /s, tan tan 0 n t V
CAER urbomachinery Chapter / urbomachinery 800 / 0 8 8 rad /s, u r 8 8 0 0 m /s, u r 8 8 0 0 8 m /s, rbv, but V u since, n n 0 0 0 0 0 0 m / s V V 0 0 m /s, rb 0 0 0 Vn u 0 8 6 77 m /s, tan tan 0 n t V
CHAPTER 3 BASIC EQUATIONS IN FLUID MECHANICS NOOR ALIZA AHMAD
 CHAPTER 3 BASIC EQUATIONS IN FLUID MECHANICS 1 INTRODUCTION Flow often referred as an ideal fluid. We presume that such a fluid has no viscosity. However, this is an idealized situation that does not exist.
CHAPTER 3 BASIC EQUATIONS IN FLUID MECHANICS 1 INTRODUCTION Flow often referred as an ideal fluid. We presume that such a fluid has no viscosity. However, this is an idealized situation that does not exist.
Performance. 5. More Aerodynamic Considerations
 Performance 5. More Aerodynamic Considerations There is an alternative way of looking at aerodynamic flow problems that is useful for understanding certain phenomena. Rather than tracking a particle of
Performance 5. More Aerodynamic Considerations There is an alternative way of looking at aerodynamic flow problems that is useful for understanding certain phenomena. Rather than tracking a particle of
Chapter Four fluid flow mass, energy, Bernoulli and momentum
 4-1Conservation of Mass Principle Consider a control volume of arbitrary shape, as shown in Fig (4-1). Figure (4-1): the differential control volume and differential control volume (Total mass entering
4-1Conservation of Mass Principle Consider a control volume of arbitrary shape, as shown in Fig (4-1). Figure (4-1): the differential control volume and differential control volume (Total mass entering
Centrifugal Machines Table of Contents
 NLNG Course 017 Table of Contents 1 Introduction and Basic Principles... 1.1 Hydraulic Machines... 1.... 1.3 Pump Geometry... 1.4 Pump Blade Geometry...3 1.5 Diffusers...5 1.6 Pump Losses...6 1.7 Example
NLNG Course 017 Table of Contents 1 Introduction and Basic Principles... 1.1 Hydraulic Machines... 1.... 1.3 Pump Geometry... 1.4 Pump Blade Geometry...3 1.5 Diffusers...5 1.6 Pump Losses...6 1.7 Example
Fluid Dynamics Midterm Exam #2 November 10, 2008, 7:00-8:40 pm in CE 110
 CVEN 311-501 Fluid Dynamics Midterm Exam #2 November 10, 2008, 7:00-8:40 pm in CE 110 Name: UIN: Instructions: Fill in your name and UIN in the space above. There should be 11 pages including this one.
CVEN 311-501 Fluid Dynamics Midterm Exam #2 November 10, 2008, 7:00-8:40 pm in CE 110 Name: UIN: Instructions: Fill in your name and UIN in the space above. There should be 11 pages including this one.
Introduction to Fluid Machines (Lectures 49 to 53)
 Introduction to Fluid Machines (Lectures 49 to 5) Q. Choose the crect answer (i) (ii) (iii) (iv) A hydraulic turbine rotates at N rpm operating under a net head H and having a discharge Q while developing
Introduction to Fluid Machines (Lectures 49 to 5) Q. Choose the crect answer (i) (ii) (iii) (iv) A hydraulic turbine rotates at N rpm operating under a net head H and having a discharge Q while developing
ENGR 4011 Resistance & Propulsion of Ships Assignment 5: A dimensional analysis of propeller thrust starting with the functional expression
 ENGR 40 Resistance & Propulsion of Ships ssignment 5: 07. -dimensional hydrofoil section is shown below. It has an incidence velocity V incidence at an angle of attack α E. For the case shown: sketch the
ENGR 40 Resistance & Propulsion of Ships ssignment 5: 07. -dimensional hydrofoil section is shown below. It has an incidence velocity V incidence at an angle of attack α E. For the case shown: sketch the
Mooring Model for Barge Tows in Lock Chamber
 Mooring Model for Barge Tows in Lock Chamber by Richard L. Stockstill BACKGROUND: Extensive research has been conducted in the area of modeling mooring systems in sea environments where the forcing function
Mooring Model for Barge Tows in Lock Chamber by Richard L. Stockstill BACKGROUND: Extensive research has been conducted in the area of modeling mooring systems in sea environments where the forcing function
Jet Aircraft Propulsion Prof. Bhaskar Roy Prof A M Pradeep Department of Aerospace Engineering Indian Institute of Technology, Bombay
 Jet Aircraft Propulsion Prof. Bhaskar Roy Prof A M Pradeep Department of Aerospace Engineering Indian Institute of Technology, Bombay Module No. #01 Lecture No. # 07 Jet Engine Cycles For Aircraft propulsion
Jet Aircraft Propulsion Prof. Bhaskar Roy Prof A M Pradeep Department of Aerospace Engineering Indian Institute of Technology, Bombay Module No. #01 Lecture No. # 07 Jet Engine Cycles For Aircraft propulsion
CENTRIFUGAL PUMP SELECTION, SIZING, AND INTERPRETATION OF PERFORMANCE CURVES
 CENTRIFUGAL PUMP SELECTION, SIZING, AND INTERPRETATION OF PERFORMANCE CURVES 4.0 PUMP CLASSES Pumps may be classified in two general types, dynamic and positive displacement. Positive displacement pumps
CENTRIFUGAL PUMP SELECTION, SIZING, AND INTERPRETATION OF PERFORMANCE CURVES 4.0 PUMP CLASSES Pumps may be classified in two general types, dynamic and positive displacement. Positive displacement pumps
FE Fluids Review March 23, 2012 Steve Burian (Civil & Environmental Engineering)
 Topic: Fluid Properties 1. If 6 m 3 of oil weighs 47 kn, calculate its specific weight, density, and specific gravity. 2. 10.0 L of an incompressible liquid exert a force of 20 N at the earth s surface.
Topic: Fluid Properties 1. If 6 m 3 of oil weighs 47 kn, calculate its specific weight, density, and specific gravity. 2. 10.0 L of an incompressible liquid exert a force of 20 N at the earth s surface.
P U M P S. The quality standard for hydraulic efficiency and suction lift. PERIPHERAL PUMPS TEP/ TSP - SERIES 50Hz
 P U M P S THE BENCHMARK FOR PERFORMANCE The quality standard for hydraulic efficiency and suction lift. PERIPHERAL PUMPS TEP/ TSP - SERIES 5Hz I N D E X TEP / TSP / TRP SERIES - PERIPHERAL PUMPS Page
P U M P S THE BENCHMARK FOR PERFORMANCE The quality standard for hydraulic efficiency and suction lift. PERIPHERAL PUMPS TEP/ TSP - SERIES 5Hz I N D E X TEP / TSP / TRP SERIES - PERIPHERAL PUMPS Page
equation 4.1 INTRODUCTION
 4 The momentum equation 4.1 INTRODUCTION It is often important to determine the force produced on a solid body by fluid flowing steadily over or through it. For example, there is the force exerted on a
4 The momentum equation 4.1 INTRODUCTION It is often important to determine the force produced on a solid body by fluid flowing steadily over or through it. For example, there is the force exerted on a
Model-Ship Correlation Method in the Mitsubishi Experimental Tank
 Model-Ship Correlation Method in the Mitsubishi Experimental Tank By Kaname Taniguchi*, Member Summary The model-ship correlation method which is developed and used in the Mitsubishi Experimental Tank
Model-Ship Correlation Method in the Mitsubishi Experimental Tank By Kaname Taniguchi*, Member Summary The model-ship correlation method which is developed and used in the Mitsubishi Experimental Tank
ENGR 4011 Resistance & Propulsion of Ships Assignment 4: 2017
 Question 1a. Values of forward speed, propeller thrust and torque measured during a propeller open water performance test are presented in the table below. The model propeller was 0.21 meters in diameter
Question 1a. Values of forward speed, propeller thrust and torque measured during a propeller open water performance test are presented in the table below. The model propeller was 0.21 meters in diameter
Numerical Analysis of Unsteady Open Water Characteristics of Surface Piercing Propeller
 Third International Symposium on Marine Propulsors smp 13, Launceston, Tasmania, Australia, May 2013 Numerical Analysis of Unsteady Open Water Characteristics of Surface Piercing Propeller Kohei Himei
Third International Symposium on Marine Propulsors smp 13, Launceston, Tasmania, Australia, May 2013 Numerical Analysis of Unsteady Open Water Characteristics of Surface Piercing Propeller Kohei Himei
4 Mechanics of Fluids (I)
 1. The x and y components of velocity for a two-dimensional flow are u = 3.0 ft/s and v = 9.0x ft/s where x is in feet. Determine the equation for the streamlines and graph representative streamlines in
1. The x and y components of velocity for a two-dimensional flow are u = 3.0 ft/s and v = 9.0x ft/s where x is in feet. Determine the equation for the streamlines and graph representative streamlines in
Dead-Downwind Faster Than The Wind (DDWFTTW) Analysis
 Dead-Downwind Faster Than The Wind (DDWFTTW) Analysis Mark Drela Jan 09 Nomenclature boat speed W wind speed F t drag force on water turbine thrust force on air prop P t shaft power of water turbine P
Dead-Downwind Faster Than The Wind (DDWFTTW) Analysis Mark Drela Jan 09 Nomenclature boat speed W wind speed F t drag force on water turbine thrust force on air prop P t shaft power of water turbine P
EXPERIMENT No.1 FLOW MEASUREMENT BY ORIFICEMETER
 EXPERIMENT No.1 FLOW MEASUREMENT BY ORIFICEMETER 1.1 AIM: To determine the co-efficient of discharge of the orifice meter 1.2 EQUIPMENTS REQUIRED: Orifice meter test rig, Stopwatch 1.3 PREPARATION 1.3.1
EXPERIMENT No.1 FLOW MEASUREMENT BY ORIFICEMETER 1.1 AIM: To determine the co-efficient of discharge of the orifice meter 1.2 EQUIPMENTS REQUIRED: Orifice meter test rig, Stopwatch 1.3 PREPARATION 1.3.1
P U M P S. The quality standard for hydraulic efficiency and suction lift. PERIPHERAL PUMPS TEP/ TSP - SERIES 50Hz
 P U M P S THE BENCHMARK FOR PERFORMANCE The quality standard for hydraulic efficiency and suction lift. PERIPHERAL PUMPS TEP/ TSP - SERIES 5Hz I N D E X TEP / TSP SERIES - PERIPHERAL PUMPS Page No. General
P U M P S THE BENCHMARK FOR PERFORMANCE The quality standard for hydraulic efficiency and suction lift. PERIPHERAL PUMPS TEP/ TSP - SERIES 5Hz I N D E X TEP / TSP SERIES - PERIPHERAL PUMPS Page No. General
ME332 FLUID MECHANICS LABORATORY (PART II)
 ME332 FLUID MECHANICS LABORATORY (PART II) Mihir Sen Department of Aerospace and Mechanical Engineering University of Notre Dame Notre Dame, IN 46556 Version: April 2, 2002 Contents Unit 5: Momentum transfer
ME332 FLUID MECHANICS LABORATORY (PART II) Mihir Sen Department of Aerospace and Mechanical Engineering University of Notre Dame Notre Dame, IN 46556 Version: April 2, 2002 Contents Unit 5: Momentum transfer
WATER DISTRIBUTION NETWORKS
 WATER DISTRIBUTION NETWORKS CE 370 1 Components of Water Supply System 2 1 Water Distribution System Water distribution systems are designed to adequately satisfy the water requirements for a combinations
WATER DISTRIBUTION NETWORKS CE 370 1 Components of Water Supply System 2 1 Water Distribution System Water distribution systems are designed to adequately satisfy the water requirements for a combinations
Jet Aircraft Propulsion Prof. Bhaskar Roy Prof. A M Pradeep Department of Aerospace Engineering Indian Institute of Technology, Bombay
 Jet Aircraft Propulsion Prof. Bhaskar Roy Prof. A M Pradeep Department of Aerospace Engineering Indian Institute of Technology, Bombay Lecture No. #03 Jet Engine Basic Performance Parameters We are talking
Jet Aircraft Propulsion Prof. Bhaskar Roy Prof. A M Pradeep Department of Aerospace Engineering Indian Institute of Technology, Bombay Lecture No. #03 Jet Engine Basic Performance Parameters We are talking
The following article was authored by Jacques Chaurette, President Fluide Design, Inc. (www.fluidedesign.com) All rights reserved.
 The following article was authored by Jacques Chaurette, President Fluide Design, Inc. (www.fluidedesign.com) All rights reserved. - HOW TO AVOID CAVITATION? CAVITATION CAN BE AVOIDED IF THE N.P.S.H. AVAILABLE
The following article was authored by Jacques Chaurette, President Fluide Design, Inc. (www.fluidedesign.com) All rights reserved. - HOW TO AVOID CAVITATION? CAVITATION CAN BE AVOIDED IF THE N.P.S.H. AVAILABLE
Useful Formulas and Calculations
 Drive Design Speed Ratio = rpm (faster) = PD = N rpm (slower) pd n Where: rpm = Revolutions per minute PD = Larger pitch diameter pd = Smaller pitch diameter N = Larger sprocket grooves n = Smaller sprocket
Drive Design Speed Ratio = rpm (faster) = PD = N rpm (slower) pd n Where: rpm = Revolutions per minute PD = Larger pitch diameter pd = Smaller pitch diameter N = Larger sprocket grooves n = Smaller sprocket
Thermodynamics I Spring 1432/1433H (2011/2012H) Saturday, Wednesday 8:00am - 10:00am & Monday 8:00am - 9:00am MEP 261 Class ZA
 Thermodynamics I Spring 1432/1433H (2011/2012H) Saturday, Wednesday 8:00am - 10:00am & Monday 8:00am - 9:00am MEP 261 Class ZA Dr. Walid A. Aissa Associate Professor, Mech. Engg. Dept. Faculty of Engineering
Thermodynamics I Spring 1432/1433H (2011/2012H) Saturday, Wednesday 8:00am - 10:00am & Monday 8:00am - 9:00am MEP 261 Class ZA Dr. Walid A. Aissa Associate Professor, Mech. Engg. Dept. Faculty of Engineering
vector H. If O is the point about which moments are desired, the angular moment about O is given:
 The angular momentum A control volume analysis can be applied to the angular momentum, by letting B equal to angularmomentum vector H. If O is the point about which moments are desired, the angular moment
The angular momentum A control volume analysis can be applied to the angular momentum, by letting B equal to angularmomentum vector H. If O is the point about which moments are desired, the angular moment
TECHNICAL INFORMATION Bulletin
 Peerless Pump Company 2005 Dr. M.L. King Jr. Street, P.O. Box 7026, Indianapolis, IN 46207-7026, USA Telephone: (317) 925-9661 Fax: (317) 924-7338 www.peerlesspump.com www.epumpdoctor.com TECHNICAL INFORMATION
Peerless Pump Company 2005 Dr. M.L. King Jr. Street, P.O. Box 7026, Indianapolis, IN 46207-7026, USA Telephone: (317) 925-9661 Fax: (317) 924-7338 www.peerlesspump.com www.epumpdoctor.com TECHNICAL INFORMATION
HYDRAULIC TURBINES. Hydraulics and Hydraulic Machines
 HYDRAULIC TURBINES Introduction: The device which converts h ydraulic energy into mechanical energy or vice versa is known as Hydraulic Machines. The h ydraulic machines which convert h ydraulic energy
HYDRAULIC TURBINES Introduction: The device which converts h ydraulic energy into mechanical energy or vice versa is known as Hydraulic Machines. The h ydraulic machines which convert h ydraulic energy
Contents. 2 Basic Components Aerofoils Force Generation Performance Parameters xvii
 Contents 1 Working Principles... 1 1.1 Definition of a Turbomachine... 1 1.2 Examples of Axial Turbomachines... 2 1.2.1 Axial Hydraulic Turbine... 2 1.2.2 Axial Pump... 4 1.3 Mean Line Analysis... 5 1.4
Contents 1 Working Principles... 1 1.1 Definition of a Turbomachine... 1 1.2 Examples of Axial Turbomachines... 2 1.2.1 Axial Hydraulic Turbine... 2 1.2.2 Axial Pump... 4 1.3 Mean Line Analysis... 5 1.4
Angular momentum equation
 Angular momentum equation For angular momentum equation, B =H O the angular momentum vector about point O which moments are desired. Where β is The Reynolds transport equation can be written as follows:
Angular momentum equation For angular momentum equation, B =H O the angular momentum vector about point O which moments are desired. Where β is The Reynolds transport equation can be written as follows:
WWW. = -o , o.. 5 S MICROCOPY RESOLUTION TEST CHART NATIONAL BUREAU OF STANDARDS-1963-A , I-
 110 ~ A14R (U XTNIN OF THELO NALESH RSEAKPIN RN FACT OONCET i 775 U DAVENIDNO HE LRNL SHEI RESEA FRC A NDE PTIEnT UI S CENTER BETHESDA 111)D R WALDEN OCT 83 DTNSRDC-83/85 UNCLSSSIED/ 13/10NL IEEE - WWW?
110 ~ A14R (U XTNIN OF THELO NALESH RSEAKPIN RN FACT OONCET i 775 U DAVENIDNO HE LRNL SHEI RESEA FRC A NDE PTIEnT UI S CENTER BETHESDA 111)D R WALDEN OCT 83 DTNSRDC-83/85 UNCLSSSIED/ 13/10NL IEEE - WWW?
DESIGN AND CONSTRUCTION OF A WATER TUNNEL. Stephen C. Ko
 i DESGN AND CONSTRUCTON OF A WATER TUNNEL By Stephen C. Ko This work has been carried out as a part of a grant from the National Science Foundation for the development of fluid mechanics laboratory equipments
i DESGN AND CONSTRUCTON OF A WATER TUNNEL By Stephen C. Ko This work has been carried out as a part of a grant from the National Science Foundation for the development of fluid mechanics laboratory equipments
Chapter 7 The Energy Equation
 Chapter 7 The Energy Equation 7.1 Energy, Work, and Power When matter has energy, the matter can be used to do work. A fluid can have several forms of energy. For example a fluid jet has kinetic energy,
Chapter 7 The Energy Equation 7.1 Energy, Work, and Power When matter has energy, the matter can be used to do work. A fluid can have several forms of energy. For example a fluid jet has kinetic energy,
I INCH- POUND j MIL-STD-1399(NAVY SECTION 302A 29 February 1988 SUPERSEDING DOD-STD-1399(NAVY) SECTION March 1972 (See 6.3) MILITARY STANDARD
 I INCH- POUND j MIL-STD-1399(NAVY SUPERSEDING DOD-STD-1399(NAVY) SECTION 302 20 March 1972 (See 6.3) MILITARY STANDARD INTERFACE STANDARD FOR SHIPBOARD SYSTEMS SECTION 302 WEATHER ENVIRONMENT AMSC N/A
I INCH- POUND j MIL-STD-1399(NAVY SUPERSEDING DOD-STD-1399(NAVY) SECTION 302 20 March 1972 (See 6.3) MILITARY STANDARD INTERFACE STANDARD FOR SHIPBOARD SYSTEMS SECTION 302 WEATHER ENVIRONMENT AMSC N/A
CALIFORNIA POLYTECHNIC STATE UNIVERSITY Mechanical Engineering Department ME 347, Fluid Mechanics II, Winter 2018
 CALIFORNIA POLYTECHNIC STATE UNIVERSITY Mechanical Engineering Department ME 347, Fluid Mechanics II, Winter 2018 Date Day Subject Read HW Sept. 21 F Introduction 1, 2 24 M Finite control volume analysis
CALIFORNIA POLYTECHNIC STATE UNIVERSITY Mechanical Engineering Department ME 347, Fluid Mechanics II, Winter 2018 Date Day Subject Read HW Sept. 21 F Introduction 1, 2 24 M Finite control volume analysis
Transactions on the Built Environment vol 24, 1997 WIT Press, ISSN
 Comparison of model test with ship sea trial results for a given vessel series C.Behrendt & T.Kucharski Institute of Marine Plant Operation, Maritime University of Szczecin, 70-500 Szczecin, Poland Abstract
Comparison of model test with ship sea trial results for a given vessel series C.Behrendt & T.Kucharski Institute of Marine Plant Operation, Maritime University of Szczecin, 70-500 Szczecin, Poland Abstract
Applied Fluid Mechanics
 Applied Fluid Mechanics 1. The Nature of Fluid and the Study of Fluid Mechanics 2. Viscosity of Fluid 3. Pressure Measurement 4. Forces Due to Static Fluid 5. Buoyancy and Stability 6. Flow of Fluid and
Applied Fluid Mechanics 1. The Nature of Fluid and the Study of Fluid Mechanics 2. Viscosity of Fluid 3. Pressure Measurement 4. Forces Due to Static Fluid 5. Buoyancy and Stability 6. Flow of Fluid and
V. MODELING, SIMILARITY, AND DIMENSIONAL ANALYSIS To this point, we have concentrated on analytical methods of solution for fluids problems.
 V. MODELING, SIMILARITY, AND DIMENSIONAL ANALYSIS To this point, we have concentrated on analytical methods of solution for fluids problems. However, analytical methods are not always satisfactory due
V. MODELING, SIMILARITY, AND DIMENSIONAL ANALYSIS To this point, we have concentrated on analytical methods of solution for fluids problems. However, analytical methods are not always satisfactory due
PROPERTIES OF FLUIDS
 Unit - I Chapter - PROPERTIES OF FLUIDS Solutions of Examples for Practice Example.9 : Given data : u = y y, = 8 Poise = 0.8 Pa-s To find : Shear stress. Step - : Calculate the shear stress at various
Unit - I Chapter - PROPERTIES OF FLUIDS Solutions of Examples for Practice Example.9 : Given data : u = y y, = 8 Poise = 0.8 Pa-s To find : Shear stress. Step - : Calculate the shear stress at various
Chapter three. Two-dimensional Cascades. Laith Batarseh
 Chapter three Two-dimensional Cascades Laith Batarseh Turbo cascades The linear cascade of blades comprises a number of identical blades, equally spaced and parallel to one another cascade tunnel low-speed,
Chapter three Two-dimensional Cascades Laith Batarseh Turbo cascades The linear cascade of blades comprises a number of identical blades, equally spaced and parallel to one another cascade tunnel low-speed,
VIBRATION ANALYSIS IN SHIP STRUCTURES BY FINITE ELEMENT METHOD
 Proceedings of COBEM 2007 Copyright 2007 by ABCM 19th International Congress of Mechanical Engineering November 5-9, 2007, Brasília, DF VIBRATION ANALYSIS IN SHIP STRUCTURES BY FINITE ELEMENT METHOD Luiz
Proceedings of COBEM 2007 Copyright 2007 by ABCM 19th International Congress of Mechanical Engineering November 5-9, 2007, Brasília, DF VIBRATION ANALYSIS IN SHIP STRUCTURES BY FINITE ELEMENT METHOD Luiz
CHAPTER 5 MASS AND ENERGY ANALYSIS OF CONTROL VOLUMES
 Thermodynamics: An Engineering Approach 8th Edition in SI Units Yunus A. Çengel, Michael A. Boles McGraw-Hill, 2015 CHAPTER 5 MASS AND ENERGY ANALYSIS OF CONTROL VOLUMES Lecture slides by Dr. Fawzi Elfghi
Thermodynamics: An Engineering Approach 8th Edition in SI Units Yunus A. Çengel, Michael A. Boles McGraw-Hill, 2015 CHAPTER 5 MASS AND ENERGY ANALYSIS OF CONTROL VOLUMES Lecture slides by Dr. Fawzi Elfghi
Pipe Flow. Lecture 17
 Pipe Flow Lecture 7 Pipe Flow and the Energy Equation For pipe flow, the Bernoulli equation alone is not sufficient. Friction loss along the pipe, and momentum loss through diameter changes and corners
Pipe Flow Lecture 7 Pipe Flow and the Energy Equation For pipe flow, the Bernoulli equation alone is not sufficient. Friction loss along the pipe, and momentum loss through diameter changes and corners
Unified Propulsion Quiz May 7, 2004
 Unified Propulsion Quiz May 7, 2004 Closed Book no notes other than the equation sheet provided with the exam Calculators allowed. Put your name on each page of the exam. Read all questions carefully.
Unified Propulsion Quiz May 7, 2004 Closed Book no notes other than the equation sheet provided with the exam Calculators allowed. Put your name on each page of the exam. Read all questions carefully.
June 9, Phosphate Conference Clearwater Convention June Abstract:
 PUMP CONSULTING & TRAINING LLC Joseph R. Askew 1811 Stonecrest Ct. Lakeland, Fl. 33813 863-644-3118-Office Phone 863-899-9896-Cell Phone E-mail: pmpcnslt@tampabay.rr.com Objectivity in pump selection,
PUMP CONSULTING & TRAINING LLC Joseph R. Askew 1811 Stonecrest Ct. Lakeland, Fl. 33813 863-644-3118-Office Phone 863-899-9896-Cell Phone E-mail: pmpcnslt@tampabay.rr.com Objectivity in pump selection,
5 ENERGY EQUATION OF FLUID MOTION
 5 ENERGY EQUATION OF FLUID MOTION 5.1 Introduction In order to develop the equations that describe a flow, it is assumed that fluids are subject to certain fundamental laws of physics. The pertinent laws
5 ENERGY EQUATION OF FLUID MOTION 5.1 Introduction In order to develop the equations that describe a flow, it is assumed that fluids are subject to certain fundamental laws of physics. The pertinent laws
ITTC Recommended Procedures
 7.5-0 -03-0. Page of 6 CONTENTS PURPOSE OF PROCEDURE EXAMPLE FOR OPEN WATER TEST. Test Design. Measurement System and Procedure.3 Uncertainty Analysis.3. ias Limit.3.. Propeller Geometry.3.. Speed of advance
7.5-0 -03-0. Page of 6 CONTENTS PURPOSE OF PROCEDURE EXAMPLE FOR OPEN WATER TEST. Test Design. Measurement System and Procedure.3 Uncertainty Analysis.3. ias Limit.3.. Propeller Geometry.3.. Speed of advance
CHAPTER TWO CENTRIFUGAL PUMPS 2.1 Energy Transfer In Turbo Machines
 7 CHAPTER TWO CENTRIFUGAL PUMPS 21 Energy Transfer In Turbo Machines Fig21 Now consider a turbomachine (pump or turbine) the total head (H) supplied by it is The power delivered to/by the fluid simply
7 CHAPTER TWO CENTRIFUGAL PUMPS 21 Energy Transfer In Turbo Machines Fig21 Now consider a turbomachine (pump or turbine) the total head (H) supplied by it is The power delivered to/by the fluid simply
Homework 6. Solution 1. r ( V jet sin( θ) + ω r) ( ρ Q r) Vjet
 Problem 1 Water enters the rotating sprinkler along the axis of rotation and leaves through three nozzles. How large is the resisting torque required to hold the rotor stationary for the angle that produces
Problem 1 Water enters the rotating sprinkler along the axis of rotation and leaves through three nozzles. How large is the resisting torque required to hold the rotor stationary for the angle that produces
Contents. Preface... xvii
 Contents Preface... xvii CHAPTER 1 Idealized Flow Machines...1 1.1 Conservation Equations... 1 1.1.1 Conservation of mass... 2 1.1.2 Conservation of momentum... 3 1.1.3 Conservation of energy... 3 1.2
Contents Preface... xvii CHAPTER 1 Idealized Flow Machines...1 1.1 Conservation Equations... 1 1.1.1 Conservation of mass... 2 1.1.2 Conservation of momentum... 3 1.1.3 Conservation of energy... 3 1.2
Reliability assessment of ship powering performance extrapolations using Monte Carlo methods
 Third International Symposium on Marine Propulsors smp 13, Launceston, Tasmania, Australia, May 2013 Reliability assessment of ship powering performance extrapolations using Monte Carlo methods Iwan M.
Third International Symposium on Marine Propulsors smp 13, Launceston, Tasmania, Australia, May 2013 Reliability assessment of ship powering performance extrapolations using Monte Carlo methods Iwan M.
Contents. 1 Introduction to Gas-Turbine Engines Overview of Turbomachinery Nomenclature...9
 Preface page xv 1 Introduction to Gas-Turbine Engines...1 Definition 1 Advantages of Gas-Turbine Engines 1 Applications of Gas-Turbine Engines 3 The Gas Generator 3 Air Intake and Inlet Flow Passage 3
Preface page xv 1 Introduction to Gas-Turbine Engines...1 Definition 1 Advantages of Gas-Turbine Engines 1 Applications of Gas-Turbine Engines 3 The Gas Generator 3 Air Intake and Inlet Flow Passage 3
Chapter 4 DYNAMICS OF FLUID FLOW
 Faculty Of Engineering at Shobra nd Year Civil - 016 Chapter 4 DYNAMICS OF FLUID FLOW 4-1 Types of Energy 4- Euler s Equation 4-3 Bernoulli s Equation 4-4 Total Energy Line (TEL) and Hydraulic Grade Line
Faculty Of Engineering at Shobra nd Year Civil - 016 Chapter 4 DYNAMICS OF FLUID FLOW 4-1 Types of Energy 4- Euler s Equation 4-3 Bernoulli s Equation 4-4 Total Energy Line (TEL) and Hydraulic Grade Line
International Journal of Research in Advent Technology Available Online at:
 A COMPUTER PROGRAMMED DESIGN OPTIMISATION AND ANALYSIS OF COMPRESSOR IMPELLER G. Naga Malleshwar Rao 1, Dr. S.L.V. Prasad 2, Dr. S. Sudhakarbabu 3 1, 2 Professor of Mechanical Engineering, Shri Shirdi
A COMPUTER PROGRAMMED DESIGN OPTIMISATION AND ANALYSIS OF COMPRESSOR IMPELLER G. Naga Malleshwar Rao 1, Dr. S.L.V. Prasad 2, Dr. S. Sudhakarbabu 3 1, 2 Professor of Mechanical Engineering, Shri Shirdi
ME 309 Fluid Mechanics Fall 2010 Exam 2 1A. 1B.
 Fall 010 Exam 1A. 1B. Fall 010 Exam 1C. Water is flowing through a 180º bend. The inner and outer radii of the bend are 0.75 and 1.5 m, respectively. The velocity profile is approximated as C/r where C
Fall 010 Exam 1A. 1B. Fall 010 Exam 1C. Water is flowing through a 180º bend. The inner and outer radii of the bend are 0.75 and 1.5 m, respectively. The velocity profile is approximated as C/r where C
Hydraulics. B.E. (Civil), Year/Part: II/II. Tutorial solutions: Pipe flow. Tutorial 1
 Hydraulics B.E. (Civil), Year/Part: II/II Tutorial solutions: Pipe flow Tutorial 1 -by Dr. K.N. Dulal Laminar flow 1. A pipe 200mm in diameter and 20km long conveys oil of density 900 kg/m 3 and viscosity
Hydraulics B.E. (Civil), Year/Part: II/II Tutorial solutions: Pipe flow Tutorial 1 -by Dr. K.N. Dulal Laminar flow 1. A pipe 200mm in diameter and 20km long conveys oil of density 900 kg/m 3 and viscosity
Fluid Flow Analysis Penn State Chemical Engineering
 Fluid Flow Analysis Penn State Chemical Engineering Revised Spring 2015 Table of Contents LEARNING OBJECTIVES... 1 EXPERIMENTAL OBJECTIVES AND OVERVIEW... 1 PRE-LAB STUDY... 2 EXPERIMENTS IN THE LAB...
Fluid Flow Analysis Penn State Chemical Engineering Revised Spring 2015 Table of Contents LEARNING OBJECTIVES... 1 EXPERIMENTAL OBJECTIVES AND OVERVIEW... 1 PRE-LAB STUDY... 2 EXPERIMENTS IN THE LAB...
Physics 3 Summer 1990 Lab 7 - Hydrodynamics
 Physics 3 Summer 1990 Lab 7 - Hydrodynamics Theory Consider an ideal liquid, one which is incompressible and which has no internal friction, flowing through pipe of varying cross section as shown in figure
Physics 3 Summer 1990 Lab 7 - Hydrodynamics Theory Consider an ideal liquid, one which is incompressible and which has no internal friction, flowing through pipe of varying cross section as shown in figure
nozzle which is fitted to a pipe through which the liquid is flowing under pressure.
 Impact of Jets 1. The liquid comes out in the form of a jet from the outlet of a nozzle which is fitted to a pipe through which the liquid is flowing under pressure. The following cases of the impact of
Impact of Jets 1. The liquid comes out in the form of a jet from the outlet of a nozzle which is fitted to a pipe through which the liquid is flowing under pressure. The following cases of the impact of
THE INFLUENCE OF SWIRL BRAKES ON THE ROTORDYNAMIC FORCES GENERATED BY DISCHARGE-TO-SUCTION LEAKAGE FLOWS 1N CENTRIFUGAL PUMPS
 FED-Vol. 154, Pumping Machinery ASME 1993 THE INFLUENCE OF SWIRL BRAKES ON THE ROTORDYNAMIC FORCES GENERATED BY DISCHARGE-TO-SUCTION LEAKAGE FLOWS 1N CENTRIFUGAL PUMPS Joseph M. Sivo, Allan J. Acosta,
FED-Vol. 154, Pumping Machinery ASME 1993 THE INFLUENCE OF SWIRL BRAKES ON THE ROTORDYNAMIC FORCES GENERATED BY DISCHARGE-TO-SUCTION LEAKAGE FLOWS 1N CENTRIFUGAL PUMPS Joseph M. Sivo, Allan J. Acosta,
BACHELOR OF TECHNOLOGY IN MECHANICAL ENGINEERING (COMPUTER INTEGRATED MANUFACTURING)
 No. of Printed Pages : 6 BME-028 BACHELOR OF TECHNOLOGY IN MECHANICAL ENGINEERING (COMPUTER INTEGRATED MANUFACTURING) Term-End Examination December, 2011 00792 BME-028 : FLUID MECHANICS Time : 3 hours
No. of Printed Pages : 6 BME-028 BACHELOR OF TECHNOLOGY IN MECHANICAL ENGINEERING (COMPUTER INTEGRATED MANUFACTURING) Term-End Examination December, 2011 00792 BME-028 : FLUID MECHANICS Time : 3 hours
COMPUTER AIDED DESIGN OF RADIAL TIPPED CENTRIFUGAL BLOWERS AND FANS
 4 th International Conference on Mechanical Engineering, December 26-28, 21, Dhaka, Bangladesh/pp. IV 55-6 COMPUTER AIDED DESIGN OF RADIAL TIPPED CENTRIFUGAL BLOWERS AND FANS Nitin N. Vibhakar* and S.
4 th International Conference on Mechanical Engineering, December 26-28, 21, Dhaka, Bangladesh/pp. IV 55-6 COMPUTER AIDED DESIGN OF RADIAL TIPPED CENTRIFUGAL BLOWERS AND FANS Nitin N. Vibhakar* and S.
Introduction to Fluid Machines and Compressible Flow Prof. S. K. Som Department of Mechanical Engineering Indian Institute of Technology, Kharagpur
 Introduction to Fluid Machines and Compressible Flow Prof. S. K. Som Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture - 1 Introduction to Fluid Machines Well, good
Introduction to Fluid Machines and Compressible Flow Prof. S. K. Som Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture - 1 Introduction to Fluid Machines Well, good
Chimney Sizing. Project Name: Location: Type Appliance: Hot Water Heater Incinerator. LP Gas #2 Oil #6 Oil Wood/Coal Waste (Type ) Appliance Input:
 Chimney Sizing Project Name: Location: Type Appliance: Type Fuel: Appliance Input: Boiler Hot Water Heater Incinerator Natural Gas LP Gas #2 Oil #6 Oil Wood/Coal Waste (Type ) BTU Hp Lbs/hr Height Above
Chimney Sizing Project Name: Location: Type Appliance: Type Fuel: Appliance Input: Boiler Hot Water Heater Incinerator Natural Gas LP Gas #2 Oil #6 Oil Wood/Coal Waste (Type ) BTU Hp Lbs/hr Height Above
Part A: 1 pts each, 10 pts total, no partial credit.
 Part A: 1 pts each, 10 pts total, no partial credit. 1) (Correct: 1 pt/ Wrong: -3 pts). The sum of static, dynamic, and hydrostatic pressures is constant when flow is steady, irrotational, incompressible,
Part A: 1 pts each, 10 pts total, no partial credit. 1) (Correct: 1 pt/ Wrong: -3 pts). The sum of static, dynamic, and hydrostatic pressures is constant when flow is steady, irrotational, incompressible,
Fachgesprach 12. HVAC Pumps. For Project Managers
 Fachgesprach 12 HVAC Pumps For Project Managers WTF Philosophy: If you don t remember a certain formula, it's OK - you can always GoogleTheS h i t. But bad engineering CONCEPTS can hurt you. WTF Institute
Fachgesprach 12 HVAC Pumps For Project Managers WTF Philosophy: If you don t remember a certain formula, it's OK - you can always GoogleTheS h i t. But bad engineering CONCEPTS can hurt you. WTF Institute
Recap: Static Fluids
 Recap: Static Fluids Archimedes principal states that the buoyant force acting on an object is equal to the weight of fluid displaced. If the average density of object is greater than density of fluid
Recap: Static Fluids Archimedes principal states that the buoyant force acting on an object is equal to the weight of fluid displaced. If the average density of object is greater than density of fluid
S.E. (Mech.) (First Sem.) EXAMINATION, (Common to Mech/Sandwich) FLUID MECHANICS (2008 PATTERN) Time : Three Hours Maximum Marks : 100
 Total No. of Questions 12] [Total No. of Printed Pages 8 Seat No. [4262]-113 S.E. (Mech.) (First Sem.) EXAMINATION, 2012 (Common to Mech/Sandwich) FLUID MECHANICS (2008 PATTERN) Time : Three Hours Maximum
Total No. of Questions 12] [Total No. of Printed Pages 8 Seat No. [4262]-113 S.E. (Mech.) (First Sem.) EXAMINATION, 2012 (Common to Mech/Sandwich) FLUID MECHANICS (2008 PATTERN) Time : Three Hours Maximum
CLASS Fourth Units (Second part)
 CLASS Fourth Units (Second part) Energy analysis of closed systems Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. MOVING BOUNDARY WORK Moving boundary work (P
CLASS Fourth Units (Second part) Energy analysis of closed systems Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. MOVING BOUNDARY WORK Moving boundary work (P
PERFORMANCE OF A CENTRAL-TYPE JET PUMP II- EXPERIMENTAL STUDY ON WATER FLOW
 Eighth International Water Technology Conference, IWTC8 24, Alexandria, Egypt PERFORMANCE OF A CENTRAL-TYPE JET PUMP II- EXPERIMENTAL STUDY ON WATER FLOW ABSTRACT EL-Otla, F. M. *, EL-Sawaf, I. A. * and
Eighth International Water Technology Conference, IWTC8 24, Alexandria, Egypt PERFORMANCE OF A CENTRAL-TYPE JET PUMP II- EXPERIMENTAL STUDY ON WATER FLOW ABSTRACT EL-Otla, F. M. *, EL-Sawaf, I. A. * and
