Least-action Principle Applied to the Kepler Problem
|
|
|
- Godwin Butler
- 5 years ago
- Views:
Transcription
1 Least-action Principle Applied to the Kepler Problem S. Olszewski Institute of Physical Chemistry of the Polish Academy of Sciences, Kasprzaka 44/5, -4 Warsaw, Poland Reprint requests to Prof. S. O.; Z. Naturforsch. 59a, (4); received March, 4 The least-action principle is examined for the two-body Kepler problem. This examination allows one to couple the eccentricity parameter of the Kepler orbit with the size of the major semiaxis of that orbit. The obtained formula is applied to an estimate of eccentricities characteristic for a set of the planetary and satellitary tracks. Key words: Eccentricity of the Kepler Orbits; Least-action Principle.. Introduction: Dependence of the Eccentricity e on the Major Semiaxis a of the Kepler Orbit The Kepler problem is one of the best known in classical mechanics. Being based partly on observations, it accounts of the motion of a planet, or satellite, along an elliptical trajectory extended about a gravitational center. The period T of the motion and the major semiaxis a are coupled by the well-known Kepler law GM S T 4π a 3, () where G is the gravitational constant, M S is the mass of the Sun in the planet case, or the mass of the planet in the satellite case. In () it is assumed for the sake of simplicity that the mass M S remains at rest. Simultaneously, the eccentricity e defining the elliptical trajectory of a planet, or satellite, is considered as independent of a or T [ 6]. In spite of the fundamental importance of the Kepler problem its mechanics seems to be discussed insufficiently. Here we have in mind the least-action principle applied to a conservative system. The principle makes reference to the variational foundations of mechanics and is based on the idea of the action function. In practice, the action variables J,J,..., considered for the Kepler problem, are parameters conjugated to the corresponding angle variables of the moving body [7, 8]. Both kinds of the action and angle variables serve to transform the Hamiltonian into a function dependent solely on J,J,.... This technique is useful because it enables one to calculate the frequencies of the periodic motion without finding a complete solution of the motion of the system. In the next step, the same action variables J,J,... occur useful in the quantization process which takes an easy form according to the well-known Bohr-Sommerfeld rules [9, ]. But beyond of J,J,... an elementary action function S can be defined, equal to double the kinetic energy of a body integrated over a time interval passed by that body along its trajectory. The least-action principle states that for a conservative system this action function should be at minimum [8, ]. In the next step, the derivative of S calculated with respect to the energy E p of the body at some time t provides us with the time interval of the motion of the body, beginning from some time t : S E p t t. () The aim of the present paper is to point out that () can be satisfied only on the condition that the eccentricity e of the planetary, or satellitary, track depends on the major semiaxis a of the Kepler orbit. The Cartesian coordinates of a body on the Kepler orbit are x a (cosu e), (3) y a ( e ) / sinu, (3a) where the coordinate u depends on the time t by the equation [8] π t ωt u esinu. T (3b) / 4 / $ 6. c 4 Verlag der Zeitschrift für Naturforschung, Tübingen
2 376 S. Olszewski Least-action Principle Applied to the Kepler Problem Here we assumed that the beginning of the motion is at the perihelion of the Kepler orbit [8]. Obviously, t at u ; the frequency of the motion about the gravitation center has been put equal to ω. For a moment let us assume that e is constant in a way similar to a. Because of (3), (3a) and (3b) we have ẋ + ẏ a [ sin u +( e )cos u ] du dt a ( e cos u)ω (4) ( e cosu) a + ecosu ω ecosu. The integral of the expression (4), extended over an interval of t beginning with t t and ending at some t t,gives t (ẋ + ẏ )dt a ω a ω since u(t )u() and t u + ecosu ecosu dt ( + ecosu)du a ω(u + esinu) u u u, (5) du dt ω ecosu ; (6) see (3b). The integral giving the elementary action S, equal to the integral of the double kinetic energy extended along the time interval (,t ), is t S m p (ẋ + ẏ )dt m p a ω(u + esinu) u u u, (7) where m p is the mass of a planet or satellite. The fundamental equation (), valid for any planet or satellite trajectory, becomes therefore t S E p S a E p a ( a ω + a ω a GM S a ) (u + esinu ) a3 ω(u + esinu ) GM S ω (u + esinu ). In the calculation of (8) we took into account (8) E p GM Sm p, (9) a which is the energy of the planet or satellite, as well as the relations () and (3b). Since from the third Kepler law given in () we have T 3 T, () a a the derivative of the expression a ω entering (7) calculated with respect to a gives (a ω) a ω + a ω a a ( a ω + πa ) 3 T T a ω. a () Our task is now to compare the result of (8) with t t (u ) calculated from (3b) for an arbitrary fraction of the period T of rotation of the celestial body about the gravitational center. This is done for different values of t λ T, () where λ is a constant: < λ. The mentioned comparison is presented in Table, where for the sake of convenience the variable u u has been taken as a parameter. It is evident that solely at λ and λ there exists an agreement between t t (u ) taken from (3b) and t calculated from (8); the case λ has been omitted as being a trivial one. A discrepancy obtained between t in (3b) and t given by Eq. (8), illustrated by the second and the third
3 S. Olszewski Least-action Principle Applied to the Kepler Problem 377 Table. A comparison of the time interval λt of the motion of a celestial body performed along the Kepler orbit with the time interval calculated from the elementary action function; see (3b), (8) and (). The orbit eccentricity e is assumed equal to a constant number. T is the circulation period of the body about the gravitational center. The beginning point of the motion is assumed in the perihelion when the position of the center of force is assumed in the Sun. u λ obtained from t λ obtained from t see (3b) for a reference calculated calculated in (8) between t and u according to (3b) 4 π 8 π π π e 4 + π e π π π π e 3 4 π e 7 4 π π column of Table, implies that e entering S should depend on a : e e(a ). (3). Equation for e(a ) This dependence can be examined when the Fourier expansion for u is applied [6,, 3]: u ωt + n n J n(ne)sin(nωt). (4) Here J n is the nth-order Bessel function of the first kind. Because e is a small number, the expansion (4) as well as the power expansions for J n can be limited to either one or two first terms. By substituting the expansion (4) for u u into the derivative of S,we obtain S m p a a ω[ωt +e +esin(ωt +e )] (5) [ e +a ω + e sin(ωt +e )+ecos(ωt +e ) e ], a a a where e esin(ωt ). (5a) In the next step, because of the relation Ep m p GM S π a t t a a t T a ω t, (6) the expression (5), substituted into the first part of (8), gives a ωe + a ωy + a ω e + a a ω y a a ω(e + y)+a ω (7) (e + y), a or e + y a (e + y), (7a) a where y esin(ωt + e ). (8) The solution of (7a) is [ ] ln a / (e + y) const (9) or a / [ e + esin(ωt + e ) ] const. (9a) It is evident from (9a) that e depends both on a and t. For example an explicit differentiation of (9a) with respect to a gives successively the equations + a / e () a ea / for ωt π and ωt 3 π, ( ) ea / + e +a / e + e (a) a for ωt π 4 and ωt 7 4π, and ea / e ( ) +a / e e (b) a for ωt 3 4 π and ωt 5 4 π. If the terms e and e entering the brackets in (a) and (b) are omitted, these equations are reduced to the same differential equation for e(a ), which is given in (). For ωt π and
4 378 S. Olszewski Least-action Principle Applied to the Kepler Problem ωt π Eq. () is fulfilled identically. A solution of () is a / e const () which is a result proportional to an average of (9a) calculated over T. Evidently, the average of (9a) calculated over the whole time period T is equal to zero. Equation () implies that the eccentricities e and e of two non-interacting bodies and circulating about a common gravitational center are referred to the major semiaxes a and a of the bodies trajectories by the equation e a/. (a) e a / The results of () and (a) are used in Section Least-action Principle for the Kepler Problem, Examined in the Framework of the Euler-Jacobi Formulation Equation () can be obtained also from a direct application of the so-called Euler-Jacobi formulation of the least-action principle [4 6]. This formulation had as its main idea, to transform the time t into some new variable τ τ(t) () [ E p + GM S m p ] / [ ma ( e cos u) ] / ( ecosu)a [ E p m p a ( e cos u)+ GM Sm p a ( e cos u) ( ecosu)a and perform the variational calculation with the aid of τ instead of t. For the case of the Kepler problem a natural substitution for τ is u u(t), (a) where u is the eccentric anomaly introduced in Sect. and coupled with t by the formula (3b). In effect, for the problem of a planar motion we obtain the requirement [5, 6] Ep δ V m p [( dx du where E p is the total energy (9) and ) ( dy ) ] + du, (3) du V GM Sm p (x + y ) / (9a) is the potential energy of the moving body. Because of (3) and (3a) we have x + y a ( ecosu), (4) and in view of (3) and (3a) dx dy + a du du [sin u +( e )cos u] (4a) a ( e cos u), so the expression submitted to variation in (3) becomes: ] / [ E p m p a + GM Sm pa + GM S m pa ecosu E p m p a e cos u ] / / GM Sm p a ( + ecosu + e cos u ) / / GM pm p a ( + ecosu). (5) In the last but one transformation in (5) we took into account the formula (9). Due to (5), the variational problem of (3) becomes / δ GM Sm p a (+ecosu)du (6) / [ δ GM Sm pa du + e ] cos udu. A full gyration of a body about a gravitational center provides us with the interval u π. (7)
5 S. Olszewski Least-action Principle Applied to the Kepler Problem 379 In this case the e-dependent component of the integral entering (6) vanishes. Consequently, by allowing for variation of a, we obtain from (6) and (7) that / δ π or GM Sm p a ( GM Sm p δa. ) / πa / δa (8) (8a) In view of (8a) the term equal to the first component of (6) can be considered as a constant. We assume that solely the second component of the expression (6) may provide us with a coupling between e and a.by neglecting the constant factor of ( GM S m / p) we obtain from the second integral in (6) between the limits u and u : δ(a / e)(sinu sinu ). (9) This gives us a dependence between e and a because the sin-difference in (9) can be considered as a multiplier which does not influence the variational process. In effect, from (9) we have a / δa e + a / δe, (9a) which when divided by δa gives the equation equivalent to (). The same result can be obtained by applying the variational procedure to the original expression of the kinetic energy [8,, 3]: δ [ (dx ) m p + dt ] dy dt, (3) dt called the Euler-Maupertuis formulation of the leastaction principle. 4. Calculation of Eccentricities for the Planet and Satellite Trajectories. Discussion Equation () or (a) can be readily applied to the calculation of e of the Kepler tracks. From the nine planets arranged according to their increasing distance from the Sun, the planet Jupiter is a central one; this is also the heaviest planet of the system [7]. Putting a Jupiter x Jupiter (3) Table. Theoretical eccentricities e theor of the planet trajectories calculated on the basis of (a) compared with the observed eccentricities e obs ; see [7]. The observed eccentricity of the Jupiter trajectory has been taken as the basic parameter in order to define e theor of the orbits of the remaining planets. The major semiaxis a x of the planet trajectories are also listed with the x value of Jupiter put equal to. Planet x e theor e obs Error of e theor see [7] see (3) Mercury Venus Earth Mars Jupiter..48 Saturn Uranus Neptune Pluto Table 3. Orbits of the satellites of Jupiter and their eccentricities. The observed eccentricity (e obs ) of Elara has been taken as a known parameter in the calculation of e theor of the remaining satellite orbits; (a). The major semiaxis x a of the orbit of Elara is taken as a unit distance. Satellite x e theor e obs Error of e theor see [7] see (3) Callisto Leda Himalia Lysithea Elara..7 Ananke Carme Pasiphae Sinope and taking into account that e Jupiter.48, (3a) the eccentricities e theor of the remainder eight planets of the solar system can be calculated. The results for e theor, together with the observed data e obs for e and the planet distances a x, are listed in Table. The error given in Table, and subsequent Tables, is defined by the relation error e >, (3) e < where e > is the larger and e < is the smaller quantity of the pair of e obs and e theor obtained for a given planet (or satellite); see Tables 5. The error (3) is below unity for Mars, Saturn and Uranus, which have their orbits closest to that of Jupiter. More distant planet orbits, which are Earth and
6 38 S. Olszewski Least-action Principle Applied to the Kepler Problem Table 4. Orbits of the satellites of Uranus and their eccentricities. The observed eccentricity (e obs ) of Umbriel has been taken as a known parameter in the calculation of e theor of the remaining satellite orbits of Uranus; (a). The major semiaxis x a of the orbit of Umbriel is taken as a unit distance. Satellite x e theor e obs Error of e theor see [7] see (3) Miranda Ariel Umbriel..35 Titania Oberon Table 5. Theoretical eccentricities e theor of the orbits taken as a basis in the calculations presented in Table, 3, and 4 (Jupiter, Elara and Umbriel). The e theor e i are calculated from (33) with the aid of the observed data (e i,e i+ for the eccentricities and a,i,a,i+ for the major semiaxes) of the orbits neighboring to i and the major semiaxis a,i of the orbit i. Considered Bodies on the e theor e obs Error of e theor celestial neighboring see [7] calculated body orbits from (3) (i) (i,i + ) Jupiter Mars, Saturn Elara Lysithea, Ananke Umbriel Ariel, Titania Neptune, have their error equal to 5.5 and., respectively. The largest error much above is obtained for Venus and Pluto. Rather accidentally, the error of e theor for Mercury is much below.. These data show that for numerous planets the dependence of e on a should be in fact much more complicated than that represented by (). The complication can be attributed to the many-body interactions between planets. A dependence of e on a, different than that given in (), should apply especially to a group of relatively light and relatively close planet orbits, like those of Mercury, Venus, and Earth. A comparison of the observed data with the theoretical values obtained for e seems to be more difficult for the satellite orbits than for the planetary ones because numerous eccentricity data for the satellite tracks are either variable, or uncertain, and the influence of the many-body effects exerted on the solution of the two-body Kepler problem is here much intensified. Many planets especially Jupiter, Saturn, Uranus and Neptune have a large number of satellites whose a are approximately equal, and the masses of these satellites are often very similar [7]. For example, the largest error of e theor is found in the case of the satellites of Saturn. These satellites are large in their number, are placed on not much distant orbits and have not very much different masses. The assumption of a coplanar position of the orbits having a common gravitational center can be another source of the error. A much better situation is attained for the satellites of Jupiter, for which the well-established observed eccentricities beginning with Callisto and the next eight satellites taken successively with an increasing distance from the Jupiter center are considered; see Table 3. The observed eccentricity of Elara, having a central position of its orbit distance from the Jupiter center, has been taken as a starting point to calculate the orbit eccentricities of the remainder of the Jupiter satellites. A very large error of e theor is found solely for Callisto, but from the seven remaining e theor, six of them (those for Leda, Himalia, Lysithea, Ananke, Carme and Sinope) have their error below, and the error of one of e theor (that of the orbit of Pasiphae) is not much above that number. A similar comparison of the eccentricities is done for the five satellites of Uranus (Miranda, Ariel, Umbriel, Titania, Oberon) for which the observed eccentricity of Umbriel has been chosen to establish the remainder of the satellite eccentricity data; Table 4. The satellites which have their orbits closest to that of Umbriel give the error of e theor much less than. (Ariel and Titania), whereas the same error for the external satellite orbits, those of Miranda and Oberon, exceeds.. An estimate of eccentricities of the orbits taken as the basis of calculations done in Table, 3, and 4 (Jupiter, Elara and Umbriel, respectively) can be attained by considering the observed data for e and a of the two neighboring orbits of these bodies (Mars and Saturn for Jupiter, Lysithea and Ananke for Elara, Ariel and Titania for Umbriel); see Table 5. The final result for e theor is calculated as the arithmetical mean of e theor obtained from any member of the mentioned orbit pair. Therefore, with the aid of (a), we have e i ( ) a / e i a /,i + e i+a /,i+, (33),i where the index i labels the examined orbit, and a,i < a,i < a,i+. (33a) The error of all e theor presented in Table 5 is much below..
7 S. Olszewski Least-action Principle Applied to the Kepler Problem Summary The least-action principle is applied to the motion of a celestial body along the Kepler orbit. This principle called also the Euler-Maupertuis principle is only a special case of more general Lagrange or Hamilton principles valid upon the following restrictions [8]: (i) the Lagrangian function should not be explicitly time dependent, so the energy of the system is a conserved quantity both on the actual and the varied paths; (ii) for the varied paths the changes of the body position at the terminal positions should vanish, which for a closed path makes this requirement applicable to the beginning-end point of the path; (iii) the potential function entering the Lagrangian should be velocity-independent. With the above restrictions, which can be assumed to be satisfied for a body moving on the Kepler orbit, the Euler-Maupertuis principle becomes equivalent to the Lagrange principle [8]. In Sect. we demonstrated that the Sommerfeld- Landau formula for the derivative of the action function with respect to energy cannot be satisfied unless the eccentricity of the orbit is a function of the major orbital semiaxis. The corresponding equation, coupling the eccentricities and major semiaxes of the orbits having a common gravitational center, is derived in Section. The same equation can be derived by a direct application of the least-action principle in both the Euler-Jacobi and conventional (Maupertuis) variational formulations; Section 3. The results of the equation which couples e and a are discussed in comparison with the observed data in Section 4. No influence of the mass ratio of the rotating body to that of the central body on the equation defining the orbit eccentricity is considered. [] V. M. Blanco and S. W. McCuskey, Basic Physics of the Solar System, Addison-Wesley, Reading, Massachusetts 96. [] E. Finlay-Freundlich, Celestial Mechanics, Pergamon, New York 958. [3] P. M. Fitzpatrick, Principles of Celestial Mechanics, Academic, New York 97. [4] S. W. McCuskey, Introduction to Advanced Dynamics, Addison-Wesley, Reading, Massachusetts 959. [5] F. R. Moulton, An Introduction to Celestial Mechanics, nd ed., Macmillan, New York 958. [6] T. E. Sterne, Introduction to Celestial Mechanics, Interscience, New York 96. [7] H. Goldstein, Classical Mechanics, nd ed., Addison- Wesley, Reading, Massachusetts 98. [8] A. Sommerfeld, Mechanik, Akademische Verlagsgesellschaft, 4th ed., Leipzig 949. [9] A. Sommerfeld, Atombau und Spektrallinien, Vol., 5th ed., Vieweg, Braunschweig 93. [] J. C. Slater, Quantum Theory of the Atomic Structure, Vol., McGraw-Hill, New York 96. [] L. D. Landau and E. M. Lifshitz, Mechanics, Pergamon Press, Oxford 96. [] H.C. Plummer, Dynamical Astronomy, Cambridge University Press, Cambridge 98 (reprinted by Dover Publ., New York 96). [3] W. Rubinowicz and W. Królikowski, Theoretical Mechanics (in Polish), 7th ed., Wydawnictwo Naukowe PWN, Warszawa 995. [4] C. Lanczos, The Variational Principles of Mechanics, 4 th ed., Dover Publications, New York 986. [5] P. Frank and R. v. Mises, Differential- und Integralgleichungen der Mechanik und Physik, Vol., Vieweg, Braunschweig 935. [6] S. Banach, Mechanics (in Polish), Vol., Czytelnik, Warszawa 947. [7] K. L. Lang, Astrophysical Data: Planets and Stars, Springer, New York 99. [8] W. Dittrich and M. Reuter, Classical and Quantum Dynamics, Springer, Berlin 99.
arxiv:astro-ph/ v1 29 Jul 2006
 On a possible regularity connecting physical characteristics of a Solar system planet and elements of its orbit. arxiv:astro-ph/0607658v1 29 Jul 2006 Z.G.Murzahanov, V.P.Merezhin e-mail: dulkyn@mail.ru
On a possible regularity connecting physical characteristics of a Solar system planet and elements of its orbit. arxiv:astro-ph/0607658v1 29 Jul 2006 Z.G.Murzahanov, V.P.Merezhin e-mail: dulkyn@mail.ru
Space Physics THE MOONS OF THE PLANETS 1
 Space Physics THE MOONS OF THE PLANETS 1 Neeke Katharina Rothe 2010/10/18 1 Kjell Rönnmark, Umeå Universitet, fysik Contents 1 Planets 2 2 Natural Satellite 2 3 The moons 3 3.1 Earth-Moon............................
Space Physics THE MOONS OF THE PLANETS 1 Neeke Katharina Rothe 2010/10/18 1 Kjell Rönnmark, Umeå Universitet, fysik Contents 1 Planets 2 2 Natural Satellite 2 3 The moons 3 3.1 Earth-Moon............................
Unit 1 Astronomy: Kepler s Laws Of Planetary Motion Assessed Activity (66 marks total)
 Name: Solutions & Marking Scheme 2009 TG: PF Unit 1 Astronomy: Kepler s Laws Of Planetary Motion Assessed Activity (66 marks total) Aim: To investigate Kepler s three laws planetary motion. Apparatus:
Name: Solutions & Marking Scheme 2009 TG: PF Unit 1 Astronomy: Kepler s Laws Of Planetary Motion Assessed Activity (66 marks total) Aim: To investigate Kepler s three laws planetary motion. Apparatus:
Observational Astronomy - Lecture 4 Orbits, Motions, Kepler s and Newton s Laws
 Observational Astronomy - Lecture 4 Orbits, Motions, Kepler s and Newton s Laws Craig Lage New York University - Department of Physics craig.lage@nyu.edu February 24, 2014 1 / 21 Tycho Brahe s Equatorial
Observational Astronomy - Lecture 4 Orbits, Motions, Kepler s and Newton s Laws Craig Lage New York University - Department of Physics craig.lage@nyu.edu February 24, 2014 1 / 21 Tycho Brahe s Equatorial
Astronomy Test Review. 3 rd Grade
 Astronomy Test Review 3 rd Grade Match the vocabulary word to its definition. Outer Planets The path a planet takes around the sun. Inner Planets Orbit Sun The center of our solar system. Small, rocky
Astronomy Test Review 3 rd Grade Match the vocabulary word to its definition. Outer Planets The path a planet takes around the sun. Inner Planets Orbit Sun The center of our solar system. Small, rocky
October 19, NOTES Solar System Data Table.notebook. Which page in the ESRT???? million km million. average.
 Celestial Object: Naturally occurring object that exists in space. NOT spacecraft or man-made satellites Which page in the ESRT???? Mean = average Units = million km How can we find this using the Solar
Celestial Object: Naturally occurring object that exists in space. NOT spacecraft or man-made satellites Which page in the ESRT???? Mean = average Units = million km How can we find this using the Solar
Section 37 Kepler's Rules
 Section 37 Kepler's Rules What is the universe made out of and how do the parts interact? That was our goal in this course While we ve learned that objects do what they do because of forces, energy, linear
Section 37 Kepler's Rules What is the universe made out of and how do the parts interact? That was our goal in this course While we ve learned that objects do what they do because of forces, energy, linear
Fractal Scaling Models of Natural Oscillations in Chain Systems and the Mass Distribution of the Celestial Bodies in the Solar System
 Fractal Scaling Models of Natural Oscillations in Chain Systems and the Mass Distribution of the Celestial Bodies in the Solar System Hartmut Müller Global Scaling Research Institute in memoriam Leonhard
Fractal Scaling Models of Natural Oscillations in Chain Systems and the Mass Distribution of the Celestial Bodies in the Solar System Hartmut Müller Global Scaling Research Institute in memoriam Leonhard
Investigating the Solar System
 Investigating the Solar System This Workbook belongs to: Our Local Star: The Sun Location in The Solar System Interesting Facts 1. 2. 3. 4. Name of Star: THE SUN 5. Draw and Color your own Sun in the blank
Investigating the Solar System This Workbook belongs to: Our Local Star: The Sun Location in The Solar System Interesting Facts 1. 2. 3. 4. Name of Star: THE SUN 5. Draw and Color your own Sun in the blank
The Kepler Problem and the Isotropic Harmonic Oscillator. M. K. Fung
 CHINESE JOURNAL OF PHYSICS VOL. 50, NO. 5 October 01 The Kepler Problem and the Isotropic Harmonic Oscillator M. K. Fung Department of Physics, National Taiwan Normal University, Taipei, Taiwan 116, R.O.C.
CHINESE JOURNAL OF PHYSICS VOL. 50, NO. 5 October 01 The Kepler Problem and the Isotropic Harmonic Oscillator M. K. Fung Department of Physics, National Taiwan Normal University, Taipei, Taiwan 116, R.O.C.
Lecture 25: The Outer Planets
 Lecture 25: The Outer Planets Neptune Uranus Pluto/Charon Uranus and three moons Neptune and two moons 1 The Outer Planets Uranus Discovered by William Herschel in 1781, who realized that this extended
Lecture 25: The Outer Planets Neptune Uranus Pluto/Charon Uranus and three moons Neptune and two moons 1 The Outer Planets Uranus Discovered by William Herschel in 1781, who realized that this extended
The Law of Ellipses (Kepler s First Law): all planets orbit the sun in a
 Team Number Team Members Present Learning Objectives 1. Practice the Engineering Process a series of steps to follow to design a solution to a problem. 2. Practice the Five Dimensions of Being a Good Team
Team Number Team Members Present Learning Objectives 1. Practice the Engineering Process a series of steps to follow to design a solution to a problem. 2. Practice the Five Dimensions of Being a Good Team
Estimation of Planetary Orbits via Vectorial Relativity (VTR)
 Universidad Central de Venezuela From the SelectedWorks of Jorge A Franco September, 8 Estimation of Planetary Orbits via Vectorial Relativity (VTR) Jorge A Franco, Universidad Central de Venezuela Available
Universidad Central de Venezuela From the SelectedWorks of Jorge A Franco September, 8 Estimation of Planetary Orbits via Vectorial Relativity (VTR) Jorge A Franco, Universidad Central de Venezuela Available
Physics Unit 7: Circular Motion, Universal Gravitation, and Satellite Orbits. Planetary Motion
 Physics Unit 7: Circular Motion, Universal Gravitation, and Satellite Orbits Planetary Motion Geocentric Models --Many people prior to the 1500 s viewed the! Earth and the solar system using a! geocentric
Physics Unit 7: Circular Motion, Universal Gravitation, and Satellite Orbits Planetary Motion Geocentric Models --Many people prior to the 1500 s viewed the! Earth and the solar system using a! geocentric
Precession of perihelion of the planet with the critical photon orbit
 Mahgoub Salih Precession of perihelion of the planet with the critical photon orbit Department of Physics, Faculty of Science and Art at al-muznab, Qassim University, KSA Abstract The solution of geodesic
Mahgoub Salih Precession of perihelion of the planet with the critical photon orbit Department of Physics, Faculty of Science and Art at al-muznab, Qassim University, KSA Abstract The solution of geodesic
A Short Essay on Variational Calculus
 A Short Essay on Variational Calculus Keonwook Kang, Chris Weinberger and Wei Cai Department of Mechanical Engineering, Stanford University Stanford, CA 94305-4040 May 3, 2006 Contents 1 Definition of
A Short Essay on Variational Calculus Keonwook Kang, Chris Weinberger and Wei Cai Department of Mechanical Engineering, Stanford University Stanford, CA 94305-4040 May 3, 2006 Contents 1 Definition of
The Solar System LEARNING TARGETS. Scientific Language. Name Test Date Hour
 Name Test Date Hour Astronomy#3 - Notebook The Solar System LEARNING TARGETS I can describe the objects that make up our solar system. I can identify the inner and outer planets. I can explain the difference
Name Test Date Hour Astronomy#3 - Notebook The Solar System LEARNING TARGETS I can describe the objects that make up our solar system. I can identify the inner and outer planets. I can explain the difference
Earth Science Unit 6: Astronomy Period: Date: Elliptical Orbits
 Earth Science Name: Unit 6: Astronomy Period: Date: Lab # 5 Elliptical Orbits Objective: To compare the shape of the earth s orbit (eccentricity) with the orbits of and with a circle. other planets Focus
Earth Science Name: Unit 6: Astronomy Period: Date: Lab # 5 Elliptical Orbits Objective: To compare the shape of the earth s orbit (eccentricity) with the orbits of and with a circle. other planets Focus
Restricted three body problems in the Solar System: simulations
 Author:. Facultat de Física, Universitat de Barcelona, Diagonal 645, 0808 Barcelona, Spain. Advisor: Antoni Benseny i Ardiaca. Facultat de Matemàtiques, Universitat de Barcelona, Gran Via de les Corts
Author:. Facultat de Física, Universitat de Barcelona, Diagonal 645, 0808 Barcelona, Spain. Advisor: Antoni Benseny i Ardiaca. Facultat de Matemàtiques, Universitat de Barcelona, Gran Via de les Corts
As part of a solar system unit, this math lesson plan uses the diameters of the planets to teach place value, rounding and ordering numbers skills.
 SOLAR SYSTEM As part of a solar system unit, this math lesson plan uses the diameters of the planets to teach place value, rounding and ordering numbers skills. Background for Solar System Math Lesson
SOLAR SYSTEM As part of a solar system unit, this math lesson plan uses the diameters of the planets to teach place value, rounding and ordering numbers skills. Background for Solar System Math Lesson
ASTR 380 Possibilities for Life in the Outer Solar System
 ASTR 380 Possibilities for Life in the Outer Solar System Possibility of Life in the Inner Solar System The Moon, Mercury, and the Moons of Mars Deimos NO LIFE NOW or EVER This is a 98% conclusion! Phobos
ASTR 380 Possibilities for Life in the Outer Solar System Possibility of Life in the Inner Solar System The Moon, Mercury, and the Moons of Mars Deimos NO LIFE NOW or EVER This is a 98% conclusion! Phobos
Advanced Newtonian gravity
 Foundations of Newtonian gravity Solutions Motion of extended bodies, University of Guelph h treatment of Newtonian gravity, the book develops approximation methods to obtain weak-field solutions es the
Foundations of Newtonian gravity Solutions Motion of extended bodies, University of Guelph h treatment of Newtonian gravity, the book develops approximation methods to obtain weak-field solutions es the
The Solar System. Name Test Date Hour
 Name Test Date Hour Astronomy#3 - Notebook The Solar System LEARNING TARGETS I can describe the objects that make up our solar system. I can identify the inner and outer planets. I can explain the difference
Name Test Date Hour Astronomy#3 - Notebook The Solar System LEARNING TARGETS I can describe the objects that make up our solar system. I can identify the inner and outer planets. I can explain the difference
Earth s Motions. Rotation -!! Period of Rotation - amount of time to make one complete rotation Example: Earth rotates in hours.
 Name: Date: Period: Earth In the Solar System The Physical Setting: Earth Science CLASS NOTES! Rotation -! Period of Rotation - amount of time to make one complete rotation Example: Earth rotates in hours
Name: Date: Period: Earth In the Solar System The Physical Setting: Earth Science CLASS NOTES! Rotation -! Period of Rotation - amount of time to make one complete rotation Example: Earth rotates in hours
Physical Science 1 Chapter 16 INTRODUCTION. Astronomy is the study of the universe, which includes all matter, energy, space and time.
 INTRODUCTION Astronomy is the study of the universe, which includes all matter, energy, space and time. Although the universe is vast and almost beyond imagination, much is known about its make-up and
INTRODUCTION Astronomy is the study of the universe, which includes all matter, energy, space and time. Although the universe is vast and almost beyond imagination, much is known about its make-up and
An Introduction to Celestial Mechanics
 An Introduction to Celestial Mechanics This accessible text on classical celestial mechanics the principles governing the motions of bodies in the solar system provides a clear and concise treatment of
An Introduction to Celestial Mechanics This accessible text on classical celestial mechanics the principles governing the motions of bodies in the solar system provides a clear and concise treatment of
Astronomy 6570 Physics of the Planets. Precession: Free and Forced
 Astronomy 6570 Physics of the Planets Precession: Free and Forced Planetary Precession We have seen above how information concerning the distribution of density within a planet (in particular, the polar
Astronomy 6570 Physics of the Planets Precession: Free and Forced Planetary Precession We have seen above how information concerning the distribution of density within a planet (in particular, the polar
Which of the following planets are all made up of gas? When a planets orbit around the Sun looks like an oval, it s called a(n)
 When a planets orbit around the Sun looks like an oval, it s called a(n) - ellipse - circle - axis - rotation Which of the following planets are all made up of gas? - Venus, Mars, Saturn and Pluto - Jupiter,
When a planets orbit around the Sun looks like an oval, it s called a(n) - ellipse - circle - axis - rotation Which of the following planets are all made up of gas? - Venus, Mars, Saturn and Pluto - Jupiter,
NAME: PERIOD: DATE: LAB PARTNERS: LAB #39 ECCENTRICITY OF PLANETARY ORBITS
 NAME: PERIOD: DATE: LAB PARTNERS: LAB #39 ECCENTRICITY OF PLANETARY ORBITS INTRODUCTION Our sun is not exactly in the center of the orbits of the planets, and therefore the planetary orbits are not circular.
NAME: PERIOD: DATE: LAB PARTNERS: LAB #39 ECCENTRICITY OF PLANETARY ORBITS INTRODUCTION Our sun is not exactly in the center of the orbits of the planets, and therefore the planetary orbits are not circular.
Planets. By Christian Bennett
 Planets By Christian Bennett Mercury The smallest planet Closest to the sun It takes 116 days to orbit around the sun At night its -208 degrees, and at day time it is 800 degrees Its axis has the smallest
Planets By Christian Bennett Mercury The smallest planet Closest to the sun It takes 116 days to orbit around the sun At night its -208 degrees, and at day time it is 800 degrees Its axis has the smallest
VISUAL PHYSICS ONLINE
 VISUAL PHYSICS ONLINE PRACTICAL ACTIVITY HOW DO THE PANETS MOVE? One of the most important questions historically in Physics was how the planets move. Many historians consider the field of Physics to date
VISUAL PHYSICS ONLINE PRACTICAL ACTIVITY HOW DO THE PANETS MOVE? One of the most important questions historically in Physics was how the planets move. Many historians consider the field of Physics to date
Shallow Water Gravity Waves: A Note on the Particle Orbits
 Journal of Oceanography Vol. 5, pp. 353 to 357. 1996 Shallow Water Gravity Waves: A Note on the Particle Orbits KERN E. KENYON 463 North Lane, Del Mar, CA 9014-4134, U.S.A. (Received 4 July 1995; in revised
Journal of Oceanography Vol. 5, pp. 353 to 357. 1996 Shallow Water Gravity Waves: A Note on the Particle Orbits KERN E. KENYON 463 North Lane, Del Mar, CA 9014-4134, U.S.A. (Received 4 July 1995; in revised
Chapter 14 Satellite Motion
 1 Academic Physics Mechanics Chapter 14 Satellite Motion The Mechanical Universe Kepler's Three Laws (Episode 21) The Kepler Problem (Episode 22) Energy and Eccentricity (Episode 23) Navigating in Space
1 Academic Physics Mechanics Chapter 14 Satellite Motion The Mechanical Universe Kepler's Three Laws (Episode 21) The Kepler Problem (Episode 22) Energy and Eccentricity (Episode 23) Navigating in Space
Gravity and the Laws of Motion
 Gravity and the Laws of Motion Mass Mass is the amount of stuff (matter) in an object. Measured in grams (kg, mg, cg, etc.) Mass will not change unless matter is added or taken away. Weight Weight is the
Gravity and the Laws of Motion Mass Mass is the amount of stuff (matter) in an object. Measured in grams (kg, mg, cg, etc.) Mass will not change unless matter is added or taken away. Weight Weight is the
Central force motion/kepler problem. 1 Reducing 2-body motion to effective 1-body, that too with 2 d.o.f and 1st order differential equations
 Central force motion/kepler problem This short note summarizes our discussion in the lectures of various aspects of the motion under central force, in particular, the Kepler problem of inverse square-law
Central force motion/kepler problem This short note summarizes our discussion in the lectures of various aspects of the motion under central force, in particular, the Kepler problem of inverse square-law
A = 6561 times greater. B. 81 times greater. C. equally strong. D. 1/81 as great. E. (1/81) 2 = 1/6561 as great Pearson Education, Inc.
 Q13.1 The mass of the Moon is 1/81 of the mass of the Earth. Compared to the gravitational force that the Earth exerts on the Moon, the gravitational force that the Moon exerts on the Earth is A. 81 2
Q13.1 The mass of the Moon is 1/81 of the mass of the Earth. Compared to the gravitational force that the Earth exerts on the Moon, the gravitational force that the Moon exerts on the Earth is A. 81 2
Tycho Brahe
 Tycho Brahe 1546-1601 At the time of Shakespeare and Elizabeth I and Champlain Lost part of his nose in a duel over who was the best mathematician At 27 he measured the distance of a supernova and a comet
Tycho Brahe 1546-1601 At the time of Shakespeare and Elizabeth I and Champlain Lost part of his nose in a duel over who was the best mathematician At 27 he measured the distance of a supernova and a comet
The two-body Kepler problem
 The two-body Kepler problem set center of mass at the origin (X = 0) ignore all multipole moments (spherical bodies or point masses) define r := r 1 r 2,r:= r,m:= m 1 + m 2,µ:= m 1 m 2 /m reduces to effective
The two-body Kepler problem set center of mass at the origin (X = 0) ignore all multipole moments (spherical bodies or point masses) define r := r 1 r 2,r:= r,m:= m 1 + m 2,µ:= m 1 m 2 /m reduces to effective
The Origin The Moons Of Uranus
 The Origin Of The Tilt Of Uranus Axis Formation and Probability Theories Examined By Paul Nethercott April 00 Abstract The planet Uranus is titled 97 degrees on its axis compared to its orbital plane.
The Origin Of The Tilt Of Uranus Axis Formation and Probability Theories Examined By Paul Nethercott April 00 Abstract The planet Uranus is titled 97 degrees on its axis compared to its orbital plane.
Use conserved quantities to reduce number of variables and the equation of motion (EOM)
 Physics 106a, Caltech 5 October, 018 Lecture 8: Central Forces Bound States Today we discuss the Kepler problem of the orbital motion of planets and other objects in the gravitational field of the sun.
Physics 106a, Caltech 5 October, 018 Lecture 8: Central Forces Bound States Today we discuss the Kepler problem of the orbital motion of planets and other objects in the gravitational field of the sun.
Lecture 4. Alexey Boyarsky. October 6, 2015
 Lecture 4 Alexey Boyarsky October 6, 2015 1 Conservation laws and symmetries 1.1 Ignorable Coordinates During the motion of a mechanical system, the 2s quantities q i and q i, (i = 1, 2,..., s) which specify
Lecture 4 Alexey Boyarsky October 6, 2015 1 Conservation laws and symmetries 1.1 Ignorable Coordinates During the motion of a mechanical system, the 2s quantities q i and q i, (i = 1, 2,..., s) which specify
PHYS 155 Introductory Astronomy
 PHYS 155 Introductory Astronomy - observing sessions: Sunday Thursday, 9pm, weather permitting http://www.phys.uconn.edu/observatory - Exam - Tuesday March 20, - Review Monday 6:30-9pm, PB 38 Marek Krasnansky
PHYS 155 Introductory Astronomy - observing sessions: Sunday Thursday, 9pm, weather permitting http://www.phys.uconn.edu/observatory - Exam - Tuesday March 20, - Review Monday 6:30-9pm, PB 38 Marek Krasnansky
Explaining Planetary-Rotation Periods Using an Inductive Method
 Explaining Planetary-Rotation Periods Using an Inductive Method Gizachew Tiruneh, Ph. D., Department of Political Science, University of Central Arkansas June 19, 2009 This paper uses an inductive method
Explaining Planetary-Rotation Periods Using an Inductive Method Gizachew Tiruneh, Ph. D., Department of Political Science, University of Central Arkansas June 19, 2009 This paper uses an inductive method
What is the Solar System?
 What is the Solar System? Our Solar System is one of many planetary systems. It consists of: The Sun Eight planets with their natural satellites Five dwarf planets Billions of asteroids, comets and meteors
What is the Solar System? Our Solar System is one of many planetary systems. It consists of: The Sun Eight planets with their natural satellites Five dwarf planets Billions of asteroids, comets and meteors
Resonance In the Solar System
 Resonance In the Solar System Steve Bache UNC Wilmington Dept. of Physics and Physical Oceanography Advisor : Dr. Russ Herman Spring 2012 Goal numerically investigate the dynamics of the asteroid belt
Resonance In the Solar System Steve Bache UNC Wilmington Dept. of Physics and Physical Oceanography Advisor : Dr. Russ Herman Spring 2012 Goal numerically investigate the dynamics of the asteroid belt
1. The two triangles shown below are similar. This means that all the angles are equal and the sides are proportional.
 1. The two triangles shown below are similar. This means that all the angles are equal and the sides are proportional. a. How many times bigger is the big triangle in comparison to the little triangle?
1. The two triangles shown below are similar. This means that all the angles are equal and the sides are proportional. a. How many times bigger is the big triangle in comparison to the little triangle?
1/13/16. Solar System Formation
 Solar System Formation 1 Your Parents Solar System 21 st Century Solar System 2 The 21 st Century Solar System Sun Terrestrial Planets Asteroid Belt Jovian Planets Kuiper Belt Oort Cloud The Solar System:
Solar System Formation 1 Your Parents Solar System 21 st Century Solar System 2 The 21 st Century Solar System Sun Terrestrial Planets Asteroid Belt Jovian Planets Kuiper Belt Oort Cloud The Solar System:
The precession of the perihelion of Mercury explained by Celestial Mechanics of Laplace Valdir Monteiro dos Santos Godoi
 The precession of the perihelion of Mercury explained by Celestial Mechanics of Laplace Valdir Monteiro dos Santos Godoi valdir.msgodoi@gmail.com ABSTRACT We calculate in this article an exact theoretical
The precession of the perihelion of Mercury explained by Celestial Mechanics of Laplace Valdir Monteiro dos Santos Godoi valdir.msgodoi@gmail.com ABSTRACT We calculate in this article an exact theoretical
Yes, inner planets tend to be and outer planets tend to be.
 1. Planet Density Make some general comments about inner and outer planets density Inner Planets Density Outer Planets Density Is there a pattern or a trend in planet density? Yes, inner planets tend to
1. Planet Density Make some general comments about inner and outer planets density Inner Planets Density Outer Planets Density Is there a pattern or a trend in planet density? Yes, inner planets tend to
Motion of the planets
 Our Solar system Motion of the planets Our solar system is made up of the sun and the 9 planets that revolve around the sun Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune & Pluto (maybe?)
Our Solar system Motion of the planets Our solar system is made up of the sun and the 9 planets that revolve around the sun Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune & Pluto (maybe?)
The first order formalism and the transition to the
 Problem 1. Hamiltonian The first order formalism and the transition to the This problem uses the notion of Lagrange multipliers and Legendre transforms to understand the action in the Hamiltonian formalism.
Problem 1. Hamiltonian The first order formalism and the transition to the This problem uses the notion of Lagrange multipliers and Legendre transforms to understand the action in the Hamiltonian formalism.
Johannes Kepler ( ) German Mathematician and Astronomer Passionately convinced of the rightness of the Copernican view. Set out to prove it!
 Johannes Kepler (1571-1630) German Mathematician and Astronomer Passionately convinced of the rightness of the Copernican view. Set out to prove it! Kepler s Life Work Kepler sought a unifying principle
Johannes Kepler (1571-1630) German Mathematician and Astronomer Passionately convinced of the rightness of the Copernican view. Set out to prove it! Kepler s Life Work Kepler sought a unifying principle
ANNEX 1. DEFINITION OF ORBITAL PARAMETERS AND IMPORTANT CONCEPTS OF CELESTIAL MECHANICS
 ANNEX 1. DEFINITION OF ORBITAL PARAMETERS AND IMPORTANT CONCEPTS OF CELESTIAL MECHANICS A1.1. Kepler s laws Johannes Kepler (1571-1630) discovered the laws of orbital motion, now called Kepler's laws.
ANNEX 1. DEFINITION OF ORBITAL PARAMETERS AND IMPORTANT CONCEPTS OF CELESTIAL MECHANICS A1.1. Kepler s laws Johannes Kepler (1571-1630) discovered the laws of orbital motion, now called Kepler's laws.
4. THE SOLAR SYSTEM 1.1. THE SUN. Exercises
 4. THE SOLAR SYSTEM 1.1. THE SUN The sun is the star located in the center of the solar system. The sun is a yellow star, since its superficial temperature is about 5.500 C (although, the temperature can
4. THE SOLAR SYSTEM 1.1. THE SUN The sun is the star located in the center of the solar system. The sun is a yellow star, since its superficial temperature is about 5.500 C (although, the temperature can
Classical Mechanics Comprehensive Exam Solution
 Classical Mechanics Comprehensive Exam Solution January 31, 011, 1:00 pm 5:pm Solve the following six problems. In the following problems, e x, e y, and e z are unit vectors in the x, y, and z directions,
Classical Mechanics Comprehensive Exam Solution January 31, 011, 1:00 pm 5:pm Solve the following six problems. In the following problems, e x, e y, and e z are unit vectors in the x, y, and z directions,
orbits Moon, Planets Spacecrafts Calculating the and by Dr. Shiu-Sing TONG
 A Science Enrichment Programme for Secondary 3-4 Students : Teaching and Learning Resources the and Spacecrafts orbits Moon, Planets Calculating the 171 of by Dr. Shiu-Sing TONG 172 Calculating the orbits
A Science Enrichment Programme for Secondary 3-4 Students : Teaching and Learning Resources the and Spacecrafts orbits Moon, Planets Calculating the 171 of by Dr. Shiu-Sing TONG 172 Calculating the orbits
Dynamical properties of the Solar System. Second Kepler s Law. Dynamics of planetary orbits. ν: true anomaly
 First Kepler s Law The secondary body moves in an elliptical orbit, with the primary body at the focus Valid for bound orbits with E < 0 The conservation of the total energy E yields a constant semi-major
First Kepler s Law The secondary body moves in an elliptical orbit, with the primary body at the focus Valid for bound orbits with E < 0 The conservation of the total energy E yields a constant semi-major
The Three Body Problem
 The Three Body Problem Joakim Hirvonen Grützelius Karlstad University December 26, 2004 Department of Engineeringsciences, Physics and Mathematics 5p Examinator: Prof Jürgen Füchs Abstract The main topic
The Three Body Problem Joakim Hirvonen Grützelius Karlstad University December 26, 2004 Department of Engineeringsciences, Physics and Mathematics 5p Examinator: Prof Jürgen Füchs Abstract The main topic
Equation of orbital velocity: v 2 =GM(2/r 1/a) where: G is the gravitational constant (G=6.67x10 11 N/m 3 kg), M is the mass of the sun (or central
 Everything in Orbit Orbital Velocity Orbital velocity is the speed at which a planetary body moves in its orbit around another body. If orbits were circular, this velocity would be constant. However, from
Everything in Orbit Orbital Velocity Orbital velocity is the speed at which a planetary body moves in its orbit around another body. If orbits were circular, this velocity would be constant. However, from
Symplectic Correctors for Canonical Heliocentric N-Body Maps
 Symplectic Correctors for Canonical Heliocentric N-Body Maps J. Wisdom Massachusetts Institute of Technology, Cambridge, MA 02139 wisdom@poincare.mit.edu Received ; accepted 2 ABSTRACT Symplectic correctors
Symplectic Correctors for Canonical Heliocentric N-Body Maps J. Wisdom Massachusetts Institute of Technology, Cambridge, MA 02139 wisdom@poincare.mit.edu Received ; accepted 2 ABSTRACT Symplectic correctors
Physics 12. Unit 5 Circular Motion and Gravitation Part 2
 Physics 12 Unit 5 Circular Motion and Gravitation Part 2 1. Newton s law of gravitation We have seen in Physics 11 that the force acting on an object due to gravity is given by a well known formula: F
Physics 12 Unit 5 Circular Motion and Gravitation Part 2 1. Newton s law of gravitation We have seen in Physics 11 that the force acting on an object due to gravity is given by a well known formula: F
Exercise 4.0 PLANETARY ORBITS AND CONFIGURATIONS
 Exercise 4.0 PLANETARY ORBITS AND CONFIGURATIONS I. Introduction The planets revolve around the Sun in orbits that lie nearly in the same plane. Therefore, the planets, with the exception of Pluto, are
Exercise 4.0 PLANETARY ORBITS AND CONFIGURATIONS I. Introduction The planets revolve around the Sun in orbits that lie nearly in the same plane. Therefore, the planets, with the exception of Pluto, are
The planet Earth moves
 TERM 4: Planet Earth AnD BEYOND Planet Earth and beyond The planet Earth moves Fossils Surface of the Earth Sedimentary rocks Unit 1 The planet Earth moves Orbits the sun The planet Earth moves Spins around
TERM 4: Planet Earth AnD BEYOND Planet Earth and beyond The planet Earth moves Fossils Surface of the Earth Sedimentary rocks Unit 1 The planet Earth moves Orbits the sun The planet Earth moves Spins around
Motion under the Influence of a Central Force
 Copyright 004 5 Motion under the Influence of a Central Force The fundamental forces of nature depend only on the distance from the source. All the complex interactions that occur in the real world arise
Copyright 004 5 Motion under the Influence of a Central Force The fundamental forces of nature depend only on the distance from the source. All the complex interactions that occur in the real world arise
arxiv:physics/ v2 [physics.gen-ph] 2 Dec 2003
![arxiv:physics/ v2 [physics.gen-ph] 2 Dec 2003 arxiv:physics/ v2 [physics.gen-ph] 2 Dec 2003](/thumbs/93/111763098.jpg) The effective inertial acceleration due to oscillations of the gravitational potential: footprints in the solar system arxiv:physics/0309099v2 [physics.gen-ph] 2 Dec 2003 D.L. Khokhlov Sumy State University,
The effective inertial acceleration due to oscillations of the gravitational potential: footprints in the solar system arxiv:physics/0309099v2 [physics.gen-ph] 2 Dec 2003 D.L. Khokhlov Sumy State University,
MATHEMATICAL PHYSICS
 MATHEMATICAL PHYSICS Third Year SEMESTER 1 015 016 Classical Mechanics MP350 Prof. S. J. Hands, Prof. D. M. Heffernan, Dr. J.-I. Skullerud and Dr. M. Fremling Time allowed: 1 1 hours Answer two questions
MATHEMATICAL PHYSICS Third Year SEMESTER 1 015 016 Classical Mechanics MP350 Prof. S. J. Hands, Prof. D. M. Heffernan, Dr. J.-I. Skullerud and Dr. M. Fremling Time allowed: 1 1 hours Answer two questions
TP 3:Runge-Kutta Methods-Solar System-The Method of Least Squares
 TP :Runge-Kutta Methods-Solar System-The Method of Least Squares December 8, 2009 1 Runge-Kutta Method The problem is still trying to solve the first order differential equation dy = f(y, x). (1) dx In
TP :Runge-Kutta Methods-Solar System-The Method of Least Squares December 8, 2009 1 Runge-Kutta Method The problem is still trying to solve the first order differential equation dy = f(y, x). (1) dx In
The Gas Giants Astronomy Lesson 13
 The Gas Giants Astronomy Lesson 13 The four outer planets: Jupiter, Saturn, Uranus, and Neptune, are much larger and more massive than Earth, and they do not have solid surfaces. Because these planets
The Gas Giants Astronomy Lesson 13 The four outer planets: Jupiter, Saturn, Uranus, and Neptune, are much larger and more massive than Earth, and they do not have solid surfaces. Because these planets
PHY321 Homework Set 10
 PHY321 Homework Set 10 1. [5 pts] A small block of mass m slides without friction down a wedge-shaped block of mass M and of opening angle α. Thetriangular block itself slides along a horizontal floor,
PHY321 Homework Set 10 1. [5 pts] A small block of mass m slides without friction down a wedge-shaped block of mass M and of opening angle α. Thetriangular block itself slides along a horizontal floor,
The Giant Planets [10]
![The Giant Planets [10] The Giant Planets [10]](/thumbs/72/67206112.jpg) The Giant Planets [10] Distance Period Diameter Mass Rotation Tilt (au) (yrs) (hrs) (deg) Earth 1 1 1 1 24.0 23 Jupiter 5.2 11.9 11.2 318 9.9 3 Saturn 9.5 29.5 9.4 95 10.7 27 Uranus 19.2 84.1 4.0 14 17.2
The Giant Planets [10] Distance Period Diameter Mass Rotation Tilt (au) (yrs) (hrs) (deg) Earth 1 1 1 1 24.0 23 Jupiter 5.2 11.9 11.2 318 9.9 3 Saturn 9.5 29.5 9.4 95 10.7 27 Uranus 19.2 84.1 4.0 14 17.2
A medium-sized star. The hottest object found in our solar system.
 A medium-sized star. The hottest object found in our solar system. It gives off heat, light, and energy. It affects the seasons, climate, and weather on Earth. The second smallest planet in our solar system.
A medium-sized star. The hottest object found in our solar system. It gives off heat, light, and energy. It affects the seasons, climate, and weather on Earth. The second smallest planet in our solar system.
AST111, Lecture 1b. Measurements of bodies in the solar system (overview continued) Orbital elements
 AST111, Lecture 1b Measurements of bodies in the solar system (overview continued) Orbital elements Planetary properties (continued): Measuring Mass The orbital period of a moon about a planet depends
AST111, Lecture 1b Measurements of bodies in the solar system (overview continued) Orbital elements Planetary properties (continued): Measuring Mass The orbital period of a moon about a planet depends
Patterns in the Solar System (Chapter 18)
 GEOLOGY 306 Laboratory Instructor: TERRY J. BOROUGHS NAME: Patterns in the Solar System (Chapter 18) For this assignment you will require: a calculator, colored pencils, a metric ruler, and meter stick.
GEOLOGY 306 Laboratory Instructor: TERRY J. BOROUGHS NAME: Patterns in the Solar System (Chapter 18) For this assignment you will require: a calculator, colored pencils, a metric ruler, and meter stick.
Exact Values of Dynamical Quantities in Planetary Motion
 International Journal of Mathematical Education. ISSN 0973-6948 Volume 6, Number 1 (2016), pp. 1-9 Research India Publications http://www.ripublication.com Exact Values of Dynamical Quantities in Planetary
International Journal of Mathematical Education. ISSN 0973-6948 Volume 6, Number 1 (2016), pp. 1-9 Research India Publications http://www.ripublication.com Exact Values of Dynamical Quantities in Planetary
4 A(n) is a small, rocky object that orbits the sun; many of these objects are located in a band between the orbits of Mars and Jupiter.
 Name Vocabulary Fill in the blank with the term that best completes the sentence., 6.11B 1 is the process in which energy is released as the nuclei of small atoms combine to form a larger nucleus., 6.11B
Name Vocabulary Fill in the blank with the term that best completes the sentence., 6.11B 1 is the process in which energy is released as the nuclei of small atoms combine to form a larger nucleus., 6.11B
(b) The period T and the angular frequency ω of uniform rotation are related to the cyclic frequency f as. , ω = 2πf =
 PHY 302 K. Solutions for problem set #9. Non-textbook problem #1: (a) Rotation frequency of 1 Hz means one revolution per second, or 60 revolutions per minute (RPM). The pre-lp vinyl disks rotated at 78
PHY 302 K. Solutions for problem set #9. Non-textbook problem #1: (a) Rotation frequency of 1 Hz means one revolution per second, or 60 revolutions per minute (RPM). The pre-lp vinyl disks rotated at 78
Perihelion Precession in the Solar System
 International Journal of Multidisciplinary Current Research ISSN: 2321-3124 Research Article Available at: http://ijmcr.com Sara Kanzi * Hamed Ghasemian! * Currently pursuing Ph.D. degree program in Physics
International Journal of Multidisciplinary Current Research ISSN: 2321-3124 Research Article Available at: http://ijmcr.com Sara Kanzi * Hamed Ghasemian! * Currently pursuing Ph.D. degree program in Physics
ISIMA lectures on celestial mechanics. 1
 ISIMA lectures on celestial mechanics. 1 Scott Tremaine, Institute for Advanced Study July 2014 The roots of solar system dynamics can be traced to two fundamental discoveries by Isaac Newton: first, that
ISIMA lectures on celestial mechanics. 1 Scott Tremaine, Institute for Advanced Study July 2014 The roots of solar system dynamics can be traced to two fundamental discoveries by Isaac Newton: first, that
Transmissions Handout #1/ Task Card #2
 Handout #1/ Task Card #1 Transmissions Specialist Handout #1 Transmissions Handout #1/ Task Card #2 At this moment, we are receiving faint radio messages from the lost ship. The messages, however, are
Handout #1/ Task Card #1 Transmissions Specialist Handout #1 Transmissions Handout #1/ Task Card #2 At this moment, we are receiving faint radio messages from the lost ship. The messages, however, are
A fully relativistic description of stellar or planetary objects orbiting a very heavy central mass
 A fully relativistic description of stellar or planetary objects orbiting a very heavy central mass Ll. Bel August 25, 2018 Abstract A fully relativistic numerical program is used to calculate the advance
A fully relativistic description of stellar or planetary objects orbiting a very heavy central mass Ll. Bel August 25, 2018 Abstract A fully relativistic numerical program is used to calculate the advance
18. Kepler as a young man became the assistant to A) Nicolaus Copernicus. B) Ptolemy. C) Tycho Brahe. D) Sir Isaac Newton.
 Name: Date: 1. The word planet is derived from a Greek term meaning A) bright nighttime object. B) astrological sign. C) wanderer. D) nontwinkling star. 2. The planets that were known before the telescope
Name: Date: 1. The word planet is derived from a Greek term meaning A) bright nighttime object. B) astrological sign. C) wanderer. D) nontwinkling star. 2. The planets that were known before the telescope
1. The bar graph below shows one planetary characteristic, identified as X, plotted for the planets of our solar system.
 1. The bar graph below shows one planetary characteristic, identified as X, plotted for the planets of our solar system. Which characteristic of the planets in our solar system is represented by X? A)
1. The bar graph below shows one planetary characteristic, identified as X, plotted for the planets of our solar system. Which characteristic of the planets in our solar system is represented by X? A)
Gravitation. Luis Anchordoqui
 Gravitation Kepler's law and Newton's Synthesis The nighttime sky with its myriad stars and shinning planets has always fascinated people on Earth. Towards the end of the XVI century the astronomer Tycho
Gravitation Kepler's law and Newton's Synthesis The nighttime sky with its myriad stars and shinning planets has always fascinated people on Earth. Towards the end of the XVI century the astronomer Tycho
Explicit gauge covariant Euler Lagrange equation
 Explicit gauge covariant Euler Lagrange equation Clinton L. Lewis a Division of Science and Mathematics, West Valley College, Saratoga, California 95070 Received 11 November 2008; accepted 22 May 2009
Explicit gauge covariant Euler Lagrange equation Clinton L. Lewis a Division of Science and Mathematics, West Valley College, Saratoga, California 95070 Received 11 November 2008; accepted 22 May 2009
9.2 - Our Solar System
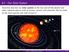 9.2 - Our Solar System Scientists describe our solar system as the Sun and all the planets and other celestial objects, such as moons, comets, and asteroids, that are held by the Sun s gravity and orbit
9.2 - Our Solar System Scientists describe our solar system as the Sun and all the planets and other celestial objects, such as moons, comets, and asteroids, that are held by the Sun s gravity and orbit
Assignment 1. Due Jan. 31, 2017
 Assignment 1 Due Jan. 31, 2017 Show all work and turn in answers on separate pages, not on these pages. Circle your final answers for clarity. Be sure to show/explain all of your reasoning and that your
Assignment 1 Due Jan. 31, 2017 Show all work and turn in answers on separate pages, not on these pages. Circle your final answers for clarity. Be sure to show/explain all of your reasoning and that your
Solar System Research Teacher Notes The Sun
 The Sun G-type main sequence star (G2V), also known as a yellow dwarf Mass = 1.99 x 10 30 kg or 333,000 Earths. Volume = 1.41 x 10 18 km 3 or 1,300,000 Earths. Density (average) = 1.41 g/cm 3 or 0.255
The Sun G-type main sequence star (G2V), also known as a yellow dwarf Mass = 1.99 x 10 30 kg or 333,000 Earths. Volume = 1.41 x 10 18 km 3 or 1,300,000 Earths. Density (average) = 1.41 g/cm 3 or 0.255
PHYS2330 Intermediate Mechanics Fall Final Exam Tuesday, 21 Dec 2010
 Name: PHYS2330 Intermediate Mechanics Fall 2010 Final Exam Tuesday, 21 Dec 2010 This exam has two parts. Part I has 20 multiple choice questions, worth two points each. Part II consists of six relatively
Name: PHYS2330 Intermediate Mechanics Fall 2010 Final Exam Tuesday, 21 Dec 2010 This exam has two parts. Part I has 20 multiple choice questions, worth two points each. Part II consists of six relatively
11 Newton s Law of Universal Gravitation
 Physics 1A, Fall 2003 E. Abers 11 Newton s Law of Universal Gravitation 11.1 The Inverse Square Law 11.1.1 The Moon and Kepler s Third Law Things fall down, not in some other direction, because that s
Physics 1A, Fall 2003 E. Abers 11 Newton s Law of Universal Gravitation 11.1 The Inverse Square Law 11.1.1 The Moon and Kepler s Third Law Things fall down, not in some other direction, because that s
Class VIII Chapter 17 Stars and the Solar System Science
 Question 1: Which of the following is NOT a member of the solar system? (a) An asteroid (b) A satellite (c) A constellation (d) A comet (c) Constellation A constellation is not a member of the solar system.
Question 1: Which of the following is NOT a member of the solar system? (a) An asteroid (b) A satellite (c) A constellation (d) A comet (c) Constellation A constellation is not a member of the solar system.
Our Fun Sun. Source: Measuring the Diameter of the Sun, The Educator s Reference Desk Enchanted Learning
 Our Fun Sun Subject: Science, Math Grades: 7 th 8 th Rational or Purpose: Students will develop an easy tool in which they are able to look at the sun and find out what its diameter is by a simple arithmetic
Our Fun Sun Subject: Science, Math Grades: 7 th 8 th Rational or Purpose: Students will develop an easy tool in which they are able to look at the sun and find out what its diameter is by a simple arithmetic
Sol o ar a r S yste t m e F o F r o m r at a i t on o The Ne N b e u b l u a a Hypothesis
 Solar System Solar system- the sun and all objects that orbit the sun due to its gravity Solar System Formation The Nebula Hypothesis Parts of the Solar System Planet- a celestial body that is in orbit
Solar System Solar system- the sun and all objects that orbit the sun due to its gravity Solar System Formation The Nebula Hypothesis Parts of the Solar System Planet- a celestial body that is in orbit
Models for locations and motions in the solar system
 Journal of Physics and Astronomy Research Vol. 2(1), pp. 054-058, March, 2015. www.premierpublishers.org, ISSN: 2123-503x JPAR Review Models for locations and motions in the solar system Lena Strömberg
Journal of Physics and Astronomy Research Vol. 2(1), pp. 054-058, March, 2015. www.premierpublishers.org, ISSN: 2123-503x JPAR Review Models for locations and motions in the solar system Lena Strömberg
Theory of mean motion resonances.
 Theory of mean motion resonances. Mean motion resonances are ubiquitous in space. They can be found between planets and asteroids, planets and rings in gaseous disks or satellites and planetary rings.
Theory of mean motion resonances. Mean motion resonances are ubiquitous in space. They can be found between planets and asteroids, planets and rings in gaseous disks or satellites and planetary rings.
Edmonds Community College ASTRONOMY 100 Sample Test #2 Fall Quarter 2006
 Edmonds Community College ASTRONOMY 100 Sample Test #2 Fall Quarter 2006 Instructor: L. M. Khandro 10/19/06 Please Note: the following test derives from a course and text that covers the entire topic of
Edmonds Community College ASTRONOMY 100 Sample Test #2 Fall Quarter 2006 Instructor: L. M. Khandro 10/19/06 Please Note: the following test derives from a course and text that covers the entire topic of
By A. M. Ilyanok and I. A. Timoshchenko.
 QUANTIZATION OF MASSES IN THE SOLAR SYSTEM. By A. M. Ilyanok and I. A. Timoshchenko. The hypothesis of quantization of masses of the solar system planets is considered. It is supposed that the solar system
QUANTIZATION OF MASSES IN THE SOLAR SYSTEM. By A. M. Ilyanok and I. A. Timoshchenko. The hypothesis of quantization of masses of the solar system planets is considered. It is supposed that the solar system
Finding Other Earths. Jason H. Steffen. Asset Earth Waubonsee Community College October 1, 2009
 Finding Other Earths Jason H. Steffen Asset Earth Waubonsee Community College October 1, 2009 True Earth Analog Necessities: 1) Main Sequence Star 2) Within the Stellar Habitable Zone 3) Roughly Earth
Finding Other Earths Jason H. Steffen Asset Earth Waubonsee Community College October 1, 2009 True Earth Analog Necessities: 1) Main Sequence Star 2) Within the Stellar Habitable Zone 3) Roughly Earth
Question number Answer Notes Marks 1 correctly; (ii) Sun X should be left of the imaginary 5-7 line, reject X placed outside the orbit
 ( a) (i) omet orbit behind Sun completed Dashed or solid correctly; curved line X marked anywhere in grey area; No need to label X as Sun X should be left of the imaginary 5-7 line, reject X placed outside
( a) (i) omet orbit behind Sun completed Dashed or solid correctly; curved line X marked anywhere in grey area; No need to label X as Sun X should be left of the imaginary 5-7 line, reject X placed outside
ASTROMATH 101: BEGINNING MATHEMATICS IN ASTRONOMY
 Name Partner(s) Section Date ASTROMATH 101: BEGINNING MATHEMATICS IN ASTRONOMY Astronomers deal with very, very large distances, some incredible temperatures, and even really, really small wavelengths.
Name Partner(s) Section Date ASTROMATH 101: BEGINNING MATHEMATICS IN ASTRONOMY Astronomers deal with very, very large distances, some incredible temperatures, and even really, really small wavelengths.
3. Period Law: Simplified proof for circular orbits Equate gravitational and centripetal forces
 Physics 106 Lecture 10 Kepler s Laws and Planetary Motion-continued SJ 7 th ed.: Chap 1., 1.6 Kepler s laws of planetary otion Orbit Law Area Law Period Law Satellite and planetary orbits Orbits, potential,
Physics 106 Lecture 10 Kepler s Laws and Planetary Motion-continued SJ 7 th ed.: Chap 1., 1.6 Kepler s laws of planetary otion Orbit Law Area Law Period Law Satellite and planetary orbits Orbits, potential,
