Proceedings of Neural, Parallel, and Scientific Computations 4 (2010) xx-xx PHASE OSCILLATOR NETWORK WITH PIECEWISE-LINEAR DYNAMICS

Transcription

1 Proceedings of Neural, Parallel, and Scientific Computations 4 (2010) xx-xx PHASE OSCILLATOR NETWORK WITH PIECEWISE-LINEAR DYNAMICS WALTER GALL, YING ZHOU, AND JOSEPH SALISBURY Department of Mathematics and Computer Science, Rhode Island College, Providence, Rhode Island 02908, USA. Department of Mathematics and Computer Science, Rhode Island College, Providence, Rhode Island 02908, USA. Neuroscience Program, Brandeis University, Waltham, Massachusetts 02454, USA. ABSTRACT. We consider a Filippov system formed from N coupled phase oscillators similar to the Kuramoto model but using a periodic sawtooth in place of the sine wave. A Hebbian rule based interaction provides for a phase oscillator associative memory network where the memorized patterns are stored as phase-locked limit-cycle attractors. AMS (MOS) Subject Classification. 37N INTRODUCTION The Kuramoto model of coupled oscillators [5] was motivated by the phenomenon of collective synchronization in some networks with a large number of oscillators [11]. Here the frequencies of the oscillations can become locked to a common frequency despite the variations in the natural frequencies of the individual oscillators [8]. Generalizations of the model can be used to form phase oscillator associative memory networks, where the memorized patterns are stored as limit-cycles, although there are problems with the stability of the limit-cycle memories that must be overcome with the addition of higher-order terms [6]. The Kuramoto model describes the dynamics of a system of N phase oscillators θ i with natural frequencies ω i. The time evolution of the i-th oscillator is given by (1.1) θi = ω i + k ij sin(θ j θ i ), i = 1,..., N, where k jk are parameters representing the coupling strengths from the j-th to the i-th oscillators. The sine function was chosen because it would be the first-order term in the Fourier expansion of more general interactions. To visualize the phases, it is helpful to think of the oscillators as points on a unit circle moving with different angular velocities. In the case of synchronization, the points on the circle move around with constant phase differences. We approximate the sine wave interaction of the Kuramoto model by a periodic piecewiselinear (but discontinuous) sawtooth, which is interesting in its own right, and is more appropriate for some applications such as wireless sensor network synchronization [10]. We investigate the finite-n case with a symmetric (self-adjoint) N N connection matrix, as occurs in some phase-oscillator network models of neurocomputers utilizing phase-lock loops [3], and optical laser oscillator technologies [4], or any neural network that learns by a Received May 30, c Dynamic Publishers, Inc.

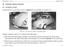
2 2 WALTER GALL, YING ZHOU, AND JOSEPH SALISBURY Hebbian rule. We will find that associative memories can be encoded by stable phase-locked limit cycles. 2. MODEL DESCRIPTION We propose a simplified model where the nonlinear sine function is replaced by a periodic piecewise-linear sawtooth-like function. Our finite-n phase oscillators are modeled as (2.1) θi = ω i + k ij saw(θ j θ i ), i = 1,..., N, where x + π (2.2) saw(x) = x π π x π is defined using the floor and ceiling functions. Here ω i and k ij are the natural frequency and the coupling strength, respectively, for the oscillator θ i. Saw is a discontinuous function, and this is a Filippov dynamical system [2]. The function saw(x) = x is the first-order term in the Taylor expansion of sin(x) on ( π, π), extended -periodically so that saw(x) = x j when j π < x < j +π, j Z, and saw((2j ± 1)π) = 0, j Z. Our definition results in saw being an odd function and the average of its right-side and left-side limits at points of discontinuity. Hence, by Dirichlet s theorem, its Fourier sine series converges point-wise to saw for all x R [9], and we can also write (2.3) saw(x) = 2 (sin(x) 12 sin(2x) + 13 sin(3x) 14 ) sin(4x) As mentioned before, we will consider each phase component ω i S 1, and thus (2.1) as a dynamical system on the N-dimensional torus T N. The terms sin(θ j θ i ) and saw(θ j θ i ) are both positive whenever the oscillator θ j is slightly ahead of the oscillator θ i, so that the term saw(θ j θ i ) contributes to the acceleration of the oscillator θ i. Similarly, they are both negative when θ j is slightly behind θ i, so that θ i slows down. The terms are both zero when the phases differ by exactly half a period, as if diametrically opposed oscillators are equally undecided whether to speed up or slow down, as was the case with Buridan s donkey. See Figure 1(a). However, the saw function is increasing on ( π, π) and so becomes increasingly larger in absolute value as the phase difference approaches either ±π. This implies that as the absolute phase difference between the oscillators θ j θ i becomes larger, saw(θ j θ i ) (or π 1 saw(θ j θ i ) to compare similar amplitudes) contributes more to the catching up or slowing down than either sin(θ j θ i ) or a smaller absolute phase difference would, encouraging coherence in comparison with the original Kuramoto dynamics. One could perhaps imagine runners on a circular track connected by elastic bands. 3. SYNCHRONIZATION It turns out that in the symmetric case k ij = k ji, i, j, for N oscillators, the space of phase-deviations is actually a gradient system (in a generalized sense) which can endow the system (2.1) with neurocomputational properties.

3 PHASE OSCILLATOR NETWORK 3 Figure 1. (a) COMPARING THE PIECEWISE-LINEAR SAWTOOTH AND π SINE WAVES. (b) THE GENERALIZED ANTIDERIVATIVE I(X) OF SAW(X) The Generalized Antiderivative of Saw. The Fourier expansion of saw can be integrated term-by-term to obtain an antiderivative I(x) for saw: ( ) (3.1) I(x) = π2 6 2 cos 2x cos 3x cos x See Figure 1(b). The function I(x) is -periodic, piecewise-smooth, and continuous, with (3.2) I(x) = 1 ( x + π ) 2 x for x (, ). 2 When x [ π, π], I(x) = x 2 /2. Now I (x) = saw(x), x R, with the derivative being taken in a generalized sense at the points {(2m + 1)π, m Z}. It is interesting to note that if we define a centered-derivative of a function f at a point x to be the limit of the centered-difference quotients: lim h 0 f(x + h) f(x h), 2h then saw(x) is the centered-derivative of I(x) for all x, including the points at which I is not differentiable in the classical sense. This can be made the basis of a simple multistep second-order numerical scheme The Phase Deviation Equations. We let (3.3) ω = 1 N be the mean natural frequency, and let (3.4) ψ i = θ i ωt, i = 1,..., N ω i

4 4 WALTER GALL, YING ZHOU, AND JOSEPH SALISBURY be the phase deviations. Let (3.5) ν i = ω i ω be the natural frequency deviations. Note that i ν i = 0. The phase deviation equations become (3.6) ψ i = ν i + k ij saw(ψ j ψ i ), i = 1,..., N. Note that if (3.7) ψ = 1 N is the mean of the phase deviations, then (3.8) in the symmetric case. d ψ dt = A Potential For the Phase Deviation Equations. When the k ij s are symmetric, a (negative) potential for the phase deviation equations can be given by (3.9) U( ψ) = ν i ψ i 1 k ij I(ψ i ψ j ), 2 ψ i where ψ is the vector of phase deviations (ψ 1,..., ψ N ). equations (3.6) is just the gradient system (3.10) d ψ dt = U( ψ). The system of phase deviation Hence, the phase deviations ψ converge to an equilibrium ψ 0 on T N. Thus, the phases θ i = ωt + ψ i converge to a limit-cycle attractor having frequency ω and phase relations ψ Hebbian Learning Rule and Neurocomputational Properties. This can form the basis of a neurocomputer with oscillatory associative memory. When N is large, there could be many such phase-locked limit-cycle attractors corresponding to many memorized patterns which are encoded into (or decoded from) the symmetric connection matrix K = k ij using the spectral theorem. Each phase-locked limit-cycle corresponds to an equilibrium of the phase deviation equations. And each equilibrium of the phase deviations corresponds to an extremum of U which corresponds to an eigenvector of K when all ν i = 0. For example, if ξ 1,..., ξ n are n orthogonal unit column N-vectors to be learned (n < N) with real weights µ 1,..., µ n, let n (3.11) K = µ j ξ j ξj t. Then, K is symmetric with eigenvectors ξ j and eigenvalues µ j on the orthogonal complement of the nullspace of K. Moreover, n (3.12) Kξ m = µ j ξ j ξj t ξ m = µ m ξ m. This results in the system asymptotically approaching the associated component at the bottom of a basin of attraction in which the initial input was located.

5 PHASE OSCILLATOR NETWORK 5 4. DISCUSSION Using the sawtooth function to model the symmetric interaction between N coupled phase oscillators, we obtain a piecewise-smooth, piecewise-linear system which can be analyzed explicitly. The phase deviations from the mean phase evolve according to a (generalized) gradient system. Stable phase-locking occurs at minimums of the potential energy function. One would expect that speed of convergence would be more rapid with sawtooth interactions compared to sine waves. Presented with a pattern close to one of the stored patterns, in the case that the ν i 0, the phase system with the symmetric connection matrix K and zero diagonal implementing a Hebbian learning rule will recall (or discriminant) by phase-locking with the closest stored pattern of phase deviations. Similarly, presented with a mixture of the stored patterns, the phase system will tend to phase-lock (or abstract) with the pattern with the largest positive weight present in the mixture, just as in principal component analysis. The use of oscillatory memories is especially interesting to neurocomputing since phaselocking has been hypothesized [1] to be important in such things as in binding gestalts, multiplexing in the thalamus, and reaching consensus by winner-take-all in the cortex. Phase oscillator networks have also been used in modeling central pattern generators for locomotion [7]. Many questions regarding capacity, retrieval, effects of forcing, inputing faster oscillation rates, possible multiplexing, and practical applications remain to be investigated. REFERENCES [1] M.A. Arbib (Ed.), Handbook of Brain Theory and Neural Networks (2ed.), MIT Press, Cambridge, [2] M. dibernardo, C.J. Budd, A.R. Champneys and P. Kowalczyk, Piecewise-smooth Dynamical Systems: Theory and Applications, Springer-Verlag, London, [3] F. Hoppensteadt and E. Izhikevich, Pattern recognition via synchronization in phase-locked loop neural networks, IEEE Transaction on Neural Network, 1: , [4] F.C. Hoppensteadt and E.M. Izhikevich, Synchronization of laser oscillators, associative memory, and optical neurocomputing, Physical Review E, 62: , [5] Y. Kuramoto, Chemical Oscillations, Waves, and Turbulence, Springer-Verlag, New York, [6] T. Nishikawa, F.C. Hoppensteadt and Y.C. Lai, Oscillatory associative memory networks with perfect retrieval, Physica D, 197: , [7] R.H. Rand, A.H. Cohen and P.J. Holmes, Systems of coupled oscillators as models of central pattern generators, in: A. Cohen (Ed.), Neural Control of Rhythmic Movements in Vertebrates, Wiley, New York, [8] S.H. Strogatz, From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators, Physica D, 143:1 20, [9] G.P. Tolstov, Fourier Series, Dover Publications, New York, [10] G. Werner-Allen, G. Tewari, A. Patel, M. Welch and R. Nagpal, Firefly-inspired sensor network synchronicity with realistic radio effects, Proceedings of the 3rd International Conference on Embedded Networked Sensor Systems, , [11] A.T. Winfree, The Geometry of Biological Time, Springer, New York, 1980.