Identifying and Classifying 2-D Shapes
|
|
|
- Matthew Doyle
- 6 years ago
- Views:
Transcription
1 Ientifying n Clssifying -D Shpes Wht is your sign? The shpe n olour of trffi signs let motorists know importnt informtion suh s: when to stop onstrution res. Some si shpes use in trffi signs re illustrte elow. Cirle Squre Retngle Otgon Tringle Knowlege n Employility Stuio Mthemtis Shpe n Spe: Ojets n Shpes: Alert Eution, Alert, Cn ( Ientifying n Clssifying -D Shpes /6
2 The tle shows how mny sies eh shpe hs. Shpe Numer of sies Cirle Tringle Retngle Squre Shpes tht hve more thn one sie re lle polygons. A stop sign is n 8-sie polygon lle n otgon n yiel sign is -sie polygon lle tringle. Qurilterls Retngles n squres hve four sies n re prt of lrger group of four-sie shpes lle qurilterls. The ngles of qurilterls totl 60. A qurilterl is ny four-sie figure. quri four lterl sie There re mny types of qurilterls, n they re lssifie oring to their shpes, ngles n lengths of sies, s shown elow. squre retngle prllelogrm rhomus trpezoi Know lege n Employility Stuio Mthemtis Shpe n Spe: Ojets n Shpes: Alert Eution, Alert, Cn ( Ientifying n Clssifying -D Shpes /6
3 Shpe Squre Retngle Prllelogrm Rhomus Trpezoi Chrteristis All sies equl in length All ngles 90 Prllel sies equl in length, ut not the sme length s the other prllel sies All ngles 90 Two prllel sies re equl in length, ut other two prllel sies re ifferent length Two ifferent sets of ngle mesurements All sies equl in length Two ifferent sets of ngle mesurements Lengths of sies my not e equl Opposite sies re not prllel Angles vry n my iffer from eh other Tringles There re three types of tringles. Tringles re lssifie oring to the length of their sies n the mesurement of their lrgest ngle. The ngles of tringles totl 80.. Length of sies Isoseles Tringle Equilterl Tringle Slene Tringle Two sies re equl in length. line of symmetry All sies re equl in length. lines of symmetry All sies re ifferent in length. 0 lines of symmetry Mesurement of the lrgest ngle Right Tringle Aute Tringle Otuse Tringle Lrgest ngle is extly 90 Lrgest ngle is <90 Lrgest ngle is >90 Knowlege n Employility Stuio Mthemtis Shpe n Spe: Ojets n Shpes: Alert Eution, Alert, Cn ( Ientifying n Clssifying -D Shpes /6
4 Think Aout Humn-me strutures suh s uilings n riges re reting using shpes suh s irles, retngles n squres. Shpes re lso foun in nture, for exmple, the sun is irle n the entre of flower is irle. Wht other shpes re foun in nture? Prtie: Mesuring n Clssifying Qurilterls. Use ruler n protrtor to mesure n reor the lengths of eh sie n ngle. Then lssify eh qurilterl. Shpe Length of eh sie Angles.. ) ) ). ) ). ) Knowlege n Employility Stuio Mthemtis Shpe n Spe: Ojets n Shpes: Alert Eution, Alert, Cn ( Ientifying n Clssifying -D Shpes /6
5 Mesure n Clssify Qurilterls (ontinue) Shpe Length of eh sie Angles.. ) ) ). ) ). ).. ) ) ) With prtner, lote vriety of lrge n smll qurilterls in your lssroom or shool, suh s oors, winows, tles n tiles. Use pproprite instruments to mesure ngles n sies (in metri n/or imperil units). Knowlege n Employility Stuio Mthemtis Shpe n Spe: Ojets n Shpes: Alert Eution, Alert, Cn ( Ientifying n Clssifying -D Shpes 5/6
6 Prtie: Mesuring n Clssifying Tringles. For eh tringle, mesure the lengths of eh sie n ngle using ruler n protrtor. Clssify eh tringle oring to the length of sies n ngles. Shpe Length of eh sie Angles. ) ). ) ). ) ) Mny is esigning tringulr errings. She mkes eh sie of the tringles ifferent length. Two of the sies join together to form n ngle of. Clssify, in two wys, the types of tringles Mny esigne. Knowlege n Employility Stuio Mthemtis Shpe n Spe: Ojets n Shpes: Alert Eution, Alert, Cn ( Ientifying n Clssifying -D Shpes 6/6
3 Angle Geometry. 3.1 Measuring Angles. 1. Using a protractor, measure the marked angles.
 3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Mathematics 10 Page 1 of 5 Properties of Triangle s and Quadrilaterals. Isosceles Triangle. - 2 sides and 2 corresponding.
 Mthemtis 10 Pge 1 of 5 Properties of s Pthgoren Theorem 2 2 2 used to find the length of sides of right tringle Tpe of s nd Some s Theorems ngles s Slene Isoseles Equilterl ute - ll ngles re less thn 90
Mthemtis 10 Pge 1 of 5 Properties of s Pthgoren Theorem 2 2 2 used to find the length of sides of right tringle Tpe of s nd Some s Theorems ngles s Slene Isoseles Equilterl ute - ll ngles re less thn 90
Area and Perimeter. Area and Perimeter. Solutions. Curriculum Ready.
 Are n Perimeter Are n Perimeter Solutions Curriulum Rey www.mthletis.om How oes it work? Solutions Are n Perimeter Pge questions Are using unit squres Are = whole squres Are = 6 whole squres = units =
Are n Perimeter Are n Perimeter Solutions Curriulum Rey www.mthletis.om How oes it work? Solutions Are n Perimeter Pge questions Are using unit squres Are = whole squres Are = 6 whole squres = units =
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Plotting Ordered Pairs Using Integers
 SAMPLE Plotting Ordered Pirs Using Integers Ple two elsti nds on geoord to form oordinte xes shown on the right to help you solve these prolems.. Wht letter of the lphet does eh set of pirs nme?. (, )
SAMPLE Plotting Ordered Pirs Using Integers Ple two elsti nds on geoord to form oordinte xes shown on the right to help you solve these prolems.. Wht letter of the lphet does eh set of pirs nme?. (, )
UNIT 31 Angles and Symmetry: Data Sheets
 UNIT 31 Angles nd Symmetry Dt Sheets Dt Sheets 31.1 Line nd Rottionl Symmetry 31.2 Angle Properties 31.3 Angles in Tringles 31.4 Angles nd Prllel Lines: Results 31.5 Angles nd Prllel Lines: Exmple 31.6
UNIT 31 Angles nd Symmetry Dt Sheets Dt Sheets 31.1 Line nd Rottionl Symmetry 31.2 Angle Properties 31.3 Angles in Tringles 31.4 Angles nd Prllel Lines: Results 31.5 Angles nd Prllel Lines: Exmple 31.6
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Applied. Grade 9 Assessment of Mathematics. Multiple-Choice Items. Winter 2005
 Applie Gre 9 Assessment of Mthemtis Multiple-Choie Items Winter 2005 Plese note: The formt of these ooklets is slightly ifferent from tht use for the ssessment. The items themselves remin the sme. . Multiple-Choie
Applie Gre 9 Assessment of Mthemtis Multiple-Choie Items Winter 2005 Plese note: The formt of these ooklets is slightly ifferent from tht use for the ssessment. The items themselves remin the sme. . Multiple-Choie
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
= x x 2 = 25 2
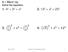 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
Perimeter and Area. Mathletics Instant Workbooks. Copyright
 Perimeter nd Are Student Book - Series J- L B Mthletis Instnt Workooks Copyright Student Book - Series J Contents Topis Topi - Plne shpes Topi 2 - Perimeter of regulr shpes Topi 3 - Perimeter of irregulr
Perimeter nd Are Student Book - Series J- L B Mthletis Instnt Workooks Copyright Student Book - Series J Contents Topis Topi - Plne shpes Topi 2 - Perimeter of regulr shpes Topi 3 - Perimeter of irregulr
MATHEMATICS AND STATISTICS 1.6
 MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Grade 6. Mathematics. Student Booklet SPRING 2008 RELEASED ASSESSMENT QUESTIONS. Assessment of Reading,Writing and Mathematics, Junior Division
 Gre 6 Assessment of Reing,Writing n Mthemtis, Junior Division Stuent Booklet Mthemtis SPRING 2008 RELEASED ASSESSMENT QUESTIONS Plese note: The formt of these ooklets is slightly ifferent from tht use
Gre 6 Assessment of Reing,Writing n Mthemtis, Junior Division Stuent Booklet Mthemtis SPRING 2008 RELEASED ASSESSMENT QUESTIONS Plese note: The formt of these ooklets is slightly ifferent from tht use
SAMPLE EVALUATION ONLY
 mesurement nd geometry topic 5 Geometry 5.1 Overview Why lern this? Geometry llows us to explore our world in very preise wy. uilders, rhitets, surveyors nd engineers use knowledge of geometry to ensure
mesurement nd geometry topic 5 Geometry 5.1 Overview Why lern this? Geometry llows us to explore our world in very preise wy. uilders, rhitets, surveyors nd engineers use knowledge of geometry to ensure
We use metres to measure length. There are 100 centimetres in a metre. a 6 m = cm b 3 m = cm c 9 m = cm
 Units of length metres We use metres to mesure length. There re 00 entimetres in metre. 00 m = m Convert these metres to entimetres: 6 m = m 3 m = m 9 m = m 600 300 900 Estimte nd then mesure the length
Units of length metres We use metres to mesure length. There re 00 entimetres in metre. 00 m = m Convert these metres to entimetres: 6 m = m 3 m = m 9 m = m 600 300 900 Estimte nd then mesure the length
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
STRAND F: GEOMETRY F1 Angles and Symmetry
 PRIMRY Mthemtis SKE, Strn F UNIT F1 ngles n Symmetry: Text STRND F: GEOMETRY F1 ngles n Symmetry Text ntents Setin F1.1 Mesuring ngles F1.2 Line n Rttinl Symmetry F1.3 ngle Gemetry F1.4 ngles with Prllel
PRIMRY Mthemtis SKE, Strn F UNIT F1 ngles n Symmetry: Text STRND F: GEOMETRY F1 ngles n Symmetry Text ntents Setin F1.1 Mesuring ngles F1.2 Line n Rttinl Symmetry F1.3 ngle Gemetry F1.4 ngles with Prllel
m m m m m m m m P m P m ( ) m m P( ) ( ). The o-ordinte of the point P( ) dividing the line segment joining the two points ( ) nd ( ) eternll in the r
 CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
Geometry of the Circle - Chords and Angles. Geometry of the Circle. Chord and Angles. Curriculum Ready ACMMG: 272.
 Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Similarity and Congruence
 Similrity nd ongruence urriculum Redy MMG: 201, 220, 221, 243, 244 www.mthletics.com SIMILRITY N ONGRUN If two shpes re congruent, it mens thy re equl in every wy ll their corresponding sides nd ngles
Similrity nd ongruence urriculum Redy MMG: 201, 220, 221, 243, 244 www.mthletics.com SIMILRITY N ONGRUN If two shpes re congruent, it mens thy re equl in every wy ll their corresponding sides nd ngles
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
Part I: Study the theorem statement.
 Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Student Book SERIES. Measurement. Name
 Student Book Nme Series Contents Topi Units of length (pp. 9) metres entimetres metres nd entimetres millimetres perimeter length nd deiml nottion onnet nd lok pply te ompleted Topi Are (pp. 0 5) squre
Student Book Nme Series Contents Topi Units of length (pp. 9) metres entimetres metres nd entimetres millimetres perimeter length nd deiml nottion onnet nd lok pply te ompleted Topi Are (pp. 0 5) squre
Trigonometry and Constructive Geometry
 Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Lesson 5.1 Polygon Sum Conjecture
 Lesson 5.1 olgon Sum onjeture me eriod te In erises 1 nd 2, find eh lettered ngle mesure. 1.,,, 2.,,, d, e d, e, f d e e d 97 f 26 85 44 3. ne eterior ngle of regulr polgon mesures 10. Wht is the mesure
Lesson 5.1 olgon Sum onjeture me eriod te In erises 1 nd 2, find eh lettered ngle mesure. 1.,,, 2.,,, d, e d, e, f d e e d 97 f 26 85 44 3. ne eterior ngle of regulr polgon mesures 10. Wht is the mesure
4. Statements Reasons
 Chpter 9 Answers Prentie-Hll In. Alterntive Ativity 9-. Chek students work.. Opposite sides re prllel. 3. Opposite sides re ongruent. 4. Opposite ngles re ongruent. 5. Digonls iset eh other. 6. Students
Chpter 9 Answers Prentie-Hll In. Alterntive Ativity 9-. Chek students work.. Opposite sides re prllel. 3. Opposite sides re ongruent. 4. Opposite ngles re ongruent. 5. Digonls iset eh other. 6. Students
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
VECTOR ALGEBRA. Syllabus :
 MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
 Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Definition :- A shape has a line of symmetry if, when folded over the line. 1 line of symmetry 2 lines of symmetry
 Symmetry Lines of Symmetry Definition :- A shpe hs line of symmetry if, when folded over the line the hlves of the shpe mtch up exctly. Some shpes hve more thn one line of symmetry : line of symmetry lines
Symmetry Lines of Symmetry Definition :- A shpe hs line of symmetry if, when folded over the line the hlves of the shpe mtch up exctly. Some shpes hve more thn one line of symmetry : line of symmetry lines
This conversion box can help you convert units of length. b 3 cm = e 11 cm = b 20 mm = cm. e 156 mm = b 500 cm = e cm = b mm = d 500 mm =
 Units of length,, To onvert fro to, ultiply y 10. This onversion ox n help you onvert units of length. To onvert fro to, divide y 10. 100 100 1 000 10 10 1 000 Convert these lengths to illietres: 0 1 2
Units of length,, To onvert fro to, ultiply y 10. This onversion ox n help you onvert units of length. To onvert fro to, divide y 10. 100 100 1 000 10 10 1 000 Convert these lengths to illietres: 0 1 2
8Similarity UNCORRECTED PAGE PROOFS. 8.1 Kick off with CAS 8.2 Similar objects 8.3 Linear scale factors. 8.4 Area and volume scale factors 8.
 8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8. re nd volume scle fctors 8. Review U N O R R E TE D P G E PR O O FS 8.1 Kick off with S Plese refer to the Resources t in the Prelims
8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8. re nd volume scle fctors 8. Review U N O R R E TE D P G E PR O O FS 8.1 Kick off with S Plese refer to the Resources t in the Prelims
ART LESSONS & EXERCISES
 RT LESSONS & EXERISES Rmón Gllego. www.diujormon.wordpress.com www.diujormon.wordpress.com English - Pge 1 www.diujormon.wordpress.com English - Pge 2 STRTING UP WITH GEOMETRY. DEFINITION OF GEOMETRY Geometry
RT LESSONS & EXERISES Rmón Gllego. www.diujormon.wordpress.com www.diujormon.wordpress.com English - Pge 1 www.diujormon.wordpress.com English - Pge 2 STRTING UP WITH GEOMETRY. DEFINITION OF GEOMETRY Geometry
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
Factorising FACTORISING.
 Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Non Right Angled Triangles
 Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Alg 3 Ch 7.2, 8 1. C 2) If A = 30, and C = 45, a = 1 find b and c A
 lg 3 h 7.2, 8 1 7.2 Right Tringle Trig ) Use of clcultor sin 10 = sin x =.4741 c ) rete right tringles π 1) If = nd = 25, find 6 c 2) If = 30, nd = 45, = 1 find nd c 3) If in right, with right ngle t,
lg 3 h 7.2, 8 1 7.2 Right Tringle Trig ) Use of clcultor sin 10 = sin x =.4741 c ) rete right tringles π 1) If = nd = 25, find 6 c 2) If = 30, nd = 45, = 1 find nd c 3) If in right, with right ngle t,
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
POLYGONS. Polygons PASSPORT
 PLYGNS PSSPRT www.mthletis.o.uk This ooklet is out ientifing n mnipulting stright sie shpes using their unique properties Mn lever people ontriute to the evelopment of moern geometr inluing: Thles of
PLYGNS PSSPRT www.mthletis.o.uk This ooklet is out ientifing n mnipulting stright sie shpes using their unique properties Mn lever people ontriute to the evelopment of moern geometr inluing: Thles of
Equivalent fractions have the same value but they have different denominators. This means they have been divided into a different number of parts.
 Frtions equivlent frtions Equivlent frtions hve the sme vlue ut they hve ifferent enomintors. This mens they hve een ivie into ifferent numer of prts. Use the wll to fin the equivlent frtions: Wht frtions
Frtions equivlent frtions Equivlent frtions hve the sme vlue ut they hve ifferent enomintors. This mens they hve een ivie into ifferent numer of prts. Use the wll to fin the equivlent frtions: Wht frtions
Mathematical Proofs Table of Contents
 Mthemtil Proofs Tle of Contents Proof Stnr Pge(s) Are of Trpezoi 7MG. Geometry 8.0 Are of Cirle 6MG., 9 6MG. 7MG. Geometry 8.0 Volume of Right Cirulr Cyliner 6MG. 4 7MG. Geometry 8.0 Volume of Sphere Geometry
Mthemtil Proofs Tle of Contents Proof Stnr Pge(s) Are of Trpezoi 7MG. Geometry 8.0 Are of Cirle 6MG., 9 6MG. 7MG. Geometry 8.0 Volume of Right Cirulr Cyliner 6MG. 4 7MG. Geometry 8.0 Volume of Sphere Geometry
Shape and measurement
 C H A P T E R 5 Shpe nd mesurement Wht is Pythgors theorem? How do we use Pythgors theorem? How do we find the perimeter of shpe? How do we find the re of shpe? How do we find the volume of shpe? How do
C H A P T E R 5 Shpe nd mesurement Wht is Pythgors theorem? How do we use Pythgors theorem? How do we find the perimeter of shpe? How do we find the re of shpe? How do we find the volume of shpe? How do
2 Calculate the size of each angle marked by a letter in these triangles.
 Cmridge Essentils Mthemtics Support 8 GM1.1 GM1.1 1 Clculte the size of ech ngle mrked y letter. c 2 Clculte the size of ech ngle mrked y letter in these tringles. c d 3 Clculte the size of ech ngle mrked
Cmridge Essentils Mthemtics Support 8 GM1.1 GM1.1 1 Clculte the size of ech ngle mrked y letter. c 2 Clculte the size of ech ngle mrked y letter in these tringles. c d 3 Clculte the size of ech ngle mrked
STRAND I: Geometry and Trigonometry. UNIT 32 Angles, Circles and Tangents: Student Text Contents. Section Compass Bearings
 ME Jmi: STR I UIT 32 ngles, irles n Tngents: Stuent Tet ontents STR I: Geometry n Trigonometry Unit 32 ngles, irles n Tngents Stuent Tet ontents Setion 32.1 ompss erings 32.2 ngles n irles 1 32.3 ngles
ME Jmi: STR I UIT 32 ngles, irles n Tngents: Stuent Tet ontents STR I: Geometry n Trigonometry Unit 32 ngles, irles n Tngents Stuent Tet ontents Setion 32.1 ompss erings 32.2 ngles n irles 1 32.3 ngles
Basic Angle Rules 5. A Short Hand Geometric Reasons. B Two Reasons. 1 Write in full the meaning of these short hand geometric reasons.
 si ngle Rules 5 6 Short Hnd Geometri Resons 1 Write in full the mening of these short hnd geometri resons. Short Hnd Reson Full Mening ) se s isos Δ re =. ) orr s // lines re =. ) sum s t pt = 360. d)
si ngle Rules 5 6 Short Hnd Geometri Resons 1 Write in full the mening of these short hnd geometri resons. Short Hnd Reson Full Mening ) se s isos Δ re =. ) orr s // lines re =. ) sum s t pt = 360. d)
8Similarity ONLINE PAGE PROOFS. 8.1 Kick off with CAS 8.2 Similar objects 8.3 Linear scale factors. 8.4 Area and volume scale factors 8.
 8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8.4 re nd volume scle fctors 8. Review Plese refer to the Resources t in the Prelims section of your eookplus for comprehensive step-y-step
8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8.4 re nd volume scle fctors 8. Review Plese refer to the Resources t in the Prelims section of your eookplus for comprehensive step-y-step
SEMI-EXCIRCLE OF QUADRILATERAL
 JP Journl of Mthemtil Sienes Volume 5, Issue &, 05, Pges - 05 Ishn Pulishing House This pper is ville online t http://wwwiphsiom SEMI-EXCIRCLE OF QUADRILATERAL MASHADI, SRI GEMAWATI, HASRIATI AND HESY
JP Journl of Mthemtil Sienes Volume 5, Issue &, 05, Pges - 05 Ishn Pulishing House This pper is ville online t http://wwwiphsiom SEMI-EXCIRCLE OF QUADRILATERAL MASHADI, SRI GEMAWATI, HASRIATI AND HESY
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
THE KENNESAW STATE UNIVERSITY HIGH SCHOOL MATHEMATICS COMPETITION PART I MULTIPLE CHOICE NO CALCULATORS 90 MINUTES
 THE 08 09 KENNESW STTE UNIVERSITY HIGH SHOOL MTHEMTIS OMPETITION PRT I MULTIPLE HOIE For ech of the following questions, crefully blcken the pproprite box on the nswer sheet with # pencil. o not fold,
THE 08 09 KENNESW STTE UNIVERSITY HIGH SHOOL MTHEMTIS OMPETITION PRT I MULTIPLE HOIE For ech of the following questions, crefully blcken the pproprite box on the nswer sheet with # pencil. o not fold,
R(3, 8) P( 3, 0) Q( 2, 2) S(5, 3) Q(2, 32) P(0, 8) Higher Mathematics Objective Test Practice Book. 1 The diagram shows a sketch of part of
 Higher Mthemtics Ojective Test Prctice ook The digrm shows sketch of prt of the grph of f ( ). The digrm shows sketch of the cuic f ( ). R(, 8) f ( ) f ( ) P(, ) Q(, ) S(, ) Wht re the domin nd rnge of
Higher Mthemtics Ojective Test Prctice ook The digrm shows sketch of prt of the grph of f ( ). The digrm shows sketch of the cuic f ( ). R(, 8) f ( ) f ( ) P(, ) Q(, ) S(, ) Wht re the domin nd rnge of
m A 1 1 A ! and AC 6
 REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
03. Early Greeks & Aristotle
 03. Erly Greeks & Aristotle I. Erly Greeks Topis I. Erly Greeks II. The Method of Exhustion III. Aristotle. Anximnder (. 60 B.C.) to peiron - the unlimited, unounded - fundmentl sustne of relity - underlying
03. Erly Greeks & Aristotle I. Erly Greeks Topis I. Erly Greeks II. The Method of Exhustion III. Aristotle. Anximnder (. 60 B.C.) to peiron - the unlimited, unounded - fundmentl sustne of relity - underlying
Geometry AP Book 8, Part 2: Unit 3
 Geometry ook 8, rt 2: Unit 3 IMRTNT NTE: For mny questions in this unit, there re multiple correct nswers, e.g. line segment cn e written s, RST is the sme s TSR, etc. Where pproprite, techers should e
Geometry ook 8, rt 2: Unit 3 IMRTNT NTE: For mny questions in this unit, there re multiple correct nswers, e.g. line segment cn e written s, RST is the sme s TSR, etc. Where pproprite, techers should e
MEP Practice Book ES3. 1. Calculate the size of the angles marked with a letter in each diagram. None to scale
 ME rctice ook ES3 3 ngle Geometr 3.3 ngle Geometr 1. lculte the size of the ngles mrked with letter in ech digrm. None to scle () 70 () 20 54 65 25 c 36 (d) (e) (f) 56 62 d e 60 40 70 70 f 30 g (g) (h)
ME rctice ook ES3 3 ngle Geometr 3.3 ngle Geometr 1. lculte the size of the ngles mrked with letter in ech digrm. None to scle () 70 () 20 54 65 25 c 36 (d) (e) (f) 56 62 d e 60 40 70 70 f 30 g (g) (h)
A B= ( ) because from A to B is 3 right, 2 down.
 8. Vectors nd vector nottion Questions re trgeted t the grdes indicted Remember: mgnitude mens size. The vector ( ) mens move left nd up. On Resource sheet 8. drw ccurtely nd lbel the following vectors.
8. Vectors nd vector nottion Questions re trgeted t the grdes indicted Remember: mgnitude mens size. The vector ( ) mens move left nd up. On Resource sheet 8. drw ccurtely nd lbel the following vectors.
Section 2.1 Special Right Triangles
 Se..1 Speil Rigt Tringles 49 Te --90 Tringle Setion.1 Speil Rigt Tringles Te --90 tringle (or just 0-60-90) is so nme euse of its ngle mesures. Te lengts of te sies, toug, ve very speifi pttern to tem
Se..1 Speil Rigt Tringles 49 Te --90 Tringle Setion.1 Speil Rigt Tringles Te --90 tringle (or just 0-60-90) is so nme euse of its ngle mesures. Te lengts of te sies, toug, ve very speifi pttern to tem
Area and Perimeter. Area and Perimeter. Curriculum Ready.
 Are nd Perimeter Curriculum Redy www.mthletics.com This ooklet shows how to clculte the re nd perimeter of common plne shpes. Footll fields use rectngles, circles, qudrnts nd minor segments with specific
Are nd Perimeter Curriculum Redy www.mthletics.com This ooklet shows how to clculte the re nd perimeter of common plne shpes. Footll fields use rectngles, circles, qudrnts nd minor segments with specific
H SERIES. Area and Perimeter. Curriculum Ready ACMMG: 109, 159, 196,
 Are n Perimeter Curriulum Rey ACMMG: 0, 5, 6, 6 www.mthletis.om Copyright 00 3P Lerning. All rights reserve. First eition printe 00 in Austrli. A tlogue reor for this ook is ville from 3P Lerning Lt. ISBN
Are n Perimeter Curriulum Rey ACMMG: 0, 5, 6, 6 www.mthletis.om Copyright 00 3P Lerning. All rights reserve. First eition printe 00 in Austrli. A tlogue reor for this ook is ville from 3P Lerning Lt. ISBN
Similar Right Triangles
 Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Something found at a salad bar
 Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Perimeter, area and volume
 6 Perimeter, re nd volume Syllus topi M. Perimeter, re nd volume This topi will develop your skills to ompetently solve prolems involving perimeter, re, volume nd pity. Outomes Clulte the re of irles nd
6 Perimeter, re nd volume Syllus topi M. Perimeter, re nd volume This topi will develop your skills to ompetently solve prolems involving perimeter, re, volume nd pity. Outomes Clulte the re of irles nd
Algebra Basics. Algebra Basics. Curriculum Ready ACMNA: 133, 175, 176, 177, 179.
 Curriulum Redy ACMNA: 33 75 76 77 79 www.mthletis.om Fill in the spes with nything you lredy know out Alger Creer Opportunities: Arhitets eletriins plumers et. use it to do importnt lultions. Give this
Curriulum Redy ACMNA: 33 75 76 77 79 www.mthletis.om Fill in the spes with nything you lredy know out Alger Creer Opportunities: Arhitets eletriins plumers et. use it to do importnt lultions. Give this
4.4 Areas, Integrals and Antiderivatives
 . res, integrls nd ntiderivtives 333. Ares, Integrls nd Antiderivtives This section explores properties of functions defined s res nd exmines some connections mong res, integrls nd ntiderivtives. In order
. res, integrls nd ntiderivtives 333. Ares, Integrls nd Antiderivtives This section explores properties of functions defined s res nd exmines some connections mong res, integrls nd ntiderivtives. In order
Log1 Contest Round 3 Theta Individual. 4 points each 1 What is the sum of the first 5 Fibonacci numbers if the first two are 1, 1?
 008 009 Log1 Contest Round Thet Individul Nme: points ech 1 Wht is the sum of the first Fiboncci numbers if the first two re 1, 1? If two crds re drwn from stndrd crd deck, wht is the probbility of drwing
008 009 Log1 Contest Round Thet Individul Nme: points ech 1 Wht is the sum of the first Fiboncci numbers if the first two re 1, 1? If two crds re drwn from stndrd crd deck, wht is the probbility of drwing
What s in Chapter 13?
 Are nd volume 13 Wht s in Chpter 13? 13 01 re 13 0 Are of circle 13 03 res of trpeziums, kites nd rhomuses 13 04 surfce re of rectngulr prism 13 05 surfce re of tringulr prism 13 06 surfce re of cylinder
Are nd volume 13 Wht s in Chpter 13? 13 01 re 13 0 Are of circle 13 03 res of trpeziums, kites nd rhomuses 13 04 surfce re of rectngulr prism 13 05 surfce re of tringulr prism 13 06 surfce re of cylinder
Surds and Indices. Surds and Indices. Curriculum Ready ACMNA: 233,
 Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
MCH T 111 Handout Triangle Review Page 1 of 3
 Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Linear Algebra Introduction
 Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Section 6: Area, Volume, and Average Value
 Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
GEOMETRY OF THE CIRCLE TANGENTS & SECANTS
 Geometry Of The ircle Tngents & Secnts GEOMETRY OF THE IRLE TNGENTS & SENTS www.mthletics.com.u Tngents TNGENTS nd N Secnts SENTS Tngents nd secnts re lines tht strt outside circle. Tngent touches the
Geometry Of The ircle Tngents & Secnts GEOMETRY OF THE IRLE TNGENTS & SENTS www.mthletics.com.u Tngents TNGENTS nd N Secnts SENTS Tngents nd secnts re lines tht strt outside circle. Tngent touches the
STRAND J: TRANSFORMATIONS, VECTORS and MATRICES
 Mthemtics SKE: STRN J STRN J: TRNSFORMTIONS, VETORS nd MTRIES J3 Vectors Text ontents Section J3.1 Vectors nd Sclrs * J3. Vectors nd Geometry Mthemtics SKE: STRN J J3 Vectors J3.1 Vectors nd Sclrs Vectors
Mthemtics SKE: STRN J STRN J: TRNSFORMTIONS, VETORS nd MTRIES J3 Vectors Text ontents Section J3.1 Vectors nd Sclrs * J3. Vectors nd Geometry Mthemtics SKE: STRN J J3 Vectors J3.1 Vectors nd Sclrs Vectors
Problem Set 9. Figure 1: Diagram. This picture is a rough sketch of the 4 parabolas that give us the area that we need to find. The equations are:
 (x + y ) = y + (x + y ) = x + Problem Set 9 Discussion: Nov., Nov. 8, Nov. (on probbility nd binomil coefficients) The nme fter the problem is the designted writer of the solution of tht problem. (No one
(x + y ) = y + (x + y ) = x + Problem Set 9 Discussion: Nov., Nov. 8, Nov. (on probbility nd binomil coefficients) The nme fter the problem is the designted writer of the solution of tht problem. (No one
PYTHAGORAS THEOREM,TRIGONOMETRY,BEARINGS AND THREE DIMENSIONAL PROBLEMS
 PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
LUMS School of Science and Engineering
 LUMS School of Science nd Engineering PH- Solution of ssignment Mrch, 0, 0 Brvis Lttice Answer: We hve given tht c.5(î + ĵ + ˆk) 5 (î + ĵ + ˆk) 0 (î + ĵ + ˆk) c (î + ĵ + ˆk) î + ĵ + ˆk + b + c î, b ĵ nd
LUMS School of Science nd Engineering PH- Solution of ssignment Mrch, 0, 0 Brvis Lttice Answer: We hve given tht c.5(î + ĵ + ˆk) 5 (î + ĵ + ˆk) 0 (î + ĵ + ˆk) c (î + ĵ + ˆk) î + ĵ + ˆk + b + c î, b ĵ nd
3 x x 3x x. 3x x x 6 x 3. PAKTURK 8 th National Interschool Maths Olympiad, h h
 PAKTURK 8 th Ntionl Interschool Mths Olmpid,.9. Q: Evlute 6.9. 6 6 6... 8 8...... Q: Evlute bc bc. b. c bc.9.9b.9.9bc Q: Find the vlue of h in the eqution h 7 9 7.. bc. bc bc. b. c bc bc bc bc......9 h
PAKTURK 8 th Ntionl Interschool Mths Olmpid,.9. Q: Evlute 6.9. 6 6 6... 8 8...... Q: Evlute bc bc. b. c bc.9.9b.9.9bc Q: Find the vlue of h in the eqution h 7 9 7.. bc. bc bc. b. c bc bc bc bc......9 h
Preliminary preparation
 Preliminry preprtion Syllus prerequisite: Preliminry preprtion This topi provies the si knowlege, skills n unerstnings require in Yer. Outomes Simplify n lgeri expression. Estlish n pply inex lws in lgeri
Preliminry preprtion Syllus prerequisite: Preliminry preprtion This topi provies the si knowlege, skills n unerstnings require in Yer. Outomes Simplify n lgeri expression. Estlish n pply inex lws in lgeri
Solutions for HW9. Bipartite: put the red vertices in V 1 and the black in V 2. Not bipartite!
 Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
11Measurement. Australian curriculum MEASUREMENT AND GEOMETRY
 11A 11B 11C 11D 11E 11F 11G 11H 11I 11J Chpter Wht you will lern Mesurement systems (Extening) Using n onverting metri lengths (Consoliting) Perimeter (Consoliting) Ares n retngles Are of tringle Are of
11A 11B 11C 11D 11E 11F 11G 11H 11I 11J Chpter Wht you will lern Mesurement systems (Extening) Using n onverting metri lengths (Consoliting) Perimeter (Consoliting) Ares n retngles Are of tringle Are of
Measurement. Chapter. What you will learn
 Chpter 11 Mesurement Wht you will lern 11.1 11.2 11.3 11.4 11.5 11.6 11.7 11.8 11.9 11.10 Mesurement systems Using nd onverting metri lengths Perimeter Ares nd retngles Are of tringle Are of prllelogrm
Chpter 11 Mesurement Wht you will lern 11.1 11.2 11.3 11.4 11.5 11.6 11.7 11.8 11.9 11.10 Mesurement systems Using nd onverting metri lengths Perimeter Ares nd retngles Are of tringle Are of prllelogrm
Lecture 6: Coding theory
 Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Pythagoras Theorem PYTHAGORAS THEOREM.
 Pthgors Theorem PYTHAGORAS THEOREM www.mthletis.om.u How oes it work? Solutions Pthgors Theorem Pge 3 questions Right-ngle tringles D E x z Hotenuse is sie: F Hotenuse is sie: DF Q k j l Hotenuse is sie:
Pthgors Theorem PYTHAGORAS THEOREM www.mthletis.om.u How oes it work? Solutions Pthgors Theorem Pge 3 questions Right-ngle tringles D E x z Hotenuse is sie: F Hotenuse is sie: DF Q k j l Hotenuse is sie:
8 Measurement. How is measurement used in your home? 8E Area of a circle 8B Circumference of a circle. 8A Length and perimeter
 8A Length nd perimeter 8E Are of irle 8B Cirumferene of irle 8F Surfe re 8C Are of retngles nd tringles 8G Volume of prisms 8D Are of other qudrilterls 8H Are nd volume onversions SA M PL E Mesurement
8A Length nd perimeter 8E Are of irle 8B Cirumferene of irle 8F Surfe re 8C Are of retngles nd tringles 8G Volume of prisms 8D Are of other qudrilterls 8H Are nd volume onversions SA M PL E Mesurement
Things to Memorize: A Partial List. January 27, 2017
 Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
1 cos. cos cos cos cos MAT 126H Solutions Take-Home Exam 4. Problem 1
 MAT 16H Solutions Tke-Home Exm 4 Problem 1 ) & b) Using the hlf-ngle formul for cosine, we get: 1 cos 1 4 4 cos cos 8 4 nd 1 8 cos cos 16 4 c) Using the hlf-ngle formul for tngent, we get: cot ( 3π 1 )
MAT 16H Solutions Tke-Home Exm 4 Problem 1 ) & b) Using the hlf-ngle formul for cosine, we get: 1 cos 1 4 4 cos cos 8 4 nd 1 8 cos cos 16 4 c) Using the hlf-ngle formul for tngent, we get: cot ( 3π 1 )
UNCORRECTED PAGE PROOFS
 mesurement mesurement n n geometry geometry UNORRETE PGE PROOFS topi 10 edutive geometry 10.1 Overview Why lern this? Lerning out geometry inludes eing le to reson dedutively nd to prove logilly tht ertin
mesurement mesurement n n geometry geometry UNORRETE PGE PROOFS topi 10 edutive geometry 10.1 Overview Why lern this? Lerning out geometry inludes eing le to reson dedutively nd to prove logilly tht ertin
Math 8 Winter 2015 Applications of Integration
 Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
Matrix- System of rows and columns each position in a matrix has a purpose. 5 Ex: 5. Ex:
 Mtries Prelulus Mtri- Sstem of rows n olumns eh position in mtri hs purpose. Element- Eh vlue in the mtri mens the element in the n row, r olumn Dimensions- How mn rows b number of olumns Ientif the element:
Mtries Prelulus Mtri- Sstem of rows n olumns eh position in mtri hs purpose. Element- Eh vlue in the mtri mens the element in the n row, r olumn Dimensions- How mn rows b number of olumns Ientif the element:
A study of Pythagoras Theorem
 CHAPTER 19 A study of Pythgors Theorem Reson is immortl, ll else mortl. Pythgors, Diogenes Lertius (Lives of Eminent Philosophers) Pythgors Theorem is proly the est-known mthemticl theorem. Even most nonmthemticins
CHAPTER 19 A study of Pythgors Theorem Reson is immortl, ll else mortl. Pythgors, Diogenes Lertius (Lives of Eminent Philosophers) Pythgors Theorem is proly the est-known mthemticl theorem. Even most nonmthemticins
Individual Contest. English Version. Time limit: 90 minutes. Instructions:
 Elementry Mthemtics Interntionl Contest Instructions: Individul Contest Time limit: 90 minutes Do not turn to the first pge until you re told to do so. Write down your nme, your contestnt numer nd your
Elementry Mthemtics Interntionl Contest Instructions: Individul Contest Time limit: 90 minutes Do not turn to the first pge until you re told to do so. Write down your nme, your contestnt numer nd your
13.4 Work done by Constant Forces
 13.4 Work done by Constnt Forces We will begin our discussion of the concept of work by nlyzing the motion of n object in one dimension cted on by constnt forces. Let s consider the following exmple: push
13.4 Work done by Constnt Forces We will begin our discussion of the concept of work by nlyzing the motion of n object in one dimension cted on by constnt forces. Let s consider the following exmple: push
