A study of Pythagoras Theorem
|
|
|
- George Webster
- 5 years ago
- Views:
Transcription
1 CHAPTER 19 A study of Pythgors Theorem Reson is immortl, ll else mortl. Pythgors, Diogenes Lertius (Lives of Eminent Philosophers) Pythgors Theorem is proly the est-known mthemticl theorem. Even most nonmthemticins hve some vgue ide tht it involves tringles nd squring something known s the hypotenuse. Becuse the ides in the previous chpters on How to red theorem nd How to red proof re so importnt we will pply them to this fmous theorem to see them in ction. So in this chpter we will pull prt the theorem nd its proof, we ll see converse for it nd lso generliztion. Sttement of Pythgors Theorem As you re udding mthemticin, you proly hve etter ide thn nonmthemticin of wht the sttement is, ut here it is gin. Theorem 19.1 For right-ngled tringle the squre of the hypotenuse is equl to the sum of the squres of the other sides. Exercise 19.2 Use the ides from Chpter 16, How to red theorem, to nlyse the theorem. Compre your nlysis with the one given elow. Study of the theorem 126 We now nlyse the theorem s though we were meeting it for the first time. Oviously we would check wht ll the words men, for exmple, wht is hypotenuse? This is firly ovious, ut wht out the other techniques in Chpter 16? We shll pply them now.
2 Study of the theorem 127 Drw in this line Figure 19.1 Any tringle gives two right-ngled tringles Find the ssumptions nd conclusions The sttement given for Pythgors Theorem is good exmple of sttement not in the form A= B or if..., then.... We cn rewrite it in this form in numer of wys. For exmple, If T is right-ngled tringle with sides, nd hypotenuse c, then c 2 = This mke it ovious tht the ssumptions concern ll right-ngled tringles: T is right-ngled tringle with sides, nd hypotenuse c nd tht the conclusion is n eqution relting the lengths: c 2 = Rte the strength of the ssumptions nd conclusions Let s rte the ssumptions nd conclusions. The ssumption is out right-ngled tringles. Certinly, there re mny exmples of these, ut they re only smll suset of ll tringles. Thus we my e tempted to sy tht this is quite wek ut not too wek. But consider this. For ny tringle we cn produce two right-ngled tringles; see Figure Thus, despite initil impressions, this theorem will tell us something out ll tringles. This mens it is very wek ssumption. Tht is good. The more exmples theorem pplies to the etter. The conclusion is very concrete nd definite sttement. It is n eqution. If we just hd n inequlity (sy c ), then the conclusion would e less impressive. This is strong conclusion. Note lso tht the conclusion llows us to clculte: given the lengths of ny two sides of right-ngled tringle we cn clculte the third. Being le to clculte is lwys good for conclusion. From this we know we hve gret theorem which will e very useful s it llows us to clculte ttriutes of lrge numer of ojects. In fct, s you my know, it llows us to clculte distnces in Crtesin coordintes. Compre with previous theorems We don t hve mny theorems to compre with s this is very simple theorem from the foundtions of geometry. Another theorem from the foundtions is tht in tringle (not necessrily right-ngled) the ngles dd up to 180 degrees (or 2π rdins if you like).
3 128 CHAPTER 19 A study of Pythgors Theorem We cn see this is similr in the sense tht given two ngles we cn clculte the third. It is different in the sense tht it is out ngles rther thn out lengths. Thus they re quite complementry! Now tht we hve oserved theorem tht dels with lengths nd one tht dels with ngles we cn sk whether there exists one tht links oth. Indeed there is one. Exercise 19.3 Find theorem tht reltes ngles nd lengths in tringle. Oserve the detil There re not mny detils to oserve in Pythgors Theorem s it is rther simple. The detil to rememer perhps is tht the tringle is right-ngled not, for exmple, isosceles. (See the exercises t the end of the chpter for some infmous exmples of mistkes with the sttement.) Clssify wht the theorem does nd how it cn e used We hve lredy discussed ove wht the theorem does: it llows us to clculte the length of side of tringle given the lengths of the other two. Drw picture Since this is geometric theorem it is out tringles then we hve good reson to drw picture. In this cse drw lots of tringles nd mesure the lengths. Do the lengths stisfy the eqution? They should do ut rememer we cn only mesure lengths pproximtely. The clssic picture is the (3, 4, 5)-tringle given in Figure This is often mistkenly given s proof of the theorem. However, it is only single exmple, not proof Figure 19.2 The clssic (3, 4, 5)-tringle
4 Study of the theorem 129 Apply the theorem to simple exmples In drwing the pictures we hve lredy pplied the theorem to simple exmples such s the (3, 4, 5)-tringle. Apply the theorem to trivil nd extreme exmples The ssumptions concern right-ngled tringles. Wht re trivil nd extreme exmples of such ojects? I would sy tht the trivil exmples re when = 1 nd = 1 so c = 2. This is tringle with two sides of rtionl lengths nd one side of irrtionl length. One could view this s counterexmple to the sttement If two sides of tringle re rtionl, then so is the third. Another useful exmple is = 1, = 2, nd so c = 5. This just shows us wht hppens when one side is twice the length of the other. Another interesting exmple is = 1, = 2, nd so c = 3. I like this, it involves the first three numers 1, 2 nd 3. The tringle = 1, = 3 nd c = 4 is good s it hs n ngle of π/6. Now for extreme exmples. Wht is n extreme right-ngled tringle? We cn view = s n extreme tringle ecuse it is very specil cse of right-ngled tringle. Here c 2 = 2 2, so c = 2. This mens tht if is rtionl, then c cnnot e rtionl (since rtionl numer times n irrtionl numer, in this cse 2, is irrtionl). Another extreme we cn go to is to mke one of the sides very ig or very smll compred with the other. If we let tend to zero, then c 2 must tend to 2 s 2 gets smll. In other words c tends to. We cn see this in digrm. Just drw tringle with very smll s compred with ; you cn see tht nd c re lmost equl. Thus we hve shown tht the lger nd the geometry re linked in the wy we would expect. The lger grees with the geometry. Note tht if equls zero, then we do not hve tringle! Apply the theorem to non-exmples Let us consider non-exmples of the theorem. Here non-exmples re tringles tht re not right-ngled. However, in this cse how do we even define hypotenuse? This is lwys defined s the length opposite the right-ngle. There is no wy of identifying specil length, so there is no wy to identify which should go on the right-hnd side of c 2 = We need nother method of identifying c. Mye we hve to tke the longest side. This is resonle since, for c 2 = to e true, we must hve c>nd c>. To see this, consider tht 2 > 0 is true, thus c 2 > 2, nd so c>. Similrly c>. If you try drwing few exmples, then you will proly see tht the eqution does not hold, even tking into ccount pproximtions in mesuring. This should led us to sk Are there ny non-right-ngled tringles for which c 2 = 2 + 2? We shll del with this in the next section when we sk Is the converse true? We shll lso look t non-exmples in Exercises
5 130 CHAPTER 19 A study of Pythgors Theorem Rewrite in symols or words We hve lredy written the theorem in s mny symols s possile when we gve the if, then sttement. Note tht is not sufficient to sy only c 2 = We hve to explin wht, nd c re, nd tht c is the hypotenuse in right-ngled tringle. Proof of Pythgors Theorem As mentioned erlier, it is not enough to show the theorem works pproximtely for some exmples or even perfectly in some specil cses such s the (3, 4, 5)-tringle. We need to prove tht it holds for ll tringles. Mye you were told tht the theorem ws true y some uthority figure in the pst nd tht is good enough for you. However, centrl im of this ook is to encourge you to think for yourself nd tht involves checking ny rgument given to you. We will now see proof of the theorem. There re literlly hundreds of proofs. 1 My fvourite proof is geometricl. Proof (of Pythgors Theorem). The proof cn e shown using the two squres in Figure To drw the first squre egin y drwing generl tringle with sides nd nd then extend these edges y lengths nd respectively. Then we cn complete the drwing to get the squre on the left-hnd side of Figure We cn drw nother squre like the one on the right-hnd side of the figure. From the figure we cn see tht oth squres hve equl re nd so we cn conclude tht Are of left squre = Are of right squre c 2 + (4 Are of (, )-tringle) = (4 Are of (, )-tringle) c 2 = c c 2 2 c 2 Figure 19.3 Proof of Pythgors Theorem 1 There re over 360 in Elish Loomis, The Pythgoren Proposition, Ntionl Council of Techers of Mthemtics, 1968.
6 Exercise 19.4 Proof of Pythgors Theorem 131 Use the ides from Chpter 18, How to red proof, to nlyse the proof. Compre your nlysis with the one given elow. Not ll the suggestions in Chpter 18 re relevnt. Let us try some of them to help pull the proof prt. Find where the ssumptions re used Where hve we used the ssumption tht the tringle is right-ngled? It is used in constructing the first squre. If sides nd did not meet t right-ngle, then we could not construct squre. And hence could not conclude tht the re ws the sme s the squre on the right. Check the text If you check the text, then you my see tht one fct hs een used ut not explicitly stted. The picture is very convincing in tht the re lelled c 2 in the left-hnd picture certinly looks squre. But notice tht we hve not proved tht it is squre. We know tht ll the edges re the sme length ut this does not men tht the shpe is squre think of dimond or kite shpe. How do we know it is truly squre? Well, we need to show tht one of the internl ngles is right-ngled, once we get it for one, the sme proof will work for ll. (Cn you see why?) Cll the internl ngle γ. Suppose tht the tringle in Figure 19.4 hs smll ngle α nd lrger ngle β. Then we cn see tht α + β + γ = 180 since we hve stright line: g Figure 19.4 But we know tht α + β + 90 = 180 since the ngles in tringle dd up to 180 nd our tringle is right-ngled. Using these two equtions we deduce tht γ is 90 s required. If we dd this explntion, then the rgument will e even more convincing. True, the picture looks convincing lredy, ut we hve to e creful with pictures they cn misled. Exercise 19.5 How else could the picture fool us?
7 132 CHAPTER 19 A study of Pythgors Theorem Wht out the converse? Let s now look t n importnt technique for exploring theorems: is the converse true? To do this it helps to write the sttement in n If, then form: If T is right-ngled tringle with sides, nd hypotenuse c, then c 2 = The converse will e If c 2 = 2 + 2, then T is right-ngled tringle with sides, nd hypotenuse c. Note tht this does not quite mke sense ecuse in the ssumptions we do not know wht, nd c re. Let s rewrite Pythgors Theorem s the following: Let T e tringle with sides of length, nd c with c the longest. If T is right-ngled tringle, then c 2 = Now the converse ecomes: Theorem 19.6 (Converse of Pythgors Theorem) Let T e tringle with sides of length, nd c with c the longest. If c 2 = 2 + 2, then T is right-ngled tringle. Is this true or not? It is! But why? Proof. Let T e tringle with sides of length, nd c where C is the ngle opposite to the side of length c, then the Cosine Rule sttes tht c 2 = cos C. Now suppose tht c 2 = 2 + 2, then we hve 2 cos C = 0. As nd cnnot e zero we must hve cos C = 0. This implies tht C = n, where n is some integer. Since 0 <C<180 we must hve C = 90, i.e. T is right-ngled tringle. Exercise 19.7 Apply the methods of Chpter 18, How to red proof, to the ove proof. Remrk 19.8 The proof of the converse used the Cosine Rule, the proof of which uses Pythgors Theorem (see pge 22 nd following). Note tht the Cosine Rule is more generl thn Pythgors Theorem, since we cn deduce Pythgors from it: if we hve right-ngled tringle, then C = 90 nd so c 2 = = Thus, we cn see tht more generl sttement cn use the simpler theorem in its proof. Since Pythgors Theorem nd its converse re true we hve two equivlent sttements (i.e. If A = B nd B = A, then A B). This mens we cn stte the following theorem. Theorem 19.9 Let T e tringle with sides of length, nd c with c the longest. Then T is right-ngled tringle if nd only if c 2 =
8 Exercises 133 Proof. We cn prove this y comining the proof of Pythgors we gve nd then using the converse rgument we just gve. Note tht we cn t just use the Cosine Rule in oth directions since Pythgors Theorem is used in the proof of the Cosine Rule! Did you spot tht? A it more on understnding converse Suppose tht we hve tringle with sides of length 2.0, 2.1 nd 2.9. We hve = The tringle is therefore right-ngled. Exercise Did we use Pythgors Theorem or its converse to deduce this? Suppose tht we hve tringle of sides of length 3.6, 7.7 nd 8.4. In this cse, = = = Thus the tringle is not right ngled. Exercise Did we use Pythgors Theorem or its converse to deduce this? A common mistke in nswering this is to mke n rgument tht the sides do not stisfy the eqution c 2 = so this cn t use Pythgors Theorem. Therefore, it must use the converse. This is wrong. The correct rgument is tht Pythgors Theorem sys tht if you hve right-ngled tringle, then it sides stisfy the eqution. Thus if the eqution is not stisfied, then there is no wy tht the tringle could e right-ngled. In effect, we re using the contrpositive sttement to Pythgors Theorem, i.e. n equivlent sttement: If c 2 = 2 + 2, then T is not right-ngled. Exercises Exercises (i) (ii) Pythgors Theorem is often misquoted. In the film The Wizrd of Oz, the Screcrow is given diplom nd to show how clever he hs ecome he points his finger to his temple nd sys The squre root of the hypotenuse is equl to the sum of the squre roots of the other sides for n isosceles tringle. This is most definitely not Pythgors Theorem s it involves squre roots nd isosceles tringles. However, just ecuse it is not Pythgors Theorem does not men tht the sttement is flse! Apply our methods to nlyse this sttement. Is it true? If not, then give counterexmple. The theorem is lso misquoted in the long-running nimted comedy The Simpsons. In the episode $pringfield (or, how I lerned to stop worrying nd love leglized gmling) Homer finds some glsses nd puts them on nd à l Screcrow puts his finger to his temple nd sttes The sum of the squre roots of ny two sides
9 134 CHAPTER 19 A study of Pythgors Theorem of n isosceles tringle is equl to the squre root of the remining side. Another chrcter then shouts Tht s right-ngled tringle, you idiot! Why re Homer nd the other chrcter oth wrong? (iii) Mny theorems from lower-level mthemtics re given without proof. Find s mny exmples of this s you cn. Try to find proofs for them from other sources nd nlyse these using the methods of Chpter 18, How to red proof. Some exmples you my like to try: () The sum of ngles in tringle is 180 degrees. () Sutrcting negtive is equivlent to dding positive. (c) The vlue of π is (d) The definition of sine nd cosine don t depend on the tringle. (You will need to know out similr tringles.) (e) For ny ngle θ, sin 2 θ + cos 2 θ = 1. (f) The re of circle of rdius r is πr 2. (iv) Consider the tringles with sides of the following lengths. Decide which re rightngled nd stte whether you used Pythgors Theorem or its converse. () 7, 24, 25, () 28, 45, 52, (c) 36.9, 80.0, 88.0, (d) 0.8, 1, 4, 1.7. (v) Construct right-ngled tringle such tht the hypotenuse hs irrtionl length ut the other two sides hve rtionl length. (vi) Construct right-ngled tringle such tht the hypotenuse hs rtionl length ut the other two sides hve irrtionl length. (vii) Let X nd Y e distinct points in plne. Drw line etween them. At the midpoint drw line perpendiculr to the line. See Figure This line is clled the perpendiculr isector of X nd Y. Show tht for every point p on the perpendiculr isector the distnce from X to p nd the distnce from Y to p re the sme. We sy p is equidistnt from X nd Y. (viii) Go ck to previous chpters nd exercises nd re-nlyse the theorems nd proofs. Did you oserve fcts tht you did not oserve efore? X Perpendiculr isector Y Figure 19.5 Perpendiculr isector
10 Summry 135 Summry Pythgors Theorem is: Let T e tringle with sides of length, nd c with c the longest. If T is right-ngled tringle, then c 2 = The converse of Pythgors Theorem is: Let T e tringle with sides of length, nd c with c the longest. If c 2 = 2 + 2, then T is right-ngled tringle.
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
13.3 CLASSICAL STRAIGHTEDGE AND COMPASS CONSTRUCTIONS
 33 CLASSICAL STRAIGHTEDGE AND COMPASS CONSTRUCTIONS As simple ppliction of the results we hve obtined on lgebric extensions, nd in prticulr on the multiplictivity of extension degrees, we cn nswer (in
33 CLASSICAL STRAIGHTEDGE AND COMPASS CONSTRUCTIONS As simple ppliction of the results we hve obtined on lgebric extensions, nd in prticulr on the multiplictivity of extension degrees, we cn nswer (in
Part I: Study the theorem statement.
 Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
1 ELEMENTARY ALGEBRA and GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE
 ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
Farey Fractions. Rickard Fernström. U.U.D.M. Project Report 2017:24. Department of Mathematics Uppsala University
 U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
set is not closed under matrix [ multiplication, ] and does not form a group.
![set is not closed under matrix [ multiplication, ] and does not form a group. set is not closed under matrix [ multiplication, ] and does not form a group.](/thumbs/78/78412113.jpg) Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Lecture 2 : Propositions DRAFT
 CS/Mth 240: Introduction to Discrete Mthemtics 1/20/2010 Lecture 2 : Propositions Instructor: Dieter vn Melkeeek Scrie: Dlior Zelený DRAFT Lst time we nlyzed vrious mze solving lgorithms in order to illustrte
CS/Mth 240: Introduction to Discrete Mthemtics 1/20/2010 Lecture 2 : Propositions Instructor: Dieter vn Melkeeek Scrie: Dlior Zelený DRAFT Lst time we nlyzed vrious mze solving lgorithms in order to illustrte
Chapter 9 Definite Integrals
 Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
Things to Memorize: A Partial List. January 27, 2017
 Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
Triangles The following examples explore aspects of triangles:
 Tringles The following exmples explore spects of tringles: xmple 1: ltitude of right ngled tringle + xmple : tringle ltitude of the symmetricl ltitude of n isosceles x x - 4 +x xmple 3: ltitude of the
Tringles The following exmples explore spects of tringles: xmple 1: ltitude of right ngled tringle + xmple : tringle ltitude of the symmetricl ltitude of n isosceles x x - 4 +x xmple 3: ltitude of the
Mathematics. Area under Curve.
 Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
7.1 Integral as Net Change and 7.2 Areas in the Plane Calculus
 7.1 Integrl s Net Chnge nd 7. Ares in the Plne Clculus 7.1 INTEGRAL AS NET CHANGE Notecrds from 7.1: Displcement vs Totl Distnce, Integrl s Net Chnge We hve lredy seen how the position of n oject cn e
7.1 Integrl s Net Chnge nd 7. Ares in the Plne Clculus 7.1 INTEGRAL AS NET CHANGE Notecrds from 7.1: Displcement vs Totl Distnce, Integrl s Net Chnge We hve lredy seen how the position of n oject cn e
Bases for Vector Spaces
 Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
1B40 Practical Skills
 B40 Prcticl Skills Comining uncertinties from severl quntities error propgtion We usully encounter situtions where the result of n experiment is given in terms of two (or more) quntities. We then need
B40 Prcticl Skills Comining uncertinties from severl quntities error propgtion We usully encounter situtions where the result of n experiment is given in terms of two (or more) quntities. We then need
The practical version
 Roerto s Notes on Integrl Clculus Chpter 4: Definite integrls nd the FTC Section 7 The Fundmentl Theorem of Clculus: The prcticl version Wht you need to know lredy: The theoreticl version of the FTC. Wht
Roerto s Notes on Integrl Clculus Chpter 4: Definite integrls nd the FTC Section 7 The Fundmentl Theorem of Clculus: The prcticl version Wht you need to know lredy: The theoreticl version of the FTC. Wht
Polynomials and Division Theory
 Higher Checklist (Unit ) Higher Checklist (Unit ) Polynomils nd Division Theory Skill Achieved? Know tht polynomil (expression) is of the form: n x + n x n + n x n + + n x + x + 0 where the i R re the
Higher Checklist (Unit ) Higher Checklist (Unit ) Polynomils nd Division Theory Skill Achieved? Know tht polynomil (expression) is of the form: n x + n x n + n x n + + n x + x + 0 where the i R re the
The area under the graph of f and above the x-axis between a and b is denoted by. f(x) dx. π O
 1 Section 5. The Definite Integrl Suppose tht function f is continuous nd positive over n intervl [, ]. y = f(x) x The re under the grph of f nd ove the x-xis etween nd is denoted y f(x) dx nd clled the
1 Section 5. The Definite Integrl Suppose tht function f is continuous nd positive over n intervl [, ]. y = f(x) x The re under the grph of f nd ove the x-xis etween nd is denoted y f(x) dx nd clled the
Calculus Module C21. Areas by Integration. Copyright This publication The Northern Alberta Institute of Technology All Rights Reserved.
 Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
4 VECTORS. 4.0 Introduction. Objectives. Activity 1
 4 VECTRS Chpter 4 Vectors jectives fter studying this chpter you should understnd the difference etween vectors nd sclrs; e le to find the mgnitude nd direction of vector; e le to dd vectors, nd multiply
4 VECTRS Chpter 4 Vectors jectives fter studying this chpter you should understnd the difference etween vectors nd sclrs; e le to find the mgnitude nd direction of vector; e le to dd vectors, nd multiply
Mathematics Number: Logarithms
 plce of mind F A C U L T Y O F E D U C A T I O N Deprtment of Curriculum nd Pedgogy Mthemtics Numer: Logrithms Science nd Mthemtics Eduction Reserch Group Supported y UBC Teching nd Lerning Enhncement
plce of mind F A C U L T Y O F E D U C A T I O N Deprtment of Curriculum nd Pedgogy Mthemtics Numer: Logrithms Science nd Mthemtics Eduction Reserch Group Supported y UBC Teching nd Lerning Enhncement
2. VECTORS AND MATRICES IN 3 DIMENSIONS
 2 VECTORS AND MATRICES IN 3 DIMENSIONS 21 Extending the Theory of 2-dimensionl Vectors x A point in 3-dimensionl spce cn e represented y column vector of the form y z z-xis y-xis z x y x-xis Most of the
2 VECTORS AND MATRICES IN 3 DIMENSIONS 21 Extending the Theory of 2-dimensionl Vectors x A point in 3-dimensionl spce cn e represented y column vector of the form y z z-xis y-xis z x y x-xis Most of the
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
Vectors , (0,0). 5. A vector is commonly denoted by putting an arrow above its symbol, as in the picture above. Here are some 3-dimensional vectors:
 Vectors 1-23-2018 I ll look t vectors from n lgeric point of view nd geometric point of view. Algericlly, vector is n ordered list of (usully) rel numers. Here re some 2-dimensionl vectors: (2, 3), ( )
Vectors 1-23-2018 I ll look t vectors from n lgeric point of view nd geometric point of view. Algericlly, vector is n ordered list of (usully) rel numers. Here re some 2-dimensionl vectors: (2, 3), ( )
8Similarity UNCORRECTED PAGE PROOFS. 8.1 Kick off with CAS 8.2 Similar objects 8.3 Linear scale factors. 8.4 Area and volume scale factors 8.
 8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8. re nd volume scle fctors 8. Review U N O R R E TE D P G E PR O O FS 8.1 Kick off with S Plese refer to the Resources t in the Prelims
8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8. re nd volume scle fctors 8. Review U N O R R E TE D P G E PR O O FS 8.1 Kick off with S Plese refer to the Resources t in the Prelims
p-adic Egyptian Fractions
 p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
2.4 Linear Inequalities and Interval Notation
 .4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
.4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
20 MATHEMATICS POLYNOMIALS
 0 MATHEMATICS POLYNOMIALS.1 Introduction In Clss IX, you hve studied polynomils in one vrible nd their degrees. Recll tht if p(x) is polynomil in x, the highest power of x in p(x) is clled the degree of
0 MATHEMATICS POLYNOMIALS.1 Introduction In Clss IX, you hve studied polynomils in one vrible nd their degrees. Recll tht if p(x) is polynomil in x, the highest power of x in p(x) is clled the degree of
Chapter 4 Contravariance, Covariance, and Spacetime Diagrams
 Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
I1 = I2 I1 = I2 + I3 I1 + I2 = I3 + I4 I 3
 2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
Chapters Five Notes SN AA U1C5
 Chpters Five Notes SN AA U1C5 Nme Period Section 5-: Fctoring Qudrtic Epressions When you took lger, you lerned tht the first thing involved in fctoring is to mke sure to fctor out ny numers or vriles
Chpters Five Notes SN AA U1C5 Nme Period Section 5-: Fctoring Qudrtic Epressions When you took lger, you lerned tht the first thing involved in fctoring is to mke sure to fctor out ny numers or vriles
6.2 The Pythagorean Theorems
 PythgorenTheorems20052006.nb 1 6.2 The Pythgoren Theorems One of the best known theorems in geometry (nd ll of mthemtics for tht mtter) is the Pythgoren Theorem. You hve probbly lredy worked with this
PythgorenTheorems20052006.nb 1 6.2 The Pythgoren Theorems One of the best known theorems in geometry (nd ll of mthemtics for tht mtter) is the Pythgoren Theorem. You hve probbly lredy worked with this
Bridging the gap: GCSE AS Level
 Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Lecture 3: Equivalence Relations
 Mthcmp Crsh Course Instructor: Pdric Brtlett Lecture 3: Equivlence Reltions Week 1 Mthcmp 2014 In our lst three tlks of this clss, we shift the focus of our tlks from proof techniques to proof concepts
Mthcmp Crsh Course Instructor: Pdric Brtlett Lecture 3: Equivlence Reltions Week 1 Mthcmp 2014 In our lst three tlks of this clss, we shift the focus of our tlks from proof techniques to proof concepts
378 Relations Solutions for Chapter 16. Section 16.1 Exercises. 3. Let A = {0,1,2,3,4,5}. Write out the relation R that expresses on A.
 378 Reltions 16.7 Solutions for Chpter 16 Section 16.1 Exercises 1. Let A = {0,1,2,3,4,5}. Write out the reltion R tht expresses > on A. Then illustrte it with digrm. 2 1 R = { (5,4),(5,3),(5,2),(5,1),(5,0),(4,3),(4,2),(4,1),
378 Reltions 16.7 Solutions for Chpter 16 Section 16.1 Exercises 1. Let A = {0,1,2,3,4,5}. Write out the reltion R tht expresses > on A. Then illustrte it with digrm. 2 1 R = { (5,4),(5,3),(5,2),(5,1),(5,0),(4,3),(4,2),(4,1),
Quadratic Forms. Quadratic Forms
 Qudrtic Forms Recll the Simon & Blume excerpt from n erlier lecture which sid tht the min tsk of clculus is to pproximte nonliner functions with liner functions. It s ctully more ccurte to sy tht we pproximte
Qudrtic Forms Recll the Simon & Blume excerpt from n erlier lecture which sid tht the min tsk of clculus is to pproximte nonliner functions with liner functions. It s ctully more ccurte to sy tht we pproximte
I do slope intercept form With my shades on Martin-Gay, Developmental Mathematics
 AAT-A Dte: 1//1 SWBAT simplify rdicls. Do Now: ACT Prep HW Requests: Pg 49 #17-45 odds Continue Vocb sheet In Clss: Complete Skills Prctice WS HW: Complete Worksheets For Wednesdy stmped pges Bring stmped
AAT-A Dte: 1//1 SWBAT simplify rdicls. Do Now: ACT Prep HW Requests: Pg 49 #17-45 odds Continue Vocb sheet In Clss: Complete Skills Prctice WS HW: Complete Worksheets For Wednesdy stmped pges Bring stmped
8. Complex Numbers. We can combine the real numbers with this new imaginary number to form the complex numbers.
 8. Complex Numers The rel numer system is dequte for solving mny mthemticl prolems. But it is necessry to extend the rel numer system to solve numer of importnt prolems. Complex numers do not chnge the
8. Complex Numers The rel numer system is dequte for solving mny mthemticl prolems. But it is necessry to extend the rel numer system to solve numer of importnt prolems. Complex numers do not chnge the
10. AREAS BETWEEN CURVES
 . AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
. AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
AQA Further Pure 1. Complex Numbers. Section 1: Introduction to Complex Numbers. The number system
 Complex Numbers Section 1: Introduction to Complex Numbers Notes nd Exmples These notes contin subsections on The number system Adding nd subtrcting complex numbers Multiplying complex numbers Complex
Complex Numbers Section 1: Introduction to Complex Numbers Notes nd Exmples These notes contin subsections on The number system Adding nd subtrcting complex numbers Multiplying complex numbers Complex
Shape and measurement
 C H A P T E R 5 Shpe nd mesurement Wht is Pythgors theorem? How do we use Pythgors theorem? How do we find the perimeter of shpe? How do we find the re of shpe? How do we find the volume of shpe? How do
C H A P T E R 5 Shpe nd mesurement Wht is Pythgors theorem? How do we use Pythgors theorem? How do we find the perimeter of shpe? How do we find the re of shpe? How do we find the volume of shpe? How do
Beginning Darboux Integration, Math 317, Intro to Analysis II
 Beginning Droux Integrtion, Mth 317, Intro to Anlysis II Lets strt y rememering how to integrte function over n intervl. (you lerned this in Clculus I, ut mye it didn t stick.) This set of lecture notes
Beginning Droux Integrtion, Mth 317, Intro to Anlysis II Lets strt y rememering how to integrte function over n intervl. (you lerned this in Clculus I, ut mye it didn t stick.) This set of lecture notes
3.1 Review of Sine, Cosine and Tangent for Right Angles
 Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
9.4. The Vector Product. Introduction. Prerequisites. Learning Outcomes
 The Vector Product 9.4 Introduction In this section we descrie how to find the vector product of two vectors. Like the sclr product its definition my seem strnge when first met ut the definition is chosen
The Vector Product 9.4 Introduction In this section we descrie how to find the vector product of two vectors. Like the sclr product its definition my seem strnge when first met ut the definition is chosen
8Similarity ONLINE PAGE PROOFS. 8.1 Kick off with CAS 8.2 Similar objects 8.3 Linear scale factors. 8.4 Area and volume scale factors 8.
 8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8.4 re nd volume scle fctors 8. Review Plese refer to the Resources t in the Prelims section of your eookplus for comprehensive step-y-step
8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8.4 re nd volume scle fctors 8. Review Plese refer to the Resources t in the Prelims section of your eookplus for comprehensive step-y-step
5: The Definite Integral
 5: The Definite Integrl 5.: Estimting with Finite Sums Consider moving oject its velocity (meters per second) t ny time (seconds) is given y v t = t+. Cn we use this informtion to determine the distnce
5: The Definite Integrl 5.: Estimting with Finite Sums Consider moving oject its velocity (meters per second) t ny time (seconds) is given y v t = t+. Cn we use this informtion to determine the distnce
On the diagram below the displacement is represented by the directed line segment OA.
 Vectors Sclrs nd Vectors A vector is quntity tht hs mgnitude nd direction. One exmple of vector is velocity. The velocity of n oject is determined y the mgnitude(speed) nd direction of trvel. Other exmples
Vectors Sclrs nd Vectors A vector is quntity tht hs mgnitude nd direction. One exmple of vector is velocity. The velocity of n oject is determined y the mgnitude(speed) nd direction of trvel. Other exmples
Torsion in Groups of Integral Triangles
 Advnces in Pure Mthemtics, 01,, 116-10 http://dxdoiorg/1046/pm011015 Pulished Online Jnury 01 (http://wwwscirporg/journl/pm) Torsion in Groups of Integrl Tringles Will Murry Deprtment of Mthemtics nd Sttistics,
Advnces in Pure Mthemtics, 01,, 116-10 http://dxdoiorg/1046/pm011015 Pulished Online Jnury 01 (http://wwwscirporg/journl/pm) Torsion in Groups of Integrl Tringles Will Murry Deprtment of Mthemtics nd Sttistics,
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
Intermediate Math Circles Wednesday, November 14, 2018 Finite Automata II. Nickolas Rollick a b b. a b 4
 Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
Section 6: Area, Volume, and Average Value
 Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Section 4: Integration ECO4112F 2011
 Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H. Thomas Shores Department of Mathematics University of Nebraska Spring 2007
 A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
UNIFORM CONVERGENCE. Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3
 UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
Improper Integrals, and Differential Equations
 Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
7.1 Integral as Net Change Calculus. What is the total distance traveled? What is the total displacement?
 7.1 Integrl s Net Chnge Clculus 7.1 INTEGRAL AS NET CHANGE Distnce versus Displcement We hve lredy seen how the position of n oject cn e found y finding the integrl of the velocity function. The chnge
7.1 Integrl s Net Chnge Clculus 7.1 INTEGRAL AS NET CHANGE Distnce versus Displcement We hve lredy seen how the position of n oject cn e found y finding the integrl of the velocity function. The chnge
Chapter 8.2: The Integral
 Chpter 8.: The Integrl You cn think of Clculus s doule-wide triler. In one width of it lives differentil clculus. In the other hlf lives wht is clled integrl clculus. We hve lredy eplored few rooms in
Chpter 8.: The Integrl You cn think of Clculus s doule-wide triler. In one width of it lives differentil clculus. In the other hlf lives wht is clled integrl clculus. We hve lredy eplored few rooms in
Review of Gaussian Quadrature method
 Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Number systems: the Real Number System
 Numer systems: the Rel Numer System syllusref eferenceence Core topic: Rel nd complex numer systems In this ch chpter A Clssifiction of numers B Recurring decimls C Rel nd complex numers D Surds: suset
Numer systems: the Rel Numer System syllusref eferenceence Core topic: Rel nd complex numer systems In this ch chpter A Clssifiction of numers B Recurring decimls C Rel nd complex numers D Surds: suset
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
An Overview of Integration
 An Overview of Integrtion S. F. Ellermeyer July 26, 2 The Definite Integrl of Function f Over n Intervl, Suppose tht f is continuous function defined on n intervl,. The definite integrl of f from to is
An Overview of Integrtion S. F. Ellermeyer July 26, 2 The Definite Integrl of Function f Over n Intervl, Suppose tht f is continuous function defined on n intervl,. The definite integrl of f from to is
MA123, Chapter 10: Formulas for integrals: integrals, antiderivatives, and the Fundamental Theorem of Calculus (pp.
 MA123, Chpter 1: Formuls for integrls: integrls, ntiderivtives, nd the Fundmentl Theorem of Clculus (pp. 27-233, Gootmn) Chpter Gols: Assignments: Understnd the sttement of the Fundmentl Theorem of Clculus.
MA123, Chpter 1: Formuls for integrls: integrls, ntiderivtives, nd the Fundmentl Theorem of Clculus (pp. 27-233, Gootmn) Chpter Gols: Assignments: Understnd the sttement of the Fundmentl Theorem of Clculus.
Exam 2, Mathematics 4701, Section ETY6 6:05 pm 7:40 pm, March 31, 2016, IH-1105 Instructor: Attila Máté 1
 Exm, Mthemtics 471, Section ETY6 6:5 pm 7:4 pm, Mrch 1, 16, IH-115 Instructor: Attil Máté 1 17 copies 1. ) Stte the usul sufficient condition for the fixed-point itertion to converge when solving the eqution
Exm, Mthemtics 471, Section ETY6 6:5 pm 7:4 pm, Mrch 1, 16, IH-115 Instructor: Attil Máté 1 17 copies 1. ) Stte the usul sufficient condition for the fixed-point itertion to converge when solving the eqution
Parse trees, ambiguity, and Chomsky normal form
 Prse trees, miguity, nd Chomsky norml form In this lecture we will discuss few importnt notions connected with contextfree grmmrs, including prse trees, miguity, nd specil form for context-free grmmrs
Prse trees, miguity, nd Chomsky norml form In this lecture we will discuss few importnt notions connected with contextfree grmmrs, including prse trees, miguity, nd specil form for context-free grmmrs
1.2 What is a vector? (Section 2.2) Two properties (attributes) of a vector are and.
 Homework 1. Chpters 2. Bsis independent vectors nd their properties Show work except for fill-in-lnks-prolems (print.pdf from www.motiongenesis.com Textooks Resources). 1.1 Solving prolems wht engineers
Homework 1. Chpters 2. Bsis independent vectors nd their properties Show work except for fill-in-lnks-prolems (print.pdf from www.motiongenesis.com Textooks Resources). 1.1 Solving prolems wht engineers
W. We shall do so one by one, starting with I 1, and we shall do it greedily, trying
 Vitli covers 1 Definition. A Vitli cover of set E R is set V of closed intervls with positive length so tht, for every δ > 0 nd every x E, there is some I V with λ(i ) < δ nd x I. 2 Lemm (Vitli covering)
Vitli covers 1 Definition. A Vitli cover of set E R is set V of closed intervls with positive length so tht, for every δ > 0 nd every x E, there is some I V with λ(i ) < δ nd x I. 2 Lemm (Vitli covering)
Chapter 0. What is the Lebesgue integral about?
 Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Chapter 1: Logarithmic functions and indices
 Chpter : Logrithmic functions nd indices. You cn simplify epressions y using rules of indices m n m n m n m n ( m ) n mn m m m m n m m n Emple Simplify these epressions: 5 r r c 4 4 d 6 5 e ( ) f ( ) 4
Chpter : Logrithmic functions nd indices. You cn simplify epressions y using rules of indices m n m n m n m n ( m ) n mn m m m m n m m n Emple Simplify these epressions: 5 r r c 4 4 d 6 5 e ( ) f ( ) 4
CM10196 Topic 4: Functions and Relations
 CM096 Topic 4: Functions nd Reltions Guy McCusker W. Functions nd reltions Perhps the most widely used notion in ll of mthemtics is tht of function. Informlly, function is n opertion which tkes n input
CM096 Topic 4: Functions nd Reltions Guy McCusker W. Functions nd reltions Perhps the most widely used notion in ll of mthemtics is tht of function. Informlly, function is n opertion which tkes n input
Algebra II Notes Unit Ten: Conic Sections
 Syllus Ojective: 10.1 The student will sketch the grph of conic section with centers either t or not t the origin. (PARABOLAS) Review: The Midpoint Formul The midpoint M of the line segment connecting
Syllus Ojective: 10.1 The student will sketch the grph of conic section with centers either t or not t the origin. (PARABOLAS) Review: The Midpoint Formul The midpoint M of the line segment connecting
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Linear Inequalities. Work Sheet 1
 Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
Infinite Geometric Series
 Infinite Geometric Series Finite Geometric Series ( finite SUM) Let 0 < r < 1, nd let n be positive integer. Consider the finite sum It turns out there is simple lgebric expression tht is equivlent to
Infinite Geometric Series Finite Geometric Series ( finite SUM) Let 0 < r < 1, nd let n be positive integer. Consider the finite sum It turns out there is simple lgebric expression tht is equivlent to
Analytically, vectors will be represented by lowercase bold-face Latin letters, e.g. a, r, q.
 1.1 Vector Alger 1.1.1 Sclrs A physicl quntity which is completely descried y single rel numer is clled sclr. Physiclly, it is something which hs mgnitude, nd is completely descried y this mgnitude. Exmples
1.1 Vector Alger 1.1.1 Sclrs A physicl quntity which is completely descried y single rel numer is clled sclr. Physiclly, it is something which hs mgnitude, nd is completely descried y this mgnitude. Exmples
Discrete Mathematics and Probability Theory Spring 2013 Anant Sahai Lecture 17
 EECS 70 Discrete Mthemtics nd Proility Theory Spring 2013 Annt Shi Lecture 17 I.I.D. Rndom Vriles Estimting the is of coin Question: We wnt to estimte the proportion p of Democrts in the US popultion,
EECS 70 Discrete Mthemtics nd Proility Theory Spring 2013 Annt Shi Lecture 17 I.I.D. Rndom Vriles Estimting the is of coin Question: We wnt to estimte the proportion p of Democrts in the US popultion,
Exponentials - Grade 10 [CAPS] *
![Exponentials - Grade 10 [CAPS] * Exponentials - Grade 10 [CAPS] *](/thumbs/88/115984632.jpg) OpenStx-CNX module: m859 Exponentils - Grde 0 [CAPS] * Free High School Science Texts Project Bsed on Exponentils by Rory Adms Free High School Science Texts Project Mrk Horner Hether Willims This work
OpenStx-CNX module: m859 Exponentils - Grde 0 [CAPS] * Free High School Science Texts Project Bsed on Exponentils by Rory Adms Free High School Science Texts Project Mrk Horner Hether Willims This work
Goals: Determine how to calculate the area described by a function. Define the definite integral. Explore the relationship between the definite
 Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Chapter 6 Techniques of Integration
 MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
List all of the possible rational roots of each equation. Then find all solutions (both real and imaginary) of the equation. 1.
 Mth Anlysis CP WS 4.X- Section 4.-4.4 Review Complete ech question without the use of grphing clcultor.. Compre the mening of the words: roots, zeros nd fctors.. Determine whether - is root of 0. Show
Mth Anlysis CP WS 4.X- Section 4.-4.4 Review Complete ech question without the use of grphing clcultor.. Compre the mening of the words: roots, zeros nd fctors.. Determine whether - is root of 0. Show
Homework 3 Solutions
 CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 3 Solutions 1. Give NFAs with the specified numer of sttes recognizing ech of the following lnguges. In ll cses, the lphet is Σ = {,1}.
CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 3 Solutions 1. Give NFAs with the specified numer of sttes recognizing ech of the following lnguges. In ll cses, the lphet is Σ = {,1}.
MTH 505: Number Theory Spring 2017
 MTH 505: Numer Theory Spring 207 Homework 2 Drew Armstrong The Froenius Coin Prolem. Consider the eqution x ` y c where,, c, x, y re nturl numers. We cn think of $ nd $ s two denomintions of coins nd $c
MTH 505: Numer Theory Spring 207 Homework 2 Drew Armstrong The Froenius Coin Prolem. Consider the eqution x ` y c where,, c, x, y re nturl numers. We cn think of $ nd $ s two denomintions of coins nd $c
= x x 2 = 25 2
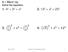 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
Exercises with (Some) Solutions
 Exercises with (Some) Solutions Techer: Luc Tesei Mster of Science in Computer Science - University of Cmerino Contents 1 Strong Bisimultion nd HML 2 2 Wek Bisimultion 31 3 Complete Lttices nd Fix Points
Exercises with (Some) Solutions Techer: Luc Tesei Mster of Science in Computer Science - University of Cmerino Contents 1 Strong Bisimultion nd HML 2 2 Wek Bisimultion 31 3 Complete Lttices nd Fix Points
SUMMER KNOWHOW STUDY AND LEARNING CENTRE
 SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
USA Mathematical Talent Search Round 1 Solutions Year 21 Academic Year
 1/1/21. Fill in the circles in the picture t right with the digits 1-8, one digit in ech circle with no digit repeted, so tht no two circles tht re connected by line segment contin consecutive digits.
1/1/21. Fill in the circles in the picture t right with the digits 1-8, one digit in ech circle with no digit repeted, so tht no two circles tht re connected by line segment contin consecutive digits.
Math 8 Winter 2015 Applications of Integration
 Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
Lecture 1. Functional series. Pointwise and uniform convergence.
 1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1
 MATH34032: Green s Functions, Integrl Equtions nd the Clculus of Vritions 1 Section 1 Function spces nd opertors Here we gives some brief detils nd definitions, prticulrly relting to opertors. For further
MATH34032: Green s Functions, Integrl Equtions nd the Clculus of Vritions 1 Section 1 Function spces nd opertors Here we gives some brief detils nd definitions, prticulrly relting to opertors. For further
Geometry AP Book 8, Part 2: Unit 3
 Geometry ook 8, rt 2: Unit 3 IMRTNT NTE: For mny questions in this unit, there re multiple correct nswers, e.g. line segment cn e written s, RST is the sme s TSR, etc. Where pproprite, techers should e
Geometry ook 8, rt 2: Unit 3 IMRTNT NTE: For mny questions in this unit, there re multiple correct nswers, e.g. line segment cn e written s, RST is the sme s TSR, etc. Where pproprite, techers should e
STRAND J: TRANSFORMATIONS, VECTORS and MATRICES
 Mthemtics SKE: STRN J STRN J: TRNSFORMTIONS, VETORS nd MTRIES J3 Vectors Text ontents Section J3.1 Vectors nd Sclrs * J3. Vectors nd Geometry Mthemtics SKE: STRN J J3 Vectors J3.1 Vectors nd Sclrs Vectors
Mthemtics SKE: STRN J STRN J: TRNSFORMTIONS, VETORS nd MTRIES J3 Vectors Text ontents Section J3.1 Vectors nd Sclrs * J3. Vectors nd Geometry Mthemtics SKE: STRN J J3 Vectors J3.1 Vectors nd Sclrs Vectors
PHYS 1114, Lecture 1, January 18 Contents:
 PHYS 1114, Lecture 1, Jnury 18 Contents: 1 Discussed Syllus (four pges). The syllus is the most importnt document. You should purchse the ExpertTA Access Code nd the L Mnul soon! 2 Reviewed Alger nd Strted
PHYS 1114, Lecture 1, Jnury 18 Contents: 1 Discussed Syllus (four pges). The syllus is the most importnt document. You should purchse the ExpertTA Access Code nd the L Mnul soon! 2 Reviewed Alger nd Strted
Coordinate geometry and vectors
 MST124 Essentil mthemtics 1 Unit 5 Coordinte geometry nd vectors Contents Contents Introduction 4 1 Distnce 5 1.1 The distnce etween two points in the plne 5 1.2 Midpoints nd perpendiculr isectors 7 2
MST124 Essentil mthemtics 1 Unit 5 Coordinte geometry nd vectors Contents Contents Introduction 4 1 Distnce 5 1.1 The distnce etween two points in the plne 5 1.2 Midpoints nd perpendiculr isectors 7 2
APPENDIX. Precalculus Review D.1. Real Numbers and the Real Number Line
 APPENDIX D Preclculus Review APPENDIX D.1 Rel Numers n the Rel Numer Line Rel Numers n the Rel Numer Line Orer n Inequlities Asolute Vlue n Distnce Rel Numers n the Rel Numer Line Rel numers cn e represente
APPENDIX D Preclculus Review APPENDIX D.1 Rel Numers n the Rel Numer Line Rel Numers n the Rel Numer Line Orer n Inequlities Asolute Vlue n Distnce Rel Numers n the Rel Numer Line Rel numers cn e represente
Lecture 3. In this lecture, we will discuss algorithms for solving systems of linear equations.
 Lecture 3 3 Solving liner equtions In this lecture we will discuss lgorithms for solving systems of liner equtions Multiplictive identity Let us restrict ourselves to considering squre mtrices since one
Lecture 3 3 Solving liner equtions In this lecture we will discuss lgorithms for solving systems of liner equtions Multiplictive identity Let us restrict ourselves to considering squre mtrices since one
HW3, Math 307. CSUF. Spring 2007.
 HW, Mth 7. CSUF. Spring 7. Nsser M. Abbsi Spring 7 Compiled on November 5, 8 t 8:8m public Contents Section.6, problem Section.6, problem Section.6, problem 5 Section.6, problem 7 6 5 Section.6, problem
HW, Mth 7. CSUF. Spring 7. Nsser M. Abbsi Spring 7 Compiled on November 5, 8 t 8:8m public Contents Section.6, problem Section.6, problem Section.6, problem 5 Section.6, problem 7 6 5 Section.6, problem
青藜苑教育 The digrm shows the position of ferry siling between Folkestone nd lis. The ferry is t X. X 4km The pos
 青藜苑教育 www.thetopedu.com 010-6895997 1301951457 Revision Topic 9: Pythgors Theorem Pythgors Theorem Pythgors Theorem llows you to work out the length of sides in right-ngled tringle. c The side opposite
青藜苑教育 www.thetopedu.com 010-6895997 1301951457 Revision Topic 9: Pythgors Theorem Pythgors Theorem Pythgors Theorem llows you to work out the length of sides in right-ngled tringle. c The side opposite
MATH STUDENT BOOK. 10th Grade Unit 5
 MATH STUDENT BOOK 10th Grde Unit 5 Unit 5 Similr Polygons MATH 1005 Similr Polygons INTRODUCTION 3 1. PRINCIPLES OF ALGEBRA 5 RATIOS AND PROPORTIONS 5 PROPERTIES OF PROPORTIONS 11 SELF TEST 1 16 2. SIMILARITY
MATH STUDENT BOOK 10th Grde Unit 5 Unit 5 Similr Polygons MATH 1005 Similr Polygons INTRODUCTION 3 1. PRINCIPLES OF ALGEBRA 5 RATIOS AND PROPORTIONS 5 PROPERTIES OF PROPORTIONS 11 SELF TEST 1 16 2. SIMILARITY
Matrix Algebra. Matrix Addition, Scalar Multiplication and Transposition. Linear Algebra I 24
 Mtrix lger Mtrix ddition, Sclr Multipliction nd rnsposition Mtrix lger Section.. Mtrix ddition, Sclr Multipliction nd rnsposition rectngulr rry of numers is clled mtrix ( the plurl is mtrices ) nd the
Mtrix lger Mtrix ddition, Sclr Multipliction nd rnsposition Mtrix lger Section.. Mtrix ddition, Sclr Multipliction nd rnsposition rectngulr rry of numers is clled mtrix ( the plurl is mtrices ) nd the
