Physics 201 Lab 9: Torque and the Center of Mass Dr. Timothy C. Black
|
|
|
- Magdalen Crawford
- 6 years ago
- Views:
Transcription
1 Theoretical Discussion Physics 201 Lab 9: Torque and the Center of Mass Dr. Timothy C. Black For each of the linear kinematic variables; displacement r, velocity v and acceleration a; there is a corresponding angular kinematic variable; angular displacement θ, angular velocity ω, and angular acceleration α, respectively. Associated with these kinematic variables are dynamical variables momentum and force for linear variables angular momentum and torque for angular variables. The rotational analogue of the inertial mass m is the moment of inertia I[1]. The relationships are summarized in table I. Linear variables displacement r velocity v d r acceleration a d v momentum p m d r m v force F m d v angular momentum analogous angular variable angular displacement θ angular velocity ω d θ angular acceleration α d ω L r p I d θ I ω τ r F I d ω I α TABLE I: Linear variables and their angular analogues According to the table, torque is the angular analogue of force: In other words, just as force acts to change the magnitude and/or direction of an object s linear velocity, torque acts to change the magnitude and/or direction of an object s angular velocity. The equation τ I d ω I α (1) describes the effect of a torque on the object s angular kinematic variables. It tells you what a torque does, but not where it comes from. A torque arises whenever a force acts upon a rigid body that is free to rotate about some axis. If the applied force is F and the displacement vector from the axis of rotation to the point where the force is applied is r, then the torque is equal to τ r F (2) Using the definition of the vector cross product, the magnitude of the torque is τ rf sin θ (3) where θ is the smallest angle between the vectors F and r. The direction of the torque vector is given by the right-hand rule place the fingers of your right hand along r and curl them into F : your thumb will point in the direction of τ. The directional relationships between F, r, and τ are shown in figure 1. So long as the total net force on an object is zero, the velocity of its center of mass will not change. However, it is possible for an object to have zero net force acting on it, but to nevertheless have a non-zero torque
2 FIG. 1: Directional relationships between F, r, and τ acting on it. Figure 2 shows one such possible scenario. The velocity of the center of mass of the object in figure 2, acted upon by two equal and opposite forces, will remain constant, but since the torque is non-zero, it will spin about its axis at an ever-increasing rate of rotation. FIG. 2: Equal forces applied to opposite sides of a rotation axis For an object to remain in static equilibrium, so that both the velocity of its center of mass and its angular velocity about any axis are constant, both the net force and the net torque on it must equal zero. The conditions for static equilibrium are: F net 0 (4) τ net 0 (5) Center of Mass The center of mass coordinate of a system or an extended object is defined so that Newton s law of motion, in the form d p F ext (6)
3 applies to the sytem or object as if it were a point particle located at the center of mass coordinate and the external force were applied at that point. If we define the center of mass coordinate as r c.m. j m j r j j m j j m j r j M tot (7) where m j is the mass of the j th particle in the system or object, r j is the position vector of the j th particle, and M tot is the system or object s total mass, we see that the center of mass so defined does indeed satisfy equation 6, since d p F ext d (M tot v c.m. ) ( ) d d r c.m. M tot d d r j m j j d p j j F j j Since the center of mass coordinate is defined so that the external force can be taken to act at that point, it is constant in time, and the geometric interpretation of Newton s Law for rotational motion (equation 8); τ ext d L c.m. d ( r c.m. p c.m. ) r c.m. d p c.m. r c.m. F ext (8) is that the displacement vector r c.m. points from the pivot point to the center of mass coordinate. Figure 3 depicts this geometric interpretation. Using the right-hand rule, we see that the torque in this case is negative (into the page), so that the celebrated swingee will rotate clockwise under the influence of gravity. Since the magnitude of the vector cross product is given by A B A B sin θ where θ is the smallest angle between A and B, then the magnitude of the torque is given by equation 9 below. τ ext r c.m. F ext sin θ (9) Equation 9 makes clear that the torque vanishes whenever the vector r c.m. from the pivot point to the center of mass is colinear with the external force F ext. For an object suspended at rest under its own weight, this implies the following results, which we will make use of in this experiment: An object suspended at rest under its own weight is in static equilibrium. Therefore, both the net force and net torque on it are zero.
4 FIG. 3: Relative orientation of the vectors r c.m. and F ext for a celebrity suspended from a pivot. Since the torque will only vanish in the gravitational field if r c.m. and F G are parallel (or anti-parallel), the object will align itself so that the vector r c.m. from the pivot point to the center of mass is vertical. It follows that in suspending a massive object from a variety of different pivot points, all vertical lines originating from the respective pivot points will intersect at the center of mass. In today s lab you will use the conditions for static equilibrium to measure the mass of a meter stick that is balanced on a knife-edge fulcrum. You will also find the center of mass coordinate of an angled bar. Procedure for Determining the Mass of a Meter Stick FIG. 4: Experimental setup for using torque to weigh a meter stick The experimental setup is shown in figure 4. Suppose you can get your meter stick in balance as shown in the figure. There are three forces acting on the left-hand side of the stick and one force acting on the right-hand side. The mass of the section of ruler on the right hand side is m rhs m l2 l, where l 100 cm is
5 the length of the ruler. The center of mass of the ruler material on the right-hand side is located a distance l 22 from the fulcrum, as illustrated in figure 5. Since the force acts at right angles to the displacement, the magnitude of the total torque acting on the right-hand side is τ right m rhs g l 2 2 mg l2 2 2l (10) FIG. 5: Illustration of the balance of torques On the left hand side, there are the gravitational forces due to m 1, m 2, and the mass of the ruler material m lhs on the left-hand side of the stick. The magnitude of the forces arising from these three sources are, respectively, F 1 F 2 m 1 g m 2 g F 3 m lhs g m l 1 l g The center-of mass of the ruler material on the left-hand side is located a distance l1 2 from the fulcrum. Since all three forces act at right angles to the displacement, the total torque on the left-hand side is τ left m 1 gr 1 + m 2 gr 2 + mg l2 1 2l All of the downward forces acting on the ruler are countered by an equal and opposite upward reaction force (normal force) that acts at the point of the fulcrum. Since it acts at the fulcrum point, it exerts no torque, so that the equation for static equilibrium is (11) τ left τ right m 1 gr 1 + m 2 gr 2 + mg l2 1 2l mg l2 2 2l Cancelling the common factor of g, and re-arranging the equation, you get an equation for the mass of the ruler: (12) m 2l(m 1r 1 + m 2 r 2 ) (l 2 2 l2 1 ) (13)
6 By varying the fulcrum point, and hence the values of l 1 and l 2, and adjusting the locations of m 1 and m 2 to achieve static equilibrium, you can obtain independent measurements of the mass of the ruler. Procedure for Finding the Center of Mass of an Angled Bar Figure 6 depicts the experimental set-up for this experiment. In brief, you will sequentially suspend the L-bracket from each of three pivot points. In each case, you will trace a vertical line along a plumb bob hanging from the pivot point. The point where all three lines intersect is the center of mass of the L-bracket. Note that the center of mass coordinate of a body need not lie within the body itself. FIG. 6: Experimental scheme for measuring the center of mass. FIG. 7: Analysis method for reporting the center of mass.
7 Summary Weighing the meter stick 1. Set the fulcrum location at approximately 30 cm. 2. Bring the meter stick into balance (static equilibrium) by varying the positions of the two masses, m 1 and m 2. The inner mass m 2 (mass closest to the fulcrum) should be about 150 g. The outer mass m 1 should be about g. You can use the position of m 1 to fine-tune the balance. 3. Record the distances r 1, r 2, l 1, l 2, m 1 and m Calculate the ruler s mass using the method of static equilibrium (equation 13) and label it m exp. 5. Weigh the ruler using the mass balance. Record this value as m b. 6. Calculate and report the fractional discrepancy δ between m exp and m b. Finding the center of mass of the angled bar 1. Tape a sheet of paper into the inside corner of the L-bracket, as shown in figure For each of the three possible pivot points: (a) Hang a plumb bob from the pivot point. (b) Mark two points along the plumb line, widely separated enough so that you can later draw an accurate line. 3. Remove the L-bracket from the hanger and carefully draw in the three lines indicated by your points. 4. The lines should intersect at a single point, or at worst, make a small triangle. In the former case, you have located the center of mass coordinate. In the later case, if all sides of the triangle are smaller than 1 cm, take the center of the triangle as the center of mass coordinate. Otherwise, repeat the measurements. 5. Report your measured center-of-mass for the object, using the origin and method shown in figure 7. [1] The moment of inertia I is defined as I r 2 dm, where the displacement r is from the axis of rotation to the location of the mass element dm.
Chapter 12 Static Equilibrium
 Chapter Static Equilibrium. Analysis Model: Rigid Body in Equilibrium. More on the Center of Gravity. Examples of Rigid Objects in Static Equilibrium CHAPTER : STATIC EQUILIBRIUM AND ELASTICITY.) The Conditions
Chapter Static Equilibrium. Analysis Model: Rigid Body in Equilibrium. More on the Center of Gravity. Examples of Rigid Objects in Static Equilibrium CHAPTER : STATIC EQUILIBRIUM AND ELASTICITY.) The Conditions
Rotational Equilibrium
 Rotational Equilibrium In this laboratory, we study the conditions for static equilibrium. Axis Through the Center of Gravity Suspend the meter stick at its center of gravity, with its numbers increasing
Rotational Equilibrium In this laboratory, we study the conditions for static equilibrium. Axis Through the Center of Gravity Suspend the meter stick at its center of gravity, with its numbers increasing
Rotational Equilibrium
 Rotational Equilibrium 6-1 Rotational Equilibrium INTRODUCTION Have you ever tried to pull a stubborn nail out of a board or develop your forearm muscles by lifting weights? Both these activities involve
Rotational Equilibrium 6-1 Rotational Equilibrium INTRODUCTION Have you ever tried to pull a stubborn nail out of a board or develop your forearm muscles by lifting weights? Both these activities involve
Chapter 9 Rotational Dynamics
 Chapter 9 ROTATIONAL DYNAMICS PREVIEW A force acting at a perpendicular distance from a rotation point, such as pushing a doorknob and causing the door to rotate on its hinges, produces a torque. If the
Chapter 9 ROTATIONAL DYNAMICS PREVIEW A force acting at a perpendicular distance from a rotation point, such as pushing a doorknob and causing the door to rotate on its hinges, produces a torque. If the
For a rigid body that is constrained to rotate about a fixed axis, the gravitational torque about the axis is
 Experiment 14 The Physical Pendulum The period of oscillation of a physical pendulum is found to a high degree of accuracy by two methods: theory and experiment. The values are then compared. Theory For
Experiment 14 The Physical Pendulum The period of oscillation of a physical pendulum is found to a high degree of accuracy by two methods: theory and experiment. The values are then compared. Theory For
Physics 1A Lecture 10B
 Physics 1A Lecture 10B "Sometimes the world puts a spin on life. When our equilibrium returns to us, we understand more because we've seen the whole picture. --Davis Barton Cross Products Another way to
Physics 1A Lecture 10B "Sometimes the world puts a spin on life. When our equilibrium returns to us, we understand more because we've seen the whole picture. --Davis Barton Cross Products Another way to
Name Section Number Team Number
 Physics 218 LAB: TORQUES and STATIC EQUILIBRIUM Name Section Number Team Number Introduction One purpose of this lab is to introduce you to quantity called torque or, as engineers cail it, moment of a
Physics 218 LAB: TORQUES and STATIC EQUILIBRIUM Name Section Number Team Number Introduction One purpose of this lab is to introduce you to quantity called torque or, as engineers cail it, moment of a
Please read this introductory material carefully; it covers topics you might not yet have seen in class.
 b Lab Physics 211 Lab 10 Torque What You Need To Know: Please read this introductory material carefully; it covers topics you might not yet have seen in class. F (a) (b) FIGURE 1 Forces acting on an object
b Lab Physics 211 Lab 10 Torque What You Need To Know: Please read this introductory material carefully; it covers topics you might not yet have seen in class. F (a) (b) FIGURE 1 Forces acting on an object
Chapter 8 continued. Rotational Dynamics
 Chapter 8 continued Rotational Dynamics 8.6 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Chapter 8 continued Rotational Dynamics 8.6 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Application of Forces. Chapter Eight. Torque. Force vs. Torque. Torque, cont. Direction of Torque 4/7/2015
 Raymond A. Serway Chris Vuille Chapter Eight Rotational Equilibrium and Rotational Dynamics Application of Forces The point of application of a force is important This was ignored in treating objects as
Raymond A. Serway Chris Vuille Chapter Eight Rotational Equilibrium and Rotational Dynamics Application of Forces The point of application of a force is important This was ignored in treating objects as
AP Physics QUIZ Chapters 10
 Name: 1. Torque is the rotational analogue of (A) Kinetic Energy (B) Linear Momentum (C) Acceleration (D) Force (E) Mass A 5-kilogram sphere is connected to a 10-kilogram sphere by a rigid rod of negligible
Name: 1. Torque is the rotational analogue of (A) Kinetic Energy (B) Linear Momentum (C) Acceleration (D) Force (E) Mass A 5-kilogram sphere is connected to a 10-kilogram sphere by a rigid rod of negligible
AP Physics Multiple Choice Practice Torque
 AP Physics Multiple Choice Practice Torque 1. A uniform meterstick of mass 0.20 kg is pivoted at the 40 cm mark. Where should one hang a mass of 0.50 kg to balance the stick? (A) 16 cm (B) 36 cm (C) 44
AP Physics Multiple Choice Practice Torque 1. A uniform meterstick of mass 0.20 kg is pivoted at the 40 cm mark. Where should one hang a mass of 0.50 kg to balance the stick? (A) 16 cm (B) 36 cm (C) 44
Rotational Kinetic Energy
 Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
Physics 101 Lab 6: Rotational Motion Dr. Timothy C. Black Fall, 2005
 Theoretical Discussion Physics 101 Lab 6: Rotational Motion Dr. Timothy C. Black Fall, 2005 An object moving in a circular orbit[1] at constant speed is said to be executing uniform circular motion. The
Theoretical Discussion Physics 101 Lab 6: Rotational Motion Dr. Timothy C. Black Fall, 2005 An object moving in a circular orbit[1] at constant speed is said to be executing uniform circular motion. The
Torques and Static Equilibrium
 Torques and Static Equilibrium INTRODUCTION Archimedes, Greek mathematician, physicist, engineer, inventor and astronomer, was widely regarded as the leading scientist of the ancient world. He made a study
Torques and Static Equilibrium INTRODUCTION Archimedes, Greek mathematician, physicist, engineer, inventor and astronomer, was widely regarded as the leading scientist of the ancient world. He made a study
= o + t = ot + ½ t 2 = o + 2
 Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
Lab 17 Torques/Moments
 Lab 17 Torques/Moments Name Partner s Name I. Introduction/Theory Terminology: The word 'torque' does not typically appear in the index to statics books such as Bedford and Fowler. For these authors, the
Lab 17 Torques/Moments Name Partner s Name I. Introduction/Theory Terminology: The word 'torque' does not typically appear in the index to statics books such as Bedford and Fowler. For these authors, the
Chapter 8. Rotational Equilibrium and Rotational Dynamics
 Chapter 8 Rotational Equilibrium and Rotational Dynamics Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related Torque The door is free to rotate about
Chapter 8 Rotational Equilibrium and Rotational Dynamics Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related Torque The door is free to rotate about
Physics A - PHY 2048C
 Physics A - PHY 2048C and 11/15/2017 My Office Hours: Thursday 2:00-3:00 PM 212 Keen Building Warm-up Questions 1 Did you read Chapter 12 in the textbook on? 2 Must an object be rotating to have a moment
Physics A - PHY 2048C and 11/15/2017 My Office Hours: Thursday 2:00-3:00 PM 212 Keen Building Warm-up Questions 1 Did you read Chapter 12 in the textbook on? 2 Must an object be rotating to have a moment
Chapter 8 Rotational Motion and Equilibrium. 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction
 Chapter 8 Rotational Motion and Equilibrium Name 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction 1. The distance between a turning axis and the
Chapter 8 Rotational Motion and Equilibrium Name 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction 1. The distance between a turning axis and the
Physics 8 Friday, November 4, 2011
 Physics 8 Friday, November 4, 2011 Please turn in Homework 7. I will hand out solutions once everyone is here. The handout also includes HW8 and a page or two of updates to the equation sheet needed to
Physics 8 Friday, November 4, 2011 Please turn in Homework 7. I will hand out solutions once everyone is here. The handout also includes HW8 and a page or two of updates to the equation sheet needed to
Structures Activity 2 Levers
 Structures Activity 2 Levers Object: The objects of this activity are to explore the concepts of torque and rotational equilibrium, study the three classes of lever, and apply the concepts of torque and
Structures Activity 2 Levers Object: The objects of this activity are to explore the concepts of torque and rotational equilibrium, study the three classes of lever, and apply the concepts of torque and
Figure Two. Then the two vector equations of equilibrium are equivalent to three scalar equations:
 2004- v 10/16 2. The resultant external torque (the vector sum of all external torques) acting on the body must be zero about any origin. These conditions can be written as equations: F = 0 = 0 where the
2004- v 10/16 2. The resultant external torque (the vector sum of all external torques) acting on the body must be zero about any origin. These conditions can be written as equations: F = 0 = 0 where the
Physics 8 Monday, October 28, 2013
 Physics 8 Monday, October 28, 2013 Turn in HW8 today. I ll make them less difficult in the future! Rotation is a hard topic. And these were hard problems. HW9 (due Friday) is 7 conceptual + 8 calculation
Physics 8 Monday, October 28, 2013 Turn in HW8 today. I ll make them less difficult in the future! Rotation is a hard topic. And these were hard problems. HW9 (due Friday) is 7 conceptual + 8 calculation
Experiment 9: Compound Pendulum
 COMSATS nstitute of nformation Technology, slamabad Campus PHYS - 108 Experiment 9: Compound Pendulum A compound pendulum (also known as a physical pendulum) consists of a rigid body oscillating about
COMSATS nstitute of nformation Technology, slamabad Campus PHYS - 108 Experiment 9: Compound Pendulum A compound pendulum (also known as a physical pendulum) consists of a rigid body oscillating about
Review for 3 rd Midterm
 Review for 3 rd Midterm Midterm is on 4/19 at 7:30pm in the same rooms as before You are allowed one double sided sheet of paper with any handwritten notes you like. The moment-of-inertia about the center-of-mass
Review for 3 rd Midterm Midterm is on 4/19 at 7:30pm in the same rooms as before You are allowed one double sided sheet of paper with any handwritten notes you like. The moment-of-inertia about the center-of-mass
General Physics (PHY 2130)
 General Physics (PHY 130) Lecture 0 Rotational dynamics equilibrium nd Newton s Law for rotational motion rolling Exam II review http://www.physics.wayne.edu/~apetrov/phy130/ Lightning Review Last lecture:
General Physics (PHY 130) Lecture 0 Rotational dynamics equilibrium nd Newton s Law for rotational motion rolling Exam II review http://www.physics.wayne.edu/~apetrov/phy130/ Lightning Review Last lecture:
Chapter 8 Rotational Equilibrium and Rotational Dynamics Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and
 Chapter 8 Rotational Equilibrium and Rotational Dynamics Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related Torque The door is free to rotate about
Chapter 8 Rotational Equilibrium and Rotational Dynamics Force vs. Torque Forces cause accelerations Torques cause angular accelerations Force and torque are related Torque The door is free to rotate about
Physics 6A Lab Experiment 6
 Biceps Muscle Model Physics 6A Lab Experiment 6 APPARATUS Biceps model Large mass hanger with four 1-kg masses Small mass hanger for hand end of forearm bar with five 100-g masses Meter stick Centimeter
Biceps Muscle Model Physics 6A Lab Experiment 6 APPARATUS Biceps model Large mass hanger with four 1-kg masses Small mass hanger for hand end of forearm bar with five 100-g masses Meter stick Centimeter
Rotational Dynamics continued
 Chapter 9 Rotational Dynamics continued 9.1 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Chapter 9 Rotational Dynamics continued 9.1 The Action of Forces and Torques on Rigid Objects Chapter 8 developed the concepts of angular motion. θ : angles and radian measure for angular variables ω :
Center of Gravity Pearson Education, Inc.
 Center of Gravity = The center of gravity position is at a place where the torque from one end of the object is balanced by the torque of the other end and therefore there is NO rotation. Fulcrum Point
Center of Gravity = The center of gravity position is at a place where the torque from one end of the object is balanced by the torque of the other end and therefore there is NO rotation. Fulcrum Point
Physics 101: Lecture 15 Torque, F=ma for rotation, and Equilibrium
 Physics 101: Lecture 15 Torque, F=ma for rotation, and Equilibrium Strike (Day 10) Prelectures, checkpoints, lectures continue with no change. Take-home quizzes this week. See Elaine Schulte s email. HW
Physics 101: Lecture 15 Torque, F=ma for rotation, and Equilibrium Strike (Day 10) Prelectures, checkpoints, lectures continue with no change. Take-home quizzes this week. See Elaine Schulte s email. HW
Chapter 8 continued. Rotational Dynamics
 Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = s = rφ = Frφ Fr = τ (torque) = τφ r φ s F to s θ = 0 DEFINITION
Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = s = rφ = Frφ Fr = τ (torque) = τφ r φ s F to s θ = 0 DEFINITION
STATIC EQUILIBRIUM. Purpose
 Purpose Theory STATIC EQUILIBRIUM a. To understand torque by experimentally measuring and manipulating them. b. To determine static equilibrium conditions by different torques that operate on a system.
Purpose Theory STATIC EQUILIBRIUM a. To understand torque by experimentally measuring and manipulating them. b. To determine static equilibrium conditions by different torques that operate on a system.
Lab 2: Equilibrium. Note: the Vector Review from the beginning of this book should be read and understood prior to coming to class!
 Lab 2: Equilibrium Note: This lab will be conducted over 2 weeks, with half the class working with forces while the other half works with torques the first week, and then switching the second week. Description
Lab 2: Equilibrium Note: This lab will be conducted over 2 weeks, with half the class working with forces while the other half works with torques the first week, and then switching the second week. Description
Chapter 10. Rotation
 Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
Chapter 19 Angular Momentum
 Chapter 19 Angular Momentum Chapter 19 Angular Momentum... 2 19.1 Introduction... 2 19.2 Angular Momentum about a Point for a Particle... 3 19.2.1 Angular Momentum for a Point Particle... 3 19.2.2 Right-Hand-Rule
Chapter 19 Angular Momentum Chapter 19 Angular Momentum... 2 19.1 Introduction... 2 19.2 Angular Momentum about a Point for a Particle... 3 19.2.1 Angular Momentum for a Point Particle... 3 19.2.2 Right-Hand-Rule
Chapter 8 Lecture. Pearson Physics. Rotational Motion and Equilibrium. Prepared by Chris Chiaverina Pearson Education, Inc.
 Chapter 8 Lecture Pearson Physics Rotational Motion and Equilibrium Prepared by Chris Chiaverina Chapter Contents Describing Angular Motion Rolling Motion and the Moment of Inertia Torque Static Equilibrium
Chapter 8 Lecture Pearson Physics Rotational Motion and Equilibrium Prepared by Chris Chiaverina Chapter Contents Describing Angular Motion Rolling Motion and the Moment of Inertia Torque Static Equilibrium
Flipping Physics Lecture Notes: Demonstrating Rotational Inertia (or Moment of Inertia)
 Flipping Physics Lecture Notes: Demonstrating Rotational Inertia (or Moment of Inertia) Have you ever struggled to describe Rotational Inertia to your students? Even worse, have you ever struggled to understand
Flipping Physics Lecture Notes: Demonstrating Rotational Inertia (or Moment of Inertia) Have you ever struggled to describe Rotational Inertia to your students? Even worse, have you ever struggled to understand
Static equilibrium. Objectives. Physics terms. Assessment. Brainstorm. Equations 6/3/14
 Static equilibrium Objectives State the conditions of static equilibrium in terms of forces and torques. Draw a free-body diagram of a lever showing all forces. Use the condition of equilibrium to solve
Static equilibrium Objectives State the conditions of static equilibrium in terms of forces and torques. Draw a free-body diagram of a lever showing all forces. Use the condition of equilibrium to solve
Rotational Kinematics
 Rotational Kinematics Rotational Coordinates Ridged objects require six numbers to describe their position and orientation: 3 coordinates 3 axes of rotation Rotational Coordinates Use an angle θ to describe
Rotational Kinematics Rotational Coordinates Ridged objects require six numbers to describe their position and orientation: 3 coordinates 3 axes of rotation Rotational Coordinates Use an angle θ to describe
Physics 111. Tuesday, November 2, Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy
 ics Tuesday, ember 2, 2002 Ch 11: Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy Announcements Wednesday, 8-9 pm in NSC 118/119 Sunday, 6:30-8 pm in CCLIR 468 Announcements This
ics Tuesday, ember 2, 2002 Ch 11: Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy Announcements Wednesday, 8-9 pm in NSC 118/119 Sunday, 6:30-8 pm in CCLIR 468 Announcements This
Rotation. Kinematics Rigid Bodies Kinetic Energy. Torque Rolling. featuring moments of Inertia
 Rotation Kinematics Rigid Bodies Kinetic Energy featuring moments of Inertia Torque Rolling Angular Motion We think about rotation in the same basic way we do about linear motion How far does it go? How
Rotation Kinematics Rigid Bodies Kinetic Energy featuring moments of Inertia Torque Rolling Angular Motion We think about rotation in the same basic way we do about linear motion How far does it go? How
When the applied force is not perpendicular to the crowbar, for example, the lever arm is found by drawing the perpendicular line from the fulcrum to
 When the applied force is not perpendicular to the crowbar, for example, the lever arm is found by drawing the perpendicular line from the fulcrum to the line of action of the force. We call torques that
When the applied force is not perpendicular to the crowbar, for example, the lever arm is found by drawing the perpendicular line from the fulcrum to the line of action of the force. We call torques that
31 ROTATIONAL KINEMATICS
 31 ROTATIONAL KINEMATICS 1. Compare and contrast circular motion and rotation? Address the following Which involves an object and which involves a system? Does an object/system in circular motion have
31 ROTATIONAL KINEMATICS 1. Compare and contrast circular motion and rotation? Address the following Which involves an object and which involves a system? Does an object/system in circular motion have
Welcome back to Physics 211
 Welcome back to Physics 211 Today s agenda: Torque Rotational Dynamics Current assignments Prelecture Thursday, Nov 20th at 10:30am HW#13 due this Friday at 5 pm. Clicker.1 What is the center of mass of
Welcome back to Physics 211 Today s agenda: Torque Rotational Dynamics Current assignments Prelecture Thursday, Nov 20th at 10:30am HW#13 due this Friday at 5 pm. Clicker.1 What is the center of mass of
11-2 A General Method, and Rolling without Slipping
 11-2 A General Method, and Rolling without Slipping Let s begin by summarizing a general method for analyzing situations involving Newton s Second Law for Rotation, such as the situation in Exploration
11-2 A General Method, and Rolling without Slipping Let s begin by summarizing a general method for analyzing situations involving Newton s Second Law for Rotation, such as the situation in Exploration
Chapter 8 - Rotational Dynamics and Equilibrium REVIEW
 Pagpalain ka! (Good luck, in Filipino) Date Chapter 8 - Rotational Dynamics and Equilibrium REVIEW TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1) When a rigid body
Pagpalain ka! (Good luck, in Filipino) Date Chapter 8 - Rotational Dynamics and Equilibrium REVIEW TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1) When a rigid body
Lecture 14. Rotational dynamics Torque. Give me a lever long enough and a fulcrum on which to place it, and I shall move the world.
 Lecture 14 Rotational dynamics Torque Give me a lever long enough and a fulcrum on which to place it, and I shall move the world. Archimedes, 87 1 BC EXAM Tuesday March 6, 018 8:15 PM 9:45 PM Today s Topics:
Lecture 14 Rotational dynamics Torque Give me a lever long enough and a fulcrum on which to place it, and I shall move the world. Archimedes, 87 1 BC EXAM Tuesday March 6, 018 8:15 PM 9:45 PM Today s Topics:
Chapter 8 continued. Rotational Dynamics
 Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = rφ = Frφ Fr = τ (torque) = τφ r φ s F to x θ = 0 DEFINITION OF
Chapter 8 continued Rotational Dynamics 8.4 Rotational Work and Energy Work to accelerate a mass rotating it by angle φ F W = F(cosθ)x x = rφ = Frφ Fr = τ (torque) = τφ r φ s F to x θ = 0 DEFINITION OF
8.012 Physics I: Classical Mechanics Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
MIT OpenCourseWare http://ocw.mit.edu 8.012 Physics I: Classical Mechanics Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS INSTITUTE
Chapter 12: Rotation of Rigid Bodies. Center of Mass Moment of Inertia Torque Angular Momentum Rolling Statics
 Chapter 12: Rotation of Rigid Bodies Center of Mass Moment of Inertia Torque Angular Momentum Rolling Statics Translational vs Rotational 2 / / 1/ 2 m x v dx dt a dv dt F ma p mv KE mv Work Fd P Fv 2 /
Chapter 12: Rotation of Rigid Bodies Center of Mass Moment of Inertia Torque Angular Momentum Rolling Statics Translational vs Rotational 2 / / 1/ 2 m x v dx dt a dv dt F ma p mv KE mv Work Fd P Fv 2 /
Dynamics of Rotational Motion
 Chapter 10 Dynamics of Rotational Motion To understand the concept of torque. To relate angular acceleration and torque. To work and power in rotational motion. To understand angular momentum. To understand
Chapter 10 Dynamics of Rotational Motion To understand the concept of torque. To relate angular acceleration and torque. To work and power in rotational motion. To understand angular momentum. To understand
Rotational Motion. 1 Purpose. 2 Theory 2.1 Equation of Motion for a Rotating Rigid Body
 Rotational Motion Equipment: Capstone, rotary motion sensor mounted on 80 cm rod and heavy duty bench clamp (PASCO ME-9472), string with loop at one end and small white bead at the other end (125 cm bead
Rotational Motion Equipment: Capstone, rotary motion sensor mounted on 80 cm rod and heavy duty bench clamp (PASCO ME-9472), string with loop at one end and small white bead at the other end (125 cm bead
Rotational Kinematics and Dynamics. UCVTS AIT Physics
 Rotational Kinematics and Dynamics UCVTS AIT Physics Angular Position Axis of rotation is the center of the disc Choose a fixed reference line Point P is at a fixed distance r from the origin Angular Position,
Rotational Kinematics and Dynamics UCVTS AIT Physics Angular Position Axis of rotation is the center of the disc Choose a fixed reference line Point P is at a fixed distance r from the origin Angular Position,
Lecture 9 - Rotational Dynamics
 Lecture 9 - Rotational Dynamics A Puzzle... Angular momentum is a 3D vector, and changing its direction produces a torque τ = dl. An important application in our daily lives is that bicycles don t fall
Lecture 9 - Rotational Dynamics A Puzzle... Angular momentum is a 3D vector, and changing its direction produces a torque τ = dl. An important application in our daily lives is that bicycles don t fall
Recap I. Angular position: Angular displacement: s. Angular velocity: Angular Acceleration:
 Recap I Angular position: Angular displacement: s Angular velocity: Angular Acceleration: Every point on a rotating rigid object has the same angular, but not the same linear motion! Recap II Circular
Recap I Angular position: Angular displacement: s Angular velocity: Angular Acceleration: Every point on a rotating rigid object has the same angular, but not the same linear motion! Recap II Circular
PHYSICS 149: Lecture 21
 PHYSICS 149: Lecture 21 Chapter 8: Torque and Angular Momentum 8.2 Torque 8.4 Equilibrium Revisited 8.8 Angular Momentum Lecture 21 Purdue University, Physics 149 1 Midterm Exam 2 Wednesday, April 6, 6:30
PHYSICS 149: Lecture 21 Chapter 8: Torque and Angular Momentum 8.2 Torque 8.4 Equilibrium Revisited 8.8 Angular Momentum Lecture 21 Purdue University, Physics 149 1 Midterm Exam 2 Wednesday, April 6, 6:30
Chapter 8. Centripetal Force and The Law of Gravity
 Chapter 8 Centripetal Force and The Law of Gravity Centripetal Acceleration An object traveling in a circle, even though it moves with a constant speed, will have an acceleration The centripetal acceleration
Chapter 8 Centripetal Force and The Law of Gravity Centripetal Acceleration An object traveling in a circle, even though it moves with a constant speed, will have an acceleration The centripetal acceleration
Parallel Forces. Forces acting in the same or in opposite directions at different points on an object.
 Parallel Forces Forces acting in the same or in opposite directions at different points on an object. Statics refers to the bodies in equilibrium. Equilibrium deals with the absence of a net force. When
Parallel Forces Forces acting in the same or in opposite directions at different points on an object. Statics refers to the bodies in equilibrium. Equilibrium deals with the absence of a net force. When
Contents. Concept Map
 Contents 1. General Notes on Forces 2. Effects of Forces on Motion 3. Effects of Forces on Shape 4. The Turning Effect of Forces 5. The Centre of Gravity and Stability Concept Map April 2000 Forces - 1
Contents 1. General Notes on Forces 2. Effects of Forces on Motion 3. Effects of Forces on Shape 4. The Turning Effect of Forces 5. The Centre of Gravity and Stability Concept Map April 2000 Forces - 1
Static Equilibrium; Torque
 Static Equilibrium; Torque The Conditions for Equilibrium An object with forces acting on it, but that is not moving, is said to be in equilibrium. The first condition for equilibrium is that the net force
Static Equilibrium; Torque The Conditions for Equilibrium An object with forces acting on it, but that is not moving, is said to be in equilibrium. The first condition for equilibrium is that the net force
Static Equilibrium and Torque
 10.3 Static Equilibrium and Torque SECTION OUTCOMES Use vector analysis in two dimensions for systems involving static equilibrium and torques. Apply static torques to structures such as seesaws and bridges.
10.3 Static Equilibrium and Torque SECTION OUTCOMES Use vector analysis in two dimensions for systems involving static equilibrium and torques. Apply static torques to structures such as seesaws and bridges.
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Torque. Introduction. Torque. PHY torque - J. Hedberg
 Torque PHY 207 - torque - J. Hedberg - 2017 1. Introduction 2. Torque 1. Lever arm changes 3. Net Torques 4. Moment of Rotational Inertia 1. Moment of Inertia for Arbitrary Shapes 2. Parallel Axis Theorem
Torque PHY 207 - torque - J. Hedberg - 2017 1. Introduction 2. Torque 1. Lever arm changes 3. Net Torques 4. Moment of Rotational Inertia 1. Moment of Inertia for Arbitrary Shapes 2. Parallel Axis Theorem
Torque and Simple Harmonic Motion
 Torque and Simple Harmonic Motion Recall: Fixed Axis Rotation Angle variable Angular velocity Angular acceleration Mass element Radius of orbit Kinematics!! " d# / dt! " d 2 # / dt 2!m i Moment of inertia
Torque and Simple Harmonic Motion Recall: Fixed Axis Rotation Angle variable Angular velocity Angular acceleration Mass element Radius of orbit Kinematics!! " d# / dt! " d 2 # / dt 2!m i Moment of inertia
Solutions to Exam #1
 SBCC 2017Summer2 P 101 Solutions to Exam 01 2017Jul11A Page 1 of 9 Solutions to Exam #1 1. Which of the following natural sciences most directly involves and applies physics? a) Botany (plant biology)
SBCC 2017Summer2 P 101 Solutions to Exam 01 2017Jul11A Page 1 of 9 Solutions to Exam #1 1. Which of the following natural sciences most directly involves and applies physics? a) Botany (plant biology)
When an object is in translational equilibrium and rotational equilibrium, we say it is in static equilibrium.
 STATIC EQUILIBRIUM I. PURPOSE In this experiment you will apply the concept of torque and learn what we mean when we say that a body is in static equilibrium. You will examine an object in static equilibrium
STATIC EQUILIBRIUM I. PURPOSE In this experiment you will apply the concept of torque and learn what we mean when we say that a body is in static equilibrium. You will examine an object in static equilibrium
PHY131H1S - Class 20. Pre-class reading quiz on Chapter 12
 PHY131H1S - Class 20 Today: Gravitational Torque Rotational Kinetic Energy Rolling without Slipping Equilibrium with Rotation Rotation Vectors Angular Momentum Pre-class reading quiz on Chapter 12 1 Last
PHY131H1S - Class 20 Today: Gravitational Torque Rotational Kinetic Energy Rolling without Slipping Equilibrium with Rotation Rotation Vectors Angular Momentum Pre-class reading quiz on Chapter 12 1 Last
are (0 cm, 10 cm), (10 cm, 10 cm), and (10 cm, 0 cm), respectively. Solve: The coordinates of the center of mass are = = = (200 g g g)
 Rotational Motion Problems Solutions.. Model: A spinning skater, whose arms are outstretched, is a rigid rotating body. Solve: The speed v rω, where r 40 / 0.70 m. Also, 80 rpm (80) π/60 rad/s 6 π rad/s.
Rotational Motion Problems Solutions.. Model: A spinning skater, whose arms are outstretched, is a rigid rotating body. Solve: The speed v rω, where r 40 / 0.70 m. Also, 80 rpm (80) π/60 rad/s 6 π rad/s.
Rotation. Rotational Variables
 Rotation Rigid Bodies Rotation variables Constant angular acceleration Rotational KE Rotational Inertia Rotational Variables Rotation of a rigid body About a fixed rotation axis. Rigid Body an object that
Rotation Rigid Bodies Rotation variables Constant angular acceleration Rotational KE Rotational Inertia Rotational Variables Rotation of a rigid body About a fixed rotation axis. Rigid Body an object that
Kinematics (special case) Dynamics gravity, tension, elastic, normal, friction. Energy: kinetic, potential gravity, spring + work (friction)
 Kinematics (special case) a = constant 1D motion 2D projectile Uniform circular Dynamics gravity, tension, elastic, normal, friction Motion with a = constant Newton s Laws F = m a F 12 = F 21 Time & Position
Kinematics (special case) a = constant 1D motion 2D projectile Uniform circular Dynamics gravity, tension, elastic, normal, friction Motion with a = constant Newton s Laws F = m a F 12 = F 21 Time & Position
Simple Harmonic Motion
 1. Object Simple Harmonic Motion To determine the period of motion of objects that are executing simple harmonic motion and to check the theoretical prediction of such periods. 2. Apparatus Assorted weights
1. Object Simple Harmonic Motion To determine the period of motion of objects that are executing simple harmonic motion and to check the theoretical prediction of such periods. 2. Apparatus Assorted weights
EXPERIMENT 7: ANGULAR KINEMATICS AND TORQUE (V_3)
 TA name Lab section Date TA Initials (on completion) Name UW Student ID # Lab Partner(s) EXPERIMENT 7: ANGULAR KINEMATICS AND TORQUE (V_3) 121 Textbook Reference: Knight, Chapter 13.1-3, 6. SYNOPSIS In
TA name Lab section Date TA Initials (on completion) Name UW Student ID # Lab Partner(s) EXPERIMENT 7: ANGULAR KINEMATICS AND TORQUE (V_3) 121 Textbook Reference: Knight, Chapter 13.1-3, 6. SYNOPSIS In
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department 8.01 Physics I Fall Term 2009 Review Module on Solving N equations in N unknowns
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department 8.01 Physics I Fall Term 2009 Review Module on Solving N equations in N unknowns Most students first exposure to solving N linear equations in N
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department 8.01 Physics I Fall Term 2009 Review Module on Solving N equations in N unknowns Most students first exposure to solving N linear equations in N
Lecture 2 - Force Analysis
 Lecture 2 - orce Analysis A Puzzle... Triangle or quadrilateral? 4 distinct points in a plane can either be arrange as a triangle with a point inside or as a quadrilateral. Extra Brownie Points: Use the
Lecture 2 - orce Analysis A Puzzle... Triangle or quadrilateral? 4 distinct points in a plane can either be arrange as a triangle with a point inside or as a quadrilateral. Extra Brownie Points: Use the
Class XI Chapter 7- System of Particles and Rotational Motion Physics
 Page 178 Question 7.1: Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie
Page 178 Question 7.1: Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie
Angular Momentum L = I ω
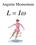 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Static Equilibrium, Gravitation, Periodic Motion
 This test covers static equilibrium, universal gravitation, and simple harmonic motion, with some problems requiring a knowledge of basic calculus. Part I. Multiple Choice 1. 60 A B 10 kg A mass of 10
This test covers static equilibrium, universal gravitation, and simple harmonic motion, with some problems requiring a knowledge of basic calculus. Part I. Multiple Choice 1. 60 A B 10 kg A mass of 10
Physics 2A Chapter 10 - Rotational Motion Fall 2018
 Physics A Chapter 10 - Rotational Motion Fall 018 These notes are five pages. A quick summary: The concepts of rotational motion are a direct mirror image of the same concepts in linear motion. Follow
Physics A Chapter 10 - Rotational Motion Fall 018 These notes are five pages. A quick summary: The concepts of rotational motion are a direct mirror image of the same concepts in linear motion. Follow
Torque and Rotational Equilibrium
 Torque and Rotational Equilibrium Theory Torque is the rotational analog of force. If you want something to move (translate), you apply a force; if you want something to rotate, you apply a torque. Torque
Torque and Rotational Equilibrium Theory Torque is the rotational analog of force. If you want something to move (translate), you apply a force; if you want something to rotate, you apply a torque. Torque
3. If you drag a rip-cord 2.0m across a wheel and it turns 10rad, what is the radius of the wheel? a. 0.1m b. 0.2m c. 0.4m d.
 1. Two spheres are rolled across the floor the same distance at the same speed. Which will have the greater angular velocity? a. the smaller sphere b. the larger sphere c. the angular velocities will be
1. Two spheres are rolled across the floor the same distance at the same speed. Which will have the greater angular velocity? a. the smaller sphere b. the larger sphere c. the angular velocities will be
CHAPTER 8 TEST REVIEW MARKSCHEME
 AP PHYSICS Name: Period: Date: 50 Multiple Choice 45 Single Response 5 Multi-Response Free Response 3 Short Free Response 2 Long Free Response MULTIPLE CHOICE DEVIL PHYSICS BADDEST CLASS ON CAMPUS AP EXAM
AP PHYSICS Name: Period: Date: 50 Multiple Choice 45 Single Response 5 Multi-Response Free Response 3 Short Free Response 2 Long Free Response MULTIPLE CHOICE DEVIL PHYSICS BADDEST CLASS ON CAMPUS AP EXAM
Chapter 8. Rotational Kinematics
 Chapter 8 Rotational Kinematics 8.3 The Equations of Rotational Kinematics 8.4 Angular Variables and Tangential Variables The relationship between the (tangential) arc length, s, at some radius, r, and
Chapter 8 Rotational Kinematics 8.3 The Equations of Rotational Kinematics 8.4 Angular Variables and Tangential Variables The relationship between the (tangential) arc length, s, at some radius, r, and
Physics 221. Exam III Spring f S While the cylinder is rolling up, the frictional force is and the cylinder is rotating
 Physics 1. Exam III Spring 003 The situation below refers to the next three questions: A solid cylinder of radius R and mass M with initial velocity v 0 rolls without slipping up the inclined plane. N
Physics 1. Exam III Spring 003 The situation below refers to the next three questions: A solid cylinder of radius R and mass M with initial velocity v 0 rolls without slipping up the inclined plane. N
The Laws of Motion. Newton s first law Force Mass Newton s second law Gravitational Force Newton s third law Examples
 The Laws of Motion Newton s first law Force Mass Newton s second law Gravitational Force Newton s third law Examples Gravitational Force Gravitational force is a vector Expressed by Newton s Law of Universal
The Laws of Motion Newton s first law Force Mass Newton s second law Gravitational Force Newton s third law Examples Gravitational Force Gravitational force is a vector Expressed by Newton s Law of Universal
STUDY GUIDE 4: Equilibrium, Angular Kinematics, and Dynamics
 PH 1110 Term C11 STUDY GUIDE 4: Equilibrium, Angular Kinematics, and Dynamics Objectives 25. Define torque. Solve problems involving objects in static equilibrium. 26. Define angular displacement, angular
PH 1110 Term C11 STUDY GUIDE 4: Equilibrium, Angular Kinematics, and Dynamics Objectives 25. Define torque. Solve problems involving objects in static equilibrium. 26. Define angular displacement, angular
Unit 1: Equilibrium and Center of Mass
 Unit 1: Equilibrium and Center of Mass FORCES What is a force? Forces are a result of the interaction between two objects. They push things, pull things, keep things together, pull things apart. It s really
Unit 1: Equilibrium and Center of Mass FORCES What is a force? Forces are a result of the interaction between two objects. They push things, pull things, keep things together, pull things apart. It s really
Motion in Two Dimensions Teacher s Guide
 Motion in Two Dimensions Teacher s Guide Objectives: 1. Use kinematic equations for motion in two dimensions to determine the range of a projectile.. Use the equation for torque to determine at what point
Motion in Two Dimensions Teacher s Guide Objectives: 1. Use kinematic equations for motion in two dimensions to determine the range of a projectile.. Use the equation for torque to determine at what point
Chapter 17 Two Dimensional Rotational Dynamics
 Chapter 17 Two Dimensional Rotational Dynamics 17.1 Introduction... 1 17.2 Vector Product (Cross Product)... 2 17.2.1 Right-hand Rule for the Direction of Vector Product... 3 17.2.2 Properties of the Vector
Chapter 17 Two Dimensional Rotational Dynamics 17.1 Introduction... 1 17.2 Vector Product (Cross Product)... 2 17.2.1 Right-hand Rule for the Direction of Vector Product... 3 17.2.2 Properties of the Vector
Simple and Physical Pendulums Challenge Problem Solutions
 Simple and Physical Pendulums Challenge Problem Solutions Problem 1 Solutions: For this problem, the answers to parts a) through d) will rely on an analysis of the pendulum motion. There are two conventional
Simple and Physical Pendulums Challenge Problem Solutions Problem 1 Solutions: For this problem, the answers to parts a) through d) will rely on an analysis of the pendulum motion. There are two conventional
Physics 111 Lecture 4 Newton`s Laws
 Physics 111 Lecture 4 Newton`s Laws Dr. Ali ÖVGÜN EMU Physics Department www.aovgun.com he Laws of Motion q Newton s first law q Force q Mass q Newton s second law q Newton s third law q Examples Isaac
Physics 111 Lecture 4 Newton`s Laws Dr. Ali ÖVGÜN EMU Physics Department www.aovgun.com he Laws of Motion q Newton s first law q Force q Mass q Newton s second law q Newton s third law q Examples Isaac
Torque and Rotational Equilibrium
 Torque and Rotational Equilibrium Name Section Theory Torque is the rotational analog of force. If you want something to move (translate), you apply a force; if you want something to rotate, you apply
Torque and Rotational Equilibrium Name Section Theory Torque is the rotational analog of force. If you want something to move (translate), you apply a force; if you want something to rotate, you apply
PHYSICS 220. Lecture 15. Textbook Sections Lecture 15 Purdue University, Physics 220 1
 PHYSICS 220 Lecture 15 Angular Momentum Textbook Sections 9.3 9.6 Lecture 15 Purdue University, Physics 220 1 Last Lecture Overview Torque = Force that causes rotation τ = F r sin θ Work done by torque
PHYSICS 220 Lecture 15 Angular Momentum Textbook Sections 9.3 9.6 Lecture 15 Purdue University, Physics 220 1 Last Lecture Overview Torque = Force that causes rotation τ = F r sin θ Work done by torque
Torque rotational force which causes a change in rotational motion. This force is defined by linear force multiplied by a radius.
 Warm up A remote-controlled car's wheel accelerates at 22.4 rad/s 2. If the wheel begins with an angular speed of 10.8 rad/s, what is the wheel's angular speed after exactly three full turns? AP Physics
Warm up A remote-controlled car's wheel accelerates at 22.4 rad/s 2. If the wheel begins with an angular speed of 10.8 rad/s, what is the wheel's angular speed after exactly three full turns? AP Physics
Rotational Dynamics Smart Pulley
 Rotational Dynamics Smart Pulley The motion of the flywheel of a steam engine, an airplane propeller, and any rotating wheel are examples of a very important type of motion called rotational motion. If
Rotational Dynamics Smart Pulley The motion of the flywheel of a steam engine, an airplane propeller, and any rotating wheel are examples of a very important type of motion called rotational motion. If
Lecture Outline Chapter 11. Physics, 4 th Edition James S. Walker. Copyright 2010 Pearson Education, Inc.
 Lecture Outline Chapter 11 Physics, 4 th Edition James S. Walker Chapter 11 Rotational Dynamics and Static Equilibrium Units of Chapter 11 Torque Torque and Angular Acceleration Zero Torque and Static
Lecture Outline Chapter 11 Physics, 4 th Edition James S. Walker Chapter 11 Rotational Dynamics and Static Equilibrium Units of Chapter 11 Torque Torque and Angular Acceleration Zero Torque and Static
Solution Only gravity is doing work. Since gravity is a conservative force mechanical energy is conserved:
 8) roller coaster starts with a speed of 8.0 m/s at a point 45 m above the bottom of a dip (see figure). Neglecting friction, what will be the speed of the roller coaster at the top of the next slope,
8) roller coaster starts with a speed of 8.0 m/s at a point 45 m above the bottom of a dip (see figure). Neglecting friction, what will be the speed of the roller coaster at the top of the next slope,
Physics 111. Lecture 22 (Walker: ) Torque Rotational Dynamics Static Equilibrium Oct. 28, 2009
 Physics 111 Lecture 22 (Walker: 11.1-3) Torque Rotational Dynamics Static Equilibrium Oct. 28, 2009 Lecture 22 1/26 Torque (τ) We define a quantity called torque which is a measure of twisting effort.
Physics 111 Lecture 22 (Walker: 11.1-3) Torque Rotational Dynamics Static Equilibrium Oct. 28, 2009 Lecture 22 1/26 Torque (τ) We define a quantity called torque which is a measure of twisting effort.
Downloaded from
 Question 4.1: A circular coil of wire consisting of 100 turns, each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil? Number of turns
Question 4.1: A circular coil of wire consisting of 100 turns, each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil? Number of turns
