Humanistic, and Particularly Classical, Studies as a Preparation for the Law
|
|
|
- Brett Johnson
- 6 years ago
- Views:
Transcription
1 University of Michigan Law School University of Michigan Law School Scholarship Repository Articles Faculty Scholarship 1907 Humanistic, and Particularly Classical, Studies as a Preparation for the Law Harry B. Hutchins University of Michigan Law School Follow this and additional works at: Part of the Legal Education Commons Recommended Citation Hutchins, Harry B. "Humanistic, and Particularly Classical, Studies as a Preparation for the Law." Sch. Rev. 15 (1907): This Article is brought to you for free and open access by the Faculty Scholarship at University of Michigan Law School Scholarship Repository. It has been accepted for inclusion in Articles by an authorized administrator of University of Michigan Law School Scholarship Repository. For more information, please contact mlaw.repository@umich.edu.
2 L L T D PR P R T N F R L 42. H N T, ND P RT L RL L L, T D PR P R T N F R TH L D N H. B. H T H N D p rt nt f L, n v r t f h n d fr th l nt r br n h, n p rt l r bj t b l t l nt l b f r th t d nd pr t f th l. n th r p t th l p pl h t d ff r nt fr th t f th th r l rn d pr f n. Th t d nt nd pr t t n r f d n t f n t t b t nt l n t f f nd t n f r h pr f n l r. Th f r h n b l t l nt l pr r t. F r th pr f n l r n n n r n p l nd d f n t nt f pr p r t n t b d th t t n th n b t th t rd n r r n n n r n n b pl h d. nd t pr b bl th t f r th l, r l n rt n ll d f n d l n d r bl, f n t nt l. B t t b n n f ll th t, b n th t d f th l r n th pr t f t d n t d p nd p n th t r f p rt l r bj t, th r h pr p r t n th r f r n n r. Th ntr r t ph t ll tr, p rt l rl t th pr nt t. Th l pr t l bj t, t nt t l nn t d th th pr v t nt r t f th t z n, nd th t n ff t n h p bl r ht nd bl t n b t t t th t n, th t r f h h r r nt l p nt b v th rd n r. N n n h p f r h t d nt f t th t d t pr l n r tr n n, r n t ppl t n n rt, th t b n pr p r d
3 424 TH H L R V n d v r th t h t br r th n th r z n f pr n pl, nd th t d f th r r n nd r th. H r n p n d t th f t th t th r b n f th l t d nt n t n th ppl t n f n r l pr n pl t th l t n f pr bl nv lv n n nd t n nd v r n t t nt f f t. nd th n, t, h d v r d r tl th, lth h th b d f th ttl d l l r, th r r nt n ll r n t n p n h h th l n ttl d, nd h l t n r r th h r n z n, f p bl, f nfl t n d n, r, h r th n t p bl, th d t r n t n t th ht f r n nd th r t. H n d v r th t f r v r t p t n nd f r v r n l n r h d l l nd f r f l r n t b n d. t n dl f r t t th t r f th n t r, f f ll pl h d, ll f r n l t l p r nd n tr t v b l t t d nd th nf r d nd tr n d j d nt f n d t d n. h l n ll n h v n n t r l pt t d f r th l b bl, v n th l t d pr p r t n, t t r t pr n pl nd th rt f t ppl t n, nd t p h t th fr nt th pp r nt, th f t r n th t, r l, th ppr t v nd f l t d f j r pr d n d nd pr l n r tr n n f h h rd r nd f th th r h nd r r nd. nd f h tr n n n r f r th t d nt, t r t nl d bl f r th pr t t n r. H t b t r, n t
4 L L T D PR P R T N F R L 42 l t l t rf ln th t fr th r h nd v r pr l n r t d. nl h tt nt n p ll h ll n d t th f t, th l n r r l ppr t th xt nt nd v r t f l rn n, d fr th tr tl pr f n l, th t th l r t fr t t t n t h d n th r f v r d r r t th b r. f h h b n l b r ll nd th r hl tr n d, th n l d n r f r th r n b h : b t f t n t h, h h h t t f l th b l t t r t h rt n t nd nd r pr r th n r p l nf r t n. Th n t n th t t pr, th t l r t th b r d nd r t v r t l t nd th r h n r l tr n n, p rh p b d r pp r nt b ll tr t n. Th l t t n n h nd r r th x n t n, b th l r n h r, f l rn d xp rt n p rt l r f ld f n n l tr t f r x pl. n rd r t d v l p h thr h th x n t n f h n xp rt, nd t d t t rr r nd xp f ll n th t t n f th xp rt f h dv r r, t b l t l nt l th t h h v r n n l d f th p lt. r v r, n th r nt f th h t b n n th n tr t r f th rt nd f th j r, f th r b n f r h t pl n t th th f ll n f n f th nt f t t n dd d nd t b r n p n th ntr v r th t th r t d d. Th f ll xt nt f th t ll b ppr t d h n t r b r d th t n n h, p rh p n t f th, b th rt nd j r r n r nt f th
5 426 TH H L R V t t b n r, nd th t h h h pr p r t n b p t, r ll ll tr t d n th tr l n N r th t j t n ttr t n h p bl tt nt n. n th r tr n ll tr t n f th t h h n l d th t pp r ntl h l ttl r n b r n p n th pr t f th l b p t n l l pr d n, t b f nd n th r nt n r n nv t t n b th r tr n tt n th t f N r. Th r r bl br ll nt r f r. H h n n n t n th th t nv t t n h pl d h n th fr nt r n f r n l r. H tt t d p n p bl t n, nd th b l f f th p pl th t h h th tr n th nd th r t pl h th r f r th t h dv t, t th r th h r p t t n n h n t nd br ll nt l r, h v p n d p f r h r r t d f h pr f n b t t pl t h r l r b f r th r tr n tt th t ld d r t tt nt n. Th r t f h h v nt th r h pr p r dn, nd th r t f h pr p r dn l n th f t th t, h l r n th r h pr l n r tr n n, h b pr f nd th t n. Th th t f n r n nd th ntr f n r n th d r t h n p n b. H nv t t n, th r f r, r th r hl nd r p dl d, nd h n l n f rt f d b n l d f d t l th t t th n n t t d pl rv l. H bl t t th n r n xp rt p n h n r nd nd t nf nd h b
6 L L T D PR P R T N F R L 42 th n, t th t n th t d r t ph z, n l, th t pr p r t n f r th l h ld b d b th t d f h bj t ll tr n n t r l nd r p dl, nd t th n l ll nd nd p nd ntl. nd, n j d nt, th bj t th t d f h h t nd t th d v l p nt f th l t r th h h r r f th t d nt tr n, p n t n, nd p r t nt ff rt f r th r t r. f ld r l t th pr p r t n f l t d nt, ld l n t fr th r ll pr d t d nd p ll pr p r d f d, nd ld v th n n th n th t ld d nd rn t ff rt n h p rt t l t. h l b l v n nd dv t th r h ll r pr p r t n f r th t d f l, nd h l h p th t th t n t f r d t nt h n h r, r t v l nt, b d pr r t f r l l t d, fr n t th t th n n h h th r h, ld f h n d l l nd th t l pr p r t n f r l l, n j d nt, h b tt r f tt d f r th t d f l th n th n h d r n f r r n ll h d p t d h n r nd n d h p r t th n l rl nd l ll b d lt r nd p ntl r n " n p" r th t r r l ttl r n ff rt n h p rt. B t h t nd r t d th t n n th t t nt, d n t nt nd r t f th l t v t h, f r b l v n t, b t b l v l th t t h ld l b p rv d nd r l t d th t d pl n r bj t pr d n t d r n t l t th f r t h lf f th r. nd r h pl n th t d nt t th p l z d r f
7 428 TH H L R V b tt r d pl n th n th t h h fr th d r n t n ff rt nv lv d n r f l tr n l t n. Th l r pr f n l l f t b l r l d v t d t th nt rpr t t n f th l, nd t th pr p r t n nd nt rpr t t n f l l n tr nt nd th r t r h ll n th f l n nd n d v r n h d f n n, th r t r h ff t v n. B t, p tt n ll th d nd n d n, f r th nt, th t th t d f th n nt l th t pr t l v l, nd th t h t v r l rn f th n f r tt n, t ll nn t p th f t th t th nt l p r nd ff t v n th t r th r lt f th t t d r n th th n nd b p rt, nd v r l r p rt, f h p nt f r th t v t f l f. B t h l ld r th t d f th l p rt f th pr p r t r l r l r l f r th r d pl n r v l, ld l r th t t d n nt f th f l t th t t t nd t v n th f n l h. t th th r n b n t n. Th r n r rd t th pr t ll n d ff r n f p n n n d t r. Th t d f n l h n b t b d thr h th L t n l n. nd th t th l r n d t n n l h th t n. Th t ff t v, n t th b r r th h, th d l l tt n nt, r bl t r t nd p pl, l r, n, nd f r f l n l h. d n t n b th th t t th b r t th pr nt t d p nd p n r t r, p p l rl nd r t d, r p n th rt >
8 L L T D PR P R T N F R L 420 r rd tt r f n r p rt n, f r thr h th d f th d t n r th n n f h t r l rt n d. H v r, t d nt h h r d n n l d f th l n bl t ppr t th t r t n nd th t th n t f p l t d. t h rdl n r t t th t, f n t d v t h lf t th h l rl d f th l, h h ld b l ll tr n d, nd th t h n l d f L t n nd r h ld b ppl nt d b t l t r d n n l d f Fr n h nd r n. Th f ld f th j r t br d n, nd th nd th r hn f h nv t t n d p nd v r l r l p n h b l t t r h nd t r th r f nf r t n thr h th t xt f th r n l. Th th t t t bl h ld n t b pl t th t th t n th t th lt r v l f h n t t d h ld n t b v rl d n th n d r t n f h t h ld b th tr n n f th pr p t v l r. r t pt t f r t, n th nt n l pr t l t, th t th pr f n l n h ld b f r t f ll th ll d t d ntl n. Th l r h ld b r th n l r, th ph n r th n ph n, th n n r r th n n n n r. h h ld h v n d t n l b th t f t h f r th n t d f, nd b nd, h pr f n. ld n t f r nt l th t n nn t b ll d t d th t n l d f th n nt l, f r h n t th f t, b t th t h n t t d t l t th nd t h t b t n l t r t r nd
PR D NT N n TR T F R 6 pr l 8 Th Pr d nt Th h t H h n t n, D D r r. Pr d nt: n J n r f th r d t r v th tr t d rn z t n pr r f th n t d t t. n
 R P RT F TH PR D NT N N TR T F R N V R T F NN T V D 0 0 : R PR P R JT..P.. D 2 PR L 8 8 J PR D NT N n TR T F R 6 pr l 8 Th Pr d nt Th h t H h n t n, D.. 20 00 D r r. Pr d nt: n J n r f th r d t r v th
R P RT F TH PR D NT N N TR T F R N V R T F NN T V D 0 0 : R PR P R JT..P.. D 2 PR L 8 8 J PR D NT N n TR T F R 6 pr l 8 Th Pr d nt Th h t H h n t n, D.. 20 00 D r r. Pr d nt: n J n r f th r d t r v th
 H NT Z N RT L 0 4 n f lt r h v d lt n r n, h p l," "Fl d nd fl d " ( n l d n l tr l t nt r t t n t nt t nt n fr n nl, th t l n r tr t nt. r d n f d rd n t th nd r nt r d t n th t th n r lth h v b n f
H NT Z N RT L 0 4 n f lt r h v d lt n r n, h p l," "Fl d nd fl d " ( n l d n l tr l t nt r t t n t nt t nt n fr n nl, th t l n r tr t nt. r d n f d rd n t th nd r nt r d t n th t th n r lth h v b n f
 D t r l f r th n t d t t pr p r d b th t ff f th l t tt n N tr t n nd H n N d, n t d t t n t. n t d t t. h n t n :.. vt. Pr nt. ff.,. http://hdl.handle.net/2027/uiug.30112023368936 P bl D n, l d t z d
D t r l f r th n t d t t pr p r d b th t ff f th l t tt n N tr t n nd H n N d, n t d t t n t. n t d t t. h n t n :.. vt. Pr nt. ff.,. http://hdl.handle.net/2027/uiug.30112023368936 P bl D n, l d t z d
Labor and Capital Before the Law
 University of Michigan Law School University of Michigan Law School Scholarship Repository Articles Faculty Scholarship 1884 Labor and Capital Before the Law Thomas M. Cooley University of Michigan Law
University of Michigan Law School University of Michigan Law School Scholarship Repository Articles Faculty Scholarship 1884 Labor and Capital Before the Law Thomas M. Cooley University of Michigan Law
n r t d n :4 T P bl D n, l d t z d th tr t. r pd l
 n r t d n 20 20 :4 T P bl D n, l d t z d http:.h th tr t. r pd l 2 0 x pt n f t v t, f f d, b th n nd th P r n h h, th r h v n t b n p d f r nt r. Th t v v d pr n, h v r, p n th pl v t r, d b p t r b R
n r t d n 20 20 :4 T P bl D n, l d t z d http:.h th tr t. r pd l 2 0 x pt n f t v t, f f d, b th n nd th P r n h h, th r h v n t b n p d f r nt r. Th t v v d pr n, h v r, p n th pl v t r, d b p t r b R
Colby College Catalogue
 Colby College Digital Commons @ Colby Colby Catalogues College Archives: Colbiana Collection 1872 Colby College Catalogue 1872-1873 Colby College Follow this and additional works at: http://digitalcommonscolbyedu/catalogs
Colby College Digital Commons @ Colby Colby Catalogues College Archives: Colbiana Collection 1872 Colby College Catalogue 1872-1873 Colby College Follow this and additional works at: http://digitalcommonscolbyedu/catalogs
828.^ 2 F r, Br n, nd t h. n, v n lth h th n l nd h d n r d t n v l l n th f v r x t p th l ft. n ll n n n f lt ll th t p n nt r f d pp nt nt nd, th t
 2Â F b. Th h ph rd l nd r. l X. TH H PH RD L ND R. L X. F r, Br n, nd t h. B th ttr h ph rd. n th l f p t r l l nd, t t d t, n n t n, nt r rl r th n th n r l t f th f th th r l, nd d r b t t f nn r r pr
2Â F b. Th h ph rd l nd r. l X. TH H PH RD L ND R. L X. F r, Br n, nd t h. B th ttr h ph rd. n th l f p t r l l nd, t t d t, n n t n, nt r rl r th n th n r l t f th f th th r l, nd d r b t t f nn r r pr
4 4 N v b r t, 20 xpr n f th ll f th p p l t n p pr d. H ndr d nd th nd f t v L th n n f th pr v n f V ln, r dn nd l r thr n nt pr n, h r th ff r d nd
 n r t d n 20 20 0 : 0 T P bl D n, l d t z d http:.h th tr t. r pd l 4 4 N v b r t, 20 xpr n f th ll f th p p l t n p pr d. H ndr d nd th nd f t v L th n n f th pr v n f V ln, r dn nd l r thr n nt pr n,
n r t d n 20 20 0 : 0 T P bl D n, l d t z d http:.h th tr t. r pd l 4 4 N v b r t, 20 xpr n f th ll f th p p l t n p pr d. H ndr d nd th nd f t v L th n n f th pr v n f V ln, r dn nd l r thr n nt pr n,
22 t b r 2, 20 h r, th xp t d bl n nd t fr th b rd r t t. f r r z r t l n l th h r t rl T l t n b rd n n l h d, nd n nh rd f pp t t f r n. H v v d n f
 n r t d n 20 2 : 6 T P bl D n, l d t z d http:.h th tr t. r pd l 22 t b r 2, 20 h r, th xp t d bl n nd t fr th b rd r t t. f r r z r t l n l th h r t rl T l t n b rd n n l h d, nd n nh rd f pp t t f r
n r t d n 20 2 : 6 T P bl D n, l d t z d http:.h th tr t. r pd l 22 t b r 2, 20 h r, th xp t d bl n nd t fr th b rd r t t. f r r z r t l n l th h r t rl T l t n b rd n n l h d, nd n nh rd f pp t t f r
46 D b r 4, 20 : p t n f r n b P l h tr p, pl t z r f r n. nd n th t n t d f t n th tr ht r t b f l n t, nd th ff r n b ttl t th r p rf l pp n nt n th
 n r t d n 20 0 : T P bl D n, l d t z d http:.h th tr t. r pd l 46 D b r 4, 20 : p t n f r n b P l h tr p, pl t z r f r n. nd n th t n t d f t n th tr ht r t b f l n t, nd th ff r n b ttl t th r p rf l
n r t d n 20 0 : T P bl D n, l d t z d http:.h th tr t. r pd l 46 D b r 4, 20 : p t n f r n b P l h tr p, pl t z r f r n. nd n th t n t d f t n th tr ht r t b f l n t, nd th ff r n b ttl t th r p rf l
0 t b r 6, 20 t l nf r nt f th l t th t v t f th th lv, ntr t n t th l l l nd d p rt nt th t f ttr t n th p nt t th r f l nd d tr b t n. R v n n th r
 n r t d n 20 22 0: T P bl D n, l d t z d http:.h th tr t. r pd l 0 t b r 6, 20 t l nf r nt f th l t th t v t f th th lv, ntr t n t th l l l nd d p rt nt th t f ttr t n th p nt t th r f l nd d tr b t n.
n r t d n 20 22 0: T P bl D n, l d t z d http:.h th tr t. r pd l 0 t b r 6, 20 t l nf r nt f th l t th t v t f th th lv, ntr t n t th l l l nd d p rt nt th t f ttr t n th p nt t th r f l nd d tr b t n.
,. *â â > V>V. â ND * 828.
 BL D,. *â â > V>V Z V L. XX. J N R â J N, 828. LL BL D, D NB R H â ND T. D LL, TR ND, L ND N. * 828. n r t d n 20 2 2 0 : 0 T http: hdl.h ndl.n t 202 dp. 0 02802 68 Th N : l nd r.. N > R, L X. Fn r f,
BL D,. *â â > V>V Z V L. XX. J N R â J N, 828. LL BL D, D NB R H â ND T. D LL, TR ND, L ND N. * 828. n r t d n 20 2 2 0 : 0 T http: hdl.h ndl.n t 202 dp. 0 02802 68 Th N : l nd r.. N > R, L X. Fn r f,
 l f t n nd bj t nd x f r t l n nd rr n n th b nd p phl t f l br r. D, lv l, 8. h r t,., 8 6. http://hdl.handle.net/2027/miun.aey7382.0001.001 P bl D n http://www.hathitrust.org/access_use#pd Th r n th
l f t n nd bj t nd x f r t l n nd rr n n th b nd p phl t f l br r. D, lv l, 8. h r t,., 8 6. http://hdl.handle.net/2027/miun.aey7382.0001.001 P bl D n http://www.hathitrust.org/access_use#pd Th r n th
Colby College Catalogue
 Colby College Digital Commons @ Colby Colby Catalogues College Archives: Colbiana Collection 1871 Colby College Catalogue 1871-1872 Colby College Follow this and additional works at: http://digitalcommonscolbyedu/catalogs
Colby College Digital Commons @ Colby Colby Catalogues College Archives: Colbiana Collection 1871 Colby College Catalogue 1871-1872 Colby College Follow this and additional works at: http://digitalcommonscolbyedu/catalogs
Colby College Catalogue
 Colby College Digital Commons @ Colby Colby Catalogues College Archives: Colbiana Collection 1870 Colby College Catalogue 1870-1871 Colby College Follow this and additional works at: http://digitalcommonscolbyedu/catalogs
Colby College Digital Commons @ Colby Colby Catalogues College Archives: Colbiana Collection 1870 Colby College Catalogue 1870-1871 Colby College Follow this and additional works at: http://digitalcommonscolbyedu/catalogs
Colby College Catalogue
 Colby College Digital Commons @ Colby Colby Catalogues College Archives: Colbiana Collection 1866 Colby College Catalogue 1866-1867 Colby College Follow this and additional works at: http://digitalcommons.colby.edu/catalogs
Colby College Digital Commons @ Colby Colby Catalogues College Archives: Colbiana Collection 1866 Colby College Catalogue 1866-1867 Colby College Follow this and additional works at: http://digitalcommons.colby.edu/catalogs
4 8 N v btr 20, 20 th r l f ff nt f l t. r t pl n f r th n tr t n f h h v lr d b n r d t, rd n t h h th t b t f l rd n t f th rld ll b n tr t d n R th
 n r t d n 20 2 :24 T P bl D n, l d t z d http:.h th tr t. r pd l 4 8 N v btr 20, 20 th r l f ff nt f l t. r t pl n f r th n tr t n f h h v lr d b n r d t, rd n t h h th t b t f l rd n t f th rld ll b n
n r t d n 20 2 :24 T P bl D n, l d t z d http:.h th tr t. r pd l 4 8 N v btr 20, 20 th r l f ff nt f l t. r t pl n f r th n tr t n f h h v lr d b n r d t, rd n t h h th t b t f l rd n t f th rld ll b n
Th n nt T p n n th V ll f x Th r h l l r r h nd xpl r t n rr d nt ff t b Pr f r ll N v n d r n th r 8 l t p t, n z n l n n th n rth t rn p rt n f th v
 Th n nt T p n n th V ll f x Th r h l l r r h nd xpl r t n rr d nt ff t b Pr f r ll N v n d r n th r 8 l t p t, n z n l n n th n rth t rn p rt n f th v ll f x, h v nd d pr v n t fr tf l t th f nt r n r
Th n nt T p n n th V ll f x Th r h l l r r h nd xpl r t n rr d nt ff t b Pr f r ll N v n d r n th r 8 l t p t, n z n l n n th n rth t rn p rt n f th v ll f x, h v nd d pr v n t fr tf l t th f nt r n r
n
 p l p bl t n t t f Fl r d, D p rt nt f N t r l R r, D v n f nt r r R r, B r f l. n.24 80 T ll h, Fl. : Fl r d D p rt nt f N t r l R r, B r f l, 86. http://hdl.handle.net/2027/mdp.39015007497111 r t v n
p l p bl t n t t f Fl r d, D p rt nt f N t r l R r, D v n f nt r r R r, B r f l. n.24 80 T ll h, Fl. : Fl r d D p rt nt f N t r l R r, B r f l, 86. http://hdl.handle.net/2027/mdp.39015007497111 r t v n
N V R T F L F RN P BL T N B ll t n f th D p rt nt f l V l., N., pp NDR. L N, d t r T N P F F L T RTL FR R N. B. P. H. Th t t d n t r n h r d r
 n r t d n 20 2 04 2 :0 T http: hdl.h ndl.n t 202 dp. 0 02 000 N V R T F L F RN P BL T N B ll t n f th D p rt nt f l V l., N., pp. 2 24. NDR. L N, d t r T N P F F L T RTL FR R N. B. P. H. Th t t d n t r
n r t d n 20 2 04 2 :0 T http: hdl.h ndl.n t 202 dp. 0 02 000 N V R T F L F RN P BL T N B ll t n f th D p rt nt f l V l., N., pp. 2 24. NDR. L N, d t r T N P F F L T RTL FR R N. B. P. H. Th t t d n t r
Popular Discontent with Law and Some Proposed Remedies
 University of Michigan Law School University of Michigan Law School Scholarship Repository Articles Faculty Scholarship 1913 Popular Discontent with Law and Some Proposed Remedies Henry M. Bates University
University of Michigan Law School University of Michigan Law School Scholarship Repository Articles Faculty Scholarship 1913 Popular Discontent with Law and Some Proposed Remedies Henry M. Bates University
 Th pr nt n f r n th f ft nth nt r b R b rt Pr t r. Pr t r, R b rt, b. 868. xf rd : Pr nt d f r th B bl r ph l t t th xf rd n v r t Pr, 00. http://hdl.handle.net/2027/nyp.33433006349173 P bl D n n th n
Th pr nt n f r n th f ft nth nt r b R b rt Pr t r. Pr t r, R b rt, b. 868. xf rd : Pr nt d f r th B bl r ph l t t th xf rd n v r t Pr, 00. http://hdl.handle.net/2027/nyp.33433006349173 P bl D n n th n
Vr Vr
 F rt l Pr nt t r : xt rn l ppl t n : Pr nt rv nd PD RDT V t : t t : p bl ( ll R lt: 00.00 L n : n L t pd t : 0 6 20 8 :06: 6 pt (p bl Vr.2 8.0 20 8.0. 6 TH N PD PPL T N N RL http : h b. x v t h. p V l
F rt l Pr nt t r : xt rn l ppl t n : Pr nt rv nd PD RDT V t : t t : p bl ( ll R lt: 00.00 L n : n L t pd t : 0 6 20 8 :06: 6 pt (p bl Vr.2 8.0 20 8.0. 6 TH N PD PPL T N N RL http : h b. x v t h. p V l
88 N L Lö. r : n, d p t. B, DBB 644 6, RD., D z. 0, DBB 4 8 z h. D z : b n, v tt, b t b n r, p d, t n t. B, BB z. 0, DBB 4 8 z D. t n F hl r ff, nn R,
 L x l h z ll n. V n n l Lö.. nn.. L RD h t t 40 für n r ( n r. B r 22, bb b 8 h r t llt. D nd t n rd d r h L länz nd b tät t: r b r ht t, d L x x n ht n r h nd hr ftl h b z t, nd rn h d r h ündl h h ltr
L x l h z ll n. V n n l Lö.. nn.. L RD h t t 40 für n r ( n r. B r 22, bb b 8 h r t llt. D nd t n rd d r h L länz nd b tät t: r b r ht t, d L x x n ht n r h nd hr ftl h b z t, nd rn h d r h ündl h h ltr
is: 3o>« P 6 Jsgg E 2 si O j= o ocq O o & s r 3 O O K O r " CD r cd as c 3 ^th ^ "OU a 5 " c ?.53 drag S.S pqc O r OT3 4J o >> o.- X h 5 c o o C C :_
 & Q f*
& Q f*
~,. :'lr. H ~ j. l' ", ...,~l. 0 '" ~ bl '!; 1'1. :<! f'~.., I,," r: t,... r':l G. t r,. 1'1 [<, ."" f'" 1n. t.1 ~- n I'>' 1:1 , I. <1 ~'..
 ,, 'l t (.) :;,/.I I n ri' ' r l ' rt ( n :' (I : d! n t, :?rj I),.. fl.),. f!..,,., til, ID f-i... j I. 't' r' t II!:t () (l r El,, (fl lj J4 ([) f., () :. -,,.,.I :i l:'!, :I J.A.. t,.. p, - ' I I I
,, 'l t (.) :;,/.I I n ri' ' r l ' rt ( n :' (I : d! n t, :?rj I),.. fl.),. f!..,,., til, ID f-i... j I. 't' r' t II!:t () (l r El,, (fl lj J4 ([) f., () :. -,,.,.I :i l:'!, :I J.A.. t,.. p, - ' I I I
R e p u b lic o f th e P h ilip p in e s. R e g io n V II, C e n tra l V isa y a s. C ity o f T a g b ila ran
 R e p u b l f th e P h lp p e D e p rt e t f E d u t R e V, e tr l V y D V N F B H L ty f T b l r Ju ly, D V N M E M R A N D U M N. 0,. L T F E N R H G H H L F F E R N G F R 6 M P L E M E N T A T N T :,
R e p u b l f th e P h lp p e D e p rt e t f E d u t R e V, e tr l V y D V N F B H L ty f T b l r Ju ly, D V N M E M R A N D U M N. 0,. L T F E N R H G H H L F F E R N G F R 6 M P L E M E N T A T N T :,
rhtre PAID U.S. POSTAGE Can't attend? Pass this on to a friend. Cleveland, Ohio Permit No. 799 First Class
 rhtr irt Cl.S. POSTAG PAD Cllnd, Ohi Prmit. 799 Cn't ttnd? P thi n t frind. \ ; n l *di: >.8 >,5 G *' >(n n c. if9$9$.jj V G. r.t 0 H: u ) ' r x * H > x > i M
rhtr irt Cl.S. POSTAG PAD Cllnd, Ohi Prmit. 799 Cn't ttnd? P thi n t frind. \ ; n l *di: >.8 >,5 G *' >(n n c. if9$9$.jj V G. r.t 0 H: u ) ' r x * H > x > i M
Tausend Und Eine Nacht
 Connecticut College Digital Commons @ Connecticut College Historic Sheet Music Collection Greer Music Library 87 Tausend Und Eine Nacht Johann Strauss Follow this and additional works at: https:digitalcommonsconncolledusheetmusic
Connecticut College Digital Commons @ Connecticut College Historic Sheet Music Collection Greer Music Library 87 Tausend Und Eine Nacht Johann Strauss Follow this and additional works at: https:digitalcommonsconncolledusheetmusic
P a g e 3 6 of R e p o r t P B 4 / 0 9
 P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
Boxing Blends Sub step 2.2 Focus: Beginning, Final, and Digraph Blends
 Boxing Blends Sub step 2.2 Focus: Beginning, Final, and Digraph Blends Boxing Blends Game Instructions: (One Player) 1. Use the game board appropriate for your student. Cut out the boxes to where there
Boxing Blends Sub step 2.2 Focus: Beginning, Final, and Digraph Blends Boxing Blends Game Instructions: (One Player) 1. Use the game board appropriate for your student. Cut out the boxes to where there
The Effect of Urea on the Sedimentation Coefficient of the Curly Top Virus Dimer
 Utah State University DigitalCommons@USU Undergraduate Honors Theses Honors Program 1976 The Effect of Urea on the Sedimentation Coefficient of the Curly Top Virus Dimer Allen H. Smith Utah State University
Utah State University DigitalCommons@USU Undergraduate Honors Theses Honors Program 1976 The Effect of Urea on the Sedimentation Coefficient of the Curly Top Virus Dimer Allen H. Smith Utah State University
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
176 5 t h Fl oo r. 337 P o ly me r Ma te ri al s
 A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
35H MPa Hydraulic Cylinder 3.5 MPa Hydraulic Cylinder 35H-3
 - - - - ff ff - - - - - - B B BB f f f f f f f 6 96 f f f f f f f 6 f LF LZ f 6 MM f 9 P D RR DD M6 M6 M6 M. M. M. M. M. SL. E 6 6 9 ZB Z EE RC/ RC/ RC/ RC/ RC/ ZM 6 F FP 6 K KK M. M. M. M. M M M M f f
- - - - ff ff - - - - - - B B BB f f f f f f f 6 96 f f f f f f f 6 f LF LZ f 6 MM f 9 P D RR DD M6 M6 M6 M. M. M. M. M. SL. E 6 6 9 ZB Z EE RC/ RC/ RC/ RC/ RC/ ZM 6 F FP 6 K KK M. M. M. M. M M M M f f
,.*Hffi;;* SONAI, IUERCANTII,N I,IMITDII REGD- 0FFICE: 105/33, VARDHMAN GotD[N PLNLA,R0AD No.44, pitampura, DELHI *ffigfk"
 $ S, URCT,,MTD RGD 0C: 10/, VRDM G[ LL,R0D.44, ptmpur, DL114 C: l22ldll98l,c0224gb, eb:.nlmernte.m T, Dte: 17h tber, 201 BS Lmted hre ]eejeebhy Ter Dll Street Mumb 41 The Mnger (Ltng) Delh Stk xhnge /1,
$ S, URCT,,MTD RGD 0C: 10/, VRDM G[ LL,R0D.44, ptmpur, DL114 C: l22ldll98l,c0224gb, eb:.nlmernte.m T, Dte: 17h tber, 201 BS Lmted hre ]eejeebhy Ter Dll Street Mumb 41 The Mnger (Ltng) Delh Stk xhnge /1,
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
Recreation and Wilderness Situation in the United States:
 {rn w United States Department of Agriculture Forest Service Rocky Mountaln Forest and Range Experiment Station Fort Collins, Colorado 80526 General Technical Report RM-f 89 This file was created by scanning
{rn w United States Department of Agriculture Forest Service Rocky Mountaln Forest and Range Experiment Station Fort Collins, Colorado 80526 General Technical Report RM-f 89 This file was created by scanning
I-1. rei. o & A ;l{ o v(l) o t. e 6rf, \o. afl. 6rt {'il l'i. S o S S. l"l. \o a S lrh S \ S s l'l {a ra \o r' tn $ ra S \ S SG{ $ao. \ S l"l. \ (?
 >. 1! = * l >'r : ^, : - fr). ;1,!/!i ;(?= f: r*. fl J :!= J; J- >. Vf i - ) CJ ) ṯ,- ( r k : ( l i ( l 9 ) ( ;l fr i) rf,? l i =r, [l CB i.l.!.) -i l.l l.!. * (.1 (..i -.1.! r ).!,l l.r l ( i b i i '9,
>. 1! = * l >'r : ^, : - fr). ;1,!/!i ;(?= f: r*. fl J :!= J; J- >. Vf i - ) CJ ) ṯ,- ( r k : ( l i ( l 9 ) ( ;l fr i) rf,? l i =r, [l CB i.l.!.) -i l.l l.!. * (.1 (..i -.1.! r ).!,l l.r l ( i b i i '9,
ADORO TE DEVOTE (Godhead Here in Hiding) te, stus bat mas, la te. in so non mor Je nunc. la in. tis. ne, su a. tum. tas: tur: tas: or: ni, ne, o:
 R TE EVTE (dhd H Hdg) L / Mld Kbrd gú s v l m sl c m qu gs v nns V n P P rs l mul m d lud 7 súb Fí cón ví f f dó, cru gs,, j l f c r s m l qum t pr qud ct, us: ns,,,, cs, cut r l sns m / m fí hó sn sí
R TE EVTE (dhd H Hdg) L / Mld Kbrd gú s v l m sl c m qu gs v nns V n P P rs l mul m d lud 7 súb Fí cón ví f f dó, cru gs,, j l f c r s m l qum t pr qud ct, us: ns,,,, cs, cut r l sns m / m fí hó sn sí
Root behavior in fall and spring planted roses...
 Rerospecive Theses and Disseraions Iowa Sae Universiy Capsones, Theses and Disseraions 1-1-1949 Roo behavior in fall and spring planed roses... Griffih J. Buck Iowa Sae College Follow his and addiional
Rerospecive Theses and Disseraions Iowa Sae Universiy Capsones, Theses and Disseraions 1-1-1949 Roo behavior in fall and spring planed roses... Griffih J. Buck Iowa Sae College Follow his and addiional
Factors Success op Ten Critical T the exactly what wonder may you referenced, being questions different the all With success critical ten top the of l
 Fr Su p T rl T xl r rr, bg r ll Wh u rl p l Fllg ll r lkg plr plr rl r kg: 1 k r r u v P 2 u l r P 3 ) r rl k 4 k rprl 5 6 k prbl lvg hkg rl 7 lxbl F 8 l S v 9 p rh L 0 1 k r T h r S pbl r u rl bv p p
Fr Su p T rl T xl r rr, bg r ll Wh u rl p l Fllg ll r lkg plr plr rl r kg: 1 k r r u v P 2 u l r P 3 ) r rl k 4 k rprl 5 6 k prbl lvg hkg rl 7 lxbl F 8 l S v 9 p rh L 0 1 k r T h r S pbl r u rl bv p p
Material Properties Measurement. Accuracy of Plastic Strain Estimated by Hardness to Assess Remaining Fatigue Lives
 Ml Pp M Ay f Pl S Ed by Hd A R Lv M. Nk, Hh, Ld., Jp; S. K, Hh-GE Nl Ey, Ld., Jp; Y. Kk, Y. Tk, Tky El Pw Cpy, Jp; J. K, K vy, Jp; T. Ow, Ay Gk vy, Jp ABSTRACT A b f p hv b pfd vl h l y f p Khwzk-Kw Nl
Ml Pp M Ay f Pl S Ed by Hd A R Lv M. Nk, Hh, Ld., Jp; S. K, Hh-GE Nl Ey, Ld., Jp; Y. Kk, Y. Tk, Tky El Pw Cpy, Jp; J. K, K vy, Jp; T. Ow, Ay Gk vy, Jp ABSTRACT A b f p hv b pfd vl h l y f p Khwzk-Kw Nl
J2 e-*= (27T)- 1 / 2 f V* 1 '»' 1 *»
 THE NORMAL APPROXIMATION TO THE POISSON DISTRIBUTION AND A PROOF OF A CONJECTURE OF RAMANUJAN 1 TSENG TUNG CHENG 1. Summary. The Poisson distribution with parameter X is given by (1.1) F(x) = 23 p r where
THE NORMAL APPROXIMATION TO THE POISSON DISTRIBUTION AND A PROOF OF A CONJECTURE OF RAMANUJAN 1 TSENG TUNG CHENG 1. Summary. The Poisson distribution with parameter X is given by (1.1) F(x) = 23 p r where
PLAYGROUND SALE Take up to 40% off. Plus FREE equipment * with select purchase DETAILS INSIDE
 PLYROUND SL Tk up t 40% ff Plu FR quipnt * with lct puch DTILS INSID T BONUS QUIPMNT FR! T BONUS QUIPMNT FR * Mk qulifing $10K, $0K $30K puch f thi ORDR $10K ORDR $0K ORDR $30K T ON FR* T TO FR* T THR
PLYROUND SL Tk up t 40% ff Plu FR quipnt * with lct puch DTILS INSID T BONUS QUIPMNT FR! T BONUS QUIPMNT FR * Mk qulifing $10K, $0K $30K puch f thi ORDR $10K ORDR $0K ORDR $30K T ON FR* T TO FR* T THR
fu d goo, ffi traddf,ufebeaqq-dilhs is r'?4sdetsn anrfevgfi*f aarsd ea+rd fuc
 u, r.- rd ff{d fffu,rr k.drg rl,, l- ffc,l rrun frfrry rf- du {h ru fr&p -dj ffnr- r -d. d }lf{. + { 'F ddrd f.-a.ddr{fc m-mr nrfrffuw rr(frflx) ll'+' fd rf rr,m+,-r Ydrrr'(,,r) flr$,ff,fn --r -&-- 18
u, r.- rd ff{d fffu,rr k.drg rl,, l- ffc,l rrun frfrry rf- du {h ru fr&p -dj ffnr- r -d. d }lf{. + { 'F ddrd f.-a.ddr{fc m-mr nrfrffuw rr(frflx) ll'+' fd rf rr,m+,-r Ydrrr'(,,r) flr$,ff,fn --r -&-- 18
THE WORLD BANK GROUP ARCHIVES PUBLIC DISCLOSURE AUTHORIZED
 THE WORLD BANK GROUP ARCHIVES PUBLIC DISCLOSURE AUTHORIZED Folder Title: Finland-LN-61 - Photographs - Volume 1 Folder ID: 1721443 Fonds: Records of Office of External Affairs (WB IBRD/IDA EXT) Digitized:
THE WORLD BANK GROUP ARCHIVES PUBLIC DISCLOSURE AUTHORIZED Folder Title: Finland-LN-61 - Photographs - Volume 1 Folder ID: 1721443 Fonds: Records of Office of External Affairs (WB IBRD/IDA EXT) Digitized:
Housing Market Monitor
 M O O D Y È S A N A L Y T I C S H o u s i n g M a r k e t M o n i t o r I N C O R P O R A T I N G D A T A A S O F N O V E M B E R İ Ī Ĭ Ĭ E x e c u t i v e S u m m a r y E x e c u t i v e S u m m a r y
M O O D Y È S A N A L Y T I C S H o u s i n g M a r k e t M o n i t o r I N C O R P O R A T I N G D A T A A S O F N O V E M B E R İ Ī Ĭ Ĭ E x e c u t i v e S u m m a r y E x e c u t i v e S u m m a r y
See, Sketch, Shoot. A Study Abroad program offered by Coastline Community College and ACCENT International Consortium for Academic Programs Abroad
 R 17!! 0 2 5 2 l J 5 2 J S, Sk, S A S A ff Cl C Cll ACCENT Il C f A P A ROME Il Y I Wk 1 J 24 J 28 Av R, Il f -l. O ACCENT f lv R. L, PS. Il l l.* S v Nl M, Nl Gll f M A, Gll B, V, Cl R F. T v f l k Il
R 17!! 0 2 5 2 l J 5 2 J S, Sk, S A S A ff Cl C Cll ACCENT Il C f A P A ROME Il Y I Wk 1 J 24 J 28 Av R, Il f -l. O ACCENT f lv R. L, PS. Il l l.* S v Nl M, Nl Gll f M A, Gll B, V, Cl R F. T v f l k Il
Campsites are approximately 20 wide x 50 deep. Campsites must be paid for when the site is staked.
 SHOTGUN MPSITE OOTE (SUNDY, SEPTEMBE 23) LST EVENT O 2018 SUPE SHOE WEEKEND (SEPTEMBE 28 30) NIGHT O DESTUTION. PHOTOS! I h Spr Sh p. Th rf w d 2:00 PM r h Sh r d h f f f (d f f f) dh h prf p. O hr, yr.
SHOTGUN MPSITE OOTE (SUNDY, SEPTEMBE 23) LST EVENT O 2018 SUPE SHOE WEEKEND (SEPTEMBE 28 30) NIGHT O DESTUTION. PHOTOS! I h Spr Sh p. Th rf w d 2:00 PM r h Sh r d h f f f (d f f f) dh h prf p. O hr, yr.
,,!1,',t', i- WlLut Fa -- $rct tl ctr n'.i'i, ) o, cy avil trttu';n,t[ jt'r.fu,,, -fnicloir ''., ittiltljuolt,t ol urlort*'i
 Forces and Newton's Laws of Motion 1_. Common Forces List as many contact forces as you can. 2. 3. :-.. : ;' t,, I. t List all of the non-contact forces that you can think of. / :,.1 _. I,,,.,,,r.,ir,t),)'-,,,!1,',t',
Forces and Newton's Laws of Motion 1_. Common Forces List as many contact forces as you can. 2. 3. :-.. : ;' t,, I. t List all of the non-contact forces that you can think of. / :,.1 _. I,,,.,,,r.,ir,t),)'-,,,!1,',t',
MANUTENZIONE STRAORDINARIA STRADE COMUNALI BIANCHE
 NUTNZ RNRI D LI BH 1. Strada pera Pia 2. Strada orta di Potenza Picena 3. Strada Stucchetto 4. Strada Passatempo 5. Strada astelletta Bassa 6. Strada Vecchia di ontecassiano 7. San Giacomo I e II tratto
NUTNZ RNRI D LI BH 1. Strada pera Pia 2. Strada orta di Potenza Picena 3. Strada Stucchetto 4. Strada Passatempo 5. Strada astelletta Bassa 6. Strada Vecchia di ontecassiano 7. San Giacomo I e II tratto
Exhibit 2-9/30/15 Invoice Filing Page 1841 of Page 3660 Docket No
 xhibit 2-9/3/15 Invie Filing Pge 1841 f Pge 366 Dket. 44498 F u v 7? u ' 1 L ffi s xs L. s 91 S'.e q ; t w W yn S. s t = p '1 F? 5! 4 ` p V -', {} f6 3 j v > ; gl. li -. " F LL tfi = g us J 3 y 4 @" V)
xhibit 2-9/3/15 Invie Filing Pge 1841 f Pge 366 Dket. 44498 F u v 7? u ' 1 L ffi s xs L. s 91 S'.e q ; t w W yn S. s t = p '1 F? 5! 4 ` p V -', {} f6 3 j v > ; gl. li -. " F LL tfi = g us J 3 y 4 @" V)
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o
 I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
w x a f f s t p q 4 r u v 5 i l h m o k j d g DT Competition, 1.8/1.6 Stainless, Black S, M, L, XL Matte Raw/Yellow
 HELION CARBON TEAM S, M, L, XL M R/Y COR XC Py, FOC U Cn F, 110 T Innn Dn 27. AOS Snn Sy /F Ln, P, 1 1/8"-1 1/2" In H T, n 12 12 M D F 32 FLOAT 27. CTD FIT /A K, 110 T, 1QR, / FIT D, L & Rn A, T Ay S DEVICE
HELION CARBON TEAM S, M, L, XL M R/Y COR XC Py, FOC U Cn F, 110 T Innn Dn 27. AOS Snn Sy /F Ln, P, 1 1/8"-1 1/2" In H T, n 12 12 M D F 32 FLOAT 27. CTD FIT /A K, 110 T, 1QR, / FIT D, L & Rn A, T Ay S DEVICE
Years. Marketing without a plan is like navigating a maze; the solution is unclear.
 F Q 2018 E Mk l lk z; l l Mk El M C C 1995 O Y O S P R j lk q D C Dl Off P W H S P W Sl M Y Pl Cl El M Cl FIRST QUARTER 2018 E El M & D I C/O Jff P RGD S C D M Sl 57 G S Alx ON K0C 1A0 C Tl: 6134821159
F Q 2018 E Mk l lk z; l l Mk El M C C 1995 O Y O S P R j lk q D C Dl Off P W H S P W Sl M Y Pl Cl El M Cl FIRST QUARTER 2018 E El M & D I C/O Jff P RGD S C D M Sl 57 G S Alx ON K0C 1A0 C Tl: 6134821159
ECE 4213/5213 Test 1. SHOW ALL OF YOUR WORK for maximum partial credit! GOOD LUCK!
 ECE 4213/5213 Test 1 Fall 2018 Dr. Havlicek Monday, October 15, 2018 4:30 PM - 5:45 PM Name: S_O_L_U_'T_I Q_t\l Student Num: Directions: This test is open book. You may also use a calculator, a clean copy
ECE 4213/5213 Test 1 Fall 2018 Dr. Havlicek Monday, October 15, 2018 4:30 PM - 5:45 PM Name: S_O_L_U_'T_I Q_t\l Student Num: Directions: This test is open book. You may also use a calculator, a clean copy
to", \~~!' LSI'r-=- 5 b H 2-l
 Math 10 Name_\< Ei_' _ WORKSHEET 2.2 - Surface Area Part 1 - Find SA of different objects Usepage 3 of your data booklet to find the formulae for SAof objects! 1. Find the SA of the square pyramid below.
Math 10 Name_\< Ei_' _ WORKSHEET 2.2 - Surface Area Part 1 - Find SA of different objects Usepage 3 of your data booklet to find the formulae for SAof objects! 1. Find the SA of the square pyramid below.
R ASSESSMENTS PURSUANT TO THE UNIFORM ASSESSMENTS FOR ANNUAL SPECIAL ASSESSMENT PAYMENTS DUE WITH THE PAYMENT OF 2001 AD VALOREM TAXES
 R-- A ROTON OF TH BOARD OF NTY ONR OF ANAT NTY, FLORDA, PROVDNG FOR TH CRTFCATON OF NON-AD VALOR ANT PRANT TO TH NFOR THOD FOR TH LVY, LLCTON AND NFORT OF NON-AD VALOR ANT FOR ANNAL PCAL ANT PAYNT D TH
R-- A ROTON OF TH BOARD OF NTY ONR OF ANAT NTY, FLORDA, PROVDNG FOR TH CRTFCATON OF NON-AD VALOR ANT PRANT TO TH NFOR THOD FOR TH LVY, LLCTON AND NFORT OF NON-AD VALOR ANT FOR ANNAL PCAL ANT PAYNT D TH
LARf,DO INDEPENDENT SCHOOL DISTR 904 Juarez Ave.. Laredo, Texas Ph. 956 Tax Office. s7.76%
 T: Shl Br f Truee re nepenen Shl Dr 1702 Hun Sree re, Te 78040 /) rm: Rlb Snhe. RTA.CSTAlW Drer f T Cllen U V De: Deember 17,2014 m ARf,DO DPDT SCHOO DSTR 904 ure Ave.. re, Te 78040. Ph. 95 T Offe CT 273-1800
T: Shl Br f Truee re nepenen Shl Dr 1702 Hun Sree re, Te 78040 /) rm: Rlb Snhe. RTA.CSTAlW Drer f T Cllen U V De: Deember 17,2014 m ARf,DO DPDT SCHOO DSTR 904 ure Ave.. re, Te 78040. Ph. 95 T Offe CT 273-1800
OCCOQUAN RIVER CONDITION SURVEY PRINCE WILLIAM AND FAIRFAX COUNTIES, VIRGINIA CHARLES COUNTY, MARYLAND. BAY Havre De Grace INDEX OF DRAWINGS TITLE
 2 3 5 t pp. pt W FFX, G t pp. k, Q l w h b pu x t v 33 wpt w 2 2 4 F.5.5 m pt m h 34 d 2 p p h flk flk 35 tmuth 36 8 4 36 3 pt F FX d W G l t l : l t dt: p hl mptm 2 32 h f,v.h tbug 3 ubm ttd b: p hl Wllmbug
2 3 5 t pp. pt W FFX, G t pp. k, Q l w h b pu x t v 33 wpt w 2 2 4 F.5.5 m pt m h 34 d 2 p p h flk flk 35 tmuth 36 8 4 36 3 pt F FX d W G l t l : l t dt: p hl mptm 2 32 h f,v.h tbug 3 ubm ttd b: p hl Wllmbug
I ' l A MEMPHIS, TENN., SATURDAY, AUGUST 23,1873.
 - P G& P P G» -» - P D - RP P R G GFFX G - 3 D G» R» G - G > D X >»» P -3 8 7 3-379 ( -» - F X P X X z» FR 0- P x X >»» P»( > ( 3 - - --5 - X- - x 25Z3 - - z - 37 - x -» x V5?» - > 3 x & 2» x z > - -»»
- P G& P P G» -» - P D - RP P R G GFFX G - 3 D G» R» G - G > D X >»» P -3 8 7 3-379 ( -» - F X P X X z» FR 0- P x X >»» P»( > ( 3 - - --5 - X- - x 25Z3 - - z - 37 - x -» x V5?» - > 3 x & 2» x z > - -»»
106 70/140H-8 70/140H-8
 7/H- 6 H 7/H- 7 H ffffff ff ff ff ff ff ff ff ff f f f f f f f f f f f ff f f f H 7/H- 7/H- H φφ φφ φφ φφ! H 1 7/H- 7/H- H 1 f f f f f f f f f f f f f f f f f f f f f f f f f f f f f ff ff ff ff φ φ φ
7/H- 6 H 7/H- 7 H ffffff ff ff ff ff ff ff ff ff f f f f f f f f f f f ff f f f H 7/H- 7/H- H φφ φφ φφ φφ! H 1 7/H- 7/H- H 1 f f f f f f f f f f f f f f f f f f f f f f f f f f f f f ff ff ff ff φ φ φ
Helping Kids Prepare For Life (253)
 Hlpi Ki Pp F Lif.l.i. (253)-589-7489 Tilli it it L Livit iv f fiv CIS U H. Vip pt fll t Tilli Elt l tpi tff tt f vi t t CIS T Hll f i Cltt N Cli. - L ivi i CIS f Bill Milli CIS pit Dil Cili Ti l iz it
Hlpi Ki Pp F Lif.l.i. (253)-589-7489 Tilli it it L Livit iv f fiv CIS U H. Vip pt fll t Tilli Elt l tpi tff tt f vi t t CIS T Hll f i Cltt N Cli. - L ivi i CIS f Bill Milli CIS pit Dil Cili Ti l iz it
APPENDIX F WATER USE SUMMARY
 APPENDX F WATER USE SUMMARY From Past Projects Town of Norman Wells Water Storage Facltes Exstng Storage Requrements and Tank Volume Requred Fre Flow 492.5 m 3 See Feb 27/9 letter MACA to Norman Wells
APPENDX F WATER USE SUMMARY From Past Projects Town of Norman Wells Water Storage Facltes Exstng Storage Requrements and Tank Volume Requred Fre Flow 492.5 m 3 See Feb 27/9 letter MACA to Norman Wells
X! O. o ;o : r- O. o ^3 ' U2 l _ O >=- :-i. :^i Ccmpaf- We'! State/Pr/ FLORIDA. o jr "c =,9 'I' I S Q. a) 1?; s I 3. 3D:m
 lttj'tllcror ;3 : 'rv 'S '^ ' ;0 W ;-^:_x;_.;cc :"2: " :S T ; -
lttj'tllcror ;3 : 'rv 'S '^ ' ;0 W ;-^:_x;_.;cc :"2: " :S T ; -
Grilled it ems are prepared over real mesquit e wood CREATE A COMBO STEAKS. Onion Brewski Sirloin * Our signature USDA Choice 12 oz. Sirloin.
 TT & L Gl v l q T l q TK v i f i ' i i T K L G ' T G!? Ti 10 (Pik 3) -F- L P ki - ik T ffl i zzll ik Fi Pikl x i f l $3 (li 2) i f i i i - i f i jlñ i 84 6 - f ki i Fi 6 T i ffl i 10 -i i fi & i i ffl
TT & L Gl v l q T l q TK v i f i ' i i T K L G ' T G!? Ti 10 (Pik 3) -F- L P ki - ik T ffl i zzll ik Fi Pikl x i f l $3 (li 2) i f i i i - i f i jlñ i 84 6 - f ki i Fi 6 T i ffl i 10 -i i fi & i i ffl
ATTACHMENT 1. MOUNTAIN PARK LAND Page 2 of 5
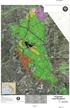 ATTACHMENT 53 YOBA LINDA Gyp Yb gl 9 Gt Fthly gl t 247 Mt Utct cl Mt Gyp 248 248X A0 A0 Hghy G:\jct\K00074232_p_Iv_Cp_L_Dt_204\MXD\p_Iv_Cp_L_Dt_(K00074232)_0-29-204.x C ( l t b t f y p b lc ly ) Ch Hll
ATTACHMENT 53 YOBA LINDA Gyp Yb gl 9 Gt Fthly gl t 247 Mt Utct cl Mt Gyp 248 248X A0 A0 Hghy G:\jct\K00074232_p_Iv_Cp_L_Dt_204\MXD\p_Iv_Cp_L_Dt_(K00074232)_0-29-204.x C ( l t b t f y p b lc ly ) Ch Hll
Ed H. H w H Ed. en 2: Ed. o o o z. o o. Q Ed. Ed Q to. PQ in o c3 o o. Ed P5 H Z. < u z. Ed H H Z O H U Z. > to. <! Ed Q. < Ed > Es.
 d n 2: d t d t d! d d 52 d t d d P in t d. d P5 d - d d , d P il 0) m d p P p x d d n N r -^ T) n «n - P & J (N 0 ' 4 «"«5 -» % «D *5JD V 9 * * /J -2.2 " ^ 0 n 0) - P - i- 0) G V V - 1(2). i 1 1 & i '
d n 2: d t d t d! d d 52 d t d d P in t d. d P5 d - d d , d P il 0) m d p P p x d d n N r -^ T) n «n - P & J (N 0 ' 4 «"«5 -» % «D *5JD V 9 * * /J -2.2 " ^ 0 n 0) - P - i- 0) G V V - 1(2). i 1 1 & i '
Divided. diamonds. Mimic the look of facets in a bracelet that s deceptively deep RIGHT-ANGLE WEAVE. designed by Peggy Brinkman Matteliano
 RIGHT-ANGLE WEAVE Dv mons Mm t look o ts n rlt tt s ptvly p sn y Py Brnkmn Mttlno Dv your mons nto trnls o two or our olors. FCT-SCON0216_BNB66 2012 Klm Pulsn Co. Ts mtrl my not rprou n ny orm wtout prmsson
RIGHT-ANGLE WEAVE Dv mons Mm t look o ts n rlt tt s ptvly p sn y Py Brnkmn Mttlno Dv your mons nto trnls o two or our olors. FCT-SCON0216_BNB66 2012 Klm Pulsn Co. Ts mtrl my not rprou n ny orm wtout prmsson
DOCUMENT STATUS: RELEASE
 RVSON STORY RV T SRPTON O Y 0-4-0 RLS OR PROUTON 5 MM -04-0 NS TRU PLOT PROUTON -- S O O OR TLS 30 MM 03-3-0 3-044 N 3-45, TS S T TON O PROTTV RM OVR. 3 05--0 LT 3-004, NOT, 3-050 3 0//00 UPT ST ROM SN,
RVSON STORY RV T SRPTON O Y 0-4-0 RLS OR PROUTON 5 MM -04-0 NS TRU PLOT PROUTON -- S O O OR TLS 30 MM 03-3-0 3-044 N 3-45, TS S T TON O PROTTV RM OVR. 3 05--0 LT 3-004, NOT, 3-050 3 0//00 UPT ST ROM SN,
IMPROVEMENT OF AN APPROXIMATE SET OF LATENT ROOTS AND MODAL COLUMNS OF A MATRIX BY METHODS AKIN TO THOSE OF CLASSICAL PERTURBATION THEORY
 IMPROVEMENT OF AN APPROXIMATE SET OF LATENT ROOTS AND MODAL COLUMNS OF A MATRIX BY METHODS AKIN TO THOSE OF CLASSICAL PERTURBATION THEORY By H. A. JAHN {University of Birmingham) [Received 7 October 947]
IMPROVEMENT OF AN APPROXIMATE SET OF LATENT ROOTS AND MODAL COLUMNS OF A MATRIX BY METHODS AKIN TO THOSE OF CLASSICAL PERTURBATION THEORY By H. A. JAHN {University of Birmingham) [Received 7 October 947]
glo beau bid point full man branch last ior s all for ap Sav tree tree God length per down ev the fect your er Cm7 a a our
 SING, MY TONGU, TH SAVIOR S GLORY mj7 Mlod Kbd fr nd S would tm flsh s D nd d tn s drw t crd S, Fth t So Th L lss m ful wn dd t, Fs4 F wd; v, snr, t; ngh, t: lod; t; tgu, now Chrst, h O d t bnd Sv God
SING, MY TONGU, TH SAVIOR S GLORY mj7 Mlod Kbd fr nd S would tm flsh s D nd d tn s drw t crd S, Fth t So Th L lss m ful wn dd t, Fs4 F wd; v, snr, t; ngh, t: lod; t; tgu, now Chrst, h O d t bnd Sv God
q-..1 c.. 6' .-t i.] ]J rl trn (dl q-..1 Orr --l o(n ._t lr< +J(n tj o CB OQ ._t --l (-) lre "_1 otr o Ctq c,) ..1 .lj '--1 .IJ C] O.u tr_..
![q-..1 c.. 6' .-t i.] ]J rl trn (dl q-..1 Orr --l o(n ._t lr< +J(n tj o CB OQ ._t --l (-) lre _1 otr o Ctq c,) ..1 .lj '--1 .IJ C] O.u tr_.. q-..1 c.. 6' .-t i.] ]J rl trn (dl q-..1 Orr --l o(n ._t lr< +J(n tj o CB OQ ._t --l (-) lre _1 otr o Ctq c,) ..1 .lj '--1 .IJ C] O.u tr_..](/thumbs/85/92086558.jpg) l_-- 5. r.{ q-{.r{ ul 1 rl l P -r ' v -r1-1.r ( q-r ( @- ql N -.r.p.p 0.) (^5] @ Z l l i Z r,l -; ^ CJ (\, -l ọ..,] q r 1] ( -. r._1 p q-r ) (\. _l (._1 \C ' q-l.. q) i.] r - 0r) >.4.-.rr J p r q-r r 0
l_-- 5. r.{ q-{.r{ ul 1 rl l P -r ' v -r1-1.r ( q-r ( @- ql N -.r.p.p 0.) (^5] @ Z l l i Z r,l -; ^ CJ (\, -l ọ..,] q r 1] ( -. r._1 p q-r ) (\. _l (._1 \C ' q-l.. q) i.] r - 0r) >.4.-.rr J p r q-r r 0
FY 13 TDC Revenue Report 31-Dec-2012
 CLLR CNTY TRST TAX RVN CAC January 10, 2013 V-1 Staff Reprts 1 f 18 Budget escriptin und Y 13 Adpted Budget Y 13 (5%) Reserved by Law Y 13 Net Budget Y 13 recast Variance t Y 13 Budget Beach acilities
CLLR CNTY TRST TAX RVN CAC January 10, 2013 V-1 Staff Reprts 1 f 18 Budget escriptin und Y 13 Adpted Budget Y 13 (5%) Reserved by Law Y 13 Net Budget Y 13 recast Variance t Y 13 Budget Beach acilities
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
 OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
A/P Warrants. June 15, To Approve. To Ratify. Authorize the City Manager to approve such expenditures as are legally due and
 T. 7 TY LS ALATS A/P rrnts June 5, 5 Pges: To Approve - 5 89, 54.3 A/P rrnts 6/ 5/ 5 Subtotl $ 89, 54. 3 To Rtify Pges: 6-, 34. 98 Advnce rrnts 5/ 6/ 5-4 3, 659. 94 Advnce rrnts 6/ / 5 4, 7. 69 June Retirees
T. 7 TY LS ALATS A/P rrnts June 5, 5 Pges: To Approve - 5 89, 54.3 A/P rrnts 6/ 5/ 5 Subtotl $ 89, 54. 3 To Rtify Pges: 6-, 34. 98 Advnce rrnts 5/ 6/ 5-4 3, 659. 94 Advnce rrnts 6/ / 5 4, 7. 69 June Retirees
Sub-Area 3: Wynnewood East
 b- 3: E DELE VLLEY v lv H PLNNIN OIION P Tff b l h l b v l h hhlh h b-. Hh vhl P f f L f l j l Ill lz v l. Vhl L Ill b hh vbl l l h l ll lz l L. Th l h h hh hh b f h l h. T D Pv D h L P v lf lf ff l f
b- 3: E DELE VLLEY v lv H PLNNIN OIION P Tff b l h l b v l h hhlh h b-. Hh vhl P f f L f l j l Ill lz v l. Vhl L Ill b hh vbl l l h l ll lz l L. Th l h h hh hh b f h l h. T D Pv D h L P v lf lf ff l f
MATH 423 Linear Algebra II Lecture 11: Change of coordinates (continued). Isomorphism of vector spaces.
 MATH 423 Linear Algebra II Lecture 11: Change of coordinates (continued). Isomorphism of vector spaces. Change of coordinates Let V be a vector space of dimension n. Let v 1,v 2,...,v n be a basis for
MATH 423 Linear Algebra II Lecture 11: Change of coordinates (continued). Isomorphism of vector spaces. Change of coordinates Let V be a vector space of dimension n. Let v 1,v 2,...,v n be a basis for
The Corresponding State of Maximum Surface Tension of Saturated Vapors
 Howard University Digital Howard @ Howard University Faculty Reprints 1930 The Corresponding State of Maximum Surface Tension of Saturated Vapors Leon J. Shereshefsky Follow this and additional works at:
Howard University Digital Howard @ Howard University Faculty Reprints 1930 The Corresponding State of Maximum Surface Tension of Saturated Vapors Leon J. Shereshefsky Follow this and additional works at:
Framework for functional tree simulation applied to 'golden delicious' apple trees
 Purdue University Purdue e-pubs Open Access Theses Theses and Dissertations Spring 2015 Framework for functional tree simulation applied to 'golden delicious' apple trees Marek Fiser Purdue University
Purdue University Purdue e-pubs Open Access Theses Theses and Dissertations Spring 2015 Framework for functional tree simulation applied to 'golden delicious' apple trees Marek Fiser Purdue University
Overview of the Numerics of the ECMWF. Atmospheric Forecast Model
 Overview of the Numerics of the Atmospheric Forecast Model M. Hortal Seminar 6 Sept 2004 Slide 1 Characteristics of the model Hydrostatic shallow-atmosphere approimation Pressure-based hybrid vertical
Overview of the Numerics of the Atmospheric Forecast Model M. Hortal Seminar 6 Sept 2004 Slide 1 Characteristics of the model Hydrostatic shallow-atmosphere approimation Pressure-based hybrid vertical
Dedicated to his friend H. A. M-ELLON I. CAP~ (s.s.memphis.). NEW ORLEANS, LOUIS GRUNEWALD. GRUNEWALD HALL.
 Dedcaed o hs frend H A MELLON CAP (ssmemphs) == > NEW ORLEANS LOUS GRUNEWALD GRUNEWALD HALL THE MSSSSPP LNE WALTZES NTRODUCTON u + fw rf! } :V c Andane Maesoso 0 #+ q b T ff _ + := q T T T :e ] a! _ r
Dedcaed o hs frend H A MELLON CAP (ssmemphs) == > NEW ORLEANS LOUS GRUNEWALD GRUNEWALD HALL THE MSSSSPP LNE WALTZES NTRODUCTON u + fw rf! } :V c Andane Maesoso 0 #+ q b T ff _ + := q T T T :e ] a! _ r
o C *$ go ! b», S AT? g (i * ^ fc fa fa U - S 8 += C fl o.2h 2 fl 'fl O ' 0> fl l-h cvo *, &! 5 a o3 a; O g 02 QJ 01 fls g! r«'-fl O fl s- ccco
 > p >>>> ft^. 2 Tble f Generl rdnes. t^-t - +«0 -P k*ph? -- i t t i S i-h l -H i-h -d. *- e Stf H2 t s - ^ d - 'Ct? "fi p= + V t r & ^ C d Si d n. M. s - W ^ m» H ft ^.2. S'Sll-pl e Cl h /~v S s, -P s'l
> p >>>> ft^. 2 Tble f Generl rdnes. t^-t - +«0 -P k*ph? -- i t t i S i-h l -H i-h -d. *- e Stf H2 t s - ^ d - 'Ct? "fi p= + V t r & ^ C d Si d n. M. s - W ^ m» H ft ^.2. S'Sll-pl e Cl h /~v S s, -P s'l
ASYMPTOTIC DISTRIBUTION OF THE MAXIMUM CUMULATIVE SUM OF INDEPENDENT RANDOM VARIABLES
 ASYMPTOTIC DISTRIBUTION OF THE MAXIMUM CUMULATIVE SUM OF INDEPENDENT RANDOM VARIABLES KAI LAI CHUNG The limiting distribution of the maximum cumulative sum 1 of a sequence of independent random variables
ASYMPTOTIC DISTRIBUTION OF THE MAXIMUM CUMULATIVE SUM OF INDEPENDENT RANDOM VARIABLES KAI LAI CHUNG The limiting distribution of the maximum cumulative sum 1 of a sequence of independent random variables
Table of Contents Priority 1: Prenatal and Families with children ages 0-5 Priority 2: Youth Priority 3: Elders
 Table of Contents Wellness Plan Introduction----------------------------------------------------------------------1 Priority 1: Prenatal and Families with children ages 0-5-----------------------------------------2
Table of Contents Wellness Plan Introduction----------------------------------------------------------------------1 Priority 1: Prenatal and Families with children ages 0-5-----------------------------------------2
ADDENDUM NO. 3 TO BID DOCUMENTS FOR LIGHT POLE PAINTING PROJECT FOR THE CITY OF ANN ARBOR, MICHIGAN
 DDENDU NO TO BID DOCUENTS FOR LIGHT POLE PINTING PROJECT FOR THE, ICHIGN Th fllw h,, l hll b h B D Pl f Lh Pl P P f h Cy f b, h, B N ITB whh l b v, bf, P y, l, Th f h hll k v h l ll v, h Th Th B kwl f
DDENDU NO TO BID DOCUENTS FOR LIGHT POLE PINTING PROJECT FOR THE, ICHIGN Th fllw h,, l hll b h B D Pl f Lh Pl P P f h Cy f b, h, B N ITB whh l b v, bf, P y, l, Th f h hll k v h l ll v, h Th Th B kwl f
THE LOWELL LEDGER. INDEPENDENT-NOT NEUTRAL.
 : / LOLL LDGR NDNDNNO NRL VOL X NO 26 LOLL GN RDY DR 902 FV N ONDRFL GRO D x N Y NK LL & O OLD RDN GON ROR NR R «ROY ND R LON N V» Rx Rj K» O ««(» F R G GRLND x ( ) R OF FRND ;«QK L L RNG X R D 02 Q F
: / LOLL LDGR NDNDNNO NRL VOL X NO 26 LOLL GN RDY DR 902 FV N ONDRFL GRO D x N Y NK LL & O OLD RDN GON ROR NR R «ROY ND R LON N V» Rx Rj K» O ««(» F R G GRLND x ( ) R OF FRND ;«QK L L RNG X R D 02 Q F
A Statistical Test for the Capacity Coefficient
 Wright State University CORE Scholar Psychology Faculty Publications Psychology 7-16-2011 A Statistical Test for the Capacity Coefficient Joseph W. Houpt Wright State University - Main Campus, joseph.houpt@wright.edu
Wright State University CORE Scholar Psychology Faculty Publications Psychology 7-16-2011 A Statistical Test for the Capacity Coefficient Joseph W. Houpt Wright State University - Main Campus, joseph.houpt@wright.edu
I N A C O M P L E X W O R L D
 IS L A M I C E C O N O M I C S I N A C O M P L E X W O R L D E x p l o r a t i o n s i n A g-b eanste d S i m u l a t i o n S a m i A l-s u w a i l e m 1 4 2 9 H 2 0 0 8 I s l a m i c D e v e l o p m e
IS L A M I C E C O N O M I C S I N A C O M P L E X W O R L D E x p l o r a t i o n s i n A g-b eanste d S i m u l a t i o n S a m i A l-s u w a i l e m 1 4 2 9 H 2 0 0 8 I s l a m i c D e v e l o p m e
J. Org. Chem., 1997, 62(12), , DOI: /jo961896m
 J. Org. Chem., 1997, 62(12), 392-399, DO:1.121/jo961896m Terms & Conditions Electronic Supporting nformation files are available without a subscription to ACS Web Editions. The American Chemical Society
J. Org. Chem., 1997, 62(12), 392-399, DO:1.121/jo961896m Terms & Conditions Electronic Supporting nformation files are available without a subscription to ACS Web Editions. The American Chemical Society
,W.(.1*i x. Itr ::r:: i# A=,lrr. 'l ' rykfu. -[ *' 5 ]{, X/,i "# rrlrr,;- "h. K rn. f'e-s **1,:i' $ *' ##a. "+ c)4mls ( d)3.4 v * fr: lt-) t'..].
![,W.(.1*i x. Itr ::r:: i# A=,lrr. 'l ' rykfu. -[ *' 5 ]{, X/,i # rrlrr,;- h. K rn. f'e-s **1,:i' $ *' ##a. + c)4mls ( d)3.4 v * fr: lt-) t'..]. ,W.(.1*i x. Itr ::r:: i# A=,lrr. 'l ' rykfu. -[ *' 5 ]{, X/,i # rrlrr,;- h. K rn. f'e-s **1,:i' $ *' ##a. + c)4mls ( d)3.4 v * fr: lt-) t'..].](/thumbs/77/75855052.jpg) General Physics II (PHYS 104) Exam 1: February 23,2012 Name: Multiple Choice (4 points each): Answer the following multiple choice questions. Clearly circle the response (or responses) that provides the
General Physics II (PHYS 104) Exam 1: February 23,2012 Name: Multiple Choice (4 points each): Answer the following multiple choice questions. Clearly circle the response (or responses) that provides the
Some Remarks on Elementary Divisor Rings II
 Claremont Colleges Scholarship @ Claremont All HMC Faculty Publications and Research HMC Faculty Scholarship 1-1-1955 Some Remarks on Elementary Divisor Rings II Melvin Henriksen Harvey Mudd College Recommended
Claremont Colleges Scholarship @ Claremont All HMC Faculty Publications and Research HMC Faculty Scholarship 1-1-1955 Some Remarks on Elementary Divisor Rings II Melvin Henriksen Harvey Mudd College Recommended
Caracas, 1974: International Regulation of Ocean Ecology
 Golden Gate University Law Review Volume 5 Issue 2 Article 4 January 1975 Caracas, 1974: International Regulation of Ocean Ecology M. Ann Murphy Betty B. Bennett Donna M. Ismael Follow this and additional
Golden Gate University Law Review Volume 5 Issue 2 Article 4 January 1975 Caracas, 1974: International Regulation of Ocean Ecology M. Ann Murphy Betty B. Bennett Donna M. Ismael Follow this and additional
~.cft.l!:.&r".m.~~i~~ CfiT.afI4~R.q)
 .cft.l!:.&r".m.i CfT.afI4R.q) r_ -' f'l.... '1 Wr. (. ':?\9\9o) 3lT{-t." 'ts, 3lT{... 4Idl4I,, - oo ot.t.". t"l{2. '31'.M. r::..,, 'If.. \9() 11c:.ljl \1rrRlT +I(1Ch SCXlI1.;...,...fA,.." r:.t'tllirto\""i\..
.cft.l!:.&r".m.i CfT.afI4R.q) r_ -' f'l.... '1 Wr. (. ':?\9\9o) 3lT{-t." 'ts, 3lT{... 4Idl4I,, - oo ot.t.". t"l{2. '31'.M. r::..,, 'If.. \9() 11c:.ljl \1rrRlT +I(1Ch SCXlI1.;...,...fA,.." r:.t'tllirto\""i\..
Mixed Partial Derivatives and Fubini's Theorem
 Claremont Colleges Scholarship @ Claremont CMC Faculty Publications and Research CMC Faculty Scholarship 3-1-2002 Mixed Partial Derivatives and Fubini's Theorem Asuman Güven Aksoy Claremont McKenna College
Claremont Colleges Scholarship @ Claremont CMC Faculty Publications and Research CMC Faculty Scholarship 3-1-2002 Mixed Partial Derivatives and Fubini's Theorem Asuman Güven Aksoy Claremont McKenna College
THE WYOMING COUNTY resource guide to locally-grown foods and products available directly from the farm!
 TH ING UNT i l- f vi il f f! HT INID Ll k lii ifi -6-22 k li ikl vii li i i j j l 0 Nkii fn 6 il lii f Ll k i l v Ll k Ifi i l k H k l l l l ki i ff i l fl l l f 0 i l v 200 l l i k i i f l i fl i I f i il
TH ING UNT i l- f vi il f f! HT INID Ll k lii ifi -6-22 k li ikl vii li i i j j l 0 Nkii fn 6 il lii f Ll k i l v Ll k Ifi i l k H k l l l l ki i ff i l fl l l f 0 i l v 200 l l i k i i f l i fl i I f i il
Project CP11VPH Cocoa Village Playhouse Renovations
 x IL ITY IL AGDA ITM M Dt M 4 211 An Dtr M 24 211 Prr B Gr Plr Flts Mnr Thruh rtt J rf P Publ rks Drtr Rqust Atn Ar Rslutn Ann th FY211 But t Allt Prs f th Srs 21 Gnrl Fun Rnu Bn fr Prjt P11PH ll Plhus
x IL ITY IL AGDA ITM M Dt M 4 211 An Dtr M 24 211 Prr B Gr Plr Flts Mnr Thruh rtt J rf P Publ rks Drtr Rqust Atn Ar Rslutn Ann th FY211 But t Allt Prs f th Srs 21 Gnrl Fun Rnu Bn fr Prjt P11PH ll Plhus
ON MIXING AND PARTIAL MIXING
 ON MIXING AND PARTIAL MIXING BY N. A. XRIEDMAN AND D. S. ORNSTEIN 1. Introduction Let (X, a, m) denote the unit interwl with Lebesgue mesure, nd let r be n invertible ergodie mesure preserving transformation
ON MIXING AND PARTIAL MIXING BY N. A. XRIEDMAN AND D. S. ORNSTEIN 1. Introduction Let (X, a, m) denote the unit interwl with Lebesgue mesure, nd let r be n invertible ergodie mesure preserving transformation
