Hashing and Amortization
|
|
|
- Randolph Sims
- 6 years ago
- Views:
Transcription
1 Lecture Hashig ad Amortizatio Supplemetal readig i CLRS: Chapter ; Chapter 7 itro; Sectio 7.. Arrays ad Hashig Arrays are very useful. The items i a array are statically addressed, so that isertig, deletig, ad lookig up a elemet each take O( time. Thus, arrays are a terrific way to ecode fuctios {,..., } T, where T is some rage of values ad is kow ahead of time. For example, takig T = {,}, we fid that a array A of bits is a great way to store a subset of {,..., }: we set Ai] = if ad oly if i is i the set (see Figure.. Or, iterpretig the bits as biary digits, we ca use a -bit array to store a iteger betwee ad 2. I this way, we will ofte idetify the set {,} with the set {,...,2 }. What if we wated to ecode subsets of a arbitrary domai U, rather tha just {,..., }? Or to put thigs differetly, what if we wated a keyed (or associative array, where the keys could be arbitrary strigs? While the workigs of such data structures (such as dictioaries i Pytho are abstracted away i may programmig laguages, there is usually a array-based solutio workig behid the scees. Implemetig associative arrays amouts to fidig a way to tur a key ito a array idex. Thus, we are lookig for a suitable fuctio U {,..., }, called a hash fuctio. Equipped with this fuctio, we ca perform key lookup: U hash fuctio {,..., } array lookup T (see Figure.2. This particular implemetatio of associative arrays is called a hash table. There is a problem, however. Typically, the domai U is much larger tha {,..., }. For ay hash fuctio h : U {,..., }, there is some i such that at least U elemets are mapped to i. The set A: Figure.. This 2-bit array ecodes the set { 2,4,5,8, } {,...2 }.
2 2 h ( key 3 = 3 key3, val 3 4 h ( key = 5 key, val h ( key 2 = 6 key2, val 2 7 Figure.2. A associative array with keys i U ad values i T ca be implemeted as a (U T-valued array equipped with a hash fuctio h : U {,..., }. h (i of all elemets mapped to i is called the load o i, ad whe this load cotais more tha oe of the keys we are tryig to store i our hash table we say there is a collisio at i. Collisios are problem for us if two keys map to the same idex, the what should we store at that idex? We have to store both values somehow. For ow let s say we do this i the simplest way possible: storig at each idex i i the array a liked list (or more abstractly, some sort of bucket-like object cosistig of all values whose keys are mapped to i. Thus, lookup takes O ( h (i time, which may be poor if there are collisios at i. Rather tha thikig about efficiet ways to hadle collisios, let s try to reaso about the probability of havig collisios if we choose our hash fuctios well..2 Hash Families Without ay prior iformatio about which elemets of U will occur as keys, the best we ca do is to choose our hash fuctio h at radom from a suitable hash family. A hash family o U is a set H of fuctios U {,..., }. Techically speakig, H should come equipped with a probability distributio, but usually we just take the uiform distributio o H, so that each hash fuctio is equally likely to be chose. If we wat to avoid collisios, it is reasoable to hope that, for ay fixed x, x 2 U (x x 2, the values h(x ad h(x 2 are completely ucorrelated as h rages through the sample space H. This leads to the followig defiitio: Defiitio. A hash family H o U is said to be uiversal if, for ay x, x 2 U (x x 2, we have Pr h(x = h(x 2 ]. If you are expectig lots of collisios, a more efficiet way to hadle thigs is to create a two-layered hash table, where each elemet of A is itself a hash table with its ow, differet hash fuctio. I order to have collisios i a two-layer hash table, the same pair of keys must collide uder two differet hash fuctios. If the hash fuctios are chose well (e.g., if the hash fuctios are chose radomly, the this is extremely ulikely. Of course, if you wat to be eve more sure that collisios wo t occur, you ca make a three-layer hash table, ad so o. There is a trade-off, though: itroducig uecessary layers of hashig comes with a time ad space overhead which, while it may ot show up i the big-o aalysis, makes a differece i practical applicatios. Lec pg. 2 of 7
3 Similarly, H is said to be ɛ-uiversal if for ay x x 2 we have Pr h(x = h(x 2 ] ɛ. The cosequeces of the above hypotheses with regard to collisios are as follows: Propositio.. Let H be a uiversal hash family o U. Fix some subset S U ad some elemet x U. Pick h H at radom. The expected umber of elemets of S that map to h(x is at most + S. I symbols, h E ( h(x ] + S. If H is ɛ-uiversal rather tha uiversal, the the same holds whe + S is replaced by + ɛ S. Proof. For a propositio ϕ with radom parameters, let I ϕ be the idicator radom variable which equals if ϕ is true ad equals otherwise. The fact that H is uiversal meas that for each x U \ {x} we have E Ih(x=h(x ]. Thus by the liearity of expectatio, we have E h ( h(x S ] = I x S + E = I x S + + S. x S x x E x S x x I h(x=h(x Ih(x=h(x ] The reasoig is almost idetical whe H is ɛ-uiversal rather tha uiversal. Corollary.2. For a hash table i which the hash fuctio ( is chose from a uiversal family, isertio, deletio, ad lookup have expected ruig time O + S, where S U is the set of keys which actually occur. If istead the hash family is ɛ-uiversal, the the operatios have expected ruig time O ( + ɛ S. Corollary.3. Cosider a hash table of size with keys i U, whose hash fuctio is chose from a uiversal hash family. Let S U be the set of keys which actually occur. If S = O(, the isertio, deletio, ad lookup have expected ruig time O(. Let H be a uiversal hash family o U. If S = O(, the the expected load o each idex is O(. Does this mea that a typical hash table has O( load at each idex? Surprisigly, the aswer is o, eve whe the hash fuctio is chose well. We ll see this below whe we look at examples of uiversal hash families. Examples.4.. The set of all fuctios h : U {,..., } is certaily uiversal. I fact, we could ot hope to get ay more balaced tha this: Lec pg. 3 of 7
4 For ay x U, the radom variable h(x (where h is chose at radom is uiformly distributed o the set {,..., }. For ay pair x x 2, the radom variables h(x, h(x 2 are idepedet. I fact, for ay fiite subset {x,..., x k } U, the tuple ( h(x,..., h(x k is uiformly distributed o { } k.,..., The load o each idex i is a biomial radom variable with parameters ( S,. Fact. Whe p is small ad N is large eough that N p is moderately sized, the biomial distributio with parameters (N, p is approximated by the Poisso distributio with parameter N p. That is, if X is a biomial radom variable with parameters (N, p, the Pr X = k ] (N pk e N p (k. k! I our case, N = S ad p =. Thus, if L i is the load o idex i, the For example, if S =, the Pr L i = k ] ( S k k! e S /. Pr L i = ] e.3679, Pr L i = ] e.3679, Pr L i = 2 ] 2 e.839,. Further calculatio shows that, whe S =, we have ] ( lg E max L i = Θ. i lglg ( lg Moreover, with high probability, max L i does ot exceed O lglg. Thus, a typical hash table with S = ad h chose uiformly from the set of all fuctios looks like Figure.3: about 37% of the buckets empty, about 37% of the buckets havig oe elemet, ad about 26% of the buckets havig more tha oe elemet, icudig some buckets with Θ elemets. 2. I Problem Set 4 we cosidered the hash family H = { h p : p k ad p is prime }, where h p : {,...,2 m } {,..., k } is the fuctio h p (x = x mod p. I Problem 4(a you proved that, for each x y, we have Pr h p (x = h p (y ] ml k. p k ( lg lglg Lec pg. 4 of 7
5 2 3 4 ( lg. Maximum load = Θ lglg. Figure.3. A typical hash table with S = ad h chose uiformly from the family of all fuctios U {,..., }. 3. I Problem Set 5, we fixed a prime p ad cosidered the hash family { } H = h a : a Z m p, where h a : Z m p Z p is the dot product h a ( x = x a = x i a i (mod p. 4. I Problem Set 6, we fixed a prime p ad positive itegers m ad k ad cosidered the hash family { } H = h A : A Z k m p, where h A : Z m p Zk p is the fuctio h A ( x = A x. 5. If H is a ɛ -uiversal hash family of fuctios {,} m {,} k ad H 2 is a ɛ 2 -uiversal hash family of fuctios {,} k {,} l, the 2 H = H 2 H = { h 2 h : h H, h 2 H 2 } is a (ɛ + ɛ 2 -uiversal hash family of fuctios {,} m {,} l. To see this, ote that for ay x x, the uio boud gives h2 h (x = h 2 h (x ] Pr h H h 2 H 2 2 To fully specify H, we have to give ot just a set but also a probability distributio. The hash families H ad H 2 come with probability distributios, so there is a iduced distributio o H H 2. We the equip H with the distributio iduced by the map H H 2 H, (h, h 2 h 2 h. You could cosider this a mathematical techicality if you wish: if H ad H 2 are give uiform distributios (as they typically are, the the distributio o H H 2 is also uiform. The distributio o H eed ot be uiform, however: a elemet of H is more likely to be chose if it ca be expressed i multiple ways as the compositio of a elemet of H 2 with a elemet of H. Lec pg. 5 of 7
6 ( ] = Pr h (x = h (x or h (x h (x ad h 2 h (x = h 2 h (x ] ] Pr h (x = h (x + Pr h (x h (x ad h 2 h (x = h 2 h (x ɛ + ɛ 2. I choosig the parameters to build a hash table, there is a tradeoff. Makig larger decreases the likelihood of collisios, ad thus decreases the expected ruig time of operatios o the table, but also requires the allocatio of more memory, much of which is ot eve used to store data. I situatios where avoidig collisios is worth the memory cost (or i applicatios other tha hash tables, whe the correspodig tradeoff is worth it, we ca make much larger tha S. Propositio.5. Let H be a uiversal hash family U {,..., }. Let S U be the the set of keys that occur. The the expected umber of collisios is at most ( S 2. I symbols, ] ( S E 2. I h(x=h(x x x U Proof. There are ( S 2 pairs of distict elemets i S, ad each pair has probability at most of causig a collisio. The result follows from liearity of expectatio. Corollary.6. If S 2, the the expected umber of collisios is less tha /2, ad the probability that a collisio exists is less tha /2. Proof. Apply the Markov boud. Thus, if is sufficietly large compared to S, a typical hash table cosists mostly of empty buckets, ad with high probability, there is at most oe elemet i each bucket. As we metioed above, choosig a large for a hash table is expesive i terms of space. While the competig goals of fast table operatios ad low storage cost are a fact of life if othig is kow about S i advace, we will see i recitatio that, if S is kow i advace, it is feasible to costruct a perfect hash table, i.e., a hash table i which there are o collisios. Of course, the smallest value of for which this is possible is = S. As we will see i recitatio, there are reasoably efficiet algorithms to costruct a perfect hash table with = O ( S..3 Amortizatio What if the size of S is ot kow i advace? I order to allocate the array for a hash table, we must choose the size at creatio time, ad may ot chage it later. If S turs out to be sigificatly greater tha, the there will always be lots of collisios, o matter which hash fuctio we choose. Luckily, there is a simple ad elegat solutio to this problem: table doublig. The idea is to start with some particular table size = O(. If the table gets filled, simply create a ew table of size 2 ad migrate all the old elemets to it. While this migratio operatio is costly, it happes ifrequetly eough that, o the whole, the strategy of table doublig is efficiet. Let s take a closer look. To simplify matters, let s assume that oly isertios ad lookups occur, with o deletios. What is the worst-case cost of a sigle operatio o the hash table? Lec pg. 6 of 7
7 Lookup: O(, as usual. Isertio: O(, if we have to double the table. Thus, the worst-case total ruig time of k operatios (k = S o the hash table is O ( + + k = O ( k 2. The crucial observatio is that this boud is ot tight. Table doublig oly happes after the secod, fourth, eighth, etc., isertios. Thus, the total cost of k isertios is k O( + O ( lg k 2 j = O (k + O (2k = O (k. j= Thus, i ay sequece of isertio ad lookup operatios o a dyamically doubled hash table, the average, or amortized, cost per operatio is O(. This sort of aalysis, i which we cosider the total cost of a sequece of operatios rather tha the cost of a sigle step, is called amortized aalysis. I the ext lecture we will itroduce methods of aalyzig amortized ruig time. Lec pg. 7 of 7
8 MIT OpeCourseWare J / 8.4J Desig ad Aalysis of Algorithms Sprig 22 For iformatio about citig these materials or our Terms of Use, visit:
1 Hash tables. 1.1 Implementation
 Lecture 8 Hash Tables, Uiversal Hash Fuctios, Balls ad Bis Scribes: Luke Johsto, Moses Charikar, G. Valiat Date: Oct 18, 2017 Adapted From Virgiia Williams lecture otes 1 Hash tables A hash table is a
Lecture 8 Hash Tables, Uiversal Hash Fuctios, Balls ad Bis Scribes: Luke Johsto, Moses Charikar, G. Valiat Date: Oct 18, 2017 Adapted From Virgiia Williams lecture otes 1 Hash tables A hash table is a
OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES
 OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES Peter M. Maurer Why Hashig is θ(). As i biary search, hashig assumes that keys are stored i a array which is idexed by a iteger. However, hashig attempts to bypass
OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES Peter M. Maurer Why Hashig is θ(). As i biary search, hashig assumes that keys are stored i a array which is idexed by a iteger. However, hashig attempts to bypass
Hashing. Algorithm : Design & Analysis [09]
![Hashing. Algorithm : Design & Analysis [09] Hashing. Algorithm : Design & Analysis [09]](/thumbs/82/84955480.jpg) Hashig Algorithm : Desig & Aalysis [09] I the last class Implemetig Dictioary ADT Defiitio of red-black tree Black height Isertio ito a red-black tree Deletio from a red-black tree Hashig Hashig Collisio
Hashig Algorithm : Desig & Aalysis [09] I the last class Implemetig Dictioary ADT Defiitio of red-black tree Black height Isertio ito a red-black tree Deletio from a red-black tree Hashig Hashig Collisio
11. Hash Tables. m is not too large. Many applications require a dynamic set that supports only the directory operations INSERT, SEARCH and DELETE.
 11. Hash Tables May applicatios require a dyamic set that supports oly the directory operatios INSERT, SEARCH ad DELETE. A hash table is a geeralizatio of the simpler otio of a ordiary array. Directly
11. Hash Tables May applicatios require a dyamic set that supports oly the directory operatios INSERT, SEARCH ad DELETE. A hash table is a geeralizatio of the simpler otio of a ordiary array. Directly
IP Reference guide for integer programming formulations.
 IP Referece guide for iteger programmig formulatios. by James B. Orli for 15.053 ad 15.058 This documet is iteded as a compact (or relatively compact) guide to the formulatio of iteger programs. For more
IP Referece guide for iteger programmig formulatios. by James B. Orli for 15.053 ad 15.058 This documet is iteded as a compact (or relatively compact) guide to the formulatio of iteger programs. For more
Lecture 4: Unique-SAT, Parity-SAT, and Approximate Counting
 Advaced Complexity Theory Sprig 206 Lecture 4: Uique-SAT, Parity-SAT, ad Approximate Coutig Prof. Daa Moshkovitz Scribe: Aoymous Studet Scribe Date: Fall 202 Overview I this lecture we begi talkig about
Advaced Complexity Theory Sprig 206 Lecture 4: Uique-SAT, Parity-SAT, ad Approximate Coutig Prof. Daa Moshkovitz Scribe: Aoymous Studet Scribe Date: Fall 202 Overview I this lecture we begi talkig about
CS / MCS 401 Homework 3 grader solutions
 CS / MCS 401 Homework 3 grader solutios assigmet due July 6, 016 writte by Jāis Lazovskis maximum poits: 33 Some questios from CLRS. Questios marked with a asterisk were ot graded. 1 Use the defiitio of
CS / MCS 401 Homework 3 grader solutios assigmet due July 6, 016 writte by Jāis Lazovskis maximum poits: 33 Some questios from CLRS. Questios marked with a asterisk were ot graded. 1 Use the defiitio of
Design and Analysis of Algorithms
 Desig ad Aalysis of Algorithms Probabilistic aalysis ad Radomized algorithms Referece: CLRS Chapter 5 Topics: Hirig problem Idicatio radom variables Radomized algorithms Huo Hogwei 1 The hirig problem
Desig ad Aalysis of Algorithms Probabilistic aalysis ad Radomized algorithms Referece: CLRS Chapter 5 Topics: Hirig problem Idicatio radom variables Radomized algorithms Huo Hogwei 1 The hirig problem
An Introduction to Randomized Algorithms
 A Itroductio to Radomized Algorithms The focus of this lecture is to study a radomized algorithm for quick sort, aalyze it usig probabilistic recurrece relatios, ad also provide more geeral tools for aalysis
A Itroductio to Radomized Algorithms The focus of this lecture is to study a radomized algorithm for quick sort, aalyze it usig probabilistic recurrece relatios, ad also provide more geeral tools for aalysis
19.1 The dictionary problem
 CS125 Lecture 19 Fall 2016 19.1 The dictioary proble Cosider the followig data structural proble, usually called the dictioary proble. We have a set of ites. Each ite is a (key, value pair. Keys are i
CS125 Lecture 19 Fall 2016 19.1 The dictioary proble Cosider the followig data structural proble, usually called the dictioary proble. We have a set of ites. Each ite is a (key, value pair. Keys are i
UC Berkeley CS 170: Efficient Algorithms and Intractable Problems Handout 17 Lecturer: David Wagner April 3, Notes 17 for CS 170
 UC Berkeley CS 170: Efficiet Algorithms ad Itractable Problems Hadout 17 Lecturer: David Wager April 3, 2003 Notes 17 for CS 170 1 The Lempel-Ziv algorithm There is a sese i which the Huffma codig was
UC Berkeley CS 170: Efficiet Algorithms ad Itractable Problems Hadout 17 Lecturer: David Wager April 3, 2003 Notes 17 for CS 170 1 The Lempel-Ziv algorithm There is a sese i which the Huffma codig was
Definitions: Universe U of keys, e.g., U N 0. U very large. Set S U of keys, S = m U.
 7 7 Dictioary: S.isertx): Isert a elemet x. S.deletex): Delete the elemet poited to by x. S.searchk): Retur a poiter to a elemet e with key[e] = k i S if it exists; otherwise retur ull. So far we have
7 7 Dictioary: S.isertx): Isert a elemet x. S.deletex): Delete the elemet poited to by x. S.searchk): Retur a poiter to a elemet e with key[e] = k i S if it exists; otherwise retur ull. So far we have
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 2 9/9/2013. Large Deviations for i.i.d. Random Variables
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 2 9/9/2013 Large Deviatios for i.i.d. Radom Variables Cotet. Cheroff boud usig expoetial momet geeratig fuctios. Properties of a momet
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 2 9/9/2013 Large Deviatios for i.i.d. Radom Variables Cotet. Cheroff boud usig expoetial momet geeratig fuctios. Properties of a momet
Skip lists: A randomized dictionary
 Discrete Math for Bioiformatics WS 11/12:, by A. Bocmayr/K. Reiert, 31. Otober 2011, 09:53 3001 Sip lists: A radomized dictioary The expositio is based o the followig sources, which are all recommeded
Discrete Math for Bioiformatics WS 11/12:, by A. Bocmayr/K. Reiert, 31. Otober 2011, 09:53 3001 Sip lists: A radomized dictioary The expositio is based o the followig sources, which are all recommeded
Posted-Price, Sealed-Bid Auctions
 Posted-Price, Sealed-Bid Auctios Professors Greewald ad Oyakawa 207-02-08 We itroduce the posted-price, sealed-bid auctio. This auctio format itroduces the idea of approximatios. We describe how well this
Posted-Price, Sealed-Bid Auctios Professors Greewald ad Oyakawa 207-02-08 We itroduce the posted-price, sealed-bid auctio. This auctio format itroduces the idea of approximatios. We describe how well this
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Recitation 4: Lagrange Multipliers and Integration
 Math 1c TA: Padraic Bartlett Recitatio 4: Lagrage Multipliers ad Itegratio Week 4 Caltech 211 1 Radom Questio Hey! So, this radom questio is pretty tightly tied to today s lecture ad the cocept of cotet
Math 1c TA: Padraic Bartlett Recitatio 4: Lagrage Multipliers ad Itegratio Week 4 Caltech 211 1 Radom Questio Hey! So, this radom questio is pretty tightly tied to today s lecture ad the cocept of cotet
Lecture 9: Hierarchy Theorems
 IAS/PCMI Summer Sessio 2000 Clay Mathematics Udergraduate Program Basic Course o Computatioal Complexity Lecture 9: Hierarchy Theorems David Mix Barrigto ad Alexis Maciel July 27, 2000 Most of this lecture
IAS/PCMI Summer Sessio 2000 Clay Mathematics Udergraduate Program Basic Course o Computatioal Complexity Lecture 9: Hierarchy Theorems David Mix Barrigto ad Alexis Maciel July 27, 2000 Most of this lecture
Problem Set 2 Solutions
 CS271 Radomess & Computatio, Sprig 2018 Problem Set 2 Solutios Poit totals are i the margi; the maximum total umber of poits was 52. 1. Probabilistic method for domiatig sets 6pts Pick a radom subset S
CS271 Radomess & Computatio, Sprig 2018 Problem Set 2 Solutios Poit totals are i the margi; the maximum total umber of poits was 52. 1. Probabilistic method for domiatig sets 6pts Pick a radom subset S
CS284A: Representations and Algorithms in Molecular Biology
 CS284A: Represetatios ad Algorithms i Molecular Biology Scribe Notes o Lectures 3 & 4: Motif Discovery via Eumeratio & Motif Represetatio Usig Positio Weight Matrix Joshua Gervi Based o presetatios by
CS284A: Represetatios ad Algorithms i Molecular Biology Scribe Notes o Lectures 3 & 4: Motif Discovery via Eumeratio & Motif Represetatio Usig Positio Weight Matrix Joshua Gervi Based o presetatios by
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Math 216A Notes, Week 5
 Math 6A Notes, Week 5 Scribe: Ayastassia Sebolt Disclaimer: These otes are ot early as polished (ad quite possibly ot early as correct) as a published paper. Please use them at your ow risk.. Thresholds
Math 6A Notes, Week 5 Scribe: Ayastassia Sebolt Disclaimer: These otes are ot early as polished (ad quite possibly ot early as correct) as a published paper. Please use them at your ow risk.. Thresholds
Amortized Analysis - Part 2 - Dynamic Tables. Objective: In this lecture, we shall explore Dynamic tables and its amortized analysis in detail.
 Idia Istitute of Iformatio Techology Desig ad Maufacturig, Kacheepuram Cheai 600 17, Idia A Autoomous Istitute uder MHRD, Govt of Idia http://www.iiitdm.ac.i COM 501 Advaced Data Structures ad Algorithms
Idia Istitute of Iformatio Techology Desig ad Maufacturig, Kacheepuram Cheai 600 17, Idia A Autoomous Istitute uder MHRD, Govt of Idia http://www.iiitdm.ac.i COM 501 Advaced Data Structures ad Algorithms
Variance of Discrete Random Variables Class 5, Jeremy Orloff and Jonathan Bloom
 Variace of Discrete Radom Variables Class 5, 18.05 Jeremy Orloff ad Joatha Bloom 1 Learig Goals 1. Be able to compute the variace ad stadard deviatio of a radom variable.. Uderstad that stadard deviatio
Variace of Discrete Radom Variables Class 5, 18.05 Jeremy Orloff ad Joatha Bloom 1 Learig Goals 1. Be able to compute the variace ad stadard deviatio of a radom variable.. Uderstad that stadard deviatio
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
Advanced Course of Algorithm Design and Analysis
 Differet complexity measures Advaced Course of Algorithm Desig ad Aalysis Asymptotic complexity Big-Oh otatio Properties of O otatio Aalysis of simple algorithms A algorithm may may have differet executio
Differet complexity measures Advaced Course of Algorithm Desig ad Aalysis Asymptotic complexity Big-Oh otatio Properties of O otatio Aalysis of simple algorithms A algorithm may may have differet executio
CS161: Algorithm Design and Analysis Handout #10 Stanford University Wednesday, 10 February 2016
 CS161: Algorithm Desig ad Aalysis Hadout #10 Staford Uiversity Wedesday, 10 February 2016 Lecture #11: Wedesday, 10 February 2016 Topics: Example midterm problems ad solutios from a log time ago Sprig
CS161: Algorithm Desig ad Aalysis Hadout #10 Staford Uiversity Wedesday, 10 February 2016 Lecture #11: Wedesday, 10 February 2016 Topics: Example midterm problems ad solutios from a log time ago Sprig
Lecture 9: Expanders Part 2, Extractors
 Lecture 9: Expaders Part, Extractors Topics i Complexity Theory ad Pseudoradomess Sprig 013 Rutgers Uiversity Swastik Kopparty Scribes: Jaso Perry, Joh Kim I this lecture, we will discuss further the pseudoradomess
Lecture 9: Expaders Part, Extractors Topics i Complexity Theory ad Pseudoradomess Sprig 013 Rutgers Uiversity Swastik Kopparty Scribes: Jaso Perry, Joh Kim I this lecture, we will discuss further the pseudoradomess
CS 332: Algorithms. Linear-Time Sorting. Order statistics. Slide credit: David Luebke (Virginia)
 1 CS 332: Algorithms Liear-Time Sortig. Order statistics. Slide credit: David Luebke (Virgiia) Quicksort: Partitio I Words Partitio(A, p, r): Select a elemet to act as the pivot (which?) Grow two regios,
1 CS 332: Algorithms Liear-Time Sortig. Order statistics. Slide credit: David Luebke (Virgiia) Quicksort: Partitio I Words Partitio(A, p, r): Select a elemet to act as the pivot (which?) Grow two regios,
Intro to Learning Theory
 Lecture 1, October 18, 2016 Itro to Learig Theory Ruth Urer 1 Machie Learig ad Learig Theory Comig soo 2 Formal Framework 21 Basic otios I our formal model for machie learig, the istaces to be classified
Lecture 1, October 18, 2016 Itro to Learig Theory Ruth Urer 1 Machie Learig ad Learig Theory Comig soo 2 Formal Framework 21 Basic otios I our formal model for machie learig, the istaces to be classified
It is always the case that unions, intersections, complements, and set differences are preserved by the inverse image of a function.
 MATH 532 Measurable Fuctios Dr. Neal, WKU Throughout, let ( X, F, µ) be a measure space ad let (!, F, P ) deote the special case of a probability space. We shall ow begi to study real-valued fuctios defied
MATH 532 Measurable Fuctios Dr. Neal, WKU Throughout, let ( X, F, µ) be a measure space ad let (!, F, P ) deote the special case of a probability space. We shall ow begi to study real-valued fuctios defied
Lecture 2: April 3, 2013
 TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 2: April 3, 203 Scribe: Shubhedu Trivedi Coi tosses cotiued We retur to the coi tossig example from the last lecture agai: Example. Give,
TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 2: April 3, 203 Scribe: Shubhedu Trivedi Coi tosses cotiued We retur to the coi tossig example from the last lecture agai: Example. Give,
Square-Congruence Modulo n
 Square-Cogruece Modulo Abstract This paper is a ivestigatio of a equivalece relatio o the itegers that was itroduced as a exercise i our Discrete Math class. Part I - Itro Defiitio Two itegers are Square-Cogruet
Square-Cogruece Modulo Abstract This paper is a ivestigatio of a equivalece relatio o the itegers that was itroduced as a exercise i our Discrete Math class. Part I - Itro Defiitio Two itegers are Square-Cogruet
Sequences and Series of Functions
 Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
MATH 320: Probability and Statistics 9. Estimation and Testing of Parameters. Readings: Pruim, Chapter 4
 MATH 30: Probability ad Statistics 9. Estimatio ad Testig of Parameters Estimatio ad Testig of Parameters We have bee dealig situatios i which we have full kowledge of the distributio of a radom variable.
MATH 30: Probability ad Statistics 9. Estimatio ad Testig of Parameters Estimatio ad Testig of Parameters We have bee dealig situatios i which we have full kowledge of the distributio of a radom variable.
The Growth of Functions. Theoretical Supplement
 The Growth of Fuctios Theoretical Supplemet The Triagle Iequality The triagle iequality is a algebraic tool that is ofte useful i maipulatig absolute values of fuctios. The triagle iequality says that
The Growth of Fuctios Theoretical Supplemet The Triagle Iequality The triagle iequality is a algebraic tool that is ofte useful i maipulatig absolute values of fuctios. The triagle iequality says that
DATA STRUCTURES I, II, III, AND IV
 Data structures DATA STRUCTURES I, II, III, AND IV I. Amortized Aalysis II. Biary ad Biomial Heaps III. Fiboacci Heaps IV. Uio Fid Static problems. Give a iput, produce a output. Ex. Sortig, FFT, edit
Data structures DATA STRUCTURES I, II, III, AND IV I. Amortized Aalysis II. Biary ad Biomial Heaps III. Fiboacci Heaps IV. Uio Fid Static problems. Give a iput, produce a output. Ex. Sortig, FFT, edit
Shannon s noiseless coding theorem
 18.310 lecture otes May 4, 2015 Shao s oiseless codig theorem Lecturer: Michel Goemas I these otes we discuss Shao s oiseless codig theorem, which is oe of the foudig results of the field of iformatio
18.310 lecture otes May 4, 2015 Shao s oiseless codig theorem Lecturer: Michel Goemas I these otes we discuss Shao s oiseless codig theorem, which is oe of the foudig results of the field of iformatio
Goodness-of-Fit Tests and Categorical Data Analysis (Devore Chapter Fourteen)
 Goodess-of-Fit Tests ad Categorical Data Aalysis (Devore Chapter Fourtee) MATH-252-01: Probability ad Statistics II Sprig 2019 Cotets 1 Chi-Squared Tests with Kow Probabilities 1 1.1 Chi-Squared Testig................
Goodess-of-Fit Tests ad Categorical Data Aalysis (Devore Chapter Fourtee) MATH-252-01: Probability ad Statistics II Sprig 2019 Cotets 1 Chi-Squared Tests with Kow Probabilities 1 1.1 Chi-Squared Testig................
Information Theory and Statistics Lecture 4: Lempel-Ziv code
 Iformatio Theory ad Statistics Lecture 4: Lempel-Ziv code Łukasz Dębowski ldebowsk@ipipa.waw.pl Ph. D. Programme 203/204 Etropy rate is the limitig compressio rate Theorem For a statioary process (X i)
Iformatio Theory ad Statistics Lecture 4: Lempel-Ziv code Łukasz Dębowski ldebowsk@ipipa.waw.pl Ph. D. Programme 203/204 Etropy rate is the limitig compressio rate Theorem For a statioary process (X i)
7.7 Hashing. 7.7 Hashing. Perfect Hashing. Direct Addressing
 Dictioary: S.isertx): Isert a elemet x. S.deletex): Delete the elemet poited to by x. S.searchk): Retur a poiter to a elemet e with key[e] = k i S if it exists; otherwise retur ull. So far we have implemeted
Dictioary: S.isertx): Isert a elemet x. S.deletex): Delete the elemet poited to by x. S.searchk): Retur a poiter to a elemet e with key[e] = k i S if it exists; otherwise retur ull. So far we have implemeted
2 Statistical Principles
 2 Statistical Priciples This lecture will serve two mai goals. First we will itroduce ad the tool of radom hash fuctios. Secod we itroduce a radomized/probabilistic view of algorithms ad data aalysis.
2 Statistical Priciples This lecture will serve two mai goals. First we will itroduce ad the tool of radom hash fuctios. Secod we itroduce a radomized/probabilistic view of algorithms ad data aalysis.
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.436J/15.085J Fall 2008 Lecture 19 11/17/2008 LAWS OF LARGE NUMBERS II THE STRONG LAW OF LARGE NUMBERS
 MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
1 Convergence in Probability and the Weak Law of Large Numbers
 36-752 Advaced Probability Overview Sprig 2018 8. Covergece Cocepts: i Probability, i L p ad Almost Surely Istructor: Alessadro Rialdo Associated readig: Sec 2.4, 2.5, ad 4.11 of Ash ad Doléas-Dade; Sec
36-752 Advaced Probability Overview Sprig 2018 8. Covergece Cocepts: i Probability, i L p ad Almost Surely Istructor: Alessadro Rialdo Associated readig: Sec 2.4, 2.5, ad 4.11 of Ash ad Doléas-Dade; Sec
Discrete Mathematics and Probability Theory Fall 2009 Satish Rao,David Tse Note 12
 CS 70 Discrete Mathematics ad Probability Theory Fall 2009 Satish Rao,David Tse Note 12 Two Killer Applicatios I this lecture, we will see two killer apps of elemetary probability i Computer Sciece. 1.
CS 70 Discrete Mathematics ad Probability Theory Fall 2009 Satish Rao,David Tse Note 12 Two Killer Applicatios I this lecture, we will see two killer apps of elemetary probability i Computer Sciece. 1.
The Binomial Theorem
 The Biomial Theorem Robert Marti Itroductio The Biomial Theorem is used to expad biomials, that is, brackets cosistig of two distict terms The formula for the Biomial Theorem is as follows: (a + b ( k
The Biomial Theorem Robert Marti Itroductio The Biomial Theorem is used to expad biomials, that is, brackets cosistig of two distict terms The formula for the Biomial Theorem is as follows: (a + b ( k
CS 270 Algorithms. Oliver Kullmann. Growth of Functions. Divide-and- Conquer Min-Max- Problem. Tutorial. Reading from CLRS for week 2
 Geeral remarks Week 2 1 Divide ad First we cosider a importat tool for the aalysis of algorithms: Big-Oh. The we itroduce a importat algorithmic paradigm:. We coclude by presetig ad aalysig two examples.
Geeral remarks Week 2 1 Divide ad First we cosider a importat tool for the aalysis of algorithms: Big-Oh. The we itroduce a importat algorithmic paradigm:. We coclude by presetig ad aalysig two examples.
Advanced Stochastic Processes.
 Advaced Stochastic Processes. David Gamarik LECTURE 2 Radom variables ad measurable fuctios. Strog Law of Large Numbers (SLLN). Scary stuff cotiued... Outlie of Lecture Radom variables ad measurable fuctios.
Advaced Stochastic Processes. David Gamarik LECTURE 2 Radom variables ad measurable fuctios. Strog Law of Large Numbers (SLLN). Scary stuff cotiued... Outlie of Lecture Radom variables ad measurable fuctios.
n outcome is (+1,+1, 1,..., 1). Let the r.v. X denote our position (relative to our starting point 0) after n moves. Thus X = X 1 + X 2 + +X n,
 CS 70 Discrete Mathematics for CS Sprig 2008 David Wager Note 9 Variace Questio: At each time step, I flip a fair coi. If it comes up Heads, I walk oe step to the right; if it comes up Tails, I walk oe
CS 70 Discrete Mathematics for CS Sprig 2008 David Wager Note 9 Variace Questio: At each time step, I flip a fair coi. If it comes up Heads, I walk oe step to the right; if it comes up Tails, I walk oe
ECE 330:541, Stochastic Signals and Systems Lecture Notes on Limit Theorems from Probability Fall 2002
 ECE 330:541, Stochastic Sigals ad Systems Lecture Notes o Limit Theorems from robability Fall 00 I practice, there are two ways we ca costruct a ew sequece of radom variables from a old sequece of radom
ECE 330:541, Stochastic Sigals ad Systems Lecture Notes o Limit Theorems from robability Fall 00 I practice, there are two ways we ca costruct a ew sequece of radom variables from a old sequece of radom
6 Integers Modulo n. integer k can be written as k = qn + r, with q,r, 0 r b. So any integer.
 6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
4.3 Growth Rates of Solutions to Recurrences
 4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
Lecture 2: Concentration Bounds
 CSE 52: Desig ad Aalysis of Algorithms I Sprig 206 Lecture 2: Cocetratio Bouds Lecturer: Shaya Oveis Ghara March 30th Scribe: Syuzaa Sargsya Disclaimer: These otes have ot bee subjected to the usual scrutiy
CSE 52: Desig ad Aalysis of Algorithms I Sprig 206 Lecture 2: Cocetratio Bouds Lecturer: Shaya Oveis Ghara March 30th Scribe: Syuzaa Sargsya Disclaimer: These otes have ot bee subjected to the usual scrutiy
MA131 - Analysis 1. Workbook 3 Sequences II
 MA3 - Aalysis Workbook 3 Sequeces II Autum 2004 Cotets 2.8 Coverget Sequeces........................ 2.9 Algebra of Limits......................... 2 2.0 Further Useful Results........................
MA3 - Aalysis Workbook 3 Sequeces II Autum 2004 Cotets 2.8 Coverget Sequeces........................ 2.9 Algebra of Limits......................... 2 2.0 Further Useful Results........................
Discrete Mathematics for CS Spring 2005 Clancy/Wagner Notes 21. Some Important Distributions
 CS 70 Discrete Mathematics for CS Sprig 2005 Clacy/Wager Notes 21 Some Importat Distributios Questio: A biased coi with Heads probability p is tossed repeatedly util the first Head appears. What is the
CS 70 Discrete Mathematics for CS Sprig 2005 Clacy/Wager Notes 21 Some Importat Distributios Questio: A biased coi with Heads probability p is tossed repeatedly util the first Head appears. What is the
Lecture 11: Hash Functions and Random Oracle Model
 CS 7810 Foudatios of Cryptography October 16, 017 Lecture 11: Hash Fuctios ad Radom Oracle Model Lecturer: Daiel Wichs Scribe: Akshar Varma 1 Topic Covered Defiitio of Hash Fuctios Merkle-Damgaård Theorem
CS 7810 Foudatios of Cryptography October 16, 017 Lecture 11: Hash Fuctios ad Radom Oracle Model Lecturer: Daiel Wichs Scribe: Akshar Varma 1 Topic Covered Defiitio of Hash Fuctios Merkle-Damgaård Theorem
Lecture 10 October Minimaxity and least favorable prior sequences
 STATS 300A: Theory of Statistics Fall 205 Lecture 0 October 22 Lecturer: Lester Mackey Scribe: Brya He, Rahul Makhijai Warig: These otes may cotai factual ad/or typographic errors. 0. Miimaxity ad least
STATS 300A: Theory of Statistics Fall 205 Lecture 0 October 22 Lecturer: Lester Mackey Scribe: Brya He, Rahul Makhijai Warig: These otes may cotai factual ad/or typographic errors. 0. Miimaxity ad least
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
7.1 Convergence of sequences of random variables
 Chapter 7 Limit theorems Throughout this sectio we will assume a probability space (Ω, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Chapter 7 Limit theorems Throughout this sectio we will assume a probability space (Ω, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Disjoint set (Union-Find)
 CS124 Lecture 7 Fall 2018 Disjoit set (Uio-Fid) For Kruskal s algorithm for the miimum spaig tree problem, we foud that we eeded a data structure for maitaiig a collectio of disjoit sets. That is, we eed
CS124 Lecture 7 Fall 2018 Disjoit set (Uio-Fid) For Kruskal s algorithm for the miimum spaig tree problem, we foud that we eeded a data structure for maitaiig a collectio of disjoit sets. That is, we eed
ECEN 655: Advanced Channel Coding Spring Lecture 7 02/04/14. Belief propagation is exact on tree-structured factor graphs.
 ECEN 655: Advaced Chael Codig Sprig 014 Prof. Hery Pfister Lecture 7 0/04/14 Scribe: Megke Lia 1 4-Cycles i Gallager s Esemble What we already kow: Belief propagatio is exact o tree-structured factor graphs.
ECEN 655: Advaced Chael Codig Sprig 014 Prof. Hery Pfister Lecture 7 0/04/14 Scribe: Megke Lia 1 4-Cycles i Gallager s Esemble What we already kow: Belief propagatio is exact o tree-structured factor graphs.
7.1 Convergence of sequences of random variables
 Chapter 7 Limit Theorems Throughout this sectio we will assume a probability space (, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Chapter 7 Limit Theorems Throughout this sectio we will assume a probability space (, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Last time, we talked about how Equation (1) can simulate Equation (2). We asserted that Equation (2) can also simulate Equation (1).
 6896 Quatum Complexity Theory Sept 23, 2008 Lecturer: Scott Aaroso Lecture 6 Last Time: Quatum Error-Correctio Quatum Query Model Deutsch-Jozsa Algorithm (Computes x y i oe query) Today: Berstei-Vazirii
6896 Quatum Complexity Theory Sept 23, 2008 Lecturer: Scott Aaroso Lecture 6 Last Time: Quatum Error-Correctio Quatum Query Model Deutsch-Jozsa Algorithm (Computes x y i oe query) Today: Berstei-Vazirii
Basics of Probability Theory (for Theory of Computation courses)
 Basics of Probability Theory (for Theory of Computatio courses) Oded Goldreich Departmet of Computer Sciece Weizma Istitute of Sciece Rehovot, Israel. oded.goldreich@weizma.ac.il November 24, 2008 Preface.
Basics of Probability Theory (for Theory of Computatio courses) Oded Goldreich Departmet of Computer Sciece Weizma Istitute of Sciece Rehovot, Israel. oded.goldreich@weizma.ac.il November 24, 2008 Preface.
Element sampling: Part 2
 Chapter 4 Elemet samplig: Part 2 4.1 Itroductio We ow cosider uequal probability samplig desigs which is very popular i practice. I the uequal probability samplig, we ca improve the efficiecy of the resultig
Chapter 4 Elemet samplig: Part 2 4.1 Itroductio We ow cosider uequal probability samplig desigs which is very popular i practice. I the uequal probability samplig, we ca improve the efficiecy of the resultig
Frequentist Inference
 Frequetist Iferece The topics of the ext three sectios are useful applicatios of the Cetral Limit Theorem. Without kowig aythig about the uderlyig distributio of a sequece of radom variables {X i }, for
Frequetist Iferece The topics of the ext three sectios are useful applicatios of the Cetral Limit Theorem. Without kowig aythig about the uderlyig distributio of a sequece of radom variables {X i }, for
The Boolean Ring of Intervals
 MATH 532 Lebesgue Measure Dr. Neal, WKU We ow shall apply the results obtaied about outer measure to the legth measure o the real lie. Throughout, our space X will be the set of real umbers R. Whe ecessary,
MATH 532 Lebesgue Measure Dr. Neal, WKU We ow shall apply the results obtaied about outer measure to the legth measure o the real lie. Throughout, our space X will be the set of real umbers R. Whe ecessary,
Fall 2013 MTH431/531 Real analysis Section Notes
 Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Induction: Solutions
 Writig Proofs Misha Lavrov Iductio: Solutios Wester PA ARML Practice March 6, 206. Prove that a 2 2 chessboard with ay oe square removed ca always be covered by shaped tiles. Solutio : We iduct o. For
Writig Proofs Misha Lavrov Iductio: Solutios Wester PA ARML Practice March 6, 206. Prove that a 2 2 chessboard with ay oe square removed ca always be covered by shaped tiles. Solutio : We iduct o. For
Lecture 14: Graph Entropy
 15-859: Iformatio Theory ad Applicatios i TCS Sprig 2013 Lecture 14: Graph Etropy March 19, 2013 Lecturer: Mahdi Cheraghchi Scribe: Euiwoog Lee 1 Recap Bergma s boud o the permaet Shearer s Lemma Number
15-859: Iformatio Theory ad Applicatios i TCS Sprig 2013 Lecture 14: Graph Etropy March 19, 2013 Lecturer: Mahdi Cheraghchi Scribe: Euiwoog Lee 1 Recap Bergma s boud o the permaet Shearer s Lemma Number
Discrete Mathematics for CS Spring 2007 Luca Trevisan Lecture 22
 CS 70 Discrete Mathematics for CS Sprig 2007 Luca Trevisa Lecture 22 Aother Importat Distributio The Geometric Distributio Questio: A biased coi with Heads probability p is tossed repeatedly util the first
CS 70 Discrete Mathematics for CS Sprig 2007 Luca Trevisa Lecture 22 Aother Importat Distributio The Geometric Distributio Questio: A biased coi with Heads probability p is tossed repeatedly util the first
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
Lecture 19: Convergence
 Lecture 19: Covergece Asymptotic approach I statistical aalysis or iferece, a key to the success of fidig a good procedure is beig able to fid some momets ad/or distributios of various statistics. I may
Lecture 19: Covergece Asymptotic approach I statistical aalysis or iferece, a key to the success of fidig a good procedure is beig able to fid some momets ad/or distributios of various statistics. I may
Linear Programming and the Simplex Method
 Liear Programmig ad the Simplex ethod Abstract This article is a itroductio to Liear Programmig ad usig Simplex method for solvig LP problems i primal form. What is Liear Programmig? Liear Programmig is
Liear Programmig ad the Simplex ethod Abstract This article is a itroductio to Liear Programmig ad usig Simplex method for solvig LP problems i primal form. What is Liear Programmig? Liear Programmig is
Lecture 4: April 10, 2013
 TTIC/CMSC 1150 Mathematical Toolkit Sprig 01 Madhur Tulsiai Lecture 4: April 10, 01 Scribe: Haris Agelidakis 1 Chebyshev s Iequality recap I the previous lecture, we used Chebyshev s iequality to get a
TTIC/CMSC 1150 Mathematical Toolkit Sprig 01 Madhur Tulsiai Lecture 4: April 10, 01 Scribe: Haris Agelidakis 1 Chebyshev s Iequality recap I the previous lecture, we used Chebyshev s iequality to get a
( ) = p and P( i = b) = q.
 MATH 540 Radom Walks Part 1 A radom walk X is special stochastic process that measures the height (or value) of a particle that radomly moves upward or dowward certai fixed amouts o each uit icremet of
MATH 540 Radom Walks Part 1 A radom walk X is special stochastic process that measures the height (or value) of a particle that radomly moves upward or dowward certai fixed amouts o each uit icremet of
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 3 9/11/2013. Large deviations Theory. Cramér s Theorem
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/5.070J Fall 203 Lecture 3 9//203 Large deviatios Theory. Cramér s Theorem Cotet.. Cramér s Theorem. 2. Rate fuctio ad properties. 3. Chage of measure techique.
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/5.070J Fall 203 Lecture 3 9//203 Large deviatios Theory. Cramér s Theorem Cotet.. Cramér s Theorem. 2. Rate fuctio ad properties. 3. Chage of measure techique.
Lecture 4 February 16, 2016
 MIT 6.854/18.415: Advaced Algorithms Sprig 16 Prof. Akur Moitra Lecture 4 February 16, 16 Scribe: Be Eysebach, Devi Neal 1 Last Time Cosistet Hashig - hash fuctios that evolve well Radom Trees - routig
MIT 6.854/18.415: Advaced Algorithms Sprig 16 Prof. Akur Moitra Lecture 4 February 16, 16 Scribe: Be Eysebach, Devi Neal 1 Last Time Cosistet Hashig - hash fuctios that evolve well Radom Trees - routig
Intermediate Math Circles November 4, 2009 Counting II
 Uiversity of Waterloo Faculty of Mathematics Cetre for Educatio i Mathematics ad Computig Itermediate Math Circles November 4, 009 Coutig II Last time, after lookig at the product rule ad sum rule, we
Uiversity of Waterloo Faculty of Mathematics Cetre for Educatio i Mathematics ad Computig Itermediate Math Circles November 4, 009 Coutig II Last time, after lookig at the product rule ad sum rule, we
Discrete Mathematics and Probability Theory Spring 2016 Rao and Walrand Note 19
 CS 70 Discrete Mathematics ad Probability Theory Sprig 2016 Rao ad Walrad Note 19 Some Importat Distributios Recall our basic probabilistic experimet of tossig a biased coi times. This is a very simple
CS 70 Discrete Mathematics ad Probability Theory Sprig 2016 Rao ad Walrad Note 19 Some Importat Distributios Recall our basic probabilistic experimet of tossig a biased coi times. This is a very simple
Lecture 12: November 13, 2018
 Mathematical Toolkit Autum 2018 Lecturer: Madhur Tulsiai Lecture 12: November 13, 2018 1 Radomized polyomial idetity testig We will use our kowledge of coditioal probability to prove the followig lemma,
Mathematical Toolkit Autum 2018 Lecturer: Madhur Tulsiai Lecture 12: November 13, 2018 1 Radomized polyomial idetity testig We will use our kowledge of coditioal probability to prove the followig lemma,
, then cv V. Differential Equations Elements of Lineaer Algebra Name: Consider the differential equation. and y2 cos( kx)
 Cosider the differetial equatio y '' k y 0 has particular solutios y1 si( kx) ad y cos( kx) I geeral, ay liear combiatio of y1 ad y, cy 1 1 cy where c1, c is also a solutio to the equatio above The reaso
Cosider the differetial equatio y '' k y 0 has particular solutios y1 si( kx) ad y cos( kx) I geeral, ay liear combiatio of y1 ad y, cy 1 1 cy where c1, c is also a solutio to the equatio above The reaso
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS
 THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
Law of the sum of Bernoulli random variables
 Law of the sum of Beroulli radom variables Nicolas Chevallier Uiversité de Haute Alsace, 4, rue des frères Lumière 68093 Mulhouse icolas.chevallier@uha.fr December 006 Abstract Let be the set of all possible
Law of the sum of Beroulli radom variables Nicolas Chevallier Uiversité de Haute Alsace, 4, rue des frères Lumière 68093 Mulhouse icolas.chevallier@uha.fr December 006 Abstract Let be the set of all possible
Lecture 11: Pseudorandom functions
 COM S 6830 Cryptography Oct 1, 2009 Istructor: Rafael Pass 1 Recap Lecture 11: Pseudoradom fuctios Scribe: Stefao Ermo Defiitio 1 (Ge, Ec, Dec) is a sigle message secure ecryptio scheme if for all uppt
COM S 6830 Cryptography Oct 1, 2009 Istructor: Rafael Pass 1 Recap Lecture 11: Pseudoradom fuctios Scribe: Stefao Ermo Defiitio 1 (Ge, Ec, Dec) is a sigle message secure ecryptio scheme if for all uppt
Skip Lists. Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 S 3 S S 1
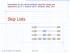 Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Skip Lists S 3 15 15 23 10 15 23 36 Skip Lists 1 What is a Skip List A skip list for
Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Skip Lists S 3 15 15 23 10 15 23 36 Skip Lists 1 What is a Skip List A skip list for
Lecture 9: Pseudo-random generators against space bounded computation,
 Lecture 9: Pseudo-radom geerators agaist space bouded computatio, Primality Testig Topics i Pseudoradomess ad Complexity (Sprig 2018) Rutgers Uiversity Swastik Kopparty Scribes: Harsha Tirumala, Jiyu Zhag
Lecture 9: Pseudo-radom geerators agaist space bouded computatio, Primality Testig Topics i Pseudoradomess ad Complexity (Sprig 2018) Rutgers Uiversity Swastik Kopparty Scribes: Harsha Tirumala, Jiyu Zhag
MA131 - Analysis 1. Workbook 2 Sequences I
 MA3 - Aalysis Workbook 2 Sequeces I Autum 203 Cotets 2 Sequeces I 2. Itroductio.............................. 2.2 Icreasig ad Decreasig Sequeces................ 2 2.3 Bouded Sequeces..........................
MA3 - Aalysis Workbook 2 Sequeces I Autum 203 Cotets 2 Sequeces I 2. Itroductio.............................. 2.2 Icreasig ad Decreasig Sequeces................ 2 2.3 Bouded Sequeces..........................
Sequences, Series, and All That
 Chapter Te Sequeces, Series, ad All That. Itroductio Suppose we wat to compute a approximatio of the umber e by usig the Taylor polyomial p for f ( x) = e x at a =. This polyomial is easily see to be 3
Chapter Te Sequeces, Series, ad All That. Itroductio Suppose we wat to compute a approximatio of the umber e by usig the Taylor polyomial p for f ( x) = e x at a =. This polyomial is easily see to be 3
Lecture Overview. 2 Permutations and Combinations. n(n 1) (n (k 1)) = n(n 1) (n k + 1) =
 COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
SDS 321: Introduction to Probability and Statistics
 SDS 321: Itroductio to Probability ad Statistics Lecture 23: Cotiuous radom variables- Iequalities, CLT Puramrita Sarkar Departmet of Statistics ad Data Sciece The Uiversity of Texas at Austi www.cs.cmu.edu/
SDS 321: Itroductio to Probability ad Statistics Lecture 23: Cotiuous radom variables- Iequalities, CLT Puramrita Sarkar Departmet of Statistics ad Data Sciece The Uiversity of Texas at Austi www.cs.cmu.edu/
 1 of 7 7/16/2009 6:06 AM Virtual Laboratories > 6. Radom Samples > 1 2 3 4 5 6 7 6. Order Statistics Defiitios Suppose agai that we have a basic radom experimet, ad that X is a real-valued radom variable
1 of 7 7/16/2009 6:06 AM Virtual Laboratories > 6. Radom Samples > 1 2 3 4 5 6 7 6. Order Statistics Defiitios Suppose agai that we have a basic radom experimet, ad that X is a real-valued radom variable
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Sequences. Notation. Convergence of a Sequence
 Sequeces A sequece is essetially just a list. Defiitio (Sequece of Real Numbers). A sequece of real umbers is a fuctio Z (, ) R for some real umber. Do t let the descriptio of the domai cofuse you; it
Sequeces A sequece is essetially just a list. Defiitio (Sequece of Real Numbers). A sequece of real umbers is a fuctio Z (, ) R for some real umber. Do t let the descriptio of the domai cofuse you; it
HOMEWORK 2 SOLUTIONS
 HOMEWORK SOLUTIONS CSE 55 RANDOMIZED AND APPROXIMATION ALGORITHMS 1. Questio 1. a) The larger the value of k is, the smaller the expected umber of days util we get all the coupos we eed. I fact if = k
HOMEWORK SOLUTIONS CSE 55 RANDOMIZED AND APPROXIMATION ALGORITHMS 1. Questio 1. a) The larger the value of k is, the smaller the expected umber of days util we get all the coupos we eed. I fact if = k
Because it tests for differences between multiple pairs of means in one test, it is called an omnibus test.
 Math 308 Sprig 018 Classes 19 ad 0: Aalysis of Variace (ANOVA) Page 1 of 6 Itroductio ANOVA is a statistical procedure for determiig whether three or more sample meas were draw from populatios with equal
Math 308 Sprig 018 Classes 19 ad 0: Aalysis of Variace (ANOVA) Page 1 of 6 Itroductio ANOVA is a statistical procedure for determiig whether three or more sample meas were draw from populatios with equal
6.046 Recitation 5: Binary Search Trees Bill Thies, Fall 2004 Outline
 6.046 Recitatio 5: Biary Search Trees Bill Thies, Fall 2004 Outlie My cotact iformatio: Bill Thies thies@mit.edu Office hours: Sat 1-3pm, 36-153 Recitatio website: http://cag.lcs.mit.edu/~thies/6.046/
6.046 Recitatio 5: Biary Search Trees Bill Thies, Fall 2004 Outlie My cotact iformatio: Bill Thies thies@mit.edu Office hours: Sat 1-3pm, 36-153 Recitatio website: http://cag.lcs.mit.edu/~thies/6.046/
Section 5.1 The Basics of Counting
 1 Sectio 5.1 The Basics of Coutig Combiatorics, the study of arragemets of objects, is a importat part of discrete mathematics. I this chapter, we will lear basic techiques of coutig which has a lot of
1 Sectio 5.1 The Basics of Coutig Combiatorics, the study of arragemets of objects, is a importat part of discrete mathematics. I this chapter, we will lear basic techiques of coutig which has a lot of
