DATA STRUCTURES I, II, III, AND IV
|
|
|
- Ralph Turner
- 5 years ago
- Views:
Transcription
1 Data structures DATA STRUCTURES I, II, III, AND IV I. Amortized Aalysis II. Biary ad Biomial Heaps III. Fiboacci Heaps IV. Uio Fid Static problems. Give a iput, produce a output. Ex. Sortig, FFT, edit distace, shortest paths, MST, max-flow,... Dyamic problems. Give a sequece of operatios (give oe at a time), produce a sequece of outputs. Ex. Stack, queue, priority queue, symbol table, uio fid,. Algorithm. Step-by-step procedure to solve a problem. Data structure. Way to store ad orgaize data. Ex. Array, liked list, biary heap, biary search tree, hash table, Lecture slides by Kevi Waye Last updated o 2/2/18 5:50 AM Appetizer Goal. Desig a data structure to support all operatios i O(1) time. INIT(): create ad retur a iitialized array (all zero) of legth. READ(A, i): retur elemet i i array. WRITE(A, i, value): set elemet i i array to value. true i C or C++, but ot Java Assumptios. Ca MALLOC a uiitialized array of legth i O(1) time. Give a array, ca read or write elemet i i O(1) time. Remark. A array does INIT i Θ() time ad READ ad WRITE i Θ(1) time. Appetizer Data structure. Three arrays A[1.. ], B[1.. ], ad C[1.. ], ad a iteger k. A[i] stores the curret value for READ (if iitialized). k = umber of iitialized etries. C[j] = idex of j th iitialized elemet for j = 1,, k. If C[j] = i, the B[i] = j for j = 1,, k. Theorem. A[i] is iitialized iff both 1 B[i] k ad C[B[i]] = i. Ahead. A[ ] ? ? 33?? B[ ]? 3 4 1? 2?? C[ ] ???? 3 k = 4 A[4]=99, A[6]=33, A[2]=22, ad A[3]=55 iitialized i that order 4
2 Appetizer Appetizer Theorem. A[i] is iitialized iff both 1 B[i] k ad C[B[i]] = i. INIT (A, ) k 0. A MALLOC(). READ (A, i) IF (IS-INITIALIZED (A[i])) RETURN A[i]. WRITE (A, i, value) IF (IS-INITIALIZED (A[i])) A[i] value. Suppose A[i] is the j th etry to be iitialized. The C[j] = i ad B[i] = j. Thus, C[B[i]] = i. B MALLOC(). ELSE ELSE C MALLOC(). RETURN 0. k k + 1. A[i] value. B[i] k. A[ ] ? ? 33?? IS-INITIALIZED (A, i) IF (1 B[i] k) ad (C[B[i]] = i) C[k] i. B[ ]? 3 4 1? 2?? RETURN true. ELSE C[ ] ???? RETURN false. k = 4 5 A[4]=99, A[6]=33, A[2]=22, ad A[3]=55 iitialized i that order 6 Appetizer Theorem. A[i] is iitialized iff both 1 B[i] k ad C[B[i]] = i. Suppose A[i] is uiitialized. If B[i] < 1 or B[i] > k, the A[i] clearly uiitialized. If 1 B[i] k by coicidece, the we still ca t have C[B[i]] = i because oe of the etries C[1.. k] ca equal i. AMORTIZED ANALYSIS biary couter multi-pop stack dyamic table A[ ]? ? 33?? B[ ] C[ ]? 3 4 1? 2?? ???? k = 4 Lecture slides by Kevi Waye A[4]=99, A[6]=33, A[2]=22, ad A[3]=55 iitialized i that order 7 Last updated o 2/2/18 5:50 AM
3 Amortized aalysis Worst-case aalysis. Determie worst-case ruig time of a data structure operatio as fuctio of the iput size. Amortized aalysis. Determie worst-case ruig time of a sequece of data structure operatios. ca be too pessimistic if the oly way to ecouter a expesive operatio is whe there were lots of previous cheap operatios Ex. Startig from a empty stack implemeted with a dyamic table, ay sequece of push ad pop operatios takes O() time i the worst case. Amortized aalysis: applicatios Splay trees. Dyamic table. Fiboacci heaps. Garbage collectio. Move-to-frot list updatig. Push relabel algorithm for max flow. Path compressio for disjoit-set uio. Structural modificatios to red black trees. Security, databases, distributed computig,... SIAM J. ALG. DISC. METH. Vol. 6, No. 2, April Society for Idustrial ad Applied Mathematics 016 AMORTIZED COMPUTATIONAL COMPLEXITY* ROBERT ENDRE TARJANt Abstract. A powerful techique i the complexity aalysis of data structures is amortizatio, or averagig over time. Amortized ruig time is a realistic but robust complexity measure for which we ca obtai surprisigly tight upper ad lower bouds o a variety of algorithms. By followig the priciple of desigig algorithms whose amortized complexity is low, we obtai "self-adjustig" data structures that are simple, flexible ad efficiet. This paper surveys recet work by several researchers o amortized complexity. ASM(MOS) subject classificatios. 68C25, 68E05 9 Biary couter CHAPTER 17 AMORTIZED ANALYSIS biary couter multi-pop stack dyamic table Goal. Icremet a k-bit biary couter (mod 2 k ). Represetatio. a j = j th least sigificat bit of couter. Couter value A[7] A[6] A[5] A[4] Cost model. Number of bits flipped. A[3] A[2] A[1] A[0] 12
4 Biary couter Aggregate method (brute force) Goal. Icremet a k-bit biary couter (mod 2 k ). Represetatio. aj = j th least sigificat bit of couter. Couter value Theorem. Startig from the zero couter, a sequece of INCREMENT operatios flips O( k) bits. A[5] A[4] A[3] A[2] A[1] A[0] At most k bits flipped per icremet. A[7] A[6] overly pessimistic upper boud Aggregate method. Aalyze cost of a sequece of operatios. Couter value A[7] A[6] A[5] A[4] A[3] A[2] A[1] A[0] Total cost Biary couter: aggregate method Startig from the zero couter, i a sequece of INCREMENT operatios: Bit 0 flips times. Bit 1 flips / 2 times. Bit 2 flips / 4 times. Theorem. Startig from the zero couter, a sequece of INCREMENT operatios flips O() bits. Bit j flips / 2 j times. The total umber of bits flipped is k 1 j=0 2 j < = j j=0 Accoutig method (baker s method) Assig (potetially) differet charges to each operatio. D i = data structure after i th operatio. c i = actual cost of i th operatio. ĉ i = amortized cost of i th operatio = amout we charge operatio i. Whe ĉ i > c i, we store credits i data structure D i to pay for future ops; whe ĉ i < c i, we cosume credits i data structure D i. Iitial data structure D 0 starts with 0 credits. Credit ivariat. The total umber of credits i the data structure 0. ĉ i c i 0 ca be more or less tha actual cost our job is to choose suitable amortized costs so that this ivariat holds Remark. Theorem may be false if iitial couter is ot zero
5 Accoutig method (baker s method) Biary couter: accoutig method Assig (potetially) differet charges to each operatio. Di = data structure after i th operatio. ci = actual cost of i th operatio. ĉ i = amortized cost of i th operatio = amout we charge operatio i. Whe ĉ i > c i, we store credits i data structure D i to pay for future ops; whe ĉ i < c i, we cosume credits i data structure D i. Iitial data structure D 0 starts with 0 credits. Credit ivariat. The total umber of credits i the data structure 0. ĉ i c i 0 Theorem. Startig from the iitial data structure D 0, the total actual cost of ay sequece of operatios is at most the sum of the amortized costs. The amortized cost of the sequece of operatios is: ca be more or less tha actual cost ĉ i Ituitio. Measure ruig time i terms of credits (time = moey). c i. credit ivariat 17 Credits. Oe credit pays for a bit flip. Ivariat. Each 1 bit has oe credit; each 0 bit has zero credits. Accoutig. Flip bit j from 0 to 1: charge 2 credits (use oe ad save oe i bit j). icremet Biary couter: accoutig method Biary couter: accoutig method Credits. Oe credit pays for a bit flip. Ivariat. Each 1 bit has oe credit; each 0 bit has zero credits. Accoutig. Flip bit j from 0 to 1: charge 2 credits (use oe ad save oe i bit j). Flip bit j from 1 to 0: pay for it with the 1 credit saved i bit j. Credits. Oe credit pays for a bit flip. Ivariat. Each 1 bit has oe credit; each 0 bit has zero credits. Accoutig. Flip bit j from 0 to 1: charge 2 credits (use oe ad save oe i bit j). Flip bit j from 1 to 0: pay for it with the 1 credit saved i bit j. icremet
6 Biary couter: accoutig method Credits. Oe credit pays for a bit flip. Ivariat. Each 1 bit has oe credit; each 0 bit has zero credits. Accoutig. Flip bit j from 0 to 1: charge 2 credits (use oe ad save oe i bit j). Flip bit j from 1 to 0: pay for it with the 1 credit saved i bit j. Theorem. Startig from the zero couter, a sequece of INCREMENT operatios flips O() bits. the rightmost 0 bit (uless couter overflows) Each INCREMENT operatio flips at most oe 0 bit to a 1 bit, so the amortized cost per INCREMENT 2. Ivariat umber of credits i data structure 0. Total actual cost of operatios sum of amortized costs 2. Potetial method (physicist s method) Potetial fuctio. Φ(Di) maps each data structure Di to a real umber s.t.: Φ(D0) = 0. Φ(Di) 0 for each data structure Di. Actual ad amortized costs. c i = actual cost of i th operatio. ĉ i = c i + Φ(D i) Φ(D i 1) = amortized cost of i th operatio. accoutig method theorem Potetial method (physicist s method) Biary couter: potetial method Potetial fuctio. Φ(D i) maps each data structure D i to a real umber s.t.: Φ(D i) 0 for each data structure D i. Potetial fuctio. Let Φ(D) = umber of 1 bits i the biary couter D. Actual ad amortized costs. c i = actual cost of i th operatio. ĉ i = c i + Φ(D i) Φ(D i 1) = amortized cost of i th operatio. Theorem. Startig from the iitial data structure D 0, the total actual cost of ay sequece of operatios is at most the sum of the amortized costs. The amortized cost of the sequece of operatios is: icremet ĉ i = = c i (c i + (D i ) (D i 1 )) c i + (D ) (D 0 ) 23 24
7 Biary couter: potetial method Potetial fuctio. Let Φ(D) = umber of 1 bits i the biary couter D. Φ(D0) = 0. Φ(Di) 0 for each Di. Biary couter: potetial method Potetial fuctio. Let Φ(D) = umber of 1 bits i the biary couter D. Φ(D0) = 0. Φ(Di) 0 for each Di. icremet Biary couter: potetial method Famous potetial fuctios Potetial fuctio. Let Φ(D) = umber of 1 bits i the biary couter D. Theorem. Startig from the zero couter, a sequece of INCREMENT operatios flips O() bits. Suppose that the i th INCREMENT operatio flips t i bits from 1 to 0. The actual cost ci ti + 1. The amortized cost ĉi = ci + Φ(Di) Φ(Di 1) ci + 1 ti operatio flips at most oe bit from 0 to 1 (o bits flipped to 1 whe couter overflows) 2. Total actual cost of operatios sum of amortized costs 2. potetial method theorem potetial decreases by 1 for ti bits flipped from 1 to 0 ad icreases by 1 for bit flipped from 0 to 1 27 Fiboacci heaps. Splay trees. Move-to-frot. Preflow push. Red black trees. (T ) = (H) = 2 trees(h) + 2 marks(h) x (f) = T (T ) = w(x) = log 2 size(x) (L) = 2 iversios(l, L ) v : excess(v) > 0 x T w(x) height(v) 0 x 1 x 0 x 2 x 28
8 Multipop stack SECTION 17.4 AMORTIZED ANALYSIS biary couter multi-pop stack dyamic table Goal. Support operatios o a set of elemets: PUSH(S, x): add elemet x to stack S. POP(S): remove ad retur the most-recetly added elemet. MULTI-POP(S, k): remove the most-recetly added k elemets. MULTI-POP(S, k) FOR i = 1 TO k POP(S). Exceptios. We assume POP throws a exceptio if stack is empty. 30 Multipop stack Goal. Support operatios o a set of elemets: PUSH(S, x): add elemet x to stack S. POP(S): remove ad retur the most-recetly added elemet. MULTI-POP(S, k): remove the most-recetly added k elemets. Theorem. Startig from a empty stack, ay itermixed sequece of PUSH, POP, ad MULTI-POP operatios takes O( 2 ) time. Use a sigly liked list. PoP ad PUSH take O(1) time each. MULTI-POP takes O() time. overly pessimistic upper boud Multipop stack: aggregate method Goal. Support operatios o a set of elemets: PUSH(S, x): add elemet x to stack S. POP(S): remove ad retur the most-recetly added elemet. MULTI-POP(S, k): remove the most-recetly added k elemets. Theorem. Startig from a empty stack, ay itermixed sequece of PUSH, POP, ad MULTI-POP operatios takes O() time. A elemet is popped at most oce for each time that it is pushed. There are PUSH operatios. Thus, there are POP operatios (icludig those made withi MULTI-POP). top
9 Multipop stack: accoutig method Multipop stack: potetial method Credits. 1 credit pays for either a PUSH or POP. Ivariat. Every elemet o the stack has 1 credit. Accoutig. PUSH(S, x): charge 2 credits. - use 1 credit to pay for pushig x ow - store 1 credit to pay for poppig x at some poit i the future POP(S): charge 0 credits. Theorem. Startig from a empty stack, ay itermixed sequece of PUSH, POP, ad MULTI-POP operatios takes O() time. Ivariat umber of credits i data structure 0. Amortized cost per operatio 2. Total actual cost of operatios sum of amortized costs 2. Potetial fuctio. Let Φ(D) = umber of elemets curretly o the stack. Φ(D0) = 0. Φ(Di) 0 for each Di. Theorem. Startig from a empty stack, ay itermixed sequece of PUSH, POP, ad MULTI-POP operatios takes O() time. [Case 1: push] Suppose that the i th operatio is a PUSH. The actual cost c i = 1. The amortized cost ĉ i = c i + Φ(D i) Φ(D i 1) = = 2. accoutig method theorem Multipop stack: potetial method Multipop stack: potetial method Potetial fuctio. Let Φ(D) = umber of elemets curretly o the stack. Theorem. Startig from a empty stack, ay itermixed sequece of PUSH, POP, ad MULTI-POP operatios takes O() time. [Case 2: pop] Suppose that the i th operatio is a POP. The actual cost ci = 1. The amortized cost ĉi = ci + Φ(Di) Φ(Di 1) = 1 1 = 0. Potetial fuctio. Let Φ(D) = umber of elemets curretly o the stack. Theorem. Startig from a empty stack, ay itermixed sequece of PUSH, POP, ad MULTI-POP operatios takes O() time. [Case 3: multi-pop] Suppose that the i th operatio is a MULTI-POP of k objects. The actual cost ci = k. The amortized cost ĉi = ci + Φ(Di) Φ(Di 1) = k k =
10 Multipop stack: potetial method Potetial fuctio. Let Φ(D) = umber of elemets curretly o the stack. Φ(D0) = 0. Φ(Di) 0 for each Di. Theorem. Startig from a empty stack, ay itermixed sequece of PUSH, POP, ad MULTI-POP operatios takes O() time. [puttig everythig together] Amortized cost ĉ i 2. 2 for push; 0 for pop ad multi-pop Sum of amortized costs ĉ i of the operatios 2. Total actual cost sum of amortized cost 2. AMORTIZED ANALYSIS biary couter multi-pop stack dyamic table potetial method theorem SECTION Dyamic table Dyamic table: isert oly Goal. Store items i a table (e.g., for hash table, biary heap). Two operatios: INSERT ad DELETE. - too may items iserted expad table. - too may items deleted cotract table. Requiremet: if table cotais m items, the space = Θ(m). Theorem. Startig from a empty dyamic table, ay itermixed sequece of INSERT ad DELETE operatios takes O( 2 ) time. Each INSERT or DELETE takes O() time. overly pessimistic upper boud 39 Whe isertig ito a empty table, allocate a table of capacity 1. Whe isertig ito a full table, allocate a ew table of twice the capacity ad copy all items. Isert item ito table. isert old capacity ew capacity isert cost copy cost Cost model. Number of items writte (due to isertio or copy). 40
11 Dyamic table: isert oly (aggregate method) Dyamic table demo: isert oly (accoutig method) Theorem. [via aggregate method] Startig from a empty dyamic table, ay sequece of INSERT operatios takes O() time. Let c i deote the cost of the i th isertio. c i = i i 1 1 Startig from empty table, the cost of a sequece of INSERT operatios is: Isert. Charge 3 credits (use 1 credit to isert; save 2 with ew item). Ivariat. 2 credits with each item i right half of table; oe i left half. isert N capacity = 16 A B C D E F G H I J K L M lg c i + j=0 < +2 2 j = Dyamic table: isert oly (accoutig method) Dyamic table: isert oly (potetial method) Isert. Charge 3 credits (use 1 credit to isert; save 2 with ew item). Ivariat. 2 credits with each item i right half of table; oe i left half. [iductio] Each ewly iserted item gets 2 credits. Whe table doubles from k to 2k, k / 2 items i the table have 2 credits. - these k credits pay for the work eeded to copy the k items - ow, all k items are i left half of table (ad have 0 credits) Theorem. [via accoutig method] Startig from a empty dyamic table, ay sequece of INSERT operatios takes O() time. slight cheat if table capacity = 1 Ivariat umber of credits i data structure 0. Amortized cost per INSERT = 3. Total actual cost of operatios sum of amortized cost 3. Theorem. [via potetial method] Startig from a empty dyamic table, ay sequece of INSERT operatios takes O() time. Let Φ(D i) = 2 size(d i) capacity(d i). umber of elemets capacity of array immediately after doublig capacity(di) = 2 size(di) size = 6 capacity = 8 Φ = 4 accoutig method theorem 43 44
12 Dyamic table: isert oly (potetial method) Dyamic table: isert oly (potetial method) Theorem. [via potetial method] Startig from a empty dyamic table, ay sequece of INSERT operatios takes O() time. Let Φ(D i) = 2 size(d i) capacity(d i). umber of elemets Case 0. [first isertio] Actual cost c 1 = 1. Φ(D 1) Φ(D 0) = (2 size(d 1) capacity(d 1)) (2 size(d 0) capacity(d 0)) = 1. Amortized cost ĉ i = c i + (Φ(D 1) Φ(D 0)) = = 2. capacity of array Theorem. [via potetial method] Startig from a empty dyamic table, ay sequece of INSERT operatios takes O() time. Let Φ(D i) = 2 size(d i) capacity(d i). umber of elemets Case 1. [o array expasio] capacity(d i) = capacity(d i 1). Actual cost c i = 1. Φ(D i) Φ(D i 1) = (2 size(d i) capacity(d i)) (2 size(d i 1) capacity(d i 1)) = 2. Amortized cost ĉ i = c i + (Φ(D i) Φ(D i 1)) = = 3. capacity of array Dyamic table: isert oly (potetial method) Dyamic table: isert oly (potetial method) Theorem. [via potetial method] Startig from a empty dyamic table, ay sequece of INSERT operatios takes O() time. Let Φ(D i) = 2 size(d i) capacity(d i). umber of elemets Case 2. [array expasio] capacity(di) = 2 capacity(di 1). Actual cost ci = 1 + capacity(di 1). Φ(Di) Φ(Di 1) = (2 size(di) capacity(di)) (2 size(di 1) capacity(di 1)) = 2 capacity(di) + capacity(di 1) = 2 capacity(di 1). Amortized cost ĉi = ci + (Φ(Di) Φ(Di 1)) = 1 + capacity(di 1) + (2 capacity(di 1)) = 3. capacity of array 47 Theorem. [via potetial method] Startig from a empty dyamic table, ay sequece of INSERT operatios takes O() time. Let Φ(D i) = 2 size(d i) capacity(d i). umber of elemets capacity of array [puttig everythig together] Amortized cost per operatio ĉi 3. Total actual cost of operatios sum of amortized cost 3. potetial method theorem 48
13 Dyamic table: doublig ad halvig Thrashig. INSERT: whe isertig ito a full table, double capacity. DELETE: whe deletig from a table that is ½-full, halve capacity. Efficiet solutio. Whe isertig ito a empty table, iitialize table size to 1; whe deletig from a table of size 1, free the table. INSERT: whe isertig ito a full table, double capacity. DELETE: whe deletig from a table that is ¼-full, halve capacity. Memory usage. A dyamic table uses Θ() memory to store items. Table is always betwee 25% ad 0% full. Dyamic table demo: isert ad delete (accoutig method) Isert. Charge 3 credits (1 to isert; save 2 with item if i right half). Delete. Charge 2 credits (1 to delete; save 1 i empty slot if i left half). Ivariat 1. 2 credits with each item i right half of table. Ivariat 2. 1 credit with each empty slot i left half of table. delete M capacity = 16 A B C D E F G H I J K L M Dyamic table: isert ad delete (accoutig method) Dyamic table: isert ad delete (potetial method) Isert. Charge 3 credits (1 to isert; save 2 with item if i right half). Delete. Charge 2 credits (1 to delete; save 1 i empty slot if i left half). discard ay existig or extra credits Ivariat 1. 2 credits with each item i right half of table. Ivariat 2. 1 credit with each empty slot i left half of table. Theorem. [via accoutig method] Startig from a empty dyamic table, ay itermixed sequece of INSERT ad DELETE operatios takes O() time. Ivariats umber of credits i data structure 0. Amortized cost per operatio 3. Total actual cost of operatios sum of amortized cost 3. accoutig method theorem to pay for expasio to pay for cotractio Theorem. [via potetial method] Startig from a empty dyamic table, ay itermixed sequece of INSERT ad DELETE operatios takes O() time. Pf sketch. Let α(d i) = size(d i) / capacity(d i). Defie (D i )= 2 size(d i) capacity(d i ) (D i ) 1/2 1 2 capacity(d i) size(d i ) (D i ) < 1/2 Φ(D0) = 0, Φ(Di) 0. [a potetial fuctio] Whe α(di) = 1/2, Φ(Di) = 0. [zero potetial after resizig] Whe α(di) = 1, Φ(Di) = size(di). [ca pay for expasio] Whe α(di) = 1/4, Φ(Di) = size(di). [ca pay for cotractio]
AMORTIZED ANALYSIS. binary counter multipop stack dynamic table. Lecture slides by Kevin Wayne. Last updated on 1/24/17 11:31 AM
 AMORTIZED ANALYSIS binary counter multipop stack dynamic table Lecture slides by Kevin Wayne http://www.cs.princeton.edu/~wayne/kleinberg-tardos Last updated on 1/24/17 11:31 AM Amortized analysis Worst-case
AMORTIZED ANALYSIS binary counter multipop stack dynamic table Lecture slides by Kevin Wayne http://www.cs.princeton.edu/~wayne/kleinberg-tardos Last updated on 1/24/17 11:31 AM Amortized analysis Worst-case
Hashing. Algorithm : Design & Analysis [09]
![Hashing. Algorithm : Design & Analysis [09] Hashing. Algorithm : Design & Analysis [09]](/thumbs/82/84955480.jpg) Hashig Algorithm : Desig & Aalysis [09] I the last class Implemetig Dictioary ADT Defiitio of red-black tree Black height Isertio ito a red-black tree Deletio from a red-black tree Hashig Hashig Collisio
Hashig Algorithm : Desig & Aalysis [09] I the last class Implemetig Dictioary ADT Defiitio of red-black tree Black height Isertio ito a red-black tree Deletio from a red-black tree Hashig Hashig Collisio
Classification of problem & problem solving strategies. classification of time complexities (linear, logarithmic etc)
 Classificatio of problem & problem solvig strategies classificatio of time complexities (liear, arithmic etc) Problem subdivisio Divide ad Coquer strategy. Asymptotic otatios, lower boud ad upper boud:
Classificatio of problem & problem solvig strategies classificatio of time complexities (liear, arithmic etc) Problem subdivisio Divide ad Coquer strategy. Asymptotic otatios, lower boud ad upper boud:
11. Hash Tables. m is not too large. Many applications require a dynamic set that supports only the directory operations INSERT, SEARCH and DELETE.
 11. Hash Tables May applicatios require a dyamic set that supports oly the directory operatios INSERT, SEARCH ad DELETE. A hash table is a geeralizatio of the simpler otio of a ordiary array. Directly
11. Hash Tables May applicatios require a dyamic set that supports oly the directory operatios INSERT, SEARCH ad DELETE. A hash table is a geeralizatio of the simpler otio of a ordiary array. Directly
OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES
 OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES Peter M. Maurer Why Hashig is θ(). As i biary search, hashig assumes that keys are stored i a array which is idexed by a iteger. However, hashig attempts to bypass
OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES Peter M. Maurer Why Hashig is θ(). As i biary search, hashig assumes that keys are stored i a array which is idexed by a iteger. However, hashig attempts to bypass
Amortized Analysis - Part 2 - Dynamic Tables. Objective: In this lecture, we shall explore Dynamic tables and its amortized analysis in detail.
 Idia Istitute of Iformatio Techology Desig ad Maufacturig, Kacheepuram Cheai 600 17, Idia A Autoomous Istitute uder MHRD, Govt of Idia http://www.iiitdm.ac.i COM 501 Advaced Data Structures ad Algorithms
Idia Istitute of Iformatio Techology Desig ad Maufacturig, Kacheepuram Cheai 600 17, Idia A Autoomous Istitute uder MHRD, Govt of Idia http://www.iiitdm.ac.i COM 501 Advaced Data Structures ad Algorithms
Hashing and Amortization
 Lecture Hashig ad Amortizatio Supplemetal readig i CLRS: Chapter ; Chapter 7 itro; Sectio 7.. Arrays ad Hashig Arrays are very useful. The items i a array are statically addressed, so that isertig, deletig,
Lecture Hashig ad Amortizatio Supplemetal readig i CLRS: Chapter ; Chapter 7 itro; Sectio 7.. Arrays ad Hashig Arrays are very useful. The items i a array are statically addressed, so that isertig, deletig,
Data Structures and Algorithm. Xiaoqing Zheng
 Data Structures and Algorithm Xiaoqing Zheng zhengxq@fudan.edu.cn MULTIPOP top[s] = 6 top[s] = 2 3 2 8 5 6 5 S MULTIPOP(S, x). while not STACK-EMPTY(S) and k 0 2. do POP(S) 3. k k MULTIPOP(S, 4) Analysis
Data Structures and Algorithm Xiaoqing Zheng zhengxq@fudan.edu.cn MULTIPOP top[s] = 6 top[s] = 2 3 2 8 5 6 5 S MULTIPOP(S, x). while not STACK-EMPTY(S) and k 0 2. do POP(S) 3. k k MULTIPOP(S, 4) Analysis
Sorting Algorithms. Algorithms Kyuseok Shim SoEECS, SNU.
 Sortig Algorithms Algorithms Kyuseo Shim SoEECS, SNU. Desigig Algorithms Icremetal approaches Divide-ad-Coquer approaches Dyamic programmig approaches Greedy approaches Radomized approaches You are ot
Sortig Algorithms Algorithms Kyuseo Shim SoEECS, SNU. Desigig Algorithms Icremetal approaches Divide-ad-Coquer approaches Dyamic programmig approaches Greedy approaches Radomized approaches You are ot
1 Hash tables. 1.1 Implementation
 Lecture 8 Hash Tables, Uiversal Hash Fuctios, Balls ad Bis Scribes: Luke Johsto, Moses Charikar, G. Valiat Date: Oct 18, 2017 Adapted From Virgiia Williams lecture otes 1 Hash tables A hash table is a
Lecture 8 Hash Tables, Uiversal Hash Fuctios, Balls ad Bis Scribes: Luke Johsto, Moses Charikar, G. Valiat Date: Oct 18, 2017 Adapted From Virgiia Williams lecture otes 1 Hash tables A hash table is a
CSE 4095/5095 Topics in Big Data Analytics Spring 2017; Homework 1 Solutions
 CSE 09/09 Topics i ig Data Aalytics Sprig 2017; Homework 1 Solutios Note: Solutios to problems,, ad 6 are due to Marius Nicolae. 1. Cosider the followig algorithm: for i := 1 to α log e do Pick a radom
CSE 09/09 Topics i ig Data Aalytics Sprig 2017; Homework 1 Solutios Note: Solutios to problems,, ad 6 are due to Marius Nicolae. 1. Cosider the followig algorithm: for i := 1 to α log e do Pick a radom
4/9/13. Fibonacci Heaps. H.min. H.min. Priority Queues Performance Cost Summary. COMP 160 Algorithms - Tufts University
 4/9/ Priority Queues Performace Cost Summary Fiboacci Heas Oeratio Liked List Biary Hea Biomial Hea Fiboacci Hea Relaed Hea make-hea COMP 60 Algorithms - Tufts Uiversity is-emty isert Origial Slides from
4/9/ Priority Queues Performace Cost Summary Fiboacci Heas Oeratio Liked List Biary Hea Biomial Hea Fiboacci Hea Relaed Hea make-hea COMP 60 Algorithms - Tufts Uiversity is-emty isert Origial Slides from
Disjoint set (Union-Find)
 CS124 Lecture 7 Fall 2018 Disjoit set (Uio-Fid) For Kruskal s algorithm for the miimum spaig tree problem, we foud that we eeded a data structure for maitaiig a collectio of disjoit sets. That is, we eed
CS124 Lecture 7 Fall 2018 Disjoit set (Uio-Fid) For Kruskal s algorithm for the miimum spaig tree problem, we foud that we eeded a data structure for maitaiig a collectio of disjoit sets. That is, we eed
Analysis of Algorithms. Introduction. Contents
 Itroductio The focus of this module is mathematical aspects of algorithms. Our mai focus is aalysis of algorithms, which meas evaluatig efficiecy of algorithms by aalytical ad mathematical methods. We
Itroductio The focus of this module is mathematical aspects of algorithms. Our mai focus is aalysis of algorithms, which meas evaluatig efficiecy of algorithms by aalytical ad mathematical methods. We
Lecture 7: Amortized analysis
 Lecture 7: Amortized analysis In many applications we want to minimize the time for a sequence of operations. To sum worst-case times for single operations can be overly pessimistic, since it ignores correlation
Lecture 7: Amortized analysis In many applications we want to minimize the time for a sequence of operations. To sum worst-case times for single operations can be overly pessimistic, since it ignores correlation
Skip Lists. Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 S 3 S S 1
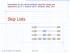 Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Skip Lists S 3 15 15 23 10 15 23 36 Skip Lists 1 What is a Skip List A skip list for
Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Skip Lists S 3 15 15 23 10 15 23 36 Skip Lists 1 What is a Skip List A skip list for
CS 332: Algorithms. Linear-Time Sorting. Order statistics. Slide credit: David Luebke (Virginia)
 1 CS 332: Algorithms Liear-Time Sortig. Order statistics. Slide credit: David Luebke (Virgiia) Quicksort: Partitio I Words Partitio(A, p, r): Select a elemet to act as the pivot (which?) Grow two regios,
1 CS 332: Algorithms Liear-Time Sortig. Order statistics. Slide credit: David Luebke (Virgiia) Quicksort: Partitio I Words Partitio(A, p, r): Select a elemet to act as the pivot (which?) Grow two regios,
Another way of saying this is that amortized analysis guarantees the average case performance of each operation in the worst case.
 Amortized Analysis: CLRS Chapter 17 Last revised: August 30, 2006 1 In amortized analysis we try to analyze the time required by a sequence of operations. There are many situations in which, even though
Amortized Analysis: CLRS Chapter 17 Last revised: August 30, 2006 1 In amortized analysis we try to analyze the time required by a sequence of operations. There are many situations in which, even though
CS583 Lecture 02. Jana Kosecka. some materials here are based on E. Demaine, D. Luebke slides
 CS583 Lecture 02 Jaa Kosecka some materials here are based o E. Demaie, D. Luebke slides Previously Sample algorithms Exact ruig time, pseudo-code Approximate ruig time Worst case aalysis Best case aalysis
CS583 Lecture 02 Jaa Kosecka some materials here are based o E. Demaie, D. Luebke slides Previously Sample algorithms Exact ruig time, pseudo-code Approximate ruig time Worst case aalysis Best case aalysis
CS / MCS 401 Homework 3 grader solutions
 CS / MCS 401 Homework 3 grader solutios assigmet due July 6, 016 writte by Jāis Lazovskis maximum poits: 33 Some questios from CLRS. Questios marked with a asterisk were ot graded. 1 Use the defiitio of
CS / MCS 401 Homework 3 grader solutios assigmet due July 6, 016 writte by Jāis Lazovskis maximum poits: 33 Some questios from CLRS. Questios marked with a asterisk were ot graded. 1 Use the defiitio of
Lecture 3: Asymptotic Analysis + Recurrences
 Lecture 3: Asymptotic Aalysis + Recurreces Data Structures ad Algorithms CSE 373 SU 18 BEN JONES 1 Warmup Write a model ad fid Big-O for (it i = 0; i < ; i++) { for (it j = 0; j < i; j++) { System.out.pritl(
Lecture 3: Asymptotic Aalysis + Recurreces Data Structures ad Algorithms CSE 373 SU 18 BEN JONES 1 Warmup Write a model ad fid Big-O for (it i = 0; i < ; i++) { for (it j = 0; j < i; j++) { System.out.pritl(
Test One (Answer Key)
 CS395/Ma395 (Sprig 2005) Test Oe Name: Page 1 Test Oe (Aswer Key) CS395/Ma395: Aalysis of Algorithms This is a closed book, closed otes, 70 miute examiatio. It is worth 100 poits. There are twelve (12)
CS395/Ma395 (Sprig 2005) Test Oe Name: Page 1 Test Oe (Aswer Key) CS395/Ma395: Aalysis of Algorithms This is a closed book, closed otes, 70 miute examiatio. It is worth 100 poits. There are twelve (12)
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
w (1) ˆx w (1) x (1) /ρ and w (2) ˆx w (2) x (2) /ρ.
 2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
Data Structures Lecture 9
 Fall 2017 Fag Yu Software Security Lab. Dept. Maagemet Iformatio Systems, Natioal Chegchi Uiversity Data Structures Lecture 9 Midterm o Dec. 7 (9:10-12:00am, 106) Lec 1-9, TextBook Ch1-8, 11,12 How to
Fall 2017 Fag Yu Software Security Lab. Dept. Maagemet Iformatio Systems, Natioal Chegchi Uiversity Data Structures Lecture 9 Midterm o Dec. 7 (9:10-12:00am, 106) Lec 1-9, TextBook Ch1-8, 11,12 How to
2. ALGORITHM ANALYSIS
 2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times 2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times Lecture slides by Kevi Waye Copyright 2005 Pearso-Addiso
2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times 2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times Lecture slides by Kevi Waye Copyright 2005 Pearso-Addiso
Data Structures and Algorithm. Xiaoqing Zheng
 Data Structures ad Algorithm Xiaoqig Zheg zhegxq@fudaeduc What are algorithms? A sequece of computatioal steps that trasform the iput ito the output Sortig problem: Iput: A sequece of umbers
Data Structures ad Algorithm Xiaoqig Zheg zhegxq@fudaeduc What are algorithms? A sequece of computatioal steps that trasform the iput ito the output Sortig problem: Iput: A sequece of umbers
Definitions: Universe U of keys, e.g., U N 0. U very large. Set S U of keys, S = m U.
 7 7 Dictioary: S.isertx): Isert a elemet x. S.deletex): Delete the elemet poited to by x. S.searchk): Retur a poiter to a elemet e with key[e] = k i S if it exists; otherwise retur ull. So far we have
7 7 Dictioary: S.isertx): Isert a elemet x. S.deletex): Delete the elemet poited to by x. S.searchk): Retur a poiter to a elemet e with key[e] = k i S if it exists; otherwise retur ull. So far we have
Advanced Course of Algorithm Design and Analysis
 Differet complexity measures Advaced Course of Algorithm Desig ad Aalysis Asymptotic complexity Big-Oh otatio Properties of O otatio Aalysis of simple algorithms A algorithm may may have differet executio
Differet complexity measures Advaced Course of Algorithm Desig ad Aalysis Asymptotic complexity Big-Oh otatio Properties of O otatio Aalysis of simple algorithms A algorithm may may have differet executio
CS 270 Algorithms. Oliver Kullmann. Growth of Functions. Divide-and- Conquer Min-Max- Problem. Tutorial. Reading from CLRS for week 2
 Geeral remarks Week 2 1 Divide ad First we cosider a importat tool for the aalysis of algorithms: Big-Oh. The we itroduce a importat algorithmic paradigm:. We coclude by presetig ad aalysig two examples.
Geeral remarks Week 2 1 Divide ad First we cosider a importat tool for the aalysis of algorithms: Big-Oh. The we itroduce a importat algorithmic paradigm:. We coclude by presetig ad aalysig two examples.
This Lecture. Divide and Conquer. Merge Sort: Algorithm. Merge Sort Algorithm. MergeSort (Example) - 1. MergeSort (Example) - 2
 This Lecture Divide-ad-coquer techique for algorithm desig. Example the merge sort. Writig ad solvig recurreces Divide ad Coquer Divide-ad-coquer method for algorithm desig: Divide: If the iput size is
This Lecture Divide-ad-coquer techique for algorithm desig. Example the merge sort. Writig ad solvig recurreces Divide ad Coquer Divide-ad-coquer method for algorithm desig: Divide: If the iput size is
Recursive Algorithm for Generating Partitions of an Integer. 1 Preliminary
 Recursive Algorithm for Geeratig Partitios of a Iteger Sug-Hyuk Cha Computer Sciece Departmet, Pace Uiversity 1 Pace Plaza, New York, NY 10038 USA scha@pace.edu Abstract. This article first reviews the
Recursive Algorithm for Geeratig Partitios of a Iteger Sug-Hyuk Cha Computer Sciece Departmet, Pace Uiversity 1 Pace Plaza, New York, NY 10038 USA scha@pace.edu Abstract. This article first reviews the
Linear chord diagrams with long chords
 Liear chord diagrams with log chords Everett Sulliva Departmet of Mathematics Dartmouth College Haover New Hampshire, U.S.A. everett..sulliva@dartmouth.edu Submitted: Feb 7, 2017; Accepted: Oct 7, 2017;
Liear chord diagrams with log chords Everett Sulliva Departmet of Mathematics Dartmouth College Haover New Hampshire, U.S.A. everett..sulliva@dartmouth.edu Submitted: Feb 7, 2017; Accepted: Oct 7, 2017;
Lecture 4 February 16, 2016
 MIT 6.854/18.415: Advaced Algorithms Sprig 16 Prof. Akur Moitra Lecture 4 February 16, 16 Scribe: Be Eysebach, Devi Neal 1 Last Time Cosistet Hashig - hash fuctios that evolve well Radom Trees - routig
MIT 6.854/18.415: Advaced Algorithms Sprig 16 Prof. Akur Moitra Lecture 4 February 16, 16 Scribe: Be Eysebach, Devi Neal 1 Last Time Cosistet Hashig - hash fuctios that evolve well Radom Trees - routig
Skip lists: A randomized dictionary
 Discrete Math for Bioiformatics WS 11/12:, by A. Bocmayr/K. Reiert, 31. Otober 2011, 09:53 3001 Sip lists: A radomized dictioary The expositio is based o the followig sources, which are all recommeded
Discrete Math for Bioiformatics WS 11/12:, by A. Bocmayr/K. Reiert, 31. Otober 2011, 09:53 3001 Sip lists: A radomized dictioary The expositio is based o the followig sources, which are all recommeded
Axioms of Measure Theory
 MATH 532 Axioms of Measure Theory Dr. Neal, WKU I. The Space Throughout the course, we shall let X deote a geeric o-empty set. I geeral, we shall ot assume that ay algebraic structure exists o X so that
MATH 532 Axioms of Measure Theory Dr. Neal, WKU I. The Space Throughout the course, we shall let X deote a geeric o-empty set. I geeral, we shall ot assume that ay algebraic structure exists o X so that
Department of Informatics Prof. Dr. Michael Böhlen Binzmühlestrasse Zurich Phone:
 Departmet of Iformatics Prof. Dr. Michael Böhle Bizmühlestrasse 14 8050 Zurich Phoe: +41 44 635 4333 Email: boehle@ifi.uzh.ch Iformatik II Midterm1 Sprig 018 3.03.018 Advice You have 90 miutes to complete
Departmet of Iformatics Prof. Dr. Michael Böhle Bizmühlestrasse 14 8050 Zurich Phoe: +41 44 635 4333 Email: boehle@ifi.uzh.ch Iformatik II Midterm1 Sprig 018 3.03.018 Advice You have 90 miutes to complete
COMP285 Midterm Exam Department of Mathematics
 COMP85 Midterm Exam Departmet of Mathematics Fall 010/011 - November 8, 010 Name: Studet Number: Please fiish withi 90 miutes. All poits above 100 are cosidered as bous poit. You ca reach maximal 1 poits.
COMP85 Midterm Exam Departmet of Mathematics Fall 010/011 - November 8, 010 Name: Studet Number: Please fiish withi 90 miutes. All poits above 100 are cosidered as bous poit. You ca reach maximal 1 poits.
Chapter 2. Asymptotic Notation
 Asyptotic Notatio 3 Chapter Asyptotic Notatio Goal : To siplify the aalysis of ruig tie by gettig rid of details which ay be affected by specific ipleetatio ad hardware. [1] The Big Oh (O-Notatio) : It
Asyptotic Notatio 3 Chapter Asyptotic Notatio Goal : To siplify the aalysis of ruig tie by gettig rid of details which ay be affected by specific ipleetatio ad hardware. [1] The Big Oh (O-Notatio) : It
Dynamic Programming. Sequence Of Decisions
 Dyamic Programmig Sequece of decisios. Problem state. Priciple of optimality. Dyamic Programmig Recurrece Equatios. Solutio of recurrece equatios. Sequece Of Decisios As i the greedy method, the solutio
Dyamic Programmig Sequece of decisios. Problem state. Priciple of optimality. Dyamic Programmig Recurrece Equatios. Solutio of recurrece equatios. Sequece Of Decisios As i the greedy method, the solutio
Dynamic Programming. Sequence Of Decisions. 0/1 Knapsack Problem. Sequence Of Decisions
 Dyamic Programmig Sequece Of Decisios Sequece of decisios. Problem state. Priciple of optimality. Dyamic Programmig Recurrece Equatios. Solutio of recurrece equatios. As i the greedy method, the solutio
Dyamic Programmig Sequece Of Decisios Sequece of decisios. Problem state. Priciple of optimality. Dyamic Programmig Recurrece Equatios. Solutio of recurrece equatios. As i the greedy method, the solutio
Design and Analysis of ALGORITHM (Topic 2)
 DR. Gatot F. Hertoo, MSc. Desig ad Aalysis of ALGORITHM (Topic 2) Algorithms + Data Structures = Programs Lessos Leared 1 Our Machie Model: Assumptios Geeric Radom Access Machie (RAM) Executes operatios
DR. Gatot F. Hertoo, MSc. Desig ad Aalysis of ALGORITHM (Topic 2) Algorithms + Data Structures = Programs Lessos Leared 1 Our Machie Model: Assumptios Geeric Radom Access Machie (RAM) Executes operatios
Graduate Analysis of Algorithms Dr. Haim Levkowitz
 UMass Lowell Computer Science 9.53 Graduate Analysis of Algorithms Dr. Haim Levkowitz Fall 27 Lecture 5 Tuesday, 2 Oct 27 Amortized Analysis Overview Amortize: To pay off a debt, usually by periodic payments
UMass Lowell Computer Science 9.53 Graduate Analysis of Algorithms Dr. Haim Levkowitz Fall 27 Lecture 5 Tuesday, 2 Oct 27 Amortized Analysis Overview Amortize: To pay off a debt, usually by periodic payments
Section 7 Fundamentals of Sequences and Series
 ectio Fudametals of equeces ad eries. Defiitio ad examples of sequeces A sequece ca be thought of as a ifiite list of umbers. 0, -, -0, -, -0...,,,,,,. (iii),,,,... Defiitio: A sequece is a fuctio which
ectio Fudametals of equeces ad eries. Defiitio ad examples of sequeces A sequece ca be thought of as a ifiite list of umbers. 0, -, -0, -, -0...,,,,,,. (iii),,,,... Defiitio: A sequece is a fuctio which
CSI 5163 (95.573) ALGORITHM ANALYSIS AND DESIGN
 CSI 5163 (95.573) ALGORITHM ANALYSIS AND DESIGN CSI 5163 (95.5703) ALGORITHM ANALYSIS AND DESIGN (3 cr.) (T) Topics of curret iterest i the desig ad aalysis of computer algorithms for graphtheoretical
CSI 5163 (95.573) ALGORITHM ANALYSIS AND DESIGN CSI 5163 (95.5703) ALGORITHM ANALYSIS AND DESIGN (3 cr.) (T) Topics of curret iterest i the desig ad aalysis of computer algorithms for graphtheoretical
CSE 5311 Notes 1: Mathematical Preliminaries
 Chapter 1 - Algorithms Computig CSE 5311 Notes 1: Mathematical Prelimiaries Last updated 1/20/18 12:56 PM) Relatioship betwee complexity classes, eg log,, log, 2, 2, etc Chapter 2 - Gettig Started Loop
Chapter 1 - Algorithms Computig CSE 5311 Notes 1: Mathematical Prelimiaries Last updated 1/20/18 12:56 PM) Relatioship betwee complexity classes, eg log,, log, 2, 2, etc Chapter 2 - Gettig Started Loop
COMP26120: Introducing Complexity Analysis (2018/19) Lucas Cordeiro
 COMP60: Itroduig Complexity Aalysis (08/9) Luas Cordeiro luas.ordeiro@mahester.a.uk Itroduig Complexity Aalysis Textbook: Algorithm Desig ad Appliatios, Goodrih, Mihael T. ad Roberto Tamassia (hapter )
COMP60: Itroduig Complexity Aalysis (08/9) Luas Cordeiro luas.ordeiro@mahester.a.uk Itroduig Complexity Aalysis Textbook: Algorithm Desig ad Appliatios, Goodrih, Mihael T. ad Roberto Tamassia (hapter )
7.7 Hashing. 7.7 Hashing. Perfect Hashing. Direct Addressing
 Dictioary: S.isertx): Isert a elemet x. S.deletex): Delete the elemet poited to by x. S.searchk): Retur a poiter to a elemet e with key[e] = k i S if it exists; otherwise retur ull. So far we have implemeted
Dictioary: S.isertx): Isert a elemet x. S.deletex): Delete the elemet poited to by x. S.searchk): Retur a poiter to a elemet e with key[e] = k i S if it exists; otherwise retur ull. So far we have implemeted
UC Berkeley CS 170: Efficient Algorithms and Intractable Problems Handout 17 Lecturer: David Wagner April 3, Notes 17 for CS 170
 UC Berkeley CS 170: Efficiet Algorithms ad Itractable Problems Hadout 17 Lecturer: David Wager April 3, 2003 Notes 17 for CS 170 1 The Lempel-Ziv algorithm There is a sese i which the Huffma codig was
UC Berkeley CS 170: Efficiet Algorithms ad Itractable Problems Hadout 17 Lecturer: David Wager April 3, 2003 Notes 17 for CS 170 1 The Lempel-Ziv algorithm There is a sese i which the Huffma codig was
Recursive Algorithms. Recurrences. Recursive Algorithms Analysis
 Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
Analysis of Algorithms -Quicksort-
 Aalysis of Algorithms -- Adreas Ermedahl MRTC (Mälardales Real-Time Research Ceter) adreas.ermedahl@mdh.se Autum 2004 Proposed by C.A.R. Hoare i 962 Worst- case ruig time: Θ( 2 ) Expected ruig time: Θ(
Aalysis of Algorithms -- Adreas Ermedahl MRTC (Mälardales Real-Time Research Ceter) adreas.ermedahl@mdh.se Autum 2004 Proposed by C.A.R. Hoare i 962 Worst- case ruig time: Θ( 2 ) Expected ruig time: Θ(
Merge and Quick Sort
 Merge ad Quick Sort Merge Sort Merge Sort Tree Implemetatio Quick Sort Pivot Item Radomized Quick Sort Adapted from: Goodrich ad Tamassia, Data Structures ad Algorithms i Java, Joh Wiley & So (1998). Ruig
Merge ad Quick Sort Merge Sort Merge Sort Tree Implemetatio Quick Sort Pivot Item Radomized Quick Sort Adapted from: Goodrich ad Tamassia, Data Structures ad Algorithms i Java, Joh Wiley & So (1998). Ruig
Generating Functions. 1 Operations on generating functions
 Geeratig Fuctios The geeratig fuctio for a sequece a 0, a,..., a,... is defied to be the power series fx a x. 0 We say that a 0, a,... is the sequece geerated by fx ad a is the coefficiet of x. Example
Geeratig Fuctios The geeratig fuctio for a sequece a 0, a,..., a,... is defied to be the power series fx a x. 0 We say that a 0, a,... is the sequece geerated by fx ad a is the coefficiet of x. Example
CS 5321: Advanced Algorithms Amortized Analysis of Data Structures. Motivations. Motivation cont d
 CS 5321: Advanced Algorithms Amortized Analysis of Data Structures Ali Ebnenasir Department of Computer Science Michigan Technological University Motivations Why amortized analysis and when? Suppose you
CS 5321: Advanced Algorithms Amortized Analysis of Data Structures Ali Ebnenasir Department of Computer Science Michigan Technological University Motivations Why amortized analysis and when? Suppose you
CS:3330 (Prof. Pemmaraju ): Assignment #1 Solutions. (b) For n = 3, we will have 3 men and 3 women with preferences as follows: m 1 : w 3 > w 1 > w 2
 Shiyao Wag CS:3330 (Prof. Pemmaraju ): Assigmet #1 Solutios Problem 1 (a) Cosider iput with me m 1, m,..., m ad wome w 1, w,..., w with the followig prefereces: All me have the same prefereces for wome:
Shiyao Wag CS:3330 (Prof. Pemmaraju ): Assigmet #1 Solutios Problem 1 (a) Cosider iput with me m 1, m,..., m ad wome w 1, w,..., w with the followig prefereces: All me have the same prefereces for wome:
Problem Set 2 Solutions
 CS271 Radomess & Computatio, Sprig 2018 Problem Set 2 Solutios Poit totals are i the margi; the maximum total umber of poits was 52. 1. Probabilistic method for domiatig sets 6pts Pick a radom subset S
CS271 Radomess & Computatio, Sprig 2018 Problem Set 2 Solutios Poit totals are i the margi; the maximum total umber of poits was 52. 1. Probabilistic method for domiatig sets 6pts Pick a radom subset S
The Boolean Ring of Intervals
 MATH 532 Lebesgue Measure Dr. Neal, WKU We ow shall apply the results obtaied about outer measure to the legth measure o the real lie. Throughout, our space X will be the set of real umbers R. Whe ecessary,
MATH 532 Lebesgue Measure Dr. Neal, WKU We ow shall apply the results obtaied about outer measure to the legth measure o the real lie. Throughout, our space X will be the set of real umbers R. Whe ecessary,
CS161: Algorithm Design and Analysis Handout #10 Stanford University Wednesday, 10 February 2016
 CS161: Algorithm Desig ad Aalysis Hadout #10 Staford Uiversity Wedesday, 10 February 2016 Lecture #11: Wedesday, 10 February 2016 Topics: Example midterm problems ad solutios from a log time ago Sprig
CS161: Algorithm Desig ad Aalysis Hadout #10 Staford Uiversity Wedesday, 10 February 2016 Lecture #11: Wedesday, 10 February 2016 Topics: Example midterm problems ad solutios from a log time ago Sprig
Lecture Notes for Chapter 17: Amortized Analysis
 Lecture Notes for Chapter 17: Amortized Analysis Chapter 17 overview Amortized analysis Analyze a sequence of operations on a data structure. Goal: Show that although some individual operations may be
Lecture Notes for Chapter 17: Amortized Analysis Chapter 17 overview Amortized analysis Analyze a sequence of operations on a data structure. Goal: Show that although some individual operations may be
Homework 9. (n + 1)! = 1 1
 . Chapter : Questio 8 If N, the Homewor 9 Proof. We will prove this by usig iductio o. 2! + 2 3! + 3 4! + + +! +!. Base step: Whe the left had side is. Whe the right had side is 2! 2 +! 2 which proves
. Chapter : Questio 8 If N, the Homewor 9 Proof. We will prove this by usig iductio o. 2! + 2 3! + 3 4! + + +! +!. Base step: Whe the left had side is. Whe the right had side is 2! 2 +! 2 which proves
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS
 THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
Lecture 5: April 17, 2013
 TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 5: April 7, 203 Scribe: Somaye Hashemifar Cheroff bouds recap We recall the Cheroff/Hoeffdig bouds we derived i the last lecture idepedet
TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 5: April 7, 203 Scribe: Somaye Hashemifar Cheroff bouds recap We recall the Cheroff/Hoeffdig bouds we derived i the last lecture idepedet
3 Gauss map and continued fractions
 ICTP, Trieste, July 08 Gauss map ad cotiued fractios I this lecture we will itroduce the Gauss map, which is very importat for its coectio with cotiued fractios i umber theory. The Gauss map G : [0, ]
ICTP, Trieste, July 08 Gauss map ad cotiued fractios I this lecture we will itroduce the Gauss map, which is very importat for its coectio with cotiued fractios i umber theory. The Gauss map G : [0, ]
CSE 332. Data Structures and Parallelism
 Aam Blak Lecture 6a Witer 2017 CSE 332 Data Structures a Parallelism CSE 332: Data Structures a Parallelism More Recurreces T () T (/2) T (/2) T (/4) T (/4) T (/4) T (/4) P1 De-Brief 1 You i somethig substatial!
Aam Blak Lecture 6a Witer 2017 CSE 332 Data Structures a Parallelism CSE 332: Data Structures a Parallelism More Recurreces T () T (/2) T (/2) T (/4) T (/4) T (/4) T (/4) P1 De-Brief 1 You i somethig substatial!
GEORGIA INSTITUTE OF TECHNOLOGY SCHOOL OF ELECTRICAL AND COMPUTER ENGINEERING
 GEORGIA INSTITUTE OF TECHNOLOGY SCHOOL OF ELECTRICAL AND COMPUTER ENGINEERING ECE 06 Summer 07 Problem Set #5 Assiged: Jue 3, 07 Due Date: Jue 30, 07 Readig: Chapter 5 o FIR Filters. PROBLEM 5..* (The
GEORGIA INSTITUTE OF TECHNOLOGY SCHOOL OF ELECTRICAL AND COMPUTER ENGINEERING ECE 06 Summer 07 Problem Set #5 Assiged: Jue 3, 07 Due Date: Jue 30, 07 Readig: Chapter 5 o FIR Filters. PROBLEM 5..* (The
Design and Analysis of Algorithms
 Desig ad Aalysis of Algorithms Probabilistic aalysis ad Radomized algorithms Referece: CLRS Chapter 5 Topics: Hirig problem Idicatio radom variables Radomized algorithms Huo Hogwei 1 The hirig problem
Desig ad Aalysis of Algorithms Probabilistic aalysis ad Radomized algorithms Referece: CLRS Chapter 5 Topics: Hirig problem Idicatio radom variables Radomized algorithms Huo Hogwei 1 The hirig problem
Section 5.1 The Basics of Counting
 1 Sectio 5.1 The Basics of Coutig Combiatorics, the study of arragemets of objects, is a importat part of discrete mathematics. I this chapter, we will lear basic techiques of coutig which has a lot of
1 Sectio 5.1 The Basics of Coutig Combiatorics, the study of arragemets of objects, is a importat part of discrete mathematics. I this chapter, we will lear basic techiques of coutig which has a lot of
Week 5-6: The Binomial Coefficients
 Wee 5-6: The Biomial Coefficiets March 6, 2018 1 Pascal Formula Theorem 11 (Pascal s Formula For itegers ad such that 1, ( ( ( 1 1 + 1 The umbers ( 2 ( 1 2 ( 2 are triagle umbers, that is, The petago umbers
Wee 5-6: The Biomial Coefficiets March 6, 2018 1 Pascal Formula Theorem 11 (Pascal s Formula For itegers ad such that 1, ( ( ( 1 1 + 1 The umbers ( 2 ( 1 2 ( 2 are triagle umbers, that is, The petago umbers
Amortized analysis. Amortized analysis
 In amortized analysis the goal is to bound the worst case time of a sequence of operations on a data-structure. If n operations take T (n) time (worst case), the amortized cost of an operation is T (n)/n.
In amortized analysis the goal is to bound the worst case time of a sequence of operations on a data-structure. If n operations take T (n) time (worst case), the amortized cost of an operation is T (n)/n.
EE260: Digital Design, Spring n Binary Addition. n Complement forms. n Subtraction. n Multiplication. n Inputs: A 0, B 0. n Boolean equations:
 EE260: Digital Desig, Sprig 2018 EE 260: Itroductio to Digital Desig Arithmetic Biary Additio Complemet forms Subtractio Multiplicatio Overview Yao Zheg Departmet of Electrical Egieerig Uiversity of Hawaiʻi
EE260: Digital Desig, Sprig 2018 EE 260: Itroductio to Digital Desig Arithmetic Biary Additio Complemet forms Subtractio Multiplicatio Overview Yao Zheg Departmet of Electrical Egieerig Uiversity of Hawaiʻi
Algorithms and Data Structures Lecture IV
 Algorithms ad Data Structures Lecture IV Simoas Šalteis Aalborg Uiversity simas@cs.auc.dk September 5, 00 1 This Lecture Aalyzig the ruig time of recursive algorithms (such as divide-ad-coquer) Writig
Algorithms ad Data Structures Lecture IV Simoas Šalteis Aalborg Uiversity simas@cs.auc.dk September 5, 00 1 This Lecture Aalyzig the ruig time of recursive algorithms (such as divide-ad-coquer) Writig
Rank Modulation with Multiplicity
 Rak Modulatio with Multiplicity Axiao (Adrew) Jiag Computer Sciece ad Eg. Dept. Texas A&M Uiversity College Statio, TX 778 ajiag@cse.tamu.edu Abstract Rak modulatio is a scheme that uses the relative order
Rak Modulatio with Multiplicity Axiao (Adrew) Jiag Computer Sciece ad Eg. Dept. Texas A&M Uiversity College Statio, TX 778 ajiag@cse.tamu.edu Abstract Rak modulatio is a scheme that uses the relative order
Today: Amortized Analysis
 Today: Amortized Analysis COSC 581, Algorithms March 6, 2014 Many of these slides are adapted from several online sources Today s class: Chapter 17 Reading Assignments Reading assignment for next class:
Today: Amortized Analysis COSC 581, Algorithms March 6, 2014 Many of these slides are adapted from several online sources Today s class: Chapter 17 Reading Assignments Reading assignment for next class:
is also known as the general term of the sequence
 Lesso : Sequeces ad Series Outlie Objectives: I ca determie whether a sequece has a patter. I ca determie whether a sequece ca be geeralized to fid a formula for the geeral term i the sequece. I ca determie
Lesso : Sequeces ad Series Outlie Objectives: I ca determie whether a sequece has a patter. I ca determie whether a sequece ca be geeralized to fid a formula for the geeral term i the sequece. I ca determie
Lecture 9: Hierarchy Theorems
 IAS/PCMI Summer Sessio 2000 Clay Mathematics Udergraduate Program Basic Course o Computatioal Complexity Lecture 9: Hierarchy Theorems David Mix Barrigto ad Alexis Maciel July 27, 2000 Most of this lecture
IAS/PCMI Summer Sessio 2000 Clay Mathematics Udergraduate Program Basic Course o Computatioal Complexity Lecture 9: Hierarchy Theorems David Mix Barrigto ad Alexis Maciel July 27, 2000 Most of this lecture
Induction: Solutions
 Writig Proofs Misha Lavrov Iductio: Solutios Wester PA ARML Practice March 6, 206. Prove that a 2 2 chessboard with ay oe square removed ca always be covered by shaped tiles. Solutio : We iduct o. For
Writig Proofs Misha Lavrov Iductio: Solutios Wester PA ARML Practice March 6, 206. Prove that a 2 2 chessboard with ay oe square removed ca always be covered by shaped tiles. Solutio : We iduct o. For
Recurrence Relations
 Recurrece Relatios Aalysis of recursive algorithms, such as: it factorial (it ) { if (==0) retur ; else retur ( * factorial(-)); } Let t be the umber of multiplicatios eeded to calculate factorial(). The
Recurrece Relatios Aalysis of recursive algorithms, such as: it factorial (it ) { if (==0) retur ; else retur ( * factorial(-)); } Let t be the umber of multiplicatios eeded to calculate factorial(). The
) n. ALG 1.3 Deterministic Selection and Sorting: Problem P size n. Examples: 1st lecture's mult M(n) = 3 M ( È
 Algorithms Professor Joh Reif ALG 1.3 Determiistic Selectio ad Sortig: (a) Selectio Algorithms ad Lower Bouds (b) Sortig Algorithms ad Lower Bouds Problem P size fi divide ito subproblems size 1,..., k
Algorithms Professor Joh Reif ALG 1.3 Determiistic Selectio ad Sortig: (a) Selectio Algorithms ad Lower Bouds (b) Sortig Algorithms ad Lower Bouds Problem P size fi divide ito subproblems size 1,..., k
ORIE 633 Network Flows September 27, Lecture 8
 ORIE 633 Network Flows September 7, 007 Lecturer: David P. Williamso Lecture 8 Scribe: Gema Plaza-Martíez 1 Global mi-cuts i udirected graphs 1.1 Radom cotractio Recall from last time we itroduced the
ORIE 633 Network Flows September 7, 007 Lecturer: David P. Williamso Lecture 8 Scribe: Gema Plaza-Martíez 1 Global mi-cuts i udirected graphs 1.1 Radom cotractio Recall from last time we itroduced the
7. Modern Techniques. Data Encryption Standard (DES)
 7. Moder Techiques. Data Ecryptio Stadard (DES) The objective of this chapter is to illustrate the priciples of moder covetioal ecryptio. For this purpose, we focus o the most widely used covetioal ecryptio
7. Moder Techiques. Data Ecryptio Stadard (DES) The objective of this chapter is to illustrate the priciples of moder covetioal ecryptio. For this purpose, we focus o the most widely used covetioal ecryptio
Algorithm Analysis. Algorithms that are equally correct can vary in their utilization of computational resources
 Algorithm Aalysis Algorithms that are equally correct ca vary i their utilizatio of computatioal resources time ad memory a slow program it is likely ot to be used a program that demads too much memory
Algorithm Aalysis Algorithms that are equally correct ca vary i their utilizatio of computatioal resources time ad memory a slow program it is likely ot to be used a program that demads too much memory
Divide & Conquer. Divide-and-conquer algorithms. Conventional product of polynomials. Conventional product of polynomials.
 Divide-ad-coquer algorithms Divide & Coquer Strategy: Divide the problem ito smaller subproblems of the same type of problem Solve the subproblems recursively Combie the aswers to solve the origial problem
Divide-ad-coquer algorithms Divide & Coquer Strategy: Divide the problem ito smaller subproblems of the same type of problem Solve the subproblems recursively Combie the aswers to solve the origial problem
Amortized Analysis. DistributeMoney(n, k) 1 Each of n people gets $1. 2 for i = 1to k 3 do Give a dollar to a random person
 Amortized Analysis DistributeMoney(n, k) 1 Each of n people gets $1. 2 for i = 1to k 3 do Give a dollar to a random person What is the maximum amount of money I can receive? Amortized Analysis DistributeMoney(n,
Amortized Analysis DistributeMoney(n, k) 1 Each of n people gets $1. 2 for i = 1to k 3 do Give a dollar to a random person What is the maximum amount of money I can receive? Amortized Analysis DistributeMoney(n,
Different kinds of Mathematical Induction
 Differet ids of Mathematical Iductio () Mathematical Iductio Give A N, [ A (a A a A)] A N () (First) Priciple of Mathematical Iductio Let P() be a propositio (ope setece), if we put A { : N p() is true}
Differet ids of Mathematical Iductio () Mathematical Iductio Give A N, [ A (a A a A)] A N () (First) Priciple of Mathematical Iductio Let P() be a propositio (ope setece), if we put A { : N p() is true}
Chapter 6. Advanced Counting Techniques
 Chapter 6 Advaced Coutig Techiques 6.: Recurrece Relatios Defiitio: A recurrece relatio for the sequece {a } is a equatio expressig a i terms of oe or more of the previous terms of the sequece: a,a2,a3,,a
Chapter 6 Advaced Coutig Techiques 6.: Recurrece Relatios Defiitio: A recurrece relatio for the sequece {a } is a equatio expressig a i terms of oe or more of the previous terms of the sequece: a,a2,a3,,a
ECEN 655: Advanced Channel Coding Spring Lecture 7 02/04/14. Belief propagation is exact on tree-structured factor graphs.
 ECEN 655: Advaced Chael Codig Sprig 014 Prof. Hery Pfister Lecture 7 0/04/14 Scribe: Megke Lia 1 4-Cycles i Gallager s Esemble What we already kow: Belief propagatio is exact o tree-structured factor graphs.
ECEN 655: Advaced Chael Codig Sprig 014 Prof. Hery Pfister Lecture 7 0/04/14 Scribe: Megke Lia 1 4-Cycles i Gallager s Esemble What we already kow: Belief propagatio is exact o tree-structured factor graphs.
Examples: data compression, path-finding, game-playing, scheduling, bin packing
 Algorithms - Basic Cocepts Algorithms so what is a algorithm, ayway? The dictioary defiitio: A algorithm is a well-defied computatioal procedure that takes iput ad produces output. This class will deal
Algorithms - Basic Cocepts Algorithms so what is a algorithm, ayway? The dictioary defiitio: A algorithm is a well-defied computatioal procedure that takes iput ad produces output. This class will deal
Lecture 2: April 3, 2013
 TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 2: April 3, 203 Scribe: Shubhedu Trivedi Coi tosses cotiued We retur to the coi tossig example from the last lecture agai: Example. Give,
TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 2: April 3, 203 Scribe: Shubhedu Trivedi Coi tosses cotiued We retur to the coi tossig example from the last lecture agai: Example. Give,
CSI 2101 Discrete Structures Winter Homework Assignment #4 (100 points, weight 5%) Due: Thursday, April 5, at 1:00pm (in lecture)
 CSI 101 Discrete Structures Witer 01 Prof. Lucia Moura Uiversity of Ottawa Homework Assigmet #4 (100 poits, weight %) Due: Thursday, April, at 1:00pm (i lecture) Program verificatio, Recurrece Relatios
CSI 101 Discrete Structures Witer 01 Prof. Lucia Moura Uiversity of Ottawa Homework Assigmet #4 (100 poits, weight %) Due: Thursday, April, at 1:00pm (i lecture) Program verificatio, Recurrece Relatios
Sequences, Mathematical Induction, and Recursion. CSE 2353 Discrete Computational Structures Spring 2018
 CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
Lecture Notes for Analysis Class
 Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Matriculation number: You have 90 minutes to complete the exam of InformatikIIb. The following rules apply:
 Departmet of Iformatics Prof. Dr. Michael Böhle Bizmühlestrasse 14 8050 Zurich Phoe: +41 44 635 4333 Email: boehle@ifi.uzh.ch AlgoDat Midterm1 Sprig 016 08.04.016 Name: Matriculatio umber: Advice You have
Departmet of Iformatics Prof. Dr. Michael Böhle Bizmühlestrasse 14 8050 Zurich Phoe: +41 44 635 4333 Email: boehle@ifi.uzh.ch AlgoDat Midterm1 Sprig 016 08.04.016 Name: Matriculatio umber: Advice You have
ECE 308 Discrete-Time Signals and Systems
 ECE 38-5 ECE 38 Discrete-Time Sigals ad Systems Z. Aliyazicioglu Electrical ad Computer Egieerig Departmet Cal Poly Pomoa ECE 38-5 1 Additio, Multiplicatio, ad Scalig of Sequeces Amplitude Scalig: (A Costat
ECE 38-5 ECE 38 Discrete-Time Sigals ad Systems Z. Aliyazicioglu Electrical ad Computer Egieerig Departmet Cal Poly Pomoa ECE 38-5 1 Additio, Multiplicatio, ad Scalig of Sequeces Amplitude Scalig: (A Costat
Math 475, Problem Set #12: Answers
 Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
IP Reference guide for integer programming formulations.
 IP Referece guide for iteger programmig formulatios. by James B. Orli for 15.053 ad 15.058 This documet is iteded as a compact (or relatively compact) guide to the formulatio of iteger programs. For more
IP Referece guide for iteger programmig formulatios. by James B. Orli for 15.053 ad 15.058 This documet is iteded as a compact (or relatively compact) guide to the formulatio of iteger programs. For more
4.3 Growth Rates of Solutions to Recurrences
 4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
Complex Numbers Solutions
 Complex Numbers Solutios Joseph Zoller February 7, 06 Solutios. (009 AIME I Problem ) There is a complex umber with imagiary part 64 ad a positive iteger such that Fid. [Solutio: 697] 4i + + 4i. 4i 4i
Complex Numbers Solutios Joseph Zoller February 7, 06 Solutios. (009 AIME I Problem ) There is a complex umber with imagiary part 64 ad a positive iteger such that Fid. [Solutio: 697] 4i + + 4i. 4i 4i
CS161 Design and Analysis of Algorithms. Administrative
 CS161 Desig ad Aalysis of Algorithms Da Boeh 1 Admiistrative Lecture 1, April 3, 1 Web page http://theory.staford.edu/~dabo/cs161» Hadouts» Aoucemets» Late breakig ews Gradig ad course requiremets» Midterm/fial/hw»
CS161 Desig ad Aalysis of Algorithms Da Boeh 1 Admiistrative Lecture 1, April 3, 1 Web page http://theory.staford.edu/~dabo/cs161» Hadouts» Aoucemets» Late breakig ews Gradig ad course requiremets» Midterm/fial/hw»
It is always the case that unions, intersections, complements, and set differences are preserved by the inverse image of a function.
 MATH 532 Measurable Fuctios Dr. Neal, WKU Throughout, let ( X, F, µ) be a measure space ad let (!, F, P ) deote the special case of a probability space. We shall ow begi to study real-valued fuctios defied
MATH 532 Measurable Fuctios Dr. Neal, WKU Throughout, let ( X, F, µ) be a measure space ad let (!, F, P ) deote the special case of a probability space. We shall ow begi to study real-valued fuctios defied
Mathematical Foundation. CSE 6331 Algorithms Steve Lai
 Mathematical Foudatio CSE 6331 Algorithms Steve Lai Complexity of Algorithms Aalysis of algorithm: to predict the ruig time required by a algorithm. Elemetary operatios: arithmetic & boolea operatios:
Mathematical Foudatio CSE 6331 Algorithms Steve Lai Complexity of Algorithms Aalysis of algorithm: to predict the ruig time required by a algorithm. Elemetary operatios: arithmetic & boolea operatios:
