Sequences and Series of Functions
|
|
|
- Juliana Jacobs
- 5 years ago
- Views:
Transcription
1 Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges (to a limit f(x)); that is, lim f (x) = f(x) x A, the we say that (f ) coverges poitwise to the limit fuctio f o A. I this case, we write f (x) f(x) or f f poitwise o A, or lim f (x) = f(x) to emphasize the limit is for. The poitwise covergece meas that, give each x A, ɛ > 0, N N such that f (x) f(x) < ɛ N. Note that the umber N here depeds o both x ad ɛ. Example 6.1. (i) Let f (x) = x2 +x, x R. For ay give x R, f (x) = x + x2 x as. Hece f (x) f(x) = x poitwise o R. (ii) Let g (x) = x o [0, 1]. Note that g (1) = 1 for all N; so (g (1)) 1. If 0 x < 1, the (g (x)) = (x ) 0. Hece the poitwise limit fuctio of g (x) o [0, 1] is give by { 0 x [0, 1) g(x) = 1 x = 1. Note that although each g is cotiuous o [0, 1], the poitwise limit fuctio g is ot cotiuous at x = 1. (iii) Let h (x) = x o [ 1, 1]. The (h (x)) x poitwise o [ 1, 1]. (iv) (Exercise 5(b)) Let f (x) = { 1 x 1 x 5 2 x x < 1. 1
2 2 6. Sequeces ad Series of Fuctios The f (x) 1 x (x 0) ad f (0) 0. The limit fuctio o [ 5, 5] is ubouded. (v) Let h (x) = cos(x). The (h (x)) coverges if ad oly if x = 2kπ for k = 0, ±1, ±2,. Proof: Let a = cos(x) a. The a 2 = cos(2x) = 2 cos 2 (x) 1 = 2a 2 1 2a 2 1 = a; so a 0. From the formula cos[( + 1)x] + cos[( 1)x] = 2 cos(x) cos x, it follows that a +1 + a 1 = 2a cos x ad hece 2a = 2a cos x. Sice a 0, we must have cos x = 1; that is, x = 2kπ with k = 0, ±1, ±2,. For all such x s, h (x) = 1 ad hece (h (x)) 1 oly for such x s. Uiform Covergece. Assume that f is cotiuous o a set A for each N ad (f (x)) f(x) poitwise o A. Whe ca we coclude that f is cotiuous o A or at some poit c A? Give c A, ad ɛ > 0, we write by the triagle iequality, f(x) f(c) f (x) f(x) + f (x) f (c) + f (c) f(c). The last term o the right-had side ca be made < ɛ/3 by choosig large eough by the covergece of (f (c)) f(c) ad, oce is fixed, by choosig x close to c from the cotiuity of f at c the secod term ca be made < ɛ/3 as well. The first term, however, is the most troublesome sice, whe is chose, the term f (x) f(x) may ot be small as x c. To deal with this term, we eed the followig defiitio. Defiitio 6.2. (Uiform Covergece) Let f : A R ad f : A R be give fuctios. We say that the sequece (f ) coverges uiformly o A to fuctio f if, for every ɛ > 0, there exists a N N such that wheever x A ad N it follows that f (x) f(x) < ɛ. Remark For poitwise covergece, give ɛ > 0, the umber N is to be foud after x A is give (so N depeds o x), while for the uiform covergece, the umber N is to be foud that works for every x A (so N is idepedet of x). 2. From the defiitios, if (f ) coverges uiformly to f o A the (f (x)) f(x) poitwise o A. Therefore, the uiform limit fuctio must be the poitwise limit fuctio. Example 6.2. Cosider f (x) = x2 +x ad f(x) = x o R. We kow (f (x)) f(x) poitwise o R. However, give ɛ > 0, ca we fid a N N such that f (x) f(x) = x2 < ɛ N, x R? If such a N existed, we would take x = N ad = N to obtai 1 < ɛ, a cotradictio if our ɛ is chose < 1. Therefore, the sequece (f ) does ot coverge uiformly to f o R. I geeral, by egatig the defiitio, (f ) does ot coverge uiformly o A to a fuctio f if ad oly if there exists a ɛ 0 > 0 ad sequeces ( k ) i N with k k ad (x k ) i A such that f k (x k ) f(x k ) ɛ 0. Example 6.3. We also cosider f (x) = x2 +x ad f(x) = x but o bouded iterval [ b, b]. Sice f (x) f(x) = x2 b2 holds for all x [ b, b], i order to make this quatity < ɛ for all such x, we ca choose N N such that N > b2 ɛ. The, for all N ad x [ b, b], it does follow that
3 6.1. Covergece of a Sequece of Fuctios 3 f (x) f(x) b2 < ɛ. Hece (f ) uiformly coverges to f o [ b, b] (but ot o whole R, as see above). Cauchy Criterio for Uiform Covergece. Like other Cauchy criteria, this criterio gives the ecessary ad sufficiet coditio for a sequece of fuctios to coverge uiformly without kowig the limit fuctio. Theorem 6.1 (Cauchy Criterio for Uiform Covergece). Let f : A R for each N. The (f ) coverges uiformly o A if ad oly if, for each ɛ > 0, there exists a N N such that (6.1) f (x) f m (x) < ɛ x A,, m N. Proof. First assume (f ) coverges uiformly o A to a limit fuctio f. The, for each ɛ > 0, there exists a N N such that f (x) f(x) < ɛ/2 x A, N. Hece, wheever, m N ad x A, it follows that provig (6.1). f (x) f m (x) f (x) f(x) + f m (x) f(x) < ɛ/2 + ɛ/2 = ɛ, We ow assume coditio (6.1) holds. The, give each x A, the sequece (f (x)) is Cauchy; hece it coverges to a limit f(x) R. This defies a fuctio f : A R, which is the poitwise covergece limit of f (x). The coditio, used with ɛ replaced by ɛ/2, implies that there exists a N N such that for all x A ad, m N we have f (x) f m (x) < ɛ/2. Hece ɛ/2 < f (x) f m (x) < ɛ/2, m N. We ow fix x A ad N ad take the limit of sequece (f m (x)) i this iequality. Use the order limit theorem, we have ɛ/2 f (x) f(x) ɛ/2 N. Hece we have proved that f (x) f(x) ɛ/2 < ɛ holds for all x A ad N. This is othig but the defiitio of the uiform covergece of (f ) to f o A. Theorem 6.2 (Cotiuity of uiform limit fuctio). Let (f ) ad f be fuctios o A ad let (f ) coverge uiformly to f o A. Assume for each N the fuctio f is cotiuous at a poit c A. The f is cotiuous at c as well. Proof. Give ɛ > 0, by the uiform covergece of (f ) to f o A, there exists a N N such that f (x) f(x) < ɛ/3 x A, N. We fix = N ad cosider fuctio f N, which is cotiuous at c A; hece, there exists a umber δ > 0 such that f N (x) f N (c) < ɛ/3 x A, x c < δ. The, wheever x A ad x c < δ, it follows that f(x) f(c) f N (x) f(x) + f N (x) f N (c) + f N (c) f(c) This proves the cotiuity of f at c A. < ɛ/3 + ɛ/3 + ɛ/3 = ɛ.
4 4 6. Sequeces ad Series of Fuctios 6.2. Uiform Covergece ad Differetiatio Theorem 6.3. Let f (x) f(x) poitwise o [a, b] ad assume each f is differetiable o a ope iterval cotaiig [a, b]. If f coverges uiformly o [a, b] to a fuctio g, the f is differetiable ad f = g o [a, b]. Proof. Let c [a, b] be give. We wat to show Note that (6.2) f(x) f(c) x c f(x) f(c) lim = g(c). x c x c g(c) f(x) f(c) f (x) f (c) x c x c + f (x) f (c) f x c (c) + f (c) g(c). Give ɛ > 0, we wat to fid a δ > 0 such that each of the three terms is < ɛ/3 for all x c < δ ad x [a, b]. The third term is idepedet of x, but depeds o. Sice f (c) g(c), there exists a N 1 N such that f (c) g(c) < ɛ/3 N 1. The secod term for fixed ca be easily hadled. The first term requires the most work. Let s do it ow. Note that by applyig the MVT to fuctio f m (x) f (x) we have, for x c, (6.3) f m (x) f m (c) x c f (x) f (c) x c = (f m(x) f (x)) (f m (c) f (c)) x c = f m(α) f (α) for some α betwee x ad c (such a umber α depeds o may thigs: m,, x, c). However, sice (f ) coverges uiformly o [a, b], by the Cauchy Criterio for Uiform Covergece, there exists a N 2 N such that f (x) f m(x) < ɛ/4 x [a, b], m, N 2. We ow use (6.3) to coclude that f m (x) f m (c) f (x) f (c) x c x c = f m(α) f (α) < ɛ/4 for all x c ad all, m N 2. Take the limit as m ad use the order limit theorem, ad we have f(x) f(c) f (x) f (c) x c x c ɛ/4 < ɛ/3 x c, N 2. Now let N = max{n 1, N 2 }. Sice f N is differetiable at c with derivative f N (c), there exists a δ > 0 such that f N (x) f N (c) f x c N(c) < ɛ/3 x [a, b], x c < δ.
5 6.2. Uiform Covergece ad Differetiatio 5 For this δ > 0, wheever x [a, b] ad x c < δ, it follows from (6.2) with = N that f(x) f(c) g(c) x c f(x) f(c) f N(x) f N (c) x c x c + f N (x) f N (c) f x c N(c) + f N(c) g(c) < ɛ/3 + ɛ/3 + ɛ/3 = ɛ. So f (c) = g(c). We also have a stroger result uder a weaker assumptio. Theorem 6.4. Let (f ) be a sequece of differetiable fuctios defied o [a, b], ad assume (f ) coverges uiformly to a fuctio g o [a, b]. If there exists a poit c [a, b] for which the sequece (f (c)) coverges, the (f ) must coverge uiformly o [a, b] ad the limit fuctio f is differetiable o [a, b] ad satisfies f (x) = g(x) o [a, b]. Proof. Let us prove the uiform covergece of (f ) o [a, b]; the the differetiatio results follow from the previous theorem. We use the Cauchy criterio to show that (f ) coverges uiformly o [a, b]. Give ay ɛ > 0, by the uiform covergece of (f ), there exists a N 1 N such that f (x) f m(x) < ɛ/2(b a) x [a, b],, m N 1. Also, by the covergece of sequece (f (c)), there exists a N 2 N such that f (c) f m (c) < ɛ/2, m N 2. We use the MVT to fuctio f (x) f m (x) to obtai (f (x) f m (x)) (f (c) f m (c)) = (f (α) f m(α))(x c) for some α betwee x ad c ad hece α [a, b]. Therefore, wheever, m N 1, (f (x) f m (x)) (f (c) f m (c)) = (f (α) f m(α)) x c f (α) f m(α) (b a) < ɛ (b a) = ɛ/2. 2(b a) Fially, let N = max{n 1, N 2 }. The, wheever, m N ad x [a, b], it follows that f (x) f m (x) (f (x) f m (x)) (f (c) f m (c)) + (f (c) f m (c)) < ɛ/2 + ɛ/2 = ɛ. Hece, by the Cauchy Criterio, (f ) coverges uiformly o [a, b] to some fuctio f. This proves the theorem. Example 6.4. Let g (x) = x o x [0, 1]. Agai (g { ) uiformly coverges to g(x) = 0, but g (x) = x x < 1 oly poitwise coverges to h(x) =, ot uiformly. 1 x = 1 Example 6.5. Let h (x) = ( 1) si(x) o R. The (h ) coverges uiformly to h(x) = 0 o R. However h (x) = ( 1) cos(x) does ot coverge for ay x R. The previous examples idicate that for a sequece of fuctios (f ) to coverge uiformly it is ot ecessary that (f ) coverge uiformly (eve poitwise).
6 6 6. Sequeces ad Series of Fuctios 6.3. Series of Fuctios A series of fuctios is a ifiite series of the form f (x) = f 1 (x) + f 2 (x) + f 3 (x) +, =1 where f 1, f 2, are fuctios defied o a commo set A R. Let the sequece of partial sums be defied by s (x) = f k (x) N. Defiitio 6.4. The series of fuctios =1 f (x) is said to coverge poitwise o A if the sequece (s (x)) coverges poitwise o A; if (s (x)) f(x) poitwise o A, the we write f (x) = f(x) x A. =1 If (s ) coverges uiformly o A the we say that the series =1 f (x) coverges uiformly o A. Theorem 6.5. Let f be cotiuous fuctios defied o a set A R, ad assume =1 f (x) coverges uiformly o A to a fuctio f. The f is cotiuous o A. Proof. Easy cosequece of the case for sequece. Theorem 6.6 (Term-by-Term Differetiatio Theorem). Let (f ) be a sequece of differetiable fuctios defied o [a, b], ad assume =1 f coverges uiformly to a fuctio g o [a, b]. If there exists a poit c [a, b] for which the series =1 f (c) coverges, the the series =1 f must coverge uiformly to a differetiable fuctio f o [a, b] satisfyig f (x) = g(x) o [a, b]. I other words, if =1 f (c) coverges at oe poit c [a, b], ad =1 f coverges uiformly o [a, b], the f(x) = f (x) =1 is well-defied for all x [a, b] ad is differetiable with f (x) = f (x) x [a, b]. Proof. Use Theorem 6.4. =1 Theorem 6.7 (Cauchy Criterio for Uiform Covergece of Series). A series =1 f coverges uiformly o a set A R if ad oly if for every ɛ > 0 there exists a N N such that for all > m N, Proof. Use Theorem 6.1. f m+1 (x) + f m+2 (x) + + f (x) < ɛ x A. Corollary 6.8 (Weierstrass M-Test). For each N, let f be a fuctio defied o A satisfyig f (x) M for all x A, where M > 0 is a real umber. If =1 M coverges, the =1 f coverges uiformly o A. Proof. Use the previous Cauchy s Criterio.
7 6.4. Power Series 7 Example 6.6. Let f(x) = si kx k 3. (a) Show f ad is differetiable ad f is cotiuous o R. (b) Ca we determie if f is twice-differetiable? Example 6.7. Let f(x) = =1 x = x + x2 2 + x The f(x) coverges o [0, 1), but f(1) =. This is a special case of the power series to be leared ext Power Series A power series is a ifiite series of power fuctios: f(x) = a (x c) = a 0 + a 1 (x c) + a 2 (x c) 2 + a 3 (x c) 3 +. =0 The poit c is called the ceter of the power series ad sequece (a ) is called the sequece of coefficiets of the power series. The power series also coverges at its ceter c. I what follows, we always assume c = 0. Theorem 6.9. If a power series =0 a x coverges at some poit x 0 0, the it coverges absolutely for all x satisfyig x < x 0. Proof. If =0 a x 0 coverges, the the sequece (a x 0 ) is bouded. Let M > 0 satisfy a x 0 M for all N. Assume x R satisfies x < x 0. The a x = a x 0 x M x. x 0 Sice x/x 0 < 1, by compariso with the geometric series, it follows easily that =0 a x coverges; hece =0 a x coverges absolutely. Radius of Covergece. Let =0 a x be a power series. Let S = {x R =0 a x coverges}. There are three cases for this set S: (a) S = {0}. I this case, the power series coverges oly at ceter 0. (b) S = R. I this case, the power series coverges at every x R. (c) S {0} ad S R. I Case (c), there exist two poits x 0, x 1 R such that x 0 0, x 0 S ad x 1 / S. By Theorem 6.9, for all x R with x > x 1, the power series diverges at x; otherwise, if it coverges at some x with x > x 1 the by the theorem, x 1 S. Therefore, the set S is icluded i the iterval [ x 1, x 1 ] ad hece S is a oempty bouded set i R. By the AoC, let R = sup S. This R satisfies x 0 R x 1 ; hece R (0, ). x 0
8 8 6. Sequeces ad Series of Fuctios Lemma I Case (c), the power series coverges at all x with x < R ad diverges at all x with x > R. Proof. 1. If x < R = sup S, the there exists x S such that x > x. Sice the power series coverges at x ad x < x = x, by Theorem 6.9, the power series coverges at x. 2. If x > R, we show that the power series diverges at x. If ot, assume the power series coverges at x. Let y = x +R 2. The R < y < x. Sice the power series coverges at x ad y < x, by Theorem 6.9 agai, the power series coverges at y; hece y S. But R = sup S; so y R, a cotradictio. Defiitio 6.5 (Radius of Covergece). Let =0 a x be a power series with the set S defied as above. The radius of covergece of this power series is the umber R [0, ] defied as follows: R = 0 i Case (a); R = i Case (b); R = sup S (0, ) i Case (c). Remark 6.6. I fact, there is a formula for the radius of covergece give by 1 R = lim sup a i all cases. However, this formula will ot be eeded for our lecture ad the homework. Example 6.8. For the power series! x, =0 the th-term is a =!x. If x 0, the a +1 a = ( + 1) x, ad hece a. Therefore, a diverges. So the give power series oly coverges at x = 0 ad diverges for all x 0. The radius of covergece for this power series is R = 0. Example 6.9. For power series =0 x! = 1 + x + x2 2! + x3 3! + the th-term is a = x!. Hece a +1 a = x +1 ( + 1)!! x = x for all x 0; thus, the power series coverges absolutely for all x 0, ad certaily it always coverges for x = 0. Therefore the give series coverges absolutely for all x. The radius of covergece for this power series is R =. Example I Case (c) above, the set S could oly be oe of the itervals ad all cases ca happe. [ R, R], [ R, R), ( R, R], ( R, R), (a) The power series =1 x / 2 has the radius of covergece R = 1 ad coverges exactly o [ 1, 1]. (b) The power series =1 x / has the radius of covergece R = 1 ad coverges exactly o [ 1, 1).
9 6.4. Power Series 9 (c) The power series =1 ( x) / has the radius of covergece R = 1 ad coverges exactly o ( 1, 1]. (d) The power series =1 x2 / has the radius of covergece R = 1 ad coverges exactly o ( 1, 1). Theorem If a power series =0 a x coverges absolutely at a poit x 0 0, the it coverges uiformly o the iterval [ x 0, x 0 ]. Proof. Use Weierstrass s M-Test. Abel s Theorem. Lemma 6.12 (Abel s Lemma). Let sequece (b ) satisfy b 1 b 2 b 3 0 ad sequece (a ) satisfy a 1 + a a A, N, for a costat A > 0. The, for all N, a 1 b 1 + a 2 b 2 + a 3 b a b Ab 1. Proof. Let s 0 = 0 ad s k = a 1 + a a k for k N. The a k = s k s k 1 for all k N. Hece a k b k = (s k s k 1 )b k = s k b k s k 1 b k = 1 s k b k s k b k+1 = k=0 1 1 s k b k + s b Sice s k A ad b k b k+1 0, it follows that 1 a k b k s k (b k b k+1 ) + s b 1 s k b k+1 = s k (b k b k+1 ) + s b. 1 1 s k (b k b k+1 ) + s b A (b k b k+1 ) + Ab = Ab 1. Theorem 6.13 (Abel s Theorem). If a power series =0 a x coverges at x = R > 0, the it coverges uiformly o the iterval [0, R]. If a power series =0 a x coverges at x = R < 0, the it coverges uiformly o the iterval [ R, 0]. Proof. Let us assume =0 a R coverges. We wat to use the Cauchy criterio to show that =0 a x coverges uiformly o [0, R]. Give ɛ > 0, from the covergece of =0 a R, there exists a umber N N such that a m+1 R m+1 + a m+2 R m a R < ɛ/2, > m N. Let x [0, R]. For ay fixed m N, cosider sequece B = ( x R )m+ ad sequece A = a m+ R m+ with N. The the sequeces (B ) ad (A ) satisfy the coditios i Abel s Lemma above with A = ɛ/2. Hece a m+1 R m+1 ( x R )m+1 + a m+2 R m+2 ( x R )m a R ( x x R ) ( R )m+1 ɛ/2 < ɛ.
10 10 6. Sequeces ad Series of Fuctios Therefore, a m+1 x m+1 + a m+2 x m a x < ɛ, x [0, R], > m N. This proves the uiform covergece of =0 a x o [0, R]. The Success of Power Series. Give a power series =0 a x, the differetiated series =1 a x 1 is also a power series. Theorem If a power series =0 a x coverges for all x ( R, R), the the differetiated series =1 a x 1 coverges for all x ( R, R) as well. Proof. Let t be such that x < t < R. The coclusio follows from the idetity a x 1 = 1 ( x 1 ) t t 1 a t. Sice r = x /t < 1, it follows that (r 1 ) 0. This ca be show by the covergece of series r usig the ratio-test. Theorem If a power series coverges poitwise o a set A, the it coverges uiformly o ay compact subset of A. Proof. Whe A cotais oe of R or R, where R is the radius of covergece, we eed the Abel s theorem. Other cases, the theorem ca be proved without it. Theorem Assume the power series g(x) = a x =0 coverges o a set A. The, g is cotiuous o A ad differetiable o ay ope iterval ( R, R) A with the derivative give by the term-by-term differetiatio g (x) = a x 1, x ( R, R). =1 Moreover, g is ifiitely differetiable o ( R, R), ad the higher-order derivatives ca be obtaied via the term-by-term differetiatio of the previous differetiated power series. Proof. Oly for the cotiuity of g at possibly the ed-poits of the iterval of covergece is the previous theorem eeded. All other coclusios ca be proved without usig the Abel s theorem. Example Let f(x) = =0 x! = 1 + x + x2 2! + x3 + (x R). 3! The, from the term-by-term differetiatio, f x 1 (x) = ( 1)! = 1 + x + x2 2! + x3 3! + = f(x). =1 Also f(0) = 1. Let g(x) = f(x)e x. The g(0) = 1 ad g (x) = f (x)e x f(x)e x = 0 for all x R. So g(x) 1; that is, f(x) = e x for all x R. I particular, with x = 1, ! + 1 3! + 1 4! + = e =
11 6.5. Taylor Series 11 Example (Exercise ) Note that the power series g(x) = x x2 2 + x3 3 = =1 1 x ( 1) has radius of covergece R = 1 ad coverges exactly for x ( 1, 1]. We ca prove this by just usig the fact g( 1) diverges ad g(1) coverges. (Explai why.) Hece g is cotiuous o ( 1, 1] ad is differetiable o ( 1, 1). The derivative is give by g (x) = ( x) 1, 1 < x < 1. =1 So, by the geometric series, g (x) = 1 that is, g(x) = 1+x x 0 for 1 < x < 1. But g(0) = 0. Hece g (t) dt = x t dt = [l 1 + t ] x 0 = l 1 + x = l(1 + x); ( 1) =1 1 x = l(1 + x), 1 < x < 1. This idetity also holds whe x = 1 sice g is cotiuous at x = 1. So we have that the value of the alterative harmoic series is give by ( 1) 1 g(1) = = = l Taylor Series =1 The power series defies a ifiitely differetiable fuctio o its ope iterval of covergece. Give a ifiitely differetiable fuctio o a ope iterval, ca we express the fuctio as a power series cetered at a iterior poit of the iterval? Such a series is called the Taylor series of the fuctio cetered at the give poit. Let f be a ifiitely differetiable fuctio defied o ( R, R). Suppose f equals a power series cetered at 0 as f(x) = a x = a 0 + a 1 x + a 2 x 2 +, x ( R, R). =0 The a 0 = f(0). By the term-by-term differetiatio, we have, for all k = 1, 2, 3,, f (k) (x) = ( 1) ( k + 1)a x k, x ( R, R). =k Hece f (k) (0) = k!a k. Therefore, with 0! = 1, we have a k = f (k) (0) k!, k = 0, 1, 2,. This shows that if a fuctio f equals a power series ear 0 the the coefficiets a k of the power series must be give by the above formula.
12 12 6. Sequeces ad Series of Fuctios Defiitio 6.7. Let f be a ifiitely differetiable fuctio ear a poit a R. The the power series f () (a) (6.4) (x a) ear a! =0 is called the Taylor series of f about a. Whe a = 0, the Taylor series iis also called the Maclauri series; but we will still call it the Taylor series. Lagrage s Remaider Theorem. Does the Taylor series of f coverge to f ear a? We assume a = 0. The followig result is useful to aswer such a questio. Theorem 6.17 (Lagrage s Remaider Theorem). Let f be ifiitely differetiable o ( R, R) ad defie N f (k) (0) S N (x) = x k x ( R, R). k! k=0 The, give ay 0 < x < R, there exists a umber c with c < x such that the error term E N (x) = f(x) S N (x) satisfies E N (x) = f (N+1) (c) (N + 1)! xn+1. Proof. Without loss of geerality, assume 0 < x < R. Cosider fuctio E N (t) = f(t) S N (t). The E () N (0) = 0 for all = 0, 1, 2,, N, ad E (N+1) N (t) = f (N+1) (t) for all t ( R, R). So, by the Geeralized Mea-Value Theorem repeatedly, we have x > x 1 > x 2 > > x N+1 > 0 such that E N (x) x N+1 = E N (x 1) (N + 1)x N 1 = E N (x 2) (N + 1)Nx N 1 2 ad this proves the theorem with c = x N+1. = = E(N+1) N (x N+1 ) (N + 1)N 2 1 = f (N+1) (c) (N + 1)!, Example Show si x = =0 ( 1) (2 + 1)! x2+1 x R. Proof. Let f(x) = si x. The f (2) (x) = ( 1) si x, for all = 0, 1, 2,.... Therefore the power series ( 1) (2 + 1)! x2+1 =0 f (2+1) (x) = ( 1) cos x is exactly the Taylor series of si x about 0. Let S N (x) be the partial sum up to power x N. The k ( 1) S 2k (x) = S 2k+1 (x) = (2 + 1)! x2+1. =0
13 6.5. Taylor Series 13 By Lagrage s Remaider Theorem, f (2k+2) (c) si x S 2k+1 (x) = E 2k+1 (x) = (2k + 2)! x2k+2 1 (2k + 2)! x 2k+2 0 as k for all x R. This proves the covergece; moreover it gives the error estimate k ( 1) (2 + 1)! x2+1 si x x 2k+2 (2k + 2)! =0 for all x R ad all k = 0, 1,. A Couterexample. The Taylor series of f may ot be equal to f ear a. Example Let f(x) = { e 1/x2 for x 0, 0 for x = 0. The f is ifiitely differetiable at all x 0. It is a good exercise to show that f has all orders of derivatives at 0 ad f () (0) = 0 for all = 0, 1, 2,. Therefore, the Taylor series of f about 0 is idetically zero; obviously f(x) 0 wheever x 0. This shows that f is ot equal to its Taylor series ear 0.
Math 341 Lecture #31 6.5: Power Series
 Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
f n (x) f m (x) < ɛ/3 for all x A. By continuity of f n and f m we can find δ > 0 such that d(x, x 0 ) < δ implies that
 Lecture 15 We have see that a sequece of cotiuous fuctios which is uiformly coverget produces a limit fuctio which is also cotiuous. We shall stregthe this result ow. Theorem 1 Let f : X R or (C) be a
Lecture 15 We have see that a sequece of cotiuous fuctios which is uiformly coverget produces a limit fuctio which is also cotiuous. We shall stregthe this result ow. Theorem 1 Let f : X R or (C) be a
M17 MAT25-21 HOMEWORK 5 SOLUTIONS
 M17 MAT5-1 HOMEWORK 5 SOLUTIONS 1. To Had I Cauchy Codesatio Test. Exercise 1: Applicatio of the Cauchy Codesatio Test Use the Cauchy Codesatio Test to prove that 1 diverges. Solutio 1. Give the series
M17 MAT5-1 HOMEWORK 5 SOLUTIONS 1. To Had I Cauchy Codesatio Test. Exercise 1: Applicatio of the Cauchy Codesatio Test Use the Cauchy Codesatio Test to prove that 1 diverges. Solutio 1. Give the series
Fall 2013 MTH431/531 Real analysis Section Notes
 Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
It is often useful to approximate complicated functions using simpler ones. We consider the task of approximating a function by a polynomial.
 Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
University of Colorado Denver Dept. Math. & Stat. Sciences Applied Analysis Preliminary Exam 13 January 2012, 10:00 am 2:00 pm. Good luck!
 Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
lim za n n = z lim a n n.
 Lecture 6 Sequeces ad Series Defiitio 1 By a sequece i a set A, we mea a mappig f : N A. It is customary to deote a sequece f by {s } where, s := f(). A sequece {z } of (complex) umbers is said to be coverget
Lecture 6 Sequeces ad Series Defiitio 1 By a sequece i a set A, we mea a mappig f : N A. It is customary to deote a sequece f by {s } where, s := f(). A sequece {z } of (complex) umbers is said to be coverget
MATH301 Real Analysis (2008 Fall) Tutorial Note #7. k=1 f k (x) converges pointwise to S(x) on E if and
 MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
sin(n) + 2 cos(2n) n 3/2 3 sin(n) 2cos(2n) n 3/2 a n =
 60. Ratio ad root tests 60.1. Absolutely coverget series. Defiitio 13. (Absolute covergece) A series a is called absolutely coverget if the series of absolute values a is coverget. The absolute covergece
60. Ratio ad root tests 60.1. Absolutely coverget series. Defiitio 13. (Absolute covergece) A series a is called absolutely coverget if the series of absolute values a is coverget. The absolute covergece
MAS111 Convergence and Continuity
 MAS Covergece ad Cotiuity Key Objectives At the ed of the course, studets should kow the followig topics ad be able to apply the basic priciples ad theorems therei to solvig various problems cocerig covergece
MAS Covergece ad Cotiuity Key Objectives At the ed of the course, studets should kow the followig topics ad be able to apply the basic priciples ad theorems therei to solvig various problems cocerig covergece
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Section 11.8: Power Series
 Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
Additional Notes on Power Series
 Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
Math 113, Calculus II Winter 2007 Final Exam Solutions
 Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
Mathematical Methods for Physics and Engineering
 Mathematical Methods for Physics ad Egieerig Lecture otes Sergei V. Shabaov Departmet of Mathematics, Uiversity of Florida, Gaiesville, FL 326 USA CHAPTER The theory of covergece. Numerical sequeces..
Mathematical Methods for Physics ad Egieerig Lecture otes Sergei V. Shabaov Departmet of Mathematics, Uiversity of Florida, Gaiesville, FL 326 USA CHAPTER The theory of covergece. Numerical sequeces..
1 Lecture 2: Sequence, Series and power series (8/14/2012)
 Summer Jump-Start Program for Aalysis, 202 Sog-Yig Li Lecture 2: Sequece, Series ad power series (8/4/202). More o sequeces Example.. Let {x } ad {y } be two bouded sequeces. Show lim sup (x + y ) lim
Summer Jump-Start Program for Aalysis, 202 Sog-Yig Li Lecture 2: Sequece, Series ad power series (8/4/202). More o sequeces Example.. Let {x } ad {y } be two bouded sequeces. Show lim sup (x + y ) lim
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MTH 142 Exam 3 Spr 2011 Practice Problem Solutions 1
 MTH 42 Exam 3 Spr 20 Practice Problem Solutios No calculators will be permitted at the exam. 3. A pig-pog ball is lauched straight up, rises to a height of 5 feet, the falls back to the lauch poit ad bouces
MTH 42 Exam 3 Spr 20 Practice Problem Solutios No calculators will be permitted at the exam. 3. A pig-pog ball is lauched straight up, rises to a height of 5 feet, the falls back to the lauch poit ad bouces
Chapter 8. Uniform Convergence and Differentiation.
 Chapter 8 Uiform Covergece ad Differetiatio This chapter cotiues the study of the cosequece of uiform covergece of a series of fuctio I Chapter 7 we have observed that the uiform limit of a sequece of
Chapter 8 Uiform Covergece ad Differetiatio This chapter cotiues the study of the cosequece of uiform covergece of a series of fuctio I Chapter 7 we have observed that the uiform limit of a sequece of
Math 113 Exam 3 Practice
 Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math 140A Elementary Analysis Homework Questions 3-1
 Math 0A Elemetary Aalysis Homework Questios -.9 Limits Theorems for Sequeces Suppose that lim x =, lim y = 7 ad that all y are o-zero. Detarime the followig limits: (a) lim(x + y ) (b) lim y x y Let s
Math 0A Elemetary Aalysis Homework Questios -.9 Limits Theorems for Sequeces Suppose that lim x =, lim y = 7 ad that all y are o-zero. Detarime the followig limits: (a) lim(x + y ) (b) lim y x y Let s
Ans: a n = 3 + ( 1) n Determine whether the sequence converges or diverges. If it converges, find the limit.
 . Fid a formula for the term a of the give sequece: {, 3, 9, 7, 8 },... As: a = 3 b. { 4, 9, 36, 45 },... As: a = ( ) ( + ) c. {5,, 5,, 5,, 5,,... } As: a = 3 + ( ) +. Determie whether the sequece coverges
. Fid a formula for the term a of the give sequece: {, 3, 9, 7, 8 },... As: a = 3 b. { 4, 9, 36, 45 },... As: a = ( ) ( + ) c. {5,, 5,, 5,, 5,,... } As: a = 3 + ( ) +. Determie whether the sequece coverges
Analytic Continuation
 Aalytic Cotiuatio The stadard example of this is give by Example Let h (z) = 1 + z + z 2 + z 3 +... kow to coverge oly for z < 1. I fact h (z) = 1/ (1 z) for such z. Yet H (z) = 1/ (1 z) is defied for
Aalytic Cotiuatio The stadard example of this is give by Example Let h (z) = 1 + z + z 2 + z 3 +... kow to coverge oly for z < 1. I fact h (z) = 1/ (1 z) for such z. Yet H (z) = 1/ (1 z) is defied for
Topics. Homework Problems. MATH 301 Introduction to Analysis Chapter Four Sequences. 1. Definition of convergence of sequences.
 MATH 301 Itroductio to Aalysis Chapter Four Sequeces Topics 1. Defiitio of covergece of sequeces. 2. Fidig ad provig the limit of sequeces. 3. Bouded covergece theorem: Theorem 4.1.8. 4. Theorems 4.1.13
MATH 301 Itroductio to Aalysis Chapter Four Sequeces Topics 1. Defiitio of covergece of sequeces. 2. Fidig ad provig the limit of sequeces. 3. Bouded covergece theorem: Theorem 4.1.8. 4. Theorems 4.1.13
Metric Space Properties
 Metric Space Properties Math 40 Fial Project Preseted by: Michael Brow, Alex Cordova, ad Alyssa Sachez We have already poited out ad will recogize throughout this book the importace of compact sets. All
Metric Space Properties Math 40 Fial Project Preseted by: Michael Brow, Alex Cordova, ad Alyssa Sachez We have already poited out ad will recogize throughout this book the importace of compact sets. All
Math Solutions to homework 6
 Math 175 - Solutios to homework 6 Cédric De Groote November 16, 2017 Problem 1 (8.11 i the book): Let K be a compact Hermitia operator o a Hilbert space H ad let the kerel of K be {0}. Show that there
Math 175 - Solutios to homework 6 Cédric De Groote November 16, 2017 Problem 1 (8.11 i the book): Let K be a compact Hermitia operator o a Hilbert space H ad let the kerel of K be {0}. Show that there
Math 113 Exam 3 Practice
 Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
MATH4822E FOURIER ANALYSIS AND ITS APPLICATIONS
 MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
SUMMARY OF SEQUENCES AND SERIES
 SUMMARY OF SEQUENCES AND SERIES Importat Defiitios, Results ad Theorems for Sequeces ad Series Defiitio. A sequece {a } has a limit L ad we write lim a = L if for every ɛ > 0, there is a correspodig iteger
SUMMARY OF SEQUENCES AND SERIES Importat Defiitios, Results ad Theorems for Sequeces ad Series Defiitio. A sequece {a } has a limit L ad we write lim a = L if for every ɛ > 0, there is a correspodig iteger
REAL ANALYSIS II: PROBLEM SET 1 - SOLUTIONS
 REAL ANALYSIS II: PROBLEM SET 1 - SOLUTIONS 18th Feb, 016 Defiitio (Lipschitz fuctio). A fuctio f : R R is said to be Lipschitz if there exists a positive real umber c such that for ay x, y i the domai
REAL ANALYSIS II: PROBLEM SET 1 - SOLUTIONS 18th Feb, 016 Defiitio (Lipschitz fuctio). A fuctio f : R R is said to be Lipschitz if there exists a positive real umber c such that for ay x, y i the domai
CHAPTER 10 INFINITE SEQUENCES AND SERIES
 CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
Taylor Series (BC Only)
 Studet Study Sessio Taylor Series (BC Oly) Taylor series provide a way to fid a polyomial look-alike to a o-polyomial fuctio. This is doe by a specific formula show below (which should be memorized): Taylor
Studet Study Sessio Taylor Series (BC Oly) Taylor series provide a way to fid a polyomial look-alike to a o-polyomial fuctio. This is doe by a specific formula show below (which should be memorized): Taylor
Lecture 8: Convergence of transformations and law of large numbers
 Lecture 8: Covergece of trasformatios ad law of large umbers Trasformatio ad covergece Trasformatio is a importat tool i statistics. If X coverges to X i some sese, we ofte eed to check whether g(x ) coverges
Lecture 8: Covergece of trasformatios ad law of large umbers Trasformatio ad covergece Trasformatio is a importat tool i statistics. If X coverges to X i some sese, we ofte eed to check whether g(x ) coverges
ANSWERS TO MIDTERM EXAM # 2
 MATH 03, FALL 003 ANSWERS TO MIDTERM EXAM # PENN STATE UNIVERSITY Problem 1 (18 pts). State ad prove the Itermediate Value Theorem. Solutio See class otes or Theorem 5.6.1 from our textbook. Problem (18
MATH 03, FALL 003 ANSWERS TO MIDTERM EXAM # PENN STATE UNIVERSITY Problem 1 (18 pts). State ad prove the Itermediate Value Theorem. Solutio See class otes or Theorem 5.6.1 from our textbook. Problem (18
Lecture Notes for Analysis Class
 Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
(a) (b) All real numbers. (c) All real numbers. (d) None. to show the. (a) 3. (b) [ 7, 1) (c) ( 7, 1) (d) At x = 7. (a) (b)
 Chapter 0 Review 597. E; a ( + )( + ) + + S S + S + + + + + + S lim + l. D; a diverges by the Itegral l k Test sice d lim [(l ) ], so k l ( ) does ot coverge absolutely. But it coverges by the Alteratig
Chapter 0 Review 597. E; a ( + )( + ) + + S S + S + + + + + + S lim + l. D; a diverges by the Itegral l k Test sice d lim [(l ) ], so k l ( ) does ot coverge absolutely. But it coverges by the Alteratig
Integrable Functions. { f n } is called a determining sequence for f. If f is integrable with respect to, then f d does exist as a finite real number
 MATH 532 Itegrable Fuctios Dr. Neal, WKU We ow shall defie what it meas for a measurable fuctio to be itegrable, show that all itegral properties of simple fuctios still hold, ad the give some coditios
MATH 532 Itegrable Fuctios Dr. Neal, WKU We ow shall defie what it meas for a measurable fuctio to be itegrable, show that all itegral properties of simple fuctios still hold, ad the give some coditios
f t dt. Write the third-degree Taylor polynomial for G
 AP Calculus BC Homework - Chapter 8B Taylor, Maclauri, ad Power Series # Taylor & Maclauri Polyomials Critical Thikig Joural: (CTJ: 5 pts.) Discuss the followig questios i a paragraph: What does it mea
AP Calculus BC Homework - Chapter 8B Taylor, Maclauri, ad Power Series # Taylor & Maclauri Polyomials Critical Thikig Joural: (CTJ: 5 pts.) Discuss the followig questios i a paragraph: What does it mea
Math 113 Exam 4 Practice
 Math Exam 4 Practice Exam 4 will cover.-.. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for
Math Exam 4 Practice Exam 4 will cover.-.. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for
Seunghee Ye Ma 8: Week 5 Oct 28
 Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
d) If the sequence of partial sums converges to a limit L, we say that the series converges and its
 Ifiite Series. Defiitios & covergece Defiitio... Let {a } be a sequece of real umbers. a) A expressio of the form a + a +... + a +... is called a ifiite series. b) The umber a is called as the th term
Ifiite Series. Defiitios & covergece Defiitio... Let {a } be a sequece of real umbers. a) A expressio of the form a + a +... + a +... is called a ifiite series. b) The umber a is called as the th term
MATH 413 FINAL EXAM. f(x) f(y) M x y. x + 1 n
 MATH 43 FINAL EXAM Math 43 fial exam, 3 May 28. The exam starts at 9: am ad you have 5 miutes. No textbooks or calculators may be used durig the exam. This exam is prited o both sides of the paper. Good
MATH 43 FINAL EXAM Math 43 fial exam, 3 May 28. The exam starts at 9: am ad you have 5 miutes. No textbooks or calculators may be used durig the exam. This exam is prited o both sides of the paper. Good
n=1 a n is the sequence (s n ) n 1 n=1 a n converges to s. We write a n = s, n=1 n=1 a n
 Series. Defiitios ad first properties A series is a ifiite sum a + a + a +..., deoted i short by a. The sequece of partial sums of the series a is the sequece s ) defied by s = a k = a +... + a,. k= Defiitio
Series. Defiitios ad first properties A series is a ifiite sum a + a + a +..., deoted i short by a. The sequece of partial sums of the series a is the sequece s ) defied by s = a k = a +... + a,. k= Defiitio
PLEASE MARK YOUR ANSWERS WITH AN X, not a circle! 1. (a) (b) (c) (d) (e) 3. (a) (b) (c) (d) (e) 5. (a) (b) (c) (d) (e) 7. (a) (b) (c) (d) (e)
 Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
Solutions to Final Exam Review Problems
 . Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
. Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
SOLUTIONS TO EXAM 3. Solution: Note that this defines two convergent geometric series with respective radii r 1 = 2/5 < 1 and r 2 = 1/5 < 1.
 SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
Archimedes - numbers for counting, otherwise lengths, areas, etc. Kepler - geometry for planetary motion
 Topics i Aalysis 3460:589 Summer 007 Itroductio Ree descartes - aalysis (breaig dow) ad sythesis Sciece as models of ature : explaatory, parsimoious, predictive Most predictios require umerical values,
Topics i Aalysis 3460:589 Summer 007 Itroductio Ree descartes - aalysis (breaig dow) ad sythesis Sciece as models of ature : explaatory, parsimoious, predictive Most predictios require umerical values,
Power Series: A power series about the center, x = 0, is a function of x of the form
 You are familiar with polyomial fuctios, polyomial that has ifiitely may terms. 2 p ( ) a0 a a 2 a. A power series is just a Power Series: A power series about the ceter, = 0, is a fuctio of of the form
You are familiar with polyomial fuctios, polyomial that has ifiitely may terms. 2 p ( ) a0 a a 2 a. A power series is just a Power Series: A power series about the ceter, = 0, is a fuctio of of the form
Advanced Analysis. Min Yan Department of Mathematics Hong Kong University of Science and Technology
 Advaced Aalysis Mi Ya Departmet of Mathematics Hog Kog Uiversity of Sciece ad Techology September 3, 009 Cotets Limit ad Cotiuity 7 Limit of Sequece 8 Defiitio 8 Property 3 3 Ifiity ad Ifiitesimal 8 4
Advaced Aalysis Mi Ya Departmet of Mathematics Hog Kog Uiversity of Sciece ad Techology September 3, 009 Cotets Limit ad Cotiuity 7 Limit of Sequece 8 Defiitio 8 Property 3 3 Ifiity ad Ifiitesimal 8 4
Read carefully the instructions on the answer book and make sure that the particulars required are entered on each answer book.
 THE UNIVERSITY OF WARWICK FIRST YEAR EXAMINATION: Jauary 2009 Aalysis I Time Allowed:.5 hours Read carefully the istructios o the aswer book ad make sure that the particulars required are etered o each
THE UNIVERSITY OF WARWICK FIRST YEAR EXAMINATION: Jauary 2009 Aalysis I Time Allowed:.5 hours Read carefully the istructios o the aswer book ad make sure that the particulars required are etered o each
4x 2. (n+1) x 3 n+1. = lim. 4x 2 n+1 n3 n. n 4x 2 = lim = 3
 Exam Problems (x. Give the series (, fid the values of x for which this power series coverges. Also =0 state clearly what the radius of covergece is. We start by settig up the Ratio Test: x ( x x ( x x
Exam Problems (x. Give the series (, fid the values of x for which this power series coverges. Also =0 state clearly what the radius of covergece is. We start by settig up the Ratio Test: x ( x x ( x x
MIDTERM 3 CALCULUS 2. Monday, December 3, :15 PM to 6:45 PM. Name PRACTICE EXAM SOLUTIONS
 MIDTERM 3 CALCULUS MATH 300 FALL 08 Moday, December 3, 08 5:5 PM to 6:45 PM Name PRACTICE EXAM S Please aswer all of the questios, ad show your work. You must explai your aswers to get credit. You will
MIDTERM 3 CALCULUS MATH 300 FALL 08 Moday, December 3, 08 5:5 PM to 6:45 PM Name PRACTICE EXAM S Please aswer all of the questios, ad show your work. You must explai your aswers to get credit. You will
Notes #3 Sequences Limit Theorems Monotone and Subsequences Bolzano-WeierstraßTheorem Limsup & Liminf of Sequences Cauchy Sequences and Completeness
 Notes #3 Sequeces Limit Theorems Mootoe ad Subsequeces Bolzao-WeierstraßTheorem Limsup & Limif of Sequeces Cauchy Sequeces ad Completeess This sectio of otes focuses o some of the basics of sequeces of
Notes #3 Sequeces Limit Theorems Mootoe ad Subsequeces Bolzao-WeierstraßTheorem Limsup & Limif of Sequeces Cauchy Sequeces ad Completeess This sectio of otes focuses o some of the basics of sequeces of
f x x c x c x c... x c...
 CALCULUS BC WORKSHEET ON POWER SERIES. Derive the Taylor series formula by fillig i the blaks below. 4 5 Let f a a c a c a c a4 c a5 c a c What happes to this series if we let = c? f c so a Now differetiate
CALCULUS BC WORKSHEET ON POWER SERIES. Derive the Taylor series formula by fillig i the blaks below. 4 5 Let f a a c a c a c a4 c a5 c a c What happes to this series if we let = c? f c so a Now differetiate
MATH 312 Midterm I(Spring 2015)
 MATH 3 Midterm I(Sprig 05) Istructor: Xiaowei Wag Feb 3rd, :30pm-3:50pm, 05 Problem (0 poits). Test for covergece:.. 3.. p, p 0. (coverges for p < ad diverges for p by ratio test.). ( coverges, sice (log
MATH 3 Midterm I(Sprig 05) Istructor: Xiaowei Wag Feb 3rd, :30pm-3:50pm, 05 Problem (0 poits). Test for covergece:.. 3.. p, p 0. (coverges for p < ad diverges for p by ratio test.). ( coverges, sice (log
Lesson 10: Limits and Continuity
 www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
Convergence of random variables. (telegram style notes) P.J.C. Spreij
 Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
NATIONAL UNIVERSITY OF SINGAPORE FACULTY OF SCIENCE SEMESTER 1 EXAMINATION ADVANCED CALCULUS II. November 2003 Time allowed :
 NATIONAL UNIVERSITY OF SINGAPORE FACULTY OF SCIENCE SEMESTER EXAMINATION 003-004 MA08 ADVANCED CALCULUS II November 003 Time allowed : hours INSTRUCTIONS TO CANDIDATES This examiatio paper cosists of TWO
NATIONAL UNIVERSITY OF SINGAPORE FACULTY OF SCIENCE SEMESTER EXAMINATION 003-004 MA08 ADVANCED CALCULUS II November 003 Time allowed : hours INSTRUCTIONS TO CANDIDATES This examiatio paper cosists of TWO
INFINITE SEQUENCES AND SERIES
 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES I geeral, it is difficult to fid the exact sum of a series. We were able to accomplish this for geometric series ad the series /[(+)]. This is
INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES I geeral, it is difficult to fid the exact sum of a series. We were able to accomplish this for geometric series ad the series /[(+)]. This is
Convergence: nth-term Test, Comparing Non-negative Series, Ratio Test
 Covergece: th-term Test, Comparig No-egative Series, Ratio Test Power Series ad Covergece We have writte statemets like: l + x = x x2 + x3 2 3 + x + But we have ot talked i depth about what values of x
Covergece: th-term Test, Comparig No-egative Series, Ratio Test Power Series ad Covergece We have writte statemets like: l + x = x x2 + x3 2 3 + x + But we have ot talked i depth about what values of x
A Proof of Birkhoff s Ergodic Theorem
 A Proof of Birkhoff s Ergodic Theorem Joseph Hora September 2, 205 Itroductio I Fall 203, I was learig the basics of ergodic theory, ad I came across this theorem. Oe of my supervisors, Athoy Quas, showed
A Proof of Birkhoff s Ergodic Theorem Joseph Hora September 2, 205 Itroductio I Fall 203, I was learig the basics of ergodic theory, ad I came across this theorem. Oe of my supervisors, Athoy Quas, showed
Arkansas Tech University MATH 2924: Calculus II Dr. Marcel B. Finan
 Arkasas Tech Uiversity MATH 94: Calculus II Dr Marcel B Fia 85 Power Series Let {a } =0 be a sequece of umbers The a power series about x = a is a series of the form a (x a) = a 0 + a (x a) + a (x a) +
Arkasas Tech Uiversity MATH 94: Calculus II Dr Marcel B Fia 85 Power Series Let {a } =0 be a sequece of umbers The a power series about x = a is a series of the form a (x a) = a 0 + a (x a) + a (x a) +
Ma 530 Introduction to Power Series
 Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
McGill University Math 354: Honors Analysis 3 Fall 2012 Solutions to selected problems
 McGill Uiversity Math 354: Hoors Aalysis 3 Fall 212 Assigmet 3 Solutios to selected problems Problem 1. Lipschitz fuctios. Let Lip K be the set of all fuctios cotiuous fuctios o [, 1] satisfyig a Lipschitz
McGill Uiversity Math 354: Hoors Aalysis 3 Fall 212 Assigmet 3 Solutios to selected problems Problem 1. Lipschitz fuctios. Let Lip K be the set of all fuctios cotiuous fuctios o [, 1] satisfyig a Lipschitz
n n 2 n n + 1 +
 Istructor: Marius Ioescu 1. Let a =. (5pts) (a) Prove that for every ε > 0 there is N 1 such that a +1 a < ε if N. Solutio: Let ε > 0. The a +1 a < ε is equivalet with + 1 < ε. Simplifyig, this iequality
Istructor: Marius Ioescu 1. Let a =. (5pts) (a) Prove that for every ε > 0 there is N 1 such that a +1 a < ε if N. Solutio: Let ε > 0. The a +1 a < ε is equivalet with + 1 < ε. Simplifyig, this iequality
MATH 6101 Fall Problems. Problems 11/9/2008. Series and a Famous Unsolved Problem (2-1)(2 + 1) ( 4) 12-Nov-2008 MATH
 /9/008 MATH 60 Fall 008 Series ad a Famous Usolved Problem = = + + + + ( - )( + ) 3 3 5 5 7 7 9 -Nov-008 MATH 60 ( 4) = + 5 48 -Nov-008 MATH 60 3 /9/008 ( )! = + -Nov-008 MATH 60 4 3 4 5 + + + + + + +
/9/008 MATH 60 Fall 008 Series ad a Famous Usolved Problem = = + + + + ( - )( + ) 3 3 5 5 7 7 9 -Nov-008 MATH 60 ( 4) = + 5 48 -Nov-008 MATH 60 3 /9/008 ( )! = + -Nov-008 MATH 60 4 3 4 5 + + + + + + +
2 Banach spaces and Hilbert spaces
 2 Baach spaces ad Hilbert spaces Tryig to do aalysis i the ratioal umbers is difficult for example cosider the set {x Q : x 2 2}. This set is o-empty ad bouded above but does ot have a least upper boud
2 Baach spaces ad Hilbert spaces Tryig to do aalysis i the ratioal umbers is difficult for example cosider the set {x Q : x 2 2}. This set is o-empty ad bouded above but does ot have a least upper boud
TR/46 OCTOBER THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION A. TALBOT
 TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
Fourier Series and their Applications
 Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
e to approximate (using 4
 Review: Taylor Polyomials ad Power Series Fid the iterval of covergece for the series Fid a series for f ( ) d ad fid its iterval of covergece Let f( ) Let f arcta a) Fid the rd degree Maclauri polyomial
Review: Taylor Polyomials ad Power Series Fid the iterval of covergece for the series Fid a series for f ( ) d ad fid its iterval of covergece Let f( ) Let f arcta a) Fid the rd degree Maclauri polyomial
Section 5.5. Infinite Series: The Ratio Test
 Differece Equatios to Differetial Equatios Sectio 5.5 Ifiite Series: The Ratio Test I the last sectio we saw that we could demostrate the covergece of a series a, where a 0 for all, by showig that a approaches
Differece Equatios to Differetial Equatios Sectio 5.5 Ifiite Series: The Ratio Test I the last sectio we saw that we could demostrate the covergece of a series a, where a 0 for all, by showig that a approaches
INFINITE SEQUENCES AND SERIES
 11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES 11.4 The Compariso Tests I this sectio, we will lear: How to fid the value of a series by comparig it with a kow series. COMPARISON TESTS
11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES 11.4 The Compariso Tests I this sectio, we will lear: How to fid the value of a series by comparig it with a kow series. COMPARISON TESTS
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Power series are analytic
 Power series are aalytic Horia Corea 1 1 The expoetial ad the logarithm For every x R we defie the fuctio give by exp(x) := 1 + x + x + + x + = x. If x = 0 we have exp(0) = 1. If x 0, cosider the series
Power series are aalytic Horia Corea 1 1 The expoetial ad the logarithm For every x R we defie the fuctio give by exp(x) := 1 + x + x + + x + = x. If x = 0 we have exp(0) = 1. If x 0, cosider the series
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.436J/15.085J Fall 2008 Lecture 19 11/17/2008 LAWS OF LARGE NUMBERS II THE STRONG LAW OF LARGE NUMBERS
 MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
Math 120 Answers for Homework 23
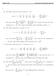 Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Math 508 Exam 2 Jerry L. Kazdan December 9, :00 10:20
 Math 58 Eam 2 Jerry L. Kazda December 9, 24 9: :2 Directios This eam has three parts. Part A has 8 True/False questio (2 poits each so total 6 poits), Part B has 5 shorter problems (6 poits each, so 3
Math 58 Eam 2 Jerry L. Kazda December 9, 24 9: :2 Directios This eam has three parts. Part A has 8 True/False questio (2 poits each so total 6 poits), Part B has 5 shorter problems (6 poits each, so 3
Chapter 3. Strong convergence. 3.1 Definition of almost sure convergence
 Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
7.1 Convergence of sequences of random variables
 Chapter 7 Limit Theorems Throughout this sectio we will assume a probability space (, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Chapter 7 Limit Theorems Throughout this sectio we will assume a probability space (, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
1.3 Convergence Theorems of Fourier Series. k k k k. N N k 1. With this in mind, we state (without proof) the convergence of Fourier series.
 .3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
.3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
PRELIM PROBLEM SOLUTIONS
 PRELIM PROBLEM SOLUTIONS THE GRAD STUDENTS + KEN Cotets. Complex Aalysis Practice Problems 2. 2. Real Aalysis Practice Problems 2. 4 3. Algebra Practice Problems 2. 8. Complex Aalysis Practice Problems
PRELIM PROBLEM SOLUTIONS THE GRAD STUDENTS + KEN Cotets. Complex Aalysis Practice Problems 2. 2. Real Aalysis Practice Problems 2. 4 3. Algebra Practice Problems 2. 8. Complex Aalysis Practice Problems
f(x)g(x) dx is an inner product on D.
 Ark9: Exercises for MAT2400 Fourier series The exercises o this sheet cover the sectios 4.9 to 4.13. They are iteded for the groups o Thursday, April 12 ad Friday, March 30 ad April 13. NB: No group o
Ark9: Exercises for MAT2400 Fourier series The exercises o this sheet cover the sectios 4.9 to 4.13. They are iteded for the groups o Thursday, April 12 ad Friday, March 30 ad April 13. NB: No group o
2.4.2 A Theorem About Absolutely Convergent Series
 0 Versio of August 27, 200 CHAPTER 2. INFINITE SERIES Add these two series: + 3 2 + 5 + 7 4 + 9 + 6 +... = 3 l 2. (2.20) 2 Sice the reciprocal of each iteger occurs exactly oce i the last series, we would
0 Versio of August 27, 200 CHAPTER 2. INFINITE SERIES Add these two series: + 3 2 + 5 + 7 4 + 9 + 6 +... = 3 l 2. (2.20) 2 Sice the reciprocal of each iteger occurs exactly oce i the last series, we would
f(x) dx as we do. 2x dx x also diverges. Solution: We compute 2x dx lim
 Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
MATH 6101 Fall 2008 Series and a Famous Unsolved Problem
 MATH 60 Fall 2008 Series ad a Famous Usolved Problem Problems = + + + + = (2- )(2+ ) 3 3 5 5 7 7 9 2-Nov-2008 MATH 60 2 Problems ( 4) = + 25 48 2-Nov-2008 MATH 60 3 Problems ( )! = + 2-Nov-2008 MATH 60
MATH 60 Fall 2008 Series ad a Famous Usolved Problem Problems = + + + + = (2- )(2+ ) 3 3 5 5 7 7 9 2-Nov-2008 MATH 60 2 Problems ( 4) = + 25 48 2-Nov-2008 MATH 60 3 Problems ( )! = + 2-Nov-2008 MATH 60
LECTURE SERIES WITH NONNEGATIVE TERMS (II). SERIES WITH ARBITRARY TERMS
 LECTURE 4 SERIES WITH NONNEGATIVE TERMS II). SERIES WITH ARBITRARY TERMS Series with oegative terms II) Theorem 4.1 Kummer s Test) Let x be a series with positive terms. 1 If c ) N i 0, + ), r > 0 ad 0
LECTURE 4 SERIES WITH NONNEGATIVE TERMS II). SERIES WITH ARBITRARY TERMS Series with oegative terms II) Theorem 4.1 Kummer s Test) Let x be a series with positive terms. 1 If c ) N i 0, + ), r > 0 ad 0
7 Sequences of real numbers
 40 7 Sequeces of real umbers 7. Defiitios ad examples Defiitio 7... A sequece of real umbers is a real fuctio whose domai is the set N of atural umbers. Let s : N R be a sequece. The the values of s are
40 7 Sequeces of real umbers 7. Defiitios ad examples Defiitio 7... A sequece of real umbers is a real fuctio whose domai is the set N of atural umbers. Let s : N R be a sequece. The the values of s are
6. Uniform distribution mod 1
 6. Uiform distributio mod 1 6.1 Uiform distributio ad Weyl s criterio Let x be a seuece of real umbers. We may decompose x as the sum of its iteger part [x ] = sup{m Z m x } (i.e. the largest iteger which
6. Uiform distributio mod 1 6.1 Uiform distributio ad Weyl s criterio Let x be a seuece of real umbers. We may decompose x as the sum of its iteger part [x ] = sup{m Z m x } (i.e. the largest iteger which
AP Calculus Chapter 9: Infinite Series
 AP Calculus Chapter 9: Ifiite Series 9. Sequeces a, a 2, a 3, a 4, a 5,... Sequece: A fuctio whose domai is the set of positive itegers = 2 3 4 a = a a 2 a 3 a 4 terms of the sequece Begi with the patter
AP Calculus Chapter 9: Ifiite Series 9. Sequeces a, a 2, a 3, a 4, a 5,... Sequece: A fuctio whose domai is the set of positive itegers = 2 3 4 a = a a 2 a 3 a 4 terms of the sequece Begi with the patter
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Assignment 5: Solutions
 McGill Uiversity Departmet of Mathematics ad Statistics MATH 54 Aalysis, Fall 05 Assigmet 5: Solutios. Let y be a ubouded sequece of positive umbers satisfyig y + > y for all N. Let x be aother sequece
McGill Uiversity Departmet of Mathematics ad Statistics MATH 54 Aalysis, Fall 05 Assigmet 5: Solutios. Let y be a ubouded sequece of positive umbers satisfyig y + > y for all N. Let x be aother sequece
Real Analysis Fall 2004 Take Home Test 1 SOLUTIONS. < ε. Hence lim
 Real Aalysis Fall 004 Take Home Test SOLUTIONS. Use the defiitio of a limit to show that (a) lim si = 0 (b) Proof. Let ε > 0 be give. Defie N >, where N is a positive iteger. The for ε > N, si 0 < si
Real Aalysis Fall 004 Take Home Test SOLUTIONS. Use the defiitio of a limit to show that (a) lim si = 0 (b) Proof. Let ε > 0 be give. Defie N >, where N is a positive iteger. The for ε > N, si 0 < si
1+x 1 + α+x. x = 2(α x2 ) 1+x
 Math 2030 Homework 6 Solutios # [Problem 5] For coveiece we let α lim sup a ad β lim sup b. Without loss of geerality let us assume that α β. If α the by assumptio β < so i this case α + β. By Theorem
Math 2030 Homework 6 Solutios # [Problem 5] For coveiece we let α lim sup a ad β lim sup b. Without loss of geerality let us assume that α β. If α the by assumptio β < so i this case α + β. By Theorem
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
1 Approximating Integrals using Taylor Polynomials
 Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
Math 210A Homework 1
 Math 0A Homework Edward Burkard Exercise. a) State the defiitio of a aalytic fuctio. b) What are the relatioships betwee aalytic fuctios ad the Cauchy-Riema equatios? Solutio. a) A fuctio f : G C is called
Math 0A Homework Edward Burkard Exercise. a) State the defiitio of a aalytic fuctio. b) What are the relatioships betwee aalytic fuctios ad the Cauchy-Riema equatios? Solutio. a) A fuctio f : G C is called
