Surface Water Waves and Tsunamis
|
|
|
- Lesley Eaton
- 6 years ago
- Views:
Transcription
1 Journal of Dynamics and Differential Equations, Vol. 18, No. 3, July 2006 ( 2006) DOI: /s Surface Water Waves and Tsunamis Walter Craig Received February 15, 2006 Because of the enormous earthquake in Sumatra on December 26, 2004, and the devastating tsunami which followed, I have chosen the focus of my mini-course lectures at this year s PASI to be on two topics which involve the dynamics of surface water waves. These topics are of interest to mathematicians interested in wave propagation, and particularly to Chilean scientists, I believe, because of Chile s presence on the tectonically active Pacific Rim. My first lecture will describe the equations of fluid dynamics for the free surface above a body of fluid (the ocean surface), and the linearized equations of motion. From this, we can predict the travel time of the recent tsunami from its epicenter off of the north Sumatra coast to the coast of nearby Thailand, the easy coasts of Sri Lanka and south India, and to Africa. In fact, the signal given by ocean waves generated by the Sumatra earthquake was felt globally; within 48 h distinguishable tsunami waves were measured by wave gages in Antarctica, Chile, Rio di Janeiro, the west coast of Mexico, the east coast of the United States, and at Halifax, Nova Scotia. To describe ocean waves, we will formulate the full nonlinear fluid dynamical equations as a Hamiltonian system [19], and we will introduce the Greens function and the Dirichlet-Neumann operator for the fluid domain along with the harmonic analysis of the theory of their regularity. From an asymptotic theory of scaling transformations, we will derive the known Boussinesq-like systems and the KdV and KP equations, which govern the asymptotic behavior of tsunami waves over an idealized flat bottom. When the bottom is no longer assumed to be perfectly flat, a related theory [6, 13] gives a family of model equations taking this into account. My second lecture will describe a series of recent results in PDE, numerical results, and experimental results on the nonlinear interactions of solitary surface water waves. In contrast with the case of the KdV equations (and certain other integrable PDE), the Euler equations for a free surface do not admit clean ( elastic ) interactions between solitary wave solutions. This has been a classical concern of oceanographers for several decades, but only recently have there been sufficiently accurate and thorough numerical simulations which quantify the degree to which solitary Department of Mathematics and Statistics, McMaster University, Hamilton, Ont., L8S 4K1 Canada. craig@math.mcmaster.ca /06/ / Springer Science+Business Media, Inc.
2 526 Craig waves lose energy during interactions [3, 4]. It is striking that this degree of inelasticity is remarkably small. I will describe this work, as well as recent results on the initial value problem which are very relevant to this phenomenon [14, 18]. KEY WORDS: Tsunamis; nonlinear surface water waves. 1. TSUNAMIS AND OCEAN WAVES The name tsunami in Japanese originally means harbor wave, but the word has come to mean a large and potentially very powerful series of ocean waves which are occasionally generated by movements of the ocean floor. Very infrequently these can be extremely large and very dangerous, and can have a destructive impact on coastal areas of the world s oceans. Small tsunamis are generated relatively often, most commonly by tectonic activity, but sometimes by other means as well, such as underwater landslides. Serious tsunamis, to the point of loss of life and major coastal destruction, take place on the order of once every several decades. I think, we were all personally touched by the deadly Boxing Day Tsunami in 2004, which was generated by the major earthquake in the Sunda Trench subduction zone off the west coast of the island of Sumatra. It is a challenge for mathematicians with interests in the hydrodynamics of ocean waves to seek a credible rôle to play in predicting and/or articulating the danger of a tsunami or in alleviating the force of their impact. Taking a naïve point of view, the most effective means to predict major tsunamis is to predict major earthquakes. However, this an ambitious objective to say the least, and despite the research of many decades of earth scientists this remains a grand challenge problem, on which major progress will take much time. The question remains, however, as to find credible aspects of tsunami prediction on which mathematicians can contribute. It seems to me that there are many important open questions in the modeling of (1) tsunami wave generation in the event of a major earthquake, (2) wave propagation across the opean ocean, and (3) wave impact upon the coastlines affected by the event. Indeed the design of tsunami early warning systems or some of its components involves mathematical modeling of solutions of the partial differential equations describing ocean wave dynamics, and computer simulation of solutions which, if they are to be an effective warning, must be performed in faster than real time. It is also an important problem to be able to clarify the character of tsunami waves, in particular those features of the waves as they impact on coastal areas which can effect tsunami safety codes in engineering and architecture.
3 Surface Water Waves and Tsunamis 527 In my first talk on tsunamis, I plan to discuss some of the elementary features of the phenomenon, most of which are essentially well know facts in the theory of surface water waves. Some however are new, or at least reflect a modern viewpoint. For the most part I will place these in the context of the Boxing Day Tsunami 2004, which is clearest in our memory, in order to bring perspective to this event. The basic details are that this tsunami was generated by a major earthquake that took place along the Sunda Trench, which is the subduction zone along of the west coast of the island of Sumatra. The earthquake took place on December 26, 2004 at 7h58 local time, and its epicenter was located approximately 250 km off shore. It was initially classified as a magnitude M w = 8.5 9, but after subsequent analysis (which took several weeks) the estimates of its strength were upgraded to M w = 9.3. The earthquake caused a rupture of the ocean floor moving essentially to the north northwest along the subduction zone, of length approximately 1200 km. The magnitude of the horizontal slip along this rupture is estimated as being 21 m in the southern parts, to 15 m in more northern locations. Vertical displacement, which is perhaps more relevant to tsunami generation, is estimated to be between 2 and 10 m. It was an unusual earthquake in the eyes of seismologists, as the rupture moved relatively slowly, acting somewhat like a zipper from the southeastern to the northwestern part of the rupture, and lasting between 15 and 20 min in all. A diagram of the northeastern Indian Ocean tectonic region gives a picture of the setting of this earthquake and allows us to put the event into perspective (Fig. 1). The slip along such an extended region acted as a line source generating tsunami waves, which propagated both through the Indian Ocean to the west, and the Andaman Basin to the east. Soon after being generated, devastating tsunami waves hit the coast of Sumatra itself and cause extensive damage and loss of life. The tsunami waves traveled at approximately 360 km/h eastwards through the Andaman Basin, to impact upon the west coast of the Malay Peninsula, including portions of Thailand and Myanmar, about 1 h after the earthquake. Waves traveling at approximately 720 km/h propagated west through the lower Bay of Bengal/Indian Ocean, impacting on Sri Lanka and the east coast of southern India approximately 2 h after the earthquake. The tsunami was in fact felt globally; within 7 h on the east African coast, within 20 h on the South Atlantic Ocean in Rio de Janeiro, within 23 h on the South Pacific Ocean in Chile, and in 29 h in Halifax, Nova Scotia. A numerical model of the global propagation of the Boxing Day Tsunami was published in Science Express on August 25, 2005, and in [17] (Fig. 2) which shows this effect.
4 528 Craig Figure 1. Northeastern Indian Ocean tectonic setting. USGS website: usgs.gov/2005/01/tectoniclg.jpg. 2. EQUATIONS OF MOTION FOR POTENTIAL FLOW Oceanographers generally treat ocean waves as free surface waves in an ideal fluid. This is to say that one works with potential flow, for which the velocity of the fluid in Eulerian coördinates is given in terms of a velocity potential ϕ, such that ϕ = 0 (2.1)
5 Surface Water Waves and Tsunamis 529 Figure 2. The global reach of the December 26, 2004 Sumatra tsunami: Science Express on August 25, 2005, Science September 23, 2005, Vol no. 5743, pp Vasily Titov, Alexander B. Rabinovich, Harold O. Mofjeld, Richard E. Thomson, Frank I. Gonzàlez. in the domain occupied by the fluid. This fluid domain is bounded below by {y = h(x), x R n 1 }, while the free surface is given in the form of a graph {y = η(x,t)}. For tsunami propagation, we should really be treating ocean waves on a sphere or on certain subsets of the sphere corresponding to ocean regions. However, for reasons of simplicity, we will simply consider the fluid domain to be x R 2, h(x) < y < η(x, t). On the bottom boundary of the fluid domain, we impose N ϕ = 0, on y = h(x) (2.2) and on the free surface, we impose the two classical boundary conditions t ϕ ϕ 2 + gη= 0, t η + x η x ϕ y ϕ = 0, on y = η(x,t). (2.3) This will describe the motion of ocean waves in the setting in which the bottom is fixed, which is in our case to be during the second phase of wave propagation of the tsunami after the time at which they have been generated. The boundary conditions describing the generation of tsunami waves are different, as the bottom boundary can no longer assumed to be stationary. In particular the sea bottom should be given as {y = h(x, t)} and one must replace the boundary conditions (2.2) by the following expression N ϕ = t h(x, t), on y = h(x,t), (2.4) where the outward normal to the bottom boundary is given by N = ( x h, 1). In studies of the generation of a tsunami from a given source, these are appropriate boundery conditions to work with.
6 530 Craig These equations can be posed in the form of a Hamilton system, a fact which is due to [19]. Zakharov s Hamiltonian can be rewritten [7] as H(η,ξ)= 1 ξg(η, h)ξ + gη 2 dx. (2.5) 2 R n 1 In this expression, we write ξ(x):= ϕ(x,η(x)), and the Dirichlet integral, which represents the kinetic energy, is expressed in terms of the Dirichlet Neumann operator G(η, h)ξ := 1 + x η 2 N ϕ, (2.6) y=η where the harmonic extension ϕ of the top boundary conditions ξ(x) to the fluid domain is required to satisfy the bottom boundary conditions (2.4). Equations (2.1) through (2.3) are written in the canonical form t ( η ξ ) ( 0 1 = 1 0 )( δη H δ ξ H ). (2.7) Explicitely, Hamilton s canonical equations (2.7) have the form t η = G(η, h)ξ, (2.8) 1 [ t ξ = gη+ 2(1 + x η 2 ( x ξ) 2 (G(η, h)ξ) 2 (2.9) ) ( 2 x η x ξ G(η, h)ξ + x ξ 2 x η 2 ( x η x ξ) 2)]. (2.10) One of the terms of the second component (2.10) of this Hamiltonian vector field has two fewer terms in the case of the water wave equations in two dimensions. The time evolution of (2.7) conserves a number of physical quantities in addition to the Hamiltonian, including the added mass M(η)= η(x,t)dx. (2.11) R n 1 Conservation of this quantity is verified by the following identity {M,H}=0, (2.12) where the Poisson bracket between two functionals F and H is given by {F,H}= δ η Fδ ξ H δ ξ Fδ η Hdx. (2.13) R n 1
7 Surface Water Waves and Tsunamis 531 The momentum, or impulse of a solution is another conserved quantity in the case that the bottom boundary of the fluid region is flat, x h = 0; I(η,ξ)= η(x,t) x ξ(x,t)dx (2.14) R n 1 and, we can verify by the calculation that {I,H}=0. (2.15) In this case, the center of mass of a solution is given by the expression C(η)= xη(x,t)dx (2.16) and it evolves linearly in time; indeed its time derivative is a constant of motion d dt C = x t η(x,t)dx = xg(η)ξ dx, R n 1 R n 1 = ξg(η)x dx = ξ( x η)dx = I(η,ξ). (2.17) R n 1 R n 1 3. LINEAR WAVE SPEED Equation (2.8) do not have the property of finite propagation speed, as does the classical wave equation, since the requirement of incompressibility for potential flow involves global information about the fluid. But solutions do have an effective propagation speed, which is finite for fluid regions which are not infinitely deep. Although, we would like to invoke this principle in an ocean basin as complicated as the Indian Ocean, it is easier to derive it in the case that the bottom is flat, and the deformations of the free surface are sufficiently small to be treated by linear theory. The fluid region is therefore {(x, y): h<y<0}, and the linearized equations of motion are given by the quadratic part of the Hamiltonian H (2) = 1 ξg(0, h)ξ + gη 2 dx. (3.1) 2 R n 1 The Dirichlet Neumann operator G(0,h) for a strip is given in terms of a Fourier multiplier operator, which can be derived by solving the boundary value problem for the velocity potential ϕ = 0, (3.2) ϕ(x,0) = ξ(x), (3.3) y ϕ(x, h) = 0. (3.4)
8 532 Craig Then the operator G is defined by the expression G(0, h)ξ(x) := y ϕ(x,0). When the particular boundary data ξ(x)=e ik x is given, the solution of the potential problem is ϕ(x,y)= from which, we deduce that cosh(k(y + h)) e ik x cosh(kh) G(0, h)e ik x k sinh(k(y + h)) = y ϕ(x,0) = y=0 e ik x = k tanh(kh)e ik x. cosh(kh) The general solution is therefore given in terms of the Fourier transform of the Dirichlet data on the linearized free surface, 1 G(0, h)ξ(x) = ( e ik x k tanh(hk)ˆξ(k)dk, 2π) n 1 R n 1 = D tanh(hd)ξ(x), (3.5) where, we use the notation D = i x. Using this information, we derive the dispersion relation for the linearized equations of motion, which is the frequency of the normal modes for the quadratic Hamiltonian H (2). Namely, the linear equations of evolution are ( ) ( )( η 0 1 δη H t = (2) ) ξ 1 0 δ ξ H (2), ( )( 0 D tanh(hd) η =. (3.6) g 0 ξ) The Fourier integral expression for the solution of this system of equations is ( ) η(x,t) = ξ(x,t) 1 (2π) (n 1)/2 R n 1 e ik x cos(ω(k)t) g k tanh(hk) sin(ω(k)t) k tanh(hk) g ( sin(ω(k)t) ˆ cos(ω(k)t) η0 (k) ˆ ξ 0 (k) ) dk, (3.7) where the frequency at wave number k is given by the dispersion relation ω(k)= gk tanh(hk). (3.8) With this dispersion relation, the phase velocity of solutions of (3.6) is c p (k) = ω(k) k 2 k
9 Surface Water Waves and Tsunamis 533 and the group velocity is c g (k) = k ω(k). The significance of these two quantities is a basic fact of the theory of linear wave propagation. Each Fourier mode e ik x component of the initial data (η 0 (x), ξ 0 (x)) T propagates as governed by the expression (3.7), with phase ( k x ω(k)t = k x t ω(k) ) k 2 k. Thus for each mode, points of constant phase propagate with the phase velocity c p. The significance of the group velocity is a bit more subtle, and involves the evolution of a wave packet. For simplicity, assume that the initial data has a smooth and compactly supported Fourier transform ( ηˆ 0 (k), ξˆ 0 (k)) T C0. If this is not the case, one could decompose more general initial data using a partition of unity on first the spatial and then the Fourier transform side, after which each component would satisfy these conditions. Individual terms in the Fourier integral expression (3.7) take the form ψ(x,t)= e ik x iω(k)t ψˆ 0 (k) dk. (3.9) R n 1 Consider points (x, t) in space time such that for all k supp ψˆ 0,wehave x t kω(k) >R. (3.10) Then we can use the identity e i(k x ω(k)t) = x kω(k)t x k ω(k)t 2 ( i k)e i(k x ω(k)t), in the integral (3.9), and because of (3.10) we can integrate by parts, to write ψ(x,t) = O R n 1 e i(k x ω(k)t) ( ( )) x k ω(k)t N i k ˆ x k ω(k)t 2 ψ 0 (k) dk ( (Rt) N ) (3.11) for all N. Thus initial data organized in a wave packet with wave numbers close to k do not travel very much into regions of space time which satisfy (3.10). That is, they essentially propagate with the group velocity k ω(k).
10 534 Craig In the case of the dispersion relation for water waves (3.8), the phase and group velocities tend as k to c p (k) g/ k, c g (k) 1 2 g/ k from which, we learn that short waves travel slowly in the ocean surface. We may also extrapolate that the individual wave crests within an evolving wavepacket will not be stationary, and will in fact travel somewhat faster than the wave packet itself (up to two times as fast for large wavenumber). On the other hand, as k 0, both the phase and group velocities tend to a constant magnitude c p (k) gh, c g (k) gh. (3.12) We will assume that large scale tsunami waves are a very low wave number phenomenon, for which the asymptotic formulae (3.12) are valid. The primary conclusion to discuss is the speed of propagation of tsunami waves in ocean basins such as the ones in which the Boxing Day tsunami occurred. Our analysis will be based on a knowledge of the bathymetry of these oceans, which is reviewed in Fig. 3 posted by the Novosibirsk Tsunami Laboratory. The distance from the epicenter of the Sumatra earthquake to the affected coast of Sri Lanka is about 1550 km, and the Bay of Bengal/Indian Ocean through which the tsunami waves traveled is a deep ocean, with depth of roughly 4 km. Making the very rough approximation that h = 4 km and taking g =9.8 m/s 2, we can approximate the speed of the tsunami over this distance to be c = gh (9.8 m/s 2 ) ( m) m/s = 720 km/h. Thus the approximation to the travel time for this process is 2.2 h, which is actually about right. Similarly, the distance from the epicenter to the Figure 3. Novosibirsk Tsunami Laboratory website:
11 Surface Water Waves and Tsunamis 535 western coast of the Malay Peninsula, which is where the principal Thai resorts were hit, and which has coastal areas of Indonesia and Myanmar, is about 700 km. However the tsunami waves generated in this direction propagated through the Andaman Basin, which is a shallower sea of quite variable depth. For purposes of our illustrative calculations let us take the approximate depth to be 1 km which is not too far off. Then, we find c = gh (9.8 m/s 2 ) 10 3 m 10 2 m/s = 360 km/h resulting in a travel time of approximately 1.9 h from the initiation at the epicenter to the impact on the coast. In any case, we see that tsunami waves can carry energy very rapidly from one coastal region to another, spanning the largest distance scales of our planet in times from hours to a little more than one day. 4. COHERENT WAVETRAINS When a sufficiently strong earthquake occurs, it may be felt without instruments almost instantly in a neighboring region, and when a large one occurs, it can be destructive over a large area. However, even very big earthquakes do not directly cause significant damage at great distances from their source. That is, disturbances in the earth s crust travel very rapidly, but as well the largest component of their energy is dissipated after having propagated a relatively short distance from their epicenter. The fact is that tsunami waves in the ocean behave differently than this. The nonlinear character of the Euler equations for the propagation of ocean waves gives rise to the possibility that tsunami waves can propagate in coherent wave packets, with little loss of amplitude over very long distances. We can deduce some aspects of the character of these nonlinear waves just from the starting point of several of the reports of witnesses of the impact of the Boxing Day Tsunami. Soon after the event there were a number of descriptions of peoples experiences posted on the web. Certain of the basic facts seemed to be common to many of these; that there were several wave crests observed, 6 or 7 in the case of the Thai coast for example, and that the period between the arrival of these crests was between 15 and 45 min. Furthermore, measured wave amplitudes at sea did not exceed 1 to 2 m, although on the coastline the tsunami in many places underwent an amplification to 3 up to maybe 7 m. This latter data is not quantified with precise observational data in most cases, apparently because not many wave gages were in place or operational in the region at the time of the event. In any case, from the basic information above, we can deduce some nontrivial facts about this tsunami s waveform.
12 536 Craig For the purpose of a sample calculation, let us take a temporal period for arrival of wave crests to be T 0 = 15 min. The spatial period of the individual crests, we can denote by X 0, so that the basic wavenumber of the tsunami wave is K 0 = 2π/X 0. The phase velocity, which we argued above is the velocity of propagation of the individual crests, is g tanh(hk 0 ) c p (K 0 ) = K 0 and the relation between the spatial and temporal periods is of course c p (K 0 )T 0 = X 0 = 2π. K 0 That is, gk 0 tanh(hk 0 )T0 2 = (2π)2. (4.1) Because, we seek a small wavenumber K 0 (and because 15 min is 900 s), (2π) 2 ghk0 2 T m/s2 ( m) (900 s) 2 K0 2. Hence, we find that 2π K m m 1, (4.2) which corresponds to a spatial wavelength of X km. The slope in mid-ocean of waves of this form is approximately x η 2 2m η X m 10 5 := ε, where applied mathematicians often think of ε as a small dimensionless parameter which would be useful in a perturbation analysis of the problem. Actually in these notes I would like to a bit more careful, and introduce two small parameters: α := a h, β:= h l, (4.3) where a is the amplitude of the solutions, we are studying, h is the fluid basin depth as before, and l is some measure of the characteristic wavelength of our solutions. The appropriate model equations for the regime of wave propagation that, we are to study are traditionally determined by the relationship between α and β; in case α β 2 1 this is the dispersive nonlinear regime, while α β 1 indicates the weakly nonlinear shallow water regime.
13 Surface Water Waves and Tsunamis 537 It is instructive to compare the parameters, we have just deduced for the 2004 Boxing Day Tsunami with these criteria. In the basin of the Indian Ocean/Bay of Bengal, we use the values of amplitude a = 1 m and depth h = 4 Km hence α = a/h On the other hand the wavelength is l=x 0 =180 Km, hence β =h/l 4Km/180 Km Therefore, in this basin of the ocean, the tsunami fits quite well into the regime α β 2 of dispersive nonlinear waves. This is of particular interest because it is this regime of the water waves problem which most clearly supports solutions of the form of coherent dispersive packets. In contrast, the same considerations in the Andaman Basin give mixed conclusions; we calculate α = a/h 10 3 while β = h/l This indicates that β 2 α β, and it is somewhat ambiguous which scaling regime is valid in order to model wave propagation. Turning to the data from the tsunami waves in the Indian Ocean taken during the event, we see that indicates that the tsunami wave is experiencing dispersive effects during its propagation. Figure 4(a) represents a trace of the satellite telemetry of wave height during one pass of the Jason 1 Altimetry Satellite (a joint NASA European Space Agency mission, which detected the Indian Ocean tsunami during track 129 of its 10 day/254 track cycle), where it is quite clearly indicated the degree to which low wave number components of the wave form are traveling faster than components with higher wave number. Figure 4(b) gives a Fourier analysis of the data from a wave gage at Syowa Station, Antarctica during the period of several days December 25 29, The data are presented in a wavelet decomposition, which indicates two strong peak responses Figure 4. (a) from E. Kulikov, Shirshov Institute of Oceanography, Moscow and Institute of Ocean Sciences, Sydney, BC: Dispersion of the Sumatra tsunami waves in the Indian Ocean detected by satellite altimetry, Fisheries and Oceans Canada, Science Pacific Region website (2005) (b) From the Tsunamis and tsunami research website of the Institute of Ocean Sciences, Sydney BC. This time/frequency plot of the Sumatra tsunami supports the wavepacket hypothesis.
14 538 Craig during the tsunami period. These are interpreted as the Fourier transform of the main wave packet, centered about the the carrier wavenumber K 0 = 3π/h of the tsunami event, and its second harmonic K 1 = 6π/h. 5. NEAR SHORE DYNAMICS At the point that tsunami waves arrive at a coastline, the can exhibit very complex near-shore wave dynamics, and there is much that is not well understood. A large wavelength ocean wave incident on a coastline can be dispersed, or its amplitude can be dramatically amplified, depending to a large part on the the width of the continental shelf, the local geometry of the coast, and the angle of incidence of the approaching tsunami. From the accounts of witnesses of the impact of a tsunami, many different things do occur. In some areas affected by the Boxing Day tsunami, the phenomenon was similar to a rising tide, with no breaking white water, but being just several times the magnitude of a normal tide, and coming in over a period of twenty minutes instead of 6 h. This sort of incidence was also observed during the impact of the 1964 Pacific Ocean tsunami on Vancouver Island, which was generated by the major earthquake in Alaska. More visible, and also more dangerous and dramatic, were the phenomenon of hydraulic jumps, or tidal bores where the mass of water in motion towards the land is rising too fast to do so smoothly, and a jump of water level, of perhaps one or several meters in height is formed. While the wave crests of the tsunami wave packet are traveling at several hundred kilometers per hour, the hydraulic jump is much slower, maybe moving at no more that several tens of kilometers per hour. This phenomemon is commonly modeled by a shock wave in the shallow water equations that characterize this near shore regime. This mass of water could possibly recede smoothly, but this is equally or more dangerous, drawing objects and people out to sea. To illustrate the wide variety of phenomena tha can occur as a tsunami wave is incident on a coastal area, I refer to a diagram compiled by N. Shunto which appears in the book of Pelinovsky [12] on the hydrodynamics of tsunami waves. The Nihonkai Chubu earthquake tsunami occurred on May 26, 1983 from a M w 7.9 earthquake with epicenter in the Sea of Japan off of the Akita Coast. The event occurred at approximately noon, so it happened that there were numerous witnesses on the beaches and shorelines, and a survey of the tsunami waves impact on the North Akita Coast, as reported by many observors, was compiled into the diagram given in Fig. 5. It is evident that the phenomena are highly varied, and include hydraulic jumps, series of breaking waves, single large breakers, and others. Another widely circulated image was taken
15 Surface Water Waves and Tsunamis 539 Figure 5. E. Pelinovsky: Dynamics of tsunami waves (1996)[Russian] Nihonkai Chubu earthquake tsunami on the north Akita coast. N. Shuto, Coastal Eng. Japan (1985), vol. 28, pp from the air over Kalutara, Sri Lanka during the Boxing Day Tsunami events (Fig. 5). One sees large waves moving in a variety of directions through the palms on plots of land ajacent to the beach. We feel that it is a challenging problem to be able to start to quantify the dynamics of large tsunami waves as they impact on coastal areas, for both the purpose of understanding the physics of the phenomenon, as well as to quatify the potential damage of their impact and the possible engineering norms that should be applied to create a tsunami-safe architecture. 6. SOLITARY WAVE INTERACTIONS The second lecture is related to the first in that it is on the topic of nonlinear water waves in the free surface of an ideal fluid. It is in fact a discussion of the classical problem of interactions between solitary water waves. We will restrict our considerations to solitary waves in two dimensions, and to the case in which the bottom boundary of the fluid region is flat. There are a number of reasons why this represents an interesting problem. One is that the dynamics of nonlinear waves is an important topic to understand, to further our basic understanding of the oceans next to which, we live, and to prepare us for its dangers. A second reason is more mathematical; from the study of the KdV equation, we know that from the apropriate point of view it is a completely integrable Hamiltonian system, whose soliton solutions interact with elastic collisions. Since the KdV equation is one of the principal model equations for
16 540 Craig Figure 6. Shoreline of Kalutara, Sri Lanka on December 26, Photo: DigitalGlobe. free surface water waves, it is therefore of interest to understand to what extent its solitary wave solutions deviate from having elastic interactions. There are two basic cases; the interaction between counter-propagating waves (either symmetric collisions or collisions between waves of different amplitudes), and co-propagating or overtaking interactions. This work updates the well-known numerical simulations of Chan and Street [2], Fenton and Reinecker [8], and Cooker et al. [3]. It has also been compared with the experimental results of Maxworthy [11] and our own experiments [4]. We work with potential flow, for which the velocity potential satisfies (2.1), and the boundary conditions (2.3) (2.2) and (Fig. 6). 7. NUMERICAL METHOD Our numerical method consists essentially in making good approximations for the Dirichlet Neumann operator (2.6), and using them in a time discretized version of the evolution equations (2.8). This approach was introduced in [7] and used in a variety of settings, including [1, 5]. It was already described by Hadamard [9] in his Collège de France lectures that Green s function for Laplace s equation is differentiable with respect to the domain on which it is given. Indeed he gave a formula for its variations, and in [10] he proposed hydrodynamical applications. In fact in the appropriate setting it has been shown that the closely related Dirichlet Neumann operator is analytic with respect to its dependence upon the domain. Putting this into practice in the neighborhood of a fluid domain at rest, we base our simulations on the Taylor expansion of the Dirichlet Neumann operator to arbitrarily high order in the equations of motion (2.8). The first several Taylor approximations to G(η) are
17 Surface Water Waves and Tsunamis 541 G (0) = D tanh(hd), G (1) = DηD G (0) ηg (0), (7.1) G (2) = 1 ( G (0) Dη 2 D D 2 η 2 G (0) 2G (0) ηg (1)). 2 In our notation, D = i x, and G (0) is a Fourier multiplier operator which is given by the expression G (0) ξ(x):= 1 e ikx k tanh(hk)ˆξ(k)dk. (7.2) 2π Such expressions can be implemented efficiently using the Fast Fourier Transform. As well, there is a recursion formula for the Taylor series for G(η) which can be incorporated into very efficient numerical schemes of arbitrarily high order in the (slope of the) surface elevation η(x). This is essentially what, we have done in [4] for our study of solitary water wave interactions. Initial data for our simulations consists of two well separated solitary water waves, of nondimensional amplitudes S 1 /h and S 2 /h, which are set to collide within the computational domain. The solitary wave profiles for this are generated using the numerical method proposed by Tanaka [16], giving us highly accurate results. 8. HEAD-ON COLLISIONS This section is concerned with collisions between two counterpropagating solitary waves, of nondimensional elevation S 1 /h and S 2 /h, respectively. The first simulations presented here are symmetric head-on collisions between two solitary waves of equal amplitudes S/h. Features of note are the degree of run-up of the wave crest during the interaction, given by sup x,t η(x,t) /h 2S/h; the phase lag due to the moment s hesitation of the crests during their interaction; the change in amplitude of the solitary waves after the interaction, S/h S + /h; their phase lag a a + ; and the residual waves η R (x, t) trailing the solitary waves as they exit the collision. We observe that the solitary waves in head-on collisions always lose a small amount of amplitude due to the collision; S + j <S j, although this is very small even for interactions between large solitary waves. The residual is clearly visible in the Fig. 7, but it is essentially too small to be detected in Fig. 8 without magnification. A snapshot plot of the computation in Fig. 8 at time t/ h/g = 90, with magnified vertical scale, is given in the Fig. 9. Viewing the interaction of two solitary waves of amplitude S/h = 0.4 after long time illustrates the asymptotic tear-shaped form of the residual,
18 542 Craig 0.4 η/h t/(h/g) 1/ x/h Figure 7. Head-on collision of two solitary waves of equal height S/h = 0.4: The amplitude after collision is S + /h= at t/ h/g = 90. The phase lag is (a j a j + )/h = η/h t/(h/g) 1/ x/h Figure 8. Head-on collision of two solitary waves of equal height S/h = 0.1: The amplitude after collision is S + /h = at t/ h/g = 90. The phase lag is (a j a j + )/h = as well as the fact that the solitary waves separate from each other and from the the residual after the collision. This is shown in Fig. 10; it is an indication of the stability of solitary waves to such head-on collisions, at least within this range of amplitudes.
19 Surface Water Waves and Tsunamis x η/h x/h Figure 9. Results of the collision of two solitary waves of equal height S/h = 0.1 after the collision, at time t/ h/g = 90. The dispersive residual wave trailing the solitary waves after the collision are visible under magnification. η/h x/h Figure 10. Results of the collision of two solitary waves of equal height S/h = 0.4 after the collision at time t/ h/g = 780. The residual has a characteristic tear-shaped envelope. 9. OVERTAKING COLLISIONS We have also run simulations of overtaking collisions with this numerical scheme, where we find yet smaller changes of amplitude S j := S j S + j, j = 1, 2 and residual η R after a collision. Normalize the notation so that the larger incoming solitary wave has amplitude S 1 and the second S 2. In these simulations, we observe that the amplitude of the first solitary wave is slightly increased, S + 1 >S 1, while the second decreases as is necessary. We also observe that the amplitude of the solution never exceeds the maximum of the amplitudes of the entering and exiting solitary waves, nor at any time does the maximum crest dip below the minimum. Just as in the situation of the two-soliton solution of the KdV equation, the solitary waves experience a positive phase shift due to the collision, as though the
20 544 Craig Figure 11. Overtaking collision of two solitary waves of height S 1 /h = 0.4, S 2 /h = 0.1: The amplitudes after collision are S + 1 /h= , S+ 2 /h= at t/ h/g = 1000 for the large, small wave, respectively. The phase shifts are (a + 1 a 1)/h = , (a + 2 a 2)/h = , respectively. two waves were repelling particles. Figure 11 shows the interaction of two solitary waves of amplitudes S 1 /h =0.4 and S 2 /h =0.1333, this being chosen so that the interaction is of the Lax category (b) in its form. The simulation is displayed in a frame of reference in motion at approximately the mean velocity of the two solitary waves. In Fig. 12, a view of this simulation with exagerated scale at a time after the interaction shown clearly the very small but nonzero residual. 10. ENERGY TRANSFER Using the conservation laws (2.11), (2.14), and the Hamiltonian (2.5), one can derive a relation between the change in amplitude through a solitary wave interaction and the energy that has been transferred to the residual. Using this, it is also possible to derive a rigorous upper bound on the energy transfer in terms of the parameters S 1 /h, S 2 /h of the initial data. The latter analysis appears in [4]. To explain the first relation, an individual solitary wave has mass M(η S ):=m(s), momentum I(η S,ξ S ) := µ(s) and energy H(η S,ξ S ) := e(s). Our initial data is given by two asymp-
21 Surface Water Waves and Tsunamis x η/h x/h Figure 12. Overtaking collision of two solitary waves of height S 1 /h = 0.4, S 2 /h = 0.1 at t/ h/g = 745, which is after the collision. The vertical scale is magnified in order to observe the dispersive trailing wave generated by the interaction. totically separated solitary waves as t, therefore the total mass, momentum and energy of our solution are given by M T = m(s 1 ) + m(s 2 ), I T = µ(s 1 ) + µ(s 2 ), (10.1) E T = e(s 1 ) + e(s 2 ). After an interaction has occurred, we will assume that the solution is composed of three distinct components; two solitary waves with possibly different amplitudes S + 1 and S+ 2, and a residual (η R(x, t), ξ R (x, t)). By conservation, their mass, momenta and energies satisfy Taking the difference, we find that M T = m(s + 1 ) + m(s+ 2 ) + m R, I T = µ(s + 1 ) + µ(s+ 2 ) + µ R, (10.2) E T = e(s + 1 ) + e(s+ 2 ) + e R. (m(s 1 ) m(s + 1 )) + (m(s 2) m(s + 2 )) = m R, (µ(s 1 ) µ(s + 1 )) + (µ(s 2) µ(s + 2 )) = µ R, (10.3) (e(s 1 ) e(s + 1 )) + (e(s 2) e(s + 2 )) = e R. Since the change in amplitude is very small, the difference m(s j ) m(s + j ) is very small, j = 1, 2, and the same for µ(s j ) and e(s j ). Approximating by the derivative, we conclude that
22 546 Craig m 1 S 1 + m 2 S 2 = m R, µ 1 S 1 + µ 2 S 2 = µ R, (10.4) e 1 S 1 + e 2 S 2 = e R, this is now three equations for the two unknowns j, j =1, 2, whose solution leads us to an absolute bound on the energy loss due to a collision [4]. Separately from this bound, Eq specify relationships between the mass, momentum and energy loss to the residual and the change in amplitude S j from the interaction. Let us consider the case of symmetric interactions as an example. In this case, µ(s 1 ) = µ(s 2 ) and therefore I T = 0 and µ R = 0. The relation (10.4) then reports that 2m (S) = m R, 2e (S) = e R. (10.5) Since in particular e(s) S 3/2 for small S, this predicts that e R S 1/2 S. (10.6) Figure 13 plots the quantity e(s) for a range of simulations ranging from S = to S = 0.5, verifying its power law behavior. Figure 14 gives our measured values of S for these simulations, while Fig. 15 gives the energy e R of the residual. The adherence of this data to the asymptotic relation (10.6) is quite convincing. The deviation of the lowest two data points from the power law behavior is due to the long relaxation time of small solutions to their asymptotic values after an interaction, we believe. Our data, particularly in Fig. 14, are at odds with the asymptotic predictions of Su and Mirie [15], who put forward that η R = O(S 3 ) while S = o(s 3 ). The relations (10.4) give a nontrivial result on the mass and energy of the residual and the quantities S j + in the case of overtaking collisions. From our simulations and from those in [8], it is observed that S 1 < 0. That is, the larger overtaking solitary wave gains a (small amount of) amplitude due to the collision, at the expense of the smaller one. We note that e(s) is a convex function of S, at least over the range of values of S being considered. The implication of (10.4) is that, since e R 0, it must be that S 1 < S 2 ; the larger solitary wave cannot gain more amplitude than the smaller one loses. Using this, a related argument applied to the relation for mass implies that m R < 0, because in this case m (S) is decreasing in S. This fact is seen in the slight depression left behind two separating solitary waves after their interaction.
23 Surface Water Waves and Tsunamis H T 10 1 S 3/ Figure 13. Total energy E T vs. wave amplitude S/h: numerical results (circles), power law (S/h) 3/2 (solid line). S/h S 3/2 S/h Figure 14. Change in amplitude S/h = (S S + )/h vs. wave amplitude S/h: numerical results (circles), power law (S/h) 3/2 (solid line). S/h
24 548 Craig H R 10 3 S S/h Figure 15. Energy of the residual e R vs. nondimensional wave amplitude S/h: numerical results (circles), power law (S/h) 2 (solid line). ACKNOWLEDGMENTS This research has been supported in part by the Canada Research Chairs Program, the NSERC under operating grant #238452, and the NSF under grant #DMS All of the numerical simulations in this note were performed by P. Guyenne. REFERENCES 1. Bateman, W. J. D., Swan, C., and Taylor, P. (2001). On the efficient numerical simulation of directionally spread surface water waves. J. Comput. Phys. 174, Chan, R. K.-C., and Street, R. (1970). A computer study of finite amplitude water waves. J. Comput. Phys. 6, Cooker, M. J., Weidman, P. D., and Bale, D. S. (1997). Reflection of a high-amplitude solitary wave at a vertical wall. J. Fluid Mech. 342, Craig, W., Guyenne, P., Hammack, J., Henderson, D., and Sulem, C. (2006). Solitary wave interactions. Phys. Fluids. 18, Craig, W., and Nicholls, D. (2000). Traveling two and three dimensional capillary gravity waves. SIAM: Math. Anal. 32, Craig, W., Guyenne, P., Nicholls, D., and Sulem, C. (2005). Hamiltonian long wave expansions for water waves over a rough bottom. Proc. R. Soc. A 461, 839.
25 Surface Water Waves and Tsunamis Craig, W., and Sulem, C. (1993). Numerical simulation of gravity waves. J. Comp. Phys. 108, Fenton, J. D., and Rienecker, M. M. (1982). A Fourier method for solving nonlinear water-wave problems: application to solitary-wave interactions. J. Fluid Mech. 118, Hadamard, J. (1910). Leçons Sur Le Calcul Des Variations, Hermann, Paris, paragraph Section Hadamard, J. (1916). Sur les ondes liquides. Rend. Acad. Lincei 5(25), Maxworthy, T. (1976). Experiments on the collision between two solitary waves. J. Fluid Mech. 76, Pelinovsky, E. (1996). Hydrodynamics of Tsunami Waves (Russian). Russian Academy of Sciences Russia. 13. Rosales, R., and Papanicolaou, G. (1983). Gravity waves in a channel with a rough bottom. Stud. Appl. Math. 68, Schneider, G., and Wayne, C. E. (2000). The long-wave limit for the water wave problem. I. The case of zero surface tension. Comm. Pure Appl. Math. 53, Su, C. H., and Mirie, R. M. (1980). On head-on collisions between two solitary waves. J. Fluid Mech. 98, Tanaka, M. (1986). The stability of solitary waves. Phys. Fluids 29, Titov, V., Rabinovich, A. B., Mofjeld, H. O., Thomson, R. E., and Gonzàlez, F. I. (2005). The global reach of the 26 December Sumatra tsunami. Science 309(5743), Wright, J. D. (2005). Corrections to the KdV approximation for water waves. SIAM J. Math. Anal. 37, Zakharov, V.E. (1968). Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9,
Tsunamis and ocean waves
 Department of Mathematics & Statistics AAAS Annual Meeting St. Louis Missouri February 19, 2006 Introduction Tsunami waves are generated relatively often, from various sources Serious tsunamis (serious
Department of Mathematics & Statistics AAAS Annual Meeting St. Louis Missouri February 19, 2006 Introduction Tsunami waves are generated relatively often, from various sources Serious tsunamis (serious
Lecture 7: Oceanographic Applications.
 Lecture 7: Oceanographic Applications. Lecturer: Harvey Segur. Write-up: Daisuke Takagi June 18, 2009 1 Introduction Nonlinear waves can be studied by a number of models, which include the Korteweg de
Lecture 7: Oceanographic Applications. Lecturer: Harvey Segur. Write-up: Daisuke Takagi June 18, 2009 1 Introduction Nonlinear waves can be studied by a number of models, which include the Korteweg de
Lecture 1: Water waves and Hamiltonian partial differential equations
 Lecture : Water waves and Hamiltonian partial differential equations Walter Craig Department of Mathematics & Statistics Waves in Flows Prague Summer School 208 Czech Academy of Science August 30 208 Outline...
Lecture : Water waves and Hamiltonian partial differential equations Walter Craig Department of Mathematics & Statistics Waves in Flows Prague Summer School 208 Czech Academy of Science August 30 208 Outline...
Tsunamis. A Large-Scale Earth and Ocean Phenomenon. Satish R Shetye
 Tsunamis A Large-Scale Earth and Ocean Phenomenon Satish R Shetye Tsunamis are surface gravity waves that are triggered due to perturbation of the ocean floor. The tsunamis that occurred in the Indian
Tsunamis A Large-Scale Earth and Ocean Phenomenon Satish R Shetye Tsunamis are surface gravity waves that are triggered due to perturbation of the ocean floor. The tsunamis that occurred in the Indian
Indian Ocean Tsunami Warning System: Example from the 12 th September 2007 Tsunami
 Indian Ocean Tsunami Warning System: Example from the 12 th September 2007 Tsunami Charitha Pattiaratchi 1 Professor of Coastal Oceanography, The University of Western Australia Email: chari.pattiaratchi@uwa.edu.au
Indian Ocean Tsunami Warning System: Example from the 12 th September 2007 Tsunami Charitha Pattiaratchi 1 Professor of Coastal Oceanography, The University of Western Australia Email: chari.pattiaratchi@uwa.edu.au
Earthquake Hazards. Tsunami
 Earthquake Hazards Tsunami Measuring Earthquakes Two measurements that describe the power or strength of an earthquake are: Intensity a measure of the degree of earthquake shaking at a given locale based
Earthquake Hazards Tsunami Measuring Earthquakes Two measurements that describe the power or strength of an earthquake are: Intensity a measure of the degree of earthquake shaking at a given locale based
Earthquake Hazards. Tsunami
 Earthquake Hazards Tsunami Review: What is an earthquake? Earthquake is the vibration (shaking) and/or displacement of the ground produced by the sudden release of energy. The point inside the Earth where
Earthquake Hazards Tsunami Review: What is an earthquake? Earthquake is the vibration (shaking) and/or displacement of the ground produced by the sudden release of energy. The point inside the Earth where
Advisors: Arcadii Grinshpan, Mathematics and Statistics Rocco Malservisi, School of Geosciences. Problem Suggested By: Rocco Malservisi
 Undergraduate Journal of Mathematical Modeling: One + Two Volume 8 2018 Spring 2018 Issue 2 Article 6 Tsunami Waves Samantha Pennino University of South Florida Advisors: Arcadii Grinshpan, Mathematics
Undergraduate Journal of Mathematical Modeling: One + Two Volume 8 2018 Spring 2018 Issue 2 Article 6 Tsunami Waves Samantha Pennino University of South Florida Advisors: Arcadii Grinshpan, Mathematics
Salmon: Introduction to ocean waves
 9 The shallow-water equations. Tsunamis. Our study of waves approaching the beach had stopped at the point of wave breaking. At the point of wave breaking, the linear theory underlying Propositions #1
9 The shallow-water equations. Tsunamis. Our study of waves approaching the beach had stopped at the point of wave breaking. At the point of wave breaking, the linear theory underlying Propositions #1
On the Whitham Equation
 On the Whitham Equation Henrik Kalisch Department of Mathematics University of Bergen, Norway Joint work with: Handan Borluk, Denys Dutykh, Mats Ehrnström, Daulet Moldabayev, David Nicholls Research partially
On the Whitham Equation Henrik Kalisch Department of Mathematics University of Bergen, Norway Joint work with: Handan Borluk, Denys Dutykh, Mats Ehrnström, Daulet Moldabayev, David Nicholls Research partially
We have previously looked at artificial seismograms such as this one here.
 We have previously looked at artificial seismograms such as this one here. S P A realistic Seismic Record Each vertical line = 1 minute Each horizontal line = 15 minutes Seismic station PMM is in Parkfield,
We have previously looked at artificial seismograms such as this one here. S P A realistic Seismic Record Each vertical line = 1 minute Each horizontal line = 15 minutes Seismic station PMM is in Parkfield,
Earthquakes and Earthquake Hazards Earth - Chapter 11 Stan Hatfield Southwestern Illinois College
 Earthquakes and Earthquake Hazards Earth - Chapter 11 Stan Hatfield Southwestern Illinois College What Is an Earthquake? An earthquake is the vibration of Earth, produced by the rapid release of energy.
Earthquakes and Earthquake Hazards Earth - Chapter 11 Stan Hatfield Southwestern Illinois College What Is an Earthquake? An earthquake is the vibration of Earth, produced by the rapid release of energy.
Earthquake Hazards. Tsunami
 Earthquake Hazards Tsunami Review: What is an earthquake? Earthquake is the vibration (shaking) and/or displacement of the ground produced by the sudden release of energy. The point inside the Earth where
Earthquake Hazards Tsunami Review: What is an earthquake? Earthquake is the vibration (shaking) and/or displacement of the ground produced by the sudden release of energy. The point inside the Earth where
Earthquakes Chapter 19
 Earthquakes Chapter 19 Does not contain complete lecture notes. What is an earthquake An earthquake is the vibration of Earth produced by the rapid release of energy Energy released radiates in all directions
Earthquakes Chapter 19 Does not contain complete lecture notes. What is an earthquake An earthquake is the vibration of Earth produced by the rapid release of energy Energy released radiates in all directions
Shoaling of Solitary Waves
 Shoaling of Solitary Waves by Harry Yeh & Jeffrey Knowles School of Civil & Construction Engineering Oregon State University Water Waves, ICERM, Brown U., April 2017 Motivation The 2011 Heisei Tsunami
Shoaling of Solitary Waves by Harry Yeh & Jeffrey Knowles School of Civil & Construction Engineering Oregon State University Water Waves, ICERM, Brown U., April 2017 Motivation The 2011 Heisei Tsunami
Earthquakes. Building Earth s Surface, Part 2. Science 330 Summer What is an earthquake?
 Earthquakes Building Earth s Surface, Part 2 Science 330 Summer 2005 What is an earthquake? An earthquake is the vibration of Earth produced by the rapid release of energy Energy released radiates in all
Earthquakes Building Earth s Surface, Part 2 Science 330 Summer 2005 What is an earthquake? An earthquake is the vibration of Earth produced by the rapid release of energy Energy released radiates in all
Lecture 4: Birkhoff normal forms
 Lecture 4: Birkhoff normal forms Walter Craig Department of Mathematics & Statistics Waves in Flows - Lecture 4 Prague Summer School 2018 Czech Academy of Science August 31 2018 Outline Two ODEs Water
Lecture 4: Birkhoff normal forms Walter Craig Department of Mathematics & Statistics Waves in Flows - Lecture 4 Prague Summer School 2018 Czech Academy of Science August 31 2018 Outline Two ODEs Water
Three Dimensional Simulations of Tsunami Generation and Propagation
 Chapter 1 Earth Science Three Dimensional Simulations of Tsunami Generation and Propagation Project Representative Takashi Furumura Authors Tatsuhiko Saito Takashi Furumura Earthquake Research Institute,
Chapter 1 Earth Science Three Dimensional Simulations of Tsunami Generation and Propagation Project Representative Takashi Furumura Authors Tatsuhiko Saito Takashi Furumura Earthquake Research Institute,
Introduction to Environmental Geology, 5e Case History: Indonesian Tsunami Indonesian Tsunami (2) Introduction Historic Tsunamis
 1 2 3 4 5 6 7 8 9 Introduction to Environmental Geology, 5e Chapter 7 Tsunami Case History: Indonesian Tsunami December 26, 2004, within a few hours, close to 250,000 people were killed With no warning
1 2 3 4 5 6 7 8 9 Introduction to Environmental Geology, 5e Chapter 7 Tsunami Case History: Indonesian Tsunami December 26, 2004, within a few hours, close to 250,000 people were killed With no warning
Earthquakes Physical Geology 2017 Part 1: Exploring Earthquake distributions. Home butto California Earthquakes: 1) 2) 3) above
 Earthquakes Physical Geology 2017 Adapted from a lab by Jennifer Wenner This lab is designed to give you experience exploring seismicity associated with different plate boundaries. You will examine seismograms
Earthquakes Physical Geology 2017 Adapted from a lab by Jennifer Wenner This lab is designed to give you experience exploring seismicity associated with different plate boundaries. You will examine seismograms
News Release December 30, 2004 The Science behind the Aceh Earthquake
 News Release December 30, 2004 The Science behind the Aceh Earthquake PASADENA, Calif. - Kerry Sieh, the Robert P. Sharp Professor of Geology at the California Institute of Technology and a member of Caltech's
News Release December 30, 2004 The Science behind the Aceh Earthquake PASADENA, Calif. - Kerry Sieh, the Robert P. Sharp Professor of Geology at the California Institute of Technology and a member of Caltech's
Physics Letters A 374 (2010) Contents lists available at ScienceDirect. Physics Letters A.
 Physics Letters A 374 00) 4 45 Contents lists available at ScienceDirect Physics Letters A www.elsevier.com/locate/pla Variational derivation of improved KP-type of equations Lie She Liam a,, E. van Groesen
Physics Letters A 374 00) 4 45 Contents lists available at ScienceDirect Physics Letters A www.elsevier.com/locate/pla Variational derivation of improved KP-type of equations Lie She Liam a,, E. van Groesen
Name: Date: Bell: The Sumatra Earthquake and Tsunami December 26, 2004
 Name: Date: Bell: The Sumatra Earthquake and Tsunami December 26, 2004 Introduction: The incredible damage and tragic loss of life resulting from the 9.0 magnitude earthquake and ensuing tsunami was shocking
Name: Date: Bell: The Sumatra Earthquake and Tsunami December 26, 2004 Introduction: The incredible damage and tragic loss of life resulting from the 9.0 magnitude earthquake and ensuing tsunami was shocking
2. Tsunami Source Details
 2. Tsunami Source Details The Northland area faces a range of potential tsunamigenic sources that include several local and distant fault systems and underwater landslides. A NIWA study (Goff et al. 2006)
2. Tsunami Source Details The Northland area faces a range of potential tsunamigenic sources that include several local and distant fault systems and underwater landslides. A NIWA study (Goff et al. 2006)
Lessons from the 2004 Sumatra earthquake and the Asian tsunami
 Lessons from the 2004 Sumatra earthquake and the Asian tsunami Kenji Satake National Institute of Advanced Industrial Science and Technology Outline 1. The largest earthquake in the last 40 years 2. Tsunami
Lessons from the 2004 Sumatra earthquake and the Asian tsunami Kenji Satake National Institute of Advanced Industrial Science and Technology Outline 1. The largest earthquake in the last 40 years 2. Tsunami
Earthquakes Earth, 9th edition, Chapter 11 Key Concepts What is an earthquake? Earthquake focus and epicenter What is an earthquake?
 1 2 3 4 5 6 7 8 9 10 Earthquakes Earth, 9 th edition, Chapter 11 Key Concepts Earthquake basics. "" and locating earthquakes.. Destruction resulting from earthquakes. Predicting earthquakes. Earthquakes
1 2 3 4 5 6 7 8 9 10 Earthquakes Earth, 9 th edition, Chapter 11 Key Concepts Earthquake basics. "" and locating earthquakes.. Destruction resulting from earthquakes. Predicting earthquakes. Earthquakes
Introduction to Environmental Geology, 5e
 Lecture Presentation prepared by X. Mara Chen, Salisbury University Introduction to Environmental Geology, 5e Edward A. Keller Chapter 7 Tsunami Case History: Indonesian Tsunami December 26, 2004, within
Lecture Presentation prepared by X. Mara Chen, Salisbury University Introduction to Environmental Geology, 5e Edward A. Keller Chapter 7 Tsunami Case History: Indonesian Tsunami December 26, 2004, within
Plates & Boundaries The earth's continents are constantly moving due to the motions of the tectonic plates.
 Plates & Boundaries The earth's continents are constantly moving due to the motions of the tectonic plates. As you can see, some of the plates contain continents and others are mostly under the ocean.
Plates & Boundaries The earth's continents are constantly moving due to the motions of the tectonic plates. As you can see, some of the plates contain continents and others are mostly under the ocean.
CHAPTER 2 THE WAY THE EARTH WORKS: EXAMINING PLATE TECTONICS
 CHAPTER 2 THE WAY THE EARTH WORKS: EXAMINING PLATE TECTONICS Coverage of plate tectonics is required early in introductory Geology as context for the mineralogy, petrology, structure, internal processes,
CHAPTER 2 THE WAY THE EARTH WORKS: EXAMINING PLATE TECTONICS Coverage of plate tectonics is required early in introductory Geology as context for the mineralogy, petrology, structure, internal processes,
THE DEPOSITS OF TSUNAMIS WESLEY PESANTEZ, CATHERINE NIELD, COLIN WINTER
 THE DEPOSITS OF TSUNAMIS WESLEY PESANTEZ, CATHERINE NIELD, COLIN WINTER AN OVERVIEW OF OUR SEMINAR WHAT IS A TSUNAMI WHY STUDY TSUNAMIS PROPERTIES OF TSUNAMIS TSUNAMI HYDRODYNAMICS IDEALIZED DEPOSITS SEDIMENT
THE DEPOSITS OF TSUNAMIS WESLEY PESANTEZ, CATHERINE NIELD, COLIN WINTER AN OVERVIEW OF OUR SEMINAR WHAT IS A TSUNAMI WHY STUDY TSUNAMIS PROPERTIES OF TSUNAMIS TSUNAMI HYDRODYNAMICS IDEALIZED DEPOSITS SEDIMENT
Earthquakes 11/14/2014. Earthquakes Occur at All Boundaries. Earthquakes. Key Aspects of an Earthquake. Epicenter. Focus
 Earthquakes Earthquakes Caused by friction and movement between Earth s tectonic plates A release of force Often caused by a catch between two plates As plates slide by, they stick to each other When the
Earthquakes Earthquakes Caused by friction and movement between Earth s tectonic plates A release of force Often caused by a catch between two plates As plates slide by, they stick to each other When the
Chapter 4 Earthquakes and Tsunamis
 Geology of the Hawaiian Islands Class 21 30 March 2004 100 100 100 96 A B C D F Exam Scores 95 94 94 90 85 83 83 83 Mean 72 67 61 59 59 55 54 41 Mean = 78.5 Median = 83 Any Questions? Chapter 4 Earthquakes
Geology of the Hawaiian Islands Class 21 30 March 2004 100 100 100 96 A B C D F Exam Scores 95 94 94 90 85 83 83 83 Mean 72 67 61 59 59 55 54 41 Mean = 78.5 Median = 83 Any Questions? Chapter 4 Earthquakes
Chapter 4 Earthquakes and Tsunamis. Geology of the Hawaiian Islands. Any Questions? Class March Mean = 78.
 Geology of the Hawaiian Islands Class 21 30 March 2004 Any Questions? 100 100 100 96 A B C D F Exam Scores 95 94 94 90 85 83 83 83 Mean 72 67 61 59 59 55 54 41 Mean = 78.5 Median = 83 Chapter 4 Earthquakes
Geology of the Hawaiian Islands Class 21 30 March 2004 Any Questions? 100 100 100 96 A B C D F Exam Scores 95 94 94 90 85 83 83 83 Mean 72 67 61 59 59 55 54 41 Mean = 78.5 Median = 83 Chapter 4 Earthquakes
Ocean and Coastal Processes. Ocean Basins. Chapter 20. Ocean Basins and Plates. Ocean Terms. Sea Arch Bay-mouth Bar Spit Tombolo Coast.
 Chapter 20 Ocean Basins and Plates Ocean and Coastal Processes Tide Wave Height Length Period Base Refraction Tsunami Beach Sea stack Ocean Terms Sea Arch Bay-mouth Bar Spit Tombolo Coast Emergent Submergent
Chapter 20 Ocean Basins and Plates Ocean and Coastal Processes Tide Wave Height Length Period Base Refraction Tsunami Beach Sea stack Ocean Terms Sea Arch Bay-mouth Bar Spit Tombolo Coast Emergent Submergent
Magnitude 8.2 NORTHWEST OF IQUIQUE, CHILE
 An 8.2-magnitude earthquake struck off the coast of northern Chile, generating a local tsunami. The USGS reported the earthquake was centered 95 km (59 miles) northwest of Iquique at a depth of 20.1km
An 8.2-magnitude earthquake struck off the coast of northern Chile, generating a local tsunami. The USGS reported the earthquake was centered 95 km (59 miles) northwest of Iquique at a depth of 20.1km
RELATION BETWEEN RAYLEIGH WAVES AND UPLIFT OF THE SEABED DUE TO SEISMIC FAULTING
 13 th World Conference on Earthquake Engineering Vancouver, B.C., Canada August 1-6, 24 Paper No. 1359 RELATION BETWEEN RAYLEIGH WAVES AND UPLIFT OF THE SEABED DUE TO SEISMIC FAULTING Shusaku INOUE 1,
13 th World Conference on Earthquake Engineering Vancouver, B.C., Canada August 1-6, 24 Paper No. 1359 RELATION BETWEEN RAYLEIGH WAVES AND UPLIFT OF THE SEABED DUE TO SEISMIC FAULTING Shusaku INOUE 1,
S e i s m i c W a v e s
 Project Report S e i s m i c W a v e s PORTLAND STATE UNIVERSITY PHYSICS 213 SPRING TERM 2005 Instructor: Dr. Andres La Rosa Student Name: Prisciliano Peralta-Ramirez Table Of Contents 1. Cover Sheet 2.
Project Report S e i s m i c W a v e s PORTLAND STATE UNIVERSITY PHYSICS 213 SPRING TERM 2005 Instructor: Dr. Andres La Rosa Student Name: Prisciliano Peralta-Ramirez Table Of Contents 1. Cover Sheet 2.
Magnitude 7.7 QUEEN CHARLOTTE ISLANDS REGION
 A major 7.7 magnitude earthquake struck at 8:04 PM local time in western British Columbia, Canada. The epicenter is located on Moresby Island, the southern large island in the Queen Charlotte Islands region.
A major 7.7 magnitude earthquake struck at 8:04 PM local time in western British Columbia, Canada. The epicenter is located on Moresby Island, the southern large island in the Queen Charlotte Islands region.
Section Forces Within Earth. 8 th Grade Earth & Space Science - Class Notes
 Section 19.1 - Forces Within Earth 8 th Grade Earth & Space Science - Class Notes Stress and Strain Stress - is the total force acting on crustal rocks per unit of area (cause) Strain deformation of materials
Section 19.1 - Forces Within Earth 8 th Grade Earth & Space Science - Class Notes Stress and Strain Stress - is the total force acting on crustal rocks per unit of area (cause) Strain deformation of materials
Unit 7: Dynamic Planet: Earthquakes & Volcanoes
 Unit 7: Dynamic Planet: Earthquakes & Volcanoes Lecture 3 Objectives: E3.4C - Describe the effects of earthquakes and volcanic eruptions on humans. E3.4f - Explain why fences are offset after an earthquake
Unit 7: Dynamic Planet: Earthquakes & Volcanoes Lecture 3 Objectives: E3.4C - Describe the effects of earthquakes and volcanic eruptions on humans. E3.4f - Explain why fences are offset after an earthquake
Dynamics of Strongly Nonlinear Internal Solitary Waves in Shallow Water
 Dynamics of Strongly Nonlinear Internal Solitary Waves in Shallow Water By Tae-Chang Jo and Wooyoung Choi We study the dynamics of large amplitude internal solitary waves in shallow water by using a strongly
Dynamics of Strongly Nonlinear Internal Solitary Waves in Shallow Water By Tae-Chang Jo and Wooyoung Choi We study the dynamics of large amplitude internal solitary waves in shallow water by using a strongly
Model Equation, Stability and Dynamics for Wavepacket Solitary Waves
 p. 1/1 Model Equation, Stability and Dynamics for Wavepacket Solitary Waves Paul Milewski Mathematics, UW-Madison Collaborator: Ben Akers, PhD student p. 2/1 Summary Localized solitary waves exist in the
p. 1/1 Model Equation, Stability and Dynamics for Wavepacket Solitary Waves Paul Milewski Mathematics, UW-Madison Collaborator: Ben Akers, PhD student p. 2/1 Summary Localized solitary waves exist in the
1.3 Short Review: Preliminary results and observations of the December 2004 Great Sumatra Earthquake Kenji Hirata
 1.3 Short Review: Preliminary results and observations of the December 2004 Great Sumatra Earthquake Kenji Hirata We give a brief review about observations and preliminary results regarding the 2004 great
1.3 Short Review: Preliminary results and observations of the December 2004 Great Sumatra Earthquake Kenji Hirata We give a brief review about observations and preliminary results regarding the 2004 great
Math 575-Lecture 26. KdV equation. Derivation of KdV
 Math 575-Lecture 26 KdV equation We look at the KdV equations and the so-called integrable systems. The KdV equation can be written as u t + 3 2 uu x + 1 6 u xxx = 0. The constants 3/2 and 1/6 are not
Math 575-Lecture 26 KdV equation We look at the KdV equations and the so-called integrable systems. The KdV equation can be written as u t + 3 2 uu x + 1 6 u xxx = 0. The constants 3/2 and 1/6 are not
UNIT - 7 EARTHQUAKES
 UNIT - 7 EARTHQUAKES WHAT IS AN EARTHQUAKE An earthquake is a sudden motion or trembling of the Earth caused by the abrupt release of energy that is stored in rocks. Modern geologists know that most earthquakes
UNIT - 7 EARTHQUAKES WHAT IS AN EARTHQUAKE An earthquake is a sudden motion or trembling of the Earth caused by the abrupt release of energy that is stored in rocks. Modern geologists know that most earthquakes
The surface of the ocean floor is as varied as the land. The five major oceans, from largest to smallest, are
 11.1 Ocean Basins The surface of the ocean floor is as varied as the land. The five major oceans, from largest to smallest, are w the Pacific w the Atlantic w the Indian w the Southern w the Arctic The
11.1 Ocean Basins The surface of the ocean floor is as varied as the land. The five major oceans, from largest to smallest, are w the Pacific w the Atlantic w the Indian w the Southern w the Arctic The
NUMERICAL SIMULATION OF TSUNAMI PROPAGATION AND INUNDATION ALONG THE RAKHINE COAST AREAS IN MYANMAR
 NUMERICAL SIMULATION OF TSUNAMI PROPAGATION AND INUNDATION ALONG THE RAKHINE COAST AREAS IN MYANMAR Su Hninn Htwe Supervisor: Bunichiro SHIBAZAKI MEE12619 Yushiro FUJII ABSTRACT This study aimed to assess
NUMERICAL SIMULATION OF TSUNAMI PROPAGATION AND INUNDATION ALONG THE RAKHINE COAST AREAS IN MYANMAR Su Hninn Htwe Supervisor: Bunichiro SHIBAZAKI MEE12619 Yushiro FUJII ABSTRACT This study aimed to assess
Topic 5: The Dynamic Crust (workbook p ) Evidence that Earth s crust has shifted and changed in both the past and the present is shown by:
 Topic 5: The Dynamic Crust (workbook p. 65-85) Evidence that Earth s crust has shifted and changed in both the past and the present is shown by: --sedimentary horizontal rock layers (strata) are found
Topic 5: The Dynamic Crust (workbook p. 65-85) Evidence that Earth s crust has shifted and changed in both the past and the present is shown by: --sedimentary horizontal rock layers (strata) are found
Earthquake Investigation
 Exploration A Earthquake Investigation 1. Obtain a piece of plastic putty and knead it into a rectangular shape. 2. Push the ends of the putty toward the middle. Draw and describe what it looks like below.
Exploration A Earthquake Investigation 1. Obtain a piece of plastic putty and knead it into a rectangular shape. 2. Push the ends of the putty toward the middle. Draw and describe what it looks like below.
Effect of the Emperor seamounts on trans-oceanic propagation of the 2006 Kuril Island earthquake tsunami
 GEOPHYSICAL RESEARCH LETTERS, VOL. 35, L02611, doi:10.1029/2007gl032129, 2008 Effect of the Emperor seamounts on trans-oceanic propagation of the 2006 Kuril Island earthquake tsunami S. Koshimura, 1 Y.
GEOPHYSICAL RESEARCH LETTERS, VOL. 35, L02611, doi:10.1029/2007gl032129, 2008 Effect of the Emperor seamounts on trans-oceanic propagation of the 2006 Kuril Island earthquake tsunami S. Koshimura, 1 Y.
Lecture 11: Internal solitary waves in the ocean
 Lecture 11: Internal solitary waves in the ocean Lecturer: Roger Grimshaw. Write-up: Yiping Ma. June 19, 2009 1 Introduction In Lecture 6, we sketched a derivation of the KdV equation applicable to internal
Lecture 11: Internal solitary waves in the ocean Lecturer: Roger Grimshaw. Write-up: Yiping Ma. June 19, 2009 1 Introduction In Lecture 6, we sketched a derivation of the KdV equation applicable to internal
Chapter 17. Ocean and Coastal Processes
 Chapter 17 Ocean and Coastal Processes Ocean Basins and Plates Ocean Basins Ocean Basins are profoundly different from the continents. Ocean crust is thin and dense and young. New ocean crust is generated
Chapter 17 Ocean and Coastal Processes Ocean Basins and Plates Ocean Basins Ocean Basins are profoundly different from the continents. Ocean crust is thin and dense and young. New ocean crust is generated
Science Starter. Describe in your own words what an Earthquake is and what causes it. Answer The MSL
 Science Starter Describe in your own words what an Earthquake is and what causes it. Answer The MSL WHAT IS AN EARTHQUAKE AND HOW DO WE MEASURE THEM? Chapter 8, Section 8.1 & 8.2 Looking Back Deserts Wind-shaped
Science Starter Describe in your own words what an Earthquake is and what causes it. Answer The MSL WHAT IS AN EARTHQUAKE AND HOW DO WE MEASURE THEM? Chapter 8, Section 8.1 & 8.2 Looking Back Deserts Wind-shaped
The Whitham Equation. John D. Carter April 2, Based upon work supported by the NSF under grant DMS
 April 2, 2015 Based upon work supported by the NSF under grant DMS-1107476. Collaborators Harvey Segur, University of Colorado at Boulder Diane Henderson, Penn State University David George, USGS Vancouver
April 2, 2015 Based upon work supported by the NSF under grant DMS-1107476. Collaborators Harvey Segur, University of Colorado at Boulder Diane Henderson, Penn State University David George, USGS Vancouver
Name Date Class. radiate in all directions, carrying some of the. of plate boundaries have different usual patterns of.
 Chapter Outline Earthquakes CHAPTER 6 Lesson 1: Earthquakes and Plate Boundaries A. What is an earthquake? 1. A(n) is the rupture and sudden movement of rocks along a fault. A fault is a fracture surface
Chapter Outline Earthquakes CHAPTER 6 Lesson 1: Earthquakes and Plate Boundaries A. What is an earthquake? 1. A(n) is the rupture and sudden movement of rocks along a fault. A fault is a fracture surface
Three Fs of earthquakes: forces, faults, and friction. Slow accumulation and rapid release of elastic energy.
 Earthquake Machine Stick-slip: Elastic Rebound Theory Jerky motions on faults produce EQs Three Fs of earthquakes: forces, faults, and friction. Slow accumulation and rapid release of elastic energy. Three
Earthquake Machine Stick-slip: Elastic Rebound Theory Jerky motions on faults produce EQs Three Fs of earthquakes: forces, faults, and friction. Slow accumulation and rapid release of elastic energy. Three
Week: 4 5 Dates: 9/2 9/12 Unit: Plate Tectonics
 clementaged.weebly.com Name: ODD Period: Week: 4 5 Dates: 9/2 9/12 Unit: Plate Tectonics Monday Tuesday Wednesday Thursday Friday 1 No School 2 E 3 O *Vocabulary *Continental Drift Notes and Sea Floor
clementaged.weebly.com Name: ODD Period: Week: 4 5 Dates: 9/2 9/12 Unit: Plate Tectonics Monday Tuesday Wednesday Thursday Friday 1 No School 2 E 3 O *Vocabulary *Continental Drift Notes and Sea Floor
Preparation for Future Earthquake and Tsunami Hazards: Lessons Learned from the 2004 Sumatra-Andaman Earthquake and the Asian Tsunami
 First International Conference of Aceh and Indian Ocean Studies Organized by Asia Research Institute, National University of Singapore & Rehabilitation and Construction Executing Agency for Aceh and Nias
First International Conference of Aceh and Indian Ocean Studies Organized by Asia Research Institute, National University of Singapore & Rehabilitation and Construction Executing Agency for Aceh and Nias
RR#8 - Free Response
 Base your answers to questions 1 through 4 on the passage and the map below and on your knowledge of Earth science. The map indicates the epicenter (*) of a major earthquake that occurred at 38 N 142 E.
Base your answers to questions 1 through 4 on the passage and the map below and on your knowledge of Earth science. The map indicates the epicenter (*) of a major earthquake that occurred at 38 N 142 E.
Dynamic Crust Practice
 1. Base your answer to the following question on the cross section below and on your knowledge of Earth science. The cross section represents the distance and age of ocean-floor bedrock found on both sides
1. Base your answer to the following question on the cross section below and on your knowledge of Earth science. The cross section represents the distance and age of ocean-floor bedrock found on both sides
Goals of this Chapter
 Waves in the Atmosphere and Oceans Restoring Force Conservation of potential temperature in the presence of positive static stability internal gravity waves Conservation of potential vorticity in the presence
Waves in the Atmosphere and Oceans Restoring Force Conservation of potential temperature in the presence of positive static stability internal gravity waves Conservation of potential vorticity in the presence
The role of resonant wave interactions in the evolution of extreme wave events
 The role of resonant wave interactions in the evolution of extreme wave events Richard Gibson & Chris Swan Department of Civil and Environmental Engineering Imperial College London SW7 2AZ United Kingdom
The role of resonant wave interactions in the evolution of extreme wave events Richard Gibson & Chris Swan Department of Civil and Environmental Engineering Imperial College London SW7 2AZ United Kingdom
Local generation of internal solitary waves in an oceanic pycnocline
 Abstract Local generation of internal solitary waves in an oceanic pycnocline Nicolas Grisouard 1,2 and Chantal Staquet 1 1 Laboratoire des Ecoulements Géophysiques et Industriels, Grenoble, France 2 Courant
Abstract Local generation of internal solitary waves in an oceanic pycnocline Nicolas Grisouard 1,2 and Chantal Staquet 1 1 Laboratoire des Ecoulements Géophysiques et Industriels, Grenoble, France 2 Courant
The shallow water equations Lecture 8. (photo due to Clark Little /SWNS)
 The shallow water equations Lecture 8 (photo due to Clark Little /SWNS) The shallow water equations This lecture: 1) Derive the shallow water equations 2) Their mathematical structure 3) Some consequences
The shallow water equations Lecture 8 (photo due to Clark Little /SWNS) The shallow water equations This lecture: 1) Derive the shallow water equations 2) Their mathematical structure 3) Some consequences
9.3. Earthquakes. Earthquakes at Divergent Boundaries
 9.3 Earthquakes Preview the headings on these two pages. What can you say about where earthquakes occur? As the plates that make up Earth s crust move, the rough edges lock together. Over time, pressure
9.3 Earthquakes Preview the headings on these two pages. What can you say about where earthquakes occur? As the plates that make up Earth s crust move, the rough edges lock together. Over time, pressure
Sendai Earthquake NE Japan March 11, Some explanatory slides Bob Stern, Dave Scholl, others updated March
 Sendai Earthquake NE Japan March 11, 2011 Some explanatory slides Bob Stern, Dave Scholl, others updated March 14 2011 Earth has 11 large plates and many more smaller ones. Plates are 100-200 km thick
Sendai Earthquake NE Japan March 11, 2011 Some explanatory slides Bob Stern, Dave Scholl, others updated March 14 2011 Earth has 11 large plates and many more smaller ones. Plates are 100-200 km thick
NUMERICAL SIMULATIONS FOR TSUNAMI FORECASTING AT PADANG CITY USING OFFSHORE TSUNAMI SENSORS
 NUMERICAL SIMULATIONS FOR TSUNAMI FORECASTING AT PADANG CITY USING OFFSHORE TSUNAMI SENSORS Setyoajie Prayoedhie Supervisor: Yushiro FUJII MEE10518 Bunichiro SHIBAZAKI ABSTRACT We conducted numerical simulations
NUMERICAL SIMULATIONS FOR TSUNAMI FORECASTING AT PADANG CITY USING OFFSHORE TSUNAMI SENSORS Setyoajie Prayoedhie Supervisor: Yushiro FUJII MEE10518 Bunichiro SHIBAZAKI ABSTRACT We conducted numerical simulations
Internal Layers of the Earth
 Lecture #4 notes Geology 3950, Spring 2006; CR Stern Seismic waves, earthquake magnitudes and location, and internal earth structure (pages 28-95 in the 4 th edition and 28-32 and 50-106 in the 5 th edition)
Lecture #4 notes Geology 3950, Spring 2006; CR Stern Seismic waves, earthquake magnitudes and location, and internal earth structure (pages 28-95 in the 4 th edition and 28-32 and 50-106 in the 5 th edition)
LECTURE 6 EARTHQUAKES AS TSUNAMI SOURCES
 LECTURE 6 EARTHQUAKES AS TSUNAMI SOURCES Northwestern University, 2007 TSUNAMI GENERATION by EARTHQUAKE SOURCES CLASSICAL APPROA CH 1. Consider model of EarthquakeRupture 2. Compute Static Deformation
LECTURE 6 EARTHQUAKES AS TSUNAMI SOURCES Northwestern University, 2007 TSUNAMI GENERATION by EARTHQUAKE SOURCES CLASSICAL APPROA CH 1. Consider model of EarthquakeRupture 2. Compute Static Deformation
Algebraic geometry for shallow capillary-gravity waves
 Algebraic geometry for shallow capillary-gravity waves DENYS DUTYKH 1 Chargé de Recherche CNRS 1 Université de Savoie Laboratoire de Mathématiques (LAMA) 73376 Le Bourget-du-Lac France Seminar of Computational
Algebraic geometry for shallow capillary-gravity waves DENYS DUTYKH 1 Chargé de Recherche CNRS 1 Université de Savoie Laboratoire de Mathématiques (LAMA) 73376 Le Bourget-du-Lac France Seminar of Computational
The Indian Ocean. Copyright 2010 LessonSnips
 The Indian Ocean One of the five major geographic divisions of the world s ocean, the Indian Ocean is located in the Eastern Hemisphere. The Indian Ocean is bounded by three continents: Africa to the west,
The Indian Ocean One of the five major geographic divisions of the world s ocean, the Indian Ocean is located in the Eastern Hemisphere. The Indian Ocean is bounded by three continents: Africa to the west,
Earthquakes & Volcanoes
 Earthquakes & Volcanoes Geology - the study of solid Earth, the rocks of which it is composed, and the processes by which they change geo = Earth; ology = study of Earth s Layers Plate Tectonics - the
Earthquakes & Volcanoes Geology - the study of solid Earth, the rocks of which it is composed, and the processes by which they change geo = Earth; ology = study of Earth s Layers Plate Tectonics - the
Week: 4 5 Dates: 9/8 9/12 Unit: Plate Tectonics
 clementaged.weebly.com Name: ODD Period: Week: 4 5 Dates: 9/8 9/12 Unit: Plate Tectonics Monday Tuesday Wednesday Thursday Friday 7 No School 8 E 9 O *Vocabulary *Frayer Vocab *Continental Drift Notes
clementaged.weebly.com Name: ODD Period: Week: 4 5 Dates: 9/8 9/12 Unit: Plate Tectonics Monday Tuesday Wednesday Thursday Friday 7 No School 8 E 9 O *Vocabulary *Frayer Vocab *Continental Drift Notes
Dangerous tsunami threat off U.S. West Coast
 Earthquakes Ch. 12 Dangerous tsunami threat off U.S. West Coast Earthquakes What is an Earthquake? It s the shaking and trembling of the Earth s crust due to plate movement. The plates move, rocks along
Earthquakes Ch. 12 Dangerous tsunami threat off U.S. West Coast Earthquakes What is an Earthquake? It s the shaking and trembling of the Earth s crust due to plate movement. The plates move, rocks along
Plate Tectonics. The Theory of Plate Tectonics. The Plate Tectonics Theory. 62 Plate Tectonics Reading Essentials
 CHAPTER 4 LESSON 3 Tectonics The Theory of Tectonics Key Concepts What is the theory of plate tectonics? What are the three types of plate boundaries? Why do tectonic plates move? What do you think? Read
CHAPTER 4 LESSON 3 Tectonics The Theory of Tectonics Key Concepts What is the theory of plate tectonics? What are the three types of plate boundaries? Why do tectonic plates move? What do you think? Read
General-Circulation- Model System for Global Tsunami Warning
 A Coupled Teleseismic Ocean-General General-Circulation- Model System for Global Tsunami Warning Y. Tony Song Jet Propulsion Laboratory, California Institute of Technology Contents:. Tsunami formation
A Coupled Teleseismic Ocean-General General-Circulation- Model System for Global Tsunami Warning Y. Tony Song Jet Propulsion Laboratory, California Institute of Technology Contents:. Tsunami formation
How Will Melting Ice Sheets Affect Us?
 PASSAGE 4 How Will Melting Ice Sheets Affect Us? Variation is normal. During the last ice age, for example, ice sheets also covered much of North America and Scandinavia. Why is what s happening now different
PASSAGE 4 How Will Melting Ice Sheets Affect Us? Variation is normal. During the last ice age, for example, ice sheets also covered much of North America and Scandinavia. Why is what s happening now different
Earthquake. What is it? Can we predict it?
 Earthquake What is it? Can we predict it? What is an earthquake? Earthquake is the vibration (shaking) and/or displacement of the ground produced by the sudden release of energy. Rocks under stress accumulate
Earthquake What is it? Can we predict it? What is an earthquake? Earthquake is the vibration (shaking) and/or displacement of the ground produced by the sudden release of energy. Rocks under stress accumulate
CHAPTER 1 BASIC SEISMOLOGY AND EARTHQUAKE TERMINOLGY. Earth Formation Plate Tectonics Sources of Earthquakes...
 CHAPTER 1 BASIC SEISMOLOGY AND EARTHQUAKE TERMINOLGY Earth Formation... 1-2 Plate Tectonics... 1-2 Sources of Earthquakes... 1-3 Earth Faults... 1-4 Fault Creep... 1-5 California Faults... 1-6 Earthquake
CHAPTER 1 BASIC SEISMOLOGY AND EARTHQUAKE TERMINOLGY Earth Formation... 1-2 Plate Tectonics... 1-2 Sources of Earthquakes... 1-3 Earth Faults... 1-4 Fault Creep... 1-5 California Faults... 1-6 Earthquake
Earthquakes and Earth s Chapter. Interior
 Earthquakes and Earth s Chapter Interior 8.1 What Is an Earthquake? An earthquake is the vibration of Earth produced by the rapid release of energy Focus and Epicenter Focus is the point within Earth
Earthquakes and Earth s Chapter Interior 8.1 What Is an Earthquake? An earthquake is the vibration of Earth produced by the rapid release of energy Focus and Epicenter Focus is the point within Earth
VALIDATION OF TSUNAMI INUNDATION MODELING FOR THE 2004 SUMATRA-ANDAMAN EARTHQUAKE FOR MAKING HAZARD MAPS IN PENANG AND LANGKAWI, MALAYSIA
 Synopses of Master Papers Bulletin of IISEE, 47, 11-16, 013 VALIDATION OF TSUNAMI INUNDATION MODELING FOR THE 004 SUMATRA-ANDAMAN EARTHQUAKE FOR MAKING HAZARD MAPS IN PENANG AND LANGKAWI, MALAYSIA Noor
Synopses of Master Papers Bulletin of IISEE, 47, 11-16, 013 VALIDATION OF TSUNAMI INUNDATION MODELING FOR THE 004 SUMATRA-ANDAMAN EARTHQUAKE FOR MAKING HAZARD MAPS IN PENANG AND LANGKAWI, MALAYSIA Noor
Prentice Hall EARTH SCIENCE
 Prentice Hall EARTH SCIENCE Tarbuck Lutgens Chapter 8 Earthquakes and Earth s Interior 8.1 What Is an Earthquake? Earthquakes An earthquake is the vibration of Earth produced by the rapid release of energy
Prentice Hall EARTH SCIENCE Tarbuck Lutgens Chapter 8 Earthquakes and Earth s Interior 8.1 What Is an Earthquake? Earthquakes An earthquake is the vibration of Earth produced by the rapid release of energy
FORCES ON EARTH. An investigation into how Newton s Laws of Motion are applied to the tectonic activity on Earth.
 FORCES ON EARTH An investigation into how Newton s Laws of Motion are applied to the tectonic activity on Earth. GEOLOGY Geologists scientists who study the forces that make and shape the Earth Geologists
FORCES ON EARTH An investigation into how Newton s Laws of Motion are applied to the tectonic activity on Earth. GEOLOGY Geologists scientists who study the forces that make and shape the Earth Geologists
Finding an Earthquake Epicenter Pearson Education, Inc.
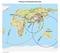 Finding an Earthquake Epicenter Measuring the Size of Earthquakes Two measurements that describe the size of an earthquake are: 1. Intensity a measure of the degree of earthquake shaking at a given locale
Finding an Earthquake Epicenter Measuring the Size of Earthquakes Two measurements that describe the size of an earthquake are: 1. Intensity a measure of the degree of earthquake shaking at a given locale
Fundamentals of Fluid Dynamics: Waves in Fluids
 Fundamentals of Fluid Dynamics: Waves in Fluids Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI (after: D.J. ACHESON s Elementary Fluid Dynamics ) bluebox.ippt.pan.pl/ tzielins/ Institute
Fundamentals of Fluid Dynamics: Waves in Fluids Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI (after: D.J. ACHESON s Elementary Fluid Dynamics ) bluebox.ippt.pan.pl/ tzielins/ Institute
Section 19.1: Forces Within Earth Section 19.2: Seismic Waves and Earth s Interior Section 19.3: Measuring and Locating.
 CH Earthquakes Section 19.1: Forces Within Earth Section 19.2: Seismic Waves and Earth s Interior Section 19.3: Measuring and Locating Earthquakes Section 19.4: Earthquakes and Society Section 19.1 Forces
CH Earthquakes Section 19.1: Forces Within Earth Section 19.2: Seismic Waves and Earth s Interior Section 19.3: Measuring and Locating Earthquakes Section 19.4: Earthquakes and Society Section 19.1 Forces
What is a tsunami? Capital Regional District Tsunami Frequently Asked Questions (FAQ s) Tsunami (soo-nah-mee)
 Tsunami (soo-nah-mee) Tsunamis (Japanese translation harbour wave ) are waves with a great distance between crests, and are caused by any widespread, sudden movement of large volumes of water. The tsunami
Tsunami (soo-nah-mee) Tsunamis (Japanese translation harbour wave ) are waves with a great distance between crests, and are caused by any widespread, sudden movement of large volumes of water. The tsunami
Geology Topics. Unit 6 Notes
 Geology Topics Unit 6 Notes Composition of the Earth Earth is layered due to density differences. Crust thin outer layer, solid, made up of continental and oceanic crust Mantle rocky layer below the crust
Geology Topics Unit 6 Notes Composition of the Earth Earth is layered due to density differences. Crust thin outer layer, solid, made up of continental and oceanic crust Mantle rocky layer below the crust
Unit 1: Water Systems on Earth Chapter 2
 Unit 1: Water Systems on Earth Chapter 2 Create a mind map with the driving question, Why are Oceans Important? Remember: Why are oceans so important? Why are oceans so important? Primary water source
Unit 1: Water Systems on Earth Chapter 2 Create a mind map with the driving question, Why are Oceans Important? Remember: Why are oceans so important? Why are oceans so important? Primary water source
What is an Earthquake?
 Earthquakes What is an Earthquake? Earthquake - sometimes violent shaking of ground caused by movement of Earth s tectonic plates; creates seismic waves Often followed by smaller earthquakes (aftershocks);
Earthquakes What is an Earthquake? Earthquake - sometimes violent shaking of ground caused by movement of Earth s tectonic plates; creates seismic waves Often followed by smaller earthquakes (aftershocks);
Seismic Activity near the Sunda and Andaman Trenches in the Sumatra Subduction Zone
 IJMS 2017 vol. 4 (2): 49-54 International Journal of Multidisciplinary Studies (IJMS) Volume 4, Issue 2, 2017 DOI: http://doi.org/10.4038/ijms.v4i2.22 Seismic Activity near the Sunda and Andaman Trenches
IJMS 2017 vol. 4 (2): 49-54 International Journal of Multidisciplinary Studies (IJMS) Volume 4, Issue 2, 2017 DOI: http://doi.org/10.4038/ijms.v4i2.22 Seismic Activity near the Sunda and Andaman Trenches
Dynamic Earth A B1. Which type of plate boundary is located at the Jordan Fault? (1) divergent (3) convergent (2) subduction (4) transform
 Dynamic Earth A B1 1. The edges of most lithospheric plates are characterized by (1) reversed magnetic orientation (2) unusually rapid radioactive decay (3) frequent volcanic activity (4) low P-wave and
Dynamic Earth A B1 1. The edges of most lithospheric plates are characterized by (1) reversed magnetic orientation (2) unusually rapid radioactive decay (3) frequent volcanic activity (4) low P-wave and
An Introduction to the Seafloor and Plate Tectonics 1
 An Introduction to the Seafloor and Plate Tectonics 1 Objectives 1) Investigate the components of the lithosphere and lithospheric plates. 2) Identify the associations among various seafloor features,
An Introduction to the Seafloor and Plate Tectonics 1 Objectives 1) Investigate the components of the lithosphere and lithospheric plates. 2) Identify the associations among various seafloor features,
A. rift valley B. deep trench C. volcanic cone D. uplifted mountain. A. a volcanic island arc B. a large watershed area
 DC Practice Test Dynamic Crust PRCTICE TEST Zimm's Earth Science 2013 1. Which feature would most likely be forming at converging continental tectonic plate boundaries?. rift valley. deep trench C.
DC Practice Test Dynamic Crust PRCTICE TEST Zimm's Earth Science 2013 1. Which feature would most likely be forming at converging continental tectonic plate boundaries?. rift valley. deep trench C.
What causes a tsunami?
 Listen: Have this page read to you [1] Have this page read to you [2] A tsunami is a series of waves in the sea caused by a movement on the sea floor. New Zealand is at risk from tsunami because it has
Listen: Have this page read to you [1] Have this page read to you [2] A tsunami is a series of waves in the sea caused by a movement on the sea floor. New Zealand is at risk from tsunami because it has
Concepts from linear theory Extra Lecture
 Concepts from linear theory Extra Lecture Ship waves from WW II battleships and a toy boat. Kelvin s (1887) method of stationary phase predicts both. Concepts from linear theory A. Linearize the nonlinear
Concepts from linear theory Extra Lecture Ship waves from WW II battleships and a toy boat. Kelvin s (1887) method of stationary phase predicts both. Concepts from linear theory A. Linearize the nonlinear
Generation of undular bores and solitary wave trains in fully nonlinear shallow water theory
 Generation of undular bores and solitary wave trains in fully nonlinear shallow water theory Gennady El 1, Roger Grimshaw 1 and Noel Smyth 2 1 Loughborough University, UK, 2 University of Edinburgh, UK
Generation of undular bores and solitary wave trains in fully nonlinear shallow water theory Gennady El 1, Roger Grimshaw 1 and Noel Smyth 2 1 Loughborough University, UK, 2 University of Edinburgh, UK
Lab 2: Plate tectonics
 Geology 101 Name(s): Lab 2: Plate tectonics Plate tectonics is the theory that is used to explain geological phenomena worldwide. For this reason, most of the useful maps that illustrate plate tectonics
Geology 101 Name(s): Lab 2: Plate tectonics Plate tectonics is the theory that is used to explain geological phenomena worldwide. For this reason, most of the useful maps that illustrate plate tectonics
Disclaimer. This report was compiled by an ADRC visiting researcher (VR) from ADRC member countries.
 Disclaimer This report was compiled by an ADRC visiting researcher (VR) from ADRC member countries. The views expressed in the report do not necessarily reflect the views of the ADRC. The boundaries and
Disclaimer This report was compiled by an ADRC visiting researcher (VR) from ADRC member countries. The views expressed in the report do not necessarily reflect the views of the ADRC. The boundaries and
LOCAL TSUNAMIS: CHALLENGES FOR PREPAREDNESS AND EARLY WARNING
 LOCAL TSUNAMIS: CHALLENGES FOR PREPAREDNESS AND EARLY WARNING HARALD SPAHN 1 1 German Technical Cooperation International Services, Jakarta, Indonesia ABSTRACT: Due to the threat of local tsunamis warning
LOCAL TSUNAMIS: CHALLENGES FOR PREPAREDNESS AND EARLY WARNING HARALD SPAHN 1 1 German Technical Cooperation International Services, Jakarta, Indonesia ABSTRACT: Due to the threat of local tsunamis warning
