Fundamentals of Fluid Dynamics: Waves in Fluids
|
|
|
- Holly Angelica Copeland
- 5 years ago
- Views:
Transcription
1 Fundamentals of Fluid Dynamics: Waves in Fluids Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI (after: D.J. ACHESON s Elementary Fluid Dynamics ) bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research of the Polish Academy of Sciences Warsaw Poland
2 Outline 1 Introduction The notion of wave Basic wave phenomena Mathematical description of a traveling wave
3 Outline 1 Introduction The notion of wave Basic wave phenomena Mathematical description of a traveling wave 2 Water waves Surface waves on deep water Dispersion and the group velocity Capillary waves Shallow-water finite-amplitude waves
4 Outline 1 Introduction The notion of wave Basic wave phenomena Mathematical description of a traveling wave 2 Water waves Surface waves on deep water Dispersion and the group velocity Capillary waves Shallow-water finite-amplitude waves 3 Sound waves Introduction Acoustic wave equation The speed of sound Sub- and supersonic flow
5 Outline 1 Introduction The notion of wave Basic wave phenomena Mathematical description of a traveling wave 2 Water waves Surface waves on deep water Dispersion and the group velocity Capillary waves Shallow-water finite-amplitude waves 3 Sound waves Introduction Acoustic wave equation The speed of sound Sub- and supersonic flow
6 The notion of wave What is a wave? A wave is the transport of a disturbance (or energy, or piece of information) in space not associated with motion of the medium occupying this space as a whole. (Except that electromagnetic waves require no medium!!!) The transport is at finite speed. The shape or form of the disturbance is arbitrary. The disturbance moves with respect to the medium.
7 The notion of wave What is a wave? A wave is the transport of a disturbance (or energy, or piece of information) in space not associated with motion of the medium occupying this space as a whole. (Except that electromagnetic waves require no medium!!!) The transport is at finite speed. The shape or form of the disturbance is arbitrary. The disturbance moves with respect to the medium. Two general classes of wave motion are distinguished: 1 longitudinal waves the disturbance moves parallel to the direction of propagation. Examples: sound waves, compressional elastic waves (P-waves in geophysics);
8 The notion of wave What is a wave? A wave is the transport of a disturbance (or energy, or piece of information) in space not associated with motion of the medium occupying this space as a whole. (Except that electromagnetic waves require no medium!!!) The transport is at finite speed. The shape or form of the disturbance is arbitrary. The disturbance moves with respect to the medium. Two general classes of wave motion are distinguished: 1 longitudinal waves the disturbance moves parallel to the direction of propagation. Examples: sound waves, compressional elastic waves (P-waves in geophysics); 2 transverse waves the disturbance moves perpendicular to the direction of propagation. Examples: waves on a string or membrane, shear waves (S-waves in geophysics), water waves, electromagnetic waves.
9 Basic wave phenomena reflection change of wave direction from hitting a reflective surface, refraction change of wave direction from entering a new medium, diffraction wave circular spreading from entering a small hole (of the wavelength-comparable size), or wave bending around small obstacles, interference superposition of two waves that come into contact with each other, dispersion wave splitting up by frequency, rectilinear propagation the movement of light wave in a straight line.
10 Basic wave phenomena reflection change of wave direction from hitting a reflective surface, refraction change of wave direction from entering a new medium, diffraction wave circular spreading from entering a small hole (of the wavelength-comparable size), or wave bending around small obstacles, interference superposition of two waves that come into contact with each other, dispersion wave splitting up by frequency, rectilinear propagation the movement of light wave in a straight line. Standing wave A standing wave, also known as a stationary wave, is a wave that remains in a constant position. This phenomenon can occur: when the medium is moving in the opposite direction to the wave, (in a stationary medium:) as a result of interference between two waves travelling in opposite directions.
11 Mathematical description of a harmonic wave T = 2π ω λ = 2π k A t A x Traveling waves Simple wave or traveling wave, sometimes also called progressive wave, is a disturbance that varies both with time t and distance x in the following way: u(x, t) = A(x, t) cos ( ) k x ω t + θ 0 = A(x, t) sin ( k x ω t + θ 0 ± π 2 }{{} θ 0 where A is the amplitude, ω and k denote the angular frequency and wavenumber, and θ 0 (or θ 0 ) is the initial phase. )
12 Mathematical description of a harmonic wave T = 2π ω λ = 2π k A t A x Traveling waves u(x, t) = A(x, t) cos ( k x ω t + θ 0 ) = A(x, t) sin ( k x ω t + θ 0 ± π 2 }{{} θ 0 Amplitude A [ e.g. m, Pa, V/m ] a measure of the maximum disturbance in the medium during one wave cycle (the maximum distance from the highest point of the crest to the equilibrium). Phase θ = k x ω t + θ 0 [rad], where θ 0 is the initial phase (shift), often ambiguously, called the phase. )
13 Mathematical description of a harmonic wave T = 2π ω A t Period T [s] the time for one complete cycle for an oscillation of a wave. Frequency f [Hz] the number of periods per unit time. Frequency and angular frequency The frequency f [Hz] represents the number of periods per unit time f = 1 T. The angular frequency ω [Hz] represents the frequency in terms of radians per second. It is related to the frequency by ω = 2π T = 2π f.
14 Mathematical description of a harmonic wave λ = 2π k A x Wavelength λ [m] the distance between two sequential crests (or troughs). Wavenumber and angular wavenumber The wavenumber is the spatial analogue of frequency, that is, it is the measurement of the number of repeating units of a propagating wave (the number of times a wave has the same phase) per unit of space. Application of a Fourier transformation on data as a function of time yields a frequency spectrum; application on data as a function of position yields a wavenumber spectrum. [ The angular wavenumber k wave-number, is defined as 1 m ], often misleadingly abbreviated as k = 2π λ.
15 Mathematical description of a harmonic wave There are two velocities that are associated with waves: 1 Phase velocity the rate at which the wave propagates: c = ω k = λ f.
16 Mathematical description of a harmonic wave There are two velocities that are associated with waves: 1 Phase velocity the rate at which the wave propagates: c = ω k = λ f. 2 Group velocity the velocity at which variations in the shape of the wave s amplitude (known as the modulation or envelope of the wave) propagate through space: c g = dω dk. This is (in most cases) the signal velocity of the waveform, that is, the rate at which information or energy is transmitted by the wave. However, if the wave is travelling through an absorptive medium, this does not always hold.
17 Outline 1 Introduction The notion of wave Basic wave phenomena Mathematical description of a traveling wave 2 Water waves Surface waves on deep water Dispersion and the group velocity Capillary waves Shallow-water finite-amplitude waves 3 Sound waves Introduction Acoustic wave equation The speed of sound Sub- and supersonic flow
18 Surface waves on deep water Consider two-dimensional water waves: u = [ u(x, y, t), v(x, y, t), 0 ]. v Suppose that the flow is irrotational: u = 0. x y Therefore, there exists a velocity potential φ(x, y, t) so that u = φ x, v = φ y. The fluid is incompressible, so by the virtue of the incompressibility condition, u = 0, the velocity potential φ will satisfy Laplace s equation 2 φ x + 2 φ 2 y = 0. 2
19 Surface waves on deep water Consider two-dimensional water waves: u = [ u(x, y, t), v(x, y, t), 0 ]. v Suppose that the flow is irrotational: u = 0. x y Therefore, there exists a velocity potential φ(x, y, t) so that u = φ x, v = φ y. The fluid is incompressible, so φ will satisfy Laplace s equation Free surface 2 φ x φ y 2 = 0. The fluid motion arises from a deformation of the water surface. The equation of this free surface is denoted by y = η(x, t).
20 Surface waves on deep water Kinematic condition at the free surface Kinematic condition at the free surface: Fluid particles on the surface must remain on the surface. The kinematic condition entails that F(x, y, t) = y η(x, t) remains constant (in fact, zero) for any particular particle on the free surface which means that DF Dt = F t and this is equivalent to + ( u ) F = 0 on y = η(x, t), η t + u η = v on y = η(x, t). x
21 Surface waves on deep water Pressure condition at the free surface Pressure condition at the free surface: The fluid is inviscid (by assumption), so the condition at the free surface is simply that the pressure there is equal to the atmospheric pressure p 0: p = p 0 on y = η(x, t).
22 Surface waves on deep water Pressure condition at the free surface Pressure condition at the free surface: The fluid is inviscid (by assumption), so the condition at the free surface is simply that the pressure there is equal to the atmospheric pressure p 0: p = p 0 on y = η(x, t). Bernoulli s equation for unsteady irrotational flow If the flow is irrotational (so u = φ and u = 0), then, by integrating (over the space domain) the Euler s momentum equation: ( φ p = t ϱ + 1 ) 2 u2 + χ, the Bernoulli s equation is obtained φ t + p ϱ u2 + χ = G(t). Here, χ is the gravity potential (in the present context χ = g y where g is the gravity acceleration) and G(t) is an arbitrary function of time alone (a constant of integration).
23 Surface waves on deep water Pressure condition at the free surface Pressure condition at the free surface: The fluid is inviscid (by assumption), so the condition at the free surface is simply that the pressure there is equal to the atmospheric pressure p 0: p = p 0 on y = η(x, t). Bernoulli s equation for unsteady irrotational flow If the flow is irrotational (so u = φ and u = 0), then, by integrating (over the space domain) the Euler s momentum equation: ( φ p = t ϱ + 1 ) 2 u2 + χ, the Bernoulli s equation is obtained φ t + p ϱ u2 + g y = G(t). Here, G(t) is an arbitrary function of time alone (a constant of integration). Now, by choosing G(t) in a convenient manner, G(t) = p 0 ϱ, the pressure condition may be written as: φ + 1 ( u 2 + v 2) + g η = 0 on y = η(x, t). t 2
24 Surface waves on deep water Small amplitude waves: the linearized surface conditions Small-amplitude waves The free surface displacement η(x, t) and the fluid velocities u, v are small. Linearization of the kinematic condition v = η + u η t }{{ x } small v(x, η, t) = η t Taylor series v(x, 0, t) + η v (x, 0, t) + = η y t }{{} small v= φ y φ y = η t v(x, 0, t) = η t on y = 0. Linearization of the pressure condition φ + 1 ( u 2 + v 2) φ +g η = 0 + g η = 0 on y = 0. t } 2 {{} t small
25 Surface waves on deep water Dispersion relation and travelling wave solution A sinusoidal travelling wave solution The free surface is of the form η = A cos(k x ω t), where A is the amplitude of the surface displacement, ω is the circular frequency, and k is the circular wavenumber.
26 Surface waves on deep water Dispersion relation and travelling wave solution A sinusoidal travelling wave solution The free surface is of the form η = A cos(k x ω t), where A is the amplitude of the surface displacement, ω is the circular frequency, and k is the circular wavenumber. The corresponding velocity potential is φ = q(y) sin(k x ω t). It satisfies the Laplace s equation, 2 φ x φ y 2 = 0. Therefore, q(y) must satisfy q k 2 q = 0, the general solution of which is q = C exp(k y) + D exp( k y). For deep water waves D = 0 (if k > 0 which may be assumed without loss of generality) in order that the velocity be bounded as y.
27 Surface waves on deep water Dispersion relation and travelling wave solution A sinusoidal travelling wave solution The free surface is of the form η = A cos(k x ω t), where A is the amplitude of the surface displacement, ω is the circular frequency, and k is the circular wavenumber. The corresponding velocity potential (for deep water waves) is φ = C exp(k y) sin(k x ω t).
28 Surface waves on deep water Dispersion relation and travelling wave solution A sinusoidal travelling wave solution The free surface is of the form η = A cos(k x ω t), where A is the amplitude of the surface displacement, ω is the circular frequency, and k is the circular wavenumber. The corresponding velocity potential (for deep water waves) is φ = C exp(k y) sin(k x ω t). Now, the (linearized) free surface conditions yield what follows: 1 the kinematic condition ( φ y = η on y = 0): t C k = A ω φ = A ω exp(k y) sin(k x ω t), k 2 the pressure condition ( φ + g η = 0 on y = 0): t C ω + g A = 0 ω 2 = g k. (dispersion relation!)
29 Surface waves on deep water Particle paths The fluid velocity components: u = A ω exp(k y) cos(k x ω t), v = A ω exp(k y) sin(k x ω t).
30 Surface waves on deep water Particle paths The fluid velocity components: u = A ω exp(k y) cos(k x ω t), v = A ω exp(k y) sin(k x ω t). Particle paths Any particle departs only a small amount (X, Y) from its mean position (x, y). Therefore, its position as a function of time may be found by integrating u = dx dt and v = dy dt ; whence: X(t) = A exp(k y) sin(k x ω t), Y(t) = A exp(k y) cos(k x ω t).
31 Surface waves on deep water Particle paths The fluid velocity components: u = A ω exp(k y) cos(k x ω t), v = A ω exp(k y) sin(k x ω t). Particle paths Any particle departs only a small amount (X, Y) from its mean position (x, y). Therefore, its position as a function of time may be found by integrating u = dx dt and v = dy dt ; whence: X(t) = A exp(k y) sin(k x ω t), Y(t) = A exp(k y) cos(k x ω t). Particle paths are circular. The radius of the path circles, A exp(k y), decrease exponentially with depth. So do the fluid velocities. Virtually all the energy of a surface water wave is contained within half a wavelength below the surface.
32 Surface waves on deep water Particle paths Particle paths are circular. The radius of the path circles, A exp(k y), decrease exponentially with depth. So do the fluid velocities. Virtually all the energy of a surface water wave is contained within half a wavelength below the surface.
33 Surface waves on deep water Effects of finite depth Effects of finite depth If the fluid is bonded below by a rigid plane y = h, so that v = φ y = 0 at y = h, the dispersion relation and the phase speed are as follows: ω 2 = g k tanh(k h), c 2 = g tanh(k h). k
34 Surface waves on deep water Effects of finite depth Effects of finite depth If the fluid is bonded below by a rigid plane y = h, so that v = φ y = 0 at y = h, the dispersion relation and the phase speed are as follows: ω 2 = g k tanh(k h), c 2 = g tanh(k h). k There are two limit cases: 1 h λ (infinite depth): k h = 2π h λ is large and tanh(k h) 1, so c 2 = g k. In practice, this is a good approximation if h > 1 3 λ. 2 h λ/2π (shallow water): k h 1 and tanh(k h) k h, so c 2 = g h, which means that c is independent of k in this limit. Thus, the gravity waves in shallow water are non-dispersive.
35 Surface waves on deep water Effects of finite depth Effects of finite depth If the fluid is bonded below by a rigid plane y = h, the dispersion relation and the phase speed are as follows: ω 2 = g k tanh(k h), c 2 = g tanh(k h). k c infinite depth g h shallow water uniform depth h 3h 10h λ
36 Dispersion and the group velocity Dispersion of waves Dispersion of waves is the phenomenon that the phase velocity of a wave depends on its frequency.
37 Dispersion and the group velocity Dispersion of waves Dispersion of waves is the phenomenon that the phase velocity of a wave depends on its frequency. There are generally two sources of dispersion: 1 the material dispersion comes from a frequency-dependent response of a material to waves 2 the waveguide dispersion occurs when the speed of a wave in a waveguide depends on its frequency for geometric reasons, independent of any frequency-dependence of the materials from which it is constructed.
38 Dispersion and the group velocity Dispersion of waves Dispersion of waves is the phenomenon that the phase velocity of a wave depends on its frequency. There are generally two sources of dispersion: 1 the material dispersion comes from a frequency-dependent response of a material to waves 2 the waveguide dispersion occurs when the speed of a wave in a waveguide depends on its frequency for geometric reasons, independent of any frequency-dependence of the materials from which it is constructed. Dispersion relation ω = ω(k) = c(k) k, c = c(k) = ω(k) k If ω(k) is a linear function of k then c is constant and the medium is non-dispersive..
39 Dispersion and the group velocity Dispersion of waves Dispersion of waves is the phenomenon that the phase velocity of a wave depends on its frequency. Dispersion relation ω = ω(k) = c(k) k, c = c(k) = ω(k) k If ω(k) is a linear function of k then c is constant and the medium is non-dispersive. deep water waves: ω = g k, c = g. k finite depth waves: ω = g k tanh(k h), c = g tanh(k h). k shallow water waves: ω = g h k, c = g h non-dispersive!.
40 Dispersion and the group velocity Dispersion relation ω = ω(k) = c(k) k, c = c(k) = ω(k) k If ω(k) is a linear function of k then c is constant and the medium is non-dispersive. deep water waves: ω = g k, c = g. k finite depth waves: ω = g k tanh(k h), c = g tanh(k h). k shallow water waves: ω = g h k, c = g h non-dispersive! Group and phase velocity c g = dω dk, c = ω k. In dispersive systems both velocities are different and frequency-dependent (i.e., wavenumber-dependent): c g = c g(k) and c = c(k). In non-dispersive systems they are equal and constant: c g = c..
41 Dispersion and the group velocity Important properties of the group velocity: 1 At this velocity the isolated wave packet travels as a whole. Discussion for a wave packet: for k in the neighbourhood of k 0 ω(k) ω(k) + (k k 0) c g, where c g = dω, dk k=k0 and ω(k) = 0 outside the neighbourhood; the Fourier integral equals [ η(x, t) = Re a(k) exp ( i (k x ω t) ) ] dk (for a general disturbance) a pure harmonic wave [ { ( }}{ Re exp i ( k 0 x ω(k 0 ) t )) a function of (x c g t) {}}{ a(k) exp ( i (k k 0 ) (x c g t) ) ] dk.
42 Dispersion and the group velocity Important properties of the group velocity: 1 At this velocity the isolated wave packet travels as a whole. 2 The energy is transported at the group velocity (by waves of a given wavelength).
43 Dispersion and the group velocity Important properties of the group velocity: 1 At this velocity the isolated wave packet travels as a whole. 2 The energy is transported at the group velocity. 3 One must travel at the group velocity to see the waves of the same wavelength. A slowly varying wavetrain can be written as η(x, t) = Re [ A(x, t) exp ( i θ(x, t) )], where the phase function θ(x, t) describes the oscillatory aspect of the wave, while A(x, t) describes the gradual modulation of its amplitude. The local wavenumber and frequency are defined by k = θ x, ω = θ t For purely sinusoidal wave θ = k x ω t, where k and ω are constants..
44 Dispersion and the group velocity Important properties of the group velocity: 1 At this velocity the isolated wave packet travels as a whole. 2 The energy is transported at the group velocity. 3 One must travel at the group velocity to see the waves of the same wavelength. The local wavenumber and frequency are defined by k = θ x, ω = θ t For purely sinusoidal wave θ = k x ω t, where k and ω are constants. In general, k and ω are functions of x and t. It follows immediately that k t + ω k = 0 x t + dω dk. k x = k k + cg(k) t x = 0 which means that k(x, t) is constant for an observer moving with the velocity c g(k).
45 Capillary waves Surface tension [ A surface tension force T N m ] is a force per unit length, directed tangentially to the surface, acting on a line drawn parallel to the wavecrests.
46 Capillary waves Surface tension [ A surface tension force T N m ] is a force per unit length, directed tangentially to the surface, acting on a line drawn parallel to the wavecrests. The vertical component of surface tension force equals T η s, where s denotes the distance along the surface. For small wave amplitudes δs δx, and then T η s T η x. y η(x) δs T η s δx δη T x
47 Capillary waves Surface tension [ A surface tension force T N m ] is a force per unit length, directed tangentially to the surface, acting on a line drawn parallel to the wavecrests. The vertical component of surface tension force equals T η s, where s denotes the distance along the surface. For small wave amplitudes δs δx, and then T η s T η x. y η(x) δs T η s A small portion of surface of length δx will experience surface tension at both ends, so the net upward force on it will be T η x T η x+δx x = T 2 η x x δx 2 Therefore, an upward force per unit area of surface is T 2 η x 2. δx δη T x
48 Capillary waves Local equilibrium at the free surface The net upward force per unit area of surface, T 2 η x 2, must be balanced by the difference between the atmospheric pressure p 0 and the pressure p in the fluid just below the surface: p 0 p = T 2 η x 2 on y = η(x, t).
49 Capillary waves Local equilibrium at the free surface The net upward force per unit area of surface, T 2 η x 2, must be balanced by the difference between the atmospheric pressure p 0 and the pressure p in the fluid just below the surface: p 0 p = T 2 η x 2 on y = η(x, t). This pressure condition at the free surface takes into consideration the effects of surface tension. The kinematic condition remains the same: fluid particles cannot leave the surface. Linearized free surface conditions (with surface tension effects) For small amplitude waves: φ y = η t, φ t + g η = T ϱ 2 η x 2 on y = 0.
50 Capillary waves Linearized free surface conditions (with surface tension effects) For small amplitude waves: φ y = η t, φ t + g η = T ϱ 2 η x 2 on y = 0. A sinusoidal travelling wave solution η = A cos(k x ω t) leads now to a new dispersion relation ω 2 = g k + T k3 ϱ. As a consequence, the phase and group velocities include now the surface tension effect: c = ω k = g k + T k ϱ, c g = dω dk = g + 3T k2 /ϱ 2 g k + T k 3 /ϱ.
51 Capillary waves Surface tension importance parameter The relative importance of surface tension and gravitational forces in a fluid is measured by the following parameter β = T k2 ϱ g. (The so-called Bond number = ϱ g L2 T ; it equals 4π2 β if L = λ.) Now, the dispersion relation, as well as the phase and group velocities can be written as g ω 2 = g k (1 + β), c = k (1 + β), c g (1 + 3β) g = 2 g k (1 + β).
52 Capillary waves Surface tension importance parameter ω 2 = g k (1 + β), c = β = T k2 ϱ g g k (1 + β), c g (1 + 3β) g = 2 g k (1 + β). Depending on the parameter β, two extreme cases are distinguished: 1 β 1: the effects of surface tension are negligible the waves are gravity waves for which ω 2 = g k, c = g k = g λ 2π, c g = c 2.
53 Capillary waves Surface tension importance parameter ω 2 = g k (1 + β), c = β = T k2 ϱ g g k (1 + β), c g (1 + 3β) g = 2 g k (1 + β). Depending on the parameter β, two extreme cases are distinguished: 1 β 1: the effects of surface tension are negligible the waves are gravity waves for which ω 2 = g k, c = g k = g λ 2π, c g = c 2. 2 β 1: the waves are essentially capillary waves for which ω 2 = g k β = T k3 g T k 2π T ϱ, c = k β = ϱ = g 3β, cg = ϱ λ 2 g k β = 3 2 c.
54 Capillary waves vs. gravity waves CAPILLARY WAVES: short waves travel faster, GRAVITY WAVES: long waves travel faster,
55 Capillary waves vs. gravity waves CAPILLARY WAVES: short waves travel faster, the group velocity exceeds the phase velocity, c g > c, GRAVITY WAVES: long waves travel faster, the group velocity is less than the phase velocity, c g < c,
56 Capillary waves vs. gravity waves CAPILLARY WAVES: short waves travel faster, the group velocity exceeds the phase velocity, c g > c, the crests move backward through a wave packet as it moves along as a whole. GRAVITY WAVES: long waves travel faster, the group velocity is less than the phase velocity, c g < c, the wavecrests move faster than a wave packet.
57 Capillary waves vs. gravity waves CAPILLARY WAVES: short waves travel faster, the group velocity exceeds the phase velocity, c g > c, the crests move backward through a wave packet as it moves along as a whole. GRAVITY WAVES: long waves travel faster, the group velocity is less than the phase velocity, c g < c, the wavecrests move faster than a wave packet. wave patterns The capillary effects predominate when raindrops fall on a pond, and as short waves travel faster the wavelength decreases with radius at any particular time. The effects of gravity predominate when a large stone is dropped into a pond, and as long waves travel faster the wavelength increases with radius at any particular time.
58 Capillary-gravity waves c c min capillary waves capillary-gravity waves gravity waves For water: 4π λ β=1 = 2 T = 17 mm g ϱ c min = 4 4g T ϱ = 231 mm s λ β=1 λ For β 1 both effects (the surface tension and gravity) are significant and the waves are capillary-gravity waves.
59 Capillary waves vs. gravity waves Example: Uniform flow past a submerged obstacle 1 U < c min there are no steady waves generated by the obstacle; 2 U > c min there are two values of λ (λ 1 > λ 2 ) for which c = U: λ 1 the larger value represents a gravity wave: the corresponding group velocity is less than c, the energy of this relatively long-wavelength disturbance is carried downstream of the obstacle. λ 2 the smaller value represents a capillary wave: the corresponding group velocity is greater than c, the energy of this relatively short-wavelength disturbance is carried upstream of the obstacle, where it is rather quickly dissipated by viscous effects, on account of the short wavelength (in fact, each wave-crest is at rest, but relative to still water it is travelling upstream with speed U).
60 Shallow-water finite-amplitude waves Assumptions: The amplitudes of waves are finite, that is, not (infinitesimally) small compared with the depth; therefore, the linearized theory does not apply. A typical value h 0 of depth h(x, t) is much smaller than a typical horizontal length scale L of the wave, that is: h 0 L. This is the basis of the so-called shallow-water approximation. The full (nonlinear) 2-D equations are: Du Dt = 1 p ϱ x, Dv Dt = 1 p ϱ y g, u x + v y = 0.
61 Shallow-water finite-amplitude waves Du Dt = 1 p ϱ x, Dv Dt = 1 p ϱ y g, u x + v y = 0. In the shallow-water approximation (when h 0 L) the vertical component of acceleration can be neglected in comparison with the gravitational acceleration: Dv Dt g 0 = 1 p ϱ y g p y = ϱ g. Integrating and applying the condition p = p 0 at y = h(x, t) gives p(x, y, t) = p 0 ϱ g [ y h(x, t) ].
62 Shallow-water finite-amplitude waves Du Dt = 1 p ϱ x, Dv Dt = 1 p ϱ y g, u x + v y = 0. In the shallow-water approximation (when h 0 L) the vertical component of acceleration can be neglected and then p(x, y, t) = p 0 ϱ g [ y h(x, t) ]. This is used for the equation for the horizontal component of acceleration: u Du h y = g =0 u Dt x t + u u h = g x x where u = u(x, t) and h = h(x, t).
63 Shallow-water finite-amplitude waves Du Dt = 1 p ϱ x, Dv Dt = 1 p ϱ y g, u x + v y = 0. A second equation linking u and h may be obtained as follows: v y = u x v(x, y, t) = u(x, t) x y+f (x, t) v=0 at y = 0 v = u x y, and using the kinematic condition at the free surface fluid particles on the surface must remain on it, so the vertical component of velocity v equals the rate of change of the depth h when moving with the horizontal velocity u: v = h t + u h x at y = h(x, t) h t + u h x + h u x = 0.
64 Shallow-water finite-amplitude waves Shallow-water equations Nonlinear equations for the horizontal component of velocity u = u(x, t) and the depth h = h(x, t) of finite-amplitude waves on shallow water: u t + u u x + g h x = 0, h t + u h x + h u x = 0. (The vertical component of velocity is v(x, y, t) = u y.) x On introducing the new variable c(x, t) = g h and then adding and subtracting the two equations the form suited to treatment by the method of characteristics is obtained [ t + (u + c) ] [ (u + 2c) = 0, x t + (u c) ] (u 2c) = 0. x
65 Shallow-water finite-amplitude waves Shallow-water equations u t + u u x + g h x = 0, h t + u h x + h u x = 0. On introducing the new variable c(x, t) = g h the form suited to treatment by the method of characteristics is obtained [ t + (u + c) x ] (u + 2c) = 0, [ t + (u c) x ] (u 2c) = 0. Let x = x(s), t = t(s) be a characteristic curve defined parametrically (s is the parameter) in the x-t plane and starting at some point (x 0, t 0). In fact, two such (families of) characteristic curves are defined such that: dt ds = 1, dx ds = u ± c. This (with +) is used for the first and (with ) for the second equation: [ dt ds t + dx ] the chain rule d (u ± 2c) = 0 (u ± 2c) = 0. ds x ds
66 Shallow-water finite-amplitude waves Shallow-water equations u t + u u x + g h x = 0, h t + u h x + h u x = 0. On introducing the new variable c(x, t) = g h the form suited to treatment by the method of characteristics is obtained [ t + (u + c) x ] (u + 2c) = 0, [ t + (u c) x ] (u 2c) = 0. Let x = x(s) = x(t), t = t(s) = s be a characteristic curve such that: [ t + dx dt dx dt ] (u ± 2c) = 0 x = u ± c. the chain rule d (u ± 2c) = 0. dt General property: u ± 2c is constant along positive / negative characteristic curves defined by dx dt = u ± c.
67 Shallow-water finite-amplitude waves Shallow-water equations u t + u u x + g h x = 0, h t + u h x + h u x = 0. On introducing the new variable c(x, t) = g h the form suited to treatment by the method of characteristics is obtained [ t + (u + c) x ] (u + 2c) = 0, [ t + (u c) x ] (u 2c) = 0. General property: u ± 2c is constant along positive / negative characteristic curves defined by dx dt = u ± c. Within the framework of the theory of finite-amplitude waves on shallow water the following problems can be solved: the dam-break flow, the formation of a bore, the hydraulic jump.
68 Outline 1 Introduction The notion of wave Basic wave phenomena Mathematical description of a traveling wave 2 Water waves Surface waves on deep water Dispersion and the group velocity Capillary waves Shallow-water finite-amplitude waves 3 Sound waves Introduction Acoustic wave equation The speed of sound Sub- and supersonic flow
69 Sound waves: introduction Sound waves propagate due to the compressibility of a medium ( u 0). Depending on frequency one can distinguish: infrasound waves below 20 Hz, acoustic waves from 20 Hz to 20 khz, ultrasound waves above 20 khz. Acoustics deals with vibrations and waves in compressible continua in the audible frequency range, that is, from 20 Hz (16 Hz) to Hz. Types of waves in compressible continua: an inviscid compressible fluid (only) longitudinal waves, an infinite isotropic solid longitudinal and shear waves, an anisotropic solid wave propagation is more complex.
70 Acoustic wave equation Assumptions: Gravitational forces can be neglected so that the equilibrium (undisturbed-state) pressure and density take on uniform values, p 0 and ϱ 0, throughout the fluid. Dissipative effects, that is viscosity and heat conduction, are neglected. The medium (fluid) is homogeneous, isotropic, and perfectly elastic.
71 Acoustic wave equation Assumptions: Gravitational forces can be neglected so that the equilibrium (undisturbed-state) pressure and density take on uniform values, p 0 and ϱ 0, throughout the fluid. Dissipative effects, that is viscosity and heat conduction, are neglected. The medium (fluid) is homogeneous, isotropic, and perfectly elastic. Small-amplitudes assumption Particle velocity is small, and there are only very small perturbations (fluctuations) to the equilibrium pressure and density: u small, p = p 0 + p ( p small), ϱ = ϱ 0 + ϱ ( ϱ small). The pressure fluctuations field p is called the acoustic pressure.
72 Acoustic wave equation Small-amplitudes assumption Particle velocity is small, and there are only very small perturbations (fluctuations) to the equilibrium pressure and density: u small, p = p 0 + p ( p small), ϱ = ϱ 0 + ϱ ( ϱ small). The pressure fluctuations field p is called the acoustic pressure. Momentum equation (Euler s equation): ( ) u ϱ t + u u = p Notice that p = (p 0 + p) = p. Continuity equation: ϱ t + (ϱ u) = 0 linearization linearization ϱ 0 u t = p. ϱ t + ϱ 0 u = 0.
73 Acoustic wave equation Momentum equation (Euler s equation): ( ) u ϱ t + u u = p Notice that p = (p 0 + p) = p. Continuity equation: ϱ t + (ϱ u) = 0 linearization linearization ϱ 0 u t = p. ϱ t + ϱ 0 u = 0. Using divergence operation for the linearized momentum equation and time-differentiation for the linearized continuity equation yields: 2 ϱ t 2 p = 0.
74 Acoustic wave equation Momentum equation (Euler s equation): ( ) u ϱ t + u u = p Notice that p = (p 0 + p) = p. Continuity equation: ϱ t + (ϱ u) = 0 linearization linearization ϱ 0 u t = p. ϱ t + ϱ 0 u = 0. Using divergence operation for the linearized momentum equation and time-differentiation for the linearized continuity equation yields: Constitutive relation: p = p( ϱ) p t = p ϱ 2 ϱ t 2 p = 0. ϱ t 2 ϱ t 2 = 1 c p t 2 where c 2 0 = p ϱ.
75 Acoustic wave equation Using divergence operation for the linearized momentum equation and time-differentiation for the linearized continuity equation yields: Constitutive relation: p = p( ϱ) p t = p ϱ 2 ϱ t 2 p = 0. ϱ t 2 ϱ t 2 = 1 c p t 2 where c 2 0 = p ϱ. Wave equation for the pressure field 1 2 p p p = 0 where c 2 c0 = 0 t2 ϱ is the acoustic wave velocity (or the speed of sound). Notice that the acoustic pressure p can be used here instead of p. Moreover, the wave equation for the density-fluctuation field ϱ (or for the compression field ϱ/ϱ 0), for the velocity potential φ, and for the velocity field u can be derived analogously.
76 The speed of sound Inviscid isotropic elastic liquid. The pressure in an inviscid liquid depends on the volume dilatation tr ε: where K is the bulk modulus. Now, p t = K tr ε t = K u p = K tr ε, u= 1 ϱ 0 ϱ t Lin. Cont. Eq. p t = K ϱ 0 ϱ t which means that the speed of sound c 0 = p/ ϱ is given by the well-known formula: K c 0 =. ϱ 0
77 The speed of sound Inviscid isotropic elastic liquid. The speed of sound is given by the well-known formula: K c 0 =. ϱ 0 Perfect gas. The determination of speed of sound in a perfect gas is complicated and requires the use of thermodynamic considerations. The final result is c 0 = γ p 0 = γ R T 0, ϱ 0 where γ denotes the ratio of specific heats (γ = 1.4 for air), R is the universal gas constant, and T 0 is the (isothermal) temperature. For air at 20 C and normal atmospheric pressure: c 0 = 343 m s.
78 Sub- and supersonic flow A steady, unseparated, compressible flow past a thin airfoil may be written in the from u = U + φ x, v = φ y, where the velocity potential φ for the small disturbance to the uniform flow U satisfies (1 M 2 ) 2 φ x + 2 φ 2 y = 0, where M = U 2 c 0 is the Mach number defined as the ratio of the speed of free stream to the speed of sound.
79 Sub- and supersonic flow A steady, unseparated, compressible flow past a thin airfoil may be written in the from u = U + φ x, v = φ y, where the velocity potential φ for the small disturbance to the uniform flow U satisfies (1 M 2 ) 2 φ x + 2 φ 2 y = 0, where M = U 2 c 0 is the Mach number defined as the ratio of the speed of free stream to the speed of sound. If M 2 1 that gives the Laplace equation which is the result that arises for incompressible theory (i.e., using u = 0).
80 Sub- and supersonic flow A steady, unseparated, compressible flow past a thin airfoil may be written in the from u = U + φ x, v = φ y, where the velocity potential φ for the small disturbance to the uniform flow U satisfies (1 M 2 ) 2 φ x + 2 φ 2 y = 0, where M = U 2 c 0 is the Mach number defined as the ratio of the speed of free stream to the speed of sound. If M 2 1 that gives the Laplace equation which is the result that arises for incompressible theory (i.e., using u = 0). Otherwise, three cases can be distinguished: 1 M < 1 the subsonic flow 2 M > 1 the supersonic flow 3 M 1 the sound barrier
81 Sub- and supersonic flow 1 M < 1 the subsonic flow: there is some disturbance to the oncoming flow at all distances from the wing (even though it is very small when the distance is large); the drag is zero (inviscid theory) and the lift = lift incompressible. 1 M 2 c 0t A Ut A
82 Sub- and supersonic flow 1 M < 1 the subsonic flow 2 M > 1 the supersonic flow: there is no disturbance to the oncoming stream except between the Mach lines extending from the ends of the airfoil and making the angle α = arcsin ( ) 1 M with the uniform stream; the drag is not zero it arises because of the sound wave energy which the wing radiates to infinity between the Mach lines. c 0t A α Ut A
83 Sub- and supersonic flow 1 M < 1 the subsonic flow: there is some disturbance to the oncoming flow at all distances from the wing (even though it is very small when the distance is large); the drag is zero (inviscid theory) and the lift = lift incompressible. 1 M 2 2 M > 1 the supersonic flow: there is no disturbance to the oncoming stream except between the Mach lines extending from the ends of the airfoil and making the angle α = arcsin ( ) 1 M with the uniform stream; the drag is not zero it arises because of the sound wave energy which the wing radiates to infinity between the Mach lines. 3 M 1 the sound barrier: sub- and supersonic theory is not valid; nonetheless, it indicates that the wing is subject to a destructive effect of exceptionally large aerodynamic forces.
Fundamentals of Fluid Dynamics: Ideal Flow Theory & Basic Aerodynamics
 Fundamentals of Fluid Dynamics: Ideal Flow Theory & Basic Aerodynamics Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI (after: D.J. ACHESON s Elementary Fluid Dynamics ) bluebox.ippt.pan.pl/
Fundamentals of Fluid Dynamics: Ideal Flow Theory & Basic Aerodynamics Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI (after: D.J. ACHESON s Elementary Fluid Dynamics ) bluebox.ippt.pan.pl/
Fundamentals of Fluid Dynamics: Elementary Viscous Flow
 Fundamentals of Fluid Dynamics: Elementary Viscous Flow Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research
Fundamentals of Fluid Dynamics: Elementary Viscous Flow Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research
Fundamentals of Acoustics
 Fundamentals of Acoustics Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research of the Polish Academy of Sciences
Fundamentals of Acoustics Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research of the Polish Academy of Sciences
OPAC102. The Acoustic Wave Equation
 OPAC102 The Acoustic Wave Equation Acoustic waves in fluid Acoustic waves constitute one kind of pressure fluctuation that can exist in a compressible fluid. The restoring forces responsible for propagating
OPAC102 The Acoustic Wave Equation Acoustic waves in fluid Acoustic waves constitute one kind of pressure fluctuation that can exist in a compressible fluid. The restoring forces responsible for propagating
Summary PHY101 ( 2 ) T / Hanadi Al Harbi
 الكمية Physical Quantity القانون Low التعريف Definition الوحدة SI Unit Linear Momentum P = mθ be equal to the mass of an object times its velocity. Kg. m/s vector quantity Stress F \ A the external force
الكمية Physical Quantity القانون Low التعريف Definition الوحدة SI Unit Linear Momentum P = mθ be equal to the mass of an object times its velocity. Kg. m/s vector quantity Stress F \ A the external force
Review of Fundamental Equations Supplementary notes on Section 1.2 and 1.3
 Review of Fundamental Equations Supplementary notes on Section. and.3 Introduction of the velocity potential: irrotational motion: ω = u = identity in the vector analysis: ϕ u = ϕ Basic conservation principles:
Review of Fundamental Equations Supplementary notes on Section. and.3 Introduction of the velocity potential: irrotational motion: ω = u = identity in the vector analysis: ϕ u = ϕ Basic conservation principles:
Lecture 1: Introduction to Linear and Non-Linear Waves
 Lecture 1: Introduction to Linear and Non-Linear Waves Lecturer: Harvey Segur. Write-up: Michael Bates June 15, 2009 1 Introduction to Water Waves 1.1 Motivation and Basic Properties There are many types
Lecture 1: Introduction to Linear and Non-Linear Waves Lecturer: Harvey Segur. Write-up: Michael Bates June 15, 2009 1 Introduction to Water Waves 1.1 Motivation and Basic Properties There are many types
Section 1 Simple Harmonic Motion. The student is expected to:
 Section 1 Simple Harmonic Motion TEKS The student is expected to: 7A examine and describe oscillatory motion and wave propagation in various types of media Section 1 Simple Harmonic Motion Preview Objectives
Section 1 Simple Harmonic Motion TEKS The student is expected to: 7A examine and describe oscillatory motion and wave propagation in various types of media Section 1 Simple Harmonic Motion Preview Objectives
Phys101 Lectures 28, 29. Wave Motion
 Phys101 Lectures 8, 9 Wave Motion Key points: Types of Waves: Transverse and Longitudinal Mathematical Representation of a Traveling Wave The Principle of Superposition Standing Waves; Resonance Ref: 11-7,8,9,10,11,16,1,13,16.
Phys101 Lectures 8, 9 Wave Motion Key points: Types of Waves: Transverse and Longitudinal Mathematical Representation of a Traveling Wave The Principle of Superposition Standing Waves; Resonance Ref: 11-7,8,9,10,11,16,1,13,16.
Chapter 15. Mechanical Waves
 Chapter 15 Mechanical Waves A wave is any disturbance from an equilibrium condition, which travels or propagates with time from one region of space to another. A harmonic wave is a periodic wave in which
Chapter 15 Mechanical Waves A wave is any disturbance from an equilibrium condition, which travels or propagates with time from one region of space to another. A harmonic wave is a periodic wave in which
Figure 1: Surface waves
 4 Surface Waves on Liquids 1 4 Surface Waves on Liquids 4.1 Introduction We consider waves on the surface of liquids, e.g. waves on the sea or a lake or a river. These can be generated by the wind, by
4 Surface Waves on Liquids 1 4 Surface Waves on Liquids 4.1 Introduction We consider waves on the surface of liquids, e.g. waves on the sea or a lake or a river. These can be generated by the wind, by
Outline. Hook s law. Mass spring system Simple harmonic motion Travelling waves Waves in string Sound waves
 Outline Hook s law. Mass spring system Simple harmonic motion Travelling waves Waves in string Sound waves Hooke s Law Force is directly proportional to the displacement of the object from the equilibrium
Outline Hook s law. Mass spring system Simple harmonic motion Travelling waves Waves in string Sound waves Hooke s Law Force is directly proportional to the displacement of the object from the equilibrium
Fundamentals of Linear Elasticity
 Fundamentals of Linear Elasticity Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research of the Polish Academy
Fundamentals of Linear Elasticity Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research of the Polish Academy
7.2.1 Seismic waves. Waves in a mass- spring system
 7..1 Seismic waves Waves in a mass- spring system Acoustic waves in a liquid or gas Seismic waves in a solid Surface waves Wavefronts, rays and geometrical attenuation Amplitude and energy Waves in a mass-
7..1 Seismic waves Waves in a mass- spring system Acoustic waves in a liquid or gas Seismic waves in a solid Surface waves Wavefronts, rays and geometrical attenuation Amplitude and energy Waves in a mass-
Oscillatory Motion and Wave Motion
 Oscillatory Motion and Wave Motion Oscillatory Motion Simple Harmonic Motion Wave Motion Waves Motion of an Object Attached to a Spring The Pendulum Transverse and Longitudinal Waves Sinusoidal Wave Function
Oscillatory Motion and Wave Motion Oscillatory Motion Simple Harmonic Motion Wave Motion Waves Motion of an Object Attached to a Spring The Pendulum Transverse and Longitudinal Waves Sinusoidal Wave Function
1 f. result from periodic disturbance same period (frequency) as source Longitudinal or Transverse Waves Characterized by
 result from periodic disturbance same period (frequency) as source Longitudinal or Transverse Waves Characterized by amplitude (how far do the bits move from their equilibrium positions? Amplitude of MEDIUM)
result from periodic disturbance same period (frequency) as source Longitudinal or Transverse Waves Characterized by amplitude (how far do the bits move from their equilibrium positions? Amplitude of MEDIUM)
Raymond A. Serway Chris Vuille. Chapter Thirteen. Vibrations and Waves
 Raymond A. Serway Chris Vuille Chapter Thirteen Vibrations and Waves Periodic Motion and Waves Periodic motion is one of the most important kinds of physical behavior Will include a closer look at Hooke
Raymond A. Serway Chris Vuille Chapter Thirteen Vibrations and Waves Periodic Motion and Waves Periodic motion is one of the most important kinds of physical behavior Will include a closer look at Hooke
Section 1 Simple Harmonic Motion. Chapter 11. Preview. Objectives Hooke s Law Sample Problem Simple Harmonic Motion The Simple Pendulum
 Section 1 Simple Harmonic Motion Preview Objectives Hooke s Law Sample Problem Simple Harmonic Motion The Simple Pendulum Section 1 Simple Harmonic Motion Objectives Identify the conditions of simple harmonic
Section 1 Simple Harmonic Motion Preview Objectives Hooke s Law Sample Problem Simple Harmonic Motion The Simple Pendulum Section 1 Simple Harmonic Motion Objectives Identify the conditions of simple harmonic
1/27/2010. With this method, all filed variables are separated into. from the basic state: Assumptions 1: : the basic state variables must
 Lecture 5: Waves in Atmosphere Perturbation Method With this method, all filed variables are separated into two parts: (a) a basic state part and (b) a deviation from the basic state: Perturbation Method
Lecture 5: Waves in Atmosphere Perturbation Method With this method, all filed variables are separated into two parts: (a) a basic state part and (b) a deviation from the basic state: Perturbation Method
V (r,t) = i ˆ u( x, y,z,t) + ˆ j v( x, y,z,t) + k ˆ w( x, y, z,t)
 IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
Exam 3 Review. Chapter 10: Elasticity and Oscillations A stress will deform a body and that body can be set into periodic oscillations.
 Exam 3 Review Chapter 10: Elasticity and Oscillations stress will deform a body and that body can be set into periodic oscillations. Elastic Deformations of Solids Elastic objects return to their original
Exam 3 Review Chapter 10: Elasticity and Oscillations stress will deform a body and that body can be set into periodic oscillations. Elastic Deformations of Solids Elastic objects return to their original
7 EQUATIONS OF MOTION FOR AN INVISCID FLUID
 7 EQUATIONS OF MOTION FOR AN INISCID FLUID iscosity is a measure of the thickness of a fluid, and its resistance to shearing motions. Honey is difficult to stir because of its high viscosity, whereas water
7 EQUATIONS OF MOTION FOR AN INISCID FLUID iscosity is a measure of the thickness of a fluid, and its resistance to shearing motions. Honey is difficult to stir because of its high viscosity, whereas water
Chapter 11 Vibrations and Waves
 Chapter 11 Vibrations and Waves 11-1 Simple Harmonic Motion If an object vibrates or oscillates back and forth over the same path, each cycle taking the same amount of time, the motion is called periodic.
Chapter 11 Vibrations and Waves 11-1 Simple Harmonic Motion If an object vibrates or oscillates back and forth over the same path, each cycle taking the same amount of time, the motion is called periodic.
Quick Recapitulation of Fluid Mechanics
 Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
PHYSICS. Course Structure. Unit Topics Marks. Physical World and Measurement. 1 Physical World. 2 Units and Measurements.
 PHYSICS Course Structure Unit Topics Marks I Physical World and Measurement 1 Physical World 2 Units and Measurements II Kinematics 3 Motion in a Straight Line 23 4 Motion in a Plane III Laws of Motion
PHYSICS Course Structure Unit Topics Marks I Physical World and Measurement 1 Physical World 2 Units and Measurements II Kinematics 3 Motion in a Straight Line 23 4 Motion in a Plane III Laws of Motion
Sound Waves. Sound waves are longitudinal waves traveling through a medium Sound waves are produced from vibrating objects.
 Sound Waves Sound waves are longitudinal waves traveling through a medium Sound waves are produced from vibrating objects Introduction Sound Waves: Molecular View When sound travels through a medium, there
Sound Waves Sound waves are longitudinal waves traveling through a medium Sound waves are produced from vibrating objects Introduction Sound Waves: Molecular View When sound travels through a medium, there
PHYSICS. Chapter 16 Lecture FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E RANDALL D. KNIGHT Pearson Education, Inc.
 PHYSICS FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E Chapter 16 Lecture RANDALL D. KNIGHT 2017 Pearson Education, Inc. Chapter 16 Traveling Waves IN THIS CHAPTER, you will learn the basic properties
PHYSICS FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E Chapter 16 Lecture RANDALL D. KNIGHT 2017 Pearson Education, Inc. Chapter 16 Traveling Waves IN THIS CHAPTER, you will learn the basic properties
Chapter 16 Waves in One Dimension
 Chapter 16 Waves in One Dimension Slide 16-1 Reading Quiz 16.05 f = c Slide 16-2 Reading Quiz 16.06 Slide 16-3 Reading Quiz 16.07 Heavier portion looks like a fixed end, pulse is inverted on reflection.
Chapter 16 Waves in One Dimension Slide 16-1 Reading Quiz 16.05 f = c Slide 16-2 Reading Quiz 16.06 Slide 16-3 Reading Quiz 16.07 Heavier portion looks like a fixed end, pulse is inverted on reflection.
Water is sloshing back and forth between two infinite vertical walls separated by a distance L: h(x,t) Water L
 ME9a. SOLUTIONS. Nov., 29. Due Nov. 7 PROBLEM 2 Water is sloshing back and forth between two infinite vertical walls separated by a distance L: y Surface Water L h(x,t x Tank The flow is assumed to be
ME9a. SOLUTIONS. Nov., 29. Due Nov. 7 PROBLEM 2 Water is sloshing back and forth between two infinite vertical walls separated by a distance L: y Surface Water L h(x,t x Tank The flow is assumed to be
4. What is the speed (in cm s - 1 ) of the tip of the minute hand?
 Topic 4 Waves PROBLEM SET Formative Assessment NAME: TEAM: THIS IS A PRACTICE ASSESSMENT. Show formulas, substitutions, answers, and units! Topic 4.1 Oscillations A mass is attached to a horizontal spring.
Topic 4 Waves PROBLEM SET Formative Assessment NAME: TEAM: THIS IS A PRACTICE ASSESSMENT. Show formulas, substitutions, answers, and units! Topic 4.1 Oscillations A mass is attached to a horizontal spring.
Wave-Body Interaction Theory (Theory of Ship Waves) Lecture Notes for Graduate Course
 Wave-Body Interaction Theory (Theory of Ship Waves) Lecture Notes for Graduate Course ( April 018 ) Lab of Seakeeping & Floating-Body Dynamics in Waves Dept of Naval Architecture & Ocean Engineering Osaka
Wave-Body Interaction Theory (Theory of Ship Waves) Lecture Notes for Graduate Course ( April 018 ) Lab of Seakeeping & Floating-Body Dynamics in Waves Dept of Naval Architecture & Ocean Engineering Osaka
The Euler Equation of Gas-Dynamics
 The Euler Equation of Gas-Dynamics A. Mignone October 24, 217 In this lecture we study some properties of the Euler equations of gasdynamics, + (u) = ( ) u + u u + p = a p + u p + γp u = where, p and u
The Euler Equation of Gas-Dynamics A. Mignone October 24, 217 In this lecture we study some properties of the Euler equations of gasdynamics, + (u) = ( ) u + u u + p = a p + u p + γp u = where, p and u
Longitudinal Waves. waves in which the particle or oscillator motion is in the same direction as the wave propagation
 Longitudinal Waves waves in which the particle or oscillator motion is in the same direction as the wave propagation Longitudinal waves propagate as sound waves in all phases of matter, plasmas, gases,
Longitudinal Waves waves in which the particle or oscillator motion is in the same direction as the wave propagation Longitudinal waves propagate as sound waves in all phases of matter, plasmas, gases,
Theory of Ship Waves (Wave-Body Interaction Theory) Quiz No. 2, April 25, 2018
 Quiz No. 2, April 25, 2018 (1) viscous effects (2) shear stress (3) normal pressure (4) pursue (5) bear in mind (6) be denoted by (7) variation (8) adjacent surfaces (9) be composed of (10) integrand (11)
Quiz No. 2, April 25, 2018 (1) viscous effects (2) shear stress (3) normal pressure (4) pursue (5) bear in mind (6) be denoted by (7) variation (8) adjacent surfaces (9) be composed of (10) integrand (11)
DIVIDED SYLLABUS ( ) - CLASS XI PHYSICS (CODE 042) COURSE STRUCTURE APRIL
 DIVIDED SYLLABUS (2015-16 ) - CLASS XI PHYSICS (CODE 042) COURSE STRUCTURE APRIL Unit I: Physical World and Measurement Physics Need for measurement: Units of measurement; systems of units; SI units, fundamental
DIVIDED SYLLABUS (2015-16 ) - CLASS XI PHYSICS (CODE 042) COURSE STRUCTURE APRIL Unit I: Physical World and Measurement Physics Need for measurement: Units of measurement; systems of units; SI units, fundamental
2 u 1-D: 3-D: x + 2 u
 c 2013 C.S. Casari - Politecnico di Milano - Introduction to Nanoscience 2013-14 Onde 1 1 Waves 1.1 wave propagation 1.1.1 field Field: a physical quantity (measurable, at least in principle) function
c 2013 C.S. Casari - Politecnico di Milano - Introduction to Nanoscience 2013-14 Onde 1 1 Waves 1.1 wave propagation 1.1.1 field Field: a physical quantity (measurable, at least in principle) function
α(t) = ω 2 θ (t) κ I ω = g L L g T = 2π mgh rot com I rot
 α(t) = ω 2 θ (t) ω = κ I ω = g L T = 2π L g ω = mgh rot com I rot T = 2π I rot mgh rot com Chapter 16: Waves Mechanical Waves Waves and particles Vibration = waves - Sound - medium vibrates - Surface ocean
α(t) = ω 2 θ (t) ω = κ I ω = g L T = 2π L g ω = mgh rot com I rot T = 2π I rot mgh rot com Chapter 16: Waves Mechanical Waves Waves and particles Vibration = waves - Sound - medium vibrates - Surface ocean
Producing a Sound Wave. Chapter 14. Using a Tuning Fork to Produce a Sound Wave. Using a Tuning Fork, cont.
 Producing a Sound Wave Chapter 14 Sound Sound waves are longitudinal waves traveling through a medium A tuning fork can be used as an example of producing a sound wave Using a Tuning Fork to Produce a
Producing a Sound Wave Chapter 14 Sound Sound waves are longitudinal waves traveling through a medium A tuning fork can be used as an example of producing a sound wave Using a Tuning Fork to Produce a
Traveling Harmonic Waves
 Traveling Harmonic Waves 6 January 2016 PHYC 1290 Department of Physics and Atmospheric Science Functional Form for Traveling Waves We can show that traveling waves whose shape does not change with time
Traveling Harmonic Waves 6 January 2016 PHYC 1290 Department of Physics and Atmospheric Science Functional Form for Traveling Waves We can show that traveling waves whose shape does not change with time
Class XI Physics Syllabus One Paper Three Hours Max Marks: 70
 Class XI Physics Syllabus 2013 One Paper Three Hours Max Marks: 70 Class XI Weightage Unit I Physical World & Measurement 03 Unit II Kinematics 10 Unit III Laws of Motion 10 Unit IV Work, Energy & Power
Class XI Physics Syllabus 2013 One Paper Three Hours Max Marks: 70 Class XI Weightage Unit I Physical World & Measurement 03 Unit II Kinematics 10 Unit III Laws of Motion 10 Unit IV Work, Energy & Power
UNIVERSITY of LIMERICK
 UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH Faculty of Science and Engineering END OF SEMESTER ASSESSMENT PAPER MODULE CODE: MA4607 SEMESTER: Autumn 2012-13 MODULE TITLE: Introduction to Fluids DURATION OF
UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH Faculty of Science and Engineering END OF SEMESTER ASSESSMENT PAPER MODULE CODE: MA4607 SEMESTER: Autumn 2012-13 MODULE TITLE: Introduction to Fluids DURATION OF
(TRAVELLING) 1D WAVES. 1. Transversal & Longitudinal Waves
 (TRAVELLING) 1D WAVES 1. Transversal & Longitudinal Waves Objectives After studying this chapter you should be able to: Derive 1D wave equation for transversal and longitudinal Relate propagation speed
(TRAVELLING) 1D WAVES 1. Transversal & Longitudinal Waves Objectives After studying this chapter you should be able to: Derive 1D wave equation for transversal and longitudinal Relate propagation speed
Chap 11. Vibration and Waves. The impressed force on an object is proportional to its displacement from it equilibrium position.
 Chap 11. Vibration and Waves Sec. 11.1 - Simple Harmonic Motion The impressed force on an object is proportional to its displacement from it equilibrium position. F x This restoring force opposes the change
Chap 11. Vibration and Waves Sec. 11.1 - Simple Harmonic Motion The impressed force on an object is proportional to its displacement from it equilibrium position. F x This restoring force opposes the change
Chapter 20: Mechanical Waves
 Chapter 20: Mechanical Waves Section 20.1: Observations: Pulses and Wave Motion Oscillation Plus Propagation Oscillation (or vibration): Periodic motion (back-and-forth, upand-down) The motion repeats
Chapter 20: Mechanical Waves Section 20.1: Observations: Pulses and Wave Motion Oscillation Plus Propagation Oscillation (or vibration): Periodic motion (back-and-forth, upand-down) The motion repeats
Waves Encountering Barriers
 Waves Encountering Barriers Reflection and Refraction: When a wave is incident on a boundary that separates two regions of different wave speed, part of the wave is reflected and part is transmitted. Figure
Waves Encountering Barriers Reflection and Refraction: When a wave is incident on a boundary that separates two regions of different wave speed, part of the wave is reflected and part is transmitted. Figure
PHYSICS 149: Lecture 24
 PHYSICS 149: Lecture 24 Chapter 11: Waves 11.8 Reflection and Refraction 11.10 Standing Waves Chapter 12: Sound 12.1 Sound Waves 12.4 Standing Sound Waves Lecture 24 Purdue University, Physics 149 1 ILQ
PHYSICS 149: Lecture 24 Chapter 11: Waves 11.8 Reflection and Refraction 11.10 Standing Waves Chapter 12: Sound 12.1 Sound Waves 12.4 Standing Sound Waves Lecture 24 Purdue University, Physics 149 1 ILQ
CHAPTER 11 VIBRATIONS AND WAVES
 CHAPTER 11 VIBRATIONS AND WAVES http://www.physicsclassroom.com/class/waves/u10l1a.html UNITS Simple Harmonic Motion Energy in the Simple Harmonic Oscillator The Period and Sinusoidal Nature of SHM The
CHAPTER 11 VIBRATIONS AND WAVES http://www.physicsclassroom.com/class/waves/u10l1a.html UNITS Simple Harmonic Motion Energy in the Simple Harmonic Oscillator The Period and Sinusoidal Nature of SHM The
J10M.1 - Rod on a Rail (M93M.2)
 Part I - Mechanics J10M.1 - Rod on a Rail (M93M.2) J10M.1 - Rod on a Rail (M93M.2) s α l θ g z x A uniform rod of length l and mass m moves in the x-z plane. One end of the rod is suspended from a straight
Part I - Mechanics J10M.1 - Rod on a Rail (M93M.2) J10M.1 - Rod on a Rail (M93M.2) s α l θ g z x A uniform rod of length l and mass m moves in the x-z plane. One end of the rod is suspended from a straight
1 POTENTIAL FLOW THEORY Formulation of the seakeeping problem
 1 POTENTIAL FLOW THEORY Formulation of the seakeeping problem Objective of the Chapter: Formulation of the potential flow around the hull of a ship advancing and oscillationg in waves Results of the Chapter:
1 POTENTIAL FLOW THEORY Formulation of the seakeeping problem Objective of the Chapter: Formulation of the potential flow around the hull of a ship advancing and oscillationg in waves Results of the Chapter:
Mathématiques appliquées (MATH0504-1) B. Dewals, Ch. Geuzaine
 Lecture 2 The wave equation Mathématiques appliquées (MATH0504-1) B. Dewals, Ch. Geuzaine V1.0 28/09/2018 1 Learning objectives of this lecture Understand the fundamental properties of the wave equation
Lecture 2 The wave equation Mathématiques appliquées (MATH0504-1) B. Dewals, Ch. Geuzaine V1.0 28/09/2018 1 Learning objectives of this lecture Understand the fundamental properties of the wave equation
Physics 142 Mechanical Waves Page 1. Mechanical Waves
 Physics 142 Mechanical Waves Page 1 Mechanical Waves This set of notes contains a review of wave motion in mechanics, emphasizing the mathematical formulation that will be used in our discussion of electromagnetic
Physics 142 Mechanical Waves Page 1 Mechanical Waves This set of notes contains a review of wave motion in mechanics, emphasizing the mathematical formulation that will be used in our discussion of electromagnetic
Introduction to Acoustics. Phil Joseph
 Introduction to Acoustics Phil Joseph INTRODUCTION TO ACOUSTICS Sound and Noise Sound waves Frequency, wavelength and wavespeed Point sources Sound power and intensity Wave reflection Standing waves Measures
Introduction to Acoustics Phil Joseph INTRODUCTION TO ACOUSTICS Sound and Noise Sound waves Frequency, wavelength and wavespeed Point sources Sound power and intensity Wave reflection Standing waves Measures
Work. Work and Energy Examples. Energy. To move an object we must do work Work is calculated as the force applied to the object through a distance or:
 Work To move an object we must do work Work is calculated as the force applied to the object through a distance or: W F( d) Work has the units Newton meters (N m) or Joules 1 Joule = 1 N m Energy Work
Work To move an object we must do work Work is calculated as the force applied to the object through a distance or: W F( d) Work has the units Newton meters (N m) or Joules 1 Joule = 1 N m Energy Work
Test 3 Preparation Questions
 Test 3 Preparation Questions A1. Which statement is true concerning an object executing simple harmonic motion? (A) Its velocity is never zero. (B) Its acceleration is never zero. (C) Its velocity and
Test 3 Preparation Questions A1. Which statement is true concerning an object executing simple harmonic motion? (A) Its velocity is never zero. (B) Its acceleration is never zero. (C) Its velocity and
Chapter 16 Mechanical Waves
 Chapter 6 Mechanical Waves A wave is a disturbance that travels, or propagates, without the transport of matter. Examples: sound/ultrasonic wave, EM waves, and earthquake wave. Mechanical waves, such as
Chapter 6 Mechanical Waves A wave is a disturbance that travels, or propagates, without the transport of matter. Examples: sound/ultrasonic wave, EM waves, and earthquake wave. Mechanical waves, such as
UNIVERSITY OF SOUTHAMPTON
 UNIVERSITY OF SOUTHAMPTON PHYS2023W1 SEMESTER 1 EXAMINATION 2016-2017 WAVE PHYSICS Duration: 120 MINS (2 hours) This paper contains 9 questions. Answers to Section A and Section B must be in separate answer
UNIVERSITY OF SOUTHAMPTON PHYS2023W1 SEMESTER 1 EXAMINATION 2016-2017 WAVE PHYSICS Duration: 120 MINS (2 hours) This paper contains 9 questions. Answers to Section A and Section B must be in separate answer
PHYS 643 Week 4: Compressible fluids Sound waves and shocks
 PHYS 643 Week 4: Compressible fluids Sound waves and shocks Sound waves Compressions in a gas propagate as sound waves. The simplest case to consider is a gas at uniform density and at rest. Small perturbations
PHYS 643 Week 4: Compressible fluids Sound waves and shocks Sound waves Compressions in a gas propagate as sound waves. The simplest case to consider is a gas at uniform density and at rest. Small perturbations
Physics 1C. Lecture 12C
 Physics 1C Lecture 12C Simple Pendulum The simple pendulum is another example of simple harmonic motion. Making a quick force diagram of the situation, we find:! The tension in the string cancels out with
Physics 1C Lecture 12C Simple Pendulum The simple pendulum is another example of simple harmonic motion. Making a quick force diagram of the situation, we find:! The tension in the string cancels out with
Chapter 16: Oscillatory Motion and Waves. Simple Harmonic Motion (SHM)
 Chapter 6: Oscillatory Motion and Waves Hooke s Law (revisited) F = - k x Tthe elastic potential energy of a stretched or compressed spring is PE elastic = kx / Spring-block Note: To consider the potential
Chapter 6: Oscillatory Motion and Waves Hooke s Law (revisited) F = - k x Tthe elastic potential energy of a stretched or compressed spring is PE elastic = kx / Spring-block Note: To consider the potential
Baccalieu Collegiate. Physics Course Outline
 Baccalieu Collegiate Physics 2204 Course Outline Course Content: Unit 1: Kinematics Motion is a common theme in our everyday lives: birds fly, babies crawl, and we, ourselves, seem to be in a constant
Baccalieu Collegiate Physics 2204 Course Outline Course Content: Unit 1: Kinematics Motion is a common theme in our everyday lives: birds fly, babies crawl, and we, ourselves, seem to be in a constant
Control Volume. Dynamics and Kinematics. Basic Conservation Laws. Lecture 1: Introduction and Review 1/24/2017
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review
 Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Webster s horn model on Bernoulli flow
 Webster s horn model on Bernoulli flow Aalto University, Dept. Mathematics and Systems Analysis January 5th, 2018 Incompressible, steady Bernoulli principle Consider a straight tube Ω R 3 havin circular
Webster s horn model on Bernoulli flow Aalto University, Dept. Mathematics and Systems Analysis January 5th, 2018 Incompressible, steady Bernoulli principle Consider a straight tube Ω R 3 havin circular
D.A.V. PUBLIC SCHOOL, UPPAL S SOUTHEND, SECTOR 49, GURUGRAM CLASS XI (PHYSICS) Academic plan for
 D.A.V. PUBLIC SCHOOL, UPPAL S SOUTHEND, SECTOR 49, GURUGRAM CLASS XI (PHYSICS) Academic plan for 2017-2018 UNIT NAME OF UNIT WEIGHTAGE 1. 2. 3. Physical World and Measurement Kinemetics Laws of Motion
D.A.V. PUBLIC SCHOOL, UPPAL S SOUTHEND, SECTOR 49, GURUGRAM CLASS XI (PHYSICS) Academic plan for 2017-2018 UNIT NAME OF UNIT WEIGHTAGE 1. 2. 3. Physical World and Measurement Kinemetics Laws of Motion
STRUCTURE OF MATTER, VIBRATIONS AND WAVES, AND QUANTUM PHYSICS
 Imperial College London BSc/MSci EXAMINATION June 2008 This paper is also taken for the relevant Examination for the Associateship STRUCTURE OF MATTER, VIBRATIONS AND WAVES, AND QUANTUM PHYSICS For 1st-Year
Imperial College London BSc/MSci EXAMINATION June 2008 This paper is also taken for the relevant Examination for the Associateship STRUCTURE OF MATTER, VIBRATIONS AND WAVES, AND QUANTUM PHYSICS For 1st-Year
196 7 atmospheric oscillations:
 196 7 atmospheric oscillations: 7.4 INTERNAL GRAVITY (BUOYANCY) WAVES We now consider the nature of gravity wave propagation in the atmosphere. Atmospheric gravity waves can only exist when the atmosphere
196 7 atmospheric oscillations: 7.4 INTERNAL GRAVITY (BUOYANCY) WAVES We now consider the nature of gravity wave propagation in the atmosphere. Atmospheric gravity waves can only exist when the atmosphere
Physical and Biological Properties of Agricultural Products Acoustic, Electrical and Optical Properties and Biochemical Property
 Physical and Biological Properties of Agricultural Products Acoustic, Electrical and Optical Properties and Biochemical Property 1. Acoustic and Vibrational Properties 1.1 Acoustics and Vibration Engineering
Physical and Biological Properties of Agricultural Products Acoustic, Electrical and Optical Properties and Biochemical Property 1. Acoustic and Vibrational Properties 1.1 Acoustics and Vibration Engineering
1 2 Models, Theories, and Laws 1.5 Distinguish between models, theories, and laws 2.1 State the origin of significant figures in measurement
 Textbook Correlation Textbook Correlation Physics 1115/2015 Chapter 1 Introduction, Measurement, Estimating 1.1 Describe thoughts of Aristotle vs. Galileo in describing motion 1 1 Nature of Science 1.2
Textbook Correlation Textbook Correlation Physics 1115/2015 Chapter 1 Introduction, Measurement, Estimating 1.1 Describe thoughts of Aristotle vs. Galileo in describing motion 1 1 Nature of Science 1.2
Introduction to Fluid Dynamics
 Introduction to Fluid Dynamics Roger K. Smith Skript - auf englisch! Umsonst im Internet http://www.meteo.physik.uni-muenchen.de Wählen: Lehre Manuskripte Download User Name: meteo Password: download Aim
Introduction to Fluid Dynamics Roger K. Smith Skript - auf englisch! Umsonst im Internet http://www.meteo.physik.uni-muenchen.de Wählen: Lehre Manuskripte Download User Name: meteo Password: download Aim
SOUND. Representative Sample Physics: Sound. 1. Periodic Motion of Particles PLANCESS CONCEPTS
 Representative Sample Physics: Sound SOUND 1. Periodic Motion of Particles Before we move on to study the nature and transmission of sound, we need to understand the different types of vibratory or oscillatory
Representative Sample Physics: Sound SOUND 1. Periodic Motion of Particles Before we move on to study the nature and transmission of sound, we need to understand the different types of vibratory or oscillatory
CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION
 CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION 7.1 THE NAVIER-STOKES EQUATIONS Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION 7.1 THE NAVIER-STOKES EQUATIONS Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
Chapter 15. Oscillatory Motion
 Chapter 15 Oscillatory Motion Part 2 Oscillations and Mechanical Waves Periodic motion is the repeating motion of an object in which it continues to return to a given position after a fixed time interval.
Chapter 15 Oscillatory Motion Part 2 Oscillations and Mechanical Waves Periodic motion is the repeating motion of an object in which it continues to return to a given position after a fixed time interval.
Shallow Water Gravity Waves: A Note on the Particle Orbits
 Journal of Oceanography Vol. 5, pp. 353 to 357. 1996 Shallow Water Gravity Waves: A Note on the Particle Orbits KERN E. KENYON 463 North Lane, Del Mar, CA 9014-4134, U.S.A. (Received 4 July 1995; in revised
Journal of Oceanography Vol. 5, pp. 353 to 357. 1996 Shallow Water Gravity Waves: A Note on the Particle Orbits KERN E. KENYON 463 North Lane, Del Mar, CA 9014-4134, U.S.A. (Received 4 July 1995; in revised
WAVES( SUB) 2. What is the property of the medium that is essential for the propagation of mechanical wave? Ans: Elasticity and inertia
 WAES( SUB). What is meant by a wave? Ans: The disturbance set up in a medium is known as a wave. What is the property of the medium that is essential for the propagation of mechanical wave? Ans: Elasticity
WAES( SUB). What is meant by a wave? Ans: The disturbance set up in a medium is known as a wave. What is the property of the medium that is essential for the propagation of mechanical wave? Ans: Elasticity
NDT&E Methods: UT. VJ Technologies CAVITY INSPECTION. Nondestructive Testing & Evaluation TPU Lecture Course 2015/16.
 CAVITY INSPECTION NDT&E Methods: UT VJ Technologies NDT&E Methods: UT 6. NDT&E: Introduction to Methods 6.1. Ultrasonic Testing: Basics of Elasto-Dynamics 6.2. Principles of Measurement 6.3. The Pulse-Echo
CAVITY INSPECTION NDT&E Methods: UT VJ Technologies NDT&E Methods: UT 6. NDT&E: Introduction to Methods 6.1. Ultrasonic Testing: Basics of Elasto-Dynamics 6.2. Principles of Measurement 6.3. The Pulse-Echo
NEW HORIZON PRE UNIVERSITY COLLEGE LESSON PLAN FOR THE ACADEMIC YEAR Department of PHYSICS ( I PUC)
 NEW HORIZON PRE UNIVERSITY COLLEGE LESSON PLAN FOR THE ACADEMIC YEAR 017 018 Department of PHYSICS ( I PUC) Week --------------------- Month: June Chapter (Physical world) Scope and excitement of Physics
NEW HORIZON PRE UNIVERSITY COLLEGE LESSON PLAN FOR THE ACADEMIC YEAR 017 018 Department of PHYSICS ( I PUC) Week --------------------- Month: June Chapter (Physical world) Scope and excitement of Physics
Exam tomorrow on Chapter 15, 16, and 17 (Oscilla;ons and Waves 1 &2)
 Exam tomorrow on Chapter 15, 16, and 17 (Oscilla;ons and Waves 1 &2) What to study: Quiz 6 Homework problems for Chapters 15 & 16 Material indicated in the following review slides Other Specific things:
Exam tomorrow on Chapter 15, 16, and 17 (Oscilla;ons and Waves 1 &2) What to study: Quiz 6 Homework problems for Chapters 15 & 16 Material indicated in the following review slides Other Specific things:
f 1/ T T 1/ f Formulas Fs kx m T s 2 k l T p 2 g v f
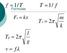 f 1/T Formulas T 1/ f Fs kx Ts 2 m k Tp 2 l g v f What do the following all have in common? Swing, pendulum, vibrating string They all exhibit forms of periodic motion. Periodic Motion: When a vibration
f 1/T Formulas T 1/ f Fs kx Ts 2 m k Tp 2 l g v f What do the following all have in common? Swing, pendulum, vibrating string They all exhibit forms of periodic motion. Periodic Motion: When a vibration
jfpr% ekuo /kez iz.ksrk ln~xq# Jh j.knksm+nklth egkjkt
 Phone : 93 93 7779, 9893 58881 Sount & Waves Page: 9 fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj
Phone : 93 93 7779, 9893 58881 Sount & Waves Page: 9 fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k flag ladyi dj] lgrs foifr vusd] ^cuk^ u NksM+s /;s; dks] j?kqcj
Maxwell s equations and EM waves. From previous Lecture Time dependent fields and Faraday s Law
 Maxwell s equations and EM waves This Lecture More on Motional EMF and Faraday s law Displacement currents Maxwell s equations EM Waves From previous Lecture Time dependent fields and Faraday s Law 1 Radar
Maxwell s equations and EM waves This Lecture More on Motional EMF and Faraday s law Displacement currents Maxwell s equations EM Waves From previous Lecture Time dependent fields and Faraday s Law 1 Radar
Magnetohydrodynamic waves in a plasma
 Department of Physics Seminar 1b Magnetohydrodynamic waves in a plasma Author: Janez Kokalj Advisor: prof. dr. Tomaž Gyergyek Petelinje, April 2016 Abstract Plasma can sustain different wave phenomena.
Department of Physics Seminar 1b Magnetohydrodynamic waves in a plasma Author: Janez Kokalj Advisor: prof. dr. Tomaž Gyergyek Petelinje, April 2016 Abstract Plasma can sustain different wave phenomena.
is a What you Hear The Pressure Wave sets the Ear Drum into Vibration.
 is a What you Hear The ear converts sound energy to mechanical energy to a nerve impulse which is transmitted to the brain. The Pressure Wave sets the Ear Drum into Vibration. electroencephalogram v S
is a What you Hear The ear converts sound energy to mechanical energy to a nerve impulse which is transmitted to the brain. The Pressure Wave sets the Ear Drum into Vibration. electroencephalogram v S
Introduction to Fluid Mechanics
 Introduction to Fluid Mechanics Tien-Tsan Shieh April 16, 2009 What is a Fluid? The key distinction between a fluid and a solid lies in the mode of resistance to change of shape. The fluid, unlike the
Introduction to Fluid Mechanics Tien-Tsan Shieh April 16, 2009 What is a Fluid? The key distinction between a fluid and a solid lies in the mode of resistance to change of shape. The fluid, unlike the
General Physics I. Lecture 14: Sinusoidal Waves. Prof. WAN, Xin ( 万歆 )
 General Physics I Lecture 14: Sinusoidal Waves Prof. WAN, Xin ( 万歆 ) xinwan@zju.edu.cn http://zimp.zju.edu.cn/~xinwan/ Motivation When analyzing a linear medium that is, one in which the restoring force
General Physics I Lecture 14: Sinusoidal Waves Prof. WAN, Xin ( 万歆 ) xinwan@zju.edu.cn http://zimp.zju.edu.cn/~xinwan/ Motivation When analyzing a linear medium that is, one in which the restoring force
Theory of linear gravity waves April 1987
 April 1987 By Tim Palmer European Centre for Medium-Range Weather Forecasts Table of contents 1. Simple properties of internal gravity waves 2. Gravity-wave drag REFERENCES 1. SIMPLE PROPERTIES OF INTERNAL
April 1987 By Tim Palmer European Centre for Medium-Range Weather Forecasts Table of contents 1. Simple properties of internal gravity waves 2. Gravity-wave drag REFERENCES 1. SIMPLE PROPERTIES OF INTERNAL
Chapter 11. Vibrations and Waves
 Chapter 11 Vibrations and Waves Driven Harmonic Motion and Resonance RESONANCE Resonance is the condition in which a time-dependent force can transmit large amounts of energy to an oscillating object,
Chapter 11 Vibrations and Waves Driven Harmonic Motion and Resonance RESONANCE Resonance is the condition in which a time-dependent force can transmit large amounts of energy to an oscillating object,
PHYS 1114, Lecture 33, April 10 Contents:
 PHYS 1114, Lecture 33, April 10 Contents: 1 This class is o cially cancelled, and has been replaced by the common exam Tuesday, April 11, 5:30 PM. A review and Q&A session is scheduled instead during class
PHYS 1114, Lecture 33, April 10 Contents: 1 This class is o cially cancelled, and has been replaced by the common exam Tuesday, April 11, 5:30 PM. A review and Q&A session is scheduled instead during class
Kelvin Helmholtz Instability
 Kelvin Helmholtz Instability A. Salih Department of Aerospace Engineering Indian Institute of Space Science and Technology, Thiruvananthapuram November 00 One of the most well known instabilities in fluid
Kelvin Helmholtz Instability A. Salih Department of Aerospace Engineering Indian Institute of Space Science and Technology, Thiruvananthapuram November 00 One of the most well known instabilities in fluid
ESS314. Basics of Geophysical Fluid Dynamics by John Booker and Gerard Roe. Conservation Laws
 ESS314 Basics of Geophysical Fluid Dynamics by John Booker and Gerard Roe Conservation Laws The big differences between fluids and other forms of matter are that they are continuous and they deform internally
ESS314 Basics of Geophysical Fluid Dynamics by John Booker and Gerard Roe Conservation Laws The big differences between fluids and other forms of matter are that they are continuous and they deform internally
Oscillatory Motion SHM
 Chapter 15 Oscillatory Motion SHM Dr. Armen Kocharian Periodic Motion Periodic motion is motion of an object that regularly repeats The object returns to a given position after a fixed time interval A
Chapter 15 Oscillatory Motion SHM Dr. Armen Kocharian Periodic Motion Periodic motion is motion of an object that regularly repeats The object returns to a given position after a fixed time interval A
UNIVERSITY OF SOUTHAMPTON. Answer all questions in Section A and two and only two questions in. Section B.
 UNIVERSITY OF SOUTHAMPTON PHYS2023W1 SEMESTER 1 EXAMINATION 2009/10 WAVE PHYSICS Duration: 120 MINS Answer all questions in Section A and two and only two questions in Section B. Section A carries 1/3
UNIVERSITY OF SOUTHAMPTON PHYS2023W1 SEMESTER 1 EXAMINATION 2009/10 WAVE PHYSICS Duration: 120 MINS Answer all questions in Section A and two and only two questions in Section B. Section A carries 1/3
ENGINEERING FLUID MECHANICS. CHAPTER 1 Properties of Fluids
 CHAPTER 1 Properties of Fluids ENGINEERING FLUID MECHANICS 1.1 Introduction 1.2 Development of Fluid Mechanics 1.3 Units of Measurement (SI units) 1.4 Mass, Density, Specific Weight, Specific Volume, Specific
CHAPTER 1 Properties of Fluids ENGINEERING FLUID MECHANICS 1.1 Introduction 1.2 Development of Fluid Mechanics 1.3 Units of Measurement (SI units) 1.4 Mass, Density, Specific Weight, Specific Volume, Specific
MAE 101A. Homework 7 - Solutions 3/12/2018
 MAE 101A Homework 7 - Solutions 3/12/2018 Munson 6.31: The stream function for a two-dimensional, nonviscous, incompressible flow field is given by the expression ψ = 2(x y) where the stream function has
MAE 101A Homework 7 - Solutions 3/12/2018 Munson 6.31: The stream function for a two-dimensional, nonviscous, incompressible flow field is given by the expression ψ = 2(x y) where the stream function has
WAVES & SIMPLE HARMONIC MOTION
 PROJECT WAVES & SIMPLE HARMONIC MOTION EVERY WAVE, REGARDLESS OF HOW HIGH AND FORCEFUL IT CRESTS, MUST EVENTUALLY COLLAPSE WITHIN ITSELF. - STEFAN ZWEIG What s a Wave? A wave is a wiggle in time and space
PROJECT WAVES & SIMPLE HARMONIC MOTION EVERY WAVE, REGARDLESS OF HOW HIGH AND FORCEFUL IT CRESTS, MUST EVENTUALLY COLLAPSE WITHIN ITSELF. - STEFAN ZWEIG What s a Wave? A wave is a wiggle in time and space
Do not turn over until you are told to do so by the Invigilator.
 UNIVERSITY OF EAST ANGLIA School of Mathematics Main Series UG Examination 2014 15 FLUID DYNAMICS - THEORY AND COMPUTATION MTHA5002Y Time allowed: 3 Hours Attempt QUESTIONS 1 and 2, and THREE other questions.
UNIVERSITY OF EAST ANGLIA School of Mathematics Main Series UG Examination 2014 15 FLUID DYNAMICS - THEORY AND COMPUTATION MTHA5002Y Time allowed: 3 Hours Attempt QUESTIONS 1 and 2, and THREE other questions.
Nicholas J. Giordano. Chapter 10 Fluids
 Nicholas J. Giordano www.cengage.com/physics/giordano Chapter 10 Fluids Fluids A fluid may be either a liquid or a gas Some characteristics of a fluid Flows from one place to another Shape varies according
Nicholas J. Giordano www.cengage.com/physics/giordano Chapter 10 Fluids Fluids A fluid may be either a liquid or a gas Some characteristics of a fluid Flows from one place to another Shape varies according
High Speed Aerodynamics. Copyright 2009 Narayanan Komerath
 Welcome to High Speed Aerodynamics 1 Lift, drag and pitching moment? Linearized Potential Flow Transformations Compressible Boundary Layer WHAT IS HIGH SPEED AERODYNAMICS? Airfoil section? Thin airfoil
Welcome to High Speed Aerodynamics 1 Lift, drag and pitching moment? Linearized Potential Flow Transformations Compressible Boundary Layer WHAT IS HIGH SPEED AERODYNAMICS? Airfoil section? Thin airfoil
Electrodynamics HW Problems 06 EM Waves
 Electrodynamics HW Problems 06 EM Waves 1. Energy in a wave on a string 2. Traveling wave on a string 3. Standing wave 4. Spherical traveling wave 5. Traveling EM wave 6. 3- D electromagnetic plane wave
Electrodynamics HW Problems 06 EM Waves 1. Energy in a wave on a string 2. Traveling wave on a string 3. Standing wave 4. Spherical traveling wave 5. Traveling EM wave 6. 3- D electromagnetic plane wave
Chapter 16 Waves in One Dimension
 Lecture Outline Chapter 16 Waves in One Dimension Slide 16-1 Chapter 16: Waves in One Dimension Chapter Goal: To study the kinematic and dynamics of wave motion, i.e., the transport of energy through a
Lecture Outline Chapter 16 Waves in One Dimension Slide 16-1 Chapter 16: Waves in One Dimension Chapter Goal: To study the kinematic and dynamics of wave motion, i.e., the transport of energy through a
PHYSICS CURRICULUM. Unit 1: Measurement and Mathematics
 Chariho Regional School District - Science Curriculum September, 2016 PHYSICS CURRICULUM Unit 1: Measurement and Mathematics OVERVIEW Summary Mathematics is an essential tool of physics. This unit will
Chariho Regional School District - Science Curriculum September, 2016 PHYSICS CURRICULUM Unit 1: Measurement and Mathematics OVERVIEW Summary Mathematics is an essential tool of physics. This unit will
