*********************************************************
|
|
|
- Dorcas Potter
- 6 years ago
- Views:
Transcription
1 Prolems Ted Eisenerg, Section Editor ********************************************************* This section of the Journl offers reders n opportunity to echnge interesting mthemticl prolems nd solutions. Plese send them to Ted Eisenerg, Deprtment of Mthemtics, Ben-Gurion University, Beer-Shev, Isrel or f to: Questions concerning proposls nd/or solutions cn e sent e-mil to <eisent@01.net>. Solutions to previously stted prolems cn e seen t < Solutions to the prolems stted in this issue should e posted efore June 15, : Proposed y Kenneth Korin, New York, NY Solve the eqution + 9 = + 9 with > : Proposed y D. M. Bătinetu-Giurgiu, Buchrest, Romni nd Neculi Stnciu, George Emil Plde School, Buzău, Romni If n 1)!! = n 1), then evlute n+1 n + 1)!n + 1)!! lim n n + 1 ) n n!n 1)!!. n 599: Proposed y Ángel Plz, University of Ls Plms de Grn Cnri, Spin Let,, c e positive rel numers. Prove tht : Proposed y Arkdy Alt, Sn Jose, CA Prove the inequlity m + m + c m c 1 R r), where,, c nd m, m, m c re respectively sides nd medins of ABC, with circumrdius R nd inrdius r. 5401: Proposed y José Luis Díz-Brrero, Brcelon Tech, Brcelon, Spin Let,, c e three positive rel numers such tht + + c =. Prove tht ) + c c) c + ) 49. 1
2 540: Proposed y Ovidiu Furdui, Technicl University of Cluj-Npoc, Cluj-Npoc, Romni Clculte ) cos) cos) d, where nd re rel numers. 0 Solutions 579: Proposed y Kenneth Korin, New York, NY Solve: + 1) 4 1) =. Solution 1 y Ed Gry, Highlnd Bech, FL Cross-multiplying nd simplifying gives = 0. Oviously 0, so dividing the polynomil y 40 gives ) = 0, )) + 1 = 0. Letting t = + 1, squring t = nd then sustituting into the ove gives 1 t ) 1t ) + 1 = 0 40 t 1t + 8 = 0, so t 1 = 1 t = ) 1 ). Since t = + 1, we hve t + 1 = 0, nd solving for gives 1 = 1 ) t 1 + t 1 4 = 1 ) t + t 4 = 1 ) t 1 t = 1 ) t t 4. Sustituting in the respective vlues of t nd simplifying gives: 1 =
3 = = = Solution y Brin D. Besley, Presyterin College, Clinton, SC Given rel numer k, we seek ll rel solutions of We require + 1) 4 1) = k k) k) + 4 k) + 1 = + + 1) + + 1) = 0, where = 4 k + k 16k)/ nd = 4 k k 16k)/. Hence there re no rel solutions unless k, 0] [16, ). Solving for, we otin = ± 4)/ or = ± 4)/. We note tht if k = 0, then there is one rel solution; if k < 0 or k = 16, then there re two rel solutions; nd if k > 16, then there re four rel solutions. For the given eqution with k =, we hve four rel solutions: Letting = 1 + )/ nd = 1 )/, we otin = ± 4)/ 4.00 or 0.8; = ± 4)/ 8.44 or Comments: Arkdy Alt of Sn Jose, CA noted in his solution tht the in the sttement of the prolem could e replced with ny of the three numers 15, 16, or 18 to otin more elegnt nswer. For emple, the eqution + 1) 4 = 18 gives the solutions 1) = 5 ± ) 6 = ± = ± = ) 6 ±. Kenneth Korin, proposer of the prolem, stted: If >, then the eqution + 1) 4 1) = 4 ) gives the solutions 1 = + + c + c = 1,
4 = + c c = 1 4, with = nd with c = 4. In the given eqution 4 =. Then = 4, = >, = =, c = 4 = 1 4. Also solved y Htef I. Arshgi, Guilford Technicl Community College, Jmestown, NC; Bruno Slgueiro Fnego, Viveiro, Spin; G.C. Greuel, Newport News, VA; Pul M. Hrms, North Newton, KS; Kee-Wi Lu, Hong Kong, Chin; Moti Levy, Rehovot, Isrel; Dvid E. Mnes, SUNY College t Oneont, Oneont, NY; Polo Perfetti, Deprtment of Mthemtics, Tor Vergt University, Rome, Itly; Boris Rys, Brooklyn, NY; Henry Ricrdo, New York Mth Circle, NY. Toshihiro Shimizu, Kwski, Jpn; Neculi Stnciu, George Emil Plde Generl School, Buzău, Romni nd Titu Zvonru, Comănesti, Romni; Alert Stdler, Herrlierg, Switzerlnd; Dvid Stone nd John Hwkins, Georgi Southern University, Sttesoro, GA; Nicusor Zlot, Trin Vui Technicl College, Focsni, Romni, nd the proposer. 580: Proposed y Arkdy Alt, Sn Jose, CA Let, y, z) = y + yz + z) + y + z ) nd,, c e the side-lengths of tringle ABC. Prove tht F 16,, c ),, c), where F is the re of ABC. Solution 1 y Toshihiro Shimizu, Kwski, Jpn From the Heron s formul, F + + c) + c )c + ) + c) = 16 =,, c ) 16 Thus, it suffices to show tht,, c ),, c),, c ) 0 cn e written s ) c)q,, c), cyc ). The l.h.s) where q,, c) = c) + c) 0. Moreover, since q,, c) q, c, ) = )c + c + c + c ), 4
5 the reltion, which is lrger q,, c) or q, c, ), depends on the vlue of or. Without loss of generlity, we ssume c. Then, q,, c) q, c, ) qc,, ). Thus, ) c)q,, c) = ) c)q,, c) c)q, c, ) ) + qc,, ) c) c) cyc 0. Therefore, ) is true. Note: It is similr to the proof of Schur s inequlity. It seems tht ) is vlid for ny,, c, even if the constrint tht,, c re the side-lengths of tringle is not stisfied. Solution y Alert Stdler, Herrlierg, Switzerlnd Denote y s the semiperimeter of the tringle put s = s, s = s, s c = s c. By the tringle inequlity, s 0, s 0, s c 0. Also = s + s c, = s c + s, c = s + s. Furthermore, we note tht,, c) = s + s c, s c + s, s + s ) = 4 s s + s s c + s c s ) 0. By Heron s formul F = s s s s c = s + s + s c ) s s s c. Therefore we need to prove tht 64 s + s + s c ) s s s c s s + s s c + s c s ) s + s c ), s c + s ), s + s ) ) which is equivlent to 7 s 4 s + 1 s s + 5 s s s c 7 s 4 s s c + 6 s s s c 1) s is seen y simply multiplying out). By Schur s inequlity which is equivlent to s s s s s s c ) s s s c s ) 0 cycl s s + s s s c s s s c ) s is seen gin y multiplying out). We hve the following inequlities 5 s s + 5 s s s c 10 s s s c, y)), 7 s 4 s 7 s 4 s s c, y Muirhed s inequlity, 16 s s 16 s s s c, y Muirhed s inequlity. 5
6 1) follows y dding these three inequlities. Solution y proposer Let s := t 1 + t + t. Since t i < s, i = 1,, tringle inequlities) then our prolem is: Find m s for which there re positive integer numers t 1, t, t stisfying t i min { i, s 1}, i = 1,,, t 1 + t + t = s. First note tht s, t i, i = 1,,. Indeed, since t i s 1, then 1 s t i, i = 1,, nd, therefore, t 1 = s t t = s t ) + s t ). Cyclic we otin t, t. Hence, s 6 s. Since t = s t 1 t, t min {, s 1} then 1 s t 1 t min {, s 1} m {s t 1, s + 1 t 1 } t s 1 t 1 nd, therefore, for t we otin the inequlity 1) m {s t 1, s + 1 t 1, } t min {s 1 t 1,, s 1} with conditions of solvility : ) s t 1 s 1 s t 1 s + 1 t 1 s 1 t 1 s + 1 t 1 s t 1 s + 1 t 1 t 1 s Since s 1 s then ) together with t 1 min { 1, s 1} it gives us ounds for t 1 : ) m {s + 1, s, s + 1, } t 1 min { 1, s 1}. Since i, i =, then s + 1 s 1, s + 1 s 1 nd solvility condition for ) ecomes s s 1 + 1, s 1 s, s s 1 + 1, s s 1 s + 1. { } Thus, s = min, 1 + 1, + 1, is the lrgest vlue of integer semiperimeter. Solution 4 y Andre Fnchini, Cntú, Itly We know tht F = ss )s )s c) where s is the semiperimeter of ABC. Now mking the sustitutions nd clering the denomintors we hve to prove 16ss )s )s c) [ + c + c) + + c ) ] [ + c + c ) c 6 ) ] now we mke the following sustitutions with, y, z > 0) = y + z, = z +, c = + y 6.
7 nd epnding out into etric sums the given inequlity yields LHS: 7 4 y + 4 z + y 4 z + y 4 + z 4 + y z 4 ) + 4 y + y z + z )+ +6 yz + y z + y z + y z + yz + y z ) + 78 y z RHS: so it remins to prove tht 8 4 yz + y 4 z + yz 4 ) or 7 4 y + 4 z + y 4 z + y 4 + z 4 + y z 4 ) 8 4 yz + y 4 z + yz 4 ) which is true ecuse it follows from Muirhed s Theorem, q.e.d. 7[4,, 0] 19[4, 1, 1] 19[4,, 0] 19[4, 1, 1] Solution 5 y Polo Perfetti, Deprtment of Mthemtics, Tor Vergt University, Rome, Itly As well known F = ss )s )s c) nd s = + + c)/. Upon setting = y + z, = + z, c = + y, the inequlity ecomes sym 7 4 y + 1y) + 5yz) ) sym The third degree Schür inequlity is + + c ) + c sym, 7 4 yz + 6 y z ). which pplied to the triple y), yz), z), yields 5 y) + 5 yz) 10 y z. sym sym sym The inequlity ecomes 7 4 yz + 16 y z ), sym 7 4 y + 16y) ) sym nd the proof is complete upon oserving tht y the AGM we hve 4 y + 4 z 4 yz, y) + y) + z) y z. Also solved y Bruno Slgueiro Fnego, Viveiro, Spin; Ed Gry, Highlnd Bech, FL; Pul M. Hrms, North Newton, KS; Kee-Wi Lu, Hong Kong, Chin; Moti Levi, Rehovot, Isrel, nd Nicusor Zlot, Trin Vui Technicl College, Focsni, Romni 7
8 581: Proposed y D.M. Btinetu-Giurgiu, Mtei Bsr Ntionl College, Buchrest, nd Neculi Stnciu George Emil Plde School, Buzău, Romni Prove: In ny cute tringle ABC, with the usul nottions, holds: ) cos A cos B m+1 m+1, where m 0 is n integer numer. Solution 1 y Nikos Klpodis, Ptrs, Greece We first recll Brrow s Inequlity: If, y, z re positive rel numers nd A + B + C = π then yz + z y + y z cos A + y cos B + z 1) This inequlity first ppered in [1]. For solution see [] or [] inequlity.0, pp. -4)). Applying inequlity 1) for = cos A, y = cos B, nd z = note tht cos A, cos B, > 0, since ABC is n cute tringle) we otin cos A cos B By the following well-known trigonometric identities cos A + cos B + = sin A sin B sin C cos A + cos B + cos C) ) nd sin A sin B sin C = r 4R nd Euler s inequlity r R) we otin tht cos A + cos B + = 1 + r R Using the AM-GM inequlity nd inequlity ) we hve ) cos A + cos B + 1 cos A cos B ) = 1 4) 8 Furthermore, y the identity cos A + cos B + cos C + cos A cos B = 1 nd inequlity 4) we otin ) cos A + cos B + cos C 4 5) By ) nd 5), we hve cos A cos B Finlly, pplying Rdon s Inequlity nd using inequlity 6) we hve tht 6) ) cos A cos B m+1 = ) m+1 cos A cos B 1 m + ) cos B m+1 cos A 1 m + 8 ) cos A m+1 cos B 1 m
9 m+1 cos A cos B ) m ) m m = m+1. References: [1] L. J. Mordell nd D. F. Brrow, Solution 740, The Americn Mthemticl Monthly Vol. 44, No. 4 Apr., 197) pp [] R. R. Jnic, On A Geometric Inequlity Of D. F. Brrow, Univ. Beogrd. Pul. Elektrotehn. Fk. Ser. Mt. Fiz. No ), pp [] O. Bottem, R. Z. Djordjevic, R. R. Jnic, D. S. Mitrinovic, nd P. M. Vsic, Geometric Inequlities, Wolters-Noordhoff Pulishing, Groningen, The Netherlnds, Remrk: Inequlities ), 4), nd 5) lso pper respectively s inequlities.16,. nd.1 in reference []. Solution yángel Plz, University of Ls Plms de Grn Cnri, Spin By the RMS-AM inequlity it is enough to prove tht cos A cos B. Tking into ccount tht A + B + C = π, then = cos π A + π B) = sin A sin B cos A cos B, so the inequlity to e proved my e written with cotngents s cot A cot B 1 cot A cot B, or 1 1 cot A cot B 9. It is well known tht if α = cot A, β = cot B, nd γ = cot C, then αβ + βγ + γα = 1. Therefore, tking = αβ, y = βγ, nd z = γα we hve to prove tht which follows y Jensen s inequlity, since function f) = 1 1 Solution y Henry Ricrdo, New York Mth Circle, NY Elementry clcultions show tht for A, B, C 0, π/) is conve for 0, 1). Furthermore, we hve cos A cos B = tn C tn A + tn B. 1) tn C tn A + tn B. ) y Nesitt s inequlity. 9
10 Finlly, 1), ), nd the power men inequlity give us ) cos A cos B m+1 = ) tn C m+1 tn A + tn B 1 tn C tn A + tn B ) 1 m+1 = m+1. Solution 4 y Nicusor Zlot, Trin Vui Technicl College, Focsni, Romni Using the inequlity m+1 + m+1 + c m+1 1 m + + c)m+1 *) we hve ) cos A cos B m+1 = ) tn C m+1 1 ) tn C m+1 tn A + tn B y ) m. ) tn A + tn B Setting tn A =, tn B = y, tn C = z, nd using Nesitt s inequlity, we hve tn C tn A + B = z, ) + y y Nesitt) The sttement of the prolem follows from ) nd ). Also solved y Bruno Slgueiro Fnego, Viveiro, Spin; Ed Gry, Highlnd Bech, FL; Kee-Wi Lu, Hong Kong, Chin; Moti Levi, Rehovot, Isrel; Toshihiro Shimizu, Kwski, Jpn, nd the proposer. 58: Proposed y Ángel Plz, University of Ls Plms de Grn Cnri, Spin Prove tht if,, c re positive rel numers, then m+1 Solution 1 y Henry Ricrdo, New York Mth Circle, NY By the rithmetic-geometric men inequlity, ech of the sums greter thn or equl to. Thus Solution y Ed Gry, Highlnd Bech, FL Clerly, if = = c, the ove product ecomes, + 8 ) + 8 ) = 7 = )) )) = + 4) + 4) = 7 = 79 = is
11 Therefore, if we show tht the product is minimum when ll vriles re equl, then the conjecture would e true. It is sufficient to clculte the product in two different wys. First, suppose tht = nd c = Second, suppose = nd c = If oth of these products eceed 79, tht would show tht if ll vriles re not equl, we do not hve minimum. Cse 1: =, c = The product ecomes ) ) ) ) Cse : =, c = The product ecomes ) ) = QED = Solution y Dionne Biley, Elsie Cmpell, nd Chrles Diminnie, Angelo Stte University, Sn Angelo, TX We egin y pplying the etension of the Arithmetic - Geometric Men Inequlity which sttes tht if α, β,, y > 0 nd α + β = 1, then α + βy α y β, with equlity if nd only if = y. It follows tht + 8 = + 8 ) = ) 9 9 ) 1 = 9 9 ) 7 9, with equlity if nd only if =, c = c, nd c =, i.e., if nd only if = = c. c Net, pply the stndrd version of the Arithmetic - Geometric Men Inequlity to get ) 7 9 ) 8 9 ) 7 9 = 7, 1) with equlity if nd only if = c =, i.e., if nd only if = = c. c 11
12 A similr set of steps yields with equlity if nd only if = = c. + 8 Therefore, y 1) nd ), + 8 with equlity if nd only if = = c. + 8 Solution 4 y Andre Fnchini, Cntú, Itly 7, ) 7 = 9, Clering the denomintors nd mking the multiplictions we hve c c + c 4 + c 4 ) c + 4 c + c 4 ) c + c )+ or which is true ecuse +16 c + c + c + c + c + c ) 54 c 16[4,, 0] + 65[4, 1, 1] + 65[,, 0] + [,, 1] 8[,, ] 16[4,, 0] 16[,, ] 65[4, 1, 1] 65[,, ] 65[,, 0] 65[,, ] [,, 1] [,, ] ech of which follows from Muirhed s Theorem, q.e.d. Also solved y Arkdy Alt, Sn Jose, CA; Htef I. Arshgi, Guilford Technicl Community College, Jmestown, NC; Michel Brozinsky solutions), Centrl Islip, NY; Bruno Slgueiro Fnego, Viveiro, Spin; Pul M. Hrms, North Newton, KS; Kee-Wi Lu, Hong Kong, Chin; Moti Levi, Rehovot, Isrel; Nikos Klpodis, Ptrs, Greece; Polo Perfetti, Deprtment of Mthemtics, Tor Vergt University, Rome, Itly; Boris Rys, Brooklyn, NY; Neculi Stnciu, George Emil Plde School, Buzău, Romni nd Titu Zvonru, Comănesti, Romni; Toshihiro Shimizu, Kwski, Jpn; Alert Stdler, Hellierg, Switzerlnd; Nicusor Zlot, Trin Vui Technicl College, Focsni, Romni, nd the proposer. 58: Proposed y José Luis Díz-Brrero, Brcelon Tech, Brcelon, Spin Let n e positive integer. Find gcd n, n ), where n nd n re the positive integers for which 1 5) n = n n 5. Solution 1 y Ethn Gegner Undergrdute student, Tylor University), Uplnd, IN 1
13 The eqution n+1 n+1 5 = n n 5)1 5) = n + 5 n n + n ) 5 yields the recurrence reltions Thus, n+1 = n + 5 n n+1 = n + n gcd n+1, n+1 ) = gcd n + 5 n, n + n ) = gcd6 n n 1, n n 1 ) = gcd16 n + 40 n, 8 n + 16 n ) = 8 gcd n + 5 n, n + n ) = 8 gcd n, n + n ) = 8 gcd n, n ) Since 1 = 1 = 1, = 6, =, = 16, = 8, we hve gcd 1, 1 ) = 0, gcd, ) = 1, gcd, ) =. It follows inductively tht { n : n gcd n, n ) = n 1 : otherwise Solution Ángel Plz, University of Ls Plms de Grn Cnri, Spin For n = 1, 1 = 1 = 1. For n > 1, ) n n 5 = n 1 n ) 5 n = n n 1 5 n 1 + n 1 ) so n = n n 1, nd n = n 1 + n 1, or in mtri form ) ) ) ) n 1 5 n 1 n 1 5 = = n 1 n ) n 1 1 Therefore, n = n 1 L n nd n = n F n, where L n nd F n+1 respectively re the nth Lucs nd the nth Fioncci numers. Since L n = F n 1 + F n+1, then gcdl n, F n+1 ) = 1 nd hence gcd n, n ) = n 1, if L n is odd, while gcd n, n ) = n if L n is even, tht is when n is multiple of. Solution y Crl Liis, Columi Southern University, Ornge Bech, AL Let 1 5 ) n = n n 5. Then ) n+1 n+1 5 = n n 5 1 ) 5 = n + 5 n ) n + n ) 5. Thus, i) n+1 = n + 5 n, ). 1
14 ii) n+1 = n + n, nd using i), nd ii) we cn show tht iii) n+1 = n + 4 n 1, iv) n+1 = n + n 1. By oservtion we note from the first few terms v) n = n 1 l n, vi) n = n 1 f n, where l n nd f n re Lucs nd Fioncci numers. We cn verify v) nd vi) y sustituting them into iii) nd iv). {, if n It is well known tht gcdf n, l n ) = 1, otherwise.. See< or < Therefore, gcd n, n ) = gcd n 1 f n, n 1 l n ) = n 1 { {, if n 1, otherwise. = n, if n n 1, otherwise. Comment y Editor: Kenneth Korin of NewYork, NY oserved connection etween this prolem nd the solution to prolem 57, tht required us to find positive integers nd y such tht = + y 5, the unique nswer of which ws, y) = He continued on s follows. Oserve tht: 1 5 ) 1 = 4096) ) = ), nd lso 161) 7 5) = 1. So, ) ) ) = ) = = ) ) 6. And dditionlly: 6 ) 6 = Also solved y Arkdy Alt, Sn Jose, CA; Dionne Biley, Elsie Cmpell, nd Chrles Diminnie, Angelo Stte University, Sn Angelo, TX; Brin D. Besley, Presyterin College, Clinton, SC; Bruno Slgueiro Fnego, Viveiro, Spin; Ed Gry, Highlnd Bech, FL; G.C. Greuel, Newport News, VA; Kenneth Korin, New York, NY; Kee-Wi Lu, Hong Kong, Chin; 14
15 Moti Levi, Rehovot, Isrel; Dvid E. Mnes, SUNY College t Oneont, Oneont, NY; Toshihiro Shimizu, Kwski, Jpn; Dvid Stone nd John Hwkins, Georgi Southern University, Sttesoro, GA, nd the proposer. 584: Proposed y Ovidiu Furdui, Technicl University of Cluj-Npoc, Cluj-Npoc, Romni Find ll differentile functions f : R R which verify the functionl eqution f ) + f ) =, for ll R. Solution 1 y Michel Brozinsky, Centrl Islip, NY We hve t once from the given eqution f ) + f ) = tht f0) = 0, nd since = ) tht f ) + f) = f ) + f) so tht f ) + f )) = f) f ) which cn e cst s G ) = G), which we lel s eqution 1) nd in which G) = f) f ). From 1) we hve G) = c for some constnt c nd thus G ) = 0, nd so f ) = f ) nd we lel this s eqution ), where we hve used the chin rule. Now, y differentiting the given eqution twice we hve nd so from ) we hve f ) + f ) + f ) + f ) = f 0) = nd f ) + f ) =. ) Letting v = f ) in ) we hve the liner differentil eqution using the integrting fctor we otin ) dv + v =, nd d dv + vd = d so tht v = + A nd f ) = v = + A 4) where the constnta = 0 since f 0) =. Integrting 4) twice we otin f) = + B + C where B nd C re constnts nd since f0) = 0, we hve C = 0. Hence, the generl solution is f) = Solution y Toshihiro Shimizu, Kwski, Jpn + B, where B is n ritrry constnt. Let P ) e the given eqution. From P ) + P ), we get d d f) + f )) + f) + f )) =. 1) 15
16 From P ) P ), we get d f) f )) f) f )) = 0. ) d First, we solve 1). Let g) = f) + f ).Then, 1) cn e rewritten s dg d = g) The root of this differentil eqution is g) = C/ for constnt C R. Net, we solve ). Let h) = f) f ). Then, ) cn e rewritten s dh d = h) The root of this differentil eqution is h) = D for constnt D R. Thus, f) = g) + / + h))/ = C/ + D + / for some constnt C, D R. Since, f) should e defined for ll R, C must e 0. Therefore, f) = D + /, where D R is constnt nd this stisfies P ). Solution y Bruno Slgueiro Fnego, Viveiro, Spin f ) + f ) =, R = f ) + f )) ), R, tht is f ) + f) =, R = f ) + f ) = = f ) + f), R = f ) f )) + f) + f ) =, R, or equivlently, g ) + g) =, R, where g : R R is the function defined y g) = f) + f ), R, tht is h ) =, with h : R R, R. h) = g), R = h) = + C, for some C R, R implies f) + f ) = g) = h) = + C, {0}. f differentile implies f differentile t = 0 = f continuous t = 0. This fct nd the equlity f) + f ) = + C imply tht C = 0. Hence, f ) = f) nd thus f ) + f) = f ) + f ) =. R {0} = f ) f) = R 0} = f ) f) = 1, R {0}. = k ) 1 f), where k : R R is the function defined y k) =, {0} = k) = + D with D R, R {0} = f) = + D, R {0}. Since ) f ) f ) + f) + f ) =, R = f0) = 0 f 0) f 0)) + f0) + f 0) = 0 = 0, so f0) = 0, we conclude tht f) = + D,, where D is ny rel constnt. Solution 4 y Moti Levy, Rehovot, Isrel The derivtive of f : R R stisfies the functionl eqution 16
17 f ) = f ), 1) hence it is lso differentile function mye ecept for = 0). Differentition of the functionl eqution gives, Sustitution of 1) into ) gives, f ) + f ) f ) =. ) or f ) + f ) + f ) =, f ) + f ) f ) =. ) All the differentile functions which stisfy the functionl eqution f ) + f ) =, must stisfy ). The solutions of the differentil eqution ) re f ) = 1 + α + 1 ) + β 1 ) Now we sustitute 4) in the left side of the originl functionl eqution: d 1 + α + 1 d ) )) + β 1 = 1 α + β ) = α β). 4) + 1 α + 1 ) ) 1 + β It follows tht α must e equl to β for 4) to e solution. All the differentile functions f : R R, which stisfy the functionl eqution f ) + f ) =, for ll R re f ) = 1 + c, c R. Solution 5 y Kee-Wi Lu, Hong Kong, Chin Denote the given functionl eqution y 1). We show tht f) = where k is n ritrry constnt. Replcing t in 1), we otin Sutrcting ) fromf 1), we otin + k, ) f ) + f) =. ) f ) + f ) ) f) f )) = 0. 4)
18 Integrting 4), we otin f) f ) =, where is n ritrry constnt. By sustituting f ) = f) ck into 1). we otin f ) + f) = +. 5) Integrting 5), we otin f) = + +, where is constnt. By putting = 0 we see tht = 0. Thus ) hold for 0. By putting = 0 into 1), we otin f0) = 0 nd so ) hold for = 0 s well. Also solved y Arkdy Alt, Sn Jose, CA; Dionne Biley, Elsie Cmpell, nd Chrles Diminnie, Angelo Stte University, Sn Angelo, TX; Ed Gry, Highlnd Bech, FL; Henry Ricrdo, New York Mth Circle, NY; Dvid Stone nd John Hwkins, Georgi Southern University, Sttesoro, GA, nd the proposer. Editor s Notes The conjecture in 575* hs een revised y its uthor Kenneth Korin of NY, NY to the following: 575* revised): Prove or disprove the following conjecture. Let k e the product of N different prime numers ech congruent to 1mod 4). The totl numer of different rectngles nd trpezoids with integer length sides nd digonls tht cn e inscried in circle with dimeter k is ectly 5N N. Toshihiro Shimizu of Kwski, Jpn provided counter emple to the originl sttement of the prolem tht did not require the digonls to lso e integers. He let k = 5 = 85 nd then developed the trpezoids 4, 4, 4, 8) nd 50, 4, 50, 8). The digonls of these two trpezoids re not of integrl length. Ken commented on Toshihiro s emples y sying tht: It never occurred to me tht trpezoid with integer length sides inscried in circle with dimeter k could hve non-integer length digonls. So with the revision, 575* remins n open prolem. 18
*********************************************************
 Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journl offers reders n opportunity to echnge interesting mthemticl problems nd solutions
Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journl offers reders n opportunity to echnge interesting mthemticl problems nd solutions
SOLUTIONS A 2 + B 2 = AB + BA = 2 4
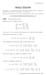 SOLUTIONS /4 SOLUTIONS No problem is ever permnently closed The editor is lwys plesed to consider for publiction new solutions or new insights on pst problems Sttements of the problems in this section
SOLUTIONS /4 SOLUTIONS No problem is ever permnently closed The editor is lwys plesed to consider for publiction new solutions or new insights on pst problems Sttements of the problems in this section
September 13 Homework Solutions
 College of Engineering nd Computer Science Mechnicl Engineering Deprtment Mechnicl Engineering 5A Seminr in Engineering Anlysis Fll Ticket: 5966 Instructor: Lrry Cretto Septemer Homework Solutions. Are
College of Engineering nd Computer Science Mechnicl Engineering Deprtment Mechnicl Engineering 5A Seminr in Engineering Anlysis Fll Ticket: 5966 Instructor: Lrry Cretto Septemer Homework Solutions. Are
7. Indefinite Integrals
 7. Indefinite Integrls These lecture notes present my interprettion of Ruth Lwrence s lecture notes (in Herew) 7. Prolem sttement By the fundmentl theorem of clculus, to clculte n integrl we need to find
7. Indefinite Integrls These lecture notes present my interprettion of Ruth Lwrence s lecture notes (in Herew) 7. Prolem sttement By the fundmentl theorem of clculus, to clculte n integrl we need to find
Chapter 6 Techniques of Integration
 MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
*********************************************************
 Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journl offers reders n opportunit to exchnge interesting mthemticl problems nd solutions
Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journl offers reders n opportunit to exchnge interesting mthemticl problems nd solutions
Section 4: Integration ECO4112F 2011
 Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
Farey Fractions. Rickard Fernström. U.U.D.M. Project Report 2017:24. Department of Mathematics Uppsala University
 U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
Torsion in Groups of Integral Triangles
 Advnces in Pure Mthemtics, 01,, 116-10 http://dxdoiorg/1046/pm011015 Pulished Online Jnury 01 (http://wwwscirporg/journl/pm) Torsion in Groups of Integrl Tringles Will Murry Deprtment of Mthemtics nd Sttistics,
Advnces in Pure Mthemtics, 01,, 116-10 http://dxdoiorg/1046/pm011015 Pulished Online Jnury 01 (http://wwwscirporg/journl/pm) Torsion in Groups of Integrl Tringles Will Murry Deprtment of Mthemtics nd Sttistics,
Polynomials and Division Theory
 Higher Checklist (Unit ) Higher Checklist (Unit ) Polynomils nd Division Theory Skill Achieved? Know tht polynomil (expression) is of the form: n x + n x n + n x n + + n x + x + 0 where the i R re the
Higher Checklist (Unit ) Higher Checklist (Unit ) Polynomils nd Division Theory Skill Achieved? Know tht polynomil (expression) is of the form: n x + n x n + n x n + + n x + x + 0 where the i R re the
Calculus of variations with fractional derivatives and fractional integrals
 Anis do CNMAC v.2 ISSN 1984-820X Clculus of vritions with frctionl derivtives nd frctionl integrls Ricrdo Almeid, Delfim F. M. Torres Deprtment of Mthemtics, University of Aveiro 3810-193 Aveiro, Portugl
Anis do CNMAC v.2 ISSN 1984-820X Clculus of vritions with frctionl derivtives nd frctionl integrls Ricrdo Almeid, Delfim F. M. Torres Deprtment of Mthemtics, University of Aveiro 3810-193 Aveiro, Portugl
SOME INTEGRAL INEQUALITIES OF GRÜSS TYPE
 RGMIA Reserch Report Collection, Vol., No., 998 http://sci.vut.edu.u/ rgmi SOME INTEGRAL INEQUALITIES OF GRÜSS TYPE S.S. DRAGOMIR Astrct. Some clssicl nd new integrl inequlities of Grüss type re presented.
RGMIA Reserch Report Collection, Vol., No., 998 http://sci.vut.edu.u/ rgmi SOME INTEGRAL INEQUALITIES OF GRÜSS TYPE S.S. DRAGOMIR Astrct. Some clssicl nd new integrl inequlities of Grüss type re presented.
Mathematics Number: Logarithms
 plce of mind F A C U L T Y O F E D U C A T I O N Deprtment of Curriculum nd Pedgogy Mthemtics Numer: Logrithms Science nd Mthemtics Eduction Reserch Group Supported y UBC Teching nd Lerning Enhncement
plce of mind F A C U L T Y O F E D U C A T I O N Deprtment of Curriculum nd Pedgogy Mthemtics Numer: Logrithms Science nd Mthemtics Eduction Reserch Group Supported y UBC Teching nd Lerning Enhncement
AN INEQUALITY OF OSTROWSKI TYPE AND ITS APPLICATIONS FOR SIMPSON S RULE AND SPECIAL MEANS. I. Fedotov and S. S. Dragomir
 RGMIA Reserch Report Collection, Vol., No., 999 http://sci.vu.edu.u/ rgmi AN INEQUALITY OF OSTROWSKI TYPE AND ITS APPLICATIONS FOR SIMPSON S RULE AND SPECIAL MEANS I. Fedotov nd S. S. Drgomir Astrct. An
RGMIA Reserch Report Collection, Vol., No., 999 http://sci.vu.edu.u/ rgmi AN INEQUALITY OF OSTROWSKI TYPE AND ITS APPLICATIONS FOR SIMPSON S RULE AND SPECIAL MEANS I. Fedotov nd S. S. Drgomir Astrct. An
Linear Inequalities. Work Sheet 1
 Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
Calculus Module C21. Areas by Integration. Copyright This publication The Northern Alberta Institute of Technology All Rights Reserved.
 Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
Section 6.1 INTRO to LAPLACE TRANSFORMS
 Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Exam 2, Mathematics 4701, Section ETY6 6:05 pm 7:40 pm, March 31, 2016, IH-1105 Instructor: Attila Máté 1
 Exm, Mthemtics 471, Section ETY6 6:5 pm 7:4 pm, Mrch 1, 16, IH-115 Instructor: Attil Máté 1 17 copies 1. ) Stte the usul sufficient condition for the fixed-point itertion to converge when solving the eqution
Exm, Mthemtics 471, Section ETY6 6:5 pm 7:4 pm, Mrch 1, 16, IH-115 Instructor: Attil Máté 1 17 copies 1. ) Stte the usul sufficient condition for the fixed-point itertion to converge when solving the eqution
QUADRATIC EQUATIONS OBJECTIVE PROBLEMS
 QUADRATIC EQUATIONS OBJECTIVE PROBLEMS +. The solution of the eqution will e (), () 0,, 5, 5. The roots of the given eqution ( p q) ( q r) ( r p) 0 + + re p q r p (), r p p q, q r p q (), (d), q r p q.
QUADRATIC EQUATIONS OBJECTIVE PROBLEMS +. The solution of the eqution will e (), () 0,, 5, 5. The roots of the given eqution ( p q) ( q r) ( r p) 0 + + re p q r p (), r p p q, q r p q (), (d), q r p q.
Chapter 9 Definite Integrals
 Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
Math 259 Winter Solutions to Homework #9
 Mth 59 Winter 9 Solutions to Homework #9 Prolems from Pges 658-659 (Section.8). Given f(, y, z) = + y + z nd the constrint g(, y, z) = + y + z =, the three equtions tht we get y setting up the Lgrnge multiplier
Mth 59 Winter 9 Solutions to Homework #9 Prolems from Pges 658-659 (Section.8). Given f(, y, z) = + y + z nd the constrint g(, y, z) = + y + z =, the three equtions tht we get y setting up the Lgrnge multiplier
Calculus AB. For a function f(x), the derivative would be f '(
 lculus AB Derivtive Formuls Derivtive Nottion: For function f(), the derivtive would e f '( ) Leiniz's Nottion: For the derivtive of y in terms of, we write d For the second derivtive using Leiniz's Nottion:
lculus AB Derivtive Formuls Derivtive Nottion: For function f(), the derivtive would e f '( ) Leiniz's Nottion: For the derivtive of y in terms of, we write d For the second derivtive using Leiniz's Nottion:
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
Thomas Whitham Sixth Form
 Thoms Whithm Sith Form Pure Mthemtics Unit C Alger Trigonometry Geometry Clculus Vectors Trigonometry Compound ngle formule sin sin cos cos Pge A B sin Acos B cos Asin B A B sin Acos B cos Asin B A B cos
Thoms Whithm Sith Form Pure Mthemtics Unit C Alger Trigonometry Geometry Clculus Vectors Trigonometry Compound ngle formule sin sin cos cos Pge A B sin Acos B cos Asin B A B sin Acos B cos Asin B A B cos
Lecture Solution of a System of Linear Equation
 ChE Lecture Notes, Dept. of Chemicl Engineering, Univ. of TN, Knoville - D. Keffer, 5/9/98 (updted /) Lecture 8- - Solution of System of Liner Eqution 8. Why is it importnt to e le to solve system of liner
ChE Lecture Notes, Dept. of Chemicl Engineering, Univ. of TN, Knoville - D. Keffer, 5/9/98 (updted /) Lecture 8- - Solution of System of Liner Eqution 8. Why is it importnt to e le to solve system of liner
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
p-adic Egyptian Fractions
 p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
Physics 116C Solution of inhomogeneous ordinary differential equations using Green s functions
 Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
63. Representation of functions as power series Consider a power series. ( 1) n x 2n for all 1 < x < 1
 3 9. SEQUENCES AND SERIES 63. Representtion of functions s power series Consider power series x 2 + x 4 x 6 + x 8 + = ( ) n x 2n It is geometric series with q = x 2 nd therefore it converges for ll q =
3 9. SEQUENCES AND SERIES 63. Representtion of functions s power series Consider power series x 2 + x 4 x 6 + x 8 + = ( ) n x 2n It is geometric series with q = x 2 nd therefore it converges for ll q =
Section 7.1 Area of a Region Between Two Curves
 Section 7.1 Are of Region Between Two Curves White Bord Chllenge The circle elow is inscried into squre: Clcultor 0 cm Wht is the shded re? 400 100 85.841cm White Bord Chllenge Find the re of the region
Section 7.1 Are of Region Between Two Curves White Bord Chllenge The circle elow is inscried into squre: Clcultor 0 cm Wht is the shded re? 400 100 85.841cm White Bord Chllenge Find the re of the region
1 ELEMENTARY ALGEBRA and GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE
 ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
2 b. , a. area is S= 2π xds. Again, understand where these formulas came from (pages ).
 AP Clculus BC Review Chpter 8 Prt nd Chpter 9 Things to Know nd Be Ale to Do Know everything from the first prt of Chpter 8 Given n integrnd figure out how to ntidifferentite it using ny of the following
AP Clculus BC Review Chpter 8 Prt nd Chpter 9 Things to Know nd Be Ale to Do Know everything from the first prt of Chpter 8 Given n integrnd figure out how to ntidifferentite it using ny of the following
MTH 505: Number Theory Spring 2017
 MTH 505: Numer Theory Spring 207 Homework 2 Drew Armstrong The Froenius Coin Prolem. Consider the eqution x ` y c where,, c, x, y re nturl numers. We cn think of $ nd $ s two denomintions of coins nd $c
MTH 505: Numer Theory Spring 207 Homework 2 Drew Armstrong The Froenius Coin Prolem. Consider the eqution x ` y c where,, c, x, y re nturl numers. We cn think of $ nd $ s two denomintions of coins nd $c
ON ALTERNATING POWER SUMS OF ARITHMETIC PROGRESSIONS
 ON ALTERNATING POWER SUMS OF ARITHMETIC PROGRESSIONS A. BAZSÓ Astrct. Depending on the prity of the positive integer n the lternting power sum T k n = k + k + + k...+ 1 n 1 n 1 + k. cn e extended to polynomil
ON ALTERNATING POWER SUMS OF ARITHMETIC PROGRESSIONS A. BAZSÓ Astrct. Depending on the prity of the positive integer n the lternting power sum T k n = k + k + + k...+ 1 n 1 n 1 + k. cn e extended to polynomil
ARITHMETIC OPERATIONS. The real numbers have the following properties: a b c ab ac
 REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
Bob Brown Math 251 Calculus 1 Chapter 5, Section 4 1 CCBC Dundalk
 Bo Brown Mth Clculus Chpter, Section CCBC Dundlk The Fundmentl Theorem of Clculus Informlly, the Fundmentl Theorem of Clculus (FTC) sttes tht differentition nd definite integrtion re inverse opertions
Bo Brown Mth Clculus Chpter, Section CCBC Dundlk The Fundmentl Theorem of Clculus Informlly, the Fundmentl Theorem of Clculus (FTC) sttes tht differentition nd definite integrtion re inverse opertions
Chapter 1: Logarithmic functions and indices
 Chpter : Logrithmic functions nd indices. You cn simplify epressions y using rules of indices m n m n m n m n ( m ) n mn m m m m n m m n Emple Simplify these epressions: 5 r r c 4 4 d 6 5 e ( ) f ( ) 4
Chpter : Logrithmic functions nd indices. You cn simplify epressions y using rules of indices m n m n m n m n ( m ) n mn m m m m n m m n Emple Simplify these epressions: 5 r r c 4 4 d 6 5 e ( ) f ( ) 4
The practical version
 Roerto s Notes on Integrl Clculus Chpter 4: Definite integrls nd the FTC Section 7 The Fundmentl Theorem of Clculus: The prcticl version Wht you need to know lredy: The theoreticl version of the FTC. Wht
Roerto s Notes on Integrl Clculus Chpter 4: Definite integrls nd the FTC Section 7 The Fundmentl Theorem of Clculus: The prcticl version Wht you need to know lredy: The theoreticl version of the FTC. Wht
Improper Integrals. Introduction. Type 1: Improper Integrals on Infinite Intervals. When we defined the definite integral.
 Improper Integrls Introduction When we defined the definite integrl f d we ssumed tht f ws continuous on [, ] where [, ] ws finite, closed intervl There re t lest two wys this definition cn fil to e stisfied:
Improper Integrls Introduction When we defined the definite integrl f d we ssumed tht f ws continuous on [, ] where [, ] ws finite, closed intervl There re t lest two wys this definition cn fil to e stisfied:
Math 113 Exam 2 Practice
 Mth Em Prctice Februry, 8 Em will cover sections 6.5, 7.-7.5 nd 7.8. This sheet hs three sections. The first section will remind you bout techniques nd formuls tht you should know. The second gives number
Mth Em Prctice Februry, 8 Em will cover sections 6.5, 7.-7.5 nd 7.8. This sheet hs three sections. The first section will remind you bout techniques nd formuls tht you should know. The second gives number
Edexcel GCE Core Mathematics (C2) Required Knowledge Information Sheet. Daniel Hammocks
 Edexcel GCE Core Mthemtics (C) Required Knowledge Informtion Sheet C Formule Given in Mthemticl Formule nd Sttisticl Tles Booklet Cosine Rule o = + c c cosine (A) Binomil Series o ( + ) n = n + n 1 n 1
Edexcel GCE Core Mthemtics (C) Required Knowledge Informtion Sheet C Formule Given in Mthemticl Formule nd Sttisticl Tles Booklet Cosine Rule o = + c c cosine (A) Binomil Series o ( + ) n = n + n 1 n 1
2.4 Linear Inequalities and Interval Notation
 .4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
.4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
MA123, Chapter 10: Formulas for integrals: integrals, antiderivatives, and the Fundamental Theorem of Calculus (pp.
 MA123, Chpter 1: Formuls for integrls: integrls, ntiderivtives, nd the Fundmentl Theorem of Clculus (pp. 27-233, Gootmn) Chpter Gols: Assignments: Understnd the sttement of the Fundmentl Theorem of Clculus.
MA123, Chpter 1: Formuls for integrls: integrls, ntiderivtives, nd the Fundmentl Theorem of Clculus (pp. 27-233, Gootmn) Chpter Gols: Assignments: Understnd the sttement of the Fundmentl Theorem of Clculus.
Discrete Mathematics and Probability Theory Summer 2014 James Cook Note 17
 CS 70 Discrete Mthemtics nd Proility Theory Summer 2014 Jmes Cook Note 17 I.I.D. Rndom Vriles Estimting the is of coin Question: We wnt to estimte the proportion p of Democrts in the US popultion, y tking
CS 70 Discrete Mthemtics nd Proility Theory Summer 2014 Jmes Cook Note 17 I.I.D. Rndom Vriles Estimting the is of coin Question: We wnt to estimte the proportion p of Democrts in the US popultion, y tking
set is not closed under matrix [ multiplication, ] and does not form a group.
![set is not closed under matrix [ multiplication, ] and does not form a group. set is not closed under matrix [ multiplication, ] and does not form a group.](/thumbs/78/78412113.jpg) Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Introduction to Algebra - Part 2
 Alger Module A Introduction to Alger - Prt Copright This puliction The Northern Alert Institute of Technolog 00. All Rights Reserved. LAST REVISED Oct., 008 Introduction to Alger - Prt Sttement of Prerequisite
Alger Module A Introduction to Alger - Prt Copright This puliction The Northern Alert Institute of Technolog 00. All Rights Reserved. LAST REVISED Oct., 008 Introduction to Alger - Prt Sttement of Prerequisite
*********************************************************
 Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to echange interesting mathematical problems and
Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to echange interesting mathematical problems and
Math 1102: Calculus I (Math/Sci majors) MWF 3pm, Fulton Hall 230 Homework 2 solutions
 Mth 1102: Clculus I (Mth/Sci mjors) MWF 3pm, Fulton Hll 230 Homework 2 solutions Plese write netly, nd show ll work. Cution: An nswer with no work is wrong! Do the following problems from Chpter III: 6,
Mth 1102: Clculus I (Mth/Sci mjors) MWF 3pm, Fulton Hll 230 Homework 2 solutions Plese write netly, nd show ll work. Cution: An nswer with no work is wrong! Do the following problems from Chpter III: 6,
Journal of Inequalities in Pure and Applied Mathematics
 Journl of Inequlities in Pure nd Applied Mthemtics GENERALIZATIONS OF THE TRAPEZOID INEQUALITIES BASED ON A NEW MEAN VALUE THEOREM FOR THE REMAINDER IN TAYLOR S FORMULA volume 7, issue 3, rticle 90, 006.
Journl of Inequlities in Pure nd Applied Mthemtics GENERALIZATIONS OF THE TRAPEZOID INEQUALITIES BASED ON A NEW MEAN VALUE THEOREM FOR THE REMAINDER IN TAYLOR S FORMULA volume 7, issue 3, rticle 90, 006.
An approximation to the arithmetic-geometric mean. G.J.O. Jameson, Math. Gazette 98 (2014), 85 95
 An pproximtion to the rithmetic-geometric men G.J.O. Jmeson, Mth. Gzette 98 (4), 85 95 Given positive numbers > b, consider the itertion given by =, b = b nd n+ = ( n + b n ), b n+ = ( n b n ) /. At ech
An pproximtion to the rithmetic-geometric men G.J.O. Jmeson, Mth. Gzette 98 (4), 85 95 Given positive numbers > b, consider the itertion given by =, b = b nd n+ = ( n + b n ), b n+ = ( n b n ) /. At ech
The area under the graph of f and above the x-axis between a and b is denoted by. f(x) dx. π O
 1 Section 5. The Definite Integrl Suppose tht function f is continuous nd positive over n intervl [, ]. y = f(x) x The re under the grph of f nd ove the x-xis etween nd is denoted y f(x) dx nd clled the
1 Section 5. The Definite Integrl Suppose tht function f is continuous nd positive over n intervl [, ]. y = f(x) x The re under the grph of f nd ove the x-xis etween nd is denoted y f(x) dx nd clled the
42nd International Mathematical Olympiad
 nd Interntionl Mthemticl Olympid Wshington, DC, United Sttes of Americ July 8 9, 001 Problems Ech problem is worth seven points. Problem 1 Let ABC be n cute-ngled tringle with circumcentre O. Let P on
nd Interntionl Mthemticl Olympid Wshington, DC, United Sttes of Americ July 8 9, 001 Problems Ech problem is worth seven points. Problem 1 Let ABC be n cute-ngled tringle with circumcentre O. Let P on
Continuous Random Variables Class 5, Jeremy Orloff and Jonathan Bloom
 Lerning Gols Continuous Rndom Vriles Clss 5, 8.05 Jeremy Orloff nd Jonthn Bloom. Know the definition of continuous rndom vrile. 2. Know the definition of the proility density function (pdf) nd cumultive
Lerning Gols Continuous Rndom Vriles Clss 5, 8.05 Jeremy Orloff nd Jonthn Bloom. Know the definition of continuous rndom vrile. 2. Know the definition of the proility density function (pdf) nd cumultive
Mathematics. Area under Curve.
 Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
MATH 573 FINAL EXAM. May 30, 2007
 MATH 573 FINAL EXAM My 30, 007 NAME: Solutions 1. This exm is due Wednesdy, June 6 efore the 1:30 pm. After 1:30 pm I will NOT ccept the exm.. This exm hs 1 pges including this cover. There re 10 prolems.
MATH 573 FINAL EXAM My 30, 007 NAME: Solutions 1. This exm is due Wednesdy, June 6 efore the 1:30 pm. After 1:30 pm I will NOT ccept the exm.. This exm hs 1 pges including this cover. There re 10 prolems.
Formulae For. Standard Formulae Of Integrals: x dx k, n 1. log. a dx a k. cosec x.cot xdx cosec. e dx e k. sec. ax dx ax k. 1 1 a x.
 Forule For Stndrd Forule Of Integrls: u Integrl Clculus By OP Gupt [Indir Awrd Winner, +9-965 35 48] A B C D n n k, n n log k k log e e k k E sin cos k F cos sin G tn log sec k OR log cos k H cot log sin
Forule For Stndrd Forule Of Integrls: u Integrl Clculus By OP Gupt [Indir Awrd Winner, +9-965 35 48] A B C D n n k, n n log k k log e e k k E sin cos k F cos sin G tn log sec k OR log cos k H cot log sin
Chapter 8.2: The Integral
 Chpter 8.: The Integrl You cn think of Clculus s doule-wide triler. In one width of it lives differentil clculus. In the other hlf lives wht is clled integrl clculus. We hve lredy eplored few rooms in
Chpter 8.: The Integrl You cn think of Clculus s doule-wide triler. In one width of it lives differentil clculus. In the other hlf lives wht is clled integrl clculus. We hve lredy eplored few rooms in
Review of Gaussian Quadrature method
 Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Goals: Determine how to calculate the area described by a function. Define the definite integral. Explore the relationship between the definite
 Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Chapter 3 Single Random Variables and Probability Distributions (Part 2)
 Chpter 3 Single Rndom Vriles nd Proilit Distriutions (Prt ) Contents Wht is Rndom Vrile? Proilit Distriution Functions Cumultive Distriution Function Proilit Densit Function Common Rndom Vriles nd their
Chpter 3 Single Rndom Vriles nd Proilit Distriutions (Prt ) Contents Wht is Rndom Vrile? Proilit Distriution Functions Cumultive Distriution Function Proilit Densit Function Common Rndom Vriles nd their
Chapter 8: Methods of Integration
 Chpter 8: Methods of Integrtion Bsic Integrls 8. Note: We hve the following list of Bsic Integrls p p+ + c, for p sec tn + c p + ln + c sec tn sec + c e e + c tn ln sec + c ln + c sec ln sec + tn + c ln
Chpter 8: Methods of Integrtion Bsic Integrls 8. Note: We hve the following list of Bsic Integrls p p+ + c, for p sec tn + c p + ln + c sec tn sec + c e e + c tn ln sec + c ln + c sec ln sec + tn + c ln
Discrete Mathematics and Probability Theory Spring 2013 Anant Sahai Lecture 17
 EECS 70 Discrete Mthemtics nd Proility Theory Spring 2013 Annt Shi Lecture 17 I.I.D. Rndom Vriles Estimting the is of coin Question: We wnt to estimte the proportion p of Democrts in the US popultion,
EECS 70 Discrete Mthemtics nd Proility Theory Spring 2013 Annt Shi Lecture 17 I.I.D. Rndom Vriles Estimting the is of coin Question: We wnt to estimte the proportion p of Democrts in the US popultion,
THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS.
 THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS RADON ROSBOROUGH https://intuitiveexplntionscom/picrd-lindelof-theorem/ This document is proof of the existence-uniqueness theorem
THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS RADON ROSBOROUGH https://intuitiveexplntionscom/picrd-lindelof-theorem/ This document is proof of the existence-uniqueness theorem
Section 7.1 Integration by Substitution
 Section 7. Integrtion by Substitution Evlute ech of the following integrls. Keep in mind tht using substitution my not work on some problems. For one of the definite integrls, it is not possible to find
Section 7. Integrtion by Substitution Evlute ech of the following integrls. Keep in mind tht using substitution my not work on some problems. For one of the definite integrls, it is not possible to find
THE QUADRATIC RECIPROCITY LAW OF DUKE-HOPKINS. Circa 1870, G. Zolotarev observed that the Legendre symbol ( a p
 THE QUADRATIC RECIPROCITY LAW OF DUKE-HOPKINS PETE L CLARK Circ 1870, Zolotrev observed tht the Legendre symbol ( p ) cn be interpreted s the sign of multipliction by viewed s permuttion of the set Z/pZ
THE QUADRATIC RECIPROCITY LAW OF DUKE-HOPKINS PETE L CLARK Circ 1870, Zolotrev observed tht the Legendre symbol ( p ) cn be interpreted s the sign of multipliction by viewed s permuttion of the set Z/pZ
M344 - ADVANCED ENGINEERING MATHEMATICS
 M3 - ADVANCED ENGINEERING MATHEMATICS Lecture 18: Lplce s Eqution, Anltic nd Numericl Solution Our emple of n elliptic prtil differentil eqution is Lplce s eqution, lso clled the Diffusion Eqution. If
M3 - ADVANCED ENGINEERING MATHEMATICS Lecture 18: Lplce s Eqution, Anltic nd Numericl Solution Our emple of n elliptic prtil differentil eqution is Lplce s eqution, lso clled the Diffusion Eqution. If
HOMEWORK SOLUTIONS MATH 1910 Sections 7.9, 8.1 Fall 2016
 HOMEWORK SOLUTIONS MATH 9 Sections 7.9, 8. Fll 6 Problem 7.9.33 Show tht for ny constnts M,, nd, the function yt) = )) t ) M + tnh stisfies the logistic eqution: y SOLUTION. Let Then nd Finlly, y = y M
HOMEWORK SOLUTIONS MATH 9 Sections 7.9, 8. Fll 6 Problem 7.9.33 Show tht for ny constnts M,, nd, the function yt) = )) t ) M + tnh stisfies the logistic eqution: y SOLUTION. Let Then nd Finlly, y = y M
Lecture 3. In this lecture, we will discuss algorithms for solving systems of linear equations.
 Lecture 3 3 Solving liner equtions In this lecture we will discuss lgorithms for solving systems of liner equtions Multiplictive identity Let us restrict ourselves to considering squre mtrices since one
Lecture 3 3 Solving liner equtions In this lecture we will discuss lgorithms for solving systems of liner equtions Multiplictive identity Let us restrict ourselves to considering squre mtrices since one
*********************************************************
 Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to exchange interesting mathematical problems
Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to exchange interesting mathematical problems
PROPERTIES OF AREAS In general, and for an irregular shape, the definition of the centroid at position ( x, y) is given by
 PROPERTES OF RES Centroid The concept of the centroid is prol lred fmilir to ou For plne shpe with n ovious geometric centre, (rectngle, circle) the centroid is t the centre f n re hs n is of smmetr, the
PROPERTES OF RES Centroid The concept of the centroid is prol lred fmilir to ou For plne shpe with n ovious geometric centre, (rectngle, circle) the centroid is t the centre f n re hs n is of smmetr, the
Some Improvements of Hölder s Inequality on Time Scales
 DOI: 0.55/uom-207-0037 An. Şt. Univ. Ovidius Constnţ Vol. 253,207, 83 96 Some Improvements of Hölder s Inequlity on Time Scles Cristin Dinu, Mihi Stncu nd Dniel Dănciulescu Astrct The theory nd pplictions
DOI: 0.55/uom-207-0037 An. Şt. Univ. Ovidius Constnţ Vol. 253,207, 83 96 Some Improvements of Hölder s Inequlity on Time Scles Cristin Dinu, Mihi Stncu nd Dniel Dănciulescu Astrct The theory nd pplictions
Taylor Polynomial Inequalities
 Tylor Polynomil Inequlities Ben Glin September 17, 24 Abstrct There re instnces where we my wish to pproximte the vlue of complicted function round given point by constructing simpler function such s polynomil
Tylor Polynomil Inequlities Ben Glin September 17, 24 Abstrct There re instnces where we my wish to pproximte the vlue of complicted function round given point by constructing simpler function such s polynomil
AQA Further Pure 2. Hyperbolic Functions. Section 2: The inverse hyperbolic functions
 Hperbolic Functions Section : The inverse hperbolic functions Notes nd Emples These notes contin subsections on The inverse hperbolic functions Integrtion using the inverse hperbolic functions Logrithmic
Hperbolic Functions Section : The inverse hperbolic functions Notes nd Emples These notes contin subsections on The inverse hperbolic functions Integrtion using the inverse hperbolic functions Logrithmic
The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a).
![The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a). The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a).](/thumbs/78/77467690.jpg) The Fundmentl Theorems of Clculus Mth 4, Section 0, Spring 009 We now know enough bout definite integrls to give precise formultions of the Fundmentl Theorems of Clculus. We will lso look t some bsic emples
The Fundmentl Theorems of Clculus Mth 4, Section 0, Spring 009 We now know enough bout definite integrls to give precise formultions of the Fundmentl Theorems of Clculus. We will lso look t some bsic emples
A basic logarithmic inequality, and the logarithmic mean
 Notes on Number Theory nd Discrete Mthemtics ISSN 30 532 Vol. 2, 205, No., 3 35 A bsic logrithmic inequlity, nd the logrithmic men József Sándor Deprtment of Mthemtics, Bbeş-Bolyi University Str. Koglnicenu
Notes on Number Theory nd Discrete Mthemtics ISSN 30 532 Vol. 2, 205, No., 3 35 A bsic logrithmic inequlity, nd the logrithmic men József Sándor Deprtment of Mthemtics, Bbeş-Bolyi University Str. Koglnicenu
2. VECTORS AND MATRICES IN 3 DIMENSIONS
 2 VECTORS AND MATRICES IN 3 DIMENSIONS 21 Extending the Theory of 2-dimensionl Vectors x A point in 3-dimensionl spce cn e represented y column vector of the form y z z-xis y-xis z x y x-xis Most of the
2 VECTORS AND MATRICES IN 3 DIMENSIONS 21 Extending the Theory of 2-dimensionl Vectors x A point in 3-dimensionl spce cn e represented y column vector of the form y z z-xis y-xis z x y x-xis Most of the
METHODS OF APPROXIMATING THE RIEMANN INTEGRALS AND APPLICATIONS
 Journl of Young Scientist Volume III 5 ISSN 44-8; ISSN CD-ROM 44-9; ISSN Online 44-5; ISSN-L 44 8 METHODS OF APPROXIMATING THE RIEMANN INTEGRALS AND APPLICATIONS An ALEXANDRU Scientific Coordintor: Assist
Journl of Young Scientist Volume III 5 ISSN 44-8; ISSN CD-ROM 44-9; ISSN Online 44-5; ISSN-L 44 8 METHODS OF APPROXIMATING THE RIEMANN INTEGRALS AND APPLICATIONS An ALEXANDRU Scientific Coordintor: Assist
Chapters Five Notes SN AA U1C5
 Chpters Five Notes SN AA U1C5 Nme Period Section 5-: Fctoring Qudrtic Epressions When you took lger, you lerned tht the first thing involved in fctoring is to mke sure to fctor out ny numers or vriles
Chpters Five Notes SN AA U1C5 Nme Period Section 5-: Fctoring Qudrtic Epressions When you took lger, you lerned tht the first thing involved in fctoring is to mke sure to fctor out ny numers or vriles
Before we can begin Ch. 3 on Radicals, we need to be familiar with perfect squares, cubes, etc. Try and do as many as you can without a calculator!!!
 Nme: Algebr II Honors Pre-Chpter Homework Before we cn begin Ch on Rdicls, we need to be fmilir with perfect squres, cubes, etc Try nd do s mny s you cn without clcultor!!! n The nth root of n n Be ble
Nme: Algebr II Honors Pre-Chpter Homework Before we cn begin Ch on Rdicls, we need to be fmilir with perfect squres, cubes, etc Try nd do s mny s you cn without clcultor!!! n The nth root of n n Be ble
378 Relations Solutions for Chapter 16. Section 16.1 Exercises. 3. Let A = {0,1,2,3,4,5}. Write out the relation R that expresses on A.
 378 Reltions 16.7 Solutions for Chpter 16 Section 16.1 Exercises 1. Let A = {0,1,2,3,4,5}. Write out the reltion R tht expresses > on A. Then illustrte it with digrm. 2 1 R = { (5,4),(5,3),(5,2),(5,1),(5,0),(4,3),(4,2),(4,1),
378 Reltions 16.7 Solutions for Chpter 16 Section 16.1 Exercises 1. Let A = {0,1,2,3,4,5}. Write out the reltion R tht expresses > on A. Then illustrte it with digrm. 2 1 R = { (5,4),(5,3),(5,2),(5,1),(5,0),(4,3),(4,2),(4,1),
On the degree of regularity of generalized van der Waerden triples
 On the degree of regulrity of generlized vn der Werden triples Jcob Fox Msschusetts Institute of Technology, Cmbridge, MA 02139, USA Rdoš Rdoičić Deprtment of Mthemtics, Rutgers, The Stte University of
On the degree of regulrity of generlized vn der Werden triples Jcob Fox Msschusetts Institute of Technology, Cmbridge, MA 02139, USA Rdoš Rdoičić Deprtment of Mthemtics, Rutgers, The Stte University of
Polynomial Approximations for the Natural Logarithm and Arctangent Functions. Math 230
 Polynomil Approimtions for the Nturl Logrithm nd Arctngent Functions Mth 23 You recll from first semester clculus how one cn use the derivtive to find n eqution for the tngent line to function t given
Polynomil Approimtions for the Nturl Logrithm nd Arctngent Functions Mth 23 You recll from first semester clculus how one cn use the derivtive to find n eqution for the tngent line to function t given
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Convex Sets and Functions
 B Convex Sets nd Functions Definition B1 Let L, +, ) be rel liner spce nd let C be subset of L The set C is convex if, for ll x,y C nd ll [, 1], we hve 1 )x+y C In other words, every point on the line
B Convex Sets nd Functions Definition B1 Let L, +, ) be rel liner spce nd let C be subset of L The set C is convex if, for ll x,y C nd ll [, 1], we hve 1 )x+y C In other words, every point on the line
*********************************************************
 Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to exchange interesting mathematical problems
Problems Ted Eisenberg, Section Editor ********************************************************* This section of the Journal offers readers an opportunity to exchange interesting mathematical problems
If we have a function f(x) which is well-defined for some a x b, its integral over those two values is defined as
 Y. D. Chong (26) MH28: Complex Methos for the Sciences 2. Integrls If we hve function f(x) which is well-efine for some x, its integrl over those two vlues is efine s N ( ) f(x) = lim x f(x n ) where x
Y. D. Chong (26) MH28: Complex Methos for the Sciences 2. Integrls If we hve function f(x) which is well-efine for some x, its integrl over those two vlues is efine s N ( ) f(x) = lim x f(x n ) where x
20 MATHEMATICS POLYNOMIALS
 0 MATHEMATICS POLYNOMIALS.1 Introduction In Clss IX, you hve studied polynomils in one vrible nd their degrees. Recll tht if p(x) is polynomil in x, the highest power of x in p(x) is clled the degree of
0 MATHEMATICS POLYNOMIALS.1 Introduction In Clss IX, you hve studied polynomils in one vrible nd their degrees. Recll tht if p(x) is polynomil in x, the highest power of x in p(x) is clled the degree of
Math 154B Elementary Algebra-2 nd Half Spring 2015
 Mth 154B Elementry Alger- nd Hlf Spring 015 Study Guide for Exm 4, Chpter 9 Exm 4 is scheduled for Thursdy, April rd. You my use " x 5" note crd (oth sides) nd scientific clcultor. You re expected to know
Mth 154B Elementry Alger- nd Hlf Spring 015 Study Guide for Exm 4, Chpter 9 Exm 4 is scheduled for Thursdy, April rd. You my use " x 5" note crd (oth sides) nd scientific clcultor. You re expected to know
The Evaluation Theorem
 These notes closely follow the presenttion of the mteril given in Jmes Stewrt s textook Clculus, Concepts nd Contexts (2nd edition) These notes re intended primrily for in-clss presenttion nd should not
These notes closely follow the presenttion of the mteril given in Jmes Stewrt s textook Clculus, Concepts nd Contexts (2nd edition) These notes re intended primrily for in-clss presenttion nd should not
Math 131. Numerical Integration Larson Section 4.6
 Mth. Numericl Integrtion Lrson Section. This section looks t couple of methods for pproimting definite integrls numericlly. The gol is to get good pproimtion of the definite integrl in problems where n
Mth. Numericl Integrtion Lrson Section. This section looks t couple of methods for pproimting definite integrls numericlly. The gol is to get good pproimtion of the definite integrl in problems where n
Math 4310 Solutions to homework 1 Due 9/1/16
 Mth 4310 Solutions to homework 1 Due 9/1/16 1. Use the Eucliden lgorithm to find the following gretest common divisors. () gcd(252, 180) = 36 (b) gcd(513, 187) = 1 (c) gcd(7684, 4148) = 68 252 = 180 1
Mth 4310 Solutions to homework 1 Due 9/1/16 1. Use the Eucliden lgorithm to find the following gretest common divisors. () gcd(252, 180) = 36 (b) gcd(513, 187) = 1 (c) gcd(7684, 4148) = 68 252 = 180 1
5.4. The Fundamental Theorem of Calculus. 356 Chapter 5: Integration. Mean Value Theorem for Definite Integrals
 56 Chter 5: Integrtion 5.4 The Fundmentl Theorem of Clculus HISTORICA BIOGRAPHY Sir Isc Newton (64 77) In this section we resent the Fundmentl Theorem of Clculus, which is the centrl theorem of integrl
56 Chter 5: Integrtion 5.4 The Fundmentl Theorem of Clculus HISTORICA BIOGRAPHY Sir Isc Newton (64 77) In this section we resent the Fundmentl Theorem of Clculus, which is the centrl theorem of integrl
( ) Same as above but m = f x = f x - symmetric to y-axis. find where f ( x) Relative: Find where f ( x) x a + lim exists ( lim f exists.
 AP Clculus Finl Review Sheet solutions When you see the words This is wht you think of doing Find the zeros Set function =, fctor or use qudrtic eqution if qudrtic, grph to find zeros on clcultor Find
AP Clculus Finl Review Sheet solutions When you see the words This is wht you think of doing Find the zeros Set function =, fctor or use qudrtic eqution if qudrtic, grph to find zeros on clcultor Find
Bernoulli Numbers Jeff Morton
 Bernoulli Numbers Jeff Morton. We re interested in the opertor e t k d k t k, which is to sy k tk. Applying this to some function f E to get e t f d k k tk d k f f + d k k tk dk f, we note tht since f
Bernoulli Numbers Jeff Morton. We re interested in the opertor e t k d k t k, which is to sy k tk. Applying this to some function f E to get e t f d k k tk d k f f + d k k tk dk f, we note tht since f
5.7 Improper Integrals
 458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
Section - 2 MORE PROPERTIES
 LOCUS Section - MORE PROPERTES n section -, we delt with some sic properties tht definite integrls stisf. This section continues with the development of some more properties tht re not so trivil, nd, when
LOCUS Section - MORE PROPERTES n section -, we delt with some sic properties tht definite integrls stisf. This section continues with the development of some more properties tht re not so trivil, nd, when
Integral points on the rational curve
 Integrl points on the rtionl curve y x bx c x ;, b, c integers. Konstntine Zeltor Mthemtics University of Wisconsin - Mrinette 750 W. Byshore Street Mrinette, WI 5443-453 Also: Konstntine Zeltor P.O. Box
Integrl points on the rtionl curve y x bx c x ;, b, c integers. Konstntine Zeltor Mthemtics University of Wisconsin - Mrinette 750 W. Byshore Street Mrinette, WI 5443-453 Also: Konstntine Zeltor P.O. Box
Bridging the gap: GCSE AS Level
 Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Mathematics Extension 1
 04 Bored of Studies Tril Emintions Mthemtics Etension Written by Crrotsticks & Trebl. Generl Instructions Totl Mrks 70 Reding time 5 minutes. Working time hours. Write using blck or blue pen. Blck pen
04 Bored of Studies Tril Emintions Mthemtics Etension Written by Crrotsticks & Trebl. Generl Instructions Totl Mrks 70 Reding time 5 minutes. Working time hours. Write using blck or blue pen. Blck pen
Anti-derivatives/Indefinite Integrals of Basic Functions
 Anti-derivtives/Indefinite Integrls of Bsic Functions Power Rule: In prticulr, this mens tht x n+ x n n + + C, dx = ln x + C, if n if n = x 0 dx = dx = dx = x + C nd x (lthough you won t use the second
Anti-derivtives/Indefinite Integrls of Bsic Functions Power Rule: In prticulr, this mens tht x n+ x n n + + C, dx = ln x + C, if n if n = x 0 dx = dx = dx = x + C nd x (lthough you won t use the second
