Exponentiated Generalized. Transformed-Transformer. Family of Distributions
|
|
|
- Alexina Hunt
- 5 years ago
- Views:
Transcription
1 Journl of Sttistil n Eonometri Methos, vol.6, no.4, 2017, 1-17 ISSN: print), online) Sienpress Lt, 2017 Exponentite Generlize Trnsforme-Trnsformer Fmily of Distributions Sulemn Nsiru 1, Peter N. Mwit 2 n Osr Nges 3 Abstrt Reently, the evelopment of generlize lss of istributions hs beome n issue of interest, to both pplie n theoretil sttistiins, ue to their wier pplition in ifferent fiels of stuies. Thus, the urrent work propose new generlize fmily of istributions lle the exponentite generlize trnsforme-trnsformer fmily. Some members of the new fmily suh s the exponentite generlize hlf logisti fmily ws isusse. Sttistil mesures suh s quntile, moment, moment generting funtion n Shnnon entropy for this new lss of istributions hve been erive. Mthemtis Subjet Clssifition: 62E15; 60E05 Keywors: Exponentite generlize T-X ; quntile; moment; moment generting funtion; Shnnon entropy 1 Pn Afrin University, Institute for Bsi Sienes, Nirobi, Keny. E-mil: sulemnstt@gmil.om/snsiru@us.eu.gh 2 Mhkos University, Deprtment of Mthemtis, Mhkos, Keny. E-mil: petermwit@mksu..ke 3 Tit Tvet University, Mthemtis n Informtis Deprtment. E-mil: osnges@ttu..ke Artile Info: Reeive : June 12, Revise : July 14, Publishe online : Deember 1, 2017
2 2 Exponentite Generlize T-X 1 Introution Myri of problems rise in ifferent fiel of stuies suh s engineering, turil siene, environmentl, biologil stuies, emogrphy, eonomis n finne tht requires moeling using suitble probbility istribution moels. However, the t generting proess is often hrterize with the problems of elongtion n symmetry, whih mkes it iffiult for the lssil istributions to provie equte fit to the rel t. In ition, the t sets my exhibit non-monotoni filure rte suh s the bthtub, unimol n moifie unimol filure rte. Hene, it is often neessry to utilize generl moel tht is likely to inlue moel suitble for the t s speil se. These hve motivte both theoretil n pplie sttistiins to evelop genertors for moifying existing sttistil istributions to mke them more flexible in moeling rel t. For this reson, reserhers in the fiel of istribution theory hve evelope n stuie mny generlize lsses of istributions. Coreiro et l. 4] evelope the exponentite generlize lss of istributions. Given rnom vrible X with umultive istribution funtion CDF) F x), the CDF of the exponentite generlize lss of istributions is efine s Gx) = 1 1 F x)) α ] β. 1) Alztreh et l. 1] reently propose new fmily of istributions lle the trnsforme-trnsformer T-X ) fmily. They use non-negtive ontinuous rnom vrible T s genertor n efine the CDF of their lss of istribution s Gx) = log1 F x)) 0 rt)t = R { log1 F x)), 2) where rt) is the probbility ensity funtion PDF) of the rnom vrible T. Alztreh et l. 1] T-X fmily of istribution extens the bet-generte fmily of 7] by repling the bet rnom vrible with ny non-negtive ontinuous rnom vrible T. The orresponing PDF of the CDF efine in eqution 2) is given by gx) = fx) r { log1 F x)). 3) 1 F x)
3 S. Nsiru, P.N. Mwit n O. Nges 3 Alzghl et l. 2] propose n extension of the T-X fmily by introuing single shpe prmeter to mke the fmily of istributions efine by 1] more flexible. Alzghl et l. 2] lle this new fmily the exponentite T-X fmily. The CDF of the exponentite T-X fmily is efine s Gx) = log1 F x)) The orresponing PDF is given by 0 rt)t = R { log1 F x)). 4) gx) = fx)f 1 x) r { log1 F x)), > 0. 5) 1 F x) It is obvious tht the upper limits use in the T-X fmily n the exponentite T-X fmily re umultive hzr funtions of ertin fmilies of istributions. Thus, new fmilies of the T-X istributions n be efine by employing new umultive hzr funtion s n upper limit. In this stuy, new T-X fmily lle the exponentite generlize EG) T-X fmily is propose by using new upper limit tht generlizes tht of 1] n 2] to provie greter flexibility in moeling rel t. 2 The New Fmily Let rt) n Rt) be the PDF n CDF of non-negtive rnom vrible T with support 0, ) respetively. The CDF of the EG T-X fmily of istributions for rnom vrible X is efine s Gx) = log1 1 F x)) ] 0 rt)t = R { log1 1 F x)) ], 6) where F x) = 1 F x) is the survivl funtion of the rnom vrible X n > 0, > 0 re shpe prmeters. The orresponing PDF of the new fmily is obtine by ifferentiting eqution 6) n is given by gx) = fx)1 F x)) 1 1 F x)) F x)) r { log1 1 F x)) ]. 7) Employing similr nming onvention s T-X istribution, eh member of the new fmily of istribution generte from 7) is nme EG T-X istribution.
4 4 Exponentite Generlize T-X When the prmeter = 1, the PDF in 7) reues to the PDF in eqution 5). In ition, when = = 1, the PDF in 7) reues to the PDF in eqution 3). The CDF n PDF of the EG T-X istribution n be written s Gx) = R { log1 1 F x)) ] = RHx)) n gx) = hx)rhx)), where Hx) n hx) re the umultive hzr n hzr funtions of the rnom vrible X with CDF 1 1 F x)) ] respetively. Thus, the EG T-X istribution n be esribe s fmily of istribution rising from weighte hzr funtion. The hzr funtion of the EG T-X fmily is given by τx) = gx) 1 Gx) = fx)1 F x)) 1 1 F { x)) 1 r log1 1 F x)) ] 1 1 F x)) ) 1 R { log1 1 F x)) ] ). Lemm 1. Let T be rnom vrible with PDF rt), then the rnom vrible X = Q X {1 1 1 e ) ] T 1 1, where Q X ) = F 1 ) is the quntile funtion of the rnom vrible X with CDF F x), follows the EG T-X istribution. Proof. Using the ft tht Gx) = R { log1 1 F x)) ] gives the reltionship between the rnom vrible T n X s T = log1 1 F X)) ]. Thus, solving for X yiels X = Q X {1 1 1 e ) ] T ) Lemm 1 mkes it esy to simulte the rnom vrible X by first generting rnom numbers from the istribution of the rnom vrible T n then omputing X = Q X {1 1 1 e ) ] T 1 1, whih hs the CDF Gx). 3 Some Exponentite Generlize Trnsforme- Trnsformer Fmilies The EG T-X fmily n be tegorize into two bro sub-fmilies. One sub-fmily hs the sme T istribution but ifferent X istributions n the other sub-fmily hs ifferent T istributions but the sme X istribution.
5 S. Nsiru, P.N. Mwit n O. Nges 5 Tble 1 isplys ifferent EG T-X istributions with ifferent T istributions but the sme X istribution. Tble 1: EG T-X Fmilies from Different T Distributions Nme Density rt) EG T-X Fmily ensity gx) Exponentil λe λt λfx)1 F x)) 1 1 F x)) F x)) ] 1 λ 1 Gmm t α 1 e t Γα)β α β fx)1 F x)) 1 1 F x)) F x)) β ] 1 1 Γα)β α { log1 1 F x)) ] 1 α Gompertz θe γt e θ γ eγt 1) θfx)1 F x)) 1 1 F x)) exp 1 θ γ {1 1 1 F x)) ] γ+1 {1 1 1 F x)) ] γ) Hlf logisti Lomx 2λe λt 1+e λt ) 2 λk 1+λt) k+1 2λfx)1 F x)) 1 1 F x)) F x)) ] λ 1 {1+1 1 F x)) ] λ 2 λkfx)1 F x)) 1 1 F x)) 1 {1 λ log1 1 F x)) ] k F x)) ] Burr XII Weibull αkt α 1 1+t α ) k+1 α γ t γ αkfx)1 F x)) 1 1 F x)) 1 { log1 1 F x)) ] α F x)) ]{1+ log1 1 F x)) )] α k+1 { ) α 1 e t γ ) α αfx)1 F x)) 1 1 F x)) 1 exp log1 1 F x)) γ ] α γ1 1 F x)) ]{ log1 1 F X)) ] 1 α 3.1 Exponentite Generlize Hlf Logisti Fmily If the rnom vrible T follows the hlf logisti istribution with prmeter λ, then rt) = 2λe λt, t > 0, λ > 0. Using eqution 7), the PDF of the 1+e λt ) 2 exponentite generlize hlf logisti EGHL) fmily is efine s gx) = 2λfx)1 F x)) 1 1 F x)) F x)) ] λ 1 { F x)) ] λ 2. 9)
6 6 Exponentite Generlize T-X Using the CDF of the hlf logisti istribution, Rt) = 1 e λt 1+e λt n eqution 6), the orresponing CDF of the EGHL fmily is given by Gx) = F x) ) ] λ F x) ) ] λ. The EGHL fmily generlizes ll hlf logisti fmilies of 2] exponentite T-X fmily n 1] T-X fmily. If the rnom vrible X follows Fréthet istribution with CDF F x) = e x) b, x > 0, > 0, b > 0, then the CDF of the EGHL-Fréthet istribution EGHLFD) is given by Gx) = { e ) x) b ] λ { e ) x) b ] λ. 10) The orresponing PDF of the EGHLFD is obtine by ifferentiting 10) n is given by gx) = 2 b bλ 1 e ) x) b e ) x) b ] 1 { e ) x) b ] λ 1 { x b+1 e x) {1 b e ) x) b ] λ 2. Some speil ses of the EGHLFD re: 11) 1. When λ = 1, the EGHLFD reues to EG stnrize hlf logisti Fréthet istribution. 2. When b = 1, the EGHLFD reues to EGHL inverse exponentil istribution. 3. When = = 1, the EGHLFD reues to hlf logisti Fréthet istribution. 4. When = = b = 1, the EGHLFD reues to hlf logisti inverse exponentil istribution. The reltionship between the EGHLFD n the uniform, Fréthet n hlf logisti istributions re given by lemm 2.
7 S. Nsiru, P.N. Mwit n O. Nges 7 Lemm If the rnom vrible Y follows the uniform istribution on the intervl 0, 1), then the rnom vrible X = log Y Y hs EGHLFD with prmeters, b,, n λ. λ 1 2. If the rnom vrible Y follows the Fréthet istribution with prmeters n b, then the rnom vrible X = log e x) b 1 + e x) b hs EGHLFD with prmeters, b,, n λ. 1 λ b 3. If the rnom vrible Y follows the hlf logisti istribution with Proof. The results follow iretly from trnsformtion of rnom vribles. prmeter λ, then the rnom vrible { X = log e ) Y 1 hs EGHLFD with prmeters, b,, n λ. ] 1 b,, 1 b, 4 Sttistil Mesures In this setion, we isuss sttistil mesures suh s quntile, moment, moment generting funtion MGF)n Shnnon entropy of the EG T-X fmily of istributions. Lemm 3. The quntile funtion of the EG T-X fmily for p 0, 1) is given by Qp) = Q X {1 1 1 e ) ] Q T p 1, where Q X ) = F 1 ) is the quntile funtion of the rnom vrible X with CDF F x) n Q T ) = R 1 ) is the quntile funtion of the rnom vrible T with CDF Rt).
8 8 Exponentite Generlize T-X Proof. Using the CDF of the EG T-X fmily efine in eqution 6), the quntile funtion is obtine by solving the eqution R { log 1 1 F Qp)) ) ] = p, for Qp). Thus, the proof is omplete. Corollry 1. Bse on lemm 3, the quntile funtion for the EGHL fmily is given by, Qp) = Q X p 1 + p λ. 1 Proposition 1. The r th non-entrl moment of the EG T-X fmily of istributions is given by i µ r = i, k, l, m=0 j=0 1) j+k+l+m l m δ r,i Γ i + 1) Γ j + 1) Γ k + 1) j! k! l! m! Γ i j + 1) Γ j k + 1) Γ k l + 1)E T m ), 12) where δ r,i = ih 0 ) 1 i s=1 s r + 1) i] h s δ r,i s with δ r,0 = h r 0, h i i = 0, 1,...) re suitbly hosen rel numbers tht epen on the prmeters of the F x) istribution, ET m ) is the m th moment of the rnom vrible T, Γ ) is the gmm funtion n r = 1, 2,.... Proof. From lemm 1, X = Q X {1 1 1 e ) ] T 1 1, where Q X ) = F 1 ) is quntile funtion. Thus, Q X ) = F 1 ) n be expresse in terms of power series using the following power series expnsion of the quntile. Q X u) = h i u i, 13) where the oeffiients re suitbly hosen rel numbers tht epen on the prmeters of the F x) istribution. For power series rise to positive i=0 integer r for r 1), we hve ) r Q X u)) r = h i u i = i=0 δ r, i u i, 14) i=0
9 S. Nsiru, P.N. Mwit n O. Nges 9 where the oeffiients δ r, i for i = 1, 2,...) re etermine from the reurrene eqution δ r,i = ih 0 ) 1 i s=1 s r + 1) i] h s δ r,i s n δ r,0 = h r 0 5]. Using equtions 13) n 14), the r th non-entrl moment of the EG T-X fmily of istributions n be expresse s { E X r ) = µ r = E δ r, i 1 Sine 0 < expnsion 1 1 e ) ) T z) η = i=0 1 1 e T ] i. 15) < 1, for T 0, ), pplying the binomil series j=0 for rel non-integer η > 0, thrie, we obtin e ) ) T 1 1 ] i i = 1) j Γ η + 1) j! Γ η j + 1) zη, z < 1, k, l=0 j=0 But the series expnsion of e lt is given by e lt 1) m l m T m =. m! 1 Thus 1 1 e T ] i = m=0 k, l m=0 j=0 1) j+k+l Γ i + 1) Γ j + 1) Γ k + 1) e lt j! k! l! Γ i j + 1) Γ j k + 1) Γ k l + 1). Substituting eqution 16) into 15) n simplifying, we obtin µ r = i i, k, l, m=0 j=0 i 1) j+k+l+m Γ i + 1) Γ j + 1) Γ k + 1) l m T m j! k! l! m! Γ i j + 1) Γ j k + 1) Γ k l + 1). 16) 1) j+k+l+m l m δ r,i Γ i + 1) Γ j + 1) Γ k + 1) j! k! l! m! Γ i j + 1) Γ j k + 1) Γ k l + 1)E T m ). Corollry 2. Bse on proposition 1, the r th moment of the EGHL fmily is given by µ r = i i, k, l, m=0 j=0 where m = 1, 2,.... 1) j+k+l+m l m δ r,i Γ i + 1) Γ j + 1) Γ k + 1) j! k! l! m! Γ i j + 1) Γ j k + 1) Γ k l + 1) { 2 n=0 1) n Γ m + 1) λ m n + 1) m,
10 10 Exponentite Generlize T-X by Proposition 2. The MGF of the EG T-X fmily of istributions is given M X z) = i r, i, k, l, m=0 j=0 1) j+k+l+m z r l m δ r,i Γ i + 1) Γ j + 1) Γ k + 1) r! j! k! l! m! Γ i j + 1) Γ j k + 1) Γ k l + 1)E T m ). Proof. By efinition the MGF is given by M X z) = E e zx). Using the series expnsion of e zx, gives us 17) M X z) = r=0 z r µ r. 18) r! Substituting µ r into eqution 18), we hve M X z) = i r, i, k, l, m=0 j=0 whih is the MGF. 1) j+k+l+m z r l m δ r,i Γ i + 1) Γ j + 1) Γ k + 1) r! j! k! l! m! Γ i j + 1) Γ j k + 1) Γ k l + 1)E T m ), Corollry 3. Bse on proposition 2, the MGF of the EGHL fmily is M X z) = { r, i, k, l, m=0 j=0 2 n=0 i 1) j+k+l+m z r l m δ r,i Γ i + 1) Γ j + 1) Γ k + 1) r! j! k! l! m! Γ i j + 1) Γ j k + 1) Γ k l + 1) 1) n Γ m + 1) λ m n + 1) m. Entropy is mesure of vrition of unertinty of rnom vrible. Entropy hs been use extensively in severl fiels suh s engineering n informtion theory. Aoring to 3], the entropy of rnom vrible X with PDF gx) is given by η X = E {log gx)).
11 S. Nsiru, P.N. Mwit n O. Nges 11 Proposition 3. The Shnnon s entropy for the EG T-X fmily of istributions is given by η X = log ) µ T + η T E 1 { log f F 1 ) E log 1 1 e ) )] T e ) T 1 1 )] + ) E log 1 e T )],19) where µ T n η T re the men n the Shnnon entropy of the rnom vrible T. Proof. By efinition { η X = 1 )E log 1 1 F X)) ] + 1)E log 1 F X))] { E log fx)] log ) + E log F X)) ) ] E { log r log 1 1 F x)) ))]. 20) From Lemm 1, we know tht T = log1 1 F X)) ] n X = F { e ) ] T 1 1. Hene, we hve E log fx)] = E E log 1 F X))] = E { log f F e ) ] T 1 1 )], 21) log 1 1 e ) ) T 1 1 ], 22) { E log 1 1 F X)) ] = E log 1 e ) ] T 1, 23) { ) ] E log F X) 1 = E T ), 24) n E { log r log 1 1 F x)) ))] = E log r T )]. 25) Substituting 21) through 25) into 20) yiels { η X = log ) µ T + η T E log f F ) E log 1 1 e ) )] T e T + ) )] 1 E log 1 e T. )] +
12 12 Exponentite Generlize T-X Substituting the men n Shnnon entropy of the hlf logisti istribution into 19), gives the Shnnon entropy of the EGHL fmily. is η X Corollry 4. From proposition 3, the Shnnon entropy of the EGHL fmily = 2 log 2λ) 2 log2) λ 1 ) E log E 1 1 e ) T 1 { log f F 1 1 )] 1 1 e T + ) )] 1 E log 1 e T. )] + The men of the hlf logisti istribution is µ T entropy is η T = 2 log2λ). = 2 log2) λ n the Shnnon 5 Prmeter Estimtion of Exponentite Generlize Hlf Logisti Fréthet Distribution Here, the estimtion of the prmeters of the EGHLFD ws one using mximum likelihoo estimtion. Let z i = e ) b n z i = 1 e ) b. Let X 1, X 2,..., X n be rnom smple of size n from EGHLFD, then the loglikelihoo funtion for the vetor of prmeters ϑ = λ,,, b, ) is given by l = n log 2 b bλ ) + 1) λ 1) b 1) log z i ) + 1) log 1 1 z i ) ] 2 log ) log1 z i )+ { log z i ) ] λ ) b. 26) Differentiting eqution 26) with respet to the prmeters λ,,, b n, respetively n equting to zero gives n λ + log 1 1 z i ) ] 1 1 z 2 i ) ] λ log 1 1 z i ) ] z i )] = 0, λ 27)
13 S. Nsiru, P.N. Mwit n O. Nges 13 n + log1 z i ) λ 1) n + log z i ) 1) z i ) log1 z i ) 1 1 z i ) + λ1 z i ) 1 1 z i ) ] λ 1 log1 z i ) z i )] λ = 0, z i log z i ) 1 z i b n2 b λ + 2 b bλ log)) 2bλ ) b ) z i log 1) 1) z i λ 1) 2 + λ 1) 28) z i 1 z i ) 1 log z i ) 1 1 z i ) λ z i 1 z i ) z i ) ] λ 1 log zi ) z i )] λ = 0, 29) log ) z i z 1 i ) b ) z i z 1 i 1 z i ) 1 log 1 1 z i ) ) b ) log + ) b log 1 z i ) λz i z 1 i 1 z i ) z i ) ] ) λ 1 b ) log z i )] = 0, 30) λ ) b 1 ) b 1 bn b bz i + 1) 1) x i x i z i ) b 1 bz i z 1 i 1 z i ) 1 + λ 1) 1 1 z i ) ] 2 ) b 1 bz i z 1 i + 1 z i ) ) b 1 bλz i z 1 i 1 z i ) z i ) ] λ 1 { 1 + = 0. 31) 1 1 z i )] λ The mximum likelihoo estimtes of ϑ = λ,,, b, ) sy ˆϑ = ˆλ, ĉ, ˆ, ˆb, â ), re obtine by solving the non-liner equtions 27), 28), 29), 30) n 31) using numeril methos.
14 14 Exponentite Generlize T-X 6 Applition In this setion, the pplition of the EGHLFD istribution is emonstrte using unensore t on 100 observtion on breking stress of rbon fibers in Gb) obtine from 6]. The t re: 0.39, 0.81, 0.85, 0.98, 1.08, 1.12, 1.17, 1.18, 1.22, 1.25, 1.36, 1.41, 1.47, 1.57, 1.57, 1.59, 1.59, 1.61, 1.61, 1.69, 1.69, 1.71, 1.73, 1.80, 1.84, 1.84, 1.87, 1.89, 1.92, 2.00, 2.03, 2.03, 2.05, 2.12, 2.17, 2.17, 2.17, 2.35, 2.38, 2.41, 2.43, 2.48, 2.48, 2.50, 2.53, 2.55, 2.55, 2.56, 2.59, 2.67, 2.73, 2.74, 2.76, 2.77, 2.79, 2.81, 2.81, 2.82, 2.83, 2.85, 2.87, 2.88, 2.93, 2.95, 2.96, 2.97, 2.97, 3.09, 3.11, 3.11, 3.15, 3.15, 3.19, 3.19, 3.22, 3.22, 3.27, 3.28, 3.31, 3.31, 3.33, 3.39, 3.39, 3.51, 3.56, 3.60, 3.65, 3.68, 3.68, 3.68, 3.70, 3.75, 4.20, 4.38, 4.42, 4.70, 4.90, 4.91, 5.08, The fit of the EGHLFD ws ompre to tht of trnsmute Mrshll-Olkin Fréthet istribution TMOFD) n Mrshll-Olkin Fréthet istribution MOFD) using ifferent gooness-of-fit tests inluing the Akike informtion riterion AIC), orrete Akike informtion riterion AIC), Byesin informtion riterion BIC), mximize log-likelihoo uner the moel 2ˆl), Anerson-Drling A ) n Crmér-Von Mises W ) sttistis. The PDF of the TMOFD n MOFD re given by gx) = αbb x b+1) e x) b α + 1 α)e x) b ] 2 λ 1, x > 0, 2λe 1 x) b + λ α + 1 α)e, > 0, b > 0, α > 0, x) b n α ) b+1 gx) = b e x) x) b α + 1 α)e ] x) b 2, > 0, b > 0, α > 0, x > 0, respetively. The mximum likelihoo estimtes MLEs) of the prmeters of the fitte istributions with their orresponing stnr errors in brket re given in Tble 2. From Tble 3, it ws ler tht the EGHLFD provies better fit to the rbon fibers t ompre to other fitte istributions sine it hs the smllest vlue for ll the gooness-of-fit sttistis.
15 S. Nsiru, P.N. Mwit n O. Nges 15 Tble 2: MLEs of the prmeters with their stnr errors Moel ˆα â ˆb ĉ ˆ ˆλ EGHLFD ) ) ) TMOFD ) 0.068) 0.206) 0.270) MOFD ) 0.489) 0.160) Tble 3: Gooness-of-fit Sttistis Moel 2ˆl AIC AIC BIC W A EGHLFD TMOFD MOFD The plot of the empiril ensity n the ensity of the fitte moels re shown in Figure 1. Figure 1: Plot of empiril ensity n ensity of fitte moels
16 16 Exponentite Generlize T-X 7 Conlusion This stuy proposes the EG T-X fmily whih is n extension of the T-X fmily of 1] n the exponentite T-X fmily of 2] istributions. The new fmily hs severl sub-fmilies s shown in Figure 2. The two extr shpe prmeters n provies greter flexibility for ontrolling skewness, kurtosis n possibly ing entropy to the enter of the EG T-X ensity funtion. Speifi exmple of member of the EG T-X fmily of istribution, nmely EGHLFD ws given n its reltionship with other bseline istributions estblishe. Some sttistil properties of the new fmily suh s the quntile, moment, moment generting funtion, n Shnnon entropy were erive. Figure 2: Fmilies of EG T-X istributions
17 S. Nsiru, P.N. Mwit n O. Nges 17 ACKNOWLEDGEMENTS. The first uthor wishes to thnk the Afrin Union for supporting his reserh t the Pn Afrin University, Institute for Bsi Sienes, Tehnology n Innovtion. Referenes 1] A. Alztreh, C. Lee n F. Fmoye, A new metho for generting fmilies of ontinuous istributions, Metron, 711), 2013), ] A. Alzghl, F. Fmoye n C. Lee, Exponentite T-X fmily of istributions with some pplitions, Interntionl Journl of Sttistis n Probbility, 23), 2013), ] C.E. Shnnon, A mthemtil theory of ommunition, Bell System Tehnil Journl, 27, 2013), ] G.M. Coreiro, E.M.M. Orteg n C.C.D. Cunh, The exponentite generlize lss of istributions, Journl of Dt Siene, 111), 2013), ] I.S. Grshteyn n I.M. Ryzhik, Tbles of integrls, series n prouts, Aemi Press, New York, ] M.D. Nihols n W. J. Pgett, A bootstrp ontrol hrt for Weibull perentiles, Qulity n Relibility Engineering Interntionl, 22, 2006), ] N. Eugene, C. Lee n F. Fmoye, The bet-norml istribution n its pplitions, Communition in Sttistis-Theory n Methos, 314), 2002),
DIFFERENCE BETWEEN TWO RIEMANN-STIELTJES INTEGRAL MEANS
 Krgujev Journl of Mthemtis Volume 38() (204), Pges 35 49. DIFFERENCE BETWEEN TWO RIEMANN-STIELTJES INTEGRAL MEANS MOHAMMAD W. ALOMARI Abstrt. In this pper, severl bouns for the ifferene between two Riemn-
Krgujev Journl of Mthemtis Volume 38() (204), Pges 35 49. DIFFERENCE BETWEEN TWO RIEMANN-STIELTJES INTEGRAL MEANS MOHAMMAD W. ALOMARI Abstrt. In this pper, severl bouns for the ifferene between two Riemn-
SOME INTEGRAL INEQUALITIES FOR HARMONICALLY CONVEX STOCHASTIC PROCESSES ON THE CO-ORDINATES
 Avne Mth Moels & Applitions Vol3 No 8 pp63-75 SOME INTEGRAL INEQUALITIES FOR HARMONICALLY CONVE STOCHASTIC PROCESSES ON THE CO-ORDINATES Nurgül Okur * Imt Işn Yusuf Ust 3 3 Giresun University Deprtment
Avne Mth Moels & Applitions Vol3 No 8 pp63-75 SOME INTEGRAL INEQUALITIES FOR HARMONICALLY CONVE STOCHASTIC PROCESSES ON THE CO-ORDINATES Nurgül Okur * Imt Işn Yusuf Ust 3 3 Giresun University Deprtment
Bivariate drought analysis using entropy theory
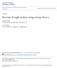 Purue University Purue e-pus Symposium on Dt-Driven Approhes to Droughts Drought Reserh Inititive Network -3- Bivrite rought nlysis using entropy theory Zengho Ho exs A & M University - College Sttion,
Purue University Purue e-pus Symposium on Dt-Driven Approhes to Droughts Drought Reserh Inititive Network -3- Bivrite rought nlysis using entropy theory Zengho Ho exs A & M University - College Sttion,
Hyers-Ulam stability of Pielou logistic difference equation
 vilble online t wwwisr-publitionsom/jns J Nonliner Si ppl, 0 (207, 35 322 Reserh rtile Journl Homepge: wwwtjnsom - wwwisr-publitionsom/jns Hyers-Ulm stbility of Pielou logisti differene eqution Soon-Mo
vilble online t wwwisr-publitionsom/jns J Nonliner Si ppl, 0 (207, 35 322 Reserh rtile Journl Homepge: wwwtjnsom - wwwisr-publitionsom/jns Hyers-Ulm stbility of Pielou logisti differene eqution Soon-Mo
F / x everywhere in some domain containing R. Then, + ). (10.4.1)
 0.4 Green's theorem in the plne Double integrls over plne region my be trnsforme into line integrls over the bounry of the region n onversely. This is of prtil interest beuse it my simplify the evlution
0.4 Green's theorem in the plne Double integrls over plne region my be trnsforme into line integrls over the bounry of the region n onversely. This is of prtil interest beuse it my simplify the evlution
More Properties of the Riemann Integral
 More Properties of the Riemnn Integrl Jmes K. Peterson Deprtment of Biologil Sienes nd Deprtment of Mthemtil Sienes Clemson University Februry 15, 2018 Outline More Riemnn Integrl Properties The Fundmentl
More Properties of the Riemnn Integrl Jmes K. Peterson Deprtment of Biologil Sienes nd Deprtment of Mthemtil Sienes Clemson University Februry 15, 2018 Outline More Riemnn Integrl Properties The Fundmentl
Continuous Random Variables
 STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 217 Néhémy Lim Continuous Rndom Vribles Nottion. The indictor function of set S is rel-vlued function defined by : { 1 if x S 1 S (x) if x S Suppose tht
STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 217 Néhémy Lim Continuous Rndom Vribles Nottion. The indictor function of set S is rel-vlued function defined by : { 1 if x S 1 S (x) if x S Suppose tht
ON THE INEQUALITY OF THE DIFFERENCE OF TWO INTEGRAL MEANS AND APPLICATIONS FOR PDFs
 ON THE INEQUALITY OF THE DIFFERENCE OF TWO INTEGRAL MEANS AND APPLICATIONS FOR PDFs A.I. KECHRINIOTIS AND N.D. ASSIMAKIS Deprtment of Eletronis Tehnologil Edutionl Institute of Lmi, Greee EMil: {kehrin,
ON THE INEQUALITY OF THE DIFFERENCE OF TWO INTEGRAL MEANS AND APPLICATIONS FOR PDFs A.I. KECHRINIOTIS AND N.D. ASSIMAKIS Deprtment of Eletronis Tehnologil Edutionl Institute of Lmi, Greee EMil: {kehrin,
ANALYSIS AND MODELLING OF RAINFALL EVENTS
 Proeedings of the 14 th Interntionl Conferene on Environmentl Siene nd Tehnology Athens, Greee, 3-5 Septemer 215 ANALYSIS AND MODELLING OF RAINFALL EVENTS IOANNIDIS K., KARAGRIGORIOU A. nd LEKKAS D.F.
Proeedings of the 14 th Interntionl Conferene on Environmentl Siene nd Tehnology Athens, Greee, 3-5 Septemer 215 ANALYSIS AND MODELLING OF RAINFALL EVENTS IOANNIDIS K., KARAGRIGORIOU A. nd LEKKAS D.F.
for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx
![for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx](/thumbs/74/70408252.jpg) Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
SOLUTIONS TO MATH38181 EXTREME VALUES EXAM
 SOLUTIONS TO MATH388 EXTREME VALUES EXAM Solutions to Question If there re norming onstnts n >, b n nd nondegenerte G suh tht the df of normlized version of M n onverges to G, i.e. ( ) Mn b n Pr x F n
SOLUTIONS TO MATH388 EXTREME VALUES EXAM Solutions to Question If there re norming onstnts n >, b n nd nondegenerte G suh tht the df of normlized version of M n onverges to G, i.e. ( ) Mn b n Pr x F n
Now we must transform the original model so we can use the new parameters. = S max. Recruits
 MODEL FOR VARIABLE RECRUITMENT (ontinue) Alterntive Prmeteriztions of the pwner-reruit Moels We n write ny moel in numerous ifferent ut equivlent forms. Uner ertin irumstnes it is onvenient to work with
MODEL FOR VARIABLE RECRUITMENT (ontinue) Alterntive Prmeteriztions of the pwner-reruit Moels We n write ny moel in numerous ifferent ut equivlent forms. Uner ertin irumstnes it is onvenient to work with
Songklanakarin Journal of Science and Technology SJST R1 Thongchan. A Modified Hyperbolic Secant Distribution
 A Modified Hyperbolic Secnt Distribution Journl: Songklnkrin Journl of Science nd Technology Mnuscript ID SJST-0-0.R Mnuscript Type: Originl Article Dte Submitted by the Author: 0-Mr-0 Complete List of
A Modified Hyperbolic Secnt Distribution Journl: Songklnkrin Journl of Science nd Technology Mnuscript ID SJST-0-0.R Mnuscript Type: Originl Article Dte Submitted by the Author: 0-Mr-0 Complete List of
Chapter 5 : Continuous Random Variables
 STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 216 Néhémy Lim Chpter 5 : Continuous Rndom Vribles Nottions. N {, 1, 2,...}, set of nturl numbers (i.e. ll nonnegtive integers); N {1, 2,...}, set of ll
STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 216 Néhémy Lim Chpter 5 : Continuous Rndom Vribles Nottions. N {, 1, 2,...}, set of nturl numbers (i.e. ll nonnegtive integers); N {1, 2,...}, set of ll
The study of dual integral equations with generalized Legendre functions
 J. Mth. Anl. Appl. 34 (5) 75 733 www.elsevier.om/lote/jm The study of dul integrl equtions with generlized Legendre funtions B.M. Singh, J. Rokne,R.S.Dhliwl Deprtment of Mthemtis, The University of Clgry,
J. Mth. Anl. Appl. 34 (5) 75 733 www.elsevier.om/lote/jm The study of dul integrl equtions with generlized Legendre funtions B.M. Singh, J. Rokne,R.S.Dhliwl Deprtment of Mthemtis, The University of Clgry,
SOME COPLANAR POINTS IN TETRAHEDRON
 Journl of Pure n Applie Mthemtis: Avnes n Applitions Volume 16, Numer 2, 2016, Pges 109-114 Aville t http://sientifivnes.o.in DOI: http://x.oi.org/10.18642/jpm_7100121752 SOME COPLANAR POINTS IN TETRAHEDRON
Journl of Pure n Applie Mthemtis: Avnes n Applitions Volume 16, Numer 2, 2016, Pges 109-114 Aville t http://sientifivnes.o.in DOI: http://x.oi.org/10.18642/jpm_7100121752 SOME COPLANAR POINTS IN TETRAHEDRON
arxiv: v1 [math.ca] 21 Aug 2018
![arxiv: v1 [math.ca] 21 Aug 2018 arxiv: v1 [math.ca] 21 Aug 2018](/thumbs/84/89276688.jpg) rxiv:1808.07159v1 [mth.ca] 1 Aug 018 Clulus on Dul Rel Numbers Keqin Liu Deprtment of Mthemtis The University of British Columbi Vnouver, BC Cnd, V6T 1Z Augest, 018 Abstrt We present the bsi theory of
rxiv:1808.07159v1 [mth.ca] 1 Aug 018 Clulus on Dul Rel Numbers Keqin Liu Deprtment of Mthemtis The University of British Columbi Vnouver, BC Cnd, V6T 1Z Augest, 018 Abstrt We present the bsi theory of
Edexcel Level 3 Advanced GCE in Mathematics (9MA0) Two-year Scheme of Work
 Eexel Level 3 Avne GCE in Mthemtis (9MA0) Two-yer Sheme of Work Stuents stuying A Level Mthemtis will tke 3 ppers t the en of Yer 13 s inite elow. All stuents will stuy Pure, Sttistis n Mehnis. A level
Eexel Level 3 Avne GCE in Mthemtis (9MA0) Two-yer Sheme of Work Stuents stuying A Level Mthemtis will tke 3 ppers t the en of Yer 13 s inite elow. All stuents will stuy Pure, Sttistis n Mehnis. A level
Generalized Kronecker Product and Its Application
 Vol. 1, No. 1 ISSN: 1916-9795 Generlize Kroneker Prout n Its Applition Xingxing Liu Shool of mthemtis n omputer Siene Ynn University Shnxi 716000, Chin E-mil: lxx6407@163.om Astrt In this pper, we promote
Vol. 1, No. 1 ISSN: 1916-9795 Generlize Kroneker Prout n Its Applition Xingxing Liu Shool of mthemtis n omputer Siene Ynn University Shnxi 716000, Chin E-mil: lxx6407@163.om Astrt In this pper, we promote
A Mathematical Model for Unemployment-Taking an Action without Delay
 Advnes in Dynmil Systems nd Applitions. ISSN 973-53 Volume Number (7) pp. -8 Reserh Indi Publitions http://www.ripublition.om A Mthemtil Model for Unemployment-Tking n Ation without Dely Gulbnu Pthn Diretorte
Advnes in Dynmil Systems nd Applitions. ISSN 973-53 Volume Number (7) pp. -8 Reserh Indi Publitions http://www.ripublition.om A Mthemtil Model for Unemployment-Tking n Ation without Dely Gulbnu Pthn Diretorte
Ranking Generalized Fuzzy Numbers using centroid of centroids
 Interntionl Journl of Fuzzy Logi Systems (IJFLS) Vol. No. July ning Generlize Fuzzy Numers using entroi of entrois S.Suresh u Y.L.P. Thorni N.vi Shnr Dept. of pplie Mthemtis GIS GITM University Vishptnm
Interntionl Journl of Fuzzy Logi Systems (IJFLS) Vol. No. July ning Generlize Fuzzy Numers using entroi of entrois S.Suresh u Y.L.P. Thorni N.vi Shnr Dept. of pplie Mthemtis GIS GITM University Vishptnm
Necessary and sucient conditions for some two. Abstract. Further we show that the necessary conditions for the existence of an OD(44 s 1 s 2 )
 Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
T b a(f) [f ] +. P b a(f) = Conclude that if f is in AC then it is the difference of two monotone absolutely continuous functions.
![T b a(f) [f ] +. P b a(f) = Conclude that if f is in AC then it is the difference of two monotone absolutely continuous functions. T b a(f) [f ] +. P b a(f) = Conclude that if f is in AC then it is the difference of two monotone absolutely continuous functions.](/thumbs/78/77085178.jpg) Rel Vribles, Fll 2014 Problem set 5 Solution suggestions Exerise 1. Let f be bsolutely ontinuous on [, b] Show tht nd T b (f) P b (f) f (x) dx [f ] +. Conlude tht if f is in AC then it is the differene
Rel Vribles, Fll 2014 Problem set 5 Solution suggestions Exerise 1. Let f be bsolutely ontinuous on [, b] Show tht nd T b (f) P b (f) f (x) dx [f ] +. Conlude tht if f is in AC then it is the differene
On the Co-Ordinated Convex Functions
 Appl. Mth. In. Si. 8, No. 3, 085-0 0 085 Applied Mthemtis & Inormtion Sienes An Interntionl Journl http://.doi.org/0.785/mis/08038 On the Co-Ordinted Convex Funtions M. Emin Özdemir, Çetin Yıldız, nd Ahmet
Appl. Mth. In. Si. 8, No. 3, 085-0 0 085 Applied Mthemtis & Inormtion Sienes An Interntionl Journl http://.doi.org/0.785/mis/08038 On the Co-Ordinted Convex Funtions M. Emin Özdemir, Çetin Yıldız, nd Ahmet
18.06 Problem Set 4 Due Wednesday, Oct. 11, 2006 at 4:00 p.m. in 2-106
 8. Problem Set Due Wenesy, Ot., t : p.m. in - Problem Mony / Consier the eight vetors 5, 5, 5,..., () List ll of the one-element, linerly epenent sets forme from these. (b) Wht re the two-element, linerly
8. Problem Set Due Wenesy, Ot., t : p.m. in - Problem Mony / Consier the eight vetors 5, 5, 5,..., () List ll of the one-element, linerly epenent sets forme from these. (b) Wht re the two-element, linerly
POSITIVE IMPLICATIVE AND ASSOCIATIVE FILTERS OF LATTICE IMPLICATION ALGEBRAS
 Bull. Koren Mth. So. 35 (998), No., pp. 53 6 POSITIVE IMPLICATIVE AND ASSOCIATIVE FILTERS OF LATTICE IMPLICATION ALGEBRAS YOUNG BAE JUN*, YANG XU AND KEYUN QIN ABSTRACT. We introue the onepts of positive
Bull. Koren Mth. So. 35 (998), No., pp. 53 6 POSITIVE IMPLICATIVE AND ASSOCIATIVE FILTERS OF LATTICE IMPLICATION ALGEBRAS YOUNG BAE JUN*, YANG XU AND KEYUN QIN ABSTRACT. We introue the onepts of positive
Conservation Law. Chapter Goal. 6.2 Theory
 Chpter 6 Conservtion Lw 6.1 Gol Our long term gol is to unerstn how mthemticl moels re erive. Here, we will stuy how certin quntity chnges with time in given region (sptil omin). We then first erive the
Chpter 6 Conservtion Lw 6.1 Gol Our long term gol is to unerstn how mthemticl moels re erive. Here, we will stuy how certin quntity chnges with time in given region (sptil omin). We then first erive the
MATH20812: PRACTICAL STATISTICS I SEMESTER 2 NOTES ON RANDOM VARIABLES
 MATH20812: PRACTICAL STATISTICS I SEMESTER 2 NOTES ON RANDOM VARIABLES Things to Know Rndom Vrible A rndom vrible is function tht ssigns numericl vlue to ech outcome of prticulr experiment. A rndom vrible
MATH20812: PRACTICAL STATISTICS I SEMESTER 2 NOTES ON RANDOM VARIABLES Things to Know Rndom Vrible A rndom vrible is function tht ssigns numericl vlue to ech outcome of prticulr experiment. A rndom vrible
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Hermite-Hadamard inequality for geometrically quasiconvex functions on co-ordinates
 Int. J. Nonliner Anl. Appl. 8 27 No. 47-6 ISSN: 28-6822 eletroni http://dx.doi.org/.2275/ijn.26.483 Hermite-Hdmrd ineulity for geometrilly usionvex funtions on o-ordintes Ali Brni Ftemeh Mlmir Deprtment
Int. J. Nonliner Anl. Appl. 8 27 No. 47-6 ISSN: 28-6822 eletroni http://dx.doi.org/.2275/ijn.26.483 Hermite-Hdmrd ineulity for geometrilly usionvex funtions on o-ordintes Ali Brni Ftemeh Mlmir Deprtment
, g. Exercise 1. Generator polynomials of a convolutional code, given in binary form, are g. Solution 1.
 Exerise Genertor polynomils of onvolutionl ode, given in binry form, re g, g j g. ) Sketh the enoding iruit. b) Sketh the stte digrm. ) Find the trnsfer funtion T. d) Wht is the minimum free distne of
Exerise Genertor polynomils of onvolutionl ode, given in binry form, re g, g j g. ) Sketh the enoding iruit. b) Sketh the stte digrm. ) Find the trnsfer funtion T. d) Wht is the minimum free distne of
Journal of Inequalities in Pure and Applied Mathematics
 Journl of Inequlities in Pure nd Applied Mthemtics MOMENTS INEQUALITIES OF A RANDOM VARIABLE DEFINED OVER A FINITE INTERVAL PRANESH KUMAR Deprtment of Mthemtics & Computer Science University of Northern
Journl of Inequlities in Pure nd Applied Mthemtics MOMENTS INEQUALITIES OF A RANDOM VARIABLE DEFINED OVER A FINITE INTERVAL PRANESH KUMAR Deprtment of Mthemtics & Computer Science University of Northern
MA10207B: ANALYSIS SECOND SEMESTER OUTLINE NOTES
 MA10207B: ANALYSIS SECOND SEMESTER OUTLINE NOTES CHARLIE COLLIER UNIVERSITY OF BATH These notes hve been typeset by Chrlie Collier nd re bsed on the leture notes by Adrin Hill nd Thoms Cottrell. These
MA10207B: ANALYSIS SECOND SEMESTER OUTLINE NOTES CHARLIE COLLIER UNIVERSITY OF BATH These notes hve been typeset by Chrlie Collier nd re bsed on the leture notes by Adrin Hill nd Thoms Cottrell. These
AP CALCULUS Test #6: Unit #6 Basic Integration and Applications
 AP CALCULUS Test #6: Unit #6 Bsi Integrtion nd Applitions A GRAPHING CALCULATOR IS REQUIRED FOR SOME PROBLEMS OR PARTS OF PROBLEMS IN THIS PART OF THE EXAMINATION. () The ext numeril vlue of the orret
AP CALCULUS Test #6: Unit #6 Bsi Integrtion nd Applitions A GRAPHING CALCULATOR IS REQUIRED FOR SOME PROBLEMS OR PARTS OF PROBLEMS IN THIS PART OF THE EXAMINATION. () The ext numeril vlue of the orret
University of Sioux Falls. MAT204/205 Calculus I/II
 University of Sioux Flls MAT204/205 Clulus I/II Conepts ddressed: Clulus Textook: Thoms Clulus, 11 th ed., Weir, Hss, Giordno 1. Use stndrd differentition nd integrtion tehniques. Differentition tehniques
University of Sioux Flls MAT204/205 Clulus I/II Conepts ddressed: Clulus Textook: Thoms Clulus, 11 th ed., Weir, Hss, Giordno 1. Use stndrd differentition nd integrtion tehniques. Differentition tehniques
MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,
![MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx, MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,](/thumbs/89/98261542.jpg) MATH3403: Green s Funtions, Integrl Equtions nd the Clulus of Vritions 1 Exmples 5 Qu.1 Show tht the extreml funtion of the funtionl I[y] = 1 0 [(y ) + yy + y ] dx, where y(0) = 0 nd y(1) = 1, is y(x)
MATH3403: Green s Funtions, Integrl Equtions nd the Clulus of Vritions 1 Exmples 5 Qu.1 Show tht the extreml funtion of the funtionl I[y] = 1 0 [(y ) + yy + y ] dx, where y(0) = 0 nd y(1) = 1, is y(x)
Math 32B Discussion Session Week 8 Notes February 28 and March 2, f(b) f(a) = f (t)dt (1)
 Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
Non-Linear & Logistic Regression
 Non-Liner & Logistic Regression If the sttistics re boring, then you've got the wrong numbers. Edwrd R. Tufte (Sttistics Professor, Yle University) Regression Anlyses When do we use these? PART 1: find
Non-Liner & Logistic Regression If the sttistics re boring, then you've got the wrong numbers. Edwrd R. Tufte (Sttistics Professor, Yle University) Regression Anlyses When do we use these? PART 1: find
Co-ordinated s-convex Function in the First Sense with Some Hadamard-Type Inequalities
 Int. J. Contemp. Mth. Sienes, Vol. 3, 008, no. 3, 557-567 Co-ordinted s-convex Funtion in the First Sense with Some Hdmrd-Type Inequlities Mohmmd Alomri nd Mslin Drus Shool o Mthemtil Sienes Fulty o Siene
Int. J. Contemp. Mth. Sienes, Vol. 3, 008, no. 3, 557-567 Co-ordinted s-convex Funtion in the First Sense with Some Hdmrd-Type Inequlities Mohmmd Alomri nd Mslin Drus Shool o Mthemtil Sienes Fulty o Siene
Time Truncated Two Stage Group Sampling Plan For Various Distributions
 Time Truncted Two Stge Group Smpling Pln For Vrious Distributions Dr. A. R. Sudmni Rmswmy, S.Jysri Associte Professor, Deprtment of Mthemtics, Avinshilingm University, Coimbtore Assistnt professor, Deprtment
Time Truncted Two Stge Group Smpling Pln For Vrious Distributions Dr. A. R. Sudmni Rmswmy, S.Jysri Associte Professor, Deprtment of Mthemtics, Avinshilingm University, Coimbtore Assistnt professor, Deprtment
University of Texas MD Anderson Cancer Center Department of Biostatistics. Inequality Calculator, Version 3.0 November 25, 2013 User s Guide
 University of Texs MD Anderson Cncer Center Deprtment of Biosttistics Inequlity Clcultor, Version 3.0 November 5, 013 User s Guide 0. Overview The purpose of the softwre is to clculte the probbility tht
University of Texs MD Anderson Cncer Center Deprtment of Biosttistics Inequlity Clcultor, Version 3.0 November 5, 013 User s Guide 0. Overview The purpose of the softwre is to clculte the probbility tht
Overview of Calculus I
 Overview of Clculus I Prof. Jim Swift Northern Arizon University There re three key concepts in clculus: The limit, the derivtive, nd the integrl. You need to understnd the definitions of these three things,
Overview of Clculus I Prof. Jim Swift Northern Arizon University There re three key concepts in clculus: The limit, the derivtive, nd the integrl. You need to understnd the definitions of these three things,
Exam 1 Study Guide. Differentiation and Anti-differentiation Rules from Calculus I
 Exm Stuy Guie Mth 26 - Clulus II, Fll 205 The following is list of importnt onepts from eh setion tht will be teste on exm. This is not omplete list of the mteril tht you shoul know for the ourse, but
Exm Stuy Guie Mth 26 - Clulus II, Fll 205 The following is list of importnt onepts from eh setion tht will be teste on exm. This is not omplete list of the mteril tht you shoul know for the ourse, but
ON SIZE BIASED KUMARASWAMY DISTRIBUTION
 ON SIZE BIASED KUMARASWAMY DISTRIBUTION rxiv:609.0978v [stt.me] 9 Sep 06 Dremlee Shrm, * nd Tpn Kumr Chkrbrty Deprtment of Sttistics, North-Estern Hill University, Shillong - 7930, Meghly, Indi Contct:
ON SIZE BIASED KUMARASWAMY DISTRIBUTION rxiv:609.0978v [stt.me] 9 Sep 06 Dremlee Shrm, * nd Tpn Kumr Chkrbrty Deprtment of Sttistics, North-Estern Hill University, Shillong - 7930, Meghly, Indi Contct:
Characterizations of the Weibull-X and Burr XII Negative Binomial Families of Distributions
 Interntionl Journl of Sttistics nd Probbility; Vol. 4, No. 2; 2015 ISSN 1927-7032 E-ISSN 1927-7040 Published by Cndin Center of Science nd Eduction Chrcteriztions of the Weibull-X nd Burr XII Negtive Binomil
Interntionl Journl of Sttistics nd Probbility; Vol. 4, No. 2; 2015 ISSN 1927-7032 E-ISSN 1927-7040 Published by Cndin Center of Science nd Eduction Chrcteriztions of the Weibull-X nd Burr XII Negtive Binomil
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Part 4. Integration (with Proofs)
 Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
4.5 THE FUNDAMENTAL THEOREM OF CALCULUS
 4.5 The Funmentl Theorem of Clculus Contemporry Clculus 4.5 THE FUNDAMENTAL THEOREM OF CALCULUS This section contins the most importnt n most use theorem of clculus, THE Funmentl Theorem of Clculus. Discovere
4.5 The Funmentl Theorem of Clculus Contemporry Clculus 4.5 THE FUNDAMENTAL THEOREM OF CALCULUS This section contins the most importnt n most use theorem of clculus, THE Funmentl Theorem of Clculus. Discovere
Particle Physics. Michaelmas Term 2011 Prof Mark Thomson. Handout 3 : Interaction by Particle Exchange and QED. Recap
 Prtile Physis Mihelms Term 2011 Prof Mrk Thomson g X g X g g Hnout 3 : Intertion y Prtile Exhnge n QED Prof. M.A. Thomson Mihelms 2011 101 Rep Working towrs proper lultion of ey n sttering proesses lnitilly
Prtile Physis Mihelms Term 2011 Prof Mrk Thomson g X g X g g Hnout 3 : Intertion y Prtile Exhnge n QED Prof. M.A. Thomson Mihelms 2011 101 Rep Working towrs proper lultion of ey n sttering proesses lnitilly
Dong-Myung Lee, Jeong-Gon Lee, and Ming-Gen Cui. 1. introduction
 J. Kore So. Mth. Edu. Ser. B: Pure Appl. Mth. ISSN 16-0657 Volume 11, Number My 004), Pges 133 138 REPRESENTATION OF SOLUTIONS OF FREDHOLM EQUATIONS IN W Ω) OF REPRODUCING KERNELS Dong-Myung Lee, Jeong-Gon
J. Kore So. Mth. Edu. Ser. B: Pure Appl. Mth. ISSN 16-0657 Volume 11, Number My 004), Pges 133 138 REPRESENTATION OF SOLUTIONS OF FREDHOLM EQUATIONS IN W Ω) OF REPRODUCING KERNELS Dong-Myung Lee, Jeong-Gon
Logic, Set Theory and Computability [M. Coppenbarger]
![Logic, Set Theory and Computability [M. Coppenbarger] Logic, Set Theory and Computability [M. Coppenbarger]](/thumbs/90/103901048.jpg) 14 Orer (Hnout) Definition 7-11: A reltion is qusi-orering (or preorer) if it is reflexive n trnsitive. A quisi-orering tht is symmetri is n equivlene reltion. A qusi-orering tht is nti-symmetri is n orer
14 Orer (Hnout) Definition 7-11: A reltion is qusi-orering (or preorer) if it is reflexive n trnsitive. A quisi-orering tht is symmetri is n equivlene reltion. A qusi-orering tht is nti-symmetri is n orer
Parabola and Catenary Equations for Conductor Height Calculation
 ELECTROTEHNICĂ, ELECTRONICĂ, AUTOMATICĂ, 6 (), nr. 3 9 Prbol nd Ctenr Equtions for Condutor Height Clultion Alen HATIBOVIC Abstrt This pper presents new equtions for ondutor height lultion bsed on the
ELECTROTEHNICĂ, ELECTRONICĂ, AUTOMATICĂ, 6 (), nr. 3 9 Prbol nd Ctenr Equtions for Condutor Height Clultion Alen HATIBOVIC Abstrt This pper presents new equtions for ondutor height lultion bsed on the
Tutorial Worksheet. 1. Find all solutions to the linear system by following the given steps. x + 2y + 3z = 2 2x + 3y + z = 4.
 Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
CS 491G Combinatorial Optimization Lecture Notes
 CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
Problem. Statement. variable Y. Method: Step 1: Step 2: y d dy. Find F ( Step 3: Find f = Y. Solution: Assume
 Functions of Rndom Vrible Problem Sttement We know the pdf ( or cdf ) of rndom r vrible. Define new rndom vrible Y = g. Find the pdf of Y. Method: Step : Step : Step 3: Plot Y = g( ). Find F ( y) by mpping
Functions of Rndom Vrible Problem Sttement We know the pdf ( or cdf ) of rndom r vrible. Define new rndom vrible Y = g. Find the pdf of Y. Method: Step : Step : Step 3: Plot Y = g( ). Find F ( y) by mpping
Compression of Palindromes and Regularity.
 Compression of Plinromes n Regulrity. Kyoko Shikishim-Tsuji Center for Lierl Arts Eution n Reserh Tenri University 1 Introution In [1], property of likstrem t t view of tse is isusse n it is shown tht
Compression of Plinromes n Regulrity. Kyoko Shikishim-Tsuji Center for Lierl Arts Eution n Reserh Tenri University 1 Introution In [1], property of likstrem t t view of tse is isusse n it is shown tht
Lecture 21: Order statistics
 Lecture : Order sttistics Suppose we hve N mesurements of sclr, x i =, N Tke ll mesurements nd sort them into scending order x x x 3 x N Define the mesured running integrl S N (x) = 0 for x < x = i/n for
Lecture : Order sttistics Suppose we hve N mesurements of sclr, x i =, N Tke ll mesurements nd sort them into scending order x x x 3 x N Define the mesured running integrl S N (x) = 0 for x < x = i/n for
Estimation of Binomial Distribution in the Light of Future Data
 British Journl of Mthemtics & Computer Science 102: 1-7, 2015, Article no.bjmcs.19191 ISSN: 2231-0851 SCIENCEDOMAIN interntionl www.sciencedomin.org Estimtion of Binomil Distribution in the Light of Future
British Journl of Mthemtics & Computer Science 102: 1-7, 2015, Article no.bjmcs.19191 ISSN: 2231-0851 SCIENCEDOMAIN interntionl www.sciencedomin.org Estimtion of Binomil Distribution in the Light of Future
Tests for the Ratio of Two Poisson Rates
 Chpter 437 Tests for the Rtio of Two Poisson Rtes Introduction The Poisson probbility lw gives the probbility distribution of the number of events occurring in specified intervl of time or spce. The Poisson
Chpter 437 Tests for the Rtio of Two Poisson Rtes Introduction The Poisson probbility lw gives the probbility distribution of the number of events occurring in specified intervl of time or spce. The Poisson
1 Probability Density Functions
 Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Establishment of Intensity-Duration-Frequency Curves for Precipitation in the Monsoon Area of Vietnam
 京都大学防災研究所年報 第 49 号 B 平成 8 年 4 月 Annuls of Diss. Prev. Res. nst., Kyoto Univ., No. 49 B, 2006 Estblishment of ntensity-durtion-frequency Curves for Precipittion in the Monsoon Are of Vietnm Le MNH NHA*,
京都大学防災研究所年報 第 49 号 B 平成 8 年 4 月 Annuls of Diss. Prev. Res. nst., Kyoto Univ., No. 49 B, 2006 Estblishment of ntensity-durtion-frequency Curves for Precipittion in the Monsoon Are of Vietnm Le MNH NHA*,
1.9 C 2 inner variations
 46 CHAPTER 1. INDIRECT METHODS 1.9 C 2 inner vritions So fr, we hve restricted ttention to liner vritions. These re vritions of the form vx; ǫ = ux + ǫφx where φ is in some liner perturbtion clss P, for
46 CHAPTER 1. INDIRECT METHODS 1.9 C 2 inner vritions So fr, we hve restricted ttention to liner vritions. These re vritions of the form vx; ǫ = ux + ǫφx where φ is in some liner perturbtion clss P, for
Definite integral. Mathematics FRDIS MENDELU
 Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová Brno 1 Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function defined on [, b]. Wht is the re of the
Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová Brno 1 Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function defined on [, b]. Wht is the re of the
Factorising FACTORISING.
 Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
COMPARISON OF DIFFERENT APPROXIMATIONS OF FUZZY NUMBERS
 Interntionl Journl of Fuzzy Loi Systems (IJFLS) Vol.5 No. Otoer 05 COMPRISON OF DIFFERENT PPROXIMTIONS OF FUZZY NUMBERS D. Stephen Dinr n K.Jivn PG n Reserh Deprtment of Mthemtis T.B.M.L. Collee Poryr
Interntionl Journl of Fuzzy Loi Systems (IJFLS) Vol.5 No. Otoer 05 COMPRISON OF DIFFERENT PPROXIMTIONS OF FUZZY NUMBERS D. Stephen Dinr n K.Jivn PG n Reserh Deprtment of Mthemtis T.B.M.L. Collee Poryr
Eigenvectors and Eigenvalues
 MTB 050 1 ORIGIN 1 Eigenvets n Eigenvlues This wksheet esries the lger use to lulte "prinipl" "hrteristi" iretions lle Eigenvets n the "prinipl" "hrteristi" vlues lle Eigenvlues ssoite with these iretions.
MTB 050 1 ORIGIN 1 Eigenvets n Eigenvlues This wksheet esries the lger use to lulte "prinipl" "hrteristi" iretions lle Eigenvets n the "prinipl" "hrteristi" vlues lle Eigenvlues ssoite with these iretions.
Lecture 1 - Introduction and Basic Facts about PDEs
 * 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
* 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
Joint distribution. Joint distribution. Marginal distributions. Joint distribution
 Joint distribution To specify the joint distribution of n rndom vribles X 1,...,X n tht tke vlues in the smple spces E 1,...,E n we need probbility mesure, P, on E 1... E n = {(x 1,...,x n ) x i E i, i
Joint distribution To specify the joint distribution of n rndom vribles X 1,...,X n tht tke vlues in the smple spces E 1,...,E n we need probbility mesure, P, on E 1... E n = {(x 1,...,x n ) x i E i, i
MATH Final Review
 MATH 1591 - Finl Review November 20, 2005 1 Evlution of Limits 1. the ε δ definition of limit. 2. properties of limits. 3. how to use the diret substitution to find limit. 4. how to use the dividing out
MATH 1591 - Finl Review November 20, 2005 1 Evlution of Limits 1. the ε δ definition of limit. 2. properties of limits. 3. how to use the diret substitution to find limit. 4. how to use the dividing out
Estimation of Parameters in Weighted Generalized Beta Distributions of the Second Kind
 Journl of Sttisticl nd Econometric Methods, vol.1, no.1, 2012, 1-12 ISSN: 2241-0384 (print), 2241-0376 (online) Interntionl Scientific Press, 2012 Estimtion of Prmeters in Weighted Generlized Bet Distributions
Journl of Sttisticl nd Econometric Methods, vol.1, no.1, 2012, 1-12 ISSN: 2241-0384 (print), 2241-0376 (online) Interntionl Scientific Press, 2012 Estimtion of Prmeters in Weighted Generlized Bet Distributions
Let s divide up the interval [ ab, ] into n subintervals with the same length, so we have
![Let s divide up the interval [ ab, ] into n subintervals with the same length, so we have Let s divide up the interval [ ab, ] into n subintervals with the same length, so we have](/thumbs/79/79376941.jpg) III. INTEGRATION Eonomists seem muh more intereste in mrginl effets n ifferentition thn in integrtion. Integrtion is importnt for fining the epete vlue n vrine of rnom vriles, whih is use in eonometris
III. INTEGRATION Eonomists seem muh more intereste in mrginl effets n ifferentition thn in integrtion. Integrtion is importnt for fining the epete vlue n vrine of rnom vriles, whih is use in eonometris
Definite integral. Mathematics FRDIS MENDELU. Simona Fišnarová (Mendel University) Definite integral MENDELU 1 / 30
 Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová (Mendel University) Definite integrl MENDELU / Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function
Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová (Mendel University) Definite integrl MENDELU / Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function
Exam 2, Mathematics 4701, Section ETY6 6:05 pm 7:40 pm, March 31, 2016, IH-1105 Instructor: Attila Máté 1
 Exm, Mthemtics 471, Section ETY6 6:5 pm 7:4 pm, Mrch 1, 16, IH-115 Instructor: Attil Máté 1 17 copies 1. ) Stte the usul sufficient condition for the fixed-point itertion to converge when solving the eqution
Exm, Mthemtics 471, Section ETY6 6:5 pm 7:4 pm, Mrch 1, 16, IH-115 Instructor: Attil Máté 1 17 copies 1. ) Stte the usul sufficient condition for the fixed-point itertion to converge when solving the eqution
Table of Content. c 1 / 5
 Tehnil Informtion - t nd t Temperture for Controlger 03-2018 en Tble of Content Introdution....................................................................... 2 Definitions for t nd t..............................................................
Tehnil Informtion - t nd t Temperture for Controlger 03-2018 en Tble of Content Introdution....................................................................... 2 Definitions for t nd t..............................................................
Lecture 6: Coding theory
 Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Section 4.4. Green s Theorem
 The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
SEMI-EXCIRCLE OF QUADRILATERAL
 JP Journl of Mthemtil Sienes Volume 5, Issue &, 05, Pges - 05 Ishn Pulishing House This pper is ville online t http://wwwiphsiom SEMI-EXCIRCLE OF QUADRILATERAL MASHADI, SRI GEMAWATI, HASRIATI AND HESY
JP Journl of Mthemtil Sienes Volume 5, Issue &, 05, Pges - 05 Ishn Pulishing House This pper is ville online t http://wwwiphsiom SEMI-EXCIRCLE OF QUADRILATERAL MASHADI, SRI GEMAWATI, HASRIATI AND HESY
( ) { } [ ] { } [ ) { } ( ] { }
![( ) { } [ ] { } [ ) { } ( ] { } ( ) { } [ ] { } [ ) { } ( ] { }](/thumbs/96/129291861.jpg) Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Mid-Term Examination - Spring 2014 Mathematical Programming with Applications to Economics Total Score: 45; Time: 3 hours
 Mi-Term Exmintion - Spring 0 Mthemtil Progrmming with Applitions to Eonomis Totl Sore: 5; Time: hours. Let G = (N, E) e irete grph. Define the inegree of vertex i N s the numer of eges tht re oming into
Mi-Term Exmintion - Spring 0 Mthemtil Progrmming with Applitions to Eonomis Totl Sore: 5; Time: hours. Let G = (N, E) e irete grph. Define the inegree of vertex i N s the numer of eges tht re oming into
I 3 2 = I I 4 = 2A
 ECE 210 Eletril Ciruit Anlysis University of llinois t Chigo 2.13 We re ske to use KCL to fin urrents 1 4. The key point in pplying KCL in this prolem is to strt with noe where only one of the urrents
ECE 210 Eletril Ciruit Anlysis University of llinois t Chigo 2.13 We re ske to use KCL to fin urrents 1 4. The key point in pplying KCL in this prolem is to strt with noe where only one of the urrents
Core 2 Logarithms and exponentials. Section 1: Introduction to logarithms
 Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
Chapter 3. Vector Spaces
 3.4 Liner Trnsformtions 1 Chpter 3. Vector Spces 3.4 Liner Trnsformtions Note. We hve lredy studied liner trnsformtions from R n into R m. Now we look t liner trnsformtions from one generl vector spce
3.4 Liner Trnsformtions 1 Chpter 3. Vector Spces 3.4 Liner Trnsformtions Note. We hve lredy studied liner trnsformtions from R n into R m. Now we look t liner trnsformtions from one generl vector spce
ON CO-ORDINATED OSTROWSKI AND HADAMARD S TYPE INEQUALITIES FOR CONVEX FUNCTIONS II
 TJMM 9 (7), No., 35-4 ON CO-ORDINATED OSTROWSKI AND HADAMARD S TYPE INEQUALITIES FOR CONVEX FUNCTIONS II MUHAMMAD MUDDASSAR, NASIR SIDDIQUI, AND MUHAMMAD IQBAL Abstrt. In this rtile, we estblish vrious
TJMM 9 (7), No., 35-4 ON CO-ORDINATED OSTROWSKI AND HADAMARD S TYPE INEQUALITIES FOR CONVEX FUNCTIONS II MUHAMMAD MUDDASSAR, NASIR SIDDIQUI, AND MUHAMMAD IQBAL Abstrt. In this rtile, we estblish vrious
The Riemann-Stieltjes Integral
 Chpter 6 The Riemnn-Stieltjes Integrl 6.1. Definition nd Eistene of the Integrl Definition 6.1. Let, b R nd < b. ( A prtition P of intervl [, b] is finite set of points P = { 0, 1,..., n } suh tht = 0
Chpter 6 The Riemnn-Stieltjes Integrl 6.1. Definition nd Eistene of the Integrl Definition 6.1. Let, b R nd < b. ( A prtition P of intervl [, b] is finite set of points P = { 0, 1,..., n } suh tht = 0
Decision Science Letters
 Decision Science Letters 8 (09) 37 3 Contents lists vilble t GrowingScience Decision Science Letters homepge: www.growingscience.com/dsl The negtive binomil-weighted Lindley distribution Sunthree Denthet
Decision Science Letters 8 (09) 37 3 Contents lists vilble t GrowingScience Decision Science Letters homepge: www.growingscience.com/dsl The negtive binomil-weighted Lindley distribution Sunthree Denthet
7 - Continuous random variables
 7-1 Continuous rndom vribles S. Lll, Stnford 2011.01.25.01 7 - Continuous rndom vribles Continuous rndom vribles The cumultive distribution function The uniform rndom vrible Gussin rndom vribles The Gussin
7-1 Continuous rndom vribles S. Lll, Stnford 2011.01.25.01 7 - Continuous rndom vribles Continuous rndom vribles The cumultive distribution function The uniform rndom vrible Gussin rndom vribles The Gussin
On the equivalence between Stein and De Bruijn identities
 On the equivlence between Stein n De Bruijn ientities Sngwoo Prk, Erchin Serpein, n Khli Qrqe rxiv:.5v4 cs.it Jul Abstrct This pper focuses on illustrting the equivlence between Stein s ientity n De Bruijn
On the equivlence between Stein n De Bruijn ientities Sngwoo Prk, Erchin Serpein, n Khli Qrqe rxiv:.5v4 cs.it Jul Abstrct This pper focuses on illustrting the equivlence between Stein s ientity n De Bruijn
a < a+ x < a+2 x < < a+n x = b, n A i n f(x i ) x. i=1 i=1
 Mth 33 Volume Stewrt 5.2 Geometry of integrls. In this section, we will lern how to compute volumes using integrls defined by slice nlysis. First, we recll from Clculus I how to compute res. Given the
Mth 33 Volume Stewrt 5.2 Geometry of integrls. In this section, we will lern how to compute volumes using integrls defined by slice nlysis. First, we recll from Clculus I how to compute res. Given the
INTRODUCTION TO INTEGRATION
 INTRODUCTION TO INTEGRATION 5.1 Ares nd Distnces Assume f(x) 0 on the intervl [, b]. Let A be the re under the grph of f(x). b We will obtin n pproximtion of A in the following three steps. STEP 1: Divide
INTRODUCTION TO INTEGRATION 5.1 Ares nd Distnces Assume f(x) 0 on the intervl [, b]. Let A be the re under the grph of f(x). b We will obtin n pproximtion of A in the following three steps. STEP 1: Divide
AP Calculus AB Unit 4 Assessment
 Clss: Dte: 0-04 AP Clulus AB Unit 4 Assessment Multiple Choie Identify the hoie tht best ompletes the sttement or nswers the question. A lultor my NOT be used on this prt of the exm. (6 minutes). The slope
Clss: Dte: 0-04 AP Clulus AB Unit 4 Assessment Multiple Choie Identify the hoie tht best ompletes the sttement or nswers the question. A lultor my NOT be used on this prt of the exm. (6 minutes). The slope
Surds and Indices. Surds and Indices. Curriculum Ready ACMNA: 233,
 Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
COUNTS OF FAILURE STRINGS IN CERTAIN BERNOULLI SEQUENCES
 COUNTS OF FAILURE STRINGS IN CERTAIN BERNOULLI SEQUENCES LARS HOLST Deprtment of Mthemtics, Royl Institute of Technology SE 100 44 Stockholm, Sween E-mil: lholst@mth.kth.se October 6, 2006 Abstrct In sequence
COUNTS OF FAILURE STRINGS IN CERTAIN BERNOULLI SEQUENCES LARS HOLST Deprtment of Mthemtics, Royl Institute of Technology SE 100 44 Stockholm, Sween E-mil: lholst@mth.kth.se October 6, 2006 Abstrct In sequence
Math Calculus with Analytic Geometry II
 orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
Bisimulation, Games & Hennessy Milner logic
 Bisimultion, Gmes & Hennessy Milner logi Leture 1 of Modelli Mtemtii dei Proessi Conorrenti Pweł Soboiński Univeristy of Southmpton, UK Bisimultion, Gmes & Hennessy Milner logi p.1/32 Clssil lnguge theory
Bisimultion, Gmes & Hennessy Milner logi Leture 1 of Modelli Mtemtii dei Proessi Conorrenti Pweł Soboiński Univeristy of Southmpton, UK Bisimultion, Gmes & Hennessy Milner logi p.1/32 Clssil lnguge theory
The Shortest Confidence Interval for the Mean of a Normal Distribution
 Interntionl Journl of Sttistics nd Proility; Vol. 7, No. 2; Mrch 208 ISSN 927-7032 E-ISSN 927-7040 Pulished y Cndin Center of Science nd Eduction The Shortest Confidence Intervl for the Men of Norml Distriution
Interntionl Journl of Sttistics nd Proility; Vol. 7, No. 2; Mrch 208 ISSN 927-7032 E-ISSN 927-7040 Pulished y Cndin Center of Science nd Eduction The Shortest Confidence Intervl for the Men of Norml Distriution
Pi evaluation. Monte Carlo integration
 Pi evlution y 1 1 x Computtionl Physics 2018-19 (Phys Dep IST, Lisbon) Fernndo Bro (311) Monte Crlo integrtion we wnt to evlute the following integrl: F = f (x) dx remember tht the expecttion vlue of the
Pi evlution y 1 1 x Computtionl Physics 2018-19 (Phys Dep IST, Lisbon) Fernndo Bro (311) Monte Crlo integrtion we wnt to evlute the following integrl: F = f (x) dx remember tht the expecttion vlue of the
On Implicative and Strong Implicative Filters of Lattice Wajsberg Algebras
 Glol Journl of Mthemtil Sienes: Theory nd Prtil. ISSN 974-32 Volume 9, Numer 3 (27), pp. 387-397 Interntionl Reserh Pulition House http://www.irphouse.om On Implitive nd Strong Implitive Filters of Lttie
Glol Journl of Mthemtil Sienes: Theory nd Prtil. ISSN 974-32 Volume 9, Numer 3 (27), pp. 387-397 Interntionl Reserh Pulition House http://www.irphouse.om On Implitive nd Strong Implitive Filters of Lttie
