7 - Continuous random variables
|
|
|
- Blake Eaton
- 6 years ago
- Views:
Transcription
1 7-1 Continuous rndom vribles S. Lll, Stnford Continuous rndom vribles Continuous rndom vribles The cumultive distribution function The uniform rndom vrible Gussin rndom vribles The Gussin cdf Collecting dt Induced probbility density functions Exmple: liner trnsformtions Exmple: non-invertible trnsformtions Simultion of rndom vribles
2 7-2 Continuous rndom vribles S. Lll, Stnford Continuous rndom vribles A continuous rndom vrible x : Ω R is specified by its (induced) cumultive distribution function (cdf) F x (z) = Prob(x z) F() 1 Then we hve Prob(x [, b]) = F x (b) F x ( )
3 7-3 Continuous rndom vribles S. Lll, Stnford Properties of the cumultive distribution function F() 1 F x () 0 for ll F x is non-decresing function F x () F x (b) if b F x is right continuous, i.e,. lim z + F x (z) = F x ()
4 7-4 Continuous rndom vribles S. Lll, Stnford Properties of the cumultive distribution function If F x is differentible, then the induced probbility density function (pdf) is p x (z) = df x (z) dz then Prob(x [, b]) = b p x (z) dz Notice tht p x (z) is not probbility; it my be greter thn 1. We use nottion x p x to men x is rndom vrible with pdf p x
5 7-5 Continuous rndom vribles S. Lll, Stnford Properties of the cumultive distribution function If x is discrete rndom vrible, then F is just stircse function 1 F() The corresponding probbility density function is sum of δ functions.
6 7-6 Continuous rndom vribles S. Lll, Stnford The uniform rndom vrible The uniform rndom vrible x U[, b] hs pdf p x (z) = 1 b if z b 0 otherwise
7 7-7 Continuous rndom vribles S. Lll, Stnford Gussin rndom vribles The rndom vrible x is Gussin if it hs pdf p(x) = 1 σ (x µ) 2 2π e 2σ 2 write this s x N(µ, σ 2 ) the men or expected vlue of x is E(x) = xp(x) dx = µ the vrince of x is E ( (x µ) 2) = (x µ) 2 p(x) dx = σ 2
8 7-8 Continuous rndom vribles S. Lll, Stnford Gussin rndom vribles pdf for x N(0, 1) is p() p is symmetric bout the men decys very fst; but p(x) > 0 for ll x
9 7-9 Continuous rndom vribles S. Lll, Stnford Computing probbilities for Gussin rndom vribles The error function is erf(x) = 2 π x 0 e t2 dt The Gussin CDF is F N () = ( ) µ 2 erf σ 2 When µ = 0 nd σ = 1, F N ()
10 7-10 Continuous rndom vribles S. Lll, Stnford Computing probbilities for Gussin rndom vribles so for x N(0, σ 2 ) we hve for 0 ( ) Prob(x [, ]) = erf σ 2 Some prticulr vlues: Prob(x [ σ, σ]) 0.68 Prob(x [ 2σ, 2σ]) Prob(x [ 3σ, 3σ])
11 7-11 Continuous rndom vribles S. Lll, Stnford Collecting dt For discrete rndom vribles, we cn collect dt nd count the frequencies of outcomes This converges to the true pmf. The nlogous procedure for continuous rndom vribles uses the cumultive distribution function. Suppose S = {z 1,..., z n } re n smples of rel-vlued rndom vrible. Let F() be the frction of smples less thn or equl to, given by F() = {z S z } n F is piecewise constnt function, clled the empiricl cdf
12 7-12 Continuous rndom vribles S. Lll, Stnford Exmple: collecting dt Suppose x N(0, 1). The plots below show 25 nd 250 dt points, respectively
13 7-13 Continuous rndom vribles S. Lll, Stnford Induced probbility density Suppose we hve x : Ω R is rndom vrible with induced pdf p x : R R. y is function of x, given by y = g(x) Wht is the induced pdf of y? The key ide is tht we need to chnge vribles for integrtion of probbilities. Recll the following. If f nd h re continuous, then h(b) h() f(x) dx = b f ( h(y) ) h (y) dy
14 7-14 Continuous rndom vribles S. Lll, Stnford Induced probbility density Assume g is continuous, nd g is strictly incresing; i.e., if < b then g() < g(b) This implies tht g is invertible, i.e., for every y there is unique x such tht y = g(x). We would like to find the pdf of y is p y, which stisfies for b, Prob(y [, b]) = b p y (y) dy We lso know tht this probbility is Prob(y [, b]) = Prob(g(x) [, b]) = Prob ( x [g 1 (), g 1 (b)] ) since g is incresing = g 1 (b) g 1 () p x (x) dx
15 7-15 Continuous rndom vribles S. Lll, Stnford Induced probbility density We hve b p y (y) dy = g 1 (b) g 1 () p x (x) dx Now we cn pply the chnge of vribles x = h(y) to the integrl on the right hnd side, where h = g 1. We hve h 1 (y) = g ( g 1 (y) ) becuse g(h(y)) = y, so d dy g(h(y)) = 1, i.e., g (h(y))h (y) = 1 Therefore, by the chnge of vribles formul b p y (y) dy = b p x( g 1 (y) ) g ( g 1 (y) ) dy
16 7-16 Continuous rndom vribles S. Lll, Stnford Induced probbility density Since this holds for ll nd b, we hve the following. If y = g(x), nd g is strictly incresing with g continuous, then the pdf of y is p y (y) = px( g 1 (y) ) g ( g 1 (y) ) More generlly, if g (x) 0 for ll x, then p y (y) = px( g 1 (y) ) g ( g 1 (y) )
17 7-17 Continuous rndom vribles S. Lll, Stnford Exmple: liner trnsformtions Suppose x : Ω R, nd y = αx + β y b g à1 () g à1 (b) x We hve p y (y) = 1 α px ( ) y β α
18 7-18 Continuous rndom vribles S. Lll, Stnford Non-invertible trnsformtions Wht hppens when g is not invertible? e.g., when y = x 2 Prob(y [, b]) = Prob(x 2 [, b]) y b = Prob(x [ b, ]) + Prob(x [, b]) = = b b p x (x) dx + p x ( y) 2 y dy + b p x (x) dx b p x ( y) 2 y dy y = x 2 = p y (y) = 1 ( 2 p x ( y) + p x ( ) y) y x
19 7-19 Continuous rndom vribles S. Lll, Stnford Simultion of rndom vribles We re given F : R [0, 1] We would like to simulte rndom vrible y so tht it hs cumultive distribution function F We hve source of uniform rndom vribles x U[0, 1] To construct y, set y = F 1 (x) Becuse Prob(y ) = Prob(F 1 (x) ) = Prob(x F()) = F() This works when F is invertible nd continuous
1 Probability Density Functions
 Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Continuous Random Variables
 STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 217 Néhémy Lim Continuous Rndom Vribles Nottion. The indictor function of set S is rel-vlued function defined by : { 1 if x S 1 S (x) if x S Suppose tht
STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 217 Néhémy Lim Continuous Rndom Vribles Nottion. The indictor function of set S is rel-vlued function defined by : { 1 if x S 1 S (x) if x S Suppose tht
Chapter 5 : Continuous Random Variables
 STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 216 Néhémy Lim Chpter 5 : Continuous Rndom Vribles Nottions. N {, 1, 2,...}, set of nturl numbers (i.e. ll nonnegtive integers); N {1, 2,...}, set of ll
STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 216 Néhémy Lim Chpter 5 : Continuous Rndom Vribles Nottions. N {, 1, 2,...}, set of nturl numbers (i.e. ll nonnegtive integers); N {1, 2,...}, set of ll
38.2. The Uniform Distribution. Introduction. Prerequisites. Learning Outcomes
 The Uniform Distribution 8. Introduction This Section introduces the simplest type of continuous probbility distribution which fetures continuous rndom vrible X with probbility density function f(x) which
The Uniform Distribution 8. Introduction This Section introduces the simplest type of continuous probbility distribution which fetures continuous rndom vrible X with probbility density function f(x) which
Expectation and Variance
 Expecttion nd Vrince : sum of two die rolls P(= P(= = 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 P(=2) = 1/36 P(=3) = 1/18 P(=4) = 1/12 P(=5) = 1/9 P(=7) = 1/6 P(=13) =? 2 1/36 3 1/18 4 1/12 5 1/9 6 5/36 7 1/6
Expecttion nd Vrince : sum of two die rolls P(= P(= = 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 P(=2) = 1/36 P(=3) = 1/18 P(=4) = 1/12 P(=5) = 1/9 P(=7) = 1/6 P(=13) =? 2 1/36 3 1/18 4 1/12 5 1/9 6 5/36 7 1/6
Lecture 3 Gaussian Probability Distribution
 Introduction Lecture 3 Gussin Probbility Distribution Gussin probbility distribution is perhps the most used distribution in ll of science. lso clled bell shped curve or norml distribution Unlike the binomil
Introduction Lecture 3 Gussin Probbility Distribution Gussin probbility distribution is perhps the most used distribution in ll of science. lso clled bell shped curve or norml distribution Unlike the binomil
CS667 Lecture 6: Monte Carlo Integration 02/10/05
 CS667 Lecture 6: Monte Crlo Integrtion 02/10/05 Venkt Krishnrj Lecturer: Steve Mrschner 1 Ide The min ide of Monte Crlo Integrtion is tht we cn estimte the vlue of n integrl by looking t lrge number of
CS667 Lecture 6: Monte Crlo Integrtion 02/10/05 Venkt Krishnrj Lecturer: Steve Mrschner 1 Ide The min ide of Monte Crlo Integrtion is tht we cn estimte the vlue of n integrl by looking t lrge number of
11 An introduction to Riemann Integration
 11 An introduction to Riemnn Integrtion The PROOFS of the stndrd lemms nd theorems concerning the Riemnn Integrl re NEB, nd you will not be sked to reproduce proofs of these in full in the exmintion in
11 An introduction to Riemnn Integrtion The PROOFS of the stndrd lemms nd theorems concerning the Riemnn Integrl re NEB, nd you will not be sked to reproduce proofs of these in full in the exmintion in
Math 118: Honours Calculus II Winter, 2005 List of Theorems. L(P, f) U(Q, f). f exists for each ǫ > 0 there exists a partition P of [a, b] such that
![Math 118: Honours Calculus II Winter, 2005 List of Theorems. L(P, f) U(Q, f). f exists for each ǫ > 0 there exists a partition P of [a, b] such that Math 118: Honours Calculus II Winter, 2005 List of Theorems. L(P, f) U(Q, f). f exists for each ǫ > 0 there exists a partition P of [a, b] such that](/thumbs/96/127235733.jpg) Mth 118: Honours Clculus II Winter, 2005 List of Theorems Lemm 5.1 (Prtition Refinement): If P nd Q re prtitions of [, b] such tht Q P, then L(P, f) L(Q, f) U(Q, f) U(P, f). Lemm 5.2 (Upper Sums Bound
Mth 118: Honours Clculus II Winter, 2005 List of Theorems Lemm 5.1 (Prtition Refinement): If P nd Q re prtitions of [, b] such tht Q P, then L(P, f) L(Q, f) U(Q, f) U(P, f). Lemm 5.2 (Upper Sums Bound
MATH20812: PRACTICAL STATISTICS I SEMESTER 2 NOTES ON RANDOM VARIABLES
 MATH20812: PRACTICAL STATISTICS I SEMESTER 2 NOTES ON RANDOM VARIABLES Things to Know Rndom Vrible A rndom vrible is function tht ssigns numericl vlue to ech outcome of prticulr experiment. A rndom vrible
MATH20812: PRACTICAL STATISTICS I SEMESTER 2 NOTES ON RANDOM VARIABLES Things to Know Rndom Vrible A rndom vrible is function tht ssigns numericl vlue to ech outcome of prticulr experiment. A rndom vrible
Math 426: Probability Final Exam Practice
 Mth 46: Probbility Finl Exm Prctice. Computtionl problems 4. Let T k (n) denote the number of prtitions of the set {,..., n} into k nonempty subsets, where k n. Argue tht T k (n) kt k (n ) + T k (n ) by
Mth 46: Probbility Finl Exm Prctice. Computtionl problems 4. Let T k (n) denote the number of prtitions of the set {,..., n} into k nonempty subsets, where k n. Argue tht T k (n) kt k (n ) + T k (n ) by
CS 109 Lecture 11 April 20th, 2016
 CS 09 Lecture April 0th, 06 Four Prototypicl Trjectories Review The Norml Distribution is Norml Rndom Vrible: ~ Nµ, σ Probbility Density Function PDF: f x e σ π E[ ] µ Vr σ x µ / σ Also clled Gussin Note:
CS 09 Lecture April 0th, 06 Four Prototypicl Trjectories Review The Norml Distribution is Norml Rndom Vrible: ~ Nµ, σ Probbility Density Function PDF: f x e σ π E[ ] µ Vr σ x µ / σ Also clled Gussin Note:
Method: Step 1: Step 2: Find f. Step 3: = Y dy. Solution: 0, ( ) 0, y. Assume
 Functions of Rndom Vrible Problem Sttement We know the pdf ( or cdf ) of rndom vrible. Define new rndom vrible Y g( ) ). Find the pdf of Y. Method: Step : Step : Step 3: Plot Y g( ). Find F ( ) b mpping
Functions of Rndom Vrible Problem Sttement We know the pdf ( or cdf ) of rndom vrible. Define new rndom vrible Y g( ) ). Find the pdf of Y. Method: Step : Step : Step 3: Plot Y g( ). Find F ( ) b mpping
7.2 Riemann Integrable Functions
 7.2 Riemnn Integrble Functions Theorem 1. If f : [, b] R is step function, then f R[, b]. Theorem 2. If f : [, b] R is continuous on [, b], then f R[, b]. Theorem 3. If f : [, b] R is bounded nd continuous
7.2 Riemnn Integrble Functions Theorem 1. If f : [, b] R is step function, then f R[, b]. Theorem 2. If f : [, b] R is continuous on [, b], then f R[, b]. Theorem 3. If f : [, b] R is bounded nd continuous
f(x)dx . Show that there 1, 0 < x 1 does not exist a differentiable function g : [ 1, 1] R such that g (x) = f(x) for all
![f(x)dx . Show that there 1, 0 < x 1 does not exist a differentiable function g : [ 1, 1] R such that g (x) = f(x) for all f(x)dx . Show that there 1, 0 < x 1 does not exist a differentiable function g : [ 1, 1] R such that g (x) = f(x) for all](/thumbs/94/119531908.jpg) 3 Definite Integrl 3.1 Introduction In school one comes cross the definition of the integrl of rel vlued function defined on closed nd bounded intervl [, b] between the limits nd b, i.e., f(x)dx s the
3 Definite Integrl 3.1 Introduction In school one comes cross the definition of the integrl of rel vlued function defined on closed nd bounded intervl [, b] between the limits nd b, i.e., f(x)dx s the
1 The fundamental theorems of calculus.
 The fundmentl theorems of clculus. The fundmentl theorems of clculus. Evluting definite integrls. The indefinite integrl- new nme for nti-derivtive. Differentiting integrls. Tody we provide the connection
The fundmentl theorems of clculus. The fundmentl theorems of clculus. Evluting definite integrls. The indefinite integrl- new nme for nti-derivtive. Differentiting integrls. Tody we provide the connection
Experiments, Outcomes, Events and Random Variables: A Revisit
 Eperiments, Outcomes, Events nd Rndom Vriles: A Revisit Berlin Chen Deprtment o Computer Science & Inormtion Engineering Ntionl Tiwn Norml University Reerence: - D. P. Bertseks, J. N. Tsitsiklis, Introduction
Eperiments, Outcomes, Events nd Rndom Vriles: A Revisit Berlin Chen Deprtment o Computer Science & Inormtion Engineering Ntionl Tiwn Norml University Reerence: - D. P. Bertseks, J. N. Tsitsiklis, Introduction
Review on Integration (Secs ) Review: Sec Origins of Calculus. Riemann Sums. New functions from old ones.
 Mth 20B Integrl Clculus Lecture Review on Integrtion (Secs. 5. - 5.3) Remrks on the course. Slide Review: Sec. 5.-5.3 Origins of Clculus. Riemnn Sums. New functions from old ones. A mthemticl description
Mth 20B Integrl Clculus Lecture Review on Integrtion (Secs. 5. - 5.3) Remrks on the course. Slide Review: Sec. 5.-5.3 Origins of Clculus. Riemnn Sums. New functions from old ones. A mthemticl description
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Section 6.1 INTRO to LAPLACE TRANSFORMS
 Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Numerical Integration
 Numericl Integrtion Wouter J. Den Hn London School of Economics c 2011 by Wouter J. Den Hn June 3, 2011 Qudrture techniques I = f (x)dx n n w i f (x i ) = w i f i i=1 i=1 Nodes: x i Weights: w i Qudrture
Numericl Integrtion Wouter J. Den Hn London School of Economics c 2011 by Wouter J. Den Hn June 3, 2011 Qudrture techniques I = f (x)dx n n w i f (x i ) = w i f i i=1 i=1 Nodes: x i Weights: w i Qudrture
Lecture 1. Functional series. Pointwise and uniform convergence.
 1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
7.2 The Definite Integral
 7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
Math 554 Integration
 Mth 554 Integrtion Hndout #9 4/12/96 Defn. A collection of n + 1 distinct points of the intervl [, b] P := {x 0 = < x 1 < < x i 1 < x i < < b =: x n } is clled prtition of the intervl. In this cse, we
Mth 554 Integrtion Hndout #9 4/12/96 Defn. A collection of n + 1 distinct points of the intervl [, b] P := {x 0 = < x 1 < < x i 1 < x i < < b =: x n } is clled prtition of the intervl. In this cse, we
Math 360: A primitive integral and elementary functions
 Mth 360: A primitive integrl nd elementry functions D. DeTurck University of Pennsylvni October 16, 2017 D. DeTurck Mth 360 001 2017C: Integrl/functions 1 / 32 Setup for the integrl prtitions Definition:
Mth 360: A primitive integrl nd elementry functions D. DeTurck University of Pennsylvni October 16, 2017 D. DeTurck Mth 360 001 2017C: Integrl/functions 1 / 32 Setup for the integrl prtitions Definition:
Problem. Statement. variable Y. Method: Step 1: Step 2: y d dy. Find F ( Step 3: Find f = Y. Solution: Assume
 Functions of Rndom Vrible Problem Sttement We know the pdf ( or cdf ) of rndom r vrible. Define new rndom vrible Y = g. Find the pdf of Y. Method: Step : Step : Step 3: Plot Y = g( ). Find F ( y) by mpping
Functions of Rndom Vrible Problem Sttement We know the pdf ( or cdf ) of rndom r vrible. Define new rndom vrible Y = g. Find the pdf of Y. Method: Step : Step : Step 3: Plot Y = g( ). Find F ( y) by mpping
63. Representation of functions as power series Consider a power series. ( 1) n x 2n for all 1 < x < 1
 3 9. SEQUENCES AND SERIES 63. Representtion of functions s power series Consider power series x 2 + x 4 x 6 + x 8 + = ( ) n x 2n It is geometric series with q = x 2 nd therefore it converges for ll q =
3 9. SEQUENCES AND SERIES 63. Representtion of functions s power series Consider power series x 2 + x 4 x 6 + x 8 + = ( ) n x 2n It is geometric series with q = x 2 nd therefore it converges for ll q =
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
f(x) dx, If one of these two conditions is not met, we call the integral improper. Our usual definition for the value for the definite integral
 Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Numerical integration
 2 Numericl integrtion This is pge i Printer: Opque this 2. Introduction Numericl integrtion is problem tht is prt of mny problems in the economics nd econometrics literture. The orgniztion of this chpter
2 Numericl integrtion This is pge i Printer: Opque this 2. Introduction Numericl integrtion is problem tht is prt of mny problems in the economics nd econometrics literture. The orgniztion of this chpter
Improper Integrals. Type I Improper Integrals How do we evaluate an integral such as
 Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
1 The fundamental theorems of calculus.
 The fundmentl theorems of clculus. The fundmentl theorems of clculus. Evluting definite integrls. The indefinite integrl- new nme for nti-derivtive. Differentiting integrls. Theorem Suppose f is continuous
The fundmentl theorems of clculus. The fundmentl theorems of clculus. Evluting definite integrls. The indefinite integrl- new nme for nti-derivtive. Differentiting integrls. Theorem Suppose f is continuous
Joint distribution. Joint distribution. Marginal distributions. Joint distribution
 Joint distribution To specify the joint distribution of n rndom vribles X 1,...,X n tht tke vlues in the smple spces E 1,...,E n we need probbility mesure, P, on E 1... E n = {(x 1,...,x n ) x i E i, i
Joint distribution To specify the joint distribution of n rndom vribles X 1,...,X n tht tke vlues in the smple spces E 1,...,E n we need probbility mesure, P, on E 1... E n = {(x 1,...,x n ) x i E i, i
38 Riemann sums and existence of the definite integral.
 38 Riemnn sums nd existence of the definite integrl. In the clcultion of the re of the region X bounded by the grph of g(x) = x 2, the x-xis nd 0 x b, two sums ppered: ( n (k 1) 2) b 3 n 3 re(x) ( n These
38 Riemnn sums nd existence of the definite integrl. In the clcultion of the re of the region X bounded by the grph of g(x) = x 2, the x-xis nd 0 x b, two sums ppered: ( n (k 1) 2) b 3 n 3 re(x) ( n These
SYDE 112, LECTURES 3 & 4: The Fundamental Theorem of Calculus
 SYDE 112, LECTURES & 4: The Fundmentl Theorem of Clculus So fr we hve introduced two new concepts in this course: ntidifferentition nd Riemnn sums. It turns out tht these quntities re relted, but it is
SYDE 112, LECTURES & 4: The Fundmentl Theorem of Clculus So fr we hve introduced two new concepts in this course: ntidifferentition nd Riemnn sums. It turns out tht these quntities re relted, but it is
Theoretical foundations of Gaussian quadrature
 Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H. Thomas Shores Department of Mathematics University of Nebraska Spring 2007
 A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
Properties of the Riemann Stieltjes Integral
 Properties of the Riemnn Stieltjes Integrl Theorem (Linerity Properties) Let < c < d < b nd A,B IR nd f,g,α,β : [,b] IR. () If f,g R(α) on [,b], then Af +Bg R(α) on [,b] nd [ ] b Af +Bg dα A +B (b) If
Properties of the Riemnn Stieltjes Integrl Theorem (Linerity Properties) Let < c < d < b nd A,B IR nd f,g,α,β : [,b] IR. () If f,g R(α) on [,b], then Af +Bg R(α) on [,b] nd [ ] b Af +Bg dα A +B (b) If
Section 6.1 INTRO to LAPLACE TRANSFORMS
 Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
3.4 Numerical integration
 3.4. Numericl integrtion 63 3.4 Numericl integrtion In mny economic pplictions it is necessry to compute the definite integrl of relvlued function f with respect to "weight" function w over n intervl [,
3.4. Numericl integrtion 63 3.4 Numericl integrtion In mny economic pplictions it is necessry to compute the definite integrl of relvlued function f with respect to "weight" function w over n intervl [,
Continuous Random Variables Class 5, Jeremy Orloff and Jonathan Bloom
 Lerning Gols Continuous Rndom Vriles Clss 5, 8.05 Jeremy Orloff nd Jonthn Bloom. Know the definition of continuous rndom vrile. 2. Know the definition of the proility density function (pdf) nd cumultive
Lerning Gols Continuous Rndom Vriles Clss 5, 8.05 Jeremy Orloff nd Jonthn Bloom. Know the definition of continuous rndom vrile. 2. Know the definition of the proility density function (pdf) nd cumultive
approaches as n becomes larger and larger. Since e > 1, the graph of the natural exponential function is as below
 . Eponentil nd rithmic functions.1 Eponentil Functions A function of the form f() =, > 0, 1 is clled n eponentil function. Its domin is the set of ll rel f ( 1) numbers. For n eponentil function f we hve.
. Eponentil nd rithmic functions.1 Eponentil Functions A function of the form f() =, > 0, 1 is clled n eponentil function. Its domin is the set of ll rel f ( 1) numbers. For n eponentil function f we hve.
Normal Distribution. Lecture 6: More Binomial Distribution. Properties of the Unit Normal Distribution. Unit Normal Distribution
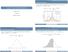 Norml Distribution Lecture 6: More Binomil Distribution If X is rndom vrible with norml distribution with men µ nd vrince σ 2, X N (µ, σ 2, then P(X = x = f (x = 1 e 1 (x µ 2 2 σ 2 σ Sttistics 104 Colin
Norml Distribution Lecture 6: More Binomil Distribution If X is rndom vrible with norml distribution with men µ nd vrince σ 2, X N (µ, σ 2, then P(X = x = f (x = 1 e 1 (x µ 2 2 σ 2 σ Sttistics 104 Colin
5 Probability densities
 5 Probbility densities 5. Continuous rndom vribles 5. The norml distribution 5.3 The norml pproimtion to the binomil distribution 5.5 The uniorm distribution 5. Joint distribution discrete nd continuous
5 Probbility densities 5. Continuous rndom vribles 5. The norml distribution 5.3 The norml pproimtion to the binomil distribution 5.5 The uniorm distribution 5. Joint distribution discrete nd continuous
INTRODUCTION TO INTEGRATION
 INTRODUCTION TO INTEGRATION 5.1 Ares nd Distnces Assume f(x) 0 on the intervl [, b]. Let A be the re under the grph of f(x). b We will obtin n pproximtion of A in the following three steps. STEP 1: Divide
INTRODUCTION TO INTEGRATION 5.1 Ares nd Distnces Assume f(x) 0 on the intervl [, b]. Let A be the re under the grph of f(x). b We will obtin n pproximtion of A in the following three steps. STEP 1: Divide
Review of Calculus, cont d
 Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Definite integral. Mathematics FRDIS MENDELU
 Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová Brno 1 Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function defined on [, b]. Wht is the re of the
Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová Brno 1 Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function defined on [, b]. Wht is the re of the
Mapping the delta function and other Radon measures
 Mpping the delt function nd other Rdon mesures Notes for Mth583A, Fll 2008 November 25, 2008 Rdon mesures Consider continuous function f on the rel line with sclr vlues. It is sid to hve bounded support
Mpping the delt function nd other Rdon mesures Notes for Mth583A, Fll 2008 November 25, 2008 Rdon mesures Consider continuous function f on the rel line with sclr vlues. It is sid to hve bounded support
The Riemann Integral
 Deprtment of Mthemtics King Sud University 2017-2018 Tble of contents 1 Anti-derivtive Function nd Indefinite Integrls 2 3 4 5 Indefinite Integrls & Anti-derivtive Function Definition Let f : I R be function
Deprtment of Mthemtics King Sud University 2017-2018 Tble of contents 1 Anti-derivtive Function nd Indefinite Integrls 2 3 4 5 Indefinite Integrls & Anti-derivtive Function Definition Let f : I R be function
Math 1431 Section M TH 4:00 PM 6:00 PM Susan Wheeler Office Hours: Wed 6:00 7:00 PM Online ***NOTE LABS ARE MON AND WED
 Mth 43 Section 4839 M TH 4: PM 6: PM Susn Wheeler swheeler@mth.uh.edu Office Hours: Wed 6: 7: PM Online ***NOTE LABS ARE MON AND WED t :3 PM to 3: pm ONLINE Approimting the re under curve given the type
Mth 43 Section 4839 M TH 4: PM 6: PM Susn Wheeler swheeler@mth.uh.edu Office Hours: Wed 6: 7: PM Online ***NOTE LABS ARE MON AND WED t :3 PM to 3: pm ONLINE Approimting the re under curve given the type
Pi evaluation. Monte Carlo integration
 Pi evlution y 1 1 x Computtionl Physics 2018-19 (Phys Dep IST, Lisbon) Fernndo Bro (311) Monte Crlo integrtion we wnt to evlute the following integrl: F = f (x) dx remember tht the expecttion vlue of the
Pi evlution y 1 1 x Computtionl Physics 2018-19 (Phys Dep IST, Lisbon) Fernndo Bro (311) Monte Crlo integrtion we wnt to evlute the following integrl: F = f (x) dx remember tht the expecttion vlue of the
The final exam will take place on Friday May 11th from 8am 11am in Evans room 60.
 Mth 104: finl informtion The finl exm will tke plce on Fridy My 11th from 8m 11m in Evns room 60. The exm will cover ll prts of the course with equl weighting. It will cover Chpters 1 5, 7 15, 17 21, 23
Mth 104: finl informtion The finl exm will tke plce on Fridy My 11th from 8m 11m in Evns room 60. The exm will cover ll prts of the course with equl weighting. It will cover Chpters 1 5, 7 15, 17 21, 23
Big idea in Calculus: approximation
 Big ide in Clculus: pproximtion Derivtive: f (x) = df dx f f(x +h) f(x) =, x h rte of chnge is pproximtely the rtio of chnges in the function vlue nd in the vrible in very short time Liner pproximtion:
Big ide in Clculus: pproximtion Derivtive: f (x) = df dx f f(x +h) f(x) =, x h rte of chnge is pproximtely the rtio of chnges in the function vlue nd in the vrible in very short time Liner pproximtion:
HW3 : Moment functions Solutions
 STAT/MATH 395 A - PROBABILITY II UW Spring Qurter 6 Néhémy Lim HW3 : Moment functions Solutions Problem. Let X be rel-vlued rndom vrible on probbility spce (Ω, A, P) with moment generting function M X.
STAT/MATH 395 A - PROBABILITY II UW Spring Qurter 6 Néhémy Lim HW3 : Moment functions Solutions Problem. Let X be rel-vlued rndom vrible on probbility spce (Ω, A, P) with moment generting function M X.
Week 10: Riemann integral and its properties
 Clculus nd Liner Algebr for Biomedicl Engineering Week 10: Riemnn integrl nd its properties H. Führ, Lehrstuhl A für Mthemtik, RWTH Achen, WS 07 Motivtion: Computing flow from flow rtes 1 We observe the
Clculus nd Liner Algebr for Biomedicl Engineering Week 10: Riemnn integrl nd its properties H. Führ, Lehrstuhl A für Mthemtik, RWTH Achen, WS 07 Motivtion: Computing flow from flow rtes 1 We observe the
Definite integral. Mathematics FRDIS MENDELU. Simona Fišnarová (Mendel University) Definite integral MENDELU 1 / 30
 Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová (Mendel University) Definite integrl MENDELU / Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function
Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová (Mendel University) Definite integrl MENDELU / Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function
Chapter 6 Notes, Larson/Hostetler 3e
 Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
Section 3.3: Fredholm Integral Equations
 Section 3.3: Fredholm Integrl Equtions Suppose tht k : [, b] [, b] R nd g : [, b] R re given functions nd tht we wish to find n f : [, b] R tht stisfies f(x) = g(x) + k(x, y) f(y) dy. () Eqution () is
Section 3.3: Fredholm Integrl Equtions Suppose tht k : [, b] [, b] R nd g : [, b] R re given functions nd tht we wish to find n f : [, b] R tht stisfies f(x) = g(x) + k(x, y) f(y) dy. () Eqution () is
Lecture 1: Introduction to integration theory and bounded variation
 Lecture 1: Introduction to integrtion theory nd bounded vrition Wht is this course bout? Integrtion theory. The first question you might hve is why there is nything you need to lern bout integrtion. You
Lecture 1: Introduction to integrtion theory nd bounded vrition Wht is this course bout? Integrtion theory. The first question you might hve is why there is nything you need to lern bout integrtion. You
AP Calculus Multiple Choice: BC Edition Solutions
 AP Clculus Multiple Choice: BC Edition Solutions J. Slon Mrch 8, 04 ) 0 dx ( x) is A) B) C) D) E) Divergent This function inside the integrl hs verticl symptotes t x =, nd the integrl bounds contin this
AP Clculus Multiple Choice: BC Edition Solutions J. Slon Mrch 8, 04 ) 0 dx ( x) is A) B) C) D) E) Divergent This function inside the integrl hs verticl symptotes t x =, nd the integrl bounds contin this
Improper Integrals, and Differential Equations
 Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
MA Handout 2: Notation and Background Concepts from Analysis
 MA350059 Hndout 2: Nottion nd Bckground Concepts from Anlysis This hndout summrises some nottion we will use nd lso gives recp of some concepts from other units (MA20023: PDEs nd CM, MA20218: Anlysis 2A,
MA350059 Hndout 2: Nottion nd Bckground Concepts from Anlysis This hndout summrises some nottion we will use nd lso gives recp of some concepts from other units (MA20023: PDEs nd CM, MA20218: Anlysis 2A,
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Handout 4. Inverse and Implicit Function Theorems.
 8.95 Hndout 4. Inverse nd Implicit Function Theorems. Theorem (Inverse Function Theorem). Suppose U R n is open, f : U R n is C, x U nd df x is invertible. Then there exists neighborhood V of x in U nd
8.95 Hndout 4. Inverse nd Implicit Function Theorems. Theorem (Inverse Function Theorem). Suppose U R n is open, f : U R n is C, x U nd df x is invertible. Then there exists neighborhood V of x in U nd
Chapter 6. Riemann Integral
 Introduction to Riemnn integrl Chpter 6. Riemnn Integrl Won-Kwng Prk Deprtment of Mthemtics, The College of Nturl Sciences Kookmin University Second semester, 2015 1 / 41 Introduction to Riemnn integrl
Introduction to Riemnn integrl Chpter 6. Riemnn Integrl Won-Kwng Prk Deprtment of Mthemtics, The College of Nturl Sciences Kookmin University Second semester, 2015 1 / 41 Introduction to Riemnn integrl
Partial Derivatives. Limits. For a single variable function f (x), the limit lim
 Limits Prtil Derivtives For single vrible function f (x), the limit lim x f (x) exists only if the right-hnd side limit equls to the left-hnd side limit, i.e., lim f (x) = lim f (x). x x + For two vribles
Limits Prtil Derivtives For single vrible function f (x), the limit lim x f (x) exists only if the right-hnd side limit equls to the left-hnd side limit, i.e., lim f (x) = lim f (x). x x + For two vribles
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
1.2. Linear Variable Coefficient Equations. y + b "! = a y + b " Remark: The case b = 0 and a non-constant can be solved with the same idea as above.
 1 12 Liner Vrible Coefficient Equtions Section Objective(s): Review: Constnt Coefficient Equtions Solving Vrible Coefficient Equtions The Integrting Fctor Method The Bernoulli Eqution 121 Review: Constnt
1 12 Liner Vrible Coefficient Equtions Section Objective(s): Review: Constnt Coefficient Equtions Solving Vrible Coefficient Equtions The Integrting Fctor Method The Bernoulli Eqution 121 Review: Constnt
The Banach algebra of functions of bounded variation and the pointwise Helly selection theorem
 The Bnch lgebr of functions of bounded vrition nd the pointwise Helly selection theorem Jordn Bell jordn.bell@gmil.com Deprtment of Mthemtics, University of Toronto Jnury, 015 1 BV [, b] Let < b. For f
The Bnch lgebr of functions of bounded vrition nd the pointwise Helly selection theorem Jordn Bell jordn.bell@gmil.com Deprtment of Mthemtics, University of Toronto Jnury, 015 1 BV [, b] Let < b. For f
Overview of Calculus I
 Overview of Clculus I Prof. Jim Swift Northern Arizon University There re three key concepts in clculus: The limit, the derivtive, nd the integrl. You need to understnd the definitions of these three things,
Overview of Clculus I Prof. Jim Swift Northern Arizon University There re three key concepts in clculus: The limit, the derivtive, nd the integrl. You need to understnd the definitions of these three things,
Section Areas and Distances. Example 1: Suppose a car travels at a constant 50 miles per hour for 2 hours. What is the total distance traveled?
 Section 5. - Ares nd Distnces Exmple : Suppose cr trvels t constnt 5 miles per hour for 2 hours. Wht is the totl distnce trveled? Exmple 2: Suppose cr trvels 75 miles per hour for the first hour, 7 miles
Section 5. - Ares nd Distnces Exmple : Suppose cr trvels t constnt 5 miles per hour for 2 hours. Wht is the totl distnce trveled? Exmple 2: Suppose cr trvels 75 miles per hour for the first hour, 7 miles
Physics 116C Solution of inhomogeneous ordinary differential equations using Green s functions
 Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
W. We shall do so one by one, starting with I 1, and we shall do it greedily, trying
 Vitli covers 1 Definition. A Vitli cover of set E R is set V of closed intervls with positive length so tht, for every δ > 0 nd every x E, there is some I V with λ(i ) < δ nd x I. 2 Lemm (Vitli covering)
Vitli covers 1 Definition. A Vitli cover of set E R is set V of closed intervls with positive length so tht, for every δ > 0 nd every x E, there is some I V with λ(i ) < δ nd x I. 2 Lemm (Vitli covering)
8 Laplace s Method and Local Limit Theorems
 8 Lplce s Method nd Locl Limit Theorems 8. Fourier Anlysis in Higher DImensions Most of the theorems of Fourier nlysis tht we hve proved hve nturl generliztions to higher dimensions, nd these cn be proved
8 Lplce s Method nd Locl Limit Theorems 8. Fourier Anlysis in Higher DImensions Most of the theorems of Fourier nlysis tht we hve proved hve nturl generliztions to higher dimensions, nd these cn be proved
Calculus in R. Chapter Di erentiation
 Chpter 3 Clculus in R 3.1 Di erentition Definition 3.1. Suppose U R is open. A function f : U! R is di erentible t x 2 U if there exists number m such tht lim y!0 pple f(x + y) f(x) my y =0. If f is di
Chpter 3 Clculus in R 3.1 Di erentition Definition 3.1. Suppose U R is open. A function f : U! R is di erentible t x 2 U if there exists number m such tht lim y!0 pple f(x + y) f(x) my y =0. If f is di
Recitation 3: More Applications of the Derivative
 Mth 1c TA: Pdric Brtlett Recittion 3: More Applictions of the Derivtive Week 3 Cltech 2012 1 Rndom Question Question 1 A grph consists of the following: A set V of vertices. A set E of edges where ech
Mth 1c TA: Pdric Brtlett Recittion 3: More Applictions of the Derivtive Week 3 Cltech 2012 1 Rndom Question Question 1 A grph consists of the following: A set V of vertices. A set E of edges where ech
F (x) dx = F (x)+c = u + C = du,
 35. The Substitution Rule An indefinite integrl of the derivtive F (x) is the function F (x) itself. Let u = F (x), where u is new vrible defined s differentible function of x. Consider the differentil
35. The Substitution Rule An indefinite integrl of the derivtive F (x) is the function F (x) itself. Let u = F (x), where u is new vrible defined s differentible function of x. Consider the differentil
Review of basic calculus
 Review of bsic clculus This brief review reclls some of the most importnt concepts, definitions, nd theorems from bsic clculus. It is not intended to tech bsic clculus from scrtch. If ny of the items below
Review of bsic clculus This brief review reclls some of the most importnt concepts, definitions, nd theorems from bsic clculus. It is not intended to tech bsic clculus from scrtch. If ny of the items below
MA123, Chapter 10: Formulas for integrals: integrals, antiderivatives, and the Fundamental Theorem of Calculus (pp.
 MA123, Chpter 1: Formuls for integrls: integrls, ntiderivtives, nd the Fundmentl Theorem of Clculus (pp. 27-233, Gootmn) Chpter Gols: Assignments: Understnd the sttement of the Fundmentl Theorem of Clculus.
MA123, Chpter 1: Formuls for integrls: integrls, ntiderivtives, nd the Fundmentl Theorem of Clculus (pp. 27-233, Gootmn) Chpter Gols: Assignments: Understnd the sttement of the Fundmentl Theorem of Clculus.
Review. April 12, Definition 1.2 (Closed Set). A set S is closed if it contains all of its limit points. S := S S
 Review April 12, 2017 1 Definitions nd Some Theorems 1.1 Topology Definition 1.1 (Limit Point). Let S R nd x R. Then x is limit point of S if, for ll ɛ > 0, V ɛ (x) = (x ɛ, x + ɛ) contins n element s S
Review April 12, 2017 1 Definitions nd Some Theorems 1.1 Topology Definition 1.1 (Limit Point). Let S R nd x R. Then x is limit point of S if, for ll ɛ > 0, V ɛ (x) = (x ɛ, x + ɛ) contins n element s S
MORE FUNCTION GRAPHING; OPTIMIZATION. (Last edited October 28, 2013 at 11:09pm.)
 MORE FUNCTION GRAPHING; OPTIMIZATION FRI, OCT 25, 203 (Lst edited October 28, 203 t :09pm.) Exercise. Let n be n rbitrry positive integer. Give n exmple of function with exctly n verticl symptotes. Give
MORE FUNCTION GRAPHING; OPTIMIZATION FRI, OCT 25, 203 (Lst edited October 28, 203 t :09pm.) Exercise. Let n be n rbitrry positive integer. Give n exmple of function with exctly n verticl symptotes. Give
Abstract inner product spaces
 WEEK 4 Abstrct inner product spces Definition An inner product spce is vector spce V over the rel field R equipped with rule for multiplying vectors, such tht the product of two vectors is sclr, nd the
WEEK 4 Abstrct inner product spces Definition An inner product spce is vector spce V over the rel field R equipped with rule for multiplying vectors, such tht the product of two vectors is sclr, nd the
Week 10: Line Integrals
 Week 10: Line Integrls Introduction In this finl week we return to prmetrised curves nd consider integrtion long such curves. We lredy sw this in Week 2 when we integrted long curve to find its length.
Week 10: Line Integrls Introduction In this finl week we return to prmetrised curves nd consider integrtion long such curves. We lredy sw this in Week 2 when we integrted long curve to find its length.
Math 113 Fall Final Exam Review. 2. Applications of Integration Chapter 6 including sections and section 6.8
 Mth 3 Fll 0 The scope of the finl exm will include: Finl Exm Review. Integrls Chpter 5 including sections 5. 5.7, 5.0. Applictions of Integrtion Chpter 6 including sections 6. 6.5 nd section 6.8 3. Infinite
Mth 3 Fll 0 The scope of the finl exm will include: Finl Exm Review. Integrls Chpter 5 including sections 5. 5.7, 5.0. Applictions of Integrtion Chpter 6 including sections 6. 6.5 nd section 6.8 3. Infinite
Mathematics 1. (Integration)
 Mthemtics 1. (Integrtion) University of Debrecen 2018-2019 fll Definition Let I R be n open, non-empty intervl, f : I R be function. F : I R is primitive function of f if F is differentible nd F = f on
Mthemtics 1. (Integrtion) University of Debrecen 2018-2019 fll Definition Let I R be n open, non-empty intervl, f : I R be function. F : I R is primitive function of f if F is differentible nd F = f on
MAA 4212 Improper Integrals
 Notes by Dvid Groisser, Copyright c 1995; revised 2002, 2009, 2014 MAA 4212 Improper Integrls The Riemnn integrl, while perfectly well-defined, is too restrictive for mny purposes; there re functions which
Notes by Dvid Groisser, Copyright c 1995; revised 2002, 2009, 2014 MAA 4212 Improper Integrls The Riemnn integrl, while perfectly well-defined, is too restrictive for mny purposes; there re functions which
Anti-derivatives/Indefinite Integrals of Basic Functions
 Anti-derivtives/Indefinite Integrls of Bsic Functions Power Rule: In prticulr, this mens tht x n+ x n n + + C, dx = ln x + C, if n if n = x 0 dx = dx = dx = x + C nd x (lthough you won t use the second
Anti-derivtives/Indefinite Integrls of Bsic Functions Power Rule: In prticulr, this mens tht x n+ x n n + + C, dx = ln x + C, if n if n = x 0 dx = dx = dx = x + C nd x (lthough you won t use the second
1.9 C 2 inner variations
 46 CHAPTER 1. INDIRECT METHODS 1.9 C 2 inner vritions So fr, we hve restricted ttention to liner vritions. These re vritions of the form vx; ǫ = ux + ǫφx where φ is in some liner perturbtion clss P, for
46 CHAPTER 1. INDIRECT METHODS 1.9 C 2 inner vritions So fr, we hve restricted ttention to liner vritions. These re vritions of the form vx; ǫ = ux + ǫφx where φ is in some liner perturbtion clss P, for
ODE: Existence and Uniqueness of a Solution
 Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.
![We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b. We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.](/thumbs/93/114277851.jpg) Mth 255 - Vector lculus II Notes 4.2 Pth nd Line Integrls We begin with discussion of pth integrls (the book clls them sclr line integrls). We will do this for function of two vribles, but these ides cn
Mth 255 - Vector lculus II Notes 4.2 Pth nd Line Integrls We begin with discussion of pth integrls (the book clls them sclr line integrls). We will do this for function of two vribles, but these ides cn
1 Techniques of Integration
 November 8, 8 MAT86 Week Justin Ko Techniques of Integrtion. Integrtion By Substitution (Chnge of Vribles) We cn think of integrtion by substitution s the counterprt of the chin rule for differentition.
November 8, 8 MAT86 Week Justin Ko Techniques of Integrtion. Integrtion By Substitution (Chnge of Vribles) We cn think of integrtion by substitution s the counterprt of the chin rule for differentition.
( dg. ) 2 dt. + dt. dt j + dh. + dt. r(t) dt. Comparing this equation with the one listed above for the length of see that
 Arc Length of Curves in Three Dimensionl Spce If the vector function r(t) f(t) i + g(t) j + h(t) k trces out the curve C s t vries, we cn mesure distnces long C using formul nerly identicl to one tht we
Arc Length of Curves in Three Dimensionl Spce If the vector function r(t) f(t) i + g(t) j + h(t) k trces out the curve C s t vries, we cn mesure distnces long C using formul nerly identicl to one tht we
Definition of Continuity: The function f(x) is continuous at x = a if f(a) exists and lim
 Mth 9 Course Summry/Study Guide Fll, 2005 [1] Limits Definition of Limit: We sy tht L is the limit of f(x) s x pproches if f(x) gets closer nd closer to L s x gets closer nd closer to. We write lim f(x)
Mth 9 Course Summry/Study Guide Fll, 2005 [1] Limits Definition of Limit: We sy tht L is the limit of f(x) s x pproches if f(x) gets closer nd closer to L s x gets closer nd closer to. We write lim f(x)
20 MATHEMATICS POLYNOMIALS
 0 MATHEMATICS POLYNOMIALS.1 Introduction In Clss IX, you hve studied polynomils in one vrible nd their degrees. Recll tht if p(x) is polynomil in x, the highest power of x in p(x) is clled the degree of
0 MATHEMATICS POLYNOMIALS.1 Introduction In Clss IX, you hve studied polynomils in one vrible nd their degrees. Recll tht if p(x) is polynomil in x, the highest power of x in p(x) is clled the degree of
Lecture 14: Quadrature
 Lecture 14: Qudrture This lecture is concerned with the evlution of integrls fx)dx 1) over finite intervl [, b] The integrnd fx) is ssumed to be rel-vlues nd smooth The pproximtion of n integrl by numericl
Lecture 14: Qudrture This lecture is concerned with the evlution of integrls fx)dx 1) over finite intervl [, b] The integrnd fx) is ssumed to be rel-vlues nd smooth The pproximtion of n integrl by numericl
Monte Carlo method in solving numerical integration and differential equation
 Monte Crlo method in solving numericl integrtion nd differentil eqution Ye Jin Chemistry Deprtment Duke University yj66@duke.edu Abstrct: Monte Crlo method is commonly used in rel physics problem. The
Monte Crlo method in solving numericl integrtion nd differentil eqution Ye Jin Chemistry Deprtment Duke University yj66@duke.edu Abstrct: Monte Crlo method is commonly used in rel physics problem. The
An instructive toy model: two paradoxes
 Tel Aviv University, 2006 Gussin rndom vectors 27 3 Level crossings... the fmous ice formul, undoubtedly one of the most importnt results in the ppliction of smooth stochstic processes..j. Adler nd J.E.
Tel Aviv University, 2006 Gussin rndom vectors 27 3 Level crossings... the fmous ice formul, undoubtedly one of the most importnt results in the ppliction of smooth stochstic processes..j. Adler nd J.E.
Integrals - Motivation
 Integrls - Motivtion When we looked t function s rte of chnge If f(x) is liner, the nswer is esy slope If f(x) is non-liner, we hd to work hrd limits derivtive A relted question is the re under f(x) (but
Integrls - Motivtion When we looked t function s rte of chnge If f(x) is liner, the nswer is esy slope If f(x) is non-liner, we hd to work hrd limits derivtive A relted question is the re under f(x) (but
Euler, Ioachimescu and the trapezium rule. G.J.O. Jameson (Math. Gazette 96 (2012), )
 Euler, Iochimescu nd the trpezium rule G.J.O. Jmeson (Mth. Gzette 96 (0), 36 4) The following results were estblished in recent Gzette rticle [, Theorems, 3, 4]. Given > 0 nd 0 < s
Euler, Iochimescu nd the trpezium rule G.J.O. Jmeson (Mth. Gzette 96 (0), 36 4) The following results were estblished in recent Gzette rticle [, Theorems, 3, 4]. Given > 0 nd 0 < s
Calculus II: Integrations and Series
 Clculus II: Integrtions nd Series August 7, 200 Integrls Suppose we hve generl function y = f(x) For simplicity, let f(x) > 0 nd f(x) continuous Denote F (x) = re under the grph of f in the intervl [,x]
Clculus II: Integrtions nd Series August 7, 200 Integrls Suppose we hve generl function y = f(x) For simplicity, let f(x) > 0 nd f(x) continuous Denote F (x) = re under the grph of f in the intervl [,x]
