A Process-Algebraic Semantics for Generalised Nonblocking
|
|
|
- Jesse Black
- 5 years ago
- Views:
Transcription
1 A Proess-Algeri Semntis for Generlise Nonloking Simon Wre Roi Mlik Deprtment of Computer Siene The University of Wikto Privte Bg 3105, Hmilton 3240, New Zeln Emil: Astrt Generlise nonloking is wek liveness property to express the ility of system to terminte uner given preonitions. This pper stuies the notions of equivlene n refinement tht preserve generlise nonloking n proposes semnti moel tht hrterises generlise nonloking equivlene. The moel n e onstrute from the trnsition struture of n utomton, n hs finite representtion for every finite-stte utomton. It is use to onstrut unique utomton representtion for ll generlise nonloking equivlent utomt. This gives rise to effetive eision proeures to verify generlise nonloking equivlene n refinement, n to metho to simplify utomt while preserving generlise nonloking equivlene. The results of this pper provie for etter unerstning of nonloking in ompositionl frmework, with possile pplitions in ompositionl verifition. 1 Introution Bloking or onflits re ommon fults in the esign of onurrent progrms tht n e very sutle n hr to etet (Dietrih et l. 2002, Wong et l. 2000). They hve long een stuie in the fiel of isrete-event systems (Cssnrs & Lfortune 1999, Rmge & Wonhm 1989), whih is pplie to the moelling of omplex, sfety-ritil systems. To improve the reliility of suh systems, tehniques re neee to etet the presene or verify the sene of loking in moels of n ever inresing size. In isrete-events theory, the sene of loking is formlise using the nonloking property, whih is use very suessfully for synthesis (Cssnrs & Lfortune 1999, Rmge & Wonhm 1989). A lot of reserh hs een onute to stuy the ompositionl semntis (Kumr & Shymn 1994, Mlik et l. 2006) of nonloking n its verifition (Florl & Mlik 2009, Su et l. 2010). Despite its wiespre use, the expressive powers of nonloking re limite. To overome its weknesses, nonloking hs een moifie n extene in severl wys (Fin & Kumr 1997, e Queiroz et l. 2004, Mlik & Leu 2008). This pper is onerne out generlise nonloking (Mlik & Leu 2008), whih s to stnr nonloking the ility to restrit the set of sttes from whih loking is heke. This is useful for the verifition of softwre omponents n of Copyright 2011, Austrlin Computer Soiety, In. This pper ppere t the 17th Computing: The Austrlsin Theory Symposium (CATS 2011), Perth, Austrli, Jnury Conferenes in Reserh n Prtie in Informtion Tehnology (CRPIT), Vol. 119, Alex Potnin n Tso Vigls, E. Reproution for emi, not-for profit purposes permitte provie this text is inlue. ertin onitions in Hierrhil Interfe-Bse Supervisory Control (Leu et l. 2005, Leu & Mlik 2010). In (Mlik & Leu 2009), set of strtion rules is propose to simplify utomt in suh wy tht generlise nonloking equivlene is preserve. Although the pproh provies useful mens for ompositionl verifition, the strtion rules re inomplete n limite in their reution potentil. In n ttempt to evelop more effetive strtion, this pper nlyses generlise nonloking using proesslgeri testing theory (Hennessy 1988, De Niol & Hennessy 1984). It hrterises generlise nonloking equivlene n refinement using proesslgeri semnti moel, n provies n lgorithm to onstrut nonil utomton representtion tht n e use s unique strtion for ll generlise nonloking equivlent utomt. These results pve the wy towrs more generl mens of strtion thn the lol strtion rules of (Mlik & Leu 2009), n in ition mke it possile to reson out refinement. The pper uses similr methos n ies s previously use for stnr nonloking (Mlik et l. 2006) n fir testing (Brinksm et l. 1995, Ntrjn & Cleveln 1995), yet the results re quite ifferent. Generlise nonloking semntis requires no interepeneny etween the possile ompletions ssoite with ifferent sttes of n utomton. This les to simpler semnti moel thn in the se of stnr nonloking or fir testing, with finite representtions n more strightforwr lgorithms. This pper is orgnise s follows. Set. 2 introues the neessry kgroun of noneterministi utomt n efines generlise nonloking. Then Set. 3 introues testing equivlene n preorer for generlise nonloking, presents semnti moel, n proves results out its equy n finiteness. Afterwrs, Set. 4 esries the nonil utomton s stnrise norml form with respet to generlise nonloking, n proposes n lgorithm to onstrut it. Finlly, Set. 5 s some onluing remrks. 2 Preliminries This setion introues the nottions use throughout this pper. Dynmi systems re moelle using multi-oloure utomt, with the possiility of noneterminism, whih nturlly rises from strtion n hiing (Hore 1985, Rosoe 1997). System ehviour is esrie using lnguges, with nottions tken from the kgroun of isrete event systems n utomt theory (Rmge & Wonhm 1989, Hoproft et l. 2001).
2 2.1 Events n Lnguges Event sequenes n lnguges re simple mens to esrie isrete system ehviours (Rmge & Wonhm 1989, Cssnrs & Lfortune 1999). Their si uiling loks re events, whih re tken from finite lphet Σ. In ition, the silent event / Σ is use, with the nottion Σ = Σ {}. Σ enotes the set of ll finite tres or strings of the form σ 1 σ 2...σ n of events from Σ, inluing the empty tre ε. A suset L Σ is lle lnguge. The ontention of two tres s,t Σ is written s st. Tres n lnguges n lso e tente, for exmple sl = {st Σ t L }. The prefix-losure of lnguge L is L = {s Σ st L for some t Σ }. Nturl projetion P : Σ Σ is the opertion tht eletes ll silent () events from tres. 2.2 Multi-oloure Automt Noneterministi multi-oloure utomt re use to moel ynmi system ehviours. Noneterminism is essentil for the strtion tehniques in this pper. Multi-oloure utomt exten the tritionl onept of mrke sttes to multiple simultneous mrking onitions, y lelling sttes with ifferent olours or propositions. The generlise nonloking onition is efine using these propositions. The following efinition ppers in (Mlik & Leu 2008), n is se on similr ies in (Clrke et l. 1999, e Queiroz et l. 2004). Definition 1 A multi-oloure utomton is tuple G = Σ,Π,Q,,Q,Ξ where Σ is finite set of events, Π is finite set of propositions or olours, Q is set of sttes, Q Σ Q is the stte trnsition reltion, Q Q is the set of initil sttes, n Ξ: Π 2 Q efines the set of mrke sttes for eh proposition in Π. G is lle finite-stte if the stte set Q is finite. The trnsition reltion is written in infix nottion x σ y, n is extene to tres in Σ in the stnr wy. For stte set Q 1 Q, the nottion Q 1 s x2 mens tht x 1 s x2 for some x 1 Q 1, n likewise Q 1 s Q2 mens x 1 s x2 for some x 1 Q 1 n x 2 Q 2. Also, x y enotes tht x s y for some tre s Σ, n x s mens x s y for some stte y Q. Finlly, G s x stns for Q s x. To support hiing of silent events, nother trnsition reltion Q Σ Q is introue, where x s y enotes the existene of tre t Σ suh tht P (t) = s n x t y. Tht is, x s y enotes pth with extly the events in s, while x s y enotes pth with n ritrry numer of events shuffle with the events of s. Nottions suh s Q 1 s Q2, x y, n x s re efine nlogously to. For stte or stte set x, the ontinution lnguge is efine s L(x) = {s Σ x s }, (1) n likewise for π Π the π-mrke lnguge is L π (x) = {s Σ x s Ξ(π) }. (2) The lnguge n the π-mrke lnguge of the utomton G re L(G) = L(Q ) n L π (G) = L π (Q ). An utomton G = Σ,Π,Q,,Q,Ξ is eterministi if it hs t most one initil stte, i.e., Q 1, if x σ y 1 n x σ y 2 lwys implies y 1 = y 2, n if G hs no trnsitions lelle. Given possily noneterministi utomton G, the well-known suset onstrution n e use to otin lngugeequivlent eterministi utomton (Hoproft et l. 2001). More preisely, where et(g) = Σ,Π, PQ, et,q et,ξ et, (3) X σ et Y for X,Y Q n σ Σ if n only if Y = {y Q X σ y } n Y ; Q et = {{x Q Q ε x }} \ { }; Ξ et (π) = {X Q X Ξ(π) }. The utomton et(g) is eterministi n stisfies L(et(G)) = L(G) n L π (et(g)) = L π (G) for eh π Π. 2.3 Opertions The proess-lgeri opertions of synhronous omposition n hiing re use in this pper to ompose utomt. Synhronous omposition moels the prllel exeution of two or more utomt, n is one using lok-step synhronistion in the style of (Hore 1985). Definition 2 Let G = Σ,Π,Q G, G,Q G,Ξ G n H = Σ,Π,Q H, H,Q H,Ξ H e multi-oloure utomt. The synhronous prout of G n H is where G H = Σ,Π,Q G Q H,,Q G Q H,Ξ (4) (x G,x H ) σ (y G,y H ) σ if σ Σ, x G G y G, n σ x H H y H ; (x G,x H ) (y G,x H ) if x G G y G ; (x G,x H ) (x G,y H ) if x H H y H ; n Ξ(π) = Ξ G (π) Ξ H (π) for eh π Π. This efinition ssumes tht the two ompose utomt shre the sme event n proposition lphets. This is suffiient for the purpose of this pper. Automt with ifferent lphets n lso e ompose y lifting them to ommon lphets first: when n event σ is e to the lphet Σ, selfloop trnsitions x σ x re e for ll sttes x Q, n when proposition π is e to Π, it is efine tht Ξ(π) = Q. It is esily onfirme tht synhronous omposition is ommuttive n ssoitive opertion. Hiing is the proess-lgeri opertion tht generlises nturl projetion of lnguges when noneterministi utomt re onsiere. Events tht re not of interest re reple y silent () trnsitions or ε-moves (Hoproft et l. 2001). Definition 3 Let G = Σ,Π,Q,,Q,Ξ e multi-oloure utomton, n let Υ Σ. The result of hiing Υ in G is G \ Υ = Σ \ Υ,Π,Q, \ Υ,Q,Ξ, (5) where \ Υ is otine from y repling ll events in Υ with the silent event.
3 G 1 : G 2 : G 3 : G 1 : G 1: G 1: T 1 :, Figure 1: Generlise nonloking vs. stnr nonloking. 2.4 Generlise Nonloking It is esirle for ontrol systems to e free from livelok n elok. This is typilly expresse n heke y esignting ertin sttes of n utomton s suess or terminl sttes n heking their rehility. In isrete event systems theory, this ie is lle the nonloking or nononfliting property, whih requires tht terminl stte e rehle from every rehle system stte (Rmge & Wonhm 1989). Nonloking is generlise in (Mlik & Leu 2008), using two propositions α n ω. The intene mening is tht ω represents terminl sttes, while α speifies set of sttes from whih terminl sttes re require to e rehle. Definition 4 Let G = Σ,Π,Q,,Q,Ξ e multi-oloure utomton with α,ω Π. G is ω-nonloking or stnr nonloking, if for ll sttes x Q suh tht G x it lso hols tht x Ξ(ω). Otherwise, G is ω-loking. G is (α,ω)-nonloking, or generlise nonloking if for ll sttes x Ξ(α) suh tht G x it lso hols tht x Ξ(ω). Otherwise, G is (α, ω)-loking. Exmple 1 Consier the utomt in Fig. 1. Sttes mrke α re grey, n sttes mrke ω re lk. Automton G 1 is oth ω-nonloking n (α,ω)-nonloking, G 2 is ω-loking n (α,ω)-nonloking, n G 3 is oth ω-loking n (α,ω)-loking. Clerly, if n utomton is ω-nonloking, it is lso (α, ω)-nonloking, ut the onverse is not true in generl. The reltionship etween generlise nonloking n stnr nonloking long with some pplitions is isusse in (Mlik & Leu 2008). 3 Generlise Nonloking Equivlene The strightforwr pproh to verify whether ompose system G 1 G 2 G n (6) is (α, ω)-nonloking onsists of expliitly onstruting the synhronous prout n heking for eh stte mrke α whether it hs rehle stte mrke ω. This n e one using CTL moel heking, n moels of sustntil size n e nlyse if the stte spe is represente symolilly (Clrke et l. 1999). Yet, the tehnique remins limite y the mount of memory ville to store representtions of the synhronous prout. In n ttempt to llevite this stte-spe explosion prolem, ompositionl verifition (Florl & Mlik 2009) seeks to rewrite iniviul system omponents n, e.g., reple G 1 in (6) y simpler version G 1, to nlyse the simpler system Figure 2: Generlise nonloking equivlene. This resoning requires tht G 1 n G 1 re relte in some wy. For exmple, utomton G 1 in Fig. 2 my e reple y G 1 while preserving the generlise nonloking property of the system (6). If the reminer G 2 G n of the system hs n α-mrke initil stte, the ompose system is (α, ω)- nonloking if n only if it n reh n ω-mrke stte fter exeuting the tre or, regrless of whether G 1 or G 1 is use. On the other hn, generlise nonloking is not preserve if G 1 is reple y G 1 in Fig. 2. If G 2 G n hs n α-mrke initil stte n n only reh n ω-mrke stte fter exeuting the tre, like utomton T 1 in Fig. 2, then (6) is (α,ω)-nonloking while (7) is (α,ω)-loking. 3.1 The Generlise Nonloking Preorer A notion of proess equivlene to perform strtions preserving generlise nonloking is esrie in (Mlik & Leu 2008). This setion generlises these efinitions n introues preorer, whih mkes it possile to reson not only out equivlene ut lso out refinement. The efinitions re se on the tritionl testing frmework (Hennessy 1988, De Niol & Hennessy 1984) tht efines preorers n equivlenes relting proesses se on their responses to tests. In the ontext of generlise nonloking, test n e n ritrry utomton, n the test s response is the oservtion whether the test is (α, ω)-nonloking in omintion with the given utomton or not. Two utomt re onsiere s equivlent, if the responses of ll tests re equl. Definition 5 Let G n H e two multi-oloure utomt with α, ω Π. G is less (α, ω)-onfliting thn H, written G (α,ω) H, if for every multi-oloure utomton T suh tht H T is (α,ω)-nonloking, G T lso is (α,ω)-nonloking. G n H re (α, ω)-onflit equivlent, written G (α,ω) H, if G (α,ω) H n H (α,ω) G. The reltion (α,ω) efines the generlise nonloking preorer. An utomton G is less (α, ω)- onfliting thn H if there re fewer tests T tht re (α, ω)-loking in omintion with G thn in omintion with H. Two utomt re (α, ω)-onflit equivlent if they re (α, ω)-loking in omintion with extly the sme tests. If G 1 (α,ω) G 1, then G 1 n e reple y G 1 in (6) without ffeting the generlise nonloking property of the omposition. Exmple 2 Automt G 1 n G 1 in Fig. 2 re (α,ω)-onflit equivlent, while G 1 n G 1 re not, euse G 1 T 1 is (α,ω)-nonloking n G 1 T 1 is (α, ω)-loking. Furthermore, it n e shown tht G 1 (α,ω) G 1. G 1 G 2 G n. (7)
4 3.2 Congruene Properties An importnt question onerning preorers suh s (α,ω) is their reltionship to proess-lgeri opertions. For ompositionl verifition, the equivlene use must e well-ehve with respet to synhronous omposition n hiing. These so-lle ongruene properties hve een estlishe in (Mlik et l. 2006) for stnr nonloking n in (Mlik & Leu 2008) for generlise nonloking equivlene, n n esily e extene to the generlise nonloking preorer. Definition 6 Let e preorer on the set of multioloure utomt. is pre-ongruene with respet to if, for ll multi-oloure utomt G, H, n T suh tht G H, it follows tht G T H T. respets (α,ω)-nonloking if, for ll multioloure utomt G n H suh tht G H, if H is (α,ω)-nonloking then G lso is (α,ω)- nonloking. Proposition 1 (α,ω) is pre-ongruene with respet to. Proof. Let G, H, n T e suh tht G (α,ω) H, n let T e n ritrry multi-oloure utomton suh tht (H T) T is (α,ω)-nonloking. Then lerly, H (T T ) = (H T) T is (α,ω)-nonloking, n sine G (α,ω) H it follows tht (G T) T = G (T T ) is (α,ω)-nonloking. Sine T ws hosen ritrrily, it follows tht G T (α,ω) H T. Proposition 2 (α,ω) respets (α,ω)-nonloking. Proof. Note tht there exists multi-oloure utomton U suh tht G U = G for every multioloure utomton G. Let G (α,ω) H, n let H e (α,ω)-nonloking. Then H U = H is (α,ω)-nonloking. Sine G (α,ω) H, it follows tht G = G U is (α,ω)-nonloking. Thus, the generlise nonloking equivlene is ongruene with respet to synhronous omposition n respets (α, ω)-nonloking. This is enough to justify the orretness of ompositionl verifition pproh suh s the one outline t the eginning of Set. 3. Similrly to stnr nonloking (Mlik et l. 2006), the generlise nonloking preorer turns out to e the orsest pre-ongruene with respet to synhronous omposition tht respets (α, ω)-nonloking. In other wors, ny preorer tht reltes multi-oloure utomt oring to their generlise nonloking ehviour n preserves synhronous omposition is ontine in the generlise nonloking preorer. Therefore, the generlise nonloking preorer is the est possile proess refinement for resoning out generlise nonloking. Proposition 3 Let e pre-ongruene with respet to whih respets (α, ω)-nonloking. Then G H implies G (α,ω) H. Proof. Let G H, n let T e multi-oloure utomton suh tht H T is (α,ω)-nonloking. Then G T H T sine is pre-ongruene with respet to. Sine respets loking it follows tht G T is (α, ω)-nonloking. Sine G, H, n T were hosen ritrrily, it follows tht G (α,ω) H. 3.3 Chrterising the Preorer In ition to the test-se efinition of proess preorer, it is esirle to hve hrteristion tht n e erive from the stte struture of n utomton (vn Gleek 2001). This setion introues the generlise nononfliting ompletion semntis s n lgeri moel of the generlise nonloking preorer n equivlene, whih n e erive from the stte n trnsitions of multi-oloure utomton in suh wy tht the moel n e represente finitely for every finite-stte utomton. This moel will e use in the following setion to onstrut nonil utomton. The following efinition resttes the generlise nonloking preorer s stte-se riterion. To hek whether n utomton G is less (α, ω)-onfliting thn nother utomton H, it is enough to ollet the ω-mrke lnguges of ll α-mrke sttes of G n hek whether H ontins lrger lnguges ssoite with the sme α-mrkings. This ie is formlise y the onept of eing stte-wise less (α, ω)- onfliting, whih turns out to e equivlent to the generlise nonloking preorer. Definition 7 Let G = Σ,Π,Q G, G,Q G,Ξ G n H = Σ,Π,Q H, H,Q H,Ξ H e multi-oloure utomt with α,ω Π. G is si to e stte-wise less (α, ω)-onfliting thn H if the following property hols for every s Σ : for every x G Ξ G (α) suh tht G s x G there exists x H Ξ H (α) suh tht H s x H n L ω (x H ) L ω (x G ). Proposition 4 Let G = Σ,Π,Q G, G,Q G,Ξ G n H = Σ,Π,Q H, H,Q H,Ξ H e multi-oloure utomt with α,ω Π. G is stte-wise less (α,ω)- onfliting thn H if n only if G is less (α,ω)-onfliting thn H. Proof. First ssume tht G is stte-wise less (α,ω)- onfliting thn H, n let T = Σ,Π,Q T, T,Q T, Ξ T e n utomton suh tht H T is (α,ω)-nonloking. Let G T s (x G,x T ) Ξ G (α) Ξ T (α). Clerly G s x G Ξ G (α), n sine G is stte-wise less (α, ω)-onfliting thn H, there exists stte x H Ξ H (α) suh tht H s x H n L ω (x H ) L ω (x G ). Thus, H T s (x H,x T ) Ξ H (α) Ξ T (α), n sine H T is (α, ω)-nonloking, there exists tre t Σ suh tht (x H,x T ) t Ξ H (ω) Ξ T (ω). Then, t L ω (x H ) L ω t (x G ), whih implies x G G t Ξ G (ω), n therefore (x G,x T ) Ξ G (ω) Ξ T (ω). Sine s, x, n x T were hosen ritrrily, it follows tht G T is (α, ω)-nonloking. Seon, ssume tht G is less (α, ω)-onfliting thn H. Let s Σ n G s x G Ξ G (α). Construt eterministi utomton T = Σ,Π,Q T, T,Q T, Ξ T suh tht L(T) = Σ, L α (T) = {s}, n L ω (T) = Σ \sl ω (x G ). Sine T is eterministi, there exists unique stte x T Q T suh tht T s x T, whih stisfies x T Ξ T (α) n L ω (x T ) = Σ \ L ω (x G ). Then G T is (α,ω)-loking, euse G T s (x G,x T ) Ξ G (α) Ξ T (α) n L ω (x G ) L ω (x T ) =. Sine G is less (α,ω)-onfliting thn H, it follows tht H T is (α,ω)-loking. This mens tht there exist u Σ, y H Q H, n y T Q T suh tht H T u (y H,y T ) Ξ H (α) Ξ T (α) n L ω (y H ) L ω (y T ) =. Then y T Ξ T (α), n y onstrution of T it follows tht u = s n y T = x T. This implies H s y H Ξ H (α) n L ω (y H ) (Σ \ L ω (x G )) = L ω (y H ) L ω (x T ) =
5 L ω (y H ) L ω (y T ) =, i.e., L ω (y H ) L ω (x G ). Thus, y H stisfies the requirements given for x H in Def. 7, so G is stte-wise less (α,ω)-onfliting thn H Prop. 4 is the key to onstruting proesslgeri moel of generlise nonloking. Essentilly, generlise nonloking n e hrterise y the sets of ω-mrke lnguges ssoite with the α-mrke sttes or, more preisely, with the tres leing to α-mrke sttes. Definition 8 Let G = Σ,Π,Q,,Q,Ξ e multi-oloure utomton with α, ω Π. The generlise nononfliting ompletion semntis for G is efine s CC (α,ω) (G) = {(,C) Σ PΣ There exists x Ξ(α) suh tht G x n L ω (x) C }. (8) If (,C) CC (α,ω) (G), then C is lle nononfliting ompletion for in G. Assume G ontins n α-mrke stte x rehle vi tre Σ, i.e., G x Ξ(α). Then the mrke lnguge L ω (x) of x lerly is nononfliting ompletion for in G, i.e., (, L ω (x)) CC (α,ω) (G). (9) Furthermore, ll superlnguges of L ω (x) re lso nononfliting ompletions, (,C) CC (α,ω) (G) for ll C L ω (x). (10) If G is finite-stte, then there exists only finite numer of α-sttes x n thus only finite numer of ssoite ω-mrke lnguges L ω (x). This mens tht ll nononfliting ompletions n e otine s supersets of the ω-mrke lnguge of some stte x, of whih there re only finitely mny. Therefore, the following losure opertions re use. Definition 9 For CC Σ PΣ, the upwr losure CC n the reue form CC re CC = {(,C ) Σ PΣ There exists (,C) CC suh tht C C } ; CC = {(,C) CC For ll (,C ) CC with C C it hols tht C = C }. (11) (12) Exmple 3 The generlise nononfliting ompletion semntis of utomton G 1 in Fig. 2 is Not every nononfliting ompletion semntis CC n e reonstrute from its reue form CC. In infinite strutures, it is not gurntee for (,C) CC tht there exists miniml suset C C suh tht (,C ) CC. However, if the set of nononfliting ompletions C tht pper in CC is finite, then the existene of miniml susets is gurntee. Thus, if G is finite-stte utomton, then it inee hols tht CC (α,ω) (G) = CC (α,ω) (G). (15) The following min result of this setion sttes tht the generlise nononfliting ompletion semntis inee hrterises the generlise nonloking preorer. If n utomton G is less (α,ω)-onfliting thn utomton H, then the generlise nononfliting ompletion semntis of G is ontine in tht of H. Proposition 5 Let G = Σ,Π,Q G, G,Q G,Ξ G n H = Σ,Π,Q H, H,Q H,Ξ H e multi-oloure utomt with α,ω Π. Then G (α,ω) H if n only if CC (α,ω) (G) CC (α,ω) (H). Proof. First let G (α,ω) H n (,C) CC (α,ω) (G). Then there exists x G Ξ G (α) suh tht G x G n L ω (x G ) C. By Prop. 4, G is stte-wise less (α,ω)- onfliting thn H, so there exists x H Ξ H (α) suh tht H x H n L ω (x H ) L ω (x G ) C. This lrey implies (,C) CC (α,ω) (H). Seon let CC (α,ω) (G) CC (α,ω) (H). By Prop. 4, it is suffiient to show tht G is stte-wise less (α,ω)-onfliting thn H. Therefore, let s Σ n x G Ξ G (α) suh tht G s x G. Then (s, L ω (x G )) CC (α,ω) (G) CC (α,ω) (H). By efinition of CC (α,ω) (H), there exists x H Ξ H (α) suh tht H s x H n L ω (x H ) L ω (x G ). Thus, x H stisfies the onitions of Def. 7, so G is stte-wise less (α,ω)-onfliting thn H. 3.4 Reltionship to Stnr Nonloking In (Mlik et l. 2006), the nononfliting ompletion semntis is introue s n lgeri moel for stnr nonloking. The moel is similr in struture to the generlise nononfliting ompletion semntis introue ove, however it nnot esily e onstrute out of the sttes n trnsitions of n utomton, so tests re referre to inste. Definition 10 (Mlik et l. 2006) Let G = Σ,Π,Q,,Q,Ξ e multi-oloure utomton with ω Π. The nononfliting ompletion semntis of G is CC (α,ω) (G 1 ) = {(ε, {,})}. (13) Exmple 4 The generlise nononfliting ompletion semntis of utomton G 4 in Fig. 3 is CC(G) = {(,C) Σ PΣ For every utomton T suh tht G T is ω- nonloking n T x, there exists t C with x t T Ξ T (ω) }. (16) CC (α,ω) (G 4 ) = {( n, + ) n 0 }. (14) The ω-mrke lnguge of the α-mrke stte q 0 is L ω (q 0 ) = +, n sine this stte n e rehe fter ny numer of events, this lnguge is ssoite with ll tres n for n 0. The ω- mrke lnguge of the seon α-mrke stte q 1 is L ω (q 1 ) = L ω (q 0 ), n s superlnguge of the lrey liste lnguge, it is utomtilly inlue in the upwr losure. The ie of the nononfliting ompletion semntis of n utomton G is tht eh nononfliting ompletion represents requirement tht nees to e stisfie y ny test tht is to e nonloking in omintion with G. If the test n exeute the tre ssoite with nononfliting ompletion C, then, in orer to e nonloking in omintion with G, the test must e le to terminte with t lest one of the tres t C. The following result shows tht the generlise nononfliting ompletion semntis n e expline in the sme wy: if pir (,C) is ontine in the
6 G 4 : T 4 : q 0 q 1 q 2 r 0 r 1 r 2 Figure 3: Stnr nononfliting ompletion semntis my e not well-foune. semntis, then every test tht n enter n α-mrke stte fter tre must e le to terminte with t lest one of the tres in C, in orer to e (α,ω)-nonloking in omintion with G. Proposition 6 Let G = Σ,Π,Q,,Q,Ξ e multi-oloure utomton with α, ω Π. The generlise nononfliting ompletion semntis n e lterntively hrterise s CC (α,ω) (G) = {(,C) Σ PΣ For every utomton T suh tht G T is (α, ω)-nonloking n T x Ξ T (α), there exists t C with x t T Ξ T (ω) }. (17) Proof. Let (,C) CC (α,ω) (G) n T = Σ,Π,Q T, T,Q T,Ξ T suh tht G T is (α,ω)-nonloking n T x T Ξ T (α). Sine (,C) CC (α,ω) (G), there exists x Ξ(α) suh tht G x n L ω (x) C. Then G T (x,x T ) Ξ(α) Ξ T (α), n sine G T is (α,ω)-nonloking there exists t Σ suh tht (x,x T ) t t Ξ(ω) Ξ T (ω). This implies x T T Ξ T (ω) n t L ω (x) C. Now let (,C) Σ PΣ, n ssume tht for every utomton T = Σ,Π,Q T, T,Q T,Ξ T suh tht G T is (α,ω)-nonloking n T x Ξ T (α), there exists t C suh tht x t T Ξ T (ω). Consier eterministi utomton T = Σ,Π,Q T, T,Q T, Ξ T suh tht L(T) = Σ, L α (T) = {}, n L ω (T) = (Σ \C). There exists extly one stte x T Ξ T (α), whih lso stisfies T x T n L ω (x T ) = Σ \ C, t so there oes not exist t C suh tht x T Ξ T (ω). By ssumption it follows tht G T is (α, ω)-loking. Then there exists stte y Ξ(α) Ξ T (α) suh tht G T y n L ω (y) =. By onstrution of T, there exists x Ξ(α) suh tht y = (x,x T ) n G T y = (x,x T ), n furthermore = L ω (y) = L ω (x) L ω (x T ) = L ω (x) (Σ \C), whih implies L ω (x) C. It follows tht (,C) CC (α,ω) (G) y efinition. This shows tht the stnr n generlise nononfliting ompletion semntis re losely relte to eh other. Yet, there re lso importnt ifferenes. While the generlise nononfliting ompletion semntis only is lose vi upwr losure, in stnr nonloking there re interepenenies etween sttes tht le to further losure properties. Exmple 5 (Mlik et l. 2006) In orer to e ω- nonloking in omintion with utomton G 4 in Fig. 3, test must initilly e le to ept t lest one of the tres,,,... Therefore, CC(G 4 ) ontins the pir (ε, { + }). Furthermore, ny suh test must e le to exeute in its initil stte, n ny test exeuting initilly must lso e le to ope with G 4 eing put k to its initil stte q 0 y exeuting the selfloop in q 0. Therefore, suh test lso hs to ept t lest one of the tres,,,... in its initil stte. It follows tht CC(G 4 ) ontins ll the pirs (ε, { n }) for n 1. This exmple shows tht, even for finite-stte utomton, the stnr nononfliting ompletion semntis is not neessrily well-foune, n in generl nnot e esrie y listing finite set of miniml nononfliting ompletions. For generlise nonloking, this is possile. Due to the presene of α- mrkings, there lwys is the possiility for test to e not α-mrke for ertin sttes. Exmple 6 Consier utomton G 4 in Fig. 3 in omintion with test T 4. Clerly, G 4 T 4 is (α,ω)- nonloking, euse the only rehle α-mrke stte of the synhronous prout G 4 T 4 is the initil stte, from whih oth utomt n terminte y exeuting tre. However, the test T 4 nnot exeute ny tre t { n } for n > 1, so unlike the se of stnr nonloking, (ε, { }) / CC (α,ω) (G 4 ). The presene of α-mrkings mkes the nononfliting ompletions for ifferent tres inepenent from eh other. This les to simpler semnti moel with finite hrteristion. It lso mens tht some strtions possile for stnr nonloking re not pplile to generlise nonloking. 4 Cnonil Automton For ompositionl resoning, it is neessry to moify utomt in suh wy tht generlise nonloking equivlene is preserve. This is filitte y the ft tht the generlise nononfliting ompletion semntis n e represente finitely. This setion explins how the generlise nononfliting ompletion semntis n e use to onstrut nonil form for ny given finite-stte utomton, whih is generlise nonloking equivlent to the originl utomton, n suh tht the nonil forms of ny two generlise nonloking equivlent utomt re equl. 4.1 Constrution from Semntis To ensure uniqueness, the nonil form is onstrute iretly from the generlise nononfliting ompletion semntis. More preisely, it is shown in the following how to onstrut nonil utomton CA(CC) for ny given moel CC Σ PΣ. (18) Afterwrs, n lgorithm will e given to ompute the nonil utomton for ny given multi-oloure utomton G. The nonil utomton onsists of two prts, lle the upper n lower utomton. The upper utomton of CC essentilly is miniml eterministi reogniser of the lnguge overe y CC, L(CC) = { Σ There exists C Σ suh tht (,C) CC }. (19) The lower utomton onsists of miniml eterministi reognisers of ll the nononfliting ompletions in CC, whih re linke to trnsitions from the orresponing sttes in the upper utomton. To ensure uniqueness, the upper utomton nees to e minimise in suh wy tht tres leing to equl nononfliting ompletions in the future re mppe to the sme stte of the upper utomton. The following efinition provies the neessry equlity for ny given moel CC.
7 Definition 11 Let CC Σ PΣ. Two tres 1, 2 Σ re si to e equivlent moulo CC, written 1 2, if for ll t Σ n ll C Σ, it hols tht ( 1 t,c) CC if n only if ( 2 t,c) CC. Given this efinition, the stte set of the upper utomton is U = L(CC)/, (20) n the trnsitions of the upper utomton re [s] σ U, [sσ] for ll sσ L(CC). (21) Here, [s] = {s L(CC) s s } enotes the equivlene lss of s moulo, n for L Σ, the nottion L/ = {[s] s L } represents its prtition into equivlene lsses. The lower utomton onsists of eterministi reognisers for ll the nononfliting ompletions. It inlues sttes epting eh of the following lnguges, V = {Cω/t There exists Σ suh tht (,C) CC, n t C }. (22) Here, L/s = {t Σ st L } enotes the ontinution lnguge of L Σ fter s Σ. To ensure minimlity n thus uniqueness, it is onvenient to ientify the sttes of the lower utomton with the lnguges in V. Aoringly, the trnsitions of the lower utomton re L σ V, L/σ for ll L V n σ Σ L. (23) A lower-utomton stte in L V is mrke ω if n only if ω L. This ensures tht the ω-mrke lnguges of these sttes re equl to the lnguges they represent, i.e., L ω (Lω) = L for eh Lω V. (24) To omplete the lower utomton, eh nononfliting ompletion in CC is ssoite with its own α-mrke stte. The α-mrke sttes my only e esse from the upper utomton n therefore nee to e istint from ny lower-utomton stte. Therefore, the following itionl sttes re use, V α = {(C,α) There exists Σ suh tht (,C) CC }. (25) Given these stte sets n trnsitions, the nonil utomton for CC is onstrute s follows, CA(CC) = Σ, {α,ω},q CA, CA,Q CA,Ξ CA (26) where Q CA = U V V α ; CA = U, V, {([],,(C,α)) (,C) CC } {((C,α),,Cω) (C,α) V α }; Q CA = {[ε] } \ { }; Ξ CA (α) = V α ; Ξ CA (ω) = {C V ω C }. The nonil utomton hs simple regulr form, ut it is not neessrily miniml. For exmple, the α-mrke sttes n e merge into their suessors, if those suessors o not hve other inoming trnsitions. The potentil for reution eomes ler in Exmple 7 elow. The following result onfirms tht the nonil utomton onstrution preserves generlise nonloking in tht the generlise nononfliting ompletion semntis of the nonil utomton is equl to the upwrs losure of the moel CC, from whih the utomton ws onstrute. Proposition 7 Let CC Σ PΣ. Then CC (α,ω) (CA(CC)) = CC. (27) Proof. First, let (,C) CC (α,ω) (CA(CC)). Then there exists x Ξ CA (α) suh tht CA(CC) x n L ω (x) C. By onstrution, this mens tht x V, α so x = (C,α) for some (,C ) CC. Also y onstrution of the upper utomton, sine CA(CC) x = (C,α), it follows tht CA(CC) [] (C,α), whih implies (,C ) CC. Furthermore y onstrution of the lower utomton, C = L ω (C ω) = L ω ((C,α)) = L ω (x) C, so it follows from (,C ) CC tht (,C) CC. Seon, let (,C) CC. Then there exists C C suh tht (,C ) CC. By onstrution of the upper utomton, CA(CC) [] (C,α) Ξ CA (α), n y onstrution of the lower utomton, (C,α) C ω n L ω ((C,α)) = L ω (C ω) = C C. Thus, given CA(CC) (C,α) Ξ CA (α) n L ω ((C,α)) C, it follows y efinition of CC (α,ω) tht (,C) CC (α,ω) (CA(CC)). The nonil utomton n e onstrute for ny moel CC, ut the result is only finite-stte if the set of nononfliting ompletions in CC is finite, n the upper utomton hs finite-stte representtion. These onitions n e ensure when CC is otine from the generlise nononfliting ompletion semntis of finite-stte utomton. In this se, the upper utomton is finite-stte euse of the finite numer of α-sttes from whih nononfliting ompletions n originte, n lthough the set of nononfliting ompletions is typilly infinite ue to upwrs losure, it is enough to onstrut the nonil utomton using only miniml nononfliting ompletions. Definition 12 The nonil form of finite-stte multi-oloure utomton G is CA(G) = CA(CC (α,ω) (G) ). (28) As expline ove, the nonil form of n utomton G is finite-stte s long s G is finite-stte. Given the previous results, it is not iffiult to show tht the nonil form is unique for ll generlise nonloking equivlent utomt. Proposition 8 Let G n H e two finite-stte multi-oloure utomt. Then G (α,ω) H if n only if CA(G) = CA(H). (29) Proof. First ssume tht G (α,ω) H. It follows tht CC (α,ω) (G) = CC (α,ω) (H) y Prop. 5, whih implies CA(G) = CA(CC (α,ω) (G) ) = CA(CC (α,ω) (H) ) = CA(H) y efinition.
8 Seon ssume tht CA(G) = CA(H). From the ft tht G is finite-stte n Prop. 7, it follows tht CC (α,ω) (G) = CC (α,ω) (G) = CC (α,ω) (CA(CC (α,ω) (G) )) = CC (α,ω) (CA(G)) = CC (α,ω) (CA(H)) = CC (α,ω) (CA(CC (α,ω) (H) )) = CC (α,ω) (H) = CC (α,ω) (H). (30) By Prop. 5, this implies G (α,ω) H. Prop. 8 shows tht the nonil utomton n e use for ientifition of generlise nonloking equivlent utomt. To etermine whether two finite-stte utomt re generlise nonloking equivlent, it is enough to onstrut their nonil utomt n hek whether they re equl. Cnonil utomt n lso e use to test the generlise nonloking preorer. To hek whether G (α,ω) H, it is possile to inspet ll α-mrke sttes of the synhronous prout of the nonil forms of G n H n ompre the ssoite lnguges. For every ω-mrke lnguge of n α-mrke stte of G, there nees to e sulnguge ssoite with some orresponing α-mrke stte of H. The lnguges n e ompre polynomilly sine they re represente eterministilly in the nonil utomt. However, the test for lnguge inlusion requires only eterministi representtion for one of the two lnguges ompre, n it is enough to onstrut only the nonil utomton of H to hek whether G (α,ω) H. 4.2 Algorithmi Constrution In the previous setion, the nonil utomton hs een onstrute from semnti moel CC, n its uniqueness hs een estlishe. This setion proposes n lgorithm tht, given finite-stte multioloure utomton G = Σ,Π,Q,,Q,Ξ, omputes its nonil form CA(G). The first step in the omputtion of the nonil utomton is the onstrution of the lower utomton, euse it ontins the lnguges ssoite with ll α-mrke sttes, whih re neee to ensure minimlity of the upper utomton. The lower utomton onsists of the miniml eterministi reognisers of ll the ω-mrke lnguges of ll α-mrke sttes of G. To onstrut it, the first step is to remove from G ll sttes from where no ω-mrke n e rehe, tht is, its stte set is restrite to R ω = {x Q x Ξ(ω) }. (31) Then suset onstrution (Hoproft et l. 2001) is use to onstrut eterministi reogniser V et of ll nononfliting ompletion lnguges of G. The suset onstrution strts with initil stte sets orresponing to eh α-mrke stte n ontinues until ll rehle stte sets hve een explore. More preisely, where V et = Σ, {ω}, PR ω, V,Q V,Ξ V (32) X σ V Y for X,Y R ω n σ Σ if n only if Y = {y R ω X σ y } n Y ; X Q V if n only if X = {x R ω x α ε x } for some x α Ξ(α); Ξ V (ω) = {X R ω X Ξ(ω) }. This utomton is then minimise using Hoproft s lgorithm (Hoproft 1971) to otin unique n miniml lower utomton V. For eh initil stte x of the minimise lower utomton, new α-mrke stte x α is rete n linke vi -trnsition to x. These α-mrke stte omprise the stte set V α. In orer to link this utomton to the upper utomton lter, mp is kept tht links the α-mrke sttes of G to their orresponing sttes in V α. Next, the upper utomton is onstrute. In orer to ensure tht it epts preisely the lnguge L(CC (α,ω) (G)) = L α (G), the stte set of G is restrite to sttes from where n α-mrke n e rehe, i.e., to R α = {x Q x Ξ(α) }. (33) Then seon suset onstrution is use to otin eterministi reogniser U et of L α (G). In orer to estlish uniqueness with respet to CC(α,ω) (G), for eh stte set X R α in this suset onstrution, the ssoite set of miniml nononfliting ompletions, CC (α,ω) (X) = {C Σ There exists Σ suh tht G X n (,C) CC (α,ω) (G) }, (34) nees to e etermine. Therefore, eh stte set X in the suset onstrution is ssoite with the set of ll initil sttes of the lower utomton V tht hve een ssoite with some α-mrke stte ontine in X. The ω-mrke lnguges of these sttes re heke for lnguge inlusion, n the initil sttes ssoite with non-miniml lnguges re remove from the set of lnguges ssoite with X. The ω-mrke lnguges of the remining sttes mke up the set CC (α,ω) (X). Now the utomton U et is minimise sujet to n initil prtition se on the sets (34). Two suset sttes X,Y R α n only e merge if CC (α,ω) (X) = CC (α,ω) (Y ). (35) This is one using Hoproft s lgorithm (Hoproft 1971) with n initil prtition se on the minimise sets of α-mrke sttes, whih stisfies (35). The result is unique miniml upper utomton with sttes prtitione in the orsest possile wy tht respets. The finl step in the onstrution of the nonil utomton is to link the upper n lower utomt. Eh stte [X] of the minimise upper utomton is linke vi -trnsition to ll the α-mrke sttes in V α tht hve een ssoite with some α-mrke stte of G ontine in one of the stte sets ssoite with the merge stte [X]. Exmple 7 Fig. 4 emonstrtes the proess of onstrution of the nonil form CA(G) of utomton G. The first step is to pply suset onstrution strting from the three α-mrke sttes q 4, q 8, n q 11. This results in the eterministi utomton V et lso shown in Fig. 4. Its three initil sttes {q 8 }, {q 11 }, n {q 4,q 5,q 8 } orrespon to the three α- mrke sttes of G, from whih the suset onstrution origintes the α-mrke stte q 4 is expne to {q 4,q 5,q 8 } euse of its outgoing -trnsitions.
9 G: q 0 q 12 q 1 q 2,, q 11 q 4 q 3 q 5 q 6 q 7 q 8 q 9 q 10 U et : {q 0, q 1 }, {q 3, q 7 },,, {q 3, q 7, q 9 } {q 3, q 6, q 7, q 9 } {q 4, q 5, q 8 }, {q 0, q 1, q 2, q 3, q 7 } U:, {q 4, q 5, q 8, q 10, q 11, q 12 } u 01 u 458,, V et : {q {q 3, q 7 } 4, q 5, q 8 } V : {q 11 } v 8,, {q, 0, q 1, q 2, q 3, q 7 } v 37, {q 3, q 6, q 7, q 9 } v, 458,, {q 8 } {q 3, q 7, q 9 } {q 4, q 5, q 8, q 10, q 11, q 12 } CA(G):, u 458 u 01,, v 8 v 458 CA :, v α 8,,, v 37 u 458 u 01,, v α 8 Figure 4: Exmple onstrution of nonil utomton. Next, the intermeite lower utomton V et is minimise using Hoproft s lgorithm, resulting in the lower utomton V. After merging, this utomton hs only two initil sttes: stte v 8 orrespons to the originl α-mrke sttes q 8 n q 11, while v 458 orrespons to the originl α-mrke stte q 4. It n lrey e seen tht the ω-mrke lnguge of v 8 is ontine in the ω-mrke lnguge of v 458. Next, to onstrut the upper utomton, suset onstrution is pplie to G to otin its eterministi form U et. Owing to the ft tht α- n ω- mrke sttes re rehle from ll sttes of G, this utomton is very similr to the intermeite lower utomton V et. The α-mrke sttes of U et re {q 4,q 5,q 8 } n {q 4,q 5,q 8,q 10,q 11,q 12 }. These sttes re oth ssoite with the lower-utomton initil sttes v 8 n v 458, however sine L ω (v 8 ) L ω (v 458 ), only v 8 is onsiere. Both α-mrke sttes re ssoite with equl sets of lower-utomton initil sttes, so they my e merge uring minimistion. An inee, minimistion results in the utomton U with only one α-mrke stte u 458. Finlly, the upper n lower utomt re linke, resulting in the nonil utomton CA(G). The only α-mrke stte of the upper utomton is u 458, whih is to e ssoite with v 8 in the lower utomton. Therefore, the new α-mrke stte v8 α is rete n linke vi silent trnsitions to u 458 n v 8. It eomes ler tht the nonil utomton, lthough unique, is not miniml. Sine v8 α hs only one outgoing -trnsition tht les to stte v 8 with no other inoming trnsitions, sttes v8 α n v 8 n e merge while preserving generlise nonloking equivlene. Furthermore, the lnguge of lowerutomton stte v 37 is equl to the lnguge of upperutomton stte u 01, n sine for lower-utomton sttes only the lnguge is relevnt, v 37 n e reple y u 01. This results in the utomton CA, whih is generlise nonloking equivlent to CA(G) n to G. The lgorithm to onstrut the nonil utomton is exponentil. The upper n lower utomton re otine through suset onstrution, n the numer of sttes of the nonil utomton is oune y U + V + V α 2 Q + 2 Q + Ξ(α) = O(2 Q ). (36) To estimte the numer of trnsitions, note tht the upper n lower utomton re eterministi utomt linke y two -trnsitions for eh α-mrke stte. Thus, the numer of trnsitions of the nonil utomton is oune y Σ U + Σ V + 2 V α = O( Σ 2 Q ). (37) The onstrution of the upper utomton requires tests for lnguge inlusion to see whether lnguges ssoite to ifferent α-mrke sttes re ontine in eh other. There re up to 1 2 Ξ(α) ( Ξ(α) 1) pirs of α-mrke sttes tht nee to e ompre, n eh test in the worst se requires onstrution of synhronous prout of two eterministi utomt with 2 Q sttes eh. The time omplexity of the lnguge inlusion hek is etermine y the numer of trnsitions of the synhronous prout, whih is oune y Σ (2 Q ) 2 = Σ 4 Q. In prtie, the test n often e omplete muh fster, euse ientil sttes of G n e reognise in the suset onstrution, n euse the test n stop erly
10 when lnguge inlusion is not stisfie. Still, the worst-se time omplexity of the lgorithm to onstrut the nonil form is O( Σ Ξ(α) 2 4 Q ) = O( Σ Q 2 4 Q ). (38) Despite its exponentil omplexity, suset onstrution is known to e well-ehve in mny prtil ses. In (Wre & Mlik 2008), suset onstrution hs een use for ompositionl verifition of sfety properties of very lrge isrete-event systems moels. Suh results suggest tht the nonil utomton my e useful tool for ompositionl verifition of generlise nonloking. 5 Conlusions The generlise nononfliting ompletion semntis hs een presente s proess-lgeri moel tht hrterises utomt oring to their generlise nonloking ehviour. The semntis n e onstrute from the trnsition struture n hs finite representtion for ny given finite-stte utomton. The generlise nononfliting ompletion semntis hs een use to efine nonil form of utomt, unique utomton tht is the sme for ll generlise nonloking equivlent utomt. An lgorithm to onstrut the nonil form hs een given. The results presente in this pper provie n lgorithmi mens to ientify generlise nonloking equivlent utomt n to perform refinement with respet generlise nonloking. In future work, the uthors woul like to stuy possile pplitions in the re of ompositionl verifition, n to exten the results to stnr nonloking. Referenes Brinksm, E., Rensink, A. & Vogler, W. (1995), Fir testing, in I. Lee & S. A. Smolk, es, Pro. 6th Int. Conf. Conurreny Theory, CONCUR 95, Vol. 962 of LNCS, Springer, Philelphi, PA, USA, pp Cssnrs, C. G. & Lfortune, S. (1999), Introution to Disrete Event Systems, Kluwer. Clrke, Jr., E. M., Grumerg, O. & Pele, D. A. (1999), Moel Cheking, MIT Press. De Niol, R. & Hennessy, M. C. B. (1984), Testing equivlenes for proesses, Theoretil Comput. Si. 34(1 2), e Queiroz, M. H., Cury, J. E. R. & Wonhm, W. M. (2004), Multi-tsking supervisory ontrol of isrete-event systems, in Pro. 7th Int. Workshop on Disrete Event Systems, WODES 04, Reims, Frne, pp Dietrih, P., Mlik, R., Wonhm, W. M. & Brnin, B. A. (2002), Implementtion onsiertions in supervisory ontrol, in B. Cillu, P. Droneu, L. Lvgno & X. Xie, es, Synthesis n Control of Disrete Event Systems, Kluwer, pp Fin, M. & Kumr, R. (1997), Mutully nonloking supervisory ontrol of isrete event systems, in Pro. 36th IEEE Conf. Deision n Control, CDC 97, Sn Diego, CA, USA, pp Florl, H. & Mlik, R. (2009), Compositionl verifition in supervisory ontrol, SIAM J. Control n Optimiztion 48(3), Hennessy, M. (1988), Algeri Theory of Proesses, MIT Press. Hore, C. A. R. (1985), Communiting Sequentil Proesses, Prentie-Hll. Hoproft, J. E. (1971), An nlog n lgorithm for minimizing sttes in finite utomton, in Z. Kohvi & A. Pz, es, Theory of Mhines n Computtions, Aemi Press, New York, NY, USA, pp Hoproft, J. E., Motwni, R. & Ullmn, J. D. (2001), Introution to Automt Theory, Lnguges, n Computtion, Aison-Wesley. Kumr, R. & Shymn, M. A. (1994), Non-loking supervisory ontrol of noneterministi isrete event systems, in Pro. Amerin Control Conf., Bltimore, MD, USA, pp Leu, R. J., Brnin, B. A., Lwfor, M. & Wonhm, W. M. (2005), Hierrhil interfe-se supervisory ontrol prt I: Seril se, IEEE Trns. Automt. Contr. 50(9), Leu, R. & Mlik, R. (2010), A ompositionl pproh for verifying hierrhil interfe-se supervisory ontrol, in Pro. 10th Int. Workshop on Disrete Event Systems, WODES 10, Berlin, Germny. Mlik, R. & Leu, R. (2008), Generlise nonloking, in Pro. 9th Int. Workshop on Disrete Event Systems, WODES 08, Göteorg, Sween, pp Mlik, R. & Leu, R. (2009), A ompositionl pproh for verifying generlise nonloking, in Pro. 7th Int. Conf. Control n Automtion, ICCA 09, Christhurh, New Zeln, pp Mlik, R., Streer, D. & Reeves, S. (2006), Conflits n fir testing, Int. J. Foun. Comput. Si. 17(4), Ntrjn, V. & Cleveln, R. (1995), Divergene n fir testing, in Pro. 22n Int. Colloquium on Automt, Lnguges, n Progrmming, ICALP 95, pp Rmge, P. J. G. & Wonhm, W. M. (1989), The ontrol of isrete event systems, Pro. IEEE 77(1), Rosoe, A. W. (1997), The Theory n Prtie of Conurreny, Prentie-Hll. Su, R., vn Shuppen, J. H., Roo, J. E. & Hofkmp, A. T. (2010), Nononflit hek y using sequentil utomton strtions se on wek oservtion equivlene, Automti 46(6), vn Gleek, R. J. (2001), The liner time rnhing time spetrum I: The semntis of onrete, sequentil proesses, in J. A. Bergstr, A. Ponse & S. A. Smolk, es, Hnook of Proess Alger, Elsevier, pp Wre, S. & Mlik, R. (2008), The use of lnguge projetion for ompositionl verifition of isrete event systems, in Pro. 9th Int. Workshop on Disrete Event Systems, WODES 08, Göteorg, Sween, pp Wong, K. C., Thistle, J. G., Mlhme, R. P. & Hong, H.-H. (2000), Supervisory ontrol of istriute systems: Conflit resolution, Disrete Event Dyn. Syst. 10,
CS 491G Combinatorial Optimization Lecture Notes
 CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
2.4 Theoretical Foundations
 2 Progrmming Lnguge Syntx 2.4 Theoretil Fountions As note in the min text, snners n prsers re se on the finite utomt n pushown utomt tht form the ottom two levels of the Chomsky lnguge hierrhy. At eh level
2 Progrmming Lnguge Syntx 2.4 Theoretil Fountions As note in the min text, snners n prsers re se on the finite utomt n pushown utomt tht form the ottom two levels of the Chomsky lnguge hierrhy. At eh level
Compression of Palindromes and Regularity.
 Compression of Plinromes n Regulrity. Kyoko Shikishim-Tsuji Center for Lierl Arts Eution n Reserh Tenri University 1 Introution In [1], property of likstrem t t view of tse is isusse n it is shown tht
Compression of Plinromes n Regulrity. Kyoko Shikishim-Tsuji Center for Lierl Arts Eution n Reserh Tenri University 1 Introution In [1], property of likstrem t t view of tse is isusse n it is shown tht
Lecture 6: Coding theory
 Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Abstraction of Nondeterministic Automata Rong Su
 Astrtion of Nondeterministi Automt Rong Su My 6, 2010 TU/e Mehnil Engineering, Systems Engineering Group 1 Outline Motivtion Automton Astrtion Relevnt Properties Conlusions My 6, 2010 TU/e Mehnil Engineering,
Astrtion of Nondeterministi Automt Rong Su My 6, 2010 TU/e Mehnil Engineering, Systems Engineering Group 1 Outline Motivtion Automton Astrtion Relevnt Properties Conlusions My 6, 2010 TU/e Mehnil Engineering,
Technische Universität München Winter term 2009/10 I7 Prof. J. Esparza / J. Křetínský / M. Luttenberger 11. Februar Solution
 Tehnishe Universität Münhen Winter term 29/ I7 Prof. J. Esprz / J. Křetínský / M. Luttenerger. Ferur 2 Solution Automt nd Forml Lnguges Homework 2 Due 5..29. Exerise 2. Let A e the following finite utomton:
Tehnishe Universität Münhen Winter term 29/ I7 Prof. J. Esprz / J. Křetínský / M. Luttenerger. Ferur 2 Solution Automt nd Forml Lnguges Homework 2 Due 5..29. Exerise 2. Let A e the following finite utomton:
Nondeterministic Automata vs Deterministic Automata
 Nondeterministi Automt vs Deterministi Automt We lerned tht NFA is onvenient model for showing the reltionships mong regulr grmmrs, FA, nd regulr expressions, nd designing them. However, we know tht n
Nondeterministi Automt vs Deterministi Automt We lerned tht NFA is onvenient model for showing the reltionships mong regulr grmmrs, FA, nd regulr expressions, nd designing them. However, we know tht n
CS311 Computational Structures Regular Languages and Regular Grammars. Lecture 6
 CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Logic, Set Theory and Computability [M. Coppenbarger]
![Logic, Set Theory and Computability [M. Coppenbarger] Logic, Set Theory and Computability [M. Coppenbarger]](/thumbs/90/103901048.jpg) 14 Orer (Hnout) Definition 7-11: A reltion is qusi-orering (or preorer) if it is reflexive n trnsitive. A quisi-orering tht is symmetri is n equivlene reltion. A qusi-orering tht is nti-symmetri is n orer
14 Orer (Hnout) Definition 7-11: A reltion is qusi-orering (or preorer) if it is reflexive n trnsitive. A quisi-orering tht is symmetri is n equivlene reltion. A qusi-orering tht is nti-symmetri is n orer
The University of Nottingham SCHOOL OF COMPUTER SCIENCE A LEVEL 2 MODULE, SPRING SEMESTER MACHINES AND THEIR LANGUAGES ANSWERS
 The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
NON-DETERMINISTIC FSA
 Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Automata and Regular Languages
 Chpter 9 Automt n Regulr Lnguges 9. Introution This hpter looks t mthemtil moels of omputtion n lnguges tht esrie them. The moel-lnguge reltionship hs multiple levels. We shll explore the simplest level,
Chpter 9 Automt n Regulr Lnguges 9. Introution This hpter looks t mthemtil moels of omputtion n lnguges tht esrie them. The moel-lnguge reltionship hs multiple levels. We shll explore the simplest level,
Nondeterministic Finite Automata
 Nondeterministi Finite utomt The Power of Guessing Tuesdy, Otoer 4, 2 Reding: Sipser.2 (first prt); Stoughton 3.3 3.5 S235 Lnguges nd utomt eprtment of omputer Siene Wellesley ollege Finite utomton (F)
Nondeterministi Finite utomt The Power of Guessing Tuesdy, Otoer 4, 2 Reding: Sipser.2 (first prt); Stoughton 3.3 3.5 S235 Lnguges nd utomt eprtment of omputer Siene Wellesley ollege Finite utomton (F)
A Disambiguation Algorithm for Finite Automata and Functional Transducers
 A Dismigution Algorithm for Finite Automt n Funtionl Trnsuers Mehryr Mohri Cournt Institute of Mthemtil Sienes n Google Reserh 51 Merer Street, New York, NY 1001, USA Astrt. We present new ismigution lgorithm
A Dismigution Algorithm for Finite Automt n Funtionl Trnsuers Mehryr Mohri Cournt Institute of Mthemtil Sienes n Google Reserh 51 Merer Street, New York, NY 1001, USA Astrt. We present new ismigution lgorithm
Necessary and sucient conditions for some two. Abstract. Further we show that the necessary conditions for the existence of an OD(44 s 1 s 2 )
 Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
CS 2204 DIGITAL LOGIC & STATE MACHINE DESIGN SPRING 2014
 S 224 DIGITAL LOGI & STATE MAHINE DESIGN SPRING 214 DUE : Mrh 27, 214 HOMEWORK III READ : Relte portions of hpters VII n VIII ASSIGNMENT : There re three questions. Solve ll homework n exm prolems s shown
S 224 DIGITAL LOGI & STATE MAHINE DESIGN SPRING 214 DUE : Mrh 27, 214 HOMEWORK III READ : Relte portions of hpters VII n VIII ASSIGNMENT : There re three questions. Solve ll homework n exm prolems s shown
Counting Paths Between Vertices. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs
 Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
Finite State Automata and Determinisation
 Finite Stte Automt nd Deterministion Tim Dworn Jnury, 2016 Lnguges fs nf re df Deterministion 2 Outline 1 Lnguges 2 Finite Stte Automt (fs) 3 Non-deterministi Finite Stte Automt (nf) 4 Regulr Expressions
Finite Stte Automt nd Deterministion Tim Dworn Jnury, 2016 Lnguges fs nf re df Deterministion 2 Outline 1 Lnguges 2 Finite Stte Automt (fs) 3 Non-deterministi Finite Stte Automt (nf) 4 Regulr Expressions
Lecture 8: Abstract Algebra
 Mth 94 Professor: Pri Brtlett Leture 8: Astrt Alger Week 8 UCSB 2015 This is the eighth week of the Mthemtis Sujet Test GRE prep ourse; here, we run very rough-n-tumle review of strt lger! As lwys, this
Mth 94 Professor: Pri Brtlett Leture 8: Astrt Alger Week 8 UCSB 2015 This is the eighth week of the Mthemtis Sujet Test GRE prep ourse; here, we run very rough-n-tumle review of strt lger! As lwys, this
POSITIVE IMPLICATIVE AND ASSOCIATIVE FILTERS OF LATTICE IMPLICATION ALGEBRAS
 Bull. Koren Mth. So. 35 (998), No., pp. 53 6 POSITIVE IMPLICATIVE AND ASSOCIATIVE FILTERS OF LATTICE IMPLICATION ALGEBRAS YOUNG BAE JUN*, YANG XU AND KEYUN QIN ABSTRACT. We introue the onepts of positive
Bull. Koren Mth. So. 35 (998), No., pp. 53 6 POSITIVE IMPLICATIVE AND ASSOCIATIVE FILTERS OF LATTICE IMPLICATION ALGEBRAS YOUNG BAE JUN*, YANG XU AND KEYUN QIN ABSTRACT. We introue the onepts of positive
Laboratory for Foundations of Computer Science. An Unfolding Approach. University of Edinburgh. Model Checking. Javier Esparza
 An Unfoling Approh to Moel Cheking Jvier Esprz Lbortory for Fountions of Computer Siene University of Einburgh Conurrent progrms Progrm: tuple P T 1 T n of finite lbelle trnsition systems T i A i S i i
An Unfoling Approh to Moel Cheking Jvier Esprz Lbortory for Fountions of Computer Siene University of Einburgh Conurrent progrms Progrm: tuple P T 1 T n of finite lbelle trnsition systems T i A i S i i
Lecture 2: Cayley Graphs
 Mth 137B Professor: Pri Brtlett Leture 2: Cyley Grphs Week 3 UCSB 2014 (Relevnt soure mteril: Setion VIII.1 of Bollos s Moern Grph Theory; 3.7 of Gosil n Royle s Algeri Grph Theory; vrious ppers I ve re
Mth 137B Professor: Pri Brtlett Leture 2: Cyley Grphs Week 3 UCSB 2014 (Relevnt soure mteril: Setion VIII.1 of Bollos s Moern Grph Theory; 3.7 of Gosil n Royle s Algeri Grph Theory; vrious ppers I ve re
CONTROLLABILITY and observability are the central
 1 Complexity of Infiml Oservle Superlnguges Tomáš Msopust Astrt The infiml prefix-losed, ontrollle nd oservle superlnguge plys n essentil role in the reltionship etween ontrollility, oservility nd o-oservility
1 Complexity of Infiml Oservle Superlnguges Tomáš Msopust Astrt The infiml prefix-losed, ontrollle nd oservle superlnguge plys n essentil role in the reltionship etween ontrollility, oservility nd o-oservility
= state, a = reading and q j
 4 Finite Automt CHAPTER 2 Finite Automt (FA) (i) Derterministi Finite Automt (DFA) A DFA, M Q, q,, F, Where, Q = set of sttes (finite) q Q = the strt/initil stte = input lphet (finite) (use only those
4 Finite Automt CHAPTER 2 Finite Automt (FA) (i) Derterministi Finite Automt (DFA) A DFA, M Q, q,, F, Where, Q = set of sttes (finite) q Q = the strt/initil stte = input lphet (finite) (use only those
Solutions for HW9. Bipartite: put the red vertices in V 1 and the black in V 2. Not bipartite!
 Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
Petri Nets. Rebecca Albrecht. Seminar: Automata Theory Chair of Software Engeneering
 Petri Nets Ree Alreht Seminr: Automt Theory Chir of Softwre Engeneering Overview 1. Motivtion: Why not just using finite utomt for everything? Wht re Petri Nets nd when do we use them? 2. Introdution:
Petri Nets Ree Alreht Seminr: Automt Theory Chir of Softwre Engeneering Overview 1. Motivtion: Why not just using finite utomt for everything? Wht re Petri Nets nd when do we use them? 2. Introdution:
22: Union Find. CS 473u - Algorithms - Spring April 14, We want to maintain a collection of sets, under the operations of:
 22: Union Fin CS 473u - Algorithms - Spring 2005 April 14, 2005 1 Union-Fin We wnt to mintin olletion of sets, uner the opertions of: 1. MkeSet(x) - rete set tht ontins the single element x. 2. Fin(x)
22: Union Fin CS 473u - Algorithms - Spring 2005 April 14, 2005 1 Union-Fin We wnt to mintin olletion of sets, uner the opertions of: 1. MkeSet(x) - rete set tht ontins the single element x. 2. Fin(x)
Minimal DFA. minimal DFA for L starting from any other
 Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
Symbolic Automata for Static Specification Mining
 Symoli Automt for Stti Speifition Mining Hil Peleg 1, Shron Shohm, Ern Yhv, n Hongseok Yng 1 Tel Aviv University, Isrel Tel Aviv-Yffo Aemi College, Isrel University of Ofor, UK Tehnion, Isrel Astrt. We
Symoli Automt for Stti Speifition Mining Hil Peleg 1, Shron Shohm, Ern Yhv, n Hongseok Yng 1 Tel Aviv University, Isrel Tel Aviv-Yffo Aemi College, Isrel University of Ofor, UK Tehnion, Isrel Astrt. We
CSE 332. Sorting. Data Abstractions. CSE 332: Data Abstractions. QuickSort Cutoff 1. Where We Are 2. Bounding The MAXIMUM Problem 4
 Am Blnk Leture 13 Winter 2016 CSE 332 CSE 332: Dt Astrtions Sorting Dt Astrtions QuikSort Cutoff 1 Where We Are 2 For smll n, the reursion is wste. The onstnts on quik/merge sort re higher thn the ones
Am Blnk Leture 13 Winter 2016 CSE 332 CSE 332: Dt Astrtions Sorting Dt Astrtions QuikSort Cutoff 1 Where We Are 2 For smll n, the reursion is wste. The onstnts on quik/merge sort re higher thn the ones
Convert the NFA into DFA
 Convert the NF into F For ech NF we cn find F ccepting the sme lnguge. The numer of sttes of the F could e exponentil in the numer of sttes of the NF, ut in prctice this worst cse occurs rrely. lgorithm:
Convert the NF into F For ech NF we cn find F ccepting the sme lnguge. The numer of sttes of the F could e exponentil in the numer of sttes of the NF, ut in prctice this worst cse occurs rrely. lgorithm:
Unfoldings of Networks of Timed Automata
 Unfolings of Networks of Time Automt Frnk Cssez Thoms Chtin Clue Jr Ptrii Bouyer Serge H Pierre-Alin Reynier Rennes, Deemer 3, 2008 Unfolings [MMilln 93] First efine for Petri nets Then extene to other
Unfolings of Networks of Time Automt Frnk Cssez Thoms Chtin Clue Jr Ptrii Bouyer Serge H Pierre-Alin Reynier Rennes, Deemer 3, 2008 Unfolings [MMilln 93] First efine for Petri nets Then extene to other
Prefix-Free Regular-Expression Matching
 Prefix-Free Regulr-Expression Mthing Yo-Su Hn, Yjun Wng nd Derik Wood Deprtment of Computer Siene HKUST Prefix-Free Regulr-Expression Mthing p.1/15 Pttern Mthing Given pttern P nd text T, find ll sustrings
Prefix-Free Regulr-Expression Mthing Yo-Su Hn, Yjun Wng nd Derik Wood Deprtment of Computer Siene HKUST Prefix-Free Regulr-Expression Mthing p.1/15 Pttern Mthing Given pttern P nd text T, find ll sustrings
I 3 2 = I I 4 = 2A
 ECE 210 Eletril Ciruit Anlysis University of llinois t Chigo 2.13 We re ske to use KCL to fin urrents 1 4. The key point in pplying KCL in this prolem is to strt with noe where only one of the urrents
ECE 210 Eletril Ciruit Anlysis University of llinois t Chigo 2.13 We re ske to use KCL to fin urrents 1 4. The key point in pplying KCL in this prolem is to strt with noe where only one of the urrents
Factorising FACTORISING.
 Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
The DOACROSS statement
 The DOACROSS sttement Is prllel loop similr to DOALL, ut it llows prouer-onsumer type of synhroniztion. Synhroniztion is llowe from lower to higher itertions sine it is ssume tht lower itertions re selete
The DOACROSS sttement Is prllel loop similr to DOALL, ut it llows prouer-onsumer type of synhroniztion. Synhroniztion is llowe from lower to higher itertions sine it is ssume tht lower itertions re selete
Bisimulation, Games & Hennessy Milner logic
 Bisimultion, Gmes & Hennessy Milner logi Leture 1 of Modelli Mtemtii dei Proessi Conorrenti Pweł Soboiński Univeristy of Southmpton, UK Bisimultion, Gmes & Hennessy Milner logi p.1/32 Clssil lnguge theory
Bisimultion, Gmes & Hennessy Milner logi Leture 1 of Modelli Mtemtii dei Proessi Conorrenti Pweł Soboiński Univeristy of Southmpton, UK Bisimultion, Gmes & Hennessy Milner logi p.1/32 Clssil lnguge theory
CIT 596 Theory of Computation 1. Graphs and Digraphs
 CIT 596 Theory of Computtion 1 A grph G = (V (G), E(G)) onsists of two finite sets: V (G), the vertex set of the grph, often enote y just V, whih is nonempty set of elements lle verties, n E(G), the ege
CIT 596 Theory of Computtion 1 A grph G = (V (G), E(G)) onsists of two finite sets: V (G), the vertex set of the grph, often enote y just V, whih is nonempty set of elements lle verties, n E(G), the ege
arxiv: v2 [math.co] 31 Oct 2016
![arxiv: v2 [math.co] 31 Oct 2016 arxiv: v2 [math.co] 31 Oct 2016](/thumbs/96/127000397.jpg) On exlue minors of onnetivity 2 for the lss of frme mtrois rxiv:1502.06896v2 [mth.co] 31 Ot 2016 Mtt DeVos Dryl Funk Irene Pivotto Astrt We investigte the set of exlue minors of onnetivity 2 for the lss
On exlue minors of onnetivity 2 for the lss of frme mtrois rxiv:1502.06896v2 [mth.co] 31 Ot 2016 Mtt DeVos Dryl Funk Irene Pivotto Astrt We investigte the set of exlue minors of onnetivity 2 for the lss
Hybrid Systems Modeling, Analysis and Control
 Hyrid Systems Modeling, Anlysis nd Control Rdu Grosu Vienn University of Tehnology Leture 5 Finite Automt s Liner Systems Oservility, Rehility nd More Miniml DFA re Not Miniml NFA (Arnold, Diky nd Nivt
Hyrid Systems Modeling, Anlysis nd Control Rdu Grosu Vienn University of Tehnology Leture 5 Finite Automt s Liner Systems Oservility, Rehility nd More Miniml DFA re Not Miniml NFA (Arnold, Diky nd Nivt
System Validation (IN4387) November 2, 2012, 14:00-17:00
 System Vlidtion (IN4387) Novemer 2, 2012, 14:00-17:00 Importnt Notes. The exmintion omprises 5 question in 4 pges. Give omplete explntion nd do not onfine yourself to giving the finl nswer. Good luk! Exerise
System Vlidtion (IN4387) Novemer 2, 2012, 14:00-17:00 Importnt Notes. The exmintion omprises 5 question in 4 pges. Give omplete explntion nd do not onfine yourself to giving the finl nswer. Good luk! Exerise
CSC2542 State-Space Planning
 CSC2542 Stte-Spe Plnning Sheil MIlrith Deprtment of Computer Siene University of Toronto Fll 2010 1 Aknowlegements Some the slies use in this ourse re moifitions of Dn Nu s leture slies for the textook
CSC2542 Stte-Spe Plnning Sheil MIlrith Deprtment of Computer Siene University of Toronto Fll 2010 1 Aknowlegements Some the slies use in this ourse re moifitions of Dn Nu s leture slies for the textook
INTRODUCTION TO AUTOMATA THEORY
 Chpter 3 INTRODUCTION TO AUTOMATA THEORY In this hpter we stuy the most si strt moel of omputtion. This moel els with mhines tht hve finite memory pity. Setion 3. els with mhines tht operte eterministilly
Chpter 3 INTRODUCTION TO AUTOMATA THEORY In this hpter we stuy the most si strt moel of omputtion. This moel els with mhines tht hve finite memory pity. Setion 3. els with mhines tht operte eterministilly
Chapter 4 State-Space Planning
 Leture slides for Automted Plnning: Theory nd Prtie Chpter 4 Stte-Spe Plnning Dn S. Nu CMSC 722, AI Plnning University of Mrylnd, Spring 2008 1 Motivtion Nerly ll plnning proedures re serh proedures Different
Leture slides for Automted Plnning: Theory nd Prtie Chpter 4 Stte-Spe Plnning Dn S. Nu CMSC 722, AI Plnning University of Mrylnd, Spring 2008 1 Motivtion Nerly ll plnning proedures re serh proedures Different
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
Data Structures LECTURE 10. Huffman coding. Example. Coding: problem definition
 Dt Strutures, Spring 24 L. Joskowiz Dt Strutures LEURE Humn oing Motivtion Uniquel eipherle oes Prei oes Humn oe onstrution Etensions n pplitions hpter 6.3 pp 385 392 in tetook Motivtion Suppose we wnt
Dt Strutures, Spring 24 L. Joskowiz Dt Strutures LEURE Humn oing Motivtion Uniquel eipherle oes Prei oes Humn oe onstrution Etensions n pplitions hpter 6.3 pp 385 392 in tetook Motivtion Suppose we wnt
Subsequence Automata with Default Transitions
 Susequene Automt with Defult Trnsitions Philip Bille, Inge Li Gørtz, n Freerik Rye Skjoljensen Tehnil University of Denmrk {phi,inge,fskj}@tu.k Astrt. Let S e string of length n with hrters from n lphet
Susequene Automt with Defult Trnsitions Philip Bille, Inge Li Gørtz, n Freerik Rye Skjoljensen Tehnil University of Denmrk {phi,inge,fskj}@tu.k Astrt. Let S e string of length n with hrters from n lphet
Model Reduction of Finite State Machines by Contraction
 Model Reduction of Finite Stte Mchines y Contrction Alessndro Giu Dip. di Ingegneri Elettric ed Elettronic, Università di Cgliri, Pizz d Armi, 09123 Cgliri, Itly Phone: +39-070-675-5892 Fx: +39-070-675-5900
Model Reduction of Finite Stte Mchines y Contrction Alessndro Giu Dip. di Ingegneri Elettric ed Elettronic, Università di Cgliri, Pizz d Armi, 09123 Cgliri, Itly Phone: +39-070-675-5892 Fx: +39-070-675-5900
Petri automata for Kleene allegories
 Petri utomt for Kleene llegories Pul Brunet, mien Pous To ite this version: Pul Brunet, mien Pous. Petri utomt for Kleene llegories. Logi in omputer Siene, Jul 205, Kyoto, Jpn. I, pp.68-79, 205, .
Petri utomt for Kleene llegories Pul Brunet, mien Pous To ite this version: Pul Brunet, mien Pous. Petri utomt for Kleene llegories. Logi in omputer Siene, Jul 205, Kyoto, Jpn. I, pp.68-79, 205, .
Descriptional Complexity of Non-Unary Self-Verifying Symmetric Difference Automata
 Desriptionl Complexity of Non-Unry Self-Verifying Symmetri Differene Automt Lurette Mris 1,2 nd Lynette vn Zijl 1 1 Deprtment of Computer Siene, Stellenosh University, South Afri 2 Merk Institute, CSIR,
Desriptionl Complexity of Non-Unry Self-Verifying Symmetri Differene Automt Lurette Mris 1,2 nd Lynette vn Zijl 1 1 Deprtment of Computer Siene, Stellenosh University, South Afri 2 Merk Institute, CSIR,
Generalized Kronecker Product and Its Application
 Vol. 1, No. 1 ISSN: 1916-9795 Generlize Kroneker Prout n Its Applition Xingxing Liu Shool of mthemtis n omputer Siene Ynn University Shnxi 716000, Chin E-mil: lxx6407@163.om Astrt In this pper, we promote
Vol. 1, No. 1 ISSN: 1916-9795 Generlize Kroneker Prout n Its Applition Xingxing Liu Shool of mthemtis n omputer Siene Ynn University Shnxi 716000, Chin E-mil: lxx6407@163.om Astrt In this pper, we promote
Implication Graphs and Logic Testing
 Implition Grphs n Logi Testing Vishwni D. Agrwl Jmes J. Dnher Professor Dept. of ECE, Auurn University Auurn, AL 36849 vgrwl@eng.uurn.eu www.eng.uurn.eu/~vgrwl Joint reserh with: K. K. Dve, ATI Reserh,
Implition Grphs n Logi Testing Vishwni D. Agrwl Jmes J. Dnher Professor Dept. of ECE, Auurn University Auurn, AL 36849 vgrwl@eng.uurn.eu www.eng.uurn.eu/~vgrwl Joint reserh with: K. K. Dve, ATI Reserh,
Mid-Term Examination - Spring 2014 Mathematical Programming with Applications to Economics Total Score: 45; Time: 3 hours
 Mi-Term Exmintion - Spring 0 Mthemtil Progrmming with Applitions to Eonomis Totl Sore: 5; Time: hours. Let G = (N, E) e irete grph. Define the inegree of vertex i N s the numer of eges tht re oming into
Mi-Term Exmintion - Spring 0 Mthemtil Progrmming with Applitions to Eonomis Totl Sore: 5; Time: hours. Let G = (N, E) e irete grph. Define the inegree of vertex i N s the numer of eges tht re oming into
Transition systems (motivation)
 Trnsition systems (motivtion) Course Modelling of Conurrent Systems ( Modellierung neenläufiger Systeme ) Winter Semester 2009/0 University of Duisurg-Essen Brr König Tehing ssistnt: Christoph Blume In
Trnsition systems (motivtion) Course Modelling of Conurrent Systems ( Modellierung neenläufiger Systeme ) Winter Semester 2009/0 University of Duisurg-Essen Brr König Tehing ssistnt: Christoph Blume In
Surds and Indices. Surds and Indices. Curriculum Ready ACMNA: 233,
 Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Solutions to Problem Set #1
 CSE 233 Spring, 2016 Solutions to Prolem Set #1 1. The movie tse onsists of the following two reltions movie: title, iretor, tor sheule: theter, title The first reltion provies titles, iretors, n tors
CSE 233 Spring, 2016 Solutions to Prolem Set #1 1. The movie tse onsists of the following two reltions movie: title, iretor, tor sheule: theter, title The first reltion provies titles, iretors, n tors
Section 2.3. Matrix Inverses
 Mtri lger Mtri nverses Setion.. Mtri nverses hree si opertions on mtries, ition, multiplition, n sutrtion, re nlogues for mtries of the sme opertions for numers. n this setion we introue the mtri nlogue
Mtri lger Mtri nverses Setion.. Mtri nverses hree si opertions on mtries, ition, multiplition, n sutrtion, re nlogues for mtries of the sme opertions for numers. n this setion we introue the mtri nlogue
Lecture 11 Binary Decision Diagrams (BDDs)
 C 474A/57A Computer-Aie Logi Design Leture Binry Deision Digrms (BDDs) C 474/575 Susn Lyseky o 3 Boolen Logi untions Representtions untion n e represente in ierent wys ruth tle, eqution, K-mp, iruit, et
C 474A/57A Computer-Aie Logi Design Leture Binry Deision Digrms (BDDs) C 474/575 Susn Lyseky o 3 Boolen Logi untions Representtions untion n e represente in ierent wys ruth tle, eqution, K-mp, iruit, et
Technology Mapping Method for Low Power Consumption and High Performance in General-Synchronous Framework
 R-17 SASIMI 015 Proeeings Tehnology Mpping Metho for Low Power Consumption n High Performne in Generl-Synhronous Frmework Junki Kwguhi Yukihie Kohir Shool of Computer Siene, the University of Aizu Aizu-Wkmtsu
R-17 SASIMI 015 Proeeings Tehnology Mpping Metho for Low Power Consumption n High Performne in Generl-Synhronous Frmework Junki Kwguhi Yukihie Kohir Shool of Computer Siene, the University of Aizu Aizu-Wkmtsu
Aperiodic tilings and substitutions
 Aperioi tilings n sustitutions Niols Ollinger LIFO, Université Orléns Journées SDA2, Amiens June 12th, 2013 The Domino Prolem (DP) Assume we re given finite set of squre pltes of the sme size with eges
Aperioi tilings n sustitutions Niols Ollinger LIFO, Université Orléns Journées SDA2, Amiens June 12th, 2013 The Domino Prolem (DP) Assume we re given finite set of squre pltes of the sme size with eges
On the Maximally-Permissive Range Control Problem in Partially-Observed Discrete Event Systems
 On the Mximlly-Permissie Rnge Control Prolem in Prtilly-Osered Disrete Eent Systems Xing Yin nd Stéphne Lfortune EECS Deprtment, Uniersity of Mihign 55th IEEE CDC, De 2-4, 206, Ls Vegs, USA X.Yin & S.Lfortune
On the Mximlly-Permissie Rnge Control Prolem in Prtilly-Osered Disrete Eent Systems Xing Yin nd Stéphne Lfortune EECS Deprtment, Uniersity of Mihign 55th IEEE CDC, De 2-4, 206, Ls Vegs, USA X.Yin & S.Lfortune
Chapter 3. Vector Spaces. 3.1 Images and Image Arithmetic
 Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
Common intervals of genomes. Mathieu Raffinot CNRS LIAFA
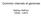 Common intervls of genomes Mthieu Rffinot CNRS LIF Context: omprtive genomis. set of genomes prtilly/totlly nnotte Informtive group of genes or omins? Ex: COG tse Mny iffiulties! iology Wht re two similr
Common intervls of genomes Mthieu Rffinot CNRS LIF Context: omprtive genomis. set of genomes prtilly/totlly nnotte Informtive group of genes or omins? Ex: COG tse Mny iffiulties! iology Wht re two similr
PREDICTABILITY IN DISCRETE-EVENT SYSTEMS UNDER PARTIAL OBSERVATION 1. Sahika Genc, Stéphane Lafortune
 PREDICTABILITY IN DISCRETE-EVENT SYSTEMS UNDER PARTIAL OBSERVATION 1 Shik Gen, Stéhne Lfortune Dertment of Eletril Engineering n Comuter Siene, University of Mihign, 1301 Bel Avenue, Ann Aror, MI 48109-2122,
PREDICTABILITY IN DISCRETE-EVENT SYSTEMS UNDER PARTIAL OBSERVATION 1 Shik Gen, Stéhne Lfortune Dertment of Eletril Engineering n Comuter Siene, University of Mihign, 1301 Bel Avenue, Ann Aror, MI 48109-2122,
A Short Introduction to Self-similar Groups
 A Short Introution to Self-similr Groups Murry Eler* Asi Pifi Mthemtis Newsletter Astrt. Self-similr groups re fsinting re of urrent reserh. Here we give short, n hopefully essile, introution to them.
A Short Introution to Self-similr Groups Murry Eler* Asi Pifi Mthemtis Newsletter Astrt. Self-similr groups re fsinting re of urrent reserh. Here we give short, n hopefully essile, introution to them.
If the numbering is a,b,c,d 1,2,3,4, then the matrix representation is as follows:
 Reltions. Solutions 1. ) true; ) true; ) flse; ) true; e) flse; f) true; g) flse; h) true; 2. 2 A B 3. Consier ll reltions tht o not inlue the given pir s n element. Oviously, the rest of the reltions
Reltions. Solutions 1. ) true; ) true; ) flse; ) true; e) flse; f) true; g) flse; h) true; 2. 2 A B 3. Consier ll reltions tht o not inlue the given pir s n element. Oviously, the rest of the reltions
Formal Languages and Automata
 Moile Computing nd Softwre Engineering p. 1/5 Forml Lnguges nd Automt Chpter 2 Finite Automt Chun-Ming Liu cmliu@csie.ntut.edu.tw Deprtment of Computer Science nd Informtion Engineering Ntionl Tipei University
Moile Computing nd Softwre Engineering p. 1/5 Forml Lnguges nd Automt Chpter 2 Finite Automt Chun-Ming Liu cmliu@csie.ntut.edu.tw Deprtment of Computer Science nd Informtion Engineering Ntionl Tipei University
Regular languages refresher
 Regulr lnguges refresher 1 Regulr lnguges refresher Forml lnguges Alphet = finite set of letters Word = sequene of letter Lnguge = set of words Regulr lnguges defined equivlently y Regulr expressions Finite-stte
Regulr lnguges refresher 1 Regulr lnguges refresher Forml lnguges Alphet = finite set of letters Word = sequene of letter Lnguge = set of words Regulr lnguges defined equivlently y Regulr expressions Finite-stte
Génération aléatoire uniforme pour les réseaux d automates
 Génértion létoire uniforme pour les réseux d utomtes Niols Bsset (Trvil ommun ve Mihèle Sori et Jen Miresse) Université lire de Bruxelles Journées Alé 2017 1/25 Motivtions (1/2) p q Automt re omni-present
Génértion létoire uniforme pour les réseux d utomtes Niols Bsset (Trvil ommun ve Mihèle Sori et Jen Miresse) Université lire de Bruxelles Journées Alé 2017 1/25 Motivtions (1/2) p q Automt re omni-present
Eigenvectors and Eigenvalues
 MTB 050 1 ORIGIN 1 Eigenvets n Eigenvlues This wksheet esries the lger use to lulte "prinipl" "hrteristi" iretions lle Eigenvets n the "prinipl" "hrteristi" vlues lle Eigenvlues ssoite with these iretions.
MTB 050 1 ORIGIN 1 Eigenvets n Eigenvlues This wksheet esries the lger use to lulte "prinipl" "hrteristi" iretions lle Eigenvets n the "prinipl" "hrteristi" vlues lle Eigenvlues ssoite with these iretions.
Chapter 2 Finite Automata
 Chpter 2 Finite Automt 28 2.1 Introduction Finite utomt: first model of the notion of effective procedure. (They lso hve mny other pplictions). The concept of finite utomton cn e derived y exmining wht
Chpter 2 Finite Automt 28 2.1 Introduction Finite utomt: first model of the notion of effective procedure. (They lso hve mny other pplictions). The concept of finite utomton cn e derived y exmining wht
A Lower Bound for the Length of a Partial Transversal in a Latin Square, Revised Version
 A Lower Bound for the Length of Prtil Trnsversl in Ltin Squre, Revised Version Pooy Htmi nd Peter W. Shor Deprtment of Mthemtil Sienes, Shrif University of Tehnology, P.O.Bo 11365-9415, Tehrn, Irn Deprtment
A Lower Bound for the Length of Prtil Trnsversl in Ltin Squre, Revised Version Pooy Htmi nd Peter W. Shor Deprtment of Mthemtil Sienes, Shrif University of Tehnology, P.O.Bo 11365-9415, Tehrn, Irn Deprtment
Coalgebra, Lecture 15: Equations for Deterministic Automata
 Colger, Lecture 15: Equtions for Deterministic Automt Julin Slmnc (nd Jurrin Rot) Decemer 19, 2016 In this lecture, we will study the concept of equtions for deterministic utomt. The notes re self contined
Colger, Lecture 15: Equtions for Deterministic Automt Julin Slmnc (nd Jurrin Rot) Decemer 19, 2016 In this lecture, we will study the concept of equtions for deterministic utomt. The notes re self contined
Automatic Synthesis of New Behaviors from a Library of Available Behaviors
 Automti Synthesis of New Behviors from Lirry of Aville Behviors Giuseppe De Giomo Università di Rom L Spienz, Rom, Itly degiomo@dis.unirom1.it Sestin Srdin RMIT University, Melourne, Austrli ssrdin@s.rmit.edu.u
Automti Synthesis of New Behviors from Lirry of Aville Behviors Giuseppe De Giomo Università di Rom L Spienz, Rom, Itly degiomo@dis.unirom1.it Sestin Srdin RMIT University, Melourne, Austrli ssrdin@s.rmit.edu.u
Chapter Five: Nondeterministic Finite Automata. Formal Language, chapter 5, slide 1
 Chpter Five: Nondeterministic Finite Automt Forml Lnguge, chpter 5, slide 1 1 A DFA hs exctly one trnsition from every stte on every symol in the lphet. By relxing this requirement we get relted ut more
Chpter Five: Nondeterministic Finite Automt Forml Lnguge, chpter 5, slide 1 1 A DFA hs exctly one trnsition from every stte on every symol in the lphet. By relxing this requirement we get relted ut more
Now we must transform the original model so we can use the new parameters. = S max. Recruits
 MODEL FOR VARIABLE RECRUITMENT (ontinue) Alterntive Prmeteriztions of the pwner-reruit Moels We n write ny moel in numerous ifferent ut equivlent forms. Uner ertin irumstnes it is onvenient to work with
MODEL FOR VARIABLE RECRUITMENT (ontinue) Alterntive Prmeteriztions of the pwner-reruit Moels We n write ny moel in numerous ifferent ut equivlent forms. Uner ertin irumstnes it is onvenient to work with
Particle Physics. Michaelmas Term 2011 Prof Mark Thomson. Handout 3 : Interaction by Particle Exchange and QED. Recap
 Prtile Physis Mihelms Term 2011 Prof Mrk Thomson g X g X g g Hnout 3 : Intertion y Prtile Exhnge n QED Prof. M.A. Thomson Mihelms 2011 101 Rep Working towrs proper lultion of ey n sttering proesses lnitilly
Prtile Physis Mihelms Term 2011 Prof Mrk Thomson g X g X g g Hnout 3 : Intertion y Prtile Exhnge n QED Prof. M.A. Thomson Mihelms 2011 101 Rep Working towrs proper lultion of ey n sttering proesses lnitilly
for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx
![for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx](/thumbs/74/70408252.jpg) Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Regular expressions, Finite Automata, transition graphs are all the same!!
 CSI 3104 /Winter 2011: Introduction to Forml Lnguges Chpter 7: Kleene s Theorem Chpter 7: Kleene s Theorem Regulr expressions, Finite Automt, trnsition grphs re ll the sme!! Dr. Neji Zgui CSI3104-W11 1
CSI 3104 /Winter 2011: Introduction to Forml Lnguges Chpter 7: Kleene s Theorem Chpter 7: Kleene s Theorem Regulr expressions, Finite Automt, trnsition grphs re ll the sme!! Dr. Neji Zgui CSI3104-W11 1
Grammar. Languages. Content 5/10/16. Automata and Languages. Regular Languages. Regular Languages
 5//6 Grmmr Automt nd Lnguges Regulr Grmmr Context-free Grmmr Context-sensitive Grmmr Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Regulr Lnguges Context Free Lnguges Context Sensitive
5//6 Grmmr Automt nd Lnguges Regulr Grmmr Context-free Grmmr Context-sensitive Grmmr Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Regulr Lnguges Context Free Lnguges Context Sensitive
Automata Theory and Infinite Transition Systems
 Automt Theory n Infinite Trnsition Systems Wolfgng Thoms Lehrstuhl Informtik 7, RWTH Ahen, Germny thoms@informtik.rwth-hen.e Astrt These leture notes report on the use of utomt theory in the stuy of infinite
Automt Theory n Infinite Trnsition Systems Wolfgng Thoms Lehrstuhl Informtik 7, RWTH Ahen, Germny thoms@informtik.rwth-hen.e Astrt These leture notes report on the use of utomt theory in the stuy of infinite
On the existence of a cherry-picking sequence
 On the existene of herry-piking sequene Jnosh Döker, Simone Linz Deprtment of Computer Siene, University of Tüingen, Germny Deprtment of Computer Siene, University of Aukln, New Zeln Astrt Reently, the
On the existene of herry-piking sequene Jnosh Döker, Simone Linz Deprtment of Computer Siene, University of Tüingen, Germny Deprtment of Computer Siene, University of Aukln, New Zeln Astrt Reently, the
#A42 INTEGERS 11 (2011) ON THE CONDITIONED BINOMIAL COEFFICIENTS
 #A42 INTEGERS 11 (2011 ON THE CONDITIONED BINOMIAL COEFFICIENTS Liqun To Shool of Mthemtil Sienes, Luoyng Norml University, Luoyng, Chin lqto@lynuedun Reeived: 12/24/10, Revised: 5/11/11, Aepted: 5/16/11,
#A42 INTEGERS 11 (2011 ON THE CONDITIONED BINOMIAL COEFFICIENTS Liqun To Shool of Mthemtil Sienes, Luoyng Norml University, Luoyng, Chin lqto@lynuedun Reeived: 12/24/10, Revised: 5/11/11, Aepted: 5/16/11,
CS261: A Second Course in Algorithms Lecture #5: Minimum-Cost Bipartite Matching
 CS261: A Seon Course in Algorithms Leture #5: Minimum-Cost Biprtite Mthing Tim Roughgren Jnury 19, 2016 1 Preliminries Figure 1: Exmple of iprtite grph. The eges {, } n {, } onstitute mthing. Lst leture
CS261: A Seon Course in Algorithms Leture #5: Minimum-Cost Biprtite Mthing Tim Roughgren Jnury 19, 2016 1 Preliminries Figure 1: Exmple of iprtite grph. The eges {, } n {, } onstitute mthing. Lst leture
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Compiler Design. Spring Lexical Analysis. Sample Exercises and Solutions. Prof. Pedro C. Diniz
 University of Southern Cliforni Computer Siene Deprtment Compiler Design Spring 7 Lexil Anlysis Smple Exerises nd Solutions Prof. Pedro C. Diniz USC / Informtion Sienes Institute 47 Admirlty Wy, Suite
University of Southern Cliforni Computer Siene Deprtment Compiler Design Spring 7 Lexil Anlysis Smple Exerises nd Solutions Prof. Pedro C. Diniz USC / Informtion Sienes Institute 47 Admirlty Wy, Suite
MCH T 111 Handout Triangle Review Page 1 of 3
 Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Separable discrete functions: recognition and sufficient conditions
 Seprle isrete funtions: reognition n suffiient onitions Enre Boros Onřej Čepek Vlimir Gurvih Novemer 21, 217 rxiv:1711.6772v1 [mth.co] 17 Nov 217 Astrt A isrete funtion of n vriles is mpping g : X 1...
Seprle isrete funtions: reognition n suffiient onitions Enre Boros Onřej Čepek Vlimir Gurvih Novemer 21, 217 rxiv:1711.6772v1 [mth.co] 17 Nov 217 Astrt A isrete funtion of n vriles is mpping g : X 1...
Maximum size of a minimum watching system and the graphs achieving the bound
 Mximum size of minimum wthing system n the grphs hieving the oun Tille mximum un système e ontrôle minimum et les grphes tteignnt l orne Dvi Auger Irène Chron Olivier Hury Antoine Lostein 00D0 Mrs 00 Déprtement
Mximum size of minimum wthing system n the grphs hieving the oun Tille mximum un système e ontrôle minimum et les grphes tteignnt l orne Dvi Auger Irène Chron Olivier Hury Antoine Lostein 00D0 Mrs 00 Déprtement
CARLETON UNIVERSITY. 1.0 Problems and Most Solutions, Sect B, 2005
 RLETON UNIVERSIT eprtment of Eletronis ELE 2607 Swithing iruits erury 28, 05; 0 pm.0 Prolems n Most Solutions, Set, 2005 Jn. 2, #8 n #0; Simplify, Prove Prolem. #8 Simplify + + + Reue to four letters (literls).
RLETON UNIVERSIT eprtment of Eletronis ELE 2607 Swithing iruits erury 28, 05; 0 pm.0 Prolems n Most Solutions, Set, 2005 Jn. 2, #8 n #0; Simplify, Prove Prolem. #8 Simplify + + + Reue to four letters (literls).
Supervisory Control under Partial Observation
 Supervisory Control under Prtil Observtion Dr Rong Su S1-B1b-59, Shool of EEE Nnyng Tehnologil University Tel: +65 6790-6042, Emil: rsu@ntu.edu.sg EE6226 Disrete Event Dynmi Systems 1 Outline Motivtion
Supervisory Control under Prtil Observtion Dr Rong Su S1-B1b-59, Shool of EEE Nnyng Tehnologil University Tel: +65 6790-6042, Emil: rsu@ntu.edu.sg EE6226 Disrete Event Dynmi Systems 1 Outline Motivtion
Assignment 1 Automata, Languages, and Computability. 1 Finite State Automata and Regular Languages
 Deprtment of Computer Science, Austrlin Ntionl University COMP2600 Forml Methods for Softwre Engineering Semester 2, 206 Assignment Automt, Lnguges, nd Computility Smple Solutions Finite Stte Automt nd
Deprtment of Computer Science, Austrlin Ntionl University COMP2600 Forml Methods for Softwre Engineering Semester 2, 206 Assignment Automt, Lnguges, nd Computility Smple Solutions Finite Stte Automt nd
On a Class of Planar Graphs with Straight-Line Grid Drawings on Linear Area
 Journl of Grph Algorithms n Applitions http://jg.info/ vol. 13, no. 2, pp. 153 177 (2009) On Clss of Plnr Grphs with Stright-Line Gri Drwings on Liner Are M. Rezul Krim 1,2 M. Siur Rhmn 1 1 Deprtment of
Journl of Grph Algorithms n Applitions http://jg.info/ vol. 13, no. 2, pp. 153 177 (2009) On Clss of Plnr Grphs with Stright-Line Gri Drwings on Liner Are M. Rezul Krim 1,2 M. Siur Rhmn 1 1 Deprtment of
SOME INTEGRAL INEQUALITIES FOR HARMONICALLY CONVEX STOCHASTIC PROCESSES ON THE CO-ORDINATES
 Avne Mth Moels & Applitions Vol3 No 8 pp63-75 SOME INTEGRAL INEQUALITIES FOR HARMONICALLY CONVE STOCHASTIC PROCESSES ON THE CO-ORDINATES Nurgül Okur * Imt Işn Yusuf Ust 3 3 Giresun University Deprtment
Avne Mth Moels & Applitions Vol3 No 8 pp63-75 SOME INTEGRAL INEQUALITIES FOR HARMONICALLY CONVE STOCHASTIC PROCESSES ON THE CO-ORDINATES Nurgül Okur * Imt Işn Yusuf Ust 3 3 Giresun University Deprtment
Analysis of Temporal Interactions with Link Streams and Stream Graphs
 Anlysis of Temporl Intertions with n Strem Grphs, Tiphine Vir, Clémene Mgnien http:// ltpy@ LIP6 CNRS n Soronne Université Pris, Frne 1/23 intertions over time 0 2 4 6 8,,, n for 10 time units time 2/23
Anlysis of Temporl Intertions with n Strem Grphs, Tiphine Vir, Clémene Mgnien http:// ltpy@ LIP6 CNRS n Soronne Université Pris, Frne 1/23 intertions over time 0 2 4 6 8,,, n for 10 time units time 2/23
Bottom-Up Parsing. Canonical Collection of LR(0) items. Part II
 2 ottom-up Prsing Prt II 1 Cnonil Colletion of LR(0) items CC_LR(0)_I items(g :ugmented_grmmr){ C = {CLOURE({ })} ; repet{ foreh(i C) foreh(grmmr symol X) if(goto(i,x) && GOTO(I,X) C) C = C {GOTO(I,X)};
2 ottom-up Prsing Prt II 1 Cnonil Colletion of LR(0) items CC_LR(0)_I items(g :ugmented_grmmr){ C = {CLOURE({ })} ; repet{ foreh(i C) foreh(grmmr symol X) if(goto(i,x) && GOTO(I,X) C) C = C {GOTO(I,X)};
Nondeterminism and Nodeterministic Automata
 Nondeterminism nd Nodeterministic Automt 61 Nondeterminism nd Nondeterministic Automt The computtionl mchine models tht we lerned in the clss re deterministic in the sense tht the next move is uniquely
Nondeterminism nd Nodeterministic Automt 61 Nondeterminism nd Nondeterministic Automt The computtionl mchine models tht we lerned in the clss re deterministic in the sense tht the next move is uniquely
On the Spectra of Bipartite Directed Subgraphs of K 4
 On the Spetr of Biprtite Direte Sugrphs of K 4 R. C. Bunge, 1 S. I. El-Znti, 1, H. J. Fry, 1 K. S. Kruss, 2 D. P. Roerts, 3 C. A. Sullivn, 4 A. A. Unsiker, 5 N. E. Witt 6 1 Illinois Stte University, Norml,
On the Spetr of Biprtite Direte Sugrphs of K 4 R. C. Bunge, 1 S. I. El-Znti, 1, H. J. Fry, 1 K. S. Kruss, 2 D. P. Roerts, 3 C. A. Sullivn, 4 A. A. Unsiker, 5 N. E. Witt 6 1 Illinois Stte University, Norml,
