1 Sterile Resources. This is the simplest case of exhaustion of a finite resource. We will use the terminology
|
|
|
- Ashlee Woods
- 5 years ago
- Views:
Transcription
1 Cmbridge Universiy Press Susinble Nurl Resource Mngemen for Scieniss nd Engineers Excerp More informion Serile Resources In his chper, we inroduce he simple concepion of scrce resource, loclly owned nd globlly rded. I is he clssic Qudrn resource, vluble nd scrce. Producion mouns o mking i vilble for sle ino n economic mrke in which is scrciy ffecs is price. Accordingly, price is endogenous o he resource sysem. Producion is he sme s consumpion, which is nmoun o desrucion: irreversible conversion o oher chemicl forms wih no recycling. The owner s bsic decision is how fs o produce. Th he resource is finie is firs principle. The fc h some porion of he resource is undiscovered ny poin in ime does no chnge is finieness. Wh does chnge, over ime, is he improving se of knowledge bou how much of he resource here is. Decisions bou how fs o produce re lwys reched wihin n environmen of imperfec knowledge nd speculion bou fuure discoveries. There is need o mke decisions in his uncerin environmen nd need o djus coninully s new informion becomes vilble. Explorion reduces, bu does no elimine, unceriny. This cse is exreme in is simpliciy. I is elbored below; he exmple of peroleum is used hroughou. Mny criicl conceps of resource economics re inroduced nd crried forwrd ino subsequen chpers.. COSTLESS PRODUCTION OF A STERILE RESOURCE.. Bse Cse This is he simples cse of exhusion of finie resource. We will use he erminology S() = moun of he resource remining o be produced nd sold X () = producion re P() = mrke price per uni of producion Cmbridge Universiy Press
2 Cmbridge Universiy Press Susinble Nurl Resource Mngemen for Scieniss nd Engineers Excerp More informion Serile Resources I is ssumed h he resource is owned unmbiguously, h i coss nohing o produce i, nd h S, X, nd P re known wih perfec ceriny. Three relions govern: Mss blnce: Price-sensiive demnd: ds d Opiml economic decision mking: = X (.) X = P β (.) dp d = rp (.) The decision equion is reched by considering rdeoff beween uni of resource produced nd sold ody versus wiing nd doing he sme ler. If P grows fser hn r, he ineres re vilble for invesmen of money, hen conserving he resource for ler sle is profible nd producers will do so he vlue of he resource grows fser hn money. If, on he oher hnd, P grows slower hn r, hen conservion is bd invesmen nd selling now is preferble money grows fser hn he vlue of he resource, nd resource owner would prefer o produce now nd inves he proceeds re r. The price equion expresses he poin of indifference beween hese wo opions; i would be relized in siuion of compeiion mong mny producers. (This is Hoelling s Rule [4]. There will be more o sy bou his ler.) The soluion for P is P = P e r (.4) nd hus we hve he producion re X, from he demnd funcion nd he iniil producion re is X = β P e βr (.5) X = P β (.6) Since ds/d = X, we hve S() = S Xd = S [ e βr ] P β (.7) βr We require wo condiions o close he sysem: S, he presen moun of he resource, nd P, he iniil price. Cmbridge Universiy Press
3 Cmbridge Universiy Press Susinble Nurl Resource Mngemen for Scieniss nd Engineers Excerp More informion. Cosless Producion of Serile Resource P Sorge, S 5 5 Producion, X P Figure.. Five differen depleion hisories, idenicl excep for iniil price. P increses by fcors of in he direcion of he rrows. S is presumed known; P is no. If P is se oo high, he demnd will be suned nd he resource will go unuilized. If P is se oo low, he demnd will be oo lrge nd he resource will be depleed premurely, leving our mhemics of decision mking invlid (Figure.). The sysem is closed by invoking he Terminl Condiion (TC): complee resource exhusion s ime goes o infiniy: S s (.8) Thus, S = P β βr (.9) The iniil price is hus P = [ ] β (.) S βr nd he iniil producion re is X = β P = βrs (.) If P is oo high (X oo low), hen S is never exhused. If P is oo low (X oo high), hen he resource is exhused premurely. In eiher cse, producion would be djused o sisfy he TC (Figure.). Ren is he inegred presen worh of ll ne revenues: R = Since P = P e r, we hve e r X ()P()d (.) R = P X ()d = P S (.) Cmbridge Universiy Press
4 Cmbridge Universiy Press Susinble Nurl Resource Mngemen for Scieniss nd Engineers Excerp More informion 4 Serile Resources Sorge, S 6 4 Producion, X Price, P Revenue, PX Figure.. Exhusion hisory h mches he TC. Demnd is X = /P β, wih (, β) = (,.5). For his simple cse, he presen worh of ll fuure producion is equl o ody s price imes ody s ol supply. Progrm Oil illusres he exhusion hisory under hese condiions. The ODE s re inegred forwrd in ime wih n explici (Euler) forwrd-difference mehod. The iniil price P needs o be djused mnully o sisfy he TC. Becuse numericl inegrion is no perfec, he relions developed bove using he clculus correspond only pproximely o he Oil simulion; he discrepncies vnish s he numericl imesep becomes infiniesimlly smll... Finie Demnd Nex, dd ceiling price P, which limis demnd (Figure.). Above his price, cusomers purchse subsiue produc. The previous soluion, in which P rises wihou bound, is invlid. Equions.. sill govern, bu he TC needs o be lered. The correc TC in his cse is S sp P (.4) Cmbridge Universiy Press
5 Cmbridge Universiy Press Susinble Nurl Resource Mngemen for Scieniss nd Engineers Excerp More informion. Cosless Producion of Serile Resource 5 () 5 Producion re, X (b) (c) 5 4 Producion re, X (d).5.5 Price, P.5.5 Price, P Figure.. Four differen demnd funcions X (P ). () bse cse X = P β ; (b) bse cse wih P P = ; (c) liner demnd X c = X ( P ); (d) bse cse shifed, X d + = P β. The dsh lines indice he coninuion of he bse cse curve beyond X. Cses b, c, nd d hve finie demnd. which leds o exhusion finie ime T. From Equions. nd., we hve from which we obin he finl resuls These relions reduce o he previous ones s P. P = P e rt (.5) S = [ P β e βrt βr (.6) [ ] β P = βrs + (.7) P β X = βrs + P β (.8) [ T = βr ln βrs P β ] + (.9) The bove relions mus govern ny ime during he exrcion hisory, else he rjecory would no be opiml nd i would be lered, conrry o hypohesis. Cmbridge Universiy Press
6 Cmbridge Universiy Press Susinble Nurl Resource Mngemen for Scieniss nd Engineers Excerp More informion 6 Serile Resources Hence, we my drop he subscrips nd i is lwys rue h [ ] β P = βrs + (.) P β X = βrs + P β (.) [ T = βr ln βrsp β ] + (.) wih S he remining unexploied resource ny ime nd P, X, T he conemporry price, producion re, nd remining ime o exhusion. Equions.,., nd. compleely chrcerize he soluion o Equions.,., nd., subjec o he TC of exhusion s price reches he ceiling P. Progrm Oil illusres hese relionships. Figure.4 displys simulion resuls for finie P nd T, chieved wih he decision rule X = X (S) (Equion.). Ren is, s bove, he inegred presen worh of ll fuure producion: R = T PXe r d = P Xd = P S (.) Sorge, S Producion, X Price, P 6 4 Revenue, PX Figure.4. Exrcion hisory wih finie demnd, X = P β wih P = 9 (cse (b) in Figure.). This leds o exhusion finie ime s shown. Cmbridge Universiy Press
7 Cmbridge Universiy Press Susinble Nurl Resource Mngemen for Scieniss nd Engineers Excerp More informion. Cosless Producion of Serile Resource 7 P S X S 4 4 T R 5 5 S 5 5 S Figure.5. P, X, nd T s funions of he ol reserve S ny ime (Equions..). Demnd: X = P β ; = ; β =.5; r =.5; P = (,, ) s indiced by he linesyles. This resul is unchnged by he imposiion of ceiling price nd he resuln finie T. Since P decreses s P decreses, ceiling price hs he effec of diminishing overll ren, in ccord wih inuiion. Equions.. give P, X, nd T s funions of he ol reserve S ny ime, ssuming complee exhusion, X = P β nd P P. Figure.5 plos hese for hree differen vlues of P. Ren peks nd begins o decline wih S high bundnce in his scenrio. Consumers Surplus Consumpion price P indices willingness o py les P h is, he vlue of he consumpion V P. The consumer obins surplus equl o he difference V P. Figure.6 illusres demnd curve mde up of individul uses X, ech wih is own vlue V. If price is se P, hose users wih higher vlue will purchse, nd hose wih lower vlue will no. The consumers surplus (CS) is heir ccumulion: CS = (V P) X (.4) for ll incremens where (V P) >. In he limi, CS(P) = X (P) (V P)dx (.5) Cmbridge Universiy Press
8 Cmbridge Universiy Press Susinble Nurl Resource Mngemen for Scieniss nd Engineers Excerp More informion 8 Serile Resources X X 6 X 5 X 4 X X X Vlue Figure.6. Demnd curve buil up of individul incremens X, ordered by decresing individul vlue, ploed on he horizonl xis. X Ren X Consumers Surplus P Vlue Figure.7. Demnd curve s in Figure.6, dding he cul price P. The re o he righ of he price line is he consumers surplus; h o he lef is he ren rnsferred o he seller. Clerly, CS is funcion of P. Grphiclly, his is illusred in Figure.7 s he re under he demnd curve, o he righ of P. The moun PX shown grphiclly is he ol ren rnsferred o he seller. So rnscions P genere consumers surplus s well s ren. Grphiclly, i is esy o see h n equivlen inegrl is P CS(P) = XdV (.6) An nlogous concep of producers surplus (PS) divides he ren ino producion cos plus surplus: ne ren. When producion is cosly, he producers surplus is he ne ren. P Cmbridge Universiy Press
9 Cmbridge Universiy Press Susinble Nurl Resource Mngemen for Scieniss nd Engineers Excerp More informion. Cosless Producion of Serile Resource 9 Consumers surplus is sic concep; ime is fixed in is consrucion. Clerly in depleion conex, s P rises over ime, CS will decrese: CS(P) = CS(P()). Suppose we hve he bse cse demnd X = P β, wih ceiling price P. Then i is esy o verify h CS my be inegred o obin CS(P) = [ P β P β] (.7) β The presen worh of he consumers surplus is explored in Problem 4... Liner Demnd As n exension of he preceding, consider he lernive demnd funcion P = P bx (.8) We sill hve he requiremen of exponenil price growh P = P e r (.9) nd hus X = P P e r b (.) Inegring ds/d = X gives S() = S + b [ ] P r (er ) P (.) The Terminl Condiion is S(T ) sp(t ) P (.) nd herefore P e rt = P (.) ( ) P rt = ln P (.4) nd S = b [ ] P r (ert ) PT (.5) Cmbridge Universiy Press
10 Cmbridge Universiy Press Susinble Nurl Resource Mngemen for Scieniss nd Engineers Excerp More informion Serile Resources.8 Compeiive.8 P.6.4 X S S 4 T S R S Figure.8. Opiml exrcion relions for he liner demnd cse: r =.5; P = X ; compeiive cse. A lile rerrngemen leds o ( ) T = r ln P S = P br X = P P b P [ ( )] P P + ln P P (.6) (.7) (.8) These ls hree equions rele S, X, nd T o P ; hey comprise implici funcions X (S), T (S), nd P (S). There re no simple closed-form soluions, bu X (S), T (S), nd P (S) cn be evlued numericlly s in Oil6M+C; he plos shown herein re reproduced in Figure.8. They chrcerize his sysem under liner demnd, s did he closed-form Equions.. for he erlier demnd funcion. As before, ren R = P S. I is ineresing o noe here h s S increses, P ulimely decreses owrd he limiing cse P ss. As resul, he R iniilly grows wih S bu ulimely peks nd hen decreses wih incresing S. The poin of mximum ren is found by seing dr/d = ; he resul is ( ) P ln P ( = P ) P (.9) Cmbridge Universiy Press
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
Average & instantaneous velocity and acceleration Motion with constant acceleration
 Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
Physics 2A HW #3 Solutions
 Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
( ) ( ) ( ) ( ) ( ) ( y )
 8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Seminar 4: Hotelling 2
 Seminar 4: Hoelling 2 November 3, 211 1 Exercise Par 1 Iso-elasic demand A non renewable resource of a known sock S can be exraced a zero cos. Demand for he resource is of he form: D(p ) = p ε ε > A a
Seminar 4: Hoelling 2 November 3, 211 1 Exercise Par 1 Iso-elasic demand A non renewable resource of a known sock S can be exraced a zero cos. Demand for he resource is of he form: D(p ) = p ε ε > A a
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
 Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
PHYSICS 1210 Exam 1 University of Wyoming 14 February points
 PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
Tax Audit and Vertical Externalities
 T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
MATH 124 AND 125 FINAL EXAM REVIEW PACKET (Revised spring 2008)
 MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
2D Motion WS. A horizontally launched projectile s initial vertical velocity is zero. Solve the following problems with this information.
 Nme D Moion WS The equions of moion h rele o projeciles were discussed in he Projecile Moion Anlsis Acii. ou found h projecile moes wih consn eloci in he horizonl direcion nd consn ccelerion in he ericl
Nme D Moion WS The equions of moion h rele o projeciles were discussed in he Projecile Moion Anlsis Acii. ou found h projecile moes wih consn eloci in he horizonl direcion nd consn ccelerion in he ericl
1 jordan.mcd Eigenvalue-eigenvector approach to solving first order ODEs. -- Jordan normal (canonical) form. Instructor: Nam Sun Wang
 jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
A 1.3 m 2.5 m 2.8 m. x = m m = 8400 m. y = 4900 m 3200 m = 1700 m
 PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
(b) 10 yr. (b) 13 m. 1.6 m s, m s m s (c) 13.1 s. 32. (a) 20.0 s (b) No, the minimum distance to stop = 1.00 km. 1.
 Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).
![INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q). INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).](/thumbs/78/77677920.jpg) INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER 2
 ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER Seion Eerise -: Coninuiy of he uiliy funion Le λ ( ) be he monooni uiliy funion defined in he proof of eisene of uiliy funion If his funion is oninuous y hen
ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER Seion Eerise -: Coninuiy of he uiliy funion Le λ ( ) be he monooni uiliy funion defined in he proof of eisene of uiliy funion If his funion is oninuous y hen
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR IAN KNOWLES
 A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
Economics 8105 Macroeconomic Theory Recitation 6
 Economics 8105 Macroeconomic Theory Reciaion 6 Conor Ryan Ocober 11h, 2016 Ouline: Opimal Taxaion wih Governmen Invesmen 1 Governmen Expendiure in Producion In hese noes we will examine a model in which
Economics 8105 Macroeconomic Theory Reciaion 6 Conor Ryan Ocober 11h, 2016 Ouline: Opimal Taxaion wih Governmen Invesmen 1 Governmen Expendiure in Producion In hese noes we will examine a model in which
S Radio transmission and network access Exercise 1-2
 S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Mathematics 805 Final Examination Answers
 . 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
. 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
P441 Analytical Mechanics - I. Coupled Oscillators. c Alex R. Dzierba
 Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Chapter Direct Method of Interpolation
 Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Solutions to Problems from Chapter 2
 Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Magnetostatics Bar Magnet. Magnetostatics Oersted s Experiment
 Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Think of the Relationship Between Time and Space Again
 Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
Math 2142 Exam 1 Review Problems. x 2 + f (0) 3! for the 3rd Taylor polynomial at x = 0. To calculate the various quantities:
 Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
MTH 146 Class 11 Notes
 8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
Version 001 test-1 swinney (57010) 1. is constant at m/s.
 Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
M r. d 2. R t a M. Structural Mechanics Section. Exam CT5141 Theory of Elasticity Friday 31 October 2003, 9:00 12:00 hours. Problem 1 (3 points)
 Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
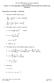 .615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
How to Prove the Riemann Hypothesis Author: Fayez Fok Al Adeh.
 How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
The neoclassical version of the Johansen-vintage (putty-clay) growth model
 Jon Vislie Sepemer 2 Lecure noes ECON 435 The neoclssicl version of he Johnsen-vinge (puy-cly) growh model The vrious elemens we hve considered during he lecures cn e colleced so s o give us he following
Jon Vislie Sepemer 2 Lecure noes ECON 435 The neoclssicl version of he Johnsen-vinge (puy-cly) growh model The vrious elemens we hve considered during he lecures cn e colleced so s o give us he following
Convergence of Singular Integral Operators in Weighted Lebesgue Spaces
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
Some Inequalities variations on a common theme Lecture I, UL 2007
 Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Chapter 2: Evaluative Feedback
 Chper 2: Evluive Feedbck Evluing cions vs. insrucing by giving correc cions Pure evluive feedbck depends olly on he cion ken. Pure insrucive feedbck depends no ll on he cion ken. Supervised lerning is
Chper 2: Evluive Feedbck Evluing cions vs. insrucing by giving correc cions Pure evluive feedbck depends olly on he cion ken. Pure insrucive feedbck depends no ll on he cion ken. Supervised lerning is
3 Motion with constant acceleration: Linear and projectile motion
 3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
14. The fundamental theorem of the calculus
 4. The funmenl heorem of he clculus V 20 00 80 60 40 20 0 0 0.2 0.4 0.6 0.8 v 400 200 0 0 0.2 0.5 0.8 200 400 Figure : () Venriculr volume for subjecs wih cpciies C = 24 ml, C = 20 ml, C = 2 ml n (b) he
4. The funmenl heorem of he clculus V 20 00 80 60 40 20 0 0 0.2 0.4 0.6 0.8 v 400 200 0 0 0.2 0.5 0.8 200 400 Figure : () Venriculr volume for subjecs wih cpciies C = 24 ml, C = 20 ml, C = 2 ml n (b) he
RESPONSE UNDER A GENERAL PERIODIC FORCE. When the external force F(t) is periodic with periodτ = 2π
 RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
A new model for limit order book dynamics
 Anewmodelforlimiorderbookdynmics JeffreyR.Russell UniversiyofChicgo,GrdueSchoolofBusiness TejinKim UniversiyofChicgo,DeprmenofSisics Absrc:Thispperproposesnewmodelforlimiorderbookdynmics.Thelimiorderbookconsiss
Anewmodelforlimiorderbookdynmics JeffreyR.Russell UniversiyofChicgo,GrdueSchoolofBusiness TejinKim UniversiyofChicgo,DeprmenofSisics Absrc:Thispperproposesnewmodelforlimiorderbookdynmics.Thelimiorderbookconsiss
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 9: The High Beta Tokamak
 .65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
.65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
3.1.3 INTRODUCTION TO DYNAMIC OPTIMIZATION: DISCRETE TIME PROBLEMS. A. The Hamiltonian and First-Order Conditions in a Finite Time Horizon
 3..3 INRODUCION O DYNAMIC OPIMIZAION: DISCREE IME PROBLEMS A. he Hamilonian and Firs-Order Condiions in a Finie ime Horizon Define a new funcion, he Hamilonian funcion, H. H he change in he oal value of
3..3 INRODUCION O DYNAMIC OPIMIZAION: DISCREE IME PROBLEMS A. he Hamilonian and Firs-Order Condiions in a Finie ime Horizon Define a new funcion, he Hamilonian funcion, H. H he change in he oal value of
The order of reaction is defined as the number of atoms or molecules whose concentration change during the chemical reaction.
 www.hechemisryguru.com Re Lw Expression Order of Recion The order of recion is defined s he number of oms or molecules whose concenrion chnge during he chemicl recion. Or The ol number of molecules or
www.hechemisryguru.com Re Lw Expression Order of Recion The order of recion is defined s he number of oms or molecules whose concenrion chnge during he chemicl recion. Or The ol number of molecules or
EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE BOUNDARY-VALUE PROBLEM
 Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Properties of Logarithms. Solving Exponential and Logarithmic Equations. Properties of Logarithms. Properties of Logarithms. ( x)
 Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples.
 Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
The Brock-Mirman Stochastic Growth Model
 c December 3, 208, Chrisopher D. Carroll BrockMirman The Brock-Mirman Sochasic Growh Model Brock and Mirman (972) provided he firs opimizing growh model wih unpredicable (sochasic) shocks. The social planner
c December 3, 208, Chrisopher D. Carroll BrockMirman The Brock-Mirman Sochasic Growh Model Brock and Mirman (972) provided he firs opimizing growh model wih unpredicable (sochasic) shocks. The social planner
Motion in a Straight Line
 Moion in Srigh Line. Preei reched he mero sion nd found h he esclor ws no working. She wlked up he sionry esclor in ime. On oher dys, if she remins sionry on he moing esclor, hen he esclor kes her up in
Moion in Srigh Line. Preei reched he mero sion nd found h he esclor ws no working. She wlked up he sionry esclor in ime. On oher dys, if she remins sionry on he moing esclor, hen he esclor kes her up in
GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS
 - TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
- TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
More on Magnetically C Coupled Coils and Ideal Transformers
 Appenix ore on gneiclly C Couple Coils Iel Trnsformers C. Equivlen Circuis for gneiclly Couple Coils A imes, i is convenien o moel mgneiclly couple coils wih n equivlen circui h oes no involve mgneic coupling.
Appenix ore on gneiclly C Couple Coils Iel Trnsformers C. Equivlen Circuis for gneiclly Couple Coils A imes, i is convenien o moel mgneiclly couple coils wih n equivlen circui h oes no involve mgneic coupling.
Lecture Notes 3: Quantitative Analysis in DSGE Models: New Keynesian Model
 Lecure Noes 3: Quaniaive Analysis in DSGE Models: New Keynesian Model Zhiwei Xu, Email: xuzhiwei@sju.edu.cn The moneary policy plays lile role in he basic moneary model wihou price sickiness. We now urn
Lecure Noes 3: Quaniaive Analysis in DSGE Models: New Keynesian Model Zhiwei Xu, Email: xuzhiwei@sju.edu.cn The moneary policy plays lile role in he basic moneary model wihou price sickiness. We now urn
REAL ANALYSIS I HOMEWORK 3. Chapter 1
 REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
Solutions Problem Set 3 Macro II (14.452)
 Soluions Problem Se 3 Macro II (14.452) Francisco A. Gallego 04/27/2005 1 Q heory of invesmen in coninuous ime and no uncerainy Consider he in nie horizon model of a rm facing adjusmen coss o invesmen.
Soluions Problem Se 3 Macro II (14.452) Francisco A. Gallego 04/27/2005 1 Q heory of invesmen in coninuous ime and no uncerainy Consider he in nie horizon model of a rm facing adjusmen coss o invesmen.
How to prove the Riemann Hypothesis
 Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Physics 235 Chapter 2. Chapter 2 Newtonian Mechanics Single Particle
 Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Estimating the population parameter, r, q and K based on surplus production model. Wang, Chien-Hsiung
 SCTB15 Working Pper ALB 7 Esiming he populion prmeer, r, q nd K bsed on surplus producion model Wng, Chien-Hsiung Biologicl nd Fishery Division Insiue of Ocenogrphy Nionl Tiwn Universiy Tipei, Tiwn Tile:
SCTB15 Working Pper ALB 7 Esiming he populion prmeer, r, q nd K bsed on surplus producion model Wng, Chien-Hsiung Biologicl nd Fishery Division Insiue of Ocenogrphy Nionl Tiwn Universiy Tipei, Tiwn Tile:
Reserves measures have an economic component eg. what could be extracted at current prices?
 3.2 Non-renewable esources A. Are socks of non-renewable resources fixed? eserves measures have an economic componen eg. wha could be exraced a curren prices? - Locaion and quaniies of reserves of resources
3.2 Non-renewable esources A. Are socks of non-renewable resources fixed? eserves measures have an economic componen eg. wha could be exraced a curren prices? - Locaion and quaniies of reserves of resources
Temperature Rise of the Earth
 Avilble online www.sciencedirec.com ScienceDirec Procedi - Socil nd Behviorl Scien ce s 88 ( 2013 ) 220 224 Socil nd Behviorl Sciences Symposium, 4 h Inernionl Science, Socil Science, Engineering nd Energy
Avilble online www.sciencedirec.com ScienceDirec Procedi - Socil nd Behviorl Scien ce s 88 ( 2013 ) 220 224 Socil nd Behviorl Sciences Symposium, 4 h Inernionl Science, Socil Science, Engineering nd Energy
Phys 110. Answers to even numbered problems on Midterm Map
 Phys Answers o een numbered problems on Miderm Mp. REASONING The word per indices rio, so.35 mm per dy mens.35 mm/d, which is o be epressed s re in f/cenury. These unis differ from he gien unis in boh
Phys Answers o een numbered problems on Miderm Mp. REASONING The word per indices rio, so.35 mm per dy mens.35 mm/d, which is o be epressed s re in f/cenury. These unis differ from he gien unis in boh
Procedia Computer Science
 Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
( ) a system of differential equations with continuous parametrization ( T = R + These look like, respectively:
 XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
HOTELLING LOCATION MODEL
 HOTELLING LOCATION MODEL THE LINEAR CITY MODEL The Example of Choosing only Locaion wihou Price Compeiion Le a be he locaion of rm and b is he locaion of rm. Assume he linear ransporaion cos equal o d,
HOTELLING LOCATION MODEL THE LINEAR CITY MODEL The Example of Choosing only Locaion wihou Price Compeiion Le a be he locaion of rm and b is he locaion of rm. Assume he linear ransporaion cos equal o d,
Physic 231 Lecture 4. Mi it ftd l t. Main points of today s lecture: Example: addition of velocities Trajectories of objects in 2 = =
 Mi i fd l Phsic 3 Lecure 4 Min poins of od s lecure: Emple: ddiion of elociies Trjecories of objecs in dimensions: dimensions: g 9.8m/s downwrds ( ) g o g g Emple: A foobll pler runs he pern gien in he
Mi i fd l Phsic 3 Lecure 4 Min poins of od s lecure: Emple: ddiion of elociies Trjecories of objecs in dimensions: dimensions: g 9.8m/s downwrds ( ) g o g g Emple: A foobll pler runs he pern gien in he
Two Coupled Oscillators / Normal Modes
 Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Macroeconomic Theory Ph.D. Qualifying Examination Fall 2005 ANSWER EACH PART IN A SEPARATE BLUE BOOK. PART ONE: ANSWER IN BOOK 1 WEIGHT 1/3
 Macroeconomic Theory Ph.D. Qualifying Examinaion Fall 2005 Comprehensive Examinaion UCLA Dep. of Economics You have 4 hours o complee he exam. There are hree pars o he exam. Answer all pars. Each par has
Macroeconomic Theory Ph.D. Qualifying Examinaion Fall 2005 Comprehensive Examinaion UCLA Dep. of Economics You have 4 hours o complee he exam. There are hree pars o he exam. Answer all pars. Each par has
Chapter 2. Motion along a straight line. 9/9/2015 Physics 218
 Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Problem Set on Differential Equations
 Problem Se on Differenial Equaions 1. Solve he following differenial equaions (a) x () = e x (), x () = 3/ 4. (b) x () = e x (), x (1) =. (c) xe () = + (1 x ()) e, x () =.. (An asse marke model). Le p()
Problem Se on Differenial Equaions 1. Solve he following differenial equaions (a) x () = e x (), x () = 3/ 4. (b) x () = e x (), x (1) =. (c) xe () = + (1 x ()) e, x () =.. (An asse marke model). Le p()
CHAPTER 2 KINEMATICS IN ONE DIMENSION ANSWERS TO FOCUS ON CONCEPTS QUESTIONS
 Physics h Ediion Cunell Johnson Young Sdler Soluions Mnul Soluions Mnul, Answer keys, Insrucor's Resource Mnul for ll chpers re included. Compleed downlod links: hps://esbnkre.com/downlod/physics-h-ediion-soluions-mnulcunell-johnson-young-sdler/
Physics h Ediion Cunell Johnson Young Sdler Soluions Mnul Soluions Mnul, Answer keys, Insrucor's Resource Mnul for ll chpers re included. Compleed downlod links: hps://esbnkre.com/downlod/physics-h-ediion-soluions-mnulcunell-johnson-young-sdler/
SOLUTIONS TO ECE 3084
 SOLUTIONS TO ECE 384 PROBLEM 2.. For each sysem below, specify wheher or no i is: (i) memoryless; (ii) causal; (iii) inverible; (iv) linear; (v) ime invarian; Explain your reasoning. If he propery is no
SOLUTIONS TO ECE 384 PROBLEM 2.. For each sysem below, specify wheher or no i is: (i) memoryless; (ii) causal; (iii) inverible; (iv) linear; (v) ime invarian; Explain your reasoning. If he propery is no
Bias in Conditional and Unconditional Fixed Effects Logit Estimation: a Correction * Tom Coupé
 Bias in Condiional and Uncondiional Fixed Effecs Logi Esimaion: a Correcion * Tom Coupé Economics Educaion and Research Consorium, Naional Universiy of Kyiv Mohyla Academy Address: Vul Voloska 10, 04070
Bias in Condiional and Uncondiional Fixed Effecs Logi Esimaion: a Correcion * Tom Coupé Economics Educaion and Research Consorium, Naional Universiy of Kyiv Mohyla Academy Address: Vul Voloska 10, 04070
LAPLACE TRANSFORMS. 1. Basic transforms
 LAPLACE TRANSFORMS. Bic rnform In hi coure, Lplce Trnform will be inroduced nd heir properie exmined; ble of common rnform will be buil up; nd rnform will be ued o olve ome dierenil equion by rnforming
LAPLACE TRANSFORMS. Bic rnform In hi coure, Lplce Trnform will be inroduced nd heir properie exmined; ble of common rnform will be buil up; nd rnform will be ued o olve ome dierenil equion by rnforming
Lecture 3: 1-D Kinematics. This Week s Announcements: Class Webpage: visit regularly
 Lecure 3: 1-D Kinemics This Week s Announcemens: Clss Webpge: hp://kesrel.nm.edu/~dmeier/phys121/phys121.hml isi regulrly Our TA is Lorrine Bowmn Week 2 Reding: Chper 2 - Gincoli Week 2 Assignmens: Due:
Lecure 3: 1-D Kinemics This Week s Announcemens: Clss Webpge: hp://kesrel.nm.edu/~dmeier/phys121/phys121.hml isi regulrly Our TA is Lorrine Bowmn Week 2 Reding: Chper 2 - Gincoli Week 2 Assignmens: Due:
Green s Functions and Comparison Theorems for Differential Equations on Measure Chains
 Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
= ( ) ) or a system of differential equations with continuous parametrization (T = R
 XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
d 1 = c 1 b 2 - b 1 c 2 d 2 = c 1 b 3 - b 1 c 3
 and d = c b - b c c d = c b - b c c This process is coninued unil he nh row has been compleed. The complee array of coefficiens is riangular. Noe ha in developing he array an enire row may be divided or
and d = c b - b c c d = c b - b c c This process is coninued unil he nh row has been compleed. The complee array of coefficiens is riangular. Noe ha in developing he array an enire row may be divided or
A LOG IS AN EXPONENT.
 Ojeives: n nlze nd inerpre he ehvior of rihmi funions, inluding end ehvior nd smpoes. n solve rihmi equions nlill nd grphill. n grph rihmi funions. n deermine he domin nd rnge of rihmi funions. n deermine
Ojeives: n nlze nd inerpre he ehvior of rihmi funions, inluding end ehvior nd smpoes. n solve rihmi equions nlill nd grphill. n grph rihmi funions. n deermine he domin nd rnge of rihmi funions. n deermine
Intermediate Macro In-Class Problems
 Inermediae Macro In-Class Problems Exploring Romer Model June 14, 016 Today we will explore he mechanisms of he simply Romer model by exploring how economies described by his model would reac o exogenous
Inermediae Macro In-Class Problems Exploring Romer Model June 14, 016 Today we will explore he mechanisms of he simply Romer model by exploring how economies described by his model would reac o exogenous
Chapter 2. First Order Scalar Equations
 Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
CHAPTER 11 PARAMETRIC EQUATIONS AND POLAR COORDINATES
 CHAPTER PARAMETRIC EQUATIONS AND POLAR COORDINATES. PARAMETRIZATIONS OF PLANE CURVES., 9, _ _ Ê.,, Ê or, Ÿ. 5, 7, _ _.,, Ÿ Ÿ Ê Ê 5 Ê ( 5) Ê ˆ Ê 6 Ê ( 5) 7 Ê Ê, Ÿ Ÿ $ 5. cos, sin, Ÿ Ÿ 6. cos ( ), sin (
CHAPTER PARAMETRIC EQUATIONS AND POLAR COORDINATES. PARAMETRIZATIONS OF PLANE CURVES., 9, _ _ Ê.,, Ê or, Ÿ. 5, 7, _ _.,, Ÿ Ÿ Ê Ê 5 Ê ( 5) Ê ˆ Ê 6 Ê ( 5) 7 Ê Ê, Ÿ Ÿ $ 5. cos, sin, Ÿ Ÿ 6. cos ( ), sin (
Inventory Management Models with Variable Holding Cost and Salvage value
 OSR Journl of Business nd Mngemen OSR-JBM e-ssn: -X p-ssn: 9-. Volume ssue Jul. - Aug. PP - www.iosrjournls.org nvenory Mngemen Models wi Vrile Holding os nd Slvge vlue R.Mon R.Venkeswrlu Memics Dep ollege
OSR Journl of Business nd Mngemen OSR-JBM e-ssn: -X p-ssn: 9-. Volume ssue Jul. - Aug. PP - www.iosrjournls.org nvenory Mngemen Models wi Vrile Holding os nd Slvge vlue R.Mon R.Venkeswrlu Memics Dep ollege
EXERCISE - 01 CHECK YOUR GRASP
 UNIT # 09 PARABOLA, ELLIPSE & HYPERBOLA PARABOLA EXERCISE - 0 CHECK YOUR GRASP. Hin : Disnce beween direcri nd focus is 5. Given (, be one end of focl chord hen oher end be, lengh of focl chord 6. Focus
UNIT # 09 PARABOLA, ELLIPSE & HYPERBOLA PARABOLA EXERCISE - 0 CHECK YOUR GRASP. Hin : Disnce beween direcri nd focus is 5. Given (, be one end of focl chord hen oher end be, lengh of focl chord 6. Focus
2. Nonlinear Conservation Law Equations
 . Nonlinear Conservaion Law Equaions One of he clear lessons learned over recen years in sudying nonlinear parial differenial equaions is ha i is generally no wise o ry o aack a general class of nonlinear
. Nonlinear Conservaion Law Equaions One of he clear lessons learned over recen years in sudying nonlinear parial differenial equaions is ha i is generally no wise o ry o aack a general class of nonlinear
FM Applications of Integration 1.Centroid of Area
 FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
ECE Microwave Engineering
 EE 537-635 Microwve Engineering Adped from noes y Prof. Jeffery T. Willims Fll 8 Prof. Dvid R. Jcson Dep. of EE Noes Wveguiding Srucures Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model
EE 537-635 Microwve Engineering Adped from noes y Prof. Jeffery T. Willims Fll 8 Prof. Dvid R. Jcson Dep. of EE Noes Wveguiding Srucures Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model
f(x) dx with An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples dx x x 2
 Impope Inegls To his poin we hve only consideed inegls f() wih he is of inegion nd b finie nd he inegnd f() bounded (nd in fc coninuous ecep possibly fo finiely mny jump disconinuiies) An inegl hving eihe
Impope Inegls To his poin we hve only consideed inegls f() wih he is of inegion nd b finie nd he inegnd f() bounded (nd in fc coninuous ecep possibly fo finiely mny jump disconinuiies) An inegl hving eihe
MAT 266 Calculus for Engineers II Notes on Chapter 6 Professor: John Quigg Semester: spring 2017
 MAT 66 Clculus for Engineers II Noes on Chper 6 Professor: John Quigg Semeser: spring 7 Secion 6.: Inegrion by prs The Produc Rule is d d f()g() = f()g () + f ()g() Tking indefinie inegrls gives [f()g
MAT 66 Clculus for Engineers II Noes on Chper 6 Professor: John Quigg Semeser: spring 7 Secion 6.: Inegrion by prs The Produc Rule is d d f()g() = f()g () + f ()g() Tking indefinie inegrls gives [f()g
ENDOGENOUS GROWTH: Schumpeter s process of creative destruction
 Jon Vislie Ocober 20, Lecure noes, ECON 4350 ENDOGENOUS GROWTH: Schumpeer s process of creive desrucion Joseph Schumpeer mde erly conribuions wih permnen influence on our undersnding of he role of R&D;
Jon Vislie Ocober 20, Lecure noes, ECON 4350 ENDOGENOUS GROWTH: Schumpeer s process of creive desrucion Joseph Schumpeer mde erly conribuions wih permnen influence on our undersnding of he role of R&D;
Neural assembly binding in linguistic representation
 Neurl ssembly binding in linguisic represenion Frnk vn der Velde & Mrc de Kmps Cogniive Psychology Uni, Universiy of Leiden, Wssenrseweg 52, 2333 AK Leiden, The Neherlnds, vdvelde@fsw.leidenuniv.nl Absrc.
Neurl ssembly binding in linguisic represenion Frnk vn der Velde & Mrc de Kmps Cogniive Psychology Uni, Universiy of Leiden, Wssenrseweg 52, 2333 AK Leiden, The Neherlnds, vdvelde@fsw.leidenuniv.nl Absrc.
The following report makes use of the process from Chapter 2 in Dr. Cumming s thesis.
 Zaleski 1 Joseph Zaleski Mah 451H Final Repor Conformal Mapping Mehods and ZST Hele Shaw Flow Inroducion The Hele Shaw problem has been sudied using linear sabiliy analysis and numerical mehods, bu a novel
Zaleski 1 Joseph Zaleski Mah 451H Final Repor Conformal Mapping Mehods and ZST Hele Shaw Flow Inroducion The Hele Shaw problem has been sudied using linear sabiliy analysis and numerical mehods, bu a novel
Final Exam. Tuesday, December hours
 San Francisco Sae Universiy Michael Bar ECON 560 Fall 03 Final Exam Tuesday, December 7 hours Name: Insrucions. This is closed book, closed noes exam.. No calculaors of any kind are allowed. 3. Show all
San Francisco Sae Universiy Michael Bar ECON 560 Fall 03 Final Exam Tuesday, December 7 hours Name: Insrucions. This is closed book, closed noes exam.. No calculaors of any kind are allowed. 3. Show all
