By convention, C > 0 for counterclockwise flow, hence the contour must be counterclockwise.
|
|
|
- Posy Hudson
- 5 years ago
- Views:
Transcription
1 Chapter The Circulation Theorem Circulation is a measure of rotation. It is calculated for a closed contour by taking the line integral of the velocity component tangent to the contour evaluated along the contour: C U dl = U cosα dl. α dl U By convention, C > 0 for counterclockwise flow, hence the contour must be counterclockwise. Consider the special case of a circular ring with radius R rotating with constant angular velocity Ω as shown. Note that Ω and R here are not for the rotation rate and radius normal to Earth s axis of rotation. Ω R U = ΩRˆλ They are defined as in the figure. Also note ˆλ is a unit vector tangent to the circle, so dl = R dλ ˆλ. For this special case where U and dl are in the same direction, so C = 2π 0 ΩR 2 dλ = 2πΩR 2. Note that ΩR 2 is the angular momentum about the axis of rotation. The derivation of the circulation theorem begins with the momentum equation without friction: D a U a = 1 ρ p + g. Recall true gravity g = g Ω 2 R. Holton forgets the star in his derivation. Fortunately the end result is the same. Taking the contour integral of the momentum equation, with g = Φ we arrive at: Da U a dl = p ρ dl Φ dl Ω 2 R dl. Intuitively, the last term must be zero because R is a position vector and therefore does not circulate. The rest of the derivation can be found in Holton to end with Kelvin s 1
2 Circulation Theorm DC a = D U a dl = ρ 1 dp The term ρ 1 dp is called the solenoid term. The word solenoid refers to the parallelograms that form when isobars and lines of constant density are drawn together for a baroclinic atmosphere. z ρ 4 ρ 3 p 4ρ2 p 3 ρ 1 p 2 p 1 y Consider a line integral around one of the parallelograms for a baroclinic atmosphere. Clearly the solenoid term is nonzero provided the parallelogram is finite. Earth dwellers usually prefer to work with the circulation relative to Earth s rotation: C = C a C E, where the circulation due to Earth s rotation Ω is C E. For a contour on Earth s surface with area A, C E = 2ΩA < sin φ > where A < sin φ > is the area of the contour projected onto the equatorial plane (see Holton Fig 4.2 to visualize) and φ = latitude. Hence, we arrive at the Bjerknes Circulation Theorem DC = where Ω is Earth s rotation rate. ρ 1 D(A < sin φ >) dp 2Ω For a barotropic atmosphere the density surfaces are also isobaric surfaces, so the parallelograms in the figure above are infinite and the solenoid term is zero. There are a couple of good examples in Holton that are worth working through. 4.2 Vorticity Circulation describes the average flow over a finite area defined by the line integral. Hence it is a macroscopic measure of rotation. In contrast vorticity is a microscopic measure of the rotation. Vorticity is a field variable (it may be unique at every point). 2
3 Absolute and relative vorticity are defined ω a U a ω U. In Cartesian coordinates U = î ĵ ˆk x y z u v w î x u ĵ y v (add the full diagnals that slope down to the right and subtract those that slope down to the left) = ( w y v z, u z w x, v x u ) y The vertical components are assigned their own variable names eta and zeta η ˆk U a ζ ˆk U. Their difference is the planetary vorticity or f = η ζ (also the Coriolis parameter), which is the local vertical component of vorticity due to Earth s rotation. (a) (b) ζ > 0 cyclone W. trough E. trough ζ < 0 anticyclone W. ridge E. ridge Think back to the worksheet on circulation where you showed that C = L 2 u/y for an easterly windfield that increased linearly to the north. By extension, if there is also a northerly component of the wind that increases linearly to the east, then C = L 2 (v/x u/y) = L 2 ζ. If we let the sides of the square approach zero length, then it is easy to show (see Holton) that where A = area inside the contour. ζ = lim A 0 C/A 3
4 From Stoke s theorem U dl = A ( U) n da where if the area is in the horizontal plane then the average ζ for an area A is C = ζ da Example: This is easy to see for a disk in solid-body motion with angular velocity ω, where C = 2πωR 2 at radius R, then ζ = C/πR 2 = 2ω. Final note: For the special cases of a disk in solid-body motion and the square around a wind field that varies linearly with distance, the vorticity at a point is equal to the average vorticity over the area, ζ = ζ. This is not true in general however. For example, a typical cyclone has decreasing ζ near the center Vorticity in natural coordinates Returning to the natural coordinates as in Ch 3: A ζ = V n + V R s The first term is called the shear vorticity and the second the curvature vorticity. (a) (b) The figure illustrates (a) shear vorticity and (b) curvature vorticity. Remember that ˆn points to left of the wind, so V/n > 0 in (a), and R s is positive so V/R s > 0 in (b). For a flow as shown, there is a combination of shear and curvature vorticity. }Shear vorticity > 0 }Shear vorticity < 0 Curvature Vorticity > 0 The subscript s on R s indicates radius of curvature of a streamline rather than the parcel trajectory. The streamline is an instantaneous snapshot of motion while a trajectory concerns 4
5 a finite length of time. If the pressure field is not time dependent, then there is no difference. Of course generally storm systems move eastward, so steamlines and trajectories are very different (more about this soon). 4.3 Potential Vorticity Not only is the solenoid term zero in a barotropic atmosphere, it is also zero on isentropic surfaces (constant θ). Flow following isentropics surfaces is adiabatic. We are motivated to follow flow on isentropic surfaces because the circulation theorem is much simpler without the solenoid term. Start with Poisson s equation θ = T(p s /p) R/cp and replace T with ρ using the ideal gas law and c v = c p R, we find ρ = (Rθ) 1 p R/cp s p cv/cp. Because ρ = ρ(p) for constant θ, the solenoid term vanishes for adiabatic flow. The circulation theorem is then D (C + 2Ω sin φδa) = 0 where we are taking only fairly small contours. If θ-surfaces are approximately horizontal so f = 2Ω sin φ and ζ C/δA, then and following the motion D [(ζ θ + f)δa] = 0 (ζ θ + f)δa = Const δa δp θ + δθ θ 5 The mass of a parcel is also constant following the motion, so our vortex, which is also a parcel, starts out stubby and wide when the isentropes are close and stretches tall and thin as the isentropes widen. If the depth of the vortex is mass weighted δp/g, then δa ( g/δp) as illustrated.
6 Between isentropes δθ = constant, so δa ( gδθ/δp) too. Hence as δp 0 following the motion the quantity ( P (ζ θ + f) g θ ) = Const p P is Ertel s potential vorticity, or isentropic PV. For the special case of a homogeneous, incompressible fluid (constant ρ) then we need not mass weight, and the depth of the fluid is simply h. Hence δa h 1 and following the motion (ζ θ + f)/h = Const For the really special case of a homogeneous, incompressible fluid with constant depth (ζ θ + f) = Const. But this is a highly idealized case. 4.4 Vorticity Eq Cartesian Coordinates Because ζ = ˆk V, gives D(ζ + f) x minus [v momentum eq. in Cartesian Coordinates] y [u momentum eq. in Cartesian Coordinates] = vorticity dilution + tilting horizontal vortices + microscopic solenoid Vorticity dilution, or the divergence term, (ζ + f) V, is due to stretching (vorticity creation) or shrinking (vorticity dilution) of vortex tubes. It is analogous to the skater who stretches out his/her arms or holds them straight up while spinning. In other words, the divergence term is the fluid analog of the conservation of angular momentum for a rigid body. Picture a purely convergent fluid that acquires rotation from the Coriolis force. The divergence term is most effective at creating vorticity in extratropical cyclones and along fronts. It probably should be called the convergence term since it appears with a minus sign, but it hard to change tradition. 6
7 Tilting horizontal vorticies is the transformation of vertical shear in the horizontal wind into vertical vorticity. The vertical shear in the horizontal wind creates a horizontal vortex tube and a horizontal gradient of the vertical wind tips the horizontal vortex tube so it develops a vertical component. This term is important in frontogenesis and supercell thunderstorms. Microscopic solenoid is like the solenoid term in the circulation theorem but in the limit that the circulating area or cell goes to zero. Imagine the sea breeze or Hadley cell circulation with at least a partial projection in the horizontal plane. This term is not significant for synoptic scale motions Isobaric Coordinates In isobaric coordinates ζ = ˆk p V. Following the same method as above except using isobaric u and v momentum eq., there is no solenoid term in the vorticity equation: D(ζ + f) = (ζ + f) V + ˆk ( ) V p ω Cartesian and isobaric ζ s differ slightly from loss of solenoid term in the isobaric vorticity eq. Scale analysis shows us that the solenoid term is small anyway Scale Analysis of Cartesian coordinate vorticity equation ζ = v x u z y U z L 10 5 s 1 The symbol indicates approximately or less than because of partial cancellation. The ratio ζ f U f o L R o 10 1 This is the Rossby number again. Recall it is also the ratio of the horizontal acceleration to the Coriolis Force. Hence, the vorticity dilution term can be approximated (ζ + f) V f V 7
8 Holton shows that the solenoid term, horizontal vortex tilting term, and vertical advection of absolute vorticity are all small compared to vorticity dilution Hence for normal synoptic scales D h (ζ + f) f V, or for particularly strong vorticity (a safe bet in any case) D h (ζ + f) (ζ + f) V. (1) where the little h on the D stands for horizontal advection only Two interesting points follow: 1) A consistency argument for estimating the scale of horizontal divergence. Recall V g = 0 for f=constant, so V V a /L 10 6 s 1 where we have assumed V a 1 m/s is the characteristic scale of the ageostrophic wind. We can compute the scale of divergence from scale analysis of the vorticity eq. D h ζ (ζ + f) t or V ζ U2 L s 2 With f 10 4 s 1, we can solve for the divergence from Eq 1 V 10 6 s 1 2) An explanation for the relative strength of highs and lows If we ignore advection for a moment so D h ζ (ζ + f) t then ζ t (ζ + f) V. In the NH for cyclonic flow, both ζ and f are positive. Converging wind ( V > 0 with ζ > 0) causes ζ/t > 0, so the vorticity increases further. 8
9 In the NH for anticyclonic flow ζ < 0 and f > 0. But normally ζ << f so ζ + f is usually positive. We normally see ζ < 0 with diverging wind ( V > 0). But cancelation between ζ and f makes the divergence not very effective at making ζ decrease further. In fact as ζ approaches f, ζ/t 0, no amount of divergence matters. 4.5 Vorticity in barotropic fluids Barotropic (Rossby) Potential Vorticity Equation You have already worked homework problems using Holton s Eq 4.13 ζ + f h = Const. Back in Holton section 4.3 this equation was derived from the circulation theorem for the special case of an incompressible homogeneous atmosphere. Implicit in this equation is that ζ is a vertical average. We arrive at this conservation law by starting from the vorticity equation, keeping just the leading term from scale analysis (Eq 1 on the previous page). The result is known as the barotropic potential vorticity equation. The name barotropic is a little misleading because we must assume the atmosphere is incompressible in the continuity equation, so Thus Eq (1) becomes V = w z. D h (ζ + f) = (ζ + f) ( ) w z From here, a small number of steps given in Holton results in D h (ζ + f) = 0 h This equation is sometimes called the incompressible barotropic vorticity equation or the Rossby potential vorticity equation. In general the fluid depth is h(x, y, t) and the height of 9
10 both the top and bottom of the fluid can also vary spatially and in time (ie neither has to be flat). This equation indicates that the creation of vorticity by vertical stretching of vortex tubes balances the horizontal advection of absolute vorticity. Recall barotropic means ρ = ρ(p) and one of the consequences is that the geostrophic wind can have no vertical shear. We also know that the geostrophic wind is divergentless, provided we take f equal to a constant, and hence there is no vertical motion for purely geostrophic flow. Thus the vertical average of ζ in a barotropic fluid can be approximated: ζ ζ g = ˆk V g. Holton has ζ g in the barotropic potential vorticity equation, but you will see it just as often with plain ζ, as it was earlier in the chapter Barotropic Vorticity Equation and the Streamfunction If a barotropic, incompressible fluid has a constant depth h, then the flow is purely horizontal, independent of depth, and V = 0. Thus Eq (1) is D h (ζ + f) = 0 Again Holton has ζ g in his equation, which is the case if we take f equal to a constant in our equation for the momentum, but only with regard to computing ζ. Keep in mind that you may compute ζ in both barotropic vorticity and potential vorticity equations from the true wind or the geostrophic wind. For divergentless horizontal wind, the flow can be represented by a streamfunction Ψ, such that u = Ψ y And as long as the horizontal wind is divergentless, and v = Ψ x ζ = v x u y = 2 Ψ x Ψ y 2 2 Ψ Thus we can use the vorticity equation to forecast the vorticity. Then we can invert the Laplacian operator to find Ψ, and we can determine the wind field as a byproduct, iff the 10
11 wind field is divergentless. Even if V is not divergentless, this procedure allows you to compute the divergentless part of V, which you might like to call V Ψ Happily the geostrophic wind is always divergentless, provided we take f equal to a constant, thus ζ g = v g x u ( g y = f o 1 2 Φ x Φ ) y 2 fo 1 2 Φ In other words, Φ is a streamfunction of the geostrophic wind, provided we take f equal to a constant. Recall that derivatives tend to yield noisy fields and integration tends to make things smoother. Thus it is natural to expect Ψ to be smooth (though wavy), while ζ often has much smaller scale features. 11
= vorticity dilution + tilting horizontal vortices + microscopic solenoid
 4.4 Vorticity Eq 4.4.1 Cartesian Coordinates Because ζ = ˆk V, gives D(ζ + f) x minus [v momentum eq. in Cartesian Coordinates] y [u momentum eq. in Cartesian Coordinates] = vorticity dilution + tilting
4.4 Vorticity Eq 4.4.1 Cartesian Coordinates Because ζ = ˆk V, gives D(ζ + f) x minus [v momentum eq. in Cartesian Coordinates] y [u momentum eq. in Cartesian Coordinates] = vorticity dilution + tilting
1/25/2010. Circulation and vorticity are the two primary
 Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Measurement of Rotation. Circulation. Example. Lecture 4: Circulation and Vorticity 1/31/2017
 Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Circulation and Vorticity
 Circulation and Vorticity Example: Rotation in the atmosphere water vapor satellite animation Circulation a macroscopic measure of rotation for a finite area of a fluid Vorticity a microscopic measure
Circulation and Vorticity Example: Rotation in the atmosphere water vapor satellite animation Circulation a macroscopic measure of rotation for a finite area of a fluid Vorticity a microscopic measure
ESCI 342 Atmospheric Dynamics I Lesson 12 Vorticity
 ESCI 34 tmospheric Dynamics I Lesson 1 Vorticity Reference: n Introduction to Dynamic Meteorology (4 rd edition), Holton n Informal Introduction to Theoretical Fluid Mechanics, Lighthill Reading: Martin,
ESCI 34 tmospheric Dynamics I Lesson 1 Vorticity Reference: n Introduction to Dynamic Meteorology (4 rd edition), Holton n Informal Introduction to Theoretical Fluid Mechanics, Lighthill Reading: Martin,
Chapter 7: Circulation and Vorticity
 Chapter 7: Circulation and Vorticity Circulation C = u ds Integration is performed in a counterclockwise direction C is positive for counterclockwise flow!!! Kelvin s Circulation Theorem The rate of change
Chapter 7: Circulation and Vorticity Circulation C = u ds Integration is performed in a counterclockwise direction C is positive for counterclockwise flow!!! Kelvin s Circulation Theorem The rate of change
t tendency advection convergence twisting baroclinicity
 RELATIVE VORTICITY EQUATION Newton s law in a rotating frame in z-coordinate (frictionless): U + U U = 2Ω U Φ α p U + U U 2 + ( U) U = 2Ω U Φ α p Applying to both sides, and noting ω U and using identities
RELATIVE VORTICITY EQUATION Newton s law in a rotating frame in z-coordinate (frictionless): U + U U = 2Ω U Φ α p U + U U 2 + ( U) U = 2Ω U Φ α p Applying to both sides, and noting ω U and using identities
Circulation and Vorticity. The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation
 Circulation and Vorticity 1. Conservation of Absolute Angular Momentum The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation V = ωr (1)
Circulation and Vorticity 1. Conservation of Absolute Angular Momentum The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation V = ωr (1)
Circulation and Vorticity. The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation
 Circulation and Vticity 1. Conservation of Absolute Angular Momentum The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation V = ωr (1)
Circulation and Vticity 1. Conservation of Absolute Angular Momentum The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation V = ωr (1)
Fixed Rossby Waves: Quasigeostrophic Explanations and Conservation of Potential Vorticity
 Fixed Rossby Waves: Quasigeostrophic Explanations and Conservation of Potential Vorticity 1. Observed Planetary Wave Patterns After upper air observations became routine, it became easy to produce contour
Fixed Rossby Waves: Quasigeostrophic Explanations and Conservation of Potential Vorticity 1. Observed Planetary Wave Patterns After upper air observations became routine, it became easy to produce contour
Using simplified vorticity equation,* by assumption 1 above: *Metr 430 handout on Circulation and Vorticity. Equations (4) and (5) on that handout
 Rossby Wave Equation A. Assumptions 1. Non-divergence 2. Initially, zonal flow, or nearly zonal flow in which u>>v>>w. 3. Initial westerly wind is geostrophic and does not vary along the x-axis and equations
Rossby Wave Equation A. Assumptions 1. Non-divergence 2. Initially, zonal flow, or nearly zonal flow in which u>>v>>w. 3. Initial westerly wind is geostrophic and does not vary along the x-axis and equations
Quasi-Geostrophic ω-equation. 1. The atmosphere is approximately hydrostatic. 2. The atmosphere is approximately geostrophic.
 Quasi-Geostrophic ω-equation For large-scale flow in the atmosphere, we have learned about two very important characteristics:. The atmosphere is approximately hydrostatic.. The atmosphere is approximately
Quasi-Geostrophic ω-equation For large-scale flow in the atmosphere, we have learned about two very important characteristics:. The atmosphere is approximately hydrostatic.. The atmosphere is approximately
Class exercises Chapter 3. Elementary Applications of the Basic Equations
 Class exercises Chapter 3. Elementary Applications of the Basic Equations Section 3.1 Basic Equations in Isobaric Coordinates 3.1 For some (in fact many) applications we assume that the change of the Coriolis
Class exercises Chapter 3. Elementary Applications of the Basic Equations Section 3.1 Basic Equations in Isobaric Coordinates 3.1 For some (in fact many) applications we assume that the change of the Coriolis
Dynamic Meteorology 1
 Dynamic Meteorology 1 Lecture 14 Sahraei Department of Physics, Razi University http://www.razi.ac.ir/sahraei Buys-Ballot rule (Northern Hemisphere) If the wind blows into your back, the Low will be to
Dynamic Meteorology 1 Lecture 14 Sahraei Department of Physics, Razi University http://www.razi.ac.ir/sahraei Buys-Ballot rule (Northern Hemisphere) If the wind blows into your back, the Low will be to
PV Thinking. What is PV thinking?
 PV Thinking CH 06 What is PV thinking? Two main approaches to solving fluid flow problems:. We can integrate the momentum, continuity and thermodynamic equations (the primitive equations) directly.. In
PV Thinking CH 06 What is PV thinking? Two main approaches to solving fluid flow problems:. We can integrate the momentum, continuity and thermodynamic equations (the primitive equations) directly.. In
Vorticity in natural coordinates
 Vorticity in natural coordinates (see Holton pg 95, section 4.2.) Let s consider the vertical vorticity component only, i.e. ζ kˆ ω, we have ω u dl kˆ ω lim --- lim ----------------- curve is in xy plane
Vorticity in natural coordinates (see Holton pg 95, section 4.2.) Let s consider the vertical vorticity component only, i.e. ζ kˆ ω, we have ω u dl kˆ ω lim --- lim ----------------- curve is in xy plane
Control Volume. Dynamics and Kinematics. Basic Conservation Laws. Lecture 1: Introduction and Review 1/24/2017
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review
 Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Note that Rossby waves are tranverse waves, that is the particles move perpendicular to the direction of propagation. f up, down (clockwise)
 Ocean 423 Rossby waves 1 Rossby waves: Restoring force is the north-south gradient of background potential vorticity (f/h). That gradient can be due to either the variation in f with latitude, or to a
Ocean 423 Rossby waves 1 Rossby waves: Restoring force is the north-south gradient of background potential vorticity (f/h). That gradient can be due to either the variation in f with latitude, or to a
Meteorology Lecture 15
 Meteorology Lecture 15 Robert Fovell rfovell@albany.edu 1 Important notes These slides show some figures and videos prepared by Robert G. Fovell (RGF) for his Meteorology course, published by The Great
Meteorology Lecture 15 Robert Fovell rfovell@albany.edu 1 Important notes These slides show some figures and videos prepared by Robert G. Fovell (RGF) for his Meteorology course, published by The Great
Lecture 12: Angular Momentum and the Hadley Circulation
 Lecture 12: Angular Momentum and the Hadley Circulation September 30, 2003 We learnt last time that there is a planetary radiative drive net warming in the tropics, cooling over the pole which induces
Lecture 12: Angular Momentum and the Hadley Circulation September 30, 2003 We learnt last time that there is a planetary radiative drive net warming in the tropics, cooling over the pole which induces
1/3/2011. This course discusses the physical laws that govern atmosphere/ocean motions.
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
BALANCED FLOW: EXAMPLES (PHH lecture 3) Potential Vorticity in the real atmosphere. Potential temperature θ. Rossby Ertel potential vorticity
 BALANCED FLOW: EXAMPLES (PHH lecture 3) Potential Vorticity in the real atmosphere Need to introduce a new measure of the buoyancy Potential temperature θ In a compressible fluid, the relevant measure
BALANCED FLOW: EXAMPLES (PHH lecture 3) Potential Vorticity in the real atmosphere Need to introduce a new measure of the buoyancy Potential temperature θ In a compressible fluid, the relevant measure
Vorticity and Potential Vorticity
 Chapter 4 Vorticity and Potential Vorticity In this chapter we explore a way of solving the shallow water equations for motions with characteristic time scales longer than the rotation period of the earth.
Chapter 4 Vorticity and Potential Vorticity In this chapter we explore a way of solving the shallow water equations for motions with characteristic time scales longer than the rotation period of the earth.
Quasi-geostrophic ocean models
 Quasi-geostrophic ocean models March 19, 2002 1 Introduction The starting point for theoretical and numerical study of the three dimensional large-scale circulation of the atmosphere and ocean is a vorticity
Quasi-geostrophic ocean models March 19, 2002 1 Introduction The starting point for theoretical and numerical study of the three dimensional large-scale circulation of the atmosphere and ocean is a vorticity
Lecture 14. Equations of Motion Currents With Friction Sverdrup, Stommel, and Munk Solutions Remember that Ekman's solution for wind-induced transport
 Lecture 14. Equations of Motion Currents With Friction Sverdrup, Stommel, and Munk Solutions Remember that Ekman's solution for wind-induced transport is which can also be written as (14.1) i.e., #Q x,y
Lecture 14. Equations of Motion Currents With Friction Sverdrup, Stommel, and Munk Solutions Remember that Ekman's solution for wind-induced transport is which can also be written as (14.1) i.e., #Q x,y
Chapter 9. Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation
 Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
Houze sections 7.4, 8.3, 8.5, Refer back to equations in Section 2.3 when necessary.
 Thunderstorm Dynamics Houze sections 7.4, 8.3, 8.5, Refer back to equations in Section.3 when necessary. Bluestein Vol. II section 3.4.6. Review article "Dynamics of Tornadic Thunderstorms" by Klemp handout.
Thunderstorm Dynamics Houze sections 7.4, 8.3, 8.5, Refer back to equations in Section.3 when necessary. Bluestein Vol. II section 3.4.6. Review article "Dynamics of Tornadic Thunderstorms" by Klemp handout.
1/18/2011. From the hydrostatic equation, it is clear that a single. pressure and height in each vertical column of the atmosphere.
 Lecture 3: Applications of Basic Equations Pressure as Vertical Coordinate From the hydrostatic equation, it is clear that a single valued monotonic relationship exists between pressure and height in each
Lecture 3: Applications of Basic Equations Pressure as Vertical Coordinate From the hydrostatic equation, it is clear that a single valued monotonic relationship exists between pressure and height in each
Atmospheric dynamics and meteorology
 Atmospheric dynamics and meteorology B. Legras, http://www.lmd.ens.fr/legras III Frontogenesis (pre requisite: quasi-geostrophic equation, baroclinic instability in the Eady and Phillips models ) Recommended
Atmospheric dynamics and meteorology B. Legras, http://www.lmd.ens.fr/legras III Frontogenesis (pre requisite: quasi-geostrophic equation, baroclinic instability in the Eady and Phillips models ) Recommended
Chapter 2. Quasi-Geostrophic Theory: Formulation (review) ε =U f o L <<1, β = 2Ω cosθ o R. 2.1 Introduction
 Chapter 2. Quasi-Geostrophic Theory: Formulation (review) 2.1 Introduction For most of the course we will be concerned with instabilities that an be analyzed by the quasi-geostrophic equations. These are
Chapter 2. Quasi-Geostrophic Theory: Formulation (review) 2.1 Introduction For most of the course we will be concerned with instabilities that an be analyzed by the quasi-geostrophic equations. These are
Balance. in the vertical too
 Balance. in the vertical too Gradient wind balance f n Balanced flow (no friction) More complicated (3- way balance), however, better approximation than geostrophic (as allows for centrifugal acceleration
Balance. in the vertical too Gradient wind balance f n Balanced flow (no friction) More complicated (3- way balance), however, better approximation than geostrophic (as allows for centrifugal acceleration
g (z) = 1 (1 + z/a) = 1
 1.4.2 Gravitational Force g is the gravitational force. It always points towards the center of mass, and it is proportional to the inverse square of the distance above the center of mass: g (z) = GM (a
1.4.2 Gravitational Force g is the gravitational force. It always points towards the center of mass, and it is proportional to the inverse square of the distance above the center of mass: g (z) = GM (a
The dynamics of high and low pressure systems
 The dynamics of high and low pressure systems Newton s second law for a parcel of air in an inertial coordinate system (a coordinate system in which the coordinate axes do not change direction and are
The dynamics of high and low pressure systems Newton s second law for a parcel of air in an inertial coordinate system (a coordinate system in which the coordinate axes do not change direction and are
( ) (9.1.1) Chapter 9. Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation. 9.1 Geostrophy and scaling.
 Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
2.5 Shallow water equations, quasigeostrophic filtering, and filtering of inertia-gravity waves
 Chapter. The continuous equations φ=gh Φ=gH φ s =gh s Fig..5: Schematic of the shallow water model, a hydrostatic, incompressible fluid with a rigid bottom h s (x,y), a free surface h(x,y,t), and horizontal
Chapter. The continuous equations φ=gh Φ=gH φ s =gh s Fig..5: Schematic of the shallow water model, a hydrostatic, incompressible fluid with a rigid bottom h s (x,y), a free surface h(x,y,t), and horizontal
The Equations of Motion in a Rotating Coordinate System. Chapter 3
 The Equations of Motion in a Rotating Coordinate System Chapter 3 Since the earth is rotating about its axis and since it is convenient to adopt a frame of reference fixed in the earth, we need to study
The Equations of Motion in a Rotating Coordinate System Chapter 3 Since the earth is rotating about its axis and since it is convenient to adopt a frame of reference fixed in the earth, we need to study
Lecture 8. Lecture 1. Wind-driven gyres. Ekman transport and Ekman pumping in a typical ocean basin. VEk
 Lecture 8 Lecture 1 Wind-driven gyres Ekman transport and Ekman pumping in a typical ocean basin. VEk wek > 0 VEk wek < 0 VEk 1 8.1 Vorticity and circulation The vorticity of a parcel is a measure of its
Lecture 8 Lecture 1 Wind-driven gyres Ekman transport and Ekman pumping in a typical ocean basin. VEk wek > 0 VEk wek < 0 VEk 1 8.1 Vorticity and circulation The vorticity of a parcel is a measure of its
2 Equations of Motion
 2 Equations of Motion system. In this section, we will derive the six full equations of motion in a non-rotating, Cartesian coordinate 2.1 Six equations of motion (non-rotating, Cartesian coordinates)
2 Equations of Motion system. In this section, we will derive the six full equations of motion in a non-rotating, Cartesian coordinate 2.1 Six equations of motion (non-rotating, Cartesian coordinates)
Chapter 6: Vector Analysis
 Chapter 6: Vector Analysis We use derivatives and various products of vectors in all areas of physics. For example, Newton s 2nd law is F = m d2 r. In electricity dt 2 and magnetism, we need surface and
Chapter 6: Vector Analysis We use derivatives and various products of vectors in all areas of physics. For example, Newton s 2nd law is F = m d2 r. In electricity dt 2 and magnetism, we need surface and
Effective Depth of Ekman Layer.
 5.5: Ekman Pumping Effective Depth of Ekman Layer. 2 Effective Depth of Ekman Layer. Defining γ = f/2k, we derived the solution u = u g (1 e γz cos γz) v = u g e γz sin γz corresponding to the Ekman spiral.
5.5: Ekman Pumping Effective Depth of Ekman Layer. 2 Effective Depth of Ekman Layer. Defining γ = f/2k, we derived the solution u = u g (1 e γz cos γz) v = u g e γz sin γz corresponding to the Ekman spiral.
ρ x + fv f 'w + F x ρ y fu + F y Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ Dv Dt + u2 tanφ + vw a a = 1 p Dw Dt u2 + v 2
 Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
Chapter 3. Stability theory for zonal flows :formulation
 Chapter 3. Stability theory for zonal flows :formulation 3.1 Introduction Although flows in the atmosphere and ocean are never strictly zonal major currents are nearly so and the simplifications springing
Chapter 3. Stability theory for zonal flows :formulation 3.1 Introduction Although flows in the atmosphere and ocean are never strictly zonal major currents are nearly so and the simplifications springing
Part 4. Atmospheric Dynamics
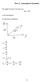 Part 4. Atmospheric Dynamics We apply Newton s Second Law: ma =Σ F i to the atmosphere. In Cartesian coordinates dx u = dt dy v = dt dz w = dt 1 ai = F m i i du dv dw a = ; ay = ; az = x dt dt dt 78 Coordinate
Part 4. Atmospheric Dynamics We apply Newton s Second Law: ma =Σ F i to the atmosphere. In Cartesian coordinates dx u = dt dy v = dt dz w = dt 1 ai = F m i i du dv dw a = ; ay = ; az = x dt dt dt 78 Coordinate
Mathematical Concepts & Notation
 Mathematical Concepts & Notation Appendix A: Notation x, δx: a small change in x t : the partial derivative with respect to t holding the other variables fixed d : the time derivative of a quantity that
Mathematical Concepts & Notation Appendix A: Notation x, δx: a small change in x t : the partial derivative with respect to t holding the other variables fixed d : the time derivative of a quantity that
The general circulation: midlatitude storms
 The general circulation: midlatitude storms Motivation for this class Provide understanding basic motions of the atmosphere: Ability to diagnose individual weather systems, and predict how they will change
The general circulation: midlatitude storms Motivation for this class Provide understanding basic motions of the atmosphere: Ability to diagnose individual weather systems, and predict how they will change
TROPICAL CYCLONE MOTION
 Chapter 3 TROPICAL CYCLONE MOTION The prediction of tropical cyclone motion has improved dramatically during the last decade as has our understanding of the mechanisms involved. Some of the basic aspects
Chapter 3 TROPICAL CYCLONE MOTION The prediction of tropical cyclone motion has improved dramatically during the last decade as has our understanding of the mechanisms involved. Some of the basic aspects
6 Two-layer shallow water theory.
 6 Two-layer shallow water theory. Wewillnowgoontolookatashallowwatersystemthathastwolayersofdifferent density. This is the next level of complexity and a simple starting point for understanding the behaviour
6 Two-layer shallow water theory. Wewillnowgoontolookatashallowwatersystemthathastwolayersofdifferent density. This is the next level of complexity and a simple starting point for understanding the behaviour
Mechanics Cycle 1 Chapter 12. Chapter 12. Forces Causing Curved Motion
 Chapter 1 Forces Causing Curved Motion A Force Must be Applied to Change Direction Coordinates, Angles, Angular Velocity, and Angular Acceleration Centripetal Acceleration and Tangential Acceleration Along
Chapter 1 Forces Causing Curved Motion A Force Must be Applied to Change Direction Coordinates, Angles, Angular Velocity, and Angular Acceleration Centripetal Acceleration and Tangential Acceleration Along
Balanced Flow Geostrophic, Inertial, Gradient, and Cyclostrophic Flow
 Balanced Flow Geostrophic, Inertial, Gradient, and Cyclostrophic Flow The types of atmospheric flows describe here have the following characteristics: 1) Steady state (meaning that the flows do not change
Balanced Flow Geostrophic, Inertial, Gradient, and Cyclostrophic Flow The types of atmospheric flows describe here have the following characteristics: 1) Steady state (meaning that the flows do not change
Fronts & Frontogenesis
 Fronts & Frontogenesis Fronts & Frontogenesis In a landmark paper, Sawyer (1956) stated that although the Norwegian system of frontal analysis has been generally accepted by weather forecasters since the
Fronts & Frontogenesis Fronts & Frontogenesis In a landmark paper, Sawyer (1956) stated that although the Norwegian system of frontal analysis has been generally accepted by weather forecasters since the
Dynamics and Kinematics
 Geophysics Fluid Dynamics () Syllabus Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3,
Geophysics Fluid Dynamics () Syllabus Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3,
The equation we worked with for waves and geostrophic adjustment of a 1-layer fluid is η tt
 GEOPHYSICAL FLUID DYNAMICS-I OC512/AS509 2015 P.Rhines LECTUREs 11-12 week 6 9-14 Geostrophic adjustment and overturning circulations with continuous stratification. The equation we worked with for waves
GEOPHYSICAL FLUID DYNAMICS-I OC512/AS509 2015 P.Rhines LECTUREs 11-12 week 6 9-14 Geostrophic adjustment and overturning circulations with continuous stratification. The equation we worked with for waves
3.1 Definition Physical meaning Streamfunction and vorticity The Rankine vortex Circulation...
 Chapter 3 Vorticity Contents 3.1 Definition.................................. 19 3.2 Physical meaning............................. 19 3.3 Streamfunction and vorticity...................... 21 3.4 The Rankine
Chapter 3 Vorticity Contents 3.1 Definition.................................. 19 3.2 Physical meaning............................. 19 3.3 Streamfunction and vorticity...................... 21 3.4 The Rankine
Geophysics Fluid Dynamics (ESS228)
 Geophysics Fluid Dynamics (ESS228) Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3, 4,
Geophysics Fluid Dynamics (ESS228) Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3, 4,
ERTH 465 Fall Lab 5. Absolute Geostrophic Vorticity. 200 points.
 Name Date ERTH 465 Fall 2015 Lab 5 Absolute Geostrophic Vorticity 200 points. 1. All labs are to be kept in a three hole binder. Turn in the binder when you have finished the Lab. 2. Show all work in mathematical
Name Date ERTH 465 Fall 2015 Lab 5 Absolute Geostrophic Vorticity 200 points. 1. All labs are to be kept in a three hole binder. Turn in the binder when you have finished the Lab. 2. Show all work in mathematical
Vortex stretching in incompressible and compressible fluids
 Vortex stretching in incompressible and compressible fluids Esteban G. Tabak, Fluid Dynamics II, Spring 00 1 Introduction The primitive form of the incompressible Euler equations is given by ( ) du P =
Vortex stretching in incompressible and compressible fluids Esteban G. Tabak, Fluid Dynamics II, Spring 00 1 Introduction The primitive form of the incompressible Euler equations is given by ( ) du P =
Dynamics Rotating Tank
 Institute for Atmospheric and Climate Science - IACETH Atmospheric Physics Lab Work Dynamics Rotating Tank Large scale flows on different latitudes of the rotating Earth Abstract The large scale atmospheric
Institute for Atmospheric and Climate Science - IACETH Atmospheric Physics Lab Work Dynamics Rotating Tank Large scale flows on different latitudes of the rotating Earth Abstract The large scale atmospheric
Part-8c Circulation (Cont)
 Part-8c Circulation (Cont) Global Circulation Means of Transfering Heat Easterlies /Westerlies Polar Front Planetary Waves Gravity Waves Mars Circulation Giant Planet Atmospheres Zones and Belts Global
Part-8c Circulation (Cont) Global Circulation Means of Transfering Heat Easterlies /Westerlies Polar Front Planetary Waves Gravity Waves Mars Circulation Giant Planet Atmospheres Zones and Belts Global
g (z) = 1 (1 + z/a) = 1 1 ( km/10 4 km) 2
 1.4.2 Gravitational Force g is the gravitational force. It always points towards the center of mass, and it is proportional to the inverse square of the distance above the center of mass: g (z) = GM (a
1.4.2 Gravitational Force g is the gravitational force. It always points towards the center of mass, and it is proportional to the inverse square of the distance above the center of mass: g (z) = GM (a
The Planetary Circulation System
 12 The Planetary Circulation System Learning Goals After studying this chapter, students should be able to: 1. describe and account for the global patterns of pressure, wind patterns and ocean currents
12 The Planetary Circulation System Learning Goals After studying this chapter, students should be able to: 1. describe and account for the global patterns of pressure, wind patterns and ocean currents
Fundamentals of Atmospheric Modelling
 M.Sc. in Computational Science Fundamentals of Atmospheric Modelling Peter Lynch, Met Éireann Mathematical Computation Laboratory (Opp. Room 30) Dept. of Maths. Physics, UCD, Belfield. January April, 2004.
M.Sc. in Computational Science Fundamentals of Atmospheric Modelling Peter Lynch, Met Éireann Mathematical Computation Laboratory (Opp. Room 30) Dept. of Maths. Physics, UCD, Belfield. January April, 2004.
 http://www.ssec.wisc.edu/data/composites.html Red curve: Incoming solar radiation Blue curve: Outgoing infrared radiation. Three-cell model of general circulation Mid-latitudes: 30 to 60 latitude MID-LATITUDES
http://www.ssec.wisc.edu/data/composites.html Red curve: Incoming solar radiation Blue curve: Outgoing infrared radiation. Three-cell model of general circulation Mid-latitudes: 30 to 60 latitude MID-LATITUDES
1/27/2010. With this method, all filed variables are separated into. from the basic state: Assumptions 1: : the basic state variables must
 Lecture 5: Waves in Atmosphere Perturbation Method With this method, all filed variables are separated into two parts: (a) a basic state part and (b) a deviation from the basic state: Perturbation Method
Lecture 5: Waves in Atmosphere Perturbation Method With this method, all filed variables are separated into two parts: (a) a basic state part and (b) a deviation from the basic state: Perturbation Method
Quick Recapitulation of Fluid Mechanics
 Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
The atmosphere in motion: forces and wind. AT350 Ahrens Chapter 9
 The atmosphere in motion: forces and wind AT350 Ahrens Chapter 9 Recall that Pressure is force per unit area Air pressure is determined by the weight of air above A change in pressure over some distance
The atmosphere in motion: forces and wind AT350 Ahrens Chapter 9 Recall that Pressure is force per unit area Air pressure is determined by the weight of air above A change in pressure over some distance
Quasi-geostrophic system
 Quasi-eostrophic system (or, why we love elliptic equations for QGPV) Charney s QG the motion of lare-scale atmospheric disturbances is overned by Laws of conservation of potential temperature and potential
Quasi-eostrophic system (or, why we love elliptic equations for QGPV) Charney s QG the motion of lare-scale atmospheric disturbances is overned by Laws of conservation of potential temperature and potential
Isentropic Analysis. We can look at weather data in other ways besides on constantpressure. Meteorology 411 Iowa State University Week 11 Bill Gallus
 Isentropic Analysis We can look at weather data in other ways besides on constantpressure surfaces! Meteorology 411 Iowa State University Week 11 Bill Gallus A brief history of meteorology In the 1930s
Isentropic Analysis We can look at weather data in other ways besides on constantpressure surfaces! Meteorology 411 Iowa State University Week 11 Bill Gallus A brief history of meteorology In the 1930s
Gravity Waves. Lecture 5: Waves in Atmosphere. Waves in the Atmosphere and Oceans. Internal Gravity (Buoyancy) Waves 2/9/2017
 Lecture 5: Waves in Atmosphere Perturbation Method Properties of Wave Shallow Water Model Gravity Waves Rossby Waves Waves in the Atmosphere and Oceans Restoring Force Conservation of potential temperature
Lecture 5: Waves in Atmosphere Perturbation Method Properties of Wave Shallow Water Model Gravity Waves Rossby Waves Waves in the Atmosphere and Oceans Restoring Force Conservation of potential temperature
The General Circulation of the Atmosphere: A Numerical Experiment
 The General Circulation of the Atmosphere: A Numerical Experiment Norman A. Phillips (1956) Presentation by Lukas Strebel and Fabian Thüring Goal of the Model Numerically predict the mean state of the
The General Circulation of the Atmosphere: A Numerical Experiment Norman A. Phillips (1956) Presentation by Lukas Strebel and Fabian Thüring Goal of the Model Numerically predict the mean state of the
Geostrophic and Quasi-Geostrophic Balances
 Geostrophic and Quasi-Geostrophic Balances Qiyu Xiao June 19, 2018 1 Introduction Understanding how the atmosphere and ocean behave is important to our everyday lives. Techniques such as weather forecasting
Geostrophic and Quasi-Geostrophic Balances Qiyu Xiao June 19, 2018 1 Introduction Understanding how the atmosphere and ocean behave is important to our everyday lives. Techniques such as weather forecasting
Internal boundary layers in the ocean circulation
 Internal boundary layers in the ocean circulation Lecture 9 by Andrew Wells We have so far considered boundary layers adjacent to physical boundaries. However, it is also possible to find boundary layers
Internal boundary layers in the ocean circulation Lecture 9 by Andrew Wells We have so far considered boundary layers adjacent to physical boundaries. However, it is also possible to find boundary layers
Atmosphere, Ocean and Climate Dynamics Answers to Chapter 8
 Atmosphere, Ocean and Climate Dynamics Answers to Chapter 8 1. Consider a zonally symmetric circulation (i.e., one with no longitudinal variations) in the atmosphere. In the inviscid upper troposphere,
Atmosphere, Ocean and Climate Dynamics Answers to Chapter 8 1. Consider a zonally symmetric circulation (i.e., one with no longitudinal variations) in the atmosphere. In the inviscid upper troposphere,
Final Examination, MEA 443 Fall 2008, Lackmann
 Place an X here to count it double! Name: Final Examination, MEA 443 Fall 2008, Lackmann If you wish to have the final exam count double and replace your midterm score, place an X in the box above. As
Place an X here to count it double! Name: Final Examination, MEA 443 Fall 2008, Lackmann If you wish to have the final exam count double and replace your midterm score, place an X in the box above. As
Dynamics of Upper-Level Waves
 Dynamics of Upper-Level Waves Atmos 5110 Synoptic Dynamic Meteorology I Instructor: Jim Steenburgh jim.steenburgh@utah.edu 801-581-8727 Suite 480/Office 488 INSCC Suggested reading: Lackman (2011) section
Dynamics of Upper-Level Waves Atmos 5110 Synoptic Dynamic Meteorology I Instructor: Jim Steenburgh jim.steenburgh@utah.edu 801-581-8727 Suite 480/Office 488 INSCC Suggested reading: Lackman (2011) section
Solution to Problems #1. I. Information Given or Otherwise Known. = 28 m/s. Heading of the ultralight aircraft!! h
 METR 520: Atmospheric Dynamics II Dr. Dave Dempsey Dept. of Geosciences, SFSU Spring 2012 Solution to Problems 1 Problem 1 An ultralight aircraft is flying. I. Information Given or Otherwise Known Horizontal
METR 520: Atmospheric Dynamics II Dr. Dave Dempsey Dept. of Geosciences, SFSU Spring 2012 Solution to Problems 1 Problem 1 An ultralight aircraft is flying. I. Information Given or Otherwise Known Horizontal
4. Atmospheric transport. Daniel J. Jacob, Atmospheric Chemistry, Harvard University, Spring 2017
 4. Atmospheric transport Daniel J. Jacob, Atmospheric Chemistry, Harvard University, Spring 2017 Forces in the atmosphere: Gravity g Pressure-gradient ap = ( 1/ ρ ) dp / dx for x-direction (also y, z directions)
4. Atmospheric transport Daniel J. Jacob, Atmospheric Chemistry, Harvard University, Spring 2017 Forces in the atmosphere: Gravity g Pressure-gradient ap = ( 1/ ρ ) dp / dx for x-direction (also y, z directions)
SIO 210: Dynamics VI (Potential vorticity) L. Talley Fall, 2014 (Section 2: including some derivations) (this lecture was not given in 2015)
 SIO 210: Dynamics VI (Potential vorticity) L. Talley Fall, 2014 (Section 2: including some derivations) (this lecture was not given in 2015) Variation of Coriolis with latitude: β Vorticity Potential vorticity
SIO 210: Dynamics VI (Potential vorticity) L. Talley Fall, 2014 (Section 2: including some derivations) (this lecture was not given in 2015) Variation of Coriolis with latitude: β Vorticity Potential vorticity
EART164: PLANETARY ATMOSPHERES
 EART164: PLANETARY ATMOSPHERES Francis Nimmo Last Week Radiative Transfer Black body radiation, Planck function, Wien s law Absorption, emission, opacity, optical depth Intensity, flux Radiative diffusion,
EART164: PLANETARY ATMOSPHERES Francis Nimmo Last Week Radiative Transfer Black body radiation, Planck function, Wien s law Absorption, emission, opacity, optical depth Intensity, flux Radiative diffusion,
The Vorticity Equation in a Rotating Stratified Fluid
 Capter 7 Te Vorticity Equation in a Rotating Stratified Fluid Te vorticity equation for a rotating, stratified, viscous fluid Te vorticity equation in one form or anoter and its interpretation provide
Capter 7 Te Vorticity Equation in a Rotating Stratified Fluid Te vorticity equation for a rotating, stratified, viscous fluid Te vorticity equation in one form or anoter and its interpretation provide
) 2 ψ +β ψ. x = 0. (71) ν = uk βk/k 2, (74) c x u = β/k 2. (75)
 3 Rossby Waves 3.1 Free Barotropic Rossby Waves The dispersion relation for free barotropic Rossby waves can be derived by linearizing the barotropic vortiticy equation in the form (21). This equation
3 Rossby Waves 3.1 Free Barotropic Rossby Waves The dispersion relation for free barotropic Rossby waves can be derived by linearizing the barotropic vortiticy equation in the form (21). This equation
Eliassen-Palm Cross Sections Edmon et al. (1980)
 Eliassen-Palm Cross Sections Edmon et al. (1980) Cecily Keppel November 14 2014 Eliassen-Palm Flux For β-plane Coordinates (y, p) in northward, vertical directions Zonal means F = v u f (y) v θ θ p F will
Eliassen-Palm Cross Sections Edmon et al. (1980) Cecily Keppel November 14 2014 Eliassen-Palm Flux For β-plane Coordinates (y, p) in northward, vertical directions Zonal means F = v u f (y) v θ θ p F will
3 Generation and diffusion of vorticity
 Version date: March 22, 21 1 3 Generation and diffusion of vorticity 3.1 The vorticity equation We start from Navier Stokes: u t + u u = 1 ρ p + ν 2 u 1) where we have not included a term describing a
Version date: March 22, 21 1 3 Generation and diffusion of vorticity 3.1 The vorticity equation We start from Navier Stokes: u t + u u = 1 ρ p + ν 2 u 1) where we have not included a term describing a
Equatorial Superrotation on Tidally Locked Exoplanets
 Equatorial Superrotation on Tidally Locked Exoplanets Adam P. Showman University of Arizona Lorenzo M. Polvani Columbia University Synopsis Most 3D atmospheric circulation models of tidally locked exoplanets
Equatorial Superrotation on Tidally Locked Exoplanets Adam P. Showman University of Arizona Lorenzo M. Polvani Columbia University Synopsis Most 3D atmospheric circulation models of tidally locked exoplanets
SIO 210: Dynamics VI: Potential vorticity
 SIO 210: Dynamics VI: Potential vorticity Variation of Coriolis with latitude: β Vorticity Potential vorticity Rossby waves READING: Review Section 7.2.3 Section 7.7.1 through 7.7.4 or Supplement S7.7
SIO 210: Dynamics VI: Potential vorticity Variation of Coriolis with latitude: β Vorticity Potential vorticity Rossby waves READING: Review Section 7.2.3 Section 7.7.1 through 7.7.4 or Supplement S7.7
EAS372 Open Book Final Exam 11 April, 2013
 EAS372 Open Book Final Exam 11 April, 2013 Professor: J.D. Wilson Time available: 2 hours Value: 30% Please check the Terminology, Equations and Data section before beginning your responses. Answer all
EAS372 Open Book Final Exam 11 April, 2013 Professor: J.D. Wilson Time available: 2 hours Value: 30% Please check the Terminology, Equations and Data section before beginning your responses. Answer all
196 7 atmospheric oscillations:
 196 7 atmospheric oscillations: 7.4 INTERNAL GRAVITY (BUOYANCY) WAVES We now consider the nature of gravity wave propagation in the atmosphere. Atmospheric gravity waves can only exist when the atmosphere
196 7 atmospheric oscillations: 7.4 INTERNAL GRAVITY (BUOYANCY) WAVES We now consider the nature of gravity wave propagation in the atmosphere. Atmospheric gravity waves can only exist when the atmosphere
Continuum Mechanics Lecture 5 Ideal fluids
 Continuum Mechanics Lecture 5 Ideal fluids Prof. http://www.itp.uzh.ch/~teyssier Outline - Helmholtz decomposition - Divergence and curl theorem - Kelvin s circulation theorem - The vorticity equation
Continuum Mechanics Lecture 5 Ideal fluids Prof. http://www.itp.uzh.ch/~teyssier Outline - Helmholtz decomposition - Divergence and curl theorem - Kelvin s circulation theorem - The vorticity equation
Vorticity Equation Marine Hydrodynamics Lecture 9. Return to viscous incompressible flow. N-S equation: v. Now: v = v + = 0 incompressible
 13.01 Marine Hydrodynamics, Fall 004 Lecture 9 Copyright c 004 MIT - Department of Ocean Engineering, All rights reserved. Vorticity Equation 13.01 - Marine Hydrodynamics Lecture 9 Return to viscous incompressible
13.01 Marine Hydrodynamics, Fall 004 Lecture 9 Copyright c 004 MIT - Department of Ocean Engineering, All rights reserved. Vorticity Equation 13.01 - Marine Hydrodynamics Lecture 9 Return to viscous incompressible
d v 2 v = d v d t i n where "in" and "rot" denote the inertial (absolute) and rotating frames. Equation of motion F =
 Governing equations of fluid dynamics under the influence of Earth rotation (Navier-Stokes Equations in rotating frame) Recap: From kinematic consideration, d v i n d t i n = d v rot d t r o t 2 v rot
Governing equations of fluid dynamics under the influence of Earth rotation (Navier-Stokes Equations in rotating frame) Recap: From kinematic consideration, d v i n d t i n = d v rot d t r o t 2 v rot
On the effect of forward shear and reversed shear baroclinic flows for polar low developments. Thor Erik Nordeng Norwegian Meteorological Institute
 On the effect of forward shear and reversed shear baroclinic flows for polar low developments Thor Erik Nordeng Norwegian Meteorological Institute Outline Baroclinic growth a) Normal mode solution b) Initial
On the effect of forward shear and reversed shear baroclinic flows for polar low developments Thor Erik Nordeng Norwegian Meteorological Institute Outline Baroclinic growth a) Normal mode solution b) Initial
where p oo is a reference level constant pressure (often 10 5 Pa). Since θ is conserved for adiabatic motions, a prognostic temperature equation is:
 1 Appendix C Useful Equations Purposes: Provide foundation equations and sketch some derivations. These equations are used as starting places for discussions in various parts of the book. C.1. Thermodynamic
1 Appendix C Useful Equations Purposes: Provide foundation equations and sketch some derivations. These equations are used as starting places for discussions in various parts of the book. C.1. Thermodynamic
Errata: Midlatitude Synoptic Meteorology (July, 2014)
 Errata: Midlatitude Synoptic Meteorology (July, 2014) My apologies for the various inevitable errors contained in this first-edition text. We are working diligently to correct them. I gratefully acknowledge
Errata: Midlatitude Synoptic Meteorology (July, 2014) My apologies for the various inevitable errors contained in this first-edition text. We are working diligently to correct them. I gratefully acknowledge
Use of dynamical concepts in weather forecasting
 Use of dynamical concepts in weather forecasting Meteorol. Appl. 4, 345 352 (1997) E B Carroll, Meteorological Office, London Road, Bracknell, Berkshire RG12 2SZ, UK A divergence-based procedure for diagnosing
Use of dynamical concepts in weather forecasting Meteorol. Appl. 4, 345 352 (1997) E B Carroll, Meteorological Office, London Road, Bracknell, Berkshire RG12 2SZ, UK A divergence-based procedure for diagnosing
ATMOSPHERIC AND OCEANIC FLUID DYNAMICS
 ATMOSPHERIC AND OCEANIC FLUID DYNAMICS Fundamentals and Large-scale Circulation G E O F F R E Y K. V A L L I S Princeton University, New Jersey CAMBRIDGE UNIVERSITY PRESS An asterisk indicates more advanced
ATMOSPHERIC AND OCEANIC FLUID DYNAMICS Fundamentals and Large-scale Circulation G E O F F R E Y K. V A L L I S Princeton University, New Jersey CAMBRIDGE UNIVERSITY PRESS An asterisk indicates more advanced
The Shallow Water Equations
 If you have not already done so, you are strongly encouraged to read the companion file on the non-divergent barotropic vorticity equation, before proceeding to this shallow water case. We do not repeat
If you have not already done so, you are strongly encouraged to read the companion file on the non-divergent barotropic vorticity equation, before proceeding to this shallow water case. We do not repeat
Nonlinear Balance on an Equatorial Beta Plane
 Nonlinear Balance on an Equatorial Beta Plane David J. Raymond Physics Department and Geophysical Research Center New Mexico Tech Socorro, NM 87801 April 26, 2009 Summary Extension of the nonlinear balance
Nonlinear Balance on an Equatorial Beta Plane David J. Raymond Physics Department and Geophysical Research Center New Mexico Tech Socorro, NM 87801 April 26, 2009 Summary Extension of the nonlinear balance
EESC V2100 The Climate System spring 2004 Lecture 4: Laws of Atmospheric Motion and Weather
 EESC V2100 The Climate System spring 2004 Lecture 4: Laws of Atmospheric Motion and Weather Yochanan Kushnir Lamont Doherty Earth Observatory of Columbia University Palisades, NY 10964, USA kushnir@ldeo.columbia.edu
EESC V2100 The Climate System spring 2004 Lecture 4: Laws of Atmospheric Motion and Weather Yochanan Kushnir Lamont Doherty Earth Observatory of Columbia University Palisades, NY 10964, USA kushnir@ldeo.columbia.edu
2. Baroclinic Instability and Midlatitude Dynamics
 2. Baroclinic Instability and Midlatitude Dynamics Midlatitude Jet Stream Climatology (Atlantic and Pacific) Copyright 26 Emily Shuckburgh, University of Cambridge. Not to be quoted or reproduced without
2. Baroclinic Instability and Midlatitude Dynamics Midlatitude Jet Stream Climatology (Atlantic and Pacific) Copyright 26 Emily Shuckburgh, University of Cambridge. Not to be quoted or reproduced without
Vortex motion. Wasilij Barsukow, July 1, 2016
 The concept of vorticity We call Vortex motion Wasilij Barsukow, mail@sturzhang.de July, 206 ω = v vorticity. It is a measure of the swirlyness of the flow, but is also present in shear flows where the
The concept of vorticity We call Vortex motion Wasilij Barsukow, mail@sturzhang.de July, 206 ω = v vorticity. It is a measure of the swirlyness of the flow, but is also present in shear flows where the
