Circulation and Vorticity
|
|
|
- Thomas Stokes
- 5 years ago
- Views:
Transcription
1 Circulation and Vorticity Example: Rotation in the atmosphere water vapor satellite animation Circulation a macroscopic measure of rotation for a finite area of a fluid Vorticity a microscopic measure of rotation at any point in a fluid Circulation is a scalar quantity while vorticity is a vector quantity. Circulation Theorem Circulation is defined as the line integral around a closed contour in a fluid of the velocity component tangent to the contour C U dl = U cosαdl By convention C is evaluated for counterclockwise integration around the contour. When will C be positive (negative)?
2 Consider a fluid in solid body rotation with angular velocity W. For a circular ring of fluid with radius R: V = WR dl = Rdl Then the circulation is: C = ΩRdl = 2πΩR 2 What is the relationship between C and angular momentum in this case? What is the relationship between C and angular velocity in this case? C can be used to describe the rotation in cases where it is difficult to define an axis of rotation and thus angular velocity. How will C change over time? Take total derivative of C in an inertial reference frame: D a C a But: D a U a = D a D a U a U a dl = dl = 1 p Φ, ρ D a U a dl + U a D a d l is just the line integral of the acceleration of wind: where we have neglected the friction force, do not need to consider the Coriolis force for an inertial reference frame, and have expressed the gravitational force as a gradient of the geopotential.
3 dl Noting that: then and: = D U a dl a = D a U a U a D adl = U a D a U a = 1 D a ( U a U a ) = 0 2 Using this the change in absolute circulation following the motion is: D a C a = 1 p d l Φ dl ρ The line integral of the gravitational force is given by: Φ dl = gk dl = gdz = dφ = 0 Then the change in circulation is given by: D a C a = 1 p d l = 1 ρ ρ dp What is the physical interpretation of each term in this equation? The sea breeze circulation What are the physical mechanisms that lead to sea breeze formation? Example: Calculate the change in circulation associated with a sea breeze
4 For a barotropic fluid r = r(p) and 1 ρ dp = 0 so: D a C a = 0 and absolute circulation is conserved following the motion. This is known as Kelvin s circulation theorem. What is the relationship between absolute and relative circulation? Ca absolute circulation Ce circulation due to the rotation of the Earth C relative circulation Ca = Ce + C The circulation due to the rotation of the Earth is given by: C e = U e = Ω r U e dl, where Stokes theorem: F ds = F is the velocity due to the rotation of the Earth A ( ) n da, where n is the unit vector normal to the area A and the direction of n is defined by the right-hand rule for counterclockwise integration of the line integral. Using Stokes theorem we can rewrite our equation for Ce as: C e = U e dl = ( U e ) A n da
5 Using the vector identity: ( U e ) = Ω r For a horizontal plane where we have used Then: is directed in the vertical direction and = 2ΩsinφA = 2ΩA e, where Ae is the area projected onto the equatorial plane and: Ae = Asinf ( ) = ( Ω R ) = Ω n ( U e ) n = 2Ω n = 2Ωsin φ = f C e = A ( U e ) n da, Ω = Ωcosφ j + Ωsin φk R = 2Ω Then: C = Ca Ce = Ca 2WAsinf = Ca 2WAe The relative circulation (C) is the difference between the absolute circulation (Ca) and the circulation due to the rotation of the Earth (Ce). Taking D of this equation gives: DC = DC a 2Ω DA e DC = dp 2Ω DA e ρ
6 For a barotropic fluid this reduces to: DC = 2Ω DA e Integrating from an initial state (1) to a final state (2) gives: C 2 C 1 = 2Ω A e2 A e1 What is the physical interpretation of this result? Vorticity Vorticity a microscopic measure of rotation at any point in a fluid Vorticity is defined as the curl of the velocity ( V ) Absolute vorticity: Relative vorticity: ω = U = ( ) ( ) = 2Ω A 2 sin φ 2 A 1 sin φ 1 ω a = U a ω = U i j k x y z u v w ' = w y v * ), ' i + u ( z+ z w * ), ' j + v ( x + x u * ), k ( y+ It is typical to consider only the vertical component of the vorticity vector: ( U a ) Vertical component of absolute vorticity: η k Vertical component of relative vorticity: ( ) = v ζ k U x u y Under what conditions will z be positive?
7 What is the relationship between absolute and relative voriticity? Vertical component of planetary vorticity: Then: η = ζ + f k ( U e ) = 2Ωsin φ = f The absolute vorticitiy is equal to the sum of the relative and planetary vorticity. What is the relationship between vorticity and circulation? Consider the circulation for flow around a rectangular area dxdy: $ δc = uδx + & v + v % x δx ' $ ) δy & u + u ( % y δy ' ) δx vδy ( $ δc = v x u ' & ) δxδy % y( δc = ζδa ζ = δc δa
8 We can also relate circulation and vorticity using Stokes theorem and the definition of vorticity: C = C = C = A A C = ζ A U dl ( U ) n da ζda ζ = C A This indicates that the average vorticity is equal to the circulation divided by the area enclosed by the contour used in calculating the circulation. For solid body rotation: C = 2ΩπR 2 and ζ = 2Ω In this case the vorticity (z) is twice the angular velocity (W)
9 Vorticity in Natural Coordinates From this figure the circulation is: [ ] ' V + V δc = V δs + d( δs) % & δc = Vd( δs) V n δnδs n δn ( * δs ) From the geometry shown in this figure: ( ) = δβδn d δs This then gives: δc = Vδβδn V n δnδs & δc = V δβ δs V ) ( + δnδs ' n * δc δnδs = V δβ δs V n In the limit as δn,δs 0: δc δnδs = ζ = V β s V n, where db is the angular change in wind direction Noting that ζ = V R s V n β s = 1 R s then What is the physical interpretation of this equation?
10 Can purely straigthline flow have non-zero vorticity? Where would this occur in the real world? Can curved flow have zero vorticity? Potential Vorticity Kelvin s circulation theorem states that circulation is constant in a barotropic fluid. Can we expand this result to apply for less restrictive conditions? Density can be expressed as a function of p and q using the ideal gas law and the definition of q. ρ = p RT and θ = T p R c # & p # s % ( T = θ p & % ( $ p ' $ ' p s R c p
11 Then: ρ = pp R c p s Rθp R c p = p ( 1 R c p ) R c p ps Rθ = pc v c p p s R c p Rθ On an isentropic surface r is only a function of p and the solenoidal term is given by: dp ρ dp ( 1 c v c p ) = 0 Then for adiabatic motion a closed chain of fluid parcels on an isentropic surface satisfies Kelvin s circulation theorem: DC a = D ( C + 2ΩδAsin φ ) = 0 For an approximately horizontal isentropic surface: C ζ θ δa, where zq is the relative vorticity evaluated on an isentropic surface. Kelvin s circulation theorem is then given by: D( C + 2ΩδAsin φ) and δa( ζ θ + f ) = Const. [ ( )] = D δa ζ θ + 2Ωsin φ [ ( )] = D δa ζ θ + f following the air parcel motion = 0
12 Consider an air parcel of mass dm confined between two q surfaces: δp From the hydrostatic equation and : δz = ρg δm = ρδv = ρδzδa δm = δp g δa For dm conserved following the air parcel motion δm = δp g δa = Const. Then: δa = δmg δp = % δθ (% ' * δmg ( % ' * = ( Const. )g δθ ( ' * & δp) & δθ ) & δp) where Const. = δm δθ Using this expression to replace da in δa( ζ θ + f ) = Const. gives: % ( Const. )g δθ ( ' * ζ θ + f & δp) ( ) = Const.
13 Ertel s Potential Vorticity (P) is defined as: P ζ θ + f ' ) ( *, δp+ ( ) g δθ Ertel s potential vorticity has units of K kg -1 m 2 s -1 and is typically given as a potential vorticity unit (PVU = 10-6 K kg -1 m 2 s -1 ) What is the sign of P in the Northern hemisphere? For adiabatic, frictionless flow P is conserved following the motion. The term potential vorticity is used for several similar quantities, but in all cases it refers to a quantity which is the ratio of the absolute vorticity to the vortex depth. For Ertel s potential vorticity the vortex depth is given by δp δθ How will ζ θ + f change if the vortex depth increases (decreases)? Potential vorticity for an incompressible fluid For an incompressible fluid r is constant and the mass, M, is given by: M = rhda, where h is the depth of the fluid being considered Rearranging gives: δa = M ρh And the potential vorticity is given by: ζ + f h As above, the potential voriticity is constant for frictionless flow following the air parcel motion.
14 For a constant depth fluid: ζ + f = η = Const. (absolute vorticity is conserved following the motion) This puts a strong constraint on the types of motion that are possible. Consider a zonal flow that has z0 = 0 initially so h0 = f0 Since ζ + f = η = Const., then at some later time z + f = h0 = f0 For a flow that turns to the north f > f0 and z = f0 f < 0 For a flow that turns to south f < f0 and z = f0 f > 0 Can these conditions be satisfied for both easterly and westerly flow?
15 For a fluid in which the depth can vary potential vorticity, rather than absolute voriticity, is conserved. Consider westerly flow over a mountain: Air column depth Change in δθ δp Increase Decrease Increase Decrease δp δp δp (return to original value) Decrease Increase Decrease Increase (return to original value) Change in ζ + f Increase Decrease Increase Decrease Sign of z Positive Negative Positive Negative Resulting northward southward lee side southward motion trough Change in f Increase Decrease Increase Decrease
16 For easterly flow over a mountain: Air column depth Change in δθ δp Decrease (Return to original value) Increase (Return to original value) Increase Decrease Increase δp δp δp Decrease Increase Decrease Change in ζ + f Decrease Increase Decrease Increase Sign of z Zero Positive Negative Positive Resulting motion westward northward southward southward Change in f Return to original value Increase Decrease Decrease As was the case for flows in which absolute vorticity was conserved the flow responds differently for easterly and westerly flow.
17 Vorticity Equation We are interested in being able to predict the time rate of change of vorticity without the constraints of adiabatic motion. To do this we will derive the vorticity equation. Since vorticity is defined as: ζ = v x u y We will subtract of the u momentum equation from of the v y x momentum equation: % v x t + u v x + v v y + w v z + fu = 1 p( ' * & ρ y) % u y t + u u x + v u y + w u z fv = 1 p( ' * & ρ x) This gives: ζ t + u ζ x + v ζ y + w ζ z + ζ + f Noting that: ( ) u 1 ρ 2 Df = f t + u f x + v f y + w f z = v f y Dζ = ζ t + u ζ x + v ζ y + w ζ z the vorticity equation becomes: D( ζ + f ) % = ( ζ + f )' u x + v ( % * ' w & y) & x $ x + v ' $ & ) + w v & % y( x z w % y $ ρ p x y ρ p' & ) % y x( v z w y u( * + 1 z ) ρ 2 u' ) + v f z ( y = % ρ p x y ρ p( ' * & y x)
18 This equation indicates that changes in absolute vorticity following the motion is due to a: Convergence term Tilting term Solenoidal term What is the physical interpretation of each of these terms? How will the vorticity change under the influence of convergence? Physical interpretation of the tilting term: What is the sign of in this example? w x and v z Does this lead to an increase or decrease in absolute vorticity?
19 The solenoidal term is the microscopic equivalent of the solenoidal term from the circulation theorem. From the circulation theorem the solenoidal term is given by: dp ρ = α p d l Applying Stokes theorem α p dl = α p A ( ) & ( F ds = F ' k da A ( ) ) n da+ * to this gives: Using the vector identity α p dl = α p A ( ) α p = α p k da gives: Expansion of the cross product gives: ( α p) Since: α x = ρ 1 x = 1 ρ ρ 2 x α y = ρ 1 y = 1 ρ ρ 2 y this gives: α p x y + α p y k = α p x y + α p y x x = 1 ρ ρ 2 x p y 1 ρ p ρ 2 y x
20 Then ( α p) k * da = 1 ρ p ρ 2 x y 1 ρ p-, + ρ 2 / A y x. A Dividing this by the area gives the solenoidal term in the vorticity equation. Vorticity equation in isobaric coordinates ζ t = V ( ζ + f ) ω ζ p ( ζ + f ) V + ) k V + * p ω,. - What do each of the terms in this equation represent? In isobaric coordinates there is no solenoidal term. Scale Analysis of the Vorticity Equation We can simplify the vorticity equation through scale analysis. Consider the scales for mid-latitude synoptic weather systems: Horizontal scale U 10 m s -1 Vertical scale W 10-2 m s -1 Length scale L 10 6 m Depth scale H 10 4 m Horizontal pressure scale dp 10 hpa Horizontal pressure scale dp/r 10 3 m 2 s -2 Mean density r 1 kg m -3 Fractional density fluctuation dr/r 10-2 Time scale T = L/U 10 5 s Coriolis parameter F 10-4 s -1 Beta parameter b m -1 s -1
21 f y = β = ( 2Ωsin φ) & 2Ωsin y ) ( ' = a + * y y β = 2Ω a cos y a = 2Ω a cosφ What is the magnitude of b in the mid-latitudes? z scales as: ζ = v, x u y < U ~ L ~ 10 5 s -1 v u where < is used since and may partially cancel ~ x y What is the relative magnitude of z compared to f0? ζ f 0 < ~ U f 0 L Ro ~ 10 1, so z is often an order of magnitude smaller than f0 (the planetary vorticity) Using this we can approximate the convergence term as: ( ) u ζ + f % x + v ( % u ' * f & y) x + v ( ' * & y) (i.e. we can neglect the relative vorticity contribution to the convergence term)
22 This approximation is not valid near the center of intense areas of low pressure where: ζ f ~ 1 and then both relative and planetary vorticity must be considered in the convergence term. What is an example of a type of flow where we cannot neglect z? Scale analysis of the terms in the vorticity equation gives: ζ t,u ζ x,v ζ y ~ U 2 L ~ s -2 w ζ z ~ WU L ~ s -2 v f y ~ Uβ ~ s -2 & f u x + v ) ( + < ' y* ~ Note that f 0 U L ~ 10 9 s -2 & w v x z + w u) W ( + < ' y z * ~ L 1 ρ 2 & ρ p x y ρ p) ( + < ' y x* ~ < ~ U H ~ s -2 δρ δp ρ ρ 1 L 2 ~ s -2 is used for the last three terms in this list since portions of each of these terms may partially cancel.
23 What is the largest term in the vorticity equation? In order for the vorticity equation to be satisfied: # f u x + v & % ( ~ s -2 < 10 9 s -2 $ y' which implies that the flow must be quasi non-divergent: # u x + v & % ( ~ 10 6 s -1 < U $ y' L ~ 10 5 s -1 How does the magnitude of the divergence compare to the magnitude of the relative and planetary vorticity? # u x + v & 10 6 s -1 % ( f 0 < $ y' ~ 10 4 s ~ ~ Ro 2 # u x + v & 10 6 s -1 % ( ζ < $ y' ~ 10 5 s ~ ~ Ro The horizontal divergence is two orders of magnitude smaller than the f and one order of magnitude smaller than z Retaining the largest terms (10-10 s -2 ) in the vorticity equation gives: ζ t + u ζ x + v ζ y + v f y = f % u x + v ( ' * & y) D h ( ζ + f ) where % = f u x + v ( ' * & y) D h t + u x + v y What is the physical interpretation of the scaled vorticity equation?
24 Near the center of intense low pressure systems, where z and f have similar magnitude the scaled vorticity equation becomes: D h ( ζ + f ) % = ( ζ + f )' u Why can cyclonic systems become more intense than anticyclonic systems? This is consistent with our analysis of the gradient wind equation where we found that the intensity of high pressure systems was limited while the intensity of low pressure systems was not. Is the scaled vorticity equation appropriate in the vicinity of fronts? Near fronts: L~10 5 m and W~10-1 m s -1 Using these scales indicates that the vertical advection, tilting, and solenoidal terms in the vorticity equation may all be as large as the divergence term, and thus must all be retained. Vorticity in Barotropic Fluids Barotropic (Rossby) Potential Vorticity Equation Consider an atmosphere that is: Barotropic: r = r(p) x + v ( * & y) Incompressible: Dρ = 0 With a depth h(x,y,t) = z2 z1, where z2 and z1 are the heights of the upper and lower boundaries of the atmosphere
25 For an incompressible fluid the continuity equation is: U = 0 u x + v y = w z Then the scaled vorticity equation becomes: D h ( ζ + f ) % = ( ζ + f )' u x + v ( * = ζ + f & y) ( ) w Approximating the vorticity (z) by the geostrophic vorticity (zg), where z ζ g = v g x u g y gives: D h ( ζ g + f ) = ( ζ g + f ) w z In a barotropic fluid V g does not vary with height and the equation above can be integrated from height z1 to z2 to give: ( ) z 2 D h ζ g + f z 2 z = ( ζ g + f ) w z 1 ( ) ( ) D h ζ g + f h D h ζ g + f z 2 z 1 z 1 ( ) = ζ g + f ( ) w z 2 = ζ g + f ( ) w z 2 [ ( ) w( z 1 )] [ ( ) w( z 1 )] Noting that w D hz gives:
26 w( z 1 ) = D hz 1 and w( z 2 ) = D hz 2 so w( z 2 ) w( z 1 ) = D hz 2 D hz 1 = D h ( z 2 z 1 ) = D hh Then: h D h ( ζ g + f ) = ( ζ g + f ) D h h 1 D h ( ζ g + f ) = 1 D h h ( ζ g + f ) h D h ln ζ g + f D h ( ) [( ζ g + f ) h] = D h ln h = 0 Rossby potential vorticity: The Rossby potential vorticity is conserved following the motion. Barotropic Vorticity Equation For a barotropic, incompressible fluid with purely horizontal flow (w = 0) the vorticity equation becomes: D h ( ζ + f ) = ( ζ + f ) w z = 0 ( ζ g + f ) h and the absolute vorticity (z + f) is conserved following the motion.
27 A more general result is that for a flow that has non-divergent horizontal # u winds % : x + v $ y = 0 & ( ' D h ( ζ + f ) = 0 For a non-divergent flow the wind can be represented by a streamfunction ψ x,y such that: [ ( )] V ψ k ψ = ψ y i + ψ x Example: Show that with this definition of the streamfunction the horizontal wind is non-divergent. The relative vorticity is then given by: ζ = v x u y = 2 ψ x + 2 ψ 2 y 2 ψ 2 j = ui + v j The vorticity equation can then be written as: D h ( ζ + f ) = 0 ( ) D h 2 ψ + f 2 ψ = V ψ ( 2 ψ + f ) t ( ) = 0 = 2 ψ + V ψ 2 ψ + f t What is the physical interpretation of this equation? This equation can be solved numerically to predict the time evolution of y. V and z can then be calculated from y.,
28 The flow in the mid-troposphere (~500 mb) is often nearly non-divergent and this equation can be used to produce a reasonable prediction of the time evolution of the flow at this level. Baroclinic (Ertel) Potential Vorticity Equation Ertel potential vorticity is given by: ( ) g θ P ζ θ + f ' ) ( *, p+ and is conserved following the motion for adiabatic, frictionless flow. We want to derive an equation for the time evolution of P in the presence of diabatic effects and friction. This equation can be derived by rewriting the horizontal momentum equation in isentropic coordinates. We can use q as a vertical coordinate in a stably stratified atmosphere since θ z > 0 and q is a monotonic function of height. The vertical velocity in isentropic coordinates is defined as: θ Dθ When will θ = 0? For an air parcel with mass dm: % δm = ρδaδz = δa' δp & g ( * = δa %, ) g p ( ' * δθ = σδaδθ & θ ) where σ = 1 p is the density in (x,y,q) space g θ
29 Then the governing equations in isentropic coordinates are given by: Horizontal momentum equation in isentropic coordinates: V t + ' V V θ ) ( 2 + Ψ *, + ζ θ + f + ( ) k V = θ V θ + F r, where Ψ = c p T + Φ is the Montgomery streamfunction Continuity equation in isentropic coordinates: σ t + θ σv ( ) = ( σ θ ) θ Hydrostatic equation in isentropic coordinates: Ψ θ = Π p ( ) c p ' p * ), ( + p s R c p T = c p, θ where P is the Exner function Isentropic vorticity equation: D ( ζ θ + f ) + ( ζ θ + f ) θ V = ) k θ F r θ V, +., * θ - D where is the total derivative following the horizontal motion = t + V θ on an isentropic surface The continuity equation can be rewritten as: D σ 1 ( ) σ 1 θ V = σ σ θ 2 θ
30 Ertel potential vorticity equation D P = P t + V θ P = P σ ( ) σ θ θ + σ ) 1 k θ F r θ V, +., * θ - where Ertel s potential vorticity is given by P = ( ζ θ + f ) σ What is the physical interpretation of this equation? For adiabatic, frictionless flow motion. D P = 0 and P is conserved following the
Chapter 7: Circulation and Vorticity
 Chapter 7: Circulation and Vorticity Circulation C = u ds Integration is performed in a counterclockwise direction C is positive for counterclockwise flow!!! Kelvin s Circulation Theorem The rate of change
Chapter 7: Circulation and Vorticity Circulation C = u ds Integration is performed in a counterclockwise direction C is positive for counterclockwise flow!!! Kelvin s Circulation Theorem The rate of change
1/25/2010. Circulation and vorticity are the two primary
 Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Measurement of Rotation. Circulation. Example. Lecture 4: Circulation and Vorticity 1/31/2017
 Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
t tendency advection convergence twisting baroclinicity
 RELATIVE VORTICITY EQUATION Newton s law in a rotating frame in z-coordinate (frictionless): U + U U = 2Ω U Φ α p U + U U 2 + ( U) U = 2Ω U Φ α p Applying to both sides, and noting ω U and using identities
RELATIVE VORTICITY EQUATION Newton s law in a rotating frame in z-coordinate (frictionless): U + U U = 2Ω U Φ α p U + U U 2 + ( U) U = 2Ω U Φ α p Applying to both sides, and noting ω U and using identities
By convention, C > 0 for counterclockwise flow, hence the contour must be counterclockwise.
 Chapter 4 4.1 The Circulation Theorem Circulation is a measure of rotation. It is calculated for a closed contour by taking the line integral of the velocity component tangent to the contour evaluated
Chapter 4 4.1 The Circulation Theorem Circulation is a measure of rotation. It is calculated for a closed contour by taking the line integral of the velocity component tangent to the contour evaluated
Circulation and Vorticity. The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation
 Circulation and Vorticity 1. Conservation of Absolute Angular Momentum The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation V = ωr (1)
Circulation and Vorticity 1. Conservation of Absolute Angular Momentum The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation V = ωr (1)
Circulation and Vorticity. The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation
 Circulation and Vticity 1. Conservation of Absolute Angular Momentum The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation V = ωr (1)
Circulation and Vticity 1. Conservation of Absolute Angular Momentum The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation V = ωr (1)
Dynamic Meteorology - Introduction
 Dynamic Meteorology - Introduction Atmospheric dynamics the study of atmospheric motions that are associated with weather and climate We will consider the atmosphere to be a continuous fluid medium, or
Dynamic Meteorology - Introduction Atmospheric dynamics the study of atmospheric motions that are associated with weather and climate We will consider the atmosphere to be a continuous fluid medium, or
= vorticity dilution + tilting horizontal vortices + microscopic solenoid
 4.4 Vorticity Eq 4.4.1 Cartesian Coordinates Because ζ = ˆk V, gives D(ζ + f) x minus [v momentum eq. in Cartesian Coordinates] y [u momentum eq. in Cartesian Coordinates] = vorticity dilution + tilting
4.4 Vorticity Eq 4.4.1 Cartesian Coordinates Because ζ = ˆk V, gives D(ζ + f) x minus [v momentum eq. in Cartesian Coordinates] y [u momentum eq. in Cartesian Coordinates] = vorticity dilution + tilting
ρ x + fv f 'w + F x ρ y fu + F y Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ Dv Dt + u2 tanφ + vw a a = 1 p Dw Dt u2 + v 2
 Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
Fixed Rossby Waves: Quasigeostrophic Explanations and Conservation of Potential Vorticity
 Fixed Rossby Waves: Quasigeostrophic Explanations and Conservation of Potential Vorticity 1. Observed Planetary Wave Patterns After upper air observations became routine, it became easy to produce contour
Fixed Rossby Waves: Quasigeostrophic Explanations and Conservation of Potential Vorticity 1. Observed Planetary Wave Patterns After upper air observations became routine, it became easy to produce contour
Dynamic Meteorology 1
 Dynamic Meteorology 1 Lecture 14 Sahraei Department of Physics, Razi University http://www.razi.ac.ir/sahraei Buys-Ballot rule (Northern Hemisphere) If the wind blows into your back, the Low will be to
Dynamic Meteorology 1 Lecture 14 Sahraei Department of Physics, Razi University http://www.razi.ac.ir/sahraei Buys-Ballot rule (Northern Hemisphere) If the wind blows into your back, the Low will be to
Chapter 9. Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation
 Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
( ) (9.1.1) Chapter 9. Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation. 9.1 Geostrophy and scaling.
 Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
The dynamics of high and low pressure systems
 The dynamics of high and low pressure systems Newton s second law for a parcel of air in an inertial coordinate system (a coordinate system in which the coordinate axes do not change direction and are
The dynamics of high and low pressure systems Newton s second law for a parcel of air in an inertial coordinate system (a coordinate system in which the coordinate axes do not change direction and are
1/18/2011. Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis ESS227 Prof. Jin-Yi Yu
 Lecture 2: Basic Conservation Laws Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed in an inertial system = rate of change of Ua following the motion in an inertial
Lecture 2: Basic Conservation Laws Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed in an inertial system = rate of change of Ua following the motion in an inertial
Lecture 14. Equations of Motion Currents With Friction Sverdrup, Stommel, and Munk Solutions Remember that Ekman's solution for wind-induced transport
 Lecture 14. Equations of Motion Currents With Friction Sverdrup, Stommel, and Munk Solutions Remember that Ekman's solution for wind-induced transport is which can also be written as (14.1) i.e., #Q x,y
Lecture 14. Equations of Motion Currents With Friction Sverdrup, Stommel, and Munk Solutions Remember that Ekman's solution for wind-induced transport is which can also be written as (14.1) i.e., #Q x,y
Class exercises Chapter 3. Elementary Applications of the Basic Equations
 Class exercises Chapter 3. Elementary Applications of the Basic Equations Section 3.1 Basic Equations in Isobaric Coordinates 3.1 For some (in fact many) applications we assume that the change of the Coriolis
Class exercises Chapter 3. Elementary Applications of the Basic Equations Section 3.1 Basic Equations in Isobaric Coordinates 3.1 For some (in fact many) applications we assume that the change of the Coriolis
Part 4. Atmospheric Dynamics
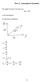 Part 4. Atmospheric Dynamics We apply Newton s Second Law: ma =Σ F i to the atmosphere. In Cartesian coordinates dx u = dt dy v = dt dz w = dt 1 ai = F m i i du dv dw a = ; ay = ; az = x dt dt dt 78 Coordinate
Part 4. Atmospheric Dynamics We apply Newton s Second Law: ma =Σ F i to the atmosphere. In Cartesian coordinates dx u = dt dy v = dt dz w = dt 1 ai = F m i i du dv dw a = ; ay = ; az = x dt dt dt 78 Coordinate
1/3/2011. This course discusses the physical laws that govern atmosphere/ocean motions.
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Balanced Flow Geostrophic, Inertial, Gradient, and Cyclostrophic Flow
 Balanced Flow Geostrophic, Inertial, Gradient, and Cyclostrophic Flow The types of atmospheric flows describe here have the following characteristics: 1) Steady state (meaning that the flows do not change
Balanced Flow Geostrophic, Inertial, Gradient, and Cyclostrophic Flow The types of atmospheric flows describe here have the following characteristics: 1) Steady state (meaning that the flows do not change
Conservation of Mass Conservation of Energy Scaling Analysis. ESS227 Prof. Jin-Yi Yu
 Lecture 2: Basic Conservation Laws Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed
Lecture 2: Basic Conservation Laws Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed
Chapter 2. Quasi-Geostrophic Theory: Formulation (review) ε =U f o L <<1, β = 2Ω cosθ o R. 2.1 Introduction
 Chapter 2. Quasi-Geostrophic Theory: Formulation (review) 2.1 Introduction For most of the course we will be concerned with instabilities that an be analyzed by the quasi-geostrophic equations. These are
Chapter 2. Quasi-Geostrophic Theory: Formulation (review) 2.1 Introduction For most of the course we will be concerned with instabilities that an be analyzed by the quasi-geostrophic equations. These are
EATS Notes 1. Some course material will be online at
 EATS 3040-2015 Notes 1 14 Aug 2015 Some course material will be online at http://www.yorku.ca/pat/esse3040/ HH = Holton and Hakim. An Introduction to Dynamic Meteorology, 5th Edition. Most of the images
EATS 3040-2015 Notes 1 14 Aug 2015 Some course material will be online at http://www.yorku.ca/pat/esse3040/ HH = Holton and Hakim. An Introduction to Dynamic Meteorology, 5th Edition. Most of the images
Gravity Waves. Lecture 5: Waves in Atmosphere. Waves in the Atmosphere and Oceans. Internal Gravity (Buoyancy) Waves 2/9/2017
 Lecture 5: Waves in Atmosphere Perturbation Method Properties of Wave Shallow Water Model Gravity Waves Rossby Waves Waves in the Atmosphere and Oceans Restoring Force Conservation of potential temperature
Lecture 5: Waves in Atmosphere Perturbation Method Properties of Wave Shallow Water Model Gravity Waves Rossby Waves Waves in the Atmosphere and Oceans Restoring Force Conservation of potential temperature
Control Volume. Dynamics and Kinematics. Basic Conservation Laws. Lecture 1: Introduction and Review 1/24/2017
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review
 Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
2.5 Shallow water equations, quasigeostrophic filtering, and filtering of inertia-gravity waves
 Chapter. The continuous equations φ=gh Φ=gH φ s =gh s Fig..5: Schematic of the shallow water model, a hydrostatic, incompressible fluid with a rigid bottom h s (x,y), a free surface h(x,y,t), and horizontal
Chapter. The continuous equations φ=gh Φ=gH φ s =gh s Fig..5: Schematic of the shallow water model, a hydrostatic, incompressible fluid with a rigid bottom h s (x,y), a free surface h(x,y,t), and horizontal
Part-8c Circulation (Cont)
 Part-8c Circulation (Cont) Global Circulation Means of Transfering Heat Easterlies /Westerlies Polar Front Planetary Waves Gravity Waves Mars Circulation Giant Planet Atmospheres Zones and Belts Global
Part-8c Circulation (Cont) Global Circulation Means of Transfering Heat Easterlies /Westerlies Polar Front Planetary Waves Gravity Waves Mars Circulation Giant Planet Atmospheres Zones and Belts Global
Atmosphere, Ocean and Climate Dynamics Answers to Chapter 8
 Atmosphere, Ocean and Climate Dynamics Answers to Chapter 8 1. Consider a zonally symmetric circulation (i.e., one with no longitudinal variations) in the atmosphere. In the inviscid upper troposphere,
Atmosphere, Ocean and Climate Dynamics Answers to Chapter 8 1. Consider a zonally symmetric circulation (i.e., one with no longitudinal variations) in the atmosphere. In the inviscid upper troposphere,
PV Thinking. What is PV thinking?
 PV Thinking CH 06 What is PV thinking? Two main approaches to solving fluid flow problems:. We can integrate the momentum, continuity and thermodynamic equations (the primitive equations) directly.. In
PV Thinking CH 06 What is PV thinking? Two main approaches to solving fluid flow problems:. We can integrate the momentum, continuity and thermodynamic equations (the primitive equations) directly.. In
Introduction to Synoptic Scale Dynamics
 Introduction to Synoptic Scale Dynamics Contents J. H. LaCasce, UiO 1 General dynamics 2 1.1 Derivatives................................. 2 1.2 Continuity equation............................. 3 1.3 Equations
Introduction to Synoptic Scale Dynamics Contents J. H. LaCasce, UiO 1 General dynamics 2 1.1 Derivatives................................. 2 1.2 Continuity equation............................. 3 1.3 Equations
1/27/2010. With this method, all filed variables are separated into. from the basic state: Assumptions 1: : the basic state variables must
 Lecture 5: Waves in Atmosphere Perturbation Method With this method, all filed variables are separated into two parts: (a) a basic state part and (b) a deviation from the basic state: Perturbation Method
Lecture 5: Waves in Atmosphere Perturbation Method With this method, all filed variables are separated into two parts: (a) a basic state part and (b) a deviation from the basic state: Perturbation Method
The Vorticity Equation in a Rotating Stratified Fluid
 Capter 7 Te Vorticity Equation in a Rotating Stratified Fluid Te vorticity equation for a rotating, stratified, viscous fluid Te vorticity equation in one form or anoter and its interpretation provide
Capter 7 Te Vorticity Equation in a Rotating Stratified Fluid Te vorticity equation for a rotating, stratified, viscous fluid Te vorticity equation in one form or anoter and its interpretation provide
Lecture 1. Equations of motion - Newton s second law in three dimensions. Pressure gradient + force force
 Lecture 3 Lecture 1 Basic dynamics Equations of motion - Newton s second law in three dimensions Acceleration = Pressure Coriolis + gravity + friction gradient + force force This set of equations is the
Lecture 3 Lecture 1 Basic dynamics Equations of motion - Newton s second law in three dimensions Acceleration = Pressure Coriolis + gravity + friction gradient + force force This set of equations is the
Using simplified vorticity equation,* by assumption 1 above: *Metr 430 handout on Circulation and Vorticity. Equations (4) and (5) on that handout
 Rossby Wave Equation A. Assumptions 1. Non-divergence 2. Initially, zonal flow, or nearly zonal flow in which u>>v>>w. 3. Initial westerly wind is geostrophic and does not vary along the x-axis and equations
Rossby Wave Equation A. Assumptions 1. Non-divergence 2. Initially, zonal flow, or nearly zonal flow in which u>>v>>w. 3. Initial westerly wind is geostrophic and does not vary along the x-axis and equations
1/18/2011. From the hydrostatic equation, it is clear that a single. pressure and height in each vertical column of the atmosphere.
 Lecture 3: Applications of Basic Equations Pressure as Vertical Coordinate From the hydrostatic equation, it is clear that a single valued monotonic relationship exists between pressure and height in each
Lecture 3: Applications of Basic Equations Pressure as Vertical Coordinate From the hydrostatic equation, it is clear that a single valued monotonic relationship exists between pressure and height in each
196 7 atmospheric oscillations:
 196 7 atmospheric oscillations: 7.4 INTERNAL GRAVITY (BUOYANCY) WAVES We now consider the nature of gravity wave propagation in the atmosphere. Atmospheric gravity waves can only exist when the atmosphere
196 7 atmospheric oscillations: 7.4 INTERNAL GRAVITY (BUOYANCY) WAVES We now consider the nature of gravity wave propagation in the atmosphere. Atmospheric gravity waves can only exist when the atmosphere
Governing Equations and Scaling in the Tropics
 Governing Equations and Scaling in the Tropics M 1 ( ) e R ε er Tropical v Midlatitude Meteorology Why is the general circulation and synoptic weather systems in the tropics different to the those in the
Governing Equations and Scaling in the Tropics M 1 ( ) e R ε er Tropical v Midlatitude Meteorology Why is the general circulation and synoptic weather systems in the tropics different to the those in the
Chapter 4: Fundamental Forces
 Chapter 4: Fundamental Forces Newton s Second Law: F=ma In atmospheric science it is typical to consider the force per unit mass acting on the atmosphere: Force mass = a In order to understand atmospheric
Chapter 4: Fundamental Forces Newton s Second Law: F=ma In atmospheric science it is typical to consider the force per unit mass acting on the atmosphere: Force mass = a In order to understand atmospheric
where p oo is a reference level constant pressure (often 10 5 Pa). Since θ is conserved for adiabatic motions, a prognostic temperature equation is:
 1 Appendix C Useful Equations Purposes: Provide foundation equations and sketch some derivations. These equations are used as starting places for discussions in various parts of the book. C.1. Thermodynamic
1 Appendix C Useful Equations Purposes: Provide foundation equations and sketch some derivations. These equations are used as starting places for discussions in various parts of the book. C.1. Thermodynamic
Chapter 1. Governing Equations of GFD. 1.1 Mass continuity
 Chapter 1 Governing Equations of GFD The fluid dynamical governing equations consist of an equation for mass continuity, one for the momentum budget, and one or more additional equations to account for
Chapter 1 Governing Equations of GFD The fluid dynamical governing equations consist of an equation for mass continuity, one for the momentum budget, and one or more additional equations to account for
6 Two-layer shallow water theory.
 6 Two-layer shallow water theory. Wewillnowgoontolookatashallowwatersystemthathastwolayersofdifferent density. This is the next level of complexity and a simple starting point for understanding the behaviour
6 Two-layer shallow water theory. Wewillnowgoontolookatashallowwatersystemthathastwolayersofdifferent density. This is the next level of complexity and a simple starting point for understanding the behaviour
The dynamics of a simple troposphere-stratosphere model
 The dynamics of a simple troposphere-stratosphere model by Jessica Duin under supervision of Prof. Dr. A. Doelman, UvA Dr. W.T.M. Verkley, KNMI August 31, 25 Universiteit van Amsterdam Korteweg-de vries
The dynamics of a simple troposphere-stratosphere model by Jessica Duin under supervision of Prof. Dr. A. Doelman, UvA Dr. W.T.M. Verkley, KNMI August 31, 25 Universiteit van Amsterdam Korteweg-de vries
4. Atmospheric transport. Daniel J. Jacob, Atmospheric Chemistry, Harvard University, Spring 2017
 4. Atmospheric transport Daniel J. Jacob, Atmospheric Chemistry, Harvard University, Spring 2017 Forces in the atmosphere: Gravity g Pressure-gradient ap = ( 1/ ρ ) dp / dx for x-direction (also y, z directions)
4. Atmospheric transport Daniel J. Jacob, Atmospheric Chemistry, Harvard University, Spring 2017 Forces in the atmosphere: Gravity g Pressure-gradient ap = ( 1/ ρ ) dp / dx for x-direction (also y, z directions)
Fluid dynamics and moist thermodynamics
 Chapter 1 Fluid dynamics and moist thermodynamics In this chapter we review the equations that represent the physical laws governing atmospheric motion. Rigorous derivations of the equations may be found
Chapter 1 Fluid dynamics and moist thermodynamics In this chapter we review the equations that represent the physical laws governing atmospheric motion. Rigorous derivations of the equations may be found
Vorticity in natural coordinates
 Vorticity in natural coordinates (see Holton pg 95, section 4.2.) Let s consider the vertical vorticity component only, i.e. ζ kˆ ω, we have ω u dl kˆ ω lim --- lim ----------------- curve is in xy plane
Vorticity in natural coordinates (see Holton pg 95, section 4.2.) Let s consider the vertical vorticity component only, i.e. ζ kˆ ω, we have ω u dl kˆ ω lim --- lim ----------------- curve is in xy plane
Lecture #2 Planetary Wave Models. Charles McLandress (Banff Summer School 7-13 May 2005)
 Lecture #2 Planetary Wave Models Charles McLandress (Banff Summer School 7-13 May 2005) 1 Outline of Lecture 1. Observational motivation 2. Forced planetary waves in the stratosphere 3. Traveling planetary
Lecture #2 Planetary Wave Models Charles McLandress (Banff Summer School 7-13 May 2005) 1 Outline of Lecture 1. Observational motivation 2. Forced planetary waves in the stratosphere 3. Traveling planetary
Dynamics Rotating Tank
 Institute for Atmospheric and Climate Science - IACETH Atmospheric Physics Lab Work Dynamics Rotating Tank Large scale flows on different latitudes of the rotating Earth Abstract The large scale atmospheric
Institute for Atmospheric and Climate Science - IACETH Atmospheric Physics Lab Work Dynamics Rotating Tank Large scale flows on different latitudes of the rotating Earth Abstract The large scale atmospheric
Introduction to Isentropic Coordinates: a new view of mean meridional & eddy circulations. Cristiana Stan
 Introduction to Isentropic Coordinates: a new view of mean meridional & eddy circulations Cristiana Stan School and Conference on the General Circulation of the Atmosphere and Oceans: a Modern Perspective
Introduction to Isentropic Coordinates: a new view of mean meridional & eddy circulations Cristiana Stan School and Conference on the General Circulation of the Atmosphere and Oceans: a Modern Perspective
BALANCED FLOW: EXAMPLES (PHH lecture 3) Potential Vorticity in the real atmosphere. Potential temperature θ. Rossby Ertel potential vorticity
 BALANCED FLOW: EXAMPLES (PHH lecture 3) Potential Vorticity in the real atmosphere Need to introduce a new measure of the buoyancy Potential temperature θ In a compressible fluid, the relevant measure
BALANCED FLOW: EXAMPLES (PHH lecture 3) Potential Vorticity in the real atmosphere Need to introduce a new measure of the buoyancy Potential temperature θ In a compressible fluid, the relevant measure
The Equations of Motion in a Rotating Coordinate System. Chapter 3
 The Equations of Motion in a Rotating Coordinate System Chapter 3 Since the earth is rotating about its axis and since it is convenient to adopt a frame of reference fixed in the earth, we need to study
The Equations of Motion in a Rotating Coordinate System Chapter 3 Since the earth is rotating about its axis and since it is convenient to adopt a frame of reference fixed in the earth, we need to study
Mathematical Concepts & Notation
 Mathematical Concepts & Notation Appendix A: Notation x, δx: a small change in x t : the partial derivative with respect to t holding the other variables fixed d : the time derivative of a quantity that
Mathematical Concepts & Notation Appendix A: Notation x, δx: a small change in x t : the partial derivative with respect to t holding the other variables fixed d : the time derivative of a quantity that
Dynamics of the Atmosphere. Large-scale flow with rotation and stratification
 12.810 Dynamics of the Atmosphere Large-scale flow with rotation and stratification Visualization of meandering jet stream Upper level winds from June 10th to July 8th 1988 from MERRA Red shows faster
12.810 Dynamics of the Atmosphere Large-scale flow with rotation and stratification Visualization of meandering jet stream Upper level winds from June 10th to July 8th 1988 from MERRA Red shows faster
Dynamics of Upper-Level Waves
 Dynamics of Upper-Level Waves Atmos 5110 Synoptic Dynamic Meteorology I Instructor: Jim Steenburgh jim.steenburgh@utah.edu 801-581-8727 Suite 480/Office 488 INSCC Suggested reading: Lackman (2011) section
Dynamics of Upper-Level Waves Atmos 5110 Synoptic Dynamic Meteorology I Instructor: Jim Steenburgh jim.steenburgh@utah.edu 801-581-8727 Suite 480/Office 488 INSCC Suggested reading: Lackman (2011) section
Goals of this Chapter
 Waves in the Atmosphere and Oceans Restoring Force Conservation of potential temperature in the presence of positive static stability internal gravity waves Conservation of potential vorticity in the presence
Waves in the Atmosphere and Oceans Restoring Force Conservation of potential temperature in the presence of positive static stability internal gravity waves Conservation of potential vorticity in the presence
Ocean currents: some misconceptions and some dynamics
 Ocean currents: some misconceptions and some dynamics Joe LaCasce Dept. Geosciences October 30, 2012 Where is the Gulf Stream? BBC Weather Center Where is the Gulf Stream? Univ. Bergen news website (2011)
Ocean currents: some misconceptions and some dynamics Joe LaCasce Dept. Geosciences October 30, 2012 Where is the Gulf Stream? BBC Weather Center Where is the Gulf Stream? Univ. Bergen news website (2011)
Quick Recapitulation of Fluid Mechanics
 Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
Goal: Use understanding of physically-relevant scales to reduce the complexity of the governing equations
 Scale analysis relevant to the tropics [large-scale synoptic systems]* Goal: Use understanding of physically-relevant scales to reduce the complexity of the governing equations *Reminder: Midlatitude scale
Scale analysis relevant to the tropics [large-scale synoptic systems]* Goal: Use understanding of physically-relevant scales to reduce the complexity of the governing equations *Reminder: Midlatitude scale
Homework 2: Solutions GFD I Winter 2007
 Homework : Solutions GFD I Winter 007 1.a. Part One The goal is to find the height that the free surface at the edge of a spinning beaker rises from its resting position. The first step of this process
Homework : Solutions GFD I Winter 007 1.a. Part One The goal is to find the height that the free surface at the edge of a spinning beaker rises from its resting position. The first step of this process
Examples of Pressure Gradient. Pressure Gradient Force. Chapter 7: Forces and Force Balances. Forces that Affect Atmospheric Motion 2/7/2019
 Chapter 7: Forces and Force Balances Forces that Affect Atmospheric Motion Fundamental force - Apparent force - Pressure gradient force Gravitational force Frictional force Centrifugal force Forces that
Chapter 7: Forces and Force Balances Forces that Affect Atmospheric Motion Fundamental force - Apparent force - Pressure gradient force Gravitational force Frictional force Centrifugal force Forces that
7 Balanced Motion. 7.1 Return of the...scale analysis for hydrostatic balance! CSU ATS601 Fall 2015
 7 Balanced Motion We previously discussed the concept of balance earlier, in the context of hydrostatic balance. Recall that the balanced condition means no accelerations (balance of forces). That is,
7 Balanced Motion We previously discussed the concept of balance earlier, in the context of hydrostatic balance. Recall that the balanced condition means no accelerations (balance of forces). That is,
Examples of Pressure Gradient. Pressure Gradient Force. Chapter 7: Forces and Force Balances. Forces that Affect Atmospheric Motion 2/2/2015
 Chapter 7: Forces and Force Balances Forces that Affect Atmospheric Motion Fundamental force - Apparent force - Pressure gradient force Gravitational force Frictional force Centrifugal force Forces that
Chapter 7: Forces and Force Balances Forces that Affect Atmospheric Motion Fundamental force - Apparent force - Pressure gradient force Gravitational force Frictional force Centrifugal force Forces that
Quasi-Geostrophic ω-equation. 1. The atmosphere is approximately hydrostatic. 2. The atmosphere is approximately geostrophic.
 Quasi-Geostrophic ω-equation For large-scale flow in the atmosphere, we have learned about two very important characteristics:. The atmosphere is approximately hydrostatic.. The atmosphere is approximately
Quasi-Geostrophic ω-equation For large-scale flow in the atmosphere, we have learned about two very important characteristics:. The atmosphere is approximately hydrostatic.. The atmosphere is approximately
Vorticity and Potential Vorticity
 Chapter 4 Vorticity and Potential Vorticity In this chapter we explore a way of solving the shallow water equations for motions with characteristic time scales longer than the rotation period of the earth.
Chapter 4 Vorticity and Potential Vorticity In this chapter we explore a way of solving the shallow water equations for motions with characteristic time scales longer than the rotation period of the earth.
Buoyancy and Coriolis forces
 Chapter 2 Buoyancy and Coriolis forces In this chapter we address several topics that we need to understand before starting on our study of geophysical uid dynamics. 2.1 Hydrostatic approximation Consider
Chapter 2 Buoyancy and Coriolis forces In this chapter we address several topics that we need to understand before starting on our study of geophysical uid dynamics. 2.1 Hydrostatic approximation Consider
d v 2 v = d v d t i n where "in" and "rot" denote the inertial (absolute) and rotating frames. Equation of motion F =
 Governing equations of fluid dynamics under the influence of Earth rotation (Navier-Stokes Equations in rotating frame) Recap: From kinematic consideration, d v i n d t i n = d v rot d t r o t 2 v rot
Governing equations of fluid dynamics under the influence of Earth rotation (Navier-Stokes Equations in rotating frame) Recap: From kinematic consideration, d v i n d t i n = d v rot d t r o t 2 v rot
The General Circulation of the Atmosphere: A Numerical Experiment
 The General Circulation of the Atmosphere: A Numerical Experiment Norman A. Phillips (1956) Presentation by Lukas Strebel and Fabian Thüring Goal of the Model Numerically predict the mean state of the
The General Circulation of the Atmosphere: A Numerical Experiment Norman A. Phillips (1956) Presentation by Lukas Strebel and Fabian Thüring Goal of the Model Numerically predict the mean state of the
Lecture 8. Lecture 1. Wind-driven gyres. Ekman transport and Ekman pumping in a typical ocean basin. VEk
 Lecture 8 Lecture 1 Wind-driven gyres Ekman transport and Ekman pumping in a typical ocean basin. VEk wek > 0 VEk wek < 0 VEk 1 8.1 Vorticity and circulation The vorticity of a parcel is a measure of its
Lecture 8 Lecture 1 Wind-driven gyres Ekman transport and Ekman pumping in a typical ocean basin. VEk wek > 0 VEk wek < 0 VEk 1 8.1 Vorticity and circulation The vorticity of a parcel is a measure of its
Lecture 2. Lecture 1. Forces on a rotating planet. We will describe the atmosphere and ocean in terms of their:
 Lecture 2 Lecture 1 Forces on a rotating planet We will describe the atmosphere and ocean in terms of their: velocity u = (u,v,w) pressure P density ρ temperature T salinity S up For convenience, we will
Lecture 2 Lecture 1 Forces on a rotating planet We will describe the atmosphere and ocean in terms of their: velocity u = (u,v,w) pressure P density ρ temperature T salinity S up For convenience, we will
TROPICAL CYCLONE MOTION
 Chapter 3 TROPICAL CYCLONE MOTION The prediction of tropical cyclone motion has improved dramatically during the last decade as has our understanding of the mechanisms involved. Some of the basic aspects
Chapter 3 TROPICAL CYCLONE MOTION The prediction of tropical cyclone motion has improved dramatically during the last decade as has our understanding of the mechanisms involved. Some of the basic aspects
+ ω = 0, (1) (b) In geometric height coordinates in the rotating frame of the Earth, momentum balance for an inviscid fluid is given by
 Problem Sheet 1: Due Thurs 3rd Feb 1. Primitive equations in different coordinate systems (a) Using Lagrangian considerations and starting from an infinitesimal mass element in cartesian coordinates (x,y,z)
Problem Sheet 1: Due Thurs 3rd Feb 1. Primitive equations in different coordinate systems (a) Using Lagrangian considerations and starting from an infinitesimal mass element in cartesian coordinates (x,y,z)
EESC V2100 The Climate System spring 2004 Lecture 4: Laws of Atmospheric Motion and Weather
 EESC V2100 The Climate System spring 2004 Lecture 4: Laws of Atmospheric Motion and Weather Yochanan Kushnir Lamont Doherty Earth Observatory of Columbia University Palisades, NY 10964, USA kushnir@ldeo.columbia.edu
EESC V2100 The Climate System spring 2004 Lecture 4: Laws of Atmospheric Motion and Weather Yochanan Kushnir Lamont Doherty Earth Observatory of Columbia University Palisades, NY 10964, USA kushnir@ldeo.columbia.edu
Scale analysis of the vertical equation of motion:
 Scale analysis of the vertical equation of motion: As we did with the hz eqns, we do for the vertical to estimate the order of magnitude of Dw/ we take the largest of the terms, Dw -- W/T h UW/L W 2 /H
Scale analysis of the vertical equation of motion: As we did with the hz eqns, we do for the vertical to estimate the order of magnitude of Dw/ we take the largest of the terms, Dw -- W/T h UW/L W 2 /H
g (z) = 1 (1 + z/a) = 1 1 ( km/10 4 km) 2
 1.4.2 Gravitational Force g is the gravitational force. It always points towards the center of mass, and it is proportional to the inverse square of the distance above the center of mass: g (z) = GM (a
1.4.2 Gravitational Force g is the gravitational force. It always points towards the center of mass, and it is proportional to the inverse square of the distance above the center of mass: g (z) = GM (a
Isentropic Analysis. Much of this presentation is due to Jim Moore, SLU
 Isentropic Analysis Much of this presentation is due to Jim Moore, SLU Utility of Isentropic Analysis Diagnose and visualize vertical motion - through advection of pressure and system-relative flow Depict
Isentropic Analysis Much of this presentation is due to Jim Moore, SLU Utility of Isentropic Analysis Diagnose and visualize vertical motion - through advection of pressure and system-relative flow Depict
( u,v). For simplicity, the density is considered to be a constant, denoted by ρ 0
 ! Revised Friday, April 19, 2013! 1 Inertial Stability and Instability David Randall Introduction Inertial stability and instability are relevant to the atmosphere and ocean, and also in other contexts
! Revised Friday, April 19, 2013! 1 Inertial Stability and Instability David Randall Introduction Inertial stability and instability are relevant to the atmosphere and ocean, and also in other contexts
ESCI 342 Atmospheric Dynamics I Lesson 12 Vorticity
 ESCI 34 tmospheric Dynamics I Lesson 1 Vorticity Reference: n Introduction to Dynamic Meteorology (4 rd edition), Holton n Informal Introduction to Theoretical Fluid Mechanics, Lighthill Reading: Martin,
ESCI 34 tmospheric Dynamics I Lesson 1 Vorticity Reference: n Introduction to Dynamic Meteorology (4 rd edition), Holton n Informal Introduction to Theoretical Fluid Mechanics, Lighthill Reading: Martin,
Note that Rossby waves are tranverse waves, that is the particles move perpendicular to the direction of propagation. f up, down (clockwise)
 Ocean 423 Rossby waves 1 Rossby waves: Restoring force is the north-south gradient of background potential vorticity (f/h). That gradient can be due to either the variation in f with latitude, or to a
Ocean 423 Rossby waves 1 Rossby waves: Restoring force is the north-south gradient of background potential vorticity (f/h). That gradient can be due to either the variation in f with latitude, or to a
Dust devils, water spouts, tornados
 Balanced flow Things we know Primitive equations are very comprehensive, but there may be a number of vast simplifications that may be relevant (e.g., geostrophic balance). Seems that there are things
Balanced flow Things we know Primitive equations are very comprehensive, but there may be a number of vast simplifications that may be relevant (e.g., geostrophic balance). Seems that there are things
SIO 210: Dynamics VI (Potential vorticity) L. Talley Fall, 2014 (Section 2: including some derivations) (this lecture was not given in 2015)
 SIO 210: Dynamics VI (Potential vorticity) L. Talley Fall, 2014 (Section 2: including some derivations) (this lecture was not given in 2015) Variation of Coriolis with latitude: β Vorticity Potential vorticity
SIO 210: Dynamics VI (Potential vorticity) L. Talley Fall, 2014 (Section 2: including some derivations) (this lecture was not given in 2015) Variation of Coriolis with latitude: β Vorticity Potential vorticity
Eliassen-Palm Theory
 Eliassen-Palm Theory David Painemal MPO611 April 2007 I. Introduction The separation of the flow into its zonal average and the deviations therefrom has been a dominant paradigm for analyses of the general
Eliassen-Palm Theory David Painemal MPO611 April 2007 I. Introduction The separation of the flow into its zonal average and the deviations therefrom has been a dominant paradigm for analyses of the general
Chapter 5. Sound Waves and Vortices. 5.1 Sound waves
 Chapter 5 Sound Waves and Vortices In this chapter we explore a set of characteristic solutions to the uid equations with the goal of familiarizing the reader with typical behaviors in uid dynamics. Sound
Chapter 5 Sound Waves and Vortices In this chapter we explore a set of characteristic solutions to the uid equations with the goal of familiarizing the reader with typical behaviors in uid dynamics. Sound
ATMOSPHERIC AND OCEANIC FLUID DYNAMICS
 ATMOSPHERIC AND OCEANIC FLUID DYNAMICS Fundamentals and Large-scale Circulation G E O F F R E Y K. V A L L I S Princeton University, New Jersey CAMBRIDGE UNIVERSITY PRESS An asterisk indicates more advanced
ATMOSPHERIC AND OCEANIC FLUID DYNAMICS Fundamentals and Large-scale Circulation G E O F F R E Y K. V A L L I S Princeton University, New Jersey CAMBRIDGE UNIVERSITY PRESS An asterisk indicates more advanced
Dynamics and Kinematics
 Geophysics Fluid Dynamics () Syllabus Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3,
Geophysics Fluid Dynamics () Syllabus Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3,
Geophysics Fluid Dynamics (ESS228)
 Geophysics Fluid Dynamics (ESS228) Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3, 4,
Geophysics Fluid Dynamics (ESS228) Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3, 4,
Chapter 10 Atmospheric Forces & Winds
 Chapter 10 Atospheric Forces & Winds Chapter overview: Atospheric Pressure o Horizontal pressure variations o Station vs sea level pressure Winds and weather aps Newton s 2 nd Law Horizontal Forces o Pressure
Chapter 10 Atospheric Forces & Winds Chapter overview: Atospheric Pressure o Horizontal pressure variations o Station vs sea level pressure Winds and weather aps Newton s 2 nd Law Horizontal Forces o Pressure
The equation we worked with for waves and geostrophic adjustment of a 1-layer fluid is η tt
 GEOPHYSICAL FLUID DYNAMICS-I OC512/AS509 2015 P.Rhines LECTUREs 11-12 week 6 9-14 Geostrophic adjustment and overturning circulations with continuous stratification. The equation we worked with for waves
GEOPHYSICAL FLUID DYNAMICS-I OC512/AS509 2015 P.Rhines LECTUREs 11-12 week 6 9-14 Geostrophic adjustment and overturning circulations with continuous stratification. The equation we worked with for waves
Transformed Eulerian Mean
 Chapter 15 Transformed Eulerian Mean In the last few lectures we introduced some fundamental ideas on 1) the properties of turbulent flows in rotating stratified environments, like the ocean and the atmosphere,
Chapter 15 Transformed Eulerian Mean In the last few lectures we introduced some fundamental ideas on 1) the properties of turbulent flows in rotating stratified environments, like the ocean and the atmosphere,
Lecture 12: Angular Momentum and the Hadley Circulation
 Lecture 12: Angular Momentum and the Hadley Circulation September 30, 2003 We learnt last time that there is a planetary radiative drive net warming in the tropics, cooling over the pole which induces
Lecture 12: Angular Momentum and the Hadley Circulation September 30, 2003 We learnt last time that there is a planetary radiative drive net warming in the tropics, cooling over the pole which induces
An Optimal Control Problem Formulation for. the Atmospheric Large-Scale Wave Dynamics
 pplied Mathematical Sciences, Vol. 9, 5, no. 8, 875-884 HIKRI Ltd, www.m-hikari.com http://dx.doi.org/.988/ams.5.448 n Optimal Control Problem Formulation for the tmospheric Large-Scale Wave Dynamics Sergei
pplied Mathematical Sciences, Vol. 9, 5, no. 8, 875-884 HIKRI Ltd, www.m-hikari.com http://dx.doi.org/.988/ams.5.448 n Optimal Control Problem Formulation for the tmospheric Large-Scale Wave Dynamics Sergei
Synoptic Meteorology II: Self-Development in the IPV Framework. 5-7 May 2015
 Synoptic Meteorology II: Self-Development in the IPV Framework 5-7 May 2015 Readings: Section 5.3.6 of Midlatitude Synoptic Meteorology. Introduction In this and other recent lectures, we have developed
Synoptic Meteorology II: Self-Development in the IPV Framework 5-7 May 2015 Readings: Section 5.3.6 of Midlatitude Synoptic Meteorology. Introduction In this and other recent lectures, we have developed
Atmospheric dynamics and meteorology
 Atmospheric dynamics and meteorology B. Legras, http://www.lmd.ens.fr/legras III Frontogenesis (pre requisite: quasi-geostrophic equation, baroclinic instability in the Eady and Phillips models ) Recommended
Atmospheric dynamics and meteorology B. Legras, http://www.lmd.ens.fr/legras III Frontogenesis (pre requisite: quasi-geostrophic equation, baroclinic instability in the Eady and Phillips models ) Recommended
( ) = 1005 J kg 1 K 1 ;
 Problem Set 3 1. A parcel of water is added to the ocean surface that is denser (heavier) than any of the waters in the ocean. Suppose the parcel sinks to the ocean bottom; estimate the change in temperature
Problem Set 3 1. A parcel of water is added to the ocean surface that is denser (heavier) than any of the waters in the ocean. Suppose the parcel sinks to the ocean bottom; estimate the change in temperature
Boundary layer controls on extratropical cyclone development
 Boundary layer controls on extratropical cyclone development R. S. Plant (With thanks to: I. A. Boutle and S. E. Belcher) 28th May 2010 University of East Anglia Outline Introduction and background Baroclinic
Boundary layer controls on extratropical cyclone development R. S. Plant (With thanks to: I. A. Boutle and S. E. Belcher) 28th May 2010 University of East Anglia Outline Introduction and background Baroclinic
On side wall labeled A: we can express the pressure in a Taylor s series expansion: x 2. + higher order terms,
 Chapter 1 Notes A Note About Coordinates We nearly always use a coordinate system in this class where the vertical, ˆk, is normal to the Earth s surface and the x-direction, î, points to the east and the
Chapter 1 Notes A Note About Coordinates We nearly always use a coordinate system in this class where the vertical, ˆk, is normal to the Earth s surface and the x-direction, î, points to the east and the
The atmosphere in motion: forces and wind. AT350 Ahrens Chapter 9
 The atmosphere in motion: forces and wind AT350 Ahrens Chapter 9 Recall that Pressure is force per unit area Air pressure is determined by the weight of air above A change in pressure over some distance
The atmosphere in motion: forces and wind AT350 Ahrens Chapter 9 Recall that Pressure is force per unit area Air pressure is determined by the weight of air above A change in pressure over some distance
Fundamentals of Atmospheric Modelling
 M.Sc. in Computational Science Fundamentals of Atmospheric Modelling Peter Lynch, Met Éireann Mathematical Computation Laboratory (Opp. Room 30) Dept. of Maths. Physics, UCD, Belfield. January April, 2004.
M.Sc. in Computational Science Fundamentals of Atmospheric Modelling Peter Lynch, Met Éireann Mathematical Computation Laboratory (Opp. Room 30) Dept. of Maths. Physics, UCD, Belfield. January April, 2004.
GFD 2 Spring 2010 P.B. Rhines Problem set 1-solns out: 5 April back: 12 April
 GFD 2 Spring 2010 P.B. Rhines Problem set 1-solns out: 5 April back: 12 April 1 The Gulf Stream has a dramatic thermal-wind signature : the sloping isotherms and isohalines (hence isopycnals) not only
GFD 2 Spring 2010 P.B. Rhines Problem set 1-solns out: 5 April back: 12 April 1 The Gulf Stream has a dramatic thermal-wind signature : the sloping isotherms and isohalines (hence isopycnals) not only
Chapter 5. Shallow Water Equations. 5.1 Derivation of shallow water equations
 Chapter 5 Shallow Water Equations So far we have concentrated on the dynamics of small-scale disturbances in the atmosphere and ocean with relatively simple background flows. In these analyses we have
Chapter 5 Shallow Water Equations So far we have concentrated on the dynamics of small-scale disturbances in the atmosphere and ocean with relatively simple background flows. In these analyses we have
