Fronts & Frontogenesis
|
|
|
- Mervin Cook
- 5 years ago
- Views:
Transcription
1 Fronts & Frontogenesis
2 Fronts & Frontogenesis In a landmark paper, Sawyer (1956) stated that although the Norwegian system of frontal analysis has been generally accepted by weather forecasters since the 1920 s, no satisfactory explanation has been given for the up-gliding motion of the warm air to which is attributed the characteristic frontal cloud and rain. Simple dynamical theory shows that a sloping discontinuity between two air masses with different densities and velocities can exist without vertical movement of either air mass....
3 Fronts & Frontogenesis In a landmark paper, Sawyer (1956) stated that although the Norwegian system of frontal analysis has been generally accepted by weather forecasters since the 1920 s, no satisfactory explanation has been given for the up-gliding motion of the warm air to which is attributed the characteristic frontal cloud and rain. Simple dynamical theory shows that a sloping discontinuity between two air masses with different densities and velocities can exist without vertical movement of either air mass.... Sawyer goes on to suggest that... a front should be considered not so much as a stable area of strong temperature contrast between two air masses, but as an area into which active confluence of air currents of different temperature is taking place.
4 Several processes including friction, turbulence and vertical motion (ascent in warm air leads to cooling, subsidence in cold air leads to warming) might be expected to destroy the sharp temperature contrast of a front within a day or two of formation. 2
5 Several processes including friction, turbulence and vertical motion (ascent in warm air leads to cooling, subsidence in cold air leads to warming) might be expected to destroy the sharp temperature contrast of a front within a day or two of formation. Therefore, clearly defined fronts are likely to be found only where active frontogenesis is in progress; i.e., in an area where the horizontal air movements are such as to intensify the horizontal temperature gradients. 2
6 Several processes including friction, turbulence and vertical motion (ascent in warm air leads to cooling, subsidence in cold air leads to warming) might be expected to destroy the sharp temperature contrast of a front within a day or two of formation. Therefore, clearly defined fronts are likely to be found only where active frontogenesis is in progress; i.e., in an area where the horizontal air movements are such as to intensify the horizontal temperature gradients. These ideas are supported by observations. 2
7 Kinematics of Frontogenesis 3
8 Kinematics of Frontogenesis Examples of two basic horizontal flow configurations which can lead to frontogenesis are shown below. The intensification of horizontal temperature by horizontal shear, and pure horizontal deformation. 3
9 A parallel shear flow and a pure deformation field can intensify temperature gradients provided the isotherms are suitably oriented. 4
10 A parallel shear flow and a pure deformation field can intensify temperature gradients provided the isotherms are suitably oriented. To understand the way in which motion fields in general lead to frontogenesis and, indeed, to quantify the rate of frontogenesis, we need to study the relative motion near a point P in a fluid, as indicated in the following figure. 4
11 Let P be at (x, y) and Q at (x + δx, y + δy). Let the velocity at P be (u 0, v 0 ) and that at Q be (u 0 + δu, v 0 + δv). 5
12 Let P be at (x, y) and Q at (x + δx, y + δy). Let the velocity at P be (u 0, v 0 ) and that at Q be (u 0 + δu, v 0 + δv). The relative motion between the flow at P and at the neighbouring point Q is δu = u u 0 u u δx + x y δy δv = v v 0 v v δx + x y δy 5
13 Let P be at (x, y) and Q at (x + δx, y + δy). Let the velocity at P be (u 0, v 0 ) and that at Q be (u 0 + δu, v 0 + δv). The relative motion between the flow at P and at the neighbouring point Q is δu = u u 0 u u δx + x y δy δv = v v 0 v v δx + x y δy In matrix form, this is ( ) [ u δu = x u y δv v x y v ] ( δx δy ) = [ ux u y v x v y ] ( δx δy ) = M ( δx δy ) 5
14 Let P be at (x, y) and Q at (x + δx, y + δy). Let the velocity at P be (u 0, v 0 ) and that at Q be (u 0 + δu, v 0 + δv). The relative motion between the flow at P and at the neighbouring point Q is δu = u u 0 u u δx + x y δy δv = v v 0 v v δx + x y δy In matrix form, this is ( ) [ u δu = x u y δv v x y v ] ( δx δy ) = [ ux u y v x v y ] ( δx δy ) = M ( δx δy ) Any matrix can be written as a sum of a symmetric matrix and an antisymmetric matrix: M = 1 2 (M + MT ) (M MT ) 5
15 We introduce a pair of matrices, S: [ 12 S = 1 2 (M + MT (u ) = x + u x 1 ( ) 2 uy + v x 1 ( ) 2 vx + u 12 ( ) y vy + v y ] and A: A = 1 2 (M MT ) = [ 12 (u x u x 1 ( ) ( ) 2 uy v x vx u 12 ( ) y vy v y 1 2 ] 6
16 We introduce a pair of matrices, S: [ 12 S = 1 2 (M + MT (u ) = x + u x 1 ( ) 2 uy + v x 1 ( ) 2 vx + u 12 ( ) y vy + v y ] and A: It follows that and therefore ( δu δv A = 1 2 (M MT ) = ) = M [ 12 (u x u x 1 ( ) ] ( ) 2 uy v x vx u 12 ( ) y vy v y 1 2 M = S + A = ( δx δy ) = S [ ux u y v x v y ( δx δy ) ] + A ( δx δy ) 6
17 We introduce a pair of matrices, S: [ 12 S = 1 2 (M + MT (u ) = x + u x 1 ( ) 2 uy + v x 1 ( ) 2 vx + u 12 ( ) y vy + v y ] and A: It follows that and therefore ( δu δv A = 1 2 (M MT ) = ) = M [ 12 (u x u x 1 ( ) ] ( ) 2 uy v x vx u 12 ( ) y vy v y 1 2 M = S + A = ( δx δy ) = S [ ux u y v x v y ( δx δy ) ] + A ( δx δy Such a decomposition is standard in developing the equations for viscous fluid motion (see e.g. Batchelor, 1970, 2.3). ) 6
18 It can be shown that S and A are second order tensors. S is symmetric (S ji = S ij ) and A antisymmetric (A ji = A ij ). 7
19 It can be shown that S and A are second order tensors. S is symmetric (S ji = S ij ) and A antisymmetric (A ji = A ij ). Note that A has only one independent non-zero component, equal to half the vertical component of vorticity, 1 2 ζ. 7
20 It can be shown that S and A are second order tensors. S is symmetric (S ji = S ij ) and A antisymmetric (A ji = A ij ). Note that A has only one independent non-zero component, equal to half the vertical component of vorticity, 1 2 ζ. We can write δu = (S 11 δx + S 12 δy) + (A 11 δx + A 12 δy) δv = (S 21 δx + S 22 δy) + (A 21 δx + A 22 δy) 7
21 It can be shown that S and A are second order tensors. S is symmetric (S ji = S ij ) and A antisymmetric (A ji = A ij ). Note that A has only one independent non-zero component, equal to half the vertical component of vorticity, 1 2 ζ. We can write δu = (S 11 δx + S 12 δy) + (A 11 δx + A 12 δy) δv = (S 21 δx + S 22 δy) + (A 21 δx + A 22 δy) Using the fact that A 11 and A 22 are zero, we have δu = S 11 δx + (S 12 + A 12 )δy δv = (S 21 + A 21 )δx + S 22 δy 7
22 It can be shown that S and A are second order tensors. S is symmetric (S ji = S ij ) and A antisymmetric (A ji = A ij ). Note that A has only one independent non-zero component, equal to half the vertical component of vorticity, 1 2 ζ. We can write δu = (S 11 δx + S 12 δy) + (A 11 δx + A 12 δy) δv = (S 21 δx + S 22 δy) + (A 21 δx + A 22 δy) Using the fact that A 11 and A 22 are zero, we have δu = S 11 δx + (S 12 + A 12 )δy δv = (S 21 + A 21 )δx + S 22 δy We now locate the origin of coordinates at the point P, so that (δx, δy) become simply (x, y). 7
23 It can be shown that S and A are second order tensors. S is symmetric (S ji = S ij ) and A antisymmetric (A ji = A ij ). Note that A has only one independent non-zero component, equal to half the vertical component of vorticity, 1 2 ζ. We can write δu = (S 11 δx + S 12 δy) + (A 11 δx + A 12 δy) δv = (S 21 δx + S 22 δy) + (A 21 δx + A 22 δy) Using the fact that A 11 and A 22 are zero, we have δu = S 11 δx + (S 12 + A 12 )δy δv = (S 21 + A 21 )δx + S 22 δy We now locate the origin of coordinates at the point P, so that (δx, δy) become simply (x, y). Also, A 21 = 1 2 (v x u y ) = 1 2 ζ and A 12 = A 21 = 1 2 ζ. 7
24 Now, in preference to the four derivatives u x, u y, v x, v y, we define the equivalent four combinations of these derivatives: D = u x + v y, the divergence (formerly δ) E = u x v y, the stretching deformation F = v x + u y, the shearing deformation ζ = v x u y, the vorticity 8
25 Now, in preference to the four derivatives u x, u y, v x, v y, we define the equivalent four combinations of these derivatives: D = u x + v y, the divergence (formerly δ) E = u x v y, the stretching deformation F = v x + u y, the shearing deformation ζ = v x u y, the vorticity Obviously, we can solve for u x, u y, v x and v y as functions of D, E, F and ζ: u x = 1 2 (D +E), u y = 2 1(F ζ), v x = 1 2 (F +ζ), v y = 1 2 (D E). 8
26 Now, in preference to the four derivatives u x, u y, v x, v y, we define the equivalent four combinations of these derivatives: D = u x + v y, the divergence (formerly δ) E = u x v y, the stretching deformation F = v x + u y, the shearing deformation ζ = v x u y, the vorticity Obviously, we can solve for u x, u y, v x and v y as functions of D, E, F and ζ: u x = 1 2 (D +E), u y = 2 1(F ζ), v x = 1 2 (F +ζ), v y = 1 2 (D E). Note that E is like D, but with a minus sign; F is like ζ, but with a plus sign. 8
27 Now, in preference to the four derivatives u x, u y, v x, v y, we define the equivalent four combinations of these derivatives: D = u x + v y, the divergence (formerly δ) E = u x v y, the stretching deformation F = v x + u y, the shearing deformation ζ = v x u y, the vorticity Obviously, we can solve for u x, u y, v x and v y as functions of D, E, F and ζ: u x = 1 2 (D +E), u y = 2 1(F ζ), v x = 1 2 (F +ζ), v y = 1 2 (D E). Note that E is like D, but with a minus sign; F is like ζ, but with a plus sign. E is called the stretching deformation because the velocity components are differentiated in the direction of the component. In F, the shearing deformation, each velocity component is differentiated at right angles to its direction. 8
28 We can write the relative velocity as ( ) [ δu u 1 = x 2 (v x + u y ) 1 2 ζ δv 1 2 (v x + u y ) ζ v y ] ( x y ) 9
29 We can write the relative velocity as ( ) [ δu u 1 = x 2 (v x + u y ) 1 2 ζ δv 1 2 (v x + u y ) ζ v y ] ( x y This equation may now be written in the form: ( ) [( ) ( ) ( ) ( δu = δv 1 D 0 E 0 0 F 0 ζ D 0 E F 0 ζ 0 ) )] ( x y ) 9
30 We can write the relative velocity as ( ) [ δu u 1 = x 2 (v x + u y ) 1 2 ζ δv 1 2 (v x + u y ) ζ v y ] ( x y This equation may now be written in the form: ( ) [( ) ( ) ( ) ( δu = δv 1 D 0 E 0 0 F 0 ζ D 0 E F 0 ζ 0 ) )] ( x y ) In component form, this is u = u (Dx + Ex + F y ζy) v = v (Dy Ey + F x + ζx) where δu = u u 0, δv = v v 0, and (u 0, v 0 ) is the translation velocity at the point P. 9
31 We can write the relative velocity as ( ) [ δu u 1 = x 2 (v x + u y ) 1 2 ζ δv 1 2 (v x + u y ) ζ v y ] ( x y This equation may now be written in the form: ( ) [( ) ( ) ( ) ( δu = δv 1 D 0 E 0 0 F 0 ζ D 0 E F 0 ζ 0 ) )] ( x y ) In component form, this is u = u (Dx + Ex + F y ζy) v = v (Dy Ey + F x + ζx) where δu = u u 0, δv = v v 0, and (u 0, v 0 ) is the translation velocity at the point P. Henceforth, we choose our frame of reference so that u 0 = v 0 = 0. That is, the frame moves with the point P. 9
32 Schematic diagram of the components of flow in the neighbourhood of a point: (a) pure divergence/convergence; (b) pure rotation; (c) pure stretching deformation; and (d) pure shearing deformation. 10
33 Decomposition of Relative Motion Clearly, the relative motion near the point P can be decomposed into four basic components, as follows. 11
34 Decomposition of Relative Motion Clearly, the relative motion near the point P can be decomposed into four basic components, as follows. (I) Pure divergence (only D nonzero). Then u = 1 2 Dx, v = 1 2 Dy or, in vector notation, u = 1 2D(r cos θ, r sin θ) = Dr, r being the position vector from P. Thus the motion is purely radial and is to or from the point P according to the sign of D. 11
35 Decomposition of Relative Motion Clearly, the relative motion near the point P can be decomposed into four basic components, as follows. (I) Pure divergence (only D nonzero). Then u = 1 2 Dx, v = 1 2 Dy or, in vector notation, u = 1 2D(r cos θ, r sin θ) = Dr, r being the position vector from P. Thus the motion is purely radial and is to or from the point P according to the sign of D. (II) Pure rotation (only ζ nonzero). Then u = 1 2 ζy, v = 1 2 ζx, whereupon u = 1 2 ( r sin θ, r cos θ) = 1 2 ζrˆθ, where ˆθ is the unit normal vector to r. Clearly such motion corresponds with solid body rotation with angular velocity 1 2 ζ. 11
36 Schematic diagram of the components of flow in the neighbourhood of a point: (a) pure divergence/convergence; (b) pure rotation; (c) pure stretching deformation; and (d) pure shearing deformation. 12
37 (III) Pure stretching deformation (only E nonzero). The velocity components are given by u = 1 2 E x, v = 1 2 E y On a streamline, dy/dx = v/u = y/x, or x dy+y dx = d(xy) = 0. Hence the streamlines are rectangular hyperbolae xy = constant. In the figure, the indicated flow directions are for E > 0. For E < 0, the directions are reversed. 13
38 (III) Pure stretching deformation (only E nonzero). The velocity components are given by u = 1 2 E x, v = 1 2 E y On a streamline, dy/dx = v/u = y/x, or x dy+y dx = d(xy) = 0. Hence the streamlines are rectangular hyperbolae xy = constant. In the figure, the indicated flow directions are for E > 0. For E < 0, the directions are reversed. (IV) Pure shearing deformation (only F nonzero). The velocity components are given by u = 1 2 F y, v = 1 2 F x The streamlines are given now by dy/dx = x/y, or d(y 2 x 2 ) = 0, so that y 2 x 2 = constant. Thus the streamlines are again rectangular hyperbolae, but with their axes of dilatation and contraction at 45 to the coordinate axes. The flow directions indicated are for F > 0. 13
39 Schematic diagram of the components of flow in the neighbourhood of a point: (a) pure divergence/convergence; (b) pure rotation; (c) pure stretching deformation; and (d) pure shearing deformation. 14
40 Total deformation. We assume that ζ = D = 0 and that E and F are nonzero). Then δu = 2 1 (+Ex + F y) δv = 1 2 ( Ey + F x) 15
41 Total deformation. We assume that ζ = D = 0 and that E and F are nonzero). Then δu = 2 1 (+Ex + F y) δv = 1 2 ( Ey + F x) We can show, by rotating the axes (x, y) to (x, y ), that we can choose the rotation angle φ so that the two deformation fields together reduce to a single field with the axis of dilatation at angle φ to the x-axis. [For details, see Roger Smith s notes, pp ]. 15
42 Total deformation. We assume that ζ = D = 0 and that E and F are nonzero). Then δu = 2 1 (+Ex + F y) δv = 1 2 ( Ey + F x) We can show, by rotating the axes (x, y) to (x, y ), that we can choose the rotation angle φ so that the two deformation fields together reduce to a single field with the axis of dilatation at angle φ to the x-axis. [For details, see Roger Smith s notes, pp ]. In other words, the stretching and shearing deformation fields may be combined to give a single total deformation field. The strength of this field is given by E = (E 2 + F 2 ) 1/2 and the axis of dilatation is inclined at an angle φ to the x-axis given by tan 2φ = F/E The total deformation field is illustrated below. 15
43 16
44 The Frontogenesis Function The frontogenetic or frontolytic tendency in a flow can be measured by the quantity d h θ /dt, which is called the frontogenesis function. 17
45 The Frontogenesis Function The frontogenetic or frontolytic tendency in a flow can be measured by the quantity d h θ /dt, which is called the frontogenesis function. This is the rate of change of horizontal potential-temperature gradient h following a fluid parcel. 17
46 The Frontogenesis Function The frontogenetic or frontolytic tendency in a flow can be measured by the quantity d h θ /dt, which is called the frontogenesis function. This is the rate of change of horizontal potential-temperature gradient h following a fluid parcel. An expression for the frontogenesis function is obtained by differentiation of the thermodynamic equation dθ dt = θ c p Q q where q represents diabatic heat sources and sinks. 17
47 The Frontogenesis Function The frontogenetic or frontolytic tendency in a flow can be measured by the quantity d h θ /dt, which is called the frontogenesis function. This is the rate of change of horizontal potential-temperature gradient h following a fluid parcel. An expression for the frontogenesis function is obtained by differentiation of the thermodynamic equation dθ dt = θ c p Q q where q represents diabatic heat sources and sinks. Differentiating with respect to x and y in turn gives ( ) d θ + u θ dt x x x + v θ x y + w θ x z = q ( ) x d θ + u θ dt y y x + v θ y y + w θ y z = q y 17
48 But we have d dt θ 2 = 2 θ d ( θ dt θ = 2 x, θ ) [ d y dt ( ) θ, d x dt ( )] θ y 18
49 But we have d dt θ 2 = 2 θ d ( θ dt θ = 2 x, θ ) [ d y dt ( ) θ, d x dt ( )] θ y Substituting from above we get d ] dt θ 2 = 2 [(θ x q x +θ y q y ) (θ x w x +θ y w y )θ z (u x θx+v 2 y θy) (v 2 x +u y )θ x θ y 18
50 But we have d dt θ 2 = 2 θ d ( θ dt θ = 2 x, θ ) [ d y dt ( ) θ, d x dt ( )] θ y Substituting from above we get d ] dt θ 2 = 2 [(θ x q x +θ y q y ) (θ x w x +θ y w y )θ z (u x θx+v 2 y θy) (v 2 x +u y )θ x θ y We now recall the formulae: u x = 2 1(D +E), u y = 2 1(F ζ), v x = 1 2 (F +ζ), v y = 1 2 (D E). 18
51 But we have d dt θ 2 = 2 θ d ( θ dt θ = 2 x, θ ) [ d y dt ( ) θ, d x dt ( )] θ y Substituting from above we get d ] dt θ 2 = 2 [(θ x q x +θ y q y ) (θ x w x +θ y w y )θ z (u x θx+v 2 y θy) (v 2 x +u y )θ x θ y We now recall the formulae: u x = 2 1(D +E), u y = 2 1(F ζ), v x = 1 2 (F +ζ), v y = 1 2 (D E). Substituting from these, we obtain d dt θ 2 = 2(θ x q x + θ y q y ) 2(θ x w x + θ y w y )θ z D θ 2 [Eθ 2 x + 2F θ x θ y Eθ 2 y] 18
52 But we have d dt θ 2 = 2 θ d ( θ dt θ = 2 x, θ ) [ d y dt ( ) θ, d x dt ( )] θ y Substituting from above we get d ] dt θ 2 = 2 [(θ x q x +θ y q y ) (θ x w x +θ y w y )θ z (u x θx+v 2 y θy) (v 2 x +u y )θ x θ y We now recall the formulae: u x = 2 1(D +E), u y = 2 1(F ζ), v x = 1 2 (F +ζ), v y = 1 2 (D E). Substituting from these, we obtain d dt θ 2 = 2(θ x q x + θ y q y ) 2(θ x w x + θ y w y )θ z D θ 2 [Eθ 2 x + 2F θ x θ y Eθ 2 y] Note that the vorticity ζ does not appear in this equation. 18
53 There are four separate effects contributing to frontogenesis. Let us write d dt θ = T 1 + T 2 + T 3 + T 4 where T 1 = (θ x q x + θ y q y )/ θ T 2 = (θ x w x + θ y w y )θ z / θ T 3 = 1 2 D θ 2 / θ T 4 = 1 2 [Eθ2 x + 2F θ x θ y Eθ 2 y]/ θ 19
54 There are four separate effects contributing to frontogenesis. Let us write d dt θ = T 1 + T 2 + T 3 + T 4 where T 1 = (θ x q x + θ y q y )/ θ T 2 = (θ x w x + θ y w y )θ z / θ T 3 = 1 2 D θ 2 / θ T 4 = 1 2 [Eθ2 x + 2F θ x θ y Eθ 2 y]/ θ Defining ˆn to be the unit vector in the direction of θ, we can write T 1 = ˆn q T 2 = θ zˆn w T 3 = 1 2 D θ T 4 = 1 2 [Eθ2 x + 2F θ x θ y Eθ 2 y]/ θ 19
55 The terms T 1 T 4 may be interpreted as follows: 20
56 The terms T 1 T 4 may be interpreted as follows: T1: represents the rate of frontogenesis due to a gradient of diabatic heating in the direction of the existing temperature gradient. 20
57 The terms T 1 T 4 may be interpreted as follows: T1: represents the rate of frontogenesis due to a gradient of diabatic heating in the direction of the existing temperature gradient. T2: represents the conversion of vertical temperature gradient to horizontal gradient by a component of differential vertical motion (vertical shear) in the direction of the existing temperature gradient. 20
58 The terms T 1 T 4 may be interpreted as follows: T1: represents the rate of frontogenesis due to a gradient of diabatic heating in the direction of the existing temperature gradient. T2: represents the conversion of vertical temperature gradient to horizontal gradient by a component of differential vertical motion (vertical shear) in the direction of the existing temperature gradient. T3: represents the rate of increase of horizontal temperature gradient due to horizontal convergence (i.e., negative divergence) in the presence of an existing gradient. 20
59 The terms T 1 T 4 may be interpreted as follows: T1: represents the rate of frontogenesis due to a gradient of diabatic heating in the direction of the existing temperature gradient. T2: represents the conversion of vertical temperature gradient to horizontal gradient by a component of differential vertical motion (vertical shear) in the direction of the existing temperature gradient. T3: represents the rate of increase of horizontal temperature gradient due to horizontal convergence (i.e., negative divergence) in the presence of an existing gradient. T4: represents the frontogenetic effect of a (total) horizontal deformation field. 20
60 T1: T 1 = ˆn q The rate of frontogenesis due to a gradient of diabatic heating in the direction of the existing temperature gradient. 21
61 T2: T 2 = θ zˆn w The conversion of vertical temperature gradient to horizontal gradient by a component of differential vertical motion (vertical shear) in the direction of the existing temperature gradient. 22
62 T3: T 3 = 1 2 D θ The rate of increase of horizontal temperature gradient due to horizontal convergence (i.e., negative divergence) in the presence of an existing gradient. 23
63 T4: T 4 = 1 2 [Eθ2 x + 2F θ x θ y Eθ 2 y]/ θ The frontogenetic effect of a (total) horizontal deformation field. 24
64 Further insight into the term T 4 may be obtained by a rotation of axes to those of the deformation field. We can show that T 4 = 1 2 E θ cos 2β (see figure above, and Roger Smith s notes for proof). 25
65 Further insight into the term T 4 may be obtained by a rotation of axes to those of the deformation field. We can show that T 4 = 1 2 E θ cos 2β (see figure above, and Roger Smith s notes for proof). This shows that the frontogenetic effect of deformation is a maximum when the isentropes are parallel with the dilatation axis (β = 0). 25
66 Further insight into the term T 4 may be obtained by a rotation of axes to those of the deformation field. We can show that T 4 = 1 2 E θ cos 2β (see figure above, and Roger Smith s notes for proof). This shows that the frontogenetic effect of deformation is a maximum when the isentropes are parallel with the dilatation axis (β = 0). It reduces to zero as the angle between the isentropes and the dilatation axis increases to
67 Further insight into the term T 4 may be obtained by a rotation of axes to those of the deformation field. We can show that T 4 = 1 2 E θ cos 2β (see figure above, and Roger Smith s notes for proof). This shows that the frontogenetic effect of deformation is a maximum when the isentropes are parallel with the dilatation axis (β = 0). It reduces to zero as the angle between the isentropes and the dilatation axis increases to 45. When the angle β is between 45 and 90, deformation has a frontolytic effect, i.e., T 4 is negative. 25
68 A number of observational studies have sought to determine the relative importance of the contributions T n to the frontogenesis function. 26
69 A number of observational studies have sought to determine the relative importance of the contributions T n to the frontogenesis function. Unfortunately, observational estimates of T 2 are noisy, since estimates for w tend to be noisy, let alone the gradient of w. Moreover, T 4 is extremely difficult to estimate from observational data currently available. 26
70 A number of observational studies have sought to determine the relative importance of the contributions T n to the frontogenesis function. Unfortunately, observational estimates of T 2 are noisy, since estimates for w tend to be noisy, let alone the gradient of w. Moreover, T 4 is extremely difficult to estimate from observational data currently available. A case study by Ogura and Portis (1982) shows that T 2, T 3 and T 4 are all important in the immediate vicinity of the front, whereas this and other investigations suggest that horizontal deformation (including horizontal shear) plays a primary role on the synoptic scale. 26
71 A number of observational studies have sought to determine the relative importance of the contributions T n to the frontogenesis function. Unfortunately, observational estimates of T 2 are noisy, since estimates for w tend to be noisy, let alone the gradient of w. Moreover, T 4 is extremely difficult to estimate from observational data currently available. A case study by Ogura and Portis (1982) shows that T 2, T 3 and T 4 are all important in the immediate vicinity of the front, whereas this and other investigations suggest that horizontal deformation (including horizontal shear) plays a primary role on the synoptic scale. Clearly, on a large scale, term T 1 must be dominant. Why? 26
72 This Figure shows a mean-sea-level isobaric analysis for the Australian region with a cold front over south-eastern Australia sandwiched between two anticyclones. 27
73 This situation is frontogenetic with warm air advection in the hot northerlies ahead of the front and strong cold air advection in the maritime southwesterlies behind it. 28
74 In an early study of many fronts over the British Isles, Sawyer (1956) found that active fronts are associated with a deformation field which leads to an intensification of the horizontal temperature gradient. 29
75 In an early study of many fronts over the British Isles, Sawyer (1956) found that active fronts are associated with a deformation field which leads to an intensification of the horizontal temperature gradient. He found also that the effect is most clearly defined at the 700 mb level, at which the rate of contraction of fluid elements in the direction of the temperature gradient usually has a well-defined maximum near the front. 29
76 A graphic illustration of the way in which flow deformation acting on an advected passive scalar quantity produces locally large gradients of the scalar was given by Welander (1955). 30
Mesoscale Atmospheric Systems. Surface fronts and frontogenesis. 06 March 2018 Heini Wernli. 06 March 2018 H. Wernli 1
 Mesoscale Atmospheric Systems Surface fronts and frontogenesis 06 March 2018 Heini Wernli 06 March 2018 H. Wernli 1 Temperature (degc) Frontal passage in Mainz on 26 March 2010 06 March 2018 H. Wernli
Mesoscale Atmospheric Systems Surface fronts and frontogenesis 06 March 2018 Heini Wernli 06 March 2018 H. Wernli 1 Temperature (degc) Frontal passage in Mainz on 26 March 2010 06 March 2018 H. Wernli
Chapter 12 Fronts & Air Masses
 Chapter overview: Anticyclones or highs Air Masses o Classification o Source regions o Air masses of North America Fronts o Stationary fronts o Cold fronts o Warm fronts o Fronts and the jet stream o Frontogenesis
Chapter overview: Anticyclones or highs Air Masses o Classification o Source regions o Air masses of North America Fronts o Stationary fronts o Cold fronts o Warm fronts o Fronts and the jet stream o Frontogenesis
Atmospheric Fronts. The material in this section is based largely on. Lectures on Dynamical Meteorology by Roger Smith.
 Atmospheric Fronts The material in this section is based largely on Lectures on Dynamical Meteorology by Roger Smith. Atmospheric Fronts 2 Atmospheric Fronts A front is the sloping interfacial region of
Atmospheric Fronts The material in this section is based largely on Lectures on Dynamical Meteorology by Roger Smith. Atmospheric Fronts 2 Atmospheric Fronts A front is the sloping interfacial region of
By convention, C > 0 for counterclockwise flow, hence the contour must be counterclockwise.
 Chapter 4 4.1 The Circulation Theorem Circulation is a measure of rotation. It is calculated for a closed contour by taking the line integral of the velocity component tangent to the contour evaluated
Chapter 4 4.1 The Circulation Theorem Circulation is a measure of rotation. It is calculated for a closed contour by taking the line integral of the velocity component tangent to the contour evaluated
Control Volume. Dynamics and Kinematics. Basic Conservation Laws. Lecture 1: Introduction and Review 1/24/2017
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review
 Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
1/3/2011. This course discusses the physical laws that govern atmosphere/ocean motions.
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Fronts in November 1998 Storm
 Fronts in November 1998 Storm Much of the significant weather observed in association with extratropical storms tends to be concentrated within narrow bands called frontal zones. Fronts in November 1998
Fronts in November 1998 Storm Much of the significant weather observed in association with extratropical storms tends to be concentrated within narrow bands called frontal zones. Fronts in November 1998
Atmospheric dynamics and meteorology
 Atmospheric dynamics and meteorology B. Legras, http://www.lmd.ens.fr/legras III Frontogenesis (pre requisite: quasi-geostrophic equation, baroclinic instability in the Eady and Phillips models ) Recommended
Atmospheric dynamics and meteorology B. Legras, http://www.lmd.ens.fr/legras III Frontogenesis (pre requisite: quasi-geostrophic equation, baroclinic instability in the Eady and Phillips models ) Recommended
Contraction Rate and Its Relationship to Frontogenesis, the Lyapunov Exponent, Fluid Trapping, and Airstream Boundaries
 MAY 2005 C O H E N A N D S C H U L T Z 1353 Contraction Rate and Its Relationship to Frontogenesis, the Lyapunov Exponent, Fluid Trapping, and Airstream Boundaries ROBERT A. COHEN Department of Physics,
MAY 2005 C O H E N A N D S C H U L T Z 1353 Contraction Rate and Its Relationship to Frontogenesis, the Lyapunov Exponent, Fluid Trapping, and Airstream Boundaries ROBERT A. COHEN Department of Physics,
The dynamics of high and low pressure systems
 The dynamics of high and low pressure systems Newton s second law for a parcel of air in an inertial coordinate system (a coordinate system in which the coordinate axes do not change direction and are
The dynamics of high and low pressure systems Newton s second law for a parcel of air in an inertial coordinate system (a coordinate system in which the coordinate axes do not change direction and are
Final Examination, MEA 443 Fall 2008, Lackmann
 Place an X here to count it double! Name: Final Examination, MEA 443 Fall 2008, Lackmann If you wish to have the final exam count double and replace your midterm score, place an X in the box above. As
Place an X here to count it double! Name: Final Examination, MEA 443 Fall 2008, Lackmann If you wish to have the final exam count double and replace your midterm score, place an X in the box above. As
A Cyclogenesis south of the Alps. Manfred Kurz Neustadt/Weinstraße
 A Cyclogenesis south of the Alps Manfred Kurz Neustadt/Weinstraße A cyclogenesis south of the Alps Surface maps 06-11-99, 00 UTC The occluded frontal system of a quasi-stationary low above the North Sea
A Cyclogenesis south of the Alps Manfred Kurz Neustadt/Weinstraße A cyclogenesis south of the Alps Surface maps 06-11-99, 00 UTC The occluded frontal system of a quasi-stationary low above the North Sea
Measurement of Rotation. Circulation. Example. Lecture 4: Circulation and Vorticity 1/31/2017
 Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Errata: Midlatitude Synoptic Meteorology (July, 2014)
 Errata: Midlatitude Synoptic Meteorology (July, 2014) My apologies for the various inevitable errors contained in this first-edition text. We are working diligently to correct them. I gratefully acknowledge
Errata: Midlatitude Synoptic Meteorology (July, 2014) My apologies for the various inevitable errors contained in this first-edition text. We are working diligently to correct them. I gratefully acknowledge
Synoptic Meteorology II: Frontogenesis Examples Figure 1
 Synoptic Meteorology II: Frontogenesis Examples The below images, taken from the 1200 UTC 17 January 2019 GFS forecast run, provide examples of the contributions of deformation and divergence to frontogenesis.
Synoptic Meteorology II: Frontogenesis Examples The below images, taken from the 1200 UTC 17 January 2019 GFS forecast run, provide examples of the contributions of deformation and divergence to frontogenesis.
= vorticity dilution + tilting horizontal vortices + microscopic solenoid
 4.4 Vorticity Eq 4.4.1 Cartesian Coordinates Because ζ = ˆk V, gives D(ζ + f) x minus [v momentum eq. in Cartesian Coordinates] y [u momentum eq. in Cartesian Coordinates] = vorticity dilution + tilting
4.4 Vorticity Eq 4.4.1 Cartesian Coordinates Because ζ = ˆk V, gives D(ζ + f) x minus [v momentum eq. in Cartesian Coordinates] y [u momentum eq. in Cartesian Coordinates] = vorticity dilution + tilting
Electric Potential (Chapter 25)
 Electric Potential (Chapter 25) Electric potential energy, U Electric potential energy in a constant field Conservation of energy Electric potential, V Relation to the electric field strength The potential
Electric Potential (Chapter 25) Electric potential energy, U Electric potential energy in a constant field Conservation of energy Electric potential, V Relation to the electric field strength The potential
V (r,t) = i ˆ u( x, y,z,t) + ˆ j v( x, y,z,t) + k ˆ w( x, y, z,t)
 IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
Quasi-Geostrophic Implications
 Chapter 10 Quasi-Geostrophic Implications When you look at a weather chart with all its isolines and plotted data, you need a framework upon which to interpret what you see. Quasi-geostrophic theory provides
Chapter 10 Quasi-Geostrophic Implications When you look at a weather chart with all its isolines and plotted data, you need a framework upon which to interpret what you see. Quasi-geostrophic theory provides
Fixed Rossby Waves: Quasigeostrophic Explanations and Conservation of Potential Vorticity
 Fixed Rossby Waves: Quasigeostrophic Explanations and Conservation of Potential Vorticity 1. Observed Planetary Wave Patterns After upper air observations became routine, it became easy to produce contour
Fixed Rossby Waves: Quasigeostrophic Explanations and Conservation of Potential Vorticity 1. Observed Planetary Wave Patterns After upper air observations became routine, it became easy to produce contour
Synoptic-Dynamic Meteorology in Midlatitudes
 Synoptic-Dynamic Meteorology in Midlatitudes VOLUME II Observations and Theory of Weather Systems HOWARD B. BLUESTEIN New York Oxford OXFORD UNIVERSITY PRESS 1993 Contents 1. THE BEHAVIOR OF SYNOPTIC-SCALE,
Synoptic-Dynamic Meteorology in Midlatitudes VOLUME II Observations and Theory of Weather Systems HOWARD B. BLUESTEIN New York Oxford OXFORD UNIVERSITY PRESS 1993 Contents 1. THE BEHAVIOR OF SYNOPTIC-SCALE,
1. COLD FRONT - CLOUD STRUCTURE IN SATELLITE IMAGES
 1. COLD FRONT - CLOUD STRUCTURE IN SATELLITE IMAGES The satellite image shows a cyclonically curved synoptic scale cloud band usually a few hundred kilometres wide; in the VIS image the cloud band mostly
1. COLD FRONT - CLOUD STRUCTURE IN SATELLITE IMAGES The satellite image shows a cyclonically curved synoptic scale cloud band usually a few hundred kilometres wide; in the VIS image the cloud band mostly
Circulation and Vorticity
 Circulation and Vorticity Example: Rotation in the atmosphere water vapor satellite animation Circulation a macroscopic measure of rotation for a finite area of a fluid Vorticity a microscopic measure
Circulation and Vorticity Example: Rotation in the atmosphere water vapor satellite animation Circulation a macroscopic measure of rotation for a finite area of a fluid Vorticity a microscopic measure
1/18/2011. Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis ESS227 Prof. Jin-Yi Yu
 Lecture 2: Basic Conservation Laws Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed in an inertial system = rate of change of Ua following the motion in an inertial
Lecture 2: Basic Conservation Laws Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed in an inertial system = rate of change of Ua following the motion in an inertial
Isentropic Analysis. Much of this presentation is due to Jim Moore, SLU
 Isentropic Analysis Much of this presentation is due to Jim Moore, SLU Utility of Isentropic Analysis Diagnose and visualize vertical motion - through advection of pressure and system-relative flow Depict
Isentropic Analysis Much of this presentation is due to Jim Moore, SLU Utility of Isentropic Analysis Diagnose and visualize vertical motion - through advection of pressure and system-relative flow Depict
Summary of High Wind Event of 7 March 2004
 Summary of High Wind Event of 7 March 2004 This event was characterized by a very strong jet streak that developed over North Carolina by 00 UTC 8 March, as seen in the Eta model analysis at 300 mb, with
Summary of High Wind Event of 7 March 2004 This event was characterized by a very strong jet streak that developed over North Carolina by 00 UTC 8 March, as seen in the Eta model analysis at 300 mb, with
t tendency advection convergence twisting baroclinicity
 RELATIVE VORTICITY EQUATION Newton s law in a rotating frame in z-coordinate (frictionless): U + U U = 2Ω U Φ α p U + U U 2 + ( U) U = 2Ω U Φ α p Applying to both sides, and noting ω U and using identities
RELATIVE VORTICITY EQUATION Newton s law in a rotating frame in z-coordinate (frictionless): U + U U = 2Ω U Φ α p U + U U 2 + ( U) U = 2Ω U Φ α p Applying to both sides, and noting ω U and using identities
Mid-Latitude Cyclones and Fronts. Lecture 12 AOS 101
 Mid-Latitude Cyclones and Fronts Lecture 12 AOS 101 Homework 4 COLDEST TEMPS GEOSTROPHIC BALANCE Homework 4 FASTEST WINDS L Consider an air parcel rising through the atmosphere The parcel expands as it
Mid-Latitude Cyclones and Fronts Lecture 12 AOS 101 Homework 4 COLDEST TEMPS GEOSTROPHIC BALANCE Homework 4 FASTEST WINDS L Consider an air parcel rising through the atmosphere The parcel expands as it
Introduction to Fluid Dynamics
 Introduction to Fluid Dynamics Roger K. Smith Skript - auf englisch! Umsonst im Internet http://www.meteo.physik.uni-muenchen.de Wählen: Lehre Manuskripte Download User Name: meteo Password: download Aim
Introduction to Fluid Dynamics Roger K. Smith Skript - auf englisch! Umsonst im Internet http://www.meteo.physik.uni-muenchen.de Wählen: Lehre Manuskripte Download User Name: meteo Password: download Aim
5 Air Mass Boundaries
 5 Air Mass Boundaries Air masses and fronts are among the main features of the long-standing Norwegian cyclone model developed in the early part of the th century. Fronts are transition zones separating
5 Air Mass Boundaries Air masses and fronts are among the main features of the long-standing Norwegian cyclone model developed in the early part of the th century. Fronts are transition zones separating
Vertical structure. To conclude, we will review the critical factors invloved in the development of extratropical storms.
 Vertical structure Now we will examine the vertical structure of the intense baroclinic wave using three visualization tools: Upper level charts at selected pressure levels Vertical soundings for selected
Vertical structure Now we will examine the vertical structure of the intense baroclinic wave using three visualization tools: Upper level charts at selected pressure levels Vertical soundings for selected
Synoptic Meteorology II: Self-Development in the IPV Framework. 5-7 May 2015
 Synoptic Meteorology II: Self-Development in the IPV Framework 5-7 May 2015 Readings: Section 5.3.6 of Midlatitude Synoptic Meteorology. Introduction In this and other recent lectures, we have developed
Synoptic Meteorology II: Self-Development in the IPV Framework 5-7 May 2015 Readings: Section 5.3.6 of Midlatitude Synoptic Meteorology. Introduction In this and other recent lectures, we have developed
Strain analysis.
 Strain analysis ecalais@purdue.edu Plates vs. continuum Gordon and Stein, 1991 Most plates are rigid at the until know we have studied a purely discontinuous approach where plates are
Strain analysis ecalais@purdue.edu Plates vs. continuum Gordon and Stein, 1991 Most plates are rigid at the until know we have studied a purely discontinuous approach where plates are
 http://www.ssec.wisc.edu/data/composites.html Red curve: Incoming solar radiation Blue curve: Outgoing infrared radiation. Three-cell model of general circulation Mid-latitudes: 30 to 60 latitude MID-LATITUDES
http://www.ssec.wisc.edu/data/composites.html Red curve: Incoming solar radiation Blue curve: Outgoing infrared radiation. Three-cell model of general circulation Mid-latitudes: 30 to 60 latitude MID-LATITUDES
WEATHER PATTERNS NAME DATE. VOCABULARY: Synoptic weather map- Isotherm- Barometric Pressure- Isobar- Convergence- Divergence- Cyclone- Anticyclone-
 NAME DATE VOCABULARY: Synoptic weather map- WEATHER PATTERNS Isotherm- Barometric Pressure- Isobar- Convergence- Divergence- Cyclone- Anticyclone- Air mass- Source region- Front- OBJECTIVE: Construct a
NAME DATE VOCABULARY: Synoptic weather map- WEATHER PATTERNS Isotherm- Barometric Pressure- Isobar- Convergence- Divergence- Cyclone- Anticyclone- Air mass- Source region- Front- OBJECTIVE: Construct a
Conservation of Mass Conservation of Energy Scaling Analysis. ESS227 Prof. Jin-Yi Yu
 Lecture 2: Basic Conservation Laws Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed
Lecture 2: Basic Conservation Laws Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed
(Refer Slide Time: 0:35)
 Fluid Dynamics And Turbo Machines. Professor Dr Shamit Bakshi. Department Of Mechanical Engineering. Indian Institute Of Technology Madras. Part A. Module-1. Lecture-4. Tutorial. (Refer Slide Time: 0:35)
Fluid Dynamics And Turbo Machines. Professor Dr Shamit Bakshi. Department Of Mechanical Engineering. Indian Institute Of Technology Madras. Part A. Module-1. Lecture-4. Tutorial. (Refer Slide Time: 0:35)
ASTR 320: Solutions to Problem Set 2
 ASTR 320: Solutions to Problem Set 2 Problem 1: Streamlines A streamline is defined as a curve that is instantaneously tangent to the velocity vector of a flow. Streamlines show the direction a massless
ASTR 320: Solutions to Problem Set 2 Problem 1: Streamlines A streamline is defined as a curve that is instantaneously tangent to the velocity vector of a flow. Streamlines show the direction a massless
ESCI 344 Tropical Meteorology Lesson 11 Tropical Cyclones: Formation, Maintenance, and Intensification
 ESCI 344 Tropical Meteorology Lesson 11 Tropical Cyclones: Formation, Maintenance, and Intensification References: A Global View of Tropical Cyclones, Elsberry (ed.) Global Perspectives on Tropical Cylones:
ESCI 344 Tropical Meteorology Lesson 11 Tropical Cyclones: Formation, Maintenance, and Intensification References: A Global View of Tropical Cyclones, Elsberry (ed.) Global Perspectives on Tropical Cylones:
u g z = g T y (1) f T Margules Equation for Frontal Slope
 Margules Equation for Frontal Slope u g z = g f T T y (1) Equation (1) is the thermal wind relation for the west wind geostrophic component of the flow. For the purposes of this derivation, we assume that
Margules Equation for Frontal Slope u g z = g f T T y (1) Equation (1) is the thermal wind relation for the west wind geostrophic component of the flow. For the purposes of this derivation, we assume that
Second Order ODEs. Second Order ODEs. In general second order ODEs contain terms involving y, dy But here only consider equations of the form
 Second Order ODEs Second Order ODEs In general second order ODEs contain terms involving y, dy But here only consider equations of the form A d2 y dx 2 + B dy dx + Cy = 0 dx, d2 y dx 2 and F(x). where
Second Order ODEs Second Order ODEs In general second order ODEs contain terms involving y, dy But here only consider equations of the form A d2 y dx 2 + B dy dx + Cy = 0 dx, d2 y dx 2 and F(x). where
CONVERGENCE, DIVERGENCE, AND VORTICITY
 CHAPTER 1 CONVERGENCE, DIVERGENCE, AND VORTICITY In your reading of the AG2 manual, volume 1, you became familiar with the terms convergence, divergence, and vorticity when used in relation to surface
CHAPTER 1 CONVERGENCE, DIVERGENCE, AND VORTICITY In your reading of the AG2 manual, volume 1, you became familiar with the terms convergence, divergence, and vorticity when used in relation to surface
vis = 74 visibility = vis - 50, for 56 vis 80
 ATSC 201 Fall 2018 Assignment 11 Answer Key Total marks out of 69 Chapter 9: A1h, A7a, A8h, A10all Chapter 12: A1h, A7h, A8h, A11g, E21, E23 Chapter 9 A1h) Find the pressure "reduced to sea level" using
ATSC 201 Fall 2018 Assignment 11 Answer Key Total marks out of 69 Chapter 9: A1h, A7a, A8h, A10all Chapter 12: A1h, A7h, A8h, A11g, E21, E23 Chapter 9 A1h) Find the pressure "reduced to sea level" using
EESC V2100 The Climate System spring 2004 Lecture 4: Laws of Atmospheric Motion and Weather
 EESC V2100 The Climate System spring 2004 Lecture 4: Laws of Atmospheric Motion and Weather Yochanan Kushnir Lamont Doherty Earth Observatory of Columbia University Palisades, NY 10964, USA kushnir@ldeo.columbia.edu
EESC V2100 The Climate System spring 2004 Lecture 4: Laws of Atmospheric Motion and Weather Yochanan Kushnir Lamont Doherty Earth Observatory of Columbia University Palisades, NY 10964, USA kushnir@ldeo.columbia.edu
Isentropic Thinking & Airstreams Analysis
 Isentropic Thinking & Airstreams Analysis Drs. James T. Moore & Sam Ng Saint Louis University & Metropolitan State College of Denver Utility of Isentropic Analysis Diagnose and visualize vertical motion
Isentropic Thinking & Airstreams Analysis Drs. James T. Moore & Sam Ng Saint Louis University & Metropolitan State College of Denver Utility of Isentropic Analysis Diagnose and visualize vertical motion
PEAT SEISMOLOGY Lecture 2: Continuum mechanics
 PEAT8002 - SEISMOLOGY Lecture 2: Continuum mechanics Nick Rawlinson Research School of Earth Sciences Australian National University Strain Strain is the formal description of the change in shape of a
PEAT8002 - SEISMOLOGY Lecture 2: Continuum mechanics Nick Rawlinson Research School of Earth Sciences Australian National University Strain Strain is the formal description of the change in shape of a
McGraw Hill Yearbook of Science & Technology Extratropical cyclone occlusion. McGraw Hill 2008 Yearbook of Science & Technology.
 McGraw Hill Yearbook of Science & Technology 0 Extratropical cyclone occlusion Journal: McGraw Hill 0 Yearbook of Science & Technology Manuscript ID: draft Manuscript Type: Date Submitted by the Author:
McGraw Hill Yearbook of Science & Technology 0 Extratropical cyclone occlusion Journal: McGraw Hill 0 Yearbook of Science & Technology Manuscript ID: draft Manuscript Type: Date Submitted by the Author:
Occlusion cyclogenesis II
 Occlusion cyclogenesis II Upper level influences on cyclogenesis Vorticity Advection (CVA) and the 4-quadrant jet streak model (Uccellini) Potential Vorticity (PV) (Hoskins Theory) Rapid cyclogenesis 14
Occlusion cyclogenesis II Upper level influences on cyclogenesis Vorticity Advection (CVA) and the 4-quadrant jet streak model (Uccellini) Potential Vorticity (PV) (Hoskins Theory) Rapid cyclogenesis 14
True or false: The atmosphere is always in hydrostatic balance. A. True B. False
 Clicker Questions and Clicker Quizzes Clicker Questions Chapter 7 Of the four forces that affect the motion of air in our atmosphere, which is to thank for opposing the vertical pressure gradient force
Clicker Questions and Clicker Quizzes Clicker Questions Chapter 7 Of the four forces that affect the motion of air in our atmosphere, which is to thank for opposing the vertical pressure gradient force
Dynamic Meteorology 1
 Dynamic Meteorology 1 Lecture 14 Sahraei Department of Physics, Razi University http://www.razi.ac.ir/sahraei Buys-Ballot rule (Northern Hemisphere) If the wind blows into your back, the Low will be to
Dynamic Meteorology 1 Lecture 14 Sahraei Department of Physics, Razi University http://www.razi.ac.ir/sahraei Buys-Ballot rule (Northern Hemisphere) If the wind blows into your back, the Low will be to
3. The linear 3-D elasticity mathematical model
 3. The linear 3-D elasticity mathematical model In Chapter we examined some fundamental conditions that should be satisfied in the modeling of all deformable solids and structures. The study of truss structures
3. The linear 3-D elasticity mathematical model In Chapter we examined some fundamental conditions that should be satisfied in the modeling of all deformable solids and structures. The study of truss structures
The Vorticity Equation in a Rotating Stratified Fluid
 Capter 7 Te Vorticity Equation in a Rotating Stratified Fluid Te vorticity equation for a rotating, stratified, viscous fluid Te vorticity equation in one form or anoter and its interpretation provide
Capter 7 Te Vorticity Equation in a Rotating Stratified Fluid Te vorticity equation for a rotating, stratified, viscous fluid Te vorticity equation in one form or anoter and its interpretation provide
THE INFLUENCE OF ROTATIONAL FRONTOGENESIS AND ITS ASSOCIATED SHEARWISE VERTICAL MOTIONS ON THE DEVELOPMENT OF AN UPPER-LEVEL FRONT
 THE INFLUENCE OF ROTATIONAL FRONTOGENESIS AND ITS ASSOCIATED SHEARWISE VERTICAL MOTIONS ON THE DEVELOPMENT OF AN UPPER-LEVEL FRONT by ANDREA A. LANG and JONATHAN E. MARTIN Department of Atmospheric and
THE INFLUENCE OF ROTATIONAL FRONTOGENESIS AND ITS ASSOCIATED SHEARWISE VERTICAL MOTIONS ON THE DEVELOPMENT OF AN UPPER-LEVEL FRONT by ANDREA A. LANG and JONATHAN E. MARTIN Department of Atmospheric and
The Kinematic Equations
 The Kinematic Equations David Roylance Department of Materials Science and Engineering Massachusetts Institute of Technology Cambridge, MA 0139 September 19, 000 Introduction The kinematic or strain-displacement
The Kinematic Equations David Roylance Department of Materials Science and Engineering Massachusetts Institute of Technology Cambridge, MA 0139 September 19, 000 Introduction The kinematic or strain-displacement
Tropical Cyclone Intensification
 Tropical Cyclone Intensification Theories for tropical cyclone intensification and structure CISK (Charney and Eliassen 1964) Cooperative Intensification Theory (Ooyama 1969). WISHE (Emanuel 1986, Holton
Tropical Cyclone Intensification Theories for tropical cyclone intensification and structure CISK (Charney and Eliassen 1964) Cooperative Intensification Theory (Ooyama 1969). WISHE (Emanuel 1986, Holton
PV Thinking. What is PV thinking?
 PV Thinking CH 06 What is PV thinking? Two main approaches to solving fluid flow problems:. We can integrate the momentum, continuity and thermodynamic equations (the primitive equations) directly.. In
PV Thinking CH 06 What is PV thinking? Two main approaches to solving fluid flow problems:. We can integrate the momentum, continuity and thermodynamic equations (the primitive equations) directly.. In
Quasi-Geostrophic ω-equation. 1. The atmosphere is approximately hydrostatic. 2. The atmosphere is approximately geostrophic.
 Quasi-Geostrophic ω-equation For large-scale flow in the atmosphere, we have learned about two very important characteristics:. The atmosphere is approximately hydrostatic.. The atmosphere is approximately
Quasi-Geostrophic ω-equation For large-scale flow in the atmosphere, we have learned about two very important characteristics:. The atmosphere is approximately hydrostatic.. The atmosphere is approximately
MA3D1 Fluid Dynamics Support Class 5 - Shear Flows and Blunt Bodies
 MA3D1 Fluid Dynamics Support Class 5 - Shear Flows and Blunt Bodies 13th February 2015 Jorge Lindley email: J.V.M.Lindley@warwick.ac.uk 1 2D Flows - Shear flows Example 1. Flow over an inclined plane A
MA3D1 Fluid Dynamics Support Class 5 - Shear Flows and Blunt Bodies 13th February 2015 Jorge Lindley email: J.V.M.Lindley@warwick.ac.uk 1 2D Flows - Shear flows Example 1. Flow over an inclined plane A
Air Masses and Fronts II
 Air Masses and Fronts II Brief review An air mass is a large body of air whose properties of temperature and humidity are fairly similar in any horizontal direction Source regions for air masses tend to
Air Masses and Fronts II Brief review An air mass is a large body of air whose properties of temperature and humidity are fairly similar in any horizontal direction Source regions for air masses tend to
NWP Equations (Adapted from UCAR/COMET Online Modules)
 NWP Equations (Adapted from UCAR/COMET Online Modules) Certain physical laws of motion and conservation of energy (for example, Newton's Second Law of Motion and the First Law of Thermodynamics) govern
NWP Equations (Adapted from UCAR/COMET Online Modules) Certain physical laws of motion and conservation of energy (for example, Newton's Second Law of Motion and the First Law of Thermodynamics) govern
Vorticity in natural coordinates
 Vorticity in natural coordinates (see Holton pg 95, section 4.2.) Let s consider the vertical vorticity component only, i.e. ζ kˆ ω, we have ω u dl kˆ ω lim --- lim ----------------- curve is in xy plane
Vorticity in natural coordinates (see Holton pg 95, section 4.2.) Let s consider the vertical vorticity component only, i.e. ζ kˆ ω, we have ω u dl kˆ ω lim --- lim ----------------- curve is in xy plane
Getting started: CFD notation
 PDE of p-th order Getting started: CFD notation f ( u,x, t, u x 1,..., u x n, u, 2 u x 1 x 2,..., p u p ) = 0 scalar unknowns u = u(x, t), x R n, t R, n = 1,2,3 vector unknowns v = v(x, t), v R m, m =
PDE of p-th order Getting started: CFD notation f ( u,x, t, u x 1,..., u x n, u, 2 u x 1 x 2,..., p u p ) = 0 scalar unknowns u = u(x, t), x R n, t R, n = 1,2,3 vector unknowns v = v(x, t), v R m, m =
Observation Homework Due 11/24. Previous Lecture. Midlatitude Cyclones
 Lecture 21 Midlatitude Cyclones Observation Homework Due 11/24 1 2 Midlatitude Cyclones Midlatitude Cyclone or Winter Storm Cyclogenesis Energy Source Life Cycle Air Streams Vertical Structure Storm Hazards
Lecture 21 Midlatitude Cyclones Observation Homework Due 11/24 1 2 Midlatitude Cyclones Midlatitude Cyclone or Winter Storm Cyclogenesis Energy Source Life Cycle Air Streams Vertical Structure Storm Hazards
p. 4, 1 st two lines should read: k-hat unit vector maintains right angles with the horizontal unit vectors.
 Reprinted with corrections August 2012. p. x, 2 nd column, 1 st full paragraph should read: In working to improve the text, constructive and insightful suggestions were provided by many colleagues, including
Reprinted with corrections August 2012. p. x, 2 nd column, 1 st full paragraph should read: In working to improve the text, constructive and insightful suggestions were provided by many colleagues, including
1/25/2010. Circulation and vorticity are the two primary
 Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
ERTH 465 Fall Lab 5. Absolute Geostrophic Vorticity. 200 points.
 Name Date ERTH 465 Fall 2015 Lab 5 Absolute Geostrophic Vorticity 200 points. 1. All labs are to be kept in a three hole binder. Turn in the binder when you have finished the Lab. 2. Show all work in mathematical
Name Date ERTH 465 Fall 2015 Lab 5 Absolute Geostrophic Vorticity 200 points. 1. All labs are to be kept in a three hole binder. Turn in the binder when you have finished the Lab. 2. Show all work in mathematical
3D Elasticity Theory
 3D lasticity Theory Many structural analysis problems are analysed using the theory of elasticity in which Hooke s law is used to enforce proportionality between stress and strain at any deformation level.
3D lasticity Theory Many structural analysis problems are analysed using the theory of elasticity in which Hooke s law is used to enforce proportionality between stress and strain at any deformation level.
Hour Exam #2 Physical Mechanics Monday, November 6, Total 100 Points Time to complete the test: 60 minutes. Answers
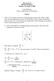 Hour Exam #2 Physical Mechanics Monday, November 6, 2000 Total 100 Points Time to complete the test: 60 minutes Answers 1. (20%) A N-S oriented cold front is passing through Norman. The surface weather
Hour Exam #2 Physical Mechanics Monday, November 6, 2000 Total 100 Points Time to complete the test: 60 minutes Answers 1. (20%) A N-S oriented cold front is passing through Norman. The surface weather
of Friction in Fluids Dept. of Earth & Clim. Sci., SFSU
 Summary. Shear is the gradient of velocity in a direction normal to the velocity. In the presence of shear, collisions among molecules in random motion tend to transfer momentum down-shear (from faster
Summary. Shear is the gradient of velocity in a direction normal to the velocity. In the presence of shear, collisions among molecules in random motion tend to transfer momentum down-shear (from faster
FLUID MECHANICS FLUID KINEMATICS VELOCITY FIELD FLOW PATTERNS
 www.getmyuni.com FLUID MECHANICS FLUID KINEMATICS Fluid Kinematics gives the geometry of fluid motion. It is a branch of fluid mechanics, which describes the fluid motion, and it s consequences without
www.getmyuni.com FLUID MECHANICS FLUID KINEMATICS Fluid Kinematics gives the geometry of fluid motion. It is a branch of fluid mechanics, which describes the fluid motion, and it s consequences without
Governing Equations and Scaling in the Tropics
 Governing Equations and Scaling in the Tropics M 1 ( ) e R ε er Tropical v Midlatitude Meteorology Why is the general circulation and synoptic weather systems in the tropics different to the those in the
Governing Equations and Scaling in the Tropics M 1 ( ) e R ε er Tropical v Midlatitude Meteorology Why is the general circulation and synoptic weather systems in the tropics different to the those in the
Dynamic Meteorology - Introduction
 Dynamic Meteorology - Introduction Atmospheric dynamics the study of atmospheric motions that are associated with weather and climate We will consider the atmosphere to be a continuous fluid medium, or
Dynamic Meteorology - Introduction Atmospheric dynamics the study of atmospheric motions that are associated with weather and climate We will consider the atmosphere to be a continuous fluid medium, or
On the effect of forward shear and reversed shear baroclinic flows for polar low developments. Thor Erik Nordeng Norwegian Meteorological Institute
 On the effect of forward shear and reversed shear baroclinic flows for polar low developments Thor Erik Nordeng Norwegian Meteorological Institute Outline Baroclinic growth a) Normal mode solution b) Initial
On the effect of forward shear and reversed shear baroclinic flows for polar low developments Thor Erik Nordeng Norwegian Meteorological Institute Outline Baroclinic growth a) Normal mode solution b) Initial
Part 4. Atmospheric Dynamics
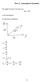 Part 4. Atmospheric Dynamics We apply Newton s Second Law: ma =Σ F i to the atmosphere. In Cartesian coordinates dx u = dt dy v = dt dz w = dt 1 ai = F m i i du dv dw a = ; ay = ; az = x dt dt dt 78 Coordinate
Part 4. Atmospheric Dynamics We apply Newton s Second Law: ma =Σ F i to the atmosphere. In Cartesian coordinates dx u = dt dy v = dt dz w = dt 1 ai = F m i i du dv dw a = ; ay = ; az = x dt dt dt 78 Coordinate
Meteorology 311. General Circulation/Fronts Fall 2017
 Meteorology 311 General Circulation/Fronts Fall 2017 Precipitation Types Rain Snow growth of ice crystals through deposition, accretion, and aggregation. Freezing Rain Rain freezes when it hits the surface.
Meteorology 311 General Circulation/Fronts Fall 2017 Precipitation Types Rain Snow growth of ice crystals through deposition, accretion, and aggregation. Freezing Rain Rain freezes when it hits the surface.
Earth Science. Lab 21: Weather Patterns
 Name: Lab 21: Weather Patterns Earth Science Date: Introduction: A basic principle in Earth Science is that energy is constantly bringing about changes. In order to understand the changing Earth, we must
Name: Lab 21: Weather Patterns Earth Science Date: Introduction: A basic principle in Earth Science is that energy is constantly bringing about changes. In order to understand the changing Earth, we must
ρ x + fv f 'w + F x ρ y fu + F y Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ Dv Dt + u2 tanφ + vw a a = 1 p Dw Dt u2 + v 2
 Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
Synoptic Meteorology I: Skew-T Diagrams and Thermodynamic Properties
 Synoptic Meteorology I: Skew-T Diagrams and Thermodynamic Properties For Further Reading Most information contained within these lecture notes is drawn from Chapters 1, 2, 4, and 6 of The Use of the Skew
Synoptic Meteorology I: Skew-T Diagrams and Thermodynamic Properties For Further Reading Most information contained within these lecture notes is drawn from Chapters 1, 2, 4, and 6 of The Use of the Skew
Cyclones and Anticyclones, Ridges and Troughs
 Cyclones and Anticyclones, Ridges and Troughs Isobars on surface maps often have a closed appearance (as illustrated) Areas of low pressure are called cyclones, while areas with high pressure are called
Cyclones and Anticyclones, Ridges and Troughs Isobars on surface maps often have a closed appearance (as illustrated) Areas of low pressure are called cyclones, while areas with high pressure are called
PV Generation in the Boundary Layer
 1 PV Generation in the Boundary Layer Robert Plant 18th February 2003 (With thanks to S. Belcher) 2 Introduction How does the boundary layer modify the behaviour of weather systems? Often regarded as a
1 PV Generation in the Boundary Layer Robert Plant 18th February 2003 (With thanks to S. Belcher) 2 Introduction How does the boundary layer modify the behaviour of weather systems? Often regarded as a
Tangent Planes, Linear Approximations and Differentiability
 Jim Lambers MAT 80 Spring Semester 009-10 Lecture 5 Notes These notes correspond to Section 114 in Stewart and Section 3 in Marsden and Tromba Tangent Planes, Linear Approximations and Differentiability
Jim Lambers MAT 80 Spring Semester 009-10 Lecture 5 Notes These notes correspond to Section 114 in Stewart and Section 3 in Marsden and Tromba Tangent Planes, Linear Approximations and Differentiability
Goal: Use understanding of physically-relevant scales to reduce the complexity of the governing equations
 Scale analysis relevant to the tropics [large-scale synoptic systems]* Goal: Use understanding of physically-relevant scales to reduce the complexity of the governing equations *Reminder: Midlatitude scale
Scale analysis relevant to the tropics [large-scale synoptic systems]* Goal: Use understanding of physically-relevant scales to reduce the complexity of the governing equations *Reminder: Midlatitude scale
Chapter 4 Water Vapor
 Chapter 4 Water Vapor Chapter overview: Phases of water Vapor pressure at saturation Moisture variables o Mixing ratio, specific humidity, relative humidity, dew point temperature o Absolute vs. relative
Chapter 4 Water Vapor Chapter overview: Phases of water Vapor pressure at saturation Moisture variables o Mixing ratio, specific humidity, relative humidity, dew point temperature o Absolute vs. relative
Quick Recapitulation of Fluid Mechanics
 Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
Lecture #14 March 29, 2010, Monday. Air Masses & Fronts
 Lecture #14 March 29, 2010, Monday Air Masses & Fronts General definitions air masses source regions fronts Air masses formation types Fronts formation types Air Masses General Definitions a large body
Lecture #14 March 29, 2010, Monday Air Masses & Fronts General definitions air masses source regions fronts Air masses formation types Fronts formation types Air Masses General Definitions a large body
Dynamics Rotating Tank
 Institute for Atmospheric and Climate Science - IACETH Atmospheric Physics Lab Work Dynamics Rotating Tank Large scale flows on different latitudes of the rotating Earth Abstract The large scale atmospheric
Institute for Atmospheric and Climate Science - IACETH Atmospheric Physics Lab Work Dynamics Rotating Tank Large scale flows on different latitudes of the rotating Earth Abstract The large scale atmospheric
Boundary layer controls on extratropical cyclone development
 Boundary layer controls on extratropical cyclone development R. S. Plant (With thanks to: I. A. Boutle and S. E. Belcher) 28th May 2010 University of East Anglia Outline Introduction and background Baroclinic
Boundary layer controls on extratropical cyclone development R. S. Plant (With thanks to: I. A. Boutle and S. E. Belcher) 28th May 2010 University of East Anglia Outline Introduction and background Baroclinic
Project 2 Fronts
 12.307 Project 2 Fronts Lodovica Illari and John Marshall March 2010 Abstract We inspect fronts crossing the country associated with day-to-day variations in the weather using real-time atmospheric observations.
12.307 Project 2 Fronts Lodovica Illari and John Marshall March 2010 Abstract We inspect fronts crossing the country associated with day-to-day variations in the weather using real-time atmospheric observations.
Atmosphere, Ocean and Climate Dynamics Answers to Chapter 8
 Atmosphere, Ocean and Climate Dynamics Answers to Chapter 8 1. Consider a zonally symmetric circulation (i.e., one with no longitudinal variations) in the atmosphere. In the inviscid upper troposphere,
Atmosphere, Ocean and Climate Dynamics Answers to Chapter 8 1. Consider a zonally symmetric circulation (i.e., one with no longitudinal variations) in the atmosphere. In the inviscid upper troposphere,
Practice Final Exam Solutions
 Important Notice: To prepare for the final exam, study past exams and practice exams, and homeworks, quizzes, and worksheets, not just this practice final. A topic not being on the practice final does
Important Notice: To prepare for the final exam, study past exams and practice exams, and homeworks, quizzes, and worksheets, not just this practice final. A topic not being on the practice final does
Continuum Mechanics Lecture 5 Ideal fluids
 Continuum Mechanics Lecture 5 Ideal fluids Prof. http://www.itp.uzh.ch/~teyssier Outline - Helmholtz decomposition - Divergence and curl theorem - Kelvin s circulation theorem - The vorticity equation
Continuum Mechanics Lecture 5 Ideal fluids Prof. http://www.itp.uzh.ch/~teyssier Outline - Helmholtz decomposition - Divergence and curl theorem - Kelvin s circulation theorem - The vorticity equation
2.2 The derivative as a Function
 2.2 The derivative as a Function Recall: The derivative of a function f at a fixed number a: f a f a+h f(a) = lim h 0 h Definition (Derivative of f) For any number x, the derivative of f is f x f x+h f(x)
2.2 The derivative as a Function Recall: The derivative of a function f at a fixed number a: f a f a+h f(a) = lim h 0 h Definition (Derivative of f) For any number x, the derivative of f is f x f x+h f(x)
Upper-Level Frontogenesis Associated with the Birth of Mobile Troughs in Northwesterly Flow
 NOVEMBER 2002 SCHULTZ AND SANDERS 2593 Upper-Level Frontogenesis Associated with the Birth of Mobile Troughs in Northwesterly Flow DAVID M. SCHULTZ NOAA/National Severe Storms Laboratory, Norman, Oklahoma
NOVEMBER 2002 SCHULTZ AND SANDERS 2593 Upper-Level Frontogenesis Associated with the Birth of Mobile Troughs in Northwesterly Flow DAVID M. SCHULTZ NOAA/National Severe Storms Laboratory, Norman, Oklahoma
AP Calculus BC - Problem Solving Drill 19: Parametric Functions and Polar Functions
 AP Calculus BC - Problem Solving Drill 19: Parametric Functions and Polar Functions Question No. 1 of 10 Instructions: (1) Read the problem and answer choices carefully () Work the problems on paper as
AP Calculus BC - Problem Solving Drill 19: Parametric Functions and Polar Functions Question No. 1 of 10 Instructions: (1) Read the problem and answer choices carefully () Work the problems on paper as
AIRBORNE DOPPLER RADAR AND DROPSONDE ANALYSIS OF AN OCEANIC COLD FRONT. Roger M. Wakimoto* National Center for Atmospheric Research Boulder, CO 80305
 A. AIRBORNE DOPPLER RADAR AND DROPSONDE ANALYSIS OF AN OCEANIC COLD FRONT Roger M. Wakimoto* National Center for Atmospheric Research Boulder, CO Hanne V. Murphey UCLA Los Angeles, CA 99. INTRODUCTION
A. AIRBORNE DOPPLER RADAR AND DROPSONDE ANALYSIS OF AN OCEANIC COLD FRONT Roger M. Wakimoto* National Center for Atmospheric Research Boulder, CO Hanne V. Murphey UCLA Los Angeles, CA 99. INTRODUCTION
The Planetary Circulation System
 12 The Planetary Circulation System Learning Goals After studying this chapter, students should be able to: 1. describe and account for the global patterns of pressure, wind patterns and ocean currents
12 The Planetary Circulation System Learning Goals After studying this chapter, students should be able to: 1. describe and account for the global patterns of pressure, wind patterns and ocean currents
Homework Two. Abstract: Liu. Solutions for Homework Problems Two: (50 points total). Collected by Junyu
 Homework Two Abstract: Liu. Solutions for Homework Problems Two: (50 points total). Collected by Junyu Contents 1 BT Problem 13.15 (8 points) (by Nick Hunter-Jones) 1 2 BT Problem 14.2 (12 points: 3+3+3+3)
Homework Two Abstract: Liu. Solutions for Homework Problems Two: (50 points total). Collected by Junyu Contents 1 BT Problem 13.15 (8 points) (by Nick Hunter-Jones) 1 2 BT Problem 14.2 (12 points: 3+3+3+3)
Fluid Mechanics II Viscosity and shear stresses
 Fluid Mechanics II Viscosity and shear stresses Shear stresses in a Newtonian fluid A fluid at rest can not resist shearing forces. Under the action of such forces it deforms continuously, however small
Fluid Mechanics II Viscosity and shear stresses Shear stresses in a Newtonian fluid A fluid at rest can not resist shearing forces. Under the action of such forces it deforms continuously, however small
Lifting Airfoils in Incompressible Irrotational Flow. AA210b Lecture 3 January 13, AA210b - Fundamentals of Compressible Flow II 1
 Lifting Airfoils in Incompressible Irrotational Flow AA21b Lecture 3 January 13, 28 AA21b - Fundamentals of Compressible Flow II 1 Governing Equations For an incompressible fluid, the continuity equation
Lifting Airfoils in Incompressible Irrotational Flow AA21b Lecture 3 January 13, 28 AA21b - Fundamentals of Compressible Flow II 1 Governing Equations For an incompressible fluid, the continuity equation
