Parallel Computing Chapter 8 Dense Matrix Computation. Jun Zhang Department of Computer Science University of Kentucky
|
|
|
- Meghan Garrison
- 5 years ago
- Views:
Transcription
1 Prllel Comuig Cher 8 Dese Mri Comuio Ju Zhg Derme of Comuer Sciece Uiversi of Keuck
2 8. Cegories of Mrices Dese mri: lmos ever elemes re ozero, or he locio of he zeros co be deeced esil d used efficiel i comuio Srse mri: locios of zero elemes re ko d such elemes re o sored or used i comuio Curre reserch focus: srse mrices Srucured or usrucured srse mrices: heher or o srse mri hs regulr srucures h m be eloied i sorge d comuio
3 8. Mig Mrices Sried riioig: mri is divided io grous of comlee ros or colums, ech grou is ssiged o oe rocessor. Mimum rocessors Block sried d (block) cclic sried Checkerbord riioig: mri is divided io smll squre or recgulr blocks d ech of hem is med o rocessor. Mimum rocessors More cocurrec m be eloied (block) cclic checkerbord
4
5 4
6 8. Mri Trsosiio Trsosig mri is o ierchge is ros d colums: T T A, Ai, j A j, i Noe h he digols re o moved. Assumig ui cos for ierchgig ir of mri elemes, he sequeil cos of rsosiio is: 8.. Checkerbord riioig A logicl mesh c be embedded io hsicl mesh or hercube (usig, e.g., MPI Cresi coordie) 5
7 6
8 Mri Trsosiio o Mesh A eleme belo he digol firs is moved u o he digol d he o he righ o is desiio rocessor A eleme bove he digol is moved do o he digol d he o he lef o is desiio rocessor No mjor commuicio cogesio Need schroizig commuicio ses Prllel ru ime: T P s 7
9 Mri Trsosiio o Hercube Recursive rsosiio lgorihm (RTA) Divide mri io four blocks d erform rsosiio Divide ech block io four smller blocks d erform rsosiio ih resec o he smll blocks. There re four ses of hem d he c be doe i rllel. Tol of log / ses, ech ih o commuicio hses d messge size / Prllel ru ime: T P ( s ) log 8
10 9
11 0
12
13 8.. Trsosiio ih Sried Priioig Block srucures c sill be used. A ll o ll ersolized commuicio is ivoked for he mri rsosiio The coss of ll o ll ersolized commuicio for differe rchiecures hve bee sudied. The messge size is /. Cos oiml for hercube ih cu hrough rouig. The rllel ru ime: T P s ( ) h log
14
15 8. Mri Vecor Mulilicio Comue Sequeil ru ime A * W b 8.. Ro ise Sriig Oe ro d oe eleme of b er rocessor. All o ll brodcs o disribue b o ll rocessors, folloed b locl comuio ih mulilicios d summios. Prllel ru ime: ll o ll brodcs (). Mulilicio d summio is ( ). Tol cos is ( ). This ssem is cosoiml 4
16 5
17 6
18 Usig < Processors / comlee ros d / elemes of b re sored i ech rocessor All o ll brodcs of messge size / is used o mke comlee b vilble o ll rocessors, folloed b locl comuio ih mulilicios d summios Prllel ru ime o hercube: ll o ll: log hich is cos oiml for s T P s ( / log )( O(). ), 7
19 Usig < Processors Prllel ru ime o mesh ih rroud: ll o ll: T ( ) ( / )( ) P s s ( ) hich is gi cos oiml for O(). We c see here is o much differece beee mesh d hercube rchiecures., Sclbili lsis Overhed fucio for hercube is T O s log, 8
20 Sclbili lsis (co.) Isoefficiec fucio is W KT, K Sere lsis, for erm, O s E E W K s log For erm, e hve W K Obviousl erm domies 9
21 Sclbili lsis (co.) Miulio so d I follos h so W W W K K K K ( (sequeil cos) ) 0
22 8.. Checkerbord Priioig Oe eleme er rocessor: rocessors c hold he mri A. The vecor is i he ls colum of rocessor..) oe o oe commuicio o lig he vecor log he ricile digol of he mri.) oe o ll brodcs o disribue he eleme mog rocessors i ech colum.) locl mulilicio ihi ech rocessor 4.) sigle ode ccumulio o obi he sum for he vecor
23
24
25 Prllel Ru Time ( rocessors) Three commuicio ses, oe o oe commuicio, oeo ll brodcs, sigle ode ccumulio, cos () o mesh d (log ) o hercube. The cos of he rllel ssem is ( ) d ( log ), resecivel. Neiher is cosoiml. Usig < rocessors Ech rocessor holds block of size ( / ) ( / ) elemes Three commuicio ses d locl comuios re sill eeded ih differe messge size. 4
26 Prllel Ru Time o Mesh ih Cu Through Rouig ihou Wrroud.) digol ligme: messge size Firs ro of rocessors s /.) columise oe o ll brodcs h / ( s / ) log( ) h.) roise sigle ode ccumulio cos he sme 4.) locl comuios cos / 5
27 Sclbili Alsis Prllel ru ime Is his rllel ssem cos oiml? Yes if T h s h s h s P ) log( ) ( ) log( ) ( ) ( log O 6
28 Sclbili Alsis (co.) Overhed fucio T O log Isoefficiec lsis, erm s s log h / erm W W K s log K log K log K log h erm W W K log K h / 7
29 Sclbili Alsis (co.) Degree of cocurrec of checkerbord riioig O( ) ( ) W ( ) Noe h / log ol for 65,56. Hece, he overll isoefficiec fucio is ( log ) 8
30 Crierio for Cos Oimli For cos oiml ssem, rllel cos is rooriol o sequeil cos log Igorig he double log erm, e hve Hece, subsiue his relioshi o he firs equio I follos h log log log log log O(log O log O( O( ) O(log ) ) ) 9
31 Mesh ih Sore d Forrd Rouig Prllel ru ime is Isoefficiec fucio is Much orse h cu hrough rouig Comrig Differe Priioigs Sried riioig ih rroud Checkerbord riioig ih cu hrough rouig T s P ) ( T s P ) ( T h s P log log 0
32 8.4 Mri Mulilicio C A B Algorihm ih rile loos: For i= 0 o do: For j = 0 o do: C[i,j] = 0 For k = 0 o do: C[i,j] = C[i,j] + A[i,k]*B[k,j] Ed do Ed do Ed do Comuio c be doe i elemeise or blockise. is relced b he umber of blocks
33 8.4. Simle Prllel Algorihm Checkerbord riioig of boh A d B. blocks of size ( / ) * ( / ). Processor P holds d i, A j i, j, Bi, j comues of he resulig mri. C i, j Comuig eeds ll d for C i, j A i, k B k, j 0 k All o ll brodcss for ech ro A ) d ech colum ) ( i,k ( B k, j Memor cos is high. Ech rocessor hs blocks of boh A d B. Ech rocessor eeds ( / ) memor, for ol of ( / ) memor.
34 Comuig Block of C Mri
35 Alsis for Hercube To ll o ll brodcs ses ih messge size / mog rocessors. ( Locl comuios, smll mri mri mulilicios Prllel ru ime ih rocessors Cos oiml if T s P log * s ( )) log O( ) 4
36 Alsis for Hercube (co.) The overll isoefficiec fucio is Mimum cocurrec is. Alsis for Mesh (sore d forrd) Commuicio cos Prllel ru ime ih rocessors Cos oiml if W K W ( s 8( ) ( / O( / TP s O( ) ) ) ) 5
37 8.4. Co s Algorihm This is memor efficie lgorihm. Tol memor requireme for Co s lgorihm is O( ). Performce o Hercube Mimum disce of ligme shifs is. O hercube ih cu hrough rouig, he cos is ( s log ) Ech sigle se shif i comue d shif cos s h 6
38 Iiil Disribuio of Mrices 7
39 Iiil Aligme d Secod Se 8
40 Third d Fourh Ses 9
41 8.4. Co s Algorihm (co.) Tol commuicio cos for shifig o mrices i ses is Locl comuio cos is Prllel ru ime ih rocessors Cos oiml if 40 s ) ( T s P ) ( O
42 8.4. Co s Algorihm (co.) Prllel Ru Time o Mesh Iiil ligme shif coss ( s ) The commuicio of comue d shif coss he sme. The ol rllel ru ime ih rocessors T P The Co s lgorihm is slighl more eesive h he simle lgorihm o boh hercube d mesh rchiecures, bu is more memor efficie 4 4 s 4
43 8.4. Fo s Algorihm Aoher memor efficie lgorihm O( ). Use oe o ll brodcs i ech ro of A, shif urd ech ro of B, ree imes. Performce o Hercube Messge size /, locl comuio / Oe o ll brodcs o hercube coss ( shifs d brodcss T P s s ) log log log 4
44 Firs d Secod Ses 4
45 Third d Fourh Ses 44
46 8.5 Solvig Lier Ssem A ssem of lier equios Wrie i mri form is d solved b Gussi elimiio d bck subsiuio 45,, 0,0,, 0,0 0 0, 0, 0 0, b b b b A,, 0 0, 0,
47 Elimiio Process 46
48 Algorihm for Gussi Elimiio For k=0 o do: For j=k+ o do: A[k,j] = A[k,j]/A[k,k] Ed do [k]=b[k]/a[k,k] A[k,k]= For i=k+ o do: For j=k+ o do: A[i,j]=A[i,j] A[i,k]*A[k,j] Ed do b[i]=b[i] A[i,k]*[k] A[i,k]=0 Ed do Ed do 47
49 Gussi Elimiio (co.) Sequeil cos of Gussi elimiio is /. Gussi elimiio does o sore he fcors h used o mulil he mri A. If e do sore hose fcors, e c rie A s fcored form (LU fcorizio, bes for m ssems ih he sme A) s L U Hece solvig A=b becomes solvig forrd elimiio d bck subsiuio A LU b L b U 48
50 Prllel Imlemeio ih Sried Priioig Suose ech rocessor holds oe ro of A. A he kh se, for rocessor k.) ll ozero elemes of he kh ro re divided b A[ k, k ].) oe o ll brodcs A[ k, j], k j o rocessors k+ o 0 Processors k+ o erform elimiio for A[ i, j] A[ i, j] A[ i, k ] A[ k, j] k i d k j 49
51 () Comuio (i) A[k,j]=A[k,j]/A[k,k] for k<j< (ii) A[k,k]= 50
52 (b) Commuicio Oe o ll brodcs of ro A[k,*] Ol he ls k colums 5
53 (c) Comuio (i) A[i,j]=A[i,j] A[i,k]*A[k,j] for k<i< d k<j< (ii) A[i,k]=0 for k<i< 5
54 Cos ih Sried Priioig Se : Divisios i he rocessor Pk, coss ( k ) Se : Oe o ll brodcs from Pk kes ( s ( k )) log Se : Locl comuio i he remiig k rocessors, ( k ) mulilicios d subrcios The ol cos of ierios is T ( k ) k 0 ( ) k 0 ( The ssem is o cos oiml, s he rocessor ime roduc is T ( log ) s log s ( ( k )) log ) log 5
55 Sriig ih feer h rocessors Processor idlig i Gussi elimiio c be llevied b usig cclicsried mig. 54
56 Gussi Elimiio ih Checkerbord Priioig Assume ech eleme is i rocessor The comuio is obviousl o cos oiml 55
57 () Comuio (i) A[k,j]=A[k,j]/A[k,k] for k<j< (ii) A[k,k]= (iii) A[i,j]=A[i,j] A[i,k]*A[k,j] 56
58 (b) Comuio (divisio) (i) A[k,j]=A[k,j]/A[k,k] for k<j< (ii) A[k,k]= (A[i,j]=A[i,j] A[i,k]*A[k,j]) 57
59 (c) Commuicio (for elimiio) (i) Oe o ll brodcs (colums) (ii) Sigle size messge (A[i,j]=A[i,j] A[i,k]*A[k,j]) 58
60 (d) Comuio (elimiio) (i) Perform elimiio i ech ro (ii) A[i,j]=A[i,j] A[i,k]*A[k,j] for k<i< d k<j< 59
61 Gussi Elimiio ih Checkerbord Priioig A ech se, oe o ll commuicio loe he rocessors i he sme ro, d oe o ll colum ise commuicio re erformed Boh commuicio ses cos O(log ) o hercube eork, d here re ses. So he rllel ssem cos is O( log ) The rllel ssem is o cos oiml 60
62 Pielied Commuicio d Comuio is Sried Priioig I ielied Gussi elimiio, ech rocessor erforms he folloig sequece of cios reeed uil ll ierios re comlee () If rocessor hs d desied for oher rocessors, i seds hose d o he rorie rocessor () If he rocessor c erform some comuio usig he d i hs, i does so () Oherise, he rocessor is o receive d o be used for oe of he bove cios 6
63 () Comuio (i) A[k,j]=A[k,j]/A[k,k] for k<j< (ii) A[k,k]= 6
64 (c) Comuio (i) A[i,j]=A[i,j] A[i,k]*A[k,j] for k<i< d k<j< (ii) A[i,k]=0 for k<i< 6
65 Cos of Pielied Commuicio d Comuio The iiiio of cosecuive ierios of he ouer loos is sered b cos umber of ses A ol of such ierios re iiied The ls ierio modifies ol he boom righ corer eleme of he coefficie mri, i comlees i cos ime I ech se, eiher O() elemes re commuiced beee direcl coeced rocessors, or divisio se is erformed o O() elemes of ro, or elimiio se is erformed o O() elemes of ro Ech of hese ses kes O() ime 64
66 Pielied Commuicio d Comuio ih Checkerbord Priioig The ides re similr o hose usig i he ielied versio ih sried riioig Commuicio d comuio c be ielied i severl s Commuicio d comuio ve fros move from he o lef corer o he boom righ corer Ech se kes cos ime There re such ses (fros) The rllel ru ime is O() Sice here re ^ rocessors re ivolved, he rllel ime cos is O(^), hich is cos oiml 65
67 66
68 67
69 68
70 69
71 Checkerbord ih feer h * rocessors Wih checkbord riioig d less h * rocessors, messge size m o be he sme i differe ros 70
72 Checkerbord ih feer h * rocessors Columise brodcs folloed b locl comuio fiishig elimiio rocess 7
73 Checkerbord ih cclic mig Beer lod blcig m be chieved b cclic mig. Hoever, commuicio overhed m icrese. A rde off is mchie deede 7
74 8.5. Pril Pivoig So, fr, e hve ssumed h he divisios i ech ro c be erformed ihou roblem. Th mes he mi digol elemes ii re lrge i bsolue vlues (relivel o off digol elemes). If ii is smll for he ih ro, e hve fid some (or ) h is lrger. ii For emle, if is smll, bu is lrge 0 ji,, 4 0,,,, 4, 0,,,, 4, 0,,,, 4, 0,4,4,4,4 4,
75 8.5. Pril Pivoig (co.) We c ierchge d (colum ivoig) Ro ivoig m be lso erformed , 4, 4, 4 4,4,,, 4,4,,, 4,4,,, 4,4 0 0, 0, 0, 4 0,4 0, 4, 4 4 4,4 4, 4, 4, 4,4,,, 4,4,,, 4,4,,, 0 4 0,4 0, 0, 0, 0
76 8.5. Pril Pivoig (co.) We c lso serch for he lrges eleme i boh he ih ro d he ih colum. This is he full ivoig sreg. Full ivoig is more robus bu is much more cosl h ril ivoig. For mos relisic licios, ril ivoig is sufficie o guree umericl sbili. Pril ivoig is srighforrd o imleme ih he simle lgorihms. Bu i is o efficie ih he ielied versios of Gussi elimiio. Wih checkerbord riioig, commuicio cos icreses subsill. A cclic mig ill lso icrese cos. 75
77 Pielied Bckrd Subsiuio The bckrd subsiuio is iherel sequeil, bu m be ielied Se ,4 4,4, 4,4,, 0 4 0,4 0, 0, 0, ,4 4,4, 4,4,, 0 4 0,4 0 0, 0, 0, 0
78 Pielied Bckrd Subsiuio (co.) Se Se ,,, 0 0, 0 0, 0, 0 ~ ~ ~ 4 4, 0 0, 0 0, 0 ~ ~ ~
79 Pielied Bckrd Subsiuio (co.) Se4 0 4 ~ 0 4 0, Comuiol cos is (). ses of cos comuio (oe ddiio d oe mulilicio) Commuicio cos is he sme s i he simle (o ielied) versio o hercube. ( ( ) log ) s 78
80 8.5.4 Differe Gussi Elimiio The versio of Gussi elimiio h e sudies is clled roorieed. Deedig uo our d srucure, Gussi elimiio c be imlemeed i colum orieed fshio. Sequeill, if he mri is sored ro b ro, he colum orieed fshio is more suible. Oherise ro orieed fshio should be used. I is lso sid h he colum orieed fshio is umericl more sble if LU fcorizio is erformed. Becuse i he columorieed fshio, he elemes of he L mri re ll smller h. 79
Week 8 Lecture 3: Problems 49, 50 Fourier analysis Courseware pp (don t look at French very confusing look in the Courseware instead)
 Week 8 Lecure 3: Problems 49, 5 Fourier lysis Coursewre pp 6-7 (do look Frech very cofusig look i he Coursewre ised) Fourier lysis ivolves ddig wves d heir hrmoics, so i would hve urlly followed fer he
Week 8 Lecure 3: Problems 49, 5 Fourier lysis Coursewre pp 6-7 (do look Frech very cofusig look i he Coursewre ised) Fourier lysis ivolves ddig wves d heir hrmoics, so i would hve urlly followed fer he
ON BILATERAL GENERATING FUNCTIONS INVOLVING MODIFIED JACOBI POLYNOMIALS
 Jourl of Sciece d Ars Yer 4 No 227-6 24 ORIINAL AER ON BILATERAL ENERATIN FUNCTIONS INVOLVIN MODIFIED JACOBI OLYNOMIALS CHANDRA SEKHAR BERA Muscri received: 424; Acceed er: 3524; ublished olie: 3624 Absrc
Jourl of Sciece d Ars Yer 4 No 227-6 24 ORIINAL AER ON BILATERAL ENERATIN FUNCTIONS INVOLVIN MODIFIED JACOBI OLYNOMIALS CHANDRA SEKHAR BERA Muscri received: 424; Acceed er: 3524; ublished olie: 3624 Absrc
Supplement: Gauss-Jordan Reduction
 Suppleme: Guss-Jord Reducio. Coefficie mri d ugmeed mri: The coefficie mri derived from sysem of lier equios m m m m is m m m A O d he ugmeed mri derived from he ove sysem of lier equios is [ ] m m m m
Suppleme: Guss-Jord Reducio. Coefficie mri d ugmeed mri: The coefficie mri derived from sysem of lier equios m m m m is m m m A O d he ugmeed mri derived from he ove sysem of lier equios is [ ] m m m m
How to Prove the Riemann Hypothesis Author: Fayez Fok Al Adeh.
 How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
Transient Solution of the M/M/C 1 Queue with Additional C 2 Servers for Longer Queues and Balking
 Jourl of Mhemics d Sisics 4 (): 2-25, 28 ISSN 549-3644 28 Sciece ublicios Trsie Soluio of he M/M/C Queue wih Addiiol C 2 Servers for Loger Queues d Blkig R. O. Al-Seedy, A. A. El-Sherbiy,,2 S. A. EL-Shehwy
Jourl of Mhemics d Sisics 4 (): 2-25, 28 ISSN 549-3644 28 Sciece ublicios Trsie Soluio of he M/M/C Queue wih Addiiol C 2 Servers for Loger Queues d Blkig R. O. Al-Seedy, A. A. El-Sherbiy,,2 S. A. EL-Shehwy
How to prove the Riemann Hypothesis
 Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
Reinforcement Learning
 Reiforceme Corol lerig Corol polices h choose opiml cios Q lerig Covergece Chper 13 Reiforceme 1 Corol Cosider lerig o choose cios, e.g., Robo lerig o dock o bery chrger o choose cios o opimize fcory oupu
Reiforceme Corol lerig Corol polices h choose opiml cios Q lerig Covergece Chper 13 Reiforceme 1 Corol Cosider lerig o choose cios, e.g., Robo lerig o dock o bery chrger o choose cios o opimize fcory oupu
Localization. MEM456/800 Localization: Bayes Filter. Week 4 Ani Hsieh
 Localiaio MEM456/800 Localiaio: Baes Filer Where am I? Week 4 i Hsieh Evirome Sesors cuaors Sofware Ucerai is Everwhere Level of ucerai deeds o he alicaio How do we hadle ucerai? Eamle roblem Esimaig a
Localiaio MEM456/800 Localiaio: Baes Filer Where am I? Week 4 i Hsieh Evirome Sesors cuaors Sofware Ucerai is Everwhere Level of ucerai deeds o he alicaio How do we hadle ucerai? Eamle roblem Esimaig a
Big O Notation for Time Complexity of Algorithms
 BRONX COMMUNITY COLLEGE of he Ciy Uiversiy of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI 33 Secio E01 Hadou 1 Fall 2014 Sepember 3, 2014 Big O Noaio for Time Complexiy of Algorihms Time
BRONX COMMUNITY COLLEGE of he Ciy Uiversiy of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI 33 Secio E01 Hadou 1 Fall 2014 Sepember 3, 2014 Big O Noaio for Time Complexiy of Algorihms Time
Extension of Hardy Inequality on Weighted Sequence Spaces
 Jourl of Scieces Islic Reublic of Ir 20(2): 59-66 (2009) Uiversiy of ehr ISS 06-04 h://sciecesucir Eesio of Hrdy Iequliy o Weighed Sequece Sces R Lshriour d D Foroui 2 Dere of Mheics Fculy of Mheics Uiversiy
Jourl of Scieces Islic Reublic of Ir 20(2): 59-66 (2009) Uiversiy of ehr ISS 06-04 h://sciecesucir Eesio of Hrdy Iequliy o Weighed Sequece Sces R Lshriour d D Foroui 2 Dere of Mheics Fculy of Mheics Uiversiy
CS623: Introduction to Computing with Neural Nets (lecture-10) Pushpak Bhattacharyya Computer Science and Engineering Department IIT Bombay
 CS6: Iroducio o Compuig ih Neural Nes lecure- Pushpak Bhaacharyya Compuer Sciece ad Egieerig Deparme IIT Bombay Tilig Algorihm repea A kid of divide ad coquer sraegy Give he classes i he daa, ru he percepro
CS6: Iroducio o Compuig ih Neural Nes lecure- Pushpak Bhaacharyya Compuer Sciece ad Egieerig Deparme IIT Bombay Tilig Algorihm repea A kid of divide ad coquer sraegy Give he classes i he daa, ru he percepro
Horizontal product differentiation: Consumers have different preferences along one dimension of a good.
 Produc Differeiio Firms see o e uique log some dimesio h is vlued y cosumers. If he firm/roduc is uique i some resec, he firm c commd rice greer h cos. Horizol roduc differeiio: Cosumers hve differe refereces
Produc Differeiio Firms see o e uique log some dimesio h is vlued y cosumers. If he firm/roduc is uique i some resec, he firm c commd rice greer h cos. Horizol roduc differeiio: Cosumers hve differe refereces
ONE RANDOM VARIABLE F ( ) [ ] x P X x x x 3
![ONE RANDOM VARIABLE F ( ) [ ] x P X x x x 3 ONE RANDOM VARIABLE F ( ) [ ] x P X x x x 3](/thumbs/87/96063720.jpg) The Cumulive Disribuio Fucio (cd) ONE RANDOM VARIABLE cd is deied s he probbiliy o he eve { x}: F ( ) [ ] x P x x - Applies o discree s well s coiuous RV. Exmple: hree osses o coi x 8 3 x 8 8 F 3 3 7 x
The Cumulive Disribuio Fucio (cd) ONE RANDOM VARIABLE cd is deied s he probbiliy o he eve { x}: F ( ) [ ] x P x x - Applies o discree s well s coiuous RV. Exmple: hree osses o coi x 8 3 x 8 8 F 3 3 7 x
CS 688 Pattern Recognition. Linear Models for Classification
 //6 S 688 Pr Rcogiio Lir Modls for lssificio Ø Probbilisic griv modls Ø Probbilisic discrimiiv modls Probbilisic Griv Modls Ø W o ur o robbilisic roch o clssificio Ø W ll s ho modls ih lir dcisio boudris
//6 S 688 Pr Rcogiio Lir Modls for lssificio Ø Probbilisic griv modls Ø Probbilisic discrimiiv modls Probbilisic Griv Modls Ø W o ur o robbilisic roch o clssificio Ø W ll s ho modls ih lir dcisio boudris
On computing two special cases of Gauss hypergeometric function
 O comuig wo secil cses of Guss hyergeomeric fucio Mohmmd Msjed-Jmei Wolfrm Koef b * Derme of Mhemics K.N.Toosi Uiversiy of Techology P.O.Bo 65-68 Tehr Ir E-mil: mmjmei@u.c.ir mmjmei@yhoo.com b* Isiue of
O comuig wo secil cses of Guss hyergeomeric fucio Mohmmd Msjed-Jmei Wolfrm Koef b * Derme of Mhemics K.N.Toosi Uiversiy of Techology P.O.Bo 65-68 Tehr Ir E-mil: mmjmei@u.c.ir mmjmei@yhoo.com b* Isiue of
Chapter 5: The pn Junction
 Cher 5: The ucio Noequilibrium ecess crriers i semicoducors Crrier geerio d recombiio Mhemicl lysis of ecess crriers Ambiolr rsor The jucio Bsic srucure of he jucio Zero lied bis Reverse lied bis No-uiformly
Cher 5: The ucio Noequilibrium ecess crriers i semicoducors Crrier geerio d recombiio Mhemicl lysis of ecess crriers Ambiolr rsor The jucio Bsic srucure of he jucio Zero lied bis Reverse lied bis No-uiformly
Integration and Differentiation
 ome Clculus bckgroud ou should be fmilir wih, or review, for Mh 404 I will be, for he mos pr, ssumed ou hve our figerips he bsics of (mulivrible) fucios, clculus, d elemer differeil equios If here hs bee
ome Clculus bckgroud ou should be fmilir wih, or review, for Mh 404 I will be, for he mos pr, ssumed ou hve our figerips he bsics of (mulivrible) fucios, clculus, d elemer differeil equios If here hs bee
Fast Fourier Transform 1) Legendre s Interpolation 2) Vandermonde Matrix 3) Roots of Unity 4) Polynomial Evaluation
 Algorithm Desig d Alsis Victor Admchi CS 5-45 Sprig 4 Lecture 3 J 7, 4 Cregie Mello Uiversit Outlie Fst Fourier Trsform ) Legedre s Iterpoltio ) Vdermode Mtri 3) Roots of Uit 4) Polomil Evlutio Guss (777
Algorithm Desig d Alsis Victor Admchi CS 5-45 Sprig 4 Lecture 3 J 7, 4 Cregie Mello Uiversit Outlie Fst Fourier Trsform ) Legedre s Iterpoltio ) Vdermode Mtri 3) Roots of Uit 4) Polomil Evlutio Guss (777
PROGRESSIONS AND SERIES
 PROGRESSIONS AND SERIES A sequece is lso clled progressio. We ow study three importt types of sequeces: () The Arithmetic Progressio, () The Geometric Progressio, () The Hrmoic Progressio. Arithmetic Progressio.
PROGRESSIONS AND SERIES A sequece is lso clled progressio. We ow study three importt types of sequeces: () The Arithmetic Progressio, () The Geometric Progressio, () The Hrmoic Progressio. Arithmetic Progressio.
F.Y. Diploma : Sem. II [CE/CR/CS] Applied Mathematics
![F.Y. Diploma : Sem. II [CE/CR/CS] Applied Mathematics F.Y. Diploma : Sem. II [CE/CR/CS] Applied Mathematics](/thumbs/89/97771715.jpg) F.Y. Diplom : Sem. II [CE/CR/CS] Applied Mhemics Prelim Quesio Pper Soluio Q. Aemp y FIVE of he followig : [0] Q. () Defie Eve d odd fucios. [] As.: A fucio f() is sid o e eve fucio if f() f() A fucio
F.Y. Diplom : Sem. II [CE/CR/CS] Applied Mhemics Prelim Quesio Pper Soluio Q. Aemp y FIVE of he followig : [0] Q. () Defie Eve d odd fucios. [] As.: A fucio f() is sid o e eve fucio if f() f() A fucio
HOMEWORK 6 - INTEGRATION. READING: Read the following parts from the Calculus Biographies that I have given (online supplement of our textbook):
 MAT 3 CALCULUS I 5.. Dokuz Eylül Uiversiy Fculy of Sciece Deprme of Mhemics Isrucors: Egi Mermu d Cell Cem Srıoğlu HOMEWORK 6 - INTEGRATION web: hp://kisi.deu.edu.r/egi.mermu/ Tebook: Uiversiy Clculus,
MAT 3 CALCULUS I 5.. Dokuz Eylül Uiversiy Fculy of Sciece Deprme of Mhemics Isrucors: Egi Mermu d Cell Cem Srıoğlu HOMEWORK 6 - INTEGRATION web: hp://kisi.deu.edu.r/egi.mermu/ Tebook: Uiversiy Clculus,
Autar Kaw Benjamin Rigsby. Transforming Numerical Methods Education for STEM Undergraduates
 Autr Kw Bejmi Rigsby http://m.mthforcollege.com Trsformig Numericl Methods Eductio for STEM Udergrdutes http://m.mthforcollege.com . solve set of simulteous lier equtios usig Nïve Guss elimitio,. ler the
Autr Kw Bejmi Rigsby http://m.mthforcollege.com Trsformig Numericl Methods Eductio for STEM Udergrdutes http://m.mthforcollege.com . solve set of simulteous lier equtios usig Nïve Guss elimitio,. ler the
EE757 Numerical Techniques in Electromagnetics Lecture 9
 EE757 uericl Techiques i Elecroeics Lecure 9 EE757 06 Dr. Mohed Bkr Diereil Equios Vs. Ierl Equios Ierl equios ke severl ors e.. b K d b K d Mos diereil equios c be epressed s ierl equios e.. b F d d /
EE757 uericl Techiques i Elecroeics Lecure 9 EE757 06 Dr. Mohed Bkr Diereil Equios Vs. Ierl Equios Ierl equios ke severl ors e.. b K d b K d Mos diereil equios c be epressed s ierl equios e.. b F d d /
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
Department of Mathematical and Statistical Sciences University of Alberta
 MATH 4 (R) Wier 008 Iermediae Calculus I Soluios o Problem Se # Due: Friday Jauary 8, 008 Deparme of Mahemaical ad Saisical Scieces Uiversiy of Albera Quesio. [Sec.., #] Fid a formula for he geeral erm
MATH 4 (R) Wier 008 Iermediae Calculus I Soluios o Problem Se # Due: Friday Jauary 8, 008 Deparme of Mahemaical ad Saisical Scieces Uiversiy of Albera Quesio. [Sec.., #] Fid a formula for he geeral erm
Section 6.3: Geometric Sequences
 40 Chpter 6 Sectio 6.: Geometric Sequeces My jobs offer ul cost-of-livig icrese to keep slries cosistet with ifltio. Suppose, for exmple, recet college grdute fids positio s sles mger erig ul slry of $6,000.
40 Chpter 6 Sectio 6.: Geometric Sequeces My jobs offer ul cost-of-livig icrese to keep slries cosistet with ifltio. Suppose, for exmple, recet college grdute fids positio s sles mger erig ul slry of $6,000.
BINOMIAL THEOREM OBJECTIVE PROBLEMS in the expansion of ( 3 +kx ) are equal. Then k =
 wwwskshieduciocom BINOMIAL HEOREM OBJEIVE PROBLEMS he coefficies of, i e esio of k e equl he k /7 If e coefficie of, d ems i e i AP, e e vlue of is he coefficies i e,, 7 ems i e esio of e i AP he 7 7 em
wwwskshieduciocom BINOMIAL HEOREM OBJEIVE PROBLEMS he coefficies of, i e esio of k e equl he k /7 If e coefficie of, d ems i e i AP, e e vlue of is he coefficies i e,, 7 ems i e esio of e i AP he 7 7 em
Existence Of Solutions For Nonlinear Fractional Differential Equation With Integral Boundary Conditions
 Reserch Ivey: Ieriol Jourl Of Egieerig Ad Sciece Vol., Issue (April 3), Pp 8- Iss(e): 78-47, Iss(p):39-6483, Www.Reserchivey.Com Exisece Of Soluios For Nolier Frciol Differeil Equio Wih Iegrl Boudry Codiios,
Reserch Ivey: Ieriol Jourl Of Egieerig Ad Sciece Vol., Issue (April 3), Pp 8- Iss(e): 78-47, Iss(p):39-6483, Www.Reserchivey.Com Exisece Of Soluios For Nolier Frciol Differeil Equio Wih Iegrl Boudry Codiios,
K3 p K2 p Kp 0 p 2 p 3 p
 Mah 80-00 Mo Ar 0 Chaer 9 Fourier Series ad alicaios o differeial equaios (ad arial differeial equaios) 9.-9. Fourier series defiiio ad covergece. The idea of Fourier series is relaed o he liear algebra
Mah 80-00 Mo Ar 0 Chaer 9 Fourier Series ad alicaios o differeial equaios (ad arial differeial equaios) 9.-9. Fourier series defiiio ad covergece. The idea of Fourier series is relaed o he liear algebra
Solutions to selected problems from the midterm exam Math 222 Winter 2015
 Soluios o seleced problems from he miderm eam Mah Wier 5. Derive he Maclauri series for he followig fucios. (cf. Pracice Problem 4 log( + (a L( d. Soluio: We have he Maclauri series log( + + 3 3 4 4 +...,
Soluios o seleced problems from he miderm eam Mah Wier 5. Derive he Maclauri series for he followig fucios. (cf. Pracice Problem 4 log( + (a L( d. Soluio: We have he Maclauri series log( + + 3 3 4 4 +...,
1. Six acceleration vectors are shown for the car whose velocity vector is directed forward. For each acceleration vector describe in words the
 Si ccelerio ecors re show for he cr whose eloci ecor is direced forwrd For ech ccelerio ecor describe i words he iseous moio of he cr A ri eers cured horizol secio of rck speed of 00 km/h d slows dow wih
Si ccelerio ecors re show for he cr whose eloci ecor is direced forwrd For ech ccelerio ecor describe i words he iseous moio of he cr A ri eers cured horizol secio of rck speed of 00 km/h d slows dow wih
An Extension of Hermite Polynomials
 I J Coemp Mh Scieces, Vol 9, 014, o 10, 455-459 HIKARI Ld, wwwm-hikricom hp://dxdoiorg/101988/ijcms0144663 A Exesio of Hermie Polyomils Ghulm Frid Globl Isiue Lhore New Grde Tow, Lhore, Pkis G M Hbibullh
I J Coemp Mh Scieces, Vol 9, 014, o 10, 455-459 HIKARI Ld, wwwm-hikricom hp://dxdoiorg/101988/ijcms0144663 A Exesio of Hermie Polyomils Ghulm Frid Globl Isiue Lhore New Grde Tow, Lhore, Pkis G M Hbibullh
Section 8 Convolution and Deconvolution
 APPLICATIONS IN SIGNAL PROCESSING Secio 8 Covoluio ad Decovoluio This docume illusraes several echiques for carryig ou covoluio ad decovoluio i Mahcad. There are several operaors available for hese fucios:
APPLICATIONS IN SIGNAL PROCESSING Secio 8 Covoluio ad Decovoluio This docume illusraes several echiques for carryig ou covoluio ad decovoluio i Mahcad. There are several operaors available for hese fucios:
Fresnel Dragging Explained
 Fresel Draggig Explaied 07/05/008 Decla Traill Decla@espace.e.au The Fresel Draggig Coefficie required o explai he resul of he Fizeau experime ca be easily explaied by usig he priciples of Eergy Field
Fresel Draggig Explaied 07/05/008 Decla Traill Decla@espace.e.au The Fresel Draggig Coefficie required o explai he resul of he Fizeau experime ca be easily explaied by usig he priciples of Eergy Field
The total number of permutations of S is n!. We denote the set of all permutations of S by
 DETERMINNTS. DEFINITIONS Def: Let S {,,, } e the set of itegers from to, rrged i scedig order. rerrgemet jjj j of the elemets of S is clled permuttio of S. S. The totl umer of permuttios of S is!. We deote
DETERMINNTS. DEFINITIONS Def: Let S {,,, } e the set of itegers from to, rrged i scedig order. rerrgemet jjj j of the elemets of S is clled permuttio of S. S. The totl umer of permuttios of S is!. We deote
Review Answers for E&CE 700T02
 Review Aswers for E&CE 700T0 . Deermie he curre soluio, all possible direcios, ad sepsizes wheher improvig or o for he simple able below: 4 b ma c 0 0 0-4 6 0 - B N B N ^0 0 0 curre sol =, = Ch for - -
Review Aswers for E&CE 700T0 . Deermie he curre soluio, all possible direcios, ad sepsizes wheher improvig or o for he simple able below: 4 b ma c 0 0 0-4 6 0 - B N B N ^0 0 0 curre sol =, = Ch for - -
( a n ) converges or diverges.
 Chpter Ifiite Series Pge of Sectio E Rtio Test Chpter : Ifiite Series By the ed of this sectio you will be ble to uderstd the proof of the rtio test test series for covergece by pplyig the rtio test pprecite
Chpter Ifiite Series Pge of Sectio E Rtio Test Chpter : Ifiite Series By the ed of this sectio you will be ble to uderstd the proof of the rtio test test series for covergece by pplyig the rtio test pprecite
1. Solve by the method of undetermined coefficients and by the method of variation of parameters. (4)
 7 Differeial equaios Review Solve by he mehod of udeermied coefficies ad by he mehod of variaio of parameers (4) y y = si Soluio; we firs solve he homogeeous equaio (4) y y = 4 The correspodig characerisic
7 Differeial equaios Review Solve by he mehod of udeermied coefficies ad by he mehod of variaio of parameers (4) y y = si Soluio; we firs solve he homogeeous equaio (4) y y = 4 The correspodig characerisic
On Absolute Indexed Riesz Summability of Orthogonal Series
 Ieriol Jourl of Couiol d Alied Mheics. ISSN 89-4966 Volue 3 Nuer (8). 55-6 eserch Idi Pulicios h:www.riulicio.co O Asolue Ideed iesz Suiliy of Orhogol Series L. D. Je S. K. Piry *. K. Ji 3 d. Sl 4 eserch
Ieriol Jourl of Couiol d Alied Mheics. ISSN 89-4966 Volue 3 Nuer (8). 55-6 eserch Idi Pulicios h:www.riulicio.co O Asolue Ideed iesz Suiliy of Orhogol Series L. D. Je S. K. Piry *. K. Ji 3 d. Sl 4 eserch
C(p, ) 13 N. Nuclear reactions generate energy create new isotopes and elements. Notation for stellar rates: p 12
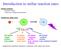 Iroducio o sellar reacio raes Nuclear reacios geerae eergy creae ew isoopes ad elemes Noaio for sellar raes: p C 3 N C(p,) 3 N The heavier arge ucleus (Lab: arge) he ligher icomig projecile (Lab: beam)
Iroducio o sellar reacio raes Nuclear reacios geerae eergy creae ew isoopes ad elemes Noaio for sellar raes: p C 3 N C(p,) 3 N The heavier arge ucleus (Lab: arge) he ligher icomig projecile (Lab: beam)
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
f(bx) dx = f dx = dx l dx f(0) log b x a + l log b a 2ɛ log b a.
 Eercise 5 For y < A < B, we hve B A f fb B d = = A B A f d f d For y ɛ >, there re N > δ >, such tht d The for y < A < δ d B > N, we hve ba f d f A bb f d l By ba A A B A bb ba fb d f d = ba < m{, b}δ
Eercise 5 For y < A < B, we hve B A f fb B d = = A B A f d f d For y ɛ >, there re N > δ >, such tht d The for y < A < δ d B > N, we hve ba f d f A bb f d l By ba A A B A bb ba fb d f d = ba < m{, b}δ
LOCUS 1. Definite Integration CONCEPT NOTES. 01. Basic Properties. 02. More Properties. 03. Integration as Limit of a Sum
 LOCUS Defiie egrio CONCEPT NOTES. Bsic Properies. More Properies. egrio s Limi of Sum LOCUS Defiie egrio As eplied i he chper iled egrio Bsics, he fudmel heorem of clculus ells us h o evlue he re uder
LOCUS Defiie egrio CONCEPT NOTES. Bsic Properies. More Properies. egrio s Limi of Sum LOCUS Defiie egrio As eplied i he chper iled egrio Bsics, he fudmel heorem of clculus ells us h o evlue he re uder
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Numbers (Part I) -- Solutions
 Ley College -- For AMATYC SML Mth Competitio Cochig Sessios v.., [/7/00] sme s /6/009 versio, with presettio improvemets Numbers Prt I) -- Solutios. The equtio b c 008 hs solutio i which, b, c re distict
Ley College -- For AMATYC SML Mth Competitio Cochig Sessios v.., [/7/00] sme s /6/009 versio, with presettio improvemets Numbers Prt I) -- Solutios. The equtio b c 008 hs solutio i which, b, c re distict
Review for the Midterm Exam.
 Review for he iderm Exm Rememer! Gross re e re Vriles suh s,, /, p / p, r, d R re gross res 2 You should kow he disiio ewee he fesile se d he udge se, d kow how o derive hem The Fesile Se Wihou goverme
Review for he iderm Exm Rememer! Gross re e re Vriles suh s,, /, p / p, r, d R re gross res 2 You should kow he disiio ewee he fesile se d he udge se, d kow how o derive hem The Fesile Se Wihou goverme
The sphere of radius a has the geographical form. r (,)=(acoscos,acossin,asin) T =(p(u)cos v, p(u)sin v,q(u) ) T.
 Che 5. Dieeil Geome o Sces 5. Sce i meic om I 3D sce c be eeseed b. Elici om z =. Imlici om z = 3. Veco om = o moe geel =z deedig o wo mees. Emle. he shee o dis hs he geoghicl om =coscoscossisi Emle. he
Che 5. Dieeil Geome o Sces 5. Sce i meic om I 3D sce c be eeseed b. Elici om z =. Imlici om z = 3. Veco om = o moe geel =z deedig o wo mees. Emle. he shee o dis hs he geoghicl om =coscoscossisi Emle. he
lecture 16: Introduction to Least Squares Approximation
 97 lecture 16: Itroductio to Lest Squres Approximtio.4 Lest squres pproximtio The miimx criterio is ituitive objective for pproximtig fuctio. However, i my cses it is more ppelig (for both computtio d
97 lecture 16: Itroductio to Lest Squres Approximtio.4 Lest squres pproximtio The miimx criterio is ituitive objective for pproximtig fuctio. However, i my cses it is more ppelig (for both computtio d
z line a) Draw the single phase equivalent circuit. b) Calculate I BC.
 ECE 2260 F 08 HW 7 prob 4 solutio EX: V gyb' b' b B V gyc' c' c C = 101 0 V = 1 + j0.2 Ω V gyb' = 101 120 V = 6 + j0. Ω V gyc' = 101 +120 V z LΔ = 9 j1.5 Ω ) Drw the sigle phse equivlet circuit. b) Clculte
ECE 2260 F 08 HW 7 prob 4 solutio EX: V gyb' b' b B V gyc' c' c C = 101 0 V = 1 + j0.2 Ω V gyb' = 101 120 V = 6 + j0. Ω V gyc' = 101 +120 V z LΔ = 9 j1.5 Ω ) Drw the sigle phse equivlet circuit. b) Clculte
Fractional Fourier Series with Applications
 Aeric Jourl o Couiol d Alied Mheics 4, 4(6): 87-9 DOI: 593/jjc446 Frciol Fourier Series wih Alicios Abu Hd I, Khlil R * Uiversiy o Jord, Jord Absrc I his er, we iroduce coorble rciol Fourier series We
Aeric Jourl o Couiol d Alied Mheics 4, 4(6): 87-9 DOI: 593/jjc446 Frciol Fourier Series wih Alicios Abu Hd I, Khlil R * Uiversiy o Jord, Jord Absrc I his er, we iroduce coorble rciol Fourier series We
1 Notes on Little s Law (l = λw)
 Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
SM2H. Unit 2 Polynomials, Exponents, Radicals & Complex Numbers Notes. 3.1 Number Theory
 SMH Uit Polyomils, Epoets, Rdicls & Comple Numbers Notes.1 Number Theory .1 Addig, Subtrctig, d Multiplyig Polyomils Notes Moomil: A epressio tht is umber, vrible, or umbers d vribles multiplied together.
SMH Uit Polyomils, Epoets, Rdicls & Comple Numbers Notes.1 Number Theory .1 Addig, Subtrctig, d Multiplyig Polyomils Notes Moomil: A epressio tht is umber, vrible, or umbers d vribles multiplied together.
Numerical Methods (CENG 2002) CHAPTER -III LINEAR ALGEBRAIC EQUATIONS. In this chapter, we will deal with the case of determining the values of x 1
 Numericl Methods (CENG 00) CHAPTER -III LINEAR ALGEBRAIC EQUATIONS. Itroductio I this chpter, we will del with the cse of determiig the vlues of,,..., tht simulteously stisfy the set of equtios: f f...
Numericl Methods (CENG 00) CHAPTER -III LINEAR ALGEBRAIC EQUATIONS. Itroductio I this chpter, we will del with the cse of determiig the vlues of,,..., tht simulteously stisfy the set of equtios: f f...
Lesson 4 Linear Algebra
 Lesso Lier Algebr A fmily of vectors is lierly idepedet if oe of them c be writte s lier combitio of fiitely my other vectors i the collectio. Cosider m lierly idepedet equtios i ukows:, +, +... +, +,
Lesso Lier Algebr A fmily of vectors is lierly idepedet if oe of them c be writte s lier combitio of fiitely my other vectors i the collectio. Cosider m lierly idepedet equtios i ukows:, +, +... +, +,
Orthogonality, orthogonalization, least squares
 ier Alger for Wireless Commuictios ecture: 3 Orthogolit, orthogoliztio, lest squres Ier products d Cosies he gle etee o-zero vectors d is cosθθ he l of Cosies: + cosθ If the gle etee to vectors is π/ (90º),
ier Alger for Wireless Commuictios ecture: 3 Orthogolit, orthogoliztio, lest squres Ier products d Cosies he gle etee o-zero vectors d is cosθθ he l of Cosies: + cosθ If the gle etee to vectors is π/ (90º),
INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
 Mthemtics Revisio Guides Itegrtig Trig, Log d Ep Fuctios Pge of MK HOME TUITION Mthemtics Revisio Guides Level: AS / A Level AQA : C Edecel: C OCR: C OCR MEI: C INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
Mthemtics Revisio Guides Itegrtig Trig, Log d Ep Fuctios Pge of MK HOME TUITION Mthemtics Revisio Guides Level: AS / A Level AQA : C Edecel: C OCR: C OCR MEI: C INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
Student Success Center Elementary Algebra Study Guide for the ACCUPLACER (CPT)
 Studet Success Ceter Elemetry Algebr Study Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d cotet of questios o the Accuplcer Elemetry Algebr test. Reviewig these smples
Studet Success Ceter Elemetry Algebr Study Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d cotet of questios o the Accuplcer Elemetry Algebr test. Reviewig these smples
f(x) dx with An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples dx x x 2
 Impope Inegls To his poin we hve only consideed inegls f() wih he is of inegion nd b finie nd he inegnd f() bounded (nd in fc coninuous ecep possibly fo finiely mny jump disconinuiies) An inegl hving eihe
Impope Inegls To his poin we hve only consideed inegls f() wih he is of inegion nd b finie nd he inegnd f() bounded (nd in fc coninuous ecep possibly fo finiely mny jump disconinuiies) An inegl hving eihe
Geometric Sequences. Geometric Sequence. Geometric sequences have a common ratio.
 s A geometric sequece is sequece such tht ech successive term is obtied from the previous term by multiplyig by fixed umber clled commo rtio. Exmples, 6, 8,, 6,..., 0, 0, 0, 80,... Geometric sequeces hve
s A geometric sequece is sequece such tht ech successive term is obtied from the previous term by multiplyig by fixed umber clled commo rtio. Exmples, 6, 8,, 6,..., 0, 0, 0, 80,... Geometric sequeces hve
A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD
 Diol Bgoo () A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD I. Itroductio The first seprtio of vribles (see pplictios to Newto s equtios) is ver useful method
Diol Bgoo () A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD I. Itroductio The first seprtio of vribles (see pplictios to Newto s equtios) is ver useful method
Union-Find Partition Structures Goodrich, Tamassia Union-Find 1
 Uio-Fid Pariio Srucures 004 Goodrich, Tamassia Uio-Fid Pariios wih Uio-Fid Operaios makesex: Creae a sileo se coaii he eleme x ad reur he posiio sori x i his se uioa,b : Reur he se A U B, desroyi he old
Uio-Fid Pariio Srucures 004 Goodrich, Tamassia Uio-Fid Pariios wih Uio-Fid Operaios makesex: Creae a sileo se coaii he eleme x ad reur he posiio sori x i his se uioa,b : Reur he se A U B, desroyi he old
Similar idea to multiplication in N, C. Divide and conquer approach provides unexpected improvements. Naïve matrix multiplication
 Next. Covered bsics of simple desig techique (Divided-coquer) Ch. of the text.. Next, Strsse s lgorithm. Lter: more desig d coquer lgorithms: MergeSort. Solvig recurreces d the Mster Theorem. Similr ide
Next. Covered bsics of simple desig techique (Divided-coquer) Ch. of the text.. Next, Strsse s lgorithm. Lter: more desig d coquer lgorithms: MergeSort. Solvig recurreces d the Mster Theorem. Similr ide
CSE 5311 Notes 12: Matrices
 CSE 5311 Noes 12: Marices Las updaed 11/12/15 9:12 AM) STRASSEN S MATRIX MULTIPLICATION Marix addiio: akes scalar addiios. Everyday arix uliply: p p Le = = p. akes p scalar uliplies ad -1)p scalar addiios
CSE 5311 Noes 12: Marices Las updaed 11/12/15 9:12 AM) STRASSEN S MATRIX MULTIPLICATION Marix addiio: akes scalar addiios. Everyday arix uliply: p p Le = = p. akes p scalar uliplies ad -1)p scalar addiios
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
Extremal graph theory II: K t and K t,t
 Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
Notes 03 largely plagiarized by %khc
 1 1 Discree-Time Covoluio Noes 03 largely plagiarized by %khc Le s begi our discussio of covoluio i discree-ime, sice life is somewha easier i ha domai. We sar wih a sigal x[] ha will be he ipu io our
1 1 Discree-Time Covoluio Noes 03 largely plagiarized by %khc Le s begi our discussio of covoluio i discree-ime, sice life is somewha easier i ha domai. We sar wih a sigal x[] ha will be he ipu io our
BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS
 BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS Opimal ear Forecasig Alhough we have o meioed hem explicily so far i he course, here are geeral saisical priciples for derivig he bes liear forecas, ad
BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS Opimal ear Forecasig Alhough we have o meioed hem explicily so far i he course, here are geeral saisical priciples for derivig he bes liear forecas, ad
Linear Programming. Preliminaries
 Lier Progrmmig Prelimiries Optimiztio ethods: 3L Objectives To itroduce lier progrmmig problems (LPP To discuss the stdrd d coicl form of LPP To discuss elemetry opertio for lier set of equtios Optimiztio
Lier Progrmmig Prelimiries Optimiztio ethods: 3L Objectives To itroduce lier progrmmig problems (LPP To discuss the stdrd d coicl form of LPP To discuss elemetry opertio for lier set of equtios Optimiztio
Unit 1. Extending the Number System. 2 Jordan School District
 Uit Etedig the Number System Jord School District Uit Cluster (N.RN. & N.RN.): Etedig Properties of Epoets Cluster : Etedig properties of epoets.. Defie rtiol epoets d eted the properties of iteger epoets
Uit Etedig the Number System Jord School District Uit Cluster (N.RN. & N.RN.): Etedig Properties of Epoets Cluster : Etedig properties of epoets.. Defie rtiol epoets d eted the properties of iteger epoets
The Eigen Function of Linear Systems
 1/25/211 The Eige Fucio of Liear Sysems.doc 1/7 The Eige Fucio of Liear Sysems Recall ha ha we ca express (expad) a ime-limied sigal wih a weighed summaio of basis fucios: v ( ) a ψ ( ) = where v ( ) =
1/25/211 The Eige Fucio of Liear Sysems.doc 1/7 The Eige Fucio of Liear Sysems Recall ha ha we ca express (expad) a ime-limied sigal wih a weighed summaio of basis fucios: v ( ) a ψ ( ) = where v ( ) =
DIFFERENCE EQUATIONS
 DIFFERECE EQUATIOS Lier Cos-Coeffiie Differee Eqios Differee Eqios I disree-ime ssems, esseil feres of ip d op sigls pper ol speifi iss of ime, d he m o e defied ewee disree ime seps or he m e os. These
DIFFERECE EQUATIOS Lier Cos-Coeffiie Differee Eqios Differee Eqios I disree-ime ssems, esseil feres of ip d op sigls pper ol speifi iss of ime, d he m o e defied ewee disree ime seps or he m e os. These
f(t)dt 2δ f(x) f(t)dt 0 and b f(t)dt = 0 gives F (b) = 0. Since F is increasing, this means that
 Uiversity of Illiois t Ur-Chmpig Fll 6 Mth 444 Group E3 Itegrtio : correctio of the exercises.. ( Assume tht f : [, ] R is cotiuous fuctio such tht f(x for ll x (,, d f(tdt =. Show tht f(x = for ll x [,
Uiversity of Illiois t Ur-Chmpig Fll 6 Mth 444 Group E3 Itegrtio : correctio of the exercises.. ( Assume tht f : [, ] R is cotiuous fuctio such tht f(x for ll x (,, d f(tdt =. Show tht f(x = for ll x [,
Tries & Suffix Tries
 Tries & Suffix Tries Be Lgmed Deprme of Compuer Sciece Plese sig guesook (www.lgmed-l.org/echig-merils) o ell me riefly how you re usig he slides. For origil Keyoe files, emil me (e.lgmed@gmil.com). Tries
Tries & Suffix Tries Be Lgmed Deprme of Compuer Sciece Plese sig guesook (www.lgmed-l.org/echig-merils) o ell me riefly how you re usig he slides. For origil Keyoe files, emil me (e.lgmed@gmil.com). Tries
SLOW INCREASING FUNCTIONS AND THEIR APPLICATIONS TO SOME PROBLEMS IN NUMBER THEORY
 VOL. 8, NO. 7, JULY 03 ISSN 89-6608 ARPN Jourl of Egieerig d Applied Sciece 006-03 Ai Reerch Publihig Nework (ARPN). All righ reerved. www.rpjourl.com SLOW INCREASING FUNCTIONS AND THEIR APPLICATIONS TO
VOL. 8, NO. 7, JULY 03 ISSN 89-6608 ARPN Jourl of Egieerig d Applied Sciece 006-03 Ai Reerch Publihig Nework (ARPN). All righ reerved. www.rpjourl.com SLOW INCREASING FUNCTIONS AND THEIR APPLICATIONS TO
Physics 2A HW #3 Solutions
 Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
FACULTY OF MATHEMATICAL STUDIES MATHEMATICS FOR PART I ENGINEERING. Lectures
 FACULTY OF MATHEMATICAL STUDIES MATHEMATICS FOR PART I ENGINEERING Lectures MODULE 0 FURTHER CALCULUS II. Sequeces d series. Rolle s theorem d me vlue theorems 3. Tlor s d Mcluri s theorems 4. L Hopitl
FACULTY OF MATHEMATICAL STUDIES MATHEMATICS FOR PART I ENGINEERING Lectures MODULE 0 FURTHER CALCULUS II. Sequeces d series. Rolle s theorem d me vlue theorems 3. Tlor s d Mcluri s theorems 4. L Hopitl
(200 terms) equals Let f (x) = 1 + x + x 2 + +x 100 = x101 1
 SECTION 5. PGE 78.. DMS: CLCULUS.... 5. 6. CHPTE 5. Sectio 5. pge 78 i + + + INTEGTION Sums d Sigm Nottio j j + + + + + i + + + + i j i i + + + j j + 5 + + j + + 9 + + 7. 5 + 6 + 7 + 8 + 9 9 i i5 8. +
SECTION 5. PGE 78.. DMS: CLCULUS.... 5. 6. CHPTE 5. Sectio 5. pge 78 i + + + INTEGTION Sums d Sigm Nottio j j + + + + + i + + + + i j i i + + + j j + 5 + + j + + 9 + + 7. 5 + 6 + 7 + 8 + 9 9 i i5 8. +
S n. = n. Sum of first n terms of an A. P is
 PROGREION I his secio we discuss hree impora series amely ) Arihmeic Progressio (A.P), ) Geomeric Progressio (G.P), ad 3) Harmoic Progressio (H.P) Which are very widely used i biological scieces ad humaiies.
PROGREION I his secio we discuss hree impora series amely ) Arihmeic Progressio (A.P), ) Geomeric Progressio (G.P), ad 3) Harmoic Progressio (H.P) Which are very widely used i biological scieces ad humaiies.
SUTCLIFFE S NOTES: CALCULUS 2 SWOKOWSKI S CHAPTER 11
 UTCLIFFE NOTE: CALCULU WOKOWKI CHAPTER Ifiite eries Coverget or Diverget eries Cosider the sequece If we form the ifiite sum 0, 00, 000, 0 00 000, we hve wht is clled ifiite series We wt to fid the sum
UTCLIFFE NOTE: CALCULU WOKOWKI CHAPTER Ifiite eries Coverget or Diverget eries Cosider the sequece If we form the ifiite sum 0, 00, 000, 0 00 000, we hve wht is clled ifiite series We wt to fid the sum
Statistics for Financial Engineering Session 1: Linear Algebra Review March 18 th, 2006
 Sttistics for Ficil Egieerig Sessio : Lier Algebr Review rch 8 th, 6 Topics Itroductio to trices trix opertios Determits d Crmer s rule Eigevlues d Eigevectors Quiz The cotet of Sessio my be fmilir to
Sttistics for Ficil Egieerig Sessio : Lier Algebr Review rch 8 th, 6 Topics Itroductio to trices trix opertios Determits d Crmer s rule Eigevlues d Eigevectors Quiz The cotet of Sessio my be fmilir to
ALGEBRA. Set of Equations. have no solution 1 b1. Dependent system has infinitely many solutions
 Qudrtic Equtios ALGEBRA Remider theorem: If f() is divided b( ), the remider is f(). Fctor theorem: If ( ) is fctor of f(), the f() = 0. Ivolutio d Evlutio ( + b) = + b + b ( b) = + b b ( + b) 3 = 3 +
Qudrtic Equtios ALGEBRA Remider theorem: If f() is divided b( ), the remider is f(). Fctor theorem: If ( ) is fctor of f(), the f() = 0. Ivolutio d Evlutio ( + b) = + b + b ( b) = + b b ( + b) 3 = 3 +
Union-Find Partition Structures
 Uio-Fid //4 : Preseaio for use wih he exbook Daa Srucures ad Alorihms i Java, h ediio, by M. T. Goodrich, R. Tamassia, ad M. H. Goldwasser, Wiley, 04 Uio-Fid Pariio Srucures 04 Goodrich, Tamassia, Goldwasser
Uio-Fid //4 : Preseaio for use wih he exbook Daa Srucures ad Alorihms i Java, h ediio, by M. T. Goodrich, R. Tamassia, ad M. H. Goldwasser, Wiley, 04 Uio-Fid Pariio Srucures 04 Goodrich, Tamassia, Goldwasser
Math 2414 Homework Set 7 Solutions 10 Points
 Mah Homework Se 7 Soluios 0 Pois #. ( ps) Firs verify ha we ca use he iegral es. The erms are clearly posiive (he epoeial is always posiive ad + is posiive if >, which i is i his case). For decreasig we
Mah Homework Se 7 Soluios 0 Pois #. ( ps) Firs verify ha we ca use he iegral es. The erms are clearly posiive (he epoeial is always posiive ad + is posiive if >, which i is i his case). For decreasig we
λiv Av = 0 or ( λi Av ) = 0. In order for a vector v to be an eigenvector, it must be in the kernel of λi
 Liear lgebra Lecure #9 Noes This week s lecure focuses o wha migh be called he srucural aalysis of liear rasformaios Wha are he irisic properies of a liear rasformaio? re here ay fixed direcios? The discussio
Liear lgebra Lecure #9 Noes This week s lecure focuses o wha migh be called he srucural aalysis of liear rasformaios Wha are he irisic properies of a liear rasformaio? re here ay fixed direcios? The discussio
Comparison between Fourier and Corrected Fourier Series Methods
 Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
Ideal Amplifier/Attenuator. Memoryless. where k is some real constant. Integrator. System with memory
 Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
M3P14 EXAMPLE SHEET 1 SOLUTIONS
 M3P14 EXAMPLE SHEET 1 SOLUTIONS 1. Show tht for, b, d itegers, we hve (d, db) = d(, b). Sice (, b) divides both d b, d(, b) divides both d d db, d hece divides (d, db). O the other hd, there exist m d
M3P14 EXAMPLE SHEET 1 SOLUTIONS 1. Show tht for, b, d itegers, we hve (d, db) = d(, b). Sice (, b) divides both d b, d(, b) divides both d d db, d hece divides (d, db). O the other hd, there exist m d
NOTES ON BERNOULLI NUMBERS AND EULER S SUMMATION FORMULA. B r = [m = 0] r
![NOTES ON BERNOULLI NUMBERS AND EULER S SUMMATION FORMULA. B r = [m = 0] r NOTES ON BERNOULLI NUMBERS AND EULER S SUMMATION FORMULA. B r = [m = 0] r](/thumbs/80/81160853.jpg) NOTES ON BERNOULLI NUMBERS AND EULER S SUMMATION FORMULA MARK WILDON. Beroulli umbers.. Defiiio. We defie he Beroulli umbers B m for m by m ( m + ( B r [m ] r r Beroulli umbers re med fer Joh Beroulli
NOTES ON BERNOULLI NUMBERS AND EULER S SUMMATION FORMULA MARK WILDON. Beroulli umbers.. Defiiio. We defie he Beroulli umbers B m for m by m ( m + ( B r [m ] r r Beroulli umbers re med fer Joh Beroulli
Inverse Transient Quasi-Static Thermal Stresses. in a Thin Rectangular Plate
 Adv Theor Al Mech Vol 3 o 5-3 Iverse Trsie Qusi-Sic Therml Sresses i Thi Recgulr Ple Prvi M Slve Bhlero Sciece College Soer Ngur Idi rvimslve@hoocom Suchir A Meshrm Derme of Mhemics PGTD RTM Ngur Uiversi
Adv Theor Al Mech Vol 3 o 5-3 Iverse Trsie Qusi-Sic Therml Sresses i Thi Recgulr Ple Prvi M Slve Bhlero Sciece College Soer Ngur Idi rvimslve@hoocom Suchir A Meshrm Derme of Mhemics PGTD RTM Ngur Uiversi
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Solving Systems of Equations
 PGE : Formultio d Solutio i Geosystems Egieerig Dr. Blhoff Solvig Systems of Equtios Numericl Methods with MTLB, Recktewld, Chpter 8 d Numericl Methods for Egieers, Chpr d Cle, 5 th Ed., Prt Three, Chpters
PGE : Formultio d Solutio i Geosystems Egieerig Dr. Blhoff Solvig Systems of Equtios Numericl Methods with MTLB, Recktewld, Chpter 8 d Numericl Methods for Egieers, Chpr d Cle, 5 th Ed., Prt Three, Chpters
is an ordered list of numbers. Each number in a sequence is a term of a sequence. n-1 term
 Mthemticl Ptters. Arithmetic Sequeces. Arithmetic Series. To idetify mthemticl ptters foud sequece. To use formul to fid the th term of sequece. To defie, idetify, d pply rithmetic sequeces. To defie rithmetic
Mthemticl Ptters. Arithmetic Sequeces. Arithmetic Series. To idetify mthemticl ptters foud sequece. To use formul to fid the th term of sequece. To defie, idetify, d pply rithmetic sequeces. To defie rithmetic
Surds, Indices, and Logarithms Radical
 MAT 6 Surds, Idices, d Logrithms Rdicl Defiitio of the Rdicl For ll rel, y > 0, d ll itegers > 0, y if d oly if y where is the ide is the rdicl is the rdicd. Surds A umber which c be epressed s frctio
MAT 6 Surds, Idices, d Logrithms Rdicl Defiitio of the Rdicl For ll rel, y > 0, d ll itegers > 0, y if d oly if y where is the ide is the rdicl is the rdicd. Surds A umber which c be epressed s frctio
Chapter 2 Infinite Series Page 1 of 9
 Chpter Ifiite eries Pge of 9 Chpter : Ifiite eries ectio A Itroductio to Ifiite eries By the ed of this sectio you will be ble to uderstd wht is met by covergece d divergece of ifiite series recogise geometric
Chpter Ifiite eries Pge of 9 Chpter : Ifiite eries ectio A Itroductio to Ifiite eries By the ed of this sectio you will be ble to uderstd wht is met by covergece d divergece of ifiite series recogise geometric
Chapter 2: Evaluative Feedback
 Chper 2: Evluive Feedbck Evluing cions vs. insrucing by giving correc cions Pure evluive feedbck depends olly on he cion ken. Pure insrucive feedbck depends no ll on he cion ken. Supervised lerning is
Chper 2: Evluive Feedbck Evluing cions vs. insrucing by giving correc cions Pure evluive feedbck depends olly on he cion ken. Pure insrucive feedbck depends no ll on he cion ken. Supervised lerning is
334 MATHS SERIES DSE MATHS PREVIEW VERSION B SAMPLE TEST & FULL SOLUTION
 MATHS SERIES DSE MATHS PREVIEW VERSION B SAMPLE TEST & FULL SOLUTION TEST SAMPLE TEST III - P APER Questio Distributio INSTRUCTIONS:. Attempt ALL questios.. Uless otherwise specified, ll worig must be
MATHS SERIES DSE MATHS PREVIEW VERSION B SAMPLE TEST & FULL SOLUTION TEST SAMPLE TEST III - P APER Questio Distributio INSTRUCTIONS:. Attempt ALL questios.. Uless otherwise specified, ll worig must be
Let s express the absorption of radiation by dipoles as a dipole correlation function.
 MIT Deparme of Chemisry 5.74, Sprig 004: Iroducory Quaum Mechaics II Isrucor: Prof. Adrei Tokmakoff p. 81 Time-Correlaio Fucio Descripio of Absorpio Lieshape Le s express he absorpio of radiaio by dipoles
MIT Deparme of Chemisry 5.74, Sprig 004: Iroducory Quaum Mechaics II Isrucor: Prof. Adrei Tokmakoff p. 81 Time-Correlaio Fucio Descripio of Absorpio Lieshape Le s express he absorpio of radiaio by dipoles
