SLOW INCREASING FUNCTIONS AND THEIR APPLICATIONS TO SOME PROBLEMS IN NUMBER THEORY
|
|
|
- Ethan Tracy Wilson
- 6 years ago
- Views:
Transcription
1 VOL. 8, NO. 7, JULY 03 ISSN ARPN Jourl of Egieerig d Applied Sciece Ai Reerch Publihig Nework (ARPN). All righ reerved. SLOW INCREASING FUNCTIONS AND THEIR APPLICATIONS TO SOME PROBLEMS IN NUMBER THEORY K. Soh Reddy, V. Kvih d V. Lkhmi Nry Vrdhm College of Egieerig, Shmhbd, Hyderbd, Adhr Prdeh, Idi E-Mil: ureddyk@gmil.com ABSTRACT Thi ricle commece wih defiiio of low icreig fucio d move o o deliee few properie of low icreig fucio. Beide, everl pplicio i ome problem of umber heory uig he heory of low icreig fucio re lo preeed o how how ueful hee fucio prove i olvig comple problem. Keyword: low icreig fucio, ympoiclly equivle, equece of poiive ieger.. INTRODUCTION Slow icreig fucio re defied follow:.. Defiiio Le f :, ) ( 0, ) be coiuouly differeible fucio uch h f > 0 d lim f. The f i id o be low f icreig fucio (.i.f. i hor) if lim 0 f Wrie F { f f } : i.i.f.... Emple (i) f log, > i.i.f. Noe h lim f lim log d f, > d f i coiuou f lim lim 0 f log (ii) f loglog, > e i lo.i.f.. SOME PROPERTIES.. Theorem Le f, g F d le > 0, c > 0 be wo co he we hve (i) f + c (ii) f c (iii) cf (iv) fg (v) f (vi) f ο g (vii) log f (viii) f + g ll lie i F. Give h f, g F d > 0, c > 0 be co. of (i), (ii), (iii), d (iv) follow he defiiio. (v) Le h f Noe h lim h lim f, d f f > 0, d i coiuou f f lim h () () () () lim Hece h f F (vi) Le h fοg ieh. f( g) f lim 0. f Noe h lim h lim f( g ), d () f (()) g g () > 0, d i coiuou f ( g) g g f ( g) g lim lim lim 0. h f( g ) f( g ) g Hece h fο g F (vii) Le h log f Noe h lim h lim log f, d f > 0, d i coiuou f f f f lim lim lim 0. h log f f log f Hece h log f F (viii) Le h f + g For ufficiely lrge, we hve 0 0 g g f + g g f f d f + g f 480
2 VOL. 8, NO. 7, JULY 03 ISSN ARPN Jourl of Egieerig d Applied Sciece Ai Reerch Publihig Nework (ARPN). All righ reerved. By ddig he bove, we ge lim 0 Hece h f + g F h () f g 0 lim lim + lim 0 h () f g.. Theorem Le f, g F. Defie h f ( ) d k f( g ) for ech, Give h f, g F. Defie h f ( ) d k f( g ) for ech. Le h () f( ) Noe h lim h lim f( ), d f ( ) > 0, d i coiuou f ( ) f ( ) lim lim lim 0 h f( ) f( ) Hece h f( ) i.i.f. Le k f( g ) Noe h lim k lim f( g ), d k f ( g) g + g > 0 d k i coiuou f ( g) g + g lim lim h f( g ) g f ( g) g f ( g) g lim + lim 0 f( g ) f( g ) g Therefore k f( g ) i.i.f. Hece hk, F.3. Theorem Le f, g F be uch h f d f f lim d 0. g d > g The F. g Give h f d f f, g F,lim d 0 g d > g f ( g ) f( g ) Le f h d g g f g f g g f g lim lim lim lim 0 h f f g g Hece f F g.4. Theorem Le h :, ) ( 0, ) be coiuouly differeible fucio uch h > 0 d lim h (i) Defie g h(log ). The g F lim 0 h (ii) Defie e. The k F lim 0 h k Give h > 0 d lim h (log ) (i) Defie g h(log ) he g Suppoe g F he g ifie g (log ) i.e. lim 0 h(log ) lim 0 g (log ) lim 0 h(log ) () Pu log o h lim 0 h () i.e. lim 0. h Coverely uppoe lim 0 h Pu e o h log d (log ) lim lim 0 h h(log ) g () (log ) Now lim lim lim 0. g () h(log ) h Hece g F (ii) Like proof of (i).5. Theorem If f F he log f lim 0. log 48
3 VOL. 8, NO. 7, JULY 03 ISSN ARPN Jourl of Egieerig d Applied Sciece Ai Reerch Publihig Nework (ARPN). All righ reerved. Give h f F, f log f f lim lim log f ' log f lim 0 i.e. lim 0 f log (byl Hopil rule)..6. Theorem f F if d oly if o ech > 0 here d f ei uch h 0, d < > We hve d f f f f f + d f f ' Suppoe f F he lim 0 f i.e. For ech > 0 here ei uch h > Ad hold. f ' d 0 <, > 0, d < > To prove he covere ume h he codiio Le > 0 be give. The here ei uch h > d f We hve, by hypohei 0 d < hi implie h f ' 0 <, > f f ie.. 0 f Therefore f F..7. Theorem If f F he f ' lim 0. f lim 0, for ll > 0 For y wih 0 < <, we ge by Theorem.6, d f 0, d < Thi implie h Hece for ll > for ome f i decreig for > f bouded bove, y, by M Th i, here ei M > 0 uch h f 0 < < M, > f f lim lim 0.8. Noe We kow h ech f F i icreig fucio., by he bove heorem, i i cler h f lim 0, >0. Thi how h he icreig ure of f i low. I oher word, f doe o icree rpidly. Thi juifie he me give o he member of F. From he bove heorem, we hve he followig reul:.9. Theorem If f F lim f 0. he f lim 0 d f I Theorem.7 pu, oge lim 0. f If f F, he lim 0 f f Sice lim 0 we mu hve lim f Theorem Le f F, he for y > d erie f diverge o. + We wrie f ( f ) we kow h he erie diverge o, he 48
4 VOL. 8, NO. 7, JULY 03 ISSN ARPN Jourl of Egieerig d Applied Sciece Ai Reerch Publihig Nework (ARPN). All righ reerved. Give > + > 0 If 0 + he lim f If > 0 he + lim lim (from Theorem.7) f f i.e. f diverge o A impor byproduc of he bove heorem i he followig reul... Theorem Le f F. The for y d lim. + f + > d, From Theorem.0, we hve + lim f + lim f, >, + From Theorem.0, we hve lim f d f () d Coider lim + f + f () lim + f () + f () f () + f lim f f + + f (By L Hopil rule) f (i) If lim, he f i id o ympoiclly g equivle o g. We decribe hi by wriig f g. (ii) f Ο( g) Me f Ag for ome A > 0. I hi ce we y h f i of lrge order g. f (ii) f ο( g) Me lim 0. I hi ce we g y h f i of mll order g..3. Emple (i) Coider f, g +, for ll > 0 f d lim lim g + Therefore f g. (ii) Ο (0 ) Becue (0 ) (iii) + + ο( ) Becue lim 0. A reul of Theorem., we ge he followig reul priculr ce..4. Theorem Le f F. The we hve he followig eme. (i) f d f (ii) f ( d ) f (iii) Le f F (i) Pu 0 i Theorem., we ge f () d lim f d f () f f () d f (ii) Pu 0, i Theorem., we ge.. Defiiio Le f, g: [, ) ( 0, ) 483
5 VOL. 8, NO. 7, JULY 03 ISSN ARPN Jourl of Egieerig d Applied Sciece Ai Reerch Publihig Nework (ARPN). All righ reerved. f () d lim f f () d f (iii) Pu 0, - i Theorem., we ge d lim d f () f f.5. Theorem Le f F. The f( + (i) lim, f (ii) If f i decreig he c Le f F For y c f( lim, for y f (i) Ce (). Suppoe c > 0 By Lgrge me vlue heorem, There ei, + c uch h f ( + f ( + c ) f f ( + f cf () 0 f f f ( + cf () 0 lim lim, (, + f () f ( + lim 0, ice lim f 0 (by Theorem.9) f () f ( + lim. f Ce (b). Suppoe c < 0 By Lgrge me vlue heorem here + c, uch h ei f f + c ( f f f + c cf () 0 f f f ( + f () 0 lim clim + c, f (), ( + ) fc lim 0, ice lim f 0 f () (by Theorem.9) f ( + lim. f (ii) Ce (). Suppoec > By Lgrge me vlue heorem here, c uch h ei f ( f ( c ) f f ( f ( c ) f 0 f f f ( f f () 0 lim ( c ) lim f f, (, Ad f ( ) i decreig f > f fc There forelim 0, ice lim f 0 (by Theorem.9) f () f c lim. f Ce (b). Suppoe c < By Lgrge me vlue heorem here c, uch h ei f f c ( f f f ( ( cf ) 0 f f f f ( f () 0 lim ( lim, f f Ad f ( ) i decreig f > f f ( There fore lim 0, f ice lim f 0 (by Theorem.9) ( c, ) f c lim. f.6. Theorem Suppoe f F i uch h f i decreig. If 0 < c c d g i fucio uch h f( g ) c g che lim. f 484
6 VOL. 8, NO. 7, JULY 03 ISSN ARPN Jourl of Egieerig d Applied Sciece Ai Reerch Publihig Nework (ARPN). All righ reerved. Suppoe f F i uch h f i decreig If 0 < c g c f ( c ) f( g ) f( c ) ice f i decreig f ( c ) f( g ) f( c ) f f f f ( c ) f( g ) f( c ) lim lim lim f f f f( g ) lim f (By Theorem.5) f( g ) lim. f 3. APPLICATIONS OF SLOW INCREASING FUNCTIONS TO SOME PROBLEMS OF NUMBER THEORY Thi ecio deil ome pplicio i problem periig o umber heory. We begi wih he followig impor defiiio. 3.. Defiiio Le f F. Through ou ( ) deoe ricly icreig equece of poiive ieger uch h > d lim for ome. f i.e. f( ) There ei everl uch equece. For emple p, he equece of prime umber i icreig order, f log d. p By prime umber heorem we hve lim log 3.. Theorem Le f :(, ) (, ) be.i.f. ( > ) f () d lim d ( b) <. Suppoe ( ) be b he equece of poiive ieger uch h f. () The.... lim. e Give h f :(, ) (, ) be.i.f. f () b Ad f > d lim d ( < b) log log + log f + ο() If i poiive ieger i iervl [, ) The log k log k+ log f( k) + ο() () k k k k Now Sice log i icreig d poiive i (, ) log k log d+ο(log ) k log +Ο (log ) log + ο (3) O he oher hd if 0 he iequliy ο() < ε Therefore for >, we hve ο() ο() k k ε( + ) < ε i.e. ο() ο k ε > we hve for ll (4) We fid h log f ( k) log f d+ο(log f) k f log f d+ο(log f) (5) f We kow h log f f lim lim (By L Hopil rule) f ( ) f lim 0. f 485
7 VOL. 8, NO. 7, JULY 03 ISSN ARPN Jourl of Egieerig d Applied Sciece Ai Reerch Publihig Nework (ARPN). All righ reerved. Ο (log f ) ο (6) Now f () d () f f lim lim 0 (By L Hopil rule) f f d ο( ) (7) f From (5), (6) d (7), we ge log f ( k) log f + ο (8) k From (), (3), (4) d (7), we ge k log ( log + ο) + log f + ο + ο k log k log + log f + ο (9) Bu k k log log + log log k log ep... ep log k k k log log log + log + ο() (By 9) k k ep ep k ( f ο ) ( f ο ) e ( f +ο ) ep log + log + () ep log + () ep log () e f e e Therefore... e... lim. e... e I view of he bove heorem d prime umber heorem implie he followig Theorem Le p be he equece of prime umber. The pp... p lim. p e d. I heorem 3. pu p, f log Le k, c be he equece of ieger which hve i heir prime fcorizio k prime fcor. Rfel Jkimczuk [ 4 ] proved h c ( k )! log ( log log ) k, ( k ) A reul of previou heorem, we hve he followig reul Theorem c, k. c, k... c, k lim. c e k, I Theorem 3. pu c,, f ( k )!log d. CONCLUSIONS We pply he reul dicued i hi ricle o look io ome of he pplicio i umber heory. ACKNOWLEDGEMENTS The uhor like o epre heir griude owrd he mgeme of Vrdhm College of Egieerig for heir coiuou uppor d ecourgeme durig hi work. Furher uhor would like o hk he oymou referee for goig hrough he ricle wih fie ooh comb d mkig criicl comme o he origil verio of hi mucrip. k 486
8 VOL. 8, NO. 7, JULY 03 ISSN ARPN Jourl of Egieerig d Applied Sciece Ai Reerch Publihig Nework (ARPN). All righ reerved. REFERENCES [] G. H. Hrdy d E. M. Wrigh A Iroducio o he Theory of Number. Fourh Ediio. [] R. Jkimczuk. 00. Fucio of low icree d ieger equece. Jourl of Ieger Sequece. 3, Aricle 0... [3] R. Jkimczuk A oe o um of power which hve fied umber of prime fcor. J. Iequl. Pure Appl. Mh. 6: 5-0. [4] R. Jkimczuk The rio bewee he verge fcor i produc d he l fcor, mhemicl ciece: Qurerly Jourl. : [5] Y. Shg. 0. O limi for he produc of power of prime. Sci. Mg. 7: [6] J. Rey Por, P. Pi Cllej d C. Trejo A lii Mem rico, Volume I, Ocv Ediio, Edioril Kpeluz
Calculus Limits. Limit of a function.. 1. One-Sided Limits...1. Infinite limits 2. Vertical Asymptotes...3. Calculating Limits Using the Limit Laws.
 Limi of a fucio.. Oe-Sided..... Ifiie limis Verical Asympoes... Calculaig Usig he Limi Laws.5 The Squeeze Theorem.6 The Precise Defiiio of a Limi......7 Coiuiy.8 Iermediae Value Theorem..9 Refereces..
Limi of a fucio.. Oe-Sided..... Ifiie limis Verical Asympoes... Calculaig Usig he Limi Laws.5 The Squeeze Theorem.6 The Precise Defiiio of a Limi......7 Coiuiy.8 Iermediae Value Theorem..9 Refereces..
Existence Of Solutions For Nonlinear Fractional Differential Equation With Integral Boundary Conditions
 Reserch Ivey: Ieriol Jourl Of Egieerig Ad Sciece Vol., Issue (April 3), Pp 8- Iss(e): 78-47, Iss(p):39-6483, Www.Reserchivey.Com Exisece Of Soluios For Nolier Frciol Differeil Equio Wih Iegrl Boudry Codiios,
Reserch Ivey: Ieriol Jourl Of Egieerig Ad Sciece Vol., Issue (April 3), Pp 8- Iss(e): 78-47, Iss(p):39-6483, Www.Reserchivey.Com Exisece Of Soluios For Nolier Frciol Differeil Equio Wih Iegrl Boudry Codiios,
arxiv:math/ v1 [math.fa] 1 Feb 1994
![arxiv:math/ v1 [math.fa] 1 Feb 1994 arxiv:math/ v1 [math.fa] 1 Feb 1994](/thumbs/93/114291597.jpg) arxiv:mah/944v [mah.fa] Feb 994 ON THE EMBEDDING OF -CONCAVE ORLICZ SPACES INTO L Care Schü Abrac. I [K S ] i wa how ha Ave ( i a π(i) ) π i equivale o a Orlicz orm whoe Orlicz fucio i -cocave. Here we
arxiv:mah/944v [mah.fa] Feb 994 ON THE EMBEDDING OF -CONCAVE ORLICZ SPACES INTO L Care Schü Abrac. I [K S ] i wa how ha Ave ( i a π(i) ) π i equivale o a Orlicz orm whoe Orlicz fucio i -cocave. Here we
Extension of Hardy Inequality on Weighted Sequence Spaces
 Jourl of Scieces Islic Reublic of Ir 20(2): 59-66 (2009) Uiversiy of ehr ISS 06-04 h://sciecesucir Eesio of Hrdy Iequliy o Weighed Sequece Sces R Lshriour d D Foroui 2 Dere of Mheics Fculy of Mheics Uiversiy
Jourl of Scieces Islic Reublic of Ir 20(2): 59-66 (2009) Uiversiy of ehr ISS 06-04 h://sciecesucir Eesio of Hrdy Iequliy o Weighed Sequece Sces R Lshriour d D Foroui 2 Dere of Mheics Fculy of Mheics Uiversiy
Hadamard matrices from the Multiplication Table of the Finite Fields
 adamard marice from he Muliplicaio Table of he Fiie Field 신민호 송홍엽 노종선 * Iroducio adamard mari biary m-equece New Corucio Coe Theorem. Corucio wih caoical bai Theorem. Corucio wih ay bai Remark adamard
adamard marice from he Muliplicaio Table of he Fiie Field 신민호 송홍엽 노종선 * Iroducio adamard mari biary m-equece New Corucio Coe Theorem. Corucio wih caoical bai Theorem. Corucio wih ay bai Remark adamard
BINOMIAL THEOREM OBJECTIVE PROBLEMS in the expansion of ( 3 +kx ) are equal. Then k =
 wwwskshieduciocom BINOMIAL HEOREM OBJEIVE PROBLEMS he coefficies of, i e esio of k e equl he k /7 If e coefficie of, d ems i e i AP, e e vlue of is he coefficies i e,, 7 ems i e esio of e i AP he 7 7 em
wwwskshieduciocom BINOMIAL HEOREM OBJEIVE PROBLEMS he coefficies of, i e esio of k e equl he k /7 If e coefficie of, d ems i e i AP, e e vlue of is he coefficies i e,, 7 ems i e esio of e i AP he 7 7 em
Types Ideals on IS-Algebras
 Ieraioal Joural of Maheaical Aalyi Vol. 07 o. 3 635-646 IARI Ld www.-hikari.co hp://doi.org/0.988/ija.07.7466 Type Ideal o IS-Algebra Sudu Najah Jabir Faculy of Educaio ufa Uiveriy Iraq Copyrigh 07 Sudu
Ieraioal Joural of Maheaical Aalyi Vol. 07 o. 3 635-646 IARI Ld www.-hikari.co hp://doi.org/0.988/ija.07.7466 Type Ideal o IS-Algebra Sudu Najah Jabir Faculy of Educaio ufa Uiveriy Iraq Copyrigh 07 Sudu
ERROR ESTIMATES FOR APPROXIMATING THE FOURIER TRANSFORM OF FUNCTIONS OF BOUNDED VARIATION
 ERROR ESTIMATES FOR APPROXIMATING THE FOURIER TRANSFORM OF FUNCTIONS OF BOUNDED VARIATION N.S. BARNETT, S.S. DRAGOMIR, AND G. HANNA Absrc. I his pper we poi ou pproximio for he Fourier rsform for fucios
ERROR ESTIMATES FOR APPROXIMATING THE FOURIER TRANSFORM OF FUNCTIONS OF BOUNDED VARIATION N.S. BARNETT, S.S. DRAGOMIR, AND G. HANNA Absrc. I his pper we poi ou pproximio for he Fourier rsform for fucios
Week 8 Lecture 3: Problems 49, 50 Fourier analysis Courseware pp (don t look at French very confusing look in the Courseware instead)
 Week 8 Lecure 3: Problems 49, 5 Fourier lysis Coursewre pp 6-7 (do look Frech very cofusig look i he Coursewre ised) Fourier lysis ivolves ddig wves d heir hrmoics, so i would hve urlly followed fer he
Week 8 Lecure 3: Problems 49, 5 Fourier lysis Coursewre pp 6-7 (do look Frech very cofusig look i he Coursewre ised) Fourier lysis ivolves ddig wves d heir hrmoics, so i would hve urlly followed fer he
A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY
 U.P.B. Sci. Bull., Series A, Vol. 78, Iss. 2, 206 ISSN 223-7027 A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY İbrahim Çaak I his paper we obai a Tauberia codiio i erms of he weighed classical
U.P.B. Sci. Bull., Series A, Vol. 78, Iss. 2, 206 ISSN 223-7027 A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY İbrahim Çaak I his paper we obai a Tauberia codiio i erms of he weighed classical
Moment Generating Function
 1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)
![th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x) th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)](/thumbs/80/81319353.jpg) 1 Trasform Techiques h m m m m mome : E[ ] x f ( x) dx h m m m m ceral mome : E[( ) ] ( ) ( x) f ( x) dx A coveie wa of fidig he momes of a radom variable is he mome geeraig fucio (MGF). Oher rasform echiques
1 Trasform Techiques h m m m m mome : E[ ] x f ( x) dx h m m m m ceral mome : E[( ) ] ( ) ( x) f ( x) dx A coveie wa of fidig he momes of a radom variable is he mome geeraig fucio (MGF). Oher rasform echiques
Linear Time Invariant Systems
 1 Liear Time Ivaria Sysems Oulie We will show ha he oupu equals he covoluio bewee he ipu ad he ui impulse respose: sysem for a discree-ime, for a coiuous-ime sysdem, y x h y x h 2 Discree Time LTI Sysems
1 Liear Time Ivaria Sysems Oulie We will show ha he oupu equals he covoluio bewee he ipu ad he ui impulse respose: sysem for a discree-ime, for a coiuous-ime sysdem, y x h y x h 2 Discree Time LTI Sysems
Reinforcement Learning
 Reiforceme Corol lerig Corol polices h choose opiml cios Q lerig Covergece Chper 13 Reiforceme 1 Corol Cosider lerig o choose cios, e.g., Robo lerig o dock o bery chrger o choose cios o opimize fcory oupu
Reiforceme Corol lerig Corol polices h choose opiml cios Q lerig Covergece Chper 13 Reiforceme 1 Corol Cosider lerig o choose cios, e.g., Robo lerig o dock o bery chrger o choose cios o opimize fcory oupu
FIXED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE
 Mohia & Samaa, Vol. 1, No. II, December, 016, pp 34-49. ORIGINAL RESEARCH ARTICLE OPEN ACCESS FIED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE 1 Mohia S. *, Samaa T. K. 1 Deparme of Mahemaics, Sudhir Memorial
Mohia & Samaa, Vol. 1, No. II, December, 016, pp 34-49. ORIGINAL RESEARCH ARTICLE OPEN ACCESS FIED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE 1 Mohia S. *, Samaa T. K. 1 Deparme of Mahemaics, Sudhir Memorial
1 Notes on Little s Law (l = λw)
 Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
HOMEWORK 6 - INTEGRATION. READING: Read the following parts from the Calculus Biographies that I have given (online supplement of our textbook):
 MAT 3 CALCULUS I 5.. Dokuz Eylül Uiversiy Fculy of Sciece Deprme of Mhemics Isrucors: Egi Mermu d Cell Cem Srıoğlu HOMEWORK 6 - INTEGRATION web: hp://kisi.deu.edu.r/egi.mermu/ Tebook: Uiversiy Clculus,
MAT 3 CALCULUS I 5.. Dokuz Eylül Uiversiy Fculy of Sciece Deprme of Mhemics Isrucors: Egi Mermu d Cell Cem Srıoğlu HOMEWORK 6 - INTEGRATION web: hp://kisi.deu.edu.r/egi.mermu/ Tebook: Uiversiy Clculus,
Economics 8723 Macroeconomic Theory Problem Set 3 Sketch of Solutions Professor Sanjay Chugh Spring 2017
 Deparme of Ecoomic The Ohio Sae Uiveriy Ecoomic 8723 Macroecoomic Theory Problem Se 3 Skech of Soluio Profeor Sajay Chugh Sprig 27 Taylor Saggered Nomial Price-Seig Model There are wo group of moopoliically-compeiive
Deparme of Ecoomic The Ohio Sae Uiveriy Ecoomic 8723 Macroecoomic Theory Problem Se 3 Skech of Soluio Profeor Sajay Chugh Sprig 27 Taylor Saggered Nomial Price-Seig Model There are wo group of moopoliically-compeiive
Positive and negative solutions of a boundary value problem for a
 Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
Supplement: Gauss-Jordan Reduction
 Suppleme: Guss-Jord Reducio. Coefficie mri d ugmeed mri: The coefficie mri derived from sysem of lier equios m m m m is m m m A O d he ugmeed mri derived from he ove sysem of lier equios is [ ] m m m m
Suppleme: Guss-Jord Reducio. Coefficie mri d ugmeed mri: The coefficie mri derived from sysem of lier equios m m m m is m m m A O d he ugmeed mri derived from he ove sysem of lier equios is [ ] m m m m
Bipartite Matching. Matching. Bipartite Matching. Maxflow Formulation
 Mching Inpu: undireced grph G = (V, E). Biprie Mching Inpu: undireced, biprie grph G = (, E).. Mching Ern Myr, Hrld äcke Biprie Mching Inpu: undireced, biprie grph G = (, E). Mflow Formulion Inpu: undireced,
Mching Inpu: undireced grph G = (V, E). Biprie Mching Inpu: undireced, biprie grph G = (, E).. Mching Ern Myr, Hrld äcke Biprie Mching Inpu: undireced, biprie grph G = (, E). Mflow Formulion Inpu: undireced,
CHAPTER 2 Quadratic diophantine equations with two unknowns
 CHAPTER - QUADRATIC DIOPHANTINE EQUATIONS WITH TWO UNKNOWNS 3 CHAPTER Quadraic diophaie equaio wih wo ukow Thi chaper coi of hree ecio. I ecio (A), o rivial iegral oluio of he biar quadraic diophaie equaio
CHAPTER - QUADRATIC DIOPHANTINE EQUATIONS WITH TWO UNKNOWNS 3 CHAPTER Quadraic diophaie equaio wih wo ukow Thi chaper coi of hree ecio. I ecio (A), o rivial iegral oluio of he biar quadraic diophaie equaio
Common Fixed Point Theorem in Intuitionistic Fuzzy Metric Space via Compatible Mappings of Type (K)
 Ieraioal Joural of ahemaics Treds ad Techology (IJTT) Volume 35 umber 4- July 016 Commo Fixed Poi Theorem i Iuiioisic Fuzzy eric Sace via Comaible aigs of Tye (K) Dr. Ramaa Reddy Assisa Professor De. of
Ieraioal Joural of ahemaics Treds ad Techology (IJTT) Volume 35 umber 4- July 016 Commo Fixed Poi Theorem i Iuiioisic Fuzzy eric Sace via Comaible aigs of Tye (K) Dr. Ramaa Reddy Assisa Professor De. of
Extremal graph theory II: K t and K t,t
 Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D. S. Palimkar
 Ieraioal Joural of Scieific ad Research Publicaios, Volue 2, Issue 7, July 22 ISSN 225-353 EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D S Palikar Depare of Maheaics, Vasarao Naik College, Naded
Ieraioal Joural of Scieific ad Research Publicaios, Volue 2, Issue 7, July 22 ISSN 225-353 EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D S Palikar Depare of Maheaics, Vasarao Naik College, Naded
ON BILATERAL GENERATING FUNCTIONS INVOLVING MODIFIED JACOBI POLYNOMIALS
 Jourl of Sciece d Ars Yer 4 No 227-6 24 ORIINAL AER ON BILATERAL ENERATIN FUNCTIONS INVOLVIN MODIFIED JACOBI OLYNOMIALS CHANDRA SEKHAR BERA Muscri received: 424; Acceed er: 3524; ublished olie: 3624 Absrc
Jourl of Sciece d Ars Yer 4 No 227-6 24 ORIINAL AER ON BILATERAL ENERATIN FUNCTIONS INVOLVIN MODIFIED JACOBI OLYNOMIALS CHANDRA SEKHAR BERA Muscri received: 424; Acceed er: 3524; ublished olie: 3624 Absrc
ONE RANDOM VARIABLE F ( ) [ ] x P X x x x 3
![ONE RANDOM VARIABLE F ( ) [ ] x P X x x x 3 ONE RANDOM VARIABLE F ( ) [ ] x P X x x x 3](/thumbs/87/96063720.jpg) The Cumulive Disribuio Fucio (cd) ONE RANDOM VARIABLE cd is deied s he probbiliy o he eve { x}: F ( ) [ ] x P x x - Applies o discree s well s coiuous RV. Exmple: hree osses o coi x 8 3 x 8 8 F 3 3 7 x
The Cumulive Disribuio Fucio (cd) ONE RANDOM VARIABLE cd is deied s he probbiliy o he eve { x}: F ( ) [ ] x P x x - Applies o discree s well s coiuous RV. Exmple: hree osses o coi x 8 3 x 8 8 F 3 3 7 x
The Inverse of Power Series and the Partial Bell Polynomials
 1 2 3 47 6 23 11 Joural of Ieger Sequece Vol 15 2012 Aricle 1237 The Ivere of Power Serie ad he Parial Bell Polyomial Miloud Mihoubi 1 ad Rachida Mahdid 1 Faculy of Mahemaic Uiveriy of Sciece ad Techology
1 2 3 47 6 23 11 Joural of Ieger Sequece Vol 15 2012 Aricle 1237 The Ivere of Power Serie ad he Parial Bell Polyomial Miloud Mihoubi 1 ad Rachida Mahdid 1 Faculy of Mahemaic Uiveriy of Sciece ad Techology
S n. = n. Sum of first n terms of an A. P is
 PROGREION I his secio we discuss hree impora series amely ) Arihmeic Progressio (A.P), ) Geomeric Progressio (G.P), ad 3) Harmoic Progressio (H.P) Which are very widely used i biological scieces ad humaiies.
PROGREION I his secio we discuss hree impora series amely ) Arihmeic Progressio (A.P), ) Geomeric Progressio (G.P), ad 3) Harmoic Progressio (H.P) Which are very widely used i biological scieces ad humaiies.
The analysis of the method on the one variable function s limit Ke Wu
 Ieraioal Coferece o Advaces i Mechaical Egieerig ad Idusrial Iformaics (AMEII 5) The aalysis of he mehod o he oe variable fucio s i Ke Wu Deparme of Mahemaics ad Saisics Zaozhuag Uiversiy Zaozhuag 776
Ieraioal Coferece o Advaces i Mechaical Egieerig ad Idusrial Iformaics (AMEII 5) The aalysis of he mehod o he oe variable fucio s i Ke Wu Deparme of Mahemaics ad Saisics Zaozhuag Uiversiy Zaozhuag 776
SUTCLIFFE S NOTES: CALCULUS 2 SWOKOWSKI S CHAPTER 11
 UTCLIFFE NOTE: CALCULU WOKOWKI CHAPTER Ifiite eries Coverget or Diverget eries Cosider the sequece If we form the ifiite sum 0, 00, 000, 0 00 000, we hve wht is clled ifiite series We wt to fid the sum
UTCLIFFE NOTE: CALCULU WOKOWKI CHAPTER Ifiite eries Coverget or Diverget eries Cosider the sequece If we form the ifiite sum 0, 00, 000, 0 00 000, we hve wht is clled ifiite series We wt to fid the sum
Fractional Fourier Series with Applications
 Aeric Jourl o Couiol d Alied Mheics 4, 4(6): 87-9 DOI: 593/jjc446 Frciol Fourier Series wih Alicios Abu Hd I, Khlil R * Uiversiy o Jord, Jord Absrc I his er, we iroduce coorble rciol Fourier series We
Aeric Jourl o Couiol d Alied Mheics 4, 4(6): 87-9 DOI: 593/jjc446 Frciol Fourier Series wih Alicios Abu Hd I, Khlil R * Uiversiy o Jord, Jord Absrc I his er, we iroduce coorble rciol Fourier series We
STK4080/9080 Survival and event history analysis
 STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
ANALYSIS HW 3. f(x + y) = f(x) + f(y) for all real x, y. Demonstration: Let f be such a function. Since f is smooth, f exists.
 ANALYSIS HW 3 CLAY SHONKWILER () Fid ll smooth fuctios f : R R with the property f(x + y) = f(x) + f(y) for ll rel x, y. Demostrtio: Let f be such fuctio. Sice f is smooth, f exists. The The f f(x + h)
ANALYSIS HW 3 CLAY SHONKWILER () Fid ll smooth fuctios f : R R with the property f(x + y) = f(x) + f(y) for ll rel x, y. Demostrtio: Let f be such fuctio. Sice f is smooth, f exists. The The f f(x + h)
Comparison between Fourier and Corrected Fourier Series Methods
 Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
Ruled surfaces are one of the most important topics of differential geometry. The
 CONSTANT ANGLE RULED SURFACES IN EUCLIDEAN SPACES Yuuf YAYLI Ere ZIPLAR Deparme of Mahemaic Faculy of Sciece Uieriy of Aara Tadoğa Aara Turey yayli@cieceaaraedur Deparme of Mahemaic Faculy of Sciece Uieriy
CONSTANT ANGLE RULED SURFACES IN EUCLIDEAN SPACES Yuuf YAYLI Ere ZIPLAR Deparme of Mahemaic Faculy of Sciece Uieriy of Aara Tadoğa Aara Turey yayli@cieceaaraedur Deparme of Mahemaic Faculy of Sciece Uieriy
Approximately Inner Two-parameter C0
 urli Jourl of ic d pplid Scic, 5(9: 0-6, 0 ISSN 99-878 pproximly Ir Two-prmr C0 -group of Tor Produc of C -lgr R. zri,. Nikm, M. Hi Dprm of Mmic, Md rc, Ilmic zd Uivriy, P.O.ox 4-975, Md, Ir. rc: I i ppr,
urli Jourl of ic d pplid Scic, 5(9: 0-6, 0 ISSN 99-878 pproximly Ir Two-prmr C0 -group of Tor Produc of C -lgr R. zri,. Nikm, M. Hi Dprm of Mmic, Md rc, Ilmic zd Uivriy, P.O.ox 4-975, Md, Ir. rc: I i ppr,
MODERN CONTROL SYSTEMS
 MODERN CONTROL SYSTEMS Lecure 9, Sae Space Repreeaio Emam Fahy Deparme of Elecrical ad Corol Egieerig email: emfmz@aa.edu hp://www.aa.edu/cv.php?dip_ui=346&er=6855 Trafer Fucio Limiaio TF = O/P I/P ZIC
MODERN CONTROL SYSTEMS Lecure 9, Sae Space Repreeaio Emam Fahy Deparme of Elecrical ad Corol Egieerig email: emfmz@aa.edu hp://www.aa.edu/cv.php?dip_ui=346&er=6855 Trafer Fucio Limiaio TF = O/P I/P ZIC
Lecture 15 First Properties of the Brownian Motion
 Lecure 15: Firs Properies 1 of 8 Course: Theory of Probabiliy II Term: Sprig 2015 Isrucor: Gorda Zikovic Lecure 15 Firs Properies of he Browia Moio This lecure deals wih some of he more immediae properies
Lecure 15: Firs Properies 1 of 8 Course: Theory of Probabiliy II Term: Sprig 2015 Isrucor: Gorda Zikovic Lecure 15 Firs Properies of he Browia Moio This lecure deals wih some of he more immediae properies
( a n ) converges or diverges.
 Chpter Ifiite Series Pge of Sectio E Rtio Test Chpter : Ifiite Series By the ed of this sectio you will be ble to uderstd the proof of the rtio test test series for covergece by pplyig the rtio test pprecite
Chpter Ifiite Series Pge of Sectio E Rtio Test Chpter : Ifiite Series By the ed of this sectio you will be ble to uderstd the proof of the rtio test test series for covergece by pplyig the rtio test pprecite
Approximately Quasi Inner Generalized Dynamics on Modules. { } t t R
 Joural of Scieces, Islamic epublic of Ira 23(3): 245-25 (22) Uiversiy of Tehra, ISSN 6-4 hp://jscieces.u.ac.ir Approximaely Quasi Ier Geeralized Dyamics o Modules M. Mosadeq, M. Hassai, ad A. Nikam Deparme
Joural of Scieces, Islamic epublic of Ira 23(3): 245-25 (22) Uiversiy of Tehra, ISSN 6-4 hp://jscieces.u.ac.ir Approximaely Quasi Ier Geeralized Dyamics o Modules M. Mosadeq, M. Hassai, ad A. Nikam Deparme
Observations on the Non-homogeneous Quintic Equation with Four Unknowns
 Itertiol Jourl of Mthemtic Reerch. ISSN 976-84 Volume, Number 1 (13), pp. 17-133 Itertiol Reerch Publictio Houe http://www.irphoue.com Obervtio o the No-homogeeou Quitic Equtio with Four Ukow S. Vidhylkhmi
Itertiol Jourl of Mthemtic Reerch. ISSN 976-84 Volume, Number 1 (13), pp. 17-133 Itertiol Reerch Publictio Houe http://www.irphoue.com Obervtio o the No-homogeeou Quitic Equtio with Four Ukow S. Vidhylkhmi
Fermat Numbers in Multinomial Coefficients
 1 3 47 6 3 11 Joural of Ieger Sequeces, Vol. 17 (014, Aricle 14.3. Ferma Numbers i Muliomial Coefficies Shae Cher Deparme of Mahemaics Zhejiag Uiversiy Hagzhou, 31007 Chia chexiaohag9@gmail.com Absrac
1 3 47 6 3 11 Joural of Ieger Sequeces, Vol. 17 (014, Aricle 14.3. Ferma Numbers i Muliomial Coefficies Shae Cher Deparme of Mahemaics Zhejiag Uiversiy Hagzhou, 31007 Chia chexiaohag9@gmail.com Absrac
Math 2414 Homework Set 7 Solutions 10 Points
 Mah Homework Se 7 Soluios 0 Pois #. ( ps) Firs verify ha we ca use he iegral es. The erms are clearly posiive (he epoeial is always posiive ad + is posiive if >, which i is i his case). For decreasig we
Mah Homework Se 7 Soluios 0 Pois #. ( ps) Firs verify ha we ca use he iegral es. The erms are clearly posiive (he epoeial is always posiive ad + is posiive if >, which i is i his case). For decreasig we
International journal of Engineering Research-Online A Peer Reviewed International Journal Articles available online
 Ieraioal joral of Egieerig Reearch-Olie Peer Reviewed Ieraioal Joral ricle available olie h://www.ijoer.i Vol.1. Ie.4. 01 RESERCH RTICLE ON TERNRY QUDRTIC EQUTION M..GOPLN S.VIDHYLKSHMI S.NIVETHITH Dearme
Ieraioal joral of Egieerig Reearch-Olie Peer Reviewed Ieraioal Joral ricle available olie h://www.ijoer.i Vol.1. Ie.4. 01 RESERCH RTICLE ON TERNRY QUDRTIC EQUTION M..GOPLN S.VIDHYLKSHMI S.NIVETHITH Dearme
On Absolute Indexed Riesz Summability of Orthogonal Series
 Ieriol Jourl of Couiol d Alied Mheics. ISSN 89-4966 Volue 3 Nuer (8). 55-6 eserch Idi Pulicios h:www.riulicio.co O Asolue Ideed iesz Suiliy of Orhogol Series L. D. Je S. K. Piry *. K. Ji 3 d. Sl 4 eserch
Ieriol Jourl of Couiol d Alied Mheics. ISSN 89-4966 Volue 3 Nuer (8). 55-6 eserch Idi Pulicios h:www.riulicio.co O Asolue Ideed iesz Suiliy of Orhogol Series L. D. Je S. K. Piry *. K. Ji 3 d. Sl 4 eserch
Asymptotic Properties of Solutions of Two Dimensional Neutral Difference Systems
 Avilble t http://pvmuedu/m Appl Appl Mth ISSN: 192-9466 Vol 8, Iue 2 (December 21), pp 585 595 Applictio d Applied Mthemtic: A Itertiol Jourl (AAM) Aymptotic Propertie of Solutio of Two Dimeiol Neutrl
Avilble t http://pvmuedu/m Appl Appl Mth ISSN: 192-9466 Vol 8, Iue 2 (December 21), pp 585 595 Applictio d Applied Mthemtic: A Itertiol Jourl (AAM) Aymptotic Propertie of Solutio of Two Dimeiol Neutrl
graph of unit step function t
 .5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
.5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
Prakash Chandra Rautaray 1, Ellipse 2
 Prakash Chadra Rauara, Ellise / Ieraioal Joural of Egieerig Research ad Alicaios (IJERA) ISSN: 48-96 www.ijera.com Vol. 3, Issue, Jauar -Februar 3,.36-337 Degree Of Aroimaio Of Fucios B Modified Parial
Prakash Chadra Rauara, Ellise / Ieraioal Joural of Egieerig Research ad Alicaios (IJERA) ISSN: 48-96 www.ijera.com Vol. 3, Issue, Jauar -Februar 3,.36-337 Degree Of Aroimaio Of Fucios B Modified Parial
ON SOME FRACTIONAL PARABOLIC EQUATIONS DRIVEN BY FRACTIONAL GAUSSIAN NOISE
 IJRRAS 6 3) Februry www.rppress.com/volumes/vol6issue3/ijrras_6_3_.pdf ON SOME FRACIONAL ARABOLIC EQUAIONS RIVEN BY FRACIONAL GAUSSIAN NOISE Mhmoud M. El-Bori & hiri El-Sid El-Ndi Fculy of Sciece Alexdri
IJRRAS 6 3) Februry www.rppress.com/volumes/vol6issue3/ijrras_6_3_.pdf ON SOME FRACIONAL ARABOLIC EQUAIONS RIVEN BY FRACIONAL GAUSSIAN NOISE Mhmoud M. El-Bori & hiri El-Sid El-Ndi Fculy of Sciece Alexdri
Special Functions. Leon M. Hall. Professor of Mathematics University of Missouri-Rolla. Copyright c 1995 by Leon M. Hall. All rights reserved.
 Specil Fucios Leo M. Hll Professor of Mhemics Uiversiy of Missouri-Roll Copyrigh c 995 y Leo M. Hll. All righs reserved. Chper 5. Orhogol Fucios 5.. Geerig Fucios Cosider fucio f of wo vriles, ( x,), d
Specil Fucios Leo M. Hll Professor of Mhemics Uiversiy of Missouri-Roll Copyrigh c 995 y Leo M. Hll. All righs reserved. Chper 5. Orhogol Fucios 5.. Geerig Fucios Cosider fucio f of wo vriles, ( x,), d
Basic Results in Functional Analysis
 Preared by: F.. ewis Udaed: Suday, Augus 7, 4 Basic Resuls i Fucioal Aalysis f ( ): X Y is coiuous o X if X, (, ) z f( z) f( ) f ( ): X Y is uiformly coiuous o X if i is coiuous ad ( ) does o deed o. f
Preared by: F.. ewis Udaed: Suday, Augus 7, 4 Basic Resuls i Fucioal Aalysis f ( ): X Y is coiuous o X if X, (, ) z f( z) f( ) f ( ): X Y is uiformly coiuous o X if i is coiuous ad ( ) does o deed o. f
Suggested Solutions to Assignment 1 (REQUIRED)
 EC 45 dvaced Macroecoomic Irucor: Sharif F ha Deparme of Ecoomic Wilfrid Laurier Uiveri Wier 28 Suggeed Soluio o igme (REQUIRED Toal Mar: 5 Par True/ Fale/ Ucerai Queio [2 mar] Explai wh he followig aeme
EC 45 dvaced Macroecoomic Irucor: Sharif F ha Deparme of Ecoomic Wilfrid Laurier Uiveri Wier 28 Suggeed Soluio o igme (REQUIRED Toal Mar: 5 Par True/ Fale/ Ucerai Queio [2 mar] Explai wh he followig aeme
S.E. Sem. III [EXTC] Applied Mathematics - III
![S.E. Sem. III [EXTC] Applied Mathematics - III S.E. Sem. III [EXTC] Applied Mathematics - III](/thumbs/92/110801020.jpg) S.E. Sem. III [EXTC] Applied Mhemic - III Time : 3 Hr.] Prelim Pper Soluio [Mrk : 8 Q.() Fid Lplce rform of e 3 co. [5] A.: L{co }, L{ co } d ( ) d () L{ co } y F.S.T. 3 ( 3) Le co 3 Q.() Prove h : f (
S.E. Sem. III [EXTC] Applied Mhemic - III Time : 3 Hr.] Prelim Pper Soluio [Mrk : 8 Q.() Fid Lplce rform of e 3 co. [5] A.: L{co }, L{ co } d ( ) d () L{ co } y F.S.T. 3 ( 3) Le co 3 Q.() Prove h : f (
Notes 03 largely plagiarized by %khc
 1 1 Discree-Time Covoluio Noes 03 largely plagiarized by %khc Le s begi our discussio of covoluio i discree-ime, sice life is somewha easier i ha domai. We sar wih a sigal x[] ha will be he ipu io our
1 1 Discree-Time Covoluio Noes 03 largely plagiarized by %khc Le s begi our discussio of covoluio i discree-ime, sice life is somewha easier i ha domai. We sar wih a sigal x[] ha will be he ipu io our
Chapter #3 EEE Subsea Control and Communication Systems
 EEE 87 Chter #3 EEE 87 Sube Cotrol d Commuictio Sytem Cloed loo ytem Stedy tte error PID cotrol Other cotroller Chter 3 /3 EEE 87 Itroductio The geerl form for CL ytem: C R ', where ' c ' H or Oe Loo (OL)
EEE 87 Chter #3 EEE 87 Sube Cotrol d Commuictio Sytem Cloed loo ytem Stedy tte error PID cotrol Other cotroller Chter 3 /3 EEE 87 Itroductio The geerl form for CL ytem: C R ', where ' c ' H or Oe Loo (OL)
e x x s 1 dx ( 1) n n!(n + s) + e s n n n=1 n!n s Γ(s) = lim
 Lecure 3 Impora Special FucioMATH-GA 45. Complex Variable The Euler gamma fucio The Euler gamma fucio i ofe ju called he gamma fucio. I i oe of he mo impora ad ubiquiou pecial fucio i mahemaic, wih applicaio
Lecure 3 Impora Special FucioMATH-GA 45. Complex Variable The Euler gamma fucio The Euler gamma fucio i ofe ju called he gamma fucio. I i oe of he mo impora ad ubiquiou pecial fucio i mahemaic, wih applicaio
An arithmetic interpretation of generalized Li s criterion
 A riheic ierpreio o geerlized Li crierio Sergey K. Sekkii Lboroire de Phyique de l Mière Vive IPSB Ecole Polyechique Fédérle de Lue BSP H 5 Lue Swizerld E-il : Serguei.Sekki@epl.ch Recely we hve eblihed
A riheic ierpreio o geerlized Li crierio Sergey K. Sekkii Lboroire de Phyique de l Mière Vive IPSB Ecole Polyechique Fédérle de Lue BSP H 5 Lue Swizerld E-il : Serguei.Sekki@epl.ch Recely we hve eblihed
Forced Oscillation of Nonlinear Impulsive Hyperbolic Partial Differential Equation with Several Delays
 Jourl of Applied Mhemics d Physics, 5, 3, 49-55 Published Olie November 5 i SciRes hp://wwwscirporg/ourl/mp hp://dxdoiorg/436/mp5375 Forced Oscillio of Nolier Impulsive Hyperbolic Pril Differeil Equio
Jourl of Applied Mhemics d Physics, 5, 3, 49-55 Published Olie November 5 i SciRes hp://wwwscirporg/ourl/mp hp://dxdoiorg/436/mp5375 Forced Oscillio of Nolier Impulsive Hyperbolic Pril Differeil Equio
Chapter 2 Infinite Series Page 1 of 9
 Chpter Ifiite eries Pge of 9 Chpter : Ifiite eries ectio A Itroductio to Ifiite eries By the ed of this sectio you will be ble to uderstd wht is met by covergece d divergece of ifiite series recogise geometric
Chpter Ifiite eries Pge of 9 Chpter : Ifiite eries ectio A Itroductio to Ifiite eries By the ed of this sectio you will be ble to uderstd wht is met by covergece d divergece of ifiite series recogise geometric
Fourier series representations of the logarithms of the Euler gamma function and the Barnes multiple gamma functions. Donal F.
 Fourier erie repreeio of he logrihm of he Euler gmm fucio d he Bre muliple gmm fucio Dol F. Coo dcoo@bopeworld.com 5 Mrch 9 Abrc Kummer Fourier erie for log Γ ( ) i well ow, hvig bee dicovered i 847. I
Fourier erie repreeio of he logrihm of he Euler gmm fucio d he Bre muliple gmm fucio Dol F. Coo dcoo@bopeworld.com 5 Mrch 9 Abrc Kummer Fourier erie for log Γ ( ) i well ow, hvig bee dicovered i 847. I
Department of Mathematical and Statistical Sciences University of Alberta
 MATH 4 (R) Wier 008 Iermediae Calculus I Soluios o Problem Se # Due: Friday Jauary 8, 008 Deparme of Mahemaical ad Saisical Scieces Uiversiy of Albera Quesio. [Sec.., #] Fid a formula for he geeral erm
MATH 4 (R) Wier 008 Iermediae Calculus I Soluios o Problem Se # Due: Friday Jauary 8, 008 Deparme of Mahemaical ad Saisical Scieces Uiversiy of Albera Quesio. [Sec.., #] Fid a formula for he geeral erm
EECE 301 Signals & Systems Prof. Mark Fowler
 EECE 31 Signal & Syem Prof. Mark Fowler Noe Se #27 C-T Syem: Laplace Tranform Power Tool for yem analyi Reading Aignmen: Secion 6.1 6.3 of Kamen and Heck 1/18 Coure Flow Diagram The arrow here how concepual
EECE 31 Signal & Syem Prof. Mark Fowler Noe Se #27 C-T Syem: Laplace Tranform Power Tool for yem analyi Reading Aignmen: Secion 6.1 6.3 of Kamen and Heck 1/18 Coure Flow Diagram The arrow here how concepual
Actuarial Society of India
 Acuarial Sociey of Idia EXAMINAIONS Jue 5 C4 (3) Models oal Marks - 5 Idicaive Soluio Q. (i) a) Le U deoe he process described by 3 ad V deoe he process described by 4. he 5 e 5 PU [ ] PV [ ] ( e ).538!
Acuarial Sociey of Idia EXAMINAIONS Jue 5 C4 (3) Models oal Marks - 5 Idicaive Soluio Q. (i) a) Le U deoe he process described by 3 ad V deoe he process described by 4. he 5 e 5 PU [ ] PV [ ] ( e ).538!
Solutions to Problems 3, Level 4
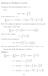 Soluios o Problems 3, Level 4 23 Improve he resul of Quesio 3 whe l. i Use log log o prove ha for real >, log ( {}log + 2 d log+ P ( + P ( d 2. Here P ( is defied i Quesio, ad parial iegraio has bee used.
Soluios o Problems 3, Level 4 23 Improve he resul of Quesio 3 whe l. i Use log log o prove ha for real >, log ( {}log + 2 d log+ P ( + P ( d 2. Here P ( is defied i Quesio, ad parial iegraio has bee used.
NOTES ON BERNOULLI NUMBERS AND EULER S SUMMATION FORMULA. B r = [m = 0] r
![NOTES ON BERNOULLI NUMBERS AND EULER S SUMMATION FORMULA. B r = [m = 0] r NOTES ON BERNOULLI NUMBERS AND EULER S SUMMATION FORMULA. B r = [m = 0] r](/thumbs/80/81160853.jpg) NOTES ON BERNOULLI NUMBERS AND EULER S SUMMATION FORMULA MARK WILDON. Beroulli umbers.. Defiiio. We defie he Beroulli umbers B m for m by m ( m + ( B r [m ] r r Beroulli umbers re med fer Joh Beroulli
NOTES ON BERNOULLI NUMBERS AND EULER S SUMMATION FORMULA MARK WILDON. Beroulli umbers.. Defiiio. We defie he Beroulli umbers B m for m by m ( m + ( B r [m ] r r Beroulli umbers re med fer Joh Beroulli
Review Exercises for Chapter 9
 0_090R.qd //0 : PM Page 88 88 CHAPTER 9 Ifiie Series I Eercises ad, wrie a epressio for he h erm of he sequece..,., 5, 0,,,, 0,... 7,... I Eercises, mach he sequece wih is graph. [The graphs are labeled
0_090R.qd //0 : PM Page 88 88 CHAPTER 9 Ifiie Series I Eercises ad, wrie a epressio for he h erm of he sequece..,., 5, 0,,,, 0,... 7,... I Eercises, mach he sequece wih is graph. [The graphs are labeled
On Almost Increasing Sequences For Generalized Absolute Summability
 Joul of Applied Mthetic & Bioifotic, ol., o., 0, 43-50 ISSN: 79-660 (pit), 79-6939 (olie) Itetiol Scietific Pe, 0 O Alot Iceig Sequece Fo Geelized Abolute Subility W.. Suli Abtct A geel eult coceig bolute
Joul of Applied Mthetic & Bioifotic, ol., o., 0, 43-50 ISSN: 79-660 (pit), 79-6939 (olie) Itetiol Scietific Pe, 0 O Alot Iceig Sequece Fo Geelized Abolute Subility W.. Suli Abtct A geel eult coceig bolute
Supplement for SADAGRAD: Strongly Adaptive Stochastic Gradient Methods"
 Suppleme for SADAGRAD: Srogly Adapive Sochasic Gradie Mehods" Zaiyi Che * 1 Yi Xu * Ehog Che 1 iabao Yag 1. Proof of Proposiio 1 Proposiio 1. Le ɛ > 0 be fixed, H 0 γi, γ g, EF (w 1 ) F (w ) ɛ 0 ad ieraio
Suppleme for SADAGRAD: Srogly Adapive Sochasic Gradie Mehods" Zaiyi Che * 1 Yi Xu * Ehog Che 1 iabao Yag 1. Proof of Proposiio 1 Proposiio 1. Le ɛ > 0 be fixed, H 0 γi, γ g, EF (w 1 ) F (w ) ɛ 0 ad ieraio
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
Computable Analysis of the Solution of the Nonlinear Kawahara Equation
 Diache Lu e al IJCSE April Vol Iue 49-64 Compuale Aalyi of he Soluio of he Noliear Kawahara Equaio Diache Lu Jiai Guo Noliear Scieific eearch Ceer Faculy of Sciece Jiagu Uiveri Zhejiag Jiagu 3 Chia dclu@uj.edu.c
Diache Lu e al IJCSE April Vol Iue 49-64 Compuale Aalyi of he Soluio of he Noliear Kawahara Equaio Diache Lu Jiai Guo Noliear Scieific eearch Ceer Faculy of Sciece Jiagu Uiveri Zhejiag Jiagu 3 Chia dclu@uj.edu.c
Math 6710, Fall 2016 Final Exam Solutions
 Mah 67, Fall 6 Fial Exam Soluios. Firs, a sude poied ou a suble hig: if P (X i p >, he X + + X (X + + X / ( evaluaes o / wih probabiliy p >. This is roublesome because a radom variable is supposed o be
Mah 67, Fall 6 Fial Exam Soluios. Firs, a sude poied ou a suble hig: if P (X i p >, he X + + X (X + + X / ( evaluaes o / wih probabiliy p >. This is roublesome because a radom variable is supposed o be
ECE 350 Matlab-Based Project #3
 ECE 350 Malab-Based Projec #3 Due Dae: Nov. 26, 2008 Read he aached Malab uorial ad read he help files abou fucio i, subs, sem, bar, sum, aa2. he wrie a sigle Malab M file o complee he followig ask for
ECE 350 Malab-Based Projec #3 Due Dae: Nov. 26, 2008 Read he aached Malab uorial ad read he help files abou fucio i, subs, sem, bar, sum, aa2. he wrie a sigle Malab M file o complee he followig ask for
Mathematical Statistics. 1 Introduction to the materials to be covered in this course
 Mahemaical Saisics Iroducio o he maerials o be covered i his course. Uivariae & Mulivariae r.v s 2. Borl-Caelli Lemma Large Deviaios. e.g. X,, X are iid r.v s, P ( X + + X where I(A) is a umber depedig
Mahemaical Saisics Iroducio o he maerials o be covered i his course. Uivariae & Mulivariae r.v s 2. Borl-Caelli Lemma Large Deviaios. e.g. X,, X are iid r.v s, P ( X + + X where I(A) is a umber depedig
LOCUS 1. Definite Integration CONCEPT NOTES. 01. Basic Properties. 02. More Properties. 03. Integration as Limit of a Sum
 LOCUS Defiie egrio CONCEPT NOTES. Bsic Properies. More Properies. egrio s Limi of Sum LOCUS Defiie egrio As eplied i he chper iled egrio Bsics, he fudmel heorem of clculus ells us h o evlue he re uder
LOCUS Defiie egrio CONCEPT NOTES. Bsic Properies. More Properies. egrio s Limi of Sum LOCUS Defiie egrio As eplied i he chper iled egrio Bsics, he fudmel heorem of clculus ells us h o evlue he re uder
STRONG DEVIATION THEOREMS FOR THE SEQUENCE OF CONTINUOUS RANDOM VARIABLES AND THE APPROACH OF LAPLACE TRANSFORM
 Joural of Statitic: Advace i Theory ad Applicatio Volume, Number, 9, Page 35-47 STRONG DEVIATION THEORES FOR THE SEQUENCE OF CONTINUOUS RANDO VARIABLES AND THE APPROACH OF LAPLACE TRANSFOR School of athematic
Joural of Statitic: Advace i Theory ad Applicatio Volume, Number, 9, Page 35-47 STRONG DEVIATION THEORES FOR THE SEQUENCE OF CONTINUOUS RANDO VARIABLES AND THE APPROACH OF LAPLACE TRANSFOR School of athematic
MATH 507a ASSIGNMENT 4 SOLUTIONS FALL 2018 Prof. Alexander. g (x) dx = g(b) g(0) = g(b),
 MATH 57a ASSIGNMENT 4 SOLUTIONS FALL 28 Prof. Alexader (2.3.8)(a) Le g(x) = x/( + x) for x. The g (x) = /( + x) 2 is decreasig, so for a, b, g(a + b) g(a) = a+b a g (x) dx b so g(a + b) g(a) + g(b). Sice
MATH 57a ASSIGNMENT 4 SOLUTIONS FALL 28 Prof. Alexader (2.3.8)(a) Le g(x) = x/( + x) for x. The g (x) = /( + x) 2 is decreasig, so for a, b, g(a + b) g(a) = a+b a g (x) dx b so g(a + b) g(a) + g(b). Sice
The Nottingham eprints service makes this work by researchers of the University of Nottingham available open access under the following conditions.
 Segi Rhm, Mohmd Rfi (2014) Iegrl rform mehod for olvig frciol dymic equio o ime cle. Abrc d Applied Alyi, 2014 (2014). pp. 1-10. ISSN 1085-3375 Acce from he Uiveriy of Noighm repoiory: hp://epri.oighm.c.uk/27710/1/iegrl%20rform%20mehod%20for
Segi Rhm, Mohmd Rfi (2014) Iegrl rform mehod for olvig frciol dymic equio o ime cle. Abrc d Applied Alyi, 2014 (2014). pp. 1-10. ISSN 1085-3375 Acce from he Uiveriy of Noighm repoiory: hp://epri.oighm.c.uk/27710/1/iegrl%20rform%20mehod%20for
L-functions and Class Numbers
 L-fucios ad Class Numbers Sude Number Theory Semiar S. M.-C. 4 Sepember 05 We follow Romyar Sharifi s Noes o Iwasawa Theory, wih some help from Neukirch s Algebraic Number Theory. L-fucios of Dirichle
L-fucios ad Class Numbers Sude Number Theory Semiar S. M.-C. 4 Sepember 05 We follow Romyar Sharifi s Noes o Iwasawa Theory, wih some help from Neukirch s Algebraic Number Theory. L-fucios of Dirichle
On The Eneström-Kakeya Theorem
 Applied Mahemaics,, 3, 555-56 doi:436/am673 Published Olie December (hp://wwwscirporg/oural/am) O The Eesröm-Kakeya Theorem Absrac Gulsha Sigh, Wali Mohammad Shah Bharahiar Uiversiy, Coimbaore, Idia Deparme
Applied Mahemaics,, 3, 555-56 doi:436/am673 Published Olie December (hp://wwwscirporg/oural/am) O The Eesröm-Kakeya Theorem Absrac Gulsha Sigh, Wali Mohammad Shah Bharahiar Uiversiy, Coimbaore, Idia Deparme
POWER SERIES R. E. SHOWALTER
 POWER SERIES R. E. SHOWALTER. sequeces We deote by lim = tht the limit of the sequece { } is the umber. By this we me tht for y ε > 0 there is iteger N such tht < ε for ll itegers N. This mkes precise
POWER SERIES R. E. SHOWALTER. sequeces We deote by lim = tht the limit of the sequece { } is the umber. By this we me tht for y ε > 0 there is iteger N such tht < ε for ll itegers N. This mkes precise
N! AND THE GAMMA FUNCTION
 N! AND THE GAMMA FUNCTION Cosider he produc of he firs posiive iegers- 3 4 5 6 (-) =! Oe calls his produc he facorial ad has ha produc of he firs five iegers equals 5!=0. Direcly relaed o he discree! fucio
N! AND THE GAMMA FUNCTION Cosider he produc of he firs posiive iegers- 3 4 5 6 (-) =! Oe calls his produc he facorial ad has ha produc of he firs five iegers equals 5!=0. Direcly relaed o he discree! fucio
Transformations. Ordered set of numbers: (1,2,3,4) Example: (x,y,z) coordinates of pt in space. Vectors
 Trnformion Ordered e of number:,,,4 Emple:,,z coordine of p in pce. Vecor If, n i i, K, n, i uni ecor Vecor ddiion +w, +, +, + V+w w Sclr roduc,, Inner do roduc α w. w +,.,. The inner produc i SCLR!. w,.,
Trnformion Ordered e of number:,,,4 Emple:,,z coordine of p in pce. Vecor If, n i i, K, n, i uni ecor Vecor ddiion +w, +, +, + V+w w Sclr roduc,, Inner do roduc α w. w +,.,. The inner produc i SCLR!. w,.,
Chapter 7. , and is unknown and n 30 then X ~ t n
 Chpter 7 Sectio 7. t-ditributio ( 3) Summry: C.L.T. : If the rdom mple of ize 3 come from ukow popultio with me d S.D. where i kow or ukow, the X ~ N,. Note: The hypothei tetig d cofidece itervl re built
Chpter 7 Sectio 7. t-ditributio ( 3) Summry: C.L.T. : If the rdom mple of ize 3 come from ukow popultio with me d S.D. where i kow or ukow, the X ~ N,. Note: The hypothei tetig d cofidece itervl re built
Theoretical Physics Prof. Ruiz, UNC Asheville, doctorphys on YouTube Chapter Q Notes. Laplace Transforms. Q1. The Laplace Transform.
 Theoreical Phyic Prof. Ruiz, UNC Aheville, docorphy o YouTue Chaper Q Noe. Laplace Traform Q1. The Laplace Traform. Pierre-Simo Laplace (1749-187) Courey School of Mhemic ad Siic Uiveriy of S. Adrew, Scolad
Theoreical Phyic Prof. Ruiz, UNC Aheville, docorphy o YouTue Chaper Q Noe. Laplace Traform Q1. The Laplace Traform. Pierre-Simo Laplace (1749-187) Courey School of Mhemic ad Siic Uiveriy of S. Adrew, Scolad
LIMITS OF FUNCTIONS (I)
 LIMITS OF FUNCTIO (I ELEMENTARY FUNCTIO: (Elemeary fucios are NOT piecewise fucios Cosa Fucios: f(x k, where k R Polyomials: f(x a + a x + a x + a x + + a x, where a, a,..., a R Raioal Fucios: f(x P (x,
LIMITS OF FUNCTIO (I ELEMENTARY FUNCTIO: (Elemeary fucios are NOT piecewise fucios Cosa Fucios: f(x k, where k R Polyomials: f(x a + a x + a x + a x + + a x, where a, a,..., a R Raioal Fucios: f(x P (x,
David Randall. ( )e ikx. k = u x,t. u( x,t)e ikx dx L. x L /2. Recall that the proof of (1) and (2) involves use of the orthogonality condition.
 ! Revised April 21, 2010 1:27 P! 1 Fourier Series David Radall Assume ha u( x,) is real ad iegrable If he domai is periodic, wih period L, we ca express u( x,) exacly by a Fourier series expasio: ( ) =
! Revised April 21, 2010 1:27 P! 1 Fourier Series David Radall Assume ha u( x,) is real ad iegrable If he domai is periodic, wih period L, we ca express u( x,) exacly by a Fourier series expasio: ( ) =
Integration and Differentiation
 ome Clculus bckgroud ou should be fmilir wih, or review, for Mh 404 I will be, for he mos pr, ssumed ou hve our figerips he bsics of (mulivrible) fucios, clculus, d elemer differeil equios If here hs bee
ome Clculus bckgroud ou should be fmilir wih, or review, for Mh 404 I will be, for he mos pr, ssumed ou hve our figerips he bsics of (mulivrible) fucios, clculus, d elemer differeil equios If here hs bee
10.5 Power Series. In this section, we are going to start talking about power series. A power series is a series of the form
 0.5 Power Series I the lst three sectios, we ve spet most of tht time tlkig bout how to determie if series is coverget or ot. Now it is time to strt lookig t some specific kids of series d we will evetully
0.5 Power Series I the lst three sectios, we ve spet most of tht time tlkig bout how to determie if series is coverget or ot. Now it is time to strt lookig t some specific kids of series d we will evetully
f(bx) dx = f dx = dx l dx f(0) log b x a + l log b a 2ɛ log b a.
 Eercise 5 For y < A < B, we hve B A f fb B d = = A B A f d f d For y ɛ >, there re N > δ >, such tht d The for y < A < δ d B > N, we hve ba f d f A bb f d l By ba A A B A bb ba fb d f d = ba < m{, b}δ
Eercise 5 For y < A < B, we hve B A f fb B d = = A B A f d f d For y ɛ >, there re N > δ >, such tht d The for y < A < δ d B > N, we hve ba f d f A bb f d l By ba A A B A bb ba fb d f d = ba < m{, b}δ
Transient Solution of the M/M/C 1 Queue with Additional C 2 Servers for Longer Queues and Balking
 Jourl of Mhemics d Sisics 4 (): 2-25, 28 ISSN 549-3644 28 Sciece ublicios Trsie Soluio of he M/M/C Queue wih Addiiol C 2 Servers for Loger Queues d Blkig R. O. Al-Seedy, A. A. El-Sherbiy,,2 S. A. EL-Shehwy
Jourl of Mhemics d Sisics 4 (): 2-25, 28 ISSN 549-3644 28 Sciece ublicios Trsie Soluio of he M/M/C Queue wih Addiiol C 2 Servers for Loger Queues d Blkig R. O. Al-Seedy, A. A. El-Sherbiy,,2 S. A. EL-Shehwy
Boundary Value Problems of Conformable. Fractional Differential Equation with Impulses
 Applied Meicl Scieces Vol 2 28 o 8 377-397 HIKARI Ld www-irico ps://doiorg/2988/s28823 Boudry Vlue Probles of Coforble Frciol Differeil Equio wi Ipulses Arisr Tgvree Ci Tipryoo d Apisi Ppogpu Depre of
Applied Meicl Scieces Vol 2 28 o 8 377-397 HIKARI Ld www-irico ps://doiorg/2988/s28823 Boudry Vlue Probles of Coforble Frciol Differeil Equio wi Ipulses Arisr Tgvree Ci Tipryoo d Apisi Ppogpu Depre of
An interesting result about subset sums. Nitu Kitchloo. Lior Pachter. November 27, Abstract
 A ieresig resul abou subse sums Niu Kichloo Lior Pacher November 27, 1993 Absrac We cosider he problem of deermiig he umber of subses B f1; 2; : : :; g such ha P b2b b k mod, where k is a residue class
A ieresig resul abou subse sums Niu Kichloo Lior Pacher November 27, 1993 Absrac We cosider he problem of deermiig he umber of subses B f1; 2; : : :; g such ha P b2b b k mod, where k is a residue class
Online Supplement to Reactive Tabu Search in a Team-Learning Problem
 Olie Suppleme o Reacive abu Search i a eam-learig Problem Yueli She School of Ieraioal Busiess Admiisraio, Shaghai Uiversiy of Fiace ad Ecoomics, Shaghai 00433, People s Republic of Chia, she.yueli@mail.shufe.edu.c
Olie Suppleme o Reacive abu Search i a eam-learig Problem Yueli She School of Ieraioal Busiess Admiisraio, Shaghai Uiversiy of Fiace ad Ecoomics, Shaghai 00433, People s Republic of Chia, she.yueli@mail.shufe.edu.c
Dynamic h-index: the Hirsch index in function of time
 Dyamic h-idex: he Hirsch idex i fucio of ime by L. Egghe Uiversiei Hassel (UHassel), Campus Diepebeek, Agoralaa, B-3590 Diepebeek, Belgium ad Uiversiei Awerpe (UA), Campus Drie Eike, Uiversieisplei, B-260
Dyamic h-idex: he Hirsch idex i fucio of ime by L. Egghe Uiversiei Hassel (UHassel), Campus Diepebeek, Agoralaa, B-3590 Diepebeek, Belgium ad Uiversiei Awerpe (UA), Campus Drie Eike, Uiversieisplei, B-260
Degree of Approximation of Conjugate of Signals (Functions) by Lower Triangular Matrix Operator
 Alied Mhemics 2 2 448-452 doi:.4236/m.2.2226 Pulished Olie Decemer 2 (h://www.scirp.org/jourl/m) Degree of Aroimio of Cojuge of Sigls (Fucios) y Lower Trigulr Mri Oeror Asrc Vishu Nry Mishr Huzoor H. Kh
Alied Mhemics 2 2 448-452 doi:.4236/m.2.2226 Pulished Olie Decemer 2 (h://www.scirp.org/jourl/m) Degree of Aroimio of Cojuge of Sigls (Fucios) y Lower Trigulr Mri Oeror Asrc Vishu Nry Mishr Huzoor H. Kh
Using Linnik's Identity to Approximate the Prime Counting Function with the Logarithmic Integral
 Usig Lii's Ideiy o Approimae he Prime Couig Fucio wih he Logarihmic Iegral Naha McKezie /26/2 aha@icecreambreafas.com Summary:This paper will show ha summig Lii's ideiy from 2 o ad arragig erms i a cerai
Usig Lii's Ideiy o Approimae he Prime Couig Fucio wih he Logarihmic Iegral Naha McKezie /26/2 aha@icecreambreafas.com Summary:This paper will show ha summig Lii's ideiy from 2 o ad arragig erms i a cerai
An Extension of Hermite Polynomials
 I J Coemp Mh Scieces, Vol 9, 014, o 10, 455-459 HIKARI Ld, wwwm-hikricom hp://dxdoiorg/101988/ijcms0144663 A Exesio of Hermie Polyomils Ghulm Frid Globl Isiue Lhore New Grde Tow, Lhore, Pkis G M Hbibullh
I J Coemp Mh Scieces, Vol 9, 014, o 10, 455-459 HIKARI Ld, wwwm-hikricom hp://dxdoiorg/101988/ijcms0144663 A Exesio of Hermie Polyomils Ghulm Frid Globl Isiue Lhore New Grde Tow, Lhore, Pkis G M Hbibullh
Arkansas Tech University MATH 2924: Calculus II Dr. Marcel B. Finan
 Arkasas Tech Uiversity MATH 94: Calculus II Dr Marcel B Fia 85 Power Series Let {a } =0 be a sequece of umbers The a power series about x = a is a series of the form a (x a) = a 0 + a (x a) + a (x a) +
Arkasas Tech Uiversity MATH 94: Calculus II Dr Marcel B Fia 85 Power Series Let {a } =0 be a sequece of umbers The a power series about x = a is a series of the form a (x a) = a 0 + a (x a) + a (x a) +
Advanced Engineering Mathematics, K.A. Stroud, Dexter J. Booth Engineering Mathematics, H.K. Dass Higher Engineering Mathematics, Dr. B.S.
 Rfrc: (i) (ii) (iii) Advcd Egirig Mhmic, K.A. Sroud, Dxr J. Booh Egirig Mhmic, H.K. D Highr Egirig Mhmic, Dr. B.S. Grwl Th mhod of m Thi coi of h followig xm wih h giv coribuio o h ol. () Mid-rm xm : 3%
Rfrc: (i) (ii) (iii) Advcd Egirig Mhmic, K.A. Sroud, Dxr J. Booh Egirig Mhmic, H.K. D Highr Egirig Mhmic, Dr. B.S. Grwl Th mhod of m Thi coi of h followig xm wih h giv coribuio o h ol. () Mid-rm xm : 3%
